陶 蔚 1 潘志松 1 朱小辉 2 陶 卿 2
1 (中国人民解放军理工大学指挥信息系统学院 南京 210007) 2 (中国人民解放军陆军军官学院十一系 合肥 230031)(wtao_plaust@163.com)
摘 要: 投影次梯度算法(projected subgradient method, PSM)是求解非光滑约束优化问题最简单的一阶梯度方法,目前只是对所有迭代进行加权平均的输出方式得到最优收敛速率,其个体收敛速率问题甚至作为open问题被提及.最近,Nesterov和Shikhman在对偶平均方法(dual averaging method, DAM)的迭代中嵌入一种线性插值操作,得到一种拟单调的求解非光滑问题的次梯度方法,并证明了在一般凸情形下具有个体最优收敛速率,但其讨论仅限于对偶平均方法.通过使用相同技巧,提出了一种嵌入线性插值操作的投影次梯度方法,与线性插值对偶平均方法不同的是,所提方法还对投影次梯度方法本身进行了适当的修改以确保个体收敛性.同时证明了该方法在一般凸情形下可以获得个体最优收敛速率,并进一步将所获结论推广至随机方法情形.实验验证了理论分析的正确性以及所提算法在保持实时稳定性方面的良好性能.
关键词: 一阶梯度方法;个体收敛速率;投影次梯度方法;线性插值操作;对偶平均方法
投影次梯度方法(projected subgradient method, PSM)是求解非光滑约束优化问题的一种简单的一阶梯度方法,在数学优化中占据着十分重要的历史地位 [1-2] ,在其基础上发展出许多具有重要影响的一阶梯度方法,如镜面下降方法(mirror descent method, MDM) [3] 和对偶平均方法(dual averaging method, DAM) [4] .相比而言,对偶平均方法的梯度权重和步长选择策略更为灵活,可以在多种不同步长情形下得到最优收敛速率.但与投影次梯度方法一样,标准的对偶平均方法也只是在一般凸情形下,将所有迭代结果进行平均,得到了最优收敛速率 [5] .
SGD(stochastic gradient descent)是梯度下降法的随机形式,由于不需要遍历样本集合,SGD在处理大规模学习问题方面具有明显优势 [6-7] .但对于强凸优化问题,即使是采用对所有迭代进行平均的输出方式,目前标准的SGD也未能证明能获得最优的收敛速率,这一问题引起了学者对SGD统治地位的质疑.为了捍卫SGD的经典与尊严,Shamir [8] 在2012年的COLT会议上把SGD的个体最优收敛速率作为open问题提出.紧接着,Shamir和Zhang [9] 提出一种由平均输出方式收敛速率得到个体收敛速率的一般技巧,尽管得到了SGD的个体收敛速率,但获得的收敛速率与最优收敛速率相差一个对数因子,仍未能达到最优.
对于强凸情形下SGD的最优收敛速率问题,已经有了相当多的研究.从总体上来看,一种思路是对算法本身进行修改,如Hazan等人 [10] 在SGD中嵌入适当数目的内循环,提出一种Epoch-GD算法,获得了平均输出方式的最优收敛速率;Chen等人 [11] 在算法每一步迭代中采用两次求解不同形式的子优化问题,提出了一种改进的随机对偶平均方法,获得了最优个体收敛速率.另一种思路是对输出方式进行修改,如Rakhlin等人 [12] 以部分迭代解平均的 α -suffix技巧来代替全部平均的输出方式;Lacoste-Julien等人 [13] 提出一种加权平均的输出方式.这些方法均获得了最优的收敛速率.
相比于强凸情形,SGD在一般凸情形下的个体收敛速率问题研究却较少,这或许是因为平均输出方式已经获得了最优收敛速率.2015年,Nesterov和Shikhman [5] 在对偶平均方法的迭代中嵌入了一种线性插值操作策略,证明了该方法在一般凸情形下具有最优的个体收敛速率,并给出了这种个体收敛结果在系统实时稳定化中的应用.从理论角度来说,这种改动与标准的对偶平均方法区别极小,是对偶平均方法很好的扩展,也是对一阶梯度方法个体最优收敛速率比较接近大家期待的一种回答.但美中不足的是,其算法设计和收敛速率分析的思路仅适用于步长策略灵活的对偶平均方法.
本文使用相同的线性插值操作,对投影次梯度方法进行适当修改,得到了一种嵌入线性插值操作投影次梯度方法,证明了在一般凸情形下这种方法具有个体最优收敛速率,并进一步得到了对应的随机方法也具有最优个体收敛速率的结论,并且该方法的个体收敛结果在系统实时稳定化中也有广泛应用前景.值得指出的是,本文对投影次梯度方法的修改也与标准投影次梯度方法的差别很小,但与文献[5]关于对偶平均算法修改还是存在着一定的差异,即如果按照该文献步骤进行简单类似的修改,得不到相关结果.由于算法形式上的不同,本文的收敛速率分析方法也与文献[5]区别很大.另外,本文的算法与文献[14]动力系统离散化后所得的算法虽然在形式上十分类似,但不仅避免了只能得到平均输出方式收敛速率的问题,还减弱了对目标函数不必要的强凸和光滑条件.作为应用,我们考虑了 l 1范数约束的hinge损失函数稀疏学习问题,实验验证了理论分析的正确性.
考虑约束的优化问题:
![]() ,
,
(1)
其中, f ( w )是凸函数, Q ⊆ ![]() n 是有界闭凸集合.记 w * 是式(1)的一个最优解.
n 是有界闭凸集合.记 w * 是式(1)的一个最优解.
对于式(1),批处理形式投影次梯度方法的迭代步骤为
w t +1 = P Q ( w t - a t ![]() f ( w t )),
f ( w t )),
(2)
其中, P Q 是 Q 上的投影算子, a t 是迭代步长, ![]() f ( w t )是 f ( w )在 w t 处的次梯度.投影次梯度方法具有如下收敛界 [4-5] :
f ( w t )是 f ( w )在 w t 处的次梯度.投影次梯度方法具有如下收敛界 [4-5] :
(3)
其中, ![]() a t .投影次梯度方法的一种推广是镜面下降方法 [3] ,其迭代步骤为
a t .投影次梯度方法的一种推广是镜面下降方法 [3] ,其迭代步骤为
![]() 〈
〈 ![]() f ( w t ), w 〉+ B ( w , w t )},
f ( w t ), w 〉+ B ( w , w t )},
(4)
其中, t ≥0,函数 B ( w , w t )是Bregman散度距离(Bregman divergence).特别可取 ![]() ,这种方法也称为近邻梯度(proximal gradient)方法.该方法具有如下收敛速率界 [15] :
,这种方法也称为近邻梯度(proximal gradient)方法.该方法具有如下收敛速率界 [15] :
(5)
在镜面下降算法的基础上,Nesterov [4-5] 提出了对偶平均算法,其主要迭代步骤为
(6)
其中, d ( w )是强凸函数,也称为近邻函数,满足:
d ( y )≥ d ( x )+〈 ![]()
![]()
x , y ∈ Q .
与投影次梯度和镜面下降方法相比,对偶平均算法引进了另外的步长参数 γ t ,使得梯度的权重的取法 a t 更加灵活.特别地可以取平均 a t =1  t ,这也是这种对偶平均算法中平均名称的由来.该方法具有收敛速率界 [5] :
t ,这也是这种对偶平均算法中平均名称的由来.该方法具有收敛速率界 [5] :
(7)
当取 a t = Θ (1 
![]() )时,投影次梯度方法和镜面下降方法的上述收敛界均可以达到最优的收敛速率 O (1
)时,投影次梯度方法和镜面下降方法的上述收敛界均可以达到最优的收敛速率 O (1 
![]() );当 a t =1且
);当 a t =1且 ![]() )时,对偶平均优化方法也取得最优收敛速率 [4-5] .另外,一些文献对这3种一阶算法分别给出了在线形式的regret界 [15-17] ,并且使用标准的在线与随机算法之间的切换技巧 [10] ,也得到了上述3种算法平均输出方式同样阶的收敛速率.
)时,对偶平均优化方法也取得最优收敛速率 [4-5] .另外,一些文献对这3种一阶算法分别给出了在线形式的regret界 [15-17] ,并且使用标准的在线与随机算法之间的切换技巧 [10] ,也得到了上述3种算法平均输出方式同样阶的收敛速率.
2013年,Shamir和Zhang [9] 未对算法进行任何改动,在平均方式输出收敛速率的基础上,运用一种得到个体收敛速率的一般技巧,在一般凸非光滑情况下得到了SGD个体收敛速率为 O (ln t 
![]() ),在强凸情形下得到SGD个体收敛速率为 O (ln t
),在强凸情形下得到SGD个体收敛速率为 O (ln t  t ),这是关于个体收敛速率方面的首批结果,也是SGD最优收敛速率open问题比较接近的一种回答 [18] .但不难发现,获得的收敛速率与最优收敛速率相差一个对数因子ln t ,仍然未能达到open问题中所期待的最优.
t ),这是关于个体收敛速率方面的首批结果,也是SGD最优收敛速率open问题比较接近的一种回答 [18] .但不难发现,获得的收敛速率与最优收敛速率相差一个对数因子ln t ,仍然未能达到open问题中所期待的最优.
为了讨论一阶梯度方法的最优个体收敛速率问题,Nesterov和Shikhman [5] 在2015年对于对偶平均算法作了如下修改:
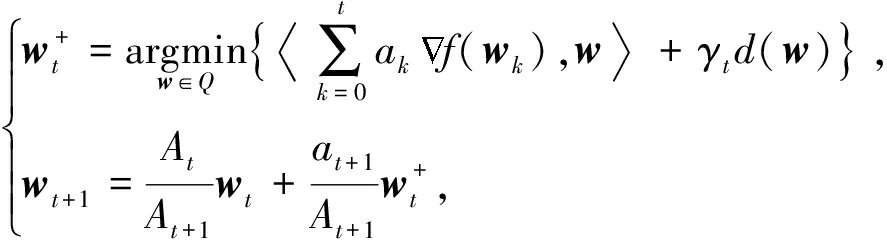
(8)
对于一般凸的情形,当 a t =1且 ![]() )或者 a t = t 且
)或者 a t = t 且 ![]() )时,该算法具有个体最优收敛速率
)时,该算法具有个体最优收敛速率 ![]()
我们沿用Nesterov和Shikhman在处理对偶平均算法个体最优收敛速率时的插值思路,提出如下嵌入线性插值操作的投影次梯度方法:
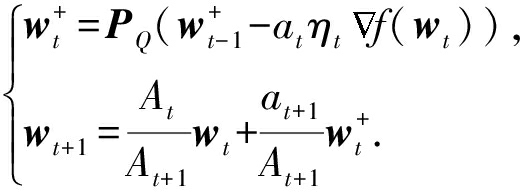
(9)
其中, t ≥1.
与标准投影次梯度方法的主要区别是该算法沿 ![]() 方向做投影梯度运算,而不是投影次梯度方法中的 w t 方向.注意到梯度运算
方向做投影梯度运算,而不是投影次梯度方法中的 w t 方向.注意到梯度运算 ![]() f ( w t )中的 w t 是由插值形式获得的,因此称该算法为嵌入插值操作的投影次梯度方法.
f ( w t )中的 w t 是由插值形式获得的,因此称该算法为嵌入插值操作的投影次梯度方法.
需要特别指出,式(9)对投影次梯度方法的修改不是显然的,因为如果使用文献[5]对于对偶平均算法的直接修改,我们一般会考虑以下算法:

(10)
但是对这种形式的算法,目前我们仍未能证明期望的个体收敛速率结果.另外,文献[14]通过对连续形式的梯度动力系统进行离散化,得到与式(10)形式上非常相似的算法:
但只能得到平均输出形式的收敛速率,并且对目标函数附加了不必要的光滑性等条件.
尽管与直接修改投影次梯度方法(式(10))存在着差异,式(9)对投影次梯度方法的修改仍然是十分微小的.下面对嵌入插值操作的投影次梯度方法(式(9))进行收敛性分析.
引理1 [1] . 假设其中 P Q 是闭凸集合 Q 上的投影算子,则对于任意 w ∈ ![]() n , w 0 ∈ Q ,则〈 w - w 0 , u - w 0 〉≤0对任意 u ∈ Q 都成立的充要条件是 w 0 = P Q ( w ).
n , w 0 ∈ Q ,则〈 w - w 0 , u - w 0 〉≤0对任意 u ∈ Q 都成立的充要条件是 w 0 = P Q ( w ).
引理2. 对于任意 w ∈ Q ,
a t η t ( f ( w t )- f ( w ))≤ a t η t 〈 ![]()
![]()
![]() .
.
具体证明见附录A.
引理3.
η t 〈 a t ![]()
![]()
![]() .
.
具体证明见附录B.
定理1. 假设 η t ≤ η t -1 ,存在 M >0,满足 ![]() ,∀ x , y ∈ Q .对于任意 w ∈ Q ,我们有
,∀ x , y ∈ Q .对于任意 w ∈ Q ,我们有 ![]() .
.
具体证明见附录C.
根据定理1,类似于文献[16],我们可以得出推论:
推论1. 假设 f ( w )是闭凸集合 Q ⊆ ![]() n 上的凸函数,存在 G >0,满足
n 上的凸函数,存在 G >0,满足 ![]() ,∀ w ∈ Q .取 a t =1和 η t =1
,∀ w ∈ Q .取 a t =1和 η t =1 
![]() ,对于任意 w ∈ Q ,有:
,对于任意 w ∈ Q ,有:
![]() .
.
推论2. 推论1条件不变,取 a t = t 和 ![]() ,有:
,有:
![]() .
.
推论2具体证明见附录D.
推论1和推论2表明嵌入插值操作投影次梯度方法对一般凸问题具有个体最优收敛速率.与标准投影次梯度方法不同的是:由于存在着插值权重,步长选择比较灵活,可以得到多种形式获得个体最优收敛速率的参数组合,这一点与对偶平均算法极为类似.因此,可以说我们将文献[5]关于个体最优收敛速率的研究思路适当修改使之适用于投影次梯度方法.
为了更加简单直接地讨论嵌入插值操作投影次梯度方法所对应的随机优化方法,我们直接考虑二分类的稀疏学习问题.假设训练样本集合 S ={( x 1 , y 1 ),( x 2 , y 2 ),…,( x m , y m )}∈ ![]() n ×{1,-1}是一些独立同分布样本组成,稀疏学习问题可以表示为求解优化问题:
n ×{1,-1}是一些独立同分布样本组成,稀疏学习问题可以表示为求解优化问题:
![]() ,
,
(11)
其中, ![]() 是对应样本( x i , y i )的损失函数,
是对应样本( x i , y i )的损失函数, ![]() ⊆
⊆ ![]() n 是有界闭凸集合.记 w * 是问题(11)的一个最优解.本文只考虑广泛使用的非光滑hinge损失函数,即: l i ( w )=max{0,1- y i 〈 w , x i 〉}.
n 是有界闭凸集合.记 w * 是问题(11)的一个最优解.本文只考虑广泛使用的非光滑hinge损失函数,即: l i ( w )=max{0,1- y i 〈 w , x i 〉}.
由于批处理形式投影次梯度方法的每一步迭代需要计算 ![]() l ( w t ),这需要计算每个 l i ( w )的次梯度,从而导致每一步迭代都需要遍历整个样本集合一次,这种操作实际上不适合大规模数据.嵌入线性插值操作的随机投影次梯度方法:
l ( w t ),这需要计算每个 l i ( w )的次梯度,从而导致每一步迭代都需要遍历整个样本集合一次,这种操作实际上不适合大规模数据.嵌入线性插值操作的随机投影次梯度方法:

(12)
其中, t ≥1, i 是从样本集合中第 t +1次迭代随机抽取样本的序号.
与批处理投影次梯度方法不同的是,随机方法的迭代步骤中 ![]() l i ( w t )是 l i ( w )在 w t 处的次梯度.显然,随机方法克服了批处理方法每一步迭代都需要计算整个样本集合上所有样本损失函数梯度的缺陷,特别是具有线性计算代价 l 1范数球
l i ( w t )是 l i ( w )在 w t 处的次梯度.显然,随机方法克服了批处理方法每一步迭代都需要计算整个样本集合上所有样本损失函数梯度的缺陷,特别是具有线性计算代价 l 1范数球 ![]() 1 ≤ λ }上的高效投影算法出现后 [19-20] ,随机投影次梯度方法已经具备求解大规模稀疏学习问题的必要条件.
1 ≤ λ }上的高效投影算法出现后 [19-20] ,随机投影次梯度方法已经具备求解大规模稀疏学习问题的必要条件.
在标准的随机优化算法中,人们往往假定可以获得目标函数梯度的一种无偏估计.对于机器学习问题,由于我们假定样本集合里的样本是独立同分布的,因此每次随机抽取样本得到的 ![]() l i ( w t )是
l i ( w t )是 ![]() l ( w t )的一个无偏估计.不难发现,随机优化算法的主要操作就是把批处理算法使用的目标函数梯度换成其无偏估计.
l ( w t )的一个无偏估计.不难发现,随机优化算法的主要操作就是把批处理算法使用的目标函数梯度换成其无偏估计.
同样,在分析随机优化算法收敛速率时,我们的主要手段就是将梯度的无偏估计在期望条件下换成整个目标函数的梯度,从而与批处理算法收敛分析方法建立密切的联系.与文献[12]引理1的证明完全类似,我们可以获得期望条件下引理1和引理2对应的结论.更进一步得到:
定理2. 假设 η t ≤ η t -1 ,存在 M >0满足 ![]() ≤ M ,∀ x , y ∈ Q ,对于式(12),有: A t E ( l ( w t )
≤ M ,∀ x , y ∈ Q ,对于式(12),有: A t E ( l ( w t ) ![]() .
.
在定理2的基础上,很容易将推论1和推论2拓广至随机情形,即嵌入线性插值操作的随机投影次梯度方法具有个体最优收敛速率.
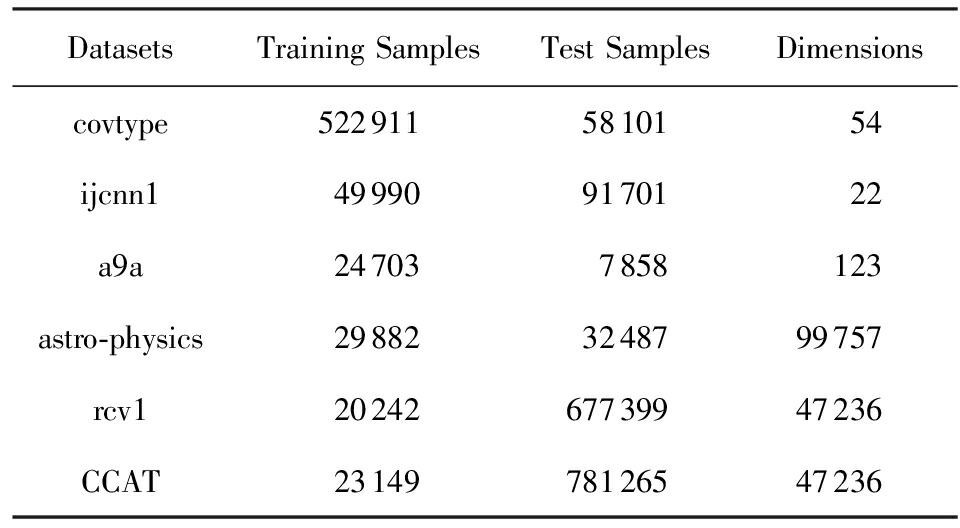
本节对随机嵌入线性插值操作投影次梯度方法的个体收敛速率及其实时稳定性进行实验验证.实验采用的是6个常用的标准数据库,其中,covtype,ijcnn1,a9a这3个数据库稀疏度较高,另外3个数据库的稀疏度均在1%以下.数据库来自于LIBSVM网站 ① .表1给出了这6个数据库的基本描述.
Table 1 Introduction of Standard Datasets
表1 标准数据库描述
在实验中,采取随机方法抽取样本,各算法均取相同的约束参数和步长,并且每个算法均运行10次,将10次输出结果的平均值作为最终输出.实验结果如图1所示,其中横坐标表示迭代次数,最大迭代次数均设置为10 000次,纵坐标表示当前目标函数值与最优目标函数值之差的平均值,这里目标函数的最优值取各算法迭代过程中10次平均后最小的目标函数值.图1中的黑色实线(PSM_average)反映了平均输出方式投影次梯度方法的收敛趋势,长虚线(PSM_individual)显示了个体输出方式投影次梯度方法的收敛趋势,带有“+”的曲线(DAM_modified)反映了文献[5]中提出的具有个体收敛速率对偶平均方法的收敛趋势,而短虚线(PSM_interpolation)表示本文提出的嵌入线性插值操作投影次梯度方法的收敛趋势.
从图1可以看出,对于6个标准数据库,嵌入线性插值操作和平均输出方式的投影次梯度方法均具有相同的收敛趋势,这就从实验上验证了本文理论分析的正确性.其次,虽然个体输出方式的随机投影次梯度稳定性也具有类似的收敛趋势,但个体输出方式的稳定性明显比嵌入线性插值操作投影次梯度方法要差.另外,文献[5]中嵌入插值操作的对偶平均方法和本文嵌入线性插值操作的投影次梯度方法具有一样的稳定性结果,因此,嵌入线性插值操作的投影次梯度方法也可以作为无限时域系统实时稳定化的一种有效工具.
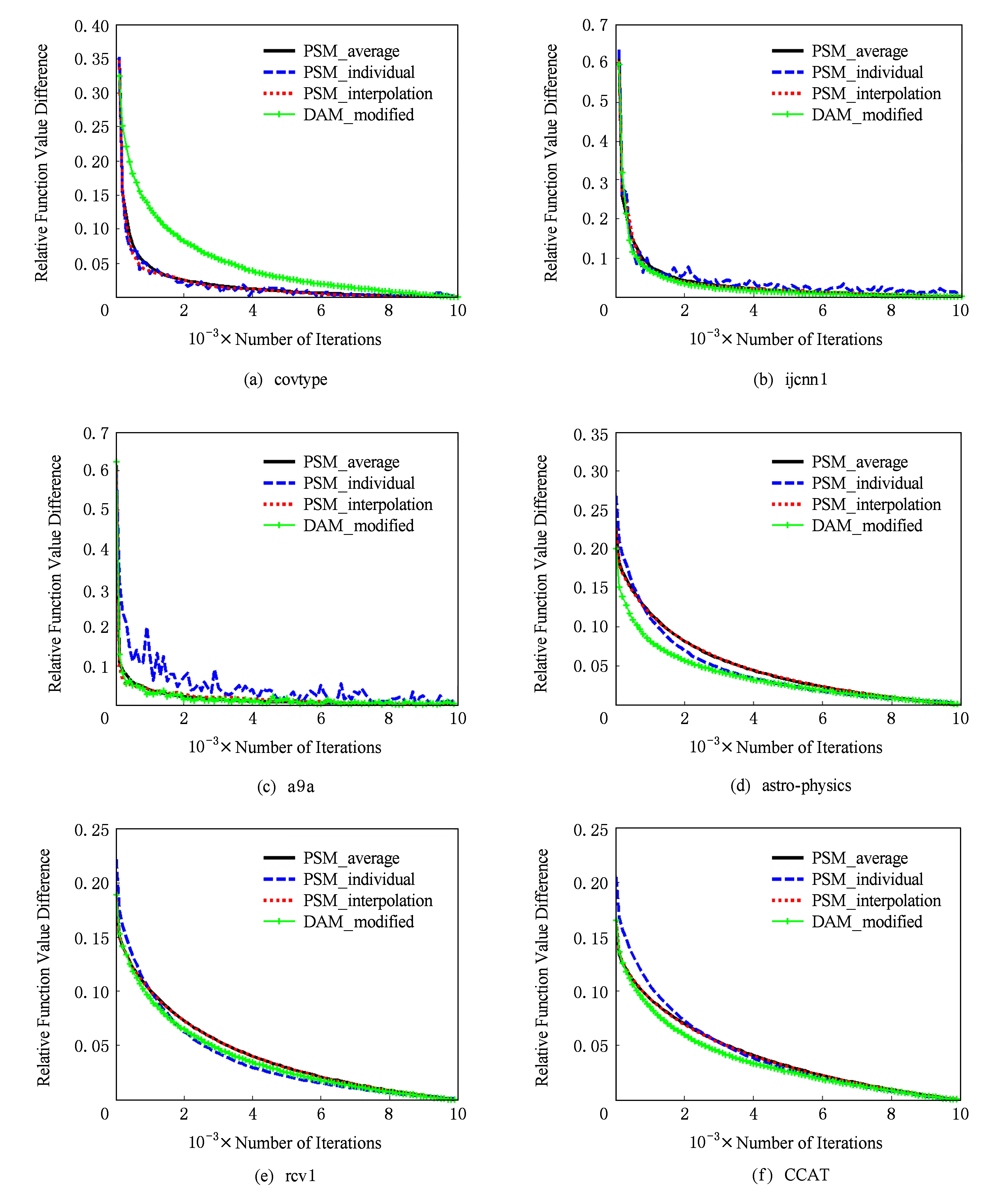
Fig. 1 Comparison of convergence rate
图1 收敛速率比较图
SGD在求解凸优化问题时能否达到个体最优收敛速率是近期提出的open问题,但在一般凸情形下的个体最优收敛速率的研究却较少.最近,Nesterov和Shikhman在对偶平均方法中直接嵌入线性插值操作,得到了个体最优收敛速率,但其结论仅限于对偶平均方法.
本文使用相同的线性插值操作策略,在投影次梯度的基础上得到了一般凸情形下的个体最优收敛速率,并进一步得到了随机方法的最优个体收敛速率.这是对投影次梯度方法在一般凸情形下是否具有个体最优收敛比较接近的一种回答.
与文献[5]不同的是,我们需要对投影次梯度算法进行一定的修改,才能结合线性插值策略,得到个体最优收敛速率的结果.
参考文献:
[1]Bertsekas D P, Nedi ![]() A, Ozdaglar A E. Convex analysis and optimization[M]. Belmont: Athena Scientific, 2003
A, Ozdaglar A E. Convex analysis and optimization[M]. Belmont: Athena Scientific, 2003
[2]Shor N Z. Minimization methods for non-differentiable functions[M]. Berlin: Springer, 1985
[3]Beck A, Teboulle M. Mirror descent and nonlinear projected subgradient methods for convex optimization[J]. Operations Research Letters, 2003, 31(2): 167-175
[4]Nesterov Y. Primal-dual subgradient methods for convex problems[J]. Mathematical Programming, 2009, 120(1): 221-259
[5]Nesterov Y, Shikhman V. Quasi-monotone subgradient methods for nonsmooth convex minimization[J]. Journal of Optimization Theory and Applications. 2015, 165(3): 917-940
[6]Zhang Tong. Solving large scale linear prediction problems using stochastic gradient descent algorithms[C] 
 Proc of the 21st Int Conf on Machine Learning. New York: ACM, 2004: 116-124
Proc of the 21st Int Conf on Machine Learning. New York: ACM, 2004: 116-124
[7]Shalev-Shwartz S, Singer Y, Srebro N, et al. Pegasos: Primal estimated sub-gradient solver for SVM[J]. Mathematical Programming, 2011, 127(1): 3-30
[8]Shamir O. Open problem: Is averaging needed for strongly convex stochastic gradient descent?[C] 
 Proc of the 25th Conf on Learning Theory. New York: ACM, 2012: 471-473
Proc of the 25th Conf on Learning Theory. New York: ACM, 2012: 471-473
[9]Shamir O, Zhang Tong. Stochastic gradient descent for non-smooth optimization: Convergence results and optimal averaging schemes[C] 
 Proc of the 29th Int Conf on Machine Learning. New York: ACM, 2012: 71-79
Proc of the 29th Int Conf on Machine Learning. New York: ACM, 2012: 71-79
[10]Hazan E, Kale S. Beyond the regret minimization barrier: An optimal algorithm for stochastic strongly-convex optimization[C] 
 Proc of the 24th Conf on Learning Theory. New York: ACM, 2011: 421-436
Proc of the 24th Conf on Learning Theory. New York: ACM, 2011: 421-436
[11]Chen Xi, Lin Qihang, Pena J. Optimal regularized dual averaging methods for stochastic optimization[G] 
 Advances in Neural Information Processing Systems. Vancouver, Canada: NIPS Foundation, 2012: 404-412
Advances in Neural Information Processing Systems. Vancouver, Canada: NIPS Foundation, 2012: 404-412
[12]Rakhlin A, Shamir O, Sridharan K. Making gradient descent optimal for strongly convex stochastic optimization[C] 
 Proc of the 29th Int Conf on Machine Learning. New York: ACM, 2012: 449-456
Proc of the 29th Int Conf on Machine Learning. New York: ACM, 2012: 449-456
[13]Lacoste-Julien S, Schmidt M, Bach F. A simpler approach to obtaining an O (1  t ) convergence rate for the projected stochastic subgradient method[OL]. (2012-12-20)[2015-9-10]. http:
t ) convergence rate for the projected stochastic subgradient method[OL]. (2012-12-20)[2015-9-10]. http: 
 arxiv.org
arxiv.org  abs
abs  1212.2002
1212.2002
[14]Tao Qing, Sun Zhengya, Kong Kang. Developing learning algorithms via optimized discretization of continuous dynamical systems[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42(1): 140-149
[15]Duchi J C, Shalev-Shwartz S, Singer Y, et al. Composite objective mirror descent[C] 
 Proc of the 23rd Conf on Learning Theory. New York: ACM, 2010: 14-26
Proc of the 23rd Conf on Learning Theory. New York: ACM, 2010: 14-26
[16]Zinkevich M. Online convex programming and generalized infinitesimal gradient ascent[C] 
 Proc of the 20th Int Conf on Machine Learning. New York: ACM, 2003: 928-936
Proc of the 20th Int Conf on Machine Learning. New York: ACM, 2003: 928-936
[17]Xiao L. Dual averaging methods for regularized stochastic learning and online optimization[J]. Advances in Neural Information Processing Systems, 2010, 11(1): 2543-2596
[18]Shao Yanjian, Tao Qing, Jiang Jiyuan, et al. Stochastic algorithm with optimal convergence rate for strongly convex optimization problems[J]. Journal of Software, 2014, 25(9): 2160-2171 (in Chinese)(邵言剑, 陶卿, 姜纪远, 等. 一种求解强凸优化问题的最优随机算法[J]. 软件学报, 2014, 25(9): 2160-2171)
[19]Duchi J, Shalev-Shwartz S, Singer Y, et al. Efficient projections onto the l 1-ball for learning in high dimensions[C] 
 Proc of the 25th Int Conf on Machine Learning. New York: ACM, 2008: 272-279
Proc of the 25th Int Conf on Machine Learning. New York: ACM, 2008: 272-279
[20]Liu Jun, Ye Jieping. Efficient Euclidean projections in linear time[C] 
 Proc of the 26th Int Conf on Machine Learning. New York: ACM, 2009: 657-664
Proc of the 26th Int Conf on Machine Learning. New York: ACM, 2009: 657-664

Tao Wei, born in 1991. Master candidate. His main research interests include convex optimization algorithm and its application in machine learning, network security.

Pan Zhisong, born in 1973. PhD. Professor and PhD supervisor. Senior member of CCF. His main research interests include pattern recognition, machine learning and network security.

Zhu Xiaohui, born in 1989. Master. His main research interests include pattern recognition and machine learning.

Tao Qing, born in 1965. PhD. Professor and PhD supervisor. Senior member of CCF. His main research interests include pattern recognition, machine learning and applied mathematics.
附录A
正文引理2证明.
![]() 〉.
〉.
(A1)
![]()
![]() f ( w t )〉-
f ( w t )〉-
![]()
![]() f ( w t )〉=
f ( w t )〉=
![]()
![]() f ( w t )〉-
f ( w t )〉-
〈 w - w t , a t η t ![]()
![]()
![]() f ( w t )〉.
f ( w t )〉.
由于 ![]()
![]() f ( w t )),根据引理1可得:
f ( w t )),根据引理1可得:
![]()
![]() f ( w t )〉≥0.
f ( w t )〉≥0.
根据次梯度的定义:
-〈 w - w t , a t η t ![]() f ( w t )〉≥ a t η t ( f ( w t )- f ( w )).
f ( w t )〉≥ a t η t ( f ( w t )- f ( w )).
所以根据式(12):
![]()
![]() f ( w t )〉.
f ( w t )〉.
(A2)
综合式(A1)和式(A2),引理2得证.
证毕.
附录B
正文引理3证明.
![]() .
.
注意到, ![]() ).
).
〈 a t ![]()
![]()
A t -1 〈 ![]() f ( w t ), w t -1 - w t 〉≤
f ( w t ), w t -1 - w t 〉≤
A t -1 f ( w t -1 )- A t -1 f ( w t ).
另一方面,
η t 〈 a t ![]()
![]()
![]() .
.
证毕.
附录C
正文定理1证明.
根据引理2和引理3,
η t ( A t -1 f ( w t -1 )- A t -1 f ( w t )).
即:
η t A t ( f ( w t )- f ( w ))≤
![]() .
.
A t ( f ( w t )- f ( w ))≤ A t -1 ( f ( w t -1 )- f ( w ))+
![]() .
.
对 A t ( f ( w t )- f ( w ))进行递归,可得:
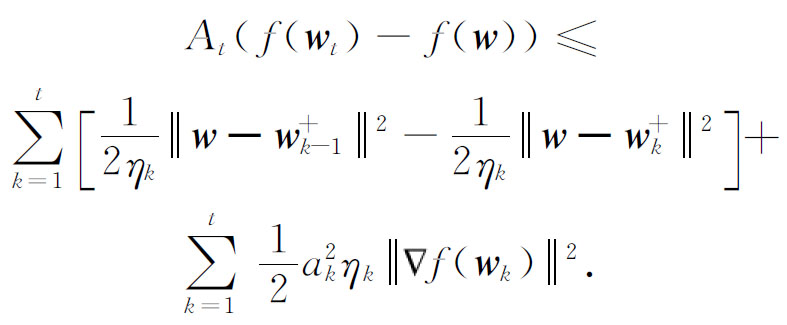
由于 η t ≤ η t -1 ,所以,
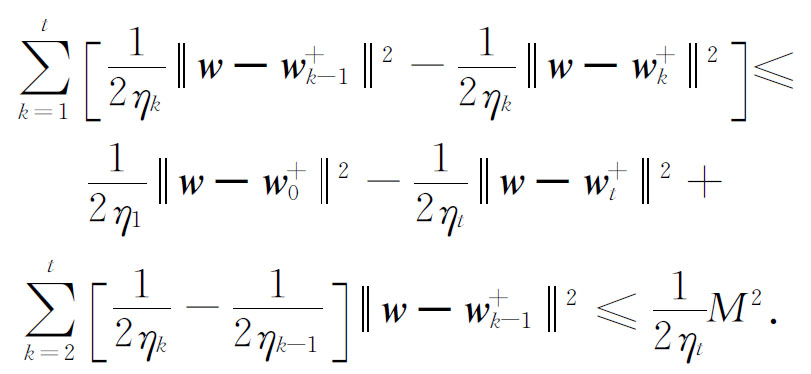
证毕.
附录D
正文推论2证明.
根据定理1:
当 a t = t 和 η t =1 
![]() 时, A t = t 2 且:
时, A t = t 2 且:
![]() ).
).
证毕.
Tao Wei 1 , Pan Zhisong 1 , Zhu Xiaohui 2 , and Tao Qing 2
1 ( College of Command Information System , PLA University of Science and Technology , Nanjing 210007) 2 (11 st Department , Army Officer Academy of PLA , Hefei 230031)
Abstract: The projected subgradient method is one of the simplest algorithms for solving nonsmooth constrained optimization problems. So far, only the optimal convergence rate in terms of the averaged output has been obtained. Its individual convergence rate is even regarded as an open problem. Recently, by incorporating a linear interpolation operation into the dual averaging methods, Nesterov and Shikhman achieved a quasi-monotone subgradient method for nonsmooth convex minimization, which is proved to have the optimal individual convergence rate. Unfortunately, their discussion is only limited to the dual averaging methods. This paper focuses on the individual convergence rate of projected subgradient methods. By employing the same technique, we present a projected subgradient method with linear interpolation operation. In contrast to the work of Nesterov and Shikhman, the projected subgradient method itself in the proposed method has to be modified slightly so as to ensure the individual convergence rate. We prove that the proposed method has the optimal individual convergence rate for solving nonsmooth convex problems. Further, the corresponding stochastic method is proved to have the optimal individual convergence rate. This can be viewed as an approximate answer to the open problem of optimal individual convergence of the projected subgradient methods. The experiments verify the correctness of our analysis and demonstrate the high performance of the proposed methods in real-time stabilization.
Key words: first-order method; individual convergence rate; projected subgradient method; linear interpolation operation; dual averaging method
收稿日期: 2016-03-11;
修回日期: 2016-05-09
基金项目: 国家自然科学基金项目(61673394,61273296) This work was supported by the National Natural Science Foundation of China (61673394, 61273296).
通信作者: 陶卿(qing.tao@ia.ac.cn)
中图法分类号: TP181