三角函数在导航、测绘、工程、物理学等科学计算类应用中使用广泛,由于三角函数算法实现的复杂性,这些函数往往是应用中最耗时的浮点计算函数,因此如何提高三角函数性能成为科研人员设计和优化浮点计算函数的一个重点.
与此同时,单指令多数据(single instruction multiple data, SIMD)向量化对发挥当今处理器浮点计算性能至关重要[1-2].从x86处理器上的SSE(streaming SIMD extensions),AVX(advanced vector extensions)到最新的AVX512F(AVX-512 founda-tion)向量指令集,从ARM处理器的ADVSIMD(advanced SIMD)到SVE(scalable vector extension)向量指令集[3],可以看出随着体系结构的发展,处理器向量宽度正在逐步加宽、并变得更加灵活可用.然而,目前主流处理器平台上的SIMD向量指令集仅包括对基础的加、减、乘、除等算术运算以及逻辑运算、访存操作、位运算等基本操作的支持,对于复杂的浮点三角函数(以及其他超越函数)没有提供直接的支持.
科研人员通常采用软件方式设计数学库以实现三角函数等超越函数.当前,应用广泛的数学库有GNU libm库(GNU math library)[4]、Intel libimf库(Intel math library)[5]、Intel SVML库(Intel short vector math library)[6]等.其中GNU libm库和Intel libimf库是标量数学库,未能利用SIMD向量部件提高函数性能,而Intel SVML库虽然是向量数学库,但属于Intel设计和开发的商用数学库,仅面向x86处理器平台实现向量化.近来,科研人员提出了Sleef开源向量数学库[7-8],该数学库具有良好的模块化和跨平台特性,可支持多种SIMD向量指令集,在多种处理器平台上实现超越函数向量化.然而,Sleef为了实现向量化,以增加冗余计算为代价,换取函数中分支语句的减少.这样,虽然增加了SIMD向量部件的利用率,但冗余计算在一定程度上还是导致了性能损失.
因此,本文基于Sleef开源向量数学库,面向飞腾处理器平台,进一步优化向量三角函数的性能.首先,我们通过完备深入的测试,发现Sleef向量三角函数实现中的性能瓶颈.然后,我们借鉴GNU libm库实现方法中的部分分支算法,针对性地提出了一种支持分支处理的向量三角函数优化方法.基于此,我们还使用了分支预测、精度削减、查表优化、条件传送优化、精度修正、性能修复等优化技术以尽可能减少引入分支后带来的向量化开销.本文所提优化方法结合Sleef向量数学库和GNU libm标量数学库各自的优势,有效提高了向量三角函数的性能.最后,我们将所提优化方法实现为Sleef的一个模块,移植入Sleef数学库中.我们在飞腾处理器上进行实验验证,结果表明我们提出的优化方法在保证向量三角函数精度的前提下,有效提高了向量三角函数性能,与原始Sleef向量三角函数相比,加速比可达1.12~3.97倍.
1 相关背景
1.1 三角函数及其软件实现
三角函数一般通过规约、近似和重建3个步骤获得近似值[9-10].1)规约.根据三角函数的对称性和周期性,将任意区间映射到[0,π/4]区间.2)近似.通过泰勒级数展开计算[0,π/4]区间的三角函数近似值.例如,sin x可以计算为
由于sin x在该区间内是收敛的,因此通过展开若干次可以获得sin x的近似值.3)重建.任意区间三角函数值可以通过[0,π/4]区间三角函数值表示.此外,对于一些特殊值的三角函数,可以绕过上述常规过程进行特殊处理(例如0、无穷大等,可以不经过计算直接返回结果).
在通用处理器上,三角函数等超越函数通常以软件方式集成在数学库中实现.程序员调用数学库中的三角函数接口,由数学库中的相关代码实现相应的函数运算.目前,常用的数学库有Linux操作系统上的GNU libm库、面向Intel处理器的Intel libimf库、ARM发布的libmathlib库(ARM optimized routines)[11]等,其中GNU libm和ARM libmathlib是开源数学库,Intel libimf是Intel特别为其处理器设计和优化的商用数学库.这些数学库都属于标量数学库,一次调用计算一个浮点操作数.因此,为了充分利用处理器上的向量部件和向量指令集以优化程序中的三角函数计算,科研人员设计和开发了向量三角函数.
1.2 向量三角函数及其软件实现
相比标量三角函数,向量三角函数内部使用SIMD指令实现向量化,根据处理器向量部件的宽度,一次调用同时计算多个浮点操作数,因而其理论性能是标量三角函数的数倍.在实现时,向量三角函数仍保留规约、近似和重建3个核心步骤,并使用SIMD指令对应的内部函数(intrinsics)或直接使用汇编指令进行向量化.
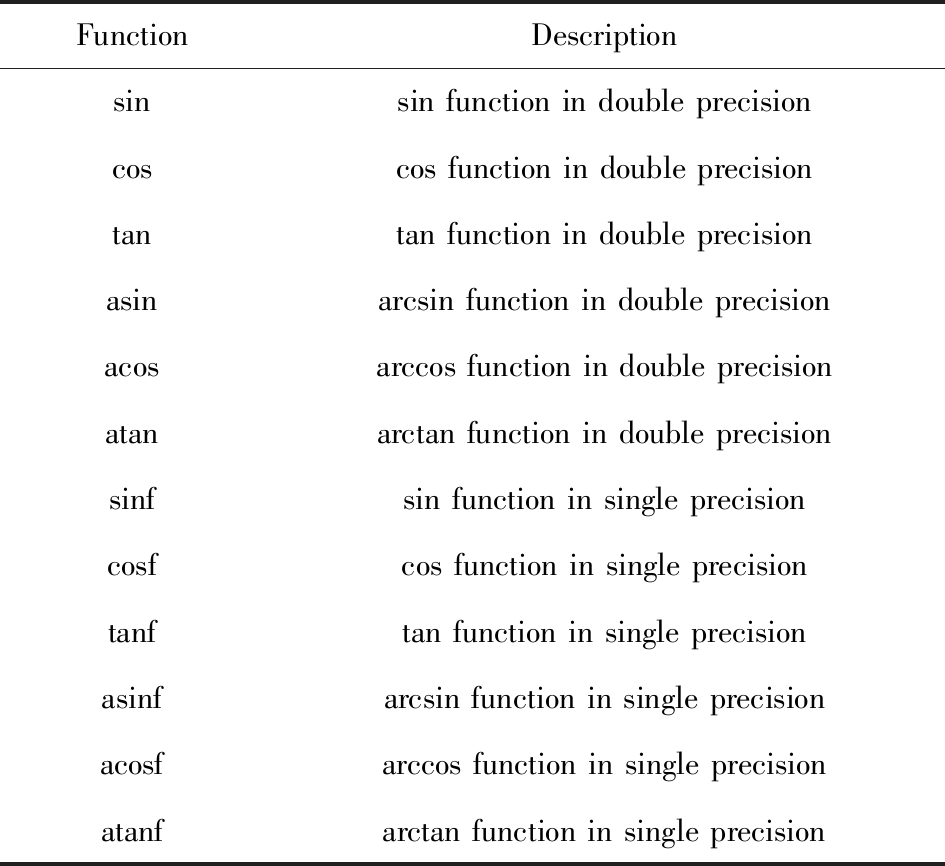
目前比较成熟的实现是Intel SVML数学库,这是Intel开发的一套商用向量数学库,虽然已经部分开源并纳入GNU的标准C库(GNU glibc)中[12],但其应用依然局限于x86平台.近来,科研人员相继实现并发布了一些开源向量数学库.其中,奈良先端科学技术大学院大学开发的Sleef开源向量数学库,为多种硬件平台上的向量超越函数实现提供了支持.Lauter[13]设计的向量libm库(vector libm)实现了双精度三角函数,但其计算精度较低.欧洲核子研究组织发布了VDT向量数学库(vectorised math),其实现依赖于第三方库进行多项式近似,因而其可向量化的程度受限[14].本文是基于Sleef向量数学库设计和优化向量三角函数的,主要针对12个三角函数进行设计实现与优化,这12个函数具体如表1所示:
Table 1 Vector Trigonometric Functions to be Optimized
表1 待优化向量三角函数
FunctionDescriptionsinsin function in double precisioncoscos function in double precisiontantan function in double precisionasinarcsin function in double precisionacosarccos function in double precisionatanarctan function in double precisionsinfsin function in single precisioncosfcos function in single precisiontanftan function in single precisionasinfarcsin function in single precisionacosfarccos function in single precisionatanfarctan function in single precision
此外,硬件实现超越函数虽然能很快返回计算结果,但仅有少量非通用体系结构提供超越函数的硬件实现[15],因而应用受限,不属于本文的研究范畴.
1.3 Sleef向量数学库

Fig. 1 The code structure of Sleef vector math library
图1 Sleef向量数学库代码结构
Sleef是一款基于C语言编写的多平台向量数学库,提供了单精度和双精度2个版本,并实现了C99标准下所有实浮点数学函数的向量化.Sleef支持多种处理器架构和SIMD指令集,目前Sleef支持x86(SSE2,SSE4.1,AVX,FMA4,AVX2+FMA3,AVX512F指令集),AArch64(ADVSIMD,SVE指令集)和PowerPC64(VSX指令集).
由于各SIMD向量指令集的向量类型和intrinsics函数存在较多差异,为了支持多种处理器平台,Sleef采用模块化封装和抽象,面向不同指令集抽象出一套通用的Sleef向量类型(包括vdouble,vfloat,vint,vint2,vopmask,vmask共6种向量类型)和Sleef intrinsics函数(包括向量浮点和整型算术运算、逻辑运算、位运算、类型转换、条件传送等函数).Sleef代码结构如图1所示,底层在头文件中实现Sleef向量类型和Sleef intrinsics函数到各指令集向量类型和intrinsics函数的映射(一个指令集对应一个头文件),上层使用Sleef向量类型和Sleef intrinsics函数实现各超越函数算法,编译器在编译时会根据所在处理器平台自动将Sleef向量类型和Sleef intrinsics函数替换为指定指令集的向量类型和intrinsics函数,从而达到编写一份Sleef超越函数算法、在不同处理器平台上编译运行的目的.正是这种封装和模块化设计使得Sleef具有良好的可扩展性和可移植性,只要符合Sleef代码规则,就可以方便地增加和修改向量数学函数或增加对新的处理器平台和指令集的支持.本文基于Sleef向量数学库在飞腾处理器平台上优化向量三角函数.
1.4 数值结果精度和误差
为了更加精确地分析向量三角函数实现的精度,本文采用ulp(unit in the last place)衡量计算结果误差.根据Goldberg定义[16-17],ulp是最接近实数真实值的2个浮点数之间的距离.假设函数真值为实数x,其对应的浮点数计算结果X可表示为d0.d1d2d3…dp-1βe,x∈[βe,βe+1),则
ulp(x)=βmax(e,emin)-p+1,
其中,β是基,e是阶数,d0.d1d2d3…dp-1是尾数,p是精度即浮点数尾数的有效位数(在IEEE754标准下单精度p=24,双精度p=53).
本文实验中,X由待测三角函数计算得出,x由任意精度算法库MPRF库[18]中对应的三角函数计算同样的操作数得出,通过计算x与X的绝对误差|x-X|的单位ulp数,从而评价待测三角函数的精度.一般情况下,三角函数等超越函数的精度需控制在0.5ulp~1.0ulp以内.
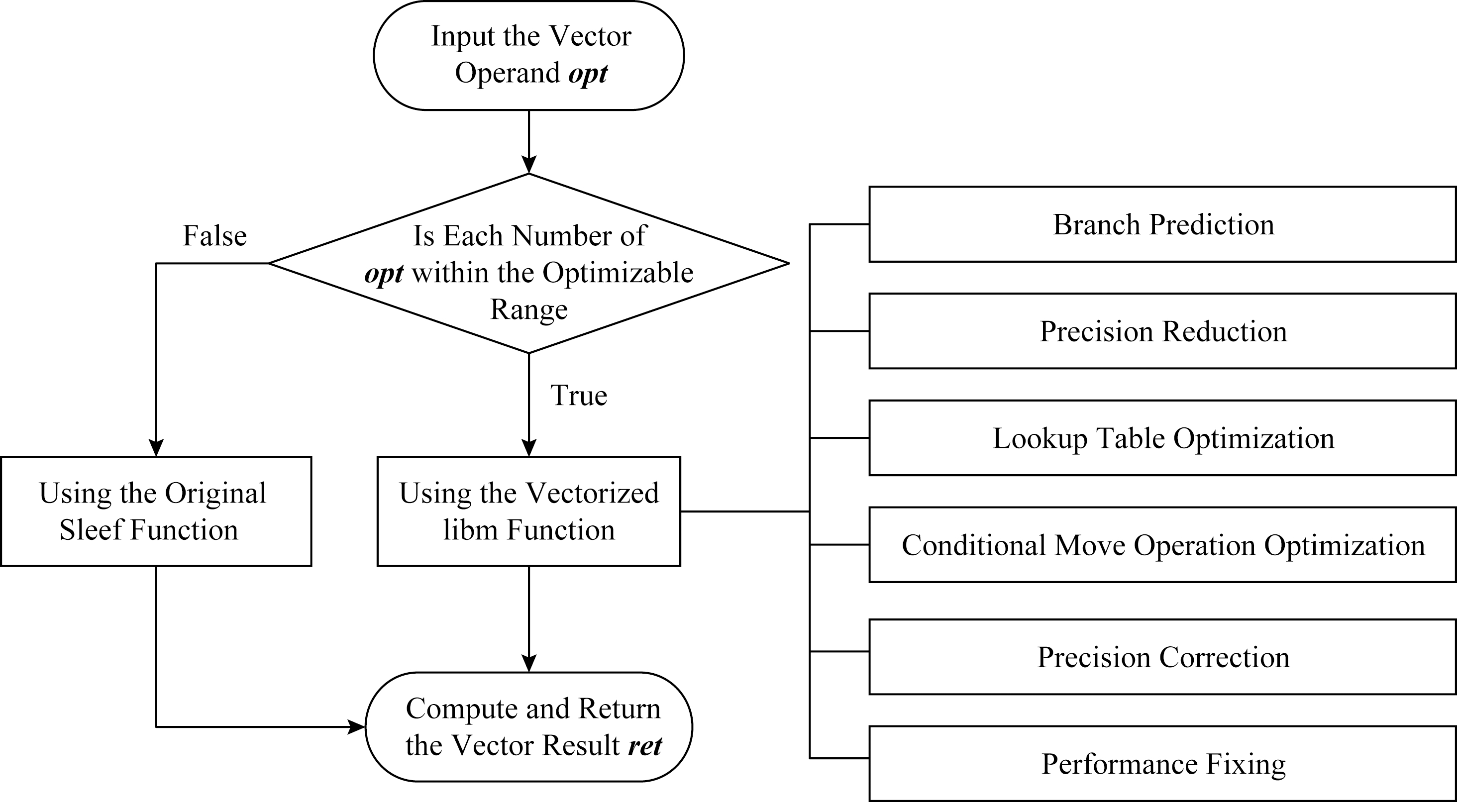
Fig. 2 Vector trigonometric function optimization
图2 向量三角函数优化方法
由于科学计算类应用中存在大量可并行的三角函数数值计算,这些计算十分耗时,因此本文将面向飞腾处理器,基于Sleef向量数学库,在保证一定精度的前提下优化向量三角函数性能.
2 向量三角函数设计与优化
2.1 优化方法
我们调研了向量数学库中三角函数的实现方法,发现虽然在算法上向量三角函数仍然采用规约、近似和重建3个步骤,但会尽量避免使用标量三角函数实现中广泛采用的分支处理,这是因为如果同一向量中的不同元素进入不同分支,那么向量化将受到影响,不同分支中的元素不能同时进行运算.Sleef向量数学库正是如此,为了充分利用SIMD指令的并行处理能力,减少分支操作,Sleef向量数学库在实现向量三角函数算法时不区分操作数的特征,采用统一算法处理所有操作数.该实现方法虽然尽可能避免了算法中的分支语句,提升了处理器SIMD向量单元的利用率,但也导致了向量三角函数在处理一些操作数时的冗余计算(例如cos函数在计算绝对值小于2-27的操作数时,可以不需要经过计算而直接将1.0作为计算结果返回).相反,libm数学库作为标量数学库,为了尽可能减少函数串行计算的计算量,对三角函数的操作数进行了分段,利用三角函数的性质,对不同的操作数范围采用不同的算法(分支)实现运算,从而提高函数运算的速度.
本文将结合Sleef向量化和libm分段计算的优势,以libm的分段计算为指导,将分段计算引入Sleef向量数学库中,从而进一步提高向量三角函数的性能.换言之,我们提出一种在向量数学库中使用分支以优化函数性能的方法.本文的基本优化方法如图2所示.
针对每个三角函数,首先我们对libm三角函数中的操作数范围分支进行筛选,当某个或某些操作数范围分支的计算量较小、执行速度较快时(也就是说该分支值得被向量化用以替换原始Sleef函数),则将其提取出来并使用Sleef intrinsics函数进行向量化.在实际应用中,优化后的三角函数在运行时会判断向量操作数opt中各元素是否均在可优化操作数范围内,如果是则进入向量化的libm分支,否则进入原始Sleef分支,最后计算出向量结果ret返回.对libm函数分支进行筛选时,既要保证函数运算的时间优于原始Sleef函数运算时间,又要保证函数运算的结果满足精度要求(最大误差控制在1.0ulp以内).在实现时,我们通过大量实验确定每个三角函数可移植的操作数范围分支,同时在向量化libm函数分支的过程中,我们还使用了分支预测、精度削减、查表优化、条件传送优化、精度修正和性能修复一系列优化技术以进一步加快函数运算速度.
1) 分支预测.如图2所示,我们的优化方法是以分支的形式添加至原始Sleef代码中的,这就在代码中引入了执行分支语句、进行分支预测所带来的开销.为了尽可能减少分支语句对函数性能的影响,降低分支预测失败的开销,我们使用各个编译器支持的分支预测函数(如gcc编译器的_builtin_expect函数)对2个分支执行的概率进行调整,以大概率执行原始Sleef分支,小概率执行向量化的libm分支,这是因为我们通过实验确定的每个函数的可优化操作数范围相对于整个实数域仍是一个小范围,因此我们认为设定以大概率执行原始Sleef分支是合理的.只有一个例外是atanf函数,因为经过实验我们发现其可优化操作数范围是整个实数域(详见2.2节),因此实现时是将原始Sleef分支整个替换为向量化的libm分支,因此不会受到分支预测优化的影响.Sleef库中已经将各个编译器的分支预测函数进行了打包,函数接口分别是LIKELY()和UNLIKELY().
2) 精度削减.libm的部分三角函数在一些操作数范围内的计算精度很高(最大误差在0.5ulp以内),代码中将对计算结果的精度进行判断,如果精度不够则进入下一层分支进行细化计算,从而达到更高的精度要求.由于Sleef的精度控制相比libm宽松一些,因此在移植libm分支时我们可以删除一些高精度分支,以降低计算开销.
3) 查表优化.标量三角函数实现时通常将函数计算所用到的常系数写在表中,并使用查表操作以减少函数计算量.原始Sleef向量数学库在实现时尽量规避了查表操作,这是因为进行向量查表会涉及到使用聚合(gather)访存指令,将内存中不同位置的常系数值加载到一个向量寄存器中,供向量中的不同元素使用,这种聚合访存因访存不连续往往需要多次访存操作才能完成,从而影响三角函数向量化的性能.我们发现当函数中需要进行查表操作,而查表所需表的大小小于向量宽度时,仍然可以使用查表操作加速函数计算.首先,使用向量load指令先将表中的数据从内存一次加载至向量寄存器中,然后使用特定的permute,blend,shuffle向量操作指令将这些数据存放至向量中的指定位置,从而代替向量gather操作,这样既保留了查表操作并减少了函数计算量,同时又降低了向量查表可能引入的多次内存读写的开销.目前支持特定permute,blend,shuffle向量操作的指令集有AVX2,AVX512F,SVE.
4) 条件传送优化.向量代码中可以使用类似三目运算符x=a?b:c功能的简单条件运算,编译器编译时会将其翻译成向量条件传送指令.例如ADVSIMD指令集中的BSL,BIT,BIF指令.本质上这些指令可以等价为若干按位逻辑操作的组合,如图3所示:
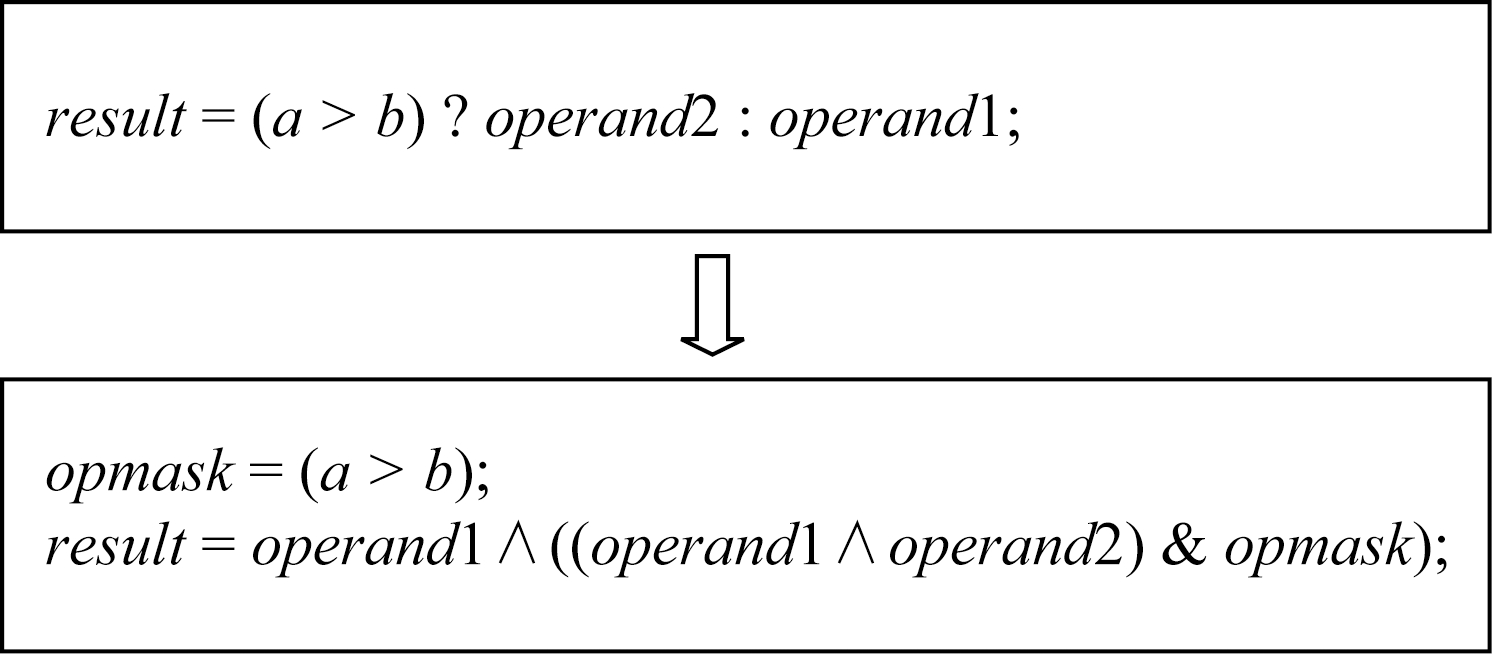
Fig. 3 Conditional move operation is implemented by bit operation
图3 条件传送操作实现为按位逻辑操作
当优化代码中使用这种条件传送运算的操作数是一些特殊值时(比如1个源操作数为0或者2个源操作数互为相反数),我们可以使用更加简单的按位逻辑操作组合而不是直接使用向量条件传送语句,从而达到提升性能的目的.向量条件传送优化如图4所示.

Fig. 4 Conditional move operation optimization
图4 条件传送优化
5) 精度修正.当计算某几个特定操作数结果有误时(如atanf函数在计算|x|≥234的操作数时),如图5我们将在代码最后使用向量条件传送语句来修正结果向量中的错误元素.
6) 性能修复.我们发现优化代码在处理可优化操作数范围内的一些特殊操作数时,在运行时可能会进入非规格化数处理的情况中而变得十分缓慢.为了解决这个问题,我们使用了类似于精度修正的方法来规避这种潜在的性能问题.如图6所示,我们的优化代码在开始计算之前会先判断操作数是否落入特殊操作数范围中,并使用条件传送语句将操作数中可能导致性能问题的元素替换为普通操作数.计算结束后再使用同样的条件传送语句将计算结果(即错误的结果)替换为正确值.由于导致被优化函数陷入非规格化数的缓慢分支对应的特殊操作数范围可以确定出来,其计算结果往往可以被近似为一个常量,因此可以提前计算得出正确的计算结果,并在代码中直接使用.
需要指出的是,原则上我们尽可能对每个向量三角函数使用上述所有优化方法,但由于各个函数内在算法的差异性,上述优化方法不一定适用于每一个函数.其中,分支预测优化应用于所有函数中,精度削减应用于所有双精度函数中,条件传送优化和精度修正只使用在asinf,acosf,atanf函数中,性能修复只使用在atanf函数中,而查表优化则因为ADVSIMD指令集不支持permute操作而只使用在了SVE指令集的atanf函数中.

Fig. 5 Precision correction
图5 精度修正

Fig. 6 Performancefixing
图6 性能修复
2.2 具体实现
结合Sleef向量数学库和libm标量数学库,我们一共对12个三角函数(包括单精度和双精度)的向量版本进行了优化.我们通过大量实验确定了各个函数可优化的操作数范围,具体如表2所示.我们发现如果libm某个函数的某个分支代码中包含大量的分支跳转语句,该分支将不值得移植和向量化,除非这些条件跳转比较简单可以转换为条件传送.另外,atanf函数的可优化操作数范围是整个实数域,因为我们发现向量化后的libm函数在整个范围内的性能均优于原始Sleef函数.
在代码移植和向量化的过程中,我们在原Sleef向量数学库的基础上增加了7个新的Sleef intrinsics函数,如表3所示.其中,vint2,vdouble,vfloat分别代表整型向量类型、双精度浮点数向量类型和单精度浮点数向量类型,vgatherr_vi2_p_vi2()与vgatherr_vf_p_vi2()为前文所提的为查表优化打包的函数.
Table 2 The Optimization Range of Vector Trigonometric Functions
表2 各向量三角函数可优化操作数范围
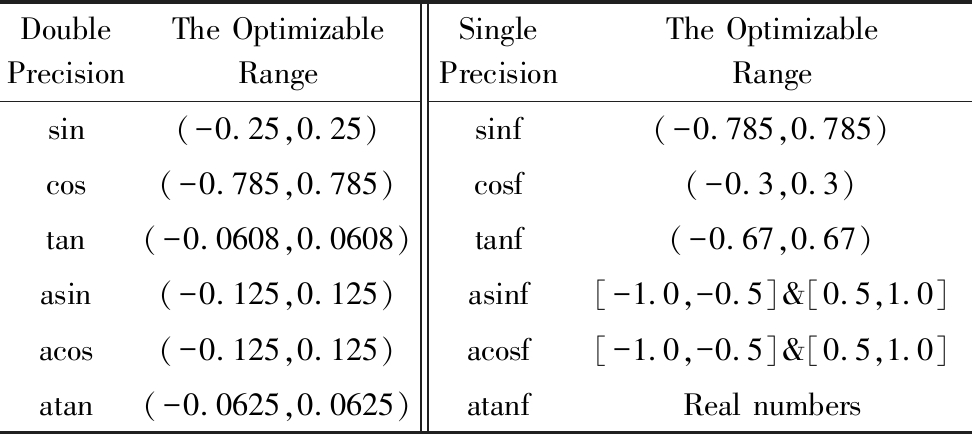
DoublePrecisionThe OptimizableRangeSinglePrecisionThe OptimizableRangesin(-0.25,0.25)sinf(-0.785,0.785)cos(-0.785,0.785)cosf(-0.3,0.3)tan(-0.0608,0.0608)tanf(-0.67,0.67)asin(-0.125,0.125)asinf[-1.0,-0.5]&[0.5,1.0]acos(-0.125,0.125)acosf[-1.0,-0.5]&[0.5,1.0]atan(-0.0625,0.0625)atanfReal numbers
Table 3 New Sleef Intrinsics
表3 优化过程中新增加的Sleef Intrinsics函数

New Sleef IntrinsicsDescriptionvint vcastou_vi_vi2(vint2x);Extract odd vector elements of the vint2 vectorvint vcasteu_vi_vi2(vint2x);Extract even vector elements of the vint2 vectorvdouble vmlanp_vd_vd_vd_vd(vdoublex,vdoubley,vdoublez);Negate multiply-substract for the vdouble vectorvfloat vmlapn_vf_vf_vf_vf(vfloatx,vfloaty,vfloatz);Multiply-substract for the vfloat vectorvint2 vgather_vi2_p_vi2(int∗ptr,vint2x);Gather operation for the vint2 vector (without loopkup table optimization)vint2 vgatherr_vi2_p_vi2(int∗ptr,vint2x);Gather operation for the vint2 vector (with loopkup table optimization)vfloat vgatherr_vf_p_vi2(const float∗ptr,vint2x);Gather operation for the vfloat vector (with loopkup table optimization)
优化的代码是以模块化方式移植入Sleef向量数学库中,从而保证这部分优化代码的独立性,也方便后续Sleef更新后,能将优化代码快速合并到新的Sleef中.具体实现时,我们将每个函数的优化代码放置于一个单独xxxx_opt.c文件中,例如单精度函数放置于opt_include/single/xxxx_opt.c文件中,而双精度函数放置于opt_include/double/xxxx_opt.c文件中,所有优化函数共同需要的常量和函数则统一放置于头文件opt_include/opt_vecf_helper.h中,为函数优化新增的intrinsics函数则放置于opt_include/sleef_arch_patch.h中,通过宏定义和include语句将这些文件导入Sleef源码中,在编译时通过控制编译选项-DCMAKE_C_FLAGS=“-DOPT_LB”来选择是否开启优化,图7显示了模块化优化方式的伪代码.
最后需要说明的是,虽然我们面向飞腾处理器进行实验,但本文所述优化方法和基于Sleef的模块化实现也可以扩展至其他处理器平台和向量指令集.

Fig. 7 Porting optimized code into Sleef
图7 以模块化方式植入优化代码
3 实验结果与分析
3.1 实验设计与环境
本文结合Sleef和libm对向量三角函数进行优化,并在飞腾处理器上对优化后的向量三角函数进行功能验证、精度实验和性能实验.其中,功能验证是验证优化后的向量三角函数功能是否正确,精度实验是具体分析优化后向量三角函数计算精度的变化,性能实验是对比我们提出的优化方法是否能进一步提升向量三角函数的性能.
本文实验主要在飞腾处理器上进行(FT-1500A/16,兼容ADVSIMD指令集,向量宽度为128 b).此外,为了进行全面的功能验证,我们还使用了x86处理器平台以验证SSE2,AVX,AVX2指令集,以及ARM Instruction Emulator模拟器以验证SVE指令集.我们使用的Sleef版本为3.3.1版本,libm版本为GNU Glibc Linaro-2.20版本.
3.2 功能验证
我们对所有优化后的向量三角函数进行严格的功能性验证,具体包括6项验证内容.
1) 优化后函数在可优化操作数范围内的计算精度是否满足设计时要求.该项验证要求待测试向量操作数中的各个元素不一致,且最终每个元素对应的计算结果的最大误差控制在1.0ulp以内.
2) 优化后函数在可优化操作数范围边界及其附近的计算精度是否满足设计时要求.同样要求待测试向量操作数中的各个元素不一致以及最终结果的最大误差控制在1.0ulp以内.这是用以检验被优化函数在算法边界处的处理是否正确.
3) 优化后函数在可优化操作数范围外的计算精度是否仍然满足设计时要求,这是用以检验本文提出的优化方法不会对可优化操作数范围外的计算产生精度方面的负面影响.
4) 优化后函数对浮点数域内的特殊浮点常量的计算结果是否正确.包括验证对浮点数±0,±∞,NaN的计算结果是否等于对应的C99标准下规定的浮点值,验证±1.0、正负最大最小非规格化数、正负最大最小规格化数的计算结果是否正确,以及验证被优化函数对大浮点数的处理是否正确(所有双精度函数检验操作数为±1E+10的计算结果,所有单精函数检验操作数为±1E+7的计算结果).
5) 优化后函数在计算与算法相关的特殊浮点常量时的计算结果是否正确.其中,双精度sin,cos,tan函数和单精度sinf,cosf,tanf函数需要检查操作数为π/4的倍数时的计算结果,双精度asin,acos函数和单精度asinf,acosf函数需要检验操作数趋于±1.0时的计算结果,这些计算结果的误差要控制在1.0ulp以内.
6) 多种情况组合下的功能验证,将前5项中列出的各种情况下的浮点操作数组合到同一向量中,测试每个向量元素的计算结果是否达到精度要求(同样要满足最大误差在1.0ulp以内),这是用以检验优化函数中的分支处理与特殊值处理等是否正确.
我们在飞腾处理器平台、x86处理器平台和ARM Instruction Emulator模拟器上对不同SIMD向量指令集进行功能验证.实验证明对于飞腾处理器平台的ADVSIMD指令集、x86平台的SSE2,AVX,AVX2指令集、以及ARM Instruction Emulator模拟器上的SVE指令集,优化后的向量三角函数均通过了功能验证,这表明我们对向量三角函数的优化达到了Sleef库的标准,可以移植入Sleef库中使用.
3.3 精度实验
对每个优化后的向量三角函数,精度实验以指定步阶从小到大测试可优化操作数范围内的浮点数,我们使用任意精度MPFR库作为参考标准,计算优化后三角函数的计算结果与MPFR库中相同函数的计算结果的具体误差(以ulp形式表示).实验将循环迭代次数控制在107次,并统计出最大误差和平均误差的ulp值.我们在飞腾处理器上进行精度实验,结果如表4所示:
Table 4 Precision Experiment Results
表4 精度实验结果
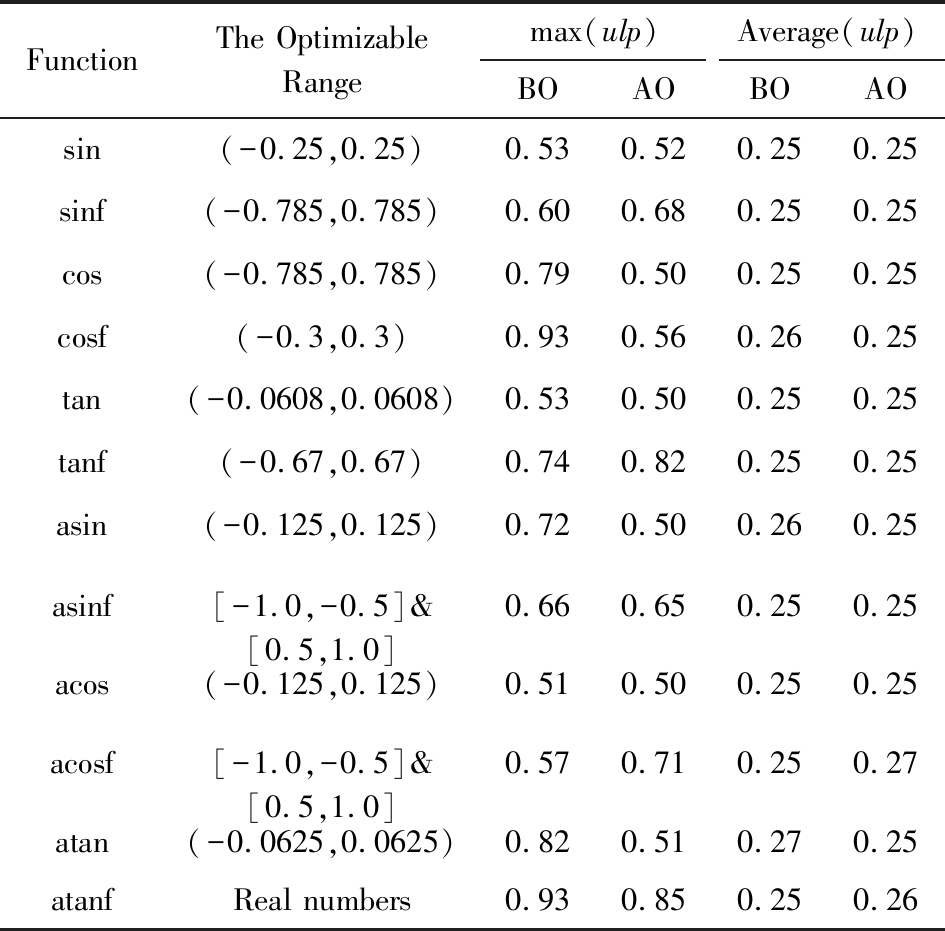
FunctionThe OptimizableRangemax(ulp)Average(ulp)BOAOBOAOsin(-0.25,0.25)0.530.520.250.25sinf(-0.785,0.785)0.600.680.250.25cos(-0.785,0.785)0.790.500.250.25cosf(-0.3,0.3)0.930.560.260.25tan(-0.0608,0.0608)0.530.500.250.25tanf(-0.67,0.67)0.740.820.250.25asin(-0.125,0.125)0.720.500.260.25asinf[-1.0,-0.5]&[0.5,1.0]0.660.650.250.25acos(-0.125,0.125)0.510.500.250.25acosf[-1.0,-0.5]&[0.5,1.0]0.570.710.250.27atan(-0.0625,0.0625)0.820.510.270.25atanfReal numbers0.930.850.250.26
Note: BO(before optimization),AO(after optimization)
可以看出,相比优化前、优化后的向量三角函数在可优化操作数范围内的精度变化很小,最大误差的变化在0.37ulp以内,平均误差的变化在0.17ulp以内,此外,除sinf,tanf,acosf函数外,其余函数在优化后的最大误差还有所降低(最大降低了0.37ulp).这说明本文所提出的优化技术对函数精度的影响较小,函数精度变化是符合要求的.
3.4 性能实验
我们从2个方面分析评估本文所提出的向量三角函数优化方法:1)通过与libm标量三角函数以及原始Sleef向量三角函数进行对比,以分析优化方法对向量三角函数的性能提升;2)分析所提优化方法所引入的开销.所有性能实验在飞腾处理上进行.
3.4.1 优化方法带来的性能提升
对于每个向量三角函数,我们在可优化操作数范围内产生单精度或双精度浮点随机数以测试函数性能.实验中,我们一共产生108个浮点随机数(存放在数组中),依次使用数组中的随机数(以向量宽度为单位,双精度为2个随机数,单精度为4个随机数)做三角函数计算,并取函数计算的平均耗时作为衡量函数性能的指标.
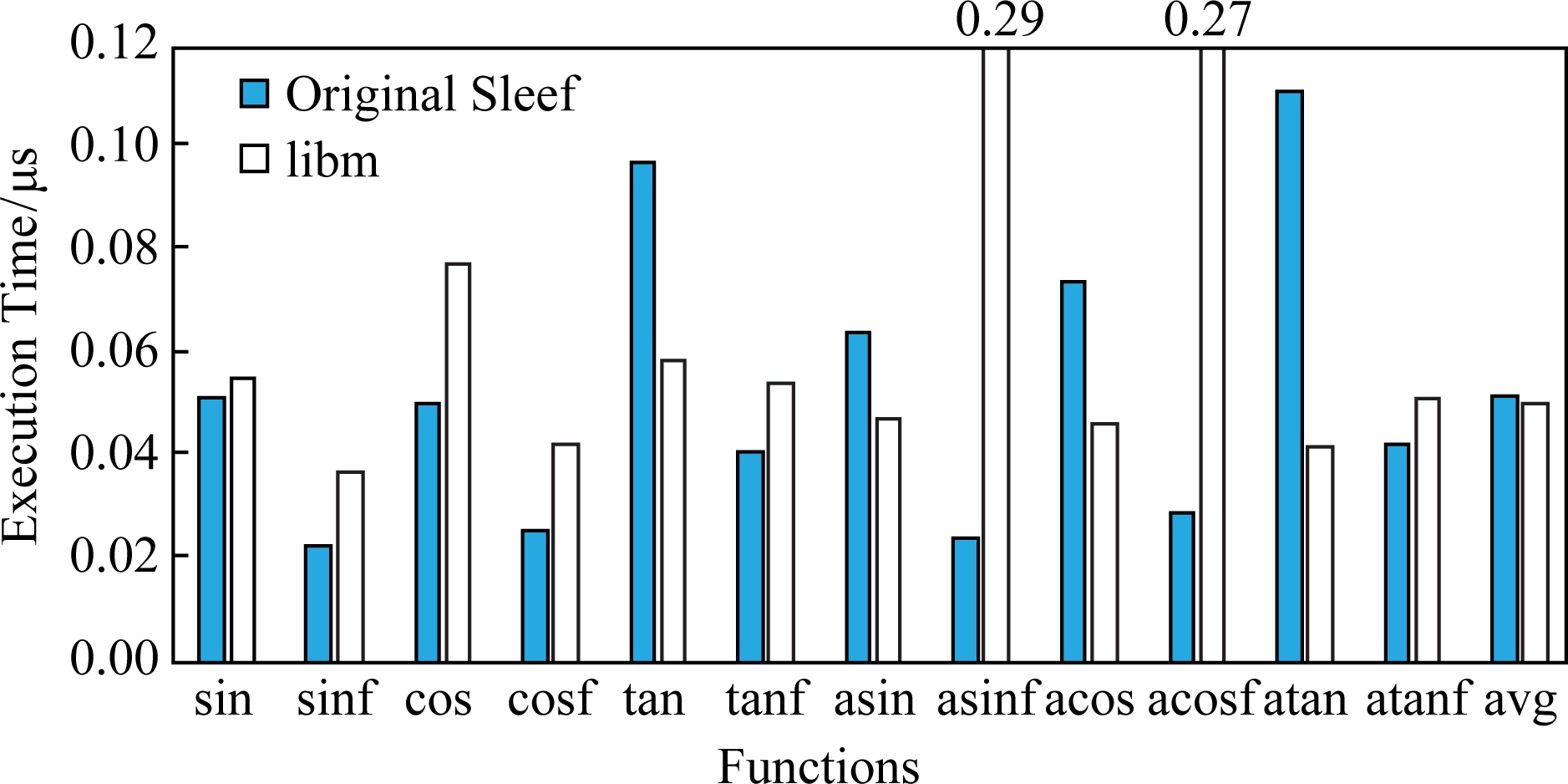
Fig. 8 Performance comparison of original Sleef functions and libm functions
图8 Sleef函数优化前与libm函数性能对比
首先,我们对比分析Sleef向量三角函数优化前与libm标量三角函数在可优化操作数范围内的性能差异,结果如图8所示.可以看出,尽管使用ADVSIMD向量指令,除异常的asinf和acosf函数外,只有一部分Sleef向量三角函数(sinf,cos,cosf,tanf)比libm标量三角函数快(最高只有1.64倍加速比),另外一部分Sleef向量三角函数与libm性能相当(sin和atanf),其余函数的性能比libm差(tan,asin,acos,atan),这是因为原始Sleef向量三角函数在计算可优化操作数范围时的算法冗余而libm采用分段计算在可优化操作数范围内降低了函数计算量.对于asinf和acosf函数,libm性能低下的原因是我们使用的libm版本内部实现时使用了软件开方(sqrt),导致函数异常耗时.
其次,我们对比分析Sleef向量三角函数优化后与libm标量三角函数的性能差异,结果如图9所示.我们发现向量三角函数优化后与libm标量三角函数相比,双精度下平均加速比为1.74倍,单精度下平均加速比为3.06倍.这一性能表现一定程度上符合飞腾处理器128 b向量宽度下向量函数与标量函数的理想加速比(双精度下2倍加速比,单精度下4倍加速比).
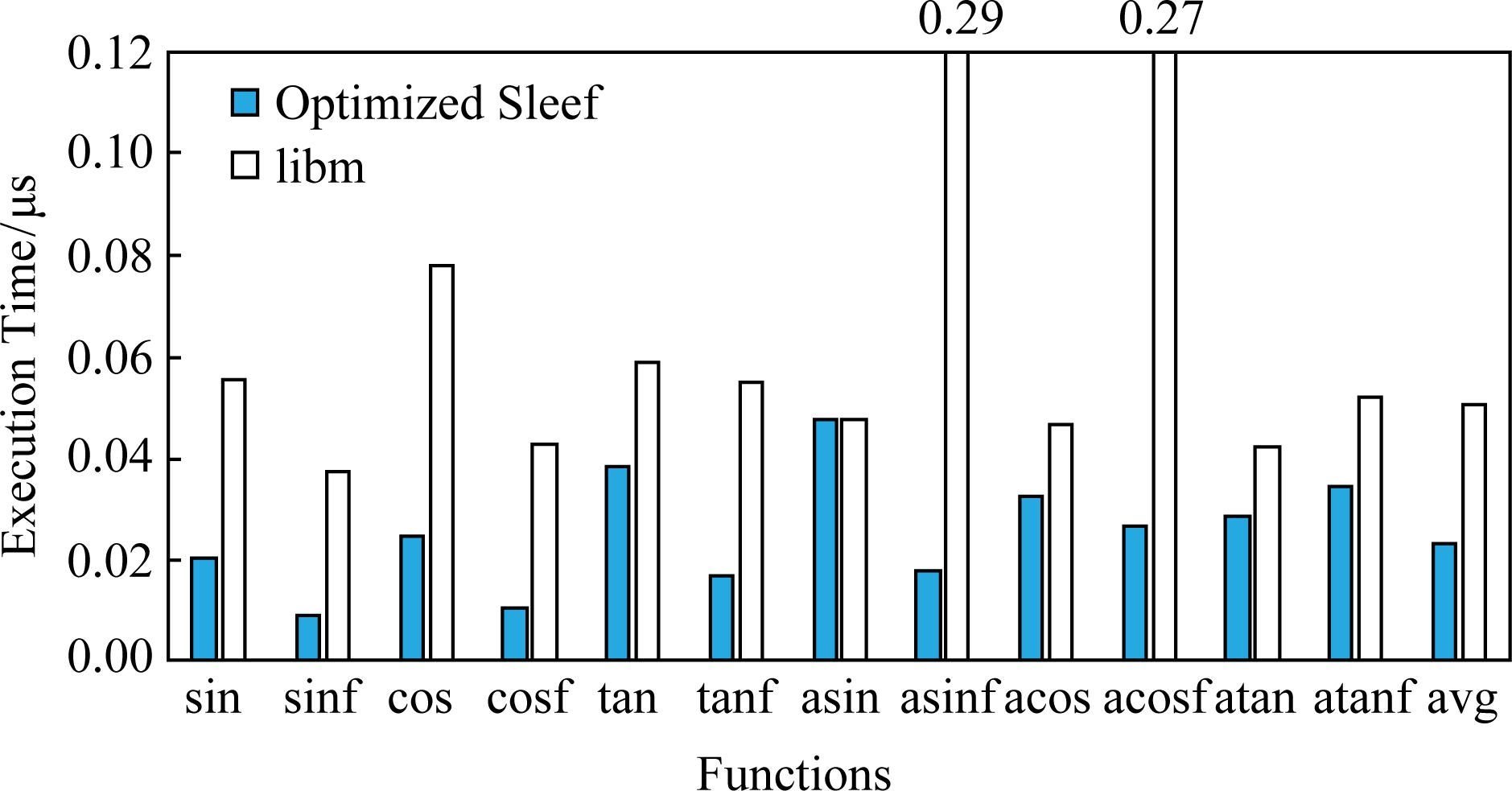
Fig. 9 Performance comparison of optimized Sleef functions and libm functions
图9 Sleef函数优化后与libm函数性能对比
最后,我们对比分析Sleef向量三角函数优化前与优化后的性能差异,结果如图10所示.可以看出使用本文所提出的优化技术,在可优化操作数范围内,所有向量三角函数的性能均得到了提升,平均加速比为2.04倍(最低加速比为1.12倍,最高可达3.97倍).
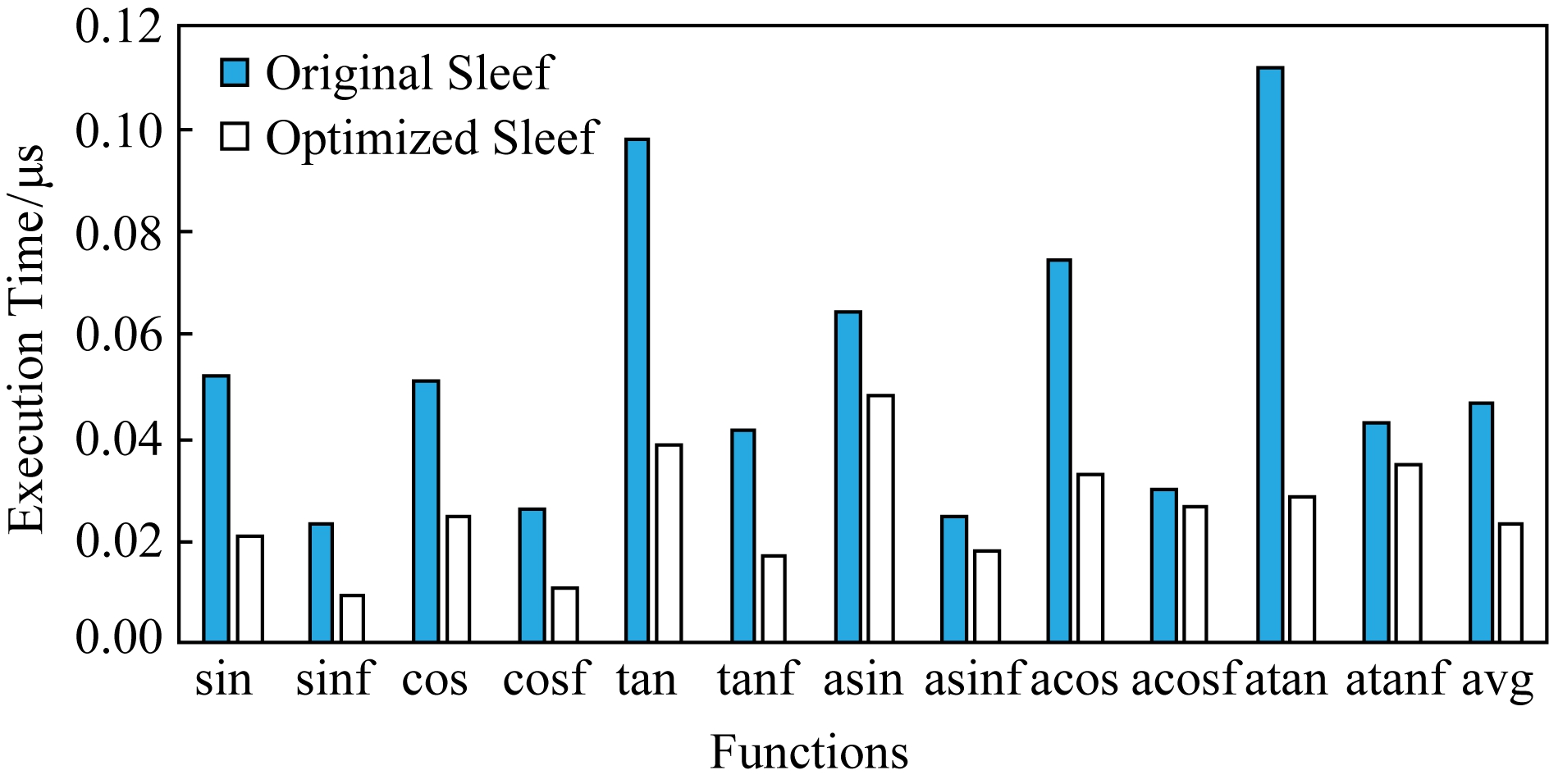
Fig. 10 Performance comparison of Sleef functions before and after optimization
图10 Sleef函数优化前与优化后性能对比
3.4.2 优化方法引入的开销
为了评估所提优化方法引入的开销,我们进行如下实验,对比分析Sleef向量三角函数优化前与优化后在可优化操作数范围之外的性能,以检查我们的优化方法在非可优化操作数范围内对原始Sleef向量三角函数的性能影响,实验结果如图11所示.可以看出使用本文所提优化方法后,在非可优化操作数范围内,所有三角函数的性能变化均很小,其中双精度三角函数的性能波动维持在4.3%以内,单精度三角函数的性能波动维持在3.8%以内(由于atanf函数的可优化操作数范围为整个实数域,因此不存在对比).换言之,我们实验确定的可优化操作数范围是正确的,并且我们的优化方法开销很低,在可优化操作数范围之外对原始Sleef向量三角函数的性能影响很小.
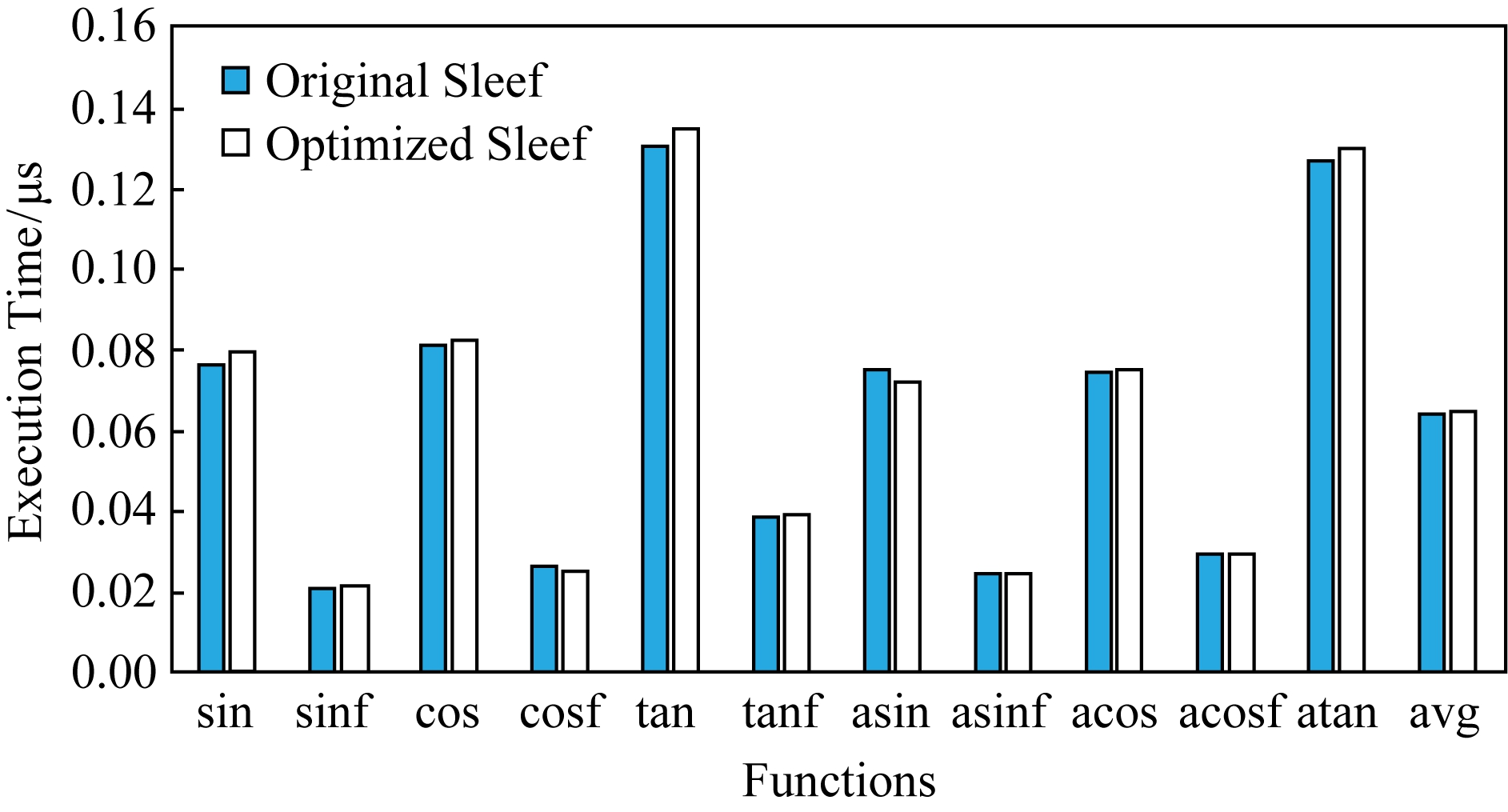
Fig. 11 Performance comparison of Sleef functions before and after optimization with operands outside the optimization range
图11 在可优化操作数范围外,Sleef函数优化前与优化后性能对比
综上所述,功能验证、精度实验和性能实验证明,本文提出的向量三角函数优化方法,在功能上满足设计要求,能够在保证计算精度和较小开销的前提下有效提高向量三角函数的性能.
4 结束语
三角函数等超越函数是科学计算类应用中最耗时的浮点计算函数,利用SIMD向量化技术提高函数性能是设计和优化数学库的一个重要研究方向.本文基于Sleef开源向量数学库,以libm分段计算为指导,设计和提出了一种支持分支处理的向量三角函数优化方法,该方法降低了原始Sleef向量三角函数中冗余计算的开销,同时保证了函数计算精度.在飞腾处理器平台上的实验表明,本文所提方法有效提高了向量三角函数性能.未来我们将进一步研究向量指数函数、对数函数、幂函数的性能优化以及代码的自动向量化工作,使得更多的科学计算应用可以得益于超越函数向量化而提升性能.
[1]Huang Libo, Ma Sheng, Shen Li, et al. Low-cost binary128 floating-point FMA unit design with SIMD support[J]. IEEE Transactions on Computers, 2012, 61(5): 745-751
[2]Wang Yongxian, Zhang Lilun, Che Yonggang, et al. Heterogeneous computing and optimization on Tianhe-2 supercomputer system for high-order accurate CFD applications[J]. Journal of Computer Research and Development, 2015, 52(4): 833-842 (in Chinese)(王勇献, 张理论, 车永刚, 等. 高阶精度CFD应用在天河2系统上的异构并行模拟与性能优化[J]. 计算机研究与发展, 2015, 52(4): 833-842)
[3]Stephens N, Biles S, Boettcher M, et al. The ARM scalable vector extension[J]. IEEE Micro, 2017, 37(2): 26-39
[4]GNU. GNU C library version 2.20[OL]. [2019-10-09]. http://www.gnu.org/software/libc/
[5]Intel. Intel libimf library[OL]. [2019-10-09]. http://software.intel.com/de-de/tags/21702
[6]Intel. Intel short vector mathematical library[OL]. [2019-10-09]. http://software.intel.com/sites/products/documentation/hpc/composerxe/en-us/cpp/win/index.htm
[7]Shibata N. Efficient evaluation methods of elementary functions suitable for SIMD computation[J]. Computer Science-Research and Development, 2010, 25: 25-32
[8]Shibata N, Petrogalli F. SLEEF: A portable vectorized library of C standard mathematical functions[J]. IEEE Transactions on Parallel and Distributed Systems, 2020, 31(6): 1316-1327
[9]Liu Chungen. Programming Principle, Implementation and Application of Floating-point Computing[M]. Beijing: China Machine Press, 2008 (in Chinese)(刘纯根. 浮点计算编程原理、实现与应用[M]. 北京: 机械工业出版社, 2008)
[10]Muller J M. Elementary Functions: Algorithms and Implementation[M]. Boston: Birkhäuser, 2006
[11]AMR. ARM optimized routines[OL]. [2019-10-09]. https://github.com/ARM-software/optimized-routines
[12]GNU. GNU C library[OL]. [2019-10-09]. https://sourceware.org/git/?p=glibc.git;a=tree;f=sysdeps/x86_64/fpu/multiarch
[13]Lauter C. A new open-source SIMD vector libm fully implemented with high-level scalar C[C] //Proc of 50th Asilomar Conf on Signals, Systems and Computers. Piscataway, NJ: IEEE, 2016: 407-411
[14]Piparo D, Innocente V, Hauth T. Speeding up HEP experiment software with a library of fast and auto-vectorisable mathematical functions[J]. Journal of Physics: Conf Series, 2014, 513(5): No.052027
[15]Lei Yuanwu, Dou Yong, Zhou Jie. FPGA-specific custom VLIW architecture for arbitrary precision floating-point arithmetic[J]. IEICE Transactions on Information and Systems, 2011, 94(11): 2173-2183
[16]Goldberg D. What every computer scientist should know about floating-point arithmetic[J]. ACM Computing Surveys, 1991, 23(1): 5-47
[17]Cornea M, Golliver R A, Markstein P. Correctness proofs outline for Newton-Raphson-based floating-point divide and square root algorithms[C] //Proc of the 14th IEEE Symp on Computer Arithmetic. Piscataway, NJ: IEEE, 1999: 96-105
[18]MPFR. The MPFR Library[OL]. [2019-10-09]. http://www.mpfr.org



