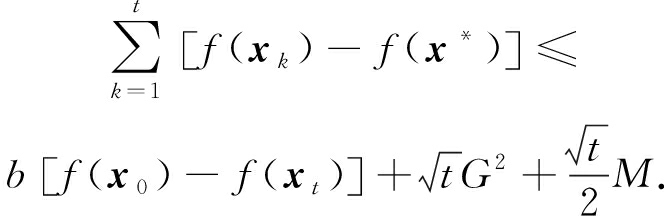无论是经典的正则化损失函数框架,如稀疏学习和支持向量机,还是当前的研究热点深度学习,如卷积和递归神经网络,都可以视为给定模型空间的参数寻优问题,随机梯度下降法(stochastic gradient descent, SGD)是解决这类参数寻优问题简单而又有效的方法.为了获得更好的收敛性能,人们开始在SGD的基础上使用动量方法.
动量实际上是物理学中的一个概念,动量原理告诉我们运动的物体会因为惯性继续保持运动,除非受到外力作用而停下来.在优化算法中,动量方法可以在梯度很小的情形下仍然保持更新,从而可以加速SGD在求解凸优化问题时的收敛速率[1-3],帮助SGD在求解非凸优化问题时摆脱局部最优点[4-5].对于随机优化问题,由于动量可以分解成过往梯度加权平均的方式,因此比SGD具有更小的方差,据此使算法获得了更好的收敛性和稳定性[6].
我们通常讨论的动量方法有2种标准形式:一种是由Polyak于1964年提出HB(heavy ball)方法[7];另一种是Nesterov于1983年提出的NAG(Nesterov’s accelerated gradient)方法[8].HB的加速性主要体现在目标函数强凸且二次可微时,尽管与梯度下降法、NAG具有相同的线性收敛速率,但HB具有最小的收敛因子.NAG的加速性主要体现在求解凸光滑目标函数时,可以将梯度下降法的收敛速率加速至最优O(1 t2),其中t是迭代步数.对于非光滑凸优化问题,SGD,HB和NAG具有相同的最优平均收敛速率,但对于个体收敛性,HB和NAG也具有加速效果,可将SGD的个体收敛速率从O(log
t2),其中t是迭代步数.对于非光滑凸优化问题,SGD,HB和NAG具有相同的最优平均收敛速率,但对于个体收敛性,HB和NAG也具有加速效果,可将SGD的个体收敛速率从O(log ![]() 加速至最优的
加速至最优的![]()
在深度神经网络训练中,使用动量优化方法替代无法选取合适步长的SGD,已经在计算机视觉等方面取得了很好的效果[9].Ochs等人通过实验验证了批处理形式的HB方法能够逃离局部最小值点[4].2019年Sun等人从理论上证明了HB方法比GD方法有更大的步长从而可以逃避鞍点[5].而NAG也表现不凡,可以提高RNN在许多任务中的性能[10].
目前,人们已经将典型的动量优化方法写进了深度学习的优化器中.随着优化方法进一步发展,出现了众多形式的动量方法.典型的有2016年Lessard等人提出的SNV(synthesized Nesterov variants)[11]、2018年Kidambi等人的AccSGD(accelerated SGD)[12]、Bryan等人的Triple动量方法[13]以及Cyrus等人提出的Robust动量方法[14]等等.
综上,无论是从理论分析还是从理解动量在优化算法中作用的角度来看,建立一个统一的动量方法的一般框架都是十分必要的.实际上,早在2013年,Sutskever等人就发现HB方法和NAG方法的区别仅仅在于计算梯度的点选取不同[15];通过引入中间变量,Yang等人于2016年提出了一种随机统一化动量方法(stochastic unified momentum, SUM),统一了SGD,HB和NAG[16];2019年Ma等人提出了QHM(quasi-hyperbolic momentum)方法,其迭代步骤可以表示成SGD与动量缓冲项的一种加权平均方式.QHM通过使用动量缓冲和加权SGD的2个折中参数将AccSGD,Triple,Robust等形式的动量方法进行统一[6].显然,SUM和QHM在统一化动量方法上的思路是不同的.
动量方法在有效提高SGD收敛性能的同时,也存在一些令人质疑的地方,即由于动量改变了SGD中梯度下降的操作,是否还能保持SGD原有的收敛性能?具体来说,对于非光滑凸问题,我们首先应该证明动量方法具有和SGD一样的最优平均收敛速率.但遗憾的是目前的研究还存在一些欠缺.特别地,对于非光滑凸目标函数,尽管SUM得到了最优的O(1 t)平均收敛速率[16],但其使用的步长严重依赖预先设定的迭代步数,这种固定总迭代步数的方法在处理大规模数据时由于不能增量地执行算法而缺少实用性.另一方面,QHM虽然在实验中的性能超越了HB和NAG,但只讨论了光滑情况下的收敛性,也没有给出具体的收敛速率[6,17].除此以外,这些方法均只适用于无约束情况,不能用于解决机器学习中如稀疏学习导致的有约束问题.据我们所知,目前还没有文献涉及详细分析动量方法在有约束非光滑情况下的平均收敛性问题.
t)平均收敛速率[16],但其使用的步长严重依赖预先设定的迭代步数,这种固定总迭代步数的方法在处理大规模数据时由于不能增量地执行算法而缺少实用性.另一方面,QHM虽然在实验中的性能超越了HB和NAG,但只讨论了光滑情况下的收敛性,也没有给出具体的收敛速率[6,17].除此以外,这些方法均只适用于无约束情况,不能用于解决机器学习中如稀疏学习导致的有约束问题.据我们所知,目前还没有文献涉及详细分析动量方法在有约束非光滑情况下的平均收敛性问题.
本文的贡献主要体现在3个方面:
1) 提出了一种含三参数的统一化动量方法TPUM(triple-parameters unified momentum),通过取不同的参数,能够同时包含SUM和QHM,是目前最一般的动量算法的统一框架.
2) 即使是对特例QHM,本文也给出约束非光滑情形的最优平均速率,而QHM目前只有光滑情形下的收敛性结论.即使是对特例SUM,本文也去掉了SUM原有收敛性中需要固定迭代步数和无约束等不合理限制.
3) 证明了所提出的TPUM方法在求解有约束非光滑凸优化问题时具有最优的平均收敛速率,并将其推广到随机情况,从而保证了添加动量不会影响标准梯度下降法的收敛性能以及动量方法对机器学习问题的可应用性.
1 TPUM方法
考虑优化问题:
min f(x), s.t. x∈Q,
(1)
其中,Q⊆![]() n是闭凸集,f是Q上的一个凸函数.
n是闭凸集,f是Q上的一个凸函数.
批处理形式的投影次梯度方法的迭代步骤为
xk+1=PQ[xk-αk![]() f(xk)],
f(xk)],
(2)
其中,αk为迭代步长,![]() f(xk)为f(x)在xk处的次梯度,P是Q上的投影算子.收敛速率通常包括个体收敛速率和平均收敛速率2种形式.经常使用的个体输出收敛速率的数学表达式为
f(xk)为f(x)在xk处的次梯度,P是Q上的投影算子.收敛速率通常包括个体收敛速率和平均收敛速率2种形式.经常使用的个体输出收敛速率的数学表达式为
f(xt)-f(x*),
其中,t是总迭代次数,x*是最优解.平均输出收敛速率的数学表达式为
其中,![]()
HB更新为
xk+1=xk-αk![]() f(xk)+β(xk-xk-1),
f(xk)+β(xk-xk-1),
(3)
其中,αk≥0为步长,β∈[0,1)为动量xk-xk-1的系数.
NAG更新为
![]() (4)
(4)
NAG等价于:
xk+1=xk-α![]() f[(1+β)xk-βxk-1]+
f[(1+β)xk-βxk-1]+
β(xk-xk-1).
(5)
显然式(3)和式(5)的区别就在于计算梯度的位置不同,在非光滑情况下,当取时变的步长αk和动量系数β时,文献[1]和[2]分别证明了这2种动量方法具有加速作用,可以得到![]() 的最优个体收敛率.
的最优个体收敛率.
为了将式(3)与式(4)统一,SUM引入中间变量![]() 在xk与yk之间进行切换,其批处理情况更新为
在xk与yk之间进行切换,其批处理情况更新为
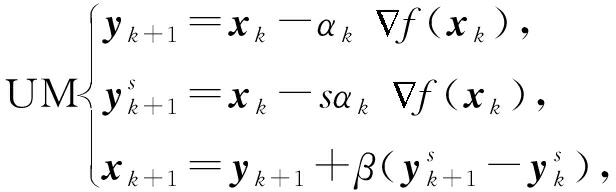 (6)
(6)
其中,s≥0为一常数,不同的s对应不同动量方法.
QHM更新如下:
![]() (7)
(7)
其中,dk称为动量缓冲器.显然,QHM也是使用当前梯度与过去梯度的凸组合,但由于折中参数vk,βk的存在,破坏了更容易理解的动量项形式β(xk-xk-1),与SUM统一动量的出发点是不同的.
然而,通过对文献[17]的研究发现,动量缓冲器与动量项β(xk-xk-1)具有密切联系,可以推出-α βkdk-1=β(xk-xk-1).正是基于这种联系,受SUM统一思路的启发,本文增加2个折中参数δ1,δ2,将QHM和SUM进行统一,提出TPUM方法:
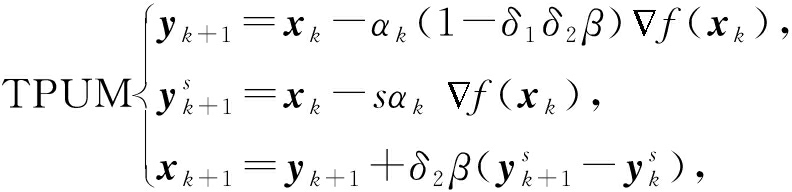 (8)
(8)
其中,步长αk>0,β∈[0,1)为动量系数,δ1,δ2∈[0,1]为折中参数.显然:
当δ1=0,s=0,δ2=1时,TPUM为HB;
当δ1=0,s=1,δ2=1时,TPUM为NAG;
当δ1=0,δ2=0时,TPUM为梯度下降法;
当δ1=1,s=0,δ2≠0,δ2≠1时,TPUM为QHM.
由此可见,TPUM是目前最一般的动量算法的统一框架.
2 TPUM方法平均收敛性分析
文献[16]给出了SUM的收敛性分析,其定理1在无约束非光滑情况下得到了![]() 的最优平均收敛速率.但是,其步长
的最优平均收敛速率.但是,其步长![]() 其中C是一正的常数,明显需要依赖于提前设定的迭代次数t.
其中C是一正的常数,明显需要依赖于提前设定的迭代次数t.
对于有约束问题(1),TPUM更新式(8)可以等价写成:
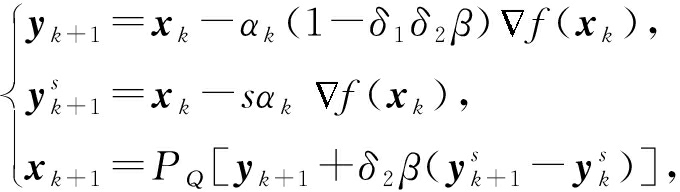 (9)
(9)
其中,P是Q上的投影算子.式(9)等价于:
xk+1=PQ[xk-αk(1-δ1δ2β)![]() f(xk)+δ2β(xk-
f(xk)+δ2β(xk-
sαk![]() f(xk)-xk-1+sαk-1
f(xk)-xk-1+sαk-1![]() f(xk-1))].
f(xk-1))].
(10)
在无约束情况下,文献[16]中定义:
![]() (11)
(11)
一个直接的优势就是利用式(11)得到:
![]()
![]() f(xk).
f(xk).
(12)
与已知的梯度优化方法十分相像[18],由式(12)出发很容易得到收敛性结论,也这正是SUM的主要证明思路.然而,这种方法仅对无约束有效,且使用的是固定步长,对于有约束情况的证明将十分困难.
为此,区别于式(11),修改动量项,得到:
引理1. 假设![]() 是由式(9)产生的,令动量项
是由式(9)产生的,令动量项
pk=b(xk-xk-1),
其中,b为一个正常数,则
xk+pk=xk+b(xk-xk-1),
xk+1+pk+1=xk+1+b(xk+1-xk),
x-(xk+1+pk+1)=x-(b+1)xk+1+bxk,
x-(xk+pk)=x-(b+1)xk+bxk-1.
引理2[19]. 对于任意x∈RN,x0∈Q:
 x-x0,y-x0
x-x0,y-x0 ≤0
≤0
当且仅当x0=P(x)时,对所有的y∈Q恒成立.
实际上,利用约束与投影的关系,与文献[18]类似,式(10)中的投影运算可以重新定义为一个优化问题:
引理3. 式(10)等价于:
![]()
![]() f(xk),x
f(xk),x +
+![]()
sαkδ2β
![]() f(xk),x
f(xk),x -
-
sαk-1δ2β
![]() f(xk-1),x
f(xk-1),x },
},
(13)
假设1. 存在![]() 对∀x∈Q恒成立,其中
对∀x∈Q恒成立,其中![]() f(xk)是f在Q上的任意次梯度.
f(xk)是f在Q上的任意次梯度.
基于上述3条引理及假设1,可以得到:
引理4. 假设![]() 是由式(9)产生的.令
是由式(9)产生的.令
![]()
b∈[0,+∞),δ2∈[0,1],
对任意的x∈Q,s≥0,δ1≥0,则
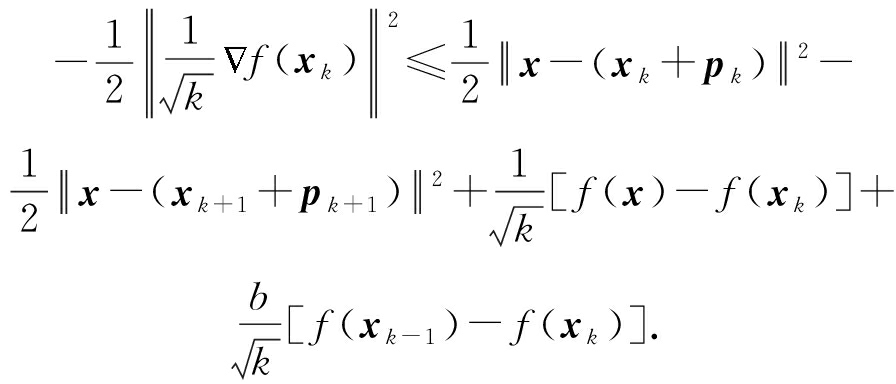 (14)
(14)
具体证明见附录A.
通过重新定义的动量项和上述引理,利用凸函数的性质,Fenchel-Young不等式,可以得到:
定理1. 假设Q有界,设![]() 由TPUM算法式(9)产生.令
由TPUM算法式(9)产生.令![]() 则存在一个正数M,使得
则存在一个正数M,使得
且对任意t>0,
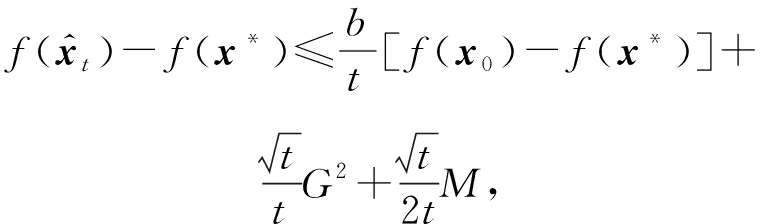 (15)
(15)
其中,![]() 是最优解.
是最优解.
具体证明见附录B.至此,针对约束非光滑凸优化问题,本文使用时变步长,证明了TPUM具有和SGD一样的![]() 最优平均收敛速率.
最优平均收敛速率.
从定理1中可以看出:
1) TPUM是更为一般的统一化动量方法,在非光滑约束情况下可以得到最优的平均收敛速率,相比特殊情形的SUM与QHM,TPUM克服了固定步长及无约束的缺陷.
2) 如果使用固定的步长,TPUM将与SUM的证明一样简洁,并且同样可以得到最优收敛速率.
3) 文献[1]证明了在非光滑情形下HB型动量对SGD的个体收敛性具有加速作用,但其证明主要是针对无约束情形,且要求动量系数是时变的.本文虽然只是得到较弱的平均收敛性,但针对的是有约束问题且考虑的是更一般的统一化动量方法.
定理1中批处理形式的TPUM在计算![]() f(xk)时需要遍历整个样本集合来获取每个fi(x)的次梯度,这种方法显然不适合处理大规模数据.为此,我们将其推广到随机形式.
f(xk)时需要遍历整个样本集合来获取每个fi(x)的次梯度,这种方法显然不适合处理大规模数据.为此,我们将其推广到随机形式.
考虑二分类的稀疏学习问题,假设训练样本集![]()
![]() n×{+1,-1},其中
n×{+1,-1},其中![]() 满足独立同分布,
满足独立同分布,![]() 表示第i次随机抽取的样本,
表示第i次随机抽取的样本,![]() 为样本标签.本文只考虑非光滑hinge损失,即:
为样本标签.本文只考虑非光滑hinge损失,即:
优化目标函数为
(16)
其中i为迭代到第t步时随机抽取的样本序号.
对于式(10),TPUM的随机形式迭代步骤为
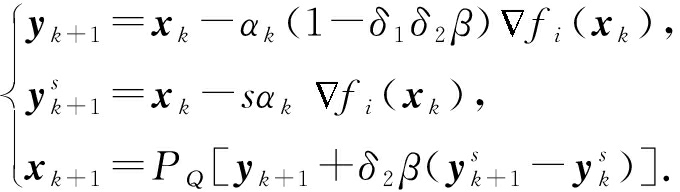 (17)
(17)
与批处理形式不同,随机优化方法的![]() fi(xt)是fi(x)在xt处的次梯度.由于hinge损失函数的次梯度不是唯一的并且有多种计算方式,这里采用文献[20]的方式进行计算,即:
fi(xt)是fi(x)在xt处的次梯度.由于hinge损失函数的次梯度不是唯一的并且有多种计算方式,这里采用文献[20]的方式进行计算,即:
![]()
![]()
(18)
其中,![]() 在实验中设置|At|=1.
在实验中设置|At|=1.
算法1. 随机TPUM算法.
输入:循环次数t;
输出:xt.
① 初始化x1=0,设定α1,δ1,δ2,s,b;
② For k=1 to t;
③ 更新![]()
④ 随机选取i∈{1,2,…,m};
⑤ 由式(18)计算![]() if(xt);
if(xt);
⑥ 由式(17)计算xk+1;
⑦ End For
当样本点满足独立同分布时,随机抽取样本计算得到的![]() if(xt)是
if(xt)是![]() f(xt)的无偏估计.从算法1中可以看出,随机形式的算法就是将批处理形式的目标函数梯度替换为其无偏估计.文献[21]直接给出了将批处理算法的收敛界转换为随机算法收敛界的技巧,该技巧对定理1同样成立.因此,可以将定理1推广至随机形式得到定理2.
f(xt)的无偏估计.从算法1中可以看出,随机形式的算法就是将批处理形式的目标函数梯度替换为其无偏估计.文献[21]直接给出了将批处理算法的收敛界转换为随机算法收敛界的技巧,该技巧对定理1同样成立.因此,可以将定理1推广至随机形式得到定理2.
定理2. 假设Q有界,设![]() 由TPUM算法式(17)产生.令
由TPUM算法式(17)产生.令
![]()
b∈(0,+∞),δ2∈[0,1],
s≥0,δ1≥0,则存在一个正数M,使得
且对任意t>0,
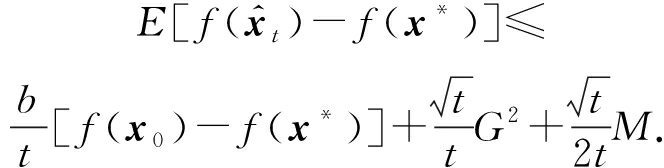 (19)
(19)
至此,在有约束非光滑情况下,得到了TPUM在批处理和随机形式下均具有了最优的![]() 平均收敛速率的结论.
平均收敛速率的结论.
3 实 验
3.1 实验目的
本节通过求解优化问题式(16),对随机TPUM式(17)平均收敛速率的理论分析结果进行实验验证.
主要实验目的有2方面:
1) 为了观察时变步长与固定步长之间的区别,验证时变步长可以达到和固定步长一样的收敛效果.为此,选取SHB,SNAG进行对比,固定步长的取法按照文献[16]中的![]() 时变步长的取法按照文中定理1中的
时变步长的取法按照文中定理1中的![]()
2) 为了验证所提出的TPUM具有最优平均收敛速率,引入DA(dual averaging)算法[22]与TPUM框架下的SHB,SNAG和QHM进行对比,同时在6个数据集中各任取了一组超参数作为TPUM.DA是一种求解非光滑约束问题的经典一阶优化方法[22],具有最优的平均收敛速率,因此实验选取DA作为基准方法,其参数选择参照文献[22]的定理3.
3.2 实验数据集与方法
实验采用的是6个常用的标准数据集,这些数据集可以在LIBSVM(1)http://www.csie.ntu.edu.tw/~cjlin/libsvm/网站中找到,详细描述如表1所示:
Table 1 Description of Standard Datasets
表1 标准数据库描述
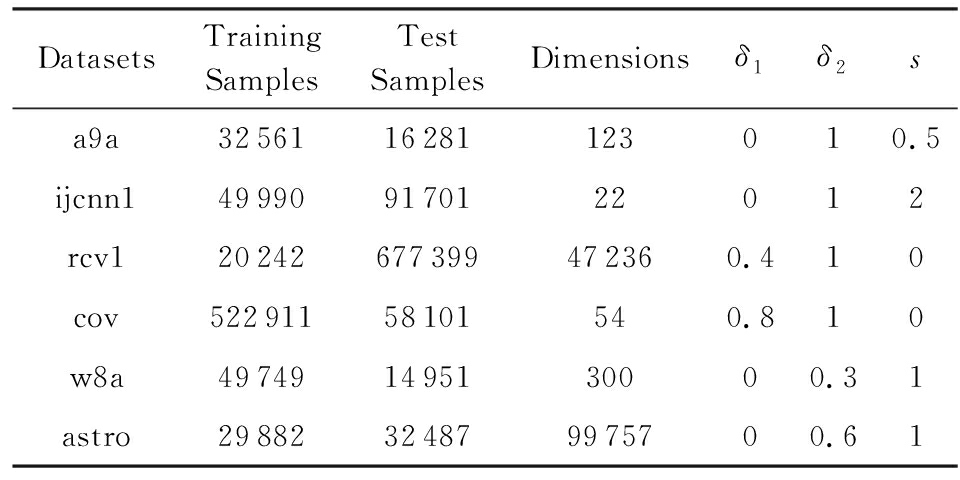
DatasetsTrainingSamplesTestSamplesDimensionsδ1δ2sa9a3256116281123010.5ijcnn1499909170122012rcv120242677399472360.410cov52291158101540.810w8a497491495130000.31astro29882324879975700.61
为了进行公平地比较,所有的实验都在随机示例序列上重复计算了10次,取平均值作为最后结果,最大迭代次数均设定为10 000次.在实验中固定β=0.9,取δ1=0,δ2=1,s=0,s=1分别表示TPUM框架下的SHB与SNAG;δ1=1,δ2=0.5,s=0时为QHM.6个数据库中的TPUM参数选取如表1所示,分别标记为TPUM1至TPUM6,可以粗略地帮助我们看出3个参数的敏感性.
实验中调用SLEP工具箱的函数来实现投影的计算[23],其中PQ为L1范数球![]() 上的投影算子,各算法取相同的约束参数z,根据数据集的不同进行调整.
上的投影算子,各算法取相同的约束参数z,根据数据集的不同进行调整.
3.3 实验结论
图1为时变步长与固定步长对于收敛性影响的比较图,其中带有time-varying的曲线表示使用的是时变步长.实验验证,尽管固定步长在计算上为常数更为简单,但时变步长可以达到和固定步长几乎一致的最优收敛速率.而在实际的机器学习问题中,如果数据集样本发生变化,或者处理大规模数据时,使用时变步长的方法无疑更具有实用性.
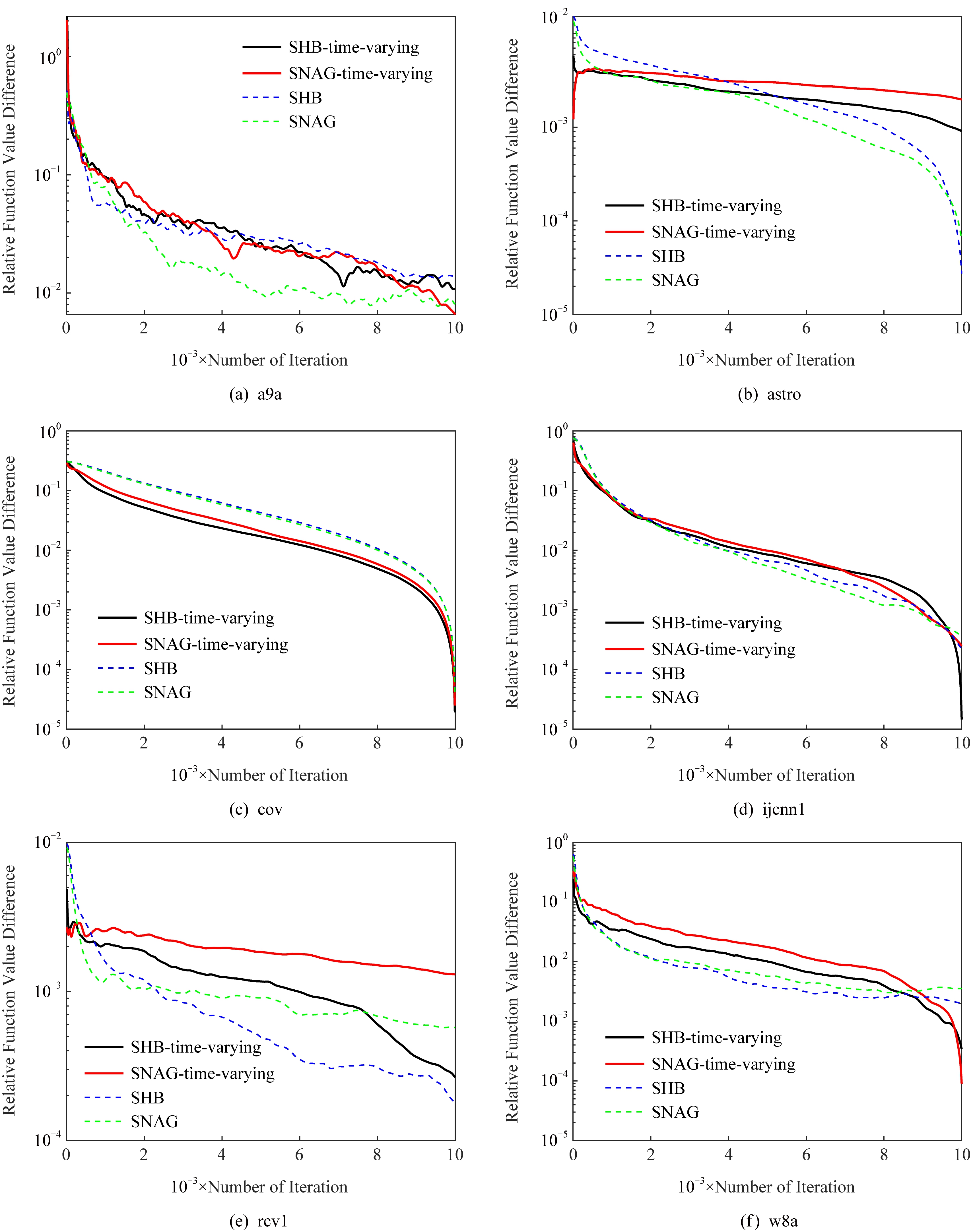
Fig. 1 Comparison of convergence rates with time-varying and constant step sizes
图1 时变步长与固定步长收敛速率比较图
图2为所提TPUM收敛性比较图.如图所示,在有约束情况下,从添加不同超参数的TPUM曲线可以看出,整体的收敛趋势没有改变.与现有的DA方法相比,TPUM方法的几种变体,即SHB,SNAG和QHM与TPUM均有一致的收敛趋势,在迭代8 000步后,5种算法基本都能达到10-2的精度,这与本文的理论分析结果是吻合的,说明了TPUM具有最优平均收敛速率.
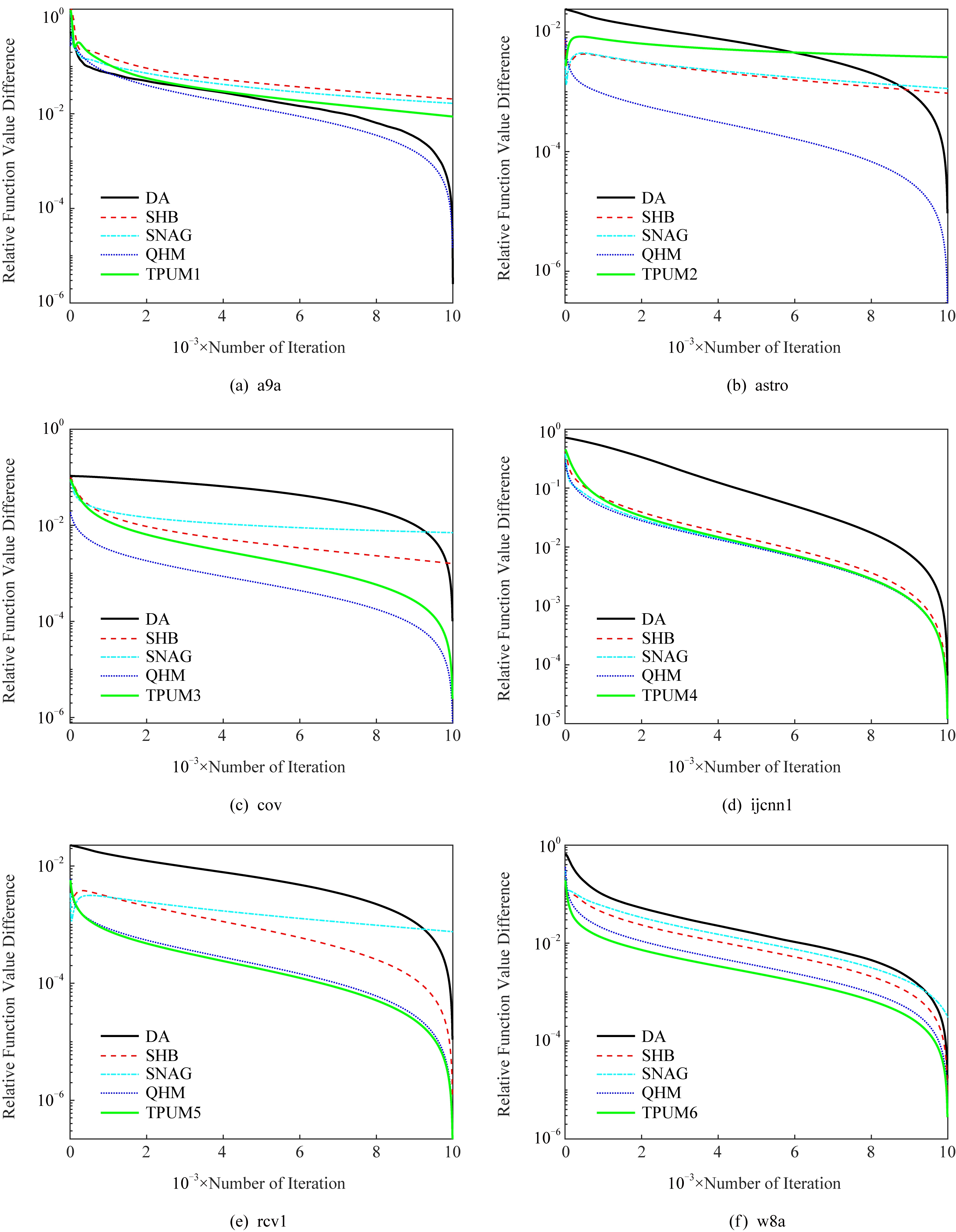
Fig. 2 Comparison of convergence rates
图2 收敛速率比较图
4 结 论
本文提出了一种更一般的统一化动量方法TPUM,包括了目前典型的统一框架SUM和QHM.其次,证明了所提出的TPUM方法在约束情况下具有最优的平均收敛速率,从而保证了添加动量不会影响标准梯度下降法的收敛性能以及动量方法对机器学习问题的可应用性.
众所周知,相比于平均输出,个体输出具有更好的稀疏性,但个体收敛性较难获得.目前对于HB,NAG的个体收敛性已经有所突破[1-3].能否得到TPUM的个体收敛性结论显然值得考虑.另一方面,2015年Kingma等人提出一种Adam(adaptive moment estimation)方法,实际上是在HB基础上对步长的设置加以改进,以得到更好的收敛性能,目前在深度学习中被广泛使用[24],而QHM与Adam的结合也已经有所研究[6].将本文提出的TPUM与Adam结合,进一步提升动量方法在深度学习中的性能将是我们下一步的研究方向.
[1]Cheng Yujia, Tao Wei, Liu Yuxiang, et al. The best individual convergence rate of Heavy-ball momentum method[J]. Journal of Computer Research and Development, 2019, 56(8): 1686-1694 (in Chinese)
(程禹嘉, 陶蔚, 刘宇翔, 等. Heavy ball型动量方法的最优个体收敛速率[J]. 计算机研究与发展, 2019, 56(8): 1686-1694)
[2]Tao Wei, Pan Zhisong, Wu Gaowei, et al. The strength of Nesterov’s extrapolation in the individual convergence of nonsmooth optimization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019. DOI: 10.1109/TNNLS.2019.2933452
[3]Tao Wei, Pan Zhisong, Chu Dejun, et al. The individual convergence of projected subgradient methods using the Nesterov’s step-size strategy[J]. Chinese Journal of Computers, 2018, 41(1): 164-176 (in Chinese)
(陶蔚, 潘志松, 储德军, 等. 使用Nesterov步长策略投影次梯度方法的个体收敛性[J]. 计算机学报, 2018, 41(1): 164-176)
[4]Ochs P, Chen Yunjun, Thomas B. Inertial proximal algorithm for nonconvex optimization[J]. SIAM Imaging Sciences, 2014, 7(2): 1388-1419
[5]Sun Tao, Li Dongsheng, Quan Zhe, et al. Heavy-ball algorithms always escape saddle points[C] //Proc of the Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2019: 3520-3526
[6]Ma J, Yarats D. Quasi-hyperbolic momentum and adam for deep learning[C/OL]. (2019-03-02) [2019-12-05]. http://arxiv.org/abs/1604.03257
[7]Polyak B T. Some methods of speeding up the convergence of iteration methods[J]. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1-17
[8]Nesterov Y. A method of solving a convex programming problem with convergence rate O(1/k2)[J]. Soviet Mathematics Doklady, 1983, 27(2): 372-376
[9]Krzhevsky A, Sutshever I, Hinton G. ImageNet classification with deep convolutional neural networks[C] //Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2012: 1097-1105
[10]Ruder S. An overview of gradient descent optimization algorithms[C/OL].(2017-06-15) [2018-10-21]. https://arxiv.org/abs/1609.04747v2
[11]Lessard L, Recht B, Packard A. Analysis and design of optimization algorithms via integral quadratic constraints[J]. SIAM Journal on Optimization, 2016, 26(1): 57-95
[12]Kidambi R, Netrapalli P, Jain P, et al. On the insufficiency of existing momentum schemes for stochastic optimization[C/OL]. (2018-07-31) [2018-12-08]. https://arxiv.org/abs/1803.05591v2
[13]Bryan V, Randy A, Kevin M. The fastest known globally convergent first-order method for minimizing strongly convex functions[J]. IEEE Control Systems Letters, 2017, 2(1): 49-54
[14]Cyrus S, Lessard L, Hu B, et al. A robust accelerated optimization algorithm for strongly convex functions[C/OL]. (2018-07-31) [2018-10-15]. https://arxiv.org/abs/1710.04753v2
[15]Sutskever J M, George E, Dahl G E, et al. On the importance of initialization and momentum in deep learning[C] // Proc of the 30th Int Conf on Machine Learning. New York: ACM, 2013: 1139-1147
[16]Yang Tianbao, Lin Qihang, Li Zhe. Unified convergence analysis of stochastic momentum methods for convex and non-convex optimization[EB/OL]. (2016-05-04) [2018-12-13]. http://arxiv.org/abs/1604.03257
[17]Gitman I, Lang H, Zhang Pengchuan, et al. Understanding the role of momentum in stochastic gradient methods[C] //Proc of 2019 Advances in Neural Information Proc Systems. Cambridge, MA: MIT Press, 2019: 9630-9640
[18]Duchi J. Introductory lectures on stochastic optimization[M]. Stanford: The Mathematics of Data, 2018: 23-32
[19]Bertsekas D, Nedic A, Ozdaglar A, et al. Convex analysis and optimization[M]. Cambridge, MA: Athena Scientific, 2003: 88-92
[20]Shalev S, Singer Y, Srebro N, et al. Pegasos: Primal estimated sub-gradient solver for svm[J]. Mathematical Programming, 2011, 127(1): 3-30
[21]Rakhlin A, Shamir O, Sridharan K. Making gradient descent optimal for strongly convex stochastic optimization[C] // Proc of the 29th Int Conf on Machine Learning. New York: ACM, 2012: 449-450
[22]Nesterov Y. Primal-dual subgradient methods for convex problems[J]. Mathematical Programming, 2019, 120(1): 221-259
[23]Liu Jun, Ji Shuiwang, Ye Jieping. SLEP: Sparse learning with efficient projections[EB/OL]. (2010-10-08) [2018-10-15]. http://www.public.asu.edu/~jye02/Software/SLEP
[24]Kingma D P, Ba J. Adam: A method for stochastic optimization[C/OL]. (2018-07-31) [2018-10-15]. https://arxiv.org/abs/1412.6980