在经典信息论中,Shannon互信息是刻画两个随机变量相互之间独立程度的度量,在信道编码中有很重要的应用且给出了信道容量[1].在量子信息论中,通过von Neumann熵形式给出了互信息的基本定义(与Shannon互信息对应,本文称作von Neumann互信息,通常也称作量子互信息[2]).在量子信息处理中,von Neumann互信息可以描述两体量子态上的全部关联[3],也用于量子信道容量的刻画[4-5],并在量子资源理论中有非常好的应用[6].von Neumann互信息可以由量子相对熵给出4种等价的定义.在量子信道容量的研究中,结合信道的n次重复使用(独立同分布)基于量子互信息来描述信道容量.而实际中较大量子系统上的操作难以实现且独立同分布的量子态难以制备等限制,一般考虑带有误差的有限情形或者one-shot情形(也就是n=1的情形).在one-shot量子信息论中,涉及到带参数的熵,量子假设检验相对熵就是非常重要的一类带参数的熵.量子假设检验相对熵来自于量子假设检验,量子假设检验类似于2个量子态的区分问题.量子假设检验是量子信息处理中的基本问题[7-8],已得到很好的发展和应用[9-18].
文献[19]在前人工作的基础上集中讨论了量子假设检验相对熵,较为系统地研究了其性质,给出了在one-shot经典-量子信道容量中的应用.文献[20]给出了与文献[19]等价的另一个量子假设检验相对熵,得到了与其他广义熵之间的关系.文献[21]基于量子假设检验相对熵[19]定义了量子假设检验条件熵,刻画了具有量子边信息的数据压缩,得到了最小压缩长度的上下界.该文献也给出了量子假设检验相对熵和其他相对熵之间的一些关系.在量子假设检验相对熵的研究相对成熟的情形下,一个自然的问题是:用量子假设检验相对熵给出量子版本互信息的定义是否等价?如果不等价,是否存在序关系?本文将采用文献[19]中关于量子假设检验相对熵的定义,较为系统地研究其性质,并讨论与其他相对熵之间的关系.在Shannon互信息中,由于贝叶斯概率,容易得到条件熵和互信息的链式法则,但是目前还不清楚量子假设检验相对熵版本的互信息是否存在链式法则。本文将重点研究基于量子假设检验相对熵的互信息定义及其相应的性质.
1 相关基础知识
本节介绍文中需要的一些基本记号以及相应的基础知识.首先介绍Shannon熵的基本概念[1].设X是一个离散型随机变量,其字母表为![]() 概率密度函数为
概率密度函数为![]() 随机变量X的Shannon熵定义为
随机变量X的Shannon熵定义为
本文均使用以2为底的对数.若2个随机变量(X,Y)服从联合分布pxy,则Shannon联合熵定义为
H(X,Y)=![]()
可以定义一个随机变量在给定另一随机变量下的条件熵,即
结合贝叶斯概率公式pxy=pxpy|x,得到联合熵和条件熵的链式法则,即
H(X,Y)=H(X)+H(Y|X).
(1)
对于同一字符集上的2个概率密度函数为px和qx,它们的相对熵定义为
(2)
其中,约定![]() ∞.对于服从联合概率密度函数为pxy的离散随机变量(X,Y),其边际概率密度函数分别为px和py,它们之间的相对熵定义为Shannon互信息,即
∞.对于服从联合概率密度函数为pxy的离散随机变量(X,Y),其边际概率密度函数分别为px和py,它们之间的相对熵定义为Shannon互信息,即
I(X;Y)=D(pxy‖pxpy).
(3)
Shannon互信息刻画一个随机变量包含另一个随机变量的信息量,也描述已知另一随机变量所含有的信息量下原随机变量不确定度的减少量.结合Shannon熵的定义,Shannon互信息表示为
I(X;Y)=D(pxy‖pxpy)=
H(X)+H(Y)-H(X,Y)=
H(X)-H(X|Y)=
H(Y)-H(Y|X).
(4)
这里,I(X;Y)=H(X)-H(X|Y)和I(X;Y)=H(Y)-H(Y|X)这2个等式是双随机变量互信息的链式法则.
量子力学的基本框架建立在Hilbert空间![]() 上,本文仅考虑有限维空间,用d表示Hilbert空间的维数.用符号A,B,C等表示相应的Hilbert空间
上,本文仅考虑有限维空间,用d表示Hilbert空间的维数.用符号A,B,C等表示相应的Hilbert空间![]() 用符号I表示空间上的恒等算子.用迹为1的半正定算子描述量子态,通常称为密度算子或密度矩阵.在本文中常用的算子集合有2类,
用符号I表示空间上的恒等算子.用迹为1的半正定算子描述量子态,通常称为密度算子或密度矩阵.在本文中常用的算子集合有2类,![]() 表示次归一化态集合;
表示次归一化态集合;![]() 表示所有量子态集合.显然,
表示所有量子态集合.显然,![]() 对于量子态ρ,其von Neumann熵定义为S(ρ)=-tr(ρ)lb ρ.对于任意2个量子态ρ和σ,von Neumann相对熵定义为
对于量子态ρ,其von Neumann熵定义为S(ρ)=-tr(ρ)lb ρ.对于任意2个量子态ρ和σ,von Neumann相对熵定义为

因为量子力学中并没有与在不同时间变量的2个变量的联合概率分布类似的概念[2-3],从而对于两体量子态ρAB,并没有类似于pxy=pxpy|x的量子态表示形式,即ρAB≠ρA⊗ρB|A,其中ρA=trB(ρA)是约化密度算子,类似于边际概率分布.算子ρB|A并不是条件量子态,甚至不是量子态.因此,没有类似于Shannon条件熵的量子条件熵的直接定义.结合链式法则(1),对于任意的两体量子态ρAB,基于子系统B的von Neumann条件熵定义为
S(A|B)=S(ρAB)-S(ρB).
(5)
显然,量子信息论中的von Neumann条件熵只是在形式上类似于经典信息论中的Shannon条件熵,在本质上它们之间有很大的区别,比如:当两体量子态为纠缠态时,S(A|B)<0.这说明von Neumann条件熵可以为负.von Neumann互信息定义为
I(A:B)=S(ρA)+S(ρB)-S(ρAB).
(6)
von Neumann条件熵和互信息在形式上都与Shannon条件熵和互信息保持一致.特别地,von Neumann互信息也有等式组(4)表示,具体讨论在第3节.
2 量子假设检验相对熵
量子假设检验问题涉及2个假设:
1)零假设(null hypothesis)H0:ρ⊗n,
2)备则假设(alternative hypothesis)H1:σ⊗n,
其中ρ⊗n=ρ⊗…⊗ρ和σ⊗n=σ⊗…⊗σ表示量子态的n次独立同分布(independent and identically distributed,i.i.d.)的拷贝态.需要解决的问题是基于量子测量结果确定哪一个假设是真的.量子测量由一个POVM(positive operator valued measure,POVM)来描述.本文仅考虑二值的POVM,相应的测量算子元为Mn和In-Mn,分别对应假设H0和H1的接受,从而产生2类误差概率:
αn(Mn)=tr((In-Mn)ρ⊗n),
βn(Mn)=tr(Mnσ⊗n),
其中,α(M)是当假设H0为真时接受假设H1的概率,β(M)是当假设H1为真时接受H0的概率.类似于经典假设检验问题,通常希望同时最小化这2类概率,但是它们之间存在均衡关系.一般情况下,约束其中一个误差概率而对另一个进行最小化.若第1类误差概率被限制在很小的参数ε∈(0,1)内,讨论第2类误差概率的最小化,量子Stein’s引理给出了渐近情形下关于误差概率的最佳可达误差指数[8-9],即
其中,![]() 且S(ρ‖σ)是量子相对熵.
且S(ρ‖σ)是量子相对熵.
在非渐近情形下,对第1类误差概率限制下第2类误差概率的变化趋势是由量子假设检验相对熵来描述的.本文后面的讨论仅考虑单次拷贝的情形,且采用文献[19]中量子假设检验相对熵的定义.
定义1.设![]() 且ε∈[0,1],量子假设检验相对熵定义为
且ε∈[0,1],量子假设检验相对熵定义为
![]()
(7)
量子假设检验相对熵是非负的,即![]() 但是若有
但是若有![]() 并不能得到ρ=σ.特别地,当ε=0时,易得tr(Mρ)=tr(Mσ)=1,这蕴含着ρ和σ具有相同的支集.特别地,令σ=I,量子假设检验相对熵退化为
并不能得到ρ=σ.特别地,当ε=0时,易得tr(Mρ)=tr(Mσ)=1,这蕴含着ρ和σ具有相同的支集.特别地,令σ=I,量子假设检验相对熵退化为
![]()
(8)
类似于von Neumann熵,该量化可以看做是量子假设检验熵.
量子假设检验相对熵满足数据处理不等式,也就是量子操作不会引起量子假设检验相对熵增加[19,22],即对于任意的量子操作Λ都有
进一步地,如果考虑n次独立同分布的情形,当n充分大时,量子假设检验相对熵等于量子相对熵[18],也就是渐近均分性(asymptotic equipartition property,AEP),即
![]()
(9)
结合文献[20]的方法,基于定义1,使用von Neumann相对熵容易给出量子假设检验相对熵的一个上界,即
![]()
(10)
其中Hb(ε)=-ε lb(ε)-(1-ε)lb(1-ε)为二元Shannon熵.
量子假设检验相对熵依赖于参数ε,量子态的ε-邻域发生变化,有可能导致量子假设检验相对熵发生变化.通过简单的计算可得性质1~4.
性质1.
a.设![]() 且σ1≤σ2,有
且σ1≤σ2,有
![]()
(11)
b.设ε1,ε2∈[0,1],且ε1<ε2,有
![]()
(12)
该结果的详细证明见文献[22]不等式(11)表明:随着备择假设的增强,第2类误差概率变大.而不等式(12)表明:误差参数的越小限制,第2类误差概率反而变大.性质1给出了备择假设的变化引起的第2类误差概率的变化,结合文献[20]的结果,容易给出零假设的微小变化和参数变化共同引起第2类误差概率的变化情形.
性质2.设![]() 且D(ρ,σ)≤δ,对于ε∈[0,1],则对于任意次归一化态τ有
且D(ρ,σ)≤δ,对于ε∈[0,1],则对于任意次归一化态τ有
![]()
(13)
及
![]()
(14)
其中,δ∈(0,1-ε).
从定义1可知,量子假设检验相对熵本质上就是一个期望值,通过零假设的一些特定限制,可以直接估算量子假设检验相对熵的界.文献[23]首先给出了这方面的讨论.
性质3.设ρ为任意满秩态,σ为任意量子态,且0≤ε<λmin(ρ),有
![]()
(15)
其中,λmin(ρ)是量子态ρ的最小特征值.
性质3仅是针对零假设为满秩态的情形,性质4给出一般量子态的情形.
性质4.对于给定的量子态ρ和任意量子态σ,设M为![]() 的最佳测量,k和d分别为量子态ρ和测量M的非零特征值数且k≤d,对于
的最佳测量,k和d分别为量子态ρ和测量M的非零特征值数且k≤d,对于![]() 则
则
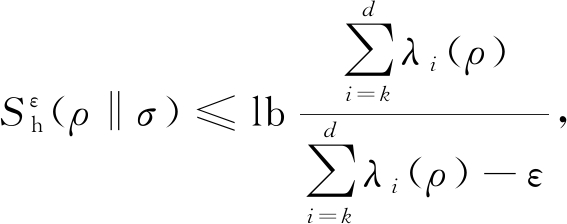
(16)
其中,λi(ρ)为ρ的特征值.
证明. 设M为![]() 的最佳测量算子元,且
的最佳测量算子元,且![]() 和
和![]() 分别为量子态ρ和最佳测量元M的非零特征值,不妨设λ1(ρ)≥λ2(ρ)≥…≥λd(ρ),μ1(M)≥μ2(M)≥…≥μk(M).令μmin(M)为M的最小特征值,则有
分别为量子态ρ和最佳测量元M的非零特征值,不妨设λ1(ρ)≥λ2(ρ)≥…≥λd(ρ),μ1(M)≥μ2(M)≥…≥μk(M).令μmin(M)为M的最小特征值,则有
![]()
![]()
![]()
结合不等式tr(Mρ)≥1-ε,有
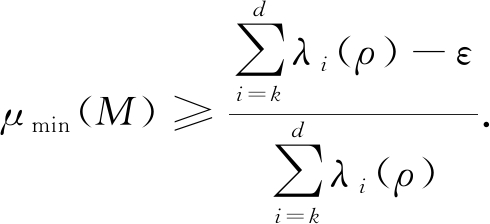
从而可得
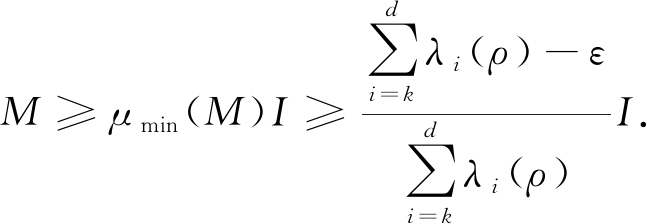
则可以得到
![]()
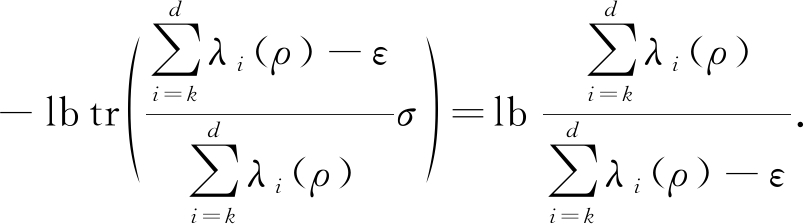
从而命题得证.
证毕.
3 量子假设检验条件熵和互信息
在经典信息论中,对于联合概率分布,依赖于贝叶斯概率,得到条件熵等于联合熵与其中一个边际分布熵的差,也就是条件熵链式法则(1).在量子信息论中,并不存在条件量子态,从而不能直接推广经典条件熵的定义.如果考虑条件量子态,只能基于某一个子系统上的测量获得另一个子系统上的量子态.但是两体量子态的局部进行测量后整体量子态会发生改变,测量前后的状态可能并不相同.依赖于测量得到的条件量子熵一般并不等于von Neumann条件熵(5).研究发现它们的差正好能刻画复合量子系统上子系统之间的非经典关联[3].本节重点讨论von Neumann条件熵的形式,不涉及测量.
量子条件熵可以通过量子相对熵来表示[5,21].对于两体量子态ρAB和次归一化态IA⊗σB,它们的von Neumann相对熵为
S(ρAB‖IA⊗σB)=
-S(ρAB)-tr[ρAB lb(IA⊗σB)]=
-S(ρAB)+S(ρB)+S(ρB‖σB).
由于von Neumann相对熵是非负的,上式两边对所有的![]() 取最小,进而得到von Neumann条件熵的相对熵表示形式,即
取最小,进而得到von Neumann条件熵的相对熵表示形式,即
![]()
(17)
由于本文采用次归一化态,从而von Neumann条件熵的相对熵表示与文献[1]的表述略有不一致.以该表示为标准形式,可以方便讨论量子假设检验相对熵性质的条件熵[19-22].
定义2.设![]() 且ε∈[0,1],则量子假设检验条件熵定义为
且ε∈[0,1],则量子假设检验条件熵定义为
![]()
(18)
从定义2易得最优化的过程并没有一个精确解,即
根据Schatten ∞-范数的半正定程序[20,22],量子假设检验条件熵也可以表示为
![]()
(19)
其中,MB=trAMAB.显然,并不能从等式(19)直接得到量子假设检验条件熵的精确解,这与von Neumann条件熵并不一致.但是对于等式(19)继续使用半正定程序易得到量子假设检验条件熵的许多性质以及和其他量化的关系,比如:数据处理不等式.该不等式的成立直接导致增加条件减小熵的结果.特别地,量子假设检验条件熵并没有类似于Shannon条件熵的链式法则(1).
在量子信息论中,对量子系统上的状态进行测量后会发生变化,测量前后的状态无法保持一致.因此无测量的von Neumann互信息是Shannon互信息形式上的直接推广.von Neumann互信息只是在形式上保持了Shannon互信息等价形式的一种,但在本质还是有所不同的.结合量子相对熵可以给出von Neumann互信息的4种等价形式,有
I(A:B)=S(ρA)+S(ρB)-S(ρAB)=![]()
![]()
(20)
其中,ρAB是两体量子系统上的任意量子态,ρA和ρB是对应子系统上的约化态,且![]() 从等式(19)可知,涉及的最优化过程都有精确解.由于von Neumann相对熵和量子假设检验相对熵具有特殊的关系式(9),那么基于量子假设检验相对熵的互信息是否也有von Neumann互信息的式(20)等价形式.下面首先给出量子假设检验互信息的不同方式定义.
从等式(19)可知,涉及的最优化过程都有精确解.由于von Neumann相对熵和量子假设检验相对熵具有特殊的关系式(9),那么基于量子假设检验相对熵的互信息是否也有von Neumann互信息的式(20)等价形式.下面首先给出量子假设检验互信息的不同方式定义.
定义3.设![]() 且ε∈[0,1],量子假设检验相对熵的互信息定义为
且ε∈[0,1],量子假设检验相对熵的互信息定义为
可知![]() 不涉及最优化,相对简单.
不涉及最优化,相对简单.![]() 和
和![]() 的定义只是交换了子系统,可以归并为一个定义.而第4种定义
的定义只是交换了子系统,可以归并为一个定义.而第4种定义![]() 涉及到2个子系统上的最优化,相对比第2个和第3个复杂.从定义3直接可得它们之间的一个序关系,即
涉及到2个子系统上的最优化,相对比第2个和第3个复杂.从定义3直接可得它们之间的一个序关系,即
由于条件熵式(18)仅涉及到某一个子系统上的最优化,本文的目标是讨论链式关系,从而下面的讨论选取第2类定义.结合量子假设检验相对熵,进一步化简![]() 有
有
进而有
![]()
(21)
其中,![]() 结合文献[20-21]的结果,得到
结合文献[20-21]的结果,得到![]() 的半正定程序,即
的半正定程序,即
原问题
s.t.0≤MAB≤IAB
tr(MABρAB)≥1-ε
对偶问题
max(1-ε)η-tr(NAB)
s.t.η ρAB≤NAB+ρA⊗σB
NAB≥0,η≥0
σB≥0,tr(σB)≤1
.
Anshu等人和Wilde在量子信道编码中提到了量子假设检验互信息的概念,并应用其刻画信道编码的最佳速率[16-17],但并没有具体讨论量子假设检验互信息的性质.下面集合量子假设检验相对熵和量子假设检验条件熵的性质来详细讨论量子假设检验互信息![]() 的性质.显然,
的性质.显然,![]() 下面讨论量子假设检验互信息
下面讨论量子假设检验互信息![]() 的单调性,也就是数据处理不等式.
的单调性,也就是数据处理不等式.
性质5.设![]() 且εA:A→A′和εB:B→B′为完全正且保迹(completely positive and trace preserving,CPTP)映射,有
且εA:A→A′和εB:B→B′为完全正且保迹(completely positive and trace preserving,CPTP)映射,有
![]()
(22)
证明. 设{NAB,σB,η}为![]() 的对偶问题最优解.由于完全正且保迹映射是保不等式关系的,从而在不等式η ρAB≤ρA⊗σB+NAB上使用映射εA⊗εB,可得
的对偶问题最优解.由于完全正且保迹映射是保不等式关系的,从而在不等式η ρAB≤ρA⊗σB+NAB上使用映射εA⊗εB,可得
其中,NA′B′=(εA⊗εB)(NAB),σB′=εB(σB),且τA′B′=(εA⊗εB)(ρAB).从而可知{NA′B′,σB′,η}是![]() 的对偶问题可行解,有
的对偶问题可行解,有
从而命题得证.
证毕.
由于量子假设检验互信息与误差参数有关,结合量子假设检验相对熵性质1直接可得量子假设检验互信息关于参数的序关系.对于0≤ε<ε′≤1,有
在三体量子系统中,对于von Neumann互信息中,丢弃一个子系统,互信息会减少.下面的结果证明量子假设检验相对熵的互信息也具有类似的性质.
性质6.设![]() 且εA:A→A′和εB:B→B′为CPTP映射,εC为子系统C上的偏迹映射,有
且εA:A→A′和εB:B→B′为CPTP映射,εC为子系统C上的偏迹映射,有
![]()
(23)
性质6的证明与性质5类似.特别地,当εA和εB均为恒等映射时,可得
![]()
(24)
该关系说明丢弃子系统减少量子假设检验互信息.
经典-量子态在具有量子边信息的信源编码中有非常重要的应用,也对应于经典-信道编码.同时,在考虑基于测量的量子条件熵时,经典-量子态仅拥有经典关联.结合量子假设检验条件熵,下面讨论三体经典-量子态的情形.
性质7.设![]() 是三体量子系统ABC上的量子态,则
是三体量子系统ABC上的量子态,则
其中,dX是经典系统X 的维数.
该结果的证明结合文献[21]中条件熵的证明过程容易得到.下面讨论两体经典-量子态的情形.不妨设![]() 是经典-量子态,则有
是经典-量子态,则有
![]()
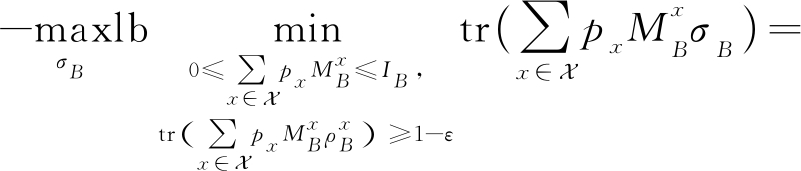
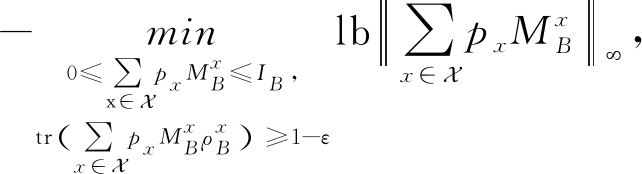
其中,第2个等号成立是由于在经典-量子态的测量可表示为![]() 又因为
又因为
进而可得
![]()
![]()
类似地可以给出经典-量子态的量子假设检验条件熵的上下界,即
其中,c=|supp{px}|表示概率分布px的支集维数.
在量子资源理论以及one-shot信息论中,常用量子最大相对熵(quantum max-relative entropy)给出所关注的量化的界,再讨论独立同分布的渐近情形[24-25].量子最大相对熵来自于最小量子Renyi散度在参数趋于无穷时的极限值[24].Ciganovic等人[26]给出了量子最大互信息的3种定义形式,目前只考虑其第2种定义形式.设![]() 且ε∈[0,1],量子最大互信息(quantum max-mutual information)和量子平滑最大互信息(quantum smoothed max-relative entropy)定义为
且ε∈[0,1],量子最大互信息(quantum max-mutual information)和量子平滑最大互信息(quantum smoothed max-relative entropy)定义为
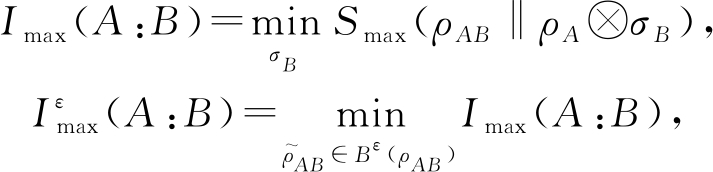
其中,![]() 且P(ρ,σ)是纯化距离[24].
且P(ρ,σ)是纯化距离[24].
下面的结果给出量子假设检验互信息与量子最大互信息之间的关系.
性质8.设![]() 且ε∈[0,1],有
且ε∈[0,1],有
![]()
Imax(A:B)-lb(1-ε).
结合文献[20-21]中结果,使用本文量子假设检验相对熵的定义,通过基本的代数运算可以完成证明.与之类似的结果,结合不等式(10),下面的结果给出量子假设检验互信息和von Neumann互信息的关系,即
![]()
(25)
根据量子条件熵和量子互信息可以由量子相对熵表示,可知量子条件熵与量子互信息有量子互信息的链式关系,即
I(A:B)=S(ρA)+S(ρB)-S(ρAB)=
S(ρB)-S(B|A)=S(ρA)-S(A|B).
(26)
一般情况下,基于其他熵度量定义的互信息并不一定有等式(26)成立[20-21,24-25].下面讨论量子假设检验互信息的链式关系.首先基于量子假设检验相对熵定义单系统上量子假设检验最大熵.
定义4.设![]() 对于ε∈[0,1],定义
对于ε∈[0,1],定义
![]()
(27)
由于该量化表示能正确识别ρ的最大熵,因此称作量子假设检验最大熵.当M=I或ε=0时,有![]() 量子假设检验最大熵与量子假设检验熵并不相同,但不等式
量子假设检验最大熵与量子假设检验熵并不相同,但不等式![]() 成立.
成立.
性质9.设![]() 且ε∈[0,1],若所有的测量算子是可分的,则有
且ε∈[0,1],若所有的测量算子是可分的,则有
![]()
(28)
其中,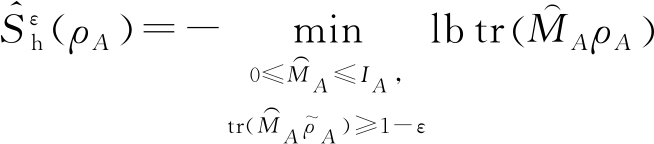 是带限制的量子假设检验最大熵.
是带限制的量子假设检验最大熵.
证明. 由等式(18),不妨设![]() 是
是![]() 的最佳测量,从而得到子系统B上的测量算子
的最佳测量,从而得到子系统B上的测量算子![]() 再结合
再结合![]() 的定义,有
的定义,有
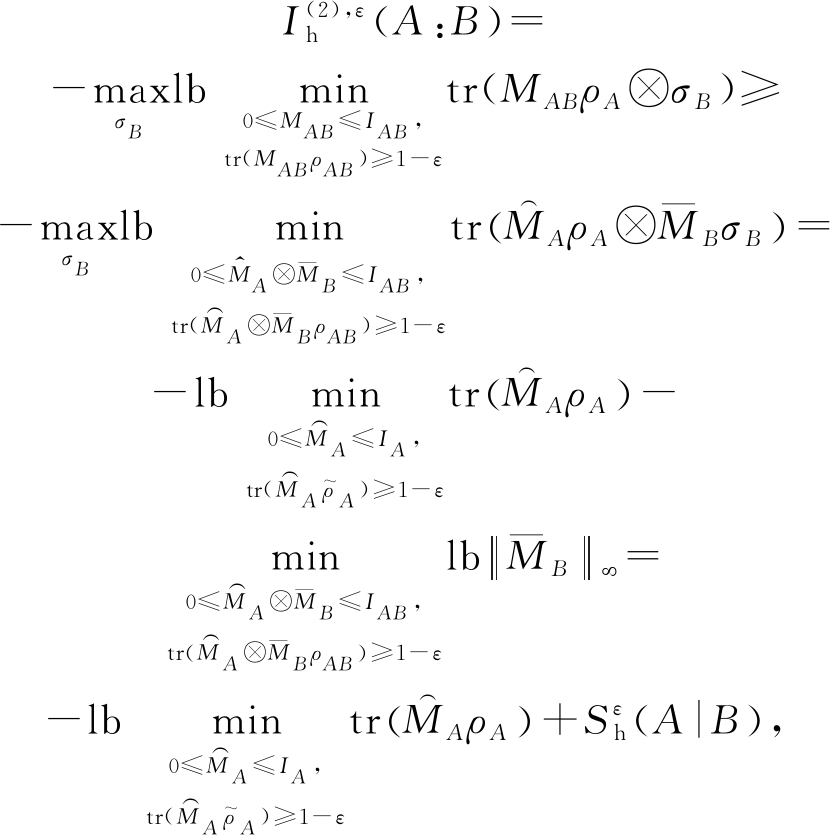
其中,![]() 第1个不等式是由于互信息
第1个不等式是由于互信息![]() 和条件熵
和条件熵![]() 的定义中有条件0≤MAB≤IAB及tr(MABρAB)≥1-ε.结合最佳测量
的定义中有条件0≤MAB≤IAB及tr(MABρAB)≥1-ε.结合最佳测量![]() 选取合适的
选取合适的![]() 满足约束条件
满足约束条件![]() 显然满足该条件的集合一定小于原始约束条件的集合,从而导致不等式成立. 第2个等式中的第2项中的约束条件与
显然满足该条件的集合一定小于原始约束条件的集合,从而导致不等式成立. 第2个等式中的第2项中的约束条件与![]() 是独立的,从而该项等于条件熵
是独立的,从而该项等于条件熵![]() 进而等到第3个等式.故而有
进而等到第3个等式.故而有
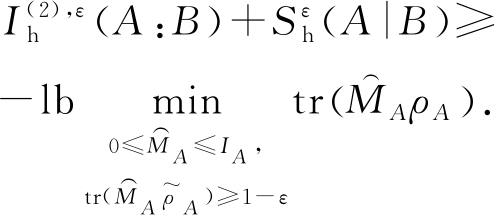
对于该不等式中右边的项,其约束条件![]() 和
和![]() 来自于
来自于![]() 和
和![]() 故可以找到相应的
故可以找到相应的![]() 使得
使得![]() 进而有
进而有
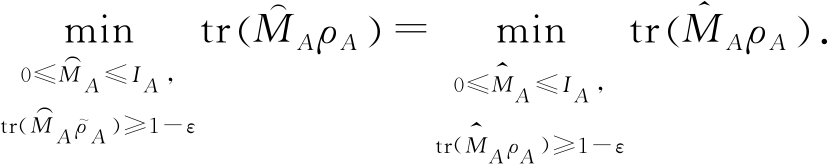
最后通过简单的代数运算,进而完成命题的证明.
证毕.
在该命题的证明过程中,得到了带限制的量子假设检验熵,该熵的测量算子依赖于条件熵的最佳测量,显然易得
另外,该命题仅给出了一个下界,但上界的证明目前还是一个开放的问题.虽然能给出互信息和条件熵的上下界,但是难以给出一个紧凑的链式关系.
4 总 结
在量子信息论中,基于von Neumann熵,可以得到类似于经典信息论中Shannon熵的好多有用量化和关系,在量子信息处理中有非常重要的应用.存在一些其他的熵在量子信息中的推广,但并不像von Neumann熵具有良好的性质或者关系,可关键是这些熵在one-shot量子信息论中有非常好的应用,比如假设检验相对熵.我们详细介绍了量子假设检验相对熵及其相关性质,并得到了新的上界.然后基于量子假设检验相对熵讨论了条件熵,得到量子假设检验相对熵形式的条件熵并没有类似Shannon熵或von Neumann熵的链式关系,这是由于假设检验相对熵或者新定义的最大熵都依赖于最优化.由于纠缠的存在同时并不存在量子版本的贝叶斯公式.对于量子假设检验相对熵,我们给出了4种不完全等价的互信息定义.结合在信息处理中常用的条件熵,主要讨论了其中一类互信息,得到了一些有意思的性质,并给出了和其他互信息之间的关系.给出了经典-量子态的量子假设检验互信息的上下界,得到了量子假设检验互信息类似于Shannon熵或von Neumann熵的互信息链式关系.
[1]Cover T M,Thomas J A.Elements of Information Theory[M].2nd ed.Hoboken,NJ:John Wiley &Sons,Inc,2006
[2]Nielson A M,Chuang L I.Quantum Computation and Quantum Information[M].Cambridge,UK:Cambridge University Press,2000
[3]Xi Zhengjun.The Entroptic Measure of Nonclassical Correlations and Quantum Coherence[M].Beijing:Science Press,2019(席政军.非经典关联和量子相干的熵度量[M].北京:科学出版社,2019)
[4]Caruso F,Giovannetti V,Lupo C,et al.Quantum channels and memory effects[J].Review Modern Physics,2014,86(4):1203-1259
[5]Wilde M M.Quantum Information Theory[M].2nd ed.Cambridge,UK:Cambridge University Press,2017
[6]Chitambar E,Gour G.Quantum resource theories[J].Review Modern Physics,2019,91(2):No.025001
[7]Helstrom C M.Quantum Detection and Estimation Theory[M].New York:Academic,1976
[8]Hiai F,Petz D.The proper formula for relative entropy and its asymptotics in quantum probability[J].Communication in Mathematical Physics,1991,143(1):99-114
[9]Ogawa T,Nagaoka H.Strong converse and Stein’s lemma in the quantum hypothesis testing[J].IEEE Transaction on Information Theory,2000,46(7):2428-2433
[10]Ogawa T,Hayashi M.On error exponents in quantum hypothesis testing[J].IEEE Transactions on Information Theory,2004,50(6):1368-1372
[11]Nagaoka H,Hayashi M.An information-spectrum approach to classical and quantum hypothesis testing for simple hypotheses[J].IEEE Transaction on Information Theory,2007,53(2):534-549
[12]Ogawa T,Nagaoka H.Making good codes for classical-quantum Channel coding via quantum hypothesis testing[J].IEEE Transactions on Information Theory,2007,53(6):2261-2266
[13]Brandão F G S L,Plenio M B.A generalization of quantum Stein’s lemma[J].Communication in Mathematical Physics,2010,295(5):791-828
[14]Ke Li.Second-order asymptotics for quantum hypothesis testing[J].The Annals of Statistics,2014,42(1):171-189
[15]Mosonyi M,Ogawa T.Two approaches to obtain the strong converse exponent of quantum hypothesis testing for general sequences of quantum states[J].IEEE Transaction on Information Theory,2015,61(12):6975-6994
[16]Wilde M M.Position-based coding and convex splitting for private communication over quantum channels[J].Quantum Information Processing,2017,16(10):264-298
[17]Anshu A,Jain R,Warsi N A.A hypothesis testing approach for communication over entanglement-assisted compound quantum channel[J].IEEE Transaction on Information Theory,2019,65(4):2623-2636
[18]Brandão F G S L,Harrow A W,Lee J R,et al.Adversarial hypothesis testing and a quantum Stein’s lemma for restricted measurements[J].IEEE Transaction on Information Theory,2020,66(8):5037-5054
[19]Wang L,Renner R.One-shot classical-quantum capacity and hypothesis testing[J].Physical Review Letters,2012,108(20):200501
[20]Dupuis F,Kramer L,Faist P,et al.Generalized entropies[OL].[ 2021-03-18].https://arxiv.org/abs/1211.3141v2
[21]Tomamichel M,Hayashi M.A hierarchy of information quantities for finite block length analysis of quantum tasks[J].IEEE Transaction on Information Theory,2013,59(11):7693-7710
[22]Khatri S,Wilde M M.Principle of quantum communication theory:A modern approach[OL].[2021-03-18].https://arxiv.org/abs/2011.04672
[23]Fang Kun,Liu Ziwen.No-go theorems for quantum resource purification[J].Physical Review Letters,2020,125(6):060405
[24]Tomamichel M.Quantum Information Processing with Finite Resources[M].Berlin:Springer,2016
[25]Vitanov A,Dupuis F,Tomamichel M,et al.Chain rules for smooth min-and max-entropies[J].IEEE Transaction on Information Theory,2013,59(5):2603-2612
[26]Ciganovic N,Beaudry J N,Renner R.Smooth max-information as one-shot generalization for mutual information[J].IEEE Transaction on Information Theory,2014,60(3):1573-1581

