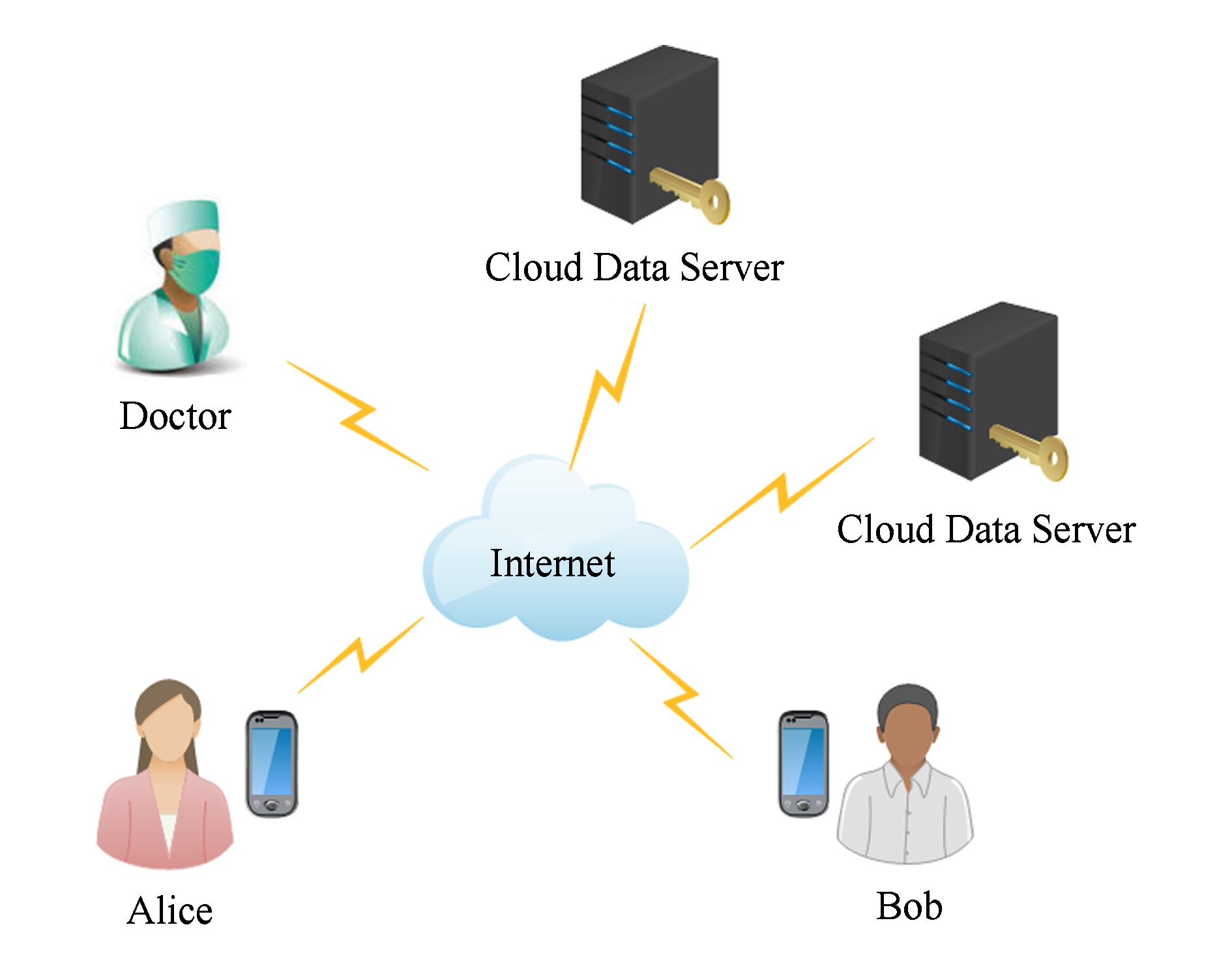
Fig. 1 A typical MHSN scenario
图1 典型的移动健康社交网络场景
收稿日期: 2017-06-11;
修回日期: 2017-07-28
基金项目: 国家自然科学基金项目(61472287);湖北省自然科学基金重点项目(2015CFA068) This work was supported by the National Natural Science Foundation of China (61472287) and the Key Program of Natural Science Foundation of Hubei Province of China (2015CFA068).
通信作者: 何德彪(hedebiao@whu.edu.cn)
吴黎兵 1,2 张宇波 2 何德彪 1,2
1 (软件工程国家重点实验室(武汉大学) 武汉 430072) 2 (武汉大学计算机学院 武汉 430072) (wu@whu.edu.cn)
摘 要 随着云存储的快速普及以及公众隐私保护意识的提升,越来越多的隐私数据被加密存储在云上.因而,如何对密文数据特别是采用公钥密码体制加密的数据进行高效检索成为了一个重要研究内容.带密文等值判定的公钥加密协议是其中一种检索方法,它可以在不泄漏明文内容的情况下判定2段密文对应的明文是否相同.最近,一系列带密文等值判定的公钥加密协议被提出.然而,在这些协议中,只用了一个服务器来执行等值判定操作,不能抵抗恶意服务器的内部关键字猜测攻击.为了解决这个问题,首次提出了基于双服务器的带密文等值判定的公钥加密协议,并在随机预言机模型下证明了它的安全性.同时,也对设计的协议进行了性能分析,分析表明:该协议适合资源受限的移动设备.
关键词 等值判定;基于身份加密;云计算;双服务器;可搜索加密
近年来,随着云计算的快速发展和普及,越来越多的用户将自己的数据存放在云端(如Dropbox、亚马逊云、阿里云、百度云等).数据上传到云端后,用户可以通过网络远程操作自己的数据(包括新增、修改、删除、检索).同时,为了保护用户的数据隐私,数据上传到云端之前会进行加密.但这使得数据检索,甚至是在同一用户上传的数据中检索变得困难.解决方法之一是将所有数据下载下来,解密之后再进行检索.显然,此方法在数据量大、网络带宽小、响应时延要求高的环境中不具有可行性.另一种解决方法是使用可搜索加密(searchable encryption)技术.
可搜索加密技术是一种允许第三方对用户上传的密文数据进行检索,同时不会泄漏除搜索模式和搜索结果以外的任何信息的技术.可分为可搜索对称加密和可搜索公钥加密技术.前者适合对用户自己拥有的数据进行加密;后者可以搜索不同用户用不同公钥加密的数据,由Boneh等人首次提出 [1] .随后,很多相关的研究成果陆续被发布 [2-11] ;最近,一些新型的带密文等值判定的可搜索公钥加密方案 [12-17] 被提出.但是这些方案都是基于单服务器的,容易遭受内部关键字猜测攻击.

Fig. 1 A typical MHSN scenario
图1 典型的移动健康社交网络场景
为此,我们设计了一个基于双服务器的带密文等值判定的公钥加密协议(dual server identity-based encryption scheme with equality test, DS-IBEET).该协议的典型应用场景如图1所示. 在一个移动健康社交网络(MHSN)中,用户(比如病人)想要通过医疗服务器和其他拥有相同症状的人建立联系,同时不泄漏他们的隐私信息.例如,Alice和Bob是2个有相同症状的病人,他们彼此不认识,但是想要建立联系,以交流病情或相互鼓励. Alice用她医生的公钥 ID DA 加密她的症状信息得到( ID A , IBEET ( ID DA , Symptom ))生成 Symptom 的陷门 td A , 发送( ID A , IBEET ( ID DA , Symptom ), td A )给服务器SA.同理,Bob发送( ID B , IBEET ( ID DB , Symptom ), td B ))给服务器SA.服务器SA首先进行初步判定,判定结果再发送给服务器SB,SB完成密文等值判定,可以得到Alice和Bob有相同的症状 Symptom ,但是服务器SA和SB都不知道 Symptom 的具体内容是什么.最后,服务器SB将判定结果发送给Alice和Bob,让他们建立联系.显然,此协议也适用于多用户环境.
本文的主要贡献有3个方面:
1) 首次提出基于双服务器的密文等值判定协议,解决了传统的单服务器环境不能抵抗恶意服务器攻击的问题;
2) 在随机预言机模型下证明了该协议的安全性;
3) 分析了该协议的性能,表明其可以适用于资源受限的移动设备.
Yang等人首次提出带密文等值判定功能的公钥加密协议(public key encryption with equality test, PKEET) [13] ,用来比较2段密文对应的明文是否相同,且在比较过程中不泄露任何明文信息.然而,该协议没有对参与密文等值判定的用户进行授权,任何用户都可以进行密文等值判定;为了解决这一问题,Tang提出了一种改进的带密文等值判定的公钥加密协议(FG-PKEET) [12] ,该协议仅允许获得授权的用户在可信第三方的帮助下执行细粒度密文等值判定,即用户可以通过授权来控制谁能对自己的密文进行等值判定,控制谁的密文可以和自己的密文进行比对;随后,为了抵抗离线消息恢复攻击,Tang将FG-PKEET扩展到了双代理版本(ADG-PKEET) [15] ;同时,为了达到粗粒度控制的目的,Tang提出了AoN-PKEET协议 [14] ,在该协议中,用户一旦授权第三方代理进行密文等值判定,则该用户的所有密文都能被该代理用来进行等值判定.
Ma等人提出了一个带委托密文等值判定的公钥加密协议(PKE-DET) [16] ,该协议中的等值判定操作被委托给第三方;Huang等人提出了一个带密文等值判定授权的公钥加密协议 [17] ,该协议的授权方式分为对用户授权和对密文授权;对用户授权模式下,测试者可以对授权用户的所有密文进行等值判定查询,对密文授权模式下,测试者只能对授权的特定密文进行等值判定查询;随后,Ma等人又提出了一种支持弹性授权的带密文等值判定的公钥加密方案 [18] ,该方案拥有4种类型的授权方式.
上述方案都是基于传统公钥加密的方案,当用户数量较大时,存在证书管理问题.为了解决这个问题,Ma首次提出了一种基于身份的带密文等值判定的公钥加密方案 [19] ,随后,在Ma的协议基础上,Wu设计了一个更高效的方案 [20] ,该方案减少了HashToPoint的使用.
然而,在已有方案中,不论是传统的公钥加密方案还是基于身份的加密方案,都不能抵抗恶意服务器的内部关键字猜测攻击.特别是在关键字数量有限的情况下,攻击更容易成功.
在本节中,我们主要介绍双线性对和CDH(computational Diffie-Hellman problem)困难问题.
2 . 1 双线性对
设 G 1 是加法循环群, G 2 是乘法循环群,且 G 1 、 G 2 的阶都为素数 q . P 是群 G 1 的一个生成元.如果 e : G 1 × G 1 → G 2 满足3个条件,则称其为双线性对.
1) 双线性性.对于任意2个点 Q , R ∈ G 1 和任意2个随机数 ![]() 存在 e ( a · Q , b · R )= e ( Q , R ) a b .
存在 e ( a · Q , b · R )= e ( Q , R ) a b .
2) 非退化性.对于任意生成元 ![]()
3) 可计算性.对于任意2个点 Q , R ∈ G 1 , e ( Q , R )是易计算的.
2 . 2 CDH问题
设 P 是群 G 1 的一个生成元, x , y ∈ Z * 是2个未知随机数,若已知{ P , xP , yP },则在多项式时间内计算出 xyP 是困难的.
3 . 1 系统模型
本文的系统模型如图2所示.系统有5个参与者:
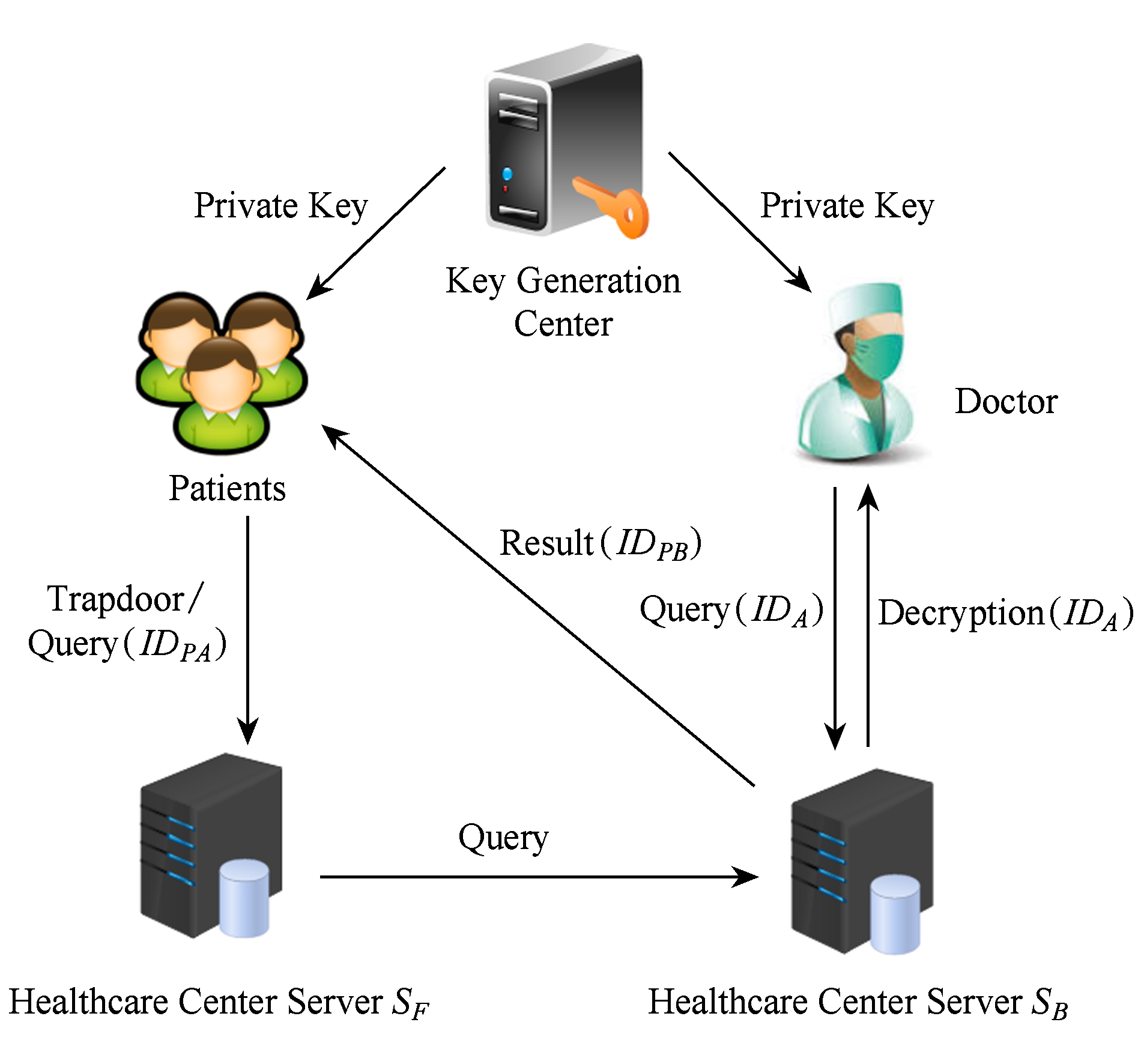
Fig. 2 System model
图2 系统模型
1) 密钥生成中心.负责生成系统主密钥、医生和病人的公私钥对以及系统参数,并将医生和病人的私钥通过安全信道分别发送给他们.
2) 病人.病人需要先在密钥生成中心注册,获得私钥.将隐私信息(例如症状)加密后发送给服务器.同时,发送一个陷门给服务器,用来执行等值判定操作.病人加密的信息只有他的医生可以解密.
3) 医生.医生需要先在密钥生成中心注册,获得私钥.医生可以解密自己的病人加密的信息.
4) 前服务器 S F .负责接收病人的密文等值判定请求,并将获得的中间结果发送给服务器 S B .
5) 后服务器 S B .负责接收服务器 S F 的中间结果,完成后续密文等值判定工作,并返回最终的结果给病人.
3 . 2 协议架构
协议包含7个算法:
1) 初始化算法 Setup (1 k ).输入安全参数 k ,产生系统参数 params .
2) 密钥生成算法 KeyGen ( params ).输入系统参数和身份 ID ,输出解密钥 dk .
3) 陷门生成算法 TrapGen ( dk ).此算法由用户执行,根据解密钥生成陷门 td .
4) 加密算法 Encrypt ( params , dk , M ).此算法由用户执行.用户对明文 M 进行加密得到密文 C .
5) 解密算法 Decrypt ( params , dk , C ).此算法由用户执行,对密文 C 进行解密.
6) 前服务器测试算法 ![]() ).此算法由前服务器 S F 执行,输出判定 MA = MB 是否成立的中间结果 X A , X B .
).此算法由前服务器 S F 执行,输出判定 MA = MB 是否成立的中间结果 X A , X B .
7) 后服务器测试算法 ![]() ).此算法由后服务器 S B 执行,判定 MA = MB 是否成立.
).此算法由后服务器 S B 执行,判定 MA = MB 是否成立.
3 . 3 安全模型
我们分别定义DS-IBEET协议面向恶意前服务器和恶意后服务器的安全模型.
3.3.1 恶意前服务器
本节我们定义恶意前服务器下的安全性.包括在选择关键字攻击下的IBEET密文语义安全和关键字猜测攻击下的陷门不可区分性.
1) 选择关键字攻击下的语义安全(SS-CKA).选择关键字攻击下的语义安全保证了敌手不能通过关键字对应的IBEET密文来区分关键字.即IBEET密文不会泄漏对应关键字的任何信息.我们用以下游戏来定义选择关键字攻击下的密文语义安全模型.
① 初始化算法( Setup ).挑战者运行初始化算法 Setup 生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
② 查询阶段1( Query - phase -Ⅰ).敌手可以适应性地对任意关键字和任意IBEET密文向挑战者发送查询请求.挑战者返回0或者1给敌手.
③ 挑战( challenge ).敌手发送2个关键字( kw 0 , kw 1 )给挑战者,挑战者随机选择 b ∈{0,1}并计算:
C ![]() ← Encrypt ( params , p
← Encrypt ( params , p ![]() , p
, p ![]() , kw b ),
, kw b ),
挑战者将 ![]() 发送给敌手.
发送给敌手.
④ 查询阶段2( Query - phase -Ⅱ).敌手继续查询除了挑战关键字( kw 0 , kw 1 )之外的任意关键字和IBEET密文.挑战者返回0或者1给敌手.
⑤ 输出( output ).最后,敌手输出它对 b 的猜测 b ′∈{0,1}.如果 b = b ′,则敌手赢得这个游戏.
我们称上述游戏中的恶意服务器 A 为SS-CKA敌手,定义它赢得游戏的优势为
![]()
 2.
2.
2) 关键字猜测攻击下的不可区分性(IND-KGA).在这个安全模型中,陷门不会泄漏关键字的任何信息给恶意前服务器.我们用以下游戏定义安 全模型:
① 初始化算法( Setup ).挑战者运行初始化算法生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
② 查询阶段1( Query - phase -Ⅰ).敌手可以适应性的对任意关键字和密文向挑战者发送查询请求.挑战者返回0或者1给敌手.
③ 挑战( challenge ).敌手发送2个关键字( kw 0 , kw 1 )给挑战者,挑战者随机选择 b ∈{0,1}并计算:
![]() ).
).
挑战者将 ![]() 发送给敌手.
发送给敌手.
④ 查询阶段2( Query - phase -Ⅱ).敌手继续查询除了挑战关键字( kw 0 , kw 1 )之外的任意关键字和IBEET密文.挑战者返回0或者1给敌手.
⑤ 输出( output ).最后,敌手输出它对 b 的猜测 b ′∈{0,1}.如果 b = b ′,则敌手赢得这个游戏.
我们称上述游戏中的恶意服务器 A 为IND-KGA敌手,定义它赢得游戏的优势为
![]()
 2.
2.
3.3.2 恶意后服务器
恶意后服务器的安全模型和恶意前服务器的安全模型类似.
1) 选择关键字攻击下的语义安全(SS-CKA).此安全模型与恶意前服务器的安全模型类似,游戏不同之处为在初始化算法( Setup )中,挑战者将 ![]() 发送给敌手.我们称该游戏中的恶意服务器 A 为SS-CKA敌手,定义它赢得游戏的优势为
发送给敌手.我们称该游戏中的恶意服务器 A 为SS-CKA敌手,定义它赢得游戏的优势为
![]()
 2.
2.
2) 关键字猜测攻击下的不可区分性(IND-KGA).此安全模型与恶意前服务器的安全模型类似,游戏不同之处为在初始化算法( Setup )中,挑战者将 ![]() 发送给敌手. 我们称该游戏中的恶意服务器 A 为IND-KGA敌手,定义它赢得游戏的优势为
发送给敌手. 我们称该游戏中的恶意服务器 A 为IND-KGA敌手,定义它赢得游戏的优势为
![]()
 2.
2.
3) 关键字猜测攻击下的不可区分性(IND-KGA-Ⅱ).为了保证恶意服务器SB不能从内部测试状态信息获取关键字的任何信息,我们通过如下游戏定义安全模型:
① 初始化算法( Setup ).挑战者运行初始化算法生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
② 查询阶段1( Query - phase -Ⅰ).敌手可以适应性地对任意关键字和密文的内部测试状态向挑战者发送查询请求.挑战者返回( X A , X B )给敌手.
③ 挑战( challenge ).敌手发送3个不同的关键字( kw 0 , kw 1 , kw 2 )给挑战者,挑战者随机选择{ b 1 , b 2 }⊂{0,1,2}并计算:
C ![]() ← Encrypt ( params , p
← Encrypt ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
), ![]() ← TrapGen ( params , p
← TrapGen ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
), ![]()
挑战者将 ![]() 发送给敌手.
发送给敌手.
④ 查询阶段1( Query - phase -Ⅱ).敌手可以适应性的对挑战关键字 ![]() 以外关键字的内部测试状态向挑战者发送查询请求.挑战者返回( X A , X B )给敌手.
以外关键字的内部测试状态向挑战者发送查询请求.挑战者返回( X A , X B )给敌手.
⑤ 输出( output ).最后,敌手输出它对{ b 1 , b 2 }的猜测{ ![]() ,
, ![]() }⊂{0,1,2}.如果{ b 1 , b 2 }={
}⊂{0,1,2}.如果{ b 1 , b 2 }={ ![]() ,
, ![]() },则敌手赢得这个游戏.
},则敌手赢得这个游戏.
我们称上述游戏中的恶意后服务器 A 为IND-KGA-Ⅱ敌手,定义它赢得游戏的优势为
Ad ![]() ( k )= Pr [{ b 1 , b 2 }={
( k )= Pr [{ b 1 , b 2 }={ ![]() ,
, ![]() }]-1
}]-1  3.
3.
在以上游戏中, b 1 和 b 2 可以相等.此时,敌手可以获知IBEET密文和陷门对应的关键字是相同的,而敌手的攻击目标是猜测3个关键字( kw 0 , kw 1 , kw 2 )中哪2个被挑战者选定了.根据以上5个游戏,我们给出DS-IBEET协议的安全性定义如下:
定义1 . 给定安全参数 k ,对任意多项式时间敌手 A i ( i =1,2,…,5),如果 ![]()
![]() 都是可以忽略的,那么我们称DS-IBEET协议是安全的.
都是可以忽略的,那么我们称DS-IBEET协议是安全的.
4 . 1 协议具体内容
该协议由7个算法组成:初始化算法、密钥生成算法、陷门生成算法、加密算法、解密算法、前服务器测试算法、后服务器测试算法.
4.1.1 初始化算法 Setup (1 k )
给定安全参数 k ∈ Z * ,Hash函数 ![]() 选择随机数( s 1 , s 2 )作为前服务器 S F 的密钥并计算
选择随机数( s 1 , s 2 )作为前服务器 S F 的密钥并计算 ![]() 选择随机数 s 3 作为后服务器 S B 的密钥并计算
选择随机数 s 3 作为后服务器 S B 的密钥并计算 ![]() 公布参数 params =( p , G 1 , G T , e , g , g 1 , g 2 , g 3 , H 1 , H 2 , h 3 , h ).
公布参数 params =( p , G 1 , G T , e , g , g 1 , g 2 , g 3 , H 1 , H 2 , h 3 , h ).
4.1.2 密钥生成算法 KeyGen ( Params , s 1 , s 2 )
给定身份 ID ∈{0,1} * ,计算 ![]() 解密钥 dk ID =(
解密钥 dk ID =( ![]() ,
, ![]() ).
).
4.1.3 陷门生成算法 TrapGen ( Params , s 1 )
用户将解密钥的一部分 td ID = ![]() 作为陷门.
作为陷门.
4.1.4 加密算法 Encrypt ( Params , M )
给定关键字明文 M ,计算 h ID = H 1 ( ID ),选择随机数 ![]() 计算密文 C =( C 1 , C 2 , C 3 , C 4 , C 5 ),其中:
计算密文 C =( C 1 , C 2 , C 3 , C 4 , C 5 ),其中:
![]()
![]()
![]()
![]()
C 5 =( M ‖ r 1 )⊕ h 3 ( ![]() ),
),
U 1 = e ( h ID , g 1 )∈ G T ,
U 2 = e ( h ID , g 2 )∈ G T ,
U 3 = e ( h ID , g 3 )∈ G T .
4.1.5 解密算法 Decrypt ( Params , C )
使用解密钥 dk ID =( ![]() ,
, ![]() )对密文 C =( C 1 , C 2 , C 3 , C 4 , C 5 )进行解密,计算为
)对密文 C =( C 1 , C 2 , C 3 , C 4 , C 5 )进行解密,计算为
C 5 ⊕ h 3 ( e ( ![]() , C 4 ))= M ‖ r 1 ,
, C 4 ))= M ‖ r 1 ,
如果 ![]() 成立,则输出 M .
成立,则输出 M .
4.1.6 前服务器测试算法 ![]()
此算法由服务器 S F 执行,给定2个密文 C A =( C 1, A , C 2, A , C 3, A , C 4, A , C 5, A )和 C B =( C 1, B , C 2, B , C 3, B , C 4, B , C 5, B )以及分别与之对应的陷门 ![]() 和
和 ![]() 得到判定 M A = M B 是否成立的中间结果 X A 和 X B .即:
得到判定 M A = M B 是否成立的中间结果 X A 和 X B .即:
X A = ![]() ,
,
X B = ![]() .
.
4.1.7 后服务器测试算法 TestSB ( C A , X A , C B , X B )
此算法由服务器 S B 执行,计算并比较下列等式是否成立:
若成立,则输出1,表明 M A = M B ,否则输出0.
4 . 2 协议正确性分析
X B = ![]() =
= ![]() × h (
× h ( ![]() )=
)=
同理:
e ( C 1, B , h ( e ( ![]() , C 4, A )) -1 × X A )= e (
, C 4, A )) -1 × X A )= e ( ![]() , M A ),
, M A ),
由于:
![]()
![]()
若等式 ![]() 成立,则有 M A = M B ,从而协议正确.
成立,则有 M A = M B ,从而协议正确.
本节我们分析上述协议的安全性.
定理1 . 本文提出的DS-IBEET协议在选择关键字攻击下是语义安全的.
上述定理能够通过下述引理1和引理2证明.
引理1 . 对于任意多项式时间敌手 ![]() 是可忽略的.
是可忽略的.
证明. 首先定义下列游戏:
Game0. 这是针对恶意前服务器的初始版本SS-CKA游戏.
1) 初始化算法( Setup ).挑战者运行初始化算法生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
2) 查询阶段1( Query - phase -Ⅰ).敌手向挑战者发送下列查询:
① h - query ( T ).此预言机维护一个初始为空的列表 L h ,给定参数 T ,随机选择 H ∈ G 1 并将〈 T , H 〉添加到列表 L h .返回 h ( T ).
② H 1 - query ( T ).此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表
给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表 ![]() 返回 H 1 ( T ).
返回 H 1 ( T ).
③ H 2 - query ( T ).此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表
给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表 ![]() 返回 H 2 ( T ).
返回 H 2 ( T ).
④ h 3 - query ( T ).此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表
给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表 ![]() 返回 h 3 ( T ).
返回 h 3 ( T ).
⑤ Encrypt - query ( Params , kw ).此预言机维护一个初始为空的列表 L Enc =〈 kw , C 〉,给定参数和明文,对明文关键字 kw 进行加密:
C ← Encrypt ( Params , kw ),
其中:
C =( C 1 , C 2 , C 3 , C 4 , C 5 ), ![]()
![]()
![]()
![]()
C 5 =( M ‖ r 1 )⊕ h 3 ( ![]() ),
),
U 1 = e ( h ID , g 1 )∈ G T ,
U 2 = e ( h ID , g 2 )∈ G T ,
U 3 = e ( h ID , g 3 )∈ G T .
并将〈 kw , C 〉添加到列表 L Enc 中,挑战者返回 C 给敌手.
3) 挑战( challenge ).敌手 A 选择2个关键字( kw 0 , kw 1 ),并将它们发送给挑战者,挑战者随机选择 b ∈{0,1}并计算密文 C kwb ,将 C kwb 发送给敌手 A .
4) 查询阶段2( Query - phase -Ⅱ).此阶段与查询阶段1一致.
5) 输出( output ).最终,敌手 A 输出对 b 的猜测值 b ′.如果 b = b ′,则 A 赢得游戏.
我们定义 A 赢得游戏Game0的优势为 ![]() ).根据3.3节定义的SS-CKA模型,有:
).根据3.3节定义的SS-CKA模型,有:
![]() ).
).
Game1. Game1与Game0基本相同,区别在于,在Game1中,挑战者用随机数 W 1 替换了Hash函数 h : G T →{0,1} * .具体游戏过程如下:
1) 初始化算法( Setup ).挑战者运行初始化算法生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
2) 查询阶段1( Query - phase -Ⅰ).敌手向挑战者发送下列查询:
① h - query ( T ): 此预言机维护一个初始为空的列表 L h ,给定参数 T ,随机选择 H ∈ G 1 并将〈 T , H 〉添加到列表 L h .返回 h ( T ).
② H 1 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表
给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表 ![]() 返回 H 1 ( T ).
返回 H 1 ( T ).
③ H 2 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表
给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表 ![]() 返回 H 2 ( T ).
返回 H 2 ( T ).
④ h 3 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表
给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表 ![]() 返回 h 3 ( T ).
返回 h 3 ( T ).
⑤ Encrypt - query ( Params , kw ).此预言机维护一个初始为空的列表 L Enc =〈 kw , C 〉,给定参数和明文,对明文关键字 kw 进行加密:
C ← Encrypt ( Params , kw ),
其中:
C =( C 1 , C 2 , C 3 , C 4 , C 5 ), ![]()
![]()
![]()
![]()
C 5 =( M ‖ r 1 )⊕ h 3 ( ![]() ),
),
U 1 = e ( h ID , g 1 )∈ G T ,
U 2 = e ( h ID , g 2 )∈ G T ,
U 3 = e ( h ID , g 3 )∈ G T ,
挑战者返回 C 给敌手.
3) 挑战( challenge ).敌手 A 选择2个关键字( kw 0 , kw 1 ),并将它们发送给挑战者,挑战者随机选择 b ∈{0,1}并计算密文 C kwb ,将 C kwb 发送给敌手 A .
4) 查询阶段2( Query - phase -Ⅱ).此阶段与查询阶段1一致,但不可查询( kw 0 , kw 1 )的密文,若 kw = kw 0 或者 kw = kw 1 ,则返回⊥并结束游戏,记为事件 Event 1.
5) 输出( output ).最终,敌手 A 输出对 b 的猜测值 b ′.如果 b = b ′,则 A 赢得游戏.
根据随机预言模型(random oracle model)的性质以及Difference Lemma [21] ,在事件 Event 1不发生的情况下,敌手 A 赢得游戏Game1的优势满足:
| Ad ![]() ( k )- Ad
( k )- Ad ![]() ( k )|≤ Pr [ Event 1].
( k )|≤ Pr [ Event 1].
由于 H 2 是随机预言机, W 1 是随机选择的,且在查询过程中未返回给敌手,故根据CDH假设, Pr [ Event 1]是可忽略的.
Game2. Game2与Game1基本相同,区别在于,在Game2中,挑战者用随机数 W 2 替换了 C 3 .具体游戏过程如下:
1) 初始化算法( Setup ).挑战者运行初始化算法生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
2) 查询阶段1( Query - phase -Ⅰ).敌手向挑战者发送下列查询:
① h - query ( T ): 此预言机维护一个初始为空的列表 L h ,给定参数 T ,随机选择 H ∈ G 1 并将〈 T , H 〉添加到列表 L h .返回 h ( T ).
② H 1 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表
给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表 ![]() 返回 H 1 ( T ).
返回 H 1 ( T ).
③ H 2 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表
给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表 ![]() 返回 H 2 ( T ).
返回 H 2 ( T ).
④ h 3 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表
给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表 ![]() 返回 h 3 ( T ).
返回 h 3 ( T ).
⑤ Encrypt - query ( Params , kw ).此预言机维护一个初始为空的列表 L Enc =〈 kw , C 〉,给定参数和明文,对明文关键字 kw 进行加密:
C ← Encrypt ( Params , kw ),
其中:
C =( C 1 , C 2 , C 3 , C 4 , C 5 ), ![]()
![]()
C 3 = W 2 , ![]()
C 5 =( M ‖ r 1 )⊕ h 3 ( ![]() ),
),
U 1 = e ( h ID , g 1 )∈ G T ,
U 2 = e ( h ID , g 2 )∈ G T ,
U 3 = e ( h ID , g 3 )∈ G T ,
挑战者返回 C 给敌手.
3) 挑战( challenge ).敌手 A 选择2个关键字( kw 0 , kw 1 ),并将它们发送给挑战者,挑战者随机选择 b ∈{0,1}并计算密文 C kwb ,将 C kwb 发送给敌手 A .
4) 查询阶段2( Query - phase -Ⅱ).此阶段与查询阶段1一致,但不可查询( kw 0 , kw 1 )对应的密文,若 kw = kw 0 或者 kw = kw 1 ,则返回⊥并结束游戏,记为事件 Event 2.
5) 输出( output ).最终,敌手 A 输出对 b 的猜测值 b ′.如果 b = b ′,则 A 赢得游戏.
根据随机预言模型的性质以及Difference Lemma [21] ,在事件 Event 2不发生的情况下,敌手 A 赢得游戏Game2的优势满足:
| Ad ![]() ( k )- Ad
( k )- Ad ![]() ( k )|≤ Pr [ Event 2].
( k )|≤ Pr [ Event 2].
由于 W 2 是随机选择的,且在查询过程中未返回给敌手,故根据CDH假设, Pr [ Event 2]是可忽略的.
证毕.
引理2 . 对于任意多项式时间敌手 ![]() 是可忽略的.
是可忽略的.
证明. 引理 2的证明过程与引理 1类似.这里不再赘述.
定理2 . 我们的DS-IBEET协议在关键字猜测攻击下是不可区分的.
上述定理可以通过引理3、引理4和引理5证明.
引理3 . 对于任意多项式时间敌手 ![]() 是可忽略的.
是可忽略的.
证明. 在我们的DS-IBEET协议中,陷门是解密钥的一部分, td ID = ![]() ,与具体的关键字无关,故陷门不会泄漏任何关键字的信息.
,与具体的关键字无关,故陷门不会泄漏任何关键字的信息.
证毕.
引理4 . 对于任意多项式时间敌手 ![]() 是可忽略的.
是可忽略的.
证明. 引理 4的证明过程与引理 3类似.这里不再赘述.
引理5 . 对于任意多项式时间敌手 ![]() 是可忽略的.
是可忽略的.
证明. 首先定义下列游戏:
Game0.这是针对恶意后服务器的初始版本游戏.
1) 初始化算法( Setup ).挑战者运行初始化算法生成密钥对对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
2) 查询阶段1( Query - phase -Ⅰ).敌手向挑战者发送下列查询:
① h - query ( T ): 此预言机维护一个初始为空的列表 L h ,给定参数 T ,随机选择 H ∈ G 1 并将〈 T , H 〉添加到列表 L h .返回$ h ( T )$.
② H 1 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表
给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表 ![]() 返回 H 1 ( T ).
返回 H 1 ( T ).
③ H 2 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表
给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表 ![]() 返回 H 2 ( T ).
返回 H 2 ( T ).
④ h 3 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表
给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表 ![]() 返回 h 3 ( T ).
返回 h 3 ( T ).
⑤ Encrypt - query ( Params , kw ).此预言机维护一个初始为空的列表 L Enc =〈 kw , C 〉,给定参数和明文,对明文关键字 kw 进行加密:
C ← Encrypt ( Params , kw ),
其中:
C =( C 1 , C 2 , C 3 , C 4 , C 5 ), ![]()
![]()
![]()
![]()
C 5 =( M ‖ r 1 )⊕ h 3 ( ![]() ),
),
U 1 = e ( h ID , g 1 )∈ G T ,
U 2 = e ( h ID , g 2 )∈ G T ,
U 3 = e ( h ID , g 3 )∈ G T ,
并将〈 kw , C 〉添加到列表 L Enc 中.挑战者返回 C 给敌手.
⑥ ![]() 此预言机维护一个初始为空的列表
此预言机维护一个初始为空的列表 ![]() 给定密文和相应的陷门,计算:
给定密文和相应的陷门,计算:
X A = ![]() ,
,
X B = ![]() .
.
3) 挑战( challenge ).敌手 A 选择3个不同的关键字( kw 0 , kw 1 , kw 2 ),并将它们发送给挑战者,挑战者随机选择{ b 1 , b 2 }⊂{0,1,2}并计算:
C ![]() ← Encrypt ( params , p
← Encrypt ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
), ![]() ← TrapGen ( params , p
← TrapGen ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
), ![]() ).
).
挑战者将 ![]() 发送给敌手.
发送给敌手.
4) 输出( output ).最后,敌手 A 输出它对{ b 1 , b 2 }的猜测{ ![]() ,
, ![]() }⊂{0,1,2}.如果{ b 1 , b 2 }={
}⊂{0,1,2}.如果{ b 1 , b 2 }={ ![]() ,
, ![]() },则 A 赢得这个游戏.
},则 A 赢得这个游戏.
我们定义 A 赢得游戏Game0的优势为 ![]() ).根据前文定义的IND-KGA-Ⅱ模型,有:
).根据前文定义的IND-KGA-Ⅱ模型,有:
![]() ).
).
Game1. Game1与Game0基本相同,区别在于,在Game1中,挑战者用随机数 W 1 , W 2 替换了Hash函数 H 2 : G T → G 1 .具体游戏过程如下:
1) 初始化算法( Setup ).挑战者运行初始化算法生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
2) 查询阶段1( Query - phase -Ⅰ).敌手向挑战者发送下列查询:
① h - query ( T ): 此预言机维护一个初始为空的列表 L h ,给定参数 T ,随机选择 H ∈ G 1 并将〈 T , H 〉添加到列表 L h ,返回 h ( T ).
② H 1 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表
给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表 ![]() 返回 H 1 ( T ).
返回 H 1 ( T ).
③ H 2 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表
给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表 ![]() 返回 H 2 ( T ).
返回 H 2 ( T ).
④ h 3 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表
给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表 ![]() 返回 h 3 ( T ).
返回 h 3 ( T ).
⑤ Encrypt - query ( Params , kw ).此预言机维护一个初始为空的列表 L Enc =〈 kw , C 〉,给定参数和明文,对明文关键字 kw 进行加密:
C ← Encrypt ( Params , kw ),
其中:
C =( C 1 , C 2 , C 3 , C 4 , C 5 ), ![]()
![]()
![]()
![]()
C 5 =( M ‖ r 1 )⊕ h 3 ( ![]() ),
),
U 1 = e ( h ID , g 1 )∈ G T ,
U 2 = e ( h ID , g 2 )∈ G T ,
U 3 = e ( h ID , g 3 )∈ G T ,
挑战者返回 C 给敌手.
⑥ ![]() 此预言机维护一个初始为空的列表
此预言机维护一个初始为空的列表 ![]() 给定密文和相应的陷门,计算:
给定密文和相应的陷门,计算:
X A = ![]() ,
,
X B = ![]() .
.
3) 挑战( challenge ).敌手 A 选择3个不同的关键字( kw 0 , kw 1 , kw 2 ),并将它们发送给挑战者,挑战者随机选择{ b 1 , b 2 }⊂{0,1,2}并计算:
C ![]() ← Encrypt ( params , p
← Encrypt ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
),
![]() ← TrapGen ( params , p
← TrapGen ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
),
挑战者将 ![]() 发送给敌手.
发送给敌手.
4) 查询阶段2( Query - phase -Ⅱ).此阶段与查询阶段1一致,但不可查询( kw 0 , kw 1 )的密文,若 kw = kw 0 或者 kw = kw 1 ,则返回⊥并结束游戏,记为事件 Event 3.
5) 输出( output ).最后,敌手 A 输出它对{ b 1 , b 2 }的猜测{ ![]() ,
, ![]() }⊂{0,1,2}.如果{ b 1 , b 2 }={
}⊂{0,1,2}.如果{ b 1 , b 2 }={ ![]() ,
, ![]() },则 A 赢得这个游戏.
},则 A 赢得这个游戏.
根据随机预言模型的性质以及Difference Lemma [21] ,在事件 Event 3不发生的情况下,敌手 A 赢得游戏Game1的优势满足:
| Ad ![]() ( k )- Ad
( k )- Ad ![]() ( k )|≤ Pr [ Event 3].
( k )|≤ Pr [ Event 3].
由于 W 1 , W 2 是随机选择的,且在查询过程中未返回给敌手,故根据 CDH 假设, Pr [ Event 3]是可忽略的.
Game2. Game2与Game1基本相同,区别在于,在Game2中,挑战者用随机数 W 3 , W 4 替换了 X A , X B .具体游戏过程如下:
1) 初始化算法( Setup ).挑战者运行初始化算法生成密钥对 ![]() 和
和 ![]() 将
将 ![]() 发送给敌手.
发送给敌手.
2) 查询阶段1( Query - phase -Ⅰ).敌手向挑战者发送下列查询:
① h - query ( T ): 此预言机维护一个初始为空的列表 L h ,给定参数 T ,随机选择 H ∈ G 1 并将〈 T , H 〉添加到列表 L h .返回 h ( T ).
② H 1 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表
给定参数 T ,随机选择 H 1 ∈ G 1 并将〈 T , H 1 〉添加到列表 ![]() 返回 H 1 ( T ).
返回 H 1 ( T ).
③ H 2 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表
给定参数 T ,随机选择 H 2 ∈ G 1 并将〈 T , H 2 〉添加到列表 ![]() 返回 H 2 ( T ).
返回 H 2 ( T ).
④ h 3 - query ( T ): 此预言机维护一个初始为空的列表 ![]() 给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表
给定参数 T ,随机选择 h 3 ∈ G 1 并将〈 T , h 3 〉添加到列表 ![]() 返回 h 3 ( T ).
返回 h 3 ( T ).
⑤ Encrypt - query ( Params , kw ).此预言机维护一个初始为空的列表 L Enc =〈 kw , C 〉,给定参数和明文,对明文关键字 kw 进行加密:
C ← Encrypt ( Params , kw ),
其中:
C =( C 1 , C 2 , C 3 , C 4 , C 5 ), ![]()
![]()
![]()
![]()
C 5 =( M ‖ r 1 )⊕ h 3 ( ![]() ),
),
U 1 = e ( h ID , g 1 )∈ G T ,
U 2 = e ( h ID , g 2 )∈ G T ,
U 3 = e ( h ID , g 3 )∈ G T ,
挑战者返回 C 给敌手.
⑥ ![]() 此预言机维护一个初始为空的列表
此预言机维护一个初始为空的列表 ![]() 给定密文和相应的陷门,计算:
给定密文和相应的陷门,计算:
X A = W 3 ,
X B = W 4 .
3) 挑战( challenge ).敌手 A 选择3个不同的关键字( kw 0 , kw 1 , kw 2 ),并将它们发送给挑战者,挑战者随机选择{ b 1 , b 2 }⊂{0,1,2}并计算:
C ![]() ← Encrypt ( params , p
← Encrypt ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
),
![]() ← TrapGen ( params , p
← TrapGen ( params , p ![]() , p
, p ![]() , k
, k ![]() ),
),
挑战者将 ![]() 发送给敌手.
发送给敌手.
4) 查询阶段2( Query - phase -Ⅱ).此阶段与查询阶段1一致,但不可查询( kw 0 , kw 1 )的密文,若 kw = kw 0 或者 kw = kw 1 ,则返回⊥并结束游戏,记为事件 Event 4.
5) 输出( output ).最后,敌手 A 输出它对{ b 1 , b 2 }的猜测{ ![]() ,
, ![]() }⊂{0,1,2}.如果{ b 1 , b 2 }={
}⊂{0,1,2}.如果{ b 1 , b 2 }={ ![]() ,
, ![]() },则 A 赢得这个游戏.
},则 A 赢得这个游戏.
根据随机预言模型的性质以及Difference Lemma [21] ,在事件 Event 4不发生的情况下,敌手 A 赢得游戏Game2的优势满足:
| Ad ![]() ( k )- Ad
( k )- Ad ![]() ( k )|≤ Pr [ Event 4].
( k )|≤ Pr [ Event 4].
由于 W 3 , W 4 是随机选择的,且在查询过程中未返回给敌手,故根据CDH假设, Pr [ Event 4]是可忽略的.
证毕.
本文从计算开销和通信开销2个方面对我们设计的协议的性能进行分析.
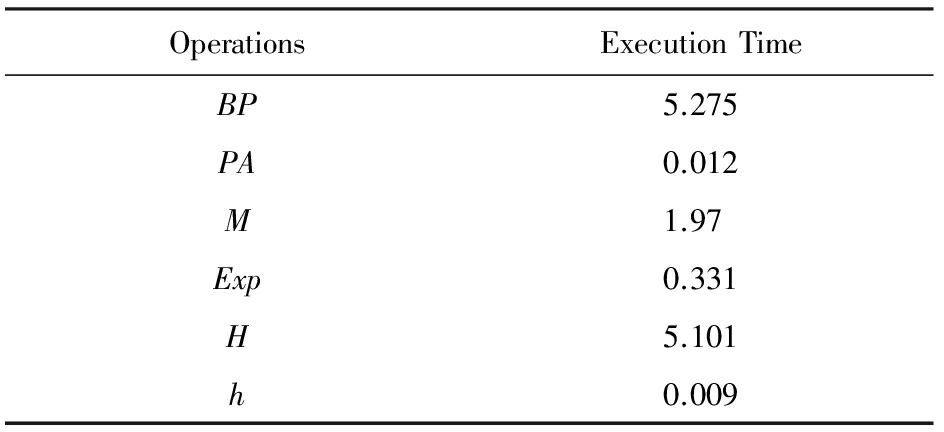
为了对协议的性能进行评估,我们在阿里巴巴的ECS云主机上调用 MIRACL库 [22] ,获得一些基本密码操作的执行时间.云主机的配置环境如表1所示,椭圆曲线参数如表2所示.我们使用Tate对,大素数 p 为512 b,大素数阶 q 为160 b.设 M , Exp , BP , H , h 和 PA 分别表示标量乘法、群 G 1 上的模指数运算、双线性对运算、HashToPoint运算、普通Hash运算和点加运算.这些基本操作的执行时间如表3所示.
Table 1 System Information
表1 系统配置信息

Table 2 Parameters of Elliptic Curve
表2 椭圆曲线参数

Table 3 Execution Time of Basic Operations
表3 基本操作执行时间 ms
根据统计,我们的DS-IBEET协议的各个算法的计算开销如表4所示.加密算法、解密算法、前服务器测试算法和后服务器测试算法的运行时间分别为24.9 ms,17.952 ms,24.692 ms和14.508 ms.显然,此协议可以运行在资源受限的移动设备上(如病人的手机  平板电脑等).
平板电脑等).
Table 4 Computation Cost
表4 计算开销 ms

本协议的通信开销如表5所示.其中,公钥长度为群 G 1 中元素比特长度的2倍,密文长度为群 G 1 中元素比特长度的4倍加上一个 Z q 上大数比特长度.陷门长度为群 G 1 中元素比特长度.
Table 5 Communication Cost
表5 通信开销
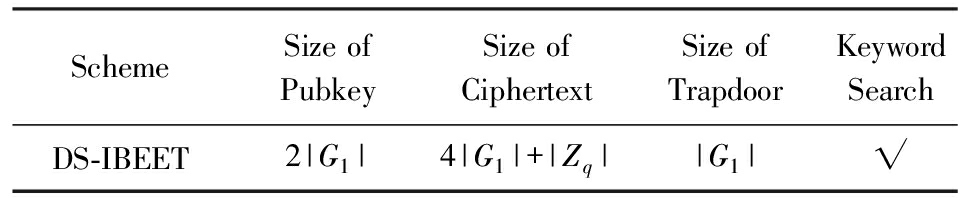
| G 1 |: The bit length of element in G 1 .
| Z q |: Bit length of number in Z q .
最近,一些带密文等值判定的公钥加密协议被提出.然而,它们仅有一个服务器参与密文等值判定过程,这种设计容易遭受恶意服务器内部关键字猜测攻击.为了解决这个问题,本文首次提出了基于双服务器的带密文等值判定的公钥加密协议,并在随机预言机模型下证明了其安全性.同时,我们利用MIRACL大数库对其计算性能进行了评估,并分析了其通信开销,结果表明我们的DS-IBEET协议性能良好,且能够在资源受限的移动设备上运行.
由于基于身份的加密协议存在密钥托管问题,我们下一步工作将尝试研究一个无证书的带等值判定的公钥加密协议.
参考文献
[1] Boneh D, Di Crescenzo G, Ostrovsky R, et al. Public key encryption with keyword search[C] //Advances in Cryptology—EUROCRYPT 2004. Berlin: Springer, 2004: 506-522
[2] Fang Liming, Willy S, Ge Chunpeng, et al. Public key encryption with keyword search secure against keyword guessing attacks without random oracle[J]. Information Sciences, 2013, 238: 221-241
[3] Abdalla M, Bellare M, Catalano D, et al. Searchable encryption revisited: Consistency properties, relation to anonymous ibe, and extensions[J]. Journal of Cryptology, 2008, 21(3): 350-391
[4] Hwang Y H, Lee P J. Public key encryption with conjunctive keyword search and its extension to a multi-user system[C] //Proc of the 1st Int Conf on Pairing-Based Cryptography. Berlin: Springer, 2007: 2-22
[5] Orencik C, Selcuk A, Savas E, et al. Multi-keyword search over encrypted data with scoring and search pattern obfuscation[J]. International Journal of Information Security, 2016, 15(3): 251-269
[6] Ibraimi L, Nikova S, Hartel P, et al. Public-key encryption with delegated search[C] //Proc of the 9th Int Conf on Applied Cryptography and Network Security (ACNS2011). Berlin: Springer, 2011: 532-549
[7] Byun J W, Rhee H S, Park H A, et al. Off-line key-word guessing attacks on recent keyword search schemes over encrypted data[C] // Proc of the 3rd VLDB Workshop on Secure Data Management (SDM 2006). Berlin: Springer, 2006: 75-83
[8] Shi Jie, Lai Junzuo, Li Yingjiu, et al. Authorized keyword search on encrypted data[C] //Proc of European Symp on Research in Computer Security (ESORICS 2014). Berlin: Springer, 2014: 419-435
[9] Cao Ning, Wang Cong, Li Ming, et al. Privacy-preserving multi-keyword ranked search over encrypted cloud data[J]. IEEE Trans on Parallel and Distributed Systems, 2014, 25(1): 222-233
[10] Wang Kaixuan, Li Yuxi, Zhou Fucai, et al. Multi-keyword fuzzy search over encrypted data[J]. Journal of Computer Research and Development, 2017, 54(2): 348-360 (in Chinese)
(王恺璇, 李宇溪, 周福才, 等. 面向多关键字的模糊密文搜索方法[J]. 计算机研究与发展, 2017, 54(2): 348-360)
[11] Chen Dongdong, Cao Zhenfu, Dong Xiaolei. Online/offline ciphertext-policy attribute-based searchable encryption[J]. Journal of Computer Research and Development, 2016, 53(10): 2365-2375 (in Chinese)
(陈冬冬, 曹珍富, 董晓蕾. 在线/离线密文策略属性基可搜索加密[J]. 计算机研究与发展, 2016, 53(10): 2365-2375)
[12] Tang Qiang. Towards public key encryption scheme supporting equality test with fine-grained authorization[C] //Proc of Australasian Conf on Information Security and Privacy. Berlin: Springer, 2011: 389-406
[13] Yang Guomin, Tan C H, Huang Qiong, et al. Probabilistic public key encryption with equality test[C] //Proc of Cryptographers’ Track at the RSA Conference. Berlin: Springer, 2010: 119-131
[14] Tang Qiang. Public key encryption supporting plaintext equality test and user-specified authorization[J]. Security and Communication Networks, 2012, 5(12): 1351-1362
[15] Tang Qiang. Public key encryption schemes supporting equality test with authorisation of different granularity[J]. International Journal of Applied Cryptography, 2012, 2(4): 304-321
[16] Ma Sha, Zhang Mingwu, Huang Qiong, et al. Public key encryption with delegated equality test in a multi-user setting[J]. The Computer Journal, 2014, 58(4): 986-1002
[17] Huang Kaibin, Tso R, Chen Y-C, et al. PKE-AET: Public key encryption with authorized equality test[J]. The Computer Journal, 2015, 58(10): 2686-2697
[18] Ma Sha, Huang Qiong, Zhang Mingwu, et al. Efficient public key encryption with equality test supporting flexible authorization[J]. IEEE Trans on Information Forensics and Security, 2015, 10(3): 458-470
[19] Ma Sha. Identity-based encryption with outsourced equality test in cloud computing[J]. Information Sciences, 2016, 328: 389-402
[20] Wu Libing, Zhang Yubo, Choo Kim-Kwang, et al. Efficient and secure identity-based encryption scheme with equality test in cloud computing[J]. Future Generation Computer Systems, 2017, 73: 22-31
[21] Victor S. Sequences of games: A tool for taming complexity in security proofs[OL]. (2004-11-30) [2017-06-10]. https://eprint.iacr.org/2004/332.pdf
[22] CertiVox. MIRACL cryptographic library: Multiprecision integer and rational arithmetic C/C++ library[OL]. (2006-08-01) [2017-06-10]. https://github.com/miracl/MIRACL
Wu Libing 1,2 , Zhang Yubo 2 , and He Debiao 1,2
1 ( State Key Laboratory of Software Engineering ( Wuhan University ), Wuhan 430072) 2 ( School of Computer Science , Wuhan University , Wuhan 430072)
Abstract With the rapid development of cloud storage and the increasing awareness of privacy, more and more private data are encrypted before outsourcing to the cloud. Thus, how to search in encrypted data has been a new research item in the scope of searchable encryption. One of the solutions is public key encryption with equality test (PKEET). It can check whether the plaintexts of two ciphertexts encrypted under different public keys are the same, without leakage any information about the plaintexts. Recently, many public key encryption schemes with equality test have been proposed. However, in these schemes, there were only one server be used to perform the equality test, which means that they could not withstand the inner keywords guessing attack. To solve this problem, we propose the first dual server identity-based encryption scheme with equality test (DS-IBEET). And we prove the security under random oracle model. In addition, performance evaluation shows that our scheme is suitable for resource-limited mobile devices.
Key words equality test; identity-based encryption; cloud computing; dual server; searchable encryption
Received his BS and MS degrees in computer science from Central China Normal University, Wuhan, China, in 1994 and 2001, respectively.
Received: his PhD degree in computer science from Wuhan University in 2006. Professor in the School of Computer Science, Wuhan University. Senior member of IEEE and CCF. His main research interests include distributed computing, trusted software and wireless sensor networks.
中图法分类号 TP391


Zhang Yubo , born in 1988. Received his BS degree in computer science and technology from Wuhan University of Science and Technology, Wuhan, China in 2011. PhD candidate in computer system architecture from Wuhan University. Student member of CCF. His main research interests include cryptography and information security.

He Debiao , born in 1980. Received his PhD degree in applied mathematics from the School of Mathematics and Statistics, Wuhan University in 2009. Professor of the State Key Laboratory of Software Engineering, School of Computer Science, Wuhan University. His main research interests include cryptography and infor-mation security, in particularly, crypto-graphic protocols.