余国先 1 王可尧 1 傅广垣 1 王 峻 1 曾 安 2
1 (西南大学计算机与信息科学学院 重庆 400715) 2 (广东工业大学计算机学院 广州 510006)
(gxyu@swu.edu.cn)
摘 要 准确预测蛋白质功能是生物信息学的核心任务之一,也是人工智能在生物数据分析中的重要应用点之一.高通量技术的广泛应用产生了大量的生物分子功能关联网络,整合这些网络可更为全面地分析理解蛋白质功能机理,提升蛋白质功能预测精度.已有多种基于数据整合的蛋白质功能预测方法,但它们通常难以应用到较大功能标签空间,未利用标签间关联性和差异性整合多个网络.提出一种基于多网络数据协同矩阵分解的蛋白质功能预测方法(ProCMF).该方法首先利用非负矩阵分解将蛋白质-功能标签关联矩阵分解为2个低秩矩阵,挖掘蛋白质与标签之间的潜在关联.其次,为利用标签间关联关系和多种蛋白质特征数据,ProCMF分别基于上述2个低秩矩阵定义平滑正则性,约束指导低秩矩阵的协同分解.为了差异性地集成多个网络,ProCMF对不同的网络设置不同的权重.最后ProCMF将上述目标统一到一个目标方程中,并用一种交替迭代的方法分别优化求解低秩矩阵和网络权重.在酵母菌、人类和老鼠3个模式物种的多网络数据集上的实验结果表明:ProCMF获得了较其他相关算法更好的预测性能,ProCMF能有效地处理大量的功能标签和区分性地整合多个网络.
关键词 蛋白质功能预测;功能关联网络;网络集成;非负矩阵分解;协同分解
蛋白质是细胞的主要成分之一,它是生命活动的主要物质基础,生物体内的各种重要功能均需要蛋白质的参与才能完成.如催化代谢反应的酶,调节物质代谢和生命活动的激素和神经递质等 [1-2] .各种高通量生物技术的应用产生了海量与蛋白质功能信息相关的数据,如蛋白质互作网络、氨基酸序列、基因微阵列和RNA-Seq数据等.蛋白质的生物功能也不断被各种生物湿实验发现,并添加到蛋白质功能标注数据库(如gene ontology, GO) [3] 中.尽管如此,蛋白质已有的功能信息并不完整、存在缺失,且受限于生物实验技术和生物学家的研究兴趣 [4-5] .如Legrain等人 [6] 指出人类目前已知约有的20 000个蛋白质中2/3蛋白质的功能信息未知或未完整标注,亟需进一步标注.传统的生物湿实验方法虽能有效测定蛋白质功能,但成本高、通量低,测定的功能范围覆盖度有限,难以对海量的蛋白质数据进行快速功能标注.
基于人工智能技术的蛋白质功能预测方法可以利用已有的蛋白质功能标注信息和各种蛋白质数据,高效且较准确地大规模预测蛋白质的功能,为后续蛋白质功能生物湿实验测定提供可靠参照,减少生物实验验证的人力和物力成本 [1-2] .这些方法有的利用蛋白质序列数据 [7-8] ,它们通常基于序列相似的蛋白质更容易共享功能这一特性.还有一些方法利用蛋白质互作网络数据 [9-11] ,这类方法普遍基于互作的蛋白质更有可能共享功能这一观察 [9] .还有一些方法通过整合多种类型的生物数据(如基因表达数据、氨基酸序列和蛋白质互作网等)进行蛋白质功能预测 [12-16] .大量研究表明有效地整合多种类型的生物数据通常能够获得更高的预测精度,原因是不同类型的数据从不同的角度刻画蛋白质功能信息,具有互补性,整合它们能够获得更为全面的蛋白质功能信息,进而提高预测精度.
Pavlidis等人 [12] 通过3种方式研究了如何整合基因微阵列数据和基因序列数据进行蛋白质功能预测:第1种方式称为前期集成方法,它通过将每个基因的微阵列数据和序列数据拼接为一个更长的特征向量,再基于这些长向量进行功能预测.第2种方式称为中期集成方法,它先将每类数据通过特定的相似性度量方法转化为对应的蛋白质功能关联网络,再对不同的网络设置不同的权重并加权整合为一个复合网络,最后在复合网络上进行功能预测.第3种方式称为后期集成方法,它首先在每种数据上单独训练一个预测器,再集成这些预测器的结果实现最终的蛋白质功能预测.他们的实验研究表明不同数据源的质量不同,应该设置不同的权重,中期集成方法能够获得较优的性能.本文工作也是围绕基于多网络集成的蛋白质功能预测展开.限于篇幅,本文仅对与本文密切相关的中期集成方法进行简单介绍.
现有基于多源异构数据中期集成的蛋白质功能预测研究工作中,部分方法仅仅是将不同类型数据计算获取的蛋白质/基因功能关联网络进行平均加权进行整合 [17-18] ,忽略了不同的网络对蛋白质功能预测任务的关联性和贡献不同.此外,若部分网络由噪声数据源计算获取,这种不加区分的多网络叠加组合会导致预测性能的极大下降 [19-20] .
Lanckriet等人 [13] 在多核学习(multiple kernel learning)框架下 [21] 进行蛋白质功能预测,他们首先将 m 类生物数据分别采用合适的核函数转为核矩阵 W d ∈ ![]() n × n ( n 为蛋白质个数, d =1,2,…, m ),该矩阵也可以看作是功能关联网络的边权重矩阵,再通过半无限规划(semi-infinite programming)优化核矩阵上的权重系数 α d ≥0,并基于优化的权重整合这些核矩阵为一个复合矩阵
n × n ( n 为蛋白质个数, d =1,2,…, m ),该矩阵也可以看作是功能关联网络的边权重矩阵,再通过半无限规划(semi-infinite programming)优化核矩阵上的权重系数 α d ≥0,并基于优化的权重整合这些核矩阵为一个复合矩阵 ![]() 再在复合矩阵上应用支持向量机进行蛋白质功能预测.Tsuda等人 [22] 通过凸优化迭代更新每个核矩阵对应的加权系数和复合核矩阵上的预测器实现蛋白质功能预测.Mostafavi等人 [23] 提出GeneMANIA方法,将该方法应用到老鼠蛋白质功能预测竞赛中取得了优异的名次 [24] .GeneMANIA通过岭回归(ridge regression)和目标矩阵对齐针对每个功能标签分别优化网络整合权重和对应的复合网络,再在复合网络上进行标签信息传播实现蛋白质功能预测.Myers和Troyanskaya [25] 观察到蛋白质的功能与不同的网络具有不同的上下文相关性,提出一种基于Bayesian统计的方法整合多个网络进行蛋白质功能预测.然而由于蛋白质功能标注非常稀疏和不平衡,针对稀疏功能标签的上下文相关性很难准确衡量,所以该方法在稀疏标签(标注的蛋白质个数小于30)上的预测精度有限.蛋白质的功能标签空间非常大和不平衡性,如最广泛用于标注蛋白质功能的GO [3] 目前包含了40 000多个功能标签,而已标注功能的蛋白质的相关标签个数通常小于10,很多稀疏标签标注的蛋白质个数小于10,并且稀疏标签的个数远大于一般的功能标签(标注的蛋白质个数大于30).上述这些方法均对每个功能标签分别优化对应的复合网络,容易出现过拟合问题.为此这些方法通常仅考虑一般的功能标签,或者采用正则化或不平衡分类技术克服标签不平衡的影响 [23,26] .
再在复合矩阵上应用支持向量机进行蛋白质功能预测.Tsuda等人 [22] 通过凸优化迭代更新每个核矩阵对应的加权系数和复合核矩阵上的预测器实现蛋白质功能预测.Mostafavi等人 [23] 提出GeneMANIA方法,将该方法应用到老鼠蛋白质功能预测竞赛中取得了优异的名次 [24] .GeneMANIA通过岭回归(ridge regression)和目标矩阵对齐针对每个功能标签分别优化网络整合权重和对应的复合网络,再在复合网络上进行标签信息传播实现蛋白质功能预测.Myers和Troyanskaya [25] 观察到蛋白质的功能与不同的网络具有不同的上下文相关性,提出一种基于Bayesian统计的方法整合多个网络进行蛋白质功能预测.然而由于蛋白质功能标注非常稀疏和不平衡,针对稀疏功能标签的上下文相关性很难准确衡量,所以该方法在稀疏标签(标注的蛋白质个数小于30)上的预测精度有限.蛋白质的功能标签空间非常大和不平衡性,如最广泛用于标注蛋白质功能的GO [3] 目前包含了40 000多个功能标签,而已标注功能的蛋白质的相关标签个数通常小于10,很多稀疏标签标注的蛋白质个数小于10,并且稀疏标签的个数远大于一般的功能标签(标注的蛋白质个数大于30).上述这些方法均对每个功能标签分别优化对应的复合网络,容易出现过拟合问题.为此这些方法通常仅考虑一般的功能标签,或者采用正则化或不平衡分类技术克服标签不平衡的影响 [23,26] .
一些基于多网络整合的方法同时考虑多个功能标签进行蛋白质功能预测.如Mostafavi和Morris在GeneMANIA的基础上提出一种效率和精度更高的SW(simultaneous weights)方法 [27] .SW综合考虑一组存在关联的多个标签(包括稀疏标签),利用这些标签及它们标注的蛋白质定义目标对齐网络,再在GeneMANIA的框架下求解对应的网络权重系数和利用标签信息传播预测蛋白质功能.他们研究还发现组合多个相关标签可在不降低其他标签上预测精度的前提下显著提升稀疏标签上的预测精度.然而,与GeneMANIA类似,SW将复合网络的优化和复合网络上的功能预测问题当作2个相互独立的目标,容易出现优化获取的复合网络不一定适宜后续的预测任务的问题.针对这一问题,Yu等人 [19] 将复合网络的优化和该复合网络上针对所有功能标签的蛋白质功能预测统一到一个目标方程中,提出一种基于多核集成的蛋白质功能预测方法ProMK,获得了比SW更高的预测精度和较高的效率.然而ProMK仅基于网络的平滑性优化网络权重,越稀疏的网络获得的权重越大,因此它易受边较少的噪声网络的干扰.为此,Yu等人 [20] 提出另一种基于多网络整合的蛋白质功能预测方法MNet.MNet结合蛋白质功能标注信息和这类信息的不完整性特点定义了一个目标网络,再将多个功能关联网络加权整合的复合网络向该目标网络对齐,在优化网络权重的同时优化复合网络上的预测器.实验对比表明MNet能够较ProMK更准确地预测蛋白质功能和克服稀疏噪声网络的干扰,但是它的计算开销非常大.蛋白质之间的特征相似度(如序列相似度,基因共表达网络和蛋白质互作网)与蛋白质之间的语义相似度存在不同程度的正相关 [16,28] ,蛋白质之间的语义相似度通常基于蛋白质已有的功能标注信息和标签间结构关系综合衡量.根据这一特点,Yu等人提出一种基于语义多网络集成的蛋白质功能预测方法SimNet [16] .SimNet首先采用一种加权的术语重合相似性度量 [29] 构建蛋白质之间的语义网络,再将该语义网络向多个网络加权整合的复合网络对齐,进而求取加权系数,再在复合网络上利用标签信息传播预测蛋白质功能.SimNet的时空开销不仅远小于MNet,其精度也通常优于后者.最近Cho等人 [18] 提出一种基于成分扩散分析 [30] 的多网络整合方法Mashup并成功应用到蛋白质功能预测中.Mashup首先在每个网络的邻接矩阵上分别进行重启动随机游走,更新邻接矩阵获得蛋白质之间的拓扑结构信息,再将这些邻接矩阵等权重相加融合为复合网络,再对该复合网络的权重邻接矩阵应用奇异值分解(singular value decomposition, SVD)获取蛋白质的低秩向量特征表示,最后在这些低维向量上应用支持向量机预测蛋白质功能.Zitnik和Zupan提出一种基于矩阵分解数据集成的蛋白质功能预测方法MFDF [17] .该方法无需对各类分子间关联数据的邻接矩阵进行以蛋白质为鞍点的映射构造蛋白质功能关联网络,它直接在这些邻接矩阵上进行协同低秩矩阵分解,实现蛋白质功能预测.虽MFDF与Mashup类似,均能较好地处理不同网络中的局部噪声数据,但它们等同看待和处理每个网络,均易受噪声和不相关网络的干扰.
综上所述,由于蛋白质功能预测问题自身的复杂性,现有基于多网络集成的方法在处理较大的标签集合、利用标签间关联和区分性整合多个网络这3方面还存在不足.在已有基于矩阵分解的多网络融合研究的 [31-32] ,为此本文提出一种基于多网络数据协同矩阵分解的蛋白质功能预测方法(protein function prediction based on multiple networks collaborative matrix factorization, ProCMF).ProCMF首先基于已有的蛋白质功能标注信息和标签间层次结构关系初始化蛋白质-功能标签关联矩阵.为处理较大的标签空间,ProCMF利用非负矩阵分解(nonnegative matrix factorization, NMF) [33] 将该关联矩阵分解为2个低秩矩阵分别挖掘蛋白质之间语义关联和标签间潜在关联,将高维标签空间通过低秩矩阵进行压缩表示.其次,为利用标签间关联关系和多个蛋白质功能关联网络,基于上述2个低秩矩阵分别定义平滑正则项,约束指导低秩矩阵的协同分解.为了区分性地集成多个网络,ProCMF对不同的网络设置不同的权重.在此基础上,ProCMF将这些目标整合到一个统一的目标方程中,再设计迭代更新策略同时优化求解低秩矩阵和网络权重.本文在酵母菌、人类和老鼠3个模式物种多网络数据集上的一系列蛋白质功能预测实验表明:ProCMF在多种评价度量上均获得了较现有相关算法更好的预测结果,ProCMF能有效地处理大量存在关联的功能标签,区分性地整合多个网络,还拥有较高的运行效率且对输入参数鲁棒.
已知有 m 个蛋白质功能关联网络,这些网络的权重邻接矩阵为 W d ∈ ![]() n × n ( d =1,2,…, m ), n 为蛋白质个数, W d ( i , j )= W d ( j , i )≥0存储第 d 个网络中成对蛋白质 i 和 j 之间的关联强度(可靠性或序列相似性大小等).这些蛋白质共计被 c 个不同的功能标签标注, Y ∈
n × n ( d =1,2,…, m ), n 为蛋白质个数, W d ( i , j )= W d ( j , i )≥0存储第 d 个网络中成对蛋白质 i 和 j 之间的关联强度(可靠性或序列相似性大小等).这些蛋白质共计被 c 个不同的功能标签标注, Y ∈ ![]() n × c 存储 n 个蛋白质的已知功能标注信息,它基于GO结构初始化.GO是目前使用最为广泛的蛋白质功能注释范式,它通过一个有向无环图存储和表示功能标签间的关联关系,图中每个节点对应一个功能标签,子节点是父节点功能信息的进一步细化,当一个蛋白质标注有标签 t 对应的功能时,该蛋白质也标注有 t 的祖先节点对应的功能,反之则不一定 [3] .根据基因本体中功能标签的结构规则,本文对蛋白质-功能标签关联矩阵 Y 进行初始化:
n × c 存储 n 个蛋白质的已知功能标注信息,它基于GO结构初始化.GO是目前使用最为广泛的蛋白质功能注释范式,它通过一个有向无环图存储和表示功能标签间的关联关系,图中每个节点对应一个功能标签,子节点是父节点功能信息的进一步细化,当一个蛋白质标注有标签 t 对应的功能时,该蛋白质也标注有 t 的祖先节点对应的功能,反之则不一定 [3] .根据基因本体中功能标签的结构规则,本文对蛋白质-功能标签关联矩阵 Y 进行初始化:
(1)
需指出的是 Y ( i , t )=0并不表示蛋白质 i 不应该标注 t ,而只是表明目前还没有证据证明该蛋白质具有 t 对应的功能.这一设置受蛋白质功能标注信息的不完整性和开放世界假设(open world assumption) [5] 的影响.GO数据库中通常仅登记蛋白质具有某个功能的信息,极少登记该蛋白质不具有的功能信息,原因是准确测定蛋白质所具有的全部功能非常困难,生物学家通常更关注蛋白质具有的功能信息.
基于功能标签的结构特性和一个蛋白质通常标注多个功能标签,一些方法利用蛋白质已有功能标注的模式信息或蛋白质之间语义相似度,进行功能预测 [34-37] .如Done等人 [37] 受SVD能够挖掘文本与单词间潜在关联的启发,将每个蛋白质看作一个文本,标注到该蛋白质上的功能标签看作构成该文本的单词,在 Y 上应用SVD分别挖掘蛋白质与标签间的潜在关联,再基于SVD的低秩近似矩阵重构新的关联矩阵,实现蛋白质功能预测.该方法通过基因本体结构和词频与逆向文件频率调整关联矩阵中不同元素的权重,并设置子节点标签与蛋白质的关联权重大于其父节点标签,以期克服标签不平衡的影响.但这种调整方式实际上并不可取,因为一个标签标注到蛋白质上的概率值不应大于其父节点标签标注到该蛋白质上的概率值.Wang等人 [38] 和余国先等人 [39] 对上千(万)个功能标签构成的有向无环图的邻接矩阵进行低秩矩阵分解,在低维标签空间进行蛋白质功能预测,最后将预测结果映射回原始标签空间,显著提升了蛋白质功能预测精度.研究表明:低秩矩阵分解可以挖掘标签间的内在关联并降低预测问题的规模和复杂性.
受上述工作启发,考虑到 Y 的稀疏高维非负特性和非负矩阵分解NMF在文本分析领域的广泛成功应用 [40] ,本文首先在蛋白质-功能标签关联矩阵 Y 上应用NMF,以期挖掘蛋白质与大量标签间内在关联,具体最小化的目标方程为
Φ 0 ( U , V )=‖ Y - UV T ‖ 2 = ![]()
(2)
其中, U =( u 1 , u 2 ,…, u n )∈ ![]() n × r 和 V =( v 1 , v 2 ,…, v c )∈
n × r 和 V =( v 1 , v 2 ,…, v c )∈ ![]() c × r 为2个低秩矩阵,它们分别在压缩的 r ( r <min( n , c ))维空间以实数化的形式描述 n 蛋白质的语义特征信息和 c 个功能标签特征信息.式(2)通过低秩矩阵分解挖掘隐藏在 Y 中蛋白质之间的语义关联和标签间内在关联,进而发现蛋白质与功能标签间的潜在关联,已被成功应用于蛋白质功能预测 [37,41] .然而式(2)并没有显式考虑标签间关联关系,蛋白质的其他特征数据(如蛋白质互作网和氨基酸序列数据等),预测精度有限.
c × r 为2个低秩矩阵,它们分别在压缩的 r ( r <min( n , c ))维空间以实数化的形式描述 n 蛋白质的语义特征信息和 c 个功能标签特征信息.式(2)通过低秩矩阵分解挖掘隐藏在 Y 中蛋白质之间的语义关联和标签间内在关联,进而发现蛋白质与功能标签间的潜在关联,已被成功应用于蛋白质功能预测 [37,41] .然而式(2)并没有显式考虑标签间关联关系,蛋白质的其他特征数据(如蛋白质互作网和氨基酸序列数据等),预测精度有限.
2.2.1 结合功能标签关联信息
一个蛋白质通常标注多个功能标签,这些标签存在不同程度的关联和共现概率 [35,42] .蛋白质功能预测问题可以转化为多标记学习问题进行研究,面向蛋白质功能预测的多标记学习方法能够利用标签间的关联关系指导蛋白质功能预测,显著提升了蛋白质功能预测精度 [42-43] .式(2)仅通过矩阵分解隐式的挖掘蛋白质与标签间的关联关系,稀疏标签容易由于标注的蛋白质个数较少而被忽略.Done等人 [37] 针对这一问题调整稀疏标签的权重,但这种调整与蛋白质功能标注的结构要求相悖 [44] .为利用标签间的关联关系,本文采用一种广泛使用的余弦相似性度量衡量成对标签间的关联关系 [14,43,45] ,该度量的定义为
C s t = ![]() ,
,
(3)
其中, Y (·, t )∈ ![]() n ×1为 Y 的第 t 个列向量,它存储功能标签 t 与 n 个蛋白质之间的已知关联.当标签 s 和 t 经常标注到同一个蛋白质上时,它们之间的关联强度较大,否则关联强度较小.上述定义还较少受标签稀疏性的影响,2个稀疏标签之间也可以有较强的关联,只要它们同时标注到同一个蛋白质上的频率较高即可.
n ×1为 Y 的第 t 个列向量,它存储功能标签 t 与 n 个蛋白质之间的已知关联.当标签 s 和 t 经常标注到同一个蛋白质上时,它们之间的关联强度较大,否则关联强度较小.上述定义还较少受标签稀疏性的影响,2个稀疏标签之间也可以有较强的关联,只要它们同时标注到同一个蛋白质上的频率较高即可.
V 中每行可以看作是对应标签的低维表示,在高维标签空间存在较强关联的标签 s 和 t ,它们的低维向量表示 v s 和 v t 应该距离靠近.为实现上述目标,受平滑性假设 [46] 启发,本文引入标签间平滑性约束项:
![]() ‖ v s - v t ‖ 2 C s t =
‖ v s - v t ‖ 2 C s t =
tr( V T ( D c - C ) V )=tr( V T L c V ),
(4)
其中, D c ∈ ![]() c × c 是对角矩阵
c × c 是对角矩阵 ![]() 通过最小化式(4)可以使得存在较强关联的标签拥有相似的低维实数向量表示,进而使得存在较强关联的功能标签更可能标注到同一个蛋白质上.
通过最小化式(4)可以使得存在较强关联的标签拥有相似的低维实数向量表示,进而使得存在较强关联的功能标签更可能标注到同一个蛋白质上.
2.2.2 结合多个蛋白质功能关联网络
U 中每行可以看作是相应蛋白质在 V 刻画的 r 维语义空间的实数向量表示,但这种向量表示并没有结合蛋白质的其他特征数据(如氨基酸序列和蛋白质互作网等).大量研究表明存在互作的蛋白质更容易共享相同的功能 [9-10] ,不同的生物数据从不同的角度反映蛋白质功能,由于蛋白质功能的时空复杂性,很有必要整合多种生物数据获取蛋白质功能信息的全局视图,进而提高功能预测精度.为此,本文拟在 U 上引入多个功能关联网络的约束:
![]() ‖ u i - u j ‖ 2 W i j =
‖ u i - u j ‖ 2 W i j =
tr( U T ( D - W ) U )=tr( U T LU ),
(5)
其中, α d ≥0为第 d 个网络的权重, D ∈ ![]() n × n 为对角矩阵
n × n 为对角矩阵 ![]() 最小化式(5)可以使得序列相似(或互作等)的成对蛋白质在低维语义空间彼此靠近,这一目标也遵循了蛋白质之间的语义相似度与蛋白质之间的特征相似度正相关的特点 [27] .因此 Φ 2 ( U , α )可以融合多个功能关联网络约束指导 U 的协同分解.
最小化式(5)可以使得序列相似(或互作等)的成对蛋白质在低维语义空间彼此靠近,这一目标也遵循了蛋白质之间的语义相似度与蛋白质之间的特征相似度正相关的特点 [27] .因此 Φ 2 ( U , α )可以融合多个功能关联网络约束指导 U 的协同分解.
式(5)存在仅只选择一个网络的风险,具体分析式(5)可改写为
![]()
![]()
(6)
其中, D d 为对角矩阵 ![]() 从式(6)可以看出,若第 d 个功能关联网络非常稀疏,则平滑性损失项tr( U T L d U )最小, α d =1即可使得式(6)达到最小.为避免仅选择单个网络的不足,本文引入在 α 上的约束项并更新式(6)为
从式(6)可以看出,若第 d 个功能关联网络非常稀疏,则平滑性损失项tr( U T L d U )最小, α d =1即可使得式(6)达到最小.为避免仅选择单个网络的不足,本文引入在 α 上的约束项并更新式(6)为

(7)
通过在式(7)中引入在 α 上的 l 2 范式约束,可以避免仅选择单个网络的不足,它还可以对平滑且含噪声少的网络设置较大的权重,对非平滑且含噪声多的网络赋予较小(甚至为0)的权重,进而实现多个网络的差异性整合和剔除噪声网络的干扰.
在2.2节分析设计的基础上,为处理较大的标签集合,利用标签间关联性和区分性整合多个网络,本文定义ProCMF最终的目标方程:
Φ ( U , V , α )=‖ Y - UV T ‖ 2 + ω 1 ![]() α d tr( U T L d U )+
α d tr( U T L d U )+
ω 2 tr( V T L c V )+ λ ‖ ![]()
(8)
其中, ω 1 >0和 ω 2 >0用于调控多个功能关联网络和标签关联性对低秩矩阵 U 和 V 的协同分解.在获取优化后的低秩矩阵 U * 和 V * 之后,本文通过
(9)
重新定义蛋白质-标签之间的关联矩阵.
2.3.1 目标方程优化求解
式(8)中 U , V 和 α 的单个求解均依赖于其中另外2个参数,为此本文引入一种类似期望最大化 [47] 的交替迭代优化方法,在固定其中2个参数的情况下优化另外1个参数,直至达到指定的迭代次数或者收敛.式(8)可以等价为
Φ ( U , V , α )=tr(( Y - UV T ) T ( Y - UV T ))+
ω 1 tr( U T LU )+ ω 2 tr( V T L c V )+ λ ‖ ![]()
tr( Y T Y )-2tr( YVU T )+tr( UV T VU T )+
ω 1 tr( U T LU )+ ω 2 tr( V T L c V )+ λ ‖ α ![]() .
.
(10)
首先,假定 α 和 V 已知,式(10)变为以 U 为参数的目标函数.由于 Y 也已知,此时式(10)中右边第1项和最后2项均为常数,可忽略,可得以 U 为参数的目标函数为
Ο u ( U )=-2tr( YVU T )+tr( UV T VU T )+
ω 1 tr( U T LU ).
(11)
令 Λ u ∈ ![]() n × r 为约束 U ≥0的拉格朗日乘数,则有:
n × r 为约束 U ≥0的拉格朗日乘数,则有:
O u ( U , Λ u )=-2tr( YVU T )+2tr( UV T VU T )+
ω 1 tr( U T LU )-tr( Λ u U T ).
(12)
对式(11)求关于 U 的偏导数:
![]() =-2 YV +2 UV T V +2 ω 1 LU - Λ u .
=-2 YV +2 UV T V +2 ω 1 LU - Λ u .
(13)
由Karush-Kuhn-Tucker(KKT) [48] 条件 ![]() 0可得:
0可得:
-( YV ) i h u i h +( UV T V ) i h u i h + ω 1 ( LU ) i h u i h =0 ![]()
(14)
由此可得 U 的迭代更新方式:
u i h ← u i h ![]() .
.
(15)
其次,假定 α 和 U 已知,式(10)变为以 V 为参数的目标函数.此时式(10)中右边第1项、第4项和第6项均为常数,可忽略,可得以 V 为参数的目标函数为
O v ( V )=-2tr( YVU T )+tr( UV T VU )+
ω 2 tr( V T L c V ).
(16)
令 Λ v ∈ ![]() c × r 为约束 V ≥0的拉格朗日乘数,则有:
c × r 为约束 V ≥0的拉格朗日乘数,则有:
O u ( U , ψ )=-2tr( YVU T )+2tr( UV T VU T )-
tr( Λ v U T ).
(17)
同样,对式(11)求关于 V 的偏导数:
![]() =-2 Y T U +2 VU T U +2 ω 2 L c V - Λ v .
=-2 Y T U +2 VU T U +2 ω 2 L c V - Λ v .
(18)
由KKT条件 ![]() 可得:
可得:
-( Y T U ) s h v s h +( VU T U ) s h v s h + ω 2 ( L c V ) s h v s h =0.
(19)
由此可得 V 的迭代更新方式:
v s h ← v s h ![]() ,
,
(20)
最后,假定 U 和 V 已知,式(10)变为以 α 为参数的目标函数.此时式(10)中右边仅第4项和第6项与 α 有关,可得以 α 为参数的目标函数:
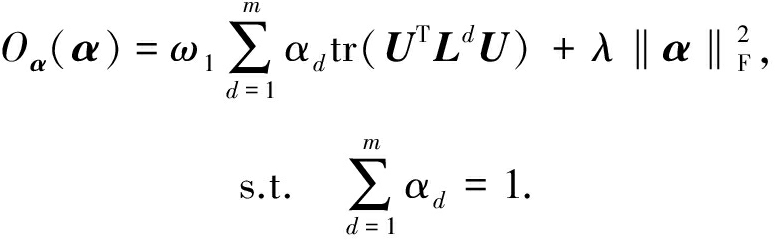
(21)
令 ![]() 式(21)可化简为
式(21)可化简为
![]()
(22)
式(22)可看作是关于 α 的二次规划问题.同样令 β ∈ ![]() m ×1和 η ≥0为 α ≥ 0 和 α T 1 =1的拉格朗日乘数,则有:
m ×1和 η ≥0为 α ≥ 0 和 α T 1 =1的拉格朗日乘数,则有:
O α ( α , β , η )= α T σ + λ α T α - α T β - η ( α T 1 -1). ![]()
(23)
基于KKT条件 [48] ,最优的 α 需满足4个条件:
1) ![]() = σ +2 λ α - β - η 1 =0,
= σ +2 λ α - β - η 1 =0,
3) β d ≥0,1≤ d ≤ m ,
4) β d α d =0,1≤ d ≤ m ,
令 O α ( α )关于 α 的导数为0,可得:
α d = ![]() ,
,
(24)
α d 依赖于 β d 和 η 的取值,其中 η 的取值对 α d 的影响为
1) 如果 η - σ d >0,由于 β d ≥0,所以 α d >0.又根据上述第4个条件 β d α d =0,得出 β d =0, α d =( η - σ d )/2 λ ;
2) 如果 η - σ d <0,由于 α d ≥0,则要求 β d >0,又因为 β d α d =0,所以 α d =0;
3) 如果 η - σ d =0,由于 β d α d =0, α d = β d /2 λ ,所以 α d =0, β d =0.
为便于讨论,假设 σ 1 ≤ σ 2 ≤…≤ σ m ,对于给定的 λ ,若 λ 不是非常大,则存在 η - σ p >0和 η - σ p +1 ≤0(1≤ p ≤ m -1), α d 存在的显示解:
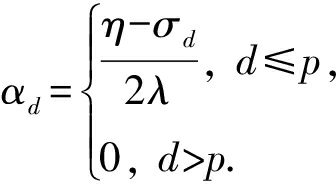
(25)
由 ![]() 可得 η 的数值解:
可得 η 的数值解:
η = 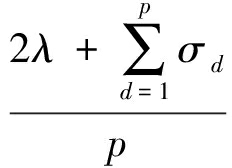 .
.
(26)
从式(25)可以看出, α d 在不同功能关联网络上的权重不同,越平滑(即tr( U T L d U )越小)的网络获取的权重越大.通常平滑的网络含有噪声边较少,这类网络中的边存在于具有功能关联的成对蛋白质之间.而非平滑网络则由于存在较多的噪声边而引入了较大的平滑损失,因而被赋予较小(甚至为0)的权重.通过式(25),还可以观察到部分功能关联网络的权重为0,原因可能是这些网络含有较多的噪声边,导致较大的平滑损失.从上述分析可以看出,ProCMF可以差异性的集成多个蛋白质功能关联网络.
为寻找 p 满足 η - σ p >0和 η - σ p +1 ≤0,对于给定的 λ ,ProCMF首先令 p = m ;再基于式(26)计算 η ,若 η > σ p 则找到符合条件的 p ,否则 p = p -1.重复上述循环直至找到符合条件的 p .可以证明当 λ 取很小值时 ![]() / p ,此时最平滑的一个或几个网络被选中;而当 λ 取值非常大时,所有的网络均被选中并赋予相似的权重.本文后续实验将对 λ 的影响做具体实验分析.
/ p ,此时最平滑的一个或几个网络被选中;而当 λ 取值非常大时,所有的网络均被选中并赋予相似的权重.本文后续实验将对 λ 的影响做具体实验分析.
在上述迭代优化的基础上,本文给出ProCMF的算法流程如算法1所示:
算法1 . 算法ProCMF.
输入:蛋白质-功能标签关联矩阵 Y , m 个蛋白质功能关联网络 ![]() 矩阵分解目标维度 r , ω 1 , ω 2 和 λ ,最大迭代次数 maxiter ,终止迭代误差 tol ;
矩阵分解目标维度 r , ω 1 , ω 2 和 λ ,最大迭代次数 maxiter ,终止迭代误差 tol ;
输出:蛋白质-功能标签关联矩阵 ![]()
① 初始化 α d =1/ m , iter =1, tol =10 -4 ,
maxiter =100, δ =10 6 ;
② ![]() ;/*初始化复合网络*/
;/*初始化复合网络*/
③ 随机初始化非负低秩矩阵 U 和 V ;
④ While iter < maxiter && δ > tol
⑤ 根据式(15)和式(20)计算更新 U 和 V ;
⑥ 根据式(25)计算新的 α ;
⑦ ![]() ;
;
⑧ δ =| Φ ( U , V , α ) iter - Φ ( U , V , α ) iter -1 |;
⑨ iter = iter +1;
⑩ End While
其中, Φ ( U , V , α ) iter 为第 iter 次迭代基于式(8)计算获取的损失大小, Φ ( U , V , α ) 0 =tr( Y T Y ).算法1中行①~③初始化 α , U , V 和 W ;行⑤~⑦计算更新 U , V , α 和 W ;行⑧~⑨计算前后2次优化迭代后损失大小的差异和迭代次数增1,用于判断是否进入下一次循环.
为验证ProCMF的性能,本文从文献[26]的附件资料中收集了酵母菌(yeast)、人类(human)和老鼠(mouse)三个模式生物的蛋白质数据集进行实验,其中每个物种的数据集均包含多个已处理好的蛋白质功能关联网络,这些网络由蛋白质结构域、基因表达数据和氨基酸序列数据等通过特定的相似性度量函数转化而来.其中Yeast包含44个网络,Human包含8个网络,Mouse包含10个网络.为标注蛋白质功能,本文下载了GO数据文件和上述物种的功能标注文件(日期:2017-07-15;地址:http://geneontology.org/),并在GO三个分支(生物过程(BP)、细胞成分(CC)、分子功能(MF))分别对蛋白质进行功能标注.特别地,本文遵循true path rule [3,49] 进行功能标注,即当蛋白质被某个功能标签所标注时,则该蛋白质也将标注该标签的祖先标签.为避免循环预测,实验中不考虑证据属性为IEA(inferred by electronic annotations)的功能标注.为评价算法预测稀疏标签的性能,所有标注蛋白质的标签个数不少于3个均予以保留进行实验分析.
传统的蛋白质功能预测实验通常将同一个蛋白质数据集划分训练集和测试集2部分,并将测试集中的蛋白质看做功能完全未知的蛋白质并对这些蛋白质进行功能预测,最后用这些蛋白质的已知功能标注信息评估预测性能 [19,43] .这种实验设置忽略了两部分蛋白质之间内在的关联,评估结果通常过于乐观 [1] .为了更好地反映蛋白质功能标注的真实场景,本文采用一种历史到现在的实验模式,首先利用2014年(history)的功能标注数据作为训练集进行功能预测,再利用2017年(recent)的功能标注数据作为评估集检验预测结果.为此本文还下载了上述3个物种的蛋白质在2014-05-15对应的GO数据文件和上述物种的功能标注文件,并用同样的预处理方法对蛋白质进行功能标注.表1中统计了2014-05和2017-07两个时间节点每个物种的蛋白质在3个分支的功能标注数和相应的标签个数.
Table 1 Statistics of Functional Annotations of Proteins
表1 蛋白质功能标注信息统计

从表1中可以看出,随着时间的推移,蛋白质的功能标注信息在不断地增多,如Yeast的3 904个蛋白质在生物过程(BP)分支的功能标注从111 094个增加到129 740个,这些蛋白质共计被2 354个不同的功能标签标注,在BP分支的标签数量跟蛋白质个数接近,从如此大的标签空间中准确预测蛋白质的功能很具有挑战性.值得指出的是,在2 354个标签中,76.4%的标签标注的蛋白质个数小于30,56.7%的标签标注的蛋白质个数小于10.
本文共选取了5个相关且具有代表性的蛋白质功能预测方法作为对比方法进行实验.这5个方法为DNN [50] ,SimNet [16] ,SW [27] ,DFMF [17] 和Mashup [18] .其中SimNet和SW均为基于多网络数据加权集成的蛋白质功能预测方法,DFMF和Mashup是矩阵分解和多网络数据等权重融合的方法.这些对比方法已经在第1节的相关工作中详细介绍,不再赘述.近期已有深度学习方法应用于蛋白质功能预测,为此本文还引入深度神经网络(DNN)作为对比算法 [50] .DNN以这些网络等权重整合的复合网络作为特征输入,它的学习率为0.02,batch大小为512个,dropout比例为0.6,并使用batch正则化技术 [51] .为更直观地研究ProCMF加权整合多个网络的效用,本文还引入ProCMF的一个变种(ProCMF-E)作为对比方法进行实验.ProCMF-E在等权重设置 α 后不再更新 α ,即ProCMF-E等权重的整合多个网络后再进行基于矩阵协同分解的蛋白质功能预测.上述对比方法的参数均参照原文作者建议的参数范围进行设置,或者优化后选取最优的参数进行实验.ProCMF中 U 和 V 的低秩系数 r =200,低秩矩阵约束项系数 ω 1 , ω 2 ∈[0.01,100]通过在训练数据集上进行5重交叉验证选择最优值, α 上的 l 2 范式约束的参数 λ =100.
为综合评价蛋白质功能预测算法的性能,本文采取CAFA(community critical assessment of protein function annotation) [1] 算法推荐的评价度量: AUC , S min 和 F max . AUC 是一种以标签为中心的评价度量,它首先计算每个标签的受试者操作特征曲线(receiver operating curve)下的面积,然后以这些标签各自曲线下面积的均值评价预测效果. F max 和 S min 是以蛋白质为中心的评价准则. F max 首先计算不同阈值下的准确率(precision)和查全率(recall)并计算该阈值对应的 F 1值,最后选择最大 F 1值作为 F max 的值; S min 结合基因本体结构首先计算不同阈值下的未被预测到的功能标签和过度预测的错误标签之间的语义距离,最后选择最小的距离值作为 S min 的值.从上述3个评价度量的定义可知当 AUC 和 F max 值越大时预测精度越高,而 S min 值越小时预测精度越高.这些度量的具体介绍可以参见文献[1].这些度量从不同的角度衡量蛋白质功能预测性能,一个蛋白质功能预测方法通常很难在这3个度量上均超过另外一个方法.
本文利用2014年5月的酵母菌、人类和小鼠3个物种的蛋白质功能标注和收集的各物种的多个蛋白质功能关联网络进行蛋白质功能预测,并用2017年5月更新的蛋白质功能标注数据对预测结果进行评价,对应实验结果汇报在表2~4中,表2~4中每种度量下最好的结果用粗体突出表示.
Table 2 Results on Yeast
表2 Yeast数据集上蛋白质功能预测结果
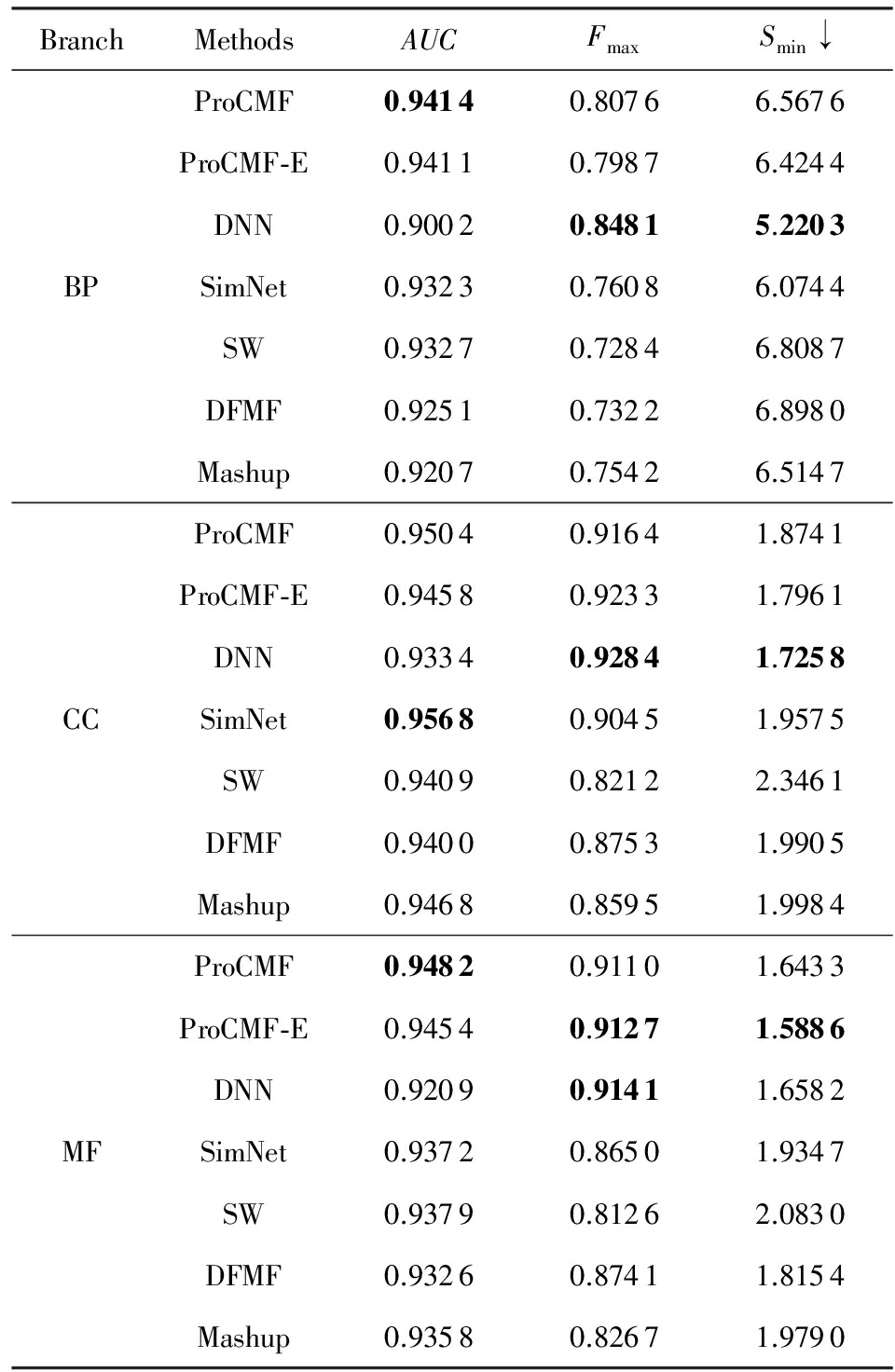
↓ means the lower the better.
从表2~4中可以看出ProCMF在整体上要优于其他对比算法以及自身变种.在3个物种的3个分支的3种度量(共3×3×3=27种)对比实验中,ProCMF分别在18,16,23,24,22,20种情况下优于
Table 3 Results on Human
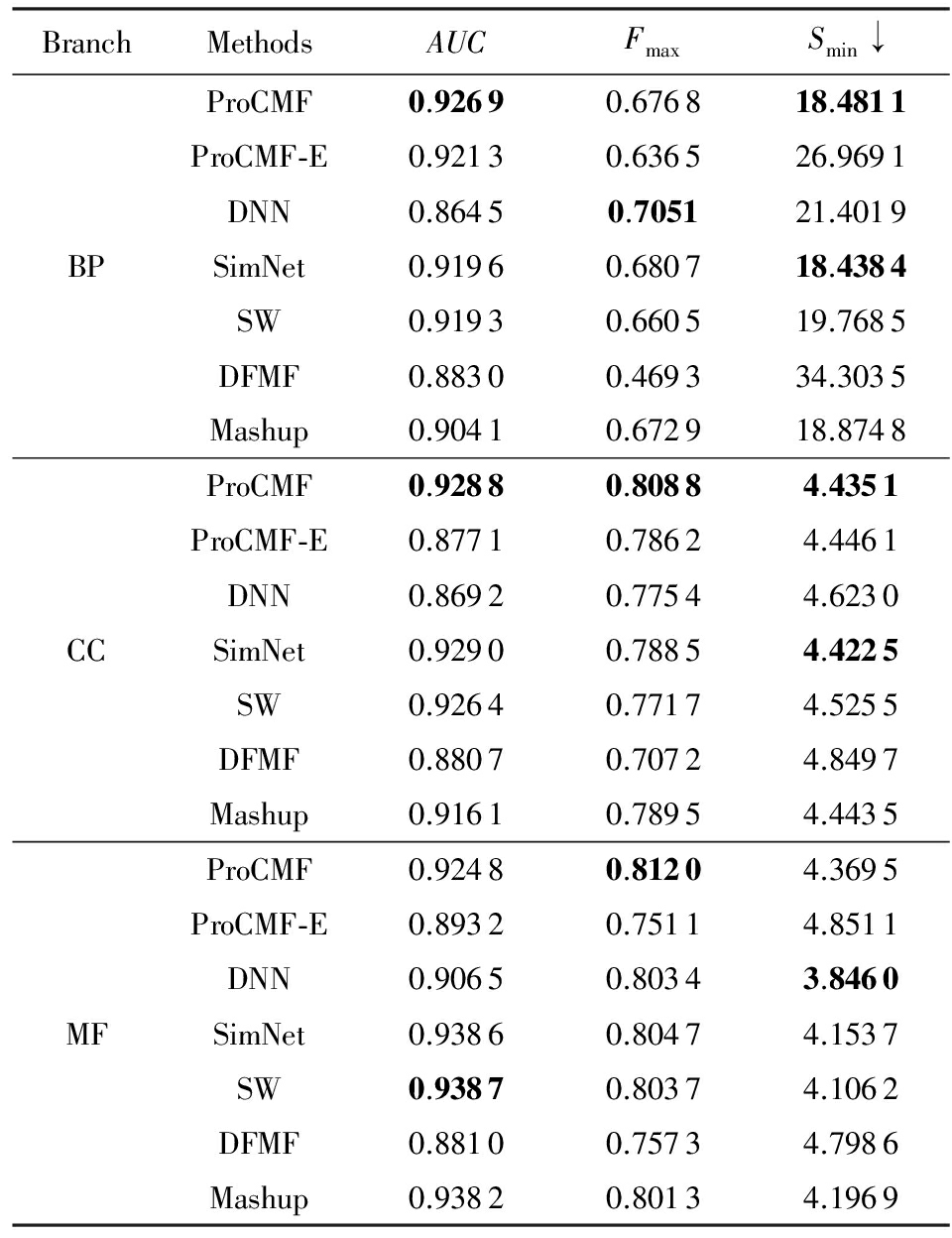
表3 Human数据集蛋白质功能预测结果
↓ means the lower the better.
Table 4 Results on Mouse
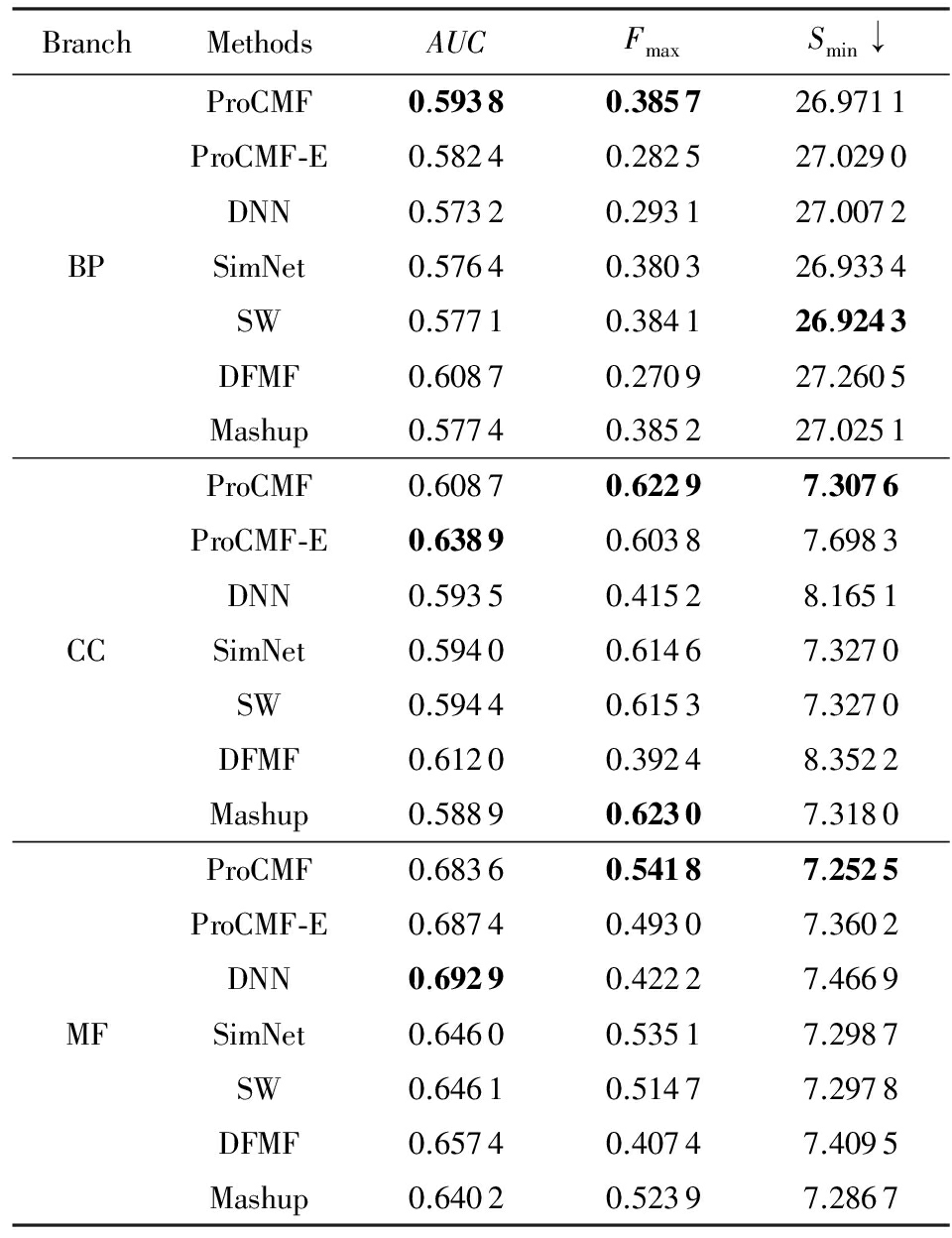
表4 Mouse数据集蛋白质功能预测结果
↓ means the lower the better.
DNN,SimNet,SW,DFMF,Mashup和ProCMF-E.由于表2~4中结果是基于历史的蛋白质功能标注数据预测并用现在的功能标注数据检验,所以结果中不存在方差,为此本文利用Wilcoxon符号秩检验 [52-53] 分析对比ProCMF与DNN,SimNet,SW,DFMF,Mashup和ProCMF-E在不同数据集和度量下的结果,对应 p 值分别为4.61%,3.24%,0.08%,0.005%,0.008和3.45%.从上述对比结果可知,ProCMF显著性优于已有基于多网络集成、矩阵分解和深度学习技术的蛋白质功能预测算法.
ProCMF的预测精度在人类和老鼠2个数据集上要优于DNN,而在酵母菌数据集中除AUC外要差于DNN.而从表1中的数据可知,在人类和老鼠2个数据集中2时间段标记数量相差较大,酵母菌数据集两时间段标记数量相差较少.因此可以发现DNN在预测大量缺失标记时的预测精度较低.
ProCMF的预测性能优于SimNet,原因是SimNet利用蛋白质已有的功能标注定义蛋白质之间的语义相似度和语义目标网络,对于功能信息完全未知的蛋白质,SimNet简单地设置它与其他蛋白质之间的语义相似度为0.SimNet通过多个网络加权整合的复合网络向该语义网络对齐进而优化各个网络上的权重.但由于蛋白质功能标注不完整,蛋白质之间的语义相似度可靠性不高,误导了SimNet各个网络上权重的优化.SW也是通过利用蛋白质的功能标注定义目标网络,再利用多网络加权整合的复合网络向该目标网络对其的方式求取网络权重,但SW的目标网络中含有权重为负的边,且SW并没有较好地考虑蛋白质功能标注信息的不完整性,所以其性能通常不及SimNet和ProCMF.本文提出的ProCMF在整合多个蛋白质功能关联网络时不依赖于目标网络的构造,而是基于2个低秩矩阵,多个网络上定义的平滑损失和标签间关联平滑损失设置网络权重,避免了SimNet和SW过度依赖目标网络的风险,所以ProCMF比SimNet和SW获得了更好的预测结果.DFMF和Mashup都是利用矩阵分解融合多源异构生物数据进行蛋白质功能预测的方法.Mashup分别在多个蛋白质功能关联网络上进行随机游走后,再将多个网络等权重相加整合,它未考虑不同网络对蛋白质功能预测的效用不同的特点,容易受噪声网络的干扰.DFMF在蛋白质与功能标签节点组成的混合网络上进行协同低秩矩阵分解挖掘蛋白质与功能标签间的潜在关联,实现蛋白质功能预测.DFMF和Mashup一样为每个网络分配相同的权重,它们均易受低质量网络的干扰.虽然ProCMF也通过低秩矩阵分解和整合多个功能关联网络进行蛋白质功能预测,但是它对不同的网络设置不同的权重,区分性地整合这些网络,所以ProCMF获得了较DFMF和Mashup更好的预测结果.从ProCMF与DNN结果间的差异可知,差异性集成不同的功能关联网络可以获得较深度学习方法更好的精度.
虽然ProCMF-E与ProCMF类似,也能够发掘利用蛋白质-功能标签关联矩阵中蛋白质与标签间的潜在关联和处理大量相关标签,但是ProCMF-E的结果通常低于ProCMF.原因是ProCMF-E与DFMF和Mashup类似,对不同的网络设置相同的权重,均忽视了不同的网络对蛋白质功能预测效用不同.
为进一步分析利用多个蛋白质功能关联网络和标签间关联性的贡献,本文引入ProCMF的3个变种(ProCMF-N,ProCMF-C和ProCMF-Y)作为对比方法进行实验.ProCMF-N只利用多个蛋白质功能关联网络( ω 1 >0, ω 2 =0);ProCMF-C只利用功能标签间的关联性( ω 1 =0, ω 2 >0);ProCMF-Y仅利用蛋白质-功能标签关联矩阵 Y 进行功能预测( ω 1 =0, ω 2 =0).与上面的实验设置类似,本文在Mouse数据集上进行了实验并将ProCMF和其3个变种在评价度量 F max 下的结果报告如图1所示:

Fig. 1 F max of ProCMF and its variants on Mouse dataset
图1 ProCMF及其变种在Mouse数据集上的F max 对比
从图1可以发现ProCMF总是获得最高的 F max ,而ProCMF-Y总是获得最低的 F max ;ProCMF-N和ProCMF-C的 F max 通常大于ProCMF-Y.这一观察表明蛋白质功能关联网络和标签间的关联性均可以提高蛋白质功能预测性能.ProCMF-C在BP分支获得了与ProCMF-Y类似的 F max ,原因是蛋白质-功能标签关联矩阵 Y 基于基因本体结构初始化,它已经嵌入了部分标签间关联关系, Y 上的低稚矩阵分解可以隐式地挖掘和利用标签间关联性.ProCMF-C在CC分支和MF分支的 F max 高于ProCMF-Y表明显示地结合标签间关联性可提高蛋白质功能预测结果.ProCMF的 F max 总是大于ProCMF-C和ProCMF-N的 F max ,表明同时利用蛋白质功能关联网络和标签间关联性可以进一步提高蛋白质功能预测性能.
ProCMF将蛋白质-功能标签关联矩阵分解为2个低秩矩阵 U 和 V ,为分析不同的低秩大小 r 对预测结果的影响,本文对 r 进行了敏感性分析并将10至300下 r 的 F max 结果值汇报在图2(Yeast)和图3(Mouse)中.ProCMF中其他参数的设置与3.3节的实验设置一致.
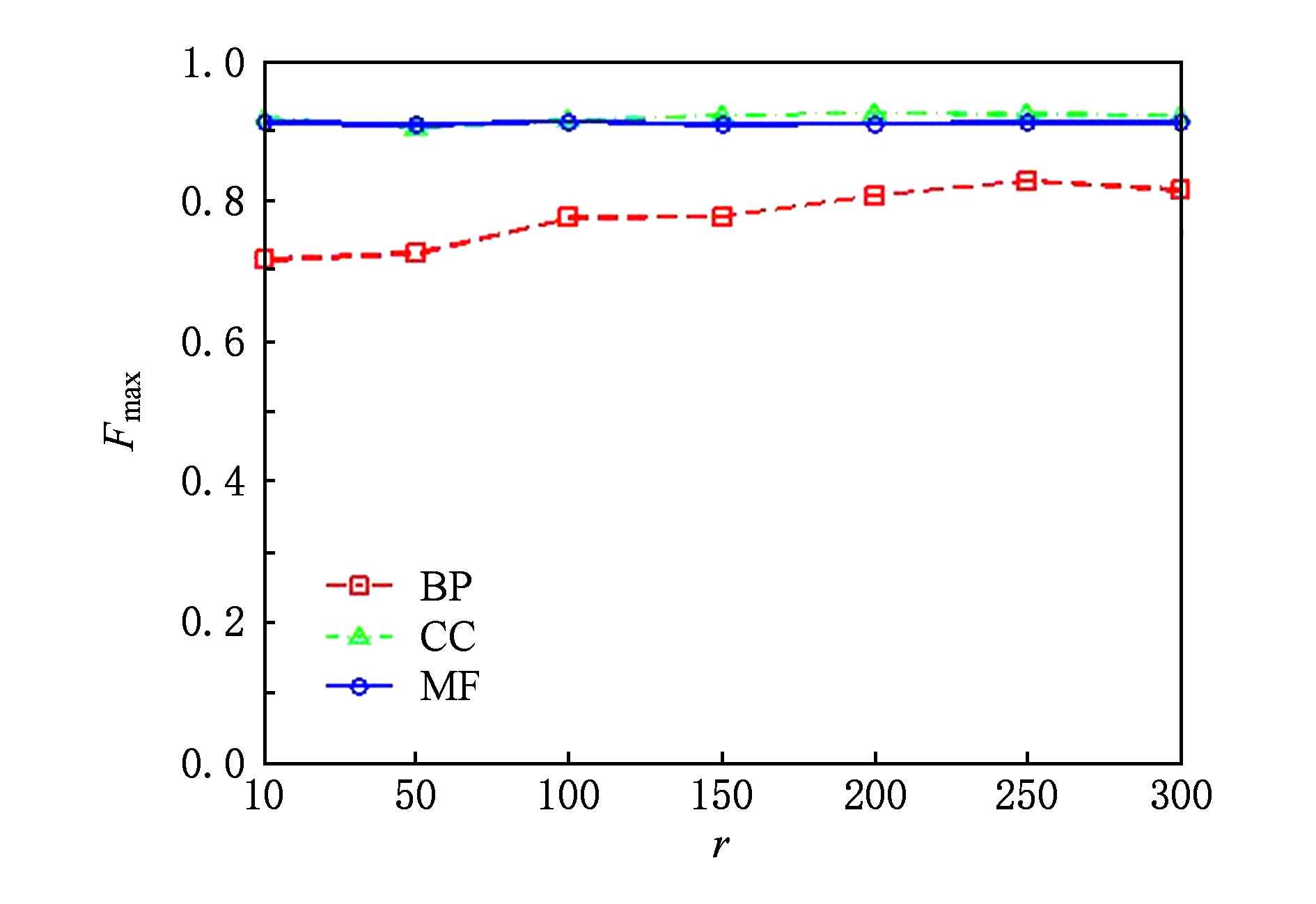
Fig. 2 Low rank parameter r analysis on Yeast
图2 酵母菌数据集上低秩参数r分析
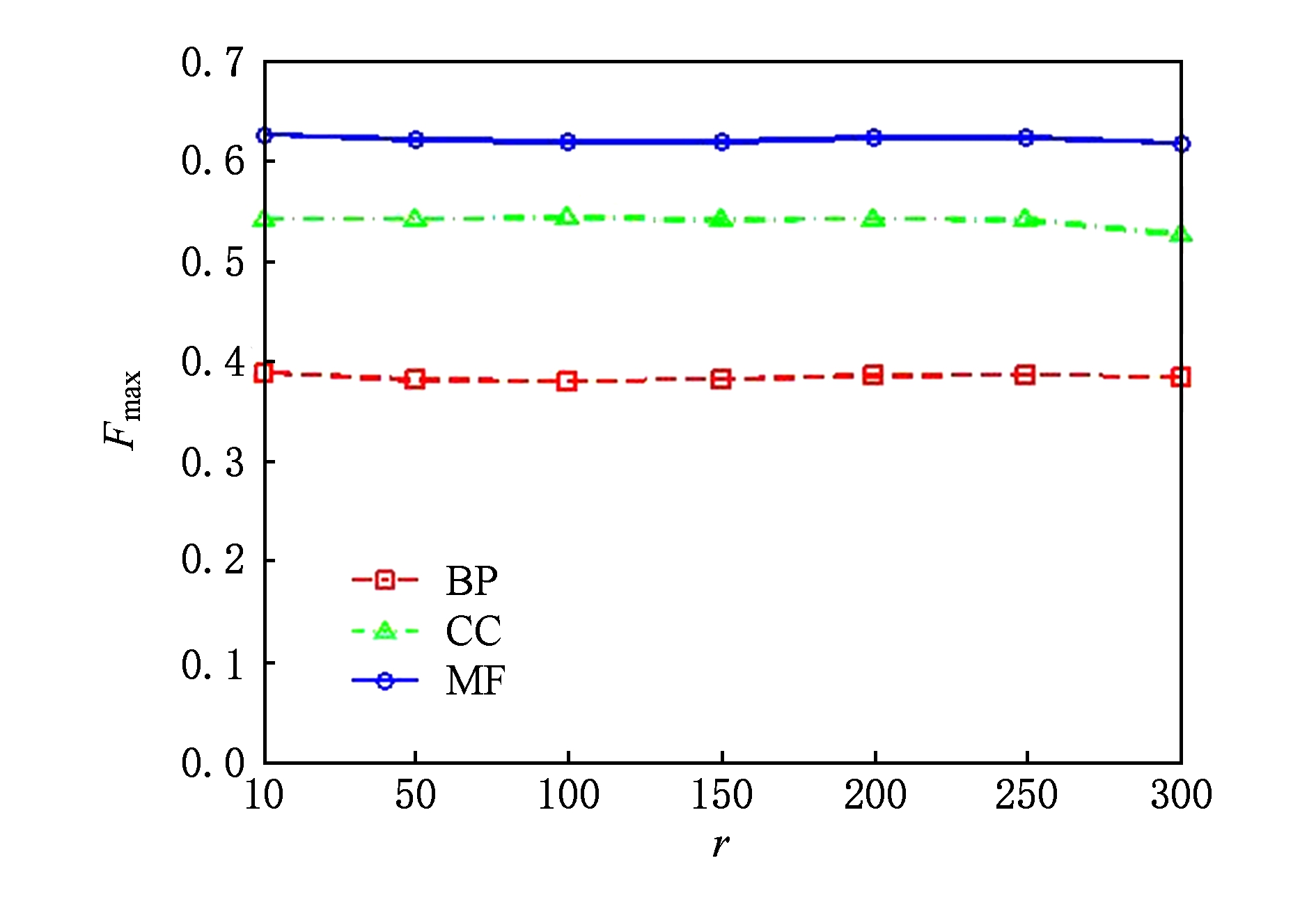
Fig. 3 Low rank parameter r analysis on Mouse
图3 老鼠数据集上低秩参数r分析
根据图2~3中曲线的趋势可以发现, r 的变化对预测的结果并没有明显的影响,这说明ProCMF对 r 是鲁棒的.ProCMF在 r 较小时就可以达到一个良好的预测效果,说明低秩矩阵 U 和 V 在很低的维度就能挖掘大量蛋白质与大量功能标签间的潜在关联. F max 在Yeast数据集的BP分支随 r 的升高有部分提升后稳定,这是因为BP分支中含有2 354个标签,而这些标签仅与3 904个蛋白质存在稀疏的关联,数据规模较小进而无法在较小的 r 下准确地挖掘蛋白质与功能标签间的关联.需指出,即使 r =10, V 也可以编码2 10 个不同的0-1标签,而 V 实际上是非负实数矩阵,因此它可以编码更多的标签.通过在蛋白质-功能标签关联矩阵上进行低秩矩阵分解可以将大量的关联标签压缩到低维空间,而显式地结合功能标签间的关联并约束低秩矩阵的分解,有助于更进一步地挖掘蛋白质与功能标签间的潜在关联.
此外,为了分析 λ 的取值对权重系数 α 的影响,本文登记了 λ 分别为1,100和10 000时 α 在人类数据集的CC分支的权重分布情况,并汇报在图4中.从图4可以看出在 λ =100时,ProCMF在8个功能关联网络上的权重不同,部分网络的权重为0,说明ProCMF能够区分性地整合多个网络.当 λ =1时,ProCMF仅选取最平滑的功能关联网络;当 λ =10 4 时,ProCMF赋予8个网络类似的权重.上述实验结果与第3节的理论分析一致,当 λ 取值过小时, α 上的 l 2 范式约束调控作用过小,ProCMF只需选择平滑性损失最小的网络即可使式(8)中的目标函数值最小;而当 λ 取值过大时, l 2 范式约束调控作用过强,为使式(8)中的目标函数值最小,ProCMF给予多个功能关联网络类似的权重.上述实验表明ProCMF的性能依赖于合适的 λ .本文实验中在训练数据上进行五重交叉验证选取合适的 λ .如何更规范化地选取合适的 λ 是本文未来研究工作之一.
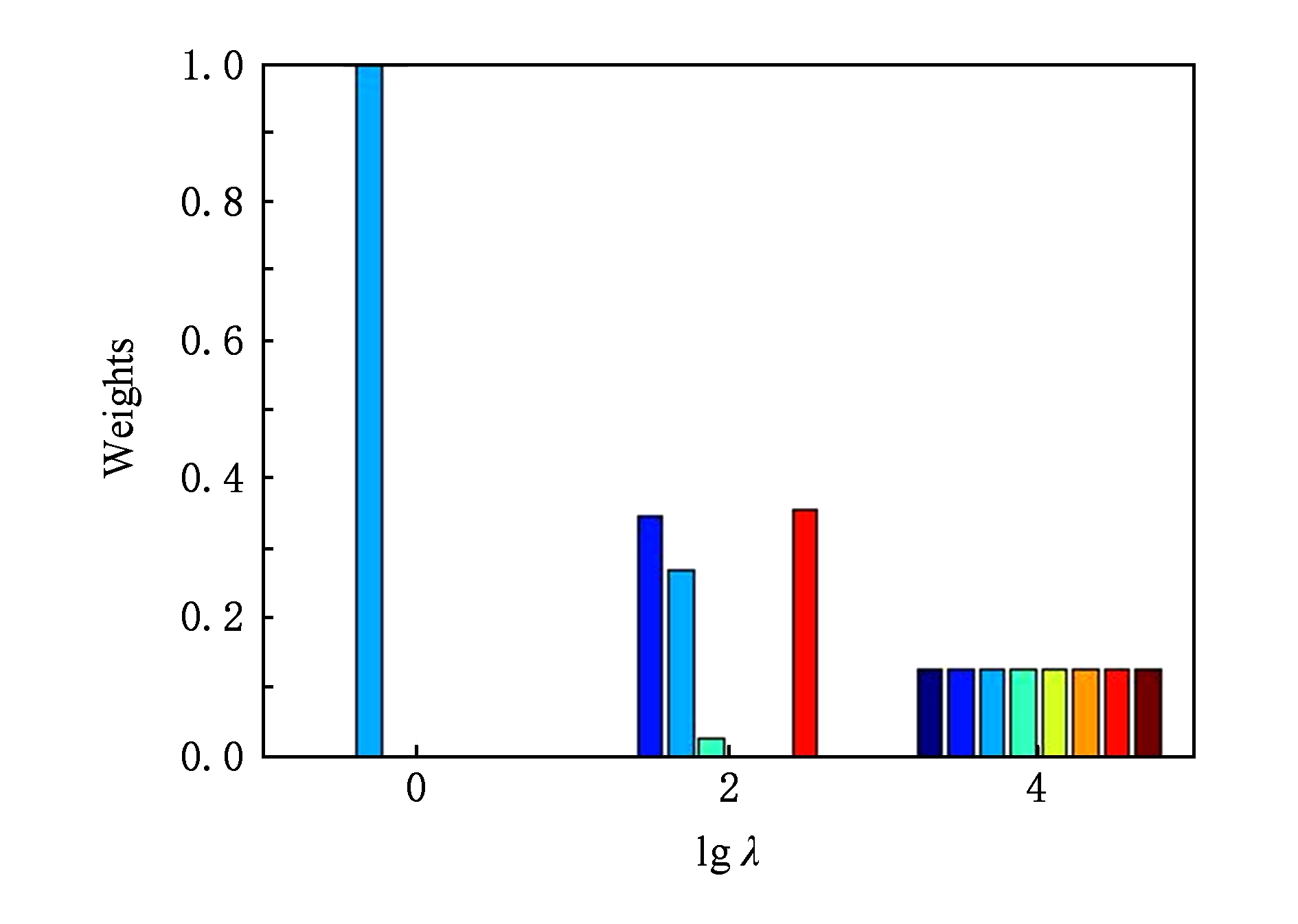
Fig. 4 Weight assignments under different input values of λ (Human, CC)
图4 不同λ值下的权重分配(人类数据集CC分支)
为了分析对比各个算法的效率,本文还登记了ProCMF及其他对算法的实际运行时间,如表5所示.实验过程中各算法参数设置与之前保持一致,各算法均基于Matlab2011b(64位)编码实现,实验运行平台配置为:Intel Xeon E5-3650v3,Linux OS 2.6.32,32 GB RAM.
Table 5 F max of ProCMF and Its Variants on Mouse Dataset
表5 ProCMF及其变种在Mouse数据集上的 F max s

从表5中的运行时间结果可以看出SimNet的运行时间耗费最小,ProCMF次之.SimNet比ProCMF更快的原因是SimNet直接通过线性回归求取多个功能关联网络上的权重,并不需要进行迭代优化,而ProCMF则需要迭代优化权重和低秩矩阵.SW在整合多个网络和预测蛋白质功能时的理论复杂度与SimNet相似,但其实际运行时间比SimNet要大很多.这是因为SW利用二分类器对每一个功能标签进行预测,并且它在定义目标网络时需要启发式地选择负样例.DFMF需要对每个网络的邻接矩阵进行低秩分解,所以其时间耗费大于ProCMF.Mashup首先在每个网络上进行随机游走,再在这些网络整合的复合网络的邻接矩阵上应用SVD,最后利用支持向量机针对每个标签进行功能预测,所以其运行时间耗费最大.
在上述实验结果的基础上,本文认为ProCMF不仅比现有基于多网络数据整合的蛋白质功能预测方法的预测结果更好,还能保持较高的效率.
本文根据合理的整合多个蛋白质功能关联网络数据和结合功能标签间关联性能提高蛋白质功能预测精度的原理,提出了一种基于多网络数据协同矩阵分解的蛋白质功能预测方法.该方法利用低秩矩阵分解挖掘蛋白质与功能标签间潜在关联信息,整合多网络数据来更完整地刻画蛋白质功能信息和融合标签间关联关系约束指导低秩矩阵的分解,获得了较其他相关算法更好的预测结果.本文研究工作为后续基于多网络数据融合的数据挖掘问题研究提供了新的思路.
通过与其他方法的对比实验和分析,验证了本文方法的有效性和合理性.如何准确地刻画标签间关联性和结合多种异构生物数据预测蛋白质功能是一个值得深入研究的问题.此外,多网络数据融合中如何有效地保持和利用每个网络的内在结构特性都有待进一步研究.
参考文献
[1]Radivojac P, Cark W, Oron T, et al. A large-scale evaluation of computational protein function prediction[J]. Nature Methods, 2013, 10(3): 221-227
[2] Shehu A, Barbará D, Molloy K. A survey of computational methods for protein function prediction[G] //Big Data Analytics in Genomics. Berlin: Springer, 2016, 225-298
[3] Gene Ontology Consortium. Expansion of the gene ontology knowledgebase and resources[J]. Nucleic Acids Research, 2017, 45(D1): D331-D338
[4] Huntley R, Sawford T, Martin M, et al. Understanding how and why the Gene Ontology and its annotations evolve: The GO within UniProt[J]. GigaScience, 2014, 3: Article No 4
[5] Schones A, Ream D, Thorman A, et al. Bias in the experimental annotations of protein function and their effect on our understanding of protein function space[J]. PLoS Computational Biology, 2013, 9(5): Article No e1003063
[6] Legrain P, Aebersold R, Archakov A, et al. The human proteome project: Current state and future direction[J]. Molecular & Cellular Proteomics, 2011, 10(7): Article No M111.009993
[7] Lee D, Redfern O, Orengo C. Predicting protein function from sequence and structure[J]. Nature Review Molecular Cell Biology, 2007, 8(12): 995-1005
[8] Lowenstein Y, Raimondo D, Redfern O, et al. Protein function annotation by homology-based inference[J]. Genome Biology, 2009, 10(2): Article No 207
[9] Schwikowski B, Uetz P, Field S. A network of protein-protein interactions in yeast[J]. Nature Biotechnology, 2000, 18(12): 1257-1261
[10] Deng M, Tu Z, Sun F, et al. Mapping Gene Ontology to proteins based on protein-protein interaction data[J]. Bioinformatics, 2004, 20(6): 895-902
[11] Li Min, Meng Xiangmao. The construction, analysis, and applications of dynamic protein-protein interaction networks[J]. Journal of Computer Research and Development, 2017, 54(6): 1281-1299(李敏, 孟祥茂. 动态蛋白质网络的构建、分析及应用研究进展[J]. 计算机研究与发展, 2017, 54(6): 1281-1299)
[12] Pavlidis P, Weston J, Cai J, et al. Learning gene functional classifications from multiple data types[J]. Journal of Computational Biology, 2002, 9(2): 401-411
[13] Lanckriet G R, De B T, Cristianini N, et al. A statistical framework for genomic data fusion[J]. Bioinformatics, 2004, 20(16): 2626-2635
[14] Yu Guoxian, Domeniconi C, Rangwala H, et al. Transductive multi-label ensemble classification for protein function prediction[C] //Proc of the 18th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2012: 1077-1085
[15] Sokolov A, Funk C, Graim K, et al. Combining hetero-geneous data sources for accurate functional annotation of proteins[J]. BMC Bioinformatics, 2013, 14(S3): S10
[16] Yu Guoxian, Fu Guangyuan, Wang Jun, et al. Predicting protein function via semantic integration of multiple networks[J]. IEEE/ACM Trans on Computational Biology & Bioinformatics, 2016, 13(2): 220-232
[17] Zitnik M, Zupan B. Data fusion by matrix factorization[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2013, 37(1): 41-53
[18] Cho H, Berger B, Peng J. Compact integration of multi-network topology for functional analysis of genes[J]. Cell Systems, 2016, 3(6): 540-548
[19] Yu Guoxian, Rangwala H, Domeniconi C, et al. Predicting protein function using multiple kernels[J]. IEEE/ACM Trans on Computational Biology and Bioinformatics, 2015, 12(1): 219-233
[20] Yu Guoxian, Zhu Hailong, Domeniconi C, et al. Integrating multiple networks for protein function prediction[J]. BMC Systems Biology, 2015, 9(S1): Article No S3
[21] Gönen M, Ethem A. Multiple kernel learning algorithms[J]. Journal of Machine Learning Research, 2011, 12(7): 2211-2268
[22] Tsuda K, Shin H J, Schölkopf B. Fast protein classification with multiple networks[J]. Bioinformatics, 2005, 21(S2): ii59-ii65
[23] Mostafavi S, Ray D, Warde-Farley D, et al. GeneMANIA: A real-time multiple association network integration algorithm for predicting gene function[J]. Genome Biology, 2008, 9(S1): Article No S4
[24] Pe  a-Castillo L, Tasan M, Myers C L, et al. A critical assessment of Mus musculus gene function prediction using integrated genomic evidence[J]. Genome Biology, 2008, 9(S1): Article No S2
a-Castillo L, Tasan M, Myers C L, et al. A critical assessment of Mus musculus gene function prediction using integrated genomic evidence[J]. Genome Biology, 2008, 9(S1): Article No S2
[25] Myers C L, Troyanskaya O G. Context-sensitive data integration and prediction of biological networks[J]. Bioinformatics, 2007, 23(17): 2322-2330
[26] Cesa-Bianchi N, Re M, Valentini G. Synergy of multi-label hierarchical ensembles, data fusion, and cost-sensitive methods for gene functional inference[J]. Machine Learning, 2012, 88(1-2): 209-241
[27] Mostafavi S, Morris Q. Fast integration of heterogeneous data sources for predicting gene function with limited annotation[J]. Bioinformatics, 2010, 26(14): 1759-1765
[28] Mazandu G K, Chimusa E R, Mulder N J. Gene Ontology semantic similarity tools: Survey on features and challenges for biological knowledge discovery[J]. Briefings in Bioinformatics, 2017, 18(5): 886-901
[29] Mistry M, Pavlidis P. Gene Ontology term overlap as a measure of gene functional similarity[J]. BMC Bioinformatics, 2008, 9: Article No 327
[30] Cho H, Berger B, Peng J. Diffusion component analysis: Unraveling functional topology in biological networks [C] //Proc of the 19th Annual Int Conf on Research in Computational Molecular Biology. Berlin: Springer, 2015: 62-64
[31] Gao Yukai, Wang Xinhua, Guo Lei, et al. Learning to recommend with collaborative matrix factorization for new users[J]. Journal of Computer Research and Development, 2017, 54(8): 1813-1823 (in Chinese)(高玉凯, 王新华, 郭磊, 等. 一种基于协同矩阵分解的用户冷启动推荐算法[J]. 计算机研究与发展, 2017, 54(8): 1813-1823)
[32] Shen Guowei, Yang Wu, Wang Wei, et al. Large-scale heterogeneous data co-clustering based on nonnegative matrix factorization[J]. Journal of Computer Research and Development, 2016, 53(2): 459-466 (in Chinese)(申国伟, 杨武, 王巍, 等. 基于非负矩阵分解的大规模异构数据联合聚类[J]. 计算机研究与发展, 2016, 53(2): 459-466)
[33] Lee D D, Seung H S. Algorithms for non-negative matrix factorization[C] //Proc of the 13th Annual Conf on Neural Information Processing Systems. Cambridge, MA: MIT Press, 2000: 535-541
[34] King O D, Foulger R E, Dwight S S, et al. Predicting gene function from patterns of annotation[J]. Genome Research, 2003, 13: 896-904
[35] Yu Guoxian, Zhu Hailong, Domeniconi C. Predicting protein function using incomplete hierarchical labels[J]. BMC Bioinformatics, 2015, 16: Article No 1
[36] Yu Guoxian, Zhu Hailong, Domeniconi C, et al. Predicting protein function via downward random walks on a gene ontology[J]. BMC Bioinformatics, 2015, 16: Article No 271
[37] Done B, Khatri P, Done A, et al. Predicting novel Human gene ontology annotations using semantic analysis[J]. IEEE/ACM Trans on Computational Biology & Bioinformatics, 2010, 7(1): 91-99
[38] Wang Sheng, Cho H, Zhai Chengxiang, et al. Exploiting ontology graph for predicting sparsely annotated gene function[J]. Bioinformatics, 2015, 31(12): i357-i364
[39] Yu Guangxian, Fu Guangyuan, Wang Jun, et al. Predicting irrelevant functions of proteins based on dimensionality reduction[J]. Science Sinica Informationis, 2017, 47(10): 1349-1368 (in Chinese) (余国先, 傅广垣, 王峻, 等. 基于降维的蛋白质不相关功能预测[J]. 中国科学: 信息科学, 2017, 47(10): 1349-1368)
[40] Wang Yuxiong, Zhang Yujin. Nonnegative matrix factorization: A comprehensive review[J]. IEEE Trans on Knowledge and Data Engineering, 2013, 25(6): 1336-1353
[41] Khatri P, Done B, Rao A, et al. A semantic analysis of the annotations of the human genome[J]. Bioinformatics, 2005, 21(16): 3416-3421
[42] Yu Guoxian, Rangwala H, Domeniconi C, et al. Protein function prediction with incomplete annotations[J]. IEEE/ACM Trans on Computational Biology & Bioinformatics, 2014, 11(3): 579-591
[43] Zhang Xiaofei, Dai Daoqing. A framework for incorporating functional interrelationships into protein function prediction algorithms[J]. IEEE/ACM Trans on Computational Biology & Bioinformatics, 2012, 9(3): 740-753
[44] Lu Chang, Wang Jun, Zhang Zili, et al. NoisyGOA: Noisy go annotations prediction using taxonomic and semantic similarity[J]. Computational Biology and Chemistry, 2016, 65: 203-211
[45] Fu Guangyuan, Yu Guoxian, Wang Jun, et al. Protein function prediction using positive and negative examples[J]. Journal of Computer Research and Development, 2016, 53(8): 1753-1765 (in Chinese)(傅广垣, 余国先, 王峻, 等. 基于正负样例的蛋白质功能预测[J]. 计算机研究与发展, 2016, 53(8): 1753-1765)
[46] Mikhail B, Niyogi P, Sindhwani V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples[J]. Journal of Machine Learning Research, 2006, 7(11): 2399-2434
[47] Dempster A P, Laird N M, Rubin D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society, Series B (methodological), 1977, 39(1): 1-38
[48] Boyd S, Vandenberghe L. Convex Optimization[M]. Cambridge, UK: Cambridge University Press, 2004
[49] Valentini, G. True path rule hierarchical ensembles for genome-wide gene function prediction[J]. IEEE/ACM Trans on Computational Biology and Bioinformatics, 2011, 8(3): 832-847
[50] Angermueller C, Pärnamaa T, Parts L, et al. Deep learning for computational biology[J]. Molecular Systems Biology, 2016, 12(7): Article No 878
[51] Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C] //Proc of the 32nd Int Conf on Machine Learning. Cambridge, MA: MIT Press, 2015: 448-456
[52] Wilcoxon F. Individual comparisons by ranking methods[J]. Biometric Bulletin, 1945, 1(6): 80-83
[53] Demsar J. Statistical comparisons of classifiers over multiple data sets[J]. Journal of Machine Learning Research, 2006, 7(1): 1-30
Yu Guoxian 1 , Wang Keyao 1 , Fu Guangyuan 1 , Wang Jun 1 , and Zeng An 2
1 ( College of Computer and Information Science , Southwest University , Chongqing 400715) 2 ( School of Computers , Guangdong University of Technology , Guangzhou 510006)
Abstract Accurately and automatically predicting biological functions of proteins is one of the fundamental tasks in bioinformatics, and it is also one of the key applications of artificial intelligence in biological data analysis. The wide application of high throughput technologies produces various functional association networks of molecules. Integrating these networks contributes to more comprehensive view for understanding the functional mechanism of proteins and to improve the performance of protein function prediction. However, existing network integration based solutions cannot apply to a large number of functional labels, ignore the correlation between labels, or cannot differentially integrate multiple networks. This paper proposes a protein function prediction approach based on multiple networks collaborative matrix factorization (ProCMF). To explore the latent relationship between proteins and between labels, ProCMF firstly applies nonnegative matrix factorization to factorize the protein-label association matrix into two low-rank matrices. To employ the correlation between labels and to guide the collaborative factorization with proteomic data, it defines two smoothness terms on these two low-rank matrices. To differentially integrate these networks, ProCMF sets different weights to them. In the end, ProCMF combines these goals into a unified objective function and introduces an alternative optimization technique to jointly optimize the low-rank matrices and weights. Experimental results on three model species (yeast, human and mouse) with multiple functional networks show that ProCMF outperforms other related competitive methods. ProCMF can effectively and efficiently handle massive labels and differentially integrate multiple networks.
Key words protein function prediction; functional association network; network integration; nonnegative matrix factorization; collaborative factorization
收稿日期: 2017-09-01;
修回日期: 2017-10-03
基金项目: 国家自然科学基金项目(61402378,61772143);重庆市自然科学基金项目(cstc2016jcyjA0351)
This work was supported by the National Natural Science Foundation of China (61402378, 61772143) and the Natural Science Foundation of Chongqing (cstc2016jcyjA0351)
通信作者: 王峻(kingjun@swu.edu.cn)
中图法分类号 TP391

Yu Guoxian , born in 1985. Associate professor. Member of CCF. His main research interests include machine learning, data mining and bioinformatics.

Wang Keyao , born in 1994. Master candidate. Student member of CCF. His main research interests include machine learning and bioinformatics (keyaowang@email.swu.edu.cn).

Fu Guangyuan , born in 1993. Master. Student member of CCF. His main research interests include machine learning and bioinformatics (fugy@email.swu.edu.cn).

Wang Jun , born in 1983. Associate professor. Member of CCF. Her main research interests include data mining and bioinformatics.

Zeng An , born in 1978. Professor. Member of CCF. Her main research interests include artificial intelligence, machinelearning and big data (zengan2010@126.com).