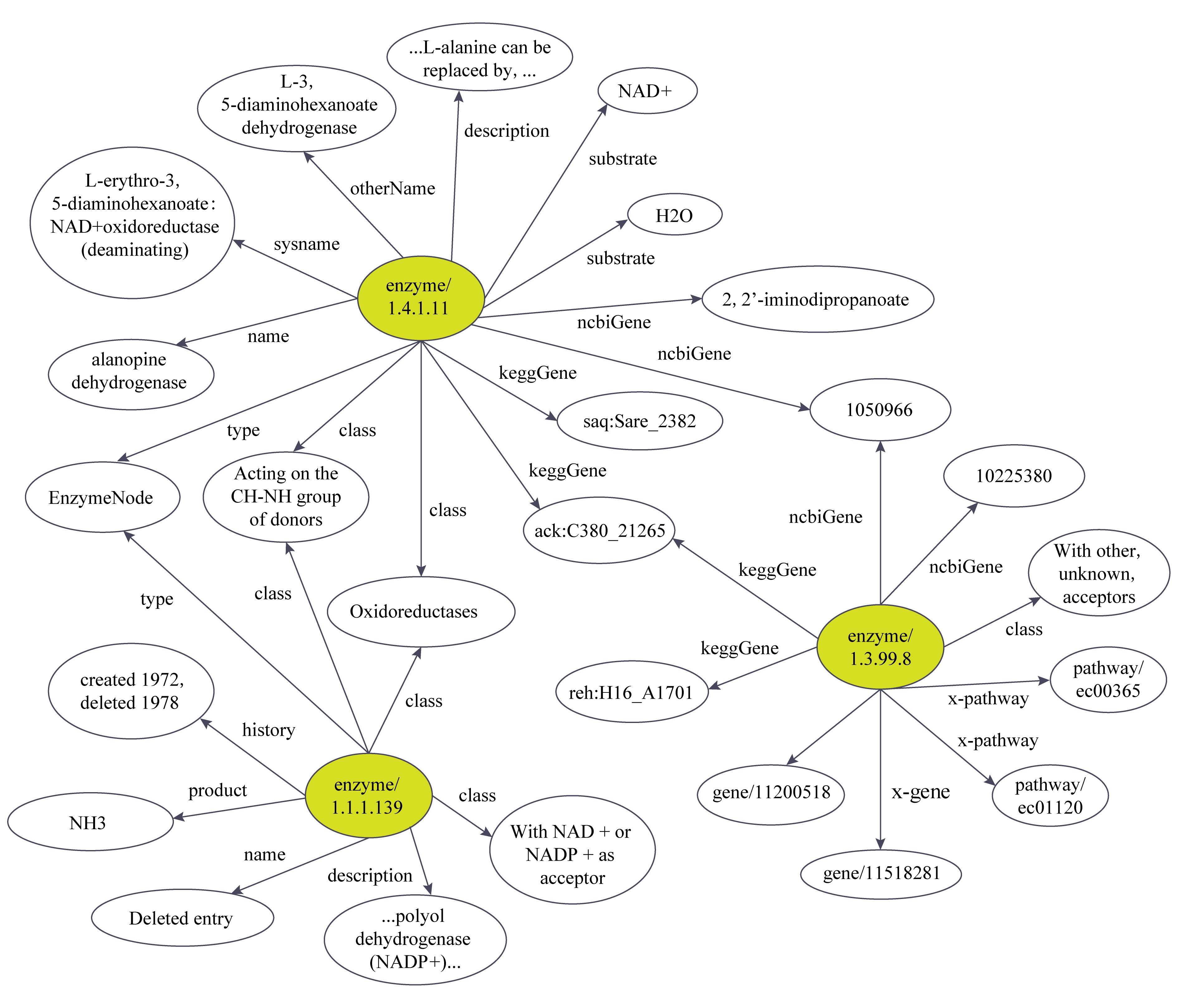
Fig. 1 The subgraph enzyme KG
图1 EKG的子图
杜治娟 张 祎 孟小峰 王秋月
(中国人民大学信息学院 北京 100872)
(2014000654@ruc.edu.cn)
摘 要 近年来,构建大规模知识图谱(knowledge graph, KG),并用其解决实际问题已经成为大趋势.KG的嵌入表示方便了机器学习在KG等关系数据上的应用,它可以促进知识分析、推理、融合、补全,甚至决策.最近,开放域知识图谱(open-domain knowledge graph, OKG)的构建和嵌入表示已经得到蓬勃发展,大大促进了开放域中大数据的智能化.与此同时,特定域知识图谱(specific-domain knowledge graph, SKG)也成为了特定领域中智能应用的重要资源.但是,SKG还不发达,其嵌入表示尚处于萌芽阶段.这主要是由于SKG与OKG的数据分布显著不同,更具体地说:1)在OKG中,如WordNet,Freebase,头/尾实体的稀疏度几乎相等;但是在Enzyme,NCI-PID等SKG中不均匀性更受欢迎,例如微生物领域的酶KG中尾实体是头实体的1 000倍.2)头实体和尾实体可以在OKG中交换位置,但是它们在SKG中是非交换的,因为大多数关系是属性.例如实体“奥巴马”可以是头实体也可以是尾实体,但是头实体“酶”总是处于头位置.3)关系的广度在OKG中具有小的偏差,而SKG中很不平衡.例如一个酶实体甚至可以链接31 809个“x-gene”实体.基于这些观察,提出了一个新方法EAE来处理这3个问题,并在链接预测和元组分类任务上评估了EAE方法.实验结果表明:EAE显著优于Trans(E,H,R,D和TransSparse),达到了最先进的性能.
关键词 特定域知识图谱;酶;嵌入表示;不均匀;非交换;不平衡
近年来,智能应用受益于实体关系构成的结构化知识 [1-2] ,比如大规模开放域知识图谱(open-domain knowledge graphs, OKGs)DBPedia [3] ,Wikidata [4] ,Freebase [5] ,YAGO [6] 和Probase [7] 等被证明是支持自然语言问答、智能搜索 [5,7] 以及知识推理、融合和补全 [8-10] 等的重要资源.构建大规模特定域知识图谱(specific-domain knowledge graph, SKG)并用于解决实际问题也受到更多关注,例如在生物医学中,诸如NCI-PID知识库 [11] 对于了解复杂疾病如癌症以及推进精密医学至关重要,又如Neurocommons [12] ,Bio2RDF [13] ,LinkedLifeData [14] 等集成了生物医学信息,并用于生命科学中的决策支持 [15-16] .虽然这些知识图谱(knowledge graphs, KG)对于解决实际问题非常重要,但是它们远不完全,并且在非静态领域,新事实的产生与日俱增,手动补全KG变得不切实际;此外,随着KG规模的增加,图表示的KG在应用中正面临着数据稀疏和计算效率低下的问题 [2,17] .更重要的是,用图表示的KG不便于机器学习 [2,17] ,而机器学习是大数据自动化和智能化的不可或缺的工具 [14] .因此,像OKG嵌入一样,SKG也需要嵌入表示,即将实体和关系表示成连续低维向量.
OKG的嵌入方法已如雨后春笋,如RESCAL [18] ,TansE [19] , HolE [20] 等.尽管这些方法在OKG上具有强大的建模能力,但由于实体不均匀、非交互和不平衡的原因,在SKG上仍然具有挑战性.
我们以中国科学院微生物研究所的酶KG(enzyme KG, EKG)来说明SKG与OKG的差异.完整的EKG包含13种关系、6 482 370个实体(其中包括6 463个头实体和6 475 907尾实体)、7 017 094个三元组.图1是EKG的子图,灰色椭圆代表头实体,空白椭圆表示尾实体 * EKG中的数据表示形式:实体表示格式如〈http://gcm.wdcm.org/data/gcmAnnotation1/enzyme/5.1.1.12〉或者“Acting on amino acids and derivatives”;关系表示格式如〈http://gcm.wdcm.org/ontology/gcmAnnotaion/v1/class 〉.为了简单起见,我们省略了url前缀“http:// gcm.wdcm.org/ontology/gcmAnnotaion/v1/”和http://gcm.wdcm.org/data/gcmAnnotation1/. .
从EKG中我们得到3个观察结果:
结果1 . 大多数实体不连通,并且头实体都是各种“酶”,如图1中的“enzyme1.4.1.11”等,而尾实体大部分是属性值,所以,头尾实体的位置是不可交换的,头实体总是处于EKG的头位置.这与OKG非常不同,在OKG中实体是可以交换的,如“奥巴马”可以是头实体,也可以是尾实体.我们把这种现象叫做实体分布的非交换性.
结果2 . 图1中有3个头实体,却有25个尾实体,这种现象在EKG中普遍存在,如表1所示,尾实体数是头实体数的1 000倍.并且头尾实体的稀疏度 * 头/尾实体的稀疏度等于头/尾实体数除以三元组总数,稀疏度小,说明出现次数少;反之亦然. 也显著不均衡,例如头数为1 085.73,但尾数为1.08.在OKG中,头尾实体的稀疏度几乎相等,比如WN18的头尾稀疏度之比是1.0,FB15K的头尾稀疏度之比是0.996 8.我们把这种现象叫做实体分布的不均匀性.

Fig. 1 The subgraph enzyme KG
图1 EKG的子图
Table 1 Feature Statistics of the Enzyme KG
表1 EKG的数据特征统计
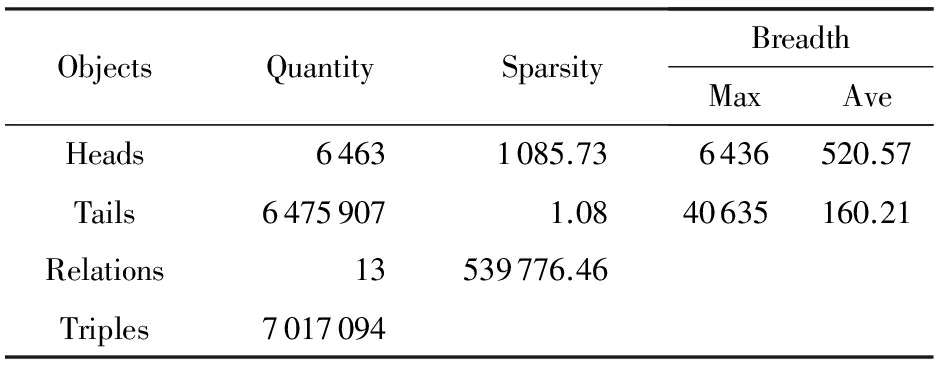
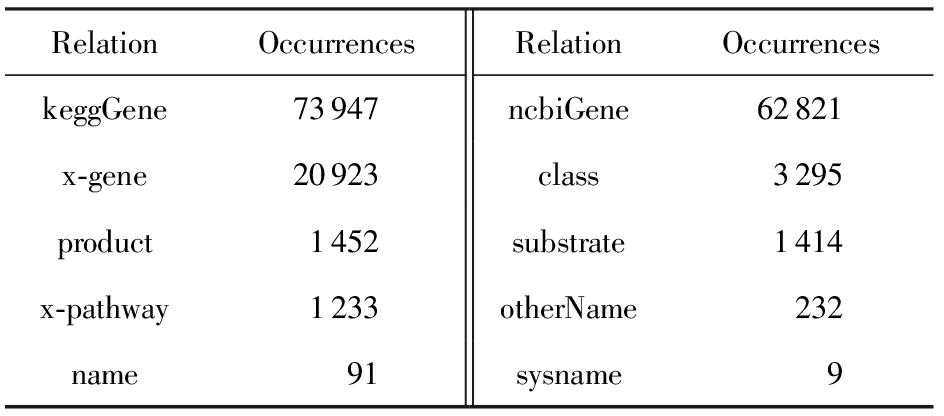
结果3 . 关系的广度 * 关系的广度分为头广度和尾广度,头广度定义为(关系,尾实体)对链接的头实体的数量,尾广度亦然.其中(关系,尾实体)表示关系和尾实体对,即它俩固定,头实体随意. 在EKG中存在严重的不平衡.如表1所示,最大头广度为6 436 ,最大尾广度是40 635,大约6.3倍.据统计,如表1~2所示,不平衡关系在EKG中占有很大的比例,特别是“KeggGene”,“ncbiGene”和“x-gene”关系,如“ncbiGene”实体平均链接821.81尾实体,最多可达39 051个,远远超过OKG.并且这种不平衡性的变化很大,比如“x-pathway”的头尾广度分别是46.08和2.39,远小于“keggGene”的.我们把现象叫做实体分布的不平衡性,对应的实体称作重头或重尾实体.
通过以上分析我们看出了SKG与OKG的数据差异,同时,我们也知道OKG的所有以前的工作,包括TransE,TransH,TransR,TransD和TransSparse都不能很好地解决这3个问题,并且它们以相同的方式对每个关系进行建模.不均匀性可能导致出现次数少的实体和关系(记作不频繁对象)在训练过程中出现拟合不足的问题,而出现次数多的实体和关系(记作频繁对象)会出现过拟合问题.同时,关系广度的严重不平衡(重头或重尾)表明需要着重区别大量头实体或者尾实体.
Table 2 Relation Distribution of EKG
表2 EKG的关系分布
为了应对上述挑战,我们提出了一种新型嵌入表示方法——酶知识图自适应嵌入(enzyme know-ledge graph adaptive embedding, EAE)方法——来学习EKG的嵌入表示,主要贡献如下:
1) 针对SKG的不均匀性、非交换性和不平衡性,提出了一种新方法EAE对EKG进行嵌入表示.
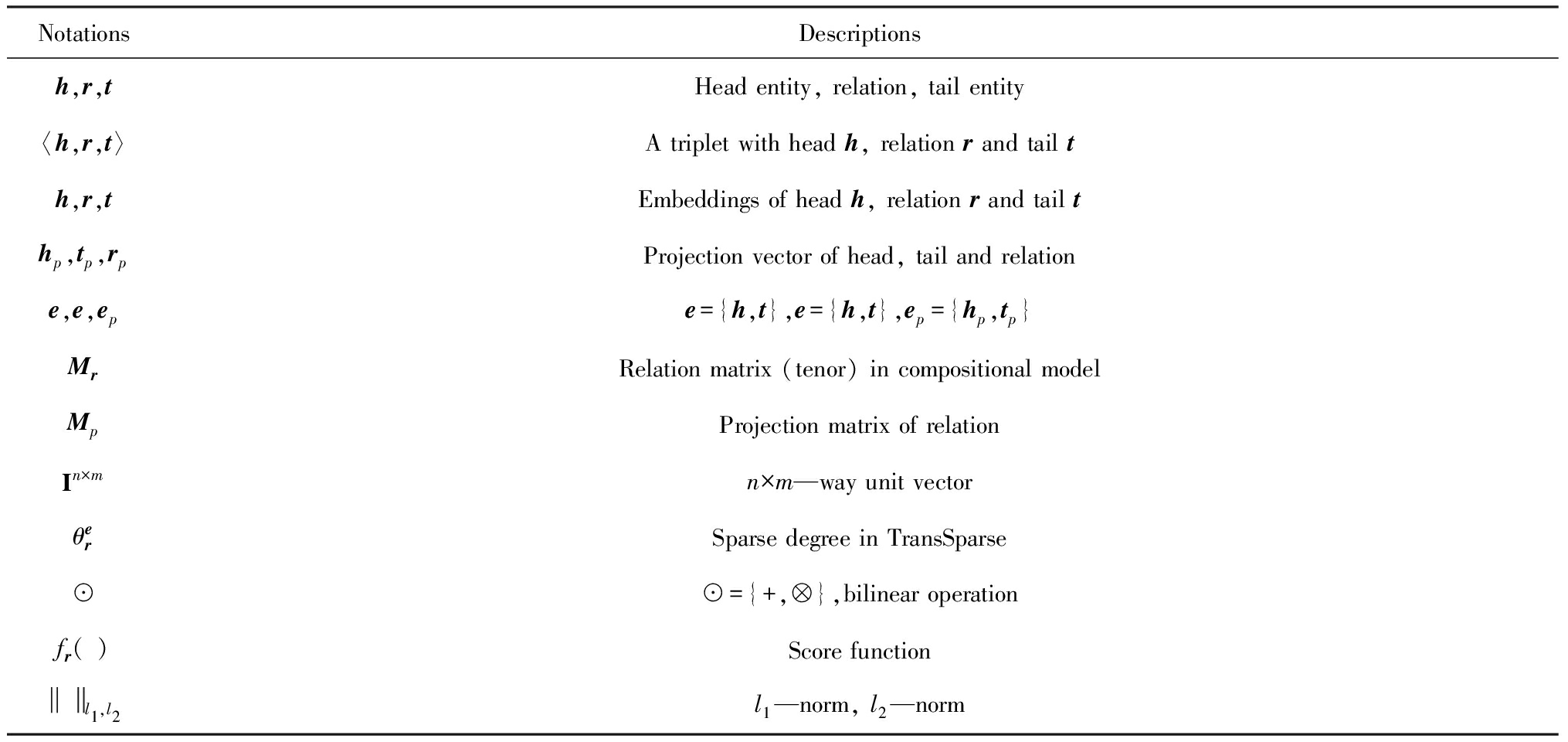
2) 为了着重区分重头或重尾实体,EAE采用了“三角形法则+点积原理”的三元组建模思想,使得 h + r 和 t 只需要保持一定的角度,而不是严格限制 h + r = t * h , r , t 依次表示头实体向量、尾实体向量和关系向量. .
3) “三角形法则”和“点积原理”都不会增加模型复杂度.所以,EAE不仅准确性高,还和TransE一样,具有参数少、时空复杂度低的优势,可以轻松扩展到大规模SKG.
4) 采用Adadelta动态调整参数,自适应地克服由于不均匀而导致的不频繁对象的拟合不足问题和频繁对象的过拟合问题.
5) 在链接预测和元组分类任务中,我们的方法取得了最先进的性能.
OKG的嵌入模型包括翻译模型、组合模型和神经网络模型.其中,翻译模型最简单,复杂性也较低.为了方便说明,我们首先给出文中使用的数学符号,如表3所示:
Table 3 Mathematical Notations
表3 文中使用的数学符号
翻译模型的灵感来自word2vec中词汇关系的平移不变性.经典模型是TransE [19] ,它认为头实体向量 h 加上关系向量 r 可以得到尾实体 t ,并且 h + r 越接近于 t ,相应的元组越有可能是正确的.所以,它的分数函数
f r ( h , t )= ![]() .
.
(1)
TransE原理很简单,对于1-to-1关系建模准确性很好.然而,它在处理复杂关系,如1-to- n , n -to-1和 n -to- n 关系时不占优势 * 这种关系分类源于TransE,对于每个关系 r ,平均链接的头实体 h 数(或者尾实体 t ),若此平均数低于1.5,则参数被标记为1,否则为 n . .因为,如式(1)所示,当一个关系 r 链接多个实体 e k , k =1,2,…, i ,…, j ,…时会出现多个实体重合的情况,即 e i = e j , i ≠ j .同理,当2个实体间有多重关系时,多个关系也会重合.为此,出现了一些改进方法,如Trans(H,R,D,Sparse) [21-24] .
TransH [21] 为了使实体面对不同关系有不同的表示,首次使用超平面和映射操作对关系进行建模,然后将头尾实体映射在超平面上:
(2)
f r ( h , t )= ![]() .
.
(3)
由式(2)可知,所有关系和实体向量建模在相同语义空间,但是一个实体可能有很多方面,不同关系关注不同的方面.所以相同的语义空间不能表达这样丰富的信息.为此,Trans(R,D,Sparse)将 r 和 e 建模在不同的语义空间中,然后通过映射矩阵 M p 将实体 e 从实体空间投射到关系空间:
e p = M p × e .
(4)
TransR [22] 中 h 和 t 共享普通映射矩阵 M p ;TransD [23] 认为应该区分 h 和 t ,并且映射矩阵 M p 应该与实体和关系都相关,所以, M p 被实体映射向量和关系映射向量所代替:
(5)
TransSparse [24] 采用稀疏矩阵 ![]() 代替 M p ,稀疏度
代替 M p ,稀疏度 ![]() 由关系 r 链接的实体数量决定.
由关系 r 链接的实体数量决定.
还有组合模型和神经网络模型.组合模型采用线性组合原理来拟合元组,例如RESCAL [18] ,LFM [25] ,DistMult [10] 和HolE [20] .其分数函数
f r ( h , t )= h T M r t .
(6)
RESCAL优化整个 M r ,带来了更多的参数.因此,LFM仅优化非零元素, DistMult使用 M r 的对角矩阵代替 M r 来减少参数,但这种方法只能建立对称关系.HolE使用点积代替张量积,并采用 h 和 t 之间的循环相关来表示实体对:
f r ( h , t )= σ ( r T ( h * t )), σ ( x )=1/(1+e - x ),
(7)
(8)
HolE在非交换关系和等价关系上优势很大,并且可以通过快速傅里叶变换加速计算.
神经网络模型包括SE [26] ,SME [27] ,NTN [28] 和SLM [28] .SE基于式(9)通过头实体特定矩阵 M rh 和尾实体特定矩阵 M r t 来转换实体空间,但是它不能捕捉实体之间的关系 [28] .SME [27] 处理实体和关系之间的相关性可以通过:
f r ( h , t )= ![]() ,
,
(9)
f r ( h , t )=( M 1 h ⊙ M 2 r + b 1 ) T ( M 3 h ⊙ M 4 r + b 2 ).
(10)
SLM [28] 使用单层神经网络的非线性运算来增强实体间关系的精确性,并减少SE的参数.但是它只提供实体和关系之间相对较弱的联系.NTN模型结合SLM [28] 和LFM [25] 定义了得分函数:
f r ( h , t )= ![]() g ( hM r t + M r ,1 h + M r ,2 t + b r ),
g ( hM r t + M r ,1 h + M r ,2 t + b r ),
(11)
其中 ![]() 是特定关系的线性层, g 是tanh()函数, M r ( M r ∈
是特定关系的线性层, g 是tanh()函数, M r ( M r ∈ ![]() d × d × k )是3阶张量.因此,这种模式需要大量训练元组,不适合稀疏KG [19] .
d × d × k )是3阶张量.因此,这种模式需要大量训练元组,不适合稀疏KG [19] .
由引言分析可知,EKG嵌入表示的困难在于:1)区分重尾实体;2)克服由于不均匀而引起的不频繁对象的拟合不足问题和频繁对象的过拟合问题.然而,翻译模型对于1-to-1关系工作良好,在复杂( n -to-1,1-to- n 和 n -to- n )关系中存在问题,组合模型表达能力强,但是复杂度高;神经网络模型又不适用.为此,我们提出了EAE模型.
对于问题1,我们可以将KG嵌入表示看作是物体成像问题,那么依据“物像原理”,我们可以把翻译模型 f r ( h , t )= ![]() 拆分成2个步骤:
拆分成2个步骤:
1) 成像.将 h 和 r 的线性操作看作 t 的像 t imag * 也可以将 t 和 r 的线性操作看作 h 的像,关系也一样. ,根据三角形法 [29] 则有式(12)成立:
t imag = h + r ,
(12)
2)计算物像相似度.采用 l 1 , l 2 —norm计算尾巴 t 与计算得到的像 t imag 之间的相似度:
sim ( t imag , t )= ![]() .
.
(13)
此时,我们可以清楚地看到,式(12)原理简单、参数少,很好地建模了实体和关系.但是式(13)中 l 1 , l 2 —norm属于赋范空间中的范数 [29] 范畴,所以当 t imag 与 t 特别像时,就会产生 t imag = t * 向量都从原点出发,长度相同,当 t imag = t 时,向量终点必然会重合,即2个向量完全重合. ,当有多个尾实体 t 1 , t 2 ,…, t i ,…时,就会出现 t imag = t 1 = t 2 =…= t i =….
为了区分众多 t 1 , t 2 ,…, t i ,…,我们想到了比范数更具有表达能力的点积 * 从数学上看,赋范空间定义了范数(范数有长度和数乘可提取),内积空间定义了内积(内积空间有角度和长度),且内积可以诱导范数,但范数不一定能诱导内积,所以范数弱于内积, n 维向量的内积也叫作点积. ,即用点积 [29] 度量 t imag 与 t 的相似度.因此,我们提出了基于“三角形法则+点积( n 维向量的点积是线性组合)原理”的EAE模型,如图2所示.数学符号如表3所示.
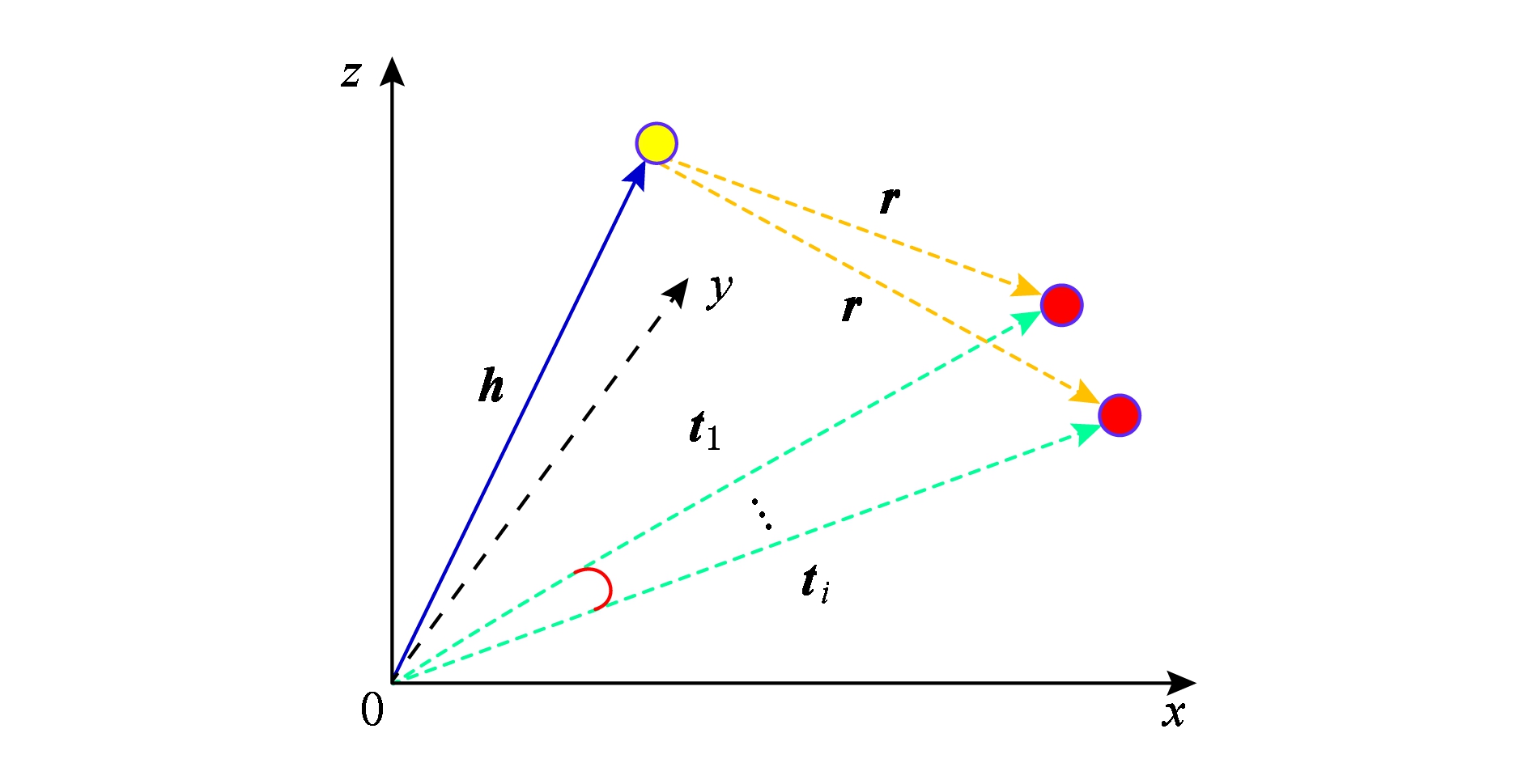
Fig. 2 EAE model
图2 EAE模型
图2中的“三角形法则”用于成像,和翻译模型一样,即式(12)所示.“点积原理”用于计算物像相似度,即用式(14)代替式(13):
sim ( t imag , t )= dot ( t imag , t ).
(14)
采用式(14)时 t imag 和 t ,或者众多 t i , i =1,2,…之间只需要保持一定的角度,而不是严格的 t imag = t .再从线性代数的角度看 [29] , dot ( t imag , t )是线性组合, t imag 是给定的权重向量, t 是特征向量,所以 t imag 与 t 之间存在式(15)的关系:
t imag =ϖ i t i .
(15)
从式(15)也可以看出,采用点积(或者线性组合)后,众多尾实体相当于被加上了权重,所以可以被区分.当然,像翻译模型一样,完整的EAE模型也可以合并式(14)(15),统一写作:
f r ( h , t )= dot ( h + r , t ).
(16)
当然, h + r 和 t 都是 n 维向量,所以式(16)也可以写作 [29] :
f r ( h , t )= dot ( h + r , t )=( h + r ) T t .
(17)
问题2出现在模型训练阶段.所以,像TransE一样,我们也将式(17)转换成带有约束条件 ![]() 的最优化问题:
的最优化问题:
![]()
γ - f r ( h ′, t ′)),
(18)
Δ ′={( h ′, r , t )| h ′∈ E ∪( h , r , t ′)| t ′∈ E },
(19)
其中, γ 是边界, Δ ′和 Δ 分别是正确和不正确的三元组的集合, Δ ′是 Δ 的负采样集.
接下来需要解决由于不均匀而引起的不频繁对象的拟合不足问题和频繁对象的过拟合问题.在传统模型中,大多数采用随机梯度下降SGD [30] 求解.SGD使用全局学习速率 η 更新所有参数,而不管数据特性如何.但是根据前面分析,我们可以看到不频繁出现的实体需要较长的时间来学习,频繁出现的实体则需要较短的时间来学习.所以,我们采用Adadelta [31] 训练模型,它可以随着时间的推移动态调整参数,使得小梯度具有较大的学习率,而大梯度具有较小的学习率.具体做法如下 [31] :
首先,Adadelta限制了过去梯度的窗口,以固定大小ϖ累积,然后将该积累表示为平方梯度的指数衰减平均值.假设在时间 epo 上,运行平均值 E [ g 2 ] epo :
(20)
其中, ρ 是衰减常数.由于在更新参数时需要这个数量的平方根,所以,将其近似转化为历史累计梯度的平方根RMS:
RMS [ g ] epo = ![]() ,
,
(21)
其中, ε 是常数.所以,参数更新:
Δ x epo =- ![]() g epo ,
g epo ,
(22)
因此,EAE的算法如算法1所示.
算法1 . EAE算法.
输入:训练集 Δ ′和 Δ 、实体和关系集 E 和 R 、边界 γ 、嵌入维度 n , m ;
输出: h , r , t .
/*初始化*/
① 对于 ![]()
② 对于 r ∈ R , r ← r / ![]()
③ 对于 ![]()
/*训练*/
④ loop
⑤ 对于每个 e ∈ E , e ← e / ![]()
⑥ Δ batch ← sample ( Δ , b ); /*采样一个大小为 b 的minibatch*/
⑦ T batch ←∅; /*初始化一组三元组*/
⑧ for 〈 h , r , t 〉∈ Δ batch do
⑨ 〈 h ′, r , t ′〉← sample ( ![]() ); /*为每个实体产生负例*/
); /*为每个实体产生负例*/
⑩ T batch ← T batch ∪{( h , r , t ),( h ′, r , t ′)};
 end for
end for
/*更新向量*/
 for
for  ∈ E ∪ R ∪ h + r in T batch
∈ E ∪ R ∪ h + r in T batch
/*归一化*/

 ←
←  /
/ ![]()
 end if
end if
 end for
end for
/*更新参数*/
 for t ∈[1, T ] do
for t ∈[1, T ] do

![]()
![]() [ γ + f r ( h ,
[ γ + f r ( h ,
t )- f r ( h ′, t ′)] + ; /*计算梯度*/

![]() ;
;
/*累计梯度*/
 Δ x epo =-
Δ x epo =- ![]() g epo ;
g epo ;
/*计算更新*/
 E [Δ x 2 ] epo = ρ E [Δ x 2 ] epo -1 +(1- ρ )
E [Δ x 2 ] epo = ρ E [Δ x 2 ] epo -1 +(1- ρ )
![]() /*累计更新*/
/*累计更新*/
 x epo ← x epo -1 +Δ x epo ; /*更新参数*/
x epo ← x epo -1 +Δ x epo ; /*更新参数*/
 end for
end for
 end loop
end loop
算法的可扩展性不仅在于高精度,而且还具有低的时间和空间复杂性.我们将EAE与其他模型进行比较,如表4所示:
Table 4 Complexities Comparison
表4 模型复杂度对比

n s =1: linear; λ =2: separate; λ =1: share.
在表4中,复杂度通过参数的数量以及每轮更新中乘法运算所需的时间和内存空间来测量. n e , n r , n t r 分别代表KG中的实体、关系和三元组的数量; n k 是神经网络的隐层节点的数量, n s 是张量的片数; d 表示 d e = d r , d e 和 d r 分别表示实体和关系嵌入空间的维度; θ (0≪ θ ≪1)表示映射矩阵的平均稀疏度.从表4中我们可以看到,EAE中的参数数量、运算所需要的内存空间与TransE相同,时间复杂度也与TransE相同,远优于神经网络模型和组合模型,同时也好于其他翻译模型,显示了我们方法的高效率.这种优势在嵌入空间越大的情况下越明显.
2.1~2.3节给出了模型定义,并分析了模型的复杂度,本节着重分析与其他翻译模型相比,我们EAE模型为什么会产生好的性能.众所周知,翻译模型的本质是利用关系向量将头实体转换为尾实体,数学表示为 h ⊥ + r = t ⊥ ,如表5所示,其几何表示如图3所示.
Table 5 The Principle of Translation - Based Models
表5 翻译模型的本质

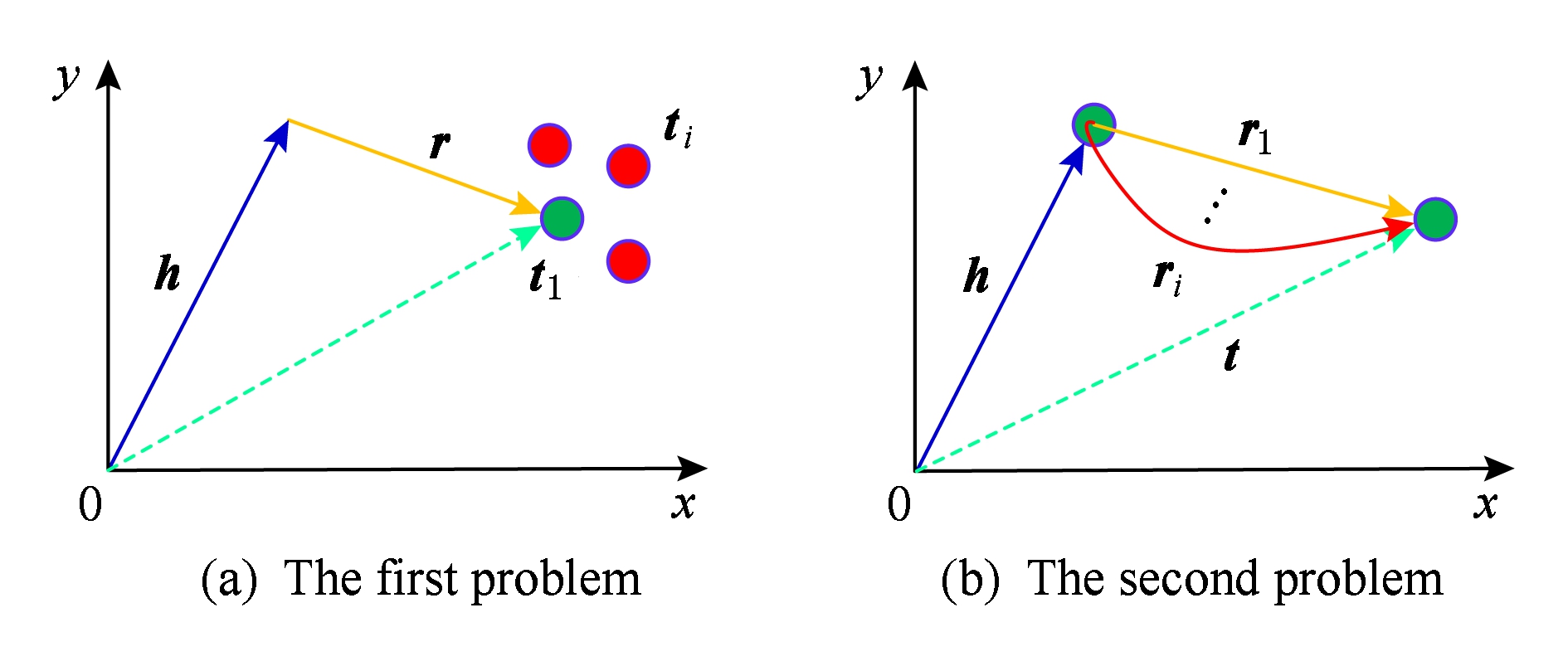
Fig. 3 The geometric representation of models
图3 翻译模型的几何表示
从图3可以看出,翻译模型存在2个问题:重头(或重尾)重合和重关系重合,如图3(a)和图3(b)所示.第1个问题的原因如下:由表4可知,在Trans(R,Sparse和H)中, M r , M r e 和 r p 由关系 r 唯一确定.这已经通过实践证明,例如在OKG的FB15K数据集上,大约只有48.9%的元组(为1-to-1和 n -to-1元组)的准确度( Hits @10 * Hits @10:预测正确的实体排在前 k 位的比例. )超过85%,而28.3%的元组(1-to- n )的元组不到60% [20] .TransD使用实体投影向量并区分头实体和尾实体.因此,可以在一定程度上解决第1个问题.但是头(尾)实体仅受实体空间中的头(尾)实体投影向量的影响.因此,它比TransSparse降低3% [20] .
然而,Trans(R,Sparse和H)很大程度上改善了第2个问题,主要是它们利用了一个投影矩阵 M r , M r e 或投影向量 r p ,而 M r , M r e 和 r p 与关系一一对应,它们不同,则关系不同.这也有实践证明:例如在OKG的FB15K数据集上,所有类型关系的准确度至少提高10% [14] .这充分说明了区分重关系的重要性.不幸的是,这个问题在EKG中不存.因此,翻译模型在EKG中没有优势.
虽然我们的EAE与翻译模式有相似之处,但EAE有优势:1) dot ( h + r , t )规定 h + r 和 t 只需要保持一定的角度,而不是严格限制 h + r 等于 t ,进而可以有效区分重头和重尾实体,解决不平衡问题.2)EAE采用Adadelta更新参数,它可以随着时间的推移动态调整参数,使得小梯度具有较大的学习率,而大梯度具有较小的学习率.因此,EAE可以自适应地克服由于不均匀而导致的不频繁对象的拟合不足问题和频繁对象的过拟合问题.3)EKG中头尾实体不存在位置交换性,所以没有必要区分头尾实体,也就不需要建立像Trans(D和Sparse)那样复杂的空间变换模型,减少了模型复杂度.4)点积不会增加时间复杂度和空间复杂度.所以,它保持了线性时间和空间复杂度,可以很容易地扩展到大规模SKG.
为证明EAE的有效性,我们选择TransE,TransH,TransR,TransD和TransSparse作为基准模型,并在链接预测、元组分类和自适应性度量任务上进行比较.
我们构建EAE模型来处理EKG中不均匀性、非交换性和不平衡性问题.因此,我们从中国科学院微生物研究所的酶知识库EKG中随机抽取139 963个实体和10种关系得到实验数据集E13M.
我们从原始数据中删除了“description”,“history”和“a(type)”3个关系, 因为:1)“description”和“history”关系对应的尾实体是长文本,不方便处理,并且这些信息作为辅助信息帮助预测更为合适;2)EKG中都是酶数据,所以a(type)对应的尾实体相同,不需要预测.此外,众所周知,训练数据、验证数据和测试数据是实验数据集包含的3个基本要素.并且在KG 嵌入中,测试时需要使用实体和关系的嵌入向量,而这些向量是训练过程中产生的,所以测试数据中的每个实体和关系必须存在于训练集中.我们删除只出现一次的所有实体和关系,然后随机抽样,得到的E13M数据集如表6~7所示:
Table 6 E13M Data Set
表6 E13M数据集

Table 7 Relation Type and Feature in E13M
表7 E13M中的关系及其特征统计
为了评估模型的性能,我们采用和TransE相同的评价指标 [15] :1) MeanRank ,正确实体的平均排序;2) Hits @ k ,预测正确的实体排在前 k 位的比例. MeanRank 越低或者 Hits @ k 越高,准确性越高.
首先,对于每个测试三元组〈 h , r , t 〉,和TransE一样,也用贝努力抽样(.bern方法)从E13M中选择实体替换头实体 h (选择实体和被替换实体不能是同一实体),并且通过 f r ( h , t )给出的相似度得分降序排列这些损坏的三元组.同样,我们重复这个过程,替换尾实体 t .
其次,实验数据包括训练数据、验证数据和测试数据.因此,三者中出现一些损坏的三元组时,上述指标中存在一个小错误.例如训练数据中损坏的三元组可能包含在验证数据和测试数据中.如果是这样,排名将是误导的.为了避免这个缺陷,我们删除所有出现在训练数据、验证数据和测试数据中损坏的三元组,记作 Filter 原始操作记作 Raw .所以,我们报告的 MeanRank 和 Hits @ k 有2种设置: Raw 和 Filter .
为了公平,所有模型的维数都设置为 d =20,迭代次数 epoch =1 000,Adadelta的参数1- ρ =10 -3 , ε =10 6 ,SGD学习率 λ ={0.001,0.01,0.1},边界 γ ={0.1,0.5,0.6,0.7,1,1.5},最小批量处理大小 B ={100,200,480,1440},EAE中不相似度量使用点积,其他的采用一阶矩离或二阶距离 d ={  1 ,
1 ,  2 },每个模型都由Adadelta [27] 和SGD [26] 分别训练.
2 },每个模型都由Adadelta [27] 和SGD [26] 分别训练.
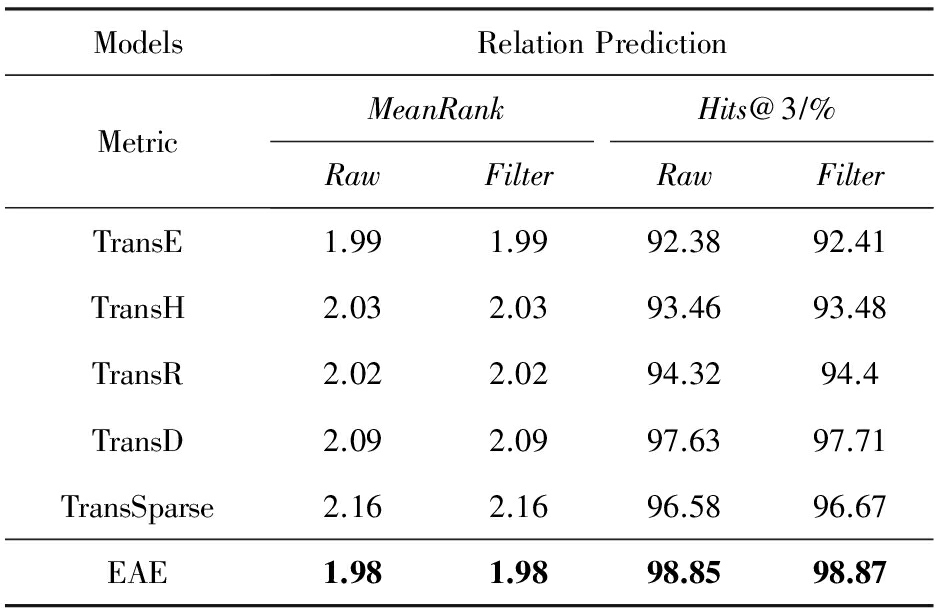
链接预测是测试补全三元组〈 h , r , t 〉的一个基准任务,即已知〈 h , r , t 〉中的任意2个,依据 f r ( h , t )最小原则预测第3个.这个任务关注相对正确性,即预测的三元组的排序,而不是获得最好的.所以这里有2个指标: MeanRank 和 Hits @ k .当预测缺失的头尾实体时,我们和之前的工作做法一样,设置 k =10.但是,对于缺失关系预测,数据集共有10个关系, k =10是无意义的.因此,我们将关系预测的 k 设置为 k =3.我们在E13M上对方法进行评估,结果如表8~10所示:
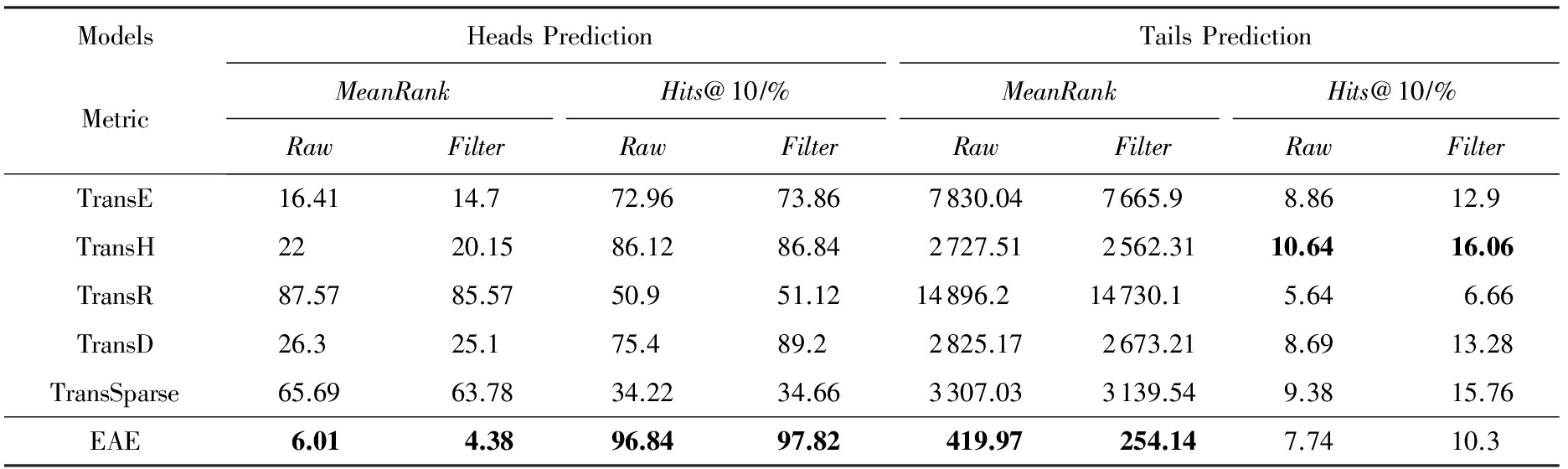
Table 8 Evaluation Results on Entity Prediction
表8 实体预测结果
Note: The bold data is the best one among all models for per metric.
Table 9 Evaluation Results on Relation Rrediction
表9 关系预测结果
Note: The bold data is the best one among all models for per metric.
从表8可以看出,EAE在预测头实体和尾实体时, MeanRank 值显著低于基准模型,而在预测头实体时, Hits @10值也显著高于基准模型.比如在预测头实体时,基准模型中最低的 MeanRank 值是14.7(TransE),而EAE降低到4.38;对于 Hits @10指标,基准模型中最高的是TransD的89.2%,我们的EAE提高了8.62%.在预测尾实体时,EAE在 MeanRank 指标上也可能比其他基准模型好10~58倍.对于关系预测任务,EAE也获得了较好的结果,在 Hits @10指标上比TransD提升了约1%,但比TransE提高了6%, MeanRank 值也得到了最小值.这些结果证明EAE模型在处理酶KG方面具有明显的优势.但是,从表8尾实体预测中我们观察到了一个现象,即在 Hits @10指标上,各种模型的最高值不超过17%,出现这种现象的主要原因应该是EKG中每个关系所链的尾实体太多,尤其是“keggGene”,“x-gene”,“ncbiGene”关系,平均可达966.31,821.81,275.54个(表2),这意味着对于这3种关系对应的尾实体,排名在前966.31,821.81,275.54的都是正确的,而目前规定排名前10是正确的,其他均按照预测错误处理,并且表7表明这3种关系的数据所占比例很大,所以会显著影响 Hits @10命中率.所以采用 MeanRank 更能评价模型的性能,并且模型具有较低的 MeanRank 或较高的 Hits @ k 都意味着更好的效果,所以,我们仍然认为EAE有很好的建模能力.
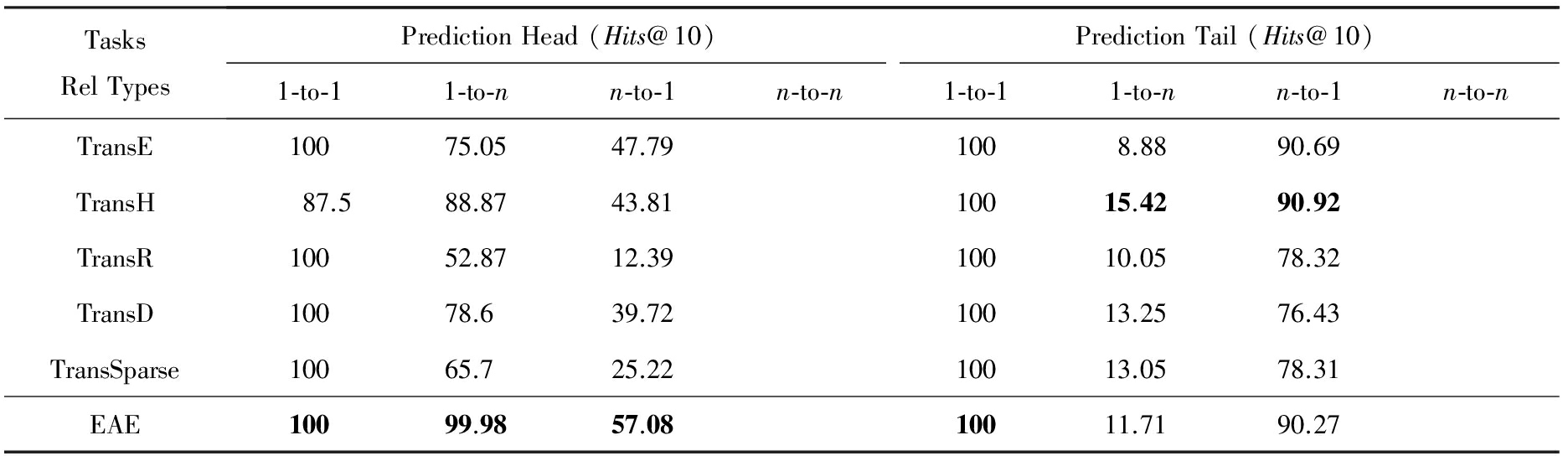
Table 10 Experimental Results on E13M by Mapping Properties of Relations
表10 E13M的映射属性关系实验结果 %
Note: The bold data is the best one among all models for per metric.
表10是按关系类别分组的链接预测结果,像TransE [14] 一样,包括1-to-1,1-to- n , n -to-1和 n -to- n .E13M包括1-to-1,1-to- n 和 n -to-1关系,不存在 n -to- n 关系.从表10中我们可以看到,当预测头实体时,EAE可以在所有基准模型中取得最优性能,并且在预测头实体方面具有更明显的优势,例如EAE可以将 Hits @10值提高10%~47.11%,甚至在预测1-to- n 关系时可以达到99.98%.但是,EAE在预测尾部实体并没有占太大优势,如表8中分析,主要是因为1-to- n 中的 n 太大,远大于10,所以各种模型没有明显区别.
元组分类是一种二元分类,其目的是判断给定的三元组〈 h , r , t 〉是否正确.因此,我们还使用E13M作为实验数据集,并按照TransParse的基本思想生成负例.对于验证数据,我们采用任意实体随机替换尾实体产生负例.同时,负例不能出现在原始验证数据集中;否则,用其他实体替换原始尾实体.测试数据也是如此.接下来,基于式(1)计算每个三元组的得分,并由阈值 θ 区分正例和负例. θ 由验证数据集中正例和负例之间的距离得分最大化决定.最后,如果一个新的三元组〈 h , r , t 〉得分高于 θ ,那是正确的;否则,是错误的.在这里,我们包括2个指标:第1个是模型在整个数据集上的分类准确性,即所有关系上的分类准确性.例如,总共有 n c 个三元组,我们正确地判断出 n s 个元组的正确性,那么整个数据集上的分类准确性是 n s / n c .类似地,通过关系名称分组三元组可以获得每个关系上的分类准确性.我们选择TransE,TransH,TransR,TransD和TransSparse作为基准模型,其结果如图4和表11所示.
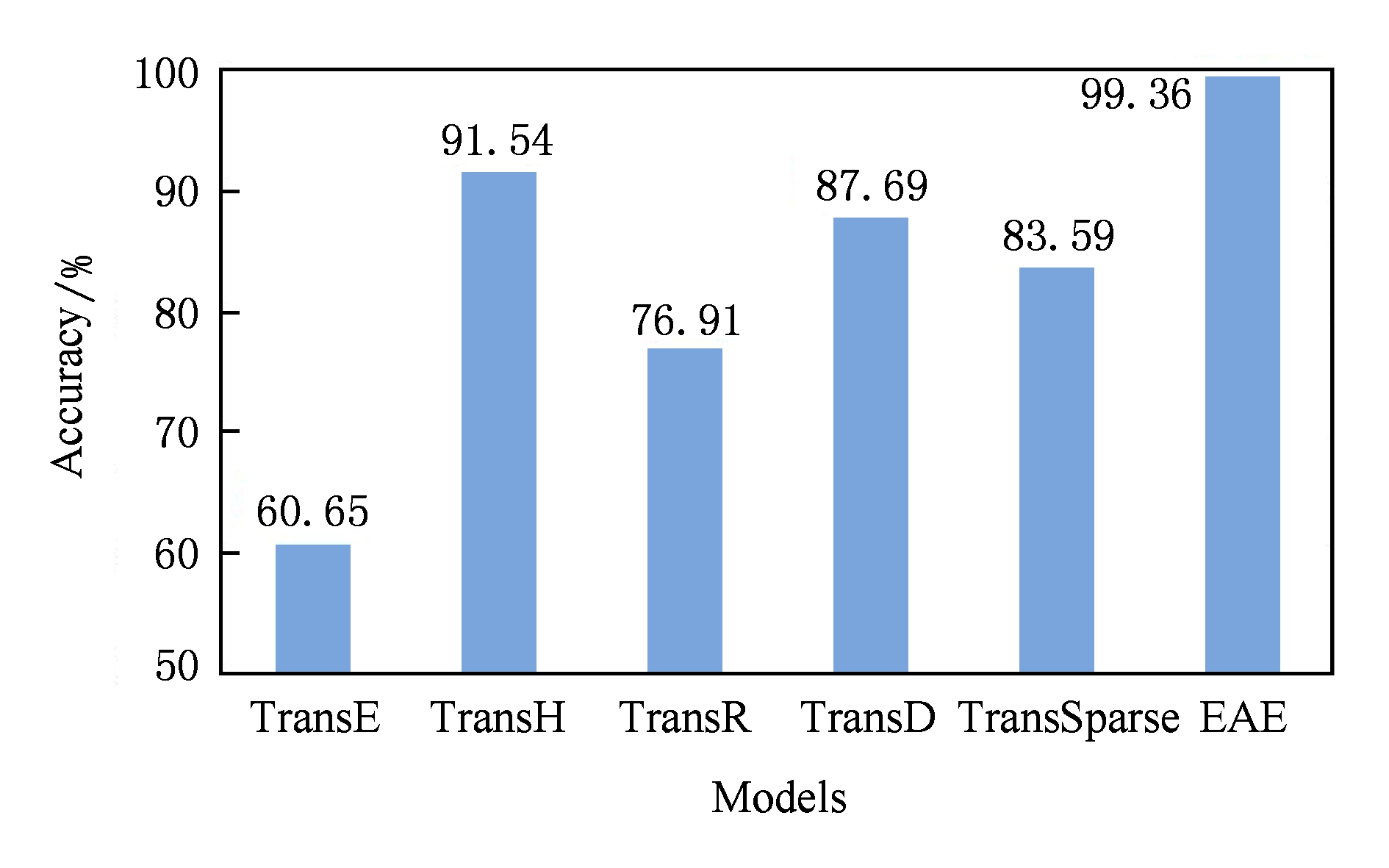
Fig. 4 Triples classification accuracies
图4 元组分类准确性
图4显示出EAE在所有基准模型中具有绝对的优势,得到最佳准确度为99.39%,几乎接近1,并且显著高于其他基准模型,最差也不比TransH高7.82%.这表明了EAE模型的正确性.
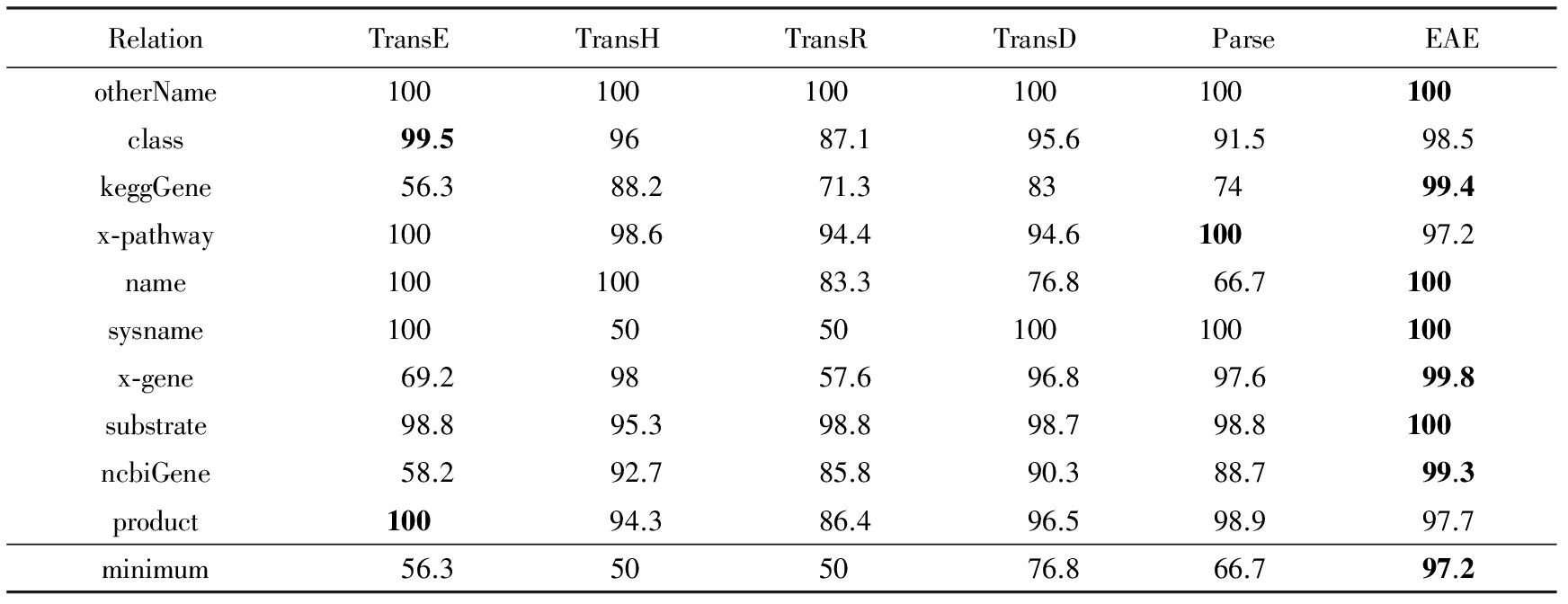
表11也明确显示出EAE在简单和复杂的关系上显著提高了性能.此外,EAE在10种关系上,分类准确率都高于97.2%,但是其他模型则差很多,比如,TransE的最低准确性为56.3%,TransH为50%,TransR为50%,TransD为76.8%,TransSparse为66.7%.这就是为什么我们使用“三角形法则和点积原理”思想.因此,我们认为EAE模型可以很好地处理重尾和重头数据,如EKG.
Table 11 Classification Accuracies of Different Relations
表11 不同关系的分类准确性
Note: The bold data is the best one among all models for per metric.
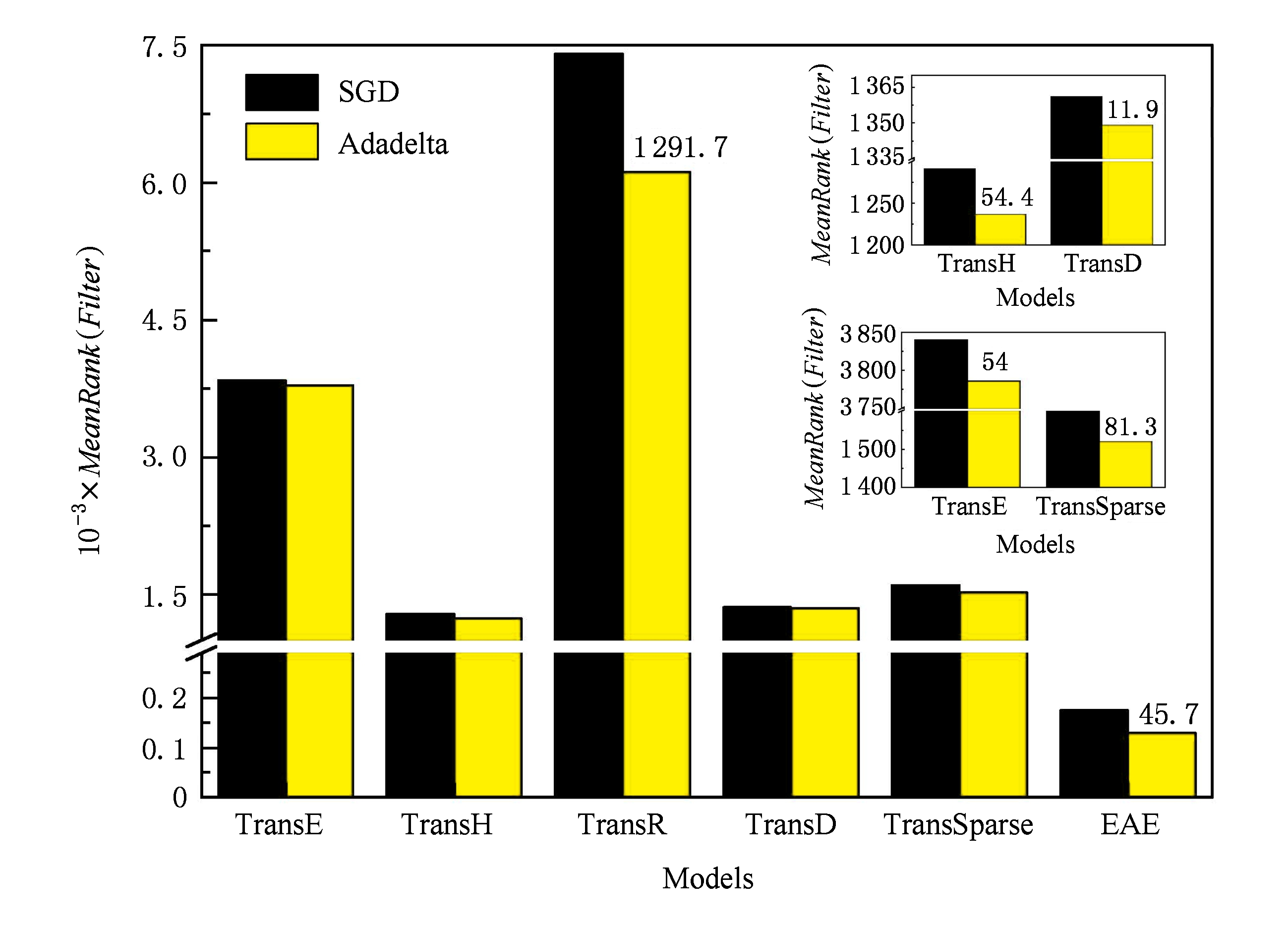
Fig. 6 MeanRank of entity prediction by SGD and Adadelta
图6 采用SGD和Adadelta训练的实体预测的MeanRank
EKG具有不均匀性,为了不让这种不均匀性影响模型准确性,使模型更容易训练,我们用Adadelta代替了SGD.为了验证Adadelta更适合这种数据, 我们将基准模型TransE,TransH,TransR,TransD,TransSparse和我们的EAE模型分别用SGD和Adadelta训练.采用实体预测和关系预测作为实验载体,度量指标仍然用 MeanRank 和 Hits @10,其结果如图5和图6所示.
从图5我们可以看出,在 Hits @10指标上,模型用Adadelta训练最少也能比用SGD提升1.3%.最好的如TransR可以提高8.5%,TransSparse提高了5.8%.这也就应证了面对不均匀数据时,Adadelta的自适应学习要比SGD使用全局学习速率 η 更新所有参数更有效,因为Adadelta对不频繁出现的实体给予较长的时间来学习,频繁出现的实体则给予较短的时间来学习,平滑了不频繁实体/关系拟合不足、简频繁实体/关系过度拟合的问题.
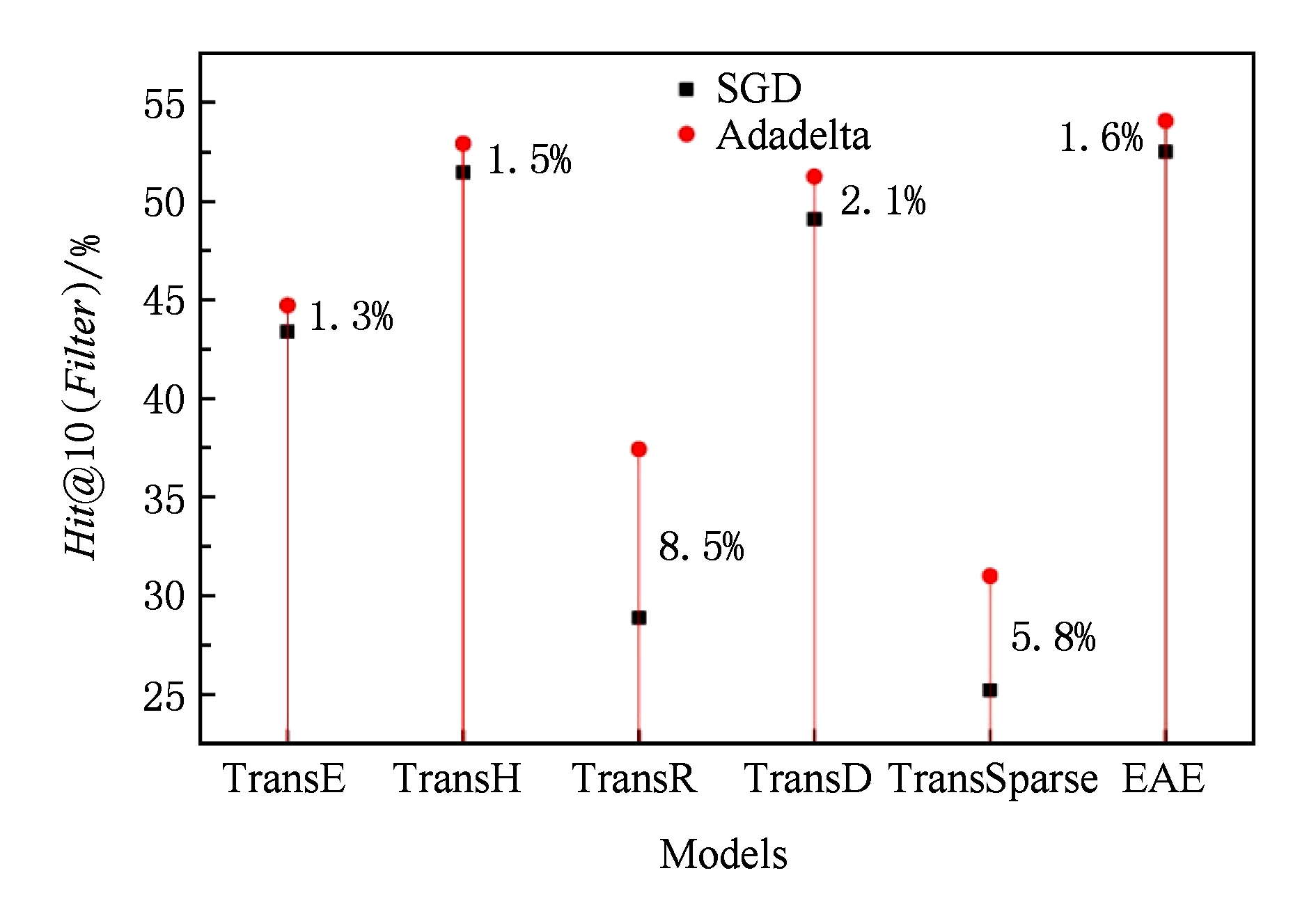
Fig. 5 Hits@10(%) of entity prediction by SGD and Adadelta
图5 采用SGD和Adadelta训练的实体预测值Hits@10(%)
同样,图6的 MeanRank 值也充分说明了这一点,每个模型在用Adadelta训练都会比用SGD有一定的改善,比如TransR最明显, MeanRank 值降低了1 291.7( MeanRank 值越低越好),这主要是TransR采用矩阵映射,参数较多,又加上数据的不均匀性较大,使用SGD的全局学习率不利于不频繁实体和频繁实体同时学习,而Adadelta可以随着时间的推移动态调整参数,使得小梯度具有较大的学习率,这样一来不频繁实体,如尾实体就有了充分的学习时间,频繁实体也不会因为训练时间过长而过拟合.同理,其他模型在采用Adadelta训练后, MeanRank 值也有不同程度的降低.而我们的EAE在采用SGD和Adadelta前后也有45.7的改进.
在本文中,我们基于“三角形法则+点积原理”思想和“自适应学习时间调整”的策略提出了EAE模型来嵌入表示EKG.其优点是:
1) dot ( h + r , t )规定 h + r 和 t 只需要保持一定的角度,而不是严格限制 h + r 等于 t ,进而可以有效区分重头和重尾实体,解决不平衡问题;
2) EAE采用Adadelta更新参数,它可以随着时间的推移动态调整参数,使得小梯度具有较大的学习率,而大梯度具有较小的学习率.因此,EAE可以自适应地克服由于不均匀而导致的复杂关系拟合不足和简单关系过度拟合地问题;
3) 点积不会增加时间复杂度和空间复杂度.所以,它可以很容易地扩展到大规模的SKG.
我们只能证明EAE对酶KG的能力很强,但当EAE遇到多个关联的微生物KG时的能力是未知的.因此,在未来的工作中,我们将考虑多个关联的微生物知识图谱的情况.
致谢 感谢中国科学院微生物研究所提供微生物数据;感谢为本论文提供修改意见的老师和同学们!
参考文献
[1]Meng Xiaofeng, Du Zhijuan. Research on the big data fusion: Issues and challenges[J]. Journal of Computer Research and Development, 2016, 53(2): 231-246 (in Chinese)(孟小峰, 杜治娟. 大数据融合研究: 问题与挑战[J]. 计算机研究与发展, 2016, 53(2): 231-246)
[2] Liu Qiao, Li Yang, Duan Hong, et al. Knowledge graph construction techniques[J]. Journal of Computer Research and Development, 2016, 53(3): 582-600 (in Chinese)(刘峤, 李杨, 段宏, 等. 知识图谱构建技术综述[J]. 计算机研究与发展, 2016, 53(3): 582-600)
[3] Walter S, Unger C, Cimiano P. DBlexipedia: A nucleus for a multilingual lexical Semantic Web[C] //Proc of the 3rd Int Workshop on NLP and DBpedia, Co-located with the 14th Int Semantic Web Conf (ISWC’15). Berlin: Springer, 2015: 87-92
[4] Vrandecic D, Krötzsch M. Wikidata: A free collaborative knowledgebase[J]. Communications of the ACM, 2014, 57(10): 78-85
[5] Bollacker K, Evans C, Paritosh P, et al. Freebase: A collaboratively created graph database for structuring human knowledge[C] //Proc of the 2008 ACM SIGMOD Int Conf on Management of Data (SIGMOD’08). New York: ACM, 2008: 1247-1250
[6] Suchanek F M, Kasneci G, Weikum G. Yago: A core of semantic knowledge[C] //Proc of the 16th Int Conf on World Wide Web (WWW’07). New York: ACM, 2007: 697-706
[7] Wu Wentao, Li Hongsong, Wang Haixun, et al. Probase: A probabilistic taxonomy for text understanding[C] //Proc of the 2012 ACM SIGMOD Int Conf on Management of Data(SIGMOD’12). New York: ACM, 2012: 481-492
[8] Dong X, Gabrilovich E, Heitz G, et al. Knowledge vault: A Web-scale approach to probabilistic knowledge fusion[C] //Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining(SIGKDD’14). New York: ACM, 2014: 601-610
[9] Neelakantan A, Roth B, McCallum A. Compositional vector space models for knowledge base completion[C] //Proc of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th Int Joint Conf on Natural Language Processing of the Asian Federation of Natural Language Processing (ACL’15). Menlo Park, CA: AAAI, 2015: 156-166
[10] Yang Bishan, Yih W, He Xiaodong, et al. Embedding entities and relations for learning and inference in knowledge bases[EB/OL]. (2014-12-20) [2017-08-01]. https://arxiv.org/abs/1412.6575
[11] Schaefer C F, Anthony K, Krupa S, et al. PID: The pathway interaction database[J]. Nucleic Acids Research, 2008, 37(Suppl_1): D674-D679
[12] Momtchev V, Peychev D, Primov T, et al. Expanding the pathway and interaction knowledge in linked life data[C] //Proc of the 8th Int Semantic Web Challenge (ISWC’09). Berlin: Springer, 2009: 1247-1250
[13] Belleau F, Nolin M A, Tourigny N, et al. Bio2RDF: Towards a mashup to build bioinformatics knowledge systems[J]. Journal of Biomedical Informatics, 2008, 41(5): 706-716
[14] Li Min, Meng Xiangmao. The construction, analysis, and applications of dynamic protein-protein interaction networks[J]. Journal of Computer Research and Development, 2017,54(6): 1281-1299 (in Chinese)(李敏, 孟祥茂. 动态蛋白质网络的构建、分析及应用研究进展[J]. 计算机研究与发展, 2017, 54(6): 1281-1299)
[15] Nickel M, Murphy K, Tresp V, et al. A review of relational machine learning for knowledge graphs[J]. Proceedings of the IEEE, 2016, 104(1): 11-33
[16] Ruttenberg A, Rees J A, Samwald M, et al. Life sciences on the semantic Web: The neurocommons and beyond[J]. Briefings in Bioinformatics, 2009, 10(2): 193-204
[17] Liu Zhiyuan, Sun Maosong, Lin Yankai, et al. Knowledge representation learning: A review[J]. Journal of Computer Research and Development, 2016, 53(2): 247-261 (in Chinese)(刘知远, 孙茂松, 林衍凯, 等. 知识表示学习研究进展[J]. 计算机研究与发展, 2016, 53(2): 247-261)
[18] Nickel M, Tresp V, Kriegel H P. A three-way model for collective learning on multi-relational data[C] //Proc of the 28th Int Conf on Machine Learning (ICML’11). Cambridge, MA: MIT Press, 2011: 809-816
[19] Bordes A, Usunier N, Garcia-Duran A, et al. Translating embeddings for modeling multi-relational data[C] // Proc of the 27th Annual Conf on Neural Information Processing Systems (NIPS’13). Cambridge, MA: MIT Press, 2013: 2787-2795
[20] Nickel M, Rosasco L, Poggio T A. Holographic embeddings of knowledge graphs[C] //Proc of the 30th AAAI Conf on Artificial Intelligence (AAAI’16). Menlo Park, CA: AAAI, 2016: 1955-1961
[21] Wang Zhen, Zhang Jianwen, Feng Jianlin, et al. Knowledge graph embedding by translating on hyperplanes[C] //Proc of the 28th AAAI Conf on Artificial Intelligence (AAAI’14). Menlo Park, CA: AAAI, 2014: 1112-1119
[22] Lin Yankai, Liu Zhiyuan, Sun Maosong, et al. Learning entity and relation embeddings for knowledge graph completion[C] //Proc of the 29th AAAI Conf on Artificial Intelligence (AAAI’15). Menlo Park, CA: AAAI, 2015: 2181-2187
[23] Ji Guoliang, He Shizhu, Xu Liheng, et al. Knowledge graph embedding via dynamic mapping matrix[C] //Proc of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th Int Joint Conf on Natural Language Processing of the Asian Federation of Natural Language Processing (ACL’15). Menlo Park, CA: AAAI, 2015: 687-696
[24] Ji Guoliang, Liu Kang, He Shizhu, et al. Knowledge graph completion with adaptive sparse transfer matrix[C] /Proc of the 30th AAAI Conf on Artificial Intelligence (AAAI’16). Menlo Park, CA: AAAI, 2016: 985-991
[25] Jenatton R, Roux N L, Bordes A, et al. A latent factor model for highly multi-relational data[C] // Proc of the 26th Annual Conf on Neural Information Processing Systems (NIPS’12). Cambridge, MA: MIT Press, 2012: 3167-3175
[26] Bordes A, Weston J, Collobert R, et al. Learning structured embeddings of knowledge bases[C] //Proc of the 25th AAAI Conf on Artificial Intelligence (AAAI’11). Menlo Park, CA: AAAI, 2011, 6(1): 301-306
[27] Bordes A, Glorot X, Weston J, et al. A semantic matching energy function for learning with multi-relational data[J]. Machine Learning, 2014, 94(2): 233-259
[28] Socher R, Chen Danqi, Manning C D, et al. Reasoning with neural tensor networks for knowledge base completion[C] // Proc of the 27th Annual Conf on Neural Information Processing Systems (NIPS’13). Cambridge, MA: MIT Press, 2013: 926-934
[29] Banchoff T, Wermer J. Linear Algebra Through Geometry[M]. Berlin: Springer, 1972: 197-254
[30] Duchi J, Hazan E, Singer Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. Journal of Machine Learning Research, 2011, 12(7): 2121-2159
[31] Zeiler M D. ADADELTA: An adaptive learning rate method [EB/OL]. (2012-12-22) [2017-08-01]. http://arxiv.org/abs/1212.5701
Du Zhijuan, Zhang Yi, Meng Xiaofeng, and Wang Qiuyue
( School of Information , Renmin University of China , Beijing 100872)
Abstract In recent years a drastic rise in constructing Web-scale knowledge graph (KG) has appeared and the deal with practical problems falls back on KG. Embedding learning of entities and relations has become a popular method to perform machine learning on relational data such as KG. Based on embedding representation, knowledge analysis, inference, fusion, completion and even decision-making could be promoted. Constructing and embedding open-domain knowledge graph (OKG) has mushroomed,which greatly promots the intelligentization of big data in open domain. Meanwhile, specific-domain knowledge graph (SKG) has become an important resource for smart applications in specific domain. However, SKG is developing and its embedding is still in the embryonic stage. This is mainly because there is a germination in SKG due to the difference for data distributions between OKG and SKG. More specifically: 1) In OKG, such as WordNet and Freebase, sparsity of head and tail entities are nearly equal, but in SKG, such as Enzyme KG and NCI-PID, inhomogeneous is more popular. For example, the tail entities are about 1 000 times more than head ones in the enzyme KG of microbiology area. 2) Head and tail entities can be commuted in OKG,but they are noncommuting in SKG because most of relations are attributes. For example, entity “Obama” can be a head entity or a tail entity, but the head entity “enzyme” is always in the head position in the enzyme KG. 3) Breadth of relation has a small skew in OKG while imbalance in SKG. For example, a enzyme entity can link 31 809 x-gene entities in the enzyme KG. Based on observation, we propose a novel approach EAE to deal with the 3 issues. We evaluate our approach on link prediction and triples classification tasks. Experimental results show that our approach outperforms Trans(E, H, R, D and TransSparse) significantly, and achieves state-of the-art performance.
Key words specific-domain knowledge graph (SKG); enzyme; embedding; inhomogeneous; nonco-mmuting; imbalance
收稿日期: 2017-09-01;
修回日期: 2017-10-17
基金项目: 国家自然科学基金项目(61379050,61532010,91646203,61532016,61762082);国家重点研发计划项目(2016YFB1000603,2016YFB1000602);2017年度河南省科技开放合作项目(172106000077);北大方正集团有限公司数字出版技术国家重点实验室开放课题
This work was supported by the National Natural Science Foundation of China (61379050, 61532010, 91646203, 61532016, 61762082), the National Key Research and Development Program of China (2016YFB1000603, 2016YFB1000602), the Science and Technology Opening up Cooperation Project of Henan Province (172106000077), and the Opening Project of State Key Laboratory of Digital Publishing Technology.
通信作者: 孟小峰(xfmeng@ruc.edu.cn)
中图法分类号 TP181

Du Zhijuan , born in 1986. PhD at Renmin University of China. Member of CCF. Her main research interests include Web data management and cloud data management.

Zhang Yi , born in 1995. Master candidate at Renmin University of China. Member of CCF. Her main research interests include Web data management.

Meng Xiaofeng , born in 1964. Professor and PhD supervisor at Renmin University of China. Fellow of CCF. His main research interests include cloud data management, Web data management,flash-based data-bases, privacy protection etc.

Wang Qiuyue , born in 1974. PhD. Assistant professor at Renmin University of China. Her main research interests include data-base and information systems, information retrieval, knowledge base, natural language questions answering, etc.