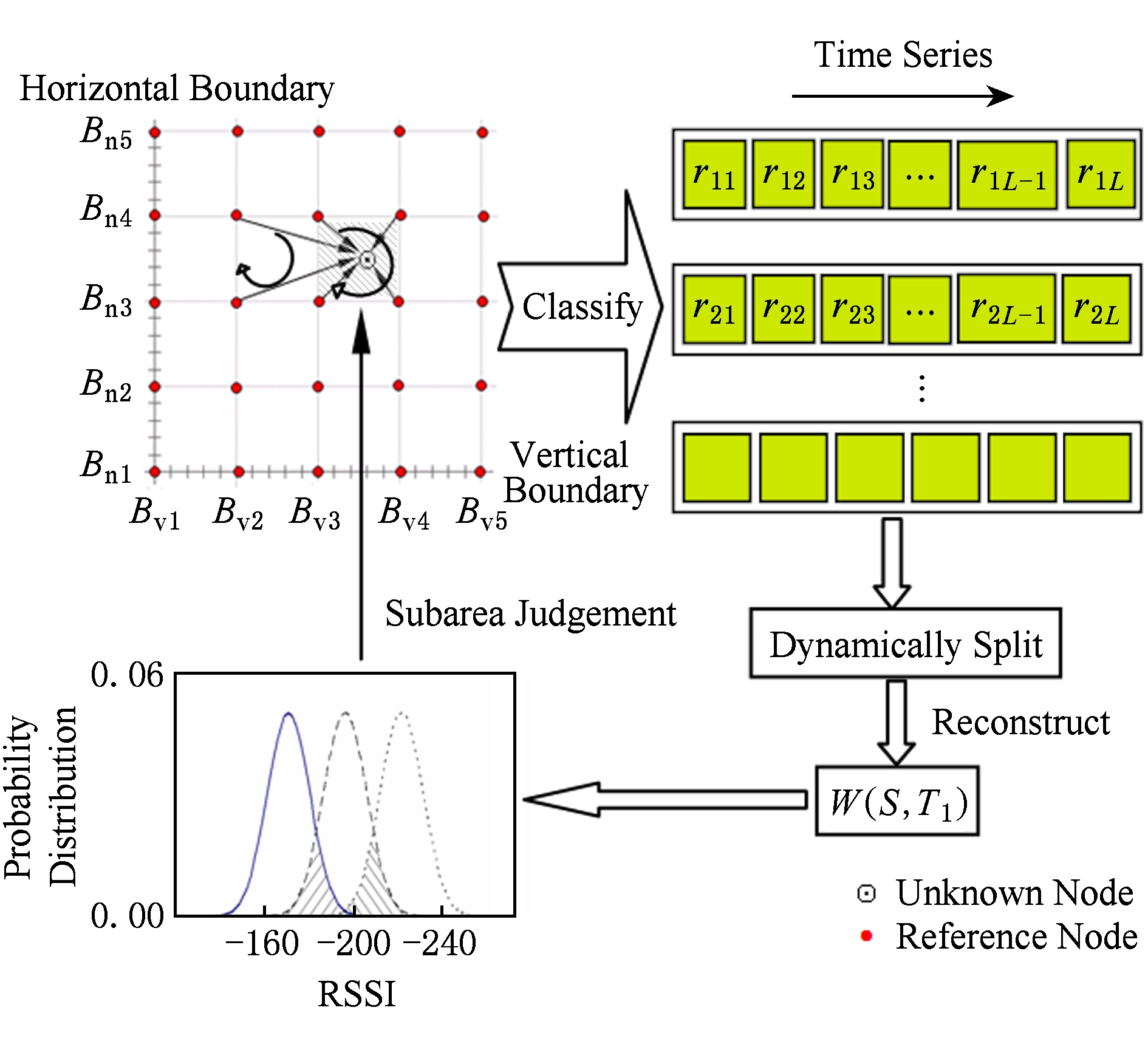
Fig. 1 Trajectory tracking model
图1 轨迹跟踪模型
秦俊平 1,2 邓庆绪 1 孙诗文 2 仁庆道尔吉 2 佟海滨 1 苏宪利 1
1 (东北大学计算机科学与工程学院 沈阳 110819) 2 (内蒙古工业大学信息工程学院 呼和浩特 010080)
(qinjuping30999@sina.com)
摘 要 现有的无线传感器网络室内轨迹跟踪算法是通过定位形成轨迹的,没有利用一定空间范围内相邻信标节点RSSI定位信息在一段时间内的启发式信息.提出了基于RSSI时间序列启发式信息的轨迹跟踪算法,该算法构建基于定位信息时空关联特性的轨迹跟踪模型,对定位信息进行一维重构边界时间序列、二维重构区域统计量、移动最小二乘法检测分别得到动态时间窗口及与之匹配的区域信息及边界信息,在此基础上完成受启发式信息约束的动态时间弯曲轨迹跟踪,并对时空关联模型轨迹跟踪算法中定位信息融合处理的原理进行了严谨的数学论证.通过现场实验与仿真实验表明:该算法轨迹光滑、误差不累积、环境适应性好,相比现有方法基于启发式信息有效克服噪声的影响、减小搜索范围,提高轨迹跟踪的准确性.
关键词 无线传感器网络;接收信号强度指示;时间序列;启发式信息;轨迹跟踪
由于成本低、部署简单、不受通视条件影响,无线传感器网络(wireless sensor network, WSN)被广泛应用于各类室内监控系统中,包括煤矿安全生产监控系统、地铁施工安全实时预警系统、室内精准导航系统等,无线传感器网络的室内应用还处于快速扩展之中.
对于许多室内应用,目标的位置与运动轨迹是最基础信息,也是基于位置服务(location based service, LBS)实现的基础.如在煤矿安全生产监控系统中,人员、移动设备的轨迹是重要的监控内容;地铁施工安全实时预警系统中根据人员与设备、设备与设备的运动轨迹预测并触发预警信号.
室内移动对象的位置信息包括当前位置与移动轨迹2个方面,目前提出的轨迹跟踪模型 [1] 大都将移动对象的轨迹定义为通过室内定位设备感知的位置序列,也就是先定位再形成轨迹.由于定位计算误差不可避免,轨迹中包含的原始位置信息在空间上不一定连续,造成这种现象的原因是定位时没有考虑定位信息是在连续的位置产生的.
研究人员提出多种室内无线传感器网络轨迹跟踪(或者预测)算法,这些算法有的是在对目标定位的基础上形成目标的运动轨迹,有的是基于视频识别形成目标的运动轨迹,还有基于加速度信息形成目标的运动轨迹.
具体到目标定位,由于接收信号强度指示(re-ceived signal strength indicator, RSSI)易于获取,基于RSSI的定位技术一直受到持续的关注 [2] .从本质上来说,基于RSSI的定位属于基于测距的定位技术,常规的作法是先建立RSSI的测距模型,在定位过程中根据所测得RSSI值换算出未知节点与信标节点之间的距离,列出3边定位方程或者多边定位方程求解得到未知节点的当前位置,持续这一过程所得一系列离散点就构成了未知节点的轨迹.这一方法的主要问题是室内RSSI的测距模型受到多径、绕射、测量技术等多种因素的影响而导致有强时变特性,其定位精度相对较低 [3] ,定位成功率不高 [4] .
未知节点在某一位置接收到信标节点发来的RSSI定位信号从而形成这一位置的指纹(fingerprinting),位置指纹定位先离线采集(位置、指纹)数据对并保存在数据库中,定位时用测量值与数据库中指纹进行匹配来确定未知节点位置.由于指纹数据库的RSSI样本是在实际环境中获取的,室内环境指纹定位法的精度明显高于基于测距的定位方法 [5] .
基于上面的原理,美国微软研究院于2000年设计了RADAR [6] 室内定位系统,在线阶段用 K NN( K nearest neighbor)算法选择与测量值最接近的 K 个指纹,取它们的中心位置作为未知节点的当前位置.鉴于RSSI的测量值一般服从一定的概率模型或者近似服从某种概率模型,通过对采集到的数据进行分析,文献[7]描述了移动设备的RSSI概率分布服从正态分布,这是移动设备概率定位法的理论基础;文献[8]对利用概率特性的方法定位与普通非概率定位方法进行了性能比较,从理论上证明概率方法可获得更高的定位精度.
美国马里兰大学的Youssef等人 [9] 提出的Horus定位系统,在离线阶段建立指纹数据库时考虑了指纹的概率分布,将RSSI信息具有相似特征的信标节点划分为一簇,形成一个定位子区域;在线阶段先将未知节点初步定位于某个子区域,再进行精确定位.
肖亚龙等人 [10] 利用不同位置之间的RSSI指纹向量差异来表征对应的物理空间距离,在获取未知节点的大概位置后,通过缩小目标对象的可能取值范围并利用最近的信标节点来进行迭代计算,算法本质上是一种区域细化的定位方法,利用了不同信标节点提供的指纹信息质量的差异来提高定位精度.算法将室内环境的未知节点在每个位置接收到的信标节点信号组织为RSSI指纹向量,则任意2个位置之间的物理距离与对应的RSSI指纹向量之间的差异存在强的相关性,多次测量的统计结果更加稳定.算法采用分层次缩小未知节点所在区域的定位策略,首先根据信标节点位置对区域进行划分,然后根据估算出的位置所属区域对应信标节点位置优化并进行精确定位.
文献[11]考虑到指纹信息的有效利用,采用主成分分析(principal component analysis, PCA)降维算法将原始的RSSI位置指纹转换为PCs(principal components)主成分.PCs模型一方面离线阶段可以减小指纹库的规模,另一方面在线匹配阶段可以减少计算量、提高精度.通过PCA降维,根据信标节点选择指纹的2个准则——最大均值与最大信息增益都被满足,其中最大均值准则优先选择距离未知节点最近的信标节点,最大增益准则选择最富含定位区分能力的信标节点进行定位,同时在降维过程中丢弃的是噪声部分,从而提高定位精度.这些算法没有利用轨迹跟踪过程中同一未知节点连续位置指纹之间的关联.
文献[12]提出的鲁棒性轨迹跟踪算法,在离线阶段采集用户的轨迹指纹信息存放在轨迹指纹数据库中,在线阶段采用鲁棒性的多元统计算法匹配实测轨迹指纹与数据库中的轨迹指纹信息.进行轨迹匹配时先将轨迹根据移动步数分成若干段,多元最小方差算法可以克服采集的低质量的轨迹数据的异常波动,提高映射轨迹指纹到物理位置的精度;为了进行轨迹分段,设备需要有加速度传感器,检测移动步数.
考虑到节点的位置变化受制于现场环境及移动速度,文献[13]引入Markov链描述的状态转移矩阵对位置指纹匹配的搜索范围加以限制,将节点定位看成贝叶斯最大后验概率计算问题;为了克服未知节点移动速度不同对定位造成的影响,文献[14]引入动态时间弯曲(dynamic time warping, DTW)算法进行位置指纹匹配.
视频轨迹跟踪是机器视觉领域中的热点研究问题,为了获得鲁棒性的跟踪效果,设计能够适应跟踪目标外观变化的外观模型成为算法研究中的一项重要内容.将机器学习理论引入外观模型检测 [15] 中的思想大大推动了视频轨迹跟踪研究的发展.文献[16]将视频跟踪问题转换成二分类问题,视频跟踪模型设计机制采用判别式外观模型学习跟踪方法,依据目标和背景的分离边界建立自适应性外观模型实现轨迹跟踪.梯度特征通常以区域统计的形式描述目标外观,尺度不变性特征转换算子 [17] 被用来描述目标的结构性外观变化并取得了不错的效果.基于外观模型的视频轨迹跟踪算法要求对场景进行全方位监控,而且光线充足才能保证轨迹精度.
对于离散的、误差较大的定位所得目标位置信息进行时空数据挖掘得到(或者预测)目标的运动轨迹.时空数据挖掘 [18] 就是从具有海量、高维、高噪声和非线性等特性的时空数据中提取出隐含的、人们事先不知道的、但又潜在有用的信息及知识的过程.时空数据挖掘的关键在于发现与具体问题相关的时空信息中蕴含的有用信息,必要时可以对原始信息进行变换或者重构 [18] .
本文提出的算法利用没有特殊硬件要求的RSSI位置指纹实现轨迹跟踪,将轨迹跟踪问题中RSSI定位信息概率分布特征与时空数据挖掘统筹考虑,通过合理部署信标节点发现启发式信息并利用基于启发式信息受限的指纹匹配算法实现高精度的轨迹跟踪.
本文的主要贡献有4个方面:
1) 算法构建基于定位信息时空关联特性的轨迹跟踪模型,采用RSSI时间序列考虑轨迹跟踪问题,将离散的定位问题转换为连续的时间序列特征发现问题;
2) 提出移动最小二乘启发式信息检测算法,对于启发式信息出现的理论依据进行了数学证明,并且根据启发式信息实现了动态时间窗口划分,与该时间窗口对应的轨迹坐落于定位空间某区域;
3) 轨迹跟踪采用受限的DTW位置指纹匹配,有效克服了噪声的影响,提高了轨迹跟踪准确度;
4) 现场实验与仿真实验证明了基于启发式信息的轨迹跟踪算法的正确性,从实践层面验证了算法的有效性.
为了充分利用移动的未知节点定位信息概率分布统计特性,针对室内应用(信标节点可人为部署),提出轨迹跟踪模型定义,以2维平面为例,如图1所示进行描述.
定义1 . 区域(subarea).2维平面由纵横相邻的4个信标节点所划分的平面子部分,图1中每个小方格为一个区域.

Fig. 1 Trajectory tracking model
图1 轨迹跟踪模型
定义2 . 边界(boundary).2维平面由水平/垂直方向的信标节点所构成的平面分界线,图1中每条横线/纵线( B h / B v )为一条边界.
模型中未知节点发送通知信号,接收到通知信号的邻近信标节点以相同频率独立地发射定位信号,未知节点接收到来自每个信标节点的定位信号按照到达时间的先后构成一个RSSI时间序列(time series)
R i =( r i 1 , r i 2 , r i 3 ,…, r ik ,…, r iL ),
(1)
其中, r ik 表示第 i 个信标节点的对应时间序列 R i 中第 k 个RSSI值.一段时间内,每个信标节点向当前未知节点发送的定位信息按照到达时间的先后组成一个 R i , i 表示信标节点ID号, R i 存放在未知节点处并进行处理.在较小范围内(相对于节点通信半径)讨论问题时,假设临近信标节点所发射定位信号未知节点都可接收到,则在同一个时间窗口内不同时间序列的长度相等,不同时间序列同一下标的分量对应几乎同一时间点,如图1所示,或者说,相当于在某个位置,未知节点几乎同时接收到其临近信标节点发射的定位信号,当未知节点移动到下一位置后,再次接收到这些信标节点发送的定位信号,以次类推.下标的分量 k 隐含表示相对时间信息,即相对于时间窗口起点的时间为 k ×(1/ f ), f 为信标节点发射定位信号频率(发射次数/秒).
时间序列 R i 的值为带有噪声的RSSI值,不同环境的噪声影响是不相同的;同一环境下,噪声的影响也是时变的 [19] .虽然有多种RSSI与距离的衰减模型,但对于实际问题,很难精确地选定模型及这些模型的参数 [20] .但有一点是研究者公认的,距离越近,RSSI值越大.
另一方面,文献[7]指出有多种RSSI测量值中噪声近似服从正态分布,文献[8]提出了基于概率分布的定位算法并进行了理论证明.
当在2维平面定义了区域与边界后,未知节点的正常移动就是从一个区域到另一个相邻区域,其间跨跃某一(几)条边界的过程.不失一般性,假设未知节点在较小范围内做近似匀速运动(较长时间的停顿可以依据RSSI变化检测出来).在现场实验中只要速度变化不剧烈,就可以取得不错的轨迹跟踪效果.
对于轨迹跟踪问题,未知节点是连续移动的,在引入区域与边界后,定义区域统计量与边界时间序列.区域与边界是按照特定位置关系形成的信标节点组合,以定位信号重构的形式考虑区域与边界所涉及的信标节点,这些定位信号蕴含丰富的时空信息.在时间窗口中分析这些统计量,可以有效地降低噪声影响,并且可以从整体上分析这些统计量的变化趋势.
定义3 . 区域RSSI时间窗口统计量.
/ L ,
(2)
其中, n 为区域 S 包含信标节点个数, L 为时间序列长度, L 与时间窗口大小 T 1 成正比例,即:
L = T 1 × f .
(3)
W ( S , T 1 )集中表示了时间窗口 T 1 内未知节点周围信标节点以区域为单位RSSI大小,是对原始定位信息的2维重构, W ( S , T 1 )反映了区域与未知节点一段时间内的相对距离关系.
定义4 . 边界RSSI时间序列.
R b =( r b 1 , r b 2 , r b 3 ,…, r bk ,…, r bJ ),
(4)
其中,
r bk =( r i 1 + r i 2 )/2.
(5)
J 为边界时间序列长度, R b 的每个分量 r bk 是从边界 b 的时间序列第 k 个分量上选择的2个信标节点(边界上相邻的、一段时间内强度最强的2个)对应的RSSI均值,边界RSSI时间序列对应时间窗口 T 2 为相邻区域时间窗口 T 1 中点之间时间段,如图2所示. R b 反映了时间窗口 T 2 以边界为单位的RSSI变化情况,是对原始定位信息的一维重构.

Fig. 2 Boundary time window and SBE detection
图2 边界时间窗口与SBE检测
定义5 . 边界跨越事件(spanning boundary event, SBE).未知节点从一个区域到达相邻区域,必然要在期间某个时间点跨跃边界( B h / B v ),如图2中虚线所示,边界跨越事件可以表示为
e span ( T 2 , t , b ),
(6)
其中, T 2 为该事件所在的时间窗口, T 2 取相邻 T 1 窗口的中间部分, t 为事件发生的时间点, b 为所跨跃的边界编号.边界跨越事件的物理含义为在 T 2 内,未知节点逐步接近、到达 b ,之后又远离 b ,期间在时间点 t 与 b 相交,下面分析跨越边界过程中 R b 的变化趋势.
定理1 . 在不考虑噪声的情况下,未知节点在边界上取得边界时间序列 R b 中最大值.
证明. 如图3所示,未知节点逐步接近边界,之后逐步离开,其中, q 为区域边长.在每个位置 p k ,未知节点接收到边界上信标节点发射的定位信号,计算 r bk 作为 R b 的第 k 个分量(下面的证明中未知节点作以水平方向为主的运动,以垂直方向为主的运动同理).
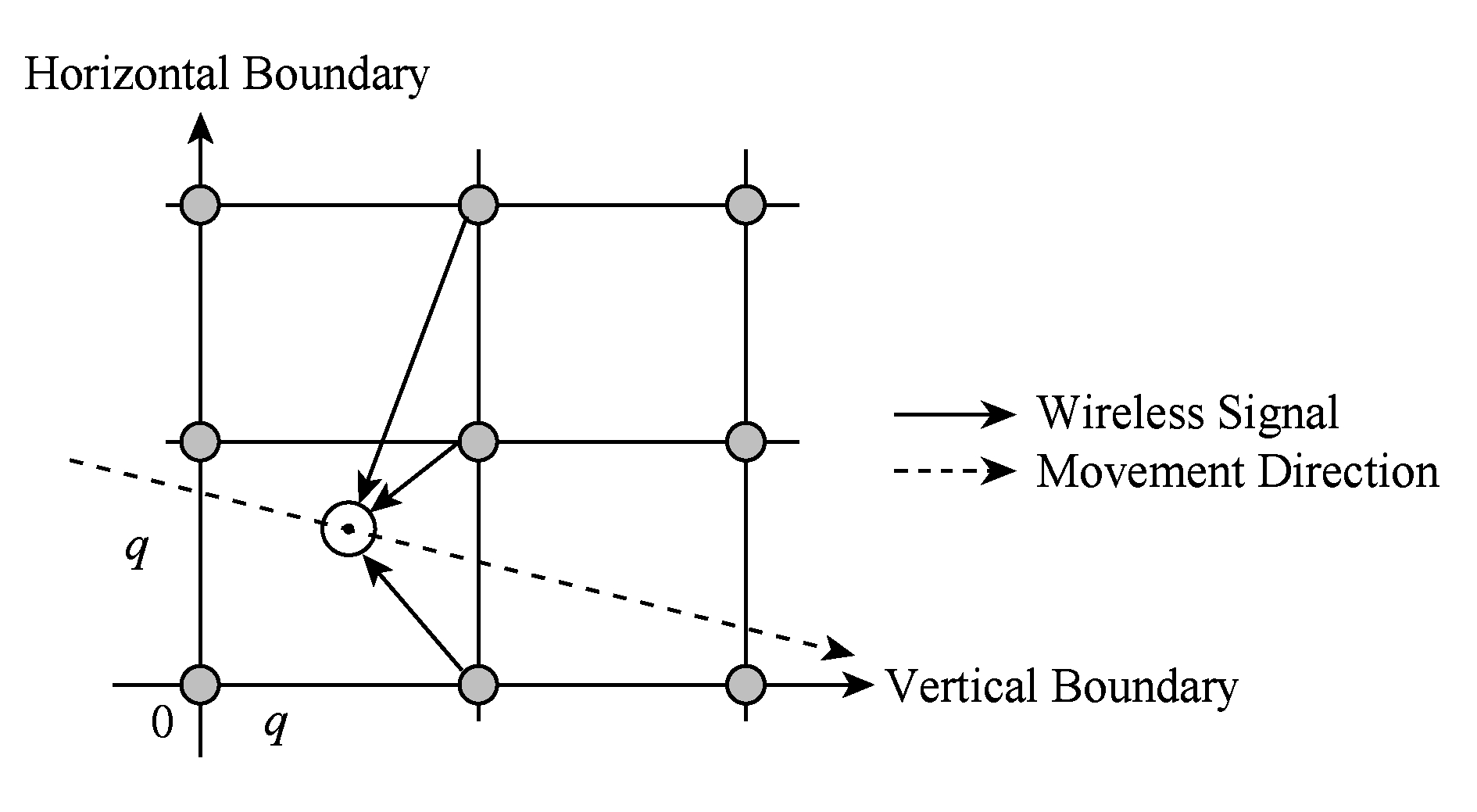
Fig. 3 Rb’s tendency
图3 Rb的变化趋势
Shadowing模型是目前在无线传感器网络研究中最普遍使用的路径损耗模型,综合考虑了信号在传输过程中衰减与距离之间的关系以及各向异性传播特征,RSSI的理论模型 [20] 为
(7)
R ( d )=10lg P ( d ),
(8)
R ( d )= R ( d 0 )-10 β lg( d / d 0 ),
(9)
其中, R ( d )表示距离为 d 处的RSSI, R ( d 0 )表示距离为 d 0 的参考点处RSSI.从理论模型可见,当 β 取值处于一定范围内时,RSSI随着 d 的增加而减小,且减小的速度先快后慢.
P ( d )表示距离信号发射点 d 处的能量均值(单位mW), P ( d 0 )表示距离 d 0 处的能量均值, d 0 =1 m, β 为路径衰减因子,环境不同, β 取值不同,在较小范围内,可以认为 β 取值不变.由式(7)可得:
P ( d )= ![]() ,
,
(10)
其中 d 0 =1 m, P ( d 0 )表示为 g ,则 P ( d )= ![]() ,将 r bk 看作位置 p k ( x , y )的函数,并对 x 求偏导数,得:
,将 r bk 看作位置 p k ( x , y )的函数,并对 x 求偏导数,得:
(11)
当 x = q 时, ![]() =0.根据该问题所表示的实际含义, x = q 作为唯一的驻点, r bk 取得极大值,意味着在未知节点跨越边界的一段时间内,在边界上取得边界时间序列的极值.
=0.根据该问题所表示的实际含义, x = q 作为唯一的驻点, r bk 取得极大值,意味着在未知节点跨越边界的一段时间内,在边界上取得边界时间序列的极值.
证毕.
实验中,由于定位信号的发射有一定间隔,未知节点可能在最接近边界处取得极大值,在定位信号发射间隔较小的情况下,引起的误差较小.
实际中,未知节点接收到的定位信号RSSI满足 [20] :
R ( d )= R ( d 0 )-10 β lg( d / d 0 )+ X ,
(12)
其中, X 表示多径、绕射、障碍物等多种因素引起的RSSI噪声, X 被看作一个以0为均值、 σ 2 为方差的高斯白噪声,即:
X ~ N ( μ , σ 2 ),
(13)
X 的概率密度函数为
(14)
随着环境不同, σ 取值不同.
假设:
1) 未知节点在时间窗口 T 1 中一直位于某个区域内部,如一直位于区域 S A ,如图4所示,接下来以 S A 周围的区域 S B , S C 作为对比,说明不同区域 W ( S , T 1 )的统计特性差异,其中 S 表示区域号, A , B , C 表示区域类别.
2) 在远小于节点通信半径的范围内,可以保证信标节点发射并且为未知节点所接收的定位信号个数是相同的且为 L ;对于次数少于 L 的区域,其位于对比范围之外.
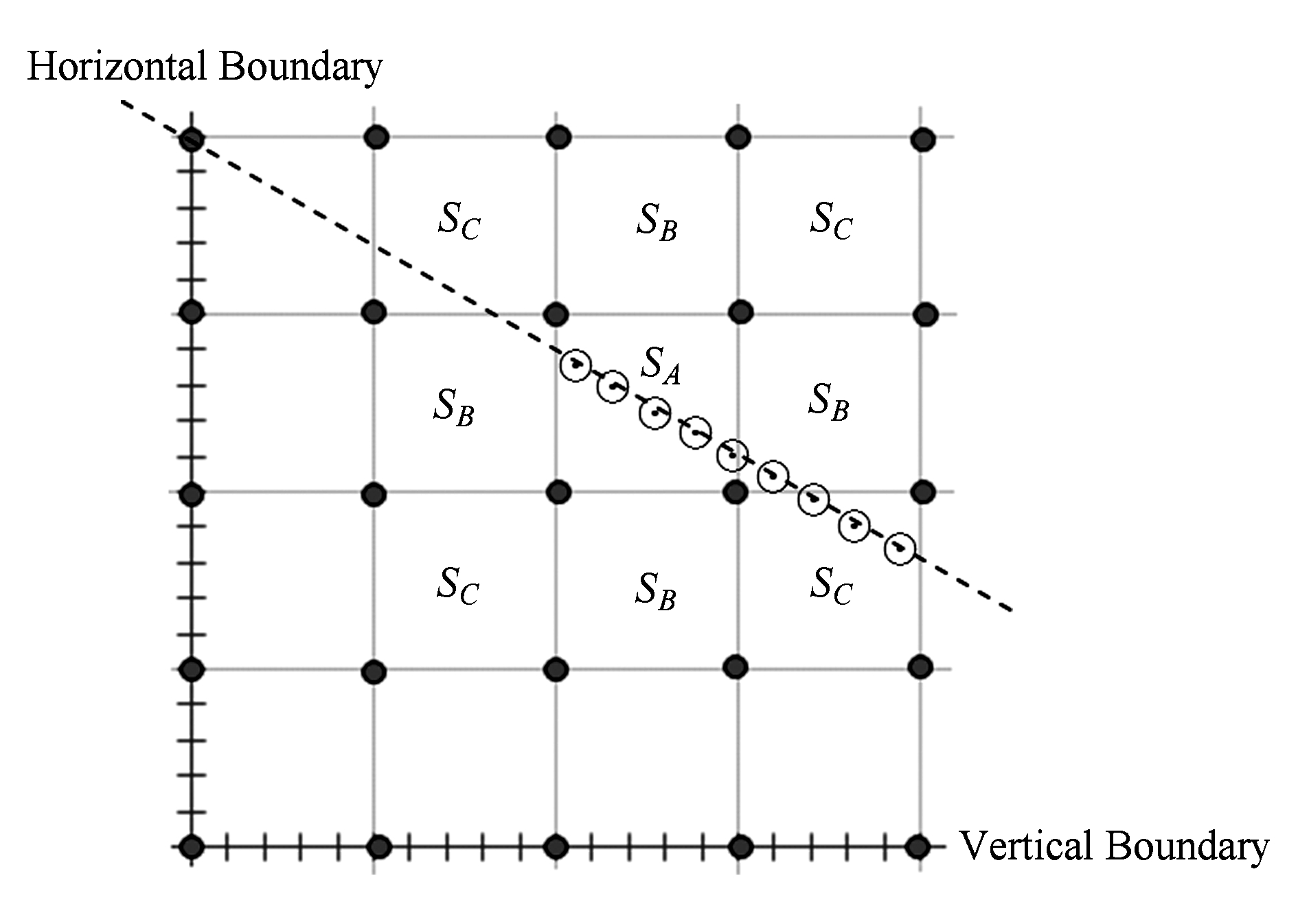
Fig. 4 Subarea relation
图4 区域关系
3) 在轨迹跟踪模型中,所有信标节点发射定位信号的参数设置(发射功率大小)相同、所配置天线相同,2维平面被划分为多个区域,区域内及区域判定算法涉及的相邻区域较小范围内(远小于节点通信半径),假设 β 与 σ 2 取值相同.
定义6 . 区域RSSI向量.
V S =( r ul , r ur , r lr , r ll ),
(15)
V S 表示某时间点未知节点所接收的来自某区域顺时针方向,见图1中弧形箭头,从左上角到左下角4个信标节点RSSI所组成向量.
定义7 . 区域RSSI向量之和.
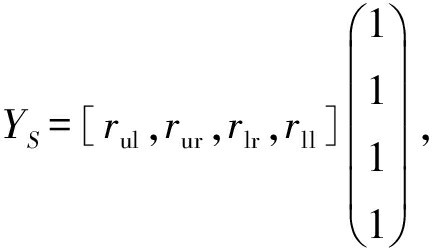
(16)
Y S 用矩阵相乘的形式表示4个分量的累加和,一方面说明在和值中每个分量的权重相同,另一方面说明 Y S 表示该时间点未知节点与区域的相对关系.
定理2 . Y S ~ N ( μ ul + μ ur + μ lr + μ ll ,(2 σ ) 2 ),其中 μ ul , μ ur , μ lr , μ ll 分别为未知节点相对于4个信标节点当前RSSI均值,均值的大小取决于信标节点与未知节点之间的距离, σ 为区域当前RSSI方差.
证明. 由式(12)可得,任一RSSI测量值 R ( d )由理论值式(8)与噪声 X 累加而成,将其看作随机变量,根据前面的假设,在较小范围内对于某个未知节点所在的某位置 p i (如图4虚线上小圆圈), d 确定后理论值 R ( d 0 )-10 β lg( d / d 0 )是确定的,相当于常量,故:
R ( d )~ N ( R ( d 0 )-10 β lg( d / d 0 ), σ 2 ),
(17)
σ 2 为噪声 X 的方差.
Y S 为4个独立信标节点对应RSSI值的累加和,各个信标节点独立地发射定位信号,未知节点接收并形成RSSI向量 V S ,故 V S 包含的4个分量相对独立,根据相互独立的随机变量之和仍然服从正态分布可得:
(18)
其中, σ ul , σ ur , σ lr , σ ll 分别为对应区域4个信标节点当前RSSI方差,根据假设, σ ul = σ ur = σ lr = σ ll = σ , σ 为所涉及区域的RSSI标准差,故:
Y S ~ N ( μ ul + μ ur + μ lr + μ ll ,(2 σ ) 2 ).
(19)
证毕.
定理3 .
(20)
其中, μ 1 , μ 2 ,…, μ L -1 , μ L 分别为在区域内不同点处 Y S 分布的均值, σ 2 为区域当前RSSI方差.
证明.
/ ![]() / L ,
/ L ,
其中, W ( S , T 1 )表示未知节点在某区域内 L 个位置时信标节点以区域为单位测量并计算的 Y S 均值,如图4所示.同样,在每个未知节点位置 p i , Y S 相互独立,
(21)
根据 E ( CX )= CE ( X )及 D ( CX )= C 2 D ( X ), ![]() /
/ ![]() 也就是 W ( S , T 1 )服从均值为
也就是 W ( S , T 1 )服从均值为 ![]() 、方差为
、方差为 ![]() 的高斯分布.
的高斯分布.
证毕.
从统计量 W ( S , T 1 )相对于 Y S 的分布均值与方差变化速率来看,在 L 个位置 p i ,如图4所示,测量 Y S 并求统计量均值 W ( S , T 1 ),分布均值与方差的变化速率是不相同的,方差有变小的趋势( L 越大效果越好),即减少了噪声的影响,这是利用 W ( S , T 1 )推断区域的重要原因.
RSSI随着 d 的增加而减小,减小的速度先快后慢, W ( S , T 1 )由 L 个位置 p i 对应 Y S 计算均值得到,对于每个 Y S ,其分布的均值仅取决于 p i 与每个区域对应4个信标节点的距离.以区域 S A , S B 为例,如图5所示,除 l 3 , l 4 这2条公共边外 ![]() 从而 W ( S A , T 1 )的分布均值大于 W ( S B , T 1 )的分布均值.
从而 W ( S A , T 1 )的分布均值大于 W ( S B , T 1 )的分布均值.
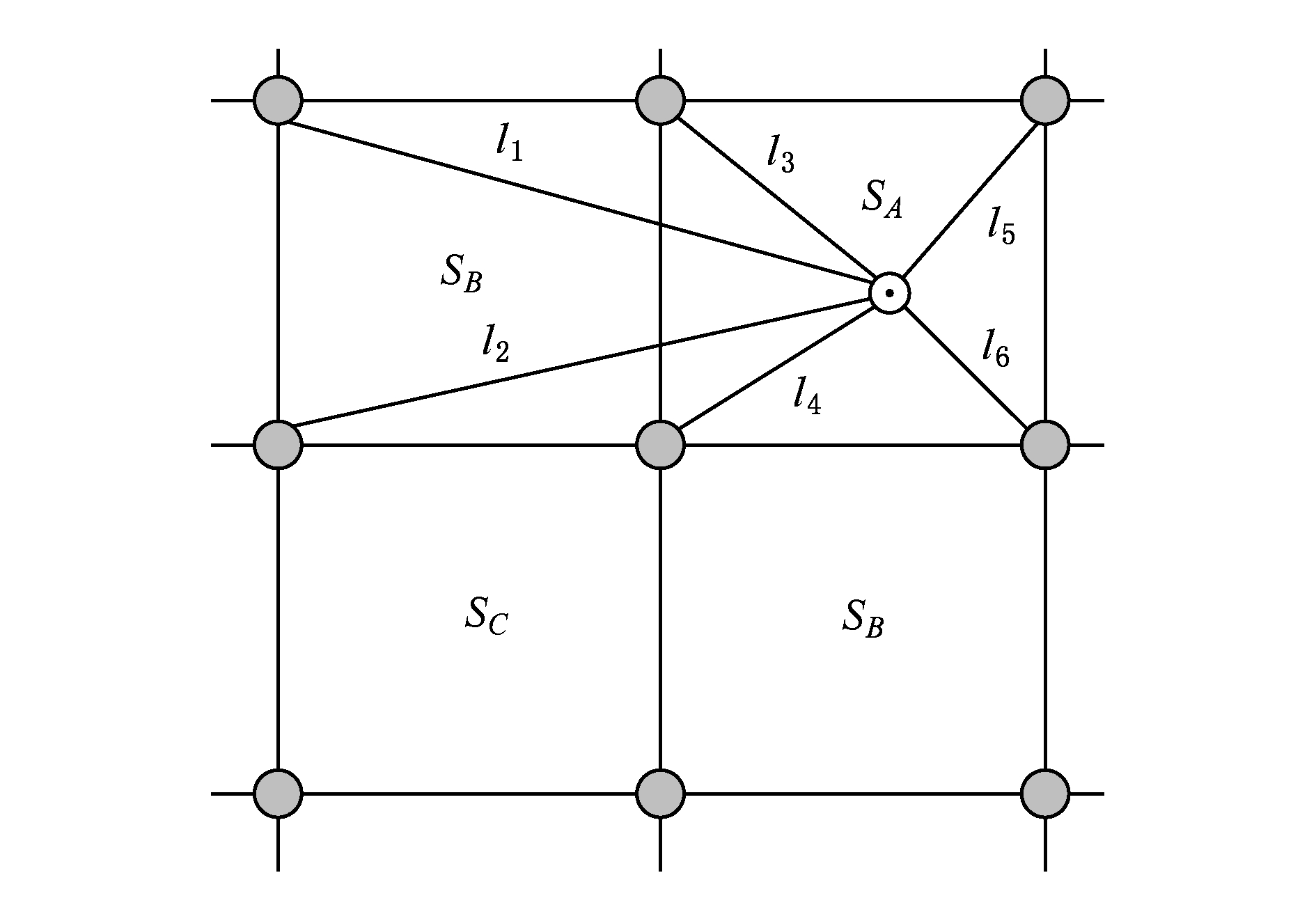
Fig. 5 Subarea W(S,T 1 ) relation
图5 区域W(S,T 1 )关系
W ( S , T 1 )由 L 个位置 p i 处 Y S 计算均值得到,根据式(22)可见, W ( S , T 1 )相当于在区域 S 内某定点多次测量计算均值的效果(从减少方差的角度看).
min( μ 1 , μ 2 ,…, μ L -1 , μ L )≤ ![]() ≤
≤
max( μ 1 , μ 2 ,…, μ L -1 , μ L ).
(22)
区域RSSI时间窗口统计量、边界RSSI时间序列与边界跨越事件 e span 都包含丰富的时间、空间信息.
下面将详细介绍用移动最小二乘法检测边界跨越事件、判定动态切分时间窗口内轨迹所在区域、计算轨迹的算法.在上述模型定义的基础上,基于启发式信息的轨迹跟踪算法步骤如下:
1) 在定位空间内按照纵横方向等间距网格状部署信标节点,将信标节点信息( Node ID ,( x , y ))保存在每个未知节点处,在未知节点形成区域信息与边界信息,其中 Node ID 为信标节点的ID,( x , y )为其坐标;
2) 接收到通知信息的信标节点以固定频率发射定位信号,未知节点接收并按照信标节点分别形成多个时间序列 R i ;
3) 各未知节点根据移动最小二乘法检测边界跨越事件、动态切分时间窗口、构建区域时间窗口统计量,推断当前区域;
4) 根据当前区域信息进行受限的位置指纹匹配,形成轨迹.
构建基于定位信息时空关联特性的轨迹跟踪模型后,未知节点在移动过程中会产生边界信息、区域信息,下面阐述启发式信息检测算法.
根据边界时间序列检测边界跨越事件,就是要根据离散数据发现时间序列的变化规律并找出一段时间内的极大值.考虑到轨迹的连续光滑要求及噪声影响,选用移动最小二乘法进行分段的曲线拟合:
线性基:
p ( x )=(1, x ) T ,
(23)
系数向量:
a ( x )= A -1 ( x ) B ( x ) y ,
(24)
其中:
A ( x )= ![]() w ( x - x j ) p ( x j ) p T ( x j ),
w ( x - x j ) p ( x j ) p T ( x j ),
(25)
n 为影响区域内节点个数,
B ( x )=( w ( x - x 1 ) p ( x 1 ),
w ( x - x 2 ) p ( x 2 ),…, w ( x - x n ) p ( x n )),
(26)
y T =( y 1 , y 2 ,…, y n ),
(27)
拟合函数为
(28)
其中, m 为线性基函数的项数,权函数选用三次样条权函数:
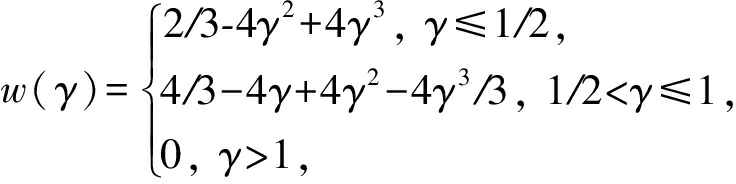
(29)
γ =( x - x i )/ γ max ,
(30)
其中, γ max 为影响区域的长度,对于每个数据点,根据权函数选择其周围的若干个数据点以不同的权值参与拟合,越靠近的数据权值越大,基函数 p ( x )的阶数决定了曲线的精度,根据实验结果选用线性阶基函数可以保证精度.
为找出极值点,要保证曲线前后的连续性,这是选用移动最小二乘法的主要原因.从理论上来说,跨越边界时 r bk 取得极大值,由于噪声的影响为了避免伪峰值对极值点加以限定引入阈值 T b , T b 要现场多次测量确定.
算法1 . SBE检测算法.
输入:边界时间序列 R b ;
输出: e span 对应时间点及边界号.
1) 对本区段 R b 进行移动最小二乘拟合处理;
2) 上一区段与本区段连接;
3) 检测极值点 m b ,要求 m b ≥ T b , m b 存在则执行4),不存在则返回1)等待新的区段边界时间序列;
4) 返回 e span 对应时间点 t b 及边界号 b ,时间点表示未知节点经过边界 b 的时间点.
检测到未知节点跨越边界的时间点后,2条相邻边界对应时间点确定出一个时间窗口 T 1 (符合定理3的假设),下面确定未知节点在 T 1 时间窗口所在区域.
对于未知节点来说,在时间窗口 T 1 内 Y S 与 W ( S , T 1 )的分布如图6所示,图6(a)为 Y S 的分布,图6(b)为 W ( S , T 1 )的分布.
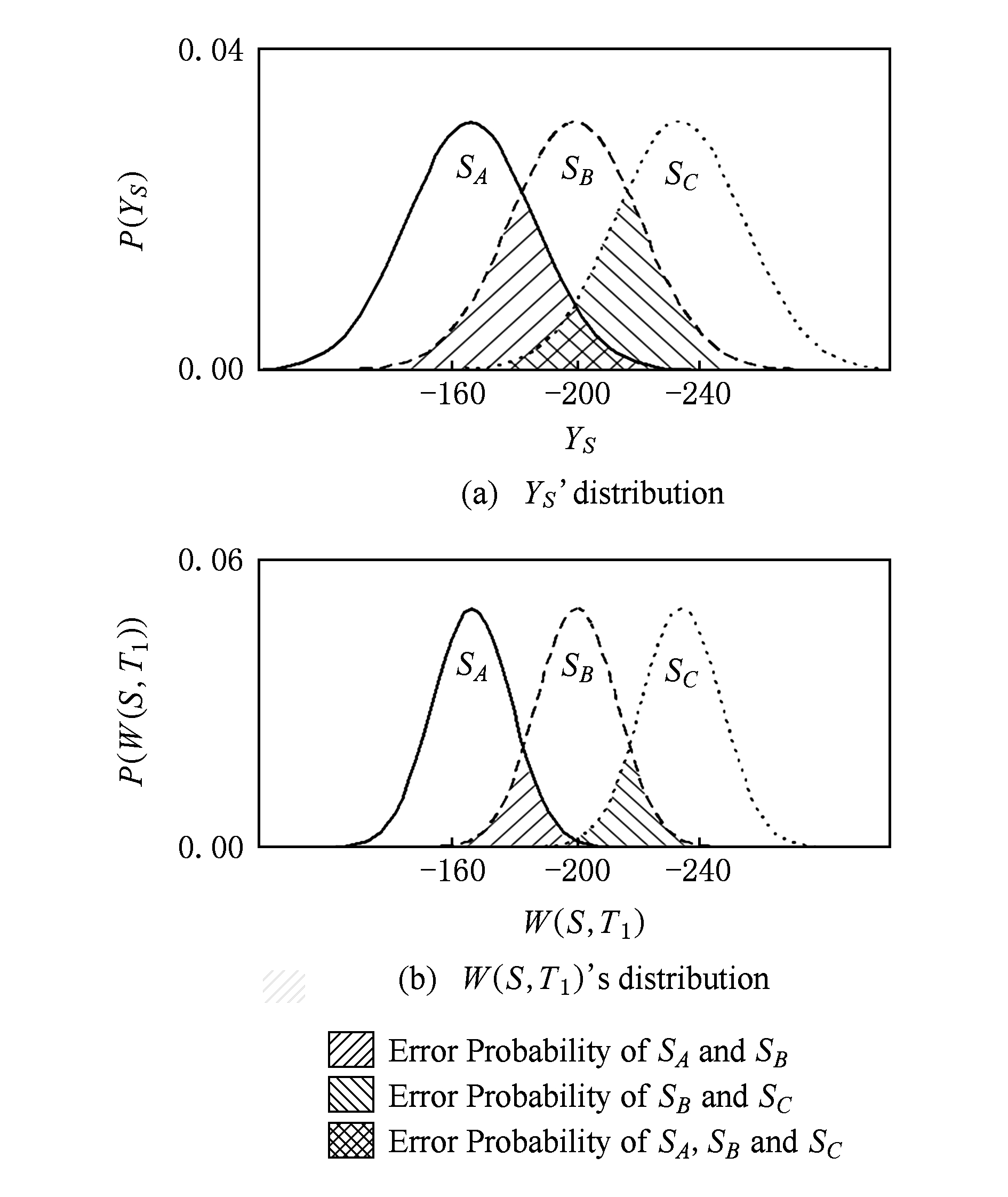
Fig. 6 W(S,T 1 ) and Y S ’ Distributions
图6 W(S,T 1 )与Y S 分布
在模式识别中,已知每类事物的总体概率分布,及类的条件概率密度,用Bayes决策理论实现分类的方法如下(假设共有2个类别ϖ 1 与ϖ 2 ),已知 p (ϖ 1 ), p (ϖ 2 )且:
p (ϖ 1 )+ p (ϖ 2 )=1,
(31)
p ( z |ϖ 1 )表示在ϖ 1 中观察到 z 的概率密度, p ( z |ϖ 2 )表示在ϖ 2 中观察到 z 的概率密度,则:
p (ϖ i | z )= 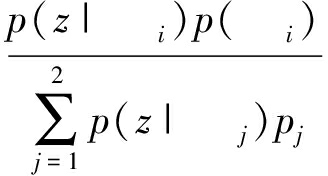 ,
,
(32)
表示观察到 z 属于哪个类别ϖ i 的概率.根据最小错误率贝叶斯决策规则,如果 p (ϖ i | z )=max ( p (ϖ i | z )),则 z ∈ϖ i .
图6中阴影区域表示发生误判的情况.显然不同类别的随机变量 μ 相距越远, σ 越小,越有利于分类.
根据 W ( S , T 1 )判定区域的算法中,对未知节点所在区域的判断,当放在时间窗口中研究时,大量现场实验证实,只需要考虑 S A , S B , S C 这3类区域,也就是:
p ( S A | W ( S , T 1 ))+ p ( S B | W ( S , T 1 ))+
p ( S C | W ( S , T 1 ))=1.
(33)
由于每类区域 W ( S , T 1 )的分布均值不固定(取决于未知节点的运动轨迹),故选定相对量进行分类.基于 W ( S , T 1 )区域判定算法,在 T 1 内以区域为单位分别计算 W ( S , T 1 ),以
arg max( W ( S i , T 1 ))
(34)
作为未知节点在 T 内所在区域.
区域判定算法准确度,在 T 内由于噪声的影响使非未知节点当前所在区域的 W ( S , T 1 )超过当前所在区域时,即发生了区域误判.下面讨论误判发生可能性的影响因素.
若区域判定正确,也就是满足:
( W ( S A , T 1 )> W ( S B , T 1 ))∩
( W ( S A , T 1 )> W ( S C , T 1 )),
(35)
区域误判也就是:
( W ( S A , T 1 )< W ( S B , T 1 ))∪
( W ( S A , T 1 )< W ( S C , T 1 )).
(36)
图6中阴影部分的面积大小表示区域误判发生的可能性,其大小取决于分布均值的差值、分布的标准差2 σ / ![]() ,而标准差2 σ /
,而标准差2 σ / ![]() 又取决于 L ( σ 是由环境决定的),减慢移动速度(增加在区域内停留时间)、增加定位信号发射次数都可以提高区域判定准确度.当边界确定后,由于仅需要考虑相邻边界之间的区域,相对于图4中区域数量减少,进一步提高区域判定准确度.
又取决于 L ( σ 是由环境决定的),减慢移动速度(增加在区域内停留时间)、增加定位信号发射次数都可以提高区域判定准确度.当边界确定后,由于仅需要考虑相邻边界之间的区域,相对于图4中区域数量减少,进一步提高区域判定准确度.
算法2 . 区域检测算法(subarea judgement algorithm, SJA).
输入:相邻边界时间点;
输出:该时间窗口对应区域号.
1) 计算时间窗口 T 内相邻边界间各窗口 W ( S , T 1 );
2) 返回arg max( W ( S i , T 1 ))对应区域.
位置指纹定位先离线采集(位置,指纹)数据对并保存在指纹数据库中,定位时根据指纹数据进行匹配来确定未知节点位置.指纹数据的噪声不可避免,在启发式信息的限定下进行位置指纹匹配,有效减小匹配范围并提高定位精度.
受样本采集、存储以及定位计算开销等的限制,基于位置指纹的定位方法需要对连续位置空间进行离散化处理,即把室内空间划分成若干个网格,如图7所示,每个网格采集其中心位置的位置指纹并存储在数据库中用于目标位置推断.位置指纹以区域RSSI向量 V S 的形式表示,采集到RSSI样本后,一旦确定其 T 1 内所属区域,则形成区域RSSI向量并进行匹配.
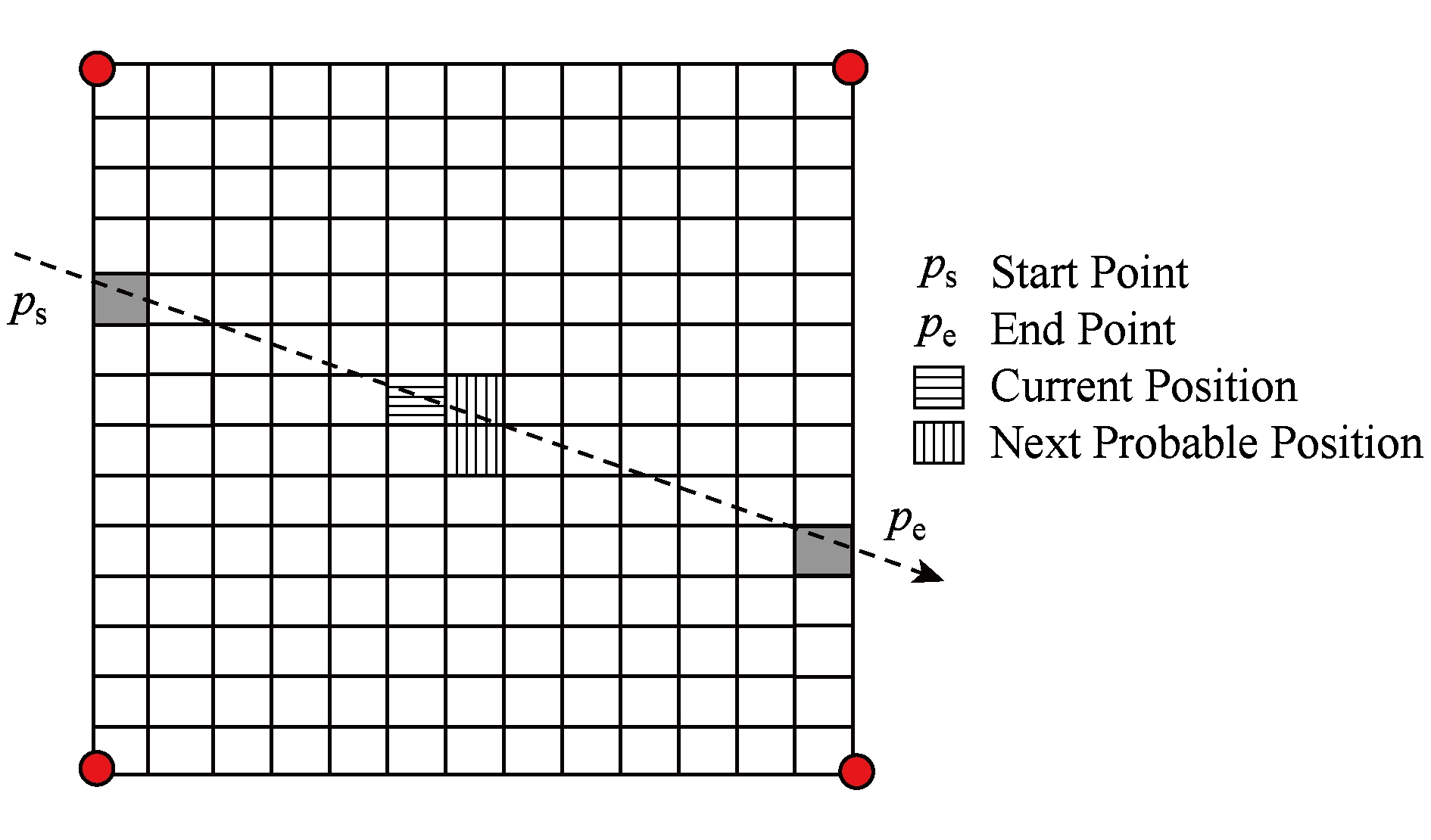
Fig. 7 Restricted position fingerprint matching
图7 受限的位置指纹匹配
为提高指纹数据的精度,离线数据库在一个位置采集多次,取其均值存放.采样位置密度高,数据库占用空间大,定位精度高;反之则精度低.本文算法用于轨迹跟踪,考虑人的正常移动速度0.7 m/s,选择采样间隔0.5 m.
单点指纹匹配用区域RSSI向量的欧几里德距离来度量测量值 ![]() 与数据库保存值 V S 之间的相似度为
与数据库保存值 V S 之间的相似度为
(37)
算法分别在边界进行单点匹配确定区域内起点位置 p s 与终点位置 p e ,如图7中深灰色位置所示.
轨迹指纹匹配用动态时间弯曲DTW算法来度量区域内RSSI向量测量值 ![]() 所形成时间序列与可能的轨迹对应时间序列的相似度(将从起点到终点的一条轨迹各位置对应指纹按序看作一时间序列),设测量值时间序列 U =( u 1, u 2,…, u n 1 ),可能轨迹时间序列
所形成时间序列与可能的轨迹对应时间序列的相似度(将从起点到终点的一条轨迹各位置对应指纹按序看作一时间序列),设测量值时间序列 U =( u 1, u 2,…, u n 1 ),可能轨迹时间序列
W =( w 1, w 2,…, w n 2 ),
n 1, n 2分别为2个序列的长度,则:
D DTW ( U , W )= D base ( u 1, w 1)+ 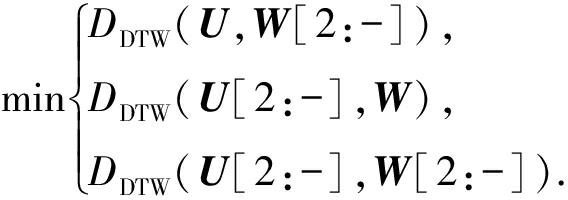
(38)
用欧几里德距离作为 D base 及2点间距离,由 D DTW 的递归定义可见, D DTW 可以衡量长度不同的2个时间序列的相似度.可能轨迹需要满足的3个基本条件:
1) 每条可能轨迹的起点为 p s ,终点为 p e ;
2) 轨迹要求连续,即如果当前时间点 t 匹配位置 p (如图7所示,横底纹位置),时间点 t +1秒(实验中每秒发射1次定位信号)仅需在其附近可能到达的范围内进行匹配,也就是在上、右上、右、右下、下、左下、左、左上等位置搜索;
3) 轨迹上相邻点要满足单调性要求,此条件与运动方向有关,例如当前时间点 t 匹配位置 p (见图7,横底纹位置),时间点 t +1秒仅需搜索其右侧、右下位置(竖底纹位置).
区域内RSSI向量测量值 ![]() 形成时间序列,选择其中相似度最高的轨迹作为轨迹跟踪的结果,相对于现有匹配算法,利用了“同一未知节点时间上连续的指纹信息对应空间位置也相邻”的特性.
形成时间序列,选择其中相似度最高的轨迹作为轨迹跟踪的结果,相对于现有匹配算法,利用了“同一未知节点时间上连续的指纹信息对应空间位置也相邻”的特性.
算法3 . 受限的DTW位置指纹匹配算法.
输入:区域RSSI向量测量值 ![]() 时间序列、位置指纹数据库;
时间序列、位置指纹数据库;
输出:区域内最匹配轨迹.
1) 以区域为单位对RSSI向量进行移动最小二乘拟合处理;
2) 依据式(37)计算起点与终点在边界上位置;
3) for 满足3个基本条件的每一条路径
计算 D DTW ;
end for
4) 输出相似度最高的可能轨迹作为轨迹跟踪结果.
算法的验证既有仿真实验,也有现场实验.现场实验信标节点信息( Node ID ,( x , y ))保存在每个未知节点处,指纹数据库保存在汇聚节点,各未知节点独立地进行边界检测与区域检测,将边界信息与区域信息上传至汇聚节点,汇聚节点据此完成指纹匹配,区域边长 q =6.5 m,信标节点部署如图1所示,现场实验采用的无线收发芯片为CC2530.
仿真实验在NS-2环境进行,采用Shadowing模型,分别选标准差 σ 为5 dBm与10 dBm、节点最大通信距离为50 m、路径损耗系数 β =3作为实验参数进行实验.
第1组实验检测边界,观察边界时间序列的变化趋势,按照图3所示运动方向进行测试.
从实验结果可见,无论是现场实验还是仿真实验,当未知节点经过边界时,边界时间序列都会出现一个明显的上升、下降过程,理论上极值点在边界(如图8中虚线所示)处取得,实验中可能会略有偏移(见图8(b)实际极值点相对边界靠右1 s),导致极值点偏移的可能原因有噪声较强,也可能是定位信号发射时错开边界位置所致.
第2组实验检测区域,依据最小错误率贝叶斯决策规则判断时间窗口内未知节点所属区域,按照图3所示运动方向进行测试.
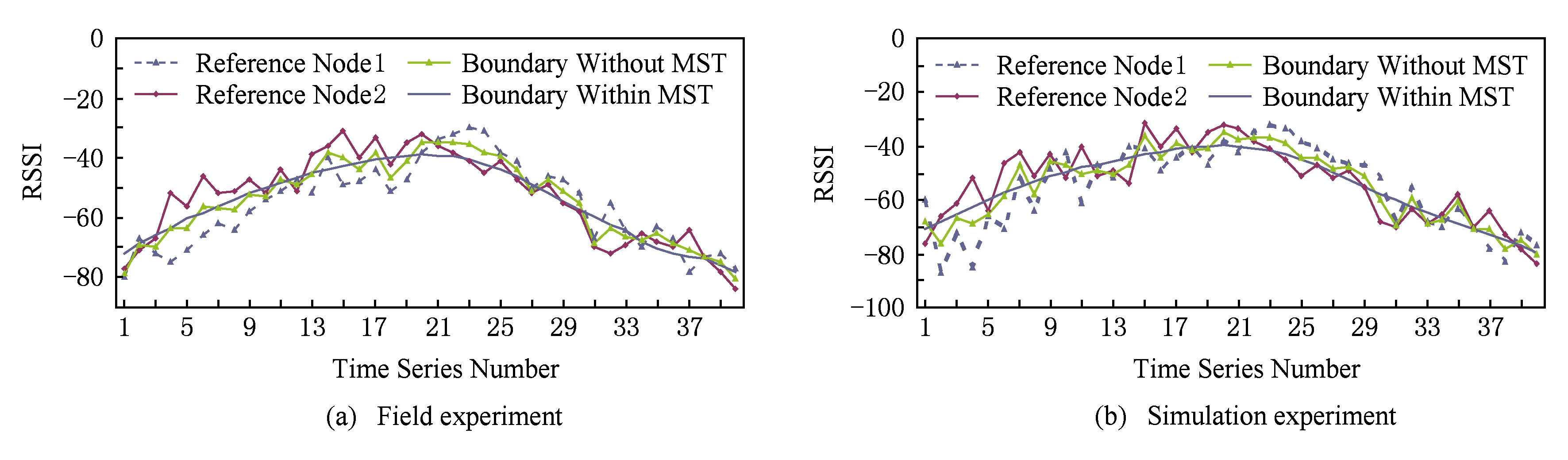
Fig. 8 Detecting boundary
图8 检测边界
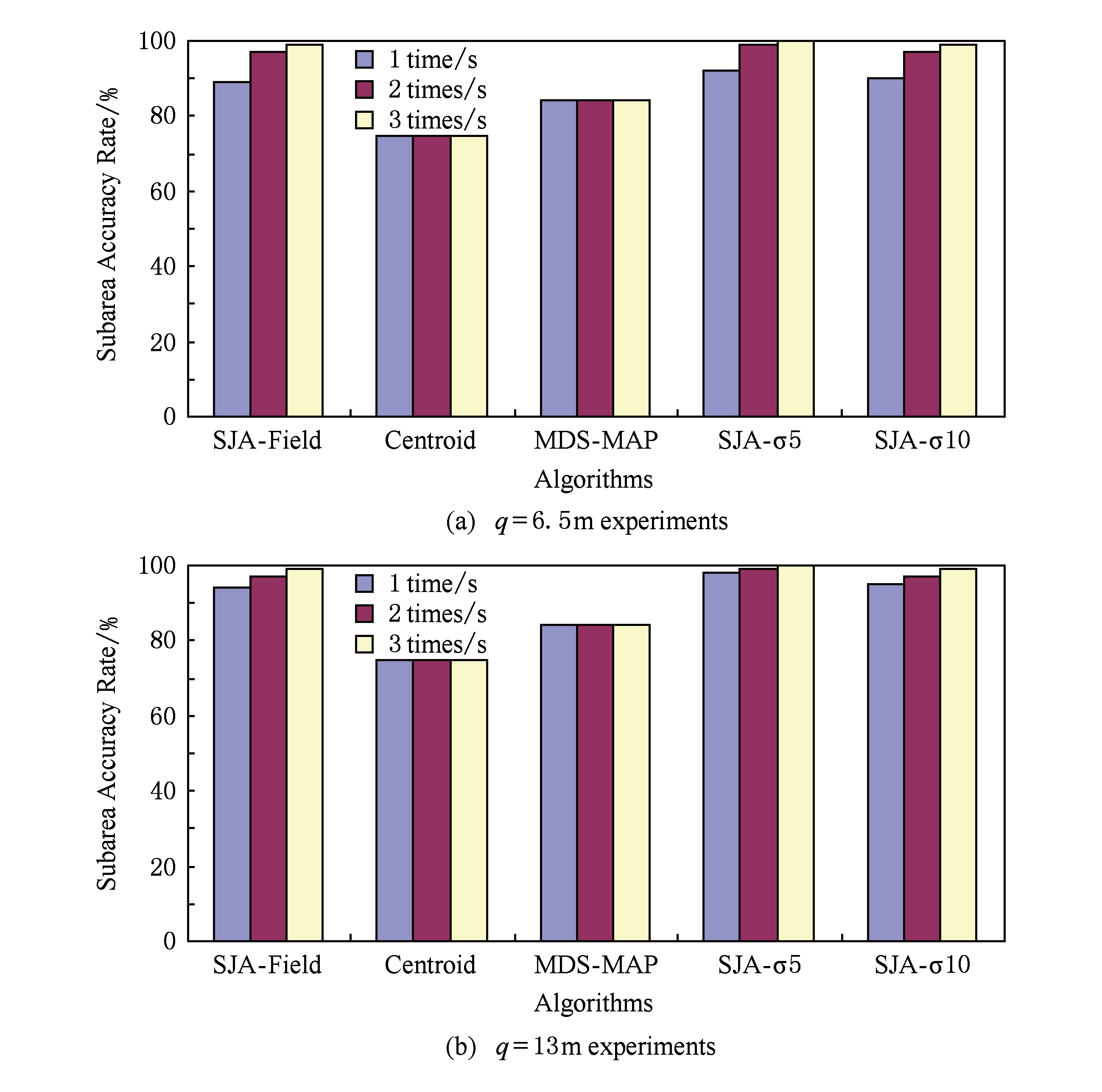
Fig. 9 Subarea judgment accuracy rate
图9 区域判定准确率
图9(a)为 q =6.5 m时的区域判定准确率,其他参数不变, q =13 m时的区域判定结果如图9(b)所示.可见,随着定位信号单位时间发射次数的增多,依据最小错误率贝叶斯决策规则判定区域的算法准确率都有所提高,但总的来说, q =13 m时的区域准确度明显好于 q =6.5 m时的情况,这主要是由于随着时间窗口的增大, W ( S , T 1 )的统计特性更好所致.算法准确率也受到RSSI噪声的影响,噪声越小、准确率越高.
质心(centroid)算法与多维标度(MDS-MAP)算法以多次定位中所在区域正确的比例衡量区域准确率,质心算法的区域判定性能比较差,因为没有利用定位信息的统计特性;多维标度算法进行多维转换确定位置,区域准确度介于质心算法与本文算法之间.
轨迹跟踪全部采用现场实验进行验证,选择 q =6.5 m间距部署信标节点,人手持未知节点以正常行走速度0.7 m/s移动,所得轨迹如图10所示.图10中实线表示真实轨迹,虚线表示本文提出基于时间序列启发式信息的室内轨迹跟踪算法所得到轨迹,三角符号表示采用质心定位算法计算所得离散点位置,在此基础上形成轨迹如点虚线所示,注意定位结果包含野值.
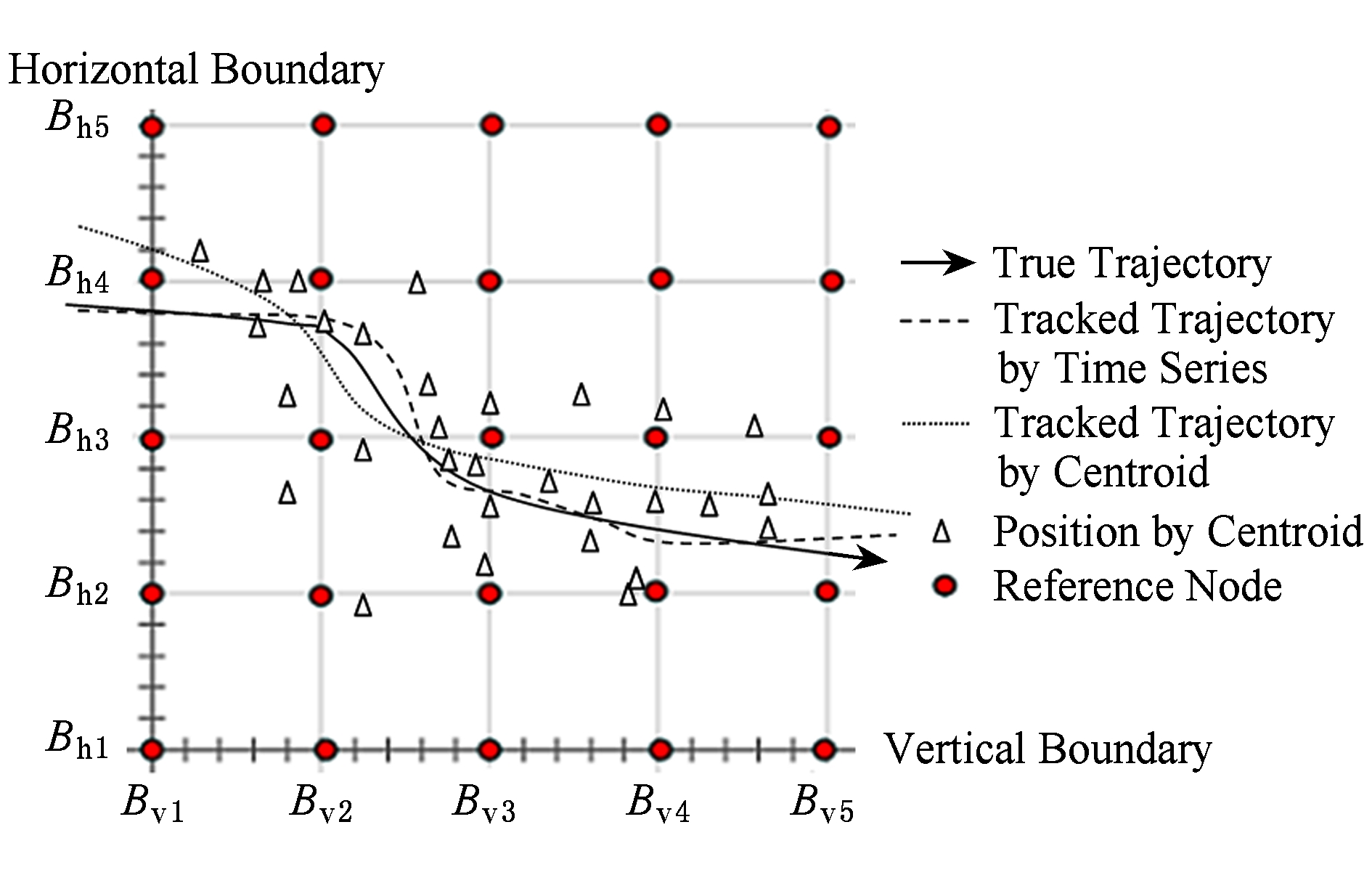
Fig. 10 Trajectory tracking
图10 轨迹跟踪
算法运行过程中,依次检测到 B v1 , B v2 , B h3 , B v3 , B v4 , B v5 各边界,判断出依次经过 S 1 , S 2 , S 3 , S 4 , S 5 各区域,区域标识如图11所示,在区域内得出的轨迹如图10所示.

Fig. 11 Trajectory tracking at the speed of 0.3 m/s
图11 0.3 m/s移动速度下的轨迹跟踪结果
从图10可见,本文算法有高的精度,现场实验轨迹精度可以达到1.0 m以内,高精度是以室内空间网格状部署信标节点从而可以获得启发式信息为基础得到的.
为了比较不同移动速度下的算法性能,在与图10相同的信标节点部署条件下,人手持未知节点以行走速度0.3 m/s移动,所得轨迹如图11所示.算法依次检出的边界、区域与行走速度0.7 m/s时相同.2次轨迹由于RSSI噪声的影响有细微差异.
对于运动速度不均匀的场合,算法是根据边界时间序列 R b 的变化趋势动态划分时间窗口并根据统计量 W ( S , T 1 )来判定所在区域的,区域检测不受影响.
区域内的轨迹是采用受限的DTW位置指纹匹配算法以区域为单位进行位置指纹匹配求取的,对于非匀速运动的目标,算法根据轨迹对应的RSSI序列与指纹数据库中的指纹进行匹配,所检测的轨迹形状没有问题,但是以时间点来看,位置会向前或者向后发生一定的偏离,这种偏离仅限于区域内,下一个区域又会以区域边界为起点/终点进行新一轮匹配计算,所以这种偏离引起的误差不会在区域间累积.如图12所示,实验中开始移动速度较快,之后速度变慢,图12中实心点表示位置有较大偏移(>1 m),但这种偏移是沿着跟踪到的轨迹方向的,从轨迹跟踪的角度来说,算法有较好的鲁棒性;从定位的角度来说,由于在每个区域内先确定起点与终点,之后进行指纹匹配,所以区域间定位误差不会累积,靠近两端的点位置偏移较少.
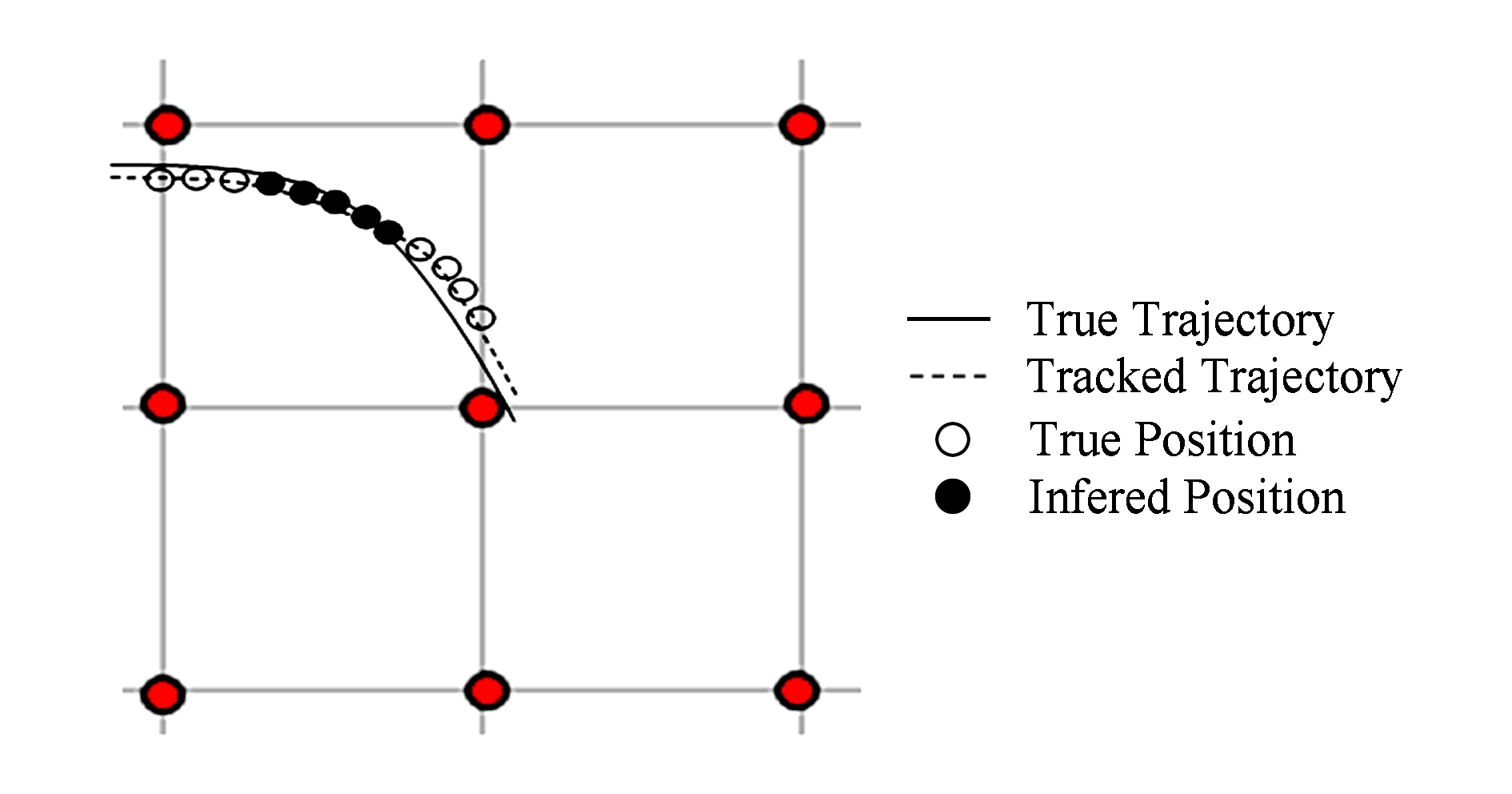
Fig. 12 Trajectory tracking at nonuniform speed
图12 非均匀移动速度下的轨迹跟踪

Fig. 13 Experimental Nodes
图13 实验节点
图13(a)所示为现场实验所用信标节点,图13(b)所示为未知节点.
算法首先完成边界检测、区域检测,再进行区域内轨迹跟踪,是分阶段实施的.其中的边界检测与区域检测各未知节点独立进行,各未知节点独立地划分动态时间窗口,时间窗口内轨迹跟踪涉及指纹数据库,在汇聚节点完成.算法仅需要将所确定区域对应RSSI数据上传,减少了定位信息通信量.
同一未知节点时间上连续的指纹信号,对应的空间位置也必然相邻.为了充分挖掘这种时空关联特性,本文构造了基于定位信息时空关联特性的轨迹跟踪模型并设计了相应算法.
边界检测算法是根据边界时间序列的变化趋势设计的,根据边界所划分的动态时间窗口内区域判定算法依据最小错误率贝叶斯决策规则设计,区域内轨迹跟踪采用动态时间弯曲位置指纹匹配算法.
算法将一段时间内的轨迹跟踪作为连续变化的时间序列来考虑,充分利用序列的变化趋势、统计特性得到重要的启发式信息.算法在时间窗口内整体判断统计量分布及边界时间序列变化趋势,可以有效降低噪声影响,减少野值出现.关于区域RSSI统计量的分布及边界时间序列的变化趋势理论上满足文中结论.区域以动态时间窗口为单位判断,误差不累积,且区域判断采用相对指标使算法能适应不同的环境.
算法采用分阶段实施的方式,充分利用节点的计算能力,只向汇聚节点传输部分信息,相关数据结构在未知节点存储需要一定的存储空间开销.
本文的轨迹跟踪模型要求信标节点网格化部署,未来的研究方向是使算法能适应信标节点位置不规律的场景.
参考文献
[1]Jin Peiquan, Wang Na, Zhang Xiaoxiang, et al. Moving object data management for indoor space[J]. Chinese Journal of Computers, 2015, 38(9): 1777-1795 (in Chinese)(金培权, 汪娜, 张晓翔, 等. 面向室内空间的移动对象数据管理[J]. 计算机学报, 2015, 38(9): 1777-1795)
[2] Yang Zheng, Liu Yunhao, Li Xiangyang. Beyond trilatera-tion: On the localizability of wireless ad-hoc networks[J]. ACM Trans on Networking, 2010, 18(6): 1806-1814
[3] Meguerdichian S, Slijepcevic S, Karayan V, et al. Localized algorithms in wireless ad-hoc networks: Location discovery and sensor exposure[C] //Proc of the 2nd ACM Int Symp on Mobile Ad-Hoc Networking & Computing. New York: ACM, 2001: 106-116
[4] Wang Fubao, Shi Long, Ren Fengyuan. Self localization systems and algorithms for wireless sensor networks[J]. Journal of Software, 2005, 16(5): 1148-1157 (in Chinese)(王福豹, 史龙, 任丰原. 无线传感器网络中的自身定位系统和算法[J]. 软件学报, 2005, 16(5): 1148-1157)
[5] Hossain AKMM, Soh WS. A survey of calibration free indoor positioning systems[J]. Computer Communications, 2015, 66(1): 1-18
[6] Bahl P, Padmanabhan V N. RADAR: An in-building RF based user location and tracking system[C] //Proc of the 19th IEEE Int Conf on Computer and Communications. Piscataway, NJ: IEEE, 2000: 775-784
[7] Kaemarungsi K, Krishnamurthy P. Analysis of WLAN’s received signal strength indication for indoor location fingerprinting[J]. Pervasive and Mobile Computing, 2012, 8(2): 292-316
[8] Roos T, Myllymaki P, Tirri H, et al. A probabilistic approach to WLAN user location estimation[J]. International Journal Wireless Information Networks, 2002, 9(3): 155-164
[9] Youssef M, Agrawala A. The Horus WLAN location determination system[C] //Proc of the 3rd Int Conf on Mobile Systems, Applications, and Services. New York: ACM, 2005: 205-218
[10] Xiao Yalong, Zhang Shigeng, Wang Jianxin. An indoor localization algorithm based on multidimensional scaling and region refinement[J]. Chinese Journal of Computers, 2017, 40(8): 1918-1932 (in Chinese)(肖亚龙, 张士庚, 王建新. 一种基于多维标度和区域细化的无线室内定位方法[J]. 计算机学报, 2017, 40(8), 1918-1932)
[11] Fang Shihhau, Lin Tsungnan. Principal component localization in indoor WLAN environments[J]. IEEE Trans on Mobile Computing, 2012, 11(1): 100-110
[12] Zhang Xinglin, Yang Zheng, Wu Chenshu, et al. Robust trajectory estimation for crowdsourcing based mobile application[J]. IEEE Trans on Parallel and Distributed Systems, 2014, 25(7): 1876-1885
[13] Zhao Fang, Luo Haiyong, Ma Yan, et al. An accurate fingerprinting localization algorithm based on common beacons[J]. Journal of Computer Research and Development, 2012, 49(2): 243-252 (in Chinese)(赵方, 罗海勇, 马严, 等. 基于公共信标集的高精度射频指纹定位算法[J]. 计算机研究与发展, 2012, 49(2): 243-252)
[14] Wang Jue, Katabi D. Dude, where’s my card: RFID positioning that works with multipath and non-line of sight[J]. ACM SIGCOMM Computer Communication Review, 2013, 43(4): 51-62
[15] Zhang Huanlong, Hu Shiqiang, Yang Guosheng. Video object tracking based on appearence models learning[J]. Journal of Computer Research and Development, 2015, 52(1): 177-190 (in Chinese)(张焕龙, 胡士强, 杨国胜. 基于外观模型学习的视频目标跟踪方法综述[J]. 计算机研究与发展, 2015, 52(1): 177-190)
[16] Song Yizhe, Li Chuan, Wang Liang, et al. Robust visual tracking using structural region hierarchy and graph matching[J]. Neurocomputing, 2012, 89(10): 12-20
[17] Hare S, Saffari A, Torr PHS. Struck: Structured output tracking with kernels[C] //Proc of the 13th IEEE Int Conf on Computer Vision. Los Alamitos, CA: IEEE Computer Society, 2011:263-270
[18] Liu Dayou, Chen Huiling, Qi Hong, et al. Advanced in spatiotemporal data mining[J]. Journal of Computer Research and Development, 2013, 50(2): 225-239 (in Chinese)(刘大有, 陈慧灵, 齐红, 等. 时空数据挖掘研究进展[J]. 计算机研究与发展, 2013, 50(2): 225-239
[19] Huang He, Chen Guoliang, Sun Yu’e, et al. Localization algorithm in complex area[J]. Journal of Computer Research and Development, 2011, 48(3): 364-373 (in Chinese)(黄河, 陈国良, 孙玉娥, 等. 复杂区域节点定位算法研究[J]. 计算机研究与发展, 2011, 48(3): 364-373)
[20] Rappaport T S. Wireless Communications: Principle and Practice[M]. Upper Saddle River, NJ:Prentice Hall, 1999
Qin Junping 1,2 , Deng Qingxu 1 , Sun Shiwen 2 , Renqing Daoerji 2 , Tong Haibin 1 , and Su Xianli 1
1 ( School of Computer Science and Engineering , Northeastern University , Shenyang 110819) 2 ( College of Information Engineering , Inner Mongolia University of Technology , Hohhot 010080)
Abstract Existing indoor trajectory tracking algorithms on wireless sensor network are based on continuous localization and can not make use of the heuristic information of RSSI time series within a certain temporal and spatial range. The heuristic information of RSSI time series is a key factor of trajectory tracking procedure. This paper proposes a new trajectory tracking algorithm on spatiotemporal correlation model based on heuristic information. According to the heuristic information related to moving trajectory, the new method contains the following essential phases. Firstly, we model the trajectory tracking model reflecting spatiotemporal correlation and statistical characteristics. Secondly, we detect spanning boundary event and judge which subarea the unknown node was in by means of information fusion of RSSI time series and moving least square method. Finally, the moving trajectory of unknown node is formed by means of dynamic time warping fingerprinting matching algorithm with heuristic information constraints. The principles of information fusion are strictly proved in mathematics. The field experiments and the simulation experiments show that the algorithm has good environment adaptability, smooth trajectory and the error does not accumulate among the subareas. Compared with the existing methods, the accuracy of trajectory tracked is improved.
Key words wireless sensor network (WSN);
received signal strength indicator (RSSI); time series; heuristic information; trajectory tracking
收稿日期: 2016-11-08;
修回日期: 2017-02-21
基金项目: 国家自然科学基金项目(61472072,61540004);内蒙古自然科学基金项目(2015MS0619,2013MS0920);内蒙古高等学校科学研究项目(NJZY091)
This work was supported by the National Natural Science Foundation of China (61472072, 61540004), the Natural Science Foundation of Inner Mongolia of China (2015MS0619, 2013MS0920), and the Higher Educational Scientific Research Project of Inner Mongolia (NJZY091).
中图法分类号 TP393

Qin Junping , born in 1974. PhD candidate. Associate professor. Member of CCF. His main research interests include pattern recognition, localization, and information fusion in WSN.

Deng Qingxu , born in 1970. PhD. Professor and PhD supervisor. Senior Member of CCF. His main research interests include reconfigurable computing systems, multi-processor real time scheduling and formal methods in real-time system analysis.

Sun Shiwen , born in 1991. Master candidate. Her main research interests include image recognition based on machine learning and localization in WSN.

Renqing Daoerji , born in 1983. PhD. Associate professor. His main research interests include moving object data mining and optimization.

Tong Haibin , born in 1986. PhD candidate. His main research interests include information security technology in WSN and industrial detection technology.

Su Xianli , born in 1980. PhD candidate. His main research interests include cyber physical systems and intelligent optimiza-tion method.