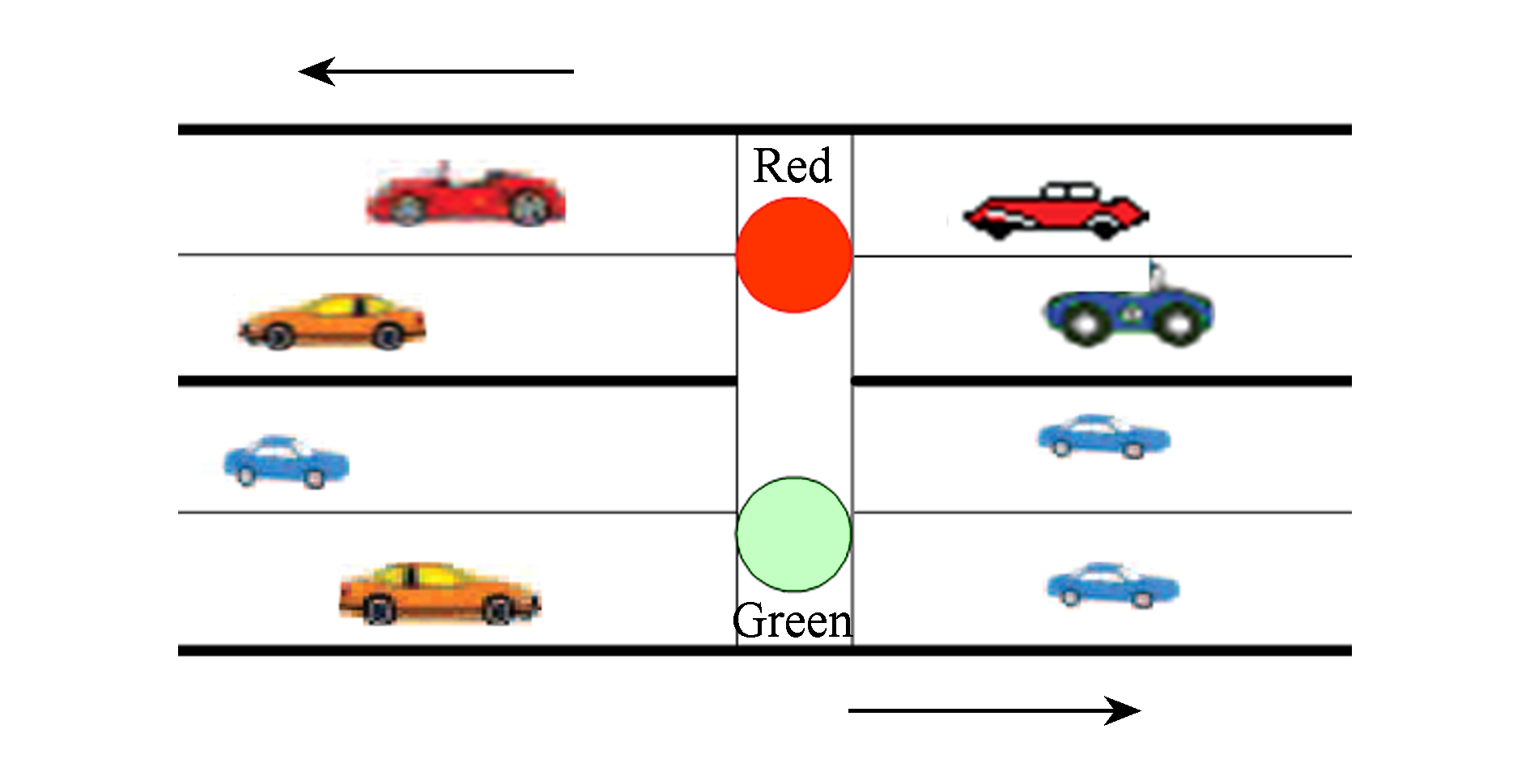
Fig. 1 Vehicles travel on the road
图1 汽车在城市道路行驶
王秀峰 崔 刚 王春萌
(哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001)
(wxf@hit.edu.cn)
摘 要 链路时延是决定车联网(vehicular ad hoc networks, VANETs)许多网络性能的重要标准.现存的VANETs基于节点移动性解决链路时延的问题,但是都没有预测的功能,不适合实际VANETs中动态预测车-车(vehicle to vehicle, V2V)链路时延.提出动态预测任意2车链路时延的数学模型DPLD,考虑2车相对速度分布、相对距离变化、交通密度和城市场景中交通灯因素对2车之间链路时延的影响,因为这些因素在链路连接过程中是变化的.通过考虑相对速度的分布,模型能够实时地调整原则自适应车速变化.通过自动调整2车之间相对距离计算方法,DPLD模型能够自适应2车间相对距离的变化.因此该模型能够有效地预测预期要发生的2车之间的链路时延.这个模型实现取决于相对速度分布参数的估计方法、指数移动平均法对车速异常处理以及交通灯对链路时延影响的概率建模并且详细给出2车遇到不同交通灯的具体链路时延预测方法.仿真结果表明:DPLD模型预测的城市环境的2车之间链路时延准确性很高.
关键词 车联网;链路时延;交通密度;预测模型;车-车
车联网(vehicular ad hoc networks, VANETs)承诺为驾乘人员提供安全和娱乐信息服务,保证道路交通的安全性、增强交通系统运行的可靠性、提高交通系统的运行效率.这种安全应用要求V2V数据实时、可靠、低延迟地传输,数据通信需要一段完整的链路时延.因此链路时延成为衡量网络性能的关键属性,也是多跳信息传输选择中继节点的重要依据之一.
关于网络性能的链路时延问题在DTN(delay tolerant networks)和MANET (mobile ad hoc networks)中研究较多 [1-2] .基于移动性模型RWP(random waypoint models) [3] ,RW(random walk) [4] ,RPGM(reference point group mobility),RVGM (reference velocity group mobility model) [5-6] ,文献[7]研究节点移动性对链路时延的影响.节点移动性的因素包括节点的速度、2节点之间的距离和节点的移动方向等对链路时延有较大的影响;文献[8-9]基于移动性提出链路时延能够有效地用指数分布近似.假设节点移动遵循RWP模型;文献[10]提出移动投影轨迹算法估计剩余链路寿命(residual link lifetime, RLL);文献[11]使用链路已经连接多久作为参数估计链路剩余的时间,提出链路剩余寿命和2节点的相对速度相关;文献[12]使用卡尔曼滤波法(unscented Kalman filter, UKF)提出一个新的RLL-预测算法预测链路寿命.但是这些在移动自组网里解决链路寿命预测的方法不能用在VANETs中,因为VANETs中的车辆移动性不遵循MANET中移动性模型.
为了给VANETs中链路时延建模,文献[13-14]提出2个分析性的研究框架.不过城市场景VAENTs中链路时延建模受多种因素的影响,包括车间距离的变化、车速、汽车在道路交叉口的转向、交通灯变化、汽车的行驶方向等因素.研究资料表明车速服从正态分布,因此,我们建模考虑相对速度的分布而不是某一车辆的瞬时速度.
现存的研究链路时延方法考虑的因素包括节点的位置、速度、距离、运动方向、速度之间的夹角、交通灯的变化,但没有预测功能,只是计算链路已经连接多久.而本文提出动态预测链路时延(dynamically predict link duration, DPLD)模型能够实时地预测城市场景VANETs中2车的链路时延.建立DPLD模型主要考虑节点的位置、相对速度的分布、节点运动方向、2车之间的距离变化、无线信号传输范围、交通灯变化对链路时延的影响,并且分析车辆速度变化对链路时延造成的影响.
目前VANETs中有一些研究链路时延的成果,Nekovee在文献[15]中假设车间的相对距离是恒定的,并且忽略汽车的移动性模型研究链路时延的概率.然后假设汽车的速度服从正态分布扩展这个研究 [16] .在文献[17]中Yan等人提出指数分布是VANETs中链路时延很好的近似.
目前,对VANETs的链路时延或连接性的研究针对某一特定的场景.文献[18]提出1维高速公路场景中的链路时延;Boban等人在文献[19]中研究高速公路场景和城市场景的单播通信的连接性时延,由于城市道路的网络拓扑结构和交通灯影响,这些链路时延的分析模型不能被扩展为城市场景所需要的;文献[20]研究上海城市汽车网络(Shanghai urban vehicular network, SUVnet)轨迹数据的特点,并且研究网络的拓扑结构、连接性和城市汽车网络的性能.这些研究是通过真实的城市汽车环境完成的;Artimy等人 [21] 研究在2维城市场景中的网络连接性,并且在道路中间设置交叉口;在文献[22]中,Taleb等人根据增加链路时延和减少链路断开事件提出一种新的路由策略,支持汽车网络的智能交通系统服务,不过并没有给出分析模型.Viriyasitavat等人基于元胞自动机模型(cellular automata model)提出一个复杂的城市VANETs网络连接性的分析框架 [23] ,考虑车辆转向频率和交通灯2种因素,并且认为2辆连续行驶的汽车遇上交通灯组合事实是独立的,这与实际情况不相符;Hu等人在文献[24]中通过考虑车间距离、车速、在交叉口的转向频率和交通灯因素提出一个具体的基于过程的Markov链模型,但是假设车辆密度和车辆速度是恒定的,这是不符合事实的.
从目前的文献研究表明,本文是唯一一篇采用2车相对速度的分布、2车间动态变化的距离并且考虑交通灯变化对链路时延的影响而建立实时预测链路时延的数学模型.本文提出的DPLD模型适合城市场景中直行的任意2车链路时延的预测.
本文只是分析汽车在道路上直行的同向行驶和对向行驶2种状况.图1给出汽车在城市环境中的4车道双向行驶的状况.

Fig. 1 Vehicles travel on the road
图1 汽车在城市道路行驶
为了实时地预测2车链路能连接多久,一个链路时延模型必须克服2个挑战: 1)能够动态地调整以适应车速的变化;2)能够解决交通灯变化对链路时延的影响.为了解决挑战1,我们提出采用2车相对速度的分布而不是某一辆汽车的瞬时速度来估计2车间预期要发生的链路时延.对于挑战2,我们为汽车到达交叉口遇上红灯或绿灯采用概率建模,然后具体考虑车辆遇上红灯或绿灯的情况而计算链路时延.
车辆在路上变速行驶,通过对车辆行驶轨迹的分析以及对以往资料研究表明,路上行驶车辆的速度服从正态分布 [16] ,其实是指速度的值服从正态分布,因为速度是矢量,即有值也有方向.假定一辆汽车的速度 v 是一个随机变量,那么| v |~ N ( u , σ 2 ),概率密度函数为
(1)
因为车辆的速度是独立地服从正态分布的随机变量,所以2车的相对速度仍然服从正态分布.2车速度的概率密度函数分别为 ![]() 和
和 ![]() 则2车相对速度的概率密度函数为
则2车相对速度的概率密度函数为 ![]() 其中
其中 ![]() 为了估计任意2车相对速度的分布,我们首先需要知道任意一辆汽车速度的分布参数 u , σ 2 ,连续采集1辆汽车速度的样本集{ v 1 , v 2 ,…, v n },估计 u 和 σ 2 采用最大化对数似然函ln L ( u , σ 2 )的最大似然法,用式(2)表示:
为了估计任意2车相对速度的分布,我们首先需要知道任意一辆汽车速度的分布参数 u , σ 2 ,连续采集1辆汽车速度的样本集{ v 1 , v 2 ,…, v n },估计 u 和 σ 2 采用最大化对数似然函ln L ( u , σ 2 )的最大似然法,用式(2)表示:
- ![]() ln(2 π )-
ln(2 π )- ![]() ln( σ 2 )-
ln( σ 2 )- ![]() (| v i |- u i ) 2 .
(| v i |- u i ) 2 .
(2)
由此衍生出 u 和 σ 2 服从最大似然估计.
![]() |.
|.
(3)
用 ![]() 估计
估计 ![]() 是样本平均值.因为
是样本平均值.因为 ![]() 是同一最小方差的无偏估计,服从正态分布 [25] ,正态分布为
是同一最小方差的无偏估计,服从正态分布 [25] ,正态分布为 ![]() N ( u , σ 2 / n ).因此
N ( u , σ 2 / n ).因此 ![]() 的标准误差是和
的标准误差是和 ![]() 成正比,样本值越多,估计误差越小.
成正比,样本值越多,估计误差越小.
采用样本方差 s 2 估计 σ 2 ,因为样本方差是方差的无偏估计 [27] ,方差为
(4)
为了减小预测误差,我们采用滑动窗口机制存取数据,每一次预测只记录最近10 s内的1辆汽车的速度样本估计 u 和 σ .
我们把任意2车之间的链路时延看作1个随机变量 T , T 的主要分布取决于3个因素:1)2车的相对速度;2)2车之间的初始距离;3)2车相对的移动方向.因为这些因素在2车链路连接过程中是变化的,因此DPLD模型需要实时调整原则才能获得更精确的预测结果.
为了确定 T 的分布,我们首先介绍相对速度驶过的距离 L 的计算方法.假设2车同向行驶,如果后面跟随的车速比前面的大,则 L = R + d , d 为初始距离, R 是通信范围;否则 L = R - d .当2车对向行驶,如果它们之间的距离逐渐增大,则 L = R - d ,否则 L = R + d .在链路连接过程中,相对速度驶过的距离是变化的.
我们给出随机变量 T 的分布函数:
(5)
2边求导得到的 T 的概率密度函数为
因为相对速度| v |服从正态分布,式(6)可以写成式(7):
(7)
其中 u 和 σ 是相对速度分布的平均值和标准差.因此,预期的链路时延能够计算为
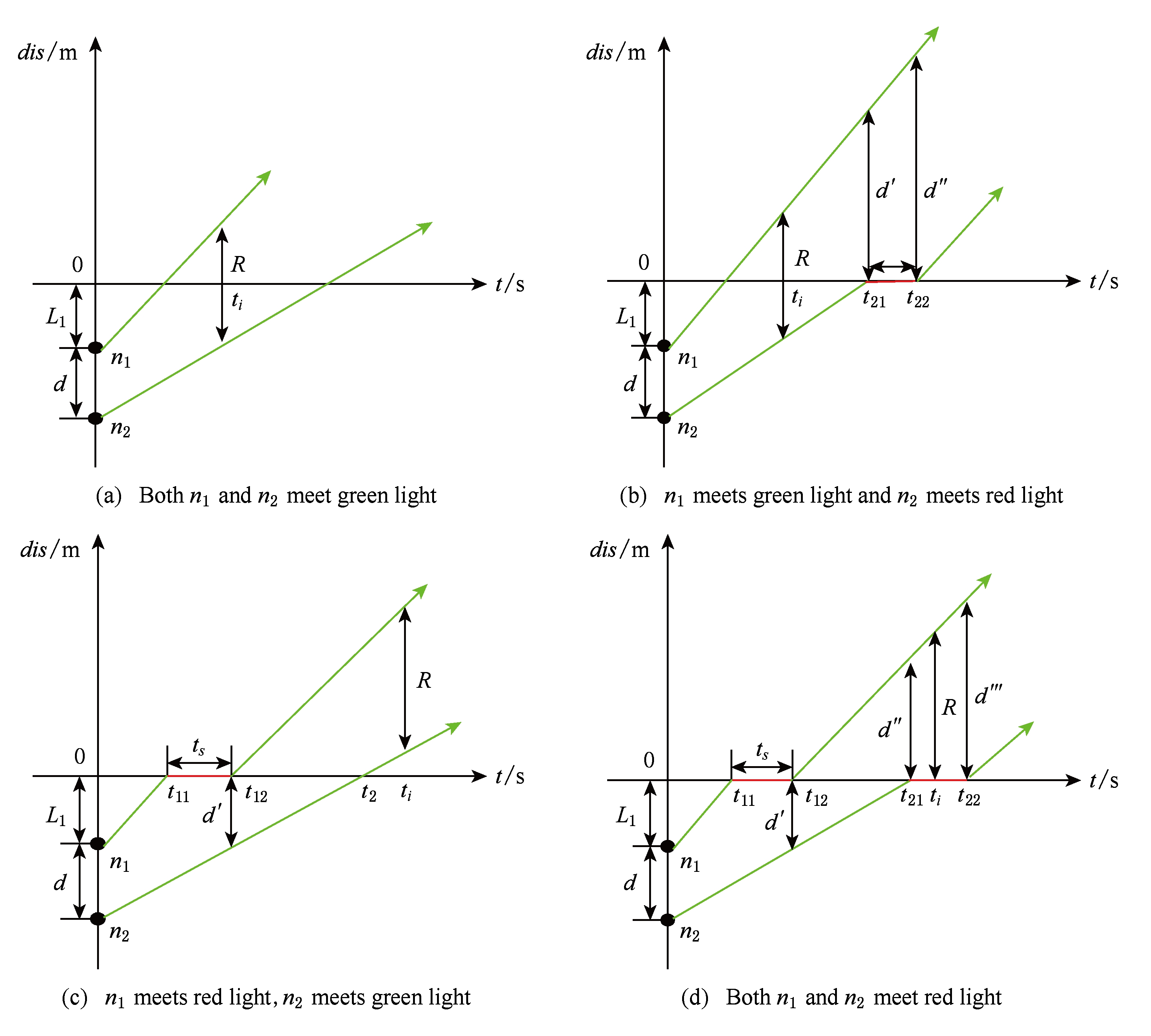
Fig. 2 Traffic lights change impact on link duration
图2 交通灯的变化对链路时延的影响
E ( t )= ![]() t ( f ( t ))d t .
t ( f ( t ))d t .
(8)
因为相对速度服从正态分布,所以99.9%的相对速度值都在[ u -4 σ , u +4 σ ]区间内.所以最小相对速度和最大的相对速度最可能的取值分别为 u -4 σ 和 u +4 σ ,因此定积分的区间缩小为[ L /( u +4 σ ), L /( u -4 σ )],所以预期的链路时延计算为
![]() t .
t .
(9)
在2.4节,我们假定汽车在路上自由地行驶,不考虑交通灯的影响.因为不可能确切地知道一辆汽车在它原始的方向继续前行或者停下来,我们使用概率为汽车遇上红灯或绿灯的机会建模.
虽然现存的一些研究成果考虑交通灯的影响,这些研究成果大多简单地认为2辆跟随行驶的汽车遇上的交通灯是独立的 [25] ,这与实际不相符.不同的是在DPLD模型里,我们认为这些事件不是独立的,这样使DPLD模型更有实际意义.
考虑实际独立的驾驶行为,2辆车在交通灯前的移动实际上是独立的,2辆紧跟着行驶的车辆遇上交通灯组合的事实是相关的 [25] .换句话说,第2辆车遇上的交通灯高度依赖于第1辆车遇上的交通灯.这个现象已经在文献[25]中建模.车辆 n 1 和车辆 n 2 遇上红灯的概率为
P r { n 1 (r)} P r { n 2 (r)| n 1 (r)},
(10)
r代表红灯,条件概率 P r { n 2 (r)| n 1 (r)}能够用相对速度和2辆车的相对距离计算:
P r { n 2 (r)| n 1 (r)}= P r {( t r - t 1 )≥ L / u 12 },
(11)
其中, L 是 n 1 到达交叉口时车间距离, L / μ 12 为汽车 n 2 到达交叉口所用的时间, t r 为红灯信号结束的时间, t 1 为汽车 n 1 到达交叉口的时间,因此 t r - t 1 是 n 1 到达交叉口后红灯信号的剩余时间.
这个概率不是一个常量,它取决于 n 1 到达交叉口的时间,假定2辆连续行驶的汽车遇上交通灯的组合事实是相关的,我们分别给出链路时延的具体计算方法.
当车辆 n 1 和车辆 n 2 到达交叉口时,车辆的运动也许极大地受到交叉口处交通灯变化的影响,如图2所示,如果车辆 n 1 遇上绿灯,也许继续前进,如果在红灯期间,它会停在交叉口.类似状况车辆 n 2 也许会发生.即使我们知道1辆汽车将会遇上哪一种类型交通灯比如红灯,也不可能知道它将会因为这个信号停多久.
幸运地是我们发现车辆 n 1 和车辆 n 2 到达交叉口的时间是可计算的值.基于 t 1 和 t 2 时间差,我们能够为1辆汽车遇上的交通信号和多久用概率建模,如图2所示,我们假设原点为交叉口,车辆 n 1 和车辆 n 2 都向交叉口驶去, d 为2车之间的初始距离, L 1 为车辆 n 1 距交叉口的距离.车辆 n 1 遇上交通灯的时延 E ( t 1 )可以用式(9)计算,用 L 1 代替 L . u , σ 是车辆 n 1 速度的平均值和均方差. E ( t 2 )也一样计算.
如图3所示假定车辆 n 1 和车辆 n 2 到达交叉口的时间差,我们能够构建一个带有汽车的“哑铃”,汽车就像2个球,哑铃条长为 t 2 - t 1 ,哑铃随意地放在由可选择的代表红绿灯时间长度的条形块构成的条形图上,条形图代表红绿灯交通信号周期.因为哑铃在图3上的位置服从均匀分布,每一个位置的概率为
P w = ![]() ,
,
(12)
其中, t g 和 t r 是红灯和绿灯的信号时间,对于哑铃被放置每一个可能位置,一辆汽车将面对的信号灯类型和长度是确定的.为了计算1个特定场景的预期链路时延,我们需要参考图2.
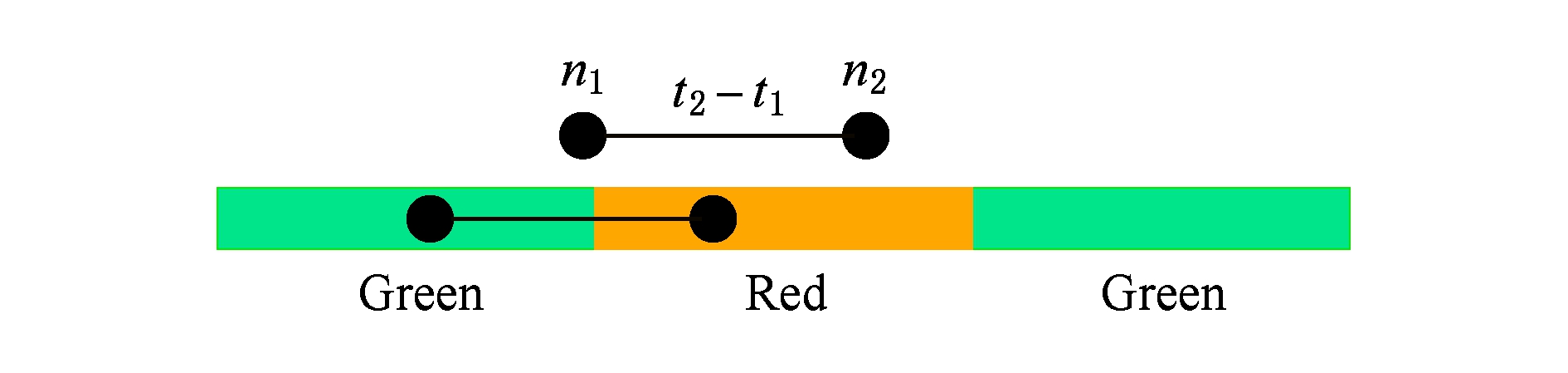
Fig. 3 Vehicles waiting time before traffic light
图3 车辆在交通灯前面等待的时间
我们假定车辆 n 1 和车辆 n 2 位于交叉口的同一侧,车辆 n 1 和车辆 n 2 同向行驶,车辆 n 1 在车辆 n 2 的前面,这意味着平均速度 μ 1 比 μ 2 大.在图2(a)中,2辆车都遇上绿灯行驶过交叉口并且在交叉口不停,则式(9)中 L = R - d ,预期的链路断开时间可计算.
在图2(b)的第2种情况中,车辆 n 2 在红灯前面停下然后驶过交叉口,链路可能断开的时间段分别为(0, t 21 ),( t 21 , t 22 ),( t 22 ,∞),如果链路在(0, t 21 )时间段内断开,在式(9)中我们使用 L = R - d 来计算预期的链路链路时延.如果链路断开发生在( t 21 , t 22 ),在式(9)中相对速度 v 被更新为 v 1 并且 L = R - d ′;否则,链路在 t 22 后断开,我们在式(9)中使用 L = R - d ″计算链路断开的时间.
对于第3种情况如图2(c)所示,车辆 n 1 遇上红灯在交叉口处停下,然后驶过交叉口,我们首先要确定链路断开发生在(0, t 11 )还是( t 12 ,∞).对于情况1,式(9)中的 L = R - d ;对于情况2, L = R - d ′.
对于情况4如图2(d)所示,比其他3种情况更复杂,2辆车都遇上红灯在交叉口停下几秒钟后驶过交叉口,链路断开的时间段有可能为(0, t 11 ),( t 12 , t 21 ),( t 21 , t 22 ), ( t 22 ,∞).如果链路在某一时间段断开,比如在 t 22 后,相对速度和相对距离应该被相应地更新.
我们只讨论车辆 n 1 和车辆 n 2 在交叉口一侧的例子,2辆车有可能在交叉口的两侧,车辆 n 1 和车辆 n 2 也许对向行驶,车辆 n 1 在车辆 n 2 的后面并且 μ 1 < μ 2 ,对于这些不同的情况,类似的方法仍然可以使用计算链路时延.由于篇幅所限,本文不再给出详细的讨论.
基于第2节建立的链路时延预测模型DPLD,任意一辆车均可以预测与其传输范围内所有车辆的链路时延.
在某一时刻,假设车辆 n i 和车辆 n j 之间的链路是连接的,基于2辆车的速度 v i , v j 的分布及2辆车之间的相对距离,2车的链路时延能够计算.每辆车存取数据的滑动窗口大小为10,车辆 n j 存储最近10 s内的速度样本{ v j 1 , v j 2 ,…, v j 10 }.这10个速度样本将在下一个信标周期内广播给车辆 n j 传输范围内所有汽车.因为车辆 n i 在车辆 n j 的传输范围内,所以它将收到这些样本.和自己的速度对比,车辆 n i 能够计算2车的相对速度{ v 1 , v 2 ,…, v 10 }, v l = v i l - v jl , l =1,2,…,10.根据{ v 1 , v 2 ,…, v 10 },车辆 n i 和车辆 n j 相对速度的分布能够通过式(3)(4)估计,在每一次信标信息内包含汽车的位置信息,车辆 n i 和车辆 n j 初始相对距离 L i j 能够计算.用 u i j , σ i j , L i j 代替式(9)中的 u , σ , L ,车辆 n i 和车辆 n j 之间的预期链路时延能够计算得到.
一辆汽车可能因为前面的车速而突然刹车,车速急剧下降,或者因为突然超车而车速突然增加,这样相对速度的突然变化会导致链路时延预测结果较大的变化,为了避免这样的问题,我们采用EMA(exponential moving average)方法预先处理速度的变化:
V l = α × v l +(1- α )× V l -1 ,
(13)
其中, V l , v l 是在时刻 l 处理的速度和瞬时速度.因为 V l 是从时刻0~ l 的速度样本的线性组合,并且 v 0 ~ v l 服从正态分布,所以 V l 仍然服从正态分布,换句话说,DPLD模型可以应用于通过EMA法处理过的速度样本.
预测车辆 n i 和车辆 n j 的链路时延的流程如图4所示:
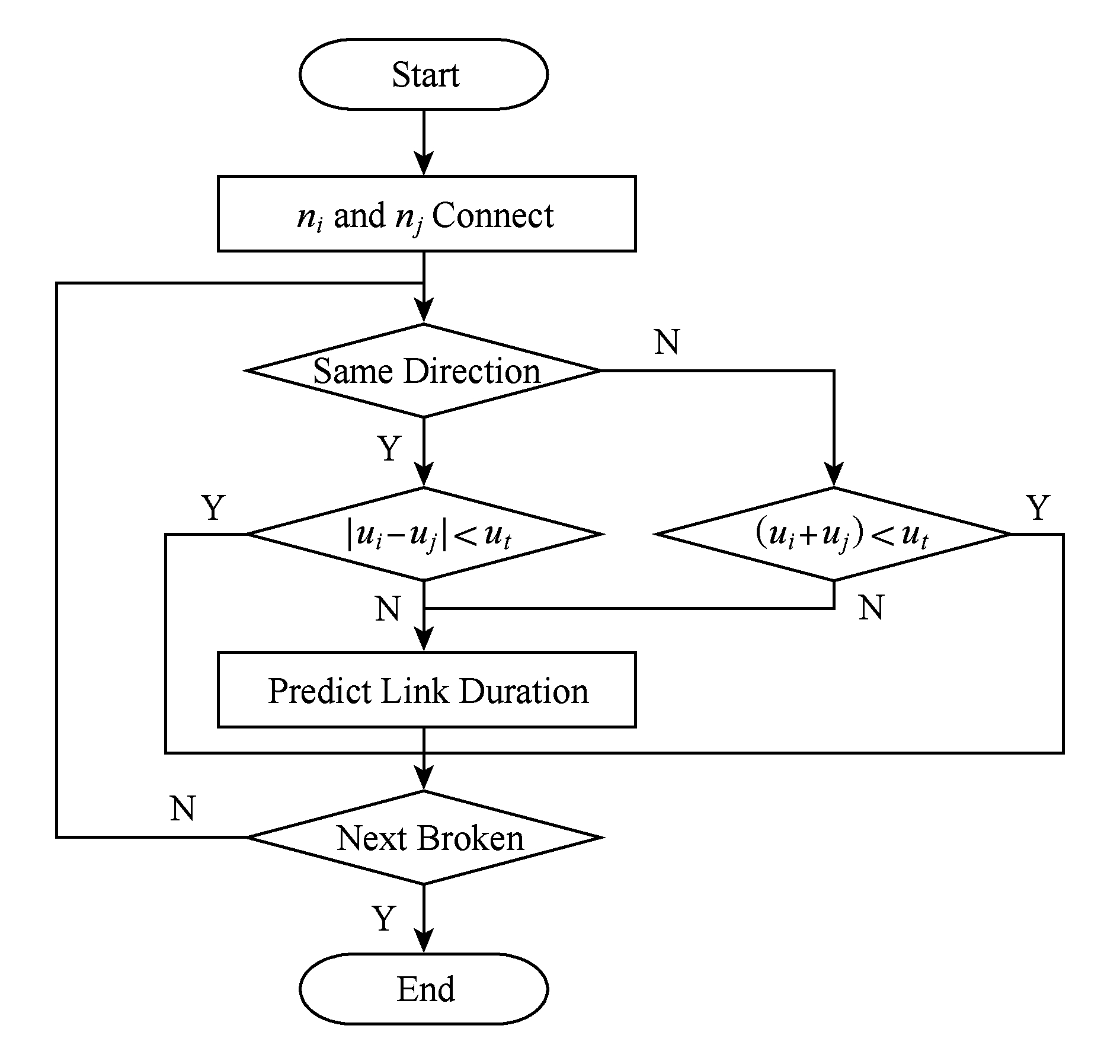
Fig. 4 Flow of n i predicting link duration
图4 车辆n i 预测链路时延流程
当节点 n i 收到一个来自节点 n j 信标信息时,首先检查节点 n j 是否和它同向行驶,如果是则平均相对速度是 u i - u j ,否则为 u i + u j .在一些特殊情况下, u i - u j 和 u i + u j 值非常小,比如2车行驶状态非常接近,这时交通密度可能是密集型的,所以2车处于跟驰状态,此时预测链路时延意义不大,这时我们采取暂时不预测而是保留上次预测的值,这个相对的平均速度 u t 的阈值设置为1 m/s.
对于该模型预测链路时延的时间复杂度而言,由于本文采用的是主节点把信标信息分发给所有的邻居节点,每个邻居节点分别采用DPLD模型计算自己和主节点的链路时延,由于定积分的概念为矩形面积的累加,所以每个节点在计算链路时延的过程是矩形面积累加过程,因此每个节点预测链路时延的时间复杂度为线性的.
因为汽车的移动性模型在VANETs中是影响DPLD模型精确性重要因素,我们通过VanetMobisim产生汽车运动轨迹 [26] , VanetMobiSim从微观和宏观层面描述真实的汽车移动性并且支持交通灯、换道和速度变化的规则.
预测城市场景中2车链路时延是一个具有挑战性的问题,因为很难预测1辆汽车将会遇上哪种类型的信号灯.为了模拟一个简单的城市场景,我们在VanetMobiSim模拟器中配置模拟场景,在长2 000 m的路上放置70辆汽车,交通流的密度是变化的.在路的中间设置交叉口,4车道、双向车流,交通灯周期为72 s,红灯和绿灯各36 s,汽车的最大速度为14 m/s,最小速度为5 m/s,加速和减速因子为3 m/s 2 ,无线通信半径为250 m,模拟时间为500 s.基于节点的移动方向,汽车对被分成2类:1)2车同向行驶;2)2车对向行驶.
1) 2车同向行驶的链路时延预测
图5给出随机抽取的一对节点预测时延和模拟时延比较,这对节点在城市场景中同向行驶.为了进一步分析预测误差,我们定义了预测误差.

Fig. 5 Link duration for a pair of nodes
图5 一对节点的链路时延
定义1 . 预测误差是指模型预测的链路时延与真实的链路时延差占真实的链路时延的百分比.
从图5可以看出:预测误差随着模拟时间的增加变小.当2辆车在第1秒开始连接时,预测误差大约20%.这是因为2车的相对距离和速度在[0,25]期间戏剧性地变化,还有交通灯的影响.当时间在25 s后,预测结果的不确定性减小,因此预测误差也减少.
为了理解图5的数据波动,我们进一步给出节点的平均速度以及相对速度的平均速度,如图6所示,第1辆车 n 1 以相对稳定的速度行驶,第2辆车 n 2 以0 m/s的速度开始(停在了交通灯前面),然后以大约12 m/s的速度线性地增加.结果导致2车之间的相对速度在3个阶段不同的变化:[0,15),[15,25),[25,45).在[0,11)期间,车辆 n 2 停在交通灯前面,车辆 n 1 朝向车辆 n 2 行驶,这样,它们的相对距离降低.在这种情况下,式(9)中的预测距离 R + d ,在第11秒时,汽车 n 2 开始移动并且2车之间相对距离慢慢地增加.因为我们不知道车辆 n 1 将会遇到的交通灯信号类型,预期的链路时延在第14秒突然下降.从15~21 s,车辆 n 1 和车辆 n 2 之间的相对距离持续减小,在22 s后,车辆 n 2 的速度变得比车辆 n 1 的速度快,车辆 n 1 和车辆 n 2 之间的距离又开始增加,在这种情况下,式(9)中的预测距离将被设置为 R - d .在第25秒后,因为 L 的计算方法不需要再改变,并且相对速度变得平稳,因此预测误差变得很小.
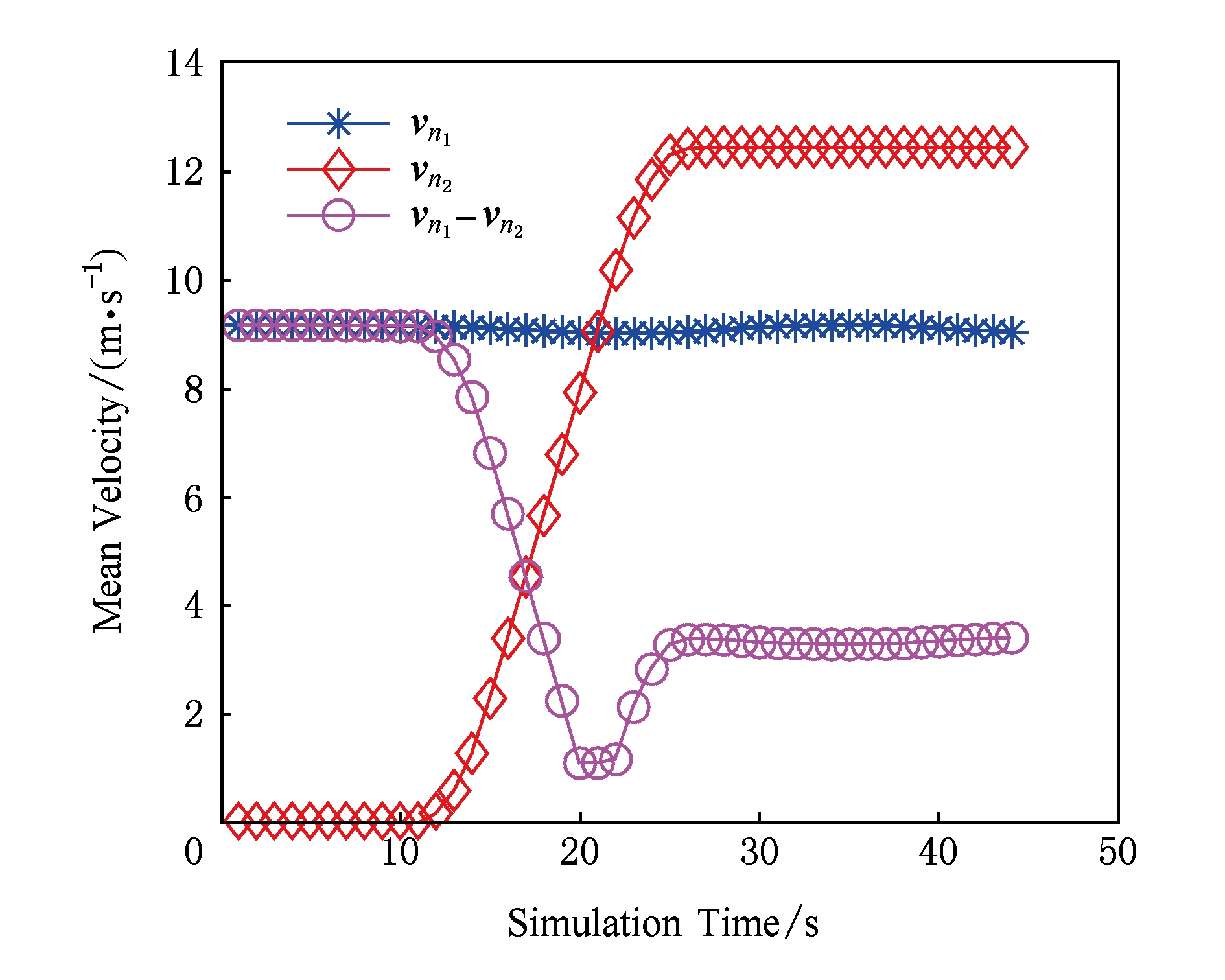
Fig. 6 u 1 ,u 2 ,u 1 -u 2 of vehicle n 1 , n 2 in same direction
图6 同向车辆n 1 ,n 2 分别的速度u 1 ,u 2 及u 1 -u 2
从以上分析,我们能够看出汽车速度的稳定性对于DLDP准确性是很重要的.正如图7所示.
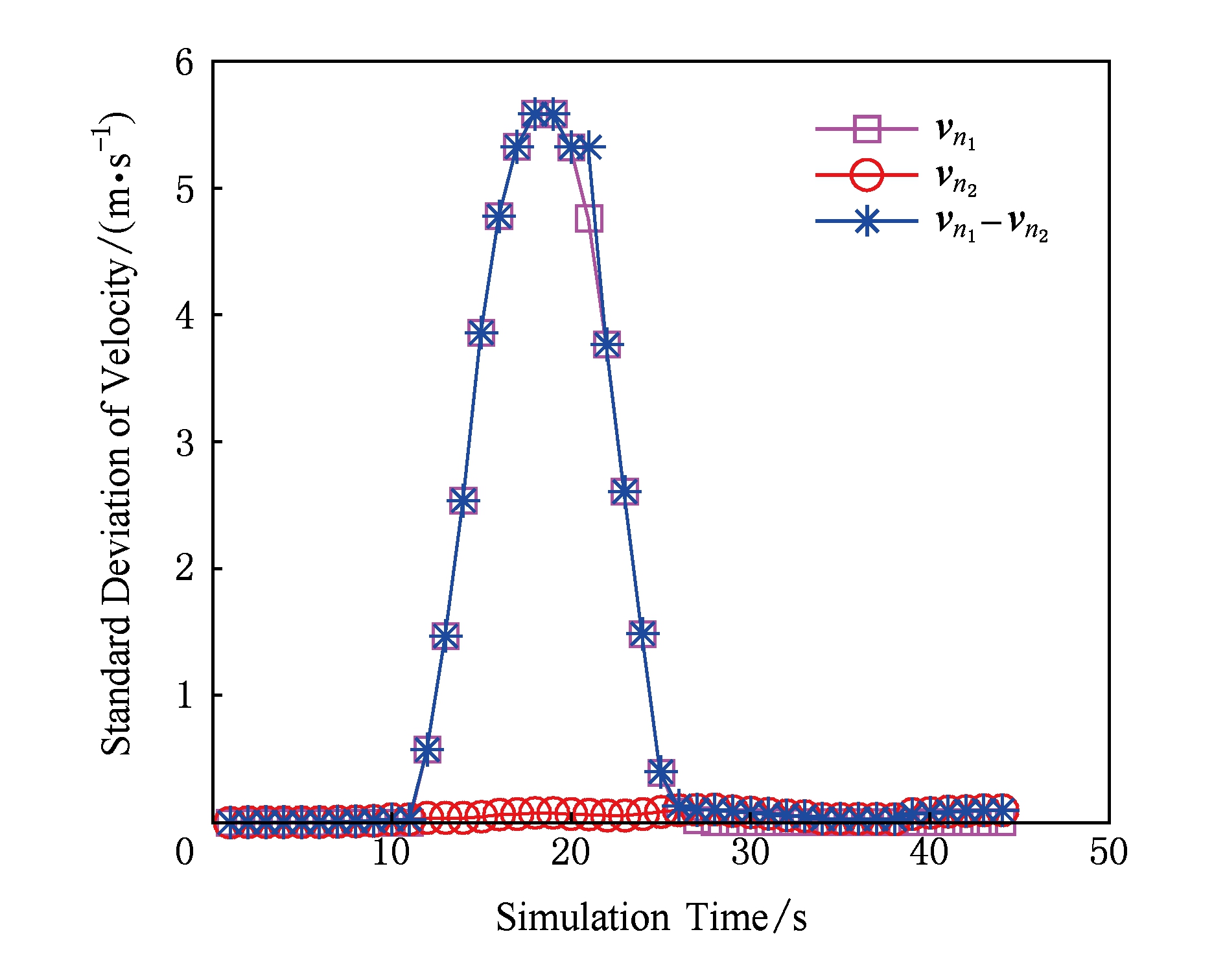
Fig. 7 σ 1 ,σ 2 ,σ 1 -σ 2 of vehicle n 1 , n 2 in same direction
图7 同向车辆n 1 ,n 2 分别的速度标准差σ 1 ,σ 2 及σ 1 -σ 2
车辆 n 2 的速度巨大变化导致预测结果的巨大误差.我们也给出所有预测结果的误差概率分布函数如图8所示,我们发现大约60%的预测误差小于20%.

Fig. 8 Probability of prediction error
图8 预测误差的概率
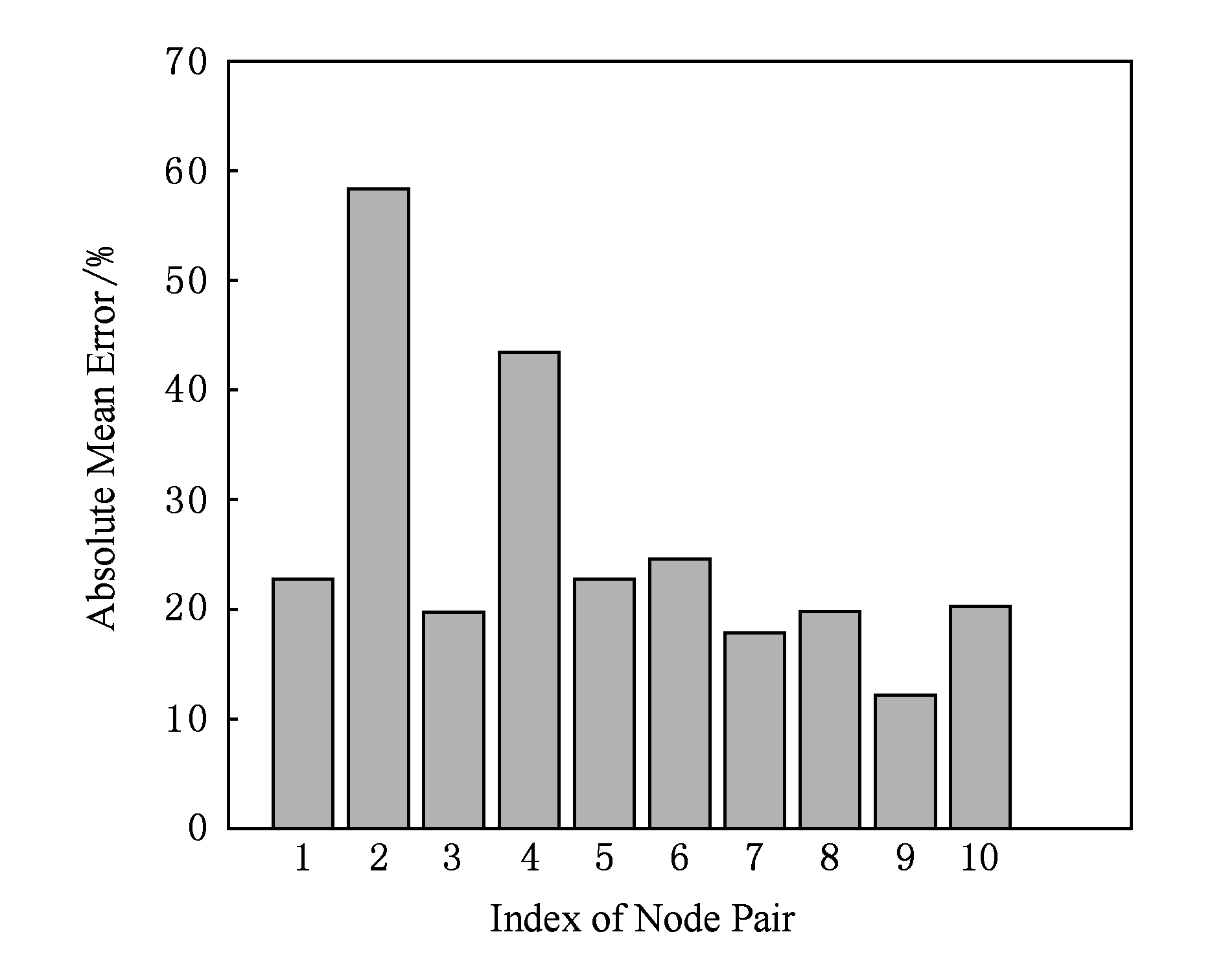
Fig. 9 Mean prediction error of 10 pairs of nodes
图9 10对节点链路时延的平均预测误差
为了分析DPLD预测城市场景中同向行驶节点链路时延的准确性,我们又随机抽取9对节点,与上面分析的1对一起给出图9所示的预测误差总体分析条形图.从图9可以看出,大多数平均预测误差大约为20%.有1对节点预测结果的误差大于50%,这主要是因为2个理由:①在交通灯前面停留太久;②速度的变化快.理由1是主要的,因为从停在交通灯前面的汽车采集不到有用的速度信息.红灯结束后,车辆开始移动导致车速变化大,因此2车的相对速度变化也会随着变大.当相对速度趋于稳定时,链路时延的预测误差逐渐变小.因此,平均的相对速度大于阈值并且相对变化小,模型可以准确的预测2车的链路时延.
2) 2车对向行驶的链路时延预测
当2车对向行驶的时候,链路时延比同向行驶的容易预测.图10给出随机选择的2辆对向行驶的每一辆汽车的平均速度和相对速度的平均速度:
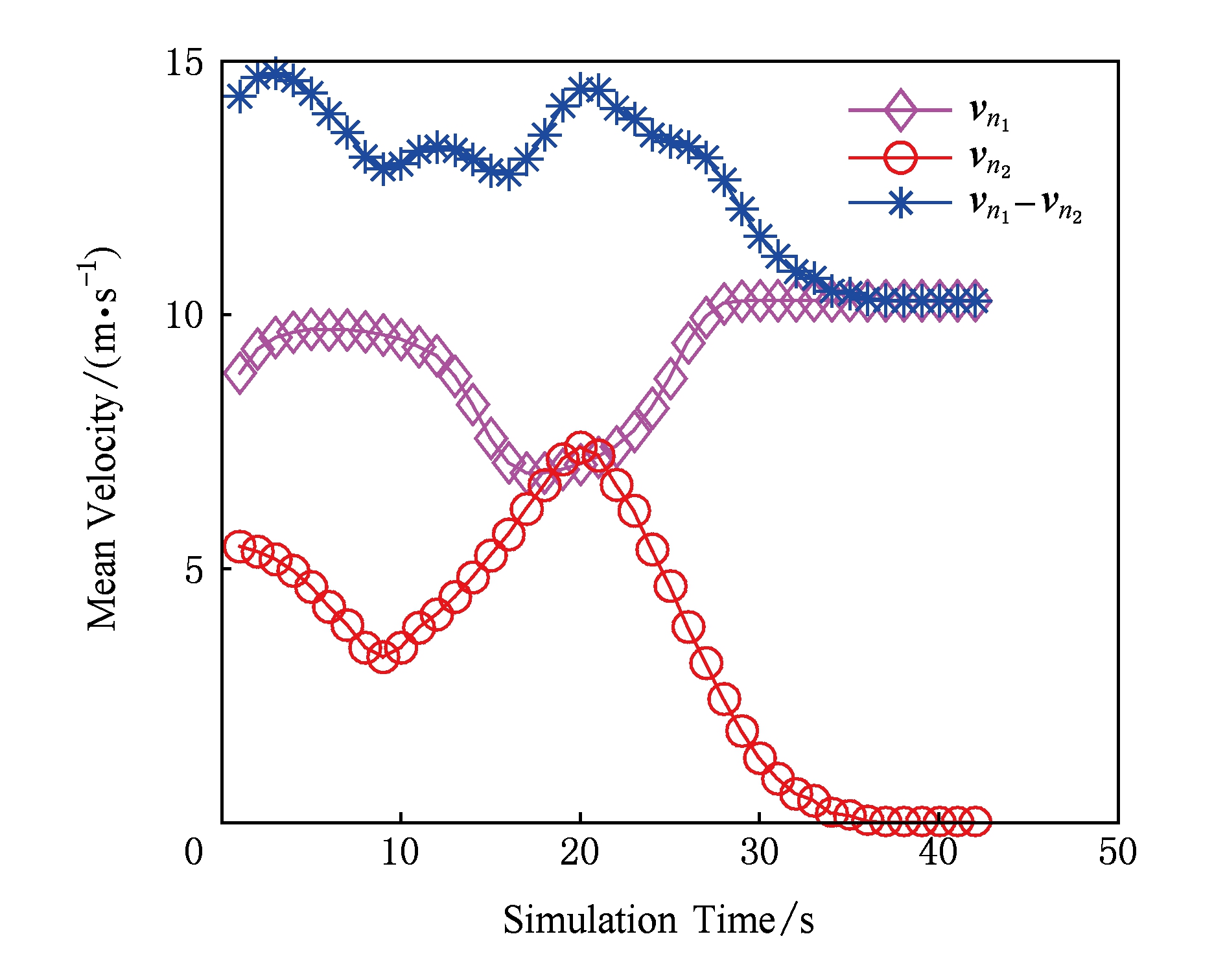
Fig. 10 u 1 ,u 2 ,u 1 -u 2 of vehicle n 1 , n 2 in opposite direction
图10 对向车辆n 1 ,n 2 分别的速度u 1 ,u 2 及u 1 -u 2
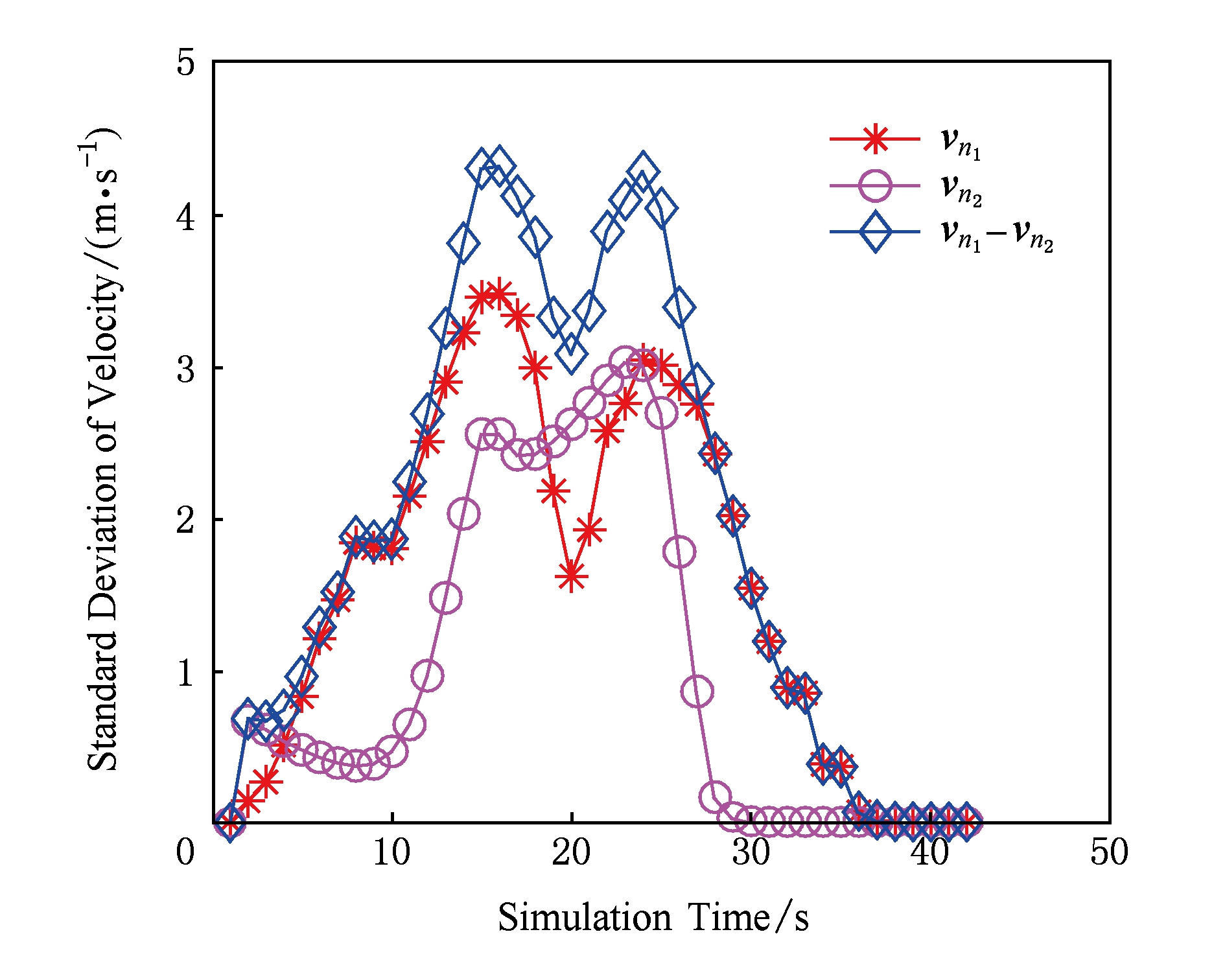
Fig. 11 σ 1 ,σ 2 ,σ 1 -σ 2 of vehicle n 1 , n 2 in opposite direction
图11 对向车辆n 1 ,n 2 分别的速度标准差σ 1 ,σ 2 及σ 1 -σ 2
图11给出节点速度的标准差和相对速度的标准差.因为它们彼此远离,相对速度实际上是它们绝对速度的和,在35 s后,第2辆车的速度变成零,停在交通灯前面.
对于这2辆车,我们给出预测的链路时延和模拟时延的比较如图12所示:
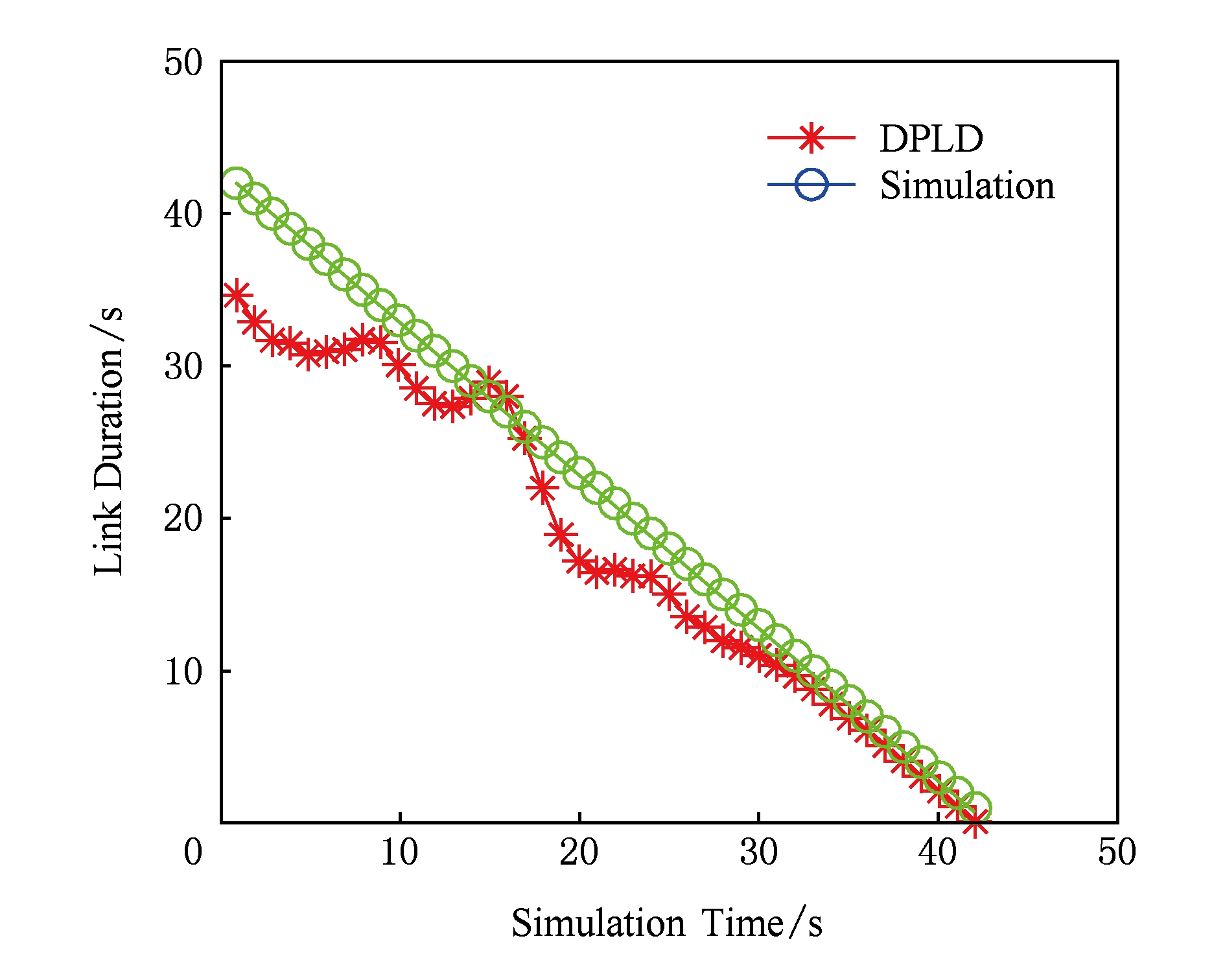
Fig. 12 Link duration for a pair of nodes
图12 一对节点的链路时延
在图13中,我们给出预测误差的分布函数,从图12中我们可以看出预测结果紧随着模拟时延,只是具有非常小的波动.图13表明大约75%的预测结果误差小于20%.

Fig. 13 Prediction error probability
图13 预测误差的概率
除了这对汽车,我们随机选择另外9对汽车,每一对汽车都是对向行驶.10对汽车的总体预测误差在图14中给出,图14中的平均误差比图9中的小.该结果又一次证明DPLD能够准确地预测对向行驶的汽车链路时延.

Fig. 14 Mean prediction error for 10 pairs of nodes
图14 10对节点链路时延的平均预测误差
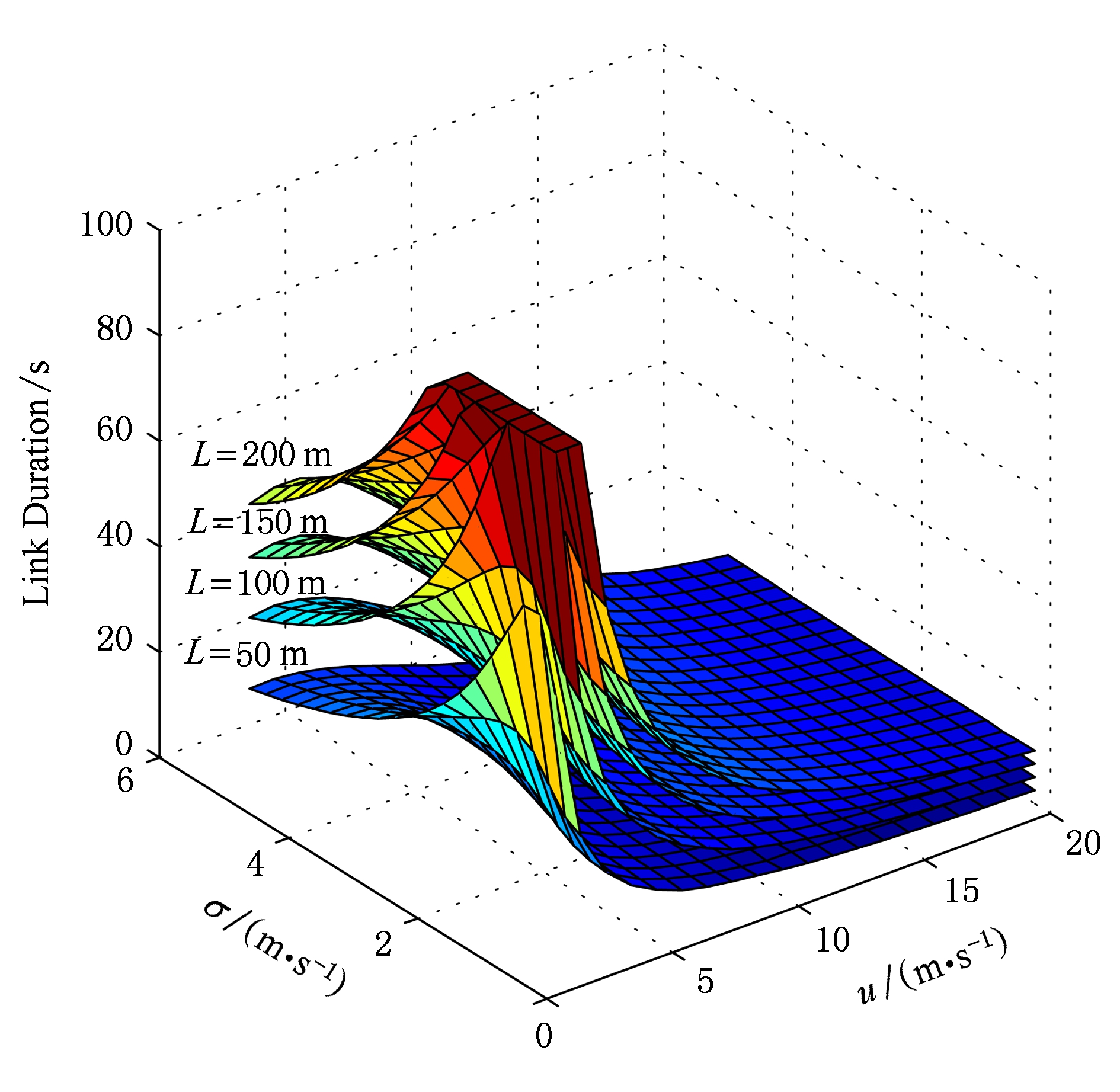
Fig. 15 u, σ, L impact on link duration prediction
图15 u, σ, L对链路时延预测的影响
图15给出DPLD的预测结果随着不同参数 u , σ , L 的变化趋势,图15中 u ∈(0,20), σ ∈(0,5), L 分别被设置为50 m,100 m,150 m,200 m.我们从图15中能够看出,当 L , σ 固定,链路时延随着 u 的减小而增加,当 u ∈(0,10),链路时延变化剧烈;当 u , L 固定,链路时延随着 σ 减小而增加,当 σ →0时变化大;如果 u , σ 不变,链路时延随着 L 增加而增加,当 u ≥10,不管 σ , L 怎样变化,链路时延的变化很小,因此我们发现 u 是影响链路时延的主要参数,其他2个次之.
通过上述对同向行驶和对向行驶的2车链路时延预测结果的分析以及该模型随着所有参数变化的趋势分析,能够证明DPLD模型可以动态地预测城市场景中的链路时延,说明该模型是正确的并且可以应用于实际的.
通过利用2车的相对速度而不是某一辆汽车的瞬时速度,本文提出VANETs中V2V的链路时延的预测模型.除了相对速度之外,模型考虑车间的相对距离和交通灯变化对预测链路时延的影响.基于该模型,1辆汽车能够动态地预测和它链接的任何节点之间的链路时延.在所有的参数中,平均相对速度是影响DPLD模型预测链路时延最重要的因子,因此,准确估计这个参数变得极其重要.为了避免车速突然变化的影响,我们采用EMA法,对于已经采集的速度样本预先处理.
模拟结果表明DPLD模型对于精确地预测VANETs中的链路时延是切合实际的.对于每一辆汽车的邻居,只需要收集和共享10 s最近的速度样本.我们计划进一步采用真实的汽车数据集来验证模型DPLD,并且通过考虑转向对链路时延的影响来扩展该模型.
参考文献
[1]Boleng J, Navidi W, Camp T. Metrics to enable adaptive protocols for mobile ad hoc networks[C] //Proc of Int Conf on Wireless Networks. Piscataway, NJ: IEEE, 2002: 293-298
[2] Jung K H, Lim W S, Jeong J P, et al. A link contact duration-based routing protocol in delay-tolerant networks[J]. Wireless Networks, 2013, 19(6): 1299-1316
[3] Tsao C, Wu Y T, Liao W, et al. Link duration of the random way point model in mobile ad hoc networks[C] //Proc of IEEE Wireless Communications and Networking Conf, Vol 1. New York: IEEE Communications Society, 2006: 367-371
[4] McDonald A B, Znati T. A path availability model for wireless ad-hoc networks[C] //Proc of IEEE Wireless Communications and Networking Conf, Vol 1. Piscataway, NJ: IEEE,1999: 35-40
[5] Hong Xiaoyan, Gerla M, Pei Guangyu, et al. A group mobility model for ad hoc wireless networks[C] //Proc of the 2nd ACM Int Workshop on Modeling, Analysis and Simulation of Wireless and Mobile Systems. New York: ACM,1999: 53-60
[6] Wang K H, Li Baochun. Group mobility and partition prediction in wireless ad-hoc networks[C] //Proc of IEEE Int Conf on Communications, Vol 2. New York: IEEE Communications Society, 2002: 1017-1021
[7] Wu Y T, Liao W, Tsao C, et al. Impact of node mobility on link duration in multihop mobile networks[J].IEEE Trans on Vehicular Technology, 2009, 58(5): 2435-2442
[8] Bai Fan, Sadagopan N, Krishnamachari B.Modeling path duration distribution in MANETs and their impact on reactive routing protocols[J]. IEEE Journal on Selected Areas in Communications, 2004, 22(7): 1357-1373
[9] Sadagopan N, Bai Fan, Krishnamachari B,et al. Paths: Analysis of path duration statistics and their impact on reactive manet routing protocols[C] //Proc of the 4th ACM Int Symp on Mobile Ad Hoc Networking & Computing. New York: ACM, 2003: 245-256
[10] Haas Z J, Hua E Y. Residual link lifetime prediction with limited information input in mobile ad hoc networks[C] //Proc of the 27th IEEE Communications Society Conf on Computer Communications. Piscataway, NJ: IEEE, 2008: 26-30
[11] Korsnes R, Ovsthus K, Li F Y, et al. Link lifetime prediction for optimal routing in mobile ad hoc networks[C] //Proc of 2005 IEEE Military Communications Conf. Piscataway, NJ: IEEE, 2005: 1245-1251
[12] Hua E, Haas Z. An algorithm for prediction of link lifetime in MANET based on unscented Kalman filter[J]. IEEE Communication Letters, 2009, 13(10): 782-784
[13] Shelly S, Babu A V. Analysis of life time in vehicular ad hoc networks of free-flow traffic state[J]. Wireless Personal Communications, 2014, 75(1): 81-102
[14] Zhu Hongzhi, Fu Luoyi, Xue Guangtao, et al. Recognizing exponential inter-contact time in VANETs[C] //Proc of IEEE Communications Society Conf on Computer Communications. Piscataway, NJ: IEEE, 2010: 1-5
[15] Nekovee M. Modeling the spread of worm epidemics in vehicular adhoc networks[C] //Proc of the 63rd Vehicular Technology Conf, Vol 2. Piscataway, NJ: IEEE, 2006: 841-845
[16] Sim M L, Nekovee M, Ko Y F. Throughput analysis of wi-fi based broadband access for mobile users on the highway[C] //Proc of the 2005 13th IEEE Int Conf on Networks Jointly Held with the 2005 7th IEEE Malaysia Int Conf on Communications. Piscataway, NJ: IEEE, 2005: 21-26
[17] Yan Gongjun, Olariu S. A probabilistic analysis of link duration in vehicular ad hoc networks[J]. IEEE Trans on Intelligent Transportation Systems, 2011,12(4): 1227-1236
[18] Rudack M, Meincke M, Lott M. On the dynamics of ad-hoc networks for inter vehicle communications[C] //Proc of Int Conf on Wireless Networks, Vol 1. New York: IEEE Communications Society, 2002: 22-27
[19] Boban M, Misek G, Tonguz O. What is the best achievable QoS for unicast routing in VANETs?[C] //Proc of 2008 Globecom Workshops. Piscataway, NJ: IEEE, 2008: 1-10
[20] Luo P E, Huang H Y, Li M L. Characteristics of trace data for a large scale ad hoc network-shanghai urban vehicular network[C] //Proc of IET Conf on Wireless, Mobile and Sensor Networks 2007. Stevenage, UK: IET, 2007: 742-745
[21] Artimy M M, Phillips W J, Robertson W. Connectivity with static transmission range in vehicular ad hoc networks[C] //Proc of Communication Networks and Services Research Conf. Los Alamitos, CA: IEEE Computer Society, 2005: 237-242
[22] Taleb T, Sakhaee E, Jamalipour A, et al. A stable routing protocol to support ITS services in VANET networks[J]. IEEE Trans on Vehicular Technology, 2007, 56(6): 3337-3347
[23] Viriyasitavat W, Bai Fan, Tonguz O. Dynamics of network connectivity in urban vehicular networks[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(3): 515-533
[24] Hu Miao, Zhong Zhangdui, Zhu Haoqing, et al. Analytical modeling of link duration for vehicular ad hoc networks in urban environment[C] //Proc of the 10th ACM Int Workshop on Vehicular Inter-networking, Systems, and Applications. New York: ACM, 2013: 61-70
[25] Krishnamoorthy K. Handbook of Statistical Distributions with Applications[M]. Oxford, Oxfordshire: Taylor & Francis, 2010: 128-135
[26] Harri J, Filali F, Bonnet C, et al. VanetMobiSim: Generating realistic mobility patterns for VANETs[C] //Proc of the 3rd Int Workshop on Vehicular Ad Hoc Networks. New York: ACM, 2006: 96-97
Wang Xiufeng, Cui Gang, and Wang Chunmeng
( School of Computer Science and Technology , Harbin Institute of Technology , Harbin 150001)
Abstract Link duration prediction is an important standard which determines many performance of network in VANETs. Existing analytical methods about link duration based on mobility of nodes in VANETs have no function to predict link duration between any two nodes in the future, so it is not practical for these methods to predict link duration between two vehicles. We propose a dynamical prediction model which considers the distribution of relative velocity, inter-vehicle distance, traffic density change and traffic light to estimate the expected link duration between any pair of connected vehicles, because these factors change continuously in the process of link connection. By taking into account the relative velocity distribution, the model is able to adjust the principle in real time to adapt variation of vehicle speed. By automatically adjusting computing method of the relative distance between two vehicles, DPLD(dynamically predict link duration) model can automatically adapt to the change of relative distance between two vehicles. Therefore, DPLD model can effectively predict the link duration between the two vehicles. Such model is implemented on each vehicle along with parameters estimation methods of relative velocity distribution, exponential moving average method processes speed exception and considering the impact of the traffic light on link duration. Simulation results show that this model predict link duration for urban scenario has the high accuracy.
Key words vehicular ad hoc networks (VANETs); link duration; traffic density; prediction model; vehicle to vehicle (V2V)
收稿日期: 2015-12-23;
修回日期: 2016-09-21
基金项目: 国家自然科学基金项目(61272130)
This work was supported by the National Natural Science Foundation of China (61272130).
中图法分类号 TP393.01

Wang Xiufeng , born in 1979. PhD in School of Computer of Harbin Institute of Technology. Her main research interest include mobile ad hoc network, vehicular ad hoc network and wireless sensor network.

Cui Gang , born in 1947. Professor and PhD supervisor in School of Computer of Harbin Institute of Technology. Senior member of CCF. His main research interest include system architecture, mobile ad hoc network, vehicular ad hoc network and wireless sensor network etc.

Wang Chunmeng , born in 1990. Master in School of Computer of Harbin Institute of Technology. His main research interest include mobile ad hoc network, vehicular ad hoc network and wireless sensor network.