吴福生 张焕国
(武汉大学计算机学院 武汉 430072) (空天信息安全与可信计算教育部重点实验室(武汉大学) 武汉 430072)
(liss@whu.edu.cn)
摘 要 协议是网络通信的规范,密码协议是信息安全的关键技术之一,安全的密码协议常常依赖于签名或消息认证技术.签名或消息认证给密钥协商协议通信带来大量计算,不利于计算能力有限设备的网络通信.设计具有计算量小又实用的安全协议是信息安全研究目标之一.故以整数乘法同态映射和二叉树为基础,提出一种新的密钥协商协议,并在开源的OpenSSL环境下实现新协议模拟实验,给出二叉树叶子结点数变化对网络通信影响的模拟实验和实验结果分析.新协议在随机预言模型下可证明安全,即在公钥加密方案中新协议满足选择明文攻击不可区分性的(IND-CPA)安全.新协议与经典的密钥协商协议相比(例如MTI,MQV,HMQV),计算量小、强安全假设少、无需额外的签名与消息认证,且可以在非安全通信信道上进行安全通信.
关键词 协议;密码学;同态;二叉树;可证明安全
密钥协商协议是网络空间信息安全研究的重点 [1] .已经在很多方面得到应用,特别是基于分布式安全多方计算的密钥协商协议的应用,引起学者们广泛的关注 [2] .Diffie和Hellman [3] 在1976年提出著名的Diffie-Hellman密钥协商协议(简称Diffie-Hellman协议),第1次在非安全的公共通信信道上实现密钥协商.此后,许多研究者以Diffie-Hellman协议为基础,提出改进的密钥协商协议,著名的有MTI系列 [4-6] 密钥协商协议、MQV [7] 密钥协商协议和KEA密钥协商协议 [8] .MQV协议的改进协议 [9] 引起研究者极大的关注,已成为IEEE P1363-2000标准 [10] .目前,以MQV为基础的最新研究成果有:HMQV [11] ,OAKE [12] ,sHMQV [13] ,YAK [14-15] 等密钥协商协议.其中,最具代表性的是HMQV密钥协商协议.
这些协议在密钥协商方面已有很大的改进,但是仍存在一些不足:Diffie-Hellman协议无法抵抗中间人攻击;MTI系列容易受到未知密钥攻击、Lim-Lee攻击、身份假冒攻击;MQV容易受到密钥泄露伪装攻击; HMQV协议及以它为基础的改进协议无法在多种移动终端设备上实行(受计算能力有限或安全性不高等因素制约).上述密钥协商协议的安全性必须依赖于签名或消息认证,因此增加协议的时间开销.更详细的密钥交换协商协议参考文献[16].
本文以整数乘法同态映射 * 整数乘法同态映射:设 α , β ∈ Z -{0}, f : Z -{0}→ Z -{0},满足 f ( α )* f ( β )= f ( α * β ). 和二叉树为基础,提出一种新的密钥协商协议,并且在OpenSSL的C语言环境下给出新协议叶子结点参数变化的网络通信模拟实验和实验结果分析.新协议无需依赖额外签名或消息认证,也能提供协议参与者之间隐式认证和抵抗中间人攻击.由于无须签名或认证,可减少通信时间开销,新协议应用于计算能力有限的设备或大数据、云计算网络环境下的通信时,在计算量的开销上有一定的优势.
本文以整数环上的乘法同态映射为基础,根据群的同态概念给出基本定义与定理.
定义1 . 群同态 [17] .设 G 1 , G 2 是2个群(半群、幺半群),“*” 为二元乘法运算. f 是 G 1 到 G 2 的映射,如果 f 满足:
∀ x , y ∈ G 1 , f ( x )∈ G 2 ,
f ( x )* f ( y )= f ( x * y ),
(1)
则称 f 是群(半群、幺半群) G 1 到群(半群、幺半群) G 2 的一个同态映射,简称同态.
设 ![]() +是整数环上的半群或幺半群,函数 f ( x )= x , x ∈
+是整数环上的半群或幺半群,函数 f ( x )= x , x ∈ ![]() +是自身的同态映射,则称 f 为自同态映射.
+是自身的同态映射,则称 f 为自同态映射.
定义2 . 映射.由于 f 是半群或幺半群 ![]() +上的一个映射,“*”为二元乘法运算, f 满足:
+上的一个映射,“*”为二元乘法运算, f 满足:
f ( x )× f ( y )= f ( x × y ) x , y ∈ ![]() +.
+.
(2)
根据定义1,称 f 是半群或幺半群 ![]() +到自身的一个整数乘法同态映射, x , y ∈
+到自身的一个整数乘法同态映射, x , y ∈ ![]() +称之为整数同态点,而对应的点 f ( x * y )∈
+称之为整数同态点,而对应的点 f ( x * y )∈ ![]() +称为整数同态值.
+称为整数同态值.
定理1 . 如果在整数环上的半群或幺半群 ![]() +上存在一个整数乘法同态映射 f ,从半群或幺半群
+上存在一个整数乘法同态映射 f ,从半群或幺半群 ![]() +任意取 n 个数 a i ∈
+任意取 n 个数 a i ∈ ![]() +, i =1,2,…, n ,则一定存在一个整数乘法同态值 f ( a 1 * a 2 *…* a n )与之对应.
+, i =1,2,…, n ,则一定存在一个整数乘法同态值 f ( a 1 * a 2 *…* a n )与之对应.
证明: 任取 n 个整数,∀ a 1 , a 2 ,… a i ,…, a n ∈ ![]() +,计算 f ( a 1 )* f ( a 2 )*…* f ( a n ),令其值为 v :
+,计算 f ( a 1 )* f ( a 2 )*…* f ( a n ),令其值为 v :
f ( a 1 )* f ( a 2 )*,…,* f ( a n )= v .
(3)
根据乘法的结合律两两结合,式(3)可变为
( f ( a 1 )* f ( a 2 ))*…*( f ( a n -1 )* f ( a n ))= v ![]()
(4)
1) 当 n 为偶数时,刚好两两匹配,适合乘法结合律,即式(4)不变.
2) 当 n 为奇数时,增加一项 f (1)=1,不影响式(4)积值.
由1)和2)可知,总是存在式(4)的表示法.由定义2,式(4)可变为
f ( a 1 * a 2 )*…* f ( a n -1 * a n )= v .
(5)
根据乘法结合律两两结合,以此类推,最后等式成立:
f ( a 1 * a 2 *…* a n -1 * a n )= v .
(6)
由此可得,式(3)与式(6)相等:
f ( a 1 )* f ( a 2 )*…* f ( a n )=
f ( a 1 * a 2 *…* a n )= v .
(7)
证毕.
二叉树在计算机科学中是一种常用的数据结构.它既可用抽象的代数理论表示,也可用程序语言伪代码表示,介于理论与程序代码之间.因此,二叉树结构非常容易转化为实际执行的计算机程序代码.
在整数集合 ![]() +中,随机选取整数 x 1 , x 2 ,…, x n ,任意两两相乘得到整数积值 v i , j ∈
+中,随机选取整数 x 1 , x 2 ,…, x n ,任意两两相乘得到整数积值 v i , j ∈ ![]() +.在集合
+.在集合 ![]() +存在整数乘法同态映射 f :
+存在整数乘法同态映射 f : ![]() +→
+→ ![]() +.整数乘法同态二叉树的构造过程为:
+.整数乘法同态二叉树的构造过程为:
1) 在 ![]() +中随机选取2个数, x i , x j ∈
+中随机选取2个数, x i , x j ∈ ![]() +, i , j ∈ n , i ≠ j ,计算 f ( x i )= v i 和 f ( x j )= v j .
+, i , j ∈ n , i ≠ j ,计算 f ( x i )= v i 和 f ( x j )= v j .
2) 根据定义2,计算 f ( x i )* f ( x j )= v i , j , f ( x i * x j )= f ( v i , j )= v i , j .
3) 由定理1,等式 f ( x i )* f ( x j )= f ( x i * x j )= v i , j 成立.
4) 以 f ( x i )= v i 为左子树、 f ( x j )= v j 为右子树、 f ( x i * x j )= v i , j 为根结点,构造1棵二叉树.下面给出任意2个结点的构造二叉树,如图1所示:
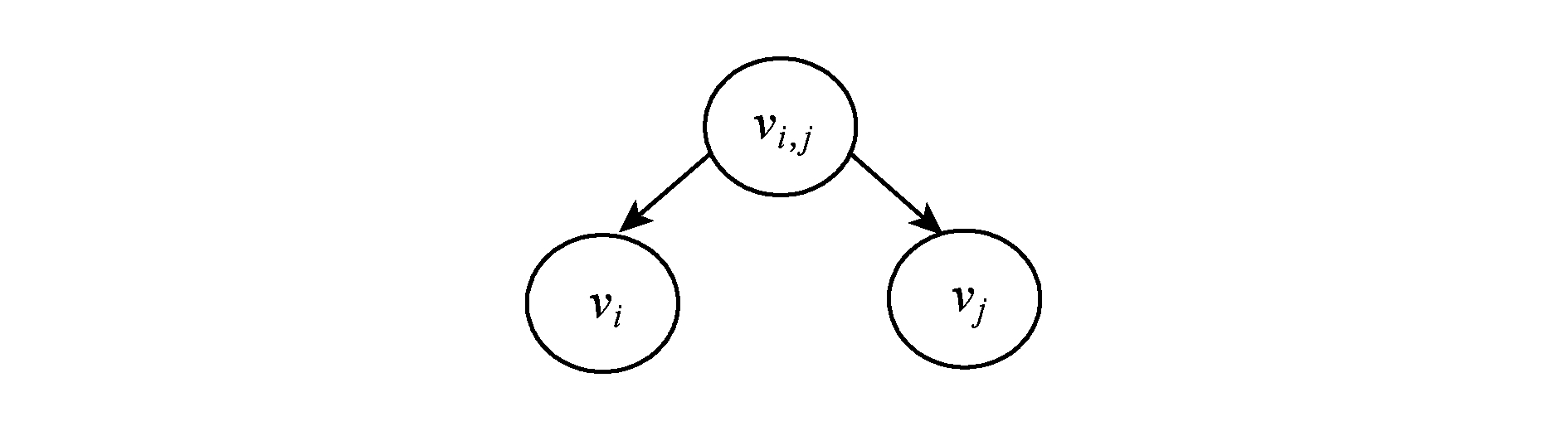
Fig. 1 The binary tree structure of any two nodes
图1 任意2结点的构造二叉树
5) 随机选取 x i +1 , x j +1 ∈ ![]() +,执行过程1)~4)构造第2棵二叉树,得到以 f ( v i +1 * v j +1 )= v i , j , i +1, j +1 为根结点的二叉树,如图2所示:
+,执行过程1)~4)构造第2棵二叉树,得到以 f ( v i +1 * v j +1 )= v i , j , i +1, j +1 为根结点的二叉树,如图2所示:
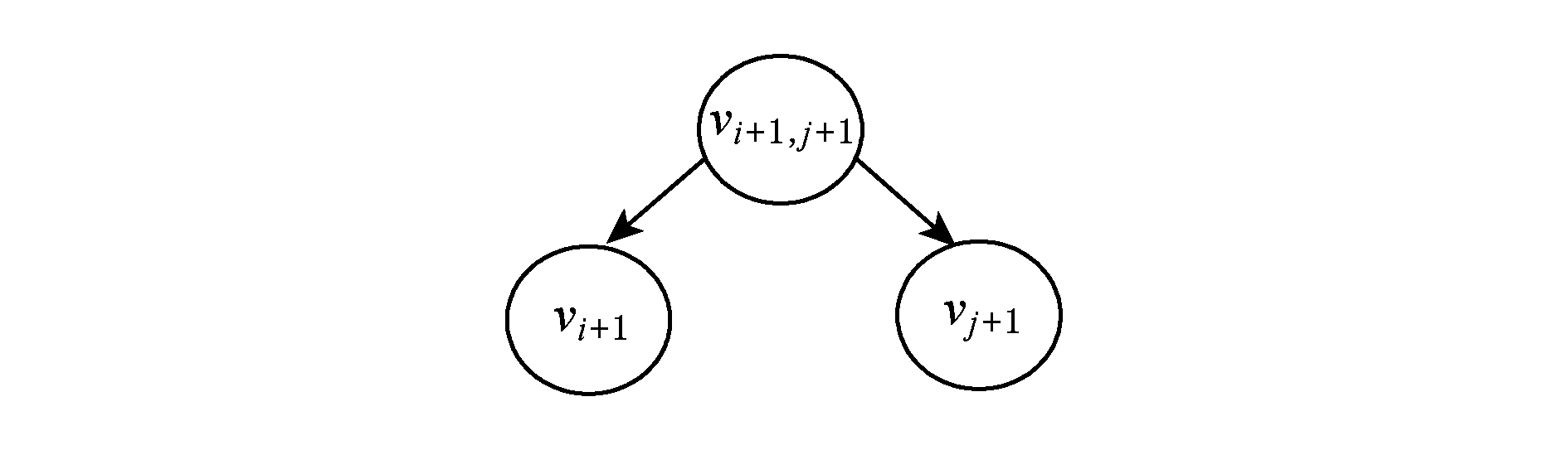
Fig. 2 The binary tree structure of any two nodes
图2 任意2结点的构造二叉树
6) 由定理1可知:
f ( x i * x j )* f ( x i +1 * x j +1 )=
f ( x i * x j * x i +1 * x j +1 )
成立,则以 f ( x i * x j )= v i , j 为根结点为左子树、以 f ( x i +1 * x j +1 )= v i +1, j +1 为根结点的右子树、以 f ( v i +1 * v j +1 )= v i , j , i +1, j +1 为根结点,构造1棵二叉树,如图3所示:
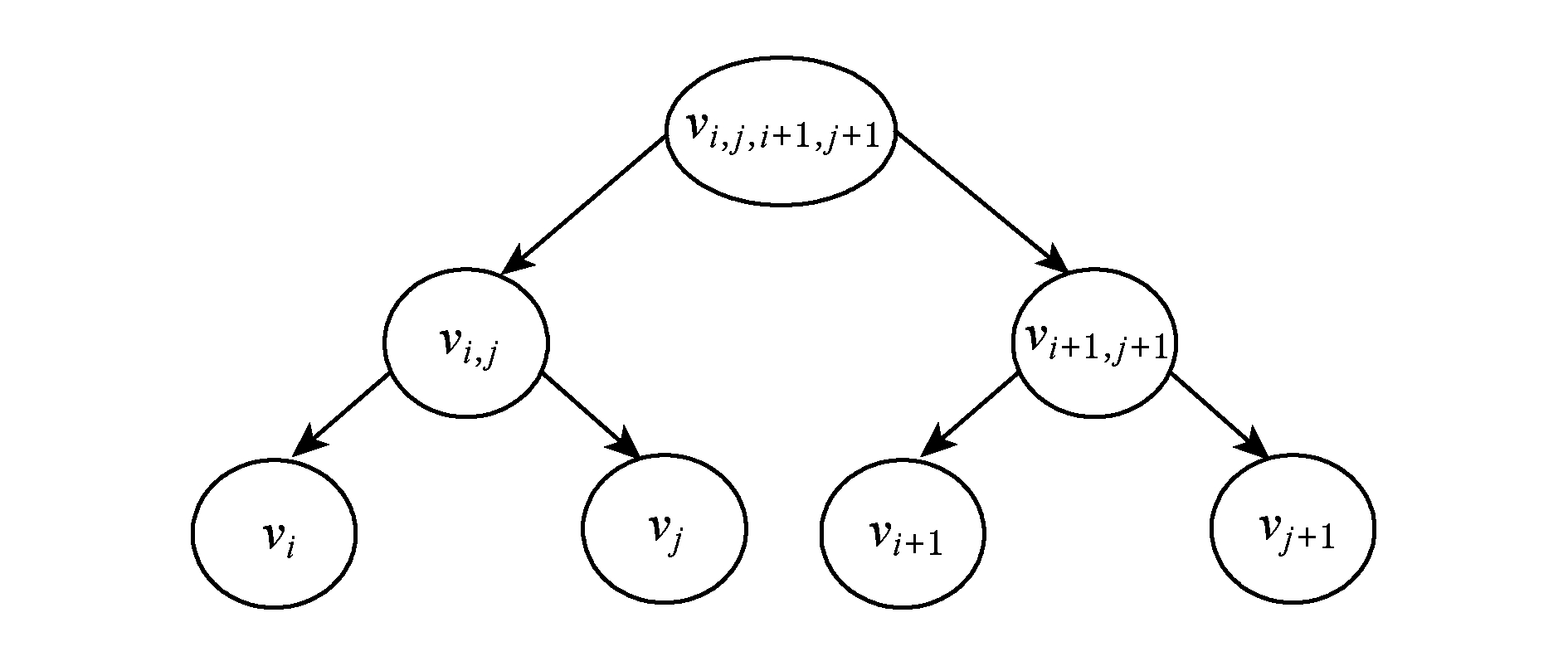
Fig. 3 A binary tree
图3 二叉树
7) 以此类推,当 n 个随机数两两匹配结束,则构造成1棵叶子结点数为 n 的二叉树 T ,称之为整数乘法同态二叉树,如图4所示:
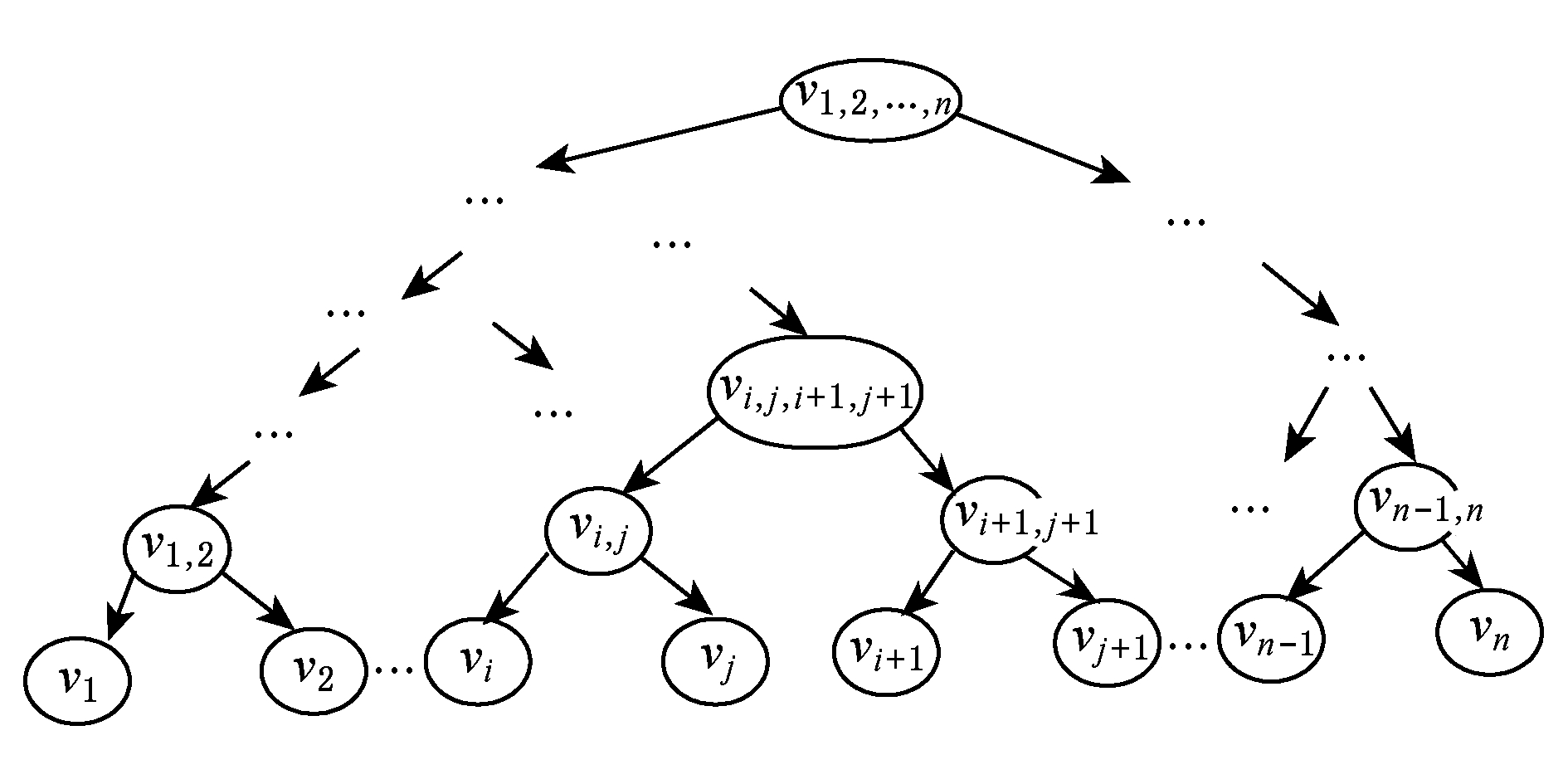
The binary tree with n leaf nodes
图4 n个叶子结点的构造二叉树
整数乘法同态二叉树没有空树,即不会有空操作.整数乘法同态二叉树的基本遍历与性质类似于数据结构 [18] 中的二叉树的基本遍历与性质.整数乘法同态二叉树的基本遍历和性质如下:
2.2.1 整数乘法同态二叉树的先序遍历
为了清楚整数乘法同态二叉树的先序遍历,给出先序遍历步骤:
1) 访问根结点;
2) 先序遍历左子树;
3) 先序遍历右子树.
① 虽然通信双方 A 与 B 注册有相同的点,但其认证结构不同于以往的Diffie-Hellman扩展协商协议,即使敌手 E 能得到 A 或 B 的所有注册点,也无法获得 A 与 B 的共享密钥.详细分析见4.3节.
2.2.2 整数乘法同态二叉树的基本性质
性质1 . 整数乘法同态二叉树的第 i 层上至多有2 i -1 个结点( i ≥1).
性质2 . 整数乘法同态二叉树的深度为 k 时,二叉树至多有2 k -1个结点( k ≥1).
通信双方 A 和 B 在可信第三方TA中一次性注册一些相同的可信同态点 ① (素数,且 A 端的同态点集合中不会有相同点,同理 B 端的同态点集合中不会有相同点).这些点数量满足2 h , h ∈ n ,即叶子结点是以2 h 配对增加,(如 h =1时叶子结点为2, h =2时叶子结点为4, h =3时叶子结点数为8,即叶子结点是以2 h 配对增加).当协议运行时,分别在 A 和 B 端构造1棵整数乘法同态二叉树(其叶子结点为素数).通过整数乘法同态二叉树的先序遍历,找到认证点(即同态值),取同态值的左、右子树根结点作为参数,然后基于Diffie-Hellman协议进行密钥协商,得到共享会话密钥 k AB ,即完成通信双方的隐式认证.该共享会话密钥 k AB 可应用于认证、加密、签名等.当协议结束时,通信双方释放构造的整数乘法同态二叉树.
根据2.1节的整数乘法同态二叉树构造方法,构造1棵叶子结点为素数的整数乘法同态二叉树.构造方法如下:
设 Z 1 ⊂ ![]() +和 Z 2 ⊂
+和 Z 2 ⊂ ![]() +是2个整数环上的半群或幺半群, Z 1 , Z 2 是
+是2个整数环上的半群或幺半群, Z 1 , Z 2 是 ![]() +上的一个划分,且 Z 1 ={ p i | p ∈ primes ∧ i ∈ n }. f 是
+上的一个划分,且 Z 1 ={ p i | p ∈ primes ∧ i ∈ n }. f 是 ![]() +到自身的一个整数乘法同态映射, p i , p j ∈ Z 1 , i , j ∈ n , i ≠ j 不同的素数.随机选取 p i , p j ,构造1棵叶子结点为素数的同态二叉树,其步骤为:
+到自身的一个整数乘法同态映射, p i , p j ∈ Z 1 , i , j ∈ n , i ≠ j 不同的素数.随机选取 p i , p j ,构造1棵叶子结点为素数的同态二叉树,其步骤为:
1) 随机选取不同的素数 p i , p j ,计算 f ( p i )= p i , f ( p j )= p j , f ( p i * p j )= v i , j .
2) 以 f ( p i )= p i 为左子树、 f ( p j )= p j 为右子树、 f ( p i * p j )= v i , j 为根结点,构造1棵叶子结点为素数的同态二叉树.
3) 随机选取 p i +1 , p j +1 ,计算 f ( p i +1 )= p i +1 , f ( p j +1 )= p j +1 , f ( p i +1 * p j +1 )= v i +1, j +1 ,以 f ( p i +1 )= p i +1 为左子树, f ( p j +1 )= p j +1 为右子树, f ( p i +1 * p j +1 )= v i +1, j +1 为根结点,构造1棵叶子结点为素数的同态二叉树.
4) 分别以步骤2)的根结点 f ( p i * p j )= v i , j 为左子树根结点、步骤3)的根结点 f ( p i +1 * p j +1 )= n i +1, j +1 为右子树根结点,构造1棵叶子结点为素数的同态二叉树.
5) 重复步骤1)~4), n 个素数叶子结点两两配对完成后,构造出1棵叶子结点为素数的同态二叉树,称之为 T i , j ,如图5所示:
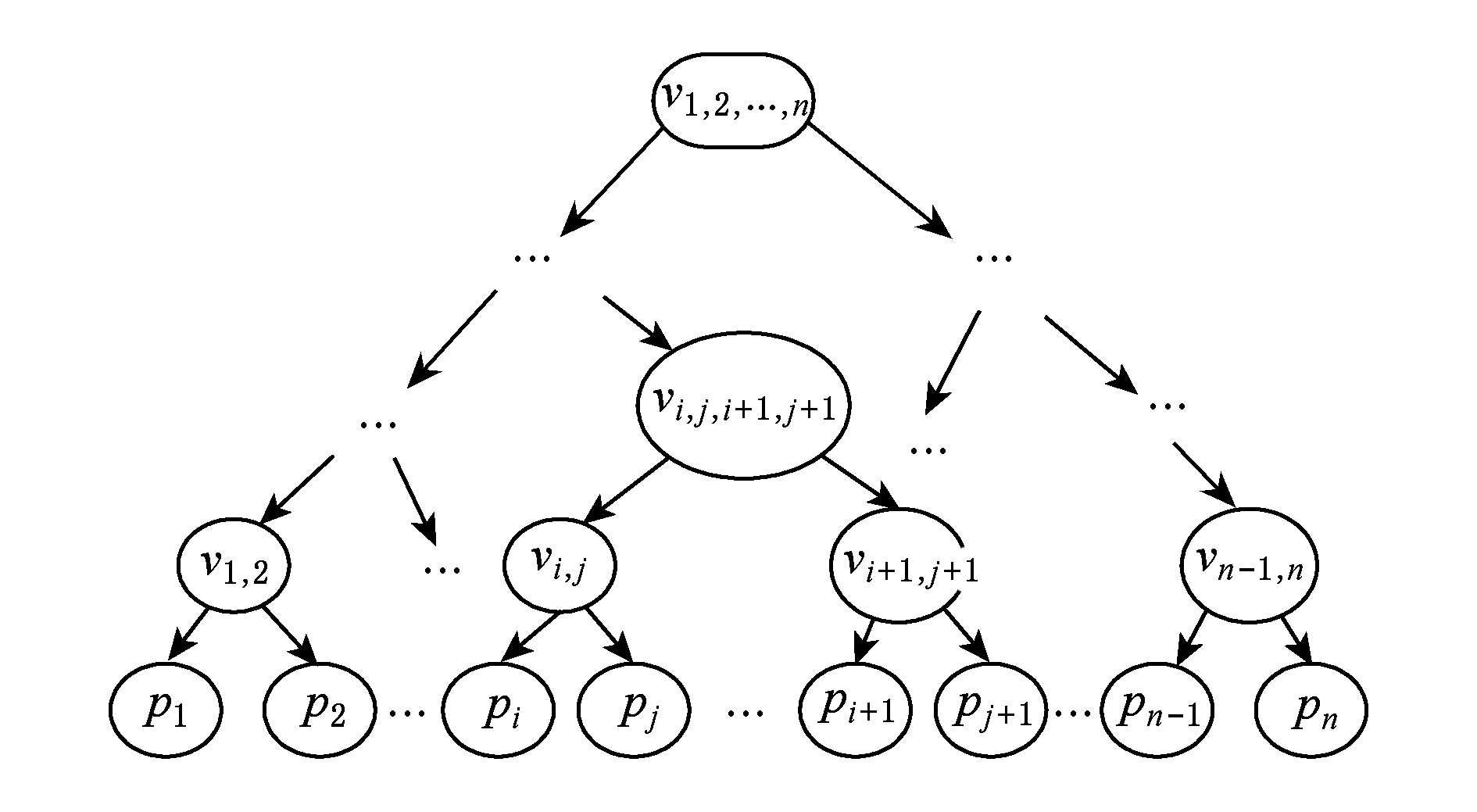
Fig. 5 The homomorphic binary tree with n leaf nodes of the primenumbers
图5 叶子结点为n个素数的同态二叉树
T i , j 是已经构造好的叶子结点为素数的同态二叉树.为证明方便,用一个集合{ T i , j }表示构造好的同态二叉树,分别存储于通信双方( A 和 B ). p i , p j ∈ Z 1 , i , j ∈ n , i ≠ j 是叶子结点(即为素数). G 是一个素数阶为 N 的循环群, g ∈ G 是群 G 的生成元.
f 为 ![]() +到自身的一个同态映射: f ( x )= x , x ∈
+到自身的一个同态映射: f ( x )= x , x ∈ ![]() +.
+.
参数设置:{ T i , j }, r i , r j ∈{ T i , j }, i , j ∈ n , i ≠ j 保密;结点 r i , j ∈{ T i , j }, G , g 公开.协议执行步骤:一轮 A 与 B 密钥协商,如图6所示,“‖”表示连接.
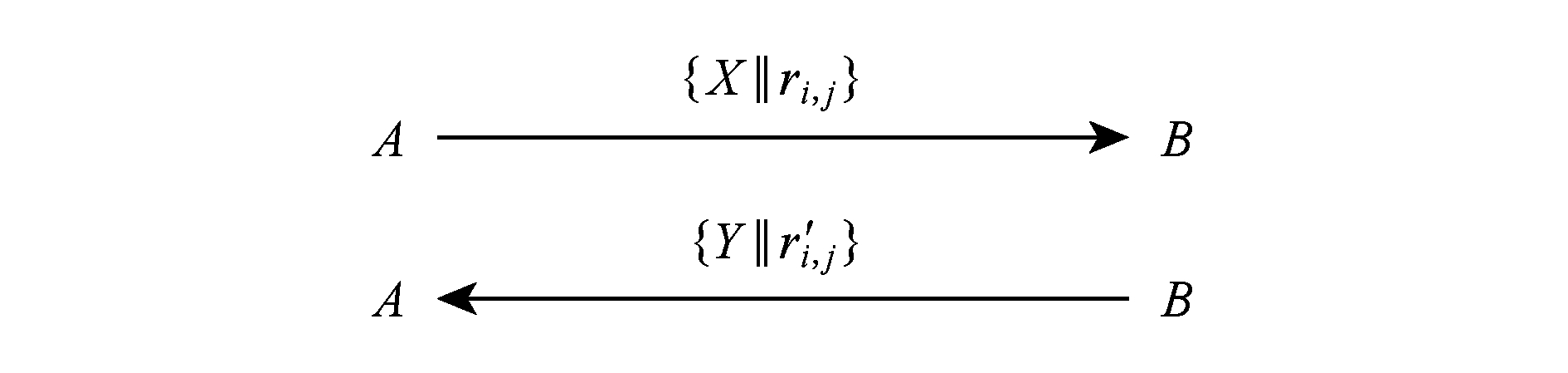
Fig. 6 One round A and B key exchange protocols
图6 一轮A与B密钥交换协议
1) A 在整数乘法同态二叉树中,如图5所示,随机选取2个兄弟结点数 r i , r j ,且计算: f ( r i )= r i , f ( r j )= r j , f ( r i )* f ( r j )= f ( r i * r j )= r i , j , X = g r i mod N ,把( X ‖ r i , j )发送给 B .
2) B 收到( X ‖ r i , j ),根据2.2.1节整数同态二叉树的先序遍历,查找 r i , j .如果查找成功,取 r i , j 的左子树根结点 r i ,计算 Y ′= g r i mod N ,然后验证等式 X = Y ′,相等则 B 相信( X ‖ r i , j )是由 A 发送.否则,终止协议执行.
3) B 在整数乘法同态二叉树中,如图5所示,随机选取2个兄弟结点数 ![]() ,
, ![]() ,计算: f (
,计算: f ( ![]() )=
)= ![]() , f (
, f ( ![]() )=
)= ![]() , f (
, f ( ![]() )* f (
)* f ( ![]() )= f (
)= f ( ![]() *
* ![]() )=
)= ![]() , Y =
, Y = ![]() 把( Y ‖
把( Y ‖ ![]() )发送给 A .
)发送给 A .
4) A 收到( Y ‖ ![]() ),根据2.2.1节整数同态二叉树的先序遍历,查找
),根据2.2.1节整数同态二叉树的先序遍历,查找 ![]() .如果查找成功,取
.如果查找成功,取 ![]() 的右子树根结点
的右子树根结点 ![]() ,计算
,计算 ![]() 然后验证等式 X ′= Y ,相等则 A 相信( Y ‖
然后验证等式 X ′= Y ,相等则 A 相信( Y ‖ ![]() )是由 B 发送.否则,终止协议执行.
)是由 B 发送.否则,终止协议执行.
5) A 计算 ![]() N .
N .
6) B 计算 ![]() N .
N .
所以 A 与 B 生成共享密钥 k AB ,即完成通信双方的密钥协商.
新协议可以抵抗中间人攻击.当只有2个大素数叶子结点时,新协议的安全性等价于大整数因式分解的困难.新协议满足CDH与DDH安全性假设及GDH [19] 假设.给出新协议结构的安全证明.
1) 建立敌手模型.设 E 是攻击者, E 具有Dolev-Yao [20] 模型的能力:①完全控制网络信息交换,即敌手可以获得网络上的任何信息;②主动攻击与被动攻击(冒充、截取、注入、重放等能力);③询问随机预言模型;④离线计算能力.
2) 假设在通信双方 A 和 B 端当且仅当取2个大素数叶子结点 p i , p j 时,即为 p i * p j = n i , j ,其安全性等同于RSA算法.
3) 新协议以Diffie-Hellman为基础,满足CDH与DDH假设.
① 满足CDH假设:存在一个PPT算法 C ,在树{ T i , j }随机选取 r i , r j ,存在:
Pr [ C  g , g r i , g r j
g , g r i , g r j 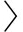 = g r i ]≤ ε ( n ),
= g r i ]≤ ε ( n ),
(8)
其中, ε ( n )为概率可忽略不计函数.即协议满足CDH假设安全.
② 满足DDH假设:存在一个PPT算法 C ,在树{ T i , j }随机选取 n i , n j ,存在:
Pr [ C  g , g r i , g r j , g r i r j
g , g r i , g r j , g r i r j 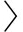 =1]-
=1]-
Pr [ C  g , g r i , g r j , g c
g , g r i , g r j , g c 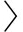 =1]≤ ε ( n ),
=1]≤ ε ( n ),
(9)
其中, ε ( n )为概率可忽略不计函数.即协议满足DDH假设安全.
4) 新协议没有使用签名与消息认证,但可以抵抗中间人攻击和具有隐式认证功能.
① 抵抗中间人攻击分析.假设敌手 E 在上述3.2节协议执行步骤1): A 发送信息{ X ‖ r i , j }给 B 时, E 截获{ X ‖ r i , j },然后假冒 A 向 B 发送 ![]() N ‖ r i , j }. B 在收到信息
N ‖ r i , j }. B 在收到信息 ![]() ‖ r i , j }后,查找 r i , j ,取其左子树根结点 r i ,计算
‖ r i , j }后,查找 r i , j ,取其左子树根结点 r i ,计算 ![]() 发现不相等.若要使等式相等,表示敌手 E 攻击成功,只有2种方法:
发现不相等.若要使等式相等,表示敌手 E 攻击成功,只有2种方法:
Ⅰ必须解决离散对数难解问题,即求解截获 X 的指数 r i ;
Ⅱ整数因式分解问题,即分解截获的大整数 r i , j 的因子 r i .故协议可以抵抗中间人攻击.
② 具有认证功能分析.当 B 收到 A 发送信息 X ,查找 r i , j ,计算 ![]() 成立,则 B 确认信息 X 是由 A 发的.同理可证, B 认证 A 过程.
成立,则 B 确认信息 X 是由 A 发的.同理可证, B 认证 A 过程.
5) 会话密钥 k AB 的前向安全.由同态二叉树可知, r i , j 是随机选择,具备新鲜度,所以每次得到的会话密钥 k AB 都不一样,且每次都是独立.故前后生成的 k AB 不会相互泄密信息,保证新协议的前向安全成立.
设DDH(·)为预言机, D 为一个求解GDH问题的算法.
定义求解的优势概率为
Pr [ D ( g , g r i , g r j , g r i )=1]-
Pr [ D ( g , g r i , g r j , g c )=1].
(10)
如果其优势概率满足:
Pr [ D ( g , g r i , g r j , g r i )=1]-
Pr [ D ( g , g r i , g r j , g c )=1]≤ ε ( n ),
(11)
r i , r j ∈ ![]() +, g ∈ G , ε ( n )可忽略不计的.则称协议满足GDH假设.
+, g ∈ G , ε ( n )可忽略不计的.则称协议满足GDH假设.
证明.敌手模型 E 完全控制通信网络,同时具有询问 DDH (·)预言机的能力. E 分别截获 ![]() 后,向 DDH (·)询问: c = r i
后,向 DDH (·)询问: c = r i ![]() 是否成立?如果 c = r i
是否成立?如果 c = r i ![]() , DDH (·)返回1,否则为0.所以 E 每次询问预言机得到的概率为
, DDH (·)返回1,否则为0.所以 E 每次询问预言机得到的概率为 ![]() .有 r i
.有 r i ![]() ∈ Z 2 ,且根据二叉树的性质,不防设叶子结点为 n ,总结点数则为2 n -1.故 E 的优势概率为
∈ Z 2 ,且根据二叉树的性质,不防设叶子结点为 n ,总结点数则为2 n -1.故 E 的优势概率为
Pr [ D ( g , g r i , g r j , g r i )=1]-
Pr [ D ( g , g r i , g r j , g c )=1]≤ ![]() ,
,
(12)
当 n →∞时,优势概率可忽略不计,协议在RO模型下是可证明安全的,即满足IND-CPA安全.
证毕.
由新协议构造可知,假设敌手 E 在2种情况下成立,则 E 可以攻破协议.
1) E 可获取 A 或 B 端的注册点,即同态点.
2) 二叉树的结点不唯一(例如存在:当 r i ≠ r j ≠ r k ≠ r m , i , j , k , m ∈ n ,有 r i r j = r k r m ).
证明.
1) 假设 E 获取了 A 或 B 端的注册点,设为{ p 1 , p 2 ,…, p 2 n }.由3.1节可知,在构造二叉树时,叶子结点是配对组成由数学的排列组合可知 h ∈ n .
(13)
由于{ p 1 , p 2 ,…, p 2 n }在 Z 1 均匀分布,因此 E 要获得与 A 或 B 完全相同二叉树的概率为 ![]() ,当 h →∞时,
,当 h →∞时, ![]() →0.故 E 不可能获得与 A 或 B 完全相同的配对组.也就是说, E 不可能获得与 A 或 B 完全相同的素数叶子结点同态二叉树.
→0.故 E 不可能获得与 A 或 B 完全相同的配对组.也就是说, E 不可能获得与 A 或 B 完全相同的素数叶子结点同态二叉树.
2) 已知叶子结点是不同的素数.反证法,假设有2个相同的结点(非叶子结点), r i = ![]() ,则一定存在结点 r i 左右子树中有1个孩子 r i 1 或 r j 1 与结点
,则一定存在结点 r i 左右子树中有1个孩子 r i 1 或 r j 1 与结点 ![]() 左右子树的孩子
左右子树的孩子 ![]() 或
或 ![]() 相同,或 gcd ( r i 1 ,
相同,或 gcd ( r i 1 , ![]() )≠1或 gcd ( r j 1 ,
)≠1或 gcd ( r j 1 , ![]() )≠1.以此类推,一定存在 p i = p j 的素数叶子结点与已知矛盾.故二叉树的结点具有唯一性.
)≠1.以此类推,一定存在 p i = p j 的素数叶子结点与已知矛盾.故二叉树的结点具有唯一性.
证毕.
本文分别从3个方面分析新协议的性能.
二叉树是计算机科学中常用的一种数据结构,其常用存储方式有2种:1)顺序存储;2)链式存储.不管是哪一种存储,在它最坏情况下空间复杂度为 O ( n ),遍历的时间复杂度为 O ( n ).
设新协议的二叉树叶子结点为 n ,分析新协议最坏情况的存储.根据性质1(见2.2.2节)得到新协议的二叉树深度为 i =lb n +1.根据性质2(见2.2.2节)得到新协议总结点数为:2 lb n +1 -1=2 n -1.由此可知,新协议存储空间为线性 O ( n ).根据其存储方式可知其遍历复杂度为线性 O ( n ),故新协议可实现.
选取4种以Diffie-Hellman协议为基础的相似协议和同类横向2种身份识别协议,比较它们在最坏情况下计算量大小和在协议中会用的安全假设个数,结果如表1所示,其中的 T exp 表示1次指数运算的时间.
Table 1 Compared Performance of the Protocols
表1 协议的性能比较
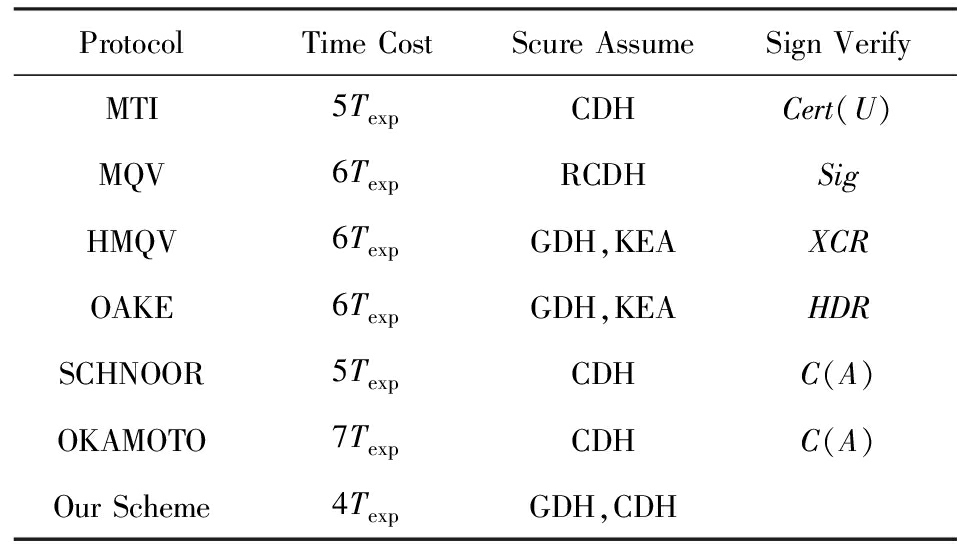
表1中协议使用的签名或消息认证为
MTI- Cert : b T = α a T = σ ;
MQV- Sig : Sig ( s A , s B )= σ ; ![]() ;
;
OAKE- HDR : H k ( g a ( bf + yc ) g x ( bd + ye ) )= σ ;
SCHNOOR- C ( A ): Sig TA ( ID ( A ), υ )= σ ;
OKAMOTO- C ( A ): Sig TA ( ID ( A ), υ )= σ .
从表1可以看出,提出的新协议在计算量的开销方面具有明显优势,原因是新协议不需要加入签名和消息认证.同时协议只使用1个强安全假设GDH,与使用2个强安全假设(GDH,KEA [21] 假设)的密钥协商协议(HMQV,OAKE)相比,新协议在实际应用中安全性更高.
参数 n 对新协议在网络通信中的影响主要表现为:1)结点的查找;2)通信时间开销.
1) 二叉树的查找平均长度.由文献[22]可知,假设树中的每个结点都是均匀分布,即等概率查找.不妨设二叉树的叶子结点为 n ,总结点数为2 n -1,查找每个结点的等概率为 P i = ![]() .其平均查找的长度为
.其平均查找的长度为
![]()
![]() lb n -1,
lb n -1,
(14)
当 n →∞时,平均查找长度为:lb n .故新协议查找长度为对数可以实现.
2) 新协议基于OpenSSL下的C语言代码模拟实验,分析参数 n 变化对新协议在网络通信中所用时间的影响.
本文给出 n 的2种变化形式对新协议在网络通信中的影响:①二叉树素数叶子结点个数(numbers of nodes, N );②叶子结点的位数(node bits, bits ).
实验环境:Intel ® CPU G3240,内存4 GB;Win7,Visual studio 2010,openSSL-1.0.1 s.使用OpenSSL函数库的大数运算,其中包括大数模指数运算函数、大素数生成函数等使用.参与者之间的通信经过Socket API的TCP连接.
采用服务器与客户端模式进行模拟实验,分别得出叶子结点个数与结点位数变化在网络通信中的时间开销,如表2所示(行表示叶子结点的位数,列表示叶子结点的个数 N ,行列交点表示网络传输花费的时间).
Table 2 The Effect of the Network Communication Based on Binary Tree Nodes
表2 二叉树结点的网络通信影响 s
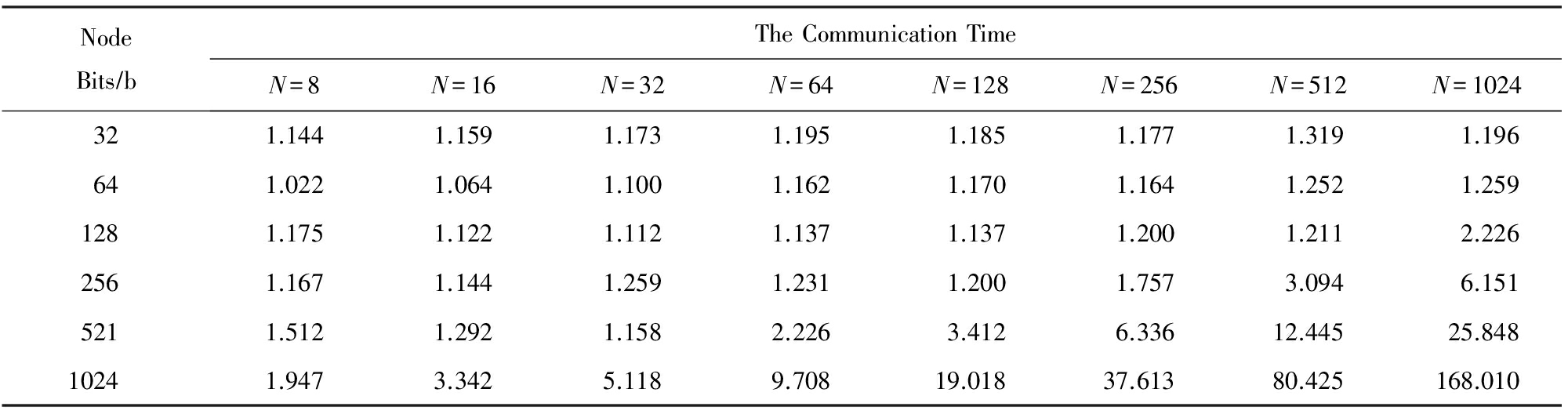
对表2的数据分别以行、列及网络通信时间(s)作为坐标进行分析.实验数据分析结果:图7表示叶子结点个数变化对网络通信时间的影响;图8表示叶子结点位数变化对网络通信时间的影响.
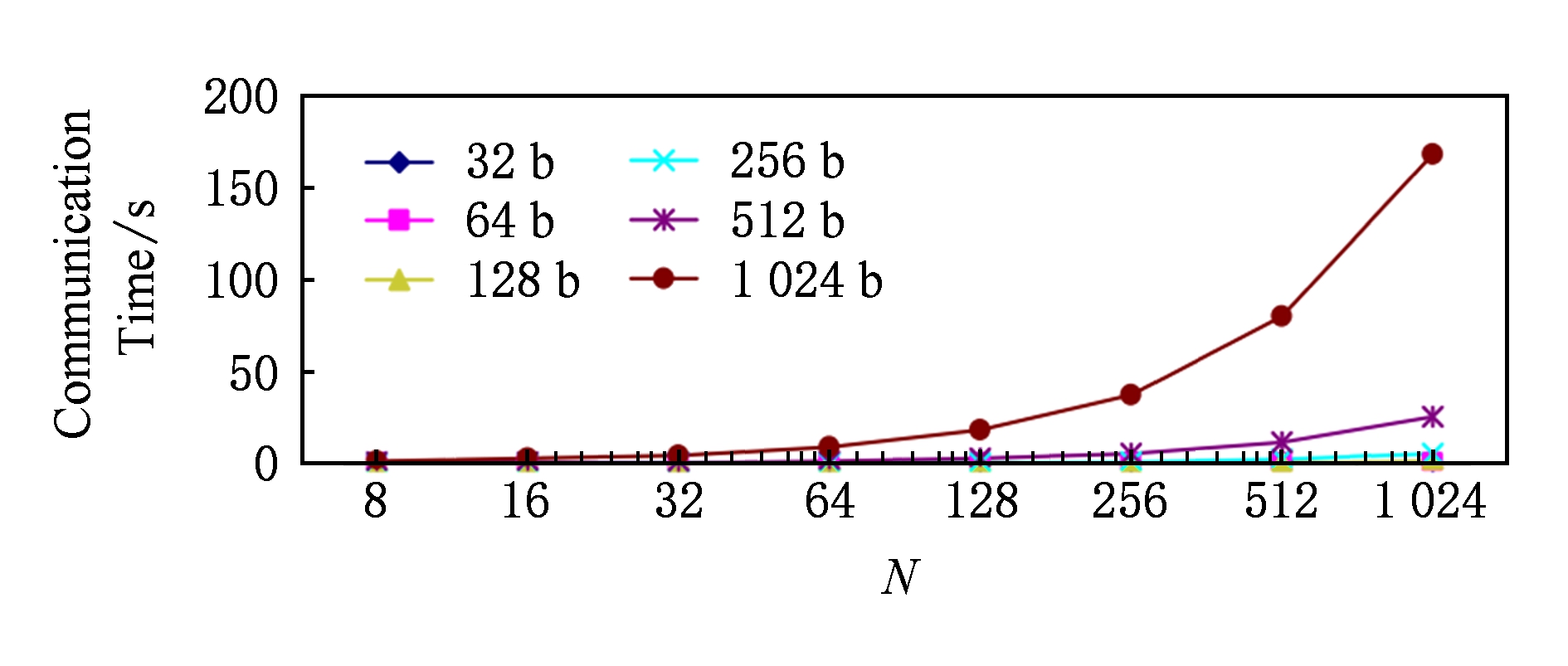
Fig. 7 The effect of the number of leaf nodes on communication time in network
图7 叶子结点个数变化对网络通信时间的影响
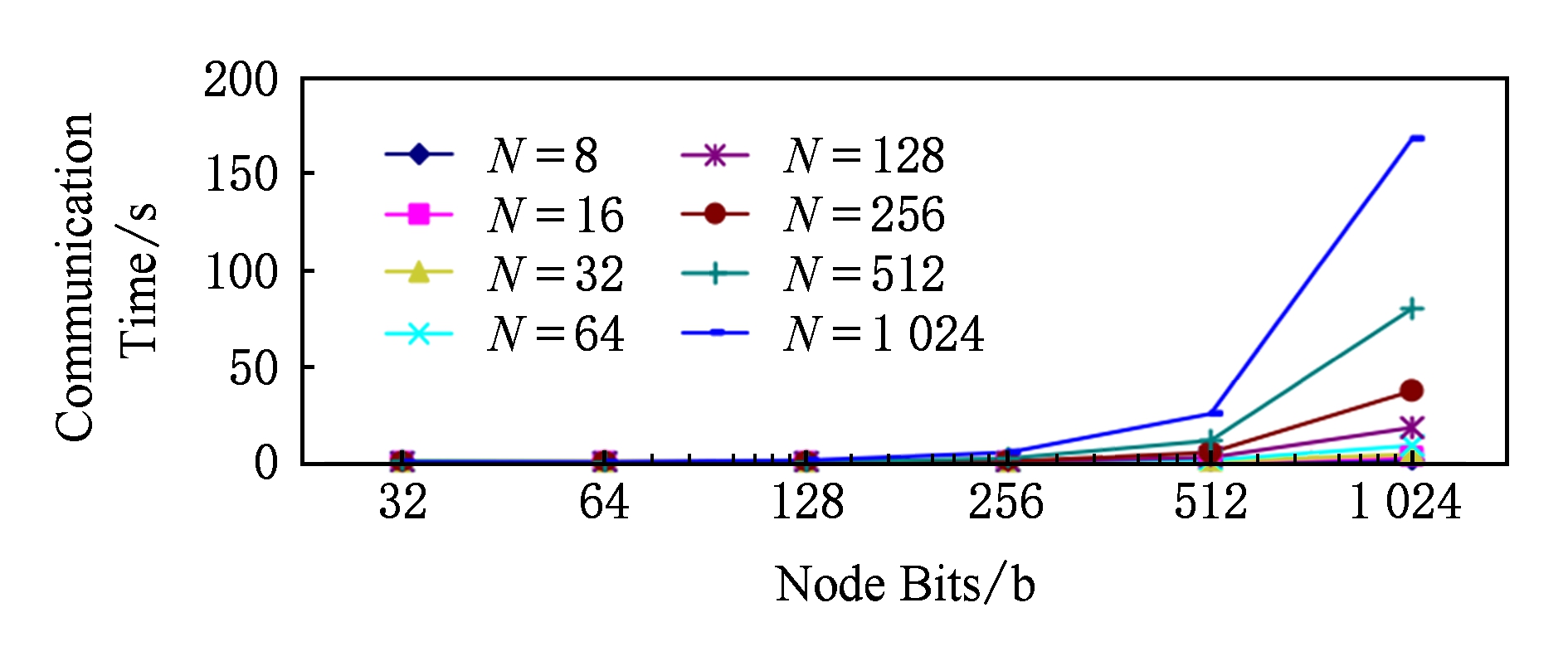
Fig. 8 The effect of the bit of leaf nodes on communication time in network
图8 叶子结点位数变化对网络通信时间的影响
3) 结果分析:
① 从图7与图8可知,结点个数 N 和结点位数 bits ,在比较小的情况下,对网络通信并没有太大的影响.但随着它们变大,网络通信时间开销随之增长.②结点位数带来的网络时间开销增长比结点的个数带来的时间开销增长快.③不防设结点个数与位数的比值为: δ = N / b .当 δ 越小,则叶子结点位数越大,需要的叶子结点个数越少.这不仅保证了新协议的安全,而且消耗的资源更少(如叶子结点的个数、二叉树结点寻找时间等).例如,如果叶子结点是1 024 b二进制素数,新协议只需要2个大素数叶子结点,就能生成1个2 048 b二进制整数根结点.这时新协议的安全等价于1个2 048 b二进制大整数因式分解的困难.故新协议的安全完全等价于RSA的安全 [23] .
本文对已有密钥协商协议进行了研究,提出一种计算量小、无需签名和消息认证等额外时间开销的密钥协商协议.提出的新协议方案具有计算量小、强安全假设少、占用资源少等优点,具有一定的创新性与适用性.其安全性依赖离散对数与大整数因式分解困难问题.新协议引入二叉树及其性质和特点,使得协议更容易转化为实际的程序语言代码,适用于云计算、 物联网、 社交网络和大数据等新兴网络通信服务.协议并发通信的安全与认证将作为未来的研究方向.
参考文献
[1]Zhang Huanguo, Han Wenbao, Lai Xuejia, et al. Survey on cyberspace security[J]. Scientia Scinica: Informations, 2116, 46(2): 125-164 (in Chinese)(张焕国, 韩文报, 来学嘉, 等. 网络空间安全综述[J]. 中国科学: 信息科学, 2016, 46(2): 125-164)
[2] Jian Han, Xu Qiuliang. Advances in key techniques of practical secure multi-party computation[J]. Journal of Computer Research and Development, 2015, 52(10): 2247-2257 (in Chinese)(蒋瀚, 徐秋亮. 实用安全多方计算协议关键技术研究进展[J]. 计算机研究与发展, 2015, 52(10): 2247-2257)
[3] Diffie W, Hellman M. New directions in cryptography[J]. IEEE Trans on Information Theory, 1976, 22(6): 644-654
[4] Lim C H, Lee P J. A key recovery attack on discrete long-based schemes using a prime order subgroup[G] //LNCS 1294: Advances in Cryptology 1997. Berlin: Springer, 1997: 249-263
[5] Just M, Vaudenay S. Authenticated multi-party key agreement[G] //LNCS 1163: Advances in Cryptology 1996. Berlin: Springer, 1996: 36-49
[6] Goss K C. Cryptographic method and apparatus for public key exchange with authentication: USA, US4956863[P]. 1990-09-11
[7] Menezes A, Qu M, Vanstone S. Some new key agreement protocols providing implicit authentication[C] //Proc of the 2nd Workshop Selected Areas in Cryptography. Berlin: Springer, 1995: 89-98
[8] Schneier B. Skipjack and kea algorithm specification version 2.0[R/OL]. Washington: National Security Agency, 1998 [2016-10-30]. http://ece.gmu.edu/coursewebpages/ECE/ECE646/F09/project/reports_1999/carlton_report.pdf
[9] Law L, Menezes A, Qu M, et al. An efficient protocol for authenticated key agreement[J]. Designs, Codes and Cryptography, 2003, 28(2): 119-134
[10] IEEE. Standard specifications for public-key cryptography[S]. New York: Institute of Electrical Electronics Engineers, 2000: 1-228
[11] Krawczyk H. Hmqv: A high-performance secure Diffie-Hellman protocol[G] //LNCS 3621: Advances in Cryptology 2005. Berlin: Springer, 2005: 546-566
[12] Yao Qizhi. Zhao Yunlei. Oake: A new family of implicitly authenticated Diffie-Hellman protocols[C] //Proc of the 2013 ACM SIGSAC Conf on Computer & Communications Security. New York: ACM, 2013: 1113-1128
[13] Zhao Shijun, Zhang Qianying. Shmqv: An efficient key exchange protocol for power-limited devices[G] //LNCS 9065: Information Security Practice and Experience ISPEC 2015. Berlin: Springer, 2015: 154-167
[14] Feng Hao. On robust key agreement based on public key authentication[J]. Security and Communication Networks, 2014, 7(1): 77-87
[15] Toorani M. Cryptanalysis of a robust key agreement based on public key authentication[J]. Security and Communi-cation Networks, 2016, 9(1): 19-26
[16] Feng Dengguo. Security Protocol—Theory and Practice[M]. Beijing: Tsinghua University Press, 2011: 273-316 (in Chinese)(冯登国. 安全协议——理论与实践[M]. 北京: 清华大学出版社, 2011: 273-316)
[17] Xu Shurun, Meng Daoji, Xiao Yongzhen, et al. Concise Mathematics Dictionary[M]. Beijing: Science Press, 2002: 45-88 (in Chinese)(徐书润, 孟道骥, 萧永震, 等. 简明数学词典[M]. 北京: 科学出版社, 2002: 45-88)
[18] Clifford A. Data Structures, Algorithm Analysis in C++[M]. 3rd ed. New York: Dover Publications, 2011: 155-160
[19] Okamoto T, Pointcheval D. The gap-problems: A new class of problems for the security of cryptographic schemes[C] //Proc of Int Workshop on Practice and Theory in Public Key Cryptography: Public Key Cryptography 2001. Berlin: Springer, 2001: 104-118
[20] Dolev D, Yao Qizhi. On the security of public key protocols[J]. IEEE Trans on Information Theory, 1983, 29(2): 198-208
[21] Bellare M, Palacio A. The knowledge-of-exponent assum-ptions and 3-round zero-knowledge protocols[G] //LNCS 3152: Advances in Cryptology 2004. Berlin, Springer: 2004: 273-289
[22] Yan Weimin, Wu Weimin. Data Structure (C Language Version)[M]. Beijing: Tsinghua University Press, 2008: 118-152 (in Chinese)(严蔚敏, 吴伟民. 数据结构(C语言版)[M]. 北京: 清华大学出版社, 2008: 118-152)
[23] Beniwal S, Yadav E, Savita. An effective efficiency analysis of random key cryptography over Rsa[C] //Proc of the 2nd Int Conf on Computing for Sustainable Global Development. Piscataway, NJ: IEEE, 2015: 267-271
Wu Fusheng and Zhang Huanguo
( School of Computer Science , Wuhan University , Wuhan 430072) ( Key Laboratory of Aerospace Information Security and Trusted Computing ( Wuhan University ), Ministry of Education , Wuhan 430072)
Abstract Protocol is the specification of the network communication. Then cryptographic protocol, whose safety is based on signature or authentication technology, is one of the key techniques of information security. The technique of signature or authentication needs huge computation during communicating, which brings barriers for many communication devices because of their limited computing power. Therefore, it is an aim of studying information security to design a secure cryptographic protocol, which is practical but doesn’t need huge computation. In this paper, a novel key agreement protocol is proposed, which is based on the binary tree and the homomorphic mapping of integer multiplication. Meanwhile, an experiment is carried out in an open source (OpenSSL) systems to test how nodes of leaf binary trees affect network communication and the result of the experiment is analyzed. Our scheme is successful because our key agreement protocol is proved to be safe in the random oracle model. That is to say, in the PKI system, our key agreement protocol meets the requirement of the indistinguishable chosen plaintext attack (IND-CPA ) security. Compared with previous protocols (like MTI, MQV, HMQV), our key agreement protocol has many advantages: the computation is small; only one strong security assumption is needed; it dispenses with extra authentication of MAC and digital signature; and communicating parties can authenticate implicitly through unsafe channels.
Key words protocols; cryptography; homomorphism; binary tree; provably secure
收稿日期: 2016-11-01;
修回日期: 2017-02-06
基金项目: 国家自然科学基金重点项目(61332019);国家“九七三”重点基础研究发展计划基金项目(2014CB340601)
This work was supported by the Key Program of the National Natural Science Foundation of China (61332019) and the National Basic Research Program of China (973 Program) (2014CB340601).
中图法分类号 TP309

Wu Fusheng , born in 1974. PhD. His main research interests include design of cryptographic protocols and security analysis of cryptographic protocols.

Zhang Huanguo , born in 1945. Professor and PhD supervisor in Wuhan University. His main research interests include cryptography and trusted computing, and cryptographic protocols.