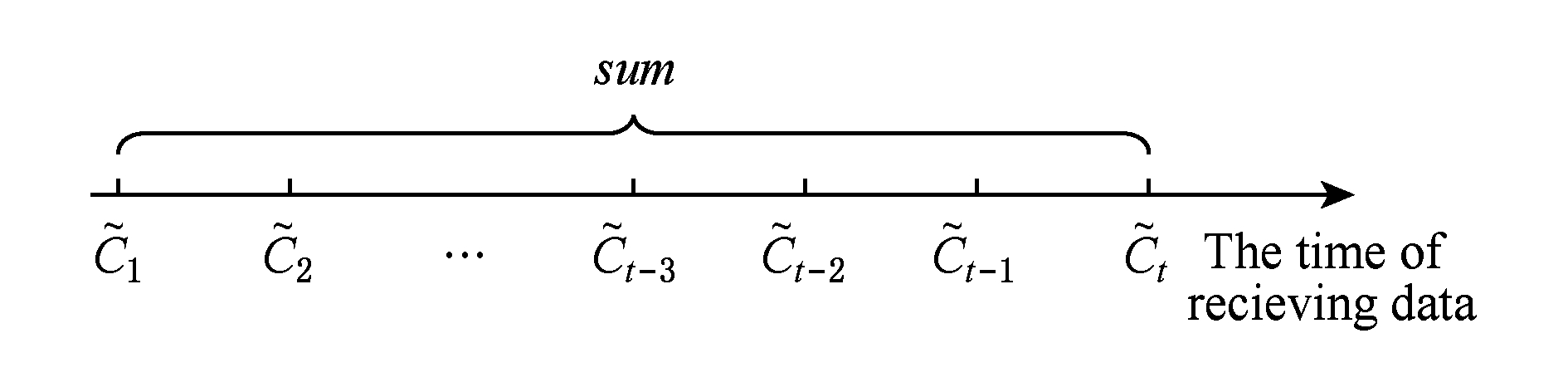
Fig. 1 The problem of noise accumulation
图1 噪声累加问题
吴英杰 张立群 康 健 王一蕾
(福州大学数学与计算机科学学院 福州 350116)
(yjwu@fzu.edu.cn)
摘 要 当前,许多实际应用需要持续地对流数据进行发布,现有关于单条流数据的差分隐私发布研究大多考虑区间的累和发布,而现实应用中往往需要对发布流数据进行任意区间计数查询,同时,用户查询往往存在特定规律,可针对历史查询进行自适应统计与分析,提高发布数据可用性.为此,提出一个基于历史查询的差分隐私流数据自适应发布算法HQ_DPSAP.算法HQ_DPSAP首先结合流数据的特性,利用滑动窗口机制动态构建窗口内流数据对应的差分隐私区间树,而后进一步分析与计算树节点的覆盖概率;接着自底向上计算隐私分配参数,再自顶向下分配隐私预算,并据此对树节点进行异方差加噪;最后根据历史查询规律自适应调整树节点的隐私预算与树结构参数,以实现流数据的自适应发布.实验对算法HQ_DPSAP的可行性及有效性进行比较分析,结果表明:算法HQ_DPSAP可有效支持任意区间计数查询,且具有较低的查询均方误差和较高的算法执行效率.
关键词 差分隐私;流数据发布;异方差加噪;历史查询;自适应算法
当前,许多实际应用需要持续地对流数据进行统计发布,如购物网站需要实时统计物品的销售额以向用户推荐热销产品,搜索引擎需要统计搜索频率较高的词组以根据用户的部分输入列出可能要搜索的词组.这些应用均需统计发布流数据在某种意义下的实时计数值.发布该类统计值在提供科学决策依据的同时,可能泄露有关用户的个体隐私信息 [1] .为此,近年来一些研究人员基于差分隐私 [2-5] 保护模型对该类流数据统计发布问题进行了研究 [6-11] ,Dwork等人 [6] 提出分段计数的方法,实现对单条流数据从时刻1到当前时刻 t 的计数值总和进行连续发布.Chan等人 [7] 进而提出了利用二叉树结构,实现了计数值总和连续发布的查询精度提高和算法效率提升.Cao等人 [8] 在系统运行前,对预先定义的查询集合进行统计分析,以实现对特定用户批次范围查询进行回答并优化查询精度.Bolot等人 [9] 提出了权重衰减下的差分隐私流数据统计发布方法,对滑动窗口内多种衰败模式的统计值加权累加和进行统计发布.在文献[10]中,采用滑动窗机制和划分等方法,提供了滑动窗口内计数值总和发布和从时刻1开始的计数值总和发布等.
在多条流数据统计发布方面,文献[11]研究如何在多个事件数据流上回答1个滑动窗查询.其研究内容关注如何更合理分配滑动窗口内的隐私预算,通过分析数据的平滑度来调整隐私分配策略.Chan等人 [12] 提出了利用二叉树结构的动态构建对多条流中具有重要影响力的流进行发布的方法(如在多部电影的点播数据中,获取本周最热门电影等).文献[13]从更一般的查询形式入手,检测数据流聚合统计值是否超过阈值,研究通信效率与隐私泄露的关系.
在现实关于单条流数据的应用中,往往需要对发布流数据进行任意区间计数查询.而在以上研究工作中,虽已从多个角度实现差分隐私流数据发布,但均未专门针对此类查询进行相关研究.为此,本文拟在滑动窗口下,实现对发布单条流数据提供灵活的任意区间计数查询,并通过对用户历史查询的分析预测,对隐私预算分配和区间树构建过程进行自适应调节,以实现发布数据精度提升和发布算法实用性的提高.本文的主要贡献有3个方面:
1) 针对流数据发布的实时性要求,提出一种在滑动窗口下进行区间树动态构建的算法;
2) 分析与计算区间树节点的覆盖概率,并据此设计隐私预算预分配策略,对动态构建的区间树节点进行异方差加噪;
3) 通过对查询区间大小和位置等用户查询偏好进行统计与分析,提出一种可自适应调节隐私预算分配与区间树结构构建的方法,从而有效提高发布数据可用性.
差分隐私保护是一种强健的隐私保护框架,由于其具有允许数据表中某条记录发生改变,对查询结果影响幅度小的特性,使得攻击者在对除某条记录外的所有信息都知情的情况下,仍无法获取到该条记录中的敏感信息.因此,能够更有效地保护隐私信息.
在差分隐私保护模型中,对兄弟数据表概念定义如下:
定义1 . 兄弟数据表.给定数据表 T 1 , T 2 ,当2个数据表之间只存在1条记录不同,则称 T 1 , T 2 为兄弟数据表.
在兄弟数据表定义基础上,Dwork给出了 ε -差分隐私定义.
定义2 . ε -差分隐私 [2] .给出任意2个兄弟数据表 T 1 , T 2 ,若发布算法 A 对该对兄弟数据表的所有可能输出均满足:
Pr [ A ( T 1 )∈ O ]≤e ε × Pr [ A ( T 2 )∈ O ],
(1)
则称算法 A 满足 ε -差分隐私.

Fig. 1 The problem of noise accumulation
图1 噪声累加问题
定义3 . 流数据.流数据为1组顺序大量、连续快速到达的数据序列,其具有实时到达、次序独立,规模随时间无限增长等特性.
在流数据中用户区间计数查询范围是[ l , r ](1≤ l ≤ r ≤ t ),其返回值公式为
(2)
根据定义2,该条件下的查询模式、噪声会随时间 t 的推移无限累加,使得隐私预算耗尽.分别如图1、图2所示:
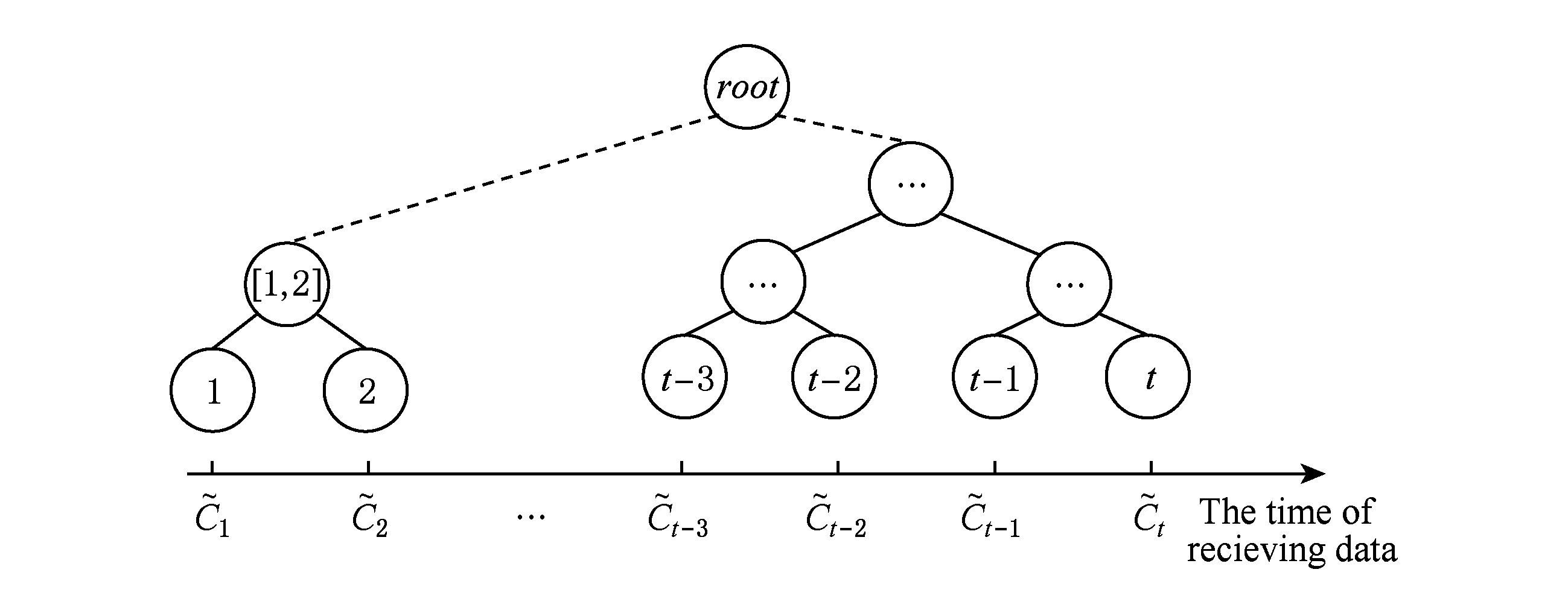
Fig. 2 The problem of privacy depletion
图2 隐私预算耗尽问题
在图1中,分别对每个时间戳的统计数据直接加噪,由于真实值 C i 与加噪值 ![]() 存在噪声误差,随着时间 t 增长,大范围区间查询会累积大量噪声,使得查询精度大幅下降,前人工作中利用差分隐私区间树构建流数据以降低查询误差.
存在噪声误差,随着时间 t 增长,大范围区间查询会累积大量噪声,使得查询精度大幅下降,前人工作中利用差分隐私区间树构建流数据以降低查询误差.
定义4 . 差分隐私区间树 [14] .对于给定计数直方图 H ={ C 1 , C 2 ,…, C n },对 H 建立差分隐私区间树 T 满足3点特性:
1) 对于所有非叶子节点,其儿子节点数大于等于2.
2) 每个节点 x 对应于 H 中的1个区间范围,表示为[ l x , r x ],根节点所代表的区间为[1, n ].
3) 每个节点 x 的隐私预算为 ε x ,真实计数值为 ![]() 通过对每个节点添加噪声(本文采用Laplace噪声 [15] ),得到加噪计数值
通过对每个节点添加噪声(本文采用Laplace噪声 [15] ),得到加噪计数值 ![]() / ε x ),使该节点满足 ε x -差分隐私.
/ ε x ),使该节点满足 ε x -差分隐私.
使用差分隐私区间树对静态数据进行重构,能有效提高数据发布的精度和查询效率.然而在流数据构建中,差分隐私区间树有其局限性.
在图2中,随着时间 t 的增长,差分隐私区间树树高将不断升高,并产生新的根节点,从而需要为新的节点分配有效的隐私预算.因此,随着隐私预算不断分配,终将导致隐私预算耗尽,降低隐私保护强度.在实际研究工作中,研究人员采用了许多方法,来降低噪声累加和隐私预算耗尽问题带来的影响.其中,Chan等人 [12] 根据实际应用背景,采用滑动窗口对流数据进行发布.滑动窗口既保证实际应用背景中被频繁访问的近期数据的发布精度,同时避免了噪声累加和隐私预算耗尽的问题.
定义5 . 滑动窗口下的流数据区间计数查询.设流数据当前时序为 t ,流数据序列为 S ={ C 1 , C 2 ,…, C t },用户可对数据源提出区间计数查询操作 q ,区间查询定义为查询某段连续时序的数据计数累和,区间查询的范围可表示为[ l q , r q ]( t - w < l q ≤ r q ≤ t ),查询结果表示为
(3)
其相当于对数据库表 S 执行查询:
Select Count (*) From S Where time ∈[ l q , r q ].
滑动窗口 W 下的流数据发布如图3所示:
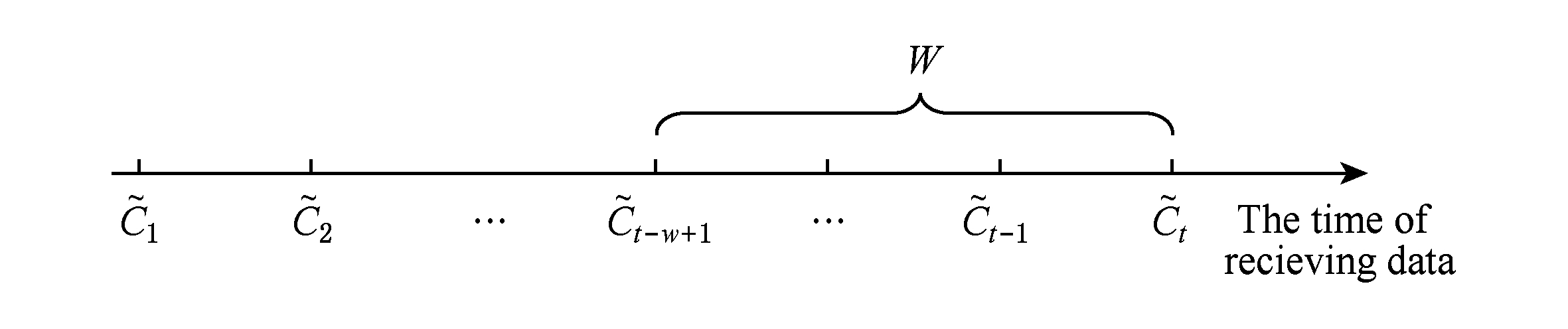
Fig. 3 Streaming data in sliding window
图3 滑动窗口下的流数据发布
对静态数据进行区间计数查询时,可采用差分隐私区间树对数据进行组织表示,现有工作 [16] 通过合理分配隐私预算,进行异方差加噪,进一步提高查询精度.异方差加噪同样适用于滑动窗口下的差分隐私流数据发布.同方差与异方差加噪方式,及其对发布精度的影响,举例如下:
如图4(a),当区间树总的隐私预算为1.0时,每个节点分配的隐私预算 ε x =0.5;而图4(b)中,节点 N 1 分配的隐私预算 ε x =0.33,它的儿子节点 N 2 , N 3 , N 4 的隐私预算 ε x =0.67.通常情况下,各个树节点的查询概率不同.例如查询区间随机分布的情况下,节点 N 2 , N 3 , N 4 的覆盖概率高于节点 N 1 ,因此,通过设计合理的隐私预设分配策略,对高覆盖概率的节点添加更少的噪声,对覆盖概率低的节点添加更多的噪声,能够有效降低整体的查询误差.
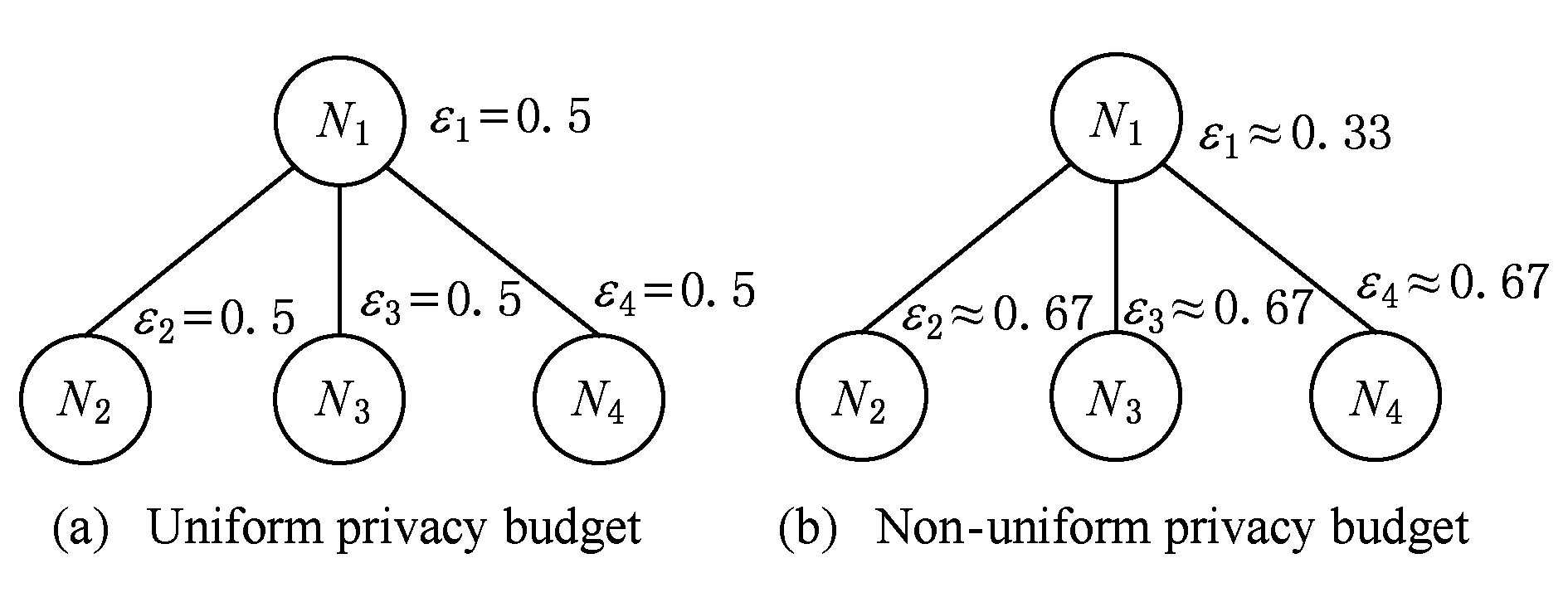
Fig. 4 Uniform/non-uniform privacy budget
图4 同/异方差加噪下的隐私预算分配
为实现流数据的自适应发布,首先需结合流数据特性,利用滑动窗口机制动态构建流数据对应的区间树.
通过在滑动窗口内进行区间树的动态构建,能够有效提高流数据发布算法的效率.在文献[11]中,采用了完全二叉树结构进行数据的组织表示.如图5所示:
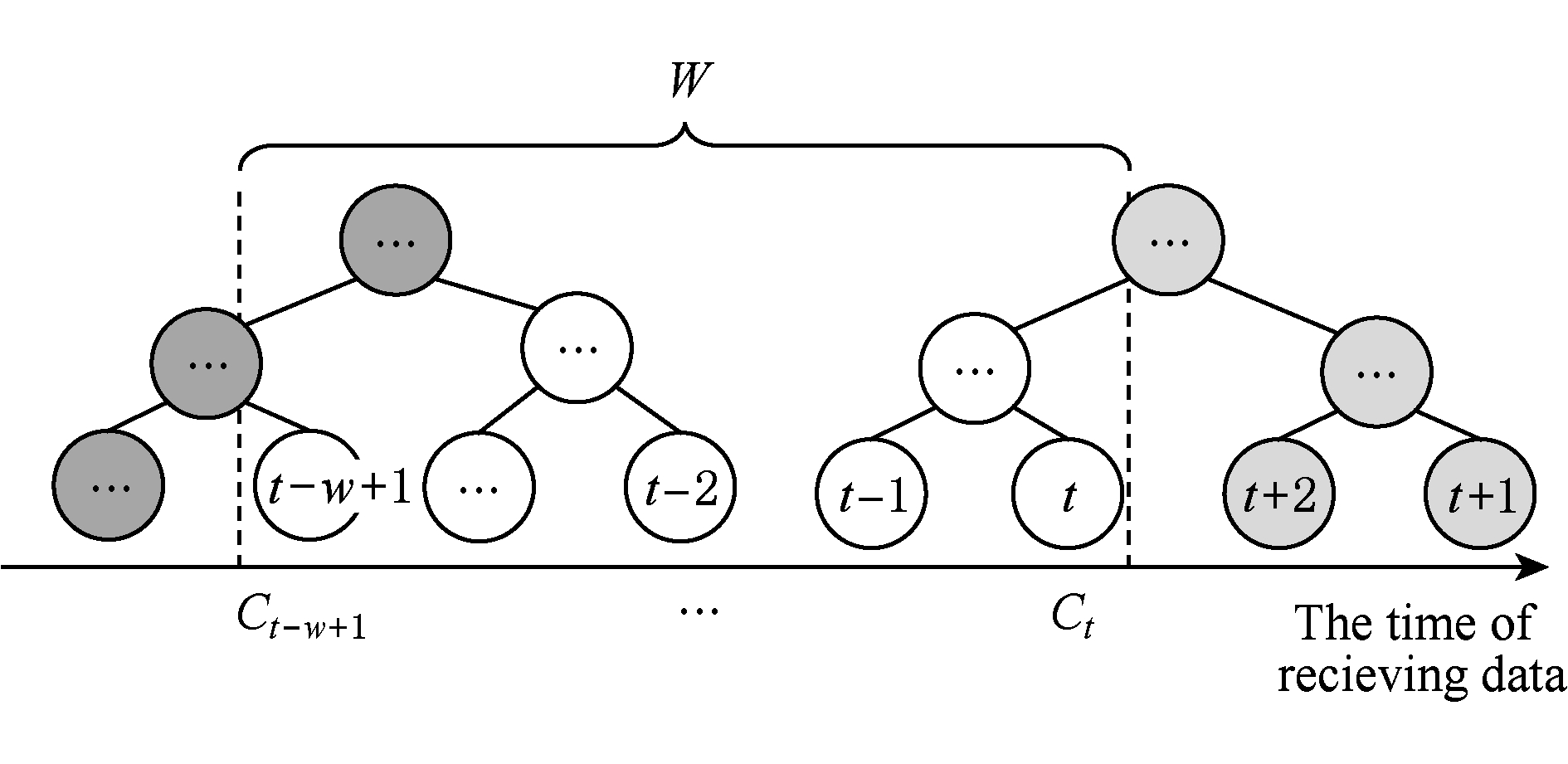
Fig. 5 Dynamic construction process of interval tree
图5 滑动窗口中的区间树动态构建过程
在图5中,滑动窗口大小为| W |,当前时刻为 t ,滑动窗口内包含2棵不完整的区间树,深灰色节点为被移出窗口的树节点,因查询集合不再覆盖这部分节点,故标记为过期节点;浅灰度节点为未来将进入窗口的虚拟树节点,随着时间 t 推移,这些节点将在动态构建过程中被激活;白色节点为正处于滑动窗口中的树节点.
由于图5中的动态构建过程对树结构要求较为严格,本文针对异方差加噪对树结构的要求,设计了更具灵活性和可扩展性的区间树动态构建算法.首先,根据建树状态不同,将区间树分为预构建树与完成构建树,定义如下.
定义6 . 预构建树.对于处于滑动窗口的区间树 T ,若该树的部分叶子节点所对应的时刻还未到来,则 T 称为预构建树.如图6所示:
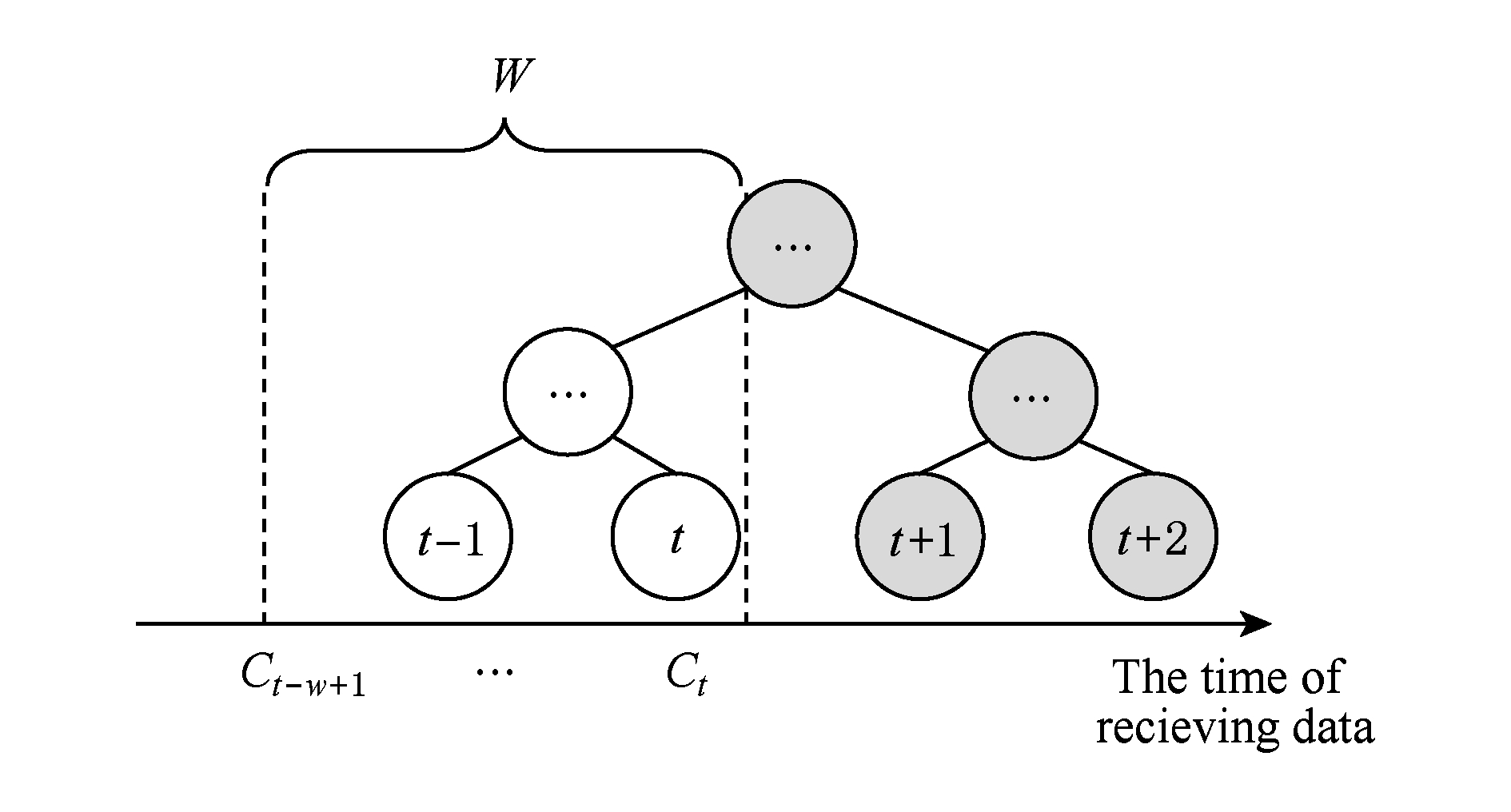
Fig. 6 Pre-building tree
图6 预构建树
定义7 . 完成构建树.对于处于滑动窗口中的区间树 T ,若该树所有节点均已完成构建,则称为完成构建树,如图7所示:
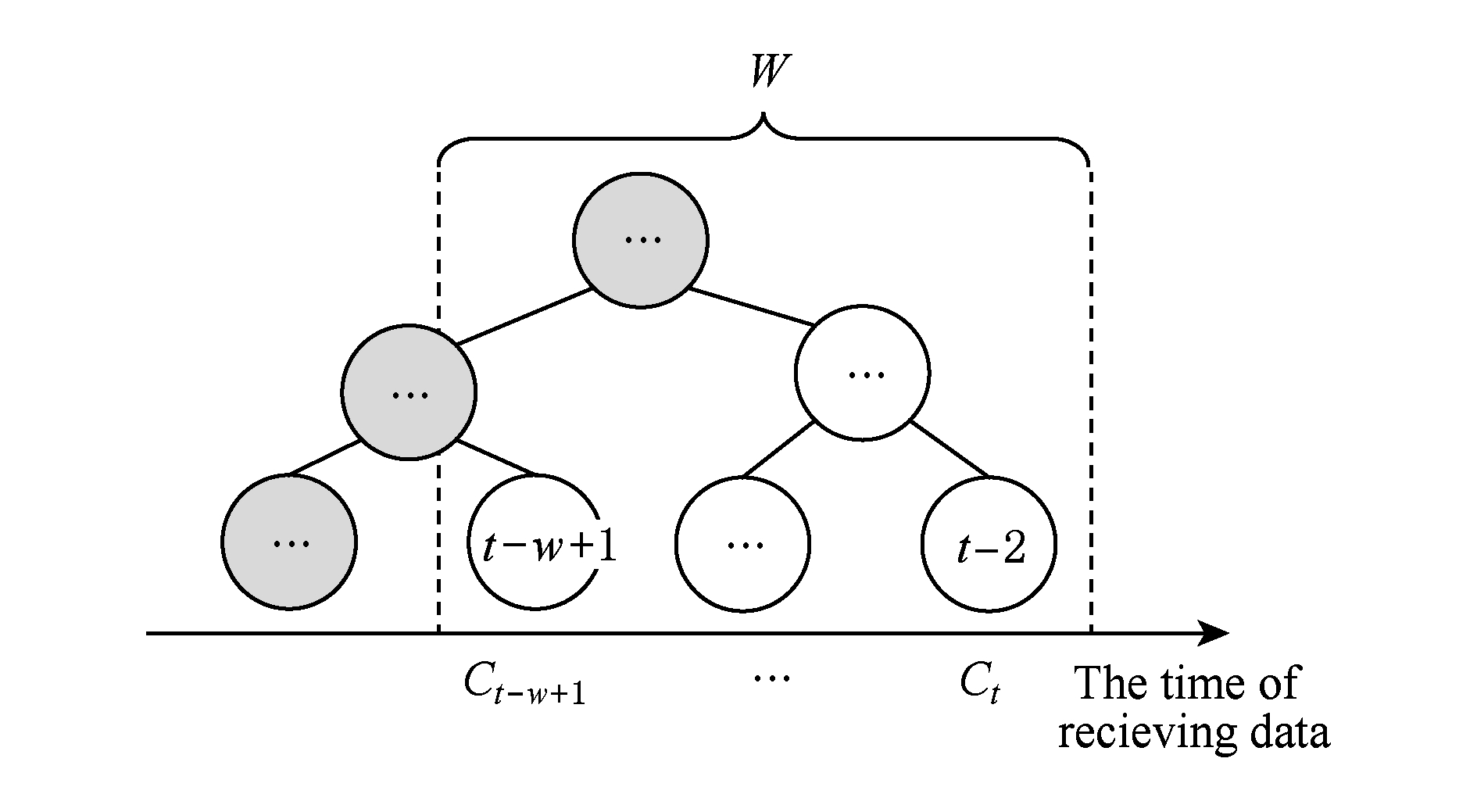
Fig. 7 Builded tree
图7 完成构建树
在流数据发布过程中,当时刻 t 推移1个单位,若滑动窗口内所有区间树均已构建完成,则可根据分叉数 k 和树高 h 等参数构建出一棵新的区间树,并进行隐私预算预分配.如图8所示:
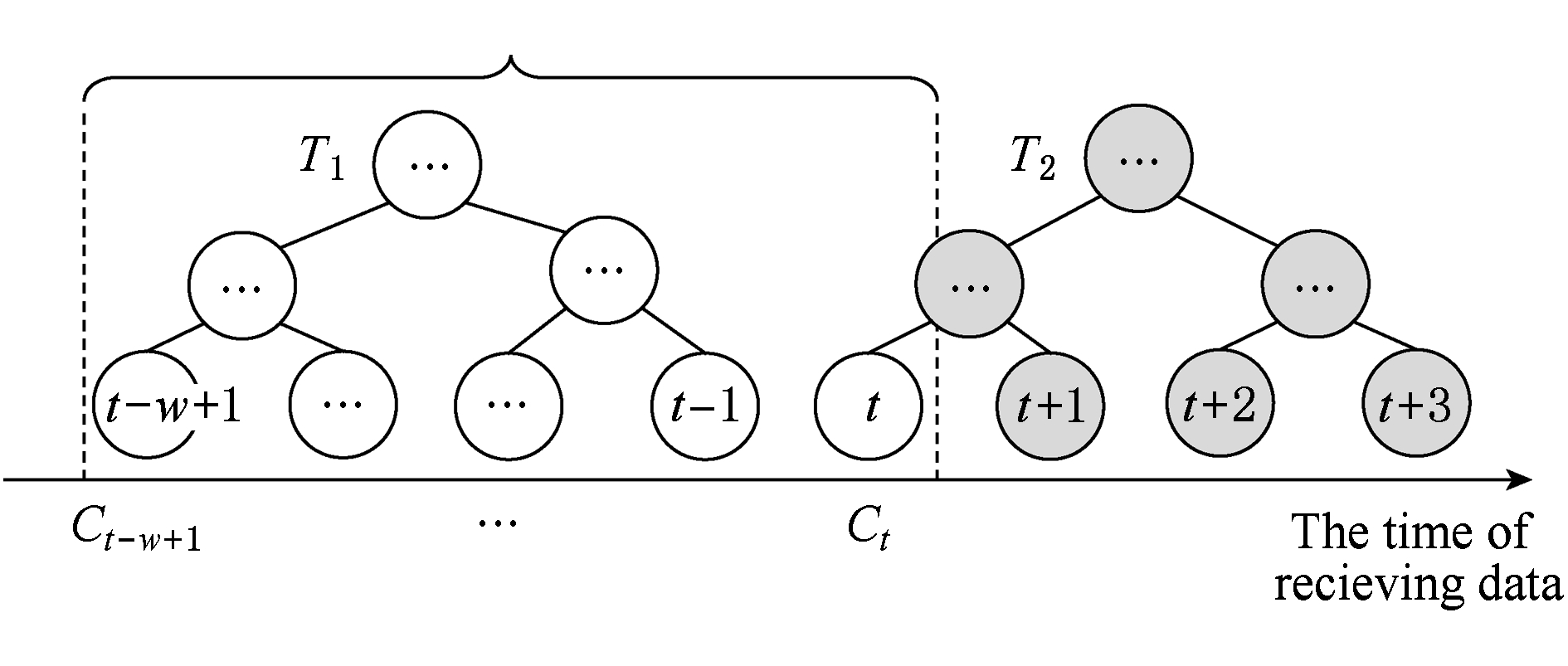
Fig. 8 Node insertion and pre-building tree
图8 节点插入并建立预构建树
在图8中,当插入新节点 t 时,滑动窗口中 T 1 为完成构建树,因此,预构建了区间树 T 2 ,并进行隐私预算预分配.
若当前滑动窗口中存在预构建树,则从树中找到对应节点位置进行节点插入操作,并根据预分配的隐私预算参数,分配隐私预算,进行加噪;再根据预构建树结构,完成父节点的递归构建操作.具体操作同样如图9所示.在图9中,当插入节点 t -1时,在滑动窗口中找到预构建树 T 2 ,将节点插入对应位置并进行加噪,同时,对节点 t 、节点 t +1的父节点进行插入、加噪.插入后的树结构如图9所示:
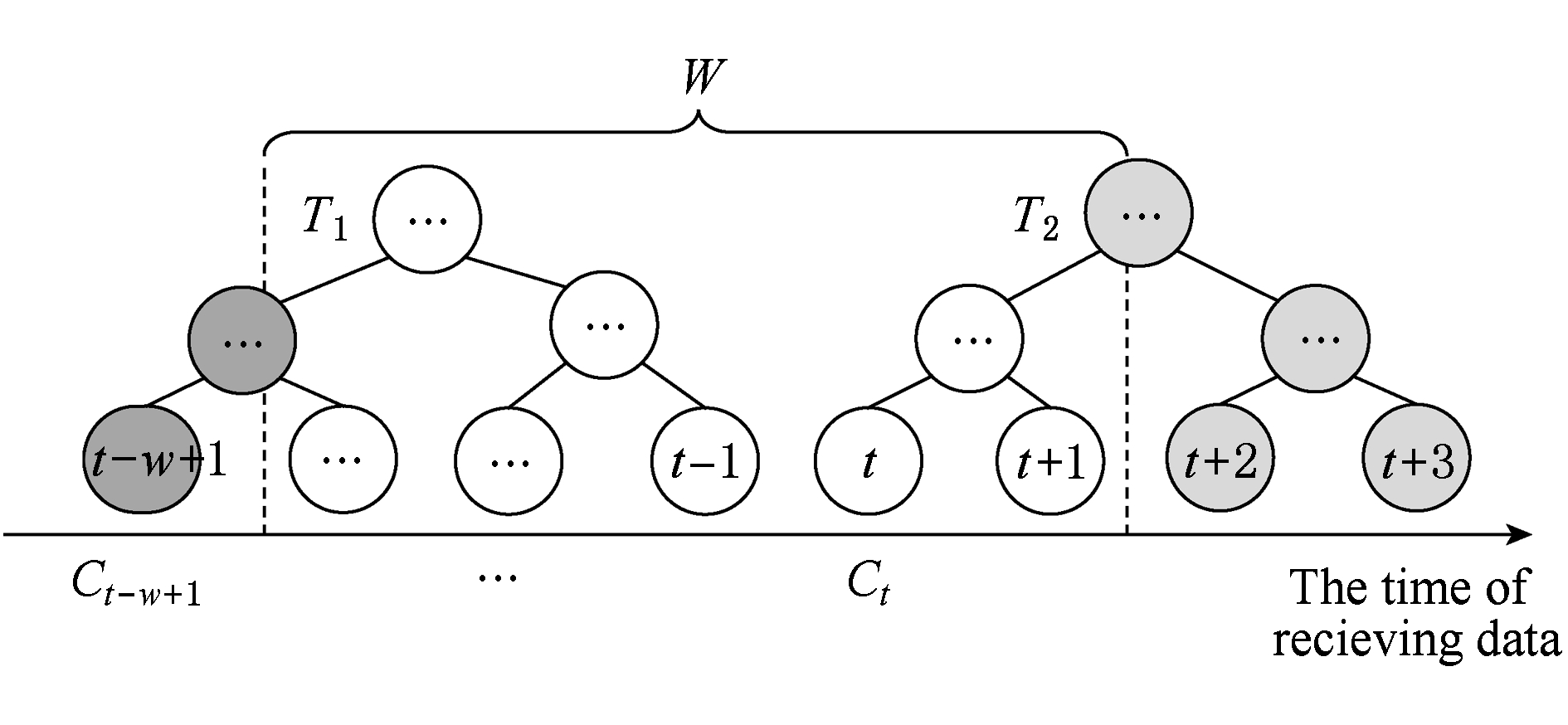
Fig. 9 Insert a node into the pre-building tree
图9 在预构建树中插入节点
在构建差分隐私区间树过程中,当新数据流入滑动窗口,将执行节点插入操作,详细过程如算法1所示.
算法1 . 节点插入算法Insert.
输入:区间树列表 TreeList 、节点真实值 v ;
输出:更新后的区间树列表.
步骤1. 判断 TreeList 中是否存在预构建树 T ,若不存在,则调用历史查询分析算法TPCalc,获得构建参数,创建预构建树,并调用节点参数计算算法NPC和隐私预算分配算法PBD,进行隐私预算预分配;
步骤2. 从节点回收池获取节点空间 Rec x ;
步骤3. 从预构建树中获取当前节点的位置和隐私预算,进行异方差加噪;
步骤4. 判断当前预构建树 T 是否满足进一步合并条件,若满足,则对 T 进行节点合并操作;
步骤5. 判断当前树是否构建完成,若构建完成,标记 T 为完成构建树.
由于滑动窗口仅对| W |长度范围内的数据进行发布,对于超出滑动窗口的树节点不再提供查询,故将作为过期节点进行移除.节点删除过程如算法2所示.
算法2 . 节点删除算法Delete.
输入:待删除节点 Del x ;
输出:更新后的区间树列表.
步骤1. 获取节点 Del x ,若节点 Del x 已移出滑动窗口,则将节点 Del x 删除并移至回收池;
步骤2. 若存在父节点,获取父节点 father ( Del x ),递归调用Delete算法.
在树结构构建过程中,采用节点回收机制提高空间利用率,所删除的节点重新进入回收池等待重新利用.
动态构建树结构的插入删除操作时间复杂度均为 O (1),满足差分隐私流数据对算法的时间效率要求,并且该算法满足差分隐私保护要求,能提供有效的区间计数查询.在实现滑动窗口下的区间树动态构建的基础上,即可进一步进行异方差加噪,提高查询精度.
在动态构建的区间树结构上进行异方差加噪前,首先需分析及计算节点的覆盖概率.以下给出节点覆盖概率计算的相关定义.
定义8 . 节点覆盖概率.设 p x 为节点 x 的查询覆盖概率, QP ( l , r )为区间[ l , r ]被查询区间覆盖的概率,则由定义3可知,节点 x 若被查询区间[ l q , r q ]覆盖,需满足2个条件:
1) 节点 x 本身被查询区间覆盖;
2) 节点的父节点不被查询区间覆盖.
因此,满足:
定义9 . 查询覆盖节点集合.设 NodeSet ( q )为查询 q 所覆盖的节点集合.同样由定义6可知,节点集合满足条件:
NodeSet ( q )=
{ x | l q ≤ l x ∧ r x ≤ r q ∧  ( l q ≤ l fx ∧ r fx ≤ r q )}.
( l q ≤ l fx ∧ r fx ≤ r q )}.
定义10 . 节点误差期望.由Laplace机制定义可知,当对节点 x 进行Laplace机制加噪时,该节点的误差期望为
根据定义8~10,设 QC ( x )为在查询全集 Q 中,节点 x 被查询区间覆盖的次数.即 QC ( x )= p x | Q |.则差分隐私区间树的整体查询误差期望为
EErr ( Q )=  =
=
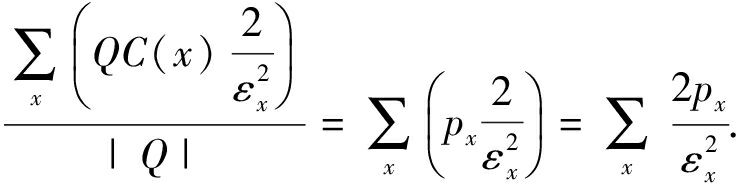
令 ![]() 表示差分隐私区间树中节点的隐私预算向量,若要最小化差分隐私区间树的区间查询期望,需在 ε -差分隐私条件约束下,对最优化问题进行求解:
表示差分隐私区间树中节点的隐私预算向量,若要最小化差分隐私区间树的区间查询期望,需在 ε -差分隐私条件约束下,对最优化问题进行求解:
s.t. ∀ ![]() .
.
根据上述定义和最优化问题的求解,得到以下结论:
结论1 . 为最小化区间计数查询误差期望,在区间树节点中隐私预算分配方案需满足:
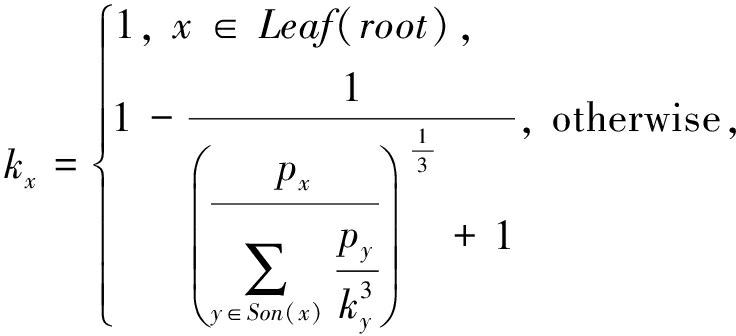
ε x = k x psum ( x ),
其中 ![]() 为节点 x 的第1个子节点.
为节点 x 的第1个子节点.
证明.
当 x 为叶节点时,结论显然成立.
当 x 非叶节点时,可通过拉格朗日乘数法构造函数求解该问题:
将 ![]() 对 ε x 求导,得:
对 ε x 求导,得:
即:
当 x 为非叶子节点,对于节点 y ∈ Son ( x ),有:
且由约束条件可知:
psum ( y )= ε - ![]() ε z = psum ( fson ( x )).
ε z = psum ( fson ( x )).
因此:
令 ε x = k x psum ( x ),则:
k x psum ( x )= 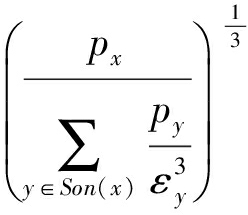 =
=
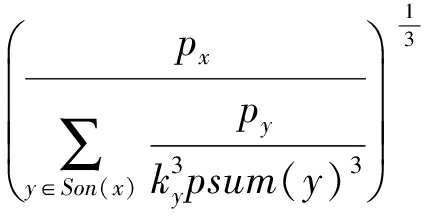 =
=
 psum ( fson ( x )),
psum ( fson ( x )),
化简,得:
k x =1- 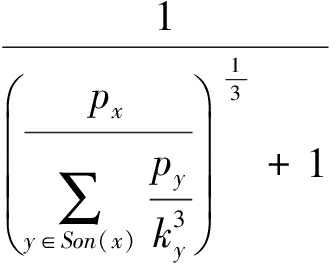 .
.
证毕.
根据结论1,即可在区间树动态构建过程中,根据节点覆盖概率计算节点系数,并进行隐私预算预分配,以实现异方差加噪,节点系数计算如算法3所示:
算法3 . 节点系数计算NPC.
输入:待计算区间树 T 、区间树中待计算节点 x ;
输出:节点系数 k x .
步骤1. 若 x 为叶节点, k x ←1,结束算法;
步骤2. 若 x 非叶节点:
For each y ∈ Son ( x )
NPC ( T , y );
End For
步骤3. k x ←1- 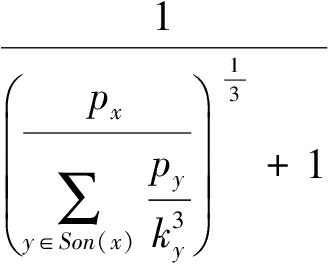 .
.
节点系数计算完成后,通过算法4进行节点隐私预算分配.
算法4 . 隐私预算预分配算法PBD.
输入:当前待分配节点 x , tot = psum ( x );
输出:最小化查询误差期望隐私预算分配方案.
步骤1. ε x ← k x tot
步骤2. For each y ∈ Son ( x )
PBD ( y , tot - ε x );
End For
在发布算法运行前,预置查询区间分布为均匀随机分布,统计节点覆盖概率,选取树结构构建参数.由于节点覆盖概率和构建参数的选取均与发布数据无关,不会造成隐私泄露,算法满足差分隐私保护要求.
通过在区间树动态构建过程中进行异方差加噪,有效降低了区间计数查询的误差,而通过对用户历史查询的统计分析,算法的发布数据精度仍有进一步的提升空间.
在算法4中,将查询区间分布假定为均匀分布,并以此进行隐私预算分配,而在不同应用场景下,用户的查询可能呈现特定规律.通过对查询区间大小和位置等用户查询偏好进行统计与分析,自适应地调整隐私预算分配与树结构构建,将有效提高发布数据可用性.首先,给出基于历史查询概率统计的节点覆盖概率计算公式:
结论2 . 基于历史查询概率统计,节点覆盖概率
其中, L x 表示节点 x 所统计区间的宽度, QSum ( L x )= 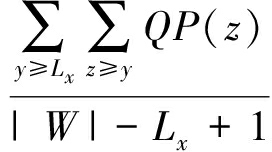 , QP ( z )表示在历史查询中,长度为 z 的查询区间出现的概率.
, QP ( z )表示在历史查询中,长度为 z 的查询区间出现的概率.
证明. 对于节点 x ,由于随时间推移,节点 x 所表示的区间[ l x , r x ]在滑动窗口 W 中的相对位置不断移动.因此,需要对整个移动过程中的覆盖概率进行统计.
设滑动窗口宽度为| W |,节点 x 所统计区间的宽度为 L x ,则节点 x 在滑动窗口中的移动步数为| W |- L x +1.设在每一步中,用户查询次数为| Q |,在无父节点时,节点 x 在全过程中被覆盖的次数为
因此,在| W |- L x +1步中节点 x 在全过程中被覆盖的概率为
![]() =
= 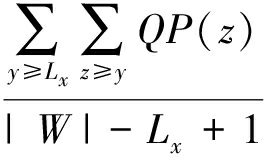 .
.
同时,由于当节点 x 存在父节点时,需去除父区间被覆盖的情况,因此,节点覆盖概率为
证毕.
通过结论2,即可在节点覆盖概率基础上分析历史查询规律,对预构建树进行隐私预算分配,进一步提高查询精度.用户进行区间查询时,更新历史查询统计并返回查询结果.如算法5所示:
算法5 . 区间计数查询RangeQuery.
输入:当前查询节点 x 、查询区间[ l , r ];
输出:区间计数统计值 ret .
步骤1. 更新查询区间概率直方图;
步骤2. 若 x 节点代表的区间与[ l , r ]无交集,则:
For each y ∈ rootlist
If l y ≤ r or r y ≥ l
ret ← RangeQuery ( y , l , r );
End If
End For
步骤3. 若 x 节点代表的区间与[ l , r ]有交集,则继续步骤4,否则结束算法;
步骤4. If l ≤ l x and r ≥ r x
![]() ;
;
Else
For each y ∈ Son ( x )
If l y ≤ r or r y ≥ l
ret ← ret + RangeQuery ( y , l , r );
End If
End For
End If
根据算法5得到的历史查询统计结果,即可使用模拟退火算法,迭代寻找新的构树参数,从而根据用户查询特性,自适应地调整区间树结构,提高查询精度.树结构的自适应调整如算法6所示:
算法6 . 树结构的自适应调整TPCalc.
输入:原构树参数;
输出:新构树参数.
步骤1. 由原构树参数产生新构树参数叉数 k 、树高 h ;
步骤2. 利用新构树参数预构建树,计算误差期望;
步骤3. 与旧构树参数误差期望对比,若误差期望更低,则接受新构树参数;
步骤4. 若误差期望更高,则以一定概率接受新构树.
综合以上算法1~6,可形成如下基于历史查询的差分隐私流数据自适应发布算法HQ_DPSAP.
算法7 . HQ_DPSAP.
输入:原始流数据、历史查询;
输出:发布流数据.
步骤1. 初始化产生构树参数叉数 k 、树高 h 、节点覆盖概率;
步骤2. 调用算法1(Insert)/算法2(Delete)动态插入/删除树节点;
步骤3. 调用过算法3(NPC)进行节点系数计算,算法4(PBD)进行隐私预算预分配,实现异方差加噪;
步骤4. 通过算法5(RangeQuery)实现滑动窗口内任意区间计数查询,进行历史查询统计,自适应地调整隐私预算,树结构参数;
步骤5. 得到新的隐私预算分配方案,并通过算法6(TPCalc)更新构树参数,返回步骤2.
基于历史查询的差分隐私流数据自适应发布算法流程图如图10所示.

Fig. 10 Flow diagram of HQ_DPSAP
图10 HQ_DPSAP算法流程图
对HQ_DPSAP算法所满足的 ε -差分隐私进行分析.
结论3 . HQ_DPSAP算法满足 ε -差分隐私.
证明. 在算法HQ_DPSAP中,滑动窗口内存在若干棵区间树,对于任意一棵区间树 T i ,由结论1知,其约束条件为∀ ![]() 故该树满足 ε -差分隐私.设 A ( T i )为对区间树 T i 的发布算法, A ( W )为对滑动窗口的发布算法,根据差分隐私并行组合特性 [5] 可知, A ( W )满足
故该树满足 ε -差分隐私.设 A ( T i )为对区间树 T i 的发布算法, A ( W )为对滑动窗口的发布算法,根据差分隐私并行组合特性 [5] 可知, A ( W )满足 ![]() 差分隐私,即 ε -差分隐私.
差分隐私,即 ε -差分隐私.
证毕.
结论4 . HQ_DPSAP算法为线性复杂度.
证明. 在HQ_DPSAP算法中,若入节点时已有预构建树,则直接从预构建树中分配已经算好的隐私参数进行加噪,故插入操作复杂度为 O (1).
若不存在预构建树,则需调用TPCalc.该算法使用模拟退火,并只生成1组新解用于树结构预构建.设新区间树的叶节点数为| W |,该算法复杂度为 O (| W |).由于每| W |个叶节点需构建1次新树,故均摊复杂度为 O (1).
在插入节点的同时需要删除窗口末尾的1个节点,如果该节点的兄弟节点已被删完,则递归删除改节点的父节点.在| W |次删除操作中,每个节点只删除1次,故均摊复杂度为 O (1).
设流数据总长度为 n ,则HQ_DPSAP算法复杂度为 O ( n ).
证毕.
现有基于滑动窗口的流数据发布方法尚无法提供窗口内的任意区间计数查询,为了检验HQ_DPSAP的精度优化效果,本节根据在流数据发布处理过程的不同,设计4种实验,命名分别为:①SW(BASE),仅基于滑动窗口,采用同方差加噪方式,不分析历史查询且固定为二叉树结构;②SW(DIFF),为在SW(BASE)基础上进行异方差加噪;③SW(DIFF,HIST),为在前者基础上,增加对历史查询规律的分析统计;④HQ_DPSAP,为本文最终形成的算法:在SW(DIFF,HIST)的基础上,根据历史查询规律,对数据进行异方差加噪和动态调整区间树结构参数.本节从查询精度和算法运行效率2个方面分析实验结果,以验证本文提出算法的性能.
实验在数据集Search Logs,NetTrace,WorldCup98上进行.其数据规模如表1所示.
在实验中,采用平均方差进行误差衡量:
Error ( Q )= 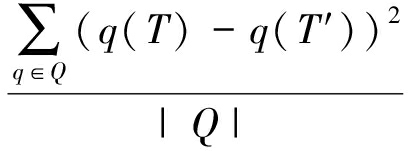 ,
,
(4)
其中,| Q |为查询集合的大小, q ( T )为区间计数查询的真实计数值, q ( T ′)为区间计数查询的加噪发布计数值.为保证实验结果更具一般性,取算法执行50次的平均值作为实验结果.
Table1 Three Common Data Set for Different Privacy Algorithm
表1 差分隐私算法常用数据集

实验环境为:Intel Core i7 930 2.8 GHz处理器,内存4 GB,Windows 8.1操作系统;算法用C++语言实现;由Matlab生成实验图表.
实验通过在Search Logs,Nettrace,WorldCup98数据集上进行不同隐私预算下的查询精度误差对比分析,并比较异方差加噪与树结构调整对算法结果的影响.
在现有流数据差分隐私数据发布工作中,为对特定时间状态发布、多条流联合统计发布、 w 事件级别隐私保护等,本文关注滑动窗口下对单条流数据进行区间计数查询数据发布.由于Search Logs与Nettrace数据集规模较小,采用其数据集长度作为滑动窗口大小.在WorldCup98数据集中,采用1 d的时长(86 400 s)作为滑动窗口大小.
1) 随机区间不同参数下的查询误差对比
随机生成1 000条长度任意的区间[ L , R ],随机生成的长度范围在滑动窗口长度内,并在不同隐私参数下,实验结果如图11~13所示:
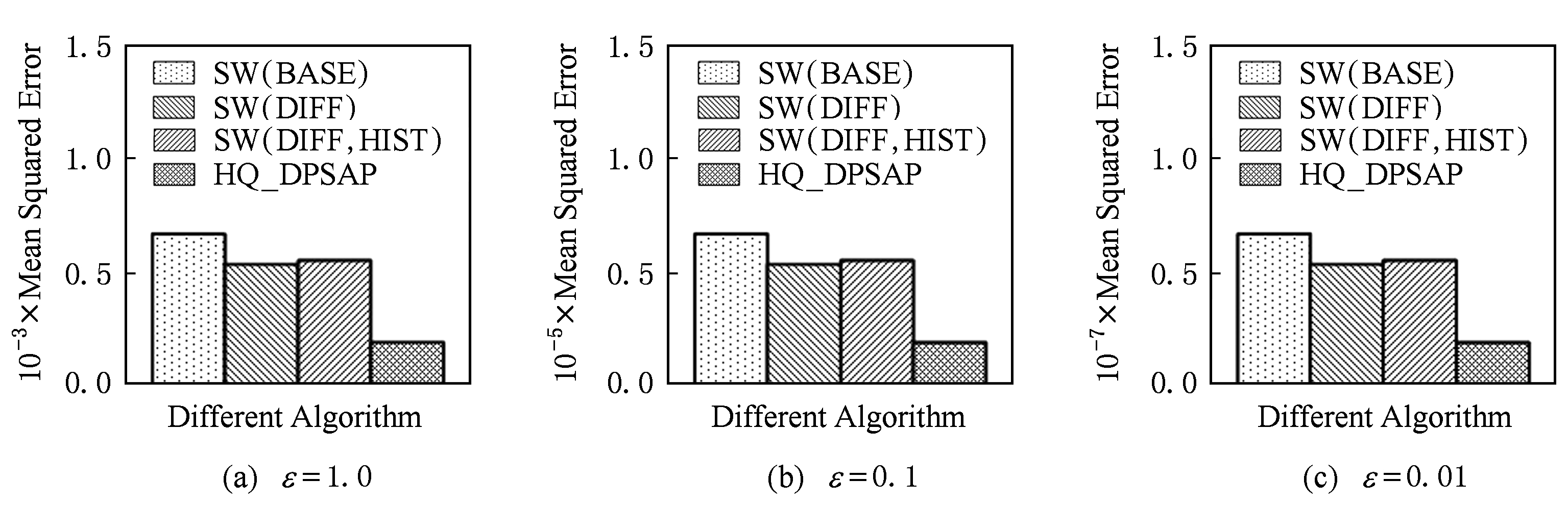
Fig. 11 Comparison of random length queries in Search Logs
图11 数据集Search Logs在随机任意长度查询区间下查询误差对比
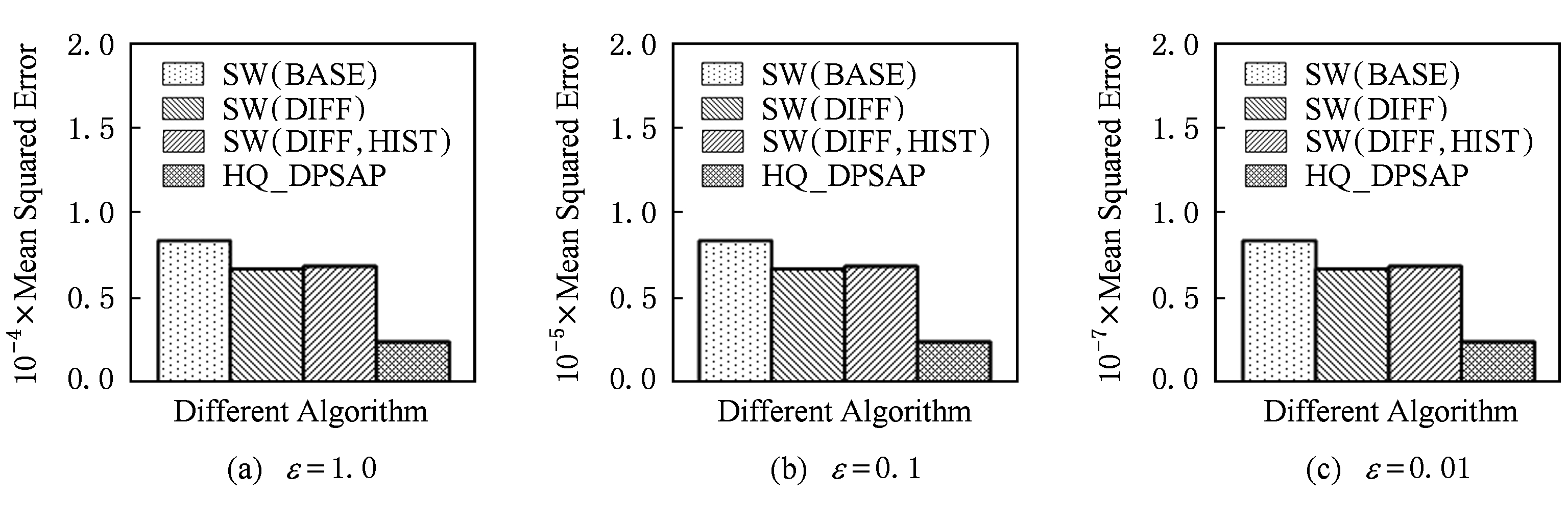
Fig. 12 Comparison of random length queries in Nettrace
图12 数据集Nettrace在随机任意长度查询区间下查询误差对比
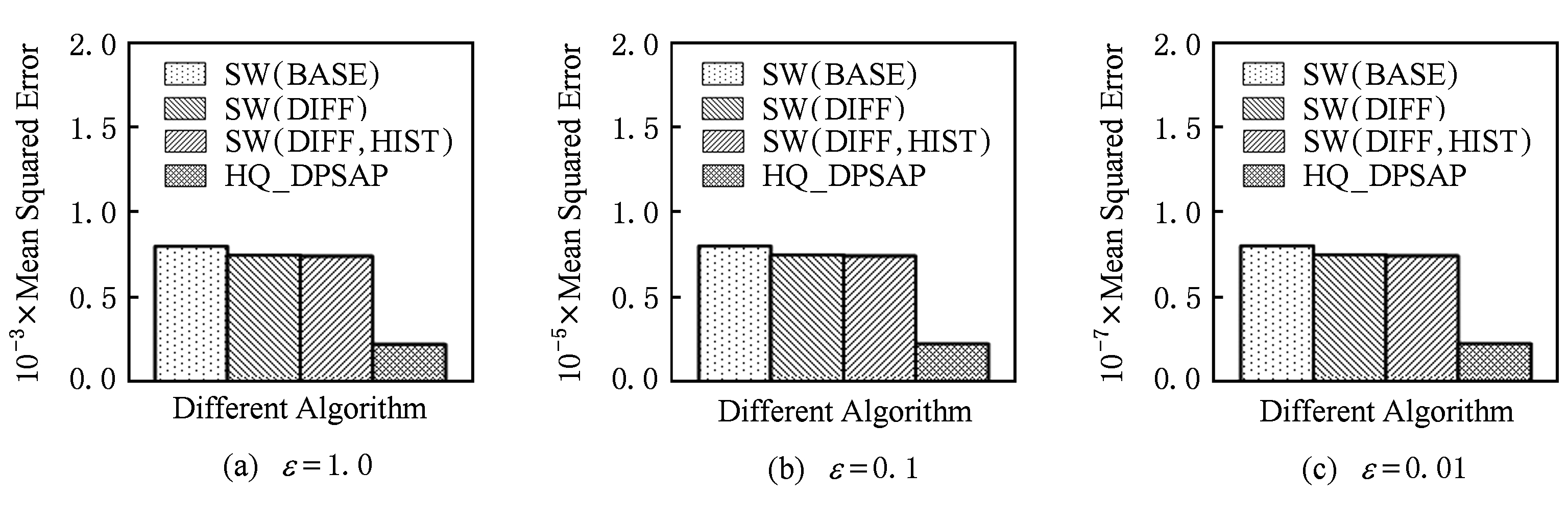
Fig. 13 Comparison of random length queries in WorldCup98
图13 数据集WorldCoup98在随机任意长度查询区间下查询误差对比
在图11~13的实验对比中,随着隐私预算减小,查询均方误差以10 2 的数量级递增.相比SW(BASE),由于采用了异方差加噪,SW(DIFF)有效降低查询误差,由于查询是随机均匀分布的,于是算法SW(DIFF,HIST)增加了对历史查询分析,并未对隐私预算产生提升.
2) 特定规律查询下的误差对比
在实际场景中,查询分布可能呈现特殊规律,本节实验设滑动窗口大小为| W |,根据区间规律分为Small,Middle,Large.其中,Small查询区间集中于1~0.33| W |;Middle查询区间集中于0.33| W |~0.67| W |;Large查询区间集中于0.67| W |~| W |.隐私预算 ε =1.0.实验结果如图14~16所示:
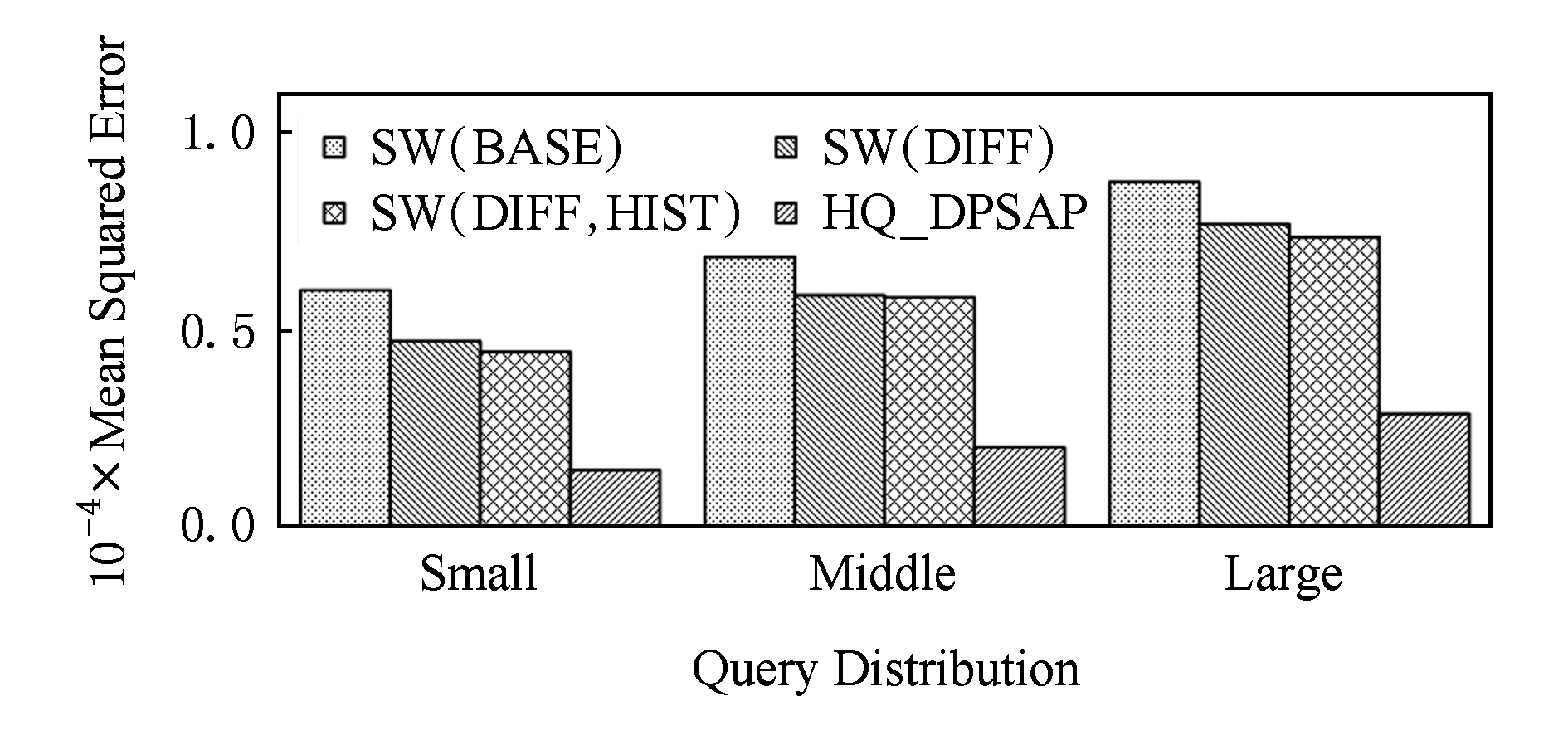
Fig. 14 Comparison of specific rule queries in Search Logs
图14 数据集Search Logs在特定规律查询区间下的误差对比
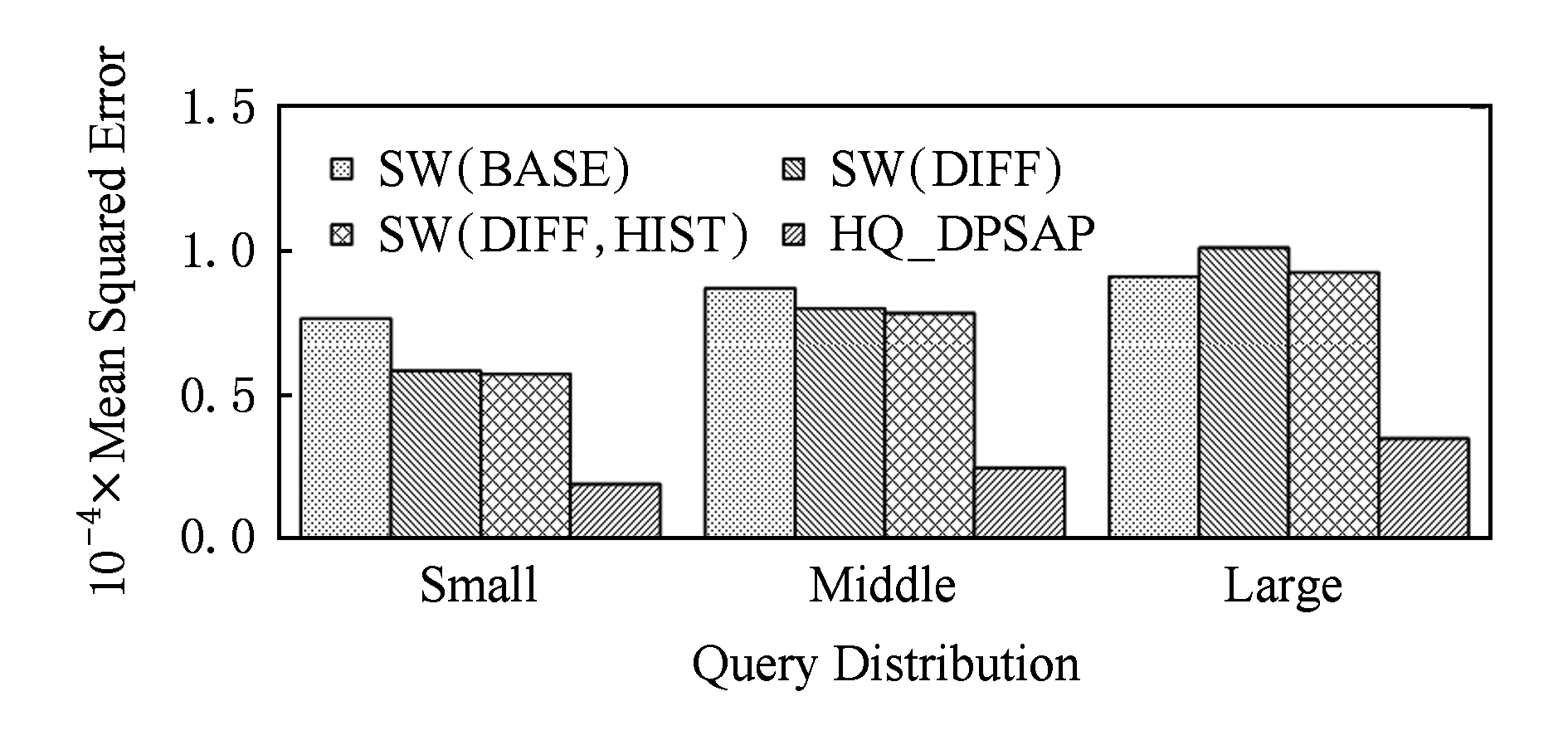
Fig. 15 Comparison of specific rule queries in Nettrace
图15 数据集Nettrace在特定规律查询区间下的误差对比
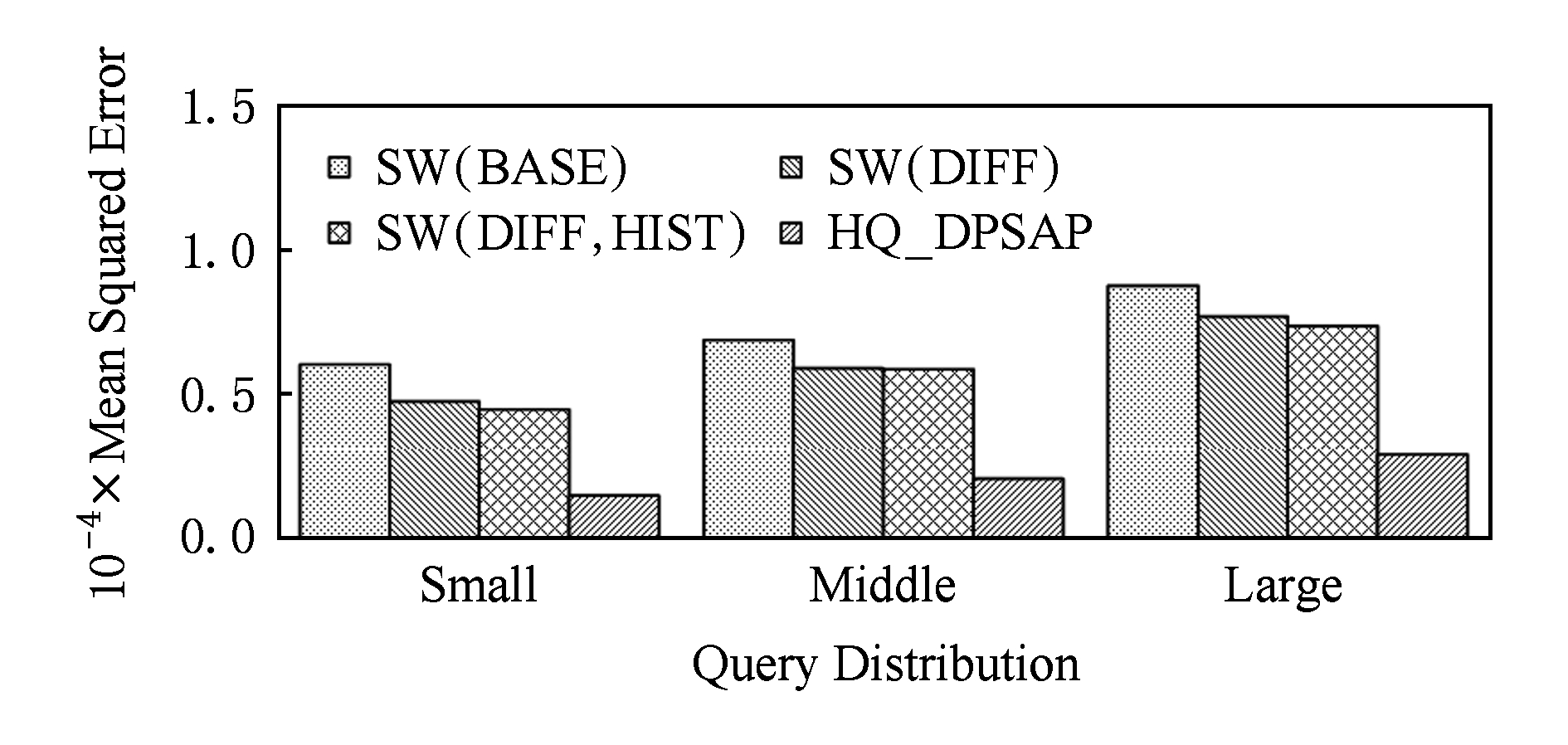
Fig. 16 Comparison of specific rule queries in WorldCup98
图16 数据集WorldCup98在特定规律查询区间下的误差对比
在图14~16的结果对比中,由于查询区间分布具备特定规律,SW(DIFF,HIST)对误差精度提升明显,在不同规律下均能在异方差加噪的基础上进一步提升.而算法HQ_DPSAP,通过对历史查询区间分布规律的统计分析和异方差加噪与区间树结构动态构建,能够有效针对不同的查询场景进行自适应的调整优化.
3) 在不同区间大小下的查询误差对
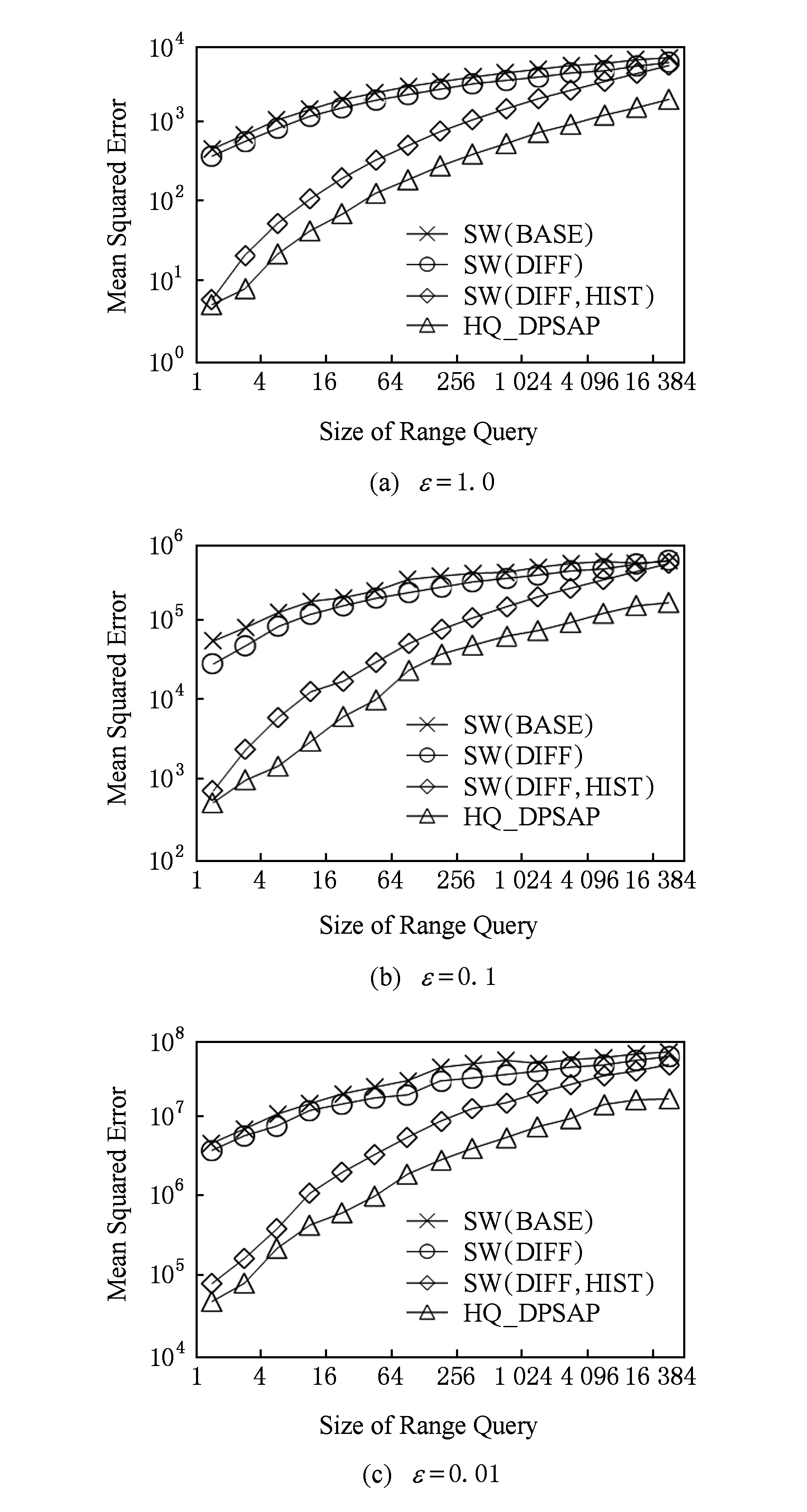
Fig.17 Comparison of different range queries in Search Logs
图17 数据集Search Logs在不同区间大小下的查询误差对比
本节实验通过随机生成固定长度的查询区间,对比分析区间查询误差.区间大小分别取2 0 ,2 1 ,…,2 13 ,…,每种长度随机生成1 000条查询.对比结果如图17~19所示.
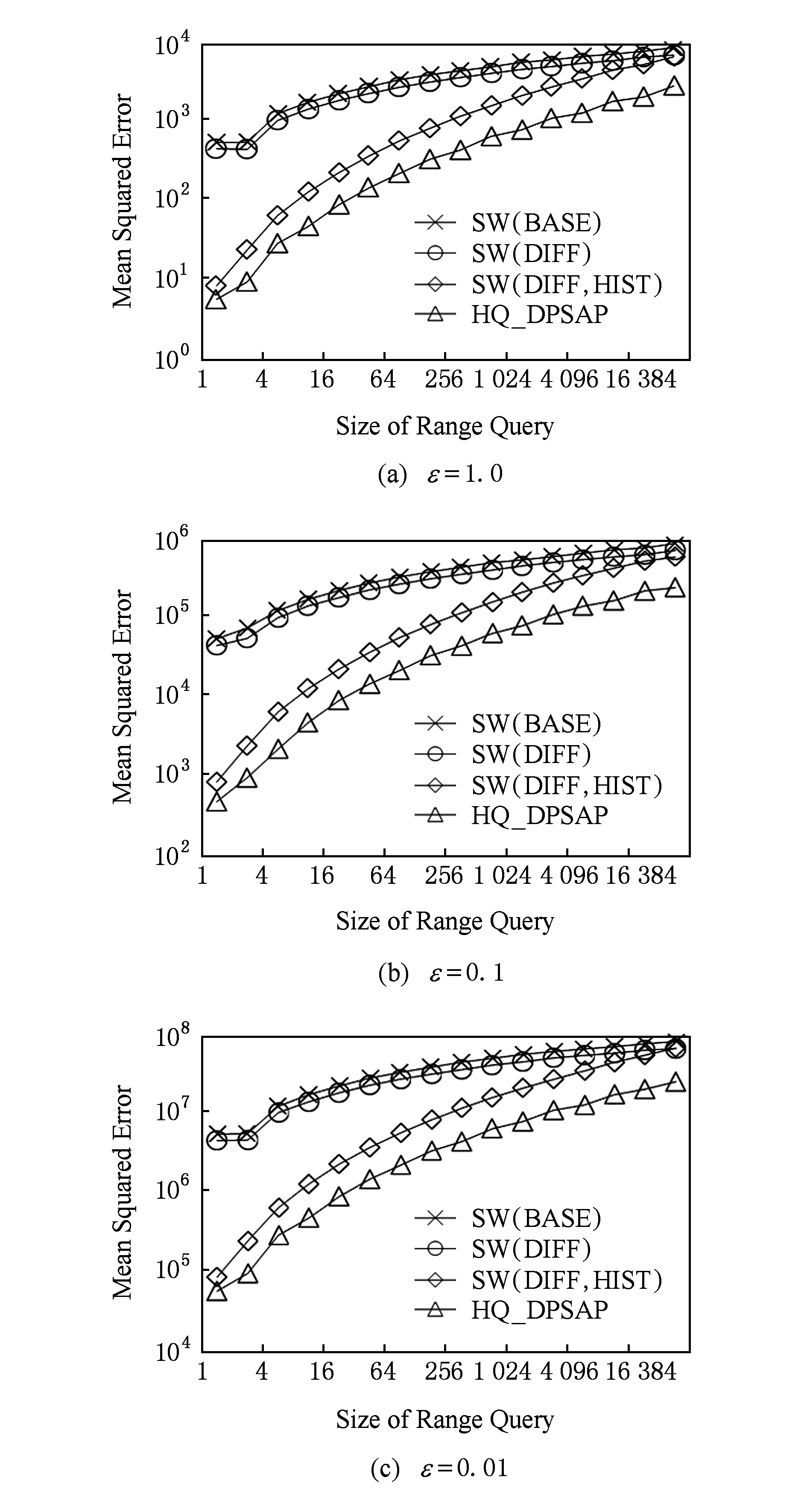
Fig. 18 Comparison of different range queries in Nettrace
图18 数据集Nettrace在不同区间大小下的查询误差对比
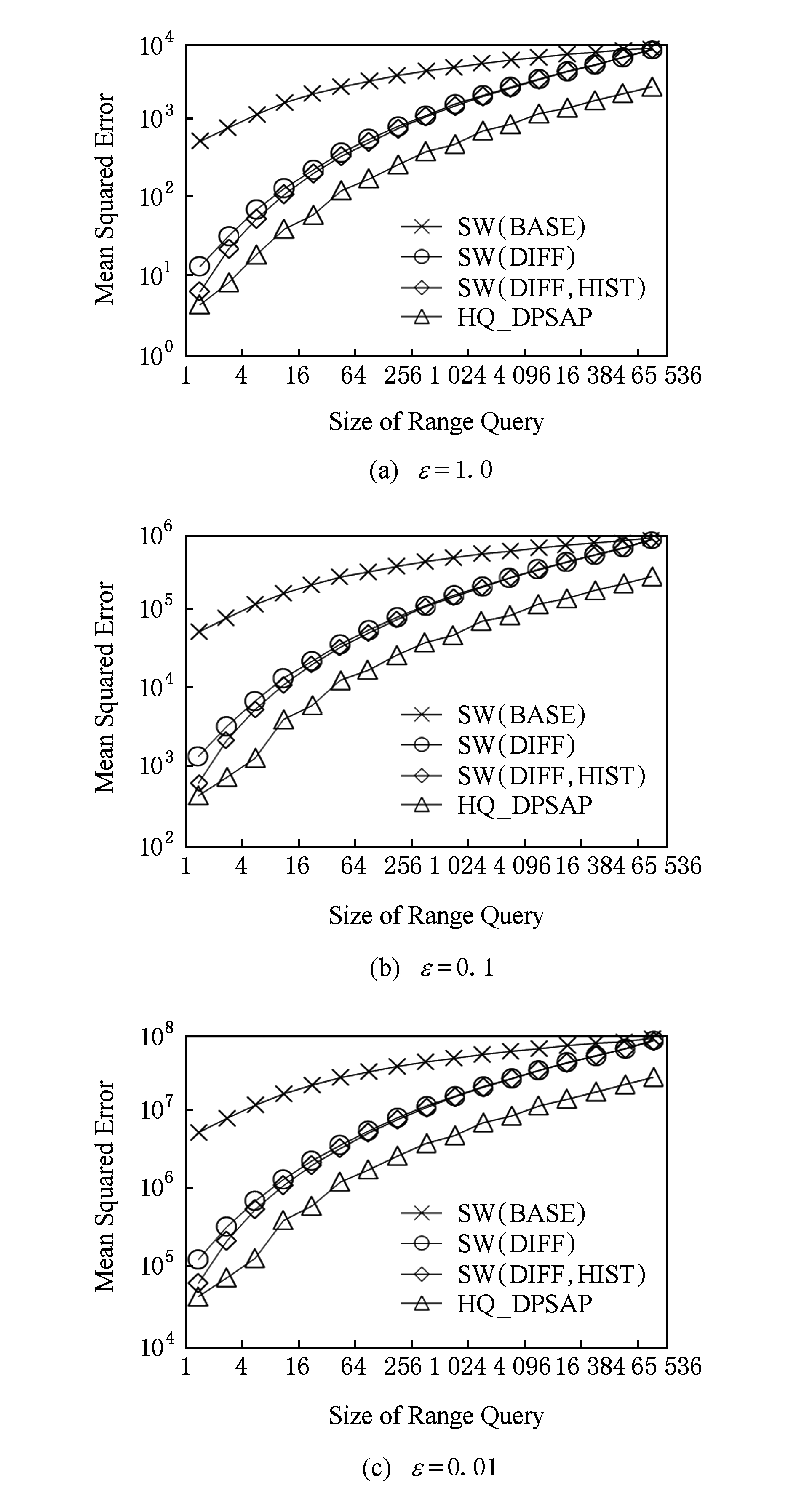
Fig. 19 Comparison of different range queries in WorldCup98
图19 数据集WorldCup98在不同区间大小下的查询误差对比
从图17~19可以看出,SW(DIFF,HIST)有效降低了数据发布误差.由于在大区间查询时,仍会覆盖许多小区间,因此优化效果有所降低.而HQ_DPSAP有对区间树结构调整,使得在大查询区间也能通过降低树高等方式降低误差.
4) 在流数据发布过程中的查询误差对比
在流数据发布背景下,用户查询区间的分布规律可能会发生变化,本文通过在数据发布过程中,动态改变用户查询区间的分布规律,并记录在流数据发布过程中,随时间 t 的增长,查询误差发生的变化,用以分析文中算法对用户查询区间规律的适应性和提升查询精度的有效性.实验结果如图20所示.
在图20中,随着时间的推移(1~7 510 000 s),查询区间分布规律由Rand改变至Small,Middle,Large.由于未对历史查询概率进行统计与分析,SW(DIFF)算法仅以区间均匀随机分布为假设,以固定的二叉区间树结构进行流数据发布,因此,不能很好地适应不同的查询分布,查询误差较大且波动较大.而算法HQ_DPSAP,能够根据不同的查询区间,调整区间树结构、调整隐私预算分配方案,因此,能够有效降低查询误差,并且降低波动使查询结果更加稳定、可用.
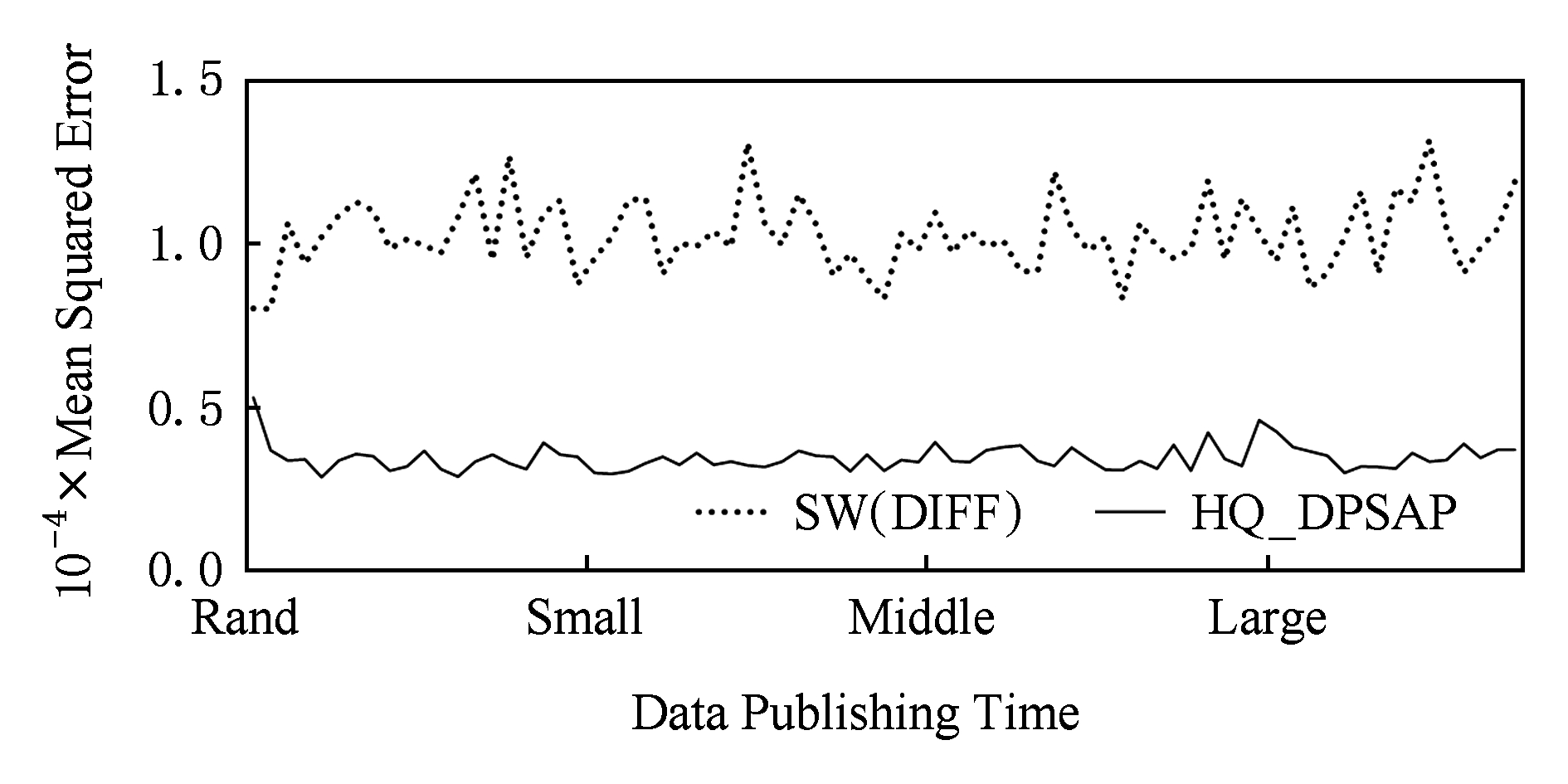
Fig. 20 Comparison of range query in stream data publications in WorldCup98
图20 数据集WorldCup98在流数据发布过程中的查询误差对比
综上实验分析表明:算法HQ_DPSAP能够适应不同的应用场景,进行自适应精度优化,有效降低了区间计数查询误差.
本节通过2个方案对算法运行效率进行对比:
1) 不同隐私参数下对运行效率的影响
使用相同大小的滑动窗口(32 768),设置不同的隐私参数(1.0,0.1,0.01),对比结果如图21所示:
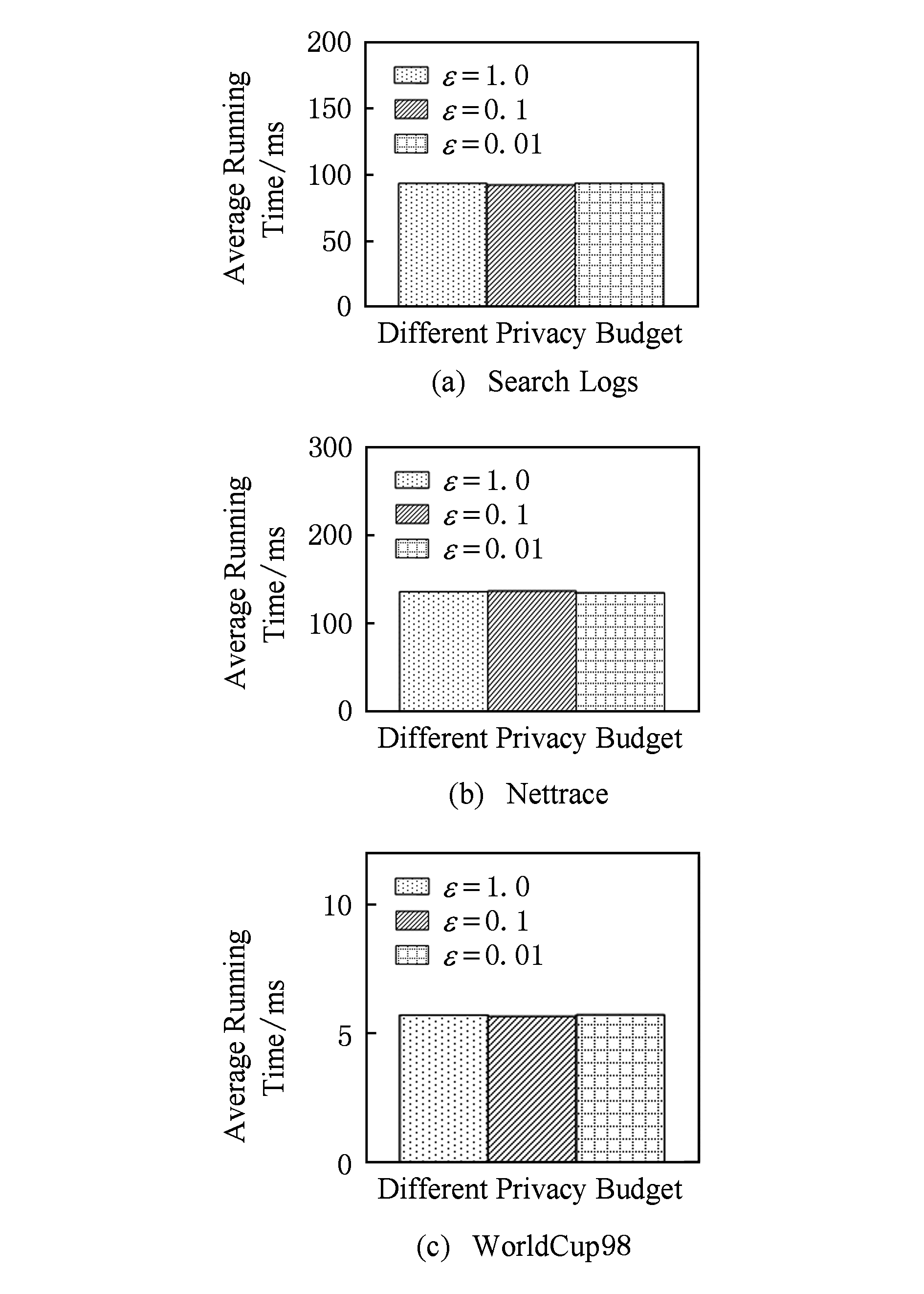
Fig. 21 Different privacy budget effect on efficiency
图21 不同隐私参数下对运行效率的影响
由图21可知,算法HQ_DPSAP运行时间不是随隐私预算不同而改变,而是随着数据集大小增加而增加.
2) 不同滑动窗口大小对运行效率的影响
固定隐私预算 ε x =1.0,设置不同大小的滑动窗口对比,结果如图22所示:

Fig. 22 Different range of window effect on efficiency under data set WorldCup98
图22 数据集WorldCoup98下不同滑动窗口大小对运行效率的影响
滑动窗口从2 8 增加到2 18 ,从图22可知,滑动窗口大小对运行时间无明显影响,与结论2一致,该算法时间复杂度为线性.
综上所述,算法HQ_DPSAP具有较高的运行效率,满足流数据实时发布要求.
为有效提高差分隐私流数据发布中的任意区间查询精度,本文提出了一种基于历史查询的差分隐私流数据自适应发布算法HQ_DPSAP.算法通过对用户历史查询的分析,可进行隐私预算与树结构的自适应调节,从而有效降低区间查询误差,提高隐私预算分配灵活性.基于真实数据集的仿真实验结果表明:HQ_DPSAP算法是有效可行的.
参考文献
[1]Fung B, Wang Ke, Chen Rui, et al. Privacy-preserving data publishing: A survey of recent developments[J]. ACM Computing Surveys, 2010, 42(4): 2623-2627
[2] Dwork C. Differential privacy[C] //Proc of the 33rd Int Colloquium on Automata, Languages and Programming. Berlin: Springer, 2006: 1-12
[3] Zhou Shuigeng, Li Feng, Tao Yufei, et al. Privacy preservation in database applications: A survey[J]. Chinese Journal of Computers, 2009, 21(5): 847-861 (in Chinese)(周水庚, 李丰, 陶宇飞. 面向数据库应用的隐私保护研究综述[J]. 计算机学报, 2009, 21(5): 847-861)
[4] Xiong Ping, Zhu Tianqing, Wang Xiaofeng. A survey on differential privacy and applications[J]. Chinese Journal of Computers, 2014, 37(1): 101-122 (in Chinese)(熊平, 朱天清, 王晓峰. 差分隐私保护及其应用[J]. 计算机学报, 2014, 37(1): 101-122)
[5] Zhang Xiaojian, Meng Xiaofeng. Differential privacy in data publication and analysis[J]. Chinese Journal of Computers, 2014. 37(4): 927-949 (in Chinese)(张啸剑, 孟小峰. 面向数据发布和分析的差分隐私保护[J]. 计算机学报, 2014, 37(4): 927-949)
[6] Dwork C, Naor M, Pitassi T, et al. Differential privacy under continual observation[C] //Proc of the 42nd ACM Symp on Theory of Computing. New York: ACM, 2010: 715-724
[7] Chan T H H, Shi E, Song D. Private and continual release of statistics[J]. ACM Trans on Information and System Security, 2011, 14(3): 26-38
[8] Cao Jianneng, Xiao Qian, Ghinita G, et al. Efficient and accurate strategies for differentially-private sliding window queries[C] //Proc of the 16th Int Conf on Extending Database Technology. New York: ACM, 2013: 191-202
[9] Bolot J, Fawaz N, Muthukrishnan S, et al. Private decayed predicate sums on streams[C] //Proc of the 16th Int Conf on Extending Database Technology. New York: ACM, 2013: 284-295
[10] Zhang Xiaojian, Meng Xiaofeng. Stream histogram publication method with differential privacy[J]. Journal of Software, 2016, 27(2): 381-393 (in Chinese)(张啸剑, 孟小峰. 基于差分隐私的流式直方图发布方法[J]. 软件学报, 2016, 27(2): 381-393)
[11] Kellaris G, Papadopoulos S, Xiao Xiaokui, et al. Differentially private event sequences over infinite streams[J]. Proceedings of the VLDB Endowment, 2014, 7(12): 1155-1166
[12] Chan T H H, Li Mingfei, Shi E, et al. Differentially private continual monitoring of heavy hitters from distributed streams[C] //Proc of the 12th Int Conf on Privacy Enhancing Technologies. Berlin: Springer, 2012: 140-159
[13] Friedman A, Sharfman I, Keren D, et al. Privacy-Preserving distributed stream monitoring[C] //Proc of the 21st Annual Network and Distributed System Security Symp. Reston, VA: ISOC, 2014: 1-12
[14] Michael H, Vibhor R, Gerome M, et al. Boosting the accuracy of differentially private histograms through consistency[J]. VLDB Endownment, 2010, 3(1): 1021-1032
[15]Dwork C, McSherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis[C] //Proc of the 3rd Theory of Cryptography Conf. Berlin: Springer, 2006: 363-385
[16] Kang Jian, Wu Yingjie, Huang Siyong, et al. An algorithm for differentially private histogram publication with non-uniform private budget[J]. Journal of Frontiers of Computer Science & Technology, 2016, 10(6): 786-798 (in Chinese)(康健, 吴英杰, 黄泗勇, 等. 异方差加噪下的差分隐私直方图发布算法[J]. 计算机科学与探索, 2016, 10(6): 786-798)
Wu Yingjie, Zhang Liqun, Kang Jian, and Wang Yilei
( College of Mathematics and Computer Science , Fuzhou University , Fuzhou 350116)
Abstract Nowadays, many practical applications need to publish streaming data continuously. Most of existing research works for differential privacy single streaming data publication focus on range accumulation. However, many practical scenarios need to answer arbitrary range counting queries of streaming data. At the same time, there exist specific rules of queries from users, so adaptive analysis and calculation for historical queries should be concerned. To improve the usability of published data, an algorithm HQ_DPASP for differential privacy streaming data adaptive publication based on historical queries is proposed. Combining the characteristics of streaming data, HQ_DPASP firstly uses the sliding window mechanism to construct the differential privacy range tree of the streaming data dynamically. Secondly, by analyzing the coverage probability of tree nodes and calculating the privacy parameters from leaves to root, HQ_DPASP allocates privacy budget from root to leaves and adds non-uniform noise on tree nodes. Finally, the privacy budget of tree nodes and tree’s parameters are adjusted adaptively based on the characteristic of historical queries. Experiments are designed for testing the feasibility and effectiveness of HQ_DPSAP. The results show that HQ_DPSAP is effective in answering arbitrary range counting queries on the published streaming data while assuring low mean squared error of queries and high algorithm efficiency.
Key words differential privacy; streaming data publication; non-uniform noise; historical query; adaptive algorithm
收稿日期: 2016-08-02;
修回日期: 2016-11-08
基金项目: 国家自然科学基金项目(61300026);福建省自然科学基金项目(2014J01230)
This work was supported by the National Natural Science Foundation of China (61300026) and the Natural Science Foundation of Fujian Province of China (2014J01230).
通信作者: 王一蕾(yilei@fzu.edu.cn)
中图法分类号 TP391

Wu Yingjie , born in 1979. PhD and professor. Member of CCF. His main research interests include data mining and data privacy preserving.

Zhang Liqun , born in 1991. Master. His main research interests include data mining and differential privacy.

Kang Jian , born in 1989. PhD candidate. His main research interests include data mining and differential privacy.

Wang Yilei , born in 1979. PhD candidate. Her main research interests include recommender systems and data privacy preserving.