卢友军 许道云
(贵州大学计算机科学与技术学院 贵阳 550025)
(yjlu111@126.com)
摘 要 相变性质是ER(Erdös-Rényi)随机图理论具有的重要性质,一个简单无向图 G =( V , E )中的 k -独立集是一个具有 k 个顶点的独立集.为更好地理解ER随机图中 k -独立集的结构特性,提出并利用一阶矩和二阶矩方法严格证明了当2≤ k = ο ( ![]() )时随机图 G ( n , p )中 k -独立集出现相变的临界概率
)时随机图 G ( n , p )中 k -独立集出现相变的临界概率 ![]() 利用
利用 ![]() 时随机图 G ( n , p )和 G ( n , m )等价的性质给出了随机图 G ( n , m )中 k -独立集出现相变的临界边数
时随机图 G ( n , p )和 G ( n , m )等价的性质给出了随机图 G ( n , m )中 k -独立集出现相变的临界边数 ![]() 实验结果表明:当2≤ k = ο (
实验结果表明:当2≤ k = ο ( ![]() )时,随机图 G ( n , p )和 G ( n , m )中存在 k -独立集的理论临界值和仿真得到的临界值一致且临界值与图节点总数 n 和独立集节点数 k 有关,而当 k = ω (
)时,随机图 G ( n , p )和 G ( n , m )中存在 k -独立集的理论临界值和仿真得到的临界值一致且临界值与图节点总数 n 和独立集节点数 k 有关,而当 k = ω ( ![]() )时,随机图 G ( n , p )和 G ( n , m )中存在 k -独立集的理论临界值和仿真临界值不一致.
)时,随机图 G ( n , p )和 G ( n , m )中存在 k -独立集的理论临界值和仿真临界值不一致.
关键词 相变性质;随机图; k -独立集;临界概率;临界边数
给定一个简单无向图 G =( V , E ), V 表示图 G 的顶点集合, E 表示图 G 的边集合.一个顶点子集 T ⊆ V 称为图 G 的独立集 [1] (independent set, IS),是指对任意的顶点 u , v ∈ T 都有( u , v )∉ E .若顶点子集 T 的元素个数为 k ,则我们称该顶点子集 T 为 k -独立集.若独立集 T 不是其他任何一个独立集 S 的真子集,则我们称该独立集 T 为图 G 的极大独立集.若独立集 T 是顶点个数最大的独立集,则我们称该独立集 T 为图 G 的最大独立集 [2] (maximum independent set, MIS).MIS问题是指在一个给定的简单无向图 G 中找一个顶点个数最大的独立集,该问题是组合优化领域中的著名NP-完全问题 [3] .MIS问题在编码理论 [4] 、计算机网络以及计算机视觉等领域都有重要应用.
20世纪50年代末,Erdös等人 [5] 首次引入了经典的随机图模型 G ( n , p ),模型中的参数 n 表示随机图的顶点数; p 表示 n 个顶点中任意2个不同顶点之间存在边的概率,通常情况下,它不是一个固定的数,而是关于顶点数 n 的函数.该模型的显著特点是任意2个不同顶点之间是否存在边的概率统计独立,容易采用解析方法对其研究.Erdös等人 [6] 系统地研究了当顶点数 n →∞时随机图 G ( n , p )的图性质 Q 与连边概率 p 之间的关系:随机图 G ( n , p )的许多图性质 Q 存在突然涌现现象,即对任一给定的连边概率 p ,要么几乎每一个图 G ∈ G ( n , p )都存在图性质 Q ,要么几乎每一个图 G ∈ G ( n , p )都不存在图性质 Q .人们把随机图 G ( n , p )中图性质 Q 的这种突然涌现现象称为图性质 Q 的相变现象,把发生相变的临界点称为相变点.如文献[7]中分析的随机图 G ( n , p )中连通性性质的相变,其临界值为 ![]() ;直径为2的性质的相变,其严格临界值为
;直径为2的性质的相变,其严格临界值为 ![]() ;孤立节点消失的性质的相变,其严格临界为
;孤立节点消失的性质的相变,其严格临界为 ![]() ;环性质的相变,其临界值为
;环性质的相变,其临界值为 ![]() ,以及文献[8]中研究的随机图着色的相变.相变现象在其他问题中同样存在,比如:随机约束满足性问题中的相变 [9-11] 以及谣言传播的相变 [12-13] 等.在文献[14]中,Culberson等人证明了随机图 G ( n , p )中存在控制团的临界概率为 p c =
,以及文献[8]中研究的随机图着色的相变.相变现象在其他问题中同样存在,比如:随机约束满足性问题中的相变 [9-11] 以及谣言传播的相变 [12-13] 等.在文献[14]中,Culberson等人证明了随机图 G ( n , p )中存在控制团的临界概率为 p c = ![]() .2012年,Nehéz等人 [15] 证明了随机图 G ( n , p )中存在 r -控制团临界值的上下界,即当概率 p ≤
.2012年,Nehéz等人 [15] 证明了随机图 G ( n , p )中存在 r -控制团临界值的上下界,即当概率 p ≤ ![]() 时,随机图 G ( n , p )中高概率不存在 r -控制团;当概率 p >
时,随机图 G ( n , p )中高概率不存在 r -控制团;当概率 p > ![]() 时,随机图 G ( n , p )中高概率存在 r -控制团,其中,log 1/ p n ≤ r ≤2log 1/ p n .
时,随机图 G ( n , p )中高概率存在 r -控制团,其中,log 1/ p n ≤ r ≤2log 1/ p n .
本文的主要工作是研究随机图 G ( n , p )和随机图 G ( n , m )中 k -独立集出现相变的临界概率和临界边数,其目的是让我们对随机图 G ( n , p )和随机图 G ( n , m )中 k -独立集的结构有更加深入的理解.
本节首先给出经典ER随机图模型的定义 [16] ,然后给出基本概念以及与ER随机图有关的一个重要结果.
随机图模型 G ( n , p ):给定 n 个顶点,任意2个不同顶点之间以概率 p 连接1条边所形成的随机图.生成一个顶点数为 n 、边数为 m 的图 G 0 ∈ G ( n , p )的概率为 ![]() 模型中的边数是一个随机变量,其期望值为
模型中的边数是一个随机变量,其期望值为 ![]()
随机图模型 G ( n , m ):给定 n 个顶点,在总共 ![]() 条可能存在的边中,随机地选取 m 条边所形成的随机图.由 n 个顶点和 m 条边构成的随机图实例总共有
条可能存在的边中,随机地选取 m 条边所形成的随机图.由 n 个顶点和 m 条边构成的随机图实例总共有 ![]() 种,全体构成一个概率空间,每一个网络在其中出现的概率是等可能的,其中
种,全体构成一个概率空间,每一个网络在其中出现的概率是等可能的,其中 ![]() N .
N .
一个图性质 Q 是指当 G ∈ Q , H ∈ G ( n , p )且 G ≅ H ( G 同构于 H )时有 H ∈ Q ,其中, G ∈ Q 表示图 G 中有图性质 Q .若该图性质满足条件: G ∈ Q 并且 G ⊂ H 时蕴含 H ∈ Q ,则称该图性质 Q 是单调递增的.
如果 F ⊆ G ⊆ H 且 F , H 都满足性质 Q ,则 G 也满足性质 Q ,称图 G 的性质 Q 是凸的.
引理1 [16] . 如果 Q 是凸的且 ![]() 则几乎每一个随机图 G ( n , p )都满足 Q 当且仅当对任意固定的 x ,几乎每一个随机图 G ( n , m )都满足 Q ,其中
则几乎每一个随机图 G ( n , p )都满足 Q 当且仅当对任意固定的 x ,几乎每一个随机图 G ( n , m )都满足 Q ,其中 ![]() ].
].
引理1的直观理解是当随机图 G ( n , m )中的边数 m 与随机图 G ( n , p )中的概率 p 满足关系 ![]() 时,二者等价,也即是说满足随机图 G ( n , p )的性质可以容易推广到随机图 G ( n , m )上.故本文的研究仅针对随机图 G ( n , p )展开.为描述随机图 G ( n , p )高概率存在某图性质 Q ,引入临界函数、严格临界函数的概念 [17] .
时,二者等价,也即是说满足随机图 G ( n , p )的性质可以容易推广到随机图 G ( n , m )上.故本文的研究仅针对随机图 G ( n , p )展开.为描述随机图 G ( n , p )高概率存在某图性质 Q ,引入临界函数、严格临界函数的概念 [17] .
设 Q 是一个图性质,如果:
成立,则称函数 h ( n )是性质 Q 的一个临界函数.如果对于任意的 ε >0,有:
成立,则称函数 h ( n )是性质 Q 的一个严格临界函数.
本节的工作是利用一阶矩和二阶矩方法分析随机图 G ( n , p )中存在 k -独立集的临界概率 p c ,给出随机图 G ( n , m )中存在 k -独立集的临界边数 m c .在引理2中先给出图 G ∈ G ( n , p )中 k -独立集个数 ![]() 的数学期望.
的数学期望.
引理2 . 在随机图 G ( n , p )中,对任意的2≤ k ≤ n ,非负整值随机变量 ![]() 的数学期望为
的数学期望为 ![]()
证明. 假设 Γ 是顶点个数为 k 的所有顶点子集构成的集合,其元素包含在 V ( G )中,其中, V ( G )表示图 G ∈ G ( n , p )的顶点集,其顶点总数为 n .为描述方便,用 α , β , γ ,…表示 Γ 中的元素.记 J α 是关于随机图 G ( n , p )的示性随机变量.
如果顶点集 α 是图 G ∈ G ( n , p )的一个 k -独立集,则 J α =1;否则, J α =0.
从顶点总数为 n 的图 G ∈ G ( n , p )中选择一个顶点个数为 k 的顶点集 α 有 ![]() 种选择方式,同时选择的顶点集 α 恰好是独立集的概率为
种选择方式,同时选择的顶点集 α 恰好是独立集的概率为 ![]() 故顶点集 α 是 k -独立集的期望为
故顶点集 α 是 k -独立集的期望为 ![]()
设 ![]() 是一个取值为非负整数的随机变量,表示图 G ∈ G ( n , p )中顶点个数为 k 的独立集个数,即
是一个取值为非负整数的随机变量,表示图 G ∈ G ( n , p )中顶点个数为 k 的独立集个数,即 ![]() 由期望的线性性质可知,对于给定的2≤ k ≤ n ,随机变量
由期望的线性性质可知,对于给定的2≤ k ≤ n ,随机变量 ![]() 的数学期望
的数学期望 ![]() 为
为
证毕.
定理1 . 对任意给定的2≤ k = o ( ![]() ),随机图 G ( n , p )中存在 k -独立集的临界值为
),随机图 G ( n , p )中存在 k -独立集的临界值为 ![]()
![]() 中存在 k -独立集]=
中存在 k -独立集]= 
证明. 设 ![]() 是一个取值为非负整数的随机变量,表示图 G ∈ G ( n , p )中顶点个数为 k 的独立集个数,即
是一个取值为非负整数的随机变量,表示图 G ∈ G ( n , p )中顶点个数为 k 的独立集个数,即 ![]() 由引理2有
由引理2有 ![]()
1) 由文献[18]可知,当 k = o ( ![]() )时,有:
)时,有:
(1)
由式(1)以及Stirling’s公式 ![]() 有:
有:
(2)
以 ![]() 代入随机变量
代入随机变量 ![]() 的期望表达式
的期望表达式 ![]() ,结合式(2)有:
,结合式(2)有:
![]()
![]()
![]()
![]()
(3)
当 c >1时,有
由一阶矩方法可知,当 ![]() 时,随机图 G ( n , p )中高概率不存在 k -独立集.
时,随机图 G ( n , p )中高概率不存在 k -独立集.
2) 当 c <1时,有 ![]() ∞.因为:
∞.因为:
(4)
其中 ![]() 表示从顶点个数为 n 的顶点集中选择2个顶点个数为 k 的顶点子集的组合数,选择的2个顶点子集的公共顶点个数为 s ;
表示从顶点个数为 n 的顶点集中选择2个顶点个数为 k 的顶点子集的组合数,选择的2个顶点子集的公共顶点个数为 s ; ![]() 表示选择的2个顶点子集同时为 k -独立集的概率.
表示选择的2个顶点子集同时为 k -独立集的概率.
又因为 ![]() 结合式(4)有:
结合式(4)有:
![]() =
= ![]() +
+
![]() + A n + B n -1.
+ A n + B n -1.
(5)
其中:
A n = ![]() ,
, ![]()
由 ![]() 可知
可知 ![]() ).于是有:
).于是有:
(6)
由 ![]() 以及
以及 ![]() 可知:
可知:
![]() =
= ![]() ×
× ![]() ×
× ![]() =
= ![]() ×
× ![]() ×
× ![]() ≤
≤ ![]() ≤
≤ ![]() ~
~ ![]() .
.
(7)
以 ![]() 带入表达式 B n ,结合式(7)有:
带入表达式 B n ,结合式(7)有:
(8)
当 c <1时,有 ![]() 结合式(8)可以得到
结合式(8)可以得到 ![]() 结合式(5)、式(6)有
结合式(5)、式(6)有 ![]() =
= ![]() ).由二阶矩方法可知,当
).由二阶矩方法可知,当 ![]() 时,随机图 G ( n , p )中高概率存在 k -独立集.
时,随机图 G ( n , p )中高概率存在 k -独立集.
综合证明1)2)的分析可知,当独立集节点数2≤ k = o ( ![]() )时随机图 G ( n , p )中存在 k -独立集的临界值为
)时随机图 G ( n , p )中存在 k -独立集的临界值为 ![]()
证毕.
注 ![]() 表示随机变量
表示随机变量 ![]() 的方差
的方差 ![]() 表示随机变量
表示随机变量 ![]() 的期望
的期望 ![]() 表示随机变量
表示随机变量 ![]() 的概率
的概率 ![]() 表示从 n 个元素中取 k 个元素的排列数.
表示从 n 个元素中取 k 个元素的排列数. ![]() 表示从 n 个元素中取出 k 个元素的组合数.
表示从 n 个元素中取出 k 个元素的组合数.
由引理1可知,当随机图 G ( n , m )中的边数 m 与随机图 G ( n , p )中的边概率 p 满足关系 ![]() 时二者等价,所以容易得到下面的定理2.
时二者等价,所以容易得到下面的定理2.
定理2 . 对任意给定的2≤ k = o ( ![]() ),随机图 G ( n , m )中存在 k -独立集的临界值为
),随机图 G ( n , m )中存在 k -独立集的临界值为
其中,[ x ]为取整函数.
![]() 中存在 k -独立集]=
中存在 k -独立集]= ![]()
给定一个图 G =( V , E ), V 表示图 G 的顶点集合, E 表示图 G 的边集合.若顶点集合 V 的顶点子集 T 中任意2个节点 u , v 之间都没有边,则称该顶点子集 T 为图 G 的独立集.若顶点子集 T 的元素个数为 k ,则称该顶点子集 T 为 k -独立集.下面给出独立集的求解算法1 [19] :
算法1 . 独立集求解算法.
输入:简单无向图 G =( V , E ),整数 k ≥2,其中,| V |= n ;
输出:独立集| S |≥ k ,其中| S |表示独立集 S 中的元素个数.
Step1. 对图 G 中的每个顶点用数字 i =1,2,…, n 标记,即 V ={1,2,…, n }.
Step2. 当 i ≤ n 时,初始化独立集 S i ={ i },同时执行 I = V - i ∪ N ( i );如果 I =∅,此时| S i |=1,那么执行 i = i +1,然后转回Step2;否则,转到Step3.
Step3. 当| S i |< k 时,对集合 I 中的所有 j ,分别执行 H j = V - N [ S i ]∪ j ∪ N ( j ),转到Step4.
Step4. 找到节点 ![]() 执行
执行 ![]() 若 I =∅,更新 S i = S i ∪{ j max },转到Step5;否则,更新 S i = S i ∪{ j max },转到Step6.
若 I =∅,更新 S i = S i ∪{ j max },转到Step5;否则,更新 S i = S i ∪{ j max },转到Step6.
Step5. 若| S i |< k ,则执行 i = i +1,转到Step2;否则,输出 S i 程序终止.
Step6. 若| S i |≥ k ,则输出 S i 程序终止;否则,转到Step3.
注:在Step2中, I = V - i ∪ N ( i )表示从图 G 的节点集 V 中去除节点 i 以及节点 i 的邻居节点之后的剩余节点集,其中, N ( i )={ j ∈ V :( i , j )∈ E }.在Step3中, N [ S i ]表示集合 S i 中节点和相应节点的邻居节点所构成的节点集合,| H j |表示去除 S i 中节点和相应节点的邻居节点,以及节点 j 和节点 j 的邻居节点之后的剩余节点集的个数 ![]() 是使得| H j |取最大值的节点.
是使得| H j |取最大值的节点.
本节的主要工作是进行数值仿真实验分析,该实验主要基于3个算法:1)随机图 G ( n , p )实例产生算法 [6,20] ;2)随机图 G ( n , m )实例产生算法 [6,20] ;3)独立集算法 [19] .数值实验的具体操作方法是首先利用随机图 G ( n , p )(或 G ( n , m ))算法产生一个随机图实例,然后调用独立集算法判断图 G ∈ G ( n , p )(或 G ∈ G ( n , m ))中是否存在 k -独立集.判断方法主要是看独立集算法在图 G 中是否能找到一个节点数不小于 k 的独立集,若独立集算法找到的独立集的节点数不小于 k ,则确定在 G ∈ G ( n , p )(或 G ∈ G ( n , m ))中存在一个 k -独立集,否则,我们确定在 G ∈ G ( n , p )(或 G ∈ G ( n , m ))中不存在 k -独立集.
从定理1可知,随机图 G ( n , p )中 k -独立集性质出现相变的临界概率 p c 与节点总数 n 和独立集节点数 k 有关.所以,在模拟随机图 G ( n , p )中 k -独立集性质的相变现象时,分别取节点总数 n 值为100,200,300,400,500,独立集节点数 k 值为5,10,15,20,25,如表1所示:
Table 1 Comparison Between the Theoretical Threshold and the Numerical Simulations for the Existence of k-Independent Set in Random Graph G(n,p)
表1 随机图 G ( n , p ) 中存在 k - 独立集的理论临界和仿真临界的对比
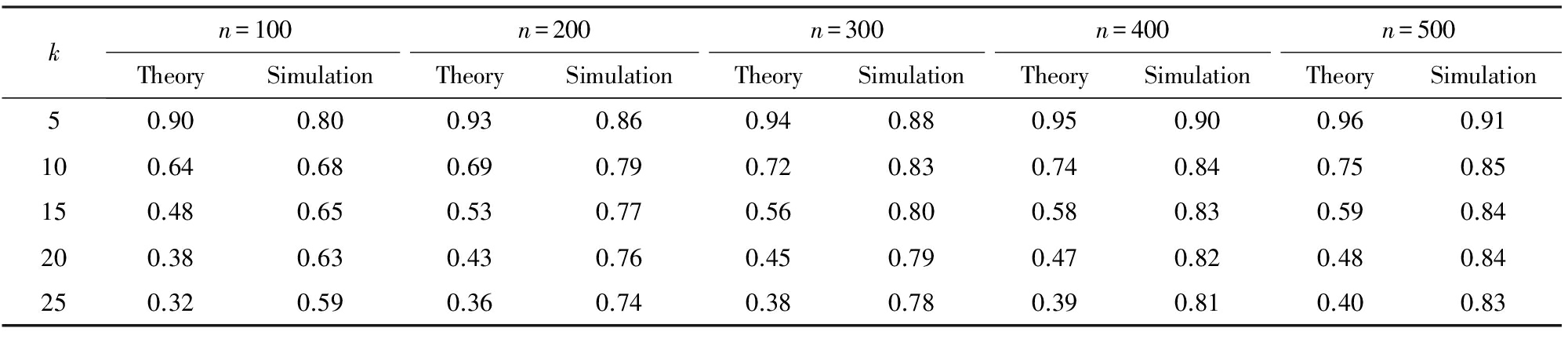
表1中的每一个理论值是取对应的 k 和 n 时利用定理1的临界概率 p c 计算得到的值,实验值是仿真得到的图 G ∈ G ( n , p )中存在 k -独立集的临界概率.从表1可以看到,当独立集的节点数 k ≪ ![]() 时,随机图 G ( n , p )中存在 k -独立集的理论临界值与仿真得到的实验值误差很小,产生这一误差的原因主要是由于我们的 n 值取得较小,因为定理1中的临界概率 p c 是在 n → ∞时的极限情况.从表1还可以看到,当 k ≫
时,随机图 G ( n , p )中存在 k -独立集的理论临界值与仿真得到的实验值误差很小,产生这一误差的原因主要是由于我们的 n 值取得较小,因为定理1中的临界概率 p c 是在 n → ∞时的极限情况.从表1还可以看到,当 k ≫ ![]() 时,随机图 G ( n , p )中存在 k -独立集的理论临界值与仿真得到的实验值之间的误差很大,而且随着 k 的增加,理论值与实验值之间的误差也在增大,说明定理1的理论临界概率对 k ≫
时,随机图 G ( n , p )中存在 k -独立集的理论临界值与仿真得到的实验值之间的误差很大,而且随着 k 的增加,理论值与实验值之间的误差也在增大,说明定理1的理论临界概率对 k ≫ ![]() 失效.
失效.
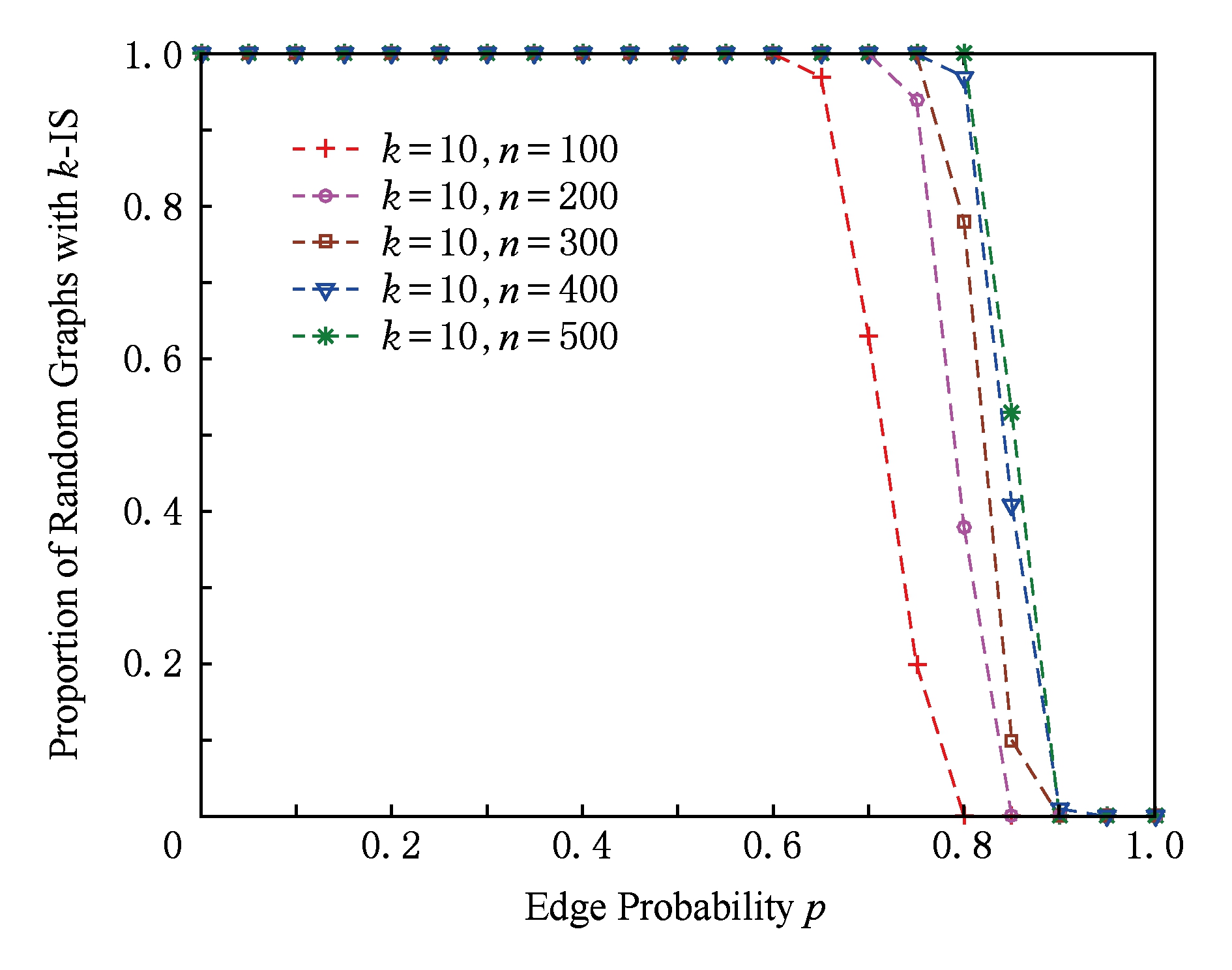
Fig. 1 Phase transition of 10-IS in random graph G(n,p)
图1 随机图G(n,p)中10-独立集的相变
图1给出了当独立集节点数 k 固定时随机图 G ( n , p )中存在 k -独立集的临界概率 p c 随节点总数 n 的变化情况,这里取独立集节点数 k =10,节点总数 n 分别取值为100,200,300,400,500.图1中的每个数据点是对每个给定的概率 p 和节点总数 n 利用随机图 G ( n , p )生成算法生成的100个图 G ∈ G ( n , p )实例中存在10-独立集的统计概率.
从图1可以看出,当独立集节点数 k =10固定时,随机图 G ( n , p )中存在10-独立集的临界概率 p c 随节点总数 n 的增加而增加,而且临界概率 p c 向右移动.
图2给出了当节点总数 n 固定时随机图 G ( n , p )中 k -独立集出现相变的临界概率 p c 随独立集节点数 k 的变化情况,这里取节点总数 n =400,独立集节点数 k 分别取值为5,10,15,20,25.图2中的每个数据点是对每个给定的概率 p 和节点总数 n 利用随机图 G ( n , p )生成算法生成的100个图 G ∈ G ( n , p )实例中存在 k -独立集的统计概率.从图2可以看出,当节点总数 n =400固定时,随机图 G ( n , p )中存在 k -独立集的临界概率 p c 随独立集节点数 k 的增加而减小,而且临界值 p c 向左移动.
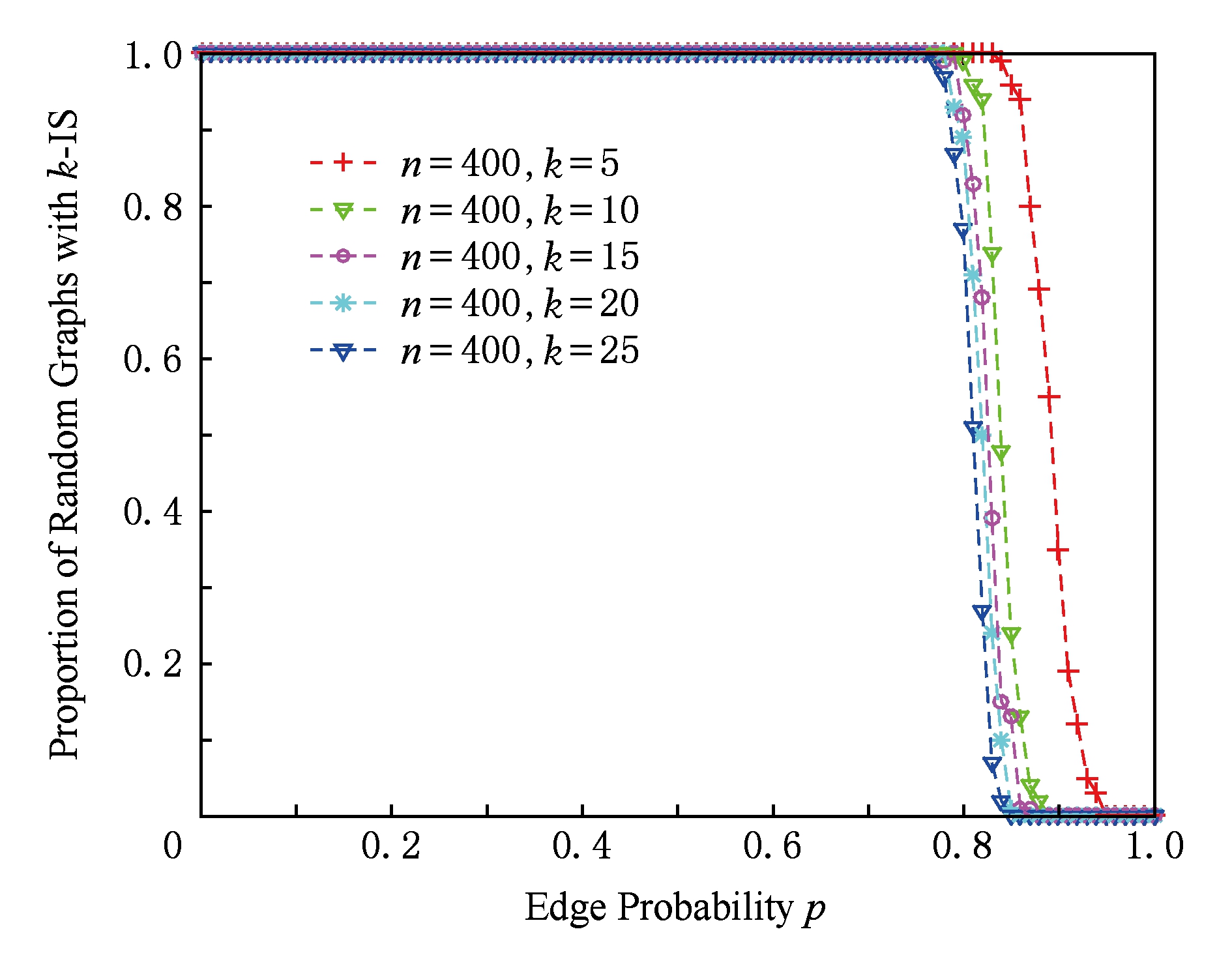
Fig. 2 Phase transition of k -IS in random graph G(n,p)
图2 随机图G(n,p)中k-独立集的相变
从定理2可知,随机图 G ( n , m )中 k -独立集性质出现相变的临界边数 m c 与节点总数 n 和独立集节点数 k 有关.所以,在模拟随机图 G ( n , m )中 k -独立集性质的相变现象时,节点总数 n 分别取值为100,200,300,400,500,独立集节点数 k 分别取值为5,10,15,20,25,如表2所示.表2中的理论值是取对应的 k 和 n 时利用定理2的临界边数 m c 计算得到的值,实验值是仿真实验得到的临界边数.从表2可以看出,当独立集的节点数 k ≪ ![]() 时,随机图 G ( n , m )中存在 k -独立集的理论临界边数 m c 与仿真实验边数之间的误差很小,理论结果与仿真结果一致.然而,当 k ≫
时,随机图 G ( n , m )中存在 k -独立集的理论临界边数 m c 与仿真实验边数之间的误差很小,理论结果与仿真结果一致.然而,当 k ≫ ![]() 时,随机图 G ( n , m )中存在 k -独立集的理论临界边数与仿真得到的实验边数之间的误差很大,而且随着 k 的增加,理论值与实验值之间的误差也在增大,说明定理2的理论临界值对 k ≫
时,随机图 G ( n , m )中存在 k -独立集的理论临界边数与仿真得到的实验边数之间的误差很大,而且随着 k 的增加,理论值与实验值之间的误差也在增大,说明定理2的理论临界值对 k ≫ ![]() 失效.
失效.
Table 2 Comparison Between the Theoretical Threshold and the Numerical Simulations for the Existence of k-Independent Set in Random Gandom Graph G(n,m)
表2 随机图 G ( n , m ) 中存在 k - 独立集的理论临界边数和仿真临界边数对比
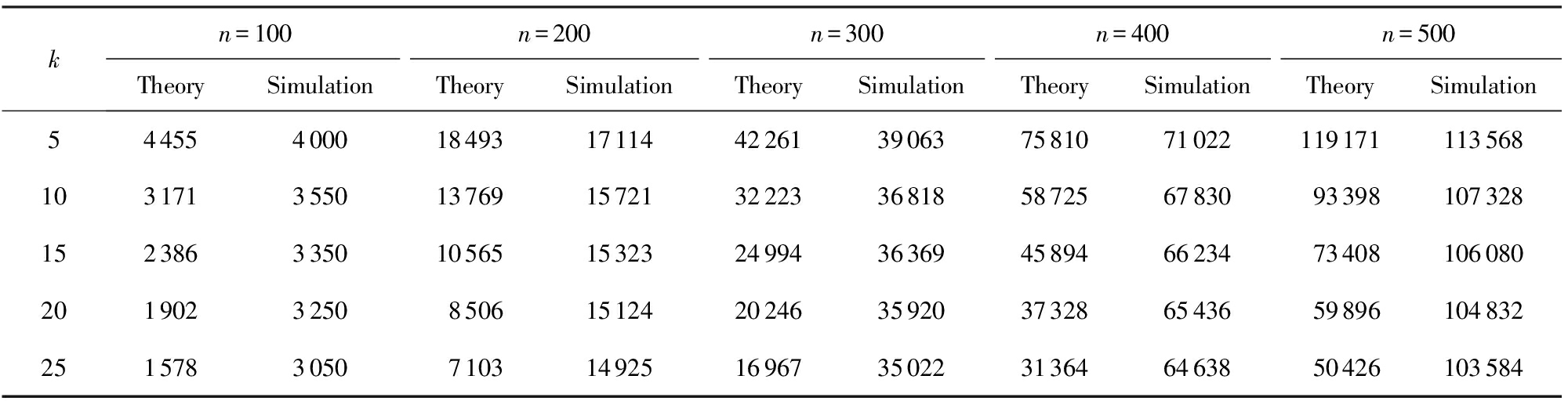
图3给出了当独立集的节点数 k 固定时随机图 G ∈ G ( n , m )中存在 k -独立集的临界边数 m c 随节点总数 n 的变化情况,这里分别取独立集节点数 k =10,节点总数 n 分别取值为100,200,300,400,500.图3中的每个数据点是对每个给定的边数 m 和节点总数 n 利用随机图 G ( n , m )生成算法生成的100个图 G ∈ G ( n , m )实例中存在 k -独立集的统计概率.从图3可以看出,当固定独立集节点数 k =10时,随机图 G ( n , m )中存在 k -独立集的临界边数 m c 随节点总数 n 的增加而增加,临界边数 m c 向右移.

Fig. 3 Phase transition of 10-IS in random graph G(n,m)
图3 随机图G(n,m)中10-独立集的相变
图4给出了当节点总数 n 固定时随机图 G ( n , m )中 k -独立集出现相变的临界边数 m c 随独立集的节点数 k 的变化情况,这里分别取节点总数 n =200,独立集节点数 k 分别取值为5,10,15,20,25.图4中的每个数据点是对每个给定的边数 m 和节点总数 n 利用随机图 G ( n , m )生成算法生成的100个图 G ∈ G ( n , m )实例中存在 k -独立集的统计概率.从图4可以看出,当固定顶点数 n =200时,随机图 G ( n , m )中存在 k -独立集的临界边数 m c 随着独立集节点数 k 的增加而减小,临界边数 m c 向左移.
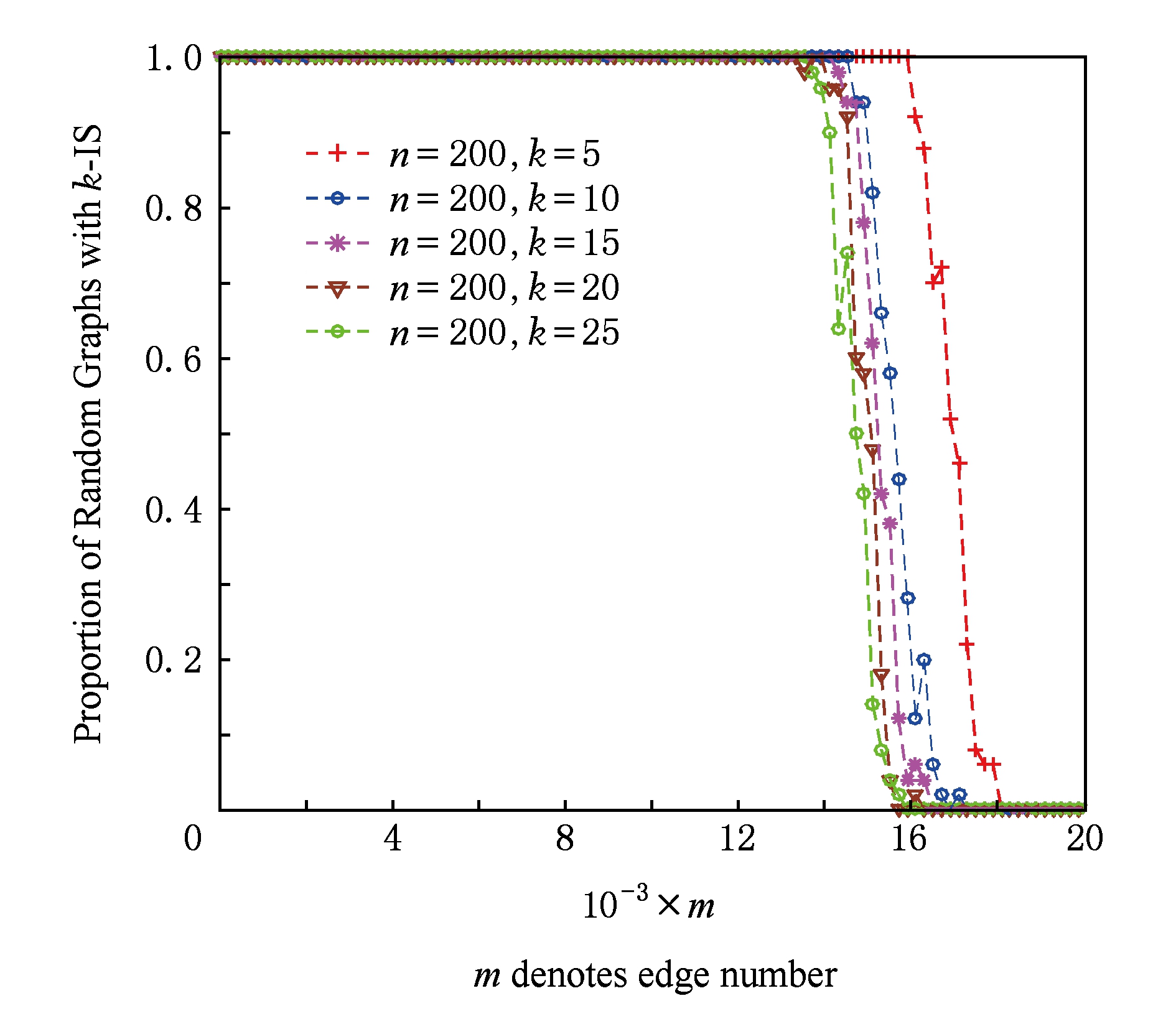
Fig. 4 Phase transition of k -IS in random graph G(n,m)
图4 随机图G(n,m)中k -独立集的相变
本文得到了当2≤ k = o ( ![]() )时随机图 G ( n , p )中存在 k -独立集的临界值
)时随机图 G ( n , p )中存在 k -独立集的临界值 ![]() 即当
即当 ![]() 时,随机图 G ( n , p )中高概率存在 k -独立集;当
时,随机图 G ( n , p )中高概率存在 k -独立集;当 ![]() 时,随机图 G ( n , p )中高概率不存在 k -独立集.同时还给出了随机图 G ( n , m )中存在 k -独立集的临界值为
时,随机图 G ( n , p )中高概率不存在 k -独立集.同时还给出了随机图 G ( n , m )中存在 k -独立集的临界值为 ![]() 其中,[ x ]为取整函数.最后,我们进行了仿真实验分析,实验结果表明,当独立集节点数2≤ k ≪
其中,[ x ]为取整函数.最后,我们进行了仿真实验分析,实验结果表明,当独立集节点数2≤ k ≪ ![]() 时,随机图 G ( n , p )和 G ( n , m )中 k -独立集性质出现相变的临界值与仿真实验结果一致且临界值与节点总数 n 和独立集节点数 k 有关,但当 k ≫
时,随机图 G ( n , p )和 G ( n , m )中 k -独立集性质出现相变的临界值与仿真实验结果一致且临界值与节点总数 n 和独立集节点数 k 有关,但当 k ≫ ![]() 时,随机图 G ( n , p )和 G ( n , m )中 k -独立集性质出现相变的临界值与仿真结果不一致.
时,随机图 G ( n , p )和 G ( n , m )中 k -独立集性质出现相变的临界值与仿真结果不一致.
参考文献
[1]Coja-Oghlan A, Efthymiou C. On independent sets in random graphs[J]. Random Structures & Algorithms, 2014, 47(3): 136-144
[2] Zhao Chunxiao, Wang Guangxing. A δ -degree-based clustering algorithm in MANET[J]. Journal of Computer Research and Development, 2005, 42(5): 818-822 (in Chinese)(赵春晓, 王光兴. 一种 δ -度约束的自组网成簇算法[J]. 计算机研究与发展, 2005, 42(5): 818-822)
[3] Garey M R, Johnson D S. Computers and Intractability: A Guide to the Theory of NP-Completeness[M]. New York: W H Freeman and Company, 1979
[4] Sloane N J A. Unsolved problem in graph theory arising from the study of codes[J]. Graph Theory Notes of New York, 1989, 18(11): 11-20
[5] Erdös P, Rényi A. On random graphs I[J]. Publicationes Mathematicae, 1959(6): 290-297
[6] Wang Xiaofan, Li Xiang, Chen Guanrong. Network Science: An Introduction[M]. Beijing: Higher Education Press, 2012: 200-201 (in Chinese)(汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育出版社, 2012: 200-201)
[7] Hopcroft J, Kannan R. Computer Science Theory for the Information Age[M]. Shanghai: Shanghai Jiao Tong University Press, 2013: 39-72
[8] Zdeborová L, Krzaka  a F. Phase transitions in the coloring of random graphs[J/OL]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007, 76(3): Article Number 031131. [2016-09-01]. https://doi.org/10.1103/PhysRevE.76.031131
a F. Phase transitions in the coloring of random graphs[J/OL]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007, 76(3): Article Number 031131. [2016-09-01]. https://doi.org/10.1103/PhysRevE.76.031131
[9] Xu Ke, Li Wei. Exact phase transitions in random constraint satisfaction problems[J]. Journal of Artificial Intelligence Research, 2000, 12(1): 93-103
[10] Xu Ke, Li Wei. Many hard examples in exact phase transitions[J]. Theoretical Computer Science, 2006, 355(3): 291-302
[11] Mertens S, Zard M, Zecchina R. Threshold values of random K-SAT from the cavity method[J]. Random Structures & Algorithms, 2006, 28(3): 340-373
[12] Nekovee M, Moreno Y, Bianconi G, et al. Theory of rumour spreading in complex social networks[J]. Physica A Statistical Mechanics & Its Applications, 2008, 374(1): 457-470
[13] Gómezgarde  es J, Lotero L, Taraskin S N, et al. Explosive contagion in networks[J/OL]. Scientific Reports, 2016, 6(1): Article Number 19767. [2016-09-01]. https://doi.org/10.1038/srep19767
es J, Lotero L, Taraskin S N, et al. Explosive contagion in networks[J/OL]. Scientific Reports, 2016, 6(1): Article Number 19767. [2016-09-01]. https://doi.org/10.1038/srep19767
[14] Culberson J, Gao Yong, Anton C. Phase transitions of dominating clique problem and their implications to heuristics in satisfiability search[DB]. Trier, Rheinland-Pfalz, Germany: DBLP, 2005 [2016-09-01]. http://dblp.org/db/conf/ijcai/ijcai2005.html
[15] Nehéz M, Olejár D, Demetrian M. A detailed study of the dominating cliques phase transition in random graphs[C] //Proc of the 9th Annual Int Conf on Theory and Applications of Models of Computation. Berlin: Springer, 2012: 594-603
[16] Bollobasi B. Random Graphs[M]. New York: Academic Press, 2001
[17] Seierstad T G. The phase transition in random graphs and random graph processes[D]. Berlin: Humboldt University, 2007
[18] Nehéz M, Olejár D, Demetrian M. On emergence of dominating cliques in random graphs[EB/OL]. 2008 [2016-09-01]. https://arxiv.org/abs/0805.2105
[19]Dharwadker A. The independent set algorithm[OL]. 2006 [2016-09-01]. http://www.dharwadker.org/independent_set/
[20] Nobari S, Lu X, Karras P, et al. Fast random graph generation[C] //Proc of the 14th Int Conf on Extending Database Technology. New York: ACM, 2011: 331-342
Lu Youjun and Xu Daoyun
( College of Computer Science and Technology , Guizhou University , Guiyang 550025)
Abstract Phase transition property is one of the most important properties of the theory of Erdös-Rényi random graphs. A subset of vertices is a k -independent set in a simple undirected graph G =( V , E ) if the subset is an independent set containing k vertex. In order to understand the structural property of k -independent sets in Erdös-Rényi random graphs, the phase transition properties of k -independent sets in Erdös-Rényi random graphs are investigated in this paper. It is shown that the threshold probability is p c =1- ![]() for the existence of k -independent sets in random graph G ( n , p ) via the first moment method and the second moment method when 2≤ k = ο (
for the existence of k -independent sets in random graph G ( n , p ) via the first moment method and the second moment method when 2≤ k = ο ( ![]() ). According to this fact that random graph G ( n , p ) is equivalent to random graph G ( n , m ) when m is close to p
). According to this fact that random graph G ( n , p ) is equivalent to random graph G ( n , m ) when m is close to p ![]() , the threshold edge number is given by m c =
, the threshold edge number is given by m c = ![]() for the existence of k -independent sets in random graph G ( n , m ). The simulation results show that the consistence between simulation and theoretical threshold value for the existence of k -independent sets in random graph G ( n , p ) and G ( n , m ) when 2≤ k = ο (
for the existence of k -independent sets in random graph G ( n , m ). The simulation results show that the consistence between simulation and theoretical threshold value for the existence of k -independent sets in random graph G ( n , p ) and G ( n , m ) when 2≤ k = ο ( ![]() ), and the threshold value is related to the total number n of vertices and the number k of vertices of independent set. However, when k = ω (
), and the threshold value is related to the total number n of vertices and the number k of vertices of independent set. However, when k = ω ( ![]() ), the theoretical threshold value is not consistent with the simulation threshold value for the existence of k -independent sets in random graph G ( n , p ) and G ( n , m ).
), the theoretical threshold value is not consistent with the simulation threshold value for the existence of k -independent sets in random graph G ( n , p ) and G ( n , m ).
Key words phase transition property; random graphs; k -independent set; threshold probability; threshold edge number
收稿日期: 2016-09-14;
修回日期: 2016-12-05
基金项目: 国家自然科学基金项目(61262006,61462001,61540050,61762019);贵州省重大应用基础研究项目(JZ20142001);贵州大学研究生创新基金项目(2016047)
This work was supported by the National Natural Science Foundation of China (61262006, 61462001, 61540050, 61762019), the Major Applied Basic Research Program of Guizhou Province (JZ20142001), and the Graduate Student Innovation Foundation of Guizhou University (2016047).
通信作者: 许道云(dyxu@gzu.edu.cn)
中图法分类号 TP301

Lu Youjun , born in 1985. PhD candidate. Student member of CCF. His main research interests include computational complexity and complex networks.

Xu Daoyun , born in 1959. Professor and PhD supervisor at the College of Computer Science and Technology, Guizhou University. Senior member of CCF. His main research interests include computability theory and computational complexity.