
Fig. 1 Directed acyclic graph of Spark job
图1 Spark作业的有向无环图
英昌甜 1,2 于 炯 2 卞 琛 2 王维庆 1,3 鲁 亮 2 钱育蓉 2
1 (新疆大学电气工程博士后科研流动站 乌鲁木齐 830046) 2 (新疆大学软件学院 乌鲁木齐 830008) 3 ((新疆大学电气工程学院 乌鲁木齐 830046)
(yingct@xju.edu.com)
摘 要 Spark默认容错机制由程序员设置检查点,并利用弹性分布式数据集(resilient distributed dataset, RDD)的血统(lineage)进行计算.在应用程序复杂度高、迭代次数多以及数据量较大时,恢复过程需要耗费大量的计算开销.同时,在执行恢复任务时,仅考虑数据本地性选择节点,并未考虑节点的计算能力,这都会导致恢复时间增加,无法最大化发挥集群的性能.因此,在建立Spark执行模型、检查点模型和RDD关键度模型的基础上,提出一种基于关键度的检查点管理(criticality checkpoint management, CCM)策略,其中包括检查点设置算法、失效恢复算法和清理算法.其中检查点设置算法通过分析作业中RDD的属性以及对作业恢复时间的影响,选择关键度大的RDD作为检查点存储;恢复算法根据各节点的计算能力做出决策,选择合适的节点执行恢复任务;清理算法在磁盘空间不足时,清除关键度较低的检查点.实验结果表明:该策略在略增加执行时间的情况下,能够选择有备份价值的RDD作为检查点,在节点失效时能够有效地降低恢复开销,提高节点的磁盘有效利用率.
关键词 内存计算;Spark;检查点管理;失效恢复;RDD属性
近年来,随着互联网的快速发展,特别是云计算的普及,全球数据量以每年约50%的速度递增,大数据 [1-3] 日益受到人们的重视.2015年9月,国务院印发《促进大数据发展行动纲要》,确定了大数据发展的国家顶层设计,大数据与各行各业的结合已是行业未来发展的必然趋势.随着大数据时代的到来,数据每天都在急剧快速膨胀,发掘这些数据的价值,需要一种高效而稳定的分布式计算框架和模型.在分布式计算框架中,Apache Spark [4-6] 由于其基于内存的高性能计算模式以及丰富灵活的编程接口,得到了广泛的支持和应用,大有逐渐取代Hadoop MapReduce成为新一代大数据计算引擎的趋势.
Spark采用了基于分布式共享内存的弹性分布式数据集(resilient distributed datasets, RDD) [7] 作为数据结构,RDD是Spark对分布式内存的抽象,具有可重构性、不变性、分区局部性以及可序列化等特性 [8-10] .作为Apache顶级的开源项目,Spark基于自身的核心部分,在迭代计算、交互式查询计算以及批量流计算等方面,开发了适应大数据处理的多种场景生态组件,如SQL处理引擎Spark SQL和Shark、流式处理引擎Spark Streaming、机器学习系统MLLib、图计算框架GraphX、统计分析工具SparkR以及分布式内存文件系统Tachyon等.
Spark是基于MapReduce算法实现的分布式计算框架,因此具有MapReduce的优点 [11-12] .同时Spark在很多方面都弥补了MapReduce的不足,比MapReduce的通用性更好、迭代运算效率更高、作业延迟更低.Spark的主要优势包括:提供了一套支持DAG图的分布式并行计算的编程框架,减少多次计算之间中间结果写到HDFS的开销;提供Cache机制来支持需要反复迭代计算或者多次数据共享,减少数据读取的I/O开销;使用多线程池模型来减少任务启动开销,shuffle过程中避免不必要的sort操作以及减少磁盘I/O操作;具有更广泛的数据集操作类型.
在Spark任务的执行过程中,首先将HDFS中存储的数据作为数据源加载到RDD中进行处理,再通过一系列的操作生成计算结果,每次操作所产生的中间结果都以RDD的形式存储在内存中.Spark通过数据集的血统(lineage)实现容错,当节点失效导致数据丢失时,Spark可以根据血统重新计算,以实现丢失数据的自动重建.为了避免错误恢复的代价与运行时间成正比增长,Spark提供了检查点(checkpoint) [13] 功能,通过设置检查点来记录中间状态,避免从头开始计算的漫长恢复.
然而,Spark集群默认的容错机制将检查点选择和设置的权利交给编程人员,而程序员往往根据经验进行选择,使结果充满不确定性.数据丢失后恢复的效果好坏和效率高低,会随着程序员的水平不同而出现巨大差异.错误的检查点策略不仅会导致程序变慢,恢复效率降低,甚至会浪费持久化存储(磁盘/固态硬盘等)的空间,影响其他作业执行效率.此外,由于现有分布式框架中的检查点策略,往往根据时间周期定时设置,并未对具体作业进行分析,考虑影响作业恢复效率的重要因素,因此选取的检查点并不一定有效,反而可能影响整体系统的计算和容错性能.
为解决这一问题,本文主要做了3方面工作:
1) 对内存计算框架的作业执行机制进行分析,建立执行效率模型,给出了RDD计算代价和任务执行时间的定义.
2) 通过分析RDD的恢复过程,建立了检查点恢复模型,给出了RDD关键度、失效恢复比的定义,并证明这些定义与任务恢复效率的关系,为算法设计提供基础模型.
3) 在相关模型定义和证明的基础上,提出了检查点管理策略的问题定义,以此作为算法设计的主要依据.
检查点/恢复策略是分布式计算广泛使用的容错技术,在国内外都有较多的相关研究 [14-19] .传统的检查点策略主要分为3类:应用级实现、用户级实现和系统级实现.
1) 应用级实现.由编程人员或自动程序将检查点代码与应用程序代码整合,检查点活动由应用程序自动执行.将检查点存储到持久化存储中,并且当节点故障后,从检查点重启.这种方法的挑战在于需要编程人员对设置检查点的应用有透彻的了解.
2) 用户级实现.需要用户级的数据库来设置检查点,并且应用程序与数据库相链接,这种方法对用户不透明,因为应用的修改、编译都链接到检查点数据库.
3) 系统级实现.检查点/恢复策略可以实现在系统级别,包括OS内核或硬件.当实现在系统级别,对用户通常是透明的,并且对应用程序不需要修改.
另外一些研究成果主要考虑分布式环境下并行计算框架的失效恢复策略.Storm [20] 是一个实时流式处理平台,运行在Java虚拟机之上;使用Clojure和Java编写,并且支持多语言编程;它依靠Nimbus在集群分发代码,并将任务分配给工作节点;由Zookeeper为其提供了容错,并与Nimbus协调重新分配任务到其他可用节点;然而,没有设置检查点机制.Apache S4 [21] 是一个开源的流处理平台,利用Zookeeper提供容错.与Storm不同,它提供了检查点机制.在一个节点出现故障时,故障转移机制重新启动一个新节点进行任务恢复.为了减少延迟,检查点是异步的,这意味着每个独立节点执行检查点,没有全局一致性.文献[22-23]提出了一种基于内存的分布式文件系统Tachyon,兼容包括Spark在内的多种计算框架.Tachyon本质上是将内存存储功能从Spark或Yarn中分离出来,使上层计算框架实现更高的执行效率.在Tachyon的实现中,文件采用兼容HDFS的Block方式进行管理,使用不同的存储媒介对数据分层次缓存,但检查点算法仅保存当前最新生成的RDD,与任务和RDD的特性无关.文献[24]提出了内存文件系统RAMCloud,将内存作为文件的存储介质,而磁盘则作为备份介质,为了提高效率,RAMCloud使用日志结构存储,利用集群的并发能力和高速带宽的Infiniband实现快速恢复,保证了数据的可用性和完整性,但Spark与RAMCloud并不兼容,因为RAMCloud的高内存占用率会影响Spark的计算性能.
因此,为了解决检查点设置的问题,其中的重点就是选择哪些有价值的RDD作为检查点存储在磁盘中,以及在数据丢失后应选择什么样的节点进行恢复.在实时系统或数据库系统中,对周期设置检查点而言,所有数据的重要性相同,仅仅根据周期设置时的时间选择最新生成的数据设置为检查点.与此不同的是,由于Spark基本存储单元为RDD,不同RDD所具有的属性如操作复杂度、血统长度、计算代价和RDD数据量大小各不相同,对于作业恢复时所产生的恢复效果不同,因此在作业执行过程中,异步存储对恢复更有价值的RDD在磁盘中,在设置检查点的同时尽量不影响作业执行效率.通过对Spark作业执行机制和执行时间进行理论分析,在恢复时根据数据本地性、节点空闲情况和节点能力选择节点,并执行恢复任务,从而缩短恢复时间.
本节通过分析Spark作业执行机制,定义了RDD和作业的执行开销,提出了作业执行模型、检查点模型和关键度模型,并且在理论基础上对目标问题进行了定义.
在Spark应用中,整个执行流程在逻辑上会形成有向无环图(DAG).Action算子触发之后,根据RDD的血统,将所有累积的算子形成一个有向无环图,然后由调度器调度该图上的任务进行运算.Spark根据RDD之间不同的依赖关系切分形成不同的阶段(stage),一个阶段包含一系列函数执行流水线.
Spark作业DAG的典型示例如图1所示, A , B , C , D , E , F 和 G 分别代表不同的RDD,RDD内的方框代表分区,虚线框为阶段.数据从HDFS输入Spark,形成RDD A 和RDD C ,RDD C 上执行 map 操作,转换为RDD D ,RDD D 和RDD E 执行 union 操作,转换为 F ,而在 B 和 F 通过 join 连接转化为 G 的过程中会执行 Shuffle ,最后RDD G 输出并保存到HDFS中.

Fig. 1 Directed acyclic graph of Spark job
图1 Spark作业的有向无环图
Spark在未设置检查点算法时,若数据失效,则需要利用血统重新计算来实现恢复.若所有需要的数据都丢失,则RDD必须重新计算生成,使任务的完成时间延长,还增加了额外的计算开销.若能为有价值的RDD设置检查点,则能有效缩减任务恢复时间.
定义1 . RDD计算代价.Spark任务中,分区由父节点为输入数据计算生成.设 Parents i jk 为分区 P i jk 的父节点集合.分区 P i jk 的计算代价为数据读取代价与数据处理代价之和,即:
T P i jk = read ( Parents i jk )+ proc ( Parents i jk ).
(1)
RDD的所有分区由集群工作节点并行计算生成,因此其计算代价为所有分区计算代价的最大值,即:
T RDD i j =max( T P i j 1 , T P i j 2 ,…, T P i jk ).
(2)
定义2 . 作业执行时间.如图1所示,Spark以宽依赖为分界点,将作业划分为多个阶段执行,因此阶段分为窄依赖和宽依赖2类.
由于Spark任务以分区为最小粒度单位,因此在任务分配时,分区计算时间与节点计算能力有关.设 cp w 为工作节点计算能力,单位是tuple/s; S P i jk 为分区 P i jk 的元组个数.
由于窄依赖的父分区为上一个RDD对应位置的一个分区,则窄依赖分区计算时间:
NT P i jk = Load ( S P i ( j -1) k )+ ![]() .
.
(3)
对于窄依赖阶段,每个阶段包括多条流水线(每条流水线包括多个RDD的不同分区).记窄依赖Stage共包含 m 个RDD,RDD相同位置的分区组成流水线,所有RDD划分为 x 条流水线,单条流水线的分区集合为 pipe i x ={ P i 1 x , P i 2 x ,…, P i jx },那么单条流水线的执行时间可表示为
(4)
对于 stage i ,记其流水线集合为 Pipes i ={ pipe i 1 , pipe i 2 ,…, pipe i x },那么该阶段的执行时间应为各流水线执行时间最大值,即:
NT stage i =max( T pipe i 1 , T pipe i 2 ,…, T pipe i x )=
![]() ).
). ![]()
宽依赖的父分区集合为上一个RDD的所有分区,即整个RDD,且宽依赖RDD的分区计算时间大于窄依赖RDD的分区计算时间,则宽依赖分区计算时间:
WT P i jk = Load ( S RDD i ( j -1) )+ ![]() .
.
(6)
由于宽依赖阶段中仅包含1个RDD,则宽依赖阶段的计算时间为
WT stage i =max{ WT P i j 1 , WT P i j 2 ,…, WT P i jk }.
(7)
一个作业由若干个阶段构成,由于Spark以宽依赖为界划分阶段,而作业的最后一个阶段必为宽依赖(所有执行均为宽依赖操作),记作业中宽、窄依赖的个数分别为 m 和 n ,那么作业执行时间可表示为
(8)
在节点故障时,会使存储在该节点内存上的多个RDD部分甚至所有分区不可用,这将导致作业无法继续正常执行,在未设置检查点的情况下,作业需要回溯,直到找到可用的RDD.极端情况下,甚至需要重新调度,之前所计算的所有工作和耗费的系统资源都会浪费.因此,对于作业而言,有必要设置检查点,从而降低节点宕机后产生的恢复开销.
定义3 . 作业恢复代价.作业执行到任意RDD,若集群中某个工作节点发生故障,作业将丢失该工作节点计算的所有中间结果.记故障的工作节点编号为 k (工作节点编号对应流水线序号和宽依赖RDD中的分区编号),那么对于所有窄依赖阶段,每个阶段丢失一条流水线的数据,则在不考虑恢复调度开销时,窄依赖阶段的恢复代价为丢失流水线的重新计算代价,即:
(9)
而对于宽依赖阶段而言,RDD的一个分区丢失,因此在不考虑恢复调度开销时,宽依赖阶段的恢复代价为该分区的重新计算代价,即:
WR i = WT P i jk .
(10)
由于工作节点故障为随机事件,发生故障时当前计算的RDD可能位于任何阶段内,因此,若故障发生在窄依赖阶段,则作业恢复代价还应考虑丢失分区在流水线的前续节点的重新计算代价.而若故障发生在宽依赖阶段,由于该阶段仅包含一个RDD,无前续节点恢复代价,仅需要恢复该RDD.
设当前作业已执行的阶段中共有 x 个窄依赖、 y 个宽依赖,正在执行的阶段共有 m 个RDD,当前正在计算 RDD i h ,在不考虑恢复调度开销时作业恢复代价可表示为
(11)
即作业恢复代价等于前续宽、窄依赖阶段的恢复代价之和,再加上丢失分区在当前阶段中父分区的计算代价之和.
定理1 . 设 Job i ={ RDD i 1 , RDD i 2 ,…, RDD i n }, RDD i ( j -1) ∈ Job i 且 RDD i j ∈ Job i .若 RDD i j 具有更长的血统,并且 RDD i ( j -1) 是 RDD i j 唯一的 parentRDD .那么,在执行 Job i 的计算节点都失效时,恢复 RDD i j 的开销较高,且为 T RDD i j .
证明. 若 RDD i j 具有更长的血统, RDD i ( j -1) 是 RDD i j 的 parentRDD .设 RDD i ( j -1) 的血统长度为 k ,则 RDD i j 的血统长度为 k +1.考虑2种情况:
1) 若 Job i 设置了检查点,则只需要从检查点处开始计算恢复.若恢复所需要的最新检查点为 RDD i p ,恢复调度开销为常量 α i 的情况下,则恢复开销分别为
![]()
![]()
2) 若 Job i 未设置检查点,在计算节点失效时,则所有RDD都需要重新计算,重新部署调度开销为常量 β i ,则恢复开销分别为
![]()
![]()
无论是情况1或情况2,明显可看出, R RDD i j > R RDD i ( j -1) 且 R RDD i j - R RDD i ( j -1) = T RDD i j .
证毕.
定理2 . 设 Job i ={ RDD i 1 , RDD i 2 ,…, RDD i n }, RDD i ( j -1) ∈ Job i ,且 RDD i j ∈ Job i . RDD i ( j -1) 为 RDD i j 的唯一 parentRDD .若节点失效时,仅丢失了 RDD i j 的第 l 个分区 P i jl ,那么在 RDD i j 的操作为窄依赖或宽依赖时,其恢复 P i jl 的开销不同,且宽依赖时恢复开销为max( R P i j 1 , R P i j 2 ,…, R P i jk ).
证明. 由于 RDD i j 的 parentRDD 为 RDD i ( j -1) ,则操作为窄依赖时可知丢失第 l 个分片 P i jl ,只需通过 RDD i ( j -1) 的对应父分片 P i j ( l -1) 通过流水线计算获得,故恢复 P i j ( l -1) 开销为
R RDD i j ( narrow )= R PT i jl =
α i + read ( PT i ( j -1) l )+ proc ( PT i jl ).
操作为宽依赖时,丢失第 l 个分片 P i jl ,需通过 RDD i ( j -1) 所有的分片计算得到 P i jl ,则恢复 PT i j ( l -1) 的开销为
R RDD i j ( wide )= R RDD i j =max( R P i j 1 , R P i j 2 ,…, R P i jk ).
因此, R RDD i j ( wide )≥ R RDD i j ( narrow ).
证毕.
定理3 . 设 Job i ={ RDD i 1 , RDD i 2 ,…, RDD i n }, RDD i ( j -1) , RDD i j , RDD i ( j +1) ∈ Job i . RDD i ( j -1) 是 RDD i ( j -1) 和 RDD i j 的唯一 parentRDD , RDD i ( j -1) 已备份为检查点并存储在正常运行节点,且计算代价 proc RDD i ( j +1) ≥ proc RDD i j .当计算节点失效时, RDD i j 和 RDD i ( j +1) 丢失,则从 RDD i ( j -1) 检查点进行恢复的代价 R RDD i ( j +1) ≥ R RDD i j .
证明. 由于 proc RDD i ( j +1) ≥ proc RDD i j ,则对于 RDD i ( j +1) 中任意第 l 个分片的计算代价 proc PT i ( j +1) l ≥ proc PT i jl .
当执行恢复计算时, RDD i ( j -1) 已备份为检查点,则恢复 RDD i j 的开销为 R RDD i j =max( R P i j 1 , R P i j 2 ,…, R P i jk ).对第 l 个分片而言,恢复该分片的开销为
R P i jl = T P i jl = α i + read ( P i ( j -1) l )+ proc ( P i jl ).
同样,恢复 RDD i ( j +1) 的开销为 R RDD i ( j +1) =max( R P i ( j +1)1 , R P i ( j +1)2 ,…, R P i ( j +1) k ).对第 l 个分片而言,恢复该分片的开销为
R P i ( j +1) l = T P i ( j +1) l =
α i + read ( P i ( j -1) l )+ proc ( P i ( j +1) l ).
由于 proc RDD i ( j +1) ≥ proc RDD i j ,可知 R P i ( j +1) l ≥ R P i jl ,同时 R RDD i ( j +1) ≥ R RDD i j .
证毕.
根据2.3节的分析,可以判断出RDD与恢复开销相关的因素有3个:
1) RDD的血统长度.在作业中具有更长血统的RDD恢复开销更大,证明详见定理1.因此当设置检查点时,应优先选择长血统的RDD,从而降低对恢复开销的影响.
2) RDD类型(指宽依赖或窄依赖).在宽依赖情况下,丢失1个子RDD分区,需重算的每个父RDD的每个分区会产生冗余计算开销,使宽依赖在恢复时开销更大,证明详见定理2.因此,应优先选择宽依赖的RDD作为检查点,从而降低恢复开销.
3) RDD计算代价.计算代价越高的RDD恢复时开销越大,应优先备份计算代价高的RDD,证明详见定理3.另外,RDD大小对数据备份时长和数据恢复读取时长都会产生影响,从而也作为考虑的关键因素.
定义4 . RDD关键度.表示RDD对任务恢复效率的重要程度.在传统的检查点策略中,并未引进权重的概念,被选择作为检查点的数据在本质上与其他数据没有区别,而在Spark中则不同,不同的RDD对恢复的重要程度不同.在RDD丢失时,需要重新计算,而不同的RDD恢复需要的计算开销不同.
综合考虑相关因素,记 LD RDD i j 表示为 LD RDD i j 血统长度, Type RDD i j 为类型, Cost RDD i j 为计算代价, Size RDD i j 为数据量大小.则RDD的关键度表示为
CR RDD i j = ![]() .
.
(12)
式(12)表明,血统长度、RDD类型、计算代价与RDD关键度成正比关系,而容量大小则成反比关系.关键度越大,恢复时对恢复效率的影响越大,因此作为检查点备份的必要性越大.
定义5 . 失效恢复比.用于表示恢复任务分配与节点计算能力的适应程度.记恢复计算节点集合 Workers ={ w 1 , w 2 ,…, w n },其计算能力 C ={ c 1 , c 2 ,…, c n }, RT 为恢复任务总量,则执行恢复任务的时间开销均值可定义为
E = 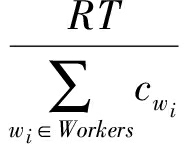 .
.
(13)
对于任意计算节点 w i ,分配给其恢复任务 RT i 时,其执行时间、均值的方差和失效恢复比分别为
T w i = ![]() ,
,
(14)
D w i =( T w i - E ) 2 ,
(15)
Ratio w i = ![]() ,
,
(16)
其中, w i ∈ Workers .
基于定义,从作业分配的角度来看,作业执行时间也可表示为
T job =max( T w 1 , T w 2 ,…, T w n ).
(17)
由于节点的失效恢复比与方差成反比,因此比值越大,方差越小,表示节点恢复作业完成时间越趋近均值,因此当所有工作节点的失效恢复比取最大值时恢复任务的执行时间最短.
2.1节至2.4节已经对作业和检查点机制作了比较详细的阐述,基于这些定义,对我们的检查点算法进行形式化表示.
优化目标:
min R job .
(18)
s.t.
(19)
其中, j ∈ jobs , w i ∈ Workers , r ∈ R .
目标是作业恢复开销最小,约束条件是资源总分配量 ![]() 符合资源需求 d j r .根据RDD关键度和恢复效率比的定义,可给出上述问题式(18)(19)等价的形式化表示.
符合资源需求 d j r .根据RDD关键度和恢复效率比的定义,可给出上述问题式(18)(19)等价的形式化表示.
优化目标:
(20)
![]() ).
).
(21)
s.t.
(22)
其中, j ∈ jobs , RDD j k ∈ job j , w i ∈ Workers , r ∈ R .
目标是最大化RDD关键度和失效恢复比,约束条件同上.因此,在设置检查点时,应选择已生成的RDD中对恢复效率影响最大,即关键度最大的RDD作为检查点进行设置.在节点失效进行恢复时,应选择节点能力更强的节点执行作业恢复.
本节提出基于关键度的检查点管理(criticality based checkpoint management,CCM)策略,其中包括检查点设置算法、失效恢复算法和检查点清理算法,具体流程图如图2所示.
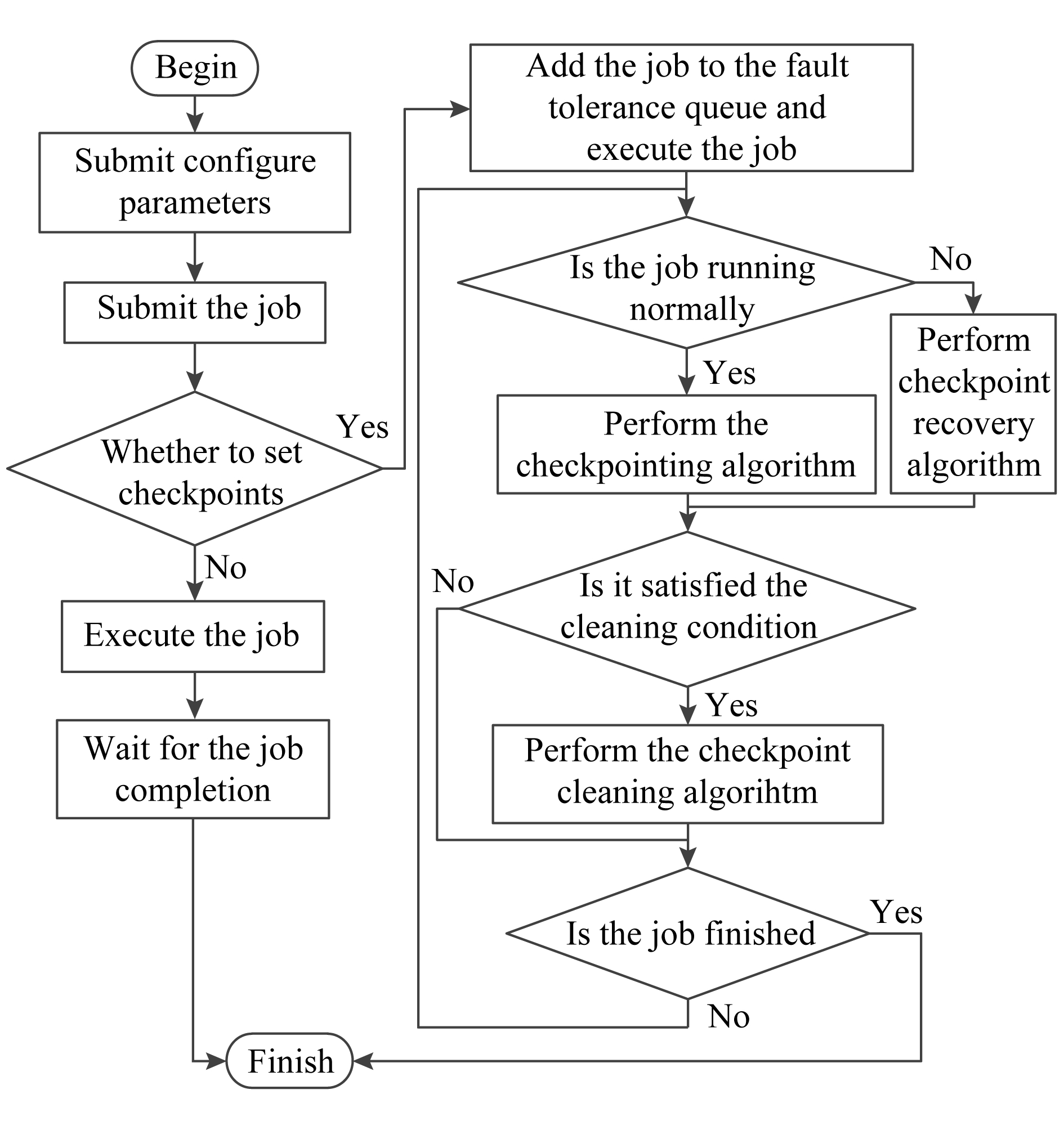
Fig. 2 Flow chart of checkpoint strategy
图2 检查点策略流程图
作业在设置检查点和恢复算法的粒度可以分为2个级别:1)RDD级别;2)分区级别.在设置检查点时,检查点选择可以在RDD级别、分区级别以权重度、固定时间间隔等多种为算法以异步检查点的方式进行设置.在算法恢复时,宕机节点上的任务需要进行恢复,以最新的检查点序列为基础,由Spark调度器重新调度执行.根据集群资源情况,分配需要的资源.
RDD级别以作业的RDD为粒度,根据RDD的重要度选择更优的检查点,问题在于粒度较大,当某个节点宕机丢失某些RDD的分区,需要重新计算所有的RDD,从磁盘中读取最新检查点信息的所有内容,浪费系统资源.分区级别以RDD的分区为粒度,根据分区的关键度,为每个分区选择异步的检查点,在丢失某些分区时不需要恢复整个RDD,只需恢复丢失的分区,无论是备份检查点时的磁盘开销,还是恢复时的读取开销和执行开销,都比较少.但问题在于,以分区为粒度和异步备份检查点时、若有多个任务同时在Spark集群中执行,检查点设置开销和管理难度明显增大.因此,采用以RDD为设置检查点的基本单位,分区为恢复检查点的基本单位.
基于关键度的检查点算法需要构建的初始化参数与基础数据如下:
1) 生成RDD结构树 treeRDDs
通过在Spark源码中插入监听代码,遍历作业的DAG图,获取DAG图中点和边的信息,以及输入 RDDId 、操作类型、输出 RDDId ,并通过DAG生成RDD结构树 treeRDDs .
2) 获取RDD深度
通过分析DAG图即可获得,实际运行时血统长度为迭代次数与血统长度相乘.
3) 获取RDD类型值
宽依赖操作的RDD具有作为检查点的意义,因此遍历RDD结构树,将操作为宽依赖的RDD写入列表,并根据该RDD分片个数获得类型值.
4) RDD计算代价
在实际的Spark环境中,作业的DAG图生成后,管理节点监控所有RDD的状态变化,通过记录各状态变化的时间点即可得出起始时间和完成时间.
5) RDD大小
在作业执行过程中,每计算完成一个RDD,即可根据其多个分区大小求和,进而获得该RDD的大小.
6) 计算关键度
通过RDD关键度公式,为RDD计算并保存.
如算法1所示,根据RDD的关键度,在作业执行时间内选择RDD作为检查点进行设置.检查点设置的时间从源RDD之后第1个生成的RDD开始作为检查点开始,到终点RDD之前最后一个生成的RDD结束为结束.在作业执行时,源RDD和终点RDD不需要进行检查点设置.由于源RDD存储在磁盘中,终点RDD为任务结束的RDD,会根据需要在结束后写入磁盘,因此不需要考虑.在作业执行过程中进行检查点设置时对比最新生成的多个RDD,并选择当前关键度最大的RDD.选择好需要备份的RDD,执行检查点设置操作,将该RDD备份.计算任务首先将检查点临时缓存在局部内存中,然后由另一个独立于计算任务的并行任务负责将缓存在内存中的检查点数据文件拷贝到HDFS.
算法1 . 检查点设置算法.
输入:结构树 treeRDDs ;
输出:检查点列表 checkpointlist .
初始化: checkpointlist ←new Array ;
checkpoint ←new Hash ;
cutlist ←new List ;
i ←0;
j ←1;
maxCR ←0.
① checkpointlist ←Null;
② checkpoint ( treeRDDs [ i ]);
③ checkpointlist . add ( treeRDDs [ i ]);
/*添加生成的第1个RDD作为检查点*/
④ while( Cfinished =1 && Tfinished =0)
⑤ for i =0 to newgenerateRDD . length do
⑥ candidateslist ← getnewRDD ;
⑦ candidates [ i ]. cost ← getRDDCost ;
⑧ calculate ( candidates [ i ]. CR );
⑨ if ( candidates [ i ]. CR > maxCR ) then
⑩ nextcheckpoint [ j ]← candidates [ i ];
 end if
end if
 end for
end for
 checkpoint ( nextcheckpoint [ j ]);
checkpoint ( nextcheckpoint [ j ]);
 checkpointlist . add ( nextcheckpoint [ j ]);
checkpointlist . add ( nextcheckpoint [ j ]);
 /*选择最大关键度RDD设置为检查点*/
/*选择最大关键度RDD设置为检查点*/
 j ++;
j ++;
 cutlist . add ( nextcheckpoint [ j ]);
cutlist . add ( nextcheckpoint [ j ]);
 curtreeRDDs ← treeRDDs . remove ( cutlist );
curtreeRDDs ← treeRDDs . remove ( cutlist );
 /*对结构树 treeRDDs 剪枝*/
/*对结构树 treeRDDs 剪枝*/
 end while
end while
管理节点在每一个固定的时间间隔要求工作节点来发送它们的当前状态.工作节点定期发送心跳给管理节点,如果在一个时间限制没有收到工作节点的心跳,标记“失败”.在这种情况下,管理节点指示工作节点利用最近的检查点进行重新启动恢复.如算法2所示,宕机后,由Spark执行恢复操作时,从最后设置的检查点RDD处进行恢复.恢复时,优先选择离执行恢复的工作节点最近的检查点副本,从而降低网络开销和恢复时延.将最新的检查点读入内存,并且可以根据需要将检查点列表中的检查点读入,从而降低恢复和执行开销.当某个RDD需要恢复但未设置检查点时,重新执行血统,通过其父节点恢复;若已将该RDD设置检查点,可以将该RDD读入内存.若有宽依赖,或丢失了RDD的所有分区,则需读取所需的RDD的所有分区到内存;若丢失了RDD的部分分区,且恢复血统中无宽依赖,则只需读取丢失分区所需检查点到内存进行计算.
算法2 . 检查点恢复算法.
输入:当前结构树 curtreeRDDs 、检查点列表 checkpointlist 、需要恢复的RDD recoveryRDDs .
初始化: parentsRDD ←new Hash ;
checkpointRDD ←new Hash ;
i , j , k ←0;
recoveryworker ← assign . freeworker .
① for i =0 to recoveryRDDs . length -1 do
② parentsRDD ← getLineage (
recoveryRDDs [ i ], curtreeRDDs );
/*获取需要恢复RDD的父RDD*/
③ for j =0 to parentsRDD . length -1 do
④ checkpointRDD ← get ( checkpointlist ,
parentsRDD );
⑤ for k =0 to recoveryRDDs . partitionnum -1 do
⑥ if ( wideDependency ( recoveryRDDs [ i ])∨ lost ( recoveryRDDs [ i ])
⑦ read ( parentsRDD [ j ]);
/*操作为宽依赖或丢失所有分区*/
⑧ end if
⑨ if (  wideDependency ( recoveryRDDs [ i ])∧ recoveryRDDs [ i ]. partition [ k ])
wideDependency ( recoveryRDDs [ i ])∧ recoveryRDDs [ i ]. partition [ k ])
⑩ read ( parentsRDD [ j ]. partition [ k ]);
/*操作为窄依赖且丢失部分分区*/
 end if
end if
 end for
end for
 end for
end for
 end for
end for
 reschedule ( recoveryworker , checkpointRDD , parentsRDD , curtreeRDDs ).
reschedule ( recoveryworker , checkpointRDD , parentsRDD , curtreeRDDs ).
/*根据血统进行恢复计算*/
随着任务执行时间的增长,保存的检查点恢复信息越来越多,其中有些恢复信息成为过时无用的恢复信息.检查点清理就是删除这些过时无用的恢复信息.检查点清理策略对恢复协议性能有直接影响.不同的恢复策略,不同的应用所需要存储的恢复信息量都会有不同,执行检查点清理会伴随有开销.因此有效的组织存储恢复信息和执行检查点清理都会对系统性能产生影响,提高集群资源利用率.
对Spark检查点机制而言,检查点存储在持久化存储磁盘或固态硬盘中.就磁盘空间而言,空间较大,并不是主要的瓶颈.因此,最简单的做法就是在任务执行完毕后,将该任务所设置的所有检查点删除.但每次检查点备份时为3个副本,因此,当系统中并行执行多个任务时,若磁盘空间有限,那么在备份过程中需要执行清理算法,可以根据检查点的关键度进行清理.
检查点清理算法,在不影响其他作业的情况下并行执行.如算法3所示,清理的2个条件为:
1) 当任务的磁盘备份空间受限时,在添加新检查点时,对已有检查点进行清理,以满足新检查点的空间需求;
2) 系统设置检查点清理周期,到达该时间周期时进行清理.
清理算法的2个步骤:
1) 新添加一个检查点,磁盘空间不足,将已有的检查点关键度进行过滤,将权重小于新检查点的对象放入候选列表.
2) 将候选列表按关键度从小到大的顺序排列.搜索候选列表,若存在目标,其容量满足新检查点的要求则进行清理;否则,当用户设定的清理时间到达时,才能将所有候列表中的检查点进行清理.
算法3 . 检查点清理算法.
输入:检查点列表 checkpointlist 、当前需添加的检查点 RDD [ i ]、存储空间空闲容量 freecapacity .
初始化: candidates ←new Hash ;
v ← RDD [ i ]. CR ;
s ← RDD [ i ]. size .
① for j =0 to checkpointlist . length -1 do
② if v > checkpointlist [ j ]. CR then
③ candidates . add ( checkpointlist [ j ]);
④ end if
⑤ end for
⑥ cancadidates . orderbyCR ();
/*对关键度进行排序*/
⑦ for j =0 to cancadidates . length -1 do
⑧ if ( freecapacity ≤ mincapacity ∧
cancadidates [ j ]. size > s )
⑨ clean ( candidates [ j ]);
⑩ checkpoint ( RDDs [ i ]);
 checkpointlist . add ( RDDs [ i ]);
checkpointlist . add ( RDDs [ i ]);
/*选择空间满足大小的检查点替换*/
 end if
end if
 end for
end for
 if time = execution
if time = execution
 cleanall ( candidates );
cleanall ( candidates );
/*到达系统清理时间*/
 end if
end if
 if taskfinishedflag =true
if taskfinishedflag =true
 cleanall ( checkpointlist );
cleanall ( checkpointlist );
/*清理所有检查点*/
 end if
end if
本节将通过实验进行比较和评价,验证检查点自动选择算法、恢复算法和检查点清理算法的有效性.
实验环境用1台服务器和8个工作节点建立计算集群,服务器作为Spark的Master和Hadoop的NameNode.为体现工作节点的计算能力不同,8个工作节点由1个高效节点、6个普通节点和1个慢节点组成,其中普通节点的配置如表1所示,高效节点配备4核CPU,16 GB内存和4个千兆网卡,而慢任务节点仅有单核CPU,1 GB内存和1个百兆网卡.
Table1 Configuration Parameters of Worker Node
表1 Worker节点配置参数

对于本文提出CCM策略进行测试,实验数据首先选取WordCount,TeraSort,K-Means,PageRank 4种算法作为作业进行分析.其中WordCount作业量为4.9 GB,TeraSort作业量为4.5 GB,K-Means输入数据总样本点为4 000 000,维度为20,点群个数为5,迭代1次.PageRank页面个数为3 000 000,迭代3次.表2为不同算法在集群失效节点个数为1时执行,且执行到第100秒时关闭1个普通节点 node 3,对比3种策略对恢复时间(execution time, ET)以及与未优化策略相比的加速时间(accelerate time, AT)和加速比(accelerate rate, AR)的影响.这3种策略分别为未优化策略(Without opt)、Tachyon检查点策略(Tachyon checkpoint)和CCM策略.
Table 2 Recovery Efficiency with Different Strategies in Single Node Failure
表2 单点失效时不同策略下的恢复效率
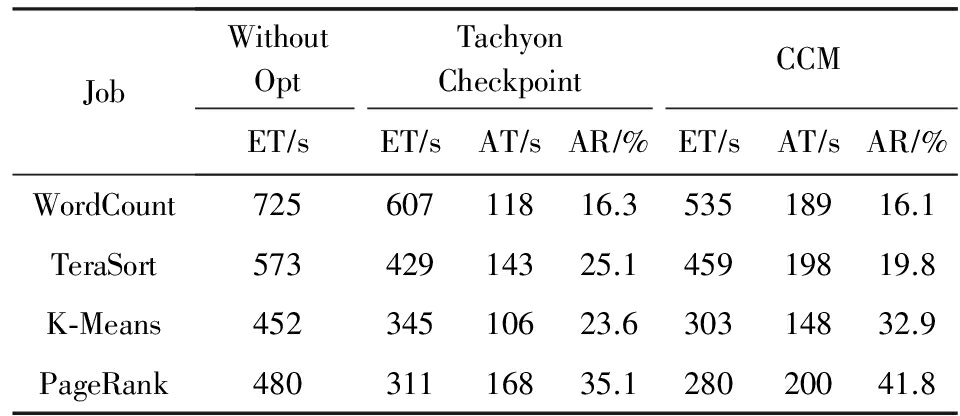
在所有的作业中,CCM策略的作业完成时间都优于传统Spark,在设置检查点的情况下,宕机恢复后,4类作业的总执行时间要小于未设置检查点的情况,从而证明了算法在多种类型作业下都具有良好的优化效果.通过观察数据发现,不同作业对恢复效率的提高程度各不相同,这是因为不同类型作业宽依赖操作个数和数据大小各不相同,因此在作业类型不同的情况下算法的优化效果无明显规律.
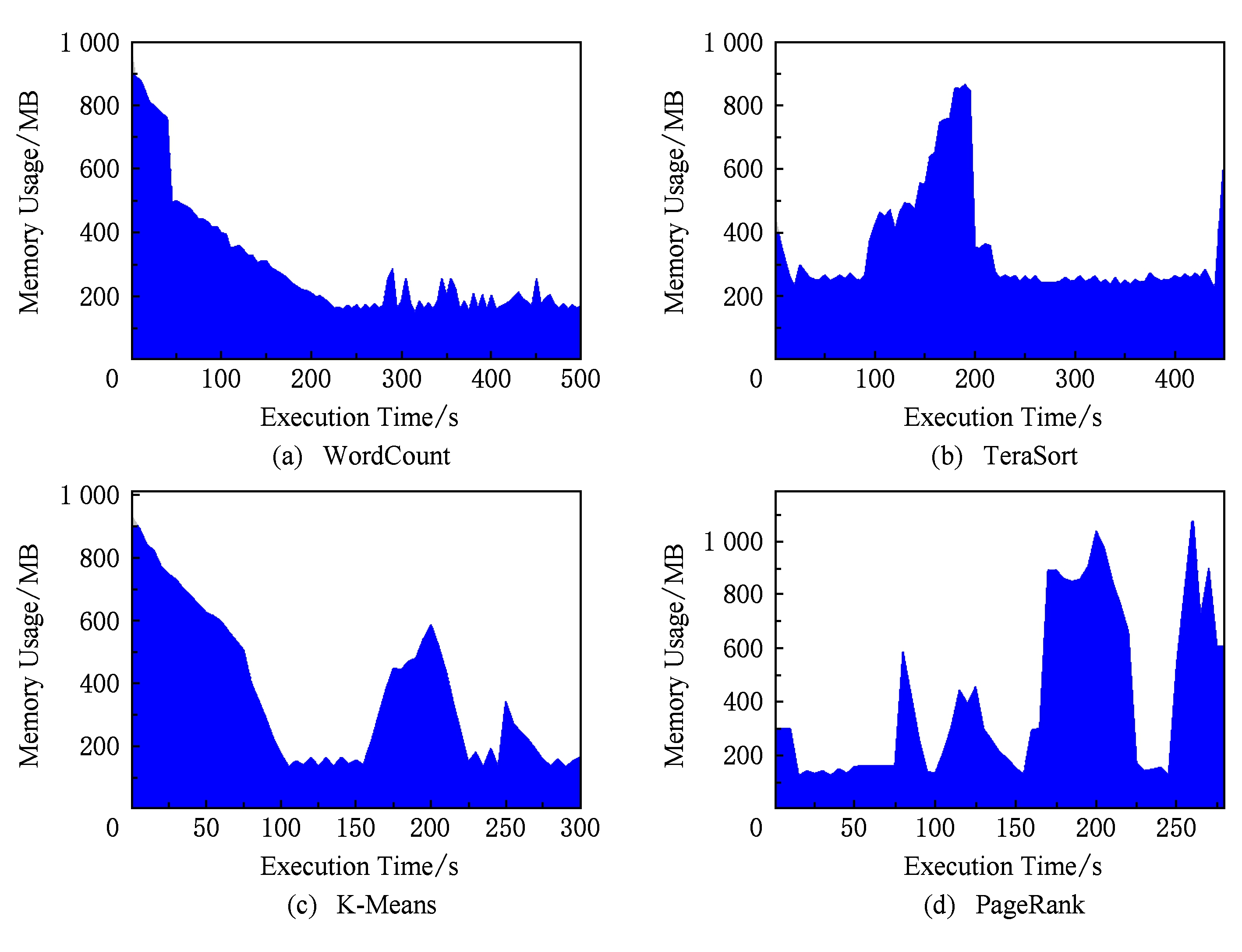
Fig. 3 Memory usage of different jobs on node3
图3 普通节点node3上不同作业的内存利用率
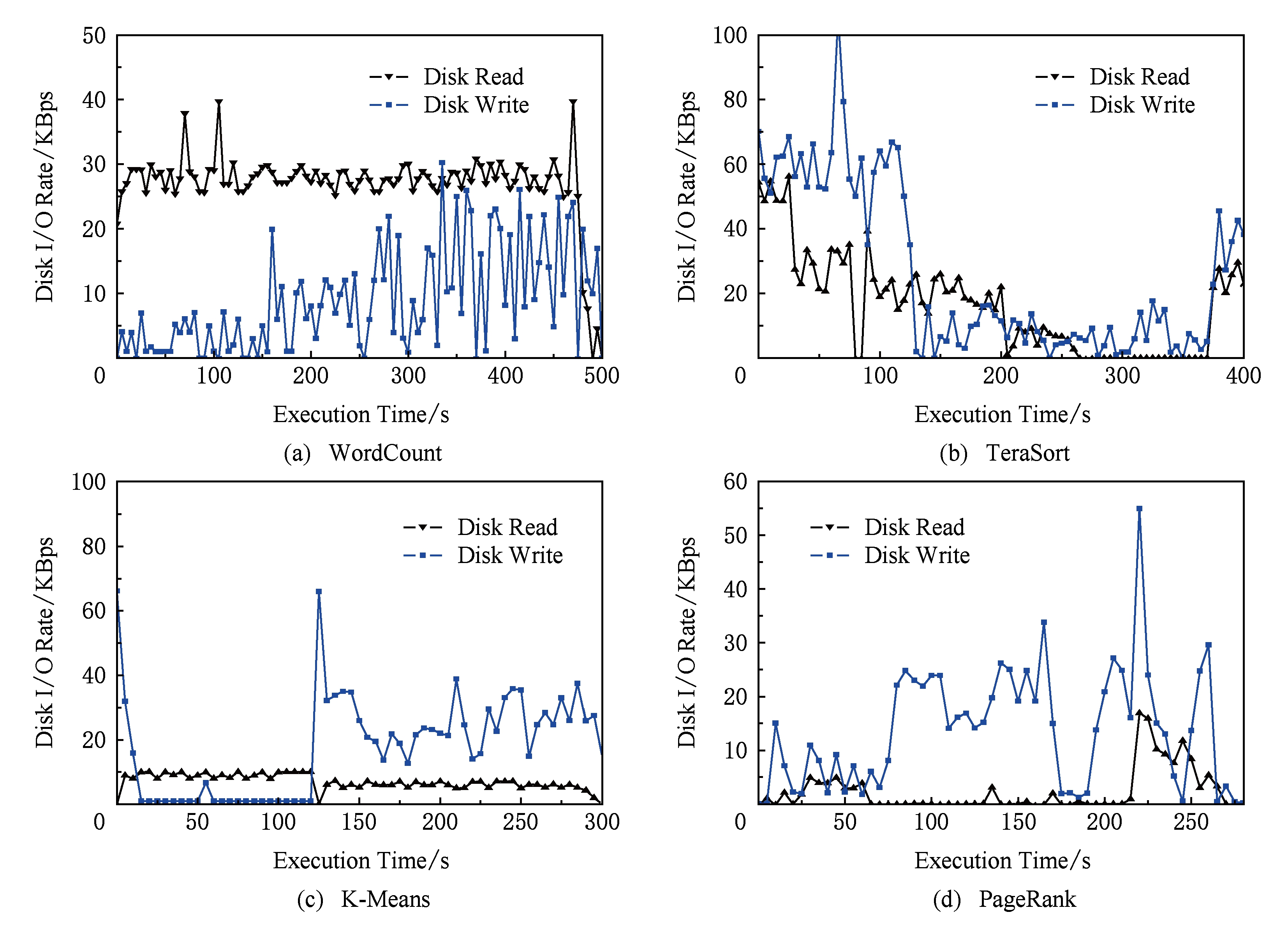
Fig. 4 Disk I/O rate of different jobs on node3
图4 普通节点node3上不同作业的磁盘I/O速率
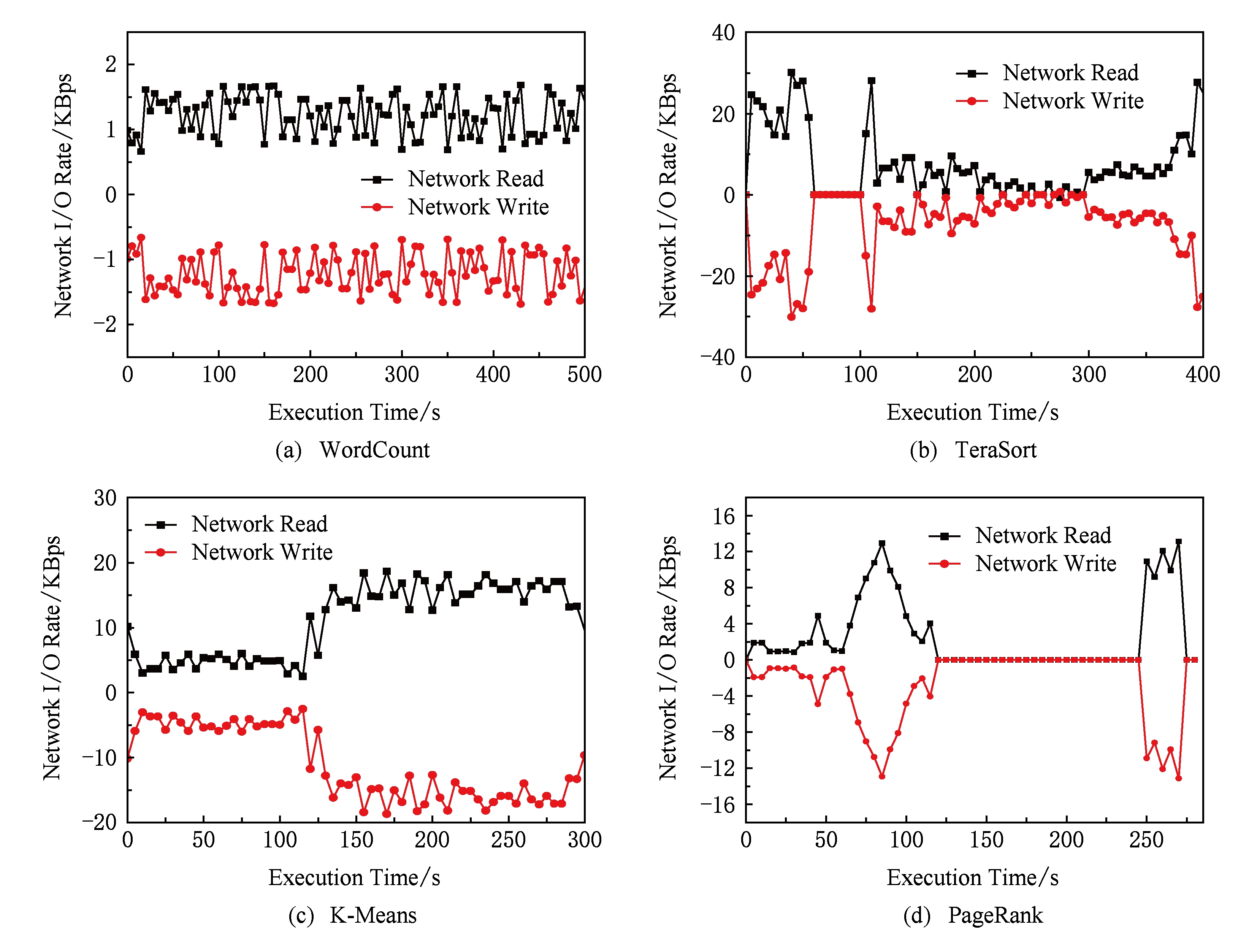
Fig. 5 The network I/O rate of different jobs on node3
图5 普通节点node3上不同作业的网络I/O速率
同样,对于内存利用率、磁盘I/O和网络I/O的情况,在作业类型变化时也具有不同的特点.图3~5分别为本文提出的CCM策略下监控普通节点 node 3在执行过程中的内存利用率、磁盘I/O速率和网络I/O速率变化情况.在内存利用率上,与作业的类型和输入数据的分布情况有关.对于相同的算法而言,所需处理的数据量越大,内存资源使用量越大.由图3可知,WordCount和TeraSort随着执行时间的增加,具有相对稳定的内存占用率;而K-Means和PageRank则随着处理任务的阶段不同,具有不同的内存占用率.
在磁盘I/O速率方面,无论任务是处理本地数据还是网络数据,都会在某个节点上产生相应的本地数据读取,消耗一定的磁盘I/O。若处理网络数据,还要产生额外的网络I/O.由于作业需要从磁盘中读取数据,并在新的RDD生成时设置检查点,因此产生了较为频繁的磁盘I/O.由图4可知,其中WordCount的磁盘I/O更为明显,其他3类作业则频率较低.K-Means在100 s后磁盘I/O有明显增加,这是由于节点失效,分配给 node 3恢复任务,此时需要从磁盘中读取相应检查点,从而实现恢复.
对于网络I/O而言,其开销大小与作业的类型和任务并行度有关.由于Spark具有数据本地性的特点,尽可能保证节点上执行的任务处理本地数据,因此网络I/O主要源于宽依赖阶段,另外小部分网络I/O则是处理远程数据.由图5可看出,对于4类不同的作业,网络I/O开销相差不大.其中WordCount作业的宽依赖阶段只需合并少量数据,因此其网络I/O开销较小.
另外,由表2可知,在设置检查点的情况下,本文提出的CCM策略的K-Means和PageRank的恢复加速情况要好于Tachyon的检查点策略,而WordCount和TeraSort与Tachyon类似,这是对比K-Means和PageRank,WordCount和TeraSort中的宽依赖操作较少,因此在使用基于lineage的检查点策略也能够较好地设置失效恢复所需检查点.并且计算开销与算法复杂度和输入数据的大小相关,当作业一定时输入数据越大,算法开销越大,在此粗略地认为输入数据越大,相应RDD的计算开销也会相应增加,同时增加磁盘读写的开销.对应不同的作业,节点的处理速度也不同.
为了进一步对比和分析CCM策略,我们选用PageRank进行性能测试、评价与比较.实验数据选用SNAP [25] 提供的有向图数据集,数据集列表如表3所示.
利用节点和连接数差异较大的2个数据集Web-Google和Wiki-Talk分别迭代1~10次对该算法性能验证,并使用nmon监测执行时间和任务检查点的大小.PageRank任务在多个数据集上执行,使用PageRank有2方面的原因:1)PageRank主要用于有向图的计算,是一个典型的迭代计算算法;2)PageRank是计算密集型算法,因此对检查点系统更敏感,更利于验证算法.对于数据密集型任务而言,代价较高,因为需在带宽远低于内存的集群网络间拷贝大量的数据,同时也将产生大量的存储开销.
Table 3 Information of Datasets
表3 测试数据集列表

图6表示与现有Spark内存系统使用不同策略的检查点设置算法的执行效率进行对比的情况.其中Web-Google和Wiki-Talk带下标Tachyon,experience,CCM分别代表:1)Tachyon设置检查点的策略,即仅考虑RDD的深度,即当选择检查点时,选择最新生成的RDD进行持久化存储;2)Spark程序员选取检查点的经验,仅考虑RDD的操作复杂度,即当设置检查点时选择宽依赖的RDD进行持久化存储;3)采用本文提出的基于关键度的检查点设置算法,即当选择检查点时选择最新生成的RDD中关键度最大的进行持久化存储.
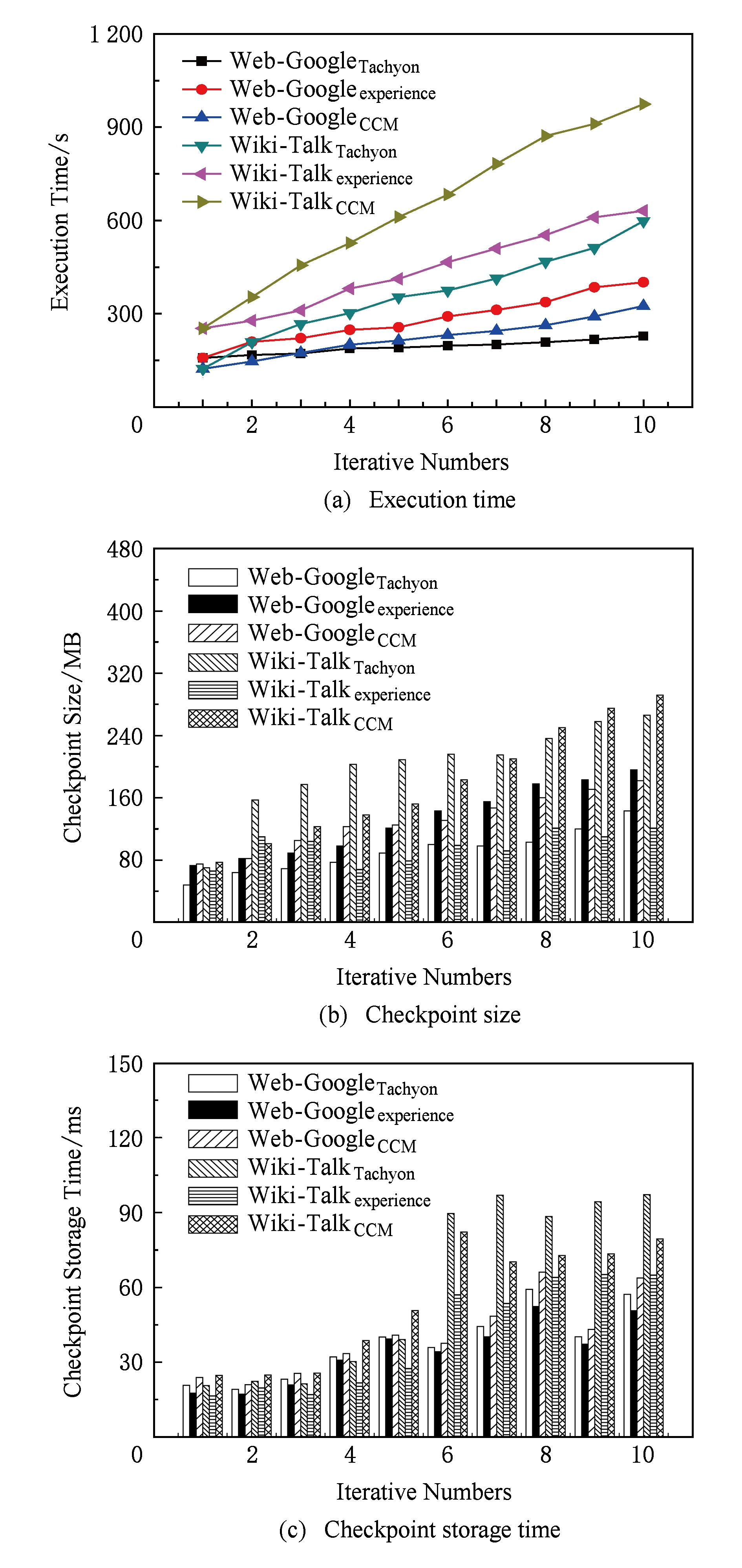
Fig. 6 Efficiency of checkpoint algorithm with different parameters
图6 不同策略下检查点设置算法的执行效率
由图6可知,对比不同数据集,Wiki-Talk具有较大的连接数和节点数,计算代价较高,因此无论采取什么样的参数设置,都使其具有较大的检查点大小,因此执行时间较长,对应检查点存储设置的平均时间开销也随之增加,并且迭代次数的增加对检查点平均时间开销的影响较小.由于全局检查点备选列表是在计算之前生成,因此对任务实际时间影响较小.随着任务和输入数据的规模不同,设置时间不同.检查点选择的大小,平均时间与所选的数据集有关.
而对比不同的参数情况,与其他情况相比,仅考虑RDD计算代价的情况下设置的检查点时间开销更大,因为计算代价与RDD的大小和复杂度都相关,因此具有更大的检查点大小.虽然可以用于宕机后RDD的恢复,但对比很长血统的RDD来说这样的恢复耗时较长.因此,将某些RDD进行检查点操作保存在稳定存储上是有帮助的.通常情况下,对于包含宽依赖的长血统的RDD设置检查点操作是非常有用的.比如PageRank算法中的排名数据集.在这种情况下,集群中某个节点的故障会使从各个父RDD得出某些数据丢失,这时候就需要重算.相反,对于那些窄依赖与稳定存储上数据的父RDD来说,对其进行检查点操作就不是必要的.
通过实验在节点的失效率(failure rate, fr )分别取值为0.125,0.25,0.375的情况下,对比Web-Google和Wiki-Talk数据集得到PageRank在不同恢复算法下的执行时间和恢复情况.
由图7可知,对比失效率不同的情况,随着失效节点个数的增加,任务执行时间也随之增加.这是由于失效率越大,意味着失效的节点越多,因此要恢复的RDD越多,需要重新计算产生相应的时间开销.对比不同数据集的情况,Wiki-Talk和Web-Google在不同算法下Wiki-Talk的时间开销差距较大,这是由于计算量大小的区别.
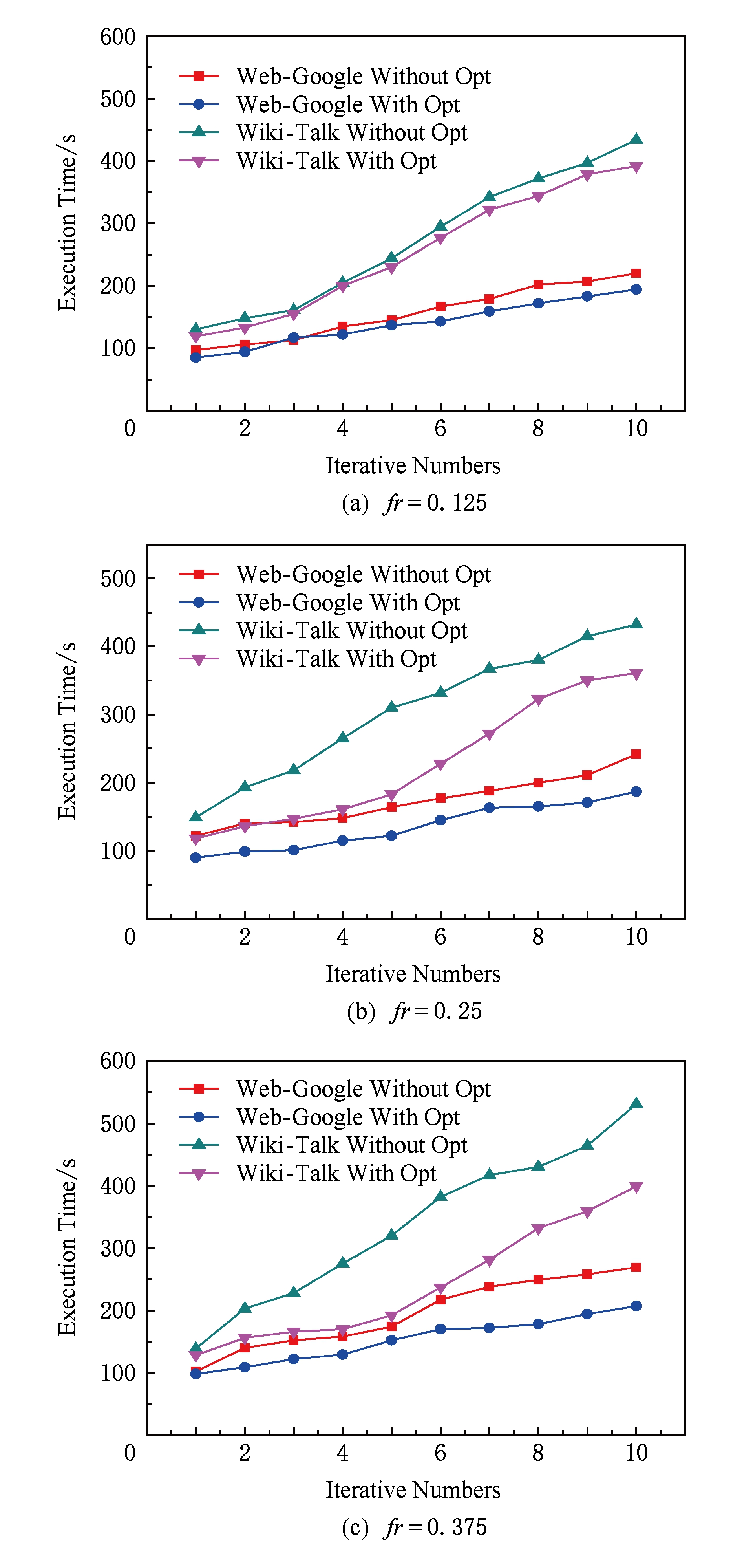
Fig. 7 Execution time of different datasets with different fr
图7 不同失效率时不同数据集的执行时间对比
对迭代次数1~10进行对比,由于未设置检查点的Spark原生系统需要利用血统进行恢复丢失的RDD,因此当迭代次数增加时时间开销随之增加.在节点失效时,同时会使运行在该节点的任务执行失败,同时丢失存储在其内存上的已生成RDD分区.在失效恢复时,Spark为了对丢失的RDD分区进行恢复,利用集群中其他主机重新执行失效任务.这些任务需要将输入数据重新读取,并利用血统进行RDD重建.随着作业迭代次数的增加,血统变长,此时需要计算RDD的时间越长,则恢复开销越大.而失效恢复策略在恢复时间开销方面没有显著的增加,因为该策略利用检查点设置算法设置了检查点,可以通过从HDFS中读取检查点进行恢复,从而减少RDD的重复计算,降低恢复时间开销.
定义6 . 有效空间利用率.在群集工作结点的备份所有检查点RDD之中,对恢复执行效率有加速作用的容量之和占检查点总容量的比率.
检查点清理(checkpoint cleaning, CC)算法是检查点选择算法的后续同步操作,同样在磁盘趋近满载时才能体现效能.图8为对比Web-Google和Wiki-Talk数据集在使用检查点清理算法策略时和未优化时的有效空间利用率.如图8所示,传统Spark框架随着并发应用数的增加,有效磁盘利用率的恶化程度也越来越高;而检查点清理算法的有效磁盘利用率则较为稳定.对比来看,采用检查点清理算法的Spark框架,其有效磁盘利用率普遍高于传统Spark框架.根据并行任务的特性,当其父RDD的所有子RDD都被设置检查点时,则该父RDD在恢复时不会被使用到,因此存储该RDD对作业恢复效率没有影响.而检查点清理算法在工作节点的某个RDD需要清理时,通知群集的其他工作节点清除该RDD的其他副本,因此能在不影响任务恢复效率的前提下提高了群集磁盘空间的有效利用率.
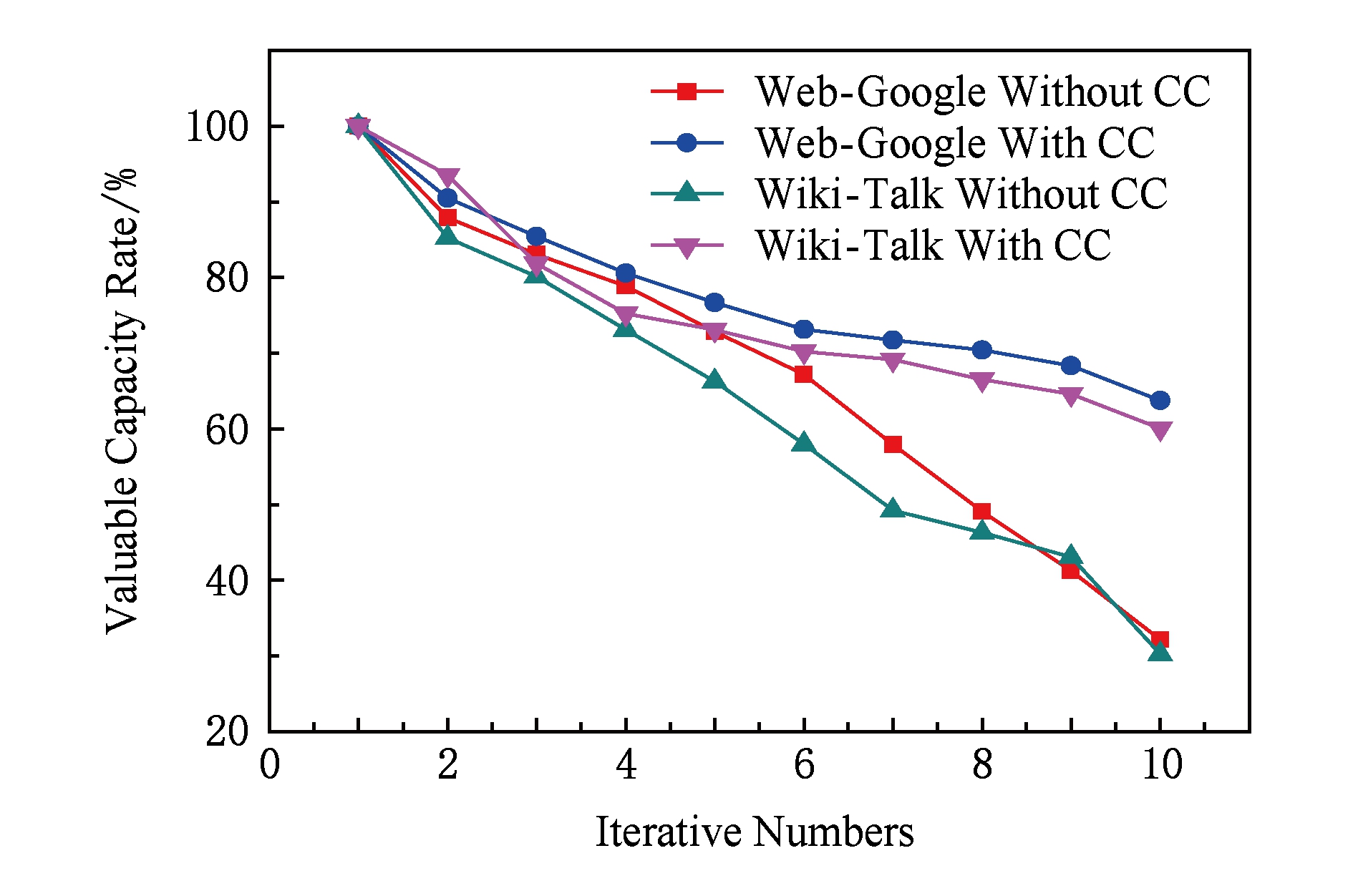
Fig. 8 Valuable capacity rate of CC
图8 检查点清理算法的有效空间利用率
综合比较表2以及图3~8,在不同数据集、策略的情况下,对比任务的执行时间和恢复时间可知,在提出失效恢复策略中,检查点策略会增加少量的时间开销,然而对比传统Spark策略中,由程序员选择检查点的不确定因素甚至是异常风险,这些额外时间和空间开销是有价值的.失效恢复算法基于检查点设置算法,在设置检查点时考虑RDD的血统长度、计算代价、操作复杂度和容量等因素.权重越大的RDD,重新计算的恢复成本也越高,优先将这些恢复成本较高的RDD设置为检查点,可以降低任务整体的重新计算代价.在执行恢复算法时,选择计算能力强的节点进行恢复,可以对任务的恢复效率进行有效的提高.
本文针对内存计算框架Spark的失效恢复问题,首先对内存计算框架的任务执行机制进行分析,建立执行模型和检查点模型.通过分析检查点恢复过程,给出了RDD关键度和失效恢复比的定义,并证明这些定义与任务恢复效率的关系,为算法设计提供基础模型.在相关模型定义和证明的基础上,提出了基于RDD关键度的检查点管理策略问题定义,以此作为算法设计的主要依据.通过算法的问题定义求解,计算RDD关键度,设计了检查点设置算法、恢复算法和并行清理算法.最后,通过不同的实验证明算法的有效性,实验结果表明,该策略优化了内存计算框架的检查点管理,提高了作业的恢复效率.
未来工作主要集中在3个方面:
1) 分析内存计算框架不同类型操作资源需求的一般规律,设计适应作业负载和类型的检查点策略;
2) 对内存计算框架的内存管理进行研究,优化Executor现有的任务内存分配策略;
3) 通过分析计算节点性能和作业DAG图,利用样本和历史记录执行预测RDD和作业的计算开销,从而协助资源分配和并行任务调度方案做决策.
参考文献
[1]Walker S J. Big data: A revolution that will transform how we live, work, and think[J]. International Journal of Advertising, 2014, 17(1): 181-183
[2] Meng Xiaofeng, Ci Xiang. Big data management: Concepts, techniques and challenges[J]. Journal of Computer Research and Development, 2013, 50(1): 146-169 (in Chinese)(孟小峰, 慈祥. 大数据管理: 概念、技术与挑战[J]. 计算机研究与发展, 2013, 50(1): 146-169)
[3] Chen C P, Zhang Chunyang. Data-intensive applications, challenges, techniques and technologies: A survey on big data[J]. Information Sciences, 2014, 275(11): 314-347
[4] Kambatla K, Kollias G, Kumar V, et al. Trends in big data analytics[J]. Journal of Parallel and Distributed Computing, 2014, 74(7): 2561-2573
[5] Zaharia M, Chowdhury M, Das T, et al. Fast and interactive analytics over Hadoop data with Spark[J]. ;Login:, 2012, 37(4): 45-51
[6] Apache. Spark overview[EB/OL]. 2011 [2016-03-18]. http://spark.apache.org
[7] Zaharia M, Chowdhury M, Das T, et al. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing[C] //Proc of the 9th USENIX Conf on Networked Systems Design and Implementation. Berkeley, CA: USENIX Association, 2012
[8] SAP. HANA overview[EB/OL]. 2011 [2016-09-21]. http://hana.sap.com/abouthana.html
[9] Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters[C] //Proc of the 6th Symp on Operating System Design and Implementation (OSDI). New York: ACM, 2004: 137-150
[10] Apache. Spark machine learning library (MLlib)[EB/OL]. 2012 [2016-03-18]. http://spark.incubator.apache.org/docs/latest/mllib-guide.html
[11] Lin Xiuqin, Wang Peng, Wu Bin. Log analysis in cloud computing environment with Hadoop and Spark[C] //Proc of the 5th IEEE Int Conf on Broadband Network & Multimedia Technology (IC-BNMT). Piscataway, NJ: IEEE, 2013: 273-276
[12] Dong Xiangyu, Xie Yuan, Muralimanohar N, et al. Hybrid checkpointing using emerging nonvolatile memories for future exascale system[J]. ACM Trans on Architecture and Code Optimization, 2011, 8(2): Article No.6
[13] Dimitriou I. A retrial queue for modeling fault-tolerant systems with checkpointing and rollback recovery[J]. Computers & Industrial Engineering, 2015, 79: 156-167
[14] Ifeanyi P E, David L, Bran S, et al. A survey of fault tolerance mechanisms and checkpoint/restart implementations for high performance computing systems[J]. Journal of Supercomputing, 2013, 65(3): 1302-1326
[15] Zhou Enqiang, Lu Yutong, Shen Zhiyu. Implementation of checkpoint system toward large scale parallel computing[J]. Journal of Computer Research and Development, 2005, 42(6): 987-992 (in Chinese)(周恩强, 卢宇彤, 沈志宇. 一个适合大规模集群并行计算的检查点系统[J]. 计算机研究与发展, 2005, 42(6): 987-992)
[16] Yi Huizhan, Wang Feng, Zuo Ke, et al. Asynchronous checkpoint/restart based on memory buffer[J]. Journal of Computer Research and Development, 2014, 51(6): 1229-1239 (in Chinese)(易会战, 王锋, 左克, 等. 基于内存缓存的异步检查点容错技术[J].计算机研究与发展, 2014, 51(6): 1229-1239)
[17] Wan Hu, Xu Yuanchao, Yan Junfeng, et al. Mitigating log cost through non-volatile memory and checkpoint optimization[J]. Journal of Computer Research and Development, 2015, 52(6): 1351-1361 (in Chinese)(万虎, 徐远超, 闫俊峰, 等. 通过非易失存储和检查点优化缓解日志开销[J]. 计算机研究与发展, 2015, 52(6): 1351-1361)
[18] Cores I, Rodríguez G, Martín M J, et al. In-memory application-level checkpoint-based migration for MPI programs[J]. Journal of Supercomputing, 2014, 70(2): 660-670
[19] Cao T, Vaz S M, Sowell B, et al. Fast checkpoint recovery algorithms for frequently consistent applications[C] //Proc of the 2011 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2011: 265-276
[20] Chardonnens T, Cudre-Mauroux P, Grund M, et al. Big data analytics on high velocity streams: A case study[C] //Proc of 2013 IEEE Int Conf on Big Data. Piscataway, NJ: IEEE, 2013: 784-787
[21] Neumeyer L, Robbins B, Nair A, et al. S4: Distributed stream computing platform[C] //Proc of the 10th IEEE Int Conf on Data Mining Workshops (ICDMW 2010). Piscataway, NJ: IEEE, 2010: 170-177
[22] Li Haoyuan, Ghodsi A, Zaharia M, et al. Tachyon: Memory throughput I/O for cluster computing frameworks[C/OL]. 2013 [2016-03-18]. https://people.eecs.berkeley.edu/~alig/papers/tachyon-workshop.pdf
[23] Li Haoyuan, Ghodsi A, Zaharia M, et al. Tachyon: Reliable, memory speed storage for cluster computing frameworks[C] //Proc of the 2014 ACM Symp on Cloud Computing. New York: ACM, 2014
[24] Ongaro D, Rumble S M, Stutsman R, et al. Fast crash recovery in RAMCloud[C] //Proc of the 23rd ACM Symp on Operating Systems Principles. New York: ACM, 2011: 29-41
[25] Jure L. Stanford network analysis project[EB/OL]. 2009 [2016-03-18]. http://snap.stanford.edu
Ying Changtian 1,2 , Yu Jiong 2 , Bian Chen 2 , Wang Weiqing 1,3 , Lu Liang 2 , and Qian Yurong 2
1 ( Postdoctoral Research Station of Electrical Engineering , Xinjiang University , Urumqi 830046) 2 ( School of Software , Xinjiang University , Urumqi 830008) 3 ( School of Electrical Engineering , Xinjiang University , Urumqi 830046)
Abstract The default fault tolerance mechanism of Spark is setting the checkpoint by programmer. When facing data loss, Spark recomputes the tasks based on the RDD lineage to recovery the data. Meanwhile, in the circumstance of complicated application with multiple iterations and large amount of input data, the recovery process may cost a lot of computation time. In addition, the recompute task only considers the data locality by default regardless the computing capabilities of nodes, which increases the length of recovery time. To reduce recovery cost, we establish and demonstrate the Spark execution model, the checkpoint model and the RDD critically model. Based on the theory, the criticality checkpoint management (CCM) strategy is proposed, which includes the checkpoint algorithm, the failure recovery algorithm and the cleaning algorithm. The checkpoint algorithm is used to analyze the RDD charactersitics and its influence on the recovery time, and selects valuable RDDs as checkpoints. The failure recovery algorithm is used to choose the appropriate nodes to recompute the lost RDDs, and cleaning algorithm cleans checkpoints when the disk space becomes insufficient. Experimental results show that: the strategy can reduce the recovery overhead efficiently, select valuable RDDs as checkpoints, and increase the efficiency of disk usage on the nodes with sacrificing the execution time slightly.
Key words memory computing; Spark; checkpoint management; failure recovery; RDD characteristics
收稿日期: 2016-09-20;
修回日期: 2017-07-04
基金项目: 国家自然科学基金项目(61262088,61462079,61363083,61562086,51667020);新疆维吾尔自治区自然科学基金项目(2017D01A20);新疆维吾尔自治区高校科研计划(XJEDU2016S106)
This work was supported by the National Natural Science Foundation of China (61262088, 61462079, 61363083, 61562086, 51667020), the Natural Science Foundation of Xinjiang Uygur Autonomous Region of China (2017D01A20), and the Higher Education Research Program of Xinjiang Uygur Autonomous Region (XJEDU2016S106).
通信作者: 于炯(yujiong@xju.edu.cn)
中图法分类号 TP311

Ying Changtian , born in 1989. PhD in Xinjiang University. Student member of CCF. Her main research interests include parallel computing, distributed system, and memory computing, etc.

Yu Jiong , born in 1964. Professor and PhD supervisor. Senior member of CCF. His main research interests include grid computing, parallel computing, etc.

Bian Chen , born in 1981. Associate professor and PhD. Senior member of CCF. His main research interests include parallel computing, distributed system, etc.

Wang Weiqing , born in 1959. Professor and PhD supervisor. His main research interests include power system relay protection, wind power generation control and grid connection technology (wwq59@xju.edu.cn).

Lu Liang , born in 1990. PhD candidate in Xinjiang University. Student member of CCF. His main research interests include flow processing, real-time computing.

Qian Yurong , born in 1981. Professor and master supervisor. Senior member of CCF. Her main research interests include data mining.