 AB ( c )| c ∈ COMPS - Δ }是可满足的.
AB ( c )| c ∈ COMPS - Δ }是可满足的. 欧阳丹彤 1,2,3 周建华 1,3 刘伯文 2,3 张立明 1,2,3
1 (吉林大学软件学院 长春 130012) 2 (吉林大学计算机科学与技术学院 长春 130012) 3 (符号计算与知识工程教育部重点实验室(吉林大学) 长春 130012)(15943054244@163.com)
摘 要: 基于模型诊断一直是人工智能领域中热门的研究问题.近些年来,随着SAT求解器效率的逐渐提高,基于模型的诊断也被转换成SAT问题进行求解.在对基于模型诊断求解方法CSSE-tree深入研究基础上,结合诊断问题和SAT求解过程的特征,给出先对包含组件个数较多的候选诊断进行求解的方法,进而减小SAT求解问题的规模;在对极小诊断解和非极小诊断解剪枝方法的基础上,首次提出非诊断解定理及非诊断解空间的剪枝方法,有效地实现了对诊断的无解空间进行剪枝.根据组件个数较多的候选诊断先求解及有解无解剪枝方法特征,构建基于反向搜索的LLBRS-tree方法.实验结果表明:与CSSE-tree算法相比,LLBRS-tree算法减少了SAT求解次数、减小了求解问题规模,效率较好,尤其是求解多诊断时效率提高更为显著.
关键词: 基于模型的诊断;无解空间剪枝;合取范式;SAT求解器;枚举树
自1980年至今,基于模型诊断(model-based diagnosis, MBD)在人工智能领域一直是一个热门的研究问题,对人工智能领域的推进起到了十分重要的作用.最早的模型诊断方法由Reiter [1] 于1987年提出,求解最终诊断结果的过程分为2个步骤:1)产生所有极小冲突集的冲突识别;2)产生所有极小碰集的候选产生.这2个步骤在得到最后的诊断结果中起着重要作用.国内外学者对碰集求解方法做了许多研究和改进.碰集的求解方法主要分为基于枚举的完备性算法 [2-5] 和基于局部搜索的非完备性算法 [6-7] .完备性算法虽然可以准确给出碰集问题的所有解,但随着碰集问题规模的增大,求解时间也会随之以指数级增加.基于局部搜索的非完备性算法虽然不确定能给出特定的解,但对于大规模问题有较好效率.
国内学者在模型诊断方法研究上也做了大量相关的工作.张健等人 [8-9] 给出了将诊断问题转换为布尔公式和数学公式的混合形式描述,然后用带有标志子句技术的求解器进行诊断;姜云飞等人 [10] 在候选诊断的分解与组合问题上给出了基于分步求解的诊断分解的方法;赵相福等人 [11-13] 提出利用SAT求解器来判断一个组件集合是否是系统的诊断解,然后结合CSSE-tree求出所有的极小诊断求解方法;陈荣等人 [14] 先利用SAT求解器得到诊断系统对应的冲突部件集,然后对冲突部件集调用碰集算法得到系统的候选诊断;欧阳丹彤等人 [15] 提出通过在诊断系统中传播元件的输出标识,来判断当前候选元件集合是否为系统的候选诊断的方法;栾尚敏等人 [16] 提出结合系统结构信息来求解极小冲突集和直接求解候选诊断的方法.以上给出的诊断方法或是提高了诊断求解效率,或是减小了求解时的内存空间消耗.
命题可满足问题(propositional satisfiability problem,SAT)是人工智能领域中很活跃的一个分支,它是NP完全问题 [17-19] .人工智能中很多NP完全问题都可以转换为SAT问题,然后进行求解,而且随着SAT求解器效率的提高,越来越多的NP问题都先转化为SAT问题,然后进行求解 [20-22] .如智能规划问题以及模型检测问题都可以转化为SAT问题进行求解 [23] .相应地,MBD问题也可以转换成SAT问题来求解.基于SAT求解器的发展,以及根据将基于模型的诊断转换成SAT问题求解的思想,国内学者赵相福等人给出的利用SAT求解器结合CSSE-tree求出所有的极小诊断解.在判断一个组件集合是否是系统的诊断时,该文将要判断的组件集合的补集中所有组件的正常行为谓词描述、系统描述和观测描述3部分文件构造成一个CNF文件,然后调用SAT求解器去判断可满足性,如果可满足,则是诊断解.基于这样的基础,该文结合CSSE-tree树模型,根据组件集合的个数,枚举出组件集合的所有幂集合,然后进行一一的判断.而且为了更加高效地求解,本文提出了2个优化策略:1)从根结点开始,利用广度优先遍历,对长度小的集合先判断,直接先得到最终的极小诊断解;2)根据CSSE-tree的生成方式,利用极小诊断解的真超集一定不是极小诊断解的剪枝规则,将极小诊断解的子结点全部剪掉.但是,给合实际的诊断实例特征,我们可以知道在CSSE-tree中只有较少的结点是极小诊断解,该方法中的修剪规则只针对有解的那些结点,所以剪掉的结点数量较少.
针对CSSE-tree中只对是解的结点进行剪枝这样的缺点,我们在本文中提出了基于反向搜索的有解无解剪枝方法LLBRS-tree.在该方法中我们不仅剪掉是解的结点,而且第1次提出了无解剪枝的思想,对不是解的那些结点也进行剪枝.并且在利用SAT求解器来判断一个组件集合是否是诊断解时,我们首先对长度比较长的组件集合进行处理,使得生成的CNF形式的文件中要判断的子句的数量较少,因此调用SAT求解器来判断时所耗费的时间也将更少.
在本节,我们首先介绍基于模型的诊断中的相关概念,而后介绍SAT问题,最后介绍将基于模型的诊断转换成SAT问题.
1.1 基于模型的诊断的相关概念
定义1. 诊断系统 [1] .一个系统定义为一个三元组( SD , COMPS , OBS ),其中: SD 为系统描述,是一阶谓词公式的集合; COMPS 为系统的组成部件集合,是一个有限常量集合;而 OBS 为观测集合,是一阶谓词公式的有限集合.
在下面我们使用一元谓词 AB (·)表示“abnormal”, AB ( c )为真当且仅当 c 反常,其中 c ∈ COMPS .
定义2. 基于一致性诊断 [1] .设组件集合 Δ ⊆ COMPS ,称 Δ 为关于( SD , COMPS , OBS )的一个基于一致性诊断,如果 SD ∪ OBS ∪{  AB ( c )| c ∈ COMPS - Δ }是可满足的.
AB ( c )| c ∈ COMPS - Δ }是可满足的.
定义3. 极小诊断集 [1] .称一个关于( SD , COMPS , OBS )的一个基于一致性诊断 Δ 是极小的,当且仅当不存在 Δ 的任何真子集也是关于( SD , COMPS , OBS )的一个基于一致性诊断.
通过上面的定义可以知道,我们要判断一个组件集合是否是系统的一个基于一致性的诊断集,只需要判定这个组件集合中的所有组件为反常的情况下,剩余组件的正常行为描述与诊断系统相关的系统描述以及系统观测描述的逻辑是否是一致的.
而且,根据基于一致性诊断的极小诊断集的定义可以得到下面的结论:如果组件集合 A 是系统的一个基于一致性诊断的极小诊断集,且组件集合 B ⊆ COMPS ,组件集合 C ⊆ COMPS ,则有2种情况:
1) 如果组件集合 A ⊂ B ,那么组件集合 B 不是基于一致性诊断的极小诊断集;
2) 如果组件集合 C ⊂ B 且 B 不是诊断解,那么组件集合 C 一定不是诊断解.
上面的情况表明一个极小诊断集的真超集一定不是极小诊断集;并且进一步说明如果一个组件集合不是诊断解,那么它的真子集一定不是诊断解.这2种情况是我们判断诊断解以及极小诊断集的基础.
1.2 SAT问题
首先,我们将要用到的符号定义如下:
变量 x i ( i =1,2,…, m )表示布尔变量; X ={ x 1 , x 2 ,…, x m }表示变量的集合;在子句中我们用符号 x i 表示与变量 x i 相对应的正文字,符号  x i 表示与变量 x i 相对应的负文字;符号 C i ( i =1,2,…, n )表示子句,子句由文字的析取构成,我们可以将子句看作是文字的集合.符号 Φ , Φ i ( i =1,2,3,…)代表CNF公式,CNF公式是由子句的合取构成,可以将它看成是子句的集合.在本文中,命题公式指的就是CNF公式.
x i 表示与变量 x i 相对应的负文字;符号 C i ( i =1,2,…, n )表示子句,子句由文字的析取构成,我们可以将子句看作是文字的集合.符号 Φ , Φ i ( i =1,2,3,…)代表CNF公式,CNF公式是由子句的合取构成,可以将它看成是子句的集合.在本文中,命题公式指的就是CNF公式.
SAT问题又叫做命题可满足问题,即判断给定的一个命题公式是不是可满足的,其形式化的定义如下:
定义4. 命题可满足问题 [19] .针对给定的一个命题公式 Φ , X ={ x 1 , x 2 ,…, x m }是该公式的变量集合,SAT问题是指是否存在一组 X 的赋值使得 Φ 的取值为真.如果存在这样的一组赋值,那么我们则称命题公式 Φ 是可满足的,否则 Φ 是不可满足的.
根据SAT问题的定义,我们只需要找到一组赋值使得给定的命题公式的取值为真,就可以判定该命题公式是可满足的.
迄今为止,许多学者都投入到SAT问题的研究中来,每年举行一次的SAT竞赛也使得很多成熟高效的SAT求解器产生.对于常规的SAT求解器,都是以CNF形式的文件作为SAT求解器的输入.针对给定的命题公式或者命题公式集合,都可以将其转化成一个CNF形式的文件描述.例如:给定的一个命题公式集合 R :{ x 1 → x 2 , x 2 → x 3 , x 3 → x 4 ,  x 4 , x 1 },我们可以将其表示为下面的一个CNF文件.使用数字1,2,3,4分别表示公式 R 中的变量 x 1 , x 2 , x 3 , x 4 :
x 4 , x 1 },我们可以将其表示为下面的一个CNF文件.使用数字1,2,3,4分别表示公式 R 中的变量 x 1 , x 2 , x 3 , x 4 :
p cnf 4 5  *CNF文件语法,p cnf都为关键字,4是 R 的变量总数,5是子句总数*
*CNF文件语法,p cnf都为关键字,4是 R 的变量总数,5是子句总数* 
-1 2 0  *负号表示该文字是负文字*
*负号表示该文字是负文字* 
-2 3 0  *一个子句都以0结尾*
*一个子句都以0结尾* 
-3 4 0
-4 0
1 0
经过上面的转化,判定命题公式集合R是否为真时,只需要将公式R转换成 CNF 文件描述,接下来调用 SAT 求解器对转换后的 CNF 文件进行求解就可以得到结果.如果 CNF 文件是可满足的,那么命题公式R为真,否则公式R为假.
根据上面的这种思想,我们要判断一个组件集合S是否是一个系统的一个基于一致性的诊断,只需要假设要判断的组件集合S为诊断解,将COMPS-S集合中每一个组件相关的正常子句描述,系统描述以及系统的观测描述一起构建成一个 CNF 形式的文件,接下来调用 SAT 求解器进行可满足性判定即可.如果 SAT 求解器返回真值,那么S是系统的一个基于一致性诊断解.否则,S不是.
1.3 基于模型的诊断转换成 SAT 问题
在本节,将介绍如何将诊断系统的模型以及系统的观测转换成 CNF 形式的文件.
给定一个诊断系统,本文中对其进行建模的方式与 Reiter [1] 建模的方法不同,我们将使用命题逻辑对该系统相关的行为进行建模.我们将使用变量来表示系统中的相关组件的输入以及输出,并且我们将对每个组件进行编号.跟诊断系统的定义一样,我们也使用AB(c)和  AB(c)来表示组件属于反常模式或者正常模式.
AB(c)来表示组件属于反常模式或者正常模式.
以图1所表示的 ISCAS -85 _c 17为例,介绍我们是如何对诊断系统进行建模,得到相对应的 CNF 文件描述.根据 ISCAS -85 _c 17的 Verilog 电路描述,我们得到图1所示的逻辑电路.在该逻辑电路中有6个组件,都是与非门,分别用N 1 ,N 2 ,N 3 ,N 4 ,N 5 ,N 6 来标识出6个逻辑与非门.而“7”,“8”,“9”,“10”,“11”分别表示系统相应的输入变量,“12”,“13”分别表示系统的输出变量,“14”,“15”,“16”,“17”分别表示组件内部的连接结点.例如变量“14”既表示组件N 2 的输出,又是组件N 3 的输入.
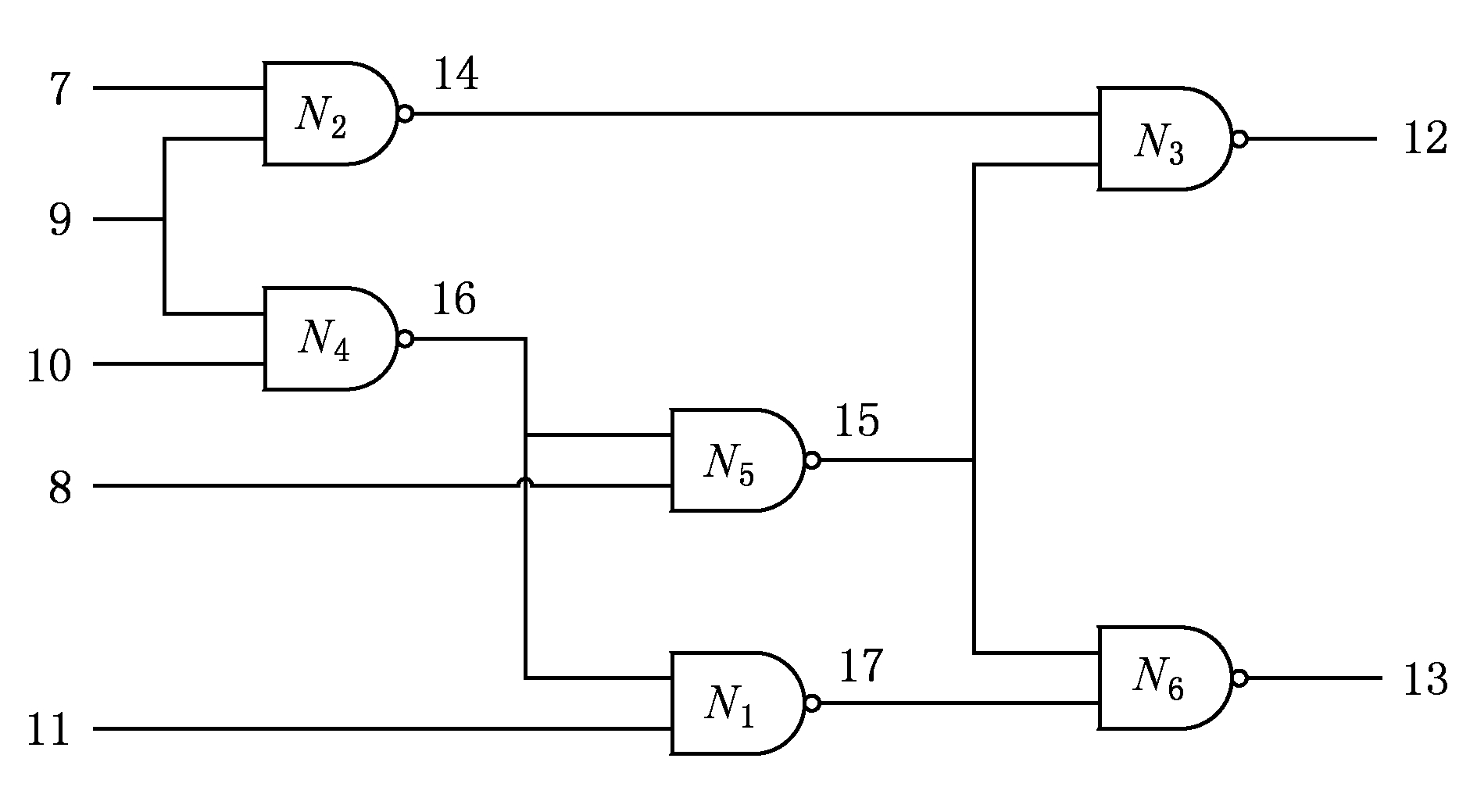
Fig. 1 Logic circuit of ISCAS-85_c17
图1 ISCAS-85_c17逻辑电路
为了将系统最后转换成CNF文件的形式进行描述,我们需将该逻辑电路ISCAS-85_c17采用CNF文件的编码,并进行相应地转换.最后,我们得到逻辑电路ISCAS-85_c17的部分CNF文件描述为C17.cnf,如图2所示.

Fig. 2 C17.cnf
图2 C17.cnf
图2所给的仅仅是部分系统描述,相应地,我们还需要对系统的观测给出CNF形式的描述.例如,当逻辑电路ISCAS-85_c17当前得到的观测值为:输入观测点“7”,“8”,“9”,“10”,“11”的观测分别为高电平,低电平,低电平,高电平,高电平;输出观测点“12”,“13”的观测值为高电平,低电平.则我们得到系统观测的CNF子句描述如下:
7 0
-8 0
-9 0
10 0
11 0
12 0
-13 0
通过上面这样的转换方式,我们就可以将一个诊断系统转换成相应的CNF文件描述,也就是转换成SAT问题,然后针对该CNF文件进行相应地处理,调用SAT求解器对其进行求解,最后得到诊断系统的诊断解,具体的算法我们在第2节进行介绍.
在第1节我们将一个诊断系统转换成SAT问题,本节将首先介绍判断一个组件集合是否是诊断解的算法ISDAG,然后讲解利用ISDAG算法,结合枚举树来求解一个给定诊断系统的所有基于一致性诊断的极小诊断解.
2.1 ISDAG算法
我们给出如下的一些定义,方便对算法进行描述.
定义5. 反常单元子句表示.对于给定的一个组件,该组件的反常单元子句表示是指用正文字单元子句描述该组件.
定义6. 正常单元子句表示.对于给定的一个组件,该组件的正常单元子句表示是指用负文字单元子句描述该组件.
例如:组件 N 1 ,我们用数字“1”代表这个组件,那么组件 N 1 的反常单元子句表示如下:
1 0  *数字0代表这行结束*
*数字0代表这行结束* 
组件 N 1 的正常单元子句表示如下:
-1 0  *负号表示负文字,0是换行*
*负号表示负文字,0是换行* 
当给定一个诊断系统后,假设系统所对应的描述以及观测都已经通过离线方式创建完成,正如在1.3节所述.假设系统描述的文件为DigSysDis.cnf以及DigSysObs.cnf,下面的ISDAG算法将介绍如何使用SAT求解器来判断一个组件集合是否是给定诊断系统的基于一致性诊断的诊断解.
算法1. ISDAG( Sub [])算法.
输入:将要判断系统的一个组件子集 Sub ;
输出:bool类型值,如果组件子集 Sub 是系统的基于一致性诊断,则返回1,否则返回0.
Step1. 将系统的观测文件DigSysObs.cnf中的子句追加到系统描述文件DigSysDis.cnf中.
Step2. 对于在组件集合 Sub 中的每一个组件,将其对应的反常单元子句表示(相当于一个选择器,表明假设该组件集合都发生故障的情况)追加到系统描述文件DigSysDis.cnf中.
Step3. 对于在组件集合( COMPS - Sub )中的每一个组件,将其对应的正常单元子句表示(表明这些组件都正常工作,没有发生故障)追加到系统描述文件DigSysDis.cnf中.
Step4. 调用SAT求解器对系统文件DigSysDis.cnf进行可满足性判断,如果得到的结果是可满足的,那么表明组件集合 Sub 是诊断解,返回1.如果得到的结果是不可满足的,那么表明组件集合 Sub 不是诊断解,返回0.
针对ISDAG算法中的Step2,Step3我们举例说明,假设 COMPS ={ N 1 , N 2 , N 3 , N 4 , N 5 , N 6 },而 Sub ={ N 1 , N 2 , N 3 }时,那么在执行Step2以及Step3后,我们加入到DigSysDis.cnf文件中的子句如下:
1 0
2 0
3 0
-4 0
-5 0
-6 0
我们要判断一个组件子集 Sub 是否是系统的诊断,首先需要将系统的观测都追加到系统描述文件中,然后在考虑组件集合 Sub 中的每一个组件都反常的情况下(相当于指定 Sub 组件集合中的组件为诊断解,即加入单元子句,将其置为正文字),也就相当于将组件集合 Sub 中的每一个组件所对应的子句置为恒真子句,接着看剩余的组件集合( COMPS - Sub )都正常的情况下,是否能正常解释系统在当前观测下面的行为(相应的这3步对应算法1的Step1,Step2,Step3).最后在Step4中调用SAT求解器,看看是否能解释系统在当前状态下的行为,如果是可满足的,返回1,表明能解释,那么我们假设组件集合 Sub 为诊断解成立, Sub 是系统的基于一致性诊断的解.如果是不可满足的,返回0,那么表明在假设组件集合 Sub 为故障的情况下,不能解释系统现在的行为,则 Sub 不是系统的基于一致性诊断的诊断解.
ISDAG算法仅仅只能判断一个组件集合是否是系统的诊断解,即只能得到系统的一个解,如果想要得到所有的诊断解,那么需要枚举出所有的组件集合,然后对这些集合进行判断,进一步得到所有解.
2.2 利用枚举树求解所有诊断解
为了求解给定诊断系统的所有基于一致性诊断的极小诊断解,我们只需要考虑所有可能出现故障的集合,假设该组件集合是故障组件集合,则调用算法ISDAG判断该组件集合是不是诊断解.这个过程其实就是一个枚举所有组件集合的过程,可以用枚举树来进行枚举,下面我们简单介绍一下枚举树.
集合枚举树(set-enumeration-tree,SE-tree)是由国外学者Rymon [24] 提出,这种树模型在很大程度上可以枚举出给定的集合中元素的所有可能的组合.例如当前集合 SS = { N 1 , N 2 , N 3 , N 4 },则集合 SS 的完全集合枚举树如图3所示.
根据图3的树模型,在求解系统的所有诊断的过程中,我们用这棵树对求解过程进行模拟.利用集合枚举树模型我们要求解所有的诊断解,只需要遍历这棵树上的所有结点,对每个结点进行相应地判断就可以得到最后的解.例如,针对集合{ N 2 , N 3 },我们表示的是当组件集合{ N 2 , N 3 }都出现故障时,组件 N 1 , N 4 正常的情况下,是否能解释系统当前的行为.那么就需要调用ISDAG算法,将组件集合{ N 2 , N 3 }作为输入参数,进行判断.如果调用ISDAG算法的返回值是1,那么表明组件集合{ N 2 , N 3 }是系统的诊断解,如果是0,那么它就不是诊断解.当然,为了求解所有的极小诊断解,我们只需要保留树中其真子集不是诊断解的所有结点,这些结点就是最后的基于一致性诊断的极小诊断解.
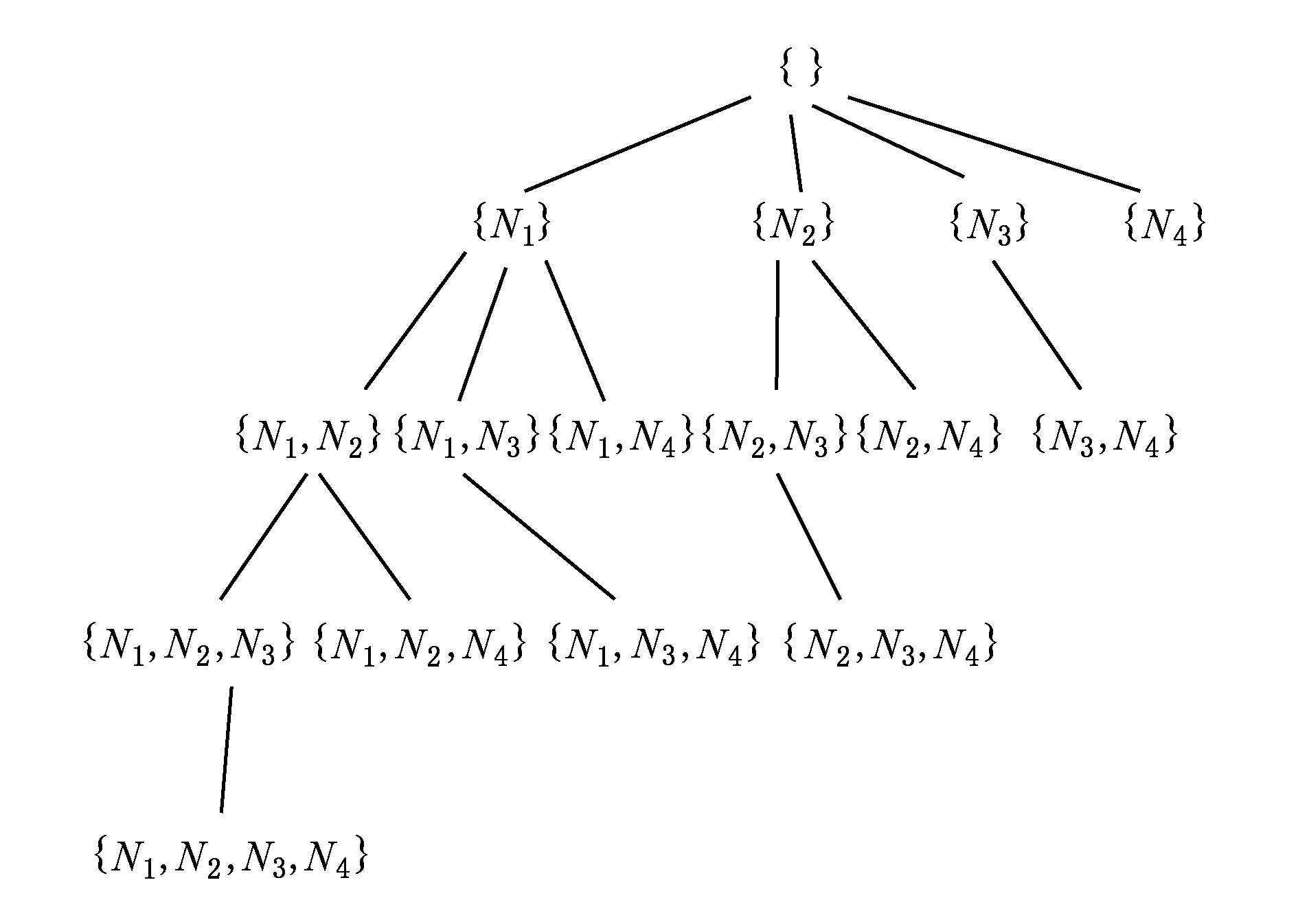
Fig. 3 SE-tree of set SS
图3 集合SS的SE-tree
近些年以来,大部分求解系统的基于一致性诊断都是根据上面的枚举树,按照广度优先遍历或者深度优先遍历,采用一定的剪枝规则,减少遍历的结点,从而得到最后的诊断解.
赵相福等人 [11-12] 提出了CSSE-tree方法,CSSE-tree也是基于这样的一棵枚举树,对整个枚举树中的结点进行遍历,然后进行相应的操作得到最后的极小诊断解.CSSE-tree的提出使得求解基于一致性诊断的求解时间得到了提升,它的优点有2点:
1) 根据系统的组件个数,系统地枚举出跟该组件集合相关幂集的所有元素,然后从根结点开始进行广度优先遍历,这样保证产生的解集是极小诊断解,并且保证了CSSE-tree的完备性,不会丢掉任何一个解.
2) 根据极小诊断解的定义可以知道,一个极小诊断解的真超集一定不是极小诊断解.CSSE-tree利用该特征作为修剪规则,避免了所有极小诊断解真超集的判断,而且由极小诊断解得定义保证了修剪规则的正确性.通过修剪规则可以减少一些不是极小诊断解的结点产生,使树中的结点数目减少,从而使得求解的效率得到相应的提高.
然而CSSE-tree也存在2个缺点:
1) 如果系统的组件个数太多,枚举出跟组件集合相关幂集合的所有元素将会使得CSSE-tree变得相当得庞大,使得空间复杂度相当得大.而且,如果在解很少的情况下,修剪规则的剪枝空间较少,效率提升较小.
2) 根据对实际例子的分析,我们知道枚举树中不是解的结点占据了枚举树中大量的结点.CSSE-tree中的修剪规则只是对是解的那些结点起作用,对于不是解的那些结点,只能进行逐个判断求解.
根据上面对CSSE-tree方法的分析,我们可以知道,在求极小诊断解时,是解的结点只是小部分,在我们判断的过程中,不是诊断解的结点占据了树中大量的结点.不能对非解的结点进行相应地处理是CSSE-tree方法最致命的缺点,如果能给出相应的策略剪掉一些不是解的结点,那么求解的效率将会得到进一步的提高.基于剪掉不是解的结点这样的思想,我们提出了基于反向搜索的有解无解剪枝方法,不仅剪掉是诊断解但非极小诊断解的一些结点,而且剪掉树中大部分不是解的结点.
2.2节描述了基于枚举树,结合ISDAG算法求诊断系统的所有基于一致性诊断的诊断解.然而我们发现枚举树中大量的结点都不是解,据此我们提出了基于反向搜索的有解无解剪枝方法.该方法不但可以剪掉是解但非极小诊断解的一些结点,而且也剪掉了不是解的结点,使得我们遍历整棵枚举树的过程中,不用遍历到所有的结点,只需要遍历少量的结点,这样可以加快求解所有解的过程.本节首先给出相关的一些定义,然后描述基于反向搜索的有解无解剪枝方法.
3.1 有解剪枝和无解剪枝
首先给出在这部分要用到的相关的定义:
定义7. 有解剪枝.给定一棵枚举树,在遍历这棵枚举树时,对于树中的某一个结点,如果先判断其父结点或者祖先结点,得到的结果是可满足的,那么该结点一定不是极小诊断解,可以不用对其进行判断.称跳过枚举树中这样结点的过程叫做有解剪枝.
定义8. 无解剪枝.给定一棵枚举树,在遍历这棵枚举树时,对于树中的某一个结点,如果先判断其子结点或者子孙结点,得到的结果是不可满足,那么可以跳过该结点,不用对这个结点进行判断.我们称跳过判断枚举树中这样结点的过程叫做无解剪枝.
定义7和定义8是基于原理基于极小诊断的定义,即如果一个组件集合是极小诊断解,那么其真超集一定不是极小诊断解;如果一个组件集合不是诊断解,那么其真子集一定不是诊断解.
定义9. 反向搜索.针对一棵枚举树,当枚举树的层数已经给定时,称从枚举树的最后一层向枚举树的根结点搜索的过程为树的反向搜索.
根据反向搜索的定义,只需要从树的最后一层向根结点进行向上搜索即可,在中间这些层之间,可以是自上向下,也可以是自下而上.并且,在访问中间层这些结点时并没有固定的顺序,只需要遍历整棵树的所有结点就可以.
为了解释上面的定义,我们举例说明,如 S ={ N 1 , N 2 , N 3 , N 4 }的部分枚举树如图4所示:

Fig. 4 Part SE-tree of set S
图4 集合S的部分枚举树
在这棵枚举树中,除了根结点以外,一共有14个结点,为了得到所有的解,我们要遍历树上的所有结点.对这棵树进行反向搜索时,我们先遍历最后一层的一些结点,如{ N 1 , N 2 , N 3 },{ N 1 , N 2 , N 4 },然后遍历第2层的结点{ N 1 , N 2 };接着再去遍历第3层的结点{ N 1 , N 3 , N 4 }、第2层的结点{ N 1 , N 3 },{ N 1 , N 4 }、第1层的结点{ N 1 }.根据这样的遍历方式,我们可以遍历结点{ N 2 },{ N 3 },{ N 4 }这些结点以及这些结点的子孙结点.
在求诊断解的过程中,在进行反向搜索时,我们需要一边遍历结点、一边对结点调用SAT求解器进行判断.在这个过程中,根据结点的判断结果,可以知道树中的某些结点可以不用遍历,那么可以跳过树中一些结点的判断过程,减少调用SAT求解器的次数,这就是剪枝过程.剪枝的过程可能是针对是解的那些结点,也有可能是针对不是解的那些结点,也就是有解剪枝和无解剪枝过程.例如,对于上面的这棵枚举树,我们基于反向搜索以及有解剪枝和无解剪枝的思想,求解极小诊断解的过程如下:
针对上面的这棵枚举树,树中一共有第1层的{ N 1 },{ N 2 },{ N 3 },{ N 4 }这4个结点以及它们的子树构成了这棵树.对这4个结点处理的方式是一样的,只对结点{ N 1 }进行举例说明.针对结点{ N 1 }及其子孙结点,我们首先判断最后一层结点{ N 1 , N 2 , N 3 }的可满足性,如果该结点是可满足的,那么向上回溯,判断{ N 1 , N 2 }结点.否则,根据无解剪枝的定义,可以剪掉结点{ N 1 , N 2 },接着继续判断结点{ N 1 , N 2 , N 4 }.如果{ N 1 , N 2 , N 3 }可满足,{ N 1 , N 2 }也可满足,那么根据有解剪枝的定义,可以剪掉结点{ N 1 , N 2 , N 4 },然后向上回溯判断结点{ N 1 }.否则如果{ N 1 , N 2 }不可满足,那么结点{ N 1 }被剪掉,接着判断{ N 1 , N 2 , N 4 },然后是{ N 1 , N 3 , N 4 }.如果结点{ N 1 , N 2 , N 3 },{ N 1 , N 2 },{ N 1 }都可满足,那么根据有解剪枝的定义,结点{ N 1 }下面的所有其他结点都被剪掉,接着判断以{ N 2 }为根的子树,判断{ N 2 , N 3 , N 4 }.否则如果{ N 1 }不可满足,那么我们接着判断{ N 1 , N 3 , N 4 }.到了判断{ N 1 , N 3 , N 4 }时,我们按照判断{ N 1 , N 2 , N 3 }的模式继续判断即可.在存储极小解的过程中,我们将可满足的解存起来,但是如果新来一个解,我们会判断是否是已经存在解的子集,如果是,那么将会更新原来的解,否则将新解加入到解集中.
根据上面的求解思路,我们在3.2节给出基于反向搜索的有解无解空间剪枝算法.
3.2 基于反向搜索的有解无解空间剪枝算法
基于有解剪枝和无解剪枝这样的思想,我们可以从枚举树的第1层最左边的第1棵子树开始,对第1层的每个结点以及子树按相同方式处理即可.针对每一棵子树,我们先判断其最左边的结点,如果是可满足的,我们反向搜索,判断其父结点,并且将其根据有解剪枝的定义,将该结点还没有访问的子孙结点都剪掉.如果是不可满足,那么可以根据无解剪枝的定义,跳过对该节点父节点的遍历,然后接着判断该结点右边的结点.
那么下面我们给出该算法的伪代码:
算法2. LLBRS-tree算法.
输入:系统描述的CNF文件DigSysDis.cnf、系统观测的CNF文件DigSysObs.cnf、极小诊断的最大诊断长度 MiniDigLen ;
输出:极小诊断解的集合.
局部变量:诊断解集合 DigRes []、诊断系统组件的个数 ComNum 、枚举树的总层数 DigTreeLevel 、待判断的第1层的某个结点及其子树 Sub - tree .
Step1. 初始化: DigRes =∅, ComNum =0, DigTreeLevel =0.
Step2. 从文件DigSysDis.cnf中的第1行中读取出诊断系统中组件的个数,赋值给变量 ComNum ,然后根据输入的最小诊断长度 MiniDigLen ,赋值给变量 DigTreeLevel .然后根据局部变量 ComNum , DigTreeLevel 的值,生成集合{1,2,3,…, ComNum }的局部集合枚举树 DigSE - tree , DigTreeLevel 是 DigSE - tree 的最大层数(根结点默认为第0层).
Step3. 将 DigSE - tree 的第1层最左边的结点及其子树赋值给 Sub - tree .
Step4. while( DigSE - tree 中存在第1层结点及其子树还没判断).
Step4.1. while( Sub - tree 判断未完成)
对该子树最底层的最左边的结点调用ISDAG算法判断;
if (该结点可满足)
① 将该结点加入到诊断解结合DigRes中,并且将在DigRes中所有该结点的真超集删除;
② 有解剪枝,将该结点的没有访问过的子孙结点剪掉;
③ 对该结点的父结点进行判断;
else
① 无解剪枝,将该结点的父结点剪掉;
② 对该结点的右边的结点进行判断;
end if
Step4.2. 将第1层的下一个结点及其子树赋值给 Sub - tree ,接着对 Sub - tree 进行判断.
Step5. 返回集合 DigRes .
在算法2的Step2中,我们其实根据输入的系统描述文件DigSysDis.cnf中组件个数以及系统输入的极小诊断的最大诊断长度 MiniDigLen 就已经知道生成的部分枚举树 DigSE - tree 中的层数以及结点个数,其结点个数为 ![]() (其中 n 代表组件的个数, m 代表极小诊断的最大诊断长度,也是 DigSE - tree 的最大层数).在Step4中,我们对枚举树第1层的所有子树进行判断即可.针对每棵子树,我们从子树的最后一层最左边的结点进行判断,按得到的结果分为2种情况:如果是可满足的,那么根据有解剪枝,将该结点的所有还没有访问的子孙结点剪掉,接着判断该结点的父结点;否则,根据无解剪枝将该结点的父结点剪掉,接着判断该结点右边的结点即可.按照这样的方式,我们跳过剪掉的结点,对所有未被访问的结点判断,然后再将其他子树按这种方式判断就可以得到最终的解.在算法的最后一步,也就是Step5,只需要将存放所有极小诊断解的集合 DigRes 返回即可.根据该算法,我们可以知道:
(其中 n 代表组件的个数, m 代表极小诊断的最大诊断长度,也是 DigSE - tree 的最大层数).在Step4中,我们对枚举树第1层的所有子树进行判断即可.针对每棵子树,我们从子树的最后一层最左边的结点进行判断,按得到的结果分为2种情况:如果是可满足的,那么根据有解剪枝,将该结点的所有还没有访问的子孙结点剪掉,接着判断该结点的父结点;否则,根据无解剪枝将该结点的父结点剪掉,接着判断该结点右边的结点即可.按照这样的方式,我们跳过剪掉的结点,对所有未被访问的结点判断,然后再将其他子树按这种方式判断就可以得到最终的解.在算法的最后一步,也就是Step5,只需要将存放所有极小诊断解的集合 DigRes 返回即可.根据该算法,我们可以知道:
1) 该算法是完备的,会得到所有的极小诊断解,不会出现丢掉一部分解的情况.因为我们用一棵枚举树的形式将所有可能出现的情况都一一列举出来,所以不会出现丢解,所有的极小诊断解在遍历完这棵树以后全部产生.
2) 通过对第2节的ISDAG算法分析可以发现,在ISDAG算法中的Step2这一步,当我们向系统描述文件DigSysDis.cnf中添加的反常单元子句的数目越多时,那么意味着单元传播的次数将会很多,文件DigSysDis.cnf中可满足的子句数目也会大大地增加,继而调用SAT求解器对该文件进行可满足性判断的时间也将会相应地缩短.在LLBRS-tree算法中,我们先对长度长的结点进行判断,这些结点的长度与极小诊断解的最大长度相等,那么相应地在调用ISDAG算法时,使得在调用SAT求解器对DigSysDis.cnf文件处理的时间缩短.同时,先对长度最长的结点进行处理,那么我们可以进行无解剪枝的过程,这样在反向搜索向上判断时可以剪掉大量不是诊断解的结点.所以,利用LLBRS-tree算法去求解给定系统的基于一致性诊断的极小诊断时,时间效率将会得到大大地提高.
3) 算法LLBRS-tree的时间复杂度以及空间复杂度主要取决于树中遍历的结点数目.在生成该树时,我们可以用自动机去模拟树中结点的生成,并且随着结点的生成与判断,树中的大量结点都会被有解剪枝和无解剪枝剪掉,从而调用SAT的次数也是大大地减少.当我们在处理组件个数不是很多,且求解的是单  双诊断时,效率可能不是很明显.但是当组件个数很多时,无解剪枝将会剪掉大量的结点,求解的时间将会得到大大地缩短.
双诊断时,效率可能不是很明显.但是当组件个数很多时,无解剪枝将会剪掉大量的结点,求解的时间将会得到大大地缩短.
本节我们对赵相福等人提出的CSSE-trees算法和本文提出的LLBRS-tree算法进行了实现,同时将2个算法进行多方面地比较.测试环境为:Dell Dimension C521,Ubuntu 12.04 LTS,GCC编译器,AMD Athlon TM 64 X2 Dual Core Processor 3600+,1.90 GHz,3 GB RAM.其中在算法ISDAG中,我们调用的SAT求解器是Picosat [25] ,该求解器在SAT比赛中也取得了不错的成绩,而且该求解器的接口写得很详细,在使用接口时很方便,所以我们选择了该求解器.
我们使用的测试用例均来自于基准电路ISCAS-85 [26] 中7个电路,它们分别是c17,c432,c499,c880,c1355,c2670,c3540.我们首先通过这些电路的电路描述得到各个电路的系统描述文件DigSysDis.cnf,然后根据给出的观测值得到系统的观测文件DigSysObs.cnf,这些CNF形式的文件都是离线构造.然后我们分别使用CSSE-tree算法和LLBRS-tree算法对ISCAS-85的这几个电路进行多次测试,记录了相关的求解时间.我们分别用2种算法对这些电路求解长度为1,2,3的极小诊断,得到的结果如表1所示:
Table 1 Solution Time
表1 求解时间 s
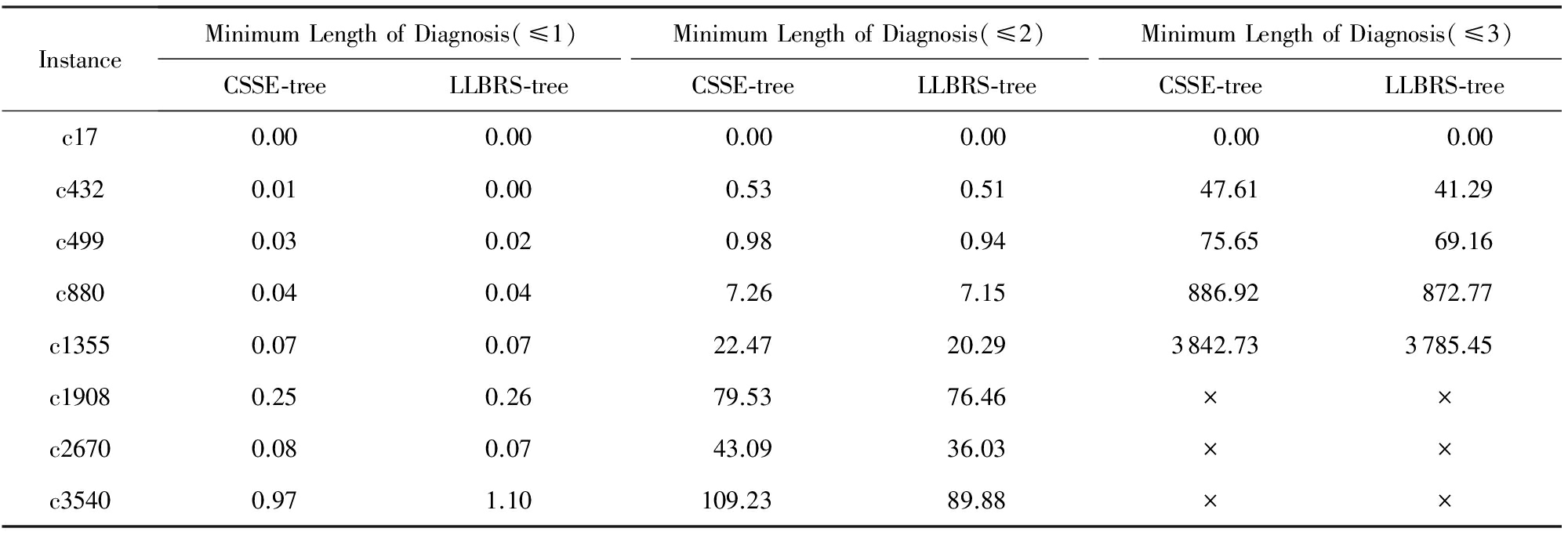
×:Timeout.
从表1中可以看出,在极小诊断解得最大长度为1时,算法LLBRS-tree跟算法CSSE-tree的求解时间基本持平,“×”表示在1 h内求解失败.这是因为当极小诊断解的最大长度为1时,2个算法都需要遍历枚举树中的所有结点,没有剪枝的情况,所以2个算法的时间基本一样.但是当极小诊断解的最大长度为2和3时,算法LLBRS-tree的求解时间比算法CSSE-tree的时间少了很多.算法LLBRS-tree的时间在平均情况下提高了5%左右,而且在极小诊断解的最大长度为3时,有些例子可以达到8%.这是因为随着极小诊断解的最大长度的增加,枚举树的层数相应地增加,树中结点的数目也增加,那么树中不是解的结点个数多于是解的结点个数.在这样的情况下,LLBRS-tree算法将会对枚举树进行无解剪枝和有解剪枝,遍历求解的结点数也将少于CSSE-tree算法,所以效率得到了提高.为了说明LLBRS-tree算法遍历的结点数目小于CSSE-tree算法遍历的结点数目,我们给出2个算法剪掉的结点个数,如表2所示.
由于单诊断并没有涉及到有解剪枝和无解剪枝的情况,所以我们在表2中只给出了2诊断和3诊断的结点剪枝情况,“×”表示在1 h内求解失败.而且针对c1908,c2670,c3540这3个电路,我们设置的求解时间限制是10 000 s,但是由于这3个电路的组件个数过多,所以2个算法都超出了时间的限制.根据表2中的双诊断剪枝结点的信息,由 Δ 这一列的差值信息 Δ =(LLBRS-tree剪掉的结点数-CSSE-tree剪掉的结点数)可以看出,由于存在无解剪枝的情况,而且伴随着有解剪枝,LLBRS-tree算法剪掉的结点数目已经多于CSSE-tree算法剪掉的结点数目.而且当我们求解3诊断时,枚举树中的结点数目急剧增加,算法LLBRS-tree的作用更加地显现出来.从3诊断的 Δ 那一列数据,我们看出:算法LLBRS-tree剪掉的结点数目已经远远大于算法CSSE-tree剪掉的结点数目,有的例子剪掉的结点数目已经高出CSSE-tree算法的十几倍.这是因为,随着枚举树的层数增加,树中不可满足的结点数目也大大地增加了,那么算法LLBRS-tree的无解剪枝策略将会发挥关键的作用,所以剪掉的结点数目远远大于算法CSSE-tree.基于这样的原因,算法LLBRS-tree在求解的过程中所消耗的时间才会小于CSSE-tree算法.而且,随着枚举树的层数增加,也就是当极小诊断解的最大长度增加时,树中不是解的结点数目还会不断地增加,远远大于是解的结点数目,那么算法LLBRS-tree的无解剪枝剪掉的结点也将会大幅度地增加,该算法的效率也会彰显出来,而CSSE-tree算法的效率将会变得越来越慢,更有可能内存溢出的情况.我们分别用2种算法针对组件个数适中的几个测试用例求解多诊断得到的结果如表3所示.
Table 2 Numbers of Cut Node
表2 剪掉结点数个数

×: Timeout.
Table 3 Time of Multi-Diagnosis
表3 多诊断时间 s

M.O: Out of memory.
从表3中可以看出,在求解多诊断时,算法LLBRS-tree的求解时间远远小于算法CSSE-tree.测试用例为c432并且诊断长度为4时,算法CSSE-tree求解时间是算法LLBRS-tree的2.6倍;但是当求解5诊断时,却是3.3倍;并且当诊断长度为6时,CSSE-tree算法出现了内存溢出的情况,而算法LLBRS-tree仍然能求解.当测试用例为c499和c880时,伴随着组件个数和诊断长度的增加,算法CSSE-tree更早的出现了内存溢出的情况,而算法LLBRS依旧能正常的工作.这是因为算法LLBRS-tree针对无解剪枝空间进行大量剪枝,加上有解空间的剪枝,使得需要判断的结点很少.而算法LLBRS生成大量的结点进行判断,导致了内存溢出.重要的是,根据LLBRS-tree算法的求解时间我们可以发现,即使诊断长度增加,该算法的求解时间也是平缓的增加,不会出现剧烈的抖动.这是由于有解无解剪枝策略在求解过程中起到重要的作用.为了更加清晰地说明这种情况,我们对测试用例c432求多诊断得到结果如图5所示:
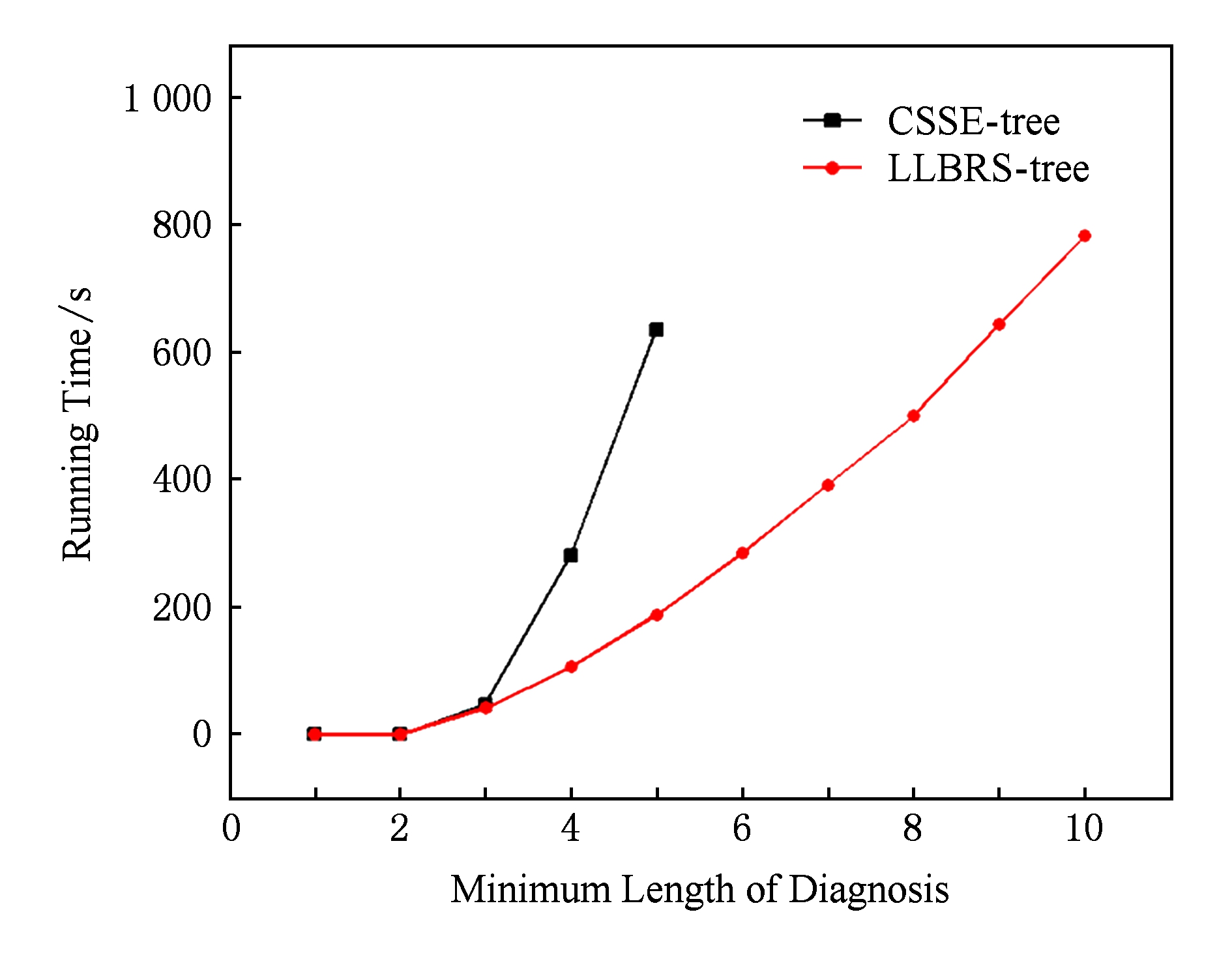
Fig. 5 Comparison chart of multi-diagnosis (ISCAS-85_c432)
图5 多诊断时间对比图(ISCAS-85_c432)
图5是算法LLBRS-tree和算法CSSE-tree针对电路c432(160个组件)求解诊断1~10的时间对比图.从图5我们可以看出,在求解3诊断以前,2个算法的时间相差几乎没有太大的差距.但是在求解4~5诊断时,从2条线的斜率可以看出,算法LLBRS-tree的时间增加很平缓,而CSSE-tree算法求解的时间急剧增加.而且更重要的是,算法LLBRS-tree在求解6~10诊断时,时间依旧很平缓地增加,不会出现急剧增加的情况,但是算法CSSE-tree却只能求到5诊断,6~10诊断出现了内存溢出的情况,不能求出结果.这是因为树中结点的数目急剧地增加,算法CSSE-tree剪掉的结点很少,随着结点的膨胀,所以算法出现了内存溢出的情况.而算法LLBRS-tree进行无解剪枝,剪掉大量不是解的结点,所以针对多诊断,依旧能正常地运行.
由上面的实验结果可以知道,对于没有应用无解空间剪枝策略的求解算法,当组件集合增加,极小诊断长度加大,并且诊断解分布在集合枚举树的右侧时,算法的时间复杂性是指数级.但是应用本文提出的有解和无解剪枝策略后,树中不是诊断解的结点将会被减掉大部分,算法的时间复杂度将小于指数级.由于受到具体诊断实例的输入和输出观测影响,基于模型诊断算法的时间复杂度将会变得十分复杂,这也将成为我们以后研究工作的一部分.
基于模型诊断在人工智能领域一直以来都备受关注,从问题的提出到现在,越来越多的人投入到该问题的研究中.基于极小诊断解的真超集一定不是极小诊断解的原理,CSSE-tree对枚举树进行了修剪,提高了诊断求解效率.但是CSSE-tree只是针对是解的结点进行剪枝,并没有考虑不是解的结点.本文首次提出对无解进行剪枝的思想,并结合有解剪枝给出LLBRS-tree诊断求解方法.
在LLBRS-tree算法中,根据包含组件个数较多的候选诊断解对应的SAT问题规模较小的特点,先对包含组件个数较多的结点进行判断,进而从减少求解问题规模的角度提高诊断求解效率.算法LLBRS-tree剪掉的结点数目远大于算法CSSE-tree,所以求解所用的时间更短,效率高于算法CSSE-tree.尤其在求解多诊断时,所要枚举结点的数目急剧增加,算法CSSE-tree只对有解进行剪枝,剪掉的结点较少.而算法LLBRS-tree进行无解和有解剪枝,在剪掉有解空间基础上还剪掉大量不是解的结点.所以,在求解多诊断时,算法LLBRS-tree剪掉的结点更多,与算法CSSE-tree相比,效率有更大提高.
在后续的工作中,我们考虑利用增量SAT求解器来求解基于模型的诊断,只需要一次调用SAT求解器,就可以得到多个解,这样求解效率会得到进一步提升.
参考文献:
[1]Raymond R. A theory of diagnosis from first principles[J]. Artificial Intelligence, 1987, 32(1): 57-95
[2]Zhao Xiangfu, Ouyang Dantong. Deriving all minimal hitting sets based on join relation[J].IEEE Trans on Systems Man Cybernetics-Systems, 2015, 45(7): 1063-1076
[3]Jiang Yunfei, Lin Li. The computation of hitting sets with boolean formulas[J]. Chinese Journal of Computers, 2003, 26(8): 919-924 (in Chinese)(姜云飞, 林笠. 用布尔代数方法计算最小碰集[J].计算机学报, 2003, 26(8): 919-924)
[4]Zhang Liming, Ouyang Dantong, Zeng Hailin. Computing the minimal hitting set based on dynamic maximum degree[J]. Journal of Computer Research and Development, 2011, 48(2): 209-215 (in Chinese) (张立明, 欧阳丹彤, 曾海林. 基于动态极大度的极小碰集求解方法[J]. 计算机研究与发展, 2011, 48(2): 209-215)
[5]Wang Yiyuan, Ouyang Dantong, Zhang Liming, et al. A method of computing minimal hitting sets using CSP[J]. Journal of Computer Research and Development, 2015, 52(3): 588-595 (in Chinese) (王艺源, 欧阳丹彤, 张立明,等. 利用CSP求解极小碰集的方法[J]. 计算机研究与发展, 2015, 52(3): 588-595)
[6]Huang Jie, Chen Lin, Zou Peng. Computing minimal diagnosis by compounded genetic and simulated annealing algorithm[J]. Journal of Software, 2004, 15(9): 1345-1350 (in Chinese)(黄杰, 陈琳, 邹鹏. 一种求解极小碰集的遗传模拟退火算法[J]. 软件学报, 2004, 15(9): 1345-1350)
[7]Liu Juan, Ouyang Dantong, Wang Yiyuan, et all. Computing minimal hitting sets with particle swarm optimization combined characteristics learning[J]. Acta Electronica Sinica, 2015, 43(5): 841-845 (in Chinese) (刘娟, 欧阳丹彤, 王艺源, 等. 结合特征学习的粒子群求解极小碰集方法[J]. 电子学报, 2015, 43(5): 841-845)
[8]Chen Yunji, Zhang Jian, Shen Haihua. A SAT-Based arithmetic circuit bug-hunting method[J]. Chinese Journal of Computers, 2007, 30(12): 2082-2089 (in Chinese) (陈云霁, 张健, 沈海华. 一种基于 SAT 的运算电路查错方法[J]. 计算机学报, 2007, 30(12): 2082-2089)
[9]Zhang Jian, Ma Feifei, Zhang Zhiqiang. Faulty interaction identification via constraint solving and optimization[G] 
 Theory and Applications of Satisfiability Testing-SAT. Berlin: Springer, 2012: 186-199
Theory and Applications of Satisfiability Testing-SAT. Berlin: Springer, 2012: 186-199
[10]Zhang Xuenong, Jiang Yunfei, Chen Aixiang, et al. A gradual approach for model-based diagnosis[J]. Journal of Software, 2008, 19(3): 584-593 (in Chinese) (张学农, 姜云飞, 陈蔼祥,等. 基于模型诊断的分步求解[J]. 软件学报, 2008, 19(3): 584-593)
[11]Zhao Xiangfu, Zhang Liming, Ouyang Dantong, et al. Deriving all minimal consistency-based diagnosis sets using SAT solvers[J]. Progress in Natural Science, 2009, 19(4): 489-494
[12]Zhao Xiangfu, Ouyang Dantong. Deriving all minimal conflict sets using satisfiability algorithms[J]. Acta Electronica Sinica, 2009, 37(4): 804-810 (in Chinese) (赵相福, 欧阳丹彤. 使用SAT求解器产生所有极小冲突部件集[J]. 电子学报, 2009, 37(4): 804-810)
[13]Zhang Liming, Zeng Hailin, Yang Fang, et al. Dynamic theorem proving algorithm for consistency-based diagnosis[J]. Expert Systems With Applications, 2011, 38(6): 7511-7516
[14]Chen Rong, Gao Jian, Zhang Weishi. Digital circuit fault diagnosis method and system based on logic compatibility [P]. Chinese: CN102156772A, 2011-08-17 (in Chinese)(陈荣, 高健, 张维石. 基于逻辑相容性的数字电路故障诊断方法及系统[P]. 中国: CN102156772A, 2011-08-17)
[15]Ouyang Dantong, Zhang Liming, Zhao Jian. Solving model-based fault diagnosis with flag propagation[J]. Chinese Journal of Scientific Instrument, 2011, 32(12): 2857-2862 (in Chinese) (欧阳丹彤, 张立明, 赵剑. 利用标志传播求解基于模型的故障诊断[J]. 仪器仪表学报, 2011, 32(12): 2857-2862)
[16]Luan Shangmin, Dai Guozhong. An approach to diagnosing a system with structure information[J]. Chinese Journal of Computers, 2005, 28(5): 801-808 (in Chinese)(栾尚敏, 戴国忠. 利用结构信息的故障诊断方法[J]. 计算机学报, 2005, 28(5): 801-808)
[17]Xu Ke, Boussemart F, Hemery F, et al. Random constraint satisfaction: Easy generation of hard (satisfiable) instances[J]. Artificial Intelligence, 2007, 171(8): 514-534
[18]Xu Ke, Li Wei. Exact phase transitions in random constraint satisfaction problems[J]. Journal of Artificial Intelligence Research, 2000, 12(1): 93-103
[19]Zhou Junping, Yin Minghao, Zhou Chunguang, New worst-case upper bound for #2-SAT and #3-SAT with the number of clauses as parameter[C] 
 Proc of the 24th AAAI Conf on Artificial Intelligence. Menlo Park: AAAI, 2010: 217-222
Proc of the 24th AAAI Conf on Artificial Intelligence. Menlo Park: AAAI, 2010: 217-222
[20] Luo Chuan, Cai Shaowei, Wu Wei, et al. Double configuration checking in stochastic local search for satisfiability[C] 
 Proc of the 28th AAAI Conf on Artificial Intelligence. Menlo Park: AAAI, 2014: 2703-2709
Proc of the 28th AAAI Conf on Artificial Intelligence. Menlo Park: AAAI, 2014: 2703-2709
[21]Cai Shaowei, Su Kaile. Comprehensive score: Towards efficient local search for SAT with long clauses[C] 
 Proc of the 23rd Int Joint Conf on Artificial Int. Menlo Park: AAAI, 2013: 489-495
Proc of the 23rd Int Joint Conf on Artificial Int. Menlo Park: AAAI, 2013: 489-495
[22]Cai Shaowei, Su Kaile. Local search for Boolean Satisfiability with configuration checking and subscore[J]. Artificial Intelligence, 2013, 204(9): 75-98
[23]Cai Dunbo, Yin Minghao. On the utility of landmarks in SAT based planning[J]. Knowledge-Based Systems, 2012, 36(6): 146-154
[24]Rymon R. Search through systematic set enumeration[C] 
 Proc of the 3rd Int conf on Principles of Knowledge Representation and Reasoning. San Franasco: Morgan Kaufmann, 1992: 539-550
Proc of the 3rd Int conf on Principles of Knowledge Representation and Reasoning. San Franasco: Morgan Kaufmann, 1992: 539-550
[25]Biere A. PicoSAT essentials[J]. Journal on Satisfiability, Boolean Modeling and Computation, 2008, 4(20): 75-97
[26]Metodi A, Stern R, Kalech M, et al. A novel SAT-based approach to model based diagnosis[J]. Journal of Artificial Intelligence Research, 2014, 51(1): 377-411

Ouyang Dantong, born in 1968. Professor and PhD supervisor of Jilin University. Senior member of CCF. Her main research interests include model-based diagnosis, model checking and automated reasoning (ouyangdantong@163.com).

Zhou Jianhua, born in 1991. Master candidate at Jilin University. His main research interests include model-based diagnosis, SAT problem and automated reasoning.

Liu Bowen, born in 1993. Master candidate at Jilin University. His main research interests include model-based diagnosis, SAT problem and automated reasoning (1591365445@qq.com).

Zhang Liming, born in 1980. PhD, Post-doctor in Jilin University. His main research interests include model-based diagnosis, model checking and Boolean satisfiability.
Ouyang Dantong 1,2,3 , Zhou Jianhua 1,3 , Liu Bowen 2,3 , and Zhang Liming 1,2,3
1 ( College of Software , Jilin University , Changchun 130012) 2 ( College of Computer Science and Technology , Jilin University , Changchun 130012) 3 ( Key Laboratory of Symbolic Computation and Knowledge Engineering ( Jilin University ), Ministry of Education , Changchun 130012)
Abstract: Model-based diagnosis has been popular in the field of artificial intelligence. In recent years, with a gradual increase of the efficiency of SAT solvers, model-based diagnosis is converted into SAT problem. After deeply studying CSSE-tree algorithm—a method for solving model-based diagnosis, combining with the characteristics of diagnose problem and SAT solving process, we solve the problem by diagnosing the candidate solutions which contain more elements first, thereby reducing the scale of SAT problem. Based on the minimal diagnostic solutions and non-minimal pruning methods on diagnostic solutions, we firstly propose a non-diagnostic solution theorem and a non-solution space pruning algorithm, which implements the non-solution space pruning effectively. We first solve the candidate solutions which contain more elements. According to the features of solution and non-solution method, we construct LLBRS-tree method based on reverse search. Experimental results show that compared with the algorithm of CSSE-tree, the algorithm of LLBRS-tree has less number of SAT solving, has smaller scale of the problem, better efficiency, especially when solving multiple diagnose problems its efficiency is more significant.
Key words: model-based diagnosis; non-solution space pruning; conjunctive normal form; SAT solver; set-enumeration-tree
收稿日期: 2015-11-03;
修回日期: 2016-04-13
基金项目: 国家自然科学基金项目(61672261,61502199,61402196,61272208);浙江省自然科学基金项目(LY16F020004) This work was supported by the National Natural Science Foundation of China (61672261, 61502199, 61402196, 61272208) and the Natural Science Foundation of Zhejiang Province of China (LY16F020004).
通信作者: 张立明(limingzhang@jlu.edu.cn)
中图法分类号: TP18