宋金凤 闻立杰 王建民
(清华大学软件学院 北京 100084)
(632230913@qq.com)
摘要针对流程模型行为相似性度量难题,提出了一种基于任务发生关系的流程模型相似性度量TOR.基于Petri网的完全前缀展开理论,提出了节点编号算法以及最近公共前驱计算方法,在此基础上定义了任务间3种基本的发生关系:因果、并行和互斥,并给出这些关系的高效计算方法和模型相似度计算公式.TOR能有效处理不可见任务和非自由选择结构,基于来自企业实际模型的实验证明了TOR具备较好的效果和性能,与已有算法相比,TOR能较好地满足行为相似性算法应具备的性质.
关键词相似性度量;任务发生关系;流程模型;完全前缀展开;Petri网
流程模型对于一个企业来说,具有十分重要的价值,它的作用不仅仅是对企业业务流程的具体刻画,而且有利于企业对业务流程进行分析、验证和优化[1].流程模型的管理包括模型分析、模型检索和模型重用等方面[2].流程模型相似性度量在流程模型管理的各个方面都发挥着非常重要的作用.目前的流程模型相似性算法主要分为3类[2]:1)元素标签映射的相似性度量;2)模型结构的相似性度量;3)行为语义的相似性度量.
元素标签映射的相似性度量,是基于节点的成对标签比较.它是通过定义2个模型的节点标签之间的映射,从而计算出相似性.标签匹配相似度等于匹配的节点数除以总节点数.为了检测标签的相似性,常常运用模式匹配算法[3]和本体匹配算法[4].Dijkman等人[5]在相似性度量方面做出了很多研究,提出了较多的相似性度量算法,最简单的一种叫标签对齐的相似性度量算法.Ehrig等人[6]提出了基于标签语义的相似性度量方法.该类算法思路简单、计算快速,但未对模型的拓扑结构和行为语义加以考虑,导致计算结果不够精准.
结构相似性度量方法,是把模型看作一个图,利用公共子图同构和图编辑距离对模型的相似性进行度量.图编辑距离详细定义了从一个图转换到另一个图所需的最小原子级图操作.Dijkman等人[7]提出了一种结构相似性度量方法,该方法定义了进行每一种编辑操作都必须付出相应代价,通过从一个模型到另一个模型的编辑距离,达到求出相似性的目的.基于上述算法,La Rosa等人[8]又提出了一种算法,结合了图的编辑距离和活动匹配的方法.Li等人[9]提出了一种基于高级变更操作来计算模型相似性的方法,这种高级变更操作可以确保模型的完整性,并且使图的编辑距离具有了高层语义上的特征.该类算法往往无法辨别行为相同或相近而结构有较大差异的模型对儿.
基于行为语义的相似性度量主要从模型的行为语义(如执行序列、任务关系)角度去考虑提取模型的行为关系,进而进行相似性的计算.Weidlich等人[10]提出了行为轮廓(behavioral profile,BP)算法的概念,行为轮廓主要是弱顺序关系、严格顺序关系、互斥关系、交叉关系等一系列关系的统称.在行为轮廓概念定义的基础上,作者提出了基于行为轮廓度量模型相似性的算法,即行为轮廓算法.该算法虽然可以在一定程度上高效提取行为关系,但是其粒度过粗,往往不能区分一些特殊结构,如互斥与循环、不可见任务等.Polyvyanyy等人[11]提出了4C(co-occurrence,conflict,causality,concurrency)算法,该算法提出了一系列关系的定义,包括共现关系、冲突关系、因果关系以及并发关系,统称为4C关系,但由于关系过多且复杂,导致了其不易于计算和理解.Zha等人[12]提出了一种变迁毗邻关系(transition adjacent relations,TAR)算法,但该算法只考虑到了变迁的紧邻关系而忽略了变迁间接影响的关系,因此导致自由选择结构与非自由选择结构可能产生相同的结果.Wang等人[13]提出基于主变迁序列(principal transition sequences,PTS)的相似性计算方法,该算法可以有效处理循环结构,但是在并发分支较多的情况下会导致空间爆炸问题.汪抒浩等人[14]提出了SSDT算法(shortest succession distance between tasks),该算法定义了任务最短跟随距离,并在此基础上定义过程模型的任务最短跟随距离矩阵,将2个过程模型的对应距离矩阵进行同维化后可以进行相似性计算.Dijkman等人[5]提出一种用因果足迹(casual footprints,CF)计算相似性的方法,该算法的主要思路是把过程模型用向量表示,但是由于向量中有过多的冗余信息,因此高维度的向量导致计算非常低效.
针对BP算法和4C算法的不足,本文提出了新的行为相似性度量方法TOR(task occurrence relations),即基于任务发生关系的流程模型相似性算法.首先定义了完全前缀展开中的前驱、公共前驱、最近公共前驱等一系列概念,并且设计了节点编号算法、最近公共前驱求解算法,提出了任务间3种发生关系,即因果、并行和互斥,据此给出了相似性计算方法.TOR算法可以很好地处理不可见任务和非自由选择结构,并且可以有效提取存在于任务间的多关系.
定义1. Petri网[15].Petri网是三元组N=(P,T,F),其中P和T是不相交的有限集合,P是所有库所的集合,而T是所有变迁的集合,它们之间的连接关系用F表示,F⊆(P×T)∪(T×P).Petri网中所有的节点集合为X=P∪T,对于任意节点x∈X,x的前置集合为·x={y∈X|(y,x)∈F},同理x的后置集合为x·={y∈X|(x,y)∈F}.
定义2. Petri网系统[15].二元组S=(N,M0)是Petri网系统,其中N=(P,T,F)为Petri网,M0
是Petri网的初始标识,M0:P→![]() ,
,![]() 是自然数集合.
是自然数集合.
定义3. 就绪[15].给定Petri网系统S=(N,M0),对于任意变迁t∈T,M是从M0可达的标识,当∀p∈·t满足M(p)≥1时,则称t就绪,记为(N,M)[t〉.若S的任意可达标识M和库所p都满足M(p)≤n(n为任意正整数),则称S是有界的.
定义4. 触发[15].给定Petri网系统S=(N,M0),M是从M0可达的标识,若t∈T且(N,M)[t〉,则t可被触发,并得到新的标识M′=M-·t+t·.
McMillan等人[16]最先提出了一种新技术来避免Petri网系统验证中无限状态造成的空间爆炸问题.他首先提出一种网展开的概念,即完全有限前缀,之后基于分支进程这一概念,对该理论进行了进一步阐述[17].该算法的创新之处在于:通过记录已经存在的标记状态,提出了截断事件的概念(即如果一个标记状态已经存在过,那么就对其之后的部分进行截断),从而避免同一状态重复出现多次的现象,确保了展开结构的简洁性.因此,该算法有着较高的效率和比较小的展开规模,在解决Petri网状态空间爆炸问题方面有着比较出色的表现.Esparza等人[18]对McMillan等人[16-17]的算法进行了改进,提出了一种新的规模更小的展开方法,即完全前缀展开.
下面对该完全前缀展开(complete prefix unfolding,CPU)技术的一些基本概念进行简要的介绍,更多相关概念和示例详见文献[18].
定义5. 出现网[18].出现网为一类特殊的Petri网O=(C,E,G),当且仅当满足如下条件:
1)O是无环的,C为条件(即库所)的集合,E为事件(即变迁)的集合,边集G⊆(C×E)∪(E×C);
2) ∀c∈C,满足|·c|≤1,即任意条件的输入都小于等于1;
3) 对于所有x∈C∪E,都有 (x#x),即所有的元素都不能是自冲突的;
(x#x),即所有的元素都不能是自冲突的;
4) ∀x∈C∪E满足{y∈C∪E|y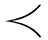 x}必须是有限的.
x}必须是有限的.
在给定出现网中,因果关系x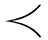 y表示x与y之间为偏序关系,即存在从x到y的路径,冲突关系x#y表示二者所在的不同路径开始于某公共条件或库所c,且从c到x的路径与从c到y的路径不相交.
y表示x与y之间为偏序关系,即存在从x到y的路径,冲突关系x#y表示二者所在的不同路径开始于某公共条件或库所c,且从c到x的路径与从c到y的路径不相交.
定义6. 分支进程[18].对于网系统S=(N,M0),其中N=(P,T,F),出现网为O=(C,E,G),则π=(O,h)为S的一个分支进程,当且仅当满足如下条件:
1)h为一个映射:C∪E|→P∪T,同时h(C)⊆P且h(E)⊆T;
2) 对于所有e∈E,·e和·h(e)之间是双射,e·和h(e)·之间是双射,即h保留了变迁的外延;
3)h使得Min(O)和M0之间为双射,Min(O)表示根据偏序关系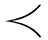 得到的C∪E中的所有最小元素集合;
得到的C∪E中的所有最小元素集合;
4) 对于所有e,f∈E,当h(e)=h(f)且·e=·f时,则必须满足e=f.
定义7. 配置[18].S=(N,M0)是Petri网系统,其中N=(P,T,F),π=(O,h)是S的一个分支进程,其中O=(C,E,G),分支进程π的某个配置C′是一组事件,满足如下关系:
1) ∀e1∈C′,e2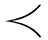 e1⟹e2∈C′,即C′是因果关系的事件组成的闭包;
e1⟹e2∈C′,即C′是因果关系的事件组成的闭包;
2) ∀e1,e2∈C′满足 (e1#e2),即e1和e2不冲突.
(e1#e2),即e1和e2不冲突.
其中,任意事件e∈E的局部配置指的是,满足条件x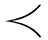 e∨x=e的所有事件x的集合,记作[e].
e∨x=e的所有事件x的集合,记作[e].
定义8. 割集[18].对于π=(O,h)的某有穷配置C′,Cut(C′)=(Min(O)∪C′·)\·C′被称为一个割集.
定义9. 充分关系[19].充分关系是在局部配置上的严格偏序关系,对于任意2个事件e,f∈E,如果有[e]⊂[f],那么[e]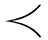 [f],且
[f],且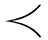 通过有穷扩展得以保持(即如果[e]
通过有穷扩展得以保持(即如果[e]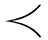 [f]且Mark([e])=Mark([f]),则对于[e]的所有有穷扩展[e]⊕E,存在同构变换
[f]且Mark([e])=Mark([f]),则对于[e]的所有有穷扩展[e]⊕E,存在同构变换![]() 使得[e]⊕E
使得[e]⊕E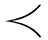 [f]⊕
[f]⊕![]() 则意味着e和f之间为充分关系.
则意味着e和f之间为充分关系.
其中,Mark(C)表示从原网的初始标识开始,依次触发配置C中的每个事件,最终得到可达标识.
定义10. 截断事件、截断条件[18].对于π=(O,h)中的一个事件e∈E,如果有一个对应事件f∈E,满足Mark([e])=Mark([f]),并且[f]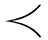 [e],那么e就是截断事件,f是其对应事件,记作f=corr(e).此时,e·被称作截断条件集合.通常来说,对于任意截断条件c∈e·,满足c·=∅,即其后的事件均被截断了.
[e],那么e就是截断事件,f是其对应事件,记作f=corr(e).此时,e·被称作截断条件集合.通常来说,对于任意截断条件c∈e·,满足c·=∅,即其后的事件均被截断了.
定义11. 完全前缀展开[18].对于有界的网系统S=(N,M0),其分支进程π=(O,h)是S基于截断技术得到的前缀展开,则π是完全的当且仅当对于S中的每个可达标识M,都存在π的一个配置C,使得:
1)Mark(C)=M,即M在π中得以表达;
2) 对于M下就绪的每个变迁t,都存在一个事件e,满足e∉C且h(e)=t且C∪{e}构成一个配置.
例1. 如图1(a)所示的Petri网,图1(b)为其完全前缀展开,也是该网的一个分支进程,其中:局部配置[A]={A},[C]={A,C},[E]={A,B,C,E},而割集Cut([A])={P1,P2},Cut([C])={P41},Cut([E])={P5};针对C与D组成的互斥结构,事件D为截断事件,其对应事件corr(D)=C,而P42为截断事件,其对应条件为P41;针对H和I构成的循环结构,事件I为截断事件,其对应事件corr(I)=F,而P72为截断条件,P71为对应条件,这是由于Mark([F])=Mark([I])且[F]={A,B,C,E,F}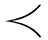 [I]={A,B,C,E,F,H,I}.
[I]={A,B,C,E,F,H,I}.
基于任务间发生关系的模型相似性度量算法TOR的主要步骤如下:
1) 基于完全前缀展开.首先把给定的Petri网模型进行完全前缀展开,这样可以保持流程模型的所有标识及任务间发生关系,便于后续提取流程模型的行为特征.
2) 节点遍历编号.逐层广度优先遍历得到的完全前缀展开,对其节点按照遍历的层次编号,并存储节点和其对应的编号.
3) 求出任务发生关系.根据最近公共前驱算法求出每2个任务的最近公共前驱并作相应的存储,从而进一步求出任务发生关系.根据求出的最近公共前驱以及特殊结构的处理方式,确定任务之间的发生关系.
4) 模型相似性计算.在相应的任务间关系集合的基础上,通过关系集合之间的加权相似性计算出模型之间的相似性.
本节主要介绍围绕任务发生关系的一系列定义,包括完全前缀展开图中任意2个节点的前驱、公共前驱、最近公共前驱以及任务发生关系.
定义12. 路径.S=(N,M0)是有界系统,π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G).a,b∈C∪E,有一条路径从a到b,即存在一条从a到b的有向通路.
例2. 在图1(b)中,A经过P1到B,则A到B可达,即存在一条从A到B的路径.
为了计算任务间发生的关系,需要对CPU节点的前驱、公共前驱以及最近公共前驱进行定义.
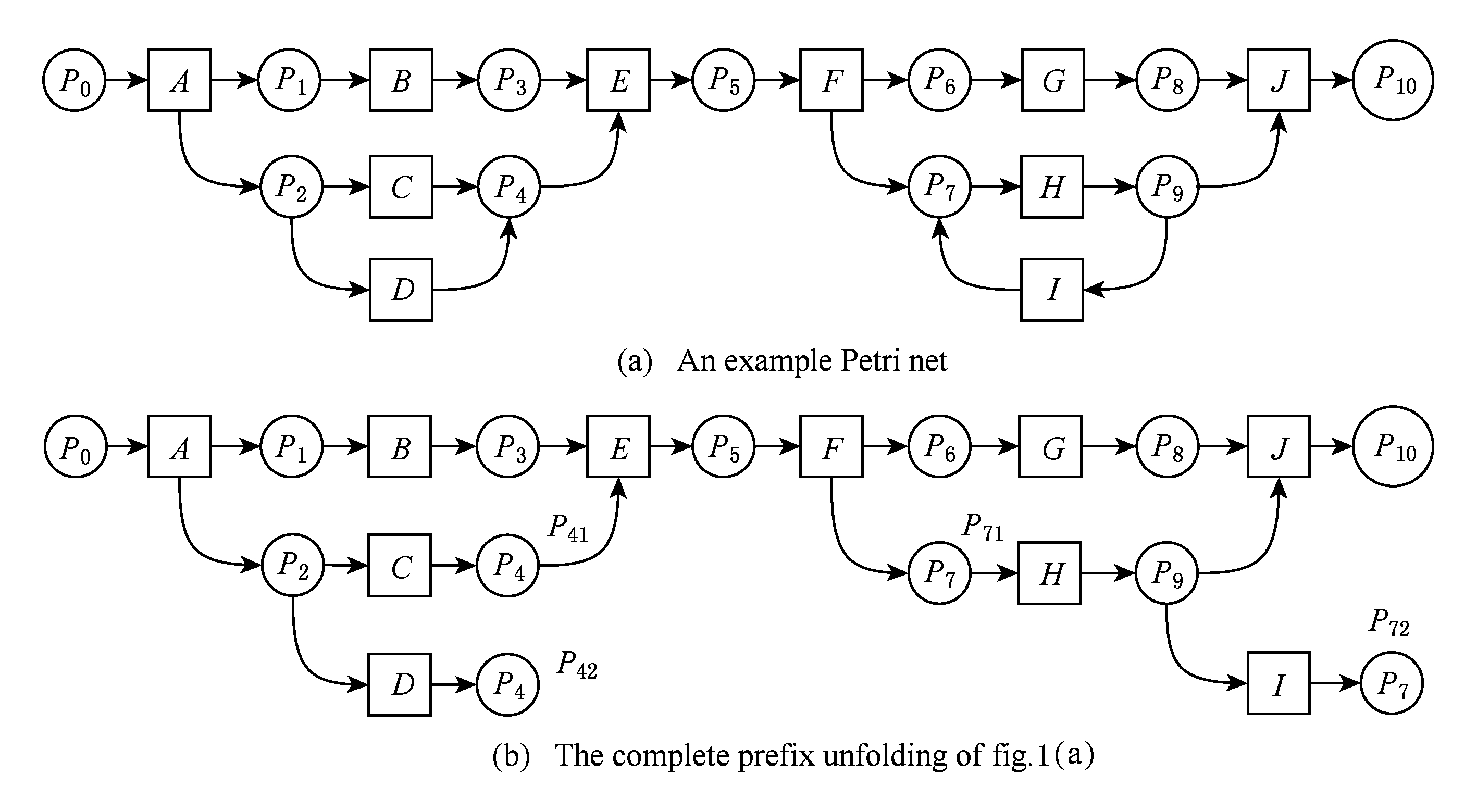
Fig. 1 An example for task occurrence relations
图1 任务发生关系示例
定义13. 前驱.S=(N,M0)是有界系统,π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G).从p到e存在一条路径,其中p∈C∪E,e∈E,那么p是e的一个前驱,记为p∈pre(e),pre(e)表示e的所有前驱节点集合.特别地,有e∈pre(e).
对于截断存在的情况,如果有一条路径从c到e,并且c,c′∈C,e∈E,如果有c=corr(c′),那么认为有一条路径从c′到e,且所有c′的前驱节点也是e的前驱,即∀p∈pre(c′),有p∈pre(e).
例3. 在图1(b)中,有一条路径从B到E,B是E的前驱.同样地,有一条路径从C到E,那么C也是E的前驱.特别地,D虽然没有直接到E的路径,但是可以通过截断条件P42跳转到P41后使得从D到E有路径相连,所以D也是E的前驱.同理,有一条路径从G到J,G是J的前驱;有一条路径从H到J,H也是J的前驱.虽然没有直接从I到J的路径,但是,可以通过截断条件P72跳转到P71后使得从I到J有路径相连,因此,I也是J的前驱.
定义14. 公共前驱.S=(N,M0)是有界系统,π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G).对任意e1,e2∈E,如果存在cp∈C∪E,并且有cp∈pre(e1)∩pre(e2),那么cp就是e1,e2的公共前驱,记作cp∈cmPre(e1,e2).
定义15. 最近公共前驱.S=(N,M0)是有界系统,π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G).对任意e1,e2∈E和lcp∈cmPre(e1,e2),若不存在lcp′∈cmPre(e1,e2),满足lcp′≠lcp而且lcp∈pre(lcp′),那么lcp是e1和e2的最近公共前驱,记为lcp∈lcPre(e1,e2).
例4. 在图1(b)中,节点A既是B的前驱,也是C的前驱,则A是B和C的公共前驱.虽然A也是C和D的公共前驱,但P2才是C和D的最近公共前驱.
定义16. 因果关系.S=(N,M0)是有界系统,π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G).e1,e2∈E,t1,t2∈T,h(e1)=t1且h(e2)=t2,则t1和t2存在因果关系,当且仅当e1∈lcPre(e1,e2)(记作t1→t2或t2←t1,即逆序关系)或者e2∈lcPre(e1,e2)(记作t2→t1或t1←t2).
定义17. 并行关系.S=(N,M0)是有界系统,π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G).e1,e2∈E,t1,t2∈T,h(e1)=t1且h(e2)=t2,则t1和t2存在并行关系,当且仅当存在e∈E,使得e≠e1且e≠e2且e∈lcPre(e1,e2),记作t1‖t2或者t2‖t1.
定义18. 互斥关系.π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G).e1,e2∈E,t1,t2∈T,h(e1)=t1且h(e2)=t2,则t1和t2存在互斥关系,当且仅当存在c∈C,使得c∈lcPre(e1,e2),记作t1#t2或者t2#t1.
例5. 在图1(b)中,A和E存在因果关系,B和C存在并行关系,C和D存在互斥关系;而对于I和J,由于lcPre(I,J)={P9},二者之间存在明显的互斥关系.
定义19. 任务发生关系.S=(N,M0)是有界系统,π=(O,h)是其包含截断事件的CPU,任务发生关系集合TOR={←,→,‖,#},统称为S的任务发生关系.
以上定义了与任务发生关系有关的一系列定义,基于上述定义才可以进行后续的模型相似性计算.
本节介绍任务发生关系的计算方法,包括节点编号算法、最近公共前驱算法以及任务发生关系的确定.
节点编号算法(其伪代码如算法1所示)主要是通过遍历CPU,确定每个节点的层级编号,是后续高效计算任意2节点最近公共前驱的基础.
算法1. 节点编号算法generateLevel.
输入: 有界系统S=(N,M0),π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G);
输出:Map(node,level). *每个节点node及其对应编号level的散列表Map*
*每个节点node及其对应编号level的散列表Map*
① 查找π中所有源节点并放入队列startNodes;
② for eachv∈startNodesdo
③Map.put(v,1);
④ end for
⑤ whilestartNodes.size()>0 do
⑥ 从startNodes中取出第1个元素,其编号为level;
⑦ for eachn∈node· do
⑧ ifn∉MaporMap.get(n)<level+1 then
⑨Map.put(n,level+1);
⑩ addntostartNodes;
 end if
end if
 end for
end for
 if节点n是互斥结构引发的截断条件且(corr(n)∉MaporMap.get(corr(n))<level) then
if节点n是互斥结构引发的截断条件且(corr(n)∉MaporMap.get(corr(n))<level) then
 Map.put(corr(n),level);
Map.put(corr(n),level);
 addcorr(n) tostartNodes;
addcorr(n) tostartNodes;
 end if
end if
 end while
end while
节点编号算法的步骤简介如下:1)取出全部首节点(一般有且仅有1个),编号为第1层;2)按照广度优先的原则,不断取出同一层次的后继节点,按照同一层编号相同的原则进行编号.同时,由于节点可从不同路径可达,因此必要时需要更新某节点及其后继节点的编号,取较大的编号作为该节点最终的编号;如果遇到循环节点,则不进行编号更新.遍历的同时,把节点和其对应的编号信息存储在散列表Map中,当所有节点遍历完成后,算法结束.针对图2(a)所示Petri网的CPU图应用节点编号算法,所得结果如图2(b)所示.
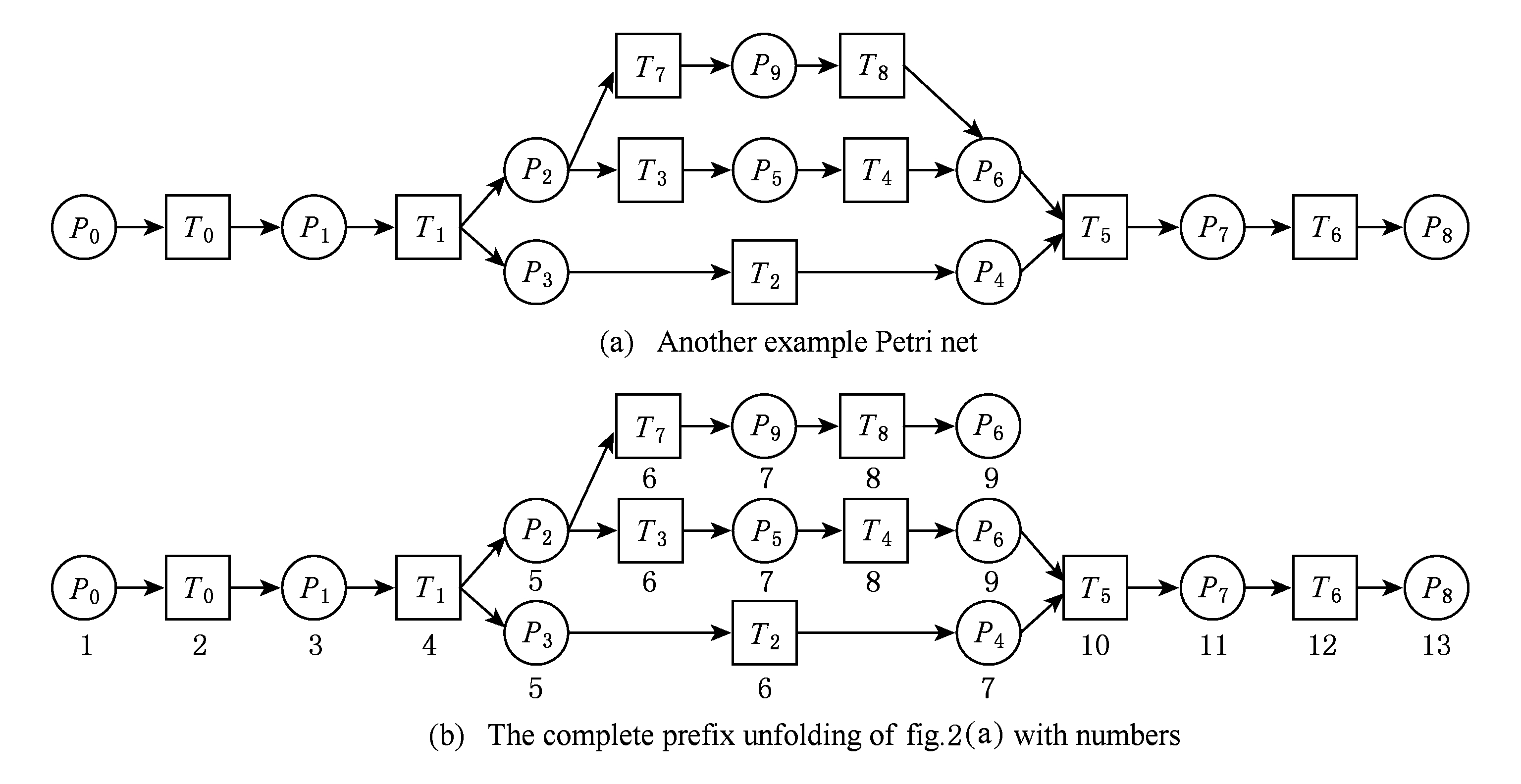
Fig. 2 An example for Algorithm 2
图2 算法2步骤举例
最近公共前驱可以在一定程度上反映任务之间的发生关系,函数computeLCP主要用于完成CPU中2节点最近公共前驱的计算,其伪代码如算法2所示,其主要思路如下:
1) 把事件e1和事件e2分别放入事件数组array1和array2中(行①~②).
2) 遍历array1求出编号最大的节点,记这个节点为node1,记最大编号为max1;同理,遍历array2求出编号最大的节点node2,记最大编号为max2(行④~⑦).
3) 比较max1和max2.若max1>max2,则node1向前回溯一步;否则node2向前回溯一步(行⑧~ ).
).
4) 不断重复思路2和思路3,直到找到公共前驱节点为止(行③~ ).
).
5) 返回公共前驱节点,这些公共节点就是e1,e2的最近公共前驱(行 ).
).
算法2. 最近公共前驱算法computeLCP.
输入: 有界系统S=(N,M0),π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G);e1∈E,e2∈E;存储CPU节点编号结果的散列表Map;
输出: 最近公共前驱数组lcpSet.
① adde1toarray1;
② adde2toarray2;
③ whilearray1∩array2=∅ do
④ getnode1fromarray1with the max number;
⑤max1=Map.get(node1);
⑥ getnode2fromarray2with the max number;
⑦max2=Map.get(node2);
⑧ ifmax1>max2then
⑨stepBackward(node1,array1);
⑩ else
 stepBackward(node2,array2);
stepBackward(node2,array2);
 end if
end if
 end while
end while
 lcpSet=array1∩array2.
lcpSet=array1∩array2.
回溯一步算法stepBackward(其伪代码如算法3所示)的主要思想是从startNode节点开始,向前回溯一步,同时更新数组array,把startNode的所有前驱节点加入数组array中,并把startNode节点从数组中移除.
算法3. 回溯一步算法stepBackward.
输入: 有界系统S=(N,M0),π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G);startNode∈C∪E;存储待遍历节点的数组array.
① for eachn∈·startNodedo
② addntoarray;
③ end for
④ ifstartNode∈Cthen
⑤ for eachc∈Cdo
⑥ ifstartNode=corr(c) then
⑦ addctoarray;
⑧ end if
⑨ end for
⑩ end if
 removestartNodefromarray.
removestartNodefromarray.
下面用一个具体的流程模型来说明2节点最近公共前驱的求解过程.
例6. 以图2(a)中的流程模型为例,求解其CPU中事件T2和T8的最近公共前驱的计算过程如下:
1) 将该模型进行完全前缀展开,并用编号算法对所有进行编号,得到的CPU如图2(b)所示;
2) 把T8放入array1中,把T2放入array2中,此时array1中节点的最大编号max1=8,array2中节点的最大编号max2=6,由于max1>max2,应该从T8向前回溯一步,调用函数stepBackward,此时array1更新为{P9},array2不变,仍为{T2};
3) 此时max1=7,max2=6,由于max1>max2,应该从P9向前回溯一步,调用函数stepBackward,此时array1更新为{T7};
4) 此时max1=6,max2=6,由于max1=max2,T2向前回溯一步,调用函数stepBackward,此时array2更新为{P3};
5) 此时max1=6,max2=5,由于max1>max2,应该从T7向前回溯一步,调用函数stepBackward,此时array1更新为{P2};
6) 此时max1=5,max2=5,由于max1=max2,应该从P3向前回溯一步,调用函数stepBackward,此时array2更新为{T1};
7) 此时max1=5,max2=4,由于max1>max2,应该从P2向前回溯一步,调用函数stepBackward,此时array1更新为{T1};
8) 到此为止,已经找到最近公共前驱集合{T1},算法结束.
根据求出的事件间最近公共前驱集合以及之前对于任务发生关系的定义,可以确定任意2个给定任务间的发生关系,对应算法的伪代码如算法4所示.
算法4. 任务发生关系的确定算法computeTOR.
输入: 有界系统S=(N,M0),π=(O,h)是其包含截断事件的CPU,其中N=(P,T,F),O=(C,E,G);t1,t2∈T;
输出: 任务发生关系集合TOR.
① for eache1∈E∧h(e1)=t1do
② for eache2∈E∧h(e2)=t2do
③lcp=computeLCP(e1,e2).get(0);
④ iflcp=e1then
⑤TOR.add(t1,t2,→);
⑥ else iflcp=e2then
⑦TOR.add(t1,t2,←);
⑧ else iflcp∈Ethen
⑨TOR.add(t1,t2,‖);
⑩TOR.add(t2,t1,‖);
 else iflcp∈Cthen
else iflcp∈Cthen
 TOR.add(t1,t2,#);
TOR.add(t1,t2,#);
 TOR.add(t2,t1,#);
TOR.add(t2,t1,#);
 end if
end if
 end for
end for
 end for
end for
通过该算法,可以基于CPU中任意2个事件间的最近公共前驱,确定流程模型中每对儿任务之间的发生关系,进一步可以求出流程模型的任务发生关系矩阵.
通过2.1节和2.2节介绍的算法和定义,已经可以确定模型的关系矩阵,基于关系矩阵可以计算过程模型的相似性.相似性计算主要思路为:首先分别介绍并行关系、互斥关系以及因果关系的权重和相似度;然后用权重乘以对应的关系相似度,从而得出整个模型的相似性.
并行关系、互斥关系以及因果关系的权重分别用如下公式计算,其中P,Q为给定的2个流程模型,P‖,P#,P→,P←分别为P的并行关系、互斥关系、因果关系和逆序关系集合.对于模型Q,亦有对应的关系集合.
w1为并行关系的权重,其计算为
w1=![]()
(1)
w2为互斥关系的权重,其计算为
w2=![]()
(2)
w3为因果关系的权重,其计算为
w3=![]()
(3)
在上述权值计算公式中,借鉴了Weidlich等人[10]在BP算法中的思路,直接采用各类二元关系个数在所有二元关系总数中的比重,认为并行关系、互斥关系和因果关系具有相同的重要性,这些权值支持用户自定义.
根据Jaccard系数,并行关系、互斥关系以及因果关系的相似性分别用如下公式计算.本文假定前任务名称、发生关系、后任务名称分别相同,为判定关系集合中元素相同的标准,如T1#T2≠T1#T3.
对于并行关系的相似性,用P模型和Q模型所有并行关系的交集元素数除以P模型和Q模型所有并行关系的并集元素数:
(4)
对于互斥关系的相似性,用P模型和Q模型所有互斥关系的交集元素数除以P模型和Q模型所有互斥关系的并集元素数:
(5)
对于因果关系的相似性,用P模型和Q模型所有因果关系的交集元素数除以P模型和Q模型所有因果关系的并集元素数:
(6)
2个模型P和Q的相似性为并行关系的权重乘以并行关系相似性、互斥关系的权重乘以互斥关系的相似性、因果关系的相似性乘以因果关系的权重这三者的累加和,其计算为
sim(P,Q)=w1×sim‖(P,Q)+
w2×sim#(P,Q)+w3×sim→(P,Q).
(7)
图3展示了包含多关系的典型实例,同时该例也体现了TOR算法对非自由选择结构的有效处理.图3(a)为Petri网表达的原模型,图3(b)是其对应的CPU.在一个分支进程里,T2和T3是并行关系,在另一分支进程里面,T2和T3是因果关系,这2种关系都是有效的.在算法的设计中已充分考虑了不同分支进程的情况,因此,在关系的提取过程中,这2种关系都会被提取出来,对应的任务发生关系矩阵如表1所示.
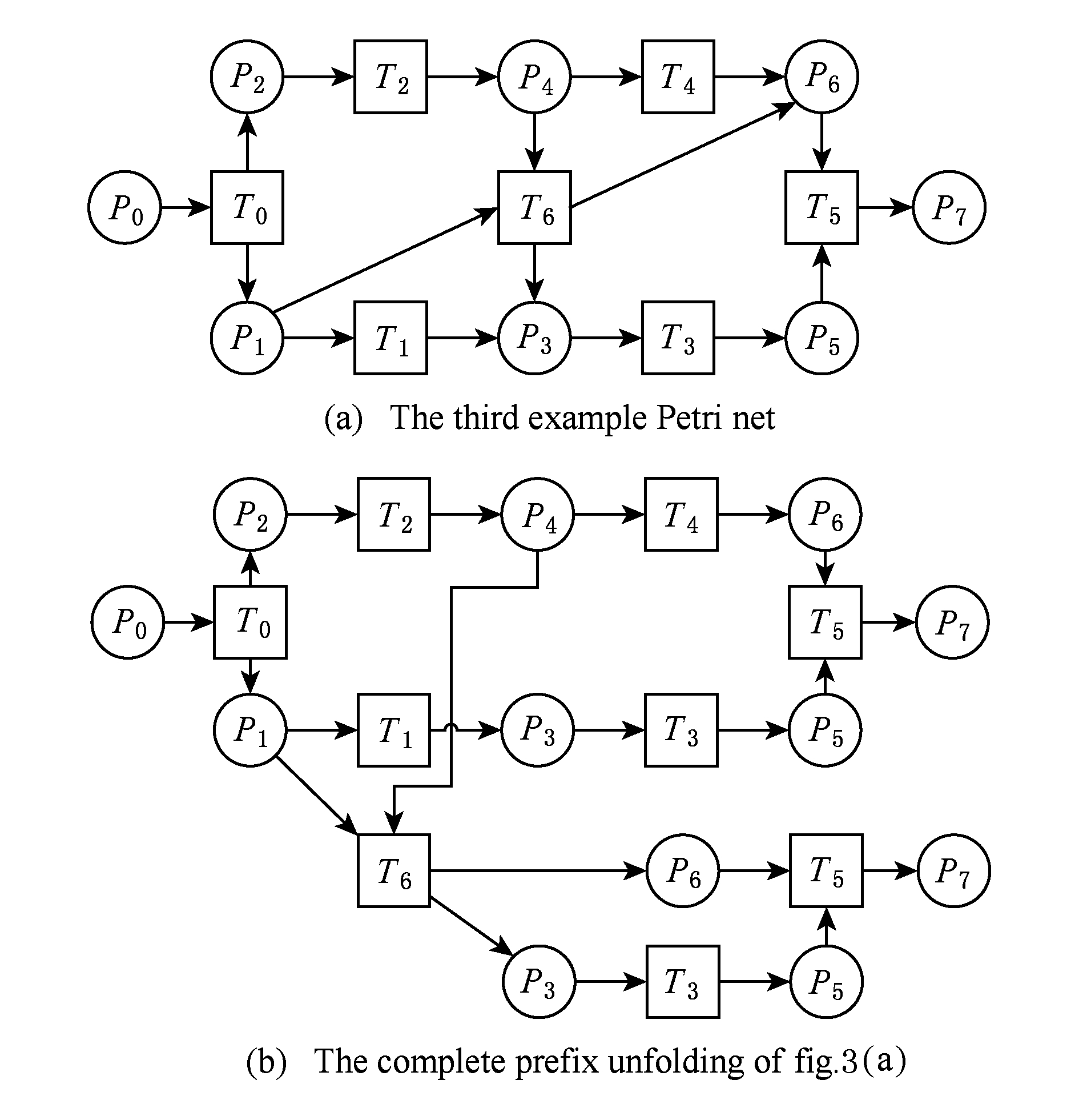
Fig. 3 An example for multiple occurrence relations between tasks
图3 任务间多发生关系实例
Table1TORMatrixoftheProcessModelinFig.3
表1图3中模型的任务发生关系矩阵
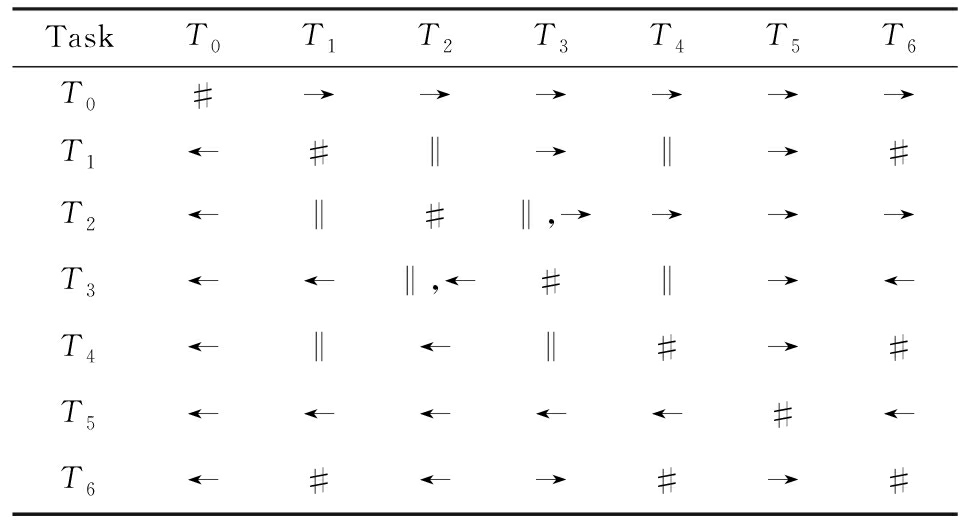
Notes: →means causality; ←means inverse causality;
#means conflict; ‖means concurrency.
在实际业务过程模型中会出现一种特殊的任务,称作不可见任务[19],即空标签任务,这种任务的存在会影响模型的行为.然而,现有的模型相似性算法大多忽略了不可见任务的处理,本文给出其具体处理方法.主要处理3种类型的不可见任务,分别是SKIP类型、REDO类型以及SWITCH类型.SKIP类型不可见任务用于跳过某些任务,如图4所示;REDO类型用于重复执行某些任务,如图5所示;SWITCH类型不可见任务,用于在过程模型的不同可选分支间进行执行顺序切换,如图6所示.关于不可见任务的详细分类,读者可参阅文献[19].
对于SKIP类型的不可见任务,可以看出在图4所示模型中,不可见任务(称其为Inv1)跳过了任务B,也就是该不可见任务的存在,导致了B被跳过.换个角度来说,该不可见任务和B是互斥关系,二者不能同时执行.在处理这一类不可见任务的时候,只需要考虑该不可见任务与其跳过范围内的可见任务的互斥关系即可.确定这个范围,就需要通过该不可见任务的输入输出边来确定其作用范围.也就是说,在SKIP类型的不可见任务处理时,不可见任务只参与互斥关系的计算,在图4中体现为B#Inv1.该模型的关系矩阵如表2所示.
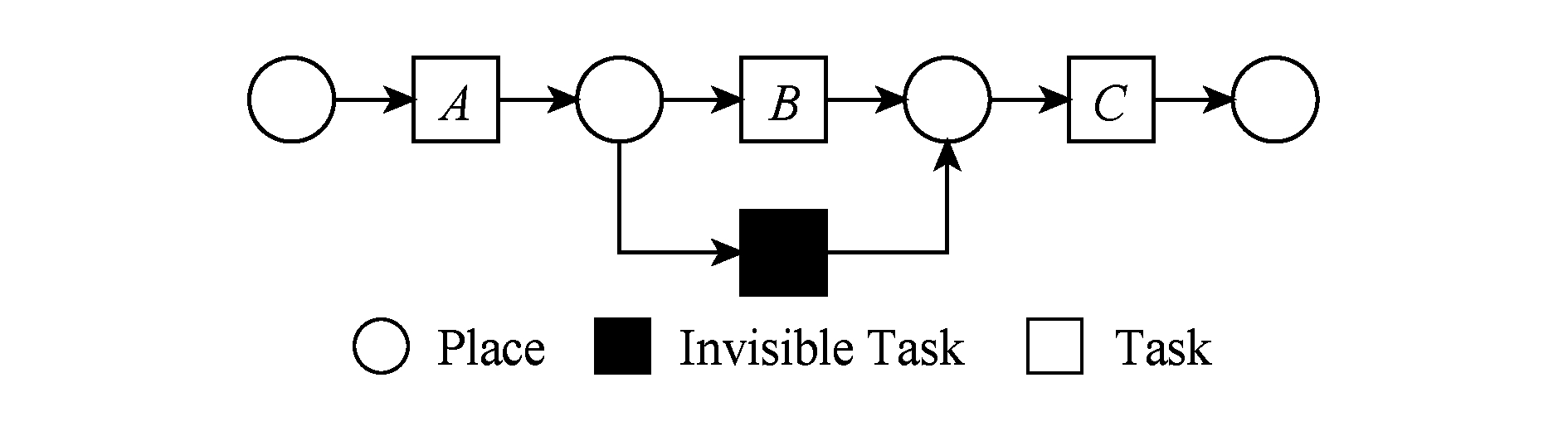
Fig. 4 An invisible task of SKIP type
图4 SKIP类型不可见任务
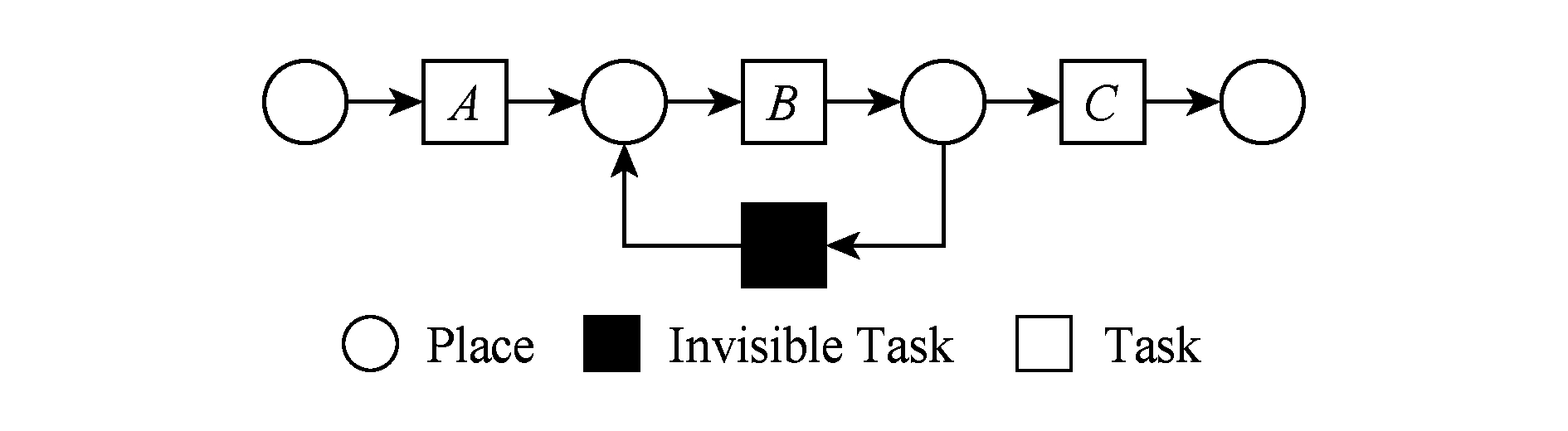
Fig. 5 An invisible task of REDO type
图5 REDO类型不可见任务
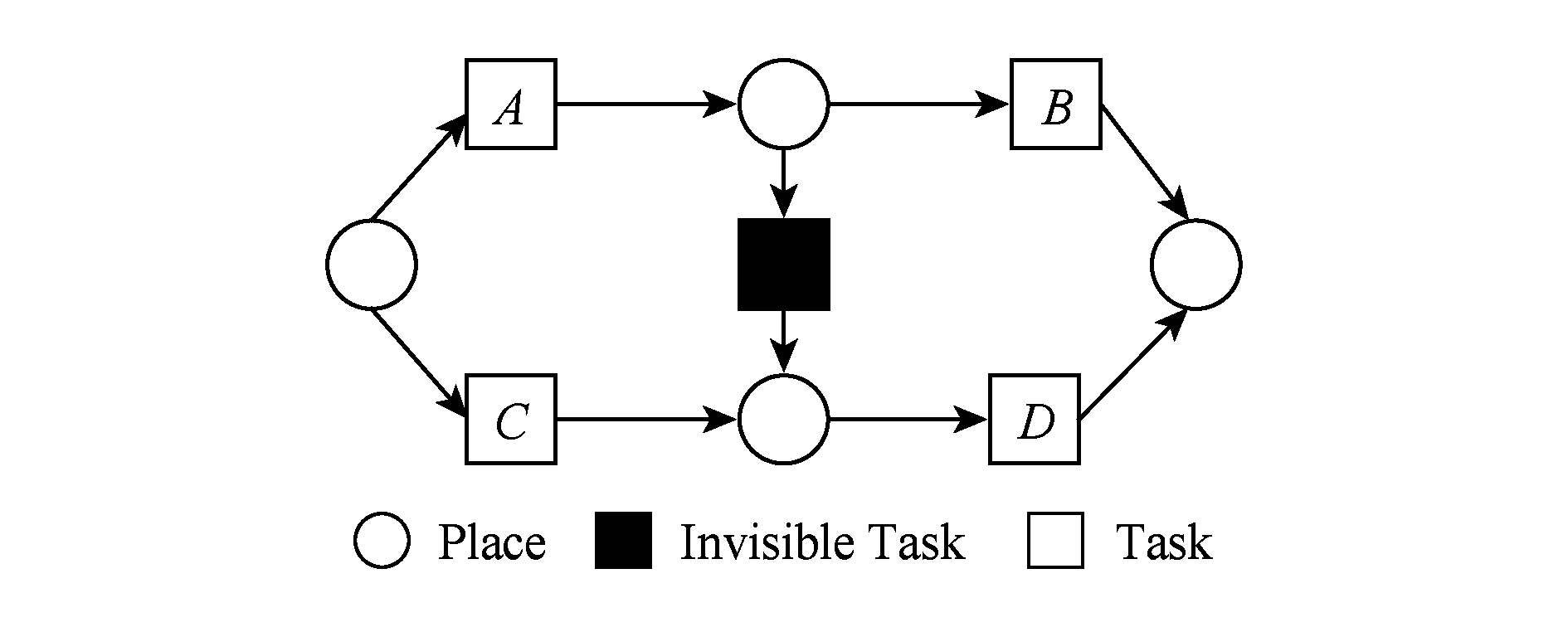
Fig. 6 An invisible task of SWITCH type
图6 SWITCH类型不可见任务
Table2TORMatrixInvolvinganInvisibleTaskofSKIPType
表2SKIP类型不可见任务的任务发生关系矩阵
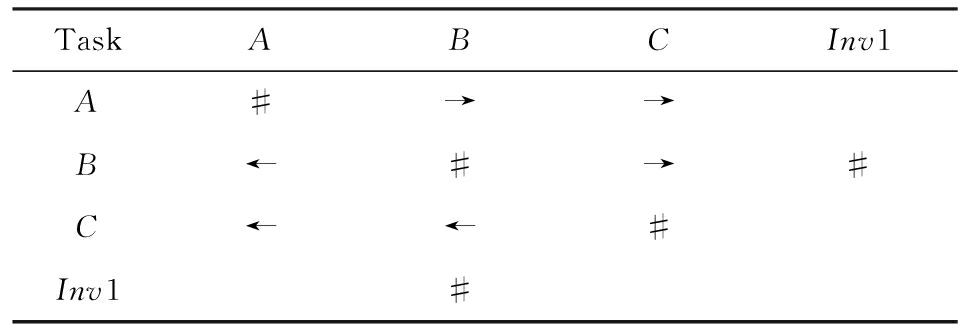
Notes: →means causality; ←means inverse causality;
#means conflict.
对于REDO类型的不可见任务,需要考虑任务间因果关系的变化.可以看出在图5所示模型中,不可见任务(称其为Inv2)和任务B构成了循环结构,导致了任务B可以重复执行.在处理这类不可见任务的时候,只需要考虑该不可见任务作用范围内可见任务的因果关系即可.虽然有Inv2→B和B→Inv2,但是最终填写矩阵的时候不考虑这2个依赖关系,而只考虑B→B.确定不可见任务的作用范围时,同样需要借助其输入输出边.将这个范围内的可见任务彼此之间的关系更新为正确的因果关系即可.该模型的关系矩阵如表3所示:
Table3TORMatrixInvolvinganInvisibleTaskofREDOType
表3REDO类型不可见任务的任务发生关系矩阵
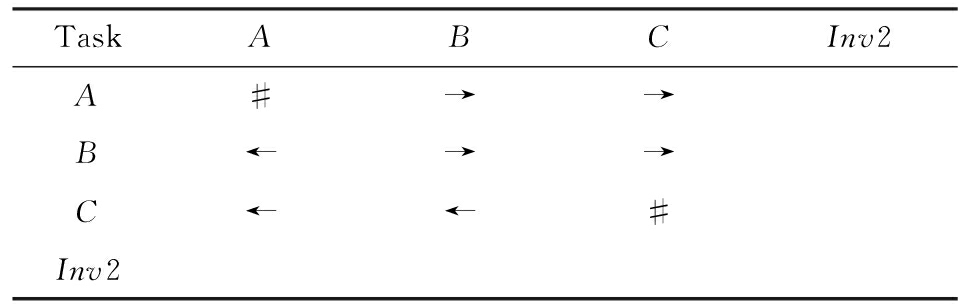
Notes: →means causality; ←means inverse causality;
#means conflict.
对于SWITCH类型的不可见任务,可以看出在图6所示模型中,不可见任务(称之为Inv3)导致了A和D之间多了一条可达路径.这种情况下,导致了A和D因果关系的产生.而不可见任务本身是不参与因果、并行和互斥3种关系中计算的.而该不可见任务的存在,使A和D之间多了一种因果关系.确定该不可见任务的作用范围,只需检测其导致了哪些任务从不可达变为可达(即因果关系).该模型的关系矩阵如表4所示:
Table4TORMatrixInvolvinganInvisibleTaskofSWITCHType
表4SWITCH类型不可见任务的任务发生关系矩阵
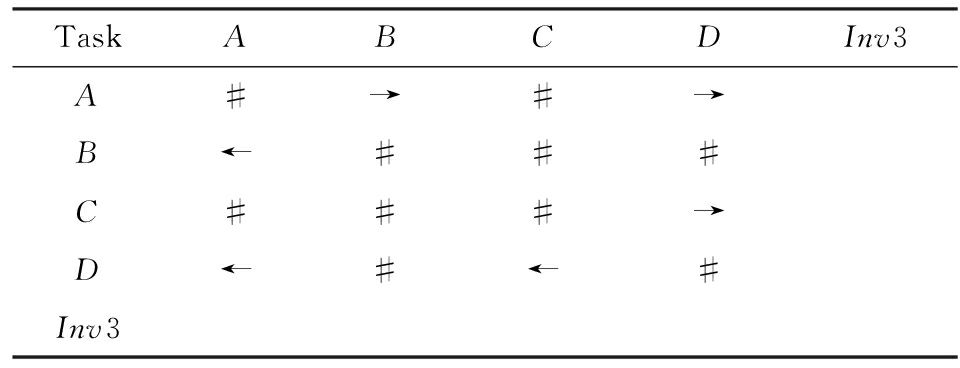
Notes: →means causality; ←means inverse causality;
#means conflict.
以上是对不可见任务造成影响的处理,通过这种方式可以很好地计算在不可见任务存在情况下的模型相似性,从而使结果更加合理和全面.
本文的实验环境如下:MacBook Pro,Intel Dual Core i5 CPU@2.6 GHz,8 GB DDR3@1 600 MHz,操作系统为OS X 10.8.3,Java Development Kit 1.8,Java虚拟机最大内存设置为2 GB.
实验所涉及的工业数据集主要包括3个:
1) 唐山轨道客车有限责任公司数据集(TC).本文实验的工业数据集包含从TC收集的91个流程模型.TC是中国第1家轨道交通制造企业,具有100多年的悠久历史,具有着超强的创新能力和研发能力,从动车组到中低速客车,从城轨车到特种车,有着完备的生产制造技术平台,其设备通用度高并且注重流程规范.
2) 东方锅炉股份有限公司数据集(DG).在本文实验的工业数据集包含从DG收集的82个流程模型.DG是国资委下属中国东方电气集团子公司下属公司,是一个热力发电系统设备、核能系统设备、煤气化设备等于一体的制造和服务供销商,拥有锅炉、核能发电、焊接、环境保护、材料、热强、自动化控制等科研机构.
3) SAP参考过程模型数据集(SAP).本文实验的工业数据集包含从SAP收集的流程381个模型.SAP是全球最大的企业资源规划和智能化解决方案的提供商,其业务包括高科技企业资源规划、消费品企业资源规划、零售企业资源规划、医疗企业资源规划、金融企业资源规划、公共事业企业资源规划、化工企业资源规划等.
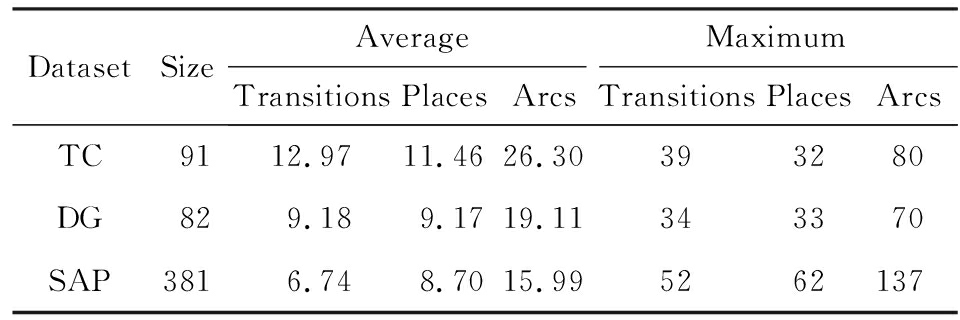
表5列出了上述3个工业数据集的基本结构特征,可以看到每个模型集中的平均 最大变迁数、平均
最大变迁数、平均 最大库所数和平均
最大库所数和平均 最大弧数.
最大弧数.
Table5TheBasicStructuralFeaturesofThreeIndustrialDatasets
表53个工业过程模型集的基本结构特征
下面通过对比TAR算法、PTS算法、BP算法、CF算法、SSDT算法及TOR算法在TC,DG,SAP这3个工业数据集上的运行时间,来评估TOR算法在实际工业数据集上的性能表现,具体实验结果如表6所示:
Table6TimeCostsofDifferentAlgorithmsontheThreeIndustrialDatasets
表6各个算法在不同工业数据集的时间消耗ms
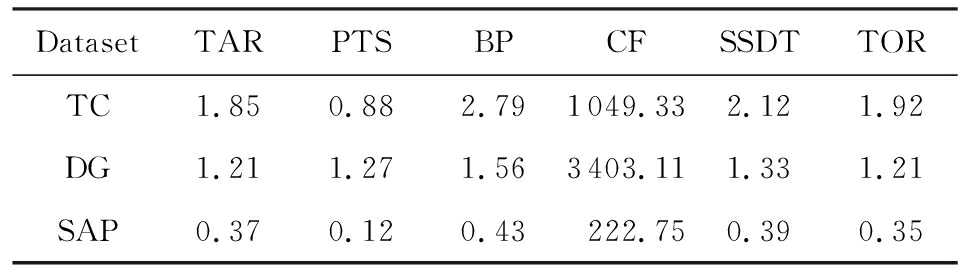
可以看出CF算法的时间复杂度较高,时间消耗远远高于其他算法;TAR算法、PTS算法、BP算法、SSDT算法、TOR算法基本在一个数量级上;TOR算法略优于BP算法、SSDT算法,与TAR算法持平,略慢于PTS算法.因此,TOR算法在实际工业数据集上运行性能表现良好.
汪抒浩等人[14]给出了流程模型行为相似性算法应当满足的5个性质,这些性质一定程度上可以作为评估不同相似性算法的依据.利用这5个性质比较TOR算法与主流模型行为相似性算法,结果如表7所示:
Table7TheSatisfactionofDifferentAlgorithmsontheFivePropertiesthataGoodSimilarityMeasureShouldHave
表7各个算法针对流程模型相似度的5个性质满足情况
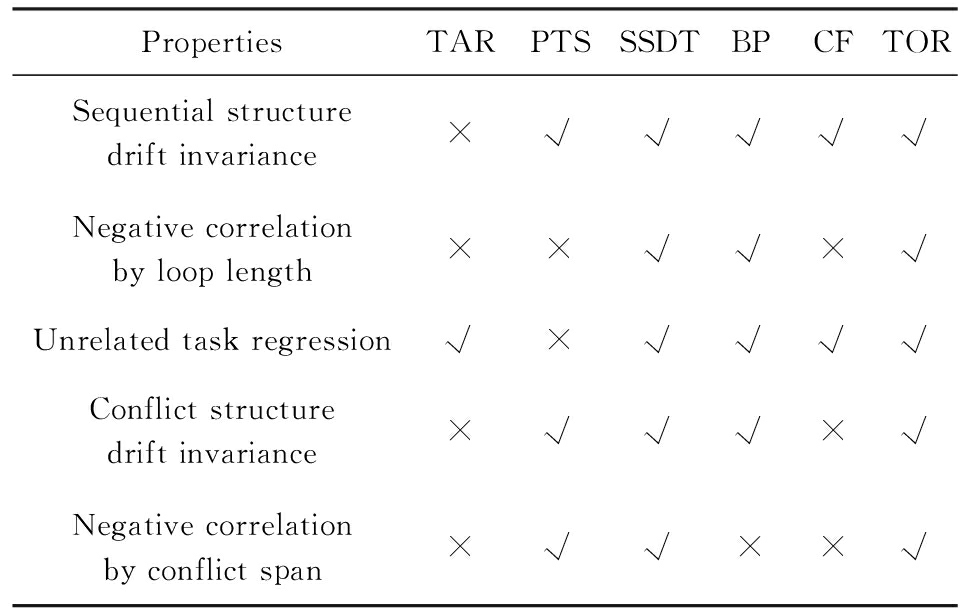
Notes: √means satisfaction; ×means unsatisfaction.
可以看出,TAR算法只满足一条性质,即互斥无关递减性;PTS算法满足3条性质,不满足循环长度负相关性和互斥无关递减性;BP算法满足4条性质,不满足互斥长度负相关性;而CF算法只满足2条性质;只有SSDT算法和TOR算法满足全部5条性质.由此可以看出,TOR算法的表现非常好,SSDT算法虽然也能满足全部5条性质,但其性能上表现得有所欠缺,且计算相似性时需要先对SSDT矩阵做同维化处理.
评估相似性算法时往往要求其对应的距离度量满足空间度量性质[20],包括非负性、对称性、恒等性以及三角不等式,非负性、对称性显而易见,恒等性要求过于苛刻,本文对三角不等式满足率进行验证.由于各个算法得到的值都是相似性,所以需要将其转化为距离,用dist(M1,M2)=1-sim(M1,M2)把相似性转化为距离.从包含n个模型的数据集中任意选出3个模型,共有![]() 种组合,对于这些组合分别验证3个不等式:
种组合,对于这些组合分别验证3个不等式:
dist(M1,M2)≤dist(M1,M3)+dist(M2,M3);
(8)
dist(M1,M3)≤dist(M1,M2)+dist(M2,M3);
(9)
dist(M2,M3)≤dist(M1,M2)+dist(M1,M3).
(10)
若针对![]() 组模型,共m组模型满足三角不等式性质,则该数据集的三角不等式满足率为
组模型,共m组模型满足三角不等式性质,则该数据集的三角不等式满足率为
(11)
TAR算法、PTS算法、SSDT算法、BP算法、CF算法以及TOR算法的三角不等式满足率如表8所示:
Table8TheSatisfactionRateofDifferentAlgorithmsontheTriangleInequality
表8各个相似性算法针对三角不等式的满足率%
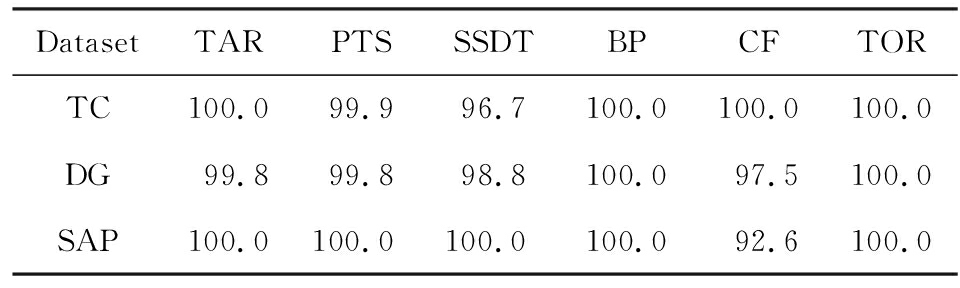
可以看出并不是所有的算法都满足三角不等式.TAR算法在DG数据集上不满足三角不等式;PTS算法在DG和TC数据集上不满足三角不等式;SSDT在TC和DG数据集上不满足三角不等式;CF算法在DG以及SAP数据集上不满足三角不等式;而BP算法和TOR算在3个数据集上均满足三角不等式.而与BP算法相比,TOR算法具有能处理不可见任务、区分循环和并发造成的任务间行为差异等优点.
针对现有流程模型行为相似性算法的不足,本文提出了一种能准确提取模型行为关系而又高效的算法——基于任务发生关系的模型相似性度量算法TOR.TOR算法首先把给定Petri网模型进行完全前缀展开,以清晰地表达模型的行为特征;接着,通过遍历对CPU图中的节点进行编号,以便于后续关系的求解;然后,对两两节点求解最近公共前驱,以确定节点对应的任务间的发生关系;最后,通过相应的公式计算模型的相似性.在算法的适用性上,TOR算法可以有效区分并发和循环的行为差异,高效处理非自由选择结构、不可见任务等复杂结构,TOR算法同时还可以有效地提取任务间多关系.基于来自3个企业的过程模型集的实验表明,TOR算法具有很好的性能优势,能满足相似性度量算法的全部5个优良性质,且其对应距离满足三角不等式.
在流程模型相似性算法评估方面,仍然缺乏一个权威的公认评估框架,在未来的工作中,将尝试提出一个合理评价相似性算法优劣的评估框架.同时,在进一步改进TOR算法以提升性能的同时,尝试将其应用于大量模型的索引方面.
参考文献
[1]Dumas M, García-Ba uelos L, Dijkman R M. Similarity search of business process models[J]. IEEE Data Engineering Bulletin, 2009, 32(3): 23-28
uelos L, Dijkman R M. Similarity search of business process models[J]. IEEE Data Engineering Bulletin, 2009, 32(3): 23-28
[2]Becker M, Laue R. A comparative survey of business process similarity measures[J]. Computers in Industry, 2012, 63(2): 148-167
[3]Rahm E, Bernstein P A. A survey of approaches to automatic schema matching[J]. The VLDB Journal, 2001, 10(4): 334-350
[4]Doan A H, Madhavan J, Domingos P, et al. Ontology matching: A machine learning approach[G]
 Handbook on Ontologies. Berlin: Springer, 2004: 385-403
Handbook on Ontologies. Berlin: Springer, 2004: 385-403
[5]Dijkman R, Dumas M, Van Dongen B, et al. Similarity of business process models: Metrics and evaluation[J]. Information Systems, 2011, 36(2): 498-516
[6]Ehrig M, Koschmider A, Oberweis A. Measuring similarity between semantic business process models[C]
 Proc of the 4th Asia-Pacific Conf on Conceptual Modeling. Sydney, Australia: ACS, 2007: 71-80
Proc of the 4th Asia-Pacific Conf on Conceptual Modeling. Sydney, Australia: ACS, 2007: 71-80
[7]Dijkman R, Dumas M, García-Ba uelos L. Graph matching algorithms for business process model similarity search[C]
uelos L. Graph matching algorithms for business process model similarity search[C]
 Proc of the 7th Int Conf on Business Process Management. Berlin: Springer, 2009: 48-63
Proc of the 7th Int Conf on Business Process Management. Berlin: Springer, 2009: 48-63
[8]La Rosa M, Dumas M, Uba R, et al. Merging business process models[C]
 Proc of OTM 2010. Berlin: Springer, 2010: 96-113
Proc of OTM 2010. Berlin: Springer, 2010: 96-113
[9]Li Chen, Reichert M, Wombacher A. On measuring process model similarity based on high-level change operations[C]
 Proc of the 27th Int Conf on Conceptual Modeling. Berlin: Springer, 2008: 248-264
Proc of the 27th Int Conf on Conceptual Modeling. Berlin: Springer, 2008: 248-264
[10]Weidlich M, Mendling J, Weske M. Efficient consistency measurement based on behavioral profiles of process models[J]. IEEE Trans on Software Engineering, 2011, 37(3): 410-429
[11]Polyvyanyy A, Weidlich M, Conforti R, et al. The 4C spectrum of fundamental behavioral relations for concurrent systems[C]
 Proc of the 35th Int Conf on Application and Theory of Petri Nets and Concurrency. Berlin: Springer, 2014: 210-232
Proc of the 35th Int Conf on Application and Theory of Petri Nets and Concurrency. Berlin: Springer, 2014: 210-232
[12]Zha Haiping, Wang Jianmin, Wen Lijie, et al. A workflow net similarity measure based on transition adjacency relations[J]. Computers in Industry, 2010, 61(5): 463-471
[13]Wang Jianmin, He Tengfei, Wen Lijie, et al. A behavioral similarity measure between labeled Petri nets based on principal transition sequences[C]
 Proc of OTM 2010. Berlin: Springer, 2010: 394-401
Proc of OTM 2010. Berlin: Springer, 2010: 394-401
[14]Wang Shuhao, Wen Lijie, Wei Daisen, et al. SSDT matrix-based behavioral similarity algorithm for process models[J]. Computer Integrated Manufacturing Systems, 2013, 19(8): 1822-1831 (in Chinese)(汪抒浩, 闻立杰, 魏代森, 等. 基于任务最短跟随距离矩阵的流程模型行为相似性算法[J]. 计算机集成制造系统, 2013, 19(8): 1822-1831)
[15]Murata T. Petri nets: Properties, analysis and applications[J]. Proceedings of the IEEE, 1989, 77(4): 541-580
[16]McMillan K L, Probst D K. A technique of state space search based on unfolding[J]. Formal Methods in System Design, 1995, 6(1): 45-65
[17]Engelfriet J. Branching processes of Petri nets[J]. Acta Informatica, 1991, 28(6): 575-591
[18]Esparza J, Römer S, Vogler W. An improvement of McMillan’s unfolding algorithm[J]. Formal Methods in System Design, 2002, 20(3): 285-310
[19]Wen Lijie, Wang Jianmin, van der Aalst W M P, et al. Mining process models with prime invisible tasks[J]. Data & Knowledge Engineering, 2010, 69(10): 999-1021
[20]Santini S, Jain R. Similarity measures[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1999, 21(9): 871-883
Song Jinfeng, Wen Lijie, and Wang Jianmin
(SchoolofSoftware,TsinghuaUniversity,Beijing100084)
AbstractSimilarity measures between process models are increasingly important for management, reuse, and analysis of process models in modern enterprises. So far, several approaches have been proposed and behavioral profile (BP) is a good concept to judge the behavioral consistency of process models, which describes the observable relations between tasks. However, all those approaches have their own advantages and disadvantages. Towards the hard problem of behavioral similarity measure between process models, especially to improve the effectiveness of BP, a new method for measuring the behavioral similarity between process models named TOR based on the occurrence relation among tasks is proposed. Based on complete prefix unfolding (CPU) technique of Petri nets, we propose the algorithms for numbering the nodes in a CPU and computing the least common precursors for each pair of nodes. Then we define the three basic occurrence relations between tasks: causal relation, concurrent relation and conflict relation. The algorithm for efficiently computing the relations and the formalism for computing the similarity are also given. TOR can handle both invisible tasks and non-free choice constructs. The experimental results show the effectiveness and efficiency of TOR. Compared with the existing mainstream behavioral similarity algorithms for process models, TOR can satisfy all the five properties that a good similarity algorithm should have.
Keywordssimilarity measure; occurrence relations of tasks; process model; complete prefix unfolding (CPU); Petri nets
This work was supported by the National Natural Science Foundation of China (61472207, 61325008).
通信作者:闻立杰(wenlj@tsinghua.edu.cn)
基金项目:国家自然科学基金项目(61472207,61325008)
修回日期:2016![]() 06
06![]() 02
02
收稿日期:2015![]() 12
12![]() 22;
22;
中图法分类号TP315

SongJinfeng, born in 1990. Master. Her main research interests include process model similarity and workflow technology.

WenLijie, born in 1977. PhD, associate professor, PhD supervisor. His main research interests include process data management, big process data, business process management and workflow technology, etc.

WangJianmin, born in 1968. PhD, professor, PhD supervisor. Senior member of CCF. His main research interests include business process management, workflow technology, big data and enterprise information systems, etc (jimwang@tsinghua.edu.cn).