陈加略 姜 远
(计算机软件新技术国家重点实验室(南京大学) 南京 210023) (软件新技术与产业化协同创新中心 南京 210023) (chenjl@lamda.nju.edu.cn)
摘 要: 脊回归(ridge regression, RR)是经典的机器学习算法之一,广泛应用于人脸识别、基因工程等诸多领域.其具有优化目标凸、存在闭合解、可解释性强以及易于核化等优点,但是脊回归的优化目标并没有考虑样本之间的结构关系.监督流形正则化学习是最具代表性的、最成功的脊回归正则化方法之一,其通过最小化每类类内方差来考虑样本之间的类内结构关系,可是单纯地只考虑类内结构仍然不够全面.以一种全新的视角重新审视最近提出的“最优间隔分布学习”原理,发现了最优间隔分布的目标可以同时优化类内间隔方差和类间间隔方差,从而同时优化了局部的类内结构和全局的类间结构.基于此提出了一种充分考虑数据结构化特征的脊回归算法——最优间隔分布脊回归(optimal margin distribution machine ridge regression, ODMRR)算法,该算法具有RR以及MRRR(manifold regularization ridge regression)的各种优势.最后通过实验验证了该方法具有优越的性能.
关键词: 脊回归;流形正则化;最优间隔分布;间隔方差;全局结构
脊回归(ridge regression, RR) [1] 的优化目标致力于最小化模型输出以及样本标记之间的二次误差,在人脸识别 [2] 、基因工程 [3] 、肝脏致癌预测 [4] 等诸多领域 [5] 有着广泛的应用.脊回归具有优化目标凸、存在闭式解、可解释性强以及易于核化等优点.但其优化目标并没有体现出数据的结构(structral)特征,这就意味着原始的脊回归算法没有考虑分类样本之间存在的潜在相互关系.在分类模型的优化目标中加入正则化约束来假设数据之间的结构关系通常可以有效地提升性能.流形正则化(manifold regularization, MR) [6] 是一种常见的做法,在诸多领域得到了广泛应用,如多标记学习 [7] 、集成学习 [8] 、特征提取 [9] 、谱图理论 [10] 、网页图像标记 [11] 等.MR是一种基于半监督 [12] 流形假设的适用于有标记和无标记样本学习的正则化框架,它的优化目标是最小化每类样本的类内方差,即要求分类器输出类内紧凑.将MR加入到有监督RR后的优化目标也是凸的,并且存在闭合解,因此具备脊回归算法所具有的各种优势.
相比于最大化最小间隔 [13] ,最优间隔分布学习理论 [14-15] 的核心思想在于通过优化“间隔分布”来有效提升模型的泛化性能.由此提出的ODM [16] ,LDM [17] 和cisLDM [18] 算法都取得了很好的性能 * 此类方法以往被称为“大间隔分布学习”方法 [17-18] ,但由于“间隔分布”本身并没有“大小”之别,因此“最优间隔分布”这个称谓比“最大间隔分布”更合适 [16] . .在最优间隔分布学习理论中,优化间隔分布是通过最大化间隔均值并同时最小化间隔方差 [13] 来实现的.本文选择了一种崭新的视角,从优化数据结构特征的角度重新分析了最优间隔理论中优化间隔分布的目标,并发现最小化间隔方差这个目标可以拆解成最小化类内间隔方差和最大化类间间隔方差2项.针对分类模型进行分析,可以发现,MR中最小化类内方差的目标和最优间隔分布学习理论中最小化间隔方差的目标是相同的,都要求类内紧凑,即两者都是在优化数据的局部类内结构.进一步对最优间隔学习理论中最大化间隔均值和最小化类间间隔方差这2项的目标进行分析,可以发现两者共同作用的目的都是为了使分类器输出类间松散.而类间松散可以看成是优化一种全局的结构关系.所以,MR的优化目标只优化了类内紧凑这一种局部分类特性,而最优间隔分布学习理论不仅考虑了类内紧凑,还进一步优化了类间松散这一种全局分类特性.换句话说,相比于MR,最优间隔分布学习理论考虑了更加全面的数据结构信息.
在本文中,我们借鉴了最优间隔分布学习理论思想,并提出了一种新的正则化方法即最优间隔分布正则化.流形正则化方法可看作为最优间隔正则化方法的特例.我们将其应用于脊回归中得到了最优间隔分布脊回归(optimal margin distribution machine ridge regression, ODMRR)算法,ODMRR算法的优化目标也是凸的,并且具有解析解,在多个真实数据集上取得很好效果.
假设X∈ ![]() d 是样本空间,Y={+1,-1}是标记集合,D是X×Y上的潜在分布,训练集是从D上随机独立同分步采样的 n 个样本,即:
d 是样本空间,Y={+1,-1}是标记集合,D是X×Y上的潜在分布,训练集是从D上随机独立同分步采样的 n 个样本,即:
S ={( x 1 , y 1 ),( x 2 , y 2 ),…,( x n , y n )}.
机器学习的目标就是通过训练集 S 学习一个分类器,使其能够预测未来从未见过的样本标记.
假设 f ( x )= w T φ ( x )+ b 是一个线性判别模型.其中 w 是线性分类面, b 是截距, φ ( x )是 x 在核 k 上的一个特征投影,并满足 k ( x i , x j )= φ ( x i ) T φ ( x j ).样本( x i , y i )的间隔可以定义为
γ i = y i ( w T φ ( x i )+ b ), ∀ i =1,2,…, n .
为了方便表示,可以将分类面 w 以及截据 b 拼接成一个增广的向量: w ′=[ w ; b ],将所有样本的特征尾部拼上一个常数1形成增广的特征 φ ( x i )′=[ φ ( x i );1].令 X ′=[ φ ( x 1 )′, φ ( x 2 )′,…, φ ( x n )′], y =[ y 1 , y 2 ,…, y n ] T .
对于线性判别分类器,其解 w *通常存在表示形式:
φ ( x i )= X α ,
(1)
其中, α =[ α 1 , α 2 ,…, α n ] T 是系数向量.可以将系数向量 α 和截距 b 拼成一个增广的向量: α ′=[ α ; b ].
为了方便将算法推广到核空间上,我们用 K 表示 n × n 的核矩阵,其第( i , j )个位置的元素为 k ( x i . x j ),可以发现 K = X T X .在 K 的最后一行拼上 K ′=[ K ; 1 1× n ],其中 1 m × n 表示维度为 m × n 的全1矩阵.
1 . 1 脊回归和流形正则化
脊回归(rigde regression, RR)的优化目标是找到一个分类面 w 和截距 b ,使得样本输出 f ( x i )和样本标记 y i 之间的二次误差之和尽量小.其优化目标可以形式化为
![]() ( y i - w ′ T φ ( x i )′) 2 + λ w ′ T Aw ′,
( y i - w ′ T φ ( x i )′) 2 + λ w ′ T Aw ′,
(2)
其中, λ 是正则化因子 ![]() 第1项的目标即是二次误差项,第2项则是为了减小模型的结构风险.
第1项的目标即是二次误差项,第2项则是为了减小模型的结构风险.
式(2)中的目标可以通过式(1)的表示定理转化成等价的形式:
![]() y T y -2 y T K ′ α ′+ α ′ T K ′ K ′ T α ′+ λ α ′ T Bα ′.
y T y -2 y T K ′ α ′+ α ′ T K ′ K ′ T α ′+ λ α ′ T Bα ′.
(3)
式(3)的优化目标是凸的,并且具有闭合的解析解,其解的形式为
α ′=( λ B + K ′ K ′ T ) -1 K ′ y ,
其中 ![]()
流形假设数据采样于高维欧式空间的一个低维流形,处于局部领域的示例具有相似的性质,即它们的标记也应该相似.对于分类问题,流形正则化的目标是减小2类样本的类内方差.所以,监督型流形正则化的脊回归(manifold regularization ridge regression, MRRR)的优化目标表示为
![]() ( y i - w ′ T φ ( x i )′) 2 + λ 1 w ′ T A w ′+
( y i - w ′ T φ ( x i )′) 2 + λ 1 w ′ T A w ′+
![]() ( w ′ T φ ( x i )′- w ′ T φ ( x j )′) 2 ),
( w ′ T φ ( x i )′- w ′ T φ ( x j )′) 2 ),
(4)
其中, λ 1 和 λ 2 是正则化因子, C 1和 C 2分别代表第1和第2类样本.式(4)中最后2项就是流形正则化项,它们分别优化了第1,2类样本的类内方差.可以发现,如果式(4)中的 λ 2 =0,MRRR将会退化为RR算法,即RR是MRRR的特例.
式(4)中的目标也可以通过式(1)中的表示定理转化成等价形式:
![]()
α ′ K ′( I n +2 λ 2 M ) K ′ T α ′+ λ 1 α ′ T Bα ′,
(5)
其中, I n 表示维度为 n 的单位阵,而:
n 1和 n 2分别表示第1,2类样本的数目.
式(5)的目标也是凸的,并且也具有闭合的解析解,其解的形式为
α ′=( λ 1 B + K ′( I n +2 λ 2 M ) K ′ T ) -1 K ′ y .
1 . 2 最优间隔分布学习理论
相比于最大化最小间隔,最优间隔分布学习理论揭示了优化间隔分布对于提升模型的泛化性能将更加显著.最优间隔分布学习理论指出优化间隔分布具体表现为最大化间隔均值和最小化间隔方差.其中,间隔均值定义为
φ ( x i )′= ![]() y T X ′ w ′.
y T X ′ w ′.
间隔方差定义为
![]() ( y i w ′ T φ ( x i )- y j w ′ T φ ( x j )) 2 =
( y i w ′ T φ ( x i )- y j w ′ T φ ( x j )) 2 =
![]() ( n w ′ T X ′ X ′ T w ′- w ′ T X ′ yy T X ′ T w ′).
( n w ′ T X ′ X ′ T w ′- w ′ T X ′ yy T X ′ T w ′).
根据间隔方差的定义可以发现,当 y i = y j 时,间隔方差的形式和流形正则化项的形式相同,即对于分类模型,类内方差即是类内的间隔方差.两者的目的都是为了使分类器输出类内紧凑.
当 y i ≠ y j 时,间隔方差的形式为
φ ( x i )′+ w ′ T φ ( x j )′) 2 ,
经过分析可以发现,这一项实际上代表了类间间隔方差.最小化间隔方差和最大化间隔均值两者共同作用的目标是为了使分类器输出类间分散.
所以最优间隔分布学习理论既考虑了使分类器输出类内紧凑这一局部分类特性,还考虑了使分类器输出类间分散这一全局分类特性.
最优间隔分布(ODM)的主要思想就是利用最优间隔分布学习理论中同时考虑分类器输出类内紧凑、类间松散这2个分类特性的优势.将最大化间隔均值和最小化间隔方差作为正则化项加入到分类模型的优化目标中.
脊回归的二次误差项表示为等价的矩阵形式:
![]() φ ( x i )′) 2 =
φ ( x i )′) 2 =
y T y -2 y T X ′ T w ′+ w ′ T X ′ X ′ T w ′,
可以发现,最小化-2 y T X ′ T w ′的目标就是最大化间隔均值,即脊回归的优化目标中本身就包含了最大化间隔均值.所以,对于脊回归问题,最优间隔分布只需要考虑最小化间隔方差一项正则化项就可以了.于是,我们将ODM运用于脊回归问题,并得到了ODMRR的优化目标:
![]() ( y i - w ′ T φ ( x i )′) 2 + λ 1 w ′ T Aw ′+
( y i - w ′ T φ ( x i )′) 2 + λ 1 w ′ T Aw ′+
λ 2 ![]() s ij ( y i w ′ T φ ( x i )′- y j w ′ T φ ( x j )′) 2 =
s ij ( y i w ′ T φ ( x i )′- y j w ′ T φ ( x j )′) 2 =
w ′ T X ′( I n +2 λ 2( D ∘ diag ( yy T )-
S ∘ yy T )) X ′ T w ′+ λ 1 w ′ T Aw ′,
(6)
其中, diag 函数的作用是用原矩阵的对角元素组成同维的新矩阵,“∘”表示Hadamard乘积, s ij 表示样本 i 和样本 j 之间的相似性度量. s ij 可以采用等价距离,即 s ij =1,那么此时第3项就是间隔方差项.也可以采用高斯距离,其定义为 ![]() / σ 2 ). S 是 n × n 维的相似性矩阵,其第( i , j )个元素即为 s ij . D 是 n × n 维的对角矩阵,其第 i 个对角元素为
/ σ 2 ). S 是 n × n 维的相似性矩阵,其第( i , j )个元素即为 s ij . D 是 n × n 维的对角矩阵,其第 i 个对角元素为 ![]()
定理1 . 优化目标(6)中的最优解 w * 存在式(1)的表示形式.
证明. w * 可以分解成有 φ ( x i )伸张以及和 φ ( x i )正交2个部分,形式为
φ ( x i )+ v = Xα + v ,
其中, X T v =0.可以发现:
X ′ T w ′= X T w + b = X T ( Xα + v )+ b = X T Xα + b ,
所以,在优化目标式(6)中,只有 w ′ T Aw ′与 v 相关,其他项都与 v 独立,可以证明:
w ′ T Aw ′= w T w =( Xα + v ) T ( Xα + v )=
α T X T Xα + v T v ≥ α T X T Xα
且不等式当且仅当 v =0时才成立.
所以,设置 v =0不会影响到优化目标式(6)的最优值,即 w * 可以表示成式(1)的表示形式.
证毕.
于是,通过定理1,可以将优化目标式(6)转换为等价的形式:
![]()
α ′ K ′( I n +2 λ 2( D ∘ diag ( yy T )-
S ∘ yy T )) K ′ T α ′+ λ 1 α ′ T Bα ′.
(7)
式(7)的优化目标是凸的,也具有闭合和解析解,其解的形式为
α ′=( λ 1 B + K ′( I n +2 λ 2( D ∘ diag ( yy T )-
S ∘ yy T )) K ′ T ) -1 K ′ T y .
为了能够控制类内间隔方差和和类间间隔方差的权重,也可以把优化目标等价表示为
![]() ( y i - w ′ T φ ( x i )′) 2 + λ 1 w ′ T Aw ′+
( y i - w ′ T φ ( x i )′) 2 + λ 1 w ′ T Aw ′+
λ 2 ![]() s ij ( w ′ T φ ( x i )′- w ′ T φ ( x j )′) 2 +
s ij ( w ′ T φ ( x i )′- w ′ T φ ( x j )′) 2 +
![]() s ij ( w ′ T φ ( x i )′- w ′ T φ ( x j )′) 2 +
s ij ( w ′ T φ ( x i )′- w ′ T φ ( x j )′) 2 +
2 λ 3 ![]() s ij ( w ′ T φ ( x i )′+ w ′ T φ ( x j )′) 2 ,
s ij ( w ′ T φ ( x i )′+ w ′ T φ ( x j )′) 2 ,
(8)
其中, λ 1, λ 2, λ 3全是正则化因子,式(8)中第2项是第1类的类内间隔分布,第3项是第2类的类内间隔分布,最后一项是2类样本的类间间隔分布,我们将式(8)的优化目标记为ODMRR-3h.可以发现,如果 λ 3=0,式(8)的优化目标就会退化为式(4)流形正则化方法的优化目标,如果 λ 2=0和 λ 3=0,式(8)的优化目标将会退化为式(2)的脊回归的优化目标.所以脊回归算法以及流形正则化的脊回归算法都可以看作最优间隔正则脊回归算法的特例.
根据定理1的证明,式(8)也存在等价的表示形式:
![]()
α ′( λ 1 B + K ′( I n + P + Q ) K ′ T ) α ′,
(9)
其中,
P = ![]() +
+ ![]() ,
,
Q = 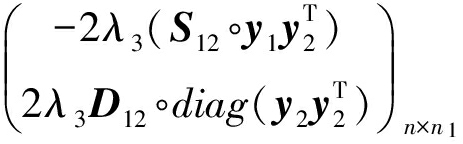 +
+ ![]() ,
,
y i 为第 i 类样本的标记向量, S ij 为第 i 类样本和第 j 类样本之间的相似性矩阵,矩阵 D 是一个对角矩阵,其第 j 个对角元上的元素是 S 矩阵中第 j 列中所有行下标 i 类别为 p 的元素之和,所以其定义式可以写为 D pq = 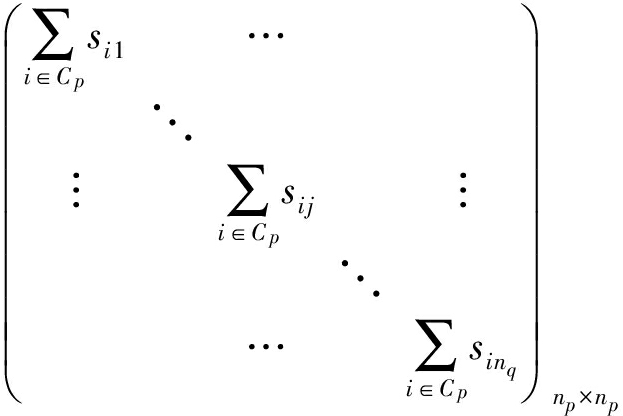 .
.
式(9)的优化目标为凸,其解也为解析解,其形式为
α ′=( λ 1 B + K ′( I n + P + Q ) K ′ T ) -1 K ′ y .
本节将先介绍实验的设置,然后给出实验的结果,并对结果进行简单地分析.
4 . 1 实验设置
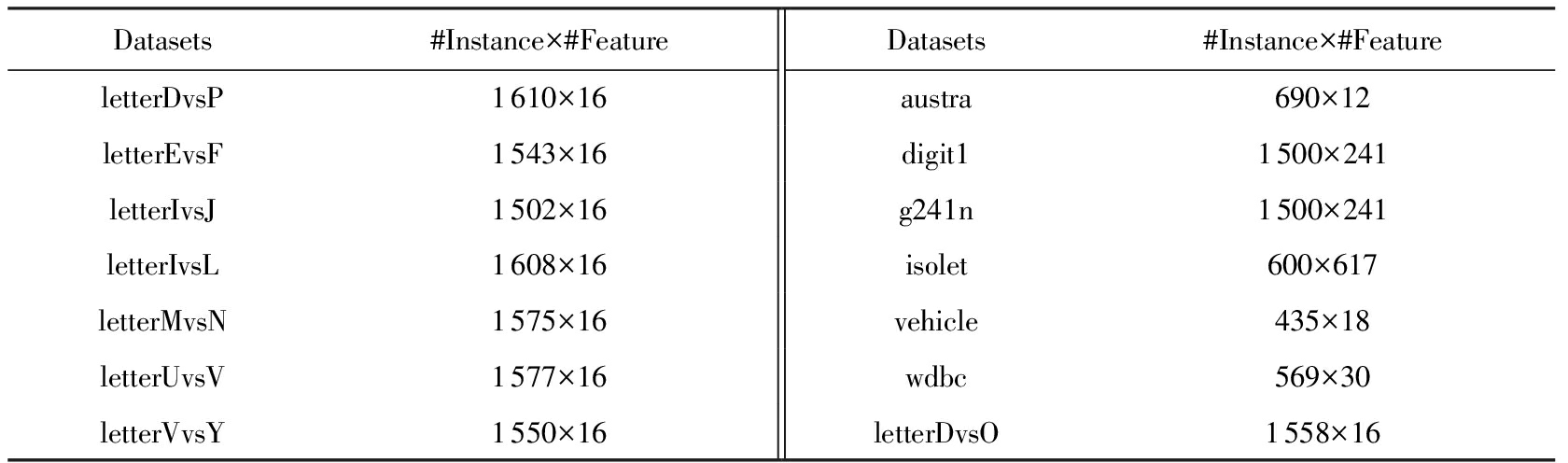
实验共选择了14个数据集,其中digit1和g241n是半监督数据集.austra,isolet,vehicle和wdbc都是UCI数据集.Letter是多标记数据集,从中选出8对相对比较难分类的字符组成了8组2分类数据集,分别记为DvsP,EvsF,IvsJ,IvsL,MvsN,UvsY,VvsY,DvsO.表1中列出了所有数据集的样本和特征维度.并且所有数据集都通过随机采样以1∶1的比例平分成训练数据和测试数据.
实验1共选择了6组对比算法:RR,MRRR,ODMRR,ODMRR_3h,ODMRR_S1,ODMRR_S1_3h.其中,在ODMRR算法中,带有_S1后缀代表相似性矩阵 S 采用全1矩阵,没有_S1后缀的相似性矩阵 S 则采用高斯距离矩阵.带有_3h的后缀表示优化目标采用式(9)的表示形式,否则采用式(6)的表示形式.
Table 1 Dataset and the Dimension of Its Instances and Features
表1 数据集及其样本和特征维度
4 . 2 实验结果
表2中的实验结果是在每个数据集上进行10次实验所得到平均精度和方差.其中,深色背景都是我们算法的实验结果.我们使用加粗字体来标明每个数据集中测试精度最高的一组算法的结果.
在每轮实验中,所有参数全部都是采用固定其余所有参数,然后通过10次交叉验证的方法选出的最优值.在交叉验证的过程中,选择80%的训练数据用于训练模型,用剩下的20%的数据来验证模型参数.10次交叉验证又包含先粗调后细调的过程,粗调的参数取值为[10 -5 ,10 -4 ,…,10 5 ],细调的参数取值为[2 -4 ,2 -3 ,…,2 4 ].而ODMRR和ODMRR_3h算法中使用到的高斯距离矩阵中的 σ 参数则采用 σ =1的默认值设置.
Table 2 Experiment Result
表2 实验结果
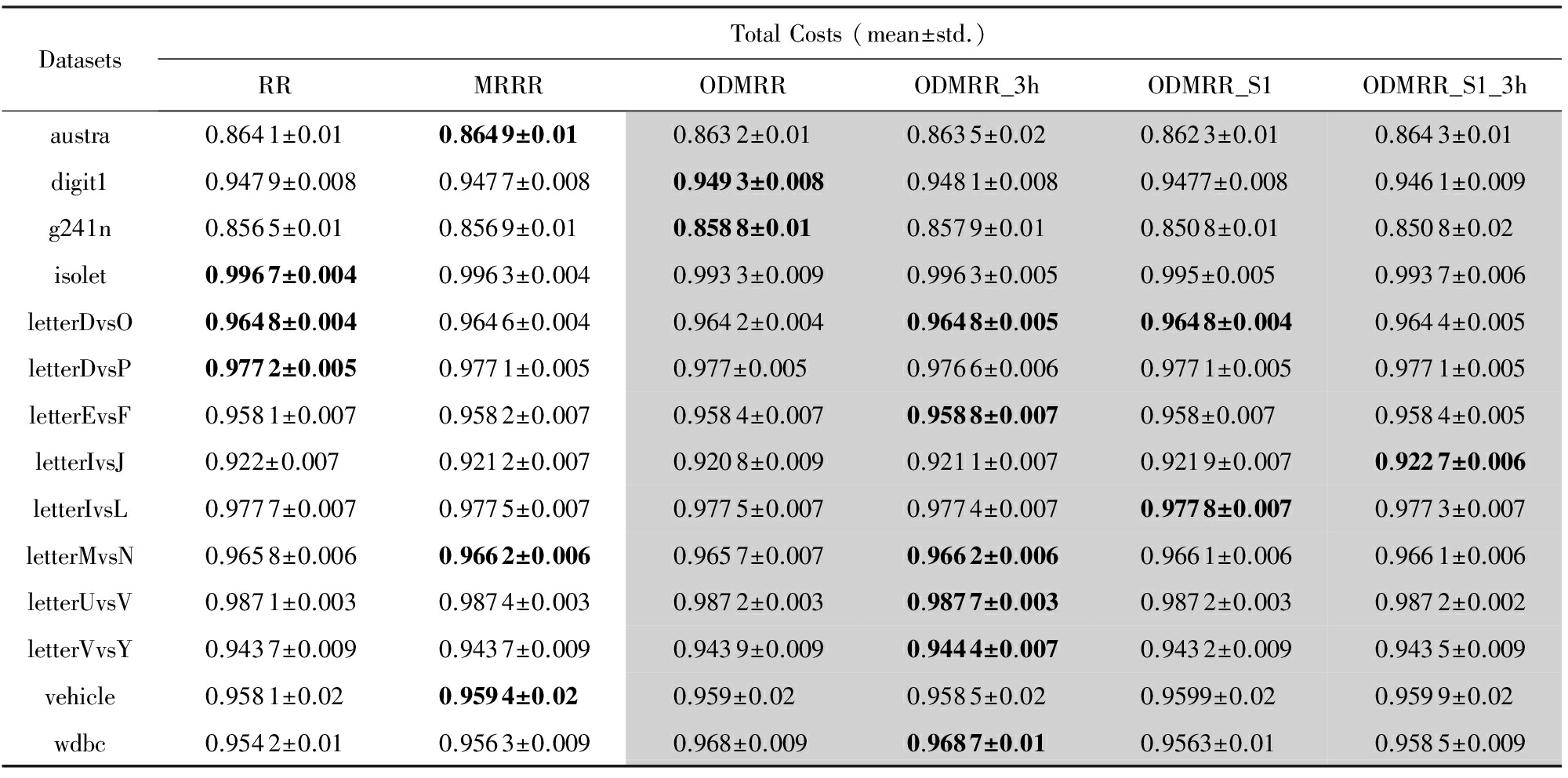
由于3个脊回归的算法都需要计算一次矩阵的求逆计算,所以这3个算法的速度都不是特别快.在这3个算法中,RR包含一个参数,MRRR包含2个参数,而ODMRR算法包含3个参数.为了减少调参的时间,我们采用固定其余参数,只调整一个参数的方法.从表2的实验结果中可以发现,即便在如此简单的调参方法下,ODMRR算法在14个数据集中有10个达到最优结果,其中2个和最优结果打平.并且可以很明显地发现对于给类内间隔分布和类间间隔分布分配不同参数的ODMRR_3h方法相比使用相同参数的ODMRR方法取得了更多的最优结果.所以这也一定程度上说明,类内结构关系和类间结构关系在对于分类器的贡献在部分数据集上可能是不同的.
脊回归算法及其流形正则化算法是机器学习领域的经典方法.这2种算法都没有充分考虑数据全局的结构化关系.我们以一种全新的视角分析了最优间隔分布学习理论对于优化间隔分布的优化目标、提出了了一种充分考虑类内结构关系和类间结构关系的正则化脊回归算法——最优间隔分布脊回归算法(ODMRR).由于脊回归算法和流形正则化的脊回归算法都是ODMRR算法的特例,所以ODMRR算法保有了脊回归和流形正则化的脊回归算法中所共有的优化目标为凸函数、有解析解、易于核化等优势.考虑到类内结构关系和类间结构关系对于模型的贡献不同,我们也提出了ODMRR算法的一种简单变形ODMRR_3算法方便用户调节两者之间的权重.最后,我们在真实数据集上进行了实验且在大部分数据集上取得了最优的结果.
参考文献:
[1] Hoerl A E, Kennard R W. Ridge regression: Biased estimation for nonorthogonal problems[J].Technometrics, 1970, 12(1): 55-67
[2] Xue Hui, Zhu Yulian, Chen Songcan. Local ridge regression for face recognition[J].Neurocomputing, 2009, 72(4): 1342-1346
[3] Cule E, Vineis P, De Iorio M. Significance testing in ridge regression for genetic data[J]. BMC Bioinformatics, 2011, 12(1): 372-378
[4] Liu Shujie, Kawamoto T, Morita O, et al. Discriminating between adaptive and carcinogenic liver hypertrophy in rat studies using logistic ridge regression analysis of toxicogenomic data: The mode of action and predictive models[J]. Toxicology and Applied Pharmacology, 2017, 318(9): 79-87
[5] Marquardt D W, Snee R D. Ridge regression in practice[J].The American Statistician, 1975, 29(1): 3-20
[6] Belkin M, Niyogi P, Sindhwani V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples[J]. Journal of Machine Learning Research, 2006, 7(11): 2399-2434
[7] Luo Yong, Tao Dacheng, Xu Chang, et al. Multiview vector-valued manifold regularization for multilabel image classification[J]. IEEE Trans on Neural Networks and Learning Systems, 2013, 24(5): 709-722
[8] Geng Bo, Tao Dacheng, Xu Chao, et al. Ensemble manifold regularization[J].IEEE Trans on Pattern Analysis and Machine Intelligence, 2012, 34(6): 1227-1233
[9] Xu Zenglin, King I, Lyu M R T, et al. Discriminative semi-supervised feature selection via manifold regularization[J]. IEEE Trans on Neural Networks, 2010, 21(7): 1033-1047
[10] Luo Siwei, Zhao Lianwei. Manifold learning algorithms based on spectral graph theory[J].Journal of Computer Research and Development, 2006, 43(7): 1173-1179 (in Chinese)(罗四维, 赵连伟. 基于谱图理论的流形学习算法[J]. 计算机研究与发展, 2006, 43(7): 1173-1179)
[11] Liu W, Liu H, Tao D, et al. Manifold regularized kernel logistic regression for Web image annotation[J]. Neurocomputing, 2016, 172(C): 3-8
[12] Zhu Xiaojin. Semi-supervised learning literature survey[J].Computer Science, University of Wiscousin-Madison, 2006, 2(3): 4-64
[13] Vapnik V. The Nature of Statistical Learning Theory[M]. Berlin: Springer, 1995
[14] Zhou Zhihua. Large margin distribution learning[C] //Proc of the Workshop on Artificial Neural Networks in Pattern Recognition. Berlin: Springer, 2014: 1-11
[15] Gao Wei, Zhou Zhihua. On the doubt about margin explanation of boosting[J].Artificial Intelligence, 2013, 203(5): 1-18
[16] Zhang Teng, Zhou Zhihua. Multi-class optimal distribution machine[C] //Proc of the 34th Int Conf on Machine Learning. 2017 [2017-04-01]. http://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/icml17mcODM.pdf
[17] Zhang Teng, Zhou Zhihua. Large margin distribution machine[C] //Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2014: 313-322
[18] Zhou Yuhang, Zhou Zhihua. Large margin distribution learning with cost interval and unlabeled data[J]. IEEE Trans on Knowledge and Data Engineering, 2016, 28(7): 1749-1763
Chen Jialüe and Jiang Yuan
( National Key Laboratory for Novel Software Technology ( Nanjing University ), Nanjing 210023) ( Collaborative Innovation Center of Novel Software Technology and Industrialization , Nanjing 210023)
Abstract: Ridge regression (RR) has been one of the most classical machine learning algorithms in many real applications such as face detection, cell prediction, etc. The ridge regression has many advantages such as convex optimization objection, closed-form solution, strong interpretability, easy to kernelization and so on. But the optimization objection of ridge regression doesn’t consider the structural relationship between instances. Supervised manifold regularized (MR) method has been one of the most representative and successful ridge regression regularized methods, which considers the instance structural relationship inter each class by minimizing each class’s variance. But considering the structural relationship interclasses alone is not a very comprehensive idea. Based on the recent principle of optimal margin distribution machine (ODM) learning with a novel view, we find the optimization object of ODM can include the local structural relationship and the global structural relationship by optimizing the margin variance interclasses and the margin variance intraclasses. In this thesis, we propose a ridge regression algorithm called optimal margin distribution machine ridge regression (ODMRR) which fully considers the structural character of the instance. Besides, this algorithm can still contain all the advantages of ridge regression and manifold regularized ridge regression. Finally, the experiments validate the effectiveness of our algorithm.
Key words: ridge regression (RR); manifold regularization; optimal margin distribution machine (ODM); margin variance; global structure
Received: n, born in 1976.
Received: her PhD degree in computer science from Nanjing University in 2004. Currently professor and PhD supervisor at the Department of Computer Science & Technology, Nanjing University. Her main research interests include machine learning and data mining.

Chen Jial ü e , born in 1991. PhD. His main research interests include machine learning and data mining.
收稿日期: 2017-05-23;
修回日期: :2017-06-25
基金项目: 国家自然科学基金项目(61673201) This work was supported by the National Natural Science Foundation of China (61673201).
通信作者: 姜远(jiangy@lamda.nju.edu.cn)
中图法分类号: TP181