 或不连约束)可资利用时,通过将其结合到相应目标所得优化模型已证明能有效提高聚类性能,然而,现有通过在目标函数中添加约束惩罚项的常用结合方式往往会破坏其原有凸目标的凸性.鉴于此,提出了一种新的结合此类弱监督辅助信息的凸聚类算法.其实现关键是代替在目标函数中添加约束,而是通过对目标函数中距离度量的改造以保持凸性,由此既保持了原凸聚类的优势同时有效提高了聚类性能.
或不连约束)可资利用时,通过将其结合到相应目标所得优化模型已证明能有效提高聚类性能,然而,现有通过在目标函数中添加约束惩罚项的常用结合方式往往会破坏其原有凸目标的凸性.鉴于此,提出了一种新的结合此类弱监督辅助信息的凸聚类算法.其实现关键是代替在目标函数中添加约束,而是通过对目标函数中距离度量的改造以保持凸性,由此既保持了原凸聚类的优势同时有效提高了聚类性能. 权祯臻 陈松灿
(南京航空航天大学计算机科学与技术学院 南京 211106) (zz.quan@nuaa.edu.cn)
摘 要: 基于目标函数的聚类是一类重要的聚类分析技术,其中几乎所有算法均是经非凸目标的优化建立,因而难以保证全局最优并对初始值敏感.近年提出的凸聚类通过优化凸目标函数克服了上述不足,同时获得了相对更稳定的解.当现实中存在辅助信息(典型的如必连和  或不连约束)可资利用时,通过将其结合到相应目标所得优化模型已证明能有效提高聚类性能,然而,现有通过在目标函数中添加约束惩罚项的常用结合方式往往会破坏其原有凸目标的凸性.鉴于此,提出了一种新的结合此类弱监督辅助信息的凸聚类算法.其实现关键是代替在目标函数中添加约束,而是通过对目标函数中距离度量的改造以保持凸性,由此既保持了原凸聚类的优势同时有效提高了聚类性能.
或不连约束)可资利用时,通过将其结合到相应目标所得优化模型已证明能有效提高聚类性能,然而,现有通过在目标函数中添加约束惩罚项的常用结合方式往往会破坏其原有凸目标的凸性.鉴于此,提出了一种新的结合此类弱监督辅助信息的凸聚类算法.其实现关键是代替在目标函数中添加约束,而是通过对目标函数中距离度量的改造以保持凸性,由此既保持了原凸聚类的优势同时有效提高了聚类性能.
关键词: 基于目标函数的聚类;凸聚类;弱监督信息;约束;距离度量;半监督聚类
聚类算法是多元数据分析的重要工具,是知识发现和数据挖掘的关键技术,已广泛用于生物信息学 [1] 、图像处理 [2] 、信息检索 [3] 等领域.聚类是依据给定的相似性度量,将数据集样本划分成若干个通常不相交的子集或簇,使得簇内相似度和簇间相异度最大 [4] .目前已有众多聚类算法被提出 [5] ,其中,基于目标函数的聚类是一类重要的聚类方法,其通过最小化或最大化一个全局目标函数实现对无标记数据的最优划分 [6] ,常见此类算法有 k 均值算法、模糊 k 均值算法、最大期望聚类算法等.然而,几乎所有基于目标函数的聚类算法都难以保证解及性能的稳定性,归咎于通过非凸目标的优化建立,易陷入局部最优解且对初始值敏感.为克服上述不足,2011年,Lindsten等人 [7] 和Hocking等人 [8] 分别将 k 均值算法和层次聚类凸松弛化,通过促使簇中心的融合获取全局最优解.鉴于凸聚类具有可求取全局最优解、对数据扰动相对不敏感及自动获取簇数的优势,近年已备受关注,相关研究集中在优化方面(如文献[9])和数据结构信息的结合方面(如文献[10-13]).
聚类本身是一种典型的无监督学习任务,然而当有一些额外的监督信息可资利用时,利用这些监督信息能获得更优的聚类效果 [14] .常用的监督信息大致有2种:1)个体的样本标记或类别;2)样本必连(must-link)和不连(cannot-link)约束,前者是指2个样本必须属于同一簇,后者则指2个样本必不属于同一簇.由于这种成对约束给出的先验信息弱于数据标记给出的先验信息 [15] ,故又被称为弱监督信息或辅助信息.本文主要关注第2种辅助型监督信息.将辅助信息结合到聚类目标所得优化模型已被证明能够有效提高聚类性能,如文献[15-20].现有的此类半监督聚类算法都基于非凸目标建模和优化,故按上述方式添加约束后目标函数的性质未改变,遗传了非凸优化对初始值敏感、难以保证全局最优的缺点.
依据上述在基于非凸目标函数的聚类中添加辅助信息可提高性能的经验,我们猜测凸聚类结合此类信息也可提高其性能.然而此方面研究尚未出现,故本文尝试弥补这一缺漏.在凸聚类中添加约束看似容易,然而研究中发现将必连约束作为惩罚项添加到目标函数中仍能保持其凸性,但将不连约束作为惩罚项添加到目标函数则会破坏其凸性,从而失去凸聚类的优势并退化为一个基于非凸目标函数的聚类任务.因此本文尝试通过对凸聚类目标函数中距离度量的改造以保持凸性.对于容易处理的必连约束,借鉴Klein等人 [15] 的方法改造距离矩阵,再恢复样本空间;对于较难处理的不连约束,受到Asafi等人 [19] 工作的启发,将不连约束转化为特征空间的增广.由此处理辅助信息后,对改变了距离度量的数据集进行凸聚类.最后,在模拟数据集和UCI数据集上的实验结果显示本文所提模型能够有效提高凸聚类的性能.
首先回顾凸聚类及相关工作.Lindsten等人 [7] 和Hocking等人 [8] 将聚类任务改造为一个凸优化问题,对于由 n 个无标记样本构成的数据集 X ={ x 1, x 2,…, x n }( x i ∈ ![]() M ),优化严格凸的目标函数:
M ),优化严格凸的目标函数:
(1)
其中,第1项是损失函数,第2项是正则化项且一般取  1 ,
1 ,  2 范数,取
2 范数,取  1 范数时式(1)与fused拉索 [21] 具有相似性.权重 w ij 非负且 w ij = w ji , u i 是样本 x i 的簇中心.对于任意参数 γ ,式(1)存在唯一的最小值,参数 γ 控制簇数:若 γ =0,则 u i = x i 时式(1)取最小值,每个簇仅有一个样本;随着 γ 的增大,簇中心逐渐融合, u i = u j 时将 x i 与 x j 归为同一簇;若 γ 过大,则将所有样本聚为一个簇.
1 范数时式(1)与fused拉索 [21] 具有相似性.权重 w ij 非负且 w ij = w ji , u i 是样本 x i 的簇中心.对于任意参数 γ ,式(1)存在唯一的最小值,参数 γ 控制簇数:若 γ =0,则 u i = x i 时式(1)取最小值,每个簇仅有一个样本;随着 γ 的增大,簇中心逐渐融合, u i = u j 时将 x i 与 x j 归为同一簇;若 γ 过大,则将所有样本聚为一个簇.
对凸聚类的研究主要在2方面展开.1)优化方面.鉴于交替迭代乘子方法(alternating direction method of multipliers, ADMM)适用于解决统计学、机器学习等领域的分布式的凸优化问题 [22] ,Chi等人 [9] 提出用ADMM方法 [22] 加速式(1)的求解过程,并提出了运行效率更高的交替最小化方法(alternating minimization algorithm, AMA) [23] ,这2种方法现已成为凸聚类相关算法的常用优化方法.2)数据结构信息的结合方面.其包括2个子方向:①改造凸聚类使其适用于特定情形:Hallac等人 [10] 提出了具有较强扩展性的network拉索,其是group拉索的泛化形式,适用于大规模图网络的聚类和优化;Wang等人 [11] 提出了适用于高维数据的稀疏凸聚类,该算法能够在凸聚类的同时进行特征选择,不仅提高凸聚类的性能而且极大地降低了算法时间复杂度;②将已有聚类算法凸松弛化:Lu等人 [12] 将谱聚类改造为凸稀疏谱聚类,并将该算法拓展为成对的稀疏谱聚类以利用数据的多视图信息提高聚类性能;Chi等人 [13] 将凸聚类拓展到凸双聚类,其目标函数的正则化项由行、列簇中心的fused拉索惩罚项共同构成,通过迭代地对行、列进行凸聚类实现算法.
将辅助信息与非凸目标结合的聚类算法,大致有3种:
1) 贪婪迭代搜索方法 [1] ,如Wagstaff等人 [16-17] 提出的COP-COBWEB算法和约束 k 均值(COP-Kmeans)算法,前者基于Fisher等人 [24] 提出的COBWEB算法,后者基于传统的 k -means算法.每次都会检查数据分配是否符合约束条件,若整个聚类过程都不违反约束,则得到的簇符合要求.其主要缺点是不能将成对约束给出的信息扩散到整个样本空间,即不能充分利用约束以反映样本空间的分布 [15] ,导致聚类结果失真.
2) 将约束作为惩罚项 [18] 添加到相应目标函数中,而后优化出模型.这是一种较为常用的半监督聚类方法,如文献[18],但此方法可能改变原目标函数的性质.
3) 改造距离度量,此方法可弥补前2种方法的不足.必连关系具有传递性且具有明显的几何特征,容易处理,然而,寻找满足不连约束的距离度量是一个NP完全的问题 [15] ,故改造距离度量的难点在于不连约束的处理.Klein等人 [15] 提出了基于层次聚类的CCL(constrained complete-link)算法,其处理不连关系的巧妙之处在于代替直接恢复样本空间的距离度量,而是在每次合并簇时获取一个新的距离度量,间接地将不连约束提供的信息扩散到样本空间.Asafi等人 [19] 提出了一种有趣的方法处理不连约束:若向特征空间为 M 维的数据集添加 N 个不连约束,则每个不连约束对应一个新的特征维度,利用扩散映射(diffusion map) [25] 将特征空间增广到 M + N 维,具体参考3.2节.鉴于相对约束衡量了3个样本之间的相似关系,能够较好地反映样本分布的局部区域信息从而指导聚类,Lesek等人 [20] 在文献[19]的基础上将相对约束转化为特征空间的增广.
结合弱监督信息的凸聚类算法具体分为2个阶段:1)通过距离度量的改造添加约束;2)对改造距离度量后的数据集进行凸聚类.本节将分别对其详细地介绍.
2 . 1 添加约束
数据集 ![]() 表示 x i 的第 m 个特征, X 的距离矩阵记为 D .向 X 添加 S 个必连约束和 N 个不连约束,具体分为2个步骤:
表示 x i 的第 m 个特征, X 的距离矩阵记为 D .向 X 添加 S 个必连约束和 N 个不连约束,具体分为2个步骤:
1) 添加必连约束.改造Klein等人 [15] 提出的all-pair-shortest-path算法,先用 D 中最小距离代替所有必连样本对之间的距离,再更新所有样本间的距离以保证直递性的满足,添加必连约束后的距离矩阵记为 ![]() 鉴于多维缩放(multiple dimensional scaling, MDS)能够在仅知样本间相似性度量的情况下恢复其空间分布 [26] ,采用此方法由
鉴于多维缩放(multiple dimensional scaling, MDS)能够在仅知样本间相似性度量的情况下恢复其空间分布 [26] ,采用此方法由 ![]() 恢复样本的相对位置
恢复样本的相对位置 ![]() 作为添加必连关系后的数据集.
作为添加必连关系后的数据集.
2) 添加不连约束.采用Asafi等人 [19] 的方法将特征空间由 M 维增广到 M + N 维,其思想基于通过扩散映射 [25] 获取的样本空间分布能更好地反映样本聚为同簇/异簇的可能性.该方法独立地处理每个不连约束:第 c 个不连约束对应增广特征空间的第 M + c 维,将 x i 在此维度的坐标记为 ![]() 若该约束介于
若该约束介于 ![]() 与
与 ![]() 之间,则
之间,则 ![]() 值分别为1与-1,除
值分别为1与-1,除 ![]() 与
与 ![]() 之外的第 i 个样本在此维度坐标为
之外的第 i 个样本在此维度坐标为
(2)
φ ( x i , x j )=| Ψ t ( x i )- Ψ t ( x j )|,
(3)
Ψ t ( x i )=( ![]() ψ 1 ( x i ),
ψ 1 ( x i ), ![]() ψ 2 ( x i ),…,
ψ 2 ( x i ),…, ![]() ψ k ( x i )),
ψ k ( x i )),
(4)
其中,式(3)是样本对( x i , x j )在扩散空间中的距离;式(4)是 x i 在扩散空间中的坐标:由高斯核计算 ![]() 的亲合矩阵
的亲合矩阵 ![]() 和 ψ i 分别是
和 ψ i 分别是 ![]() 特征分解后对应的第 i 个特征值和特征向量, t 是时间参数.由该不连约束导出的约束距离矩阵元素记为
特征分解后对应的第 i 个特征值和特征向量, t 是时间参数.由该不连约束导出的约束距离矩阵元素记为 ![]() |.
|.
最后,得到添加所有约束后的数据集 ![]() 其第 i 个样本为
其第 i 个样本为
(5)
其中,参数 α 决定了不连约束的相对重要性,本文取 α = d max , d max 是原始距离矩阵 D 中的最大值.同时,可得到添加所有约束后的距离矩阵 ![]() 其中
其中
(6)
2 . 2 凸聚类
对添加约束后的数据集 ![]() 进行凸聚类,即优化式(1).本节对凸聚类中权重的计算做了改进,并基于聚类稳定性理论选取正则化参数,最后简要描述用于优化的AMA算法.
进行凸聚类,即优化式(1).本节对凸聚类中权重的计算做了改进,并基于聚类稳定性理论选取正则化参数,最后简要描述用于优化的AMA算法.
2.2.1 权重
采用谱聚类中相似度图的构造方法 [27] 计算权重集合.Eric等人 [9] 将 k 近邻图与高斯核结合以反映样本分布的局部密度,权重 ![]() 并将其归一化.其中
并将其归一化.其中 ![]() 是指示函数:
是指示函数:
(7)
kNN ( x i )是 x i 的 k 个最近邻的集合 ![]() 由高斯核得到的
由高斯核得到的 ![]() 的亲合矩阵.
的亲合矩阵.
然而,若样本分布呈现多尺度性,选择一个固定的尺度参数 σ 不能有效反映样本局部分布,故本文采用局部尺度化(local sacling)方法 [28] 改造高斯核:为每个样本 x i 选取一个局部尺度参数 σ i = d ( x i , x k ),其中, d ( x i , x k )是样本对( x i , x k )之间的距离, x k 是 x i 的第 k 个近邻,则样本对( x i , x j )之间的亲合度为 ![]() / σ i σ j ).为保证图中存在若干连通分量,鉴于结合 k 近邻图构造的相似度图在 k 明显大于lb n 时连通 [27] ,本文一般取 k =| δ lb n |, δ ∈[1.5,2].
/ σ i σ j ).为保证图中存在若干连通分量,鉴于结合 k 近邻图构造的相似度图在 k 明显大于lb n 时连通 [27] ,本文一般取 k =| δ lb n |, δ ∈[1.5,2].
2.2.2 正则化项参数的选择
Lange等人 [29] 提出用聚类稳定性理论评价模型的有效性:从同一数据源抽取若干组样本进行聚类时,结果应具有可重现性、对于抽取的样本不敏感.Wang等人 [30] 用此理论选择簇数:每次将包含 n 个样本的数据集划分成2组训练集和1组验证集,用验证集衡量训练得到的2个模型的稳定性.这种方法的缺点是训练样本数量缩减为 n  3,所得模型不可靠.为提高训练模型的可靠性,Fang和Wang等人 [31] 对上述方法做出改进:每次用Bootstrap方法抽取2组各包含 n 个样本的训练集,得到2个训练模型并计算其聚类距离,如式(8).推广上述理论:一个好的正则化参数也应对于微小的数据扰动不敏感,故将Bootstrap方法用于式中正则化参数的选取,具体如算法1所示:
3,所得模型不可靠.为提高训练模型的可靠性,Fang和Wang等人 [31] 对上述方法做出改进:每次用Bootstrap方法抽取2组各包含 n 个样本的训练集,得到2个训练模型并计算其聚类距离,如式(8).推广上述理论:一个好的正则化参数也应对于微小的数据扰动不敏感,故将Bootstrap方法用于式中正则化参数的选取,具体如算法1所示:
算法1 . 选取正则化参数 γ .
输入:改造距离度量后的数据集 ![]() 权重集合 W 、候选正则化参数 γ 1 , γ 2 ,…, γ G ;
权重集合 W 、候选正则化参数 γ 1 , γ 2 ,…, γ G ;
输出:最优正则化参数 γ .
/*第1阶段:抽样*/
① for b =1,2,…, B do
② for j =1,2 do
③ 用Bootstrap方法从 ![]() 中独立有重复地抽取 n 个样本,记作
中独立有重复地抽取 n 个样本,记作 ![]()
④ end for
⑤ end for
/*第2阶段:计算各正则化参数对应的聚类不稳定性*/
⑥ for g =1,2,…, G do
⑦ for b =1,2,…, B do
⑧ 分别对 ![]() 和
和 ![]() 进行凸聚类,聚类结果记为
进行凸聚类,聚类结果记为 ![]() 计算二者的聚类距离:
计算二者的聚类距离:
![]()
![]()
![]()
(8)
⑨ end for
⑩ end for
 for g =1,2,…, G do
for g =1,2,…, G do
(9)
 end for
end for
/*第3阶段:获取最优正则化参数*/
 γ = γ
γ = γ ![]() .
.
其中,式(8)的 ![]() 是指示函数,若
是指示函数,若 ![]() 将 x i 与 x j 聚为同一簇,则其值为1,否则为0.
将 x i 与 x j 聚为同一簇,则其值为1,否则为0.
2.2.3 AMA算法
本文涉及的凸聚类均用AMA算法优化.首先,给出式(1)的增广拉格朗日形式:
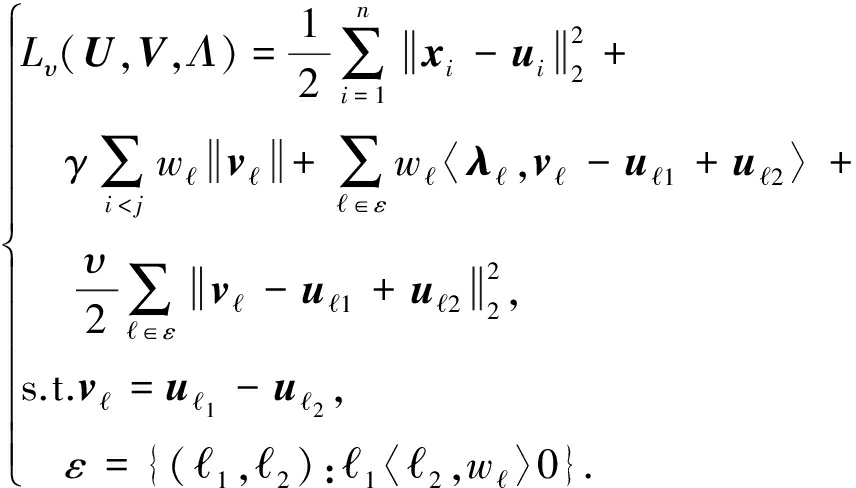
(10)
再用对偶上升方法迭代地更新各变量,第 m 次迭代过程如下:
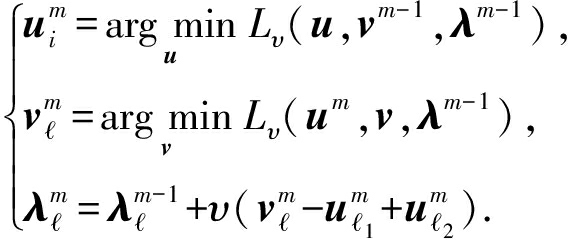
(11)
AMA算法的具体推导过程可参考文献[9].由于其实际迭代过程中只需更新 U , Λ ,且更新 Λ 的复杂度取决于权重集合 W 的稀疏性,故相比式(11)极大地减少了算法运行时间.具体如算法2所示:
算法2 . AMA.
输入:数据集 X 、权重集合 W 、正则化参数 γ ;
输出:变量 V .
① 初始化 Λ 0 ;
② repeat
③ for i =1,2,…, n
④ ![]()
(12)
⑤ end for
⑥ for all  =(
=(  1 ,
1 ,  2 )∈ ε
2 )∈ ε
⑦ ![]()
(13)
⑧ end for
⑨ until满足收敛条件.
⑩ for all  =(
=(  1 ,
1 ,  2 )∈ ε ,
2 )∈ ε ,
![]() ;
;
(14)
 end for
end for
其中,式(13)的 ![]() 是 z 到闭凸集 C
是 z 到闭凸集 C  的映射, C
的映射, C  ={ λ
={ λ 
![]() 是
是 ![]() 的对偶范数, υ 是迭代步长;式(14)是范数
的对偶范数, υ 是迭代步长;式(14)是范数 ![]() 的近端映射(proximal
的近端映射(proximal ![]() [ σ
[ σ 
![]()
![]()
![]() ],常数 σ
],常数 σ  =
= ![]() ,
,  1 ,
1 ,  2 范数的近端映射可用其软阈值函数 [33] 计算.
2 范数的近端映射可用其软阈值函数 [33] 计算.
优化结束后进行簇的分配.首先,由 X 构造包含 n 个顶点的图,并将满足 v  =0的第
=0的第  对样本用一条边连接;再对该图进行广度优先搜索,得到若干连通分量,每个联通分量对应一个簇.
对样本用一条边连接;再对该图进行广度优先搜索,得到若干连通分量,每个联通分量对应一个簇.
3 . 1 实验设置
实验中发现对数据集进行Z-score标准化 [34] 后再建模能够提高聚类性能. X 经标准化处理后记作 X ′, x i 的第 m 个特征 ![]() 经处理后为
经处理后为
x ![]() i =
i = ![]() ,
,
(15)
其中 ![]() 和 σ x ( m ) 分别是所有样本第 m 维的均值和标准差. X ′的每列都符合均值为0,标准差为1的正态分布.
和 σ x ( m ) 分别是所有样本第 m 维的均值和标准差. X ′的每列都符合均值为0,标准差为1的正态分布.
为方便叙述,将必连约束记为ML,不连约束记为CL.弱监督信息可通过2种方法获取:1)随机获取.从同一/不同类中随机抽取的2个样本构成一个ML/CL.2)由样本真实分布获取.用 L ( x i )表示 x i 的真实类号,设定 k 1 , k 2 且 k 1 > k 2 .对于每个样本 x i ,若 k 1 NN ( x i )中满足 L ( x i )= L ( x j )( x j ∈ k 1 NN ( x i ))的样本数目小于 k 2 ,则选取距 x i 较近且满足 L ( x i )≠ L ( x j )的样本 x j 构成CL,记为( x i , x j ).若( x i , x j )、( x i , x t )都是与 x i 相关的CL,且 D i , j < D i , t ,则约束( x i , x j )的重要性比( x i , x t )大.类似可获取ML并定义其重要性.有时,方法2所获约束对凸聚类的指导作用未必大于方法1所获约束对应的指导作用,故采用2种方法所得约束集的并集.
对 X ′进行3种实验:仅添加ML、仅添加CL、同时添加2种约束(ML与CL各 占1  2).逐渐增加约束数目,并针对每个约束数目随机选取4~5组不同的约束进行实验.每次实验等同于将 X ′按照第2节进行建模与优化,其凸聚类阶段的相关设置具体如下:正则化项取
2).逐渐增加约束数目,并针对每个约束数目随机选取4~5组不同的约束进行实验.每次实验等同于将 X ′按照第2节进行建模与优化,其凸聚类阶段的相关设置具体如下:正则化项取  2 范数;结合高斯核(用局部尺度化方法改造)与 k 近邻计算权重集合 W ,且 k =
2 范数;结合高斯核(用局部尺度化方法改造)与 k 近邻计算权重集合 W ,且 k =
2 ![]() log( n )
log( n ) ![]() ±1;正则化参数 γ 由算法1获取,候选参数集合由 G 个升序排列的数值构成,其取值范围依数据集而定,且
±1;正则化参数 γ 由算法1获取,候选参数集合由 G 个升序排列的数值构成,其取值范围依数据集而定,且 ![]() 最后,将聚类结果与无约束的凸聚类对比,采用芮氏指标(RI) [15-16] 和调整后的芮氏指标(ARI) [35] 对聚类结果进行性能评估,RI和ARI的值越大,表明聚类效果越好.
最后,将聚类结果与无约束的凸聚类对比,采用芮氏指标(RI) [15-16] 和调整后的芮氏指标(ARI) [35] 对聚类结果进行性能评估,RI和ARI的值越大,表明聚类效果越好.
实验均在配置为英特尔i5-3470 CPU,16 GB内存的计算机上执行,由R语言实现,且用R的多线程实现正则化参数选择模块的加速.
3 . 2 实验结果
本文在模拟数据集和真实数据集上实验:模拟生成的2个圆圈数据集和2个半月数据集,如图1所示,4个真实数据集取自UCI [36] (Iris选取了难分的2类数据),具体如表1所示:
Table 1 Data Sets
表1 数据集


Fig. 1 Simulated data sets
图1 模拟数据集
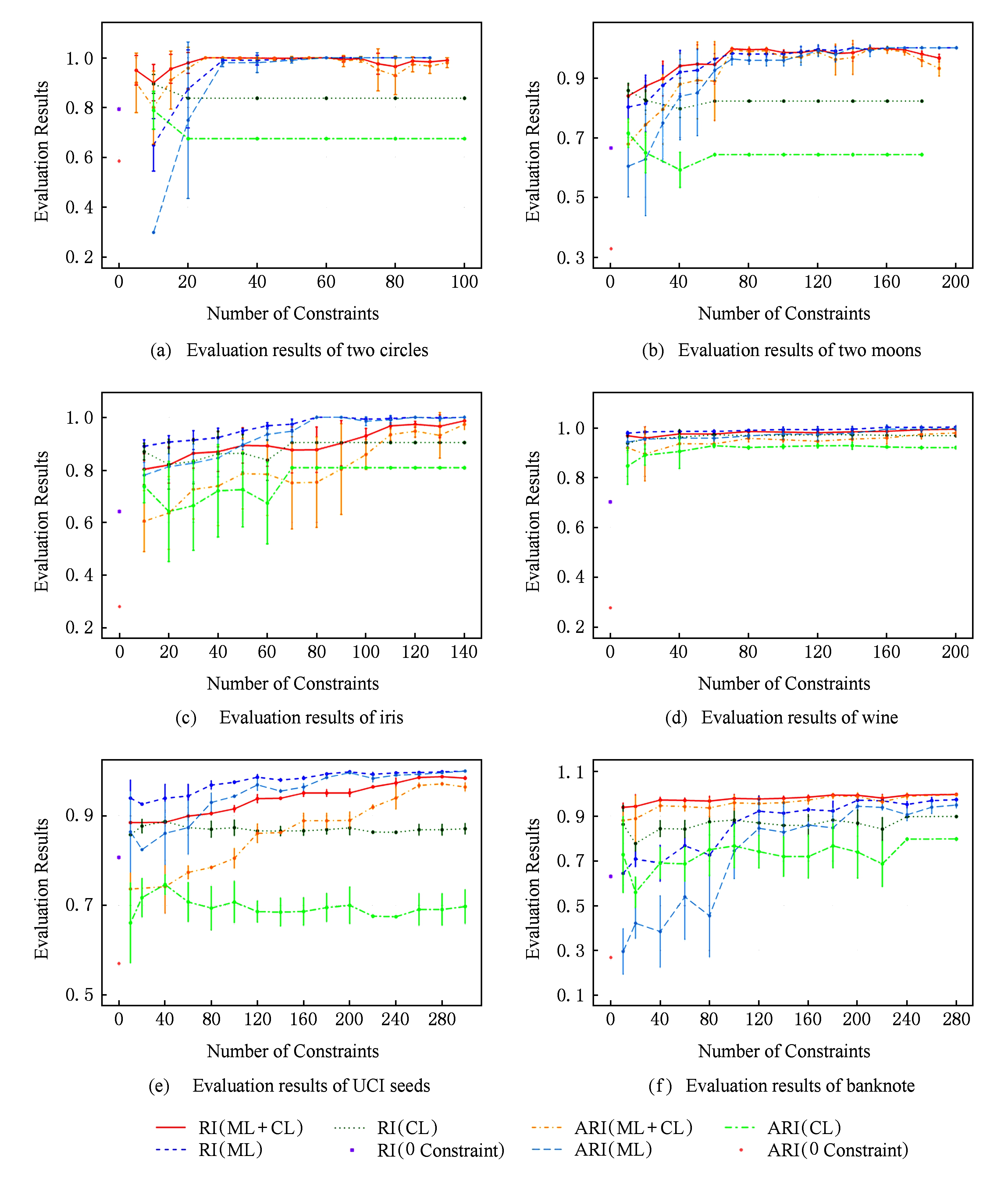
Fig. 2 Evaluation on clustering performance
图2 聚类性能评价结果
聚类性能的比较结果如图2所示,横坐标为约束数目,纵坐标为聚类性能评价结果,由图和实验数据可获得5种信息:
1) 结合弱监督信息的凸聚类性能优于无约束的凸聚类.随着约束的增多,聚类效果更优,这与直觉吻合.部分数据集在添加少量约束时就已获得较高性能,反映了约束的稀疏性.
2) 具体比较3种实验的性能.仅添加ML时,性能的提高幅度较明显并趋于最优;仅添加CL时,性能相对稳定;同时添加ML和CL时,性能的提高幅度也较明显,有时优于仅添加ML或CL时的情形.整体而言,性能在约束较少时波动较大,随约束的增多趋于稳定,ARI的波动比RI大.
3) 比较聚类所得簇数与真实类数.表2为部分数据集在不同约束下的平均簇数,可见:仅添加ML的实验在约束较少时簇数偏多,约束增多时簇数趋于真实类数;只添加CL时簇数相对稳定,约束过多时簇数相对较多;同时添加ML和CL时簇数稳定,约束较多时更逼近真实类数.
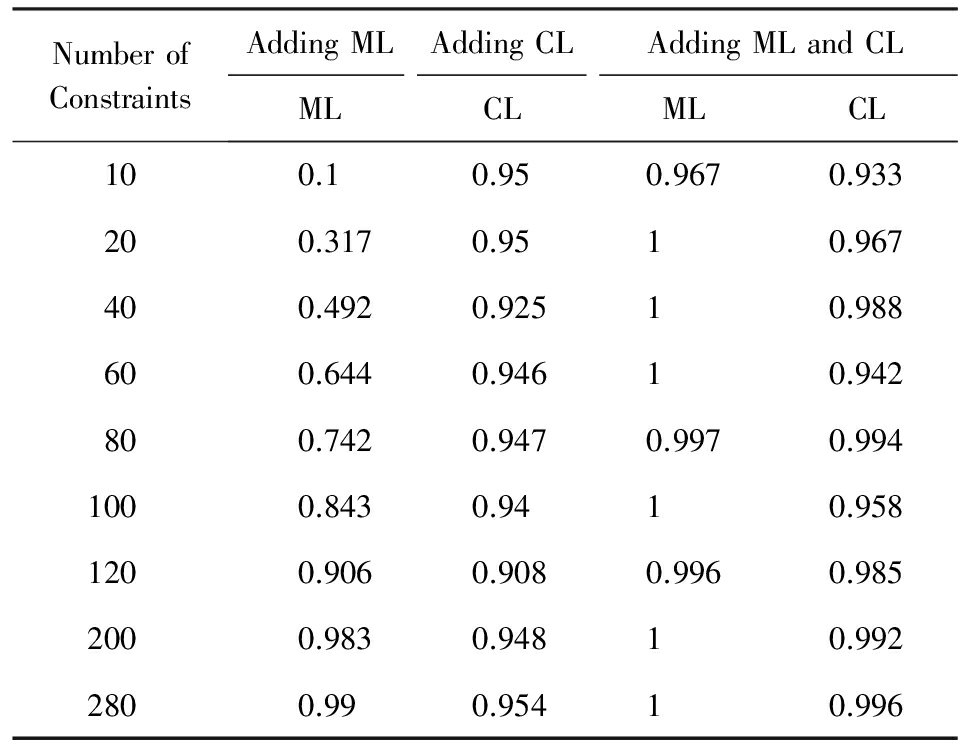
4) 比较聚类结果的约束符合率,即符合约束条件的样本对的数目与所添约束总数的比值.表3为Banknote在3种实验中的平均约束符合率,可见:仅添加ML的实验在约束较少时符合率较低,另外2种实验的约束符合率一直保持较高水平;在约束较少时,同时添加ML和CL使得ML的约束符合率也很高,故联合使用CL可提高约束符合率.
Table 2 Average Number of Clusters
表2 平均簇数
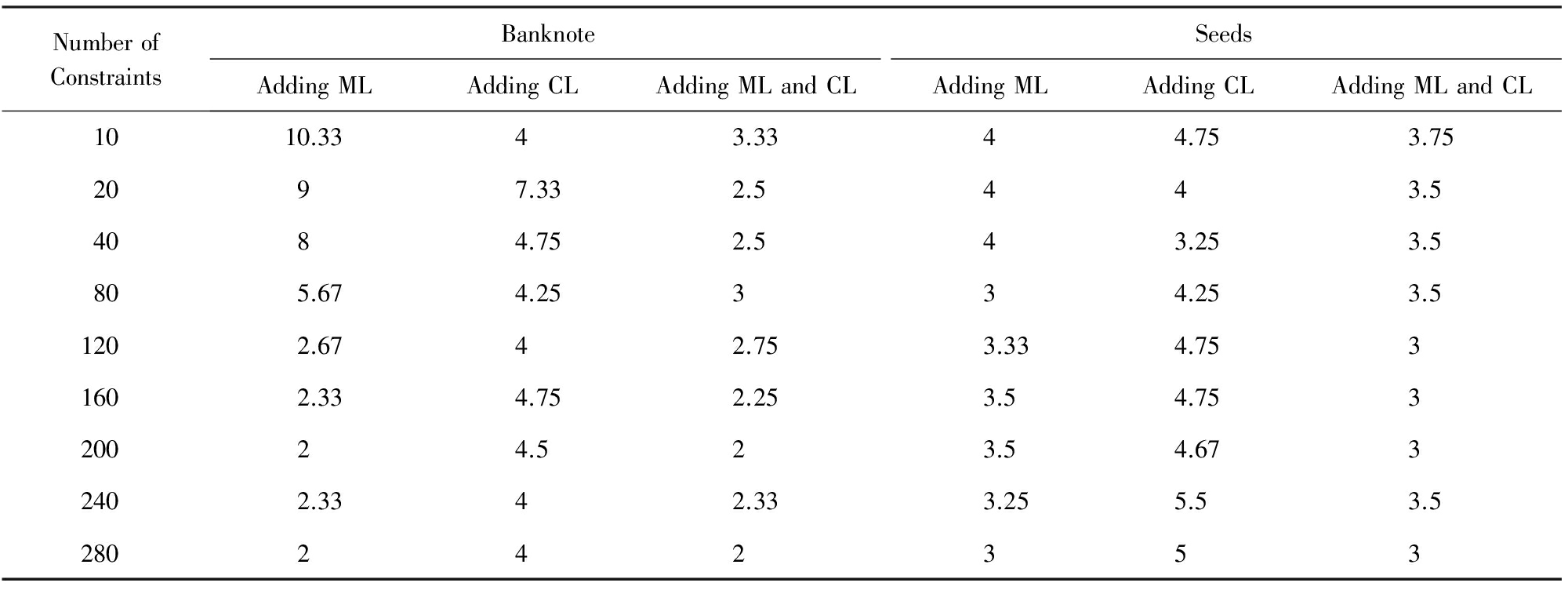
Table 3 Average Coincidence of Constraints in Banknote
表3 Banknote的平均约束符合率
5) 比较约束的重要性对聚类性能的影响.表4为将Iris数据集依照样本分布获取的约束按重要性降序排序后,相同约束数目下前3组实验的RI值.可见:约束数目相同时,聚类性能与约束的重要性呈正相关关系,约束数目增多时性能趋于稳定,故弱监督信息的质量对聚类结果有重要影响.
Table 4 RI of Iris with Constraints Sorted
表4 Iris的芮氏指标 ( 约束依重要性排序 )

本文鉴于凸聚类的优势及基于非凸目标函数的半监督聚类算法可获取更优聚类效果的经验,提出了一种结合必连与不连辅助信息的凸聚类算法,通过对凸聚类目标函数中距离度量的改造保持了其凸性,并通过实验证明了此算法能够有效提高聚类性能.此算法存在2个缺点:1)不连约束过多时算法运行时间较长,影响算法效率;2)遗传了凸聚类不允许聚簇重叠的缺点.针对缺点1,可考虑2个层面:1)实验结果反映了约束的稀疏性,即添加相对少的约束就可获得较高的聚类性能,故实际应用中毋须添加过多约束以避免冗余;2)结合聚类集成 [37] 方法,将约束集合划分为若干允许重叠的子集,并行地运行凸聚类再集成聚类结果.针对缺点2,可将模糊C均值算法与凸聚类结合,进行建模与优化.故下一步工作是聚类集成以及模糊C均值算法与凸聚类的结合.
参考文献:
[1] Madeira S C, Oliveira A L. Biclustering algorithms for biological data analysis: A survey[J]. IEEE/ACM Trans on Computational Biology and Bioinformatics, 2004, 1(1): 24-45
[2] Oliveira D, Valente J, Pedrycz W, et al. Advances in fuzzy clustering and its applications[M]. New York: John Wiley & Sons, 2007: 285-311
[3] Liu Ming, Liu Bingquan, Liu Yuanchao. A fast clustering algorithm for information retrieval[J]. Journal of Computer Research and Development, 2013, 50(7): 1452-1463 (in Chinese)(刘铭, 刘秉权, 刘远超. 面向信息检索的快速聚类算法[J]. 计算机研究与发展, 2013, 50(7): 1452-1463)
[4] Wong K C. A short survey on data clustering algorithms[C] //Proc of the 2nd Int Conf on Soft Computing and Machine Intelligence (ISCMI). Piscataway, NJ: IEEE, 2015: 64-68
[5] Xu Rui, Wunsch D. Survey of clustering algorithms[J]. IEEE Trans on Neural Networks, 2005, 16(3): 645-678
[6] Hall L O. Objective function-based clustering[J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2012, 2(4): 326-339
[7] Lindsten F, Ohlsson H, Ljung L. Just Relax and Come Clustering!: A Convexification of k -means Clustering[M]. Linköping: Linköping University Electronic Press, 2011
[8] Hocking T D, Joulin A, Bach F, et al. Clusterpath an algorithm for clustering using convex fusion penalties[C] //Proc of the 28th Int Conf on Machine Learning. New York: ACM, 2011: 1
[9] Chi E C, Lange K. Splitting methods for convex clustering[J]. Journal of Computational and Graphical Statistics, 2015, 24(4): 994-1013
[10] Hallac D, Leskovec J, Boyd S. Network lasso: Clustering and optimization in large graphs[C] //Proc of the 21st ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2015: 387-396
[11] Wang Binhuan, Zhang Yilong, Sun Wei, et al. Sparse Convex Clustering[OL]. arXiv preprint arXiv: 1601.04586, 2016 [2016-05-01]. http: / /arxiv.org /abs /1601.04586
[12] Lu Canyi, Yan Shuicheng, Lin Zhouchen. Convex sparse spectral clustering: Single-view to multi-view[J]. IEEE Trans on Image Processing, 2016, 25(6): 2833-2843
[13] Chi E C, Allen G I, Baraniuk R G. Convex biclustering[J]. Biometrics, 2016, 73(1): 10-19
[14] Zhou Zhihua. Machine Learning[M]. Beijing: Tsing University Press, 2016: 293-312 (in Chinese)(周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 293-312 )
[15] Klein D, Kamvar S D, Manning C D. From instance-level constraints to space-level constraints: Making the most of prior knowledge in data clustering [R]. Stanford, CA: Stanford University InfoLab, 2002
[16] Wagstaff K, Cardie C, Rogers S, et al. Constrained k -means clustering with background knowledge[C] //Proc of the 18th Int Conf on Machine Learning. New York: ACM, 2001: 577-584
[17] Wagstaff K, Cardie C. Clustering with instance-level constraints[C] //Proc of the 17th Int Conf on Machine Learning, New York: ACM, 2000: 1103-1110
[18] Fang Ling, Chen Songcan. Semi-supervised clustering learning combined with feature preferences[J]. Journal of Frontiers of Computer Science and Technology, 2015, 9(1): 105-111 (in Chinese)(方玲, 陈松灿. 结合特征偏好的半监督聚类学习[J]. 计算机科学与探索, 2015, 9(1): 105-111)
[19] Asafi S, Cohen-Or D. Constraints as features[C] //Proc of the 31st IEEE Conf on Computer Vision and Pattern Recognition (CVPR). Piscataway, NJ: IEEE, 2013: 1634-1641
[20] Lasek P, Lasek K. Relative constraints as features[C] //Proc of the 23rd Int Workshop on Concurrency, Specification and Programming. Berlin: Humboldt University, 2014: 121-125
[21] Tibshirani R, Saunders M, Rosset S, et al. Sparsity and smoothness via the fused lasso[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 2005, 67(1): 91-108
[22] Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends ® in Machine Learning, 2011, 3(1): 1-122
[23] Tseng P. Applications of a splitting algorithm to decomposition in convex programming and variational inequalities[J]. SIAM Journal on Control and Optimization, 1991, 29(1): 119-138
[24] Fisher D H. Knowledge acquisition via incremental conceptual clustering[J]. Machine Learning, 1987, 2(2): 139-172
[25] Lafon S, Lee A B. Diffusion maps and coarse-graining: A unified framework for dimensionality reduction, graph partitioning, and data set parameterization[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2006, 28(9): 1393-1403
[26] Wickelmaier F. An introduction to MDS[M]. Denmark: Aalborg University, 2003
[27] Von Luxburg U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395-416
[28] Zelnik-Manor L, Perona P. Self-tuning spectral clustering[C] //Advances in Neural Information Processing System. Berlin: Springer, 2005: 1601-1608
[29] Lange T, Roth V, Braun M L, et al. Stability-based validation of clustering solutions[J]. Neural Computation, 2004, 16(6): 1299-1323
[30] Wang Junhui. Consistent selection of the number of clusters via crossvalidation[J]. Biometrika, 2010, 97(4): 893-904
[31] Fang Yixin, Wang Junhui. Selection of the number of clusters via the bootstrap method[J]. Computational Statistics and Data Analysis, 2012, 56(3): 468-477
[32] Parikh N, Boyd S. Proximal algorithms[J]. Foundations and Trends ® in Optimization, 2014, 1(3): 127-239
[33] Donoho D L. De-noising by soft-thresholding[J]. IEEE Trans on Information Theory, 1995, 41(3): 613-627
[34] Al Shalabi L, Shaaban Z, Kasasbeh B. Data mining: A preprocessing engine[J]. Journal of Computer Science, 2006, 2(9): 735-739
[35] Hubert L, Arabie P. Comparing partitions[J]. Journal of Classification, 1985, 2(1): 193-218
[36] Asuncion A, Newman D. UCI machine learning repository[DB].
[37] Strehl A, Ghosh J. Cluster ensembles-a knowledge reuse framework for combining partitionings[C] //Proc of the 18th National Conf on Artificial Intelligence. New York: ACM, 2002: 93-99
Quan Zhenzhen and Chen Songcan
( College of Computer Science and Technology , Nanjing University of Aeronautics and Astronautics , Nanjing 211106)
Abstract: Objective function-based clustering is a class of important clustering analysis techniques, of which almost all the algorithms are built by optimization of non-convex objective. Thus, these algorithms can hardly get global optimal solution and are sensitive to the provided initialization. Recently, convex clustering has been proposed by optimizing a convex objective function, not only does it overcome the insufficiency illustrated above, but it also obtains a relatively stable solution. It has been proven that clustering performance can be improved effectively by combining useful auxiliary information (typically must-links and  or cannot-links) obtained from reality with the corresponding objective. To the best of our knowledge, all such semi-supervised objective function-based clustering algorithms are based on non-convex objective, semi-supervised convex clustering has not been proposed yet. Thus, we attempt to combine pairwise constraints with convex clustering. However, the existing methods usually make the original convex objectives lose their convexity, which add constraint penalty terms to the objective function. In order to deal with such problem, we introduce a novel semi-supervised convex clustering model by using the weakly-supervised information. In particular, the key idea is to change distance metric instead of adding constraint penalty terms to the objective function. As a result, the proposed method not only maintains the advantages of convex clustering, but also improves the performance of convex clustering.
or cannot-links) obtained from reality with the corresponding objective. To the best of our knowledge, all such semi-supervised objective function-based clustering algorithms are based on non-convex objective, semi-supervised convex clustering has not been proposed yet. Thus, we attempt to combine pairwise constraints with convex clustering. However, the existing methods usually make the original convex objectives lose their convexity, which add constraint penalty terms to the objective function. In order to deal with such problem, we introduce a novel semi-supervised convex clustering model by using the weakly-supervised information. In particular, the key idea is to change distance metric instead of adding constraint penalty terms to the objective function. As a result, the proposed method not only maintains the advantages of convex clustering, but also improves the performance of convex clustering.
Key words: objective function-based clustering; convex clustering; weakly-supervised information; constraints; distance metric; semi-supervised clustering

Quan Zhenzhen , born in 1991. Master candidate. Student member of CCF. Her main research interests include machine learning and pattern recognition.

Chen Songcan , born in 1962. Professor and PhD supervisor of pattern recognition and artificial intelligence. Senior member of CCF. His main research interests include pattern recognition, machine learning and neural computing.
收稿日期: 2017-05-23;
修回日期: :2017-06-19
基金项目: 国家自然科学基金项目(61672281) This work was supported by the National Natural Science Foundation of China (61672281).
通信作者: 陈松灿(s.chen@nuaa.edu.cn)
中图法分类号: TP391.4