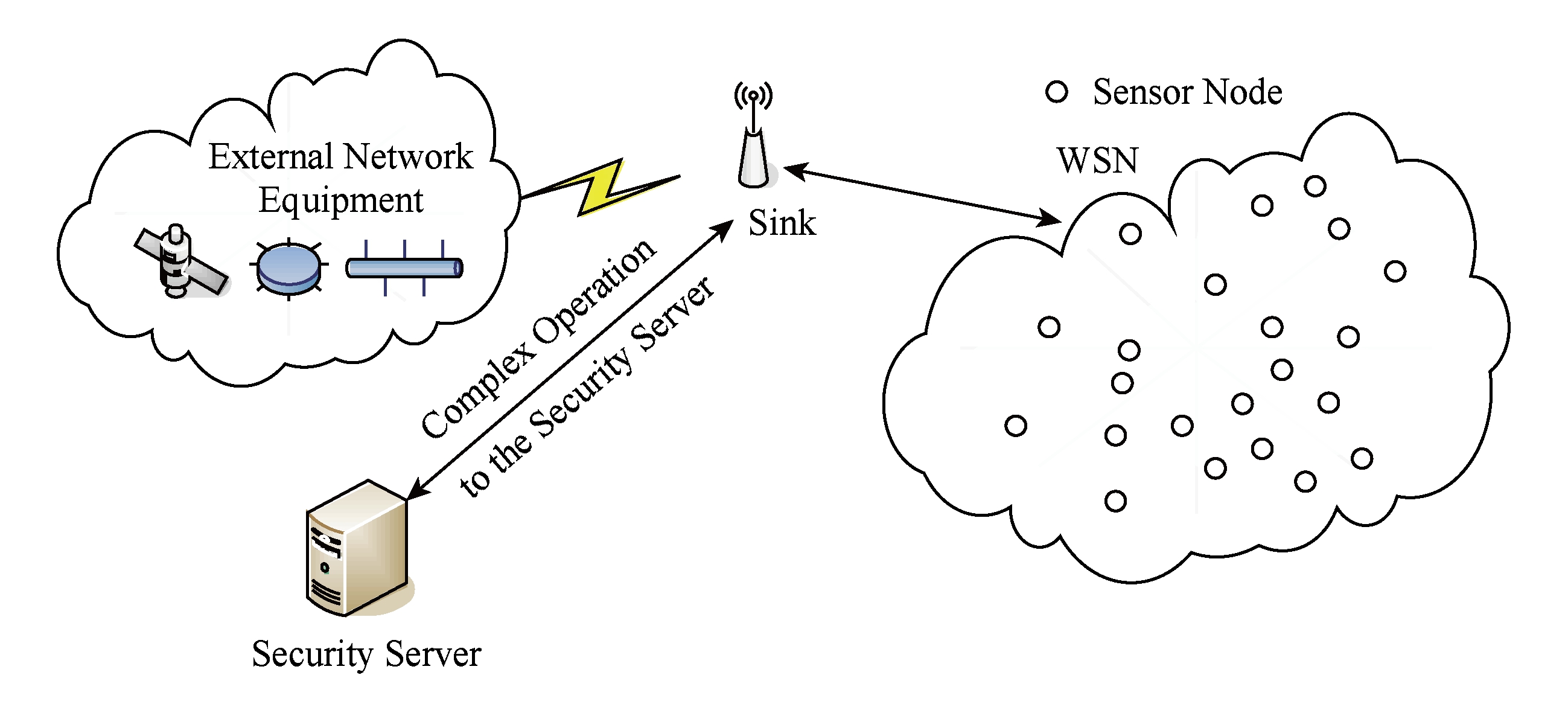
Fig. 1 Wireless sensor network model
图1 无线传感器网络模型
常 芬 1,2 崔 杰 1,2 王良民 1,3
1 (安徽大学计算机科学与技术学院 合肥 230601) 2 (安徽大学信息保障技术协同创新中心 合肥 230601) 3 (江苏大学计算机科学与通信工程学院 江苏镇江 212013)
(1198813216@qq.com)
A Traceable and Anonymous Authentication Scheme Based on Elliptic Curve for
摘 要 在无线传感器网络中,传感器节点布置在相应的应用领域,用于检测周边环境并发送检测值给Sink.消息在转发的过程中,消息的完整性及消息源的敏感信息应该受到保护.一方面,消息认证是阻止未经授权和损坏的消息转发的最有效的方法;另一方面,采用匿名通信的方式可以隐藏敏感节点的身份信息,实现节点位置的隐私保护.然而,匿名通信也为攻击者提供了利用匿名技术进行违法活动的机会.因此,追踪恶意节点的身份就显得尤为重要.为了解决无线传感器网络络中的发送节点身份隐私泄露和恶意节点追踪问题,提出基于椭圆曲线的可追踪匿名认证方案.方案将椭圆曲线和环签名相结合,实现节点匿名通信,提供中间节点的认证.仿真实验结果表明,与现有方法相比,在签名产生和认证开销相当的情况下,利用环签名的可链接特性能够实现对恶意节点的可追踪性,提高网络的性能和安全性.
关键词 无线传感器网络;匿名认证;可追踪;环签名;公钥密码体制
无线传感器网络(wireless sensor network, WSN)一般由一个或多个资源丰富的基站和大量资源受限的传感器节点组成 [1] ,通过无线通信方式形成多跳的自组织的网络系统.无线传感器网络中的隐私主要分为2类 [2] :内容隐私(content privacy)和上下文隐私(contextual privacy).内容隐私是对传感器网络中传输的消息提供完整性、不可抵赖性及保密性保护,具体细化为数据融合和数据查询2方面的隐私,一般情况下内容的隐私可以用加密认证技术实现.上下文隐私通常是对通信实体的身份、位置和节点间流量信息的保护.位置隐私包括对数据源节点和汇聚节点的位置隐私.
在实际应用中,由于传感器节点资源受限、部署环境恶劣而且采用无线多跳通信方式等特点,易受到攻击者攻击,引发严重的敏感节点身份隐私泄露问题.例如:在珍稀动物监测领域,攻击者可以对源节点进行ID分析攻击,通过对获取的源节ID信息分析,进而获得源节点的位置信息,从而发现珍稀动物的位置对其进行捕捉 [3] ;在军事领域,身份隐私的泄露和篡改会导致战术决策的失误,使军友陷入危险之中;在智能家居和智能交通领域,传感器采集的相关信息往往关联到用户实体,一旦敏感节点的ID信息泄露,将导致用户信息泄露.因此,对无线传感器网络中敏感节点身份信息的保护意义重大.
针对攻击者发起的ID分析攻击,可以采取匿名通信的方式进行抵御,通过匿名隐藏敏感节点的身份信息来实现节点位置的隐私保护 [4-8] .匿名通信固然能为节点提供隐私保护,但也为攻击者提供了利用匿名技术进行违法活动的机会.因此,在为节点提供匿名通信的同时,一旦有恶意节点发送无效或伪造信息,追踪恶意节点的身份就显得尤为重要.
如图1所示,无线传感器网络(WSN)由大量传感器节点组成,假定每个节点都知道它在传感器领域的相对位置,而且可以和邻居节点直接通过地理路由通信.整个网络通过多跳通信全链接.假定安全服务器(security server, SS)负责在整个网络内产生、存储、分配安全参数,该服务器不可能被破解.在网络部署后,传感器节点可能被破解.一旦被破解,则完全被攻击者控制.已经破解的节点不能产生能被SS和其他节点接受的新公钥.

Fig. 1 Wireless sensor network model
图1 无线传感器网络模型
在图1所示的网络模型基础上,本文考虑恶意节点或对手可发动2种类型的攻击:主动攻击和被动攻击.
主动攻击可能只是被破解的传感器节点发射的.一旦传感器节点被破解,敌人将获得存储在破解节点的所有信息,其中包括被破解节点的安全参数.对手可以修改信息的内容;也可以假装成其他节点,在协议中引入新的消息,删掉原有的消息,用另外的消息代替原来的消息,并重放旧的消息,破坏通信信道;或注入自己的消息等.
采用各种方法对协议进行攻击,与协议无关的人能够窃听协议的部分或全部.通过被动攻击,敌人可以窃听网络中的信息传播和进行交通分析.如ID分析,攻击者通过获得先验消息或窃听数据包信息的方式来获得节点的ID信息,并通过监听分析得出节点ID与网络拓扑之间的对应关系.
本文研究的重点是对上下文隐私中的敏感节点身份信息进行保护的同时,必要时对恶意节点的身份进行追踪,提出基于椭圆曲线的可追踪恶意节点的匿名认证方案.本方案将椭圆曲线加密技术与可链接环签名技术相结合,用以隐藏敏感节点的身份信息.当发现有恶意节点发送了未通过验证的消息后,Sink节点和环中成员节点将进行合作,利用环签名的可链接特性找出恶意节点的身份.
本文的主要贡献:
1) 将椭圆曲线加密技术与可链接环签名技术相结合,保证了节点身份信息的隐私,降低了签名和验证过程所需的计算开销,提高了通信效率.
2) 利用环签名的可链接特性,实现对恶意节点的可追踪性,以保证高效准确地找到恶意节点,提高网络的安全性.
无线传感器网络中对敏感节点身份信息的保护,可以采用环签名技术实现.认证作为无线传感器网络中基本的安全服务,它主要包括实体认证和消息认证2方面.在之前的研究中,提出了大量的消息认证和完整性验证的认证方案.这些方案基本上可分为2类:基于对称密钥的方案 [9-13] 和基于公钥的方案 [4,14-16] .其中,基于对称密钥和Hash函数的认证方案 [9-10] 中的节点共享密钥,攻击者可以通过俘获单个传感器节点来获得共享的密钥.因此,这些方案对俘获节点的攻击不具有恢复力.其他类型的对称密钥方案包括TESLA [17] 和它的改进方案 [18-19] ,这些方案可以提供消息发送者的认证,但都需要节点之间的初始时间同步,在大规模无线传感器网络中实现起来比较困难.另外,在消息认证过程中引入了延迟,而且延迟随传感器规模的增大而增加.
为了解决上述方案的局限性,基于多项式的消息认证方案 [11] 被提出,该方案采用多项式对消息认证,在传统的多项式方案中增加了干扰因素,以阻止攻击者通过计算多项式系数恢复多项式.与基于多重MACs [9-10] 的方案相比适应性更高,而且保持了中间节点认证的优点.然而,可使用错误校正码技术 [20] 完全消除方案中增加的干扰因素.因此,多项式的消息认证方案中存在的阈值问题仍然没能解决.阈值的大小取决于多项式阶的大小,当单个节点被俘获时,该节点只要接收到多于阈值个消息便可解出多项式,当多于阈值个节点被被俘获时,共谋也可以解出多项式.
Li等人 [4] 针对传统的多项式报文加密技术存在的最大阈值问题,给出了一种基于椭圆曲线加密技术的网络匿名协议.该协议可阻止攻击者通过获取报文消息内容来确定源节点的ID信息.源节点从一组不可区分的公钥组中进行密钥选择,加密消息在传输过程中进行逐跳身份认证,因此,当节点中存在俘获节点时,节点的ID信息也不会被泄露.由于协议中使用的椭圆曲线加密技术确保了数据的完整性,当基站连续接收到不完整信息时,可以通过对密钥取交集操作来确定被俘获节点的ID.然而,协议中发送节点发送每条消息都要动态选择环成员,开销较大.当被俘获的节点每次发送消息都选取相同的匿名集时,再对密钥取交集操作来确定被俘获节点的ID的做法就不可取.
针对消息发送者的匿名,Rivest等人 [21] 首次提出了环签名匿名方案.随后,许多结构改进、性能提高的环签名方案 [22-27] 被相继提出.环签名方案允许签名者与其他成员协作匿名签名信息,消息的真正签名者与其他成员构成的匿名集被称为环.环中任何一个成员使用自己的私钥和其他环成员的公钥,而不需要经过他们的同意即可代表整个环进行签名,而对于验证者只知道签名来自这个环并不知道谁是真正的签名者,也不能确定2个环签名是由相同的签名者产生.对此,Liu等人 [28] 提出了一种变体的环签名方案,创造了可链接环签名.这个概念下,环签名的签名者的身份仍然是匿名的,但是如果2个环签名是由相同的签名者签名,那么这2个签名是可链接的.
因为无线传感器网络中没有权威中心或可信第三方,群的形成是自发的,所以可链接的环签名在无线传感器网络中的应用受到关注.当接收方想知消息的发送节点是否是同一节点时,可链接环签名便可以满足这个场景下的需求.因此,在无线传感器网络中环签名是作为匿名认证工具的一个很好的候选 [28] .又因为基于公钥的方案在密钥管理上更为简单,基于椭圆曲线密码(elliptic curve cryptography)的公钥方案在计算复杂度、内存使用和安全的弹性上表现更高效 [21] .据此,考虑将以上2种技术相结合,以适合资源受限的无线传感器网络.
2.1 椭圆曲线加密技术
椭圆曲线密码系统作为一个公钥加密系统,它也具有公钥加密系统的所有特点.公钥加密系统的加密双方都需要2个密钥:公钥和私钥.每一方的公钥都是通过自己的私钥得到的,加密明文时都要用到对方的公钥,解密密文时使用自己的私钥.椭圆曲线的公钥密码系统加密和解密过程:
p 是一个大于3的素数, F p 是模 p 的有限域. F p 上的曲线 E 定义为: y 2 = x 3 + ax + b mod p .其中 a , b ∈ F p 且满足4 a 2 +27 b 3 ≠0 mod p .若数偶( x , y )满足上式,则是曲线 E 上的点,定义∞为 E 上的无穷远点.假定 G =( x G , y G )是曲线上的生成元,其阶为 N 足够大.
1) 密钥生成算法.设( E ,+)是有限域 F p 上的椭圆曲线, G 是 E 的循环子群,生成元为 P ,其阶 n 足够大,使得 G 上的离散对数是难解的.随机挑选一个整数 a ,使得 a ∈[1, n -1],计算公钥 Q = aP ;公开( Q , P , G ),保存私钥 a .
2) 加密算法.假设 B 想把明文 m ∈ F p 加密发送给 A , B 首先获取 A 的公钥( Q , P , G ),(必要时重复)选取随机数 r , r ∈[1, n -1],计算( x 2 , y 2 )= rQ ,直到 x 2 ≠0;然后计算: c 1 = rP =( x 1 , y 1 ), c 2 = m x 2 mod p ,则密文为( c 1 , c 2 ).
3) 解密算法. A 收到( c 1 , c 2 )后,利用私钥 a 计算出( x 2 , y 2 )= ac 1 ,再利用 F p 的元素 c 2 和非零元 x 2 ,计算明文 ![]() p .
p .
2.2 环签名
给定环 S ={ A 1 , A 2 ,…, A k ,…, A n },环中的每个节点的公私钥对为( pk i , sk i ), i =1,2,…, n ,不失一般性,假定 A k 是真正签名人.除密钥生成算法以外,环签名还包括环签名产生算法和环签名验证算法:
1) 环签名产生算法.其输入是待签名的消息 m 、环中所有成员的公钥 pk i ( i ∈[1, n ])、真正签名人的私钥 sk k ;其输出是 A k 对消息 m 的环签名 σ .记作 σ ← ring - sign ( m , pk 1 , pk 2 ,…, pk n , sk k ).
2) 环签名验证算法.其输入是待验证的消息签名对( m , σ )、环中所有成员的的公钥;其输出是0或1,1表示该签名有效,0表示该签名无效.记作1或0← ring - verify ( m , pk 1 , pk 2 ,…, pk n , σ ).
一个安全的环签名一般要满足以下3个性质:
1) 正确性.环中的任一成员执行环签名算法后,输出的签名都能通过该体制中的签名验证算法.
2) 匿名性.若环中成员为 n 个,验证者不会以大于1  n 的概率识别产生该签名的真正签名者.
n 的概率识别产生该签名的真正签名者.
3) 不可伪造性.任意不在环 S ={ A 1 , A 2 ,…, A k ,…, A n }中的节点不能产生一个使得 ring - verify ( m , pk 1 , pk 2 ,…, pk n , σ )=1的有效的签名对( m , σ ).
在本文中不区分节点 A i 与它的公钥 Q i .因此,也有环 S ={ Q 1 , Q 2 ,…, Q k ,…, Q n }.
2.3 基于离散对数的签名方案
如图1的网络模型中,包括一个Sink和 N 个传感器节点 Node ={ N 1 , N 2 ,…, N N }组成.对于每一个要发送的消息 m ,发送节点 N k 都要对消息 m 产生一个消息签名.假定环中成员只有发送者 N k 一个时, N k 和 N j 的通信过程如下:
1) 密钥生成阶段.发送节点 N k 选择一个大素数 p 和乘法群 ![]() * p 上的生成元 g .随机选取私钥 x ∈
* p 上的生成元 g .随机选取私钥 x ∈ ![]() * p ,计算公钥: y = g x mod p .这里 g 和 p 是系统公开参数.
* p ,计算公钥: y = g x mod p .这里 g 和 p 是系统公开参数.
2) 签名产生阶段.设 m ∈ ![]() * p 是待签名的消息,签名者 N k 随机选择一个秘密整数 k ∈
* p 是待签名的消息,签名者 N k 随机选择一个秘密整数 k ∈ ![]() * p -1,计算: r = g k mod p , s = xh ( m , r )- rk mod ( p -1).这里的 h 是单向Hash函数,对消息 m 的签名为 sig ( m )=( r , s )∈
* p -1,计算: r = g k mod p , s = xh ( m , r )- rk mod ( p -1).这里的 h 是单向Hash函数,对消息 m 的签名为 sig ( m )=( r , s )∈ ![]() * p ×
* p × ![]() * p .随后,签名者 N k 将数据( m ,( r , s ))发送给接受者 N j .
* p .随后,签名者 N k 将数据( m ,( r , s ))发送给接受者 N j .
3) 签名认证阶段.接收方 N j 收到签名( m ,( r , s ))后,验证等式 y h ( m , r ) = r r g s mod p 是否成立,如果等号成立,则确认( r , s )是 m 的有效签名.
本文提出的基于椭圆曲线的可追踪匿名认证方案,将椭圆曲线和可链接环签名相结合,实现节点匿名通信,同时在环签名中附加一些额外的信息,在必要时可通过环中所有节点的协作追踪签名者的真实身份,用以解决无线传感器网络络中的发送节点身份隐私泄露和恶意节点追踪问题.该方案由系统初始化与密钥生成、匿名签名产生、签名认证和恶意节点追踪4个部分组成.
图1是本文的网络模型,其中包括一个Sink和 N 个传感器节点 Node ={ N 1 , N 2 ,…, N N }组成.对于每一个要发送的消息 m ,发送节点 N k 都要对消息 m 产生一个消息签名.签名的产生是基于椭圆曲线上的离散对数问题.图2是本方案的系统流程图.
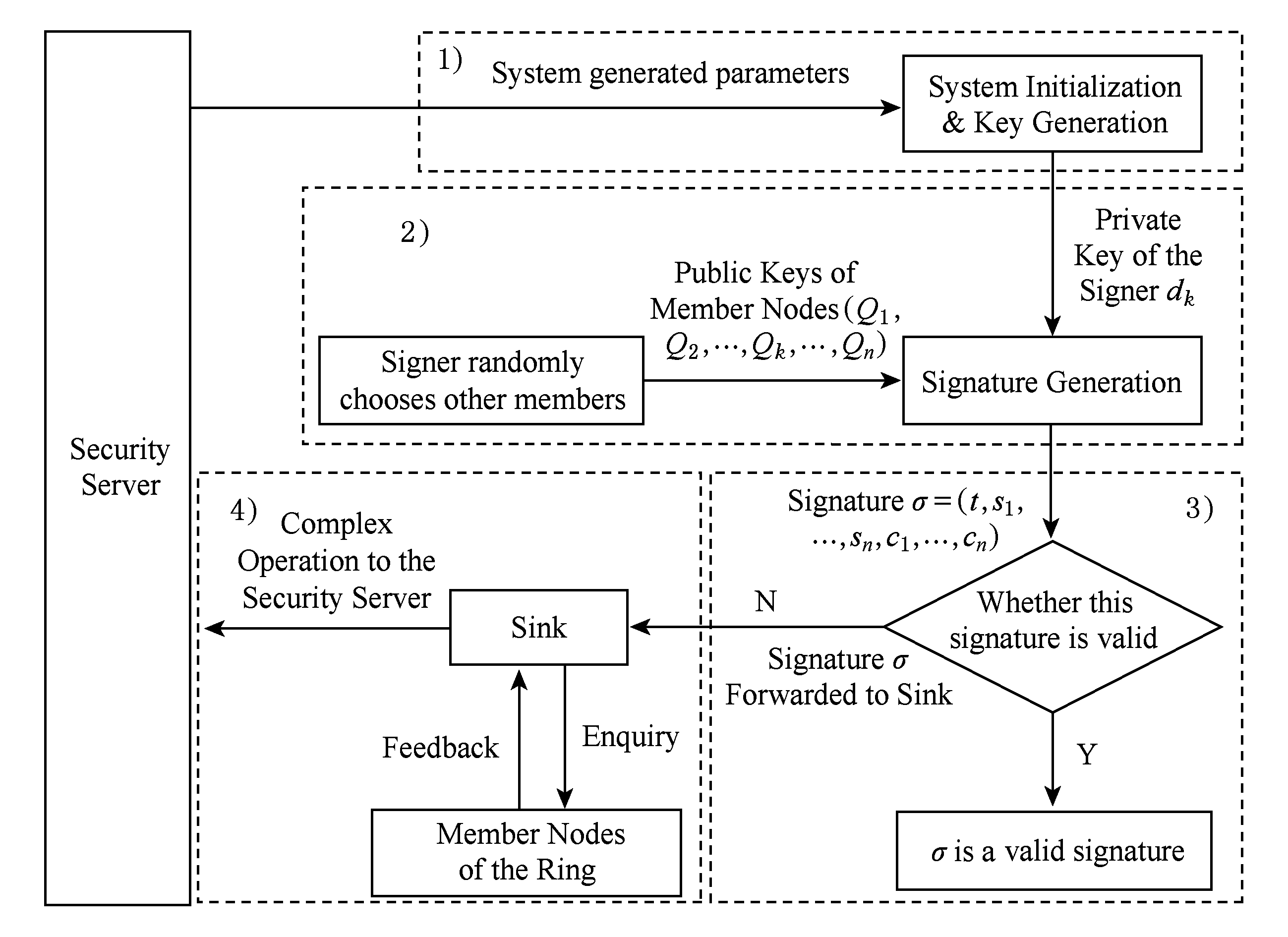
Fig. 2 System flow chart of this scheme
图2 本方案系统流程图
下面结合流程图给出本方案各个阶段的具体过程:
1) 系统初始化与密钥生成阶段
假设 G =( x G , z G )是椭圆曲线上的生成元,其中基于椭圆曲线的离散对数问题是难解问题,假设 H :{0,1} * → G 和 H 1 :{0,1} * → ![]() p 是2个Hash函数.公共参数为: param =( G , H , H 1 ).假定消息的发送者 N k 要匿名发送消息 m 给其他的节点 N j ,不失一般性, N k 要随机选取其他 n -1个节点和自身共同组成环成员节点. N k 的匿名节点集一旦选定,就不再改变. A k 表示发送消息的节点 N k 的身份,匿名节点集 S ={ A 1 , A 2 ,…, A k ,…, A n }.注意,本文不区分节点 A i 与它的公钥 Q i .因此,也有 S ={ Q 1 , Q 2 ,…, Q k ,…, Q n }.节点 N k 随机挑选一个整数 d k ∈[1, N -1]作为私钥,计算公钥 Q k = d k × G .
p 是2个Hash函数.公共参数为: param =( G , H , H 1 ).假定消息的发送者 N k 要匿名发送消息 m 给其他的节点 N j ,不失一般性, N k 要随机选取其他 n -1个节点和自身共同组成环成员节点. N k 的匿名节点集一旦选定,就不再改变. A k 表示发送消息的节点 N k 的身份,匿名节点集 S ={ A 1 , A 2 ,…, A k ,…, A n }.注意,本文不区分节点 A i 与它的公钥 Q i .因此,也有 S ={ Q 1 , Q 2 ,…, Q k ,…, Q n }.节点 N k 随机挑选一个整数 d k ∈[1, N -1]作为私钥,计算公钥 Q k = d k × G .
2) 签名产生阶段
假定节点 A k 要发送消息 m ,其私钥为 d k ∈[1, N -1],为了产生一个有效的匿名签名, A k 做以下步骤:
① 计算 h = H ( Q 1 , Q 2 ,…, Q k ,…, Q n ),这里的 H 是Hash函数,例如SHA-1;
② 计算 t = h d k ;
③ 由随机函数产生随机数 r , s i , c i ∈ ![]() * p , i ∈[1, n ], i ≠ k ;
* p , i ∈[1, n ], i ≠ k ;
④ 计算( x i , z i )= s i G + c i Q i , y i = h s i t c i mod N ( i =1,2,…, k -1, k +1,…, n );
⑤ 计算( x k , z k )= rG , y k = h r mod N ;
⑥ 计算 c k = H 1 ( m , t , x 1 ,…, x n , y 1 ,…, y n )-
![]() ,
,
其中,i≠k,计算s k =r-c k d k mod N ;
⑦ 输出签名 σ =( t , s 1 ,…, s n , c 1 ,…, c n ).
3) 认证阶段
给定环 S ={ Q 1 , Q 2 ,…, Q k ,…, Q n }、消息 m 以及待验证的签名 σ =( t , s 1 ,…, s n , c 1 ,…, c n ).当消息的接受者接收到签名消息后,接收者要检查:
检查公钥 Q i ≠∞, i =1,2,…, n ,否则无效;
检查公钥 S ={ Q 1 , Q 2 ,…, Q k ,…, Q n }, i =1,2,…, n ,是否在椭圆曲线上,否则无效;
检查 nQ i =∞, i =1,2,…, n ,否则无效.
在此之后,接收者做以下操作:
首先计算 h = H ( Q 1 , Q 2 ,…, Q k ,…, Q n ),( x i , z i )= s i G + c i Q i , y i = h s i t c i ( i =1,2,…, n );
然后检查等式
是否成立,其中 i =1,2,…, n .如果等式成立,则输出1,否则输出0.
4) 恶意节点追踪阶段
对于签名认证阶段中未通过认证的签名,消息的接收节点将收到的消息转发给Sink节点.Sink节点收到转发来的消息后,假设其收到的签名是 σ =( t , s 1 ,…, s n , c 1 ,…, c n ),Sink节点进行以下操作:
根据消息签名的环 S ={ Q 1 , Q 2 ,…, Q k ,…, Q n },Sink节点与环中的成员节点逐一进行一次交互,即Sink节点向环中成员发送查询命令,环中成员向Sink节点发送经匿名的消息.将未通过签名认证的签名与当前环成员发送来的匿名消息的签名进行逐一比较.由于同一发送节点所选环成员集相同,故而同一节点签名不同消息的签名中 t 值相同,据此即可找到未通过验证的消息的节点,从而完成节点的追踪.
图3是环成员节点为5时的恶意节点追踪过程.此时, S ={ Q 1 , Q 2 , Q 3 , Q 4 , Q 5 },真正的发送节点是 N 4 .若发送节点 N 4 产生的签名未认证通过,则将签名 σ 发送给Sink.Sink节点向环中成员节点{ N 1 , N 2 , N 3 , N 4 , N 5 }发送查询命令,然后环中成员逐一发送各自签名{ σ 1 , σ 2 , σ 3 , σ 4 , σ 5 }给Sink.然后,Sink将 σ 和{ σ 1 , σ 2 , σ 3 , σ 4 , σ 5 }交由安全服务器进行比较,从而找出真正的发送节点 N 4 .安全服务器对签名进行对比,如 σ =( t , s 1 ,…, s 5 , c 1 ,…, c 5 )和 ![]() 5),分别提取2个签名中的 t 和 t ′,然后比较 t 和 t ′是否相等,如果相等,则这2个签名是由同一个签名人产生,否则这2个签名不可链接,即非同一签名人产生.
5),分别提取2个签名中的 t 和 t ′,然后比较 t 和 t ′是否相等,如果相等,则这2个签名是由同一个签名人产生,否则这2个签名不可链接,即非同一签名人产生.
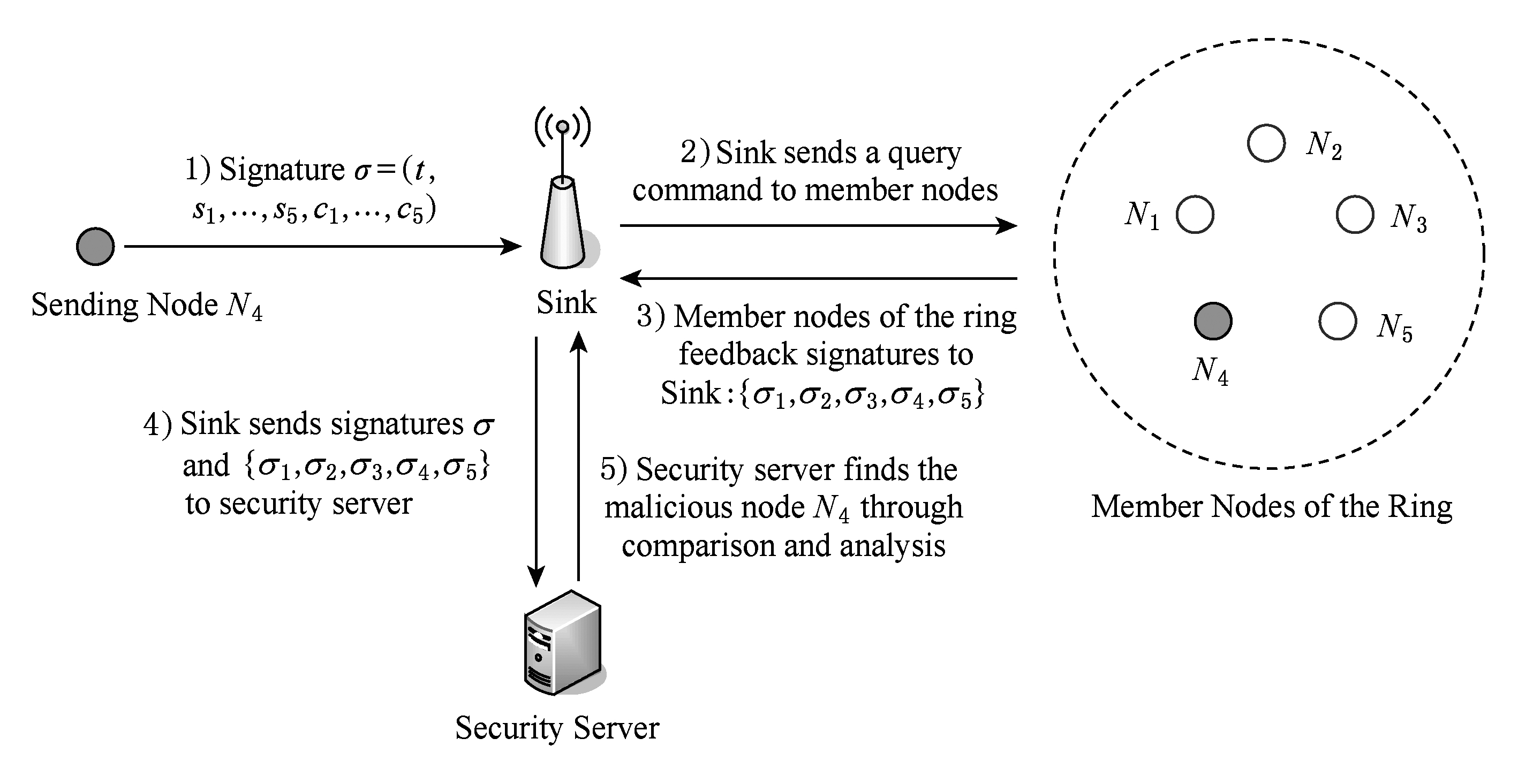
Fig. 3 Tracking process of malicious nodes (n=5)
图3 恶意节点追踪过程(n=5)
在本节中,将给出基于椭圆曲线的可追踪匿名认证方案的安全性证明.假设以下数学问题是难解的:Hash函数和离散对数问题.
定理1. 确定性.环中的任一成员执行环签名算法后,输出的签名都能通过该体制中的签名验证算法.
证明. 当接受者接收到签名消息后,要验证签名的正确性,也就是验证等式
![]() ,
,
i =1,2,…, n
成立.
因为
c k = H 1 ( m , t , x 1 , x 2 ,… x n , y 1 , y 2 ,… y n )-
![]() ,
,
可推出 ![]() , y 2 ,…, y n ),( i =1,2,…, n ).其中:( x i , z i )= s i G + c i Q i , y i = h ( s k + c k d k ) ,( i =1,2,…, n ), i ≠ k ;( x k , z k )= rG , y k = h r .为了方便推导,这里将( x i , z i )= s i G + c i Q i 表示成 x i = s i G + c i Q i .
, y 2 ,…, y n ),( i =1,2,…, n ).其中:( x i , z i )= s i G + c i Q i , y i = h ( s k + c k d k ) ,( i =1,2,…, n ), i ≠ k ;( x k , z k )= rG , y k = h r .为了方便推导,这里将( x i , z i )= s i G + c i Q i 表示成 x i = s i G + c i Q i .
因为, s k = r - c k d k , r = s k + c k d k .所以可推得,
x k = s k G + c k Q k , y k = h s k t c k .
因此,输出的签名都能通过该体制中的签名验证算法.
证毕.
定理2. 匿名性.本文提出的可追踪恶意节点的基于椭圆曲线的可追踪匿名认证方案提供无条件消息发送者匿名.
证明. 首先,本文方案产生的签名 σ 是由签名者利用其私钥和随机数生成的,签名者的私钥是随机分布的.其次,签名中的 t 是由单向Hash函数得到,签名中除 s k 和 c k 外其他均是随机选取.而 s k 和 c k 也是经椭圆曲线上点的横坐标值、Hash函数和随机数得到,没有泄露签名者身份的任何信息.最后,即使攻击者获得了环中成员的私钥,攻击者也不会以大于1  n 的概率识别产生该签名的真正签名者.故而,本文提出的方案满足无条件匿名性.
n 的概率识别产生该签名的真正签名者.故而,本文提出的方案满足无条件匿名性.
证毕.
定理3. 在无线传感器网络 SN ={Sink, Node }中,其中 Node ={ N 1 , N 2 ,…, N N }.对任意2个节点( N i , N j )之间采用本文签名产生算法的签名方案满足不可伪造性.即任意不在环 S ={ A 1 , A 2 ,…, A k ,…, A n }中的节点不能产生一个使得 ring - verify ( m , G , Q 1 , Q 2 ,…, Q k ,…, Q n , σ )=1的有效的签名.
证明. 在签名的生成阶段,要用到环成员中签名者的私钥.因此,攻击者 A ′想要伪造出合法的签名 σ ′,就要得到某个环成员的私钥 d k .环成员的私钥 d k 是由随机函数产生,攻击者若想从公钥 Q k = d k × G 得出私钥 d k 是解椭圆曲线上的离散对数问题.故而,签名人的私钥是安全的,攻击者不能假冒环中节点去生成签名.
假定攻击者不属于环 S ={ A 1 , A 2 ,…, A k ,…, A n },他想伪造 S 的签名,他可随机选择 n 个随机数 ![]() i .伪造签名为
i .伪造签名为 ![]() ,
, ![]() ,他在环中任选环成员节点 A c ,可计算出( x i , z i )= s i G + c i Q i , y i = h s i t c i ( i =1,2,…, n ).但由于他没有环成员节点 A c 的私钥,无法计算 s c = r - c c d c .从而,伪造的签名无法通过签名认证算法.故而可证,任意不在环 S ={ A 1 , A 2 ,…, A k ,…, A n }中的节点不能产生一个使得 ring - verify ( m , G , Q 1 , Q 2 ,…, Q k ,…, Q n , σ )=1的有效的签名.即可证对任意2个节点( N i , N j )之间采用本文签名产生算法的签名方案满足不可伪造性.
,他在环中任选环成员节点 A c ,可计算出( x i , z i )= s i G + c i Q i , y i = h s i t c i ( i =1,2,…, n ).但由于他没有环成员节点 A c 的私钥,无法计算 s c = r - c c d c .从而,伪造的签名无法通过签名认证算法.故而可证,任意不在环 S ={ A 1 , A 2 ,…, A k ,…, A n }中的节点不能产生一个使得 ring - verify ( m , G , Q 1 , Q 2 ,…, Q k ,…, Q n , σ )=1的有效的签名.即可证对任意2个节点( N i , N j )之间采用本文签名产生算法的签名方案满足不可伪造性.
证毕.
本节通过理论和仿真2个方面对我们提出的方案进行分析.本文提出的方案将与一种基于椭圆曲线加密技术的网络匿名协议 [4] 和基于二项式的方案 [11] 作比较.
5.1 理论分析
在认证方案中私钥的管理是个主要问题,尤其是在规模比较大的无线传感器网络中.现有的一些方案利用2节点间共享私钥提供端到端的节点认证,这就意味着只有接受者才能验证消息的真实性.也就是说,中间节点不能进行消息认证,只能转发消息直到消息最终被接受节点认证.这不仅消耗额外的传感器的能量,而且还增加了网络碰撞、降低了消息传输率.我们提出的方案实现中间节点的认证,可抵抗ID分析攻击.在发送节点的可连接性和追踪恶意节点方面比文献[4]的性能要好.
下面从安全性、计算开销和通信开销这3个方面进行分析:
1) 从安全性方面分析,当环成员 n =1时( n 为环成员的个数),我们提出的方案至少提供与文献[4]相同的安全性.随着 n 的增大,针对文献[4]中当基站连续接收到不完整信息时,可以通过对密钥取交集操作来确定被俘获节点的ID.显然,当被俘获的节点每次发送消息都选取相同的匿名集时,再对密钥取交集操作来确定被俘获节点的ID的做法就不可取.假设被俘获的节点 N A 每次发送消息都选取相同的匿名集 S ={ Q 1 , Q 2 ,…, Q A ,…, Q n },Sink连续接收到不完整信息后,对不完整消息的发送节点匿名集取交集,得到的结果仍然是 S ={ Q 1 , Q 2 ,…, Q A ,…, Q n },无法确定被俘获节点的ID.而在我们的方案中,产生签名的环成员是随机选择的,发送节点的环成员一旦选定,发送每条消息的环就固定.这就比文献[4]中发送每条消息都要动态选择环成员节省开销,而且根据消息签名的环 S ={ Q 1 , Q 2 ,…, Q A ,…, Q n },Sink节点与环中的成员节点逐一进行一次交互,即Sink节点向环中成员发送查询命令,环中成员向Sink节点发送经匿名的消息,再利用环签名的可链接特性,实现对恶意节点的可追踪性,保证高效准确地找到恶意节点,提高了网络的安全性.
2) 对于基于公钥的认证方案,计算开销是性能测量的最重要的指标之一.因此,我们首先仿真一次签名产生阶段和认证阶段的运行时间.表1所示2个方案的计算开销,其中MP用以表示标量点乘, n 是环中成员个数.从表1可看出,2个方案在一次签名产生阶段,其做椭圆曲线乘的次数相同,我们的方案只做2次Hash,而文献[4]需做 n 次;在认证阶段,文献[4]的各项计算次数都呈线性增长,而我们方案仍只做2次Hash.这里的乘、加和指数的计算开销相对椭圆曲线乘较小,对其影响不大.
Table 1 Computational Overhead for the Two Schemes
表1 2方案的计算开销

3) 对于通信开销,这里对消息的大小进行分析.文献[4]中的消息格式:( m , S , r 1 , y 1 ,…, r n , y n , s ),其中 m , s , r i , y i 的长度均为 L , S 是所有环成员的ID列表.假定组成网络的总节点数为 λ ,那么每个节点的ID大小为 ![]() lb
lb ![]() ,故S的长度是
,故S的长度是 ![]() .因此,文献[4]的一个消息的总长度为
.因此,文献[4]的一个消息的总长度为 ![]() +2L(n+1).
+2L(n+1).
定理4. 基于椭圆曲线的可追踪匿名认证方案的消息格式为( m , t , S , s 1 , s 2 ,…, s n , c 1 , c 2 ,…, c n ),假定 m , t , s i , c i 的长度均为 L ,组成网络的总节点数为 λ ,则发送节点 N k 发送一个消息的总长度为 ![]() +2L(n+1).
+2L(n+1).
证明. 由于m,t,s i ,c i 的长度均为L,这里s i ,c i 的长度为2nL,i∈[1,n],故而m,t,s i ,c i 的长度之和为2L+2nL.在图1网络模型中,有N个传感器节点Node={N 1 ,N 2 ,…,N N },因此,每个节点的ID大小为 ![]() .消息格式中的S是所有环成员的ID列表, S 中环成员的个数为 n ,因此, S 的长度是
.消息格式中的S是所有环成员的ID列表, S 中环成员的个数为 n ,因此, S 的长度是 ![]()
故而可证,发送节点 N k 发送一个消息的总长度为 ![]() +2L(n+1).
+2L(n+1).
证毕.
因此,当我们提出方案的网络总节点数N小于文献[4]的总节点数λ时,发送节点N k 发送一个消息的总长度 ![]() lb
lb ![]() +2L(n+1)小于文献[4]的总长度,此时的通信代价较小.当我们提出方案的网络总节点数N等于文献[4]的总节点数λ时,发送节点N k 发送一个消息的总长度
+2L(n+1)小于文献[4]的总长度,此时的通信代价较小.当我们提出方案的网络总节点数N等于文献[4]的总节点数λ时,发送节点N k 发送一个消息的总长度 ![]() lb
lb ![]() +2L(n+1)和文献[4]的总长度等长,两方案的通信代价相同.
+2L(n+1)和文献[4]的总长度等长,两方案的通信代价相同.
5.2 仿真分析
本节通过仿真实验比较文献[4]、文献[11]和本方案在签名产生和认证阶段的执行时间.我们选择4 MHz Telosb作为仿真平台,并采用SHA-1作为单向Hash函数.基于二项式的方案 [11] 是在对称密钥下实现,基于椭圆曲线加密技术的网络匿名协议方案 [4] 和我们提出的方案均是基于ECC,这里我们选定对称密钥长度 l =80 b,我们方案的密钥长度 L =2 l =160 b.根据文献[4]中对匿名成员个数 n 的选取,本方案同样选取 n =1,10,15,20.
图4所示我们提出的方案和对比方案在签名产生和认证阶段的处理时间.其中:图4(a)是基于多项式的方案和基于椭圆曲线加密技术的网络匿名协议及本文方案在产生一个签名阶段所需的时间;图4(b)是3个方案认证单个签名所需的时间.文献[11]中二项式的阶 d x , d y 取80,100,50分别对应本文方案的 n 取10,15,20.
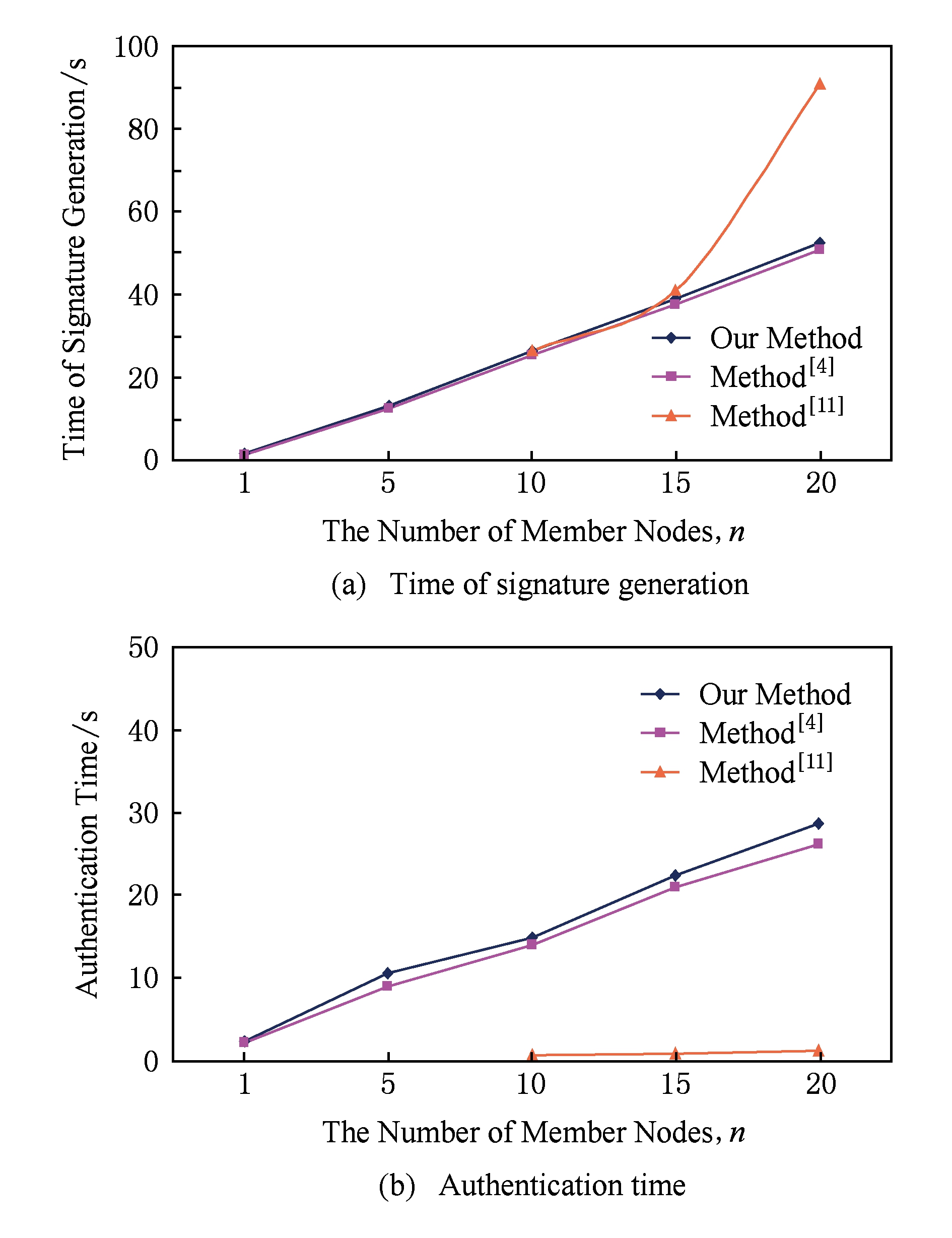
Fig. 4 Process time for the three schemes (16 b,4 MHz TelosB Mote)
图4 3个方案的处理时间(16 b,4 MHz TelosB Mote)
从图4曲线可看出,本文提出的方案在签名阶段的用时大于认证阶段的用时.随着环中成员的增多,签名产生阶段和认证阶段的处理时间呈线性增加.文献[11]的签名产生阶段曲线呈非线性斜率逐渐增加,相比我们的方案在签名产生阶段的时间相对较短.与文献[4]相比,我们的方案在产生和认证阶段的处理时间相差不大,符合以上进行的理论分析.
经过理论和仿真分析,与对比方案比较显示,我们提出的基于椭圆曲线的可追踪匿名认证方案可实现节点匿名通信,提供中间节点的认证,而且在签名产生和认证开销相当的情况下,利用环签名的可链接特性实现对恶意节点的可追踪性,提高性能和网络的安全性.
在本文中,我们提出基于椭圆曲线提出可追踪恶意节点的匿名认证方案,本方案将椭圆曲线和环签名相结合,实现节点匿名通信,同时在环签名中附加一些额外的信息,在必要时可通过环中所有节点的协作追踪签名者的真实身份,用以解决无线传感器网络络中的发送节点身份隐私泄露和恶意节点追踪问题,本方案实现中间节点的认证.现有的一些方案利用2节点间共享私钥提供端到端的节点认证,这就意味着只有接受者才能验证消息的真实性.也就是说,中间节点不能进行消息认证,只能转发消息直到消息最终被接受节点认证.这不仅消耗额外的传感器的能量,而且还增加网络碰撞、降低消息传输率.利用环签名的可链接特性,实现对恶意节点的可追踪性.仿真实验结果表明,与现有方法相比,本方案在签名产生和认证开销相当的情况下,利用环签名的可链接特性实现对恶意节点的可追踪性,提高性能和网络的安全性.
参考文献
[1]Akyildiz I F, Su Weilian, Sankarasubramaniam Y, et al. A survey on sensor networks[J]. IEEE Communications Magazine, 2002, 40(8): 102-114
[2]Gottumukkala V P V, Pandit V, Li Hailong, et al. Base-station location anonymity and security technique (BLAST) for wireless sensor networks[C] 
 Proc of IEEE Int Conf on Communications (ICC). Piscataway, NJ: IEEE, 2012: 6705-6709
Proc of IEEE Int Conf on Communications (ICC). Piscataway, NJ: IEEE, 2012: 6705-6709
[3]Peng Hui, Chen Hong, Zhang Xiaoying, et al. Location privacy preservation in wireless sensor networks[J]. Journal of Software, 2015, 26(3): 617-639 (in Chinese)(彭辉, 陈红, 张晓莹, 等. 无线传感器网络位置隐私保护技术[J]. 软件学报, 2015, 26(3): 617-639)
[4]Li Jian, Li Yun, Ren Jian,et al. Hop-by-Hop message authentication and source privacy in wireless sensor networks[J]. IEEE Trans on Parallel and Distributed Systems, 2014, 25(5): 1223-1232
[5]Christin D, Pons-Sorolla D R, Hollick M, et al. TrustMeter: A trust assessment scheme for collaborative privacy mechanisms in participatory sensing applications[C] 
 Proc of the 9th Int Conf on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP). Piscataway, NJ: IEEE, 2014: 1-6
Proc of the 9th Int Conf on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP). Piscataway, NJ: IEEE, 2014: 1-6
[6]Nezhad A A, Miri A, Makrakis D. Location privacy and anonymity preserving routing for wireless sensor networks[J]. Computer Networks, 2008, 52(18): 3433-3452
[7]Chen Juan, Du Xiaojiang, Fang Binxing. An efficient anonymous communication protocol for wireless sensor networks[J]. Wireless Communications and Mobile Computing, 2012, 12(14): 1302-1312
[8]Di Pietro R, Viejo A. Location privacy and resilience in wireless sensor networks querying[J]. Computer Communications, 2011, 34(3): 515-523
[9]Ye Fan, Luo Haiyun, Lu Songwu,et al. Statistical en-route filtering of injected false data in sensor networks[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(4): 839-850
[10]Zhu Sencun, Setia S, Jajodia S, et al. An interleaved hop-by-hop authentication scheme for filtering of injected false data in sensor networks[C] 
 Proc of IEEE Symp on Security and Privacy. Piscataway, NJ: IEEE, 2004: 259-271
Proc of IEEE Symp on Security and Privacy. Piscataway, NJ: IEEE, 2004: 259-271
[11]Zhang Wensheng, Subramanian N, Wang Guiling. Lightweight and compromise-resilient message authentication in sensor networks[C] 
 Proc of the 27th Conf on Computer Communications (INFOCOM). Piscataway, NJ: IEEE, 2008: 1418-1426
Proc of the 27th Conf on Computer Communications (INFOCOM). Piscataway, NJ: IEEE, 2008: 1418-1426
[12]Panda M. Data security in wireless sensor networks via AES algorithm[C] 
 Proc of the 9th Int Conf on Intelligent Systems and Control (ISCO). Piscataway, NJ: IEEE, 2015: 1-5
Proc of the 9th Int Conf on Intelligent Systems and Control (ISCO). Piscataway, NJ: IEEE, 2015: 1-5
[13]Yu Lei, Li Jianzhong. Grouping-based resilient statistical en-route filtering for sensor networks[C] 
 Proc of the 28th Conf on Computer Communications (INFOCOM). Piscataway, NJ: IEEE, 2009: 1782-1790
Proc of the 28th Conf on Computer Communications (INFOCOM). Piscataway, NJ: IEEE, 2009: 1782-1790
[14]Verma D, Jain R, Shrivastava A. Performance analysis of cryptographic algorithms RSA and ECC in wireless sensor networks[J]. IUP Journal of Telecommunications, 2015, 7(3): 51-65
[15]Lavanya M, Natarajan V. An improved authentication framework for wireless sensor network using elliptic curve cryptography[J]. IUP Journal of Computer Sciences, 2015, 9(1): 25-31
[16]Wang Haodong, Sheng Bo, Tan C C, et al. Comparing symmetric-key and public-key based security schemes in sensor networks: A case study of user access control[C] 
 Proc of the 28th Int Conf on Distributed Computing Systems. Piscataway, NJ: IEEE, 2008: 11-18
Proc of the 28th Int Conf on Distributed Computing Systems. Piscataway, NJ: IEEE, 2008: 11-18
[17]Perrig A, Canetti R, Tygar J D, et al. Efficient authentication and signing of multicast streams over lossy channels[C] 
 Proc of IEEE Symp on Security and Privacy. Piscataway, NJ: IEEE, 2000: 56-73
Proc of IEEE Symp on Security and Privacy. Piscataway, NJ: IEEE, 2000: 56-73
[18]Liu Donggang, Ning Peng, Zhu Sencun, et al. Practical broadcast authentication in sensor networks[C] 
 Proc of the 2nd Annual Int Conf on Mobile and Ubiquitous Systems: Networking and Services. Piscataway, NJ: IEEE, 2005: 118-129
Proc of the 2nd Annual Int Conf on Mobile and Ubiquitous Systems: Networking and Services. Piscataway, NJ: IEEE, 2005: 118-129
[19]Perrig A, Szewczyk R, Tygar J D, et al. SPINS: Security protocols for sensor networks[J]. Wireless Networks, 2002, 8(5): 521-534
[20]Albrecht M, Gentry C, Halevi S, et al. Attacking cryptographic schemes based on perturbation polynomials[C] 
 Proc of the 16th ACM Conf on Computer and Communications Security. New York: ACM, 2009: 1-10
Proc of the 16th ACM Conf on Computer and Communications Security. New York: ACM, 2009: 1-10
[21]Rivest R L, Shamir A, Tauman Y. How to leak a secret[C] 
 Proc of Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2001: 552-565
Proc of Int Conf on the Theory and Application of Cryptology and Information Security. Berlin: Springer, 2001: 552-565
[22]Chow S S M, Yiu S M, Hui L C K. Efficient identity based ring signature[C] 
 Proc of Int Conf on Applied Cryptography and Network Security. Berlin: Springer, 2005: 499-512
Proc of Int Conf on Applied Cryptography and Network Security. Berlin: Springer, 2005: 499-512
[23]Wang Huaqun, Zhang Futai, Sun Yanfei. Cryptanalysis of a generalized ring signature scheme[J]. IEEE Trans on Dependable and Secure Computing, 2009, 6(2): 149-151
[24]Liu J K, Au M H, Susilo W, et al. Linkable ring signature with unconditional anonymity[J]. IEEE Trans on Knowledge and Data Engineering, 2014, 26(1): 157-165
[25]Fujisaki E, Suzuki K. Traceable ring signature[C] 
 Proc of Int Workshop on Public Key Cryptography. Berlin: Springer, 2007: 181-200
Proc of Int Workshop on Public Key Cryptography. Berlin: Springer, 2007: 181-200
[26]Debnath A, Singaravelu P, Verma S. Privacy in wireless sensor networks using ring signature[J]. Journal of King Saud University-Computer and Information Sciences, 2014, 26(2): 228-236
[27]Au M H, Liu J K, Susilo W, et al. Secure ID-based linkable and revocable-iff-linked ring signature with constant-size construction[J]. Theoretical Computer Science, 2013, 469: 1-14
[28]Liu J K, Wei V K, Wong D S. Linkable spontaneous anonymous group signature for ad hoc groups[C ] 
 Proc of
Proc of
Australasian Conf on Information Security and Privacy. Berlin: Springer, 2004: 325-335

Chang Fen, born in 1989. Master. Her main research interests include network security, privacy protection for wireless sensor network.

Cui Jie, born in 1980. Associate professor and master supervisor. His main research interests include wireless sensor network, Internet of vehicles, software defined network, security multi-party computation, privacy for big data and cloud security.

Wang Liangmin, born in 1977. Professor and PhD supervisor. Member of IEEE, ACM, and senior member of CCF. His main research interests include security protocols for wireless sensor networks and privacy & security of big data.
Chang Fen 1,2 , Cui Jie 1,2 , and Wang Liangmin 1,3
1 ( School of Computer Science and Technology , Anhui University , Hefei 230601) 2 ( Co - Innovation Center for Information Supply & Assurance Technology , Anhui University , Hefei 230601) 3 ( School of Computer Science and Communication Engineering , Jiangsu University , Zhenjiang , Jiangsu 212013)
Abstract In wireless sensor network (WSN), sensor nodes are deployed in the corresponding application fields, in order to observe their environment and send their observations to the Sink. The message source should be protected in the process of transmission between nodes and Sink. On one hand, message authentication is one of the most effective ways to keep unauthorized and corrupted messages from being forwarded in wireless sensor network; on the other hand, anonymous communication can hide sensitive nodes identity information to implement the privacy protection of nodes location. However, anonymous communication has incurred a series of problems, such as, it gives the attacker an opportunity to use anonymous technology for illegal activities. Thus, it is particularly important to track the identity of the malicious nodes. In order to solve the problems above, a traceable and anonymous authentication scheme based on elliptic curve is proposed in this paper. The scheme combines elliptic curve with ring signature, implements nodes’ anonymous communication and provides the intermediate nodes’ authentication. The simulation results demonstrate that this scheme is equal to the existing schemes on the signature and certification cost. While, by using the linkable characteristics of ring signature, the proposed scheme can realize the traceability of malicious nodes, and improve the performance and security of the network.
Key words wireless sensor network (WSN); anonymous authentication; traceability; ring signature; public-key cryptosystem
收稿日期: 2016-08-22;
修回日期: 2016-12-15
基金项目: 国家自然科学基金项目(61472001,61272074) This work was supported by the National Natural Science Foundation of China (61472001, 61272074).
通信作者: 崔杰(cuijie@mail.ustc.edu.cn)
中图法分类号 TP393