刘怡然1柯俊明1蒋 瀚2宋祥福1
1(山东大学计算机科学与技术学院 济南 250000)2(山东大学软件学院 济南 250000)
摘要区块链由于其去中心化、防篡改、可验证等显著特点,引起人们的普遍关注. 其中,去中心化的共识机制在区块链中尤为关键.目前常见的典型共识机制有工作量证明机制(proof of work, PoW)、权益证明机制(proof of stake, PoS)和行动证明机制(proof of activity, PoA)等.但是这些共识机制几乎没有对参与生成区块节点的收益分配给出一种具体的方案.基于博弈论中计算沙普利值的原理对权益证明机制(PoS)中的收益分配方式进行改进,使得PoS机制中参与生成区块的节点的收益分配更加公平合理,改善现在区块链中的社会分层现象,大幅度提高新加入的小节点获得收益的可能性,抵制系统中心化的趋势.此外还将该思想应用到了Ouroboros协议中,对Ouroboros协议的收益分配算法进行了改进,使其满足存活性和持久性.
关键词权益证明机制;沙普利值;收益分配;Ouroboros协议;博弈论
自2008年中本聪[1]发表了名为“比特币:一种点对点的电子现金系统”的文章后,一种新型的“货币”——比特币由此诞生.它被称为“密码货币”或“数字货币”.历经10年发展,目前已经出现了上千种数字货币,一定程度上得到社会承认的不下百种,支撑这些数字货币运行的核心技术就是区块链.由于它具备去中心化、防篡改、可验证等优点,迅速成为社会和研究机构的热门研究对象.区块链是一个链式分布式存储结构,每一块中包括了交易的信息以及前一块的Hash值[2],正是这些Hash值将这些区块连接在一起就构成了区块链.
共识机制的作用正是保障系统的一致性并保证系统安全、稳定运行.共识机制描述了区块链系统的核心工作——节点竞争记账即产生新块并获得一定数目交易费的过程[3],目前比特币中使用的共识机制称为工作量证明机制(proof of work, PoW).系统中的每个节点都对系统提供计算能力,由能够完成计算工作的节点获得记账权即创建一个新的区块并获得交易费.与工作量证明机制比拼算力不同,权益证明(proof of stake, PoS)是根据钱包中的货币数目及货币存在天数来确定一个新的度量单位,即“币龄”来实现的.它根据币龄大小的关系降低了计算机进行Hash计算的难度,一定程度上缓解了资源浪费问题.之后又出现了PoS的进化版本PoA(行动证明),在权益持有者中选取挖块者.这种共识机制又大大缩短了达到共识的时间.
工作量证明机制PoW这个概念由Cynthia 和Moni 在1993年的学术论文中首次提出.而工作量证明这个名词则是在1997年AdamBack的文章[4]中才被真正提出用来防止DOS攻击.2008年中本聪发表的比特币白皮书再次使用了工作量证明机制来保证比特币系统的一致性.其核心机制是通过竞争计算能力来保证系统中的数据一致性以此来达到共识.整个系统中的每个节点为整个系统提供计算能力(简称算力),节点通过解决一个难求解易验证的SHA256的问题来获得相应的奖励(也就是通过挖块来获得收益)[5].完成这个困难工作并向大家证明的机制就叫做工作量证明机制.另外,这个工作的难度会随着时间不断增长,以保持每10 min出1个新块的速度.在比特币中,这个工作就是找到一个Hash值,同时这个Hash必须要满足一定的条件.即满足:
Hash(data,counter)<T.
在PoW中,最后能够最先给出满足条件Hash值的节点将会获得最终的挖块收益,而付出过算力但却最终没有挖块成功的人一无所获.这样某些拥有超过全网50%以上算力的人就极有可能发动51%攻击进而操控整个区块链,而其余参与挖块的人一无所获.综上,工作量证明机制逻辑简单,但并非完美,其缺点主要在于资源的浪费和51%攻击等安全问题,并且会加剧区块链中的贫富差距.
权益证明PoS最早由Sunny在2012年提出[6],最早在PPcoin系统中被实现.PPcoin系统混合了PoW机制和PoS机制.PoS机制中引入了币龄的概念,一个人拥有的币龄与拥有的钱数和时间成正比.在PPcoin网络中,币龄表示为钱数和时间的乘积:
Coinage=Coins×Timeweight.
PPcoin沿用了PoW的挖矿机制[7],不允许矿工穷举所有counter值而是在1 s之内只允许计算1次Hash值,这个步骤可以通过时间计数器TimeCounter实现,PoS中Hash值的满足条件修改为
Hash(data,TimeCounter)<d0×
Coins×Timeweight,
若符合该条件,持有这些数据的矿工获得挖矿资格和收益.因此,持币数越多且持币时间越长的人就拥有更大的币龄,从而更有可能使得上述不等式成立,即更容易挖矿成功进而获得收益.不仅如此,为了改善“富者更富”的现象,PoS规定,每当一个矿工挖到一块奖励时,PPcoin就将该矿工已经出示的币龄清零重新计算.
目前以太坊在Serenity阶段使用了Casper协议,它是一种改进的PoS机制.Casper是一种基于保证金的经济激励共识协议(security-deposit based economic consensus protocol).每个节点必须先缴纳一定数量的保证金才可以参与出块和共识的形成,恶意参与节点将存在保证金被罚没的风险,损失一定的经济利益.一般来说,需要掌握超过全网1/3的币龄才能左右最终的结果.也就是说3人投票,前2人分别支持一方,这个时候的结果就和第三方的投票结果有关. 不仅如此在PoS机制中,挖块成功的收益仍然是由某一节点独享,其余节点虽然付出了相应的努力,但是并不会获得收益.
PoS机制虽然考虑了PoW机制的不足,在一定程度上减轻了资源浪费和节点之间的贫富差距问题,也在一定程度上解决了大算力节点垄断问题,对新加入的节点更友好,而且各节点达成共识的时间缩短了.但是也存在一定的缺点,它需要依照权益的结余来选择,这就会导致首富账户的权力更大,它就很有可能支配记账权和收益.并且PoS很容易产生分叉,所以每一笔交易的产生需要多个交易进行确认.
然而,现在的PoW机制和PoS机制几乎是挖块成功的节点独享获得的交易费,而其余付出过工作量或者币龄的节点一无所得.在这种情况下,区块链中的大节点更容易发起51%攻击,获得全部收益进而控制整个区块链.不仅如此,这样还可能加剧区块链中“富者更富,穷者更穷”的现象,不利于区块链的健康持续发展.
经过上面的分析和论述可以发现,虽然共识机制不断进化,达到共识的时间也不断缩短,并且还能够实现一定的扩展性[8],但是目前常见的共识机制如PoW,PoS以及后面将要介绍的PoA对于挖矿成功后的收益分配都没有一个具体的方案.在PoW中,计算出符合条件的Hash值节点获得全部收益;在PoS中,币龄越大的人获得挖块权并获得全部收益的概率越大;对于PoW而言,如果某个节点掌握了超过全网50%的算力,它就有可能操纵整个区块链从而获得全部收益[9];对于PoS而言,如果某个节点掌握了超过了全网50%的币龄,它就有可能瓜分所有的收益.
因此本文基于博弈论中计算沙普利值的原理对权益证明机制(PoS)中的收益分配方式进行改进,使得PoS机制中参与生成区块的节点的收益分配更加公平合理,改善现在区块链中的社会分层现象,大幅度提高新加入的小节点获得收益的可能性,抵制系统中心化的趋势.
行动证明PoA是由Bentov等人在2014年提出[10].行动证明协议结合了工作量证明协议和权益证明协议,是比特币协议的扩展.在PoA协议中,全网节点需要进行更复杂的验证,由于这些复杂的验证,PoA才表现出了一些额外的优势.
PoA协议中主要的执行过程是follow-the-satoshi[10].这个过程主要是通过选取一些伪随机数来生成一个satoshi(数字货币流通的最小单位)值.这个选择过程也是与PoS中的币龄相关,币龄越大,被选中为权益持有者的可能性越大[11].比如说Alice持有6个币,Bob持有3个币,那么Alice在上述过程中的胜出概率为Bob的2倍.这个过程与这些钱的积累过程无关,只与总金额有关.
下面简述PoA协议中区块产生的过程:
1) 每个矿工首先使用自身的Hash算力通过工作量证明机制生成一个空块头(empty block header).这个空块头中不包含任何交易信息,其余信息与普通块相同.
2) 当某一个矿工成功生成一个空块头后,矿工将此空块头广播全网.
3) 全网节点通过此块头的Hash值来确定n个随机的权益持有者.选取权益持有者的过程:首先将此块头的Hash值与前一个块的Hash值连接,并在后面加上n个固定的后缀值.然后,将得到的n个值进行再一次的Hash.最后,将这n个值作为输入,调用follow-the-satoshi子程序.
4) 在线的权益持有者检查此空块头是否有效,即检查Hash值是否符合现在的难度系数.若合法,权益持有者检查自己是否被选中,当全网有n-1个权益持有者发现自己被选中时,他们就对空块头的Hash值签名,这样就表明他们掌握了目前的satoshi值.当第n个权益持有者发现自己被选中后,他就可以在空块头的基础上创建一个新块,即在空块头中添加交易的信息,其余n-1个权益持有者的签名和自己对整个块的签名信息.
5) 第n个权益持有者将新块广播全网,全网节点检查此块的有效性.权益持有者每次都是在最长链后产生新块.
6) 矿工与n个权益持有者共享第n个权益持有者挖块成功获得的交易费.
在PoA协议中,最后生成区块的第n个权益持有者获得交易费将分给选出的n个权益持有者和产生空块头的矿工.这样线上的矿工即使不挖矿,作为权益持有者也可以拥有一部分收益,这促使矿工保持线上运行,有利于货币的健康运行.但是对于每个节点的收益分配方式,并没有给出具体的方案.
CoA系统[12]采用了PoA的思想,对PoS机制进行改进,在一定程度上克服了PoS中的分叉问题.在CoA系统中,区块产生的过程与PoA协议中产生区块的过程类似.CoA系统中的协议叫做CoA协议,它主要基于PoS协议和PoA协议.此协议主要保证,在一定时间内,只有一名随机选取的权益持有者可以创建新的区块.其执行过程类似于一个线上抽奖程序,所有权益持有者遵循CoA协议进行线上抽奖.每个权益持有者每次执行follow-the-satoshi过程.
首先给出一些参数定义:挖矿所得的satoshi总额为2K;一个子分组的长度ω≥1;一个分组的总长度n=K×ω;comb函数:{0,1}n→{0,1}K;出块的最小间隔时间G0;原始块金额C0;块奖励金C1(0≤C1≤C0);防双花时间间隔T0.
CoA协议具体描述如下:
1) 所有的区块可以看做是每个长度为l的连续区块构成:每个区块由一个权益持有者产生,他的身份必须是公开可验证的,这个权益持有者收集满足条件的交易向全网广播,并创建第Bi块.这个新块中包含的信息有:这些交易的信息、前一块的Hash值、目前的时间戳、索引i,以及用自己私钥对这部分信息的签名等.
2) 每个新产生的第Bi块都和一个假定均匀分布的比特bi联系起来,比如说取Hash(Bi)的第1个比特.
3) 第Bj块和第Bi块之间的时间间隔应该为|j-i-1|×G0.这就意味着如果存在连续的4块分别为Bi,Bi+1,Bi+2,Bi+3,4个块分别由Ai,Ai+1,Ai+2,Ai+3产生,但是如果Ai+1,Ai+2不想参与,那么第Bi+3块和第Bi块之间时间戳的间隔至少为2G0.如果出现的新块的时间戳与当前时间相差太多,全网节点会认为此块无效.
4) 产生前一个区块的n个人可以选择下一部分产生区块的人,即生成一组长度为n的候选区块Bi1,Bi2,…,Bin.全网节点使用comb函数生成一系列K比特的种子:
SBin=comb(bi1,bi2,…,bin).
即是将长度n和它的输入联系在一起的一个函数(如果ω=1).
5) 种子SBil用交替的方式通过执行follow-the-satoshi过程来产生l个权益持有者.也就是说如果l个有效块为
Bil+j1,Bil+j2,…,Bil+jl.
那么遵循协议的节点就可以通过执行follow-the-satoshi过程并且将Hash(il,z,SBil)(z∈{1,2,…})作为输入,就可以得知产生区块Bil+jl+z的节点身份.
6) 如果satoshi的金额c是来自未花费输出的一部分(c<C0),此时权益持有者必须添加一个附加签名来证明他控制了额外的C0-c金额,否则他不能去产生一个有效块.即在第1个T0时间段内,块内的所有金额必须是权益持有者本身合法拥有的,只有这样其输出才能够延伸到新产生的块中.一旦产生第i块权益持有者Ai对他创建的2个区块Bi和![]() 同时签名,在接下来的T0时间内任意一个权益持有者Aj创建新块,都可以根据新块中的信息发现Ai的违规行为,一旦确认Ai违规,Aj就可以没收至少为C0的金额.对于Aj,他可以得到C1金额的奖励金,并且Ai剩余的金额要全部销毁.
同时签名,在接下来的T0时间内任意一个权益持有者Aj创建新块,都可以根据新块中的信息发现Ai的违规行为,一旦确认Ai违规,Aj就可以没收至少为C0的金额.对于Aj,他可以得到C1金额的奖励金,并且Ai剩余的金额要全部销毁.
7) “三次”列入黑名单法则:若一个控制了输出为txout0的权益持有者连续3次都没有创建新块,那么这个txout0就被列入了黑名单.也就是说,在下一组n个权益持有者开始创建新块时,如果他们在执行follow-the-satoshi过程,并且得到的Hash(in,z,SBil)指向了txout0,但是这个此时掌握txout0的人3次都没有创建新块,那么全网所有的诚实节点就会从第z-1步直接跳到了第z+1步重新执行协议.假若txout0通过了一个正常的交易,那么构成输出txout0的这笔钱就不再在黑名单中了.
如果全网节点遇到了很多竞争的长链,那么会将拥有最多块数的那条链作为最终的一条链.
CoA协议中,在n个候选产生区块的人中执行follow-the-satoshi过程选取后一块的生成人,生成区块的人获得收益与n个人共享收益.但是关于n个人中每个人具体的收益是多少并没有给出分配方案.现在,我们希望对参与共识的每一个节点最终获得的收益给出一个具体的描述,并且是一种直观的表示方法.在博弈论中,Shapley使用公理的方法提出了沙普利值的概念.使用求解沙普利值的方法可以计算出每个节点的收益情况.由于沙普利值具有很好的经济意义,并且其求解方法浅显易懂,所以其实用意义巨大.下面我们介绍博弈论中一些基本知识和定义.
博弈也叫对策,指的是带有竞争或对抗性质的行为.博弈的基本要素包括:局中人、策略、收益、信息和行动顺序[13].局中人就是在博弈中决策并最后获得结果的团体,在CoA系统中,每个权益持有者就可以看做一个局中人.策略是局中人完整的相机抉择的计划[14].一个博弈结束后,每个局中人从这个博弈中的获得就叫做收益.在博弈中,如果各个局中人达成了具有约束力的协议,则称该博弈为合作博弈[15].在区块链中各节点相互约束,共识机制规定了各个节点之间的约束条件,所以各节点执行共识协议就可以看做是各节点之间进行合作博弈的过程.在合作博弈中,主要的讨论对象是联盟.下面,给出联盟博弈的具体表示方法.
1.3.1 联盟博弈
一个联盟的博弈可以定义为一个二元组(N,v)[16]:
1) 有限集N表示局中人集合;
2) 函数v:2N|→![]() 是为每个联盟(N的一个子集称为一个联盟)S⊆N定义了价值v(S).一个联盟的收益也叫做联盟的价值.函数v也称为价值函数,并且我们规定v(φ)=0.
是为每个联盟(N的一个子集称为一个联盟)S⊆N定义了价值v(S).一个联盟的收益也叫做联盟的价值.函数v也称为价值函数,并且我们规定v(φ)=0.
根据特征函数性质的不同,可以将博弈分为4类[13]:
1) 可加博弈.若对于任意的联盟S,T⊆N,S∩T=∅,满足:v(S∪T)=v(S)+v(T),则博弈G=(N,v)就是一个可加博弈.
2) 超可加博弈.若对于任意的联盟S,T⊆N,S∩T=∅,满足:v(S∪T)≥v(S)+v(T),则博弈G=(N,v)就是一个超可加博弈.
3) 次可加博弈.若对于任意的联盟S,T⊆N,S∩T=∅,满足:v(S∪T)≤v(S)+v(T),则博弈G=(N,v)就是一个次可加博弈.
4) 标准化博弈.若∀i∈N,有v({i})=0,则称博弈G=(N,v)是0标准化博弈;若∀i∈N,有v({i})=0,且v(N)=1,则称博弈G=(N,v)是0-1标准化博弈.
特殊地,在一个投票博弈中,|N|个局中人进行投票,若联盟总的投票数过半,则获胜.用W⊆2N表示获胜的联盟.对于任意属于W的联盟S,可以将价值函数v(S)定义成:
![]()
1.3.2 联盟博弈收益分配
在联盟博弈中,要解决的核心问题就是联盟中的每个局中人的如何分配收益.在给出一个公平的分配方式之前,先给出博弈分析中的一些专有符号.首先,ψ:N×![]() 2|N||→
2|N||→![]() |N|表示从一个联盟博弈的集合(包括局中人集合N和一个价值函数v)到|N|个实数值的映射.对于x∈
|N|表示从一个联盟博弈的集合(包括局中人集合N和一个价值函数v)到|N|个实数值的映射.对于x∈![]() |N|,xi表示在联盟中局中人i∈N的收益份额.在本文中将ψi(N,v)简写为xi.现在给出收益分配的一些基本定义.
|N|,xi表示在联盟中局中人i∈N的收益份额.在本文中将ψi(N,v)简写为xi.现在给出收益分配的一些基本定义.
定义1. 有效收益.给定联盟博弈(N,v),有效收益集合被定义为{x∈![]()
![]() 即有效价值集合是指每个局中人的收益不能超过联盟的总价值.
即有效价值集合是指每个局中人的收益不能超过联盟的总价值.
定义2. 预估算(pre-imputation).给定联盟博弈(N,v),预估算集合用p表示,预估算集合被定义为{x∈![]()
![]() 由此可以看出,预估算集合是有效收益集合中收效最大的集合.即局中人分配了联盟中所有的价值.
由此可以看出,预估算集合是有效收益集合中收效最大的集合.即局中人分配了联盟中所有的价值.
定义3. 估算(imputation).给定联盟博弈(N,v),估算集合用ρ表示,估算集合被定义为{x∈ρ|∀i∈N,xi≥v(i)}.在估算集合中,每个局中人必须保证他们在联盟中的收益要不少于他们自己作为一个联盟的收益.
1.3.3 沙普利的公理化方法[16]
首先,如果对于任何既不包含局中人i,也不包含局中人j的联盟S中,N中的2个局中人i和j在函数v的意义上都有v(S∪{i})=v(S∪{j}),则i,j称为可以相互替代的.下面对称性公理表明对于可以相互替代的局中人,他们获得的收益应该是相等的.
公理1. 对称性(symmetry).对于任意v,如果i,j是可以相互替代的,则:
ψi(N,v)=ψj(N,v).
接着,给出载体(carrier)的概念.
定义4. 载体(carrier).给定联盟博弈(N,v),若对于∀S∈N,T∈N,存在v(S)=v(S∩T),则称T为博弈(N,v)的一个载体.
载体通常不唯一,如果T为博弈(N,v)的一个载体,T⊆T1,则T1也是博弈(N,v)的一个载体.载体之外的局中人i称为哑元(dummy player).哑元对于任何联盟没有贡献,即哑元加入任何联盟,该联盟的收益不会发生变化.下面的公理说明在进行收益分配时,不必要考虑哑元的存在,即不需要分配收益给哑元.
公理2. 有效性(effective).对于任意v的任何载体T,都有:
最后,考虑2个不同的博弈,即对于同一个局中人集合分别定义2个不同的价值函数v1,v2.下面给出可加性公理.
公理3. 可加性(additivity).给定2个价值函数v1,v2,对于任意局中人i,都有ψi(N,v1+v2)=ψi(N,v1)+ψi(N,v2),并且对于联盟S,博弈(N,v1+v2),(N,v1)和(N,v2)满足:
(v1+v2)(S)=v1(S)+v2(S).
介绍完上述3个公理后,将引出一个重要结论:总是存在一个预估算满足公理1~3.
引理1. 对于一个联盟博弈(N,v),总是存在一个特定的预估算φ(N,v)=φ(N,v),满足对称性、哑元和可加性公理.这个特定的收益估算φ(N,v),就是沙普利值.
定义5. 沙普利值.给定一个联盟博弈(N,v),每个局中人的沙普利值为
![]()
[v(S∪{i})-v(S)].
这个等式可以看做是计算局中人i的“平均边际效益”[17].假设N个局中人被排序了,并且假设根据顺序,在联盟S(不包含i)中,每一个局中人获取其之前的局中人形成的联盟的边际递增价值.那就是第i个局中人获得的价值为v(S∪{i})-v(S),然后计算局中人i的边际递增价值的数目,在联盟S(不包含i)中,所有排在局中人i之前的排列方式一共有|S|!种,在局中人i之后,剩余局中人的排列方式一共有(|N|-|S|-1)!种.最后对所有可能联盟S中的边际递增价值求和,求均值.
现在我们详细描述改进后的CoA协议,并给出每个权益持有者收益的计算方式.假设区块链中有n个候选权益持有者,每个权益持有者标号为1,2,…,i,…,n.这n个权益持有者可以构成一个大的集合:
N={1,2,…,i,…,n}.
这n个权益持有者的总币龄可以表示为
在n个权益持有者中,把每个节点的币龄占比看做每个节点的投票权,可表示为
ω1,ω2,ω3,…,ωi,…,ωn,
则:
此时,每个节点竞争挖块并获得收益的过程就可以看作是节点进行合作博弈的过程.权益持有者手中的币龄代表他本身的投票权,每个人投票选出下一块出块的权益持有者.即若存在某个节点获得的总投票权大于![]() 则v(S)=1,获得挖块权力;若总投票权占比小于等于
则v(S)=1,获得挖块权力;若总投票权占比小于等于![]() 则v(S)=0.现在可以根据前面给出的沙普利值的定义计算每个节点的沙普利值φi(N,v):
则v(S)=0.现在可以根据前面给出的沙普利值的定义计算每个节点的沙普利值φi(N,v):
![]()
[v(S∪{i})-v(S)].
记挖块所得的收益为R,所以每个权益持有者i获得的收益为
Ri=φi(N,v)×R.
这样,就给出了改进的CoA协议中每个权益持有者收益的计算公式,所以就可以给出一个完整的CoA的改进方案. 改进后的CoA协议描述如下:
1) 每个矿工通过工作量证明机制生成一个不包含任何交易信息空块头,其余信息与普通块相同.
2) 当某一个矿工成功生成一个空块头后,矿工将此空块头广播全网.
3) 产生此块头的矿工通过调用follow-the-satoshi子程序来确定n个随机的权益持有者.
4) 在线的权益持有者检查此空块头是否有效,即检查Hash值是否符合现在的难度系数.若合法,权益持有者检查自己是否被选中,当全网有n个权益持有者发现自己被选中时,他们就对空块头签名,这样就表明他们掌握了目前的satoshi值.
5)n个权益持有者进行投票,选出生成块的人.每个人的币龄占比就为其投票权.每个权益持有者出示的币龄必须为他合法拥有的币龄.
6) 当第i个权益持有者发现自己被选中后,他就可以在空块头的基础上创建一个新块,即在空块头中添加交易的信息,其余n-1个权益持有者的签名和自己对整个块的签名信息.
7) 第i个权益持有者将新块广播全网,全网节点检查此块的有效性.权益持有者每次都是在最长链后产生新块.
8) 若一个被选举出的权益持有者连续3次都没有创建新块,他就被列入了黑名单,然后再次进行投票,重新选举出创建新块的人.
n个权益持有者共享第i个权益持有者挖块成功获得的交易费,并按照每个节点的沙普利值进行分配.
2.2.1 合理性分析
对于改进后的CoA协议,候选出块的每个权益持有者分红占比和此节点的币龄占比息息相关.
下面考虑这样的例子.假设在区块链中存在4个节点,每个节点的币龄占比可以组成一个权重向量![]() 这样问题就转化成了计算权重向量为
这样问题就转化成了计算权重向量为![]() 的加权多数博弈的沙普利值.根据前面的沙普利定理可以得到节点沙普利值的向量组为
的加权多数博弈的沙普利值.根据前面的沙普利定理可以得到节点沙普利值的向量组为![]() 由此可以看出
由此可以看出![]() 币龄占比的节点可以拿到
币龄占比的节点可以拿到![]() 的收益.现在,考虑另一种简单的情况,区块链中存在2个大节点的情况,每个大节点的币龄占比为
的收益.现在,考虑另一种简单的情况,区块链中存在2个大节点的情况,每个大节点的币龄占比为![]() 剩下的3个小节点,每一个小节点的币龄占比为
剩下的3个小节点,每一个小节点的币龄占比为![]() 也就是每个节点的币龄占比组成的权重向量为
也就是每个节点的币龄占比组成的权重向量为![]() 现在来计算这2个大节点的沙普利值.
现在来计算这2个大节点的沙普利值.
将这2个拥有最大币龄占比的2个节点分别计做x和y.对于每个小的节点的排序,我们可以使用数组(a,b)来表示所有节点的排序情况[15],a(或b)代表x(或y)出现之前的小节点的个数.对应于数组(a,b),所有节点有2种排序:x先于y,或者y先于x.对应于每一种其他的数对,只有一种排序,因此可能的排序如图1所示.
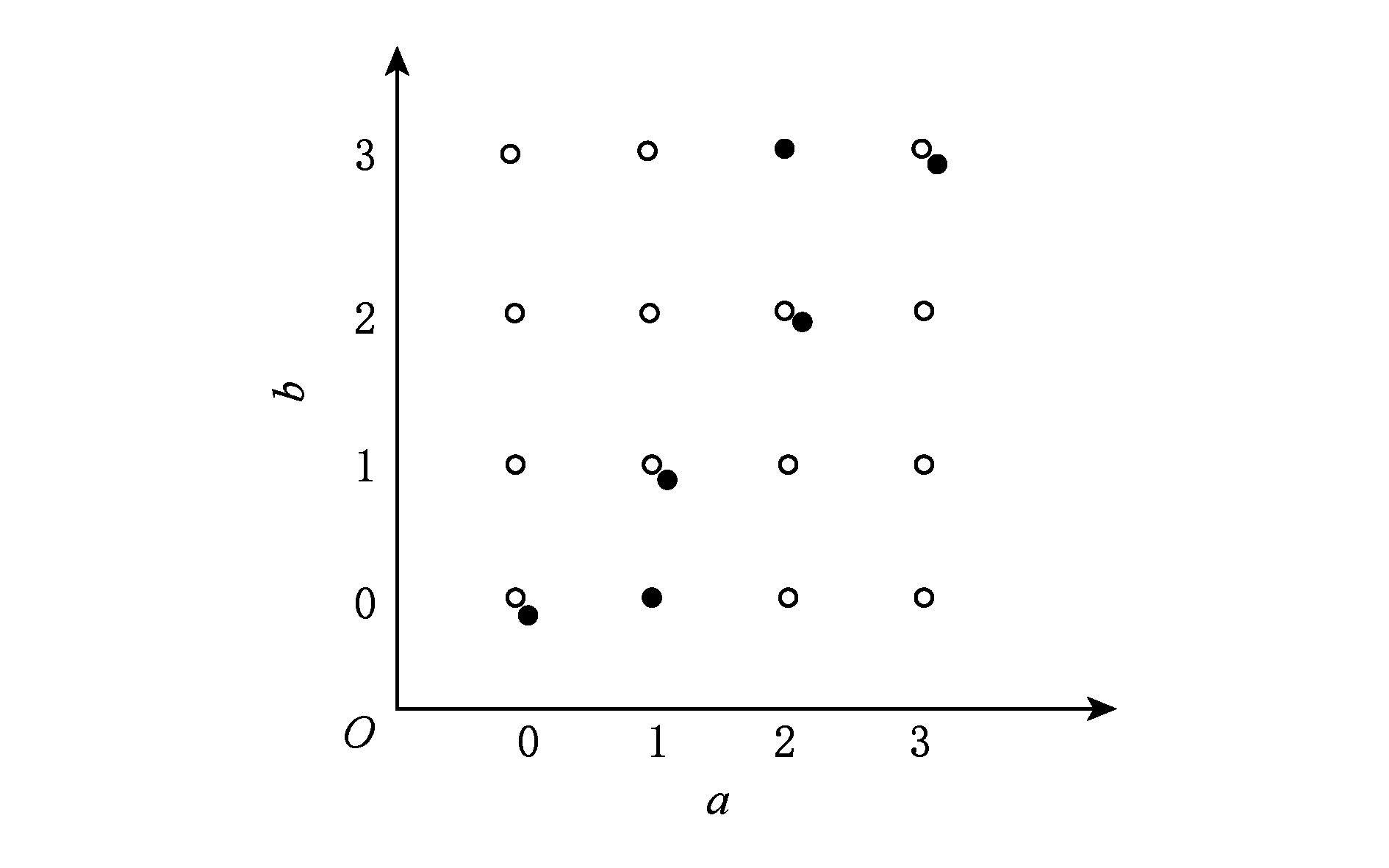
Fig. 1 Sort representation of each node
图1 各节点的排序表示
例如点A的排序就和排序(p1,y,p2,x,p3)一致(其中(p1,p2,p3)代表了小节点的排序).对角线上的每一个位置相应地表示了对所有节点的2种可能的顺序,所以对小节点的每一种排序都对应于所有局中人20种可能的顺序,在6个实心圆点的位置,x是一个关键局中人.因为目前小节点的排序是不相关的,x的值是![]() 由对称性质可得,y的值也是
由对称性质可得,y的值也是![]() 因此我们可以得到这个加权大多数的博弈结果为
因此我们可以得到这个加权大多数的博弈结果为
所以,在这种情况下,2个币龄占比大约为33%的大节点所得的收益为30%.对比前面描述的存在一个币龄占比为50%大节点所得的收益大约为66.7%的情况,我们可以发现多个大节点数目增加的时候,每个大节点得到相对收益会降低.这种现象当然是我们现在比较喜欢的,如果在区块链中的拥有大量算力或者币龄的大节点不断增加,这些节点的收益不会随着大节点的增多而获得更多的收益,这样就能有效改善“富者更富,穷者更穷”的局面.
现在,考虑一个更加常见的情形,在候选出块者中存在2个大节点(每一个大节点拥有![]() 的投票权)和n-2个同等大小的小节点.现在我们感兴趣的是对于任意大小的n,这些节点博弈的沙普利值即收益值.计算沙普利值的方法和我们讨论的上一种的情况相似.当x和y分别出现之后,上述使用的排序的描述可以通过小节点的a和b的比例来修正.图2说明了这样的情况,阴影区域对应于x是关键局中人的排序.由图2可知,阴影部分占比为
的投票权)和n-2个同等大小的小节点.现在我们感兴趣的是对于任意大小的n,这些节点博弈的沙普利值即收益值.计算沙普利值的方法和我们讨论的上一种的情况相似.当x和y分别出现之后,上述使用的排序的描述可以通过小节点的a和b的比例来修正.图2说明了这样的情况,阴影区域对应于x是关键局中人的排序.由图2可知,阴影部分占比为![]() 也就是说大节点的沙普利值为
也就是说大节点的沙普利值为![]() 所以我们可以知道当n很大时,每个大节点获得收益大约是
所以我们可以知道当n很大时,每个大节点获得收益大约是![]()
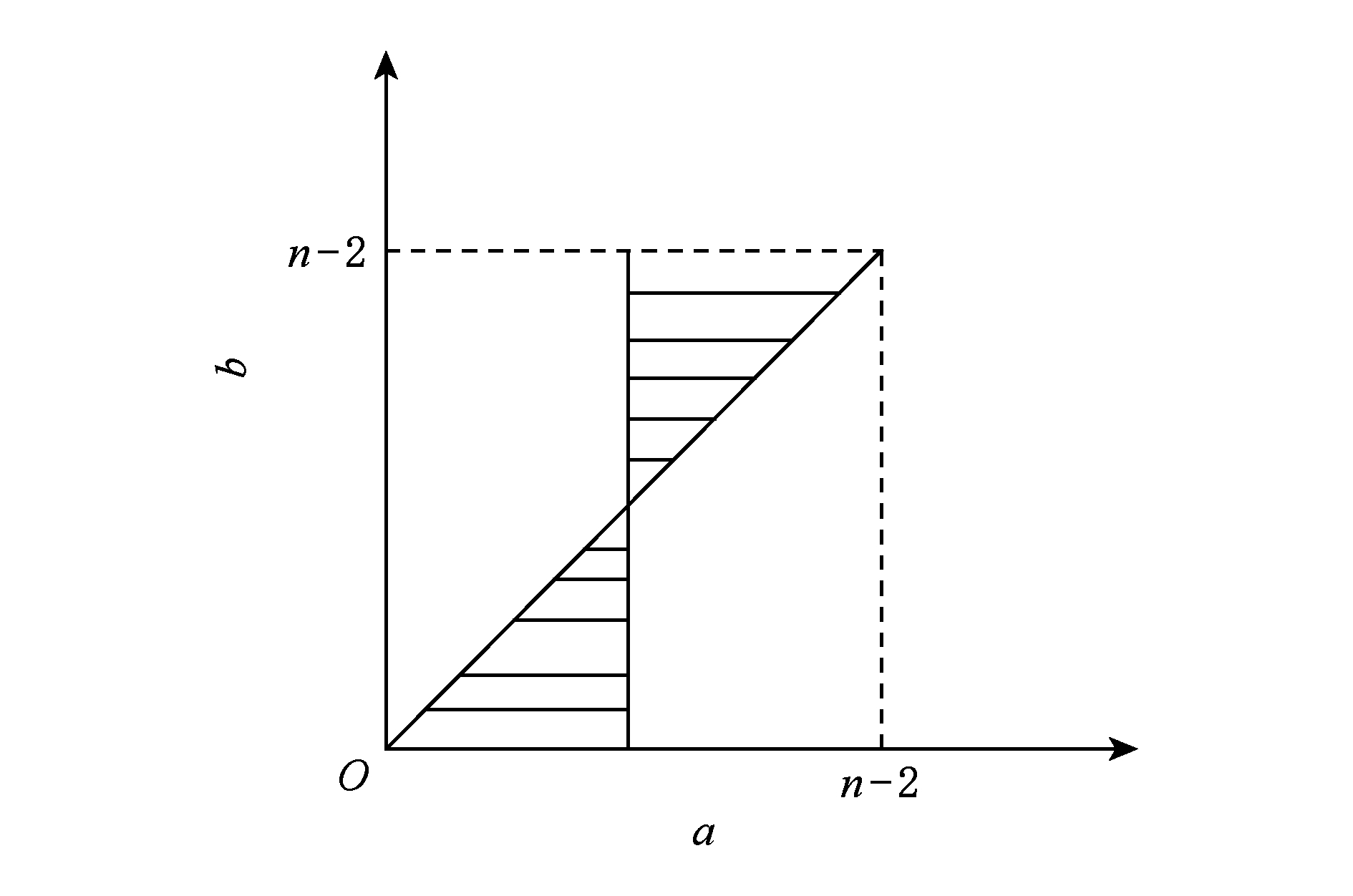
Fig. 2 Sort representation of each node
图2 多节点下各节点的排序表示
该合作博弈的币龄占比和博弈结果可以表示为
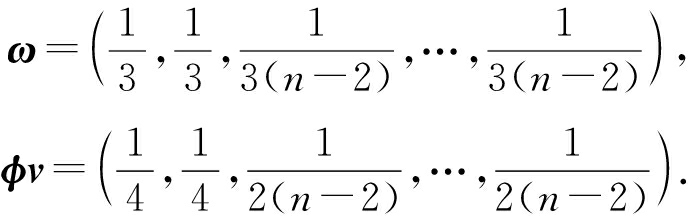
可以明显看出,当大节点数目大于2时,小节点的收益会增大,大节点的收益会减小,此时,由于存在相互制衡的大节点数目,大节点的收益将会减少,相应的小节点的收益将会增多,这将会有利于小节点的健康发展;从另一个角度出发,所有小节点此时总的币龄占比为![]() 得到的总收益为
得到的总收益为![]() 小节点没有动力聚集在一起(因为聚集在一起形成大节点的收益会减少),相反,大节点有动力分散自己的投票权,使得自己的总收益增大.
小节点没有动力聚集在一起(因为聚集在一起形成大节点的收益会减少),相反,大节点有动力分散自己的投票权,使得自己的总收益增大.
虽然我们的模型对现有的各节点情况进行了简化,但是仍然可以发现,在候选出块者中的大节点数目大于2时,小节点数目的增加会使得大节点的收益下降.现在综合所有情况,可得出以下结论:如果存在大量的小节点,大节点只需要得到它们需要数量的小币龄节点的跟随,就能获得较大收益.事实上,在这种改进的机制中,小节点的收益将会变得更多.并且相对较小的节点并不会聚集在一起,而是保持独立,游走于各大节点之间.这种现象有利于使节点独立运行,小节点之间不容易形成团体,有利于共识机制的健康运行.
2.2.2 公平性分析
现在我们从2个角度来说明沙普利值按照各个局中人的币龄占比来进行收益分配的公平性[11].
从节点被选取出的随机顺序的角度来考虑,设n个权益持有者(局中人)必须在一个确定的时间选举出产生区块的人,但是由于网络延迟等各种各样的原因,他们给出结果的顺序是由先后的,这样的顺序一共有n! 种.假设各种可能的到达顺序是等可能的,即各种可能的到达顺序都有相同的概率![]() 又设当局中人i到达时,在他面前到达的局中人已经一起形成了一个联盟M,则i的加入使得联盟的收益从v(M)变成了v(M∪{i}),这个增加值v(M∪{i})-v(M)作为局中人i的分配.记M中的局中人的人数为|M|,则局中人i是第|M|+1个到达的可能性共有|M|!×(|N|-|M|-1)!种,则局中人i的期望收益就为
又设当局中人i到达时,在他面前到达的局中人已经一起形成了一个联盟M,则i的加入使得联盟的收益从v(M)变成了v(M∪{i}),这个增加值v(M∪{i})-v(M)作为局中人i的分配.记M中的局中人的人数为|M|,则局中人i是第|M|+1个到达的可能性共有|M|!×(|N|-|M|-1)!种,则局中人i的期望收益就为
![]()
[v(M∪{i})-v(M)],
此期望收益就是沙普利值.
从节点之间组成的随机联盟的角度来考虑,设:
![]()
[v(M∪{i})-v(M)],![]()
记:
yi(m)=![]() xm(1-x)n-1-mdx
xm(1-x)n-1-mdx
和
φi(v)=![]() Ri(t)dt.
Ri(t)dt.
设t∈[0,1],并设所有局中人都以概率t(即币龄占比)来参加博弈,这一个局中人i不参加的联盟M⊆N\{i}是一个“随机联盟”,这个“随机联盟”形成的概率为t|M|(1-t)|N|-|M|-1,Ri(t)是在这种随机机制下局中人i对可能形成的有i参加的联盟的贡献的期望值.由于博弈进行时并没有指定t的值,所以取Ri(t)关于t的平均值作为应该分配给i的份额,即Ri(t)在[0,1]上的积分,即φi(v)=![]() Ri(t)dt,就可以得到局中人i的平均收益为
Ri(t)dt,就可以得到局中人i的平均收益为
![]()
[v(M∪{i})-v(M)],
即期望收益就是沙普利值.
由此可以看出某一节点的沙普利值即为此节点的期望收益,所以沙普利值是按照每个节点的币龄大小来进行收益分配的一种公平性分配方案.
Ouroboros是Aggelos等人在Crypto 2017提出的基于PoS的可证明安全协议[18],本文引用该协议模型,对协议的权益部分进行改进.
Ouroboros协议及改进描述如下:
1) 初始阶段.初始化节点k和公钥vk,vk对应的权益sk,初始种子真随机数ρ,定义当前的时期epoch,定义时间段slot.
2) 执行阶段.
① 每个节点根据当前的时期epoch对应的ρ执行f(follow-the-satoshi),根据每个节点k对应的公钥vk和权益sk决定区块并返回每个节点对应的分红占比sk*.
② 节点k′生成区块,将区块收益按照每个节点对应的分红占比sk*分给对应的节点,同时根据安全多方计算生成真随机数ρ和下一个时期的epoch,对随机数ρ进行承诺.
Ⅰ. 其余的节点等待节点k′生成区块;
Ⅱ. 时间段slot内收到区块,验证节点k′生成区块;
Ⅲ. 超过时间段slot未收到区块,认为节点k′放弃区块.
③ 重复②直到更新时期epoch.
④ 所有节点对随机数ρ进行检验.开启下个时期epoch,进入②.
follow-the-satoshi(4个节点的情况)[8]描述如下:
输入:节点k对应的权益sk、真随机数ρ执行:
① 根据每个节点k对应的权益sk构造FTS-Merkle树.原始版本的Merkle树如图3所示.改进后的Merkle树如图4所示.
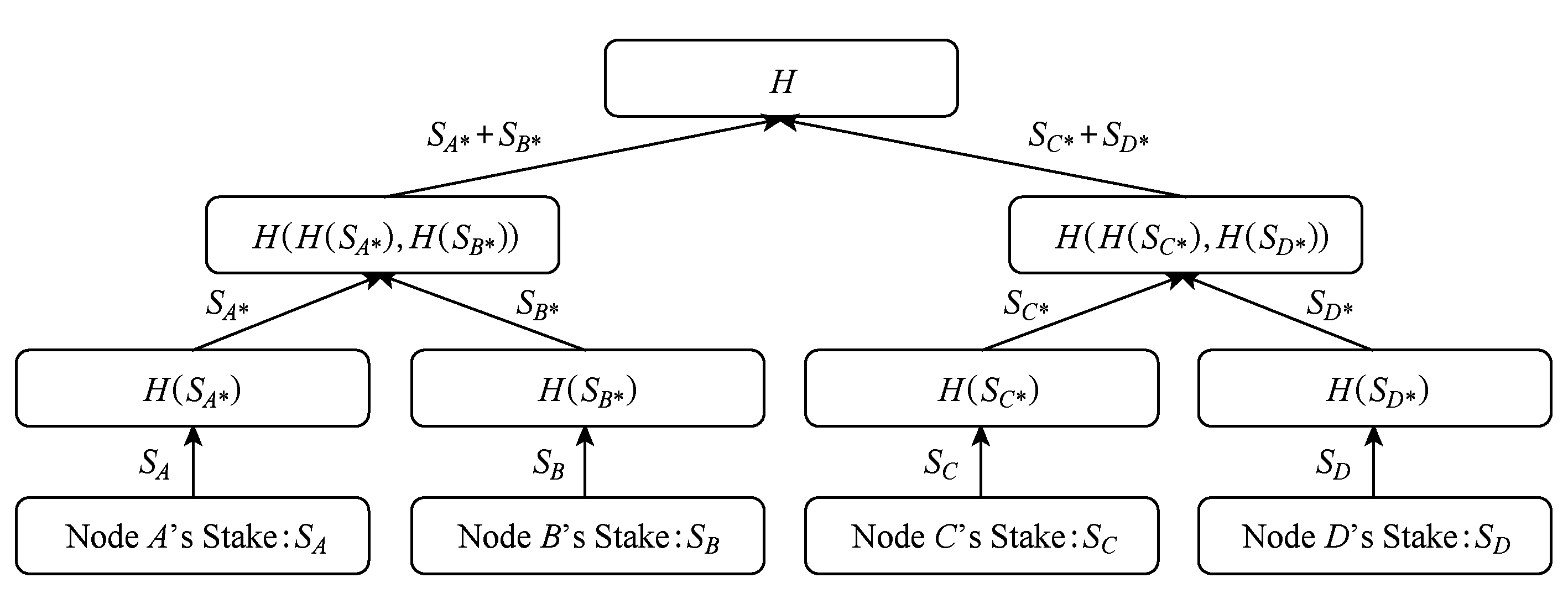
Fig. 3 Original version of FTS-Merkle tree
图3 原始版本的FTS-Merkle
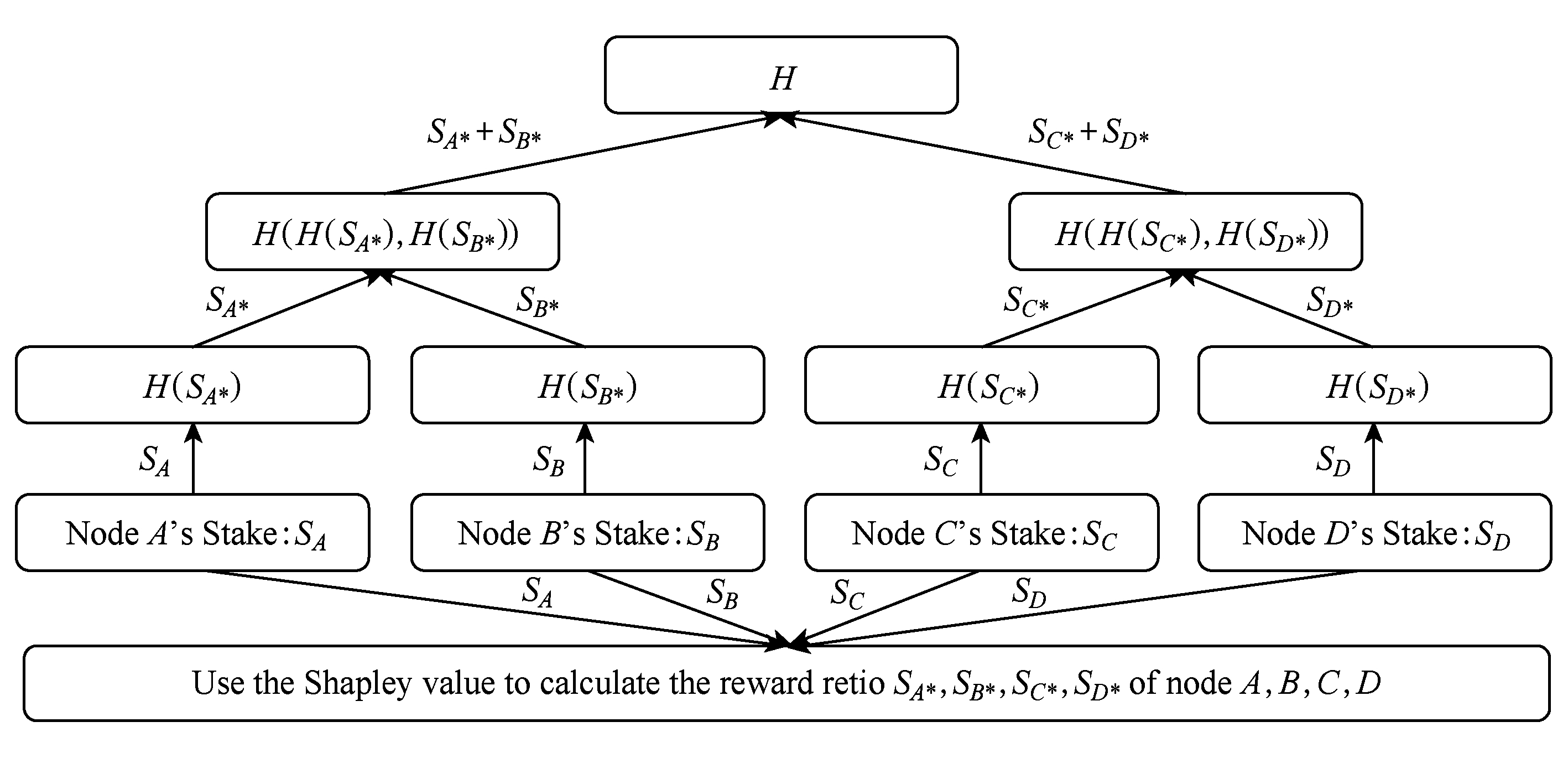
Fig. 4 Improved version of FTS-Merkle tree
图4 改进后的FTS-Merkle树
② 利用真随机数ρ生成![]() 区间内的伪随机数ρ′
区间内的伪随机数ρ′
Ⅰ. 若![]() 则进入左边,继续使用真随机数ρ生成
则进入左边,继续使用真随机数ρ生成![]() 区间内的伪随机数ρ′决定下一步进入的树干,直到到达叶节点k′.
区间内的伪随机数ρ′决定下一步进入的树干,直到到达叶节点k′.
Ⅱ. 若![]() 则进入右边,继续使用真随机数ρ生成
则进入右边,继续使用真随机数ρ生成![]() 区间内的伪随机数ρ′决定下一步进入的树干,直到到达叶节点k′.
区间内的伪随机数ρ′决定下一步进入的树干,直到到达叶节点k′.
③ 根据每个节点k的权益sk计算沙普利值得到每个节点对应的分红占比sk*
④ 返回节点k′的值和每个节点对应的分红占比sk*
输出:某个节点k′和每个节点k的分红占比sk*.
改进后的协议利用每个节点k对应的权益sk计算对应的沙普利值φ(vk),利用φ(vk)计算每个节点k对应的收益占比
利用改进后的![]() 执行协议的剩余部分.
执行协议的剩余部分.
我们引用Garay关于比特币主干协议的要求[19]:
① 存活性(liveness)
如果交易是城实的,改进的协议满足经过一段时间的确认,该交易将保证持续稳定,即不会再更改.存活性可以保证交易的有效时间,当经过一段时间之后,交易必须得到处理——接受或被抛弃.
② 持久性(persistence)
如果网络中存在某个诚实的节点声称接受了某个交易,那么如果剩下的节点诚实的执行协议,则剩下的节点也会回应该交易是稳定的.在保证持久性的过程中,需要确定一些安全参数k.持久性可以保证区块的不可更改性,如果某个区块之后有k个块被确认,则该区块的交易不可更改.
如果Ouroboros协议满足以上2条性质,基于沙普利值的Ouroboros协议依然满足以上2条性质,只是在区块的确认时间上有小的调整,但依然满足存活性和持久性.
本文使用改进的CoA系统中的收益分配方案,通过计算每个节点沙普利值对收益进行了公平分配,并在一定程度上缓解了51%攻击.不仅如此,如果大节点的数量不断增加的话,并不会出现“强者更强”的局面.因此,此种改进后的收益分配方式也对小节点有利,这就从根本上扭转了区块链中“弱者更弱”的局面.
重新基于计算币龄的沙普利值对收益进行分配的方法有效的解决了区块链中存在的大矿池们一家独大的情况,实现了收益分配的均衡化. 不仅如此,在这种分配方式下,新加入的小节点获得收益的可能性较原来有所提高.同时将相同的思想应用到Ouroboros协议中,对Ouroboros协议的收益分配算法进行了改进,并满足了存活性和持久性.
对于改进后的方案,其中很多的细节部分还需要进一步的改进与优化.比如在分配币龄方案中每一次进行挖块之前都要计算各节点的币龄占比,必将耗费一定时间代价,若存在挖矿成功节点不遵守协议独吞收益的情况,如何设置惩罚措施等.
参考文献
[1]Nakamoto S. Bitcoin: A peer-to-peer electronic cash system[OL]. [2018-06-01]. https://bitcoin.org/bitcoin.pdf
[2]Narayanan A, Bonneau J, Felten E, et al. Bitcoin and cryptocurrency technologies: A comprehensive introduction[OL].[2018-06-03]. https://www.zentralblatt-math.org/ioport/en/?q=an%3A06610102
[3]Turek J, Shasha D. The many faces of consensus in distributed systems[J]. Computer, 1992, 25(6): 8-17
[4]Dai W. B-Money[OL]. [2018-06-06]. http://www.weidai.com/bmoney.txt
[5]Dinur I, Nadler N. Time-memory tradeoff attacks on the MTP proof-of-work scheme[OL]. [2018-06-03]. https://link.springer.com/content/pdf/10.1007%2F978-3-319-63715-0_13.pdf
[6]Sunny K, Scott N. PPCoin: Peer-to-peer crypto-currency with proof-of-stake[OL].[2018-05-15]. https://peercoin.net/assets/paper/peercoin-paper.pdf
[7]Finney H. RPoW-Reusable proofs of work[OL].[2018-05-15]. http://cryptome.org/rpow.htm
[8]Schwartz D, Youngs N, Britto A. The ripple protocol consensus algorithm[OL]. (2017-04-15) [2018-06-02]. http://ripple.com/files/ripple_consensus_whitepaper.pdf
[9]Zhu Liehuang, Gao Feng, Shen Meng, et al. Survey on privacy preserving techniques for blockchain technology[J]. Journal of Computer Research and Development, 2017, 54(10): 2170-2186 (in Chinese)
(祝烈煌, 高峰, 沈蒙, 等. 区块链隐私保护研究综述[J]. 计算机研究与发展, 2017, 54(10): 2170-2186)
[10]Bentov I, Lee C, Mizrahi A, et al. Proof of activity: Extending bitcoin’s proof of work via proof of stake[OL].[2018-06-02]. http://www.cs.cornell.edu/~iddo/PoAslides.pdf
[11]Ren L. Proof of stake velocity: Building the social currency of the digital age[OL]. [2018-06-02]. http://www.reddcoin.com/papers/PoSV.pdf
[12]Bentov I, Gabizon A, Mizrahi A. Cryptocurrencies without proof of work[OL].[2018-06-02]. http://arxiv.org/pdf/1406.5964.pdf
[13]Ma Hongkuan. Game theory[M]. Shanghai: Tongji University Press, 2015 (in Chinese)
(马洪宽. 博弈论[M]. 上海: 同济大学出版社, 2015)
[14]Xie Zheng, Dai Li, Li Jianping. Game theory[M]. Beijing: Higher Education Press, 2018 (in Chinese)
(谢政, 戴丽, 李建平. 博弈论[M]. 北京: 高等教育出版社, 2018)
[15]Tian Youliang, Peng Changgen, Ma Jianfeng, et al. Game-theoretic mechanism for cryptographic protocol[J]. Journal of Computer Research and Development, 2014, 51(2): 344-352 (in Chinese)
(田有亮, 彭长根, 马建峰, 等. 安全协议的博弈论机制[J]. 计算机研究与发展, 2014, 51(2): 344-352)
[16]Kevin L, Yoav S. Essentials of game theory: A concise,multidisciplinary introduction[M]. Australia: Morgan & Claypool Publisers, 2008
[17]Robert J. Lectures on game theory[M]. Translated by Zhou huaren. 1st ed. Beijing: China Renmin University Press, 2017 (in Chinese)
(Roger S. 博弈论讲义[M]. 周华任, 译. 1版. 北京: 中国人民大学出版社, 2017)
[18]Kiayias A, Russell A, David B, et al. Ouroboros: A provably secure proof-of-stake blockchain protocol[G] //LNCS 10401: Advances in Cryptology (CRYPTO 2017). Berlin: Springer, 2017: 357-388
[19]Garay J, Kiayias A, Leonardos N. The bitcoin backbone protocol: Analysis and applications[G] //LNCS 9057: Advances in Cryptology (EUROCRYPT 2015). Berlin: Springer, 2015: 281-310
Liu Yiran1, Ke Junming1, Jiang Han2, and Song Xiangfu1
1(SchoolofComputerScienceandTechnology,ShandongUniversity,Jinan250000)2(SoftwareCollege,ShandongUniversity,Jinan250000)
AbstractBlockchain has attracted much attention for its decentralization, tamper-proof, easy to verify and other notable advantages. But for the blockchain, its most fundamental attribute is decentralization. This requires a good consensus mechanism to be established. At present, the common consensus mechanisms include the proof-of-work (PoW) consensus mechanism, the proof-of-stake (PoS) consensus mechanism, the proof-of-activity (PoA) consensus mechanism, and so on. However, these consensus mechanisms didn’t give a specific scheme for the reward distribution of participating nodes. Based on the principle of calculating Shapley value in Game Theory, this paper improves the distribution of reward in the mechanism of the PoS consensus mechanism, makes the reward distribution of the nodes participated in the generated block in the PoS mechanism more fair and reasonable, and it can also reverse the social stratification in the blockchain, thus greatly improving the possibility of the new small node gaining the benefit. In addtion, we apply the same ideas in the Ouroboros protocol to improve its revenue distribution algorithm so that it satisfies survivability and durability.
Keywordsproof-of-stake; Shapley value; reward distribution; Ouroboros protocol; game theory
通信作者:蒋瀚(jianghan@sdu.edu.cn)
This work was supported by the Key Program of the National Natural Science Foundation of China (61632020), the National Natural Science Foundation of China (61572294, 61602287), the Natural Science Foundation of Shandong Province of China (ZR2017MF021), the Key Research and Development Program of Shandong Province (2018GGX101037), the Major Innovation Project of Science and Technology in Shandong Province (2018CXGC0702), the Fundamental Research Funds for the Central Universities (2017JC019), and the Project of Shandong Province Higher Educational Science and Technology Program (J15LN16).
基金项目:国家自然科学基金重点项目(61632020);国家自然科学基金项目(61572294,61602287);山东省自然科学基金项目(ZR2017MF021);山东省重点研发计划(2018GGX101037);山东省科技重大创新工程项目(2018CXGC0702);中央高校基本科研业务费专项资金项目(2017JC019);山东省高等学校科学技术计划项目(J15LN16)
修回日期:2018-08-07
收稿日期:2018-06-12;
中图法分类号TP301
(sdnulyr@126.com)

LiuYiran, born in 1996. Master candidate. Her main research interests include blockchanin and cryptocurrencies.

KeJunming, born in 1994. Master candidate. His main research interests include computer security and crypto-currencies (Junmingke1994@gmail.com).

JiangHan, born in 1974. PhD and lecturer. His main research interest includes theory of cryptography, side-channel attacks and cryptographic protocols.

SongXiangfu, born in 1992. PhD candidate. His main reasearch interests include secure multi-party computation and cryptocuurencies (bintasong@gmail.com).