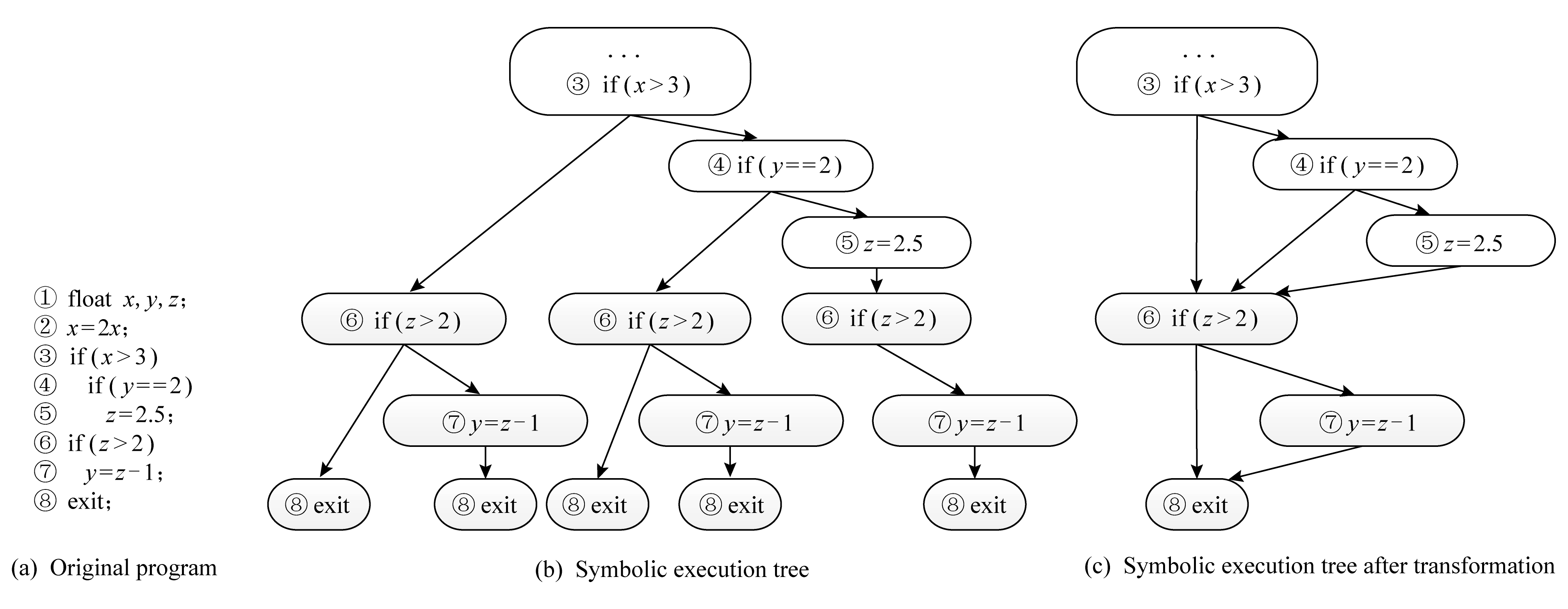
Fig. 1 Symbolic execution tree
图1 符号执行树
郭 曦1王 盼2
1(华中农业大学信息学院计算机科学系 武汉 430070)2(武汉电力职业技术学院电力工程系 武汉 430079)
摘要程序分析的主要目标是对程序的性质进行研究,符号执行作为目前主流的分析方法在生成高效的测试用例集或提高路径覆盖率等方面发挥着重要的作用,其中路径条件表达式的提取以及约束求解是路径分析过程中的关键步骤.现有的路径分析方法普遍存在约束求解效率不高而导致的路径覆盖率较低的问题.由于符号执行引擎所采用的搜索策略不尽相同,在符号执行分析过程中存在状态合并的过程,该抽象过程可能导致产生不正确的测试用例.以提高路径分析效率为目标,提出一种高效的程序分析方法:首先对传统的符号执行树的表示方法进行改进,提取不同路径共享的符号表达式和路径约束条件以提高符号执行过程中状态合并的效率,然后采用隐式关联分析方法,产生逆向分析中的依赖条件集合,并给出基于依赖条件重构的算法以提高路径覆盖率.实验结果表明:相对于传统的状态合并以及符号执行方法,该方法有更为高效的状态合并效率以及更高的路径约束条件分析精度.
关键词路径分析;状态合并;依赖条件;符号执行;约束求解
程序分析的一个主要目标是提高路径的覆盖率,从而对程序的行为、状态和属性等特征进行分析.然而在实际操作过程中,穷尽地覆盖分析往往导致过大的时空开销,并且伴随有极大的状态冗余以及约束条件精度丢失.现有的程序分析方法通常采用符号执行和约束求解的方法来开展各种分析,其中存在的问题主要有状态空间爆炸和约束求解器对于路径约束求解能力的限制等.导致状态空间爆炸的原因,除了程序本身的规模决定了搜索空间呈指数级增长之外,程序状态合并的效率、输入集合的优化程度以及约束求解器对于不同类型符号表达式的求解能力等,都会导致分析的时空开销激增,从而极大地影响分析的效率.
状态合并作为减少状态空间爆炸的常见方法,其思路是对不同的执行路径进行分析,在合并点通过引入辅助变量[1]来对目标变量进行表示,从而区分输入的符号值.但是引入的辅助变量往往会极大影响后期的约束求解器的求解效果,因为目前的约束求解器对于线性约束有较好的处理效果,但当约束条件中存在浮点类型数据、函数调用等结构时,约束求解器为了能够持续运行,可能会删除部分路径条件或者停止工作从而导致分析结果不完备.同时在逆向符号执行过程中,路径条件在改变执行路径过程中,可能会导致部分路径条件丢失的问题,从而遗漏部分执行分支使分析结果不够精确.
本文针对符号执行过程中通常使用的状态合并方法进行优化研究,使用改进符号表达式表示形式的方法,提高约束求解器的分析效果,从而减少状态空间爆炸对于路径分析效率的影响.在该过程中,针对路径条件在迭代分析过程中存在条件丢失的问题,提出改进的路径条件优化组合方法,以提高路径分析的精度.本文主要贡献有2个方面:
1) 通过对状态合并的符号表示方式进行改进,将路径约束与目标变量作为一个整体参与分析,从而精简符号执行树的表示形式;
2) 基于该符号执行树,根据基本块的之间的依赖关系对路径条件进行优化组合,减少路径条件的丢失,提高逆向分析的精度.
符号执行作为主流的程序分析方法在路径覆盖、测试用例生成等研究方向发挥了重要的作用.符号执行的主要思路是使用符号替代具体的数值作为程序的输入,模拟程序的执行,通过收集、求解路径中的条件表达式来研究程序的状态和性质.随着程序规模的增大,其状态搜索空间呈指数增长,同时大量冗余的执行分支以及因为约束求解器的分析性能导致的路径遗漏等问题严重影响了分析的效果.为了缓解状态空间爆炸带来的影响,状态合并[2]作为目前主要的分析方法得到了广泛的应用,它通过分析不同路径的符号表达式在合并点的状态来研究各种合并策略[2-5].SMART[2]通过计算程序的函数摘要的方法生成测试用例集,并使用辅助变量来对不同路径的符号状态进行合并.MergePoint[3]采用符号执行和状态合并的搜索方法,状态合并的操作只能在没有函数调用、跳转语句的程序中才能使用.SMASH[4]使用不可达分析的方法对程序状态进行分析,并删除与需求不相关的执行路径.这几种方法都在函数调用时引入了辅助变量,它会增加符号变量分析的难度,从而进一步制约了约束求解器的求解性能[5].ROSSETTE[6]使用减少辅助变量引入的方法对状态合并展开分析,但该方法只能适用于对等的数据结构.对于状态空间中的冗余状态以及不可达状态,主要通过分析当前状态是否出现在之前的分析结果中,以及将状态空间分解为若干独立的子空间的方法进行研究.JPF[7]使用状态匹配的方法减少状态规模,Boonstoppel等人[8]使用读写集的方法来简化状态匹配条件.文献[9-10]使用程序切片的方法对状态空间进行分组.函数摘要[11-12]作为一种静态分析方法,主要对接口符号变量开展分析,该过程可以与别名分析、可达分析、指向分析等方法进行协同工作.这些方法都存在对程序行为推理不够精确的问题.静态单赋值(static single assignment, SSA)通过改变变量的下标,获得不同变量的定义,使得每个变量只有惟一的定义,同时每个变量只有一条定义-使用链,主要应用于程序分析、编译器优化等领域[13].文献[14]提出将变量转换为守卫符号表达式集合的符号执行方法,但该方法并未分析路径条件的顺序对约束求解的影响.文献[15]基于程序输出的符号将程序的执行路径进行划分,从而对回归测试和程序版本进行测试,该方法并没有对路径条件的表示形式进行优化,易导致约束求解器停止工作.文献[16]通过分析缺陷的类型以及关联的路径,以计算不同上下文中危险操作的覆盖能力为目标,使用符号执行的分析方法来生成高效输入.文献[17]采用抽象引导的半形式化方法框架对候选状态进行评估,生成能够覆盖多个目标状态的状态序列.文献[18]从最短路径、条件约束集概率和可达路径数量的角度,通过推迟变量实例化的方法缓解路径组合爆炸问题.

Fig. 1 Symbolic execution tree
图1 符号执行树
针对状态合并分析过程中由于辅助变量的引入带来的约束求解困难问题,以及路径约束条件在求解过程中存在条件遗漏的问题,本文以传统的符号执行树为起点,以基本块为单位对符号执行树进行优化表示,将相同的基本块进行合并,从形式上约简符号执行树的规模.在状态合并过程中,将约束条件和目标变量作为整体向目标变量提供反馈信息,从而避免辅助变量的引入.在路径条件的约束求解阶段,本文以程序输出语句为起点,采用逆向符号执行和流敏感的数据流的分析方法,提取能够改变输出变量值的隐式语句集合,再通过对路径约束条件的重新组合,使得约束条件在新的路径分析过程中得以完整地保留,避免因约束条件丢失带来的路径搜索不完备的问题.与传统基于状态合并的符号执行方法相比,本文方法可以减少符号表达式和路径约束条件的数量,同时在约束条件求解过程中有更高的分析精度.
符号执行的基本思想是使用变量符号来代替具体的输入值,模拟程序的执行.这种抽象的分析方法相对于具体的执行可以获得更多的路径信息,从而可以更加高效地生成测试用例,以及挖掘未执行的路径.
定义1. 路径条件(path condition).对于一个程序P、一个测试输入t,设π为P在t作用下的执行路径,其对应的路径条件φ是由π中的分支条件等信息组成的一阶逻辑公式.
路径条件的生成是符号执行中的一个重要步骤,在程序的一次执行过程中,当遇到条件分支时,符号执行工具会收集当前的分支条件,并计算在t作用下的约束公式,该约束公式由该路径中所有分支条件进行连接得出.任何输入只要符合t所对应的路径约束条件都会产生与t一致的执行路径.
对于图1(a)所示的程序,传统符号执行所生成的符号执行树如图1(b)所示.符号执行在执行过程中需要保存当前的符号状态:由符号表达式组成的变量,以及当前路径条件φ.当执行过程中遇到分支条件时,符号执行工具使用可达的分支对应的当前路径条件φ更新当前的符号状态.
对于图1(a)所示的程序,传统的符号执行采用符号值x0,y0,z0分别替代输入变量x,y,z.对于图1(b)所示的每条执行路径,符号执行会记录该路径所对应的状态,图1(b)所对应的状态集合如表1所示.同时将图1(b)转换为图1(c)所示的形式,即将相同的结点进行合并,可以有效减少执行路径集合中结点存储的次数,第3节的分析也是基于转换后的符号执行树.
Table1StateSetofSymbolicExecution
表1符号执行状态集合

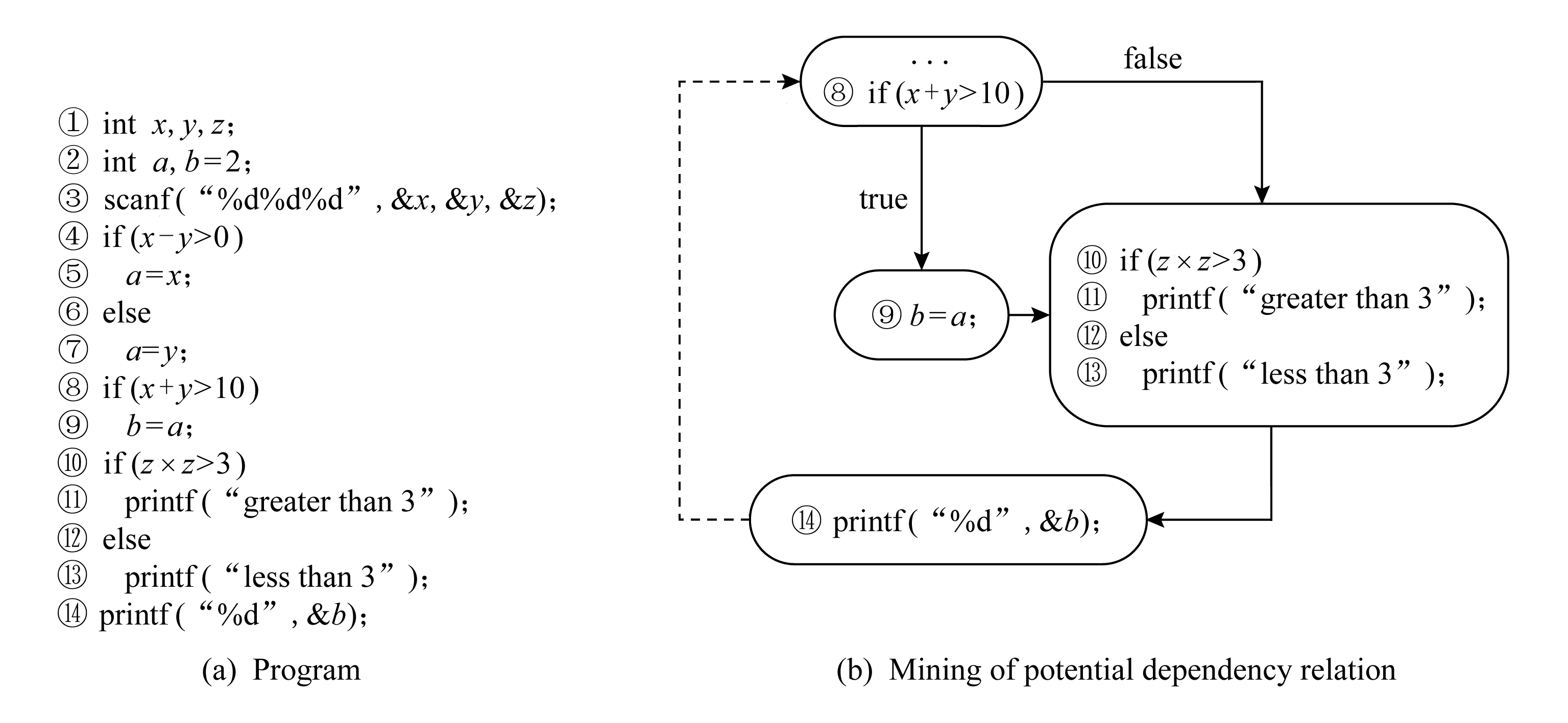
Fig. 2 Potential dependent analysis
图2 隐式依赖分析
符号执行在遇到新的路径分支时,会将该路径条件加入到状态集合中,并依据路径的可达性对各符号变量的值进行更新.路径条件φ可以表示为φ=φ1∨φ2∨φ3∨φ4∨φ5.由于符号执行对于路径的搜索依赖于路径条件φ,即通过反转最近新增的路径条件符号的值来进行,例如对于程序ifkthena=0.3 elsea=fun(b),其符号执行状态可以表示为(k=k0)∧((k∧a=0.3)∨( k∧a=fun(b))).图1(a)中的程序具有嵌套分支条件,可以产生类似的执行状态.注意到表1中φ5所在的行对应的输入变量存在浮点数,在现实程序中除了浮点数以外,存在函数返回以及库函数调用等方式对变量的赋值,目前的约束求解器在处理浮点数以及函数调用等类型的约束条件时,其分析性能受到很大限制.故这种符号执行状态表示方法在实际分析过程中,存在较高的概率使得约束求解器丢弃不能求解的约束条件,从而影响分析的精度.本文使用一种新的状态表示方法,将状态表达式中的路径条件φ和输入变量符号作为2个独立的部分进行表示,从而缓解因约束求解器性能而导致的求解不完备或中断问题,第3节将详细分析该方法的工作过程.
k∧a=fun(b))).图1(a)中的程序具有嵌套分支条件,可以产生类似的执行状态.注意到表1中φ5所在的行对应的输入变量存在浮点数,在现实程序中除了浮点数以外,存在函数返回以及库函数调用等方式对变量的赋值,目前的约束求解器在处理浮点数以及函数调用等类型的约束条件时,其分析性能受到很大限制.故这种符号执行状态表示方法在实际分析过程中,存在较高的概率使得约束求解器丢弃不能求解的约束条件,从而影响分析的精度.本文使用一种新的状态表示方法,将状态表达式中的路径条件φ和输入变量符号作为2个独立的部分进行表示,从而缓解因约束求解器性能而导致的求解不完备或中断问题,第3节将详细分析该方法的工作过程.
逆向符号分析由于具有明确的分析目标,故在路径挖掘、程序调试等方向有广泛的应用.在逆向分析过程中,目标语句一般选取最后一条表达式语句,也可以通过设置断言的方法将某一可疑语句设为目标语句.从目标语句开始,对程序进行逆向分析直到程序的入口语句,该过程中目标语句可以表示为程序输入的符号表达式,从而枚举出与目标语句相关的路径条件表达式集合.
与目标语句相关的符号分析方法可以精简地表示程序全部执行路径,该处用与目标语句中变量b相关的3个符号表达式就可以概括图2(a)的全部8条执行路径.依据程序输出,将程序执行路径集合进行分组,即2条执行路径π1,π2对应的输出符号有相同的表达式形式,则π1和π2有相同的关联切片[19].关联切片对数据依赖、控制依赖进行传递闭包运算.数据依赖和控制依赖依据执行路径π中修改目标语句中变量值的语句集合进行分析.
定义2. 直接依赖.设b1和b2为符号执行树中的2个结点,v为目标语句中的变量,如果:
1)b1重新定义了变量v的值;
2)b2中的语句使用了变量v的值;
3)b1和b2之间存在一条可达路径π,同时在π中的所有语句均没有重定义变量v的值;
则称b2直接依赖于b1.直接依赖是符号执行树中最常见的依赖形式,图2(b)中实线表示2个结点存在直接依赖关系,但是在逆向符号执行分析过程中,目标语句中的变量在不同的执行路径π中会有不同的语句对其符号值进行重定义,故存在如下定义:
定义3. 隐式依赖.对于程序P中的一条执行路径π,目标语句为s,π中某条语句s′对应的路径条件为φ,称s隐式依赖于s′,当且仅当以下条件成立:
1)s具有与φ一致的路径条件s φ;
φ;
2)s中的变量v在π中的语句集合中都没有被重新定义,但v在s与s′之间另一条路径π′中被重定义了;
3) 通过反转φ中某个逻辑公式的值,可以触发新路径π′的执行.
图2(b)中的虚线体现了语句⑧和语句 之间存在隐式依赖关系[14]:目标语句
之间存在隐式依赖关系[14]:目标语句 中的变量b在路径π=[⑧,⑩,
中的变量b在路径π=[⑧,⑩, ,
, ,
, ,
, ]中没有被重定义,但是在路径π′=[⑧,⑨,⑩,
]中没有被重定义,但是在路径π′=[⑧,⑨,⑩, ,
, ,
, ,
, ]中,语句⑨对变量b进行了重定义操作.同时由于改变语句⑧处路径条件φ中关于路径谓词x+y>10的当前真值,可以使得语句⑨成为可达的语句.依据定义3,语句
]中,语句⑨对变量b进行了重定义操作.同时由于改变语句⑧处路径条件φ中关于路径谓词x+y>10的当前真值,可以使得语句⑨成为可达的语句.依据定义3,语句 隐式依赖于语句⑧,如图2(b)中的虚线箭头.在实际分析过程中为了能够挖掘出与目标路径相关的隐式依赖语句,需要挖掘出能够逆向执行到对目标语句中符号变量有重定义操作的语句位置的路径条件,我们将其定义为依赖条件.
隐式依赖于语句⑧,如图2(b)中的虚线箭头.在实际分析过程中为了能够挖掘出与目标路径相关的隐式依赖语句,需要挖掘出能够逆向执行到对目标语句中符号变量有重定义操作的语句位置的路径条件,我们将其定义为依赖条件.
定义4. 依赖条件(dependency condition).对于程序P中的一条执行路径π,目标语句为s,π中某条语句s′对应的路径条件为φ,若s隐式依赖于s′,同时经修改φ中若干分支谓词表达式的真值,得到φ′,使得s与s′之间另一条路径π′可达,则该分支谓词φ′表达式构成路径π的依赖条件.
以图2(a)所示的程序为例,对比传统符号执行、传统逆向分析和依赖条件分析在路径条件φ表达方面的区别.设图2(a)所示的程序的一组输入为{x=6,y=2,z=2},记语句④,⑧,⑩对应的谓词表达式分别为p1,p2,p3,它们在当前输入下的真值分别为true,false,true,对应的执行路径π可以标记为[p1,t,p2,f,p3,t].在当前输入值的作用下,传统符号执行的路径条件为(x-y>0)∧ (x+y>10)∧(z×z>3).对于传统逆向分析,以语句
(x+y>10)∧(z×z>3).对于传统逆向分析,以语句 为目标语句进行逆向分析,由于p2的真值为false,故语句⑨没有对目标语句中的符号变量b进行重定义操作,此时与符号变量b相关的路径为[
为目标语句进行逆向分析,由于p2的真值为false,故语句⑨没有对目标语句中的符号变量b进行重定义操作,此时与符号变量b相关的路径为[ ,②],p1,p2,p3均不出现在该路径条件中,故逆向分析的路径条件为true.依赖条件分析在收集路径条件的过程中,加入了流敏感的数据流分析方法,故可以通过“定义-使用链”分析来提取对变量b有重定义操作的符号语句位置,这些对目标变量有隐式作用的语句集合S′成为隐式依赖分析的依据,在p1,p2,p3的取值过程中,通过修改部分谓词表达式的真值能够实现对S′可达,则这些谓词表达式构成目标语句的依赖条件.本例中若p2的当前真值经修改为true,则语句⑨对目标语句
,②],p1,p2,p3均不出现在该路径条件中,故逆向分析的路径条件为true.依赖条件分析在收集路径条件的过程中,加入了流敏感的数据流分析方法,故可以通过“定义-使用链”分析来提取对变量b有重定义操作的符号语句位置,这些对目标变量有隐式作用的语句集合S′成为隐式依赖分析的依据,在p1,p2,p3的取值过程中,通过修改部分谓词表达式的真值能够实现对S′可达,则这些谓词表达式构成目标语句的依赖条件.本例中若p2的当前真值经修改为true,则语句⑨对目标语句 中的符号变量b有重定义操作,从而改变程序的输出结果,此时逆向分析的路径为[
中的符号变量b有重定义操作,从而改变程序的输出结果,此时逆向分析的路径为[ ,⑧,②],对应的依赖条件为
,⑧,②],对应的依赖条件为 (x+y>10).只要输入符合该依赖条件,则可以使目标语句中的符号变量b有相同的符号表达式.
(x+y>10).只要输入符合该依赖条件,则可以使目标语句中的符号变量b有相同的符号表达式.
基于路径条件的程序分析主要用来提高语句或者分支的覆盖率.隐式依赖分析可以将程序的输入符号以及依赖条件与目标语句中的变量符号进行关联,对于依赖条件φ1∧φ2∧…∧φn,每次路径分析时通过取反最近加入的条件表达式来获取不同的路径,即通过约束求解器对集合{φ1∧φ2∧…∧φi|1≤i≤n}的可满足性进行分析,若某个路径条件可解,则将其从集合中删除,当集合为空时分析结束.对于程序2(a)以及一组输入{x=6,y=2,z=2},其路径分析过程如表2所示:
Table2PathsAnalysisBasedonDependentCondition
表2基于依赖条件的路径分析
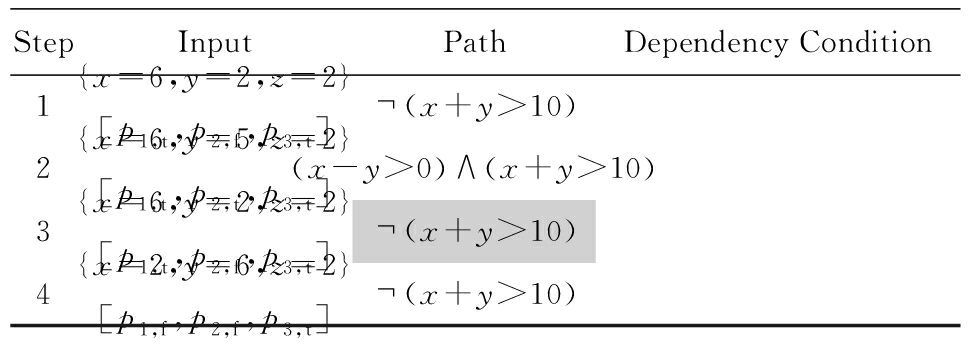
表2枚举了经隐式依赖分析的路径挖掘结果,路径条件 (x-y>0)∧(x+y>10)对应的执行路径并没有出现在“Path”栏中.约束求解器通过判断路径条件表达式是否可解来反馈路径的可达性.但现有的约束求解器在逆向分析过程中存在路径条件丢失的情况.故该方法需要进行完善,第3节中将提出对依赖条件表示的修改算法.
(x-y>0)∧(x+y>10)对应的执行路径并没有出现在“Path”栏中.约束求解器通过判断路径条件表达式是否可解来反馈路径的可达性.但现有的约束求解器在逆向分析过程中存在路径条件丢失的情况.故该方法需要进行完善,第3节中将提出对依赖条件表示的修改算法.
经过第2节的分析可以将一段程序生成精简的符号执行树,并在其基础上进行路径条件的生成以及路径搜索操作,从而提高语句和分支覆盖率.但在上述分析过程中存在2个问题:
1) 现有的路径条件中常包含较为复杂的数据结构和方法调用,这种表示形式对于主流的约束求解器难以求解,故约束求解器需要删除某些不能求解的逻辑公式从而保持求解过程的连续性,但这种直接删除的逻辑公式往往包含关键的路径信息,从而使得求解的结果不完备.
2) 新路径的生成需要对依赖分析后的路径条件进行增量修改,但在增量修改过程中存在部分约束表达式丢失的现象.其原因是约束求解器在增量求解过程中,对依赖条件产生的输入符号可能与之前增量过程所产生的输入符号相同,导致该依赖条件在下一步的增量分析中被删除,这种间接删除的逻辑公式会屏蔽部分新路径的发掘,从而对约束求解器的分析精度产生影响.
对于第1个问题,本文使用符号签名的方法,使用新的路径条件表示形式,将路径条件中目标语句包含的符号表达式抽出,从而避免状态合并中辅助变量对于约束求解器的干扰,提高约束求解器的执行效率.对于第2个问题,本文提出依赖条件的优化表示算法,减少因间接删除逻辑公式所产生的影响.
符号执行的方法在一次计算过程中,对每个变量只保存一个符号表达式,故在状态合并时,对于在多次执行过程中有多个符号表达式的变量,需要引入辅助变量来代替该变量的符号表达式.例如对于图1(a)中语句⑥,对应的符号执行状态如表3所示,由于变量z在3条路中有不同的符号表达式(z0,2.5),则在状态合并时,需要引入辅助变量z′来表示[14],如表4所示,状态合并后的路径条件φ为每条路径对应的路径条件与当前变量z的符号值的合取操作进行析取.
若基于表4的结果进行约束求解,由于路径条件中存在诸如z′=2.5这样带有浮点数运算的表达式,则约束求解器在计算过程中可能受制于求解能力而导致状态合并失败,故下面给出在不影响路径条件逻辑含义的基础上删除辅助变量的方法.对于图1(a)的程序,其符号执行的最终状态如表1所示.这种表示方法难以直观地获得每个变量对应的符号值集合以及每个符号值对应的约束条件.
Table3ExampleofIntermediateState(Statement⑥in
Fig.1(a))
表3中间状态示例(图1(a)中语句⑥)
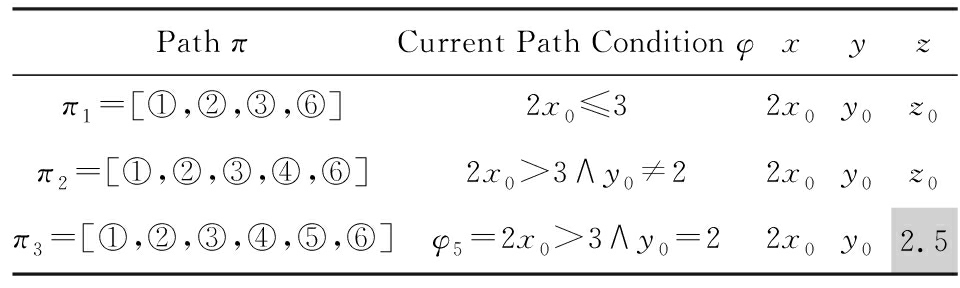
Table4ExampleofStateMerging
表4状态合并示例

对于一个程序P,其输入变量集合为T(t1,t2,…,tm),P的路径条件集合记为Φ(Φ=φ1∨φ2∨…∨φn),设某个输入变量t(t∈T)在状态合并点对应的符号值集合为V(V=v1∨v2∨…∨vi),则有如下定义.
定义5[14]. 符号签名(symbol signature).令某个符号表达式vk对应的路径条件Φvk为:
{φx∨φy∨…∨φz|1<x,y,z<n,x≠y,x≠z,y≠z},其中φx,φy,φz表示到达vk的不同路径所对应的路径条件,则t在状态合并时对应的符号签名vs定义为{(φ,vk)|φ∈Φvk}.
例如对于图1(a)的程序,依据表1所示的状态表和符号签名的定义,可以将其转换为符号签名视图[14],该视图反映了图1(a)中语句⑧位置经状态合并后程序的最终状态:
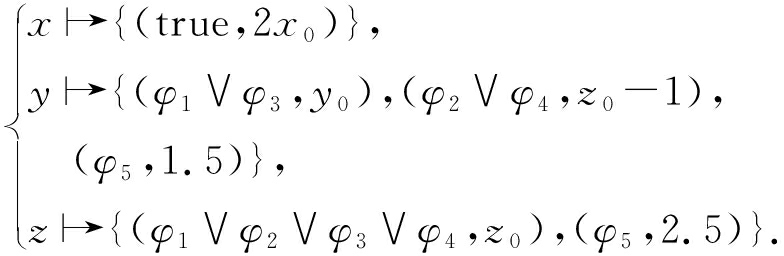
(1)
注意式(1)中没有辅助变量,且逻辑上与含有辅助变量的状态一致.下面分析式(1)的产生过程.首先对于图1(a)中的状态合并点语句⑥,语句①~⑥对应的符号执行状态如表3所示.
对于即将执行的语句⑥,其逻辑表达式z>2需要进行运算以求出下一个合并点,即语句⑧处的符号签名视图.对于变量z对应的符号表达式z0和2.5,进行z>2的运算,即此时语句⑥对应的符号签名为{( φ5,z0>2),(φ5,2.5>2)},由于 (2.5>2)恒为真,故可以表示为{(
φ5,z0>2),(φ5,2.5>2)},由于 (2.5>2)恒为真,故可以表示为{( φ5,z0>2),(φ5,true)}.此时语句⑥对应的路径条件为φ6=(
φ5,z0>2),(φ5,true)}.此时语句⑥对应的路径条件为φ6=( φ5∧z0>2)∨(φ5∧true).
φ5∧z0>2)∨(φ5∧true).
当φ6可满足时语句⑦可达,此时的y=z-1运算存在对变量y的重定义,变量y在目标语句⑧处对应的符号签名为:y={( φ6,y0),(
φ6,y0),( φ5∧φ6,z0-1),(φ5∧φ6,1.5)},这和式(1)中的y的符号签名在逻辑上是等价的.此时依据前一个状态合并点的符号执行状态信息和符号签名信息,计算出程序最终状态的符号签名信息,这与依据程序最终状态的符号执行状态获得的签名信息在逻辑上是一致的.
φ5∧φ6,z0-1),(φ5∧φ6,1.5)},这和式(1)中的y的符号签名在逻辑上是等价的.此时依据前一个状态合并点的符号执行状态信息和符号签名信息,计算出程序最终状态的符号签名信息,这与依据程序最终状态的符号执行状态获得的签名信息在逻辑上是一致的.
这种符号签名视图可以直观地获得每个输入变量在合并点处的符号值以及对应的路径条件,对于表2中不同的符号值,采用灰色背景进行标记.符号签名的特点如下.
1) 对于某个符号表达式的符号签名vs,设(φ1,v1)和(φ2,v2)是vs中的2个不同元素,若v1=v2,则这2个元素可以合并为(φ1∨φ2,v1),且此时的符号签名等价于vs\{(φ1,v1),(φ2,v2)}∪{φ1∨φ2,v1};
2) 如果vs中存在形如(false,v)的元素,则可以将其从vs中删除.
符号签名的表示形式相对于传统符号执行的状态表示形式,其最大优点在于不同执行路径的路径条件表达式和变量的符号表达式,在符号签名中的表达形式中可以共享,例如在图1(a)中语句⑥处,传统符号执行依据路径条件有3条不同的执行路径,但通过符号签名分析,可以获得在此处变量z的2个不同符号值(r0,2.5),从而减少对约束求解器的调用次数.
本文将变量符号与符号签名之间建立起关联,使用符号签名的常用符号执行语义[14]表示如图3所示:
![]()
Binary Operation:
Condition Operation:
![]()
![]()
Fig. 3 Symbol execution semantic
图3 符号执行语义
其中v1⊙v2表示对2个符号签名v1和v2进行合并操作,但与普通的合并运算的区别于v1⊙v2还进行重复的路径条件和约束表达式的共享,从而减少对求解器的调用.更新操作主要使用⊙运算符进行运算,其中当路径条件φ可满足时,则将符号签名v1作用于后续路径中的符号签名,当 φ可满足时,将v2作用于后续路径中的符号签名.当存在对变量符号进行赋值操作时,常量操作和符号输入操作对该变量符号值进行更新,该过程中⊙运算只对满足路径条件φ的执行路径中的赋值操作进行运算.二元运算主要对2个符号变量(a,b)间存在二元运算符时进行操作,运算结果为变量a的符号表达式与变量b的符号表达式的笛卡儿积.在条件运算中,当条件表达式e可满足时,则对e和后续可达语句s的各自符号签名进行笛卡儿积运算,并将e对应的符号表达式并入到当前的路径条件中,当e不可满足时,则需要对x的每个符号签名中的符号变量进行分析.
φ可满足时,将v2作用于后续路径中的符号签名.当存在对变量符号进行赋值操作时,常量操作和符号输入操作对该变量符号值进行更新,该过程中⊙运算只对满足路径条件φ的执行路径中的赋值操作进行运算.二元运算主要对2个符号变量(a,b)间存在二元运算符时进行操作,运算结果为变量a的符号表达式与变量b的符号表达式的笛卡儿积.在条件运算中,当条件表达式e可满足时,则对e和后续可达语句s的各自符号签名进行笛卡儿积运算,并将e对应的符号表达式并入到当前的路径条件中,当e不可满足时,则需要对x的每个符号签名中的符号变量进行分析.
对于程序的一次执行,传统的路径发掘方法具有如下性质:如果φ1∧φ2∧…∧φn为该执行对应路径条件的一个前缀,则满足条件φ1∧φ2∧…∧ φn的输入,其对应的路径条件均以φ1∧φ2∧…∧
φn的输入,其对应的路径条件均以φ1∧φ2∧…∧ φn为前缀.通过第2节分析,该性质对于依赖条件不成立.由于依赖条件dc在逻辑上要弱于路径条件pc,即φ⟹dc,故对于依赖条件所具有的性质:如果φ1∧φ2∧…∧φn为程序一次执行对应依赖条件的一个前缀,则满足条件φ1∧φ2∧…∧
φn为前缀.通过第2节分析,该性质对于依赖条件不成立.由于依赖条件dc在逻辑上要弱于路径条件pc,即φ⟹dc,故对于依赖条件所具有的性质:如果φ1∧φ2∧…∧φn为程序一次执行对应依赖条件的一个前缀,则满足条件φ1∧φ2∧…∧ φn的输入,其对应的依赖条件均以φ1∧φ2∧…∧
φn的输入,其对应的依赖条件均以φ1∧φ2∧…∧ φn为前缀,由于φ⟹dc,此时该性质也适用于路径条件.
φn为前缀,由于φ⟹dc,此时该性质也适用于路径条件.
在表2中,路径条件 (x-y>0)∧(x+y>10)对应的执行路径并没有出现在“路径”栏中,其原因是表2中行③通过对行②的依赖条件中最近加入的条件表达式x+y>10进行取反操作,即得到行③的依赖条件(x-y>0)∧
(x-y>0)∧(x+y>10)对应的执行路径并没有出现在“路径”栏中,其原因是表2中行③通过对行②的依赖条件中最近加入的条件表达式x+y>10进行取反操作,即得到行③的依赖条件(x-y>0)∧ (x+y>10),该依赖条件的一组输入可以是{x=6,y=2,z=2},注意到该组输入对应的依赖条件是
(x+y>10),该依赖条件的一组输入可以是{x=6,y=2,z=2},注意到该组输入对应的依赖条件是 (x+y>10),这样行③的部分依赖条件,即(x-y>0)并未出现在行③的“路径”栏中(表2中的灰色区域),这也是导致新路径分析不够精确的重要原因.
(x+y>10),这样行③的部分依赖条件,即(x-y>0)并未出现在行③的“路径”栏中(表2中的灰色区域),这也是导致新路径分析不够精确的重要原因.
导致依赖信息丢失的原因是依赖条件的表示方法,为了能够获得遗漏路径的依赖条件,需要将现有的依赖条件表示方法进行修改,即采用依赖条件重构的方法对目前的依赖条件进行重新排序.依赖条件重构的算法[15]如下所示.
算法1. 依赖条件重构算法.
输入:程序P、测试集t、目标语句C;
输出:重构后的依赖条件DCR.
①Stack=∅;
② 执行函数Execute(t,0);
③ whileStack≠∅
④ 将pop(Stack)的值赋给(f,j);
⑤ iff不能被满足
⑥a是一个可以满足f的输入;
⑦ 将a赋值给T;
⑧ 执行函数Execute(a,j);
⑨ end if
⑩ end while
 return DCR;
return DCR;
 ProcedureExecute(t,n)
ProcedureExecute(t,n)
 计算关于C的依赖条件;
计算关于C的依赖条件;
 dc=φ1∧φ2∧…∧φm;
dc=φ1∧φ2∧…∧φm;
 dc′=Reorder(dc);
dc′=Reorder(dc);
 for all从n+1到m中的变量i
for all从n+1到m中的变量i
![]()

![]()
 将函数值(k,j)压入到栈Stack中;
将函数值(k,j)压入到栈Stack中;
 end for
end for
 return
return
 end Procedure
end Procedure
 ProcedureReorder(seq)
ProcedureReorder(seq)
 ifseq的长度为0
ifseq的长度为0
 returnseq;
returnseq;
 end if
end if
 seq=φ1∧φ2∧…∧φk;
seq=φ1∧φ2∧…∧φk;
 将seq1和seq2的值都赋值为true;
将seq1和seq2的值都赋值为true;
 for all从1 tok-1中的变量i
for all从1 tok-1中的变量i
 ifbr(φi)⊆br(φk)
ifbr(φi)⊆br(φk)
 seq1=seq1∧φi;
seq1=seq1∧φi;
 else
else
 seq2=seq1∧φi;
seq2=seq1∧φi;
 end if
end if
 end for
end for
 returnReorder(seq1)∧Reorder(seq2)∧φk;
returnReorder(seq1)∧Reorder(seq2)∧φk;
 end Procedure
end Procedure
其中函数Reorder( )用来对现有的依赖条件序列进行重构,其工作过程类似于快速排序算法.对于由多个逻辑表达式序列seq组成的待重组的依赖条件dc,该算法依据最近加入的条件表达式e将待重组的序列seq分解为2个子序列seq1和seq2,seq中与e存在隐式依赖的逻辑表达式依据seq中的相对顺序存放到seq1中,对应地将seq中与e不存在隐式依赖的逻辑表达式依据seq中的相对顺序存放到seq2中,并将e存入到一个栈Stack中.然后分别对seq1和seq2重复上述过程,直到栈Stack=∅,最后程序输出为重组后的路径分支表达式.图4表示该算法的执行过程[15].其中图4(a)表示待重组的序列seq中逻辑表达式之间的隐式依赖关系,其中每个逻辑表达式用一个结点表示,例如e6→e1,则表示e6隐式依赖于e1.初始时,由于e6与其他结点存在隐式依赖关系,故将e6存入栈Stack中,并以e6为中心结点,将其余结点依据是否存在依赖关系依据原始相对顺序移到e6两侧.由于e1和e3均与e6存在隐式依赖,故将e1和e3依据原始序列seq中的顺序存放到e6左侧,记为seq1,e2,e5,e6则存放到e6右侧,记为seq2.然后分别对seq1和seq2重复上述过程,直到栈Stack=∅,此时重构后的依赖条件序列.当每次从栈Stack中弹出一个依赖条件,函数Execute( )需要对该依赖条件的可满足性进行分析,若该依赖条件可解,则可以计算出对应的输入i,该输入i可以生成新的依赖条件,并对该依赖条件进行分析.为了提高分析速度,在函数Execute( )的参数中加入了一个参数n,该参数用以指示分析从当前序列第n个结点开始,如该节开头分析,前n个结点的作为前缀时,分析结果能够得以传递到下一次迭代分析中,从而提高分析的速度.在表2的分析结果基础上,算法1的执行步骤如表5所示,其中第3个函数中生成了表2中未能发掘的路径[p1,f,p2,t,p3,t],如表5中灰色背景标记所示.
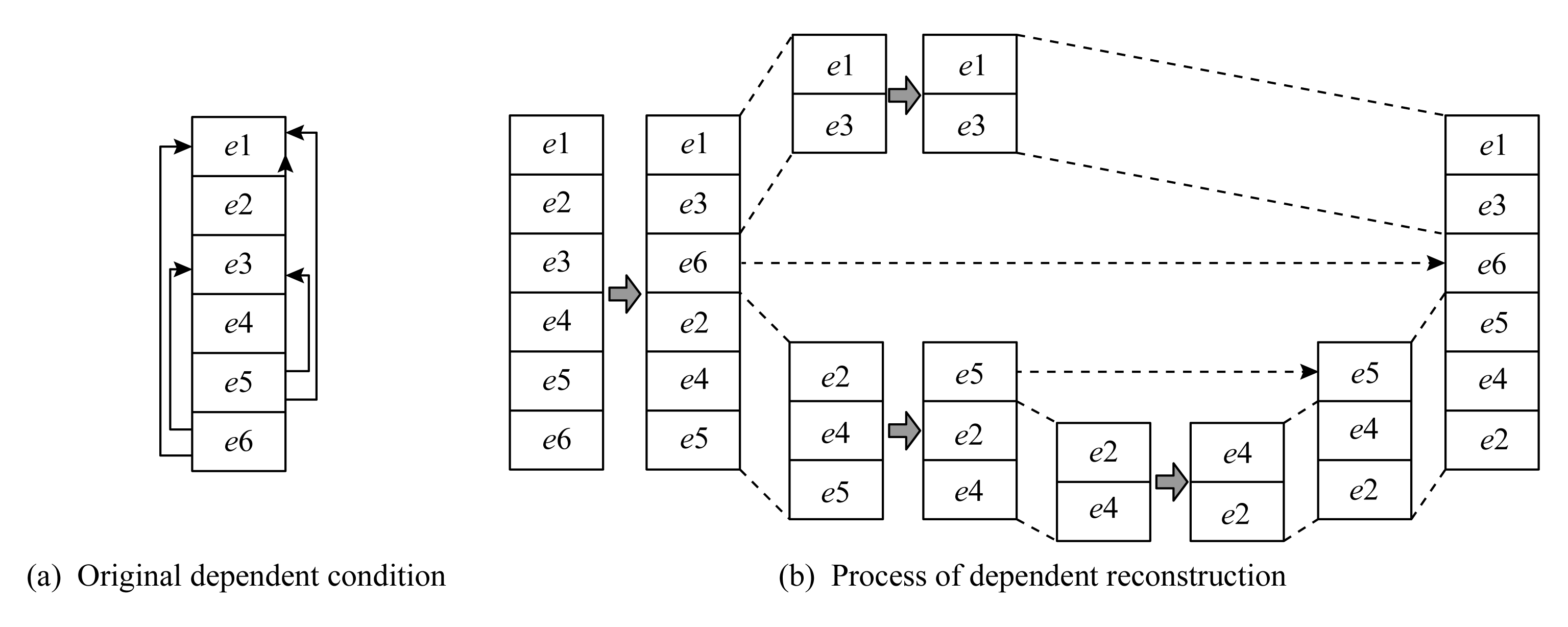
Fig. 4 Example of dependent condition reconstruction
图4 依赖条件重组示例
Table5ProcessofDependentConditionReconstruction
表5依赖条件的重构过程

通过符号签名的分析方法对路径条件的表示形式进行修改,并在此基础上使用依赖条件重组算法对路径中的依赖关系进行分析,可以有效减少传统符号执行方法和状态合并方法因直接删除或间接删除路径条件所带来的分析精度上的损失.
记→为语句中符号变量间的直接依赖, 为语句中符号变量间的传递依赖,dc(s,π)表示路径π的目标语句s对应的依赖条件,则有如下定理.
为语句中符号变量间的传递依赖,dc(s,π)表示路径π的目标语句s对应的依赖条件,则有如下定理.
定理1. 对于程序P对应的2个输入t1和t2,ti(i=1,2)对应的执行路径为π(ti),设s是π(t1)中的一条语句,但s不在π(t2)中.设b为π(t1)中的最后一个分支条件,且有s b,同时b也在π(t2)中,此时b在π(t1)和π(t2)中有不同的表达形式.
b,同时b也在π(t2)中,此时b在π(t1)和π(t2)中有不同的表达形式.
证明. 采用反证法.依据已有条件s b,设b′→b为π(t1)中从s到b的路径中的最后一个连接,此时有s
b,设b′→b为π(t1)中从s到b的路径中的最后一个连接,此时有s b′→b.此时假设b在π(t1)和π(t2)中有相同的表达形式,则b同样也在路径π(t2)中,故在π(t2)中b也满足s
b′→b.此时假设b在π(t1)和π(t2)中有相同的表达形式,则b同样也在路径π(t2)中,故在π(t2)中b也满足s b,即b也出现在路径π(t2)中,这与定理中b为π(t1)中的最后一个满足s
b,即b也出现在路径π(t2)中,这与定理中b为π(t1)中的最后一个满足s b分支条件的条件相矛盾,故b在π(t1)和π(t2)中有不同的表达形式.
b分支条件的条件相矛盾,故b在π(t1)和π(t2)中有不同的表达形式.
证毕.
定理2. 对于程序P对应的2个输入t1和t2,ti(i=1,2)对应的执行路径为π(ti),设s是π(t1)中的一条语句,若t2=dc(s,π(t1)),则s是路径π(t2)中一条语句.
证明. 设si和sj是2条有先后顺序的语句,即si→sj,则由sj和π(t1)共同决定的路径π(sj,π(t1))中的语句都会包含在由si和π(t1)共同决定的路径π(sj,π(t1))中,故dc(si,π(t1))⟹dc(sj,π(t1)).因t2 dc(si,π(t1)),故t2
dc(si,π(t1)),故t2 dc(sj,π(t1)),从而sj将包含在π(t1)和π(t2)中,即任意的si是路径π(t2)中一条语句.
dc(sj,π(t1)),从而sj将包含在π(t1)和π(t2)中,即任意的si是路径π(t2)中一条语句.
证毕.
定理1使得依赖条件可以确保在目标语句中,每个符号变量只有惟一的符号值.定理2使得对于一个可达路径π,本文方法可以发掘一条路径π′,使得π′和π有相同的依赖条件.
本文在WALA平台上构建实验原型系统,该平台可以读取待分析的程序,构建程序调用图和控制流图,同时采用Z3作为约束求解器,对线性约束表达式和字符串进行求解操作.Java语言由于具有动态类型,使得变量在分析过程中可以方便地替换为符号表达式或者具体的数值,故本文以Java程序为测试集.实验方案如图5所示:
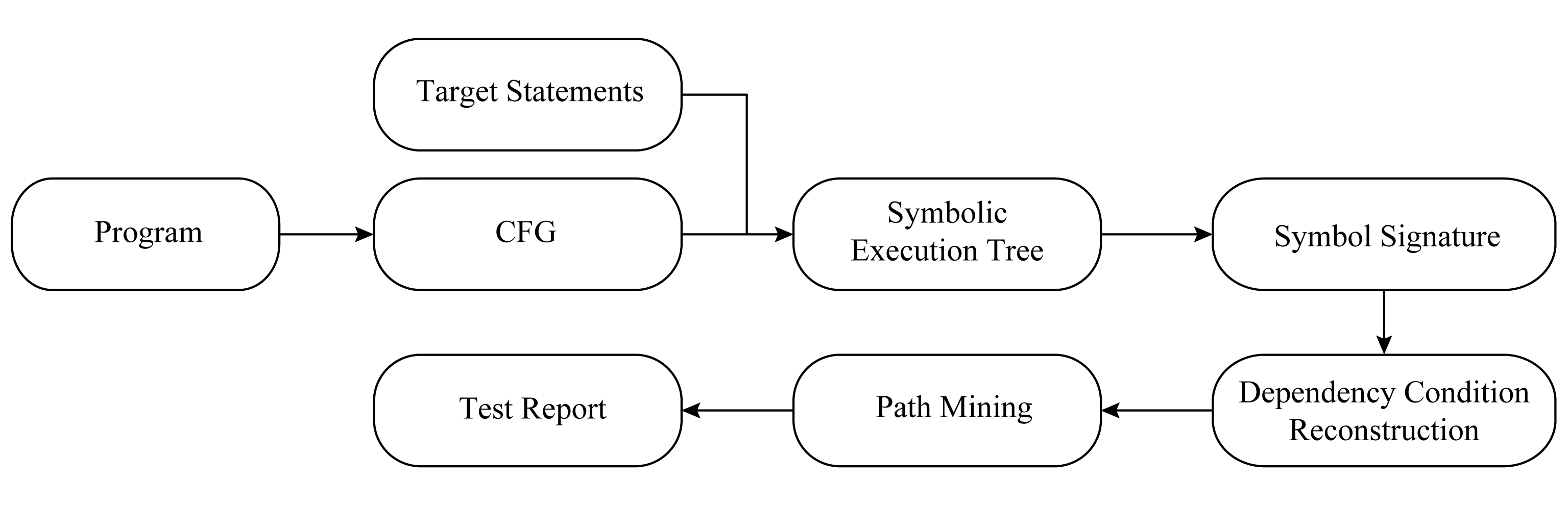
Fig. 5 Experimental setup
图5 实验方案
依赖条件是在逆向符号执行过程中生成的.对于目标语句中的符号变量,主要分析与其有重定义操作的语句集合.实验以状态合并和符号执行作为分析工具,主要实验内容包括:对比传统状态合并方法和本文方法在状态合并上的数量,以及相对于传统符号执行方法,本文方法在发掘可行的隐式路径数量上性能的提升.同时验证了路径条件和符号表达式的共享在符号签名的分析方法中的有效性.
表6中“符号签名均值”表示程序中各符号变量在不同路径中对应的不同符号表达式个数的平均值,符号签名的平均值不超过6.该值越小,表明程序变量间的隐式依赖数量越少.“符号签名共享比率”表示达到目标位置的不同路径的数量与该目标位置的符号签名个数的比值,表明路径表达式和符号表达式在不同路径中存在相同的前缀,故在新路径发掘过程中,可以有效利用相同的前缀从而减少重复分析带来的额外计算开销.“传统合并方法合并程度”表示对当前程序进行传统合并方式与本文方法在状态合并数量上的比值.从表6中可以看出除了3个程序,本文方法在其余程序中均可以较传统方法有更多的状态合并.在进行符号执行过程中,本文方法相对于传统的符号执行方法DART,均可以减少时间开销.其中“有效路径对比”表示传统符号执行方法所生成的路径数量与本文方法所生成的路径数量的比值,由于本文方法采用了符号签名和依赖条件重组的分析方法,能够有效减少因直接删除和间接删除依赖条件所导致的路径分析精度上的损失.约束求解器在程序分支条件处需要对当前的分支条件表达式进行求解,由于约束求解器在计算过程中有较大的时间开销,故在实际分析过程中需要尽可能减少约束求解器的调用次数.“求解次数比率”表示传统符号执行方法与本文方法在调用约束求解器时数量的对比.由于采用了共享路径条件和符号表达式的分析方法,故本文方法能够较少地调用约束求解器.
Table6ComparisonofStateMergingandSymbolicExecution
表6状态合并和符号执行的对比
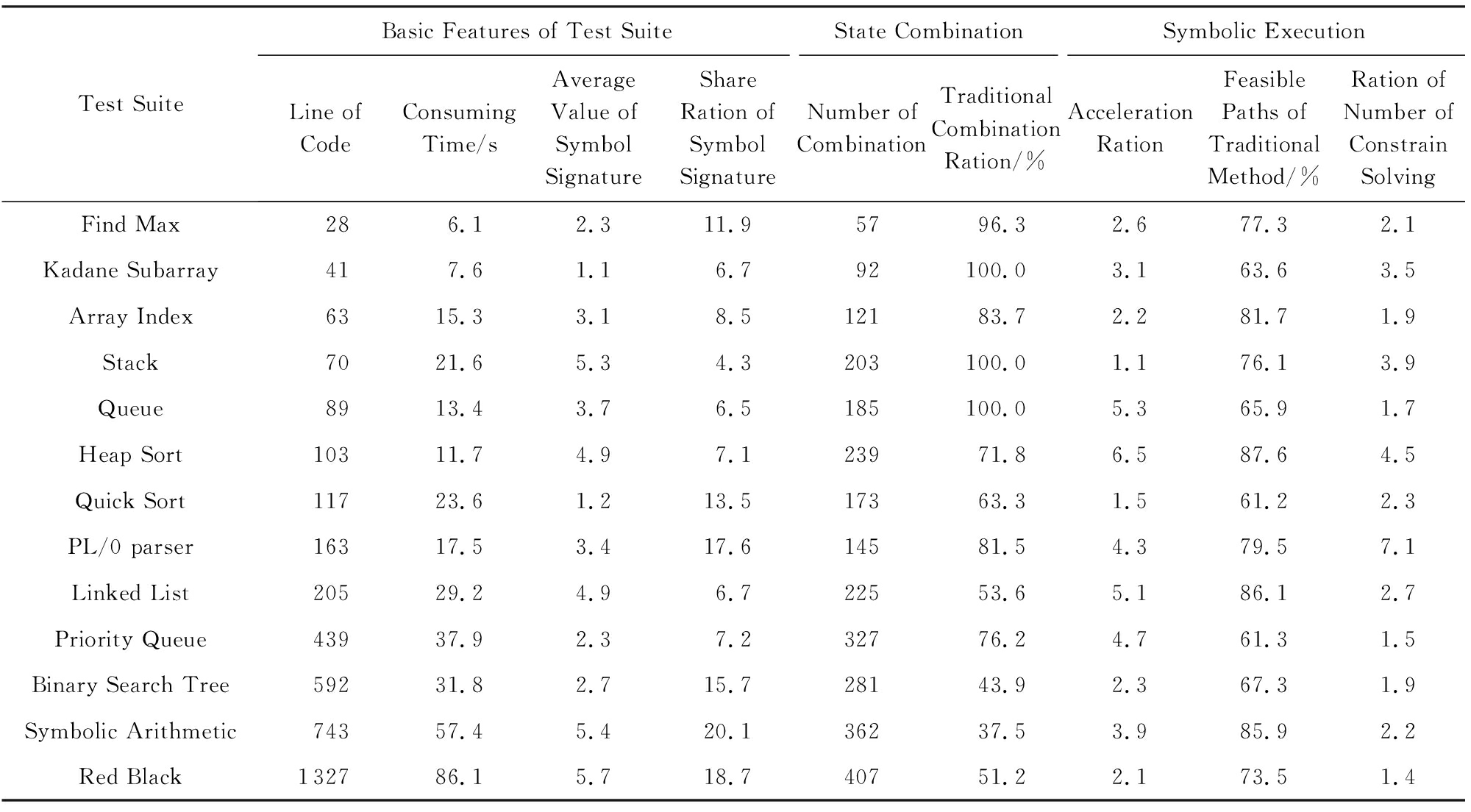
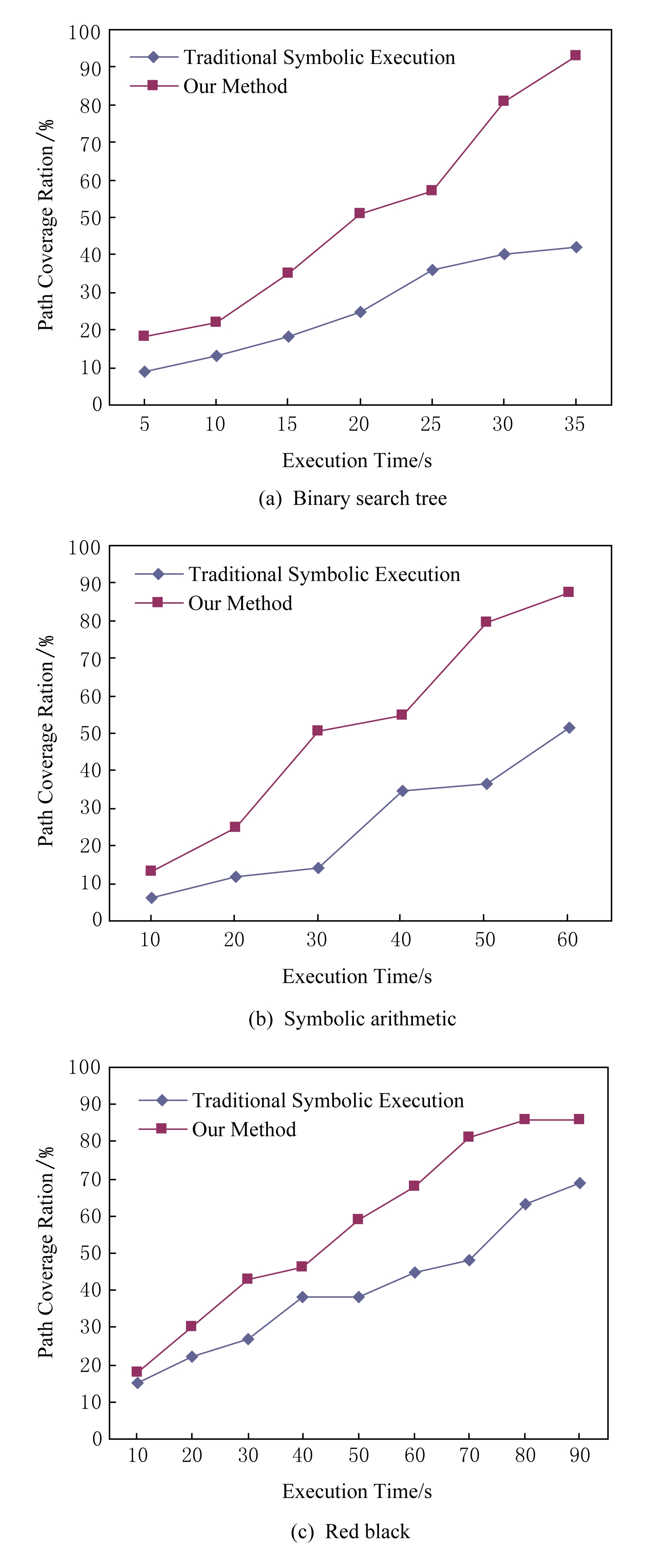
Fig. 6 Comparison of path coverage
图6 路径覆盖率对比
为了对比在路径发掘方面的效率,本文以表6中规模最大的3个程序为例,实验结果如图6所示:
本文方法使用了基于依赖条件重组的路径分析方法,相对于传统符号执行方法可以发掘更多的可达路径.本文方法较传统符号执行方法在路径覆盖率方面有较大提高,但没有达到100%,其原因是对于程序执行语义的建模精度还有待提高,尤其是对于数组下表、内存地址访问、循环终止条件等符号表达式的处理还有待进一步完善.另一个原因是约束求解器的性能对于依赖条件的求解有直接的影响,虽然本文采用路径条件和变量符号分离的表示方法来提高约束求解器的求解性能,但同样由于数组下表等复杂数据结构的影响,在一定程度上影响了路径的覆盖率,这是本文将来主要的研究工作.对于程序中一条具有n个分支条件的执行路径,本文的方法需要约束求解器对该路径对应的依赖条件进行n次分析,另外不同执行路径的依赖条件之间有相似性,将来工作中可以采用并行符号执行的方法以提高这2个过程的分析效率.
符号执行是路径分析中的传统方法,但状态空间爆炸和约束求解器性能严重制约了其性能的发挥.状态合并作为一种有效的状态约简方法得到了广泛的应用,但因路径条件的表示形式影响了约束求解器求解的性能.本文采用一种基于改进符号执行树的分析方法,在其基础上通过分离路径条件和符号表达式,从而可以提高约束求解器的求解性能而提高状态合并的效率.在约束求解器的求解过程中,本文还提出了基于依赖条件的重构算法,从而避免因路径条件的直接删除和间接删除所导致的路径分析不够完备的问题.如实验部分所述,本文方法在路径分析的性能方面较传统方法有较大提高,但由于对程序中数组下标、地址解析等复杂结构执行语义建模还不够精确,故影响了路径覆盖率的进一步提升.将来的工作中主要是复杂数据结构语义建模,例如可以加入静态单赋值(SSA)的分析方法,减少路径条件分析时引入临时变量的数量及变量间命名的冲突,从而可以构建更为精确的路径条件.
参考文献
[1]Kuznetsov V, Kinder J, Bucur S, et al. Efficient state merging in symbolic execution[J]. ACM SIGPLAN Notices, 2012, 47(6): 193-204
[2]Godefroid P. Compositional dynamic test generation[C] //Proc of the 34th ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 2007: 47-54
[3]Avgerinos T, Rebert A, Cha S K, et al. Enhancing symbolic execution with veritesting[C] //Proc of the 36th Int Conf on Software Engineering. New York: ACM, 2014: 1083-1094
[4]Godefroid P, Nori A V, Rajamani S K, et al. Compositional may-must program analysis: Unleashing the power of alternation[C] //Proc of the 37th ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 2010: 43-56
[5]Wang Chong, Lü Yinrun, Chen Li, et al. Survey on development of solving methods and state-of-the-art application of satisfiability modulo theories[J]. Journal of Computer Research and Development, 2017, 54(7): 1405-1425 (in Chinese)
(王翀, 吕荫润, 陈力, 等. SMT求解技术的发展及最新应用研究综述[J]. 计算机研究与发展, 2017, 54(7): 1405-1425)
[6]Torlak E, Bodik R. A lightweight symbolic virtual machine for solver-aided host languages[J]. ACM SIGPLAN Notices, 2014, 49(6): 530-541
[7]Visser W, Reanu C S, Nek R. Test input generation for java containers using state matching[C] //Proc of the 5th Int Symp on Software Testing and Analysis. New York: ACM, 2006: 37-48
[8]Boonstoppel P, Cadar C, Engler D. RWset: Attacking path explosion in constraint-based test generation[C] //Proc of the 14th Int Conf on TOOLS and Algorithms for the Construction and Analysis of Systems. Berlin: Springer, 2008: 351-366
[9]Majumdar R, Xu Rugang. Reducing test inputs using information partitions[C] //Proc of the 21st Int Conf on Computer Aided Verification. Berlin: Springer, 2009: 555-569
[10]Chakrabarti A, Godefroid P. Software partitioning for effective automated unit testing[C] //Proc of the 6th Int Conf on Embedded Software. New York: ACM, 2006: 262-271
[11]Sharir M, Pnueli A. Two Approaches to Interprocedural Dataflow Analysis[M]. Englewood: Prentice-Hall, 1981: 189-234
[12]Reps T, Horwitz S, Sagiv M. Precise interprocedural dataflow analysis via graph reachability[C] //Proc of the 22nd ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 1995: 49-61
[13]Tu Peng, Padua D. Gated SSA-based demand-driven symbolic analysis for parallelizing compilers[C] //Proc of the 9th Int Conf on Supercomputing. New York: ACM, 1995: 414-423
[14]Sen K, Necula G, Gong Liang, et al. MultiSE: Multi-path symbolic execution using value summaries[C] //Proc of the 10th Joint Meeting on Foundations of Software Engineering. New York: ACM, 2015: 842-853
[15]Qi Dawei, Nguyen H D T, Roychoudhury A. Path exploration based on symbolic output[J]. ACM Trans on Software Engineering and Methodology, 2011, 22(4): 278-288
[16]Wang Weiguang, Zeng Qingkai, Sun Hao. Dynamic symbolic execution method oriented to critical operation[J]. Journal of Software, 2016, 27(5): 1230-1245 (in Chinese)
(王伟光,曾庆凯,孙浩.面向危险操作的动态符号执行方法[J].软件学报. 2016, 27(5): 1230-1245)
[17]Zhou Yanhong, Wang Tiancheng, Li Huawei, et al. Test generation for multiple target states using path constraint solving[J]. Chinese Journal of Computers, 2016, 39(9): 1829-1842 (in Chinese)
(周艳红, 王天成, 李华伟, 等. 基于路径约束求解的多目标状态激励生成方法[J]. 计算机学报, 2016, 39(9): 1829-1842)
[18]Qin Xiaojun, Zhou Lin, Chen Zuoning, et al. Software vulnerable trace’s solving algorithm based on lazy symbolic execution[J]. Chinese Journal of Computers, 2015, 38(11): 2290-2300 (in Chinese)
(秦晓军, 周林, 陈左宁, 等. 基于懒符号执行的软件脆弱性路径求解算法[J]. 计算机学报, 2015, 38(11): 2290-2300)
[19]Gyimothy T, Beszedes A, Forgacs I. An efficient relevant slicing method for debugging[C] //Proc of the 7th Int Symp on Foundations of Software Engineering. New York: ACM, 1999: 303-321
Guo Xi1and Wang Pan2
1(DepartmentofComputerScience,CollegeofInformatics,HuazhongAgricultureUniversity,Wuhan430070)2(DepartmentofPowerEngineering,WuhanElectricPowerTechnicalCollege,Wuhan430079)
AbstractThe main purpose of program analysis is researching the properties of programs. Symbolic execution, which is the current popular analysis method, plays an important role in the aspects of generating efficient test cases, improving the path coverage ratio and so on. The key processes are extracting the path constraint and constraint solving. The current analysis methods have the shortcomings with low efficient of constraint solving, which results to low path coverage ratio. Due to different search strategies used by symbolic execution engine, the process of state merging may exist during symbolic execution, which may result to incorrect path information. This paper aims at improving the efficiency of path analysis, and a high efficient program analysis method is proposed. The shape of conventional symbolic execution tree is improved, and extracting the symbolic expression and path constraints in different paths to improve the efficiency of state merging; and then we use the potential relation analysis to generate the dependent relation set in backward analysis. The algorithm of dependent relation reorder is proposed to improve the path coverage ratio. Experimental results demonstrate that our method can improve the efficiency of state merging and improve the accuracy of path constraint analysis compared with conventional methods of state merging and symbolic execution.
Keywordspath analysis; state merging; dependency condition; symbolic execution; constrain solving
This work was supported by the National Natural Science Foundation of China (61502194) and the Fundamental Research Funds for the Central Universities (2662018JC028).
基金项目:国家自然科学基金项目(61502194);中央高校基本科研业务费专项资金(2662018JC028)
修回日期:2017-12-08
收稿日期:2017-07-24;
中图法分类号TP311
(xguo@mail.hzau.edu.cn)

GuoXi, born in 1983. PhD, associate professor. His main research interests include information security, software testing, and software engineering.

WangPan, born in 1987. PhD, lecturer. Her main research interest is power electronics transformation.