基因表达数据中的局部模式挖掘研究综述
姜 涛1李战怀2
1(河南财经政法大学计算机与信息工程学院 郑州 450046)2(西北工业大学计算机学院 西安 710129) (jiangtaoxxx@126.com)
摘要基因微阵列(DNA microarray)是实验分子生物学中的一个重要突破,其使得研究者可以同时监测多个基因在多个实验条件下表达水平的变化,进而为发现基因协同表达网络、研制药物、预防疾病等提供技术支持.研究者们提出了大量的聚类算法来分析基因表达数据,但是标准的聚类算法(单向聚类)只能发现少量的知识.因为基因不可能在所有实验条件下共表达,也不可能展示出相同的表达水平,但是可能参与多种遗传通路.在这种情况下,双聚类方法应运而生.这样就将基因表达数据的分析从整体模式转向局部模式,从而改变了只根据数据的全部对象或属性将数据聚类的局面.主要从局部模式的定义、局部模式类型与标准、局部模式的挖掘与查询等方面进行了梳理.介绍了基因表达数据中局部模式挖掘当前的研究现状与进展,详细总结了基于定量和定性的局部模式挖掘标准以及相关的挖掘系统,分析了存在的问题,并深入探讨了未来的研究方向.
关键词基因微阵列;基因表达;局部模式;保序子矩阵;双聚类;数据挖掘
基因微阵列(DNA microarray)技术是DNA重组与聚合酶链式反应(polymerase chain reaction, PCR)扩增这两大技术出现之后产生的一项重大生物技术[1].通过微阵列实验,生物学家能够同一时间内监测大量基因在特定生理过程中的动态表达水平,进而将基因的活动状态相对全面地展示出来.同以往的单基因表达研究模式相比,基因微阵列技术使得人们能够在基因组层面上以全局的、系统的视角来解释生命现象与本质.自从其发明以来,该技术已经应用到生物和医学研究等许多应用中.例如,在癌症研究中,它的出现使得人们能够更好地理解肿瘤发生的生物学机制,进而发现新的目标和新的药物,并制定可以裁剪的个性化治疗方案.然而,基因在某一生理过程中的表达数据只是某一状态下的表型数据,如何揭示大量基因表型数据背后的基因功能及其生命现象的本质才是设计微阵列实验的初衷.因为数据挖掘技术能够从大量的数据中发现不易觉察的信息,或者挖掘出某些潜在的有价值的模式,所以在生物医学等领域的探索中有着广泛的应用.
基因表达数据反映的是直接或间接测量得到的基因转录产物mRNA在细胞中的丰度[2].检测细胞中 mRNA 丰度的方法主要有4种:cDNA 微阵列、寡核苷酸芯片、基因表达系列分析(serial analysis of gene expression, SAGE)、反转录PCR(reverse transcription-PCR, RT-PCR).由于生物体中的细胞种类繁多且基因表达随着时空的改变而变化,与其他数据相比,基因表达数据要更为复杂、数据量要更大、数据的增长速度也要更快.基因微阵列之上的基因表达数据可以看作n×m的矩阵,其中n为基因数目(行数)、m为实验条件个数(列数)、矩阵中的每个属性值代表某个基因在某个实验条件下的表达水平.基因表达数据中蕴藏着基因活动的信息,如细胞处于何种状态(正常、恶化等)、药物对癌细胞的作用是否见效,能够从很大程度上反映细胞的当前生理状态.通过对基因表达数据的分析能够达到预测基因功能与获取基因表达调控网络等信息的目的,这也是基因微阵列在生物医学等领域广泛应用的关键因素之一.
自从Hartigan[3]发表重要研究成果,即将矩阵分为若干个含有近似值的子矩阵之后,双聚类方法得到巨大的发展.在基因表达数据分析应用中,其旨在从中找出在若干实验条件下展示出同样趋势的若干基因所组成的键值对(键为基因,值为实验条件).之前,层次聚类和K均值等传统方法通过“最大程度上增大组间的差异,同时最大程度上减小组内的差异”的标准,来鉴别在所有实验条件下具有相似表达水平的基因组合.然而,基因不可能在所有实验条件下共表达,也不大可能展示出相同的表达水平,但是可能参与多种表达通路.在这种情况下,双聚类方法应运而生.之后,出现了大量的用于基因表达数据分析的模型、算法与软件.然而,国内鲜有关于基因表达数据中局部模式挖掘方法的系统阐述.本文主要从局部模式的定义、局部模式类型与标准、局部模式的挖掘与查询等方面,介绍了基因表达数据中局部模式挖掘当前的研究现状与进展,详细总结了基于定量和定性的局部模式挖掘标准以及相关的挖掘系统与工具,分析了存在的问题,并深入探讨了未来的研究方向.
1问题定义
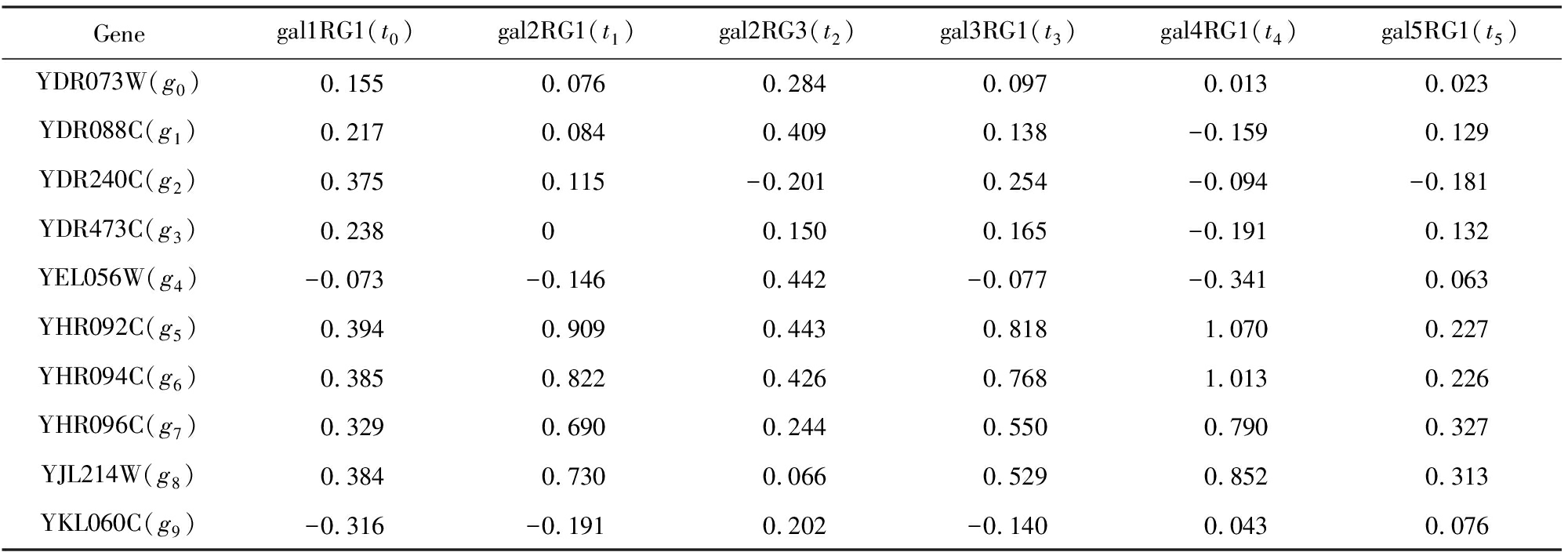
挖掘局部模式所需要的源数据是一个n×m的矩阵A,其中元素aij为实数,aij表示基因i在实验条件j下的表达值.表1给出了一个基因表达数据矩阵.
本文用A表示一个基因表达数据矩阵,其中基因的集合用行集合X={x1,x2,…,xi,xi+1,…,xn}表示,实验条件的集合用列集合Y={y1,y2,…,yj,yj+1,…,ym}表示,aij表示行i(或xi)和列j(或yj)之间的关系值.这样,矩阵A的另一种表示方法就是(X,Y).假设I⊆X,J⊆Y,I与J分别表示部分行与部分列.于是AIJ=(I,J)表示A中的子矩阵,其中只包含矩阵A中的部分aij元素.
Table1ExampleofGeneExpressionDataMatrix
表1基因表达数据矩阵举例
Genegal1RG1(t0)gal2RG1(t1)gal2RG3(t2)gal3RG1(t3)gal4RG1(t4)gal5RG1(t5)YDR073W(g0)0.1550.0760.2840.0970.0130.023YDR088C(g1)0.2170.0840.4090.138-0.1590.129YDR240C(g2)0.3750.115-0.2010.254-0.094-0.181YDR473C(g3)0.23800.1500.165-0.1910.132YEL056W(g4)-0.073-0.1460.442-0.077-0.3410.063YHR092C(g5)0.3940.9090.4430.8181.0700.227YHR094C(g6)0.3850.8220.4260.7681.0130.226YHR096C(g7)0.3290.6900.2440.5500.7900.327YJL214W(g8)0.3840.7300.0660.5290.8520.313YKL060C(g9)-0.316-0.1910.202-0.1400.0430.076
现有大部分聚类算法主要挖掘行聚类与列聚类,本文将行或列聚类称为整体模式(单向聚类).行聚类是部分行在所有列下具有相似行为或趋势,如图1(a)所示,表示为AIY=(I,Y),其中I={x1,x2,…,xp}(I⊆X,|I|<|X|=n),即行模式为|I|×m的矩阵.列聚类是部分列在所有行下展现出相同的行为或趋势,如图1(b)所示,表示为AXJ=(X,J),其中J={y1,y2,…,yq}(J⊆Y,|J|<|Y|=m),即列模式为n×|J|的矩阵.
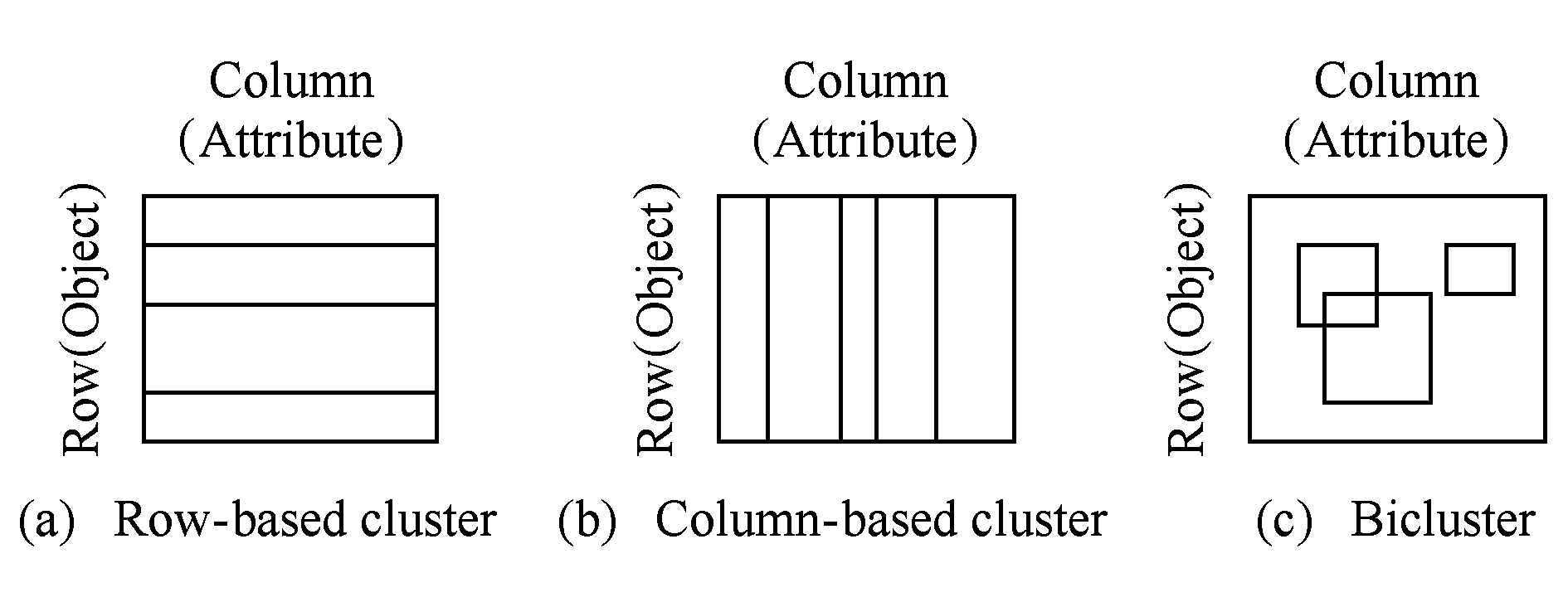
Fig. 1 Diagram of clustering and biclustering
图1 单向聚类与双聚类示意图
近年来出现了一种称为双聚类[1]的方法,其将标准聚类(单向聚类)算法的挖掘结果从整体模式转变为局部模式.在双聚类中,部分行在部分列下具有相同的行为或趋势,或者部分列在部分行下展现出相似的行为或趋势如图1(c)所示.因此,双聚类AIJ=(I,J),包含了矩阵A中的部分行I和部分列J,其中I={x1,x2,…,xp}(I⊆X,|I|<|X|=n),J={y1,y2,…,yq}(J⊆Y,|J|<|Y|=m).这样,双聚类AIJ=(I,J)定义为矩阵A中一个|I|×|J|的子矩阵,有时也将其称为保序子矩阵(order-preserving submatrix, OPSM)[4].
本文重点关注的双聚类问题的定义如下:给定矩阵A,发现符合某些共同特点的子矩阵的集合.但是,关于共同特点,不同的方法具有不同的定义,将在第2节中进行总结.下面以OPSM[4]为例进行介绍.其输入为基因表达数据,如表1所示;输出为多个局部模式OPSM,如表2所示;运算过程为先将每个基因的表达值按大小排序,接着替换为列标签,最后寻找列标签序列的最长公共子序列(频繁模式).表2为从表1中挖掘出来的2个局部模式OPSM,将其记为由基因和实验条件序列所组成的键值对.
Table2ExampleofLocalPattern
表2局部模式举例

Genet0t1t3t4Genet0t1t2t3g00.1550.0760.0970.013g50.3940.9090.8181.070g10.2170.0840.138-0.159g60.3850.8220.7681.013g20.3750.1150.254-0.094g70.3290.6900.5500.790g30.23800.165-0.191g80.3840.7300.5290.852
Notes: Index lables ofg0,g1,g2andg3after permutation aret4t1t3t0, and the OPSM isg0g1g2g3:t4t1t3t0. Similarly, index lables ofg5,g6,g7andg8after permutation aret0t3t1t4, and the OPSM isg5g6g7g8:t0t3t1t4.
标准聚类(单向聚类)与双聚类(双向聚类)的差异主要体现在3个方面:
1) 聚类方向不同.单向聚类仅在数据矩阵的单一方向(行或列)上聚类;双聚类则可对数据的对象(行)与属性(列)同时聚类,如图1所示.这样,双聚类解决了摘要中指出的“基因不可能在所有实验条件下共表达”的问题.
2) 聚类结果相关度不同.单向聚类结果可能存在属性(列)与某些对象(行)不相关的情况;而双聚类结果中的属性(列)与该聚类所属对象(行)一定相关.
3) 聚类结果互异性不同.单向聚类分析所得到的结果是互异的,即一个对象(行)存在且仅存在于一个类中;双聚类分析所得到的结果具有相容性,即一个对象(行)可以存在于多个类中,也可以不存在于任何一个类中.这样,双聚类解决了摘要中指出的“基因可能参与多种遗传通路”的问题.
单向聚类与双聚类的优劣主要体现在3个方面:
1) 双聚类利用了聚类的二元性.单向聚类从行或列中的一个维度进行数据的划分,但不能同时从行与列这2个维度进行数据的划分;而双聚类可以同时从行与列这2个维度对数据进行划分.这样,双聚类解决了摘要中指出的“标准聚类只能发现少量的知识的问题”.
2) 双聚类可发现隐藏的潜在模式.单向聚类将所有的行或列划分成若干类,即发现整体模式,该特性使得其隐藏了若干潜在模式;而双聚类从行与列这2个维度进行数据划分的特性,使得行或列不必属于同一类,即发现局部模式,那么就可以发现不明显的潜在模式.这样,双聚类解决了摘要中指出的“标准聚类只能发现少量的知识的问题”.
3) 双聚类可降低数据的维度.单向聚类只在单轴方向(行或列)上降低数据的维度;双聚类则可同时降低双轴方向上的维度.
2局部模式类型与标准
现有的局部模式主要包括两大类:恒值双聚类(图2中的A1,A2,A3)和相干双聚类(图2中的A4,A5,A6)[5].恒值双聚类又可以细分为三小类:恒值双聚类(图2中的A1)、行恒值双聚类(图2中的A2)和列恒值双聚类(图2中的A3).相干双聚类也可以细分为三小类:加性相干双聚类(图2中的A4)、乘性相干双聚类(图2中的A5)和相干演化双聚类(图2中的A6)[5].
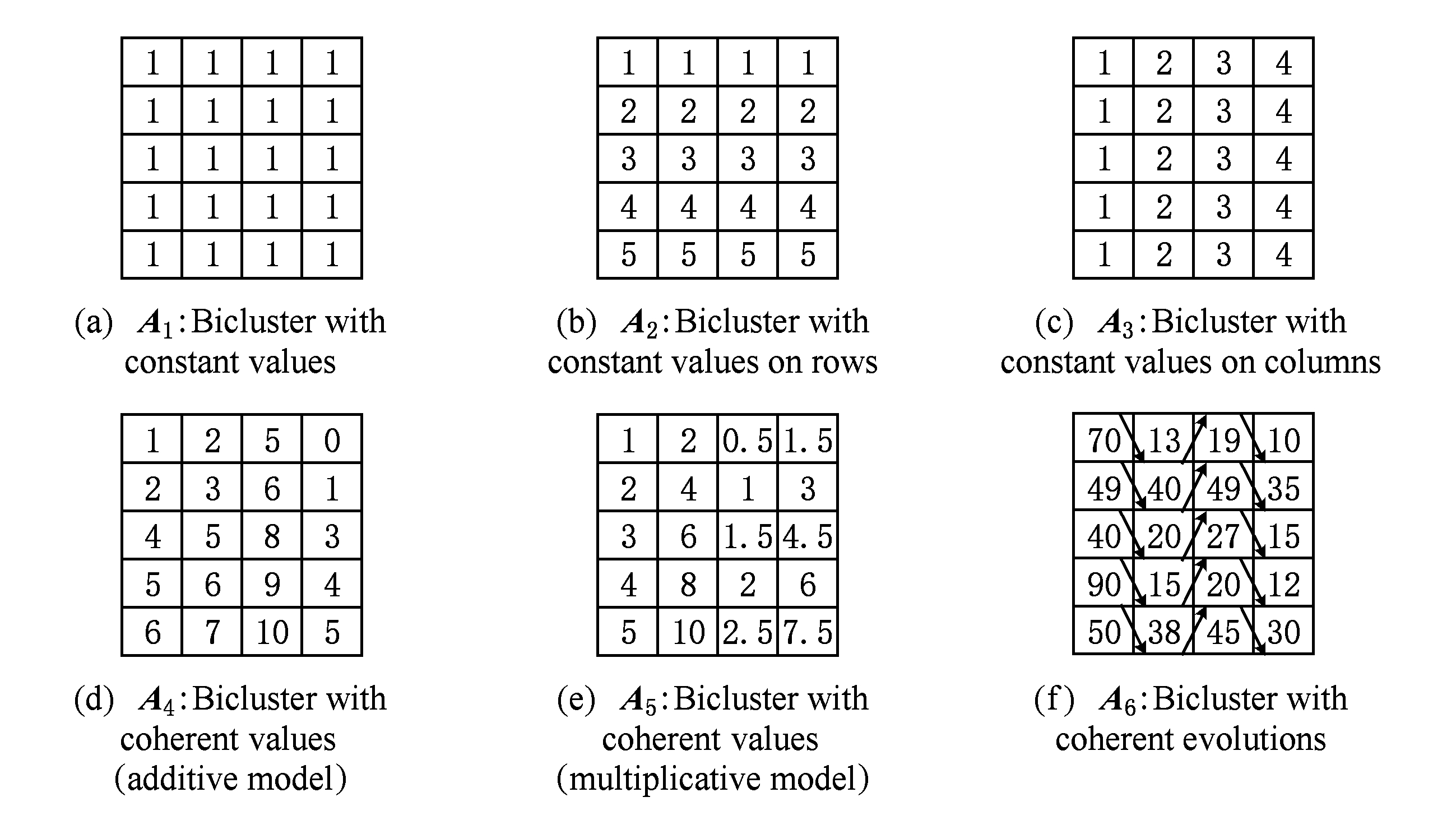
Fig. 2 Examples of different types of biclusters
图2 双聚类模式类型举例
恒值双聚类和相干双聚类各自的特点如表3所示.
恒值双聚类是一种特殊的双聚类,其中的所有元素值都相同,即aij=μ;行恒值双聚类中的每一行元素值分别相同,行与行之间相差一个常数或者倍数,即aij=μ+ai或aij=μ×ai,其中ai表示行常数或倍数;列恒值双聚类中的每一列元素值分别相同,列与列之间相差一个常数或者倍数,即aij=μ+βj或aij=μ×βj,其中βj表示列常数或倍数.
相干双聚类与恒值双聚类有所不同.加性相干双聚类中的每个元素值基本上不相同,每一行与列值是在一个基准值μ的基础上加上行常数ai和列常数βj,即aij=μ+ai+βj;乘性相干双聚类中的每个元素值基本上也不相同,每一行与列值是在一个基准值μ的基础上乘以行倍数ai和列倍数βj,即aij=μ×ai×βj;相干演化双聚类不太在意每个元素值,重在关注前后行或列之间的表达值的升降,如果2行或列具有相同和相反的趋势,那么二者可以聚为一类.
根据双聚类间的关系,一组双聚类可分为如下类型[5],如图3所示.
1) 单独的双聚类,如图3(a)所示;2)互斥行与列的双聚类组,如图3(b)所示;3)无重叠的棋盘型双聚类组,如图3(c)所示;4)互斥行的双聚类组,如图3(d)所示;5)互斥列的双聚类组,如图3(e)所示;6)无重叠的树形双聚类组,如图3(f)所示;7)无重叠的非排它的双聚类组,如图3(g)所示;8)层次型重叠双聚类组,如图3(h)所示;9)任意位置重叠的双聚类组,如图3(i)所示.
Table3TypesofBiclusters
表3双聚类类型
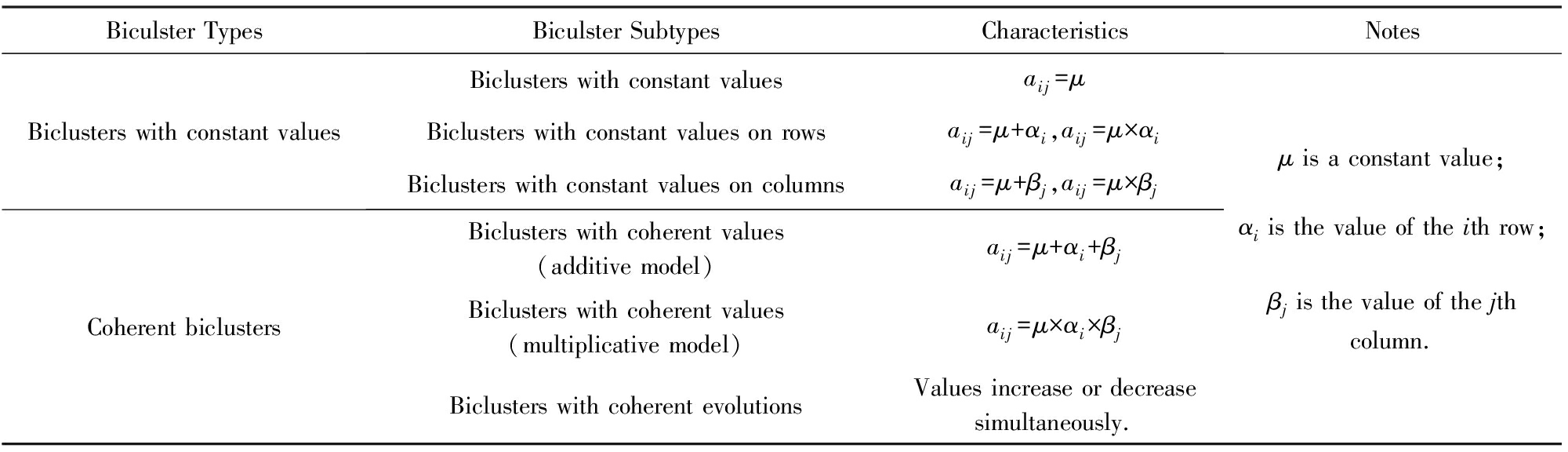
Biculster TypesBiculster SubtypesCharacteristicsNotesBiclusters with constant valuesBiclusters with constant valuesaij=μBiclusters with constant values on rowsaij=μ+αi,aij=μ×αiBiclusters with constant values on columnsaij=μ+βj,aij=μ×βjCoherent biclustersBiclusters with coherent values(additive model)aij=μ+αi+βjBiclusters with coherent values(multiplicative model)aij=μ×αi×βjBiclusters with coherent evolutionsValues increase or decreasesimultaneously.μ is a constant value;αi is the value of the ith row;βj is the value of the jthcolumn.
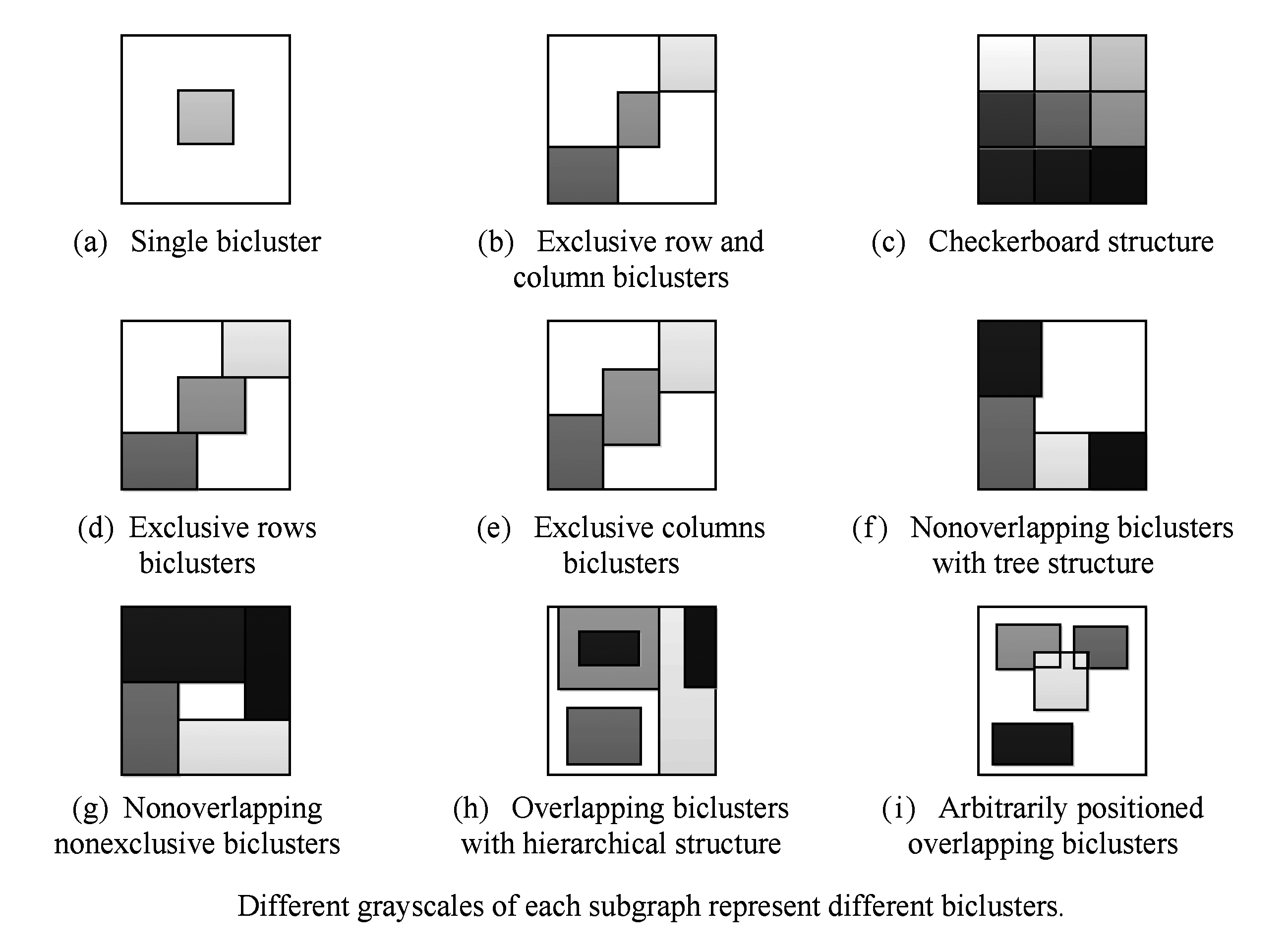
Fig. 3 Group types of biclusters
图3 双聚类组的类型
3研究现状
双聚类的概念最初由Hartigan[3]提出,其作为对矩阵中的行与列同时聚类的一种方法,并将其命名为Direct聚类.Cheng和Church[1]提出了基因表达数据的双聚类,并引入了元素残差以及子矩阵的均方残差(mean squared residue,MSR)[1]的概念.文献[1]展示出MSR在发现行恒值双聚类、列恒值双聚类、加性相干双聚类(shift biclusters)方面具有良好的性能.然而,其在发现乘性相干双聚类(scale biclusters)方面的表现却差强人意.该算法是一种贪婪方法.首先将整个数据矩阵作为初始化数据;接着删除元素残差或者均方残差最大元素或者行列,依次递归下去直到剩余矩阵的MSR低于某个阈值;然后增加部分元素或者行列,保证所得矩阵的MSR也低于该阈值.该方法效率较低,因为一次只能挖掘一个双聚类.Ben-Dor等人[4,6]介绍了一种特殊的双聚类模型OPSM,并证明了其是NP难问题.OPSM与双聚类的关系如下:本质上OPSM属于双聚类,只是一个更特殊的双聚类而已.大部分双聚类主要是在实数数据上做恒值模式、行/列恒值模式、加性相干模式、乘性相干模式、相干演化模式等的挖掘工作.OPSM首先对每一行数据进行从小到大的排列,再替换成相应的列标签,这样就将实数数据转化序列数据,具体的序列操作有频繁集挖掘、最长公共子序列查找等.大部分的OPSM挖掘主要操作对象是序列数据,少部分OPSM挖掘工作的操作对象是未经预处理的实数数据.这种转化可以从一定程度上减少噪声数据的影响,同时也可以减少计算量.随后,人们给出了基于定量测度和定性测度的双聚类挖掘方法.定量测度包括均方残差(MSR)[1]、方差和(sum of squares,SSQ)[3]、残差均值(mean residue,MR)[7]、平方残差和(sum squared residue,SSR)[8]、平均相关值(average correlation value,ACV)[9]、平均斯皮尔曼秩相关系数(average spearman’s rho,ASR)[10-11]、平均一致性相关指数(average corres-pondence similarity index,ACSI)[12]等.定性测度包括上升、下降、相似、相反、同步、异步、重叠、位置、冗余、对称、非对称、非线性等[13-14].
近年来,基因表达数据挖掘得到生物医学与学术界的重点关注,取得一定的研究成果[5,15-18].本节主要从基于定量测度的双聚类、基于定性测度的双聚类、基于查询的双聚类和约束型双聚类等方面对基因表达数据中局部模式的挖掘方法的研究现状进行梳理和介绍.
3.1基于定量测度的双聚类
主要从噪声与缺失值问题、双聚类算法、双聚类理论研究、现有方法的比较、相关系统与工具等方面介绍基于定量测度的双聚类.
1) 解决噪声与缺失值问题的工作.由于基因表达数据的来源不同且数据是由基因微阵列图像数据转化而来的,其中不可避免地会产生噪声,所以减少噪声数据的影响也是一项有意义的研究工作[18].这方面也有一些研究成果.基于Cheng等人[1]提出的δ-bicluster模型,Yang等人[7]为减少数据缺失值的影响,给出一种δ-cluster模型来发现相干模式,继而设计了柔性重叠聚类(flexible overlapped clustering, FLOC)算法来挖掘任意位置有重叠的双聚类,其中用到残差均值MR测度.Deodhar等人[19]提出一种鲁棒的有重叠的双聚类方法,将其命名为鲁棒重叠双聚类(robust overlapping co-clustering, ROCC),能有效地从大量的含有噪声的数据中挖掘出稠密的、任意位置的有重叠的双聚类.Sun等人[20]为了减少基因表达数据中噪声的影响,提出名为Auto-Decoder的模型,利用神经网络技术来发现隐藏在噪声基因表达数据中的具有重叠的双聚类.
2) 挖掘各种类型双聚类的工作.对于一个局部模式而言,双聚类的类型主要包括如表3所示的两大类与六小类[5].而对于局部模式的组合来说,双聚类组的类型又包括如图3所示的9种情况[5].Cho[8]给出了数据转换的方法来解决现有的平方残差和SSR测度方法只能有效地挖掘出在数值上具有偏移的双聚类(加性相干双聚类),却不能很好地解决在数值上有缩放的双聚类(乘性相干双聚类)的问题.Ayadi等人[10]发现大多数现有方法主要关注正相关双聚类,而研究表明负相关双聚类也出现在具有重要生物学意义的双聚类中.为了弥补现有算法的不足,给出文化基因双聚类算法(memetic biclustering algorithm, MBA).Divina等人[21]给出一种基于进化计算的双聚类方法(sequential evolu-tionary biclustering, SEBI),用来发现尺寸较大、重叠较少且MSR小于某阈值的双聚类.Odibat等人[22]发现现有方法并不能有效地挖掘矩阵数据中任意位置有重叠的双聚类,提出一种确定性双聚类算法,称之为基于正负相关的重叠双聚类(positive and negative correlation based overlapping co-clustering, PONEOCC).该算法可以有效地发现正负相关的任意位置上有重叠的双聚类.同样,该算法也可以应用于含有噪声的基因表达数据分析.Truong等人[23]观察到现有大多数方法要么挖掘无重叠的双聚类,要么发现重叠区域比较大的双聚类,而不允许用户指定双聚类之间的最大重叠比例.为此,提出一种可以产生K个重叠的双聚类的算法,并且这些重叠的比例低于预设阈值.与现有算法产生所有双聚类结果的方式不同,该算法每次发现一个与已产生的结果不同的并且带有一定重叠比例的双聚类.实验也表明该算法可以返回许多大的高质量的双聚类.Chen等人[24]发现现有研究已为线性模式(即相干模式)提出若干种定量相干测度,但是其缺乏挖掘所有相干模式的能力且容易被噪声所干扰.为此,提出一种通用的线性模式相干测度最小均方误差(minimal mean squared error,MMSE).利用该测度,双聚类算法可以发现所有类型的线性模式,包括偏移(加性相干模式)、缩放(乘性相干模式)、偏移与缩放联合模式等.Wang等人[25]提出并设计基于pScore测度和pCluster模型的方法,发现具有相似升降趋势的模式.Bhattacharya等人[26]介绍了一种基于双相关系数的聚类算法(bi-correlation clustering algorithm, BCCA).其发现的模式不仅具有相似的表达趋势,而且具有共同的转录因子结合位点.这项工作之所以有意义,是因为现有工作只考虑了前者,而忽略了后者,即在相应的启动子序列上拥有共同的转录因子结合位点是一项能证明这些基因共表达的证据.Xiao等人[27]提出一种有效的投票算法从带有任意背景的矩阵中发现加性相干双聚类.Xie等人[28]提出一种有效的方法来不间断地检测数值数据流之间的相关性.该方法基于离散傅里叶转换,能快速计算时滞(异步)相关模式.Murali等人[29]提出非确定性贪婪方法xMOTIFs来发现具有行恒定值的双聚类.Bergmann等人[30]提出一种大规模基因表达数据分析的迭代签名算法(iterative signature algorithm, ISA),其通过多次迭代来发现具有重叠的转录模块.Pandey等人[31]利用范围支持框架(range support pattern, RAP)来挖掘恒值双聚类和行恒值双聚类.定量测度如表4所示:
Table4QuantitativeMeasuresofBiclusters
表4双聚类的定量测度

ReferencesMethodsQuantitativeMeasuresFormulasNotesRef [1,21]CC,SEBIMSRMSR=1|I||J|∑i∈I,j∈J(aij-aiJ-aIj+aIJ)aiJ,aIj,aIJ are the values of the ith row, the jth column, and the mean value of bicluster, respectively.Ref [3]BlockClusteringSSQSSQ(I,J)=∑i∈I,j∈J(aij-aIJ)2Ref [7]FLOCMRMR=∑i∈I,j∈J|rij|vIJrij is the residue of aij, and vIJ is the count of element.Ref [8]RESIDUE(Ⅱ)SSRSSR=‖HIJ‖2=∑i∈I,j∈Jh2ijhij is the residue.Ref [9]HomogeneityClusteringACVACV(A)=max∑ni=1∑nj=1|rrowij|-nn′-n{,∑mk=1∑ml=1|rcolkl|-mm′-m}ACV(A) ∈ [0, 1], rrowijis the correlation of the ith row and the jth row in matrix A.Similarly, we have rcolkl.Ref [10-11]MBA,BiMineASRASR(I′,J′)=2×max∑i∈I′∑j∈I′,j≥i+1ρij|I′|(|I′|-1){,∑k∈J′∑l∈J′,l≥k+1ρkl|J′|(|J′|-1)}ρij(i≠j), ρkl(k≠l) are Spearman s rank correlation coefficients.Ref [12]BicFinderACSIACSIi(I′,J′)=2×∑j∈I′,j≥i+1∑k∈I′,k≥j+1CSI(i,j,k)|I″|(|I″|-1)CSI is the coefficient of similarity index, which refers to Ref [12].Ref [24]MMSEMMSEMMSE(A)=minα,π,β(1|I||J|∑i∈I,j∈J(αiπj+βi-di,j)2)π,αi,βi are base vector, multiplicative factor vector, and additive factor vector. dij=aij.Ref [25]δ-pClusterpScorepScore(A)=|(ai1j1-ai1j2)-(ai2j1-ai2j2)|Ref [26]BCCACorrCorr(ai,aj)=∑ml=1(ail-ai)(ajl-aj)∑ml=1(ail-ai)2∑ml=1(ajl-aj)2Pearson correlation coefficient
3) 主要进行双聚类理论研究的工作.Teng等人[9]提出一种测度方法ACV来发现同质聚类.实验表明其更适用于加性与乘性相干模式的搜索.Ayadi等人[11]提出一种枚举算法BiMine来挖掘基因表达数据中的双聚类.其有3个新特点:①其依赖于ASR评价函数;②其利用双聚类枚举树BET来索引挖掘出来的双聚类;③设计了减少搜索空间的剪枝规则.Ayadi等人[12]利用平均一致性相关指数,ACSI来评估相干双聚类,并利用有向无环图组建这些双聚类.Denitto等人[32]为了解决双聚类与生俱来的高复杂度问题,提出一种新的二元因子图方法.其将双聚类问题转化成序列搜索问题,每次挖掘一个双聚类,同时利用Max Sum算法缓解以往方法的扩展性问题.Lee等人[33]提出一种稀疏奇异值分解方法(sparse singular value decomposition, SSVD),作为一种探索分析工具来发现髙维度数据矩阵中棋盘形状的双聚类.棋盘形状的双聚类如图3(c)所示.Tanay等人[34]提出一种带有统计模型的图理论的方法——支持双聚类分析的统计方法(statistical-algorithmic method for bicluster analysis, SAMBA),来发现基因表达数据中具有重要意义的双聚类.Sill等人[35]引入稳定性选择的因素来改善稀疏奇异值分解方法的性能,之后提出了基于抽样的支持稀疏奇异值分解的稳定性选择方法(stability selection for sparse singular value de-composition, S4VD)来发现稳定性双聚类.Tchagang等人[36]受排序保序框架与最小均方残留测度MSR的启发,提出了基于阶次保持的短时序列分析(analysis of short time-series using rank order preservation, ASTRO)与最小均方残差(minimum mean squared residue, MiMeSR)方法,从短时间序列基因表达数据中挖掘具有生物学意义的模式.Tan等人[37]详细给出了基因表达数据分析中3个聚类方法的算法,并分析了复杂度问题.Humrich等人[38]发现精确的双聚类算法复杂度为指数级、多项式级的算法却是非精确的.为了减少在寻找最大精确OPSM过程中得到精确结果、有理论保证、算法可扩展、不受噪声数据影响,提出一种新的精确算法,即固定参数可解整数规划方法.Joung等人[39]为降低在发现基因表达数据中相干模式的计算复杂度,提出一种概率共同演化双聚类算法(probabilistic coevolutionary biclustering algorithm, PCOBA).Cho等人[40]利用规范化、确定谱的初始化和增量本地搜索等策略,给出双聚类软件Co-clustering,解决前期提出的最小平方和残差双聚类(minimum sum-squared residue coclustering, MSSRCC)模型的局部极小化问题以及划分聚类算法中的退化严重等问题.Cho等人[41]介绍了2种与MSR相似的平方残差测度,同时提出2种有效的基于K均值的双聚类算法.Yang等人[42]观察到当遇到大量的异质数据时,现有的聚类方法往往得不到满意的结果.为此,介绍了一种应用范围更为普遍的方法correlated双聚类,来发现具有直观生物学意义的聚类.其首先利用奇异值分解来鉴别相关聚类,接着将问题转化为2种全局聚类问题,最后利用混合聚类算法与Lift算法来生成双聚类δ-corBiclusters.Roy等人[43]提出双聚类挖掘方法——共调控双聚类(co-regulated biclustering, CoBi),基于BiClust树,其只需一次遍历就可发现所有的正负相关的双聚类.
4) 对现有算法进行全方位比较的工作.Roy等人[44]介绍了可能从基因表达数据中观察到的感兴趣的模式,同时讨论了检测具有相似表达模式的基因功能组的双聚类技术.Eren等人[45]观察到每种新提出的双聚类方法在文献中只和少量的现有方法作了比较,这样对于不同的局部模式挖掘任务,往往不知道选用哪种双聚类方法更合适.为评估现有方法的优缺点,利用BiBench包比较了12种算法在不同实验条件、噪声、重叠比例等指标下的性能.Saber等人[46]给出微阵列数据分析方面的双聚类方法的综述.
5) 双聚类挖掘系统设计与实现的工作.Barkow等人[47]设计并实现了一个名为BicAT的工具,其中包括若干现有算法的实现,方便用户比较并选用合适的算法.同时还提供了数据的预处理、聚类、数据的可视化、后期处理等步骤.其他相关系统的总结如表5所示:
Table5SystemsorToolsofBiclustersBasedonQuantitativeMeasures
表5基于定量测度的双聚类系统或工具

Systems∕ToolsFunctionsWebsitesBicFinder[12] It is a heuristic algorithm, which relies on a new evaluation function called ACSI (average correspondence similarity index) to assess the coherence of a given bicluster and utilizes a directed acyclic graph to construct its biclusters.URL①AutoDecoder[20] It uses a neural network to find overlapped biclusters from noise gene expression data.URL②BCCA [26] It discoveries biclusters that have a similar change of expression pattern, and finds the genes that have common transcription factor binding sites.URL③xMOTIFs [29] The method discoveries the constant row biclusters.URL④ISA[30] It proposes an iterative signature algorithm for the analysis of large-scale gene expression data, i.e., through multiple iterations to find overlapping transcription modules.URL⑤RAP[31] It utilizes the range measurements to discovery constant value biclusters and constant row biclusters.URL⑥SSVD [33] It seeks a low-rank, checkerboard structured matrix approximation to data matrices.URL⑦SAMBA [34] The method is graph theoretic coupled with statistical modelling of the data, and finds the most significant biclusters.URL⑧S4VD [35] It incorporates stability selection to find stable biclusters.URL⑨ASTRO, MiMeSR[36] It extracts biologically significant patterns from short time series gene expression data.URL⑩
Continued(Table5)

Systems∕ToolsFunctionsWebsitesCo-clustering[40] It proposes specific strategies that enable MSSRCC to escape poor local minima and resolve the degeneracy problem in partitional clustering algorithms.URL CoBi[43] It is a greedy method, which finds positively and negatively co-regulated gene clusters from gene expression data.URL BicAT [47] The tool includes the implements of some existing algorithms, and supports data preprocessing, clustering, data visualization, etc.URL
① http://www.info.univ-angers.fr/pub/hao/BicFinder.html
② http://grafia.cs.ucsb.edu/autodecoder/
③ http://www.isical.ac.in/~rajat/
④ http://genomics10.bu.edu/murali/xmotif
⑤ http://www2.unil.ch/cbg/index.php?title=ISA
⑥ http://vk.cs.umn.edu/gaurav/rap/
⑦ http://www.unc.edu/?haipeng
⑧ http://www.cs.tau.ac.il/~rshamir/biclust.html, http://acgt.cs.tau.ac.il/expander/
⑨ http://s4vd.r-forge.r-project.org/,https://github.com/mwsill/s4vd
⑩ http://www.benoslab.pitt.edu/astro/
 http://www.cs.utexas.edu/users/dml/Software/cocluster.html
http://www.cs.utexas.edu/users/dml/Software/cocluster.html
 https://sites.google.com/site/swarupnehu/publications/resources
https://sites.google.com/site/swarupnehu/publications/resources
 http://www.tik.ee.ethz.ch/sop/bicat
http://www.tik.ee.ethz.ch/sop/bicat
3.2基于定性测度的双聚类
本节也从噪声与缺失值问题、双聚类算法、双聚类理论研究、现有方法的比较、相关系统等方面来介绍基于定性测度的双聚类.需要指出的是,该类方法解决了摘要中指出的“基因不可能展示出相同的表达水平”的问题.
1) 解决噪声与缺失值问题的工作.Chui和Yip等人[13,48]试图利用多份数据的保序子矩阵挖掘方法(OPSM-repeated measurements, OPSM-RM)来消除数据噪声的影响.Fang等人[14]为了挖掘放松的OPSM,提出包含以行或列为中心的OPSM-Growth方法.Zhang等人[49]为减少数据中噪声的影响,提出了一种近似保序聚类模型(approximate order preserving clusters, AOPC).随后,Fang等人[50-51]基于桶和概率的方法,来发现非严格的聚类OPSM.Peng等人[52]设计实现了一个利用多份数据来挖掘基因表达数据的软件包.其给出几种转换模型,支持不同种类的扩展性非相似/距离测度,提供了一些K均值聚类方法的变种,介绍了3种流行的聚类质量的评价方法.Abdullah等人[53]为了从含有噪声的数据中发现非对称重叠双聚类,提出了基于交叉最小化与图形绘制的双聚类技术.Henriques等人[54]提出一种基于序列模式挖掘的双聚类(biclu-stering based on sequential pattern mining, BicSPAM)的方法,它是第1个试图解决OPSM允许对称并且能够容忍不同级别噪声的方法.Li等人[55]提出确定性算法——定性双聚类(qualitative biclustering, QUBIC),从含有噪声的数据中高效地发现重叠的乘性相干双聚类.
2) 挖掘各种类型双聚类的工作.其主要挖掘具有同样升降趋势、反向趋势、同步(无时间延迟)、异步(具有时间延迟)、重叠、对称、非对称、非线性等特性的局部模式.每个算法包含上述特性中的一个或多个.Liu等人[56]发现现有的相似测度大多数基于欧氏距离或余弦距离,提出一种灵活有效的聚类模型,命名为保序双聚类(order preserving cluster, OP-Cluster).该模型判断2个对象相似的标准是不同实验条件下基因表达值排序的顺序相同,也就是共调控的基因表达水平在同样条件下同升同降.Wang等人[57]给出一种基于最近邻(nearest neighbor, NN)的新的测度方法来指导相似模式聚类.Zhao等人[58]观察到基于模式和趋势的聚类方法不能直接应用于同时具有正相关和负相关的共调控基因聚类.为此设计了一种编码模式,其中有相同编码的基因是正相关或负相关调控基因.在此基础上提出共表达基因聚类(coregulated gene cluster, CO-GCLUSTER)算法,来发现最大共调控基因聚类的.Jiang等人[59]发现基于模式的聚类方法返回大量高重复度的聚类,使得用户很难鉴别感兴趣的模式,同时不同的模式或测度需要不同的算法,而没有一个通用的基于模式的聚类模型.为此,提出一种通用的质量驱动的top-k模式挖掘模型Q-Clustering,来提升所发现的双聚类的质量.闫雷鸣等人[60]为挖掘非线性相关的模式,引入二次互信息的相似性度量,建立了一种时序数据非线性相关模型,提出基于互信息的时间序列双聚类算法(mutual-information-based time series biclustering algorithm, MI-TSB).印莹等人[61-62]提出一种从时序微阵列数据中挖掘同步和异步共调控基因聚类的方法Reg-Cluster.印莹等人[63]发现现有方法只适用于相同列下的双聚类,而非相同列下的聚类也具有重要意义.为此,提出异步(具有时间偏移)的共表达模式的挖掘方法——时间偏移聚类(time-shifting cluster, ts-Cluster).赵宇海等人[64-65]提出双聚类方法g-Cluster来发现具有正负相关的共调控基因聚类.Wang等人[66]设计了发现缩放、偏移、反转时滞表达模式的模型——时滞聚类(time-delayed cluster, td-Cluster),并且很容易地从2维数据扩展到3维数据.Wang等人[67]给出具有恒定值的子矩阵,又称局部保守聚类的方法(local conserved cluster, LC-Cluster),其实际上是OPSM中的一种特殊情况.Ji等人[68]提出一种正负相关共调控基因聚类的模型(positive and negative co-regulated gene cluster, PNCGC).该模型可以鉴别关联规则丢失的共调控聚类,减少了被Apriori模型引入的不相关聚类.Ji等人[69]发现现有双聚类方法1次只能比较2个基因间的相似度,且相似度打分函数使得聚类方法丢失了许多重要信息.为此,提出了一种时滞共调控双聚类的方法q-Cluster,其每次可以比较多个基因且可以产生完整的双聚类.Ji等人[70]为了发现具有一致或者相似波动趋势的双聚类,给出一种快速层次双聚类算法(quick hierarchical biclustering, QHB).该算法不仅能生成双聚类,而且能够产生已发现的双聚类间关系的层次图.Chen等人[71]为了提高正负相关模式挖掘的性能,提出一种名为上下位模式(up-down bit pattern, UDB),将挖掘算法的时间复杂度从指数级别减少到多项式等级.姜涛等人[72]为了快速挖掘基因表达数据中的保序子矩阵(OPSM),提出了基于蝶形网络的基因表达数据的并行分割与挖掘方法.其扩展了Hama BSP 框架,使得节点在每个超步中只需要与指定的某个节点通信即可,且最多使用lbN个超步,N为集群中计算节点数目.实验表明所提出方法弥补了Apache Hama系统的处理框架BSP 的不足,减少了信息传递量,加速了处理速度,同时从理论上证明了该方法能保证挖掘结果的完整性.
3) 主要进行双聚类理论研究的工作.Trapp等人[73]发现现有方法在解决NP难问题OPSM时都不能保证结果最优,为此提出了基于线性规划的确定性方法,同时讨论了挖掘特定类型模式的计算复杂度问题.Kriegel等人[74]提出基于局部密度阈值的OPSM挖掘方法,试图改变现有的基于全局密度阈值方法并不能适用于每种OPSM的现状.安平[75]利用互信息和核密度进行双聚类挖掘.Zhang等人[76]发现现有的大多数方法假设基因表达数据是同质的,并不适用于异质数据.为了挖掘异质数据中的相干模式,提出称为F-cluster的模型.Cho等人[77]给出一种基于坏字符规则的KMP算法(the Knuth-Morris-Pratt algorithm),其试图快速地匹配保序模式.Hochbaum等人[78]转换了最大OPSM的挖掘思路,由原来的发现最多行列的双聚类转化成如何从源数据中减少行列的问题.设计了参数为5的OPSM挖掘方法MinOPSM,将双聚类问题转化为一个2次不可分离的集合覆盖问题.接着,给出另一种结合原始对算法的公式化方法将近似系数提升为3.Yoon等人[79]为解决双聚类的高时间复杂度问题,利用零抑制二元决策图(zero-suppressed binary decision diagrams, ZBDDs),从基因表达数据中发现相干双聚类.Painsky等人[80-81]为了发现“每行只属于一类,而每列可以属于多个聚类”的双聚类,如图3(d)所示,介绍了基于最优集合覆盖的方法.Ji等人[82]为了解决密集数据中闭合模式的发现问题,提出了2种压缩层次挖掘方法.该方法首先压缩源挖掘空间,接着将整个挖掘任务层次化地分割成独立的子任务,最后单独挖掘每一个子任务.薛云等人[83-84]发现现有方法在挖掘局部模式Deep OPSM的过程中计算代价较大,提出了基于所有公共子序列的方法,实验证明所提方法具有良好的有效性与高效性.Kuang等人[85]观察得到大多数现有OPSM挖掘方法是基于贪婪策略或者Apriori原理,使得挖掘结果丢失了包括Deep OPSM在内的一些有意义的OPSM.为此,提出了基于序列模式挖掘的精确OPSM搜索算法.同时,利用动态规划、后缀树和分支界限规则来增强算法的性能.Kim等人[86]为解决数字字符串之上的保序匹配,定义了模式的前缀和最近邻表示,提出了单模式与多模式匹配算法.前者在一般情况下的时间复杂度为O(nlogm),经过优化后的时间复杂度为O(n+mlogm),后者的时间复杂度为O(nlogm).Bruner等人[87]为了解决保序模式匹配的NP完全问题,提出固定参数算法,其在最坏情况下的时间复杂度为O(1.79run(T)nk).当T具有少量的上升与下降趋势时,该算法的时间复杂度为O(1.79nnk).Crochemore等人[88]为解决保序模式匹配问题,给出一种时间复杂度为O(nlog logn)的非完整保序后缀树的创建方法.同时给出一种时间复杂度为O(nlogn/log logn)的完整保序后缀树的创建方法.Chen等人[89]发现现有方法在鉴别具有恒定表达水平的双聚类时表现不佳,提出了一种2阶段双聚类方法,其在二进制数据与定性数据上具有良好的性能.对定性测度的总结如表6所示:
Table6QualitativeMeasuresofBiclusters
表6双聚类的定性测度
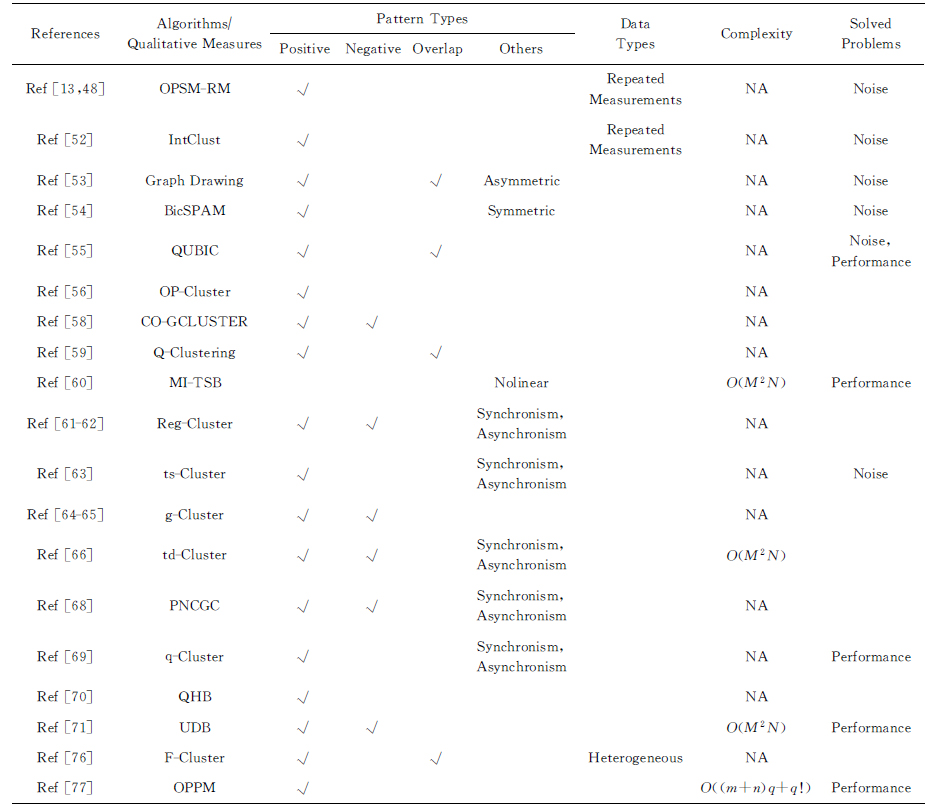
ReferencesAlgorithms∕Qualitative MeasuresPattern TypesPositiveNegativeOverlapOthersDataTypesComplexitySolvedProblemsRef [13,48]OPSM-RM√Repeated MeasurementsNANoiseRef [52]IntClust√Repeated MeasurementsNANoiseRef [53]Graph Drawing√√AsymmetricNANoiseRef [54]BicSPAM√SymmetricNANoiseRef [55]QUBIC√√NANoise, PerformanceRef [56]OP-Cluster√NARef [58]CO-GCLUSTER√√NARef [59]Q-Clustering√√NARef [60]MI-TSBNolinearO(M2N)PerformanceRef [61-62]Reg-Cluster√√Synchronism,AsynchronismNARef [63]ts-Cluster√Synchronism, AsynchronismNANoiseRef [64-65]g-Cluster√√NARef [66]td-Cluster√√Synchronism, AsynchronismO(M2N)Ref [68]PNCGC√√Synchronism, AsynchronismNARef [69]q-Cluster√Synchronism, AsynchronismNAPerformanceRef [70]QHB√NARef [71]UDB√√O(M2N)PerformanceRef [76]F-Cluster√√HeterogeneousNARef [77]OPPM√O((m+n)q+q!)Performance
Notes: “√” means yes; “NA” means unavailable.
4) 对现有算法进行全方位比较的工作.文献[5,15-18]从相关算法所挖掘模式的生物学意义及其难点、各种算法的优缺点、相关应用等方面进行了详细的归纳、比较、总结,同时对进一步可以研究的方向进行了展望.
 等人[90]提出一种快速的分治方法BiMax来发现基因表达数据中的双聚类,同时与其他5种表现突出的双聚类方法(CC[1],OPSM[4,6],xMotif[29],ISA[30],SAMBA[34])在生成数据与真实数据上进行了系统的比较.
等人[90]提出一种快速的分治方法BiMax来发现基因表达数据中的双聚类,同时与其他5种表现突出的双聚类方法(CC[1],OPSM[4,6],xMotif[29],ISA[30],SAMBA[34])在生成数据与真实数据上进行了系统的比较.
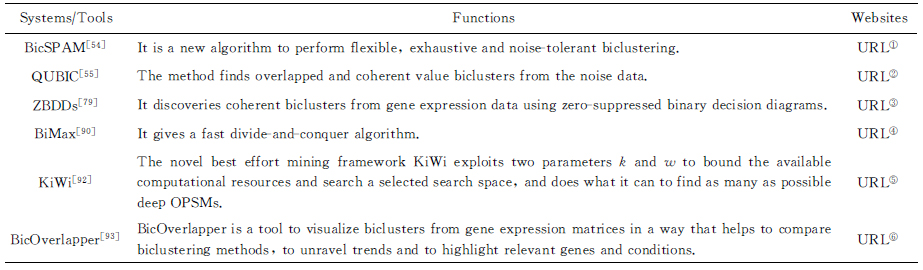
5) 双聚类挖掘系统设计与实现的工作.Gao等人[91-92]提出并实现了一种KiWi框架与系统工具,该方法利用k和w这2个参数来约束计算资源和搜索空间.Santamaría等人[93]设计并实现了一种基因表达数据中双聚类的可视化工具BicOverlapper.其他相关系统的总结如表7所示:
Table7SystemsorToolsofBiclustersBasedonQualitativeMeasures
表7基于定性测度的双聚类系统或工具
Systems∕ToolsFunctionsWebsitesBicSPAM[54] It is a new algorithm to perform flexible, exhaustive and noise-tolerant biclustering.URL①QUBIC[55] The method finds overlapped and coherent value biclusters from the noise data.URL②ZBDDs[79] It discoveries coherent biclusters from gene expression data using zero-suppressed binary decision diagrams.URL③BiMax[90] It gives a fast divide-and-conquer algorithm.URL④KiWi[92] The novel best effort mining framework KiWi exploits two parameters k and w to bound the available computational resources and search a selected search space, and does what it can to find as many as possible deep OPSMs.URL⑤BicOverlapper[93] BicOverlapper is a tool to visualize biclusters from gene expression matrices in a way that helps to compare biclustering methods, to unravel trends and to highlight relevant genes and conditions.URL⑥
① http://web.ist.utl.pt/rmch/software/bicspam
② http://csbl.bmb.uga.edu/~maqin/bicluster/, http://csbl.bmb.uga.edu/publications/materials/ffzhou/QServer/, http://csbl.bmb.uga.edu/~maqin/bicluster/web.html
③ http://akebono.stanford.edu/users/sryoon/tcbb05
④ http://people.ee.ethz.ch/~sop/bimax/
⑤ http://www.bcgsc.ca/platform/bioinfo/ge/kiwi/
⑥ http://vis.usal.es/bicoverlapper
3.3基于查询的双聚类
基于查询的双聚类[94]来自生物信息领域[95-98],应用对象是基因表达数据.首先由用户根据经验来提供功能相关或共表达的种子基因,接着利用该种子对搜索空间剪枝或者对双聚类的挖掘与搜索进行指导.Hochreiter等人[99]设计了双聚类获取的因素分析框架(factor analysis for bicluster acquisition, FABIA).该框架是一种乘性相干值模型,衡量不同基因在相关实验条件下的线性相关性,并捕捉从数据中观察到的重尾分布,还允许利用有充分依据的模型选择方法和应用贝叶斯技术.Jiang等人[100]设计了一种基因模式搜索(gene pattern explorer, GPX)的可视化工具,其利用图形化界面对OPSM数据进行上钻或者下翻,方便生物学家分析基因表达数据.Dhollander等人[101]为使现有挖掘方法能利用先验知识并回答指定的问题,提出一种基于贝叶斯的查询驱动的双聚类方法(query-driven biclustering, QDB).同时给出一种基于实验条件列表的联合方法,来实现关键词的多样性并免除必须事先定义阈值等问题.随后,Zhao等人[102]对QDB方法进行了改进,提出了ProBic方法.虽然二者在概念上相似,但是也有不同之处.QDB方法利用概率关系模型扩展贝叶斯框架,并采用基于期望最大化的直接指定方法来学习该概率模型.Alqadah等人[103]提出一种利用低方差和形式概念分析优势组合的方法,命名为基于查询的双聚类算法(query based biclustering algorithm, QBBC),来发现在部分实验条件下具有相同表达趋势的基因.由用户给出共表达或具有同样功能的种子基因,来缩减搜索空间并指导双聚类的挖掘.姜涛等人[104]观察到保序子矩阵OPSM的快速检索对生物学家寻找某种生理功能模块起着重要作用,但现有大多数方法需要通过挖掘来实现.为了避开挖掘而直接通过索引源数据来检索OPSM,提出带有行列表头的前缀树索引方法、基于行/列关键词的精确/模糊查询技术的OPSM查询方法.姜涛等人[105]为了提升局部模式挖掘结果中检索少量符合用户要求的双聚类OPSM查询的相关性,提出了基于枚举序列与多维索引的2种查询方法.其利用自定义约束从提出的2种索引中搜索相关结果.在真实数据集上的实验结果表明:与蛮力搜索方法相比,基于枚举序列与多维索引的2种查询方法能够更准确、更有效地检索OPSM.姜涛等人[106]为进一步减少文献[105]的索引大小,提出了基于数字签名与Trie的OPSM索引与查询方法.实验结果证明了所提出查询方法的有效性与准确性.姜涛等人[107]设计和实现了基于蝶形网络和带有行与列表头的前缀树索引的OPSM挖掘、索引与检索工具(order-preserving submatrix mining, indexing and search tool, OMEGA).姜涛等人[108]对文献[104]的工作进行了扩展,将原来的正相关模式的搜索增加为正相关、负相关、时滞正负相关等模式的查询.其他相关工具的总结如表8所示:
Table8SystemsorToolsofBiclustersBasedonQuery
表8基于查询的双聚类系统或工具

Systems∕ToolsFunctionsWebsitesFABIA[99] FABIA is based on a multiplicative model, captures heavy tailed distributions as observed in real-world transcriptomic data, and is allowed to utilize well-founded model selection methods and to apply Bayesian techniques.URL①GPX [100] It is an integrated environment for interactive exploration of coherent expression patterns and co-expressed genes in gene expression data.URL②QDB [101] It introduces a novel Bayesian query-driven biclustering framework, which allows introducing knowledge from a set of seed genes (query) to guide the pattern search.URL③QBBC[103] It allows the users to give tightly co-expressed or functionally related seeds to prune the search space and guide biclustering.QBBC is proposed by a new formulation that combines the advantages of low-variance biclustering techniques and formal concept analysis.URL④OMEGA[107] It utilizes prefix-tree to index the gene expression data, and queries OPSMs based on genes or conditions.URL⑤
① http://www.bioinf.jku.at/software/fabia/fabia.html
② http://www.cse.buffalo.edu//DBGROUP/bioinformatics/GPX/
③ http://homes.esat.kuleuven.be/tdhollan/Supplementary_Information_Dhollander_2007/index.html, http://homes.esat.kuleuven.be/?kmarchal
④ http://faris-alqadah.heroku.com
⑤ https://sites.google.com/site/jiangtaonwpu/
3.4约束型双聚类
目前,约束型双聚类的相关研究相对较少,它是一种对基因表达数据挖掘与分析的新方法.Pensa等人[109-110]提出一种从局部到整体的方法来建立间隔约束的二分分区,该方法是通过扩展从0/1数据集中提取出来的一些局部模式来实现的.基本思想是将间隔约束转换成一个放松的局部模式,接着利用K均值算法来获得一个局部模式的分区,最后对此分区做后续处理来确定数据之上的协同聚类结构.随后,Pensa等人[111]对文献[109-110]进行了扩展,主要的不同点有:1)作者同时在行列之上应用目标函数来评价双聚类的好坏;2)文献[111]将文献[109-110]中的数据从0/1矩阵扩展到了实数数据;3)提升must-link与cannot-link这2类约束在行列之上的处理性能.Tseng等人[112]发现现有约束聚类方法大多是类K均值方法,且只能解决基于距离的相似度问题,为此提出一种约束层次聚类方法,并将其命名为相关约束的完整链接(correlational-constrained complete link, C-CCL).该方法利用相关系数作为测度,相比现有算法具有较好的性能.
3.5存在的问题
当前关于基因表达数据挖掘与管理的研究取得了一定的进展,但是还存在着一些问题.例如,基因表达数据中局部模式的快速挖掘、基因表达数据中局部模式的索引、基因表达数据中基于关键词的局部模式查询、基因表达数据中局部模式的约束型查询.具体问题有4点:
1) 随着数据密集型计算平台的出现,如何在分布式并行环境下快速挖掘基因表达数据中的局部模式.
2) 随着高通量测序技术的飞速发展,大量的基因表达数据以前所未有的速度增长.同时,由于基因表达数据分析代价不断减小,大规模的局部模式分析结果也得到累积.如何为这2种数据集设计一个通用的索引结构和查询方法显得尤为迫切.据我们所知,从基因表达数据中挖掘局部模式的耗时远远超过从局部模式数据中搜索局部模式,但是,局部模式的数据量远远大于基因表达数据.如何保证索引能容纳于内存中、索引更新更高效、基于索引的查询更快且具有可扩展性是一项具有挑战性的工作.
3) 虽然局部模式的检索可以通过关键词的查询来处理,但是查询结果大的相关性很难满足.
4) 假如问题1~3都可以圆满解决,如何设计同时满足索引数据量小且查询性能又较高的方法有待研究.
4未来研究方向
尽管现有方法实现了一些研究突破,但是在一些方面仍需要进一步思考和拓展.笔者认为在局部模式的挖掘、索引与检索领域,还有如下3个方面可以进行尝试与探索:
1) 现有的局部模式挖掘大多数是针对单机而设计的,且不管从挖掘结果的数量还是效率上都很难令人满意.目前云计算等分布式并行计算环境正在如火如荼的发展中,为基因表达数据等生物信息挖掘提供了有利的平台.然而,现有方法还不能简单地移植到新的环境中,亟待设计与实现新的计算与通信框架来提高计算的效率与保证计算结果的完整性.
2) 现有的大多数方法关注的是局部模式的批量挖掘,且挖掘出的大量结果很难得到有效的利用.研究与实践表明,基于索引与查询等数据管理和检索技术能够从海量数据中有效地提取想要的信息,且能在很大程度上提高结果的利用效率以及检索结果的相关度.
3) 现有局部模式挖掘方法没有做到领域知识的抽取与有效利用.文献中存在大量来自不同专家的领域知识,其若被有效地提取出来,将从本质上改变缺乏先验知识的现状.另外,现有的爬虫技术与知识抽取方法并不一定适用于本研究,所以还需要进一步的优化与扩充.从分析中可以看出,有必要研究新的数据挖掘与管理方法来对基因之间相互作用的情况进行研究,进一步为生物医学探索提供关键的引导性知识.
随着高通量测序技术的大规模应用推广、大数据应用的兴起和数据密集型等大规模计算平台的普及,局部模式的挖掘、索引与查询方法的研究必将得到更为广泛的关注,同时也将面临新的未知挑战,需要科研工作者结合业界的动态不断地探索与解决.
5总结
基因微阵列技术使得基因表达数据的产生速度加快和数量的增大.双聚类技术又将挖掘结果的类型从单向聚类的整体模式转换为局部模式.因为双聚类在基因表达数据分析方面的成果同样可以移植或转化到商品推荐、直销与选举分析等领域,所以很有必要对现阶段双聚类的研究成果加以整理与总结.本文从局部模式定义、局部模式类型与标准、研究现状、未来的研究方向等方面梳理了基因表达数据中的局部模式挖掘技术.同时指出虽然局部模式的研究已经开展了很多年,也涌现出大量的重要研究成果,但是随着大数据技术与系统的产生与发展,现有局部模式挖掘方法并不一定完全适用于新形势与新情况.本文针对局部模式挖掘的综述研究希望能够为关注大数据中局部模式挖掘理论与应用的研究者与实践领域专家提供借鉴.
参考文献
[1] Cheng Yizong, Church G M. Biclustering of expression data[C] //Proc of the 8th Int Conf on Intelligent Systems for Molecular Biology (ISMB). Menlo Park, CA: AAAI, 2000: 93-103
[2]Wang Zhenjia, Li Guojun, Robinson R W, et al. UniBic: Sequential row-based biclustering algorithm for analysis of gene expression data[J]. Scientific Reports, 2016, 6: 23466
[3]Hartigan J A. Direct clustering of a data matrix[J]. Journal of the American Statistical Association, 1972, 67(337): 123-129
[4]Ben-Dor A, Chor B, Karp R, et al. Discovering local structure in gene expression data: The order-preserving submatrix problem[C] //Proc of the 6th Annual Int Conf on Computational Biology (RECOMB). New York: ACM, 2002: 49-57
[5]Madeira S C, Oliveira A L. Biclustering algorithms for biological data analysis: A survey[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2004, 1(1): 24-45
[6]Ben-Dor A, Chor B, Karp R, et al. Discovering local structure in gene expression data: The order-preserving submatrix problem[J]. Journal of Computational Biology, 2003, 10(3/4): 373-384
[7]Yang Jiong, Wang Wei, Wang Haixun, et al. δ-Clusters: Capturing subspace correlation in a large data sets[C] //Proc of the 18th Int Conf on Data Engineering (ICDE). Piscataway, NJ: IEEE, 2002: 517-528
[8]Cho H. Data transformation for sum squared residue[C] //Proc of the 14th Pacific-Asia Conf on Advances in Knowledge Discovery and Data Mining (PAKDD). Berlin: Springer, 2010: 48-55
[9]Teng Li, Chan Laiwan. Discovering biclusters by iteratively sorting with weighted correlation coefficient in gene expression data[J]. Journal of Signal Processing Systems, 2008, 50(3): 267-280
[10]Ayadi W, Hao Jinkao. A memetic algorithm for discovering negative correlation biclusters of DNA microarray data[J]. Neurocomputing, 2014, 145: 14-22
[11]Ayadi W, Elloumi M, Hao Jinkao. A biclustering algorithm based on a bicluster enumeration tree: Application to DNA microarray data[J]. BioData Mining, 2009, 2(1): 9
[12]Ayadi W, Elloumi M, Hao Jinkao. BicFinder: A biclustering algorithm for microarray data analysis[J]. Knowledge and Information Systems, 2012, 30(2): 341-358
[13]Chui C K, Kao Ben, Yip K Y, et al. Mining order-preserving submatrices from data with repeated measurements[C] //Proc of the 8th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2008: 133-142
[14]Fang Qiong, Ng W, Feng Jianlin. Discovering significant relaxed order-preserving submatrices[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (SIGKDD). New York: ACM, 2010: 433-442
[15]Sim K, Gopalkrishnan V, Zimek A, et al. A survey on enhanced subspace clustering[J]. Data Mining and Knowledge Discovery, 2013, 26(2): 332-397
[16]Jiang Daxin, Tang Chun, Zhang Aidong. Cluster analysis for gene expression data: A survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(11): 1370-1386
[17]Kriegel H P, Kroger P, Zimek A. Clustering of high-dimensional data: A survey on subspace clustering, pattern-based clustering, and correlation clustering[J]. ACM Transactions on Knowledge Discovery Data, 2009, 3(1): 1
[18]Yue Feng, Sun Liang, Wang Kuanquan, et al. State-of-the-art of cluster analysis of gene expression data[J]. Acta Automatica Sinica, 2008, 34(2): 113-120 (in Chinese)
(岳峰, 孙亮, 王宽全, 等. 基因表达数据的聚类分析研究进展[J]. 自动化学报, 2008, 34(2): 113-120)
[19]Deodhar M, Gupta G, Ghosh J, et al. A scalable framework for discovering coherent co-clusters in noisy data[C] //Proc of the 26th Annual Int Conf on Machine Learning (ICML). New York: ACM, 2009: 241-248
[20]Sun Huan, Miao Gengxin, Yan Xifeng. Noise-resistant bicluster recognition[C] //Proc of the 13th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2013: 707-716
[21]Divina F, Aguilar-Ruiz J S. Biclustering of expression data with evolutionary computation[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(5): 590-602
[22]Odibat O, Reddy C K. A generalized framework for mining arbitrarily positioned overlapping co-clusters[C] //Proc of the 19th SIAM Int Conf on Data Mining (SDM). Philadelphia, PA: SIAM, 2011: 343-354
[23]Truong D T, Battiti R, Brunato M. Discovering non-redundant overlapping biclusters on gene expression data[C] //Proc of the 13th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2013: 747-756
[24]Chen Shuhua, Liu Juan, Zeng Tao. MMSE: A generalized coherence measure for identifying linear patterns[C] //Proc of the 8th IEEE Int Conf on Bioinformatics and Biomedicine (BIBM). Piscataway, NJ: IEEE, 2014: 489-492
[25]Wang Haixun, Wang Wei, Yang Jiong, et al. Clustering by pattern similarity in large data sets[C] //Proc of the 28th ACM SIGMOD Int Conf on Management of Data (SIGMOD). New York: ACM, 2002: 394-405
[26]Bhattacharya A, De R K. Bi-correlation clustering algorithm for determining a set of co-regulated genes[J]. Bioinformatics, 2009, 25(21): 2795-2801
[27]Xiao Jing, Wang Lusheng, Liu Xiaowen, et al. An efficient voting algorithm for finding additive biclusters with random background[J]. Journal of Computational Biology, 2008, 15(10): 1275-1293
[28]Xie Qing, Shang Shuo, Yuan Bo, et al. Local correlation detection with linearity enhancement in streaming data[C] //Proc of the 22nd ACM Int Conf on Information and Knowledge Management (CIKM). Piscataway, NJ: IEEE, 2013: 309-318
[29]Murali T M, Kasif S. Extracting conserved gene expression motifs from gene expression data[C] //Proc of the 8th Pacific Symp on Biocomputing (PSB). Singapore: World Scientific Publishing, 2003, 8: 77-88
[30]Bergmann S, Ihmels J, Barkai N. Iterative signature algorithm for the analysis of large-scale gene expression data[J]. Physical Review E, 2003, 67(3): 031902
[31]Pandey G, Atluri G, Steinbach M, et al. An association analysis approach to biclustering[C] //Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (SIGKDD). New York: ACM, 2009: 677-686
[32]Denitto M, Farinelli A, Bicego M. Biclustering gene expressions using factor graphs and the max-sum algorithm[C] //Proc of the 24th Int Joint Conf on Artificial Intelligence (IJCAI). Menlo Park, CA: AAAI, 2015: 925-931
[33]Lee M, Shen Haipeng, Huang Jianhua Z, et al. Biclustering via sparse singular value decomposition[J]. Biometrics, 2010, 66(4): 1087-1095
[34]Tanay A, Sharan R, Shamir R. Discovering statistically significant biclusters in gene expression data[J]. Bioinformatics, 2002, 18(Suppl 1): S136-S144
[35]Sill M, Kaiser S, Benner A, et al. Robust biclustering by sparse singular value decomposition incorporating stability selection[J]. Bioinformatics, 2011, 27(15): 2089-2097
[36]Tchagang A B, Bui K V, McGinnis T, et al. Extracting biologically significant patterns from short time series gene expression data[J]. BMC Bioinformatics, 2009, 10(1): 255
[37]Tan Jinsong, Chua K S, Zhang Louxin, et al. Algorithmic and complexity issues of three clustering methods in microarray data analysis[J]. Algorithmica, 2007, 48(2): 203-219
[38]Humrich J, Gärtner T, Garriga G C. A fixed parameter tractable integer program for finding the maximum order preserving submatrix[C] //Proc of the 11th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2011: 1098-1103
[39]Joung J G, Kim S J, Shin S Y, et al. A probabilistic coevolutionary biclustering algorithm for discovering coherent patterns in gene expression dataset[J]. BMC Bioinformatics, 2012, 13(Suppl 17): S12
[40]Cho H, Dhillon I S. Coclustering of human cancer microarrays using minimum sum-squared residue coclustering[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2008, 5(3): 385-400
[41]Cho H, Dhillon I S, Guan Yuqiang, et al. Minimum sum-squared residue co-clustering of gene expression data[C] //Proc of the 12th SIAM Int Conf on Data Mining (SDM). Philadelphia, PA: SIAM, 2004: 114-125
[42]Yang Wenhui, Dai Daoqing, Yan Hong. Finding correlated biclusters from gene expression data[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(4): 568-584
[43]Roy S, Bhattacharyya D K, Kalita J K. CoBi: Pattern based co-regulated biclustering of gene expression data[J]. Pattern Recognition Letters, 2013, 34(14): 1669-1678
[44]Roy S, Bhattacharyya D K, Kalita J K. Analysis of gene expression patterns using biclustering[J]. Methods in Molecular Biology, 2015, 1375: 91-103
[45]Eren K, Deveci M, Küçüktunç O, et al. A comparative analysis of biclustering algorithms for gene expression data[J]. Briefings in Bioinformatics, 2013, 14(3): 279-292
[46]Saber H B, Elloumi M. DNA microarray data analysis: A new survey on biclustering[J]. International Journal for Computational Biology, 2015, 4(1): 21-37
[47]Barkow S, Bleuler S, Prelic A, et al. BicAT: A biclustering analysis toolbox[J]. Bioinformatics, 2006, 22(10): 1282-1283
[48]Yip K Y, Kao Ben, Zhu Xinjie, et al. Mining order-preserving submatrices from data with repeated measurements[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(7): 1587-1600
[49]Zhang Mengsheng, Wang Wei, Liu Jinze. Mining approximate order preserving clusters in the presence of noise[C] //Proc of the 24th Int Conf on Data Engineering (ICDE). Piscataway, NJ: IEEE, 2008: 160-168
[50]Fang Qiong, Ng W, Feng Jianlin, et al. Mining bucket order-preserving submatrices in gene expression data[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(12): 2218-2231
[51]Fang Qiong, Ng W, Feng Jianlin, et al. Mining order-preserving submatrices from probabilistic matrices[J]. ACM Transactions on Database Systems, 2014, 39(1): 6
[52]Peng Wei, Li Tao. IntClust: A software package for clustering replicated microarray data[C] //Proc of the 6th IEEE Int Symp on BioInformatics and BioEngineering (BIBE). Piscataway, NJ: IEEE, 2006: 103-109
[53]Abdullah A, Hussain A. A new biclustering technique based on crossing minimization[J]. Neurocomputing, 2006, 69(16): 1882-1896
[54]Henriques R, Madeira S C. BicSPAM: Flexible biclustering using sequential patterns[J]. BMC Bioinformatics, 2014, 15(1): 130
[55]Li Guojun, Ma Qin, Tang Haibao, et al. QUBIC: A qualitative biclustering algorithm for analyses of gene expression data[J]. Nucleic Acids Research, 2009, 37(15): e101
[56]Liu Jinze, Wang Wei. OP-Clustering by tendency in high dimensional space[C] //Proc of the 3rd IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2003: 187-194
[57]Wang Haixun, Pei Jian, Yu P S. Pattern-based similarity search for microarray data[C] //Proc of the 11th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (SIGKDD). New York: ACM, 2005: 814-819
[58]Zhao Yuhai, Yu J X, Wang Guoren, et al. Maximal subspace coregulated gene clustering[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(1): 83-98
[59]Jiang Daxin, Pei Jian, Zang Aidong. A general approach to mining quality pattern-based clusters from microarray data[C] //Proc of the 10th Int Conf on Database Systems for Advanced Applications (DASFAA). Berlin: Springer, 2005: 188-200
[60]Yan Leiming, Sun Zhihui, Wu Yingjie, et al. Biclustering nonlinearly correlated time series gene expression data[J]. Journal of Computer Research and Development, 2008, 45(11): 1865-1873 (in Chinese)
(闫雷鸣, 孙志挥, 吴英杰, 等. 联合聚类非线性相关的时序基因表达数据[J]. 计算机研究与发展, 2008, 45(11): 1865-1873)
[61]Yin Ying, Zhao Yuhai, Zhang Bin, et al. Mining synchronous and asynchronous co-regulated gene clusters from time series microarray data[J]. Chinese Journal of Computers, 2007, 30(8): 1302-1314 (in Chinese)
(印莹, 赵宇海, 张斌, 等. 时序微阵列数据中的同步和异步共调控基因聚类[J]. 计算机学报, 2007, 30(8): 1302-1314)
[62]Yin Ying, Zhao Yuhai, Zhang Bin. Identifying synchronous and asynchronous co-regulations from time series gene expression data[C] //Proc of the 11th Pacific-Asia Conf on Advances in Knowledge Discovery and Data Mining (PAKDD). Berlin: Springer, 2007: 1046-1054
[63]Yin Ying, Zhao Yuhai, Zhang Bin, et al. Mining time-shifting co-regulation patterns from gene expression data[C] //Proc of the Joint 9th Asia-Pacific Web Conf on Advances in Data and Web Management (APWeb) and 8th Int Conf on Web-Age Information Management (WAIM). Berlin: Springer, 2007: 62-73
[64]Zhao Yuhai, Wang Guoren, Yin Ying, et al. Mining positive and negative co-regulation patterns from microarray data[C] //Proc of the 6th IEEE Int Symp on BioInformatics and BioEngineering (BIBE). Piscataway, NJ: IEEE, 2006: 86-93
[65]Zhao Yuhai, Wang Guoren, Yin Ying, et al. A novel approach to revealing positive and negative co-regulated genes[J]. Journal of Computer Science and Technology, 2007, 22(2): 261-272
[66]Wang Guoren, Yin Linjun, Zhao Yuhai, et al. Efficiently mining time-delayed gene expression patterns[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 2010, 40(2): 400-411
[67]Wang Guoren, Zhao Yuhai, Zhao Xiangguo, et al. Efficiently mining local conserved clusters from gene expression data[J]. Neurocomputing, 2010, 73(7/8/9): 1425-1437
[68]Ji Liping, Tan K L. Mining gene expression data for positive and negative co-regulated gene clusters[J]. Bioinformatics, 2004, 20(16): 2711-2718
[69]Ji Liping, Tan K L. Identifying time-lagged gene clusters using gene expression data[J]. Bioinformatics, 2005, 21(4): 509-516
[70]Ji Liping, Mock K W L, Tan K L. Quick hierarchical biclustering on microarray gene expression data[C] //Proc of the 6th IEEE Int Symp on BioInformatics and BioEngineering (BIBE). Piscataway, NJ: IEEE, 2006: 110-120
[71]Chen J R, Chang Y I. An up-down bit pattern approach to coregulated and negative-coregulated gene clustering of microarray data[J]. Journal of Computational Biology, 2011, 18(12): 1777-1791
[72]Jiang Tao, Li Zhanhuai, Chen Qun, et al. Parallel partitioning and mining gene expression data with butterfly network[C] //Proc of the 24th Int Conf on Database and Expert Systems Applications (DEXA): Part I. Berlin: Springer, 2013: 129-144
[73]Trapp A C, Prokopyev O A. Solving the order-preserving submatrix problem via integer programming[J]. INFORMS Journal on Computing, 2010, 22(3): 387-400
[74]Kriegel H P, Kröger P, Renz M, et al. A generic framework for efficient subspace clustering of high-dimensional data[C] //Proc of the 5th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2005: 250-257
[75]An Ping. Research on biclustering methods for gene expression data analysis[D]. Suzhou, Jiangsu: Soochow University, 2013 (in Chinese)
(安平. 基因表达数据的双聚类分析方法研究[D]. 江苏苏州: 苏州大学, 2013)
[76]Zhang Xiang, Wang Wei. An efficient algorithm for mining coherent patterns from heterogeneous microarrays[C] //Proc of the 19th Int Conf on Scientific and Statistical Database Management (SSDBM). Piscataway, NJ: IEEE, 2007: 32
[77]Cho S, Na J C, Park K, et al. A fast algorithm for order-preserving pattern matching[J]. Information Processing Letters, 2015, 115(2): 397-402
[78]Hochbaum D S, Levin A. Approximation algorithms for a minimization variant of the order-preserving submatrices and for biclustering problems[J]. ACM Transactions on Algorithms, 2013, 9(2): 19
[79]Yoon S, Nardini C, Benini L, et al. Discovering coherent biclusters from gene expression data using zero-suppressed binary decision diagrams[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2005, 2(4): 339-354
[80]Painsky A, Rosset S. Exclusive row biclustering for gene expression using a combinatorial auction approach[C] //Proc of the 12th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2012: 1056-1061
[81]Painsky A, Rosset S. Optimal set cover formulation for exclusive row biclustering of gene expression[J]. Journal of Computer Science and Technology, 2014, 29(3): 423-435
[82]Ji Liping, Tan K L, Tung A K H. Compressed hierarchical mining of frequent closed patterns from dense data sets[J]. IEEE Transactions on Knowledge and Data Engineering, 2007, 19(9): 1175-1187
[83]Xue Yun, Liao Zhengling, Li Meihang, et al. A new approach for mining order-preserving submatrices based on all common subsequences[J]. Computational and Mathematical Methods in Medicine, 2015, 2015: 680434
[84]Xue Yun, Fu Juntong, Li Jiejin, et al. A new OPSM algorithm based on all common subsequences[J]. Journal of South China Normal University: Natural Science Edition, 2015, 47(4): 165-171 (in Chinese)
(薛云, 傅俊橦, 李杰进, 等. 基于公共子序列的 OPSM 双聚类算法[J]. 华南师范大学学报: 自然科学版, 2015, 47(4): 165-171)
[85]Kuang Qiuhua, Zhang Meizhen, Ma Zhihao, et al. An algorithm for discovering deep order preserving submatrix in gene expression data[C] //Proc of the 9th IEEE Int Conf on Bioinformatics and Biomedicine (BIBM). Piscataway, NJ: IEEE, 2015: 1678-1683
[86]Kim J, Eades P, Fleischer R, et al. Order-preserving matching[J]. Theoretical Computer Science, 2014, 525: 68-79
[87]Bruner M L, Lackner M. A fast algorithm for permutation pattern matching based on alternating runs[J]. Algorithmica, 2016, 75(1): 84-117
[88]Crochemore M, Iliopoulos C S, Kociumaka T, et al. Order-preserving incomplete suffix trees and order-preserving indexes[C] //Proc of the 20th Int Symp on String Processing and Information Retrieval (SPIRE). Berlin: Springer, 2013: 84-95
[89]Chen H C, Zou Wen, Tien Y J, et al. Identification of bicluster regions in a binary matrix and its applications[J]. PloS One, 2013, 8(8): e71680
 A, Bleuler S, Zimmermann P, et al. A systematic comparison and evaluation of biclustering methods for gene expression data[J]. Bioinformatics, 2006, 22(9): 1122-1129
A, Bleuler S, Zimmermann P, et al. A systematic comparison and evaluation of biclustering methods for gene expression data[J]. Bioinformatics, 2006, 22(9): 1122-1129
[91]Gao B J, Griffith O L, Ester M, et al. Discovering significant OPSM subspace clusters in massive gene expression data[C] //Proc of the 12th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining (SIGKDD). New York: ACM, 2006: 922-928
[92]Gao B J, Griffith O L, Ester M, et al. On the deep order-preserving submatrix problem: A best effort approach[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(2): 309-325
[93]Santamaría R, Therón R, Quintales L. BicOverlapper: A tool for bicluster visualization[J]. Bioinformatics, 2008, 24(9): 1212-1213
[94]Smet R D, Marchal K. An ensemble method for querying gene expression compendia with experimental lists[C] //Proc of the 4th IEEE Int Conf on Bioinformatics and Biomedicine (BIBM). Piscataway, NJ: IEEE, 2010: 314-318
[95]Zou Quan, Li Xubin, Jiang Wenrui, et al. Survey of MapReduce frame operation in bioinformatics[J]. Briefings in Bioinformatics, 2014, 15(4): 637-647
[96]Zou Quan, Guo Maozu, Liu Yang, et al. A classification method for class-imbalanced data and its application on bioinformatics[J]. Journal of Computer Research and Development, 2010, 47(8): 1407-1414 (in Chinese)
(邹权, 郭茂祖, 刘扬, 等. 类别不平衡的分类方法及在生物信息学中的应用[J]. 计算机研究与发展, 2010, 47(8): 1407-1414)
[97]Chen Wei, Cheng Yongmei, Zhang Shaowu, et al. Heuristic clustering method based on neighbor-seeds for 454 sequencing data[J]. Journal of Software, 2014, 25(5): 929-938 (in Chinese)
(陈伟, 程咏梅, 张绍武, 等. 邻域种子的启发式454序列聚类方法[J]. 软件学报, 2014, 25(5): 929-938)
[98]Zou Quan, Hu Qinghua, Guo Maozu, et al. HAlign: Fast multiple similar DNA/RNA sequence alignment based on the centre star strategy[J]. Bioinformatics. 2015, 31(15): 2475-2481
[99]Hochreiter S, Bodenhofer U, Heusel M, et al. FABIA: Factor analysis for bicluster acquisition[J]. Bioinformatics, 2010, 26(12): 1520-1527
[100]Jiang Daxin, Pei Jian, Zhang Aidong. GPX: Interactive mining of gene expression data[C] //Proc of the 30th Int Conf on Very Large Data Bases (VLDB). New York: ACM, 2004: 1249-1252
[101]Dhollander T, Sheng Q Z, Lemmens K, et al. Query-driven module discovery in microarray data[J]. Bioinformatics, 2007, 23(19): 2573-2580
[102]Zhao Hui, Cloots L, Bulcke T V, et al. Query-based biclustering of gene expression data using probabilistic relational models[J]. BMC Bioinformatics, 2011, 12(Suppl 1): S37
[103]Alqadah F, Bader J S, Anand R, et al. Query-based biclustering using formal concept analysis[C] //Proc of the 12th SIAM Int Conf on Data Mining (SDM). Philadelphia, PA: SIAM, 2012: 648-659
[104]Jiang Tao, Li Zhanhuai, Chen Qun, et al. Towards order-preserving submatrix search and indexing[C] //Proc of the 20th Int Conf on Database Systems for Advanced Applications (DASFAA): Part II. Berlin: Springer, 2015: 309-326
[105]Jiang Tao, Li Zhanhuai, Shang Xuequn, et al. Constrained query of order-preserving submatrix in gene expression data[J]. Frontiers of Computer Science, 2016, 10(6): 1052-1066
[106]Jiang Tao, Li Zhanhuai, Shang Xuequn, et al. Constrained query of order-preserving submatrix based on signature and Trie[J]. Journal of Software, 2017, 28(8): 2175-2195 (in Chinese)
(姜涛, 李战怀, 尚学群, 等. 基于数字签名与Trie的保序子矩阵约束查询[J]. 软件学报, 2017, 28(8): 2175-2195)
[107]Jiang Tao, Li Zhanhuai, Chen Qun, et al. OMEGA: An order-preserving submatrix mining, indexing and search[C] //Proc of the European Conf on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML/PKDD): Part III. Berlin: Springer, 2015: 303-307
[108]Jiang Tao, Li Zhanhuai, Shang Xuexun, et al. Local pattern query from gene expression data[J]. Computer Science, 2016, 43(7): 191-196, 223 (in Chinese)
(姜涛, 李战怀, 尚学群, 等. 基因表达数据中局部模式的查询[J]. 计算机科学, 2016, 43(7): 191-196, 223)
[109]Pensa R G, Robardet C, Boulicaut J F. Towards constrained co-clustering in ordered 0/1 data sets[C] //Proc of the 16th Int Symp on Methodologies for Intelligent Systems (ISMIS). Berlin: Springer, 2006: 425-434
[110]Pensa R G, Robardet C, Boulicaut J F. Constraint-driven co-clustering of 0/1 data[G] //Constrained Clustering: Advances in Algorithms, Theory and Applications, Data Mining and Knowledge Discovery Series. London: Chapman & Hall, 2008: 123-148
[111]Pensa R G, Boulicaut J F. Constrained co-clustering of gene expression data[C] //Proc of the 8th SIAM Int Conf on Data Mining (SDM). Philadelphia, PA: SIAM, 2008: 25-36
[112]Tseng V S, Chen L C, Kao C P. Constrained clustering for gene expression data mining[C] //Proc of the 12th Pacific-Asia Conf on Advances in Knowledge Discovery and Data Mining (PAKDD). Berlin: Springer, 2008: 759-766
ASurveyonLocalPatternMininginGeneExpressionData
Jiang Tao1and Li Zhanhuai2
1(SchoolofComputerandInformationEngineering,HenanUniversityofEconomicsandLaw,Zhengzhou450046)2(SchoolofComputerScience,NorthwesternPolytechnicalUniversity,Xi’an710129)
AbstractAs an unprecedented breakthrough in experimental molecular biology domain, DNA microarray enables simultaneously monitoring of the expression level of thousands of genes over many experimental conditions. Studies have shown that analyzing microarray data is essential for finding gene co-expression network, designing new types of drugs, preventing disease, and so on. To analyze gene expression datasets, the researchers design many clustering methods, which can only find fewer of useful knowledge. Due to a subset of genes co-regulate and co-express only under a subset of experimental conditions, and also not co-express at the same level, they can belong to several genetic pathways that are not apparent. In this situation, the biclustering method is proposed. At the same time, the direction of gene expression analysis changes from the whole pattern mining to the local pattern discovery, and then it changes the situation of clustering data only based on all the objects or attributes of the data. The paper introduces the state-of-the-art progress, which includes the definition of local pattern, the types and criteria of local pattern, mining and query methods of local pattern. Then it concludes the mining criteria based on quantity and quality, and related software. Further, it gives the problems in the existing algorithms and tools. Finally, we discuss the research direction in the future.
KeywordsDNA microarray; gene expression; local pattern; order-preserving submatrix; biclustering; data mining
中图法分类号TP311.13
基金项目:国家自然科学基金项目(61702161,61732014,61502146,91746115,61602153);河南省重点研发与推广专项(科技攻关)(182102210213);河南省高等学校重点科研项目(18A520003,18A520015,18B510004) This work was supported by the National Natural Science Foundation of China (61702161, 61732014, 61502146, 91746115, 61602153), the Key Research and Development and Promotion Program of He’nan Province (182102210213), and the Key Research Found for Higher Education of He’nan Province (18A520003, 18A520015, 18B510004).
修回日期:2018-03-05
收稿日期:2017-09-01;

JiangTao, born in 1983. PhD, lecturer. Member of CCF. His main research interests include data management, data mining, and information retrieval.

LiZhanhuai, born in 1961. PhD, professor, PhD supervisor. Senior member of CCF. His main research interests include data management, data mining, big data analysis, and information retrieval.









 http://www.cs.utexas.edu/users/dml/Software/cocluster.html
http://www.cs.utexas.edu/users/dml/Software/cocluster.html https://sites.google.com/site/swarupnehu/publications/resources
https://sites.google.com/site/swarupnehu/publications/resources http://www.tik.ee.ethz.ch/sop/bicat
http://www.tik.ee.ethz.ch/sop/bicat



