董学士 董文永 蔡永乐
(武汉大学计算机学院 武汉 430072) (dxs_cs@163.com)
摘要基于着色旅行商问题(colored traveling salesman problem, CTSP),给出了一种适用性更加宽泛的组合优化问题模型:着色瓶颈旅行商问题(colored bottleneck traveling salesman problem, CBTSP).CBTSP可建模含有部分重合工作区域的规划问题,譬如有合作任务和单独任务的人员与车辆的路线规划,此类问题由于目标函数与旅行商问题不一样,因此不能够用CTSP模型来建模.由于CBTSP属于NP难问题,对于规模大的此类问题,自然启发式算法是个合适的选择.基于此,提出了一种自然启发式算法求解CBTSP,该算法是基于伊藤过程的粒子群算法(particle swarm optimization, PSO)、模拟退火算法(simulated annealing, SA)和遗传算法(genetic algorithm, GA)的混合算法(PSGA).PSGA首先用二重染色体编码来构建问题的解,然后运用遗传算法的交叉操作进行更新,其中交叉长度由伊藤过程的活动强度来控制,而活动强度由粒子半径和环境温度来决定.为了充分验证算法的有效性,使用小尺度到大尺度不同规模的数据进行实验,通过广泛的实验与分析表明:PSGA求解CBTSP问题的求解质量要优于对比算法.
关键词混合算法;遗传算法;着色瓶颈旅行商问题;着色旅行商问题;瓶颈旅行商问题
着色旅行商问题(colored traveling salesman problem, CTSP)是旅行商问题(traveling salesman problem, TSP)与多旅行商问题(multiple traveling salesman problem, MTSP)的一种扩展模型,CTSP是一种来源于但不局限于多机器工程系统(multi-machine engineering system, MES)的模型,可应用在具有部分重合工作区域的规划[1].为建模有部分重合区域的人员与车辆调配的路线优化问题,本文给出了一种新的模型——着色瓶颈旅行商问题(colored bottleneck traveling salesman problem, CBTSP),可应用于有合作与单独任务的人员与车辆的路线规划等问题,其目标是最小化所有旅行路线的最大边,具体的应用场景参见1.3节的论述.在智能交通、多任务协作等领域,一些实际问题可用CBTSP来建模,所构建模型的尺度(对应着CBTSP的城市数量)往往趋于大尺度(城市数量1 000或以上),因此,研究大尺度的CBTSP及其求解算法有一定的意义.
由于CBTSP是本文提出的模型,尚没有相应的求解算法,算法方面的研究主要集中在CTSP模型.东南大学Li等人[2]提出CTSP模型,并用遗传算法求解该问题;之后,Li等人[1]将贪心遗传算法(genetic algorithm with greedy initialization, GAG)、爬山法遗传算法(hill-climbing genetic algorithm, HCGA)与模拟退火遗传算法(simulated annealing genetic algorithm, SAGA)应用在求解小规模的CTSP,即CTSP的城市数量小于等于101.瓶颈旅行商(bottleneck traveling salesman problem, BTSP)[3-10]相关工作有:Vairaktarakis[3]给出了 BTSP是NP完全问题,可应用在工作流的规划领域;BTSP也可应用在重构相邻信息的排序序列[4];Garfinkel等人[5]将BTSP应用在集成线路的排序;BTSP另一种应用就是最小化状态变化机的排序[7];BTSP也可以应用于最小化机器的最大变化状态[8];Ahmed[10]应用遗传算法求解BTSP.元启发式算法的其他相关应用:Liao等人[11]将蚁群算法应用于混合可变的优化问题;Ferreira[12]将一种蚁群优化方法用于眼底图像渗出物的分割.
本文在提出CBTSP模型的基础上,进一步设计了一种混合粒子群优化算法(particle swarm optimi-zation, PSO)、模拟退火(simulated annealing, SA)和遗传算法(genetic algorithm, GA)的启发式算法PSGA来求解该问题.PSGA算法首先用二重染色体编码来产生问题的解,然后用遗传算法的交叉操作来更新该解,在求解过程中,活动强度控制着交叉长度,并受粒子半径和环境温度的影响.通过使用小尺度到大尺度CBTSP实例的实验与分析表明:PSGA求解CBTSP是有效的,该算法的求解质量要好于对比算法.
本文的创新点包括:给出了一种问题模型CBTSP,该模型可对一类组合优化问题进行建模,并将该模型的规模扩展到大尺度;提出了一种新的混合算法PSGA用于求解CBTSP问题.
着色旅行商问题(CTSP)[1]有m个旅行者和n个城市,其中m,n∈![]() +={1,2,…},且m<n.该问题可以被定义为一个完全图G(V,E),V={0,1,…,n-1}表示城市集,每个边(i,j)∈E,i≠j,该边(i,j)与权重Wij表示城市i与城市j之间的距离.城市数据集V被分成m+1个非空集:1个数据集U表示一个共享的城市集;m个数据集Vi∈V,表示第i个旅行商的独享城市集,即只有旅行者i才能访问,∀i∈Zm={1,2,…,m}.定点di∈V表示站点,是旅行者i开始和结束的地方.颜色i着色的城市只能被旅行者i访问.被i着色的城市集Vi表示只有旅行者i才能访问,其中i=1,2,…,m.共享集U的城市a被颜色集c(a)着色,表示只有旅行者i∈c(a)才能访问它.
+={1,2,…},且m<n.该问题可以被定义为一个完全图G(V,E),V={0,1,…,n-1}表示城市集,每个边(i,j)∈E,i≠j,该边(i,j)与权重Wij表示城市i与城市j之间的距离.城市数据集V被分成m+1个非空集:1个数据集U表示一个共享的城市集;m个数据集Vi∈V,表示第i个旅行商的独享城市集,即只有旅行者i才能访问,∀i∈Zm={1,2,…,m}.定点di∈V表示站点,是旅行者i开始和结束的地方.颜色i着色的城市只能被旅行者i访问.被i着色的城市集Vi表示只有旅行者i才能访问,其中i=1,2,…,m.共享集U的城市a被颜色集c(a)着色,表示只有旅行者i∈c(a)才能访问它.
在CTSP中,共享数据U有相关定义,U可被多个旅行者访问,∀a∈U,c(a)=Zm.如果di=0∈U且∀a∈U,c(a)=Zm,该对应的CTSP整数编码模型:变量xijk(i≠j,i,j∈V,k∈Zm)表示第k个旅行者是否经过城市i到j,变量uik(i∈V,k∈Zm)表示第k个旅行者从起点到城市i的城市数目[1].
CBTSP的定义与CTSP的定义基本相同,但两者有不同的目标函数.
CTSP的目标函数[1]:
(1)
CBTSP的目标是最小化旅行回路的最大边,其表达式为minf=maxedge(i,j)(i,j=0,1,…,n-1).
CBTSP与CTSP虽有不同的目标函数,但有相同的限制条件.
CBTSP的限制条件为
![]()
(2)
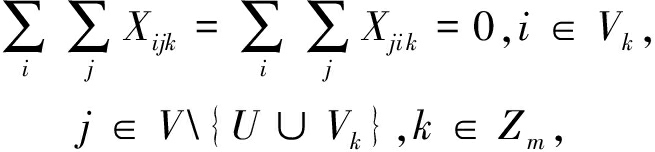
(3)
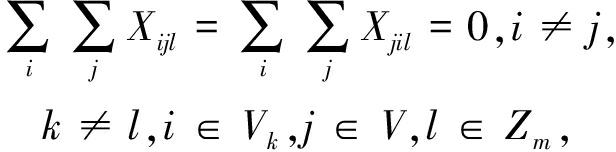
(4)

(5)
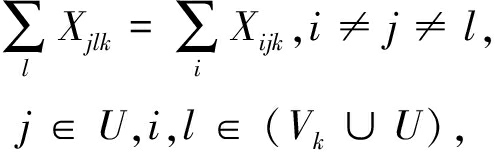
(6)
式(2)表示每个旅行者开始和结束该起点(起始点 0);式(3)表示旅行者k不能访问其他旅行者的独享城市,另外,其他的旅行者也不能访问旅行者k的独享城市;式(4)表示旅行者l(l≠k)既不是开始于第k个城市数据集也不返回到该集;式(5)表示除了起始点0之外,每个城市必须只被访问一次;式(6)表示每个旅行者必须同时访问和退出共享城市集.
1) 相同点.CBTSP和CTSP一样,都有独享城市集和共享城市集、多个旅行者和多个城市,其中独享城市只能被指定的旅行者访问,共享城市可以被所有的旅行者访问,每个城市只能被访问一次.2个问题都是NP难问题,两者可共用相同的数据集.
2) 不同点.2个问题的目标函数不同,CBTSP的目标是使所有旅行回路的最大的边最小化,CTSP的目标是使所有旅行回路的总的距离最小.
CTSP可以较容易地转化为CBTSP,改变CTSP的目标函数即可.BTSP转化为CBTSP,需要经过更为复杂的过程:1)由BTSP单个旅行商变为CBTSP的多个旅行商;2)将BTSP的数据划分成独享城市集和共享城市集;3)增加式(2)~(6)的限制条件.
CTSP可以应用在多机器工程系统MES的规划问题.CBTSP可用来建模一类具有协作与单独任务的人员和车辆的路线规划优化问题,该类问题一般具有一些特点:它们通常有多个人或车辆,个体不仅需要执行共同区域的合作任务,而且需要执行个体所属区域的独立任务,在行动过程中,因某些需要或原因,个体需要被增员,为了能被更容易地找到,需最小化旅行回路的最大边.该问题的目标、个人和任务可与CBTSP的目标、旅行者和任务相匹配,因此可以用CBTSP来建模.
最大离散旅行商问题(maximum scatter traveling salesperson problem, MSTSP)[13-15]的目标是最大化旅行回路的最小边,MSTSP是根据制造业与医学图像等方面的应用需要而提出的一种模型.例如MSTSP的一个应用实例[13]:假如有一个被冤枉的犯人,没有违法却可能会面临着指控,于是他从警察局越狱逃跑,为了避免被拒捕他开始在全国流窜,当他的一些通缉信息如名字与照片在电视上播放后,一般来说,他在一个地方逗留的时间越长,就会越容易引起当地人的怀疑,有的人可能会到警察局报案,在相信他无辜的全国范围朋友们的帮助下,他会采取从一个安全的地方到另外一个安全的地方的方式来逃跑,并尽可能地远离之前安全的地方.用更准确的术语来表达,他需要寻找一个穿过安全地方的旅行回路,即任意相邻2点的最小距离需尽可能最大化,这个问题的模型称之为MSTSP.与MSTSP相反,BTSP是最小化旅行回路的最大边长,使最大的相邻点距离尽可能最小.如果上面的被误指控的犯人的实例用BTSP建模,该犯人将会更容易被警察抓到.
本文给出了CBTSP的一类应用,它可以应用在具有合作与单独任务的人员和车辆路线的规划.以军队(装甲车)路线规划为例,有1支军队需执行歼敌或其他任务,譬如它可被分成6组,每组包括几个人(装甲车),一方面,这6组需要在自己独有的区域内执行单独的任务;另一方面他们需要在共同的或共享的区域内互相合作来完成合作或协作的任务.如果在一个区域内有太多敌人或任务,这6组需要在这个共享的区域相互合作来完成任务,如果在某些区域敌人或任务非常少,每个组将负责一个独立的区域来独立完成自己所属区域的单独任务.因此,这6组不仅要在共同区域内执行合作的任务,而且需要在独有区域内执行独立任务.在共享的区域与独立区域,分别有许多地点,对于共享区域,其地点可被所有组访问,并且一个地点只能被访问一次,一个地点的任务被完成之后,该地点无需再次被访问,对于独有的区域,每个地点只能被指定的组访问.在执行任务的过程中,因为某些原因,例如遇到太多的敌人或新的作战任务,需要增员或加派人员到某个组,在这几组执行任务的行程过程中,为了能被增援人员更容易找到,他们需要在整个旅行路线中寻找一个旅行回路,使得旅行路线的最大边尽可能最小,这个问题就可以通过CBTSP来建模.CBTSP的应用不仅仅局限于上面实例的路线规划问题,它还可应用在一类具有协作与单独任务的人员和车辆的路线规划问题,该问题具有一些特征:它们一般包括多个人员与车辆,每个个体(人员或车辆)不仅需要执行共同区域或共享区域的协作任务,而且需要执行自己区域的独立任务,在执行任务的行程过程当中,因为某些原因,单独的个体需要增加人员或支援,为了能被其他人更容易地找到,需最小化旅行路线的最大边.
定理1. CBTSP是NP难问题.
证明. 根据CBTSP的定义可知,CBTSP可由CTSP变化而来,改变CTSP的目标函数,也就是使所有旅行回路中最大的边最小化,即可转化为CBTSP.CBTSP可理解成有相同起始点的含部分重合区域(共享城市集)的多个BTSP问题的组合模型,因为BTSP是NP难问题,所以CBTSP也属于NP难问题.从另一角度来讲,CBTSP可由CTSP通过改变目标函数变化而来,因为CTSP属于NP难问题[1],而改变目标函数操作不会引起CBTSP的时间复杂度的变化,因此,CBTSP也属于NP难问题.
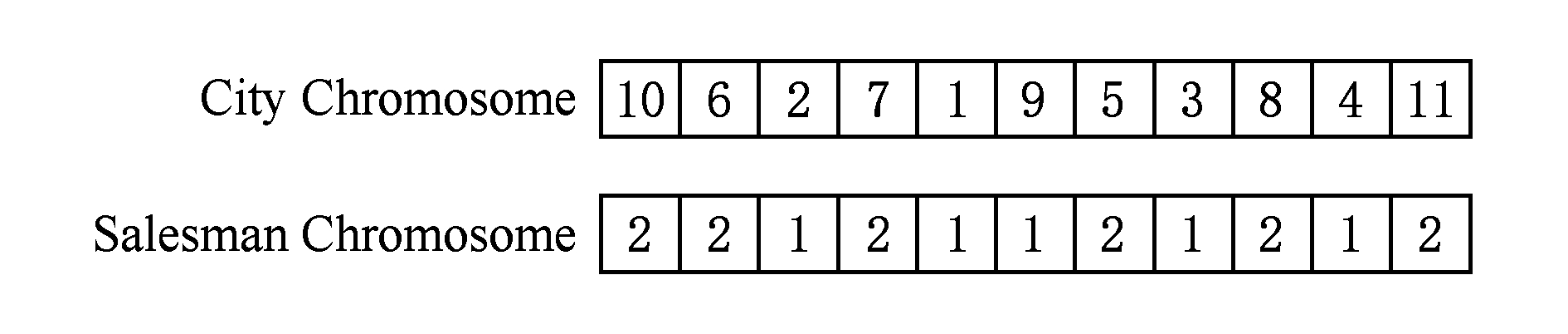
Fig. 1 Example of dual-chromosome coding
图1 二重染色体编码的实例
文献[1]使用二重染色体对遗传算法求解CTSP的解编码,本文也采用该编码方法对CBTSP进行编码.如图1所示,城市染色体是n-1个城市的排列,而旅行商染色体是城市染色体的城市所对应的旅行商的排列.
我们给出一个实例来说明该编码方法,如图1所示,例如一个11个城市和2个旅行商的CBTSP,城市1~4为旅行商1的独享城市集,城市5~8为旅行商2的独享城市集,城市9~11为2个旅行商的共享城市集.如果起始点城市0也加入在内,则旅行商1的访问路径为0→2→1→9→3→4→0,旅行商2的访问路径为0→10→6→7→5→8→11→0.
本文提出的算法是一种基于伊藤过程的混合算法,粒子的活动强度受粒子半径和环境温度的影响,半径越小、温度越高则粒子的运动强度越剧烈,反之,运动强度越弱.粒子的运动强度控制着交叉操作中的交叉长度,强度越大,交叉长度越长.在求解过程中,将第i个粒子与最优解进行交叉,产生新的解.
PSGA求解CBTSP的步骤如算法1所示.
算法1. PSGA求解CBTSP的步骤.
① 参数初始化;
② 初始化M个粒子和环境温度T;
③ 读取CBTSP数据;
④ 计算粒子的适应度值,并保存最优值;
⑤ 用式(8)计算粒子半径;
⑥ 通过式(9)计算环境温度;
⑦ 用式(10)计算活动强度;
⑧ 根据适应度值,对粒子进行分类;
⑨ 用式(11)计算交叉长度;
⑩ while判断终止条件是否满足do
 for 遍历每个粒子do
for 遍历每个粒子do
 执行交叉操作产生新解;
执行交叉操作产生新解;
 end for
end for
 计算适应度值,并保存最好值;
计算适应度值,并保存最好值;
 根据适应度值进行分类;
根据适应度值进行分类;
 更新退火温度;
更新退火温度;
 更新所有粒子的交叉长度;
更新所有粒子的交叉长度;
 end while
end while
 返回最优解.
返回最优解.
在算法1中,步骤①为算法参数的初始化;步骤②表示初始化种群M和初始温度T;步骤③读取CBTSP数据;步骤④计算粒子的适应度值,并保存最优值;步骤⑤~⑦计算粒子半径、环境温度和活动强度;步骤⑧为根据适应度值对粒子进行分类;步骤⑨根据式(11)计算粒子的交叉长度;步骤⑩~ 执行交叉操作;步骤
执行交叉操作;步骤
 对环境温度、交叉长度更新.
对环境温度、交叉长度更新.
PSGA算法有4个部分:粒子半径、环境温度、活动强度、交叉算子.该混合算法具体设计如下:
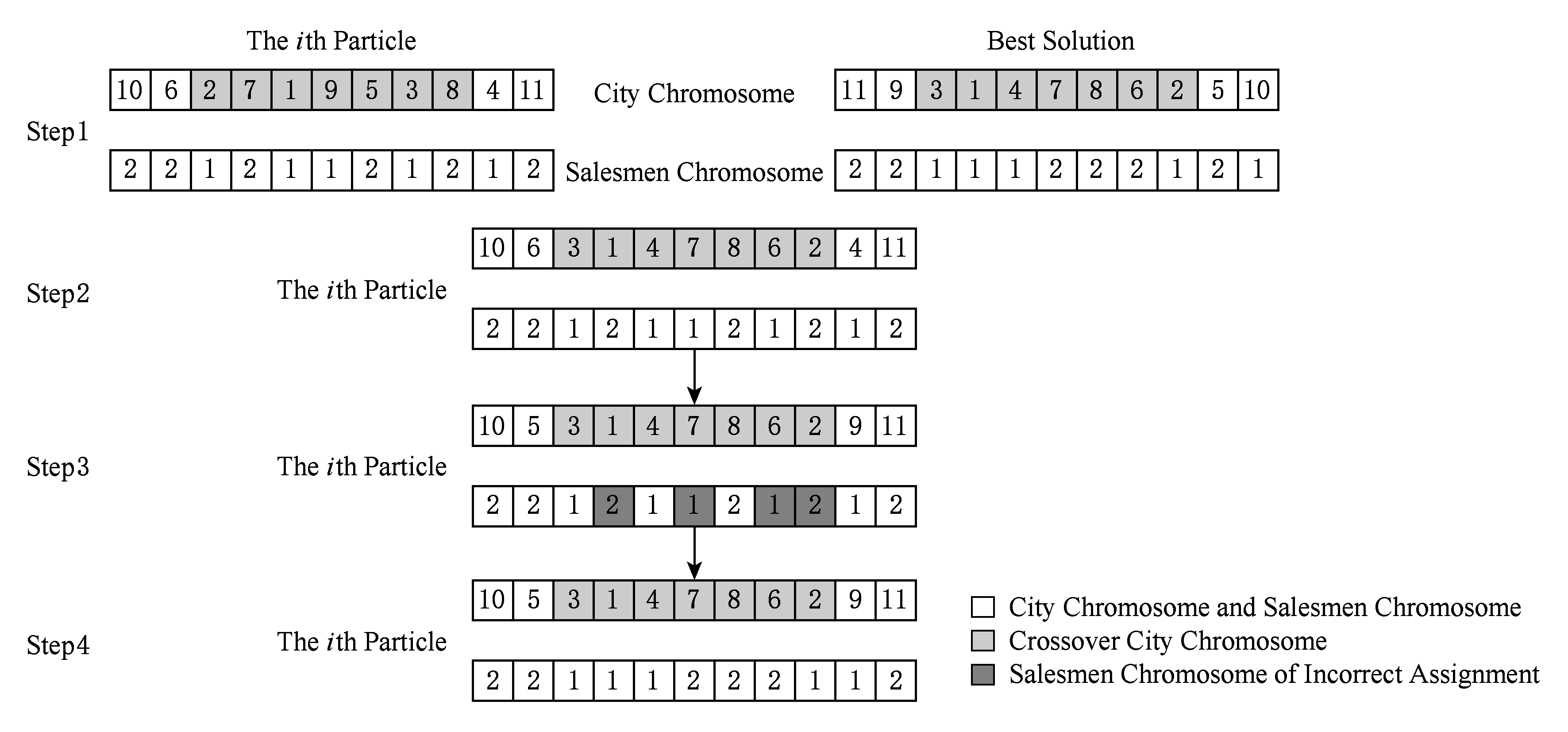
Fig. 2 Example of crossover operator
图2 交叉算子的实例
1) 粒子半径
根据爱因斯坦等人的大分子的运动定律,粒子半径越小,环境温度越高,粒子的随机性运动就越激烈;相反,当粒子半径越大和温度越低,随机运动会越弱.对于优化算法,拥有差的适应度值的粒子,其运动越剧烈;反之,有好的适应度值的粒子运动强度越弱.适应度值越好,越会降低运动强度保持当前解,因此,可以增加大的半径;相反,可以使半径变小,考虑到粒子的优缺点,动态调整粒子半径可计算为[16-19]:
r(x)=g(f(x)),
(7)
其中,x表示当前种群的一个粒子,f(x)代表适应度值,g(x)表示单调函数.因为CBTSP是求最小化的问题,所以g(x)是一个单调递减函数,该函数有许多选择,包括线性转换函数和基于分类的方法等.本文采用分类的方法来计算粒子半径,首先,N个当前种群的粒子根据适应度值的等级按照最好到最差的顺序分类,结果用x1,x2,…,xN来表示.粒子半径计算为
![]()
(8)
其中,rmax和rmin分别表示最大和最小的半径,所有的半径被均匀分布在rmax和rmin之间.如果是缺省值,rmax=1,rmin=0.
2) 环境温度
宏观世界中,分子运动的剧烈程度是受外界环境温度影响.当温度越高,粒子运动越剧烈;当温度越低,粒子运动越弱.模拟退火算法,在迭代过程中,环境温度会被逐渐地降低,因此,环境温度可计算为
Ti=ρ×Ti-1,
(9)
其中,Ti表示第i个规划时间的温度;ρ表示退火系数,它能控制温度降低的速度,缺省值的情况下ρ=0.9.
3) 活动强度
活动强度控制着粒子的运动强度,根据爱因斯坦的分子运动和粒子热力学运动定律,该强度与粒子半径成反比、与温度成正比,因此,当前种群微粒xi的活动强度δ计算为[16-19]
![]()
(10)
其中,δ表示粒子的活动强度,ri表示粒子xi的半径,T表示温度.
4) 交叉算子
因为交叉操作,粒子可以在解的空间中随机变化,在环境影响下,将粒子与最优解进行交叉并产生新的解,从而避免陷入局部最优,保持解的多样性.交叉操作有2部分:交叉长度和交叉过程.交叉长度由活动强度决定,通过环境温度和粒子半径计算,即:
li=γ×δi×n,
(11)
其中,li表示第i个粒子的交叉长度;γ为随机服从均匀分布数,取值在0~1之间;n为二重染色体长度.
如图2所示,混合算法PSGA的交叉过程的计算步骤如下:
步骤1. 在城市染色体的[1,n-li]之间随机选择一个起始位置,将灰色区域的连续li位置与最优解交叉.
步骤2. 用最优解中对应的城市替换灰色区域相应的城市.
例如城市替换的对应关系为:2—3,7—1,1—4,9—7,5—8,3—6,8—2.
步骤3. 根据交换规则,对第i个粒子的灰色区域之外的冗余城市进行替换,直到没有冗余城市为止.
例如步骤2的灰色区域外的城市染色体4,灰色区域内也存在4,即为冗余,所以要对灰色区域外的4进行替换,根据交换关系,最优解中的4对应第i个粒子的1,于是4被1替换,但1仍然与灰色区域的城市染色体重复,继续根据对应关系进行替换,最优解中的1对应着第i个粒子的7,但仍不满足条件,7继续被9替换,结果满足条件,因此该操作的最终值为9.
步骤4. 对旅行商染色体错误的赋值进行校正.例如,在步骤3中,城市染色体中的1,7,6,2分别对应错误的旅行商染色体,因此需要校正,修正之后的结果,如步骤4所示.
通过以上4个步骤,粒子完成交叉过程,实现了对问题的解更新.
实验的运行环境为:AMD AthlonTMⅡ X4 640 3.01 GHz处理器和3.25 GB内存.实验是用Java进行设计与开发.
表1为CBTSP的小尺度实验数据.
在表1中,n的取值范围是21~76,m的取值范围是2~6,s表示共享城市的数量,e表示独有城市的数量.
表1和表2中,城市数量n的取值为21~101的数据来自CTSP的论文[1].
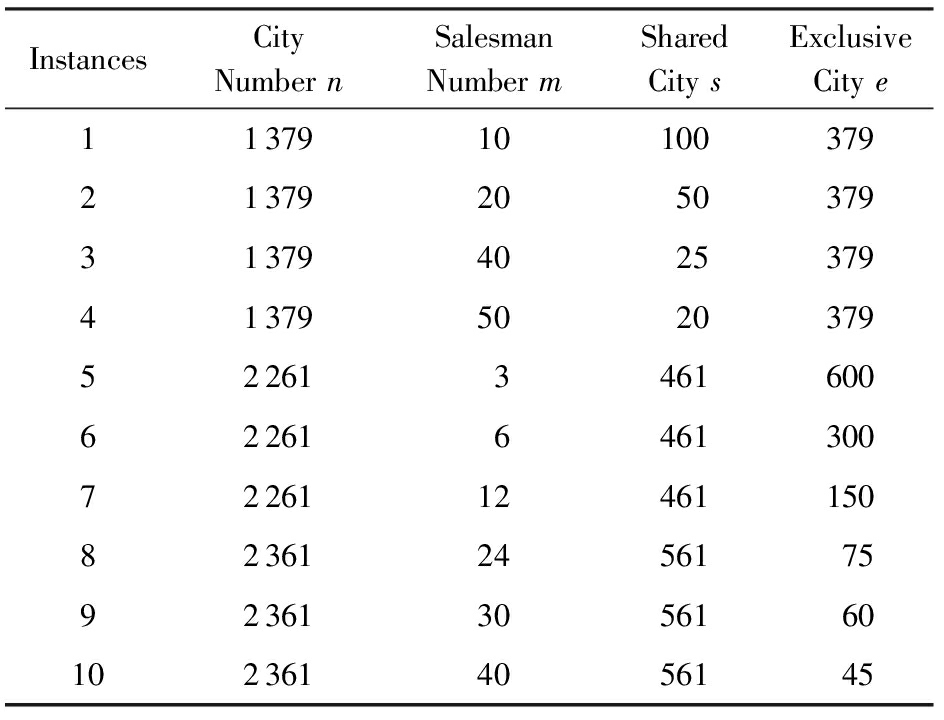
表2和表3为中尺度和大尺度CBTSP的实验数据.在表2中,n的取值为101~665,m的取值为4~33;在表3中,n的取值为1 379~2 361,m的取值为3~50.表3是根据CBTSP的要求,由TSPLIB TSP数据制作而成,TSPLIB TSP标准数据集已在网上共享.
Table1SmallScaleExperimentDataforCBTSP
表1CBTSP的小尺度实验数据
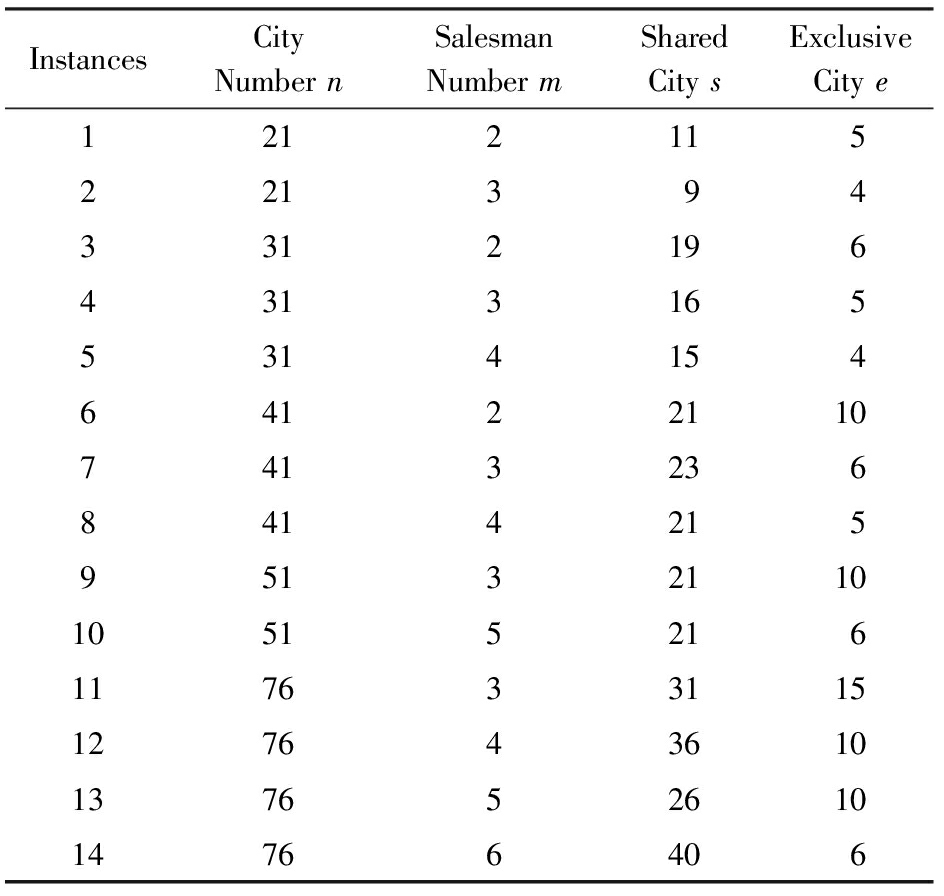
Table2MediumScaleExperimentDataforCBTSP
表2CBTSP的中尺度实验数据
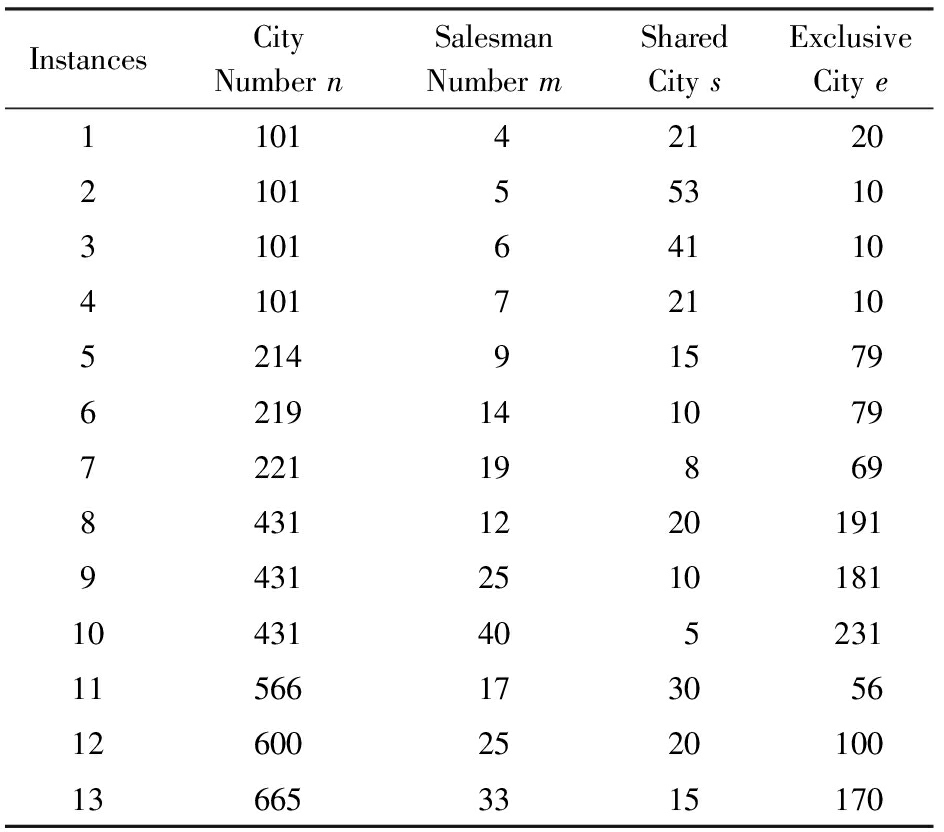
Table3LargeScaleExperimentDataforCBTSP
表3CBTSP的大尺度实验数据
混合算法参数的设置情况为:种群M=150,初始温度T=1 000.遗传算法和改进遗传算法的参数设置情况为:种群大小为30,交叉概率0.7,变异概率0.1;模拟退火的遗传算法参数情况,初始温度100,总的冷却时间60,每个温度的步长为30,模拟系数0.9.以上算法的运行时间相同,即为算法的终止条件,其中算法求解小尺度、中尺度和大尺度CTSP的运行时间分别为20 s,40 s,60 s.
图3所示为当n=31与m=4时,算法GAG,HCGA,SAGA,PSGA求解CBTSP的运行界面.
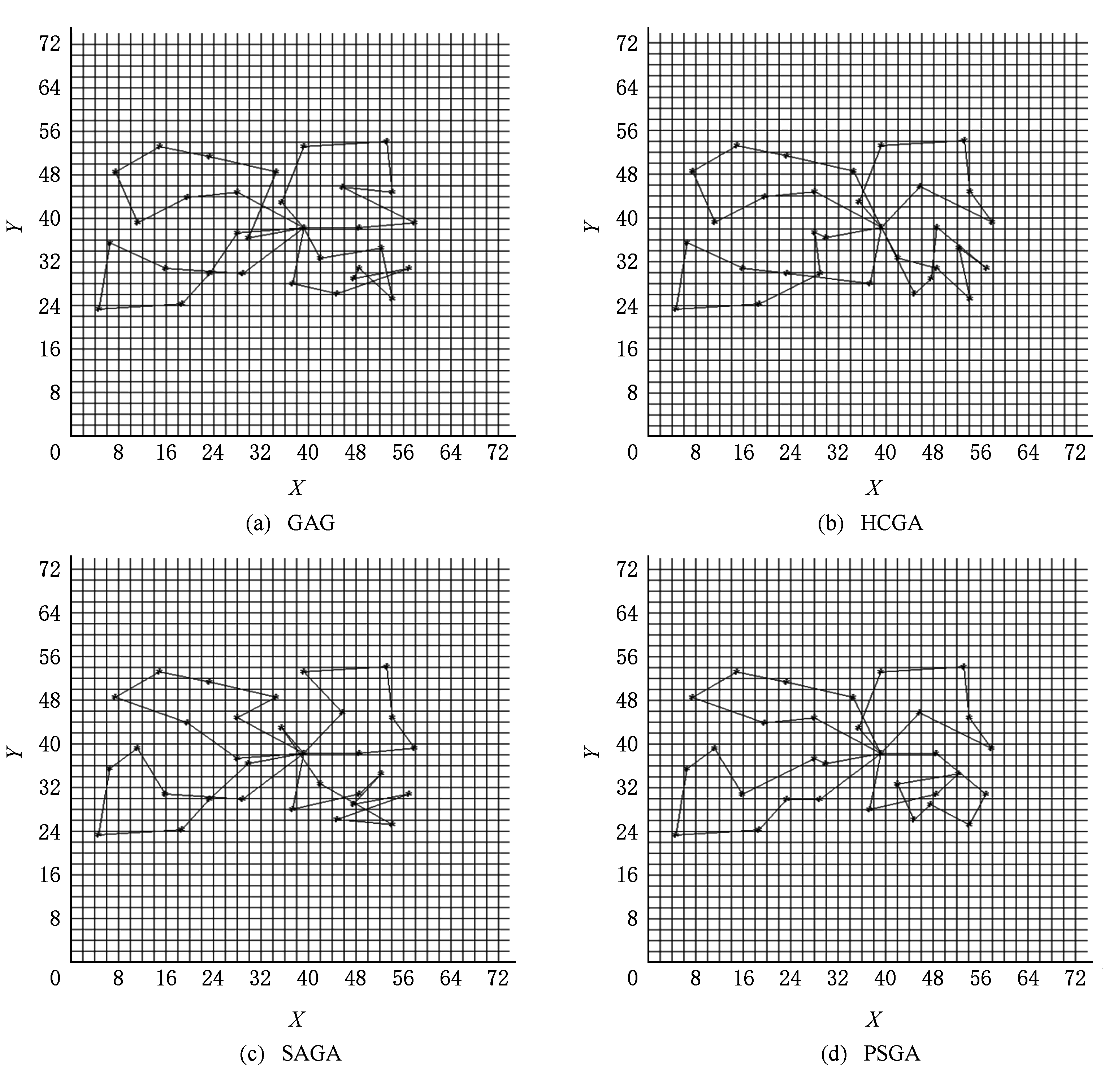
Fig. 3 Optimal routes of GAG, HCGA, SAGA and PSGA for CBTSP with n=31 and m=4
图3 当n=31和m=4时GAG,HCGA,SAGA,PSGA求解CBTSP最优路线图
图4所示为当n=51与m=5时,算法GAG,HCGA,SAGA,PSGA求解CBTSP的运行界面.GAG:最优解24.0,平均解27.8,迭代次数13 278;HCGA:最优解17.0,平均解23.0,平均求解最优解的迭代次数18 198;SAGA:最优解20.0,平均求解最优解的迭代次数22.4,平均求解最优解的迭代次数1 386;PSGA:最优解20.0,平均解21.8,迭代次数6 088.
图5为当n=101与m=7时,4个算法求解CBTSP的运行界面.GAG:最优解25.0,最差解35.0,平均解31.1,平均求解最优解的迭代次数14 349;HCGA:最优解21.0,最差解34.0,平均解是27.7,平均求解最优解的迭代次数19 842;SAGA:最优解22.0,最差解27.0,平均解24.9,平均求解最优解的迭代次数2 378;PSGA:最优解21.0,最差解25.0,平均解22.5,平均求解最优解的迭代次数5 720.从该案例数据分析可看出,PSGA的求解质量最好.
表4~6为GA,GAG,HCGA这3种算法求解小尺度、中尺度和大尺度CBTSP的实验结果对比数据.
表4~6中,n表示城市数量;m表示旅行者数目;best,worst,average为算法求解该问题运行10次的最优解、最差解和平均解;iterations表示算法运行10次的平均求解最优解的迭代次数.从表4~6中可看出,算法HCGA求解CBTSP的求解质量要好于算法GAG和GA.
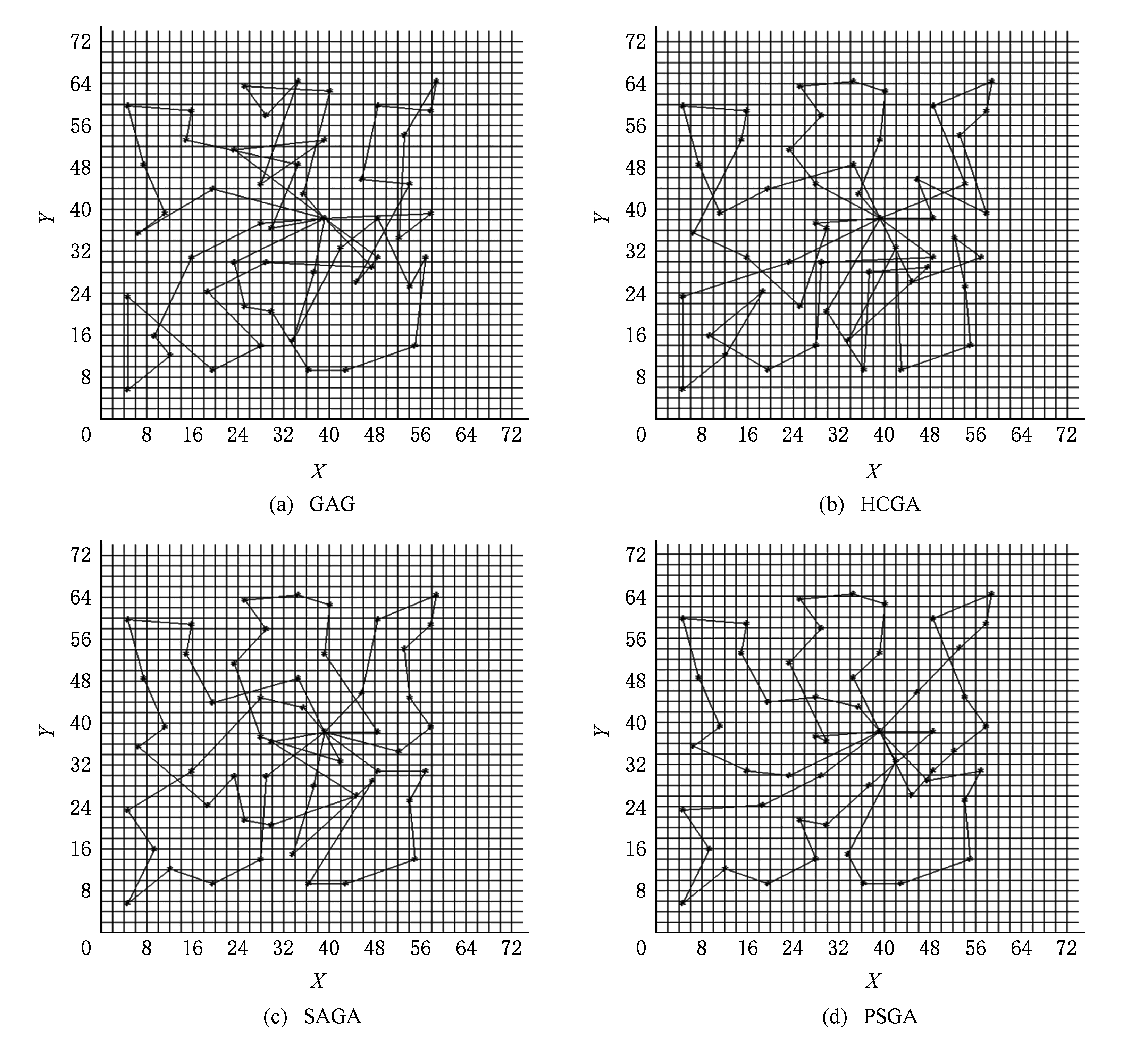
Fig. 4 Optimal routes of GAG, HCGA, SAGA and PSGA for CBTSP with n=51 and m=5
图4 当n=51和m=5时GAG,HCGA,SAGA,PSGA求解CBTSP最优路线图
Table4ExperimentalResultsofGA,GAGandHCGAforSmallScaleCBTSP
表4GA,GAG,HCGA求解小尺度CBTSP的实验结果数据
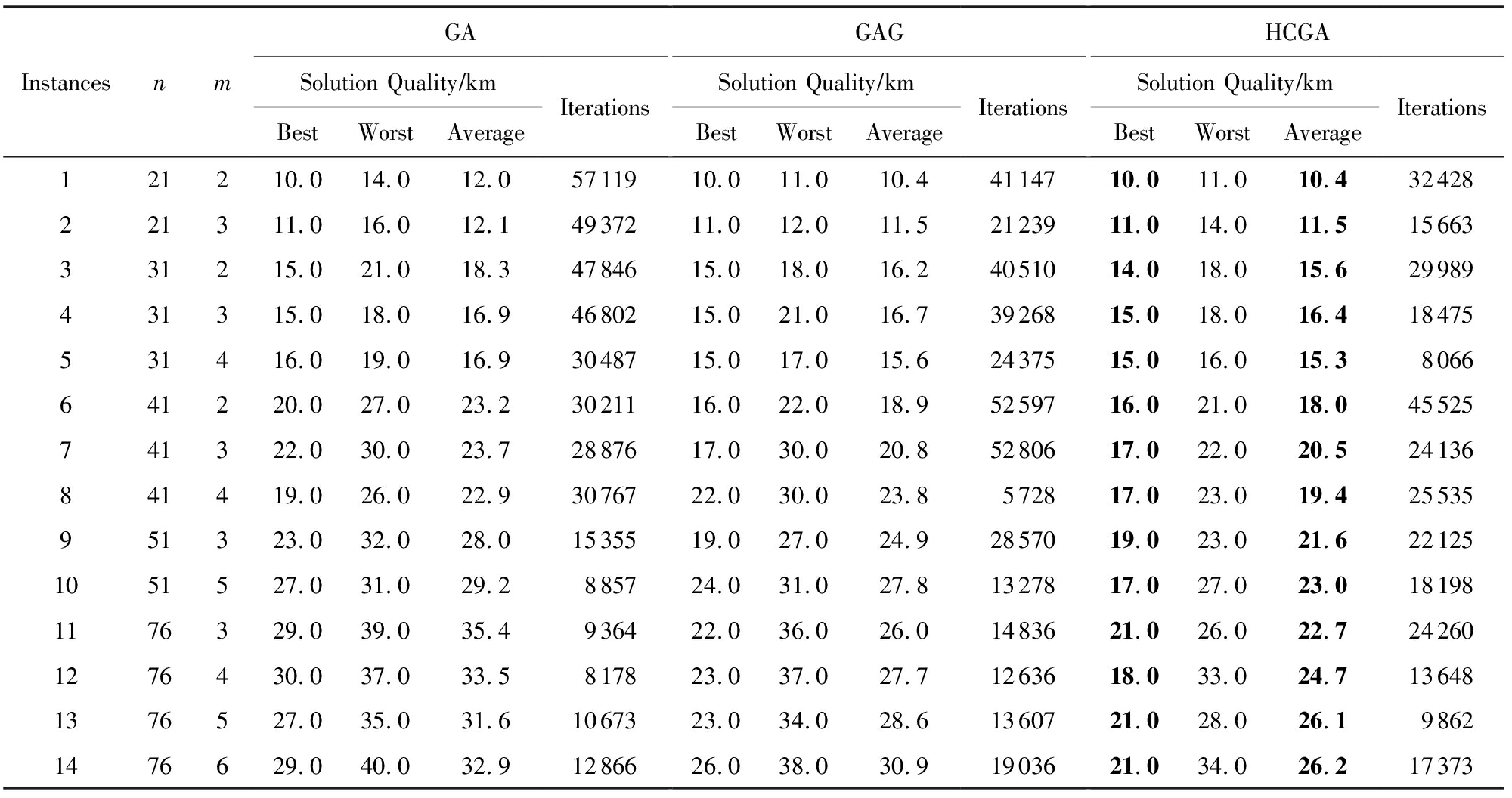
Notes: Bold number stands for the best values of best solution or average solution in the table.
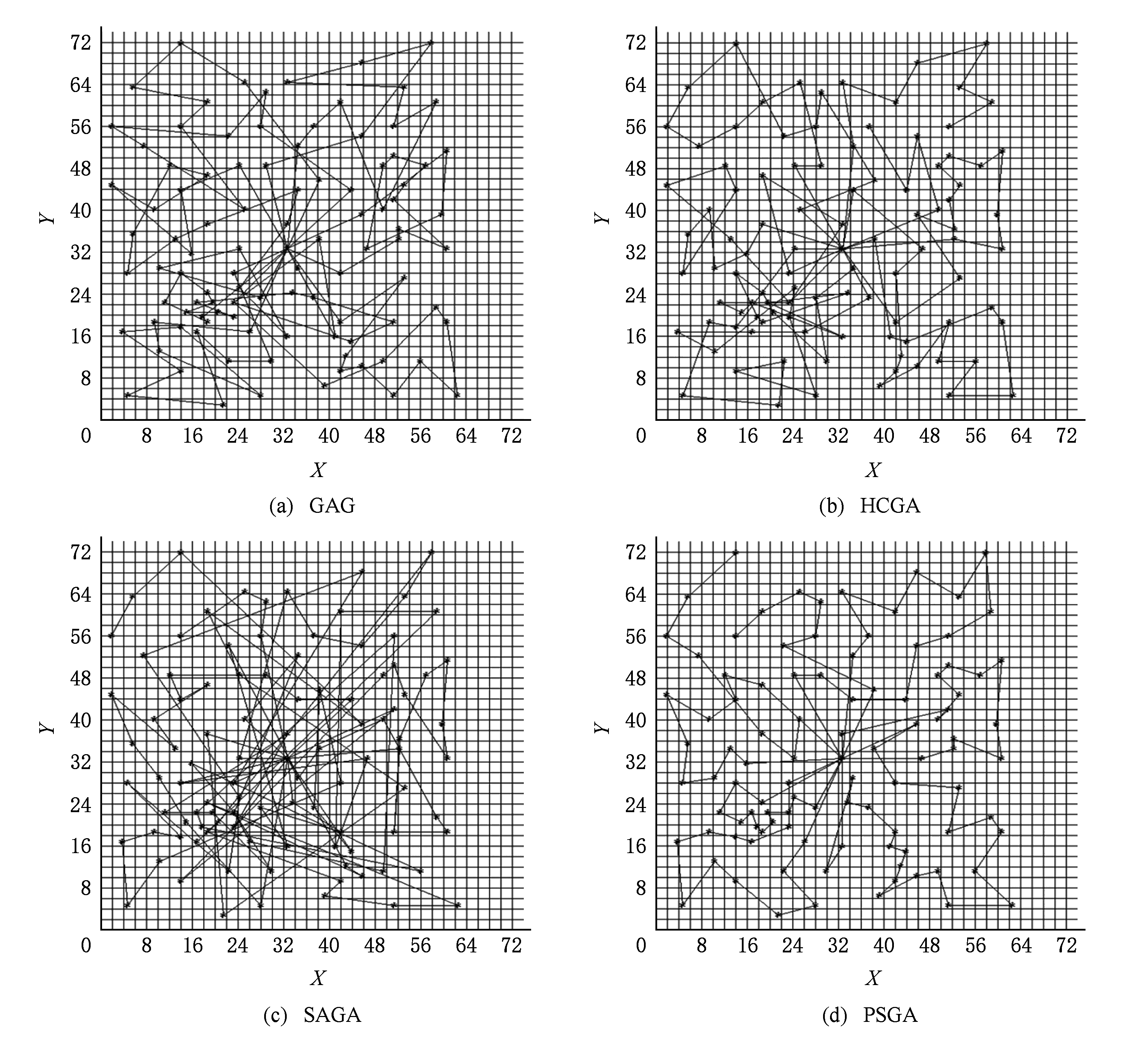
Fig. 5 Optimal routes of GAG, HCGA, SAGA and PSGA for CBTSP with n=101 and m=7
图5 当n=101与m=7时 GAG,HCGA,SAGA,PSGA求解CBTSP最优路线图
Table5ExperimentalResultsofGA,GAGandHCGAforMediumScaleCBTSP
表5GA,GAG,HCGA求解中尺度CBTSP的实验结果数据
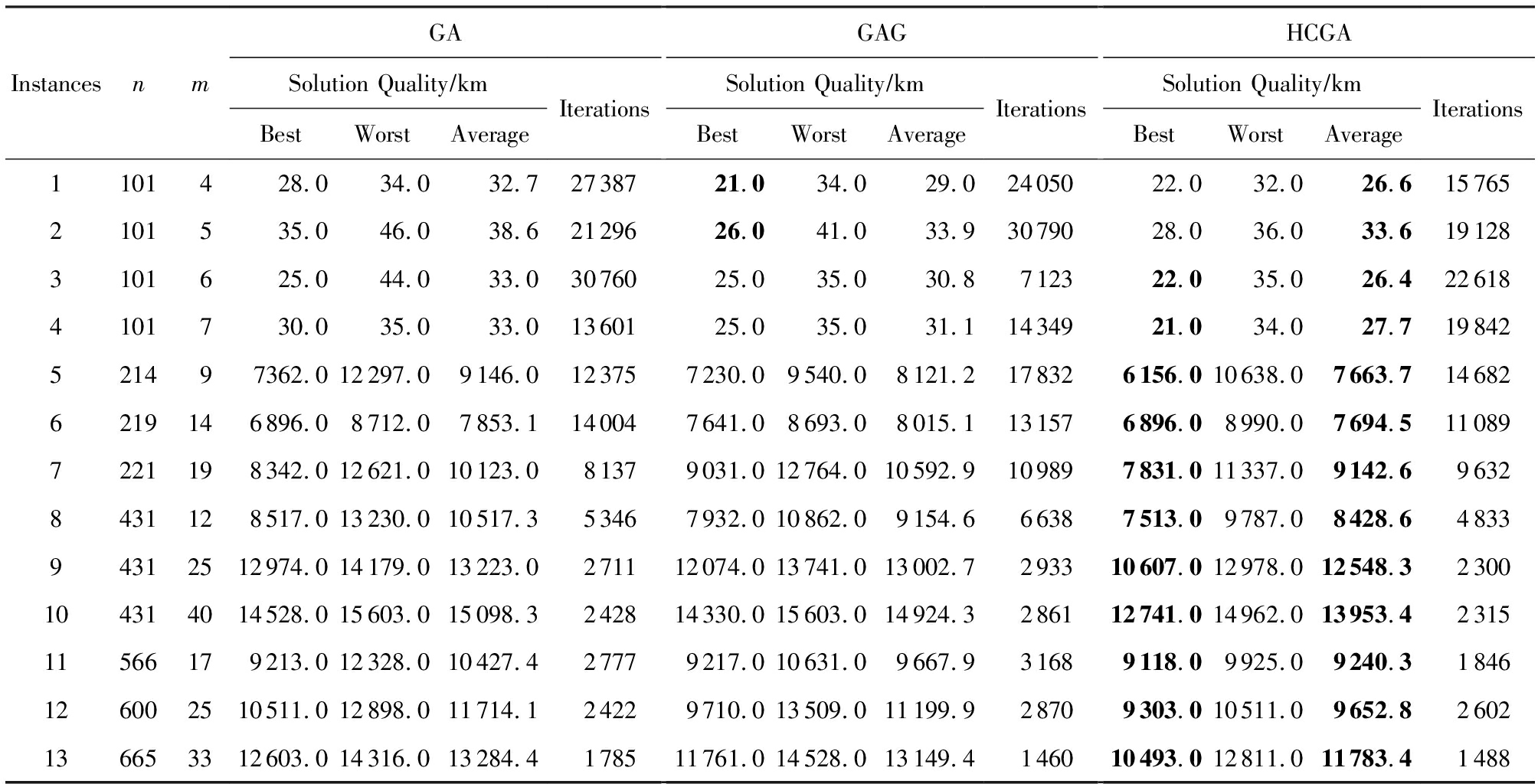
Notes: Bold number stands for the best values of best solution or average solution in the table.
Table6ExperimentalResultsofGA,GAGandHCGAforLargeScaleCBTSP
表6GA,GAG,HCGA求解大尺度CBTSP的实验结果数据
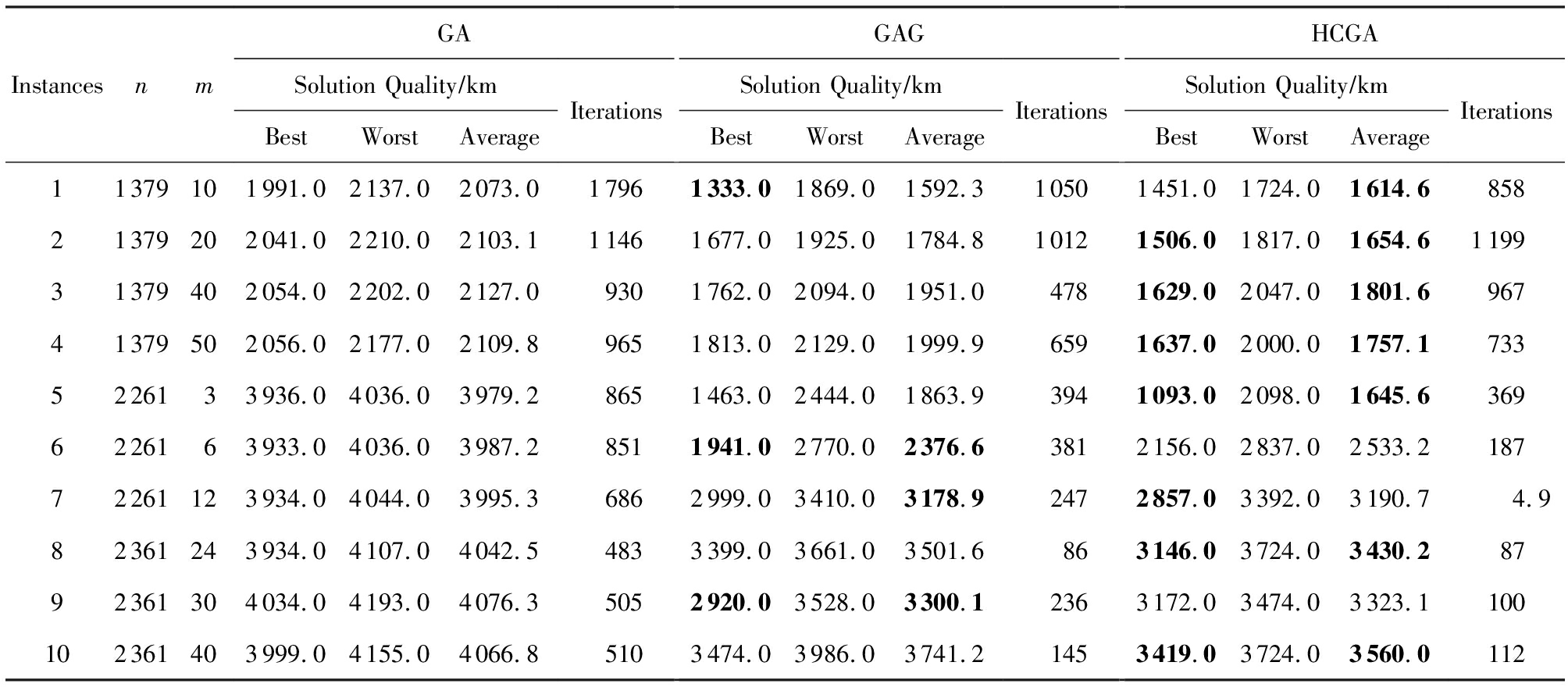
Notes: Bold number stands for the best values of best solution or average solution in the table.
表7~9为算法SAGA和PSGA求解CBTSP的数据.表7~9中,best,worst,average分别为算法求解CBTSP运行10次的最优解、最差解和平均解;iterations为算法运行10次的平均求解最优解的迭代次数.从表7~9中数据可以看出,PSGA求解该问题的求解质量好于SAGA.
图6和图7为5种算法求解该问题的平均求解质量对比图,数据来自于表4~9.图6和图7中X轴表示实例的序号,每个序号对应着具体实例数据;Y轴表示算法的平均求解质量.从图6~7可以看出,PSGA求解CBTSP的解的质量要好于GA,GAG,HCGA,SAGA.
Table7ExperimentalResultsofSAGAandPSGAforSmallScaleCBTSP
表7SAGA与PSGA求解小尺度CBTSP的实验结果数据
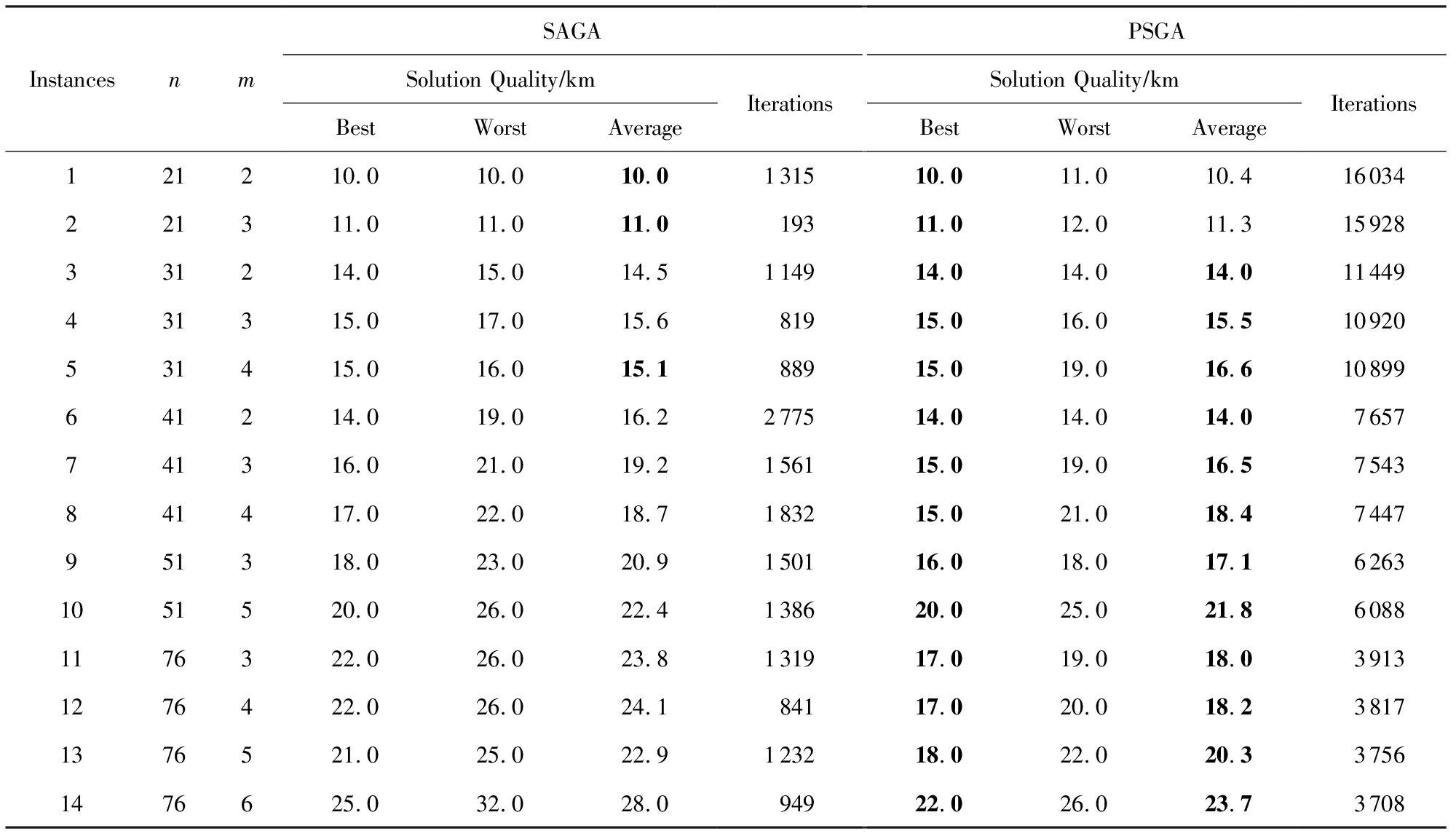
Notes: Bold number stands for the best values of best solution or average solution in the table.
Table8ExperimentalResultsofSAGAandPSGAforMediumScaleCBTSP
表8SAGA与PSGA求解中尺度CBTSP的实验结果数据
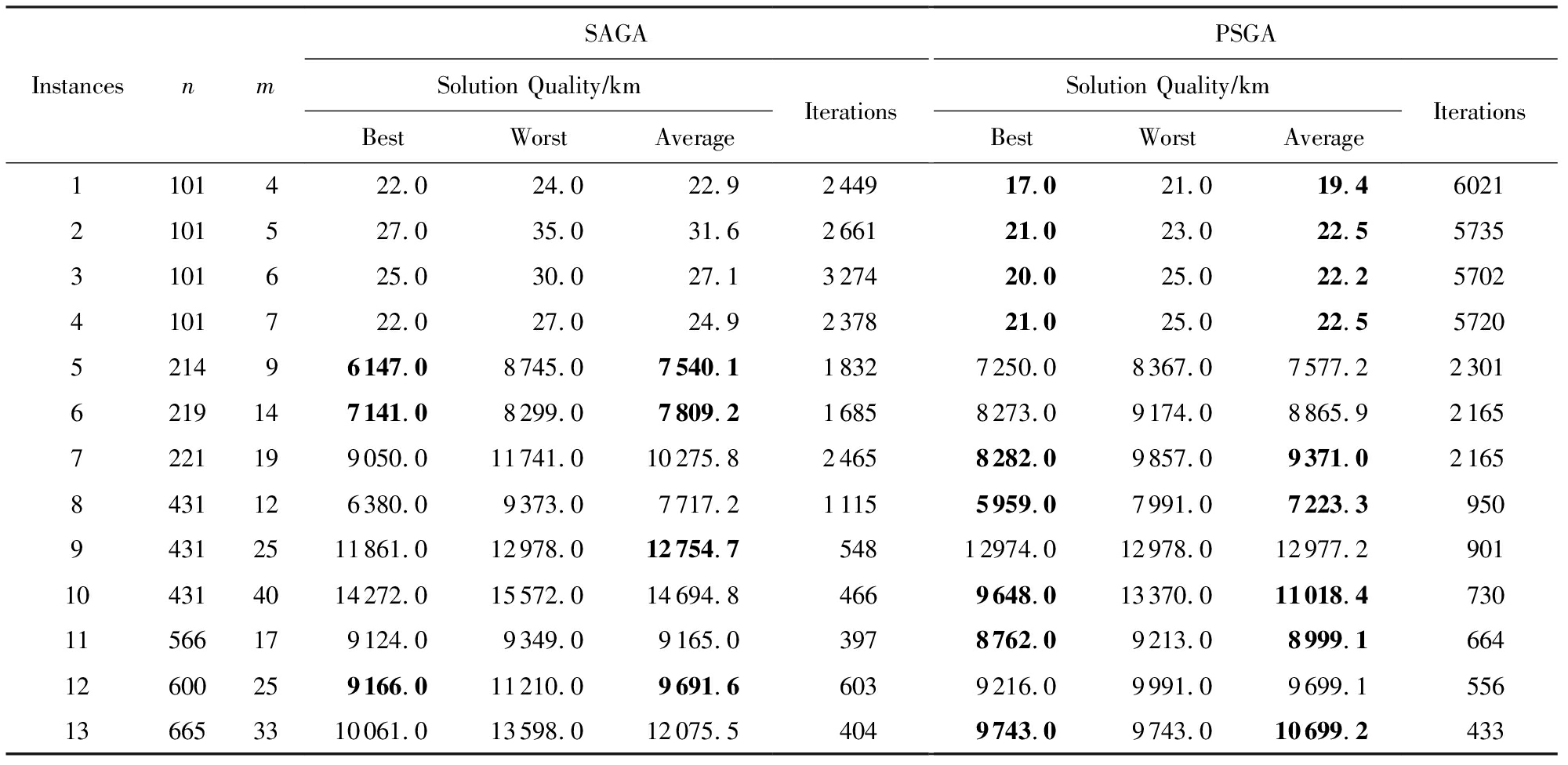
Notes: Bold number stands for the best values of best solution or average solution in the table.
Table9ExperimentalResultsofSAGAandPSGAforLargeScaleCBTSP
表9SAGA与PSGA求解大尺度CBTSP的实验结果数据

Notes: Bold number stands for the best values of best solution or average solution in the table.
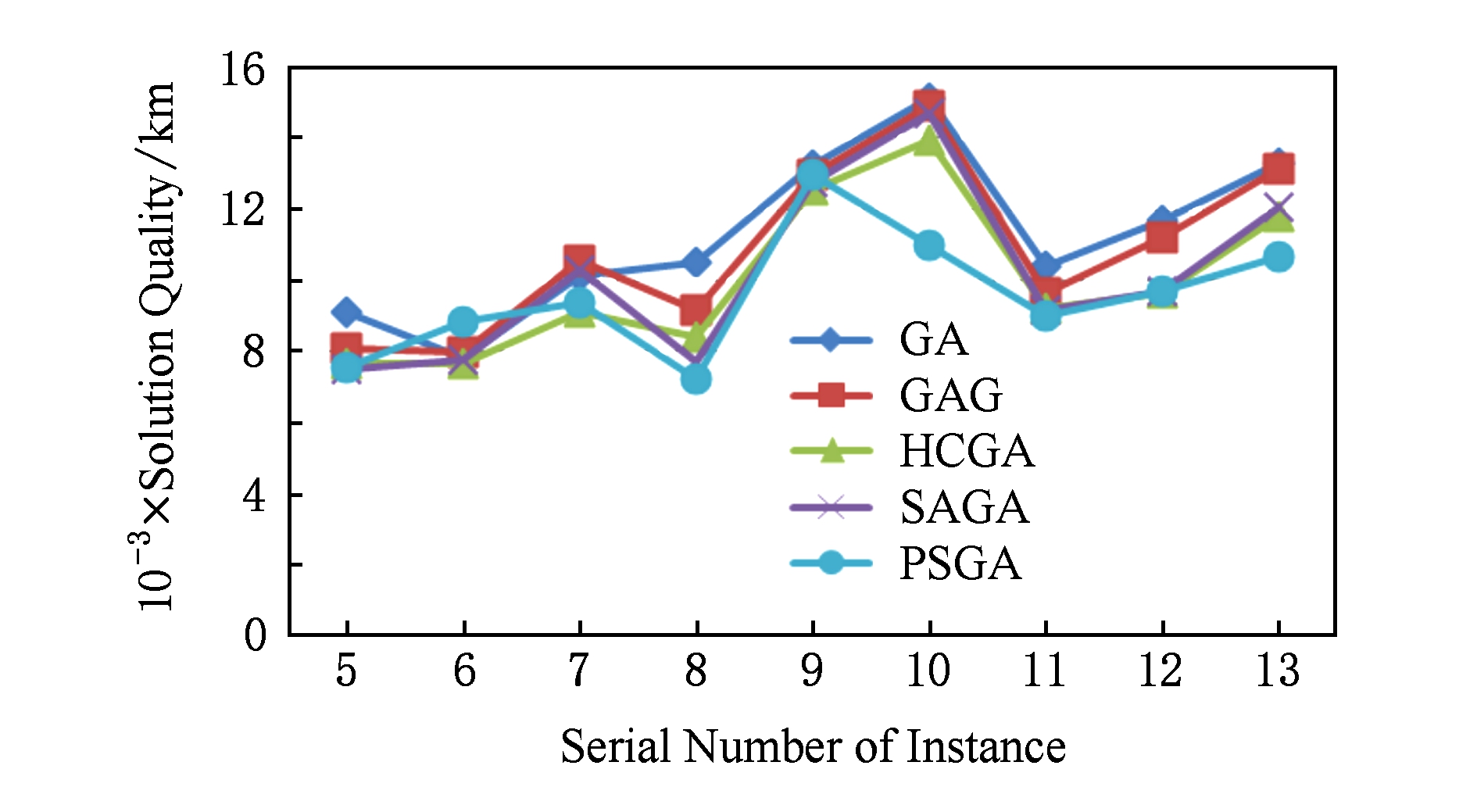
Fig. 6 Average solution quality of the algorithms for medium scale CBTSP
图6 算法求解中尺度CBTSP的平均求解质量对比图
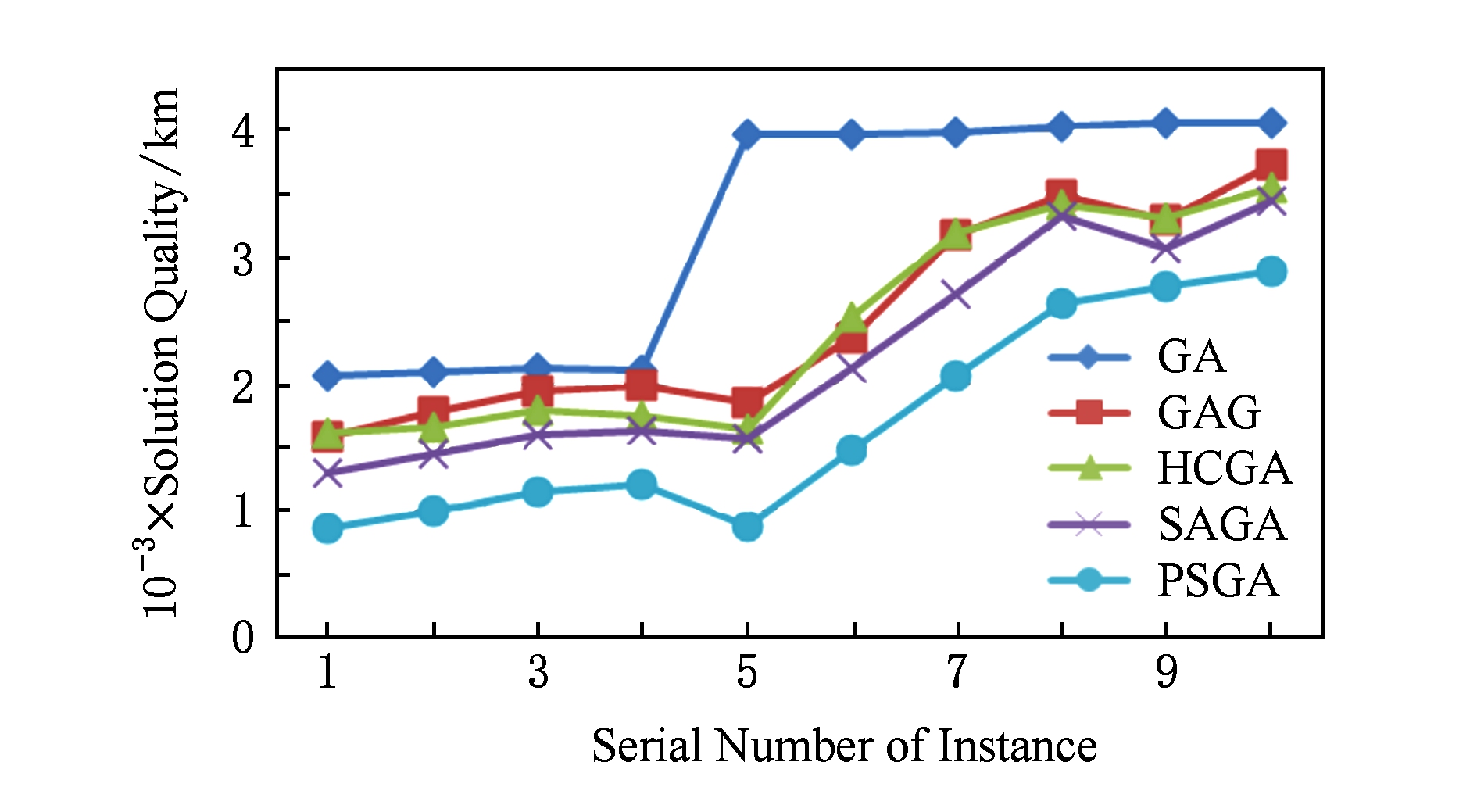
Fig. 7 Average solution quality of the algorithms for large scale CBTSP
图7 算法求解大尺度CBTSP的平均求解质量对比图
为了验证算法的有效性,引入文献[20]的百分偏差对算法的求解质量进行对比分析.表10为5种算法求解3种不同尺度的CBTSP的百分偏差,PDbest表示最优解百分偏差,PDav表示平均解百分偏差.从表10可以看出,PSGA的PDbest与PDav的值在5种算法中最小,表明PSGA求解该问题的最优解和平均解要优于SAGA,HCGA,GAG,GA.
Table10PercentageDeviationoftheAlgorithmsforDifferentScaleCBTSPProblem
表10算法求解不同尺度CBTSP的百分偏差数据
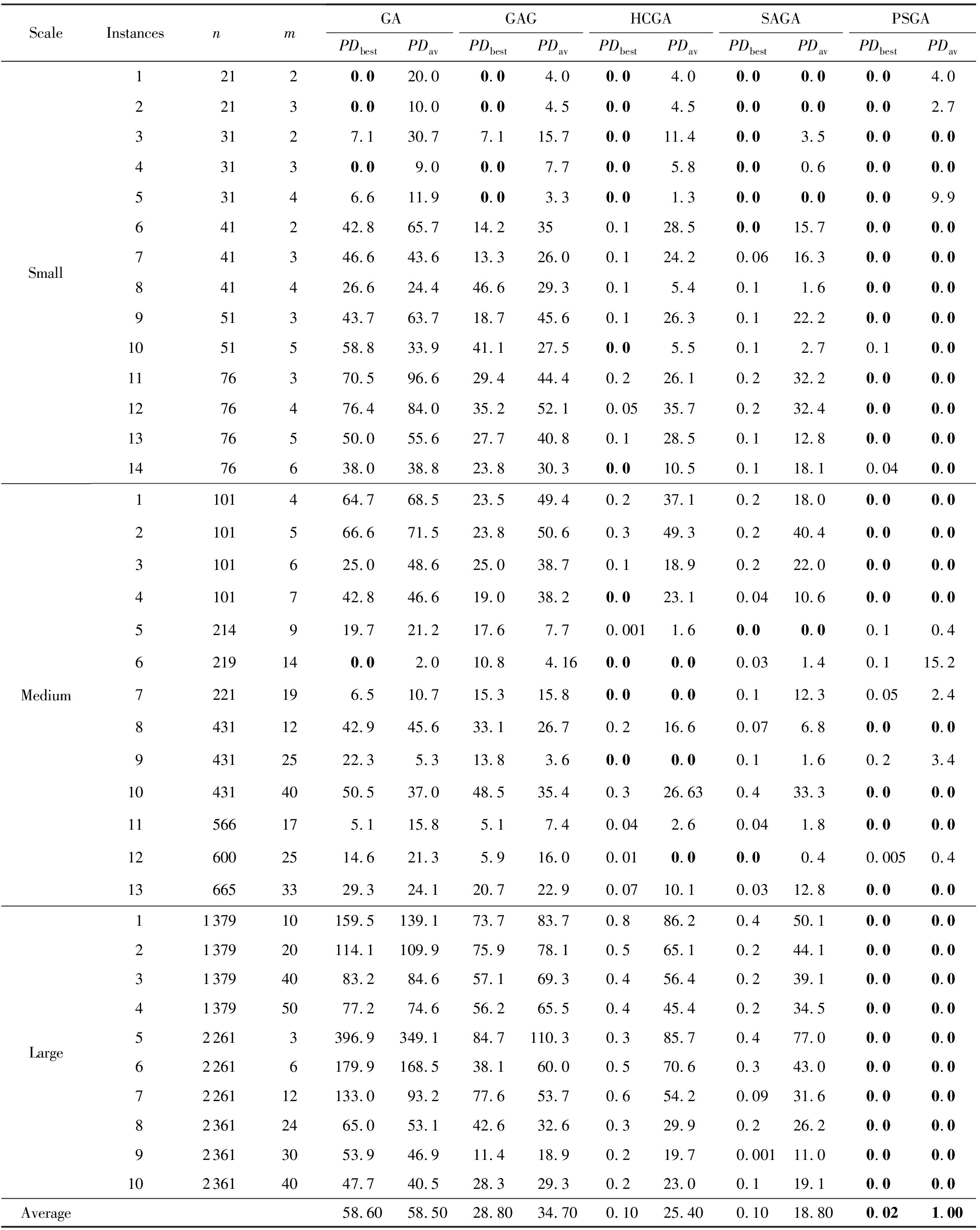
Notes: Bold number stands for the best values of best solution or average solution in the table.
PSGA是先进的群体智能算法,在求解组合优化等问题方面可表现出较好的性能,从本节分析可看出,PSGA求解CBTSP要好于其他算法.PSGA用二重染色体构建问题的解,并用交叉算子对问题的解动态更新,具有较强的求解问题的能力.为验证本文所提混合算法的性能,使用小尺度、中尺度和大尺度的CBTSP实例数据进行实验与对比分析,结果表明PSGA求解CBTSP是有效的,其求解质量要优于SAGA,HCGA,GAG,GA算法.
针对实际应用需求,本文给出一种CBTSP模型,可应用在具有部分重合工作区域的人员与车辆的路线规划问题,为拓展该模型的应用领域,开发与研究高性能的求解算法具有一定的意义.本文提出一种新的混合算法,并将其应用在求解CBTSP之中,通过3种不同尺度的实验表明:PSGA算法求解CBTSP解的质量要优于相关的对比算法.
今后的可能工作包括2方面:1)继续研究与探索CBTSP的应用领域,开发更先进的算法和模型来求解该问题,使求解质量与速度得到进一步的提升;2)本文研究CBTSP的规模或尺度有限,以后的工作可集中在探讨各种算法在求解更大尺度CBTSP的特点和规律.
参考文献
[1] Li Jun, Zhou Mengchu, Sun Qirui, et al. Colored traveling salesman problem[J]. IEEE Transactions on Cybernetics, 2015, 45(11): 2390-2401
[2]Li Jun, Sun Qirui, Zhou Mengchu, et al. A new multiple traveling salesman problem and its genetic algorithm-based solution[C] //Proc of the 2013 IEEE Int Conf on Systems Man and Cybernetics. Piscataway, NJ: IEEE, 2013: 627-632
[3]Vairaktarakis G L. On Gilmore-Gomorys open question for the bottleneck TSP[J]. Operations Research Letters, 2003, 31(6): 483-491
[4]Kao Mingyang, Sanghi M. An approximation algorithm for a bottleneck traveling salesman problem[J]. Journal of Discrete Algorithms, 2009, 7(3): 315-326
[5]Garfinkel R S, Gilbert K C. The bottleneck traveling salesman problem: Algorithms and probabilistic analysis[J]. Journal of the Association for Computing Machinery, 1978, 25(3): 435-448
[6]Kao Mingyang, Sanghi M. An approximation algorithm for a bottleneck traveling salesman problem[G] //LNCS 3998: Proc of the 6th Italian Conf on Algorithms and Complexity. Berlin: Springer, 2006: 223-235
[7]Gilmore P C, Gomory R E. Sequencing a one state-variable machine: A solvable case of the traveling salesman problem[J]. Operations Research, 1964, 12(5): 655-679
[8]Kabadi S N. Polynomial Solvable Cases of the TSP[M]. Berlin: Springer, 2007: 489-583
[9]Plante R D, Lowe T J, Chhandrasekaran R. The product matrix traveling salesman problem: An application and solution heuristic[J]. Operations Research, 1987, 35(5): 772-783
[10]Ahmed Z H. A hybrid genetic algorithm for the bottleneck traveling salesman problem[J]. ACM Transactions on Embedded Computing Systems, 2013, 12(1): 9:1-9:10
[11]Liao Tianjun, Socha K, Oca M A M D, et al. Ant colony optimization for mixed-variable optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2013, 18(4): 503-518
[12]Ferreira M. Exudate segmentation in fundus images using an ant colony optimization approach[J]. Information Sciences, 2015, 296: 14-24
[13]Arkin E M, Chiang Y J, Mitchell J S B, et al. On the maximum scatter traveling salesman problem[J]. SIAM Journal on Computing, 1999, 29(2): 515-544
[14]Chiang Y J. New approximation results for the maximum scatter TSP[J]. Algorithmica, 2005, 41(4): 309-341
[15]John L R. The bottleneck traveling salesman problem and some variants[D]. Burnaby, BC: Master of Science of Simon Fraser University, 2010: 21-23
[16]Dong Wenyong, Zhang Wensheng, Yu Ruiguo. Convergence and runtime analysis of ITÖ algorithm for one class of combinatorial optimization[J]. Chinese Journal of Computers, 2011, 34(4): 636-646 (in Chinese)
(董文永, 张文生, 于瑞国. 求解组合优化问题伊藤算法的收敛性和期望收敛速度分析[J]. 计算机学报, 2011, 34(4): 636-646)
[17]Yi Yunfeng, Cai Yongle, Dong Wenyong, et al. Improved ITÖ for multiobjective real-time vehicle routing problem with customers satisfaction[J]. Acta Electronica Sinica, 2015, 43(10): 2053-2061 (in Chinese)
(易云飞, 蔡永乐, 董文永, 等. 求解带用户满意度的多目标实时车辆路径问题的改进伊藤算法[J]. 电子学报, 2015, 43(10): 2053-2061)
[18]Dong Wenyong, Cai Yongle, Wang Yufeng, et al, Discrete ITÖ algorithm to the colored traveling salesman problem[J]. International Journal of Wireless and Mobile Computing, 2016, 11(2): 157-165
[19]Dong Xueshi, Dong Wenyong, Wang Yufeng. Hybrid algorithms for multi-objective balanced traveling salesman problem[J]. Journal of Computer Research and Development, 2017, 54(8): 1751-1762 (in Chinese)
(董学士, 董文永, 王豫峰. 混合算法求解多目标平衡旅行商问题[J]. 计算机研究与发展, 2017, 54(8): 1751-1762)
[20]Zhang Hongguang, Zhou Jie. Dynamic multiscale region search algorithm using vitality selection for travelling salesman problem[J]. Expert Systems with Applications, 2016, 60: 81-95
Dong Xueshi, Dong Wenyong, and Cai Yongle
(ComputerSchool,WuhanUniversity,Wuhan430072)
AbstractBased on colored traveling salesman problem (CTSP), this paper gives a more widely applicable combination optimization problem (COP) model named colored bottleneck traveling salesman problem (CBTSP), which can be used to model the planning problems with the partially overlapped workspace such as the route planning of persons and vehicles with cooperative and independent tasks. The objective function of these problems is different from the one of traveling salesman problems (TSPs), therefore it can’t be modeled by CTSP. Since CBTSP is NP-hard problem, for this kind of large scale problem, nature-inspired algorithms are good choice for solving it. Based on these, the paper proposes a nature-inspired algorithm to solve CBTSP, and the new algorithm named PSGA is a hybrid algorithm of particle swarm optimization (PSO), simulated annealing (SA) and genetic algorithm (GA) based on ITÖ process. PSGA firstly uses dual-chromosome coding to generate solution of CBTSP, and then updates the solution by using the crossover operator of GA. During this process, the length of crossover is controlled by the activity intensity, which is affected by the particle radius and environment temperature. In order to test the effectiveness of PSGA algorithm, the paper makes experiments by using small scale to large scale CBTSP data, and the extensive experiments show that PSGA can demonstrate better solution quality than the compared algorithms.
Keywordshybrid algorithm; genetic algorithms (GA); colored bottleneck traveling salesman problem (CBTSP); colored traveling salesman problem (CTSP); bottleneck traveling salesman problem
中图法分类号TP301
通信作者:董文永(dwy@whu.edu.cn)
基金项目:国家自然科学基金项目(61672024,61170305)This work was supported by the National Natural Science Foundation of China (61672024, 61170305).
修回日期:2018-06-12
收稿日期:2018-01-08;

DongXueshi, born in 1985. PhD candidate. His main research interests include intelli-gent computing and simulation optimization.

DongWenyong, born in 1973. Professor. His main research interests include intelli-gent computing, system control and simu-lation optimization.

CaiYongle, born in 1991. Master. His main research interests include intelligent optimization and simulation optimization.