 D={X1,X2,…,Xm}为D确定的决策等价分类.
D={X1,X2,…,Xm}为D确定的决策等价分类.周艳红1,2,3张贤勇1,3莫智文1,3
1(四川师范大学数学与软件科学学院 成都 610068)2(中国民用航空飞行学院计算机学院 四川广汉 618307)3(四川师范大学智能信息与量子信息研究所 成都 610068) (zhouyanhong515@163.com)
摘要在邻域粗糙集中,基于信息度量的属性约简具有重要应用意义.然而,条件邻域熵具有粒化非单调性,故其属性约简具有应用局限性.对此,采用粒计算技术及相关的3层粒结构,构建具有粒化单调性的条件邻域熵,进而研究其相关属性约简.首先,揭示条件邻域熵的粒化非单调性及其根源;其次,采用3层粒结构,自底向上构建一种新型条件邻域熵,获得其粒化单调性;进而,基于粒化单调的条件邻域熵,建立属性约简及启发式约简算法;最后,采用UCI(University of CaliforniaIrvine)数据实验,验证改进条件邻域熵的单调性与启发式约简算法的有效性.所得结果表明:新建条件邻域熵具有粒化单调性,改进了条件邻域熵,其诱导的属性约简具有应用前景.
关键词邻域粗糙集;条件邻域熵;粒计算;3层粒结构;属性约简
粗糙集理论是一种有效处理不确定性问题的新型数学工具[1],已经广泛应用于机器学习与模式识别等领域[2].属性约简是粗糙集理论进行知识发现与优化处理的基础,具有重要的应用意义,近年来呈现诸多研究成果.文献[3]提出基于正域的启发式属性约简算法;文献[4]研究4种不同熵的属性重要度秩保持性质,并提出增量式属性约简算法;文献[5]基于最大依赖性、最大相关性与最小冗余性原则提出基于互信息的启发式算法;文献[6-7]利用双量化思想探讨层次约简,提出3层粒结构(微观底层、中观中层、宏观高层)的构建方法;文献[8]提出一种基于相对决策熵的属性约简算法.
经典粗糙集主要以等价关系与等价类为基础,能够有效处理离散型数据,但在处理连续型数据方面具有局限性.对此,邻域粗糙集拓展经典粗糙集并适用于数值型及混合型数据分析.文献[9]提出邻域关系,文献[10]提出邻域互信息,文献[11]提出邻域类,文献[12-19]则对邻域信息系统进行了深入研究.其中,文献[12]在邻域信息系统中提出邻域熵,并进行系列研究;文献[13]将Shannon 熵与邻域熵结合提出邻域互信息并做属性约简;文献[15]利用邻域互信息[10]发展属性约简;文献[16]提出基于3支决策的邻域熵与条件邻域熵并做属性约简;文献[17]构造基于邻域粗糙集的多标记分类任务的特征选择算法;文献[18]开发基于邻域粒化与粗糙逼近的数值属性约简算法;文献[19]利用邻域粗糙集中的熵度量来研究基因选择.
综上可见,在邻域粗糙集中,基于信息度量的属性约简具有研究价值与应用意义.事实上,邻域熵、条件邻域熵与邻域互信息已经系统地存在[10].但是,其中的条件邻域熵具有粒化非单调性,不能建立约简的核与启发式算法;此外,鉴于对数函数定义域,该条件邻域熵没有考虑“0概率信息项”,从而带来不自然的熵值突变;进而,这些具体情况阻碍了相关属性约简的后续发展.本文主要针对经典条件邻域熵[10]及其缺陷,进行改进并提出具有粒化单调性的条件邻域熵,进而依托信息增量的可控性来研究相关的属性约简.
邻域信息系统是邻域粗糙集的基本背景,本节复习其基本知识.
定义1[11]. 邻域信息系统.IS=(U,C,V,f,δ)被称为邻域信息系统.其中,U为非空有限论域;C为非空属性集;V为所有属性的值域,即![]() 表示属性c所有取值的集合);δ∈[0,1]为邻域参数.特别地,DS=(U,C∪D,V,f,δ)表示邻域决策系统,其中,C与D分别为条件属性集与决策属性集,U
表示属性c所有取值的集合);δ∈[0,1]为邻域参数.特别地,DS=(U,C∪D,V,f,δ)表示邻域决策系统,其中,C与D分别为条件属性集与决策属性集,U D={X1,X2,…,Xm}为D确定的决策等价分类.
D={X1,X2,…,Xm}为D确定的决策等价分类.
本文主要涉及邻域决策系统DS.针对DS与IS,设A,B⊆C={c1,c2,…,cn}.
定义2[11]. 距离函数.在IS中,设x,y∈U,则C的距离函数为
![]()
(1)
若p=1,dC(x,y)为Manhattan距离;若p=2,dC(x,y)为Euclidean距离;若p=∞,dC(x,y)为Chebychev距离.
距离函数在邻域粗糙集中起着核心作用,这里dC自然诱导dA,dB.本文主要采用Chebychev距离(详细计算参见文献[20]).
定义3[11]. 邻域和邻域关系.在IS中,x∈U在B上的δ邻域为
B决定的邻域关系为
NRδ(B)={(x,y)∈U×U|dB(x,y)≤δ}.
U NRδ(B)记U上基于B的覆盖,即由邻域关系决定的邻域集.
NRδ(B)记U上基于B的覆盖,即由邻域关系决定的邻域集.
性质1[12]. 邻域是邻域粗糙集中的基本粒,具有2项单调性质:
1) 若A⊆B,则![]() ⊇
⊇![]()
2) 若0≤γ≤δ≤1,则![]() ⊆
⊆![]()
基于邻域,文献[10]研究了IS中的信息度量,包括邻域熵、条件邻域熵与邻域互信息等,相关定义与性质如下.
定义4[10]. 邻域熵.在IS中,B的邻域熵为
(2)
定义5[10]. 条件邻域熵、联合邻域熵、邻域互信息.在IS中,A关于B的条件邻域熵为
NHδ(A/B)=![]()
(3)
A与B的联合邻域熵为
NHδ(A∪B)=![]()
(4)
A与B的邻域互信息为
NMIδ(A;B)=![]()
(5)
定理1[10].
1)NMIδ(A;B)=NMIδ(B;A);
2)NMIδ(A;B)=NHδ(A)+NHδ(B)-NHδ(A∪B).
文献[10]还考虑条件B的邻域结构与决策D的分类结构,将IS中的条件邻域熵落实到了DS中.为了更好地分析信息本质与层次机制,定义6给出一种范化形式.
定义6. 条件邻域熵.在DS中,D关于B的条件邻域熵为
NHδ(D/B)![]()
(6)
针对DS中的条件邻域熵(式(6)),下面采用3层粒化技术[6]进行“高层→中层→底层”层次分解(如图1左列),以待改进与比较.
式(6)位于宏观高层,能够转换为等价形式:
NHδ(D/B)![]() /
/![]()
其中:
NHδ(Xj
![]()
如此,图1左列中的中层度量与底层度量具有相关的符号描述.
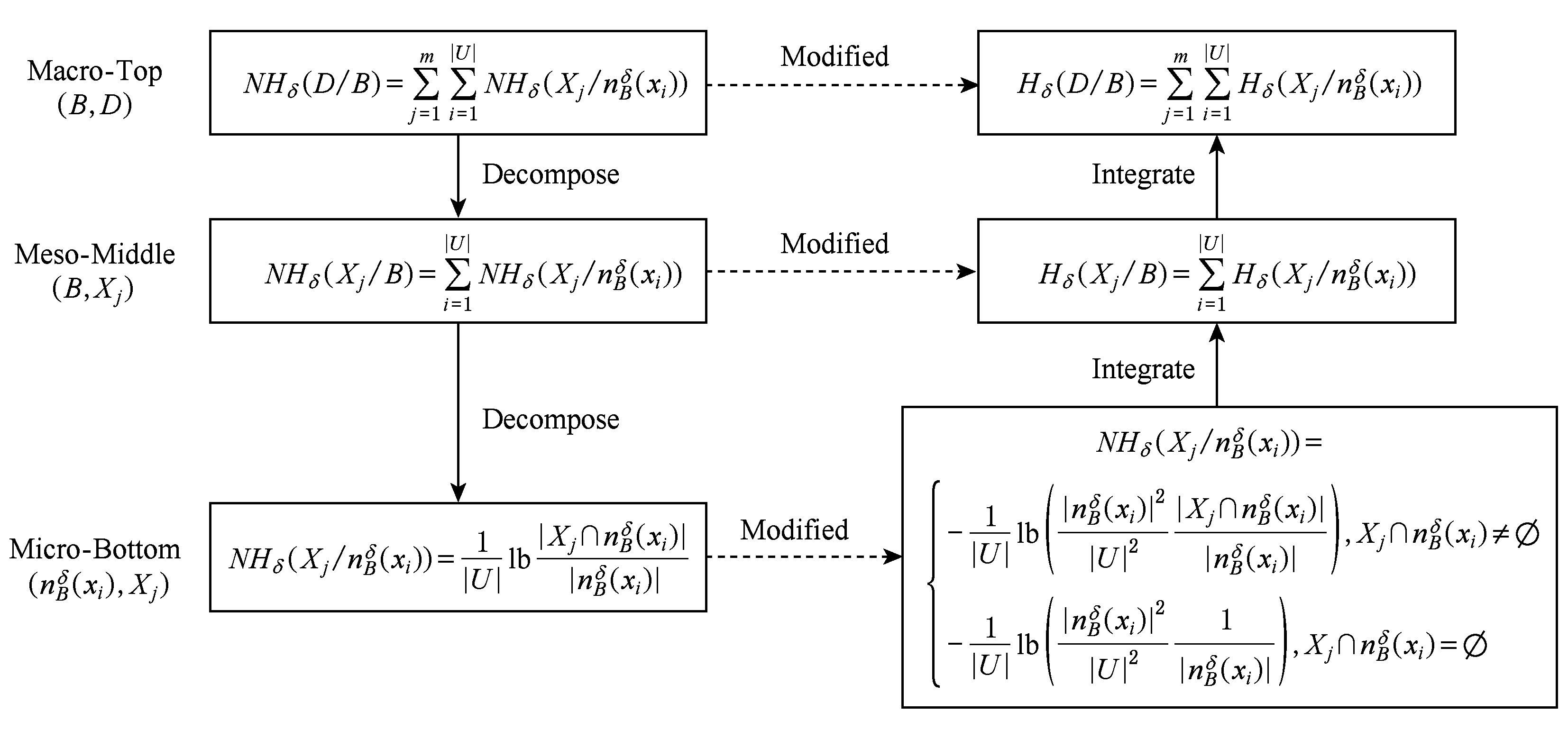
Fig. 1 Conditional neighborhood entropy and its improvement relationship based on three-layer granular structure
图1 基于3层粒结构的条件邻域熵及其改进关系
由图1左列可知,高层NHδ(D B)由NHδ(Xj
B)由NHδ(Xj
![]() 通过“ΣΣ” 表示;通过一次分解,中层NHδ(Xj
通过“ΣΣ” 表示;通过一次分解,中层NHδ(Xj B)由NHδ(Xj
B)由NHδ(Xj
![]() 通过“Σ” 表示;底层则由NHδ(Xj
通过“Σ” 表示;底层则由NHδ(Xj
![]() 直接表示.可见,条件邻域熵具有3层分解形式,其粒化非单调性主要位于高层且具有如下层次诱因.
直接表示.可见,条件邻域熵具有3层分解形式,其粒化非单调性主要位于高层且具有如下层次诱因.
在DS中,若A⊆B,则![]() ⊇
⊇![]() 即邻域随着属性减少而粗化.在底层,当粒度变粗时,
即邻域随着属性减少而粗化.在底层,当粒度变粗时,![]() 和
和![]() 的值都在变大,但概率值
的值都在变大,但概率值![]() 可能变大也可能变小,故条件邻域熵对应的底层度量在粗化过程中是不确定的进而是非单调的.关于粗化过程,这一底层不确定性机制决定着中高层集成度量的非单调性表现.因此,条件邻域熵自然具有粒化非单调性,支撑实例如例1所示.
可能变大也可能变小,故条件邻域熵对应的底层度量在粗化过程中是不确定的进而是非单调的.关于粗化过程,这一底层不确定性机制决定着中高层集成度量的非单调性表现.因此,条件邻域熵自然具有粒化非单调性,支撑实例如例1所示.
例1.DS=(U,C∪D,V,f,δ)如表1所示.其中,U={x1,x2,…,x7},C={c1,c2,…,c5},U D={X1,X2}={{x1,x2,x4,x5},{x3,x6,x7}},δ=0.4.
D={X1,X2}={{x1,x2,x4,x5},{x3,x6,x7}},δ=0.4.
Table1DecisionTableofExample1
表1例1决策表
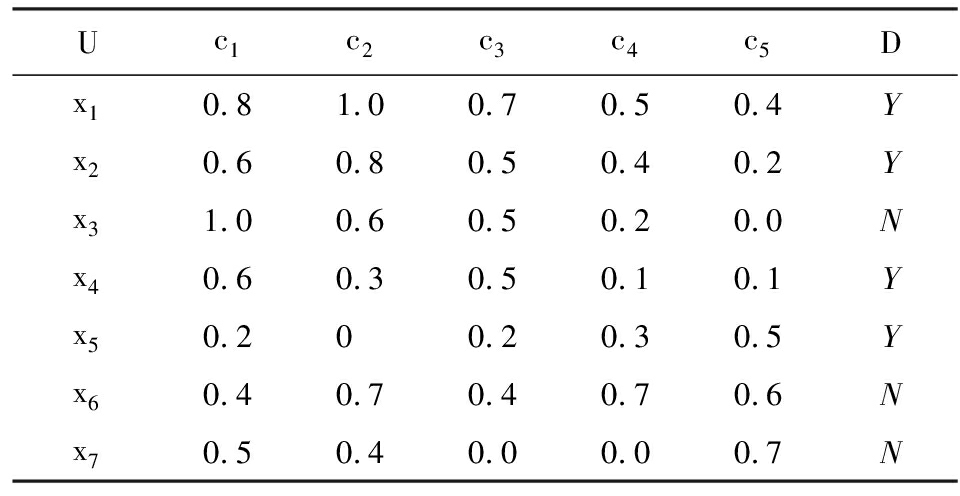
条件邻域熵(式(6))可以直接计算,其等价于实施“ΣΣ”集成图1左列中的底层度量.现选取粗化过程{c1,c2,c3,c4}→{c1,c2,c3}→{c1,c2},经计算3个条件邻域熵值可得:
NHδ(D {c1,c2})-NHδ(D
{c1,c2})-NHδ(D {c1,c2,c3})=
{c1,c2,c3})=
9.6515×10-4>0;
NHδ(D {c1,c2,c3})-NHδ(D
{c1,c2,c3})-NHδ(D {c1,c2,c3,c4})=
{c1,c2,c3,c4})=
-0.0157<0.
因此,在粗化{c1,c2,c3}→{c1,c2}中,
NHδ(D {c1,c2})>NHδ(D
{c1,c2})>NHδ(D {c1,c2,c3}),
{c1,c2,c3}),
而在粗化{c1,c2,c3,c4}→{c1,c2,c3}中,
NHδ(D {c1,c2,c3})<NHδ(D
{c1,c2,c3})<NHδ(D {c1,c2,c3,c4}).
{c1,c2,c3,c4}).
可见,条件邻域熵是粒化非单调的.
基于上述分析与实例,条件邻域熵(式(6))具有客观的粒化非单调性,这根源于基础概率![]() 的结构.下面,利用图2深入分析该概率度量,以揭示条件邻域熵的不足之处及改进空间.
的结构.下面,利用图2深入分析该概率度量,以揭示条件邻域熵的不足之处及改进空间.
如图2所示,对于粗化过程B→A有![]() ⊇
⊇![]() (性质1);设起始
(性质1);设起始![]() ∅,但最后
∅,但最后![]() ∅.这一粗化过程涉及邻域粒交概念Xj的质变,即从非交到相交.鉴于对数函数定义域,条件邻域熵开始没有考虑
∅.这一粗化过程涉及邻域粒交概念Xj的质变,即从非交到相交.鉴于对数函数定义域,条件邻域熵开始没有考虑![]() 而后又考虑
而后又考虑![]() 从而形成了交信息的突变.事实上,“非交到交”的质变关联于交信息的渐变,自然地过程涉及
从而形成了交信息的突变.事实上,“非交到交”的质变关联于交信息的渐变,自然地过程涉及![]() 对比地,条件邻域熵没有考虑“0概率信息项”,相当于采用不合理的
对比地,条件邻域熵没有考虑“0概率信息项”,相当于采用不合理的![]() 导致“交信息突变”,这种情况体现了条件邻域熵的不足,进而成为导致粒化非单调性的又一根源.从函数平滑性来看,条件邻域熵没有涉及“0概率信息项”,从而不能平稳地处理“交信息质变”,事实上其带来了“交信息突变”从而也导致了其粒化非单调性.
导致“交信息突变”,这种情况体现了条件邻域熵的不足,进而成为导致粒化非单调性的又一根源.从函数平滑性来看,条件邻域熵没有涉及“0概率信息项”,从而不能平稳地处理“交信息质变”,事实上其带来了“交信息突变”从而也导致了其粒化非单调性.
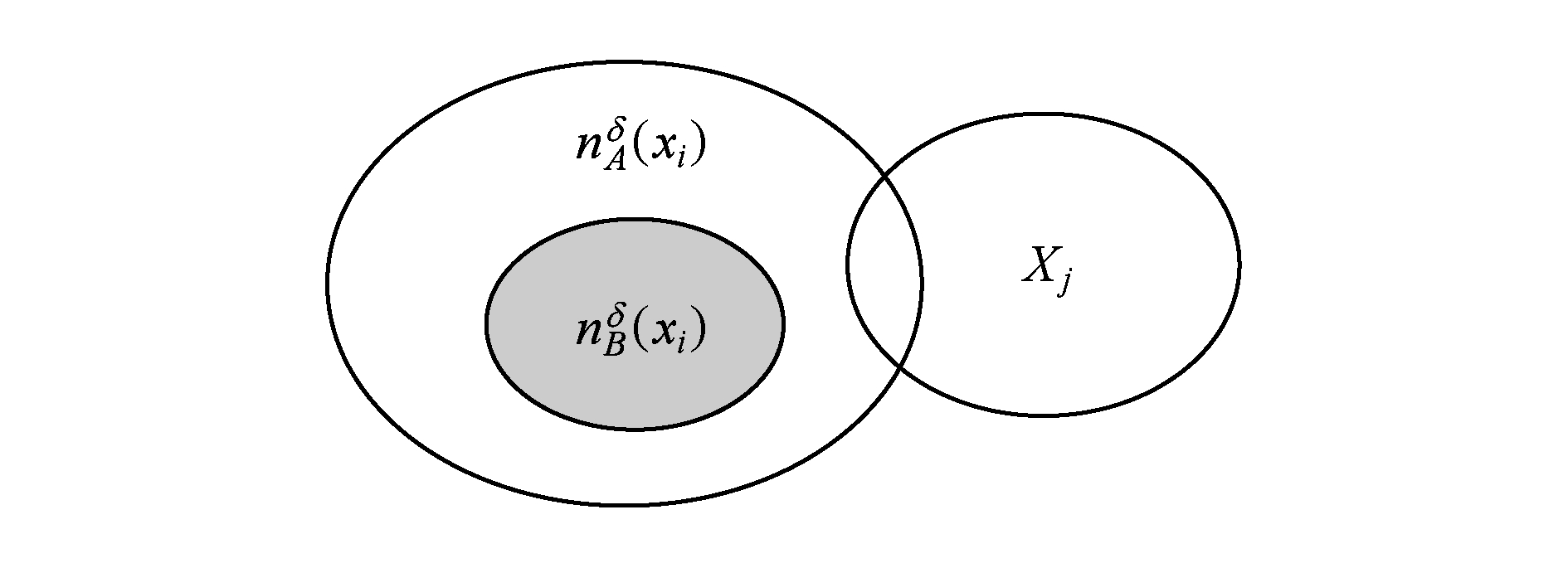
Fig. 2 Qualitative change of intersection information in knowledge coarsening
图2 知识粗化中的交信息质变
条件邻域熵(式(6))具有粒化非单调性的不足,相关的两大底层概率诱因是:1) 底层概率在粗化中的不确定性,2) 底层0概率没有被考虑.对此,本节采用3层粒结构[6]与自底向上粒计算策略,先改进条件邻域熵对应的底层度量,再集成构建具有粒化单调性的新型条件邻域熵.
定义7. 底层度量.对于DS=(U,C∪D,V,f,δ),在底层![]() 上定义度量:
上定义度量:
Hδ(Xj
![]()
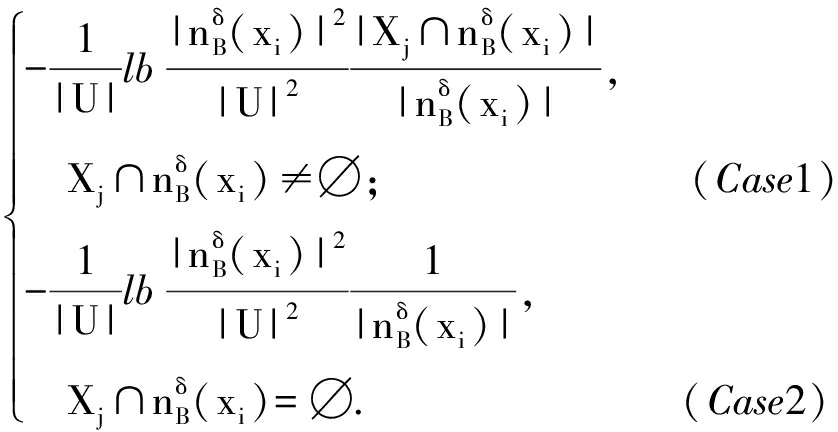
针对条件邻域熵(定义6)及其底层分解度量(图1),定义7引入![]() 来构造了底层度量Hδ(Xj
来构造了底层度量Hδ(Xj
![]() 对应
对应![]() ∅,此时
∅,此时![]() 即
即![]() 具有明显的粒化单调性;Case2对应具有“0概率信息项”的
具有明显的粒化单调性;Case2对应具有“0概率信息项”的![]() ∅,此时考虑
∅,此时考虑![]() 而其蕴含着粒化单调性.可见,Case1利用
而其蕴含着粒化单调性.可见,Case1利用![]()
![]() 为粒化单调性奠定基础,Case2给出“0概率信息项”的具体处理方法且考虑了粒化单调性,两者基于信息渐变来实现平稳衔接.从而,性质2自然表明了新建底层度量的粒化单调性.可见,定义7的新型底层度量从机制上与结果上改进了条件邻域熵(式(6))对应的底层度量,这一结论也标注于图1底层.特别地,Case1考虑了“绝对粒度比例”与“相对包含概率”的双量化信息集成[7],得到
为粒化单调性奠定基础,Case2给出“0概率信息项”的具体处理方法且考虑了粒化单调性,两者基于信息渐变来实现平稳衔接.从而,性质2自然表明了新建底层度量的粒化单调性.可见,定义7的新型底层度量从机制上与结果上改进了条件邻域熵(式(6))对应的底层度量,这一结论也标注于图1底层.特别地,Case1考虑了“绝对粒度比例”与“相对包含概率”的双量化信息集成[7],得到
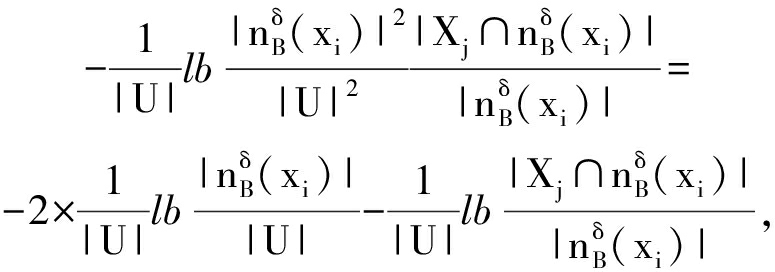
即底层度量可以能够表示为不确定性信息
的线性集成(或者表示为其中一个的线性变换),故关联于集成的不确定性信息;基于Case1的设置,Case2利用“近似逼近”来获取信息度量变化的平稳性.因此,定义7所建度量主要具有数学优势.
性质2. 若A⊆B,则
Hδ(Xj
![]()

![]()
证明. 在B→A粗化过程中,若![]() ∅,则有
∅,则有![]() ∅;若
∅;若![]() ∅,则有
∅,则有
![]() ∅,
∅,![]() ∅.
∅.
因此,粗化过程涉及3种粒相交情形,相关的分类与证明如下:
1) 考虑情形![]() ∅
∅
由于A⊆B,有![]() ⊆
⊆![]() (性质1),则
(性质1),则![]() 进而:
进而:
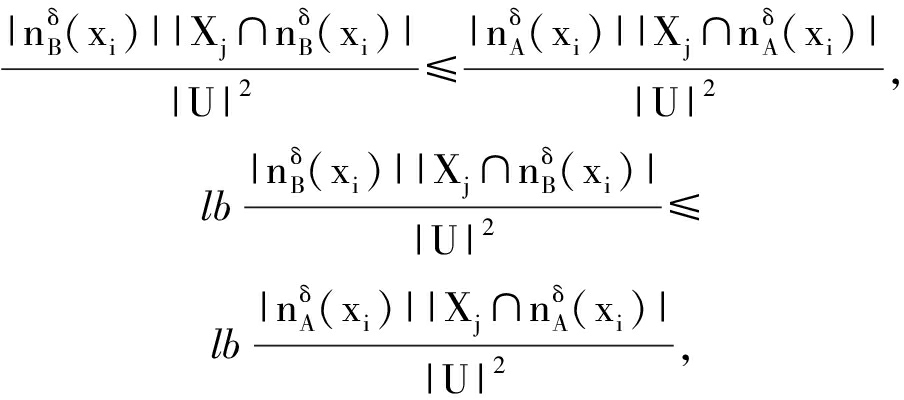
因此:
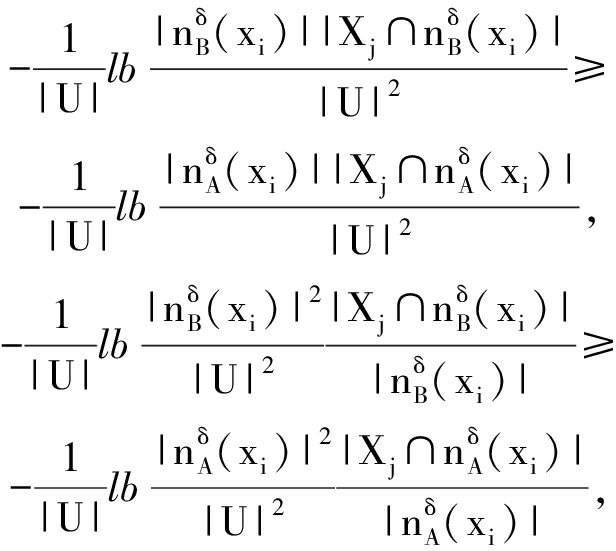
即Hδ(Xj
![]()

![]()
2) 考虑情形![]() ∅,
∅,![]() ∅
∅
当![]() ∅,则
∅,则![]() 从而
从而
类似于情形1的证明过程,可得:
Hδ(Xj
![]()

![]()
3) 考虑情形![]() ∅,
∅,![]() ∅
∅
此时,![]()
因此,Hδ(Xj
![]()

![]()
综上情形1~3,得证.
证毕.
性质2表明底层度量Hδ(Xj
![]() 具有粒化单调性.特别地,证明中的情形2恰好可用图2来解释,故也说明定义7考虑了图2的“交信息质变”这一特殊情况.
具有粒化单调性.特别地,证明中的情形2恰好可用图2来解释,故也说明定义7考虑了图2的“交信息质变”这一特殊情况.
性质3. 若0≤γ≤δ≤1,则
Hδ(Xj
![]()

![]()
定义7构建了新型底层度量,性质2与性质3分别体现了其相关的粒化单调性及参数单调性,因此其对条件邻域熵的底层分解度量具有改进性.下面,对该底层度量实施自然集成,获取中高层度量及其单调性,最终在高层改进条件邻域熵.特别地,基于底层度量的科学构造与信息集成,中高层度量也具有可解释性与相关不确定性语义.
定义8. 中层度量.在中层(B,Xj)定义度量
Hδ(Xj/![]() /
/![]()
(7)
性质4. 若A⊆B,则
Hδ(Xj B)≥Hδ(Xj
B)≥Hδ(Xj A).
A).
性质5. 若0≤γ≤δ≤1,则
Hδ(Xj B)≤Hγ(Xj
B)≤Hγ(Xj B).
B).
定义8集成定义7底层度量构建了中层度量,其具有粒化单调性与参数单调性,这2条性质(即性质4与性质5)自然来源于底层的相应性质(即性质2与性质3).类似地,下面将中层的度量及其性质自然集成演化到高层.
定义9. 单调条件邻域熵.在高层(B,D)上定义单调条件邻域熵:
Hδ(D/B)![]() /B)=
/B)=![]() /
/![]()
(8)
性质6. 若A⊆B,则Hδ(D B)≥Hδ(D
B)≥Hδ(D A).
A).
性质7. 若0≤γ≤δ≤1,则
Hδ(D B)≤Hγ(D
B)≤Hγ(D B).
B).
定义9最终建立了具有粒化单调性(性质6)的条件邻域熵,其“自底向上”的集成演化标注于图1的右列.利用图1对条件邻域熵(定义6)与单调条件邻域熵(定义9)进行比较总结.
1) 图1左列体现了条件邻域熵的“高层→中层→底层”分解过程,即高层度量NHδ(D B)通过“Σ”分解到中层度量NHδ(Xj
B)通过“Σ”分解到中层度量NHδ(Xj B),再通过“Σ”分解到底层度量NHδ(Xj
B),再通过“Σ”分解到底层度量NHδ(Xj
![]()
2) 图1右列体现了单调条件邻域熵的“底层→中层→高层”集成过程,即底层度量Hδ(Xj
![]() 通过“Σ”集成到中层度量Hδ(Xj
通过“Σ”集成到中层度量Hδ(Xj B),再通过“Σ”集成到高层度量Hδ(D
B),再通过“Σ”集成到高层度量Hδ(D B).
B).
3) 定义6的条件邻域熵的“自顶向下分解”与定义9的单调条件邻域熵的“自底向上集成”具有相反性与对比性,但两者在3种粒度层次上具有横向改进性.具体地,在底层上Hδ(Xj
![]() 改进NHδ(Xj
改进NHδ(Xj
![]() 在中层上Hδ(Xj
在中层上Hδ(Xj B)改进NHδ(Xj
B)改进NHδ(Xj B),在高层上Hδ(D
B),在高层上Hδ(D B)改进NHδ(D
B)改进NHδ(D B).
B).
综上3点可见,现有工作已经涉及3项内容:1)对条件邻域熵进行3层分解,并揭示高层粒化非单调性及其底层诱因;2)自底向上构建新型条件邻域熵,从粒化机制上得到粒化单调性;3)从粒化单调性的角度,新型条件邻域熵在3个层次上都具有改进性.
目前,属性约简主要集中在粒化高层,其中的粒化单调度量是构建属性约简的重要基础.第2节通过底层的单调构造与0概率处理,在粒化高层建立了具有粒化单调性的条件邻域熵,其具有特定的不确定性语义.进而,本节采用新建单调条件邻域熵来自然研究属性约简,包括建立相关的定义、性质及算法等.
定理2. 2个条件等价:
(N1)Hδ(D B)≠Hδ(D
B)≠Hδ(D (B-{b})),∀b∈B;
(B-{b})),∀b∈B;
(N2)Hδ(D B′)≠Hδ(D
B′)≠Hδ(D B),∀B′⊂B.
B),∀B′⊂B.
证明. 1) 若∀B′⊂B,则∃b∈B-B′⊂B,使得B′⊆B-{b}⊂B.由粒化单调性(性质6)与N1,可知Hδ(D B′)≤Hδ(D
B′)≤Hδ(D (B-{b}))<Hδ(D
(B-{b}))<Hδ(D B).因此,Hδ(D
B).因此,Hδ(D B′)≠Hδ(D
B′)≠Hδ(D B),即N1⟹N2成立.
B),即N1⟹N2成立.
2) ∀b∈B,设B′=B-{b}⊂B.由N2知Hδ(D B)≠Hδ(D
B)≠Hδ(D (B-{b})),即N2⟹N1成立.
(B-{b})),即N2⟹N1成立.
综上2点得证.
证毕.
定义10. 约简.引入新条件:
(S)Hδ(D B)=Hδ(D
B)=Hδ(D C),
C),
若子集B满足条件S与N1或条件S与N2,则称为C的一个相对D约简,所有相对约简组成的集合记为RedC(D).
基于单调条件邻域熵,定理2提供2条等价的独立必要性条件,即N1与N2.再加上联合充分性条件S,定义10自然定义相关的属性约简.
定义11. 核.若Hδ(D (C-{c}))≠Hδ(D
(C-{c}))≠Hδ(D C),则称c在C中是必要的,否则是不必要的.C中所有必要属性组成的集合称为核,记为CoreC(D),即:
C),则称c在C中是必要的,否则是不必要的.C中所有必要属性组成的集合称为核,记为CoreC(D),即:
CoreC(D)={c∈C|Hδ(D (C-{c}))≠Hδ(D
(C-{c}))≠Hδ(D C)}.
C)}.
(9)
定理![]()
证明. 1) 若c∉![]() 则∃B∈RedC(D),使得c∉B.
则∃B∈RedC(D),使得c∉B.
Hδ(D B)=Hδ(D
B)=Hδ(D C),B⊆C-{c}⊂C,
C),B⊆C-{c}⊂C,
由粒化单调性(性质6)可得:
Hδ(D (C-{c}))=Hδ(D
(C-{c}))=Hδ(D C).
C).
由定义11知,c∉CoreC(D).因此
CoreC(D)⊆![]()
2) 若c∉CoreC(D),由定义11知:
Hδ(D (C-{c}))=Hδ(D
(C-{c}))=Hδ(D C).
C).
∃B∈RedC(D),B⊆C-{c},使得:
Hδ(D (C-{c}))=Hδ(D
(C-{c}))=Hδ(D B).
B).
由粒化单调性(性质6)知,Hδ(D B)=Hδ(D
B)=Hδ(D C),故B∈RedC(D).由B⊆C-{c}有c∉B,从而
C),故B∈RedC(D).由B⊆C-{c}有c∉B,从而![]() 因此:
因此:
![]() ⊆CoreC(D).
⊆CoreC(D).
综上2点得证.
证毕.
类似于经典情形,定义11提供核计算公式,并可生成相关算法(如算法1);定理3表明核在所有约简中,因此可计算的核可以作为构建约简的基础.定义12首先利用单调条件邻域熵来建立属性重要度,进而设计基于核的启发式属性增加算法(如算法2).
定义12. 属性重要度.设c∈C-B,则属性c对条件属性集B相对于D的重要度为
Sig(c,B,D)=Hδ(D B∪{c})-Hδ(D
B∪{c})-Hδ(D B).
B).
(10)
其表征“B上增加属性c”增加过程中单调条件邻域熵的变化.
算法1. 求核算法.
输入:决策表DS=(U,C∪D,V,f,δ);
输出:CoreC(D).
Step1. 计算Hδ(D C),设置CoreC(D)=∅;
C),设置CoreC(D)=∅;
Step2. for ∀ck∈C(k=1,2,…,n) do
Step3. 计算Hδ(D (C-{ck}));
(C-{ck}));
Step4. ifHδ(D (C-{ck}))≠Hδ(D
(C-{ck}))≠Hδ(D C)
C)
then
Step5.CoreC(D)=CoreC(D)∪{ck};
Step6. end if
Step7. end for
Step8. returnCoreC(D).
算法2. 基于核的属性增加启发式约简算法.
输入:决策表DS=(U,C∪D,V,f,δ);
输出:B∈RedC(D).
Step1. 计算Hδ(D C);
C);
Step2. 由算法1,计算CoreC(D),取B=
CoreC(D),计算Hδ(D B);
B);
Step3. whileHδ(D B)≠Hδ(D
B)≠Hδ(D C) do
C) do
Step4. ∀ck∈C-B,计算Sig(ck,B,D),取
c0=arg maxSig(ck,B,D);
Step5. 令B=B∪{c0},计算Hδ(D B);
B);
Step6. end while
Step7. returnB.
算法1通过逐个删除条件属性,并基于式(9)进行求核计算.算法2在算法1求核的基础上,采用属性重要度进行启发式搜索,快速增加条件属性来最终获取一个属性约简.具体地,Step3~6循环增加属性直至粒化单调条件邻域熵值达到最初C所在的最高水平,其中主要加入具有最大Sig值的属性(即Step4中的c0),以提升整个算法的收敛速度.
最后指出,算法1基本地计算核而算法2启发地搜索约简,两者都依托了改进条件邻域熵及其粒化单调性.对比地,传统条件邻域熵具有粒化非单调性,不能进行相关约简算法的有效构建与具体实现.
本节提供UCI(University of CaliforniaIrvine)数据实验,验证新建条件邻域熵的改进单调性与相关约简算法的有效性.
这里验证改进条件邻域熵的粒化单调性.为此,选取3类UCI数据集:Wdbc,Pima,Sonar[21].其中,Wdbc数据集包含569个对象、30个条件属性、1个决策属性;Pima数据集包含768个对象、8个条件属性、1个决策属性;Sonar数据集包含208个对象、60个条件属性、1个决策属性.
对每一类数据集,主要在确定邻域参数δ后选择一条属性扩充增链,从而计算条件邻域熵与改进条件邻域熵并分析它们的粒化单调性.
1) Wdbc数据集采用阈值δ=0.8,只关注前12个条件属性并构建一条具有自然序的属性增链
{c1}→{c1,c2}→{c1,c2,c3}→…→
{c1,c2,c3,…,c12};
2) Pima数据集采用δ=0.95,并关注自然增链
{c1}→{c1,c2}→{c1,c2,c3}→…→
{c1,c2,c3,…,c8};
3) Sonar数据集采用δ=0.4,只关注前15个条件属性及其构成的自然增链
{c1}→{c1,c2}→{c1,c2,c3}→…→
{c1,c2,c3,…,c15}.
在这些实验设计下,3种数据集的2种条件邻域熵值分别列入表2~4,它们对应地描绘于图3~5;其中,图3~5中横坐标及属性数目对应着属性增链,纵坐标熵值记录
NH=NHδ(D/B)与H=Hδ(D/B).
Table2ValuesofTwoTypesofConditionalNeighborhoodEntropyinWdbcDataset(δ=0.8)
表2Wdbc数据集的2种条件邻域熵值(δ=0.8)
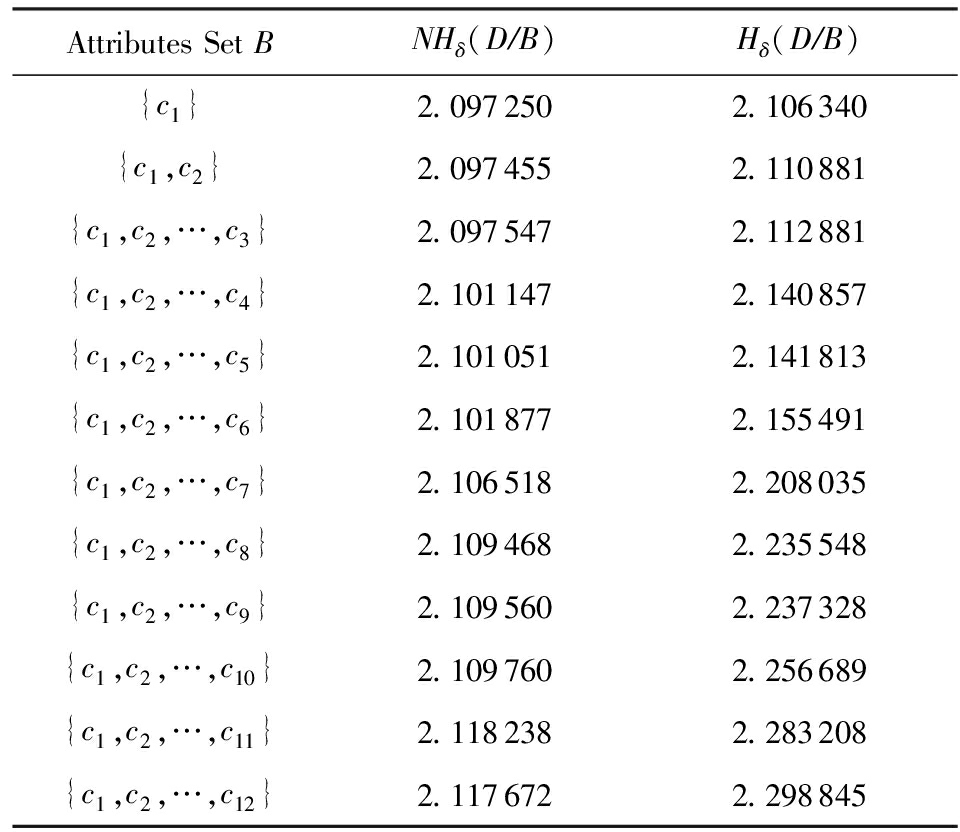
Table3ValuesofTwoTypesofConditionalNeighborhoodEntropyinPimaDataset(δ=0.95)
表3Pima数据集的2种条件邻域熵值(δ=0.95)
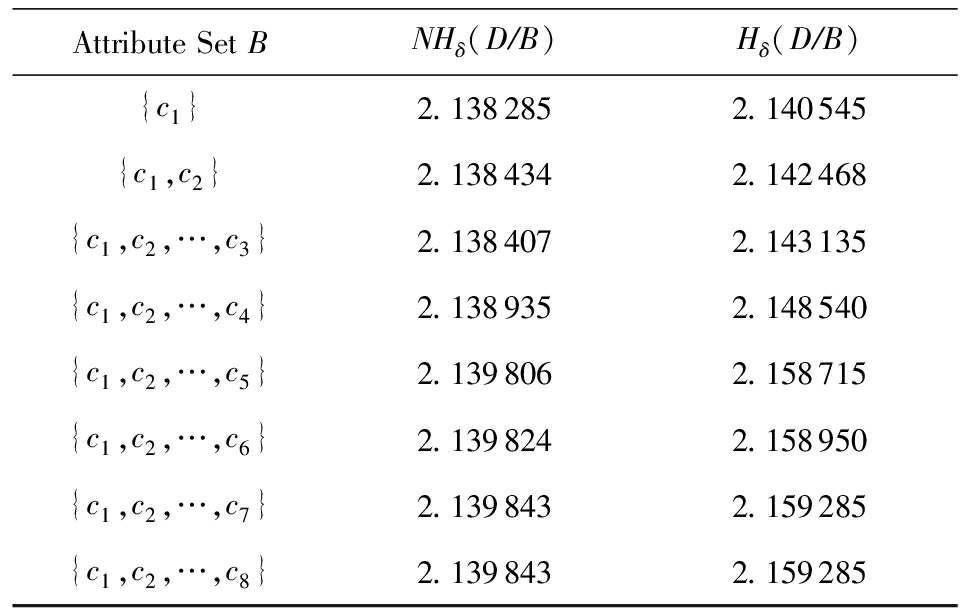
Table4ValuesofTwoTypesofConditionalNeighborhoodEntropyinSonarDataset(δ=0.4)
表4Sonar数据集的2种条件邻域熵值(δ=0.4)

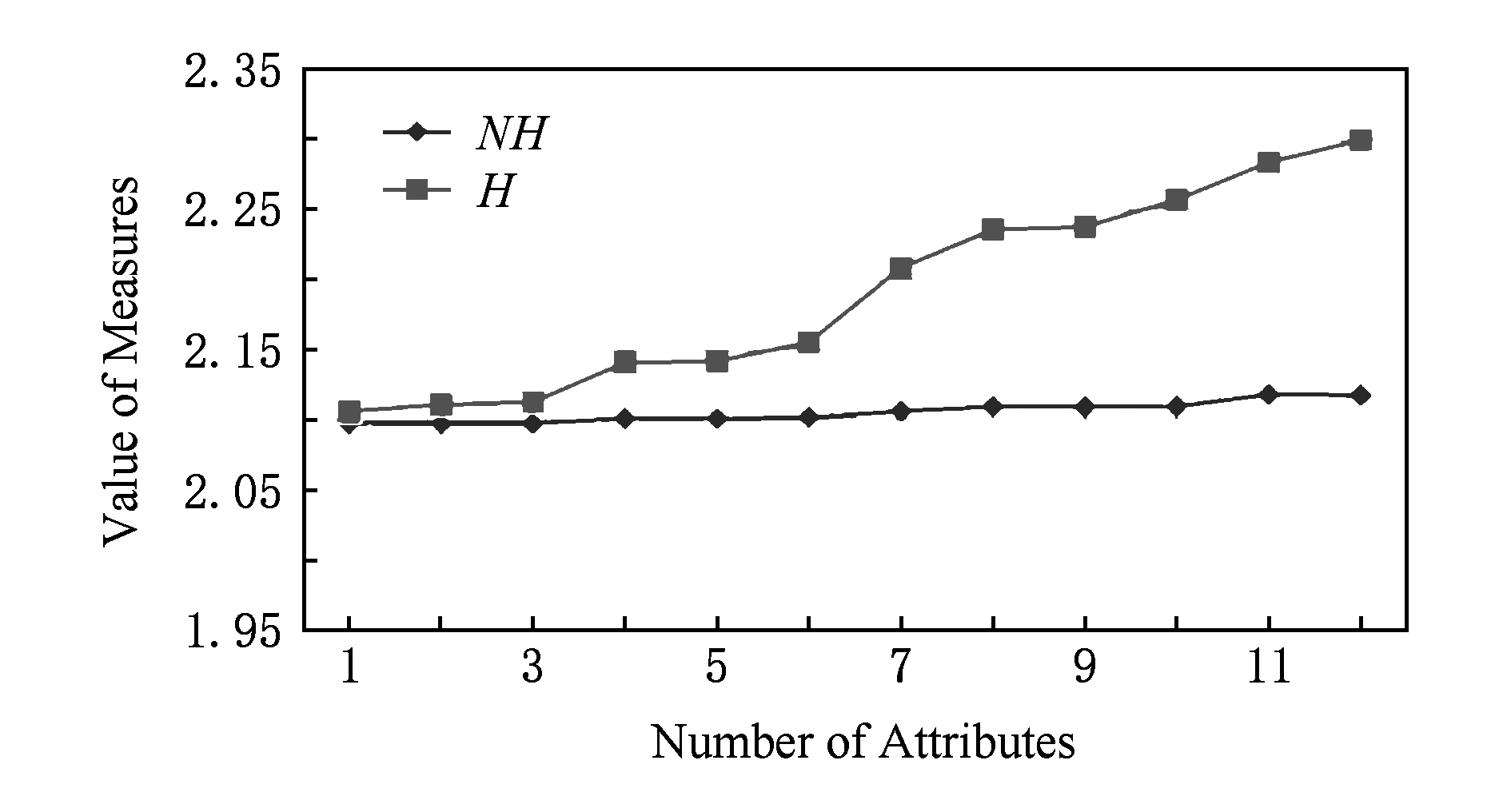
Fig. 3 Changing curves of two types of conditional neighborhood entropy in Wdbc dataset (δ=0.8)
图3 Wdbc数据集的2种条件邻域熵的变化曲线 (δ=0.8)
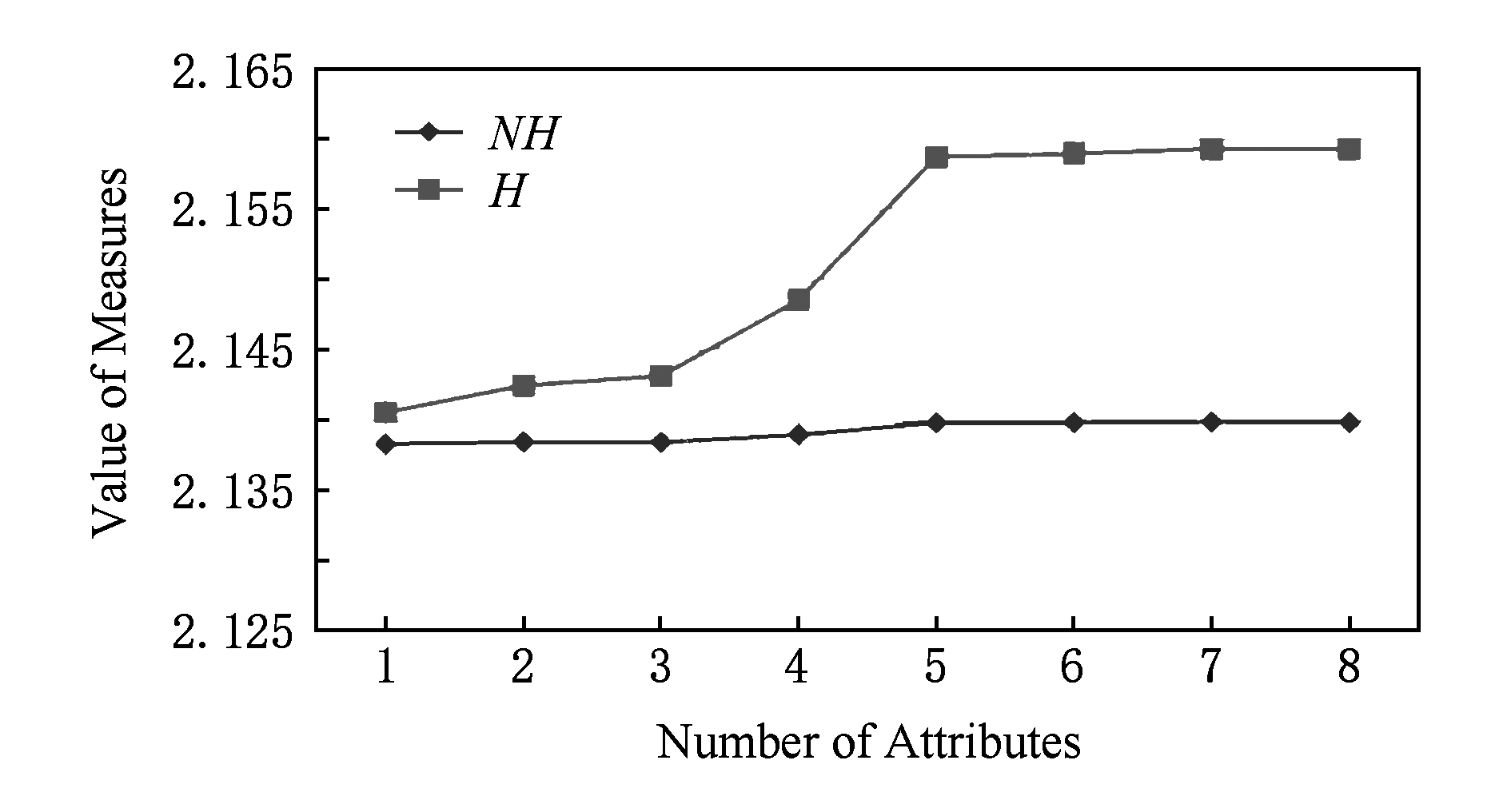
Fig. 4 Changing curves of two types of conditional neighborhood entropy in Pima dataset (δ=0.95)
图4 Pima数据集的2种条件邻域熵的变化曲线 (δ=0.95)
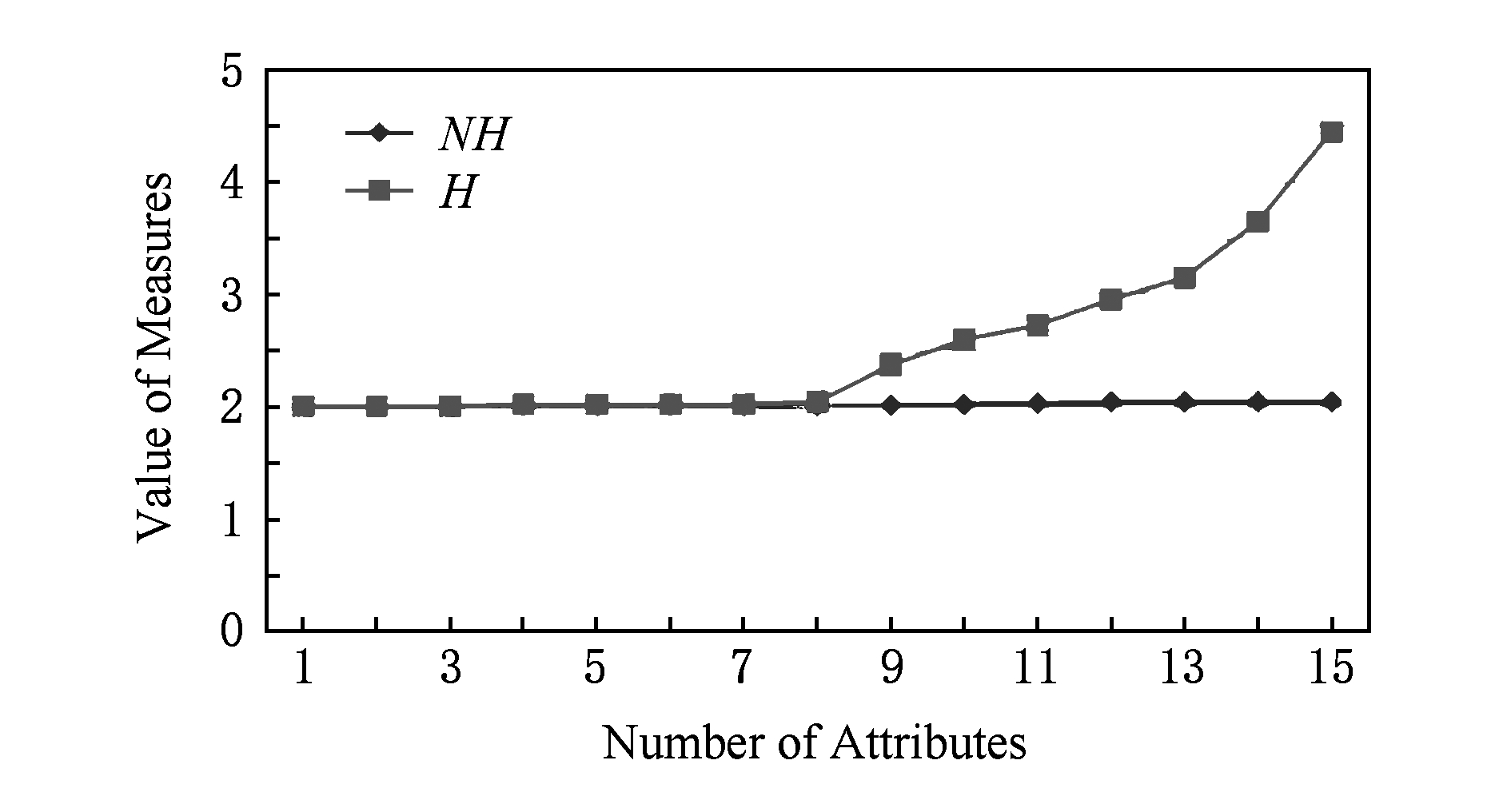
Fig. 5 Changing curves of two types of conditional neighborhood entropy in Sonar dataset (δ=0.4)
图5 Sonar数据集的2种条件邻域熵的变化曲线 (δ=0.4)
基于表2~4与图3~5结果,容易验证2种条件邻域熵的粒化单调性.
1) 在表2中,属性增链
{c1,c2,c3}→{c1,c2,c3,c4}→{c1,c2,c3,c4,c5}
涉及NHδ(D B)非单调变化
B)非单调变化
2.097 547→2.101 147→2.101 050
与Hδ(D B)单增变化
B)单增变化
2.112 881→2.140 857→2.141 813;
而属性增链
{c1,c2,…,c10}→{c1,c2,…,c11}→{c1,c2,…,c12}
涉及NHδ(D B)非单调变化
B)非单调变化
2.109 760→2.118 238→2.117 672
与Hδ(D B)单增变化
B)单增变化
2.256 689→2.283 208→2.298 845.
2) 在表3中,而属性增链
{c1}→{c1,c2}→{c1,c2,c3}
涉及NHδ(D B)非单调变化
B)非单调变化
2.138 285→2.138 434→2.138 407
与Hδ(D B)单增变化
B)单增变化
2.140 545→2.142 468→2.143 135.
3) 在表4中,而属性增链
{c1,c2,…,c13}→{c1,c2,…,c14}→{c1,c2,…,c15}
涉及NHδ(D B)非单调变化
B)非单调变化
2.045 410→2.047 744→2.046 308
与Hδ(D B)单增变化
B)单增变化
3.153 038→3.648 269→4.447 961.
由此可见,条件邻域熵不具备粒化单调性,而新建条件邻域熵具有改进性.事实上,图3~5比较清晰地展现了Hδ(D B)在所选属性增链上的粒化单调性,这也说明了Hδ(D
B)在所选属性增链上的粒化单调性,这也说明了Hδ(D B)的有效性;对比地,NHδ(D
B)的有效性;对比地,NHδ(D B)由于数值变化较小因而其粒化非单调性表现不是太明显.总之,3个UCI实验较好地说明了新建条件邻域熵的粒化单调性及相关改进性.
B)由于数值变化较小因而其粒化非单调性表现不是太明显.总之,3个UCI实验较好地说明了新建条件邻域熵的粒化单调性及相关改进性.
基于粒化单调的条件邻域熵,下面说明相关属性约简的有效性.为此,主要在5类UCI数据集(Wdbc,Pima,Sonar,Wpbc,Wine)[21]上实施算法1与算法2,并得到核与约简的最终结果.
针对5类UCI数据集,实验中采用了3种邻域参数,即δ分别取0.3,0.5,0.8.首先利用算法1求出核,再利用算法2求出一个约简(其中属性重要度充当了启发式信息,用以加速整个搜索算法的收敛速度).表5给出了算法1与算法2的具体实验结果,即提供了相关的核与约简;进而,表6给出了相关的数目统计.
Table5ExperimentalResultsofCoreandReductBasedonFiveTypesofUCIDataSets
表55类UCI数据集上的核与约简的实验结果
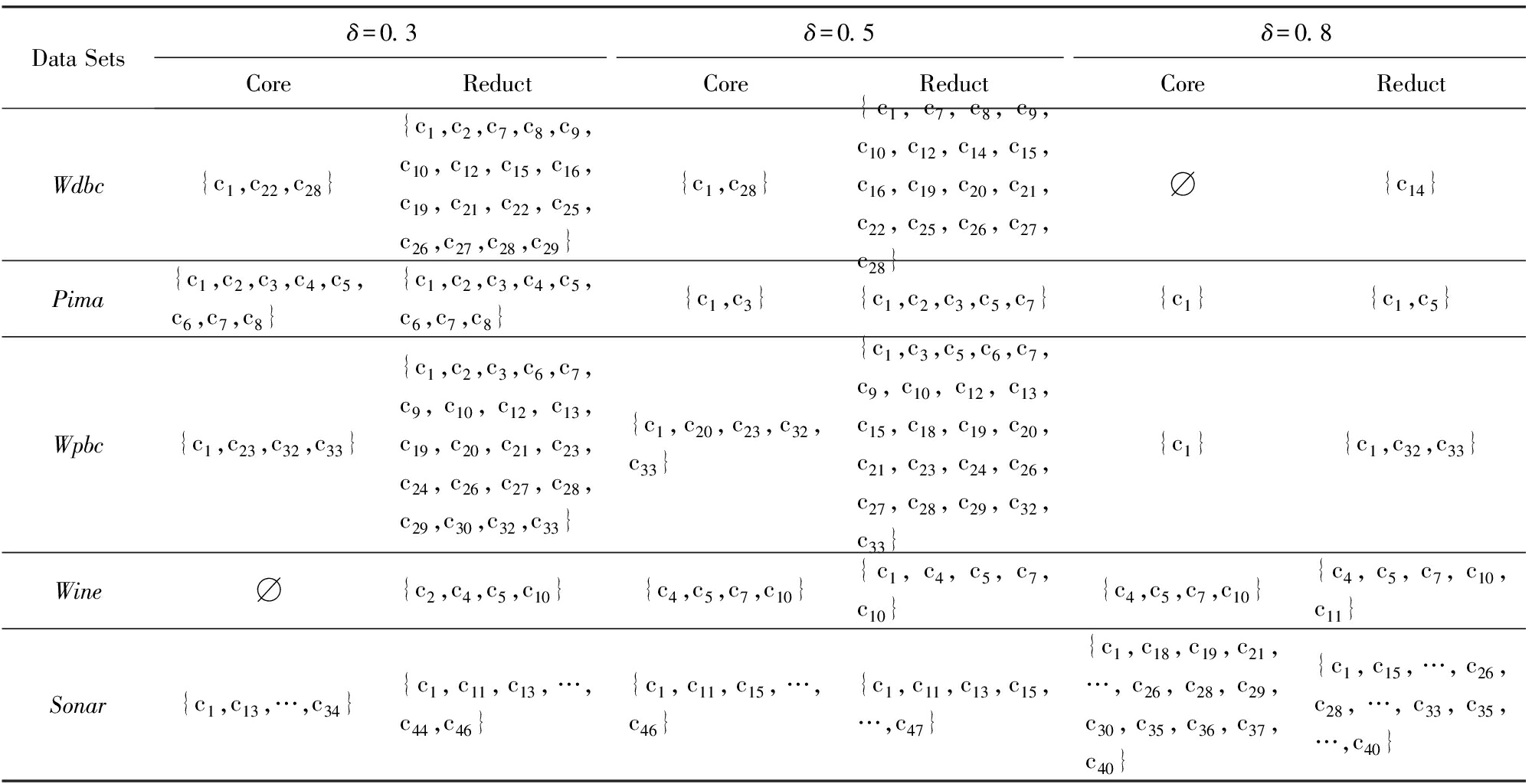
Table6NumberInformationofFiveTypesofUCIDataSetsandTheirExperimentResults
表65类UCI数据集及其实验结果的数目信息
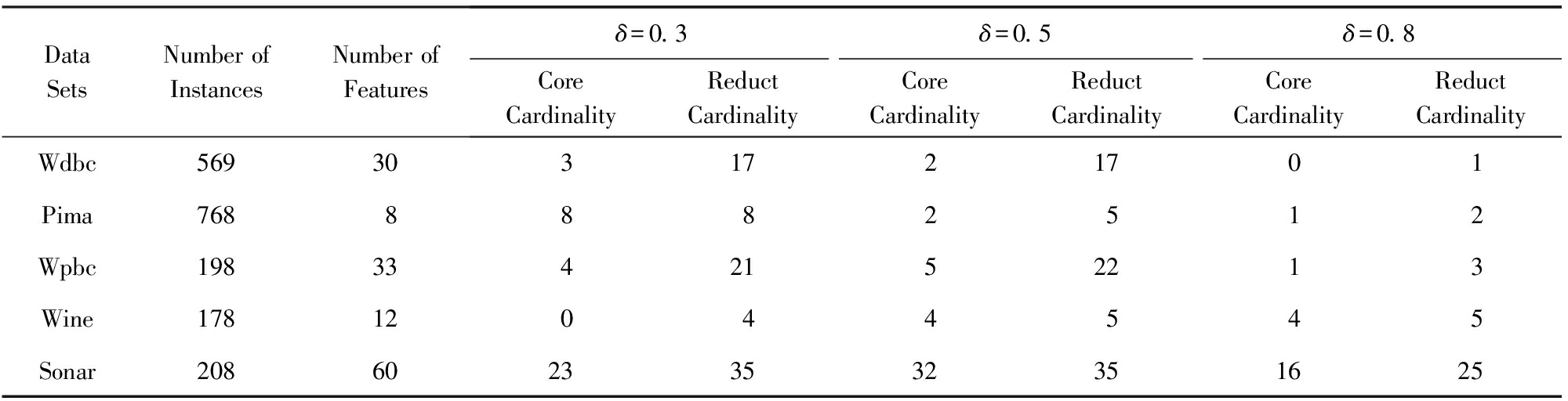
基于表5与表6,这里的数据集已经具有一定规模,但算法1与算法2都能够有效地得到基本结果.下面,针对相同的数据集进行相关分析.
核都在所得的相关约简中,表明算法1的核为约简构建的基础.当然,也有核为空的情况(如Wdbc数据集在δ=0.8时),此时算法2只能直接利用属性重要度进行启发搜索.
基于粒化单调的条件邻域熵,利用算法2可以有效地删除部分冗余属性,保留有效属性.例如,Sonar具有60个条件属性,核包括大约20多个,而约简包括大约30多个,相关属性约简比较合理.
实验结果还依赖于参数δ的取值.随着参数0.3→0.5→0.8的增大,核有扩大或缩小的结果;属性约简一般没有扩大或缩小的变化,但约简基数总体有变小的趋势.
基于大规模数据实验及其结果,本文所构造的属性约简算法是有效的,基于改进条件邻域熵的约简算法可以具体实现,这也充分说明了改进所得粒化单调性的应用价值.
条件邻域熵不具备粒化单调性,其中1个基本诱因是“0概率信息项”未处理导致的信息突变性;从而,粒化非单调性及其诱因阻碍了相关的属性约简发展,例如没法建立约简的核与启发式算法.对此,本文主要进行单调改进与约简构建.通过采用3层粒结构[6],“自顶向下”分解剖析条件邻域熵,“自底向上”集成构建新型条件邻域熵,并在每个层面获取粒化单调性从而实现基本改进.进而,基于高层所建的条件邻域熵及其粒化单调性,深入研究属性约简,并挖掘属性重要度来构造基于核的启发式约简算法(算法2).最后,通过大规模数据实验,有效验证了相关的粒化单调性与属性约简算法.总之,本文所建的条件邻域熵具有粒化单调性,改进了传统条件邻域熵,其诱导的属性约简具有应用前景,但相关的理论探讨与实际应用还值得深入,比如相关的度量保持条件、度量近似应用、与其他约简目标的结合等,度量的分段性还值得实际处理.
参考文献
[1] Pawlak Z. Rough sets[J]. International Journal of Parallel Programming, 1982, 11(5): 341-356
[2]Liu Dun, Li Tianrui, Li Huaxiong. A multiple-category classification approach with decision-theoretic rough sets[J]. Fundamenta Informaticae, 2012, 115(2/3): 173-188
[3]Qian Yuhua, Liang Jiye, Pedrycz W, et al. Positive approximation: An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence, 2010, 174(9/10): 597-618
[4]Liang Jiye, Mi Junrong, Wei Wei, et al. An accelerator for attribute reduction based on perspective of objects and attributes[J]. Knowledge -Based Systems, 2013, 44: 90-100
[5]Peng Hanchuan, Long Fuhui, Ding C H. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8): 1226-1238
[6]Zhang Xianyong, Miao Duoqian. Three-layer granular structures and three-way informational measures of a decision table[J]. Information Sciences, 2017, 412/413: 67-86
[7]Zhang Xianyong, Miao Duoqian. Double-quantitative fusion of accuracy and importance: Systematic measure mining, benign integration construction hierarchical attribute reduction[J]. Knowledge -Based Systems, 2016, 91: 219-240
[8]Jiang Feng, Sui Yuefei, Zhou Lin. A relative decision entropy-based feature selection approach[J]. Pattern Recognition, 2015, 48(7): 2151-2163
[9]Lin T Y. Neighborhood systems and relational database[C] //Proc of the 16th ACM Annual Computer Science Conf. New York: ACM, 1988: 725-725
[10]Hu Qinhua, Yu Daren. Neighborhood entropy[C]//Proc of the 8th Int Conf on Machine Learning and Cybernetics. Piscataway, NJ: IEEE, 2009: 1776-1782
[11]Hu Qinghua, Yu Daren, Xie Zongxie. Neighborhood classifiers[J]. Expert Systems with Applications, 2008, 34(2): 866-876
[12]Chen Yuming, Wu Keshou, Chen Xuhui, et al. An entropy-based uncertainty measurement approach in neighborhood systems[J]. Information Sciences, 2014, 279: 239-250
[13]Hu Qinhua, Zhang Lei, Zhang D, et al. Measuring relevance between discrete and continuous features based on neighborhood mutual information[J]. Expert Systems with Applications, 2011, 38(9): 10737-10750
[14]Zheng Tingting, Zhu Linyun. Uncertainty measures of neighborhood system-based rough sets[J]. Knowledge -Based Systems, 2015, 86: 57-65
[15]Liu Yao, Xie Hong, Chen Yuehua, et al. Neighborhood mutual information and its application on hyperspectral band selection for classification[J]. Chemonmetrics and Intelligent Laboratory Systems, 2016, 157: 140-151
[16]Chen Yuming, Zeng Zhiqiang, Zhu Qingxin, et al. Three-way decision reduction in neighborhood systems[J]. Applied Soft Computing, 2016, 38: 942-954
[17]Duan Jie, Hu Qinghua, Zhang Lingjun, et al. Feature selection for multi-label classification based on neighborhood rough sets[J]. Journal of Computer Research and Development, 2015, 52(1): 56-65 (in Chinese)
(段洁, 胡清华, 张灵均, 等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展, 2015, 52(1): 56-65)
[18]Hu Qinghua, Yu Daren, Xie Zongxia. Numerical attribute reduction based on neighborhood granulation and rough approximation[J]. Journal of Software, 2008, 19(3): 640-649 (in Chinese)
(胡清华, 于达仁, 谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简[J]. 软件学报, 2008, 19(3): 640-649)
[19]Chen Yuming, Zhang Zunjun, Zheng Jianzhong, et al. Gene selection for tumor classification using neighborhood rough sets and entropy measures[J]. Journal of Biomedical Informatics, 2017, 67: 59-68
[20]Hu Qinhua, Yu Daren, Liu Jinhu, et al. Neighborhood rough set based heterogeneous feature selection[J]. Information Sciences, 2008, 178(18): 3577-3594
[21]Bay S D. The UCI KDD repository[DB/OL]. [2017-05-10]. http://kdd.ics.uci.edu
Zhou Yanhong1,2,3, Zhang Xianyong1,3, and Mo Zhiwen1,3
1(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610068)2(CollegeofComputer,CivilAviationFlightUniversityofChina,Guanghan,Sichuan618307)3(InstituteofIntelligentInformationandQuantumInformation,SichuanNormalUniversity,Chengdu610068)
AbstractIn the neighborhood rough sets, the attribute reduction based on information measures holds fundamental research value and application significance. However, the conditional neighborhood entropy exhibits granulation non-monotonicity, so its attribute reduction has the research difficulty and application limitation. Aiming at this issue, by virtue of the granular computing technology and its relevant three-layer granular structure, a novel conditional neighborhood entropy with granulation monotonicity is constructed, and its relevant attribute reduction is further investigated. At first, the granulation non-monotonicity and its roots of the conditional neighborhood entropy are revealed; then, the three-layer granular structure is adopted to construct a new conditional neighborhood entropy by the bottom-up strategy, and the corresponding granulation monotonicity is gained; furthermore, relevant attribute reduction and its heuristic reduction algorithm are studied, according to this proposed information measure with the granulation monotonicity; finally, data experiments based on the UCI (University of CaliforniaIrvine) machine learning repository are implemented, and thus they verify both the granulation monotonicity of the constructed conditional neighborhood entropy and the calculation effectiveness of the related heuristic reduction algorithm. As shown by the obtained results, the established conditional neighborhood entropy has the granulation monotonicity to improve the conditional neighborhood entropy, and its induced attribute reduction has broad application prospects.
Keywordsneighborhood rough set; conditional neighborhood entropy; granular computing; three-layer granular structure; attribute reduction
中图法分类号TP18
通信作者:张贤勇(xianyongzh@sina.com)
基金项目:国家自然科学基金项目(61673285,61203285,11671284);高等学校博士学科点专项科研基金项目(20135134110003);四川省科技计划项目(2017JY0197,2017JQ0046)This work was supported by the National Natural Science Foundation of China (61673285, 61203285, 11671284), the Specialized Research Fund for the Doctoral Program of Higher Education of China (20135134110003), and the Science and Technology Project of Sichuan Province of China (2017JY0197, 2017JQ0046).
修回日期:2018-03-16
收稿日期:2017-08-25;

ZhouYanhong, born in 1982. PhD. Her main research interests include rough sets and granular computing.

ZhangXianyong, born in 1978. PhD, professor, master supervisor. His main research interests include rough sets, granular computing, and data mining.

MoZhiwen, born in 1963. PhD, professor, PhD supervisor. His main research interests include uncertainty data analysis and quantum information processing.