刘 勇 谢胜男 仲志伟 李金宝 任倩倩
(黑龙江大学计算机科学技术学院 哈尔滨 150080) (黑龙江省数据库与并行计算重点实验室(黑龙江大学) 哈尔滨 150080) (acliuyong@sina.com)
摘要影响最大化问题是在社交网中寻找对传播项最具影响力的种集,使得传播项的传播范围最大.目前的研究只考虑了传播项上主题的分布,而忽略了用户本身的兴趣分布.在传播项的主题分布和用户的兴趣分布都被考虑的条件下,研究如何选取最具影响力的种集.首先提出了基于主题兴趣的独立级联传播模型TI-IC,并利用期望最大化算法求学习TI-IC模型参数;然后在TI-IC模型基础上提出了基于主题兴趣的影响最大化问题TIIM,并提出了求解TIIM问题的启发式算法ACG-TIIM.ACG-TIIM首先构造以每个用户为根的可达路径树,快速粗略预估每个用户的影响范围;然后根据预估的影响范围排序所有结点并选择少量结点作为候选种子;最后使用带有EFLF优化的贪心算法从候选种子中选择最具影响力的种集.多个真实数据集上的实验结果表明:在描述传播规律和预测传播结果方面,TI-IC模型优于经典的IC模型和TIC模型.ACG-TIIM算法可以有效并高效地求解基于主题兴趣的影响最大化问题.
关键词社会网;影响最大化;主题分布;传播模型;期望最大化
近年来,随着社交应用的普及,人们信息获取的方式发生了很大的改变.通过在线社交网络转发和分享消息逐渐成为了人们获取信息的主要方式.很多在线社交网站允许用户对信息进行转发、评论、标记或其他一些类似的操作.如果能充分挖掘社交网络中这些海量数据并发现传播规律,将促进新思想、新产品在社交网上快速传播.
为了利用社交网进行病毒式营销, Kempe等人[1]首次提出了影响最大化问题:选取一个大小为k的初始用户集合,使得在给定传播模型下最终被影响的用户数量最大.文献[1]同时在独立级联(independent cascade, IC)模型和线性阈值(linear threshold, LT)模型上给出了贪心算法.此后,影响最大化及其相关问题被广泛研究.一方面,为了扩展到大规模社交网络上,经典传播模型上高效地影响最大化算法[2-5]相继被提出;另一方面,为了更准确地模拟信息传播过程,一些新的传播模型[6-8]相继被提出.
现有的传播模型几乎都是利用朋友之间的影响来模拟传播过程.例如:基于主题的独立级联(topic-aware independent cascade, TIC)模型[6]利用传播项的主题分布和用户在不同主题上的影响程度来计算朋友之间的影响概率.然而,在现实生活中,我们发现这样一个现象:相对于朋友之间的影响,人们更容易被其感兴趣的信息所吸引.例如:用户使用新浪微博转发好友发布的内容时,用户更多的是被内容本身所吸引,被好友影响的可能性相对较小.即使一个不经常联系的好友发布了令用户感兴趣的内容时,用户也有很大可能性转发该内容.
根据上述分析,在求解社会网中的影响最大化问题时理应考虑用户对传播项的兴趣.使用用户的兴趣分布和传播项的主题分布建立传播模型,可以更精确地描述信息传播过程,得到更准确的预测结果,具有重要的理论意义和广泛的应用价值.
本文利用用户兴趣的主题分布和传播项的主题分布,在传统独立级联模型的基础上,提出了基于主题-兴趣的独立级联传播(topic-interest independent cascade, TI-IC)模型,并在该模型的基础上设计了基于主题兴趣的影响最大化算法ACG-TIIM.通过在2个真实数据集上的实验结果表明:TI-IC模型在均方根误差MSE,F1-score,ROC曲线下面积等多个指标上均优于传统的IC模型和TIC模型.ACG-TIIM算法可以得到和传统贪心算法几乎一样的种集,但比传统贪心算法快2个数量级以上.本文主要贡献有4个方面:
1) 提出了基于主题兴趣的传播模型TI-IC,并使用期望最大化(expectation maximization, EM)算法学习该模型的参数.
2) 提出了新传播项主题分布向量的学习算法.
3) 在TI-IC基础上,提出了基于主题兴趣的影响最大化问题(topic-interest based influence maxi-mization, TIIM),并给出了高效启发式算法ACG-TIIM.ACG-TIIM算法也可用于求解其他传播模型上的影响最大化问题.
4) 多个真实数据集上的实验结果表明,TI-IC模型比IC模型和TIC模型能更准确地描述信息传播规律, ACG-TIIM算法可高效求解影响最大化问题.
Domingos等人[9]最先考虑社会网中具有影响力的结点选择问题.2003年,Kempe等人[1]首次提出了影响最大化问题,证明了影响最大化问题在独立级联模型和线性阈值模型上都为NP-hard问题,并且设计出具有(1-1/e)近似比的贪心算法.贪心算法虽然简单,但是由于在每次迭代选择种子结点的过程中都需要进行大量的蒙特卡洛模拟来估计影响范围,导致贪心算法的效率较低.为了扩展到大规模社交网络上,很多高效的影响最大化算法[2-5]被提出.例如Li等人[5]提出了在线广告的实时影响最大化问题,对于一个给定关键字的广告,在线寻找k个结点的种集,利用反向可达集的概念设计了一个基于采样的算法,不仅有近似比保证,也提升了算法的效率.
任何影响最大化算法都依赖于特定的传播模型.社交网传播模型大致可以分为带有拓扑结构的传播模型和无拓扑结的传播模型两大类.
带有拓扑结构的传播模型将社交网拓扑结构看作前置条件,要求信息沿着边进行传播.经典的IC模型和LT模型均属于此类模型.Barbieri等人[6]扩展了传统IC模型,提出了主题感知的独立级联模型TIC.Aslay等人[10]在该模型的基础上,提出了基于主题的影响最大化问题,设计了一个树形框架,利用索引来减少新传播项的计算量,使得算法效率得到很大提升.Chen等人[11]估计每个用户的影响上界,利用该上界对影响力小的用户进行剪枝,并设计了高效的计算上界方法.文献[12]考虑了时间因素的影响,在IC模型和LT模型基础上提出了AsIC和AsLT模型.文献[13]通过分析传播内容来构造传播模型.文献 [14]考虑内在因素和外在因素的作用来模拟传播过程.文献[7]同时考虑外部影响、朋友影响和用户兴趣的联合作用利用随机过程构建传播模型CMPP.文献[8]考虑结点和结点之间的交互作用,在IC模型基础上提出了情感交互模型OI.
无拓扑结构的传播模型假定社交网拓扑结构无法获取,只根据观察到的事件序列来推断传播轨迹,预测传播趋势.文献[15]推断用户之间的信息传播速率,使得观察事件序列出现概率最大.文献[16]根据观测的事件序列来推断信息传播路径和网络拓扑结构,通过追踪新闻站点之间的新闻流通路径验证算法有效性.文献[17]将用户映射到一个连续隐藏空间中,根据与感染源的距离远近来计算每个用户被感染的概率.通过从观察到的事件序列中学习传播核函数来预测信息传播.文献[18]使用表示学习的方式将用户映射到连续潜在空间.如果2个用户在潜在空间的距离越近,则这2个用户的影响概率越大.通过这种方式来构造传播模型Embedded IC.
本文传播模型是一种带有拓扑结构的传播模型.与现有模型的主要区别是,本文传播模型只关注用户的兴趣,如果用户对传播项感兴趣,则用户接受传播项.本文传播模型在预测效果方面优于IC模型和TIC模型,因此更适合作为求解影响最大化问题的传播模型.
本节介绍基于主题兴趣的传播模型TI-IC.该模型是IC模型的扩展,假设每个传播项存在一个主题分布,并且每个用户存在一个兴趣分布.例如,一个电影可能会包含:喜剧、爱情、动作等基本的主题,一个用户也会存在一个兴趣分布,如对喜剧的喜爱程度是0.6,对爱情剧的喜爱程度是0.1,对动作片的喜爱程度是0.3.
社交网用有向图G=(V,E)表示,社交网用户的历史动作日志记为D.日志D中每条记录格式为(u,i,t),代表用户u在时间t接收传播项i.对于每个主题z∈[1,Z],每个传播项i都有一个主题分量![]() 每个用户u都有一个兴趣分量
每个用户u都有一个兴趣分量![]() 因此每个传播项i存在主题分布向量θi=(θ1i,θ2i,…,θZi),每个用户u存在不同主题上的兴趣分布向量θu=(θ1u,θ2u,…,θZu).
因此每个传播项i存在主题分布向量θi=(θ1i,θ2i,…,θZi),每个用户u存在不同主题上的兴趣分布向量θu=(θ1u,θ2u,…,θZu).
TI-IC模型的工作原理如下:每个结点仅有一次机会由不活跃状态变为活跃状态,并且该过程不可逆.在时刻t= 0,只有种集S⊆V中的结点为传播项i上的活跃结点;在时刻t≥1,如果结点u的任何邻居v在时刻t-1变得活跃,那么它有一次机会去激活它的邻居结点u,激活的概率为θi·θu.那么,在结点u的多个邻居同时活跃的条件下,结点u被激活的概率为
![]()
![]()
(1)
其中,![]() 表示在传播项i的传播过程中,可能影响结点u的邻居结点集合,即
表示在传播项i的传播过程中,可能影响结点u的邻居结点集合,即![]() 其中,ti(u)表示用户u接收传播项i的时间;Δ为时延阈值,即在此时间段之内的传播为有效的,如果影响时间间隔超过了此阈值,则此次传播无效.每个被激活的结点仅有一次机会去激活它的不活跃邻居结点,该传播过程持续到没有被激活的结点为止.
其中,ti(u)表示用户u接收传播项i的时间;Δ为时延阈值,即在此时间段之内的传播为有效的,如果影响时间间隔超过了此阈值,则此次传播无效.每个被激活的结点仅有一次机会去激活它的不活跃邻居结点,该传播过程持续到没有被激活的结点为止.
IC模型和TI-IC模型最主要的区别在于:IC模型只考虑了活跃结点对相邻目标结点的影响概率,而不考虑传播项的具体情况,IC模型假定对所有传播项边上的影响概率都是相同的;而TI-IC模型在描述信息传播过程中关注目标结点对传播项的兴趣,不同的传播项对目标结点会有不同的兴趣,从而产生不同的影响概率.
TIC模型和TI-IC模型最主要的区别在于:TIC模型考虑了传播项的主题分布和用户在不同主题上对相邻目标用户的影响,因此不同的朋友对目标用户会产生不同的影响;而TI-IC模型只关注目标用户对传播项的兴趣,而不考虑不同朋友对目标用户的影响.当目标用户看到他的任何朋友接受传播项时,目标用户都会以相同的概率被影响.
本节使用EM算法求解基于主题兴趣的传播模型参数.该学习算法的输入是:社会网络G(V,E)、用户历史动作日志D(u,i,t)以及主题个数Z.在学习中我们假设每个用户只能接受相同传播项一次.另外,D中的u都属于G中的结点集合V.我们令I代表传播项集合,Di代表传播项i的传播轨迹.
学习算法的输出结果是TI-IC模型的参数,我们记为Θ.现假设TI-IC传播模型的每个传播轨迹都是独立的,则给定模型参数Θ的对数似然函数表示为
(2)
其中,L(Θ;Di)表示传播项i的传播轨迹的似然函数.现假设u在时刻ti(u)接收了传播项i,令ti(u)=∞代表u不接收![]() 表示在i的传播过程中可能影响u的邻居集合.当结点
表示在i的传播过程中可能影响u的邻居集合.当结点![]() 结点v在传播项i上一定活跃,结点u在传播项i上也一定活跃.
结点v在传播项i上一定活跃,结点u在传播项i上也一定活跃.![]() 表示在i的传播过程中,一定不会影响u的邻居集合.当结点
表示在i的传播过程中,一定不会影响u的邻居集合.当结点![]() 结点v在传播项i上一定活跃,结点u在传播项i上可能活跃、也可能不活跃.
结点v在传播项i上一定活跃,结点u在传播项i上可能活跃、也可能不活跃.
传播轨迹Di在第z个主题分量上的似然函数定义为![]() 其中,
其中,![]() 表示在传播项i传播过程中主题z使结点u被激活的概率,即
表示在传播项i传播过程中主题z使结点u被激活的概率,即![]() 表示传播项i的传播过程中,在主题z上结点u的邻居没有激活结点u的概率.
表示传播项i的传播过程中,在主题z上结点u的邻居没有激活结点u的概率.![]() 具体定义如下:
具体定义如下:

(3)
显然,在传播项i传播过程中,当结点![]() 时,在主题z上结点v激活结点u的概率为
时,在主题z上结点v激活结点u的概率为![]() 参照标准EM算法的符号表示,
参照标准EM算法的符号表示,![]() 表示参数Θ的当前估计.完全数据的似然函数表示如下:
表示参数Θ的当前估计.完全数据的似然函数表示如下:
![]()
![]()
![]()
(4)
其中,πz表示传播项i在主题z上的先验概率,![]() 表示在当前参数条件下,在传播项i传播过程中主题z占全部主题作用的百分比.具体推导过程如下:
表示在当前参数条件下,在传播项i传播过程中主题z占全部主题作用的百分比.具体推导过程如下:
![]()
![]()
⟹![]()
![]()
⟹![]()
⟹![]()
![]() ⟹
⟹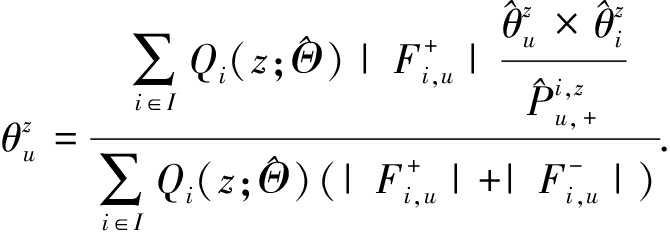
(5)
学习TI-IC模型参数的EM算法伪代码如算法1所示.开始随机地初始化参数![]() 和πz,需保证
和πz,需保证![]() 和
和![]() 算法1不断执行E步和M步直到收敛为止.算法1结束后,
算法1不断执行E步和M步直到收敛为止.算法1结束后,![]() 的值即为
的值即为![]()
算法1. 学习兴趣主题模型TI-IC参数的EM算法.
输入:社会网G(V,E)、传播轨迹D、主题个数Z;
输出:TI-IC参数Θ={θu(∀u∈V),θi(∀i∈I)}.
①![]()
② repeat
③ for alli∈Ido
④ for allz={1,2,…,Z} do
⑤
⑥ end for
⑦ end for *E-Step结束*
*E-Step结束*
⑧ for allz={1,2,…,Z} do
⑨![]()
⑩ for allu∈Vdo


 end for
end for
 end for
end for *M-step结束*
*M-step结束*
 until convergence
until convergence
从历史数据中学习TI-IC模型参数之后,在实际应用之前还需要获得传播项的主题分布向量.如果传播项是一个已经存在的传播项,TI-IC模型学习算法的输出同时包含了传播项的主题分布向量.然而,实际应用中的任务通常是促销新产品.如何针对新产品选择合适的主题分布向量是一个关键问题.下面给出3种新产品的主题分布向量构造方法:
1) 新产品的主题分布向量取自一个均分分布向量.这种方法显然没有考虑不同产品的特征,通常不能达到最佳的促销效果.
2) 由领域专家为新产品选择合适的主题分布向量.这种方法增加了人工的工作量,而且TI-IC模型中每个维度的具体含义,很难给出准确的定义,使得领域专家很难做出合适的选择.
3) 利用少量新产品的销售数据学习新产品的主题分布向量.假设有少量用户{u1,u2,…,un}购买了新产品i,这些用户的兴趣分布向量![]() 已经在学习TI-IC模型参数之后获得.直觉上这些用户应该对产品i感兴趣,这些用户的兴趣向量的对应分量应与产品i的主题分布向量的对应分量比较接近.为此,我们应选择产品i的主题分布向量θi使得下面的目标最小化:
已经在学习TI-IC模型参数之后获得.直觉上这些用户应该对产品i感兴趣,这些用户的兴趣向量的对应分量应与产品i的主题分布向量的对应分量比较接近.为此,我们应选择产品i的主题分布向量θi使得下面的目标最小化:
(6)
对式(6)的优化目标,我们使用梯度下降算法求解.具体求解过程如算法2所示,其中λ是学习步长.
算法2. 学习新传播项的算法.
输入:接收新传播项i的部分用户兴趣分布向量![]() 主题个数Z;
主题个数Z;
输出:新传播项i的主题分布向量θi.
①![]()
② repeat
③![]()
④ until convergence
本节首先提出了基于主题兴趣的影响传播最大化问题,然后给出了求解该问题的一个新的启发式算法.
本节在基于主题兴趣的传播模型TI-IC基础上,提出了基于主题兴趣的影响最大化问题TIIM,并给出了该问题的形式化定义.
基于主题兴趣的影响最大化问题TIIM:给定有向图G(V,E)、用户的历史动作日志D(u,i,t)、种集大小k、传播项i.基于兴趣主题的影响最大化问题是寻找大小为k的种集S,使得传播项i的影响范围最大.种集S形式化地表示为
![]()
(7)
其中,δi(S)表示种集S在传播项i上的影响范围.在TI-IC模型中,尽管边上的影响概率需考虑主题和兴趣,而传播的机制并没有发生变化.所以对于TI-IC模型而言,影响范围函数δi(S)的单调性和子模性可直接由IC模型继承而来.
对TIIM问题,完全可以使用传统贪心算法[1]求解.但是在大规模网络上由于多次蒙特卡洛模拟而使得贪心算法复杂度太高变得实际上并不可行.
贪心算法每次从所有结点中选择影响增益最大的结点直到达到k个结点为止.假设图中有|V|个结点、|E|条边,每次估计影响范围使用R次蒙特卡洛模拟,则贪心算法时间复杂度为O(kR|V||E|).实验中我们发现影响增益大的结点基本上都是本身影响范围大的结点.如果我们有一个启发式算法预先排序每个结点的影响范围,从中选中少量影响范围大的结点构成候选集,再使用贪心算法从候选集中选择结点,也可以获得和贪心算法一样的结果.下面给出候选集的选择过程.
从社交网中每个结点v出发,进行深度优先搜索,寻找影响概率大于等于阈值ε的所有路径,可构造一棵以v为根的可达路径树,则结点v的影响范围可以近似地估计为
(8)
其中,PATH(v,u)表示从结点v到结点u的可达路径集合;p(path)表示沿着路径path,结点v对结点u的影响概率.定义候选集合C,C中存储δv值最大的前λk结点,我们仅对C中的结点利用蒙特卡洛模拟计算影响范围,贪心选择k个结点作为种集.实验中λ=3就取得了和传统贪心算法几乎一样的实验结果.例1给出了生成候选集合的一个实例.
例1. 如图1(a),给定有向图G(V,E),边上概率已学习获得,期望选择2个种子结点进行影响最大化,设置阈值ε=0.03.构造结点a的可达路径树T(a),如图1(b)所示.由式(8)可得δa=0.878 5(没有包括对自身结点a的影响).以此类推,可以计算出图1(a)中所有结点的影响范围,δb=0.1,δc=0.9, 其余结点的影响范围都为0,因此C={a,c,b},再通过蒙特卡洛模拟方法贪心选择2个具有最大影响范围的结点作为种集.
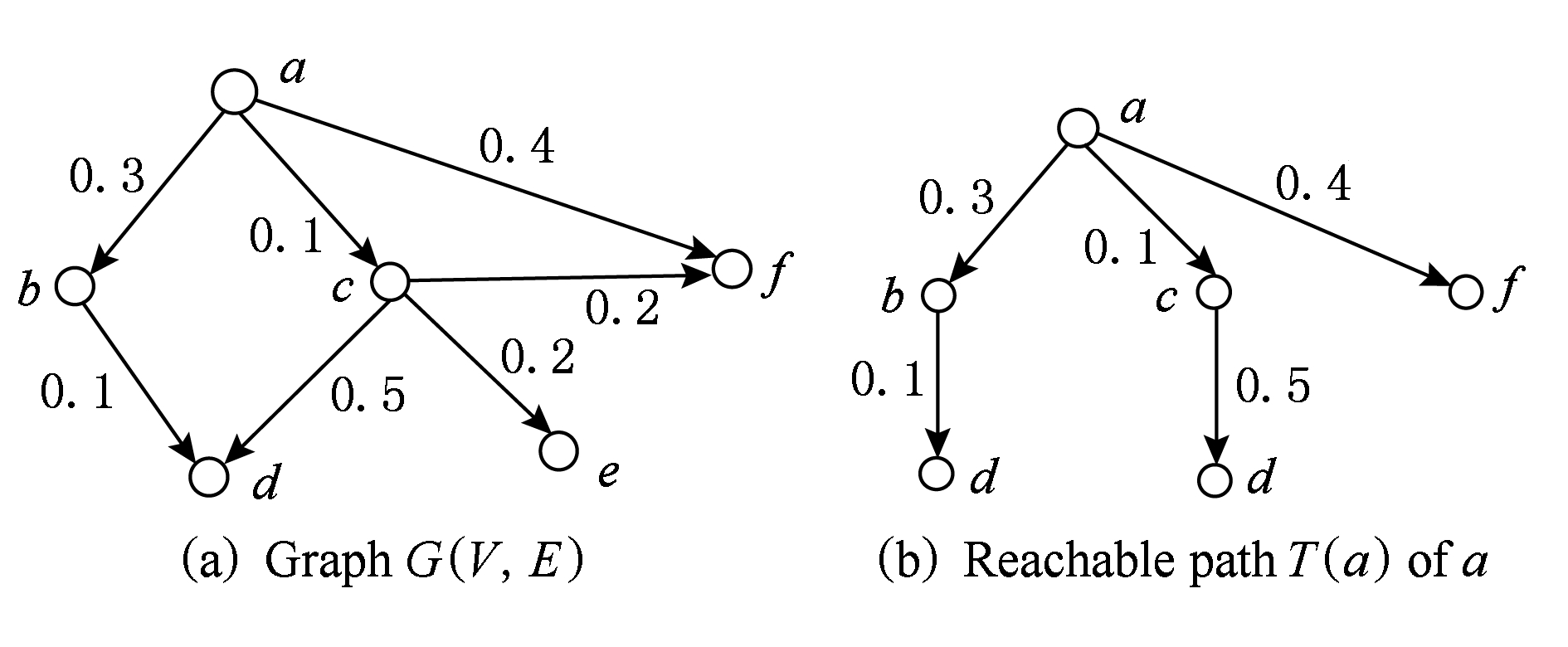
Fig. 1 An example for reachable paths
图1 可达路径的例子
在生成候选集之后,使用带有CELF优化的贪心算法选择种集,可得到有效解决TIIM问题的启发式算法ACG-TIIM.算法的伪代码如算法3所示.
算法3. 求解TIIM问题的启发式算法ACG-TIIM.
输入:图G(V,E)、用户兴趣向量集合{θu|u∈V}、传播项i的主题分布θi、种集大小k、主题个数Z、模拟次数R;
输出:种集S.
①S=∅,C=∅;
② for (u,v)∈E
③![]()
④ end for
⑤ for eachv∈V
⑥ CreateT(v);
⑦![]()
⑧ end for
⑨Sort(V,δv);
⑩ fori=1 toλkdo
 pushviintoC;
pushviintoC;
 end for
end for
 for eachv∈C
for eachv∈C
 Q.push(v,δi(v),0);
Q.push(v,δi(v),0);
 end for
end for
 while (|S|≤k)
while (|S|≤k)
 u=Q.pop( );
u=Q.pop( );
 if (u.round≠|S|)
if (u.round≠|S|)
 u.mg=δi(S∪{u})-δi(S);
u.mg=δi(S∪{u})-δi(S);
 Q.push(u,u.mg,|S|);
Q.push(u,u.mg,|S|);
 else
else
 S=S∪{u};
S=S∪{u};
 end if
end if
 end while
end while
 returnS.
returnS.
算法3的输入是一个有向图G(V,E)、由TI-IC模型学习得到的用户兴趣向量集合(其中向量θu表示用户u的兴趣分布)、传播项i的主题分布θi、一个正整数k、代表蒙特卡洛模拟次数的正整数R.输出具有最大影响范围的种集S(|S|=k).
步骤②~④利用由TI-IC模型学习得到的用户兴趣分布向量及传播项的主题分布向量来计算结点间的影响概率.步骤⑤~⑧预先估计每个结点本身的影响范围,实际上这种估计只需要保证排序正确即可.步骤⑨~ 按照每个结点的估计范围进行排序,将λk个结点放入候选集合C.步骤
按照每个结点的估计范围进行排序,将λk个结点放入候选集合C.步骤 ~
~ 将候选集合C的结点(连同当前增益、当前迭代次数)放入优先级队列Q.步骤
将候选集合C的结点(连同当前增益、当前迭代次数)放入优先级队列Q.步骤 ~
~ 使用CELF优化[19]的贪心算法选择大小为k的种集S.
使用CELF优化[19]的贪心算法选择大小为k的种集S.
步骤②~④的复杂度为O(Z|E|).步骤⑤~⑧的复杂度为O(|V||E|).步骤⑨的复杂度为O(|V|log|V|).步骤 ~
~ 是传统贪心过程,复杂度为O(kR|C||E|).所以ACG-TIIM算法总的复杂度为O(|V||E|+kR|C||E|).传统贪心算法时间复杂度为O(kR|V||E|).因为|C|≪|V|,所以ACG-TIIM算法要比传统贪心算法快很多.
是传统贪心过程,复杂度为O(kR|C||E|).所以ACG-TIIM算法总的复杂度为O(|V||E|+kR|C||E|).传统贪心算法时间复杂度为O(kR|V||E|).因为|C|≪|V|,所以ACG-TIIM算法要比传统贪心算法快很多.
本节在2个真实数据集上测试和评估本文提出的模型和算法,并且与多个现有的模型及算法进行比较.
我们使用2个真实数据集进行实验.2个数据集都包含社会网G(V,E)和一组动作日志D(u,i,t).数据集分别是Digg[6]和Last.fm[6].其中,Digg数据集是一个社交新闻网站,用户在网站上对文章进行投票评论,D中包含的元组(u,i,t)代表用户u在时刻t投票给了故事i.如果用户u投票给故事i,用户u的朋友v在之后不久也投票给了故事i,采用与文献[6]相同的处理方式,认为这个投票的动作从用户u传播到了朋友v.数据集Last.fm是世界最大的社交音乐平台,用户可以在这个网站中搜索、收听以及评论自己喜欢的音乐.D中包含的元组(u,i,t)代表用户u在时刻t评论了歌手i.
我们从Digg数据集中提取了15 000个结点和395 513条边以及相应的动作日志.从Last.fm数据集中提取了5 100个结点和23 453条边以及相应的动作日志.在2个数据集的动作日志上各选择了1 000个传播项,并且每个传播项的传播范围都超过50.在2个数据集中,我们都不考虑孤立结点,即在D中有动作记录,但是在图G中却没有朋友的结点.
实验中所有算法均用C++编写,在Microsoft Visual Studio 2005环境下编译.所有实验都在Intel Core i7 6700 3.4 GHz-主频 CPU、8 GB主存的台式机上运行.
本文模型主要与下面6个模型进行对比.
1) 独立级联模型(IC模型).传统的独立级联模型工作原理如下.网络中结点共有2个状态,活跃结点与不活跃结点,每个活跃结点有且仅有一次机会去激活未活跃的结点,并且该过程不可逆,传播的停止条件是当前时刻没有再被激活的结点.该模型的参数为结点间的影响传播概率,由文献[20]中的EM算法学习而来.
2) 基于主题的独立级联模型(TIC模型[6]).TIC模型工作原理与IC模型一致,与IC模型不同的是,活跃结点激活不活跃结点的概率为基于主题的影响传播概率.该模型的参数为结点间基于主题的影响传播概率,由文献[6]中的EM算法学习而来.
3) 固定传播概率的IC模型(NIC).固定边上影响概率为0.02(多次实验测试最佳的影响概率值),工作原理与IC模型一致.
3个模型共同需要设置的参数是延迟阈值Δ,通常的做法是设置Δ在3~5之间,但是通过实验我们发现Δ的变化对3个模型的影响不大,为了减少模型的计算量,在实验中我们都把Δ的值设置为无穷大.
4) 使用混合泊松过程建模社交影响、外部影响和内部影响的CMPP模型[7].取社交影响权重为0.3,内部影响权重为0.7,不考虑外部影响,这种配置是CMPP模型在本文实验数据上的最好效果.
5) 本文基于兴趣主题的传播模型TI-IC-UN.在模拟传播之前,对新传播项的特征向量直接取均匀分布.
6) 本文基于兴趣主题的传播模型TI-IC.在模拟传播之前,对新传播项的特征向量使用梯度下降算法(算法2)进行学习.
对于新的传播项i,我们通过限制条件选取感染源集合:首先找到传播项i的所有活跃结点;然后依次检查这些活跃结点,如果活跃结点v的任何邻点在传播项i上都没有在v之前活跃,就把活跃结点v加入到感染源集合中.
对于TIC模型和TI-IC模型,如果没有明确说明,我们设置传播项主题分布个数Z=10.TIC模型也使用算法2学习了新传播项的主题分布向量.
我们将所有传播项按照8∶2的比例分成训练集和测试集,保证一个传播项的传播轨迹或者全在训练集或者全在测试集.显然测试集中的每个传播项都是新传播项.首先在训练集上学习模型中的参数,然后根据学习得到的模型预测测试集中每个新传播项的传播结果.具体预测过程为:对每个传播项i,首先确定它的感染源集合(如果结点v接受了传播项i,但是v的任何邻居没有在v之前接受传播项i,则结点v是感染源);然后让感染源中的结点为初始活跃结点,使用2 000次蒙特卡洛模拟模拟传播项i的传播过程,计算每个结点被激活的概率,最后根据预测的概率值计算如下10个指标.
1) 均方误差(mean squared error,MSE).计算每个结点预测的概率值与真实值(被激活是1,没被激活是0)差的平方,然后求平均值.
2) 准确率(Accuracy).给定一个激活阈值τ,如果预测的概率值大于等于τ,则预测该结点活跃;否则预测该结点不活跃.对每个传播项i,计算预测正确的结点数占所有结点数的百分比.
3) 真正例(true positive,TP).预测为活跃实际为活跃的结点数.
4) 假正例(false positive,FP).预测为活跃实际为不活跃的结点数.
5) 真负例(true negative,TN).预测为不活跃实际为不活跃的结点数.
6) 假负例(false negative,FN).预测为不活跃实际为活跃的结点数.
7) 精确率(precision,P):
8) 召回率(recall,R):
9)F1分数(F1-score):
10) ROC曲线下面积AUC.按照预测的概率值对所有结点排序,计算ROC曲线下面积.
注意:对每个传播项,都按照上述公式先计算MSE,Accuracy,F1-score,AUC;然后在所有传播项上求均值.
5.3.1 在MSE上的对比
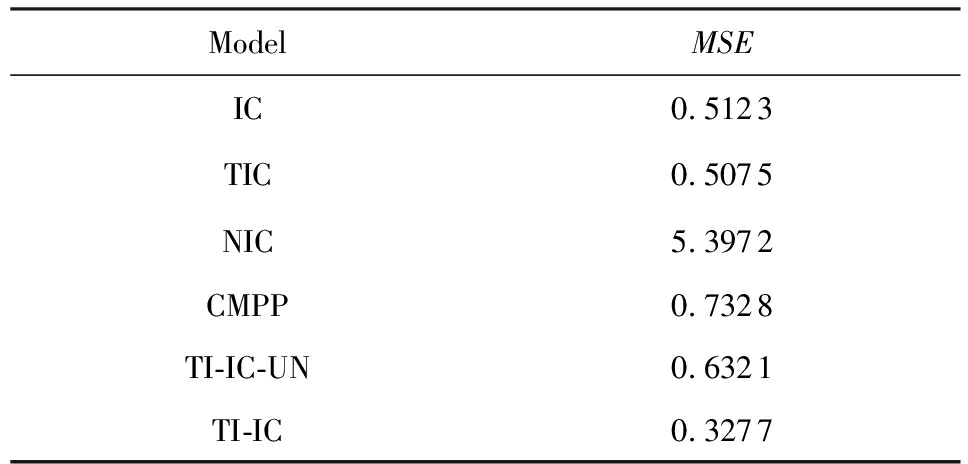
表1和表2分别给出了不同模型在2个数据集合上的MSE.可以看出,NIC模型的误差最大,因为NIC模型使用了固定的影响概率,使得预测效果较差.CMPP模型明显优于NIC模型,但是比IC模型和TIC模型要差.在Digg数据集上,IC模型明显优于TIC模型;而在Last.fm数据集上,IC模型与TIC模型差别不大.TI-IC-UN模型由于没有学习新传播项的主题分布向量,使得MSE要大于IC模型.但是当学习了新传播项的分布向量后得到的TI-IC模型要明显优于IC模型和TIC模型.这说明不同的传播项有不同的特征,在传播之前学习其特征是必要的.
Table1MeanSquaredErrorofDifferentModelsinDigg
表1Digg上不同模型的均方误差

Table2MeanSquaredErrorofDifferentModelsinLast.fm
表2Last.fm上不同模型的均方误差
5.3.2 在准确率和F1分数上的对比
图2和图3分别给出了不同模型在数据集Digg和Last.fm上在不同激活阈值τ下的准确率.由图2和图3可知,在准确率性能的度量上设置激活阈值τ>0.1时,我们新提出的模型TI-IC都明显高于其他模型.其中NIC模型性能最差,IC模型和TIC模型次于TI-IC模型,但是明显高于其他模型;TI-IC-UN模型由于没有考虑新传播项的主题分布,与IC模型和TIC模型相比,在准确率方面仍然处于劣势.
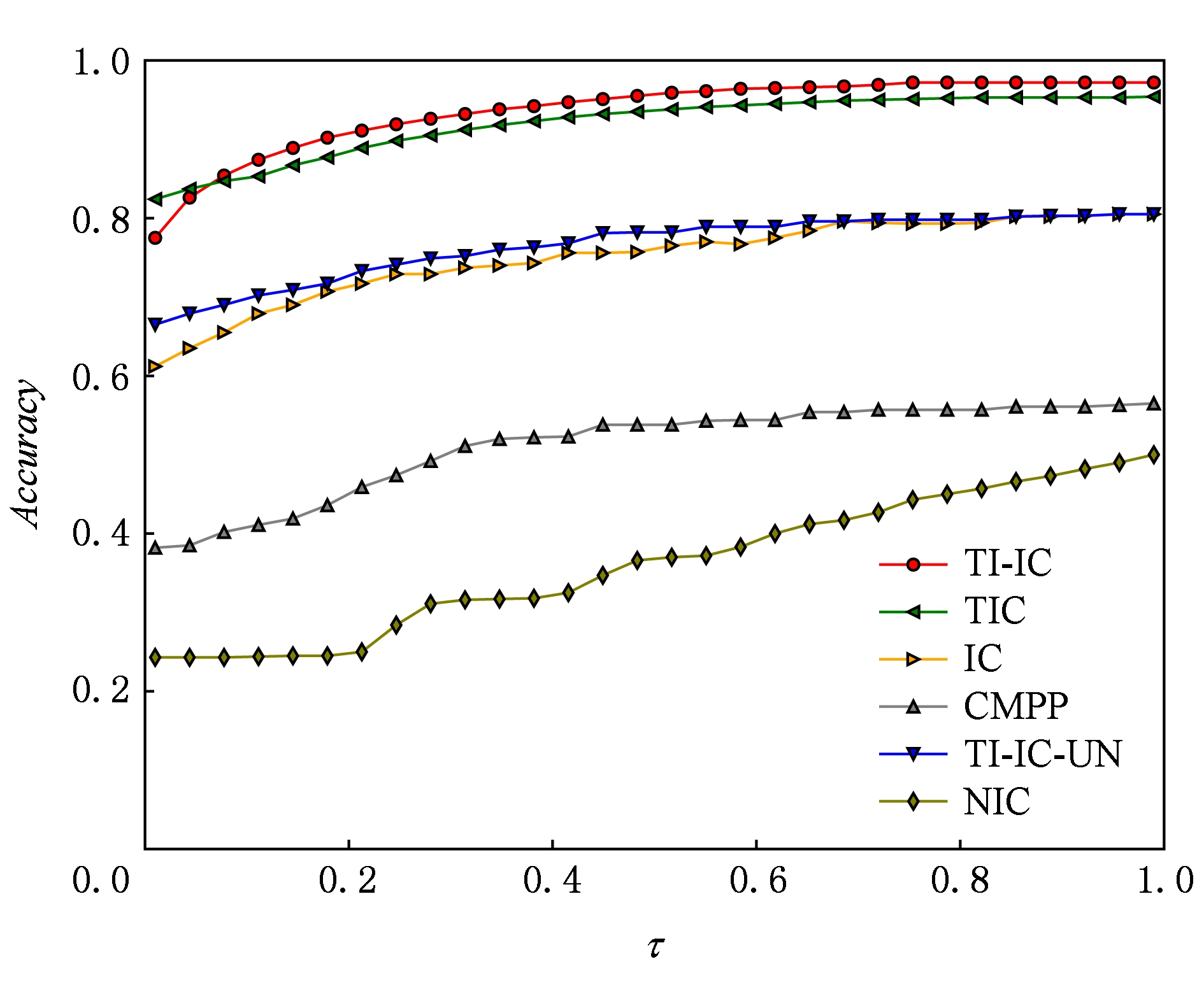
Fig. 2 Accuracy of different models in Digg dataset
图2 Digg数据集上不同模型下的准确率
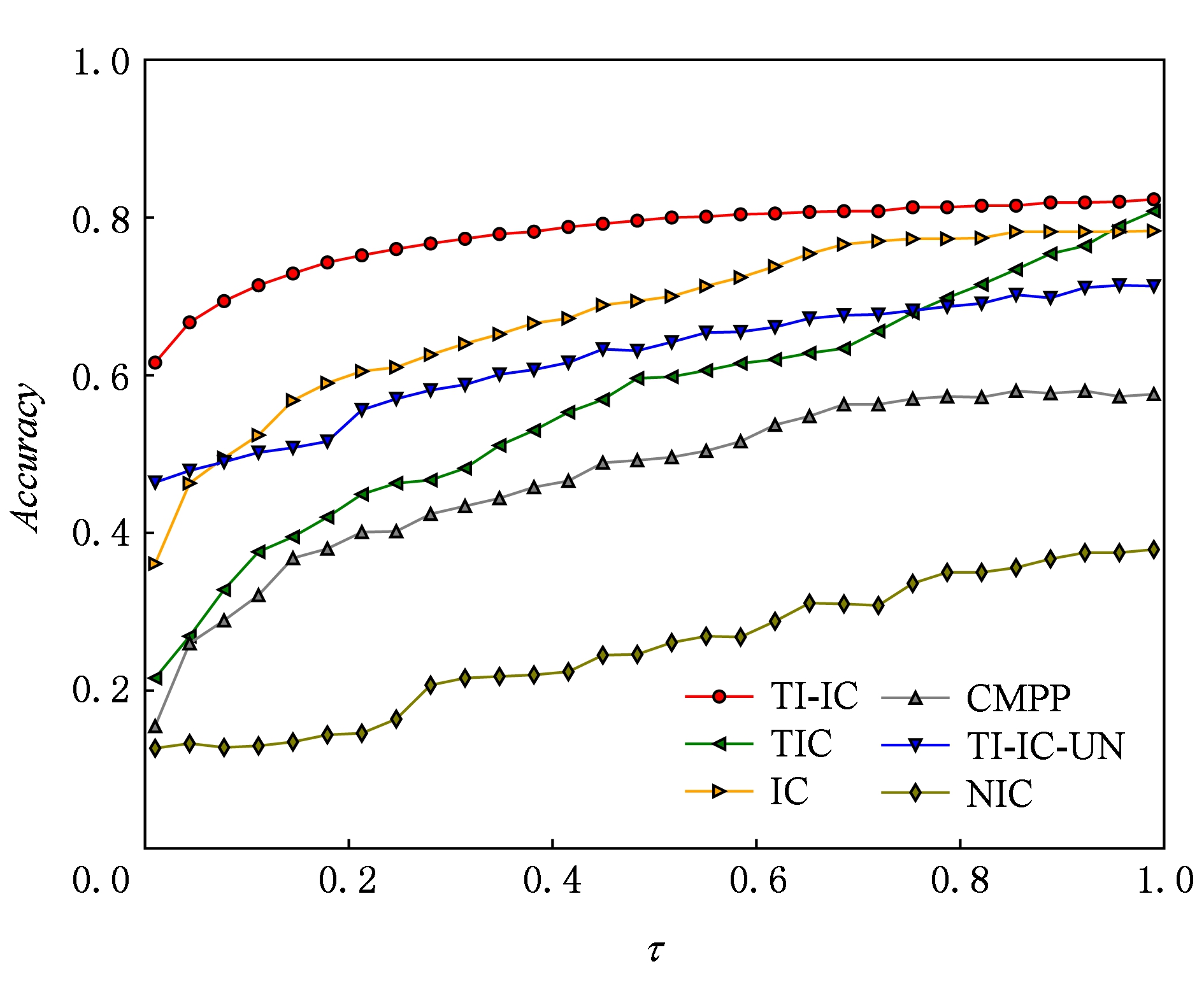
Fig. 3 Accuracy of different models in Last.fm dataset
图3 Last.fm数据集上不同模型下的准确率
图4和图5分别给出了不同模型在数据集Digg和Last.fm 上在不同激活阈值τ下的F1-score.从图4和图5可以看出,TI-IC模型的F1-score始终高于其他模型;TI-IC-UN模型由于没有考虑新传播项的主题分布,在F1-score上也不具有优势.
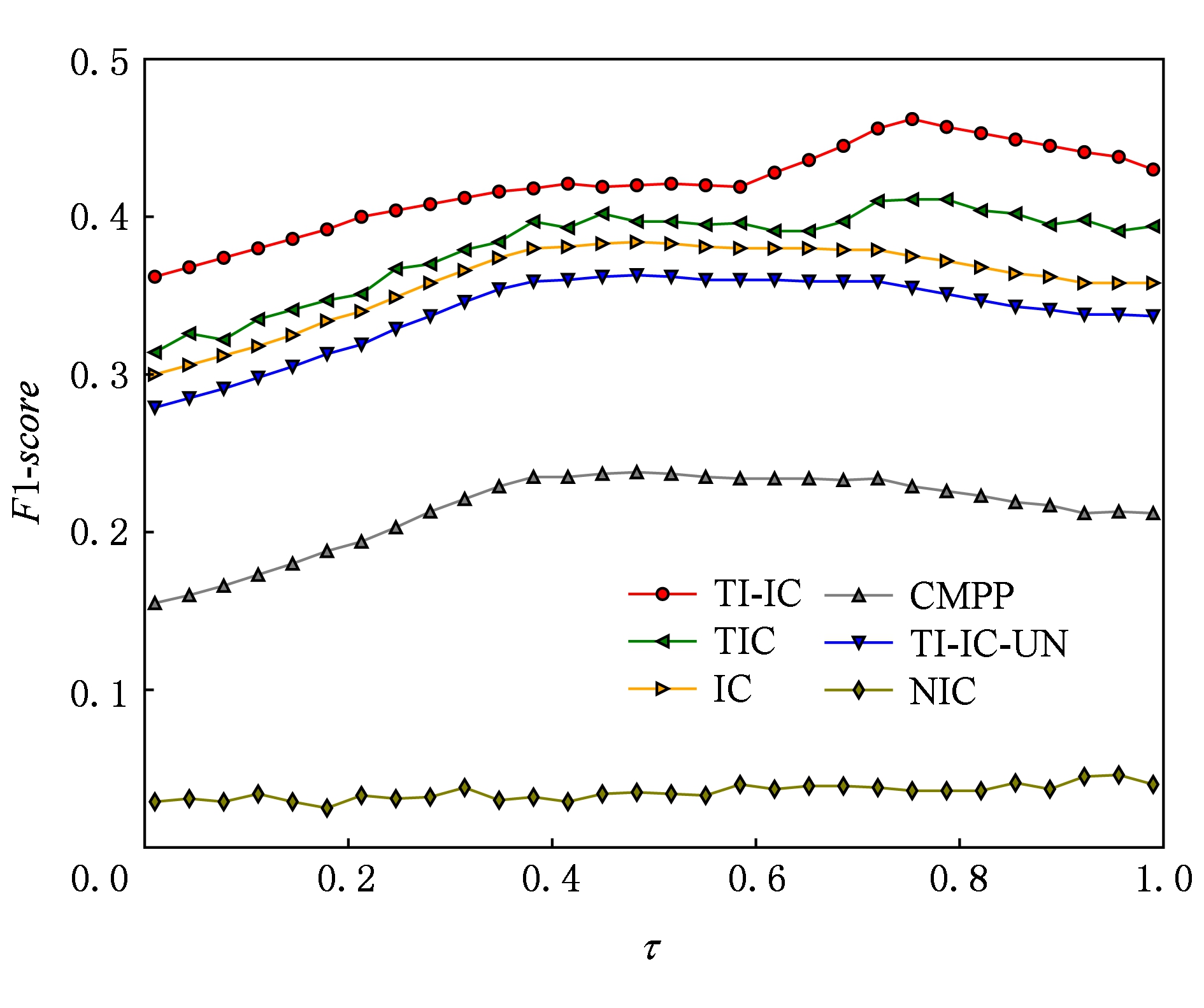
Fig. 4 F1-score of different models in Digg dataset
图4 Digg数据集上不同模型下的F1-score
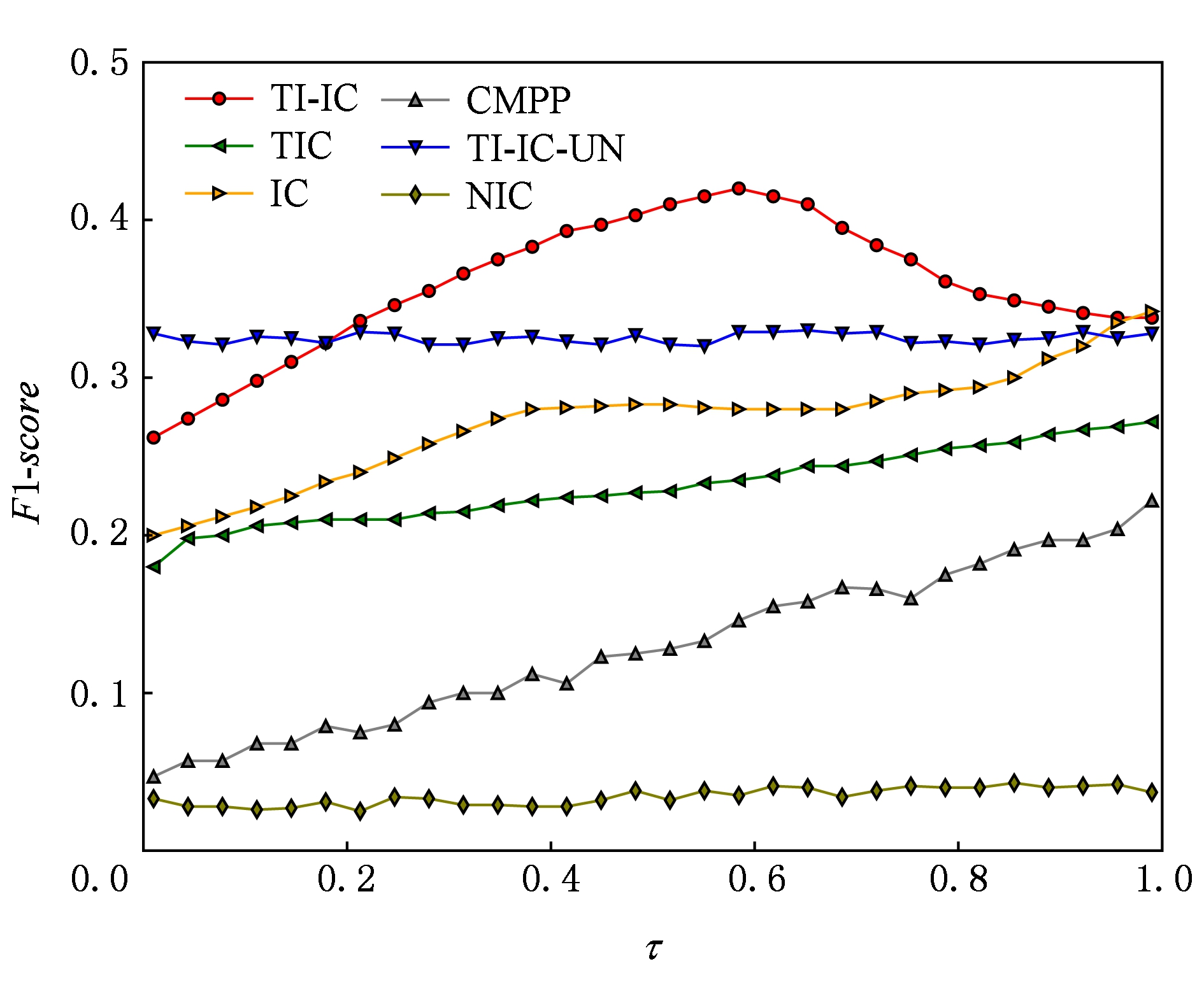
Fig. 5 F1-score of different models in Last.fm dataset
图5 Last.fm数据集上不同模型下的F1-score
综上所述,我们新提出的模型TI-IC在准确率和F1-score上均好于现有的IC模型和TIC模型,并且TI-IC,IC,TIC模型的预测效果明显好于CMPP模型和固定影响概率的NIC模型.
5.3.3 在ROC曲线上的对比
我们对比了不同模型的ROC曲线,如图6和图7所示.在数据集Digg上TI-IC模型与IC模型、TIC模型在ROC曲线上有多处重叠,但是TI-IC模型在ROC曲线下面积仍然大于IC模型和TIC模型.在数据集Last.fm上,TI-IC模型的优势更明显.在2个数据集上,TI-IC-UN模型的ROC曲线下面积仍然低于IC模型和TIC模型,再次说明学习新传播项自身特征的重要性.
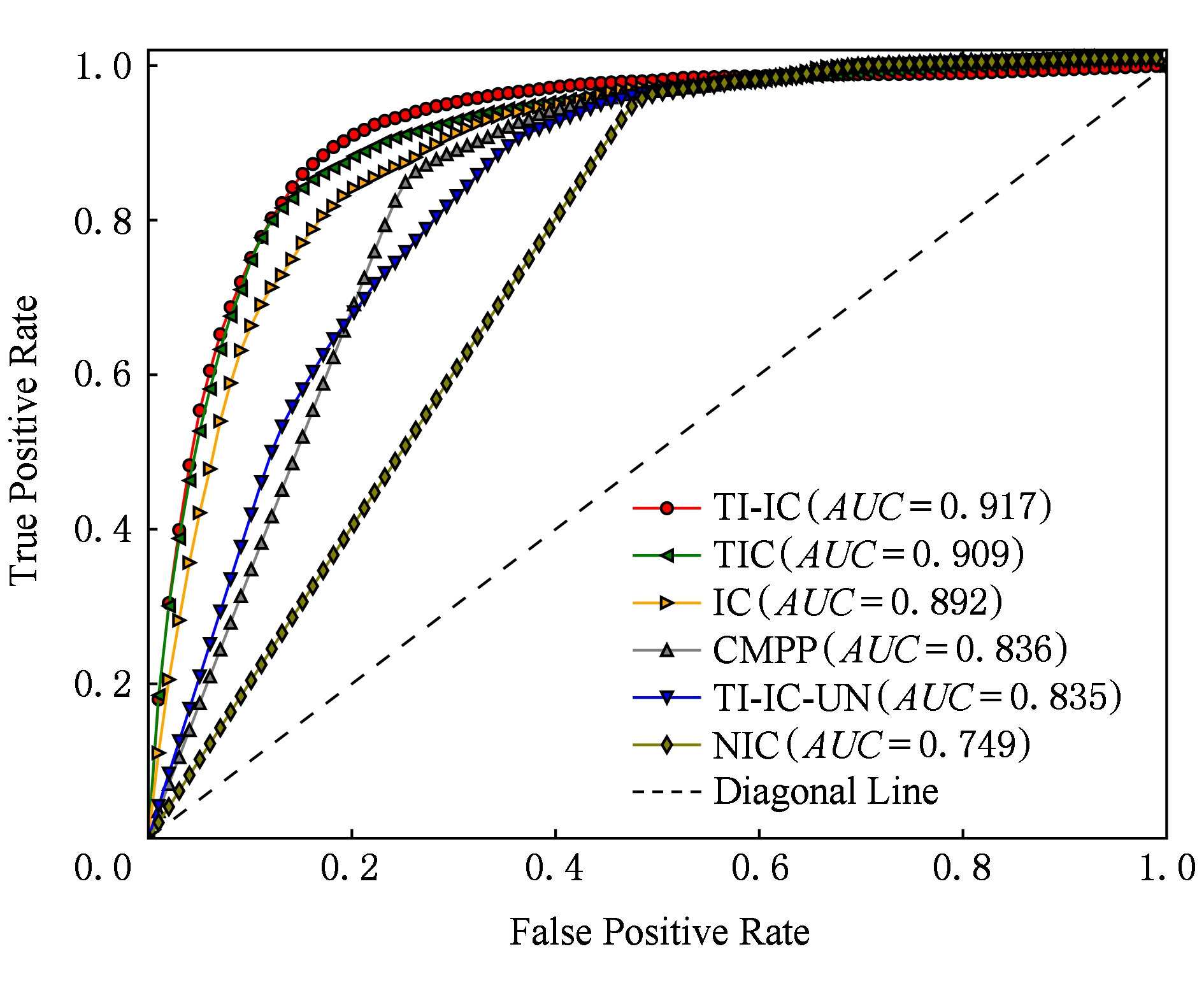
Fig. 6 ROC curve of different models in Digg dataset
图6 Digg数据集上不同模型下的ROC曲线
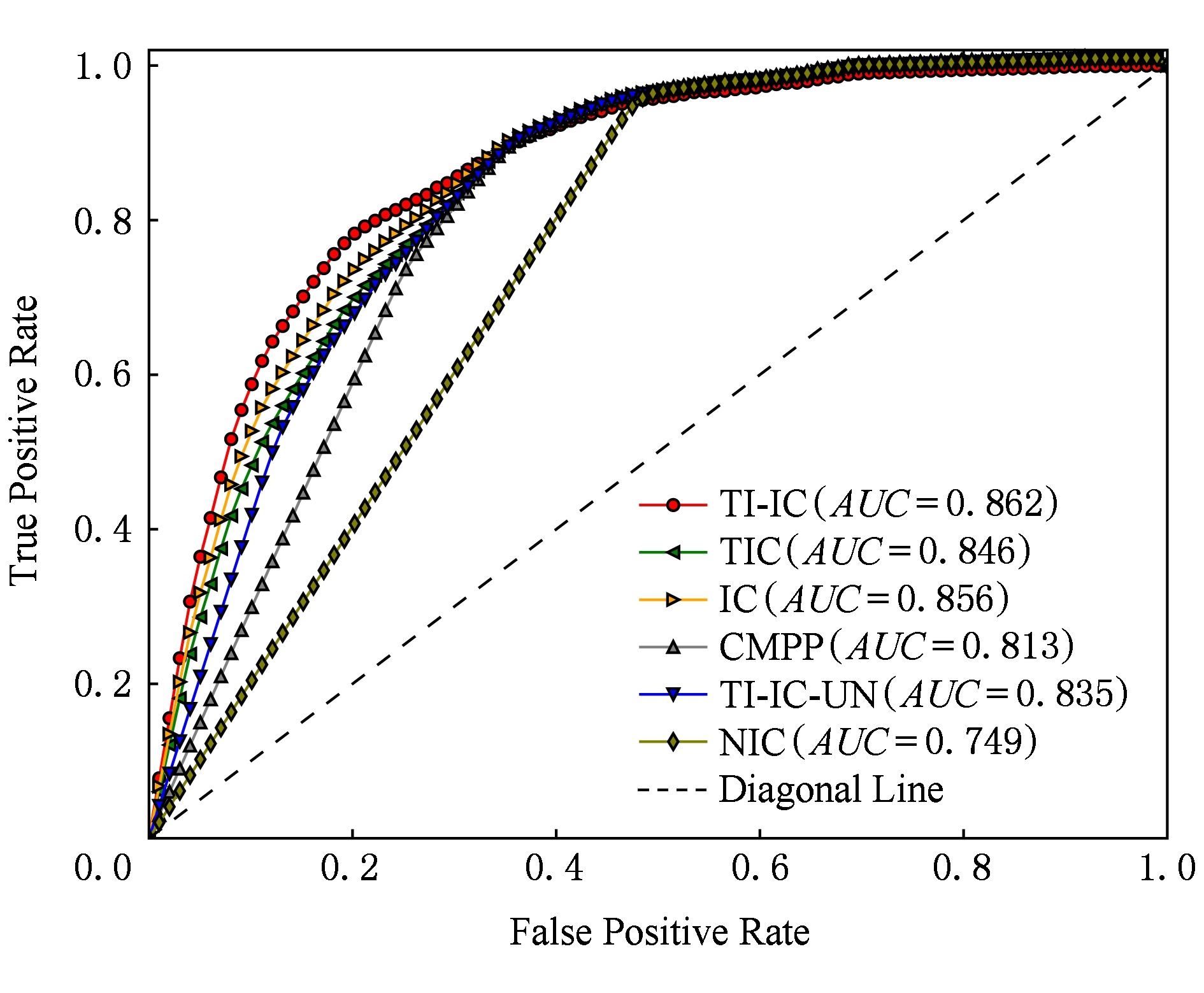
Fig. 7 ROC curve of different models in Last.fm dataset
图7 Last.fm数据集上不同模型下的ROC曲线
综合5.3.1~5.3.3节中的实验结果和分析,我们可以得出如下结论:TI-IC模型相比于其他现有模型能更有效地模拟传播过程,更准确地预测传播结果.
本节实验主要验证不同主题个数对实验结果的影响.图8和图9分别给出了数据集Digg和Last.fm上TI-IC模型和TIC模型在不同主题数下的ROC面积,其他模型没有主题个数选项.从实验图中可以看出:当主题个数是10时,基本达到了理想的实验结果;当主题个数大于10时,实验效果没有明显改善.考虑到学习效率,本文设置主题个数为10.
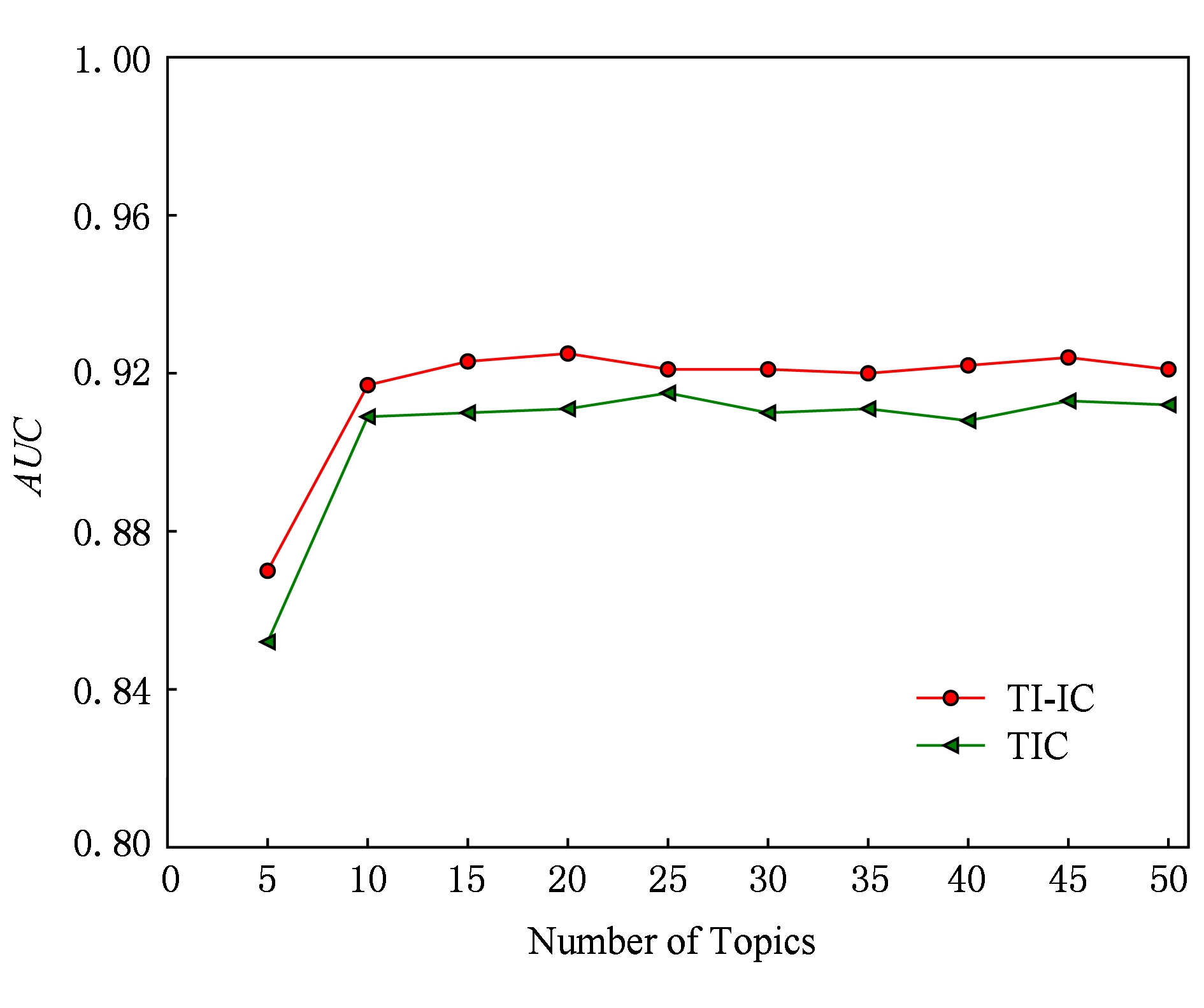
Fig. 8 ROC area vs topic number in Digg dataset
图8 Digg数据集上主题个数对ROC面积的影响

Fig. 9 ROC area vs topic number in Last.fm dataset
图9 在Last.fm数据集上主题个数对ROC面积的影响
本文提出的启发式算法ACG-TIIM,主要与如下影响最大化算法进行比较.
1) LDegree算法.在这个算法中,我们简单选择具有最大度的k个结点作为种集,再使用蒙特卡洛模拟估计影响范围.
2) CELF-Gre算法.使用带有CELF优化[19]的贪心算法选择k个结点作为种集,该算法在影响最大化问题中被广泛应用.
3) ACG-TIIM-UN算法.本文提出启发式算法ACG-TIIM,但是不学习新传播项的主题分布,直接取均匀分布.
本节实验中,涉及蒙特卡洛模拟估计影响范围时都将设置模拟次数R=2 000.CELF-Gre算法和ACG-TIIM算法在应用到TI-IC模型之前,都用本文EM算法获取用户的兴趣分布以及新传播项的主题分布,然后转换成边上的影响概率.新传播项取自测试集合,并对所有传播项的结果计算均值.CELF-Gre算法和ACG-TIIM算法在应用到IC模型之前,都用文献[20]中算法直接获取边上的影响概率.CELF-Gre算法和ACG-TIIM算法在应用到TIC模型之前,都用文献[6]中算法获取边上分主题的影响概率,再用本文算法学习新传播项的主题分布,转换成边上的影响概率.在实验中,我们将统一设置算法中的主题数目Z=10,选择候选集合时设置λ=3.
5.5.1 种集大小与影响范围的关系
本节实验主要验证种影响范围与种集大小的关系.首先在TI-IC模型下,运行上述对比算法选择不同大小的种集,在数据集Digg和Last.fm上的影响范围如实验图10和图11所示.
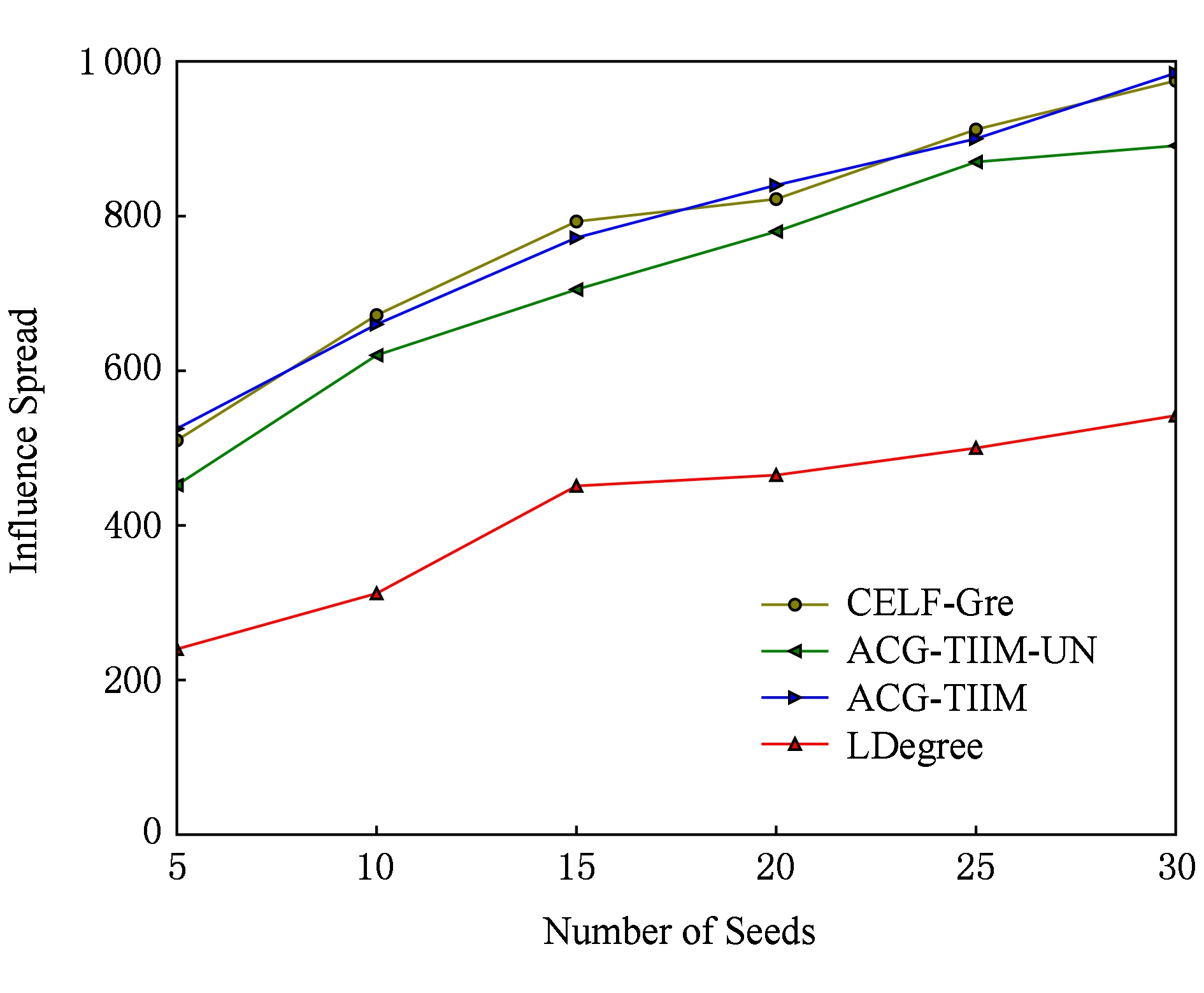
Fig.10 Influence spread vs seeds number in Digg dataset
图10 Digg数据集上种集大小对影响范围的影响
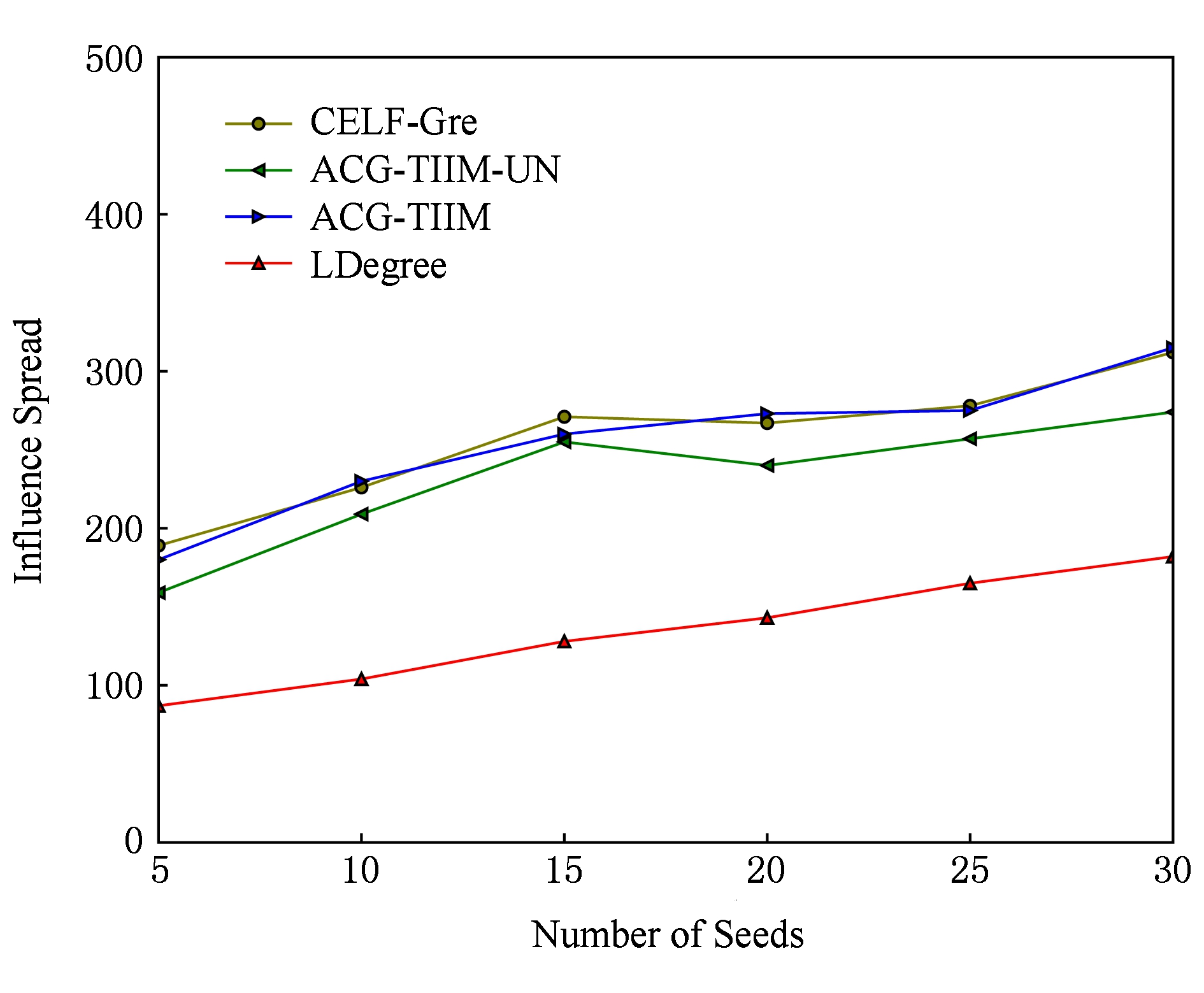
Fig. 11 Influence spread vs seeds number in Last.fm dataset
图11 Last.fm数据集上种集大小对影响范围的影响
从图10和图11可得出如下结论:LDegree算法的运行效果最差,是由于该算法只考虑社会网中的拓扑结构,选择了全局具有最大度的结点,既没有考虑用户之间的影响,也没有考虑用户对传播项的兴趣.ACG-TIIM-UN算法得到的影响范围远远好于LDegree算法,是由于该算法在真实的数据上学习了用户的兴趣,转换成了影响概率,使得影响范围计算更准确.然而,ACG-TIIM-UN算法获得的影响范围仍旧小于CELF-Gre算法和ACG-TIIM算法,这是因为CELF-Gre算法和ACG-TIIM算法除了学习用户的兴趣分布,还学习了新传播项的主题分布,从而使得影响范围更广.而且,我们进一步检查了算法ACG-TIIM-UN和算法ACG-TIIM返回的种集,在所有传播项上,算法ACG-TIIM-UN返回的种集几乎都一样;但是算法ACG-TIIM在不同的传播项上返回的种子集合差异很大,这再次说明在促销新产品时,应该针对特定的产品选择特定的用户.CELF-Gre算法和ACG-TIIM算法得到几乎相同的影响范围.我们进一步检查了这2个算法返回的种集,发现在不同的种集大小条件下,这2个算法返回的种集几乎全完一样.这是因为这2个算法在计算种集之前,学习了相同的参数(包括用户兴趣分布和新传播项的主题分布).但是ACG-TIIM算法只考察了部分候选结点,而CELF-Gre算法需要考察全部候选结点,这使得这2个算法的运行效率会差别很大,具体差别见5.5.2节的实验.
在IC模型和TIC模型下,我们也运行了上述对比算法.在IC模型下,ACG-TIIM算法和CELF-Gre算法的影响范围几乎完全一样.在TIC模型下,ACG-TIIM-UN的影响范围稍微低于ACG-TIIM算法和CELF-Gre算法,ACG-TIIM算法和CELF-Gre算法的影响范围几乎完全一样.
5.5.2 种集大小与运行时间的关系
本节主要对影响最大化算法的运行时间进行比较.在TI-IC模型上,运行上述对比算法选择不同大小的种集,在数据集Digg和Last.fm上的运行时间如实验图12和图13所示:

Fig.12 Running time vs seeds number in Digg dataset
图12 Digg数据集上种集大小对运行时间的影响
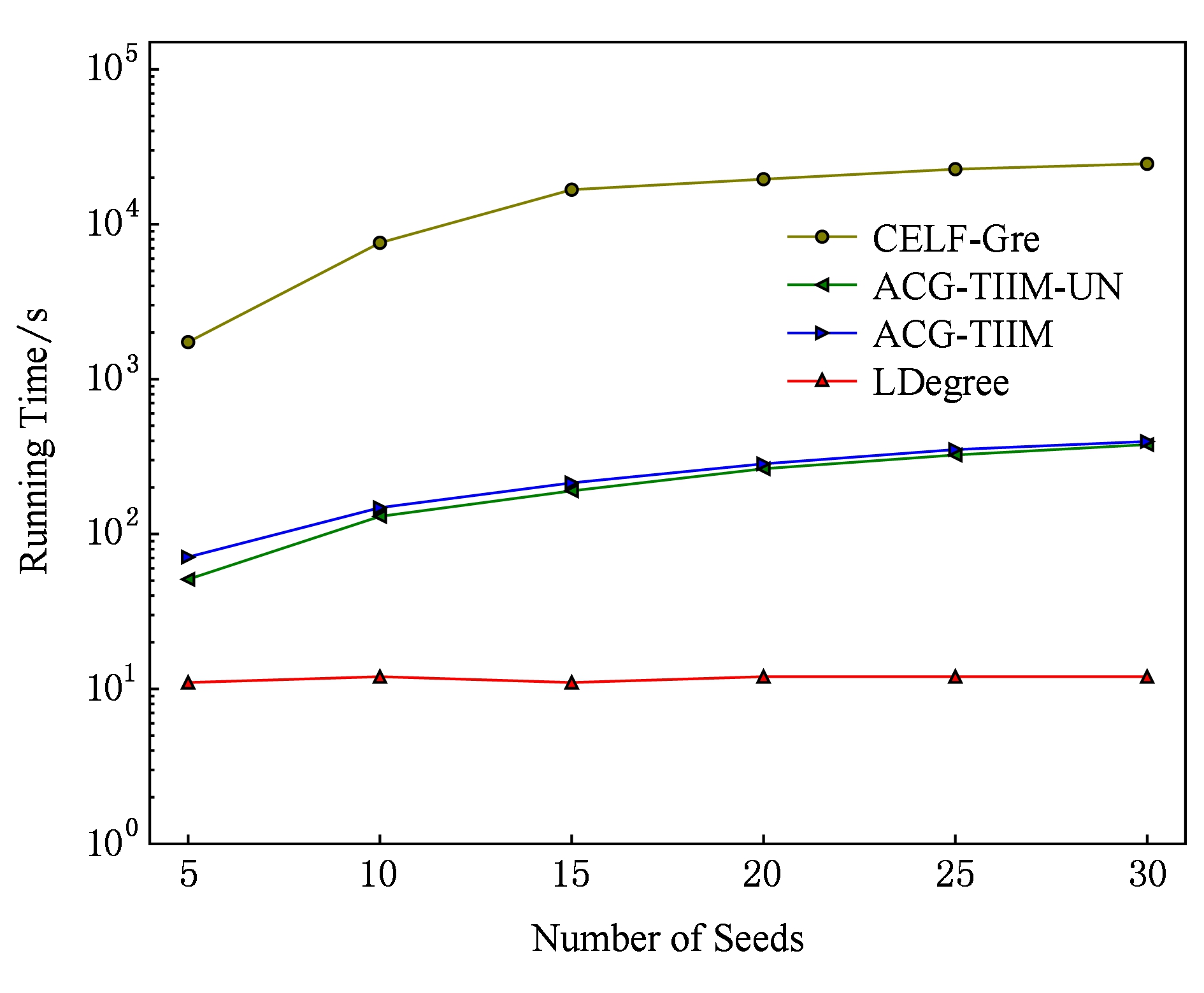
Fig. 13 Running time vs seeds number in Last.fm dataset
图13 Last.fm数据集上种集大小对运行时间的影响
从实验图中可得出如下结论:LDegree算法的运行时间是最短的,由于该算法只是从整个网络中选择具有最大度的k个结点作为种集.ACG-TIIM算法和ACG-TIIM-UN算法的运行效率较为接近,ACG-TIIM算法在选择种集之前需要学习新传播项的主题分布,所以ACG-TIIM算法比ACG-TIIM-UN算法稍慢.但是ACG-TIIM算法比CELF-Gre算法快2个数量级,这是因为ACG-TIIM算法在选择种集之前,先生成候选结点,仅对候选结点进行蒙特卡洛模拟估计影响范围.候选结点数要远远小于所有结点数,所以ACG-TIIM算法效率比CELF-Gre算法高很多,这与4.2节算法复杂性分析结果基本一致.
在IC模型和TIC模型下,我们也运行了上述对比算法,ACG-TIIM算法效率远远优于CELF-Gre算法.
本文提出了基于用户兴趣和传播项主题分布的传播模型TI-IC,并给出了基于TI-IC模型的影响最大化算法ACG-TIIM.实验结果表明,本文提出的模型TI-IC在多个测试指标上都优于现有的模型,能更准确地预测传播结果.ACG-TIIM算法可高效求解TI-IC模型的影响最大化问题,而且ACG-TIIM算法也适用于IC模型和TIC模型上的影响最大化问题.
未来的研究工作拟对用户的兴趣分布和用户之间的影响进行联合建模,希望能获得更有效的社交网传播模型.
参考文献
[1] Kempe D, Kleinberg J. Maximizing the spread of influence through a social network[C] //Proc of the 9th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2003: 137-146
[2]Chen Wei, Wang Yajun, Yang Siyu. Efficient influence maximization in social networks[C] //Proc of the 15th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 199-208
[3]Chen Wei, Wang Chi, Wang Yajun. Scalable influence maximization for prevalent viral marketing in large-scale social networks[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 1029-1038
[4]Kim J, Kim S K, Yu H. Scalable and parallelizable processing of influence maximization for large-scale social networks[C] //Proc of the 29th Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2013: 266-277
[5]Li Yuchen, Zhang Dongxiang, Tan Kian-Lee. Real-time targeted influence maximization for online advertisements[J]. Proceedings of the VLDB Endowment, 2015, 8(10): 1070-1081
[6]Barbieri N, Bonchi F, Manco G. Topic-aware social influence propagation models[C] //Proc of the 12th Int Conf on Data Mining. Piscataway, NJ: IEEE, 2012: 81-90
[7]Rong Yu, Cheng Hong, Mo Zhiyu, et al. Why it happened: Identifying and modeling the reasons of the happening of social events[C] //Proc of the 21st ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2015: 1015-1024
[8]Galhotra S, Arora A, Roy S. Holistic influence maximiza-tion-combining scalability and efficiency with opinion-aware models[C] //Proc of the 2016 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2016: 743-758
[9]Domingos P, Richardson M. Mining the network value of customers[C] //Proc of the 7th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2001: 57-66
[10]Aslay C, Barbieri N, Bonchi F, et al. Online topic-aware influence maximization queries[C] //Proc of the 17th Int Conf on Extending Database Technology. New York: ACM, 2014: 92-101
[11]Chen Shuo, Fan Jun, Li Guoliang, et al. Online topic-aware influence maximization[J]. Proceedings of the VLDB Endowment, 2015, 8(6): 666-677
[12]Saito K, Kimura M, Ohara K, et al. Generative models of information diffusion with asynchronous time-delay[C/OL] //Proc of the 2nd Asian Conf on Machine Learning. 2010 [2017-05-01]. http://www.ar.sanken.osaka-u.ac.jp/~motoda/papers/acml_10.pdf
[13]Lagnier C, Denoyer L, Gaussier E, et al. Predicting information diffusion in social networks using content and user’s profiles[C] //Proc of the 35th European Conf on Information Retrieval. Berlin: Springer, 2013: 74-85
[14]Myers S A, Zhu Chenguang, Leskovec J. Information diffusion and external influence in networks[C] //Proc of the 18th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2012: 33-41
[15]Rodriguez M G, Leskovec J, Scholkopf B. Modeling information propagation with survival theory[C] //Proc of the 30th Int Conf on Machine Learning. New York: ACM, 2013: 666-674
[16]Gomez-Rodriguez M, Leskovec J, Krause A. Inferring networks of diffusion and influence[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 1019-1028
[17]Bourigault S, Lagnier C, Lamprier S, et al. Learning social network embeddings for predicting information diffusion[C] //Proc of the 7th ACM Int Conf on Web Search and Data Mining. New York: ACM, 2014: 393-402
[18]Bourigault S, Lamprier S, Gallinari P. Representation learning for information diffusion through social networks: An embedded cascade model[C] //Proc of the 9th ACM Int Conf on Web Search and Data Mining. New York: ACM, 2016: 573-582
[19]Leskovec J, Krause A, Guestrin C, et al. Cost-effective outbreak detection in networks[C] //Proc of the 13th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2007: 420-429
[20]Saito K, Nakano R, Kimura M, et al. Prediction of information diffusion probabilities for independent cascade model[C] //Proc of Int Conf on Knowledge-Based Intelligent Information & Engineering Systems. Amsterdam: IOS Press, 2008: 67-75
Liu Yong, Xie Shengnan, Zhong Zhiwei, Li Jinbao, and Ren Qianqian
(SchoolofComputerScienceandTechnology,HeilongjiangUniversity,Harbin150080) (KeyLaboratoryofDatabaseandParallelComputingofHeilongjiangProvince(HeilongjiangUniversity),Harbin150080)
AbstractInfluence maximization is a problem of finding a small set of seed nodes in a social network that maximizes the spread scope of a propagation item. Existing works only take into account the topic distribution on propagation items, but ignore the interest distribution on users. This paper focuses on how to select the most influential seeds when both the topic distribution of propagation items and the interest distribution of users are taken into consideration. A topic-interest independent cascade (TI-IC) propagation model is proposed, and an expectation maximization (EM) algorithm is proposed to learn the parameters of the TI-IC model. Based on the TI-IC model, a topic-interest influence maximization (TIIM) problem is proposed, and a new heuristic algorithm called ACG-TIIM is presented to solve TIIM. ACG-TIIM first takes each user as a root node to construct a reachable path tree, roughly estimate the influence scope of each user, and then sorts all the users according to the estimated influence scope to select a small number of users as candidate seeds, finally uses the greedy algorithm with EFLF optimization to select the most influential seeds from candidate seeds. The experimental results on real datasets show that TI-IC model is superior to classical IC and TIC models in describing propagation law and predicting propagation results. ACG-TIIM can solve the TIIM problem effectively and efficiently.
Keywordssocial networks; influence maximization; topic distribution; propagation model; expectation maximization
中图法分类号TP311.1
通信作者:任倩倩(rqian99@163.com)
基金项目:国家自然科学基金项目(61370222,61602159);黑龙江省自然科学基金项目(F201430);哈尔滨科技创新人才研究专项资金项目(2017RAQXJ094);黑龙江省高校基本科研业务费专项资金(HDJCCX-201608)This work was supported by the National Natural Science Foundation of China (61370222,61602159), the Natural Science Foundation of Heilongjiang Province of China (F201430), the Innovation Talents Project of Science and Technology Bureau of Harbin (2017RAQXJ094), and the Fundamental Research Funds for the Central Universities of Heilongjiang Province (HDJCCX-201608).
修回日期:2018-03-20
收稿日期:2017-09-12;

LiuYong, born in 1975. Associate professor at Heilongjiang University. His main research interests include data mining and social network.

XieShengnan, born in 1991. Master at Heilongjiang University. Her main research interest is social network.

ZhongZhiwei, born in 1993. Bachelor at Heilongjiang University. His main research interest is social network.

LiJinbao, born in 1969. Professor and PhD supervisor at Heilongjiang University. His main research interest include sensor network, mobile social network and big data.

RenQianqian, born in 1980. Associate professor at Heilongjiang University. Her main research interests include database and information processing.