 g1
g1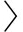 ,e是可高效计算的双线性映射,e:G1×G1→G2,有关双线性映射性质如下[17,19-20]:
,e是可高效计算的双线性映射,e:G1×G1→G2,有关双线性映射性质如下[17,19-20]:张启坤1甘 勇1王锐芳1郑家民2谭毓安2
1(郑州轻工业学院计算机与通信工程学院 郑州 450002)2(北京理工大学计算机学院 北京 100081)
摘要无线传感器网络中传感器节点资源受限,传感器节点的通信能力及范围限制了其协同操作的规模,该环境下的群组密钥协商往往以簇为单元,群组之间的安全信息交换也限制于簇内通信.针对传感器通信能力及计算能力的限制,提出一种簇间轻量级非对称群组密钥协商协议(inter-cluster lightweight asymmetric group key agreement, CL-AGKG),为簇间传感器节点间建立一条安全高效的群组通信信道.该协议首先建立簇头间的联盟共享密钥,以簇头为桥接节点,实现不同簇的传感器节点具有相同的群组密钥因子信息,进而实现跨簇非对群组密钥协商.全网节点都可以与群组内部节点共享其秘密信息,实现消息发送者不受群组约束的群组安全通信机制.通过非对称计算将更多传感器节点的计算与通信量迁移到能量较大的簇头节点,确保传感器节点的计算及通信开销轻量级性.并实现密钥自证实性,不需要额外的通信轮数,传感器节点可自证实其计算群组密钥的正确性.经分析并证明:该协议在安全及性能方面具有较高的优势.
关键词无线传感网;非对称群组密钥协商;可认证;密钥自证实性;非对称计算
传感器网络中节点共同收集信息、协同处理数据是传感器网络群组通信的应用体现,如何保障传感器网络群组通信的安全是当前研究的一个重要问题.群组密钥协商是为群组成员之间建立一条安全的通信信道.多年来无线传感器网络密钥协商机制一直是传感网络安全研究的重点技术,典型的研究有潘耘等人[1]融合了基于CA 的公钥认证框架和基于身份的公钥认证框架二者的优点,提出了适合于无线传感器网络环境的轻量级的、高效的密钥预分配方案;夏戈明等人[2]提出基于对称平衡不完全区组设计的密钥预分配方案,安全强度有所提高,并在能量消耗方面进行了优化;黄海平等人[3]提出基于逻辑网格的密钥预分配方案,传感器节点间通过求解网格矩阵系数,计算共同的密钥参数,进而实现共享对称加密密钥;Walid等人[4]提出一个高度可扩展性密钥预分配方案,有效地提高了共享密钥节点的连通性,提高节点存储共享密钥的性能;Monjul等人[5]通过扩展图论的方法设计一个密钥预分配方案,密钥预分配方案有其固有的缺陷.
传感器节点之间通过在线计算生成它们之间的共享密钥,是传感网密钥协商的另一种可行技术.近年来典型的方案有Tseng 等人[6]提出一种非平衡环境下群组密钥协商协议,但其不具有可认证性和动态性;张启坤等人[7]对Tseng等人[6]的群组密钥协商协议进行了改进,提出一种新的动态可认证群组密钥协商协议,具有可认证性和动态性;Cheng等人[8]采用双线映射技术对Tseng 等人[6]的协议进行改进,使之能够抵抗密钥临时泄露攻击;张启坤等人[9-10]采用组合密钥技术实现密钥协商,但其容易遭受密钥信息共谋攻击;Teng等人[11]提出无线网络环境下可认证的群组密钥协商协议,协议具有动态灵活性,能抵御积极攻击;Thomas等人[12]提出无线传感网络中一种节约资源的群组密钥协商,其主要是针对特定的无线网络环境下在计算量尽可能少、信息传播轮数尽可能少的节能性群组密钥协商;Walid等人[13]提出无线传感网络中一种可扩展的密钥管理机制,该方案针对传感器存储资源受限及传感网节点易变性提出的密钥管理机制,适用于传感网特定的应用环境.
非对称群组密钥协商的主要特点是群组成员协商一对公/私密钥对,分别用于群组交换信息的加密与解密.伍前红等人[14]在2009年EUROCRYPT 会议上提出非对称群组密钥协商(asymmetric group key agreement, AGKA)协议,由于群组加密密钥和解密密钥不相同,加密密钥可以对外公开,这使得消息发送者不局限于群组内部人员,该方案具有较高的安全性,但在效率方面没有优势,该方案只适用于静态群组;2011年伍前红等人[15]对其EUROCRYPT 会议提出的AGKA进行了扩展与改进,使其具有动态性,增强了方案的灵活性和实用性;张磊等人[16-17]提出可认证的非对称群组密钥协商,提高了非对称群组密钥协商的安全性;Zhao等人[18]提出一种应用于ad hoc 网络的动态ASGKA,该方案的群组间认证采用多方签名技术来实现,增加了较大的计算量.在移动设备资源受限的环境下,该方案有待于进一步简化计算量与通信量;徐畅等人[19]提出具有隐藏特性的可认证非对称群组密钥协商协议,对参与群组密钥协商的成员隐私信息具有一定的保护能力;Lü等人[20]提出基于无证书密码系统的可认证非对称群组密钥协商方案,避免了基于身份密码系统中密钥托管问题,在Diffie-Hellman困难假设下可证明安全的;2014年张启坤等人[21]利用短签名技术实现动态可认证非对称群组密钥协商,进一步提高了群组密钥协商的安全性及效率,但群组密钥协商的计算量及通信消耗比较大,不适用于移动网络环境中.
综上分析,无线传感网中基于预置的密钥分配方案,由于传感器节点存储能力的限制,使其在大规模的无线网络中的应用受到限制;基于在线计算的对称群组密钥协商,其安全度不高,且灵活性较差,不适用于网络易受攻击及节点易被捕获的传感网络;当前非对称群组密钥协商,其计算量及通信量较大,有待进一步优化以适用节点资源受限的无线传感网.
本文提出可认证非对称群组密钥协商具有3项优势:
1) 可跨簇性.参与群组密钥协商的传感器节点可分布在不同的簇,在传感器节点通信能力受限的情况下通过桥接技术实现跨簇非对称群组密钥协商,完成传感器节点远距离信息安全交换与信息安全传输;
2) 轻量级计算.由于非对称群组密钥涉及的通信与计算较对称群组密钥协商要大,通过不对等计算技术,将传感器节点的计算与通信负载迁移簇头节点来完成,弥补传感器节点资源受限的限制问题,达到非对称群组密钥协商的性能,具有对称群组密钥协商的轻量级计算和非对称群组密钥协商的安全性及灵活性;
3) 群组密钥自证实性.群组成员计算完群组密钥后,不需要经过额外的通信广播轮数,只需通过简单函数映射关系,自己能够验证其所计算的群组密钥的正确性.
首先给出双线性映射的定义[15-16],假设G1为加法群,G2为乘法循环群,其具有共同的大素数阶q,q≥2k+1,k是安全参数,且G1和G2上的离散对数是困难的.群G1和G2是一对双线性群,设G1= g1
g1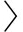 ,e是可高效计算的双线性映射,e:G1×G1→G2,有关双线性映射性质如下[17,19-20]:
,e是可高效计算的双线性映射,e:G1×G1→G2,有关双线性映射性质如下[17,19-20]:
性质1. 双线性.对所有的g1,g2∈G1,及a,b∈![]()
![]() 有e(ag1,bg2)=e(g1,g2)ab.
有e(ag1,bg2)=e(g1,g2)ab.
性质2. 非退化性.即e(g1,g2)≠1.
性质3. 可高效计算性.存在有效的算法,对于g1,g2∈G1可高效计算e(g1,g2).
假设1. 离散对数问题[17,19-20].设![]() 寻找一个整数a使得
寻找一个整数a使得![]() 在计算上是困难的.
在计算上是困难的.
假设2. DCDH(divisible computational Diffie-Hellman)问题[17,19-20].假设一个三元组(g1,ag1,bg1)∈G1,对于未知数a,b∈![]()
![]() 计算(a
计算(a b)g1是困难的.
b)g1是困难的.
1.2.1 安全模型与安全假设
本节参考了文献[18,21],在其基础上给出了非对称群组密钥协商协议参与者安全模型属性,然后给出安全模型的形式化定义及要实现的安全目标.
1) 安全模型属性及相关符号
假设U是参与密钥协商协议的传感器节点组成的集合,该集合的大小为多项式有界,U中每个传感器节点都有自己的身份信息及对应的公 私密钥对,U的任意子集Usub={u1,u2,…,un}中的节点可以随时执行密钥协商协议Π,用
私密钥对,U的任意子集Usub={u1,u2,…,un}中的节点可以随时执行密钥协商协议Π,用![]() 表示节点ui与其伙伴节点{u1,u2,…,ui-1,ui+1,…,un}执行非对称密钥协商的第π个实例,π∈
表示节点ui与其伙伴节点{u1,u2,…,ui-1,ui+1,…,un}执行非对称密钥协商的第π个实例,π∈![]()
![]() 每个参与节点实例
每个参与节点实例![]() 拥有多个属性,定义如下:
拥有多个属性,定义如下:
![]() 实例
实例![]() 的会话密钥身份标识,参与本次会话密钥协商的所有伙伴具有相同的会话密钥身份.
的会话密钥身份标识,参与本次会话密钥协商的所有伙伴具有相同的会话密钥身份.
![]() 实例
实例![]() 的伙伴身份标识,是所有与实例
的伙伴身份标识,是所有与实例![]() 建立一个会话密钥的参与者身份的集合,包括实例
建立一个会话密钥的参与者身份的集合,包括实例![]() 自己.
自己.
![]() 实例
实例![]() 执行密钥协商协议Π后,参与者计算出的群组会话加密密钥.
执行密钥协商协议Π后,参与者计算出的群组会话加密密钥.
![]() 实例
实例![]() 执行密钥协商协议Π后,计算出的群组会话解密密钥.
执行密钥协商协议Π后,计算出的群组会话解密密钥.
![]() 实例
实例![]() 在执行密钥协商过程中接收和发送所有消息的链接.
在执行密钥协商过程中接收和发送所有消息的链接.
![]() 实例
实例![]() 的当前状态,如果执行协议结束,实例
的当前状态,如果执行协议结束,实例![]() 执行完所有接收和发送的消息,并且它已经成功计算出参数
执行完所有接收和发送的消息,并且它已经成功计算出参数![]() 和
和![]() 则该协议成功终止,实例
则该协议成功终止,实例![]() 进入接受状态,否则进入终止状态.
进入接受状态,否则进入终止状态.
定义1. 伙伴关系(partnering).实例![]() 的伙伴定义为与实例
的伙伴定义为与实例![]() 一起参与本次会话密钥的所有实例,实例
一起参与本次会话密钥的所有实例,实例![]() 与其伙伴
与其伙伴![]() 满足4个条件:
满足4个条件:
1) 实例![]() 与其伙伴不能为同一实体,即ui≠uj;
与其伙伴不能为同一实体,即ui≠uj;
2) 他们成功的完成群组会话密钥协商;
1.2.2 敌手模型
本文所设计的跨簇非对称密钥协商协议方案中,参与群组密钥协商的传感器节点所计算的公开群组密钥是群组加密密钥,而群组解密密钥是由各不相同的传感器节点自身的密钥参数计算的.本文把保密性定义为任意概率多项式时间的敌手区分用群组加密密钥加密的2个等长消息的优势是可忽略的.通过一个挑战者C与一个敌手A之间的游戏规则来定义该群组密钥协商协议的安全性,安全模型中包括一个主动攻击者和一个协议参与者集合,每个参与者被模拟成一个随机预言机,该游戏分为3个步骤:
1) 初始化阶段.该阶段挑战者C运行系统函数Setup( )(
)( 是一个安全参数),输出相关的系统参数及主密钥.然后将系统参数发给敌手A,并保留主密钥.
是一个安全参数),输出相关的系统参数及主密钥.然后将系统参数发给敌手A,并保留主密钥.
2) 训练阶段.敌手A通过以下询问与挑战者C进行交互:
![]() 敌手A伪装成
敌手A伪装成![]() 向预言机
向预言机![]() 发送消息m,如果消息m=null(null表示空串),则预言机
发送消息m,如果消息m=null(null表示空串),则预言机![]() 作为会话的主动发起者发起一次会话.否则它作为一个响应者,按照协议规则对敌手相应的询问做出回应,并做出接受或拒绝该会话的决定,并将每次接收和发送的消息记录下来.
作为会话的主动发起者发起一次会话.否则它作为一个响应者,按照协议规则对敌手相应的询问做出回应,并做出接受或拒绝该会话的决定,并将每次接收和发送的消息记录下来.
![]() 预言机
预言机![]() 收到此查询后,返回群组密钥协商执行计算出的群组加密密钥
收到此查询后,返回群组密钥协商执行计算出的群组加密密钥![]() 如果预言机状态不接受,则返回一个终止符号⊥.
如果预言机状态不接受,则返回一个终止符号⊥.
![]() 预言机
预言机![]() 收到此查询后,返回群组密钥协商执行计算出的群组解密密钥,如果预言机状态不接受,则返回一个终止符号⊥.用它来模拟已知密钥安全性.
收到此查询后,返回群组密钥协商执行计算出的群组解密密钥,如果预言机状态不接受,则返回一个终止符号⊥.用它来模拟已知密钥安全性.
Corrupt(ui)—— 该查询要求被询问的参与者返回它的长期私钥![]() 敌手一旦拥有参与者ui的长期私钥,便可以通过Send伪装成参与者ui.响应过Corrupt询问的实体状态被称为“已腐化”.用它来模拟密钥的向前安全性.
敌手一旦拥有参与者ui的长期私钥,便可以通过Send伪装成参与者ui.响应过Corrupt询问的实体状态被称为“已腐化”.用它来模拟密钥的向前安全性.
![]() 在游戏的某个时刻,A发送2个消息(m0,m1)(|m0|=|m1|),向一个新鲜的(新鲜定义,见定义2)预言机
在游戏的某个时刻,A发送2个消息(m0,m1)(|m0|=|m1|),向一个新鲜的(新鲜定义,见定义2)预言机![]() 发出Test询问,只允许敌手A进行一次Test查询.预言机
发出Test询问,只允许敌手A进行一次Test查询.预言机![]() 随机选择一个比特b∈{0,1},然后将mb用群组加密密钥加密后返回给敌手A.
随机选择一个比特b∈{0,1},然后将mb用群组加密密钥加密后返回给敌手A.
3) 输出.游戏结束后,敌手A输出一个对比特b的猜测值(记为b′).若b′=b,则称敌手A赢得了此游戏.定义敌手A成功赢得游戏的概率为AdvA( )=|2Pr[b′=b]-1|(
)=|2Pr[b′=b]-1|( 为安全参数).
为安全参数).
定义2. 新鲜性(freshness).一个随机预言机![]() 在游戏结束时满足以下条件,则称该预言机
在游戏结束时满足以下条件,则称该预言机![]() 满足
满足![]() 是新鲜的:
是新鲜的:
![]() 处于接受状态;
处于接受状态;
2) A没有对预言机![]() 及搭档预言机
及搭档预言机![]() 做过
做过![]() 或者
或者![]() 查询;
查询;
3) 未对参与实体集合Pj做过Corrupt查询.
定义3. 安全性.称该非对称群组密钥协商协议具有 适应性选择挑战ID和选择明文攻击下的语义不可区分性(indistinguishability against identity-based chosen plaintext attack, IND-ID-CPA),如果没有概率多项式时间(probabilistic polynomial time, PPT)内敌手A以不可忽略的优势赢得以上游戏,或者任意概率多项式时间IND-ID-CPA敌手A赢得该游戏的优势AdvA( )=|2Pr[b′=b]-1|可以忽略.
)=|2Pr[b′=b]-1|可以忽略.
在无线传感网中簇间非对称群组密钥协商协议分为2个部分:1)簇头之间的联盟密钥建立;2)簇间传感器节点非对称群组密钥协商协议.
假设G1和G2分别是具有相同大素数阶q的加法群和乘法群,q≥2 +1,
+1, 是安全参数,且G1和G2上的离散对数是困难的,设G1=
是安全参数,且G1和G2上的离散对数是困难的,设G1= g1
g1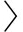 .e是可高效计算的双线性映射,e:G1×G1→G2,H1,H2:G2→
.e是可高效计算的双线性映射,e:G1×G1→G2,H1,H2:G2→![]()
![]() 为2个散列函数.系统的参数为params=(q,G1,G2,g1,e,H1,H2).
为2个散列函数.系统的参数为params=(q,G1,G2,g1,e,H1,H2).
设N个簇的簇头集合为φ={U1,U2,…,UN},任意簇头Ui(1≤i≤N)随机选择SKi∈![]()
![]() 并计算PKi=SKig1,则Ui(1≤i≤N)的公
并计算PKi=SKig1,则Ui(1≤i≤N)的公 私密钥对为(PKi,SKi),SKi由簇头秘密保存,PKi广播出去并对外公开.
私密钥对为(PKi,SKi),SKi由簇头秘密保存,PKi广播出去并对外公开.
将N个簇的簇头Ui(1≤i≤N)作为三叉树的叶子节点,构建一个完全三叉树,如图1所示.其中Th,l表示非叶子节点,h为分枝节点Th,l在树中的高度(层数),l为该分枝节点Th,l在h层中的第l个节点,且
1≤h≤![]() log3N
log3N![]() +1,0≤l≤
+1,0≤l≤![]() N/3
N/3![]() .
.

Fig. 1 The logical structure of key agreement for cluster heads
图1 簇头联盟密钥建立的逻辑结构
每个左孩子叶子节点Ui(1≤i≤N),用自己的私钥及其兄弟节点的公钥可计算出其父节点![]() (0≤i≤N)的私钥,即其父节点私钥表示为
(0≤i≤N)的私钥,即其父节点私钥表示为![]()
![]()
![]() 秘密保存,其父节点对应的公钥
秘密保存,其父节点对应的公钥![]() 对外广播.每个叶子节点逐层向上计算,直到根节点T0,0.当某个叶子节点Ui(1≤i≤N)没有兄弟节点,可计算其父节点的私钥
对外广播.每个叶子节点逐层向上计算,直到根节点T0,0.当某个叶子节点Ui(1≤i≤N)没有兄弟节点,可计算其父节点的私钥![]() 其父节点对应的公钥
其父节点对应的公钥![]() 当某个叶子节点Ui(1≤i≤N)缺少一个兄弟节点时,其可计算其父节点的私钥
当某个叶子节点Ui(1≤i≤N)缺少一个兄弟节点时,其可计算其父节点的私钥![]() H1(e(g1,g1)SKiSKi+1),其父节点对应的公钥
H1(e(g1,g1)SKiSKi+1),其父节点对应的公钥![]()
![]() 根据双线性映射的性质可知,所有簇头节点(叶子节点)都能计算出一个共同的树根节点T0,0私钥,把该私钥作为簇头节点之间共享的联盟密钥.
根据双线性映射的性质可知,所有簇头节点(叶子节点)都能计算出一个共同的树根节点T0,0私钥,把该私钥作为簇头节点之间共享的联盟密钥.
为简述方便,以9个簇头的传感网为例,由9个簇头组建的三叉树分3层,假设簇头分别为U0,U1,U2,U3,U4,U5,U6,U7,U8其对应的公 私密钥对分别为(SK0,PK0),(SK1,PK1),(SK2,PK2),(SK3,PK3),(SK4,PK4),(SK5,PK5),(SK6,PK6),(SK7,PK7),(SK8,PK8),则簇头间联盟密钥生成过程如下:
私密钥对分别为(SK0,PK0),(SK1,PK1),(SK2,PK2),(SK3,PK3),(SK4,PK4),(SK5,PK5),(SK6,PK6),(SK7,PK7),(SK8,PK8),则簇头间联盟密钥生成过程如下:
1)U0,U1,U2通过各自自己的私钥和其兄弟节点的公钥可计算出其父节点T1,0的私钥TX1,0.如U0计算TX1,0=H1(e(PK1,PK2)SK0)=H1(e(g1,g1)SK0SK1SK2)及对应公钥TY1,0=H1(e(g1,g1)SK0SK1SK2)g1,并广播TY1,0.U1计算TX1,0=H1(e(PK0,PK2)SK1)=H1(e(g1,g1)SK1SK0SK2);U2计算TX1,0=H1(e(PK0,PK1)SK2)=H1(e(g1,g1)SK2SK0SK1).
2) 同理,U3,U4,U5各自计算出其父节点私钥TX1,1=H1(e(PK4,PK5)SK3)=H1(e(PK3,PK5)SK4)=H1(e(PK3,PK4)SK5)=H1(e(g1,g1)SK3SK4SK5),U3计算对应的公钥TY1,1=TX1,1g1,并广播出去.
3) 同理,U6,U7,U8,U5各自计算出其父节点私钥TX1,2=H1(e(PK7,PK8)SK6)=H1(e(PK6,PK8)SK7)=H1(e(PK6,PK7)SK8)=H1(e(g1,g1)SK6SK7SK8),U6计算对应的公钥TY1,2=TX1,2g1,并广播出去.
4) 所有叶子节点收到U0,U3和U6的广播后,可计算出根节点T0,0的私钥
TX0,0=H1(e(TY1,1,TY1,2)H1(e(g1,g1)SK2SK0SK1))=
H1(e(TY1,0,TY1,2)H1(e(g1,g1)SK3SK4SK5))=
H1(e(TY1,0,TY1,1)H1(e(g1,g1)SK6SK7SK8)),
则传感器网络中每个簇头可协商出一个共同的联盟密钥TX0,0.
本节提出一种轻量级的关于无线传感器节点之间的跨簇可认证的非对称群组密钥协商协议,以一个簇的传感器节点的群组密钥协商为例,有2种假设需要考虑:
1) 每个簇有一个簇头和n个传感器节点组成.簇头Ui内的低能量节点集合表示为u={ui,1,ui,2,…,ui,n},其对应的身份集合表示为I={idui,1,idui,2,…,idui,n},任意节点ui,j(1≤j<n)的公私密钥对(ski,j,pki,j),其中ski,j∈![]()
![]() 为本簇能量较大的簇头,其对应的身份表示为
为本簇能量较大的簇头,其对应的身份表示为![]() Ui的公私密钥对(SKi,PKi),其中SKi∈
Ui的公私密钥对(SKi,PKi),其中SKi∈![]()
![]() SKig1.
SKig1.
2) 每个节点在执行协议之前都能知道其他成员的身份信息.
定义4. 非对称群组密钥协商(asymmetric group key agreement, AGKA)[21].一个群组密钥协商Σ是非对称的,如果该协议成功终止,有等式ekui,t=ekui,k,ekui,t≠dkui,t或ekui,t=ekuj,k,ekuj,k≠dkuj,k,其中ekui,t dkui,t,ekuj,k
dkui,t,ekuj,k dkuj,k分别是ui,t和ui,k及ui,t和uj,k分别是同簇和不同簇的2个不同的节点,其计算出的群组加密
dkuj,k分别是ui,t和ui,k及ui,t和uj,k分别是同簇和不同簇的2个不同的节点,其计算出的群组加密 解密密钥(t,k,i,j∈
解密密钥(t,k,i,j∈![]() +,1≤t≤n,1≤k≤n,t≠n,1≤i≤N,1≤j≤N,i≠j).
+,1≤t≤n,1≤k≤n,t≠n,1≤i≤N,1≤j≤N,i≠j).
2.3.1 跨簇传感器节点间群组密钥计算
如果参与群组密钥协商的传感器节点分布在不同的簇,则跨簇群组密钥协商过程如下:
1) 每个传感器节点ui,t(1≤i≤N,1≤t≤n)随机选择2个数mi,t,qi,t∈![]()
![]() 然后计算Qi,t=qi,tg1,Ti,t=((mi,t+ski,t)
然后计算Qi,t=qi,tg1,Ti,t=((mi,t+ski,t) qi,t)g1,Mi,t=mi,tPKi.并将(idui,t,Qi,t,Ti,t,Mi,t)发送给簇头Ui(注:(idui,t,Qi,t,Ti,t,Mi,t)提前存储在对应传感器内存卡上,以减少在线计算量,延长传感器使用寿命).
qi,t)g1,Mi,t=mi,tPKi.并将(idui,t,Qi,t,Ti,t,Mi,t)发送给簇头Ui(注:(idui,t,Qi,t,Ti,t,Mi,t)提前存储在对应传感器内存卡上,以减少在线计算量,延长传感器使用寿命).
2) 收到(idui,t,Qi,t,Ti,t,Mi,t)(1≤i≤N,1≤t≤n)后,簇头节Ui(1≤i≤N)验证等式![]() 是否成立,如果成立,则Ui可以确保消息(idui,t,Qi,t,Ti,t,Mi,t)是由ui,t发送的,然后令
是否成立,如果成立,则Ui可以确保消息(idui,t,Qi,t,Ti,t,Mi,t)是由ui,t发送的,然后令![]() 计算
计算![]()
3) 各簇头Ui(1≤i≤N)之间,将各簇内参与群组密钥协商的传感器节点信息fi,t相互传递共享.为描述方便,假设有2个簇的传感器节点参与群组密钥协商,分别是以簇头Ui和簇头Uj为首的跨簇群组密钥协商.则Ui将其内部参与密钥协商的节点信息(fi,t,Qi,t,Ti,t,pki,t)(1≤t≤n)发送给Uj,Uj将其内部参与密钥协商的节点信息(fj,t,Qj,t,Tj,t,pkj,t)(1≤t≤n)发送给Ui.
①Ui选择一个随机数![]()
![]()
![]() 计算
计算![]()

 可以计算出群组加密密钥
可以计算出群组加密密钥![]() 和群组解密密钥
和群组解密密钥![]() 然后,Ui将
然后,Ui将![]() 广播给簇内传感器节点.
广播给簇内传感器节点.
② 同理,Uj选择一个随机数![]()
![]()
![]() 计算
计算![]() /
/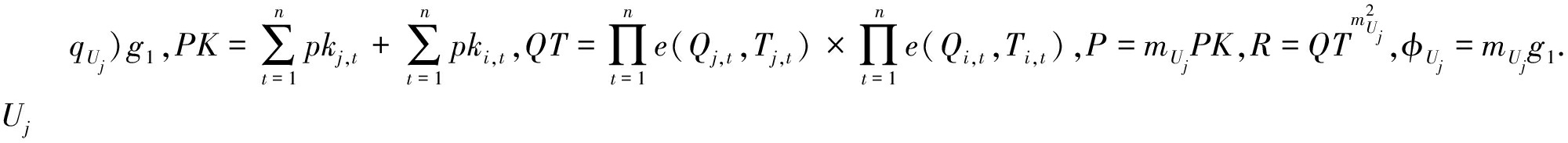 可以计算出群组加密密钥
可以计算出群组加密密钥![]() 和群组解密密钥
和群组解密密钥![]() 然后,Uj将
然后,Uj将![]() 广播给簇内传感器节点.
广播给簇内传感器节点.
4) 群组密钥计算.各簇内每个节点ui,t(1≤i≤N,1≤t≤n)在接收到各自簇头Ui(1≤i≤N)广播之后,验证等式![]() 是否立,如果成立,则每个ui,t(1≤i≤N,1≤t≤n)可以确保
是否立,如果成立,则每个ui,t(1≤i≤N,1≤t≤n)可以确保![]()
![]() 是由簇头Ui发送过来的.然后各个ui,t(1≤i≤N,1≤t≤n)可获得群组加密密钥ekui,t=(R,P),并通过自己的密钥参数mi,t计算
是由簇头Ui发送过来的.然后各个ui,t(1≤i≤N,1≤t≤n)可获得群组加密密钥ekui,t=(R,P),并通过自己的密钥参数mi,t计算![]() 及群组解密密钥
及群组解密密钥![]()
5)ui,t(1≤i≤N,1≤t≤n)通过验证等式![]() 是否成立,来验证ekui,t和dkui,t计算的正确性.此方案的示意图如图2所示.
是否成立,来验证ekui,t和dkui,t计算的正确性.此方案的示意图如图2所示.
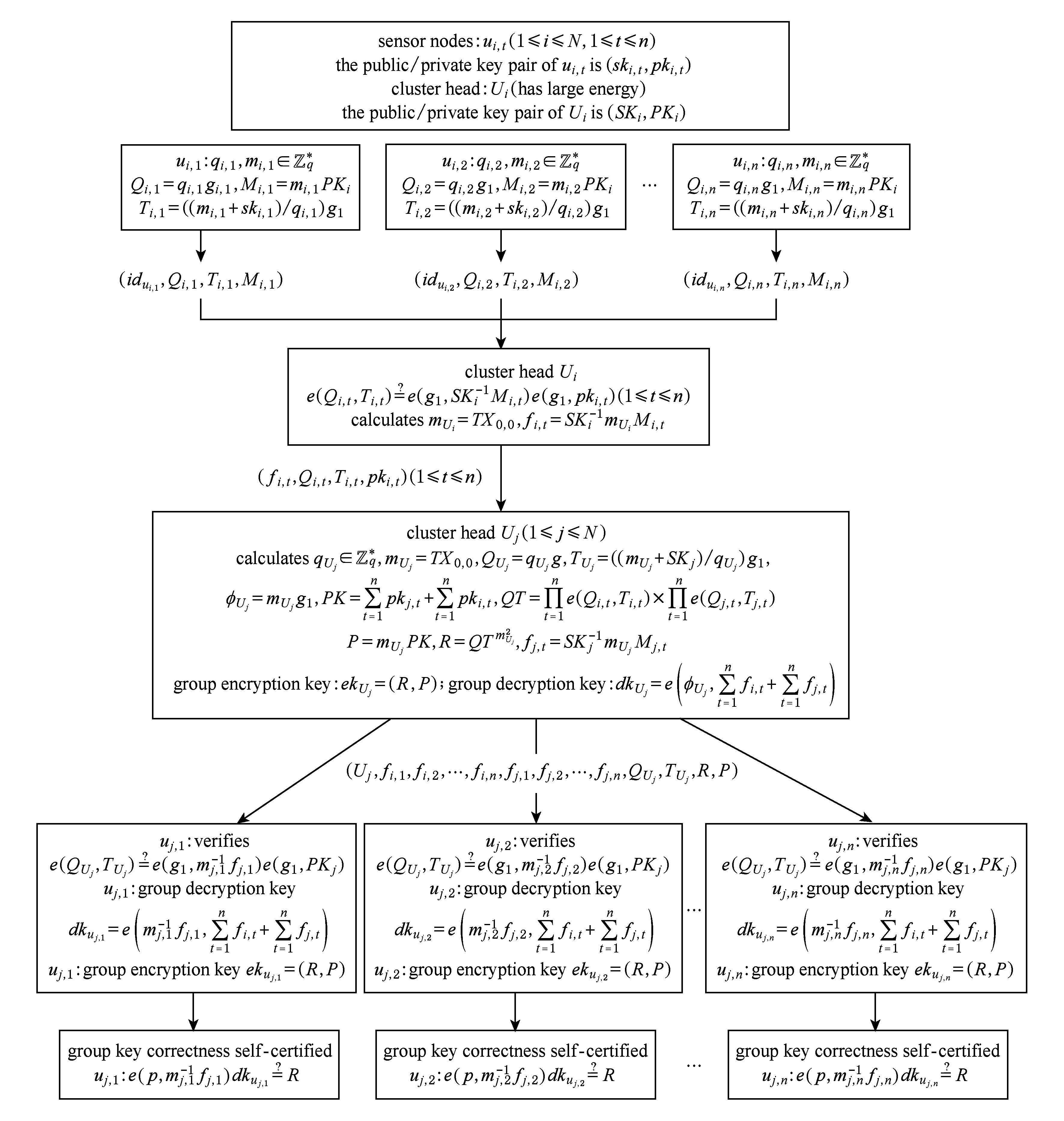
Fig. 2 Cross-cluster sensor node group key agreement
图2 簇间传感器节点群组密钥协商
对任意明文信息m∈M*(M*:明文空间),任意成员ui,t拥有群组加密密钥ekui,t和群组解密密钥dkui,t作如下操作.
加密:消息发送者ui,t随机选择整数γi,t∈![]()
![]() 算δi,t=γi,tg1,ηi,t=m⊕H2(e(g1,(H2(Re(P,φi,t)-1)g1)γi,t).然后广播密文c=
算δi,t=γi,tg1,ηi,t=m⊕H2(e(g1,(H2(Re(P,φi,t)-1)g1)γi,t).然后广播密文c= δi,t,ηi,t
δi,t,ηi,t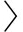 ,簇间传感器节点的通信,可由簇头进行转发广播.
,簇间传感器节点的通信,可由簇头进行转发广播.
解密:当收到消息发送者广播的密文c= δi,t,ηi,t
δi,t,ηi,t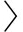 ,群组内任意成员uj,t可用计算的群组私钥dkuj,t计算出明文m=ηi,t⊕H2(e(δi,t,H2(dkuj,t)g1)).
,群组内任意成员uj,t可用计算的群组私钥dkuj,t计算出明文m=ηi,t⊕H2(e(δi,t,H2(dkuj,t)g1)).
本节首先给出相关等式的正确性证明,其次对提出的协议进行安全性分析,最后给出协议的性能比较与分析.
定理1. 正确性.群组密钥协商阶段,如果参与群组密钥协商的任意传感器节点ui,t计算无误,则都可计算出一致的群组解密密钥dkui,t,即:
![]()
1≤t≤n,1≤k≤n,t≠n.
证明.
由于![]() 和双线性配对的特性,有:
和双线性配对的特性,有:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
观察上述公式,群组解密密钥dkui,t是一个固定量,与具体成员自身的固定参数有关.只要每个成员计算无误,则群组解密密钥dkui,t是一个定值.
证毕.
定理2. 贡献性.该群组密钥协商是贡献性群组密钥协商.
证明. 根据定理1的证明,如果参与群组密钥协商的成员在密钥协商过程中计算无误的情况下都可计算出一致的群组解密密钥,即![]() 最终的群组密钥包含每个参与者ui,t(1≤t≤n)的贡献参数mi,t(1≤t≤n).即只有所有群组成员全部参与协商才能最终获得群组密钥,任何群组成员事先不知群组密钥或也不能控制群组密钥.
最终的群组密钥包含每个参与者ui,t(1≤t≤n)的贡献参数mi,t(1≤t≤n).即只有所有群组成员全部参与协商才能最终获得群组密钥,任何群组成员事先不知群组密钥或也不能控制群组密钥.
证毕.
定理3. 一致性自证实.如果等式e(P,φi,t)dkui,t=R(1≤t≤n)成立,因为参数P和R是公开的,φi,t是通过公开参数fi,t和成员自身的保留参数简单计算的.因此,如果φi,t计算无误,则只要等式成立,簇内每个群组成员ui,t就可以验证群组解密密钥dkui,t计算的正确性.
证明. 由![]() 和双线性映射的特性,有:
和双线性映射的特性,有:
![]()
![]()
![]()
![]()
![]()
![]() /
/![]()
![]()
![]()
所以,等式e(P,φi,t)dkui,t=R.
证毕.
定理4. 如果公式![]() 成立,ui,t(1≤t≤n)可以确保信息
成立,ui,t(1≤t≤n)可以确保信息![]() 是Ui发送的,因为消息经过Ui的签名认证.
是Ui发送的,因为消息经过Ui的签名认证.
证明. 由![]()

![]()
![]() 和双线性配对的特性,则有:
和双线性配对的特性,则有:
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以,等式![]() 成立.ui,t(1≤t≤n)可以确保信息
成立.ui,t(1≤t≤n)可以确保信息![]()
![]() 是Ui签名的.
是Ui签名的.
证毕.
定理5. 对于一个DCDH问题实例(G1,G2,q,g1,ag1,bg1,e,h,H1,H2),我们构造一个多项式时间模拟器C,利用攻击者A来解决DCDH问题.假如存在能成功攻击协议CL-AGKG,我们可以证明C可以不可忽略的优势解决DCDH问题,首先,我们假设敌手A在攻击实验中请求为q0个用户私钥,对Dk.Reveal进行q1次询问.对Corrupt进行q2次询问,A最多建立q3协议运行.敌手A以优势Adv(A)=ε赢得这场游戏,则存在一个算法以优势![]() 解决DCDH问题.
解决DCDH问题.
证明. 设挑战者C是一个挑战者,A是一个能破译该协议的敌手.给定C一个实例(G1,G2,q,g1,ag1,bg1,e,h,H1,H2),未知数a,b∈![]()
![]() 是公开的散列函数,H1和H2是C所控制的2个随机预言机.C利用A来求解DCDH问题.定义一个新的会话,他将有一个唯一的会话ID.挑战者C随机选择一个会话,该会话的ID用符号sidt表示.对应的模拟会话的ID用Csidt表示,则该会话被选中的概率设为Pr[Csidt=0]=σ,对应的Pr[Csidt=1]=1-σ.同时该挑战者C记下二元组(sidt,Csidt).
是公开的散列函数,H1和H2是C所控制的2个随机预言机.C利用A来求解DCDH问题.定义一个新的会话,他将有一个唯一的会话ID.挑战者C随机选择一个会话,该会话的ID用符号sidt表示.对应的模拟会话的ID用Csidt表示,则该会话被选中的概率设为Pr[Csidt=0]=σ,对应的Pr[Csidt=1]=1-σ.同时该挑战者C记下二元组(sidt,Csidt).
1) 初始化阶段.游戏开始,C选择系统参数params=(G1,G2,q,g1,ag1,bg1,e,h,H1,H2),C将参数发送给敌手A.
2) 训练阶段.挑战者C与敌手A交互如下:
KG(ui)模拟用户私钥生成—— A询问预言机H1.C维护一个列表![]() 其中,
其中,![]() 是用户ui的身份标识,
是用户ui的身份标识,![]() 是对应用户私钥,
是对应用户私钥,![]() 是对应用户公钥,
是对应用户公钥,![]() 为用户类型标识(其中,
为用户类型标识(其中,![]() 表示用户C不能计算该用户密钥,
表示用户C不能计算该用户密钥,![]() 表示用户C可以计算该用户密钥).对于用户u的密钥请求,C查找列表CL1,如果存在匹配的列表
表示用户C可以计算该用户密钥).对于用户u的密钥请求,C查找列表CL1,如果存在匹配的列表![]() 则返回对应的
则返回对应的![]() 和
和![]() 否则,作如下处理:
否则,作如下处理:
① C随机选择![]()
![]()
![]() 计算
计算![]() 并把
并把![]() 插入列表CL1.
插入列表CL1.
② C无法为该用户产生密钥,C设置该用的列表为![]()
③ C检查用户列表CL1,如果列表存在多个![]() 或者列表长度等于qg但不存在
或者列表长度等于qg但不存在![]() 的列表项,C则终止模拟(Event1).
的列表项,C则终止模拟(Event1).
![]() 保留一个初始化为空的列表CL2.假设
保留一个初始化为空的列表CL2.假设![]() 初始化定义一个与
初始化定义一个与![]() 相对应的会话身份
相对应的会话身份![]() 然后将
然后将![]() 提交给随机预言机H2,如果该成员以前没有询问过.则如同询问预言机H1一样,做相应处理后将
提交给随机预言机H2,如果该成员以前没有询问过.则如同询问预言机H1一样,做相应处理后将![]() 加入CL1.C开始模拟如下预言:
加入CL1.C开始模拟如下预言:
1) 如果![]() 且
且![]()
① C选择系统参数pC=bg1作为公钥返回给A,并保留参数b;
② A随机选择ai,ri∈![]()
![]() 并根据查询列表CL1获得的私钥
并根据查询列表CL1获得的私钥![]() 计算
计算![]()

![]() 并将
并将![]() 发送给C;
发送给C;
③ C收到![]() 随机选择c∈
随机选择c∈![]()
![]() 计算
计算![]() 并将
并将![]() 加入列表CL2.
加入列表CL2.
2) 如果![]() 且
且![]()
① C选择系统参数![]() 作为公钥返回给A,并保留参数b′;
作为公钥返回给A,并保留参数b′;
② A随机选择ai,ri∈![]()
![]() 并根据查询列表CL1获得的私钥
并根据查询列表CL1获得的私钥![]() 计算
计算![]()

![]() 并将
并将![]() 发送给C;
发送给C;
③ C收到![]() 随机选择c∈
随机选择c∈![]()
![]()
计算![]() 并将
并将![]() 加入列表CL2.
加入列表CL2.
![]() 如果
如果![]() 为成功结束,则C计算根据列表CL2和c计算出R′,P′,并返回ek′=(R′,P′),否则返回null.
为成功结束,则C计算根据列表CL2和c计算出R′,P′,并返回ek′=(R′,P′),否则返回null.
![]() 如果
如果![]() 没有成功结束,则返回null.如果
没有成功结束,则返回null.如果![]() 计算tc=cg1,并查找CL2列表,计算
计算tc=cg1,并查找CL2列表,计算![]() 输出dk′=e(tc,X);否则如果
输出dk′=e(tc,X);否则如果![]() 则输出符号⊥(Event2).
则输出符号⊥(Event2).
Corrupt(uj)—— C收到Corrupt询问后,首先在CL1中查找uj对应的身份![]() 如果列表中没有,则表示该询问是第1次询问.然后向询问预言机H1一样,做相应处理后将
如果列表中没有,则表示该询问是第1次询问.然后向询问预言机H1一样,做相应处理后将![]() 加入CL1.如果
加入CL1.如果![]() 则输出符号⊥(⊥表示是终止)(Event3);否则返回
则输出符号⊥(⊥表示是终止)(Event3);否则返回![]()
![]() 敌手A相关的询问结束后,他向C发起挑战,A选择一个新鲜的预言机
敌手A相关的询问结束后,他向C发起挑战,A选择一个新鲜的预言机![]() 和2个消息m0,m1,且有|m0|=|m1|.假设
和2个消息m0,m1,且有|m0|=|m1|.假设![]() 作如下应答:
作如下应答:
1) C在CL1列表中查询相关的信息![]()
2) 如果![]() 则在CL2列表中提取信息
则在CL2列表中提取信息![]() 计算
计算![]() 否则输出符号⊥(Event4).
否则输出符号⊥(Event4).
3) C选择一个随机数![]()
![]()
![]() 计算
计算![]() 然后加密
然后加密![]() ⊕
⊕![]()
4) 返回c*= δ*,η*
δ*,η*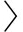 给A.
给A.
Response——A完成所有的询问后,返回一个b′∈{0,1}作为对b的猜测.如果A能获得一定的优势正确猜测b′=b,A必须询问H2获取列表CL2中的信息![]() 计算
计算![]() 以及dk*=e(L,cg1),从而获取mb=η*⊕h(e(δ*,dk*))的猜测优势.则C可以根据A的方法计算DCDH问题,因为
以及dk*=e(L,cg1),从而获取mb=η*⊕h(e(δ*,dk*))的猜测优势.则C可以根据A的方法计算DCDH问题,因为![]() 根据系统参数(g1,ag1,bg1),C可高效计算cg1=(ac
根据系统参数(g1,ag1,bg1),C可高效计算cg1=(ac a)g1的值.
a)g1的值.
证毕.
引理1. 如果C没有终止上述模拟游戏,则敌手A无法区分模拟世界和真实世界环境.
证明.
在上述的模拟游戏中的所有输出都符合协议CL-AGKG的规则要求,同时实体输出的消息符合消息空间上的均匀分布.因此,敌手A无法觉察到模拟世界和真实世界的不一致性.
证毕.
C成果的概率为

由于传感器节点资源受限,协议设计过程中除安全性外,协议的计算量、通信量及能量消耗是衡量协议性能的重要指标.本文就近年来可以进行量化计算的文献进行对比分析.这些协议都适用于无线传器网络,具有可比性及代表性.依据这些协议所提供的数据,分别从计算与通信复杂度及协议消耗的总能量进行对比分析.表1列举了本文协议与这些具有可比性和代表性的4个群组密钥协商协议在计算复杂度及通信量方面进行比较分析.
Table1ComplexityAnalysisofAuthenticatedProtocols
表1可认证协议的复杂度分析

ProtocolModular ExponentiationTate PairingScalar MultiplicationLength of Message SentLength of Message ReceivedRef [22]30n2|G1|n|G1|Ref [23]2333|G1|(n+1)|G1|Ref [24]n44n+1(2n+3)|G1|(2n+3)|G1|Ref [25]n+545n+2(n+4)|G1|(n+4)|G1|Ours524|G1|(n+4)|G1|
从表1可以看出计算复杂度较小的是Tsai[23]及本文方案,其计算复杂度不随节点的数量变化而变化.Chen等人[24]及张磊等人[25]计算复杂度最高,通信复杂度Chen等人[24]最高.
从协议执行时间上看,我们通过文献[26]提供的数据进行分析,该文献通过PBC实验室提供的实验程序pbc-0.5.12版本,在硬件Intel®CoreTM2 Duo E8400 CPU(3.00 GHz),操作系统ubuntu-10.04上运行相关算法,结果显示在G1上的乘法平均运行时间为0.016 ms,在G1和G2上的指数平均运算时间分别是3.886 ms和0.489 ms,双线对的平均运行时间为4.354 ms.总结如表2所示:
Table2CostTimeofSomeAlgorithms
表2运算消耗时间

AlgorithmCost Time∕msScalar Multiplication Over G1 0.016Modular Exponentiation Over G1 3.886Modular Exponentiation Over G2 0.489Tate Pairing4.354
无线传感器网络中根据以上计算复杂度和相关算法运行的时间分析,我们的方案和前期4种研究成果的时间消耗对比分析如图3所示.
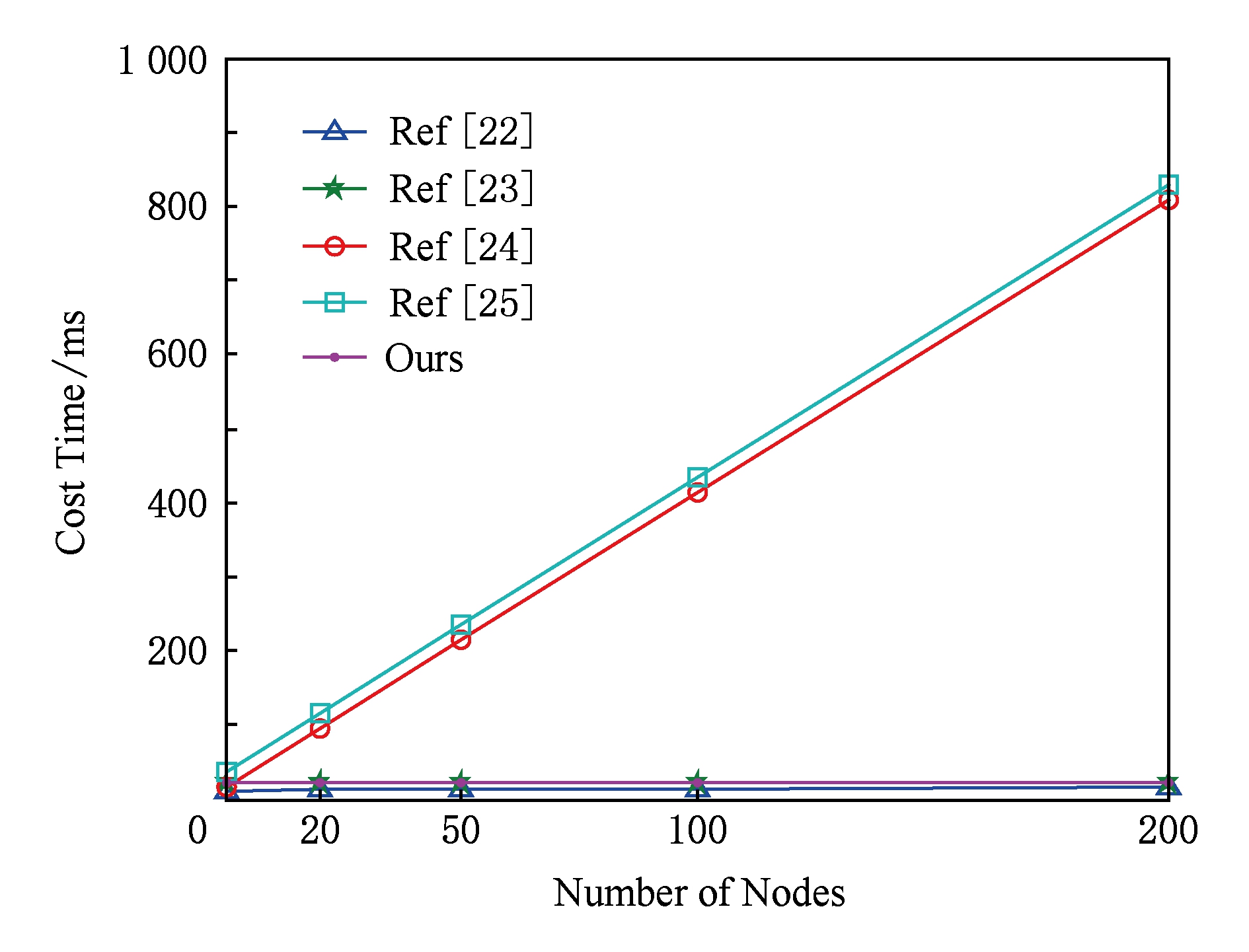
Fig. 3 The time cost of the five protocols
图3 5种协议运行时间对比
从图3可以看出协议运行时间最长为张磊等人[25]提出的方案.其次是Chen等人[24]方案这2种方案的运行时间远远比其他3种方案消耗时间长.运行时间最短的是Lee等人[22]和本文提出的协议,这2种协议运行时间相当.
从协议的能量消耗上分析,本文把群组密钥协商所消耗的总能量简单地量化成群组成员在协商过程中的计算量消耗和通信量消耗的总和.不失一般性,根据文献[21]提供的资料,一个133 MHz“Strong ARM”微处理器执行一个模幂运算需要消耗9.1 mJ能量,执行一个纯标量乘法运算需要消耗8.8 mJ能量,执行一个Tate对运算需要消耗47 mJ能量.一个IEEE 802.11频谱24 WLAN卡发送1 b信息需要消耗0.66 μm能量,其接收1 b信息需要消耗0.31 μm能量,如表3所示:
Table3EnergyCostsforComputationandCommunication
表3计算与通信能量消耗

Type of CommunicationEnergy Costs∕mJComputation Cost of Modular Exponentiation9.1Computation Cost of Scalar Multiplication8.8Computation Cost of Tate Pairing47.0Communication Cost for Transmitting 1bit0.66×10-3Communication Cost for Receiving 1bit0.31×10-3
假设群组密钥协商协议在有限域Fp上交换一个单位信息的信息长度为1 024 b.由于传统加密方法用1 024 b长度的密钥加密信息的安全度等同于椭圆曲线加密方法采用160 b长度的密钥加密的安全性.假设基于椭圆曲线加密方案的群组密钥协商协议的单个信息量为160 b.由于这5个有效的协议均为160 b的加密密钥.设每个信息量的大小为160 b,则这5个协议的计算消耗如图4所示:
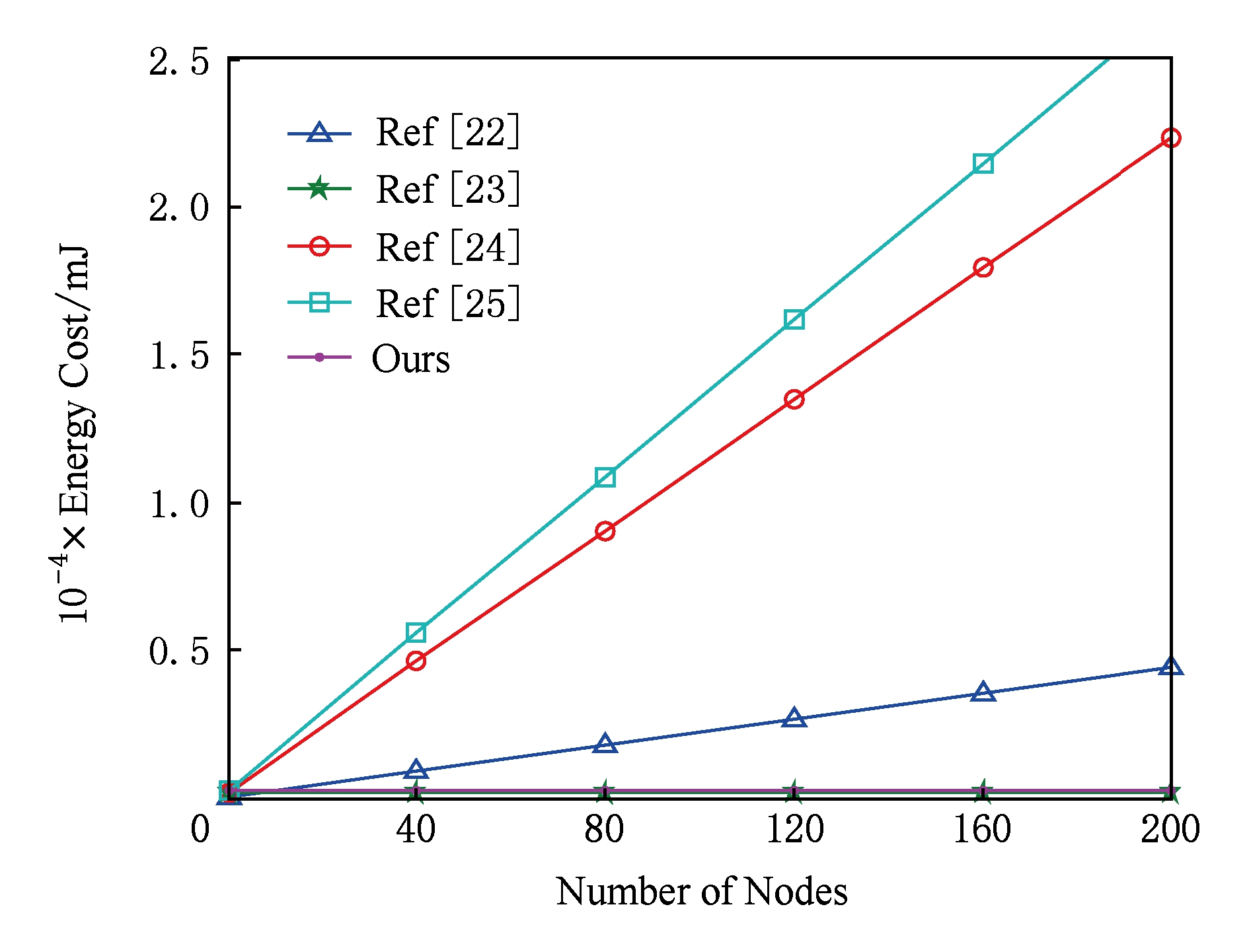
Fig. 4 Computation cost of the unauthenticated protocols
图4 协议计算所消耗能量
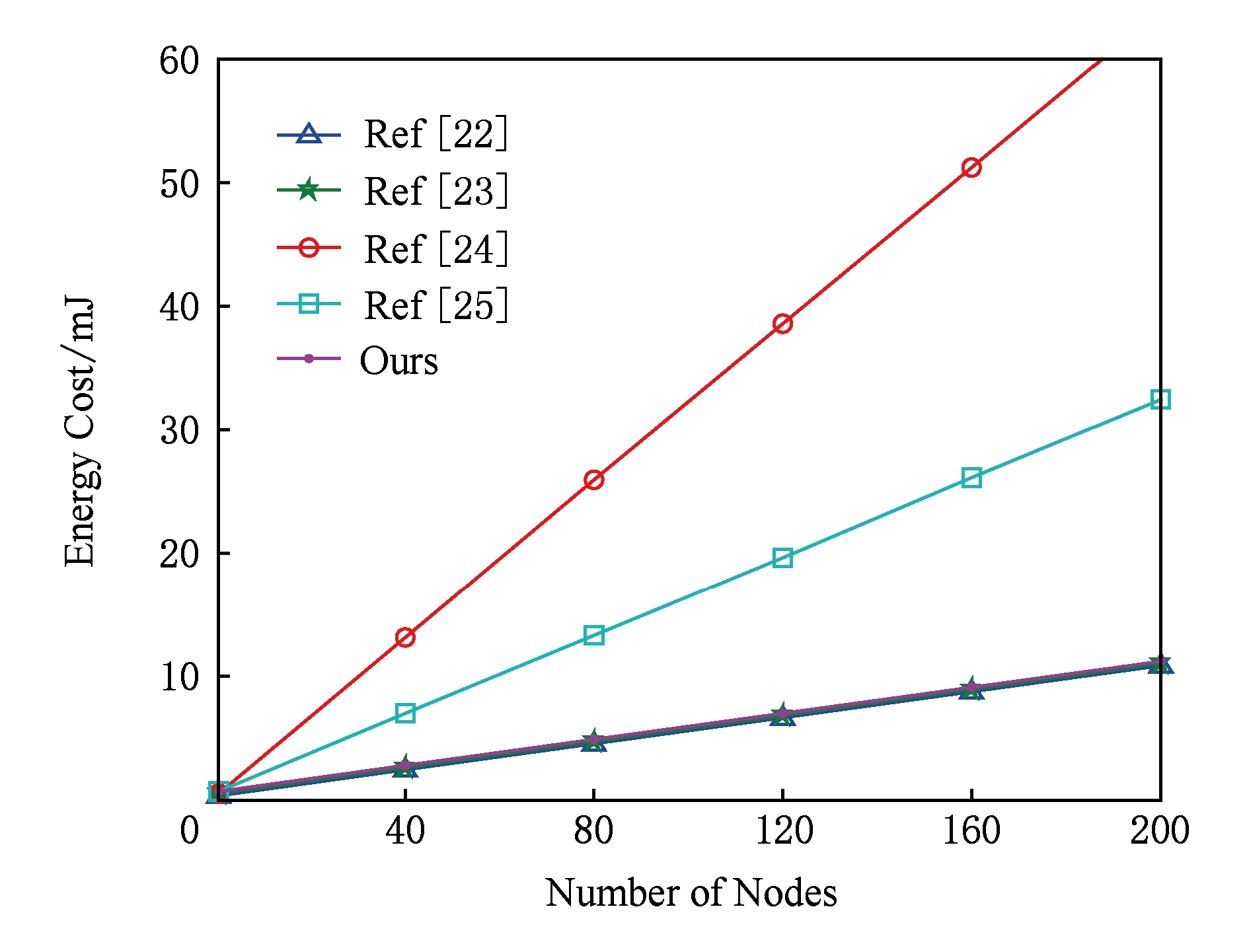
Fig. 5 Communication cost of the unauthenticated protocols
图5 协议通信所消耗能量
由图4可以看出,计算消耗能量最大的为张磊等人[25]提出的协议,计算消耗能量最低的为Tsai 等人[23]及本文提出的协议,两者的计算能量消耗线几乎重叠.Chen等人[24]和张磊等人[25]计算量消耗的原因是因为其计算量随着参与群组密钥协商的成员数量的增加而增加,且幂指数计算消耗能量较大.
通信能量消耗如图5所示,Lee等人[22],Tsai[23]与本文这3种方案的通信能量消耗相当,通信消耗曲线几乎重合,通信消耗较少,具有明显的优势.Chen等人[24]方案通信消耗较大.
总能量消耗分析如图6所示,Chen等人[24]及张磊等人[25]这2种方案的总能耗随着群组成员的规模增大上升较快,因此不适用于大规模的群组密钥协商协议.Tsai[23]及本文协议总能量消耗处于明显优势,该方案适用于大规模的大规模群组密钥协商协议,如网格计算及云计算等大型分布式协同计算.但本文方案与Tsai[23]具有较大性能的优势体现在,本文方案是可认证的非对称群组密钥协商,与对称群组密钥协商相比具有加大的灵活性和较高的安全性.
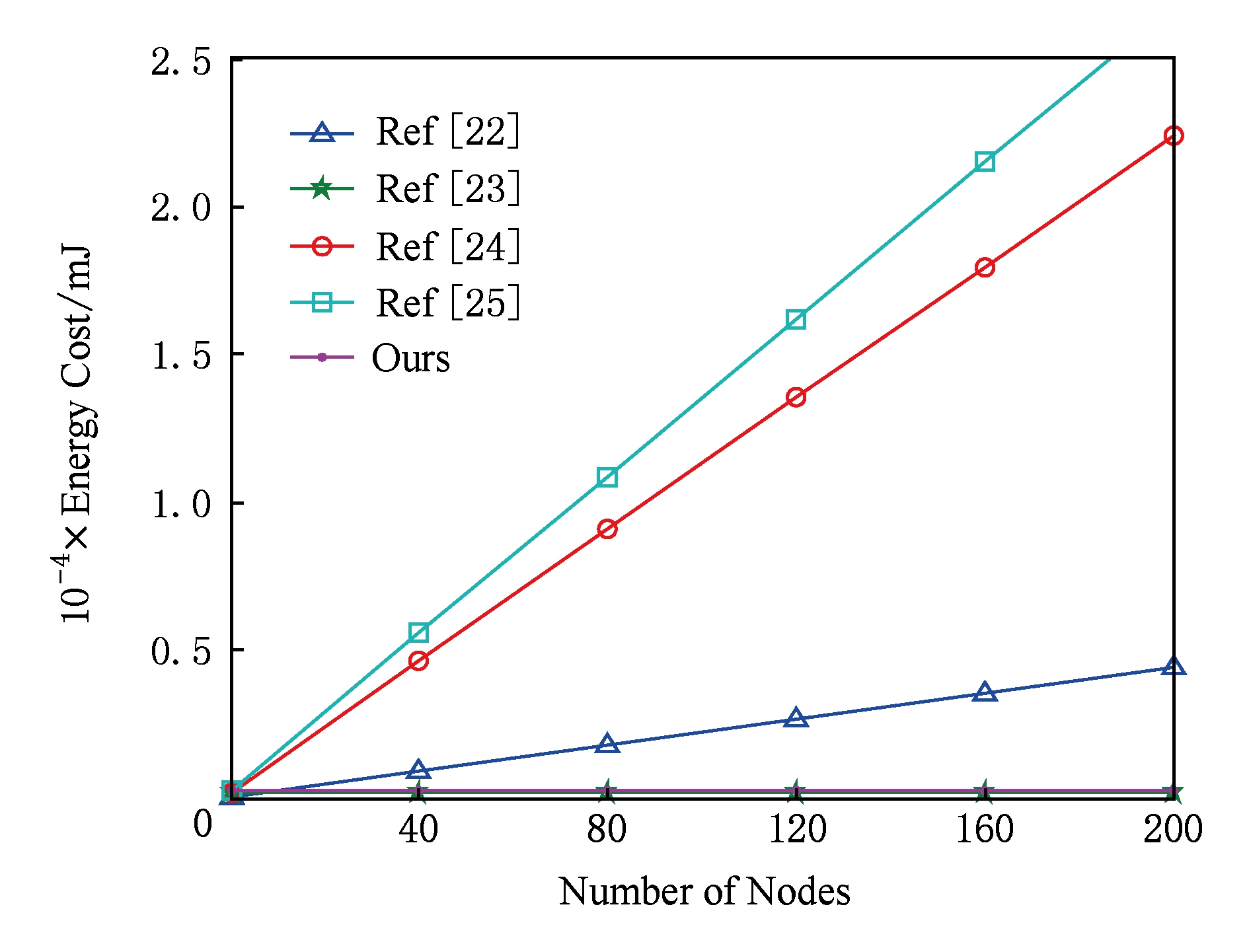
Fig. 6 Total energy cost of the authenticated protocols
图6 总能量消耗
分析了现有的群组密钥协商协议的方案,为适用新型网络应用需求,如移动云计算网络、无线传感器网络等,其网络终端易受攻击、网络节点资源受限、计算能力和通信范围有限等特性,提出跨簇非对称群组密钥协商协议,即传感器节点的信息交换采用非对称密码体制,具有更高的安全性和灵活性; 跨簇群组密钥协商使得通信范围有限的资源节点更容易扩展簇间协同计算的范围;采用了非对称计算,使得传感器节点承担轻量级的计算及通信量.经证明和分析验证了协议的安全性及能耗性能具有较好的优势.
参考文献
[1]Pan Yun, Wang Licheng, Cao Zhenfu, et al. Lite-CA based key pre-distribution scheme in wireless sensor network[J]. Journal on Communications, 2009, 30(3): 130-134 (in Chinese)(潘耘, 王励成, 曹珍富, 等. 基于轻量级CA的无线传感器网络密钥预分配方案[J]. 通信学报, 2009, 30(3): 130-134)
[2]Xia Geming,Huang Zunguo, Wang Zhiying. A key pre-distribution scheme for wireless sensor networks based on the symmetric balanced incomplete block design[J]. Journal of Computer Research and Development, 2008, 45(1): 154-164 (in Chinese)(夏戈明, 黄遵国, 王志英. 基于对称平衡不完全区组设计的无线传感器网络密钥预分配方案[J]. 计算机研究与发展, 2008, 45(1): 154-164)
[3]Huang Haiping, Wang Ruchuan, Sun Lijuan, et al. Key distribution scheme of wireless sensor networks based on logic grid[J]. Journal on Communications, 2009, 30(8): 131-140 (in Chinese)(黄海平, 王汝传, 孙力娟, 等. 基于逻辑网格的无线传感器网络密钥分配方案[J]. 通信学报, 2009, 30(8): 131-140)
[4]Bechkit W, Challal Y, Bouabdallah A, et al. A highly scalable key pre-distribution scheme for wireless sensor networks[J]. IEEE Transactions on Wirelss Communications, 2013, 12(2): 948-959
[5]Monjul S, Irani A, Hussain M A. A review on desirable measures for good key pre-distribution scheme in wireless sensor network[C] //Proc of Int Conf on Green Computing and Internet of Things. Piscataway, NJ: IEEE, 2016: 129-134
[6]Tseng Y M. A resource-constrained group key agreement protocol for imbalanced wireless networks[J]. Computer Security, 2007, 26(4): 331-333
[7]Zhang Qikun, Zhang Quanxin, Ma Zhongmei, et al. An authenticated asymmetric group key agreement for imbalanced mobile networks[J]. Chinese Journal of Electronics, 2014, 23(4): 827-835
[8]Cheng Qingfeng, Ma Changui, Wei Fushan. Analysis and improvement of a new authenticated group key agreement in a mobile environment[J]. Annals of Telecommunications, 2011, 64(11/12): 331-337
[9]Zhang Qikun, Yuan Junling, Guo Ge, et al. An authentication key establish protocol for WSNs based on combined key[J]. Wireless Personal Communication, 2018, 99(1): 95-110
[10]Zhang Qikun, Tan Yu’an, Zhang Li, et al. A combined key management scheme in wireless sensor networks[J]. Sensor Letters, 2011, 9(4): 1501-1506
[11]Teng Jikai, Wu Chuankun. Efficient group key agreement for wireless mobile networks[C] //Proc of the IET Int Conf on Wireless Sensor Network. Herts, UK: IET, 2010: 323-330
[12]Thomas R H, Thomas A C, Keith M C, et al. Energy-efficient group key agreement for wireless networks[J]. IEEE Transactions on wireless Communication, 2015, 14(10): 5552-5564
[13]Walid A, Noureddine B. An efficient and scalable key management mechanism for wireless sensor networks[J]. ICACT Transactions on Advanced Communications Technology, 2014, 3(4): 480-493
[14]Wu Qianhong, Mu Yi, Susilo W, et al. Asymmetric group key agreement[C] //Proc of the 28th EUROCRYPT 2009. Berlin: Springer, 2009: 153-170
[15]Wu Qihong, Zhang Xinyu,Tang Ming, et al. Extended asymmetric group key agreement for dynamic groups and its applications[J]. China Communications, 2011, 8(4): 32-40
[16]Zhang Lei, Wu Qianhong, Qin Bo, et al. Identity-based authenticated asymmetric group key agreement protocol[G] //LNCS 6196: Proc of Int Computing and Combinatorics. Berlin: Springer, 2010: 510-519
[17]Zhang Qikun, Li Yuanzhang, Song Danjie, et al. Alliance authentication protocol in clouds computing environment[J]. China Communications, 2012, 9(7): 42-54
[18]Zhao Xingwen, Zhang Fangguo, Tian Haibo. Dynamic asymmetric group key agreement for ad hoc networks[J]. Ad Hoc Networks, 2011, 9(5): 928-939
[19]Xu Chang,Li Zhoujun,Mu Yi, et al. Affiliation-hiding authenticated asymmetric group key agreement based on short signature[J]. Computer Journal, 2014, 57(10): 1580-1590
[20]Lü Xixiang, Li Hui, Wang Baocang. Authenticated asymmetric group key agreement based on certificateless cryptosystem[J]. International Journal of Computer Mathematics, 2014, 91(3): 447-460
[21]Zhang Qikun, Wang Ruifang, Tan Yu’an. Identity-based authenticated asymmetric group key agreement[J]. Journal of Computer Research and Development, 2014, 51(8): 1727-1738 (in Chinese)(张启坤, 王锐芳, 谭毓安. 基于身份的可认证非对称群组密钥协商协议[J]. 计算机研究与发展, 2014, 51(8): 1727-1738)
[22]Lee C C, Lim T H, Tsai C S. A new authenticated group key agreement in a mobile environment[J]. Annals of Telecommunications, 2011, 64(11/12): 735-744
[23]Tsai J L. A novel authenticated group key agreement protocol for mobile environment[J]. Annals of Telecommunications, 2011, 64(11/12): 663-669
[24]Chen Yong, He Mingxing, Zeng Shengke, et al. Universally composable asymmetric group key agreement protocol[C] //Proc of the 10th Int Conf on Information, Communications and Signal Processing (ICICS). Piscataway, NJ: IEEE, 2015: 1-6
[25]Zhang Lei, Wu Qianhong, Josep D F. Round-efficient and sender-unrestricted dynamic group key agreement protocol for secure group communications[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(11): 2352-2364
[26]Wei Guiyi, Yang Xianbo, Jun Shao. Efficient certificateless authenticated asymmetric group key agreement protocol[J]. KSII Transactions on Internet and Information System, 2012, 6(12): 3352-3365
Zhang Qikun1, Gan Yong1, Wang Ruifang1, Zheng Jiamin2, and Tan Yu’an2
1(InstituteofComputerandCommunicationEngineering,ZhengzhouUniversityofLightIndustry,Zhengzhou450002)2(SchoolofComputerScienceandTechnology,BeijingInstituteofTechnology,Beijing100081)
AbstractWireless sensor networks have some obvious characteristics, such as communication range is limited, energy-constraint, network is vulnerable et al. Group key agreement in this environment requires a cross-cluster, and computation and communication overhead are lightweight and highly safe group key agreement protocol. Aiming at these demands, the paper proposes a cross-domain lightweight asymmetric group key agreement, in order to establish a safe and efficient group communication channel among sensor nodes. Firstly, the protocol establishes the secret information among the cluster heads, and the cluster head as the bridge node to realize the sensor nodes in different cluster have the same group key information, thus realizing the cross cluster asymmetric group key agreement. The whole network node can share the secret information with the internal nodes of the group, which realizes the group security communication mechanism of the message sender unconstraint; proposed an asymmetric calculation to achieve computation and communication migration technologies to ensure that the sensor nodes are lightweight computing and communication consumption. For our asymmetric GKA protocol, the key confirmation is simple and requires no additional rounds if the protocol has been correctly executed. Proven and analysis show that the proposed protocol has the advantages in security and energy consumption.
Keywordswireless sensor networks; asymmetric group key agreement; authenticated; key self-confirmation; asymmetric calculation
This work was supported by the National Natural Science Foundation of China (U1636213, 61772477, 61572445, 61501406), the Natural Science Foundation of Henan Province of China (162300410322), the Science and Technology Project of He’nan Province (172102210059), and the Beijing Natural Science Foundation (4172053).
通信作者:王锐芳(wangruifang29@163.com)
基金项目:国家自然科学基金项目(U1636213,61772477,61572445,61501406);河南省自然科学基金项目(162300410322);河南省科技攻关项目(172102210059); 北京市自然科学基金项目(4172053)
修回日期:2018-04-08
收稿日期:2017-09-06;
中图法分类号TP309
(zhangqikun04@163.com)

ZhangQikun, born in 1980. PhD. His main research interests include information security and cryptography.

GanYong, born in 1965. PhD, professor, senior member of CCF. His main research interests include multimedia communications, image processing, coding and network engineering.

WangRuifang, born in 1982. Master, Her main research interests include information security and cryptography.

ZhengJiamin, born in 1975. PhD. His main research interests include information security and cloud computing.

TanYuan, born in 1972. PhD, professor. His main research interests include infor-mation security and network storage.