姚 晟 徐 风 赵 鹏 纪 霞
(计算智能与信号处理教育部重点实验室(安徽大学) 合肥 230601) (安徽大学计算机科学与技术学院 合肥 230601) (fisheryao@126.com)
随着计算机和互联网的迅速发展,数据急剧增加.然而,现实中的很多数据包含着大量的冗余特征(又称为属性),这些特征不仅降低了数据的分类性能,而且还增加了计算的复杂程度,因此需要对它们进行消除.特征选择(又称为属性约简)是数据预处理中很重要的一项技术,其基本思想是在没有降低数据分类精度的情形下尽可能去消除那些冗余的特征,最终得到一个特征子集.近年来,特征选择方法广泛地运用于机器学习、模式识别和数据挖掘等领域中 [1-3] .
特征评估是特征选择方法中一个很关键的环节,如何构建一个有效的评估函数一直是特征选择研究的重点.目前,学者们提出了很多关于特征评估的方法,如信息熵 [4-5] 、依赖度 [6] 和相关性 [7] 等.基于不同评估方法得到的特征选择结果也可能不同.
粗糙集理论是波兰学者Pawlak [8] 提出的一种处理模糊和不确定性知识的方法,目前已被广泛运用于特征选择方法中 [4,6,9] .传统的粗糙集理论建立在等价关系的基础上,把依赖度作为属性的评估依据.这种方法只适用于符号型属性的评估,由于现实中很多数据是连续型的,因此基于传统粗糙集理论的特征选择方法具有一定的局限性.Lin [10-11] 运用邻域关系代替等价关系,提出邻域粗糙集模型,这种模型可以直接处理连续型属性,放宽了粗糙集理论的适用范围.同时,基于邻域粗糙集模型的特征选择算法也相继提出 [6,9,12] .
目前,基于邻域粗糙集模型的特征选择算法中,利用邻域关系刻画对象之间的相似性 [10] 进行特征评估,并通过邻域半径来限定对象的邻域,这种方式虽然可以直接处理连续型数据,但是也存在一些问题.由于现实中很多的数据集是海量高维的,且有些数据可能是分布式的,因此这可能导致不同特征下的数据分布不均,甚至同一特征下不同类别的数据分散程度也不一样,而传统的邻域粗糙集模型只是通过距离函数和邻域半径来构造邻域关系,这样会产生许多误分类现象,从而影响到最终特征选择的结 [6,12] .Min [13] 等学者提出误差范围的覆盖粗糙集模型,在这个模型中利用一个误差范围来修正对象的邻域,并同时提出了相应的特征选择算法.Zhao [14] 等学者在假设这个误差满足高斯分布的情形,提出了自适应邻域粒模型,并提出基于该模型的特征选择算法.可以看出关于邻域误差的问题,目前越来越受到研究人员的关注.
本文针对目前邻域粗糙集模型存在的不足,引入二元邻域空间理论的定义 [15] ,用方差刻画数据的分布情况,依据方差将邻域半径分配到各个属性下,使每个属性对应的邻域半径能够自适应数据的分布状况,利用这种方法我们定义了自适应二元邻域空间理论,同时提出了对应的粗糙集模型.随后再结合邻域直觉模糊熵 [16] 来构造评估函数,并给出相应的特征选择算法.在实验分析中,我们分别将提出的算法和目前已有的特征选择算法进行实验对比,最终结果表明本文提出的特征选择算法具有更好的性能.
在经典粗糙集模型 [8] 中,信息系统 IS 表示为一个四元组的形式,即 IS =( U , AT , V , f ).其中, U 为非空有限对象集; AT 为非空有限属性集(又称为特征集); V 为全体属性集的值域, ![]() 其中, V a 为属性 a ∈ AT 的值域; f 满足函数映射关系 f : U × A → V , f a ( x )→ V a ,即属性到属性值域上的映射,简写为 a ( x ).此外,当信息系统 IS =( U , AT ∪{ d }, V , f )时,此信息系统又被称为决策信息系统( DIS ),其中 AT , d 分别被称为信息系统的条件属性和决策属性.
其中, V a 为属性 a ∈ AT 的值域; f 满足函数映射关系 f : U × A → V , f a ( x )→ V a ,即属性到属性值域上的映射,简写为 a ( x ).此外,当信息系统 IS =( U , AT ∪{ d }, V , f )时,此信息系统又被称为决策信息系统( DIS ),其中 AT , d 分别被称为信息系统的条件属性和决策属性.
定义1 [8] . 信息系统.设信息系统 IS =( U , AT , V , f ),∀ B ⊆ AT ,由属性子集 B 诱导的等价关系 IND ( R B )定义为
IND ( R B )={( x , y )∈ U × U | a ( x )= a ( y ),∀ a ∈ B },
等价关系 IND ( R B )满足对称性、自反性和传递性.由 IND ( R B )诱导出的划分表示为 U  IND ( R B ),其中包含对象 x 的等价类[ x ] B 定义为
IND ( R B ),其中包含对象 x 的等价类[ x ] B 定义为
[ x ] B ={ y ∈ U |( x , y )∈ IND ( R B )}.
定义2 [8] . 近似集.设信息系统 IS =( U , AT , V , f ), B ⊆ AT ,∀ X ⊆ U 关于 B 的下近似和上近似分别定义为
![]() ⊆ X };
⊆ X }; ![]() ∅}.
∅}.
另外∀ X ⊆ U 关于 B 的正区域、负区域和边界域分别定义为
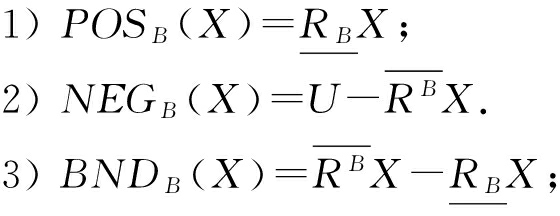
经典粗糙集理论是建立在等价关系的基础上,因此只适用于符号型属性,而无法处理连续型属性.Lin [10-11,15] 通过引入邻域的概念,将粗糙集理论推广到邻域空间,邻域空间可以直接处理数值型属性.本节我们主要介绍二元邻域空间 [15] 的基本内容.
定义3 [10] . 邻域.设邻域信息系统 NIS =( U , AT , V , f ),其中 U 为有限对象集, AT 为属性集且均为连续型, V 为属性的值域, f 为函数映射: U × AT → V .∀ x ∈ U 关于属性集 B ⊆ AT 的 δ 邻域定义为
其中, δ 称为邻域半径,是一个非负常数; Δ B ( x , y )被称为对象 x 和 y 之间的距离.常用的距离公式为闵可夫斯基距离,设属性集 B ={ a 1 , a 2 ,…, a m },闵可夫斯基距离定义为
闵可夫斯基距离有3种常用的形式:
1) 当 P =1时,
此距离又称为 Manhattan距离;
2) 当 P =2时,
此距离又称为Euclidean距离;
3) 当 P =∞时,
此距离又称为Chebychev距离.
定义4 [15] . 邻域系统.对于邻域信息系统 NIS =( U , AT , V , f ), A ⊆ AT ,设 B 1 , B 2 ,…, B m ⊆ A ,称 β ={ R B i |1≤ i ≤ m }为二元邻域关系集,这里满足 R B i ={( x , y )| Δ B i ( x , y )≤ δ B i }.那么∀ x ∈ U 基于 β 中二元邻域关系 R B i (1≤ i ≤ m )的邻域定义为 n B i ( x )={ y ∈ U |( x , y )∈ R B i },对象 x 在 β 下的所有邻域的集合 NS B ( x )称为对象 x 的邻域系统,即 NS B ( x )={ n B i ( x )|1≤ i ≤ m },并且称{ NS B ( x )| x ∈ U }为 U 上的邻域系统,用 NS B ( U )表示.那么( U , β )称为二元粒计算模型;( U , NS ( U ))称为 β 上的二元邻域空间,简称邻域空间.
定义5 [15-16] . 邻域空间近似集.设邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT 诱导的邻域空间为( U , NS B ( U )),则 X ⊆ U 基于该邻域空间的下近似 ![]() 和上近似
和上近似 ![]() 分别定义为
分别定义为
![]() ∃ N ( x )∈ NS B ( x ), N ( x )⊆ X };
∃ N ( x )∈ NS B ( x ), N ( x )⊆ X }; ![]() ∀ N ( x )∈ NS B ( x ),
∀ N ( x )∈ NS B ( x ),
N ( x )∩ X ≠∅}.
当 ![]() 时,称 X 在邻域空间( U , NS B ( U ))是可定义的,否则称为粗糙的.
时,称 X 在邻域空间( U , NS B ( U ))是可定义的,否则称为粗糙的.
同样地, X 关于邻域空间( U , NS B ( U ))的正区域、负区域和边界域分别定义为

可以看出,邻域空间的下近似、上近似和边界将论域 U 划分成3个区域.
设邻域信息系统 NIS =( U , AT , V , f ),在 B ⊆ AT 诱导的二元邻域空间( U , NS B ( U ))中,对象 x ∈ U 的邻域系统 NS B ( x )由 x 的邻域构成,通常邻域空间中的距离函数大多选取闵可夫斯基距离,对于对象 x ,如果∀ y ∈ U 与 x 的距离不超过给定的邻域半径 δ ,那么 y 将被包含在 x 的邻域中,这样却存在一定缺陷.设属性集 C ={ a 1 , a 2 ,… a m },对于对象 x , y ∈ U ,因此闵可夫斯基距离定义为
可以看出,对象 x , y 在属性集 C 下的距离是由各属性下距离分量| a i ( x )- a i ( y )| p 的共同结果.实际上,数据集的每个属性表示的是不同的指标,这些属性下取值的分布情况可能会不同,有的属性值比较集中,有的属性值就比较发散,甚至对于同一个属性,不同类别下数据的分布情况也不一样.正是由于这种因素,使得对象之间在各属性下的距离占总距离的比重不一样,如果统一设定一个邻域半径,导致聚集程度较大的属性对最终总距离的贡献较小,使得对象之间距离主要取决于发散程度较大的数据,这显然是不合理的,同时构造的邻域存在着一定误分类情形.具体情形可以观察例1.
例1 . 表1所示的是一个邻域决策信息系统 NIS =( U , AT ∪{ d }, V , f ), AT ={ a 1 , a 2 , a 3 }.
Table 1 Neighborhood Decision Information System
表1 邻域决策信息系统
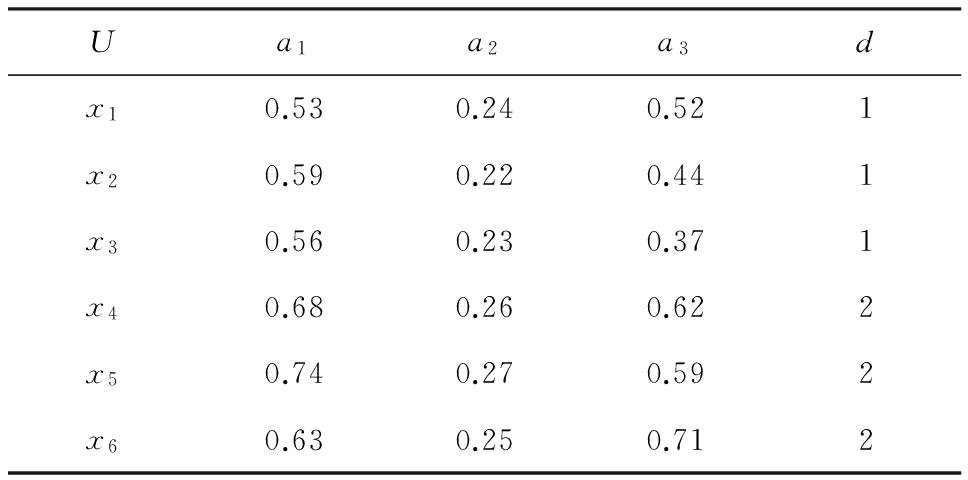
我们设 B ={ a 1 , a 2 },分别计算 δ =0.05和 δ =0.1下每个对象的邻域:
当 δ =0.05时,
n B ( x 1 )={ x 1 , x 3 },
n B ( x 2 )={ x 2 , x 3 },
n B ( x 3 )={ x 1 , x 2 , x 3 },
n B ( x 4 )={ x 4 },
n B ( x 5 )={ x 5 },
n B ( x 6 )={ x 6 }.
当 δ =0.1时,
n B ( x 1 )={ x 1 , x 2 , x 3 },
n B ( x 2 )={ x 1 , x 2 , x 3 , x 6 },
n B ( x 3 )={ x 1 , x 2 , x 3 , x 6 },
n B ( x 4 )={ x 4 , x 5 , x 6 },
n B ( x 5 )={ x 4 , x 5 },
n B ( x 6 )={ x 2 , x 3 , x 4 , x 6 }.
观察表1可以发现,属性 a 1 和 a 3 的数据较为分散,而属性 a 2 的数据较为聚集,这使得在计算的结果中,当邻域半径取值较小时,每个对象刻画的邻域类较为精细,但是在邻域粗糙集中,较细的邻域类往往是不能选择出最优特征子集 [6,12] .而当邻域半径取值较大时,很多的邻域类中出现了误包含现象,即邻域类中出现了不属于同一个类的对象,如对象 x 2 , x 3 , x 6 的邻域类.同样,这样也不能选择出最优的特征子集 [6,12] .
为了解决以上存在的问题,本文定义一种自适应邻域空间( U , aNS ( U )),其中对象 x ∈ U 的自适应邻域系统表示为 aNS B ( x ).自适应邻域空间的主要思想是对于一个给定的邻域半径,我们按照数据的方差将邻域半径分割到每个属性下,然后对象按照每个属性下的对应邻域半径求取邻域,最终的自适应邻域系统 aNS B ( x )由对象 x 在每个属性下的邻域构成.
定义6 . 自适应邻域系统.设邻域决策信息系统为 NIS =( U , AT ∪{ d }, V , f ), B ⊆ AT ,给定 B 下的邻域半径为 δ ,∀ a i ∈ B (1≤ i ≤| B |), x ∈ U 有集合:
Var B ( D x )={ Var a 1 ( D x ), Var a 2 ( D x ),…, Var a | B | ( D x )},
其中, D x ={ D ∈ U  { d }| x ∈ D }(即包含对象 x 的决策类), Var a i ( D x )表示 D x 中各对象在属性 a i 下取值的方差.我们定义由 B 诱导出的对象 x 的自适应邻域系统
{ d }| x ∈ D }(即包含对象 x 的决策类), Var a i ( D x )表示 D x 中各对象在属性 a i 下取值的方差.我们定义由 B 诱导出的对象 x 的自适应邻域系统 ![]() 为
为
其中, n a i ( x )={ y ∈ U | a i ∈ B ,| a i ( x )- a i ( y )|≤ δ a i },并且这里的 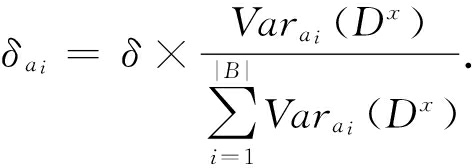 在不出现混淆的情况下,下文中我们运用 aNS B ( x )代替
在不出现混淆的情况下,下文中我们运用 aNS B ( x )代替 ![]()
通过定义6可以看出,对象 x 的自适应邻域系统 aNS B ( x )里的元素为对象 x 在每个属性下的邻域,并且邻域半径按照类的方差来进行分配,因此邻域半径满足关系 ![]()
定义7 . 自适应近似集.设邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT ,并且 B 下的邻域半径为 δ ,∀ X ⊆ U 关于自适应邻域空间( U , aNS B ( U ))的下近似和上近似分别定义为
![]() ∃ N ( x )∈ aNS B ( x ), N ( x )⊆ X };
∃ N ( x )∈ aNS B ( x ), N ( x )⊆ X }; ![]() ∀ N ( x )∈ aNS B ( x ), N ( x )∩ X ≠∅}.
∀ N ( x )∈ aNS B ( x ), N ( x )∩ X ≠∅}.
此外, X 关于自适应邻域空间( U , aNS B ( U ))的正区域、负区域和边界域分别定义为

当 ![]() 即 BUN B ( X )=∅,称 X 在自适应邻域空间( U , aNS B ( U ))是可定义的,否则称为粗糙的.
即 BUN B ( X )=∅,称 X 在自适应邻域空间( U , aNS B ( U ))是可定义的,否则称为粗糙的.
性质1 . 对于邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT ,设 B 下的邻域半径为 δ 1 , δ 2 ,并且满足 δ 1 ≤ δ 2 ,由 B 和 δ 1 诱导的自适应邻域空间为( U , aN ![]() ( U )),由 B 和 δ 2 诱导的自适应邻域空间为
( U )),由 B 和 δ 2 诱导的自适应邻域空间为 ![]() 那么存在关系:
那么存在关系:
aN ![]() ( U )⪯ aN
( U )⪯ aN ![]() ( U ).
( U ).
证明. 根据定义6我们有∀ a i ∈ B ,都有 ![]() 其中:
其中:
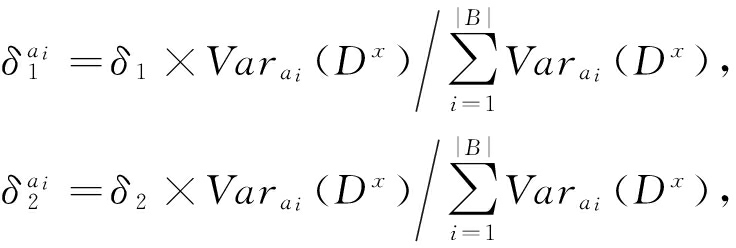
那么,∀ ![]() ∀
∀ ![]() 满足
满足 ![]() ⊆
⊆ ![]() 即 aN
即 aN ![]() ( x )⪯ aN
( x )⪯ aN ![]() ( x ),所以有 aN
( x ),所以有 aN ![]() ( U )⪯ aN
( U )⪯ aN ![]() ( U ).
( U ).
证毕.
性质2 . 对于邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT ,设 B 下的邻域半径为 δ 1 , δ 2 ,由 B 诱导的自适应邻域空间满足 aN ![]() ( U )⪯ aN
( U )⪯ aN ![]() ( U ),∀ X ⊆ U 满足关系:
( U ),∀ X ⊆ U 满足关系:
BU ![]() ( X )⊆ BU
( X )⊆ BU ![]() ( X ).
( X ).
证明. 由 aN ![]() ( U )⪯ aN
( U )⪯ aN ![]() ( U )根据定义6有∀ x ∈ U , aN
( U )根据定义6有∀ x ∈ U , aN ![]() ( x )⪯ aN
( x )⪯ aN ![]() ( x ),所以根据定义7有
( x ),所以根据定义7有 ![]() ⊆
⊆ ![]() ⊆
⊆ ![]() 即 BU
即 BU ![]() ( X )⊆ BU
( X )⊆ BU ![]() ( X ).
( X ).
证毕.
直觉模糊集是由Atanassov [17] 在模糊集理论的基础上进行的推广.直觉模糊集理论中,首先分别定义一对关于对象的粗糙直觉隶属度函数,即隶属度 μ ( x )和非隶属度 ν ( x ),然后在这2个函数的基础上进一步定义了犹豫度函数 π ( x )=1- μ ( x )- ν ( x ),利用这3个函数,直觉模糊集的熵理论可以很好地运用于数据的不确定性分析 [18-20] .我们在Zheng等人 [16] 的基础上,定义了自适应二元邻域空间粗糙集模型中的隶属度 μ ( x )和非隶属度 ν ( x )函数.
定义8 . 粗糙直觉隶属函数.设邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT , B 诱导的自适应邻域空间为( U , aNS B ( U )), X ⊆ U ,∀ x ∈ U 在 B 下关于 X 的一对粗糙直觉隶属函数 ![]() 分别定义为
分别定义为

在定义8中, ![]() 表示粗糙直觉模糊集中对象 x 隶属于 X 的程度,
表示粗糙直觉模糊集中对象 x 隶属于 X 的程度, ![]() 表示为 x 不隶属于 X 的程度,根据这2个函数可以得到对象 x 关于 X 的犹豫程度
表示为 x 不隶属于 X 的程度,根据这2个函数可以得到对象 x 关于 X 的犹豫程度 ![]() 通过这3个量去描述对象与集合之间的关系,这样不仅符合我们人类的认知观,而且能更好地反映出集合的不确定性 [17] .
通过这3个量去描述对象与集合之间的关系,这样不仅符合我们人类的认知观,而且能更好地反映出集合的不确定性 [17] .
性质3 . 设邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT ,∀ X ⊆ U ,对于 x ∈ U 满足:
1) 如果 x ∈ POS B ( X ),有 ![]() 0;
0;
2) 如果 x ∈ NEG B ( X ),有 ![]() 1;
1;
3) 如果 x ∈ BUN B ( X ),有 ![]()
证明. 根据定义8可以直接得到.
证毕.
信息熵作为信息系统中一种重要的不确定性度量方法,学者们对它作了大量的研究 [4,21-22] .近年来,学者们将模糊熵和直觉模糊熵运用于信息系统的不确定性度量,取得了很多不错的成果 [16,23] .接下来,我们在Zheng等人 [16] 提出的邻域直觉模糊熵的基础上结合自适应邻域空间,提出基于自适应邻域空间粗糙集的邻域直觉模糊熵.
定义9 . 邻域直觉模糊熵.设邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT , B 诱导的自适应邻域空间为( U , aNS B ( U )),∀ X ⊆ U ,则 X 关于 B 的邻域直觉模糊熵 ![]() 定义为
定义为
这里的
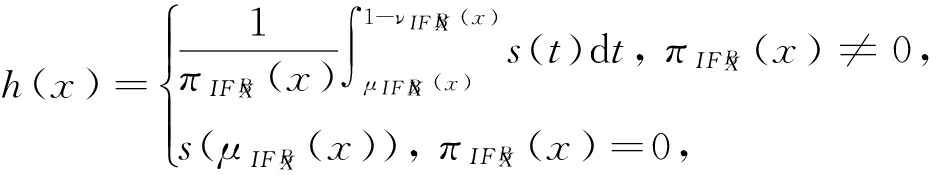
其中
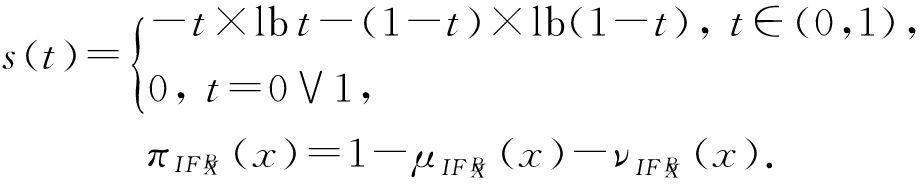
特别地,对于邻域决策信息系统 NIS =( U , AT ∪{ d }, V , f ), U  d 关于 B 的直觉模糊熵 IE ( I
d 关于 B 的直觉模糊熵 IE ( I ![]() )定义为
)定义为
其中, U  d ={ D 1 , D 2 ,…, D m }.
d ={ D 1 , D 2 ,…, D m }.
性质4 . 设邻域信息系统 NIS =( U , AT , V , f ), B ⊆ AT , B 诱导的自适应邻域空间为( U , aNS B ( U )),∀ X ⊆ U 关于 B 的邻域直觉模糊熵 ![]() 满足3个性质:
满足3个性质:
2) ![]() 当且仅当∀ x ∈ U ,有
当且仅当∀ x ∈ U ,有 ![]()
![]() 或者
或者 ![]() 当且仅当∀
当且仅当∀ ![]()
证明. 首先,我们分析一下函数
的单调性,对 s ( t )求导为 ![]() 那么当0< t <0.5时函数 s ( t )单调递增,当0.5< t <1时函数 s ( t )单调递减,所以
那么当0< t <0.5时函数 s ( t )单调递增,当0.5< t <1时函数 s ( t )单调递减,所以
0≤ s ( t )≤1. ![]()
当 ![]() 时,那么
时,那么 ![]()
![]() 即
即 ![]() 所以性质1)得证.然后运用反证法,假设∃
所以性质1)得证.然后运用反证法,假设∃ ![]() 根据定义8有 h ( x )>0,则
根据定义8有 h ( x )>0,则 ![]() 所以性质2)成立.假设∃
所以性质2)成立.假设∃ ![]() 根据定义8有 h ( x )<1,则
根据定义8有 h ( x )<1,则 ![]() <1,所以性质3)成立.
<1,所以性质3)成立.
证毕.
性质5 . 设邻域信息系统 NIS =( U , AT , V , f ), B 2 ⊆ B 1 ⊆ AT , B 1 , B 2 诱导的自适应邻域空间分别为( U , aNS B 1 ( U )),( U , aNS B 2 ( U )),∀ X ⊆ U 关于 B 1 , B 2 的直觉模糊熵 ![]() 满足以下关系:
满足以下关系:
IE ( I ![]() )≤ IE ( I
)≤ IE ( I ![]() ).
).
证明. 如果 ![]() 根据定义9显然成立.如果
根据定义9显然成立.如果 ![]() 由性质3可知,当0< t <0.5,函数 s ( t )单调递增,0.5< t <1,函数 s ( t )单调递减,如果
由性质3可知,当0< t <0.5,函数 s ( t )单调递增,0.5< t <1,函数 s ( t )单调递减,如果 ![]() 保持不变,那么当
保持不变,那么当 ![]() 时
时 ![]() 达到最大.当
达到最大.当 ![]()
![]() 是关于
是关于 ![]() 的单调递增函数,当
的单调递增函数,当 ![]() 是关于
是关于 ![]() 的单调递减函数,那么我们将讨论
的单调递减函数,那么我们将讨论 ![]() 的4种情形:
的4种情形:
1) 当 ![]() 并且
并且 ![]()
![]() 所以我们有
所以我们有 ![]()
![]() 又
又 ![]() 因此
因此 ![]()
2) 当 ![]() 并且
并且 ![]()
![]() 所以我们有
所以我们有 ![]() 又
又 ![]() 因此
因此 ![]()
3) 当 ![]() 并且
并且 ![]() 所以我们有
所以我们有 ![]() 和
和 ![]() 又
又 ![]() 我们有
我们有 ![]() 且
且 ![]()
4) 当 ![]() 并且
并且 ![]() 我们有
我们有 ![]() 和
和 ![]()
![]() 又
又 ![]() 我们有
我们有 ![]() 且
且 ![]()
综上所述,有:
因此 IE ( I ![]() )≤ IE ( I
)≤ IE ( I ![]() ).
).
证毕.
例2 . 继续例1,设邻域决策信息系统 NIS =( U , AT ∪{ d }, V , f )如表1所示,设 B 3 ={ a 1 }, B 2 ={ a 1 , a 2 }, B 1 ={ a 1 , a 2 , a 3 },这里我们可以得到 U  d 关于 B 1 , B 2 , B 3 的邻域直觉模糊熵.
d 关于 B 1 , B 2 , B 3 的邻域直觉模糊熵.
U  { d }={ D 1 , D 2 },其中 D 1 ={ x 1 , x 2 , x 3 }, D 2 ={ x 4 , x 5 , x 6 }.那么:
{ d }={ D 1 , D 2 },其中 D 1 ={ x 1 , x 2 , x 3 }, D 2 ={ x 4 , x 5 , x 6 }.那么:
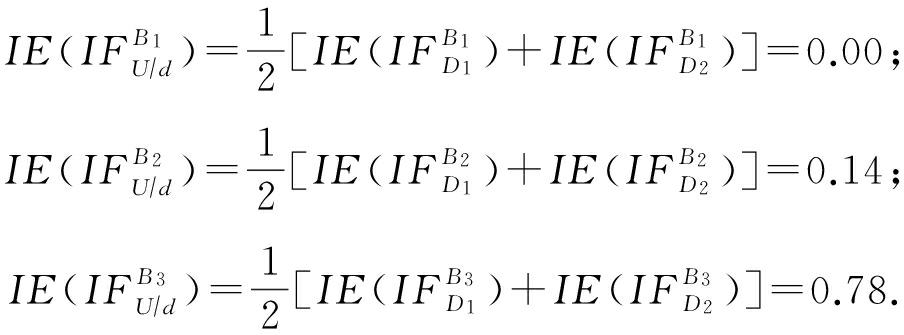
最终结果满足性质5中的关系 ![]()
从性质5可以看出,随着属性子集的增加,其邻域直觉模糊熵的值单调不增,这是一个很重要的性质,它为我们构造基于邻域直觉模糊熵的特征选择算法提供了理论依据.
特征选择作为粗糙集理论的一个重要的应用,许多研究人员在这方面作了深入的研究 [4,6,9] ,尤其在邻域粗糙集模型中,目前已有多种特征选择算法,例如基于属性依赖度的特征选择算法 [6] 、基于邻域熵的特征选择算法 [24] 、基于模糊集的特征选择算法 [5,25] .
由于在直觉模糊集中,对象与集合之间的关系通过隶属度、非隶属度和犹豫度3个方面来描述,这3个方面表现出了对象对集合的支持、反对和中立3个观点,它进一步增强了模糊集的表示能力,处理模糊性具有更多的优势 [17] .同时文献[16]指出了直觉模糊熵具有更好的信息系统不确定性度量效果.因此我们将自适应二元邻域空间粗糙集模型融合邻域直觉模糊熵来构造相应的特征选择算法.
定义10 . 相对约简.设邻域决策信息系统 NIS =( U , AT ∪{ d }, V , f ), B ⊆ AT ,如果 ![]() 并且∀ a ∈ B ,都有
并且∀ a ∈ B ,都有 ![]() 那么称 B 是关于 AT 的相对约简.
那么称 B 是关于 AT 的相对约简.
定义11 . 属性重要度.设邻域决策信息系统 NIS =( U , AT ∪{ d }, V , f ), B ⊆ AT ,∀ a ∈ B ,定义 a 在 B 下基于决策属性 d 的重要度为
在本文提出的特征选择算法中,我们把定义11中的属性重要度作为特征评估函数.其算法的具体构造过程如下所述.
对于邻域决策信息系统 NIS =( U , AT ∪{ d }, V , f ),为了降低算法的时间复杂度,根据定义6,我们首先计算出 AT 中每个属性下各个决策类的方差.
算法1 . 计算方差 Var B ( D i )( D i ∈ U  { d })和 Var B .
{ d })和 Var B .
输入: NIS =( U , AT ∪{ d }, V , f ), AT ={ a 1 , a 2 ,…, a | AT | };
输出:方差 Var AT .
Step1. 计算决策属性 d 的划分 U  { d }={ D 1 , D 2 ,…, D m }.
{ d }={ D 1 , D 2 ,…, D m }.
Step2. 对于 U  { d }中每个决策类 D i ,计算在所有条件属性下的方差,即属性集 AT 下 D i 的方差表示为
{ d }中每个决策类 D i ,计算在所有条件属性下的方差,即属性集 AT 下 D i 的方差表示为
Var AT ( D i )={ Var a 1 ( D i ), Var a 2 ( D i ),…, Var a | AT | ( D i )}.
Step3. 由Step2的结果可以得到:
Var AT ={ Var AT ( D 1 ), Var AT ( D 2 ),…, Var AT ( D m )}.
设| U |= n ,| AT |= c ,那么算法1的时间复杂度为 O (( c +1) n ).
我们计算 U 上的自适应邻域系统 aNS B ( U ),即计算∀ x ∈ U 的 aNS B ( x ),其中 B ⊆ AT ,具体过程如算法2所示.
算法2 . 计算 aNS B ( U ).
输入: NIS =( U , AT ∪{ d }, V , f )、 B ⊆ AT 且 B ={ a 1 , a 2 ,…, a | B | }、邻域半径 δ 、 Var AT ;
输出: aNS B ( U ).
Step1. 根据算法1的结果,计算所有决策类 D i 在 B ={ a 1 , a 2 ,…, a | B | }下每个属性的邻域半径 ![]()
 *根据定义6*
*根据定义6* 
Step2. 对于对象 x i ∈ U ,计算其在 B 下每个属性的邻域 ![]() 这里的 a j ∈ B , x i ∈ D t .
这里的 a j ∈ B , x i ∈ D t .  *邻域采用文献[26]的计算方法*
*邻域采用文献[26]的计算方法* 
Step3. 根据Step2得到
aNS B ( U )={ aNS B ( x 1 ), aNS B ( x 2 ),…,
aNS B ( x | U | )}.
这里的
算法2中,设| U |= n ,| U  { d }|= m ,则Step1的时间复杂度为 O ( m ×| B |),由于Step2采用文献[26]提出的排序方法计算邻域,使得时间复杂度为 O ( n ×lb n ),那么Step2的时间复杂度为 O (| B |× n ×lb n ),因而算法2的时间复杂度为 O (| B |×( m + n ×lb n )).
{ d }|= m ,则Step1的时间复杂度为 O ( m ×| B |),由于Step2采用文献[26]提出的排序方法计算邻域,使得时间复杂度为 O ( n ×lb n ),那么Step2的时间复杂度为 O (| B |× n ×lb n ),因而算法2的时间复杂度为 O (| B |×( m + n ×lb n )).
通过算法2求得 aNS B ( U ),那么就可以计算出自适应邻域直觉模糊熵,具体如算法3所示.
算法3 . 计算自适应邻域直觉模糊熵 ![]()
输入: NIS =( U , AT ∪{ d }, V , f )、 B ⊆ AT 且 B ={ a 1 , a 2 ,…, a | B | },邻域半径 δ 、 Var AT ;
输出: ![]()
Step1. 根据算法2得到 aNS B ( U ).
Step2. 对于决策类 D i ∈ U  { d }:
{ d }:
Step2.1. 计算∀ x j ∈ U 的 ![]()
![]()
 *根据定义8*
*根据定义8* 
Step2.2. 如果 ![]() 那么进行
那么进行 ![]()
![]() 否则进行
否则进行 ![]()
Step2.3. 对于Step2.2的计算结果进一步计算 ![]()
 *根据定义8*
*根据定义8* 
Step3. 对于Step2中的所有决策类计算 ![]()
Step4.返回最终结果
算法3中,| U |= n ,| U  { d }|= m ,在算法2的结果上,Step2时间复杂度为 O (| B |× n ),则Step2至Step3的时间复杂度为 O (| B |× mn ),由于Step1的时间复杂度为算法2的时间复杂度,所以整个算法3的时间复杂度为 O (| B |× mn +| B |×( m + n ×lb n )).
{ d }|= m ,在算法2的结果上,Step2时间复杂度为 O (| B |× n ),则Step2至Step3的时间复杂度为 O (| B |× mn ),由于Step1的时间复杂度为算法2的时间复杂度,所以整个算法3的时间复杂度为 O (| B |× mn +| B |×( m + n ×lb n )).
下面构造出本文所提出的特征选择算法,其基本思想是:利用邻域直觉模糊熵来评价属性的重要度,然后每次在剩余的属性中选择属性重要度最大的属性加入约简集合中,直到最后满足算法的终止条件后终止算法,此时约简集合即为最终的特征选择结果.具体流程如算法4所示.
算法4 . 基于邻域直觉模糊熵的特征选择算法(feature selection based on neighborhood intuitionistic fuzzy entropy, FSNIFE).
输入: NIS =( U , AT ∪{ d }, V , f )、邻域半径 δ 、终止阈值 λ =0.001;
输出:约简集合 red .
Step1. 初始化: red =∅, n =0, IE ( I ![]() )=1.
)=1.  *其中 n 用来记录约简集的基数*
*其中 n 用来记录约简集的基数* 
Step2. 计算 Var AT .  *根据算法1*
*根据算法1* 
Step3. 对于属性∀ a i ∈ AT - red :
Step3.1. 计算属性 a i 的重要度 SIG ( a , red , d )= ![]()
 *根据算法3和定义11*
*根据算法3和定义11* 
Step3.2. 选择Step3.1中属性重要度最大的属性,记为 a t ,将属性 a t 加入 red 中.
Step4. 重复进行Step3,直到满足 SIG ( a t , red , D )≤ λ 或 red = AT 时停止.
Step5. 返回结果 red .
设| U |= n ,| AT |= c ,| U  { d }|= m ,在算法4中,假设最终的特征选择的结果为 l 个属性,那么Step4的时间复杂度为
{ d }|= m ,在算法4中,假设最终的特征选择的结果为 l 个属性,那么Step4的时间复杂度为
O ( c × mn + m + n ×lb n )+( c -1)×
(2 mn +2( m + n ×lb n ))+…+( c - l +1)×
( lmn + l ( m + n ×lb n )))= ![]()
因此整个算法的时间复杂度为
O (( mn + m + n ×lb n )× ![]()
即:
![]()
( mn + m + n ×lb n )+( c +1)× n ).
当 l = c 时,此时算法的计算次数最多,因此最坏的时间复杂度为
通常情况下, m ≪ n ,因此本文所提出的特征选择算法的时间复杂度不超过 O ( c 3 × n ×lb n ).
为了验证本文所提的特征选择算法的有效性,我们首先选取目前已有的3个特征选择算法 [5,12,25] ;然后将它们和本文提出的特征选择算法分别对同一数据集进行实验;最后通过对比各个算法的实验结果来评估算法的性能,其中性能的评估分别通过特征选择的数量、算法运行的时间和特征子集的分类精度3个指标体现.
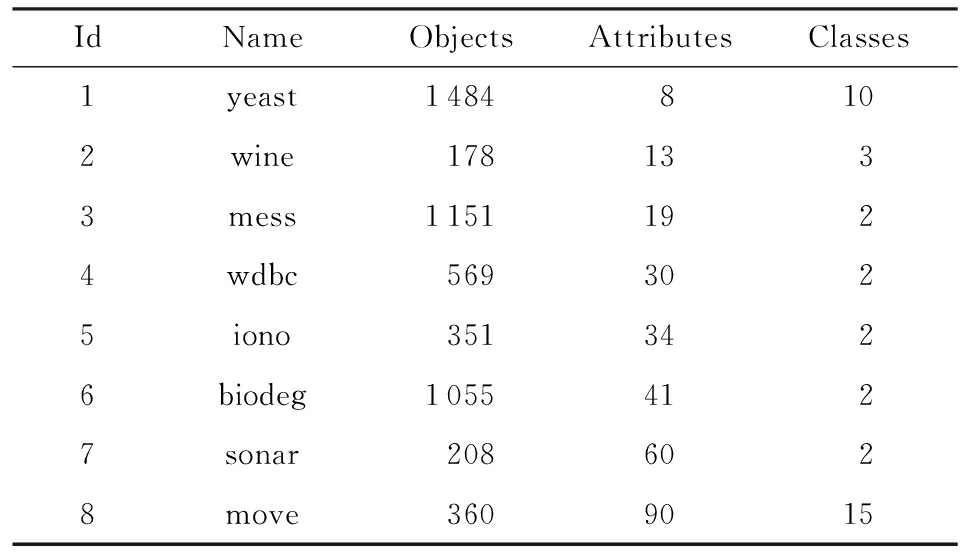
本文从UCI数据库获取了8个数据集,具体信息如表2所示.选择已有的特征选择算法分别为:基于信息熵的一种新的模糊粗糙集特征选择(feature selection based on information entropy of fuzzy rough set, FSFRSIE)算法 [5] 、基于模糊粗糙集的特征选择(feature selection based on fuzzy rough set, FSFRS)算法 [25] 和基于模糊邻域粗糙集的特征选择(feature selection based on fuzzy neighborhood rough set, FSFNRS)算法 [12] .这些算法可以直接运用于连续型属性,同时为了消除属性量纲的影响,我们需要将数据进行标准化,但是为了保证数据的方差相对不变,我们这里采用极差正规化变换,变换公式为 x * =( x - x min )  ( x max - x min ),变换后的数据全部位于[0,1]之间.
( x max - x min ),变换后的数据全部位于[0,1]之间.
本实验所有算法运行的硬件环境为Intel ® Core TM i3 CPU 550,3.2 GHz 和2.0 GB RAM的PC机上,操作系统为Windows 7,实验所采用的编译工具为Java.分类精度的计算采用支持向量机(support vector machine, SVM)和决策树(decision tree, DT)这2种分类器.
Table 2 UCI Data Set
表2 UCI数据集
由于邻域半径 δ 的取值对特征选择的结果具有很重要的影响,因此在本文的算法(FSNIFE)开始计算之前,我们需要确定 δ 的参数.为了能选择出合适的特征子集,我们首先将 δ 在某个邻域半径区间上依次选取等步长的值进行实验,由于每个数据集的特征数目不一样,邻域半径区间的选取也不一样.初步实验后我们得到,yeast,wine,mess数据集的区间选取为[0.01,0.3],步长为0.01;wdbc,iono,biodeg数据集的区间选取为[0.01,0.5],步长为0.01;sonar数据集的区间选取为[0.01,1],步长为0.01;move数据集的区间选取为[0.1,8],步长为0.1.然后对数据集在每个邻域半径下进行特征选择实验,并采用支持向量机(SVM)和决策树(DT)这2种分类器对特征子集结果采用十折交叉验证法计算其分类精度.FSNIFE算法在所有数据集的结果如图1~8所示.最终的实验结果选取为分类精度最高且邻域半径 δ 最小的特征子集,由于同一个特征子集在不同分类器下的分类精度并不一样,因此本实验会得到2个特征选择结果,分别为SVM和DT这2种分类器选择出的特征子集.
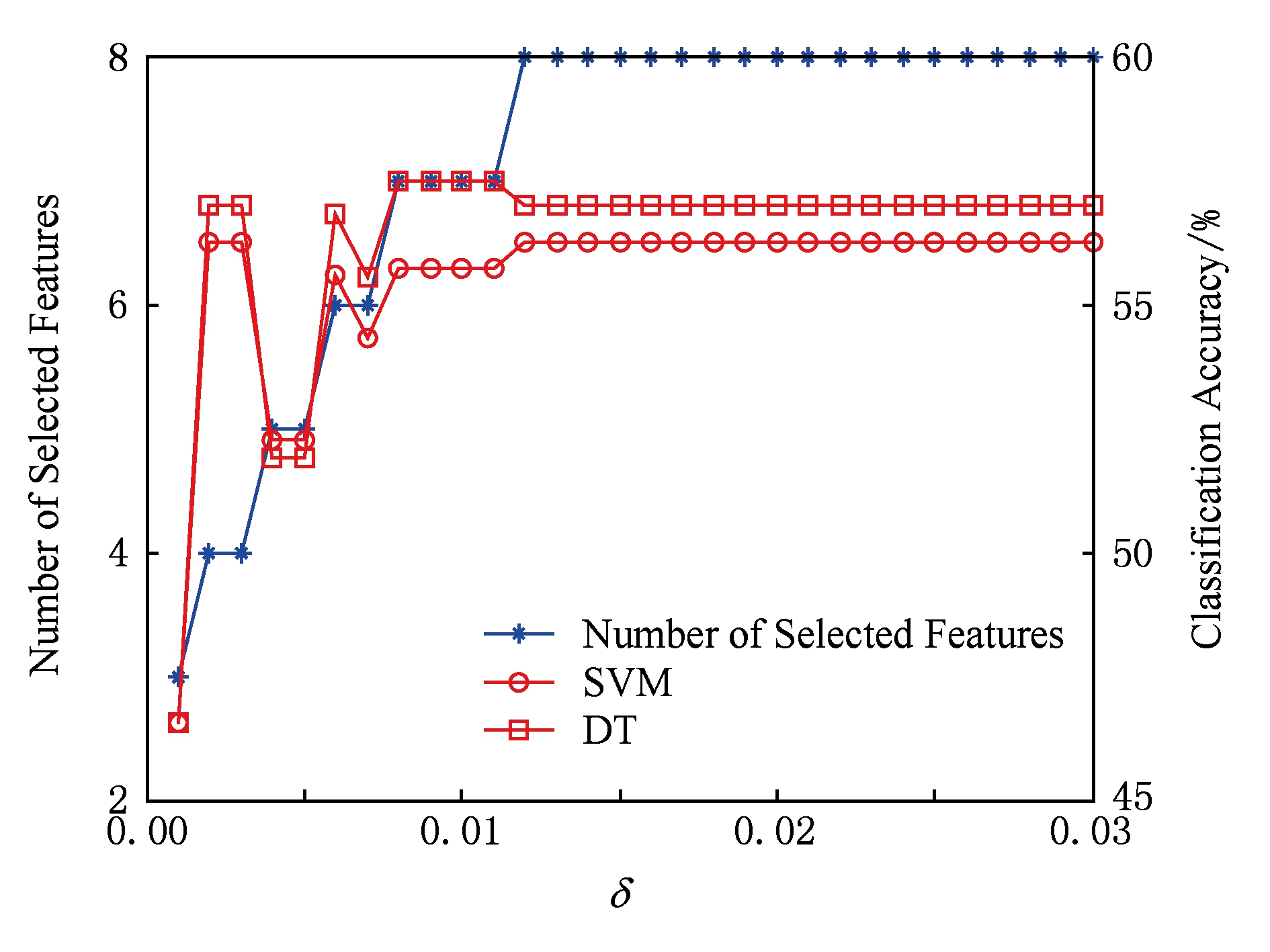
Fig. 1 yeast data set result
图1 yeast数据集结果
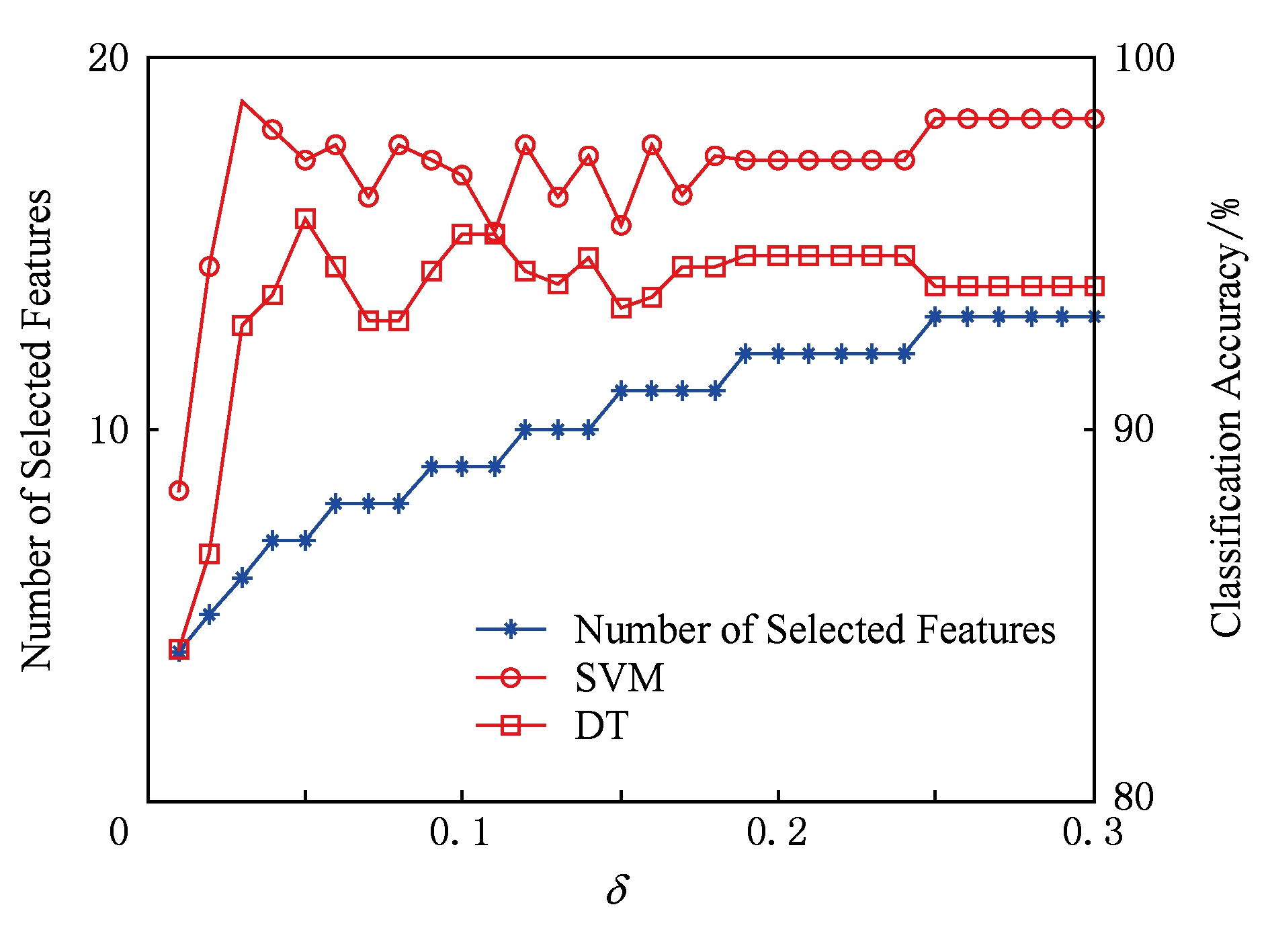
Fig. 2 wine data set result
图2 wine数据集结果
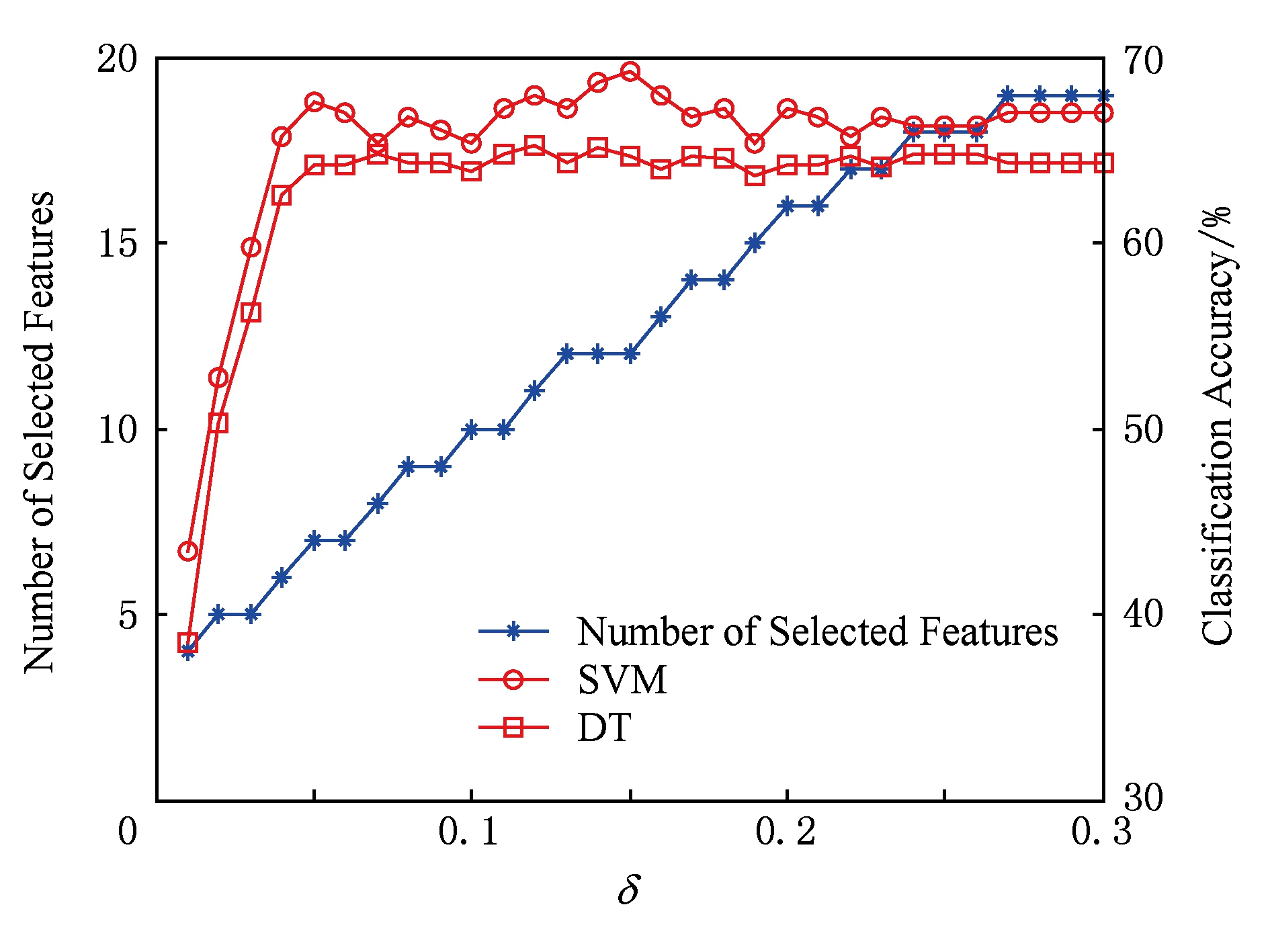
Fig. 3 mess data set result
图3 mess数据集结果
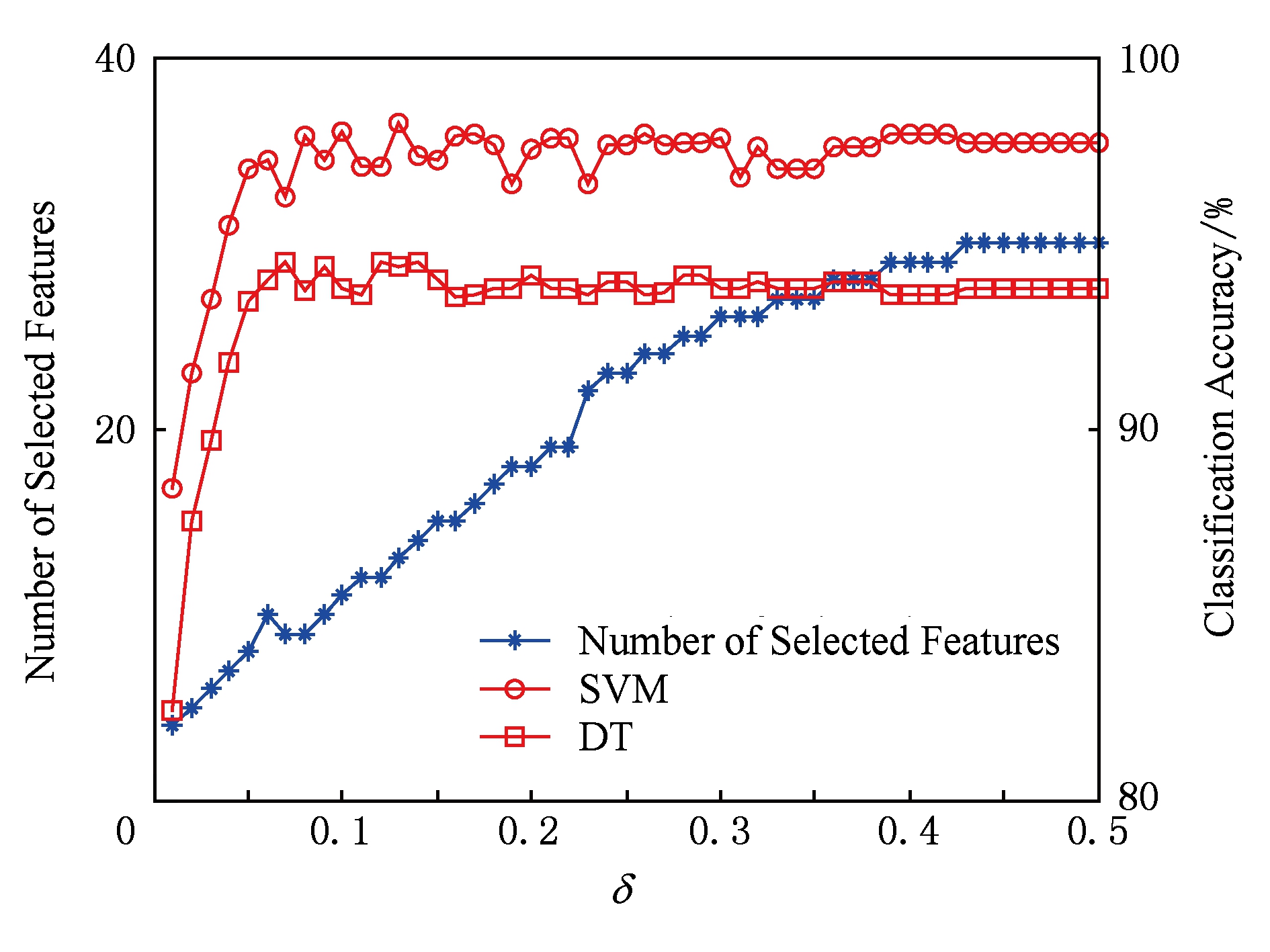
Fig. 4 wdbc data set result
图4 wdbc数据集结果
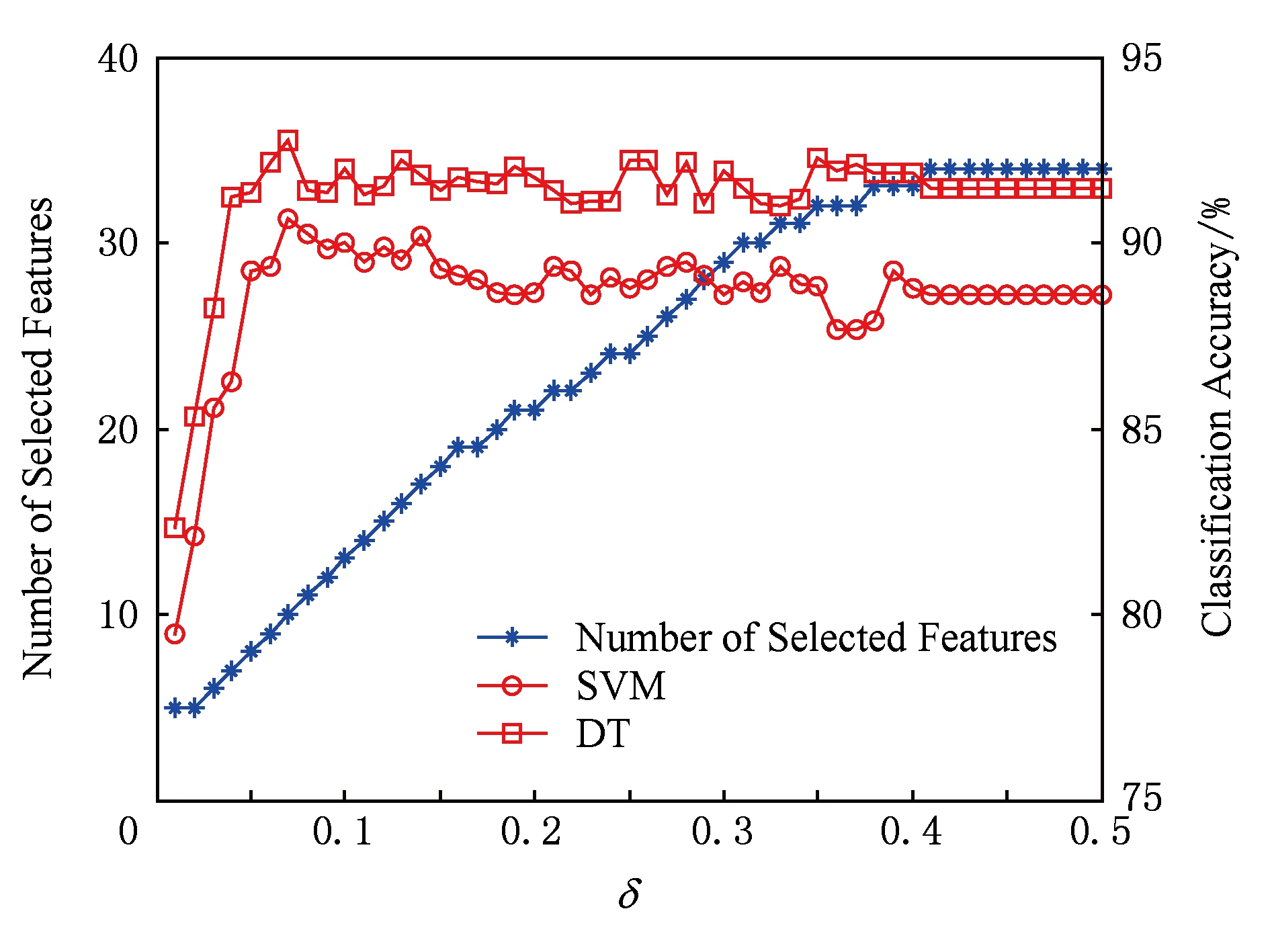
Fig.5 iono data set result
图5 iono数据集结果
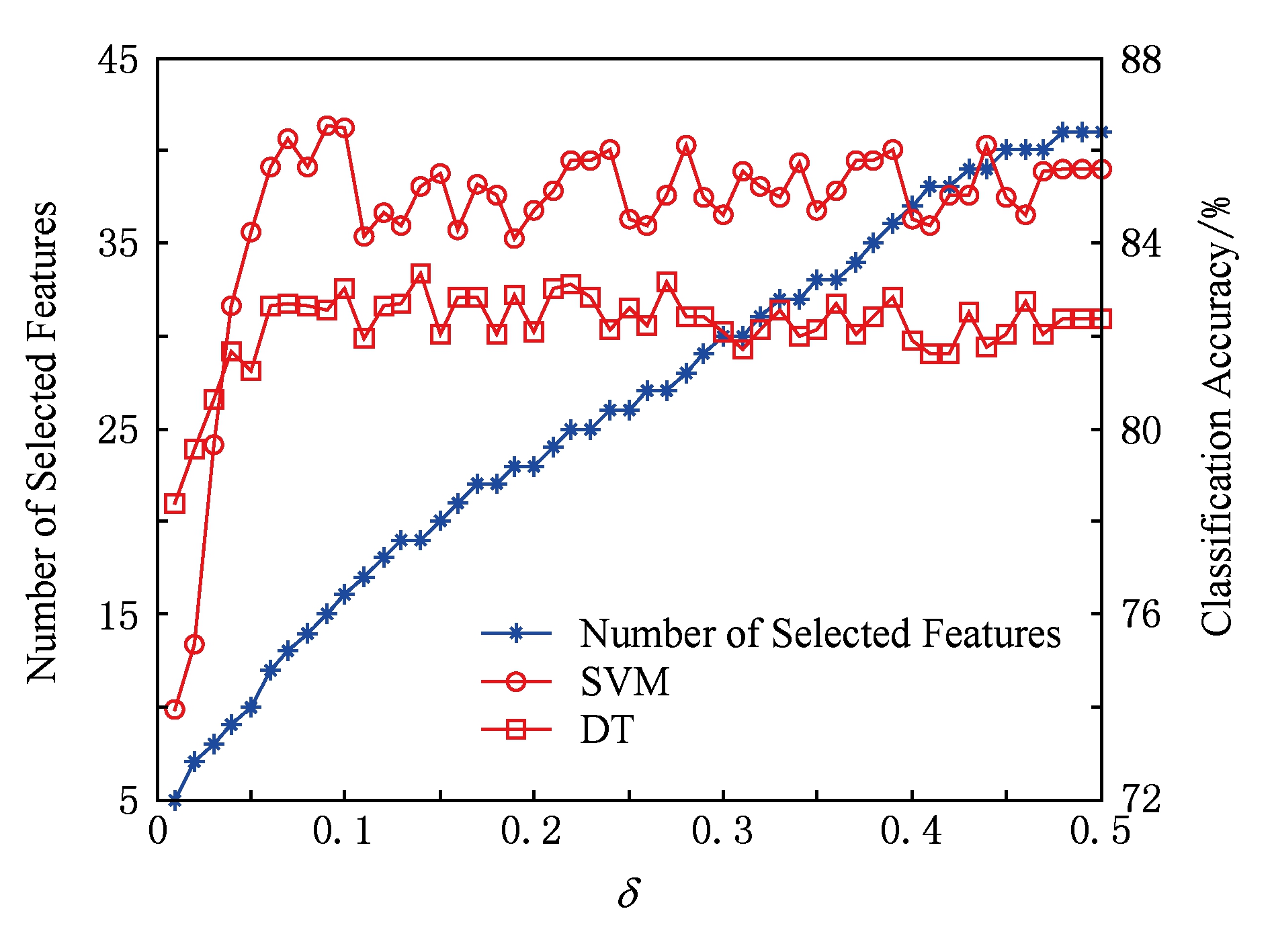
Fig. 6 biodeg data set result
图6 biodeg数据集结果
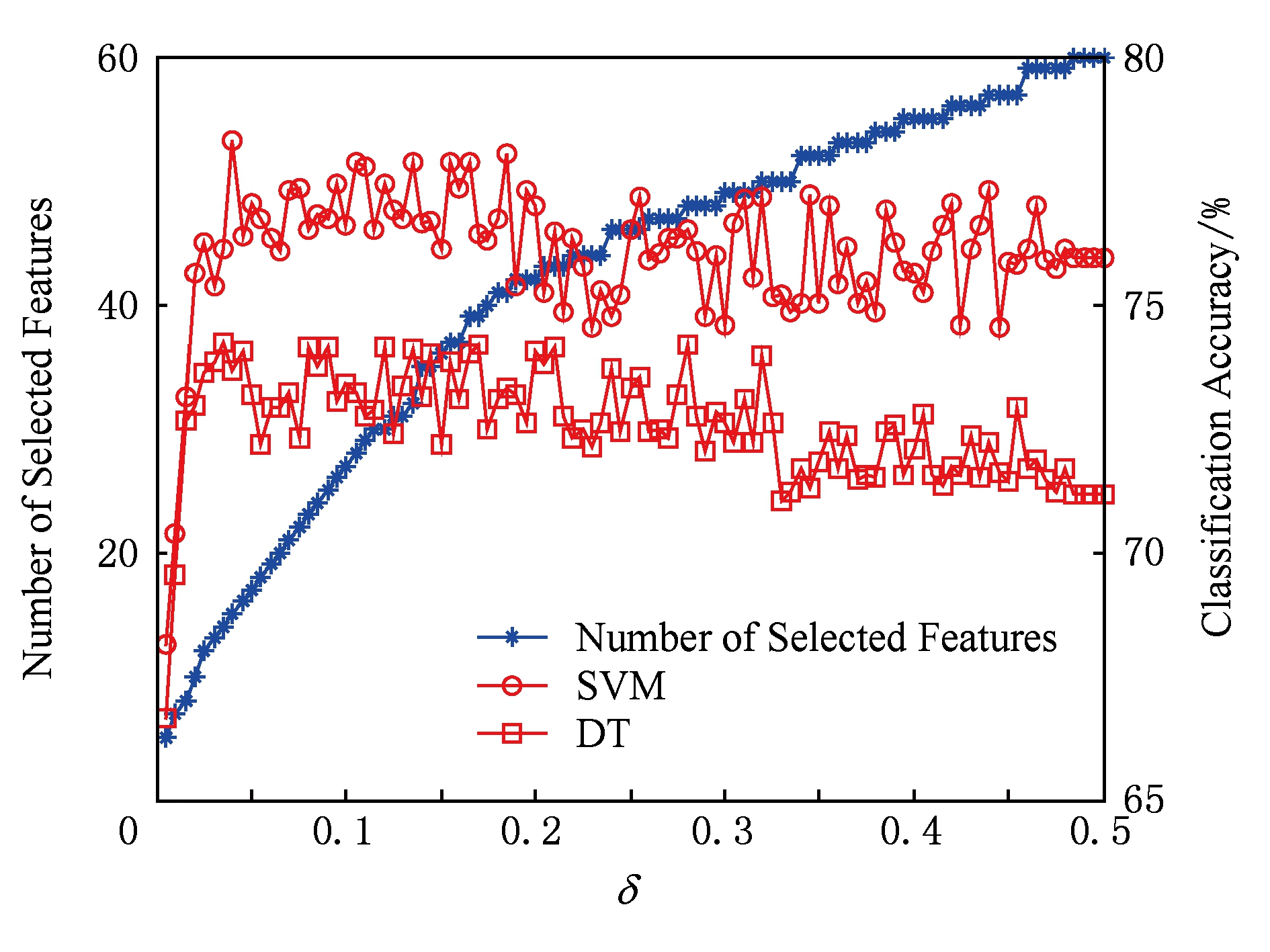
Fig. 7 sonar data set result
图7 sonar数据集结果
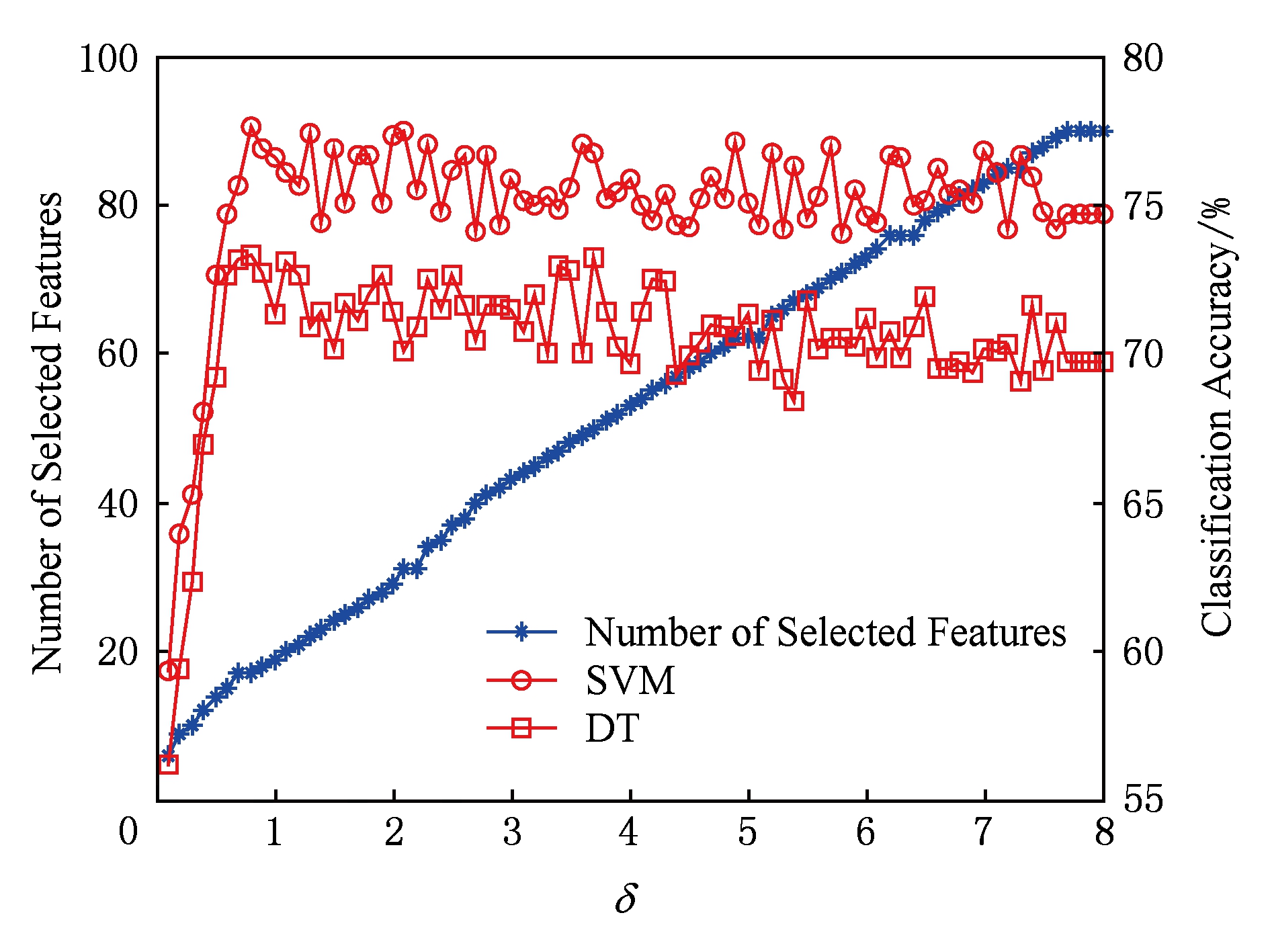
Fig. 8 move data set result
图8 move数据集结果
表3是4种算法在SVM分类器下选择的特征子集的基数结果,表4是4种算法在DT分类器下选择的特征子集的基数结果.相比较于原数据集属性的数目,这4种算法都能很有效地删去多余的属性,尤其对于数据集sonar,move.这说明现实中的很多数据集都存在着大量的冗余属性,从而体现出特征选择的重要性.另外比较这4种算法的2类特征选择结果,可以发现在大部分数据集中,本文所提出的FSNIFE算法选择的特征数目比其他算法要更加的少,说明用FSNIFE算法能更高效地筛选出数据集中少又有效的特征.因此在属性的约简基数方面,FSNIFE算法更具优越性.
Table 3 Feature Selection Results of 4 Algorithms in SVM
表3 分类器SVM的4种算法特征选择结果
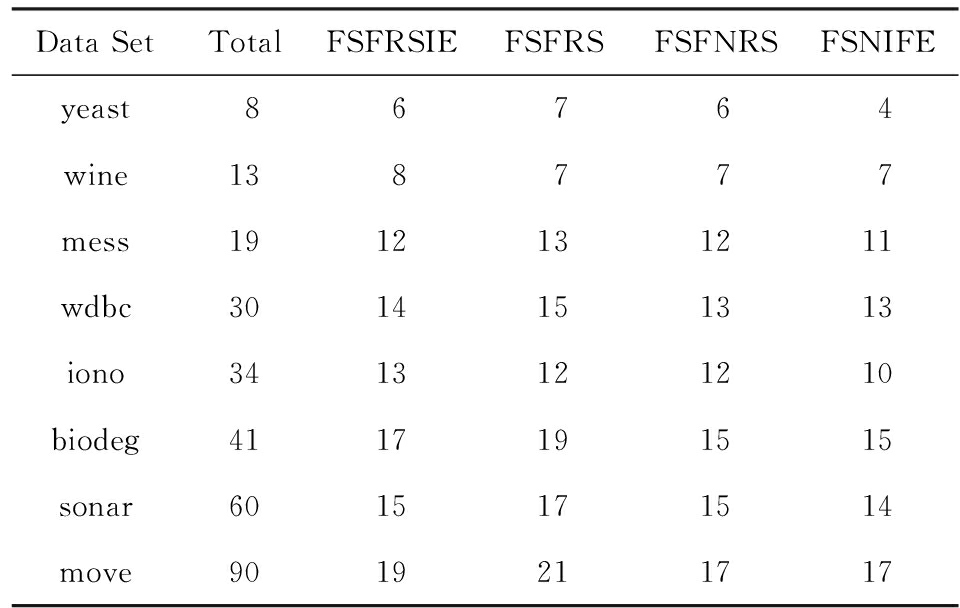
Table 4 Feature Selection Results of 4 Algorithms in DT
表4 分类器DT的4种算法特征选择结果
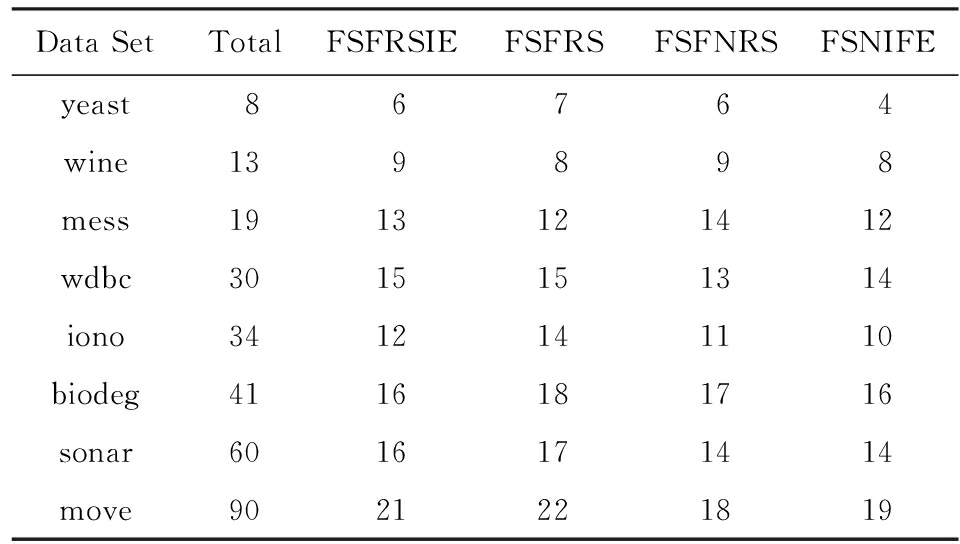
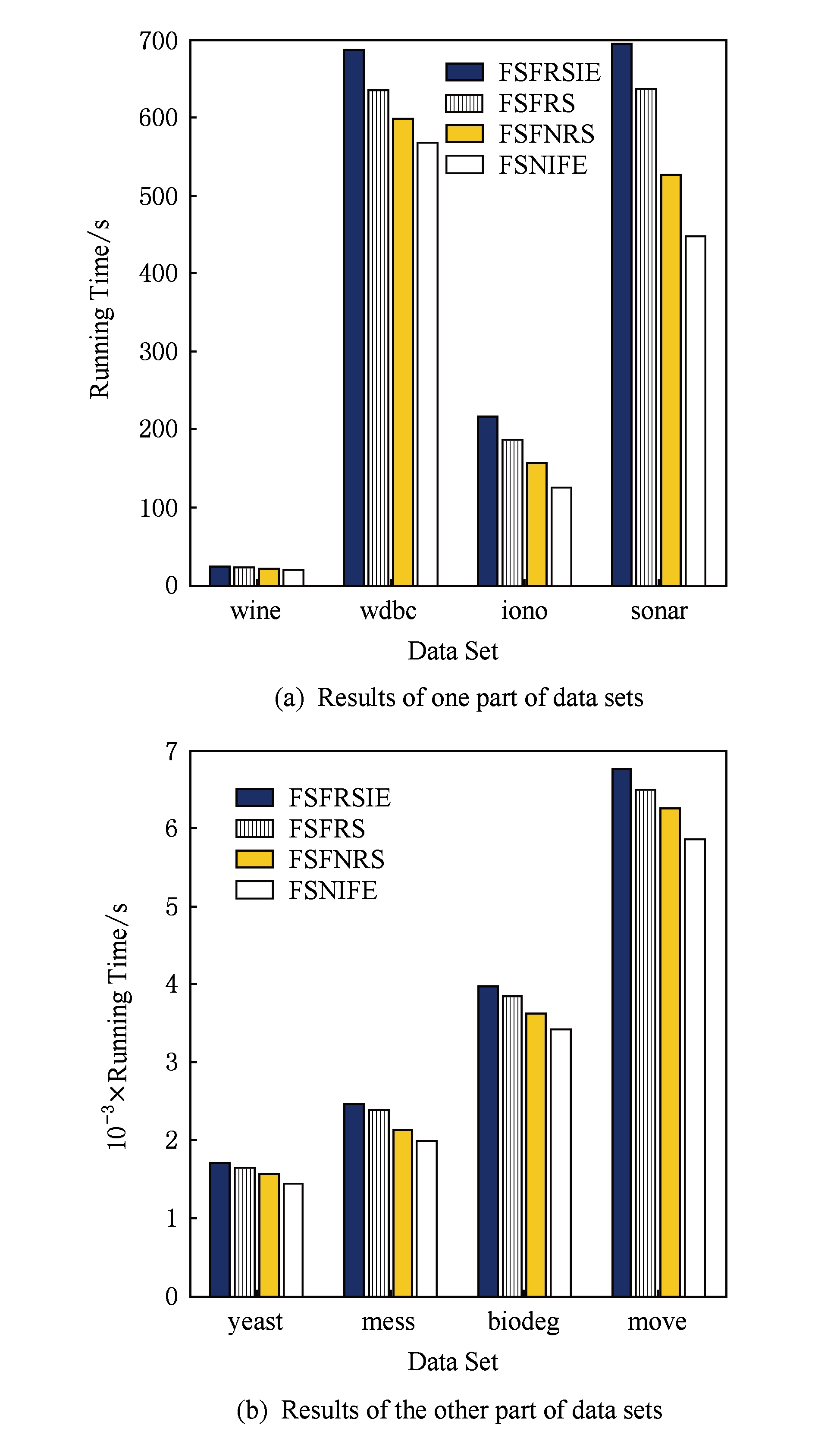
Fig. 9 Running time comparison of 4 algorithms in each data set
图9 4种算法在各数据集运行时间比较
图9展示的是4种算法在所有数据集上特征选择运行所消耗的时间对比,这个时间是每个算法运行10次后取得的平均时间.由于不同数据集算法消耗时间的数量级不一样,因此我们分开表示.通过图9可以看出,相较于其他3种算法,本文所提出的FSNIFE算法所消耗的时间最短.这是由于这4种算法中,FSFRSIE算法和FSFRS算法的时间复杂度为 O ( c 2 × n 2 ),FSFNRS算法的时间复杂度为 O ( c × n 2 ),而本文的FSNIFE算法的时间复杂度为 O ( c 3 × n ×lb n ),其中 c 表示数据集属性的数量, n 表示对象的数量,因此当 c ≪ n 时,FSNIFE算法的时间复杂度即为 O ( n ×lb n ),是这4种算法中最低的.因而在实际运用中,FSNIFE算法将会更快速地选择出特征子集.
为了进一步测试4种特征选择的性能,我们分别运用支持向量机(SVM)和决策树(DT)这2种分类器对5.2节中对应的特征选择结果进行分类训练,并得到相应的分类精度,重复实验10次,最终的分类精度采用这10次实验的均值,所有结果如表5和表6所示.在SVM分类器的分类精度结果中,除了yeast,wine数据集外,其余数据集特征子集的分类精度高于全部特征的分类精度;在DT分类器的分类精度结果中,所有数据集特征子集的分类精度均高于全部特征的分类精度.这说明在数据集中存在很多噪声数据,这些数据对我们的分类有负面影响,因此,对数据进行特征选择很有必要.表5和表6中,黑体数值是该行分类精度的最大值.可以看出,表3和表4中FSNIFE算法选择出的特征子集在大部分数据集具有更高的分类精度.
Table 5 Average Classification Accuracy in SVM of All Feature Selection Results in Table 3
表5 表3中所有特征选择结果在SVM的平均分类精度 %
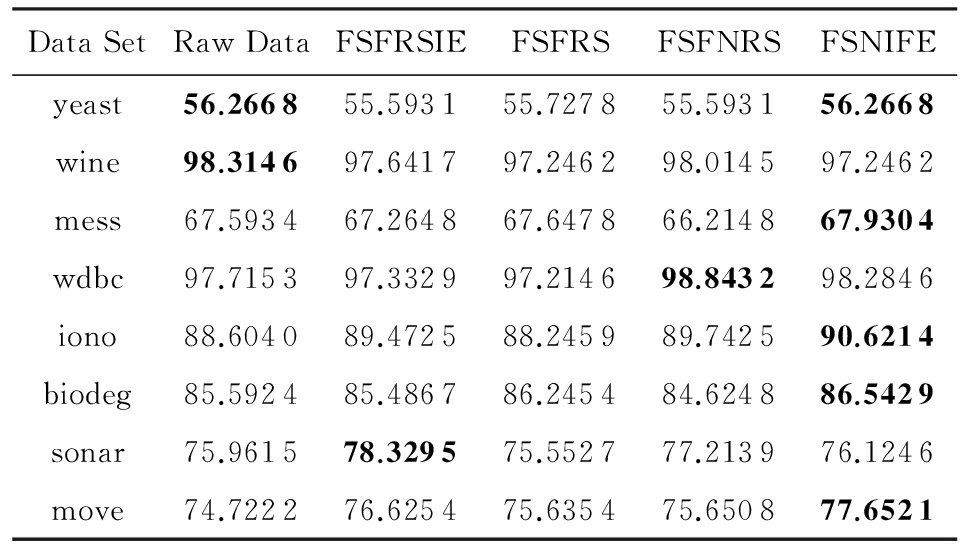
Notes:Bold data represent maximum value.
Table 6 Average Classification Accuracy in DT of All Feature Selection Results in Table 4
表6 表4中所有特征选择结果在DT的平均分类精度 %

Notes:Bold data represent maximum value.
综合特征选择结果、算法运行时间和分类精度这3个方面,相比于其他3种特征选择算法,本文提出的FSNIFE算法可以选择出更少的有效特征,并使对应的分类精度几乎相等甚至更高,而且算法的运行时间也更短.因此FSNIFE算法对于数据的特征选择是适合的,相比较于其他算法更具优越性.
由于本文所提的算法时间复杂度为 O ( c 3 × n ×lb n ),而实验中选取的均为属性较少的数据集,因而当数据集属性的数目远大于对象的数目时,该算法的计算效率将会变得很低,因此本文所提的特征选择算法适用于维度较低的数据集,而对于高维的数据并不是很适用.
本文针对目前邻域粗糙集模型没有考虑到数据分布问题,首先通过方差刻画数据的分布情况,并重新定义了二元邻域空间,使得新的邻域空间能够自适应数据的分布;然后提出了自适应二元邻域空间的粗糙集模型;最后将新提出的模型结合邻域直觉模糊熵,定义了一种新的特征评估方式,并给出相应的特征选择算法.UCI实验结果表明,与现有的算法相比,新提出的算法在特征选择的数量、算法运行时间和分类精度都有着更高的性能.本文将邻域半径取各个值分别计算,然后根据计算结果来寻找最佳的邻域半径.接下来需要进一步探索更好的邻域半径选取方法.
参考文献
[1]Han Xiaohong, Chang Xiaoming, Quan Long, et al. Feature subset selection by gravitational search algorithm optimization[J]. Information Sciences, 2014, 281(10): 128-146
[2]Lu Shuxia, Wang Xizhao, Zhang Guiqiang, et al. Effective algorithms of the Moore-Penrose inverse matrices for extreme learning machine[J]. Intelligent Data Analysis, 2015, 19(4): 743-760
[3]Antonelli M, Ducange P, Marcelloni F, et al. On the influence of feature selection in fuzzy rule-based regression model generation[J]. Information Sciences, 2016, 329(1): 649-669
[4]Liang Jiye, Wang Feng, Dang Chuangyin, et al. A group incremental approach to feature selection applying rough set technique[J]. IEEE Trans on Knowledge & Data Engineering, 2014, 26(2): 294-308
[5]Zhang Xiao, Mei Changlin, Chen Degang, et al. Feature selection in mixed data: A method using a novel fuzzy rough set-based information entropy[J]. Pattern Recognition, 2016, 56(1): 1-15
[6]Hu Qinghua, Yu Daren, Liu Jinfu, et al. Neighborhood rough set based heterogeneous feature subset selection[J]. Information Sciences, 2008, 178(18): 3577-3594
[7]Koprinska I, Rana M, Agelidis V G. Correlation and instance based feature selection for electricity load forecasting[J]. Knowledge -Based Systems, 2015, 82: 29-40
[8]Pawlak Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341-356
[9]Duan Jie,Hu Qinghua,Zhang Lingjun,et al.Feature selection for multi-label classification based on neighborhood rough sets[J].Journal of Computer Research and Development, 2015, 52(1): 56-65 (in Chinese)(段洁, 胡清华, 张灵均, 等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展, 2015, 52(1): 56-65)
[10]Lin T Y. Rough sets, neighborhood systems and approxima-tion[J]. World Journal of Surgery, 1986, 10(2): 189-194
[11]Lin T Y. Granular computing on binary relations I: Data mining and neighborhood systems[J]. Rough Sets in Knowledge Discovery, 1998(2): 165-166
[12]Wang Changzhong, Shao Mingwen, He Qiang, et al. Feature subset selection based on fuzzy neighborhood rough sets[J]. Knowledge-Based Systems, 2016, 111: 173-179
[13]Min Fan,Zhu W. Attribute reduction of data with error ranges and test costs[J]. Information Sciences, 2012, 211(30): 48-67
[14]Zhao Hong, Wang Ping, Hu Qinghua. Cost-sensitive feature selection based on adaptive neighborhood granularity with multi-level confidence[J]. Information Sciences, 2016, 366(20): 134-149
[15]Lin T Y. Granular computing: Practices, theories, and future directions[C] 
 Proc of Encyclopedia on Complexity of Systems Science. Berlin: Springer, 2012: 4339-4355
Proc of Encyclopedia on Complexity of Systems Science. Berlin: Springer, 2012: 4339-4355
[16]Zheng Tingting, Zhu Linyun. Uncertainty measures of neighborhood system-based rough sets[J]. Knowledge-Based Systems, 2015, 86(C): 57-65
[17]Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems, 1986, 20(1): 87-96
[18]Szmidt E, Kacprzyk J. Entropy for intuitionistic fuzzy sets[J]. Fuzzy Sets & Systems, 2001, 118(3): 467-477
[19]Vlachos I K, Sergiadis G D. Intuitionistic fuzzy information-applications to pattern recognition[J]. Pattern Recognition Letters, 2007, 28(2): 197-206
[20]Zhang Huimin . Entropy for intuitionistic fuzzy sets based on distance and intuitionistic index[J]. International Journal of Uncertainty Fuzziness and Knowledge-Based Systems, 2013, 21(1): 181-196
[21]Chen Yumin, Wu Keshou, Chen Xuhui, et al. An entropy-based uncertainty measurement approach in neighborhood systems[J]. Information Sciences, 2014, 279(20): 239-250
[22]Zhang Zhenhai,Li Shining,Li Zhigang,et al.Multi-label feature selection algorithm based on information entropy[J].Journal of Computer Research and Development, 2013, 50(6): 1177-1184 (in Chinese)(张振海, 李士宁, 李志刚, 等. 一类基于信息熵的多标签特征选择算法[J]. 计算机研究与发展, 2013, 50(6): 1177-1184)
[23]Wei Wei, Liang Jiye, Qian Yuhua, et al. Can fuzzy entropies be effective measures for evaluating the roughness of a rough set?[J]. Information Sciences, 2013, 232(5): 143-166
[24]Zhao Hua, Qin Keyun. Mixed feature selection in incomplete decision table[J]. Knowledge-Based Systems, 2014, 57(2): 181-190
[25]Wang Changzhong, Qi Yali, Shao Mingwen, et al. A fitting model for feature selection with fuzzy rough sets[J]. IEEE Trans on Fuzzy Systems, 2017, 25(4): 741-753
[26]Liu Yong, Huang Wenliang, Jiang Yunliang, et al. Quick attribute reduct algorithm for neighborhood rough set model[J]. Information Sciences, 2014, 271(1): 65-81

Yao Sheng , born in 1979. PhD. Lecturer, master supervisor. Her main research interests include rough set, granular computing, big data.

Xu Feng , born in 1993. Master candidate. His main research interests include rough set, granular computing, big data.

Zhao Peng , born in 1976. PhD. Associate professor, master supervisor. Her main research interests include intelligent information processing (zhaopeng_ad@ahu.edu.cn).

Ji Xia , born in 1983. PhD. Lecturer, master supervisor. Her main research interests include rough set (jixia1983@163.com).
Yao Sheng, Xu Feng, Zhao Peng, and Ji Xia
( Key Laboratory of Intelligent Computing & Signal Processing ( Anhui University ), Ministry of Education , Hefei 230601) ( College of Computer Science and Technology , Anhui University , Hefei 230601)
Abstract Feature selection is a very vital technology in data preprocessing.In this method, some most effective features are mainly selected from the features of original data sets, which is aimed to reduce the dimension of data sets.Accordingly, the performance of the learning algorithm can be improved.In the feature selection algorithms based on the neighborhood rough set model, without considering data uneven distribution, there currently exist some defects in the neighborhood of object.To solve this problem of data uneven distribution, variance is adapted to measure the distribution of the data, and the binary neighborhood space is redefined, then the rough set model of the adaptive binary neighborhood space is proposed according to this binary neighborhood space.As well as, the new rough set model of the adaptive binary neighborhood space is combined with the neighborhood intuitionistic fuzzy entropy as the method of the evaluation of features, and then the corresponding feature selection algorithm is also constructed.The experimental results of UCI show that the proposed intuitionistic fuzzy entropy feature selection algorithm can select smaller feature subsets which have higher accuracy of classification, at the same time, the intuitionistic fuzzy entropy feature selection algorithm based on adaptive neighborhood space rough set model also has less time consumption.Therefore, the proposed feature selection algorithm has stronger superiority in this paper.
Key words rough set; neighborhood; variance; binary neighborhood space; neighborhood intuitionistic fuzzy entropy; feature selection
摘 要 特征选择是数据预处理中一项很重要的技术,主要从原始数据集的特征中选出一些最有效的特征以降低数据集的维度,从而提高学习算法性能.目前基于邻域粗糙集模型的特征选择算法中,由于没有考虑数据分布不均的问题,对象的邻域存在一定的缺陷.为了解决这个问题,采用方差来度量数据的分布情况,重新定义二元邻域空间,基于此提出自适应二元邻域空间的粗糙集模型,并将该模型与邻域直觉模糊熵结合作为特征评估的方式,进而构造相应的特征选择算法.UCI实验结果表明:所提出的算法能够选出更小且具有更高分类精度的特征子集,同时算法拥有更少的时间消耗.因此所提的特征选择算法具有更强的优越性.
关键词 粗糙集;邻域;方差;二元邻域空间;邻域直觉模糊熵;特征选择
中图法分类号 TP18
收稿日期: 2016-12-02;
修回日期: 2017-06-14
基金项目: 国家自然科学基金项目(61602004,61300057);安徽省自然科学基金项目(1508085MF127);安徽省高等学校自然科学研究重点项目(KJ2016A041,KJ2017A011);安徽大学信息保障技术协同创新中心公开招标课题(ADXXBZ2014-5,ADXXBZ2014-6);安徽大学博士科研启动基金项目(J10113190072)
This work was supported by the National Natural Science Foundation of China (61602004, 61300057), the Natural Science Foundation of Anhui Province (1508085MF127), the Natural Science Foundation of Anhui Higher Education Institutions (KJ2016A041, KJ2017A011), the Public Bidding Project of Co-Innovation Center for Information Supply & Assurance Technology of Anhui University (ADXXBZ2014-5, ADXXBZ2014-6), and the Doctoral Scientific Research Foundation of Anhui University (J10113190072).
通信作者: 徐风(xuf_2015@163.com)