Fig. 1 Two distance measurement methods
图1 2种距离度量方式
赵 亮 1 王永利 1 杜仲舒 1 陈广生 2
1 (南京理工大学计算机科学与工程学院 南京 210094) 2 (华电能源股份有限公司佳木斯热电厂 黑龙江佳木斯 154005) (845203965@qq.com)
近年来,近似最近邻(approximate nearest neighbor, ANN)查询被广泛地应用于机器学习以及相关的应用领域中,包括机器视觉、信息检索等.随着数据的爆炸性增长,越来越多的关注集中到ANN查询的Hash技术上,希望通过Hash技术将原始数据映射成简洁的二进制编码串的形式,再进行比较查询,从而降低计算复杂度.同时,为了使Hash码尽可能地保持原始数据间的近邻关系,保证近似查询的准确度,因而引入了Hash学习的概念.基于Hash学习的ANN技术主要包括2个阶段 [1] :投影阶段和量化阶段.投影阶段的主要目的是将原始高维数据映射到低维表示,并保存原始数据的相似性,本质上,近邻结构的保持是通过构建一个包含原始数据的邻域信息的近邻图,并使用图的拉普拉斯算子概念计算出一个变换矩阵,然后将原始数据通过此变换矩阵映射到低维空间表示 [2] ,Hash学习的目的即在于学习此变换矩阵.量化阶段通过将降维后得到的实数值使用二进制稀疏表示,从而降低计算复杂度.量化也是一个有损变换,因此可能会对二进制编码的最终质量产生显著影响.尽管目前学者们提出了许多Hash学习方法,但大多数方法都仅聚焦于第1阶段(投影阶段)的信息损失,而忽略了第2阶段(量化阶段)的信息损失,只是简单地采用单位编码阈值划分方法,并使用海明距离进行相似性度量.事实上,量化阶段所要考虑的信息损失并不比投影阶段所要考虑的信息损失少,甚至一个不好的量化策略,即使采用了较好的投影策略,也会造成最后的Hash效果非常差 [3] .
目前已有的ANN查询方法所采用的量化策略基本都是使用统一位数来编码每一个投影维度,但对于实际应用而言,不同的维度所包含的信息量必然不同,某些维度上的数据比较分散,信息量比较大,为了保持原始数据相互之间的相似性,就需要使用更多的位数来编码这一维度;某些维度上的数据比较集中,甚至基本一致,就可以使用较少的位数来编码这一维度,或者不需要对这一维度进行编码.
另一方面,现有的量化策略基本都是采用阈值划分的方法,并通过计算二进制编码之间的海明距离来度量相似性.例如普遍使用的单位编码量化(single-bit quantization, SBQ)策略通过设定一个阈值 θ ,第 i 位的数值为 f i ( x ),如果 f i ( x )≥ θ ,则该位编码为1,否则编码为0,当数据已经被归一化且均值为0时,阈值 θ 通常被设置为0.少数使用2 b编码量化的,如分层量化(hierarchical quantization, HQ) [4] 和双比特位量化(double-bit quantization, DBQ) [1] ,将投影后的某一维数据编码成2 b二进制,但此时仍使用海明距离来对二进制编码的相似性进行度量,例如00与01的距离为1,00与10的距离也为1,而实际上00与10的距离应该要比00与01的距离大,因此破坏了原始数据的相似性,违反了Hash方法要保持原始数据相似性的初衷.
提出一种Hash学习的动态自适应的编码量化(Hash learning-dynamic adaptive quantization, HL-DAQ)方法,根据每一维度的离散系数来为该维度动态分配编码位数,以保证更多的原始信息被保留下来.同时,还提出一种根据编码位数分配情况动态计算各编码之间相似性距离的方法,主要工作概述有3个方面:
1) 提出一种动态自适应编码量化策略,首先计算每一投影维度的离散系数,然后通过约束条件,最大限度地保持原始数据的近邻结构,为尽量多的维度编码,解决原始数据的局部结构保持问题.同时,信息量越大的维度使用更多的编码位数,并使用动态规划方法求得总信息熵最大的二进制编码分配方式,解决原始数据的全局结构保持问题.
2) 提出一种动态自适应距离度量方式来度量自然二进制编码的相似性,改进了原始基于海明距离的相似性度量方式只适用于单位量化以及近邻结构保持不够好等弊端,可以证明,利用动态自适应距离较海明距离而言更能保持原始数据的相似性.
3) 公开数据集上进行的实验证明,HL-DAQ方法与其他已有的量化方法相比,能更好地保持原始数据的相似性,提高查询准确率,并在图像与非图像数据集上具有通用性.
目前已有的Hash算法基本可以分为两大类:1)与数据集无关的Hash方法,例如局部敏感Hash(locality-sensitive Hash, LSH) [5] 、位移不变的内核Hash(shift invariant kernel Hash, SIKH) [6] 等,生成与数据集无关的随机投影.与数据集无关的Hash方法通常需要比较长的二进制编码来保证Hash函数的性能.2)与数据集有关的Hash方法,例如光谱Hash(spectral Hash, SH) [7] 、主成分分析Hash(principal component analysis Hash, PCAH) [8] 、快速Hash(fast Hash, FastH) [9] 、迭代量化(iterative quantization, ITQ) [10] 、监督离散Hash(supervised discrete Hash, SDH) [11] 、可扩展离散Hash(scalable discrete supervised Hash, COSDISH) [12] 等,其特征在于通过训练数据集学习投影函数.一般来说,与数据集有关的Hash方法要比与数据集无关的Hash方法性能较好 [13-14] ,然而这些方法的主要目的都是希望找到一个高质量的投影方法,以达到最大限度保持原始数据相似性的目的,却很少把注意力集中到量化阶段.典型的量化方法为SBQ,它首先设定一个阈值,将投影后的每一维度的数值与此阈值进行比较,然后使用一个二进制位对此维度进行编码.然而量化也是一个有损变换,降低了所表示数据的精度,并且使用简单的单位量化方法会对所获得的二进制编码的检索质量带来显著影响.近年来,一些研究者也相继提出了一些更高位数的量化方法来解决这一局限性.
Liu等人 [15] 提出了一种用于锚点图Hash(anchor graph Hash, AGH)的HQ方法,HQ通过将投影划分为4种状态,并使用2个位来对每个投影维度进行编码.
Kong等人 [1] 提出了另一种称之为DBQ的量化策略,更有效地保留了数据的近邻结构,但是通过2 b编码量化仅将投影维度量化为3个状态,而不是可以编码的4个2 b编码.Lee等人 [16] 也提出了一种类似的方法,通过采用专门的距离度量方式来对4个2 b状态进行度量.
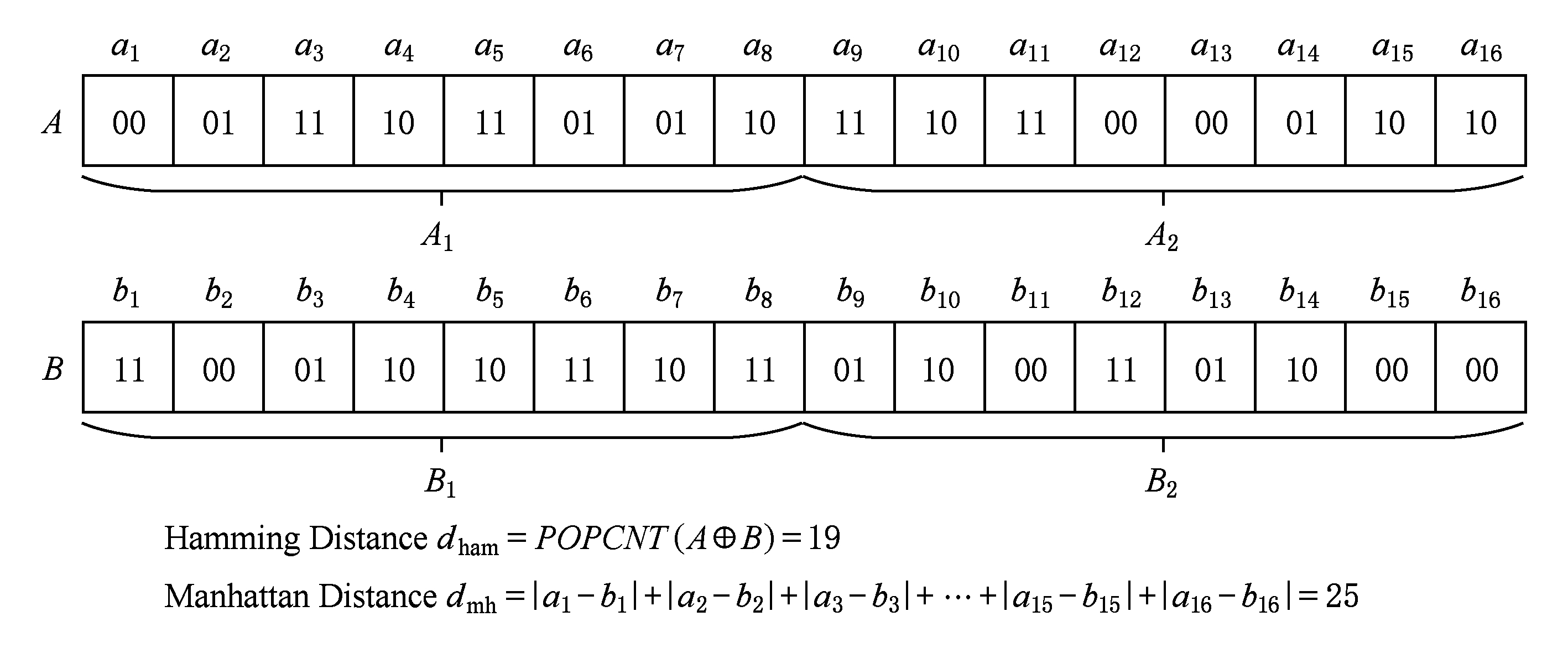
Kong等人 [17] 还提出了一种更为灵活的量化方法称为曼哈顿量化(Manhattan quantization, MQ),它能够将每个投影维度编码成多个位组成的自然二进制码(natural binary code, NBC),并且曼哈顿距离度量方式有效地保留了数据的近邻结构,该方法首次提出使用NBC的十进制距离来对原始数据距离进行度量.曼哈顿距离和海明距离的比较如图1所示,可以看出,2 b曼哈顿距离度量方式的距离度量粒度显然比海明距离度量方式更精细.

Fig. 1 Two distance measurement methods
图1 2种距离度量方式
上述提出的量化方法在标准SBQ上均有所改进,能够显著提高量化性能.然而,所有这些策略都具有明显的局限性,即它们对每个预测维度采用固定的 k 位来进行编码量化,没有考虑到不同投影维度的信息量与数据分布不同.
基于离散系数的动态自适应编码量化技术解决了这2个限制,提出了一种有效的编码量化方法和信息离散性度量标准,并通过在每个投影维度上动态分配二进制编码,解决保留最大原始数据信息量问题.
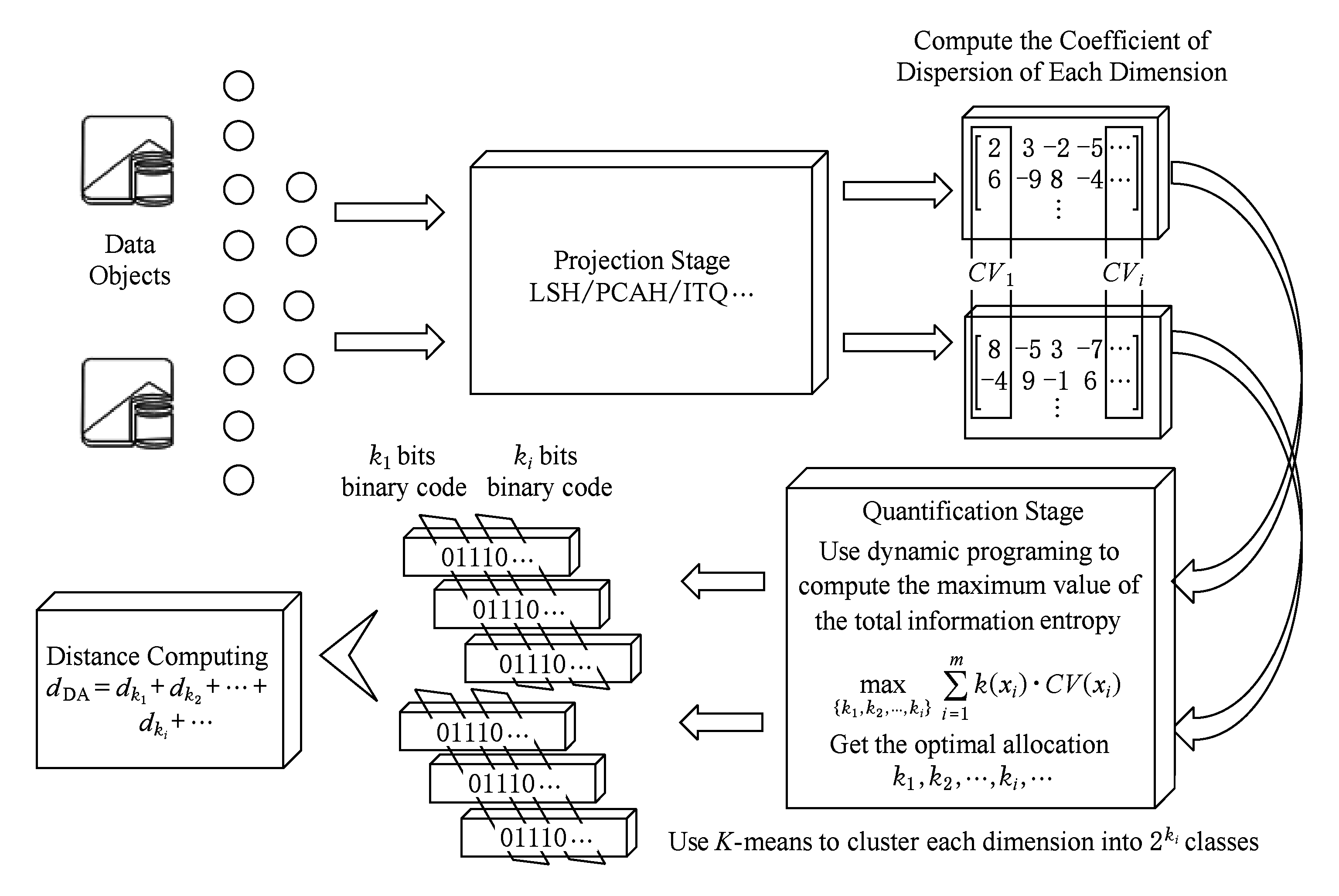
Fig. 2 HL-DAQ overall framework diagram
图2 HL-DAQ模型整体流程框架图
本节给出HL-DAQ模型的执行流程框架图以及一些相关概念的定义.HL-DAQ方法主要分为投影和量化2个阶段,如图2所示.首先从数据集中取出的数据经过诸如LSH  PCAH
PCAH  ITQ等投影方法进行降维,投影到低维矩阵上;然后再通过计算每一维度的离散系数值,根据离散系数值动态为每一维度分配编码位数,使得总信息熵最大.进一步地,根据所分配的编码位数,使用 K -means [18] 对每一维度进行聚类,根据聚类结果进行编码得到二进制串,最后通过所提出的动态自适应距离度量方式计算数据对象之间的距离.
ITQ等投影方法进行降维,投影到低维矩阵上;然后再通过计算每一维度的离散系数值,根据离散系数值动态为每一维度分配编码位数,使得总信息熵最大.进一步地,根据所分配的编码位数,使用 K -means [18] 对每一维度进行聚类,根据聚类结果进行编码得到二进制串,最后通过所提出的动态自适应距离度量方式计算数据对象之间的距离.
定义1 . 离散系数.给定一组数据分布 f ( X ),其离散系数表示为其标准差与均值的比值,定义为
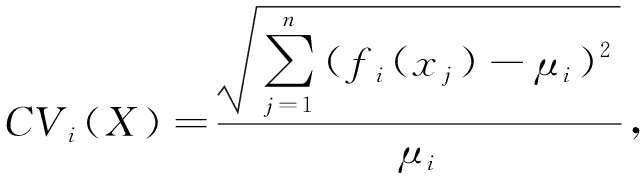
(1)
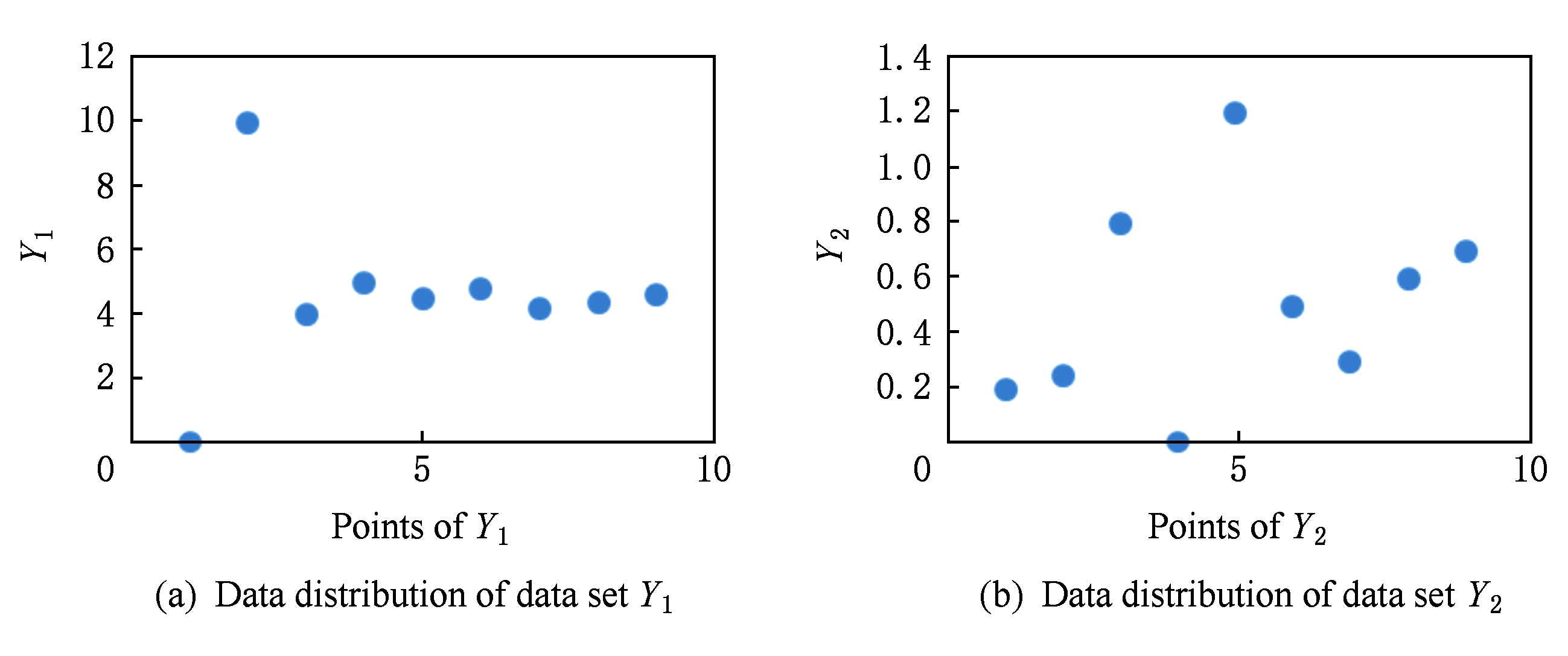
Fig. 3 Two different sets of data with different ranges on different dimensions
图3 2个不同维度上值域不同的2类数据分布
其中, μ i = E ( f i ( X )); E ( f i ( X ))是表示 X 在投影 f i ( X )下的数据分布中心,即均值,数学上该式被称为标准差系数,标准差系数是衡量数据中各观测值离散程度的一个统计量 [19] .当进行2个或多个数据离散程度的比较时,如果度量单位与平均数相同,可以直接利用标准差来比较.如果单位和(或)平均数不同,比较其离散程度就不能采用标准差,而需采用标准差与平均数的比值(相对值).离散系数较大的表明数据的分布情况差异也大,从而需要分配更多的编码位进行编码,反之则较少.离散系数可以消除单位和(或)平均数不同对2个或多个数据离散程度比较的影响.
假设从诸如PCAH或LSH等某种Hash方法中得到了 m 维投影{ f 1 ( x ), f 2 ( x ),…, f m ( x )},首先定义这些投影信息量的度量方式.在信息理论中,方差和熵都是公认的信息量的度量方式 [20] ,可以作为每个投影的信息量度量选择,但实际上由于不同维度所表达的信息不一样,其取值范围也不一样,例如:
如图3所示, Y 1 的方差为6.386,而 Y 2 的方差为0.13,如果使用方差来表示信息量并为投影维度分配二进制编码位, Y 1 的编码位数将比 Y 2 大许多倍,然而从整体分布来看,显然 Y 1 的分布比较集中,而 Y 2 的分布比较分散,使用方差来度量信息量并对编码位数进行分配的话,显然不能很好地保持 Y 2 的近邻结构,一种更为合理的方案是,根据原始数据计算其数据的离散程度,用离散系数表示,如定义1所示.
对于图3中的2组数据,根据式(1)计算可得, Y 1 的离散系数为0.548, Y 2 的离散系数为0.724,因此使用离散系数对信息量进行度量并分配编码位数的情况下, Y 2 所分配的编码位数将比 Y 1 的多或至少相当,因此更能保证原始数据的近邻结构.
根据生成投影的独立性,所有投影的总离散系数可计算得到:
(2)
通过计算每一投影维度离散系数占总离散系数的比重,来为该维度动态分配可变数量的位.如果该维度的离散系数足够小,那么分配给该维度的位可以为0;如果该维度的离散系数足够大,分配给该维度的位也可以是总位数.
将 k 位分配给某一维投影,对于该投影维度将产生2 k 个不同的二进制编码.因此,在该维度中应该有2 k 个质心,将其分成2 k 个间隔或簇.每个数据点被分配给这些簇之一并由其对应的二进制编码表示.
为了准确度量二进制编码串所能保持的近邻结构信息量,定义一种新的近邻结构信息熵概念.
定义2 . 近邻结构信息熵.给定数据集 X ={ x i }, i =1,2,…, n ,其近邻结构信息熵定义为每一投影维度量化后的编码位数与该维度的信息量的乘积:
(3)
其中, CV ( x i )表示第 i 维投影的离散系数,即信息量; k ( x i )表示第 i 维投影所分得的量化编码位数.由此可知,要使得最终二进制编码所包含的原始数据近邻结构信息量最大,就得使信息熵最大,即使得每一投影维度的编码位数与其离散系数的乘积之和最大.
根据每一维度的离散系数动态地选择每个投影的位数.假设有 m 个投影{ f 1 ( x ), f 2 ( x ),…, f m ( x )}和对应的离散系数 CV i ( X ),以及每一维度所分配得到的位数 k i ( x ),目标函数 ![]() 标是找到最佳位分配方案,使得整个数据集的所有投影的总信息熵最大化,因此目标函数可以确定为
标是找到最佳位分配方案,使得整个数据集的所有投影的总信息熵最大化,因此目标函数可以确定为
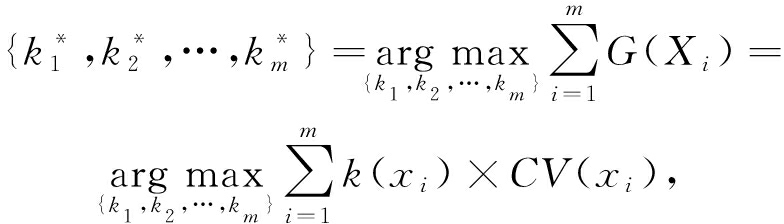
s.t. ∀ i ∈{1,2,…, m }, k i ∈{0,1,…, L },
(4)
其中, k i 是分配给投影 f i ( x )的位数, L 是所有二进制码的总长度; ![]() 是来自所有投影维度的总信息熵, G ( X i )是投影 f i ( x )中 k i 位相应的信息熵.另外,因为投影是独立的,因此可以简单地将每个投影的信息熵相加.
是来自所有投影维度的总信息熵, G ( X i )是投影 f i ( x )中 k i 位相应的信息熵.另外,因为投影是独立的,因此可以简单地将每个投影的信息熵相加.
对于总长度为 L 位的 m 维投影{ f 1 ( x ), f 2 ( x ),…, f m ( x )}和对应的信息熵,通过求解式(4),可以找到每个投影的最佳位分配,使得来自 m 维投影的总信息熵最大化.然而,优化该目标函数是一个组合问题,可能的分配方式是指数级的,如何得到最佳分配方式成为问题关键.
一种较简单的方式实现最优位分配问题如下:
给定二进制散列长度 L 和 m 维投影,其总信息熵表示为
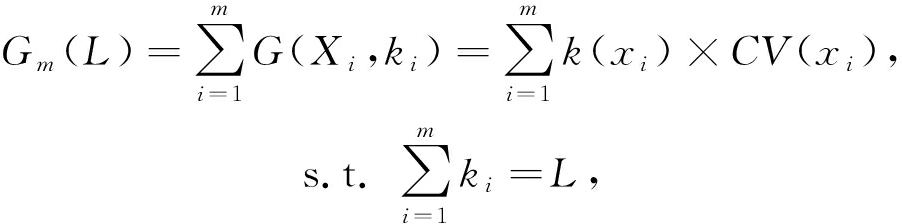
(5)
然后近邻结构信息熵由如下贝尔曼方程 [21] 来表示:
(6)
其中, ![]() 即为所寻求的最优位分配(最大信息熵),
即为所寻求的最优位分配(最大信息熵), ![]() 表示第 m 维被编码成 ν m 位二进制时的信息熵,
表示第 m 维被编码成 ν m 位二进制时的信息熵, ![]() 表示剩余的 m -1维在编码总长度为 L - ν m 下的最优位分配,不论
表示剩余的 m -1维在编码总长度为 L - ν m 下的最优位分配,不论 ![]() 的状态如何,
的状态如何, ![]() 必须是余下 m -1维的最优分配,满足最优子结构性质;另一方面,各维度信息具有独立性,对于某个分配的
必须是余下 m -1维的最优分配,满足最优子结构性质;另一方面,各维度信息具有独立性,对于某个分配的 ![]() 其并不影响后续维度的最优分配,满足无后效性;最后,对于一个给定的离散系数 CV i ( x i )和编码位数 k ( x i ),其信息熵便是一定的,并且在
其并不影响后续维度的最优分配,满足无后效性;最后,对于一个给定的离散系数 CV i ( x i )和编码位数 k ( x i ),其信息熵便是一定的,并且在 ![]() 的求解中将会多次用到此结果,满足重叠子问题性质.基于此设置,此问题可以使用动态规划来解决,由 m 个子问题(计算
的求解中将会多次用到此结果,满足重叠子问题性质.基于此设置,此问题可以使用动态规划来解决,由 m 个子问题(计算 ![]() 的值)表征,每个子问题最多有 L 种组合方式,由约束条件1≤ i ≤ m 和0≤ ν m ≤ L ,其时间复杂度为 O ( mL ).因此,使用动态规划,可以快速找到给定编码长度和投影的全局最优位分配.下面证明基于离散系数的动态自适应量化方法所获得最优位分配较传统的固定位数编码量化方法而言,能更多地保留原始数据信息量.
的值)表征,每个子问题最多有 L 种组合方式,由约束条件1≤ i ≤ m 和0≤ ν m ≤ L ,其时间复杂度为 O ( mL ).因此,使用动态规划,可以快速找到给定编码长度和投影的全局最优位分配.下面证明基于离散系数的动态自适应量化方法所获得最优位分配较传统的固定位数编码量化方法而言,能更多地保留原始数据信息量.
定理1 . 假设使用 L 位二进制对一个 m 维的数据 X ={ x 1 , x 2 ,…, x m }进行编码,设传统固定位数编码量化方法的近邻结构信息熵为 G 1( X ),基于离散系数的动态自适应量化方法的近邻结构信息熵为 G 2( X ),那么 G 2( X )≥ G 1( X )恒成立.
证明. 根据式(3)计算近邻结构信息熵,当使用传统固定位数编码量化方法时,每一维度被编码成 L  m 位,那么总信息熵为
m 位,那么总信息熵为 ![]() 当使用基于离散系数的动态自适应量化编码方法时,由于编码位数根据离散系数进行分配,根据动态规划求解最优分配思想,同时需满足离散系数越大所对应的编码位数也越多,因此当离散系数为 CV ( x i )时,设编码位数为 a × CV ( x i ),并且满足
当使用基于离散系数的动态自适应量化编码方法时,由于编码位数根据离散系数进行分配,根据动态规划求解最优分配思想,同时需满足离散系数越大所对应的编码位数也越多,因此当离散系数为 CV ( x i )时,设编码位数为 a × CV ( x i ),并且满足 ![]() 此时的总信息熵为
此时的总信息熵为 ![]() 根据计算:
根据计算:
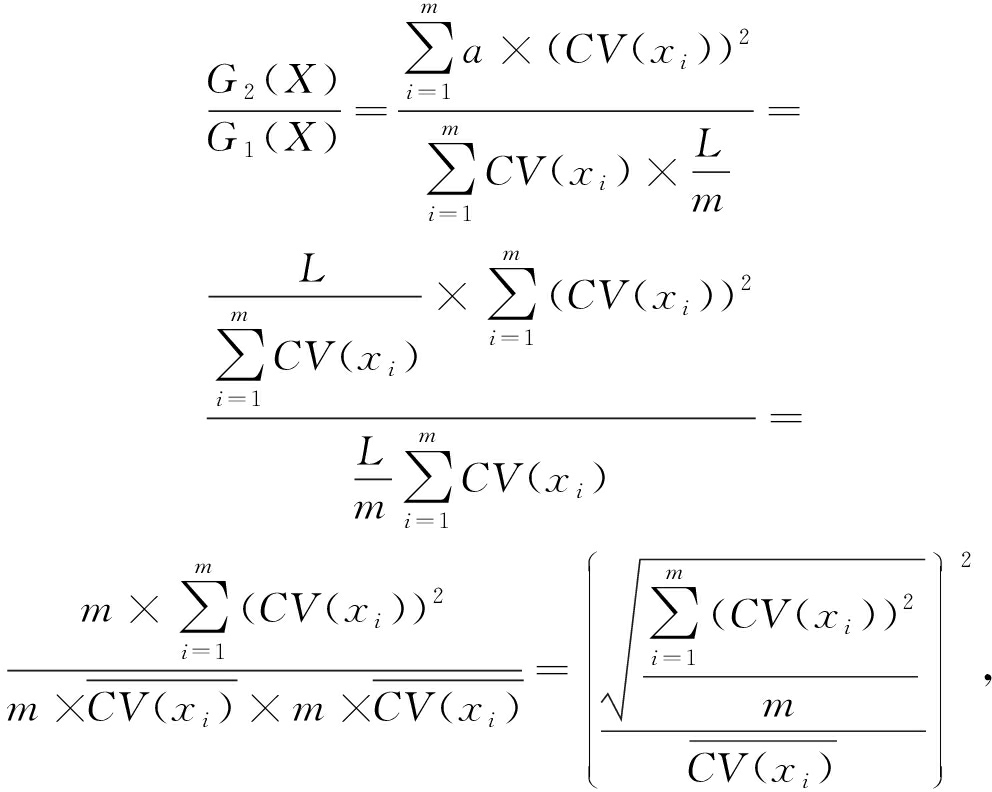
(7)
其中, ![]() 为 CV ( x i )的算术平均数,
为 CV ( x i )的算术平均数, 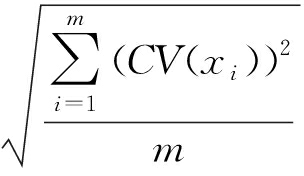 为平方平均数,由均值不等式 [22] 可知,平方平均数大于等于算术平均数,因此式(7)的结果大于等于1,即 G 2( X )≥ G 1( X ).
为平方平均数,由均值不等式 [22] 可知,平方平均数大于等于算术平均数,因此式(7)的结果大于等于1,即 G 2( X )≥ G 1( X ).
证毕.
当原始数据本身均匀分布,度量单位也一致,即信息量均匀分布,那么采用固定位编码方式时复杂度为 O (1),而使用此编码方式复杂度将大大增加,因此此方法在信息量均匀分布的数据集上不具有优势.然而,原始数据均分分布的数据集在现实场景下几乎是不存在的.
引言提到,现阶段已有的二进制编码距离度量方式主要包括海明距离和曼哈顿距离.2种方法都是采用固定编码长度的度量方式,需要首先确定每一投影所使用的二进制编码长度 [23] ,其中曼哈顿距离第1次提出使用NBC的十进制距离来对二进制编码进行度量.海明距离只适用于单位量化,例如当某一维度被编码成2 b二进制时,其海明距离和十进制距离如图4、图5所示:
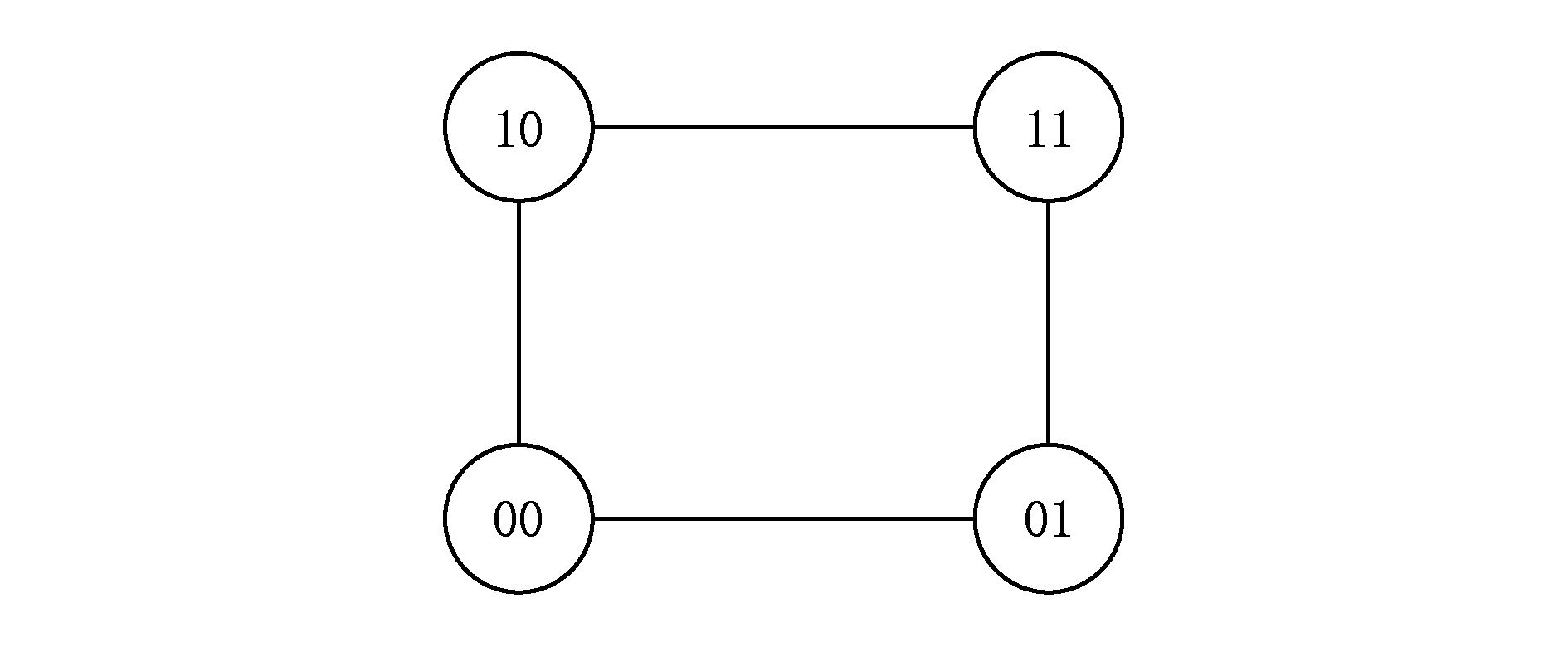
Fig. 4 Hamming distance under two binary codes
图4 2 b二进制编码下的海明距离

Fig. 5 Decimal distance under two natural binary codes
图5 2 b自然二进制编码下的十进制距离
其中每条线段表示距离为1,但在这种距离度量模式下,00—10的距离与00—01的距离是相等的,都为1,而实际上2 b自然二进制编码下00—10的距离应该要比00—01的距离大.并且,01—10的距离由实际上的1被扩大到了2,00—11的距离也由实际上的3被缩小到了2,使得00—11的距离与01—10的距离相等,这显然破坏了原始数据的相似性,给距离度量结果造成了很大的误差 [24] .
定义3 . 动态自适应距离.给定量化时每一投影维度所分配的NBC长度,以及每一投影维度量化后得到的二进制串,2点之间的动态自适应距离即为它们各个维度上二进制编码所对应的NBC之间的十进制距离的差的总和.令 x =( x 1 , x 2 ,…, x m ) T , y =( y 1 , y 2 ,…, y m ) T ,编码分配方式为 K =( k 1 , k 2 ,…, k m ),那么 x 和 y 之间的动态自适应距离定义如下:
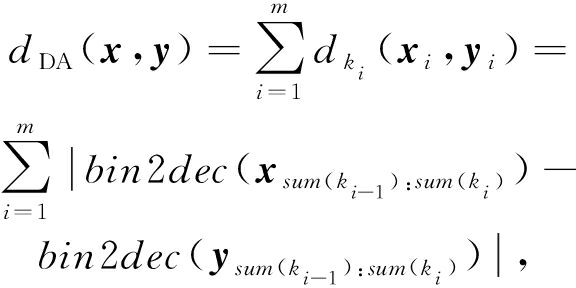
(8)
其中,| exp |表示 exp 的绝对值; sum ( k i )表示 k 1 到 k i 的和; ![]() 表示 x 下标从 sum ( k i -1 )到 sum ( k i )的子串所构成的向量; bin 2 dec ( X i )表示向量 X i 所构成二进制串的十进制值.在动态自适应距离中,使用十进制距离而不是海明距离来测量每个投影维度之间的距离,然后对所有投影维度的距离进行求和.NBC码的十进制距离被定义为相应NBC码的十进制值之间的差.
表示 x 下标从 sum ( k i -1 )到 sum ( k i )的子串所构成的向量; bin 2 dec ( X i )表示向量 X i 所构成二进制串的十进制值.在动态自适应距离中,使用十进制距离而不是海明距离来测量每个投影维度之间的距离,然后对所有投影维度的距离进行求和.NBC码的十进制距离被定义为相应NBC码的十进制值之间的差.
定理2 . 动态自适应距离对于原始数据近邻结构的保持优于海明距离.
证明. 假设某一维度被编码成 k 位, A 与 B 表示在原始空间中相邻的2个数据经过投影并转换到[0,2 k ]区间范围内的2点,并且 A > B ,根据编码规则,相邻的数据被编码成相同或者相近的二进制码,假设2 i -1< A <2 i ,其中1< i < k ,那么数据 A 编码后的二进制为 ![]() 数据 B 编码后的二进制为
数据 B 编码后的二进制为 ![]() 当使用海明距离进行度量时, d ham ( A , B )= i ;当使用动态自适应距离进行度量时, d DA ( A , B )=1.显然,使用动态自适应距离更好地保持了原始数据的相似性.又假设另一原始数据点被投影并转换成 C =1,那么数据 C 编码后的二进制为
当使用海明距离进行度量时, d ham ( A , B )= i ;当使用动态自适应距离进行度量时, d DA ( A , B )=1.显然,使用动态自适应距离更好地保持了原始数据的相似性.又假设另一原始数据点被投影并转换成 C =1,那么数据 C 编码后的二进制为 ![]() 当使用海明距离进行度量时, d ham ( A , C )=2;当使用动态自适应距离进行度量时, d DA ( A , C )=2 i -2.显然,使用动态自适应距离对原始数据的近邻结构保持得更好.同时,可以看出,在动态自适应距离下, k 位编码之间的最大距离是2 k -1,可以有效地保持2 k 个不同编码值(区域)的相对距离.而海明距离下的最大距离为 k ,对编码距离的表示粒度显然较动态自适应距离差很多.
当使用海明距离进行度量时, d ham ( A , C )=2;当使用动态自适应距离进行度量时, d DA ( A , C )=2 i -2.显然,使用动态自适应距离对原始数据的近邻结构保持得更好.同时,可以看出,在动态自适应距离下, k 位编码之间的最大距离是2 k -1,可以有效地保持2 k 个不同编码值(区域)的相对距离.而海明距离下的最大距离为 k ,对编码距离的表示粒度显然较动态自适应距离差很多.
证毕.
本节对所提出的相关算法进行了详细的描述,包括动态自适应编码量化算法和动态自适应距离度量算法,分别对应图2中的量化阶段和距离度量阶段.
由式(5)(6),首先描述根据动态规划求最佳位分配的算法,为了保证每一维的信息被同等对待,本算法引入约束条件 ![]() 其中 CV i 和 CV j 分别表示第 i 维和第 j 维的离散系数, k i 和 k j 分别表示第 i 维和第 j 维的编码位数.算法描述如下:
其中 CV i 和 CV j 分别表示第 i 维和第 j 维的离散系数, k i 和 k j 分别表示第 i 维和第 j 维的编码位数.算法描述如下:
算法1 . 动态规划获取最优二进制编码分配算法.
输入:离散系数 CV i 、目标函数 ![]() CV i ;约束条件∀
CV i ;约束条件∀ ![]()
输出:二进制编码最优分配方案 K =( k 1 , k 2 ,…, k m ).
① for each i =1: m
② for each integer of k i =0: k max
③ if ( G ( X i , k i ))= k i × CV i 没有被计算过)
④ temp [ k i , CV i ]= k i × CV i ;
⑤ else G ( X i , k i )= temp [ k i , CV i ];
⑥ end if
⑦ if ![]()
G ( X i , k i )
⑧ ![]()
G ( X i , k i );  * G ( X i , k i ))表示数据 X 的第 i 维被编码成 k i 位时的信息熵,
* G ( X i , k i ))表示数据 X 的第 i 维被编码成 k i 位时的信息熵, ![]() 表示余下 m -1维的总信息熵,
表示余下 m -1维的总信息熵, ![]() 初值为0 *
初值为0 * 
⑨ end if
⑩ end for
 end for
end for
 return K =( k 1 , k 2 ,…, k m ).
return K =( k 1 , k 2 ,…, k m ).
对于给定的维度 m 、编码长度 L ,算法1的行③~⑨的计算复杂度为 O (1),加之嵌套的2重循环,因此总时间复杂度为 O ( mL ).
给定经过某个具有 m 维投影的现有投影方法(如LSH,PCAH,ITQ等)学习过后的训练与测试数据集,一个固定的Hash编码长度 L ,基于离散系数的动态自适应编码量化方法可以描述如下:
算法2 . 动态自适应量化编码算法.
输入:投影矩阵 U_trn 、为所有投影维度编码的二进制总长度 L ;
输出:编码好的二进制编码矩阵 U_trn .
① for each dimension of the matrix U_trn
② 计算离散系数
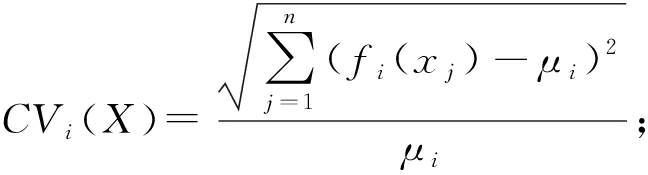
③ end for
④ 计算总离散系数 ![]()
⑤ 给定信息熵的计算公式 G ( x i )= k ( x i )- CV ( x i )以及目标函数
其中∀ ![]()
⑥ 根据算法1得到最优分配 K =( k 1 , k 2 ,…, k m );
⑦ for each dimension of the matrix U_trn i =1: m
⑧ if k i >0
⑨ 使用 K -means将此维度中的点聚类到 ![]() 类中
类中 ![]()
⑩ end if
 end for
end for
 UX_trn =[ ];
UX_trn =[ ];
 for each row of the matrix U_trn j =1:
for each row of the matrix U_trn j =1:
size ( U_trn ,1)  *训练数据集大小*
*训练数据集大小* 
 U_temp =[ ];
U_temp =[ ];
 for each dimension of the matrix U_trn i =1: size ( U_trn ,2)
for each dimension of the matrix U_trn i =1: size ( U_trn ,2)  *数据维数*
*数据维数* 
 if k i >0
if k i >0
 if U_trn ( j , i )∈ C n
if U_trn ( j , i )∈ C n
 U_trn ( j , i )= n , U_temp =[ U_ temp , dec 2 bin ( U_trn ( j , i ), k i )];
U_trn ( j , i )= n , U_temp =[ U_ temp , dec 2 bin ( U_trn ( j , i ), k i )];  *其中[ A , B ]表示将 矩阵 A 和矩阵 B 横向拼接*
*其中[ A , B ]表示将 矩阵 A 和矩阵 B 横向拼接* 
 end if
end if
 end for
end for
 end if
end if
 end for
end for
 UX_trn =[ UX_trn ; U_temp ];
UX_trn =[ UX_trn ; U_temp ];  *其中[ A ; B ]表示将矩阵 A 和矩阵 B 纵向拼接*
*其中[ A ; B ]表示将矩阵 A 和矩阵 B 纵向拼接* 
 end for
end for
假设训练数据集大小为 n ,数据维度为 m 维,对各阶段时间复杂度进行分析,行①~③计算离散系数为 O ( m );行⑥动态规划求最佳编码分配为 O ( mL ),其中 L 是编码长度,为编码前指定的定值;对于给定迭代次数 T ,行⑦~  对每一维度使用 K -means聚类并对所有数据进行分类为
对每一维度使用 K -means聚类并对所有数据进行分类为 ![]() 其中 k i 最大为常数 L ,因此时间复杂度为 O ( mn );行
其中 k i 最大为常数 L ,因此时间复杂度为 O ( mn );行  ~
~  对训练数据集进行编码为 O ( mn ).综上,总时间复杂度为 O ( mn ),受数据规模影响不大,适合处理大规模数据.
对训练数据集进行编码为 O ( mn ).综上,总时间复杂度为 O ( mn ),受数据规模影响不大,适合处理大规模数据.
对于根据动态自适应算法编码好的二进制串,使用动态自适应距离对各编码之间的相似度进行度量,动态自适应距离度量算法描述如算法3.
算法3 . 动态自适应距离度量算法.
输入:编码好的训练集二进制矩阵 UX_trn 、编码好的测试集二进制矩阵 UX_tst 、二进制编码分配 K =( k 1 , k 2 ,…, k m );
输出:距离矩阵 D .
① D = zeros [ size ( UX_trn ,1), size ( UX_tst )];
② for each row of the matrix UX_trn i =1: size ( UX_trn ,1)  *训练数据集大小*
*训练数据集大小* 
③ for each row of the matrix UX_tst i =1: size ( UX_tst ,1)  *测试数据集大小*
*测试数据集大小* 
④ for each dimension of the matrix UX_trn m =1: size ( UX_trn ,2)  *数据对象维度*
*数据对象维度* 
⑤ if k m >0
⑥ ![]()
⑦ D ( i , j )= D ( i , j )+| UX_trn ( i , a : b )- UX_tst ( j , a : b )|;  * UX_trn ( i , a : b )表示数据集中第 i 行(第 i 个数据)的第 a 列到第 b 列(第 a 维到第 b 维)*
* UX_trn ( i , a : b )表示数据集中第 i 行(第 i 个数据)的第 a 列到第 b 列(第 a 维到第 b 维)* 
⑧ end if
⑨ end for
⑩ end for
 end for
end for
对于 m × n 1 维的训练数据集和 m × n 2 维测试数据集,算法3行⑦的计算复杂度为 O (1),对于3重循环,因此总复杂度为 O ( mn 1 n 2 ).
为了验证所述方法的性能,利用4个公开图像数据集及1个非图像数据集与已有方法进行比较实验:
① http: 
 www.cs.utoronto.ca
www.cs.utoronto.ca  ~kriz
~kriz  cifar.html ② http:
cifar.html ② http: 
 lms.comp.nus.edu.sg
lms.comp.nus.edu.sg  research
research  NUS-WIDE.htm
NUS-WIDE.htm
③ http: 
 corpus-texmex.irisa.fr
corpus-texmex.irisa.fr  ④ http:
④ http: 
 labelme.csail.mit.edu
labelme.csail.mit.edu  Release3.0
Release3.0  browserTools
browserTools  php
php  publications.php
publications.php
⑤ http: 
 qwone.com
qwone.com  ~jason
~jason  20Newsgroups
20Newsgroups 
1) CIFAR-10 ① .该数据集是8 000万个微小图像数据集中的一个子集,总大小174 MB,包括6万幅图像,分成10个类别,每幅图像由3 072个特征描述(32×32 RGB像素图像),其中5万幅为训练图像,1万幅为测试图像.
2) NUS-WIDE ② .由大约27万幅图像组成,总大小1.1 GB,包括5 018个类别,每幅图像有634个特征.
3) Gist-1M-960 ③ .由960个gist特征描述的100万幅图像,总大小5.37 GB.
4) 22K-LabelMe ④ .从大的LabelMe数据集中采样的22 019幅图像,总大小5.94 GB,每幅图像由512个GIST特征描述符表示.
5) 20Newsgroups ⑤ .包括大约2万个新闻文档,分成20个类别,总大小16.5 MB.
采用普遍的方案,将到每个点的前50个最近邻点的平均距离设置为确定点对于查询点是否是真实“命中”的阈值.对于所有实验,随机选择1 000个点作为查询点,其余点作为训练点.最终结果是由10组随机训练  查询分区的平均值.评价指标包括查准率( Precision )、召回率( Recall )和平均准确率( mAP ),定义如下:
查询分区的平均值.评价指标包括查准率( Precision )、召回率( Recall )和平均准确率( mAP ),定义如下:
Precision =检索相关点的数量÷所有检索点的数量,
Recall =检索相关点的数量÷所有相关点的数量, ![]()
其中, Q 是查询点 q i 组成的集合; n i 是在数据集中与 q i 相关点的数量,相关点被排序为 ![]() R i k 是排列好的检索结果中从最顶端的结果到得到数据点 p k 的集合.通过查准率-召回率(PR)曲线,考察样本数与查准率、召回率的关系,平均准确率( mAP )与编码长度的关系来对量化方法进行评价.
R i k 是排列好的检索结果中从最顶端的结果到得到数据点 p k 的集合.通过查准率-召回率(PR)曲线,考察样本数与查准率、召回率的关系,平均准确率( mAP )与编码长度的关系来对量化方法进行评价.
为了测试HL-DAQ策略的影响,对现有的Hash量化方法进行改进,提取已有Hash方法的投影方法,将它们组合到不同的量化方法中,并比较其性能,所采用的Hash投影方法有:
1) LSH—通过从标准高斯函数随机采样获得投影;
2) PCAH—使用数据的主方向作为投影;
3) ITQ—找到使量化损失最小的正交旋转矩阵的迭代法;
4) 将HL-DAQ方法与SBQ,DBQ,2-MQ这3种量化方法进行比较:
5) SBQ—单位数量化,大多数Hash方法使用的标准技术;
6) DBQ—2 b量化;
7) 2-MQ—使用曼哈顿距离的2 b量化.
测试多种Hash方法和量化方法的组合,表示为每个“XXX-YYY”,其中XXX表示Hash方法,YYY表示量化方法.例如PCAH-DBQ表示使用DBQ量化的PCAH方法.
为了说明动态自适应量化方法的一般性和有效性,将3种不同的投影方法与4种不同的量化方法进行组合,并且在5个不同的数据集上进行同样的测试,测试结果如表1~5所示.其中表1~5分别给出了3种Hash投影方法与4种编码量化方法的不同组合在22K-LabelMe,CIFAR-10,Gist-1M-960,NUS-WIDE,20Newsgroups数据集上,就编码位数分别为32 b,64 b,128 b情况下的平均准确率 mAP .由表1~5可知,在不同的Hash投影方法和不同的编码位数下,HL-DAQ方法均比其他量化编码算法具有更高的 mAP ,由此可知,动态自适应量化编码方法与动态自适应距离在大多数情况下实现了较好性能.
图6~9给出了4种量化编码方法分别组合LSH,PCAH,ITQ这3种Hash投影方法在CIFAR-10,Gist-1M-960,NUS-WIDE,20Newsgroups数据集下的某一次实验结果,其中每幅图中的第1个坐标系给出的是 Recall 与 Precision 的关系,第2个坐标系给出的是检索样本数与 Recall 的关系,第3个坐标系给出的是检索样本数与 Precision 的关系,第4个坐标系给出的是编码位数与 mAP 的关系.由图6可知,数据集采用CIFAR-10、Hash投影方法采用LSH时,在相同 Recall 下,HL-DAQ比其他量化方法具有更高的 Precision ;在相同 Precision 下,HL-DAQ比其他量化方法具有在更高的 Recall ;但在相同检索样本点数量情况下,HL-DAQ的 Precision 与 Recall 均稍逊于DBQ;在所有编码位数情况下,HL-DAQ均比其他方法具有更高的 mAP .图7采用的数据集为Gist-1M-960,Hash投影方法采用的是PCAH,其结果与图6基本一致,只是在相同 Recall 情况下,HL-DAQ的 Precision 稍逊于DBQ和MQ.图8给出的是数据集采用NUS-WIDE、Hash投影方法采用ITQ时的实验结果,HL-DAQ各项性能明显均优于其他3种量化编码方法.图9给出的是数据集采用20Newsgroups、Hash投影方法采用LSH时的实验结果,其结果与图6基本一致,证明提出的方法不仅仅适用于图像数据集,对非图像数据集具有通用性.
Table 1 The mAP Comparison under Different Hash Projection Methods Combined with Different Quantitative Coding Methods on 22K - LableMe Dataset
表1 22K - LableMe数据集上不同Hash投影方法与不同量化编码方法组合的 mAP 比较

Table 2 The mAP Comparison under Different Hash Projection Methods Combined with Different Quantitative Coding Methods on CIFAR - 10 Dataset
表2 CIFAR - 10数据集上不同Hash投影方法与不同量化编码方法组合的 mAP 比较

Table 3 The mAP Comparison under Different Hash Projection Methods Combined with Different Quantitative Coding Methods on Gist - 1M - 960 Dataset
表3 Gist - 1M - 960数据集上不同Hash投影方法与不同量化编码方法组合的 mAP 比较

Table 4 The mAP Comparison under Different Hash Projection Methods Combined with Different Quantitative Coding Methods on NUS - WIDE Dataset
表4 NUS - WIDE数据集上不同Hash投影方法与不同量化编码方法组合的 mAP 比较

Table 5 The mAP Comparison under Different Hash Projection Methods Combined with Different Quantitative Coding Methods on 20Newsgroups Dataset
表5 20Newsgroups数据集上不同Hash投影方法与不同量化编码方法组合的 mAP 比较

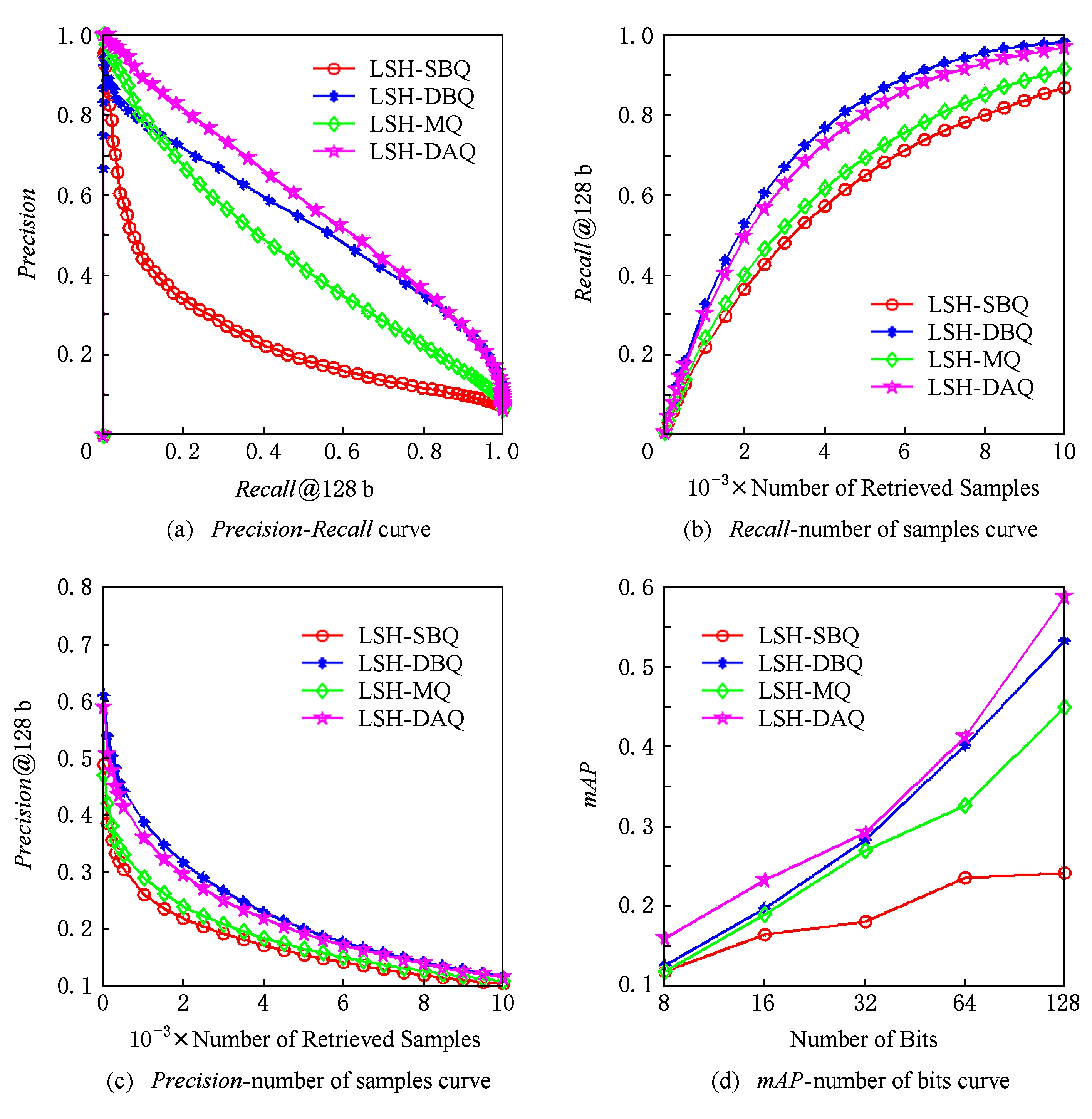
Fig. 6 Comparison of four quantization effects combined with LSH projection method on CIFAR-10 dataset
图6 CIFAR-10数据集下LSH投影方法4种量化效果比较
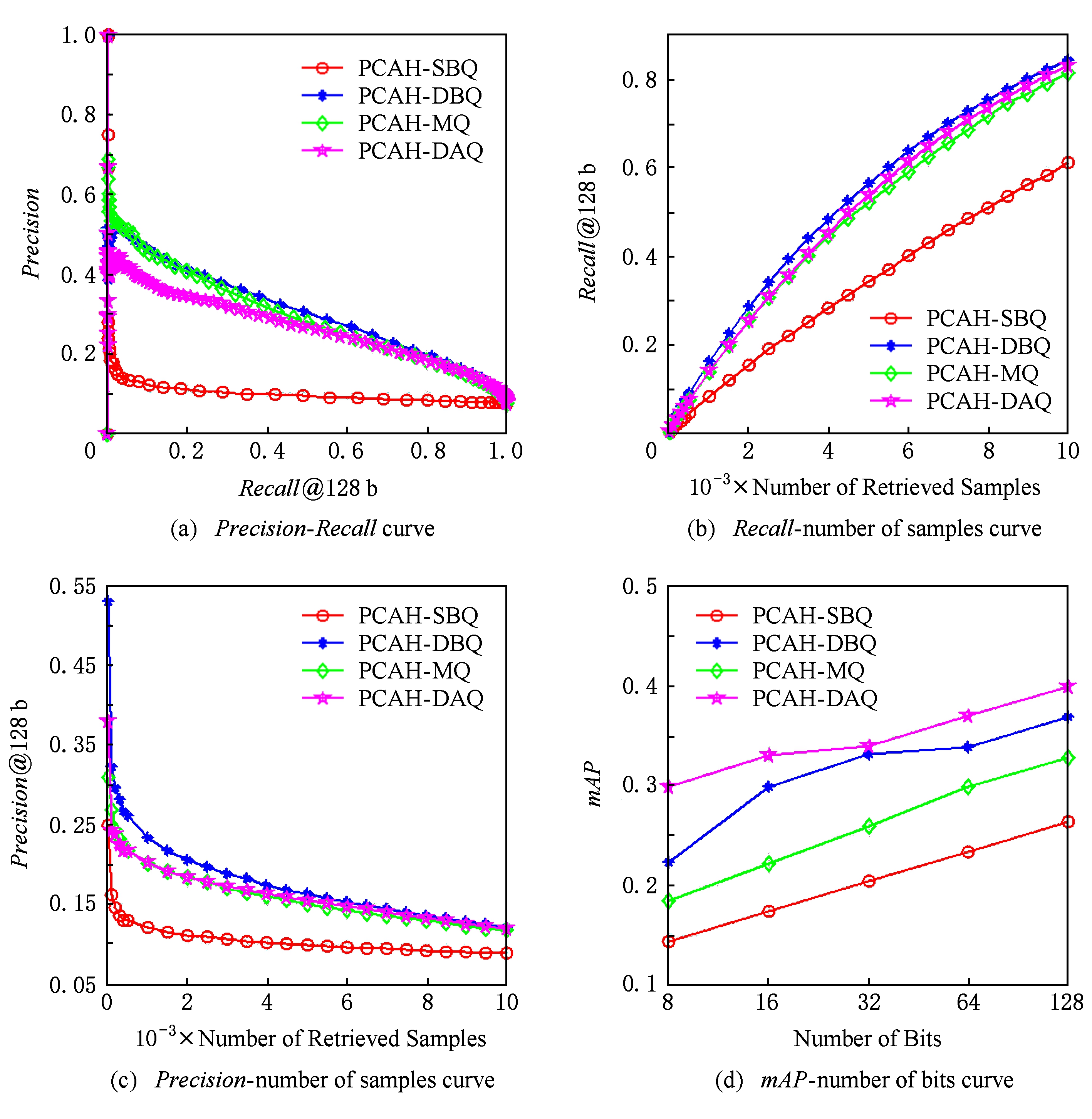
Fig. 7 Comparison of four quantization effects combined with PCAH projection method on Gist-1M-960 dataset
图7 Gist-1M-960数据集下PCAH投影方法4种量化效果比较
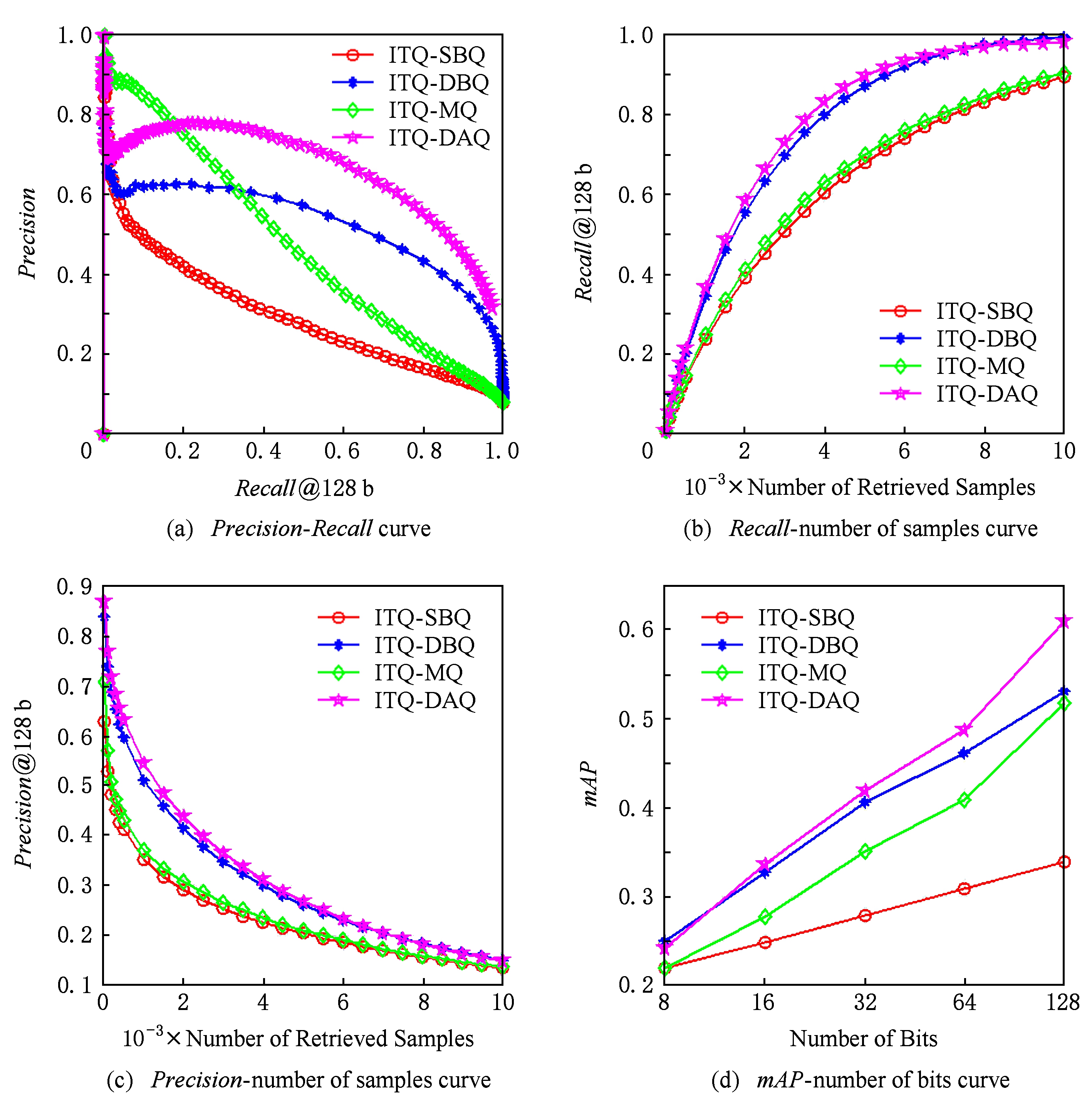
Fig. 8 Comparison of four quantization effects combined with ITQ projection method on NUS-WIDE dataset
图8 NUS-WIDE数据集下ITQ投影方法4种量化效果比较
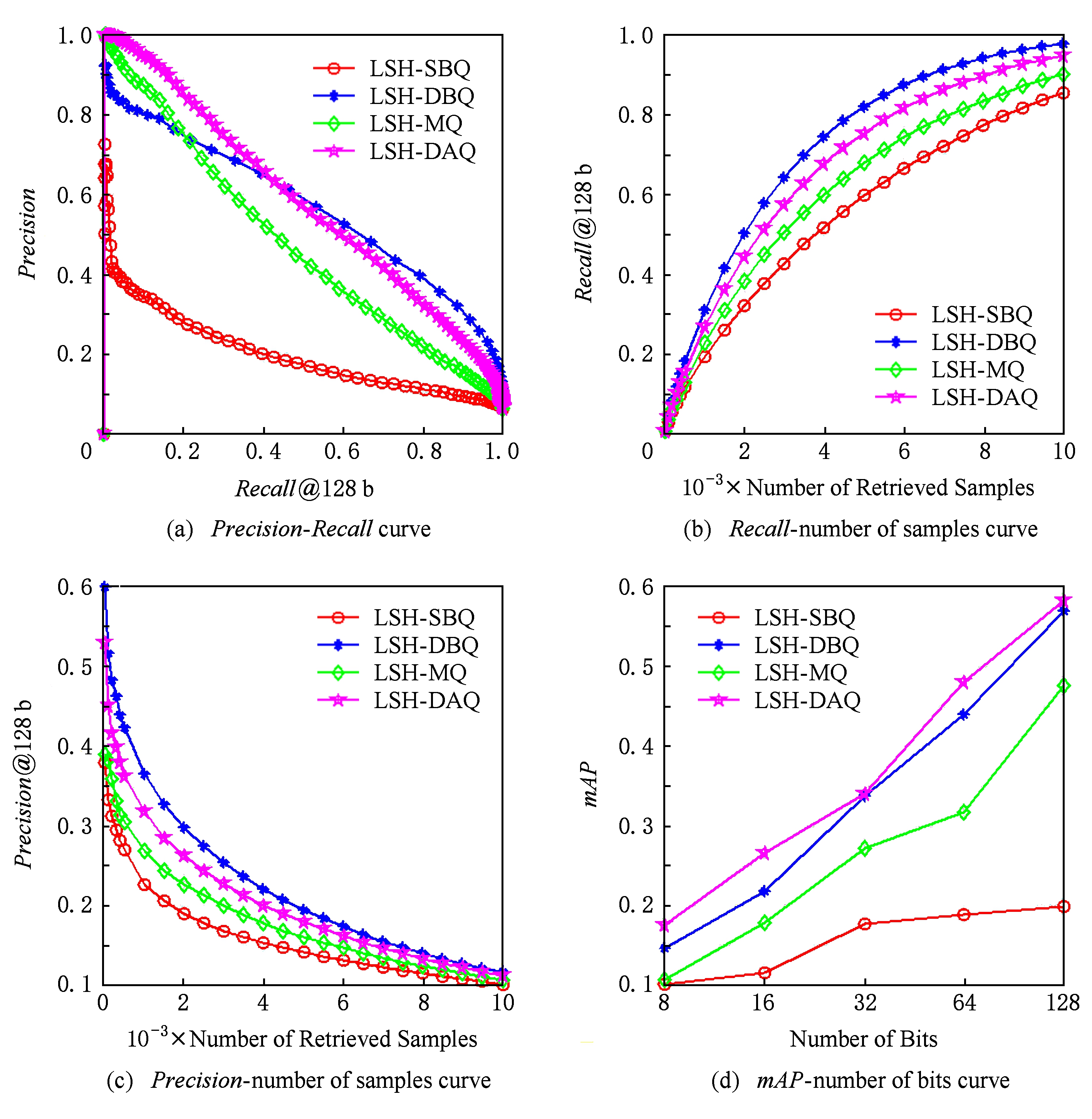
Fig. 9 Comparison of four quantization effects combined with LSH projection method on 20Newsgroups dataset
图9 20Newsgroups数据集下LSH投影方法4种量化效果比较
根据典型的实验结果,LSH通常比其他现有技术的Hash方法(例如ITQ,PCAH,SH)性能更差.为了演示量化阶段的重要性,将HL-DAQ方法添加到LSH中,并将得到的“LSH-DAQ”方法与其他最先进的技术进行比较.在22K-LabelMe数据集上运行实验,实验结果如图10所示.结果表明,虽然标准LSH算法平常效果比较差,简单地替换其默认量化方案与HL-DAQ方法相结合产生的结果显著优于其他的先进Hash方法.
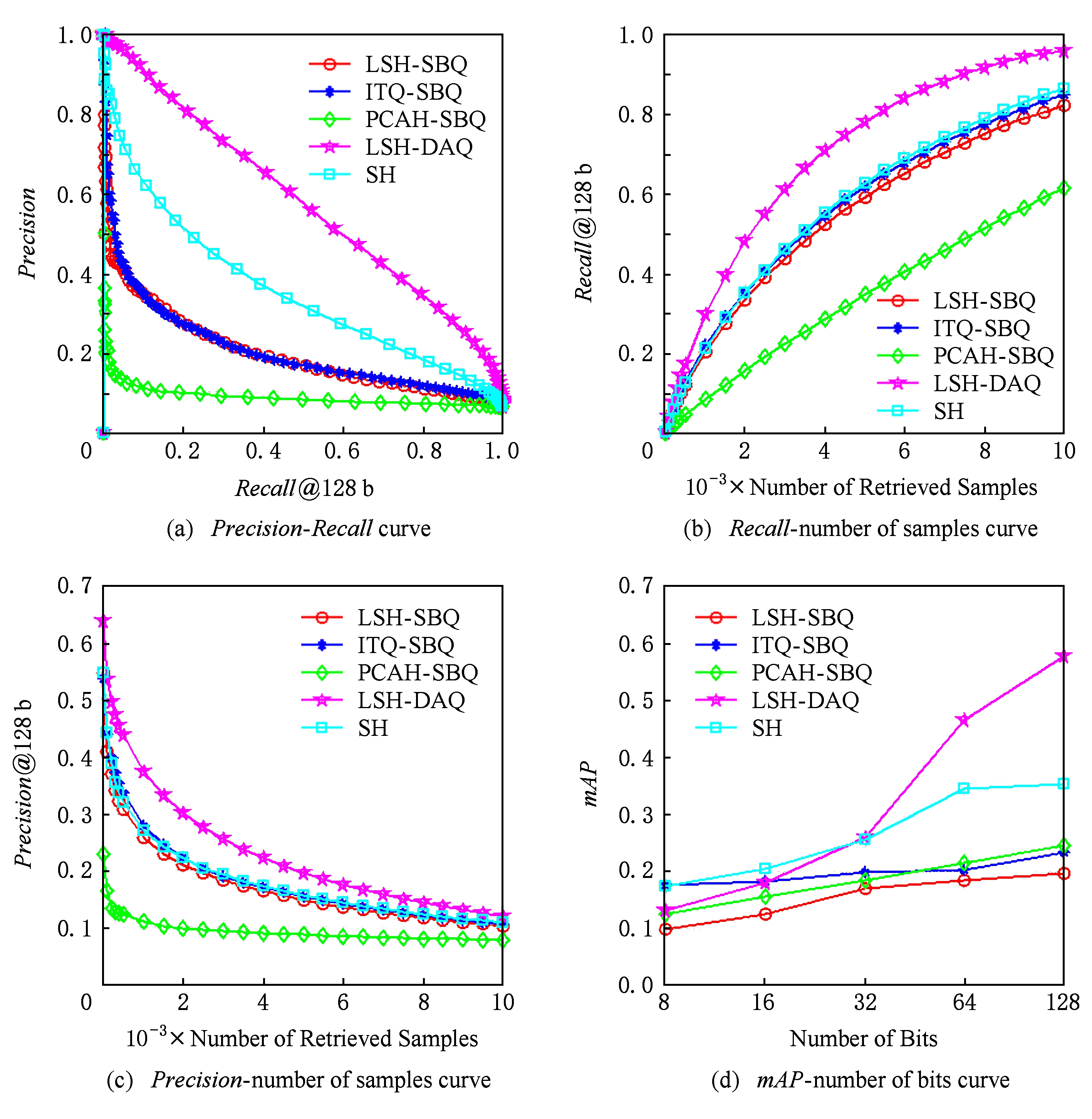
Fig. 10 Comparison of LSH projection combination DAQ quantization method and other methods
图10 LSH投影组合DAQ量化方法与其他方法效果比较
现有的Hash方法通常忽略在量化阶段学习和适应的重要性.HL-DAQ方法较以前的算法具有更好的效果.对现有的Hash应用带来了显著改善,并且表明量化学习在很大程度上还没有被研究,是亟需要发展突破的研究领域.有理由相信,量化学习的研究定将促进数据挖掘和信息检索方面准确率的更大提升.
参考文献
[1]Kong Weihao, Li Wujun. Double-bit quantization for hashing[C] 
 Proc of the 26th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2013: 137-138
Proc of the 26th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2013: 137-138
[2]He Xiaofei, Cai Deng, Yan Shuicheng, et al. Neighborhood preserving embedding[C] 
 Proc of the 10th IEEE Int Conf on Computer Vision. Los Alamitos, CA: IEEE Computer Society, 2005: 1208-1213
Proc of the 10th IEEE Int Conf on Computer Vision. Los Alamitos, CA: IEEE Computer Society, 2005: 1208-1213
[3]Li Wujun, Zhou Zhihua. Learning to Hash for big data: Current status and future trends[J]. Chinese Science Bulletin, 2015, 60(5): 485-490 (in Chinese)(李武军, 周志华. 大数据哈希学习: 现状与趋势[J]. 科学通报, 2015, 60(5): 485-490)
[4]Wang Wei, Yang Xiaoyan, Ooi B C, et al. Effective deep learning-based multi-modal retrieval[J]. The VLDB Journal, 2016, 25(1): 79-101
[5]Long Mingsheng, Cao Yue, Wang Jianmin, et al. Composite correlation quantization for efficient multimodal retrieval[C] 
 Proc of the 39th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2016: 579-588
Proc of the 39th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2016: 579-588
[6]Heo Jae-Pil, Lee Youngwoon, He Junfeng, et al. Spherical hashing: Binary code embedding with hyperspheres[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2015, 37(11): 2304-2316
[7]Wang Jun, Liu Wei, Kumar Sanjiv, et al. Learning to Hash for indexing big data—A survey[J]. Proceedings of the IEEE, 2015, 104(1): 34-57
[8]Tsai Yi-Hsuan, Yang Ming-Hsuan. Locality preserving hashing[C] 
 Proc of the 2014 IEEE Int Conf on Image Processing. Piscataway, NJ: IEEE, 2014: 2988-2992
Proc of the 2014 IEEE Int Conf on Image Processing. Piscataway, NJ: IEEE, 2014: 2988-2992
[9]Zhong Zisha, Fan Bin, Ding Kun, et al. Efficient multiple feature fusion with hashing for hyperspectral imagery classification: A comparative study[J]. IEEE Trans on Geoscience & Remote Sensing, 2016, 54(8): 4461-4478
[10]Liu Haomiao, Wang Ruiping, Shan Shiguang, et al. Deep supervised hashing for fast image retrieval[C] 
 Proc of the 2016 IEEE Conf on Computer Vision and Pattern Recognition. Los Alamitos, CA: IEEE Computer Society, 2016: 2064-2072
Proc of the 2016 IEEE Conf on Computer Vision and Pattern Recognition. Los Alamitos, CA: IEEE Computer Society, 2016: 2064-2072
[11]Shen Fumin, Shen Chunhua, Liu Wei, et al. Supervised discrete hashing[C] 
 Proc of the 2015 IEEE Conf on Computer Vision and Pattern Recognition. Los Alamitos, CA: IEEE Computer Society, 2015: 37-45
Proc of the 2015 IEEE Conf on Computer Vision and Pattern Recognition. Los Alamitos, CA: IEEE Computer Society, 2015: 37-45
[12]Zhang Shifeng, Li Jianmin, Guo Jinma, et al. Scalable discrete supervised Hash learning with asymmetric matrix factorization[C] 
 Proc of the 16th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2016: 1347-1352
Proc of the 16th IEEE Int Conf on Data Mining (ICDM). Piscataway, NJ: IEEE, 2016: 1347-1352
[13]Qian Jiangbo, Zhu Qiang, Chen Huahui. Multi-granularity locality-sensitive Bloom filter[J]. IEEE Trans on Computers, 2015, 64(12): 3500-3514
[14]Qian Jiangbo, Zhu Qiang, Chen Huahui. Integer-granularity locality-sensitive Bloom filter[J]. IEEE Communications Letters, 2016, 20(11): 2125-2128
[15]Liu Wei, Wang Jun, Kumar S, et al. Hashing with graphs[C  OL]
OL] 
 Proc of the 28th Int Conf on Machine Learning. 2011[2017-02-01]. http:
Proc of the 28th Int Conf on Machine Learning. 2011[2017-02-01]. http: 
 machinelearning.wustl.edu
machinelearning.wustl.edu  mlpapers
mlpapers  paper_files
paper_files  ICML2011Liu_6.pdf
ICML2011Liu_6.pdf
[16]Lee Youngwoon, Heo Jae-Pil, Yoon Sung-Eui. Quadra-embedding: Binary code embedding with low quantization error[J]. Computer Vision and Image Understanding, 2014, 125(8): 214-222
[17]Kong Weihao, Li Wujun, Guo Minyi. Manhattan hashing for large-scale image retrieval[C] 
 Proc of the 35th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2012: 45-54
Proc of the 35th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2012: 45-54
[18]Silva J A, Faria E R, Barros R C, et al. Data stream clustering: A survey[J]. ACM Computing Surveys, 2013, 46(1): 1-31
[19]Moran S, Lavrenko V, Osborne M. Variable bit quantisation for LSH[C  OL]
OL] 
 Proc of the 51st Annual Meeting of the Association for Computational Linguistics. 2013 [2017-02-01]. https:
Proc of the 51st Annual Meeting of the Association for Computational Linguistics. 2013 [2017-02-01]. https: 
 www.aclweb.org
www.aclweb.org  anthology
anthology  P13-2132
P13-2132
[20]Duan Lingyu, Lin Jie, Wang Zhe, et al. Weighted component hashing of binary aggregated descriptors for fast visual search[J]. IEEE Trans on Multimedia, 2015, 17(6): 1-1
[21]Groeneveld R A, Meeden G. The mode, median, and mean inequality[J]. The American Statistician, 1977, 31(3): 120-121
[22]Dolcetta I C, Ishii H. Approximate solutions of the Bellman equation of deterministic control theory[J]. Applied Mathematics & Optimization, 1984, 11(1): 161-181
[23]Li Peng, Wang Meng, Cheng Jian, et al. Spectral hashing with semantically consistent graph for image indexing[J]. IEEE Trans on Multimedia, 2013, 15(1): 141-152
[24]Moran S, Lavrenko V, Osborne M. Neighbourhood preserving quantisation for LSH[C] 
 Proc of the 36th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2013: 1009-1012
Proc of the 36th Int ACM SIGIR Conf on Research and Development in Information Retrieval. New York: ACM, 2013: 1009-1012

Zhao Liang , born in 1992. Master in Nanjing University of Science and Technology. His main research interests include approxi-mate nearest neighbor search, intelligent computing and system.

Wang Yongli , born in 1974. Professor, PhD supervisor. His main research interests include big data analysis, intelligent services and cloud computing.

Du Zhongshu , born in 1993. Master candidate in Nanjing University of Science and Technology. His main research interests include approximate nearest neighbor search, distributed system and hashing.

Chen Guangsheng , born in 1971. Technician. His main research interests include machine learning, electronic instrument designing and intelligent computing.
Zhao Liang 1 , Wang Yongli 1 , Du Zhongshu 1 , and Chen Guangsheng 2
1 ( School of Computer Science and Engineering , Nanjing University of Science and Technology , Nanjing 210094) 2 ( Jiamusi Thermal Power Plant of Huadian Energy Company Limited , Jiamusi , Heilongjiang 154005)
Abstract The existing binary coding methods for Hash learning usually learn a set of hypergraphs for data projection, and then simply translate the result data into binary code from the division of each hyperplane. While these methods all ignore the fact that the information may be distributed unevenly in the whole projection dimension, and the range of data value in each projection dimension may not be the same. In order to solve this problem, we propose a dynamic adaptive quantization coding method called HL-DAQ, which allocates the corresponding binary coding bits to each projection dimension dynamically according to the amount of information of it. And HL-DAQ maximizes the total information of all the projections through the dynamic programming method with the purpose to preserve the neighbor structure of the original data as much as possible. Experiments prove that the dynamic adaptive quantization coding for Hash learning method proposed in this paper has significant improvement over the traditional quantization methods for Hash. It is proved that the dynamic adaptive coding for Hash learning method and the dynamic adaptive distance measurement method keep the neighbor structure of the original data better than the original quantization coding methods that fix bit and the original distance measurement method such as Hamming distance.
Key words quantization; approximate nearest neighbor (ANN); dynamic adaptive coding; dynamic programming; dynamic adaptive distance; binary encoding
摘 要 现有基于Hash学习二进制编码方法通常学习一组用于数据投影的超平面,并且简单地对来自每个超平面划分的结果进行二值化编码,而忽视了信息可能不均匀地分布在整个投影中且每一维投影中数据取值范围可能不一样的事实.为了解决此问题提出一种动态自适应编码量化方法,根据投影维度的信息量动态地为该维度分配相应的二进制编码位数,并通过动态规划方法使得所有投影的总信息量最大,以尽可能地保留原始数据的近邻结构.经实验验证,动态自适应编码量化方法较传统的Hash量化方法有显著的改进,理论证明:动态自适应编码方法和距离度量方式对原始数据的近邻结构保持优于传统固定位数量化编码及海明距离度量方式.
关键词 量化;近似最近邻;动态自适应编码;动态规划;动态自适应距离;二进制编码
中图法分类号 TP212.9
收稿日期 : 2017-04-05;
修回日期: 2017-10-11
基金项目 : 国家自然科学基金项目(61170035);“江苏省六大人才高峰”高层次人才项目(WLW-004);中央高校基本科研业务费专项资金项目(30916011328);江苏省科技成果转化专项资金项目(BA2013047)
This work was supported by the National Natural Science Foundation of China (61170035), the Six Talent Peaks Project in Jiangsu Province (WLW-004), the Fundamental Research Funds for the Central Universities (30916011328), and the Jiangsu Province Special Funds for Transformation of Science and Technology Achievement (BA2013047).