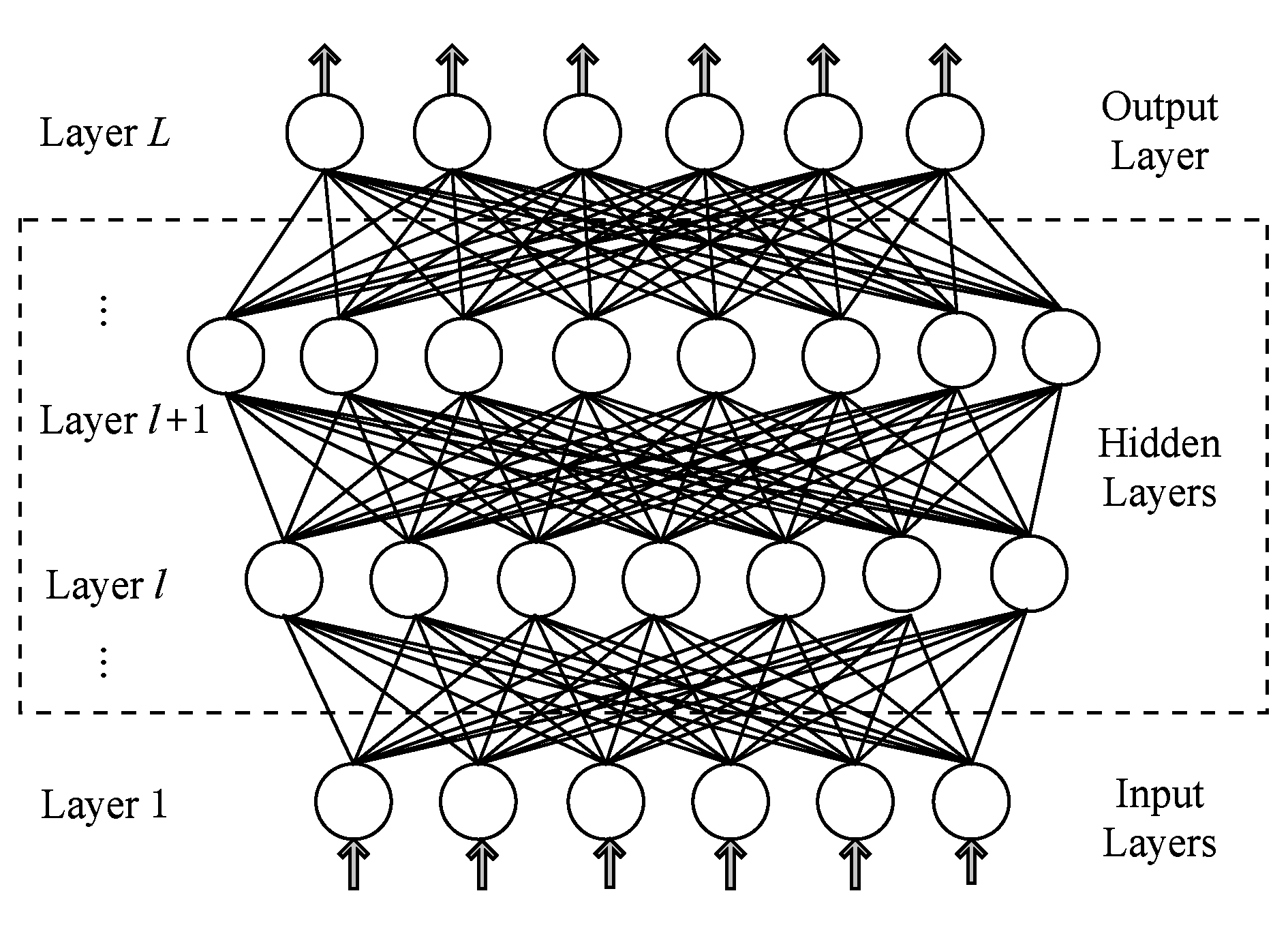
Fig. 1 Fully connected multiple layer network
图1 全连接多层神经网络
任 刚 1,2,3 邓 攀 2 杨 超 2 吴长茂 2
1 (河南工学院计算机科学与技术系 河南新乡 453003) 2 (中国科学院软件研究所并行软件与计算科学实验室 北京 100190) 3 (中国科学院大学 北京 100049) (rengang2013@iscas.ac.cn)
神经网络(neural networks, NNs)也称神经元计算网络,是机器学习中的一类重要算法,其由许多具有层次关系的神经节点构成,能够通过样本学习实现权值调整从而模拟非线性映射关系 [1] .它借助于人类神经系统活动能够实现处理、存储和检索外界信息的原理,来实现自动学习、存储和运行等智能行为.从出现到现在的几十年里,学术界和工业界对其进行了广泛的研究并取得了大量成果 [2] .目前,神经网络已成为一个强大的计算模型,可以有效地解决复杂的模式分类 [3-5] 、图形图像识别 [6-8] 、语义理解 [9-11] 和语音识别 [12-14] 等问题.
BP(back propagation)算法是一种经典的神经网络学习算法,它采用随机选定网络初始值、梯度逐步下降的方法完成神经网络的训练.该算法训练过程包含大量计算,属于典型计算密集型算法,因此,BP算法的并行化成为神经网络热点研究方向之一.目前,其并行方法主要包括数据并行和结构并行2类.数据并行方法将样本数据平均分配到多个计算节点,实现数据的并行处理,而单个计算节点包含整个神经网络结构,因此该方法又称为粗粒度并行 [15-17] ,它适合于大数据样本训练.结构并行方法是将整个神经网络划分为多个结构,各结构之间并行训练,因此又称为细粒度并行 [18-19] ,该方法适用于大规模神经网络训练.
近年来,神经网络的数据训练集规模越来越大,维度也越来越高,呈现出明显的大数据特点 [1] .因此,基于Hadoop集群系统 [20] MapReduce并行模型 [21] 的BP算法受到广泛重视.文献[22]于2006年首次提出了基于MapReduce并行模型的BP (MapReduce back propagation, MRBP)算法.文献[23]针对大规模移动数据相似度较高的问题,将Adaboost算法 [24] 引入MRBP算法中,有效地提高相似性大数据的学习效率.文献[25-27]在基本MRBP算法上又提出了具有局部迭代功能的MRBP算法,进一步优化了MRBP算法的效率.最近,又有学者利用智能算法提高MRBP算法训练效率.比如,文献[28]提出了基于遗传算法(genetic algorithm, GA) [29] 的MRBP算法.文献[30]利用粒子群优化(particle swarm optimization, PSO)算法 [31] 优化MRBP算法的训练效率.
从并行方式来讲,上述MRBP算法均采用粗粒度并行方式,面对样本较多的情况,表现出良好的性能.但是,该类算法缺乏细粒度结构并行的能力,当训练数据维度较高、网络中神经节点较多时,训练效率仍显不足.因此,如何实现MRBP算法的结构并行成为一个亟需解决的问题.
然而,现有基于消息传递集群系统的结构并行方法 [32-33] 不适用于基于Hadoop集群的MRBP算法.其原因在于Hadoop集群系统的MapReduce编程模型中没有显式的消息通信指令,其计算节点之间的通信由Hadoop系统自动完成.为此,本文尝试提出一种适合Hadoop集群MapReduce编程模型的结构并行方法,来提高MRBP算法的训练效率.本文的主要贡献在于:
1) 提出了一个适合于MapReduce 编程模型的结构并行策略,即逐层并行-逐层集成(layer-wise parallelism and layer-wise ensemble, LPLE)结构并行策略.根据该并行策略,设计了基于结构并行的MRBP算法——SP-MRBP(structure parallelism based MRBP),并给出了该算法主要实现代码.据作者所知,这是首次将结构并行方法引入MRBP算法;
2) 推导出了SP-MRBP算法与经典MRBP算法计算时间解析表达式,并以此分析了这2种算法的计算时间差和SP-MRBP算法最优并行结构数;
3) 通过并行结构规模扩展性、计算节点规模扩展性、样本规模扩展性和网络规模扩展性4组实验,验证了SP-MRBP算法的有效性.
人工神经网络是一种全连接多层网络,一个 L 层神经网络如图1所示.底层( l =1)为输入层,顶层 ( l = L )为输出层,中间层又称为隐含层.第 l 层包含 n l 个神经节点.每个神经节点都与上一层和下一层的所有神经节点相连.每个神经节点有一个激活值和一个误差值,我们把 l 层上节点 i 的激活值记为 a i ( l ),误差值记为 δ i ( l ). l +1层的神经节点 i 和 l 层的神经节点 j 之间的权值表示为 w i j ( l +1).

Fig. 1 Fully connected multiple layer network
图1 全连接多层神经网络
BP算法是一个有导师的机器学习训练算法,它使用一组样本集合去训练一个多层神经网络.训练过程的实质是寻找网络权重的过程.该算法包括3个阶段:信号向前传播、误差向后反馈和权值更新.1)在信号向前传播阶段,一个样本的输入部分从输入层输入,然后逐层传播,计算出每层节点的输出值,最后在输出层,每个节点的激活值与该样本的输出部分的差值作为该节点的误差.2)在误差反馈阶段,输出层的误差逐层向底层传播,计算出下面每层节点的误差.3)在权值更新阶段,根据新的激活值和误差更新权值矩阵.第1阶段计算过程如图2所示,第2阶段和第3阶段这2个阶段可以合并计算,其详细过程如图3所示.
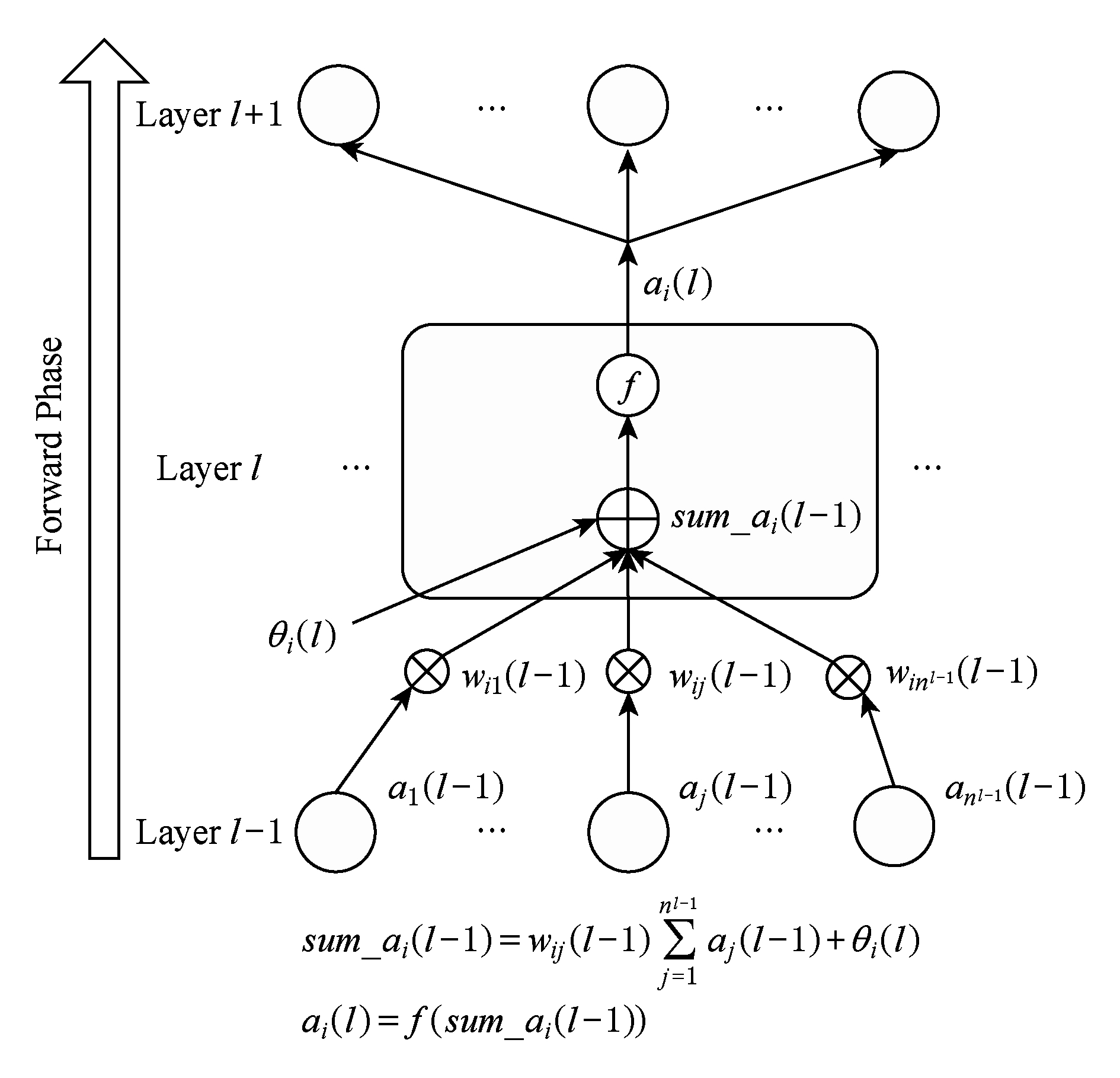
Fig. 2 Forward stage of signal transmission
图2 信号向前传播阶段
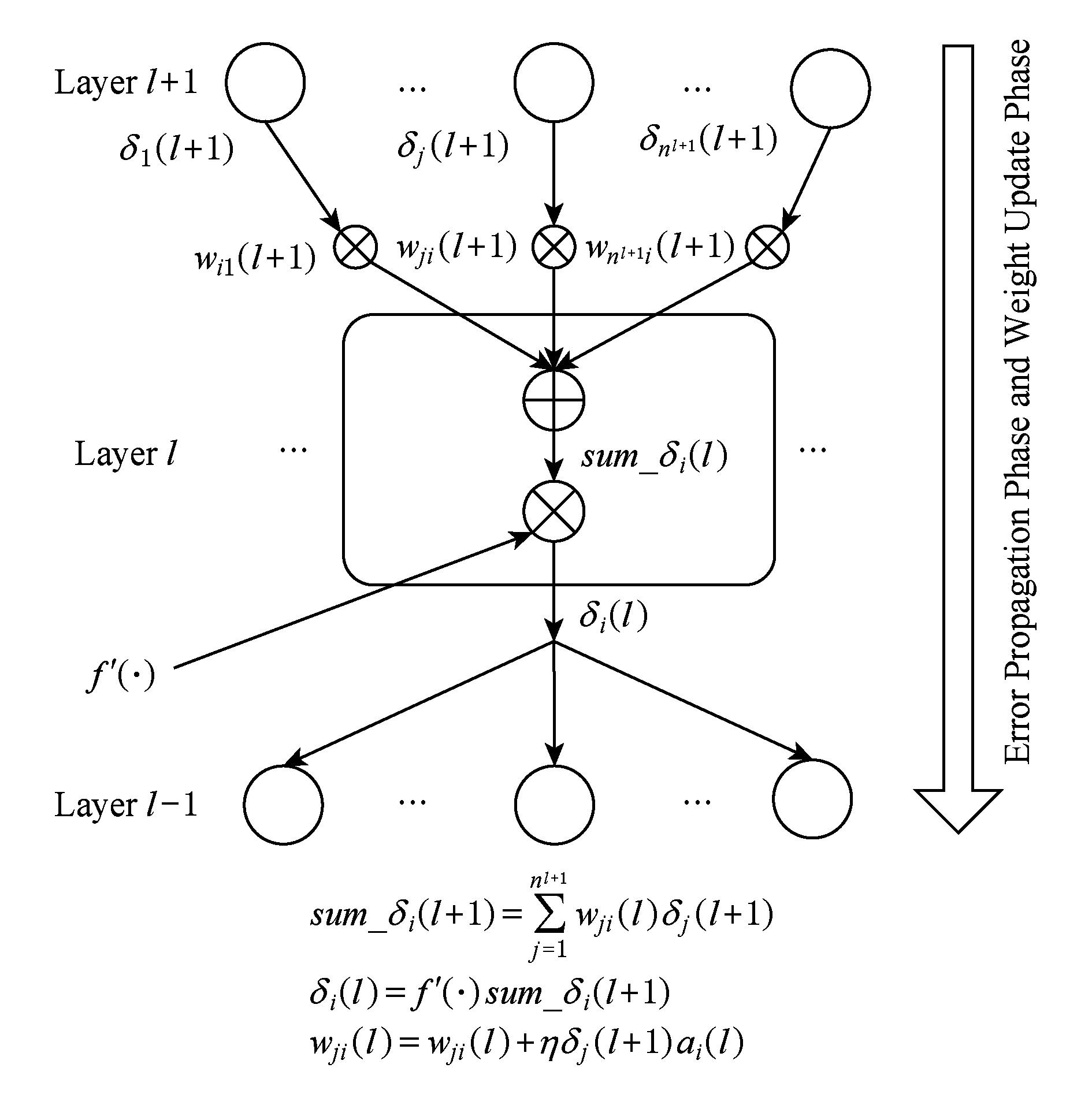
Fig. 3 Backward and weight update stage
图3 误差向后传播与权值矩阵更新阶段
具有单隐含层的多层神经网络,只要具有足够多的神经节点,就足以逼近任意一个输入输出函数 [34] .因此,本文以3层( l =1,2,3),每层有 n l 个神经节点的多层神经网络为例,来分析上述3个阶段的时间复杂度.
信号向前传播阶段如图2所示,对于给定的输入样本 P ,隐含层和输出层的激活值计算公式如下:
![]()
(1)
i =1,2,…, n l , l =2,3,
其中, f (·)为sigmod函数, θ 为阈值常数.我们分别用 t m , t a 和 t ac 表示浮点数乘法、加法和计算激活值所消耗的时间.同时,不失一般性,忽略 θ 的计算时间,那么向前阶段所消耗时间可近似表示为
t 1 = n 2 ( n 1 + n 3 )( t m + t a )+ t ac ( n 2 + n 3 ),
(2)
令 M a = t m + t a , t ac = αM a ,则:
t 1 = n 2 ( n 1 + n 3 ) M a + αM a ( n 2 + n 3 )=
n 2 ( n 1 + n 3 + α ) M a + αn 3 M a .
(3)
误差向后反馈阶段如图3所示,该阶段网络输出值与期望值的误差通过权值矩阵向底层神经节点反馈.输出层第 i 个节点的误差值 δ i (2)可表示如下:
δ i (3)=( a i (3)- t i )) f ′(·), i =1,2,…, n 3 ,
(4)
其中, f ′(·)是激活函数的一阶导数, a i (3)是输出层神经节点 i 的实际输出, t i 是其期望输出.
中间层误差项 δ i (2)可表示如下:
(5)
整个过程所需要的时间 t 2 可近似表示为
t 2 = n 2 n 3 M a .
(6)
权值更新阶段利用误差项 δ j ( l +1)和激活值 a i ( l )来更新 w j i ( l ).
w j i ( l )= w j i ( l )+ ηδ j ( l +1) a i ( l ),
(7)
其中, η 表示学习率.权值矩阵更新时间可表示为
t 3 = n 2 ( n 1 + n 3 ) M a .
(8)
输入样本 P 的1次训练时间 T seq 可表示为
T seq = t 1 + t 2 + t 3 =(2 n 2 n 1 +3 n 2 n 3 +
αn 2 + αn 3 ) M a =( n 2 K + αn 3 ) M a ,
(9)
其中, K =2 n 1 +3 n 3 + α .
Hadoop集群系统是一种为实现大数据处理的云计算系统,主要由Hadoop分布式文件系统(Hadoop distributed file system, HDFS) [35] 和MapReduce编程模型 [21] 构成.HDFS文件系统总体框架如图4所示,它包含名称节点(NameNode)和数据节点(DataNode)2个角色.一个文件被分为若干个块(Block),分布存储在多个数据节点.通常情况下,为了提高系统可靠性,每个文件块还会有2个副本.文件块的位置信息由名称节点管理.当客户端需要写入文件时,首先向名称节点请求写入位置,然后按照名称节点指定的位置写入文件,而另外的2个副本则由数据节点负责写入.当客户端读取文件时,则向名称节点请求文件位置信息,然后按照指定位置信息读取文件.HDFS集群节点之间通过Java socket组播传输模式通信.另外,名称节点和数据节点上分别有1个JobTracker进程和1个TaskTracker进程,负责作业指派和任务管理.
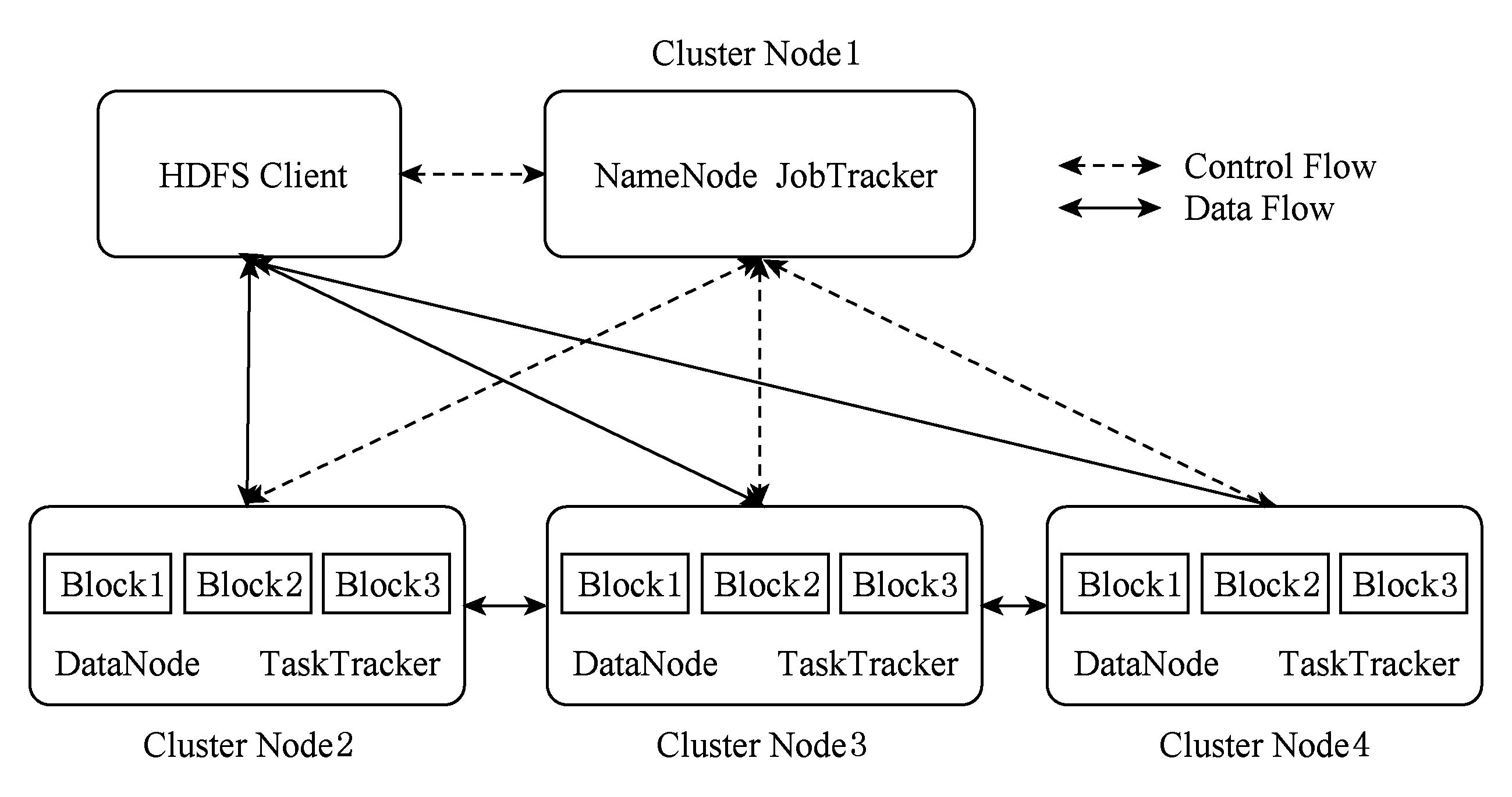
Fig. 4 HDFS file system
图4 HDFS文件系统

Fig. 5 MapReduce programming model
图5 MapReduce编程模型
MapReduce编程模型包括Mapper和Reducer这2个任务,其详细处理流程如图5所示:首先,在每个数据节点上,由TaskTracker进程启动Mapper任务,1个Mapper依次读取1个数据分片(Split)中的每个键值对,该数据分片一般对应于1个数据块,读取完毕后,按具体业务逻辑产生新的键值对,如下所示:
Mapper ∷( key 1 , value 1 )→
list ( key 2 , value 2 ).
(10)
在Mapper任务完成后,根据具体的业务逻辑,可以直接将计算结果存入HDFS供下次迭代使用;或者把( key 2 , value 2 )合并成链表形式发送给Reducer节点,进行规约处理.其Reducer处理逻辑如下所示:
Reducer ∷( key 2 , list ( value 2 ))→
list ( key 3 , value 3 ).
(11)
目前存在的基于消息传递集群结构并行方法,常采用垂直分割的方法 [32-33] ,该方法将每层神经节点平均映射到多个集群计算节点上,逐层计算,每计算一层,各计算节点彼此通信,交换计算结果,以此提高训练效率.但是,由于Hadoop集群中各计算节点的通信不由用户直接控制,现有方法并不能直接应用于MapReduce编程模型.为了在Hadoop集群环境下实现结构并行,本文提出逐层并行-逐层集成(LPLE)策略.
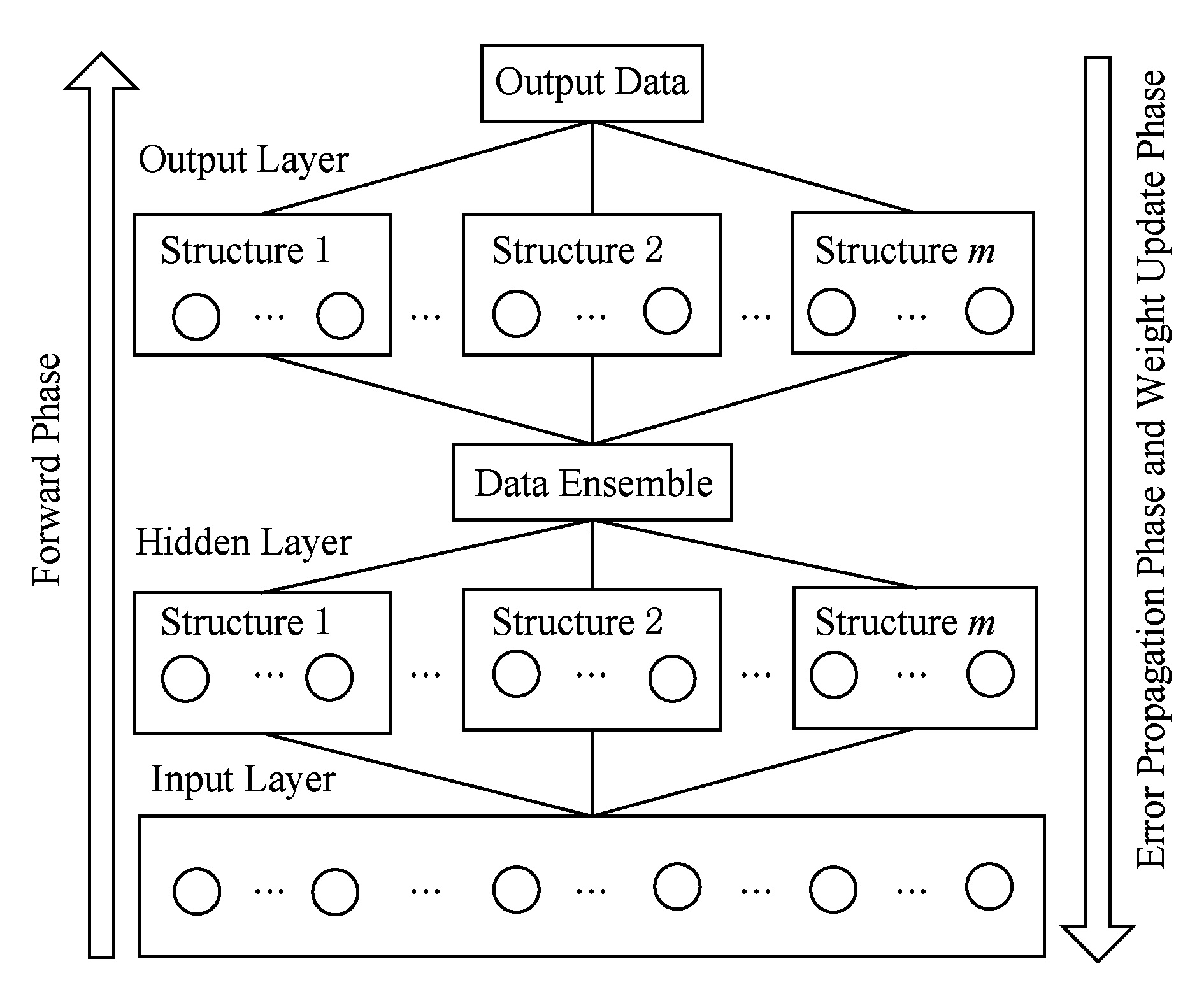
Fig. 6 LPLE strategy
图6 逐层并行-逐层集成结构并行策略
图6显示了基于3层神经网络的LPLE并行策略,该策略将隐含层和输出层均分为 m 个并行结构;而输入层不进行结构划分.在信号向前传播阶段,隐含层各结构首先根据输入层数据,计算出各自神经节点激活值;然后集成各结构结果,为输出层激活值计算提供数据.在误差反馈阶段,输出层各并行结构根据已计算出的激活值,计算出本结构所有节点误差值,然后集成所有结构的输出,为隐含层误差值计算提供准备.
在具体MapReduce模型的实现上,LPLE策略中每个结构的计算任务都由1个MapReduce作业完成,并行结构输出结果集成由另一个MapReduce作业来完成.这样,每层计算由 m 个并行结构作业和1个集成作业完成.下面给出代码实现中主要符号含义.
P i :输入样本 i ;
y j :输出层第 j 个神经节点期望输出;
A ( l )=( a 1 ( l ), a 2 ( l ),…, a nl ( l )): l 层激活值向量;
Infor_A ( l )=( A (1), A (2),…, A ( l )):从输入层到 l 层激活值向量集合;
δ ( l )=( δ 1 ( l ), δ 2 ( l ),…, δ nl ( l )): l 层各节点误差值;
Infor_δ ( l )=( δ ( L ), δ ( L -1),…, δ ( l )):从输出层到 l 层的误差值集合;
Structure_F k =( a s tart ( l ),…, a e nd ( l )):向前阶段 l 层并行结构 k 各神经节点激活值集合, start 为开始神经节点, end 为结尾神经节点;
Structure_B k =( δ s tart ( l ),…, δ e nd ( l )):向后阶段 l 层并行结构 k 神经节点误差值集合.
2.3.1 结构并行作业
向前阶段并行结构的Mapper从HDFS的文件分片中依次读取样本数据,计算出该结构所有节点激活值,再存回HDFS中,待后继集成作业处理.若当前层是输出层的话,为了提高计算速度,本文把误差值 δ i ( l )计算及权值增量Δ w i j ( l )计算也一并完成,并把Δ w i j ( l )作为 key 2 , δ i ( l ) a j ( l -1)作为 value 2 ,发送给Reducer任务. l 层Mapper任务主要算法如下.
算法1 . 前向阶段第 l 层第 k 个并行结构Mapper算法.
输入:  P i , Infor_A ( l -1)
P i , Infor_A ( l -1)  ; start 为起始节点, end 为结束节点.
; start 为起始节点, end 为结束节点.
① for ( i = start ; i + +; i < end +1) do
② for ( j =1; j + +; j < n l -1 ) do
③ sum_a i ( l )= a j ( l -1) w i j ( l );
④ end for
⑤ a i ( l )= f ( sum_a i ( l )+ θ );
⑥ Structure_F k = Structure_F k ∪ a i ( l );
⑦ if l = L then
⑧ δ i ( l )=( a i ( l )- y i ) f ′(·);
⑨ Structure_B k = Structure_B k ∪ a i ( l );
⑩ EMIT (  Δ w i j ( l ), δ i ( l ) a j ( l -1)
Δ w i j ( l ), δ i ( l ) a j ( l -1)  );
);
 Write
Write  P i , Infor_A ( l -1), Structure_f k ( l ), Structure_b k ( l )
P i , Infor_A ( l -1), Structure_f k ( l ), Structure_b k ( l )  to HDFS;
to HDFS;
 end if
end if
 Write
Write  P i , Infor_A ( l -1), Structure_f k ( l )
P i , Infor_A ( l -1), Structure_f k ( l )  to HDFS;
to HDFS;
 end for
end for
本文算法中,权值矩阵采用全局变量形式.值得注意的是,由于在计算 l 误差值时,还需要用到 l +1层权值矩阵,因此, l +1层权值矩阵必须在 l 层误差值全部计算完毕后,才能更新.为此,本文设置2个权值矩阵,一个是权值矩阵( w i j ( l )),一个是权值增量矩阵(Δ w i j ( l )).这里,Reducer任务只负责更新输出层权值增量矩阵(Δ w i j ( l )),而权值矩阵在后继作业中更新.
算法2 . 向前阶段第l层Reducer算法.
输入:  (Δ w i j ( l )), ValueList
(Δ w i j ( l )), ValueList  , w i j ( l )是待更新权值, ValueList 是样本权值列表.
, w i j ( l )是待更新权值, ValueList 是样本权值列表.
① for each value in ValueList do
② sum = sum + value ;
③ num + +;
④ end for
⑤ avg = sum  num ;
num ;
⑥ Update Δ w i j ( l ) with avg .
2.3.2 结构集成作业
向前阶段集成作业中,Mapper负责将各个数据节点的结构信息发送给Reducer数据节点.
算法3 . 向前阶段第l层结构集成Mapper算法.
输入:  key 2 , value 2
key 2 , value 2  设置为
设置为  P i , Infor_A ( l -1), Structure_F k ( l ), Structure_B k ( l )
P i , Infor_A ( l -1), Structure_F k ( l ), Structure_B k ( l )  .
.
① if l = L then
② EMIT (  P 1 , Infor_A ( l -1), Structure_F k ( l ), Structure_B k ( l )
P 1 , Infor_A ( l -1), Structure_F k ( l ), Structure_B k ( l )  );
);
③ else
④ EMIT (  P 1 , Infor_A ( l -1), Structure_F k ( l )
P 1 , Infor_A ( l -1), Structure_F k ( l )  );
);
⑤ end if
Reducer收到Mapper发送来的结构数据后,将各结构数据集成后,重新写回HDFS,为下层计算提供数据.若当前层是输出层,则还需集成误差值.
算法4 . 向前阶段第 l 层结构集成Reducer算法.
输入:  P i , Infor_A ( l -1), Structure_F 1 ( l ),…, Structure_F m ( l ), Structure_B 1 ( l ),…, Structure_B m ( l )
P i , Infor_A ( l -1), Structure_F 1 ( l ),…, Structure_F m ( l ), Structure_B 1 ( l ),…, Structure_B m ( l )  .
.
① if l = L then
② for ( k =1; k + +; k < m ) do
③ A ( l )= A ( l )∪ Structure_F k ( l );
④ δ ( l )= δ ( l )∪ Structure_B k ( l );
⑤ end for
⑥ Infor_A ( l )= Infor_A ( l -1)∪ A ( l );
⑦ Infor_δ ( l )= Infor_δ ( l -1)∪ δ ( l );
⑧ Write  P i , Infor_A ( l ), Infor_δ ( l )
P i , Infor_A ( l ), Infor_δ ( l )  to HDFS;
to HDFS;
⑨ else
⑩ for ( k =1; k + +; k < m ) do
 A ( l )= A ( l )∪ Structure_F k ( l );
A ( l )= A ( l )∪ Structure_F k ( l );
 end for
end for
 Infor_A ( l )= Infor_A ( l -1)∪ A ( l );
Infor_A ( l )= Infor_A ( l -1)∪ A ( l );
 Write
Write  P i , Infor_A ( l )
P i , Infor_A ( l )  to HDFS;
to HDFS;
 end if
end if
向后阶段负责逐层计算各结构神经节点误差值并集成各结构输出,同时更新相应权值矩阵,为下一层计算提供数据.下面分别给出向后阶段结构并行和结构集成MapReduce模型实现主要代码.
2.4.1 结构并行作业
在求得样本 P i 各层激活值及其输出层误差值后,开始向后求隐含层误差值并更新权值矩阵.假设 l 层被平均分割为 m 个并行结构,则每个并行结构对应1个MapReduce作业,其Mapper有3个任务:1)计算结构内节点误差值;2)计算神经节点权值增量,并发送给Reducer;3)更新上一层权值矩阵.
算法5 . 向后阶段第 l 层第 k 个并行结构Mapper算法.
输入:  P i , Infor_A ( L ), Infor_δ ( l +1)
P i , Infor_A ( L ), Infor_δ ( l +1)  .
.
① num + +;
② for ( i = start ; i + +; i < end +1) do
③ for ( j =1; j + +; j < n l +1 ) do
④ sum_δ i ( l +1)= sum_δ i ( l +1)+ δ j ( l +1) w j i ( l +1);
⑤ Update w j i ( l +1) with Δ w j i ( l +1);
⑥ end for
⑦ δ i ( l )= f ′(·) sum_δ i ( l +1);
⑧ Structure_B k = Structure_B k ∪ δ i ( l );
⑨ for ( j =1; j + +; j < n l -1 ) do
⑩ EMIT (  Δ w i j ( l ), δ i ( l ) a j ( l -1)
Δ w i j ( l ), δ i ( l ) a j ( l -1)  );
);
 end for
end for
 end for
end for
 Write
Write  P i , Infor_A ( L ), Infor_δ ( l +1), Structure_B k ( l )
P i , Infor_A ( L ), Infor_δ ( l +1), Structure_B k ( l )  to HDFS.
to HDFS.
Reducer对收到的所有权值增量取平均值,并更新权值增量矩阵Δ w i j ( l ).如果当前层是隐含层最后一层(2层),直接更新权值矩阵 w i j ( l ).
算法6 . 向后阶段第 l 层结构并行Reducer算法.
输入:  Δ w i j ( l ), ValueList
Δ w i j ( l ), ValueList  .
.
① for each value in ValueList do
② sum = sum + value ;
③ num + +;
④ end for
⑤ avg = sum  num ;
num ;
⑥ if l =2 then
⑦ Update w i j ( l ) with avg ;
⑧ else
⑨ Update Δ w i j ( l ) with avg ;
⑩ end if
2.4.2 结构集成作业
该阶段由1个MapReduce作业来完成,其Mapper从HDFS读取 l +1层的各结构数据后,发送给Reducer.
算法7 . 向后阶段第 l 层第 k 个结构Mapper算法.
输入:  P i , Infor_A ( L ), Infor_δ ( l +1), Structure_B k ( l )
P i , Infor_A ( L ), Infor_δ ( l +1), Structure_B k ( l )  .
.
① EMIT (  P i , Infor ( l +1), Infor_δ ( l +1), Structure_B k ( l )
P i , Infor ( l +1), Infor_δ ( l +1), Structure_B k ( l )  ).
).
Reducer接收到经过系统整理过的样本结构数据后,合并各结构误差值,并存入HDFS,为下层计算做好数据准备.
算法8 . 向后阶段第l层结构集成Reducer算法.
输入:  P i , Infor_A ( L ), Infor_δ ( l +1), Structure_B 1 ( l ),…, Structure_B m ( l )
P i , Infor_A ( L ), Infor_δ ( l +1), Structure_B 1 ( l ),…, Structure_B m ( l )  .
.
① for ( k =1; k + +; k < m ) do
② δ ( l )= δ ( l )∪ Structure_B k ( l );
③ end for
④ Infor_δ ( l )= Infor_δ ( l +1)∪ δ ( l );
⑤ Write  P i , Infor_A ( L ), Infor_δ ( l )
P i , Infor_A ( L ), Infor_δ ( l )  to HDFS.
to HDFS.
准确的算法执行时间涉及众多因素,很难准确表示.为了分析影响算法效率的主要因素,本节以3层网络为例,给出SP-MRBP算法和MRBP算法复杂度近似解析表达式,旨在分析影响SP-MRBP算法和MRBP算法时间差及SP-MRBP算法最优并行结构数的主要因素.
假设神经网络隐含层和输出层都被分为 m 个并行子结构,则1个样本的训练时间可计算如下.
3.1.1 向前激活值计算阶段
该阶段时间 ![]() 可分为结构并行计算时间
可分为结构并行计算时间 ![]() 和结构集成时间
和结构集成时间 ![]() 按照式(3),则有:
按照式(3),则有:
![]()
(12)
3层网络的向前阶段包括隐含层结构集成时间 ![]() 和输出层结构集成时间
和输出层结构集成时间 ![]() 每个结构完成计算后,将计算结果存入HDFS.其数据节点之间信息通过Java套接字组播模式传输,该模式把要被广播所有值组合在一起发送.这里, m 个节点广播一条长度为 w 的消息的通信时间可近似表示为
每个结构完成计算后,将计算结果存入HDFS.其数据节点之间信息通过Java套接字组播模式传输,该模式把要被广播所有值组合在一起发送.这里, m 个节点广播一条长度为 w 的消息的通信时间可近似表示为
t com ( w )= m ( t ini + t c g ( w )),
(13)
其中, t c 表示发送或接收一个浮点数的时间, t ini 是通信启动时间, g ( w )是分组广播模式的规模大小.通常 g ( w )≪ w .根据式(13),可得:
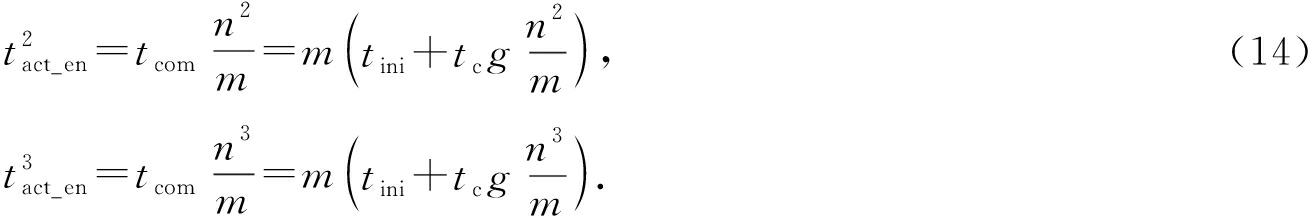
(15)
根据式(14)(15)则有:
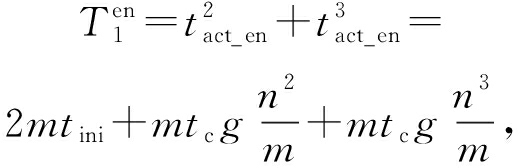
(16)
这里,令 t ini ![]() M a , t c = ρ M a 则有:
M a , t c = ρ M a 则有:
![]()
(17)
则第1阶段时间可近似表示为
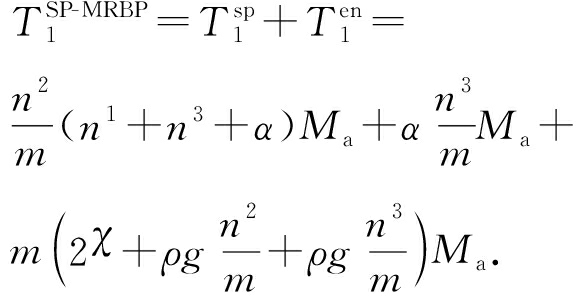
(18)
3.1.2 误差向后反馈阶段
该阶段时间 ![]() 可分为结构并行时间
可分为结构并行时间 ![]() 和结构集成时间
和结构集成时间 ![]() 按照式(18),则有:
按照式(18),则有:
![]()
(19)
与向前阶段类似,误差向后传播阶段结构集成包含输出层结构集成时间 ![]() 和隐含层结构集成2部分
和隐含层结构集成2部分 ![]() 这里直接给出结果:
这里直接给出结果:
![]()
(20)
根据式(19)(20),可得:
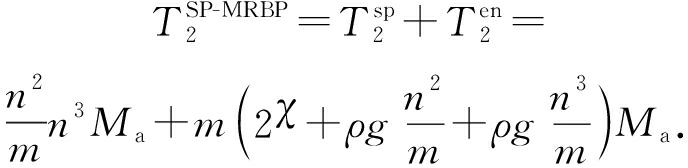
(21)
3.1.3 权值更新阶段
该阶段时间 ![]() 包括权值计算时间
包括权值计算时间 ![]() 和权值在Mapper和Reducer传送时间
和权值在Mapper和Reducer传送时间 ![]() 由式(8)可得:
由式(8)可得:
![]()
(22)
权值传输时间 ![]() 由隐含层权值传输时间
由隐含层权值传输时间 ![]() 和输出层权值传输时间
和输出层权值传输时间 ![]() 构成.
构成.

(23)
由式(22)(23)可得:
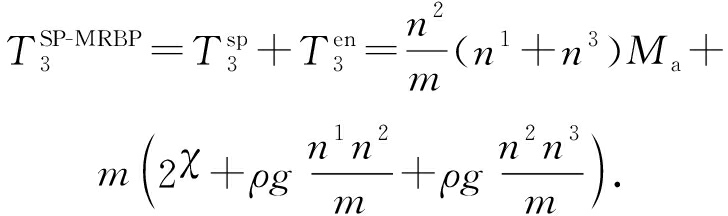
(24)
从上述分析可知,SP-MRBP算法1次训练时间 T SP-MRBP 可近似表示为
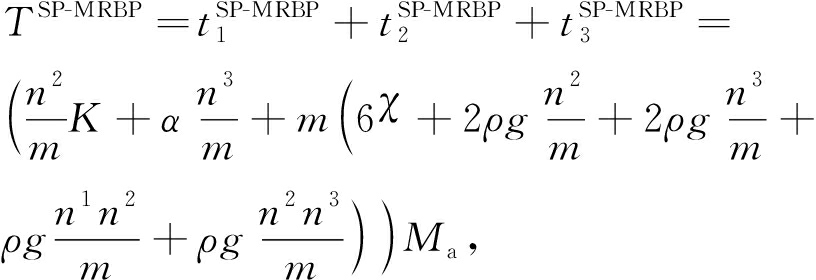
(25)
这里令 ![]() 则式(25)可表示为
则式(25)可表示为
![]()
(26)
假设共有 A 条样本, p 个数据节点,则每个数据节点有 A  p 条样本,则整个训练时间为
p 条样本,则整个训练时间为
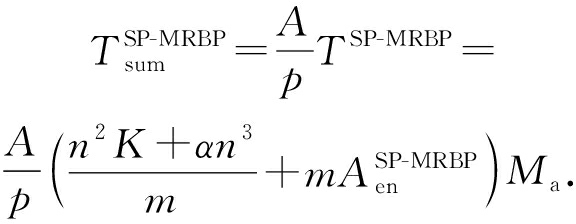
(27)
式(27)由2项构成,第1项可以认为是样本计算时间,第2项可以认为是样本通信时间.可知,在样本总数和计算节点一定的情况下,随着并行结构数 m 增加,其计算时间会随之减少,而通信时间会随之增加.
MRBP算法由Mapper完成整个神经网络激活值计算、误差计算及其权值更新,然后将权值增量发送给Reducer节点进行更新;Reducer接收所有权值之后求出均值,并更新权值矩阵.因此,MRBP 算法时间 ![]() 可以近似表示为数据节点训练
可以近似表示为数据节点训练 ![]() 和通信时间
和通信时间 ![]() 之和.根据式(9),样本训练时间可近似表示为
之和.根据式(9),样本训练时间可近似表示为
![]()
(28)
1个样本训练还包括1次通信过程,每次广播大小为 n 2 ( n 1 + n 3 ),根据式(13),其通信时间可表示为
![]()
(29)
这里,仍令 t ini ![]() M a , t c = ρ M a ,则有:
M a , t c = ρ M a ,则有:
![]()
(30)
令 ![]() 则式(30)可表示为
则式(30)可表示为
![]()
(31)
假设样本数为 A ,数据节点数为 p ,则每个数据节点有 A  p 个样本.整个MRBP算法所需时间为
p 个样本.整个MRBP算法所需时间为
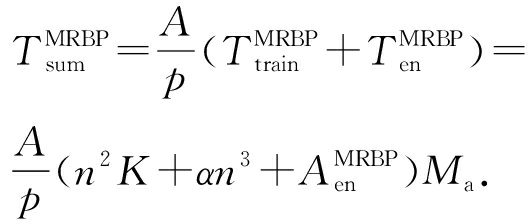
(32)
根据式(27)(32),可得MRBP算法和SP-MRBP算法时间差如下:
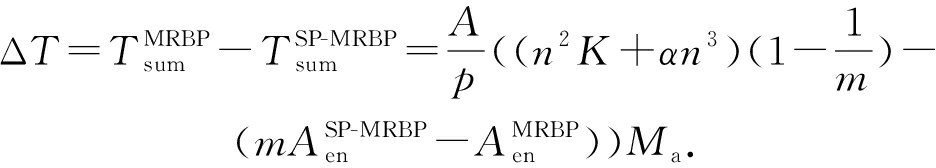
(33)
式(33)包含4项,前2项差值可以认为是结构并行带来的时间收益,后2项差值是并行计算带来的通信成本.由于组播模式下,一般 g ( w )≪ w ,在神经网络结构确定的情况下,该值趋向一个常数,为分析方便,假设 g ( w )= C ,则 ![]() 和
和 ![]() 可近似表示为
可近似表示为
![]()
(35)
则式(33)可进一步简化为
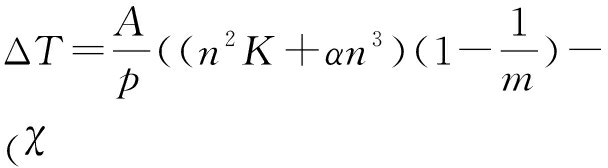 + ρ C )(6 m -1)) M a .
+ ρ C )(6 m -1)) M a .
(36)
当 m 逐步增大,1-1  m 趋近1,6 m -1趋近6 m ,则进一步简化为
m 趋近1,6 m -1趋近6 m ,则进一步简化为
![]()
(37)
根据式(37),不难推出,当
![]()
(38)
时,SP-MRBP算法计算时间会小于原MRBP算法时间.
从式(27)来看,当不断增加并行结构数 m ,计算时间会不断减少,而通信成本会不断增加.总计算时间呈现出先减少后增加的趋势,对式(27)求 m 的一阶偏导数,可得:
![]()
(39)
令式(39)等于零,求出最优并行结构数 m * :
![]()
(40)
本节给出SP-MRBP算法与经典MRBP算法 [22] 和PSO-MRBP算法 [30] 的性能比较实验.
实验集群包括16个计算节点,通过100  1 000 MB交换机连接,每个计算节点含4组4核处理器,包含32 GB内存和2 TB硬盘,整个Hadoop集群系统形成一个2×32
1 000 MB交换机连接,每个计算节点含4组4核处理器,包含32 GB内存和2 TB硬盘,整个Hadoop集群系统形成一个2×32  3=21.3 TB镜像文件系统.软件系统采用Ubuntu 14.10;JDK 1.7;Hadoop 2.2.每次实验测试1次训练时间,取50次平均值.每个计算节点最多启动4个Mapper任务和1个Reducer任务.
3=21.3 TB镜像文件系统.软件系统采用Ubuntu 14.10;JDK 1.7;Hadoop 2.2.每次实验测试1次训练时间,取50次平均值.每个计算节点最多启动4个Mapper任务和1个Reducer任务.
本实验用于测试并行结构数对算法性能的影响,实验数据包括100万条样本.计算节点数为16.整个系统包含Mapper任务总数为16×4=64个.神经网络设置为3层.各层神经节点数都设置相同.实验考虑小型网络、中型网络和大型网络3种规模,其单层节点数分别为50,100,200.并行结构数从1增加到16.
实验结果如图7所示,可以看出,随着并行结构数的增多,计算时间总体下降,证明了本文算法的有效性.但是,随着并行结构数的增加,计算时间反而会小幅增长,其原因有2个:首先,并行结构数的增加会造成通信成本的增大.其次,并行结构数增加会导致在单个数据节点上待运行的Mapper任务数超过最大并发数.
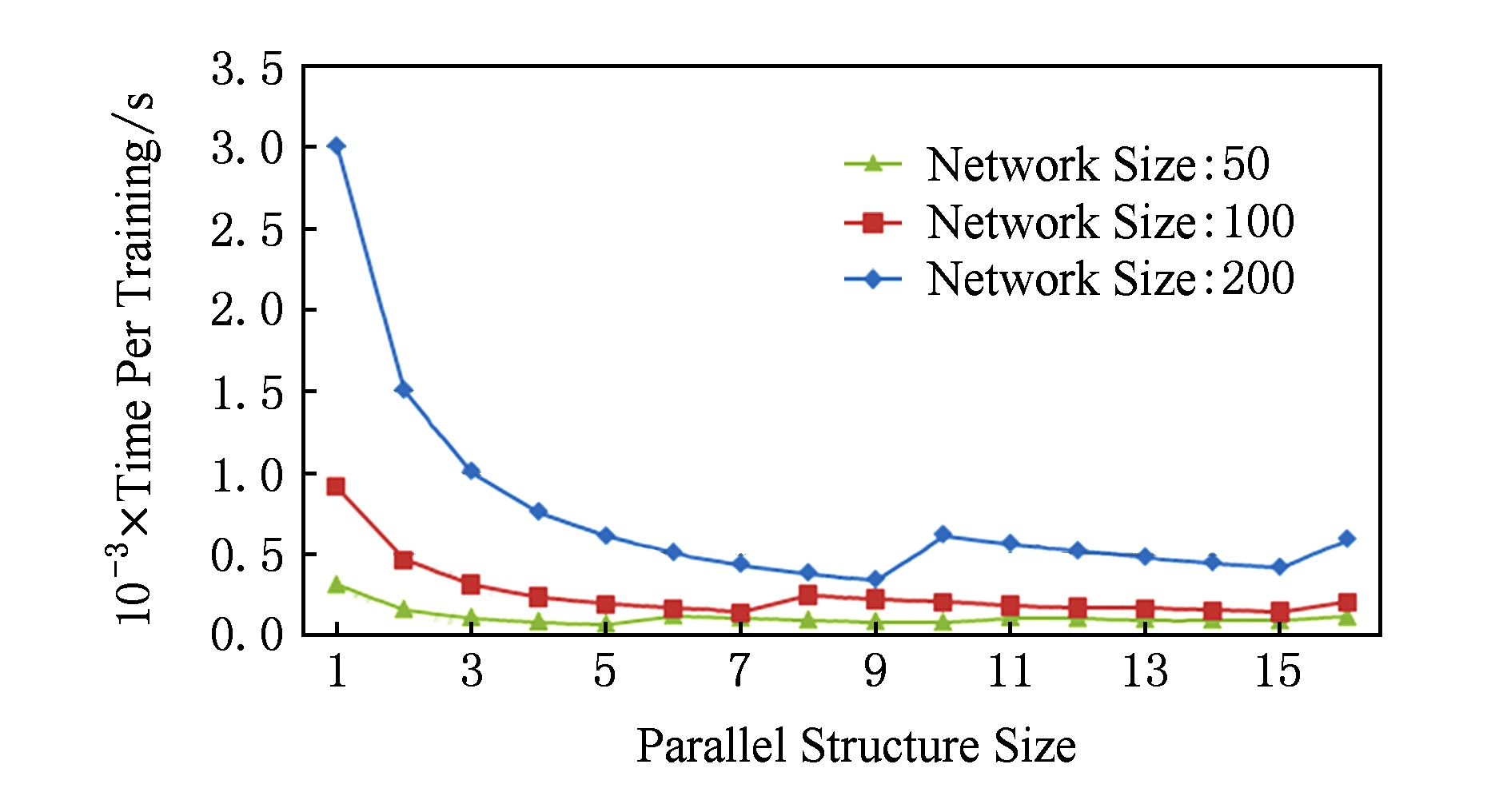
Fig. 7 Scalability of parallel structure size
图7 并行结构扩展性
同时,我们观察到,对于大规模网络来说,其系统瓶颈要大于小规模网络,说明本文算法对大规模网络更有效.
本实验用于测试计算节点数对计算时间的影响.此实验中,神经网络设置为3层,每层100个神经节点,样本总数控制在100万条,根据上个实验得到的结果,单层并行结构数设置为7.集群节点数从1增加到16,这样系统Mapper任务总数从4逐步增加到64.
实验结果如图8所示,可以看出,随着计算节点的增加,3个算法计算时间都随之减少,这是因为计算任务被平均分配到个节点,从而缩短了计算时间.同时又注意到,在计算节点较小时,3个算法计算时间差别不大,这是由于在计算节点较少的情况下,计算节点满负载工作,结构并行优势不能发挥.而随着计算节点的进一步增加,原算法得到了足够多的资源,计算时间就不再下降,而本文算法仍然保持下降趋势,表明本文算法具有更好的扩展性.
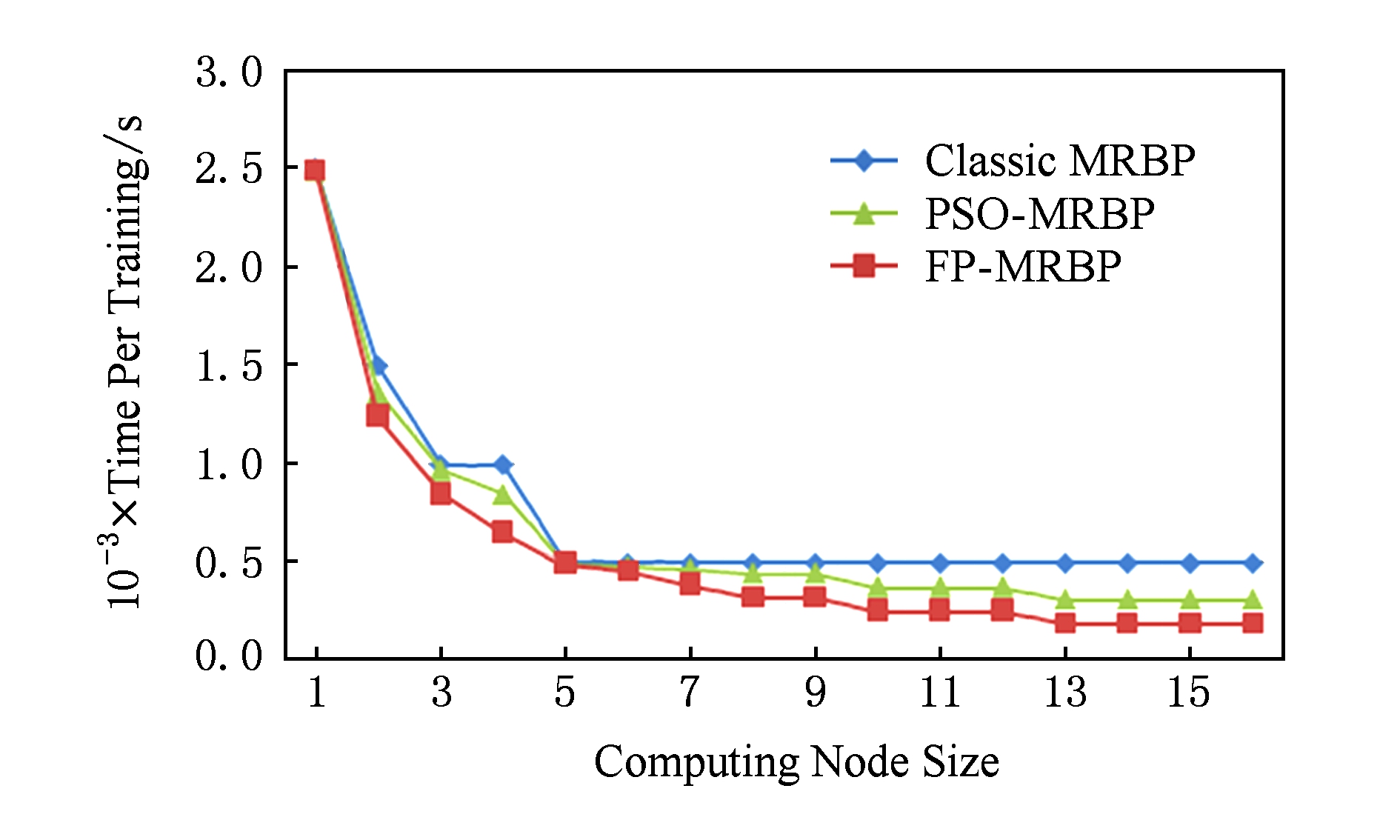
Fig. 8 Scalability of computing node size
图8 计算节点扩展性
本实验用于测试样本规模对算法性能的影响.实验中,神经网络设置为3层,每层100个神经节点,单层并行结构为7,使用16个计算节点,整个系统包含16×4=64个Mapper任务,样本数从10万增加到100万.
实验结果如图9所示,可以看出,3种算法计算时间都随着样本数的增加而增加.但是本文算法的增加幅度更小、更平稳.其原因在于,增加的计算量被平均分配到本文算法的各个并行结构中.
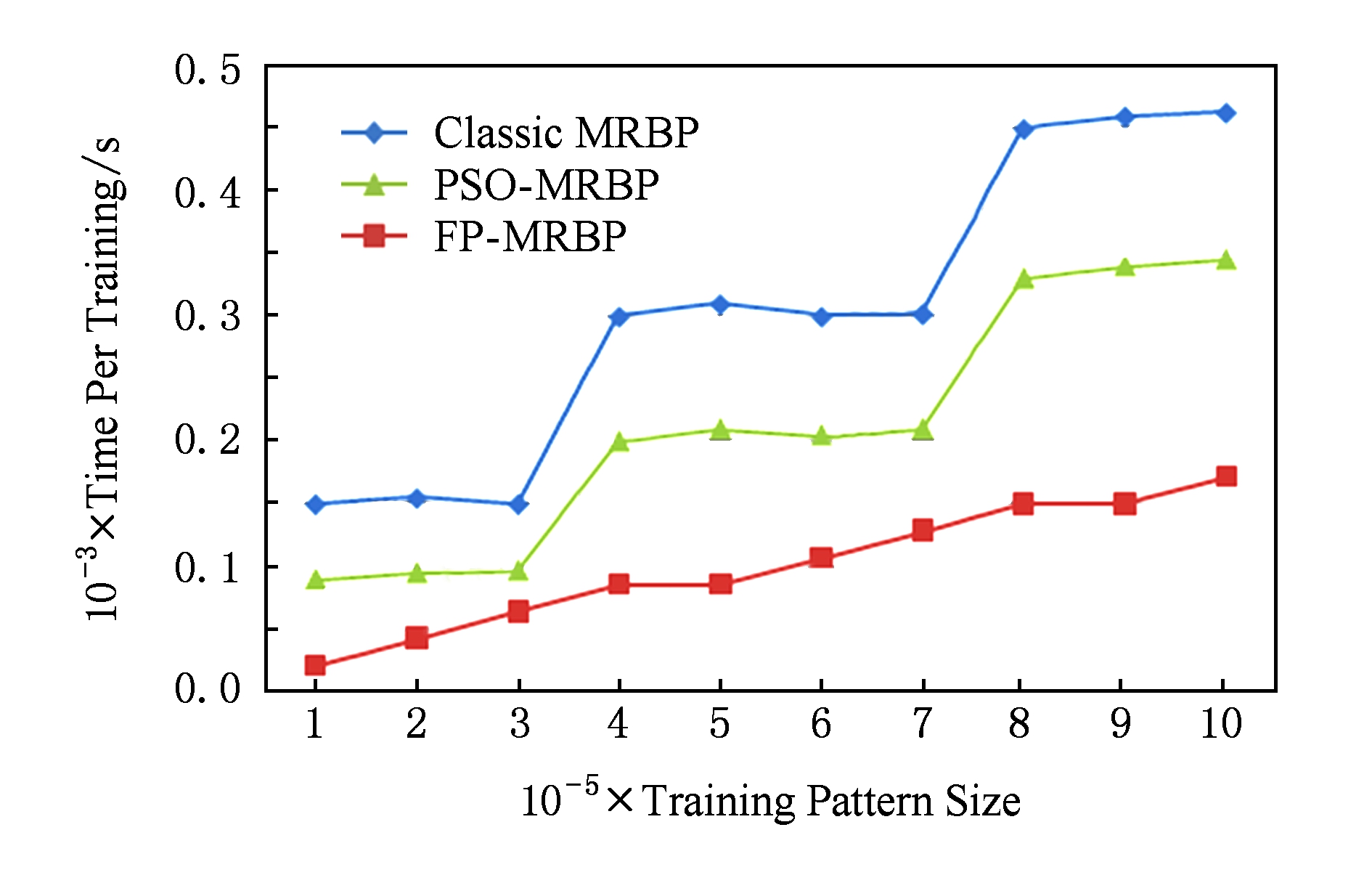
Fig. 9 Scalability of sample size
图9 样本规模扩展性
本实验用于测试网络规模对算法性能的影响,样本总数100万条,使用全部16个计算节点,整个系统共运行16×4=64个Mapper任务,SP-MRBP并行结构数设置为7,神经网络设置为3层,每层节点从50逐步增加到500.
实验结果图10所示,可以看出,随着网络规模增加,3种算法计算时间都大幅增加,但是本文算法的增加幅度远小于原算法,这是因为本文算法的并行结构可以平均分配增加的计算量.
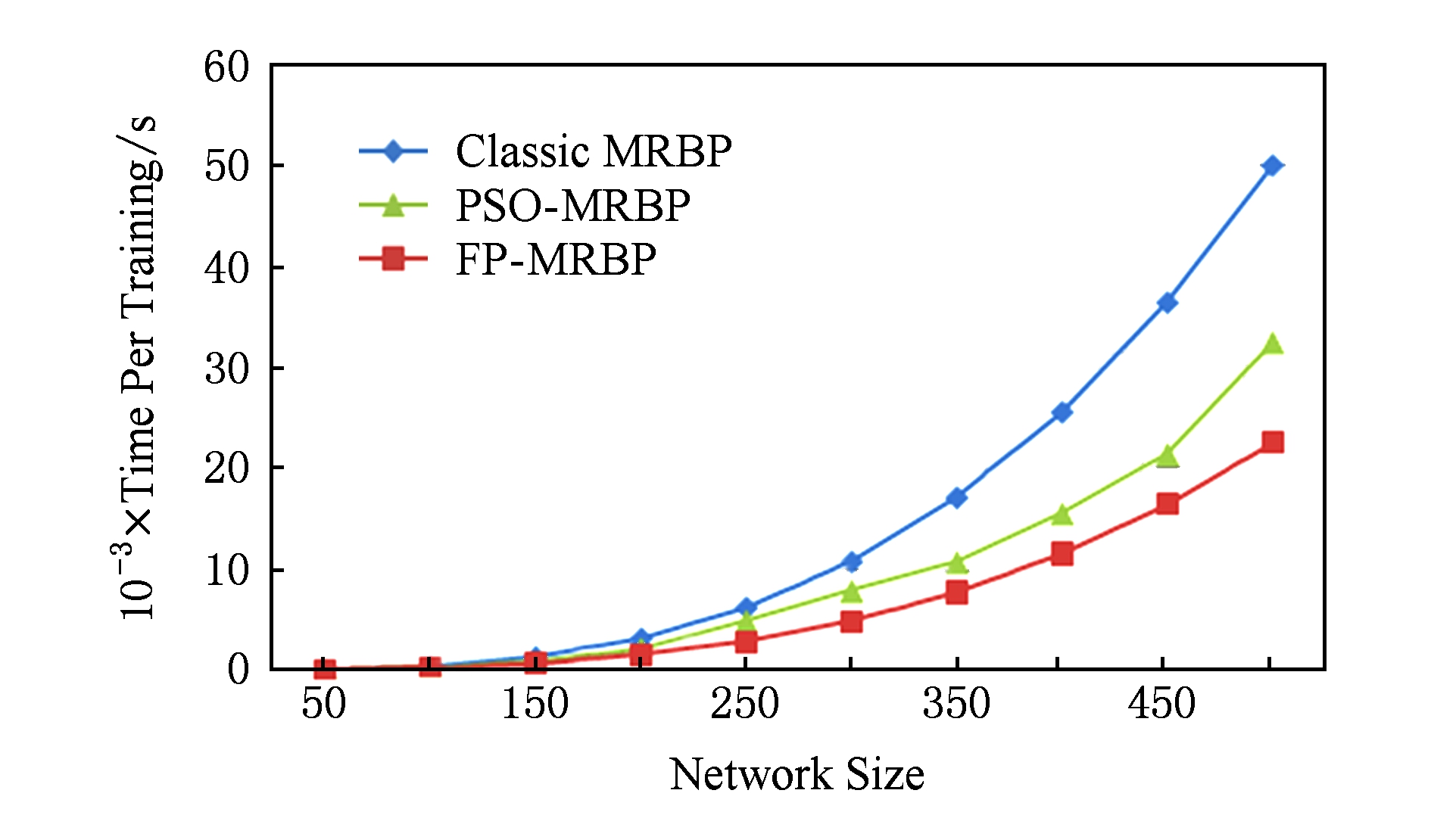
Fig. 10 Scalability of network size
图10 网络规模扩展性
为了解决经典MRBP算法处理较大规模神经网络时性能不足的问题,本文提出了一种支持结构并行的MRBP算法:SP-MRBP.该算法采用逐层并行-逐层集成(LPLE)的结构并行策略,来提高神经网络的学习效率.同时,推导出了SP-MRBP算法和MRBP算法执行时间解析表达式,并据此分析了2种算法的时间差和SP-MRBP算法的最优并行结构数.实验结果说明,对于规模较大的神经网络,较之经典MRBP算法,本文算法具有较高效率.
参考文献
[1]Zhang Lei, Zhang Yi. Big data analysis by infinite deep neural networks[J]. Journal of Computer Research and Development, 2015, 53(1): 68-79 (in Chinese)(张蕾, 章毅. 大数据分析的无限深度神经网络方法[J]. 计算机研究与发展, 2015, 53(1): 68-79)
[2]Jiao Licheng, Yang Shuyuan, Liu Fang, et al. Seventy years Beyond neural networks: Restrospect and prospect[J]. Chinese Journal of Computers, 2016, 39(8): 1697-1707 (in Chinese)(焦李成, 杨淑媛, 刘芳, 等. 神经网络七十年:回顾与展望[J]. 计算机学报, 2016, 39(8): 1697-1707)
[3]Urszula M K, Mateusz K. Spiking neural network vs multilayer perceptron: Who is the winner in the racing car computer game[J]. Soft Computing, 2014, 23(5): 44-56
[4]Xu Jin, Yang Gugang, Yin Yafei, et al. Sparse-representation-based classification with structure-preserving dimension reduction[J]. Cognitive Computation, 2014, 6(3): 608-621
[5]Murphey Y L, Luo Yun. Feature extraction for a multiple pattern classification neural network system[C] 
 Proc of the 16th Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 2002: 220-223
Proc of the 16th Int Conf on Pattern Recognition. Piscataway, NJ: IEEE, 2002: 220-223
[6]Ciresan D C, Meier U, Gambardella L M, et al. Deep, big, simple neural nets for bandwritten digit recognition[J]. Neural Computation, 2010, 22(12): 3207-3220
[7]Graves A, Liwicki M, Fernández S, et al. A novel connectionist system for unconstrained handwriting recognition[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2009, 31(5): 855-868
[8]Farabet C, Couprie C, Najman L, et al. Learning hierarchical features for scene labeling[J]. IEEE Trans on Pattern Analysis & Machine Intelligence, 2013, 35(8): 1915-1925
[9]Wang Lijun, Lu Huchuan, Xiang Ruan, et al. Deep networks for saliency detection via local estimation and global search[C] 
 Proc of IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 3183-3192
Proc of IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 3183-3192
[10]Li Guangbin, Yu Yizhou. Visual saliency based on multiscale deep features[C] 
 Proc of IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 5455-5463
Proc of IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 5455-5463
[11]Zhao Rui, Ouyang Wanli, Li Hongsheng, et al. Saliency detection by multi-context deep learning[C] 
 Proc of IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 1265-1274
Proc of IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 1265-1274
[12]Mohamed A R, Dahl G E, Hinton G. Acoustic modeling using deep belief networks[J]. IEEE Trans on Audio Speech & Language Processing, 2012, 20(1): 14-22
[13]Caceres N, Wideberg J P, Benitez F G. Deriving origin-destination data from a mobile phone network[J]. IET Intelligent Transport Systems, 2007, 1(1): 15-26
[14]Dahl G E, Yu Dong, Deng Li, et al. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition[J]. IEEE Trans on Audio Speech & Language Processing, 2012, 20(1): 30-42
[15]Tallada M G. Coarse grain parallelization of deep neural networks[C] 
 Proc of the 21st ACM SIGPLAN Symp on Principles and Practice of Parallel Programming. New York: ACM, 2016: 1-12
Proc of the 21st ACM SIGPLAN Symp on Principles and Practice of Parallel Programming. New York: ACM, 2016: 1-12
[16]Volodymyr T, Anatoly S. Efficiency of parallel large-scale two-layered MLP training on many-core system[C] 
 Proc of the 8th Int Conf on Neural Networks and Artificial Intelligence. Berlin: Springer, 2014: 201-210
Proc of the 8th Int Conf on Neural Networks and Artificial Intelligence. Berlin: Springer, 2014: 201-210
[17]Turchenko V, Grandinetti L, Efficiency analysis of parallel batch pattern NN training algorithm on general-purpose supercomputer [G] 
 LNCS 5518: Proc of Int Conf on Artificial Neural Networks. Berlin: Springer, 2009: 223-226
LNCS 5518: Proc of Int Conf on Artificial Neural Networks. Berlin: Springer, 2009: 223-226
[18]Pethick M, Liddle M, Werstein P, et al. Parallelization of a backpropagation neural network on a cluster computer[J]. Parallel and Distributed Computing Systems, 2003, 23(1): 44-56
[19]Suresh S, Omkar S N, Mani V. Parallel implementation of back-propagation algorithm in networks of workstations[J]. IEEE Trans on Parallel & Distributed Systems, 2005, 16(1): 24-34
[20]White T. Hadoop: The Definitive Guide[M]. Sebastopol, CA: O’Reilly Media Inc, 2012
[21]Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters[J]. ACM Communication, 2008, 51(1): 107-113
[22]Chu Chengtao, Kim S K. Map-Reduce for machine learning on multicore[J]. Advances in Neural Information Processing Systems, 2006, 19(3): 281-288
[23]Liu Zhiqiang, Li Hongyan, Miao Gaoshan. MapReduce-based backpropagation neural network over large scale mobile data[C] 
 Proc of the 6th Int Conf on Natural Computation. Piscataway,NJ: IEEE, 2010: 1726-1730
Proc of the 6th Int Conf on Natural Computation. Piscataway,NJ: IEEE, 2010: 1726-1730
[24]Cao Ying, Miao Qiguang, Liu Jiachen, et al. Advance and prospects of AdaBoost algorithm[J]. Acta Electronica Sinica, 2013, 39(6): 745-758 (in Chinese)(曹莹, 苗启广, 刘家辰, 等. AdaBoost 算法研究进展与展望[J]. 自动化学报, 2013, 39(6): 745-758)
[25]Zhang Haijun. Research on parallel implementation of neural networks based on cloud computing and their learning methods [D]. Guangzhou: South China University of Technology, 2015 (in Chinese)(张海军. 基于云计算的神经网络并行实现及其学习方法研究[D]. 广州:华南理工大学, 2015)
[26]Zhang Haijun, Xiao Nanfeng. Parallel implementation of multilayered neural networks based on Map-Reduce on cloud computing clusters[J]. Soft Computing, 2016, 20(4): 1471-1483
[27]Zhu Chenjie, Yang Yongli. Research of MapReduce based on BP neural network algorithm[J]. Microcomputer Applications, 2012, 10(3): 44-56 (in Chinese)(朱晨杰, 杨永丽. 基于MapReduce 的BP 神经网络算法研究[J]. 微型计算机应用, 2012, 10(3): 44-56)
[28]Zhu Chenje, Rao Ruonan. The improved BP algorithm based on MapReduce and genetic algorithm[C] 
 Proc of Int Conf on Computer Science and Service System. Piscataway, NJ: IEEE, 2012: 1567-1570
Proc of Int Conf on Computer Science and Service System. Piscataway, NJ: IEEE, 2012: 1567-1570
[29]Wang Qing, Ma Guangfu, Mi Man. Research on neural network control based on genetic algorithm[J]. Journal of System Simulation, 2006, 18(4): 1070-1072 (in Chinese)(王清, 马广富, 弥曼. 一种基于遗传算法的神经网络控制方法研究[J]. 系统仿真学报, 2006, 18(4): 1070-1072)
[30]Cao Jianfang, Cui Hongyan, Shi Hao, et al. Big data: A parallel particle swarm optimization-back-propagation neural network algorithm Based on MapReduce[J]. Plos One, 2016, 11(6): 1134-1143
[31]Li Zuoyong, Wang Jiayang, Guo Chen. A new method of BP network optimized based on particle swarm optimization and simulation test[J]. Acta Electronica Sinica, 2008, 36(11): 2224-2228 (in Chinese)(李祚泳, 汪嘉杨, 郭淳. PSO算法优化BP网络的新方法及仿真实验[J]. 电子学报, 2008, 36(11): 2224-2228)
[32]Wah B W, Chu Lonchuan. Efficient mapping of neural networks on multicomputers[C] 
 Proc of Int Conf on Parallel Processing. Piscataway, NJ: IEEE, 1990: 234-241
Proc of Int Conf on Parallel Processing. Piscataway, NJ: IEEE, 1990: 234-241
[33]Sudhakar V, Murthy C S. Efficient mapping of back-propagation algorithm onto a network of workstations[J]. IEEE Trans on Systems Man & Cybernetics, 1998, 28(6): 841-848
[34]Haykins S, Neural Networks: A Comprehensive Foundation[M]. New York: Prentice Hall, 1999
[35]Ghemawat S, Gobioff H, Leung S T. The google file system[C] 
 Proc of the 9th ACM Symp on Operating Systems Principles. New York: ACM, 2003: 29-43
Proc of the 9th ACM Symp on Operating Systems Principles. New York: ACM, 2003: 29-43

Ren Gang , born in 1978. PhD and associate professor. His main research interests include intelligent algorithm, parallel algorithm and formal methods.

Deng Pan , born in 1983. PhD and associate professorr. Her main research interests include smart city, big data, cloud computing, parallel computing, and the Internet of things.

Yang Chao , born in 1979. Professor and PhD supervisor. His main research interests include numerical analysis and modeling, large-scale scientific computing, and parallel numerical software.

Wu Changmao , born in 1974. PhD, research assistant. Member of CCF. Currently, his main research interests include parallel software and parallel algorithm.
Ren Gang 1,2,3 , Deng Pan 2 , Yang Chao 2 , and Wu Changmao 2
1 ( Department of Computer Science and Technology , Henan Institute of Technology , Xinxiang , Henan 453003) 2 ( Laboratory of Parallel Software and Computational Science , Institute of Software , Chinese Academy of Sciences , Beijing 100190) 3 ( University of Chinese Academy of Sciences , Beijing 100049)
Abstract Back propagation (BP) algorithm is a widely used learning algorithm that is used for training multiple layer neural networks. BP algorithm based on Hadoop cluster and MapReduce parallel programming model (MRBP) shows good performance on processing big data problems. However, it lacks the capability of fine-grained parallelism. Thus, when confronted with high dimension data and neural networks with large nodes, the performance is low relatively. On the other hand, since the users can’t control the communication of Hadoop computing nodes, the existing structure parallel scheme based on clusters can’t be directly applied to MRBP algorithm. This paper proposes a structure parallelism based MRBP algorithm (SP-MRBP), which adopts layer-wise parallelism, layer-wise ensemble (LPLE) strategy to implement structure parallel computing. Also, we derive the analytical expressions of the proposed SP-MRBP algorithm and the classic MRBP algorithm, and obtain the time differences between the both algorithms as well as the optimal number of parallel structures of SP-MRBP algorithm. To the best knowledge of the authors, it is the first time to introduce the structure parallelism scheme to the MRBP algorithm. The experimental results show that, compared with the classic MRBP algorithm, our algorithm has better performance on processing efficiency when facing large neural networks.
Key words MapReduce model; structure parallelism; back propagation (BP) algorithm; multiple layer neural networks; MapReduce back propagation (MRBP) algorithm
摘 要 BP(back propagation)算法是一种常用的神经网络学习算法,而基于Hadoop集群MapReduce编程模型的BP(MapReduce back propagation, MRBP)算法在处理大数据问题时,表现出良好的性能,因而得到了广泛应用.但是,由于该算法缺乏神经节点之间细粒度结构并行的能力,当遇到数据维度较高、网络节点较多时,性能还显不足.另一方面,Hadoop集群计算节点通信不能由用户直接控制,现有基于集群系统的结构并行策略不能直接用于MRBP算法.为此,提出一种适合于Hadoop集群的结构并行MRBP (structure parallelism based MapReduce back propagation, SP-MRBP)算法,该算法将神经网络各层划分为多个结构,通过逐层并行-逐层集成(layer-wise parallelism,layer-wise ensemble, LPLE)的方式,实现了MRBP算法的结构并行.同时,推导出了SP-MRBP算法和MRBP算法计算时间解析表达式,以此分析了2种算法时间差和SP-MRBP算法最优并行规模.据了解,这是首次将结构并行策略引入MRBP算法中.实验表明,当神经网络规模较大时,SP-MRBP较之原算法,具有较好的性能.
关键词 MapReduce模型;结构并行;BP算法;多层神经网络;MRBP算法
中图法分类号 TP183
收稿日期 : 2017-01-17;
修回日期: 2017-09-04
基金项目 : 国家自然科学基金项目(61100066)
This work was supported by the National Natural Science Foundation of China (61100066).