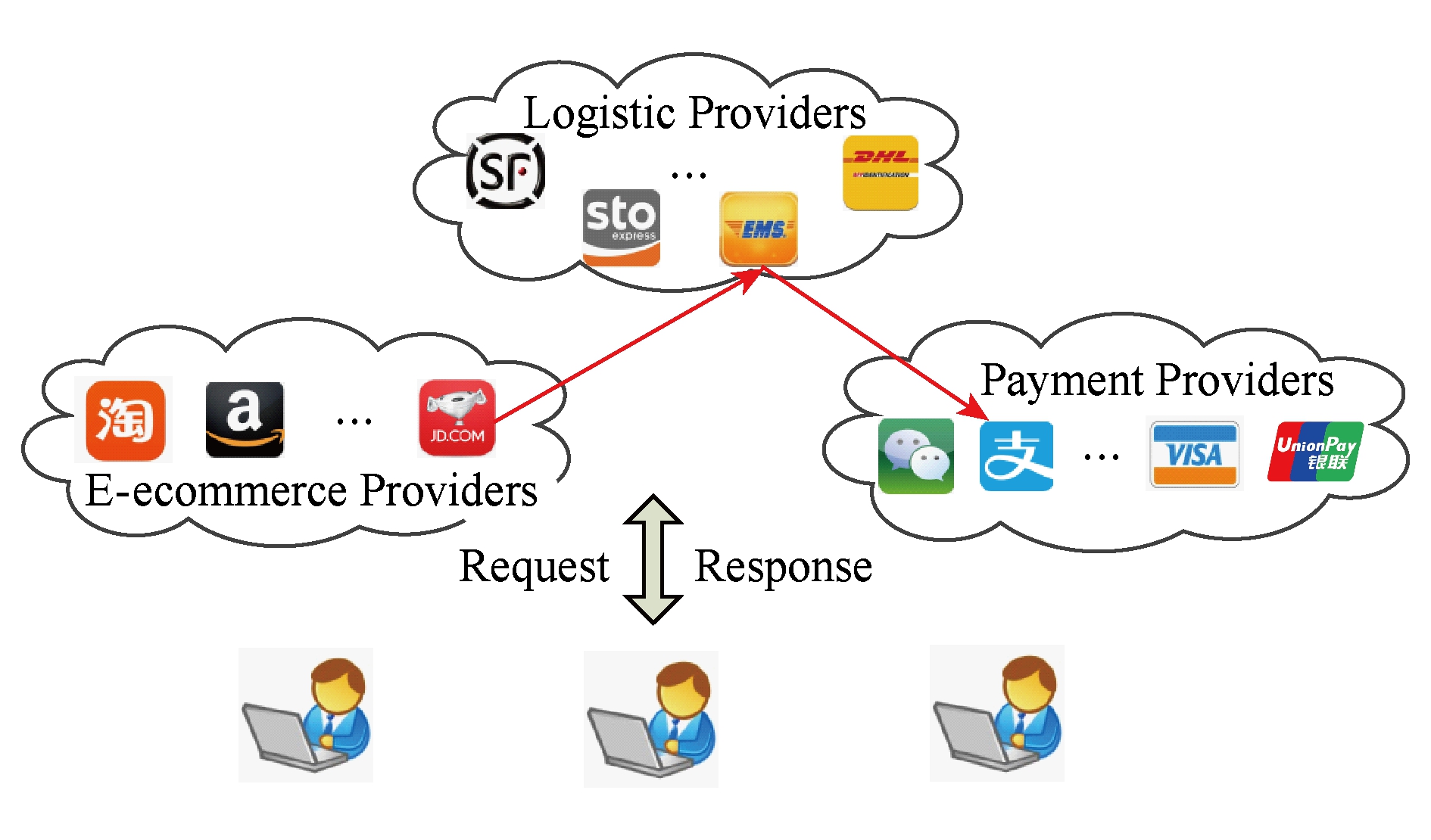
Fig. 1 Case of online shopping
图1 网上购物案例
张以文 1,2 崔光明 2 严远亭 2 赵 姝 1,2 张燕平 1,2
1 (计算智能与信号处理教育部重点实验室(安徽大学) 合肥 230031) 2 (安徽大学计算机科学与技术学院 合肥 230601) (zhangyiwen@ahu.edu.cn)
服务计算作为一种新的计算范式,凭借其以服务为基本构建块,支持异构环境下分布式应用的快速、低成本、便捷组合的特点得到快速发展,其核心思想是通过重用已有的网络服务而不是重新开发构造新的企业应用,使得分布在企业内部或跨越企业边界的不同商业应用系统能得到快捷的实现、灵活的无缝集成和相互协作 [1] .但随着越来越多的网络资源以服务的形式发布与使用,具有相同功能的服务数量迅速增加,加之用户需求的多样化、动态化和复杂化等特点,导致服务组合方案呈现出指数增长趋势,服务组合问题也逐渐演变为NP完全问题.
随着服务质量(quality of service, QoS)的提出,不同服务之间的衡量更加科学化与规范化,越来越多的有关QoS感知的服务组合方法被应用到服务组合问题求解过程中 [2] .传统的服务计算多认为不同服务的QoS具有相互独立性,且服务之间不存在相互影响.但在实际应用背景下,服务之间往往存在质量约束,例如在图1所示的网上购物案例中,购物时往往会涉及到商家与部分物流方的协同合作关系,即商家包邮,导致在服务组合优化过程中,同一候选服务在不同的服务组合实例中具有不同的QoS值.

Fig. 1 Case of online shopping
图1 网上购物案例
除此之外,在图1所示的购物案例中,不同的任务由不同的主体去操作,例如物流服务由不同的物流方进行操作,但物流方如何内部操作,包括取货、运输等用户无需关心,但整体的配送速度会影响用户的购物体验.因此,图1所示的购物案例中,不同的任务之间既存在相互协同合作关系,即服务间的QoS约束问题也存在相互独立性,即各提供商的内部操作互不影响.现有的服务组合研究较少同时关注这2种现象,尤其在big service [3-4] 环境下,这一现象更加普遍.为解决这一问题,本文提出一种任务粒化的质量约束模型,通过将图1所示的任务按照质量约束进行粒化处理,分解为多个任务粒,然后通过每个任务粒的局部最优选择逐步逼近全局最优,同时,通过子模态理论,论证了任务粒化模型求解过程的完备性.本文的主要贡献如下:
1) 提出基于商空间任务粒化的质量约束感知服务组合优化方法,构建了基于任务粒化的分层递阶服务组合模型,可有效解决大规模服务组合优化问题.
2) 总结了现有的QoS属性聚合方式,从理论上验证每种聚合方法都具有子模态性质,以及多属性服务组合问题的效用函数仍具有子模态性质.
3) 提出一种任务粒化的质量约束感知的服务组合算法Tg-QcA,并通过大量的仿真实验验证了算法的可行性、高效性和稳定性.
为更直观地描述质量约束感知的服务组合优化问题,基于商空间理论 [5-6] ,结合服务组合优化问题的常用模型 [7-8] ,首先给出分层递阶服务组合模型如图2所示.
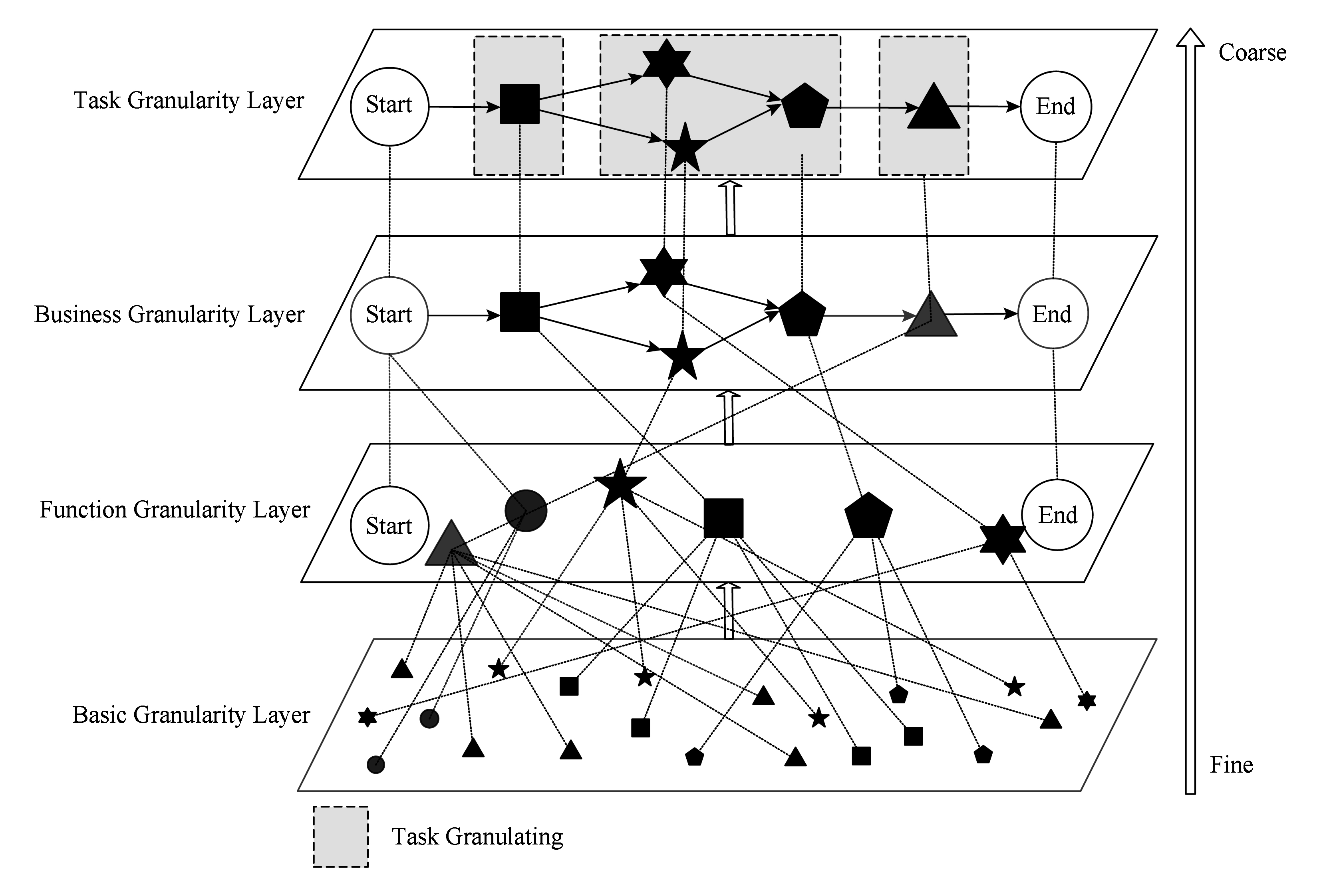
Fig. 2 Hierarchical model of service composition
图2 分层递阶服务组合模型
由图2可知,质量约束的服务组合问题可以分为4层,分别为基本粒层(候选服务层)、功能粒层(任务层)、业务粒层(用户需求)以及任务粒层(质量约束).其中,前3层均为服务组合问题的描述层,主要用于服务组合优化问题的模型描述,任务粒层则为质量约束感知的服务组合优化问题的求解层,用以形式化表示质量感知的任务粒化方法及求解方法.
服务组合问题粒化描述是指为形象直观地描述服务组合问题而构建的分层递阶链模型,对应于图2中基本粒层、功能粒层以及业务粒层,其详细定义如下:
定义1 . 基本粒.是服务组合问题的最小粒,表示每个原子服务,可以描述为一个五元组: s =( id , I , desc , O , Q ).其中:
1) id 表示每个服务的唯一标识;
2) I 表示输入参数,其定义为 I ={ I s 1 , I s 2 ,…, I s n };
3) desc 表示功能描述;
4) O 表述输出参数,定义为 O ={ O s 1 , O s 2 ,…, O s n };
5) Q 表示每个服务的服务质量QoS,定义 Q ={ cost ( Cost ), availability ( Ava ),…}.
基本粒表示每个任务的候选服务,在图1所示的网上购物案例中,每个候选服务均为基本粒.基本粒作为服务组合问题的基本元素,即服务提供者提供的服务都属于基本粒.基本粒的数量不断增加,其组织、存储、最优化选择日益困难.所以,为简化求解用户需求所包含功能问题的搜索空间,将基本粒按照其功能聚合成功能粒,其定义如下.
定义2 . 功能粒.指具有相同功能属性的基本粒聚类后的粒度表示,对应于服务组合问题的某个特定任务,功能粒包含基本粒.可采用四元组 T =( I , desc , S , O ) 进行描述.其中:
1) I 表示输入参数,其定义为 I ={ I s 1 , I s 2 ,…, I s n };
2) desc 表示功能粒描述;
3) S 表示基本粒的集合;
4) O 表述输出参数,定义为 O ={ O s 1 , O s 2 ,…, O s n }.
功能粒包含基本粒,其功能属性、接口一致,且在服务质量上有所差别.在图1所示的案例中,将服务组合论域按照功能聚合之后,产生的功能粒个数为3,分别对应每个任务.
在基本粒层中,每个候选服务都是一个基本元素,获得满足用户业务需求的组合服务较难,通过将粒度适度粗化,可以减少问题求解的时间和空间开销.功能粒层是建立在任务之上,所以,在获得用户任务需求时,只需将功能粒商空间中部分任务按照某些逻辑结构有限次组合从而完成特定业务需求,即业务粒.
定义3 . 业务粒.表示在某特定业务流程基础上,满足用户需求功能粒的聚类集合,可以使用三元组 B =( desc , T , U )表示.其中:
1) desc 表示业务粒描述;
2) T 表示实现某特定业务流程的功能粒集合;
3) U 表示该业务粒的评价函数.
业务粒是解决服务组合问题的桥梁,以及与其应用领域知识的交互接口,在求解服务组合优化问题中是不可或缺的阶段.服务组合是建立在业务需求之上,对于不同用户需求获得不同的业务流最优解是服务组合的目标.
在服务组合问题的逐层建模过程中,从基本粒到业务粒是问题的逐渐粗化过程,通过筛选用户需求任务减少问题搜索空间.例如,对于图1所示的服务组合案例,其对应的分层递阶商空间链模型论域描述如下.基本粒商空间论域可表示为{Taobao,…,JD,SF,…,DHL,WeChat,…,UnionPay},元素个数为候选服务数.将候选服务按照所属功能进行聚合,可得功能粒商空间的论域为{ t 1 , t 2 , t 3 },其中 t 1 ={Taobao,…,JD}, t 2 ={SF,…,DHL}, t 3 ={WeChat,…,UnionPay}.将功能粒按照用户业务需求进行2次筛选,可得业务粒商空间.服务组合的分层递阶模型每一层都有实际意义,都可解决本层次的问题.基本粒层是原服务组合问题,可以获得较多、较细的关于候选服务的信息,例如,基本粒层可以获得每个候选服务按照输入输出构成的拓扑关系,而功能粒层则只有任务级别的拓扑关系;功能粒层相比于基本粒层更易于获得用户任务需求;业务粒层可以获得用户需求的最优候选服务序列.
在图2所示的模型中,利用分层递阶模型逐步获得业务粒层服务组合问题模型,可以大幅度降低服务组合求解的问题搜索域.但在具体的实际应用中,基本粒服务之间往往存在质量约束关系,例如,购物与物流服务之间会存在包邮现象.为解决这一问题,本部分在图2中业务粒层的基础上构建任务粒层,其中任务粒的划分是由基本粒服务之间的质量约束决定.基于此,先给出质量约束定义如下:
定义4 . 质量约束.指基本粒服务之间具有的QoS约束关系,可以用三元组 qc =( id , S , p )表示.其中:
1) id 表示每个质量约束的唯一标识;
2) S 表示具有该质量约束的基本粒服务集合;
3) p 表示该质量约束的QoS约束值.
质量约束是用于描述服务与服务之间的QoS约束关系,例如图1所示的服务组合案例,可以抽象为如下服务模型: SC ={ t 1 ={ s 1,1 , s 1,2 , s 1,3 , s 1,4 }, t 2 ={ s 2,1 , s 2,2 , s 2,3 }, t 3 ={ s 3,1 , s 3,2 , s 3,3 }}.质量约束可以抽象为表1(以价格为例)所示:
Table 1 Quality Constraint
表1 质量约束

表1所示的质量约束是指基本粒服务 s 1,1 与 s 2,1 之间存在质量约束关系,QoS约束值为服务价格减少$14.
定义5 . 隶属度.指任务与任务之间的耦合度,通过候选服务之间的质量约束数量决定,表示为: M = h ( t i , t j ).其中, h ( t i , t j )表示任务 t i 和 t j 之间具有质量约束的数量.通过隶属度,可以判断每2个任务间的耦合程度,隶属度值越大表明该任务之间耦合关系越强,不利于划分至不同的任务粒.
定义6 . 任务粒.指业务粒根据隶属度函数值将原组合服务问题分解为多个简单子服务组合问题,可以用三元组 Tg =( id , sc ′, F )表示.其中:
1) id 表示每个粒度划分的唯一标识;
2) sc ′表示原问题业务粒 sc 的子集,即 sc 中功能粒的子集;
3) F 表示每个粒度划分的评估函数.
任务粒是对服务组合问题按照粒化需求进行问题分解的形式化表示.例如,图1所示的网上购物案例,原问题粒表示为{( t 1 , t 2 , t 3 )},按照任务执行主体,可以将3个任务分为3类,分别为电商平台方、支付方以及物流方,即任务粒表示为{( t 1 ),( t 2 ),( t 3 )}.在服务组合问题求解过程中,首先获得每个子问题的最优解,然后将这些局部最优解进行组合成原问题可行解.若假设每个任务的候选服务数为 n ,则原问题求解规模为 n 3 ,而基于任务粒的求解规模则为 n + n + n .尤其在big service环境下, n 3 ≻( n + n + n ),原问题的求解复杂度从指数级降为任务线性级,问题的求解规模大幅度降低.
在数学上,子模态是集合函数的一种性质,其定义如下:
给定集合 U ={ u 1 , u 2 ,…, u i ,…, u n },其包含 n 个元素,给定任意函数 g :2 U → ![]() ,即 g ( x )的定义域是集合 U 的任意子集.若集合 U 满足以下3个等价条件之一,则该集合具有子模态性质 [9] .
,即 g ( x )的定义域是集合 U 的任意子集.若集合 U 满足以下3个等价条件之一,则该集合具有子模态性质 [9] .
1) 对于任意一个 X , Y ⊂ U ,且 X ⊂ Y ,以及对任意 x ∈ U ,满足
g ( X ∪{ x })- g ( X )≥ g ( Y ∪{ x })- g ( Y );
(1)
2) 对于任意一个 X , Y ⊂ U ,且满足
g ( X )+ g ( Y )≥ g ( X ∪ Y )+ g ( X ∩ Y );
(2)
3) 对于任意一个 X ⊂ U 及 x 1 , x 2 ∈ U\X ,且满足
g ( X ∪{ x 1 })+ g ( X ∪{ x 1 })≥
g ( X ∪{ x 1 , x 2 })+ g ( X ).
(3)
集合 U 具有子模态性质时,就是当添加一个新的元素进入集合 U 时,函数值 g 的增益随着集合规模的增大而减小,即函数 g 满足边际效用递减.从优化问题角度看,服务组合问题属于多目标优化问题且为NP完全问题,若判断效用函数满足子模态性质,则基于简单的寻优策略,如贪心算法,就可以在多项式时间内获得高精度的解.基于此,接下来从服务组合效用函数的计算方式入手,其子模态性质分析如下.
QoS感知的服务组合问题,不同的QoS属性拥有不同的组合计算方式,但常用的可以归纳为表2所示的5类情况 [10-13] :
Table 2 Calculation Method of QoS Combination
表2 QoS组合计算方式

在表2所示的QoS组合计算方式中,同一属性在不同的组合逻辑模型中存在不同的计算方式.例如,响应时间(response time)在顺序模型中,一般计算各个任务响应时间之和,但在并行模型中通常取各任务响应时间的最大值.
根据表2所列的5种QoS聚合方式,假设服务组合问题的基本粒集合为 U ,对于任意一个 U 的子集 X ,即 X ⊂ U ,且 x 1 , x 2 ∈ U\X ,可得每种QoS聚合方式的子模态性质分析如下.
情况1 . 和. Sum ( X ∪{ x 1 })+ Sum ( X ∪{ x 2 })≥ Sum ( X ∪{ x 1 , x 2 })+ Sum ( X ),其中 Sum ( X )表示集合 X 中各元素的和.
由于 x 1 , x 2 ∈ U\X ,即 x 1 , x 2 ∉ X ,可得 Sum ( X ∪{ x 1 })= Sum ( X )+ Sum ({ x 1 }),所以, Sum ( X ∪{ x 1 })+ Sum ( X ∪{ x 2 })=2 Sum ( X )+ Sum ({ x 1 })+ Sum ({ x 2 }), Sum ( X ∪{ x 1 , x 2 })+ Sum ( X )≤2 Sum ( X )+ Sum ({ x 1 })+ Sum ({ x 2 })(当 x 1 ≠ x 2 时取等号).因此,和式成立.
情况2 . 积. Pro ( X ∪{ x 1 })+ Pro ( X ∪{ x 2 })≥ Pro ( X ∪{ x 1 , x 2 })+ Pro ( X ),其中 Pro ( X )表示集合 U 中各元素的积.
在候选服务的QoS中, QoS信息均可进行标准化处理,使其恒大于等于1,则 Pro 类型可以转换为 Sum 类型,情况1已证,即也成立.
情况3 . 均值. Avg ( X ∪{ x 1 })= Sum ( X ∪{ x 1 })  (| X |+1),其中,| X |表示集合 X 中元素的个数, Sum ( X ∪{ x 1 })表示集合{ X ∪{ x 1 }}中各元素的和, Avg ( X ∪{ x 1 })表示集合{ X ∪{ x 1 }}中各元素的均值,对于同一服务组合优化问题而言,任务数唯一,则 Avg 转换为 Sum 问题,情况1已证.
(| X |+1),其中,| X |表示集合 X 中元素的个数, Sum ( X ∪{ x 1 })表示集合{ X ∪{ x 1 }}中各元素的和, Avg ( X ∪{ x 1 })表示集合{ X ∪{ x 1 }}中各元素的均值,对于同一服务组合优化问题而言,任务数唯一,则 Avg 转换为 Sum 问题,情况1已证.
情况4 . 最大值.max( X ∪{ x 1 })+max( X ∪{ x 2 })≥max( X ∪{ x 1 , x 2 })+max( X ),其中max( X )表示集合 X 中各元素最大值,则令 y 1 =max( X ∪{ x 1 })+max( X ∪{ x 2 }), y 2 =max( X ∪{ x 1 , x 2 })+max( X ), y 1 与 y 2 间详细比较如下:
1) 当max( X )≥max({ x 1 }∪{ x 2 }),则max( X ∪{ x 1 })=max( X ∪{ x 2 })=max( X ∪{ x 1 , x 2 })=max( X ),即 y 1 =2max( X )= y 2 .
2) 当max({ x 1 })>max( X )>max({ x 2 }),则max( X ∪{ x 1 })=max( X ),max( X ∪{ x 2 })=max( X ∪{ x 1 , x 2 }),即 y 1 =max( X ∪{ x 1 })+max( X ∪{ x 2 })=max( X ∪{ x 1 , x 2 })+max( X )= y 2 .
3) 当max({ x 1 })>max({ x 2 })>max( X ),则max( X ∪{ x 1 })=max( X ∪{ x 1 , x 2 }),max( X ∪{ x 2 })>max( X ),即 y 1 > y 2 .
4) 当max({ x 2 })>max({ x 1 })>max( X ),则与3)类似,可得 y 1 > y 2 .
5) 当max( X )=max({ x 1 })=max({ x 2 }),则 y 1 = y 2 .
综上分析可知, y 1 ≥ y 2 .
情况5 . 最小值.min( X ∪{ x 1 })+min( X ∪{ x 2 })≥min( X ∪{ x 1 , x 2 })+min( X ),其中min( X )表示集合 X 中各元素最小值,由于min与max类型可相互转换,则根据情况4易知,显然成立.
通过上述分析可知,表2所列的组合服务QoS聚合方式均可进行粒化计算,对应于服务组合问题,即原问题可以分解为多个子问题,表明在任务粒化处理过程中QoS聚合方式均满足子模态性质.
在服务组合优化问题中,每个基本粒服务对应的QoS属性往往存在多个,即组合服务的效用函数是若干个聚合计算的线性加权,记为多目标效用函数.例如,QoS包含Cost和Availability,其中Cost采用 Sum 聚合方式,Availability采用 Pro 的聚合方式,在效用函数的计算时,则是2种方式的线性加权.为验证多目标效用函数仍满足子模态性质,引入如下引理1.
引理1 . 设 g 1 ({ x }), g 2 ({ x }),…, g k ({ x })都具有子模态性质, c 1 , c 2 ,…, c k 是非负实数,则函数
(4)
仍具有子模态性质.
证明. 因为 g 1 ({ x }), g 2 ({ x }),…, g k ({ x })均具有子模态性质,对于任意一个 U 的子集 X ,即 X ⊂ U ,且 x 1 , x 2 ∈ U\X ,可得:
g 1 ( X ∪{ x 1 })+ g 1 ( X ∪{ x 2 })≥
g 1 ( X ∪{ x 1 , x 2 })+ g 1 ( X ),
g 2 ( X ∪{ x 1 })+ g 2 ( X ∪{ x 2 })≥
g 2 ( X ∪{ x 1 , x 2 })+ g 2 ( X ),
⋮
g k ( X ∪{ x 1 })+ g k ( X ∪{ x 2 })≥
g k ( X ∪{ x 1 , x 2 })+ g k ( X ).
由上式左右分别加权相加可得:
c 1 ( g 1 ( X ∪{ x 1 })+ g 1 ( X ∪{ x 2 }))+ c 2 ( g 2 ( X ∪{ x 1 })+ g 2 ( X ∪{ x 2 }))+…+ c k ( g k ( X ∪{ x 1 })+ g k ( X ∪{ x 2 }))≥ c 1 ( g 1 ( X ∪{ x 1 , x 2 })+ g 1 ( X ))+ c 2 ( g 2 ( X ∪{ x 1 , x 2 })+ g 2 ( X ))+…+ c k ( g k ( X ∪{ x 1 , x 2 })+ g k ( X )),即函数 ![]() 满足子模态性质.
满足子模态性质.
证毕.
通过上述分析可知,在服务组合优化问题中,常用的QoS聚合方式均满足子模态性质,多目标效用函数计算仍满足子模态性质.所以可得,任务粒化的质量约束感知服务组合问题,可以采用贪心算法,并且可以在多项式时间内获得高精度的解.
本节主要介绍基于任务粒化的质量约束感知服务组合优化算法,记为Tg-QcA.首先,通过隶属度进行任务粒的划分;其次,基于满足子模态QoS计算方式,并根据每个任务粒的局部寻优获得top- k 解;最后,将每个局部最优组合进行组合获取全局最优解.由于,每个基本粒服务的QoS存在单属性和多属性之分,且多属性包含单属性情况,因此,本节将任务粒的划分和多属性任务粒化分别进行阐述.
本文所提的粒化思想是基于任务间的隶属度动态划分,即对于不同的数据集以及不同的质量约束关系集,所得的任务粒化结果不同.其大致过程可以分为以下3步:首先,统计每个任务的隶属度值,即每个任务对其他任务而言,存在质量约束的数量;其次,根据隶属度阈值,对任务粒进行划分;最后,输出最终的任务粒.其详细描述如算法1所示:
算法1 . 任务粒化算法.
输入:任务数 n 、隶属度矩阵 M 、隶属度阈值 γ ;
输出:任务粒集合 TS .
① 初始化 TS =∅,任务粒 T =∅;
② for each t 1 ≤ n ∧ t 1 ∉ TS do
③ T =∅;
④ T . add ( t 1 );
⑤ for each t 2 ≤ n ∧ t 2 ∉ TS ∧ t 2 ≠ t 1 do
⑥ if ∃ t 3 ∈ T ∧ M ( t 3 , t 2 )≥ γ then
⑦ T . add ( t 2 );
⑧ end if
⑨ end for
⑩ TS . add ( T );
 end for
end for
 return TS .
return TS .
其中, M ( t 3 , t 2 )表示隶属度矩阵 M 中的 t 3 行的 t 2 列的隶属度值.由算法1可知,任务粒划分的对象是每个任务,即确定每个任务的归属任务粒.以图1和表1为例,可以构造任务之间的隶属度矩阵如下所示:
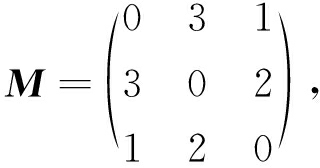
(5)
其中,矩阵 M 的行列均表示任务 t 1 至 t 3 ,且第 i 行第 j 列对应的数值表示任务 t i 和 t j 的隶属度值.若设置隶属度阈值为3,则式(5)所示的隶属度矩阵可将任务 t 1 至 t 3 分为2个任务粒( t 1 , t 2 )与( t 3 ),若将隶属度阈值设为2,则只可分为一个任务粒( t 1 , t 2 , t 3 ),这是由于任务 t 1 与 t 2 的隶属度大于等于2,虽然任务 t 1 和 t 3 的隶属度不大于2,但任务 t 2 与 t 3 的隶属度大于等于2,因此任务 t 1 , t 2 , t 3 均属于同一任务粒.
多属性是指每个候选服务的QoS不唯一,其计算方式是表2所列的计算方式的线性组合.由于多属性服务组合问题,在每一维度上均最优的候选服务不一定存在,本部分则利用候选服务的效用函数(式(4))作为衡量指标,然后取每个任务粒的top- k 个最优解.最后将各个任务粒的top- k 个最优解进行枚举,取其最优解作为原问题的解,其详细过程如算法2所示:
算法 2 . 多属性任务粒化验证算法.
输入:每个任务粒;
输出:服务组合最优解.
① 初始化 bestfit =0;
② Get the k value of the top- k ;
③ Generate an array best [ n , k ] to keep the best services;
④ for each s i ∈ s do
⑤ for each s i , j ∈ s i do
⑥ Keep the top- k best services s i , j ;
⑦ end for
⑧ Add s i , j into best [ i , k ];
⑨ end for
⑩ for each s i , j ∈ best [ n , k ] do
 Enumerate the bestfit = Enume ( best [ n , k ]);
Enumerate the bestfit = Enume ( best [ n , k ]);
 end for
end for
 return bestfit .
return bestfit .
其中, best [ n , k ]表示保存每个任务粒中top- k 最优解, Enume ( best [ n , k ])表示获得 best [ n , k ]中的枚举最优解.在任务粒的枚举过程中,对每一种服务组合方式均须进行质量约束计算,并取约束之后的结果作为最优化选择依据.
为验证基于任务粒化的质量约束感知的服务组合优化模型的可行性,以及本文算法Tg-QcA的高效性和稳定性,本部分以公共数据集QWS为测试数据 [14-15] .通过与考虑质量约束的粒子群算法(Qc-PSO [16] )、采用剪枝优化的质量感知服务选择算法(CASP [7] )以及没考虑质量约束的粒子群算法(PSO)进行对比,验证本文所提求解方案的可行性、高效性以及稳定性.
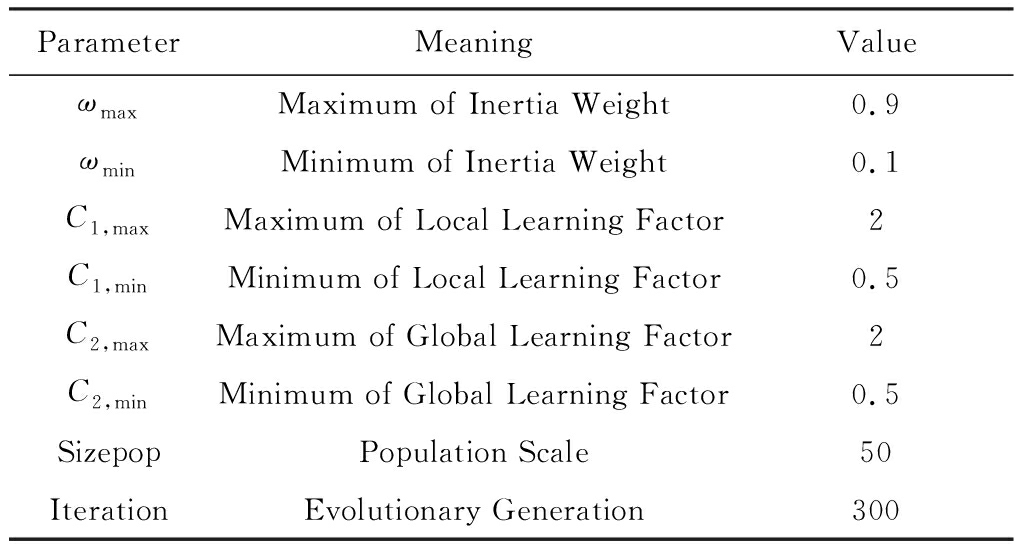
本实验环境是Microsoft Visual Studio 2010,编程语言为C#,实验机器配置为16 GB内存、core i7 3.6 GHz处理器、Windows 7操作系统.任务数为5,每个任务的候选服务数从100递变到500,每次实验进行100次重复实验,取其均值作为最终衡量指标,对比算法PSO中参数设置如表3所示:
Table 3 Experimental Parameter Settings
表3 PSO算法实验参数表
对于混合多属性计算方式而言,TgA- k 表示每个任务粒度中取top- k 个最优解.
针对本文所提任务粒化算法,本节首先验证不同规模的质量约束数据集对服务组合问题寻优结果的影响;其次,验证不同的QoS维数对任务粒化服务组合寻优结果的影响;最后,验证不同候选服务数量对服务组合寻优结果的影响证.其中,采用均方差 RMSE 验证不同算法的稳定性,定义如下:
(6)
其中, x i 表示第 i 次实验结果, x 表示 n 次实验的平均结果.
4.2.1 质量约束的影响
为验证质量约束对服务组合优化问题的影响,本节通过在如下实验参数设置下进行100次重复实验,取其均值,结果如图3所示.其中,每个任务的候选服务数量为450,QoS的维度为2,任务数量为5,质量约束比例以5%为步长从5%递增到30%.
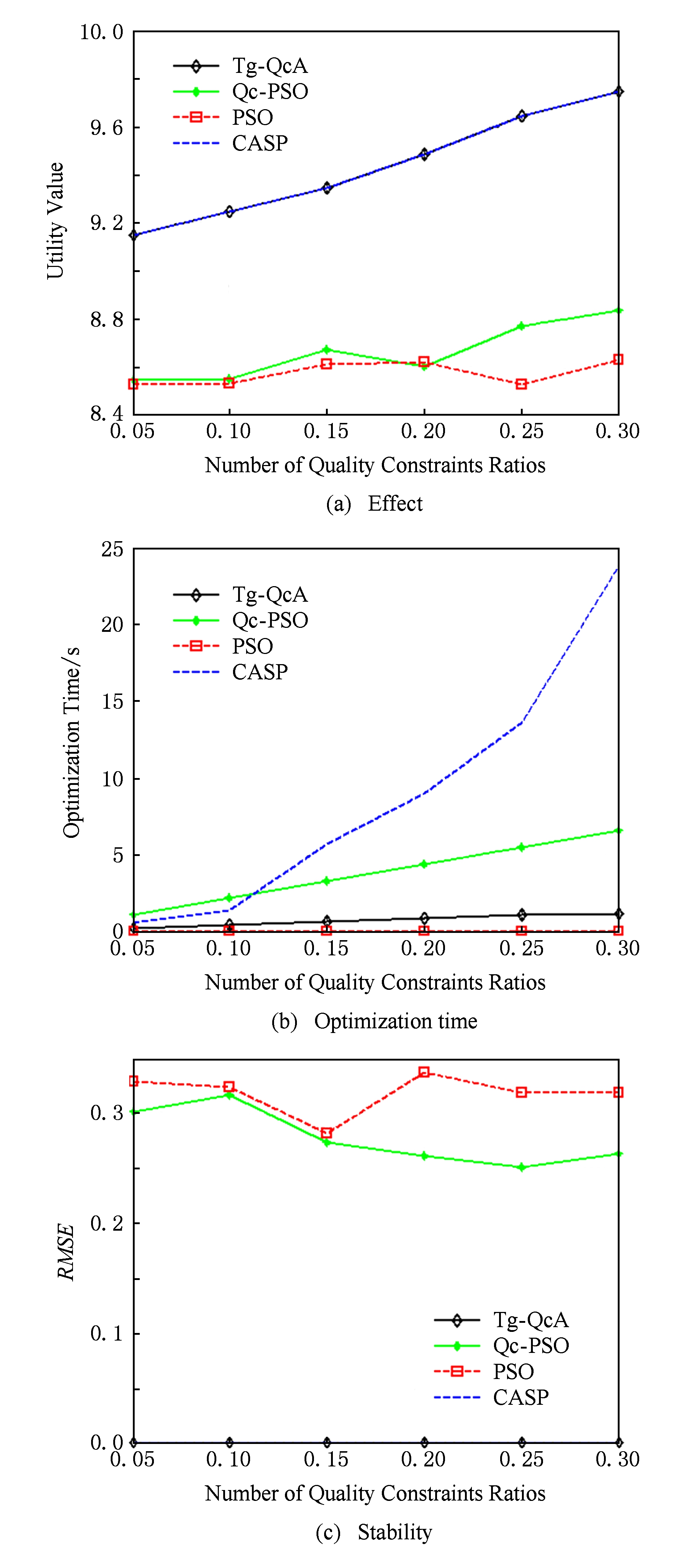
Fig. 3 Impact of quality constraints
图3 质量约束的影响
从图3(a)可以看出,存在质量约束的情况下,服务组合问题的优化结果显著提高,并且,随着质量约束比例的增加,服务组合问题优化精度越来越高,表明质量约束的影响越来越大.CASP是基于剪枝的服务选择算法,属于一种枚举的优化算法,因此,在图3(a)中CASP与Tg-QcA寻优结果一致,表明本文算法具有优秀的全局寻优能力.尤其,从图3(b)可以看出,本文算法相比于CASP而言,寻优时间显著较低,综合表明本文算法寻优能力强的同时具有很高的寻优效率.虽然从图3(b)可以看出,存在质量约束的服务组合寻优时间相比于没质量约束的要长,但是相比于其精度提升而言,在任务粒化方法中,其时间开销可以忽略,对比Tg-QcA和Qc-PSO 2条时间曲线可以看出,在解决质量约束的服务组合优化问题时,任务粒化的时间优势非常明显.从图3(c)可以看出,Tg-QcA算法是基于任务粒化的服务组合优化方法,其均方差近乎于0,显著低于其他2种算法,表明本算法具有很好的稳定性,并且结合图3(a)的寻优结果可知,本文算法在质量约束逐渐增加的情形下,具有优秀的寻优精度、寻优效率和寻优稳定性.

Fig. 4 Impact of QoS dimension
图4 QoS维数的影响
4.2.2 QoS维数的影响
为验证QoS维数对质量约束感知服务组合优化问题的影响,本节通过在表3实验参数设置下进行100次重复实验,取其均值,实验结果如图4所示.其中,每个任务的候选服务数量为450,任务数量为5,质量约束比例为20%,QoS维数从1变化到9,其递增步长为1.
从图4(a)可以看出,随着QoS维数的增加,服务组合优化问题的寻优结果逐步提高,实验结果表明在QoS维度变化过程中,质量约束仍起到至关重要的作用,尤其随着QoS维度的增加,质量约束的效果更明显,即曲线间的差距越大.与质量约束影响结果类似,本文算法取得了与CASP一致的寻优精度,并且其时间开销显著低于CASP.由图4(b)可以看出,随着QoS维度的增加,寻优时间几乎不增加,这是由于QoS维度只用于每个服务组合实例的效用值计算,其影响甚微,乃至于在大刻度的坐标轴下变化近乎为0,但从曲线的间距可以看出,采用任务粒化的质量感知服务组合优化算法的时间开销远小于Qc-PSO.由图4(c)可以看出,Tg-QcA的均方差近乎于0,显著低于其他2种算法,表明本算法具有很好的稳定性.综上可知,本文算法在QoS维度逐渐增加的情形下,同样具有很好的寻优精度、寻优效率和寻优稳定性.
4.2.3 候选服务数量的影响
为验证候选服务数对质量约束感知服务组合优化问题的影响,本节通过在如下实验参数设置下进行100次重复实验,取其均值,实验结果如图5所示.其中,QoS的维度为2,任务数量为5,质量约束比例为20%,候选服务数量以50为步长,从50递增到450.

Fig. 5 Impact of candidate service number
图5 候选服务数的影响
由图5(a)可以看出,随着候选服务数量的增加,Tg-QcA获得的效用值最大,表明该算法的寻优精度最高,而且远大于其他2种算法.Qc-PSO在任务数量较小的情况下,寻优效果不高于PSO,这是由于候选服务较少,对应的质量约束较少,而PSO又是一种随机的启发式群体智能算法,以至于结果具有随机性.虽然随着候选服务数量的增加,Qc-PSO的寻优效果逐步上升,但仍远小于Tg-QcA.同样,本文算法的寻优精度与CASP一致的同时,本文算法的时间效率远高于CASP.从图5(b)可以看出,随着候选服务数的增加,Tg-QcA的时间开销增大,但远小于Qc-PSO,表明本文算法具有很好的时间性能.图5(c)的实验结果同样反映了Tg-QcA的均方差接近于0,显著低于其他2种算法,同样表明本文算法具有很好的稳定性.
本文旨在利用任务粒化思想解决质量约束感知的服务组合优化问题,通过对候选服务间的质量约束判断任务间的隶属度值,然后进行任务粒的划分,进一步降低问题的求解规模,并逐步获得原问题的最优解.从粒化角度,现有质量约束感知的服务组合优化方法主要可以分为2类:基于非粒化思想质量约束求解算法和基于粒化思想质量约束求解算法.
1) 基于非粒化思想质量约束求解算法
随着QoS衡量方式的出现,考虑QoS之间关联的研究成果也随之出现.文献[17]中利用了整数规划表达式求解服务组合优化问题,而且构建适用于多QoS约束的整数规划模型.文献[18]在文献[17]的基础上给出有状态的Web服务组合优化约束表达式.文献[19]给出了服务质量依赖于其他可选服务,即提出支持服务关联的QoS模型,而且利用整数规划与启发式求解问题最优解,但其关系模型构建较为复杂,尤其当候选服务数量较大时,其关系描述较为臃肿,不利于推广.文献[20]提出业务约束模型,并且利用改进遗传算法解决QoS约束服务组合优化问题,但该文只限于2个而且是抽象的任务之间进行组合优化,实用性极大受限.文献[7]提出一种QoS关联的服务组合优化问题研究,在文章中通过以Response time为例构建系统的场景分析和同一个服务提供商的QoS约束模型,但没能系统考虑QoS在整个组合服务中的关联关系.
2) 基于粒化思想质量约束求解算法
近年来,考虑粒度的服务组合问题也有相关研究,但只是将粒度概念引入服务组合问题,而且解决的是服务组合中的特定问题.例如,文献[21]利用多粒度方法分析一个提供商提供多个服务问题,并且采用图的思路解决最优化问题.文献[22]提出多粒度服务组合模型,利用粒度思想进行服务发现,并采用改进遗传算法解决服务组合问题.文献[23]提出一种多粒度上下文模型,获得更多的上下文信息,用以解决更复杂的服务组合问题.在这类研究中,只是将服务组合部分过程进行粒度化处理,没有系统考虑粒度下的服务组合问题.在质量约束感知的服务组合优化方面,文献[16]引入粒度思想,但属于将质量约束进行聚合操作,而不是对问题进行分解.
通过对质量约束感知的服务组合优化问题的分析,发现服务组合优化问题可以进行粒化处理,以便将复杂的服务组合过程分解为多个简单的服务组合子问题.基于此,本文利用商空间理论将服务间的质量约束进行任务间的粒度划分,即根据任务间的隶属度值决定每个任务的归属.从理论方面分析了每个候选服务的QoS聚合方式均具有子模态性质,从而保证了任务粒化的精度和问题的完备性.进一步地,通过对任务粒化分析,提出基于任务粒化的质量约束感知服务组合优化算法Tg-QcA,并通过大量的仿真实验,在质量约束数量、QoS维数以及候选服务数量3个方面验证了本文算法的性能.本文模型对大数据驱动的大服务生态系统环境下大规模、高频实时、跨领域协同的服务组合问题求解具有重要的理论和实践参考价值.
参考文献
[1]Wu Quanwang, Zhu Qingsheng. Transactional and QoS-aware dynamic service composition based on ant colony optimization[J]. Future Generation Computer Systems, 2013, 29(5): 1112-1119
[2]Ma You, Wang Shangguang, Hung P C K, et al. A highly accurate prediction algorithm for unknown Web service QoS values[J]. IEEE Trans on Services Computing, 2016, 9(4): 511-523
[3]Zheng Zibin, Zhu Jieming, Lyu M R. Service-generated big data and big data-as-a-service: An overview[C] 
 Proc of IEEE Int conf on Big Data. Piscataway, NJ: IEEE, 2013: 403-410
Proc of IEEE Int conf on Big Data. Piscataway, NJ: IEEE, 2013: 403-410
[4]Xu Xiaofei, Sheng Quan, Zhang Liangjie, et al. From big data to big service[J]. Computer, 2015, 48(7): 80-83
[5]Zhang Ling, Zhang Bo. The quotient space theory of problem solving[J]. Fundamenta Informaticae, 2004, 59(2  3): 287-298
3): 287-298
[6]Zhang Yanping, Zhang Ling, Xu Chenchu. The property of different granule and granular methods based on quotient space[M] 
 Information Granularity, Big Data, and Computational Intelligence. Berlin: Springer, 2015: 171-190
Information Granularity, Big Data, and Computational Intelligence. Berlin: Springer, 2015: 171-190
[7]Deng Shuiguang, Wu Hongyue, Hu Daning, et al. Service selection for composition with QoS correlations[J]. IEEE Trans on Services Computing, 2016, 9(2): 291-303
[8]Deng Shuiguang, Huang Longtao, Hu Daning, et al. Mobility-enabled service selection for composite services[J]. IEEE Trans on Services Computing, 2016, 9(3): 394-407
[9]Kempe D, Kleinberg J, Tardos é. Maximizing the spread of influence through a social network[C] 
 Proc of the 9th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2003: 137-146
Proc of the 9th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2003: 137-146
[10]Zhang Yiwen, Cui Guangming, Zhao Shu, et al. IFOA4WSC: A quick and effective algorithm for QoS-aware service composition[J]. International Journal of Web and Grid Services, 2016, 12(1): 81-108
[11]Al-Helal H, Gamble R. Introducing replaceability into Web service composition[J]. IEEE Trans on Services Computing, 2014, 7(2): 198-209
[12]Zhang Yiwen, Cui Guangming, Wang Yan, et al. An optimization algorithm for service composition based on an improved FOA[J]. Tsinghua Science & Technology, 2015, 20(1): 90-99
[13]Jatoth C, Gangadharan G R, Buyya R. Computational intelligence based QoS-aware Web service composition: A systematic literature review[J]. IEEE Trans on Services Computing, 2017, 10(3): 475-492
[14]Al-Masri E, Mahmoud Q H. Discovering the best Web service[C] 
 Proc of the 16th Int Conf on World Wide Web. New York: ACM, 2007: 1257-1258
Proc of the 16th Int Conf on World Wide Web. New York: ACM, 2007: 1257-1258
[15]Al-Masri E, Mahmoud Q H. Qos-based discovery and ranking of Web services[C] 
 Proc of the 16th Int Conf on Computer Communications and Networks. Piscataway, NJ: IEEE, 2007: 529-534
Proc of the 16th Int Conf on Computer Communications and Networks. Piscataway, NJ: IEEE, 2007: 529-534
[16]Zhang Yiwen, Cui Guangming, Deng Shuiguang, et al. Alliance-aware service composition based on quotient space[C] 
 Proc of Int Conf on Web Services. Piscataway, NJ: IEEE, 2016: 340-347
Proc of Int Conf on Web Services. Piscataway, NJ: IEEE, 2016: 340-347
[17]Zeng L, Benatallah B, Ngu A H H, et al. Qos-aware middleware for Web services composition[J]. IEEE Trans on Software Engineering, 2004, 30(5): 311-327
[18]Ardagna D, Pernici B. Adaptive services composition in flexible processes[J]. IEEE Trans on Software Engineering, 2007, 33(6): 369-384
[19]Ren Lifang, Wang Wenjian, Xu Hang. Uncertainty-aware adaptive service composition in cloud computing[J]. Journal of Computer Research and Development, 2016, 53(12): 2867-2881 (in Chinese)(任丽芳, 王文剑, 许行. 不确定感知的自适应云计算服务组合[J]. 计算机研究与发展, 2016, 53(12): 2867-2881)
[20]Wu Quanwang, Zhu Qingsheng, Zhou Mingqiang. A correlation-driven optimal service selection approach for virtual enterprise establishment[J]. Journal of Intelligent Manufacturing, 2014, 25(6): 1441-1453
[21]Barakat L, Miles S, Poernomo I, et al. Efficient multi-granularity service composition[C] 
 Proc of IEEE Int Conf on Web Services. Piscataway, NJ: IEEE, 2011: 227-234
Proc of IEEE Int Conf on Web Services. Piscataway, NJ: IEEE, 2011: 227-234
[22]Wu Quanwang, Zhu Qingsheng, Jian Xing. Qos-aware multi-granularity service composition based on generalized component services[C] 
 Proc of Int Conf on Service-Oriented Computing. Berlin: Springer, 2013: 446-455
Proc of Int Conf on Service-Oriented Computing. Berlin: Springer, 2013: 446-455
[23]Niu Wenjia, Li Gang, Zhao Zhijun, et al. Multi-granularity context model for dynamic Web service composition[J]. Journal of Network and Computer Applications, 2011, 34(1): 312-326

Zhang Yiwen , born in 1976. Received his PhD degree from Hefei University of Technology in 2013. Associate professor. Member of CCF. His main research interests include service computing, big data and cloud computing.

Cui Guangming , born in 1991. Master in Anhui University. His main research interests include service computing, evolutionary computing etc.

Yan Yuanting , born in 1986. Received his PhD degree in Anhui University. Lecturer. His main research interests include machine learning granular computing and bioinformatics.

Zhao Shu , born in 1979. Received her PhD degree from Anhui University. Professor. Her main research interests include machine learning, quotient space theory and social network.

Zhang Yanping , born in 1962. PhD and professor in Anhui University. Her main research interests include computational intelligence, quotient space theory, granular computing and machine learning.
Zhang Yiwen 1,2 , Cui Guangming 2 , Yan Yuanting 2 , Zhao Shu 1,2 , and Zhang Yanping 1,2
1 ( Key Laboratory of Intelligent Computing and Signal Processing ( Anhui University ), Ministry of Education , Hefei 230031) 2 ( School of Computer Science and Technology , Anhui University , Hefei 230601)
Abstract With the development of service computing, more and more sources are released and utilized as services. Competition between service providers grows increasingly fierce. Hence, the win-win cooperation between services becomes an inevitable trend. Moreover, the consideration of the quality constraint correlation between businesses further complicates the service composition optimization problem. To solve it, this paper uses task granulation on service composition business process, and presents a quality constraint-aware service composition method based on task granulation (Tg-QcA) when considering the quality constraint between candidate services. Firstly, this paper makes theoretical analysis and verifies that each QoS aggregation has component mode and the utility function of multi-attribute service composition problem still has component mode, thereby guaranteeing the completeness of task-granulation optimization method. Secondly, a quality constraint based model is built and then a task granulation partition is made through the subjection degree between tasks to decompose the original problem, thereby reducing the solving scale of problem. Finally, it is demonstrated by computer simulation that this algorithm and this model have strong feasibility, efficiency and stability.
Key words service composition; task granulating; quality constraints; submodular; quality of service (QoS)
摘 要 随着服务计算的发展,越来越多的资源以服务的形式发布与使用,服务提供商间的竞争日趋激烈,合作共赢成为必然趋势,但考虑质量约束关系服务组合优化问题复杂性大大增强.为解决这一问题,在充分考虑候选服务间质量约束的同时,对服务组合业务流程进行任务粒化,提出基于任务粒化的质量约束感知服务组合优化方法(Tg-QcA).首先,通过理论分析,验证每种QoS聚合方式均具有子模态性质以及多属性服务组合问题的效用函数仍具有子模态性质,保证了基于任务粒化优化方法的完备性;其次,通过质量约束建模,利用任务间的隶属度进行任务粒化划分,对原问题进行分解,有效降低了问题求解规模;最后,大量的仿真模拟实验结果表明:所提模型与算法具有很好的可行性、高效性和稳定性.
关键词 服务组合;任务粒化;质量约束;子模;服务质量
中图法分类号 TP391
收稿日期 : 2017-04-01;
修回日期: 2017-08-09
基金项目 : 国家科技支撑计划基金项目(2015BAK24B01);国家自然科学基金项目(71601001,61673020);教育部人文社会科学基金项目(15YJAZH112);安徽省高校自然科学基金重点项目(KJ2016A038);安徽省自然科学基金项目(1808085MF197)
This work was supported by the National Key Technology Research and Development Program of China (2015BAK24B01) , the National Natural Science Foundation of China (71601001, 61673020), the General Research for Humanities and Social Sciences Project of Ministry Education of China(15YJAZH112), the Key Project of Natural Science Research for Universities of Anhui Province of China (KJ2016A038), and the Natural Science Foundation of Anhui Province of China (1808085MF197).
通信作者 : 赵姝(zhaoshuzs2002@hotmail.com)