
 github.com
github.com  dqiong
dqiong  CUDA-TP.
CUDA-TP. 段 琼 1 田 博 1 陈 征 1 王 洁 1,2 何增有 1,2
1 (大连理工大学软件学院 辽宁大连 116620) 2 (辽宁省泛在网络与服务软件重点实验室(大连理工大学) 辽宁大连 116620) (wangjie1003@163.com)
摘 要 蛋白质及蛋白质翻译后修饰(post-translational modifications, PTMs)的鉴定是蛋白质组学研究的基础,对整个领域的进一步发展有着十分重要的意义.近年来,质谱设备的快速发展使得获取“自顶向下”(top-down,TD)的高精度完整蛋白质质谱数据成为可能.目前基于TD质谱数据的完整蛋白质鉴定算法虽然在匹配精度、PTM位点的推断上取得了一些成效,但它们运行时间还有很大的不足和提升空间.利用图形处理器(graphics processing unit, GPU)可以将大规模的重复计算并行化,提高串行程序的执行速度.CUDA-TP算法基于通用并行计算架构(compute unified device architecture, CUDA)来计算蛋白质与TD质谱数据的匹配分数.首先,对每一个质谱数据,CUDA-TP利用优化的MS-Filter算法在蛋白质数据库中过滤出其对应的少数候选蛋白质集合,然后通过AVL(adelson-velskii and landis)树加速质谱匹配过程.GPU中的多线程技术被用来并行化谱图网格及最终数组中所有元素的前驱结点的求解.同时,该算法还使用target-decoy策略来控制蛋白质与质谱图匹配结果的错误发现率(false discovery rate, FDR).实验结果表明:CUDA-TP算法能够有效地加速完整蛋白质的鉴定,速度分别比MS-TopDown和MS-Align+快10倍与2倍.到目前为止,这是唯一能够利用CUDA架构来加速完整蛋白质鉴定的研究工作.CUDA-TP源代码公布在https: 
 github.com
github.com  dqiong
dqiong  CUDA-TP.
CUDA-TP.
关键词 “自顶向下”蛋白质组学;蛋白质鉴定;图形处理器;通用并行计算架构;谱图比对
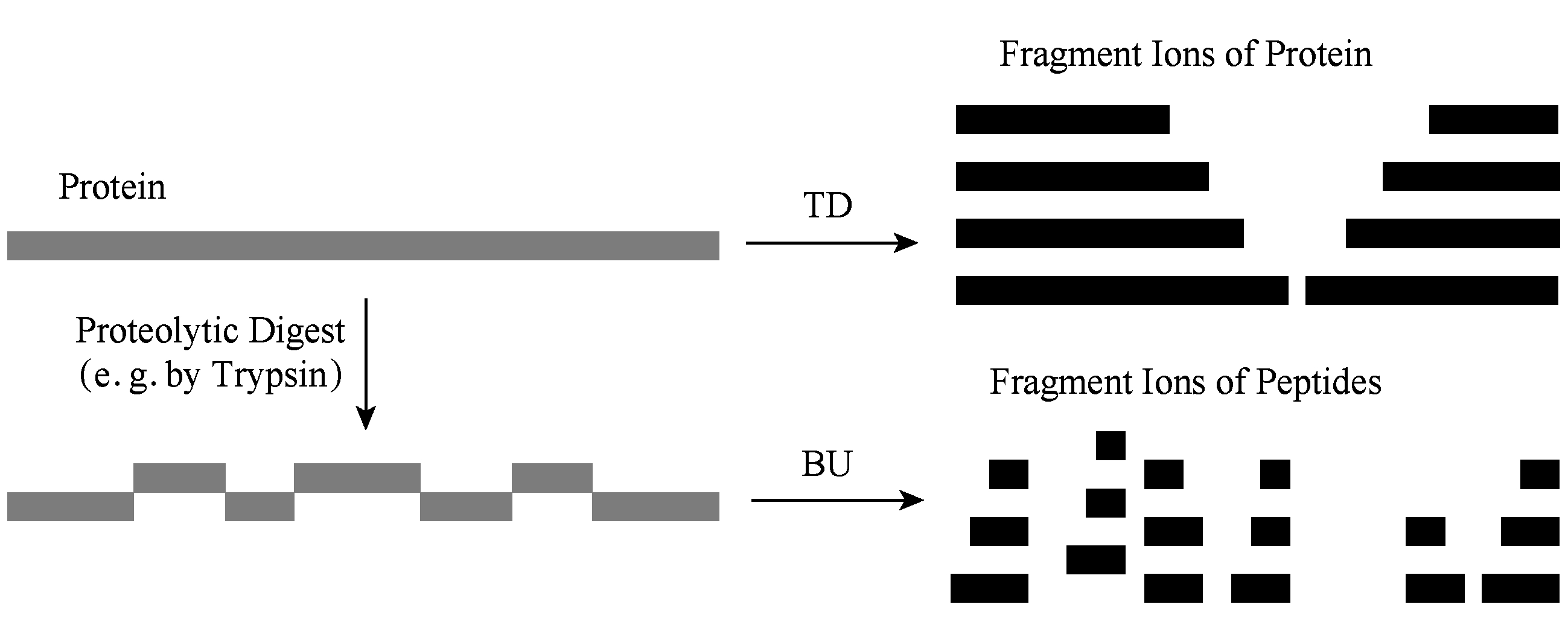
Fig. 1 Comparison between TD and BU for protein identification
图1 蛋白质鉴定中的TD与BU方法对比
蛋白质组学(proteomics)是一门新兴学科,主要研究细胞内表达的所有蛋白质及其活动规律 [1] .由于基因的作用最终是由蛋白质(protein)来体现,所以蛋白质组学的研究有着更为重要的实际意义和价值.蛋白质组学的一个重要目标是能够快速有效地进行蛋白质鉴定,即确定一个样本中表达的所有的蛋白质.蛋白质是由氨基酸分子链接而成的生物大分子,蛋白质的一级结构(氨基酸序列)唯一确定了蛋白质的身份,因此可以通过识别氨基酸序列达到鉴定蛋白质的目的.只有鉴定到生物样品中真实表达的蛋白质,才能准确获得蛋白质相互作用、亚细胞定位等信息,为进一步的疾病标记物发现和新药开发提供强有力的支持 [2] .因此,蛋白质鉴定是蛋白质组学研究的基础,对整个领域的进一步发展和应用有着十分重要的意义.
为解决蛋白质鉴定问题,目前以生物质谱为基础的蛋白质组学分析方法主要有“自底向上”(bottom-up, BU)和“自顶向下”(top-down, TD)二种方法 [3] ,2种方法比对如图1所示.BU方法通常先将蛋白质的复杂样品进行酶切产生肽段的混合物;然后通过液相色谱等技术将这些肽段的混合物进行分离,进而通过质谱技术将肽段碎裂,并根据碎裂谱图中的离子峰信息进行数据库搜索来鉴定肽段;最后将鉴定到的肽段进行组装、推理获得样品中所含有的蛋白质 [4-6] .
BU是由肽段推测蛋白质序列,属于“从局部推断整体”.尽管BU已经在当前的蛋白质组学研究中广泛使用,但该类方法同样存在着一系列的局限 [7] :
1) 由于并不是所有的肽段都可以有效地被捕捉到并生成二级谱图,导致很多蛋白质没有相应的肽段鉴定结果,进而无法鉴定到该蛋白质的存在;
2) 即使可以通过少数几个鉴定得到的肽段信息来推断蛋白质的存在与否,但是却不能测绘出整个蛋白质序列的全部信息,这主要包括蛋白质各种氨基酸位点上的翻译后修饰(post-translational modification, PTM);
3) 由于是通过肽段的鉴定结果间接地得到蛋白质的鉴定结果,而同一个肽段可以映射到多个不同的蛋白质序列,这就需要解决一个复杂的计算问题:蛋白质推断 [8] .而蛋白质推断问题目前尚未彻底解决,仍有很多计算上的挑战需要克服.
与BU策略相反,TD方法不需要将蛋白质“切割”成更短的肽段序列,而是直接将完整的蛋白质进行分离和离子化,然后对其进行碎裂并利用串联质谱测量由每个蛋白质生成的二级谱图.在数据分析阶段,通过比对数据库中的蛋白质序列和实验二级谱图进行蛋白质鉴定 [9-10] .这样,通过完整蛋白质的质量及其碎裂谱的信息可以实现真正意义上的蛋白质鉴定.另外,TD能够保留多种PTM之间的关联信息,逐渐成为蛋白质组学研究中的热点 [5] .
鉴于TD方法对于蛋白质鉴定具有重要的生物学意义,针对TD策略中完整蛋白质与谱图的匹配问题,已经提出了一些有效的算法.在这些方法中,ProSight [11-12] 采用泊松分布概率打分模型计算蛋白质与谱图的匹配概率,用“鸟枪标注”的方法生成所有可能的蛋白质变体数据库.这种方法最大的问题是扩展性差,如果变体增多可能导致“组合爆炸”.Frank等人 [13] 借鉴谱图比对方法,以动态规划为基础开发了MS-TopDown算法,该算法能有效的鉴定蛋白质及未知的PTM.Liu等人 [14] 在此基础上通过优化动态规划显著提高了计算速度并提供了匹配的统计显著性评估方法.在此后,TopPIC [15] ,MASH suit [16] ,MSpathFinder [17] ,Ptop [18] 等工具都是以动态规划为主体进行蛋白质数据库搜索并在不同的方面做了改进.然而,其面临的最大问题还是匹配时间不尽如人意,这是由动态规划算法所固有的时间复杂度决定的.
高性能计算的发展对计算速度的提升做出了巨大贡献.自2003年开始,图形处理器(graphics proc-essing units, GPU)就在浮点运算性能和存储器带宽上飞速发展.通用并行计算架构(compute unified device architecture, CUDA) [19] 是由英伟达公司推出的高性能运算平台,它能够充分发挥GPU并行计算的优势.随着GPU可编程性的增强,GPU突破仅应用于图形处理领域的局限,开始用于一些通用计算领域 [20-21] ,尤其是在生物信息学领域,为研究人员提供了新的思路.例如翟艳堂等人 [22] 提出的PTM鉴定算法MS-Alignment的并行架构,有效地提高了在肽段上检测PTM的效率;对于肽段鉴定问题,Zhang等人 [23] 通过CUDA架构将肽段鉴定算法RT-PSM [24] 的速度提升了26倍;Baumgardner等人 [25] 成功对SpectraST [26] 算法进行了并行计算加速;Li等人 [27] 也顺利地将谱图点积算法并行化.近几年来,CUDA并行计算架构更是在基因序列比对方面取得了全新的进展 [28-30] .
鉴于完整蛋白质与质谱数据匹配存在高耗时的缺点,本文借鉴谱图比对的思想,以MS-TopDown算法为基础,选择CUDA编程模型设计CUDA-TP算法核心步骤,即完整蛋白质与TD质谱匹配分数的计算.同时在计算步骤中引入平衡二叉搜索(adelson-velskii and landis, AVL)树来保存每个路径点上的信息并对MS-Filter [31] 进行改进以加速蛋白质过滤.最后,本文选取常用的target-decoy [32-33] 方法对结果进行错误发现率(false discovery rate, FDR)控制.实验结果表明:在1%的FDR下CUDA-TP运行速度分别是MS-TopDown和MS-Align+算法的10倍与2倍.
本文的主要贡献有3个方面:
1) 提出了一种新型的基于GPU的完整蛋白质与谱图打分算法,该算法是对MS-TopDown的并行优化,它继承了可以鉴定未知PTM的特点,同时得到的最终分数是谱图网格中的全局分数,并没有使用MS-Align+方法中缩减谱图网格搜索空间的策略.
2) 对MS-Filter算法进行改进加速了蛋白质过滤过程.
3) 使用真实数据集进行实验,验证了本文所提出的CUDA-TP算法的高效性.
通常情况下,可以把一个谱图转换为其相应的前缀残基质量(prefix residue mass, PRM)谱图来表示完整蛋白质的前缀肽段.例如二级串联谱图中一个质量为 ma 的 y 离子单同位素谱峰在PRM谱图中对应的质量为 M - ma ( M 表示完整蛋白质质量).本文中,谱图中所有谱峰都为单同位素谱峰,每个谱峰的单同位素质量包含2个值: ma 和其对应的 M - ma .同时,谱图还包含1个空质量0与代表完整蛋白质PRM值的 M -18(18表示1个水分子质量).具体而言,可以把谱图 S 表示为一个有序序列:
a 0 < a 1 <…< a n ,
其中, a 0 =0, a n = M -18.相应地,长度为 m 的蛋白质序列 P 表示为
b 0 < b 1 <…< b m ,
其中, b i 表示蛋白质序列 P 中从第1个氨基酸到第 i 个氨基酸的质量之和(假设 b 0 =0, b m = M ′-18, M ′为蛋白质 P 未加任何修饰物的质量).给定一个蛋白质序列 P 和一个谱图 S ,定义它们所组成的谱图网格(spectra grid)为( a 0 , b 0 ),( a 0 , b m ),( a n , b 0 ),( a n , b m )四个点所组成的2维矩形方格,其共包含( n +1)( m +1)个点.为了降低复杂性和方便计算,大部分的TD方法不包含谱峰强度,本文也将不考虑谱图中谱峰强度.
蛋白质序列 P 和谱图 S 之间的匹配可以看作谱图网格中的一条如图2所示的路径.路径中一个点与其相邻点的连接包含3种情况:
1) 如果从( a i , b j )到( a i ′ , b j ′ )满足 a i = a i ′ , b j = b j ′ ,则呈斜对角线;
2) 如果从( a i , b j )到( a i ′ , b j ′ )满足 a i ′ > a i ,则为垂直线,垂直线表示蛋白质质量增大,例如氨基酸位点上产生一个质量大于0的PTM;
3) 如果从( a i , b j )到( a i ′ , b j ′ )满足 b i ′ > b i ,则为水平线,水平线表示蛋白质质量减少,例如氨基酸位点上产生1个质量小于0的PTM.匹配路径上所经过的点即为共享谱峰数量 [34] (shared peak count),也称为匹配分数.图2(a)表示完美匹配,没有发生任何PTM;图2(b)表示第5和第6个氨基酸位点上分别产生-80Da和+90Da的PTM.
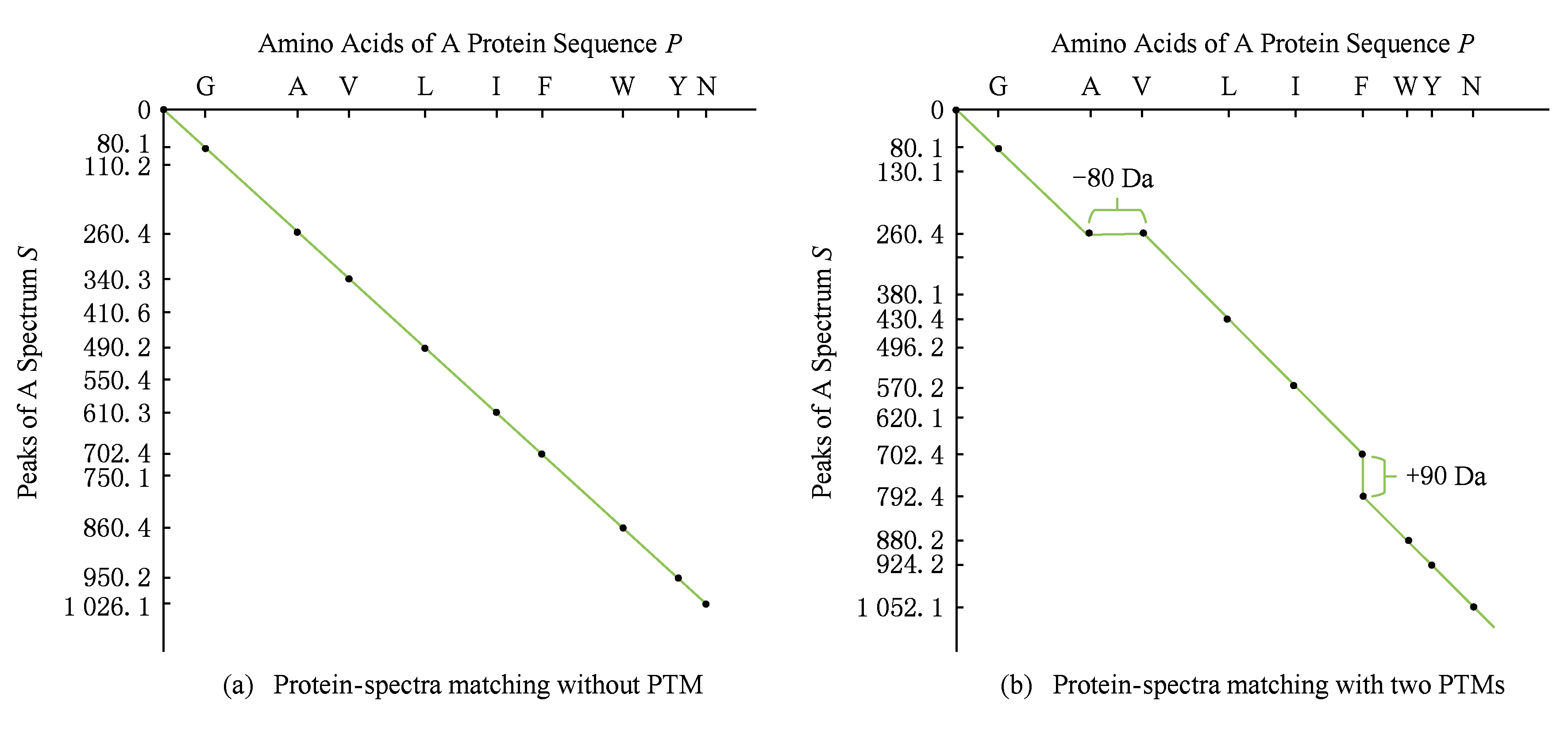
Fig. 2 Illustration of protein-spectra matching
图2 蛋白质与谱图之间的匹配
通过观察可知,每条从( a 0 , b 0 )到( a n , b m )的路径都可能是蛋白质序列 P 和谱图 S 的一个有效匹配,而且匹配的路径数目随着质量变化个数 F (质量变化对应路径中垂直与水平线)的增加而呈现指数增长.为了避免这种情况的发生,通常采用动态规划算法寻找谱图网格中的最优路径 [14-18] ,这样,算法的运行时间只会随着 F 的增加呈线性增长.
动态规划算法在寻找最优路径的过程中需要迭代地填充大小为 n × m × F 的数组 D , D 中的元素 D i j ( f )表示在最多允许发生 f 个质量变化的前提下从( a 0 , b 0 )到( a i , b j )的最高匹配分数.数组 D 填充完成后, D nm ( F )的值即为蛋白质序列 P 和谱图 S 的匹配分数.在最优路径中, D i ′ j ′ ( f ′)的前驱点标记为 D i j ( f ),如果2个数值对( a i , b j )和( a i ′ , b j ′ )满足条件:
| a i - a i ′ - b j ′ + b j |< β ,
(1)
则称它们是余对角的(codiagonal),其中 β 为误差值.
通常,如果 i < i ′且 j < j ′,则( i , j )<( i ′, j ′),定义 diag ( i , j )为( i , j )余对角线上使路径匹配分达最大的点且满足 diag ( i , j )<( i , j ),即 diag ( i , j )是( a i ′ , b j ′ )同对角线的前驱节点,若( a i ′ , b j ′ )没有这样的前驱节点,把 diag ( i , j )置为初始点(0,0).定义数组 H 为
![]()
(2)
D i j ( f )的计算为
D i j ( f )=max( D diag ( i , j ) ( f )+1,
H i -1, j -1 ( f -1)+1).
(3)
H i j ( f )的状态转移方程为
H i j ( f )=max( D i j ( f ), H i -1, j ( f ), H i , j -1 ( f )).
(4)
路径起始点 D 0,0 ( f )=0.可以看出,质量变化数 F 仅会让数组 D 中的元素个数线性增加,算法的时间复杂度为 O ( nmF ), n 和 m 分别表示谱图 S 中谱峰数量与蛋白质序列 P 的长度.
为了减小匹配误差,算法中的质量变化可以选取已知的PTM(如双氧化、磷酸化、甲基化)集合 Δ PTM 中的数值 δ .因此,质量变化分为了2部分:已知的PTM与未知的PTM.用 F s 和 F g 分别表示二者在匹配中所允许的最大个数.至此,可以将 diag ( i , j )扩展为 diag ( δ ) ( i , j )并使之满足条件:
- β <| a i - a i ′ - b j ′ + b j |- δ < β ,
(5)
则之前的数组 D 和 H 大小变为 n × m × F g × F s , D i j ( g , s )中的值仍然表示从(0,0)到( i , j )的最大分数.把式(3)转化成:
D i j ( g , s )=max( D diag ( i , j ) ( g , s )+1,
H i -1, j -1 ( g -1, s ), D diag ( δ ) ( i , j ) ( g , s -1)+1).
(6)
状态转移方程式(4)更新成
H i j ( g , s )=max( D i j ( g , s ),
H i -1, j ( g , s ), H i , j -1 ( g , s )).
(7)
通过式(6),可以利用动态规划算法,最终求得全局谱图网格中完整蛋白质序列 P 与谱图 S 的匹配分数.
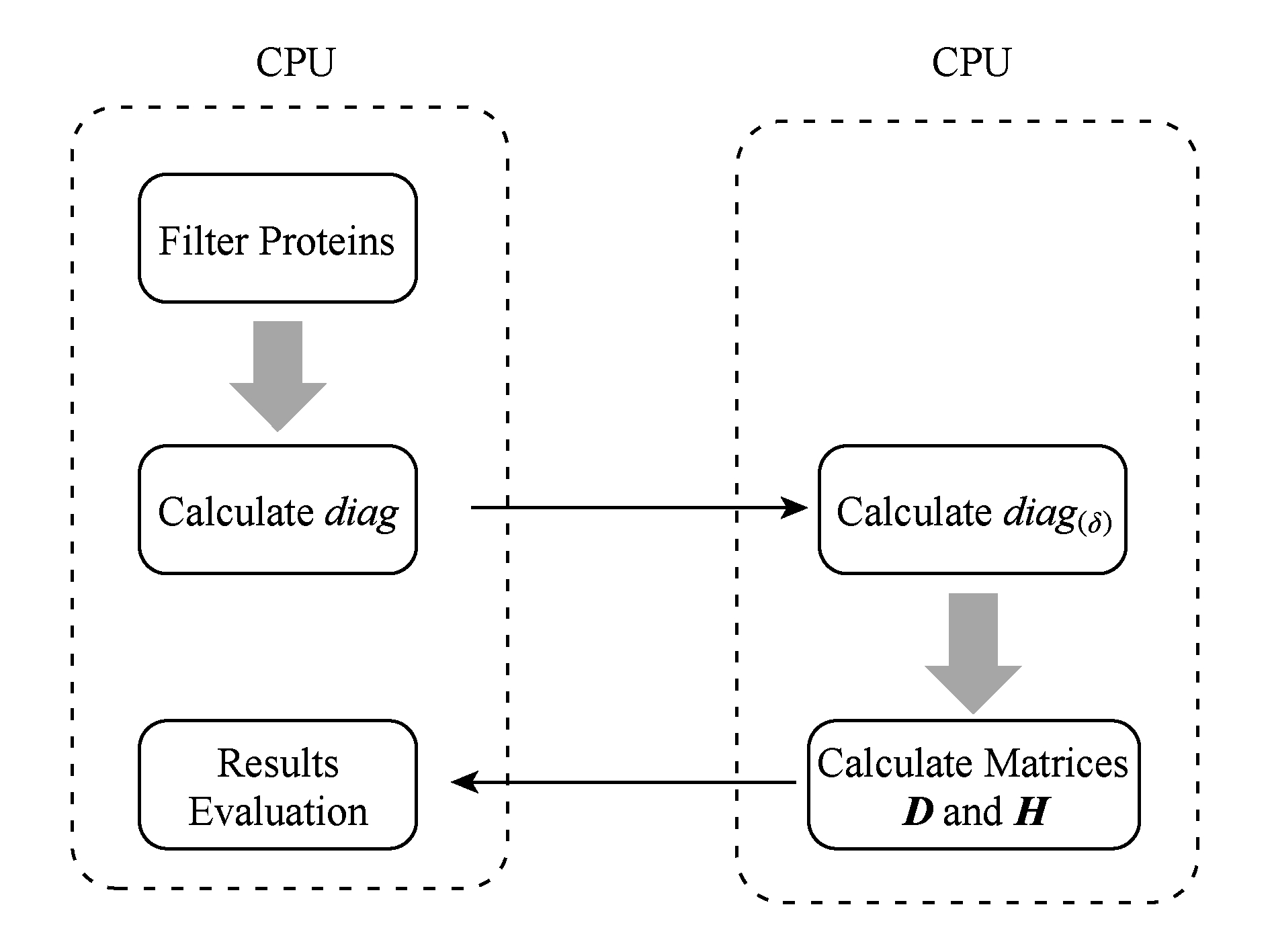
Fig. 3 The flowchart of CUDA-TP algorithm
图3 CUDA-TP算法流程图
如第1节所述的算法虽然能在线性时间内计算出匹配分数,但当蛋白质数据库变大或者谱图数量增多时,其时间开销依然不容乐观.为了加速计算过程,本文提出了基于GPU的CUDA-TP算法,该算法首先在CPU端使用AVL树优化前驱节点的求取,然后设计并行模型加速式(6)的计算.同时,为了加快蛋白质过滤,CUDA-TP还对蛋白质过滤算法MS-Filter [31] 做了改进.算法的整体流程如图3所示.
在谱图网格中寻找最优路径时,首先要计算网格中每个点的前驱坐标 diag ( i , j ).由定义可知 diag ( i , j )必是( i , j )左上部余对角线上的点.如图4所示,为求 A 的前驱点,首先需要找到其左上部区域 Z 中与 A 在同一条余对角线上的点的集合{ A 0 , A 1 , A 2 },然后再在该集合内选取 diag ( i , j )的坐标.在选取坐标时,由式(6)可知,由于 A 1 的 diag 值为 A 0 的坐标,所以匹配路径中 A 1 的匹配分数(对应 D 中元素)至少比 A 0 大1,依次类推,得到点 A 的 diag 取值是离 A 最近点 A 2 的坐标值.因此,求谱图网格中每个点的 diag 即为求距离该点最近且和它呈余对角的点的坐标.最简单的方法是遍历满足要求区域中的所有点,如图4所示, A 的遍历区域为 Z ,但时间开销巨大.
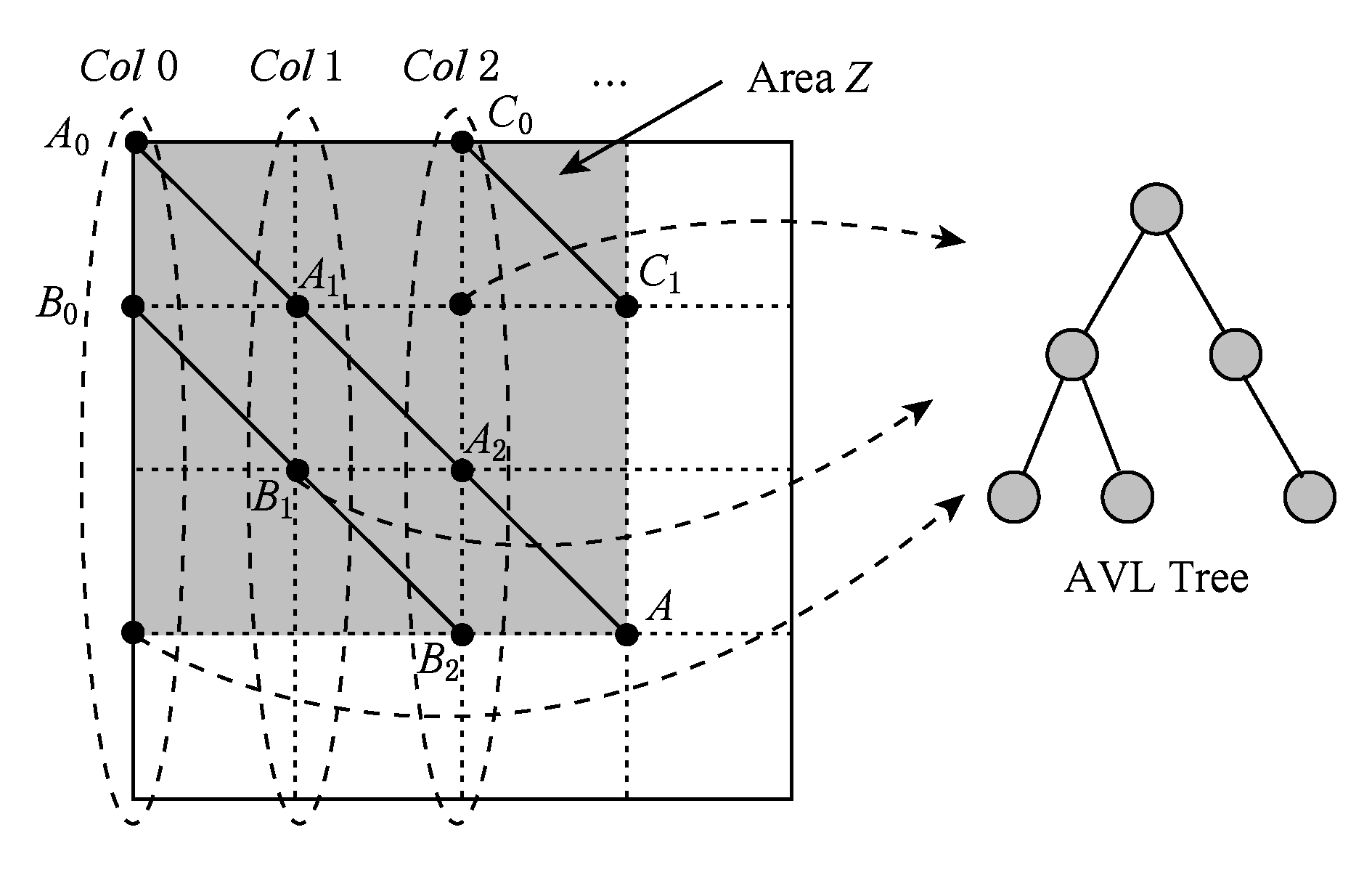
Fig. 4 Calculate diag of all nodes in the spectra grid
图4 计算谱图网格中所有点的diag
由式(1)易知,如果2个点是余对角的,那么它们所在坐标对应的数值对( a i , b j )的差值 d 在误差范围内是相等的.也就是说,集合{ A 0 , A 1 , A 2 }对应相同的 d .利用这条性质,可以通过AVL树只遍历一遍谱图网格求取所有点的 diag ,如图4所示.计算分步骤:
1) 将谱图网格从左到右按列进行划分,每列元素的顺序从上到下;
2) 建立一棵空的AVL树,树的节点包含1个坐标和1个 d 值;
3) 从第1列的第1个元素开始,依次计算坐标元素的 d 值.如果AVL树中没有这个元素的 d 值,则把此值和它的坐标作为新节点插入AVL树.如果查找到已经有节点的 d 值与它相等,则把该元素的 diag 置为此节点所存储的坐标,同时更新节点的坐标为该元素的坐标.
当步骤3运行至最后1列的最后1个元素时,所有点的 diag 求取完毕.由于AVL树节点个数等于谱图网格中所有节点的不同的 d 值数量,所以AVL树的查找速度≪ O (lb nm ),能极大加快 diag 的计算.伪代码如下:
算法1 . 在CPU端计算 diag .
输入:谱图 a [ n ]、蛋白质序列 b [ m ]、误差值 β 、AVL树 avl_tree ;
输出:所有点的 diag .
① InitializeAVLtree ( avl_tree )  *将输入的 avl_tree 初始化为null*
*将输入的 avl_tree 初始化为null* 
② for i =0 to m do
③ for j =0 to n do
④ d ← b [ i ]- a [ j ];
⑤ if avl_tree include d
⑥ diag ( i , j )← avl_tree [ d ]( i , j );
⑦ avl_tree [ d ]( i , j )←( i , j );
⑧ else
⑨ Insert ( avl_tree , d , i , j );
⑩ end if
 end for
end for
 end for
end for
 return diag .
return diag .
需要注意的是,伪代码中行⑤AVL树在查找 d 值时,如果AVL树节点中的值与该值的差的绝对值小于 β ,就认为它们是相等的. avl_tree [ d ]( i , j )表示AVL树中查找到的等于 d 值的节点所包含的坐标.
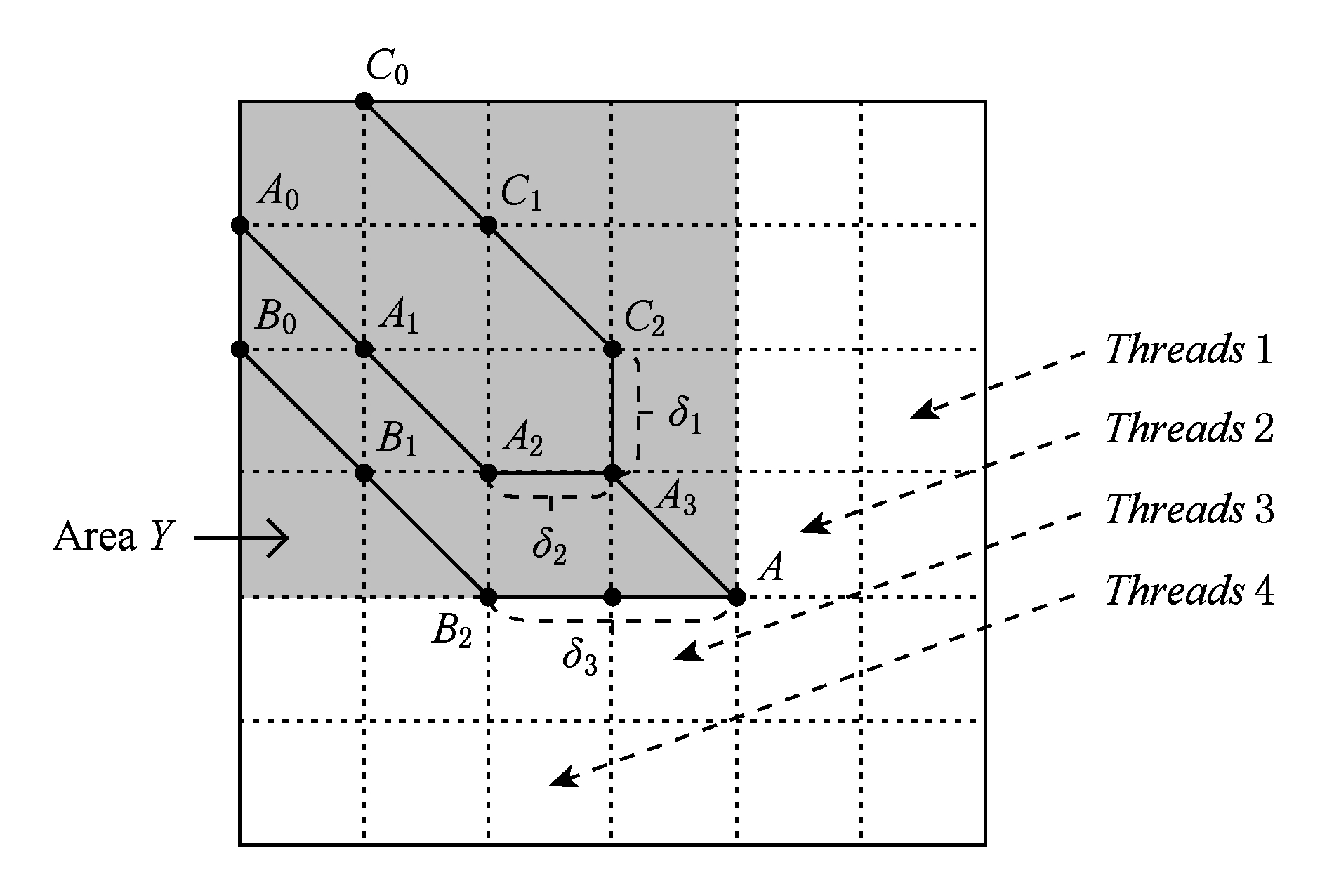
Fig. 5 Calculate diag (δ) of all nodes in the spectra grid
图5 计算谱图网格中所有点的diag (δ)
不同于 diag 的计算,求解 diag ( δ ) 需要知道PTM集合 Δ PTM 中的所有数值 δ .如果 Δ PTM 中有 k 个值,那么,求某个点的 diag ( δ ) 之前必须找出该点谱图网格左上部与该点满足式(5)的 k 个点集合,然后在这 k 个点集合中选取使匹配分值最大,即距离所求点最近的 k 个点的坐标作为最终结果.如图5所示,假设 k =3,集合 Δ PTM ={ δ 1 , δ 2 , δ 3 },在求 A 点的 diag ( δ ) 时,首先在区域 Y 中寻找满足条件的点集合{ A 0 , A 1 , A 2 },{ B 0 , B 1 , B 2 },{ C 0 , C 1 , C 2 },然后选取集合中距离 A 最近的3个点 A 2 , B 2 , C 2 的坐标作为返回值.显然,算法1无法满足这样的计算要求.
由 diag ( δ ) 的计算过程可知,网格中的每个元素在求解时,其结果互不影响,即所有元素可以同时计算.这种性质很好地符合了CUDA并行架构要求.在CUDA架构中,CPU作为主机(host),GPU作为主机的协处理器(co-processor),它被看作执行高度线程化并行处理任务的计算设备(device).运行在GPU上的CUDA并行计算函数称为内核(kernel),以线程栅格(grid)形式组织,线程栅格由若干个线程块(block)组成,每个线程块又包含若干个线程(threads).实际运行时,线程块被分割成更小的线程束(wrap)来执行运算任务,1个线程束由连续的32个线程组成.
diag ( δ ) 并行算法如图5所示,网格中每个点的计算分配1个线程,线程之间并行执行,线程块与线程块之间不需要同步,将所有的元素存入GPU的全局存储器.对一个点左上部的搜索区域,仍然按照算法1进行划分.算法执行过程中,始终维护1个包含 k 个点坐标的数组 g ,该数组的元素为坐标值且映射 Δ PTM 中的某个 δ 值.遍历搜索区域时,如果2个点在同一个集合中,那么它们所对应的 δ 必是相等的,则把后遍历到的节点坐标更新到数组 g .如图5中的点集合{ A 0 , A 1 , A 2 },它们都对应 δ 2 ,当遍历至 A 1 时,更新 g [ δ 2 ]为 A 1 的坐标,依次类推,遍历完成时,数组 g 即为 A 的最终结果.算法2描述了计算 diag ( δ ) 的具体过程.
算法2 . 在GPU端计算 diag ( δ ) .
输入:谱图 a [ n ]、蛋白质序列 b [ m ]、误差值 β 、PTM的集合 Δ PTM ;
输出:存储所有点的 diag ( δ ) 数组 g .
① ( n_left , m_left )← GetCoord ( blockDim . x , blockIdx . x , blockIdx . y );  *根据线程块,线程信息获取要处理的元素*
*根据线程块,线程信息获取要处理的元素* 
② d ←fbs( b [ m_left ]- a [ n_left ]);
③ for i =0 to m_left do
④ for j =0 to n_left do
⑤ delta ←fbs( b [ i ]- a [ j ]- d );
⑥ if Δ PTM include delta
⑦ g [ delta ]←( i , j );
 *存储所得结果*
*存储所得结果* 
⑧ end if
⑨ end for
⑩ end for
 return g .
return g .
算法2中的行①表示从当前的线程获取所要计算的点坐标;行②保存该坐标对应的 d 值;行③④开始遍历坐标左上部区域的所有点;行⑤~  求当前遍历点的 delta 值,如果PTM集合 Δ PTM 包含此值,则将其更新到数组 g ,最后返回的数组 g 即为最终结果;代码的行⑥检测 Δ PTM 中是否存在 δ 与 delta 之差的绝对值小于 β ,如果存在,则判断集合 Δ PTM 包含 delta .
求当前遍历点的 delta 值,如果PTM集合 Δ PTM 包含此值,则将其更新到数组 g ,最后返回的数组 g 即为最终结果;代码的行⑥检测 Δ PTM 中是否存在 δ 与 delta 之差的绝对值小于 β ,如果存在,则判断集合 Δ PTM 包含 delta .
为求蛋白质序列 P 与谱图 S 的匹配分数,需要对式(6)和式(7)进行计算,即求解数组 D 和数组 H .在CUDA-TP算法中, D 和 H 在逻辑上被聚集为数组 E , E 中每个元素包含2个值: D i , j , H i , j .在计算 E i , j 之前,需要得到 E i -1, j , E i , j -1 , E i -1, j -1 这3个值.如图6所示,每次计算一个对角线上的元素,依次向下进行,直至最后1个元素.不难发现,对角线上的元素计算时互相之间是并行的,某个对角线上的元素全部计算完成后,再进行下一个对角线的计算.由此,可以设计并行架构求解数组 E .
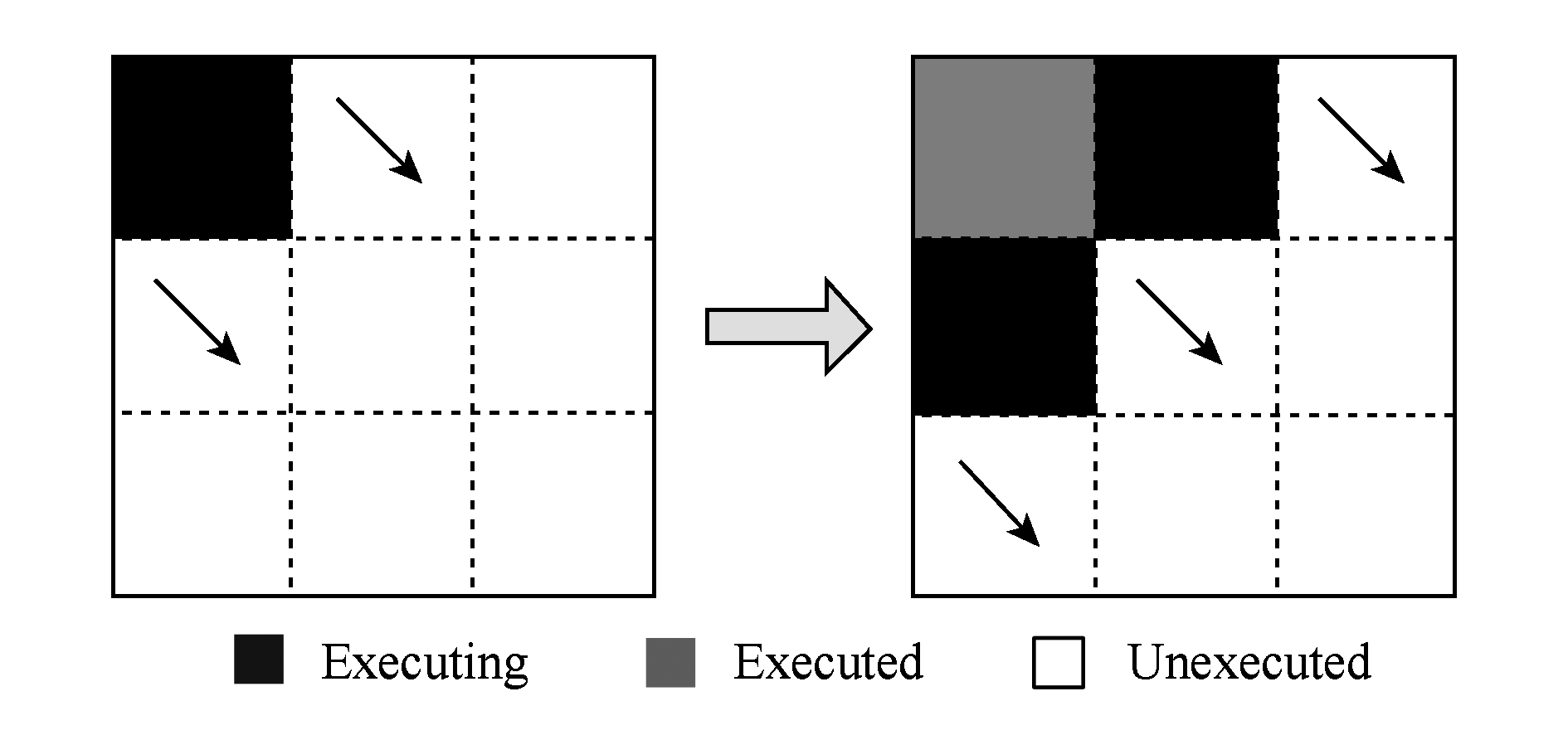
Fig. 6 Execution of CUDA-TP algorithm
图6 CUDA-TP算法的执行顺序
若蛋白质序列 P 的长度为 m ,谱图 S 的谱峰数量为 n ,则数组 E 的元素个数为 nm .当 n 或者 m 变得很大时, E 的元素就会相应的增多,导致要求解的空间很“庞大”,而GPU中同时并行执行的线程数量是受限的,给每个元素指定1个线程显然是不科学的.为了合理地利用GPU性能,可以把 r × c 个元素分为1个计算单元,每个单元分别分配1个线程, r 和 c 根据GPU计算能力来指定大小(本文 r 和 c 均设置为2).线程按照标号顺序计算单元格中的元素,以保证在计算当前元素时其左上部的所有元素是已知的.同时,并行的线程运行在同一个线程块内,这样能够将数组 E 放到GPU的共享存储器中.如图7所示,计算单元 A , B , C 中的元素互不影响,它们是并行的,3个线程同时对其进行计算且每个线程按顺序计算4个元素.
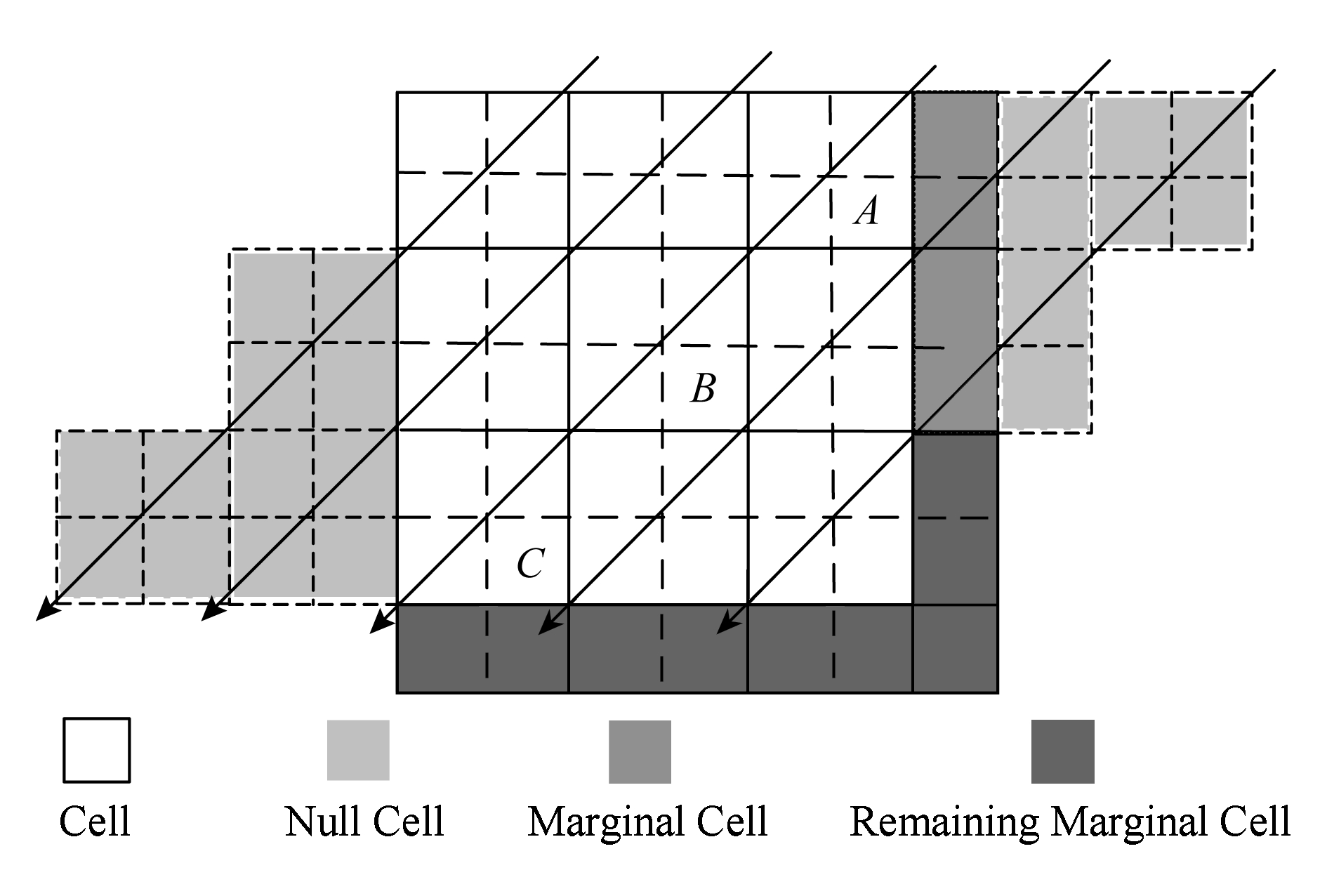
Fig. 7 Parallel processing architecture
图7 并行计算架构
在大多数情况下, n 和 m 不是 r 与 c 的整数倍,本文把不能分配到单元格中的元素称为边界元素.显然,计算单元的最大并行数量 ![]() 但很多时候不能为所有线程分配计算单元.因此,当某个对角线上的计算单元不足 p 时,对不足的空间进行填充并把这些填充进去的元素称为空元素,空元素中没有实际值,只是为了并行架构中的线程能更加有效地识别自身所对应的计算单元.同时,算法只对1个维度的边界填充空元素,所填充的维度取 n 和 m 中的较小值所在的维度,这样能够尽可能地减少空元素数量,提升线程执行效率.填充完成后,边界元素还剩余的部分称为剩余边界元素,由于剩余边界元素的数量必小于( r -1) n +( c -1) m ,远小于数组 E 的元素个数 nm ,所以GPU线程执行完毕后将这部分元素交由CPU端处理.如图7所示,对 m 所在的横向维度填充空元素, r =2和 c =2,并行单元数 p =3,3个线程依次向右进行运算,至第5次GPU结束返回给CPU结果,CPU继续完成剩余边界元素的计算.GPU计算数组 E 的算法如算法3所示:
但很多时候不能为所有线程分配计算单元.因此,当某个对角线上的计算单元不足 p 时,对不足的空间进行填充并把这些填充进去的元素称为空元素,空元素中没有实际值,只是为了并行架构中的线程能更加有效地识别自身所对应的计算单元.同时,算法只对1个维度的边界填充空元素,所填充的维度取 n 和 m 中的较小值所在的维度,这样能够尽可能地减少空元素数量,提升线程执行效率.填充完成后,边界元素还剩余的部分称为剩余边界元素,由于剩余边界元素的数量必小于( r -1) n +( c -1) m ,远小于数组 E 的元素个数 nm ,所以GPU线程执行完毕后将这部分元素交由CPU端处理.如图7所示,对 m 所在的横向维度填充空元素, r =2和 c =2,并行单元数 p =3,3个线程依次向右进行运算,至第5次GPU结束返回给CPU结果,CPU继续完成剩余边界元素的计算.GPU计算数组 E 的算法如算法3所示:
算法3 . 在GPU端计算数组 E .
输入:谱图 a [ n ]、蛋白质序列 b [ m ]、计算单元大小 r 和 c , diag , diag ( δ );
输出:所求数组 E .
① idx ← GetIdx ( blockDim . x , blockIdx . x , blockIdx . y );
② p ←min( n  r , m
r , m  c );
c );
③ for i =0 to r do
④ for j =0 to c do
⑤ ( e i , e j )← GetEIndex ( E , p , idx , i , j );
⑥ if ( e i , e j )≠∅
⑦ E [ e i , e j ]← GetMax ( E , e i , e j , diag , diag ( δ ));  *获取结果并填充进数组 E *
*获取结果并填充进数组 E * 
⑧ end if
⑨ end for
⑩ end for
 return E .
return E .
算法3的行①首先获取当前的线程标号;行②求得最大并行数 p ;行③④表示线程按顺序计算 r × c 个元素;行⑤得到要处理的元素坐标,如果该坐标代表的元素不为空元素,则将数组 E 中此元素的数值更新;最后的行  返回数组 E .需要注意的是,更新数组元素值的函数 GetMax 中的参数 diag 为算法1的结果, diag_delta 即为3.2节所述的 diag ( δ ) , E 包含的数组 D 和 H 值严格按照式(6)和式(7)求解.
返回数组 E .需要注意的是,更新数组元素值的函数 GetMax 中的参数 diag 为算法1的结果, diag_delta 即为3.2节所述的 diag ( δ ) , E 包含的数组 D 和 H 值严格按照式(6)和式(7)求解.
由第1节描述可知,谱图网格中的元素个数为 nm ,这里记为 N ,所允许的最大已知PTM与未知PTM的组合数量 F s × F g 记为 F .计算 diag 的过程中,若直接对每个元素点遍历其左上部区域,时间复杂度为 O ( N 2 ).算法1引入AVL树后,不再需要查找谱图网格,而是根据 d 值搜索整个AVL树,假设谱图网格中有 d ′个不同的 d 值,则一个元素的搜索时间上限为 O ( N lb d ′),因此算法1时间复杂度为 O ( N lb d ′).CPU通过PEI总线与GPU交互数据,本文中的数据传输时间几乎可以忽略不计,因此只对运算的时间复杂度进行分析.在引入并行线程之前,计算 diag ( δ ) 的时间复杂度与计算 diag 类似,同为 O ( N 2 ).引入并行线程之后,假设GPU所有线程块总共可同时运行 p ′个线程,那么时间复杂度将降低至 ![]()
数组填充时,串行程序依次计算数组 E 中的元素,完成 F 个 E 数组的计算需要 O ( NF ).由2.3节可知,CUDA-TP算法将 E 划分为 F  ( r × c )个单元格,每次有 p 个线程同时运行且每个线程在单元格中串行执行,但由于空元素的存在,平均同时运行线程的数量约为 p
( r × c )个单元格,每次有 p 个线程同时运行且每个线程在单元格中串行执行,但由于空元素的存在,平均同时运行线程的数量约为 p  2, GPU执行完毕后最多剩余( r -1) n +( c -1) m 个元素,于是CUDA-TP计算 E 的时间复杂度为
2, GPU执行完毕后最多剩余( r -1) n +( c -1) m 个元素,于是CUDA-TP计算 E 的时间复杂度为
![]()
(8)
因此,质谱匹配的总时间复杂度由 O ( N 2 + FN )变为
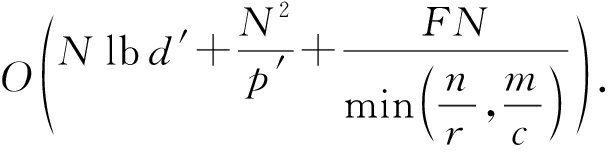
(9)
对谱图 S 来说,要从蛋白质数据库中寻找1个蛋白质 P ,使得它与这个蛋白质的匹配分数最高.蛋白质数据库通常包含很多个蛋白质,让所有蛋白质与谱图 S 进行匹配分值计算,时间开销是巨大的.常用的方法是为每个谱图挑选出 L 个候选蛋白质,然后谱图与这 L 个候选蛋白质计算匹配分数并以最高分值的蛋白质作为鉴定结果.MS-Filter [31] 是目前进行蛋白质过滤很有效的方法(蛋白质过滤问题定义及相关算法参见文献[31]),它为每个蛋白质与谱图 S 计算过滤分数,以分数高低作为是否过滤蛋白质的条件.CUDA-TP通过优化MS-Filter算法3个计算步骤中的步骤2来加速蛋白质过滤,优化后的计算过程:
1) 在低精度下计算谱图与蛋白质的卷积数组;
2) 查找对角线分值大于阈值的候选区域,如果相邻候选区域的最大边界与最小边界值之差小于所有氨基酸中甘氨酸的最小质量75.05,则将这2个区域合并;
3) 在高精度下依次对合并后的候选区域计算卷积数组,如果卷积数组中对角线分值大于设定的阈值,则将阈值更新为此分值,最后的阈值即为蛋白质的过滤分数.
蛋白质的过滤加速体现在步骤2的候选区域合并,通过合并分散的小区域来减少步骤3高精度卷积数组的个数.
CUDA-TP创建 L 个流(stream)对过滤出的候选蛋白质与谱图的匹配分数并行计算,CUDA架构的流并行是粗粒度的并行,它能够使GPU运算的同时与CPU进行数据交换.如图8所示,为每个候选蛋白质分配1个流,流与流之间并行执行.
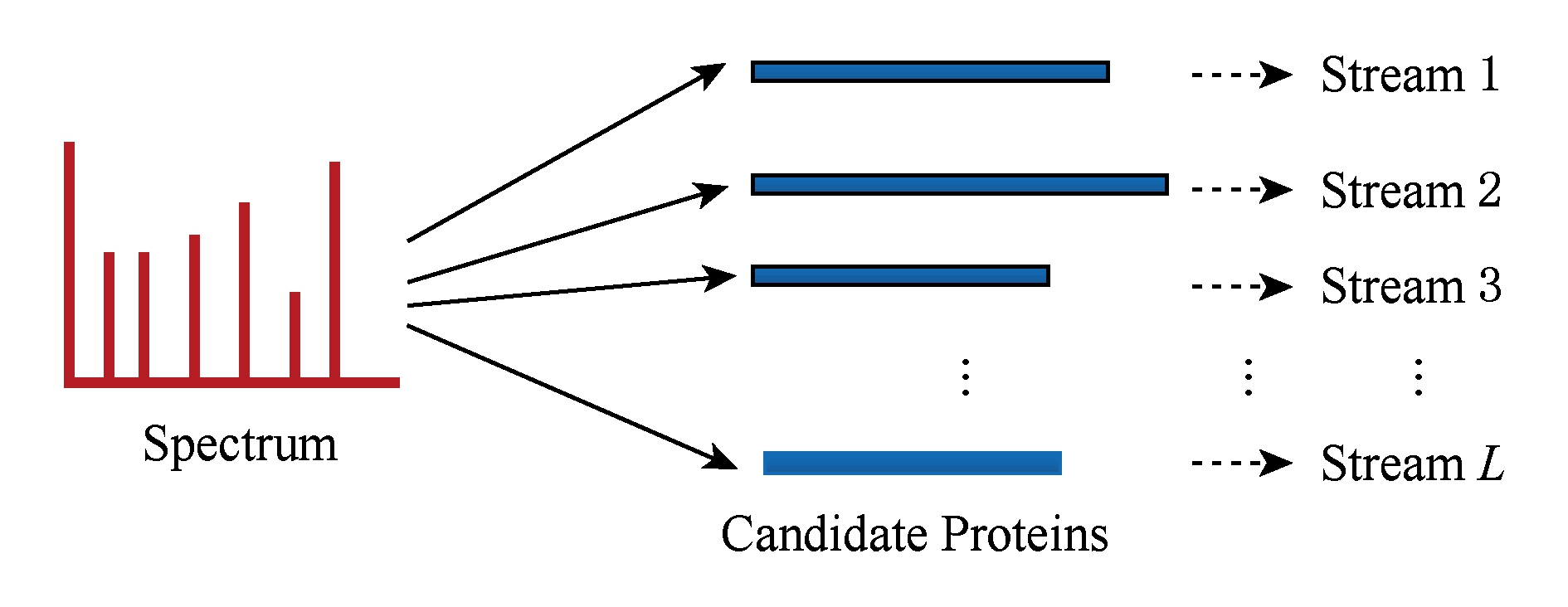
Fig. 8 Stream parallelism for calculating the matching
score between the spectrum and candidate proteins
图8 谱图与候选蛋白质匹配分数计算的流并行
① https: 
 www.ncbi.nlm.nih.gov
www.ncbi.nlm.nih.gov 
② http: 
 www.ionsource.com
www.ionsource.com 
③ http: 
 bix.ucsd.edu
bix.ucsd.edu  projects
projects  msalign
msalign 
本文采用人类细胞蛋白p65 [35] 、大肠杆菌蛋白 [36] (escherichia coli, Ecoli)、人类核心组蛋白(human core histones)H4 [37] 和鼠伤寒沙门氏菌 [38] (salmonella typhimurium, ST)质谱数据来进行实验,所有的蛋白质数据库均来自美国国立生物信息中心NCBI ① .原始质谱数据文件使用ReAdw ② 和MS-Deconv [39] 转化为只包含单同位素谱峰的谱图.
由于TD方法是对完整蛋白质的鉴定,谱峰数量太少会导致匹配分数过低,所以只保留前体质量(precursor mass)大于2500Da且至少包含10个谱峰的谱图 [14] .最终的实验数据集及其分布如表1和图9所示.
Table 1 The Number of Spectra from Four Datasets and the Number of Proteins in the Corresponding Databases
表1 数据集中的谱图数量及数据库中蛋白质个数
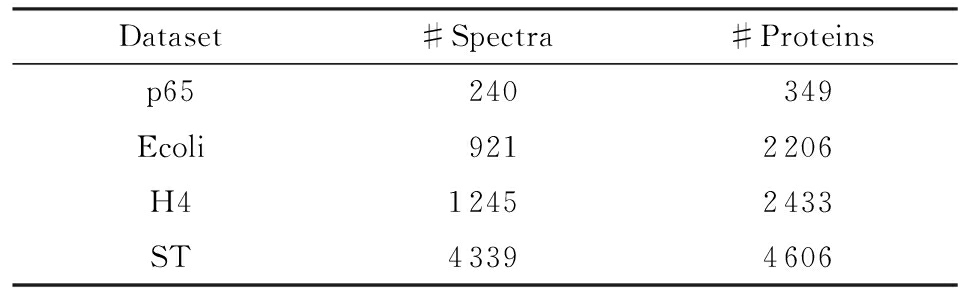
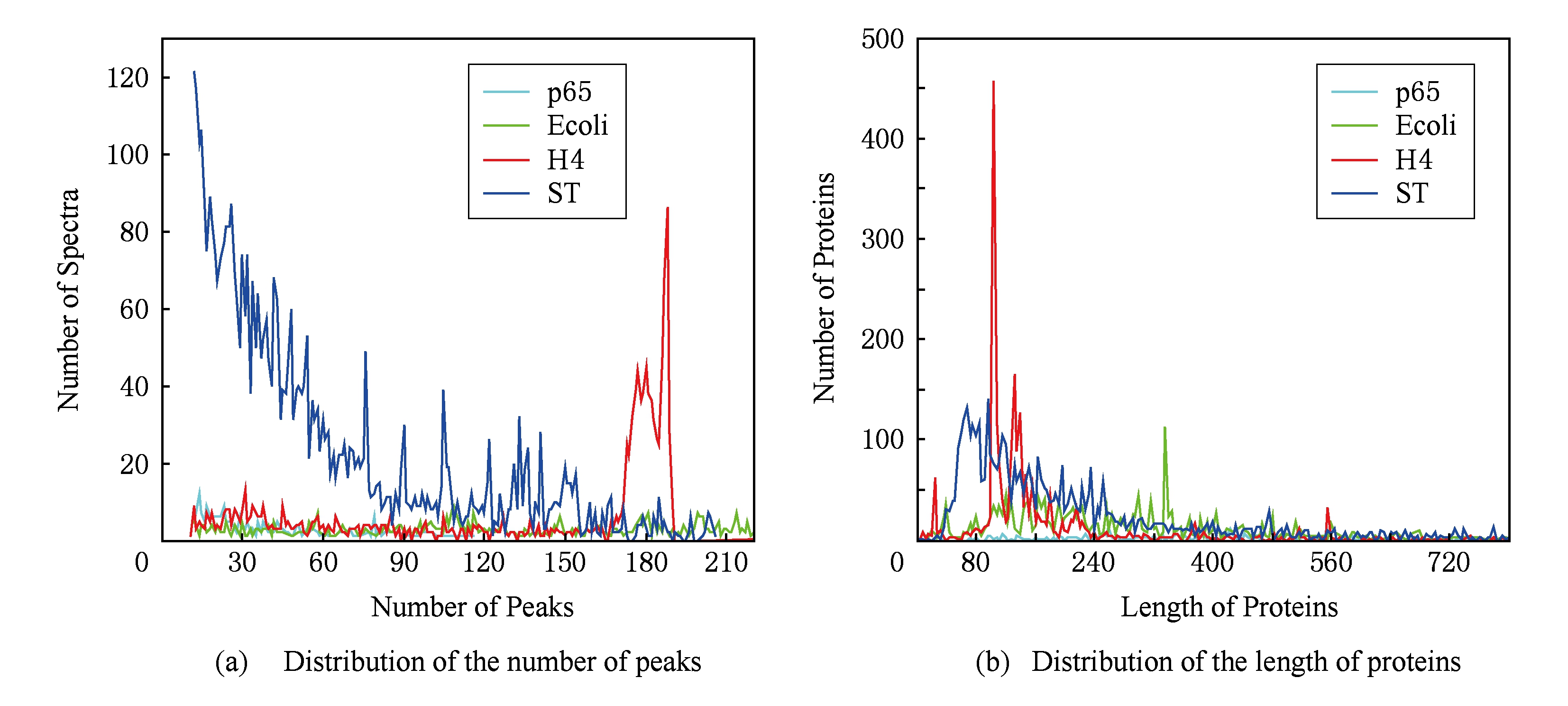
Fig. 9 Distribution of the number of peaks and the length of proteins
图9 谱峰数量和蛋白质长度分布
p65数据集包含240个谱图,Ecoli数据集包含921个谱图,H4和ST分别包含1 245,4 339个谱图,谱图中的谱峰数量分布如图9(a)所示.p65与Ecoli数据集的谱峰较为均匀地分布在20~190之间;ST数据集的谱峰数量大多在20~80之间,占比57.2%,为2 482个;而H4数据集的谱峰数量多数分布在160~200之间,占比57.8%,为720个.
4个实验数据集的蛋白质数据库分别含有349,2 206,2 433,4 606个蛋白质,蛋白质序列长度分布如图9(b)所示.p65蛋白质数据库中的蛋白质长度大多分布在240~480之间,占比60.2%,共211个;ST蛋白质数据库中的蛋白质长度在40~240之间的有2 947个,占整个数据库的64.1%;H4和Ecoli蛋白质数据库中的蛋白质长度多集中在80~340,H4包含1 989个,Ecoli包含1 883个,各自占比为81.4%,83.3%.
CUDA-TP基于谱图比对思想,与MS -Align+ ③ 通过减少搜索谱图网格空间以达到运行时间降低的策略不同,它是串行算法MS-TopDown的并行加速算法.本文通过设置不同的参数 F (常用策略是固定 F g ,改变 F s )和 L 来对CUDA-TP与MS-TopDown的运行时间进行比对,实验环境如表2所示:
Table 2 The Running Environment
表2 实验环境

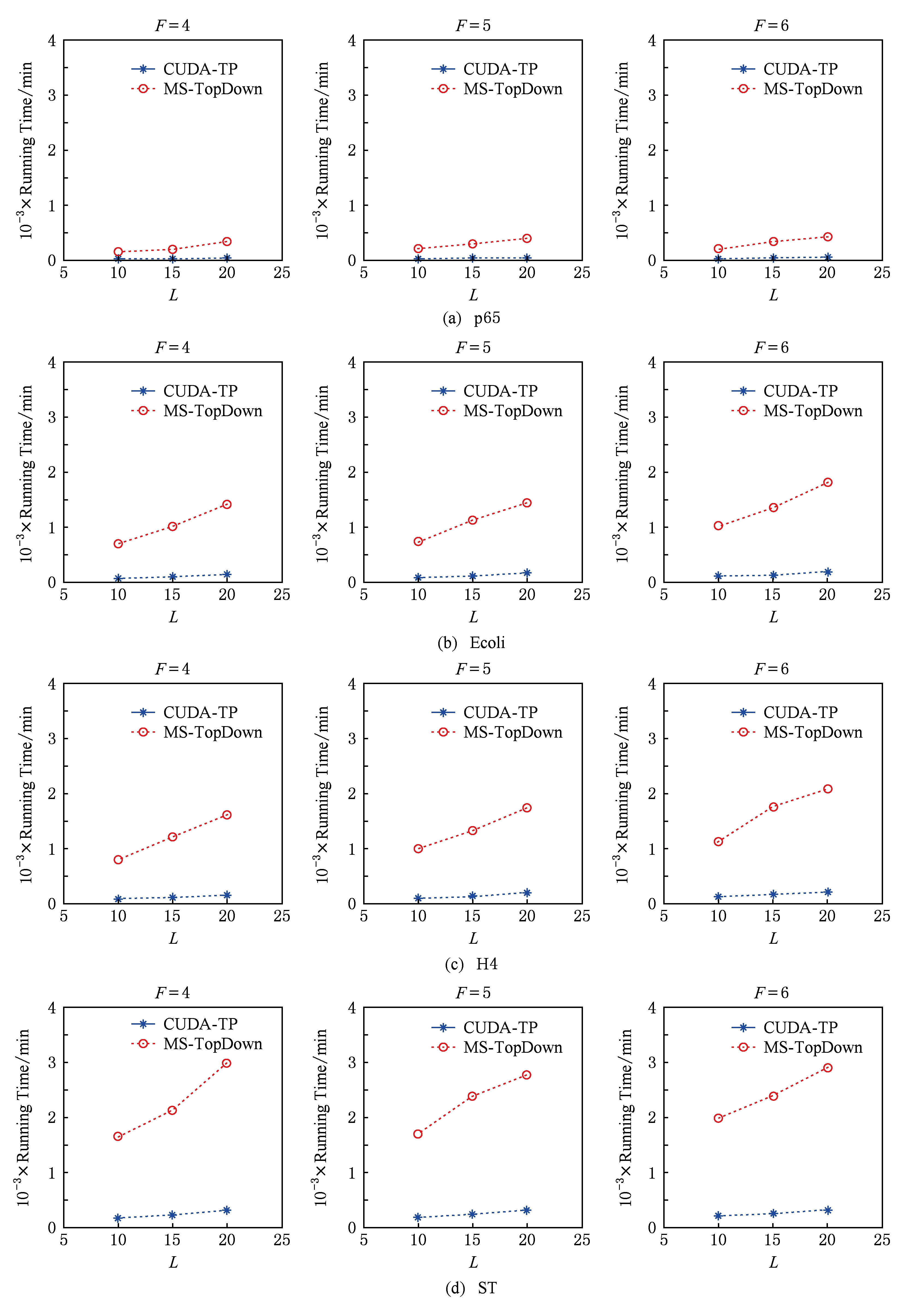
Fig. 10 Running time of CUDA-TP and MS-TopDown on four datasets with different parameters
图10 4个数据集上CUDA-TP与MS-TopDown在不同参数下的运行时间
MS-TopDown没有蛋白质过滤步骤,选用2.5节改进的MS-Filter算法进行蛋白质过滤.MS-Align+从官方网站下载,MS-Align+只提供参数 F 的设置,运行时 L 为软件中的默认参数,因此只对比不同 F 参数下的运行时间.同时,实验采用常用的target-decoy [32-33] 进行FDR控制,所得实验结果FDR值均小于1%.本文首先设定不同的允许最多发生的PTM个数 F 和蛋白质过滤数量 L ,从多角度对比CUDA-TP与MS-TopDown的运行时间,4个数据集的实验结果如图10所示:
在p65数据集上,CUDA-TP平均运行时间为22 min,MS-TopDown平均运行时间为212 min,CUDA-TP速度是MS-TopDown的9.6倍;在Ecoli数据集上,CUDA-TP平均运行时间为110 min,MS-TopDown平均运行时间为1 212 min,CUDA-TP速度是MS-TopDown的11倍;在ST数据集上,CUDA-TP平均运行时间为243 min,MS-TopDown平均运行时间为2 315 min,CUDA-TP速度是MS-TopDown的9.5倍;在H4数据集上,CUDA-TP平均用时139 min,MS-TopDown用时1 405 min,CUDA-TP速度是MS-TopDown的10.1倍.可以看出,虽然质谱数据集ST是H4的将近4倍,但是用时却只是H4的2倍,这是由于H4谱图中谱峰数量与其数据库蛋白质长度普遍比ST的高,导致要求解的谱图网格元素增多,增加了运行时间.
MS-Align+只可以调整 F 的大小, L 默认固定为20,因此本文对比分析了3种方法在不同 F 参数下的运行时间,实验结果如图11所示:
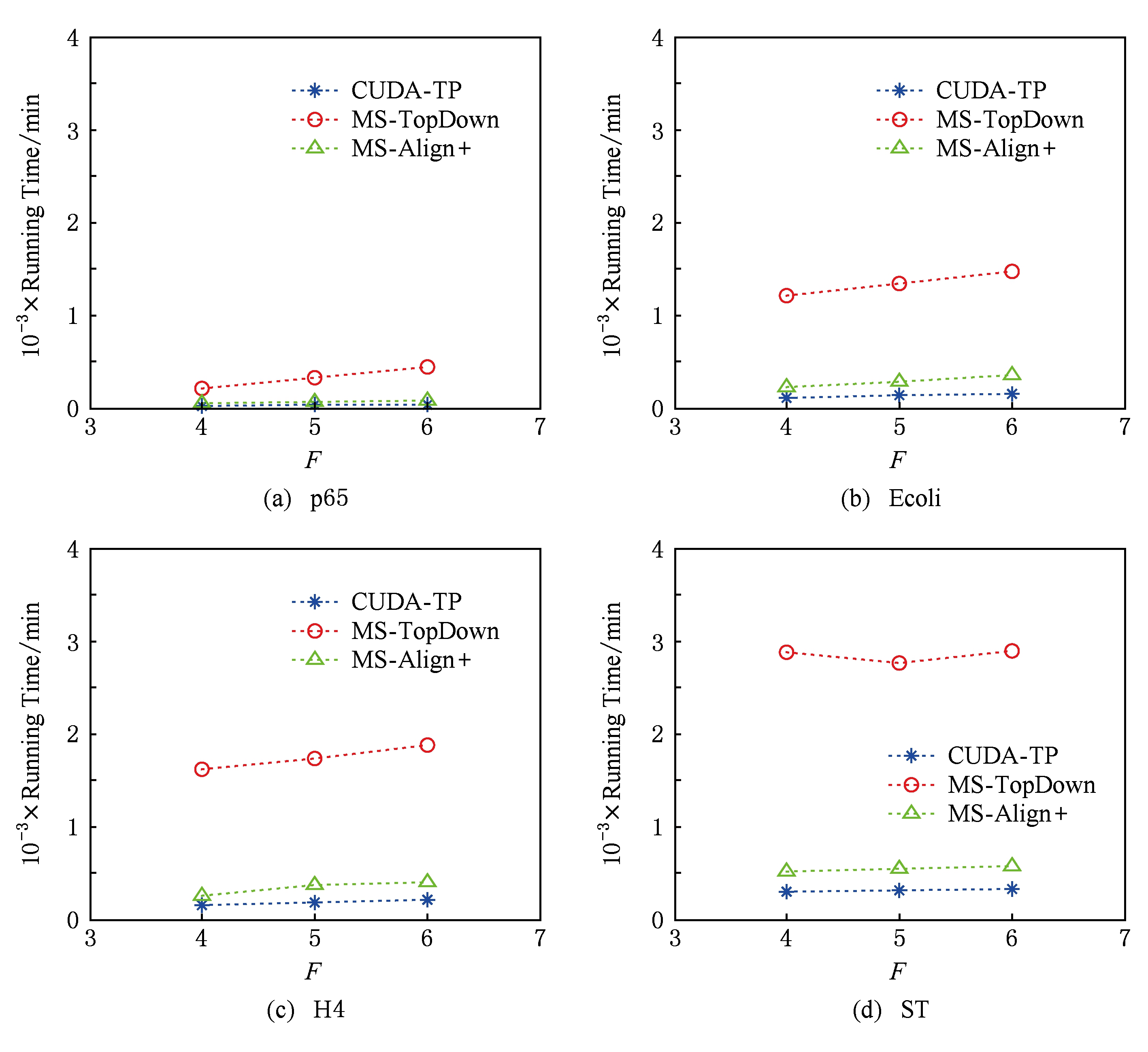
Fig. 11 Running time of three methods on four datasets with different parameters
图11 4个数据集上3种方法在不同参数下的运行时间
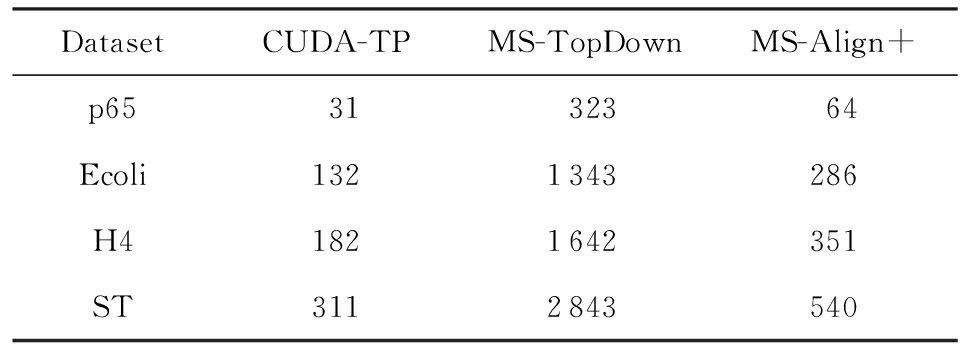
3种方法的平均运行时间在表3中给出,从表3中可以看到CUDA-TP的运行速度约是MS-Align+的2倍,这证明基于谱图比对思想的并行计算方法明显优于通过减少谱图网格搜索空间来加速计算过程的策略.
Table 3 Average Running Time of Three Methods
表3 3种方法平均运行时间 min
并行算法除了运行时间,有时更加关心其运行时的吞吐率.MS-TopDown与MS-Align+是单核CPU 程序,并没有进行多线程优化,这是由于2种方法采用以空间换取时间的策略,单核运行时就几乎达到了电脑资源的占用极限,实验中二者平均内存使用率在90%以上,多核CPU的运行几乎是不可完成的.文献[18]也指出单核MS-Align+运行大规模人类蛋白质质谱数据时,内存需求甚至高达40 GB.而CUDA-TP并行算法可以在显存1 GB的电脑上流畅运行,其内存占用不超过4 GB,因此具有更广的适用性.
① https: 
 github.com
github.com  dqiong
dqiong  CUDA-TP.
CUDA-TP.
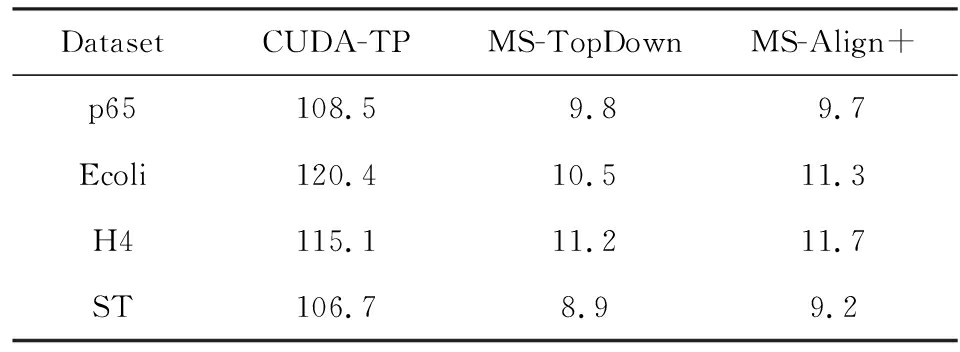
CUDA-TP的时间复杂度已经在2.4节详细给出,3种方法在不同数据集上的吞吐率如表4所示,吞吐率指单位时间内算法执行的计算单元数量.从表4中可以看出CUDA-TP吞吐率约为MS-TopDown和MS-Align+的11倍,这在Ecoli和H4数据上表现尤为明显,说明谱图网格元素的增多虽然增加了运行时间,但吞吐率并没有随着降低.MS-Align+通过减少求取网格的数量来减少计算时间,但吞吐率并没有实质提升.因此,CUDA-TP在运行时间和算法的吞吐率上要明显优于目前的MS-TopDown和MS-Align+方法.
Table 4 Throughput of Three Methods
表4 3种方法的吞吐率 10 -6 cell 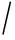 s
s
MS-TopDown在数据集上的执行时间通常要花费大量时间(本文中MS-TopDown在最大数据集上的运行时间在2 d左右),这大大降低了其在蛋白质鉴定中的实用性,而本文提出的基于GPU的蛋白质鉴定并行算法运行速度是其10倍,有效地解决了谱图比对思想应用于大规模数据的弊端,与现有的MS-Align+算法相比具有明显优势,通过上述多种不同的实验测试,验证了CUDA-TP的优秀性能.CUDA-TP源代码托管在github公共服务网站 ① .
当前,“自顶向下”的蛋白质组学飞速发展,已经成为大规模鉴定蛋白质及定位PTM的关键技术,但这些技术的应用算法在运行时间上还存在瓶颈.本文研究了TD策略下的蛋白质鉴定问题,提出了一种新型的基于GPU的完整蛋白质鉴定并行算法CUDA-TP.1)该算法通过流并行和优化MS-Filter来加速蛋白质过滤;2)引入AVL树降低谱图网格中每个元素前驱节点的求取时间;3)在GPU端设计了计算迭代公式的CUDA并行架构.实验结果表明CUDA-TP可以有效地加速完整蛋白质鉴定,与通过减少谱图搜索空间来换取效率的MS-Align+相比具有明显优势.
在TD策略下对完整蛋白质进行鉴定,除了计算蛋白质与谱图的匹配分数,还需要进一步评估匹配结果的统计显著性.因此如何计算匹配分数的同时得到蛋白质与谱图匹配的统计显著性评估结果,并且不降低时间运行效率,这将是我们下一步的研究工作.
参考文献
[1]Nilsson T, Mann M, Asbersold R, et al. Mass spectrometry in high-throughput proteomics: Ready for the big time[J]. Nature Methods, 2010, 7(9): 681-685
[2]Noble W S, MacCoss M J. Computational and statistical analysis of protein mass spectrometry data[J]. PLoS Computational Biology, 2012, 8(1): 291-319
[3]Chait B T. Mass spectrometry: Bottom-up or top-down[J]. Science, 2006, 314(5796): 65-66
[4]Aebersold R, Mann M. Mass spectrometry-based proteomics[J]. Nature, 2003, 422(6928): 198-207
[5]Sun Ruixiang, Luo Lan, Chi Hao, et al. Top-down proteomics: The large-scale proteoform identification[J]. Progress in Biochemistry and Biophysics, 2015, 42(2): 101-114 (in Chinese)(孙瑞祥, 罗兰, 迟浩, 等. “自顶向下(top-down)”的蛋白质组学—蛋白质变体的规模化鉴定[J]. 生物化学与生物物理进展, 2015, 42(2): 101-114)
[6]Wang Haipeng, Fu Yan, Sun Ruixiang, et al. pepReap: A peptide identification algorithm using support vector machines[J]. Journal of Computer Research and Development, 2005, 42(9): 1511-1518 (in Chinese)(王海鹏, 付岩, 孙瑞祥, 等. pepReap: 基于支持向量机的肽鉴定算法[J]. 计算机研究与发展, 2005, 42(9): 1511-1518)
[7]Siuti N, Kelleher N L. Decoding protein modifications using top-down mass spectrometry[J]. Nature Methods, 2007, 4(10): 817-821
[8]Huang Ting, Wang Jingjing, Yu Weichuan, et al. Protein inference: A review[J]. Briefings in Bioinformatics. 2012, 13(5): 586-614
[9]Arnaud C H. Top-down proteomics becomes reality[J]. Chemical & Engineering News, 2013, 91(20): 11-17
[10]Whitelegge J. Intact protein mass spectrometry and top-down proteomic[J]. Expert Review of Proteomics, 2013,10(2): 127-129
[11]LeDuc R D, Taylor G K, Kim Y B, et al. ProSight PTM: An integrated environment for protein identification and characterization by top-down mass spectrometry[J]. Nucleic Acids Research, 2004, 32(Suppl 2): 340-345
[12]Zamdborg L, LeDuc R D, Glowacz K J, et al. ProSight PTM 2.0: Improved protein identification and characteri-zation for top down mass spectrometry[J]. Nucleic Acids Research, 2007, 35(Suppl 2): 701-706
[13]Frank A M, Pesavento J J, Mizzen C A, et al. Interpreting top-down mass spectra using spectral alignment[J]. Analytical Chemistry, 2008, 80(7): 2499-2505
[14]Liu Xiaowen, Sirotkin Y, Shen Yufeng, et al. Protein identification using top-down spectra[J]. Molecular & Cellular Proteomics, 2012, 11(6): 1377-1391
[15]Kou Qiang, Xun Likun, Liu Xiaowen. TopPIC: A software tool for top-down mass spectrometry-based proteoform identification and characterization[J]. Bioinformatics, 2016, 32(22): 3495-3497
[16]Cai Wenxuan, Guner H, Gregorich Z R, et al. MASH suite pro: A comprehensive software tool for top-down proteomics[J]. Molecular & Cellular Proteomics, 2016, 15(2): 703-714
[17]Joshua N A. MSPathFinder: A database search engine for top-down proteomics[CP  OL]. Washington: Pacific Northwest National Laboratory, 2015 [2016-10-11]. http:
OL]. Washington: Pacific Northwest National Laboratory, 2015 [2016-10-11]. http: 
 omics.pnl.gov
omics.pnl.gov  software
software  pathfinder
pathfinder
[18]Sun Ruixiang, Luo Lan, Wu Long, et al. pTop 1.0: A high-accuracy and high-efficiency search engine for intact protein identification[J]. Analytical Chemistry, 2016, 88(6): 3082-3090
[19]NVIDIA Corporation. NVIDIA CUDA Programming Guide, version 7.5: Reference Description[OL]. [2016-10-11]. http: 
 docs.nvidia.com
docs.nvidia.com  cuda-
cuda-  cuda-c-programming-guide
cuda-c-programming-guide  index.html
index.html
[20]Li Tao, Liu Xuechen, Zhang Shuai, et al. Parallel support vector machine training with hybrid programming model[J]. Journal of Computer Research and Development, 2015, 52(5): 1098-1108 (in Chinese)(李涛, 刘学臣, 张帅, 等. 基于混合编程模型的支持向量机训练并行化[J]. 计算机研究与发展, 2015, 52(5): 1098-1108)
[21]Li Zhe, Li Zhanshan, Li Ying. A constraint network model and parallel arc consistency algorithms based on GPU[J]. Journal of Computer Research and Development, 2017, 54(3): 514-528 (in Chinese)(李哲, 李占山, 李颖. 基于GPU的约束网络模型和并行弧相容算法[J]. 计算机研究与发展, 2017, 54(3): 514-528)
[22]Zhai Yantang, Tu Qiang, Lang Xianyu, et al. Research of CUDA-based acceleration of MS-Alignment for identification of post-translation modifications[J]. Appication Research of Computers, 2010, 27(9): 3409-3414 (in Chinese)(翟艳堂, 涂强, 郎显宇, 等. 基于CUDA的蛋白质翻译后修饰鉴定MS-Alignment算法加速研究[J]. 计算机应用研究, 2010, 27(9): 3409-3414)
[23]Zhang Jian, McQuillan I, Wu Fangxiang. Parallelizing peptide-spectrum scoring using modern graphics processing units[C] 
 Proc of the 1st IEEE Int Conf on Computational Advances in Biological and Medical Sciences. Piscataway, NJ: IEEE, 2011: 208-213
Proc of the 1st IEEE Int Conf on Computational Advances in Biological and Medical Sciences. Piscataway, NJ: IEEE, 2011: 208-213
[24]Wu Fangxiang, Gagné P, Droit A, et al. RT-PSM, a real-time program for peptide-spectrum matching with statistical significance[J]. Rapid Commu-nications in Mass Spectrometry, 2006, 20(8): 1199-1208
[25]Baumgardner L A, Shanmugam A K, Lam H, et al. Fast parallel tandem mass spectral library searching using GPU hardware acceleration[J]. Journal of Proteome Research, 2011, 10(6): 2882-2888
[26]Lam H, Deutsch E W, Eddes J S, et al. Building consensus spectral libraries for peptide identification in proteomics[J]. Nature Methods, 2008, 5(10): 873-875
[27]Li You, Chi Hao, Xia Leihao, et al. Accelerating the scoring module of mass spectrometry-based peptide identification using GPUs[J]. BMC Bioinformatics, 2014, 15(1): 121-131
[28]Sandes E F O, Miranda G, Martorell X, et al. CUDAlign 4.0: Incremental speculative traceback for exact chromosome-wide alignment in GPU clusters[J]. IEEE Trans on Parallel & Distributed Systems, 2016, 27(10): 2838-2850
[29]Liu Yongchao, Wirawan A, Schmidt B. CUDASW++ 3.0: Accelerating smith-waterman protein database search by coupling CPU and GPU SIMD instructions[J]. BMC Bioinformatics, 2013, 14(14): 117-127
[30]Jain C, Kumar S. Fine-grained GPU parallelization of pairwise local sequence alignment[C] 
 Proc of the 21st Int Conf on High Performance Computing (HiPC). Piscataway, NJ: IEEE, 2014: 1-10
Proc of the 21st Int Conf on High Performance Computing (HiPC). Piscataway, NJ: IEEE, 2014: 1-10
[31]Alessandro M. Protein identification from top-down mass spectra, a fast filtering algorihm[D]. Padova, Umbria, Italy: Università degli Studi di Padova, 2011
[32]Elias J E, Gygi S P. Target-decoy search strategy for increased confidence in large-scale protein identifications by mass spectrometry[J]. Nature Methods, 2007, 4(3): 207-214
[33]Reiter L, Claassen M, Schrimpf S P, et al. Protein identification false discovery rates for very large proteomics data sets generated by tandem mass spectrometry[J]. Molecular & Cellular Proteomics, 2009, 8(11): 2405-2417
[34]Pevzner P A, Dancik V, Tang C L. Mutation-tolerant protein identification by mass spectrometry[J]. Journal of Computational Biology, 2000, 7(6): 777-787
[35]Savaryn J P, Skinner O S, Fornelli L, et al. Targeted analysis of recombinant NF kappa B (RelA  p65) by denaturing and native top down mass spectrometry[J]. Journal of Proteomics, 2016, 134: 76-84
p65) by denaturing and native top down mass spectrometry[J]. Journal of Proteomics, 2016, 134: 76-84
[36]Cannon J R, Cammarata M, Robotham S A, et al. Ultraviolet photodissociation for characterization of whole proteins on a chromato-graphic time scale[J]. Analytical Chemistry, 2011, 86(4): 2185-2192
[37]Tian Zhixin, ![]() Zhao Rui, et al. Enhanced top-down characterization of histone post-translational modifications[J]. Genome Biology, 2012, 13(10): R86
Zhao Rui, et al. Enhanced top-down characterization of histone post-translational modifications[J]. Genome Biology, 2012, 13(10): R86
[38]Tsai Y S, Scherl A, Shaw J L, et al. Precursor ion independent algorithm for top-down shotgun proteomics[J]. Journal of the American Society for Mass Spectrometry, 2009, 20(11): 2154-2166
[39]Liu Xiaowen, Inbar Y, Dorrestein P C, et al. Deconvolution and database search of complex tandem mass spectra of intact proteins: A combinatorial approach[J]. Molecular & Cellular Proteomics, 2010, 9(12): 2772-2782
Duan Qiong 1 , Tian Bo 1 , Chen Zheng 1 , Wang Jie 1,2 , and He Zengyou 1,2
1 ( School of Software , Dalian University of Technology , Dalian , Liaoning 116620) 2 ( Key Laboratory for Ubiquitous Network and Service Software of Liaoning Province ( Dalian University of Technology ), Dalian , Liaoning 116620)
Abstract Identifying proteins and their post-translational modifications are critical to the success of proteomics. Recent advances in mass spectrometry (MS) instrumentation have made it possible to generate high-resolution mass spectra of intact proteins. The existing algorithms for identifying proteins from top-down MS data are able to achieve good performance with respect to protein-spectrum matching precision and prediction accuracy of PTM locations, but their efficiencies in terms of running time are still far from satisfactory. Graphics processing unit (GPU) can be applied to parallelize large-scale replication computations and reduce the running time of serial programs. Based on compute unified device architecture (CUDA), this paper proposes an algorithm called CUDA-TP for computing alignment scores between proteins and mass spectra. Firstly, CUDA-TP uses the optimized MS-Filter algorithm to quickly filter out proteins in the database that cannot possibly attain high score for a given mass spectrum, thus only a small number of candidate proteins are obtained. Then, an AVL tree is introduced into the algorithm to speed up the computation of protein-spectrum matching. Multi-thread technique on GPU is applied to get the previous diagonal points of all nodes in the spectra grid created from mass spectra and proteins as well as the final array. Meanwhile, this algorithm utilizes target-decoy approach to control false discovery rate (FDR) of proteins and mass spectral matching results. Experimental results demonstrate that CUDA-TP can significantly accelerate protein identification such that its running time is about 10 times and 2 times faster than that of MS-TopDown and MS-Align+. To our knowledge, there are still no existing methods in the literature that can perform protein identification from top-down spectra using CUDA architecture. The source codes of the algorithm are available at https: 
 github.com
github.com  dqiong
dqiong  CUDA-TP.
CUDA-TP.
Key words top-down proteomics; protein identification; graphics processing unit(GPU); compute unified device architecture(CUDA); spectral alignment
中图法分类号 TP391
通信作者 : 何增有(zyhe@dlut.edu.cn)
This work was supported by the National Natural Science Foundation of China (61572094) and the Fundamental Research Funds for the Central Universities (DUT14QY07).
修回日期: 2017-05-03
基金项目 : 国家自然科学基金项目(61572094);中央高校基本科研业务费专项资金(DUT14QY07)

收稿日期 : 2017-02-21;
Duan Qiong , born in 1990. Master candidate. His main research interests include data mining, bioinformatics, parallel computing.

Tian Bo , born in 1992. Master candidate. Her main research interests include machine learning, bioinformatics.

Chen Zheng , born in 1994. Master candidate. His main research interests include machine learning, data mining.

Wang Jie , born in 1979. PhD. Associate professor. Member of CCF. His main research interests include parallel computing, parallel architecture.

He Zengyou , born in 1976. PhD. Professor, PhD supervisor. Senior member of CCF. His main research interests include bioin-formatics, data mining, machine learning.