刘 佩 1,2 蒋梓逸 1 曹 袖 1,2
1 (复旦大学计算机科学与技术学院 上海 201203) 2 (网络信息安全审计与监控教育部工程研究中心(复旦大学) 上海 200433) (13210240020@fudan.edu.cn)
摘 要 在分布式存储系统中,如何优化失效数据的修复时间以保证系统的高可靠性,已引起了人们的广泛关注.近几年的研究发现修复过程中不同的节点选择机制对数据的再生时间产生很大的影响,已有工作提出了单节点失效场景下的节点选择SPSN (select provider select newcomer)算法,系统中往往存在多个节点同时修复的情况,此时,SPSN算法巨大的时空开销使得数据的再生时间不再最优.对已有真实系统的失效数据及原因进行统计;基于已有算法特点和修复模型,提出了具有更优的多节点选择B-WSJ(bandwidth based weak and strong judgement)算法.为了更好地描述算法,对带宽中节点的关系进行分类,算法利用节点关系分别实现了修复模型中目标节点的浅度和深度判断,并加入一定的预处理和剪枝策略,最终快速选择出具有较优带宽的节点集合.为了评估B-WSJ算法性能,使用Waxman算法产生网络拓扑,依据FTA(failure trace archive)网站所给的真实系统的节点失效模型进行多次实验,仿真结果表明:B-WSJ算法使得节点修复性能得到了很大的提升.
关键词 分布式存储系统;数据修复;再生时间;多节点失效;节点选择
随着云计算和“互联网+”应用的普及,分布式存储系统在各行各业中得到广泛的应用,用户访问不良特征和系统软硬件的错误导致节点的失效非常之多.Kondo等人 [1] 跟踪27个不同规模系统在一段时间内的节点失效状况,并给出了的真实失效数据集FTA(failure trace archive),如微软公司的桌面计算机系统数据集Microsoft99、P2P系统PlanetLab的数据集、高性能计算机PNNL等.本文通过用Mysql和Matlab对所得到的数据进行分析和统计得到云存储中节点的失效情况,经过归一化处理得到平均每个系统每周内的失效率为60.29%.从FTA中可以看出节点的失效率是非常高的,如何保证系统的可靠性是一项非常重要的课题.
为了提高分布式存储系统的可靠性,系统通常引入良好的数据冗余机制和数据修复策略.经典的冗余方式为副本机制 [2] ,例如HDFS [2] 系统和Ceph [3] 系统.在大数据时代,因纠删码(erasure coding)比副本机制具有更低的存储成本,广泛应用于实际系统中 [4-5] .当系统发生节点失效时,保证持续的可靠性,系统需要将失效节点上的数据重新修复到新的节点上.修复时提供数据下载的存活节点称为供应节点,修复时存储再生数据的新节点称为新生节点.传统纠删码方式的失效数据修复需要先将源文件恢复出来,因此会引入不必要的修复带宽开销 [6] .在此基础之上,Dimakis等人 [7] 通过研究节点存储开销和修复带宽开销之间的关系,提出了再生码,其可以下载比纠删码更少的数据块把失效的数据再生出来.在拥有相似的存储效率的情况下,再生码可以很好地降低数据修复时的修复带宽(数据传输量) [8] .
然而降低修复过程中链路上数据传输量,并不意味着降低数据的修复时间(也叫再生时间).假设在分布式存储系统中,节点失效后数据在传输的同时进行修复,因此节点的计算能力等可以忽略,数据的修复时间由瓶颈带宽决定.每条链路的数据修复时间由数据量和带宽大小的商计算得出,则整个再生修复过程中数据修复时间由最大的单条链路修复时间决定.如图1所示,我们需要选择任意2个节点来传输数据给节点1,从而修复出失效节点上的数据.节点4传输给节点1的数据量为64 MB,传统的方式考虑降低链路上传输的数据量 [7,9] .图1(a)将节点3传给节点1的数据减少为32 MB,此时数据的修复时间为 ![]() 即25.6 s.当选择节点2和节点4时,图1(b)中表示数据的修复时间为
即25.6 s.当选择节点2和节点4时,图1(b)中表示数据的修复时间为 ![]() 即17.07 s.实际系统中由于其他背景应用的竞争或同一节点的邻接带宽之间互相影响,链路的可用带宽具有异构性.因此在数据修复时,不同节点的选择对于数据的修复时间有很大的影响.
即17.07 s.实际系统中由于其他背景应用的竞争或同一节点的邻接带宽之间互相影响,链路的可用带宽具有异构性.因此在数据修复时,不同节点的选择对于数据的修复时间有很大的影响.

Fig. 1 The performance of data repair progress with different methods
图1 数据修复过程中不同优化方法的性能
存储系统的修复过程中默认参与修复的节点已经给定,传统的算法包括具有随机性的BHS(blind helper selection)算法和SHS [10] (static helper selection)算法.Gong等人 [11] 首次提出了单个节点失效场景下的最优节点选择机制SPSN(select provider select newcomer).其本质为贪心算法,对已有带宽进行排序之后,优先选择带宽较大的节点进行传输数据,从而降低了数据的修复时间.
理论研究和实际系统中,往往存在多个节点同时修复(也叫延迟修复)的情况.此时SPSN算法由于具有串行选择的特征而不再最优.随着系统中节点失效规模的扩大,这将给数据修复带来很大的时间开销和空间开销.基于这些问题,本文提出了多节点失效场景下的节点选择机制B-WSJ(bandwidth based weak and strong judgement),其对节点关系的运算进行建模,利用此模型并行地进行新生节点的强弱判断,在很大程度上优化了多节点失效时的数据修复时间.实验结果表明B-WSJ较SPSN算法有很大的性能提升.
Ahmad等人 [10] 研究在什么条件下,再生码修复时对节点进行动态选择优于随机选择.本文提出了一个FR(family repair)模型,并分析得到在某些情况下,应用此节点选择机制的数据修复比随机选择能够获得更低的存储开销和修复带宽开销.Ahmad等人 [12] 继续针对本地修复再生码(locally repairable regenerating codes, LRRC)提出了动态供应节点选择机制(dynamic helper selection, DHS),并分析在特定的编码状况下,DHS节点选择机制比SHS算法和BHS算法具有更低的存储开销和带宽开销.
Gong等人 [11] 针对单节点失效场景提出了最优节点选择算法SPSN,其特征为优先选取带宽较大的节点作为供应节点和新生节点,本文分别探讨了在固定的修复带宽和弹性修复带宽场景下的节点选择机制.研究结果表明SPSN算法较随机选择算法有很大的性能提升.齐凤林等人 [13] 在此基础上,将节点的计算能力考虑进来,提出了不同拓扑模型上的供应节点的选择,结果表明节点的选择机制对修复性能具有较好的性能提升.Jia等人 [14] 考虑节点之间的实际物理链路,将同时选择供应节点和节点传输数据的路由路径建模成整数线性规划问题,并提出了近似最优解.
以上的研究针对单节点失效场景,然而理论研究和实际系统均表明多节点失效的延迟修复非常常见.在实际存储系统 [15] 中,由于软硬件错误或用户不良的访问需求等,节点的性能相差很大.Shen等人 [16] 利用Lyapunov方法,根据失效节点的等待时间和网络拓扑中的可用带宽,确定延迟修复何时开始.此研究成果表明,与逐个修复相比,延迟修复可以很好地降低系统的再生时间.在Wuala [17] ,Total Recall [18] 等实际系统中,当节点失效的个数达到设定的阈值时,失效数据才开始再生;因此多节点失效的延迟修复是一种非常常见的现象.Hu等人 [19] 基于单节点失效时修复的性能,首次提出了多节点失效场景下的合作修复编码(mutually cooperative recovery, MCR).理论证明,与单节点失效时的MSR码和MBR码相比,MCR码消耗更小的存储成本和修复带宽.为了进一步降低修复带宽,Shum等人 [20] 基于合作修复编码,应用信息流图的最大流最小割定理得到关于修复带宽和节点存储量的权衡曲线,满足此曲线上的编码方式被称为线性合作再生码.曲线上2个极点分别为存储开销最低的编码(minimum-storage cooperative regenerating, MSCR) [21] 和修复带宽最小的编码(minimum-bandwidth cooperative regenerating, MBCR).
已有的延迟修复过程中,SPSN算法的性能不再最优.随着系统中节点失效规模的扩大,这将给数据修复带来很大的时间开销和空间开销.
系统中文件的存储方式为( n , k , d ),文件被切分成 k 个数据块,通过某种编码方式,放置到 n 个节点中;当分布式存储系统中的节点失效时,系统需要从 d 个存活节点中下载信息准备恢复失效节点上的数据.假设文件存储方式为 (4,2,2)MDS码,即文件通过编码成块放置到4个节点上,文件的冗余度为2的网络拓扑如图2(a)所示,数据修复过程中供应节点只传输数据给新生节点,新生节点不但从供应节点下载数据,而且需要传输数据给其他新生节点.因此拓扑网络并没有展示新生节点到供应节点的传输带宽和供应节点之间的传输带宽.图2(a)中直线上的数字表示任意2个节点之间的可用带宽 C ,其可以由系统的主节点获取并满足 C ~U(0.3,120) [22] ,单位为Mbps [11] .任意节点之间链路通过公式 ![]() 计算得到传输数据量为64 MB [7] .当2个节点失效时,需要从3个候选新生节点中选择出2个节点作为新生节点,并从剩下3个存活节点中为每个新生节点选择2个供应节点.
计算得到传输数据量为64 MB [7] .当2个节点失效时,需要从3个候选新生节点中选择出2个节点作为新生节点,并从剩下3个存活节点中为每个新生节点选择2个供应节点.
SPSN算法将所有的带宽进行排序 [11] ,当修复第1个失效节点上的数据时,此算法依据节点的入度信息选择了具有较大带宽集合的节点4作为新生节点,节点5和节点6作为供应节点,修复时间为 ![]() 修复第2个失效节点时,继续选择了具有较大带宽集合的节点3作为新生节点,节点1和节点6作为供应节点,修复时间为
修复第2个失效节点时,继续选择了具有较大带宽集合的节点3作为新生节点,节点1和节点6作为供应节点,修复时间为 ![]() 因此图2(b)选择出节点集合的数据修复时间约为14.89 s.如果新生节点之间互相传输信息,则供应节点给每个新生节点传输数据量可以得到减少,从而有效地降低了链路中的数据冗余.B-WSJ算法基于此思想,考虑新生节点之间的带宽,同时选择具有较大带宽的供应节点和新生节点.最终得到的较优带宽集合的节点2和节点3作为新生节点,节点1和节点6作为供应节点.此时图2(c)选择出节点集合的数据修复时间为12.19 s.已有的多节点失效场景下,默认随机选择新生节点来修复失效的数据,即BHS算法;如图2(d)选择节点2和节点4作为新生节点,节点1和节点6作为供应节点,修复时间为
因此图2(b)选择出节点集合的数据修复时间约为14.89 s.如果新生节点之间互相传输信息,则供应节点给每个新生节点传输数据量可以得到减少,从而有效地降低了链路中的数据冗余.B-WSJ算法基于此思想,考虑新生节点之间的带宽,同时选择具有较大带宽的供应节点和新生节点.最终得到的较优带宽集合的节点2和节点3作为新生节点,节点1和节点6作为供应节点.此时图2(c)选择出节点集合的数据修复时间为12.19 s.已有的多节点失效场景下,默认随机选择新生节点来修复失效的数据,即BHS算法;如图2(d)选择节点2和节点4作为新生节点,节点1和节点6作为供应节点,修复时间为 ![]() 约25.6 s.
约25.6 s.
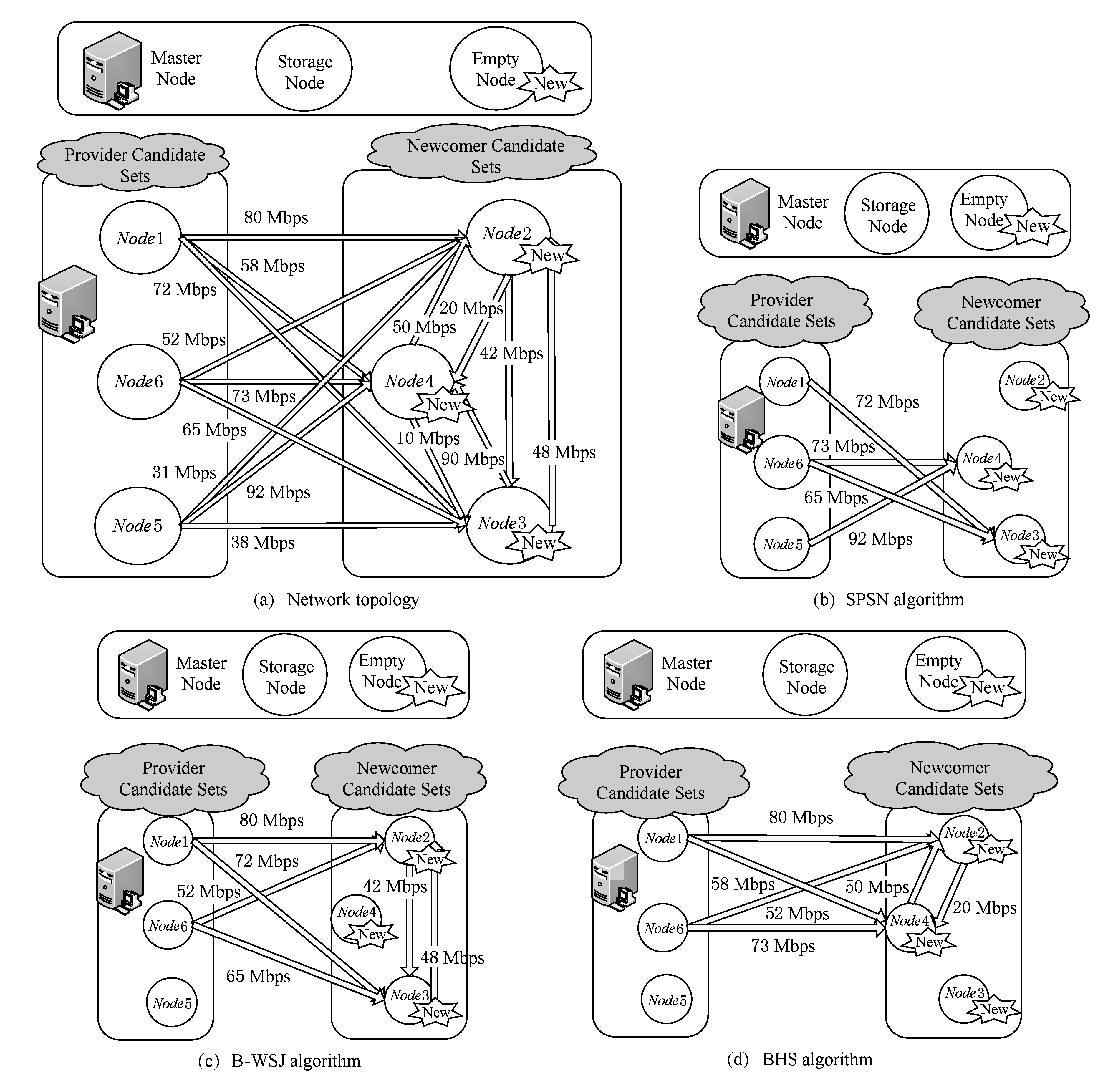
Fig. 2 Example of node selection algorithm
图2 节点选择算法示例
从图2可知,节点选择机制对于数据的修复性能具有很大的影响,已有的节点选择算法在多节点修复场景下具有很大的局限性.首先,SPSN算法仅仅考虑供应节点和新生节点之间带宽的选择,而没有考虑到新生节点之间带宽的选择.这将使得新生节点之间的带宽在后续多节点修复过程中造成性能瓶颈;其次,SPSN算法串行选择节点,使得数据再生过程中产生很多冗余信息,增加了网络的负担;最后,SPSN算法由于其具有串行贪心选择的特征,随着系统中节点失效规模的扩大,这将给数据修复带来很大的时间开销和空间开销.
基于这些问题,本文提出了多节点失效场景下的节点选择机制B -WSJ,主要贡献有4个方面:1)算法对带宽中节点的关系进行分类,并在操作中将已有算法所忽略的节点关系存储起来;2)算法分为浅度和深度判断,逐层过滤,去掉冗余信息,浅度判断中加入了已有算法忽略新生节点信息;3)算法继续对弱判断结果进行强判断操作,找出两两相连的 r 个节点,随着失效节点规模增大,这将具有很大的挑战性;4)算法中加入了大量的预处理和剪枝思想,从而有效地降低算法的时空复杂度.实验结果表明,B-WSJ较SPSN算法有很大的性能提升.下面我们对算法进行详细的描述,并进行多维度的分析和验证.
分布式存储系统利用一定的通信技术,将文件分布到物理位置独立的服务器中 [4] ,最终提供相应的接口给用户端上传、下载或更新.
定义1 . 网络拓扑.实际系统中网络拓扑结构有星型、树形、网状等,基于已有的研究,不失一般性,本文将网络拓扑抽象成overlay结构,记为 G ( V , E ).其中:
1) V = V p ∪ V f ∪ V n . V 为所有节点的集合; V p 为存活节点的集合; V f 表示失效节点的集合; V n 表示空闲的节点集合,此处的空闲是指相对于目标文件空闲.
2) E ={ C ( u , v )| u ∈ V p ∪ V n , v ∈ V }. E 表示网络中所有带宽.实际分布式存储系统中,块服务器间歇性的向主节点发送信息,数据中心的链路带宽可以由主节点获取 [11,17] .根据文献[22]可知带宽满足 C ( u , v )~U[0.3,120].
定义2 . 链路上节点之间关系.网络中某节点 w ,我们对其邻居节点关系记录如下:
1) 其下游的邻居节点集合被记作 T ( w ),集合中的元素个数记为 count + T ( w ).即对于拓扑中任意节点 v ∈ T ( w ),存在一条从节点 w 到节点 v 链路带宽;
2) 其上游的邻居节点如果属于集合 V n ,即候选新生节点集合,我们将这些邻居节点的集合记为 H n ( w ),集合中的元素个数记为 count + H n ( w ).即对于拓扑中任意节点 v ∈ H n ( w ),存在一条从节点 v 到节点 w 链路带宽;
3) 其上游的邻居节点如果属于集合 V p ,即候选供应节点集合,我们将这些邻居节点的集合记为 H p ( w ),集合中的元素个数记为 count + H p ( w ).即对于拓扑中任意节点 v ∈ H p ( w ),存在一条从节点 v 到节点 w 链路带宽;
4) 既为其上游邻居节点,也为下游邻居节点集合记为 HT ( w ),集合中的元素个数记为 count + HT ( w ).即对于拓扑中任意节点 v ∈ HT ( w ),既存在一条从节点 v 到节点 w 链路带宽,也存在一条从节点 w 到节点 v 链路带宽.
定理1 . 假设集合 ![]() 有
有 ![]() 即
即 ![]() 若条件成立:∀
若条件成立:∀ ![]() 且
且 ![]() 则此时 S 个节点两两相连,即这些节点构成有向完全图,记作 DCG S .
则此时 S 个节点两两相连,即这些节点构成有向完全图,记作 DCG S .
证明.
① 当 S =1时,假设这个节点为 v 1 ,很明显1个节点两两相连,结论是成立的;
② 当 S = k 时( k ≥1),则 ![]() ∀
∀ ![]() 假设这 k 个节点两两相连,结论成立.
假设这 k 个节点两两相连,结论成立.
③ 当 S = k +1时, ![]() 且
且 ![]() ∀
∀ ![]() count + T ( v i )= k , count + H n ( v i )+ count + H p ( v i )= k .
count + T ( v i )= k , count + H n ( v i )+ count + H p ( v i )= k .
下面我们用反证法来证明这 k 个节点是两两相连的.由于 v 1 , v 2 ,…, v k 节点两两相连,首先我们假设 v k +1 至少与 ![]() 中某个节点不是两两相连的.因为
中某个节点不是两两相连的.因为 ![]() 且
且 ![]() 则 v k +1 只能
则 v k +1 只能 ![]() 中某些节点相连.由于假设中 v k +1 至少与
中某些节点相连.由于假设中 v k +1 至少与 ![]() 中某个节点不是两两相连,则 count + T ( v i )< k 或者 count + H n ( v i )+ count + H p ( v i )< k .这与已知条件是违背的,因此假设不成立,即这 k +1个节点是两两相连的.定理得证.
中某个节点不是两两相连,则 count + T ( v i )< k 或者 count + H n ( v i )+ count + H p ( v i )< k .这与已知条件是违背的,因此假设不成立,即这 k +1个节点是两两相连的.定理得证.
证毕.
文件以( n , k , d )的编码方式存储到此拓扑网络中.存储模型可以描述为源文件从虚拟节点VS发出,系统首先将其均匀分成 k 块;然后经过某种编码方式将这 k 个数据块编成 n 块;最后将通过Hash或者其他分布算法将这些数据块放到 n 个存储节点上,每个节点上存储的数据量为 α .我们设定源文件的存储具有MDS性质,即目标节点DS可以访问 n 个存储节点中任意 k 个节点上的数据,经过相应的解码操作将源文件还原出来.当节点失效时,每个新选择出的节点需要从 d 供应节点下载数据.
在分布式存储系统中节点失效的个数达到 r ( r ≤ n )时,我们才对其进行合作修复.时间被切割成不同的阶段,直到此时间段内所有的数据修复完才进入到下一个时间段 [20-21] .已有文献对分布式存储系统中带宽的预测方法表明未来带宽大小的变化与历史带宽大小是相关联的 [23-24] ,在很短时间内带宽大小变化很小.因此,我们假设系统中主节点获得的带宽大小在此修复时间段内保持不变,而且修复过程中每个节点之间传输的数据量均为 β .
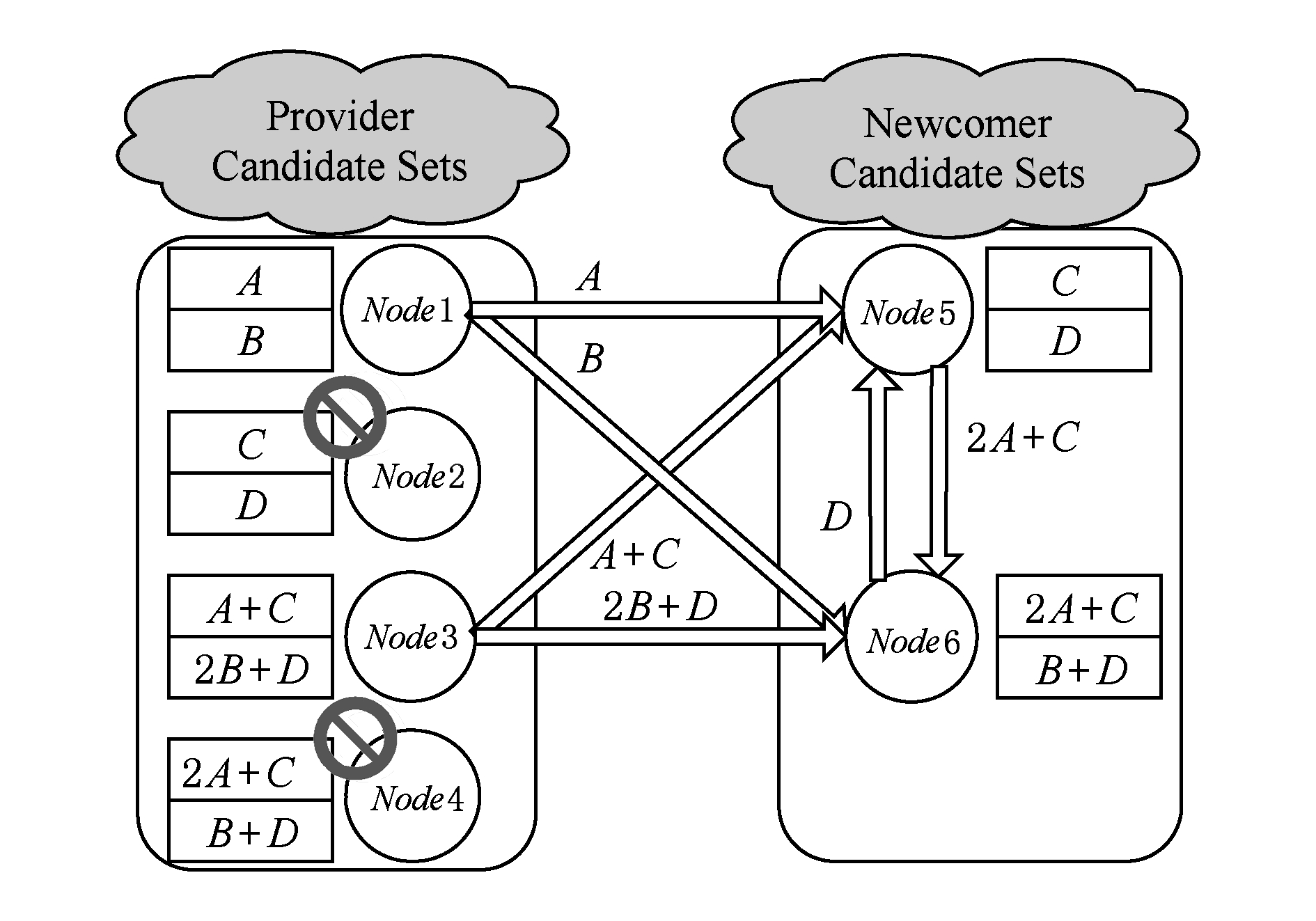
Fig. 3 Cooperative recovery of distributed storage systems from multiple losses
图3 分布式存储系统中多节点失效时的合作修复
定义3 . 多节点修复模型.首先,系统从空闲节点集 V n 中找出| V f |个节点作为新生节点(被称为newcomer),并且为每个newcomer从存活节点集合 V p 中选出 d 个节点( n - r ≥ d ≥ k )作为供应节点(被称为provider).其次,每个newcomer从每个provider下载相应的数据量 β 并存储到newcomer上,这个操作记为 ψ α → ψ β ;与此同时,每个newcomer需要从其他 r -1个newcomer下载的数据,此过程可以记录为 ψ d β → ψ β ;最后,每个newcomer通过计算所得到的数据量,恢复出失效的数据,记录为 ψ ( d + r -1) β → ψ α .
下面通过图3来详细说明多节点修复模型(合作修复模型),源文件被均分为4个块 A , B , C , D ,这些原始文件块经过编码生成8个数据块,新数据块中每2块作为一个包按照某种布置策略分布到4个节点上.那么节点1将存储数据块 A , B ;节点2存储数据块 C , D ;节点3存储数据块 A + C ,2 B + D ;节点4存储数据块2 A + C , B + D .此时文件存储采用的编码方式( n , k , d )为(4,2,2),鉴于文件存储具有MDS性质,即任取拓扑中2个节点上的数据可以将源文件恢复出来,因此,所用文件存储模型可以容忍2个节点失效.
在某个时间点,节点2和节点4上的数据失效了,即 r =2,此时系统的数据修复开始.假设选定的新生节点为节点5和节点6,供应节点为节点1和节点3,每一个所选新节点需要从2个供应节点上下载数据.新生节点5需要从节点1下载数据块 A ,从节点3下载数据块 A + C ,计算出数据块 C ,并将中间计算结果2 A + C 传输给节点6;与此同时,从节点6下载数据块 D ,此时节点2上的失效数据被再生出来.新生节点6从节点1下载数据块 B ,从节点3下载数据块2 B + D ,计算出数据块 D ,并将中间结算结果 D 传输给节点5;与此同时,从节点6下载数据块2 A + C ,此时节点4上的失效数据被再生出来.通过此种新生节点之间互相交换信息的合作修复方式,可以很大程度上降低链路上传输的数据量.
定义4 . 多节点修复模型的目标函数.基于上述合作修复模型,我们对多节点失效场景下的修复性能问题进行优化.理论和实际系统均表明修复过程中节点在传输的同时进行修复 [8,10] ,我们将修复过程中源文件的修复过程构建成一个信息流图 [7] ,即数据以比特流传输.当每个文件中多个失效节点被同时修复时,数据的计算和存储将在数据的传输过程中流水线式地进行,因此,计算开销和存储开销可以忽略不计.多个失效节点被同时修复时,由于所传输的数据量是固定的,因此,每个文件中失效节点的数据修复时间将由比特流中瓶颈带宽决定.由于每个节点之间传输的数据量均为 β ,我们可以得到修复模型的目标函数为 ![]() 其中 u ∈ V p ∪ V n , v ∈ V .
其中 u ∈ V p ∪ V n , v ∈ V .
当分布式存储系统中失效节点个数达到某个阈值时,系统开始进行修复操作.从3.2节多节点失效的修复模型中可以看到,在节点修复期间我们假定带宽大小几乎不变.因此为了优化修复的性能,我们需要提出相应的算法使得瓶颈带宽尽量偏大.记 ![]() 为目标函数的结果,表示第 t 时间段,失效节点个数达到阈值 r ,修复过程中所选带宽集合
为目标函数的结果,表示第 t 时间段,失效节点个数达到阈值 r ,修复过程中所选带宽集合 ![]() 确定的节点集合:
确定的节点集合:
![]() ∀ E ′⊆
∀ E ′⊆ ![]()
C ( HN , TN )~U[0.3,120],
HN ∈ V p ∪ V n , TN ∈ V n }.
为了选择出带宽集合 ![]() 已有的算法逐个选择节点,这样会产生很大的时间开销和空间开销.本文基于多节点失效场景下修复模型的特性,对已有算法进行改进,提出了B -WSJ算法.
已有的算法逐个选择节点,这样会产生很大的时间开销和空间开销.本文基于多节点失效场景下修复模型的特性,对已有算法进行改进,提出了B -WSJ算法.
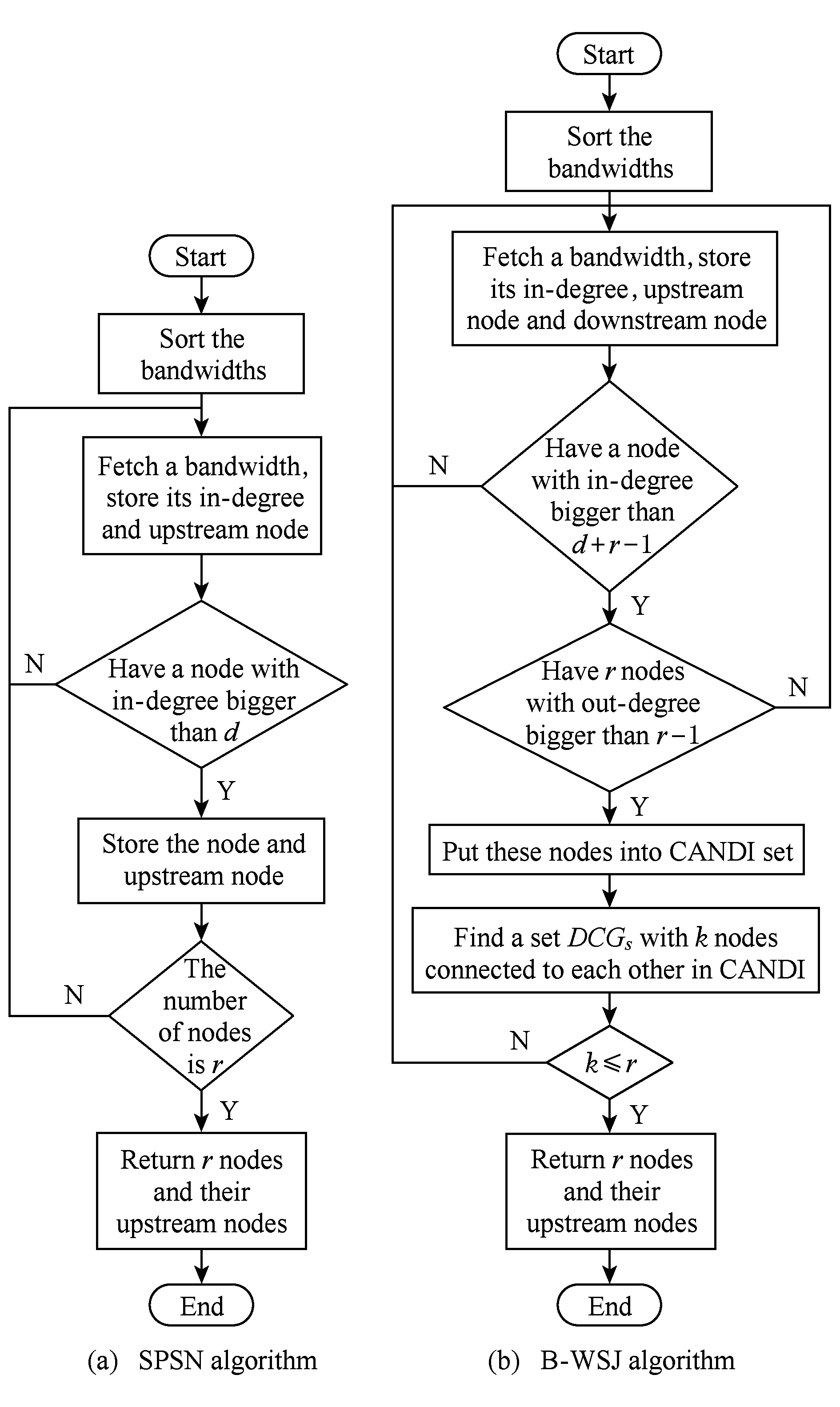
Fig. 4 Algorithm design idea
图4 算法设计思想
算法将贪心思想引入,全局选择较优带宽集合;运算分成两大部分包括浅度弱判断和深度强判断;弱判断是找出满足供应节点和新生节点个数条件的候选新生节点集合,见图4(b)的第1、第2个判断条件.弱判断是基于定义2找出满足 count + H p ( v i )= d , count + T ( v i )= r -1公式的候选新生节点 v i .在此集合上,强判断进一步筛选出 r 个两两通信的节点集合,见图4(b)中 DCG S 的形成.强判断是基于定理1,找出满足 ![]() 的新生节点集合
的新生节点集合 ![]() 最终,算法选择出了具有较优带宽集合的 r 个新生节点和对应 d 个供应节点.
最终,算法选择出了具有较优带宽集合的 r 个新生节点和对应 d 个供应节点.
从图4还可以看出,对比已有的算法,B-WSJ算法有很多特征:
1) 算法不但存储节点的入度,而且存储了节点的出度和相邻节点信息用于后续判断;
2) 算法在弱判断过程中考虑了对每个节点的出度信息,以初步满足新生节点的个数;
3) 算法继续对弱判断选择出的节点集合进行强判断操作,确定是否存在 r 个节点两两相连,找出满足合作修复的新生节点.强判断的过程具有很大的挑战性,算法利用定义2以及定理1可以快速找出两两相连的 r 个新生节点;
4) 算法中加入了大量的预处理和剪枝思想,从而有效地降低算法的时空复杂度.
算法1 . B-WSJ算法.
输入:网络拓扑 G ( V , E )、带宽 E ={ C ( u , v )| u ∈ V p ∪ V n , v ∈ V n };
输出: ![]() 及带宽的邻接节点.
及带宽的邻接节点.
① 初始化队列 ![]() ∅,hashset类型的 H p , H n , T , CANDI , DCG S , v n 分别为空, count + H p ( v )=0, count + T ( v )=0;
∅,hashset类型的 H p , H n , T , CANDI , DCG S , v n 分别为空, count + H p ( v )=0, count + T ( v )=0;
② ![]() ← Sort ({ C ( u , v ), u ∈ V p ∪ V n , v ∈ V n }, desc );
← Sort ({ C ( u , v ), u ∈ V p ∪ V n , v ∈ V n }, desc );
③ fo ![]()
 *对带宽的弱判断*
*对带宽的弱判断* 
④ if ( count + H p ( v )≥ d + r -1 &&
count + T ( v )≥ r -1) then
⑤ CANDI ← v ;
 *对节点的强判断*
*对节点的强判断* 
⑥ if ( CANDI . size ≥ r ) then
⑦ DCG S ←∪ s HT ( v i ), v i ∈ CANDI ;
⑧ if ( s ≥ r ) then
⑨ v n ← DCG S ;
⑩ return v n 及相应 H p 的前 d 个元素;
 end if
end if
 end if
end if
 end if
end if
 end for
end for
关于算法1中实现弱判断的步骤④, T ( v )是通过计算所有选取带宽中上游节点的出度来实现的. H p 和 H n 是通过计算所有选取带宽中下游节点的入度来实现的.并把候选新生节点邻接供应节点存储进集合 H p ,邻接新生节点存储进对应的 H n 和 T .
算法2 . 弱判断中 count + H p ( v )和 count + T ( v )的实现.
① for each C ( u , v ) ![]() do
do
② if ( v ∈ V n )
③ if ( u ∈ V n ) then
④ T ( u )← v ;
⑤ count + T ( u )++;
⑥ H n ( v )← u ;
⑦ count + H n ( v )++;
⑧ else if ( u ∈ V p ) then
⑨ H p ( v )← u ;
⑩ count + H P ( v )++;
 end if
end if
 end if
end if
 end for
end for
算法1中实现强判断的步骤⑧是通过判断2节点是否均在彼此的邻接新生节点集合 H n 中得到的,直到最后得到 r 个相互连接的节点.
算法3 . 强判断中 DCG S 的实现.
① for each i in CANDI do
② if ( H P ( i ). size ≥ d && H n ( i ). size ≥ r -1) then
③ for each j in hashset v n do
④ if ( v n . size =0)
⑤ v n . add ( i );
⑥ break;
⑦ else if ( j = i ‖!( j ∈ H n ( i ))‖!( i ∈ H n ( j )))
⑧ continue;
⑨ else
⑩ v n . add ( i );
 if ( v n . size = r )
if ( v n . size = r )
 return v n ;
return v n ;
 end if
end if
 end if
end if
 end for
end for
 end if
end if
 end for
end for
下面列举一个实例来对强判断进行说明.假设弱判断选择出的节点如图5所示,图5(a)表示弱判断选择出的集合 CANDI 包含元素为{ Node 2, Node 1, Node 4, Node 3},它们是满足供应节点和新生节点个数条件的候选新生节点,并且每个节点 i 的 H n 集合里的元素为图5(a)所示.假设失效节点个数为3,我们进行4项强判断:①取集合 CANDI 中第1个元素 Node 2,由于此时集合为空, Node 2将被放入集合中 v n ;②取 CANDI 中下一个元素 Node 1,由于 Node 2∈ H n ( Node 1),并且 Node 1∈ H n ( Node 2),因此将 Node 1加入集合.由于 v n 的长度未到达2,算法继续进行;③取元素 Node 4,由于 Node 4∈ H n ( Node 2),而 Node 2∉ H n ( Node 4),故忽略 Node 4;④取最后一个元素 Node 3,由于 Node 3∈ H n ( Node 1),并且 Node 1∈ H n ( Node 3), Node 3∈ H n ( Node 2),并且 Node 2∈ H n ( Node 3),因此将 Node 3加入集合如图5(b)所示.此时集合中元素的个数满足条件,算法终止,并输出最后集合 v n 及相应 H n 的前 d 个元素.

Fig. 5 An example of strong judgement
图5 强判断的实例
本算法由Gong等人 [11] 所作研究的思想拓展而成,其核心想法是优先选取最大的带宽传输数据,下面对算法的性能进行分析.首先对B -WSJ算法的最优性进行证明;然后对其时间复杂度进行分析;最后我们考虑算法对不同编码方式的影响.
1) 证明算法的最优性
定理2 . 分布式存储系统中多节点失效场景下,对于已有的修复模型,节点选择算法B -WSJ为最优.
证明. 我们把B-WSJ算法得出的最优结果记录为 ![]() 本算法一旦寻找到满足条件的结果则终止,因此最后一个被遍历的链路带宽 C 1 为瓶颈带宽.为方便使用反证法证明,此处假设B-WSJ算法继续运行并查找到更优的带宽集合,并记录为
本算法一旦寻找到满足条件的结果则终止,因此最后一个被遍历的链路带宽 C 1 为瓶颈带宽.为方便使用反证法证明,此处假设B-WSJ算法继续运行并查找到更优的带宽集合,并记录为 ![]() 时的瓶颈带宽,则 C 1 < C 2 ,此时 t 1 < t 2 ;然而B-WSJ算法从大到小遍历带宽队列
时的瓶颈带宽,则 C 1 < C 2 ,此时 t 1 < t 2 ;然而B-WSJ算法从大到小遍历带宽队列 ![]() 由于队列中带宽降序排列,因此如果 t 1 < t 2 则 C 1 > C 2 ,这与假设得到的条件矛盾,故假设不成立.因此B-WSJ算法所求出的
由于队列中带宽降序排列,因此如果 t 1 < t 2 则 C 1 > C 2 ,这与假设得到的条件矛盾,故假设不成立.因此B-WSJ算法所求出的 ![]() 是最优的.
是最优的.
证毕.
2) 算法时间复杂度的分析
实际分布式存储系统中,链路带宽可以通过数据中心的主节点获取 [17] ,带宽包括集合 V p 中节点到集合 V n 中节点的带宽,集合 V n 中两两节点的带宽.相关研究测量得出获取带宽的时间很短 [22] ,只需2~4个往返时延(round-trip time, RTT),因此获取带宽的时间对于再生修复时间来说可以忽略不计.
当进行多个失效节点的修复时,已有算法SPSN的时间复杂度为 O ( r × N );B-WSJ算法时间复杂度为 O (( CANDI . size )× N ),因此算法的时间复杂度是相似的.然而B-WSJ算法的平均时间复杂度远远小于最坏的时间复杂度.一方面,B-WSJ引入了一定的预处理机制,当算法1中步骤③队列 ![]() 中带宽至少从获取 r × d + r ( r -1)-1个并存储相应的节点信息时,步骤④的弱判断操作才开始执行.通过这种方式,可以在很大程度上降低算法执行的规模 N .另一方面,B-WSJ多次引入剪枝思想,算法1中步骤④按照节点的出入度情况筛选新生节点放入 CANDI ,使得集合 CANDI 的范围得到了很大的缩小;算法3中步骤②根据每个节点的 H p 和 H n 的信息来去掉集合 CANDI 中不合格的元素时,进一步缩小集合 CANDI 的范围,使得其大小不超过 r .
中带宽至少从获取 r × d + r ( r -1)-1个并存储相应的节点信息时,步骤④的弱判断操作才开始执行.通过这种方式,可以在很大程度上降低算法执行的规模 N .另一方面,B-WSJ多次引入剪枝思想,算法1中步骤④按照节点的出入度情况筛选新生节点放入 CANDI ,使得集合 CANDI 的范围得到了很大的缩小;算法3中步骤②根据每个节点的 H p 和 H n 的信息来去掉集合 CANDI 中不合格的元素时,进一步缩小集合 CANDI 的范围,使得其大小不超过 r .
综上分析可知,B-WSJ算法加入各种机制降低了节点选择的时间复杂度.一方面,分布式存储系统中,单个文件的存储节点是有限的,例如Google文件系统编码方式为(6,3,3),此时,失效节点个数 r 满足条件: r ≤3, r ≪ N ;因此,失效节点的个数相对系统节点来说是一个很小的值.另一方面,算法中设计的预处理机制和剪枝策略,涉及了节点出入度和连接关系,删除了大量随机孤立或连接稀疏的节点,从而大批量地缩小了算法的选择范围.分布式存储系统中,等待节点失效个数达到 r 时进行修复.Garraghan等人在文献[25]中指出系统的节点修复时间以小时(h)为单位,大部分节点失效可以通过重启服务器或者其他方式来进行修复,因此其修复时间可以少于30 min;而有些不能通过重启服务器进行修复的失效则需要几天时间.基于此,算法的复杂度是可以接受的.
3) 编码性质的影响
当失效节点的个数达到阈值 r 时,这些失效的数据将被再生到新的空节点上.根据定义5可知多节点失效时的合作修复模型.我们将此修复过程建模成信息流图,即最大流等于最小割.使用B-WSJ算法选择新生节点集合 v n 和相应 H p 之后,系统继续开始修复数据.修复过程中修复带宽最小割的大小至少为文件的大小,修复过程中的数据传输量可以保证源文件被恢复.因此B -WSJ算法选择出的节点与文件的MDS性质是独立的.
本节根据第3节的系统模型和4.1节的算法思路,进行了仿真实验.由于Waxman算法 [26] 在许多研究中被广泛的应用,本实验使用其来随机生成网络拓扑.在一个 n × n 平面上随机产生 N 个节点;节点之间的链路根据概率 p ( u , v )给出, ![]() 为节点 u 和节点 v 之间的欧几里德距离,
为节点 u 和节点 v 之间的欧几里德距离, ![]() 指平面上2点之间最大的距离; γ 和 δ 是大小为0到1范围内的权重系数, γ 越大,所产生的网络拓扑中带宽的密度越稠密, δ 则控制了平面远距离和近距离带宽的分布.依据FTA中真实数据的失效模型,随后用Java语句实现了B-WSJ算法,为了尽可能真实地验证参考因素的变化会怎样影响算法的性能,我们将每一个对比实验做了200次,最终结果为200次实验数据的平均值,算法的性能指标由修复过程中数据的再生时间来衡量.
指平面上2点之间最大的距离; γ 和 δ 是大小为0到1范围内的权重系数, γ 越大,所产生的网络拓扑中带宽的密度越稠密, δ 则控制了平面远距离和近距离带宽的分布.依据FTA中真实数据的失效模型,随后用Java语句实现了B-WSJ算法,为了尽可能真实地验证参考因素的变化会怎样影响算法的性能,我们将每一个对比实验做了200次,最终结果为200次实验数据的平均值,算法的性能指标由修复过程中数据的再生时间来衡量.
设定拓扑网络中结点的总个数 N =600, n =6 000, γ 和 δ 分别为0.7和0.05.文件大小为128 MB,带宽的值服从U[0.3,120]分布,单位为Mbps [22] .存储文件以 n =10, k =4的MDS码进行编码,失效节点修复过程中节点之间传输量的数据量 β ,其计算方式为 ![]() 实验分成2批进行.第1批实验中,为了验证多节点失效场景下,B-WSJ算法相对已有算法,对异构分布式存储系统数据修复性能的影响.此场景下设定节点的失效阈值为2,理由如下:1)现实场景中常见分布式存储系统具有编码特性而使得存储节点有一定的限制,例如Google文件系统 [27] 编码方式为(6,3,3),这将使得文件存储于6个节点中,为了保证数据可被恢复,失效节点的个数将不大于3;2)已有分布式存储相关的研究中均设置节点失效1个.基于以上讨论,为了在更逼近真实分布式系统的场景下,对比所提算法和已有算法的性能,此处失效节点个数阈值被设定为2.第2批实验中,为了研究算法的稳定性,我们设定不同环境参数来进行实验,如不同的节点失效个数、变化供应节点的个数、选择不同的带宽范围.
实验分成2批进行.第1批实验中,为了验证多节点失效场景下,B-WSJ算法相对已有算法,对异构分布式存储系统数据修复性能的影响.此场景下设定节点的失效阈值为2,理由如下:1)现实场景中常见分布式存储系统具有编码特性而使得存储节点有一定的限制,例如Google文件系统 [27] 编码方式为(6,3,3),这将使得文件存储于6个节点中,为了保证数据可被恢复,失效节点的个数将不大于3;2)已有分布式存储相关的研究中均设置节点失效1个.基于以上讨论,为了在更逼近真实分布式系统的场景下,对比所提算法和已有算法的性能,此处失效节点个数阈值被设定为2.第2批实验中,为了研究算法的稳定性,我们设定不同环境参数来进行实验,如不同的节点失效个数、变化供应节点的个数、选择不同的带宽范围.
在实验1中,主要变化网络拓扑中带宽分布,以探索多节点失效场景下,B-WSJ算法与已有的算法的性能变化.设定节点的失效阈值为2,每个供应节点需要从4新生节点中下载数据,即 d =4.实验分别在网络拓扑中带宽均匀分布范围为[0.3,120],[1,120],[10,120],[30,120],[50,120],[70,120],[90,120]的情况下进行.如图6所示:
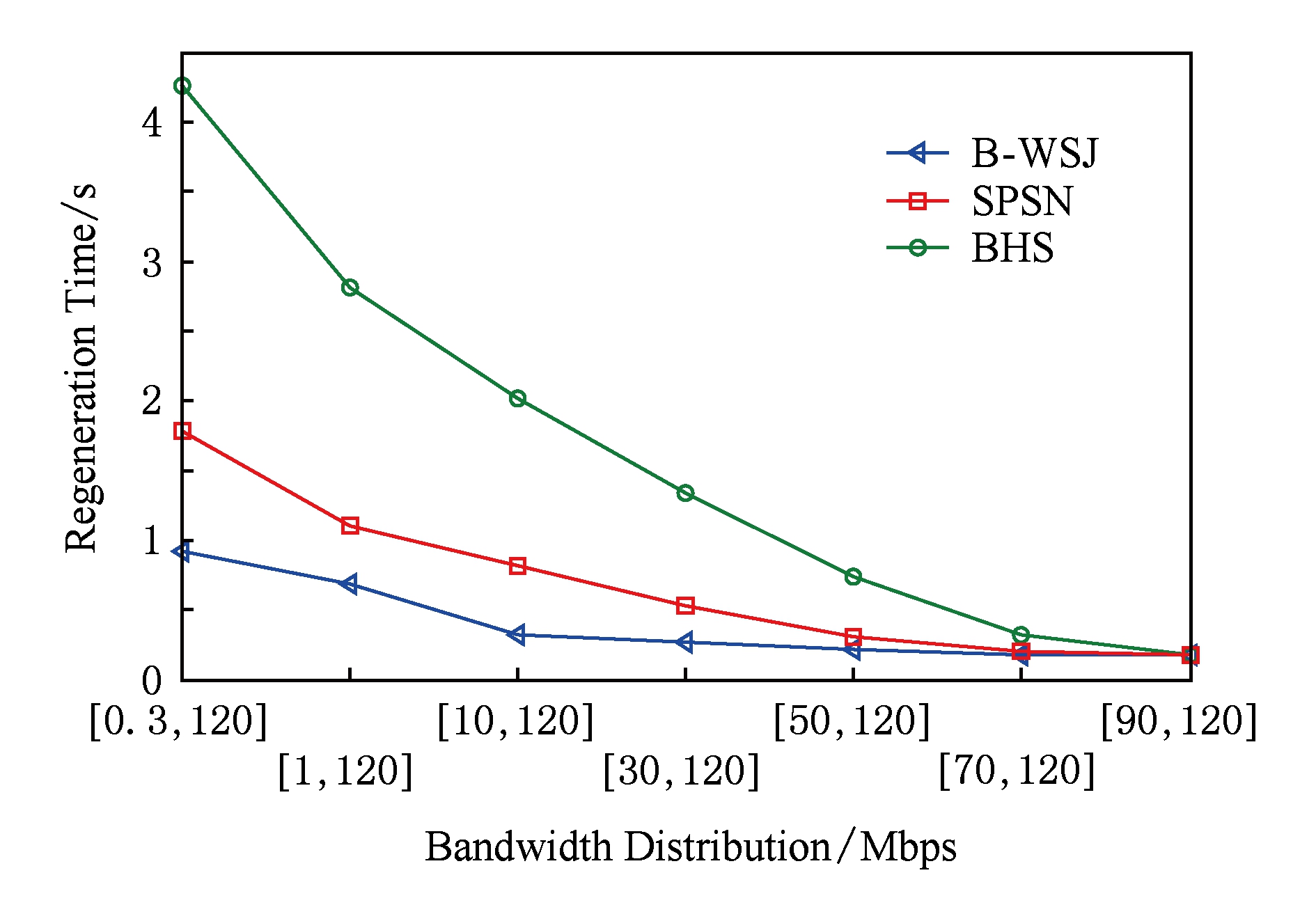
Fig. 6 Performance of different node selection algorithm with different network topologies
图6 不同带宽分布情况下不同节点选择算法的性能
在带宽异构明显的情况下,已有的节点选择机制性能相差越来越大.当带宽分布为[90,120]时,即带宽变化不明显时,B -WSJ算法比SPSN算法性能提高了5.27%,比BHS算法性能提高了21.73%.当带宽分布为[0.3,120]时,B -WSJ算法比SPSN算法性能提高了45.93%,比BHS算法性能提高了78.95%.结果证明节点的选择机制对于数据的再生时间具有很大的影响.从图6中还可以看出,B -WSJ算法在带宽异构明显时的性能要好于带宽异构不明显时的性能,这是由B -WSJ算法的对带宽进行贪心择优的特征决定的.
为了验证环境参数对算法性能的影响,我们对不同供应节点个数进行变化.文献相关参考文献网络拓扑中带宽服从均匀分布U[0.3,120] .实验依次变换 d 的取值,即 d 分别取值为4,5,6,7,8,结果如图7所示:
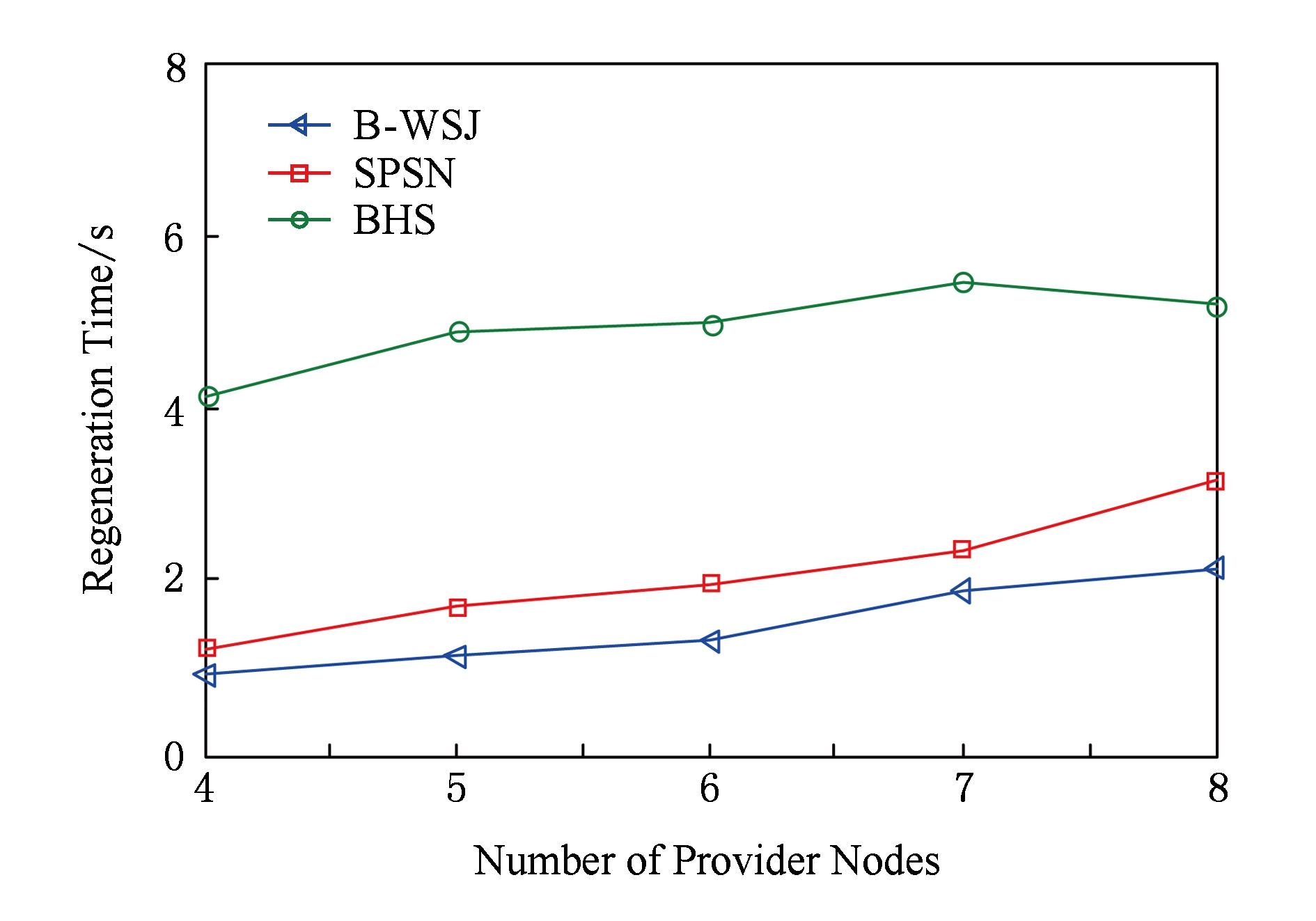
Fig. 7 Performance of different node selectionalgorithm with different providers
图7 不同供应节点个数时不同节点选择算法的性能
从图7中可以看出随着供应节点个数的增加,算法的再生时间均增加,这是由于算法不但选择新生节点而且同时选择供应节点的个数决定的;从图7中可以清晰看出,B-WSJ算法所选结果的再生时间比SPSN算法增长幅度较慢,这是符合算法的特征的;BHS算法的结果没有特别明显的增长趋势.
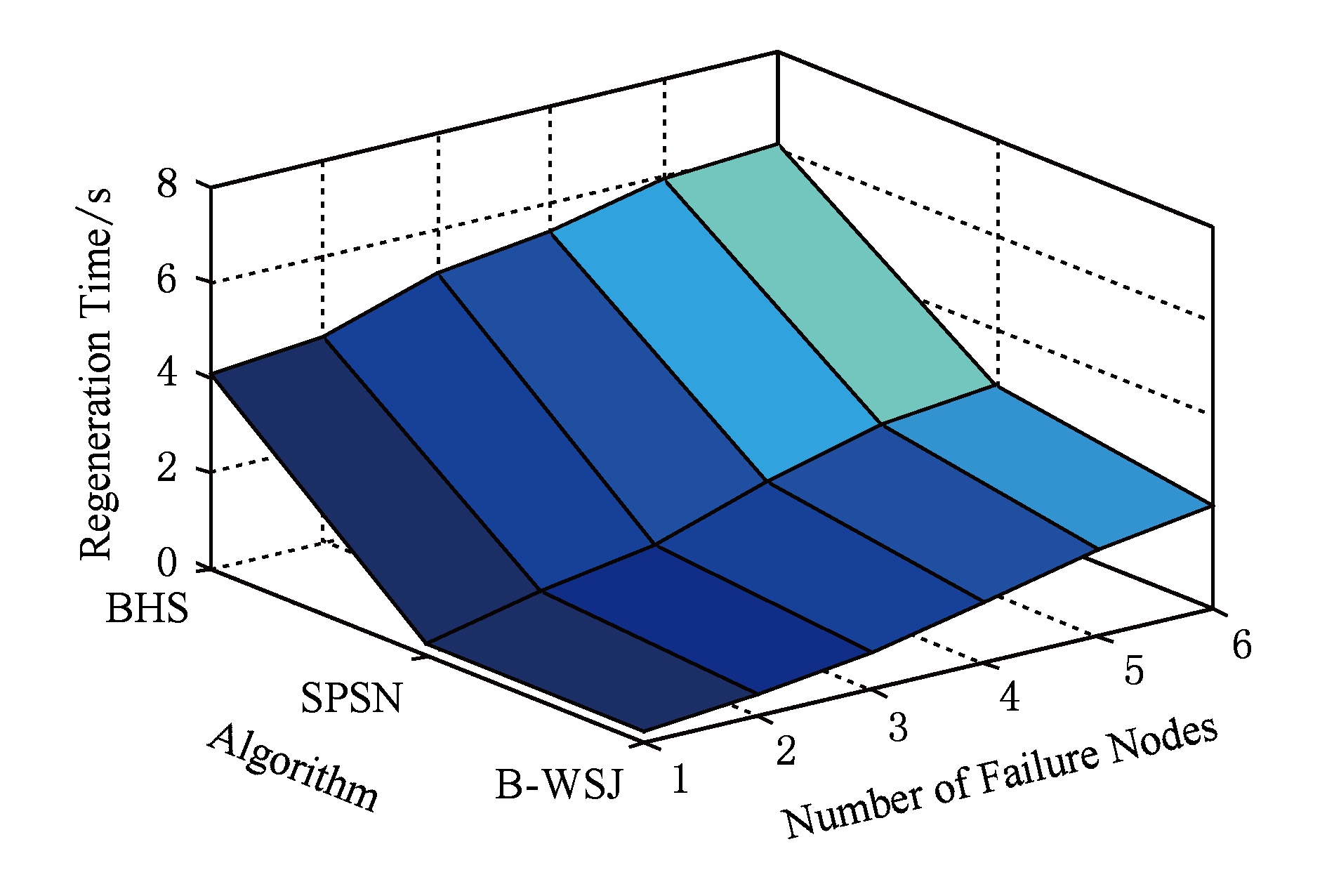
Fig. 8 Performance of different node selection algorithmwith different numbers of failure nodes
图8 不同失效节点个数时不同节点选择算法的性能
为了继续验证环境参数中节点失效个数对B -WSJ算法性能的影响,我们在失效不同节点个数的场景进行了实验.设定 d =4,带宽服从均匀分布U[0.3,120].由于单个文件需要能够被恢复出来,因此不能超过6个节点同时失效,故实验中阈值 r 分别取值为1,2,3,4,5,6.图8表明:随着节点失效个数的增加,已有节点选择算法的性能越来越差.从图8中可看出B-WSJ算法性能最优,而SPSN算法性能较差.当 r =1时,SPSN算法和B-WSJ算法性能相同,这是由于SPSN算法为B-WSJ算法在失效一个节点情况下的特例.随着失效个数越多,由于SPSN算法为逐个失效节点的修复,其选择到的节点性能越来越差,因此其再生时间越来越长,而B-WSJ算法具有全局并行性的特征而性能相对较优.BHS算法为随机选择算法,性能不稳定,因此平均性能最差.
在大数据环境下,分布式存储系统通常引进冗余来提高可靠性.在多节点失效场景下,当失效节点个数达到一个阈值时,系统才进行修复.为了优化修复时间,相关研究验证了单节点失效场景中节点选择机制对修复时间的影响.然而已有的算法不适用于多节点失效的场景,其串行性特征会使得数据的修复性能不再最优.基于此问题,本文继续探索了多节点失效场景下,节点选择机制对数据修复性能的影响.在分析多节点失效的延迟修复模型之后,本文提出了B-WSJ算法,并对算法性能进行多维度的分析和最优性证明.最后通过在不同的参数环境下对比已有算法,结果证明节点选择机制对于数据的修复性能具有很大的影响;通过对不同的实际文件存储方式和失效模型进行实验,结果表明:算法在失效个数比较多或带宽异构明显的情况下,B-WSJ算法比已有算法的性能更优.本文的研究模型比较理想,后续我们将继续扩展环境,考虑传输不同数据量场景下的节点选择机制.
参考文献
[1]Kondo D, Javadi B, Losup A, et al. The failure trace archive: Enabling comparative analysis of failures in diverse distributed systems[C] 
 Proc of the 10th IEEE
Proc of the 10th IEEE  ACM Conf on Cluster, Cloud and Grid Computing. Piscataway, NJ: IEEE, 2010: 398-407
ACM Conf on Cluster, Cloud and Grid Computing. Piscataway, NJ: IEEE, 2010: 398-407
[2]Shvachko K, Kuang H, Radia S, et al. The Hadoop distributed file system[C] 
 Proc of the 26th Symp on Mass Storage Systems and Technologies. Piscataway, NJ: IEEE, 2010: 1-10
Proc of the 26th Symp on Mass Storage Systems and Technologies. Piscataway, NJ: IEEE, 2010: 1-10
[3]Weil S A, Brandt S A, Miller E L, et al. Ceph: A scalable, high-performance distributed file system[C] 
 Proc of the 7th Symp on Operating Systems Design and Implementation. Berkeley, CA: USENIX Association, 2010: 307-320
Proc of the 7th Symp on Operating Systems Design and Implementation. Berkeley, CA: USENIX Association, 2010: 307-320
[4]Luo Xianghong, Shu Jiwu. Summary of research for erasure code in storage system[J]. Journal of Computer Research and Development, 2012, 49(1): 1-11 (in Chinese)(罗象宏, 舒继武. 存储系统中的纠删码研究综述[J]. 计算机研究与发展, 2012, 49(1): 1-11)
[5]Wang Yijie, Sun Weidong, Zhou Song, et al. Key technologies of distributed storage for cloud computing[J]. Journal of Software, 2012, 23(4): 962-986 (in Chinese)(王意洁, 孙伟东, 周松, 等. 云计算环境下的分布存储关键技术[J]. 软件学报, 2012, 23(4): 962-986)
[6]Sathiamoorthy M, Asteris M, Papailiopoulos D, et al. XORing elephants: Novel erasure codes for big data[C] 
 Proc of the 39th Int Conf on Very Large Data Bases. New York: ACM, 2013: 325-336
Proc of the 39th Int Conf on Very Large Data Bases. New York: ACM, 2013: 325-336
[7]Dimakis A G, Godfrey P B, Wu Yunnan, et al. Network coding for distributed storage systems[J]. IEEE Trans on Information Theory, 2008, 56(9): 4539-4551
[8]Wei Dongsheng, Li Jun, Wang Xin. Performance study of exact minimum bandwidth regenerating codes in distributed storage system[J]. Journal of Computer Research and Development, 2014, 51(8): 1671-1680 (in Chinese)(卫东升, 李钧, 王新. 分布式存储中精确修复最小带宽再生码的性能研究[J]. 计算机研究与发展, 2014, 51(8): 1671-1680)
[9]Wang Yan, Wei Dongsheng, Yin Xunrui, et al. Hetero-geneity-aware data regeneration in distributed storage systems[C] 
 Proc of IEEE INFOCOM 2014. Piscataway, NJ: IEEE, 2014: 1878-1886
Proc of IEEE INFOCOM 2014. Piscataway, NJ: IEEE, 2014: 1878-1886
[10]Ahmad I, Wang Chih-Chun. When and by how much can helper node selection improve regenerating codes[C] 
 Proc of the 52th Annual Allerton Conf on Communication, Control and Computing. Piscataway, NJ: IEEE, 2014: 459-466
Proc of the 52th Annual Allerton Conf on Communication, Control and Computing. Piscataway, NJ: IEEE, 2014: 459-466
[11]Gong Qingyuan, Wang Jiaqi, Wang Yan, et al. Optimal node selection for data regeneration in heterogeneous distributed storage systems[C] 
 Proc of the 44th Conf on Parallel Processing. Piscataway, NJ: IEEE, 2015: 390-399
Proc of the 44th Conf on Parallel Processing. Piscataway, NJ: IEEE, 2015: 390-399
[12]Ahmad I, Wang Chih-Chun. When locally repairable codes meet regenerating codes-what if some helpers are unavailable[C] 
 Proc of the Int Symp on Information Theory. Piscataway, NJ: IEEE, 2015: 849-853
Proc of the Int Symp on Information Theory. Piscataway, NJ: IEEE, 2015: 849-853
[13]Qi Fenglin, Gong Qingyuan, Zhou Yangfan, et al. Hetero-geneity-aware node selection for data repair in distributed storage systems[J]. Journal of Computer Research and Development, 2015, 52(Suppl Ⅱ): 68-74 (in Chinese)(齐凤林, 宫庆媛, 周扬帆, 等. 分布式存储再生码数据修复的节点选择方案[J]. 计算机研究与发展, 2015, 52(增刊Ⅱ): 68-74)
[14]Jia Chengjin, Wang Jun, Zhu Yanqin, et al. On the optimal provider selection for repair in distributed storage system with network coding[C] 
 Proc of the 15th Int Conf on Algorithms and Architectures for Parallel Processing. Piscataway, NJ: IEEE, 2015: 506-520
Proc of the 15th Int Conf on Algorithms and Architectures for Parallel Processing. Piscataway, NJ: IEEE, 2015: 506-520
[15]Ford D, Labelle F, Popovici FI, et al. Availability in globally distributed storage systems[C] 
 Proc of the 9th USENIX Conf on Operating Systems Design and Implementa-tion. Berkeley, CA: USENIX Association, 2010: 61-74
Proc of the 9th USENIX Conf on Operating Systems Design and Implementa-tion. Berkeley, CA: USENIX Association, 2010: 61-74
[16]Shen Jiajie, Gu Jiazhen, Zhou Yangfan, et al. Bandwidth-aware delayed repair in distributed storage systems[C] 
 Proc of the 24th Int Symp on Qualigy of Service. Piscataway, NJ: IEEE, 2016
Proc of the 24th Int Symp on Qualigy of Service. Piscataway, NJ: IEEE, 2016
[17]Lam I, Szebeni S, Szilagyi G, et al. Wuala[EB  OL]. [2016-02-13]. https:
OL]. [2016-02-13]. https: 
 tresorit.com
tresorit.com  business
business  wuala- alternative
wuala- alternative
[18]Bhagwan J R, Tati K, Cheng Yuchung, et al. Total recall: System support for automated availability management[C] 
 Proc of the 1st Symp on Networked Systems Design and Implementation. Berkeley, CA: USENIX Association, 2004: 337-350
Proc of the 1st Symp on Networked Systems Design and Implementation. Berkeley, CA: USENIX Association, 2004: 337-350
[19]Hu Yuchong, Xu Yinlong, Wang Xiaozhao, et al. Cooperative recovery of distributed storage systems from multiple losses with network coding[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(2): 268-276
[20]Shum K W, Hu Yuchong. Cooperative regenerating codes[J]. IEEE Trans on Information Theory, 2012, 59(11): 7229-7258
[21]Li Jun, Li Baochun. Cooperative repair with minimum-storage regenerating codes for distributed storage[C] 
 Proc of the 33rd IEEE Int Conf on Computer Communications. Piscataway, NJ: IEEE, 2014: 316-324
Proc of the 33rd IEEE Int Conf on Computer Communications. Piscataway, NJ: IEEE, 2014: 316-324
[22]Lee S J, Sharma P, Banerjee S, et al. Measuring bandwidth between planetLab nodes[C] 
 Proc of the 6th Int Workshop on Passive and Active Network Measurement. Berlin: Springer, 2005: 292-305
Proc of the 6th Int Workshop on Passive and Active Network Measurement. Berlin: Springer, 2005: 292-305
[23]Eswaradass A, Sun Xianhe, Wu Ming. A neural network based predictive mechanism for available bandwidth[C] 
 Proc of the 19th Parallel and Distributed Processing Symp. Piscataway, NJ: IEEE, 2005
Proc of the 19th Parallel and Distributed Processing Symp. Piscataway, NJ: IEEE, 2005
[24]Cong Xin, Shuang Kai, Su Sen, et al. SBDP: Bandwidth prediction mechanism towards server demands in P2P-VoD system[J]. Journal of Peer-to-Peer Networking and Applications, 2015, 8(3): 501-511
[25]Garraghan P, Townend P, Xu J. An empirical failure-analysis of a large-scale cloud computing environment[C] 
 Proc of the 15th Int Symp on High-Assurance Systems Engineering. Piscataway, NJ: IEEE, 2014: 113-120
Proc of the 15th Int Symp on High-Assurance Systems Engineering. Piscataway, NJ: IEEE, 2014: 113-120
[26]Waxman B. Routing of multipoint connections[J]. IEEE Journal on Selected Areas in Communications, 1988, 6(9): 1617-1622
[27]Ghemawat S, Gobioff H, Leung S T. The Google file system[C] 
 Proc of the 19th ACM Symp on Operating Systems Principles. New York: ACM, 2003: 29-43
Proc of the 19th ACM Symp on Operating Systems Principles. New York: ACM, 2003: 29-43
Liu Pei 1,2 , Jiang Ziyi 1 , and Cao Xiu 1,2
1 ( School of Computer Science and Technology , Fudan University , Shanghai 201203) 2 ( Engineering Research Center of Cyber Security Auditing and Monitoring ( Fudan University ), Ministry of Education , Shanghai 200433)
Abstract In distributed storage systems, how to optimize the regeneration time of lost data so as to keep high reliability has attracted attention increasingly. Recent researches reveal that node selection mechanism during repair progress has great impact on regeneration time. SPSN (select provider select newcomer) algorithm has put forward by some studies, which suits the scenario of single node failure well. However, it is very common to repair many modes at the same time in actual system. In this scenario, SPSN algorithm will no longer be optimal taking large time and space consumption into consideration. By analyzing the data failure trace of real distributed file system, we propose a node selection algorithm B-WSJ (bandwidth based weak and strong judgement) based on the existing algorithms and repairing model with the characteristic of parallelism which is suitable for multi-failure scenario. In order to describe the algorithm better, we firstly define several concepts of node-relationship on a link. Secondly we use these concepts to realize the weak and strong judgment of target node with pre-process and pruning strategy added. Finally, the nodes with better bandwidth will be chosen. To evaluate the performance of NS algorithm, we use Waxman algorithm to generate network topology and do many experiments with node failure models in real system provided by FTA (failure trace archive). The experimental results show the performance of B-WSJ algorithm can be improved greatly compared with the existing algorithms.
Key words distributed storage system; data repair; regeneration time; multi-node failure; node selection
中图法分类号 TP333
修回日期: 2017-07-04

收稿日期 : 2016-11-29;
Liu Pei , born in 1991. Master. Her main research interests include distributed storage system, network coding, cloud computing.

Jiang Ziyi , born in 1990. Received his master degree in science and technology from Fudan University in 2015. His main research interests include distributed storage system, network coding, Internet of things.

Cao Xiu , born in 1968. Master. Senior engineer. His main research interests include distributed system, computer network, smart grid.