F 1 ( s 1 , s 2 ,…, s p )+ F 2 ( s 1 , s 2 ,…, s p ),
郭颖婕 1 刘晓燕 1 吴辰熙 2 郭茂祖 1,3 李 傲 1
1 (哈尔滨工业大学计算机科学与技术学院 哈尔滨 150001) 2 (Rutgers大学数学系 美国新泽西洲皮斯卡特维 08854) 3 (建筑大数据智能处理方法研究北京市重点实验室(北京建筑大学) 北京 100044) (yjguo0625@gmail.com)
摘 要 在全基因组关联研究GWAS中,多数方法对疾病与单核苷酸多态性位点之间的互作关系形式给出了强假设,这降低了相关方法的挖掘能力.近几年,以基因作为研究单位的基因-基因相互作用检测方法,因其在统计效力与生物可解释性方面的优势受到重视.针对已有方法检测相互作用类型时存在的局限性,提出一种基于U统计值与集成学习器的假设检验方法GBUtrees,通过构造统计量用于表征疾病性状与2个基因之间关系偏离加性模型的程度,检测以基因为单位的基因-基因相互作用.该统计量在不同子样例集下结果的平均值满足U统计量理论,从而可以利用U统计量的渐进正态分布性质获得所构造统计量的分布信息.GBUtrees对相互作用的形式不作假设,增强该方法对不同形式相互作用的挖掘能力.仿真与真实实验结果表明:该方法能够有效地进行不同类型相互作用的挖掘,可以应用于全基因组关联研究.
关键词 U统计量;集成学习;基因相互作用;单核苷酸多态性位点;全基因组关联研究
复杂疾病如癌症、糖尿病等,因其发病率高、治愈率低的问题,长期危害人类健康.对此类疾病遗传变异致病机理的研究是生命科学界的重大课题.全基因组关联研究(Genome-Wide Association Studies,GWAS)作为一种发现遗传变异——单核苷酸多态性位点(single nucleotide polymorphism, SNP)的新兴研究模式,自2005年《Science》杂志发表首例关于GWAS的研究成果——老年性黄斑变性以来,GWAS的研究已经超过1 800项,并发表了关于237种不同疾病研究成果,共计24 000余个SNP被证实与这些疾病显著相关 [1] .但对于大多数复杂遗传相关疾病而言,这些成果仅仅阐释了遗传因素很小的一部分.例如,已发现的与老年性黄斑变性、高胆固醇、阿兹海默症疾病相关的致病风险基因,分别只占相应遗传致病因素的50%,25%及23%.这一现象被称为“失踪遗传(the missing heritability)”,是目前GWAS研究的热点.该现象的发生是由于复杂疾病由多对微效基因与环境因素共同作用所致,即基因之间存在复杂的相互作用关系.而传统的GWAS主要基于单位点模型,独立检测单个SNP与给定表型之间的关系,从而导致一些存在基因互作的性状相关基因无法被单独检测出来.因此,识别与分析基因相互作用,成为解决“失踪遗传”的可行方案之一.尽管利用基因相互作用不能完全解决“失踪遗传”,但此类研究依然可以通过辅助构建新的基因通路为复杂性状的遗传与调控机理提供生物学解释.
基因相互作用又称为“上位效应”(epistasis).此概念最早由Bateson在1909年提出 [2] ,后由Fisher进一步给出定义 [3] :上位效应是指2个位点之间相互作用形式,使用2个位点建模产生的性状值与单独使用每个位点得到的性状值的和之间产生的差值来衡量上位效应的强度.后续研究中,对上位效应的定义变得更为宽泛,不同的方法对于相互作用也有不同的定义.初期的上位效应研究主要着眼于2个SNP位点间的相互作用关系.在精神分裂症、阿兹海默症、乳腺癌等复杂疾病中均有关于2个SNP之间交互作用的报道.因此产生了许多以2个SNP、或者3个SNP乃至多个SNP为研究单位的上位效应检测方法.统计类的检测方法通过设计一些表征相互作用强度的统计量,检测显著的相互作用关系,例如基于优势比(odds ratio, OR )的统计量、基于连锁不平衡(linkage disequilibrium, LD)的统计量以及基于熵的统计量等.另一类方法则采用计算机方法的思想,例如采用降维技术的多因子降维方法 [4] 、基于树模型的TEAM(tree-based epistasis associa-tion mapping)方法 [5] 、通过优化存储策略加速计算的BOOST(Boolean operation-based screening and testing)方法 [6] ,以及BEAM(Bayesian epistasis asso-ciation mapping),pRF等.这些基于位点的检测方法面临最大的挑战是维数灾难.由于必须考虑所有的SNP或SNP组,成对或者高阶的相互作用关系检测次数随互作关系阶数呈指数级增长,随之而来的对统计显著性的校正会导致统计效力的弱化.因此,本文研究以基因为单位,将一个基因中的所有SNP看作一个组来检测基因之间的相互作用.
基于基因的相互作用研究有以下3个明显的优势:
1) 基于基因的方法可以大大减少所需的检测次数,例如,对于20 000个基因,成对检测基因之间相互作用是可行的;而对于300万SNP,成对检测显然不现实.
2) 2组基因之间可能存在多对SNP的相互作用,组内的SNP之间也可能存在连锁不平衡关系,这些同时存在的作用关系会隐性地呈现在以基因为单位的模型中,更利于相互作用的检测.
3) 基于基因的方法可以更好地利用已有的生物学背景知识,缩小研究范围.例如可以检测那些蛋白质互作网络(protein-protein interaction, PPI)中已经呈现互作关系的蛋白质编码基因之间的关系,或者某个通路内基因之间的相互作用关系.
目前,在以基因为单位的相互作用研究中,Peng等人 [7] 在疾病组与对照组中分别对2个基因进行典型相关性分析(canonical correlation analysis, CCA),并设计统计量CCU(canonical correlation-based U statistic)来度量2个基因在疾病与对照组中相关性指标的差异程度,用于表征相互作用的强度.该方法的局限性在于CCA只能度量2个基因之间的线性关系.Yuan等人 [8] 和Larson等人 [9] 针对Peng等人的方法存在的问题,将CCU扩展到KCCU(kernel canonical correlation-based U statistic),在做典型相关性分析之前,将核函数作用在疾病和对照组中2个基因的数据上,从而增强模型对非线性关系的解释能力.Li等人 [10] 提出了一种基于熵的非参数假设检验方法GBIGM(gene based informa-tion gain method).通过分析2个基因共同作用时与考虑只有单个基因时熵的变化(即信息增益),并利用随机置换类标签的方式获得相互作用的显著性 p 值.Emily [11] 开发了AGGrEGATOr(a gene-based gene-gene interaction)方法,该方法首先计算两基因间所有SNP对的Wald统计值,并将一组Wald统计值结合成为一个显著性 p 值用于度量2个基因之间是否存在相互作用.此前,Ma等人 [12] 成功地将这一策略用于数量型性状的基因互作检测中.
本文的主要贡献有4个方面:
1) 提出了一种基于U统计量与集成学习结合的假设检验方法GBUtrees(gene-based gene-gene interaction detection based on U statistics and tree-based ensemble learners),将基因相互作用问题转化为检验2组SNP与疾病性状的对数优势比(log odds ratio, LOR)之间是否满足加性模型关系;
2) 利用以树为基分类器的集成学习方法作为底层学习方法,充分发挥该类方法对非线性关系的建模能力,有效学习2组基因之间可能存在的相互作用关系;
3) 通过多次采样子样例集使得预测模型的结果满足U统计值框架,利用其满足渐进正态分布的性质设计表征基因相互作用强度的统计量;
4) 利用8种不同相互作用模式疾病模型生成的模拟数据集与真实人类类风湿关节炎数据的实验结果表明,我们提出的GBUtrees方法可以有效挖掘基因-基因之间不同形式的相互作用关系.
本文以基因作为基本研究单位.假设基因 G 1 和 G 2 分别包含 p 和 q 个SNP,每个SNP位点只有高频等位基因(major allele)与低频等位基因(minor allele)两种碱基形式,分别记为A和a,则对于人类二倍体而言,每个SNP位点存在3种可能的基因型AA,Aa,aa.数据中使用0,1,2分别对应上述3种基因型.则基因 G 1 可表示为
G 1 =( s 1 , s 2 ,…, s p ),
(1)
其中 s i ∈{0,1,2}, i =1,2,…, p .
同理,包含 q 个SNP的基因 G 2 可表示为
G 2 =( s 1 , s 2 ,…, s q ),
(2)
其中 s i ∈{0,1,2}, i =1,2,…, q .
本文方法主要针对疾病-对照数据,因此我们的目标值 y ∈{0,1},其中1表示疾病组,0表示对照组.如果对于 G 1 , G 2 与 y 的LOR之间存在以下的关系:
![]()
F 1 ( s 1 , s 2 ,…, s p )+ F 2 ( s 1 , s 2 ,…, s p ),
(3)
其中 F 1 , F 2 可以是任意形式的函数.我们则称 G 1 , G 2 与 y 之间满足加性关系,即 G 1 , G 2 之间没有相互作用关系.换言之,当基因 G 1 中变量发生改变时,并不会改变基因 G 2 对性状的影响.因此,想要判断2个基因之间是否有相互作用关系,可以通过建立如下假设检验来衡量观测数据是否可以被建模成为加性模型:
H 0 :
∃ F 1 , F 2 , F ( G 1 , G 2 )=
F 1 ( G 1 )+ F 2 ( G 2 ),∀( G 1 , G 2 )∈ X TEST ,
(4)
H 1 :
∀ F 1 , F 2 , F ( G 1 , G 2 )≠
F 1 ( G 1 )+ F 2 ( G 2 ),∃( G 1 , G 2 )∈ X TEST ,
(5)
其中, X TEST 表示测试集.
使用监督学习中的集成学习方法对目标值进行建模,同时获得集成学习方法中的统计指标,来完成上述假设检验.Mentch等人 [13] 在2016年提出了基于U统计理论度量随机森林方法中的不确定性,并于2017年进一步完善该方法 [14] .本文利用该假设检验框架实现对基因互作的检测.下面将分别介绍U统计理论、集成学习方法以及基于该假设检验框架提出的基因互作检测方法.
给定样本 ![]() 假设参数 θ 存在如下的无偏估计:
假设参数 θ 存在如下的无偏估计:
θ = Ε ( h ( Z 1 , Z 2 ,…, Z k ))
(6)
其中, h 是一个函数,有 k ≤ n 个变量,则参数 θ 的最小无偏估计如下:
(7)
其中, h 称为U统计量 [15] 的核函数, k 称为阶.当核函数与阶数固定时,这些U统计量的分布是渐进正态的,其方差为 ![]() 其中 ζ 1, k 计算为
其中 ζ 1, k 计算为
![]()
(8)
其中, ![]() 这里 Z 1 表示2次重采样中存在一个相同样本.通常 ζ c , k 表示重采样中有 c 个公共样本.
这里 Z 1 表示2次重采样中存在一个相同样本.通常 ζ c , k 表示重采样中有 c 个公共样本.
集成学习使用多个分类器来解决同一问题,通过组合多个弱监督的基分类器以期得到一个更为全面的强监督模型.通过合理的选择并组合基分类器,集成学习可以在显著提高一个学习系统的泛化能力的同时提高学习器的分类精度.该方法已在多个领域成功应用 [16-17] .在1.2节U统计量的框架下,任何类型基分类器,只要能够写成式(7)的形式,均可以应用到本文的方法中.考虑到基因互作问题中存在严重的非线性相互作用,本文选取决策树模型作为集成学习中的基分类器.假设训练集有 n 个样本,
Z 1 =( X 1 , y 1 ), Z 2 =( X 2 , y 2 ),…, ![]()
(9)
其中 X =( X 1 , X 2 ,…, X d )是一个特征向量, y ∈ ![]() 是目标函数值.选取一个小于 n 的 k 值,( X i 1 , y i 1 ),( X i 2 , y i 2 ),…,( X i k , y i k )是训练样本的一个子样例集.给定一个待测样本 x * ,我们把一个树模型在该子样例集上的预测模型记为 T x * .为
是目标函数值.选取一个小于 n 的 k 值,( X i 1 , y i 1 ),( X i 2 , y i 2 ),…,( X i k , y i k )是训练样本的一个子样例集.给定一个待测样本 x * ,我们把一个树模型在该子样例集上的预测模型记为 T x * .为 ![]() 个子样例集都训练一棵树,那么最终待测样本 x * 的预测可表示为
个子样例集都训练一棵树,那么最终待测样本 x * 的预测可表示为
![]()
( X i 2 , y i 2 ),…,( X i k , y i k )).
(10)
实际中,选取 ![]() 并不现实,通常只需构建
并不现实,通常只需构建 ![]() 个树模型即可.在这种情况下,式(10)中 b n ( x * )被称为不完全U统计量.当 m n 个子样例集通过有放回的方式从
个树模型即可.在这种情况下,式(10)中 b n ( x * )被称为不完全U统计量.当 m n 个子样例集通过有放回的方式从 ![]() 个子样例集中抽取时,不完全U统计量仍然满足渐进正态的性质.
个子样例集中抽取时,不完全U统计量仍然满足渐进正态的性质.
针对1.1节中式(4),(5)对应的假设检验问题,我们设计如下方法:
首先,我们要构建一个用于作为测试集的测试网格(test grid).测试网格中的数据并非真实数据,其重点在于模拟真实数据中特征的分布.例如本文研究的是2个基因相互作用,所以设计一个二维网格.网格大小为 N 1 × N 2 ,网格中每个位置代表 G 1 , G 2 的一组取值情况.为了避免测试数据与真实数据重复,我们预先从原始数据中抽取 N 1 + N 2 个样本用于构建网格.将前 N 1 个样本的 G 1 与后 N 2 个样本的 G 2 分别组合,从而生成 N 1 × N 2 的网格.
网格中每个点的预测值为 ![]() 所有网格的预测值记为向量形式:
所有网格的预测值记为向量形式:
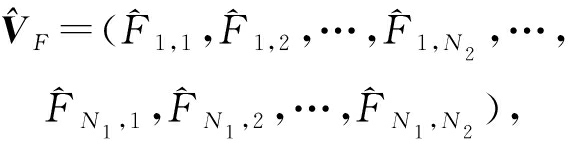
(11)
则有:
(12)
(13)
式(12)表示 G 1 取第 i 个SNP组合时,遍历测试网格上所有 G 2 时的预测平均值,同理可得式(13)是 G 2 取第 j 个SNP组合时,遍历测试网格上所有 G 1 时的预测平均值.如果 G 1 , G 2 之间是加性关系,则网格中所有的点( g 1 i , g 2 j )都可以表示成 F i , j = f i · + f · j - μ ,其中 μ 表示测试网格中所有点预测值的真实期望.因此,1.1节中的假设检验也可以表示为
H 0 : F i , j - f i · - f · j + μ =0,
∀( g 1 i , g 2 j )∈ X TEST .
(14)
H 1 : F i , j - f i · - f · j + μ ≠0,
∃( g 1 i , g 2 j )∈ X TEST .
(15)
令 N = N 1 × N 2 ,我们引入一个维度为 N × N 的差异矩阵 D :
D = I N -( I N 1 ⊗ ![]()
( 1 N 1 × N 1 ⊗ ![]()
(16)
其中⊗表示张量乘积.则检验值 ![]() 可以表示为
可以表示为 ![]() 此时自由度为 P =1+( N 1 -1)+( N 2 -1), D 矩阵的秩为 N - P .令 Σ 表示
此时自由度为 P =1+( N 1 -1)+( N 2 -1), D 矩阵的秩为 N - P .令 Σ 表示 ![]() 的协方差,
的协方差,
![]()
(17)
我们使用 ![]() 作为表征相互作用强度的统计值.
作为表征相互作用强度的统计值.
实验中存在一个问题,当测试网格数据样本量超过50时,方法性能会大幅下降,因此考虑降低测试网格的维度.Johnson-Lindenstrauss定理保证了任何降维方法的精度上下限.影响降维精度的因素主要是维数、数据大小等,与降维方法本身无关.在维数差不是特别大时,用任何方法都可以保证一个较高的精度.本文采用随机投射(random projec-tion)方法.该方法是机器学习中常见的降维方法.通过随机生成一个 ![]() p × q 的投射矩阵,并对矩阵中的每一个轴(即每一行)归一化,之后左乘数据,便可将 X ∈
p × q 的投射矩阵,并对矩阵中的每一个轴(即每一行)归一化,之后左乘数据,便可将 X ∈ ![]() q 降至
q 降至 ![]() p .实验中我们构造1 000个随机矩阵,降维的维数设为15.详细方法描述见算法1.
p .实验中我们构造1 000个随机矩阵,降维的维数设为15.详细方法描述见算法1.
算法1 . 基于U统计量的基因互作检测方法GBUtrees.
输入:2个基因的基因型数据 X =( X 1 , X 2 )、样本的类标签 Y ∈[0,1] n ;
输出: χ ![]() 检验的 p 值.
检验的 p 值.
① 将原始样本集划分为训练集和测试集,测试集样本个数为 N 1 + N 2 ;
② 计算差异矩阵 D ;
③ 选取测试网格约简的维度 r =15;
④ 生成 M =1 000个随机映射矩阵 R 1 , R 2 ,…, R M ;
⑤ ![]()
⑥ 随机从训练集中选取一个公共样本 ![]()
⑦ For j =1,2,…, N do
⑧ 随机选取 k -1个样本,并连同公共样本构成一个大小为 k 的子训练集 ![]()
⑨ 使用 ![]() 构建一个树模型;
构建一个树模型;
⑩ 使用构建的树模型对test grid中每一个点做测试,获得预测向量 ![]()
 对每一个随机映射矩阵,记录
对每一个随机映射矩阵,记录 ![]()
 End For
End For
 对每一个随机映射矩阵,记录
对每一个随机映射矩阵,记录 ![]()
![]()
 N ;
N ;
 End For
End For
 计算 m 次预测均值之间的方差 ζ 1, k ;
计算 m 次预测均值之间的方差 ζ 1, k ;
 计算所有预测之间的方差 ζ k , k ;
计算所有预测之间的方差 ζ k , k ;
 计算所有预测的均值
计算所有预测的均值 ![]()
 对 M 个随机映射矩阵,分别计算统计值
对 M 个随机映射矩阵,分别计算统计值 ![]()
 根据自由度为 r 的 χ
根据自由度为 r 的 χ ![]() 检验,为 M 个统计值 T R i 求 p 值 θ 1 , θ 2 ,…, θ M ;
检验,为 M 个统计值 T R i 求 p 值 θ 1 , θ 2 ,…, θ M ;
 返回 p 值均值作为相互作用关系强度的显著性.
返回 p 值均值作为相互作用关系强度的显著性.
算法1中涉及到的主要参数分为以下2个部分:
1) GBUtrees框架下,选取子样例集的次数 ![]() 每个子样例集包含样本的个数 k ,以及每次集成学习中包含树的个数 N .其中,根据文献[11]中的定理1, k 满足
每个子样例集包含样本的个数 k ,以及每次集成学习中包含树的个数 N .其中,根据文献[11]中的定理1, k 满足 ![]() 为训练集样本的个数.因此,模拟实验中样本数为4 000的训练集每次选取120个样本用于构造每棵树.此外,表征基因作用强度的统计量的显著性水平 α 需满足
为训练集样本的个数.因此,模拟实验中样本数为4 000的训练集每次选取120个样本用于构造每棵树.此外,表征基因作用强度的统计量的显著性水平 α 需满足 ![]() ( n
( n  m ).而
m ).而 ![]() 因此,实验中我们选取
因此,实验中我们选取 ![]() 用以控制 α =0.05.
用以控制 α =0.05.
2) 构造每一棵树时,需要考虑每个分裂节点至少包含样本个数( minsplit )以及树的最大深度( maxdepth ).利用网格搜索(grid search)方式,对每个 minsplit 与 maxdepth 组合做5重交叉验证(5-fold cross-validation),最终选取 minsplit =3, maxdepth =4.
本文实验分为仿真模拟数据与真实数据2部分.
2.1.1 仿真数据来源
仿真实验选用经典的基于重采样仿真的SNP遗传数据生成软件gs2.0.该软件以单体型数据为模板,通过设定疾病优势比( OR )、人群患病率(population prevalence)以及样本大小,可以高效产生大量疾病-对照SNP仿真数据.
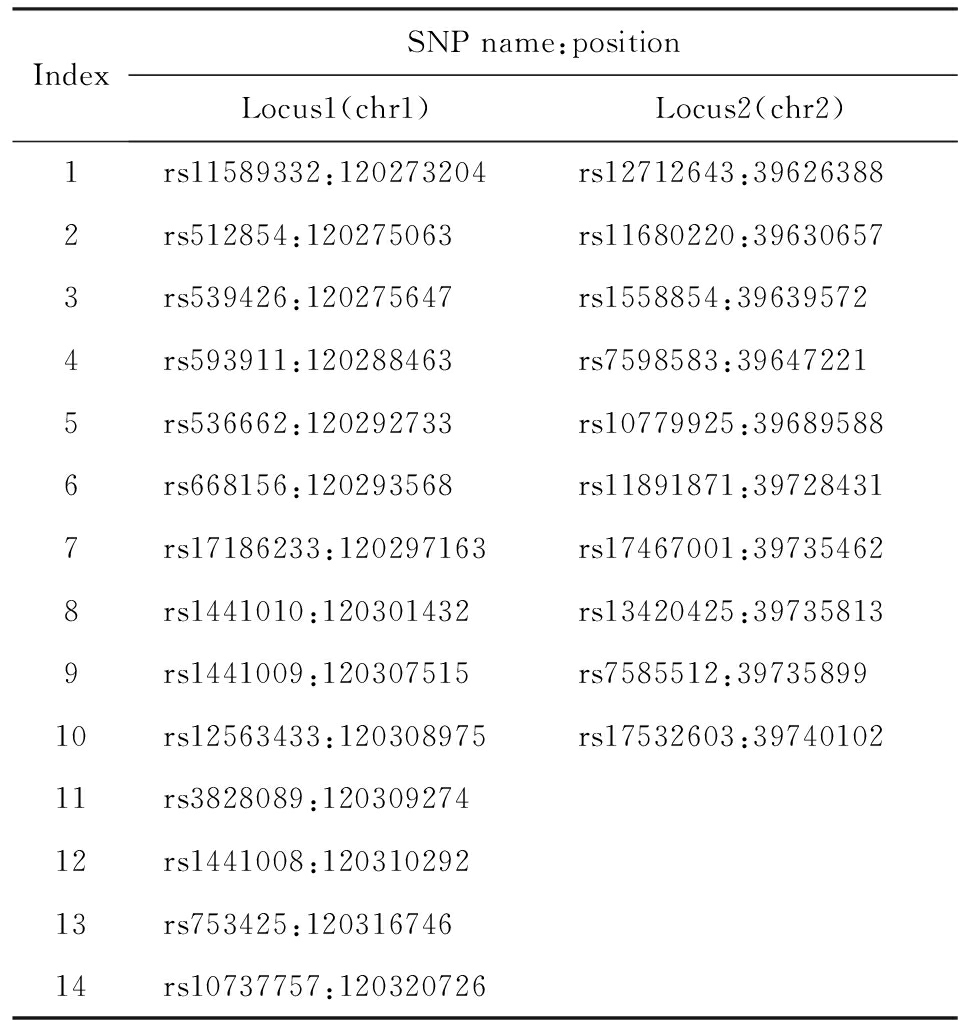
本文使用的模板数据是Hapmap 高加索人群(CEU)数据,使用NCBI build37作为参照基因组进行注释.该数据共有90个单体型,以1 000 Genome数据为参考基因组,通过使用SHAPEIT [18] 与IMPUTE2,对缺失的位点进行基因型填充.随后分别在一号染色体与二号染色体上各选取了一个基因 [11-12] ,一号染色体上基因选取了14个tag SNP,二号染色体上基因选取了10个tag SNP.2个基因内部连锁不平衡(LD)模式见图1.选取SNP的详细信息见表1.
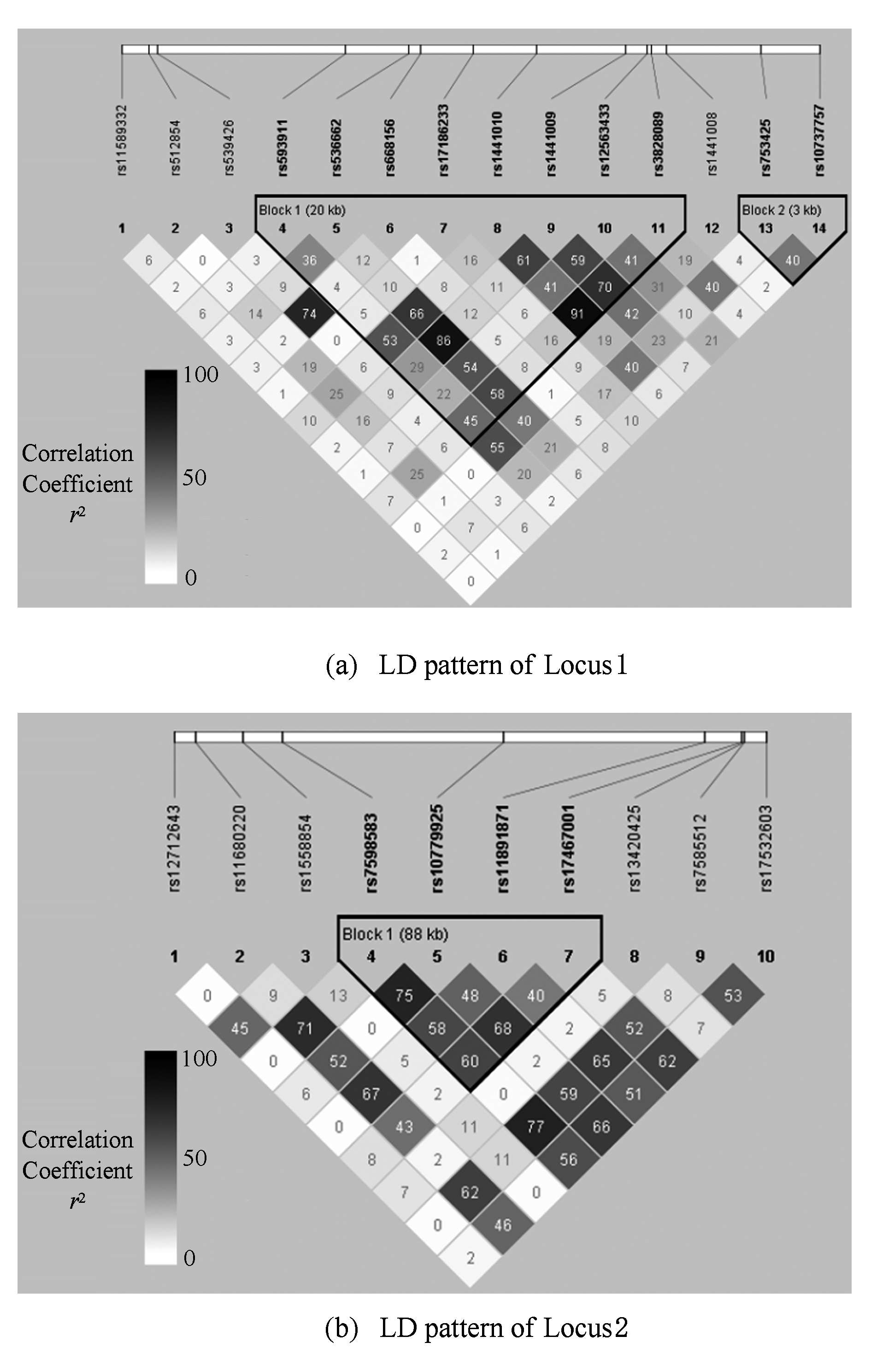
Fig. 1 LD patterns of two empirical loci used in simulation studies
图1 仿真数据2个基因模板的连锁不平衡模式图
Table 1 Details of the SNPs Used in Simulation Studies
表1 仿真数据2个基因模板选取SNP的信息
2.1.2 仿真模型
gs2.0共有8种可选的两位点疾病遗传风险模型.根据方法不同性能的考量,实验分为以下2个方面:
1) 为了考察方法第1类错误率的表现,设定优势比 OR =1.0,此时生成不存在相互作用.分别生成样本数为1 000,2 000,3 000,4 000,5 000的样本集各100个,观察第1类错误率在不同样本规模时的变化规律.
2) 为了考察方法在不同交互程度时的表现,将优势比设为1.5,2,2.5,3,3.5,4共6个取值,人群患病率(population prevalence)设为0.1,样本由2 000疾病样本、2 000对照样本组成.8种疾病模型共有48种组合,每种组合生成100个数据集.
2.1.3 实验结果分析
为了验证基于U统计框架方法的有效性,本文采用功效(power)与假阳率2个指标.功效即在每种参数设置下,可以成功检测到模拟数据中插入的相互作用的数据集占100个数据集的比例.GBUtrees与GBIGM [10] ,KCCU [8-9] ,AGGrEGATOr [11] 共4种方法进行了比较.其中,GBIGM与AGGrEGATOr两种方法没有参数限制;KCCU方法采用文献中推荐的参数,设定修剪摺刀法(trimmed jackknife)的修剪比例为 ω =0.15.
在假阳性方面,设定显著性阈值 α =0.05,随着样本规模增加,GBUtrees犯第1类错误的概率均可控制在显著性阈值以内,可以用于后续的相互作用检验.
在不同的 OR 值下,由图2可以看到,在8种模型下,随着 OR 值的增大,GBUtrees的检测能力表现为单调递增,且检测能力均高于其他3种方法.隐性-隐性模型相较于其他模型,检测能力略低, OR 最大时只能维持在30%左右,其余模型中最大的检测率可以达到90%.隐性-隐性模型的比率表见表2,表2中每个位置表示特定基因型组合下个体罹患疾病的几率. Pr ( D | g i )表示个体在基因型 g i 下患病的概率, ![]() 表示个体在基因型 g i 下不患病的概率,则有:
表示个体在基因型 g i 下不患病的概率,则有:
![]()
(18)
则基因型 g i 的外显率为
![]()
(19)
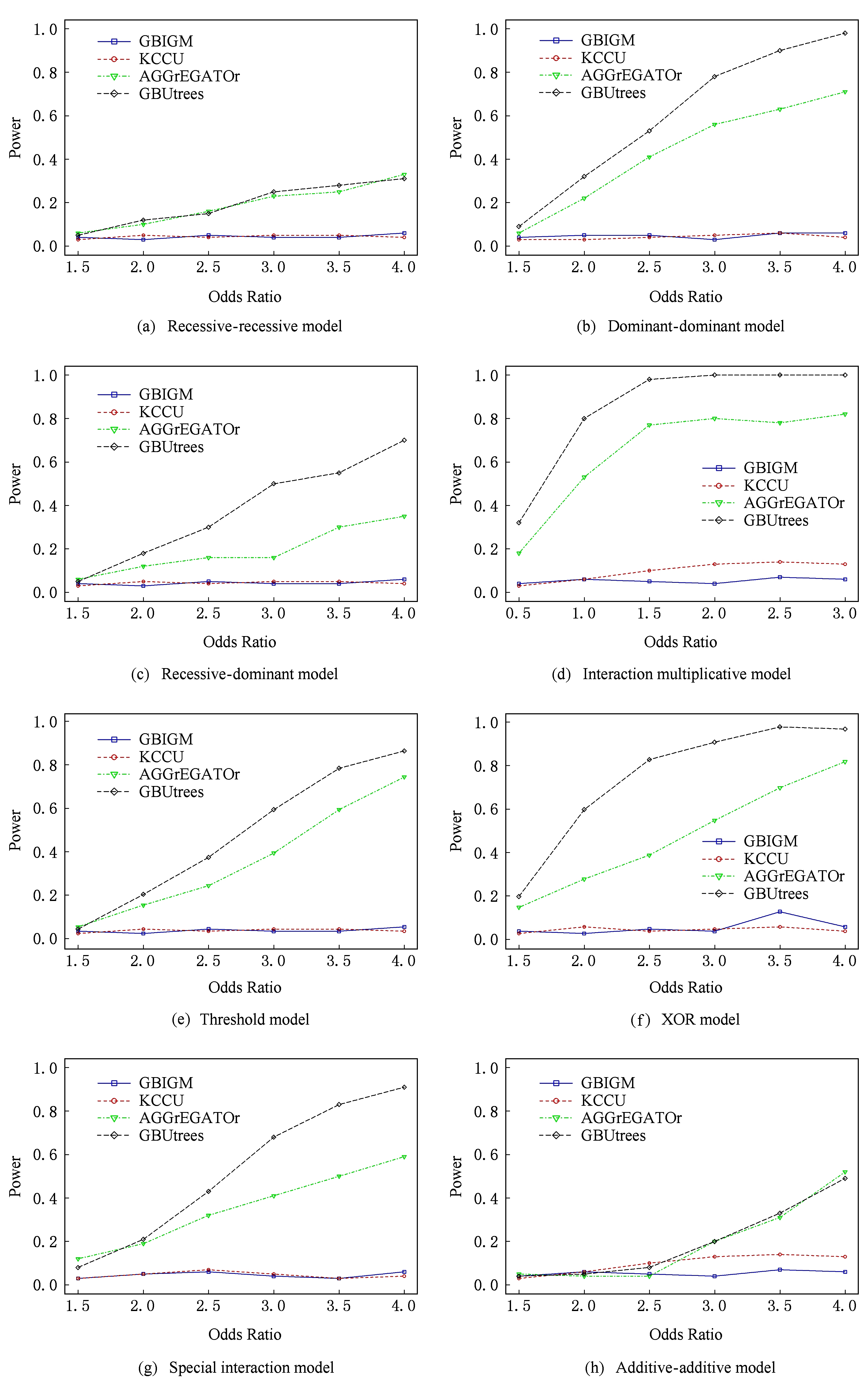
Fig. 2 Power comparison between GBUtrees and competitive methods under four disease models with different odds ratio
图2 4种交互作用检测方法在8种疾病模型的不同OR值下的功效比较
由此我们可以得到2个位点基因型组合的外显率表,见表3.
Table 2 Table of Odds for Recessive - Recessive Model
表2 隐性 - 隐性模型的疾病比率表
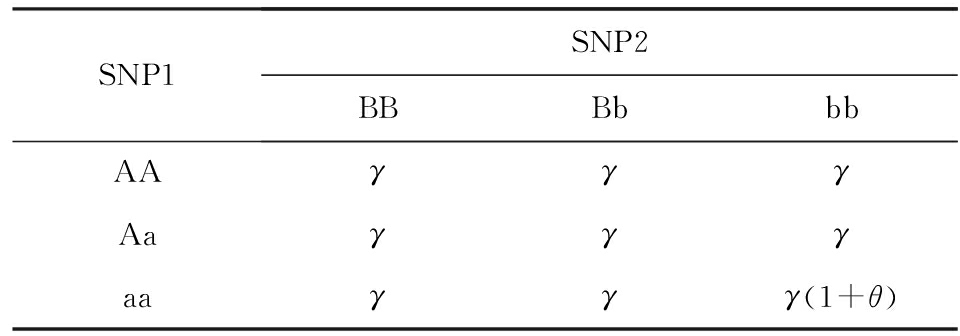

Fig. 3 Power comparison between GBUtrees and competitive methods under four disease models with different sample size
图3 4种交互作用检测方法在4种疾病模型的不同样本量下的功效比较
表2中γ是比率的基准值.实验中通常我们设定疾病在人群患病率 p =0.01, ![]() 因此 γ 是个较小的值.可以看出在我们的方法中,9种基因型组合中的前8种log( Pr ( D | g i ))=log( γ )-log(1+ γ )都接近于0,而唯一产生变化的基因型组合位点aabb全部都是低频基因位点,而一般的SNP的次等位基因频率(minor allele frequency, MAF )处于0.2~0.4之间,从而导致最后一种产生作用的基因型组合在数据中几乎不会出现.隐性-隐性模型本身所具有的难检出性是导致本文及对比方法普遍失效的重要原因.
因此 γ 是个较小的值.可以看出在我们的方法中,9种基因型组合中的前8种log( Pr ( D | g i ))=log( γ )-log(1+ γ )都接近于0,而唯一产生变化的基因型组合位点aabb全部都是低频基因位点,而一般的SNP的次等位基因频率(minor allele frequency, MAF )处于0.2~0.4之间,从而导致最后一种产生作用的基因型组合在数据中几乎不会出现.隐性-隐性模型本身所具有的难检出性是导致本文及对比方法普遍失效的重要原因.
Table 3 Penetrance Table for Recessive - Recessive Model
表3 隐性 - 隐性模型的疾病外显率表
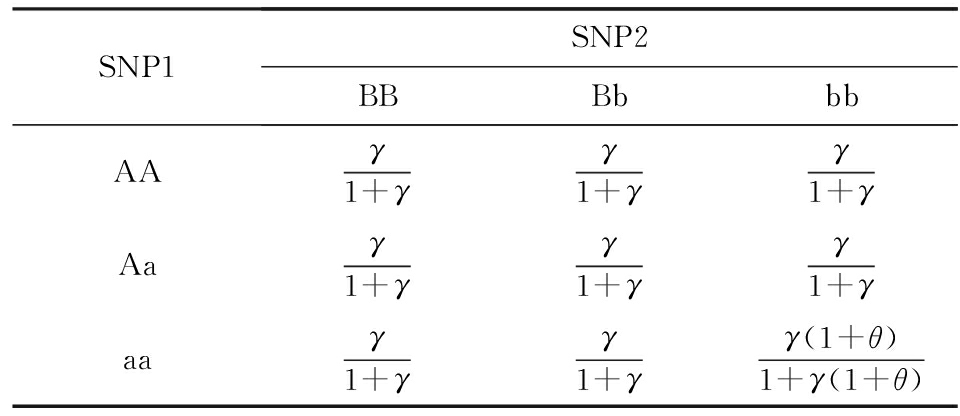
3种对比方法中,AGGrEGATOr在8种疾病模型下均表现出与GBUtrees相似的变化趋势与性质,而KCCU与GBIGM在该模拟实验中几乎无法检测出相互作用.本文中仿真实验与GBIGM中模拟实验 [8] 的区别在于选取的模板数据不同,不同的模板数据由于内部不同的连锁不平衡结构会对方法的性能产生影响.
此外,样本量对方法性能影响的结果如图3所示.随着样本量增加,GBUtrees与AGGrEGATOr性能均呈现单调递增的趋势,另外2种方法性能没有随样本数量的增加而发生改变.图3只展示了4个模型下方法的表现,GBUtrees在剩余疾病模型上均表现出类似的变化趋势,且优于其他3种方法.
① https: 
 www.genome.jp
www.genome.jp  kegg
kegg  pathway.html
pathway.html
2.2.1 真实数据描述及预处理
为了评估方法在处理真实疾病对照数据时的表现,我们选用了一组类风湿关节炎(rheumatoid arth-ritis, RA)的真实基因型数据.RA是一种遗传相关的慢性的自身免疫性疾病,持续性的炎症会影响骨重塑,进一步导致骨坏死.我们使用WTCCC(2007) 数据集,该数据使用Affymetrix GeneChip 500K进行基因型鉴定.为了验证潜在的基因之间的相互作用,我们参考了KEGG ① 上的RA 通路hsa05323.该通路共包含90个基因,其中MHCII与V-ATP是2个蛋白质结合体,内部存在许多的相互作用.因此,对这2个复合体各选取了一个代表基因.通过使用NCBI发布的人类基因组序列NCBI build36的注释文件确定每个基因在染色体上的起始终止位置,并为每个基因的上下游增加了10 kb的缓冲区,我们从RA数据中为最终剩余的48个基因确定其包含的SNP.随后借助软件PLINK对数据进行质量控制,共包括3个步骤:1)删除性别与性染色体不匹配的数据;2)设置SNP缺失率(missing rate)小于10%、低频等位基因频率 MAF >5%,以及显著影响表型的缺失;3)删除不满足Hardy-Weinberg平衡的SNP.经过质量控制之后,共剩余385个SNP和4 966个样本,其中4 966个样本包括1 973个病例样本以及2 993个对照样本.
2.2.2 真实数据结果分析
为了避免人群结构、性别成为干扰因素,我们将性别作为变量加入数据.随后使用软件GCTA对数据做主成分分析,并将前10个分量加入数据用于校正潜在人群结构带来的影响.
我们总共评估了 ![]() 对基因的相互作用(gene-gene interaction, GGI).为了避免方法中存在的随机效应,每个方法都执行了10次.通过显著性水平和多重检验校正,对于KCCU和GBIGM方法,分别获得了43和65个重要的基因互作关系对.其中有30和65个GGI的 p 值为0.AGGrEGATOr方法在进行多重校正之后,没有任何达到显著性的结果.参考Emily [11] 文中的建议,我们取消对结果的多重校正,获得了16个重要的GGI,并根据 p 值对这些结果排序.对于我们的方法,同样取消多重校正,获得了13个重要的GGI.我们选择GBUtrees的前10个结果与AGGrEGATOr的前10个结果进行比较(见表4),大约占所有相互作用关系的1%.
对基因的相互作用(gene-gene interaction, GGI).为了避免方法中存在的随机效应,每个方法都执行了10次.通过显著性水平和多重检验校正,对于KCCU和GBIGM方法,分别获得了43和65个重要的基因互作关系对.其中有30和65个GGI的 p 值为0.AGGrEGATOr方法在进行多重校正之后,没有任何达到显著性的结果.参考Emily [11] 文中的建议,我们取消对结果的多重校正,获得了16个重要的GGI,并根据 p 值对这些结果排序.对于我们的方法,同样取消多重校正,获得了13个重要的GGI.我们选择GBUtrees的前10个结果与AGGrEGATOr的前10个结果进行比较(见表4),大约占所有相互作用关系的1%.
Table 4 Ranking of Significant GGI Results in the WTCCC Rheumatoid Arthritis Dataset Analysis
表4 WTCCC人类类风湿数据集上显著相互作用关系在不同方法中的秩次
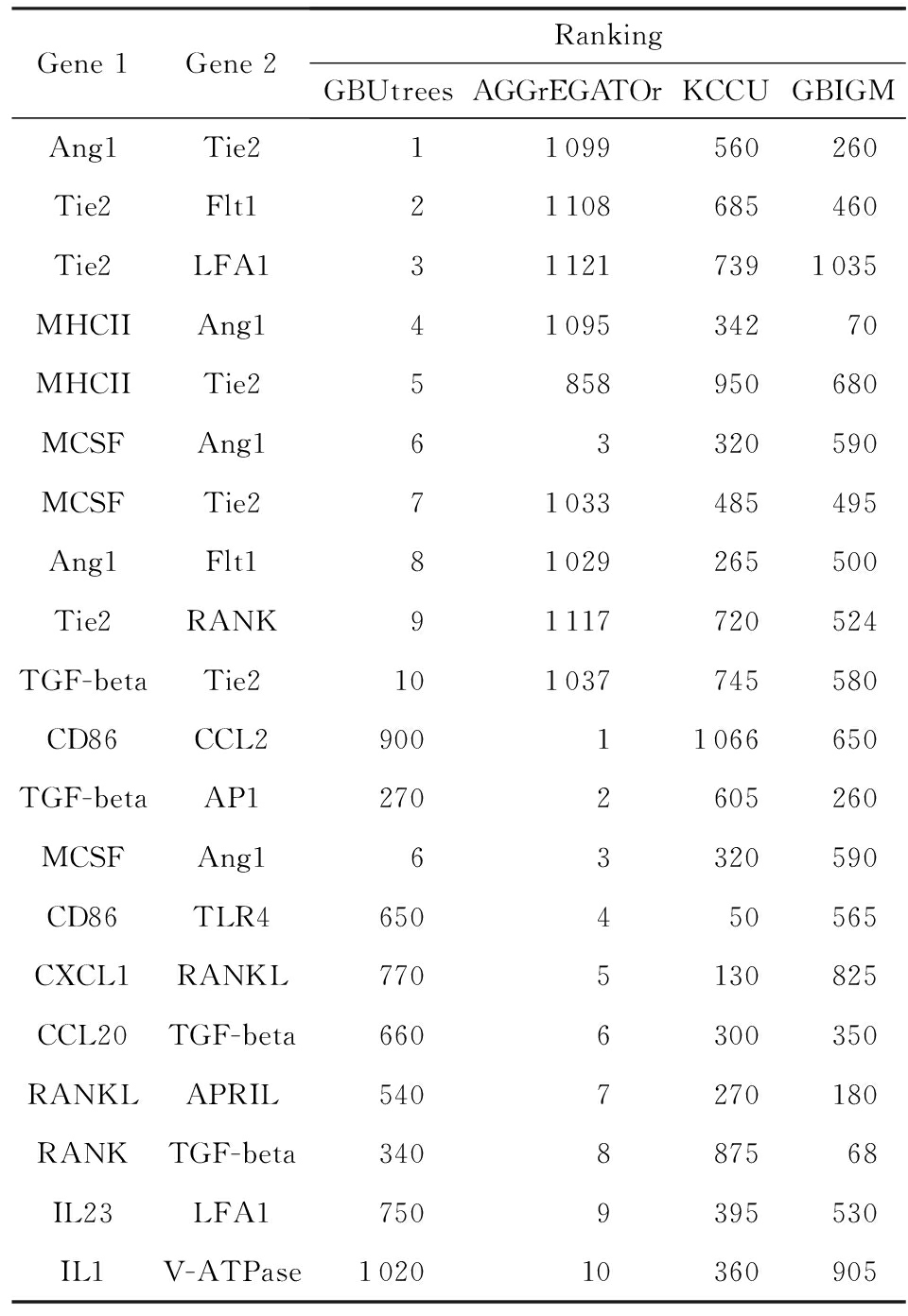
GBUtrees检测出最显著的相互作用来自血管生成素(Ang1)与Tie2.该相互作用是一对RA致病机制中已被证实的互作关系 [19] .血管翳是RA病变过程中的一个特征性的病例产物.滑膜血管增生是RA早期关键事件,是促进和维持血管翳的重要因素.而RA血管生成是由滑膜组织髓细胞和纤维母细胞(包括血管生成素Ang1)释放的促血管生成因子驱动和维持的.内皮细胞(EC)的特异性因子Ang1及其酪氨酸激酶受体Tie2在生理性和病理性的血管生成发育中至关重要.Ang1/Tie2在RA滑膜组织中上调表达.有研究表明Ang1/Tie2信号通路介导了肿瘤坏死因子(TNF-)、白介素(IL)以及toll类受体TLR2在RA中促进血管生成的作用.AGGrEGATOr方法发现的第7对是RANKL与APRIL之间的互作 [20] .研究表明纤维细胞样滑膜细胞FLS是RA发病机制中的主要效应细胞,而APRIL促进了RANKL的FLS表达.KCCU与GBIGM方法给出了太多显著性结果,因此没有对这2种方法的结果进行进一步分析.
检测基因-基因相互作用的研究在理解人类复杂疾病致病机理方面具有重要意义.本文提出一种基于U统计量与集成学习结合的假设检验方法GBUtrees用于基因相互作用检测.我们将检测基因之间的相互作用问题转化为假设检验问题,定义零假设为2个基因与疾病标签的LOR之间满足加性关系.这一假设对基因之间互作的形式没有限制,增强了方法对不同类型作用关系的检测能力.仿真数据实验结果表明,在可控第1类错误率的前提下,GBUtrees在模拟的8种疾病模型上均优于相比较的其他方法,且方法效力随着作用强度的增大以及样本量的增大呈现单调递增.此外,在真实类风湿关节炎数据验证实验中,GBUtrees成功复现了已被证实的Ang1/Tie2相互作用.以上结果表明该方法在基因相互作用挖掘中的有效性.
GBUtrees采用集成学习方法作为底层学习方法,增强了方法的泛化能力.同时,以树模型作为基分类器,发挥其强大的非线性建模能力,大大增加了方法检出不同类型相互作用的功效.此外,通过设计重采样的策略,使预测结果具有U统计量的渐进正态性质,从而可以设计用于表征相互作用关系强度的统计量.获得相互作用关系强度 p 值对于检验结果的复现以及应用到后续的全基因组关联研究中都具有至关重要的意义.仿真模拟数据以及真实人类疾病数据的实验结果表明,本文提出的GBUtrees方法在检测效力方面优于现有的方法,可以有效用于疾病相关基因相互作用的挖掘研究.
参考文献
[1]Macarthur J, Bowler E, Cerezo M, et al. The new NHGRI-EBI Catalog of published genome-wide association studies (GWAS Catalog)[J]. Nucleic Acids Research, 2016, 45(Database issue): D896-D901
[2]Bateson W. Mendel’s Principles of Heredity[M]. Cambridge, UK: Cambridge University Press, 1909
[3]Fisher R. The correlation between relatives on supposition of mendelian inheritance[J]. Royal Society of Edinburgh, 1918, 52: 399-433
[4]Ritchie M D, Hahn L W, Moore J H. Power of multifactor dimensionality reduction for detecting gene-gene interactions in the presence of genotyping error, missing data, pheno-copy, and genetic heterogeneity[J]. Genetic Epidemiology, 2003, 24(2): 150-157
[5]Zhang Xiang, Huang Shunping, Zou Fei, et al. TEAM: Efficient two-locus epistasis tests in human genome-wide association study[J]. Bioinformatics, 2010, 26(12): i217-i227
[6]Wan Xiang, Can Yang, Qiang Yang, et al. BOOST: A fast approach to detecting gene-gene interactions in genome-wide case-control studies [J]. American Journal of Human Genetics, 2010, 87(3): 325-340
[7]Peng Qianqian, Zhao Jinghua, Xue Fuzhong. A gene-based method for detecting gene-gene co-association in a case-control association study [J]. European Journal of Human Genetics, 2010, 18: 582-587
[8]Yuan Zhongshang, Gao Qingsong, He Yungang, et al. Detection for gene-gene co-association via kernel canonical correlation analysis [J]. BMC Genetics, 2012, 13(1): 83-88
[9]Larson N B, Jenkins G D, Larson M C, et al. Kernel canonical correlation analysis for assessing gene-gene interactions and application to ovarian cancer[J]. European Journal of Human Genetics, 2014, 22: 126-131
[10]Li Jin, Huang Dongli, Guo Maozu, et al. A gene-based information gain method for detecting gene-gene interactions in case-control studies [J]. European Journal of Human Genetics, 2015, 23: 1566-1572
[11]Emily M. AGGrEGATOr: A Gene-based GEne-Gene interActTiOn test for case-control association studies [J]. Statistical Applications in Genetics & Molecular Biology, 2016, 15(2): 151-171
[12]Ma Li, Clark A G, Keinan A. Gene-based testing of interactions in association studies of quantitative traits [J]. Plos Genetics, 2013, 9(2): e1003321
[13]Mentch L, Hooker G. Quantifying uncertainty in random forests via confidence intervals and hypothesis tests [J]. Journal of Machine Learning Research, 2016, 17(1): 841-881
[14]Mentch L, Hooker G. Formal hypothesis tests for additive structure in random forests [J]. Journal of Computational & Graphical Statistics, 2017, 26(3): 589-597
[15]Lee A J. U-Statistics: Theory and Practice[M]. New York: CRC Press, 1990
[16]Zhang Hu, Tan Hongye, Qian Yuhua, et al. Chinese text deception detection based on ensemble learning [J]. Journal of Computer Research and Development, 2015, 52(5): 1005-1013 (in Chinese)
(张虎, 谭红叶, 钱宇华, 等. 基于集成学习的中文文本欺骗检测研究[J]. 计算机研究与发展, 2015, 52(5): 1005-1013)
[17]Fu Yiqi, Dong Wei, Yin Liangze, et al. Software defect prediction model based on the combination of maching learning algorithms[J]. Journal of Computer Research and Development, 2017, 54(3): 633-641 (in Chinese)
(傅艺绮, 董威, 尹良泽, 等. 基于组合机器学习算法那的软件缺陷预测模型[J]. 计算机研究与发展, 2017, 54(3): 633-641)
[18]Delaneau O, Marchini J, The 1000 Genomes Project Consortium. Integrating sequence and array data to create an improved 1000 genomes project haplotype reference panel[J]. Nature Communications, 2014, 5: 3934
[19]Elshabrawy H A, Chen Z, Volin M V, et al. The pathogenic role of angiogenesis in rheumatoid arthritis [J]. Angiogenesis, 2015, 18(4): 433-448
[20]Kayakabe K, Kuroiwa T, Sakurai N, et al. Interleukin-6 promotes destabilized angiogenesis by modulating angiopoietin expression in rheumatoid arthritis [J]. Rheumatology, 2012, 51(9): 1571-1579

Guo Yingjie , born in 1987. PhD candidate. Her main research interests include machine learning and bioinformatics.

Liu Xiaoyan , born in 1963. PhD. Associaate professor and master supervisor. Her main research interests include bioinformatics and data mining.(liuxiaoyan@hit.edu.cn).

Wu Chenxi , born in 1988. PhD. Assistant professor. His main research interests include flat surface, three dimension topology.

Guo Maozu , born in 1966. Professor. PhD supervisor. Member of CCF. His main research interests include machine learning, smart city and bioinformatics.

Li Ao , born in 1995. Master. His main research interests include machine learning and deep learning.
Guo Yingjie 1 , Liu Xiaoyan 1 , Wu Chenxi 2 , Guo Maozu 1,3 , and Li Ao 1
1 ( School of Computer Science and Technology , Harbin Institute of Technology , Harbin 150001) 2 ( Department of Mathematics , Rutgers University , Piscataway , NJ , USA 08854) 3 ( Beijing Key Laboratory of Intelligent Processing for Building Big Data ( Beijing University of Civil Engineering and Architecture ), Beijing 100044)
Abstract In qualitative genome-wide association studies (GWAS), most existing methods make strong assumptions on the interaction form between genes which limited their power. Lately, many methods for detecting gene-gene interaction have been developed, and among them, the gene-based methods have grown in popularity as they confer an advantage in both statistical power and biological interpretability. In this paper, we propose a hypothesis testing framework for gene-based gene-gene interaction detection based on U statistics and tree-based ensemble learners (GBUtrees). We construct a statistic that detects the deviation from the additive structure in the prediction of log odds ratio of a qualitative trait from each base learner, then average it for learners trained using different subsamples to turn it into the form of U statistics. GBUtrees benefits from both the non-linear modeling power of tree-based ensemble model and the asymptotic normality of U statistics. Our method makes no assumption on the form of interaction, which strengthens its power for detecting different kinds of interactions. Based on simulated studies of eight disease models and real data from the RA pathway in WTCCC dataset, we conclude that it is effective in detecting different kinds of interactions and can be useful for genome-wide association studies.
Key words U statistics; ensemble learning; gene-gene interaction; single nucleotide polymorphism; genome-wide association studies
中图法分类号 TP391
通信作者 : 郭茂祖(guomaozu@bucea.edu.cn)
基金项目 : 国家自然科学基金项目(61571163,61532014,61671189);国家重点研发计划项目(2016YFC0901902)
This work was supported by the National Natural Science Foundation of China (61571163, 61532014, 61671189) and the National Key Research and Development Plan of China (2016YFC0901902).
收稿日期 : 2018-05-18;
修回日期: 2018-06-13
DOI: 10.7544/issn1000-1239.2018.20180365