王 博 刘惊雷
(烟台大学计算机与控制工程学院 山东烟台 264005) (bob8190@163.com)
摘 要 布尔Game是一种重要的多Agent合作求解框架,它利用命题逻辑来表达静态的Agent博弈场景.其中每个Agent的目标采用命题公式来表示,其目标是否满足取决于命题公式的赋值.目前布尔Game多从知识表示角度和纳什均衡计算的角度来研究,从联盟角度研究核的求解却不多.布尔Game求核是生成策略组合然后在策略组合内对比的过程.首先,通过以布尔Game的决策变量为顶点、以目标为超边,构成布尔Game上的超图结构来求满足核的约束满足的解.其次,以Agent为顶点、以Agent间的依赖关系为边构成的有向依赖图,可以将布尔Game根据稳定集分解为规模上更小的布尔Game.这2种结构简化了求核的生成过程和比较过程,进而在一定程度上提高了布尔Game求核效率.然后基于超图的超树分解和依赖图的稳定集分解,给出了不同的布尔Game的求核算法.最后实验验证了算法的有效性.
关键词 布尔Game;核求解;约束可满足问题;超图;超树分解;稳定集
正则形式的Game通过矩阵来表示博弈,其中Agent的目标被描述为收益函数的形式,这使得在有很多可能结果的Game中对目标的理解复杂化.布尔Game是一种表示博弈的新兴框架,由Harrenstein等人于2001年首先给出在双人零和博弈上的确定性逻辑描述 [1] .后来由Bonzon推广为多Agent的一般博弈的框架 [2] .布尔Game是一种逻辑推理的框架,它通过命题公式来使Agent的理性行为形式化.布尔Game包含一个Agent的集合和一个决策变量的集合,其中每个Agent理性地控制一组决策变量,每个决策变量有且仅有一个Agent控制,并且每个Agent都有一个明确的目标,这目标是由连接词连接决策变量而构成的命题公式来表示,命题公式是一种二元偏好关系的表示.如果存在约束,每个Agent的约束是由这个Agent所控制的决策变量表示的命题公式.因此相对于正则形式描述Game的方式,布尔Game具有很明显的优势,布尔Game更加透明和简洁.对于每个策略组合,布尔Game不需要收益函数,而是使用每个Agent的目标,因为策略的收益源于Agent的目标.但是布尔Game也存在缺点,就是在计算纯策略纳什均衡和核时,布尔Game比其他的Game表示方法更困难.因为判断布尔Game是否存在核的问题属于NP完全问题,同时也属于 ![]() 完全问题 [3] .
完全问题 [3] .
在布尔Game中比较有名的2个均衡解为纯策略纳什均衡(pure Nash equilibrium, PNE)和核(core),但是均衡解不一定是最优解.PNE和核都是策略组合的集合,不同的是PNE是非合作Game下的均衡,而核是在合作Game下通过联盟达到的一种均衡.PNE特征是没有Agent会因为单独地脱离这个PNE而获得更好的收益;而核的特征是Agent中的联盟不会因为共同地脱离而都取得更好的收益.以著名的囚徒困境为例来说明这2种均衡解,假设2个小偷共谋闯入民宅作案后,被警察逮捕,被分别单独审讯,警察对每个犯罪嫌疑人都给出如下的判罚规则:若小偷1和2都坦白了罪行,则两人各被判刑3年;若两者一方坦白,一方抵赖,则抵赖者被判5年,而坦白者因如实交代有功,减刑3年,立即释放;若两人都抵赖,则警方证据不足,因私闯民宅,各被判刑1年.不同的策略对应的效应如表1所示:
Table 1 Strategy Table for the Prisoner ’ s Dilemma
表1 囚徒困境的策略表
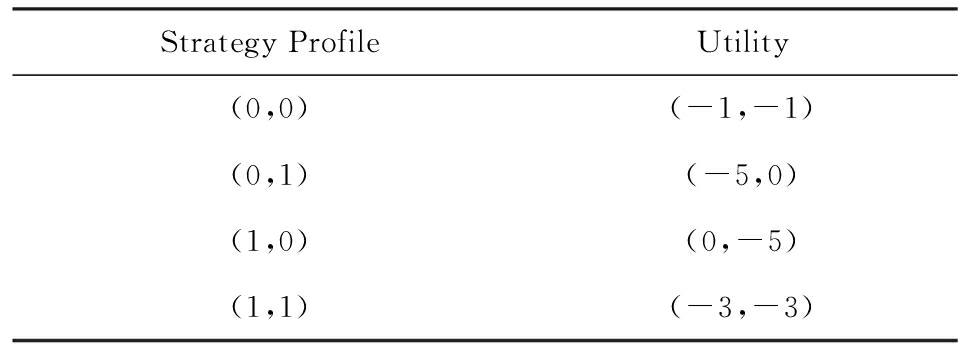
表1中第1列的序数对的第1个序数为小偷1的策略,第2个序数为小偷2的策略,以“0”表示抵赖,“1”表示坦白.表1中第2列的序数对分别对应于小偷1的效用和小偷2的效用.可以明显地看出囚徒困境问题存在一个PNE,就是策略组合(1,1),因为在该策略组合下任一小偷单独改变自己的策略都不会获得更高的收益.即使2个嫌犯可以联盟合作,该问题也不存在核,因为即使对于属于PNE的策略组合(1,1)来说,当小偷1和小偷2联盟来改变策略时,他们却能获得更好的收益,因此该问题没有核解.
本文主要研究以布尔Game为输入的核求解的问题.事实上布尔Game的核求解问题就是合作Game以布尔Game为框架的求解问题.Dunne等人使用非合作布尔Game的表示方法表示了合作布尔Game,本文也采用这样的布尔Game的表示方式,它们的Agent都是由命题公式来代表目标,并且这些Agent都控制一组决策变量,合作布尔Game的不同之处在于包含了成本 [3] .
目前,布尔Game已经着重从知识表示的角度和纯策略纳什均衡的角度进行了大量的研究,而在计算以核为解的表示和算法问题上研究不多.现在有2种现有的方法可以应用在这个计算问题上:1)把布尔Game转换成正则形式的Game是可用的,这样就能容易地解出正则形式的Game.但是,这样的转换在决策变量的数量上是指数级的.尤其是需要计算整个效用矩阵的方法可能只适用于Agent和行动的数量足够小时.避免使用所有收益矩阵中条目的方法可能更加适用于布尔Game.2)布尔Game中隐藏着很多图结构,通过这些图的结构可以提高布尔Game的求解效率,也能迅速地得出Game中的联盟结构并以此来求核.通常,计算布尔Game的核的问题可以看做策略组合的产生和对比测试的问题,即产生策略然后检测这个策略是否与后面的定义5所描述的一致.因此核求解的算法主要通过简化生成过程或测试过程来在一定程度上降低算法复杂度.在布尔Game的相关研究方面,本文的主要贡献在于:
1) 给出了布尔Game解的PNE、核和约束满足问题(CSP)三者之间的关系,即布尔Game满足核的赋值,一定是PNE,但不一定满足CSP(参见第2节的例1).反之,布尔Game中的策略组合一旦满足CSP,就一定是核,进而一定是PNE.
2) 将布尔Game中的决策变量看作超图中的顶点,Agent目标中包含的决策变量看作超图中的超边,构成布尔Game的超图结构.通过超图的超树分解算法求核,即求解布尔Game的约束可满足问题的解(参见5.3节的命题3).
3) 使用Agent之间存在的依赖关系,即一个Agent的目标中的决策变量依赖于另一个Agent所控制的决策变量.以Agent为顶点、以相关Agent为边构成的有向依赖图,根据稳定集将图分解,得到规模上更小的子图,这一定程度地降低了核求解的时间复杂度,简化了布尔Game的核求解问题.
本节从布尔Game框架的提出发展以及布尔Game的求解2方面,简要地描述布尔Game研究的相关工作.Harrenstein等人于2001年首先提出了二元偏好的双人零和Game上的布尔Game的模型,并在布尔Game的确定性上进行了逻辑描述 [1] .Dunne等人主要给出了以布尔Game的形式表示的一些Game实例在决策问题上的计算复杂性 [4] .Bonzon等人将布尔Game扩展为多Agent参与的未必是零和博弈的框架,并且描述了纳什均衡和劣势策略,并对相关问题的计算复杂性进行了研究 [2] .Dunne等人提出了一种表示合作Game的新模型,即合作布尔Game.此模型是在原有的布尔Game上添加了成本,使得Agent的目的除了达成自己的目标外,还要使成本最小化 [3] .Bonzon等人通过优先化的目标和命题化的CP-nets中表达Agent的偏好,扩展了二元的偏好关系,并给出了纳什均衡在布尔Game中的语义描述和确定了一些问题的计算复杂度 [5] .后来又提出布尔Game可以用来分析联盟的形成,而且证明了如果联盟能够保证联盟成员的所有目标都得到满足,那么布尔Game中的联盟就是高效的 [6] .Wooldridge等人在合作布尔Game上应用税收方案促使整个Game达到稳定状态,并提出了一个合适的税收方案的方法 [7] .
Clercq等人给出了布尔Game扩展为Agent之间相互不确定彼此目标的模型,使用了概率论中的不确定量度在语义上定义了不完全信息的布尔Game,并给出了这些语义的语法特征 [8] .Harrenstein等人研究了在带成本的布尔Game中转换的效果,Agent在成本上主要是为了追求某个目标的满意,其次是为了将他们的决策成本降到最低 [9] .引入并定义了迭代布尔Game,研究了其决策问题的计算复杂性 [10] ,又有不严格的准备方案可以通过适当的激励机制来消除.除了考虑在Game中不受限制地控制Agent的成本功能外,还研究了几种机制,即使是在税收或补贴不可能的情况下,允许Agent组成联盟,并消除Game中的不良结果 [11] .之后通过用可能的逻辑来代替传统逻辑的使用,以一种自然的方式来解决一些不切实际的假设,运用可能性逻辑设置了2种不同的环境,并通过一个面向谈判的程序说明了如何让掌握较多知识的Agent获得比其他一般的Agent更多有价值的结果 [12] .在国内也有一些关于Game联盟的研究有助于求核,杨威等人在协作感知系统的多目标非线性优化问题上,基于联盟博弈理论构建了一个不可转移支付的联盟构造博弈模型,提出了一种分布式多目标联盟构造算法DMCF [13] .徐广斌等人基于DP算法来求最优联盟的问题,提出了CCDP算法 [14] .
在布尔Game解的计算问题上,Bonzon等人定义了布尔Game中的Agent之间的依赖关系图,给出了在无环依赖关系图求PNE的算法,而且证明了这种依赖图简化了纯策略纳什均衡的计算 [15] .Sauro和Villata引入了稳定联盟和 Δ -约简,提出了基于二者的算法,并通过实验展示了它们有效地改善了核的计算 [16] .Dunne等人定义了 k 界纳什均衡的概念:没有Agent可以通过改变小于 k 个决策变量来阻塞当前策略组合而更加受益,而且证明了布尔Game在纳什均衡相关的计算问题上,比一般的表示Game的框架要容易得多 [17] .Clercq等人提出了一种基于析取回答集编程的求解纯策略纳什均衡的方法,并通过实验验证了该方法的有效性 [18] .2017年他们又给出了求一般布尔Game均衡解的方法.该方法基于析取回答集编程(ASP)并解出任何布尔Game的解,而且还扩展到了对带约束和成本的布尔Game求解 [19] .
本文则研究和计算了布尔Game核的求解问题,与已有的求核算法的主要区别在于:
1) 对比于Sauro等人的包含成本的求核方法,本文的布尔Game没有添加成本,是更加一般化的布尔Game.而且根据布尔Game的核与约束满足问题之间的关系,运用了布尔Game的超图形式简化了求解约束满足解的过程.
2) 对比于Clercq等人提出的判断布尔Game中是否存在核的方法,本文研究的是求布尔Game中的所有核.总的来说本文吸取了Bonzon等人的稳定集的概念 [15] ,将其求纳什均衡的方法扩展到布尔Game的核求解中,通过Agent间的依赖关系得到稳定集,再以稳定集分解布尔Game,从而简化了部分核的求解过程,提高了求解效率.
本节对布尔Game的相关概念进行形式化描述,并统一了第3~5节中所用到的标记.
布尔Game是一种逻辑推理的框架,它通过使用命题公式来使Agent的理性行为形式化.本文给出如下定义:
定义1 . 布尔Game.布尔Game是一个四元组 G =( N , V , π , Φ ).其中, N ={1,2,…, n }表示 n 个Agent的集合; V ={ p 1 , p 2 ,…}是一组原子命题,即决策变量的集合; π : V → N 为控制赋值函数; Φ ={ φ 1 , φ 2 ,…, φ n }表示Agent所对应的目标公式.
控制赋值函数 π 将每一个决策变量映射到控制这个决策变量的Agent上.Agent i 控制的所有决策变量记作 π i ={ p ∈ V | π -1 ( p )= i }.每个决策变量有且只有一个Agent控制,即{ π 1 , π 2 ,…, π n }是决策变量集 V 的一个划分.上述中控制的意思是只有Agent i 才可以设置 π i 中每个决策变量的真值.
定义2 . 策略组合.给定布尔Game G =( N , V , π , Φ ). G 中的Agent i 上所有策略的集合 S i ={ s i ∈2 π i },那么Game G 中所有的策略组合 S = S 1 × S 2 ×…× S i × S i +1 ×…× S n .对于∀ i , s i ∈ S i , G 的一个策略组合 s =( s 1 , s 2 ,…, s i , s i +1 ,…, s n ).一个策略组合也称作一组赋值.
定义2中,2 π i 表示 π i 上解释的集合. s i 是Agent i 的策略,即 i 控制的所有决策变量 π i 上的一个解释, s 是所有决策变量 V 上的一个解释,即 s ∈2 V .
定义3 . 效用函数.给定一个布尔Game G =( N , V , π , Φ ).对于每个Agent i ∈ N 和 G 的每个策略组合 s ,效用函数 u i 被定义为 u i ( s )=1当且仅当 s  φ i ,否则 u i ( s )=0.
φ i ,否则 u i ( s )=0.
定义4 . 纯策略纳什均衡(PNE).布尔Game G 的一个策略组合 s =( s 1 , s 2 ,…, s n )是PNE,当且仅当∀ i ∈ N , s i 是对 s - i 最好的回应,即对于Agent i 所有的策略 ![]() ⊆
⊆ ![]() 是 i 之外的Agent的策略组合.
是 i 之外的Agent的策略组合.
定义5 . 核 core ( G ).策略组合 s ∈ S 被联盟 C ⊆ N ( C ≠∅)阻塞,如果存在一个策略组合 s ′∈ S 使得:
![]() 即在联盟以外的所有Agent在 s 和 s ′中执行相同的策略;
即在联盟以外的所有Agent在 s 和 s ′中执行相同的策略;
2) ∀ ![]() 就是说在 C 内的所有Agent对于 s 更偏向于 s ′,即它们在 s ′的收益明显比在 s 中高.
就是说在 C 内的所有Agent对于 s 更偏向于 s ′,即它们在 s ′的收益明显比在 s 中高.
于是布尔Game的核 core ( G )就包含不受任何非空的联盟 C ⊆ N 阻塞的策略组合 s .
定义5也蕴含着 core ( G )不会受单独的Agent阻塞,所以每个核都是PNE.
例1 . 给定一个布尔Game G 1 =( N , V , π , Φ ),其中 N ={1,2,3}, V ={ p 1 , p 2 , p 3 }.而且 π 1 ={ p 1 }, π 2 ={ p 2 }, π 3 ={ p 3 },即Agent 1控制 p 1 ,Agent 2控制 p 2 ,Agent 3控制 p 3 .Agent 1,2和3的目标分别是 φ 1 =  p 1 ∨( p 1 ∧ p 2 ∧
p 1 ∨( p 1 ∧ p 2 ∧  p 3 )=1, φ 2 = p 1 ↔( p 2 ↔ p 3 )=1和 φ 3 =( p 1 ∧
p 3 )=1, φ 2 = p 1 ↔( p 2 ↔ p 3 )=1和 φ 3 =( p 1 ∧  p 2 ∧
p 2 ∧  p 3 )∨(
p 3 )∨(  p 1 ∧ p 2 ∧ p 3 )=1.
p 1 ∧ p 2 ∧ p 3 )=1.
例1可以理解为:假设有3个Agent分别是1,2和3.他们都可以选择去打球(设这样的决策变量为真)或者选择待在家里(设这样的决策变量为假),他们自己决定自己的行为,即控制是否去打球.他们的选择也就是每个Agent所控制的决策变量.而且他们对于去打球或者待在家里没有优先的偏好,只要他们完成了他们的目标即可(即命题公式为真).因此,Agent 1的目标是只跟Agent 2一起打球或者待在家里.Agent 2的目标是跟Agent 1和Agent 3一起去打球或者他们3个只有其中一个Agent去打球.而Agent 3想要只和Agent 2一起打球或者只让Agent 1单独去球场.对于这个问题的PNE和核都只有一个:唯独Agent 3一个人去打球,即策略组合 ![]() 此时,没有一个Agent会改变自己的行动而让最终的策略变得更好,也不会有任何Agent的联盟通过改变他们策略阻塞这个策略.
此时,没有一个Agent会改变自己的行动而让最终的策略变得更好,也不会有任何Agent的联盟通过改变他们策略阻塞这个策略.
定义6 . 约束满足问题(CSP).可通过三元组 I =( X , Y ,C)来表示.其中, X 是一个有限的变量集合, Y 表示有限的值域集合,C={ C 1 , C 2 ,…, C m }表示由 m 个约束组成的约束集合.对于每个约束 C i (1≤ i ≤ m ),由二元组( S i , r i )表示.其中, S i ⊆ X 是约束的范围,它是一个长度为 l i 的变量集合; r i 是 l i 个变量 S i 在值域 Y 上的关系,被称作约束关系.而CSP的解为一组满足所有约束的在 X 上的赋值.
定义7 . 布尔Game的约束满足问题表示.给定一个布尔Game G =( N , V , π , Φ ).布尔Game的约束满足问题表示 CSP ( G )=( V ,{0,1},C),其中∀ i ∈ N , C i =( RV ( i ), φ i =1), RV ( i )表示Agent i 的相关变量,其具体介绍参见定义11.
通过定义7可知,在布尔Game G 中,Agent i 的策略 S i 就是约束 C i 的待定解集,只有满足约束关系 r i 的才是约束 C i 的解,在布尔Game层次上就是Agent i 为了满足目标所采取的策略.
例2 . 对于例1的布尔Game G 1 中的约束满足问题 CSP ( G 1 )可表示为 X ={ p 1 , p 2 , p 3 }, Y ={0,1},C={(( p 1 , p 2 , p 3 ), φ 1 =1),(( p 1 , p 2 , p 3 ), φ 2 =1),(( p 1 , p 2 , p 3 ), φ 3 =1)},而 CSP ( G 1 )的解为使 φ 1 ∧ φ 2 ∧ φ 3 =1的赋值集合.
超树树宽是专门为超图设计的一种环性的度量.约束可满足问题在结构上最合适的表示方式之一是与之相对应的超图 [20] .因此在CSP下的布尔Game可以通过超图结构表示.
定义8 . 超图.超图表示为 H =( P , HE ),其中 P 是顶点集, HE ={ e ≠∅| e ⊆ P }是超边的集合,即每条超边是顶点集 P 的非空子集.
对于一个CSP I =( X , Y ,C),它相对应的超图表示为 H ( I )=( P , HE ),其中 P = X ,并且 HE ={ var ( S )|( S , r )∈C}, var ( S )表示在约束C的约束范围 S 中的变量集合.那么给定一个布尔Game G =( N , V , π , Φ ).根据定义7, G 的超图表示为 H ( G )=( V , RV ).其中布尔Game中的决策变量的集合 V 视为超图中的顶点集; RV 是所有Agent的相关变量的集合,它被看做超图中的超边的集合.
定义9 . 超树.超图 H 的超树为一个三元组 HT =( T , ![]() , λ ).其中 T =( D , E )是一棵有根树, D 是超树中的节点集合, E 是树的边集合,对应于超图的超边集;
, λ ).其中 T =( D , E )是一棵有根树, D 是超树中的节点集合, E 是树的边集合,对应于超图的超边集; ![]() 和 λ 都是标签函数,分别为对于每个顶点 d ∈ D 的集
和 λ 都是标签函数,分别为对于每个顶点 d ∈ D 的集 ![]() ( d )⊆ P 和 λ ( d )⊆ HE .
( d )⊆ P 和 λ ( d )⊆ HE .
超树的定义中, ![]() 和 λ 表示超树中节点内所包含的项,所
和 λ 表示超树中节点内所包含的项,所 ![]() ( d )表示在超树的节点 d 中所包含的对应超图中的点的集合, λ ( d )就是超树的节点 d 中所包含的对应超图中的超边的集合.
( d )表示在超树的节点 d 中所包含的对应超图中的点的集合, λ ( d )就是超树的节点 d 中所包含的对应超图中的超边的集合.
定义10 . 超树分解.超图 H 的超树分解结果是一棵超树 HT =( T , ![]() , λ ),需要满足以下条件:
, λ ),需要满足以下条件:
1) ∀超边 h ∈ HE ,∃节点 d ∈ D ,使得 var ( h ) ![]() ( d );
( d );
2) ∀ p ∈ P ,集合{ d ∈ D | p ![]() ( d )}可以诱导 T 的一棵连通子树;
( d )}可以诱导 T 的一棵连通子树;
3) ∀ d ∈ D , ![]() ( d )⊆ var ( λ ( d ));
( d )⊆ var ( λ ( d ));
4) ∀ d ∈ D , var ( λ ( d )) ![]() ( T d )⊆ χ ( d ).
( T d )⊆ χ ( d ).
定义10中, var 表示超边中包含的点的集合, T d 表示以超树中节点 d 为根节点的子树.若 T d 中节点的集合表示为 D ′,那 ![]() ( T d )=∪
( T d )=∪ ![]() ( d ),即 T d 的每个节点中包含的对应超图中点的并集.需要注意的是一个超图的超树分解可能不止一个.
( d ),即 T d 的每个节点中包含的对应超图中点的并集.需要注意的是一个超图的超树分解可能不止一个.
超图的超树分解 HT =( T , ![]() , λ ),它的宽度为
, λ ),它的宽度为 ![]() 对于超图 H 的超树宽度 hw ( H )是在所有 H 的超树分解中最小的宽度.那么对于一个宽度为 k 的超树分解,当 k = hw ( H )时,这个宽度为 k 的超树分解为最优.布尔Game目标的超树宽度是对应超图的超树宽度.布尔Game目标的超树宽度为1时,布尔Game对应超图就是无环的.也可以称布尔Game的目标是无环的.无环超图的超树分解是连接树 [21] .
对于超图 H 的超树宽度 hw ( H )是在所有 H 的超树分解中最小的宽度.那么对于一个宽度为 k 的超树分解,当 k = hw ( H )时,这个宽度为 k 的超树分解为最优.布尔Game目标的超树宽度是对应超图的超树宽度.布尔Game目标的超树宽度为1时,布尔Game对应超图就是无环的.也可以称布尔Game的目标是无环的.无环超图的超树分解是连接树 [21] .
对于布尔Game G 的连接树 J ( G ),因为它属于宽度为1的超树分解,所以它的每个节点中都只有一条超边.而连接树中顶点的连接条件为:当2条超边 h 1 和 h 2 共同包含一个决策变量 v 时,在 J ( G )中 h 1 和 h 2 就可以被连通,而且 v 也一定会出现在连通 h 1 和 h 2 唯一路径上的每个节点中.换言之,在 J ( G )中包含 v 的所有节点可以诱导一棵 J ( G )的(连通)子树.
例3 . 给定布尔Game G 3 ,其中有一组Agent N ={1,2,3}和一组决策变量 V ={ p 1 , p 2 , p 3 , p 4 }.其中Agent 1控制 p 1 ,Agent 2控制 p 2 ,Agent 3控制 p 3 和 p 4 .Agent 1的目标是使公式 φ 1 = p 1 ↔ p 3 为真,而Agent 2和Agent 3的目标分别是使 φ 2 = p 2 ∧( p 1 ∧  p 4 )和 φ 3 =( p 3 ∨ p 1 )→ p 2 为真.那么该布尔Game的超图如图1所示,表示为 H ( G 3 )=( V , HE ),其中 V ={ p 1 , p 2 , p 3 , p 4 }, HE ={ e 1 , e 2 , e 3 }, e 1 ={ p 1 , p 3 }, e 2 ={ p 1 , p 2 , p 4 }, e 3 ={ p 1 , p 2 , p 3 }.这是一个无环超图,所以根据连接树中顶点的连接条件可以得到一个超树分解,即连接树 J ( G 3 ),如图2所示,对于根节点 φ 3 ,
p 4 )和 φ 3 =( p 3 ∨ p 1 )→ p 2 为真.那么该布尔Game的超图如图1所示,表示为 H ( G 3 )=( V , HE ),其中 V ={ p 1 , p 2 , p 3 , p 4 }, HE ={ e 1 , e 2 , e 3 }, e 1 ={ p 1 , p 3 }, e 2 ={ p 1 , p 2 , p 4 }, e 3 ={ p 1 , p 2 , p 3 }.这是一个无环超图,所以根据连接树中顶点的连接条件可以得到一个超树分解,即连接树 J ( G 3 ),如图2所示,对于根节点 φ 3 , ![]() ( φ 3 )={ p 1 , p 2 , p 3 }, λ ( φ 3 )={ e 3 }.
( φ 3 )={ p 1 , p 2 , p 3 }, λ ( φ 3 )={ e 3 }.
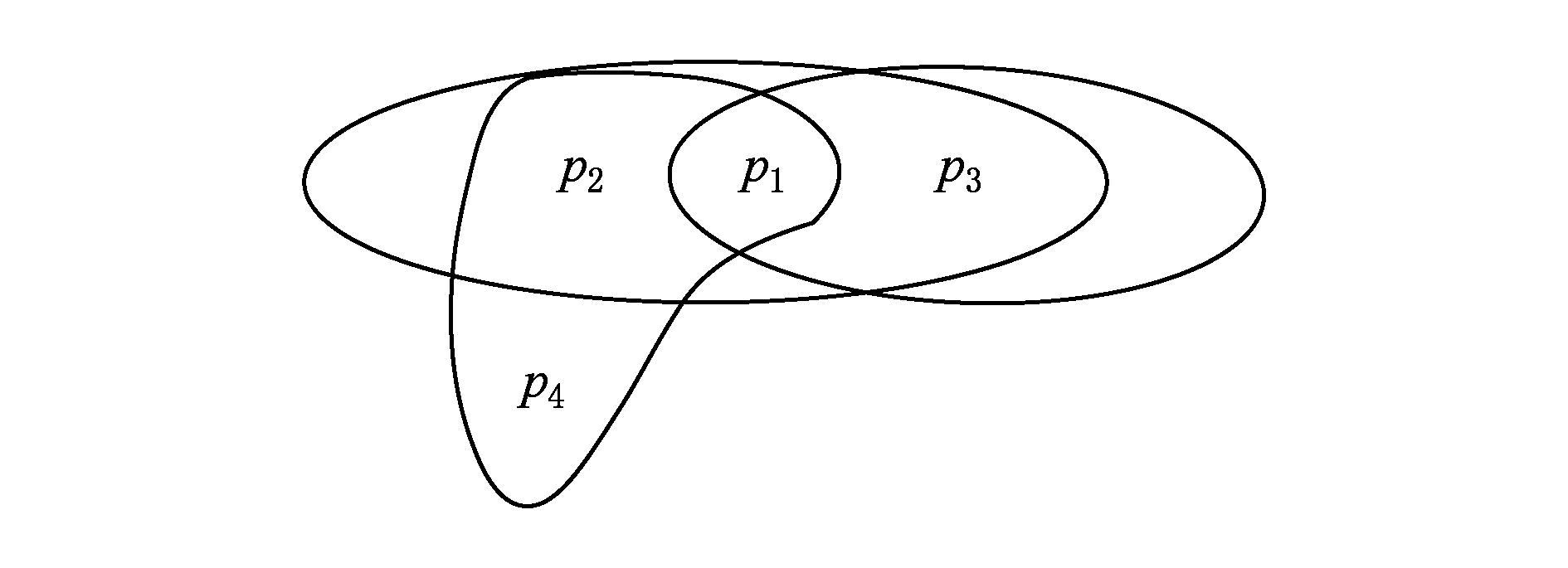
Fig. 1 The hypergraph structure of G 3
图1 G 3 的超图结构
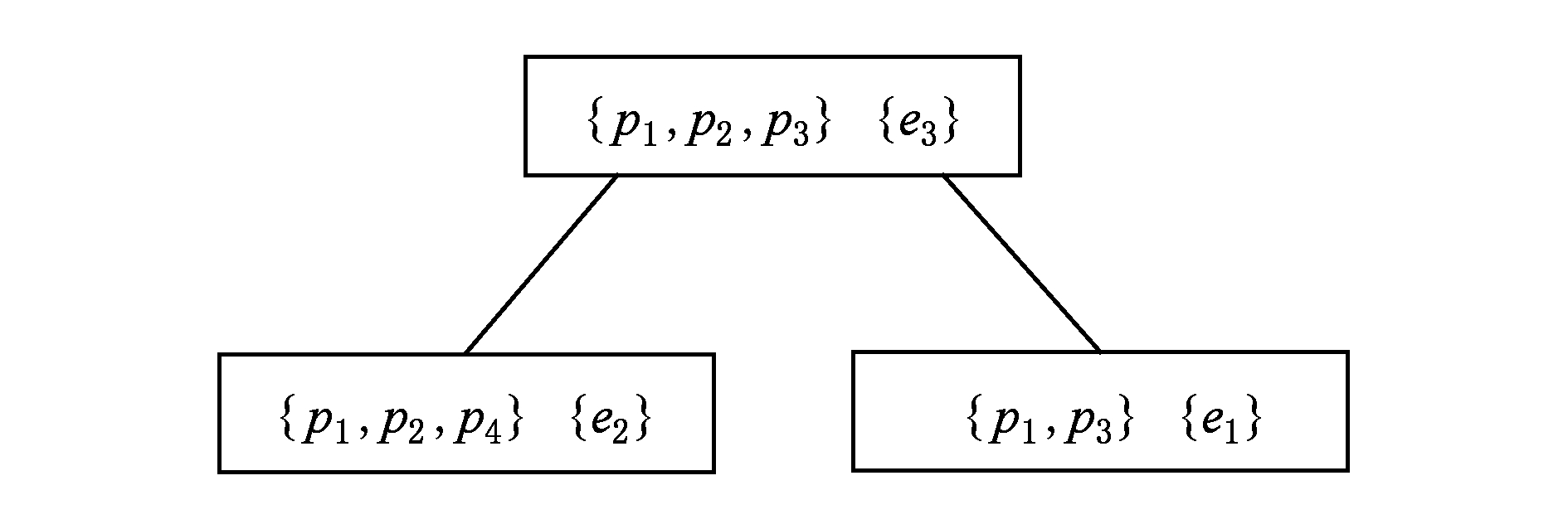
Fig. 2 The join tree J(G 3 )
图2 连接树J(G 3 )
定义11 . 相关变量,相关Agent.给定布尔Game G =( N , V , π , Φ ).Agent i 的相关变量 RV ( i )为 φ i 中不能继续约简的原子变量的集合. i 的相关Agent RA ( i )={ π -1 ( p )∈ N | p ∈ RV ( i )}.Agent上的依赖关系图是有向图 DG =( N , R ),其中∀ i , j ∈ N ,如果 j ∈ RA ( i ),那么有向边( i , j )∈ R .
Agent i 的相关Agent是控制着Agent i 的相关变量的一组Agent集合.布尔Game的依赖关系图为图( N , R ),其中顶点集合 N 对应于Agent的集合,并且 R 是所有有向边( i , j )的集合,其中∀ i , j ∈ N , j ∈ RA ( i ),即Agent i 依赖于Agent j , R 也是一种在 N 上的二元关系. R 上的传递闭包记作 TC , TC ( i , j )表示在关系 R 上Agent i 和Agent j 之间是否存在一条路径,那么 TC ( i )就表示Agent i 直接或间接依赖的Agent的集合.若依赖关系图 DG 上的一组Agent稳定,需要在关系 R 上闭合 [15] .
定义12 . 稳定集.给定布尔Game G =( N , V , π , Φ ).对于 B ⊆ N , B 是稳定集当且仅当 R ( B )⊆ B ,即∀ i ∈ B ,对于任意的Agent j 使得( i , j )∈ R ,同时 j ∈ B .
稳定集就是 N 的子集 B ,其中 B 中的Agent不依赖于 B 以外任何的Agent. R ( B )表示∀ i ∈ B , RA ( i )⊆ R ( B ).即集合 B 中所有Agent的相关Agent的集合.所以稳定集 B 的 R ( B )运算时在 B 上是闭合的.稳定集的概念最早是由Neumann等人于1953年提出的,它是一种策略标准,但是与本文中稳定集的概念是不同的 [22] .
引理1 . 令 C ⊆2 N ,若存在布尔Game G 使得 C 在 G 上是稳定的,需要满足以下4个性质:
1) ∅∈ C ;
2) N ∈ C ;
3) 若 B , B ′∈ C ,则 B ∪ B ′∈ C ;
4) 若 B , B ′∈ C ,则 B ∩ B ′∈ C .
通过引理1可知,稳定集在交、并运算上是闭合的.
命题1 . 给定布尔Game G =( N , V , π , Φ ),∀ i ∈ N , TC ( i )一定是稳定集.
证明. 假设 TC ( i )不是稳定集,那么一定∃ j ∈ TC ( i )依赖于 TC ( i )以外的Agent k ∈ N ,但是因为 TC ( i )是 i 所依赖的所有的Agent集合,若 j 依赖于 k ,则 k ∈ TC ( i ).这与假设矛盾,所以命题成立.
证毕.
定义13 . 依赖关系图映射.给定布尔Game G =( N , V , π , Φ ). DG ( G )=( N , R )是与 G 对应的依赖关系图,并且 B ⊆ N 是稳定集,那么布尔Game G 在 B 上的映射为 G B ={ B , V B , π B , Φ B },其中 ![]()
通过定义13可以看出,布尔Game在稳定集 B 上的映射 G B 中,Agent的目标是不包含稳定集以外的Agent所控制的决策变量,因此映射 G B 也是一个布尔Game.
如果布尔Game G 上在 B 的映射 G B 的一个策略组合 s B 不是 G B 上的纳什均衡,那么在 G 中以 s B 为基础的任一策略组合 s 都不是 G 中的纳什均衡 [15] .同样地,本文将这样的结论推广到核的求解上.
命题2 . 给定布尔Game G =( N , V , π , Φ )和一个稳定集 B ,如果 s ∈ core ( G ),那么 s B ∈ core ( G B ),其中 s B ⊆ s ,即 s B 是 s 在 B 控制决策变量上的映射.
证明. 假设对于一个稳定集 B , s ∈ core ( G )时, s B ∉ core ( G B ).于是一定存在一个策略组合 ![]() 阻塞 s B ,即存在一个联盟 B ′⊆ B 使得联盟 B ′以外的Agent在
阻塞 s B ,即存在一个联盟 B ′⊆ B 使得联盟 B ′以外的Agent在 ![]() 和 s B 执行相同决策,而且∀ i ∈ B ′,
和 s B 执行相同决策,而且∀ i ∈ B ′, ![]() ≻ i s B .那么,令 s - B 为稳定集 B 以外的Agent上的
≻ i s B .那么,令 s - B 为稳定集 B 以外的Agent上的
策略,并且 ![]() 于是, s ′就是联盟 B ′以外Agent上的策略.因此∀ i ∈ B ,若 u i ( s )≤ u i ( s ′),当且仅当
于是, s ′就是联盟 B ′以外Agent上的策略.因此∀ i ∈ B ,若 u i ( s )≤ u i ( s ′),当且仅当 ![]() 那么 s 就被联盟 B ′通过 s ′阻塞了.这与 s ∈ core ( G )矛盾,所以命题2成立.
那么 s 就被联盟 B ′通过 s ′阻塞了.这与 s ∈ core ( G )矛盾,所以命题2成立.
证毕.
例4 . 给定一个布尔Game G 2 ={ N , V , π , Φ },其中 N ={1,2,3}, V ={ p 1 , p 2 , p 3 }, π i ={ p i }, φ 1 = p 2 , φ 2 = p 1 ∨  p 2 并且 φ 3 = p 1 ∧ p 2 ∧ p 3 .于是对于相关变量, RV (1)={ p 2 }, RV (2)={ p 1 , p 2 }, RV (3)={ p 1 , p 2 , p 3 }.而 RA (1)={2}, RA (2)={1,2}, RA (3)={1,2,3}.于是 G 2 的依赖关系图可以表示为: DG ( G 2 )=( N , R ),其中 R ={(1,2),(2,1),(2,2),(3,1),(3,2),(3,3)}.所以 G 2 的依赖关系图如图3所示:
p 2 并且 φ 3 = p 1 ∧ p 2 ∧ p 3 .于是对于相关变量, RV (1)={ p 2 }, RV (2)={ p 1 , p 2 }, RV (3)={ p 1 , p 2 , p 3 }.而 RA (1)={2}, RA (2)={1,2}, RA (3)={1,2,3}.于是 G 2 的依赖关系图可以表示为: DG ( G 2 )=( N , R ),其中 R ={(1,2),(2,1),(2,2),(3,1),(3,2),(3,3)}.所以 G 2 的依赖关系图如图3所示:

Fig. 3 The dependencies between Agents of G 2
图3 布尔Game G 2 的Agent依赖关系
图3中从Agent 3到Agent 1有一个箭头,表示3依赖于1,即Agent 1是Agent 3的相关Agent.在 G 2 中集合{1,2}是在 R 上除空集和 N 外唯一的稳定集.
本节对基于超树分解的无环布尔Game的可满足核的求解算法以及通过稳定集分解布尔Game的求核算法,进行了具体的算法描述和分析.
通过第3节引入的在CSP下的布尔Game,本节采用超图的超树分解算法得到超树,即Gottlob等人提出的det- k -decomp算法 [23] .该算法可以在多项式时间内判断一个宽度为 k 的超树分解是否存在,而且如果存在这样的有界超树,可以通过递归构造出一个宽度为 k 的超树分解.因为本文研究的是超图上无环的布尔Game,所以需要构造一个宽度为1的超树分解,即一个连接树.得到的超树通过类数据库内连接查询的方式,求解满足布尔Game的约束满足问题的核,参见算法1.
算法1 . traverseJoinTree ( J ( G ), G , RV , S ).
输入:布尔Game G =( N , V , π , Φ )、 G 中所有Agent的相关变量集 RV ;
输出:布尔Game约束满足问题下的解 S .
① J ( G )← det - k - decomp ();
② p ← J ( G )的根节点;
③ if( public ←( RV ( p )∩ CV ))≠∅
④ S p ← S public ×2 RV ( p )- public ;
⑤ else
⑥ S p ←2 p ;
⑦ end if
⑧ S s ←∅;
⑨ for each s ∈ S p
⑩ if s  φ p
φ p
 S s ← S s ∪{ s };
S s ← S s ∪{ s };
 end if
end if
 end for
end for
 CV ← CV ∪ RV ( p );
CV ← CV ∪ RV ( p );
 if S =∅
if S =∅
 S ← S ∪ S s ;
S ← S ∪ S s ;
 else
else
 S ← S 的内连接 S s ;
S ← S 的内连接 S s ;
 end if
end if
 return S ;
return S ;
 if p 是叶子结点
if p 是叶子结点
 return false;
return false;
 end if
end if
 for each p 的所有子结点 c
for each p 的所有子结点 c
 把 J ( G ) c 作为以 c 为根结点的 J ( G )的子树;
把 J ( G ) c 作为以 c 为根结点的 J ( G )的子树;
 traverseJoinTree ( J ( G ) c , G , RV , S );
traverseJoinTree ( J ( G ) c , G , RV , S );
 end for
end for
第1步,算法1的行①~⑦,在递归的过程中获得当前结点的待验证策略集合 S p . S p 的存储结构类似于数据库的表,由决策变量和其对应的赋值组成,决策变量相当于数据表中的属性行,决策变量上的赋值相当于字段.该过程是依据引理2执行的.首先将 J ( G )的根节点赋值给中间变量 p . CV 是已生成并测试过的决策变量的集合.在生成当前结点的待验证策略之前,可以通过判断 CV 和 RV ( p )是否存在交集来减少该结点生成的待验证策略集的大小. CV 和 RV ( p )存在交集就意味着当前结点中的一部分决策变量已经参与过生成待验证策略.所以可以在之前求得的结点目标可满足的解的基础上,只是生成在 RV ( p )中未和 CV 相交的部分决策变量.而因为连接树的构成特点,若之前的结点已经生成过策略,当前结点的决策变量和之前的结点的决策变量之间一定存在交集.具体过程可以参见5.4节的例5.
第2步,在算法1的行⑧~  ,逐一测试待验证策略是否满足当前结点Agent的目标,若满足,则将该策略写入策略集 S s 中. S p 中所有的策略都检验完后,更新 CV ,将新的参加过生成策略的决策变量加入 CV .接着就是将得到的策略集 S s 和之前的结点得到的可满足解通过数据库连接操作中的内连接,从而更新策略集 S ,当然在程序的一开始 S =∅时,需要直接将 S s 赋值给 S .
,逐一测试待验证策略是否满足当前结点Agent的目标,若满足,则将该策略写入策略集 S s 中. S p 中所有的策略都检验完后,更新 CV ,将新的参加过生成策略的决策变量加入 CV .接着就是将得到的策略集 S s 和之前的结点得到的可满足解通过数据库连接操作中的内连接,从而更新策略集 S ,当然在程序的一开始 S =∅时,需要直接将 S s 赋值给 S .
第3步,在算法1的行  ~
~  ,递归地调用当前结点的叶子结点,直到当前结点为叶子结点时退出递归.
,递归地调用当前结点的叶子结点,直到当前结点为叶子结点时退出递归.
引理2 . 一个合取范式是重言式,当且仅当它的每一个简单析取范式都是重言式.
对于布尔Game G 的约束满足问题 CSP ( G ),根据引理2,对 φ 1 ∧ φ 2 ∧…∧ φ n =1的求解,可以转化为对每个Agent的目标单独求可满足解,最后通过内连接操作合并得到所有目标的解,即求得约束解的核.
算法1的目的是求解布尔Game的约束满足问题,即求 φ 1 ∧ φ 2 ∧…∧ φ n =1的解.通过建立布尔Game G 上通过建立布尔Game G 上的超图结构,然后超树分解得到连接树 J ( G ),在 G 的连接树 J ( G )上递归地遍历求得所有Agent都可满足的解.
一般的穷举方法的求核算法是在所有Agent上生成所有的策略组合,然后调用函数1判断每个策略组合 s 是否满足核的定义.由于一般的穷举算法的时间复杂度是指数级的,所以在较大规模的布尔Game上求解是相当消耗时间的.所以本节根据稳定集分解布尔Game,可以将布尔Game的规模缩小,提高运算效率.
根据命题2的逆否命题,即如果 s B ∉ core ( G B ),那么 s ∉ core ( G ),可以通过稳定集分解布尔Game为规模更小的在原始布尔Game上的映射.通过这样的方法可以提前排除很多不必要的策略上的测试,产生待检测的子策略组合,从而缩小测试的策略范围.接下来根据命题2、命题1和定义12来设计算法2.
算法2的目的是通过稳定集分解布尔Game得到一些规模更小的布尔Game,然后从规模最小的布尔Game开始,在具有包含和被包含关系的布尔Game上迭代求核.这样就降低了核求解过程的策略测试范围,以此来提高求解布尔Game的核的效率.因为一个布尔Game可能存在很多规模不一的稳定集,所以算法2按照稳定集间的包含关系从规模最小的非空稳定集分解布尔Game,最后求得原布尔Game的核.算法2的详细描述如下:
算法2 . 基于稳定集的布尔Game分解求核算法.
输入:布尔Game G =( N , V , π , Φ )、 G 中Agent间的依赖关系图 DG =( N , R );
输出: G 的核 core ( G ).
① ![]() ←∅;
←∅;
② TC ← warshall ( DG );
③ for each i ∈ N
④ ![]() ←
← ![]() ∪ TC ( i );
∪ TC ( i );
⑤ end for
⑥ ![]() ←
← ![]() ∪{ N };
∪{ N };
⑦ B pre ←∅;
⑧ core ( G )←∅;
⑨ for each B ∈ TC
⑩ if B pre ⊂ B
 把 G 映射到 B ,得到 G B ={ B , V B , π B , Φ B };
把 G 映射到 B ,得到 G B ={ B , V B , π B , Φ B };
 if isEmpty ( core ( G ))
if isEmpty ( core ( G ))
 S B ←2 V B ;
S B ←2 V B ;
 else
else
 end if
end if
 core ( G )←∅;
core ( G )←∅;
 for each s ∈ S B
for each s ∈ S B
 if isCore ( G B , s )
if isCore ( G B , s )
 core ( G )← core ( G )∪{ s };
core ( G )← core ( G )∪{ s };
 end if
end if
 end for
end for
 end if
end if
 end for
end for
 return core ( G ).
return core ( G ).
第1步,在算法2的行①~⑥,先通过 warshall 算法求解布尔Game上存在的关系 R 的传递闭包的关系矩阵 TC [24] .然后根据命题1和引理1,由 TC 得到所有稳定集,对于 TC ( i ),其中 i ∈ N .将这些稳定集和全集 N 写入稳定集的集合 ![]() .得到的稳定集的集合按照从小到大的次序排序.
.得到的稳定集的集合按照从小到大的次序排序.
第2步,算法2的行⑦~  ,是算法的核心.变量 B pre 是当前稳定集的前一个遍历过的稳定集. core ( G )用来记录每个子布尔Game的核,当遍历到最后一个稳定集时, core ( G )就表示整个布尔Game的核.首先遍历稳定集的集合,现在第1个稳定集上生成子布尔Game,之后的稳定集之间需要存在包含和被包含的关系,即算法中 B pre 和 B 的关系,如果有则将 G 映射到当前稳定集 B 上得到 G B ,否则就跳过当前的稳定集,查看下一个是否存在这样的关系.然后就是在当前子布尔Game G B 上生成策略组合,若是 TC 中的第1个稳定集,则直接在 G B 上生成策略组合,否则要在上一个求得的核的基础上生成策略.最后调用函数1来测试上面生成的策略是否符合核的定义,并将当前求得的核保存在 core ( G )中,以便下一次循环调用.按照上述描述直到最后一个稳定集,即 G 中的Agent的全集 N ,此时求得的就是布尔Game G 的核.
,是算法的核心.变量 B pre 是当前稳定集的前一个遍历过的稳定集. core ( G )用来记录每个子布尔Game的核,当遍历到最后一个稳定集时, core ( G )就表示整个布尔Game的核.首先遍历稳定集的集合,现在第1个稳定集上生成子布尔Game,之后的稳定集之间需要存在包含和被包含的关系,即算法中 B pre 和 B 的关系,如果有则将 G 映射到当前稳定集 B 上得到 G B ,否则就跳过当前的稳定集,查看下一个是否存在这样的关系.然后就是在当前子布尔Game G B 上生成策略组合,若是 TC 中的第1个稳定集,则直接在 G B 上生成策略组合,否则要在上一个求得的核的基础上生成策略.最后调用函数1来测试上面生成的策略是否符合核的定义,并将当前求得的核保存在 core ( G )中,以便下一次循环调用.按照上述描述直到最后一个稳定集,即 G 中的Agent的全集 N ,此时求得的就是布尔Game G 的核.
函数1 . isCore ( G , s ).
输入:布尔Game G =( N , V , π , Φ )、 G 的一个策略组合 s ;
输出:布尔变量 flagCore .
① C ←∅;
② for i ←1 to | N |
③ if s ![]() φ i
φ i
④ C ← C ∪{ i };
⑤ end if
⑥ end for
⑦ S C ←{ s - C }×2 π C ;
⑧ flagCore ←true;
⑨ for each s ′∈ S C
⑩ if s ′≻ s
 flagCore ←false;
flagCore ←false;
 break;
break;
 end if
end if
 end for
end for
 return flagCore .
return flagCore .
函数1的功能是检测布尔Game G 中的一个策略组合是否符合核的定义,即对于当前策略组合,是否存在一个联盟所引起的另一个策略组合阻塞当前策略组合,若没有联盟阻塞当前策略组合,则该策略组合就是核,否则就不属于核.下面是对函数1的具体描述.2 π C 表示在联盟 C 上生成的策略组合, s - C 表示联盟 C 以外的Agent的策略组合.首先生成联盟 C ,构成联盟的原则是目标未满足的Agent可以构成联盟;然后改变联盟 C 中Agent的策略,而保持 C 以外的Agent的策略不变,通过和2 π C 的笛卡尔积,构成新的策略组合 S C ;最后检测 S C 中是否存在策略组合 s ′阻塞 s ,即 s ′是否使联盟 C 的效用相对 s 得到提高,若 S C 中不存在一个 s ′阻塞 s ,那么 s 就是布尔Game G 的核,否则不属于核.
命题3 . 如果布尔Game G 的策略组合 S s 是 CSP ( G )的解集,那么 S s ⊆ core ( G ).
证明. s ∈ S s 为布尔Game G 的核,即 s ∈ core ( G ), C ⊆ N 是任意的一个联盟, S 是 G 上的所有的策略组合.假设存在一个策略组合 s ′∈ S ,使联盟 C 以外的所有Agent在 s 和 s ′执行相同的决策,并且联盟 C 内的Agent在 s ′所得的收益比在 s 中的收益多.但是因为 s 是 CSP ( G )的解,也就是对于每个Agent的目标都会被满足,即 φ 1 ∧ φ 2 ∧…∧ φ n =1.而且本文的布尔Game G 的收益是二元的,即非1即0.所以联盟 C 内的Agent在 s ′所得的收益最多和在 s 中的收益一样多,结论与假设和核的定义相互矛盾,因此 S s ⊆ core ( G ).
证毕.
算法1的成立完全是以命题3为前提的.需要说明的是,命题3只满足充分性,而必要性不一定满足,比如例1中的布尔Game G 1 唯一地满足核的解为 ![]() 而此时 φ 1 ∧ φ 2 ∧ φ 3 =0.
而此时 φ 1 ∧ φ 2 ∧ φ 3 =0.
一般求核问题可以看做产生策略和比较测试的过程,即先产生策略然后再比较检测该策略是否符合 φ 3 ∧ φ 1 =1,如定义5所述.而算法1根据命题3,可以不必考虑比较检测的步骤,因此大大缩短了算法的时间复杂度.同样地,算法1也同样适用于布尔Game求纯策略纳什均衡.
定理1 . 在最坏情况下,算法1的时间复杂度为 O (| N |×2 k ),其中 k 表示布尔Game目标中决策变量的最大值.
证明. 直观来看,在布尔Game G 的超图结构的超树分解 J ( G )中,每个结点都需要生成它们的策略,即在每个Agent目标上生成策略,因为只有根结点能生成所有的策略,其他结点生成的策略是在之前结点的基础上完成的,所以第1个结点中目标的决策变量数在算法的运行效率上起决定性作用.那么最坏的情况就是根结点的目标中决策变量数最大且每个结点都包含这样的决策变量数 k 时,此时每个结点生成策略的时间复杂度是2 k .最后需要在所有结点上生成策略,于是算法的复杂度为| N |×2 k .
证毕.
定理2 . 在最坏情况下,函数1的时间复杂度为 O (2 | V C | ),其中| V C |表示该策略中可以组成联盟中的决策变量数.
证明. 函数1的关键步骤是对新生成的带联盟的策略组合集 S C 进行逐个检测,而 S C 的个数就是2 | V C | .所以在最坏情况下需遍历完整个 S C ,所以函数1的时间复杂度为 O (2 | V C | ).
证毕.
例5 . 给定一个布尔Game G 4 =( N , V , π , Φ ),其中 N ={1,2,3,4}, V ={ a , b , c , d , e , f }, π 1 ={ a , b }, π 2 ={ c , d }, π 3 ={ e }, π 4 ={ f }. φ 1 =( a ∧ b )∨ c , φ 2 = b ↔( c ↔ d ), φ 3 =( a → b )∧ e , φ 4 =(  c ∧ d ∧ f )∨( c ∧
c ∧ d ∧ f )∨( c ∧  d ∧
d ∧  f ).
f ).
根据例5描述,由定义7, G 4 可以被表示为 CSP ( G 4 )=( V ,{0,1}, C ),其中 V ={ a , b , c , d , e , f }, C ={ C 1 , C 2 , C 3 , C 4 }而 C 1 ={( a , b , c ), φ 1 =1}, C 2 ={( b , c , d ), φ 2 =1}, C 3 ={( a , b , e ), φ 3 =1}, C 4 ={( c , d , f ), φ 4 =1}.对于 CSP ( G 4 )的超图表示 H ( G 4 )如图4所示:
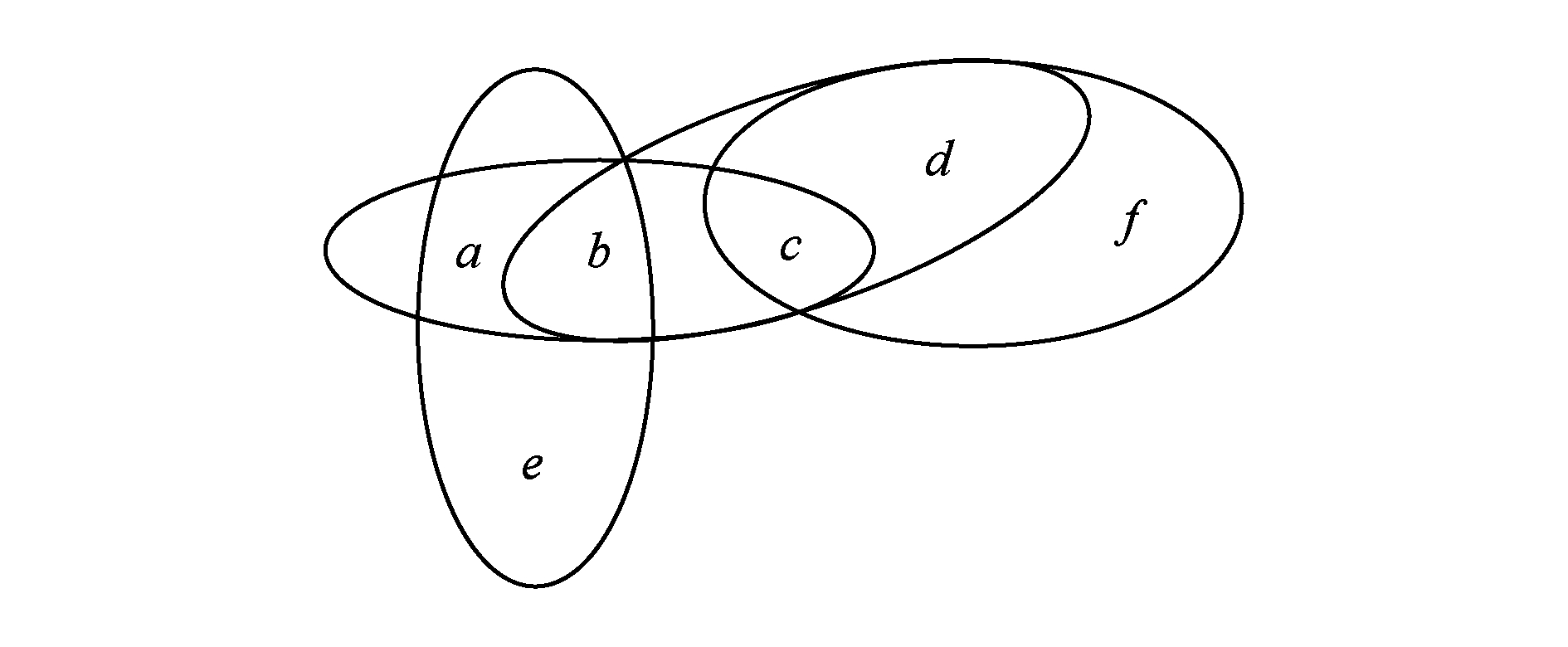
Fig. 4 The hypergraph structure of G 4
图4 G 4 的超图结构
把每个Agent的目标所包含的决策变量视作一条超边,那么可以得到与 H G 4 相对应的超树分解.因为 H G 4 是无环超图,它的超树分解就是它所对应的连接图 JT ( G 4 ),如图5所示.
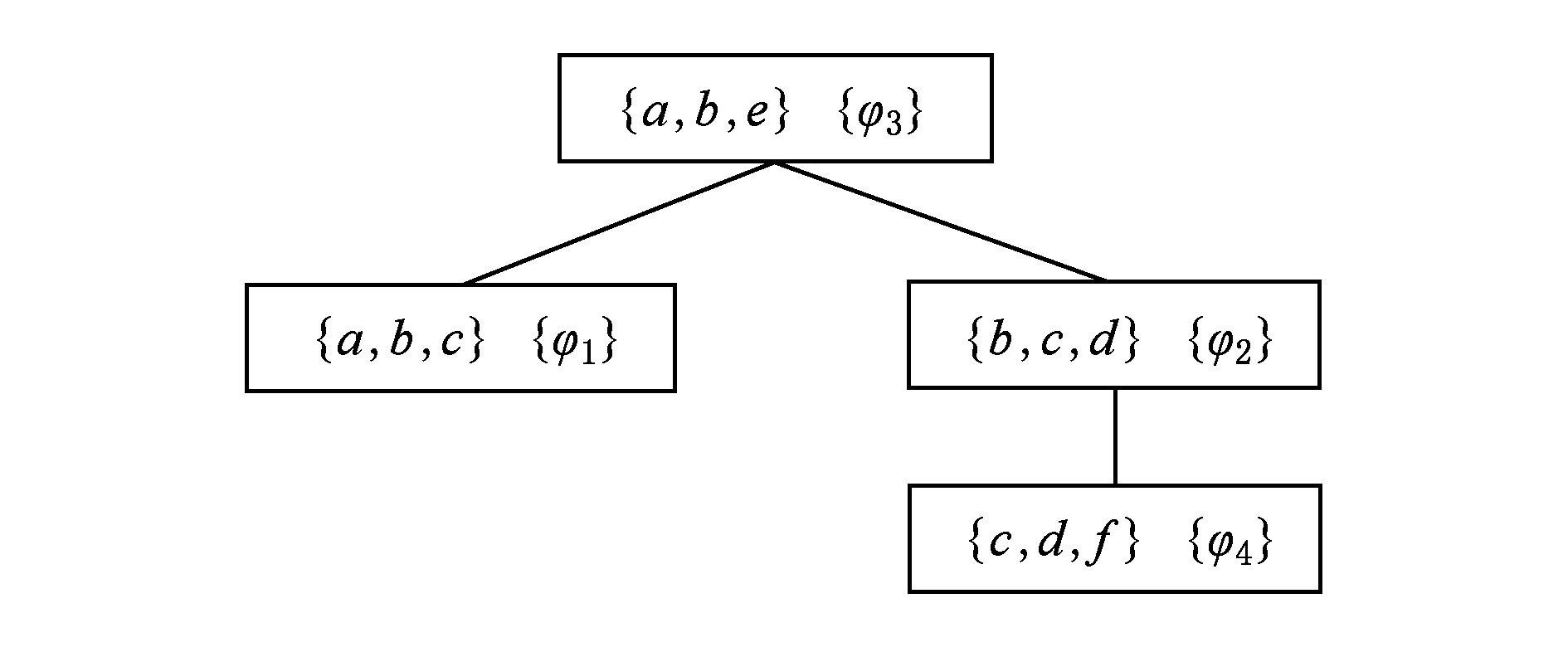
Fig. 5 The join tree on H(G 4 )
图5 H(G 4 )生成的连接树
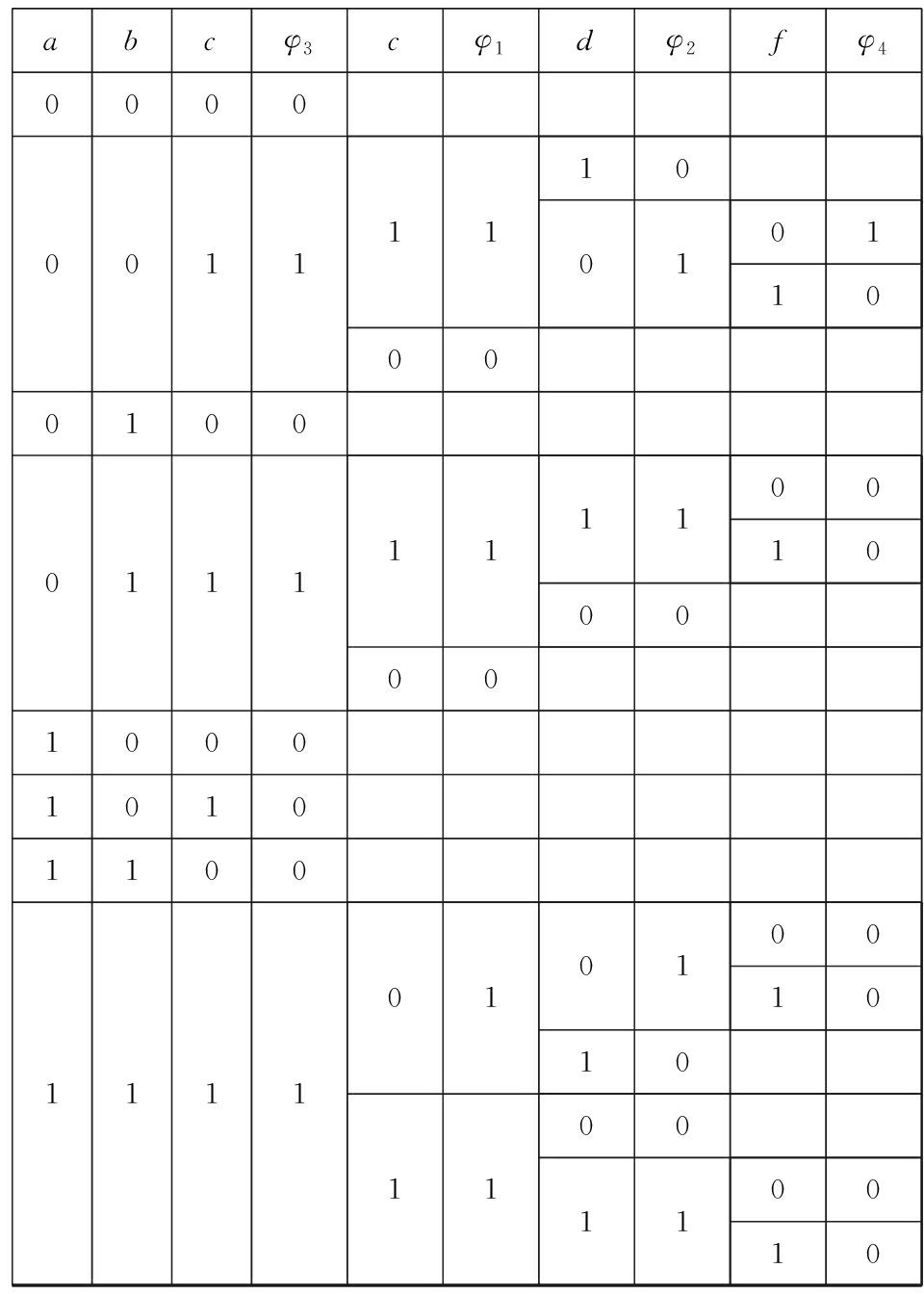
下面求解 G 4 的属于约束满足解的核.根据算法1得到图6的执行过程,图6是从左到右执行的.详细描述如下:根据命题3,可以得到满足布尔Game G 4 中的 φ 1 ∧ φ 2 ∧ φ 3 ∧ φ 4 =1的赋值一定是 G 4 的核.1)根据 G 4 的连接树结构,得到 r 3 ={(0,0,1),(0,1,1),(1,1,1)},即满足 φ 3 =1的赋值.2)生成和测试 φ 3 的子结点 φ 1 ,根据命题3,在以上的结果中只需以 r 3 的结果为基础连续生成和测试,那么生成决策变量 a , b , c 的策略是(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,1,0),(1,1,1).3)经过测试得到满足的策略集{(0,0,0,1),(0,0,1,1),(0,1,0,1),(0,1,1,1),(1,1,0,1),(1,1,1,1)}.同理,每个结点都需要在之前求得的结果上生成策略并进行测试,这在很大程度上降低了生成策略和测试的时间.每个结点都遍历过后得到满足 φ 1 ∧ φ 2 ∧ φ 3 ∧ φ 4 =1的策略,也是 G 4 的核,对应于 a , b , c , d , e , f 为{(0,0,1,0,1,0)}.
![]()
Fig. 6 Truth table of the process of algorithm 1
图6 算法1 执行过程的真值表
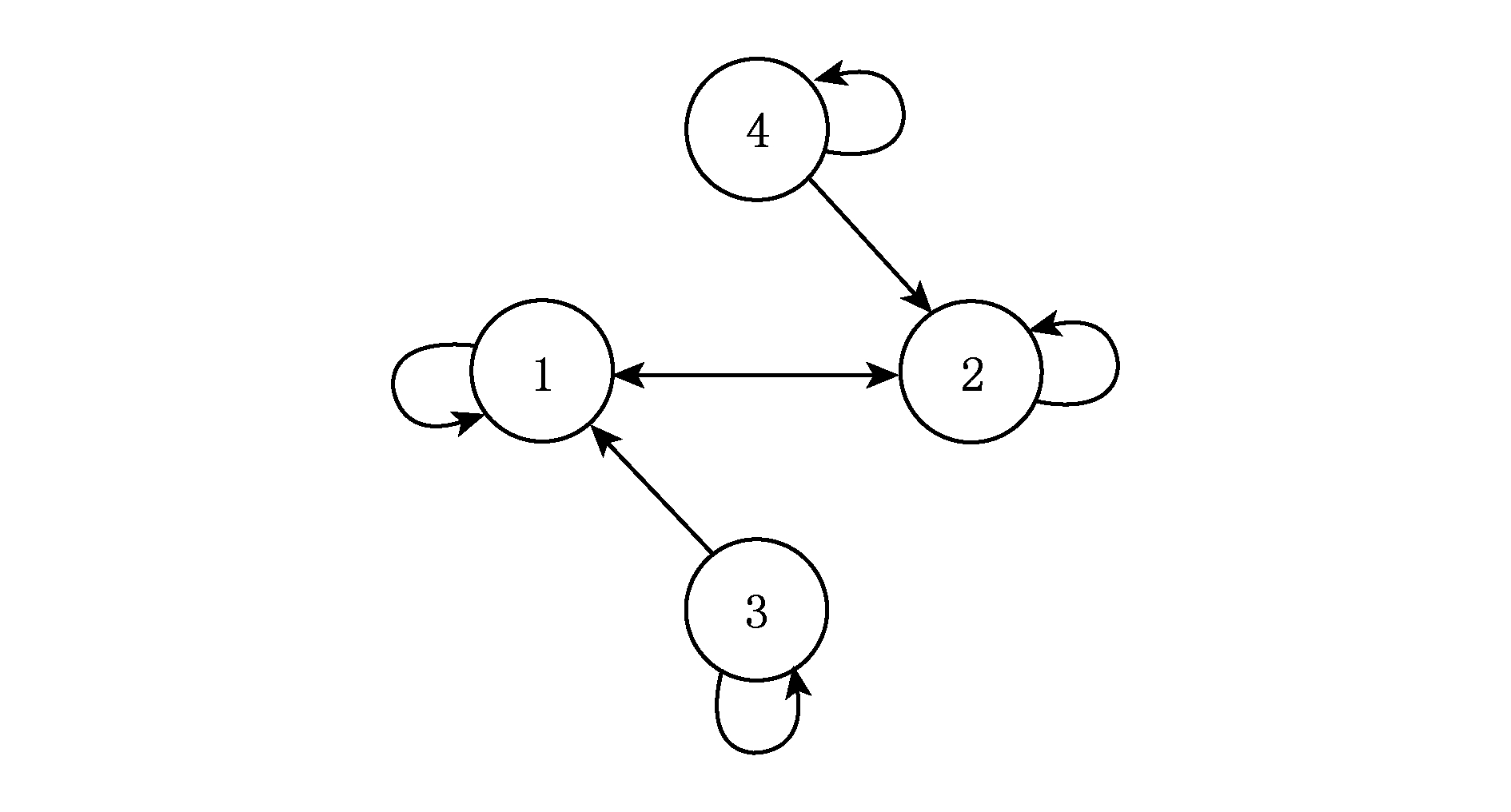
Fig. 7 Dependency graph among Agent of G 4
图7 G 4 中Agent间的依赖图
根据算法2,从小到大地遍历集合 ![]() ,需要上一个稳定集是下一个的真子集.首先将 G 4 映射到 B 1 上得到子布尔Game G B 1 .然后在 G B 1 中求核,并将求得的核记录下来以备下一步使用.在 G B 1 中求核具体过程如表2所示,其中最后一列中的“Y”表示是核,“N”表示不是核.从左到右执行,遍历所有的策略,对于每个策略生成可能阻塞该策略的联盟,而生成联盟的Agent条件是它们的目标未达成.以对应于( a , b , c , d )的策略(0,0,0,0)为例, G B 1 中Agent 1和Agent 2的目标分别是 φ 1 =0和 φ 2 =0,因此构成联盟 C ={1,2}.接着检验策略(0,0,0,0)是否被联盟 C 阻塞,就是在 C 以外的Agent保持策略 s - C 不变,而改变 C 中Agent的策略 s C 来看新的策略( s C ,
,需要上一个稳定集是下一个的真子集.首先将 G 4 映射到 B 1 上得到子布尔Game G B 1 .然后在 G B 1 中求核,并将求得的核记录下来以备下一步使用.在 G B 1 中求核具体过程如表2所示,其中最后一列中的“Y”表示是核,“N”表示不是核.从左到右执行,遍历所有的策略,对于每个策略生成可能阻塞该策略的联盟,而生成联盟的Agent条件是它们的目标未达成.以对应于( a , b , c , d )的策略(0,0,0,0)为例, G B 1 中Agent 1和Agent 2的目标分别是 φ 1 =0和 φ 2 =0,因此构成联盟 C ={1,2}.接着检验策略(0,0,0,0)是否被联盟 C 阻塞,就是在 C 以外的Agent保持策略 s - C 不变,而改变 C 中Agent的策略 s C 来看新的策略( s C ,
s - C )是否优于(0,0,0,0).比较得出(0,0,0,1)≻(0,0,0,0),于是(0,0,0,0)被联盟 C 阻塞了,所以(0,0,0,0)不是 G B 1 的核.和上述过程相同,对于其他的策略也需要被检验是否被某个联盟阻塞,进而得到核.于是最后得到 G B 1 的核 core ( G B 1 )={(0,0,1,0),(0,1,1,1),(1,0,1,0),(1,1,0,0),(1,1,1,1)}.
Table 2 The First Process of Algorithm 2
表2 算法2的第1步执行过程

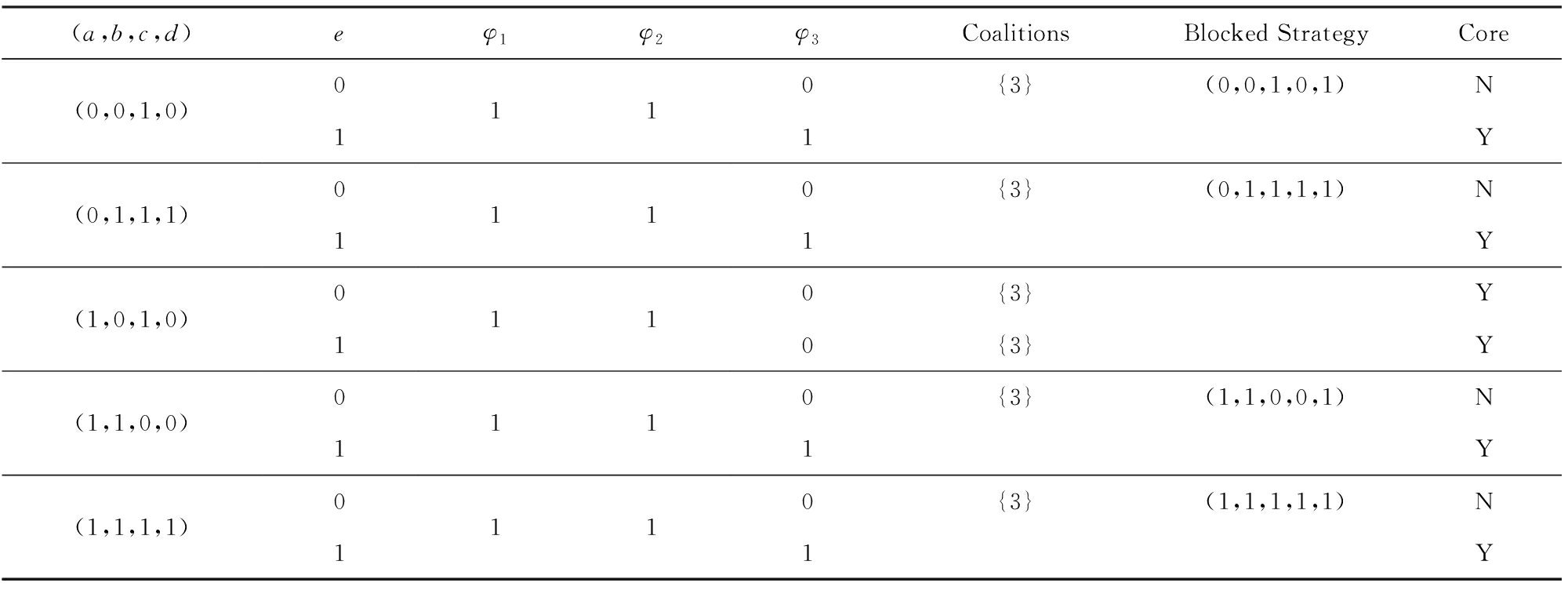
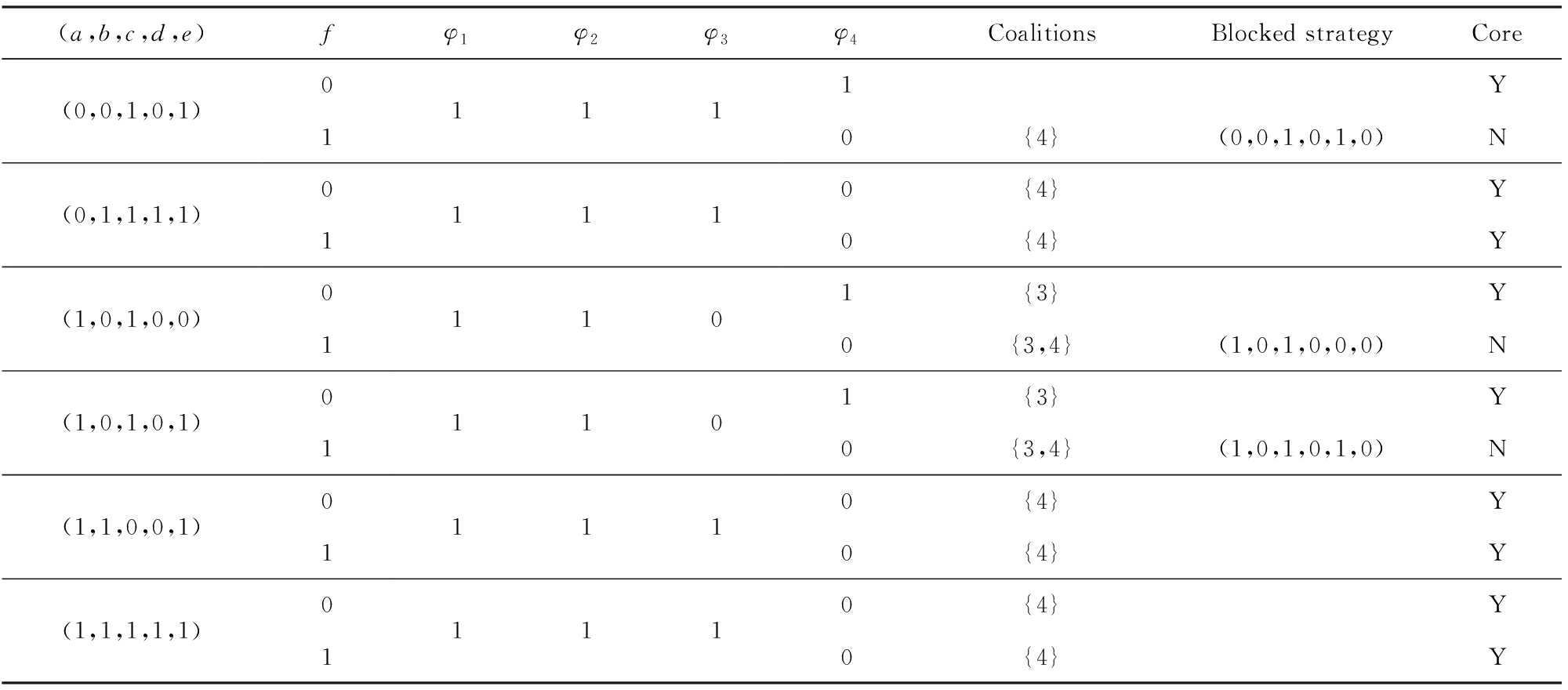
因为 B 1 ⊂ B 2 ,所以求解 G 4 映射在 B 2 上的子布尔Game G B 2 的核.此时根据命题2,通过 core ( G B 1 )×2 π 3 得到 G B 2 需要判断的策略集,2 π 3 是 π 3 上的解释.与求 G B 1 的核的过程相同,遍历所有策略,在每个策略上生成联盟,再检测联盟是否阻塞该策略,具体的执行过程如表3所示.最后得到 G B 2 的核为 core ( G B 2 )={(0,0,1,0,1),(0,1,1,1,1),(1,0,1,0,0),(1,0,1,0,1),(1,1,0,0,1),(1,1,1,1,1)}.
Table 3 The Second Process of Algorithm 2
表3 算法2 的第2步执行过程
因为 B 2 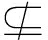 B 3 且 B 2 ⊂ N ,所以最后求解布尔Game G 的核.与求 G B 1 的核的过程相同,通过 core ( G B 2 )×2 f 得到在 G 上的待验证策略集.然后遍历所有策略,在每个策略上生成联盟,再检测联盟是否阻塞该策略.具体的执行过程如表4所示.最终求得的布尔Game G 的核对应于( a , b , c , d , e , f )为 core ( G )={(0,0,1,0,1,0),(0,1,1,1,1,0),(0,1,1,1,1,1),(1,0,1,0,0,0),(1,0,1,0,1,0),(1,1,0,0,1,0),(1,1,0,0,1,1),(1,1,1,1,1,0),(1,1,1,1,1,1)}.
B 3 且 B 2 ⊂ N ,所以最后求解布尔Game G 的核.与求 G B 1 的核的过程相同,通过 core ( G B 2 )×2 f 得到在 G 上的待验证策略集.然后遍历所有策略,在每个策略上生成联盟,再检测联盟是否阻塞该策略.具体的执行过程如表4所示.最终求得的布尔Game G 的核对应于( a , b , c , d , e , f )为 core ( G )={(0,0,1,0,1,0),(0,1,1,1,1,0),(0,1,1,1,1,1),(1,0,1,0,0,0),(1,0,1,0,1,0),(1,1,0,0,1,0),(1,1,0,0,1,1),(1,1,1,1,1,0),(1,1,1,1,1,1)}.
Table 4 The Last Process of Algorithm 2
表4 算法2的最后一步执行过程
本节对算法1、算法2和已有的求核算法进行实验对比,并进行相应的分析,来证明本文提出算法的有效性.由于布尔Game是新兴的框架,在实际中应用不多,数据较缺乏,所以本节采用随机生成的布尔Game来模拟数据,以此来验证本文给出的算法的效率.
本节构建了一个随机生成的布尔Game模型 [19] ,该模型可以根据需要构建适用于算法1的无环超图的布尔Game,也可以构造无特殊结构的布尔Game.
通过以下8个参数的约束下随机生成布尔Game:
1) Agent的数量| N |;
2) 每个Agent控制决策变量的数量 b ;
3) 目标中二元运算符(∨和∧)的最大值 m ;
4) 目标存在一个合取运算符的概率 p (相反的是析取运算符);
5) 目标中决策变量取非的概率 n ;
6) 每个Agent是否包含至少一个自己所控制的变量(默认为否,以 s 表示);
7) 是否附加超图无环的约束(默认为否,以0表示);
8) 为保证每次运行程序时得到的布尔Game相同,设置 seed .
按上述约束,设置参数| N |=5, b =2, m =3, p =0.5, n =0.5, seed =1,其他取默认值,生成的随机的布尔Game的数据格式如下:
① bg Agent 5
② a 1 p 1 p 2 0
③ a 2 p 3 p 4 0
④ a 3 p 5 p 6 0
⑤ a 4 p 7 p 8 0
⑥ a 5 p 9 p 10 0
⑦ 1 (- p 6 & ( p 7 ;( p 7 ; p 9 )))
⑧ 2 (- p 8 & p 6 )
⑨ 3 ( p 6 ;- p 2 )
⑩ 4 ( p 5 ;( p 10 ; p 7 ))
 5 ( p 5 & p 7 )
5 ( p 5 & p 7 )
数据的行①以 bg 来表示一个布尔Game的开始,后面表示Agent的个数.行②~⑥格式相同,其中 p 1 , p 2 ,…, p 10 表示决策变量, a 表示一个Agent的开始的标识,以行②为例,Agent 1控制的决策变量为 p 1 和 p 2 ,最后都以0为该Agent的结束标识.而行⑦~  格式相同,以行⑦为例开头的数字1表示Agent 1,后面便是Agent 1的目标,其中,“-”表示取否,“;”表示析取,“&”表示合取,即Agent的目标为
格式相同,以行⑦为例开头的数字1表示Agent 1,后面便是Agent 1的目标,其中,“-”表示取否,“;”表示析取,“&”表示合取,即Agent的目标为  p 6 ∧( p 7 ∨( p 7 ∨ p 9 )).
p 6 ∧( p 7 ∨( p 7 ∨ p 9 )).
这里考虑的二元运算符只有合取和析取.因为根据蕴含等值等式 A → B ⟺  A ∨ B 和等价等值式 A ↔ B ⟺( A → B )∧( B → A )⟺( A ∧ B )∨(
A ∨ B 和等价等值式 A ↔ B ⟺( A → B )∧( B → A )⟺( A ∧ B )∨(  A ∧
A ∧  B ),可以将目标中的蕴含符和等价符转换为只包含析取和合取的命题公式.为了使得随机布尔Game具有多样性,这里通过设置参数 m 把不同Agent的目标的长度设置一定的差异,并且对于每个Agent目标中的二元运算符的数量都在[1, m ]区间.
B ),可以将目标中的蕴含符和等价符转换为只包含析取和合取的命题公式.为了使得随机布尔Game具有多样性,这里通过设置参数 m 把不同Agent的目标的长度设置一定的差异,并且对于每个Agent目标中的二元运算符的数量都在[1, m ]区间.
本文的实验的环境为:计算机操作系统是Windows7 64 b,硬件内存为8 GB DDR 3,主频为3.2 GHz的i5-4700英特尔处理器.程序的实现通过C++程序语言实现.实验的数据是根据6.1节描述随机生成的模拟数据.
本文以算法的运行时间为算法效率优劣的评估标准,分别设置2组实验,即对算法1和算法2进行实验.1)在超图无环的布尔Game上对算法1和可满足性问题的穷举算法进行实验对比,来验证算法1的相对效率和影响算法效率的因素.2)在一般布尔Game上运用本文提出的算法2和一般的穷举算法进行实验对比,和检验不同参数对算法效率的影响.考虑到实验中影响实验结果的变量比较多,所以采用控制变量法进行实验对比.本实验的主要自变量为Agent的数量| N |、决策变量的数量| V |以及每个目标中存在的二元运算符的个数.为了降低特殊布尔Game对算法的影响和方便观察实验结果,每个自变量对应因变量的取值为不同的100个布尔Game运行时间的中位数的对数,时间的单位为毫秒(ms).而且为了防止程序运行时间过长,设置超时时间为5 min,无论是否求得核,只要超过5 min就终止程序.
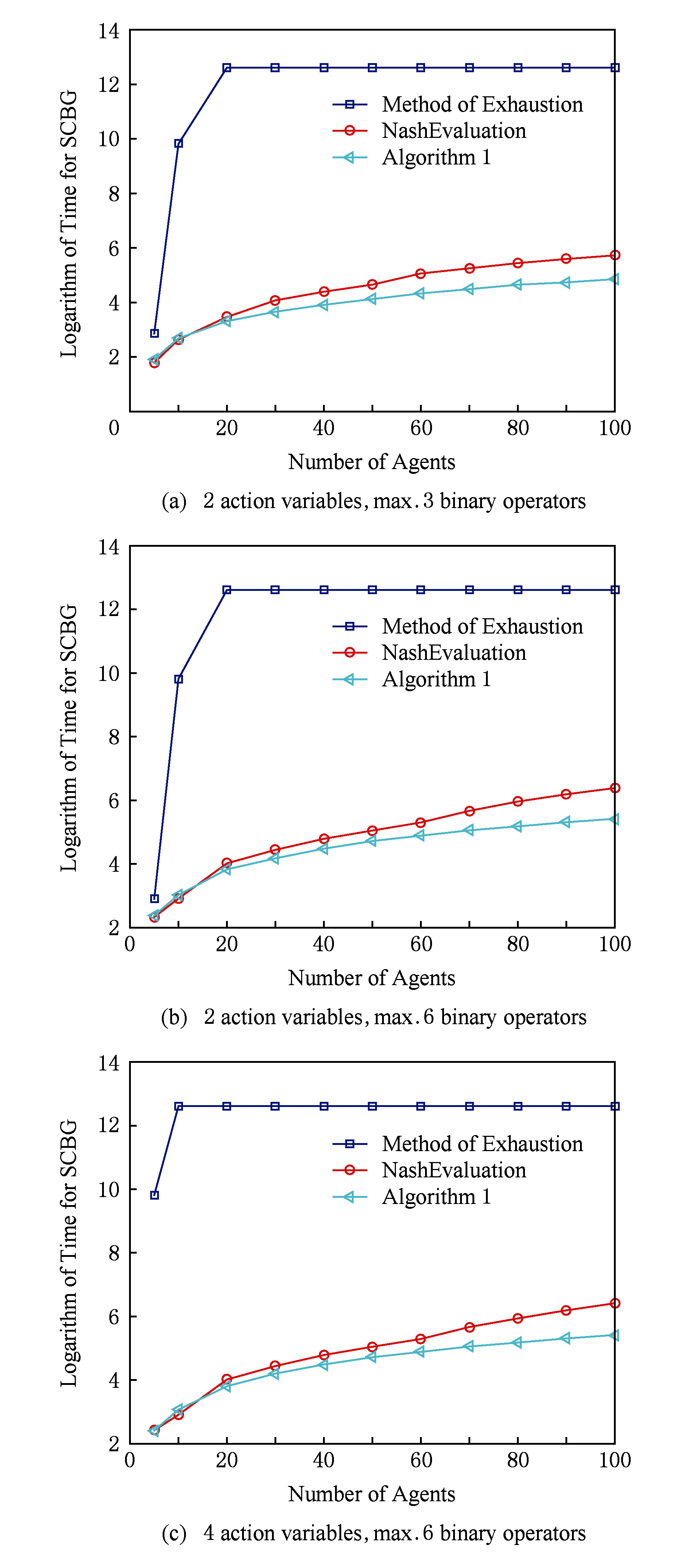
Fig. 8 Experiment of solving core of Boolean games with a constraint satisfaction solution
图8 无环布尔Game求可满足核的实验
本节在存在约束满足解的无环布尔Game的数据集上进行实验,实验结果如图8所示.该实验对一般的穷举法、NashEvaluation算法 [25] 和算法1进行比较.这里的NashEvaluation算法是通过多次遍历超图的超树分解,最后通过半连接操作求得约束满足解的算法.以Agent的数量为自变量进行3组实验,每组实验分设不同的决策变量数和最多二元运算符数,纵向对比这2个参数对算法的影响.通过每个Agent i 控制相同的决策变量数目| π i |来决定总的决策变量数| V |,目标 φ i 中的决策变量数可以通过二元运算符的个数得到.分别设置(2,3),(2,6),(4,6)三组参数对进行实验,以参数对(2,3)为例,其中参数2表示每个Agent控制的决策变量数为2个,参数3表示每个Agent目标中最多包含的二元运算符的数目为3个.
通过图8的实验结果可以得出,在存在约束满足解的无环布尔Game中,算法1明显比一般的穷举法高效得多.穷举法和算法1的运行时间都随着Agent的数量的增加而增加,穷举法的运算时间变化比较剧烈的原因是它需要穷举出所有的策略组合,而这样的过程所耗的时间是指数级增长的.当决策变量的个数达到40时,穷举法就超出了5 min.反观算法1的曲线比较平滑,图8的(a)和(b)可以看出,算法1的时间复杂度和所有决策变量的数目的关系不大,而与目标中二元运算符的数目有关,即包含决策变量最多的目标有关系.所以一旦固定了二元运算符的数量,算法1就只受到Agent个数的影响,这也从实验的角度验证了定理1的正确性.与穷举法对比,算法1的效率较高是因为它考虑了每个Agent目标之间的关系,即不同Agent之间的相关变量存在相交的部分,而且通过超树分解,将所有的决策变量分解为更小的组,从而大大降低了策略生成的次数.
在NashEvaluation算法和算法1的比较中,可以发现本文提出的算法1比NashEvaluation算法更高效.这是因为NashEvaluation算法对超树进行了3次遍历并进行了半连接处理;而算法1只是对超树进行了一次的遍历,因为在这个过程中,每个结点被遍历时都是在先前结点计算得到的解上计算,这在一定程度上减少了策略的检测个数.而且可以发现,在中小规模的布尔Game中2个算法的效率相差不大,而在大规模的布尔Game求解中算法1相对较好.从图8的(a),(b)和(c)可以看到,NashEvaluation算法和算法1一样,都是受 m 和Agent个数 N 的影响比较大.需要说明的是图8中纵坐标中SCBG是“求解布尔Game的核”的缩写.
本节在不存在任何限制的布尔Game的数据集上进行实验,测试算法2的效率.这里只在每个Agent上控制2个决策变量,目标中包含3个二元操作符的布尔Game上进行实验测试.
通过图9可得,对于2个算法,当Agent个数增加到30个,相应的决策变量数就增加到了60个,这时布尔Game的核的求解就到了一定的界限.但在30个Agent之前,算法2所达到的效果还是相对明显的,在一定程度上提高了计算核的效率.所以算法2只是适用于Agent的个数和决策变量的数目不太多的情况下,虽然在通过Agent间的依赖关系分解了原始布尔Game,但在局部的子布尔Game的求核算法中仍然是指数级的.对于剩余的待检测策略,在比较的过程中,每个策略需要的对比次数至少是2 | V | .所以该算法只能适用于中小规模的无约束满足解的布尔Game求核.
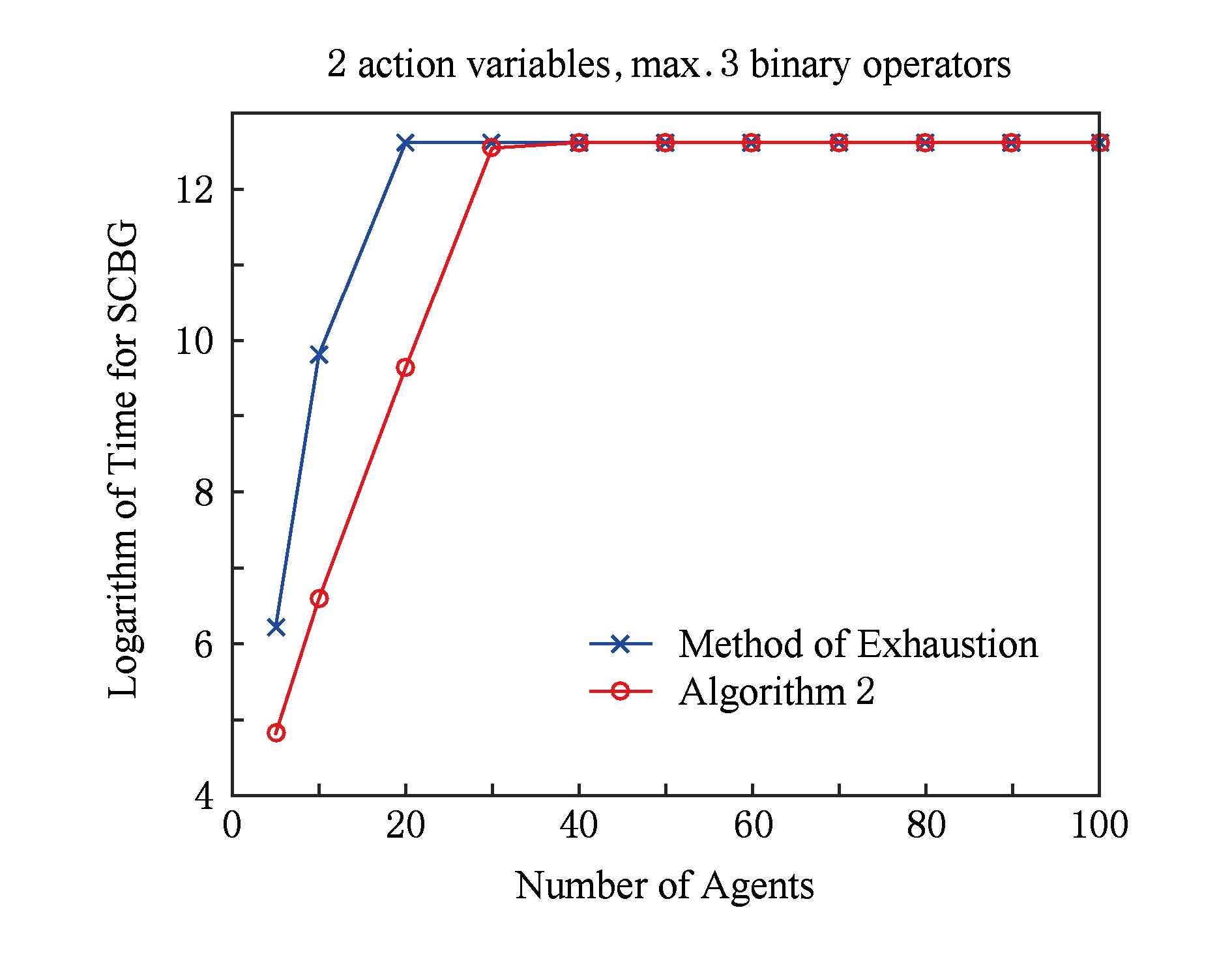
Fig. 9 Experiment of solving core of general Boolean games
图9 一般布尔Game求核实验
通过6.3节、6.4节的实验分析,可以得出本文给出的算法1适用于求解超图无环布尔Game的约束满足解,算法1受Agent和对应相关变量(目标中的决策变量)的影响比较大,而跟整个决策变量集的大小无关.当相关变量数固定时,算法1与Agent数属于线性关系;当Agent数固定时,算法1与最大相关变量是指数关系.实验证明这种将布尔Game的决策变量集通过目标分解的方法,大大降低了生成策略组合的过程,从而提高了求核的效率.并且在与NashEvaluation算法的比较中,算法1在大规模的布尔Game的可满足核的求解上相对高效.
算法2适用于中小规模的布尔Game,规模是指布尔Game的Agent数量和决策变量数的大小.通过稳定集分解布尔Game的方法,在一定程度上降低了求核的运行时间,但是也存在弊端,就是当布尔Game规模过大时,被分解得到的子布尔Game规模虽然相对于较小,但规模相对于一般问题还是过大.所以该算法对于中小规模的布尔Game是适用的.
本文主要研究了2个问题:1)求解布尔Game的可满足性问题的解;2)求解布尔Game的所有核.在问题1上引入约束满足问题的超图表示,对于有无环超图的布尔Game,利用超树分解来降低求可满足解的可行空间,给出了基于超树分解的求布尔Game可满足解的算法,该算法在很大程度上缩小了问题的规模,提高了求解效率.在问题2上通过Agent间的依赖关系图得到稳定集,利用稳定集分解布尔Game来降低求核的可行空间,给出了基于稳定集分解的布尔Game求核算法,提高了求解核的效率.最后以随机生成的布尔Game实验验证了上述2种算法的有效性.
本文的未来工作包括:
1) 将Agent间的依赖关系加入到布尔Game的超树分解中,将超图的结构更接近于布尔Game,研究该结构的核求解问题,找到高效率的核求解算法.
2) 在布尔Game的超图表示中,研究在超图的超树分解的树宽大于等于2时,布尔Game的核求解方法.
3) 在执行决策变量时将单个Agent的操作细分化,将税收、决策变量的约束关系、成本加入到布尔Game中,使得更贴近现实中的博弈.
参考文献
[1]Harrenstein P, Hoek W, Meyer J J, et al. Boolean games[C] 
 Proc of the 8th Conf on Theoretical Aspects of Rationality and Knowledge. San Francisco, CA: Morgan Kaufmann, 2001: 287-298
Proc of the 8th Conf on Theoretical Aspects of Rationality and Knowledge. San Francisco, CA: Morgan Kaufmann, 2001: 287-298
[2]Bonzon E, Lagasquie-Schiex M C, Lang J et al. Boolean games revisited[C] 
 Proc of the 17th European Conf on Artificial Intelligence. Amsterdam: IOS Press, 2006: 265-269
Proc of the 17th European Conf on Artificial Intelligence. Amsterdam: IOS Press, 2006: 265-269
[3]Dunne P E, Hoek W, Kraus S et al. Cooperative Boolean games[C] 
 Proc of the 7th Int Joint Conf on Autonomous Agents and Multiagent Systems-Volume 2. Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems, 2008: 1015-1022
Proc of the 7th Int Joint Conf on Autonomous Agents and Multiagent Systems-Volume 2. Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems, 2008: 1015-1022
[4]Dunne P E, Hoek W V D. Representation and complexity in Boolean games[C] 
 Proc of Logics in Artificial Intelligence. Berlin: Springer, 2004: 347-359
Proc of Logics in Artificial Intelligence. Berlin: Springer, 2004: 347-359
[5]Bonzon E, Lagasquie-Schiex M C, Lang J. Compact preference representation and Boolean games[J]. Autonomous Agents and Multi-Agent Systems, 2009, 18(1): 1-35
[6]Bonzon E, Lagasquie-Schiex M C, Lang J. Effectivity functions and efficient coalitions in Boolean games[J]. Synthese, 2012, 187(1): 73-103
[7]Wooldridge M, Endriss U, Kraus S. Incentive engineering for Boolean games[J]. Artificial Intelligence, 2013, 195(2): 418-439
[8]Clercq S D, Schockaert S, Cock M D. Possibilistic Boolean games: Strategic reasoning under incomplete information[C] 
 Proc of Logics in Artificial Intelligence. Berlin: Springer, 2014: 196-209
Proc of Logics in Artificial Intelligence. Berlin: Springer, 2014: 196-209
[9]Harrenstein P, Turrini P, Wooldridge M. Hard and soft equilibria in Boolean games[C] 
 Proc of the 2014 Int Conf on Autonomous Agents and Multi-Agent Systems. Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems, 2014: 845-852
Proc of the 2014 Int Conf on Autonomous Agents and Multi-Agent Systems. Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems, 2014: 845-852
[10]Gutierrez J, Harrenstein P, Wooldridge M. Iterated Boolean games[C] 
 Proc of the 23rd Int Joint Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2013: 932-938
Proc of the 23rd Int Joint Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2013: 932-938
[11]Harrenstein P, Turrini P, Wooldridge M. Hard and soft preparation sets in Boolean games[J]. Studia Logica, 2016, 104(4): 813-847
[12]Clercq S D, Schockaert S, Nowé A. Modelling incomplete information in Boolean games using possibilistic logic[J]. International Journal of Approximate Reasoning, 2018, 93(2): 1-23
[13]Yang Wei, Ban Dongsong, Guan Donglin et al. Coalition formation based distributed algorithm for multi-objective cooperative sensing in cognitive radio networks[J]. Chinese Journal of Computers, 2012, 35(4): 730-740 (in Chinese)
(杨威, 班冬松, 管东林. 基于联盟构造博弈的认知无线电网络分布式多目标协作感知算法[J]. 计算机学报, 2012, 35(4): 730-740)
[14]Xu Guangbin, Liu Jinglei, The optimal coalition strcture generation with the constrained number of coalition[J]. Journal of Nanjing University: Natural Sciences, 2015, 51(4): 601-613 (in Chinese)
(徐广斌, 刘惊雷. 带有联盟个数约束的最优联盟结构生成[J]. 南京大学学报: 自然科学, 2015, 51(4): 601-613)
[15]Bonzon E, Lagasquie-Schiex M C, Lang J. Dependencies between players in Boolean games[J]. International Journal of Approximate Reasoning, 2009, 50(6): 899-914
[16]Sauro L, Villata S. Dependency in cooperative Boolean games[J]. Journal of Logic and Computation, 2013, 23(2): 425-444
[17]Dunne P E, Wooldridge M. Towards tractable Boolean games[C] 
 Proc of the 11th Int Conf on Autonomous Agents and Multiagent Systems-Volume 2. Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems, 2012: 939-946
Proc of the 11th Int Conf on Autonomous Agents and Multiagent Systems-Volume 2. Richland, SC: International Foundation for Autonomous Agents and Multiagent Systems, 2012: 939-946
[18]Clercq S D, Cock M D, Bauters K. Using answer set programming for solving Boolean games[C] 
 Proc of 14th Int Conf on Principles of Knowledge Representation and Reasoning. Palo Alto, CA: AAAI, 2014: 602-605
Proc of 14th Int Conf on Principles of Knowledge Representation and Reasoning. Palo Alto, CA: AAAI, 2014: 602-605
[19]Clercq S D, Bauters K, Schockaert S. Exact and heuristic methods for solving Boolean games[J]. Autonomous Agents and Multi-Agent Systems, 2017, 31(1): 66-106
[20]Gottlob G, Leone N, Scarcello F. A comparison of structural CSP decomposition methods[J]. Artificial Intelligence, 1999, 124(2): 243-282
[21]Gottlob G, Leone N, Scarcello F. Hypertree decompositions and tractable queries[J]. Journal of Computer and System Sciences, 2002, 64(3): 579-627
[22]Neumann J V, Morgenstern O. Theory of Games and Economic Behavior[M]. Princeton, NJ: Princeton University Press, 1953
[23]Gottlob G, Samer M. A backtracking-based algorithm for hypertree decomposition[J]. Journal of Experimental Algorithmics, 2009, 13(1): 1-19
[24]Warshall S. A theorem on Boolean matrices[J]. Journal of the ACM, 1962, 9(1): 11-12
[25]Gottlob G, Greco G, Scarcello F. Pure Nash equilibria: Hard and easy games[J]. Journal of Artificial Intelligence Research, 2005, 24(1): 357-406

Wang Bo , born in 1994. Master candidate. His main research interests include computation of a core on Boolean games.

Liu Jinglei , born in 1970. PhD, professor, and master supervisor. His main research interests include artificial intelligent and theoretical computer science.
Wang Bo and Liu Jinglei
( School of Computer and Control Engineering , Yantai University , Yantai , Shandong 264005)
Abstract Boolean game is an important framework to compute the solution of multi-agent cooperation, which represents the static agent games scenario based on propositional logic. In Boolean games, every agent uses propositional formulas to represent its goals, so whether its goals can be satisfied depending on the propositional formulas’ truth value. At present, Boolean game is mainly studied from the knowledge representation perspective and solving pure Nash equilibrium, but computing core from coalitional view is not enough. Computing core of Boolean games is the procedure of generating strategy profiles and comparing with strategy profiles. Firstly, in order to solve the solution of constraint satisfaction problem of Boolean games, we structure hypergraph on Boolean games where the action variables are regarded as the vertices and the goals are regarded as the hyperedge. Secondly, we see agents as the vertices and the dependence relationship between agents as edge to structure a directed dependency graph, which can get a set of stable sets to decompose Boolean games as smaller Boolean games on the scale. These two structures simplify the generation process and comparison process, and then improve the efficiency of computing core of Boolean games to some extent. Then, based on the hypertree decomposition and the stable set decomposition of the dependent graph, we give different methods of computing core of Boolean game. Finally, we verify the validity of this algorithm through the experimental evaluation.
Key words Boolean game; computing core; constraint satisfaction problems; hypergraph; hypertree decomposition; stable set
中图法分类号 TP18
通信作者 : 刘惊雷(jinglei_liu@sina.com)
基金项目 : 国家自然科学基金项目(61572419,61773331,61703360);山东省高等学校科技计划项目(J17KA091)
This work was supported by the National Natural Science Foundation of China (61572419, 61773331, 61703360), and the Project of Shandong Province Higher Educational Science and Technology Program (J17KA091).
收稿日期 : 2018-05-18;
修回日期: 2018-06-11
DOI: 10.7544/issn1000-1239.2018.20180360