田 泽 杨 明 李爱师
(南京师范大学计算机科学与技术学院 南京 210023) (zetian_edu@126.com)
摘 要 字典学习是重要的特征表示方法之一,在人脸识别等方面有广泛的应用,特别适合解决姿态变化下的人脸识别问题,因而倍受研究者的关注.为有效增强字典的判别能力,研究者结合领域知识和抗噪等策略提出大量的字典学习模型,其中包括最近提出的同时进行降维和字典学习的方法,但这些方法侧重考虑样本中特定类的信息,未能有效考虑训练样本间的共享信息.因此,提出了一种稀疏约束下快速低秩共享的字典学习方法.该方法采用降维和字典联合进行学习的方式,并嵌入Fisher判别准则获得特定类字典和编码系数,同时施加低秩约束获得低秩共享字典,以此增强字典和编码系数的判别能力.此外,运用Cayley变换保护投影矩阵的正交性来获得紧凑的特征集合.在AR,Extended Yale B,CMU PIE和FERET四个数据集上的人脸识别实验验证所提方法的优越性.实验结果表明所提方法在表情变化下的人脸识别具有很强的鲁棒性,并对光照起到了抑制作用,尤其适合解决光照、表情变化下的小样本问题.
关键词 人脸识别;字典学习;稀疏约束;低秩模型;共享特征
人脸识别存在光照、表情、姿态、小样本等挑战性问题,同时,人脸识别的高维问题也增加了人脸识别的难度,通常使用经典的降维方法主要有LDA [1] ,LPP [2] 和PCA [3] ,降维得到的子空间能够提高人脸识别的准确率.但是这些方法对人脸识别存在的光照、表情等问题不具有良好的鲁棒性.稀疏表示可以较好地解决这些问题.
稀疏表示 [4] 已经成为信号处理领域的强大工具.应用包括压缩感知 [5] 、稀疏信号恢复 [6] 、图像分割 [7] 以及信号分类.在这些应用领域中,信号通常可以由固定的字典来表示.基于这一理论,稀疏表示分类器被提出并应用于人脸识别.然而,固定的字典对于分类任务并没有足够的鉴别力,这就促进基于稀疏约束的字典学习研究.
字典学习可以分为无监督字典学习和有监督字典学习.KSVD [8] 算法为无监督字典学习的典型代表,通过奇异值分解对字典原子进行更新.文献[9]提出DKSVD算法,将线性分类器加入KSVD字典学习模型,促使KSVD算法具有分类能力.文献[10]将鉴别性稀疏编码误差项加入DKSVD算法促使稀疏编码的判别能力进一步加强.文献[11]将Fisher判别准则嵌入到字典和稀疏编码中,这促使稀疏编码和字典都具有判别能力,但其仅考虑样本中特有的信息,没有考虑样本间的共享信息.针对这一问题,文献[12]提出利用低秩约束字典来获得样本间的共享信息,这增强了字典和稀疏编码的判别能力.
此外,大部分有监督字典学习 [9-12] 都是先对数据进行降维再进行字典学习,这些方法不能从原数据集中获得更为重要的特征,从而降低字典的学习能力.针对这一问题,稀疏嵌入框架 [13] 被提出,通过同时降维和字典学习的策略来增强字典和稀疏编码的判别能力.文献[14]通过约束投影矩阵正交来获得紧凑的特征,但其投影矩阵的求解是不恰当的且收敛性不能被保证,因此降低了字典的学习能力.针对此问题,SEDL [15] 通过Cayley [16] 变换来保护投影矩阵的正交性,从而获得重要和紧凑的特征.
针对上述所提字典学习的不足,本文提出一种稀疏约束下快速低秩共享的字典学习(FLRSDLSC)方法,并将其用于人脸图像分类.本文的主要贡献有3个方面:
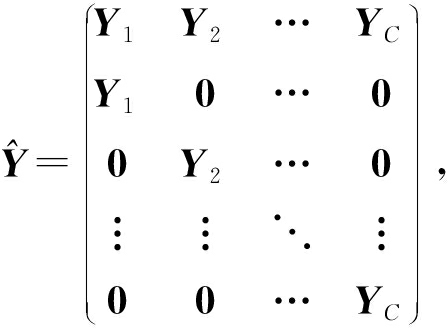
1) 字典学习框架由特定类的字典和共享的子字典所组成.对于特定类的字典,嵌入Fisher判别准则;对于共享的子字典,嵌入低秩约束.因此,该方法能从样本中获得共享和特定类的特征,以此增强字典和稀疏编码的判别能力.
2) 通过Cayley变换保护投影矩阵的正交性来获得紧凑的特征.
3) 采用降维和字典学习同时进行的方法,增强字典对降维后样本的表示能力.
Chen等人于2017年提出一种同时降维和字典学习的方法(SEDL)应用于人脸识别.其目标函数如下:
![]() g ( X )+ λ 3
g ( X )+ λ 3 ![]() ,
,
(1)
s.t. P T P = I ,
其中, f ( P , Y , D , X )为变量 P , Y , D , X 的函数,
(2)
γ ( P , Y c , D , X c )= ![]() +
+ ![]()
(3)
![]()
![]() )+
)+ ![]() ;
;
(4)
Y =( Y 1 ,…, Y c ,…, Y C )∈ ![]() d × N 表示大小为 N 的训练数据集, Y c ∈
d × N 表示大小为 N 的训练数据集, Y c ∈ ![]()
![]() 表示第 c 类训练样本,其中 N = n 1 +…+ n c +…+ n C .降维的目标是学习投影矩阵 P ∈
表示第 c 类训练样本,其中 N = n 1 +…+ n c +…+ n C .降维的目标是学习投影矩阵 P ∈ ![]() p × d ( p < d ), p 表示数据降维后的维度大小. D =( D 1 ,… D c ,…, D C )∈
p × d ( p < d ), p 表示数据降维后的维度大小. D =( D 1 ,… D c ,…, D C )∈ ![]() p × k 表示结构化的字典,其中 D c ∈
p × k 表示结构化的字典,其中 D c ∈ ![]()
![]() 为第 c 类子字典.让 X =( X 1 ,…, X c ,…, X C )∈
为第 c 类子字典.让 X =( X 1 ,…, X c ,…, X C )∈ ![]() k × N 表示 Y 在字典 D 下的编码系数,其中 X c 表示 Y c 在字典 D 下的编码系数.令 X , X c 列的平均向量分别为 m 与 m c ,则 X c , X 平均稀疏编码矩阵分别为 M c =( m c ,…, m c )与 M =( m ,…, m ).
k × N 表示 Y 在字典 D 下的编码系数,其中 X c 表示 Y c 在字典 D 下的编码系数.令 X , X c 列的平均向量分别为 m 与 m c ,则 X c , X 平均稀疏编码矩阵分别为 M c =( m c ,…, m c )与 M =( m ,…, m ).
式(1)由4部分组成:重构误差项 f ( P , Y , D , X )、 l 1 范数正则化项 ![]() 鉴别性稀疏编码项 g ( X )和F范数正则化项.式(1)等号右边第1项希望降维后的训练样本 Y c 能由字典 D 表示,也可以由子字典 D c 表示,但不能由其他类子字典表示,从而增强字典的判别能力;第2项促使编码系数尽可能稀疏;第3项最小化稀疏编码的类内离散度,最大化稀疏编码的类间离散度,因此稀疏编码系数具有判别能力,
鉴别性稀疏编码项 g ( X )和F范数正则化项.式(1)等号右边第1项希望降维后的训练样本 Y c 能由字典 D 表示,也可以由子字典 D c 表示,但不能由其他类子字典表示,从而增强字典的判别能力;第2项促使编码系数尽可能稀疏;第3项最小化稀疏编码的类内离散度,最大化稀疏编码的类间离散度,因此稀疏编码系数具有判别能力, ![]() 确保式(4)是凸和稳定的;第4项最小化由降维引起的源数据域的重构误差,防止降维时引起病态投影.约束项希望降维矩阵 P 尽可能正交,以此获得更为紧凑的特征信息.SEDL只考虑特定类的样本信息,忽略样本间的相关性,导致字典和稀疏编码判别能力的降低.
确保式(4)是凸和稳定的;第4项最小化由降维引起的源数据域的重构误差,防止降维时引起病态投影.约束项希望降维矩阵 P 尽可能正交,以此获得更为紧凑的特征信息.SEDL只考虑特定类的样本信息,忽略样本间的相关性,导致字典和稀疏编码判别能力的降低.
Natarajan于2006年提出用稀疏近似解 [17] 去求解矩阵最小化问题,其目标函数如下:
![]()
(5)
其中 H ∈ ![]() s × d t 是决策变量, L 是线性映射, L 将 H 从 s 维映射到 p 维.然而式(5)的求解是NP难问题.当
s × d t 是决策变量, L 是线性映射, L 将 H 从 s 维映射到 p 维.然而式(5)的求解是NP难问题.当 ![]() 式(5)的解就是核范数
式(5)的解就是核范数 ![]() (即所有奇异值之和)的解.人们转而求解如下凸优化问题:
(即所有奇异值之和)的解.人们转而求解如下凸优化问题:
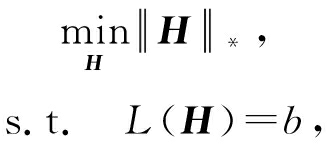
(6)
式(6)通过奇异值阈值 [18] 算法近似求解.
( FLRSDLSC )
针对SEDL方法的不足,本文提出一种稀疏约束下快速低秩共享的字典学习方法.该方法学习特定类字典和共享子字典,以此增强字典和稀疏编码的判别能力,同时采用字典学习和降维同时进行的方式.其模型定义如下:
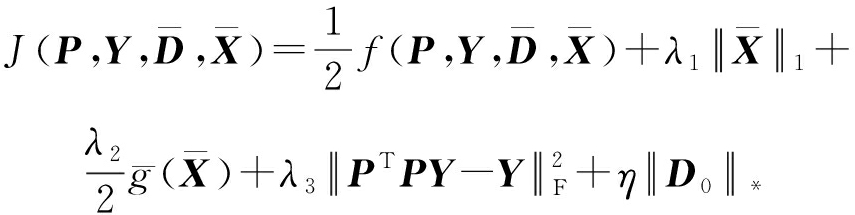
(7)
s.t. P T P = I ,
其中,
![]()
![]()
(8)
![]()
(9)
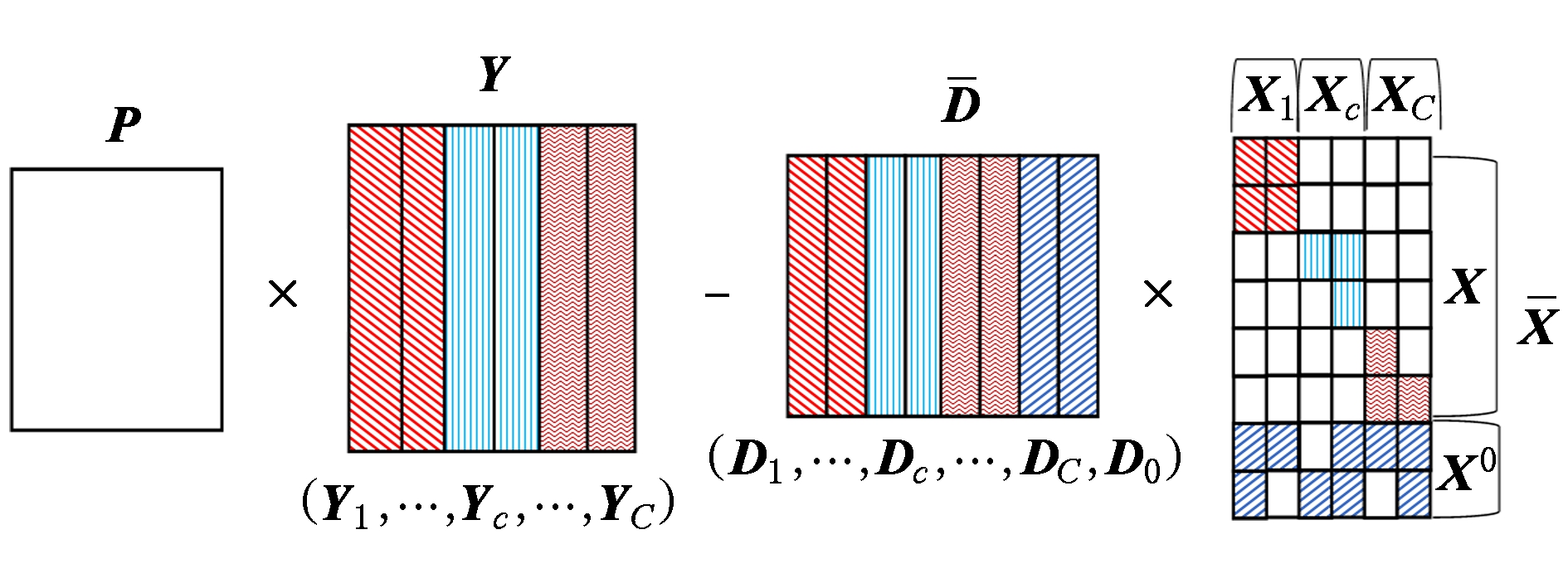
Fig. 1 The relationship between variables in term (8)
图1 式(8)变量间的关系
λ 1 , λ 2 , η , λ 3 为正则化参数; X 0 列的均值向量为 m 0 , X 0 的均值矩阵为 M 0 =( m 0 ,…, m 0 ); D 0 ∈ ![]()
![]() 为共享子字典,
为共享子字典, ![]() 为总字典,
为总字典, ![]() 为核范数正则化促使子字典 D 0 具有低秩结构. X 0 代表 Y 在共享字典 D 0 下的编码系数,
为核范数正则化促使子字典 D 0 具有低秩结构. X 0 代表 Y 在共享字典 D 0 下的编码系数, ![]() 代表 Y 在总字典
代表 Y 在总字典 ![]() 下的编码系数.
下的编码系数.
式(7)中的目标函数的第2项、第4项以及约束项与式(1)一致,不同处在于第1项、第3项,还增加了第5项,这源于将共享字典加入到SEDL模型.第1项不同处在于希望样本 Y 可以由总字典 ![]() 表示,也可以由第 c 类子字典 D c 和共享子字典 D 0 表示,以此增强字典的判别能力(图1解释了式(8)中变量间的关系).第3项不同处在于嵌入共享字典所对应的稀疏编码,由于该字典是低秩的,其对应的稀疏编码应该是相似的(图2解释了式(9)变量间的关系),以此增强稀疏编码的判别能力.
表示,也可以由第 c 类子字典 D c 和共享子字典 D 0 表示,以此增强字典的判别能力(图1解释了式(8)中变量间的关系).第3项不同处在于嵌入共享字典所对应的稀疏编码,由于该字典是低秩的,其对应的稀疏编码应该是相似的(图2解释了式(9)变量间的关系),以此增强稀疏编码的判别能力.
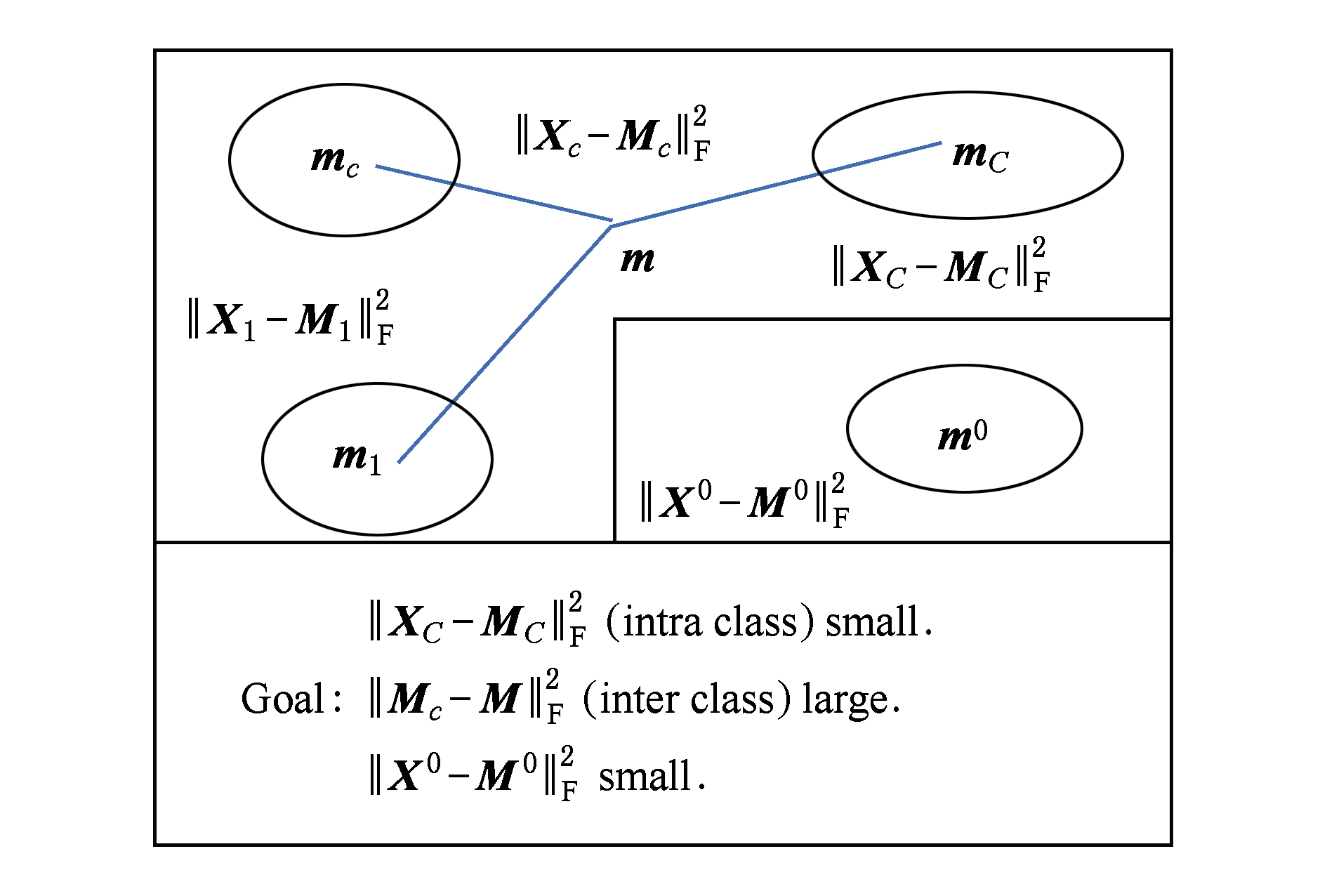
Fig. 2 The relationship between variables in term (9)
图2 式(9)变量间的关系
式(7)是一个非凸的问题,其求解通过反复更新稀疏编码 ![]() 字典
字典 ![]() 降维矩阵 P 这3个过程,直至收敛.
降维矩阵 P 这3个过程,直至收敛.
2.2.1 更新稀疏编码 ![]()
固定 ![]() 更新
更新 ![]() 式(7)重新定义如下:
式(7)重新定义如下:
![]()
(10)
其中
![]()
(11)
f P ( D )= f ( P , D )代表 P 固定 D 的函数,用式(11)求导后的结果和FISTA [19] 算法对式(10)进行求解,式(11)求导如下:
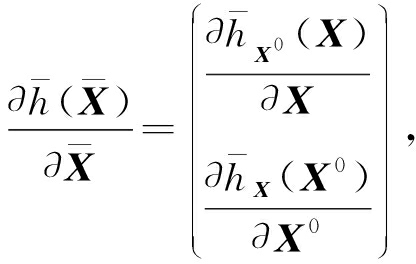
(12)
式(12)的第1分量推导如下:
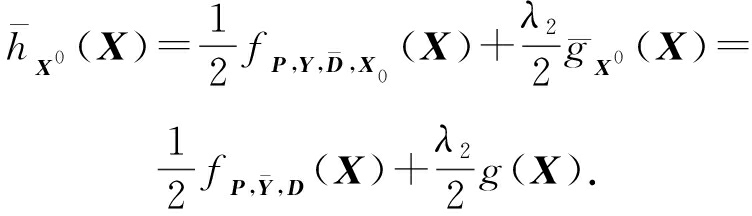
(13)
引理 ![]()
![]()
(14)
其中, ![]() 代表单位矩阵;
代表单位矩阵; ![]() 定义为函数,对于矩阵
定义为函数,对于矩阵
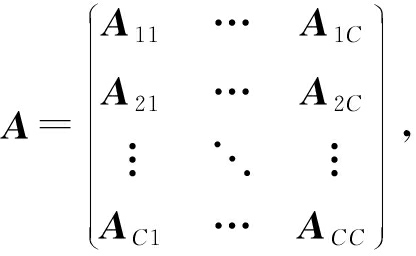
![]() 定义为 A 的2倍对角矩阵,即:
定义为 A 的2倍对角矩阵,即:
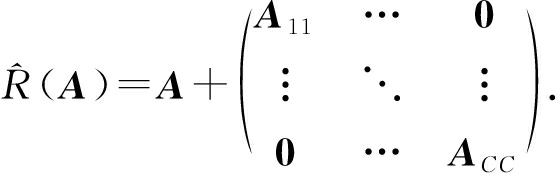
(15)
证明. 见附录A.
式(12)的第2分量,使用引理3,推导如下:
![]()
(16)
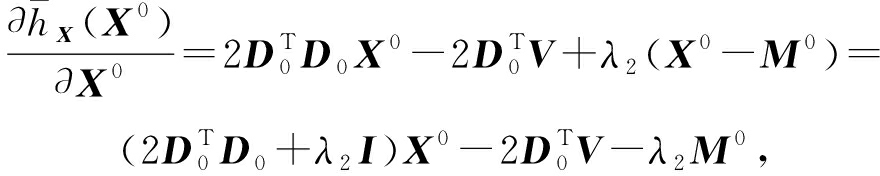
(17)
其中 ![]()
式(14)和式(17)组合求解式(12).
2.2.2 更新字典 ![]()
引理2 . 固定 ![]() 更新
更新 ![]() 提出如下方法分别解决 D , D 0 .更新 D ,式(7)简化如下:
提出如下方法分别解决 D , D 0 .更新 D ,式(7)简化如下:
![]()
(18)
其中 ![]() 和
和 ![]()
证明. 见附录B.
式(18)运用ODL [20] 算法进行求解.
引理3 . 固定 ![]() 更新 D 0 ,式(7)简化如下:
更新 D 0 ,式(7)简化如下:
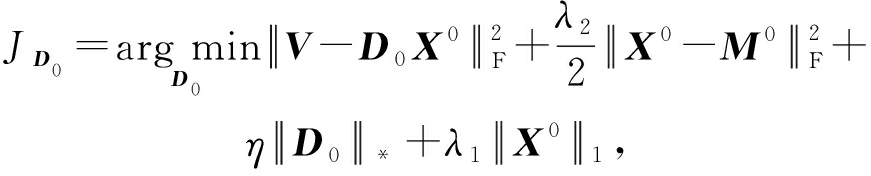
(19)
其中 ![]()
证明. 见附录C.
基于引理3,式(19)简化如下:
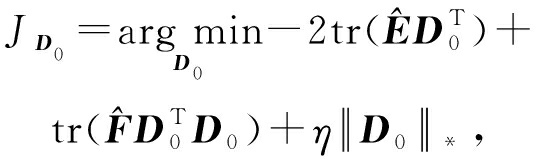
(20)
其中 ![]()
式(20)使用ADMM [21] 模型和奇异值阈值算法.ADMM过程如下:首先选择一个正数 ρ ,初始化 Z = U = D 0 ,然后迭代求解如下子问题直到收敛:
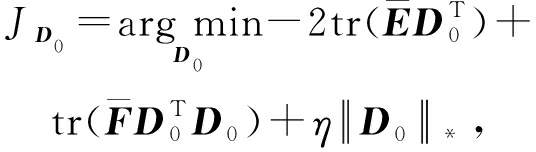
(21)
其中
![]()
(22)
![]()
(23)
Z = K n  ρ ( D c + U ),
ρ ( D c + U ),
(24)
U = U + D 0 - Z ,
(25)
其中 K 为软阈值运算符.式(21)的优化问题运用ODL算法进行求解.
2.2.3 更新降维矩阵 P
固定 ![]() 更新 P ,式(7)重新定义如下:
更新 P ,式(7)重新定义如下:
![]()
s.t. P T P = I ,
(26)
式(26)使用Cayley变换求解 P ,其求解简化为
![]()
(27)
其中 i 初始值为1; P 1 为训练样本的PCA降维矩阵; P i 代表第 i 次迭代的降维矩阵; τ 是一个恰当的步长; ![]() 为斜对称矩阵,
为斜对称矩阵, ![]()
![]() J P T - P
J P T - P ![]() J T ,
J T , ![]() J 为式(26)的导数,求导简化成如下形式:
J 为式(26)的导数,求导简化成如下形式:
![]()
![]()
λ 3 (-4 PYY T +2 PYY T P T P +2 PP T PYY T ),
(28)
通过对上述变量的更新,输出 P , D , D 0 , X , X 0 .
基于2.2节,利用学习得到降维矩阵 P 、总字典 ![]() 和其对应的稀疏编码
和其对应的稀疏编码 ![]() 则FLRSDLSC分类方法定义如下:
则FLRSDLSC分类方法定义如下:
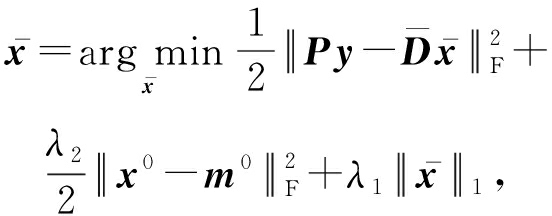
(29)
其中 y 为测试样本; m 0 为稀疏编码系数 x 0 的列平均向量.式(29)运用FISTA算法可求得 ![]() 从
从 ![]() 提取 x 0 和 x c ,通过如下最小化重构误差来预测 y 的类别:
提取 x 0 和 x c ,通过如下最小化重构误差来预测 y 的类别:
![]()
(1- w ) ![]() ,
,
(30)
其中, w 为平衡参数, m c 为 x c 的列平均向量.
输入:训练集 Y ,参数 λ 1 , λ 2 , λ 3 , η 和最大迭代次数 T ;
步骤1. 初始化 P 为训练样本的PCA降维矩阵, ![]() 为随机矩阵;
为随机矩阵;
步骤2. 固定 ![]() 更新 X ,使用FISTA算法及式(14)对式(10)求解编码系数 X ;
更新 X ,使用FISTA算法及式(14)对式(10)求解编码系数 X ;
步骤3. 固定 ![]() 更新 X 0 ,使用FISTA算法及式(17)对式(10)求解编码系数 X 0 ;
更新 X 0 ,使用FISTA算法及式(17)对式(10)求解编码系数 X 0 ;
步骤4. 固定 ![]() 更新 D ,使用ODL算法对式(18)求解字典 D ;
更新 D ,使用ODL算法对式(18)求解字典 D ;
步骤5. 固定 ![]() 更新 D 0 ,使用ODL算法对式(21)求解共享子字典 D 0 ;
更新 D 0 ,使用ODL算法对式(21)求解共享子字典 D 0 ;
步骤6. 固定 ![]() 更新 P ,使用式(27)求解降维矩阵 P ;
更新 P ,使用式(27)求解降维矩阵 P ;
7) 重复步骤2到步骤6,直到达到收敛条件或者满足最大迭代次数;
输出:降维矩阵 P 、字典 ![]() 稀疏编码系数
稀疏编码系数 ![]() 结合2.3节,利用式(30)对测试样本进行分类.
结合2.3节,利用式(30)对测试样本进行分类.
我们的算法快速主要体现在更新稀疏编码 X 和结构化(特定类)字典 D 上,本节比较了原始和高效的FDDL字典学习方法的复杂度.每个算法的复杂度被估计为一次迭代所需乘法的数量.假设:1)每类样本数量是特定类字典数量的2倍,特定类字典数量与共享类字典数量是相同的.令 n c = n , k c = k 0 = k ;2)每类字典的个数、训练样本的数量都远小于样本维数,即 k < d , n < d ;3)每个算法需要 q 次迭代才能收敛.
在本节分析中使用以下事实:1)如果 A 1 ∈ ![]() m 1 × n 1 , B 1 ∈
m 1 × n 1 , B 1 ∈ ![]() n 1 × p 1 ,则矩阵乘法 A 1 B 1 具有复杂度 O ( m 1 n 1 p 1 );2)如果 A 1 ∈
n 1 × p 1 ,则矩阵乘法 A 1 B 1 具有复杂度 O ( m 1 n 1 p 1 );2)如果 A 1 ∈ ![]() n × n 是非奇异的,则矩阵求逆
n × n 是非奇异的,则矩阵求逆 ![]() 的复杂度为 O ( n 3 );3)矩阵的奇异值分解 A 1 ∈
的复杂度为 O ( n 3 );3)矩阵的奇异值分解 A 1 ∈ ![]() p × q , p > q ,其复杂度 Ο ( pq 2 ).
p × q , p > q ,其复杂度 Ο ( pq 2 ).
1) 更新 X (O-FDDL-X)
参考文献[12],原始的稀疏编码更新被分为 C 个子问题O-FDDL-X的复杂度:
C 2 k ( dn + qCkn + Cdk ).
(31)
2) 更新 X (E-FDDL-X)
由引理1可知,
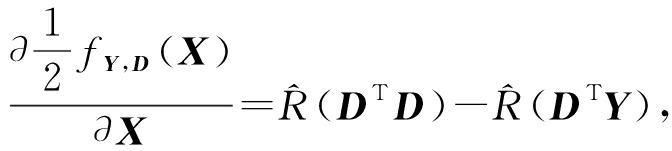
(32)
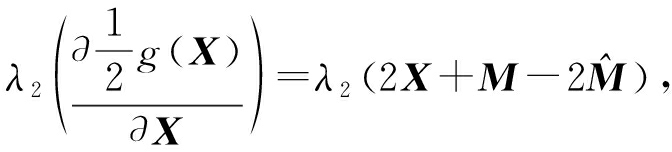
(33)
其中, ![]() 计算代价不是很高, M 与 M c 的计算可以忽略,因为都是列运算.将式(32)和式(33)组合起来得到该算法的复杂度:
计算代价不是很高, M 与 M c 的计算可以忽略,因为都是列运算.将式(32)和式(33)组合起来得到该算法的复杂度:
![]()
C 2 k ( dk + dn + qCnk ).
(34)
3) 更新 D (O-FDDL-D)
参考文献[12],原始的字典更新被分为 C 个子问题,O-FDDL-D的复杂度:
Cdk ( qkn + C 2 n ).
(35)
4) 更新 D (E-FDDL-D)
参考文献[12],E-FDDL-D的复杂度:
Cdk ( Cqk + Cn )+ C 3 k 2 n .
(36)
表1,2分别展示原始的FDDL算法和高效的FDDL算法的复杂度分析与不同字典学习方法的总体复杂度分析.
Table 1 Complexity Analysis for the Proposed Efficient
Algorithms and Their Original Versions
表1 高效算法和原始算法的复杂度分析

Table 2 Complexity Analysis for Different Dictionary
Learning Methods
表2 不同字典学习方法的复杂度分析
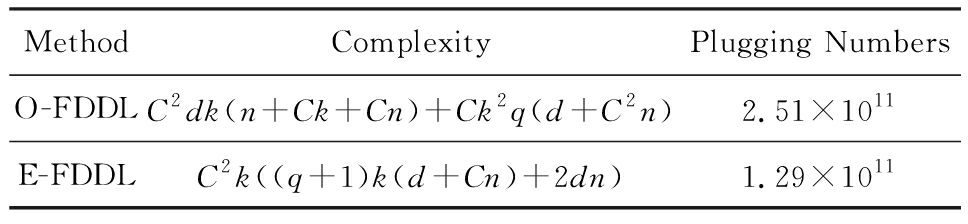
选择一系列参数集合:类别数为100、数据降维后的维度为50、数据维度为500、迭代次数为50、特定类与共享类字典数为10、每类训练样本为20,也就是 C =100, n =20, d =500, q =50, k =10.假设 q 2 =50.从表1,2可以得出高效FDDL算法相比原始FDDL算法实现低复杂度.
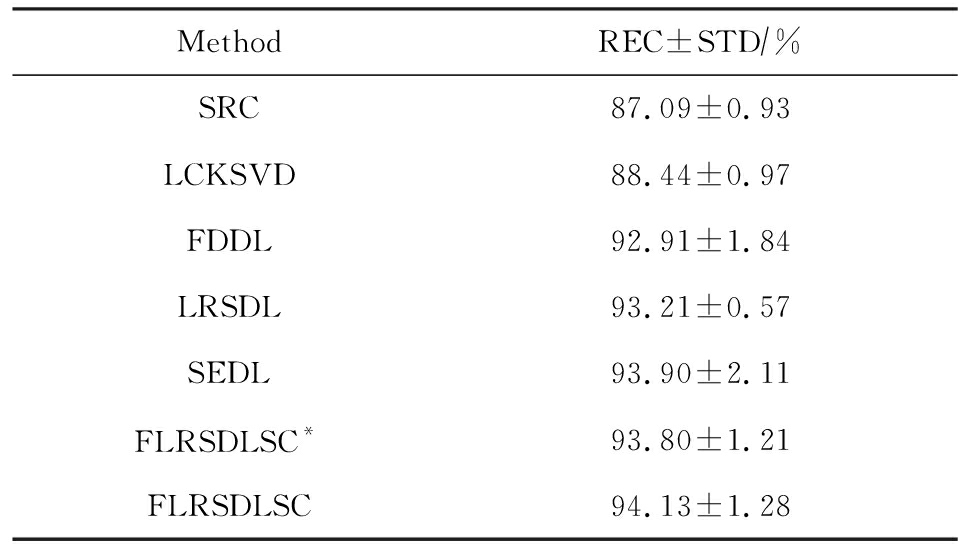
本文在4个公开的数据集上进行实验:AR [22] ,Extended Yale B [23] ,CMU PIE [24] ,FERET [25] 人脸数据集.对比的方法主要有SRC [4] ,LCKSVD [10] ,FDDL [11] ,LRSDL [12] ,SEDL [15] ,FLRSDLSC * .为了解释联合降维和字典学习的能力,固定降维矩阵的FLRSDLSC * 的方式被提出.在所有实验中,主成分分析的方法应用于数据的降维或者初始化SEDL,FLRSDLSC * 的降维矩阵.在AR,the Extended Yale B,CMU PIE,FERET和AR性别数据集下,FLRSDLSC模型的训练参数设置如下: λ 1 , η 统一设置为0.001与0.003; λ 2 分别设置为0.2,0.2,0.2,0.001,0.2; λ 4 分别设置为0.5,0.3,0.4,0.3,0.5.其分类参数设置如下: w 分别设置为1.2,0.1,1,1,0.1; λ 1 分别设置为0.001,0.3,0.001,0.01,0.01; λ 2 分别设置为0.1,10,1,1,1.
由实验参数的设置可以看出,式(7)的第1项与第4项对FLRSDLSC的贡献几乎同等重要,说明获得结构化(特定类)字典和防止病态降维的重要性;式(7)的第2,3,5项对FLRSDLSC的贡献相对较小.
AR数据库由126个个体的4 000多幅图像组成,这些图像在照明、表情和配件方面各不相同.如文献[15]中所述,使用包含100个个体中的1 400张图像,其中50名男性,50名女性,其人脸图像只存在表情和光照问题.图3展示AR数据集中第1个人的样本图像.每一个个体随机选择7张图片用于训练,剩下的7张图片用于测试.重复实验10次以计算识别率的平均值和相应的标准偏差.所有实验人脸图像大小调整为60×43.在AR数据集上的对比实验中,特征的维度通过PCA降至300.
Fig. 3 Sample images of the first subject on AR dataset
图3 AR数据集第1个人的样本图像
表3展示不同的方法的识别率.在SRC,LCKSVD,FDDL和LRSDL字典学习方法中,LRSDL达到最佳性能为97.34%,比FLRSDLSC方法低0.5%左右.基于特征和字典联合学习的SEDL方法获得了第3高的识别率为94.21%,比LRSDL方法低3.1%左右,可以得出样本间共享信息的重要性,比FLRSDLSC方法低3.7%,这是因为未考虑样本中共享信息.实验验证我们的方法在光照、表情变化下人脸识别具有鲁棒性.
图4展示了不同维度的识别率.PCA+FDDL,PCA+LRSDL,JDDRDL,SEDL作为基准线进行比较.FLRSDLSC方法与其他方法相比在不同维度下都实现了最佳性能,并且在低维特征的人脸识别上仍然能获得高分类性能,说明在表情和光照下的人脸图像上具有良好的鲁棒性.SEDL和FLRSDLSC方法在特征维数为450~600时识别率缓慢增加,到600维时开始降低,这说明增加维数对字典学习方法可能无效.
Table 3 Recognition Rate on AR Dataset
表3 在AR数据集下的识别率
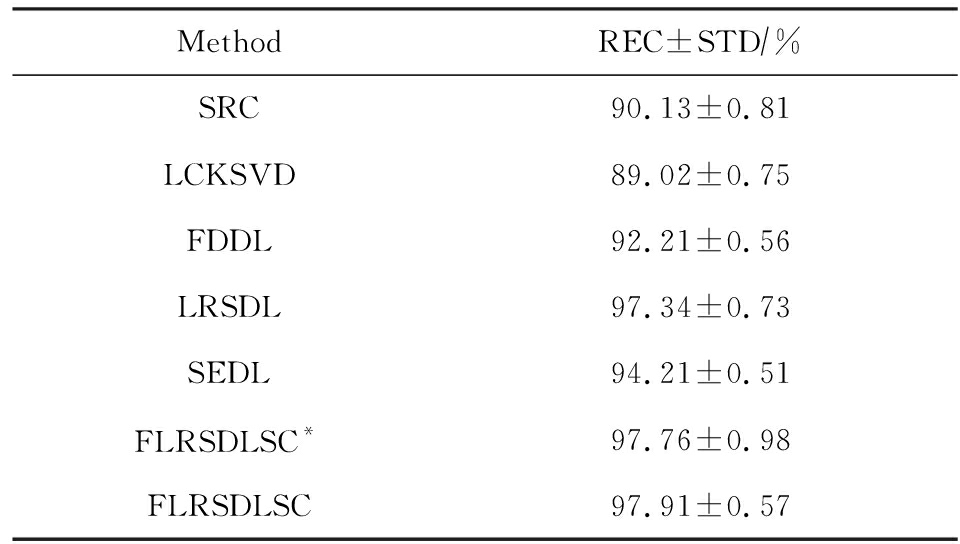
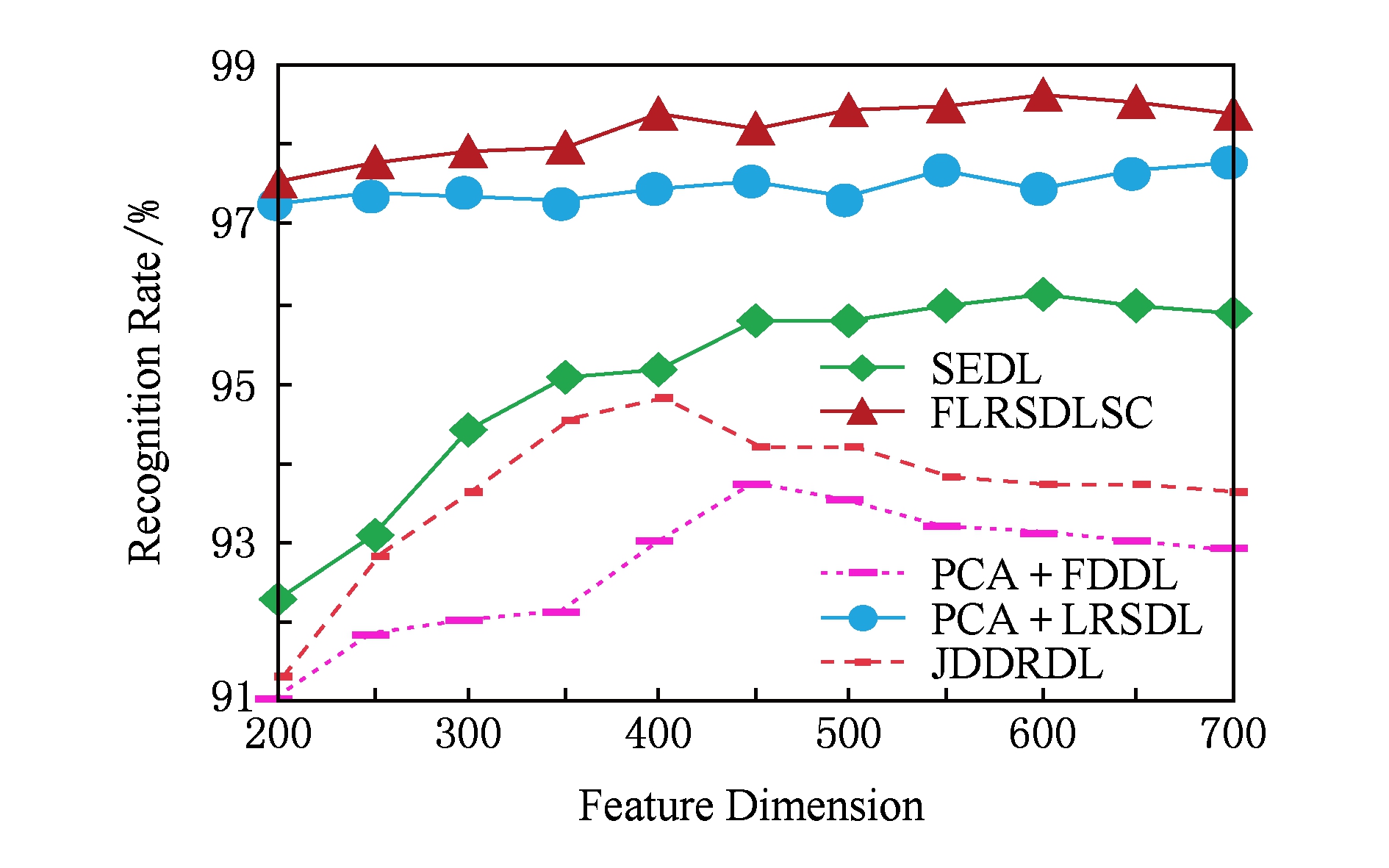
Fig. 4 Recognition rate under different dimensions of features on AR dataset
图4 AR数据集下不同特征维度的识别率
表4展示用不同数量的样本(4~7)进行训练获得的识别率.FLRSDLSC方法与3种经典方法(FDDL,JDDRDL,SEDL)进行比较,在不同数量的训练样本下都实现了最好的性能.当样本为4时,
Table 4 Recognition Rate with Different Numbers of Training Samples on AR Dataset
表4 AR数据集下不同数量的训练样本的识别率
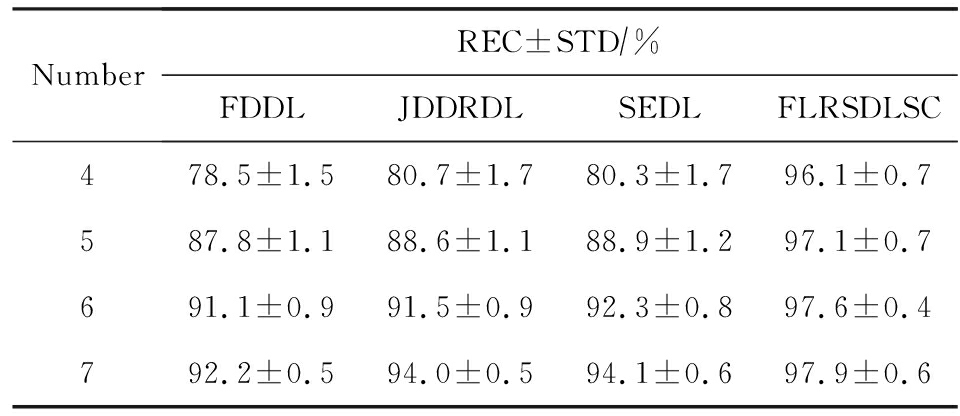
FLRSDLSC方法在识别率上比SEDL高出15%左右,并且实现96.1%的准确率,说明对小样本的人脸识别也是有效的.当样本为5~7时,识别率增长地缓慢,但仍然要比其他方法要高至少3%.
图5绘制了FLRSDLSC的收敛图.如图5所示,迭代次数从1增加到100,目标函数值从18.9下降到18.62且函数值在每次迭代中都下降并最终收敛.
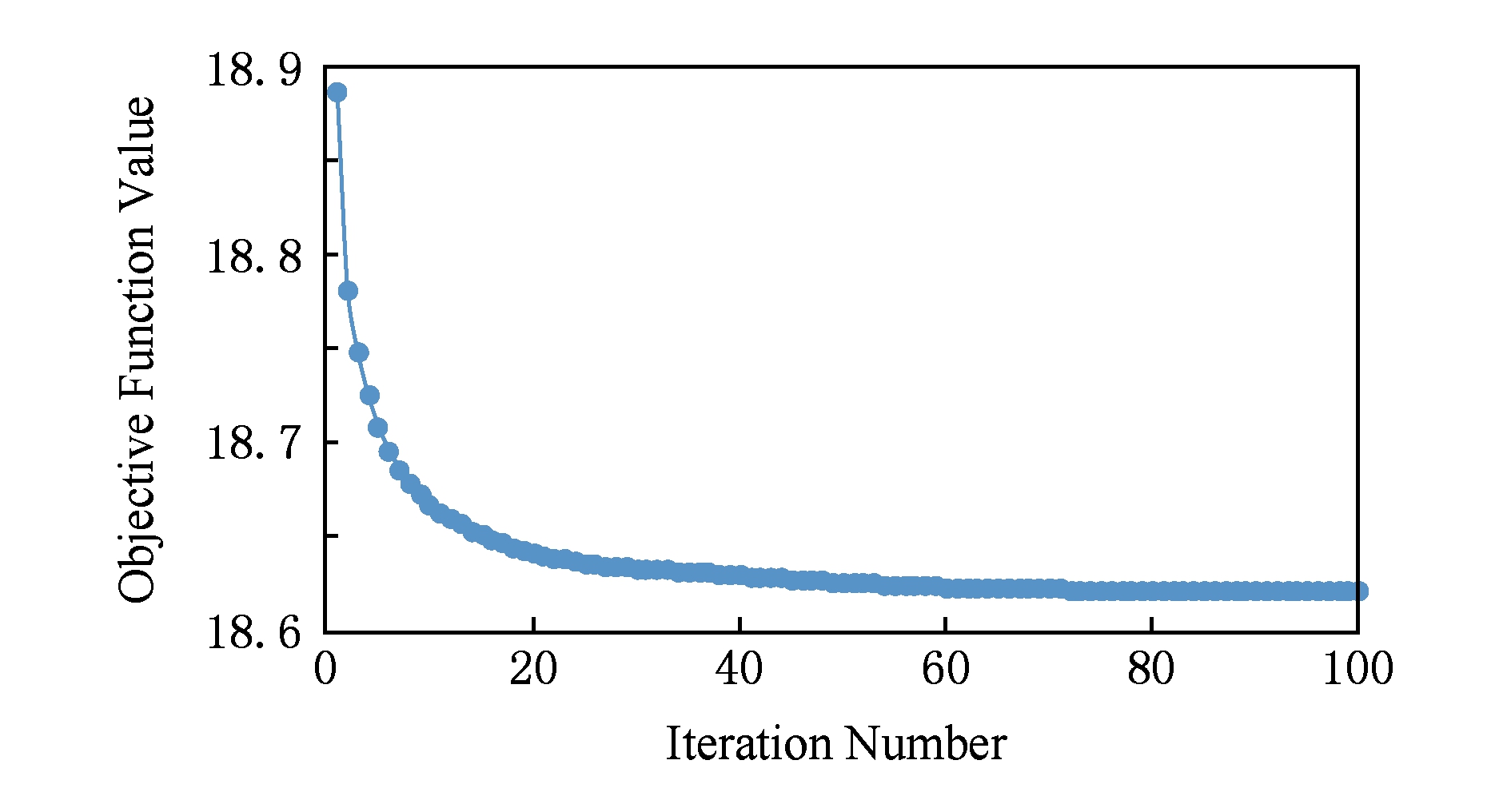
Fig. 5 The convergence of FLRSDLSC on AR dataset
图5 在AR数据集下FLRSDLSC的收敛性
Extended Yale B数据库包含38个个体在各种光照条件下的2 414张图像.图6展示第1个个体在各种照明条件下的样本图像.对于每个个体,随机选择20张图像进行训练,其余用于测试.实验重复10次,所有人脸图像大小都调整为54×48.在Extended Yale B数据库的对比实验中,特征的维度通过PCA降至500.

Fig. 6 Sample images of the first subject from Extended Yale B dataset
图6 Extended Yale B数据集中第1个人的样本图像
表5展示了不同算法下的识别率.在SRC,LCKSVD,FDDL和LRSDL字典学习方法中,LRSDL达到最佳性能为95.23%,但比基于联合学习的SEDL模型低了1.3%左右.FLRSDLSC * 的识别率高于SEDL大约0.2%,说明样本间共享信息对字典学习的重要性.FLRSDLSC方法比FLRSDLSC * 高出0.3%左右,这是因为降维时能获得更为紧凑的特征.
图7展现了不同维度下the Extended Yale B数据的识别率,对比方法有PCA+FDDL,PCA+LRSDL,JDDRDL,SEDL.在200~400维时,FLRSDLSC方法比其他算法有显著的提升,再次说明其算法在低维特征人脸识别的有效性.当特征维度为700时,识别率达到最高,说明提高特征维数对字典学习起到了促进作用.与AR数据集不同的是SEDL在不同维度下的识别率比LRSDL高,展示在该数据集下SEDL通过降维和字典学习同时进行的方法能获得更重要的特征,从而加强字典的判别能力.
Table 5 Recognition Rate on Extended Yale B Dataset
表5 在Extended Yale B数据集下的识别率
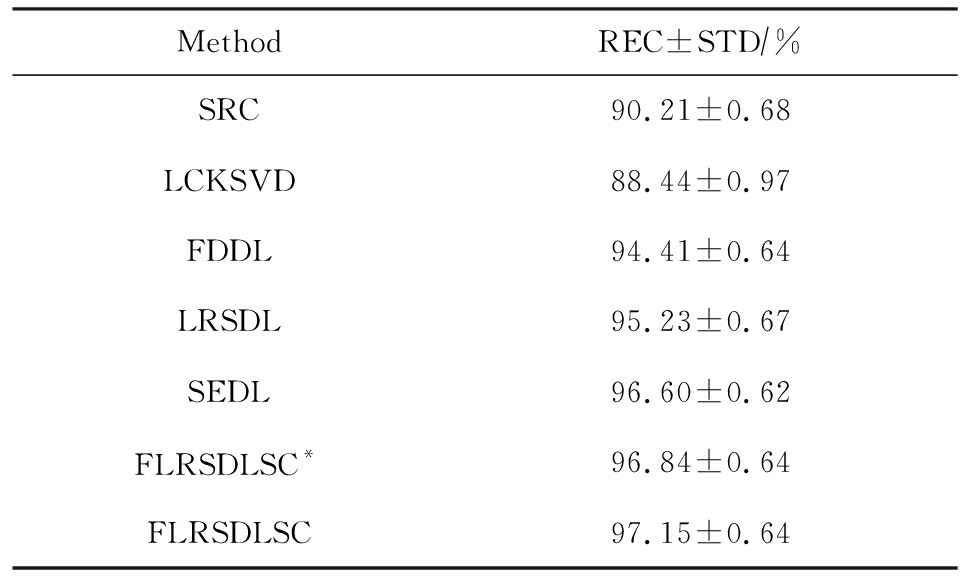
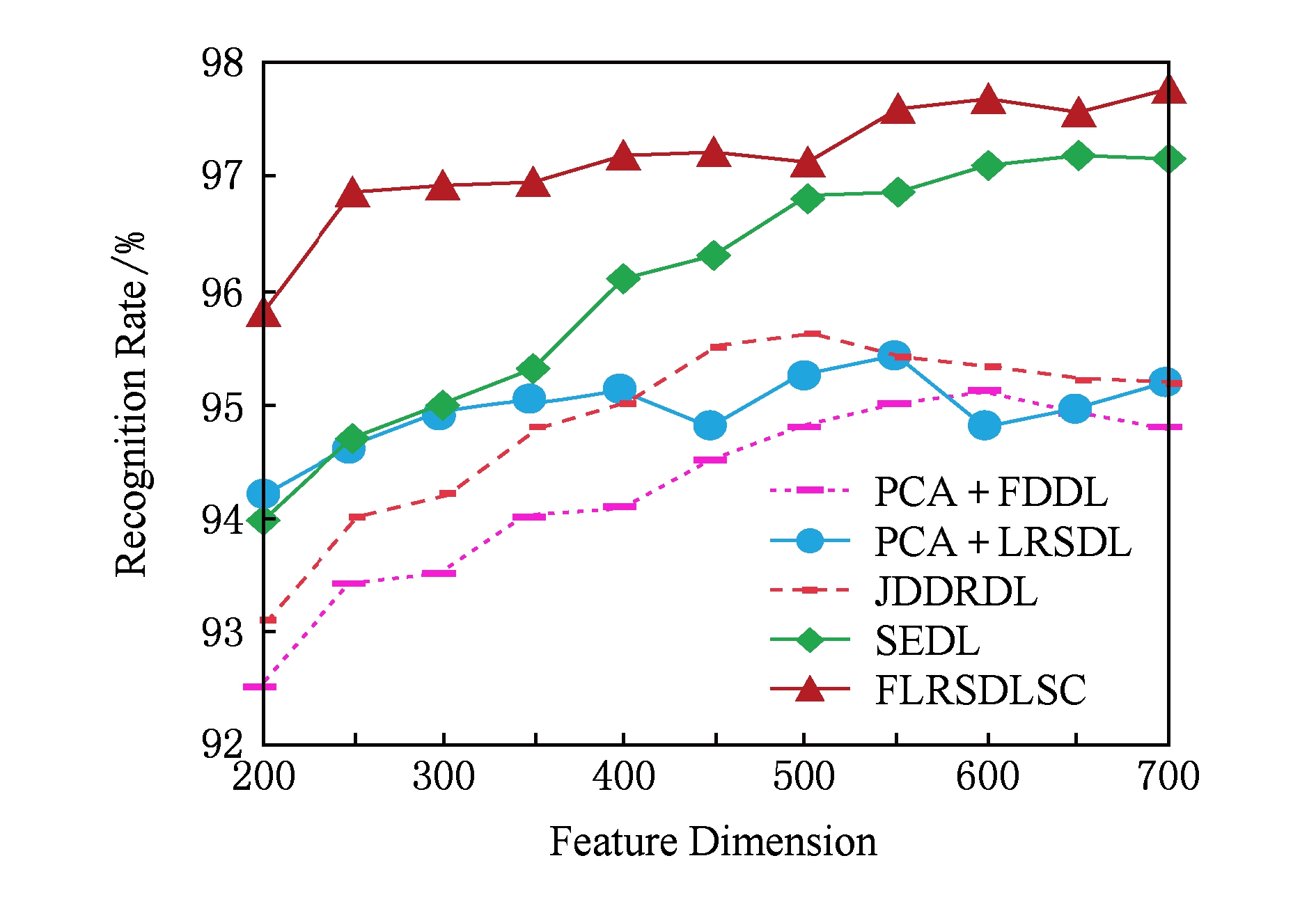
Fig. 7 Recognition rate under different dimensions of features on Extended Yale B dataset
图7 Extended Yale B数据集下不同特征维度的识别率
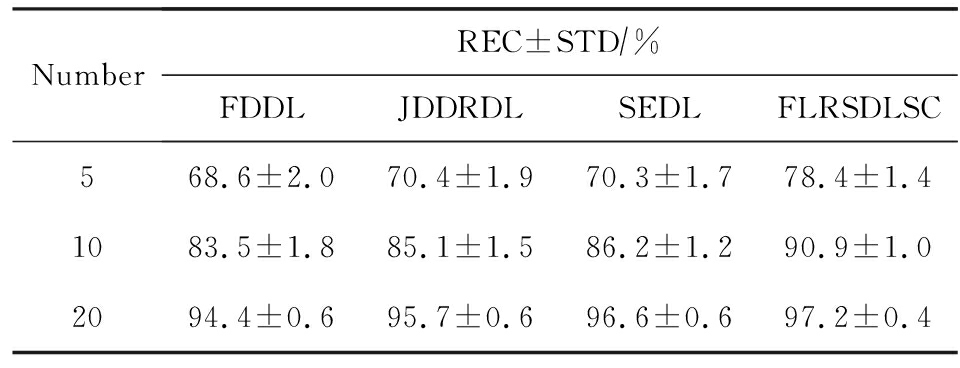
表6展示用不同数量的样本进行训练获得的识别率,FLRSDLSC方法实现了最好的实验效果,对比方法有PCA+FDDL,JDDRDL,SEDL.当训练样本为5时,JDDRDL获得第2高的性能,但比FLRSDLSC方法少8%,说明了FLRSDLSC方法对于光照、小样本问题的人脸识别具有鲁棒性.在不同数量的训练样本下,FLRSDLSC都实现了最高的性能.当训练样本为20时,FLRSDLSC只比SEDL高出0.6%,展示了从样本间提取共享信息的重要性.
Table 6 Recognition Rate with Different Number of Training Samples on Extended Yale B Dataset
表6 Extended Yale B数据集下不同数量的训练样本的识别率
CMU PIE数据集包含68个个体的41 368张图像,图像中含有不同的姿态、光照、表情等问题.如文献[15]所述,取CMU PIE数据集的子集(C05,C07,C09,C27,C29)并且每个个体有170张图片.图8展示第1个个体不同姿态下的样本图像.每个个体随机挑选20张图片进行训练,剩下的图片作为测试样本.重复实验10次计算识别率的平均值和相应的标准偏差.所有人脸图像大小调整成60×45.在CMU PIE数据库的对比实验中,特征的维度通过PCA降至500.

Fig. 8 Sample images of the first subject from CMU PIE dataset
图8 CMU PIE数据集第1个人的人脸图像
表7显示我们的方法实现了最佳性能,识别率为94.21%,比SEDL高出约0.8%,说明样本间的共享信息增强了在姿态、光照、表情问题下的人脸识别.LRSDL与SEDL的性能基本相同,意味着样本间的共享信息与降维和字典学习同时进行的方式都能对鉴别性字典的学习起到促进作用.
图9展示了不同维度下CMU PIE数据集的识别率,对比方法有PCA+FDDL,PCA+LRSDL,JDDRDL,SEDL.我们的方法在200,250维下的识别率要小于PCA+LRSDL的实验结果,但在其他维度上都要好于其他算法,展示了姿态问题对降维和字典同时进行学习的影响.PCA+LRSDL的性能整体上要好于SEDL和JDDRDL,说明LRSDL模型中样本间的共享信息对于解决人脸识别的姿态问题有着重要作用.
Table 7 Recognition Rate on CMU PIE Dataset
表7 CMU PIE数据集下的识别率
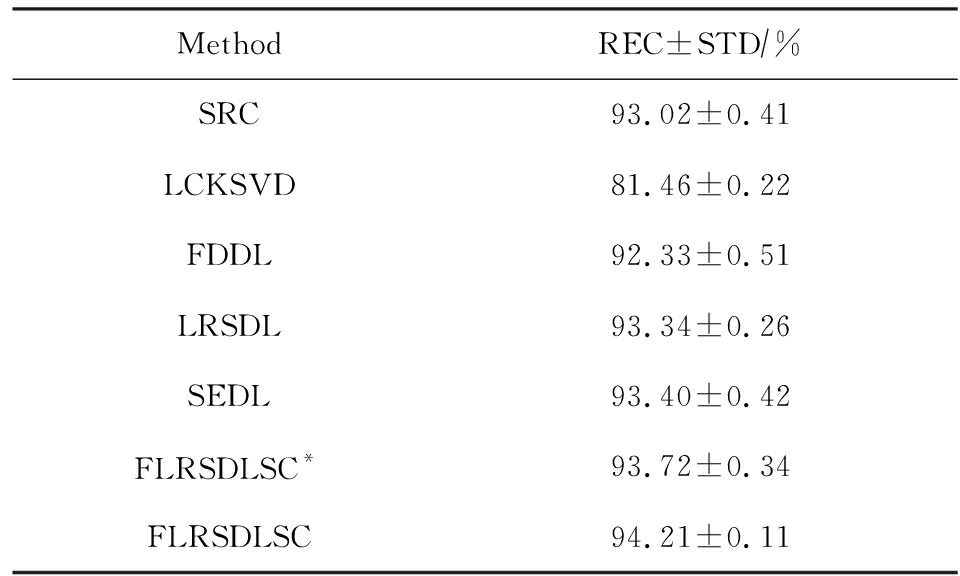
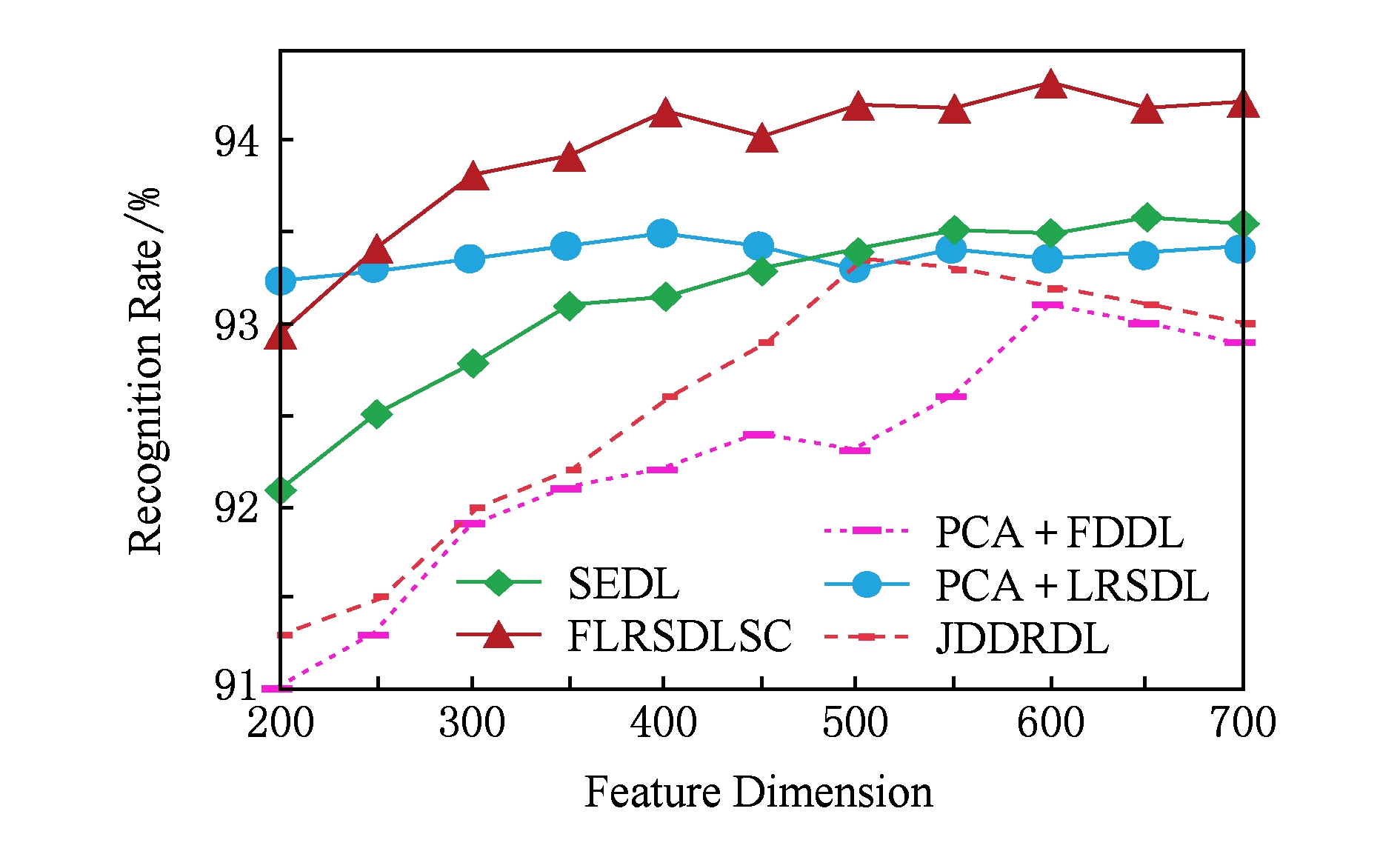
Fig. 9 Recognition rate under different dimensions of features on the CMU PIE dataset
图9 CMU PIE数据集下不同特征维度的识别率

Fig. 10 Sample images from FERET dataset
图10 FERET数据集样本图像
FERET数据库由14 051张具有不同姿态、光照和表情的图像组成.如文献[15]所述,使用200个个体中带有“ba”,“bj”和“bk”的图像,即使用600张图像进行实验.图10展示了FERET 数据集的部分样本,每个个体使用“ba”和“bj”的图像作为训练集,剩下的一张图片作为测试集.所有图像大小调整成70×60.在FERET数据库的对比实验中,特征的维度通过PCA降至400.
表8展示了在FERET数据集下的识别率.SEDL实现第二高性能比FLRSDLSC * 高出0.5%,它保护了投影矩阵的正交性,获得了更紧凑的特征.FLRSDLSC实现了最高的识别率,展示了该方法在光照、表情下人脸识别的鲁棒性.
Table 8 Recognition Rate with Different Number of Training Samples on FERET Dataset
表8 FERET数据集下不同数量的训练样本的识别率
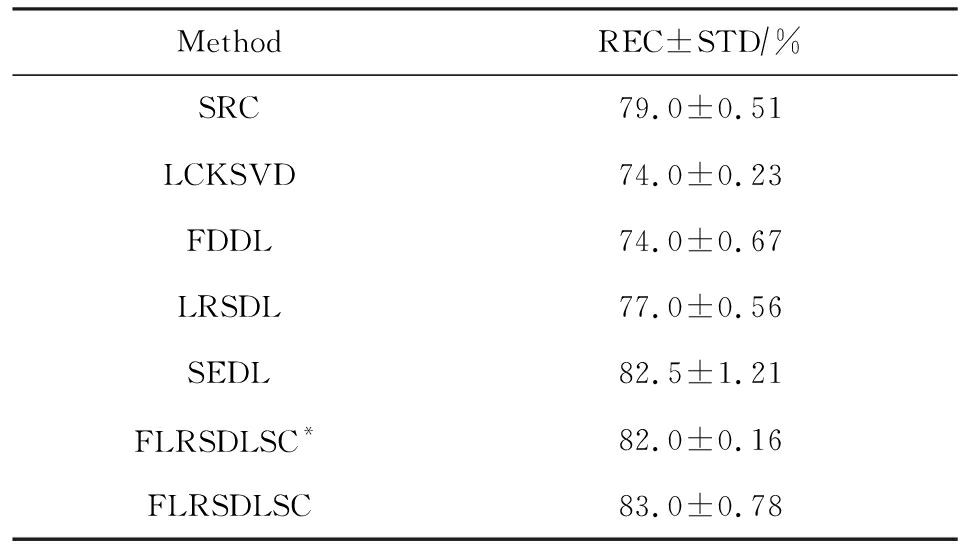
图11展示了不同维度下FERET数据集的识别率,对比方法有PCA+FDDL,PCA+LRSDL,JDDRDL,SEDL.与AR,Extended Yale B数据集相似,FLRSDLSC在光照、表情下的人脸识别都要高于其他方法且在200维时高于其他方法5%,说明该方法适合解决光照、表情下的小样本问题.
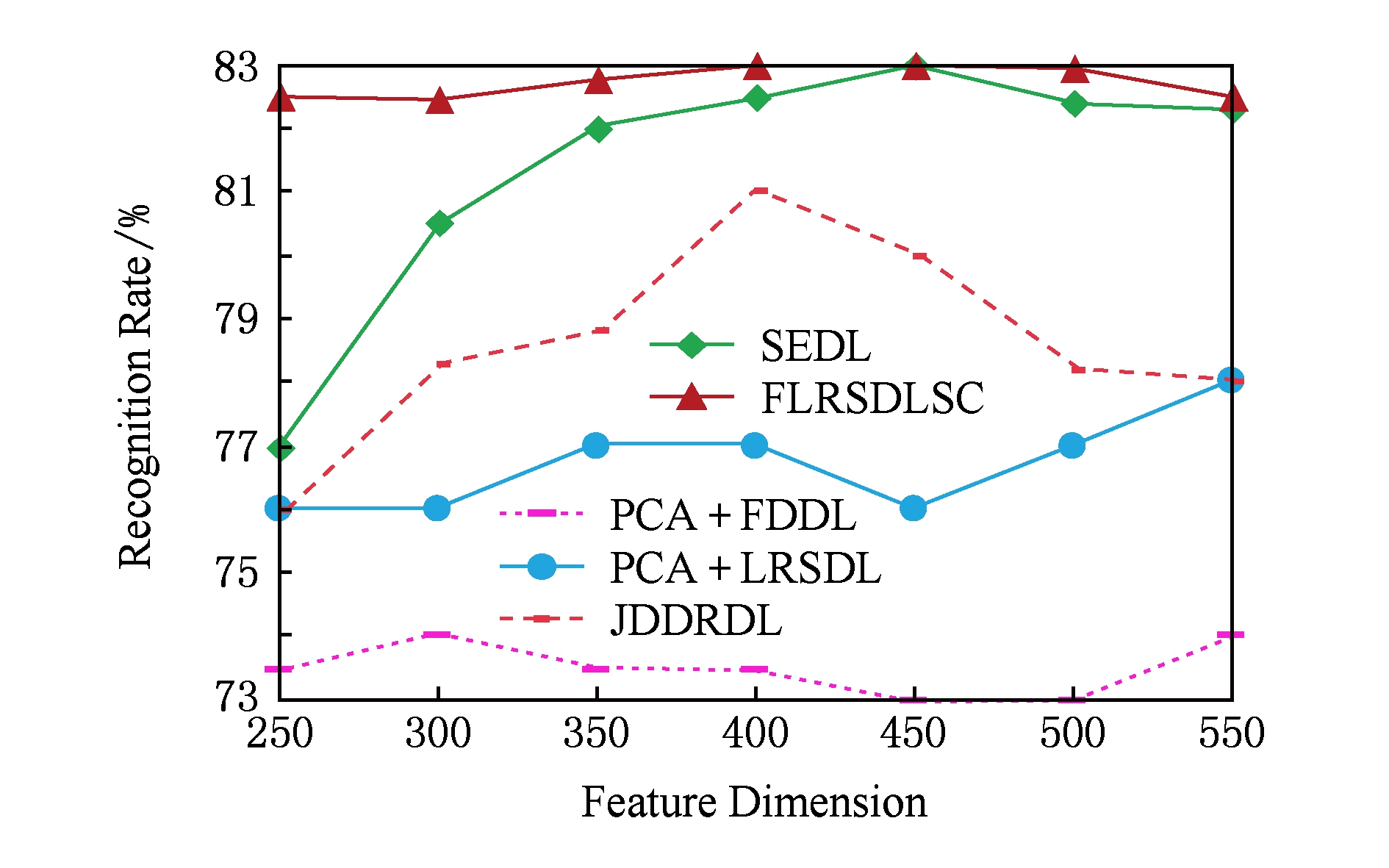
Fig.11 Recognition rate under different dimensions of features on FERET dataset
图11 FERET数据集下不同特征维度的识别率
AR数据集通常用于性别分类的研究.如文献[15]所述,使用1 400张图像进行实验,其中50名男性和50名女性.我们选择随机选择25名男性和25名女性的图像进行训练,其余图像进行测试,实验重复10次.所有图像大小调整为60×43.在AR性别数据集下的对比实验中,特征的维度通过PCA降至300.
表9展示FLRSDLSC在AR性别数据集下取得最高的识别率并且高于SEDL方法,说明了该方法对光照、表情问题下的人脸识别具有鲁棒性.
Table 9 Recognition Rate with Different Numbers of Training Samples on AR Gender Dataset
表9 AR性别数据集下不同数量的训练样本的识别率
本文提出了一种稀疏约束下快速低秩共享的字典学习(FLRSDLSC)方法.在字典学习阶段,嵌入Fisher判别准则来获得结构化字典,同时嵌入低秩约束获得低秩共享字典;在特征学习阶段,利用Cayley变换保护投影矩阵的正交性来获得紧凑的特征信息.最后,特征和字典进行联合学习促使字典获得更为重要的特征信息,以此增强字典和稀疏编码的判别能力.实验结果表明该方法在表情变化下的人脸识别具有很强的鲁棒性,并对光照起到了抑制作用,尤其适合解决光照、表情变化下的小样本问题.
参考文献
[1]Belhumeur P N, Hespanha J P, Kriegman D J. Eigenfaces vs. Fisherfaces: Recognition using class specific linear projection[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2002, 19(7): 711-720
[2]He Xiaofei, Niyogi P. Locality preserving projections[J]. Advances in Neural Information Processing Systems, 2004, 16(1): 186-197
[3]Turk M, Pentland A. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience, 1991, 3(1): 71-86
[4]Wright J, Ma Y, Mairal J, et al. Sparse representation for computer vision and pattern recognition[J]. Proceedings of the IEEE, 2010, 98(6): 1031-1044
[5]Peng Yigang, Suo Jinli, Dai Qionghai, et al. From compressed sensing to low rank matrix recovery: Theory and application [J]. Acta Automatica Sinica, 2013, 39(7): 981-994 (in Chinese)
(彭义刚, 索津莉, 戴琼海, 等. 从压缩传感到低秩矩阵恢复: 理论与应用[J]. 自动化学报, 2013, 39(7): 981-994)
[6]Mousavi H S, Monga V, Tran T D. Iterative convex refinement for sparse recovery[J]. IEEE Signal Processing Letters, 2015, 22(11): 1903-1907
[7]Spratling M W. Image segmentation using a sparse coding model of cortical area V1[J]. IEEE Trans on Image Processing, 2013, 22(4): 1631-1643
[8]Aharon M, Elad M, Bruckstein A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation[M]. Piscataway, NJ: IEEE, 2006: 4311-4322
[9]Zhang Qiang, Li Baoxin. Discriminative K-SVD for dictionary learning in face recognition[C] 
 Proc of IEEE Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2010: 2691-2698
Proc of IEEE Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2010: 2691-2698
[10]Jiang Zhuolin, Lin Zhe, Davis L S. Label consistent K-SVD: Learning a discriminative dictionary for recognition[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2013, 35(11): 2651-2664
[11]Yang Meng, Zhang Lei, Feng Xiangchu, et al. Fisher discrimination dictionary learning for sparse representation[C] 
 Proc of 2011 IEEE Int Conf on Computer Vision (ICCV2011). Piscataway, NJ: IEEE, 2011: 543-550
Proc of 2011 IEEE Int Conf on Computer Vision (ICCV2011). Piscataway, NJ: IEEE, 2011: 543-550
[12]Vu T H, Monga V. Fast low-rank shared dictionary learning for image classification[J]. IEEE Trans on Image Processing, 2017, 26(11): 5160-5175
[13]Nguyen H V, Patel V M, Nasrabadi N M, et al. Sparse Embedding: A Framework for Sparsity Promoting Dimensionality Reduction[C] 
 Proc of European Conf on Computer Vision (ECCV 2012). Berlin: Springer, 2012: 414-427
Proc of European Conf on Computer Vision (ECCV 2012). Berlin: Springer, 2012: 414-427
[14]Feng Zhizhao, Yang Meng, Zhang Lei, et al. Joint discriminative dimensionality reduction and dictionary learning for face recognition[J]. Pattern Recognition, 2013, 46(8): 2134-2143
[15]Chen Yefei, Su Jianbo. Sparse embedded dictionary learning on face recognition[J]. Pattern Recognition, 2017 (64): 51-59
[16]Wen Zaiwen, Yin Wotao. A feasible method for optimization with orthogonality constraints[J]. Mathematical Programming, 2013, 142(1  2): 397-434
2): 397-434
[17]Natarajan B K. Sparse approximate solutions to linear systems[J]. SIAM Journal on Computing, 2006, 24(2): 227-234
[18]Cai Jianfeng, Candès E J, Shen Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2008, 20(4): 1956-1982
[19]Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202
[20]Mairal J, Bach F, Ponce J, et al. Online learning for matrix factorization and sparse coding[J]. Journal of Machine Learning Research, 2009, 11(1): 19-60
[21]Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations & Trends in Machine Learning, 2010, 3(1): 1-122
[22]Martinez A M. The AR face database[J]. CVC Technical Report, 1998, 24
[23]Georghiades A S, Belhumeur P N, Kriegman D J. From few to many: Illumination cone models for face recognition under variable lighting and pose[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2001, 23(6): 643-660
[24]Sim T, Baker S, Bsat M. The CMU pose, illumination, and expression database[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2003, 25(12): 1615-1618
[25]Phillips P J, Moon H, Rizvi S A, et al. The FERET evaluation methodology for face-recognition algorithms[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2000, 22(10): 1090-1104

Tian Ze , born in 1994. Master candidate. His main research interests include machine learning, pattern recognition and computer vision.

Yang Ming , born in 1964. PhD, professor. Member of CCF. His main research interests include machine learning, pattern recognition, image processing and computer vision.

Li Aishi , born in 1994. Master candidate. His main research interests include machine learning and computer vision(liamgsal@gmail.com).
附录
附录A 证明引理1.
先求 f ( Y , D , X )和 g ( X )的梯度.
![]()
![]()
的梯度,其函数重写如下:
其中,

然后我们获得
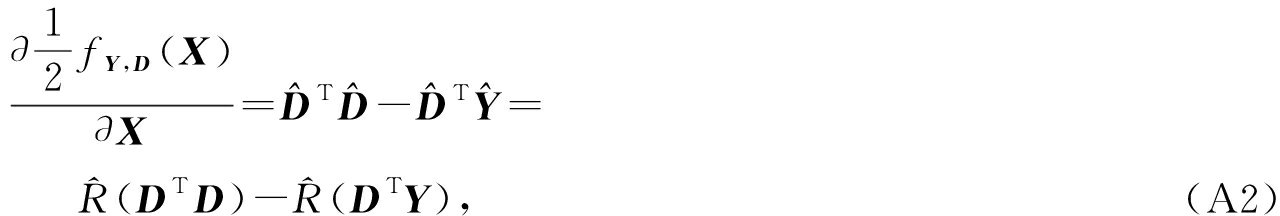
当目标函数定义如下:
![]() 的求导公式如下:
的求导公式如下:
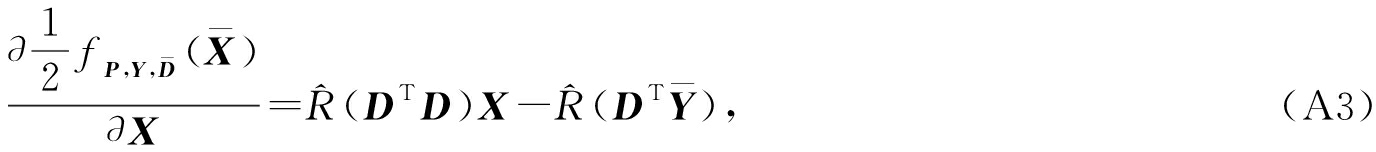
其中 ![]()
g 的梯度 ![]()
![]() p × q 为全1矩阵,很容易验证如下公式:
p × q 为全1矩阵,很容易验证如下公式:
我们推导出:
因此我们获得:

其中, ![]()
M c - M 我们重写为如下2个式子:
(A11)
然后推导如下:
![]() ⟹
⟹ ![]()
![]()
![]()
![]()
![]()
![]()
![]()
现在我们证明
![]()
![]()
(A12)
其中, 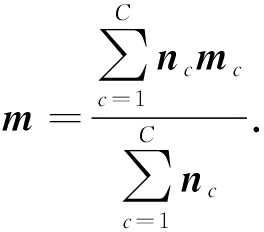
然后我们推导出:
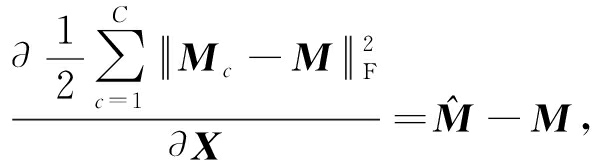
(A13)
其中, ![]()
组合(A10),(A13)和 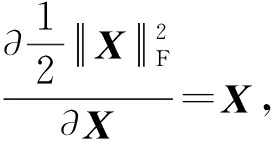 得到:
得到:

证毕.
附录B . 证明引理2.
令 w c ∈{0,1} K 为二值化向量,其第 j 个元素为1当且仅当 D 的第 j 列属于 D c . W c = diag ( w c ),我们观察 ![]() 重写 f ( Y , X , D )如下:
重写 f ( Y , X , D )如下:
![]() +
+ ![]()
![]() +
+ ![]()
![]()
![]()
-2tr( ED T )+tr( FD T D )+constant,
(B1)
其中,
![]()
![]()
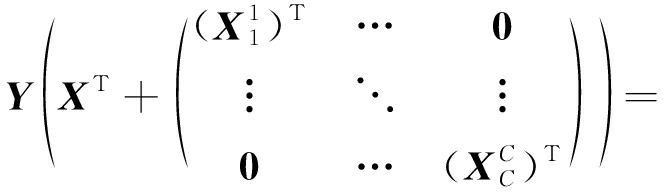
![]()
(B2)
![]()
![]()
![]()
(B3)
令:
(B4)
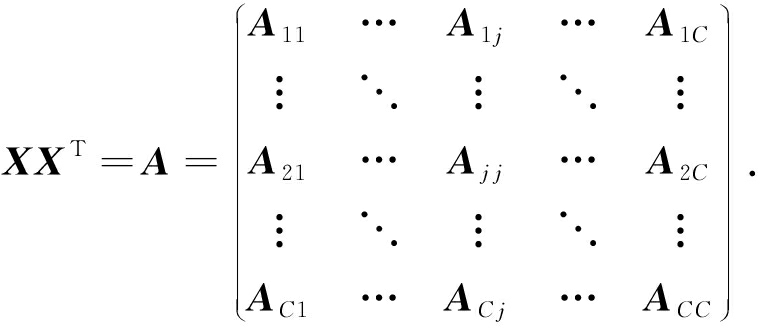
根据 W j 的定义,我们观察到“左乘”矩阵 W j 迫使矩阵在除了第 j 个块行之外的任何地方都为零.同样,“右乘”矩阵将只保留其 j 块列.从而得到如下结果:
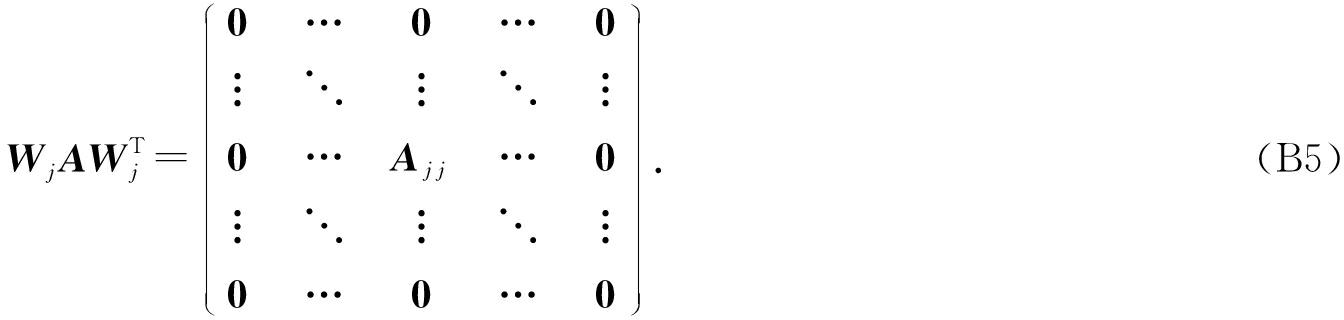
然后 ![]()
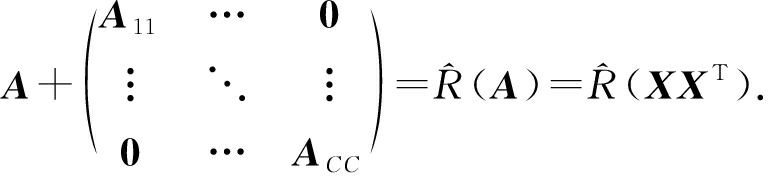
(B6)
根据 f ( Y , X , D )公式的重写过程, ![]() 简化如下:
简化如下:
![]()
![]()
-2tr( ED T )+tr( FD T D ),
(B7)
其中,
证毕.
附录C . 证明引理3.
当 P , Y , D , X 固定,我们有
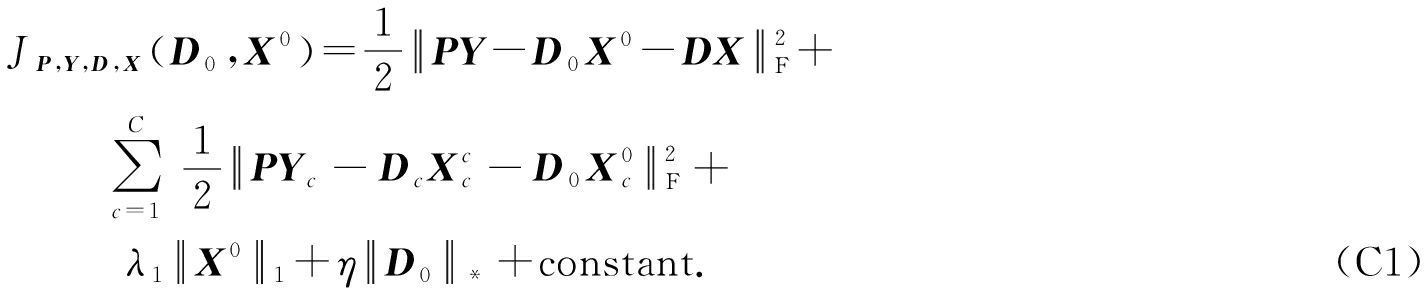
令 ![]() 和
和 ![]() 式(C1)简化如下:
式(C1)简化如下:

我们得到:
现在令 ![]() 式(C2)简化如下:
式(C2)简化如下:
证毕.
Tian Ze, Yang Ming, and Li Aishi
( College of Computer Science and Technology , Nanjing Normal University , Nanjing 210023)
Abstract Dictionary learning is one of the most important feature representation methods. It has a wide range of applications in face recognition and other aspects. It is particularly suitable for solving face recognition problems under the change of pose, and has attracted much attention from many researchers. In order to enhance the discriminative ability of dictionary, researchers have put forward a large number of dictionary learning models in combination with domain knowledge and anti-noise strategies, including the recently proposed methods for simultaneous dimensionality reduction and dictionary learning, but these methods focus on the specific-class samples and fail to consider the sharing information between training samples. Therefore, we propose a fast low-rank shared dictionary learning with sparsity constraints approach. The method learns dimensionality reduction and dictionary jointly, and embeds Fisher discriminant criteria to obtain specific-class dictionary and coding coefficients. At the same time, we enforce a low-rank constraint to obtain the low-rank shared dictionary to enhance the discriminative ability of dictionary and coding coefficients. In addition, the Cayley transform is used to protect the orthogonality of the projection matrix to catch a compact feature set. Face recognition experiments on AR, Extended Yale B, CMU PIE, and FERET datasets demonstrate the superiority of our approach. The experimental results show that the proposed method has strong robustness to face recognition under facial expression changes, and plays an inhibitory role in lighting. It is especially suitable for solving small sample problems under illumination and expression changes.
Key words face recognition; dictionary learning; sparsity constraints; low-rank models; shared features
中图法分类号 TP181
通信作者 : 杨明(m.yang@njnu.edu.cn)
基金项目 : 国家自然科学基金重点项目(61432008);国家自然科学基金项目(61272222)
This work was supported by the Key Program of the National Natural Science Foundation of China (61432008) and the National Natural Science Foundation of China (61272222).
收稿日期 : 2018-05-18;
修回日期: 2018-06-06
DOI: 10.7544/issn1000-1239.2018.20180364