当今信息技术已经进入人工智能技术飞速发展的时代,新一代人工智能技术是建立在大数据计算基础上的.而大数据计算技术发展速度可以说是日新月异.在云计算、雾计算、边缘计算等计算模式下,大数据处理技术可以在海量的分散数据中迅速发现有价值的数据,极大地提高生产力水平,给经济发展带来巨大推动力,目前大数据技术已经成为云计算之后信息技术领域的另一个信息产业增长点.
大数据强大的数据计算处理能力,也对数据安全带来了巨大的安全风险,大数据的机密性、认证性以及隐私保护等数据安全问题,目前受到高度关注[1].大数据的生命周期大概可以分成数据的采集、存储、挖掘和发布4个主要环节.数据的采集是指数据的采集和聚合过程,需要关注的安全问题是数据汇聚过程中是传输安全问题;数据的存储则需要保证数据的机密性以及加解密的性能;数据的挖掘则需要关注数据的敏感信息的隐私保护问题,以及挖掘者的身份认证问题;数据的发布则需要对数据进行安全审计以及数据溯源问题.可以看出,在大数据的每个应用环节,都有可能遇到安全问题,而密码技术则是解决大数据安全问题的核心技术.
海量数据的应用背景,为密码学提出了新的要求,其中最重要的就是密码算法的效率问题.本文分析了大数据安全方案逻辑架构,抽取了关键的密码底层算法以及运算模块,提出了3个快速密码部件的快速实现算法,并在基于Xilinx公司的KC705开发板上进行了验证,同时给出实验数据.具体有3方面内容:
1) 针对国产分组密码算法标准SM4-XTS,进行了快速实现,该工作可以对海量的数据进行快速地加解密,性能可达31.5 Gbps,同时有效地保证数据安全;
2) 针对国产数字签名算法标准SM2,进行了快速实现,该工作可以解决高并发的用户身份认证问题;
3) 针对大整数模幂运算,进行了快速实现,大整数模幂运算可以作为同态加密的协处理器,可以直接对大数据密文进行处理,解决了大数据隐私保护的问题.
1 相关工作
Elbirt等人[2]在2000年提出了一种在FPGA的快速AES的流水线实现方式,最高能到10 Gbps.负责对储存媒介信息保护进行算法标准开发的IEEE 1619安全储存委员会(SISWG)于2008年4月正式公布了XTS-AES算法标准[3],XTS-AES算法是一种可调整的窄式块分组密码,该算法主要用于以数据单元(包括扇区、逻辑磁盘块等)为基础结构的存储设备中静止状态数据的加密.XTS-AES的公布解决了大数据存储一系列的安全威胁,并且允许在算法实现上应用并行化和流水线结构,提高性能.随着国密算法SM4标准的发布,国内的芯片厂商也生产了相应的SM4算法芯片并应用于国密市场.比较代表性的产品有北京宏思电子技术有限责任公司的HSM4A高性能分组密码算法芯片和清华大学微电子学研究所的高性能SM4芯片.这几款芯片大都只支持ECB和CBC模式,并不支持XTS模式,国内并没有直接支持SM4-XTS模式的产品.
2006年Ansari等人[4]在X86架构上实现快速ECC算法,并在OpenSSL上提供了开源代码的实现,单核CPU上ECC签名的性能可以达到2万次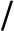 秒的级别.国外很多公司和高校也投入到ECC的快速实现当中[5-6].随着国密标准算法SM2的发布,国内的芯片厂商也推出了相应的SM2芯片产品,比较具有代表性的是北京宏思电子技术有限责任公司的HSM2A高性能公钥密码算法芯片和北京华大信安科技有限公司的高性能ISECMM1521SV1芯片.
秒的级别.国外很多公司和高校也投入到ECC的快速实现当中[5-6].随着国密标准算法SM2的发布,国内的芯片厂商也推出了相应的SM2芯片产品,比较具有代表性的是北京宏思电子技术有限责任公司的HSM2A高性能公钥密码算法芯片和北京华大信安科技有限公司的高性能ISECMM1521SV1芯片.
1999年Paillier[7]提出了一种新的同态加密算法,即Paillier加密算法,该方案在提出后受到了广泛的关注.2001年Choi等人[8]通过选取特殊的参数改进了Paillier加密体制.基于Paillier体制的加法同态性可以有效地设计应用于大数据环境下的隐私保护方案.而Paillier算法的核心运算为大整数模幂.2012年Gueron[9]在X86架构上实现快速的大整数模幂运算,并在OpenSSL上提供了开源代码的实现,单核CPU上512 b的大整数模幂性能可以达到8 000次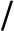 秒的级别.国内支持大整数模幂运算的产品主要有北京芯光天地集成电路设计有限公司的SSX26芯片和北京华大信安科技有限公司的高性能ISRSAMM11KBV1芯片.
秒的级别.国内支持大整数模幂运算的产品主要有北京芯光天地集成电路设计有限公司的SSX26芯片和北京华大信安科技有限公司的高性能ISRSAMM11KBV1芯片.
2 相关知识
2.1 SM4密码算法及XTS模式
2012年3月国家密码管理局正式公布了SM4分组密码算法行业标准.与DES和AES算法类似,SM4算法是一种分组密码算法,其分组长度为128 b,密钥长度也为128 b.加密算法与密钥扩展算法均采用32轮非线性迭代结构,以字(32 b)为单位进行加密运算,每一次迭代运算均为一轮变换函数F.SM4算法加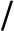 解密算法的结构相同,只是使用轮密钥相反,其中解密轮密钥是加密轮密钥的逆序.SM4算法的整体结构如图1所示.
解密算法的结构相同,只是使用轮密钥相反,其中解密轮密钥是加密轮密钥的逆序.SM4算法的整体结构如图1所示.
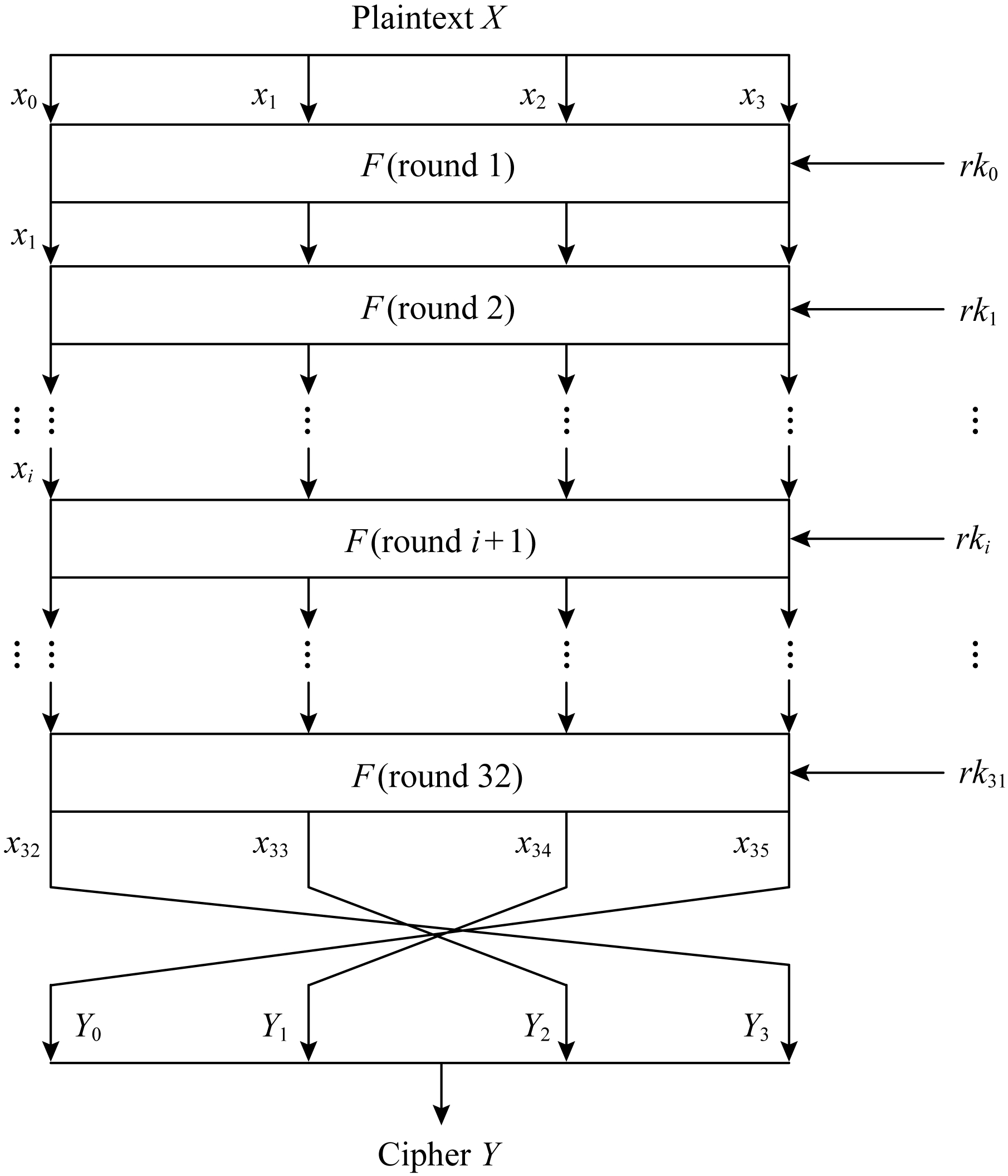
Fig. 1 The overall architecture of SM4
图1 SM4的整体结构图
XTS模式是可调整的分组密码模式,跟传统的分组密码相比,除了密钥和明文这2个输入以外,XTS模式还多了一个输入,这个输入被称作调整值[10](Tweak).Tweak的作用类似于CBC模式中的初始向量和OCB模式中的Nonce[11].引入这个调整值的原因是在一般情况下,密钥的改变对整个加密系统来说是一项开销很大的事情,所以在保持密钥不变的情况下,通过改变这个调整值,能够对整个加密系统提供多变性,相比于改变密钥来说,改变调整值对整个加密系统开销更少,并且没有任何风险性,因为调整值可以公开[12],而不用担心像密钥那样泄漏的问题.对于不同的Tweak,XTS模式就代表2个不同的分组密码,优点体现在改变Tweak比改变密钥的代价更小;因为改变密钥,就意味着要重新进行密钥扩展算法.XTS模式的作用主要体现在存储加密,尤其是磁盘扇区加密上.
2.2 SM2算法简介
SM2是2010年12月国国家密码管理局发布的具有自主知识产权的国产密码算法.该算法是基于椭圆曲线离散对数难题提出的公钥密码算法.SM2签名算法可满足大数据应用中身份认证的安全需求.SM2具体的签名流程如下.
设待签名的消息为M,用户A的身份信息为ZA,为了获取消息M的数字签名(r,s),作为签名者的用户A应实现运算步骤为:
① 置M=ZA‖M;
② 计算e=SM3(M);
③ 用随机数发生器产生随机数k∈[1,n-1];
④ 计算椭圆曲线点(x1,y1)=[k]G;
⑤ 计算r=(e+x1) mod n,若r=0或r+k=n,则返回步骤③;
⑥ 计算s=(1+dA)-1(k-r.dA) mod n,若s=0则返回步骤③;
⑦ 消息M的签名为(r,s).
2.3 Paillier同态密码算法
同态加密机制分为3个阶段[13],分别为初始化阶段、加密阶段和解密阶段.
1) 初始化阶段.令n=p×q,其中p,q为2个大素数,选择![]() 使得gcd(L(gγmod n2),n)=1,L为求商函数,L(x)=(x-1)
使得gcd(L(gγmod n2),n)=1,L为求商函数,L(x)=(x-1) n,公钥为(n,g),私钥为(p,q),等价为γ(γ=lcm(p-1,q-1)).
n,公钥为(n,g),私钥为(p,q),等价为γ(γ=lcm(p-1,q-1)).
2) 加密阶段.设有明文m∈Zn,且m<n.随机选取一个随机数r<n,则密文为c=gm.rnmod n2.
3) 解密阶段.因为密文c<n2,解密过程为明文![]()
加法同态的定义:如果已知密文E(x)和E(y),通过一系列运算可以计算出E(x+y),而不需要知道x,y的值.即C(E(x),E(y))=E(x+y),此处C代表任意运算.
Paillier算法的加同态性质证明:
已知密文E(x)和E(y),则:
D(E(x)×E(y) mod n2)=
D(gx+y(r1r2)nmod n2)=
x+y mod n=D(E(x+y)),
由此式可以推出,在不知道x和y的情况下可以求出E(x+y),所以说Paillier算法满足加法同态性质.
3 大数据安全方案逻辑架构
本文分析了基于高性能密码实现的大数据安全方案逻辑架构,如图2所示,该方案从逻辑上分为3层:密码算法层、密码服务层和应用层.
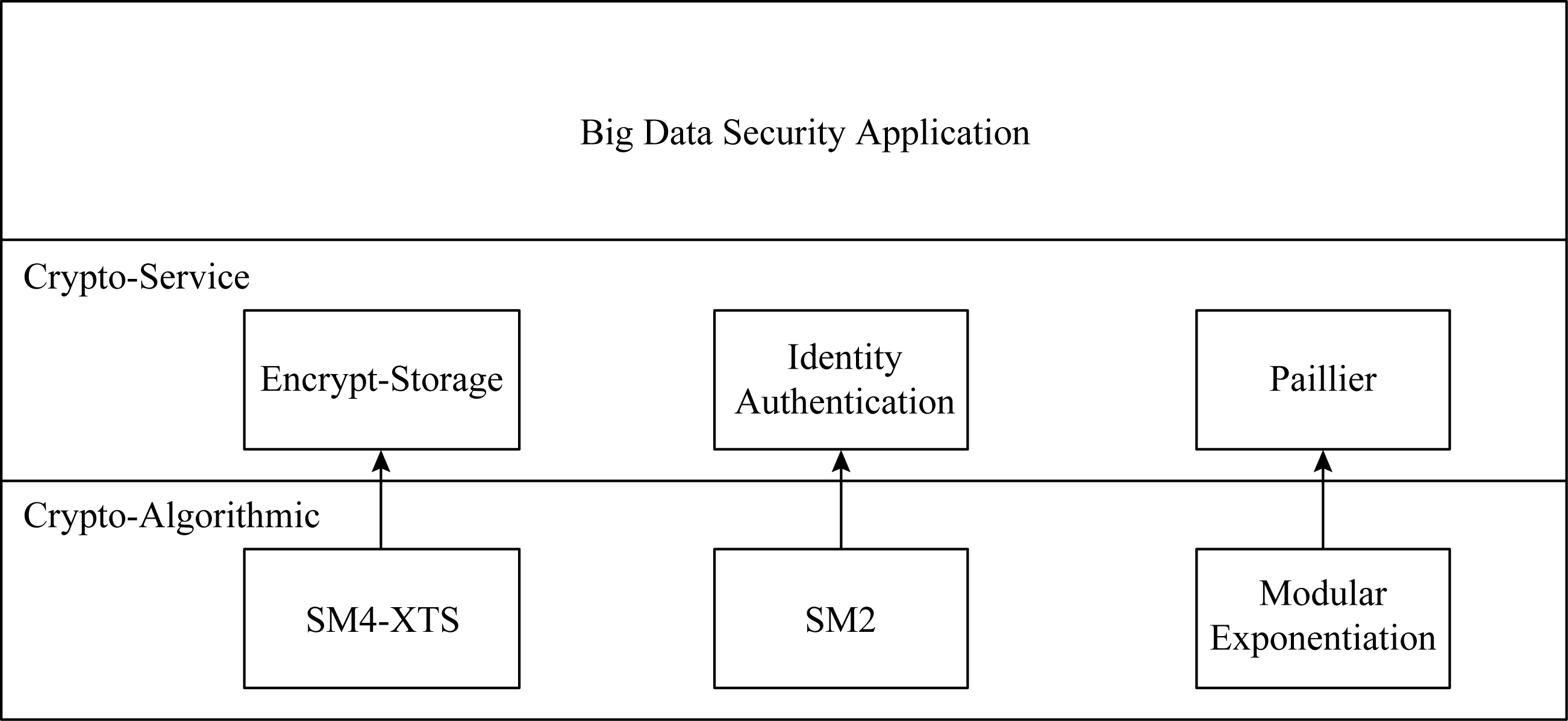
Fig. 2 The logic architecture of big data scheme
图2 大数据安全方案逻辑架构
密码算法层是整个大数据安全方案的核心层,为整个大数据安全方案提供技术支撑,在该层实现了安全方案需要的所有密码算法,包括SM4-XTS存储加解密算法、SM2签名验签算法、大整数的模幂算法.在密码算法层,重点研究高性能密码实现技术,研究大整数运算、椭圆曲线计算等优化算法以及众核并行技术,实现FPGA高性能密码运算.
通过改进众核并行和流水线技术,优化智能调度和协同计算,提高并发、多任务密码处理阵列,在FPGA平台实现高速密码算法,保证满足大数据安全方案对高性能密码运算的需求.
密码服务层是对密码算法层的封装,对外提供应用接口.在这一层,用户可以自定义指令来调用密码算法层实现密码服务,如身份认证、存储加密、Paillier同态加解密运算等.
应用层是调用密码服务层的接口来解决大数据应用中存在的实际问题.调用存储加密接口可以对海量的大数据进行高速地加解密;调用身份认证接口可以处理高并发用户的身份认证需求;调用大整数模幂运算可以快速封装成Paillier同态算法,完成一些加同态加解密的业务需求.
4 大数据安全方案的快速实现
本文的核心工作是密码算法层在FPGA上的快速实现.本方案中密码算法层主要支持3种快速算法的实现:SM4-XTS模式、SM2签名验签、大整数的模幂.下面分别介绍3种算法的快速实现方案.
4.1 SM4-XTS的快速实现
SM4-XTS模式的快速实现分为2个步骤:1)32级流水线SM4的高速实现;2)伽罗华域乘法的快速实现,并与32级流水线的配合.
4.1.1 32级流水线SM4的高速实现
S-BOX是SM4实现中最影响性能的部分.S-BOX的实现有2种方式[14]:1)采用多个S-BOX的组合逻辑方式;2)基于ROM的查找表实现方式.如果选择多个S-BOX,整个轮函数可以由组合逻辑实现,中间不需要插入寄存器,一次迭代可以在一个时钟周期内完成.此时,多个S-BOX虽然多占用了资源,但是控制逻辑可减少复杂度,而且方便使用流水线处理;如果只用一个S-BOX实现,为了完成非线性变换,需要对S-BOX进行分时复用,此时必须在S-BOX的输入和输出端插入2级寄存器,此时虽然省去了S-BOX占用的资源,但是控制逻辑复杂很多,而且增加了大量的寄存器资源,并且花费的时间也大大增加,一次迭代至少需要多个时钟周期才能完成.所以我们选择采用多个S-BOX的组合逻辑实现方式,即可以在一个周期内完成轮函数,又支持流水线方式.
对于SM4的密钥扩展,我们采用动态即时轮密钥扩展技术,每个周期都可以使用一个单独密钥加解密一个分组而不影响性能,这为我们使用流水线技术打下了基础.
在这种硬件架构下,可以采用流水线的方式提升性能.通过即时轮密钥扩展技术,SM4运算时,轮密钥扩展和加解密运算是可以同时进行的.通过精密设计的流水线,使得每个周期都可以使用一个单独密钥加解密一个分组而不影响性能.这样,我们就可以在算法工作前期花费少量的周期建立起流水线,当流水线填满后可以充分发挥部分逻辑电路的运算能力,大幅度提升算法性能.
在本文的快速实现方案中,我们使用了32级流水线技术来完成SM4算法的高速实现[15],为SM4-XTS的快速实现提供了技术基础.
4.1.2 SM4-XTS的高速实现
XTS加密算法示意图如图3所示,其中SM4-ENC为标准的SM4加密算法,Key2为调整值的密钥,Key1为待加密数据的密钥.伽罗华域模乘中的α为有限域GF(2128)域上的本原元,该有限域的生成多项式为x127+x7+x2+x+1.计算的顺序步骤:
① T=SM4-ENC(Key2,i)⊗αj;
② PP=P⊕T;
③ CC=SM4-ENC(Key1,PP);
④ C=CC⊕T.

Fig. 3 The overall architecture of SM4-XTS
图3 SM4-XTS的整体结构图
步骤①中伽罗华域模乘在j是迭代递增的情况下相当于移位加异或运算,所以可以每个时钟周期更新一次结果.故在SM4流水线建立完成后,每个周期j递增1,然后计算出来的T可以用于步骤②③的运算中,依然保证SM4-XTS模式可以每个周期都向外输出128 b的结果,实现高速SM4-XTS模式.
4.2 SM2的快速实现
SM2协议可分为4层,如图4所示,最顶层是SM2协议(包括签名、验签、加解密和密钥协商等),所有协议的基础都是点乘操作.点乘操作是基于点加、倍点运算来实现的.最底层是最基本的算术运算,包括模加、模减、模逆、模乘.针对SM2协议的每一层我们都可以使用一定的优化策略来加速运算,减少运算时间从而提升性能.
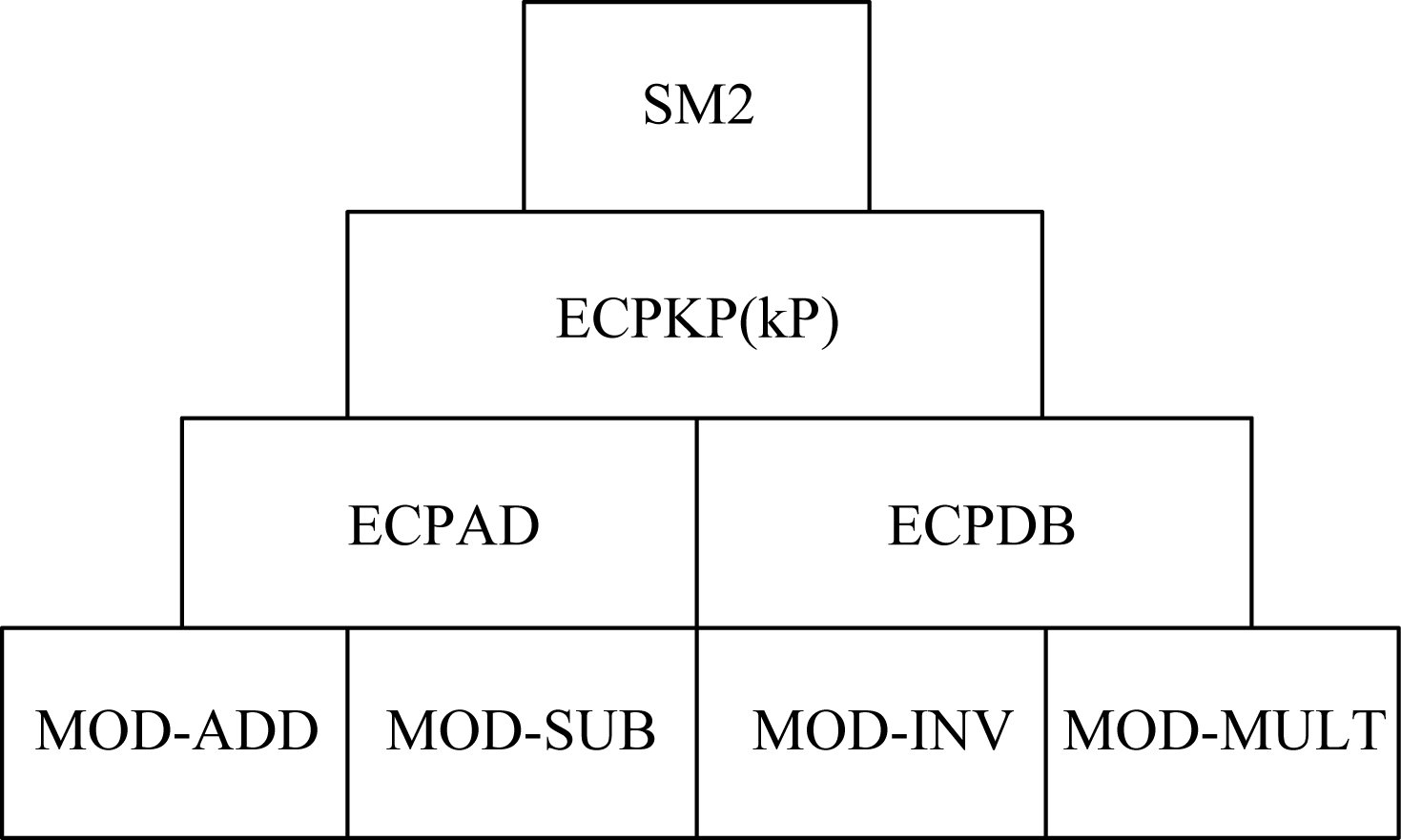
Fig. 4 The overall architecture of SM2
图4 SM2的总体架构
1) 模乘器的优化
在最底层的4种算术运算中,模乘运算是整个SM2协议使用频率最高、最核心,也是最重要的模块,大约占用90%的运算时间.模加和模减逻辑结构相对简单,模逆使用频率低,所以模乘器的优化是我们在实现中关注的重点.优化策略主要包括3点:
① 利用FPGA内部的高速DSP运算单元构建模乘器.DSP是FPGA内置的算术运算单元,可以支持(25 b×18 b+48 b)的乘累加运算.通过精心设计DSP的组合,尽量减少关键路径的延时,以支持高速的模乘运算.
② 利用Karastusba算法减少部分积数量.模乘运算的运算时间由部分积数量决定.构建256 b的乘法,Karastusba算法只需要3个128 b乘法生成的部分积和少量加法,相对传统简单乘法减少了25%运算量.同理,采用分而治之的方法,对N采取同样的策略,最终可大幅降低模乘运算时间.
③ 针对SM2特殊参数优化模约减运算.模乘中的模约减过程可以针对SM2协议定义的素数P的特殊性来实现.我们可以采用若干次加法和减法运算来得到模约减结果,与目前普遍通用的Montgomery算法相比,节省了数次256 b的乘法运算,性能可以明显提升.
2) 点加和倍点的优化
在点加和倍点的运算过程中,为了避免耗时的模逆运算,需要将普通坐标转换成雅可比坐标下运算.在SM2协议中,倍点需要8次模乘、6次模加、4次模减,而点加需要11次模乘、2次模加和6次模减.优化策略主要包括2点:
① 利用模乘器流水线能力提高点加和倍点的运算效率.
② 降低倍点和点加运算的模乘相关性.为了充分发挥模乘器流水线的性能,需要对点加和倍点运算的公式进行数据相关性分析,设计详细的计算顺序,使连续的模乘模加运算不存在输入输出数据的相关性.
3) 点乘的优化
对签名来说,最费时的操作为点乘操作(x1,y1 )=[k]G.系数k按二进制展开为256位0和1的组合,我们可以采用NAF(非线性相关)编码的方式,对点乘系数k进行编码,增加系数k中0的数量,降低系数k的汉明重量,从而减少运算次数,提升签名速度.
4.3 大整数模幂的快速实现
同态加密算法能够保持数据明文与密文之间的同态关系,包括支持加法、乘法的单同态加密算法,以及支持加法和乘法的全同态加密算法.全同态的运算具有速度慢、密文规模大、效率低等缺点,使其很难适用于大规模业务场景;RSA,Paillier等单同态加密算法,因为其实现相对简单,所以有比较具体的应用场景.所以本文主要研究Paillier单同态加密方案[16-17].
众所周知,Paillier算法的核心难题是大整数的模幂问题.而模幂的基本运算是大整数的模乘,所以在本节中重点介绍大整数模乘的快速实现.
如图5的算法所示,大整数模乘算法[18],采用蒙哥马利模乘算法的FIOS实现方式,便于FPGA实现.在该算法中,w=128,即基本的运算是128 b的乘法运算,这样s=4,8,12,16就分别代表512,1024,1536,2048位长度的模乘运算,可以通过定义s的不同值来实现模乘器长度的动态配置.

Fig. 5 Montgomery multiplication (FIOS)
图5 蒙哥马利模乘的FIOS实现
在实现的具体过程中,需要注意中间结果的存储问题.对于一个大整数,用寄存器存储的话可能会带来很大的资源浪费,随着数据宽度的增加导致需要的寄存器硬件资源飞速增加.所以本节的实现中,可以用FPGA自带的BRAM来存储A,B,M以及中间结果Z.实验证明,可以减少60%的资源消耗,而且随着数据宽度的增加,效果会更加明显.
总之,本方案提供了一个可以动态配置长度的大整数模幂处理器[19].通过FIOS算法的深度优化以及BRAM的充分利用,可以高效、高速地完成大整数模幂的运算.
5 实验与结果
本方案在FPGA芯片上实现一个高性能的密码协处理器,该协处理器支持3种密码功能:SM4-XTS模式加解密、SM2签名、大整数的模幂运算.通过输入不同的密令码来调用不同的密码功能.该密码协处理器的实现为整个大数据安全方案提供单芯片解决方案,便于产品化的推广.
5.1 实验环境
我们基于Xilinx公司的KC705开发板快速实现了各个算法,并实际测试了我们的方法,取得了实验数据.
KC705是Xilinx公司提供的7系列FPGA的开发套件,开发板上的FPGA芯片是Kintex-7系列 的XC7K325T-2,属于中端系列,是Xilinx公司最具性价比的产品,便于产业推广,具有实际的推广价值.
本方案在KC705开发板上实现同时支持3种密码运算的密码协处理器,对3种算法的资源共享、异步时钟、地址分配等做了优化处理,通过输入不同的命令码便可以支持相应的密码功能.
5.2 实验结果
本方案实现了一个高性能的密码协处理,同时支持3种密码功能:SM4-XTS、SM2签名以及大整数模幂运算.通过输入不同的命令码来调用不同的密码功能.
该密码协处理器内部包含3个密码模块,各个模块在功能上相互独立;但是每个密码模块运行的时钟频率各不相同,需要做异步时钟处理,同时为3个不同的算法模块分配不同的访问地址.表1列举了该密码协处理各密码模块的实验结果.
Table 1 Results of Cryptographic Co-processor
表1 密码协处理器的实验结果

FunctionOperation Frequency∕MHzUtilization∕LUTsTime of One Operation∕μsSM4-XTS250186430.004SM2 Signature1503006938.5Modular Exponentiation(512b) 6627382149.2
由表1可以看出,这3种算法运行在不同的时钟频率、资源占有率也各不相同.SM4-XTS模式可以运行在250 MHz的时钟频率,处理一个SM4分组需要的时间为0.004 μs,SM4-XTS加密性能可达31.5 Gbps;而SM2签名运行在150 MHz的时钟频率,做一次签名运算需要的时间为38.5 μs,SM2签名速度可达每秒26 063次;512 b大整数模幂运行在66 MHz的时钟频率,做一次模幂运算需要时间为149.2 μs,大整数模幂速度可达每秒6 702次.
表2列举的密码协处理器的资源使用情况.LUT是(look-up-table)的缩写,DSP是FPGA内部实现的乘法器,二者都是FPGA的基本逻辑单元.本方案实现的密码协处理充分利用了FPGA的元器件特性,提高各个模块的实现效率.表2可以看出本方案切实可行,在实现高性能算法的同时,预留了大量的资源便于逻辑调度、访问控制等控制逻辑的实现.
Table 2 Utilization of FPGA
表2 FPGA的资源使用情况

FPGA Resource In UseTotalUsage Rate∕%LUT 7609420380037.34DSP65684078.10
5.3 相关工作比较
1) SM4-XTS性能比较
SM4是我国专用的对称密码算法,目前国内的产品基本都不支持SM4-XTS模式,只是支持ECB和CBC模式.其他产品的ECB模式与本文方案性能对比如表3所示:
Table 3 Performance Comparison of SM4-XTS Encryption with Other Works
表3 SM4-XTS加密性能与其他工作的比较果

WorksEncryption Speed∕GbpsOurs 31.5HSM4A2.5SSX1510 2.0
HSM4A芯片是北京宏思电子技术有限责任公司生产的一款SM4算法芯片,加密性能可达2.5 Gbps.
SSX1510是清华微电子所芯片研发的一款SM4芯片,其加密性能可达2.0 Gbps.
可以看出:本文的工作首先填补了国内该方向的空白,同时由表3的结果可以看出,本文采用32级流水线的高速实现方式,每个周期都可以输出128 b的密文,加密性能已经基本达到了极限,远超于其他产品的性能.所以本文提出的方案具有比较好的性价比,优势巨大.
2) SM2和大整数模幂性能比较
如表4、表5所示,SM2与大整数模幂性能与国内其他厂商产品性能对比结果.
Table 4 Performance Comparison of SM2 Signature with Other Works
表4 SM2签名性能与其他工作的对比

WorksNumbers of Signatures per SecondOurs 26063HSM2A20000ISECMM1521SV1 14000
Table 5 Performance Comparison of 512 b Modular Exponentiation with Other Works
表5 512 b大数模幂性能与其他工作的对比

Works Numbers of 512b Modular Exponentiations per SecondOurs 6702SSX261400ISRSAMM11KBV1 231
HSM2A芯片是北京宏思电子技术有限责任公司生产的一款SM2算法芯片,签名速度可达每秒20 000次.
ISECMM1521SV1是北京华大信安科技有限公司开发的椭圆曲线公钥密码芯片产品,其签名速度可达每秒14 000次.
SSX26芯片是北京芯光天地集成电路设计有限公司设计的一款RSA算法芯片,支持大整数模幂运算,512 b的大整数模幂速度可达每秒1 400次.
ISECMM1521SV1是北京华大信安科技有限公司开发的一款RSA算法芯片,支持大整数模幂运算,其512 b的大整数模幂速度可达每秒231次.
由以上结果可以看出:SM2和大整数模幂的性能比较,本文的工作都处于比较明显的领先地位.所以本文的方案具有一定的优势,可以良好地满足该方案密码算法的需求.
6 总 结
本文提出了基于高性能密码实现的大数据安全方案,主张用密码技术来解决大数据安全问题.实验结果表明,本文提出的方案主要解决了大数据技术中存在的3个技术难题:1)大规模的海量数据高速加解密问题;2)高并发的用户身份认证问题;3)大数据的部分隐私保护问题.而且该方案在安全性、易用性、性能方面都具有较大优势,优于目前已知的其他方案.因此本文提出的方案是行之有效的.
未来可以继续添加数据溯源和数据确权的解决方案,如此可以解决大数据全生命周期的安全问题,方案会更加完整、有效.
[1]Feng Dengguo, Zhang Min, Zhang Yan, et al. Study on cloud computing security[J]. Journal of Software, 2011, 22(1): 71-83 (in Chinese)
(冯登国, 张敏, 张妍, 等. 云计算安全研究[J].软件学报, 2011, 22(1): 71-83)
[2]Elbirt J, Chetwynd B, Paar C, et al. An FPGA implementation and performance evaluation of the AES block cipher candidate algorithm finalist[C] 
 Proc of the 3rd AES Conf (AES3). Piscataway, NJ: IEEE, 2000: 192-201
Proc of the 3rd AES Conf (AES3). Piscataway, NJ: IEEE, 2000: 192-201
[3]IEEE Std. P1619-2007 the XTS -AES Tweakable Block Cipher[S]. Piscataway, NJ: IEEE, 2008
[4]Ansari B, Hasan M. High performance architecture of elliptic curve scalar multiplication, CACR-2006-01[R]. Waterloo, Canada: Department of Electrical and Computer Engineering, University of Waterloo, 2006
[5]Damgard I, Jurik M. A generalisation, a simplication and some applications of Paillier’s probabilistic public-key system [J]. Lecture Notes in Computer Science, 2001, 7(45): 119-136
[6]Bao Kejin, Song Yonggang. Optimizing and realization of the finite field inversion algorithm based on FPGA [J]. Computer Engineering, 2006, 32(23): 156-159 (in Chinese)
(鲍可进, 宋永刚. 基于FPGA的有限域求逆算法的改进及实现[J]. 计算机工程, 2006, 32(23): 156-159)
[7]Paillier P. Public-key cryptosystems based on composite degree residuosity classes[G] 
 LNCS 1592: Proc of Eurocrypt’99. Berlin: Springer, 1999: 223-238
LNCS 1592: Proc of Eurocrypt’99. Berlin: Springer, 1999: 223-238
[8]Choi S, Won D. Improvement of probabilistic public key cryptosystems using discrete logarithm[C] 
 Proc of Int Conf on Information Security and Cryptology. Berlin: Springer, 2001: 72-80
Proc of Int Conf on Information Security and Cryptology. Berlin: Springer, 2001: 72-80
[9]Gueron S. Efficient software implementations of modular exponentiation [J]. Journal of Cryptographic Engineering, 2012, 9(2): 31-43
[10]Kazuhiko M. Improved security analysis of XEX and LRW modes[G] 
 LNCS 4356: Proc of SAC 2006. Berlin: Springer, 2007: 96-113
LNCS 4356: Proc of SAC 2006. Berlin: Springer, 2007: 96-113
[11]Li Meng. Differentially private publication scheme for trajectory data[C] 
 Proc of IEEE Int Conf on Data Science in Cyberspace (ICDSC). Piscataway, NJ: IEEE, 2017: 596-601
Proc of IEEE Int Conf on Data Science in Cyberspace (ICDSC). Piscataway, NJ: IEEE, 2017: 596-601
[12]Halevi S. Extending EME to handle arbitrary-length messages with associated data[C] 
 Proc of INDOCRYPT 2004. Berlin: Springer, 2004: 315-327
Proc of INDOCRYPT 2004. Berlin: Springer, 2004: 315-327
[13]Montgomery P. Modular multiplication without trial division [J]. Mathematics of Computation, 1985,12(44): 519-523
[14]Moses L, Ronald L, David W. Tweakable block ciphers[G] 
 LNCS 2442: Proc of CRYPTO 2002. Berlin: Springer, 2002: 31-46
LNCS 2442: Proc of CRYPTO 2002. Berlin: Springer, 2002: 31-46
[15]Halevi S, Rogaway P. A tweakable enciphering mode[G] 
 LNCS 2729: Proc of CRYPTO 2003. Berlin: Springer, 2007: 482-499
LNCS 2729: Proc of CRYPTO 2003. Berlin: Springer, 2007: 482-499
[16]Cuauhtemoc M, Debrup C, Francisco R. Efficient implementations of some tweakable enciphering schemes in reconfigurable hardware[G] 
 LNCS 4859: Proc of Indocrypt 2007. Berlin: Springer, 2007: 414-424
LNCS 4859: Proc of Indocrypt 2007. Berlin: Springer, 2007: 414-424
[17] Akoglu L, Tong H, Koutra D. Graph based anomaly detection and description [J]. Data Mining and Knowledge Discovery, 2015, 29(3): 626-688
[18]Coron J, Mandal A, Naccache D, et al. Fully homomorphic encryption over the integers with shorter public keys[C] 
 Proc of Conf on Advances in Cryptology. Berlin: Springer, 2011: 487-504
Proc of Conf on Advances in Cryptology. Berlin: Springer, 2011: 487-504
[19]Cheon J H, Kim J, Lee M S, et al. CRT-based fully homomorphic encryption over the integers[J]. Information Sciences, 2015, 310(C): 149-162




