近年来,随着监控、传感、控制和通信等技术的不断发展,传统电网正在逐步被智能电网(smart gird)所取代[1],相较于前者,后者可以在公共电力供应商与其用户之间实时传输信息[2],以实现高效的配电与输电[3].总的来说,智能电网就是将信息技术、通信技术、计算机技术和原有的输电、配电基础设施高度集成而形成的新型电网[4],可以提高能源效率、减少对环境的影响、提高供电的安全性和可靠性、降低输电网的电能损耗[4].
智能电网能够通过由智能电表等实体组成的高级计量基础设施(advanced metering infrastructure, AMI)进行周期性、高频率的数据采集[3],以监测实体的各种状态,如电力消耗、负载平衡、资源分配等.这种细粒度的能源相关数据可以支持智能配电、能耗监管和能源管理[1],但也带来了安全和隐私方面的挑战.例如,恶意用户通过远程访问电表或捕获智能电表和供应商之间的计量数据可以访问用户能耗数据.对这种精细的高频能量使用数据进行分析可以得到消费者的行为和生活习惯等隐私信息,如工作时间、用餐时间、娱乐时间、房屋占用时间等[5].解决安全与隐私问题已成为智能电表部署的关键要求[6].
由美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)智能电网互操作性小组发布的智能电网网络安全综合指南[7]指出,智能电网最重要的安全目标为CIA[8],即机密性(confidentiality)、完整性(integrity)和可用性(availability).机密性限制未经授权的对信息的访问和披露,以保护个人隐私和专有信息.数据完整性是智能电网系统信息安全的支柱[9],确保防止未经授权的信息修改和破坏,以保证信息的不可抵赖性和真实性.完整性丧失是指未经授权修改或破坏信息,并可能进一步导致有关能源管理的错误决策.可用性的目标是确保授权用户可以对信息进行及时、可靠的访问和使用.可用性的丧失是对信息的访问或使用的中断,可能进一步破坏电力传输[10].
基于上述智能电网的隐私问题和安全目标,并综合考量方案的可用性、可扩展性和可进化性等关键事项[11],相关学者对其隐私保护方案的设计进行了大量研究.目前智能电网隐私保护方法可分为非密码的和基于密码的2类.
非密码技术使用工程基础设施来混淆消费者的实际电能使用量.主要包括基于电池的负载隐藏(battery-based load hiding, BLH)和基于物理不可克隆函数(physical unclonable functions, PUF)两种方法[3].BLH使用可充电电池部分供应能量需求,以控制仪表读数来隐藏实际的能量消耗.第2类非密码学方法PUF通过使用物理结构中的单向功能来实现消费者隐私[12].但此类方法大都需要额外安装与维护设备,成本较高.故研究者希望能在现有的智能电网架构下设计出合理的用户隐私保护方案,基于密码技术的方法多是根据这种思想来设计的.
基于密码技术的隐私保护方法可以定义为将分布式计算泄露的信息限制为可从指定的计算输出中学习到的信息的方法[13],分为数据混淆、数据聚合和身份匿名3类.数据混淆可以通过应用随机噪声[14]或对细粒度能耗数据使用适当的代数变换来掩盖原始数据[15].第2种方法是数据聚合,使用网络中的聚合器,通过sum或average等函数连接和汇总来自多个设备的数据包,再将聚合后的数据发送到电力服务公司.数据匿名的目的是将用户身份与其能耗数据分开[16-17].其想法为电力供应商将收到足够的信息来计算所需的信息,但不足以将数据与某一特定的智能电表或用户相关联.可以利用(可链接)匿名证书[18-19]、群签名[20-21]、(可链接)环签名[22-23]等密码技术实现数据匿名.
而现有的隐私保护研究工作少有考虑到量子安全性.量子计算技术正在飞速发展,基于格(lattice)的密码学是一类经典的后量子密码,被公认为是后量子密码算法标准最有力的竞争者[24],在安全性方面拥有很大的潜力[25].
结合当前智能电表的数据传输机制安全性不高以及量子信息科学快速发展的实际情况,本文提出了一个后量子的智能电网隐私保护方案.我们的方案改进了现有的应用于智能电网的数据采集阶段的基于静态可链接环签名的可以追踪非法用户的保护用户隐私的数据采集方案[23],利用格密码将其隐私性扩展到量子计算领域,并且将签名尺寸由同用户数目N成线性关系改进到对数级别.并且方案通过使用基于格的后量子签名方案拥有动态用户加入与删除的功能,加强其灵活性和可用性.
为了构造本文方案,我们选择目前基于格的签名尺寸为对数级别的环签名方案中较为先进的工作[26],并对其进行了改进以增加可链接性.将此可链接环签名方案用于智能电表隐私保护系统,使得系统即使面对量子计算机也能很好地保护用户的个人隐私,同时也可以实现异常用户的检测.
1 预备知识
1.1 符号说明
n维向量x=(x0,x1,…,xn-1)的欧氏范数为![]() 多项式
多项式![]() 的欧氏范数为
的欧氏范数为![]() 无穷范数为
无穷范数为![]() 个多项式组成的向量p=(p0,p1,…,pm-1)的欧氏范数为
个多项式组成的向量p=(p0,p1,…,pm-1)的欧氏范数为![]()
a←Z表示从集合Z中随机均匀或者分布Z中随机选取元素a.对正整数t,在Rt上的连续正态分布为![]() 在Zt上中心在v、标准差为σ的离散高斯分布的概率质量函数为
在Zt上中心在v、标准差为σ的离散高斯分布的概率质量函数为![]() Zt),其中
Zt),其中![]() Z
Z![]() 是为了得到概率分布而使用的一个归一化因子.若
是为了得到概率分布而使用的一个归一化因子.若![]() 将被简写为
将被简写为![]()
δl,i表示克罗内克函数,对于l=i,δl,i=1;对l≠i,δl,i=0.函数v=negl(λ)表示函数v(λ)是可以忽略的,即v(λ)<1 λc对于任意c>0和任何足够大的λ都成立.
λc对于任意c>0和任何足够大的λ都成立.
1.2 承诺方案
承诺方案(commitment scheme)的概念由Chor等人[27]提出,主要用于可验证的秘密分享.承诺者随机选择r值以构造对消息值m的承诺c=Comck(m;r)并将c发送给接收者.发送者后来透露被承诺值的相关消息给接收者,以供接收者确认这个打开值(opening)并检查它确实就是最初承诺过的那个值.
此类承诺方案的基本安全性质为隐藏性和绑定性.隐藏性(hiding)为承诺不会泄露被承诺值的任何信息,即不能通过c得到关于m或r的信息.绑定性(binding)则是不能打开一个承诺到2个不同的值,即打开c=Comck(m;r)到m′,r′(m≠m′或r≠r′)发生的概率是可以忽略的.
定义1. 基于格的同态承诺方案[26].令![]() 为随机数域,其中γr为正实数;
为随机数域,其中γr为正实数;![]() 是消息域,其中γM为正实数;则对一个随机数r∈Sr(γr)和一个消息m=(m1,m2,…,mv)∈SM(γM)的承诺为
是消息域,其中γM为正实数;则对一个随机数r∈Sr(γr)和一个消息m=(m1,m2,…,mv)∈SM(γM)的承诺为
Comck(m;r)=Comck(m1,m2,…,mv;r)=
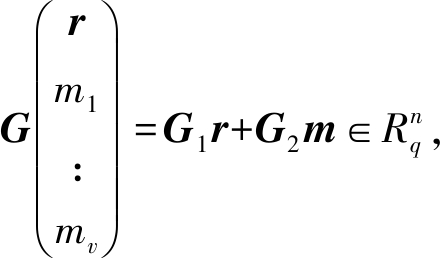
承诺密钥![]() 是一个随机均匀选取的公共矩阵,可以拆分成2个矩阵G1,G2来表示,
是一个随机均匀选取的公共矩阵,可以拆分成2个矩阵G1,G2来表示,![]()
此承诺方案拥有加法同态性:Comck(a;r1)+Comck(b;r2)=Comck(a+b;r1+r2),且对∀γ∈Rq都有:γ Comck(m;r)=Comck(γ
Comck(m;r)=Comck(γ m;γ
m;γ r).它对素数
r).它对素数![]() 是统计隐藏的,其计算绑定性依赖于当
是统计隐藏的,其计算绑定性依赖于当![]() 时Module-SISn,m+v,q,θ问题的困难性[26].
时Module-SISn,m+v,q,θ问题的困难性[26].
定义2. Module-SISn,m,q,θ问题[28].令Rq=Zq[X] (Xd+1).给
(Xd+1).给![]() 它的每个分量随机均匀且独立的选取.问题要求找到
它的每个分量随机均匀且独立的选取.问题要求找到![]() 使得Az=0 mod q且
使得Az=0 mod q且![]()
1.3 Σ协议
Σ协议是一类两方之间的三步零知识证明系统,允许证明者(prover)使验证者(verifier)相信某声明为真.对关系![]() 的Σ协议,即对声明(statement)u存在证据(witness)w使得
的Σ协议,即对声明(statement)u存在证据(witness)w使得![]() 成立.
成立.
定义3[26].![]() 是一个两方协议,其中
是一个两方协议,其中![]() 是多项式时间(probability polynomial time, PPT)算法.
是多项式时间(probability polynomial time, PPT)算法.![]() 与
与![]() 是2个关系且
是2个关系且![]() 则协议
则协议![]() 被称为是一个对于关系
被称为是一个对于关系![]() 与
与![]() 的,挑战值空间为
的,挑战值空间为![]() 公共输入为u,秘密输入为w,完备性误差为α,稳健性误差为
公共输入为u,秘密输入为w,完备性误差为α,稳健性误差为![]() 的Σ协议,当且仅当满足4个条件:
的Σ协议,当且仅当满足4个条件:
1) 3-move形式.
①![]() 以(u,w)作为输入,生成初始消息t,将其发送给
以(u,w)作为输入,生成初始消息t,将其发送给![]()
②![]() 选择挑战
选择挑战![]() 并发送给
并发送给![]()
③![]() 收到x后,向
收到x后,向![]() 给出相应答复s;
给出相应答复s;
④![]() 根据协议记录(t,x,s)决定是否接受(即证明是否有效).
根据协议记录(t,x,s)决定是否接受(即证明是否有效).
2) 完备性.若![]() 以至少1-α的概率接受证明.
以至少1-α的概率接受证明.
3) k-特殊稳健性.存在PPT算法ε(称为知识提取器)以k个可通过验证的证明记录(t,x1,s1)(t,x2,s2)…(t,xk,sk)为输入,其中xi互不相同,输出w′满足![]()
4) 特殊诚实验证者零知识(special honest verifier zero-knowledge, SHVZK)存在一个PPT算法S(称为模拟器)以![]() 和
和![]() 为输入,输出一个协议记录(t,x,s).其分布与实际运行协议所产生的可接受的协议记录是不可区分的.
为输入,输出一个协议记录(t,x,s).其分布与实际运行协议所产生的可接受的协议记录是不可区分的.
1.4 拒绝采样
拒绝采样技术[29]可以防止泄露信息,其想法是以一个确定的概率输出响应,否则终止.
定理1. 拒绝采样[29].![]() 是Zd的子集,且
是Zd的子集,且![]() 中所有元素的范数小于T,h是在
中所有元素的范数小于T,h是在![]() 上的一个概率分布,定义算法:
上的一个概率分布,定义算法:
![]() 采样
采样![]() 然后以
然后以![]() 的概率输出(v,z);
的概率输出(v,z);
![]() 然后以1
然后以1 M的概率输出(v,z).
M的概率输出(v,z).
其中,σ=12T,M=e1+1 288.则
288.则![]() 会输出向量的概率大于
会输出向量的概率大于![]() 与
与![]() 的输出之间的统计距离为
的输出之间的统计距离为![]()
1.5 基于格的环签名方案
环签名的概念是由Rivest,Shamir和Tauman在2001年[30]提出的,环签名中的每个用户都可以选择包括自己的任何一组可能的签名者组成环,并通过使用自己的密钥和其他成员的公钥来代表整个环对任意消息进行签名,而无需获得他们的批准或帮助.
一个安全的环签名的性质有正确性、不可伪造性和匿名性.正确性为环中任意成员进行环签名过程后得到的签名不能通过验证的概率可以忽略.不可伪造性为任何不在环中的成员生成代表该环的签名并且通过验证的概率可以忽略.匿名性体现在任何人无法知道签名的真正签名者,在大小为N的环中,验证者能够确定签名者真正身份的概率不超过1 N.
N.
Esgin等人提出的环签名方案[26]是体现目前最先进水平的基于格的环签名方案之一,环签名大小与环成员个数N成对数关系,即O(log N),其安全性基于Module-SIS问题的困难性.该环签名方案将one-out-of-many证明从离散对数设置[31-32]扩展到了格设置,并以基于格的one-out-of-many证明作为构建块来设计基于格的环签名方案.one-out-of-many证明中证明者的目标是说服验证者他知道一组承诺中的一个承诺的打开值,而不透露他具体拥有哪一个.
Esgin等人介绍了一个基于格的one-out-of-many协议,其可以证明证明者知道一组承诺(共N=βk个)中的一个打开为0的承诺中的随机数,即证明cl是一个打开为0的承诺且知道其随机数r,即cl=Comck(0;r),其中下标l∈{0,1,…,N-1}.
为证明l∈{0,1,…,N-1},将序列(δlj,0,δlj,1,…,δlj,β-1)承诺,沿用Bootle的思想[31]证明它们都分别是一个汉明重量为1的二元序列,即对于![]() 且存在唯一的t∈[0,β-1]使得δlj,t=1,lj∈[0,β-1]对∀j成立;则可证明l=(l0,l1,…,lk-1)是l以β为基的表示方法,故l∈{0,1,…,βk-1}.
且存在唯一的t∈[0,β-1]使得δlj,t=1,lj∈[0,β-1]对∀j成立;则可证明l=(l0,l1,…,lk-1)是l以β为基的表示方法,故l∈{0,1,…,βk-1}.
证明cl是一个打开为0的承诺的思路沿用Groth和Kohlweiss的思![]() 其中
其中![]() 和i=(i0,i1,…,ik-1)分别是l和i以β为基的表示方法.对挑战x,fj,i=xδlj,i+aj,i可看作关于x的一次多项式,对于所有的i∈[0,N-1],连乘积
和i=(i0,i1,…,ik-1)分别是l和i以β为基的表示方法.对挑战x,fj,i=xδlj,i+aj,i可看作关于x的一次多项式,对于所有的i∈[0,N-1],连乘积![]() 是一个形如式(1)的关于x的多项式,
是一个形如式(1)的关于x的多项式,
![]()
![]()
(1)
其中,pi,j为多项式j次项的系数,当![]() 和l已知时,pi,j在未接受到挑战x时就可以求出.由式(1)可知,对于所有的pi(x),i∈[0,N-1],其中仅有pl(x)是k次的多项式.证明思想是向验证者发送初始消息Ej,j∈[0,k-1],以在后续验证过程中消去
和l已知时,pi,j在未接受到挑战x时就可以求出.由式(1)可知,对于所有的pi(x),i∈[0,N-1],其中仅有pl(x)是k次的多项式.证明思想是向验证者发送初始消息Ej,j∈[0,k-1],以在后续验证过程中消去![]() 中低阶项1,x,x2,…,xk-1的系数,仅保留xk的系数为
中低阶项1,x,x2,…,xk-1的系数,仅保留xk的系数为![]() 也就是证明者的承诺.
也就是证明者的承诺.
协议中的响应是取决于某些秘密值的,所以响应不能在域中均匀分布,这妨碍了此协议的零知识性,故使用到1.4节介绍的拒绝采样.协议以p1 N的概率(参见文献[26]的定理2)为一个(k+1)-特殊稳健性的Σ协议.
N的概率(参见文献[26]的定理2)为一个(k+1)-特殊稳健性的Σ协议.
此one-out-of-many协议允许构造短的环签名方案,用户对其私钥sk进行承诺得到用户公钥pk,签名者证明他知道一组用于构造环的承诺(公钥)中的一个的打开为0的承诺中的随机数(即知道私钥).环签名方案为了达到一个不可忽略的可靠性误差重复运行了r次Σ协议,拒绝采样应用于r-联通的向量.
当承诺方案为计算绑定且统计隐藏时,此环签名方案在相关参数设置下拥有统计正确性、匿名性和不可伪造性.
1.6 可链接环签名
可链接环签名(linkable ring signature)为环签名增添了可链接性[33].一个可链接环签名方案包括5个有效的算法(RSetup,RKgen,RSign,RVerify,RLink):
1) pp←RSetup(1λ).输入安全参数λ,生成并公开系统参数pp.
2) (pk,sk)←RKgen(pp).根据系统参数生成环成员的公私钥对(pk,sk).
3) σ←Rsignpp,sk(M,L).输出关于消息M、环L的签名σ,要求sk是由RKgen(pp)生成的,且其对应公钥pk在环L中.
4) {0,1}←RVerifypp(M,L,σ).输入关于消息M、环L的签名σ,验证其有效性.若有效输出1,否则输出0.
5) {0,1}←RLinkpp(σ1,σ2).输入2个可以通过验证的签名σ1和σ2,若2个签名是可以链接起来的,输出1,否则输出0.
可链接环签名的安全性除了不可伪造性和匿名性之外增添了可链接性:签名者的身份仍保持匿名但由同一签名者签署的2个签名可以链接起来.它的可链接性和签名者匿名性的属性在各种现实应用场景中是非常理想的.
2 基于格的可链接环签名方案
基于智能电表隐私保护系统的异常检测需求,我们通过增添可链接元素来为1.5节描述的环签名方案增加可链接性.具体思想为在签名过程中加入一个用于证明可链接性的元素K=G2r,并向验证者发送消息Fj(j∈[0,k-1]),以消去多项式G2z中低阶项1,x,x2,…,xk-1的系数,仅保留xk的系数为K,以满足![]()
2.1 方案详述
我们的基于格的可链接环签名LRS由算法五元组(LRS_Setup,LRS_Keygen,LRS_Sign,LRS_Verify,LRS_Link)组成.
我们改造1.5节提到的one-out-of-many证明,即文献[26]中的协议2,以期为LRS提供底层Σ协议Σ0,如图1所示.协议Σ0服务于关系:
![]()
![]()
cl=Comck(0;r)∧K=G2r},![]()
![]()
![]()
定理2. 若承诺方案为计算上绑定且统计上隐藏的,协议Σ0在参数设置为常数M=e1+1 288,d≥7,md≥86,2U≥qn
288,d≥7,md≥86,2U≥qn m×22λ
m×22λ (md),素数q≡5 mod 8且
(md),素数q≡5 mod 8且![]() 时对于关系
时对于关系![]() 和
和![]() 为一个SHVZK且有(k+1)-特殊稳健性的Σ协议的概率(也就是此协议证明者
为一个SHVZK且有(k+1)-特殊稳健性的Σ协议的概率(也就是此协议证明者![]() 的步骤
的步骤 ~
~ 会输出响应而不至于终止协议的概率):
会输出响应而不至于终止协议的概率):
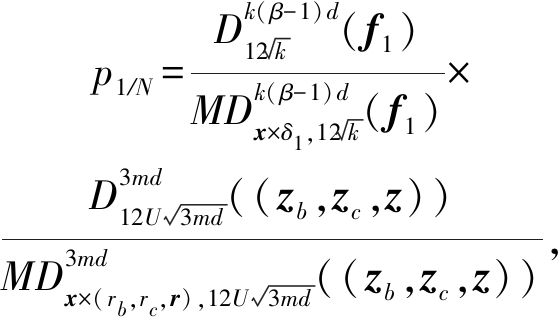
(2)
其中,f1=(f0,1,f0,2,…,fk-1,β-1),δ1=(δl0,1,δl0,2,…,δlk-1,β-1).
证明. 相较于文献[26]中SHVZK和(k+1)-特殊稳健性的协议2,协议Σ0增添了用于实现可链接性的元素K以及{Fj![]() ,故只需对文献[26]中的证明进行简单的扩展.
,故只需对文献[26]中的证明进行简单的扩展.
SHVZK:对于模拟出的证明记录,由于Fj=G2ρj中![]() 是随机选取的,故不会影响SHVZK.
是随机选取的,故不会影响SHVZK.
(k+1)-特殊稳健性.对互不相同的挑战x0,x1,…,xk,有k+1个可接受协议记录,它们有相同的初始消息CMT,K和k+1个不同的响应z0,z1,…,zk.故有K=G2r以及![]() 可得:
可得:

(ck,(c0,c1,…,cN-1),(l,r)) (ck,(c0,c1,…,cN-1))① rb←{-U,-U+1,…,U-1,U}md;② δ=(δl0,0,δl0,1,…,δlk-1,β-1);③ B=Comck(δ;rb);④ a0,1,a0,2,…,ak-1,β-1←Dd12k;⑤ rc←{-U,U+1,…,U-1,U}md;⑥ ra,rd←Dmd12U3md;⑦ forj=0,1,…,k-1 do⑧ aj,0=-∑β-1i=1aj,i;⑨ end for⑩ A=Comck(a0,0,a0,1,…,ak-1,β-1;ra);C=Comck({aj,i(1-2δlj,i)}k-1,β-1j,i=0;rc);D=Comck(-a20,0,-a20,1,…,-a2k-1,β-1;rd);forj=0,1,…,k-1 doρj←Dmd12U3md∕k;Ej=∑N-1i=0pi,jci+Comck(0;ρj);∕∗using pi,jin formula(1)∗∕Fj=G2ρj;end forK=G2r;A,B,C,D,{Ej}k-1j=0,{Fj}k-1j=0,K→ ←x=Xωω←{0,1,…,2d-2,2d-1} fj,i=xδlj,i+aj,i∀j,∀i≠0;zb=x∙rb+ra;zc=x∙rc+rd;z=xk∙r-∑k-1i=0xjρj;abort with probability(1-p1∕N) from formula(2); if aborted Return ⊥; end ifA,B,C,D,{Ej}k-1j=0,{Fj}k-1j=0,K,{fj,i}k-1,β-1j=0,i=1,zb,zc,z→Accept if and only if all the following statements are satisfied:① forj=0,1,…,k-1 do②fj,0=x-∑β-1i=1fj,i;③ end for④ ∀j,∀i≠0:fj,i≤?60dk⑤ ∀j:fj,0≤?60dk(β-1)⑥ z,zb,zc≤?243mdU;⑦ f=(f0,0,f0,1,…,fk-1,β-1);⑧ g={fj,i(x-fj,i)}k-1,β-1j,i=0;⑨ xB+A=?Comck(f;zb);⑩ xC+D=?Comck(g;zc);∑N-1i=0∏k-1j=0fj,ij()ci-∑k-1j=0Ejxj=?Comck(0;z);Kxk-∑k-1j=0Fjxj=?G2z.
Fig. 1 Lattice -based Σ-protocol Σ0 for ![]()
图1 基于格的证明关系![]() 的Σ协议Σ0
的Σ协议Σ0
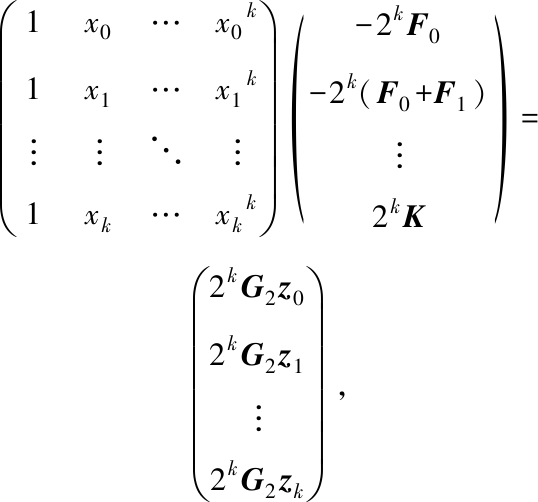
(3)
式(3)等号左侧第1个矩阵(记为V)为范德蒙矩阵.已知V可逆且其逆矩阵V-1的最后一行的元素记为α0,α1,…,αk,在式(3)两侧左乘V-1得到的矩阵最后一行的元素为
当![]() 时,
时,![]() 成立[26],且
成立[26],且![]() 即可以证明
即可以证明![]()
证毕.
记![]() 为协议Σ0中对应的值.LRS详细描述如下:
为协议Σ0中对应的值.LRS详细描述如下:
1) 系统建立算法LRS_Setup(1λ).
输入:安全参数λ;
输出:全局参数pp=(ck,H).
①![]()
② 选取Hash函数H:{0,1}*→Cr,H将任意长度的01字符串映射为Cr中的元素,![]() 为挑战空间;
为挑战空间;
③ ck=(G1,G2)  *承诺密钥*
*承诺密钥*
④ return pp=(ck,H).
2) 密钥生成算法LRS_Keygen(pp).
输入:全局参数pp=(ck,H);
输出:公私钥对(pk,sk).
① r←{-U,…,U}md;
② c=Comck(0;r)=G1r  *0是全0向量*
*0是全0向量* ;
;
③ return(pk,sk)=(c,r).
3) 签名算法LRS_Signpp,sk(M,L).
输入:消息M和环L=(c0,c1,…,cN-1),其中cl=Com(0;skl),l∈{0,1,…,N-1};
输出:用户l(l∈{0,1,…,N-1})使用其私钥skl代表环L对消息M的签名σ.
① 重复运行r次协议Σ0的![]() 的步骤①~
的步骤①~ 以生成(CMT1,CMT2,…,CMTr)
以生成(CMT1,CMT2,…,CMTr)  *将r次运行时得到的响应fj,i,z,zb,zc看做r连通的向量共同存储,以便于拒绝采样*
*将r次运行时得到的响应fj,i,z,zb,zc看做r连通的向量共同存储,以便于拒绝采样*
② K=G2 skl;
③ x=(x1,x2,…,xr)=H(ck,M,L,(CMT1,CMT2,…,CMTr),K);
④ for i=1 to r do
RSPi←协议Σ0的![]() 步骤
步骤
 ~
~
 *中止概率p1
*中止概率p1 N来自式(4)*
N来自式(4)*
end for
⑤ if ∀i∈{1,2,…,r},RSPi≠⊥, do
![]()
return σ
⑥ else返回步骤①;
 *最多重复
*最多重复![]() 次*
次*
⑦ end if
⑧ return ⊥.
 *若达到最大迭代次数
*若达到最大迭代次数![]() 停止*
停止*
4) 签名验证算法LRS_Verifypp,sk(M,L,σ).
输入:消息M和环L以及环L对消息M签署的签名![]()
输出:1或0. *签名有效输出1,否则输出0*
*签名有效输出1,否则输出0*
① if σ=⊥ return 0;
② if x≠H(ck,M,L,(CMT1,CMT2,…,CMTr),K) return 0;
③ for i=1 to r do
用CMTi,xi和RSPi运行协议Σ0中![]() 的步骤①~
的步骤①~ ,若输出
,若输出![]() 步骤⑥改为
步骤⑥改为![]()
④ return 1.
5) 链接性验证算法LRS_Link(pp,σ1,σ2).
输入:2个合法的签名σ1和σ2;
输出:1或0. *表示是否可以链接*
*表示是否可以链接*
① σ1=(…,K1,…),σ2=(…,K2,…);
② if K1=K2do
③ return 1;
④ else return 0.
根据协议Σ0构造可链接环签名时,依然重复运行r次协议Σ0以达到不可忽略的完备性误差.拒绝采样应用于r-联通的向量![]() 和
和![]() 也就是说在参数设置为常数M=e1+1
也就是说在参数设置为常数M=e1+1 288,d≥7,md≥86,2U≥qn
288,d≥7,md≥86,2U≥qn m×22λ
m×22λ (md),素数q≡5 mod 8且
(md),素数q≡5 mod 8且![]() 时,协议证明者会输出响应而不至于终止协议的概率为
时,协议证明者会输出响应而不至于终止协议的概率为
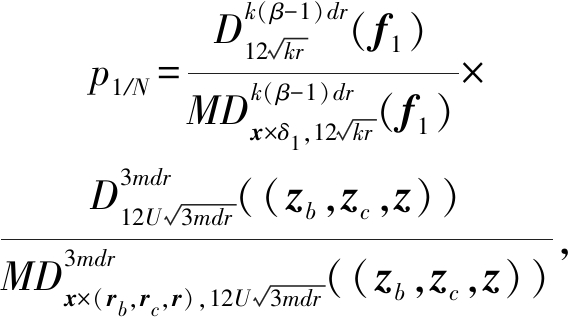
(4)
由于此可链接环签名只在文献[26]的环签名方案中增添了可链接性,且可链接标签也可以以概率1通过验证步骤![]() 故可链接环签名方案LRS依然拥有可忽略的正确性误差,它是统计上正确的,LRS_Sign的迭代次数的期望值为M2=O(1).
故可链接环签名方案LRS依然拥有可忽略的正确性误差,它是统计上正确的,LRS_Sign的迭代次数的期望值为M2=O(1).
2.2 安全性分析
由于此可链接环签名只是在1.5节中描述的环签名方案中增添了可链接性,由协议Σ0的SHVZK,易知添加的可链接元素K并不会影响环签名的匿名性和不可伪造性,故LRS的安全性是可以继承文献[26]中的环签名方案的,其拥有匿名性和不可伪造性.
定理3. 可链接性.若承诺方案是统计隐藏和计算绑定的,可链接环签名LRS在随机预言机下具有可链接性.正式地讲,若PPT敌手只拥有一个密钥对(pk,sk)=(Comck(0;r),r),它可以生成一个合法的签名![]() 使得K≠G2r的概率是可以忽略的.
使得K≠G2r的概率是可以忽略的.
证明.证明LRS的可链接性的思想是证明若存在一个PPT敌手![]() 在只拥有一个密钥对(pk,sk)的情况下可以一个不可忽略的概率生成合法签名
在只拥有一个密钥对(pk,sk)的情况下可以一个不可忽略的概率生成合法签名![]() 使得K≠G2sk,则可以击破消息和随机数域的最大范数分别为2k和
使得K≠G2sk,则可以击破消息和随机数域的最大范数分别为2k和![]() 的承诺方案的绑定性.
的承诺方案的绑定性.
使用文献[26]的定理4中证明不可伪造性的思想来构造矛盾以证明可链接性.证明中将用到PKGen,Sign,Corrupt和随机预言机H这4类预言机:
1) pki←PKGen(⊥).当第i次询问时,PKGen以新的随机硬币值运行RKgen(pp)并返回公钥pki.
2) skj←Corrupt(pkj).若pkj是由PKGen生成的,返回对应的私钥skj.
3) σ←Sign(skj,M,L).运行RSignpp,skj(M,L)以获得一个签名σ.(skj,pkj)是由PKGen生成的.
4) 随机预言机H.以其定义域中的一个元素为输入,返回其值域中对应的元素.
假设PPT敌手![]() 可以分别对预言机PKGen,Sign和随机预言机H进行最多qP,qS,qH次询问,且
可以分别对预言机PKGen,Sign和随机预言机H进行最多qP,qS,qH次询问,且![]() 只询问预言机Corrupt一次,获得的密钥对为(pk*,sk*),则可以以ε=1
只询问预言机Corrupt一次,获得的密钥对为(pk*,sk*),则可以以ε=1 poly(n)的概率生成一个代表环L对消息m的有效签名σ=(…,K,…)且pk*∈L,K≠G2sk*.
poly(n)的概率生成一个代表环L对消息m的有效签名σ=(…,K,…)且pk*∈L,K≠G2sk*.
令Ψ和Φ分别为![]() 和随机预言机H可用的随机纸带的集合,记xj=(xj,1,xj,2,…,xj,r)为第j次询问H给出的答复,则可将Φ划分成Φj-(第j次询问之前),xj和Φj+(第j次询问之后),故三元组(Φj-,xj,Φj+)可以表示随机预言机的输出.
和随机预言机H可用的随机纸带的集合,记xj=(xj,1,xj,2,…,xj,r)为第j次询问H给出的答复,则可将Φ划分成Φj-(第j次询问之前),xj和Φj+(第j次询问之后),故三元组(Φj-,xj,Φj+)可以表示随机预言机的输出.
构造PPT算法![]() 来证明矛盾:
来证明矛盾:
1) j←{1,2,…,qH+qS}
2) ψ←Ψ
4) 运行![]() 可以询问由
可以询问由![]() 模拟的预言机PKGen,Sign,Corrupt和随机预言机
模拟的预言机PKGen,Sign,Corrupt和随机预言机![]()
① PKGen(⊥).当![]() 询问PKGen时,
询问PKGen时,![]() 以新的随机硬币值运行LRS_Keygen(pp)并返回公钥pk.
以新的随机硬币值运行LRS_Keygen(pp)并返回公钥pk.
② Corrupt(pkj).若pkj是由PKGen生成的,返回对应的私钥skj.Corrupt仅允许被查询一次.
③ Sign(pkj,M,L).![]() 运行LRS_Signpp,sk(M,L)以获得一个签名σ,但签名中的挑战值x是由询问随机预言机获得的.返回σ.
运行LRS_Signpp,sk(M,L)以获得一个签名σ,但签名中的挑战值x是由询问随机预言机获得的.返回σ.
④ H1(ck,M,L,(CMT1,CMT2,…,CMTr),K).若元组之前被询问过,返回之前设定的x值.否则给出新的输出为H(ck,M,L,(CMT1,CMT2,…,CMTr),K)=x并记录.
若![]() 输出签名
输出签名![]() 且K≠G2sk*,固定ψ和φj-;否则提前终止程序.
且K≠G2sk*,固定ψ和φj-;否则提前终止程序.
5) 对于![]()
6) 对于![]()
① 运行![]() 其可以询问PKGen,Sign,Corrupt和
其可以询问PKGen,Sign,Corrupt和![]()
② 输出签名![]() 其中yi可能不等于
其中yi可能不等于![]()
7) 若存在i*∈{1,2,…,r}和![]() 且|S*|=i*+1,使得
且|S*|=i*+1,使得![]() 包含k+1个不同挑战,并且对于所有的u∈S*,σu是挑战为
包含k+1个不同挑战,并且对于所有的u∈S*,σu是挑战为![]() 的合法签名,且有K≠G2sk*.
的合法签名,且有K≠G2sk*.
8) 以{σu}u∈S*为输入运行(k+1)特殊稳健性知识提取器可以提取证据l′和![]() 满足
满足![]() 由定理2中对(k+1)-特殊稳健性的讨论可知2kpkl′=
由定理2中对(k+1)-特殊稳健性的讨论可知2kpkl′=![]() 且
且![]()
情况1. 若![]() 则由于skl′是由
则由于skl′是由![]() 生成的,则将与承诺方案计算上的绑定性产生矛盾.
生成的,则将与承诺方案计算上的绑定性产生矛盾.
情况2. 若![]() 且skl′≠vk*,则有
且skl′≠vk*,则有![]() 即
即![]() 拥有关于skl′的知识,与
拥有关于skl′的知识,与![]() 仅询问Corrupt一次矛盾.
仅询问Corrupt一次矛盾.
情况3. 若![]() 且skl′=vk*,则有
且skl′=vk*,则有![]() 2kvk*,由于K≠G2sk*,有
2kvk*,由于K≠G2sk*,有![]() 2kK,得出矛盾.
2kK,得出矛盾.
因此,由于![]() 仅询问Corrupt一次且{σu}u∈S*是挑战为
仅询问Corrupt一次且{σu}u∈S*是挑战为![]() 的合法签名且有K≠G2sk*,那么情况2与情况3均不可能发生.所以可以从情况1中得出一个与承诺方案计算上的绑定性相矛盾的结论.
的合法签名且有K≠G2sk*,那么情况2与情况3均不可能发生.所以可以从情况1中得出一个与承诺方案计算上的绑定性相矛盾的结论.
参考文献[26]中对不可伪造性的讨论易知击破承诺方案绑定性的概率为1 poly(n).
poly(n).
证毕.
2.3 性能分析
依照文献[26]的方法,可以分析可链接环签名LRS的签名尺寸,如表1所示:
Table 1 The Analysis of Our Linkable Ring Signature Size
表1 可链接环签名尺寸分析

ObjectNumberSizeNoteRandomness VectorNR=3md log(144U3mdr)z,zb,zc∈D3md12U3mdCommitmentNc=4+2knd logqA,B,C,D,E0,…,Ek-1,F0,…,Fk-1fj,iNf=(β-1)kd log(144kr)f0,1,…,fj,i,∈D12krUser Secret Key md log(2U)A randomness vector in a commitmentUser Public Keynd logqA commitment in RnqRing Signaturer[Nc(nd logq)+Nf d log(144kr)+NR md log(144U3mdr)]+nd logq
当安全参数设置为λ=100时,此可链接环签名的表现如表2所示,签名的尺寸随着环大小N的增加而增加,且是次线性关系,为O(log N).
Table 2 Our Linkable Ring Signature Size Growth with Respect to Ring Zize
表2 签名大小与环尺寸的关系
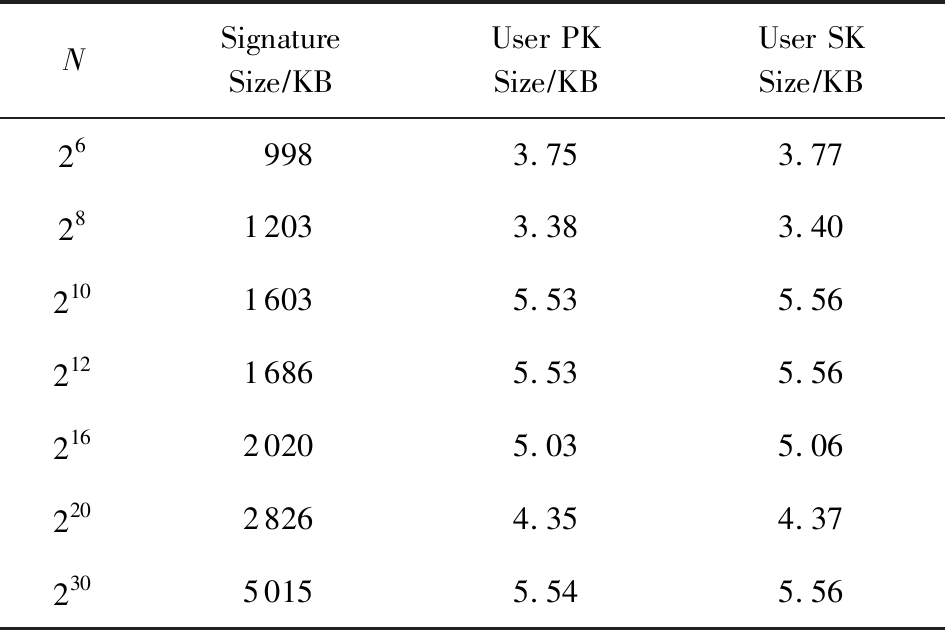
NSignatureSize∕KBUser PKSize∕KBUser SKSize∕KB269983.753.772812033.383.4021016035.535.5621216865.535.5621620205.035.0622028264.354.3723050155.545.56
3 后量子的隐私保护数据采集方案
3.1 方案简介
我们的隐私保护方案基于3层的智能电网结构,主要包括主站、数据集中器与智能电表3种数据传输设备,结构如图2所示.电力服务公司在每个小区建立基站作为电力服务公司的代理,即小区数据集中器Con,该小区的数据先由用户智能电表发送到集中器做处理,再发送到电力服务公司.
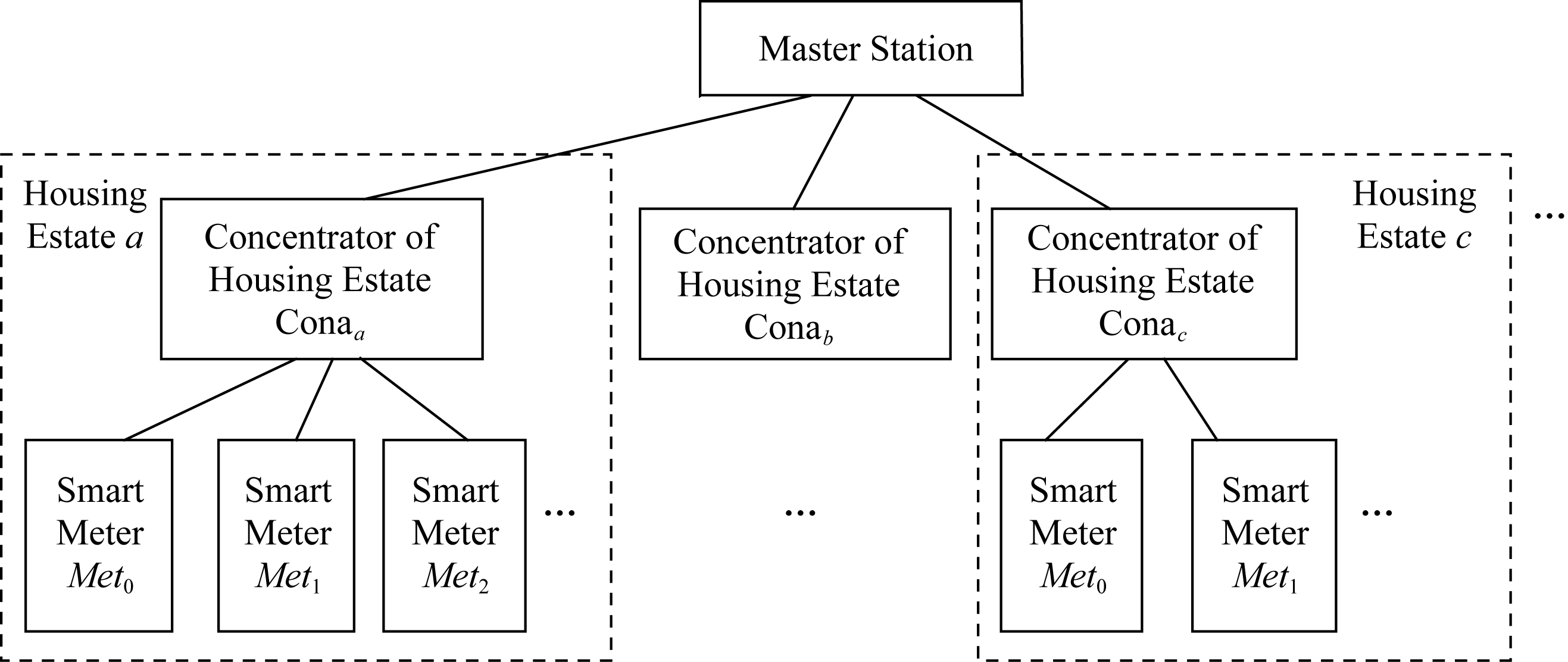
Fig. 2 Three-tier structure of smart grid
图2 智能电网3层结构示意图
我们利用在第2节中介绍的基于格的可链接环签名LRS,将文献[23]中提出的保护用户隐私的数据采集方案改进为抗量子计算的,并且选取一个后量子签名方案(如已经通过NIST后量子密码学标准项目[24]第2轮筛选的基于格的数字签名方案qTESLA[34]),以提供动态用户加入和撤销功能.
本数据采集方案主要关注用户的能耗数据自智能电表上传到小区集中器的传输过程中的隐私保护.同一小区集中器下辖的所有智能电表构成一个环,收集这些智能电表的公钥信息后公开.智能电表采集到实时数据后用可链接环签名对数据信息进行签名,然后将信息-签名对发送给小区集中器,通过集中器验证及异常检测后,数据将被上传至后台主站作进一步处理.基于可链接环签名的性质,签名用户具有匿名性,集中器或其他用户无法将用电情况和真实用户身份一一对应,实现了用户的隐私保护.
集中器持有签名私钥,公开其签名公钥.当有用户动态加入或撤销时,集中器将该用户的公钥在环中增加或删除,更新环组成.集中器对更新后的环进行签名,并将消息-签名对广播给各成员.各用户收到信息后,使用集中器的公钥进行验证,若验证通过则更新智能电表所存储的系统公共参数中的环组成,就可以实现智能电表的动态加入与撤销,而不需要重新初始化整个系统.
3.2 方案详述
本方案主要包括系统初始化、数据上传、数据认证、异常检测和用户动态加入(撤销)共5个阶段.
记一个小区内的N个用户为{U0,U1,…,UN-1},该小区装有一台数据集中器Con,其下安装N台智能电表,记为{Met0,Met1,…,MetN-1},分别安装到用户U0,U1,…,UN-1家中.在时刻t,智能电表采集到的用户数据记为M(t).
1) 系统建立
在实际应用场景中,一个集中器管辖一个小区的智能电表,基于小区的实际构造,小区中用户的最大数量多在最初小区建设时就已经固定,我们估计这个最大值,并设定其为环大小N*=βk,为了使接下来的用户动态加入和撤销操作时的计算不至于繁复,固定这个环大小.根据β和k的值选取满足LRS的参数设置要求的相关参数m,d等.
本系统的初始化需要电力服务公司参与,可将其看作一个可信第三方(CA),初始化完成后,采集过程不需要CA参与.初始化过程为:
① 根据安全参数,CA调用LRS_Setup(1λ)以获得全局参数pp.
② 对于用户Ui,i∈{0,1,…,N-1},安装电表过程中调用LRS_Keygen(pp)来为Meti选取密钥对(ski,pki),私钥ski由智能电表Meti自行保存.
③ CA为集中器Con选取签名私钥skC,并获得公钥pkC.以基于格的签名方案qTESLA为例来描述我们的方案,可以将Nina等人在文献[34]中给出的qTESLA的实现程序预植入集中器的计算模块,使用时直接调用.
④ 令L0=(pk0,pk1,…,pkN-1),由于实际用户数量N不等于预设定的固定环尺寸N*,复制公钥pkN-1以填充环到N*=βk大小,填充后的环为L=(pk0,pk1,…,pkN-1,…,pkN-1)=(pk0,pk1,…,pkN-1,…,pkN*-1).由于此签名方案对环公钥没有不可重复的要求,这种扩充方式不会破坏其安全性.且匿名性仍然为验证者能够确定签名者真正身份的概率不超过1 N.
N.
⑤ 公开系统参数PSP=(pp,L,pkC).在系统初始化阶段,电力服务公司通过物理手段在电表安装过程中将该小区的公开系统参数PSP预置入智能电表内,以减少初始数据传输量.
2) 数据上传
在时刻t,用户Ul的智能电表Metl采集到的用户数据为Ml(t),其中l∈{0,1,…,N-1}.数据上传流程为:智能电表Metl拥有的公私钥对为(pkl,skl),且根据密钥分配有pkl=Comck(0;skl).根据预置入的PSP,电表计算模块调用算法LRS_Signpp,skl(Ml(t),L),输出对消息的签名σl(t).然后Metl将消息-签名对(Ml(t),σl(t))发送给该小区的集中器Con.
3) 数据验证
集中器Con收到下辖电表发送的消息-签名对(M(t),σ(t))后需对其是否来自本小区的合法电表进行验证,验证流程为:
根据存储的系统公开参数PSP,Con调用算法LRS_Verifypp(M(t),L,σ(t)),根据其输出判定是否接受此信息签名对为合法数据.输出1时,通过验证,即可以签名确为该小区内的某台合法电表生成,留存以做进一步处理;否则删除该消息.
4) 异常检测
根据我国标准,每隔15 min小区的数据集中器Con会收集由小区内的智能电表采集的用户数据信息.对于Con收集到的时刻t小区内所有的由下辖智能电表上传的通过认证的数据,Con会进行集中检测,判定是否存在异常,具体流程为:
① 调用LRS_Link算法对所有签名进行链接性检测,Con对比时刻t收到的所有数据的合法签名,当检测到2个(或以上)签名可以链接时,即合法签名σ1=(…,K1,…),σ2=(…,K2,…),…中K1=K2=…,则可以判定它们为同一台电表所签署.
Ⅰ. 若多条已链接的合法签名对应的数据M(t)一致,则判定为同一电表重复发送,取其中一条作为该电表在时刻t上传的数据留存,其余删除.
Ⅱ. 若2个或多个已链接的合法签名对应的数据M(t)不相同,则可以判定该电表工作异常.集中器对下辖小区内的智能电表逐个发送时刻t数据重传命令,检测重传签名与该签名的链接性以确定此故障电表的位置,电力服务公司将对其进行硬件检测和安全监测,排除安全隐患,进行故障维修.
② 记剩余合法签名的数目为n.若n=N,Con整理所有数据(共N个)上传至主站,完成时刻t的数据采集.否则,在时刻t有(N-n)台智能电表的未正常发送数据,集中器对小区内的智能电表逐一发送时刻t数据重传命令,并检测重传数据与已有数据的链接性.如果存在链接,则该智能电表已经发送时刻t数据,工作正常;如果不存在链接,则该智能电表之前并未成功上传时刻t数据,记录该数据并检测其通信模块以确定是否正常工作.
5) 用户动态加入及撤销
当有新用户加入时,电力服务公司为新用户安装电表,并通过线下的物理手段将新用户的公钥提供给集中器以更新系统公开参数PSP中的环为L′,为新电表和集中器更新PSP′=(pp,L′,pkC)并存储.使用集中器私钥skC为L′签名,获得信息-签名对并广播给环成员,其他电表在接受到此消息签名对之后,使用集中器的公钥pkC进行签名验证,验证通过则更新其中存储的系统公开参数PSP=(pp,L′,pkC).此后新用户便可以作为该小区的成员使用其智能电表进行数据采集,具体过程为:
① 参数更新.由于用户动态加入和删除多为小幅度变更,我们最开始设定了固定的环大小,所以小区中用户数量的小幅改变不会导致计算参数m,d,k,β等都发生变化,也不会造成用户电表的私钥的改变.所以对于系统公开参数PSP来说,仅有环的组成需要改变.对环L,去除掉其中重复的公钥以还原原本的初始环L0=(pk0,pk1,…,pkN-1).假设加入的新用户个数为Njoin,Njoin≥1,公钥分别为npk0,npk1,…,npkNjoin-1.新用户加入后环成员个数变为N′=N+Njoin.将新用户的公钥加入环,得到新的环![]() 同样复制公钥pkN′-1来扩充环大小到N*,得到更新后的环L′.将L′存入新用户的电表和集中器中.
同样复制公钥pkN′-1来扩充环大小到N*,得到更新后的环L′.将L′存入新用户的电表和集中器中.
② 集中器Con使用其签名私钥skC对更新后的环L′进行签名.调用签名程序qTESLA.Sign(L′,skC)得到签名SigC(L′),然后将信息-签名对(L′,SigC(L′))广播给集中器下辖的所有用户.
③ 环内用户的电表收到签名后,使用集中器公钥pkC对签名SigC(L′)进行验证.调用植入电表计算模块的签名验证程序qTESLA.Ver(L′,SigC(L′)),若验证通过则更新其中存储的系统公开参数PSP=(pp,L′,pkC).
用户动态撤销的过程同用户加入相似,将用户的公钥从环中删除,集中器更新环后对其进行签名然后广播给各智能电表以更新系统公开参数,故不再赘述.
4 系统分析
4.1 安全性分析
我们给出智能电网中关于个人用户隐私性的形式化定义:在数据采集过程中,智能电表Met向集中器Con发送数据,任何实体(包括集中器)都无法将每个合法用户的身份与它的数据消息相匹配.也就是说,数据的上传和认证不会泄露电表的身份信息.
本文提出的数据采集方案拥有用户身份匿名性和消息认证性,其安全性基于第2节所讨论的可链接环签名方案LRS的正确性和安全性.LRS的安全性是可以归约到Module-SIS困难问题上的,由于此问题在量子计算机上仍是困难的,所以此可链接环签名方案面对量子攻击仍然可以正确的隐藏签名者的身份信息.故数据采集方案也同样满足身份匿名性,并且可以实现抗量子计算的隐私保护.
4.2 性能分析
由于用户动态加入和撤销并不会频繁进行,故我们主要集中分析对智能电表要求更高的数据发送阶段.
我们对3.2节中数据上传阶段每个智能电表的通信量进行分析,此阶段电表将发送对数据的签名给集中器.记用户个数为N,根据2.3节的讨论我们得知每个智能电表在发送数据阶段的通信量为O(log N)级别,对于单次协议Σ0,其计算量为O(N log N)级别,而签名时LRS_Sign的迭代次数的期望值为M2=O(1),故电表计算量为O(N log N).
将本文方案同相关工作进行比较,如表3所示:
Table 3 The Comparisons of Different Schemes on Function and Performance
表3 相关工作功能与性能对比

SchemeComputationof meterCommunicationtrafficQuantumResistantDynamicUsersTrackingFaulty UsersWhether a trusted third partyis required during operationRef [22]O(N)O(N)NoNoYesYesRef [23]O(N)O(N)NoNoYesNoOursO(N logN)O(logN)YesYesYesNo
4.3 本文方案的优势
我们的后量子的智能电表隐私保护方案利用了基于格的可链接环签名方案的匿名性和可链接性以及格密码的抗量子计算能力,从而构造一个拥有隐私保护、异常检测和用户动态加入及撤销功能的隐私保护系统.本方案的优势有3个方面:
1) 良好的可行性.分析结果显示,我们的方案在有效保护用户隐私的同时,可以在一轮通信的条件下实现数据采集.并且由于选取的可链接环签名大小为对数级别,所以在通信量上具有优势.
2) 可扩展性.具有可行性的后量子签名方案(如qTESLA)使得本方案支持用户的动态加入与撤销.所以当用户规模改变时,可以支持用户设备数量的改变.并且本文方案以小区为单位,利于监管.
3) 抗量子计算.由于供电设备的使用寿命往往会持续数十年,本方案采用基于格的密码学后量子密码体制,面对或将到来的量子计算时代仍然可以实现隐私保护,满足抗量子计算的安全需求.
5 总结及展望
本文提出了一个后量子的智能电表隐私保护系统并对其进行了安全分析.此系统在保护用户隐私的前提下,可以支持动态用户加入与撤销和异常检测以及故障用户追踪等功能,并且拥有抗量子计算的隐私保护能力.为了实现此系统,我们选择了一个基于格的短的环签名方案,为其增添可链接性.该可链接环签名方案的尺寸在基于格的次线性大小的环签名中有很大的优势,所以本文的隐私保护方案在抗量子隐私保护领域具有很大的实用性.未来我们将致力于提高方案效率并且完善方案的功能.
由于当今智能生活的普及,除智能电表之外,智能水表以及智能燃气表等设备也逐渐应用于现实生活并且取代传统水表和燃气表,它们同智能电表拥有相似的安全与隐私问题,未来我们的工作或将扩展到这些领域.
[1]Tan Song, De D, Song Wenzhan, et al. Survey of security advances in smart grid: A data driven approach[J]. IEEE Communications Surveys & Tutorials, 2017, 19(1): 397-422
[2]Zhao Jia, Liu Jiqiang, Qin Zhan, et al. Privacy protection scheme based on remote anonymous attestation for trusted smart meters[J]. IEEE Transactions on Smart Grid, 2018, 9(4): 3313-3320
[3]Sanket D, Rabei A, Naveen C, et al. A survey of privacy preserving schemes in IoE enabled smart grid advanced metering infrastructure[J]. Cluster Computing, 2019, 22(1): 43-69
[4]Zhang Wenliang, Liu Zhuangzhi, Wang Mingjun, et al. Research status and development trend of smart grid[J]. Power System Technology, 2009, 33(13): 1-11 (in Chinese)
(张文亮, 刘壮志, 王明俊, 等. 智能电网的研究进展及发展趋势[J]. 电网技术, 2009, 33(13): 1-11)
[5]Mcdaniel P, Mclaughlin S. Security and privacy challenges in the smart grid[J]. IEEE Security AND Privacy, 2009, 7(3): 75-77
[6]Ericsson G N. Cyber security and power system communication—essential parts of a smart grid infrastructure[J]. IEEE Transactions on Power Delivery, 2010, 25(3): 1501-1507
[7]National Institute of Standards and Technology. Guidelines for smart grid cybersecurity[OL]. 2014. [2019-05-10]. https:
 nvlpubs.nist.gov
nvlpubs.nist.gov nistpubs
nistpubs ir
ir 2014
2014 NIST.IR.7628r1.pdf
NIST.IR.7628r1.pdf
[8]National Institute of Standards and Technology. Standards for security categorization of federal information and information systems[OL]. 2004. [2019-03-06]. https:
 www.nist.gov
www.nist.gov publications
publications standards-security-categorization-federal-information-and-information-systems
standards-security-categorization-federal-information-and-information-systems
[9]Pathan A S K, Fadlullah Z M, Fouda M M, et al. Information integrity in smart grid systems[J]. Information Systems, 2015, 53: 145-146
[10]Wang Wenye, Lu Zhou. Cyber security in the smart grid: Survey and challenges[J]. Computer Networks, 2013, 57(5): 1344-1371
[11]Khurana H, Hadley M, Lu Ning, et al. Smart-grid security issues[J]. IEEE Security and Privacy, 2010, 8(1): 81-85
[12]Alam A. A novel non-cryptographic security services for advanced metering infrastructure in smart grid[J]. Communications on Applied Electronics, 2015, 3(7): 35-39
[13]Sharma A, Vibha O. Implementation of cryptography for privacy preserving data mining[J]. International Journal of Database Management Systems, 2010, 2(3): 57-65
[14]Vukovic O, Dan G, Bobba R B. Confidentiality-preserving obfuscation for cloud-based power system contingency analysis[C] 
 Proc of IEEE Int Conf on Smart Grid Communications. Piscataway, NJ: IEEE, 2013: 432-437
Proc of IEEE Int Conf on Smart Grid Communications. Piscataway, NJ: IEEE, 2013: 432-437
[15]Borden A R, Molzahn D K, Ramanathan P, et al. Confidentiality-preserving optimal power flow for cloud computing[C] 
 Proc of the 2012 50th Annual Allerton Conf on Communication, Control, and Computing (Allerton). Piscataway, NJ: IEEE, 2012: 1300-1307
Proc of the 2012 50th Annual Allerton Conf on Communication, Control, and Computing (Allerton). Piscataway, NJ: IEEE, 2012: 1300-1307
[16]Sun Xiaoxun, Wang Hua, Li Jiuyong, et al. Satisfying privacy requirements before data anonymization[J]. Computer Journal, 2012, 55(4): 422-437
[17]Zhang Ji, Li Hongzhou, Liu Xuemei, et al. On efficient and robust anonymization for privacy protection on massive streaming categorical information[J]. IEEE Transactions on Dependable and Secure Computing, 2017, 14(5): 507-520
[18]Cheung J, Chim T, Yiu S, et al. Credential-based privacy-preserving power request scheme for smart grid network[C] 
 Proc of 2011 IEEE Global Telecommunications Conf. Piscataway, NJ: IEEE, 2011: 1-5
Proc of 2011 IEEE Global Telecommunications Conf. Piscataway, NJ: IEEE, 2011: 1-5
[19]Diao Feng, Zhang Fangguo. Full privacy preserving smart metering system[J]. Journal of Cryptologic Research, 2014, 1(4): 400-409 (in Chinese)
(刁凤, 张方国. 智能电表的完整隐私保护系统[J]. 密码学报, 2014, 1(4): 400-409)
[20]Zargar S H M, Yaghmaee M H. Privacy preserving via group signature in smart grid[C OL]
OL] 
 Proc of the 1st Congress of Electric Industry Automation. 2013 [2019-06-01]. http:
Proc of the 1st Congress of Electric Industry Automation. 2013 [2019-06-01]. http:
 confnews.um.ac.ir
confnews.um.ac.ir images
images 41
41 conferences
conferences eiac2013
eiac2013 207_2.pdf
207_2.pdf
[21]Zhang Muling. Security and privacy issues in smart grid[D]. Shanghai: Shanghai Jiao Tong University, 2014 (in Chinese)
(张木玲. 智能电网中若干安全和隐私问题的研究[D]. 上海: 上海交通大学, 2014)
[22]Wang Wei. Smart grid payment scheme based on ring signature and certificateless signature[D]. Qingdao: Ocean University of China, 2015 (in Chinese)
(王玮. 基于环签名和无证书签名的智能电网缴费方案[D]. 青岛: 中国海洋大学, 2015)
[23]Liu Wenming. Research on security mechanism of smart meter in data transmission[D]. Guangzhou: Sun Yat-sen University, 2013 (in Chinese)
(刘文明. 智能电能表数据传输的安全机制研究[D]. 广州: 中山大学, 2013)
[24]Chen L, Jordan S, Liu Yikai, et al. Report on Post-Quantum Cryptography[M]. Gaithersburg: US Department of Commerce, National Institute of Standards and Technology, 2016
[25]Zhang Pingyuan, Jiang Han, Cai Jie, et al. Recent advances in lattice-based cryptography[J]. Journal of Computer Research and Development, 2017, 54(10): 2121-2129 (in Chinese)
(张平原, 蒋瀚, 蔡杰, 等. 格密码技术近期研究进展[J]. 计算机研究与发展, 2017, 54(10): 2121-2129)
[26]Esgin M F, Steinfeld R, Sakzad A, et al. Short lattice-based one-out-of-many proofs and applications to ring signatures[OL C]
C] 
 Cryptology ePrint Archive, 2018. [2018-10-15]. https:
Cryptology ePrint Archive, 2018. [2018-10-15]. https:
 eprint.iacr.org
eprint.iacr.org 2018
2018 773
773
[27]Chor B, Goldwasser S, Micali S, et al. Verifiable secret sharing and achieving simultaneity in the presence of faults (extended abstract)[C] 
 Proc of the 26th Annual Symp on Foundations of Computer Science. Piscataway, NJ: IEEE, 1985: 383-394
Proc of the 26th Annual Symp on Foundations of Computer Science. Piscataway, NJ: IEEE, 1985: 383-394
[28]Langlois A, Stehlé D. Worst-case to average-case reductions for module lattices[J]. Designs, Codes and Cryptography, 2015, 75(3): 565-599
[29]Lyubashevsky V. Lattice signatures without trapdoors[G] 
 LNCS 7237: Advances in Cryptology-EUROCRYPT 2012. Berlin: Springer, 2012: 738-755
LNCS 7237: Advances in Cryptology-EUROCRYPT 2012. Berlin: Springer, 2012: 738-755
[30]Rivest R L, Shamir A, Tauman Y. How to leak a secret[C] 
 Proc of the 7th Int Conf on the Theory and Application of Cryptology and Information Security: Advances in Cryptology. Berlin: Springer, 2001: 552-565
Proc of the 7th Int Conf on the Theory and Application of Cryptology and Information Security: Advances in Cryptology. Berlin: Springer, 2001: 552-565
[31]Bootle J, Cerulli A, Chaidos P, et al. Short accountable ring signatures based on DDH[G] 
 LNCS 9326: Computer Security (ESORICS 2015). Berlin: Springer, 2015: 243-265
LNCS 9326: Computer Security (ESORICS 2015). Berlin: Springer, 2015: 243-265
[32]Groth J, Kohlweiss M. One-out-of-many proofs: Or how to leak a secret and spend a coin[G] 
 LNCS 9057: Advances in Cryptology (EUROCRYPT 2015). Berlin: Springer, 2015: 253-280
LNCS 9057: Advances in Cryptology (EUROCRYPT 2015). Berlin: Springer, 2015: 253-280
[33]Liu J K, Wei V K, Wong D S. Linkable spontaneous anonymous group signature for ad hoc groups[G] 
 LNCS 3108: Information Security and Privacy. Berlin: Springer, 2004: 325-335
LNCS 3108: Information Security and Privacy. Berlin: Springer, 2004: 325-335
[34]Bindel N, Akleylek S, Alkim E, et al. Submission to NIST’s post-quantum project (2nd round): Lattice-based digital signature scheme qTESLA[OL]. 2019. [2019-04-09]. https:
 qtesla.org
qtesla.org wp-content
wp-content uploads
uploads 2019
2019 04
04 qTESLA_round2_04. 26.2019.pdf
qTESLA_round2_04. 26.2019.pdf



