高斯噪声(Gaussian noise, GN)和脉冲噪声(impulse noise, IN)是2种常见且在各类文献中广为讨论的参数化噪声模型,高斯噪声模型常用噪声水平值(noise level)[1-2]来反映图像受噪声干扰的严重程度,脉冲噪声模型则以噪声比例(noise ratio)[3]作为描述噪声严重程度的指标.研究者们已经针对这2种类型的噪声提出了大量行之有效的降噪算法,但这些算法多是针对图像仅受高斯[4-5]或者脉冲噪声[6-7]单一干扰情况下所设计的.在现实中,图像极易同时受高斯和脉冲噪声干扰,简单地先后利用脉冲降噪算法和高斯降噪算法对其降噪很难实现高质量降噪的目的[8].这是因为当图像受高斯和脉冲噪声混合干扰后,2种噪声互相影响,难以将两者完全区分开并逐一处理.
近10年来,高斯-脉冲混合噪声降噪逐渐成为图像降噪领域的热点问题[9-15].早期Cai等人[9]在变分框架(variational framework)下基于l1数据保真项(data-fidelity term)以及引入了包含图像边缘局部相似先验信息的Mumford-shah正则项对混合噪声处理.为降低实现难度,该算法首先将当前像素点的亮度值与局部窗口中值滤波器的输出值进行比较,检测并移除图像中可能被脉冲噪声破坏的像素点,然后在变分框架下对图像进行复原.Cai算法的降噪效果在很大程度上依赖于对脉冲噪声检测的精度,这意味着其降噪效果会随着图像受噪声干扰严重程度的加重而显著降低.随后,Liu等人[12]基于最大似然估计(maximum likelihood estimation)和稀疏表示(sparse representation)技术提出了一种通用加权l2-l0范数能量最小化模型(energy minimi-zation model),并利用更容易逼近求解的加权保真度(weighting data fidelity)函数解决了高斯-脉冲混合噪声的降噪问题.该算法能够在很好保持图像纹理的同时有效地去除高斯-脉冲混合噪声,但由于字典学习和稀疏编码均需要耗费大量计算资源,且当噪声水平较高时,需要多次迭代才能获得较好的降噪效果,导致该算法的执行效率比较低.近期,Jiang等人[13]提出了一种稀疏非局部正则化的加权编码(weighted encoding with sparse nonlocal regulari-zation, WESNR)混合降噪算法.该算法没有显式的脉冲噪声检测过程,而是采用加权编码(weighted encoding)的方式隐式地统一处理高斯和脉冲噪声,通过将图像稀疏性先验和非局部相似先验信息集成到正则项中并引入到变分框架下完成图像降噪任务.稀疏表示和非局部相似技术的联合使用,使得该算法对高斯-脉冲混合噪声的降噪效果达到了比较高的水平,但执行效率仍然较低.类似地,Huang等人[14]利用自然图像所具有的非局部自相似性(nonlocal self-similarity)和低秩性(low-rank),提出了一种基于拉普拉斯尺度混合(Laplacian scale mixture, LSM)模型和非局部低秩正则化(nonlocal low-rank regularization, NLR)的LSM-NLR高斯-脉冲混合噪声降噪算法.虽然文献[13-14]中的工作考虑了图块之间的相似性,但忽略了图块之间其实也存在差异.为此,Liu等人[15]提出了一个加权联合稀疏表示非局部正则化(weighted joint sparse nonlocal regularization, WJSR)模型对高斯-脉冲混合噪声建模,并采用加权正交匹配追踪(weighted simultaneous orthogonal matching pursuit, W-SOMP)贪婪算法求解高度非凸的WJSR模型全局最优解.最后,基于WJSR模型、稀疏错误(sparse errors)和全局图像先验知识定义目标函数,并通过求解这个目标函数的最优值实现高斯-脉冲混合噪声的去除.该算法的执行效率受制于图像大小和噪声严重程度.综上所述,现有的各类高斯-脉冲混合降噪算法多是在主流高斯降噪算法的基础上进行扩展,使其也可以同时处理脉冲噪声.这些混合噪声降噪算法通常基于反映各种图像先验信息的正则化项来构建目标函数,在迭代优化技术支撑下通过求解目标函数最优值的方式完成降噪任务.由于算法中字典学习、非局部估计、低秩逼近等关键模块的计算复杂度太高,导致执行时间过长.而降噪算法作为诸多图像处理任务的前置预处理模块,较长的执行时间将严重拖累图像处理系统的整体性能.因此,现有的高斯-脉冲混合噪声降噪算法在执行效率方面亟待提高.
近年来,卷积神经网络(convolutional neural network, CNN)因其强大的学习能力在图像降噪领域[4-5,16-17]得到了大量的应用,所获得的性能指标超越了许多经典的算法.例如,Zhang等人[4]提出了一个端到端的CNN卷积神经网络高斯降噪(denoising convolutional neural network, DnCNN)算法,能在给定高斯噪声水平值的情况下获得令人满意的降噪效果.基于CNN训练技术的各类降噪算法在执行效率和降噪效果2个方面(尤其是执行效率方面)具有显著的综合优势,使其有望成为解决高斯-脉冲混合噪声降噪问题的新途径,但也存在若干问题需要进一步解决.例如,虽然DnCNN降噪算法可以完成盲降噪任务,但是其降噪效果会有一定程度的下降且只能处理噪声水平值在[0,55]范围内的高斯噪声.究其原因在于:DnCNN本质上是基于训练策略(training-based approach)实现的,其降噪性能在很大程度上受制于训练降噪模型时所使用的图像与待降噪图像受噪声干扰的模式、程度是否趋于一致,两者越接近,则DnCNN算法的降噪效果越好.为训练盲降噪模型,训练图像集合中就必须涵盖各种受不同噪声水平干扰的噪声图像,这必然导致模型收敛比较困难,故盲降噪版DnCNN算法的降噪效果要比非盲降噪版的差一些.为提高基于训练的降噪算法的降噪效果,一个自然的想法就是利用某种划分机制,将训练图像集合划分为多个在噪声失真程度上大致相同的子集,并在各个图像子集上训练相适应的降噪模型.这样对于给定的待降噪图像,只要能找到一个合适的降噪模型(训练集合中图像受噪声干扰的程度与待降噪图像近似)对其进行复原处理,就能保证降噪效果.近期,文献[18]中提出了一种基于类感知(class-aware)的全连接卷积神经网络(fully-convolutional neural network, FCNN)降噪算法,根据图像所表达的语义内容(例如人脸、宠物、花、起居室、街道等)的不同,将训练的图像集合细分为若干个具有不同语义主题的子集并训练与之相匹配的精调模型(fine-tuning model).虽然这种实现策略确实在一定程度上提高了降噪效果,但根据图像语义内容构建图像子集的方法的普适性不强,因为自然图像内容的种类远远大于文献[18]中提到的那几种.另外,即便图像语义内容相同,如果训练降噪模型所用图像的噪声严重程度与待降噪图像相差比较大,仍然不能获得令人满意的降噪效果.故需要寻找一种普适性更好的划分图像训练子集的标准.
通过对大量受不同高斯-脉冲混合噪声模式(各种不同噪声水平的高斯噪声与不同噪声比例的脉冲噪声组合)干扰图像的峰值信噪比(peak signal to noise ratio, PSNR)统计分析后发现:图像受到混合模式近似(噪声水平或者噪声比例值相近)的混合噪声干扰后,其PSNR值ζPSNR分布范围非常接近且分布在特定的区间范围内,受图像内容的影响不大.因此,图像的PSNR质量值可以作为衡量混合噪声类型和强度的标准,它是一种比基于图像语义内容划分模型训练图像子集更具有普适性的分类依据.为此,提出了一种基于图像质量感知的快速盲降噪算法(image quality-aware fast blind denoising algorithm, IQA-FBDA).该算法首先利用基于相对浅层的CNN卷积神经网络训练的图像质量评估模型估计给定待降噪图像的ζPSNR值,然后依据该值查找预先构建的混合噪声模式分类字典(mixed noise pattern classification dictionary, MNPCD)以确定其所属子类类别,最后调用预先训练好的与该类别相匹配的深层CNN降噪模型快速而高质量地完成盲降噪任务.大量的实验数据表明:所提出的IQA-FBDA算法在降噪效果上达到了当前主流混合降噪算法的同等水平,而在执行效率方面则比现有的主流高斯-脉冲混合降噪算法有显著提升,更适用于那些对执行时间有严格要求的系统.
1 相关工作
1.1 脉冲噪声模型
脉冲混合噪声模型可以定义为
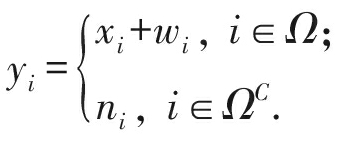
(1)
其中,yi,xi,wi,ni分别表示第i个位置的噪声像素点、原始像素点、高斯噪声和脉冲噪声;Ω和ΩC分别代表受高斯噪声和脉冲噪声干扰的像素点位置集合.假定像素点亮度值的取值范围为[mmin,mmax](对于8 b的灰度图像,mmin=0,mmax=255),那么固定脉冲噪声(fixed-valued impulse noise, FVIN)的取值为mmin或者mmax,随机脉冲噪声(random-valued impulse noise, RVIN)的像素值为整个灰度空间[mmin,mmax]之间的随机值,高斯噪声服从零均值正态分布![]()
1.2 DnCNN降噪算法简介
Zhang等人[4]通过对VGG(visual geometry group)网络模型[19]进行修改,设计出了一个端到端的DnCNN前馈去噪卷积神经网络模型来实现噪声图像与噪声信号的分离(即图像降噪)任务.DnCNN降噪算法将残差图像作为网络的输出,利用残差学习(residual learning)技术达到图像降噪的目的.形式上,假设共有N张原始无失真图像,对其中任一图像x添加噪声得到噪声图像y,将噪声图像y和残差图像v=y-x分别作为网络的输入输出对(training pairs, TP),训练DnCNN降噪模型.在降噪时,对于给定的噪声图像y,采用DnCNN模型得到残差图像R(y)≈v,降噪后的图像为![]() 即只要将噪声图像减去通过网络模型获得的残差图像即可得到降噪后的复原图像.CNN模型训练的目标函数为残差图像v与估计残差图像R(y)之间的平均均方误差
即只要将噪声图像减去通过网络模型获得的残差图像即可得到降噪后的复原图像.CNN模型训练的目标函数为残差图像v与估计残差图像R(y)之间的平均均方误差
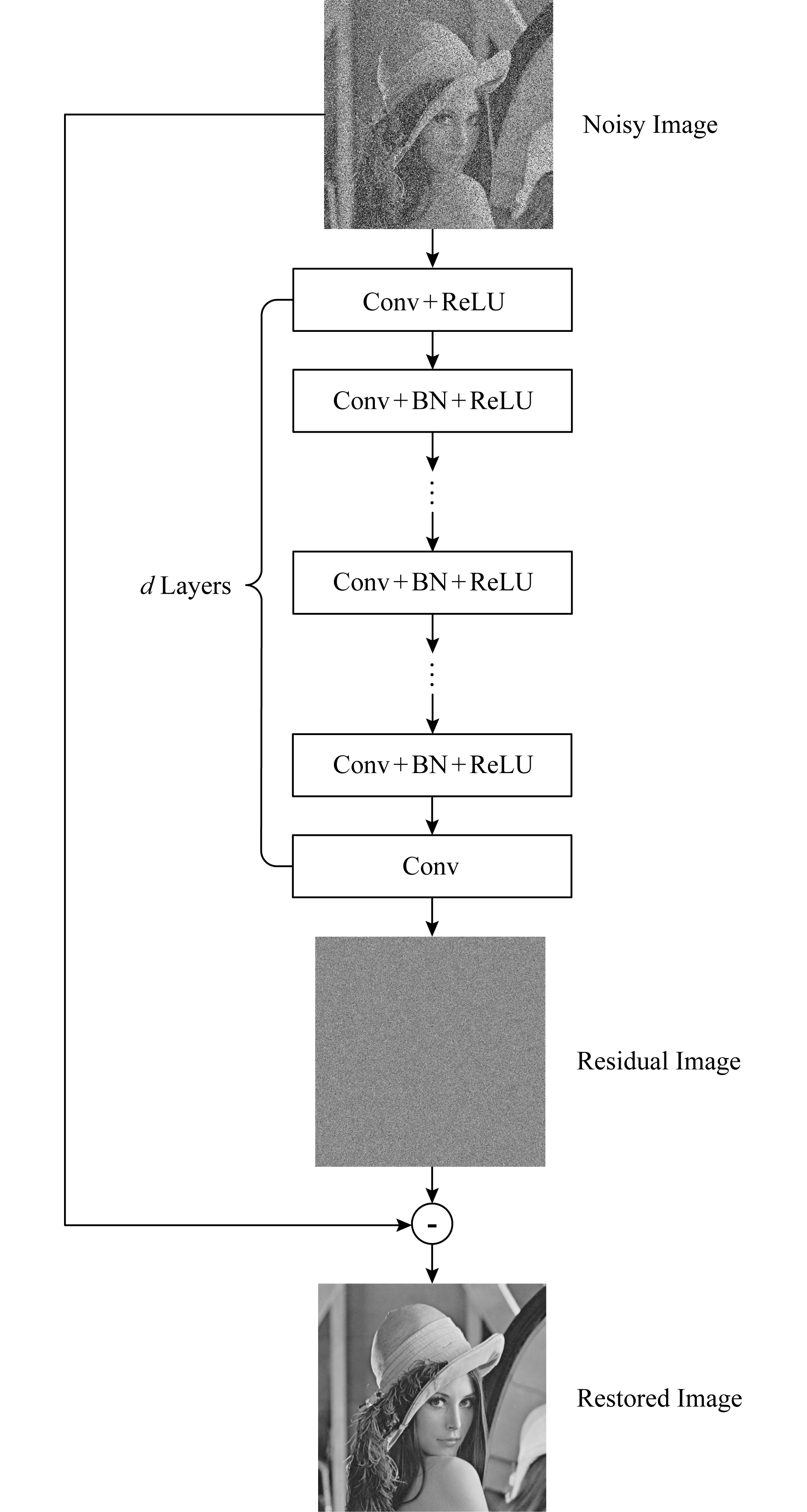
Fig. 1 The network architecture of DnCNN
图1 DnCNN网络的组成架构
(2)
其中,yi,xi分别表示第i(i=1,2,…,N)张噪声图像及其对应的原始无失真图像,Θ为CNN网络参数.
如图1所示,DnCNN网络模型框架的核心由3种不同类型的卷积层构建而成.假设网络深度为d,第1层采用卷积层(convolutional layer, Conv)加修正线性单元(rectified linear unit, ReLU)[20],即图1所示的(Conv+ReLU).其中,ReLU是作为激活函数为网络提供非线性.该层使用了64个大小为3×3×1的滤波器产生64个特征映射图;第2~(d-1)层在卷积层和ReLU之间加入了批归一化(batch normalization, BN)操作,即图1所示的(Conv+BN+ReLU),中间层使用64个大小为3×3的滤波器.BN操作可缓解随机梯度下降(stochastic gradient descent, SGD)训练算法产生的内部协变量转移(internal covariate shift)现象,以提高网络的训练效率[21];最后1层只用了1个卷积层(Conv)输出残差图像.
2 IQA-FBDA算法
2.1 设计思想与技术路线
由引言可知,基于训练策略实现的CNN降噪算法其性能取决于模型的训练集,依据图像的ζPSNR值划分噪声图像子集比文献[18]中基于图像语义内容进行划分更具普适性.因此,提出了一种基于图像质量感知的高斯-脉冲混合噪声降噪算法.该算法流程框图如图2所示,实现过程共分为2个阶段:
1) 训练阶段.首先在大量无失真图像上添加不同噪声水平和噪声比例的高斯-脉冲混合噪声构成噪声图像总集,基于对应的无失真图像计算各个噪声图像的ζPSNR值.然后将整个ζPSNR值的动态变化空间细分为16个子范围,记录每个子范围内图像的高斯噪声水平值和脉冲噪声比例值以构建MNPCD噪声模式分类字典.此外,利用深层DnCNN网络架构(对DnCNN网络架构进行扩展训练,使其可用于高斯-脉冲混合噪声的降噪)训练与各个子集相匹配的专用精调降噪模型.考虑到实际降噪时仅有待降噪图像本身可用(没有无失真图像作为参考图像,无法计算ζPSNR值),本文利用噪声图像总集及其对应的图像质量值,基于CNN卷积神经网络技术构建了1个预测能力强大的图像质量评估模型,直接基于待降噪图像本身无参考地估计它的ζPSNR值作为图像受混合噪声干扰严重程度的度量.
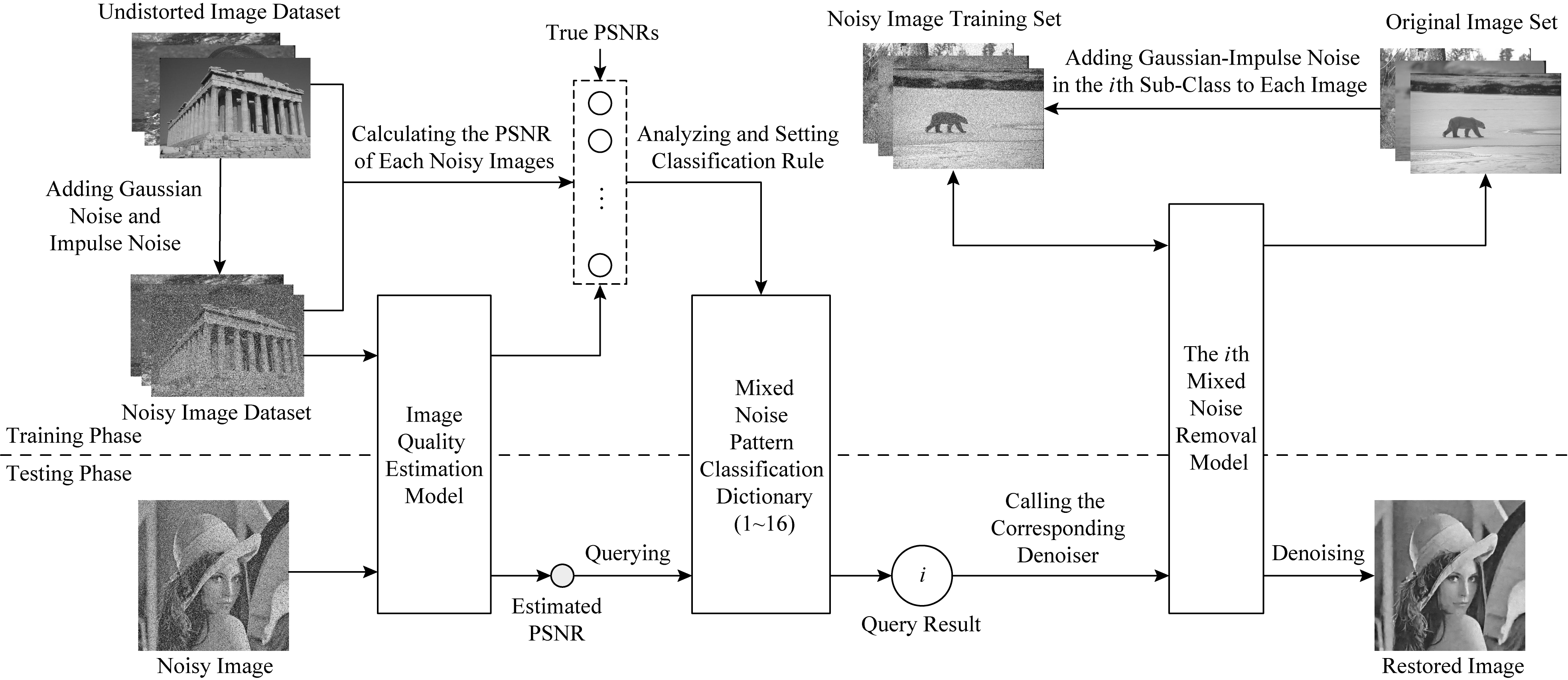
Fig. 2 The overall framework of IQA-FBDA
图2 IQA-FBDA算法的流程框图
2) 降噪阶段.对于1张给定的噪声图像,首先利用图像质量评估模型估计图像的ζPSNR值,然后根据该质量值查询MNPCD噪声模式分类字典即可确定待降噪图像所属图像子集的类别,从而调用预先训练好的对应类别的混合噪声降噪模型实现盲降噪任务.所获得的降噪算法在降噪效果和执行效率2方面都表现出令人满意的性能.
2.2 混合噪声模式分类字典的构建
不同级别的高斯噪声(噪声水平为5~30,间隔5)和脉冲噪声(噪声比例为0.1~0.5,间隔0.05)构成了54种混合组合情况的高斯-脉冲混合噪声,分别加入到BSD数据库[22]中的200张原始无失真图像上构成噪声图像集合,计算每张噪声图像的ζPSNR值作为评价图像质量的指标.根据ζPSNR值某一区段内混合噪声模式出现的种类和频率相对固定的特点,将所有的组合情况分为16类(其中,将高斯噪声水平σ<5、脉冲噪声比例r<0.1的图像单独分为第16类,该类图像受混合噪声干扰的程度比较小),每一类别具体包括的噪声组合模式以及相应的图像质量值范围列在表1~2中.
由表1可知:脉冲噪声比例相同时,高斯噪声水平相差10以内的图像往往划分到同一个类中,表明高斯噪声水平的变化对图像质量的影响不大,且脉冲噪声比例越大,高斯噪声对图像质量的影响越不明显;当高斯噪声水平相同时,脉冲噪声比例仅仅相差0.05却没有划分到同一类,表明脉冲噪声对图像质量的影响非常大.当高斯噪声水平与脉冲噪声比例都不相同时,图像在某些时候有可能划分到同一个类中.例如σ=30,r=0.15和σ=15,r=0.20的噪声图像都被划分为第5类.由表2可知:各类图像质量值的变化范围在1.0以内,当脉冲噪声比例较小时、图像质量值相差较大(0.6~0.9)、脉冲噪声比例较大时,图像质量值相差较小(0.3~0.5).图3给出了不同类别的噪声图像的视觉对比图,其中,图3(a)~(c)被划分第5类,图3(d)~(f)被划分为第10类.由图3可知:类别不同的图像在视觉上差异比较明显,而属于同一类的图像虽然受不同模式的混合噪声干扰,但是视觉效果差别甚微,只有通过图像的ζPSNR值才能发现图像受不同模式的噪声干扰后发生了细微变化.综上所述,基于表1~2可以构建MNPCD混合噪声模式分类字典,对于任意给定的某个图像质量值,直接查找该分类字典(即表1和表2)就可以判定图像所属类别,并可以知道该类别主要包括哪些混合组合模式.这样,在准备深层降噪模型所需要的训练数据时,就可以按照各个子类中的混合模式生成相应的训练数据(适当地在该类噪声水平值和噪声比例值变化范围内通过插值法生成部分训练图像),从而确保所获得的训练图像集合与待降噪图像降质程度近似.
Table 1 Noise Combination Patterns Corresponding to theClasses of Noisy Images Subsets
表1 各类噪声图像子集对应的噪声组合模式

NoiseRatios rGaussian Noise Levels σ510152025300.101122340.153334450.204455670.256667880.3088899100.35910101011110.401111111212130.451313131314140.50141414151515
Table 2 The PSNR Range of Each Noisy Image Subset
表2 各类噪声图像子集所对应的PSNR值范围 dB

ClassζPSNRClassζPSNRClassζPSNRClassζPSNRClassζPSNR117.8-18.5415.3-16.0713.9-14.31012.75-13.101311.8-12.1216.9-17.8514.7-15.3813.4-13.91112.40-12.751411.5-11.8316.0-16.9614.3-14.7913.1-13.41212.10-12.4015<11.5

Fig. 3 Visual comparison of different categories of noisy images
图3 不同类别的噪声图像在视觉上的对比
2.3 图像质量评估模型
考虑到执行复杂度,采用浅层的CNN卷积神经网络结构在图块级(patch level)上实现图像质量评估模型,网络结构如图4所示.为训练该模型,选取了BSD数据库[22]中的200张图像作为训练集,加入不同模式的混合噪声后将其分解成大小为28×28的图块,将图块及其对应的ζPSNR值分别作为图4所示的网络结构的输入和输出.该预测模型执行预测任务时以图块作为输入,对于1张待降噪的噪声图像,随机从图像不同位置抽取30个大小为28×28的图块输入到网络,以获得的30个图块质量值的平均值代表整张待降噪图像最终的图像质量(可有效克服欠估计和过估计对预测结果的影响,排除图像内容对预测结果的影响,且执行效率高).图块大小设置为28×28以及每张图像选取的图块个数为30个是根据多次实验结果选择出的最优值.这样,根据估计出的图像质量值对照所创建的混合噪声模式分类字典就能确定待降噪图像的所属混合噪声类别.
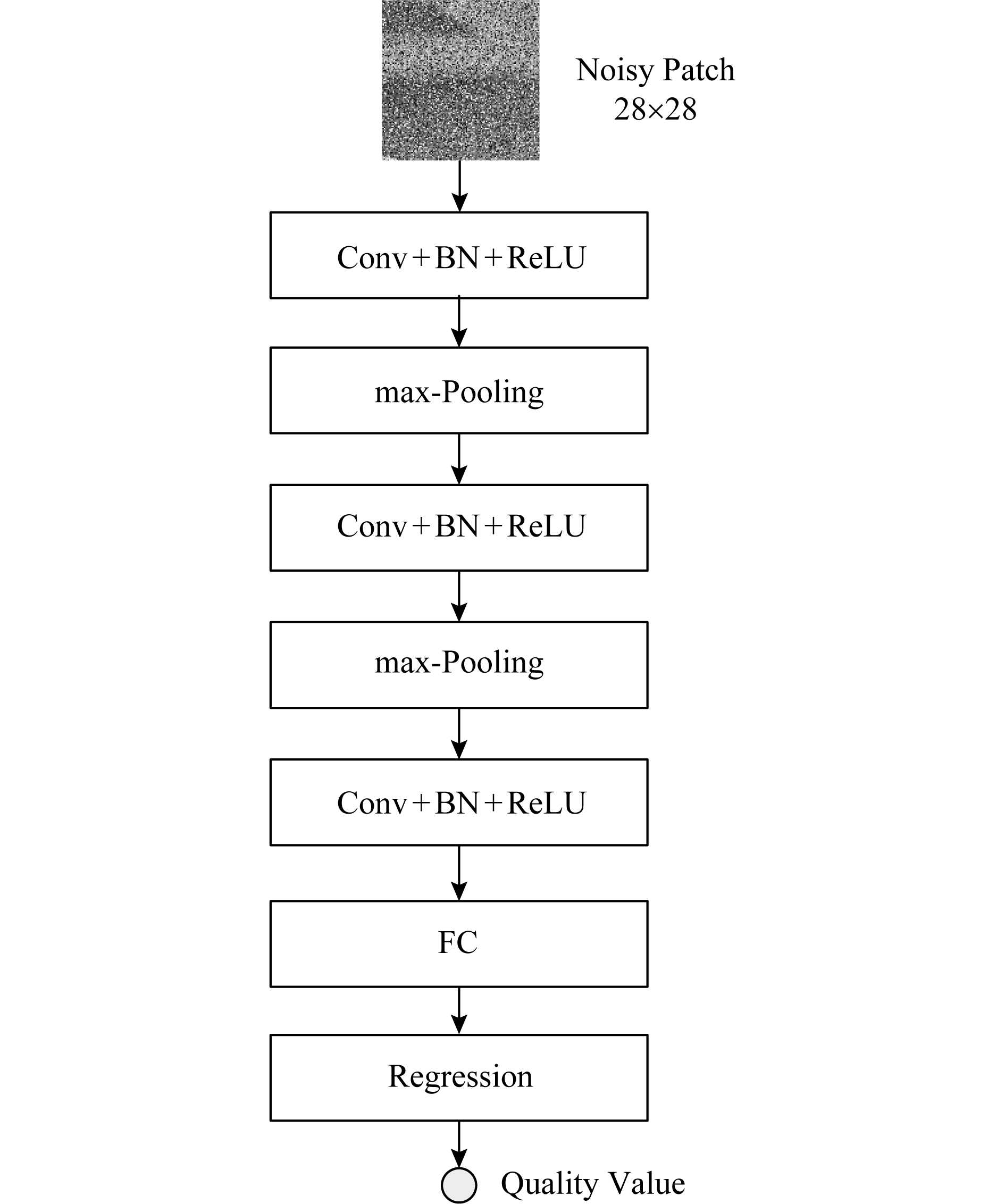
Fig. 4 The architecture of patch-based imagequality estimator
图4 基于图块级的图像质量评估模型
为了验证图像质量评估模型的准确性和混合噪声模式分类字典的有效性,在BSD数据库[22]中随机选取100张图像(与训练集不重叠)分别加入5种不同组合的混合噪声(如表3所示,以这5种模式组合为例),基于预测模型并根据分类字典确定各个噪声图像的类别,通过分类正确率衡量其有效性,具体实验数据列于表3中(σ表示高斯噪声水平,r代表脉冲噪声比例).由表3可知:分类正确率都在83%以上,最佳的结果达到了97%,说明所创建的噪声模式分类字典和训练的图像质量估计模型是可靠的.
Table 3 Classification Accuracy of the Image QualityEstimator
表3 图像质量评估模型的分类准确性

Gaussian-Impulse Mixed NoiseσrCorrectClassificationIncorrectClassificationAccuracyRate∕%100.30831783100.5095595200.40851585300.30831783300.5097397
2.4 深层降噪模型

Fig. 5 Some representative images in BSD database
图5 BSD数据库中部分代表性图像
IQA-FBDA算法中完成混合噪声降噪功能的模型是以DnCNN算法中的深层网络结构为基础,对网络的训练数据(输入-输出)进行适当变更,使其能去除图像中的高斯-脉冲混合噪声.为了训练各个子类别对应的混合噪声降噪模型,从BSD数据库中选取200张图像构成原始图像集,对于MNPCD混合噪声模式分类字典第i个子类,对这些图像添加该子类包括的各种模式的高斯-脉冲混合噪声(为了获得更好的降噪效果,根据该子类噪声水平和噪声比例值变化范围用插值方法生成一定量的噪声图像作为训练数据),以滑动窗口的方式从准备好的训练集图像中提取若干个大小为40×40的图块作为网络的输入(所采用的参数均与DnCNN模型相同,训练图块个数达到240 000个),以噪声图块与对应无失真图块之间的残差映射图块作为输出.在降噪阶段,以整张噪声图像作为输入,将噪声图像减去降噪模型输出的残差图像即可直接得到复原图像.
2.5 降噪后再评估策略
鉴于图像质量评估模型预测精度,IQA-FBDA算法在实际应用时存在少量调用相邻子类降噪模型完成降噪任务的情况,导致在某些时候不能获得最优的降噪效果.为此,提出降噪后再评估策略进一步提升IQA-FBDA算法的降噪效果.具体地,在使用图像质量评估模型得到待降噪图像的ζPSNR值后,调用MNPCD混合噪声模式分类字典中与[ζPSNR-v,ζPSNR+v]区段内所重叠的各个降噪模型对噪声图像进行降噪,搜索范围参数v=0.7.然后,通过文献[1]中的算法评价各个降噪模型对噪声图像的降噪效果(该算法是噪声水平评估算法,其值越小,说明降噪后的图像质量越好).最后,选择最小评估值对应的复原图像作为最终的降噪结果.虽然降噪后再评估的策略使得算法的执行时间有所增加,但是基于CNN预训练的IQA-FBDA算法的全部执行时间相比于传统的混合噪声降噪算法来说仍然是非常少的.
3 实验结果与分析
3.1 实验设置
为了验证所提出IQA-FBDA算法的性能,分别在10张常用图像(被各经典文献采用,包括Lena,Boat,Barbara,House,Peppers等)、100张BSD纹理分割数据库[22]图像(不同于训练时所使用的图像,部分图像如图5所示)和100张自然场景图像(由文献[23-24]分别提供的90张和10张用于图像质量评价的图像构成)共3种不同图像类型的数据集上进行测试.参与对比的算法包括M-BM3D(median BM3D[25]),WESNR[13],LSM-NLR[14],WJSR[15]共4种具有代表性的降噪算法.其中,考虑到BM3D算法不适用于处理脉冲噪声且需要以已知噪声水平值作为入口参数,本文采用与文献[13]类似的做法,首先利用中值滤波移除噪声图像中的脉冲噪声,然后通过文献[1]的工作对去除脉冲噪声后的图像进行噪声水平估计,最后以该估计值作为BM3D算法的入口参数对已滤除脉冲噪声后的图像再次降噪以去除高斯噪声,改进后的算法记为M-BM3D.降噪效果的衡量指标为PSNR.所有算法运行的硬件平台均为Intel CoreTM i7-6700 3.40 GHz CPU处理器,16 GB内存.软件配置均为Windows 7操作系统,Matlab 2017b编程环境.
3.2 降噪效果比较
首先,为了验证IQA-FBDA算法去除高斯-随机脉冲混合噪声的有效性,对10张常用图像分别添加不同水平的高斯噪声(σ)和不同比例的脉冲噪声(r)构成混合噪声图像集,比较每张噪声图像使用各个对比算法复原后图像的ζPSNR值.限于篇幅,表4仅列出各算法在Lena,Barbara,Peppers这3张图像上的具体实验数据,表5则给出了各个算法在不同配置下在10张图像上所获得ζPSNR值的平均值.从表4~5可以看出,所提出的IQA-FBDA算法的降噪效果大部分情况下排在前2名,且复原图像的ζPSNR值与最优值相差甚微.
Table 4 PSNR Performance of Different Algorithms on Lena, Barbara, and Peppers Image
表4 各算法在单张噪声图像上的降噪效果对比
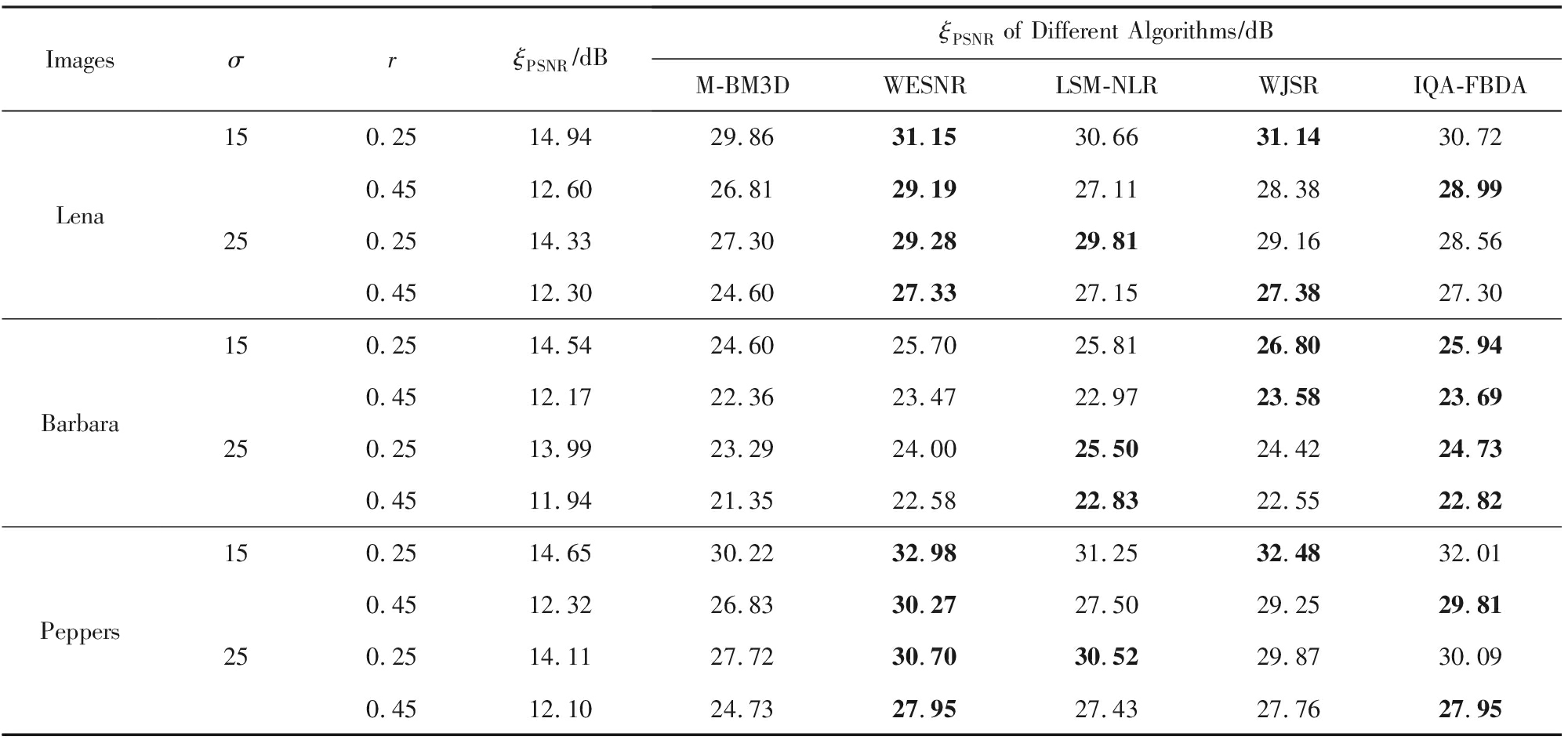
ImagesσrξPSNR∕dBξPSNR of Different Algorithms∕dBM-BM3DWESNRLSM-NLRWJSRIQA-FBDALenaBarbaraPeppers150.2514.9429.8631.1530.6631.1430.720.4512.6026.8129.1927.1128.3828.99250.2514.3327.3029.2829.8129.1628.560.4512.3024.6027.3327.1527.3827.30150.2514.5424.6025.7025.8126.8025.940.4512.1722.3623.4722.9723.5823.69250.2513.9923.2924.0025.5024.4224.730.4511.9421.3522.5822.8322.5522.82150.2514.6530.2232.9831.2532.4832.010.4512.3226.8330.2727.5029.2529.81250.2514.1127.7230.7030.5229.8730.090.4512.1024.7327.9527.4327.7627.95
Note: The top 2 results are bold.
Table 5 Average PSNR Performance of Each Algorithm on 10 Commonly Used Images
表5 各算法在10张常用图像上的平均降噪效果对比 dB
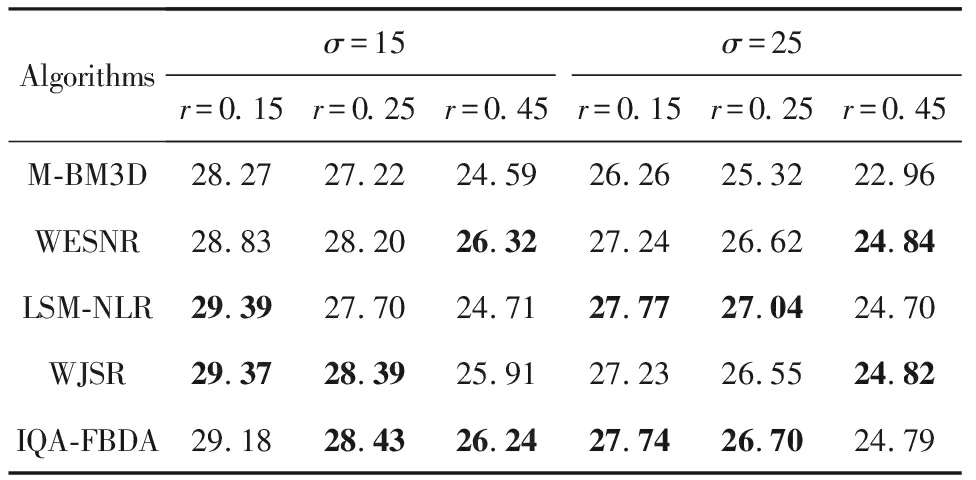
Algorithmsσ=15σ=25r=0.15r=0.25r=0.45r=0.15r=0.25r=0.45M-BM3D28.2727.2224.5926.2625.3222.96WESNR28.8328.2026.3227.2426.6224.84LSM-NLR29.3927.7024.7127.7727.0424.70WJSR29.3728.3925.9127.2326.5524.82IQA-FBDA29.1828.4326.2427.7426.7024.79
Note: The top 2 results are bold.
其次,为了验证IQA-FBDA算法的鲁棒性,在100张纹理图像和100张自然图像上分别进行测试,表6和表7分别列出了各算法在这2个测试图像集上不同高斯-脉冲混合噪声下的平均降噪效果.从表6~7可以看出,IQA-FBDA算法的降噪效果在大多数情况下是最优的.特别地,图像受到混合噪声干扰的程度越大,算法的降噪性能越好.考虑到表8所列的关于执行效率的数据,总体上IQA-FBDA算法在降噪效果和执行效率2个方面的综合性能要显著优于其他对比算法.需要说明的是:1) IQA-FBDA算法属于盲降噪算法,而WESNR算法、LSM-NLR算法和WJSR算法都是非盲降噪算法,需要人工设置参数,其真实性能在实际应用中并不能达到表4~7中所列数据的水平;2)固定脉冲噪声作为随机脉冲噪声的特例,所提出的IQA-FBDA算法也适用于-固定脉冲混合噪声的去除,且同样能获得令人满意的降噪效果.限于篇幅,这里不再给出具体实验数据.

Fig. 6 Visual comparison of denoising effect on Barbara image
图6 在Barbara图像上的降噪效果的视觉对比
Table 6 Average PSNR Performance of Each Algorithm on 100 Images from BSD Database
表6 各算法在100张BSD图像上的平均降噪效果对比 dB
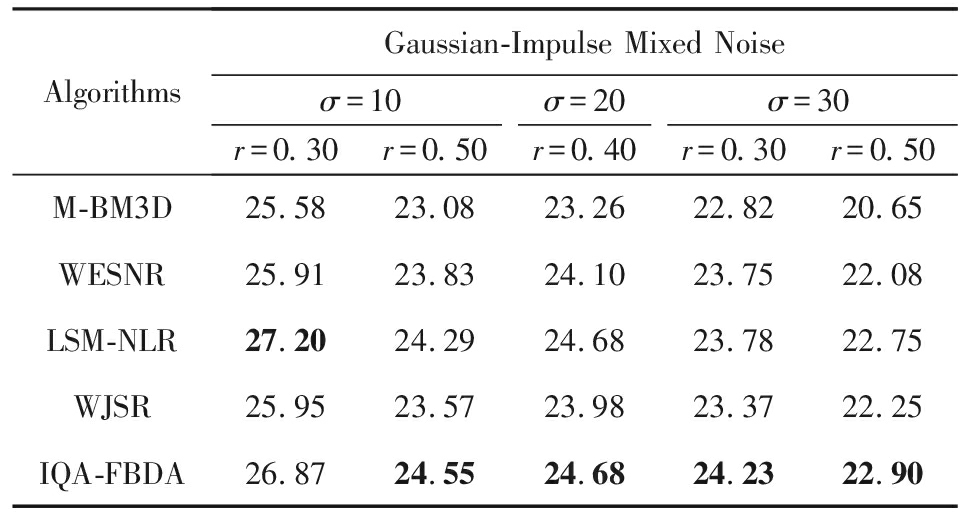
AlgorithmsGaussian-Impulse Mixed Noiseσ=10σ=20σ=30r=0.30r=0.50r=0.40r=0.30r=0.50M-BM3D25.5823.0823.2622.8220.65WESNR25.9123.8324.1023.7522.08LSM-NLR27.2024.2924.6823.7822.75WJSR25.9523.5723.9823.3722.25IQA-FBDA26.8724.5524.6824.2322.90
Note: The best values are bold.
最后,为了从视觉上对比各个算法的降噪效果,图6给出了各算法对添加了高斯-随机脉冲混合噪声(σ=15,r=0.25)的Barbara图像的降噪效果视觉对比图.从图6中可以看出,IQA-FBDA算法的降噪效果仅次于WJSR算法(但所提出的算法具有极高的执行效率),在视觉效果上两者相差甚微,表明IQA-FBDA算法在降噪效果方面是令人满意的.
Table 7 Average PSNR Performance of Each Algorithm on100 Natural Images
表7 各算法在100张自然图像上的平均降噪效果对比 dB
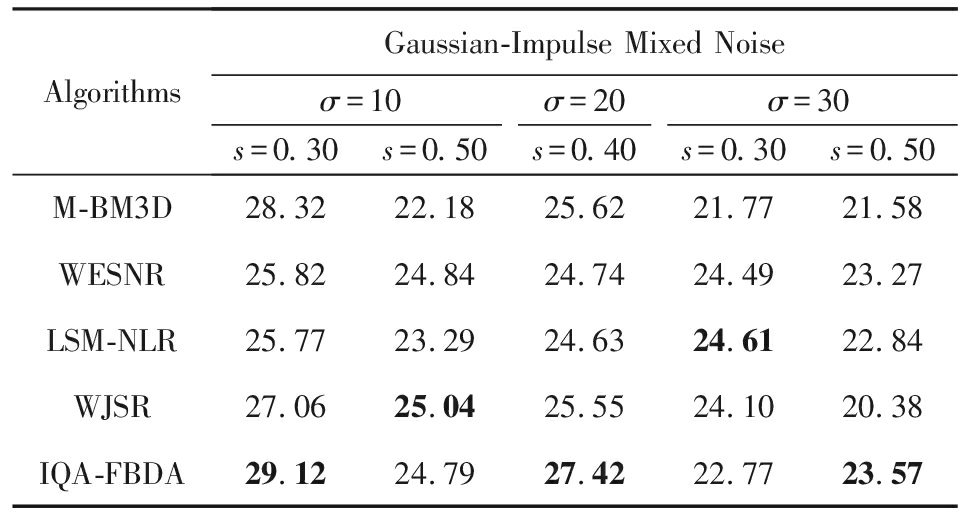
AlgorithmsGaussian-Impulse Mixed Noiseσ=10σ=20σ=30s=0.30s=0.50s=0.40s=0.30s=0.50M-BM3D28.3222.1825.6221.7721.58WESNR25.8224.8424.7424.4923.27LSM-NLR25.7723.2924.6324.6122.84WJSR27.0625.0425.5524.1020.38IQA-FBDA29.1224.7927.4222.7723.57
Note: The best values are bold.
3.3 执行时间比较
执行效率直接影响到降噪算法的实用性,是评价算法性能的另一个重要指标.因此,将各个对比算法对10张大小为512×512的图像进行降噪处理,以平均执行时间作为评价算法执行效率的指标,各算法在不同高斯高斯-随机脉冲混合噪声下的执行时间列于表8中.由表8可知,IQA-FBDA算法的平均执行时间在所有参与比较的算法中具有显著优势,仅次于M-BM3D算法,但其降噪效果显著优于M-BM3D算法,故IQA-FBDA算法在降噪效果和执行效率2个方面的综合性能是所有参与比较算法中最优的.其实,表8所给出的IQA-FBDA算法实验数据是在没有使用图形处理器(graphics processing unit, GPU)硬件加速条件下获得的.若使用硬件加速技术,则执行时间能进入200 ms内,其执行效率将是最高的,可以达到实时应用标准.
Table 8 Average Execution Time of Different Algorithms
表8 各算法平均执行时间对比 s
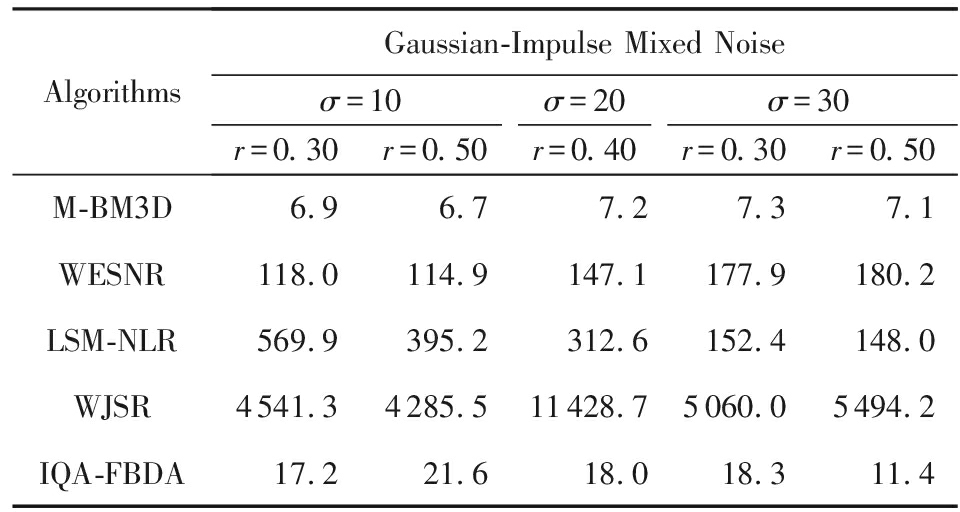
AlgorithmsGaussian-Impulse Mixed Noiseσ=10σ=20σ=30r=0.30r=0.50r=0.40r=0.30r=0.50M-BM3D6.96.77.27.37.1WESNR118.0114.9147.1177.9180.2LSM-NLR569.9395.2312.6152.4148.0WJSR4541.34285.511428.75060.05494.2IQA-FBDA17.221.618.018.311.4
4 总 结
对于任意给定的受高斯-脉冲混合噪声干扰的图像,所提出的IQA-FBDA算法通过设计无参考PSNR值预测模型以及MNPCD混合模式分类字典,能保证自动调用与之最匹配的精调深层CNN降噪模型进行降噪,在降噪效果和执行效率2个方面可取得最佳平衡.与当前主流的高斯-脉冲混合噪声降噪算法相比,IQA-FBDA算法无需为高斯-脉冲混合噪声设计复杂的理论描述模型,也无需设计复杂的迭代求解算法对其降噪,实现复杂度更低.一旦模型训练完成,整个执行过程无需人工干预,属于盲降噪算法.此外,该算法以图像质量值作为划分训练图像子集的标准,是一种比图像语义内容更具有普适性的方法,具有更广的应用范围.
[1]Xu Shaoping, Zeng Xiaoxia, Tang Yiling. Fast noise level estimation algorithm based on two-stage support vector regression[J]. Journal of Computer-Aided Design & Computer Graphics, 2018, 30(3): 447-458 (in Chinese)
(徐少平, 曾小霞, 唐祎玲. 基于两阶段支持向量回归的快速噪声水平估计算法[J]. 计算机辅助设计与图形学学报, 2018, 30(3): 447-458)
[2]Wu Jiang, You Fei, Jiang Ping. Noise variance estimation method based on regression analysis and principal component analysis[J]. Journal of Electronics & Information Technology, 2018, 40(5): 1195-1201 (in Chinese)
(吴疆, 尤飞, 蒋平. 基于回归分析和主成分分析的噪声方差估计方法[J]. 电子与信息学报, 2018, 40(5): 1195-1201)
[3]Xu Shaoping, Yang Rongchang, Liu Xiaoping. Adaptive switching median filter based on noise ratio estimation[J]. Journal of Optoelectronics·Laser, 2014, 25(4): 792-800 (in Chinese)
(徐少平, 杨荣昌, 刘小平. 基于噪声估计的自适应开关型中值滤波器[J]. 光电子·激光, 2014, 25(4): 792-800)
[4]Zhang Kai, Zuo Wangmeng, Chen Yunjin, et al. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155
[5]Zhang Kai, Zuo Wangmeng, Zhang Lei. FFDNet: Toward a fast and flexible solution for CNN based image denoising[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4608-4622
[6]Singh N, Thilagavathy T, Lakshmipriya R T, et al. Some studies on detection and filtering algorithms for the removal of random valued impulse noise[J]. IET Image Processing, 2017, 11(11): 953-963
[7]Taherkhani F, Jamzad M. Restoring highly corrupted images by impulse noise using radial basis functions interpolation[J]. IET Image Processing, 2018, 12(1): 20-30
[8]Velayudhan D, Paul S. Two-phase approach for recovering images corrupted by Gaussian-plus-impulse noise[C] 
 Proc of 2016 Int Conf on Inventive Computation Technologies (ICICT). Piscataway, NJ: IEEE, 2016 [2018-08-23]. https:
Proc of 2016 Int Conf on Inventive Computation Technologies (ICICT). Piscataway, NJ: IEEE, 2016 [2018-08-23]. https:
 ieeexplore.ieee.org
ieeexplore.ieee.org document
document 7824875
7824875
[9]Cai Jianfeng, Chan R H, Nikolova M. Two-phase approach for deblurring images corrupted by impulse plus Gaussian noise[J]. Inverse Problems and Imaging, 2008, 2(2): 187-204
[10]Xiao Yu, Zeng Tieyong, Yu Jian, et al. Restoration of images corrupted by mixed Gaussian-impulse noise via l1-l0 minimization[J]. Pattern Recognition, 2011, 44(8): 1708-1720
[11]Zhang Jian, Xiong Ruiqin, Zhao Chen, et al. Exploiting image local and nonlocal consistency for mixed Gaussian-impulse noise removal[C] 
 Proc of 2012 IEEE Int Conf on Multimedia and Expo. Piscataway, NJ: IEEE, 2012: 592-597
Proc of 2012 IEEE Int Conf on Multimedia and Expo. Piscataway, NJ: IEEE, 2012: 592-597
[12]Liu Jun, Tai Xuecheng, Huang Haiyang, et al. A weighted dictionary learning model for denoising images corrupted by mixed noise[J]. IEEE Transactions on Image Processing, 2013, 22(3): 1108-1120
[13]Jiang Jielin, Zhang Lei, Yang Jian. Mixed noise removal by weighted encoding with sparse nonlocal regularization[J]. IEEE Transactions on Image Processing, 2014, 23(6): 2651-2662
[14]Huang Tao, Dong Weisheng, Xie Xuemei, et al. Mixed noise removal via Laplacian scale mixture modeling and nonlocal low-rank approximation[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3171-3186
[15]Liu Licheng, Chen Long, Chen C L P, et al. Weighted joint sparse representation for removing mixed noise in image[J]. IEEE Transactions on Cybernetics, 2017, 47(3): 600-611
[16]Ren Jingjing, Fang Xianyong, Chen Shangwen, et al. Image deblurring based on fast convolutional neural networks[J]. Journal of Computer-Aided Design & Computer Graphics, 2017, 29(8): 1444-1456 (in Chinese)
(任静静, 方贤勇, 陈尚文, 等. 基于快速卷积神经网络的图像去模糊[J].计算机辅助设计与图形学学报, 2017, 29(8): 1444-1456)
[17]Zhang Fu, Cai Nan, Wu Jixiu, et al. Image denoising method based on a deep convolution neural network[J]. IET Image Processing, 2018, 12(4): 485-493
[18]Remez T, Litany O, Giryes R, et al. Class-aware fully convolutional Gaussian and Poisson denoising[J]. IEEE Transactions on Image Processing, 2018, 27(11): 5707-5722
[19]Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[OL]. [2018-09-10]. http:
 arxiv.org
arxiv.org abs
abs 1409.1556v6
1409.1556v6
[20]Nair V, Hinton G E. Rectified linear units improve restricted Boltzmann machines[C] 
 Proc of the 27th Int Conf on Int Conf on Machine Learning. New York: ACM, 2010: 807-814
Proc of the 27th Int Conf on Int Conf on Machine Learning. New York: ACM, 2010: 807-814
[21]Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C] 
 Proc of the 32nd Int Conf on Int Conf on Machine Learning. New York: ACM, 2015: 448-456
Proc of the 32nd Int Conf on Int Conf on Machine Learning. New York: ACM, 2015: 448-456
[22]Arnelaez P, Maire M, Fowlkes C, et al. Contour detection and hierarchical image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(5): 898-916
[23]Zhang Lin, Zhang Lei, Bovik A C. A feature-enriched completely blind image quality evaluator[J]. IEEE Transactions on Image Processing, 2015, 24(8): 2579-2591
[24]Ponomarenko N, Jin L, Ieremeiev O, et al. Image database TID2013: Peculiarities, results and perspectives[J]. Signal Processing: Image Communication, 2015, 30: 57-77
[25]Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080-2095




