众所周知,若敌手访问一个解密预言机,则能引起对基本的Regev[1]或GPV(Gentry,Peikert,Vaikuntanathan)[2]加密以及各种全同态加密(fully homomorphic encryption, FHE)方案[3-6]的攻击.这些攻击能够让敌手直接获得私钥.因此,与那些获得并利用消息的某些比特信息而进行的攻击相比,上述攻击形式更为严重.实际上,如果不要求方案具有同态加密的功能,那么存在一些基于格的IND-CCA2加密方案(如文献[2]),但是这些方法与同态加密并不兼容.因此,本文关心的是如何获得这些方案CCA1安全的变体.此外,Brakerski等人,如文献[7-9]利用密钥交换、自举等方法获得的一系列全同态加密方案,但这些方案并不能实现IND-CCA1安全,因为在这些方案中,其公钥包含了对私钥信息的加密.随后,GSW(Gentry-Sahai-Waters)方案[10]能够实现层级全同态加密而不需要任何密钥交换过程,因此其方案为实现FHE方案的IND-CCA1安全性提供了一种可能,因为对于那些使用密钥交换、自举或者其他方法的全同态加密方案来说,该方案避免了在公钥中包含对私钥加密的信息.

LMSV(Loftus,May,Smart,Vercauteren)[6]研究了Gentry[11]基于理想格的同态加密方案(及其变体[12])在自适应攻击下私钥的安全性,同时,他们证明了如果敌手能够访问解密预言机,那么就能确定私钥.此外,Loftus等人[12]给出了Smart-Vercauteren密码系统的一个变体,在该方案中,即使敌手有一个解密预言机,私钥仍旧安全；该结果是基于“有效密文”的概念由解密算法所保证,并且其安全性依赖于一个非常强的知识假设.随后,由于构造Smart-Vercauteren密码系统所依赖的计算假设,即短主理想(the short principal ideal)问题被攻破[13-16],因此LMSV方案不再被认为是安全的.近来,Cannitte等人[17]提出了第1个真正意义上的IND-CCA1安全的FHE方案,但他们并没有完全解决密文长度仍然依赖于电路输入长度的问题.因此IND-CCA1安全的层级全同态加密问题仍旧没有得到完全解决.值得注意的是,Loftus等人[12]着重解释了密文有效性攻击(ciphertext validity attacks, CVA)的相关性,即该模型允许敌手访问一个能够决定密文是否有效的预言机.同时,他们证明了敌手在CVA预言机的帮助下解密挑战密文的可能性(至少私钥仍是安全的.然而该攻击不是CCA1攻击,而是CCA2攻击).Loftu等人[6]认为对同态加密方案的CCA1和CVA攻击在实践中是可实现的(他们在文献[6]第6节中写道“在真实世界中,通常是敌手将其选择的密文先发给某一参与方,然后通过观察该参与方的行为获得该预言机”).例如考虑一个场景,给出了一个CVA预言机的精确描述.如果使用者正在将一个加密的数据库储存在云端并且进行查询,那么攻击者能够发送其选择的密文作为回应.如果这些密文是无效的,那么使用者可能重新发送相同的查询直到收到一个有效的密文作为回应.Bleichenbacher[18]利用CVA预言机来攻击RSA的某些变体就是一个典型的例子.由此可以认为,提出新的技术来让同态加密方案的私钥变得安全,从而抵抗CVA攻击、密钥恢复攻击(key recovery attacks, KRA)是非常必要且紧迫的.

为解决这个问题,李增鹏等人[19]提出一个不同于Loftus等人[6]的方案.他们给出了GSW方案[11]的一个变体,即多私钥GSW方案(MGSW),该变体允许有一个公钥对应着多个私钥.即通过使用“一次”一私钥的方法来避免私钥完全暴露的风险,从而不再依赖于“有效密文”的概念.其核心思想是,即使敌手能够从每个解密查询中得到一次私钥的某些比特,但他们也不可能将从多个解密查询中得来的信息结合起来计算出真正的私钥.但是,该方案也存在风险,即当解密查询时,利用噪声信息可能恢复出私钥信息.在本文3.1节给出该攻击方案的具体描述.此外,不禁要问：是否存在这样一种全同态加密方案，它可有效抵抗一些已知的密钥恢复攻击?

为了解决上述问题,本文提出了MGSW方案的一种“对偶”版本,记为DMGSW方案,并着重解释了该DMGSW方案如何能够结合多个私钥有效抵抗一些已知的自适应密钥恢复攻击.

此外,为证明方案能够抵抗特定类(或某些已知攻击)的自适应攻击,本文利用剩余Hash引理和向量空间投影论证给出理论框架.遗憾的是,不能证明该方案的IND-CCA1安全性.但希望本文的方案对于完全实现可证明安全的IND-CCA1全同态加密方案来说是一块垫脚石.

诚然,证明全同态加密的IND-CCA1安全性是一个非常有挑战性的工作,最接近的解决方案是Loftus等人[6]的结果,他们使用了一个非常强的知识假设,但是该结果现在已经被攻破了.Cannitte等人[17]基于multi-key的全同态加密方案[20-21],实现了IND-CCA1安全,但他们的方案依赖复杂的multi-key技术,且密文长度仍依赖于电路输入长度,使得该问题并未完全解决.

1 预备知识

本节着重介绍本文需用到的数学符号.

1.1 符 号

令n∈,[n]表示集合{1,2,…,n}.令X为平均值μ:E[X]=μ的一个随机变量,这里E表示X的平均值或期望值.X的标准差是本文中,列向量以粗体小写字母表示,如x.用转置来表示行向量xT.用粗体大写字母,如R来表示矩阵.此外,本文用到的内积和范数定义如下：〈x,y〉=xTy表示2个向量x和y的标准欧几里得内积.对于向量v=(v1,v2…,vn)T,∞范数是|v2|,…,|vn|},1范数是欧几里得范数是对于一个向量v，用表示其2范数.

引理1[10]. 矩阵向量剩余Hash引理.令κ∈,n∈,q∈,且m≥n lb q+2κ.令是一个均匀随机矩阵(注意R是随机选取),令且那么：

Δ((A,AT·r),(A,y))≤2-κ,

(1)

其中，Δ(A,B)表示分布A和B的统计距离.

1.2 离散高斯

实际上,格密码方案[22]主要依赖于格上的高斯概率分布.在本文中,依然需要分析高斯分布上错误元素的行为.首先给出高斯分布的相关定义.

定义1[23]. 令L为m的一个子集.对于向量c∈m和参数σ∈,定义：

以c为均值、以σ为参数L的离散高斯分布是：

∀

为了方便表示,将ρσ,0和DL,σ,0简写为ρσ和Dσ,将Dm,σ,0简写为

定义2[9]. B -界分布.n}n∈是整数上的高斯分布,如果满足:

则称之为B -界分布.

对于整数上的一个分(λ),且整数界为B=B(λ),如果存在那么是B -界的.

引理2[23]. 噪声边界满足2个条件：

1) 对于∀k>0,参数ei(i∈[m])满足

2) 对于∀k>0,向量e=[e1,e2,…,em]满足

注1. 本文中,假设因此,如果那么在平均情况下由引理2中的2)可知,

1.3 容错学习(learning with errors, LWE)

LWE问题是全同态加密GSW方案[10]及本文方案的主要计算假设.具体如下：

定义3. 对于一个秘密向量si∈通过均匀随机地选择向量ai∈选取噪声变量ei,并输出(ai,bi=〈si,ai〉+ei(mod q)),从而选取q上的LWE分布

LWE问题有2个版本：搜索(search)版本,是已知LWE样本来寻找秘密向量；判定(decision)版本,是用来区分LWE实例和均匀随机样本.

定义4. 对于i∈[m]，任一均匀随机的si∈对于所有抽样来说是固定的),给定了从中选取的m个独立样本(ai,bi)∈q,从而找到si.

定义5. 给定m个独立样本(ai,bi)∈q,其中每个抽样取自2个分布：1)LWE分布其中s∈是一个均匀随机的秘密向量(对所有的抽样来说是固定的)；2)均匀分布.即(以不可忽略的优势)区分以上2个分布.

Regev[1]及文献[20-21,24]证明了对于恰当的参数,LWE问题与格的近似最短向量(shortest vector problem, SVP)问题同样困难.

1.4 层级全同态加密

定义6. 令L=L(κ)为一个固定的函数.为深度是L的一类电路{Cκ}κ∈构造的一个L-层级全同态加密(leveled-FHE)方案,该方案包括4个PPT算法(KeyGen,Enc,Dec,Eval)：

1) 密钥生成算法KeyGen.是一个随机化算法,它以安全参数1κ为输入,并输出一个公钥pk和私钥sk.

2) 加密算法Enc.是一个随机化算法,它以一个公钥pk和一个消息μ∈{0,1}为输入,并输出一个密文c.

3) 解密算法Dec.是一个确定性算法,它以一个私钥sk和一个密文ct为输入,并输出一个消息μ∈{0,1}.

4) 同态运算算法Eval.输入一个公钥pk,一个运算电路C∈Cκ,和一个密文列表ct1,ct2,…,ct(κ),并输出一个密文ct*.

并要求2个正确性成立：

1) 对于任意κ,μ∈{0,1}和由KeyGen(1κ)输出的任意(pk,sk),有:

μ=Dec(sk,(Enc(pk,μ))).

2) 对于任意κ,μ1,μ2,…,μ,和C∈Cκ,有:

C(μ1,μ2,…,μ)=Dec(sk,(Eval(pk,C,Enc(pk,μ1),Enc(pk,μ2),…,Enc(pk,μ))).

使用选择明文攻击(chosen plaintext attacks, CPA)安全性的标准概念来定义安全性.

定义7. 如果对于任意多项式时间敌手A来说,下面的公式在κ上是可忽略的,那么说一个同态加密方案是不可区分选择明文攻击安全的(也称为IND-CPA安全的)：

|Pr[A(pk,Enc(pk,0))=1]-
Pr[A(pk,Enc(pk,1))=1]|,

其中,(pk,sk)←KeyGen(1κ).

此外,根据选择密文安全(chosen ciphertext attacks, CCA1)的概念,在其攻击的第1阶段中,敌手A已知一个公钥,然后访问一个解密预言机.它可以获得任意输入的解密.在第2阶段中,敌手已知一个挑战密文Enc(pk,μ)并且不再需要对解密预言机进行查询.CCA1安全性模型适用于分析敌手是否能从解密查询中得到私钥.因此,CCA1是很适合用来研究同态加密的一个安全模型.

1.5 基本工具

下面回顾一下Brakerski等人如文献[7-8,10]提出的一些基本工具.令q,m∈.令=lb q+1,因此,2-1≤q<2且N=m×.

定义8. PowerOf2的幂运算.算法PowerOf2输入一个m维向量v=[v1,v2,…,vm]∈输出中的一个N维向量：

(v1,2v1,…,2-1v1,v2,2v2,…,
2-1v2,…,vm,2vm,…,2-1vm)T.

定义9. BitDecomp比特分解.算法BitDecomp输入一个向量v∈输出一个N维向量,其中params←MGSW.Setup(1κ,1L)是vi二进制表示中的第j位(按最低有效位到最高有效位排列).换句话说：

定义10. BitDecomp逆比特分解.算法BitDecomp-1输入一个向量

v=(v1,0,v1,1,…,v1,-1,v2,0,v2,1,…,
v2,-1,…,vm,0,vm,1,…,vm,-1)T∈

输出:

这里,输入向量v不需要是{0,1}-向量,可以是N上的任意向量.

定义11. Flatten展平运算.算法Flatten输入一个向量v∈并输出一个N维二元向量(即{0,1}N的一个元素).将该算法定义为

Flatten(v)=BitDecomp(BitDecomp-1(v)).

注2. 令x,y∈且x′∈那么:

〈BitDecomp(x),PowersOf2(y)〉=〈x,y〉且〈x′,PowersOf2(y)〉=〈BitDecomp-1(x′),y〉=〈BitDecomp(BitDecomp-1(x′)),PowersOf2(y)〉=〈Flatten(x′),PowersOf2(y)〉.

以上算法可以从向量扩展到矩阵.可以根据Micciancio和Peikert[25]的工具矩阵(gadget matrix)G来解释上面的函数.首先定义G=Im⊗g∈其中,g=(1,2,4,…,2-1)T.对于v∈有PowersOf2(v)=vTG.对于v∈有BitDecomp-1(v)=G v.对于x∈算法BitDecomp(x)可以重命名为G-1(x).上面的定义和结果能够用G和G-1的方式来解释,参见引理3.

引理3[25]. 对于任意的N≥mlb q,存在一个固定的有效可计算矩阵G∈和一个有效可计算确定性“短原象”函数G-1(·)满足如下条件.对于任意的m′,输入一个矩阵M∈逆函数G-1(M)输出一个矩阵G-1(M)∈{0,1}N×m′使得G G-1(M)=M.

因此,可以将G看作一个具有“公共陷门”的特殊矩阵,它允许解决最小整数解(short integer solution, SIS)问题.这里,G-1(·)是一个有效可计算的函数.

2 GSW方案

本节首先介绍全同态加密GSW方案[10],然后介绍李增鹏等人[19]对该方案的自适应攻击,该攻击与Chenal和Tang[3]的攻击类似.

2.1 GSW方案

令κ为安全参数,L为同态加密的层级数.leveled-FHE方案的层级数.给出GSW[10]方案的简要描述,该方案最初是根据函数BitDecomp,BitDecomp-1,Flatten定义的,但是本文采用Alperin-Sheriff等人[27]的简化方式,即使用工具矩阵G定义.

1) GSW初始化算法GSW.Setup(1κ,1L)：

① 选择κ比特的一个模q,参数n=n(κ,L)∈和上的错误分(κ,L),使得LWE问题对于已知攻击实现至少2κ的安全性,选择一个参数m=m(κ,L)=O(n lb q).

② 输出参数params=(n,q,,m)，并令=lb q+1和N=(n+1).

2) GSW密钥生成算法GSW.KeyGen(params):

① 均匀选取t=(t1,t2,…,tn)T←并计算:

s←(1,-tT)T=(1,-t1,-t2,…,-tn)T∈

② 均匀选取随机公共矩阵B←和一个错误向量em.

③ 计算向量b=B t+e∈并构造矩阵A=(b|B)∈并满足:

④ 返回私钥sk←s和公钥pk←A.

3) GSW加密算法C←GSW.Enc(pk,μ):

① 令G为上述(n+1)×N维的工具矩阵,并均匀选取一个随机矩阵R←{0,1}m×N.

② 加密单比特消息μ∈{0,1},并生成密文

C=μ G+ATR(mod q)∈

需注意的是,在原GSW方案中,加密算法使用:

Flatten(μ I+BitDecomp(R A))∈{0,1}N×N，

其中,I是一个单位矩阵.

4) GSW解密算法μ′←GSW.Dec(sk,C):

① 输入私钥sk=s∈令k满足q4<2k-1≤q2,其中C[k]为C的第k列.

② 在(-q2,q2]范围内计算x←〈C[k],s〉(mod q)，这里有〈C[k],s〉=C[k]Ts,并有:

CTs=μ GTs+RTA s=μ(1,2,4,…)T+RTe.

由上,可以看出,计算时所选择密文矩阵C的第k列,对应着向量〈C[k],s〉的第k个坐标,即

③ 输出因此,如果|x|<2k-2≤q4,则返回0;否则返回1.

5) GSW运算算法

GSW.Eval(pk,(C1,C2,…,Cl)):

① 加法运算GSW.Add(C1,C2)∈输出:

C1+C2=(μ1+μ2)G+AT(R1+R2).

② 乘法运算GSW.Mult(C1,C2)计算并输出:

C1G-1(C2)=(μ1G+ATR1)G-1(C2)=μ1C2+
ATR1G-1(C2)=μ1μ2G+ATR1G-1(C2)+
μ1ATR2=μ1μ2G+AT(R1G-1(C2)+μ1R2).

注意C1G-1(C2)∈此外,利用G-C1G-1(C2)计算同态NAND门.

注3. Mukherjee等[20]方案中的解密算法公式是为了选择一个特定的向量w来计算s C G-1(w)T,但相比原GSW方案的解密算法效率要低得多(无论是计算时间还是噪声项的大小).因此本文仍将采用原GSW方案的解密算法.此外,当q为2的幂时,还存在另外一种方式处理q上的信息.具体细节参见文献[10].

2.2 安全性

定理1. 对于参数m=O(n lb q),令参数(m,n,q,)使得LWE困难假设成立,那么该GSW方案是IND-CPA安全的.

该证明的主要步骤是证明(A,RA)和均匀分布计算不可区分,本文不再赘述.

2.3 密钥恢复攻击

本节着重介绍能够恢复GSW方案私钥的2种自适应攻击.尽管该类攻击方式超出了原始GSW方案[10]安全模型的范围,但这种类型的攻击却是众所周知的.

1) 自适应攻击1.该类自适应密钥恢复攻击,类似于Chenal和Tang[3]的攻击.敌手通过询问一些解密预言机来恢复私钥s=(1,-tT)T.

敌手选择密文矩阵C并询问解密预言机,并且该预言机将返回〈C[k],s〉的“最高有效位(most signification bit, MSB)”,其中C[k]是C的第k列并且k对于敌手来说是已知的.实际计算C[k]Ts (mod q)2k-1，即MSB.

简单来说,敌手选择适当M值放在指定的密文位置,即敌手选择C[k]=(0,0,…,0,M,0,…,0)T,并逐位计算得到该私钥的各位.例如为了计算t1∈q,令C[k]=(0,1,0,…,0)T,然后对该密文矩阵进行一次解密预言机查询.因此:

〈C[k],s〉=-t1,

所以敌手能够得到t1的MSB之后,重新计算(例如通过选择密文向量C[k]=(0,2,0,…,0))获得2(-t1)(mod q)的MSB,这样就产生了关于下一个MSB的信息(但是,如果当MSB=1时,敌手需要考虑到规约,即进行降模处理).而实际攻击时,为了区分正负值,敌手可以选择形如C[k]=(M,1,0,…,0)的密文向量,因为该向量提供〈C[k],s〉=M-t1的MSB.本文不再赘述,有关该类攻击的详细讨论可参见文献[3].

如上描述,调用解密预言机所查询矩阵的第k列是一个单位向量.因此,一个通用的方法是通过禁止选择这种形式的密文来避免这种攻击.但是由于GSW方案是同态的,攻击者总能够将一个随机的0的加密添加到密文上,使得该修改后的密文矩阵C与其他密文矩阵一样,不能被解密算法区分而正常解密.当然,正如Loftus等人[6]所做的工作,考虑其他形式的解密算法,只需确定一个密文是否“正确地形成”即可,即是否是“有效密文”.但李增鹏等人[19]则提出“多密钥的同态加密”方案来抵抗上述自适应攻击1,将在第4节给出更详细的描述.

2) 自适应攻击2.上述攻击1的主要目标是得到b=B t+e中的秘密值t.然而,如果能够计算出噪声向量e,然后利用公共矩阵B和LWE实例b所存在的运算关系,也能够确定秘密向量t的值.因此本文给出了一个方法来确定噪声向量e.具体步骤为：

步骤1. 对于任意的1≤j≤m,为了得到噪声向量e的第j个噪声项ej,首先考虑公钥矩阵A的第j行,并记为aj=(bjt+ej(mod q)|bj)∈.然后,将这一行插入到密文矩阵的第k列中,因此设C[k]=(aj)T,并令C的其他列为0.

步骤2. 在上述情况下,解密预言机计算：

〈C[k],s〉=C[k]Ts=ajs=
(bjt+ej(mod q)|bj)(1,-tT)T=
bjt+ej-bjt=ej,

并返回因此能够得到ej的MSB(因为该位肯定为0,因为ej应该是小于q的).

步骤3. 为了扩展该攻击,敌手选择一个整数-q2<μ<q2，并利用来替换aj，并通过逐步尝试μ=1,2,4,…,2d值来重复进行解密计算,以此实现对方案的自适应攻击.因此解密预言机返回并确定该不等式|ej+μ|<2k-2是否成立.

步骤4. 通过尝试μ=1,2,4,…,2d能够确定使得ej+2d≥2k-2成立的2的最小乘幂.这意味着不等式2k-2-2d≤ej<2k-2-2d-1成立.此外,利用二进制搜索类型算法,使用大约d次解密预言机查询,可以精确地确定噪声项ej.

3 MGSW方案

第3节中已经概述了对GSW全同态加密方案的2种自适应攻击方法.本节首先概述李增鹏等人[19]抵抗自适应攻击1的多私钥GSW全同态加密方案(MGSW).然后,给出对MGSW方案的自适应攻击2.

3.1 MGSW方案

为抵抗该攻击1,李增鹏等人[19]改进了GSW方案的密钥生成算法.而GSW方案的密钥生成算法是选择形如[B t+e|B]的公钥A,其中私钥t是均匀随机选取的,e是一个短噪声向量,而李增鹏等人[19]则不再仅使用只包含单个LWE实例的公钥,而是采用结构的新公钥矩阵:

A′=[B t1+e1|B t2+e2|…|B t+e|B],

其中,秘密向量t1,t2,…,t均匀取自分布噪声向量e1,e2,…,e取自离散高斯分m.为方便,记噪声元素为基于此,令私钥为s1=(1,0,…,0,-(t1)T)T,…,s=(0,…,0,1,-(t)T)T.因此A′si=ei(mod q),其中1≤i≤.最后,每运行一次解密算法,生成一个新的随机一次秘密:

当整数λi很小(例如可以取λi∈{0,1}或{-1,0,1}或取自一个离散高斯分布),那么:

是一个短向量,且至少存在2个可能的私钥.因此,在这种情况下,即使为了确保在实际使用过程中,方案中所有的私钥使用次数不超过一次,那么也并不需要很大的取值.

简要回顾李增鹏等人[19]的MGSW方案.

1) MGSW初始化算法

params←MGSW.Setup(1κ,1L):

① 与GSW方案的初始化算法相同,区别在于选择参数φ=O(lb n)(私钥的数量).

② 输出公共参数params=(n,q,,m,φ),并令=lb q+1且N=(φ+n).

2) MGSW密钥生成算法

(pk,sk)←MGSW.KeyGen(params):

① 均匀选取ti←并输出:

si←(Ii|-(ti)T)T=

其中,Ii是(φ×φ)维单位矩阵I的第i行且使得si的第i个坐标等于1.

② 对于i∈[φ],均匀选取公共矩阵B←和φ个噪声向量eim.

③ 计算bi=B ti+ei∈并生成公钥矩阵A′=[bi|b2|…|bφ|B]∈

④ 输出pk←A′和sk←{s1,s2,…,sφ}.

3) MGSW加密算法C←MGSW.Enc(pk,μ):

① 加密一个消息μ∈q,均匀选取一个随机矩阵R′∈{0,1}m×N.

② 计算并输出密文C=μ G+A′TR′∈其中G为(n+φ)×N维工具矩阵.

4) MGSW解密算法μ′←MGSW.Dec(sk,C):

① 从{0,1}均匀选择非0的λ1,λ2,…,λφ,并生成一个一次密钥

② 选择一个整数1≤i≤φ,使得λi=1,且令k=(i-1)+j,使得G的第k列的第i个数是2j-1,其中q4<2j-1≤q2.

③ 在(-q2,q2]范围内计算:

x=〈C[k],s〉(mod q)=C[k]Ts(mod q).

④ 输出

同态运算跟原始GSW方案完全相同.

3.2 对MGSW方案的自适应攻击(自适应攻击2)

该类攻击的主要目标是利用噪声向量e来恢复秘密向量t,为实现该目标,需要将C的第k列设成A的第j行aj的转置,并将C的所有其他列设为0.实际上,与对MGSW方案的自适应攻击1的最主要不同在于k值是变化的,且攻击者并不知晓.显然,该攻击方法比自适应攻击1要困难的多.重复使用上述方法去计算向量e1的第j个元素攻击者便可以获得向量e1,那么敌手就能通过使用格算法来解决LWE的一个更简单的实例从而完成密码分析.

对该攻击的具体描述如下，令：

且一次私钥是令k′使得q4<2k′-1≤q2成立,将aj放入C的第k′列,并且将其他所有列全设为0.攻击者希望解密算法选择λ1=1和k=k′.那么有12的概率使得λ1=1,平均情况下大约有φ2的概率使得λi=1.

这里需注意的是,对于攻击者为什么能够获知λi=1,其原因在于,当解密者选择一些i并令λi=1,进而计算和而攻击者则选择一个C使得除第k列C[k]外其他所有列均为0.那么,如果λi≠1,解密返回值为0.而如果攻击者从解密预言机中获得一个非零值,那么他就确定λi=1.

因此,解密预言机选择k=k′的概率大约为(12)(2φ)=1φ.若k=k′那么解密预言机计算:

换句话说,尽管攻击者可以“看到”但实际却是一个含有噪音项的而这里,由于项是固定的,噪音项E的分布主要在于λi的选择.然而,因为最初取自离散高斯,这使得E的均值接近于0且E的分布类似于高斯分布.因此,很自然地希望噪音项E能够通过重复进行解密预言机查询而被“平均掉”,从而恢复出

具体来说,攻击者选择一个恰当的整数-q2<u<q2,并对密文矩阵C调用解密预言查询,这里的密文矩阵C的第k′列是向量的转置.因此,解密预言机(假设k=k′)计算其中E是噪音项,并返回

为获得的MSB,采取与Chenal和Tang[3]相同的方法来获得的MSB.因此攻击者在得知后判定是否成立.因此,重复进行相同的查询(同时要求k=k′)将给出相同的计算但对应相同的噪音值E是不同的,直到满足上述不等式,即可获得的MSB.

显然该攻击方法比自适应攻击1要困难的多.因此,李增鹏等人[26]的多密钥GSW方案仅能抵抗部分自适应攻击.由上述描述,需要考虑一个不同的解决方案.

注4：实际上,完全使用该方法去计算可能是非常困难的,因为至少对于攻击者而言,并不知道分布E的均值,上述方式仅是近似获得E的均值.但攻击者一旦获得噪声向量e1足够多的信息,那么他们就能通过使用格算法来解决LWE的一个更简单的实例从而完成密码分析,其中

4 DMGSW方案

在本节中,提出一个具有多私钥DMGSW方案,DMGSW方案的安全性基于非齐次短整数解(inhomogeneous short integer solution, ISIS)问题,而非LWE问题.

定义12. ISIS.令q,n,m∈,m>n.为上一个分布.将上的ISIS分布定义为

(B t(mod q),B),

其中,B为在q中均匀选择的一个n×m矩阵,tm是一个长度为m的整数向量.类似于decision-LWE问题,判定版本ISIS问题(decision-ISIS)是将取自ISIS分布中的样本(u,B)区分于取自均匀分布的样本

Ajtai[28](或Micciancio[29])已经证明了存在一个分使得对于恰当选取的参数来说,ISIS问题是困难的.实际上,分可以取自一个离散高斯分布或取自均匀分布{0,1}.(详见文献[29]).

定理2[19]. 令m>n∈,q∈,是上的一个离散高斯分布,它使得ISIS问题是困难的,φ为整数且满足φ=O(lb q).定义2个分布X和Y:

① X是n×(φ+m)矩阵上的分布[u1|u2|…|uφ|B],其中B∈是均匀随机选取的,并且对于所有的1≤i≤φ满足,ui=B ti(mod q),这里ti取自离散高斯分m.

② Y是 上的均匀分布，那么2个分布X和Y是计算不可区分的.

证明. 令D是一个PPT敌手,他能够以不可忽略的概率区分X和Y.对于1≤i≤φ+1来说,引入中间分布Xi如下:

[d1|d2|…|di-1|ui|…|uφ|B],

其中，ui如上所述,di是从中均匀选取的.因此X1=X且Xφ+1=Y.

由上假设,D能够以明显的概率ε区分X1和Xφ+1,因此,通过一系列游戏序列,存在某个i使得D能以至少εφ的概率将分布Xi和Xi+1区分开来.

显然,D给出了一个ISIS区分器：即给出一个ISIS挑战(y,B),均匀地选取d1,d2,…,di-1,从ISIS分布中选取ui+1,ui+2,…,uφ,生成分布

[d1|d2|…|di-1|y|ui+1|ui+2|…|uφ|B],

并调用D对该分布进行区分.

通过假设,显然不存在这样的区分器.

证毕.

4.1 DMGSW方案

本节中给出一个DMGSW方案.在原GSW方案中,公钥是基于LWE实例,形如A=(B t+e,B),密文是基于ISIS问题,形如ATR.如Regev的加密方案,其对偶方案有基于ISIS问题的公钥(BT,BTT)和基于类似LWE实例BR+X的密文.

1) DMGSW初始化算法

params←DMGSW.Setup(1κ,1L):

① 选择模q=q(κ),格维参数m=m(κ,L)和n,以及分(κ,L),对于已知ISIS攻击,参数的合理选择可以实现至少2κ的安全性.

② 令=lb q+1且N=(φ+m)，输出params=(m,q,,n).

2) DMGSW密钥生成算法

(pk,sk)←DMGSW.KeyGen(params):

① m分布中选取向量计算ei=(Ii|-(ti)T)T,其中行向量Ii是φ×φ维单位矩阵的第i行.

② 均匀选取矩阵B∈计算向量ui=B ti,1≤i≤φ,令矩阵

A=[u1|u2|…|uφ|B]∈

这里A ei=0.

③ 输出公钥A和私钥(e1,e2,…,eφ).

3) DMGSW加密算法

C←DMGSW.Enc(pk,μ):

① 均匀选取矩阵R←和X(φ+m)×N.

② 加密消息μ∈{0,1},计算

C=μ G+ATR+X(mod q)∈

其中G为(φ+m)×N维工具矩阵.

③ 输出密文C.

注5. DMGSW方案中密文C可以记为

Flatten(μ I+BitDecomp(ATR+X))=

BitDecomp(BitDecomp-1(μ I)+ATR+X)=

BitDecomp(μ G+ATR+X)(mod q).

4) DMGSW解密算法

μ′←DMGSW.Dec(ski,C):

① 从 选择λ1,λ2,…,λφ且λi,i∈[φ]并不全为0,那么生成一次私钥使得很短.这里,同样有

② 确定整数1≤k=(i-1)+j≤φ ,使得λi=1且2j-1∈(q4,q2].

③ 令C[k]为C的第k列,并计算这里:

因此:

μ λi2j-1+E.

其中,为一个小噪音项.

④ 返回

注6. 针对步骤1)，需特别强调的是,有不同的方法来选择参数λi.其中可以采用从{0,1}分布中均匀选取的方法.该方法可以得到恰当的值,因此本文分析中采用该方法.另一种是采取从上离散高斯分布中选取的方法,该方法使得取值具有小的标准差且得到更高的安全性(详见第6节中的讨论).此外,还可采用拒绝抽样(rejection sampling)的某些形式来获得向量为更好控制λi的大小并防止泄露关于向量ei信息.

5) 同态运算DMGSW.Eval(pk,(C1,C2,…,C)):

同态操作与GSW方案类似,具体如下：

① 同态加法DMGSW.Add(C1,C2)输出:

C1+C2=(μ1+μ2)G+AT(R1+R2)+
(X1+X2)∈

② 同态乘法DMGSW.Mult(C1,C2)计算N×N的矩阵G-1(C2),并输出C1G-1(C2).即:

C1G-1(C2)=(μ1G+ATR1+X1)G-1(C2)=
μ1C2+ATR1G-1(C2)+X1G-1(C2)=
μ1μ2G+(ATR1G-1(C2)+μ1ATR2)+
X1G-1(C2)+μ1X2)∈

③ 与非运算DMGSW.NAND(C1,C2)计算G-1(C2),并输出G-C1G-1(C2).

4.2 正确性

本节中分析解密和同态运算的正确性并确定参数大小.假设是由均匀随机选取的λi∈{0,1}所构成.而ei中的元素取自标准差为σ的离散高斯分,是B -界的,且B=6σ,使得不等式成立.因此,向量中的元素是以B′=tB为界且满足

由加密算法对消息加密输出的密文称为第0层的密文C.而层级i≥1的密文C则是由密文运算算法Eval生成.且至多对0层密文执行i次运算.

定义13. 如果那么称密文C∈是E噪音的,这里如果具有E噪音的密文C满足E<q8,那么有使得不等式|ξ|≤E<q8<2j-2成立,且

其中,

引理4. 为上的一个B界分布.如果E≥φ B+m B2成立,那么层级为0的密文是E噪音.

证明. 对于密文C=μ G+ATR+X其中X取自高斯分(φ+m)×N.为方便分析,将X记为 其中噪声矩阵X#∈φ×N且X*∈m×N.由于因此有:

因为和由Cauchy-Schwarz不等式可知:

因此,有综上,无穷范数的误差边界为φ B+m B2.

证毕.

下面分析同态运算噪声规模.具体来说，对于第i层的密文噪声(N+1)iE,记E为层级0的噪声.如果满足条件(N+1)LE≤q8,那么执行L层同态操作后,解密正确.

引理5. 令符号和参数如上所述(特别是,E≥φ B+m B2).令C为层级i≤L上的任意密文,那么C的噪音是(N+1)iE(无穷范数).

证明. 令C1和C2为μ1,μ2∈{0,1}的2个密文,满足

对于密文加法,假设其i层密文噪声为(N+1)iE.计算Cadd=C1+C2.那么:

且

2(N+1)iE≤(N+1)i+1E.

对于密文乘法,Cmult=C1G-1(C2)满足:

使得:

证毕.

同样的计算对NAND门来说同样成立.假设q8>(N+1)LE,计算包含NAND门且电路深度为L的布尔电路.输入噪声为E层级0的密文,每执行一次同态运算,噪声乘以至多为(N+1)的一个因子.因此,经过L次同态运算后,最终密文中的噪声大小为(N+1)L,且能够正确地解密.

4.3 DMGSW方案的安全性

DMGSW方案的安全性依赖于ISIS和LWE假设.利用定理2来证明该方案DMGSW在ISIS假设下是安全的.

定理3. 如果ISIS假设和LWE假设是困难的,那么DMGSW方案是IND-CPA安全的,对于φ=O(lb q)及参数m,n,q,.

证明. 安全性证明以hybrid hop形式,分2步给出.可以用hybrid hop形式表述.

1) 使用一个均匀随机矩阵A替换公钥.

2) 使用一个均匀随机矩阵C替换密文.当C是一个均匀随机矩阵时,敌手在IND-CPA游戏中不具有不可忽略的优势,因此C独立于消息μ.有必要说明的是,敌手的行为在不同的游戏步骤之间是相同的.

① Hybird.1.在本游戏中,用均匀矩阵代替公钥.挑战密文与方案中的相同.如果这2个游戏中,敌手成功的概率是不可忽略的,那么敌手是一个能够将含有ISIS实例的公钥与均匀随机矩阵区分开的算法.然而,由ISIS假设和定理2可知,该算法不存在.

② Hybird.2.在本游戏中,用上的均匀随机的矩阵来替换密文C.如果在这个游戏中,敌手成功的概率明显区别于Hybird.1中成功的概率,那么存在一个区分器来区分LWE分布ATR+X(mod q)和均匀分布.

由LWE假设,不存在这样的PPT区分器.最后,Hybird.2与消息位μ无关,因此敌手在这个游戏中获得的优势为0.

证毕.

5 抵抗自适应攻击的DMGSW方案的安全性

在DMGSW方案中,与MGSW方案的主要区别在于没有噪音项.因此自适应攻击2不可能发生.下面,证明自适应攻击1同样不适用于DMGSW方案.

该安全性分析依赖于剩余Hash引理(leftover hash lemma, LHL)的高斯版本,而不同于之前的平均情况.下面,给出Agrawal等人[30]的定理2的一种特殊情况.

定理4. 一维剩余Hash引理LHL.令ε,σ∈,使得对于所有的绝对常数ε>0,σ>C(详见文献[30]).令φ≥10 lb(8φ1.5σ)且s′≤4φ lb(1ε).那么统计距离为2ε的2个分布：

① 选择1个长度为t的向量X∈φ,其每个元素均选自φ上参数为σ的离散高斯分布；选择1个长度为φ的向量z∈φ,其每个元素选自φ上的参数为s′的离散高斯分布,计算并输出XTz.

② 从 上参数为σ s′的离散高斯分布选择并输出一个元素.实际上,对于一次私钥

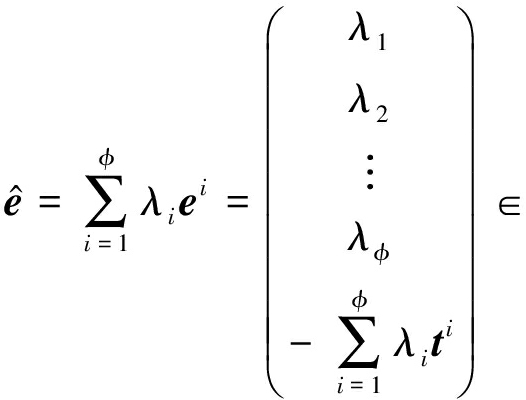
执行解密计算如果敌手将其选择的一个向量插入到密文矩阵C的第k列中并进行一次解密查询.如自适应攻击1,敌手不知道k,但却能以很高的概率猜出该值.实际上,敌手有12的概率获得λ1=1,当λ1=1时,将C的所有其他列设置为0,能够确保解密预言机仅返回一个非0值.

采取与自适应攻击1相同的方式.对于线性映射L:q,对应着与密文C[k]T的乘法.此时,敌手可以获得：

的1位.正如自适应攻击1,可以声明,几乎所有的向量(Ii,-(ti)T)T并不在L的核中.依据是否含有L个有缺陷的向量.需要考虑2种情况：

1) 当L(ei)值与在q上均匀选取的元素一样时,那么在该情况下,基于在自适应攻击1中的剩余Hash引理(并假设L是满射且大部分私钥不会失效)足以推断上值与L(ei)上值无关且敌手不能从该形式的查询中得到私钥.

2) 如果投影L将L((w1,w2,…,wφ+m)T)=wi投影到坐标φ<i≤φ+m上.在这种情况中,L(ei)值取自离散高斯分布且不能使用剩余Hash引理来判定不携带关于L(ei)的任何信息.不同的是,对于该情形,可以使用定理4来证明.在这种情况中,需假设λi是从一个参数为σ的离散高斯分中选取的.

那么假设攻击者看到这里L(ei)独立取自离散高斯分.那么由定理4可知,对于φ=O(lb q)(由于使得LWE假设是困难的并满足φ=O(lb σ)=O(lb q),并且该整数φ与取自参数为σ2的离散高斯中的样本不可区分.而在本文中,L(ei)是固定的而不是独立选取的,且敌手不可获得.

而从敌手的视角,仅可以看到但是高斯剩余Hash引理仍能保证该值与L(ei)相互独立.此外,正如前面所解释的,攻击者仅能看到一个位而不是整个值因此,本文的DMGSW方案抵抗自适应攻击.

6 总 结

自适应攻击是威胁目前主流全同态加密安全性的一种有力的攻击模式.本文给出了对李增鹏等人[19]的多私钥GSW方案的一种自适应攻击方法,并构造了一个抵抗该类自适应攻击的对偶多私钥GSW(DMGSW)方案.该方案安全性基于ISIS假设和LWE假设,同时本文给出详细的安全性分析,并证明了该方案对“一些已知”的自适应攻击的抵抗性.

参考文献

[1]Regev O. On lattices, learning with errors, random linear codes, and cryptography[C]//Proc of the 37th ACM Symp on the Theory of Computing (STOC’05). New York: ACM, 2005: 84-93

[2]Gentry C, Peikert C, Vaikun-tanathan V. Trapdoors for hard lattices and new cryptographic constructions[C]//Proc of the 40th ACM Symp on the Theory of Computing (STOC’08). New York: ACM, 2008: 197-206

[3]Chenal M, Tang Qiang. On key recovery attacks against existing somewhat homomorphic encryption schemes[C]//Proc of the 3rd Cryptology and Information Security in Latin (LaintCrypt’14). Berlin: Springer, 2014: 239-258

[4]Chenal M, Tang Qiang. Key recovery attacks against NTRU-based somewhat homomorphic encryption schemes[C]//Proc of the 18th Information Security Conf (ISC’15). Berlin: Springer, 2015: 397-418

[5]Dahab R, Galbraith D S, Morais E. Adaptive key recovery attacks on NTRU-based somewhat homomorphic encryption schemes[C]//Proc of the 8th Int Conf on Information Theoretic Security (ICITS’15). Berlin: Springer, 2015: 283-296

[6]Loftus J, May A, Smart P N, et al. On CCA-secure somewhat homomorphic encryption[C]//Proc of the 18th Selected Areas in Cryptography (SAC’11). Berlin: Springer, 2011: 55-72

[7]Zhang Zhenfei, Plantard T, Susilo W. On the CCA-1 security of somewhat homomorphic encryption over the integers[C]//Proc of the 8th Information Security Practice and Experience (ISPEC’12). Berlin: Springer, 2012: 353-368

[8]Brakerski Z. Fully homomorphic encryption without modulus switching from classical gapsvp[C]//Proc of the 32nd Int Cryptology Conf (CRYPTO’12). Berlin: Springer, 2012: 868-886

[9]Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) Fully homomorphic encryption without bootstrapping[C]//Proc of Innovations in (Theoretical) Computer Science (ITCS’12). New York: ACM, 2012: 309-325

[10]Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE[C]//Proc of the 52nd IEEE Annual Symp on Foundations of Computer Science (FOCS’11). Piscataway, NJ: IEEE, 2011: 97-106

[11]Gentry C, Sahai A, Waters B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptoti-cally-faster, attribute-based[C]//Proc of the 33rd Int Cryptology Conf (CRYPTO’13). Berlin: Springer, 2013: 75-92

[12]Gentry C. Fully homomorphic encryption using ideal lattices[C]//Proc of the 41st ACM Symp on the Theory of Computing (STOC’09). New York: ACM, 2009: 169-178

[13]Smart P N, Vercauteren F. Fully homomorphic encryption with relatively small key and ciphertext sizes[C]//Proc of the 13th Int Conf on Theory and Practice of Public Key Cryptography (PKC’10). Berlin: Springer, 2010: 420-443

[14]Biasse F J, Fieker C. Subexponential class group and unit group computation in large degree number fields[J]. LMS Journal of Computation & Mathematics, 2014, 17(A): 385-403

[15]Biasse J F, Song Fang. Efficient quantum algorithms for computing class groups and solving the principal ideal problem in arbitrary degree number fields[C]//Proc of the 27th ACM-SIAM Symp on Discrete Algorithms (SODA’16). New York: ACM, 2016: 893-902

[16]Cramer R, Ducas L, Peikert C, et al. Recovering short generators of principal ideals in cyclotomic rings[C]//Proc of the 35th Annual Int Conf on the Theory and Applications of Cryptographic Techniques (EUROCRYPT’16). Berlin: Springer, 2016: 559-585

[17]Canetti R, Raghuraman S, Richelson S, et al. Chosen-ciphertext secure fully homomorphic encryption[C]//Proc of the 20th Int Conf on Theory and Practice of Public Key Cryptography (PKC’17). Berlin: Springer, 2017: 213-240

[18]Bleichenbacher D. Chosen ciphertext attacks against protocols based on the RSA encryption standard PKCS #1[C]//Proc of the 18th Int Cryptology Conf (CRYPTO’98). Berlin: Springer, 1998: 1-12

[19]Li Zengpeng, Galbraith D S, Ma Chunguang. Preventing adaptive key recovery attacks on the GSW levelled homomorphic encryption scheme[C]//Proc of the 10th Provable Security (ProvSec’16). Berlin: Springer, 2016: 373-383

[20]Clear M, McGoldrick C. Multi-identity and multi-key leveled FHE from learning with errors[C]//Proc of the 35th Int Cryptology Conf (CRYPTO’15). Berlin: Springer, 2015: 630-656

[21]Mukherjee P, Wichs D. Two round multiparty computation via multi-key FHE[C]//Proc of the 35th Annual Int Conf on the Theory and Applications of Cryptographic Techniques (EUROCRYPT’16). Berlin: Springer, 2016: 735-763

[22]Peikert C. Public-key cryptosystems from the worst-case shortest vector problem: Extended abstract[C]//Proc of the 41st ACM Symp on the Theory of Computing (STOC’09). New York: ACM, 2009: 333-342

[23]Agrawal S, Boneh D, Boyen X. Efficient lattice (H)IBE in the standard model[C]//Proc of the 29th Annual Int Conf on the Theory and Applications of Cryptographic Techniques (EUROCRYPT’10). Berlin: Springer, 2010: 553-572

[24]Lyubashevsky V. Lattice signatures without trapdoors[C]//Proc of the 31st Annual Int Conf on the Theory and Applications of Cryptographic Techniques (EUROCRYPT’12). Berlin: Springer, 2012: 738-755

[25]Peikert C, Waters B. Lossy trapdoor functions and their applications[J]. SIAM Journal on Computing, 2011, 40(6): 1803-1844

[26]Li Zengpeng, Galbraith D S, Ma Chunguang. Preventing adaptive key recovery attacks on the gentry-sahai-waters leveled homomorphic encryption scheme, 2016/1146[R/OL]. New York: IACR Cryptology ePrint Archive, 2016 [2017-06-01]. https://eprint.iacr.org/2016/1146.pdf

[27]Alperin-Sheriff J, Peikert C. Faster bootstrapping with polynomial error[C]//Proc of the 34th Int Cryptology Conf (CRYPTO’14). Berlin: Springer, 2014: 297-314

[28]Ajtai M. Generating hard instances of lattice problems (extended abstract)[C]//Proc of the 8th ACM Symp on the Theory of Computing (STOC’96). New York: ACM, 1996: 99-108

[29]Micciancio D. Generalized compact knapsacks, cyclic lattices, and efficient one-way functions from worst-case complexity assumptions[C]//Proc of the 43rd IEEE Annual Symp on Foundations of Computer Science (FOCS’02). Los Alamitos, CA: IEEE Computer Society, 2002: 356-365

[30]Agrawal S, Gentry C, Halevi S, et al. Discrete gaussian leftover hash lemma over infinite domains[C]//Proc of the 19th Int Conf on the Theory and Application of Cryptology and Information Security (ASIACRYPT’13). Berlin: Springer, 2013: 97-116

Leveled Fully Homomorphic Encryption Against Adaptive Key Recovery Attacks

Li Zengpeng1,2, Ma Chunguang1, and Zhao Minghao3

1(College of Computer Science and Technology, Harbin Engineering University, Harbin 150001)2(College of Computer Science and Technology, Qingdao University, Qingdao, Shandong 266071)3(School of Software, Tsinghua University, Beijing 100084)

Abstract A major open problem is to protect leveled homomorphic encryption from adaptive attacks that allow an adversary to learn the private key. In order to achieve the goal of preventing key recovery attacks on fully homomorphic encryption (FHE), Li Zengpeng et al (PROVSEC’16) proposed an multiple secret keys fully homomorphic encryption scheme under the learning with errors (LWE) assumption to prevent key recovery attacks on FHE, which did not use the notion of “valid ciphertexts” of Loftus et al (SAC’11). However, utilizing the information of noise, the attacks can still recover the information of the secret key. Li Zengpeng et al.’s scheme cannot provide an efficient method to protect the secret key. In this paper, Inspired by the work of Li Zengpeng et al (EPRINT’16), we first give a new method of key recovery attacks to Li Zengpeng et al.’s scheme; then, we propose a new FHE scheme with multiple secret keys which differs from EPRINT’16, and prove our new scheme against key recovery attacks. Our main idea is to adopt the dual version of encryption algorithm and generate a “one-time” secret key every time, so that even if an attacker can learn some bits of the one-time private key from each decryption query and cannot obtain some bits of noise, the scheme still does not allow them to compute a valid private key.

Key words adaptive key recovery attacks; lattice-based cryptography; learning with errors; fully homomorphic encryption; multiple secret keys

收稿日期：2017-06-12；

修回日期：2018-12-26

基金项目：国家自然科学基金项目(61472097,61802214)

This work was supported by the National Natural Science Foundation of China (61472097, 61802214).

通信作者：马春光(machunguang@hrbeu.edu.cn)

中图法分类号 TP391

Li Zengpeng, born in 1989. Assistant professor in the College of Computer Science and Technology of Qingdao University. Member of ACM, CCF, CACR, IEEE and IEICE. His main research interests include data security, data privacy and cryptography. In particular, his research focus are lattice-based cryptography, fully homomorphic encryption and cryptography protocol.

Ma Chunguang, born in 1974. Professor of the College of Computer Science and Tech-nology of Harbin Engineering University. His main research interests include cryptography and information security.

Zhao Minghao, born in 1992. PhD candidate in Tsinghua University. Student member of ACM, CCF and CACR. His main research interests include cloud computing, storage system, mobile computing, privacy preserving techniques and applied cryptography.