无线传感器网络(wireless sensor networks,WSNs)是由多个传感器节点组成的自组织网络,用于在部署区域内进行信息采集、处理和传输等.WSNs的许多应用需要知道传感器节点的位置信息[1-2],例如目标区域感兴趣事件的实时检测和目标追踪、环境监测等.此外,位置信息还可以提高网络中路由的效率[3-4],实现网络拓扑自配置等.因此,位置信息在WSNs的应用中极其重要,节点定位技术已经成为当前WSNs研究的热点之一[5-6].
1 相关工作
根据定位过程中是否需要测距可以将定位算法分为基于测距(range-based)定位和无需测距(range-free)定位2类[7-8].在基于测距的定位中,节点需要配备特殊硬件获得其与已知位置的节点之间的距离或角度信息,然后根据距离或角度信息计算自己的位置,代表性的测距算法有TOA(time of arrival)[9],AOA(angle of arrival)[10],RSSI(received signal strength indication)[11]等.在无需测距的定位中,节点仅仅通过网络连接信息来计算自己的位置,代表性的算法如APIT(approximate point-in-triangulation)[12],DV-Hop(distance vector hop)[13-21],LAEP(a novel range-free localization algorithm using expected hop progress)[22]等.相对于基于测距定位,无需测距定位简单易行、成本低廉,但是定位精度相比前者较低.
本文主要针对DV-Hop定位算法进行位置求精.DV-Hop是一种经典的无需测距定位算法,具有算法简单、易实现等优点,但定位精度一般.DV-Hop自提出之后有许多文献都对其进行了改进.基于调节邻居信息的DV-Hop改进算法(an improved DV-Hop localization algorithm, DV-RND)[13]改进了DV-Hop节点之间的距离估计方法,它是采用2个邻居节点之间的共同邻居节点的个数来表示它们的相近程度,进而估计出距离.基于优化算法的DV-HOP改进算法(an improved DV-Hop localization algorithm based on evolutionary)[14]利用3种进化算法改进DV-Hop,包括用蛙跳算法(shuffled frog leaping algorithm, SFLA)优化DV-Hop每个锚点的每跳距离,利用遗传算法(genetic algorithm, GA)和粒子流优化算法(particle swarm optimization, PSO)求精DV-Hop计算得到的位置节点坐标.文献[15]提出用平均每跳距离代替所有锚点的每跳距离,再用2维双曲算法代替DV-Hop中用几何方法求解节点坐标,最后利用PSO算法继续求精DV-Hop.文献[16]研究多通信半径条件下的DV-Hop算法设计问题.文献[17]提出了一种基于蝙蝠算法的DV-Hop改进定位算法(improved DV-Hop localization algorithm based on bat algorithm in WSNs, IBDV-Hop),不仅提高了平均跳距的精度,还引入了非线性动态惯性权重方法来扩展算法的全局搜索范围以及局部搜索精度.文献[18]提出基于邻居节点信息梯度化的距离估计算法(a distance estimating algorithm based on gradient neighbors in wireless sensor net-works, DV-GNN),通过将邻居节点信息梯度化来提高节点距离测量.文献[19]通过跳距修正和粒子群优化来提高DV-Hop的定位精度.文献[20]提出用GA优化提高DV-Hop的定位精度.文献[21]将传统意义上的跳数换成用来指示未知节点相对于锚点的接近度,最后利用邻近算法得出未知节点的坐标.
本文所提算法与上述DV-Hop改进算法的区别在于,本文不是改进DV-Hop的计算过程,而是对DV-Hop的定位结果进行位置求精,因此本文算法与上述DV-Hop改进算法是互补关系.文献[14-15,20]虽然也对DV-Hop的定位结果求精,但是它们是以锚点为参考节点;本文是以未知节点周围的邻居节点为参考节点对DV-Hop的定位结果进行求精.本文算法借鉴基于测距的Malguki[23] 定位算法:利用节点间定位距离和测距距离构建校正矢量,然后在校正矢量方向通过迭代方式得到节点的定位位置.本文将Malguki算法思想应用到DV-Hop改进中,提出一种基于校正矢量的分布式迭代求精算法(CVLR),它可以解决DV-Hop的定位模糊问题,从而大幅度改进DV-Hop的定位精度.CVLR和Malguki的区别在于:1)Malguki是基于RSSI测距的定位算法,而CVLR是基于DV-Hop的无需测距定位算法;2)CVLR与Malguki的目标函数不一样;3)搜索方法不一样,CVLR提出一种简单的基于校正矢量的搜索方法.CVLR的贡献主要有3个方面:
1) 提出一种基于DV-Hop的定位过程的伪测距方法,它利用节点保存的每跳距离的校正值去估计其与1跳或2跳邻居节点之间的距离;
2) 提出一种基于节点间的伪测距距离和定位距离(定位位置之间的距离)的位置校正矢量构建方法,并将求精过程建模为使这2个距离的差值的平方和在校正矢量方向上的最小化问题,通过一种简单的搜索方法来求解这个最小化问题;
3) 提出利用节点的1跳邻居节点信息的CVLR1和利用1跳与2跳邻居节点信息CVLR2求精算法.
2 DV-Hop定位过程及其定位模糊问题
2.1 DV-Hop定位过程
DV-Hop定位主要包括3个阶段:1)未知节点通过广播保存到锚点跳数最小的数据并转发给邻居节点;2)广播结束后锚点每跳距离的校正值由式(1)确定;3)未知节点根据保存的校正值和到锚点的最小跳数值就可以计算到相应锚点的距离.当得到3个以上距离时,可以用3边定位等几何算法求得未知节点坐标.
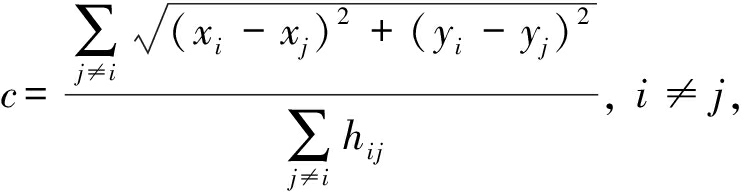 ∀j,
∀j,
(1)
其中,(xi,yi),(xj,yj)表示锚点i和j的坐标,hi j表示锚点i和j之间的最小跳数值.
2.2 DV-Hop定位模糊问题
DV-Hop的定位模糊问题[13]是导致DV-Hop定位算法精度低的原因之一.如图1所示,A1,A2,A3是锚点,其余的都是未知节点,dA1A2,dA1A3,dA2A3分别为锚点A1,A2,A3之间的物理距离.那么可以得到A1,A2,A3的校正值为:cA1=(dA1A2+dA1A3) (4+4),cA2=(dA1A2+dA2A3)
(4+4),cA2=(dA1A2+dA2A3) (4+4),cA3=(dA1A3+dA1A3)
(4+4),cA3=(dA1A3+dA1A3) (4+4).未知节点B2距离锚点A3较近,所以节点B2将会保存A3的校正值,相应的节点B3距离A2较近,所以将会保存A2的校正值,由此可以得到节点B2到3个锚点的距离为:
(4+4).未知节点B2距离锚点A3较近,所以节点B2将会保存A3的校正值,相应的节点B3距离A2较近,所以将会保存A2的校正值,由此可以得到节点B2到3个锚点的距离为:![]() 相应的节点B3到3个锚点的距离为:
相应的节点B3到3个锚点的距离为:![]() 那么当dA1A2≈dA1A3≈dA2A3时,cA1≈cA2≈cA3,进而
那么当dA1A2≈dA1A3≈dA2A3时,cA1≈cA2≈cA3,进而![]() 因此节点B2和节点B3的最终定位将会十分接近(如图1中节点p,q),甚至如果节点B2和节点B3接收到的校正值相同,它们的最终定位将会重叠.
因此节点B2和节点B3的最终定位将会十分接近(如图1中节点p,q),甚至如果节点B2和节点B3接收到的校正值相同,它们的最终定位将会重叠.
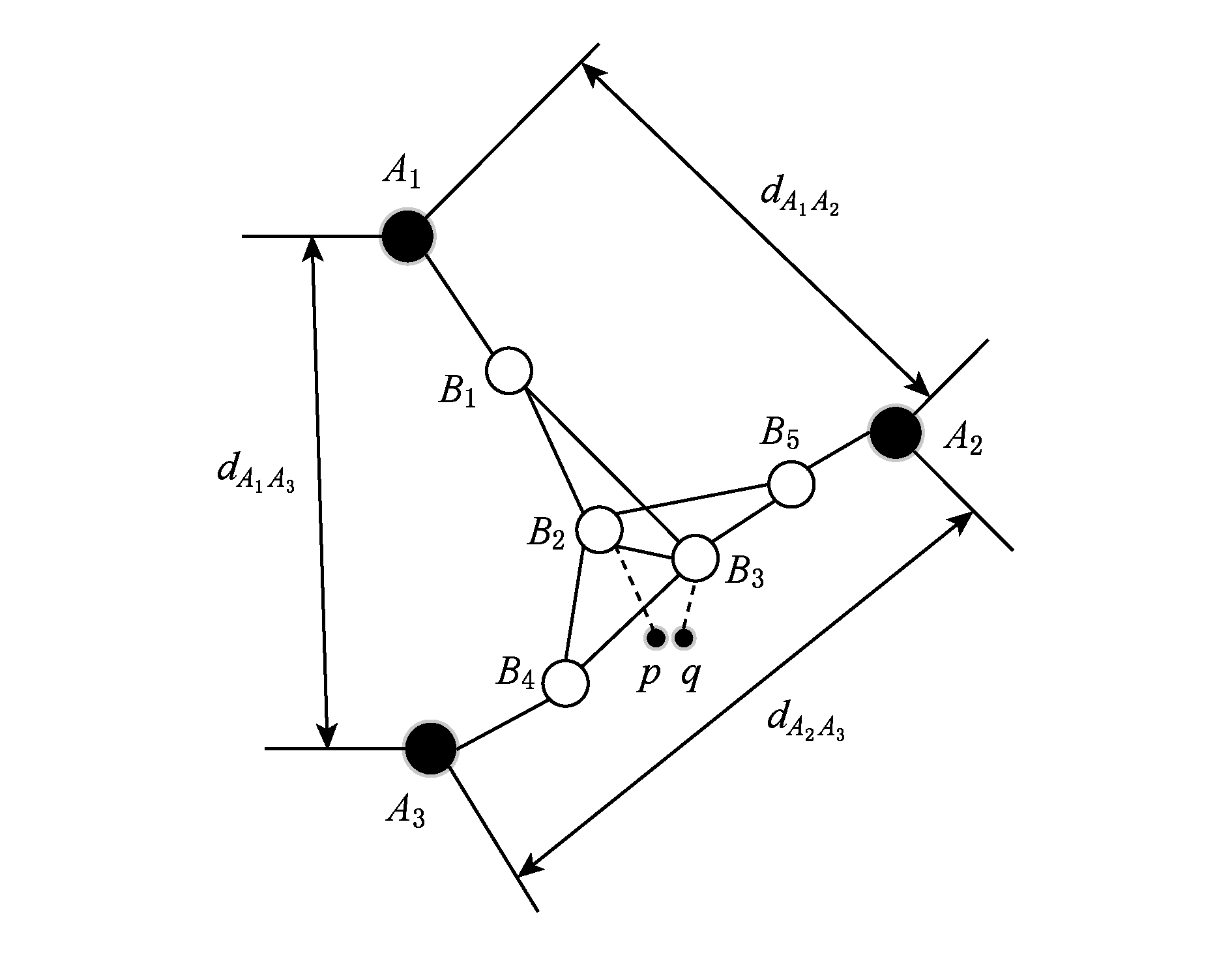
Fig. 1 The hop-distance ambiguity problem of DV-Hop
图1 DV-Hop定位模糊问题
现有DV-Hop改进算法都不能很好地解决以上DV-Hop算法的定位模糊问题.我们注意到DV-Hop定位过程中仅利用了锚点的信息,但没有利用本地的邻居节点的信息.因此,我们提出在DV-Hop定位完成后,再继续利用节点的1跳或2跳邻居节点信息去进行位置求精,从而解决DV-Hop定位模糊问题.
3 CVLR算法
针对第2节描述的问题,本节提出CVLR算法,它包括3个步骤:1)根据每个节点保存的校正值计算得到它与1跳和2跳邻居节点的距离,我们称之为“伪测距距离”(pseudo ranging distance, PRD);2)利用“伪测距距离”和“定位距离”(利用节点定位坐标计算得到的距离)构建校正矢量,将定位结果求精建模为使这2个距离的差值的平方和在校正矢量方向上最小;3)使用一种简单的搜索算法对这个最小化问题进行迭代求解.
3.1 伪测距距离
伪测距距离根据节点和它的1跳邻居节点各自所保存的校正值的平均值来进行计算,具体表示为
![]()
(2)
其中,Γ1i表示节点i 的1跳邻居节点的集合,ci和cj分别表示节点i和j保存的校正值,![]() 表示节点i和j之间的伪测距距离.
表示节点i和j之间的伪测距距离.
相应的节点i和它任意的2跳邻居节点的伪测距距离被定义为
![]()
(3)
其中,Γ2i表示节点i 的2跳邻居节点的集合,![]() 表示节点i和j之间的伪测距距离.节点k是节点i到j最短路径上的一个节点.
表示节点i和j之间的伪测距距离.节点k是节点i到j最短路径上的一个节点.
3.2 位置校正矢量
我们利用节点间的定位距离和伪测距距离的差值来构建位置校正矢量.假设节点j是当前需要求精的节点i的1跳邻居节点,并且节点i和节点j的初始定位坐标为![]() 那么节点i和节点j之间定位距离和伪测距距离的差值可以表示为
那么节点i和节点j之间定位距离和伪测距距离的差值可以表示为
![]()
(4)
其中,![]() 表示节点间的定位距离,它可以被定义为
表示节点间的定位距离,它可以被定义为
![]()
(5)
进而节点i和节点j之间的位置校正矢量可以被定义为
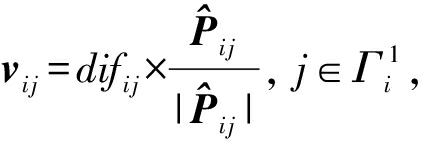
(6)
其中,![]() 表示节点i指向节点j的向量,
表示节点i指向节点j的向量,![]() 表示向量的长度.相似的节点i和它的2跳邻居节点j之间位置校正矢量可以表示为
表示向量的长度.相似的节点i和它的2跳邻居节点j之间位置校正矢量可以表示为
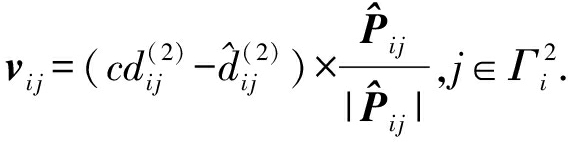
(7)
图2描述了位置校正矢量的原理,图中三角形和圆形分别表示节点i和它1跳或2跳邻居节点j的估计位置,cdi j和![]() 分别为定位距离和伪测距距离.图2(a)中,当
分别为定位距离和伪测距距离.图2(a)中,当![]() 时,位置校正矢量vi j的方向和
时,位置校正矢量vi j的方向和![]() 的方向相反,也就是说合力会使得节点i的求精位置远离节点j的位置.在图2(b)中,当
的方向相反,也就是说合力会使得节点i的求精位置远离节点j的位置.在图2(b)中,当![]() 时,位置校正矢量vi j的方向和
时,位置校正矢量vi j的方向和![]() 的方向相同,也就是说合力会使得节点i的求精位置靠近节点j的位置.特别地,当定位距离等于伪测距距离时,相应的位置校正矢量也为0,意味着向量不参与节点i的求精过程.
的方向相同,也就是说合力会使得节点i的求精位置靠近节点j的位置.特别地,当定位距离等于伪测距距离时,相应的位置校正矢量也为0,意味着向量不参与节点i的求精过程.
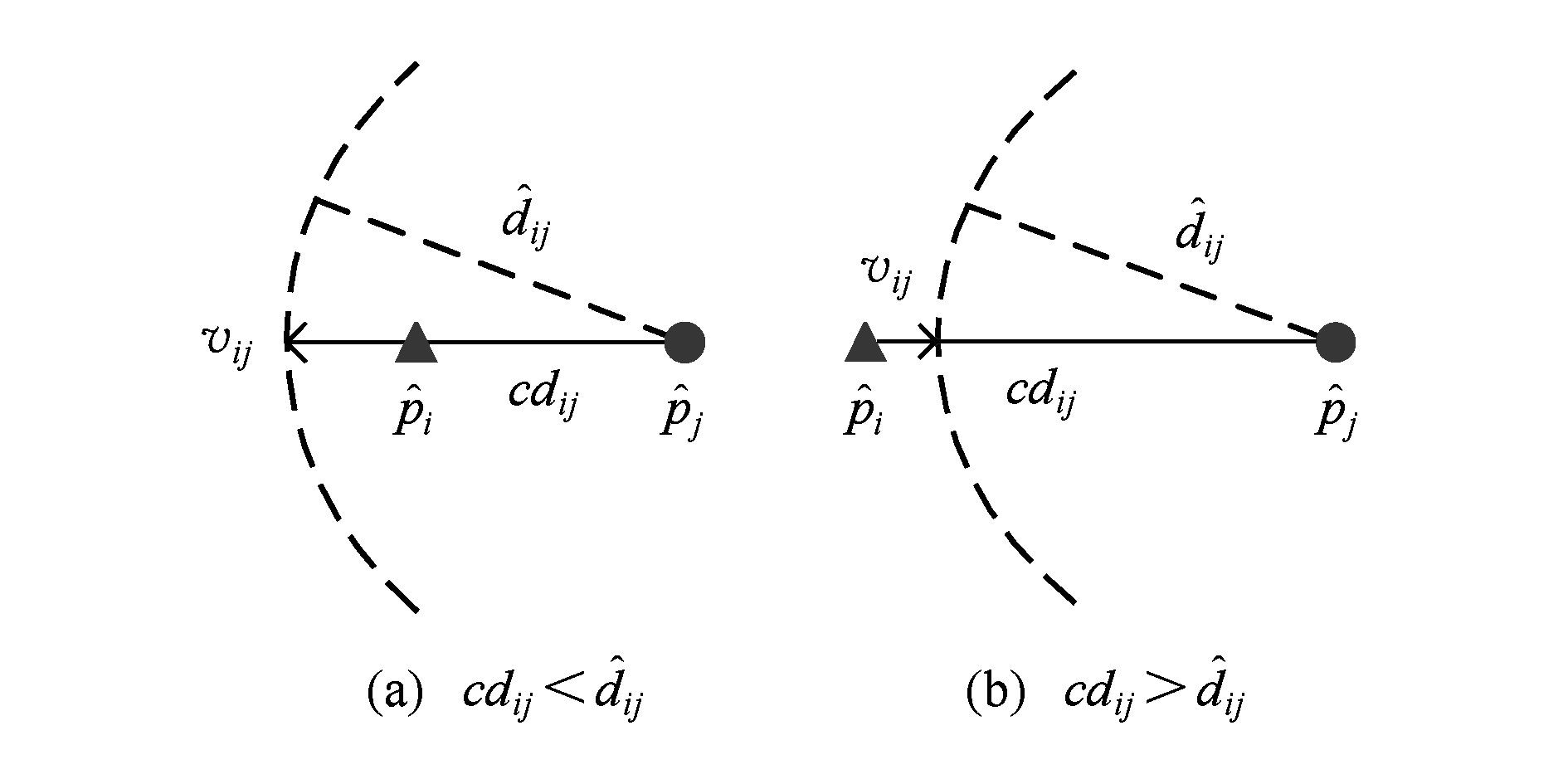
Fig. 2 The principle of correction vector
图2 位置校正矢量的原理
节点i的位置校正矢量的合成矢量可以表示为
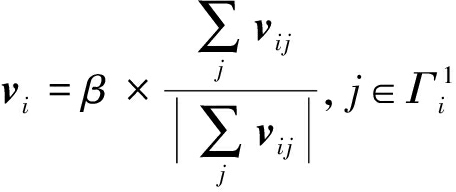 或j∈Γ1i∪Γ2i,
或j∈Γ1i∪Γ2i,
(8)
其中,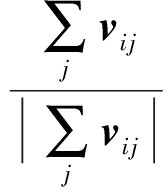 表示矢量的单位化结果,β表示校正因子,用来调整节点的修正幅度以得到更优的求精位置,它主要对CVLR算法的收敛速度产生影响.
表示矢量的单位化结果,β表示校正因子,用来调整节点的修正幅度以得到更优的求精位置,它主要对CVLR算法的收敛速度产生影响.
3.3 基于搜索的求精方法
在知道节点i的位置校正矢量的方向之后,我们设置了一个目标函数,目的是使伪测距距离和定位距离的差值的平方和在校正矢量方向上最小,然后提出一种简单的搜索方法来求解上述最小化问题.CVLR的目标函数定义为
![]()
j∈Γ1i或j∈Γ1i∪Γ2i,
(9)
其中,![]() 表示节点i在k次迭代求精之后的结果,
表示节点i在k次迭代求精之后的结果,![]() 表示用DV-Hop进行的原始定位结果;
表示用DV-Hop进行的原始定位结果;![]() 表示节点j和点p之间的“定位距离”,这个点p的坐标Pp∈P的集合,集合P表示为
表示节点j和点p之间的“定位距离”,这个点p的坐标Pp∈P的集合,集合P表示为
![]()
(10)
式(10)表示在第k次求精时,以节点i前一次求精后的位置![]() 为起点,在位置校正矢量
为起点,在位置校正矢量![]() 方向上均匀地取M个点作为本次求精的坐标点集合,我们的M=10.最终CVLR在这些点中找到使得目标函数值达到最小的那个点作为本次求精的结果.
方向上均匀地取M个点作为本次求精的坐标点集合,我们的M=10.最终CVLR在这些点中找到使得目标函数值达到最小的那个点作为本次求精的结果.
3.4 CVLR算法定位流程

Fig. 3 The distributed refinement procedure of unknown node in CVLR
图3 CVLR算法流程图
图3为CVLR算法的定位求精流程图,整个CVLR算法分为2个阶段:初始化阶段和迭代求精阶段.图3中的DV-Hop Initialization是算法的初始化阶段,进行DV-Hop定位,其余部分是算法的迭代求精阶段,下面依次详细介绍:
Step1. 每个节点广播自身初始位置坐标(DV-Hop定位结果)和自身保存的校正值给邻居节点.
Step2. 根据自身的校正值和接收到的邻居节点的校正值,每个节点由式(2)(3)计算出它和邻居节点的伪测距距离.
Step3. 根据自身和邻居节点的定位坐标,每个节点由式(5)计算出它和邻居节点之间的定位距离.
Step4. 根据Step2的伪测距距离和Step3的定位距离,每个节点由式(6)~(8)计算出自己的合成位置校正矢量.
Step5. 根据Step4的合成位置校正矢量,每个节点由式(9)(10)计算出自己的求精坐标.
Step6. 如果迭代次数k小于设定的阈值,每个节点广播各自的求精坐标给邻居节点并且重复Step3~Step6.如果迭代次数k达到设定的阈值则结束算法.
如果所用到的邻居节点仅包含1跳邻居节点,我们把这种算法称作CVLR1;如果包含1跳和2跳邻居节点,我们称作CVLR2.
3.5 复杂度分析
本节从时间开销和通信开销2个方面来分析CVLR的复杂度,其中通信开销用需要发送的消息数量来衡量.对于CVLR1,从通信开销来说,每个节点在每一次迭代求精过程中都会向它的1跳邻居节点广播它的本次求精坐标,因此CVLR1每次求精过程的通信开销为O(m),其中m表示网络中未知节点的数量;从时间开销来看,在CVLR1的求精过程中,式(5)(8)(9)的计算都是![]() 的单层循环,其中
的单层循环,其中![]() 表示1跳邻居节点的平均数量,因此,CVLR1单个节点的时间开销为
表示1跳邻居节点的平均数量,因此,CVLR1单个节点的时间开销为![]() 同理可得CVLR2的时间开销为
同理可得CVLR2的时间开销为![]() 其中
其中![]() 表示2跳邻居节点的平均数量.对于CVLR2的通信开销,由于每个节点会广播它的求精坐标给1跳和2跳邻居节点,所以CVLR2的通信开销为
表示2跳邻居节点的平均数量.对于CVLR2的通信开销,由于每个节点会广播它的求精坐标给1跳和2跳邻居节点,所以CVLR2的通信开销为![]() 可以看出CVLR2的通信开销远大于CVLR1的开销,特别是当节点密度很大时,通信开销增长很快,这也意味着CVLR2的能耗较大.因此,当实际应用场景需要高定位精度时,可以采用CVLR2算法;当定位精度要求不高,而能量消耗尽量少时,可以采用CVLR1算法.
可以看出CVLR2的通信开销远大于CVLR1的开销,特别是当节点密度很大时,通信开销增长很快,这也意味着CVLR2的能耗较大.因此,当实际应用场景需要高定位精度时,可以采用CVLR2算法;当定位精度要求不高,而能量消耗尽量少时,可以采用CVLR1算法.
4 CVLR性能仿真分析
4.1 仿真环境和参数设置
我们用N来表示节点的数量,r来表示节点的通信半径,Pi=(xi,yi)和![]() 分别表示节点i的真实坐标和估计坐标.此外,我们用式(11)来表示节点的归一化平均定位误差,用式(12)来表示不同算法的定位性能比较:
分别表示节点i的真实坐标和估计坐标.此外,我们用式(11)来表示节点的归一化平均定位误差,用式(12)来表示不同算法的定位性能比较:
(11)
![]()
(12)
默认的实验参数为:我们考虑在100m ×100 m的区域随机部署N个未知节点,默认在区域的4个角落上布置锚点,它们的坐标分别为(0,0),(0,100),(100,0),(100,100).
4.2 CVLR性能研究
1) 校正因子β设置
式(8)中的β值是不确定的,本节我们将通过实验来确定β的取值.图4显示了CVLR算法中不同仿真环境下β值对定位误差的影响,其中仿真参数为:图4(a)未知节点数量从190~290之间变化,所有节点通信半径都是22 m,β值从0.5~3之间变化;图4(b)未知节点数量都为190个,所有节点通信半径从16~28 m之间变化,β值从0.5~3之间变化.
从图4中我们可以看到,当β值从1.5~2.5之间变化时,定位误差相差不大,且比其他值的误差要小,尤其在不同数量的未知节点环境中体现更明显.此外,我们通过大量仿真实验发现,当β=1.5时算法收敛速度较慢,当β值为2或2.5时算法收敛速度不相上下,且均比1.5时快.但从图4中还可以看到,当β=2.5时,在未知节点数过少或者通信半径过小的仿真环境下定位误差反而上升,具有不稳定性.综合考虑,我们在仿真实验中取β=2.
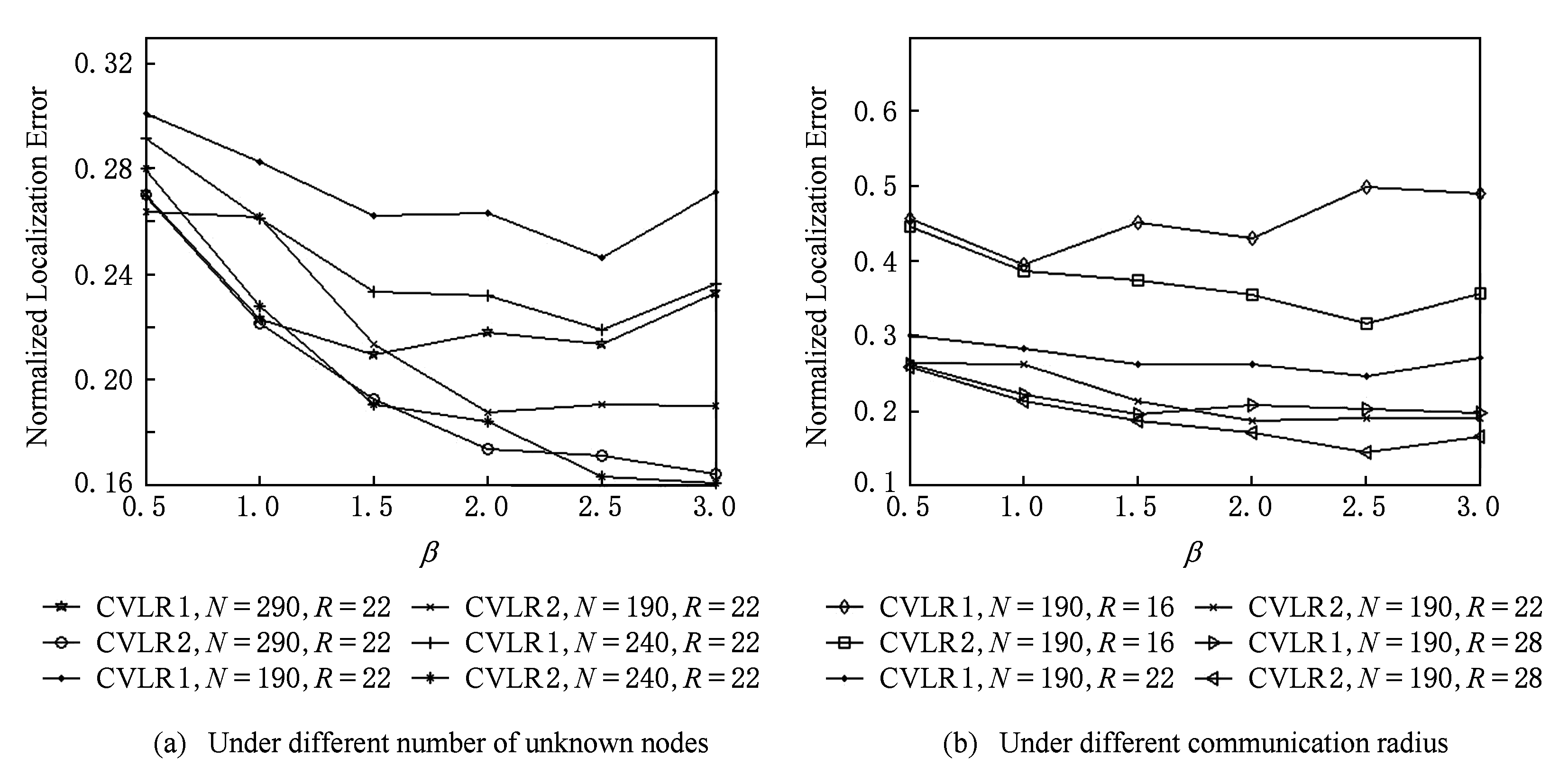
Fig. 4 Influence of β on positioning error
图4 β对定位误差的影响
2) 理想测距和伪测距下的收敛性
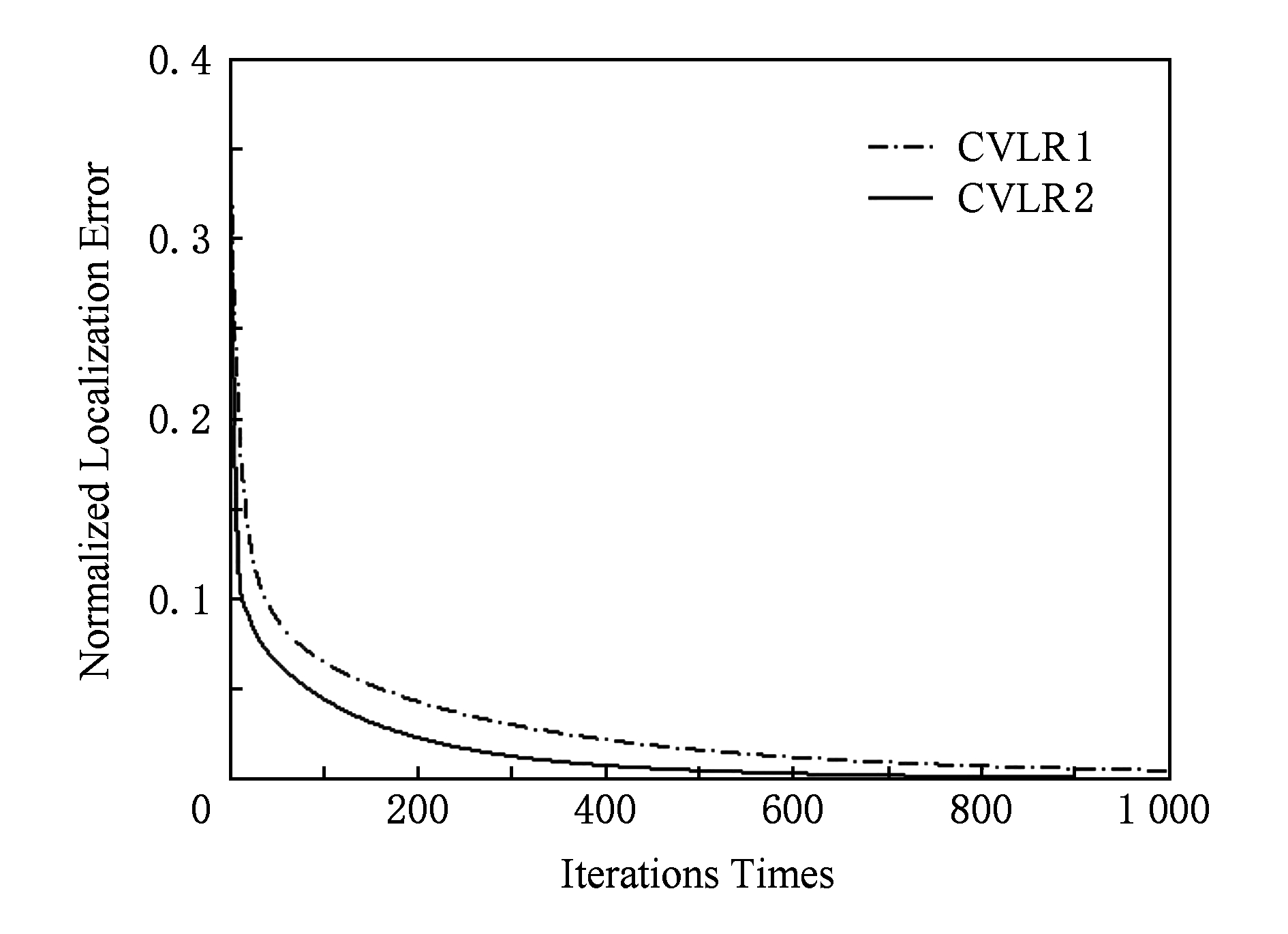
Fig. 5 The CVLR algorithm under ideal ranging condition
图5 理想测距条件下的CVLR算法
考虑一种特殊的理想情况:相邻节点之间的伪测距距离等于它们之间的真实距离.如图5所示,随着迭代次数的增加,归一化平均定位误差逐渐趋向于0,这意味着如果知道节点间的真实距离,CVLR能够对DV-Hop的定位结果进行位置求精.同时,也可以看到CVLR2的收敛性能是要好于CVLR1.
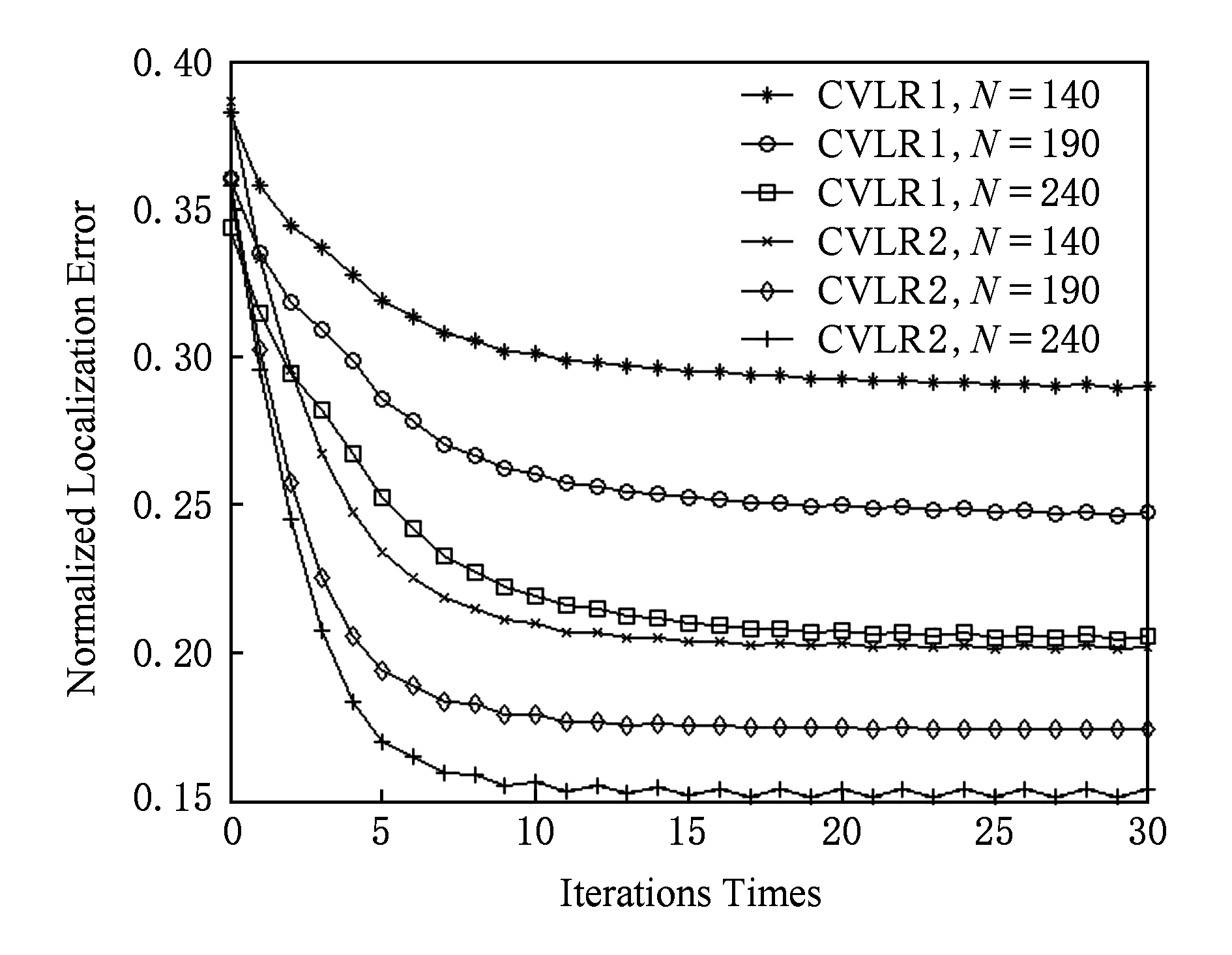
Fig. 6 The relation between the number of iterations and the positioning error
图6 迭代次数与定位误差之间的关系
图6给出了CVLR在伪测距条件下的收敛性情况,其中迭代次数为0时表示DV-Hop的定位结果,N表示未知节点数量.从图6中可以看到:1)伪测距条件下,CVLR仍然能收敛,只是不能收敛到0;2)CVLR的归一化定位误差随着迭代次数和未知节点数量的增加而减少;3)CVLR2的收敛速度和定位精度优于CVLR1.从图6还可以看到,CVLR1和CVLR2的定位误差在迭代次数12次和5次之后基本收敛,因此在之后的仿真中本文设置CVLR1和CVLR2的最大迭代次数分别为12次和5次.
3) 理想测距和伪测距下的性能对比
为展示CVLR在伪测距PRD下与理想测距(ideal ranging distance, IRD)的性能差异,以及相对于DV-Hop的定位性能优势,图7中比较了DV-Hop,CVLR-PRD,CVLR-IRD在相同场景下的归一化定位误差.仿真实验中,未知节点数量设为190,通信半径从15~35 m之间变化.
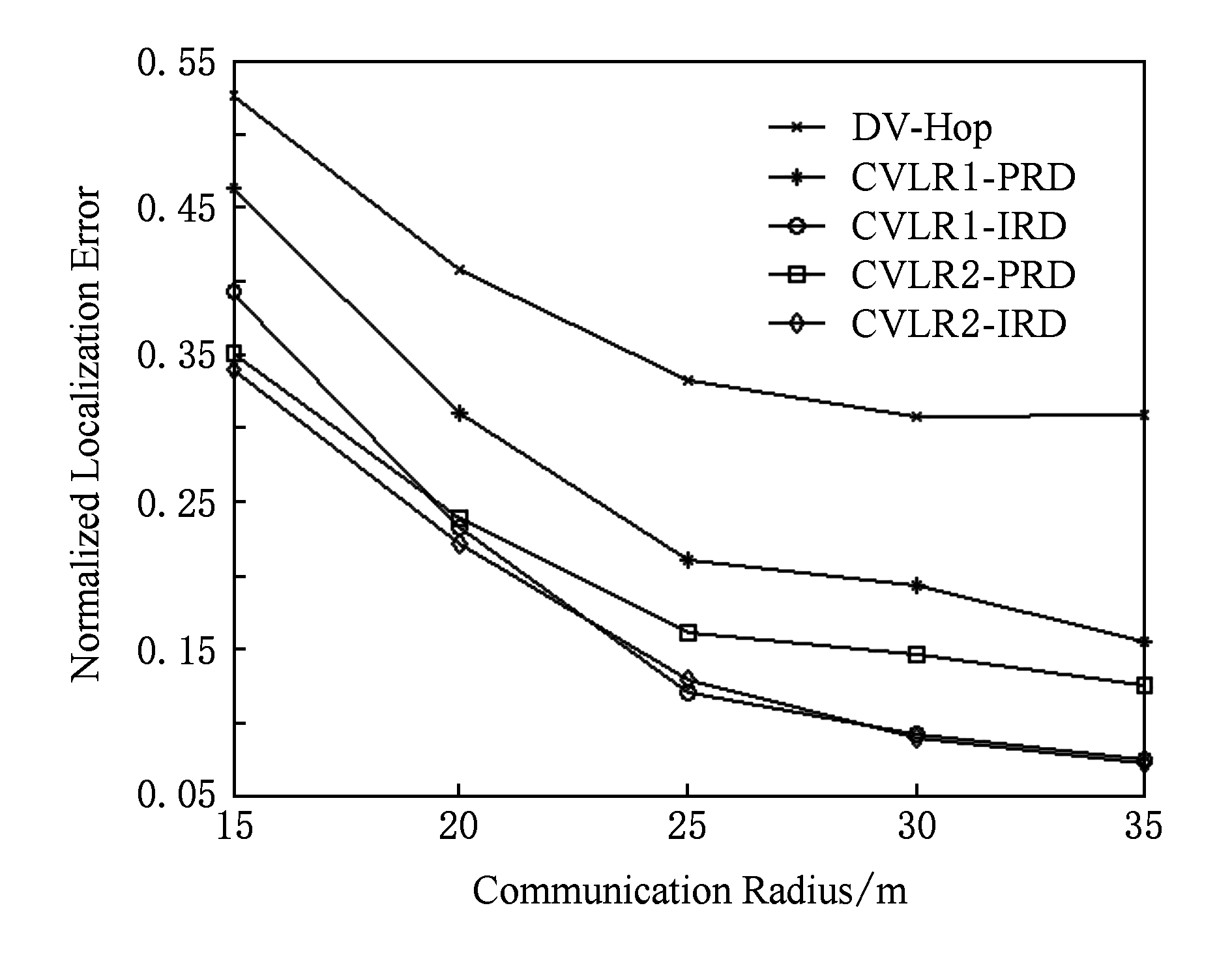
Fig. 7 The influence of the communication radius on positioning error
图7 节点通信半径对定位误差的影响
从图7中可以看到,CVLR-PRD的定位精度相对于DV-Hop要提高许多.平均而言,相对于DV-Hop,CVLR1-PRD和CVLR2-PRD的定位精度分别提高31.83%和47.59%.另外,相对于对应的CVLR-IRD,CVLR1-PRD和CVLR2-PRD的定位精度分别有37.33%和22.06%的差距.
4.3 CVLR与其他定位算法的性能比较
图8比较了DV-Hop,CVLR1,CVLR2,DV-RND,DV-EA的定位性能.DV-RND[13]和DV-EA[14]都是基于DV-Hop的改进定位算法.DV-RND主要解决DV-Hop中定位模糊问题,这与CVLR要解决的问题一致;DV-EA利用3种优化算法来提高DV-Hop定位精度,特别是它也包括对DV-Hop的定位结果进行位置求精,这点与CVLR一致.图8(a)中,未知节点数量为190,通信半径从15~35 m变化;图8(b)中,节点通信半径是22 m,未知节点数量从100~400变化.

Fig. 8 The performance comparison among CVLR, DV-Hop, DV-RND and DV-EA
图8 CVLR,DV-Hop,DV-RND,DV-EA的定位误差比较
从图8中我们可以看到:1)DV-RND,DV-EA,CVLR的定位精度都优于DV-Hop;2)CVLR1和CVLR2的定位性能明显比DV-Hop,DV-RND,DV-EA好,CVLR2定位性能最好.具体来说,在图8(a)中,CVLR1和CVLR2较DV-Hop的定位精度平均提高31.83%和47.59%,较DV-RND的定位精度平均提高21.20%和39.31%,较DV-EA的定位精度平均提高21.26%和39.45%;在图8(b)中,CVLR1和CVLR2较DV-Hop的定位精度平均提高34.23%和48.54%,较DV-RND的定位精度平均提高30.64%和45.60%,较DV-EA的定位精度平均提高22.30%和39.26%.
CVLR性能优于DV-RND和DV-EA的原因在于:1)DV-RND仅优化了未知节点到锚点的距离估计,它不能完全解决节点定位模糊问题.2)DV-EA虽然既优化了锚点的每跳距离,也对DV-Hop的定位结果进行了位置求精.但是,它与DV-RND一样,仅仅利用了锚点的消息,因而它要取得好的性能需要较多的锚点.3)CVLR在求精过程中,能够利用未知节点的周围邻居节点的信息,通过多轮迭代方式对每个节点定位位置进行优化,因而能够如2.2节所描述的那样,较好地解决DV-Hop的定位模糊问题.同样,CVLR2性能高于CVLR1也是因为这个原因.
5 结束语
本文针对典型的无需测距算法DV-Hop存在的定位模糊问题,提出了一种基于校正矢量的分布式迭代求精CVLR算法.CVLR能充分利用节点的1跳邻居节点和2跳邻居节点信息对节点的位置进行求精,其基本思想为利用节点接收到的锚点的校正值来计算节点间伪测距距离,然后通过定位距离和伪测距距离的偏差来构建位置校正矢量,最后利用一种简单的搜索算法来获得求精坐标.仿真实验显示,CVLR1和CVLR2较好地解决DV-Hop的定位模糊问题,其定位精度远高于DV-Hop算法,也优于DV-RND和DV-EA.
具体仿真结果表明:在相同通信半径不同未知节点数量下,CVLR1和CVLR2较DV-Hop的定位精度平均提高31.83%和47.59%,较DV-RND的定位精度平均提高21.20%和39.31%,较DV-EA的定位精度平均提高21.26%和39.45%;在相同未知节点数量不同通信半径下,CVLR1和CVLR2较DV-Hop的定位精度平均提高34.23%和48.54%,较DV-RND的定位精度平均提高30.64%和45.60%,较DV-EA的定位精度平均提高22.30%和39.26%.
在未来工作中,可以从3个方面继续改进本文的工作:1)结合其他DV-Hop改进算法,改进本文提出的节点之间的伪测距距离的估计,从而提高定位精度; 2)利用其他优化方法来解决本文提出的最小化问题,减少迭代次数,从而降低定位能耗;3)本文算法虽然用MATLAB进行仿真实验得出的结果较好,但是毕竟不是真实场景,后续也可以考虑使用ZigBee进行组网,在真实场景中测试和改进本文提出的算法.
[1]Xu Yang, Liu Fugui. Application of wireless sensor network in water quality monitoring [C]//Proc of the 20th IEEE Int Conf on Computational Science and Engineering. Piscataway, NJ: IEEE, 2017: 368-371
[2]Wang Haohan, Dong Linxi, Wei Wei, et al. The WSN monitoring system for large outdoor advertising boards based on ZigBee and MEMS sensor [J]. IEEE Sensors Journal, 2018, 18(3): 1314-1323
[3]Gurumoorthy K B, Kumar A N. Mutual constraint based GA suggested routing algorithm for improving QoS in clustered MANETS [J]. Wireless Personal Communications, 2018, 98(3): 2975-2991
[4]Manap Z, Ali BM, Ng CK, et al. A Review on hierarchical routing protocols for wireless sensor networks [J]. Wireless Personal Communications, 2013, 72 (2): 1077-1104
[5]Mao Keji, Fan Congling, Ye Fei, et al. Node localization algorithm in wireless sensor networks based on SVM [J]. Journal of Computer Research and Development, 2014, 51(11): 2427-2436 (in Chinese)(毛科技, 范聪玲, 叶飞, 等. 基于支持向量机的无线传感器网络节点定位算法[J]. 计算机研究与发展, 2014, 51(11): 2427-2436)
[6]Xiao Fu, Sha Chaoheng, Chen Lei, et al. Localization algorithm for wireless sensor networks via norm regularized matrix completion[J]. Journal of Computer Research and Development, 2016, 53(1): 216-227 (in Chinese)(肖甫, 沙朝恒, 陈蕾, 等. 基于范数正则化矩阵补全的无线传感网定位算法[J]. 计算机研究与发展, 2016, 53(1): 216-227)
[7]Yao Yingbiao, Jiang Nanlan. Distributed wireless sensor network localization based on weighted search[J]. Computer Networks, 2015, 86(5): 57-75
[8]Ahmadi Y, Neda N, Ghazizadeh R. Range free localization in wireless sensor networks for homogeneous and non-homogeneous environment[J]. IEEE Sensors Journal, 2016, 16(22): 8018-8026
[9]Yeredor A. Decentralized TOA-based localization in non-synchronized wireless networks with partial, asymmetric connectivity[C]//Proc of the 15th IEEE Int Workshop on Signal Processing Advances in Wireless Communications. Piscataway, NJ: IEEE, 2014: 165-169
[10]Shao Huajie, Zhang Xiaoping, Wang Zhi. Efficient closed-form algorithms for AOA based self-localization of sensor nodes using auxiliary variables[J]. IEEE Transactions on Signal Processing, 2014, 62(10): 2580-2594
[11]Yao Yingbiao, Han Qi, Xu Xiaorong, et al. A RSSI-based distributed weighted search localization algorithm for WSNs [J]. International Journal of Distributed Sensor Networks, 2015: Article ID 293403
[12]Tang Wenliang, Zhou Linying. An improved APIT localization algorithm based on triangle-circumcircle cover [J]. Chinese Journal of Sensors and Actuators, 2015, 28(1): 121-125 (in Chinese)(汤文亮, 周琳颖. 基于三角形外接圆覆盖的改进APIT定位算法[J]. 传感技术学报, 2015, 28(1): 121-125)
[13]Wu Guang, Wang Shu, Wang Bang, et al. A novel range-free localization based on regulated neighborhood distance for wireless ad hoc and sensor networks[J]. Computer Networks, 2012, 56(16): 3581-3593[14]Mehrabi M, Taheri H, Taghdiri P. An improved DV-Hop localization algorithm based on evolutionary algorithms [J]. Telecommunication System, 2017, 64(4): 639-647
[15]Singh S P, Sharma S C. A PSO based improved localization algorithm for wireless sensor network [J]. Wireless Personal Communications, 2018, 98(1): 487-503
[16]Ma Shuli, Zhao Jianping. Multi communication ranges DV-Hop localization algorithm for wireless sensor network [J]. Chinese Journal of Sensors and Actuators, 2016, 29(4): 593-600 (in Chinese)(马淑丽, 赵建平. 多通信半径的无线传感器网络DV-Hop定位算法[J]. 传感技术学报, 2016, 29(4): 593-600)
[17]Liu Yuan, Chen Junjie, Xu Zhenfeng. Improved DV-Hop localization algorithm based on bat algorithm in wireless sensor networks [J]. KSII Transactions on Internet & Information Systems, 2017, 11(1): 215-236
[18]Zheng Mingcai, Zhang Dafang, Zhao Jinqin, et al. Distance estimating algorithm based on gradient neighbors in wireless sensor networks [J]. Journal on Communications, 2008, 29(11): 237-245 (in Chinese)(郑明才, 张大方, 赵晋琴, 等. 基于梯度化邻居节点信息的传感器网络节点距离测量[J]. 通信学报, 2008, 29(11): 237-245)
[19]Zhao Yanhang, Qian Zhihong, Shang Xiaohang, et al. PSO localization algorithm for WSN nodes based on modifying average hop distances [J]. Journal on Communications, 2013, 34(9): 105-114 (in Chinese)(赵雁航, 钱志鸿, 尚小航, 等. 基于跳距修正粒子群优化的 WSN 定位算法[J]. 通信学报, 2013, 34(9): 105-114)
[20]Peng Bo, Li Lei. An improved localization algorithm based on genetic algorithm in wireless sensor networks [J]. Cognitive Neurodynamics, 2015, 9(2): 249-256
[21]Gurung S, Hossain A K, Kanchanasut K. A hop-count based positioning algorithm for wireless ad-hoc networks [J]. Wireless Networks, 2014, 20(6): 1431-1444
[22]Wang Yun, Wang Xiaodong, Wang Demin, et al. Range-free localization using expected hop progress in wireless sensor networks [J]. IEEE Transactions on Parallel & Distributed Systems, 2009, 20(10): 1540-1552
[23]Arias J, Zuloaga A, Lazaro J. Malguki: An RSSI based ad hoc location algorithm [J]. Microprocessors and Microsystems, 2004, 28(8): 403-409




