强化学习(reinforcement learning, RL)是智能体从环境状态到动作映射的学习,以使动作从环境中获得的累积奖赏值最大[1-3].强化学习通过试错与环境交互获得策略的改进,这就导致一个问题:哪一种试错策略可以产生最有效的学习.因此强化学习面临探索(exploration)和利用(exploitation)的两难问题:长期来看,探索可能获得更高的累积奖赏,帮助智能体收敛到最优策略;而利用总是最大化短期奖赏,但可能收敛到次优解上[4-5].多臂赌博机(multi-armed bandit, MAB)问题是强化学习中研究探索与利用平衡的经典问题.
随机多臂赌博机(stochastic multi-armed bandit, SMAB)问题是一类经典的MAB问题,该问题最早由Robbins提出[6].一个MAB问题中包括K个臂,玩家每次只能选择其中一个臂,并获得相应的奖赏.n轮游戏后,玩家的目标是最大化奖赏的期望值.其中,玩家选择某个臂之后只能知道该臂的奖赏,且各个臂的奖赏是相互独立的,服从某种未知的分布.为了达到目标,玩家需要在获得奖赏的同时去学习该奖赏的分布.因此,每个时间步,玩家都必须在以下两者做出选择:利用,选择目前为止已知奖赏最高的臂;探索,尝试其他未来奖赏可能更高的臂.这样,在游戏过程中玩家面临着探索与利用间的平衡问题.
作为一个序列化的决策问题,MAB被应用于很多实际场景中,最早的应用就是Robbins提出的诊治试验[6].诊治试验中各个患者的治疗方案对应MAB问题中的各个臂.诊治试验的目标是最小化患者的健康损失.近来,MAB问题有了更多广泛的应用,比如推荐算法[7-9]、众包机制[10-12]、搜索引擎关键字选择[13]、网络信道选择[14]等.除了SMAB问题,MAB问题还存在多个变种,例如Markov赌博机(Markovian bandit)[15],对抗式赌博机(adversarial bandit)[15]和上下文相关的赌博机(contextual bandit)[16]等.在上下文相关的赌博机问题中,玩家选择一个臂之后,除了获得相应的奖赏之外,还可以获得该臂的上下文信息.本文将研究SMAB问题,提出一种自适应的MAB算法,并将其推广到上下文相关的场景中.
目前已有很多策略来平衡MAB问题中探索与利用的难题.Watkins首次引入ε -贪心(ε -greedy)算法[17],ε -greedy算法以一个很小的概率ε进行探索,以1-ε的概率利用.但是ε -greedy算法将在所有臂中均等选择进行探索,没有利用选择臂之后获得的信息,比如各个臂的平均奖赏和选择次数.软最大化(SoftMax)算法最早由Luce提出[18],SoftMax算法是基于当前已知臂的平均奖赏来对探索和利用的程度进行折中.然而SoftMax算法只考虑了平均奖赏,这种较为单一的信息可能导致错误的概率分配,比如某个臂第一次被选择,随机得到一个很低的奖赏,SoftMax算法根据这一次的奖赏为该臂分配了很低的选择概率,但该臂有可能是初期奖赏低而实际平均奖赏很高的臂.置信上界 (upper-confidence-bound, UCB)动作选择方法[19]则根据各个臂已知的平均奖赏和选择次数直接计算出要选择的臂,不利用随机性来选择臂.使用UCB算法时必须在初期轮流选择所有臂各一次,那么当实验次数小于等于臂的数量时,难以使用UCB方法,因此UCB方法泛化能力较弱.LinUCB算法[20-21]是经典的上下文相关的MAB算法,利用上下文信息最大化奖赏的期望值.然而LinUCB算法只适用于上下文可用的场景中.
本文针对上述随机多臂赌博机算法未能充分使用反馈信息以及泛化能力较弱的问题,提出了一种自适应的多臂赌博机算法,利用当前估计值最小的动作被选择的次数(chosen number of arm with minimal estimation, CNAME)来调整探索和利用的概率,记为CNAME算法.本文的主要贡献有3个方面:
1) 提出了一种自适应的随机多臂赌博机算法CNAME,其探索概率由一个简单分式给出,该分式由当前平均奖赏最小的臂被选择的次数和参数w构成,充分利用了选择臂之后的信息.该算法不依赖上下文信息,因此在各个应用场景中具有更强的推广能力和泛化能力.
2) 通过理论分析给出了CNAME算法的悔值(regret)上界,并与其他算法的悔值上界进行对比,为CNAME算法提供了有力的效果保证.
3) 通过实验研究给出了CNAME算法中关键参数的参考取值范围.在无上下文的随机数据集和内容分发网络(content distribution network, CDN)[22]数据集以及带有上下文的雅虎公司R6A数据集上的实验结果表明:利用估计值最小的动作被选择的次数能有效平衡探索和利用,并且在上下文相关的场景中依然表现良好.
1 背景和相关工作
1.1 随机多臂赌博机问题
随机多臂赌博机问题,又称为K-臂赌博机问题, K即为臂的数量,下文把各个臂统称为动作.K-臂赌博机的目标是最大化获得的累积奖赏.若时刻t动作i被选择,则获得随机奖赏Xi,t.各个动作的奖赏相互独立且服从均值为μ=[μ1,μ2,…,μK]的某种分布,μi是动作i的真实值.假设已知各个动作的真实值,只要一直选择有最高真实值的动作便可以获得最大的累积奖赏,这种情况下多臂赌博机问题自然得解.然而,事实上随机多臂赌博机问题可以通过获得的奖赏来估计各个动作的值,但动作的真实值是未知的.
悔值是K-臂赌博机的一种典型的度量标准[15].在动作真实值未知的情况下,任何算法都不可能每次都选到奖赏最高的动作,悔值就是实际得到的奖赏与期望得到的最大奖赏之间的差值.给定n次操作后的悔值定义为
![]()
![]()
(1)
其中,Nn(i)是前n次操作中动作i被选择的次数.悔值越小,则该算法产生的策略越接近最优策略.
1.2 估计值函数
动作的真实值是选择动作后期望得到的平均奖赏,因此一种估计动作值的简单方法是计算选择动作之后实际获得的平均奖赏.假设第n次操作之后,动作i已经被选择Nn(i)次,得到的奖赏分别是r1,r2,…,rNn(i),这时动作i的估计值为
(2)
Qn+1(i)是到第n次操作之后的动作i的估计值,即动作i实际获得的平均奖赏.根据式(2),Qn+1(i)的更新需要记录每次选择动作i之后获得的奖赏,为了减小需要的存储空间,估计值的更新可以转化为增量式的更新:
(3)
根据式(3),估计值的更新只需要存储立即奖赏和上一时刻的估计值.若Nn(i)=0,Qn(i)为初始值;当Nn(i)→∞时,根据大数定理可知Qn(i)收敛到动作i的真实值.这种方法叫作抽样平均(sample average)[23],每个估计值都是奖赏的简单平均值.因此,通过以上方法得到动作的估计值后,可以根据估计值作出动作选择.
1.3 动作选择方法
本节主要介绍已有的3类经典随机多臂赌博机算法.
1.3.1 ε -greedy方法及其变种
最简单的动作选择方法是一直选择估计值最高的动作,即贪心动作a*,这种方法称为贪心(greedy)方法[1].贪心方法利用当前知识最大化立即奖赏,没有探索的过程.
一个简单的代替贪心的办法是在大多数时间内采用a*,但是以一个很小的概率ε进行探索,即与估计动作值无关地随机均匀地选择一个动作,该方法为ε -greedy[17],ε位于开区间(0,1)上.
ε -greedy算法的一个变种是ε -优先(ε -first)算法[24],ε -first算法在实验初期先做完所有的探索工作.例如对于一个给定实验次数为n的实验,在最初的εn次实验中随机选择动作,即纯探索阶段,在余下的(1-ε)n次实验中,选择平均奖赏最高的动作,即纯利用阶段.
ε -greedy算法的另一个变种是ε -递减(ε -decreasing)算法[25].ε -decreasing算法用一个递减的概率来接近最优策略,递减变量εt由εt=min{1,ε0 t}给出,其中t是时间步,初始参数ε0>0.此外,Cesa-Bianchi等人[25]提出了混合贪心(greedy mix)算法,用递减因子1
t}给出,其中t是时间步,初始参数ε0>0.此外,Cesa-Bianchi等人[25]提出了混合贪心(greedy mix)算法,用递减因子1 ln t代替了ε -decreasing算法的递减因子1
ln t代替了ε -decreasing算法的递减因子1 t.类似地,Strens[26]提出了Least Taken算法,Vermorel等人[27]则在Least Taken算法的基础上添加了初始参数ε0.
t.类似地,Strens[26]提出了Least Taken算法,Vermorel等人[27]则在Least Taken算法的基础上添加了初始参数ε0.
1.3.2 SoftMax方法及其变种
尽管ε -greedy算法是一类有效的方法,但是ε -greedy算法在探索的时候是在所有的动作中均等选择.这就意味着ε -greedy算法选择下一个动作时有可能选到最差的动作.为了避免这种情况,SoftMax方法将探索概率更改为与估计值相关的一个分级函数:贪心动作仍然具有最高的选择概率,其他动作则根据其估计值进行分级并分配权重.SoftMax算法广泛使用Gibbs或Boltzmann分布,时刻t选择动作i的概率为

(4)
其中,τ是温度(temperature)参数[28].高温可以使得各动作的选择概率趋于相等,低温则使具有不同估计值的动作的选择概率趋于不同.当τ→0时,SoftMax算法的作用与greedy方法一致.
与ε -greedy算法相似,SoftMax算法可以变形为递减的软最大化(decreasing SoftMax)算法[25],decreasing SoftMax算法的温度随时间步的增加而递减,即τt=τ0 t.类似地,可以用递减因子1
t.类似地,可以用递减因子1 ln t代替decreasing SoftMax算法的递减因子1
ln t代替decreasing SoftMax算法的递减因子1 t[25].作为一个更复杂的SoftMax算法变种,Exp3算法的关键在于利用了累计奖赏与动作选择概率的比值[25].
t[25].作为一个更复杂的SoftMax算法变种,Exp3算法的关键在于利用了累计奖赏与动作选择概率的比值[25].
1.3.3 UCB方法
由于动作值的估计具有不确定性,因此,需要在动作选择过程中引入探索.然而,非贪心动作中有接近贪心的动作,也有很差的动作.如果能根据非贪心动作成为最优动作的可能性进行探索,探索的效果往往会更好.
基于上述的思想,UCB算法动作选择方法同时考虑非贪心动作估计值对最优动作估计值的接近程度和估计值的不确定性:
(5)
其中,t是时间步,At是时刻t应该被选择的动作,Nt(i)表示动作i在时间步t之前已经被选择的次数,参数c>0控制探索的程度.若Nt(i)=0,则把动作i看作最优动作At.参数![]() 时,为UCB1算法[19].本文后续对比实验中采用的是UCB1算法.
时,为UCB1算法[19].本文后续对比实验中采用的是UCB1算法.
雅虎公司的科学家在UCB算法的基础上引入了上下文信息,提出了LinUCB算法[20],并应用于雅虎公司的新闻推荐中.LinUCB算法假设一个玩家选择一个动作之后,其奖赏和上下文信息成线性关系.于是学习过程就变成:用玩家和动作的上下文信息预估奖赏及其置信区间,选择置信区间上界最大的动作,观察奖赏后更新线性关系的参数,以此达到最大化奖赏期望值的目的.
1.3.4 已有算法存在的问题
基于上述讨论可知:ε -greedy算法是一个简单有效的方法,其存在的问题是在所有动作中均等探索,没有利用选择动作后获得的反馈信息.SoftMax算法仅基于当前已知动作的估计值对各动作的选择概率进行分级,因此SoftMax算法容易被误导.ε -greedy算法和SoftMax算法都仅需要设置一个参数,计算相对简单.与上述2种方法不同的是,UCB动作选择方法充分利用了动作的估计值和被选择次数,每次都根据已有信息直接计算出要选择的动作,其计算开销相对较大.另外,UCB动作选择方法必须在实验初期轮流选择所有动作各一次,因此当实验次数小于等于动作的数量时,UCB动作选择方法将不适用.LinUCB算法则只适用于上下文信息可用的场景中,实际应用中存在着大量没有先验信息的环境,此时LinUCB算法的使用将受限.
2 算法描述
本文针对已有的随机多臂赌博机算法存在的不足,提出了一种自适应的随机多臂赌博机算法(CNAME).
2.1 CNAME算法描述
探索概率的变化将直接影响探索和利用的平衡.针对该问题,本文提出一种新的探索概率计算方法:
p=w 
![]()
其中,mt是当前平均奖赏最小的动作被选择的次数,参数w>0用来控制探索概率衰减的速率,起到宏观调控的作用.w和mt共同控制探索概率.该计算方法可以充分利用选择动作之后的信息,根据环境自适应地调整探索概率,平衡探索和利用.本文3.1节将通过实验讨论参数w对CNAME算法效果的影响及其参考取值范围.
CNAME算法以w
![]() 的概率选择目前最少被选择的动作,即探索;或者选择当前估计值最大的动作,即利用.具体如算法1所示:
的概率选择目前最少被选择的动作,即探索;或者选择当前估计值最大的动作,即利用.具体如算法1所示:
算法1. CNAME算法.
输入:动作集合;
输出:估计值.
① 设置参数w;
② for 每个动作i∈[1,2,…,K] do
③ Q0(i)=0;
④ N0(i)=0;
⑤ end for
⑥ for 每个时间步t≤n do
⑦![]()
⑧![]()
⑨ 在开区间(0,1)上产生一个随机数x;
⑩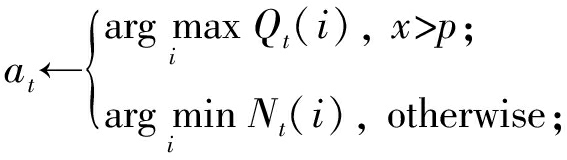
 获得立即奖赏
获得立即奖赏![]()
 Nt(at)=Nt-1(at)+1;
Nt(at)=Nt-1(at)+1;
 Qt
Qt![]()
Qt-1(at)];
 end for
end for
根据算法1,步骤①首先设置CNAME算法的关键参数w,参数w影响着探索概率衰减的速率.步骤②~⑤初始化动作的估计值和被选择的次数,即Q0(i)=0,N0(i)=0.这里也可以使用乐观初始值,比如Q0(i)=1,乐观初始值在实验初期可以临时地促进探索[1].步骤⑥~⑩为动作选择的过程,n是实验次数,mt是时刻t估计值最小的动作已经被选择的次数,p是当前的探索概率.步骤⑩在选择动作时,同时考虑了实际获得的平均奖赏和动作选择的次数.步骤 是选择动作at后获得立即奖赏
是选择动作at后获得立即奖赏![]() 该奖赏服从某种概率分布.步骤
该奖赏服从某种概率分布.步骤
 对动作被选择的次数和估计值进行更新,其中,估计值更新方法采用的是增量式抽样平均方法.
对动作被选择的次数和估计值进行更新,其中,估计值更新方法采用的是增量式抽样平均方法.
2.2 CNAME算法分析
在任何一个特定环境下,探索的效果更优还是利用的效果更优取决于估计的精确值、环境不确定性和剩余操作次数等复杂的具体情况[1].
CNAME算法充分利用了用户反馈,即动作估计值和动作选择的次数,自适应地根据实际情况来调整探索概率.同时,通过参数w控制探索概率下降的速率,并根据mt来改变探索概率.具体从3个方面分析:
1) 当参数w的取值较大时,mt对探索概率的影响较小;当参数w的取值较小时,mt对探索概率的影响则较大.由于不同环境中mt的实际影响也不同,本文设计参数w来削弱或者增强mt在调整探索概率时起到的作用.
2) 每当mt增加一次,说明估计值最小的动作又被选择了一次,估计值最小的动作是对整个累积奖赏贡献最少的动作,应尽量减少该动作被选择的次数.随着mt的增加,探索概率降低,贪心动作的选择概率增加,这样有助于提高实际获得的累积奖赏.
3) CNAME算法在探索时选取的是当前最少被选择的动作,这样就保证每个动作都有被选择到的机会,同时避免了随机选择动作的盲目性.
2.3 CNAME算法的悔值上界证明
基于2.1~2.2节的算法描述和分析,本节将通过证明给出CNAME算法的悔值上界.悔值用来评价算法的好坏,悔值上界越小,说明该算法的效果越好.
Lai等人[29]发现,对于均值为单一参数的奖赏分布,所有算法都满足:
(6)
其中,![]() /p*(x)dx是pi和p*之间的KL散度,pi指任意次优动作i在随机变量X上的概率分布,p*指最优动作在随机变量X上的概率分布,x∈X.KL散度可度量pi和p*的接近程度,2个概率分布越接近,KL散度值越小,则式(1)中的悔值也越小,pi越接近最优策略p*.
/p*(x)dx是pi和p*之间的KL散度,pi指任意次优动作i在随机变量X上的概率分布,p*指最优动作在随机变量X上的概率分布,x∈X.KL散度可度量pi和p*的接近程度,2个概率分布越接近,KL散度值越小,则式(1)中的悔值也越小,pi越接近最优策略p*.
对于某个算法A,根据式(1)(6),若已知算法中pi的上界,便可得到算法A的悔值上界.为了方便证明,给出已知的2个不等式:
引理1. Chernoff-Hoeffding不等式.
设X1,X2,…,Xn为[0,1]之间的随机变量,且E[Xt|X1,X2,…,Xt-1]=μ,Sn=X1+X2+…+Xn.那么对于所有的a≥0都有:
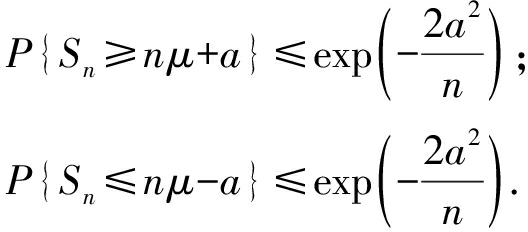
引理2. Bernstein不等式.
设X1,X2,…,Xn为[0,1]之间的随机变量,且![]() 么对于所有的a≥0都有:
么对于所有的a≥0都有:
定理1. 第n次操作时,CNAME算法的次优动作选择概率pi不超过:
证明. 首先,对于所有的动作1≤i≤K,定义Xi,n为动作i在第n次操作得到的立即奖赏,显然E[Xi,n]=μi.另外,拥有μ*的动作叫作最优动作.类似地,![]() 表示最优动作在前n次操作被选择的次数,
表示最优动作在前n次操作被选择的次数,![]() 表示最优动作在第n次操作时的平均奖赏.最优动作值与次优动作值的差值为Δi=μ*-μi.动作i在第n次操作时的平均奖赏定义为
表示最优动作在第n次操作时的平均奖赏.最优动作值与次优动作值的差值为Δi=μ*-μi.动作i在第n次操作时的平均奖赏定义为
令前n次操作中动作i被选择次数的期望为:![]() 其中P{at=i}为时刻t动作i的选择概率.
其中P{at=i}为时刻t动作i的选择概率.
令εn表示第n次操作的探索概率,即
其中,w>0.同时,令![]() 则动作i在第n次操作的选择概率满足:
则动作i在第n次操作的选择概率满足:
(7)
根据式(7),要求解P{at=i},只需要求出概率![]() 即可.已知:
即可.已知:
![]()
![]() },
},
令![]() 为动作i在前n次操作中随机被选到的次数,结合Chernoff-Hoeffding不等式(引理1),可得:
为动作i在前n次操作中随机被选到的次数,结合Chernoff-Hoeffding不等式(引理1),可得:
![]() }=
}=![]() }=
}=![]() }×
}×![]() }≤
}≤![]()
![]() }+
}+![]()
![]()
![]()
(8)
根据式(7)(8),求解P{an=i}的问题可以转化为求解x0和![]() 的问题.其中,
的问题.其中,![]() x0}的求解过程为:
x0}的求解过程为:
已知![]() 而且
而且![]() 的方差
的方差
根据Bernstein不等式(引理2)可以得到:
(9)
求解x0,具体过程为
![]()
![]()
![]()
![]()
(10)
当n≥K时,结合式(7)~(10)可得:
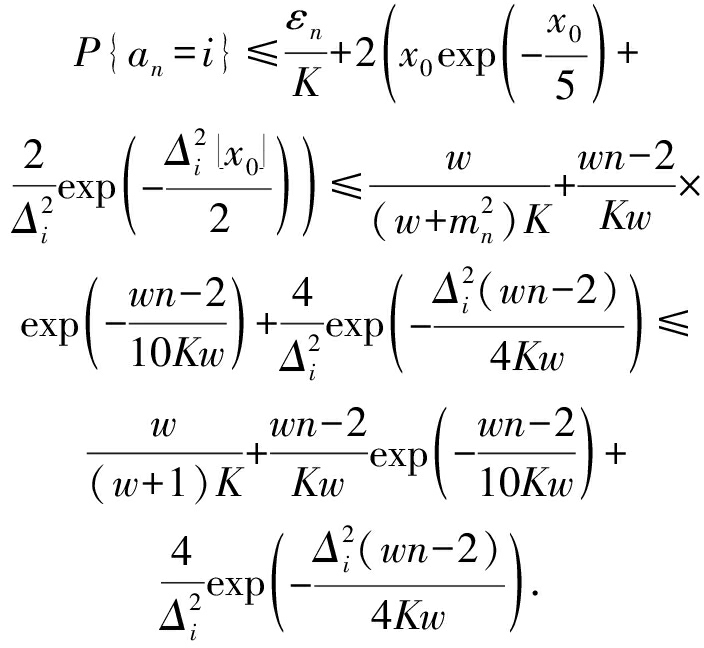
那么对于CNAME算法,w>0,若n≥K,那么在第n次操作时动作i的选择概率pi有:

(11)
证毕.
定理2. 第n次操作时,CNAME算法的悔值满足:
![]()
![]()
证明. 结合式(6)(11)可得到E[Nn(i)]的下界为
![]()
![]() )).
)).
(12)
最后,根据式(1)(12)可得出CNAME算法的悔值上界:
![]()
![]()
证毕.
① https:
 webscope.sandbox.yahoo.com
webscope.sandbox.yahoo.com
值得注意的是,不同于其他算法的悔值上界,例如ε -decreasing算法的悔值上界O(log n)和Exp3算法的悔值上界![]() 本节给出了CNAME算法的次优动作选择概率的上界,基于此可以得到某一时刻动作选择概率的分布,进而得到该时刻的悔值上界,即瞬时的悔值上界.此时,若要进一步知道某个时刻的悔值,只需要知道最优动作与次优动作之间的差值.
本节给出了CNAME算法的次优动作选择概率的上界,基于此可以得到某一时刻动作选择概率的分布,进而得到该时刻的悔值上界,即瞬时的悔值上界.此时,若要进一步知道某个时刻的悔值,只需要知道最优动作与次优动作之间的差值.
3 实验部分
本节通过4组实验来分别研究CNAME算法中参数w的影响以及CNAME算法与其他算法的效果比较.在对比实验中,使用3个数据集:服从正态分布的随机数据集、内容分发网络数据集[22]和带有上下文信息的雅虎公司R6A数据集①.
3.1 实验1:CNAME算法中参数w的影响
本节的实验对象是一组有1 000个随机产生的K-臂赌博机的任务,其中K=10.具体实验设置如下:
1) 每个任务的真实值μ=[μ1,μ2,…,μK]服从均值为0、方差为1的正态分布.
2) 每个动作i的奖赏服从一个均值为μi、方差为1的正态分布.
3) 1 000个K-臂赌博机任务通过1 000次重复随机选择μ产生,选取1 000个不同的K-臂赌博机任务是为了克服任务和环境本身的随机性.
在上述实验条件下取不同的w值,分别记录1 000个随机任务的平均奖赏和平均每轮的悔值.
首先,在闭区间[0.01,100]以10的倍率分别取5组不同的w值,图1给出了相应的平均奖赏和平均每轮的悔值.
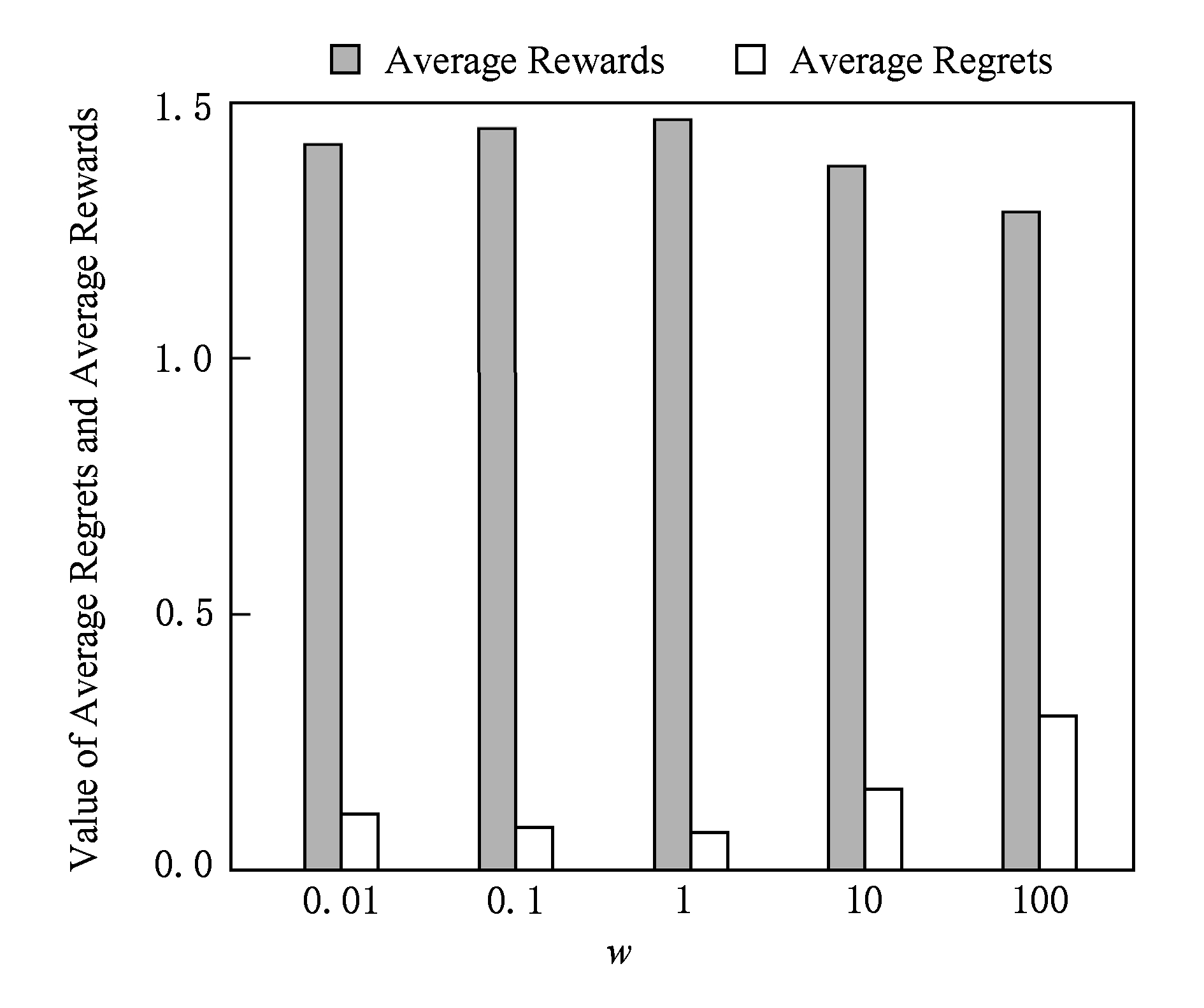
Fig. 1 Average rewards and average regrets of algorithm CNAME with different values of parameter w
图1 不同w值下CNAME算法的平均奖赏和平均悔值
从图1可以看出:当w∈[1,100]时,随着w的减小,平均奖赏呈增加趋势,而平均每轮的悔值呈下降趋势.然而当w=0.1和w=0.01时获得的平均奖赏却小于w=1时的平均奖赏,即平均奖赏并不是随着w的减小而无限增加的.同时,平均每轮的悔值的下降也存在下限.基于图1的数据,可以猜测,w=1是CNAME算法效果的分界线,w<1或w>1时,效果均下降.较之其他w的取值,当w取值为0.1和1时,CNAME算法的平均奖赏较高,平均每轮的悔值较低.
为进一步研究当w∈[0.1,1]时,CNAME算法的性能,下面以0.1为间隔分别取10组不同的w值展开实验.表1给出了对应的实验结果数据,加粗部分是效果最好的参数及结果.
Table 1 Average Rewards and Average Regrets of
CNAME (w∈[0.1,1])
表1 CNAME算法的平均奖赏和平均悔值(w∈[0.1,1])
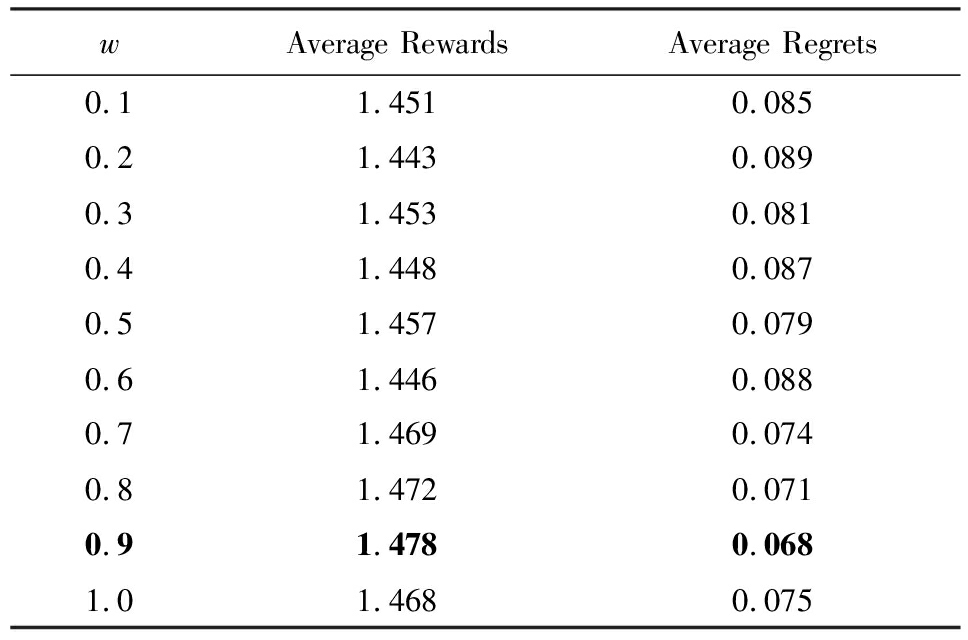
wAverage RewardsAverage Regrets0.11.4510.0850.21.4430.0890.31.4530.0810.41.4480.0870.51.4570.0790.61.4460.0880.71.4690.0740.81.4720.0710.91.4780.0681.01.4680.075
Note: The best result is highlighted in bold.
基于图1和表1的数据,可以确认当w∈[0.1,1]时,CNAME算法能够获得较高的平均奖赏和较低的平均悔值.此外,根据表1可知,当w取值较为接近1时,比如w=0.9时,获得的平均奖赏更大,平均每轮的悔值更小,即CNAME算法的效果更好.
仅以平均奖赏为例对图1和表1的实验结果进行分析,主要有2个原因:
1) 当w的取值过小时,探索概率的衰减速率过快,导致没有足够的探索,无法得到最高的累积奖赏.
初始时刻m0=0,CNAME算法探索的概率为1,此时接近随机策略.一定时间步之后,当mt≠1时,探索概率开始衰减,w越小,衰减的速率越高.例如当w=1,mt=1时,探索概率为0.5;当mt=2时,探索概率降为0.2,算法效果近似于ε -decreasing.而当w=0.01,mt=1时,探索概率为0.009 9;当mt=2时,探索概率衰减到0.002 5,这时算法效果类似于greedy,可能会忽略更优的动作,从而不能获得最高的平均奖赏.因此,w取值过小,平均奖赏反而会有所下降.
2) 当w的取值较大时,探索概率的衰减速率过慢,导致过度探索,平均奖赏相对较小.
例如当w=100,mt=1时,探索概率为0.990;mt=2,探索概率为0.962.mt的增加对探索概率的影响过小,不能及时地减少探索概率,导致了过多的探索,使得平均奖赏较小.因此w取值过大,平均奖赏相对较小.
综上所述,参数w应根据实际环境适当取值,不宜过大也不宜过小.根据实验结果,该环境下CNAME算法的参数w取闭区间[0.1,1]中的值较好.
3.2 实验2:随机数据集上的比较
本节基于随机数据集,比较CNAME算法和其他3类经典算法及其变种的算法性能.
与实验1相似,本实验同样采用随机产生的服从正态分布的数据集:1 000个随机产生的多臂赌博机任务.具体地,K=10,n=2 000;μ=[μ1,μ2,…,μK]服从均值为0、方差为1的正态分布;每个动作i的奖赏服从一个均值为μi、方差为1的正态分布.根据实验1的结果,本次实验中,参数w=0.95.
在上述实验条件下,分别记录各个算法的平均奖赏和平均每轮的悔值.表2列出了实验中6种算法的参数设置、对应1 000个任务在2 000个时间步下的平均奖赏和平均每轮的悔值.各个算法均采用的是该实验条件下效果较好的参数,表2中加粗部分是效果最好的结果.
从表2可以看出,该实验条件下,CNAME算法获得的平均奖赏最高,平均每轮的悔值最低.变种ε -decreasing算法的效果明显优于ε -greedy算法的效果;类似地,变种decreasing SoftMax算法的效果优于SoftMax算法.
Table 2 Parameters and Experimental Results of
Six Algorithms
表2 6种算法的参数设置及实验结果
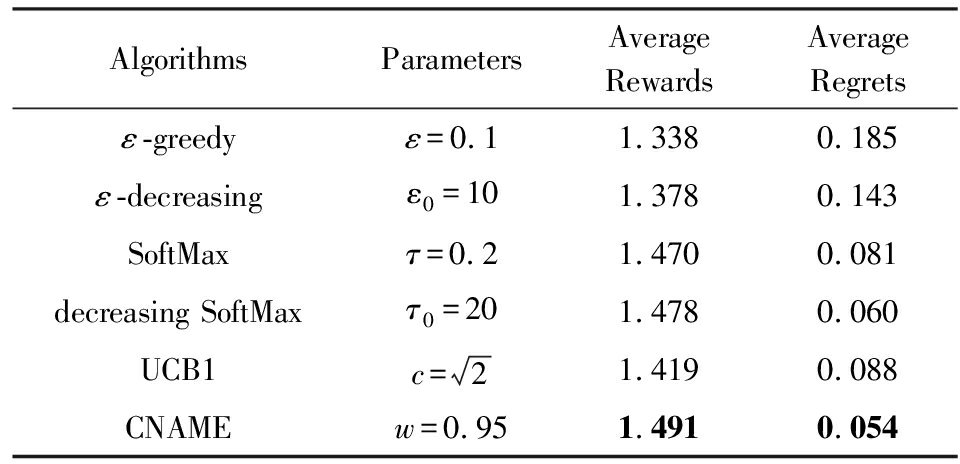
AlgorithmsParametersAverageRewardsAverageRegretsε-greedyε=0.11.3380.185ε-decreasingε0=101.3780.143SoftMaxτ=0.21.4700.081decreasing SoftMaxτ0=201.4780.060UCB1c=21.4190.088CNAMEw=0.951.4910.054
Note: The best result is highlighted in bold.
为了简洁清晰地表示这几种算法的对比效果,图2和图3仅分别展示了ε -decreasing,decreasing SoftMax,UCB1,CNAME这4种算法运行至1 000个时间步时的实验数据.图2是CNAME算法与其他3种算法平均奖赏的结果比较.图3为CNAME算法与其他3种算法的悔值的比较,同时给出了CNAME算法平均悔值的上界(upper bound).基于2.3节得出的悔值上界,upper bound是平均每轮的悔值上界.由图3可知,随着时间步的增加,upper bound的值保持平稳,可见CNAME算法非常稳定.另一方面,CNAME算法各个时间步的平均悔值均在upper bound之下,符合2.3节的理论结论.
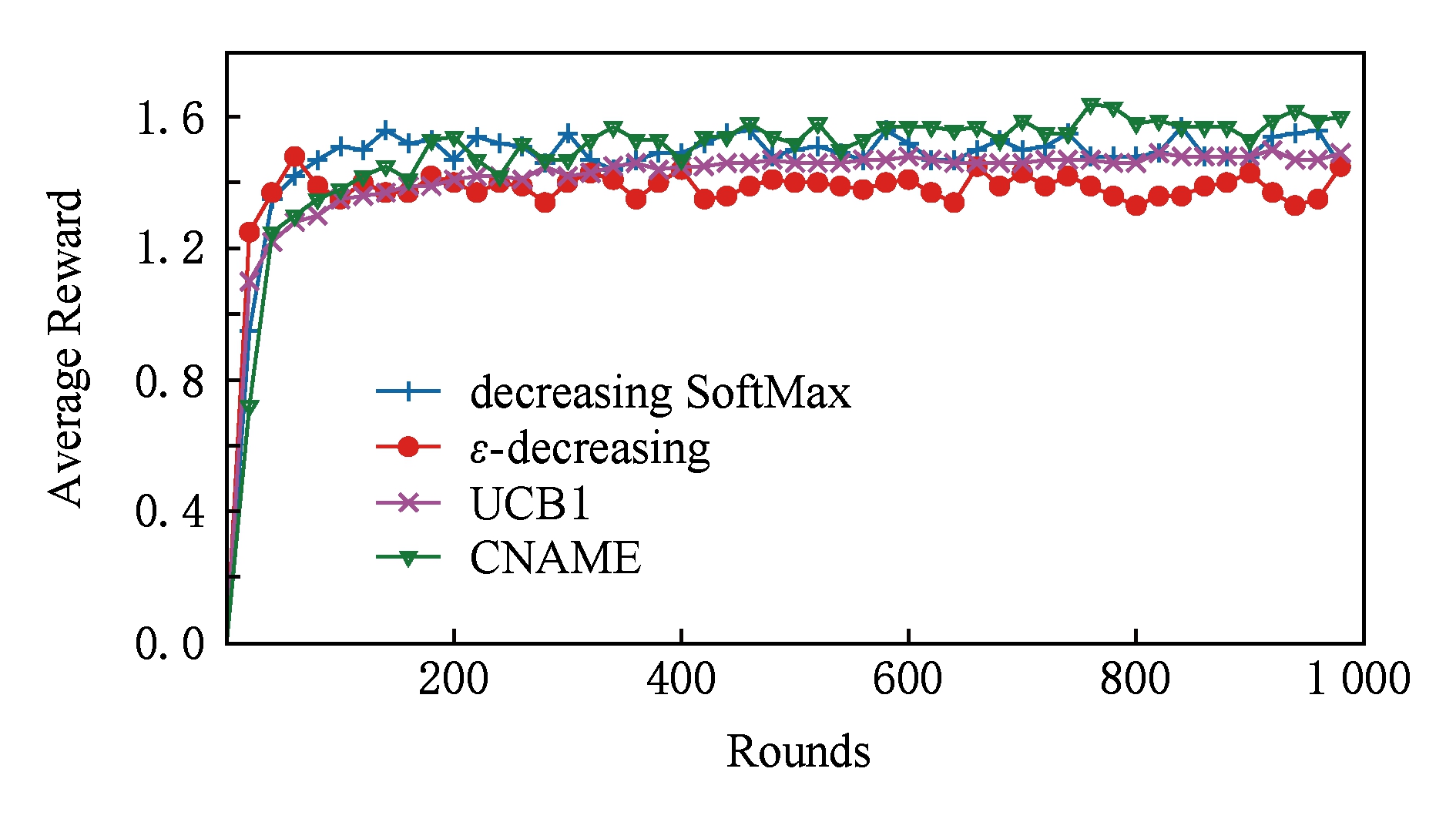
Fig. 2 Average rewards of CNAME and the other three algorithms
图2 CNAME算法与其他3种算法的平均奖赏
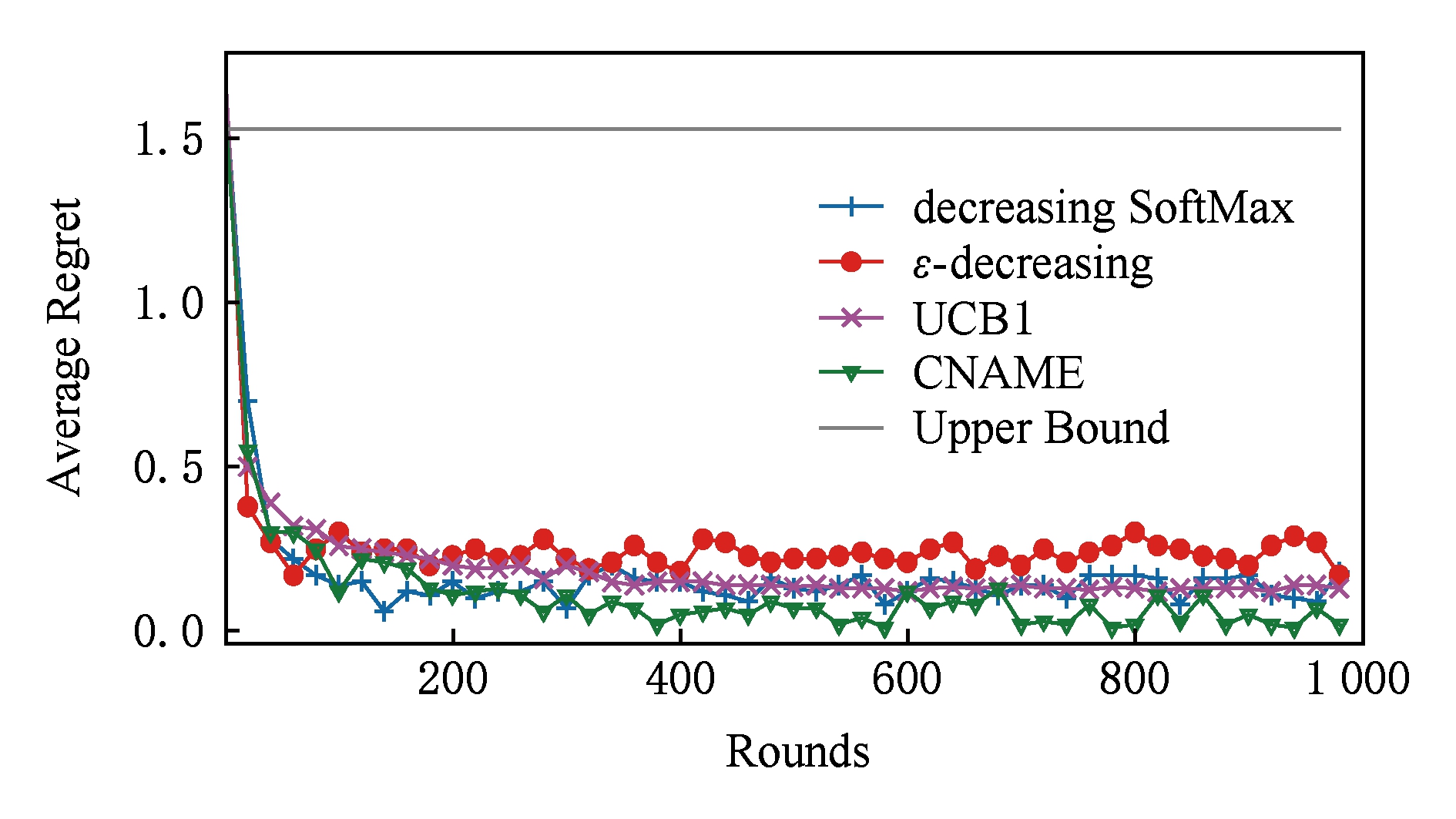
Fig. 3 Average regrets of CNAME and the other three algorithms
图3 CNAME算法与其他3种算法的平均每轮的悔值
表2、图2和图3中的数据均是1 000个随机任务的平均值.结合图表,本文从3方面进行比较:
1) CNAME算法和ε -greedy算法及其变种
CNAME算法的收敛速度略低于ε -decreasing算法,但其平均奖赏明显高于ε -greedy算法和ε -decreasing算法,平均每轮悔值也明显低于ε -greedy算法和ε -decreasing算法.CNAME算法的效果与ε -greedy算法和ε -decreasing算法相比有了很大的提高.
这是因为CNAME算法利用了用户反馈,虽然收敛速度有所减小,但效果比探索概率固定不变的ε -greedy算法好很多.同理,ε -decreasing算法的探索概率虽然是随着时间降低的,但是没有利用选择动作之后的信息,因此其效果比CNAME算法差.
2) CNAME算法和SoftMax算法及其变种
CNAME算法的收敛速度略低于decreasing SoftMax算法,但其平均奖赏高于SoftMax算法和decreasing SoftMax算法,且平均每轮的悔值较低.因此,CNAME算法的效果与SoftMax算法和decreasing SoftMax算法相比有所提高.
这是因为与SoftMax算法相比,CNAME算法除了考虑动作估计值,还考虑了动作被选择的次数,比SoftMax算法和decreasing SoftMax算法利用的信息多,虽然收敛速度略有降低,但不易被前期的估计值误导.因此CNAME算法最终获得的平均奖赏和平均每轮悔值均优于SoftMax算法和decreasing SoftMax算法.
3) CNAME算法和UCB1算法
CNAME算法的收敛速度与UCB1算法相当,但其平均奖赏高于UCB1算法,且平均每轮的悔值低于UCB1算法.值得注意的是,通过分析实验数据的变化,我们发现:CNAME算法的数据波动较小,而UCB1算法在实验初期的数据会出现尖峰.
这是因为CNAME算法和UCB1算法均充分利用了选择动作之后的信息,两者收敛速度相当.但是UCB1算法在初期的前K次操作中,先将每个动作轮流选择一次,在第K+1次操作时选择贪心动作,因此UCB1算法会在第K+1操作时出现尖峰.而CNAME算法在第K+1次操作时,依然根据当前的探索概率选择动作,因此CNAME算法的数据不会出现尖峰.
综上所述,CNAME算法是一种有效的多臂赌博机算法.
3.3 实验3:内容分发网络数据集上的比较
实验3采用的数据集对应于真实环境中可用资源冗余情况下的数据检索问题.例如在内容分发网络中,agent必须通过一个可用资源冗余的网络来检索数据.假设每次检索agent只选择一个资源,直到检索到数据,agent的目标是最小化检索的累积延时.该问题可转换为随机多臂赌博机问题进行处理[27],3项具体说明如下:
1) 实验3用超过700个学校的主页作为资源,每一个主页对应多臂赌博机中的一个臂(动作).
2) 这些主页约每隔10 min被检索一次,共记录了10 d的检索延迟信息(约1 300条),单位为ms.
3) 每一个延时对应一个负奖赏,因此,平均延时越小,对应算法越有效.
上述延时数据来源于实际问题,数据范围广、波动大,而且隐含了实际环境中的各种干扰和影响.本文分别利用各个算法对该数据集进行处理,更能体现各个算法性能的差异和各自的稳定性.
表3是6种算法平均每轮的检索延时,这些数据是1 000次模拟的平均结果.考虑到实际环境的随机性,每次模拟中延时的顺序都是随机的.
Table 3 Average Latency of Six Algorithms
表3 6种算法的平均延时

AlgorithmsParametersAverage Latency∕msε=0.05427ε-greedyε=0.1494ε=0.15475ε0=5424ε-decreasingε0=10397ε0=15389τ=0.1411SoftMaxτ=0.15410τ=0.2409τ0=15401decreasing SoftMaxτ0=20392τ0=25388UCB1c= 2373w=0.1372CNAMEw=0.5374w=1376
Note: The best result is highlighted in bold.
从表3可以看出,使用ε -greedy,ε -decreasing,SoftMax,decreasing SoftMax这4种算法得到的平均延时明显高于UCB1和CNAME算法.这主要是因为关于延时的网络数据通常波动很大,而且延时数据的取值范围很广,可能是10 ms,也可能是1 000 ms.对于这样的数据,需要非常小心地探索,因为尝试一个动作有可能得到很小的延时,但也有可能得到一个突增的延时.这种情况下,UCB1算法和CNAME算法的优势很明显,这2种算法同时根据动作的估计值和被选择的次数自适应地调整探索和利用,充分利用了反馈信息.
虽然UCB1算法和CNAME算法最后得到的平均延时相当,但CNAME算法只需要约2 min就可以完成计算,而UCB1算法则需要约6 h.这主要是因为UCB1算法相对复杂,计算负担较大,所以需要较长的计算时间;而CNAME算法的计算则相对简单,计算负担较小,极大地节约了计算时间.
可见,CNAME算法可以更加高效地平衡随机多臂赌博机问题中的探索和利用.
3.4 实验4:雅虎公司 R6A数据集上的比较
在线内容推荐是交互式机器学习问题的重要内容,需要在探索和利用之间进行有效的平衡.实验4将推荐系统建模为多臂赌博机模型.雅虎公司R6A数据集包含45 811 883个用户访问雅虎公司首页Today模块的点击日志.对于每次访问,用户和每个候选文章都有关联的6维的特征向量.
本节对比了CNAME算法与其他3种算法在雅虎公司R6A数据集上的推荐效果,实验结果如图4所示,纵坐标表示累计奖赏,对应推荐系统中的点击次数.其中,Random算法作为基准算法,每次为用户随机推荐物品,LinUCB算法为上下文相关的多臂赌博机算法.
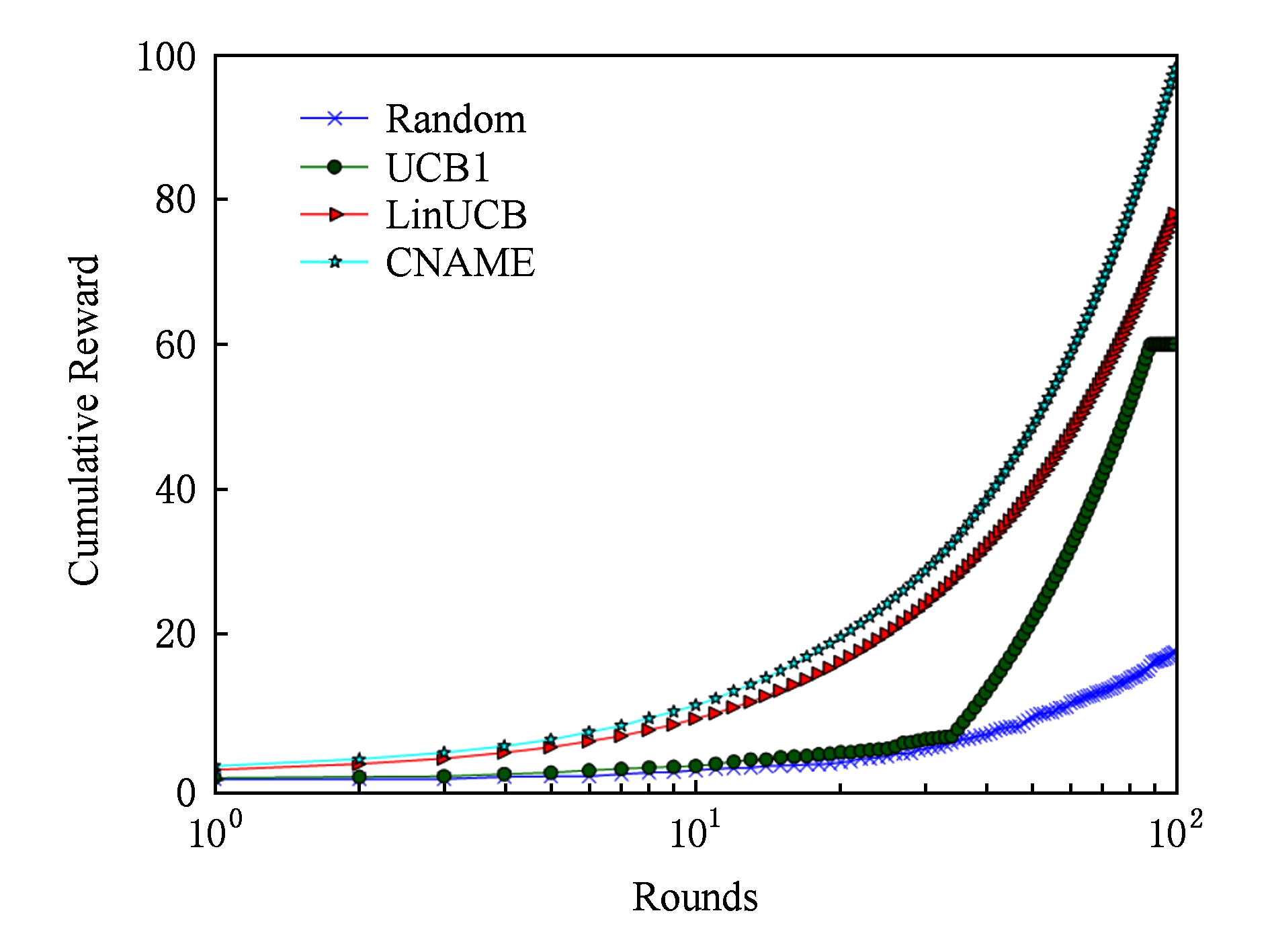
Fig. 4 Cumulative rewards of CNAME and the other three algorithms
图4 CNAME算法与其他3种算法的累计奖赏
从图4可以看出,Random算法的累计奖赏最低,这是因为Random算法只是随机产生推荐,没有利用用户反馈信息.CNAME算法获得的累计奖赏明显高于UCB1算法.UCB1算法在初期将各个物品轮流推荐给用户,在物品数量较大的情况下不能及时地学习到用户的兴趣.因此,UCB1算法在初期获得的累计奖赏接近Random算法,后期获得的累计奖赏则快速增加.
LinUCB算法作为经典的上下文相关的多臂赌博机算法,主要结合数据集中的6维特征向量进行推荐,在100个时间步后获得的累计奖赏为78.由于LinUCB算法依赖用户和物品的特征向量,而不同推荐系统中的特征向量维度和含义不同,LinUCB算法无法方便地推广到不同的应用场景.CNAME算法基于探索概率,在利用用户反馈进行推荐的同时,探索可能为用户带来惊喜的物品.因此CNAME算法获得的累计奖赏很高且稳定增长,100个时间步后获得的累计奖赏高达98,累计奖赏高于基于上下文信息的LinUCB算法.CNAME算法在推荐的过程中,一方面根据用户反馈,自适应地调整探索概率,另一方面不依赖上下文信息,可以方便地应用到各个场景中.
4 总 结
本文提出了一种自适应的随机多臂赌博机算法,即CNAME算法.该算法充分利用选择动作之后获得的信息,同时考虑动作的估计值和被选择的次数,简便高效地解决了随机多臂赌博机中探索和利用的平衡问题.CNAME算法根据当前估计值最小的动作(即实际获得的平均奖赏最小的动作)已经被选择的次数mt和参数w共同控制探索的概率,自适应地根据实际环境调整探索和利用的程度.同时,CNAME算法在探索时选择目前最少被选择的动作,避免了随机选择动作的盲目性.
一方面,本文通过理论分析和证明给出了CNAME算法的悔值上界,为CNAME算法的性能提供了有力的理论支持.另一方面,本文通过4组实验讨论了CNAME算法的关键参数w的影响及参考取值范围并分别在随机数据集,内容分发网络数据集和带有上下文信息的雅虎公司 R6A数据集上与其他3类经典算法及其变种进行了对比实验.实验表明CNAME算法与ε -greedy算法和ε -decreasing算法相比有了很大的提高,效果比SoftMax算法和decreasing SoftMax算法略好,比UCB1算法更高效.此外,CNAME算法的泛化能力较强,在雅虎公司R6A数据集上获得了与LinUCB算法相当甚至更好的效果.综上所述,CNAME算法是一种效果稳定、高效且泛化能力强的多臂赌博机算法.
未来工作尝试将CNAME算法应用到更加复杂的多臂赌博机问题中,比如带有预算的多臂赌博机问题[30]、定性的多臂赌博机问题等[31];同时,探讨CNAME算法解决复杂问题的可能性,尝试提出有实际应用的新型多臂赌博机问题.此外,考虑与深度学习相结合,生成深度网络多臂赌博机,以解决更加复杂的问题.
[1]Sutton R, Barto G. Reinforcement Learning: An Introduction[M]. Cambridge, MA: MIT Press, 1998: 1-20
[2]Gao Yang, Zhou Ruyi, Wang Hao, et al. Study on an average reward reinforcement learning algorithm[J]. Chinese Journal of Computers, 2007, 30(8): 1372-1378 (in Chinese)(高阳, 周如益, 王皓, 等. 平均奖赏强化学习算法研究[J]. 计算机学报, 2007, 30(8): 1372-1378)
[3]Zhao Fengfei, Qin Zheng. A multi-motive reinforcement learning framework[J]. Journal of Computer Research and Development, 2013, 50(2): 240-247 (in Chinese)(赵凤飞, 覃征. 一种多动机强化学习框架[J]. 计算机研究与发展, 2013, 50(2): 240-247)
[4]Liu Quan, Fu Qiming, Yang Xudong, et al. A scalable parallel reinforcement learning method based on intelligent scheduling[J]. Journal of Computer Research and Development, 2013, 50(4): 843-851 (in Chinese)(刘全, 傅启明, 杨旭东, 等. 一种基于智能调度的可扩展并行强化学习方法[J]. 计算机研究与发展, 2013, 50(4): 843-851)
[5]Liu Zhibin, Zeng Xiaoqin, Liu Huiyi, et al. A heuristic two-layer reinforcement learning algorithm based on BP neural networks[J]. Journal of Computer Research and Development, 2015, 52(3): 579-587 (in Chinese)(刘智斌, 曾晓勤, 刘惠义, 等. 基于BP神经网络的双层启发式强化学习方法[J]. 计算机研究与发展, 2015, 52(3): 579-587)
[6]Robbins H. Some aspects of the sequential design of experiments[J]. American Mathematical Society, 1952, 58(5): 527-535
[7]Devanur N R, Kakade S M. The price of truthfulness for pay-per-click auctions[C]//Proc of ACM Conf on Electronic Commerce. New York: ACM, 2009: 99-106
[8]Cheng Shi, Mao Luhong, Chang Peng. Multi-armed bandit recommender algorithm with matrix factorization[J]. Journal of Chinese Computer Systems, 2017, 38(12): 2754-2758 (in Chinese)(成石, 毛陆虹, 常鹏. 融合矩阵分解的多臂赌博机推荐算法[J]. 小型微型计算机系统, 2017, 38(12): 2754-2758)
[9]Yu Yonghong, Gao Yang, Wang Hao, et al. Integrating user social status and matrix factorization for item recommendation[J]. Journal of Computer Research and Development, 2018, 55(1): 113-124 (in Chinese)(余永红, 高阳, 王皓, 等. 融合用户社会地位和矩阵分解的推荐算法[J]. 计算机研究与发展, 2018, 55(1): 113-124)
[10]Jain S, Gujar S, Zoeter O, et al. A quality assuring multi-armed bandit crowdsourcing mechanism with incentive compatible learning[C]//Proc of the 13th Int Conf on Autonomous Agents and Multi-Agent Systems. New York: ACM, 2014: 1609-1610
[11]Jain S, Narayanaswamy B, Narahari Y. A multi-armed bandit incentive mechanism for crowdsourcing demand response in smart grids[C]//Proc of the 28th AAAI Conf on Artificial Intelligence and the 26th Innovative Applications of Artificial Intelligence Conf. Menlo Park, CA: AAAI, 2014: 721-727
[12]Sun Xinxin. Research on task assignment technology in crowdsourcing environment[D]. Yangzhou: Yangzhou University, 2016 (in Chinese)(孙信昕. 众包环境下的任务分配技术研究[D]. 扬州: 扬州大学, 2016)
[13]Zhou Baojian. Research on search engine keyword optimal selection strategy based on multi-armed bandit[D]. Harbin: Harbin Institute of Technology, 2014 (in Chinese)(周保健. 基于多臂赌博机的搜索引擎关键字最优选择策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2014)
[14]Chen Hongcui. Research on channel selection mechanism based on multi-armed bandit in cognitive network[D]. Chongqing: Chongqing University of Posts and Telecommu-nications, 2016 (in Chinese)(陈红翠. 认知网络中基于赌博机模型的信道选择机制研究[D]. 重庆: 重庆邮电大学, 2016)
[15]Bubeck S, Cesabianchi N. Regret analysis of stochastic and nonstochastic multi-armed bandit problems[J]. Foundations and Trends in Machine Learning, 2012, 5(1): 1-22
[16]Slivkins A. Contextual bandits with similarity information[J]. Journal of Machine Learning Research, 2014, 15(1): 2533-2568
[17]Watkins C J C H. Learning from delayed rewards[J]. Robotics & Autonomous Systems, 1989, 15(4): 233-235
[18]Luce R D. Individual choice behavior[J]. American Economic Review, 1959, 67(1): 1-15
[19]Auer P, Cesa-Bianchi N, Fischer P. Finite-time analysis of the multiarmed bandit problem[J]. Machine Learning, 2002, 47(2/3): 235-256
[20]Li Lihong, Chu Wei, Langford J, et al. A contextual-bandit approach to personalized news article recommendation[C]//Proc of ACM Int Conf on World Wide Web. New York: ACM, 2010: 661-670
[21]Chu Hongmin, Lin Hsuan Tien. Can active learning experience be transferred?[C]//Proc of IEEE Int Conf on Data Mining. Piscataway, NJ: IEEE, 2017: 841-846
[22]Krishnamurthy B, Wills C, Zhang Yin. On the use and performance of content distribution networks[C]//Proc of the 1st ACM SIGCOMM Internet Measurement Workshop. New York: ACM, 2001: 169-182
[23]Thathachar M A L, Sastry P S. A new approach to the design of reinforcement schemes for learning automata[J]. IEEE Transactions on Systems Man & Cybernetics, 1985, SMC-15(1): 168-175
[24]Even-Dar E, Mannor S, Mansour Y. PAC bounds for multi-armed bandit and Markov decision processes[C]//Proc of the 15th Annual Conf on Computational Learning Theory (COLT). Berlin: Springer, 2002: 255-270
[25]Cesa-Bianchi N, Fischer P. Finite-time regret bounds for the multi-armed bandit problem[C]//Proc of the Int Conf on Machine Learning. New York: ACM, 1998: 100-108
[26]Strens M. Learning Cooperation and feedback in pattern recognition[D]. London: Physics Department, King’s College London, 1999
[27]Vermorel J, Mohri M. Multi-armed bandit algorithms and empirical evaluation[C]//Proc of the European Conf on Machine Learning. Berlin: Springer, 2005: 437-448
[28]Kirkpatrick B S, Gelatt C, Vecchi D. Optimization by simulated annealing[J]. Science, 1983, 220(4598): 671-680
[29]Lai T L, Robbins H. Asymptotically efficient adaptive allocation rules[J]. Advances in Applied Mathematics, 1985, 6(1): 4-22
[30]Xia Yingce, Qin Tao, Ding Wenkui, et al. Finite budget analysis of multi-armed bandit problems[J]. Neurocomputing, 2017, 258: 13-29
[31]Szörényi B, Busa-Fekete R, Weng P. Qualitative multi-armed bandits: A quantile-based approach[C]//Proc of the 32nd Int Conf on Machine Learning. New York: ACM, 2015: 1660-1668



