随着经济不断的发展,城市中私家车数量的增加,交通环境变得日益拥堵[1],并伴随着严重的环境污染问题.同时养车压力居高不下,以及社交网络不断深入生活等多方面因素相互作用下,越来越多的人选择拼车出行.参与拼车离不开拼车系统[2-4](软件),决定拼车软件效率主要是其背后的拼车算法性能.然而目前市场上的拼车软件的拼车算法仍存在较多不足之处,如:1)拼车方式不合理,只选取乘客周围的司机进行匹配;2)拼车路线规划随意,没有指向性,导致司机绕路距离增加;3)拼车请求不人性化,不能保证乘客的出发时间、司机的到达时间等.为此本文提出一种高效的大规模多对多拼车匹配算法Uroad来弥足现有算法的不足.
算法从全局角度出发,以所有司机产生的绕路距离总和最小为考量目标,对拼车请求中的乘客和司机进行匹配.Uroad在匹配乘客和司机的过程中,除了考虑到双方的时间和费用条件之外,还将所有司机因为拼车产生的绕路距离也作为拼车过程中的考虑要素之一.司机在提出拼车申请时,除了要提供自身行程的出发位置和目的地位置之外,还可以提出自身行程开始的出发时间和要求到达自身目的地的最晚到达时间.同样乘客在发出拼车请求时,除了需要包含行程的出发位置和目的地位置之外,还可以提出2方面的约束:1)时间约束即出发时间段,乘客可以提出一个出发时间段,表明司机可以在该时间内前来接乘客;2)费用约束即最大拼车费用,乘客可以提出一个最大拼车费用值,表明对此次拼车服务乘客最多愿意支付的费用.Uroad则会根据自身的拼车计费模型为乘客来估算车费.除了考虑乘客自身行程距离之外,该计费模型还将因为乘客拼车而对司机产生的绕路距离也考虑在内.根据乘客的拼车要求,Uroad会尽可能为每一名乘客匹配一名符合双方拼车条件的司机为其服务,最终使得所有司机因为拼车而产生的绕路距离之和最小.
不同于基本方法中直接计算大量最短路径距离,Uroad在前期增加了一系列的基于时间、欧氏距离、路网距离的空间剪枝策略,以加快算法的整体运行速度和效率.其中拼车匹配过程共分为两大阶段:1)单乘客对多司机匹配,为每一名乘客找出所有符合其拼车要求的司机集合;2)多乘客与多司机最优组合匹配,尽可能为每一名乘客在其司机集合中指定一名司机,使得所有司机产生的绕路距离最小.在第1阶段中,Uroad通过连续的3种空间剪枝策略,能高效实现单个乘客与多司机的匹配,即基于乘客出发时间约束筛选、基于2点间欧氏距离筛选、基于路网真实距离筛选.第1阶段匹配结果中每名乘客可以被多名司机服务,同时单个司机也可以服务多名乘客,因此Uroad在第2阶段借鉴组合优化的思想,利用Kuhn-Munkres(KM)算法[5]进行多乘客与多司机的全局最优匹配,使最后的匹配结果产生的绕路路程之和最小.同时我们利用切分矩阵算法来提高这一阶段的匹配速度.实验结果显示,算法能在2 min内实现1 000名乘客在100 000名司机中找出最优的拼车匹配组合方案,与直接计算最短路径的基本方法相比,整体耗时缩短了40%.和现有算法中乘客随机选择司机的策略相比,加入了全局优化策略,之后本文算法中所有司机的拼车距离总和可减少60%左右.同时实验也显示了各阶段的剪枝技术较好的性能和较低的开销,以及我们可以通过少量的路网距离计算来完成拼车匹配的优势.综上,本文的贡献主要有4个方面:
1) 定义了一种多对多拼车匹配问题,在拼车过程中加入了时间约束和费用约束,并且将所有司机绕路距离最小作为整体的拼车目标.
2) 通过3种空间剪枝技术缩小最短路径的计算量,从而提高算法的整体效率.
3) 证明了切分矩阵算法的合理性,大幅加快了在确定乘客与司机的最优匹配组合阶段的运行速度,提高了算法整体的效率.
4) 基于真实路网信息,进行了大量大规模的仿真实验,验证了Uroad算法的有效性和高效性.
1 预备知识
本节将介绍一些预备知识,以便于更好地理解Uroad所研究的拼车场景和拼车方式,包括乘客和司机的定义、拼车中的计费模型以及拼车问题的定义.
1.1 乘客和司机
1.1.1 乘客
乘客指的是向Uroad提出拼车服务请求的人员.为了能够获得较好的拼车服务,Uroad要求乘客r在拼车请求中除了表明自己的出发位置Orig(r)和目的地位置Dest(r)这2个必要的位置信息之外,还需要提出一个出发时间段,即最早出发时间departureTimeMin(r)和最晚出发时间departure-TimeMax(r),以此来确定乘客r的出发时间范围,乘客r只在该时间范围内接受司机的拼车服务.同时,乘客r需要在拼车请求中提出一个最大拼车费用maxPrice(r),以此来限定本次拼车服务的费用.在乘客设定最大拼车费用maxPrice(r)时,系统会根据乘客提供的出发位置Orig(r)和目的地位置Dest(r)来预估一个最低拼车费用值,以此为乘客设定拼车费用提供参考,同时也保证了司机的最低收益.乘客在根据要求向Uroad提出自己的拼车请求之后,Uroad会自动反馈乘客的拼车匹配结果,乘客只需在出发时间段内等待相应的拼车司机来接送即可.
1.1.2 司机
司机指的是能够提供拼车服务的通勤人员.为了能够顺利地提供拼车服务,司机d需要提供自己的出发位置Orig(d)和目的地位置Dest(d).此外,司机还需要提出一个出发时间DepartureTime(d)和一个最晚达到时间ArrivalTime(d),分别代表司机会在时刻DepartureTime(d)从自身的出发位置出发,并且必须要在ArrivalTime(d)之前达到自己的目的地位置.
根据乘客提出的拼车要求,Uroad为每一名乘客尽可能确定一名能够满足双方拼车要求的司机作为拼车对象.当司机确定了拼车匹配结果后,从司机的出发位置出发到乘客的出发位置,接上乘客之后将其送达到目的地,最后再返回司机自己的目的地位置.期间,司机获得的车费收入,主要是根据乘客自身的行程距离和司机因为接送乘客产生的绕路距离这两部分来决定的.车费的具体计算方式,将在2.2节中展开.
1.2 计费模型
图1是拼车过程的一个示意图.其中,黑点分别代表司机d的出发位置Orig(d)和目的地位置Dest(d).白点代表了乘客r的出发位置Orig(r)和目的地位置Dest(r).虚线表示司机原本的行程路线,即从司机的出发位置直接到其目的地位置的行程,记为DriverTrip(d).实线代表实际拼车过程中的行程路线,主要分为3部分:1)从司机的出发位置Orig(d)到乘客的出发位置Orig(r),记为Pickup(d,r);2)从乘客的出发位置Orig(r)到乘客的目的地位置Dest(r),记为RiderTrip(r);3)从乘客的目的地位置Dest(r)到司机的目的地位置Dest(d),记为Return(d,r).显然,为了给乘客r提供拼车服务,司机d在接送乘客r的过程中,相比于司机原本的行程DriverTrip(d),势必会产生一定的绕路距离,将其记为Detour(d,r).

Fig. 1 Carpooling process diagram
图1 拼车过程示意图
以图1为例,乘客r在获得了司机d提供的拼车服务后,需要支付的拼车费用记为Price(d,r).拼车费用Price(d,r)主要分为2部分:一部分是RiderTrip(r)所对应的费用.这部分费用是乘客r至少需要支付的费用,只与行程RiderTrip(r)有关.另一部分费用是因为司机d接送乘客r而产生的绕路距离Detour(d,r)所对应的费用.因为不同的司机,对应的绕路距离不同.所以对乘客而言,这部分费用是会发生变化的.综上所述,车费Price(d,r)表示为
Price(d,r)=RiderTrip(r)+Detour(d,r),
(1)
其中绕路距离Detour(d,r)代表的是司机拼车实际路程(图1中的实线)与司机原本的路程(图1中的虚线)的距离之差.所以绕路距离Detour(d,r)表示为
Detour(d,r)=Pickup(d,r)+RiderTrip(r)+
Return(d,r)-DriverTrip(d).
(2)
根据式(1)和式(2),拼车车费Price(d,r)可以直接表示为
Price(d,r)=Pickup(d,r)+2×RiderTrip(r)+
Return(d,r)-DriverTrip(d).
(3)
需要说明的是,式(3)中所有行程的金额,即2点之间的行程所代表的金额,都是其对应的最短路径距离的倍数.例如Pickup(d,r)代表的是从司机出发位置Orig(d)到乘客出发位置Orig(r)这段路程所代表的距离,费用即是从司机出发位置Orig(d)到乘客出发位置Orig(r)的最短路径距离的某一个倍数值,这个倍数即实际情景中每公里定价.
1.3 问题定义
在拼车计费模型的基础上,我们对研究的拼车问题做出了如下定义:
定义1. 给定一个司机的集合D,任一司机d∈D包含出发位置Orig(d)、目的地位置Dest(d)、出发时间DepartureTime(d)、最晚达到时间ArrivalTime(d)这4部分信息.给定一个乘客的集合R,任一乘客r∈R包含5部分信息:出发位置Orig(r)、目的地位置Dest(r)、最大拼车费用maxPrice(r)、最早出发时间departureTime-Min(r)、最晚出发时间departureTimeMax(r).feedbackTime(D,R)表示拼车匹配结果反馈给乘客与司机的时间.那么我们的目标是,为∀r∈R找出一名司机d∈D能够满足双方的拼车要求,即需要满足5点要求:
1) departureTimeMin(r)≤DepartureTime(d)+Pickup(d,r)≤departureTimeMax(r);
2) DepartureTime(d)+Pickup(d,r)+RiderTrip(r)+Return(d,r)≤ArrivalTime(d);
3) Price(d,r)≤maxPrice(r);
4) feedbackTime(D,R)<DepartureTime(d);
其中,需要注明的是,第1)2)条要求中的Pickup(d,r),RiderTrip(r),Return(d,r)虽然代表的是最短路径距离,但是Uroad可以根据拼车时道路上的实时平均车速来转换成对应的行驶时间.所以这里指代的是其对应的行驶时间,是对应的最短路径距离的某一个倍数值,这个倍数是可以根据计算时的具体情况调整:
1) 表示的是司机必须要在乘客的出发时间范围内到达乘客的出发位置,以方便乘客能够合理规划自己的行程;
2) 表示的是司机在完成乘客的拼车订单之后,还能在自己的最晚到达时间之前到达司机自身的目的地,保证了司机的行程不被耽误;
3) 表示的是乘客支付的车费必须小于他提出的最大拼车费用;
4) 司机和乘客出发时间之前获得拼车反馈信息,确保司机在出行时能够明确自己的具体行程安排;
5) 表示所有司机因为拼车产生的绕路距离最小.
1.4 数据结构
1.4.1 司机信息列表(driver table)
司机信息列表中存储了当前所有已经提出拼车请求但是还没有匹配到乘客的司机.每当一名新的司机提出了拼车服务请求之后,他就会被添加进司机信息列表中.作为司机信息列表中的一个实体,它需要包含6项属性:
1) ID为一名司机的唯一标识;
2) Origin为司机当前的出发位置,通常可以通过手机等移动设备获取;
3) Destination为司机的目的地位置信息;
4) DriverTrip为从司机的出发位置到其目的地位置的最短路径距离;
5) DepartureTime为出发时间;
6) ArrivalTime为最晚到达目的地的时间.当司机匹配到乘客之后,会自动将该司机从司机列表中删除.
1.4.2 网格索引(grid index)
我们将地图划分成m×n个相同大小的正方形网格.根据司机的出发位置来确定其所属的网格,并将司机存入该网格内.当要查询某一范围的司机时,只要确定该范围所覆盖的网格,直接获取这些网格内的所有司机并进行筛选即可.这就避免了对所有司机进行检验筛选,降低了查询过程中的时间消耗.这里选择使用网格索引是因为它易于实现和较低的更新开销.因为在拼车场景中司机信息会被频繁地创建和删除,所以更新和构建索引的开销会极大影响算法的效率.因此,在更新频率较高的拼车场景中,通过建立更新和建立索引开销较低的网格索引则比较合适.
1.4.3 时间索引(time index)
我们采用hashmap的数据结构来实现时间索引的构建.根据司机的出发时间构建一个司机出发时间索引(driver departure time index),将出发时间点作为key值,其对应的value值是所有在出发时刻的司机所构成的司机集合.当要获取某一出发时间的所有司机时,只要根据时间在司机出发时间索引中直接获取该时间下的所有司机即可.相应地根据乘客的最晚出发时间来建立一个乘客的出发索引(rider departure time index),同样是将乘客的最晚出发时间点作为key值,所有最晚出发时间相同的乘客构成乘客集合作为value值存储在对应位置中.通过时间索引可以快算查找对应时刻的司机和乘客,就可以降低根据时间查找司机和乘客的时间,从而提高整体算法的运行速度.
1.4.4 绕路距离记录表(detour distance table)
为了记录下乘客与司机之间是否能够匹配以及匹配成功后的绕路距离等信息,我们设计并采用绕路距离记录表来存储匹配的绕路距离,如表1所示:
Table 1 Detour Distance Diagram
表1 绕路距离记录表

Riderd1d2…r15km∞…︙︙︙
绕路距离记录表中的行表示乘客,列表示司机每个空格的数据值代表司机与乘客进行匹配时产生的绕路距离.例如司机d1与乘客r1可以进行拼车匹配,匹配后的绕路距离为5 km,填在司机d1和乘客r1相交的空格中;如果司机d2与乘客r1不能匹配,则空格的值为无穷大∞.由于拼车条件的限制,并不是任意一名乘客与司机都能成功匹配,即表格中存在大量的∞.所以考虑到这一特性,我们采用稀疏矩阵的形式来实现绕路距离记录表,在缩小存储空间的同时,也能加快搜索和查找的速度.
2 Uroad查询过程
本文算法可以分为两大步骤执行:1)单乘客对多司机匹配,每一名乘客找出所有既能符合乘客拼车要求又能满足自身拼车要求的司机;2)多乘客与多司机最优组合匹配,每一名乘客在满足要求的司机中指定一名司机与之匹配,使得最终所有司机的拼车绕路距离之和最小.
2.1 单乘客对多司机匹配
筛选出满足某一乘客拼车要求的司机,现有较为简单的方法是:直接计算所有司机出发位置到乘客出发位置的Pickup(d,r)距离,以及乘客目的地位置到所有司机目的地位置的Return(d,r)距离.根据计算获得的每一名乘客与所有司机匹配后各路段行程的最短距离,来筛选出所有既能符合乘客出发时间和最大拼车费用约束,又能保证自身时间约束的司机.虽然这个方法看上去十分简单,但是它需要进行大量的路网距离计算.计算量非常巨大,极大影响算法的性能.这对于需要快速反馈的拼车场景来说并不可取.为了避免出现以上情况,我们通过运用一些空间剪枝技术来缩小需最短路径距离计算量.Find Drivers Algorithm算法主要分为3部分:出发时间筛选(departure time pruning, DTP)、欧氏距离筛选(Euclidean pruning, EP)、最短路径距离筛选(shortest path pruning, SP).
2.1.1 基于乘客出发时间筛选
在这一步骤中,输入的是司机的出发时间索引和乘客的最晚出发时间索引.输出是每一名乘客对应的所有出发时间在其最晚出发时间之前的司机集合,记为D1.这一步主要是删去所有出发时间不符合要求的司机.
因为乘客和司机都有各自的特定出发时间,所以如果司机能够为乘客提供拼车服务,那么司机的出发时间DepartureTime(d)必定要早于乘客的最晚出发时间departureTimeMax(r),才有可能满足乘客的出发时间要求.

Fig. 2 Rider departure time index and driver departure time index diagram
图2 乘客最晚出发时间索引和司机出发时间索引示意图
为了找出所有早于乘客最晚出发时间departure-TimeMax(r)的司机,最直接的方法就是遍历所有的司机,判断他们的出发时间符合乘客的要求.但是这需要消耗大量的时间,所以这个方法并不可取.所以我们通过建立司机出发时间索引(driver departure time index)和乘客最晚出发时间索引(rider max departure time index),实现查询速度的提升.其中2个索引的key值按从早到晚的顺序进行排序.2个索引的结构具体如图2所示.
出发时间筛选的伪代码如算法1所示.
算法1. 出发时间筛选算法.
输入:司机出发时间索引ddti、乘客最晚出发时间索引rmdti;
输出:符合双方时间要求的司机集D1.
① DS=null;  *司机集合*
*司机集合*
② ddti.keySet()→dtArray;  *从小到大进行排列*
*从小到大进行排列*
③ rmdti.keySet()→rtArray;  *从小到大进行排列*
*从小到大进行排列*
④ Start=0;  *在dtArray中标记第1个索引*
*在dtArray中标记第1个索引*
⑤ FOR(i=0;i<rtArray.length;i++)
⑥ rTime=rtArray[i];
⑦ FOR(j=Start;j<rTime‖Start>
dtArray[length-1];i++)
⑧ Put all ddti.get(dtArray[j]) into
DS;
⑨ ENDFOR
⑩ RS←rmdti.get(rTime);  *乘客集合*
*乘客集合*
 WHILE RS.hasnext() DO
WHILE RS.hasnext() DO
 r=RS.next();
r=RS.next();
 DS→r.D1;
DS→r.D1;
 ENDWHILE
ENDWHILE
 ENDFOR
ENDFOR
出发时间筛选的5个主要步骤为:
1) 按顺序遍历乘客最晚出发时间索引,先获取出发时间最早的乘客集合和对应的时刻记为rTime(行⑥).
2) 顺序遍历司机出发时间索引并获取合并对应的司机集合,直到出发时间与rTime相等为止(行⑦~⑨).将此时的合并后获得的司机集合记为D1,那么D1就是出发时间筛选后时刻rTime对应的乘客集合中所有乘客的目标司机集合(行 ).
).
3) 完成时刻rTime后,继续为乘客最晚出发时间索引中下一时刻rTime′乘客集合进行出发时间筛选.
4) 从时刻rTime开始遍历并获取对应时刻的司机集合与D1合并,一直遍历到出发时间为rTime′为止.将新合并获得的司机集合记为![]() 该司机集合则是时刻rTime′对应的乘客集合中所有乘客经过出发时间筛选后的目标司机集合.
该司机集合则是时刻rTime′对应的乘客集合中所有乘客经过出发时间筛选后的目标司机集合.
5) 直到遍历完乘客最晚出发时间索引位为止.
通过以上5个步骤我们只需遍历一遍乘客最晚出发时间索引和司机出发时间索引就可完成整个出发时间筛选步骤.
例1. 以图2为例,出发时间筛选的具体操作为:
根据乘客最晚出发时间索引获取第1个出发时刻rTime=07:40,顺序遍历司机出发时间索引直到时刻07:40为止.获取并合并该时刻之前的所有司机集合,即获取07:25,07:30,07:35,07:40这4个出发时刻对应的司机集合,并合并获得新司机集合D1={d1,d2,d3,d4,d5,d6,d7,d8,d9,d10,d11,d12,d13,d14,d15}.时刻07:40对应的最晚出发时间乘客r1经过出发时间筛选后的司机集合为D1.接着按顺序遍历乘客最晚出发时间索引,获取第2个rTime′=07:45.然后继续从07:40之后遍历司机出发时间索引,直到07:45为止,并将这2个时刻时间的所有司机与D1合并成新的司机集合![]() 就是乘客经过出发时间筛选之后获得的司机集合.之后在继续遍历乘客最晚出发时间索引,直到完成该索引的最后一个时刻对应的乘客集合的出发时间筛选操作.
就是乘客经过出发时间筛选之后获得的司机集合.之后在继续遍历乘客最晚出发时间索引,直到完成该索引的最后一个时刻对应的乘客集合的出发时间筛选操作.
2.1.2 基于欧氏距离筛选
在这一计算步骤中,输入为一名乘客r的拼车请求和该乘客通过出发时间筛选后获得的司机集合D1.输出的是所有在欧氏距离上满足了乘客r的拼车要求,并且也满足自身到达时间要求的所有司机D3.
为了能够更加清晰地说明我们的算法,我们将用图3中的例子来配合解释.黑色的点代表的是乘客,白色的点代表的是司机.图3(a)中的点表示的是司机和乘客的出发位置,图3(b)中的点表示的是他们的目的地位置.
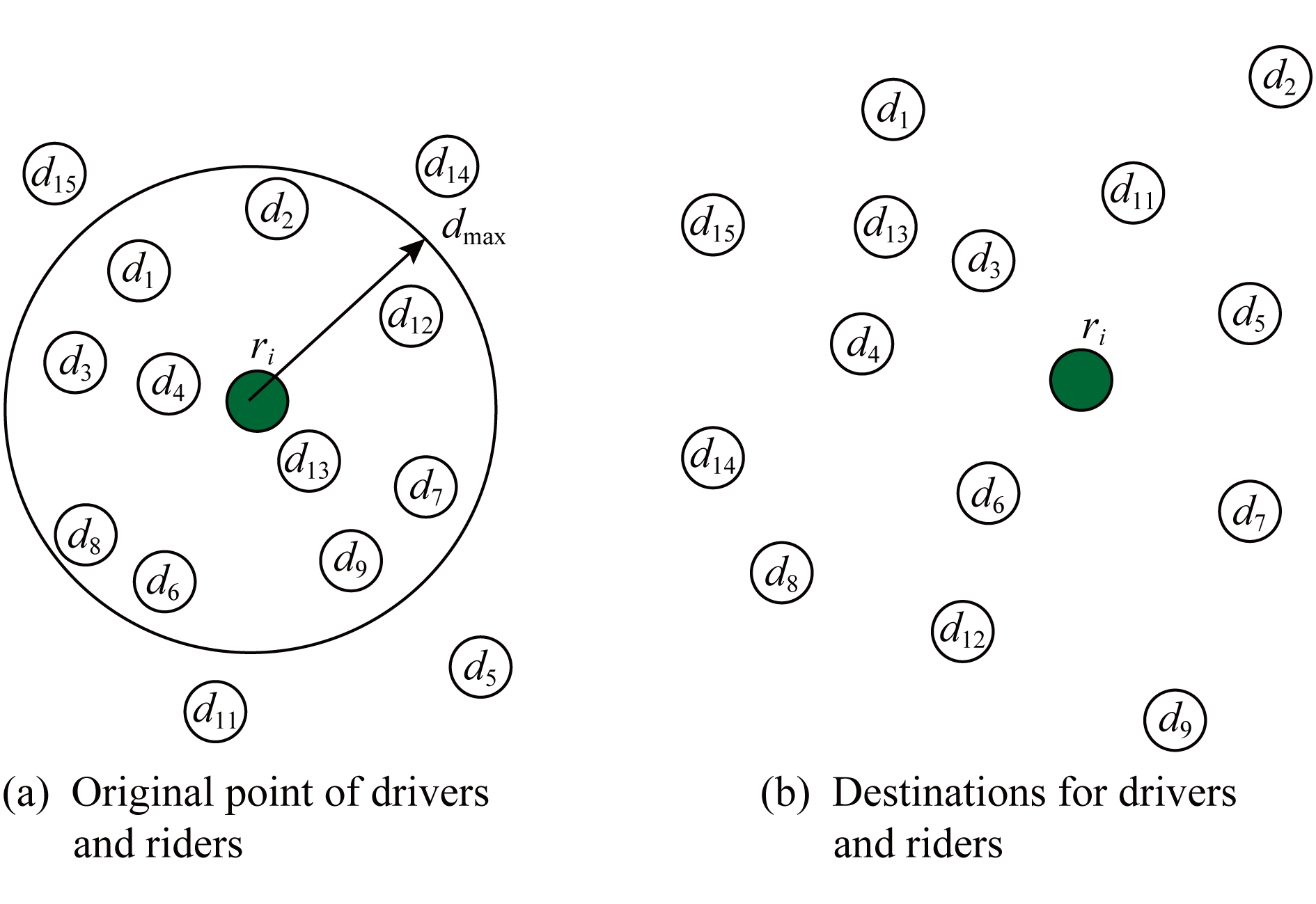
Fig. 3 Euclidean distance screening diagram
图3 欧氏距离筛选说明图
众所周知,欧氏距离指2点之间的线段距离,它必定是小于或等于2点之间的路网距离.而且相比于计算2点之间的最短路径距离而言,计算2点之间的欧氏距离花费的时间就要短得多.因此,在计算实际路网距离之前,通过欧氏距离排除一部分不可能匹配的司机,这是一种时间代价较低的剪枝方法.
欧氏距离筛选的伪代码如算法2所示:
算法2. 欧氏距离筛选算法.
输入:司机集合D1、1名乘客r、当前时刻Now;
输出:司机集合D3.
① Build the grid index g for D1;
② riderTimeMax←departureTimeMax(r)-Now;
③ dmax←riderTimeMax;  *dmax是一个距离*
*dmax是一个距离*
④ D1←RangeQuerry(g,orig(r),dmax);
⑤ FOR d∈D1DO
⑥ Compute EuclideanPickup(d,r);
⑦ IF DepartureTime(d)+EuclideanPickup(d,r)≤departureTimeMax(r) THEN
⑧ Add d into D2;
⑨ EndIF
⑩ ENDFOR
 FOR d∈D2DO
FOR d∈D2DO
 Compute EuclideanReturn(d,r);
Compute EuclideanReturn(d,r);
 IF EuclideanPickup(d,r)+2×
IF EuclideanPickup(d,r)+2×
RiderTrip(r)+EuclideanReturn(d,r)-DriverTrip(d)≤maxPrice(r) &&
DepartureTime(d)+EuclideanPickup(d,r)+RiderTrip(r)+EuclideanReturn(d,r)≤ArrivalTime(d) THEN
 Put d into D3;
Put d into D3;
 ENDIF
ENDIF
 ENDFOR
ENDFOR
 RETURN D3.
RETURN D3.
欧氏距离筛选的主要步骤为
1) 根据D1中司机的出发位置,为他们建立网格索引g(行①).计算从当前时刻Now起到乘客r最晚出发时间departureTimeMax(r)的时长,即departureTimeMax(r)-Now,记为riderTimeMax(行②).根据目前道路平均时速Speed和rider-TimeMax相乘计算获得能够满足乘客出发时间要求的最远距离dmax(行③).
2) 通过grid index筛选出所有落在以乘客出发位置Orig(r)为圆心、以dmax为半径的圆范围内的所有司机,记为D1(行④),并记录下乘客r出发位置Orig(r)与这些司机出发位置的欧氏距离,记为EuclideanPickup(d,r).
3) 从这些司机中筛选出在欧氏距离上满足:
DepartureTime(d)+EuclideanPickup(d,r)≤
departureTimeMax(r).
(4)
式(4)的乘客出发时间要求的司机,组成司机集合D2(行⑤~⑩).
需要特别说明的是,在步骤3中不使用乘客的出发时间约束departureTimeMin(r)≤depar-tureTime(d)+EuclideanPickup(d,r)这一条件,是因为2点之间的路网距离是大于等于欧氏距离的,所以可能存在有些司机虽然在欧氏距离上不满足乘客的这一出发时间约束,但是在路网距离上确实满足.为了避免将这些司机误删,所以不采用departureTimeMin(r)≤DepartureTime(d)+EuclideanPickup(d,r)这一时间约束条件,但是在之后的路网距离筛选上,会用到乘客的最晚出发时间来作为筛选条件.
4) 计算从乘客r的目的地位置Dest(r)到集合D2中所有司机目的地位置的欧氏距离,并记为EuclideanReturn(d,r).判断这些司机在欧氏距离上是否都满足乘客r的拼车费用约束,即是否满足:
EuclideanPickup(d,r)+2×RiderTrip(r)+
EuclideanReturn(d,r)-DriverTrip(d)≤
maxPrice(r),
(5)
同时是否满足司机自身的到达时间约束,即是否满足:
DepartureTime(d)+EuclideanPickup(d,r)+
RiderTrip(r)+EuclideanReturn(d,r)≤
ArrivalTime(d).
(6)
将同时满足式(5)(6)的司机保留下来,组成司机集合D3(行 ~
~ ).司机集合D3就是满足欧氏距离筛选的乘客r的司机集合.
).司机集合D3就是满足欧氏距离筛选的乘客r的司机集合.
例2. 乘客r1根据出发时间筛选后,获得的司机集合D1中的司机分布如图3所示.进行欧氏距离筛选计算时的时刻Now=07:20,平均道路时速Speed=60 km h,rate=1yuan
h,rate=1yuan km.乘客r1的departureTimeMin(r1)=7:30,departureTime-Max(r1)=7:40;RiderTrip(r1)=12 km;maxPrice(r1)=20yuan.计算可得乘客r1的riderTimeMax=20 min,则dmax=20 km.为司机集合D1中的司机建立grid index后,根据dmax筛选出司机{d1,d2,d3,d4,d6,d7,d8,d9,d10,d12,d13}是在圆范围内的.接着计算乘客r1的出发位置与这些司机的Euclid-eanPickup(d,r)的距离,并检验是否满足式(4)乘客出发时间的要求,各司机的计算结果如表2所示:
km.乘客r1的departureTimeMin(r1)=7:30,departureTime-Max(r1)=7:40;RiderTrip(r1)=12 km;maxPrice(r1)=20yuan.计算可得乘客r1的riderTimeMax=20 min,则dmax=20 km.为司机集合D1中的司机建立grid index后,根据dmax筛选出司机{d1,d2,d3,d4,d6,d7,d8,d9,d10,d12,d13}是在圆范围内的.接着计算乘客r1的出发位置与这些司机的Euclid-eanPickup(d,r)的距离,并检验是否满足式(4)乘客出发时间的要求,各司机的计算结果如表2所示:
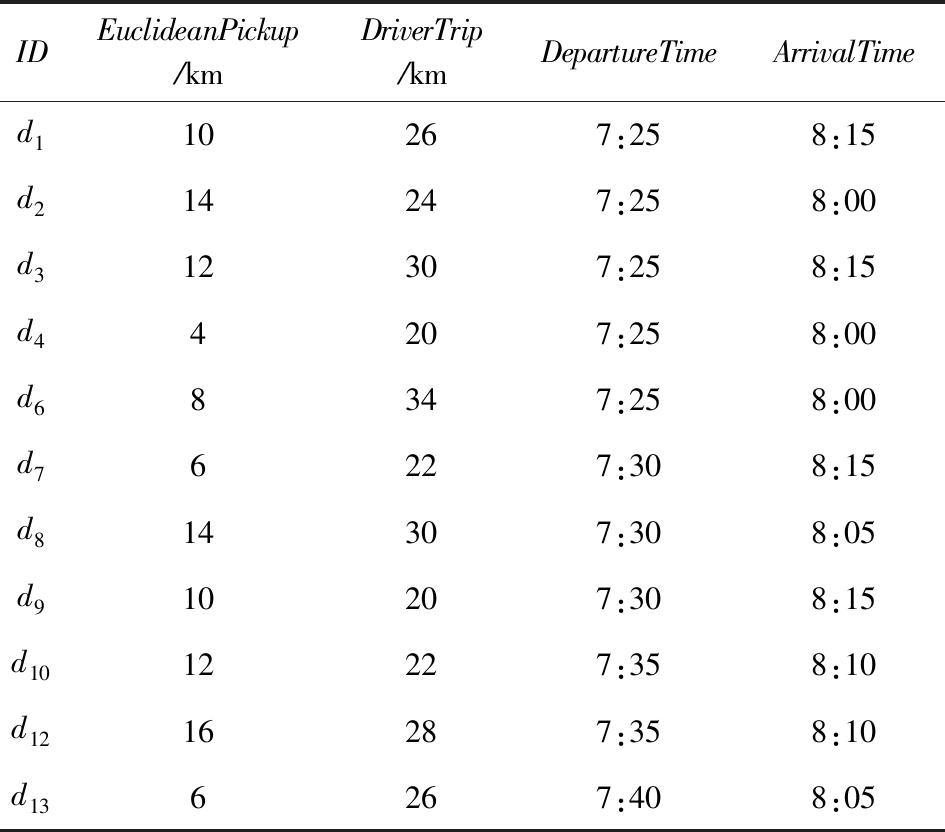
Table 2 Euclidean Distance Screening Step 1
表2 欧氏距离筛选步骤1
IDEuclideanPickup∕kmDriverTrip∕kmDepartureTimeArrivalTimed110267:258:15d214247:258:00d312307:258:15d44207:258:00d68347:258:00d76227:308:15d814307:308:05d910207:308:15d1012227:358:10d1216287:358:10d136267:408:05
所以满足式(4)的司机集合D2为{d1,d2,d3,d4,d6,d7,d9}.
接着计算司机集合D2中所有司机目的地位置与乘客r1目的地位置Dest(r)之间的Euclidean-Return(d,r)距离,并检验是否满足式(5)(6)的乘客拼车费用和司机到达时间约束,计算结果如表3所示:
Table 3 Euclidean Distance Screening Step 2
表3 欧氏距离筛选步骤2

IDPickupReturnDriverTripDepartureTimeArrivalTimed11010267:258:15d21412247:258:00d3126307:258:15d448207:258:00d686347:258:00d768227:308:15d91014207:308:15
同时满足式(5)(6)的司机集合D3为{d1,d3,d4,d6,d7},所以经过欧氏筛选之后获得的司机集合为D3={d1,d3,d4,d6,d7}.
2.1.3 基于路网距离筛选
这一步的输入是一名乘客r的拼车和通过欧氏距离筛选的司机集合D3;输出是通过路网距离筛选的司机集合D5,即所有满足乘客拼车要求的司机组成的集合.
路网距离筛选和欧氏距离筛选大致相同,分别是计算乘客与司机之间的路网Pickup(d,r)距离和Return(d,r)距离来对司机进行筛选,主要的差别在于约束条件上有略微的调整.
路网距离筛选的伪代码如算法3所示:
算法3. 路网距离筛选.
输入:司机集合D3、1个乘客r;
输出:司机集合D5.
① FOR d∈D3DO
② Compute Pickup(d,r);
③ IF DepartureTime(d)+Pickup(d,r)≤departureTimeMax(r) && Pickup(d,r)+2×RiderTrip(r)+Euclidean-Return(d,r)-DriverTrip(d)≤maxPrice(r) && departureTime(d)+Pickup(d,r)+RiderTrip(r)+EuclideanReturn(d,r)≤Arrival-Time(d) THEN
④ Put d into D4;
⑤ ENDIF
⑥ ENDFOR
⑦ FOR d∈D4DO
⑧ Compute Return(d,r);
⑨ IF Pickup(d,r)+2×RiderTrip(r)+Return(d,r)-DriverTrip(d)≤maxPrice(r) && DepartureTime(d)+Pickup(d,r)+RiderTrip(r)+Return(d,r)≤ArrivalTime(d) THEN
⑩ Put d into D5;
 ENDIF
ENDIF
 ENDFOR
ENDFOR
 FOR d∈D5DO
FOR d∈D5DO
 Compute Detour(d,r);
Compute Detour(d,r);
 Put Detour(d,r) into Detour Distance
Put Detour(d,r) into Detour Distance
Table;
 ENDFOR
ENDFOR
 RETURN D5.
RETURN D5.
路网距离筛选的主要步骤有3个:
1) 计算乘客r与D3中所有司机的Pickup(d,r)距离,并检验是否满足时间约束,即:
departureTimeMin(r)≤DepartureTime(d)+
Pickup(d,r)≤departureTimeMax(r).
(7)
2) 利用路网距离Pickup(d,r)和欧氏距离EuclideanReturn判断司机是否符合式(8)(9):
Pickup(d,r)+2×RiderTrip(r)+
EuclideanReturn(d,r)-
DriverTrip(d)≤maxPrice(r);
(8)
DepartureTime(d)+Pickup(d,r)+
RiderTrip(r)+EuclideanReturn(d,r)≤
ArrivalTime(d).
(9)
这一步是为了删除更多不符合要求的司机,这里利用司机的到达时间约束和乘客的费用约束,通过半欧氏的方法删除一部分不符合要求的司机.将经过这一步筛选之后得到的司机集合记为D4,该集合中的所有司机都满足乘客的拼车时间要求.但是由于用到了EuclideanReturn,所以并不是所有司机在乘客的费用约束和司机的到达时间约束上都满足要求,还需进一步的筛选.
3) 计算司机集合D4中所有司机与乘客r的Return距离,并判断是否符合乘客r的费用约束和司机的到达时间约束,即是否满足式(10)(11):
Pickup(d,r)+2×RiderTrip(r)+
Return(d,r)-DriverTrip(d)≤
maxPrice(r);
(10)
DepartureTime(d)+Pickup(d,r)+
RiderTrip(r)+Return(d,r)≤
ArrivalTime(d).
(11)
将满足式(10)(11)的司机组成集合D5,则该集合就是所求的所有满足乘客r的拼车条件的司机集合.
最后根据式(2)计算出乘客r1与司机集合D5中所有司机的绕路距离Detour(d,r),并将结果写入绕路距离记录表中.伪代码如例3所示:
例3. 在欧氏距离筛选结果的基础上对路网距离筛选进行进一步的说明计算司机集合D3中所有司机的出发位置到乘客r1出发位置的Pickup(d,r)距离,并判断是否在路网距离上满足式(7)~(9)乘客的出发时间约束,各司机的计算结果如表4所示.
Table 4 Road Network Distance Screening Step 1
表4 路网距离筛选步骤1

IDEuclideanPickupPickupReturnDriverTripDepartureTimeArrivalTimed1101110267:258:15d312146307:258:15d4488207:258:00d68126347:258:00d7698227:308:15
所以满足式(7)~(9)的司机集合D4为{d1,d3,d6,d7}.
接着计算司机集合D4中所有司机目的地位置分别与乘客r1目的地位置Dest(r)之间的Return(d,r)距离,并检验是否满足式(10)(11)的乘客拼车费用和司机到达时间约束,各司机的计算结果如表5所示.
同时满足式(10)(11)的司机集合D为{d1,d3},所以经过路网距离筛选之后获得的司机集合D5={d1,d3},即D5为所有满足乘客r1拼车要求的司机集合.然后将乘客r1的匹配结果填写入绕路距离记录表Detour Distance Table中.
Table 5 Road Network Distance Screening Step 2
表5 路网距离筛选步骤2

IDEuclideanPickupPickupEuclideanReturnReturnDriverTripDepartureTimeArrivalTimed110111010267:258:15d3121468307:258:15d6812613347:258:00d769810227:308:15
对每一名乘客都按照以上的步骤进行一次欧氏距离筛选和路网距离筛选,为其找出对应的符合拼车要求的所有司机集合,并将结果填入绕路距离记录表中.最后补全整张绕路距离记录表的内容.
2.2 多乘客与多司机最优组合匹配
在为每一名乘客找出对应的符合拼车要求的司机集合之后,为了达到所有司机拼车绕路距离最小的目标,Uroad会尽可能为每一名乘客在其司机集合中选派一名司机组成拼车匹配组合,使得所有司机最后产生的绕路距离最少.
但是在实际情况中,每一名乘客对应符合要求的司机会有m名,那么n名乘客与司机的匹配组合方案就会有m×n种情况.同时,每一名司机对应能够提供服务的乘客也有数十名,这会使得乘客之间出现争夺司机资源的情况.而当乘客和司机数量达到数百甚至数万名时,要将每一名乘客与其中一名司机匹配起来的组合方案就会有数万种.要在这数万种可能情况中找出一种所有司机绕路距离最少的匹配组合方案,就非常具有挑战性.
像这类从多种具有可能性的组合中挑选出一种最优的组合方案的问题,称为“组合优化”问题或者是“指派问题”.针对这类问题,Kuhn[5]提出了一种经典的解决方案——KM算法,可以获得组合优化中的最优匹配方案.之后经过Edmonds等人[6]不断的研究,将KM算法针对n×n矩阵的运行时间复杂度简化到O(n3),使得算法的性能得到大幅度的提升.其中,n代表匹配组合矩阵的大小.
但是在面对大规模乘客与司机的拼车匹配场景中,同一时间需要进行优化组合的乘客和司机数量将达到数千甚至数万名.即使是时间复杂度为O(n3)的KM算法,也需要消耗大量的时间进行计算,所以直接简单地运用KM算法并不适合.
针对上述问题,我们提出一种基于KM算法的改进方案,称之为拆分矩阵算法(split matrix algorithm, SM).通过将完整的KM矩阵拆分成多个子矩阵,再对子矩阵进行KM算法操作获取最优匹配组合方案.这一方法通过缩小矩阵规模来达到加快速度的目的.
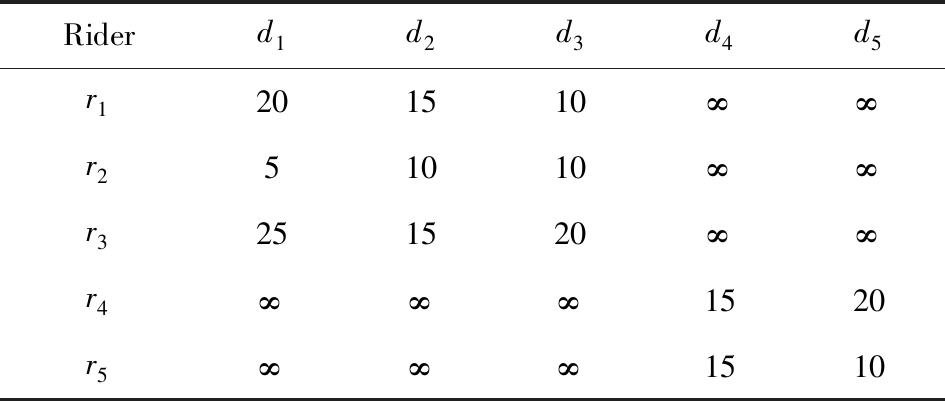
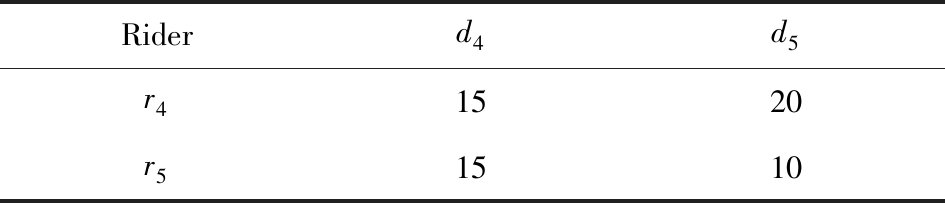
在拼车场景中符合每名乘客拼车要求的司机只有少数,所以整个绕路距离记录表会十分稀疏.如表6所示,我们可以直观地看到,乘客r1,r2,r3只能够与司机d1,d2,d3进行拼车匹配组合,而乘客r4,r5只能够与司机d4,d5进行拼车匹配组合.根据KM优化算法,我们将绕路距离记录表拆分成如表7、表8中的2个绕路距离子矩阵,即将所有相互有匹配关联可能的乘客和司机拆分到同一个绕路距离子矩阵中.拆分之后再采用KM算法来计算获得乘客与司机的拼车匹配组合结果.在这一例子中,复杂度从表6的O(53)降低到了表7、表8中的O(33)+O(23).通过上述方式,算法的复杂度大为降低.
Table 6 Detour Distance Diagram
表6 绕路距离记录表
Riderd1d2d3d4d5r1201510∞∞r251010∞∞r3251520∞∞r4∞∞∞1520r5∞∞∞1510
Table 7 Detour Sub-Matrix1 Diagram
表7 绕路距离子矩阵1

Riderd1d2d3r1201510r251010r3251520
Table 8 Detour Sub-Matrix2 Diagram
表8 绕路距离子矩阵2
Riderd4d5r41520r51510
在SM算法中的输入是乘客与司机的绕路距离记录表Detour Distance Table,输出是一组由绕路距离子矩阵Detour Sub-Matrix构成的矩阵列表List.SM算法具体实现如算法4所示:
算法4. 拆分矩阵.
输入:绕路距离表;
输出:矩阵列表.
① FOR every rider r in Recording Table DO
② Get r and r’s candidate drivers D;
③ IF r has been checked
④ CONTINUE;
⑤ ELSE
⑦ Create a new Matrix M;
⑧ Add r and all drivers in D into M;
⑨ FOR every driver d in M DO
⑩ Get d and d’s candidate riders R;
 ENDFOR
ENDFOR
 FOR every rider r′ in R DO
FOR every rider r′ in R DO
 Get r′’s candidate drivers D′;
Get r′’s candidate drivers D′;
 IF r′ is in M
IF r′ is in M
 CONTINUE;
CONTINUE;
 ELSE
ELSE
 Add r′ into M;
Add r′ into M;
 FOR every driver d′ in D′
FOR every driver d′ in D′
 IF d′ is in M
IF d′ is in M
 CONTINUE;
CONTINUE;
 ELSE
ELSE
 Add d′ into M;
Add d′ into M;
 ENDIF
ENDIF
 ENDFOR
ENDFOR
 ENDIF
ENDIF
 ENDFOR
ENDFOR
 Add Matrix into Matrix List;
Add Matrix into Matrix List;
 ENDIF
ENDIF
 ENDFOR
ENDFOR
 RETURN Matrix List.
RETURN Matrix List.
按照从上到下的顺序遍历绕路距离记录表Detour Distance Table中的每一个乘客r,有3种操作情况:
1) 若乘客r已经被检查过,将直接检查Detour Distance Table中的下一个乘客.
2) 若乘客r还未被检查过,则将新建一个Detour Sub-Matrix,并将r和r关联的司机集合D5加入到子矩阵中,并遍历集合D5中的每个司机d.
3) 找出d能够服务的所有乘客集合R(即Detour Distance Table中d所在列中绕路距离值不为∞的乘客).对于R中的每个乘客r′,则乘客r′可能有2种情况:
① 如果r′已经在Detour Sub-Matrix中,将直接检查R中的下一个乘客,直到所有乘客都检查完毕.
② 如果r′不在Detour Sub-Matrix中,将r′加入到Detour Sub-Matrix中,并找出r′对应的关联司机集合![]() 遍历
遍历![]() 中的每个司机d′,则司机d′可能有2种情况:
中的每个司机d′,则司机d′可能有2种情况:
i) 若d′已经在Detour Sub-Matrix中,将对应的Detour(d′,r′)填入Detour Sub-Matrix后检查D′中的下一个司机,直到所有司机都检查完毕.
ii) 若d′不在Detour Sub-Matrix中,将d′加入到Detour Sub-Matrix中,并跳转到步骤3).
将Detour Sub-Matrix存入到List中,并跳转到步骤1).
定理1. 通过算法4获得的匹配组合方案与单纯KM算法获得的匹配组合方案相同.
证明. 假设2种方案获得的匹配组合方案不同,即至少存在1名乘客匹配后的绕路不同.有3种情况:
1) 只有1名乘客匹配后的绕路不同,即2种方案仅有1名乘客匹配了不同的司机导致绕路距离不同.但是由于2种方案都是通过KM算法来选择绕路距离最小的司机,不可能存在有2个最小绕路距离值的情况,所以假设不成立.
2) 有多名乘客互相交换了司机,导致2种方案总绕路距离不同,但是这些乘客匹配的司机集合是不变的.相同的乘客集合与相同的司机集合通过KM算法仅有一种最小绕路距离的方案,不可能出现2种最小值,所以假设不成立.
3) 情况1)和情况2)的结合,同样原理,假设不成立.
综上,假设不成立,即过SM+KM算法获得的匹配组合方案与单纯KM算法获得的匹配组合方案相同.
证毕.
例4. 以表6中的Detour Distance Table为例,对其进行SM算法的过程为:
1) 遍历Detour Distance Table中的第1名乘客r1.因为r1还没有被检查过,所以建立一个新的Detour Sub-Matrix1,将乘客r1以及其对应的关联司机集合D5={d1,d2,d3}加入到Detour Sub-Matrix1中.此时矩阵Detour Sub-Matrix1如表9所示:
Table 9 Detour Sub-Matrix1 Diagram
表9 绕路距离子矩阵1
Riderd1d2d3r1201510
2) 遍历D5中的第1个司机d1,找到其能够服务的所有乘客集合R={r1,r2,r3},并检验R中的第1名乘客r1.因为r1已经检查过了,所以直接跳过r1检查r2.
因为r2不在Detour Sub-Matrix1,将r2加入Detour Sub-Matrix1,并找出r2对应的关联司机集合![]() 遍历
遍历![]() 中的所有司机,发现d1,d2,d3都已经在Detour Sub-Matrix1中.将r2与司机d1,d2,d3的Detour填入Detour Sub-Matrix1.此时矩阵Detour Sub-Matrix1如表10所示:
中的所有司机,发现d1,d2,d3都已经在Detour Sub-Matrix1中.将r2与司机d1,d2,d3的Detour填入Detour Sub-Matrix1.此时矩阵Detour Sub-Matrix1如表10所示:
Table 10 Detour Sub-Matrix1 Diagram
表10 绕路距离子矩阵1

Riderd1d2d3r1201510r251010
3) 遍历乘客r3,因为r3不在Detour Sub-Matrix1,将r3加入Detour Sub-Matrix1,并找出r3对应的关联司机集合![]() 遍历
遍历![]() 中的所有司机,发现d1,d2,d3都已经在Detour Sub-Matrix1中.将r3与司机d1,d2,d3的Detour填入Detour Sub-Matrix1.此时矩阵Detour Sub-Matrix1如表11所示:
中的所有司机,发现d1,d2,d3都已经在Detour Sub-Matrix1中.将r3与司机d1,d2,d3的Detour填入Detour Sub-Matrix1.此时矩阵Detour Sub-Matrix1如表11所示:
Table 11 Detour Sub-Matrix1 Diagram
表11 绕路距离子矩阵1

Riderd1d2d3r1201510r251010r3251520
遍历完成司机集合D5中的第1个司机d1之后,接着遍历司机d2,找到其能够服务的所有乘客集合R′={r1,r2,r3}.顺序检查乘客r1,r2,r3,发现都已经检查过.
4) 遍历司机d3,找到其能够服务的所有乘客集合R″={r1,r2,r3}.顺序检查乘客r1,r2,r3,发现也都已经检查过.最后将构成的Detour Sub-Matrix1加入List.
5) 在检查Detour Distance Table中的第2,3名乘客r2,r3,发现已经检查过了.直接跳过检查后一名乘客r4,发现还没有被检查过,所以建立一个新的Detour Sub-Matrix2,将乘客r4以及其对应的关联司机集合D5={d4,d5}加入到Detour Sub-Matrix2中.此时矩阵Detour Sub-Matrix2如表12所示:
Table 12 Detour Sub-Matrix2 diagram
表12 绕路距离子矩阵2
Riderd4d5r41520
6) 遍历D5中的第1个司机d4,找到其能够服务的所有乘客集合R={r4,r5},并检验R中的第1名乘客r4.因为r4已经检查过了,所以直接跳过r4检查r5.
因为r5不在Detour Sub-Matrix2,将r5加入Detour Sub-Matrix2,并找出r5对应的关联司机集合![]() 遍历
遍历![]() 中的所有司机,发现d4,d5都已经在Detour Sub-Matrix2中.将r5与司机d4,d5的Detour填入Detour Sub-Matrix2.此时矩阵Detour Sub-Matrix2如表13所示:
中的所有司机,发现d4,d5都已经在Detour Sub-Matrix2中.将r5与司机d4,d5的Detour填入Detour Sub-Matrix2.此时矩阵Detour Sub-Matrix2如表13所示:
Table 13 Detour Sub-Matrix2 diagram
表13 绕路距离子矩阵2

Riderd4d5r41520r51510
遍历完成司机集合D5中的第1个司机d4之后,接着遍历司机d3,找到其能够服务的所有乘客集合R″={r4,r5}.顺序检查乘客r4,r5,发现也都已经检查过.最后将构成的Detour Sub-Matrix2加入Matrix List.
7) 检查Detour Distance Table中的最后乘客r5,发现已经检查过了,结束完成整个SM算法.
3 实验与分析
本节将通过2部分实验来检验分析Uroad的拼车匹配算法的性能.1)与多个基准算法进行比较,分析Find Drivers算法(算法1~4)在各个阶段中的性能;2)分析在KM算法处理之前采用SM算法优化处理的性能比较.
实验用到的路网数据来自于洛杉矶市(City of Los Angeles)路网[7]:总共包含193 948个节点和530 977条边.实验中用到的司机与乘客数据是采用Brinkhoff生成器[8]在洛杉矶市路网上生成的,总共产生了1 000个乘客的请求和100 000名司机.这里不使用出租车轨迹数据的主要原因是出租车司机是没有出发位置和目的地位置设定的,并不适用于我们研究的问题,所以采用的是模拟数据.
所有实验中都假设路网的平均速度为60 km/h,拼车费率为1 yuan/km.实验中,模拟拼车匹配计算的时间为7:00,司机的出发时间为7:00—9:00之间的一个随机时间,乘客的出发时间段为7:00—9:00之间的一个随机时间段.实验中用到的网格索引结构,其每个网格的边长为经度(或纬度)0.01°所对应的路网距离,即边长约为1km.实验中计算实际路网距离是基于Dijkstra算法[9]实现的.
所有实验均在Dell工作站中完成,处理器为Intel® Xeon® CPU E3-1220 v3@3.10 GHz,内存为4 GB,系统为Windows 10专业版.
3.1 单乘客对多司机匹配环节
实验对比了3个算法的性能和特点,除了Uroad中包含的本文提出的方法(DTP+EP+SP)外,另有2种基准算法与其比较,以便于查看分析每一个计算步骤的性能:
1) SP(最短路径距离筛选).对所有司机直接进行Dijkstra算法,计算司机与乘客出发位置之间的距离和目的地位置之间的距离,并通过拼车约束条件筛选出符合要求的司机集合.
2) DTP+SP(出发时间筛选+最短路径距离筛选).先对所有乘客和司机进行出发时间筛选,缩小乘客的候选司机集合;然后进行最短路径计算,并通过拼车约束条件筛选出符合要求的司机集合.
3) DTP+EP+SP(出发时间筛选+欧氏距离筛选+最短路径距离筛选).即本文提出的方法.
3.1.1 整体性能比较
本节通过改变匹配司机规模数量、乘客拼车费用、司机到达时间等,考察比较3种算法的总体计算时间.
1) 匹配司机规模数量对性能的影响
如图4所示,固定乘客数量1 000人,乘客拼车费用为1.2×RiderTrip(r)即乘客RiderTrip对应费用的1.2yuan/km,司机的到达时间为DepartureTime(d)+1.3×DriverTrip(d),即其出发时间加上DriverTrip对应时间的1.3倍.设置司机数量N=20 000~100 000人.图4中横坐标为司机数量,纵坐标为所有乘客总体的匹配时间.

Fig. 4 Different driver’s quantity
图4 不同司机数量
从图4可见,DTP+EP+SP是3个算法中效率最高的算法.在相同数量的司机规模下,DTP+EP+SP表现最为有益.同时,随着司机数量的增加,DTP+EP+SP增加的时间也更少,增加的时间比例最低.这是因为,DTP+EP+SP在计算最短路径之前,从出发时间和欧氏距离2个方向对司机进行了筛选,使得参与最短路径计算的司机数量大幅减少,从而提高了效率.同时,当司机数量大于8万时,DTP+SP算法时间的增加速率有明显的提升趋势.这也说明,当司机数量过大时,DTP阶段的优化也会出现一定的瓶颈阶段.
2) 乘客拼车费用和司机到达时间对性能的影响
如图5所示,固定乘客数量为1 000人,匹配司机的规模数量为100 000人,司机的到达时间为DepartureTime(d)+1.5×DriverTrip(d).设置乘客拼车费用约束为P=1.1×RiderTrip(r)~1.5×RiderTrip(r).图5中横坐标为乘客拼车费用约束,纵坐标为所有乘客总体的匹配时间.

Fig. 5 Different passengers carpooling costs constraints
图5 不同乘客拼车费用约束
如图6所示,固定乘客数量为1 000人,匹配司机的规模数量为100 000人,乘客拼车费用为1.2×RiderTrip(r).设置司机到达时间约束为T=DepartureTime(d)+1.1×DriverTrip(d)~DepartureTime(d)+1.5×DriverTrip(d).图6中横坐标为司机到达时间约束,纵坐标为所有乘客总体的匹配时间.
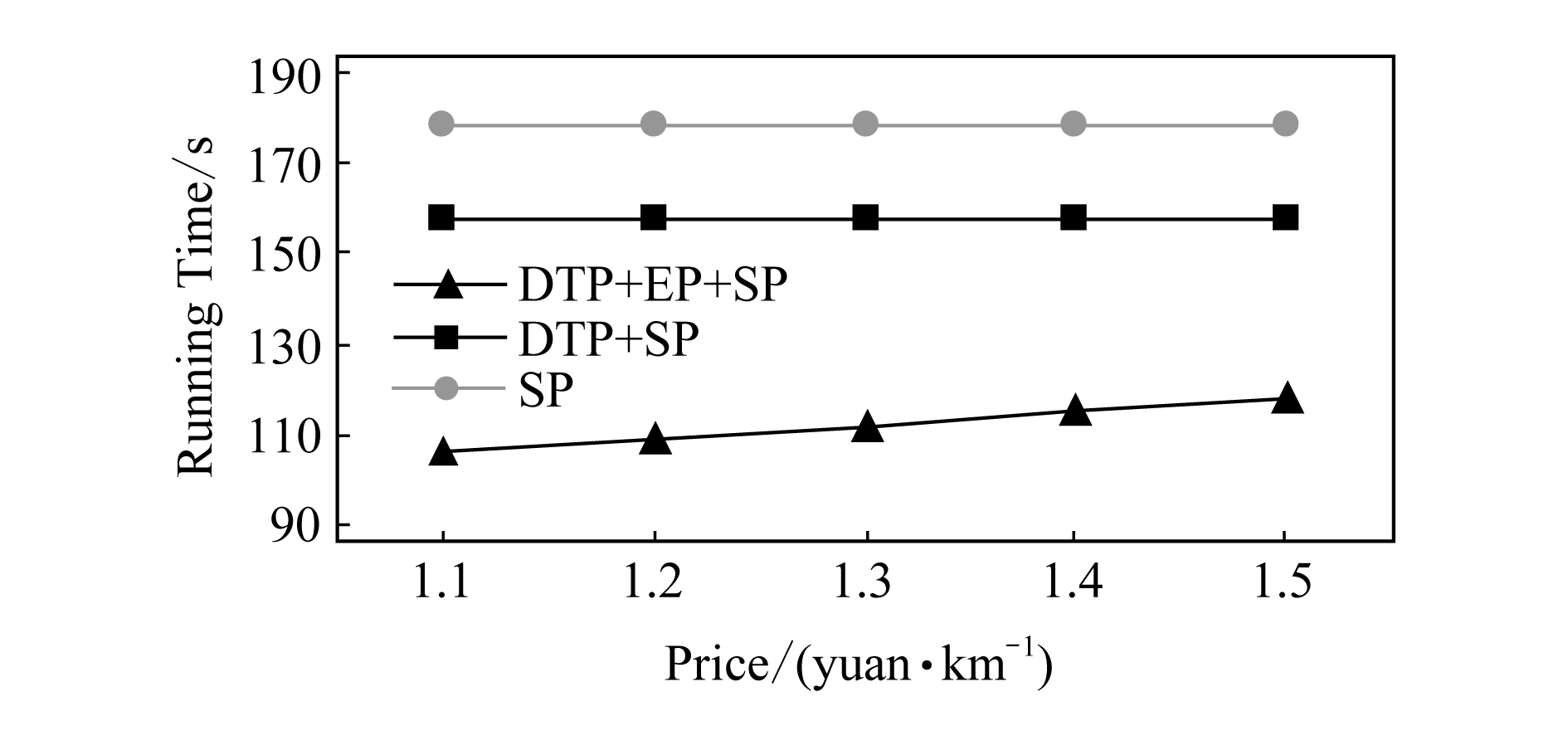
Fig. 6 Different driver arrival time constraints
图6 不同司机达到时间约束
可以看到图5和图6差别不大.随着乘客费用的增加或者司机到达时间的增加,DTP+SP和SP几乎没有明显的时间变化,这是因为2个算法在最短路径之前的筛选过程中没有运用到乘客费用和司机到达时间这2个约束条件,导致每次SP阶段的司机数量没有明显的差异.而DTP+EP+SP随着乘客费用约束的增加和司机到达时间的增加而略有上升.这是由于约束条件的放宽,使得在欧氏距离筛选过程中排除的司机数量略有减少,在最短路径计算阶段的计算量略有上升.
3.1.2 各阶段性能分析
本节主要分析DTP+EP+SP在各个阶段的性能表现,包括各个阶段耗时和占总时间的比例.DTP+EP+SP的3个阶段分别为:1)DTP,出发时间筛选;2)EP,欧氏距离筛选;3)SP,路网距离筛选.
实验中,固定乘客数量1 000人,乘客拼车费用为1.2×RiderTrip(r)即乘客RiderTrip对应费用的1.2 yuan/km,司机的到达时间为DepartureTime(d)+ 1.3×DriverTrip(d),即其出发时间加上DriverTrip对应时间的1.3倍.设置司机数量N=20 000~100 000人.图7中横坐标为司机数量,纵坐标为所有乘客总体的匹配时间.图8中横坐标为司机数量,纵坐标为各个阶段运行时间所占整体的比例.图9中横坐标为司机数量,纵坐标为各个阶段删除司机数量所占整体的比例.

Fig. 7 Time consuming in each step
图7 各阶段运行时间

Fig. 8 Ratio of running time in each step
图8 各阶段运行时间比例
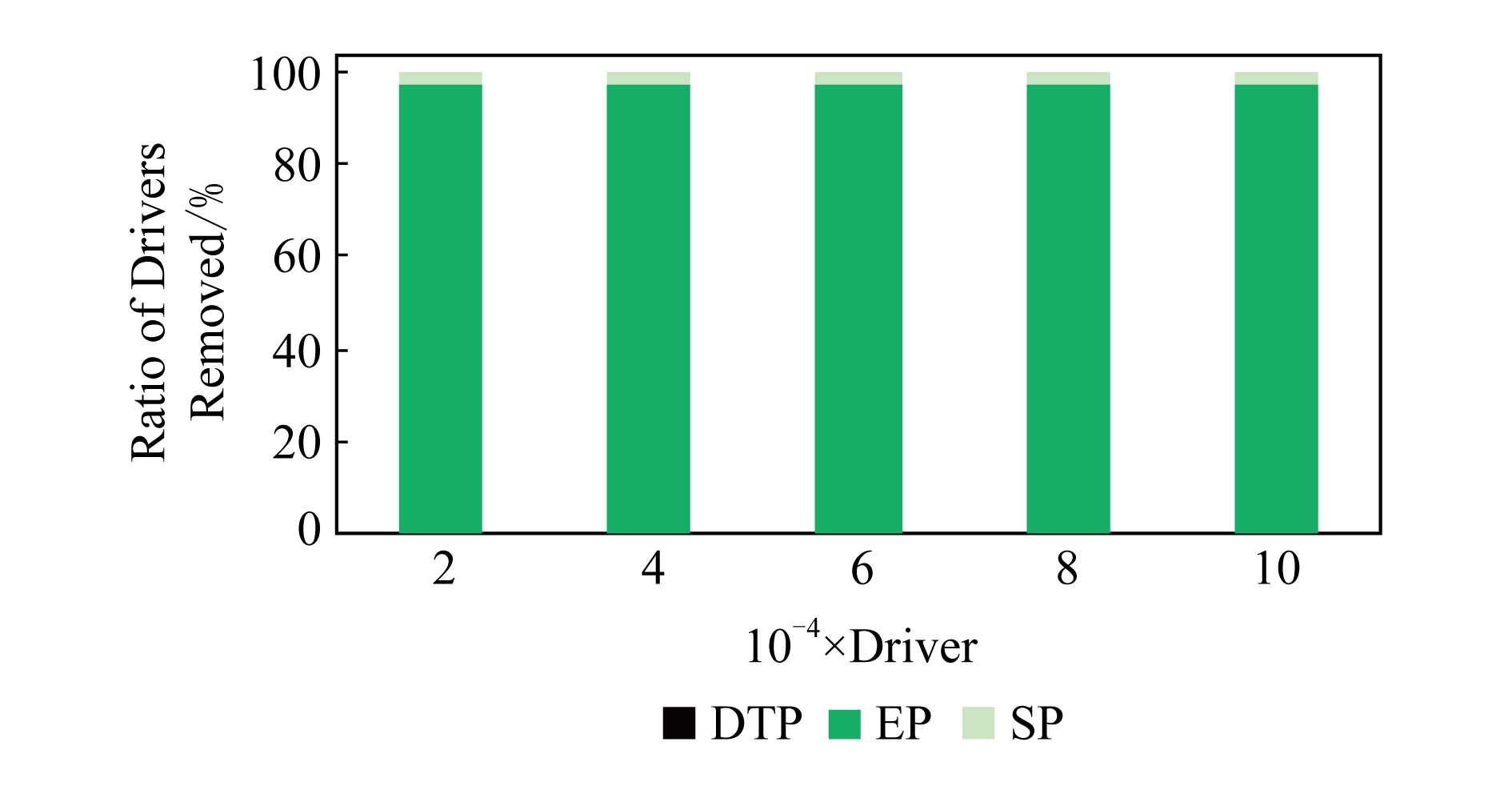
Fig. 9 Proportion of drivers removed at each stage
图9 各阶段排除司机数量比例
从图7、图8中都可以看到,DTP阶段无论是用时还是所占比例都是最少的,几乎可以忽略.但是从图9中可以看到,虽然用时少,但是筛选排除的司机数量占整体35%左右,DTP的筛选效果还是十分明显的.
从图7、图8中都可以看到,EP阶段消耗的时间和所占比例相对较少,主要是因为在EP阶段中没有最短路径距离计算,只进行了欧氏距离计算,计算代价比较小,所以用时相对而言比较少.但是随着司机数量的增长,EP阶段用时比例逐步上升.这是因为在EP阶段删除了大量的不可匹配的司机,即使司机数量增加了,通过EP阶段筛选的司机并没有明显的增加,所以EP阶段耗时比例会有所上升.从图9也可以明显看出,在筛选司机数量过程中,EP阶段负责了大部分司机的筛选.
从图7、图8中都可以看到,SP阶段是耗时最多的,占了绝大多数的运行时间比例.但是从图9中可以看出,实际进入SP阶段的司机数量其实只有少数,这直接说明了最短路径计算十分耗时.这也是我们在最短路径计算之前设计各种剪枝技术,以减少最短路径计算量的原因.
同时我们针对小规模数据量对于本文算法的性能测试.从图10可以看出,在规模较小的情况下,固定司机人数之后,算法的整体运行时间随着乘客人数的增加有明显的增长.这表明算法的耗时主要与最短路径距离筛选相关.从图11可以看出,在较小规模的情况下,算法的整体运行时间随着司机数量的增加而缓慢增加,最终趋于稳定.这表明本算法的剪枝技术十分有效.

Fig. 10 The impact of small-scale riders on the running time of each stage
图10 小规模乘客对各阶段运行时间的影响
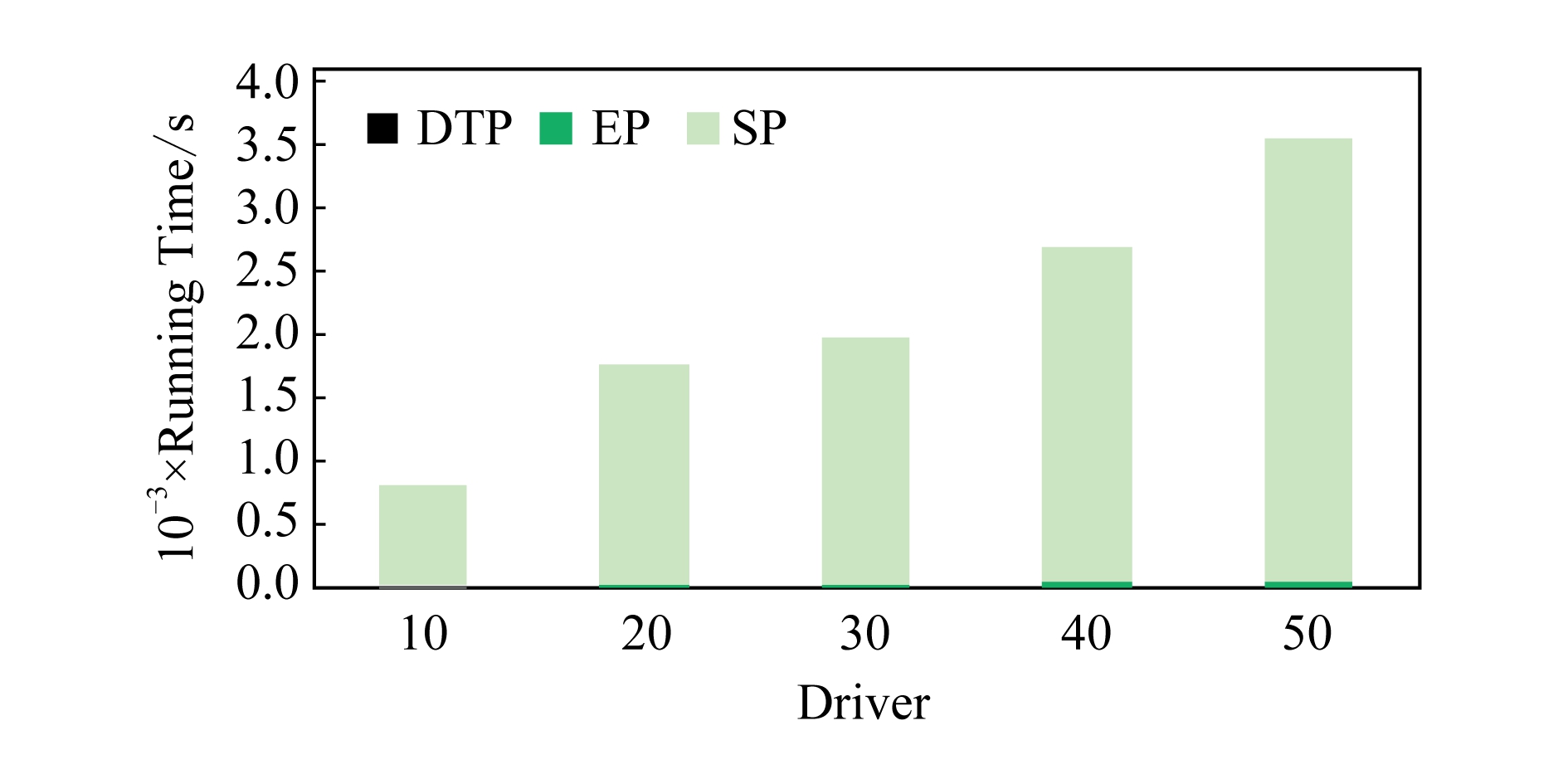
Fig. 11 The impact of small-scale drivers on the running time of each stage
图11 小规模司机对各阶段运行时间的影响
3.2 SM算法
实验对比了随机匹配算法、KM算法、SM+KM算法之间的性能,主要通过改变司机和乘客数量来考察比较3种算法的运行时间和绕路距离总和.
1) 随机匹配算法.通过乘客ID顺序,为每一名乘客随机匹配一名符合要求的司机.
2) KM算法.对Detour Distance Table直接采用KM找出最优拼车匹配组合.
3) SM+KM算法.先对Detour Distance Table采用SM将其拆分成多个小矩阵,并对小矩阵采用KM,找出最优拼车匹配组合.
3.2.1 改变乘客数量
如图12所示,固定司机数量100 000,乘客拼车费用1.2×RiderTrip(r),司机的到达时DepartureTime(d)+1.3×DriverTrip(d).设置乘客数量N=100~1 000.

Fig. 12 Impact of the quantity of riders on running time and detour distance
图12 乘客数量对运行时间和绕路距离的影响
图12中横坐标为乘客数量,图12(a)纵坐标为运行时间,图12(b)纵坐标为绕路距离.
根据图12(a)可以发现,在乘客数量300以内,KM与其他2种算法时间相差不大;而在乘客300以上(即Detour Distance Table中乘客数量增加)时,KM的运行时间出现指数型增长.而SM+KM和随机匹配的运行时间始终平稳变化不大,并且在实际数据上,SM+KM和随机匹配的运行时间都在1 s以内.
图12(b)可以发现,KM和SM+KM两种算法的绕路距离是一样的,这也验证了定理1的正确性.同时,随机匹配算法的绕路距离则始终都比其他2种算法要高出很多.KM和SM+KM两者的绕路距离总和基本保持在随机匹配算法的40%.这说明加入全局优化策略之后,SM+KM算法能够在保证时间不增加的情况下,使得所有司机的总体绕路距离减少60%左右,这也体现了本文全局优化策略的有效性.
综上所述,在司机数量相同、改变乘客数量的情况下,SM+KM算法在运行时间和绕路距离中的总体表现均优于其他2种算法.
3.2.2 改变司机数量
如图13,固定乘客数量1 000,乘客拼车费用1.2×RiderTrip(r),司机的到达时间departureTime(d)+1.3×DriverTrip(d).设置司机数量N=10 000~100 000.图13(a)(b)中横坐标为司机数量,图13(a)纵坐标为运行时间,图13(b)纵坐标为绕路距离.
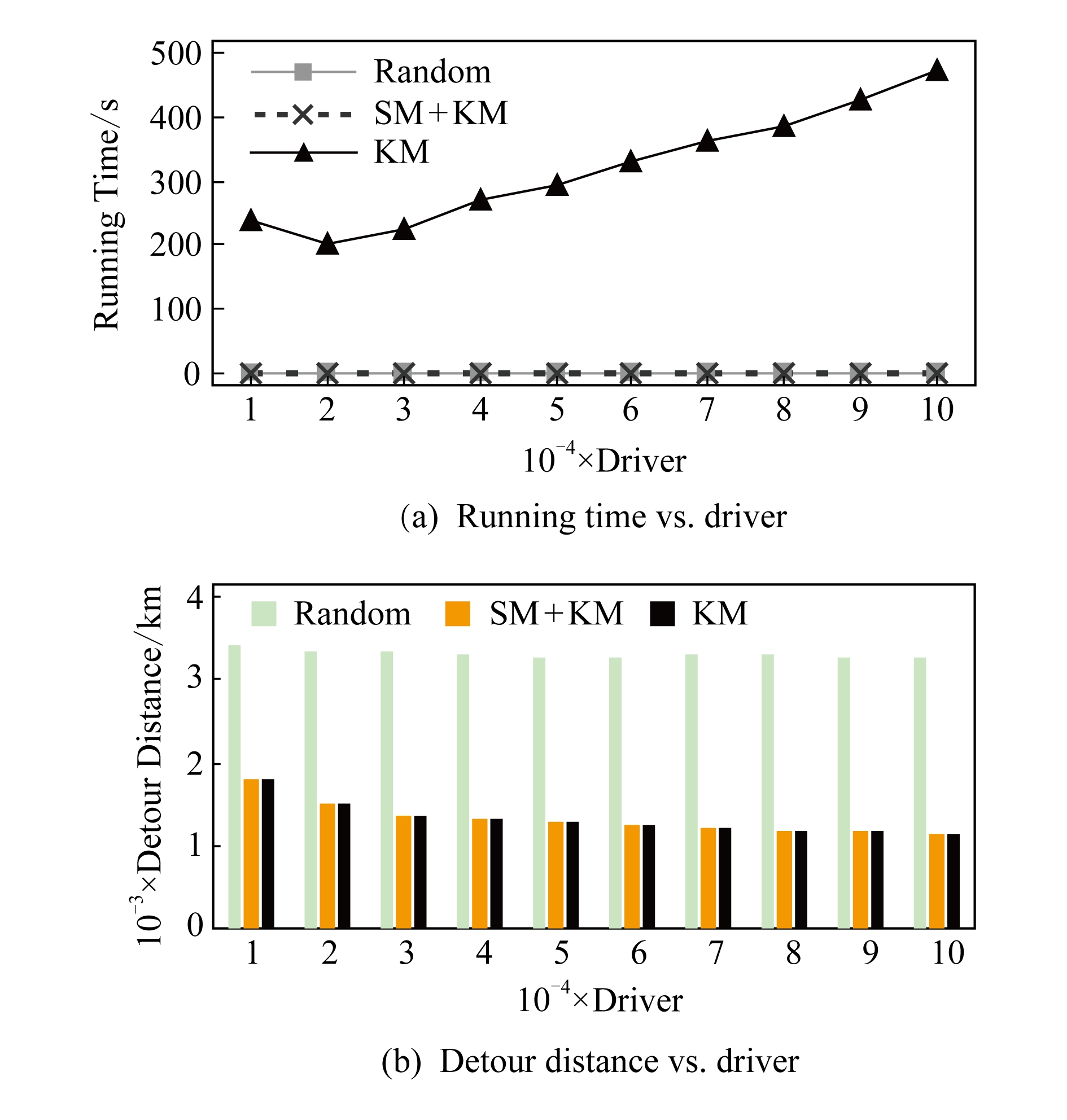
Fig. 13 Impact of the quantity of drivers on running time and detour distance
图13 司机数量对运行时间和绕路距离的影响
根据图13(a)可以发现,无论司机的数量如何增长(即Detour Distance Table中司机数量增加),SM+KM和随机匹配始终能表现优异,计算10 000名司机与计算100 000名司机的运行时间相差不大,均在1 s以内,但是KM则相差十分巨大.结合图12(a)可以发现,KM对司机和乘客规模的改变都十分敏感,无论是增加司机数量还是增加乘客数量,都会使得KM的计算时间显著增加.这是因为KM本身较高的时间复杂度所决定的.这里体现了SM+KM的一个特点:无论Detour Distance Table中司机和乘客的数量有多少,通过SM分解矩阵之后,能够使得进入KM中的子矩阵控制在小规模内(乘客与司机数量约300以内),以此降低了整体算法的运行时间.
根据图13(b)可以发现,KM和SM+KM的绕路距离是在同样条件下随机匹配绕路距离的50%~65%之间.同时,随着司机数量的增加,KM和SM+KM的绕路距离会随之有略微的减少.这是因为随着司机数量的增加,乘客可以匹配的司机数量增加,乘客对应的最优司机的绕路距离也降低了,所以整体的绕路距离会减少.但是随机匹配的绕路距离没有明显的趋势变化,基本维持在3 300左右.这是因为虽然每一名乘客的候选司机数量增加了,但是由于随机匹配是随机分配司机的策略,所以在总体绕路距离中并不会有明显的趋势变化.
综上所述,在乘客数量相同、改变司机数量的情况下,SM+KM算法在运行时间和绕路距离的总体变现均优于其他2种算法.并且无论Detour Distance Table中司机和乘客的数量有多少,SM+KM的运行时间都控制在1 s以内.
4 相关工作
与本文有关的现有工作主要分为3部分:1)拼车匹配方法;2)全局优化;3)拼车计费模型.本文的相关工作也将从这3方面展开.
拼车匹配方式主要分为4类[10],其中一名司机接送一名乘客和一名司机接送多名乘客为主这两类方式为大家所接受.
Cao等人[1]提出了一种针对私家车拼车的算法SHAREK.他们的目的是在大量的司机中,为乘客找出符合其拼车要求的一系列满足Skyline要求的司机.主要是利用欧氏距离设计了一些剪枝和筛选技术来降低最短路径的计算时间,从而提高整体拼车匹配算法的运行效率.Zhang等人[11]提出了一种多用户路径规划问题,并提出了相应的解决方案.他们的目的是为乘客和司机设计规划一条共同行驶的路径,使他们从各自出发位置出发在某一点汇合之后共同行驶一段距离,再前往到达各自目的地位置.同时,在这一条路径中,司机和乘客的共同行驶距离能够达到最长.但是和Uroad相比,这2个算法都没有考虑到司机出发时间限制这一因素,同时也没有从整体出发考虑全局最优化的拼车结果,所以和Uroad相比是不同的,并不能直接用于解决本文问题.
Ota等人[12]主要解决的问题是为乘客匹配一辆出租车,要求这辆出租车在接上新乘客之后产生的绕路最少.他们的解决方案是通过为拼车匹配中2点之间的最短路径构建索引的方式,来加快拼车匹配过程中最短路径的查询速度以提高整体效率.微软Zheng等人[13]提出了针对出租车拼车设计实现的T-Share系统,为了帮助乘客找到最佳的出租车,以大规模的出租车轨迹数据为依据来预测出租车司机的未来位置,并以预测结果作为匹配的主要依据.Huang等人[14]提出了一种基于分支界定的动态树生成方法来实现拼车过程中的快速匹配.出租车下一步所有可能的匹配方案以树的分支来表示,并通过各项约束条件来进行分支路径的筛选.他们将上海市某一天所有出租车的行程构造成对应的路径树,并模拟生成新到来的拼车请求,以此来检验拼车匹配所需要的完成时间.但是这项工作主要针对的是出租车的拼车场景,实验中用到的都是已知的出租车历史轨迹数据,和Uroad解决的司机也有出发位置目的地位置的问题设定具有本质上的区别.
针对全局优化,主要的相关工作有:Armant 等人[15]通过实验对比了MIP模型和CP模型在解决最大化拼车参与人数问题上的表现.实验结果表明,虽然MIP模型比较复杂,但是在性能上要优于CP模型.Alonsomora等人[16]提出了一种量化拼车中乘客等待时间、拼车延迟时间等参数的数学模型.并通过贪心算法来分配拼车资源,使得最后得到的分配方案能够达到最优的效果,以此来获得最优解.Maciejewski等人[17]提出了一种启发式出租车分配方案,为的是能够在减少乘客的平均等车时间的同时,提高出租车的载客率.实验结果表明在模拟器中,他们的分配方法比传统的“为乘客就近分配出租车”的方案表现更好.虽然这3项工作都是以全局优化为目标,但是他们的优化目标分别是最大化拼车参与人数、优化拼车等待和延迟时间、提高出租车的载客率,和Uroad追求的最小化所有司机绕路距离并不相同.
在拼车计费模型方面,Gopalakrishnan等人[18]提出了一种主要用于多人拼车的计费模型.他们在论文中指出,由于是多名乘客共同拼车,所以新加入拼车行列的乘客势必会对车上已有乘客造成一定影响.所以,新加入的乘客应该对车上已有乘客给予一定的费用作为对其造成行程延迟的补偿.Ma等人[19]针对多人共乘出租车的拼车模式提出了相应的计费模型.在他们的计费模型中,乘客的车费主要是根据其加入拼车行列中之后,对司机原有行程产生的绕路距离来决定的.针对车上已有乘客,根据与新乘客共乘的时间,将新乘客的一部分车费作为补偿支付给车上已有乘客.和Uroad不同的是,他们主要针对的是多人拼车场景提出的计费模型,而Uroad主要针对的是一名司机接送一名乘客的拼车场景,所以这些拼车计费模型并不适用.
5 总结与展望
本文提出了一种高效的大规模顺风车拼车匹配算法Uroad.司机可在拼车之前表明自己的出发时间和最晚到达时间.乘客也可在拼车请求中注明自身的出发时间段和愿意支付的最大拼车费用.除了乘客本身的行程之外,Uroad在计费模型中将乘客造成的绕路距离也考虑在内,使得拼车计费模型更加合理.Uroad通过出发时间筛选、欧氏距离筛选和路网距离筛选3部分操作,为每一名乘客匹配1名符合双方拼车要求的司机,使得最后所有司机产生的绕路距离最小.实验结果显示,在大规模情况下,平均只需要不到2 min,Uroad就能为1 000名乘客在100 000名司机中找出最优的拼车匹配组合方案,比直接计算最短路径缩短了40%的时间.在小规模情况下,平均只需要不到3.5 s,就能完成50名乘客在5 000名司机中找到最优拼车匹配方案,说明本文算法在不同场景中均有优异的性能.
虽然本文提出了高效的多对多拼车算法,但是在算法的公平性方面在未来还需要进行进一步的研究,主要包括2方面:
1) 本文所提算法是从所有司机绕路距离总和最小的全局最优目标从发,并不能保证每一位乘客所承担费用最小的局部最优结果,仅仅是对产生的拼车费用满足乘客拼车约束,所以未来可能需要进入竞价机制等方案,优化拼车定价模型;
2) 虽然本文算法能保证匹配结果中司机和乘客的绕路距离最短,但并未对路径进行具体规划,这可能导致多个拼车服务中同时包含同一段路径,从而引起该路段发生拥堵现象,进而影响到实际的拼车耗时.因此在未来的工作中,我们也需要结合路径的具体规划和道路资源竞争情况对算法进行优化.
[1]Cao Bin, Alarabi L, Mohamed F M, et al. SHAREK: A scalable dynamic ride sharing system[C] //Proc of the 16th IEEE Int Conf on Mobile Data Management. Washington, DC: IEEE Computer Society, 2015: 4-13
[2]Charles T, Huang Yan, Liu Zhi, et al. Noah: A dynamic ridesharing system[C] //Proc of the 29th ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2013: 985-988
[3]Cici B, Markopoulou A, Laoutaris N. SORS: A scalable online ridesharing system[C] //Proc of the 9th ACM SIGSPATIAL Int Workshop on Computational Transportation Science. New York: ACM, 2016: 13-18
[4]Yeung S, Miller E, Madria S. A flexible real-time ridesharing system considering current road conditions[C] //Proc of the 17th IEEE Int Conf on Mobile Data Management. Piscataway, NJ: IEEE, 2016: 186-191
[5]Kuhn H W. Statement for naval research logistics:“The hungarian method for the assignment problem”[J]. Journal of the Royal Statistical Society, 2015, 64(4): 611-633
[6]Edmonds J, Karp R M. Theoretical improvements in algorithmic efficiency for network flow problems[J]. Journal of the ACM, 1972, 19(2): 248-264
[7]US Department of Commerce, US Census Bureau, Geography Division. All lines shapefile [Modified Roads][OL]. 2010[2017-04-12]. https://www.ofm.wa.gov/sites/default/Files/public/legacy/pop/geographic/tiger10/metadata/roads10.html
[8]Brinkhoff T. A framework for generating network-based moving objects[J]. GeoInformatica, 2002, 6(2): 153-180
[9]Fredman M L,Tarjan R E. Fibonacci heaps and their uses in improved network optimization algorithms[J]. Journal of the ACM, 1987, 34(3): 596-615
[10]Agatz N, Erera A, Savelsbergh M, et al. Optimization for dynamic ride-sharing: A review[J]. European Journal of Operational Research, 2012, 223(2): 295-303
[11]Zhang Xinpeng,Asano Y,Yoshikawa M. Mutually beneficial confluent routing[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(10): 2681-2696
[12]Ota M,Vo H,Silva C, et al. A scalable approach for data-driven taxi ride-sharing simulation[C] //Proc of the 14th IEEE Int Conf on Big Data. Washington, DC: IEEE Computer Society, 2015: 888-897
[13]Wolfson O, Zheng Yu, Ma Shou. T-Share: A large-scale dynamic taxi ridesharing servic[C] //Proc of the 29th Int Conf on Data Engineering. Washington, DC: IEEE Computer Society, 2013: 410-421
[14]Huang Yan,Jin Ruoming, Bastani F, et al. Large scale real-time ridesharing with service guarantee on road networks[J]. Proceedings of the VLDB Endowment, 2013, 7(14): 2017-2028
[15]Armant V,Mahbub N,Brown K N. Maximising the number of participants in a ride-sharing scheme: MIP Versus CP formulations[C] //Proc of the 27th Int Conf on TOOLS with Artificial Intelligence. Piscataway, NJ: IEEE, 2016: 836-843
[16]Alonsomora J,Samaranayake S, Wallar A, et al. On-demand high-capacity ride-sharing via dynamic trip-vehicle assignment[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(3): 462-467
[17]Maciejewski M, Bischoff J,Kai N. An assignment-based approach to efficient real-time city-scale taxi dispatching[J]. IEEE Intelligent Systems, 2016, 31(1): 68-77
[18]Gopalakrishnan R, Mukherjee K, Tulabandhula T. The costs and benefits of sharing: Sequential individual rationality and sequential fairness[OL]. 2016[2017-08-10]. https://arxiv.org/abs/1607.07306
[19]Ma Shuo, Zheng Yu,Wolfson O. Real-time city-scale taxi ridesharing[J]. IEEE Transactions on Knowledge & Data Engineering, 2015, 27(7): 1782-1795





