多重签名[1]是指2个以上的签名者对同一则消息进行签名,同时要求签名的长度不会因为签名者数目增多而呈线性增长,该类方案在电子商务领域被广泛应用.目前多重签名主要使用RSA(rivest shamir adleman)[2]、ElGamal[3-4]、双线性对[5]、离散对数[6-7]等思想来设计.1994年Harn[8]提出了Meta-ElGamal多重签名.1996年Wu等人[9]依据签名的签署顺序不同,将多重签名区分为顺序多重签名和广播多重签名.顺序多重签名意味着签名者必须按照特有的顺序依次对消息进行签名;广播多重签名是指签名者不必拘泥于固有的顺序,按广播的方式对消息进行签名,由收集者合并且输出签名.广播多重签名相比顺序多重签名应用更为广泛,ElGamal 型多重签名的安全性基于DL(discrete logarithm)问题的难解性,满足不可伪造性,缺点是不具备签名者的身份验证,不能抵制多个签名者的联合攻击.
1997年Zheng[10]提出了签密方案.签密方案相对于传统的签名方案而言,能够同时完成签名和加密2项功能.签名方案只是确保设计方案的不可伪造性,在安全性分析时,只要方案满足选择消息攻击的不可伪造性,那么就说设计的方案是语义安全的.签密方案能够在一个合理的逻辑步骤内同时完成签名和加密，在安全性分析时,不仅要分析方案的保密性,还要分析方案的不可伪造性.
2002年Baek等人[11]对Zheng的签密方案进行了改进,同时给出了随机预言模型下的安全性证明.2011年Fan等人[12]改进了2002版本的签密方案,在Hash函数的输入中添加了接收方和发送方的公钥.近年来,越来越多的学者将签密和具有特殊性质的签名结合起来进行研究,使用不同的认证方法来认证用户公钥[13-19].2016年周才学[20]指出很多签密方案还存在安全问题,同时他认为在解签密算法的验证等式中不应出现明文信息,加密部分应该包含发送者的公钥或身份信息,签名部分应包含接收者的公钥或身份信息,在无证书密码体制的签名部分中不要让部分私钥和秘密值之间只是存在简单的线性关系.
UC(universally composalble)安全框架[21]满足协议的模块化设计要求,可以单独用来设计协议.只要协议满足UC安全性,则可以保证和其他协议并发组合运行的安全性.设计一个UC安全协议,首先要将协议所希望完成的功能抽象为一个理想函数,该理想函数相当于现实世界中一个不可攻破的可信第三方.2003年Canetti等人[22]纠正了自己在2001年提出的签名理想函数的定义,通过添加SID(session identifier)来编码签名者的身份,允许被收买的签名者对合法的签名进行验证,对公钥、签名、验证消息进行储存;2007年Kristian等人[23]利用用户友好交互提出了一个安全消息传递理想函数,给出了签密的理想函数;2012年Canetti等人[24]提出了不经意传输(oblivious transfer, OT)协议的理想函数,同时给出了使用OT协议的双向认证协议的通用方法.国内对UC安全的研究也取得了一些成果,冯涛等人[25]利用可否认加密体制和可验证平滑投影Hash函数提出了一个UC安全的高效不经意传输协议;苏婷等人[26]基于密钥注册模型形式化定义了签密协议的安全模型(即签密协议的理想函数),设计了一般化的签密协议,给出了UC框架下的证明;张忠等人[27]形式化定义了信息处理集合和无线射频识别(radio frequency identification, RFID)组证明的理想函数,然后设计了一个组证明RFID协议,证明了该协议安全地实现了理想功能;田有亮等人[28]利用身份签密机制提出了一个UC安全的群通信协议,解决了多播群组通信的组合安全问题,之后,他们又设计了一个通用可组合的安全多方计算协议[29],即在UC框架下能实现公平的安全两方计算协议,使人们认为的两方公平安全计算不能实现的问题得到解决.
本文结合自认证公钥和Meta-ElGamal多重签名协议的思想,在UC框架下设计了一个ElGamal型广播多重签密(ElGamal broadcasting multi-sign-cryption, EBMSC)协议,进而在UC安全框架下分析了该协议的安全性.也给出了ElGamal型广播多重签密协议的UC安全性证明.
1 预备知识
1.1 困难假设
定义1. DL假设.设G是阶为素数p的循环群, g是G的一个生成元.已知(p,G,w),找到一个a∈Z
使得w∈ga是困难的.
定义2. CDH假设.设G是素数阶p的循环群,g是G的一个生成元.已知(ga,gb∈G*,其中a,b∈Z
找到ga b∈G是困难的.
1.2 UC安全框架
UC安全框架是由现实模型、理想模型和混合模型组成.在UC框架中,用交互式图灵机(inter-active turing machine, ITM)来描述协议的参与方、敌手和环境机等实体.每个ITM的运行都被限定在概率多项式时间内.在现实模型中,包括了参与方P、敌手A、协议π和环境机Z等实体,参与方P不仅诚实地执行协议π,而且相互之间还可以直接通信.在理想模型中,包括了参与方P、模拟者S、理想函数F和环境机Z等实体.和现实模型不一样的是,参与方P相互之间不能直接通信,而是通过理想函数F来转发信息,现实模型和理想模型的外部环境Z相同.由于模块化的设计思想,只要证明某个协议能满足UC安全性,则和其他协议并发运行也能保证其安全性.
定义3. 不可区分性[21].X和Y是2个不可区分的二元分布集合(记作X≈Y),如果任何c∈N都有k0∈N,使得所有k>k0和所有的a,都有:
|Pr(X(k,a)=1)-Pr(Y(k,a)=1)|<k-c.
定义4. UC仿真[21].设n∈N,令F是理想函数,π具有n个参与方的协议,τ是现实中某类敌手.若对任何现实攻击者A∈τ都存在一个理想过程中的敌手S,使得任何环境机Z都不能区分它是与(π,A)交互还是与(F,S)交互，则称π安全实现了F,记作:
IDEALF,S,Z≈REALπ,A,Z.
定义5. 组合定理[21].令F和G是理想函数,π是F-混合模型下的一个协议,ρ协议在G-混合模型下可以安全地实现F.则对于任何敌手AG,都存在一个AF,使得对于任何环境机Z,都有:
1.3 基于离散对数的多重签名回顾
Harn[8]利用离散对数提出了一种有效的多重签名方案.假设n个签名者对同一消息m进行签名.
1) 每一个签名者ui从[1,p-1]中随机选取ki,计算
然后将ri广播给所有的签名者.一旦来自所有签名者的ri(i=1,2,…,n),汇聚在广播通道中,每一签名者计算r的值:
2) 签名者ui用秘钥zi和ki对消息m运行签名算法.即si=(zi(m′+r)-ki) mod p,其中0≤si≤p-2和m′=f(m).签名者把元组(m,si)发送给消息收集者.
3) 收集者收到来自各个ui的签名(m,si),验证
这里m′=f(m)，yi是ui的公钥.
4) 消息收集者将对通过验证的消息进行合并：s=(s1+s2+…+sn) mod p，得到完整的签名(r,s).
5) 验证者计算公钥:
6) 验证ym′+r=r αsmod p,这里m′=f(m).
2 EBMSC协议的形式化定义
2.1 EBMSC算法定义
一个EBMSC协议由4个算法组成:参与方包括消息发起者或签密收集者UC、签密者U1,U2,…,Un、接收者UV.
系统设置算法:输入安全参数1k,生成系统主密钥s和系统参数params.
密钥提取算法:身份IDu的用户随机选择秘密钥生成其公钥yu,而密钥生成中心(key generator central, KGC)随机选择秘密钥ηu,然后根据用户身份IDu和公钥yu生成其部分私钥Tu,之后安全的形式发给用户.用户收到部分私钥Tu后,计算完整私钥xu.
多重签密算法:输入系统的参数params、明文m、签密者Ui的私钥xi及接收者UV的公钥yV,输出多重签密密文σ.
解签密算法:输入密文σ、参数params、签密者Ui的公钥yi及接收者UV的私钥xV,输出明文m或者解签密符号⊥.
2.2 安全模型
一个EBMSC协议有2类敌手,即A1和A2.敌手A1无法得到系统的主密钥,但是可以替换用户的公钥(敌手A1相当于模拟了不诚实的用户);敌手A2可以得到系统的主密钥,但不能替换用户的公钥(敌手A2相当于模拟了恶意的KGC).
定义6. 如果存在任何多项式有界的敌手A1和A2赢得游戏IND-CCA2-I和IND-CCA2-II的优势是可忽略的,则称EBMSC 协议是具有适应性选择密文攻击下的不可区分性(indistinguishability against adaptive chosen ciphertext attacks, IND-CCA2).
IND-CCA2-I:这是挑战者C和敌手A1之间的交互游戏.
初始化.C运行系统设置算法得到系统参数params和系统主密钥s,之后将系统参数params发给A1,但保留主密钥s.
阶段1. A1进行多项式有限次询问.
公钥询问:当收到A1的公钥询问时,C运行密钥提取算法中的用户公钥生成算法得到yi,返回给A1.
部分私钥提取询问:A1可以请求身份IDu的部分私钥询问,C运行密钥提取算法中的部分密钥生成算法得到Tu,之后把Tu返回给A1.
私钥提取询问:A1可以请求身份IDu的私钥询问,C运行密钥提取算法中的私钥生成算法得到xu,之后把xu返回给A1.
签密询问:A1收到(IDi,IDV,m)的签密询问时,C通过调用签密算法得到多重签密密文σ,之后将σ发给A1.
解签密询问:A1收到(IDi,IDV,σ)时,C通过调用解签密算法得到的消息mi之后返给A1.
挑战阶段.A1生成2个等长的消息(mo,m1)及2个身份
但要求接收者
的部分私钥不能被询问.C随机选择δ∈{0,1},然后执行对δ的多重签密,之后将δ*发给A1.
阶段2. A1可以像阶段1那样进行多项式有界次询问,但仍然要求的私钥不能被询问,此外不能做σ*的解签密询问.
最后,输出δ′={0,1}作为对δ的猜测.如果δ′=δ,则A1赢得游戏.
IND-CCA2-II: 前面各阶段和敌手A1一样,只是敌手A2最后赢得游戏的条件是的私钥不能被询问,而且不能做σ*的解签密询问,除非接收者的公钥被替换.
定义7. 如果存在任何多项式有界的敌手A1和A2赢得游戏UF-CMA-I和UF-CMA-II的优势是可忽略的,则称EBMSC协议是具有适应性选择消息攻击下的不可伪造性(unforgeability against adaptive chosen message attacks, UF-CMA).
UF-CMA-I:C和伪造者A1之间的交互游戏.
初始化. C运行系统设置算法得到系统参数params和系统主密钥s,之后将系统参数params发给A1,但保留主密钥s.
训练. A1进行的多项式有界次询问和定义6中IND-CCA2-I的阶段1一样.
伪造. 当询问结束后,A1输出伪造的多重签密密文
询问期间,不能做
的部分私钥询问.如果密文通过解签密验证,则定义A1在游戏中获胜.
UF-CMA-II:C和伪造者A2之间的交互游戏.
初始化. C运行系统设置算法得到系统参数params和系统主密钥s,之后将系统参数params发给A2,但保留主密钥s.
训练. A2进行的多项式有界次询问和定义6中IND-CCA2-II游戏的阶段1一样.
伪造. 询问结束后,A2输出伪造多重签密密文询问期间,不能做的秘密钥询问.如果σ*通过解签密验证，则定义A2在游戏中获胜.
3 一个具体的EBMSC协议
3.1 初始化(Setup)
密钥生成中心(KGC)随机选择大素数p,g是Z
上阶为p的生成元.定义4个安全Hash函数H1:{0,1}*×Z
Z
ZZ
Z
Z
Z
随机选择系统主密钥s∈Z
计算系统公钥PPub=gsmod p.最后KGC保密系统主密钥s,公开系统参数(p,g,l,PPub,H1,H2,H3,H4).
3.2 密钥生成(Extract)
1) 用户Ui随机选择ki∈Z并进一步计算公钥
之后返回给KGC.
2) KGC选择ηi∈RZ计算
mod p, Ti=(ηi+sH1(IDi,λi,yi)) mod (p-1)，将(λi,Ti)返回给用户Ui.
3) 用户Ui验证
mod p, 如果等式成立,则Ui计算xi=kiTimod (p-1),并把xi作为其私钥.通过以上步骤,签密者Ui将得到公私钥(xi,yi),接收者UV将获得公私钥(xV,yV).
3.3 广播多重签密(MultiSC)
签密者Ui选择ri∈RZ计算
然后广播给其他的签密者,通过下面步骤得到密文,并发送给签密收集者UC.
2) h=H2(m,α).
4) Ci=m⊕H3(Wi).
5) μi=H4(m,Ti,TV,Wi).
6) βi=(ki(μi+Ti+h α)-ri) mod (p-1).
7) 输出(αi,α,βi,h,Ti,TV,Ci),通过验证
是否成立,若等式成立,则计算:
8) 签密收集者UC将进一步输出签密密文σ=(α,βi,h,Ti,TV,{C1,C2,…,Cn}) 给接收者UV.
3.4 解签密(USC)
接收者UV收到签密密文σ后,执行步骤.
2) m=Ci⊕H3(Wi).
3) μi=H4(m,Ti,TV,Wi).
4) 验证：
其中,
若等式成立,则接受明文m;否则,输出⊥符号表示广播多重签密无效.
3.5 正确性分析
可通过验证等式确保所提协议的正确性:
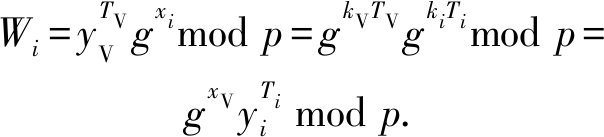
3.6 ROM下的安全性分析
3.6.1 保密性
在随机预言模型(ROM)下的安全性分析,我们参考文献[18]的思路.
定理1. 在ROM中,如果没有任何多项式有界的敌手A1能以不可忽略的优势ε赢得定义6中的游戏IND-CCA2-I(至多进行qi次Hi询问(i=1,2,3,4),qPK次公钥替换询问,qPSK次部分私钥提取询问,qSK次私钥提取询问,qSC次签密询问,qUSC次解签密询问),则存在一个挑战者C能至少以ε′的优势解决CDH问题,这里:
证明. 给定一个随机的CDH问题实例(p,g,ga,gb),其中a,b∈Z目标为了计算ga b mod p.为了达到这个目标,A1作为C的子程序在交互游戏中充当敌手.游戏开始之时,C运行Setup(1k),得到参数:
params={p,g,l,PPub=ga,H1,H2,H3,H4},
同时将params发给A1.在交互游戏中,表L1到L4用于记录H1至H4的询问与应答值,Lk用于记录公私钥的询问与应答值.
阶段1.A1进行多项式有界次适应性询问.
H1询问:C从个身份q1中选择第i个身份作为挑战的目标身份,A1发出H1询问.如果A1向C询问的Hash函数值已经在L1中存在,则返回相应的值给A1;否则,C选取ψ∈R{0,1}.如果ψ=1,则将(IDi,yi,-,ψ)记录到L1中;否则选择h1∈RZ返回
将(IDi,yi,λi,h1,ψ)记录到L1表中.这里设ψ=0的概率是ρ,即ρ=Pr[ψ=0].
H2询问:A1发出H2询问时.C检查元组(m,α,h2)是否存在于L2,如果存在,则返回h2;否则,C随机选取h2∈Z然后将h2发给A1,并将(m,α,h2)记录到L2中.
H3询问:A1发出H3询问.C检查元组(Wi,h3)是否存在于L3表中,如果存在,则返回h3;否则,C随机选取h3∈R{0,1}l,然后将h3发给A1,记录(Wi,h3)到L3中.
H4询问:A1发出H4询问时,检查元组(m,Ti,TV,Wi,μ)是否存在于L4中,如果存在,则返回μ;否则,C选取h4∈RZ然后将h4发给A1,记录(m,Ti,TV,Wi,μ)到L4中.
公钥询问:收到A1公钥询问时,C随机选择ki,并计算公钥
之后将其添加到Lk表中.
部分私钥询问:A1询问身份IDi的部分私钥.若ψ=0,则C选择Ti∈Z
将(IDi,Ti,ψ)记录到L1中,并返回Ti;否则,放弃仿真.
私钥询问:A1询问身份IDi的私钥.假设已经询问过H1预言机.若ψ=0,则返回完整私钥xi=kiTimod p;否则,放弃仿真,之后将私钥添加到Lk中.
公钥替换询问:A1对身份IDi进行公钥替换询问时.C用
来替换Lk中的原有记录.
多重签密询问:A1可对任何消息m及签密人的身份IDi、接收者的身份IDV进行签密询问.假设在此之前已经做过Hash函数值询问和密钥提取询问.如果ψ=0,则正常执行多重签密算法;否则执行操作:
1) 挑战者C选择ri∈RZ计算:
继续执行操作:
2) 计算
3) 计算Ci=m⊕H3(Wi).
4) 计算μi=H4(m,TV,Ti,Wi).
5) 计算βi=(ki(μi+Ti+h α)-ri) mod (p-1).验证：
是否成立.如果成立,则计算:
6) 计算
7) 输出σ=(α,β,h,Ti,TV,{C1,C2,…,Cn}).
解签密询问:A1通过提供的多重签密密文,当A1询问σ是否合法时,挑战者C先从表中查找出记录yi,再查找表L1.如果ψ=0,则正常执行解签密算法;否则,挑战者C计算
⊕H3(Wi),μi=H4(m,TV,Ti,Wi),然后将(Wi,m)提交给预言机.如果:
则通过解签密;否则认为不合法.
挑战阶段.通过上面的询问过后,如果ψ=0.则放弃仿真;否则挑战者C随机选择δ={0,1},计算
⊕
然后提交多重签密密文
阶段2. A1可以像阶段1那样进行多项式有界次适应性询问.但是要求身份IDV的私钥仍然不能被询问,此外不能做σ*的解签密询问.
猜测.最后,输出δ′={0,1},用δ′作为对δ的猜测.如果δ′=δ,那么C计算
输出
作为CDH问题实例的解答,原因如下:
概率分析[14]在阶段1或阶段2挑战者C不放弃仿真的概率是
即在密钥提取阶段,至少有一个身份IDV的私钥xV没被A1询问,C不放弃游戏的概率为1
e(qSK+qPSK),同时,A1对
做H3询问的概率为1q3,那么C将成功.所以C解决CDH问题的概率是
证毕.
定理2. 在ROM中,如果没有任何多项式有界的敌手A2能以不可忽略的优势ε赢得定义6中的游戏IND-CCA2-Ⅱ(至多进行qi次Hi询问(i=1,2,3,4),qPK次公钥替换询问,qSK次私钥提取询问,qSC次签密询问,qUSC次解签密询问),则存在一个挑战者C能够至少以ε′的优势解决CDH问题,这里:
证明. 给定一个随机的CDH问题实例(p,g,ga,gb),其中a,b∈Z目标为了计算ga b mod p.为了达到这个目的,A2作为C的子程序,在交互游戏IND-CCA2-II中充当敌手.游戏开始后,C运行Setup(1k),得到参数:
params={p,g,l,PPub=gs,H1,H2,H3,H4},
同时将params发给A2.在游戏中,表L1到L4用于记录H1至H4的询问与应答值,Lk用于记录公私钥的询问与应答值.
阶段1.除了部分私钥询问,其他询问同定理1.
挑战阶段. 通过上面的询问过后,若ψ=0.则放弃游戏;否则挑战者C随机选择δ∈{0,1},计算,yi=ga,
⊕返回密文
阶段2. A2可以像阶段1那样进行多项式有界次适应性询问.但是要求身份为IDV的私钥仍然不能被询问,并且不能做关于σ*的解签密询问.
猜测. 最后,输出δ′∈{0,1},用δ′作为对δ的猜测.如果δ′=δ,那么挑战者C计算
即C输出
作为CDH问题实例的应答,因为:
⟺
⟺
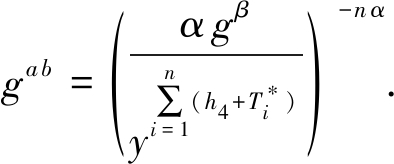
概率分析在阶段1或阶段2挑战者C不放弃仿真的概率是
因为不进行部分私钥询问，即C不放弃游戏的概率为1e(qPK+qSK),同时,A1对做H3询问的概率为1q3,那么C将成功.所以C解决CDH问题的概率是
证毕.
3.6.2 不可伪造性
定理3. 如果任何多项式有界的敌手A1和A2赢得定义7中的游戏UF-CMA-I和UF-CMA-II的优势是可忽略的,则EBMSC协议具有适应性选择消息攻击下的不可伪造性(至多进行qi次Hi询问(i=1,2,3,4),qPK次公钥替换询问,qPSK次部分私钥提取询问,qSK次私钥提取询问,qSC次签密询问,qUSC次解签密询问),在UF-CMA-I中,则存在一个挑战者C至少能够以
的优势解决离散对数问题;在UF-CMA-II中,则存在一个挑战者C至少能够以
的优势解决离散对数问题.
证明. 给定一个随机的离散对数问题实例(p,g,ga)，目标为了计算a∈Z为了达到这个目的,A1作为挑战者C的子程序,在交互游戏UF-CMA-I中充当敌手,C充当敌手A1的挑战者.
在交互游戏开始之时,游戏开始后,C运行Setup(1k),得到参数:
params={p,g,l,PPub,H1,H2,H3,H4},
并将params发给A1.在游戏中,表L1到L4记录H1至H4的预言机,Lk用于追踪公私钥的询问与应答值.
询问阶段.和定理1相同.
伪造. 对于不同的敌手伪造的过程不一样.
1) A1输出一个伪造的广播多重签密密文σ*.如果A1没做过身份的私钥或部分私钥询问,σ*通过解签密验证,则A1赢得定义7中UF-CMA-I.
设A1输出有效的伪造广播多重签密密文
计算:
①
② PPub=ga.
调用预言机H1可以得到h1,输出:
作为离散对数问题实例的解答,原因如下:
⟺
⟺
分析C成功解决离散对数问题的概率,A1没做过IDi的私钥或部分私钥询问的概率为
通过解签密验证的概率为1qUSC,所以C解决离散对数问题的概率为ε′,这里:
2) A2输出有效的伪造广播多重签密密文σ*.如果A2没有做过的私钥询问,同时σ*通过解签密验证,则A2赢得定义7中UF-CMA-II.
设A2输出有效的伪造广播多重签密密文
这里:
① 
②
③ yi=gamod p.
分别调用预言机H2和H4得到h和h4.C输出:
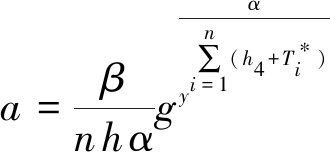
作为离散对数问题实例的应答,因为:
⟺
⟺
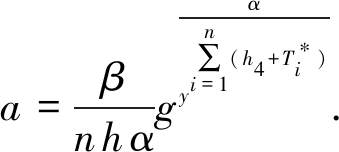
分析C成功解决离散对数问题的概率,A2没有作过私钥询问的概率为1e qSK,σ*通过解签密验证的概率为1qUSC,所以C解决离散对数问题的概率为ε′,这里:
证毕.
4 EBMSC协议的UC安全性分析
4.1 理想函数FEBMSC
理想模型中,EBMSC协议的理想函数FEBMSC、参与方P1,P2,…,Pn及敌手S一起运行,执行过程如下:
① 在收到(KGC,Setup,sid)请求后验证,若验证sid=(KGC,sid′)成功,则将此消息发送给敌手S.
② 在收到敌手S回复的(Setup,Verify,sid,params)后,记录下Verify.
③ 在收到Pi的(Key,sid,Pi)请求后,验证sid=(Pi,sid′),若验证成功,则将此消息发送给敌手S,然后收到敌手S回复的(Pi,sid,yi).
④ 在收到PV的(Key,sid,PV)请求后,验证sid=(PV,sid′),若验证成功,则将此消息发送给敌手S.在收到敌手S回复的yV后,将yV发送给Pi.一旦收到来自Pi的消息(Key,sid,PV),则将此消息发送给敌手S,从敌手S处收到yi时,将yi发送给PV.之后,忽略所有的(Key,sid,PiPV).
⑤ 在收到Pi多重签密者的
请求后,验证sid=(Pi,sid′),若验证不成功,则将忽略发送过来的消息;否则,执行如下:
如果
同时参与方PV是诚实的,则发送(MultiSC,sid,|m|)给敌手S,这里|m|是消息长度;否则,发送(MultiSC,sid,m)给敌手.
当从敌手S处收到σ时,将(MultiSC,sid,m,σ)给PV,并存储(m,σ).
⑥ 在收到接受者PV的(USC,sid,σ,yi)请求后,验证sid=(PV,sid′),若验证不成功,则将忽略发送过来的消息;否则,执行如下:
如果(m,σ)已经记录过,则验证Verify((params,sid,m,σ),f=1),并把(m,f)发给S.
否则,将(USC,sid,σ,yi)发给敌手S,并从敌手S处得到m,并以(m,f=0)的形式发送给PV.
4.2 协议πEBMSC
下面是设计的ElGamal型广播多重签密协议πEBMSC=(Setup,Extract,MultiSC,USC),在UC框架下该协议运行如下:
① 一旦收到(KGC,Setup,sid)消息请求,则验证sid=(KGC,sid′),运行Setup(1k)得到(s,params),返回参数params.
② 收到(U,Key,sid),运行Extract(params,s,ID),得到(xID,yID),然后将(xID,yID)返回.
③ 收到(MultiSC,m,yV,sid)消息请求后,运行MultiSC(params,m,xi,yV)→σ,并将σ返回.
④ 收到(USC,sid,σ),运行USC(params,m,yi,xV),得到消息m,若收到(Verify,sid,m,σ)请求,则运行Verify(params,sid,m,σ)→f,并返回f的值.
4.3 UC框架下协议的安全性证明
定理4. 协议πEBMSC实现了广播多重签密理想函数FEBMSC.
证明. 假设A为现实模型中的敌手.现在构造一个理想敌手S,使得对于任何环境机Z都不能区分是与FEBMSC和S在理想模型下的交互,还是与πEBMSC和A在现实过程中的交互.理想敌手S、环境机Z、敌手A以及参与方P1,P2,…,Pn一起运行.
构造敌手S:在理想过程中,敌手S可以调用A的副本来与FEBMSC和S交互,模拟A在现实过程与协议πEBMSC的交互.首先,敌手S把输出带上的内容写到A的输入带上,并把A输出带的内容拷贝到Z的输出带上.
模拟签密者Pi和接收者PV都不被入侵.当S收到FEBMSC的消息(Setup,sid),运行Setup算法生成公钥yV,并把消息(Verify,v)输出给FEBMSC.当S收到来自FEBMSC的一个消息(MultiSC,sid,m),运行多重签密算法MultiSC,得到签密σ并把(MultiSC,sid,m)输出给FEBMSC.当S收到来自FEBMSC的一个消息(Verify,sid,m,σ,v′)后,运行验证签名算法Verify,得到验证结果f,把(Verify,sid,m,f)输出给FEBMSC.现实环境下签密者对消息进行签密,并将签密结果发送给接收者.接收者验证签密的有效性.理想环境中仿真器S对真实过程进行仿真,仿真签密过程和验证过程,同样发送签密和验证结果,因而,环境机Z不能区分出是FEBMSC与S在理想模型中的交互,还是πEBMSC与A在现实过程中的交互.
模拟签密者Pi被入侵.敌手S模拟A伪装成参与方Pi把(Setup,sid)发送给FEBMSC.同样,当S收到来自FEBMSC的消息(Extract,sid)后.运行密钥生成算法Setup,得到签密者公钥yi并将其返回给FEBMSC.当S收到来自FEBMSC的消息(MultiSC,sid),运行多重签密算法,得到密文并将其返回给FEBMSC.S模拟A入侵参与方Pi,并将(MultiSC,sid,m′)发送给FEBMSC.同样,当S接收到(MultiSC,sid,m′)时,可以得到多重签密σ′,即把(MultiSC,sid,m′,σ′)发送给FEBMSC.由此看来,环境Z并不能区分现实过程和理想模型.
模拟接收者PV被入侵.若参与方PV被收买,敌手S可以模拟参与方的身份把(Verify,sid,m′,σ′,v′)发送给FEBMSC,随后,当S接收到(Verify,sid,m′,σ′,v′)时,计算验证结果f,把(Verify,sid,m′,σ′,v′,f) 发送给FEBMSC.此时,环境机Z不能区分(m,σ)与(m′,σ′).
模拟签密者Pi和接收者PV都被入侵.当多重签密者Pi和解签密者PV都被攻陷时,S将获得双方的所有输入信息,即Z可产生真实的数据来仿真协议的运行.
综合上述4种情形,环境机Z不能区分出是FEBMSC与S在理想模型中的交互,还是πEBMSC与A在现实过程中的交互.即协议πEBMSC能够实现广播多重签密理想函数FEBMSC.
证毕.
定理5. 在UC安全框架下,协议πEBMSC满足选择消息攻击下的不可伪造性.
证明. 假设存在伪造者F,则构造环境机Z和敌手A,使得对于任何敌手A,Z都以不可忽略的概率区分它是与(πEBMSC,A)交互还是与(FEBMSC,S)交互.
构造环境机Z.当收到来自A的多重签密请求时,则Z激活Pi,然后输出多重签密密文σ,并返回给A.当收到来自A的解签密请求时,Z激活Pi,并输出(m,f)给A.
构造敌手A.当A要求对消息m进行多重签密时,敌手A首先要求环境机Z对m进行多重签密,然后把多重签密密文σ给F;当F需要对σ′解签密时,敌手A首先要求环境机Z对σ′进行解签密,然后把(m′,f)返回给A,再发给伪造者F.一旦F收到了m′,并且f=1,则F伪造的多重签密是有效的,此时,Z输出f=1.显然,如果F以可忽略的概率赢得了 定理3中的UF-CMA-I和UF-CMA-II游戏,则F能够成功地伪造出有效的F, 假设伪造者F以可忽略的概率存在,则Z以可忽略的概率输出f=1.而在理想模型中,Z输出f=1的概率总是等于0.换句话说,如果存在这样的伪造者F,Z总以可忽略的概率区分它是与(πEBMSC,A)交互还是与(FEBMSC,S)交互,故与定理5的假设矛盾.所以,不存在这样的伪造者F,也就是说,在UC安全框架下,协议πEBMSC满足选择消息攻击下的不可伪造性.
证毕.
5 性能分析
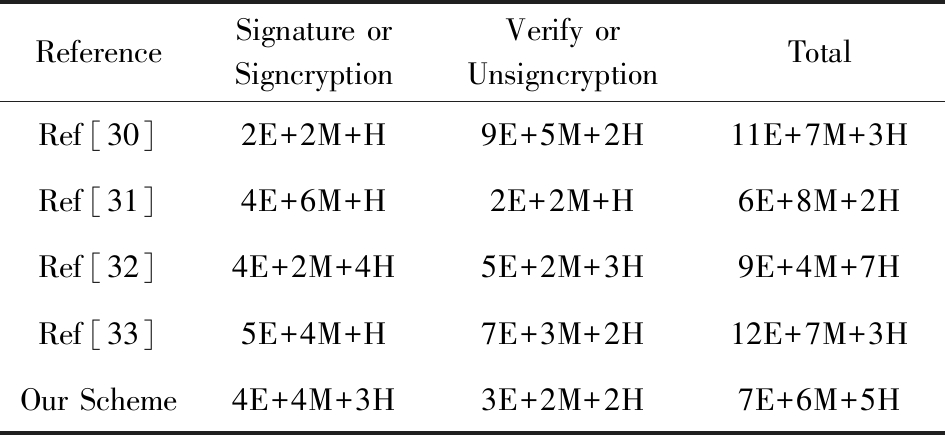
ElGamal型广播多重签密协议的计算开销主要集中在模指数和Hash函数运算.表1中E表示1次模指数运算,H表示1次Hash函数运算,M表示1 次乘法运算.本文方案与文献[30-33]中的方案效率比较如表1所示.从表1中看出,本文分案明显好于文献[30,32-33],并且本文还实现了广播多重签密功能.本文与文献[31]的效率相当, 但文献[31]只实现了多重数字签名,而本文方案不仅实现了多重签密功能,还在UC框架证明了该协议是安全的.
Table 1 Efficiency of this Paper Compared with Others References
表1 本文方案与其他文献的效率比较
ReferenceSignature or SigncryptionVerify or UnsigncryptionTotalRef[30]2E+2M+H9E+5M+2H11E+7M+3HRef[31]4E+6M+H2E+2M+H6E+8M+2HRef[32]4E+2M+4H5E+2M+3H9E+4M+7HRef[33]5E+4M+H7E+3M+2H12E+7M+3HOur Scheme4E+4M+3H3E+2M+2H7E+6M+5H
Notes: E: 1 exponential operation; M: 1 multiplication operation; H: 1 hash operation.
6 总 结
目前设计的ElGamal型广播多重签密协议的安全性一般是基于DL问题的难解性,虽然满足了不可伪造性,但是不具备签名者的身份验证,使得该类协议容易遭受多个签名者的联合攻击.本文设计了一个新的ElGamal型广播多重签密协议,由于本文是采用自认证方式来认证用户的公钥,克服了密钥管理问题以及能够抵抗文献[5-7]的攻击.在随机预言模型中证明了该协议在离散对数和CDH假设下是语义安全的.为了使所提协议适应更加复杂的网络环境,本文引入UC安全技术,而在UC安全框架下分析了该协议的安全性.我们定义了ElGamal型广播多重签密协议的理想函数FEBMSC,进而证明了UC安全的ElGamal型广播多重签密协议的通用可组合安全性.下一步将对集合相交协议进行研究.
[1]Itakura K, Nakamura K. A public-key cryptosystem suitable for digital multi-signatures[J]. NEC Research & Development, 1983,71(1): 474-480
[2]Zhang Jianhong, Wei Yongzhuang, Wang Yumin. Digital multisignatrues scheme based on RSA[J]. Journal on Communications, 2003, 24(8): 150-154 (in Chinese)(张键红, 韦永壮, 王育民. 基于RSA的多重数字签名[J]. 通信学报, 2003, 24(8): 150-154)
[3]Li Zichen, Yang Yixian. ELGamal’s multisignature digital signature scheme[J]. Journal of Beijing University of Posts and Telecommunications, 1999, 22(2): 30-34 (in Chinese)(李子臣, 杨义先. ElGamal多重数字签名方案[J]. 北京邮电大学学报, 1999, 22(2): 30-34)
[4]Burmester M, Desmedt Y, Doi H, et al. A structured ELGamal-Type multisignature scheme[G] //LNCS 1751: Proc of the 3rd Int Workshop on Practice and Theory in Public Key Cryptography. Berlin: Springer, 2000: 466-483
[5]Zhang Qiupu, Ye Dingfeng. Cryptanalysis and improvemen of an identity-based multi-signcryption scheme[J]. Acta Electronica Sinica, 2011, 39(12): 2713-2720 (in Chinese)(张秋璞, 叶顶峰. 对一个基于身份的多重签密方案的分析和改进[J]. 电子学报, 2011, 39(12): 2713-2720)
[6]Lu Langru, Zeng Junjie, Kuang Youhua, et al. A new multisignature scheme based on discrete logarithm problem and its distributed computation[J]. Chinese Journal of Computers, 2002, 25(12): 1419-1420 (in Chinese)(陆浪如, 曾俊杰, 匡友华, 等. 一种新的基于离散对数多重签名方案及其分布式计算[J]. 计算机学报, 2002, 25(12): 1419-1420)
[7]Han Xiaoxi, Wang Guilin, Bao Feng, et al. An attack to multisignature schemes based on discrete logarithm[J]. Chinese Journal of Computers, 2004, 27(8): 1147-1152 (in Chinese)(韩小西, 王贵林, 鲍丰, 等. 针对基于离散对数多重签名方案的一种攻击[J]. 计算机学报, 2004, 27(8): 1147-1152)
[8]Harn L. New digital signature scheme based on discrete logarithm[J]. Electronics Letters, 1994, 30(5): 396-398
[9]Wu Tzongchen, Chou Shulin, Wu Tzongsun. Two ID-based multi-signature protocols for sequential and broadcasting architectures[J]. Computer Communications, 1996, 19(9
10): 851-856
[10]Zheng Yuliang. Digital signcryption or how to achieve cost (signature and encryption) cost (signature)+cost (encryption)[C] //LNCS 1294: Proc of the 17th Annual Int Cryptology Conf. Berlin: Springer, 1997: 165-179
[11]Baek J, Steinfeld R, Zheng Yuliang. Formal proofs for the security of Signcryption[C] //LNCS 2274: Proc of the 5th Int Workshop on Practice and Theory in Public Key Cryptosystems. Berlin: Springer, 2002: 80-98
[12]Fan Jia, Zheng Yuliang, Tang Xiaohu. A single key pair is adequate for the Zheng signcryption[C] //LNCS 6812: Proc of the 16th Australasian Conf on Information Security and Privacy. Berlin: Springer, 2011: 371-388
[13]Zhou Kai, Peng Changgen, He Jianqiong, et al. Provable secure trajectory privacy protection scheme for continuous queries in location-based services[J]. Netinfo Security, 2017, 17(1): 43-47 (in Chinese)(周凯, 彭长根, 何建琼, 等. 可证明安全的LBS中连续查询的轨迹隐私保护方案[J]. 信息网络安全, 2017, 17(1): 43-47)
[14]Yu Huifang, Yang Bo. Identity-based hybird signcryption scheme using ECC[J]. Journal of Software, 2015, 26(12): 3174-3182 (in Chinese)(俞惠芳, 杨波. 使用ECC的身份混合签密方案[J]. 软件学报, 2015, 26(12): 3174-3182)
[15]Zhou Yanwei, Yang Bo, Wang Qinglong. Provable secure leakage-resilient certificateless hybird signcryption scheme[J]. Journal of Software, 2016, 27(11): 2898-2911 (in Chinese) (周彦伟, 杨波, 王青龙. 可证明安全的抗泄露无证书混合签密机制[J]. 软件学报, 2016, 27(11): 2898-2911)
[16]Shi Min, Ye Weiwei, Ou Qingyu. Identity-based authenticated protocol without bilinear pairing[J]. Netinfo Security, 2016, 16(10): 21-27 (in Chinese)(矢敏，叶伟伟，欧庆于. 不需双线性对的基于身份的认证密钥协商协议[J]. 信息网络安全, 2016(10): 21-27)
[17]Li Jianmin, Yu Huifang, Zhao Chen. Self-certified blind signcryption protocol with UC security[J]. Journal of Frontiers of Computer Science and Technology, 2017, 11(6): 932-940 (in Chinese)(李建民, 俞惠芳, 赵晨. UC安全的自认证盲签密协议[J]. 计算机科学与探索, 2017, 11(6): 932-940)
[18]Yu Huifang, Yang Bo. Provably secure certificateless hybrid signcryption[J]. Chinese Journal of Computers, 2015, 37(4): 804-813 (in Chinese)(俞惠芳, 杨波. 可证安全的无证书混合签密[J]. 计算机学报, 2015, 37(4): 804-813)
[19]Yu Huifang, Yang Bo. Low-computation certificateless hybrid signcryption scheme[J]. Frontiers of Information Technology Electric Engineering, 2017, 18(7): 928-940
[20]Zhou Caixue. Cryptanalysis and improvement of some signcryption scheme[J]. Computer Engineering and Science, 2016, 38(11): 2246-2253 (in Chinese)(周才学. 几个签密方案的密码学分析与改进[J]. 计算机工程与科学, 2016, 38(11): 2246-2253)
[21]Canetti R. Universally composable security: A new paradigm for cryptographic protocols[C] //Proc of the 42nd IEEE Symp on Foundation of Computer Science. Los Alamitos, CA: IEEE Computer Society, 2001: 136-145
[22]Canetti R, Lindaell Y, Ostrovky R, et al. Universally compusable two-party and multi-party secure computation[C] //Proc of the 34th Annual ACM Symp on Theory of Computing. New York: ACM, 2003: 219-233
[23]Kristian G, Lillian K. Universally composable signcryption[C] //LNCS 4582: EuroPKI 2007. Berlin: Springer, 2007: 346-353
[24]Canetti R, Dachman D, Vaikuntanathan V, et al. Efficient password authenticated key exchange via oblivious transfer[C] //LNCS 7293: Proc of the 15th Int Conf on Practice and Theory in Public Key Cryptograhy. Berlin: Springer, 2012: 449-466
[25]Feng Tao, Li Fenghua, Ma Jianfeng, et al. A new method for concurrent deniable authentication of UC Security[J]. Science in China Series F: Informations Sciences, 2008, 38(8): 1220-1233 (in Chinese)(冯涛, 李风华, 马建峰, 等. UC安全的并行可否认认证新方法[J]. 中国科学F辑: 信息科学, 2008, 38(8): 1220-1233)
[26]Su Ting, Xu Qiuliang. UC secure signcryption protocol with public verifiability[J]. Journal of Southeast University: Natural Science Edition, 2008, 38(Suppl): 55-58 (in Chinese)(苏婷, 徐秋亮. 可证明安全的UC安全签密协议[J]. 东南大学学报: 自然科学, 2008, 38(增刊): 55-58)
[27]Zhang Zhong, Xu Qiuliang. Universal composable grouping-proof protocol for RFID tags in the Internet of things[J]. Chinese Journal of Computers, 2011, 34(7): 1188-1194 (in Chinese)(张忠, 徐秋亮. 物联网环境下UC安全的组证明RFID协议[J]. 计算机学报, 2011, 34(7): 1188-1194)
[28]Tian Youliang, Ma Jianfeng, Peng Changgen, et al. Universally composable mechanism for group communication[J]. Chinese Journal of Computers, 2012, 35(4): 645-653 (in Chinese)(田有亮, 马建峰, 彭长根, 等. 群组通信的通用可组合机制[J]. 计算机学报, 2012, 35(4): 645-653)
[29]Tian Youliang, Peng Changgen, Ma Jianfeng, et al. Universally composable secure multiparty computation protocol with fairness[J]. Journal on Communications, 2014, 35(7): 54-62 (in Chinese)(田友亮, 彭长根, 马建峰, 等. 通用可组合公平安全多方计算协议[J]. 通信学报, 2014, 35(7): 54-62)
[30]Zhang Xinghua. A new multi-proxy multi-signature scheme based on discrete logarithm problem[J]. Computer Applica-tions and Software, 2014, 31(2): 317-320 (in Chinese)(张兴华. 一个新的基于离散对数问题的多重代理多重签名方案[J]. 计算机应用与软件, 2014, 31(2): 317-320)
[31]Cao Yang. ElGamal multiple digital signature scheme based on identity[J]. Bulletin of Science and Technology, 2015, 31(5): 197-199 (in Chinese)(曹阳. 基于身份的ElGamal多重数字签名方案[J]. 科技通报, 2015, 31(5): 197-199)
[32]Wang Caifen, Jianghong, Yang Xiaodong, et al. Multi-message and multi-receiver hybrid signcryption scheme based on discrete logarithm[J]. Computer Engineering, 2016, 42(1): 150-155 (in Chinese)(王彩芬, 姜红, 杨小东, 等. 基于离散对数的多消息接收者混合签密方案[J]. 计算机工程, 2016, 42(1): 150-155)
[33]Hu Jianghong. A certificateless broadcasting multi-proxy signature scheme based on RSA[J]. Computer and Modernization, 2016(6): 113-116 (in Chinese)(胡江红. 基于RSA的无证书广播多重代理签名方案[J]. 计算机与现代化, 2016(6): 113-116)
