随着Twitter、Facebook、微博等社交应用的兴起,社交网络已成为信息传播的重要媒介,许多公司也开始将其作为广告推广和产品营销的主要工具.与传统大众营销方式不同,作为数字广告领域中发展最快的行业,社交广告不仅关注消费者的固有价值,还注重其在信息传播中的作用.在现实世界中,人们对于是否购买一种产品或接受一种想法多受其朋友、同事或同龄人的影响.因此一些公司会采用免费试用或利益回报的方式在整个网络中寻找意见领袖,即寻找最具影响力的种子,以便通过这些种子个体的社交影响力来扩大产品或广告的影响范围,从而获得更大收益.这种基于“口碑”[1]的营销方式,利用成员间推介的“级联”效应使产品的潜在客户不断增多.与影响力最大化(influence maximization, IM)问题[2-3]类似,社交广告要解决的问题是,在特定传播模型下,找到k个最具影响力的节点集合,从而最大化产品或广告的影响范围.近年来,病毒营销[4]中的影响力最大化问题被广泛研究,但由于所用数据集的限制,大多数现有研究成果只能用于分析用户在虚拟世界中的行为,而忽略了位置信息的作用.幸运的是,随着无线通信设备和定位技术的发展,人们可以通过网络随时分享位置和想法,由此产生了海量的时空数据,从而使得在传统社交网络中加入空间这一维度成为可能.
举个例子,许多现实世界中的营销活动都增加了对营销位置[5-6]这一因素的考量,比如,图1解释了与营销位置有关的用户进行信息传播的过程,其中u1和u2分别代表2个传播种子,他们可以继续向自己的下层传播,如黑线所示.当营销活动主办方在位置V进行营销活动时,距离V较近的用户(如图1中的u1),相比距离V较远的用户(如图1中的u2),往往更有可能成为营销活动的成功推广者或参与者,因为较近的距离是影响决策的重要因素之一.此时,距离营销位置不同的用户应给予不同权重的考虑.类似地,在信息传播过程中,与u1距离较近的朋友(圆圈所示),因同处于营销位置附近而更可能受其影响成为潜在顾客.进一步而言,用户间的影响概率也应根据二者间的物理距离进行动态推演,但遗憾的是,现有IM模型由于未考虑空间位置信息,因此不能直接用于解决该问题.
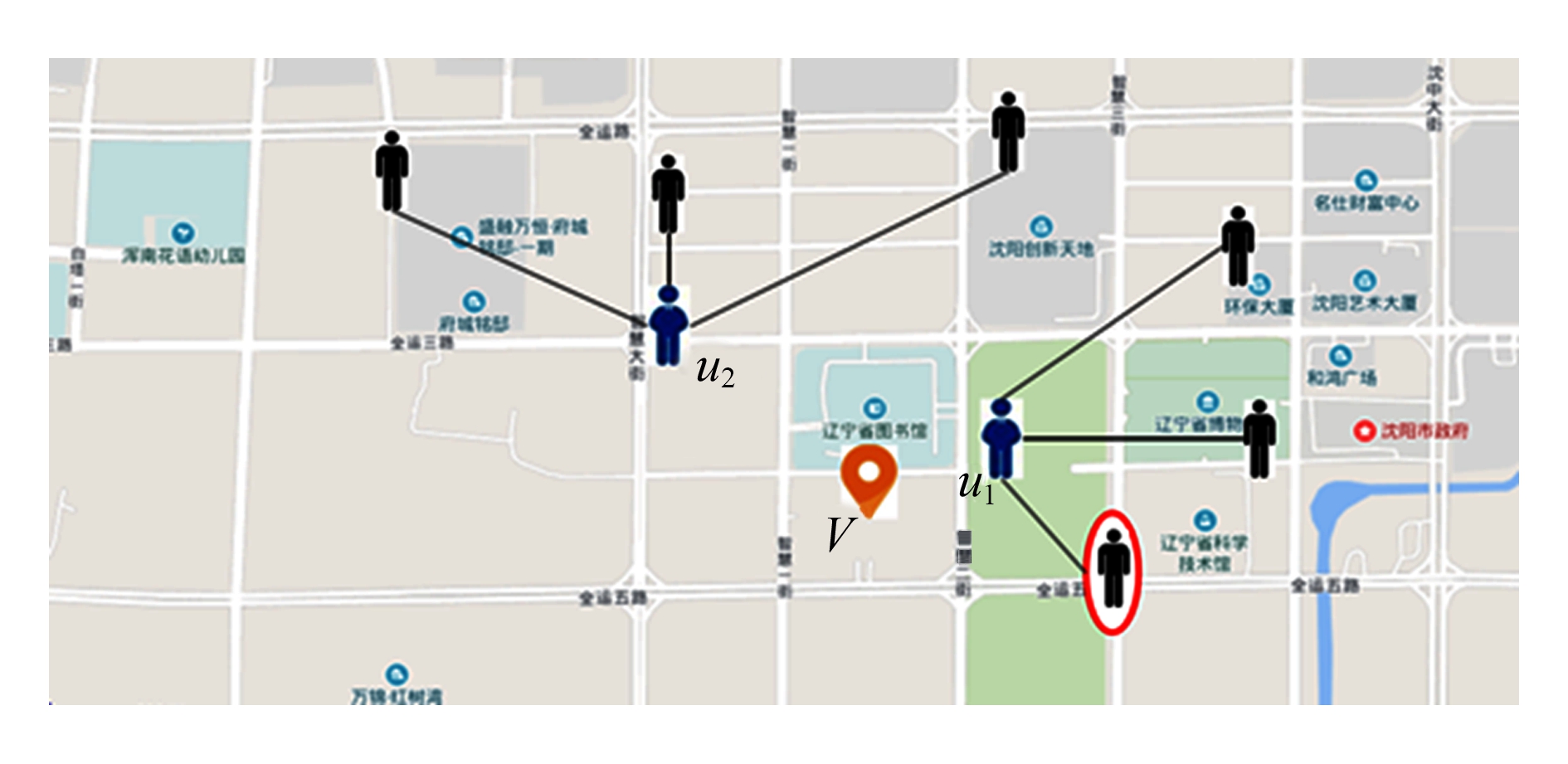
Fig. 1 Location-aware promotion
图1 考虑位置信息的营销活动示意图
基于上述问题,本文首先提出一种位置敏感独立级联模型(distance-aware independent cascade, DAIC),并基于该模型对地理社交网络中的影响力最大化(location-aware influence maximization, LAIM)问题进行了重新定义,进而提出一种在贪婪框架下的位置敏感影响力最大化算法LA_Greedy(location-aware greedy).
值得注意的是,大多数IM问题的研究工作是在“忽略竞争”情况下展开[7-9],即假定1家公司可以在网络中独立于其他公司进行种子挑选,但实际上几家公司常常在同一市场相互竞争(例如宝马、奔驰、奥迪在汽车市场中的竞争),并在同一网络挑选种子,由此,针对竞争网络的影响力最大化问题得到了广泛关注与研究[10-11].虽说如此,研究者们在解决竞争环境下的IM问题时,做出了许多不切实际的假设[12-13],比如1家公司可以在知道竞争对手的种子挑选结果后再做出最有利本公司的选择.然而在现实世界中,公司的营销策略和种子选择结果都是重要的商业秘密,不可能轻易地被他人获知.因此,同一领域的2家公司常常要在无任何辅助信息情况下完成种子挑选工作,这往往会导致种子重叠现象[14],使得一些种子个体不能实现预期的传播范围,从而造成影响力的损失[15].
考虑图2(a)中的无竞争网络,为了扩大新款车型的影响,假定公司甲选择节点A和节点B作为初始推广者,期待利用A和B的个人影响扩大该款汽车的市场影响力,进而得到更多消费者青睐,并最终可以影响到7人.在图2(b)所示的竞争网络中,假设甲公司竞争对手即乙公司,也要推出一款新车型,在无法获知竞争对手甲公司的选择结果下,同样可将节点A和节点B作为推销甲公司的车的初始推广者,继而在信息传播过程中,二级推广者C将受到A和B的共同影响.但由于受到现有广告传播机制的限制,C往往只会选择一款汽车进行推荐,因为公司只与初始推广者(即种子个体)存在利益交互(如免费试用或根据最终影响范围给予一定利益回报),二级推广者C仅仅靠与种子个体之间的往来关系决定是否继续进行推荐.因此相对自由的二级推广者在做推荐选择时会受到更多因素的影响(如对重叠种子的信任程度,甚至可能直接被其他竞争公司选为其产品或广告的推广者).
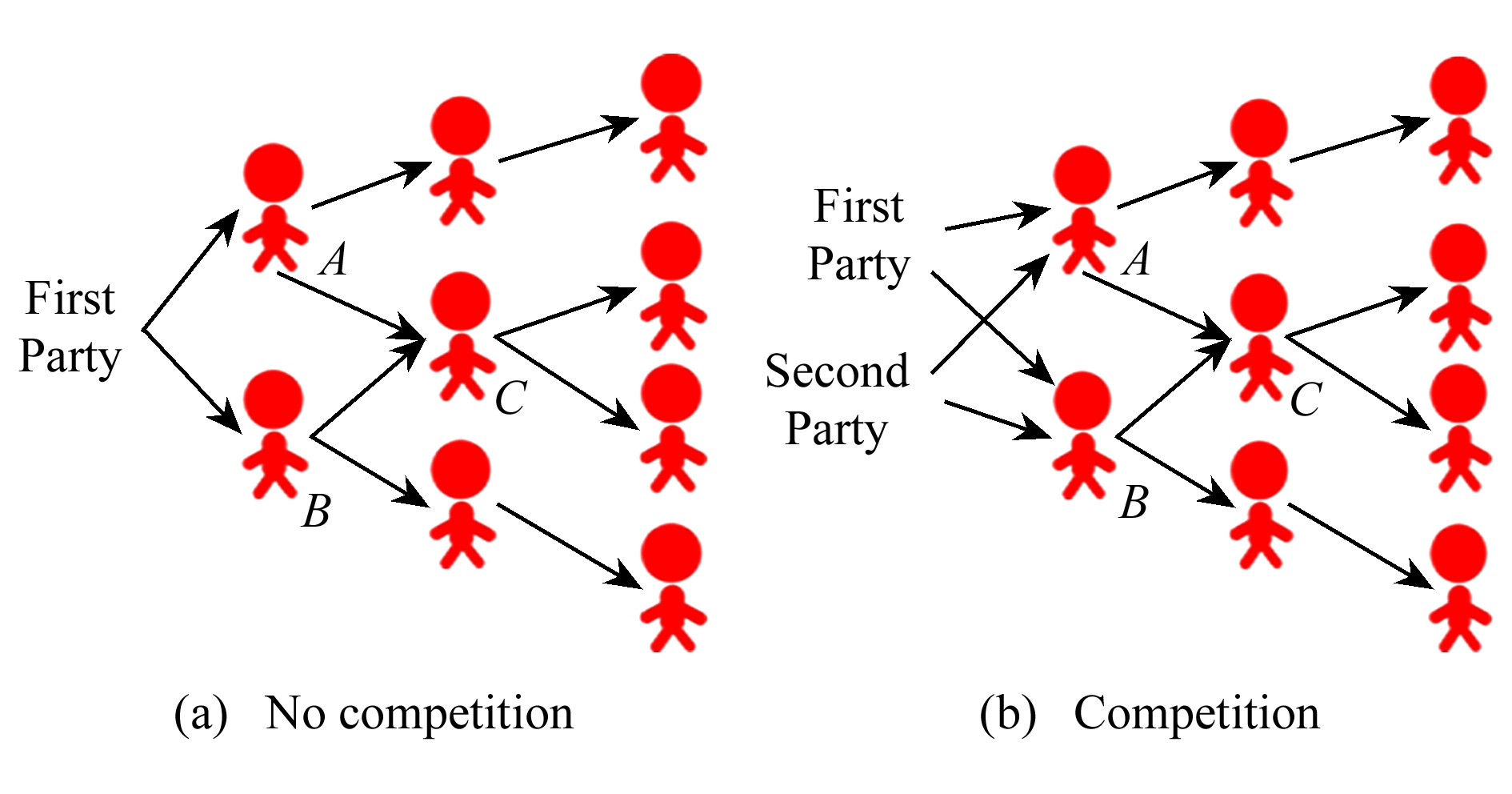
Fig. 2 Information propagation in social network
图2 社交网络信息传播示意图
综上所述,无论是重叠种子个体(overlapping seeds)A与B的出现,还是二级推广者C不确定的选择结果,都会使同一网络中相互竞争的2家公司不能达到预期的影响力传播范围.同样地,作为被公司寄予厚望的种子个体也会因其推广效果不佳而受到相应损失.为解决该问题,本文通过分析重叠种子与其邻居节点的支付矩阵,首次为重叠种子个体提供了选择公司的博弈决策机制,使重叠种子在博弈中找到纳什均衡点,进而决策出将为其推销产品的最佳公司,相应地,该博弈决策机制也降低了种子集合的重叠率和影响力的损失.
综上所述,本文主要贡献有3个方面:
1) 提出了一种距离敏感独立级联模型DAIC,该模型将用户间物理距离引入独立级联模型(independent cascade, IC)中,量化了距离因素对传播概率的影响,解决了地理社交网络中用户间影响力概率的动态推演问题.
2) 提出了一种贪婪框架下位置敏感影响力最大化算法LA_Greedy,该算法基于DAIC模型将营销物理位置引入影响力最大化(IM)的定义中,解决了传统IM由于未考虑位置信息所导致的影响力传播范围与实际可用范围间的距离偏差问题.
3) 提出了一种面向重叠种子的竞争博弈决策机制(game decision-making mechanism, GDMM),该机制首次立足广告重叠种子角度,通过分析重叠种子与其邻居节点的支付矩阵,对竞争选择进行决策博弈,最终找到纳什均衡点,从而降低了种子重叠率和影响力损失.
1 基于DAIC模型的IM问题
本节首先介绍距离敏感独立级联模型DAIC,然后基于该模型重新定义了地理社交网络中的影响力最大化问题.为清楚起见,表1给出了本文用到的一些符号及其含义:
Table 1 Notation of Symbols
表1 符号及含义
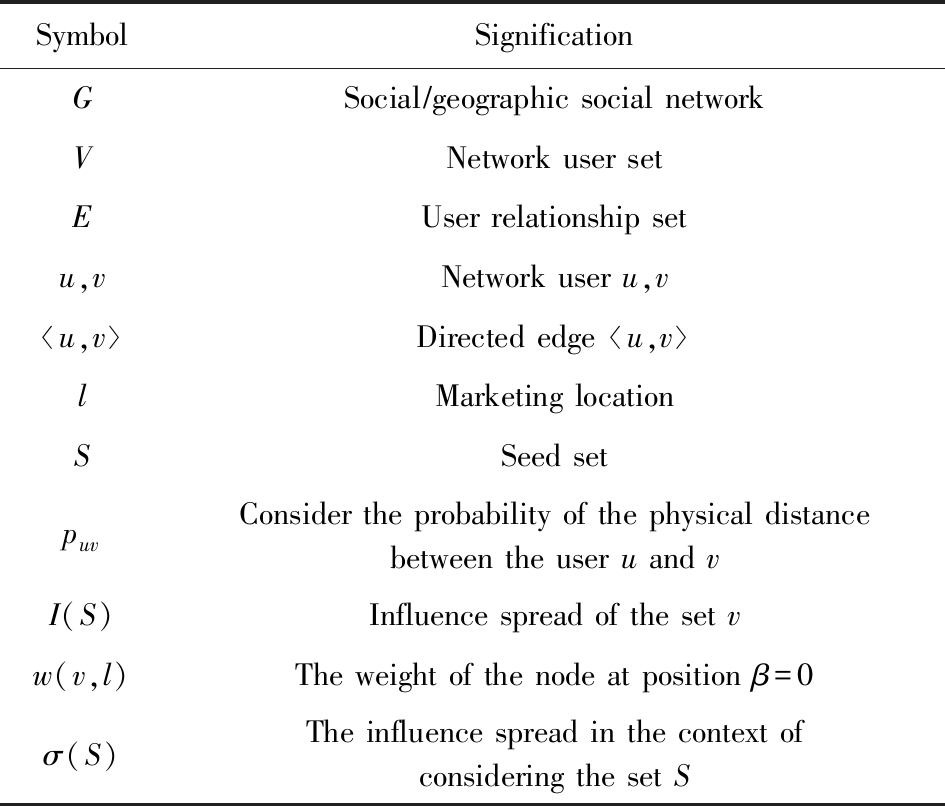
SymbolSignificationGSocial∕geographic social networkVNetwork user setEUser relationship setu,vNetwork user u,vu,vDirected edge u,vlMarketing locationSSeed setpuvConsider the probability of the physical distancebetween the user u and vI(S)Influence spread of the set vw(v,l)The weight of the node at position β=0σ(S)The influence spread in the context ofconsidering the set S
1.1 距离敏感独立级联模型DAIC
网络用户间影响概率的大小是决定传播范围的关键因素之一,同一节点其传播能力在不同的影响概率下具有很大差异.在IC模型中,用户间的影响概率通常被随机指定,但在携带位置信息的地理社交网的营销活动中,用户间影响概率还会受到彼此间物理距离的作用,因此,不能直接套用IC模型对影响概率值的随机指派方法.基于此,本文提出一种距离敏感独立级联模型DAIC,旨在有效量化位置距离对传播概率的影响.直观地,当用户u要在位置lu进行产品推荐时,在其朋友中,与之距离较近的用户会因同处于营销位置附近而更可能被影响,从而成为潜在顾客,因此有理由认为,u对邻居v的影响力会随着彼此间物理距离的增加而减弱,即用户间位置距离与影响概率成反比.下面,对用户间影响概率的理论计算推演过程做详细阐述.
不失一般性,假定地理社交网络中u对v的影响概率为puv,u的地理位置为lu,pu→v(l,lu)表示当用户v处在位置l时u对v的影响概率,简写为p(l).令dl>0表示一个极小的距离增量,则当用户v处在位置l+dl时,u对v的影响概率为p(l+dl),影响概率的改变量则为dp=p(l+dl)-p(l).如前所述,节点u对v的影响力会随着距离的增加而减弱,于是有dp=p(l+dl)-p(l)<0,表示对应于距离增量dl的影响概率损失.与放射性衰变[16-17]类似(微粒越大,衰变越快),理论上, dp正比于p(l):
![]() ∝p(l).
∝p(l).
(1)
等式形式:
![]()
(2)
其中,负号表示p(l)随着距离的增加而减小,比例常数为τ,整理式(2),得:
![]()
(3)
整理式(3),得:
![]()
(4)
将式(4)两边同时积分,得:
(5)
整理式(5),得:
![]()
(6)
整理式(6),得:
![]()
(7)
其中,c为积分常数,整理式(7),得:
![]()
(8)
令l(u)=0,则在式(8)中,Δ=l-lu=l(在二维空间中Δ表示l与lu之间的欧氏距离),即式(8)从理论上证明了u对v的影响概率随着距离的增加呈指数衰减.通过简化,定义用户间位置敏感的影响概率计算公式为
puv=e-α l.
(9)
与IC模型类似,DAIC模型的信息传播过程如下:给定初始活跃集合A,当不活跃节点u在时间步t变为活跃状态后,该节点将尝试激活每个处在不活跃状态的邻居.但无论激活结果如何,在以后的时间步中,u都不会再对其邻居产生任何影响.若成功,则邻居节点v在时间步t+1变为活跃状态.当节点v有多个邻居节点变为活跃状态时,这些节点可以按任意顺序尝试激活v.当不再存在激活可能时,传播过程结束.
1.2 基于DAIC模型的影响力最大化问题
在社交网络研究中,通常将有向图G(V,E)作为抽象研究对象,其中V为节点的集合,E为边的集合.
定义1. 影响力传播范围.给定一个网络G(V,E)和一个集合S⊂V,集合S的影响力传播范围I(S)代表S最终影响的人数,也可通过![]() 进行计算.
进行计算.
定义2. 位置敏感影响力传播范围.给定一个地理社交网络G(V,E)和一个营销位置l,以及集合S⊂V.考虑位置的影响力传播范围
其中,w(v,l)表示节点v对应营销位置l的权值.
如上所述,营销位置附近的用户应该具有更高的权值,即w(v,l)与v和l间的距离成反比.为了简化,本文令w(v,l)=ce-β d(v,l),其中c>0表示节点能够达到的最大权值,d(v,l)为节点v与营销位置l间的欧氏距离,β>0为衰减速率.
问题1. 影响力最大化(IM)问题. 给定一个社交网络G(V,E)和种子个数k,求一个节点集合S⊂V,|S|=k,使得以S作为初始种子集合时,在特定信息传播模型下具有最大的影响力传播范围,即对于任意大小为k的节点集合S′,I(S)≥I(S′),集合S为
![]()
(10)
问题2. 位置敏感影响力最大化(LAIM)问题. 给定一个地理社交网络G(V,E)、营销位置l及种子个数k,要求找到一个节点集合S⊂V,|S|=k,使得以S作为初始种子集合在DAIC模型上进行影响力最大化传播时,其位置敏感的影响力传播范围σ(S)最大,即对于任意大小为k的节点集合S′,σ(S)≥σ(S′),集合S为
![]()
(11)
2 位置敏感影响力最大化算法LA_Greedy
算法1. LA_Greedy算法.
输入:地理社交网络G、种子集合大小k、营销位置l;
输出:种子集合S.
① Off-line compute puv for  u,v
u,v ∈E;
∈E;  *计算每对用户间影响概率puv*
*计算每对用户间影响概率puv*
② compute w(v,l) for v∈V;  *为用户分配不同权值*
*为用户分配不同权值*
③ S←∅;  *给定种子集合S,初始为空*
*给定种子集合S,初始为空*
④ for i=1 to k do  *根据种子个数k进行循环计算*
*根据种子个数k进行循环计算*
⑤ u![]()
 *获得最大边际收益节点u*
*获得最大边际收益节点u*
⑥ S←S∪{u};  *将u加入种子集合S*
*将u加入种子集合S*
⑦ end for
⑧ return S.
在位置敏感影响力最大化问题LAIM中,当权值函数w(v,l)=ce-β d(v,l)的参数c=1,β=0时,网络中所有节点的权值都变为与位置无关的常量1,这时LAIM就等价于IM,因此,LAIM问题是NP-难的[19].类似地,可以证明计算位置敏感的影响力传播范围也是一个NP-难问题[20].基于影响力传播函数的性质,本文提出一种贪婪框架下位置敏感影响力最大化算法LA_Greedy,算法1给出了其详细步骤.
步骤1. 以网络个体间的位置距离为输入,利用式(9)计算每对用户u和v间的影响概率puv;
步骤2. 根据网络中各用户v与特定营销推广位置l之间的距离,为用户分配不同的权值,即w(v,l)=ce-β d(v,l).
步骤3. 给定种子集合S,初始为空,根据种子个数k进行循环运算.
步骤4. 基于目标函数σ(S),在每次迭代过程中,将具有最大边际收益的节点u加入到集合S中.
步骤5. 循环结束,将集合S作为初始种子集合返回.
3 重叠种子个体的博弈决策机制GDMM
现实世界同一领域中不可避免的竞争往往引发种子重叠现象,导致一些种子个体不能实现预期的传播范围,造成影响力损失.通过分析重叠种子与其邻居节点的支付矩阵,本文首次为重叠种子个体制定选择公司的博弈决策机制GDMM,使其在博弈中找到纳什均衡点并作出最佳公司选择决策.GDMM博弈过程如下.
根据重叠种子个体和二级推广者做出不同决策时的利益得失情况,分别给出双方的支付矩阵SSeed与NNeighbor:
![]()
(12)
NNeighbor=![]()
(13)
其中,γk∈[0,1](k=1,2,…,8)为博弈分析的参数因子,主要取决个体间的信任程度,可以根据具体要求进行调整.
![]() 表示种子个体选择A公司,邻居节点也受其影响为A推荐产品或传播广告时,种子从A公司获得的收益(如免费试用新品或得到约定的回报).
表示种子个体选择A公司,邻居节点也受其影响为A推荐产品或传播广告时,种子从A公司获得的收益(如免费试用新品或得到约定的回报).
![]() 表示种子个体选择A公司,邻居节点受其他因素影响转而为B推荐产品或传播广告时,种子个体遭受的损失(如未达到预期影响范围阻碍了与A公司日后的合作,从而造成一定的经济损失).
表示种子个体选择A公司,邻居节点受其他因素影响转而为B推荐产品或传播广告时,种子个体遭受的损失(如未达到预期影响范围阻碍了与A公司日后的合作,从而造成一定的经济损失).
![]() 表示种子个体选择B公司,邻居节点受其他因素影响转而为A推荐产品或传播广告时,种子个体遭受的损失(如未达到预期影响范围阻碍了与B公司日后的合作,从而造成一定的经济损失).
表示种子个体选择B公司,邻居节点受其他因素影响转而为A推荐产品或传播广告时,种子个体遭受的损失(如未达到预期影响范围阻碍了与B公司日后的合作,从而造成一定的经济损失).
![]() 表示种子个体选择B公司,邻居节点也受其影响为B推荐产品或传播广告时,种子从B公司获得的收益(如免费试用新品或得到约定的回报).
表示种子个体选择B公司,邻居节点也受其影响为B推荐产品或传播广告时,种子从B公司获得的收益(如免费试用新品或得到约定的回报).
![]() 表示种子个体选择A公司,邻居节点(二级推广者)受其他因素影响或直接被竞争公司选中为B推荐产品或传播广告时,二级推广者获得的收益.
表示种子个体选择A公司,邻居节点(二级推广者)受其他因素影响或直接被竞争公司选中为B推荐产品或传播广告时,二级推广者获得的收益.
![]() 表示种子个体选择B公司,邻居节点(二级推广者)受其他因素影响或直接被竞争公司选中为A推荐产品或传播广告时,二级推广者获得的收益.
表示种子个体选择B公司,邻居节点(二级推广者)受其他因素影响或直接被竞争公司选中为A推荐产品或传播广告时,二级推广者获得的收益.
![]() 表示种子个体选择A公司,邻居节点(二级推广者)受其他因素影响转而为B推荐产品或传播广告时,二级传播者受到的损失.(由于公司只与种子存在利益关系,故该损失是对2个体间信任缺失的量化).
表示种子个体选择A公司,邻居节点(二级推广者)受其他因素影响转而为B推荐产品或传播广告时,二级传播者受到的损失.(由于公司只与种子存在利益关系,故该损失是对2个体间信任缺失的量化).
![]() 表示种子个体选择B公司,邻居节点(二级推广者)受其他因素影响转而为A推荐产品或传播广告时,二级传播者受到的损失.(由于公司只与种子存在利益关系,故该损失是对2个体间信任缺失的量化).
表示种子个体选择B公司,邻居节点(二级推广者)受其他因素影响转而为A推荐产品或传播广告时,二级传播者受到的损失.(由于公司只与种子存在利益关系,故该损失是对2个体间信任缺失的量化).
为计算方便,对Neighbor在原支付矩阵的基础上进行了转置.通过简单的画线法可以得出该博弈模型不存在纯策略均衡,但可求出混合策略的纳什均衡.假定重叠种子个体以概率x选择A公司,以概率1-x选择B公司,即重叠种子个体的混合策略为PSeed=(x,1-x);二级推广者以概率y选择A公司,以概率1-y选择B公司,即二级推广者的混合策略为PNeighbor=(y,1-y).则重叠种子个体的预期支付函数为
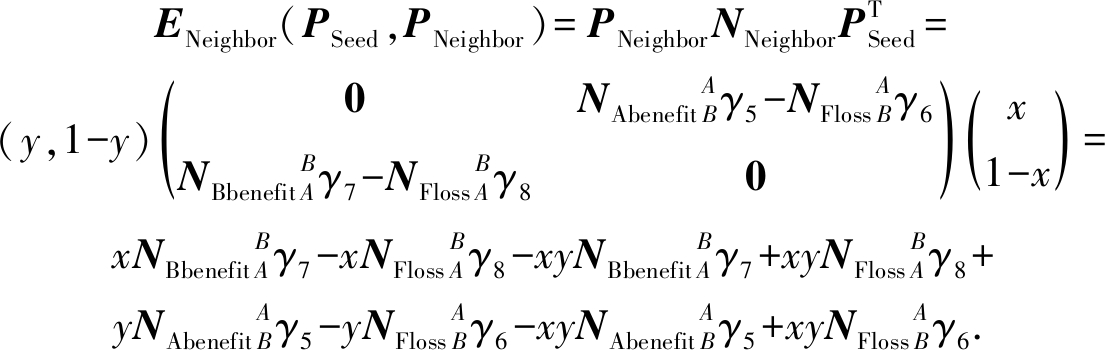
(14)
对式(14)关于y求偏导,可得重叠种子个体最优化一阶条件:

解得x:
即在博弈过程中,重叠种子个体选择公司的最佳混合策略为PSeed=(x,1-x).可以看出,重叠种子个体选择A公司的概率x与其邻居节点被A公司选中时获得的收益有关,邻居节点从A公司获得的收益越多,重叠种子选择A公司的概率越大;反之,则更倾向于选择B公司.
4 实验数据集与性能测试
4.1 实验数据与测试环境
为验证所提算法和策略的有效性,利用Twitter官方提供的API接口采集了2016年10月内1周的数据.经过清洗得到有效节点6 046个、节点间关系数据14 487条.由于所采数据的用户地理位置比较紧密(各节点距中心位置的平均距离约为72.99 km).为了检测所提算法在不同类型测试集上的效果,又模拟了具有12 000个节点、28 320条边的位置较为疏远(各节点距中心位置的平均距离约为341.03 km)的数据集,具体情况如表2所示.
在实验中,采用Java语言编程,CPU为Intel Core i5-4590 3.3 GHz,内存为8 GB,操作系统为Windows 7.
Table 2 Experimental Data Set
表2 实验数据集

DataTypeNodeNumberNumber ofRelationshipsBetween NodesAverage Distance ofthe Node from theCenter Position∕kmTwitter60461447872.99Analog Data1200028320341.03
4.2 参数设置
实验中,营销位置l与各节点的公司选择通过随机指定.设用户间影响概率计算公式n=|V|的参数α为经验值0.02,权值函数w(v,l)=ce-β d(v,l)中c=10,β=0.02.通常每个重叠种子个体对应多个邻居,故在博弈分析中将邻居得失的均值作为支付函数参数,γk∈[0,1](k=1,2,…,8)暂设为1.
4.3 实验结果与性能分析
为体现社交网用户之间关系紧密程度,本文用网络聚类系数来评测,Cv表示节点聚类系数,CG表示网络聚类系数,具体计算:
![]()
(15)
其中,|Ev|表示网络用户v的邻居节点间的实际连接数,kv为用户v的邻居个数.
(16)
其中,V={v1,v2,…,vn}表示网络G中的所有个体集合,n=|V|为个体数目.
通过计算发现,与具有相同节点数和边数的一个完全随机化网络相比,采集的Twitter数据所构建的社交网有着明显较高聚类系数,说明Twitter网用户间关系比较紧密,有利于信息传播.
为验证GDMM策略对重叠种子在进行公司选择时的指导效果,分别针对真实Twitter数据以及模拟数据,在DAIC与IC 这2种传播模型下对种子集合的重叠率进行了测试(此处将Greedy与LA_Greedy算法分别作为A和B这2家公司挑选种子时所用的策略予以指定),实验结果分别如图3和图4所示,其中,横坐标代表种子个数k,纵坐标代表种子集合的重叠率.从图3和图4中可以看出,尽管随着k的增大,2家公司的种子集合的重叠率都呈变大趋势,但相比于没有使用纳什平衡的方法,GDMM策略却可以明显降低种子集合的重叠率,从而更好地保证传播效果.
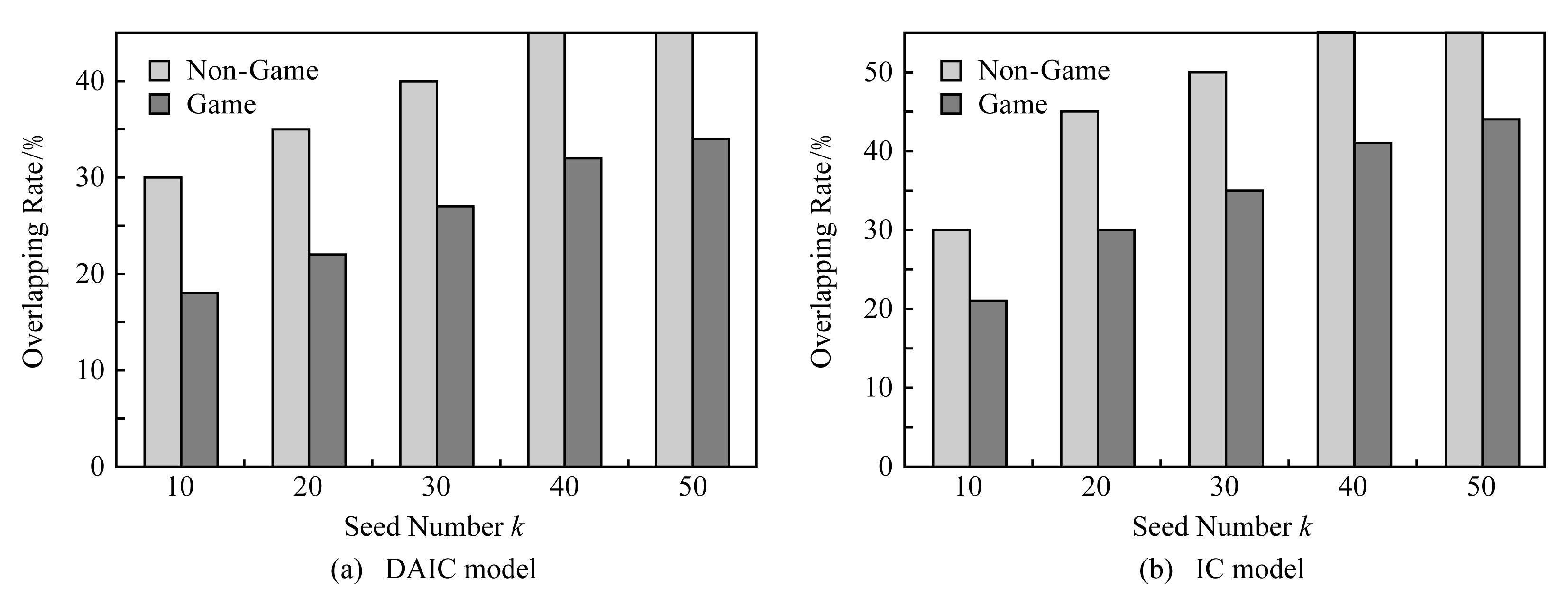
Fig. 3 Overlapping rate of Twitter data based on different models
图3 Twitter数据在不同传播模型下的种子重叠率
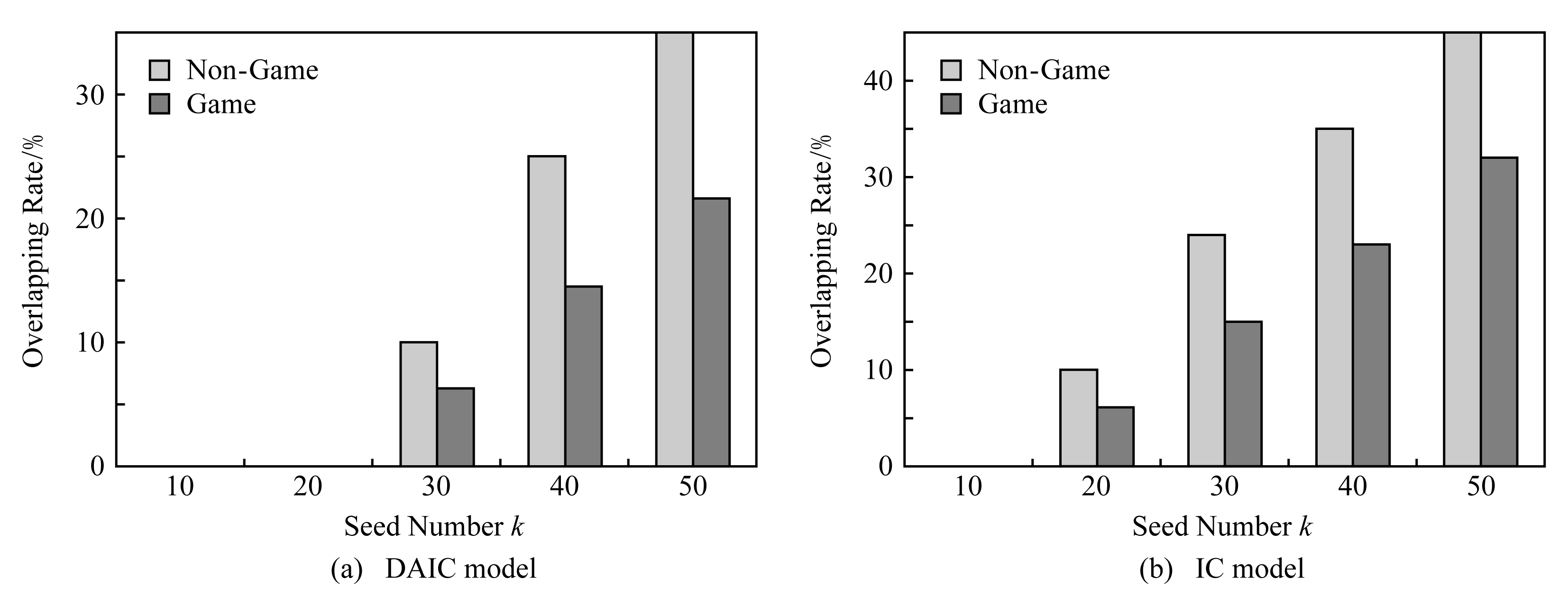
Fig. 4 Overlapping rate of simulated data based on different models
图4 模拟数据在不同传播模型下的种子重叠率
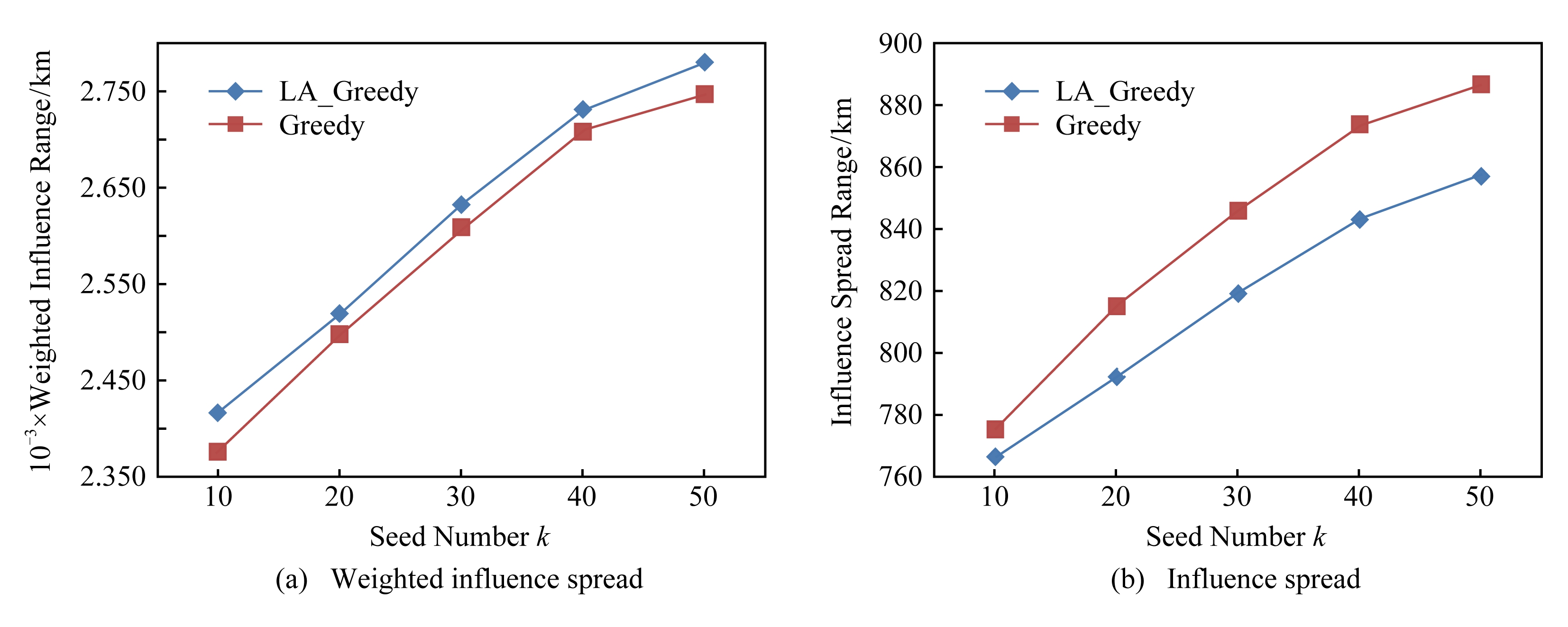
Fig. 5 Influence spread of Twitter data based on DAIC model
图5 Twitter数据在DAIC模型下的影响力传播
为验证LA_Greedy算法的影响力传播范围,实验对种子集合的影响力传播过程进行了20 000次模拟,然后将此过程所得平均值作为种子节点最终的影响范围,并体现在影响人数和影响人数权值这2个指标上.图5和图6为Greedy和LA_Greedy这2种算法在Twitter数据集上分别在DAIC模型和IC模型下的测试结果,其中横坐标代表种子个数k,纵坐标代表传播过程结束后种子集合的影响范围和加权影响范围.
首先,从图5和图6中可以看出,随着k的增加,种子集合的影响范围与加权影响范围也随之增加,但当k增至一定规模后,其增长速度开始变得缓慢.这是因为随着具有较大影响力的节点不断地被选入到集合后,新加入种子的边际影响力也越来越小.
其次,从图5和图6中还可以看出,虽然通过LA_Greedy算法所求种子集合的最终影响人数略少于Greedy算法,但是LA_Greedy算法所影响节点的加权影响范围却高于Greedy算法,这说明LA_Greedy算法确实更加适用于解决地理社交网络中位置敏感的影响力最大化问题,即通过LA_Greedy算法所找到的种子集合可以影响更多网络中权值较大的用户,也就是营销位置附近的潜在顾客,解决了传统IM中由于缺少位置信息所导致的传播范围与实际需求不符问题.
图7和图8则给出了Greedy和LA_Greedy这2种算法在模拟数据集上分别在DAIC模型和IC模型下的测试结果.与Twitter数据类似,横坐标代表种子个数k,纵坐标代表传播过程结束后种子集合的影响范围和加权影响范围.分别对比图5(a)与图7(a)、图5(b)与图7(b),可以看出,用户在地理位置比较疏远的模拟数据集上的种子集合的影响范围与加权影响范围,要远远小于用户地理位置比较紧密的Twitter数据集上的传播结果,这是因为模拟数据集中各节点距中心位置的平均距离约为341.03 km,类似于日常生活中相距较远的2个城市之间的距离,因此当给定营销位置后,网络中各用户的权值与用户间的影响概率的计算结果都非常小,导致种子集合的影响范围不理想.不过,此结果也符合日常生活中人们的行为习惯,即当用户受到线上影响而进入线下环节后,是否参与线下体验将取决于用户和推荐产品的位置特征,这是因为用户的消费行为受到地理位置影响,存在对消费位置的偏好,此偏好由用户的生活习惯和交通能力的因素决定,体现了用户的日常生活范围,推荐产品的位置越超出用户的日常生活范围,用户去尝试的概率就会越低,这也说明所提算法确实可以用于日常生活中针对某一特定范围内的营销推广活动.
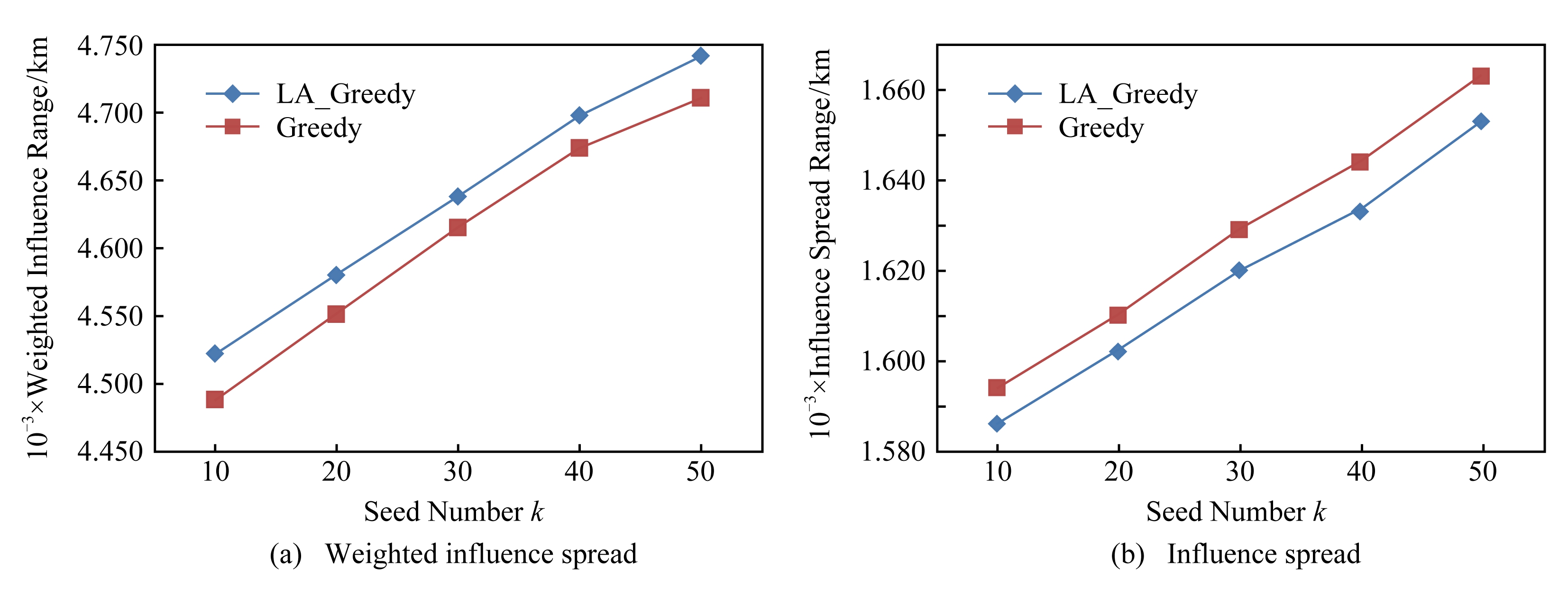
Fig. 6 Influence spread of Twitter data based on IC model
图6 Twitter数据在IC模型下的影响力传播
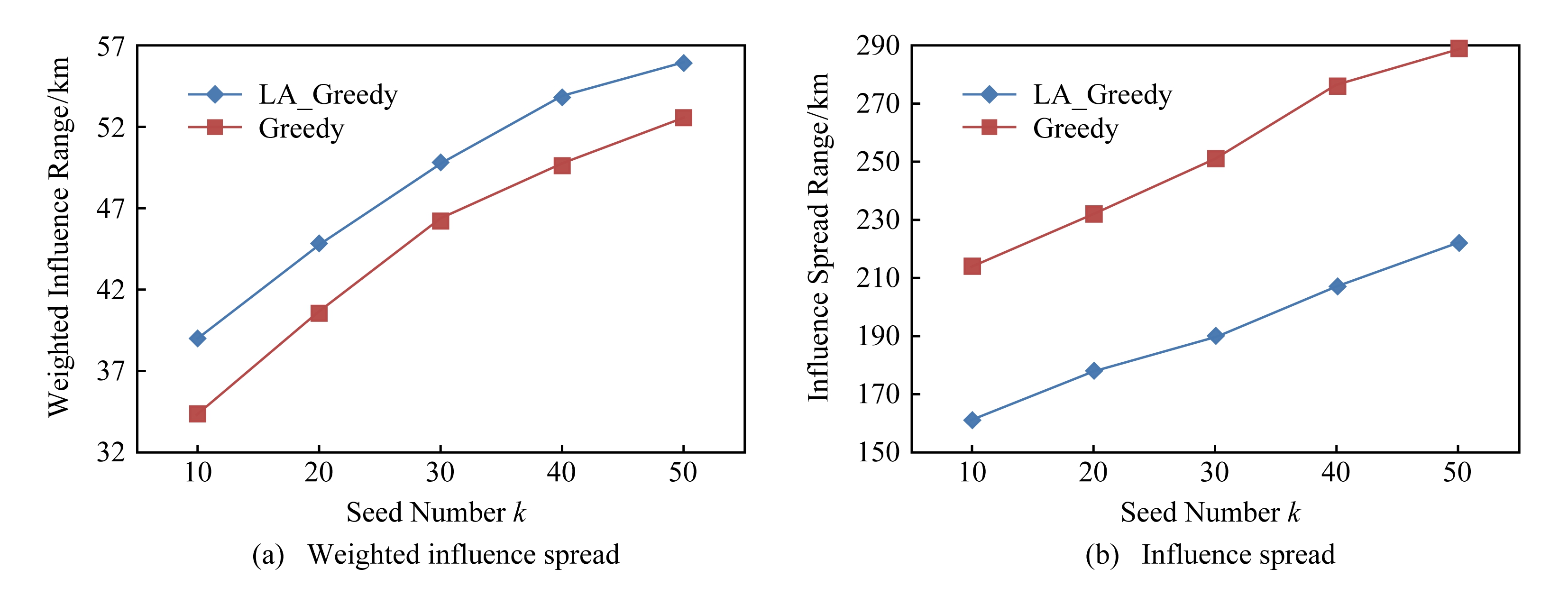
Fig. 7 Influence spread of simulated data based on DAIC model
图7 模拟数据在DAIC模型下的影响力传播
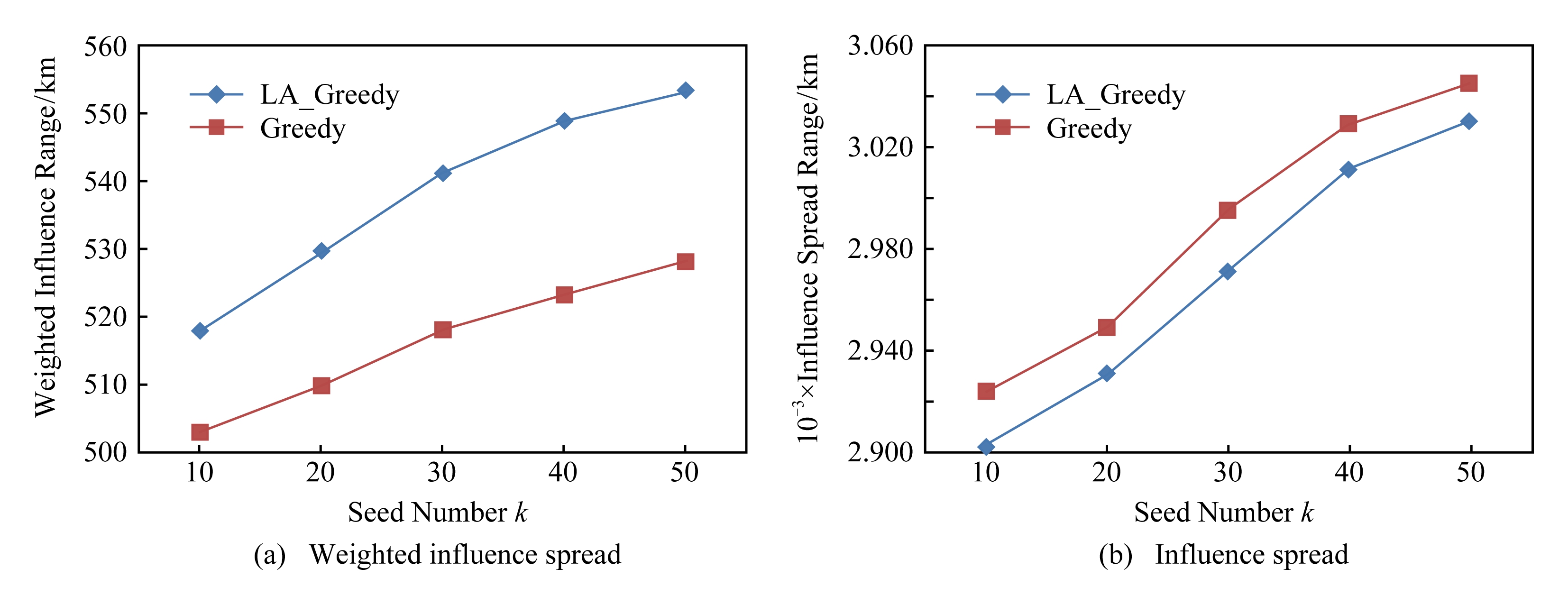
Fig. 8 Influence spread of simulated data based on IC model
图8 模拟数据在IC模型的实验结果
5 总 结
基于放射性衰变定律,首先对地理社交网中用户间影响概率的计算公式进行了理论推导,并提出了一种距离敏感的DAIC传播模型,进一步,基于该模型又提出了贪婪框架下位置敏感的影响力最大化算法LA_Greedy.实验证明,在求解位置敏感的影响力最大化问题时,LA_Greedy算法与传统Greedy算法相比,前者可以吸引更多营销位置附近的用户,确保了用户的精准推荐.此外,当重叠种子根据所提的GDMM机制进行公司选择时,种子集合的重叠率确实得以明显下降,从而保证了有效的传播效果.未来工作将考虑把Twitter以外更多其他社交网数据纳入研究,并加强对部分垂直领域的数据分析处理,以体现本文工作可扩展性和实际应用价值.
[1]Steffes E M, Burgee L E. Social ties and online word of mouth[J]. Internet Research, 2013, 19(1): 42-59
[2]Domingos P, Richardson M. Mining the network value of customers[C] //Proc of the 7th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2001: 57-66
[3]Kempe D, Kleinberg J. Maximizing the spread of influence through a social network[C] //Proc of the 9th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2003: 137-146
[4]Aslay C, Lu Wei, Bonchi F, et al. Viral marketing meets social advertising: Ad allocation with minimum regret[J]. Proceedings of the VIDB Endowment, 2014, 8(7): 814-825
[5]Li Guoliang, Chen Shuo, Feng Jianhua, et al. Efficient location-aware influence maximization[C] //Proc of ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2014: 87-98
[6]Zhu Wenyuan, Peng Wenchih, Zheng Kai, et al. Modeling user mobility for location promotion in location-based social networks[C] //Proc of the 21st ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2015: 1573-1582
[7]Goyal A, Lu Wei, Lakshmanan L V S. An efficient algorithm for influence maximization under the linear threshold model[C] //Proc of the 11th IEEE Int Conf on Data Mining. Piscataway, NJ: IEEE, 2012: 211-220
[8]Chen Wei, Wang Yajun, Yang Siyu. Efficient influence maximization in social networks[C] //Proc of ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2009: 199-208
[9]Wang Yaxuan, Wang Hongzhi, Li Jianzhong, et al. Efficient influence maximization in weighted independent cascade model[M] //Database Systems for Advanced Applications. Berlin: Springer, 2016: 49-64
[10]Bharathi S, Kempe D, Salek M. Competitive influence maximization in social networks[M] //Internet and Network Economics. Berlin: Springer, 2007: 306-311
[11]Carnes T, Nagarajan C, Wild S M, et al. Maximizing influence in a competitive social network: A follower’s perspective[C] //Proc of the 9th Int Conf on Electronic Commerce. New York: ACM, 2007: 351-360
[12]Wu Hong, Liu Weiyi, Yue Kun, et al. Maximizing the spread of competitive influence in a social network oriented to viral marketing[M] //Web-Age Information Management. Berlin: Springer, 2015: 516-519
[13]Li Hui, Bhowmick S S, Cui Jiangtao, et al. GetReal: Towards realistic selection of influence maximization strategies in competitive networks[C] //Proc of ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2015: 1525-1537
[14]Yu Zhiyong, Zhang Daqing, Yu Zhiwen, et al. Participant selection for offline event marketing leveraging location-based social networks[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2015, 45(6): 853-864
[15]Zeng Yifeng, Chen Xuefeng, Cong Gao, et al. Maximizing influence under influence loss constraint in social networks[J]. Expert Systems with Applications, 2016, 55: 255-267
[16]Krane K S, Ruby L, Williams R E. Post use review: Introductory nuclear physics[J]. American Journal of Physics, 1990, 58(2): 191-192
[17]Ginzburg V L, Levin L M, Rabinovich M S, et al. Chapter I—Molecular physics and thermodynamics[M] //Molecular Physics, Thermodynamics, Atomic and Nuclear Physics, Amsterdam: Elsevier, 1965: 115-176
[18]Hu Jie, Meng Kun, Chen Xiaomin, et al. Analysis of influence maximization in large-scale social networks[J]. ACM SIGMETRICS Performance Evaluation Review, 2014, 41(4): 78-81
[19]Wang Xiaoyang, Zhang Ying, Lin Xuemin, et al. Distance-aware influence maximization in geo-social network[C] //Proc of the 32nd Int Conf on Data Engineering. Los Alamitos, CA: IEEE Computer Society, 2016: 1-12
[20]Chen Wei, Wang Chi, Wang Yajun. Scalable influence maximization for prevalent viral marketing in large-scale social networks[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 1029-1038

