随着数据量的爆发式增长[1],人们对数据的处理识别能力并没有因为计算资源和存储能力的提高而提升.图结构数据[2]能够在许多应用中表现实体对象之间复杂的关系,如用户交互形成的社交网络[3]、电话信息组成的通信网络[4]、学者合作形成的研究网络[5]、网页浏览形成的Web网络[6]、用户产品和服务购买的交易网络[7]、行程和道路组成的交通网络[8]、垃圾噪音数据组成的过滤网路[9],以及化学化合物互相作用的生物网络[10]等.图数据随处可见,在大数据背景下图数据的规模日益增大,截至2017年6月Facebook的月活跃用户数已达20亿,Twitter的月活跃用户数保持在3.2亿,腾讯的QQ保持8.61亿月活跃用户,微信则超过9.6亿[11-12],社交网络已成为连接网络信息空间和人类现实世界不可或缺的桥梁.
然而,这种连接关系所构成的大规模图结构数据具有上亿顶点和千亿条边,对于这样的社交网络图是无法直接加载内存进行处理;现有的大多数算法对于这类大图不能有效处理,尤其是涉及到图流实时分析决策时,无法及时反馈给用户需要的信息;现实生活中的数据往往含有很多隐藏的错误信息标签,例如WEB网络图中错误的链接以及一些垃圾邮件的传播[13]、病毒的扩散[14]等,这种噪音阻碍了用户对原始图真实结构特征的挖掘,增加了计算资源的消耗.大图数据的这些缺陷使得用户难以直接管理,给社会网络分析和数据挖掘带来了挑战.
针对大规模图数据的概要化是潜在的解决方案,图的概要化(graph summarization)[15],简称图概要,运用各种图形操作技术,寻找一组简洁的超图或稀疏图,阐明原始图的主要结构信息或变化趋势,代替原始大图进行数据分析.它一般针对大规模的图数据,在一定的应用背景下,考虑时间、空间和信息之间的权衡,量化顶点或边缘的属性相似性和邻域相似性,缩小原始图的规模,保留一些应用价值属性,支持用户的互动分析,或者滤除噪声数据.一个优秀的概要图涵盖了原始图中主要的结构特征,其顶点称为超级顶点(简称超点),它代表原始图中一组相近顶点的集合;其边称为超级边(简称超边),它代表2个顶点集合之间的联系.图概要既可以揭露实体之间隐藏的复杂关系,又可以保持原图的性质,有效减少图的存储空间,提高图计算的效率.
通常,图概要概念的不同表述还有图概括(graph synposis)[16]、图聚集(graph aggregation)[17]、图规约(graph simplification)[18-19]等,而图采样(graph sampling)[20-21]、图聚类(graph clustering)[22-23]、图压缩(graph compression)[24-25]与图概要有紧密的联系,但最终的目标又不尽相同.
图采样与图概要的目标都是创建一个原始图的简短表示[26],进行有效的算法分析.不同点在于图采样是通过局部子图特征来估计原始图的属性,例如顶点采样和边采样,进行图的稀疏化以缩小图的规模,如何进行有代表性、有普遍性的采样是其研究的核心,但会导致图结构特征大量丢失;而图概要则从全局出发,合并高度相似的顶点减小图的规模,能维持图结构特征.
图聚类和图概要都通过顶点的分组合并得到子图.不同点在于图聚类是组合密集连接的顶点,侧重寻找局部稠密的结构,图聚类没有特定的目标和任务;而图概要立足于整体结构,侧重寻找属性和结构相似的集合,它不仅概括稠密的结构,还概括稀疏的结构,相较于图聚类,图概要一般都具有特定的任务,与实际应用联系更为紧密.
图概要和图压缩主要目的都是节省大量的空间开销.但是图压缩旨在寻找输入图的最小空间存储,忽视了图结构和属性隐藏的语义特征,可解释性差;图概要旨在寻找高质量的超图代替原始图进行分析.当然,图概要中部分方法基于图压缩的理念寻找输入图的较小表示,兼顾了其结构特征的相似性.
总之,图采样通过局部结构评估整体特征,图聚类合并局部稠密的顶点,图压缩寻找原始图的最小表示模型,它们更注重处理大型数据时计算效率的提升和内存资源的利用,但往往忽略了图数据的真实结构信息.而图概要技术的根本目的在于通过小规模的超图或稀疏图替代原始图进行特征分析,更注重挖掘用户未知的结构模式和隐藏的信息特征,一个优秀的图概要技术往往需要结合特定的应用背景和需求.因此当我们面对一个真实世界的大型网络数据时,如何去发现一些有趣的结论或者未知的结构,图概要技术是最佳的选择.例如关于维基百科的编辑网络概要图,图采样只能评估其编辑网络中各个话题的热度级别;图聚类将相近的话题进行分组;图压缩则将其转化为无法解释的最小存储模型;而图概要能描述了一些群体在对某些敏感问题上多次互相编辑,形成“冲突-战争”导致两极分化的特殊结构,有助于人们寻找文化差异较大甚至对立的特殊社会群体.
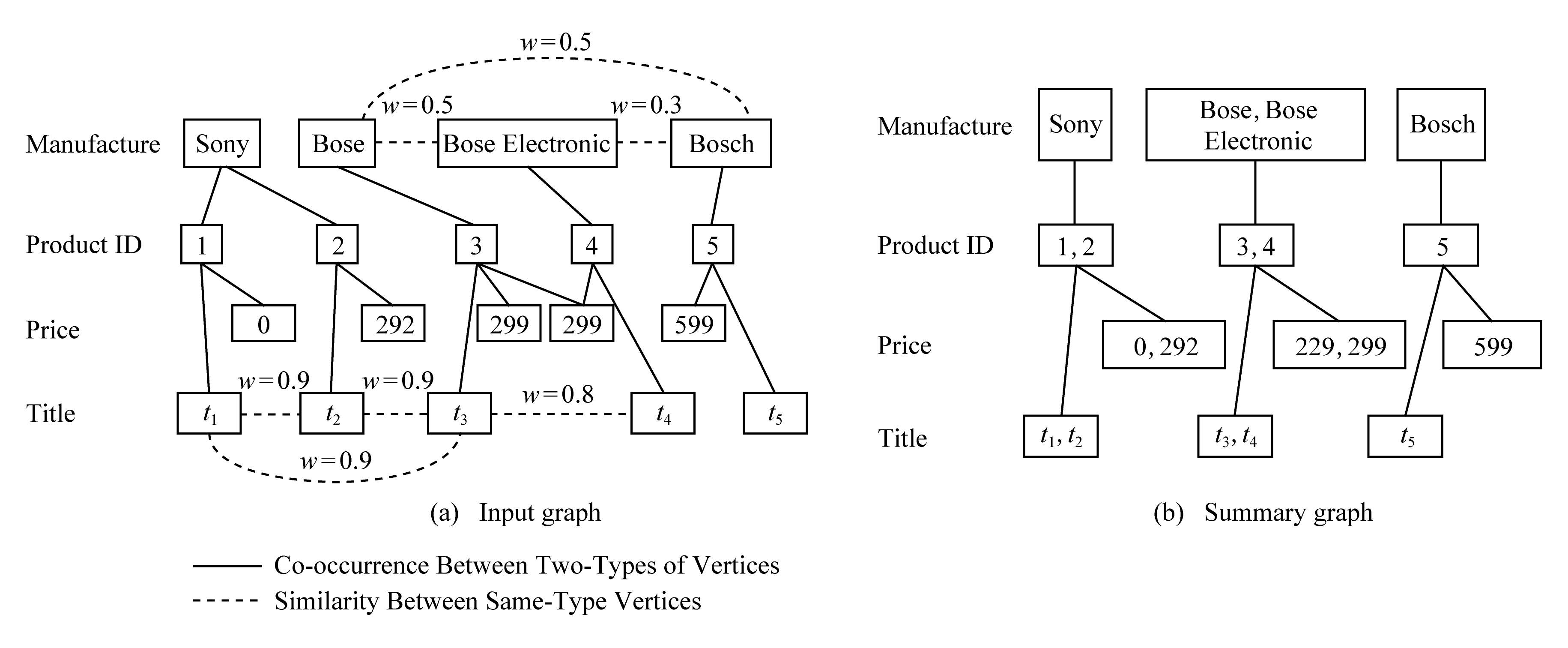
Fig. 1 Cosum entity relationship summary[32]
图1 Cosum实体关系概要图[32]
1 图概要技术
本文从图概要的解决方案及应用需求,将现有的概要技术分为:基于空间压缩的图概要、基于查询优化的图概要、基于模式可视化的图概要和基于影响分析的图概要.图结构数据主要有静态图和动态图,静态图的边和顶点保持一致,动态图由于其自身的边或顶点不断变化,具有时间维度属性.
1.1 基于空间压缩的图概要
基于空间压缩的图概要方案,旨在减少输入图的规模,降低网络的异构性[27],滤除噪音数据,保留原始图的主要结构信息,用较小的、有代表性的超图代替原始图进行数据分析.主要采用图压缩和图聚类2种方法.
1) 基于图聚类的方法
图聚类将每个密集连接的集群映射到超级顶点,确保不同集群的顶点性质不相同,生成的概要图仅凸显集群内部边缘信息的顶点集合,以近似邻接矩阵表示.聚类技术最初不能保证概要图的质量,启发式算法的出现,通过给定输入图和期望超点的数量k,重建误差最小化,使得概要图的质量得以提高.
文献[28]提出的关于加权图的概要化WGC(compression of weighted graphs),从“简单”和“广义”进行扩展,主要寻找实体关系结构相似的顶点合并,在保持最小化误差的条件下追求压缩最大化,关键在于合并一定跳数顶点的过程中保持边权重或连接强度,以获得压缩图.在简单加权图概要任务中,通过为每个边分配其代表所有边的平均权重,逼近原始图使误差最小化.在广义加权图压缩任务中生成保持连通性的子图,即任何2个顶点的最佳路径在概要图中与原始图相等,但路径不一定一样.
文献[29]提出的概要技术GRAC(graph clust-ering)采用多层次的聚类算法,主要分为粗化阶段、初始聚类阶段以及细化阶段.当顶点合并成超点时,超边的权重为包含的所有边的权重之和.粗化阶段首先随机遍历所有未标记的顶点,如果顶点v的所有邻居顶点已标记,则标记此顶点;若该顶点存在未标记的邻居顶点,则合并顶点v与某一邻居顶点使其最大化:
![]()
(1)
其中,e(u,v)对应边的权值,w(v)对应顶点的权值,直到所有顶点粗化完成.聚类阶段则采用光谱算法[30]参数进行划分.细化阶段受核k-means[31]和谱聚类的启发,采用增量式加权核k-means保证算法优化相应的图聚类目标,采用本地搜索来提升批量细化的质量.
Cosum[32]将RDF(resource description frame-work)图转化为多类型图,并将实体解析问题转化为多类型图概要问题.其关键方法是输入k-型图转换为由超顶点组成的另一个k-型概要图,使用不同类型的顶点集链接来提高顶点分辨率的准确性.Cosum将顶点联合成超顶点,使得每个超级顶点是相干的(即顶点具有相同类型并且具有高相似性),并且根据其组成顶点之间的原始边缘创建超级边缘.已经表明:Cosum优于最先进的通用实体解决方法,特别是在具有缺失值和一对多或多对多关系的数据集中.如图1所示,RDF图被建模为多类型图,输入图顶点表示不同对象,实线表示关系,虚线上方的权重w表示实体之间的相似度,相似度可通过邻居顶点相似或者内容相似度(字符串)计算.概要图显示对于产品1,2而言,合并超顶点时制造商是更重要的特征,而对于产品3,4而言价格特征则更重要.
2) 基于图压缩的方法
压缩是数据概要中的常用技术,其目标是通过压缩技术最小化描述输入图,通常基于最小描述长度 [33](minimum description length, MDL)原则,构造输入图的模型及模型规则下存储的数据,辨别各种结构模式.问题在于如何利用MDL去选择最合适的模型,一般应用相关的优化函数将顶点或边缘递归合并到超级顶点中.关键策略是合并过程中保持边缘权重或连接的强度,最小化误差并最大化压缩获得压缩图.在属性图概要化中,压缩技术也利用了顶点结构和属性.初始的策略是优先选取一个维度(属性信息)进行概要化压缩,然后再根据拓扑结构进行修正,后期从信息论的角度统一度量结构和属性的差异化.
文献[34]是第1个基于MDL原则提出了全新的图概要模型,该模型在可控有界误差内生成概要图,其概要图由2部分组成:通过聚合顶点生成S和校正C.校正指精确重建G的边缘校正列表.成本R是S和C的存储成本总和:Cost(R)=E(S)+C.该模型在计算最大压缩图的同时生成了最佳概要图,核心策略有2种:1)基于贪心策略遍历所有顶点,寻找全局最佳顶点对,迭代合并成超点,最大限度地降低顶点的成本;2)随机策略则是一种轻量级的随机化方案,选择顶点与附近的最佳顶点对合并.此模型针对概要图的误差进一步扩展研究,定义了误差参数度量:
![]()
(2)
其中,![]() 为概要图中顶点v的邻接边,Nv为概要图中顶点v的邻接边,但目前无法扩展到属性图或者动态图中.如图2所示,当合并高度相似的顶点(g,h)时,由于原始图中包含边(h,d),此时需要在较正列表C中新增边(h,d),最后一步当合并时生成额外的边(g,d)时需要在较正列表删减此边.文献[35]针对上述方法的贪心和随机策略提出了新的迭代算法加速了概要化进程,解决其概要稠密大图时执行时间过长的问题.
为概要图中顶点v的邻接边,Nv为概要图中顶点v的邻接边,但目前无法扩展到属性图或者动态图中.如图2所示,当合并高度相似的顶点(g,h)时,由于原始图中包含边(h,d),此时需要在较正列表C中新增边(h,d),最后一步当合并时生成额外的边(g,d)时需要在较正列表删减此边.文献[35]针对上述方法的贪心和随机策略提出了新的迭代算法加速了概要化进程,解决其概要稠密大图时执行时间过长的问题.
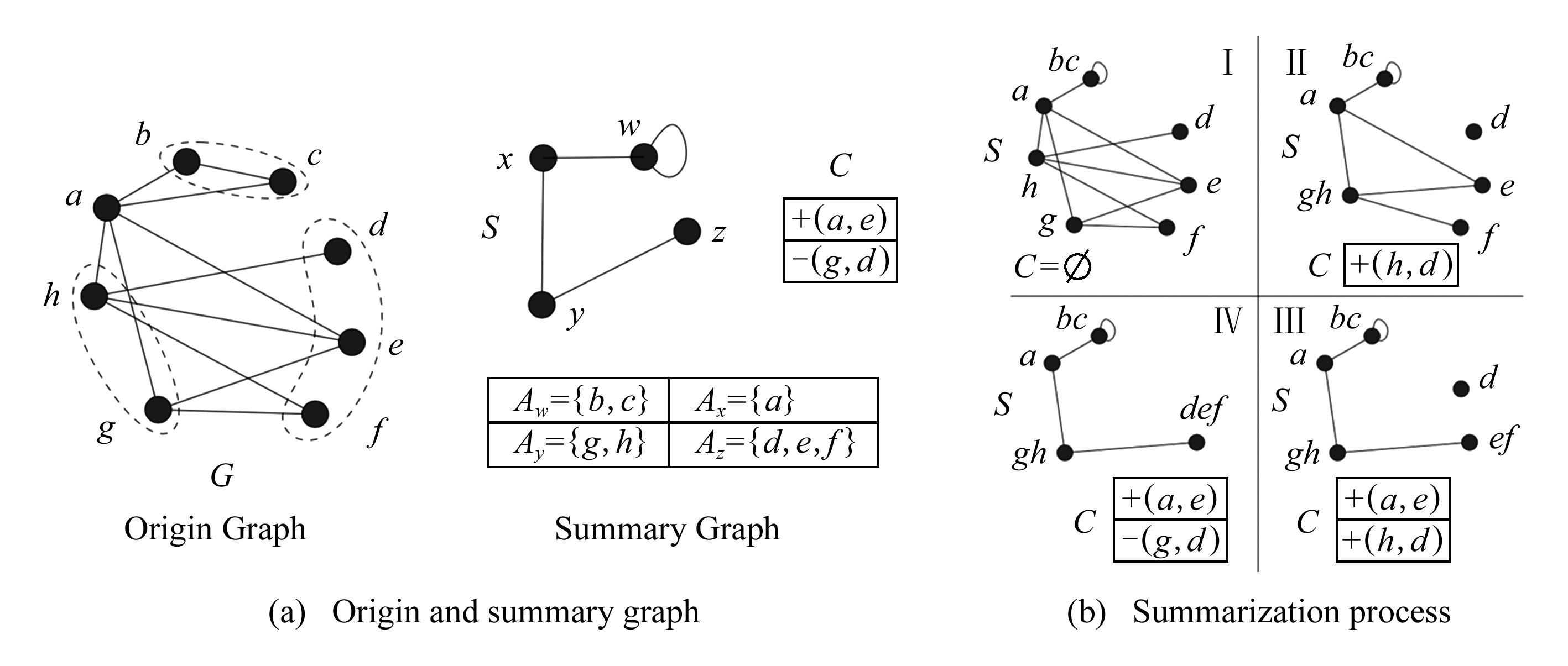
Fig. 2 MDL compression of origin graph[34]
图2 原始图的MDL压缩[34]
文献[36]提出了概要化模型——SlashBurn.现实世界的图很容易被高度顶点(集线器)断开,可以通过寻找高度顶点和邻居(辐条),对其顶点进行排序,递归地将一个图分割成仅由集线器连接的超级集线器和超级辐条,快速地压缩原始图,以MDL的原则生成概要模型,该方法支持任何幂律图上工作,而不需要任何领域特定的知识或者在图上定义良好的自然排序以实现更好的排列.图3是SlashBurn概要化1次之后的图形,通过删除集线器顶点创建许多较小的“辐条”和GCC(giant connected com-ponent),集线器顶点获得最低的ID,辐条中的顶点按照它们所属的连接组件大小递减顺序获得最高的ID即(9,16),并且GCC获得剩余的ID(2,8),下一次迭代从GCC开始.
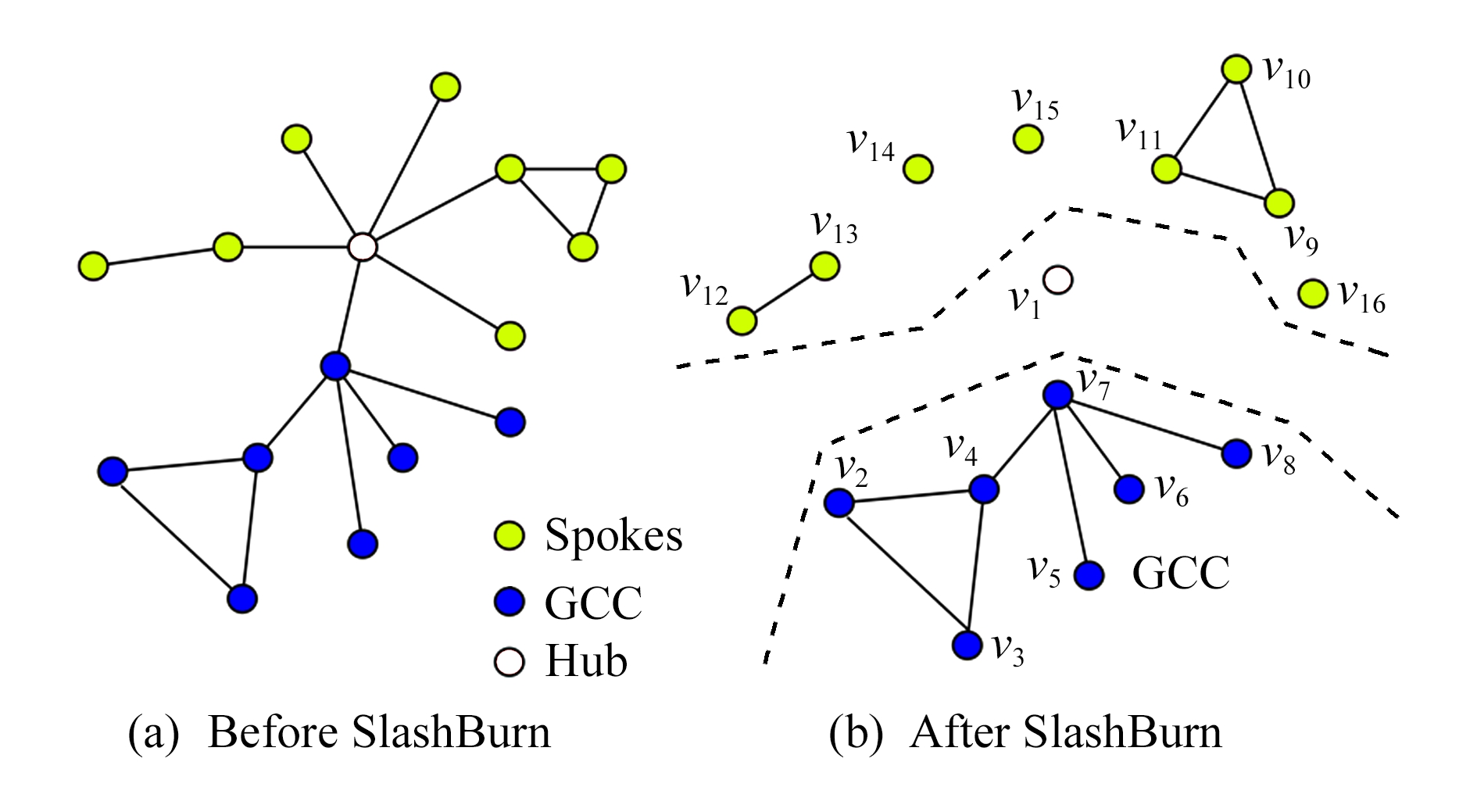
Fig. 3 Graph summary with hub model 图3 集线器模型
与SlashBurn类似的有文献[37],提出一种基于无损压缩高度顶点的G-Dedensified方法,认为高度顶点附近存在大量的冗余信息,引入公共的压缩顶点去除多余的边缘,加速查询处理,问题的关键在于如何寻找公共连接的高度顶点.通常情况下将所有高度顶点邻居划分为2个集合,遵循MDL的原则使高度顶点和输入顶点分开,且确保输入顶点包含所有高度顶点的输出边,称之为“解密”操作.
SAGS(set-based approximate graph summariza-tion)[38]使用统一的局部敏感散列(unified locality sensitive Hash, ULSH)[39]和MDL来压缩大型网络,以进行内存处理,生成概要图.在这项工作中,ULSH通过在顶点邻域上执行一组minhash函数来处理图形,计算散列码,然后聚合基于多个散列函数输出相同的顶点,添加新的虚拟顶点.
AGSUM(attribute graph summarization)[40]基于MDL最小化模型和模型数据,模型成本代价主要由3部分组成:顶点、属性和顶点之间的链接.核心策略是通过贪心算法结合拓扑结构和属性信息度量顶点相似性,结构信息相似度则根据2跳顶点对进行衡量,属性相似度基于Jaccard相似度构建,初始化时通过属性传播算法对原始图初始化,基于贪心策略反复迭代合并使成本最小化,如图4所示.图4(a)为原始图,图4(b)为概要图,其中不同标签的顶点分别被合并为超点,最后将原始图划分为3个子图G1,G2,G3;图4(c)为还原后的原始图,由于概要化中可能导致结构信息的丢失,重构的原始图具有一定的误差率.
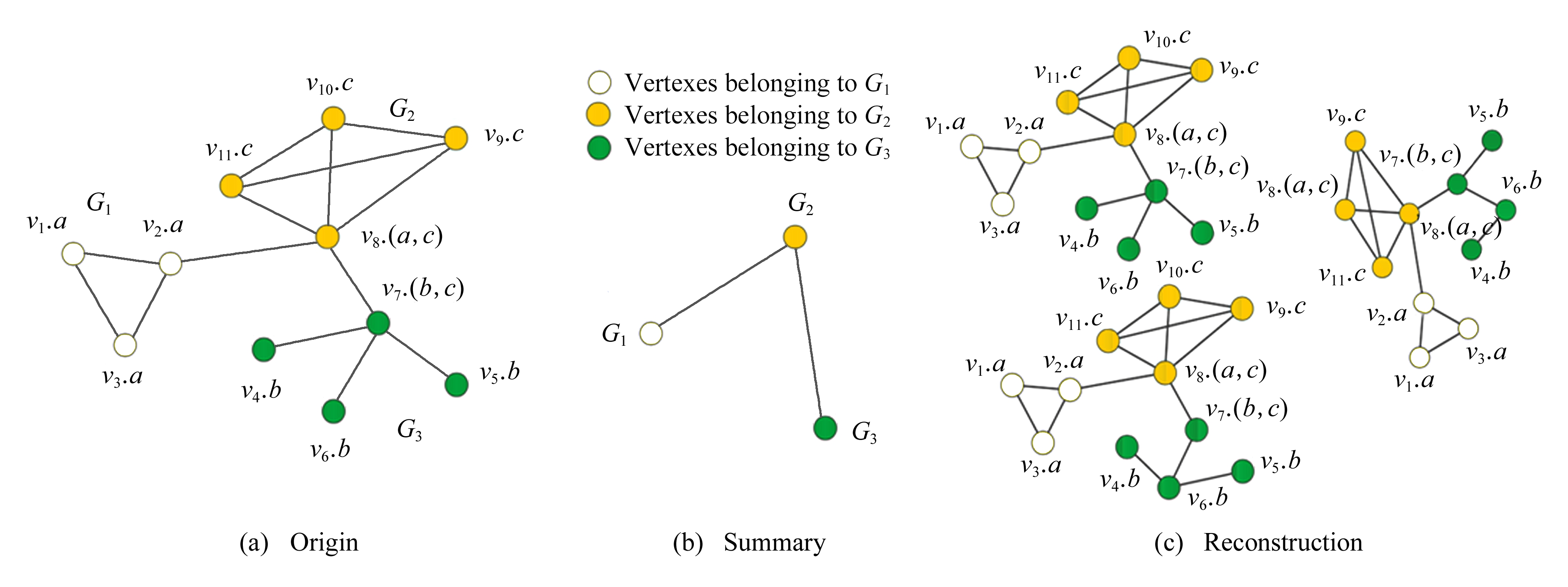
Fig. 4 AGSUM graph summary[40]
图4 AGSUM概要示意图[40]
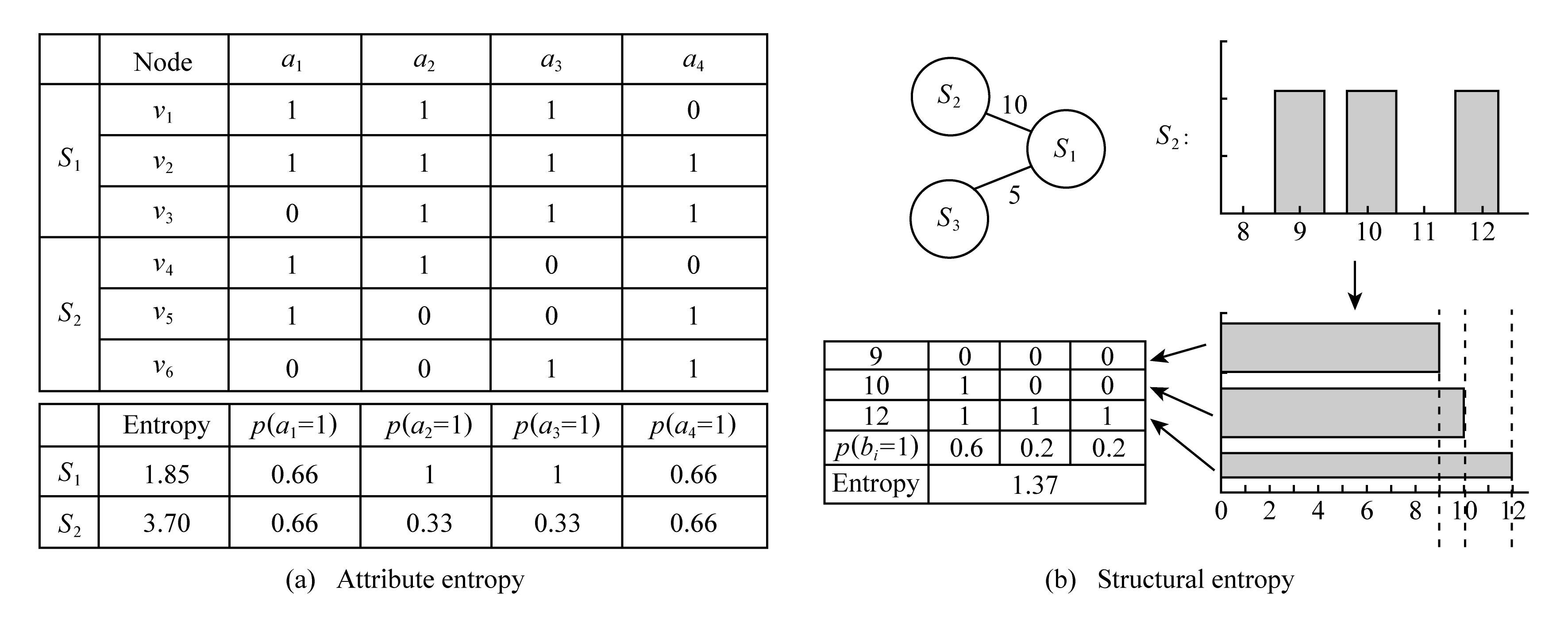
Fig. 5 Structural entropy and attribute entropy[41]
图5 结构熵与属性熵[41]
文献[41]由信息论启发,提出了统一熵模型S-Entropy和分区同质性度量,核心思想是把属性转化为顶点,通过概率分布对其进行编码计算分区之间的熵差,再基于标准放松,根据用户自身偏好,转化为加权熵,最终产生精确同质分区和近似同质分区.加权熵主要是由边熵和顶点属性熵组成,熵的计算方式为
(3)
图5(a)表格表示了属性熵的计算,超点S1内含顶点v1,v2,v3,顶点具有属性a1,a2,a3,a4,则超点S1属性熵为1.85,超点S2的属性熵为3.7,即表明S1内部属性相似度大于S2;右侧则根据邻居边的频数分布转化为二进制表示,S2超点到S1超点的平均边数为10,其中2个顶点9条边、2个顶点10条边、1个顶点12条边,转化为直方图,基于直方图的视觉将9,10,11转化为全1的二进制向量,去除一样的列,只关心其中的差异,计算结构熵.
文献[42]在文献[34]的基础上提出了最新的成本定义,添加了新的压缩成本,创建一个原始图的概要图,通过成本模型重复选择最优顶点对合并.成本模型由概要成本和压缩成本组成,基于贪心算法重复选择最低总成本.成本模型为
![]()
(4)
其中,Costs(u)属于概要成本,Costc(u)属于压缩成本,Costsc(u)选择其中的最小值.如图6所示,超点ID从90起标记,观察到顶点对(27,2)具有最大的压缩率,彼此共享所有的邻居顶点,当超点90合并后,继续根据成本模型选择最优压缩顶点对(51,60),此次压缩新增了多余的边(60,24),需要在较正列表中删去此边.

Fig. 6 Iterative steps of cost model[42]
图6 成本模型迭代步骤[42]
1.2 基于查询优化的图概要
基于查询优化的图概要以维持原始图的特定结构信息为主要目的,解决超大规模图下针对某些查询任务的快速响应,支持现有或特定的图形算法加速查询,尽可能地减少磁盘的访问,得到精确的结果,降低平均误差.
文献[43]提出的层次聚类GRASS(graph structure summarization)针对查询效率,通过贪心法分组顶点,归一化差异性,支持顶点的邻接关系和特征向量中心查询,并在误差允许内重构原始图:
![]()
(5)
其中,A(i,j)表示原始图顶点(i,j)存在的边.
文献[44]提出一种基于质量保证的超点合并策略S2A,给定期望的超点数量,使重建误差最小化.这种针对如三角形或者子图查询计数进行优化的启发式策略,可用于如Grass等概要化方法的改进.
SNAP和K-SNAP[45]是用于概要图形的2种经典模型,其核心思想首先基于顶点属性对所有顶点进行迭代分组,直到分组中的顶点属性一样,最终产生最大关系属性图,启发式算法K-SNAP允许用户控制概要化的精确度,通过不同层次的概要图进行查询优化,这2种图形聚合与数据库操作风格类似,引入了顶点分组的概念,并提供了2个启发式算法(自上而下和自下而上)来评估SNAP.如图7左侧图所示,每个顶点代表学生,学生具有性别、班级等属性,学生之间包含朋友、同学的关系,SNAP操作生成右边的概要图,这个概要图表明了4组学生及其关系,每个小组学生属于同一性别且同一班级,直观上说,SNAP根据用户选择的属性和顶点生成一个满足以下条件的概要图:该概要图的顶点对应于最大的兼容分组,该概要图的边缘关系满足从原始图R中推导出的群组关系.图7右侧图显示了根据属性分组构建的概要图,但该方法在结构一致性上缺乏更好的表现.
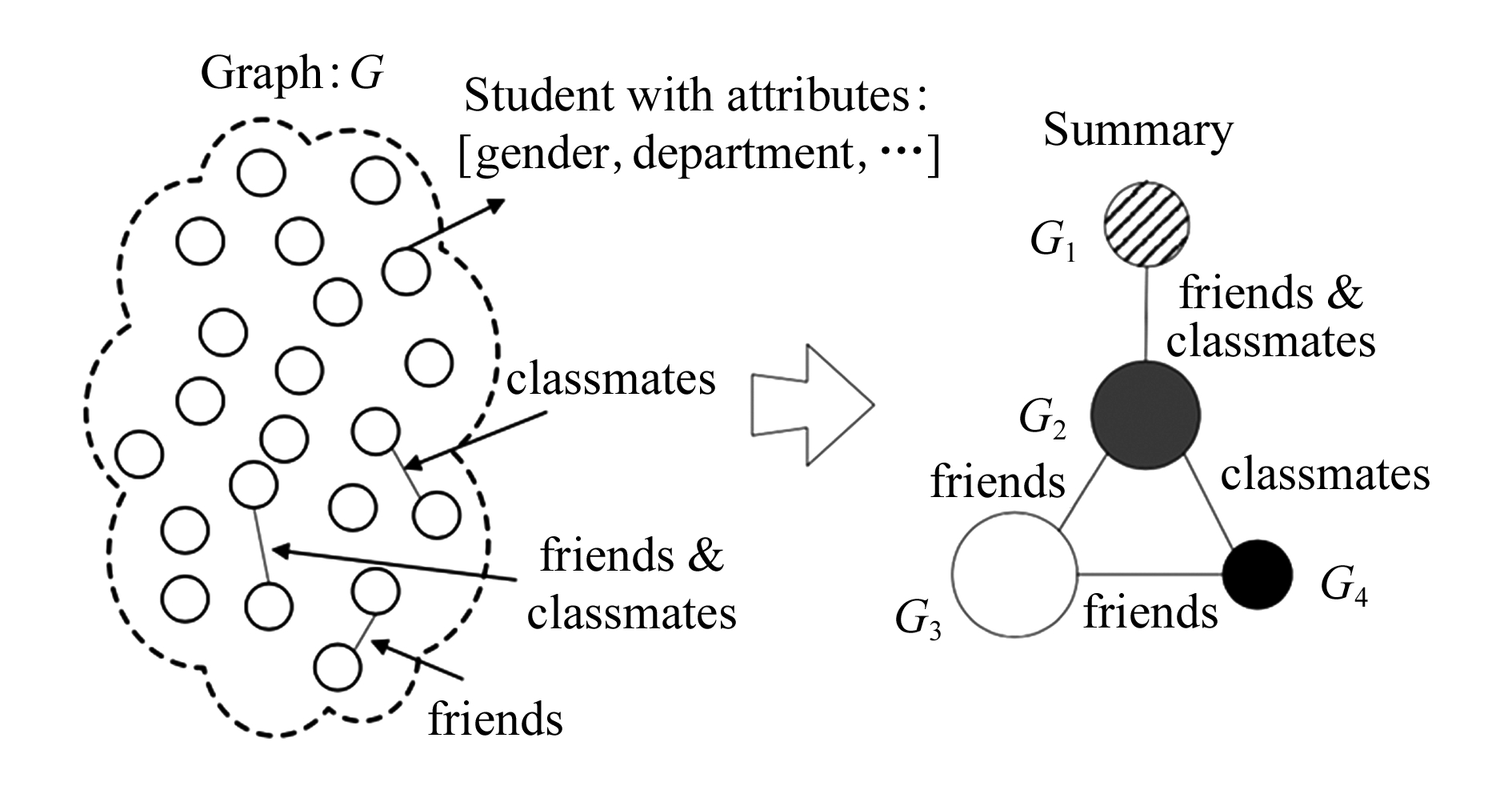
Fig. 7 SNAP-graph summary[45]
图7 SNAP-概要化[45]
CANAL[46]在K-SNAP的基础上,针对顶点属性为连续值时,利用链接结构和隐藏的信息实现自动化分类,评估概要图的兴趣度,帮助用户自动找出有意义的概要图,而这一行为在K-SNAP中可能需要用户对多个分辨率的概要图进行汇总.
存在一些特殊应用背景的概要技术,查询优化只是其次要任务,例如关于隐私保护的概要化,一个零知识隐私框架(zero knowledge private, ZKP).文献[47]在图概要中使用ZKP保护用户的个人隐私,引入了合成属性,将拉普拉斯噪声[48]标度λ设置为与灵敏度和采样误差之和成正比,并且与ZKP隐私级别成反比,简化图概要中ZKP机制的构建和分析,生成概率图.概率图[49]将具有相同属性值的顶点分组一起,提出一个概率图概要化框架,当中涉及复杂的概率推理,通过计算每个分组之间的期望值(所有链接边的概率值之和)生成一个概要图.其核心操作可使用R-DBMS中的关系运算符来实现.因为关系数据库是一个已经被证明可以扩展到非常大的数据的完善和成熟的技术,这是其自身优势之一.概率图定义了一组可能的实例PI.将概率图G的所有可能实例的集合表示为E(PI).每个PI是从概率图导出的正则图,其中每个边或者存在或者不存在.每个PI的存在概率计算为
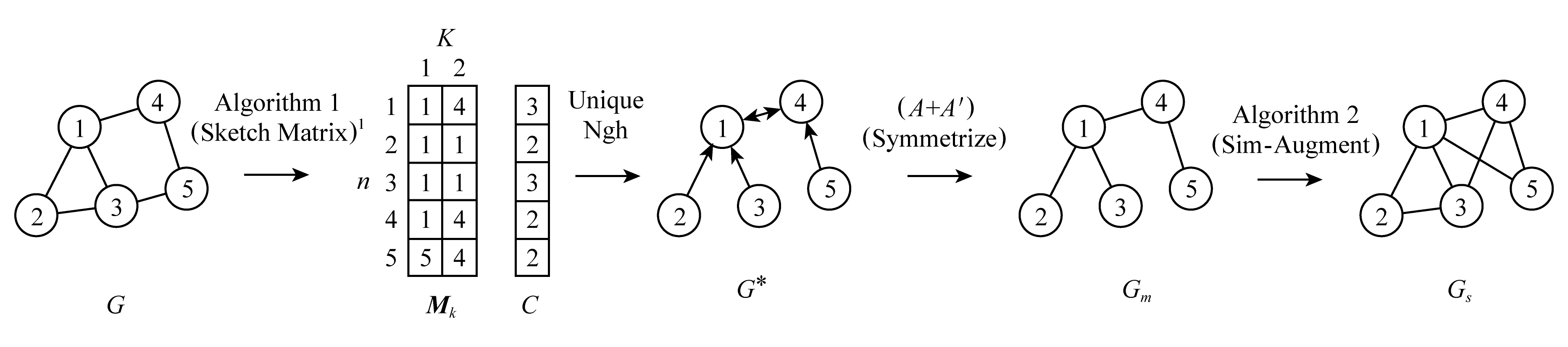
Fig. 9 Topological model of incremental sketch[55]
图9 增量概要图的拓扑模型[55]
(6)
其中对于给定边存在所有实例集合的概率和为1.
查询随时间动态变化的大型复杂图形数据面临更多的挑战,例如通过电话或社交网络与其他人的通信模式、网络服务器之间的连接、信息流动、新闻传播、信息在智能家居环境中的设备之间传输.目前,动态图的概要技术研究刚刚起步,采用的方案往往是将数据线性投影到保持数据显著特征低维空间.
频率动态图概要具有3个特征:更小的次线性空间、线性构建时间以及边缘更新时恒定的维护成本,以便提升查询效率性能.广泛的做法是基于散列[50]或基于样本的方法独立处理每个流元素,而不用维护元素之间的连接.现有的算法假设查询存在,建立索引加速,但只能解决临时问题,而不支持对图流进行多样化和复杂的分析,例如CountMin[51]和Bottom-k[52]等工作受限于查询数据假设存在,G-sketch[53]通过假设存在更好的划分输入图流数据进一步改善了CountMin.
由Tang等人[54]提出的TCM模型则适用于众多图流数据,其采用多个独立的散列函数对流图生成多个草图,并满足4个条件:1)概要图S的尺寸远小于G;2)在线性时间内构造S;3)S的更新成本是恒定的;4)S满足原始图的结构特征.如图8所示,S1和S2是由2个独立的散列函数生成的概要图,当执行查询顶点g到顶点b的权重时,2个概要图均显示为1,根据选取的聚合函数选择最小权值为1,实践证明使用多个独立散列函数能提高查询的准确性.
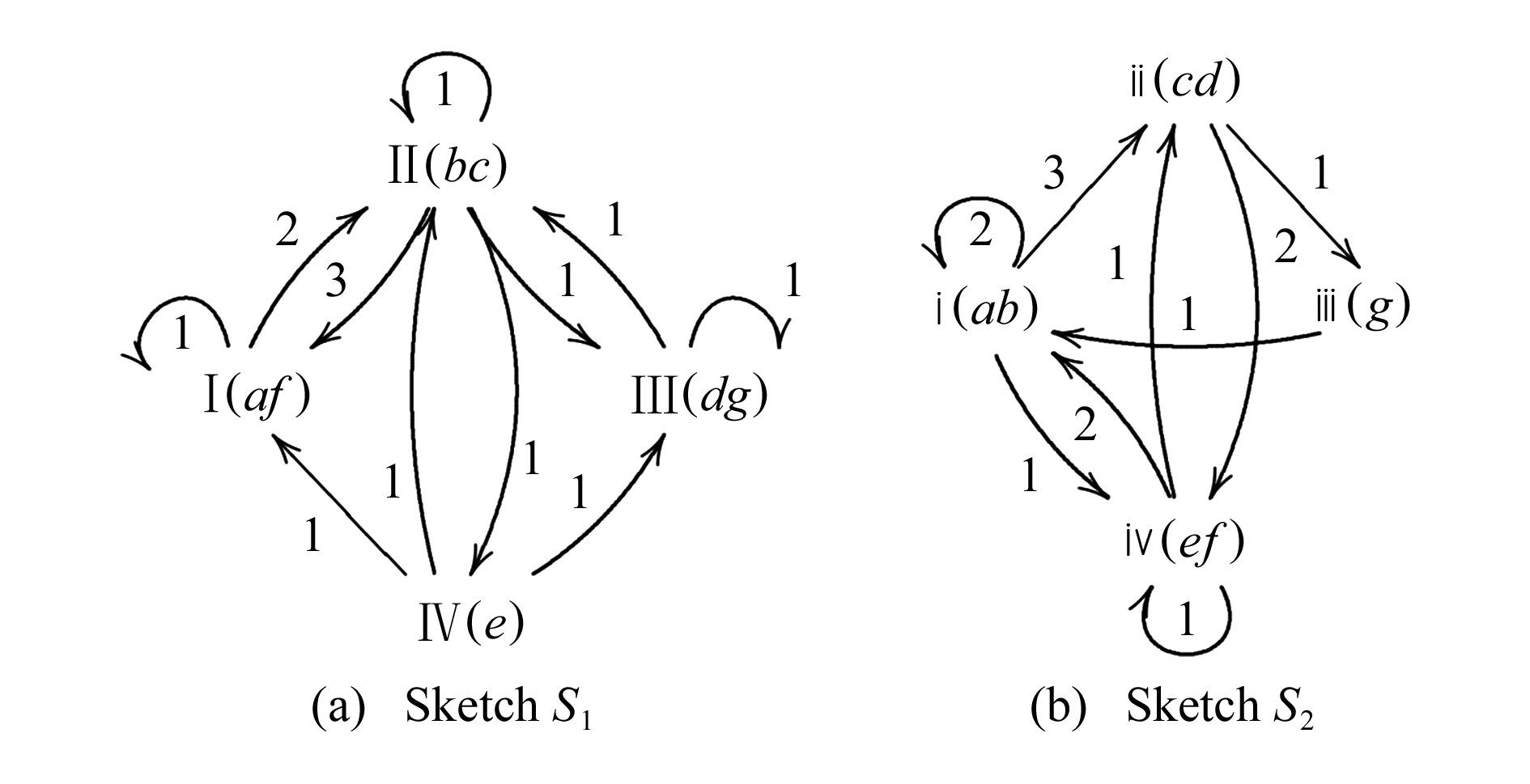
Fig. 8 Iterative steps of cost model[54]
图8 TCM模型概要图[54]
TCM模型在查询优化方面比基于频率计数或者单一样本的概要图更优越,同时在针对各种类型的流数据处理时,其自身具备更好的适用性和普遍性.
Bandyopadhyay等人[55]提出的一种基于局部邻域最小散列的可扩展概要图,使用k个散列函数维护一个最小邻居顶点的采样子图,对于每一个散列函数选取具有最小散列值的数据作为局部样本,滤除单个数据流中的频繁更新对采样偏斜的影响.然后,对于相同散列函数产生的样本,选取具有最小散列值的样本作为全局样本,完成局部样本集在中心顶点的合并,滤除在分布顶点上的重复更新对样本偏斜的影响,同时可以导出图结构的无偏估计量,例如三角形.如图9所示,散列函数的结果H1:1,5,2,4,3;H2:4,1,5,2,3;此时更新矩阵Mk和计数表C,当新来一条边(i,j)时,判断H1(j)<H1(M1(i,1)),是则更新M(i,1)=j,同理下一步更新M(j,1),然后更新第2列.C表则统计了每一顶点的更新次数,从Mk到G*,则直接根据每一行的顶点构造有向图,最后利用对称性还原原始图.
1.3 基于模式可视化的图概要
基于可视化的概要方法通过删除或合并不重要的顶点或边缘对原始图进行高度的抽象描述,产生一个可直观理解的概要图,帮助用户在特定应用场景下理解分析原始图的实际意义.这里的概要图由原始顶点和边缘的子集组成.通常,基于可视化[56]生成概要图主要有基于顶点边缘的可视化和基于模式结构可视化2种策略.
基于顶点边缘的可视化是通过特定顶点的语义对网络进行剪枝、结构抽象或性质过滤,比较典型的有OntoVis[57],一种依靠顶点过滤的视觉分析工具,用于分析不同的大型异构社交网络,使用与社交网络相关联的本体中的信息从语义上修剪大的异构网络[58],获得语义抽象.除语义抽象外,OntoVis允许用户进行结构抽象和重要性过滤,使用统计度量来评估顶点类型之间的连通性和相关性,以使大型网络易于管理分析.
文献[59]提出了一种无监督的机制,可用于自我中心信息抽象,根据网络子结构自动筛选,即k-hop邻域渐进地构建了一个自我中心抽象图,允许用户可视化结果.针对与OntoVis相同类型的图形,采用边缘而不是顶点过滤,提出了一种无监督机制建立中心抽象图.
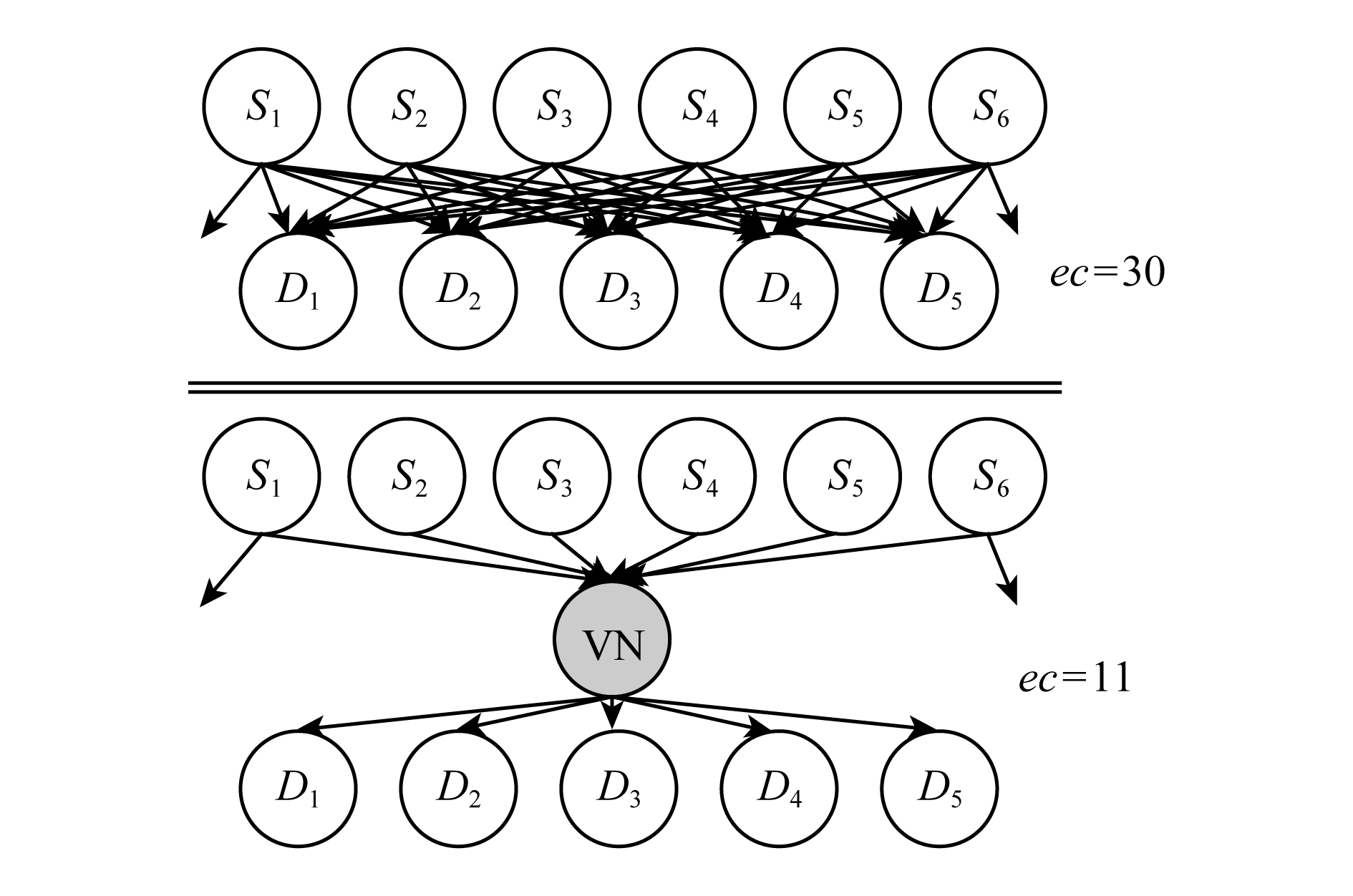
Fig. 10 VNM graph summarization
图10 VNM概要化
虚拟顶点挖掘(virtual node miner, VNM)[60]是Web图形的有损压缩方案,VNM使用频繁挖掘方法通过将每个顶点的出入边作为事务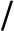 项集来提取有意义的连接.对于每个循环模式,它从其顶点中删除链接,并在S中生成一个新的顶点(虚拟顶点),添加一个出边,从而允许增量图表更新.相关地,引入了主题简化的思想来增强网络可视化,其中顶点和链接的常见模式被紧凑的字形替换以帮助可视化和了解实体及其属性之间复杂的关系,如图10所示,原始图共30条边,添加VN后只需要11条边,并完整地保留原始图信息.
项集来提取有意义的连接.对于每个循环模式,它从其顶点中删除链接,并在S中生成一个新的顶点(虚拟顶点),添加一个出边,从而允许增量图表更新.相关地,引入了主题简化的思想来增强网络可视化,其中顶点和链接的常见模式被紧凑的字形替换以帮助可视化和了解实体及其属性之间复杂的关系,如图10所示,原始图共30条边,添加VN后只需要11条边,并完整地保留原始图信息.
基于模式结构的可视化是面向图形挖掘应用领域和用户兴趣形成的一些特殊的图形概要方法,为了满足特定的需求,以一个或多个固定的结构作为核心特征合并成超顶点,寻找“异常”模式,通过可视化揭露实体属性的特征关系.
Motif[61]是一种依靠图简化技术,利用网络中的重复图案来减少可视化的复杂性,提高可阅读性.该技术采取易于理解的结构来替换网络中的图案,结构必须具有3个特征:1)需要较少的屏幕空间,确保可视化的阅读性;2)易于理解的结构性;3)可展示隐藏的关系.文献[61]中提出2个结构:扇形图案和并行图案,并设计有效的算法进行可视化,如图11所示:
Fig. 11 Motif: graph summary of sector structure[61]
图11 Motif:扇形结构的概要化[61]
文献[62]基于MDL原理,将原始图拆分为多个可能重复的子图,再与6种基本结构词汇表匹配压缩,分别是星、链、完全团、近似团、二分核、近似二分核.每一步压缩的过程中追求代价最小化,最后选择多个算法结合提出的质量度量依次选择候选结构,生成最适合的概要模型,图12显示了维基百科的编辑网络图的可视化结果,旨在发现用户争议分歧最大的相关主题.

Fig. 12 Wikipedia editor conflict war visualization[62]
图12 维基百科编辑-冲突战争可视化[62]
针对动态图,基于模式挖掘的概要方法从时间数据中提取有意义的模式.TIME-C[63]描述了具有1组重要时间结构的大型动态图.文献[63]的作者将时间图概要问题正式转化为信息理论优化问题,其目标是确定时间行为的局部静态结构,最小化动态图的全局描述长度.它引入了很多基于时间行为的词典(闪烁、周期、单词),主要分为4步:1)识别每个时间戳中的静态结构;2)使用静态词典标记它们;3)链接在一起查找时间结构;4)时间词典标记它们;5)选择最小化描述时间成本的时间结构.缝合静态结构对应于进化跟踪,其通过迭代奇异值分解(SVD)处理以找到潜在的时间相干结构,然后利用余弦相似性度量所发现的结构的时间相干性.
1.4 基于影响扩散的图概要

Fig. 13 Cluster graph of COARSENET[67]
图13 COARSENET的聚类图[67]
影响和扩散趋势分析是图挖掘长期研究的重点,其本质是随着时间演变,如何在动态网络中总结影响扩散的主要过程.基于影响扩散的图概要旨在寻找原始大图中影响力的动态描述,方便理解影响传播的模式,主要通过概要化过程中维持优化与应用相关的信息实现.
影响和扩散过程本质上是时间的演变对社会网络的影响.OSNet[64]总结了动态图中有趣的扩散过程.输入时间有序的交互流,表示为标记顶点间的无向边.OSNet的目标是在有向图中捕获级联(即扩散过程,如新闻传播),从而显示动态的流动.输出概要图由原始输入图中“有趣”顶点的子图组成,其中将兴趣定义为顶点扩散程度的线性组合(即扩散过程中感染的顶点数量),以及最大“传播半径”(即从扩散过程根到顶点的路径长度).OSNet的关键思想是:1)构建传播树;2)通过其熵和阈值来计算摘要的特征表现.文献[65]侧重于了解社会团体随着时间推移的集体活动.该文作者提出了通过多图(用户照片、用户评论、照片标签和评论标签图)非负矩阵分解[66]来提取活动主题,以获得用户和概念的潜在空间.潜在空间中的顶级用户和术语定义了与活动主题相对应的“重要”动作,应用余弦相似性来随着时间的演变跟踪主题.
一种近线性时间算法COARSENET[67]使用评分技术反复合并2个相邻顶点对获得加权图,寻找对网络扩散性能影响不大的边缘,使得概要图保留其主要性质,实验表明其空间缩小至原始图的10%而不会丢失主要信息.为了表示网络的扩散特性,最近的研究表明当邻接矩阵的第一特征值为与原始图的第一特征值相似时表明它们是自然相近的,当合并顶点对时需要重新对边进行权值计算,权值的更新取其删减边缘和邻接边的平均值,选择使特征值变化最小的顶点(阈值限制)对进行合并.如图13所示,计算当前原始图每一条边的评分,当特征值变化低于阈值时用实线框标注,视为一次成功的合并,高于阈值时则用虚线框标注,视为一次失败的合并,其中顶点4,5,8,9,12,15合并为超点,6,11合并为超点,右侧则显示了一次迭代后的概要图.
文献[68]基于图谱理论提出了一个图概要框架,对于大型图而言,具有相近光谱特性的网络图具有相似的结构模式,并提出光谱距离来度量概要图与原始图的结构相似性.其中光谱距离定义为
SD(G,Gs,l)=![]()
(7)
其中,λ为归一化拉普拉斯矩阵的特征值,光谱距离将粗化图的特征值与原始网络的头尾进行比较,参数l则控制匹配的位置.
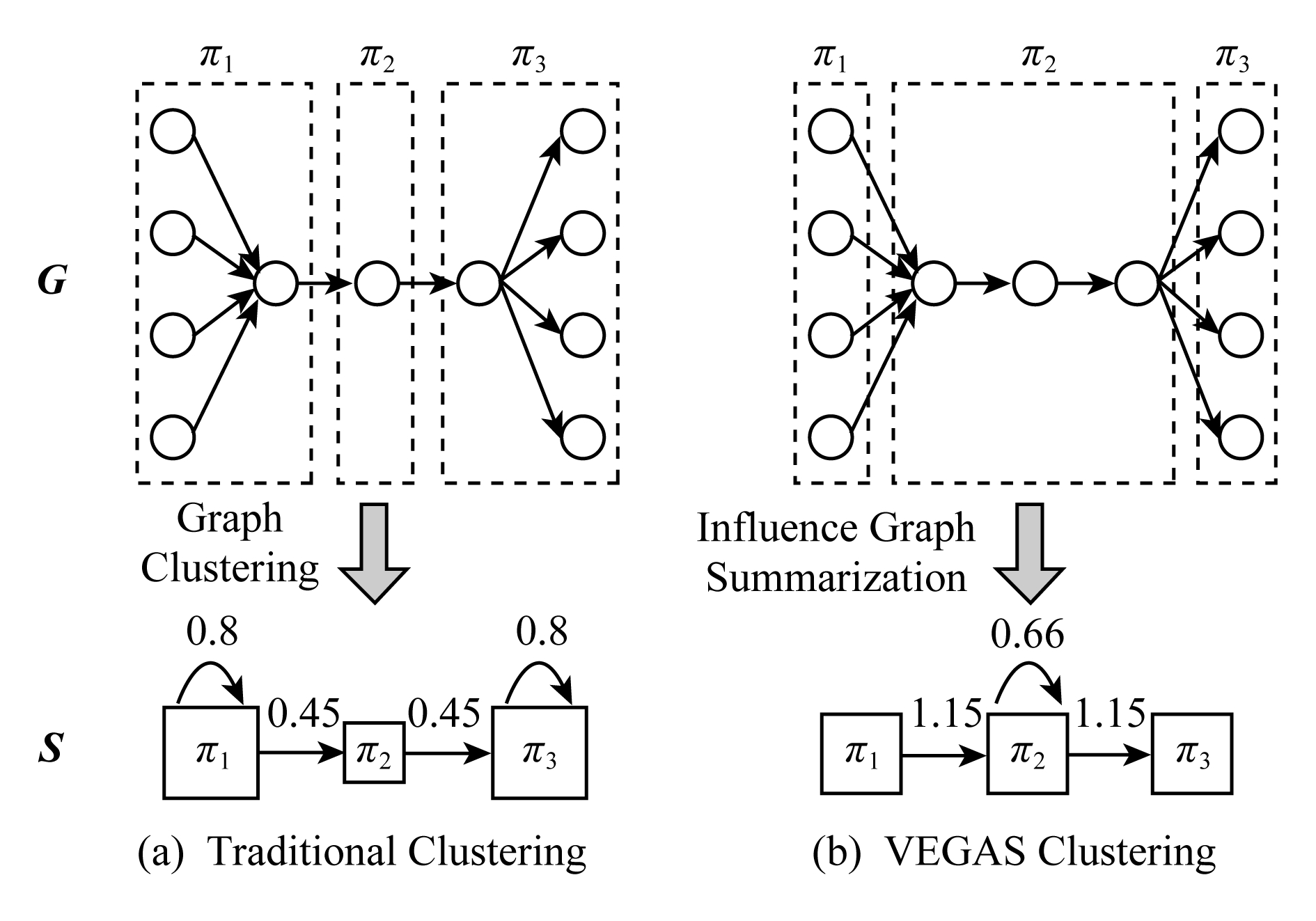
Fig. 14 Difference between VEGAS and traditional clustering
图14 VEGAS聚类和传统的图聚类的区别
VEGAS[69]是一个典型的针对引文网络图的最大化影响分析的概要方法,其核心算法是基于k-means,通过矩阵分解生成概要图,并支持基于流的影响模式,支持丰富的属性信息扩展.为了流影响的最大化,生成的顶点簇内的一致性不再取决于密集的内部连接,而是由同一簇中的高度顶点拓扑相似性来定义.在这个目标中,跨越群集的边缘会比传统方法更多,从而突出描绘影响模式的流程.如图14所示,假设原始图存在统一的权值,原始图中虚线框内顶点聚类为概要图中的正方形超点,超点上方标记了影响流的大小,左侧是传统的图聚类,导致了更大的影响内流,其值是0.8,而右侧的VEGAS聚类,则更好地表示了群内和群间的影响流.
1.5 图概要算法小结
为了综合比较主流的图概要方法,本节对1.1~1.4节提到的各类算法从输入图的类型、结构、参数、输出图等进行综合比较,比较结果如表1所示:
Table 1 Comparison of Graph Summarization Methods
表1 图概要方法对比

CategoryMethodInput GraphUnweightedWeightedUndirectedDirectedHomogeneousHeterogeneousDynamicParameter-freeLinearOutputSpatialCompressionQueryOptimizationImpactAnalysisVisualizationEDS[70]√××√√×××√Structure List WGC[28]×√√√√××××Super GraphSZIP[71]√√√×√×××√Compressed GraphCosum[32]√√√××√×√√Super GraphMDL-R[34]√×√√√××√×Super GraphGRAC[29]√×√×√××××Super GraphAGSUM[40]√×√×√××√√Super GraphREF[72]√×√√√××√×Super GraphGBASE[73]√√√√√×××√Compressed GraphSAC[74]√√√×√××√√Super GraphS-Entropy[41]√×√×√××√√Super Graphk-SNAP[45]√×√√√××√√Super GraphTCM[54]√×√××√√××Temporal StructuresGRASS[43]√×√×√××××Super GraphCANAL[46]√×√√√××√×Super GraphG-sketch[53]√×√√√×√√×Structure ListBortik[55]√×√√√×√××Structure ListS2A[44]√×√×√×√××Super GraphG-Dedensified[36]√×√√×√×√√Sparsified GraphOSNet[64]√×√×√×√×√Temporal StructuresCOARSENT[67]×√×√√×××√Super GraphSPINE[65]×√×√√××××Sparsified GraphVEGAS[69]√√×√√×××√Super GraphVNM[60]√××√√××××Sparsified GraphTIME-C[63]√×√×√√√×√Structure ListMotif[61]√×√×√√×××Sparsified GraphOntoVis[57]√×√××√×√√Sparsified GraphVOG[59]√×√×√×√√√Structure List
Notes:“√” stands for support; “×” stands for non-support.
表1主要从输入图的类型区分加权图、无权图、有向图、无向图、同质图、异构图以及是否需要给定参数和时间复杂度来区分各个图概要技术,其中√代表支持,×代表不支持.
1) 大部分主流概要技术应用于无向无权的简单图数据,针对加权和异构图的概要技术较少.
2) 在基于空间压缩的图概要技术中,支持加权图的概要技术一般采用图聚类的思想,但能胜任异构网络概要化的研究方法比较匮乏.
3) 在查询优化的图概要技术中尚未考虑到加权图的查询,大部分方法的算法复杂度是非线性的,只解决了某些特定查询的优化,在动态图流上图概要查询优化技术取得不小的进展,领先于其他应用领域的动态概要技术.
4) 影响分析的图概要技术除了OSNet外,都是针对有向图,无需输入参数,能客观地分析网络结构中顶点间的影响关系,实际应用中影响分析扩散传播往往需要考虑时间粒度.
5) 模式可视化的概要技术不支持加权的图数据,除了VNM算法外,都是针对无向图,算法TIME-C和Moitif能同时处理同构图和异构图.
2 分布式环境下的图概要化
随着图数据规模的扩大、属性的多样化和结构的复杂化,有学者开始致力于分布式图概要的研究.当前关于分布式下图形概要化的工作刚刚起步,相关文献较少.分布式图概要主要面临3个问题:
1) 由于顶点和边缘分布在不同的设备内存中,集中式图形摘要算法中看似简单的操作需要在分布式环境中跨多个顶点的消息传递和仔细协调.
2) 集中式算法不需要担心计算如何分布,但是一个好的分布式图表汇总方法应该在不同的机器上完全分配计算,以实现高效的并行化.
3) 计算量和通信成本成为分布式图概要的主要因素.
文献[75]首次提出了分布式下的图概要,在Apache Graph上实现了3种分布式算法:1)第1种对应于文献[34]的集中式贪心策略,寻找超级顶点对,但造成了大量的通信和计算成本.2)第2种采用随机策略寻找顶点对,但随机性负面地影响了概要的准确性.3)第3种为Dist-LSH,采用Striped-minhash的技术,新增了权值归一化处理,快速比较2个集合的相似度,直接找出合适的候选人进行检查,从而完全消除了与不必要检查相关的计算和网络成本.如图15所示,将权重向量{ai:wi}作为输入除以权值范围[0,1]进行归一化处理,以顶点个数作为桶数进行区域划分,如图15中w1=0.53,给定集合A和B,在每个纵轴上应用不同的散列函数,如果散列到同一桶中则视为命中1次,总的命中次数越高则代表集合的相似性越高,即采用这种方案寻找最相似的加权候选集.
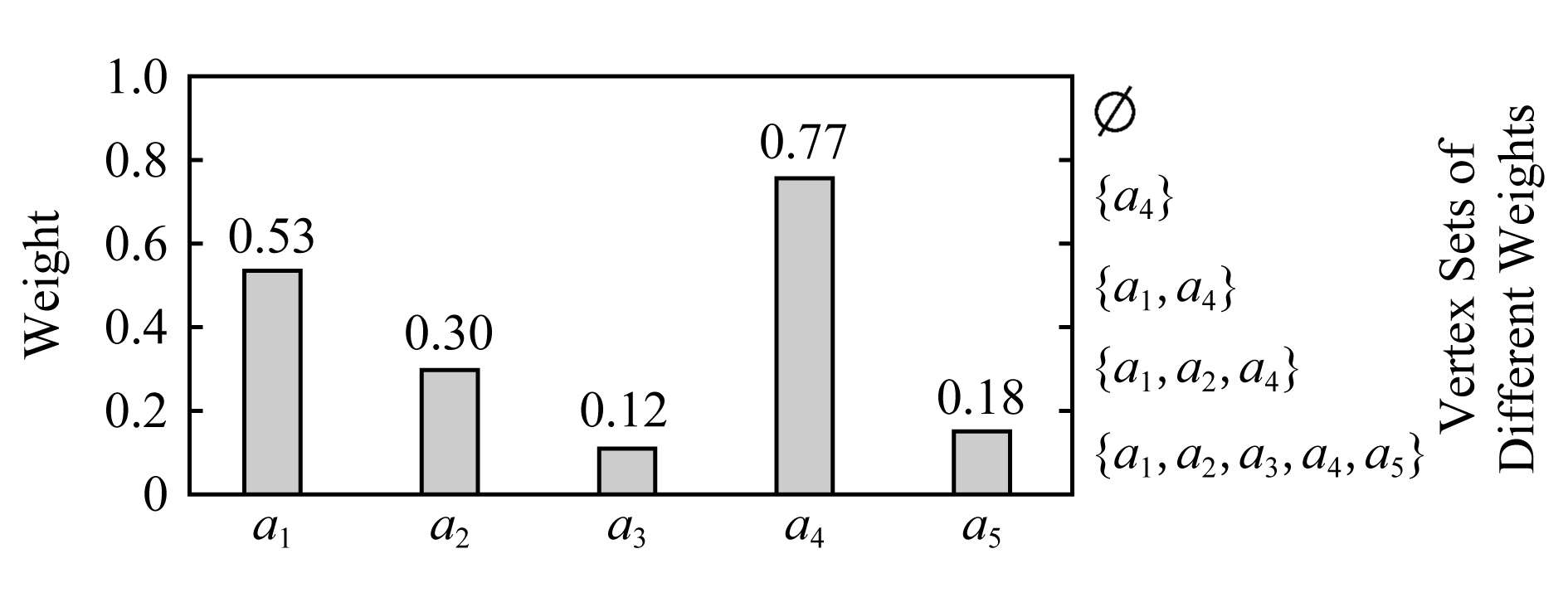
Fig. 15 Normalization of Striped-minhash weights
图15 R=5时Striped-minhash权值归一化
文献[76]提出了一种新的度量主干的概念来提高大型图形数据的分析效率,度量主干即为保留权值的最短路径的最小子图,用于替代原始图精确或近似进行各个指标的度量.计算度量主干需要解决所有顶点对的最短路径问题 (all-pairs-shortest-paths, APSP)问题,该文献通过算法避免APSP并证明了半度量子图依然能提升计算性能.同时,可作为一种有损压缩机制,半度量边数量作为存储的边.最后给出了算法在Apache Graph上的分布式实现:1)检测第1阶半度量边;2)迭代标记局部度量边;3)标记所有剩余的度量边.
3 部分图概要算法实验
图的概要化是一个相对广泛的概念,其核心技术本身与用户的兴趣和应用目的紧密联系,导致不同应用领域的概要技术无法客观地对比,原因在于解决主要问题的技术方案不同,不同维度的评价指标无法展示各个图概要技术的优越性.
相对而言,基于空间压缩的概要图技术,核心任务基本一致,对比的指标相同.本文在无属性的图上选取了经典的基于MDL压缩的MDL-R[34],REF[72],GBASE[73],GRAC[29]四种算法进行了实验性能的比较.
1) MDL-R.第1个基于MDL的压缩概要技术,虽然在大型图数据下效率偏低,但提供了高质量的概要图.
2) REF.一个流行的Web压缩技术,该方法由2个逻辑部分组成:第1部分减少每个顶点邻居列表的大小;第2部分使用复杂的比特级编码进行压缩.为了实验对比的公平性,去除比特级编码运行该算法.
3) GBASE.一个针对大型图存储压缩的查询优化系统方案,本研究只采用其压缩技术——块存储编码,将邻接矩阵转换为二进制字符串.
4) GRAC.加权图的图聚类算法,将给定的加权图进行划分使得权重最小.
实验的数据集为CNR,RouteView,Wordnet,Facebook四种数据集.
1) CNR.该网络是从CNR域网爬虫提取的,由有向边转化为无向边,最大的CNR数据集具有10万顶点和40万余条边.
2) RouteView.这是一个表示Internet拓扑系统的模型,这个数据集是由俄勒岗大学路线视图项目组收集,大约具有1万个顶点和3万条边.
3) Wordnet.自然语言处理应用程序中常用的英语单词的大型词汇数据库,将每个单词对应于1个顶点,如果每个单词具有相近或包含或前置的关系,则顶点之间存在边,该图大约有7万个顶点和12万条边.
4) Facebook.该数据集是2005年康奈尔大学从自身大学社区提取的Facebook网络图,有1.5万顶点和14万条边,每个顶点存在边即表示学生之间为朋友关系.

Fig. 16 Experiment on information retention rate and compression ratio of non-attribute graph
图16 无属性图信息保持率和压缩率的对比实验
图16显示了无属性图上4种算法的信息保持率和压缩率的实验结果.信息保持率上,GRAC的性能相对优越,值得关注的是REF在Facebook数据集上几乎没有丢失信息,但结合压缩率指标可知,该现象是由压缩效果不理想引起.对于另外2种算法,概要化过程中为了追求一定的压缩率都采取了误差阈值进行扩展:MDL-R在各类数据集上均可以取得最大化压缩的结果,主要原因在于根据MDL信息理论,其在迭代压缩过程中始终基于贪心策略寻找最大化压缩顶点,而GRAC的压缩效果相对最差, Facebook数据集由于其顶点和边缘的高度比,压缩性明显最差.值得关注的是GRAC在该数据集上效果最好,其核心是基于聚类的分区思想,在这种高度密集的图数据上更有优势.
图17是针对无属性图的运行时间比较.MDL-R时间开销最大,因为采用贪心策略,重心永远关注在如何全局最大化降低成本上,MDL-R可以扩展基于局部最优的随机策略进行概要化,减少时间开销的增大,其生成的概要模型忽略了顶点存储的自身信息.在时间代价上GRAC表现最为优异,主要通过权值相同聚类降低有限的成本,但缺陷在于需要重复给定分类参数,寻找合适的压缩率.
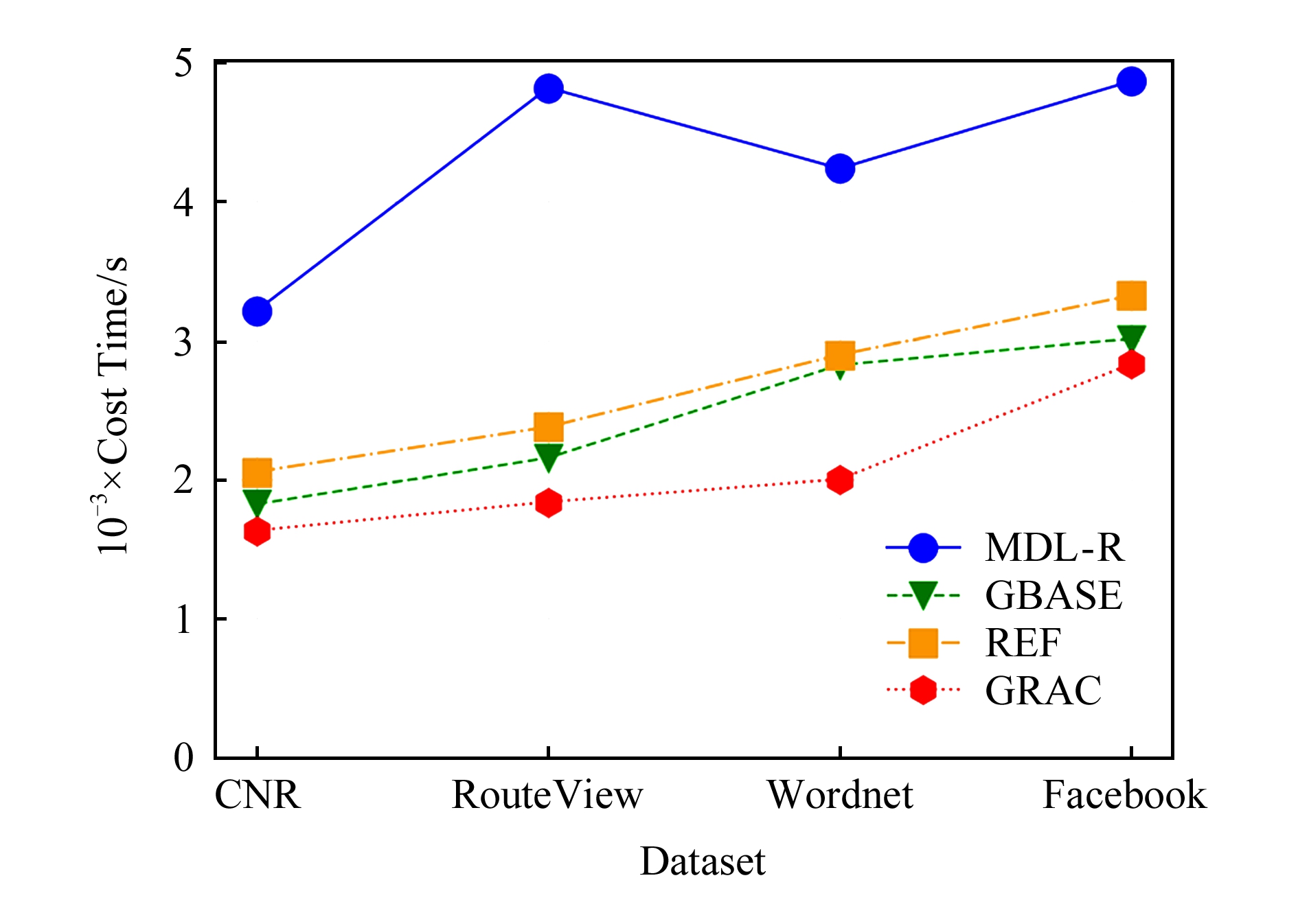
Fig. 17 Experiments on time cost of non-attributed graphs
图17 无属性图时间代价的对比实验
在属性图上进行了实验,选取压缩率、属性熵[77]以及时间代价进行对比.算法选择SAC[74],K-SNAP[45],AGSUM[40],S-Entropy[41]这4种算法.
1) SAC.一种针对属性图的聚类算法,通过随机游走距离度量属性相似性和结构相似性.
2) K-SNAP.第1个基于用户属性分组进行概要技术的经典方案.
3) AGSUM.在K-SNAP基础上进一步优化了结构一致性的压缩.
4) S-Entropy.是一种基于属性熵和结构熵的统一模型,产生近似同质分区.
数据集采用Political Books(PB)和DBLP[78]数据集.
1) Political Books(PB).政治家的博客数据集,具有1 500顶点、2万条边和3个属性,其中平均度8.
2) DBLP.是计算机领域内以作者为核心的一个计算机类英文文献的数据库系统,按年代列出了作者科研成果、国际期刊和会议等发表的论文.实验选择的数据集包括3个DBLP数据集,DBLP1只包含选定的数据库出版物,具有7 000顶点和2万条边,DBLP2新增了AL出版物,具有1.5万个顶点和3.8万条边,DBLP3包含了所有会议和期刊的出版物,具有10万顶点和24万条边.
图18显示了4种图概要技术在属性图上压缩率和信息熵的实验.在图18(b)熵的指标上K-SNAP性能最好,主要原因在于K-SNAP单纯通过顶点的属性进行概要汇总,未考虑网络的结构,因此结构性能上表现最差,压缩率最高;而AGSUM充分考虑了属性和结构的一致性,生成了紧凑的概要图,压缩率降低,熵比较大是因为牺牲了属性的一致性;SAC是基于距离的一般聚类方法,将属性顶点转化为增广顶点,导致不同属性的顶点放在一起从而产生较高的熵;S-Entropy基于熵的维度平衡结构和属性一致性,概要图的结构性能降低.
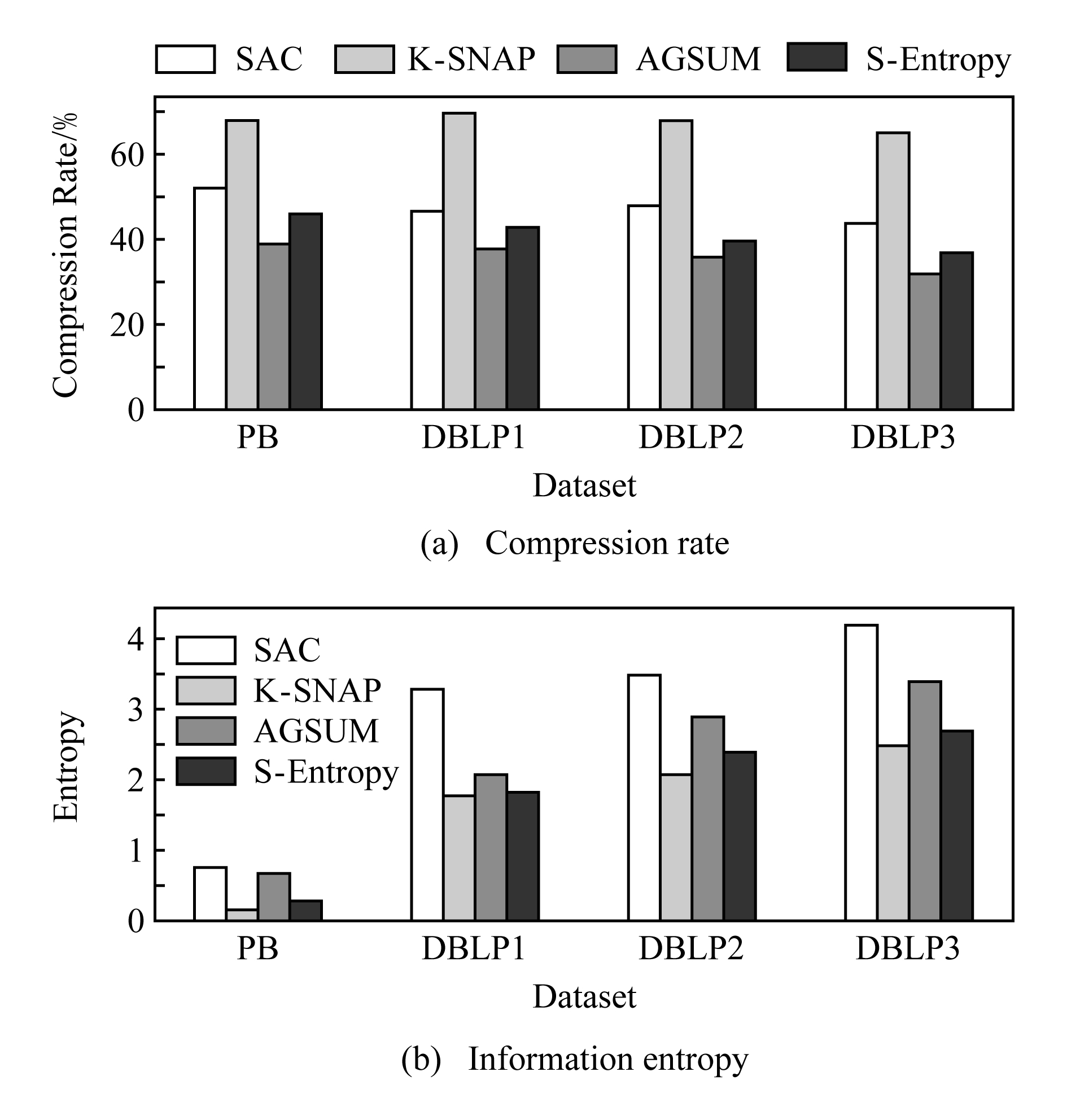
Fig. 18 Experiments on entropy and compression ratio of attribute graph
图18 属性图信息熵和压缩率的对比实验
由图19可知,K-SNAP时间开销最低,主要原因是只考虑一个维度的概要化,计算量明显低于其他方法;S-Entropy比其他性能更为优异.随着数据集的增大,S-Entropy的时间性能更接近线性增长,表明了该技术在大型数据集上良好的扩展性,相比较AGSUM,S-Entropy更重视属性的一致性,对于结构熵的度量缺乏更多有力的说明,这也是概要技术评价需要考虑的标准之一.
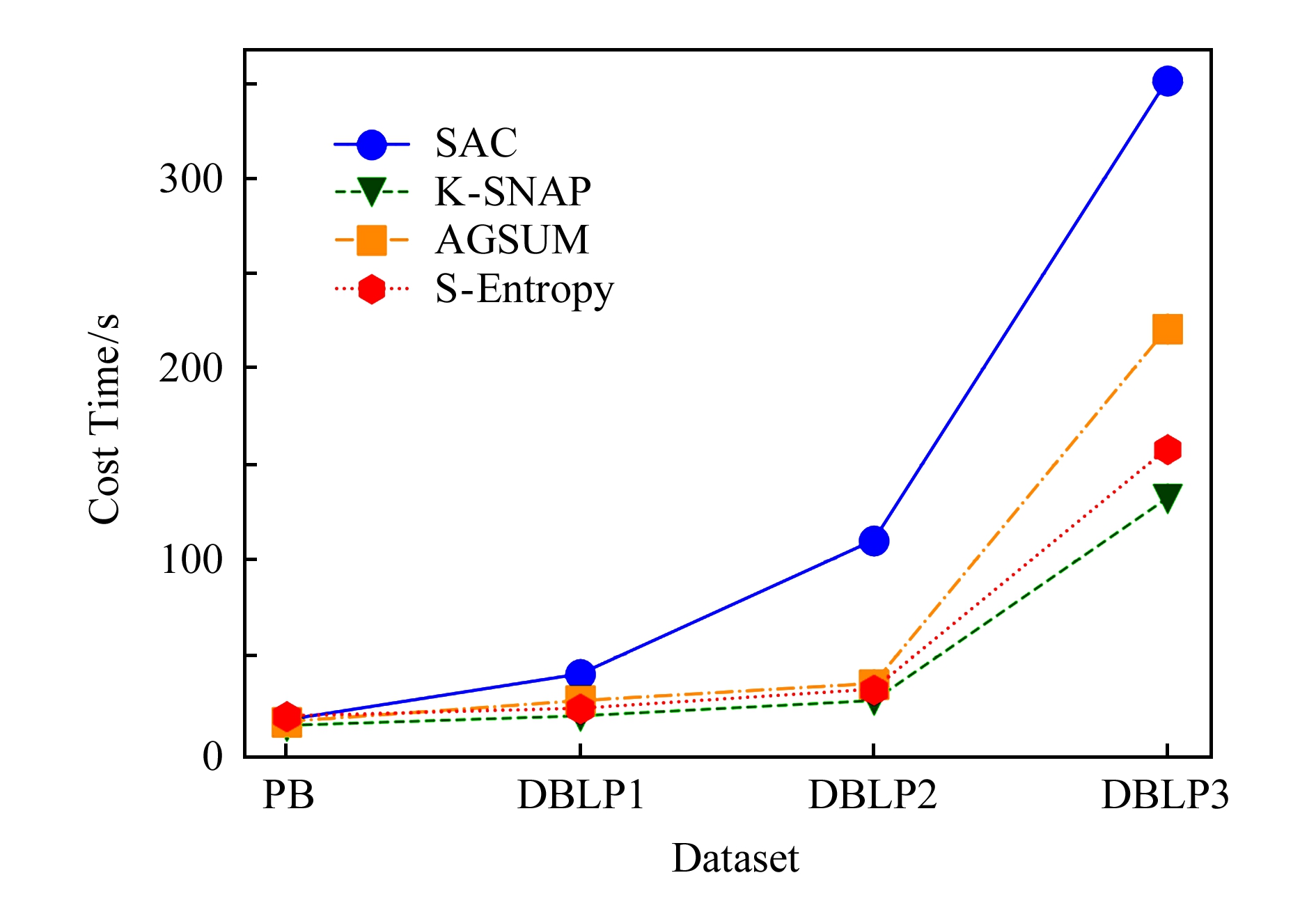
Fig. 19 Experiments on time cost of attribute graph
图19 属性图时间代价的对比实验
4 图概要应用
随着互联网的迅速发展,实际生活中图数据量不断增加,研究者识别大规模图数据的模式和隐藏意义的困难持续增加,从而影响决策过程.图概要技术为理解和识别图数据中的结构和意义提供了可能.图概要的应用与现实生活紧密联系、息息相关,主要有5个方面的应用领域:
1) 减少数据量和存储空间.现实世界图形数据集往往极为庞大,例如Facebook的社交网络超过30亿的用户,每天邮件的发送投递超过1 000亿,这些应用所产生的图数据已经超出内存的限制,大多数图算法无法直接作用于原始图去提炼潜在的结构特征.图概要技术下的社交网络图具有更小的空间,且让研究者在更高层次对原始图进行分析研究,准确揭露隐藏结构.
2) 图数据的查询优化.大量通用的图数据查询算法在解决庞大的复杂数据图时面临着效率低下、准确性降低的弊端,特定的概要技术可以极大提高查询的效率和准确性,例如社交网络图上最经典的查询可能询问2个顶点是否存在边或者路径.这样的查询通过邻接矩阵概要化技术可以比最先进的图查询算法提速50倍,减少平均错误率.其他类似的提高查询效率的有三角形查询、权重估计等.然而,针对常见的查询尚缺乏能取得优化效果的通用型图概要技术.
3) 可视化分析.在交互式图形界面领域,图概要技术作为可视化的重要手段,解决原始图过大而无法加载到屏幕的弊端,帮助用户直观地理解原始图的结构特征,加速分析.比较经典的可视化技术,通过结合用户自身的兴趣结构,给定一些特殊的结构去压缩原始图,例如文献[61]通过一些特定词汇结构针对维基百科编辑图进行可视化,旨在寻找用户分歧较大的主题,这往往能发现许多额外的有趣现象.
4) 影响分析和扩散.部分文献通过图概要技术,试图寻找大型图中影响力的动态扩散模式,以便理解影响传播的模式和重要条件,一般结合实际背景维持一些与影响有关的全局因子并捕捉变化模式,经典应用有网络作品的影响力分析[68]、社交图谱的概要化[79]、图表抽象从模拟异构犯罪数据集中提取影响流、高效识别犯罪团伙.
5) 噪声过滤和隐私保护.真实的图数据通常是大规模、具有很多噪声的数据,例如错误的连接或者标签属性,这种数据阻碍了分析,隐藏了重要信息,增加了数据工作的处理量.概要化技术有利于滤除噪声,揭示隐藏模式.同样,针对现实网络图的真实信息,概要技术可以滤出与应用需求无关的部分用户敏感信息,加强对用户的隐私保护[49].
5 存在的问题及挑战
近年来,尽管涌现了许多图数据概要方面的研究工作,但该领域仍然是新兴的,需要更多的深入研究,目前尚面临许多问题和挑战:
1) 图概要化评价标准的确立[80-81].图数据的概要化是一个相对广泛的概念,尚没有明确的定义,其本身是依赖于用户的兴趣和应用需求,不同应用领域的概要技术无法直观地对比,因此缺乏统一标准的概要评估技术.如果概要化的目的是为了解决存储空间的限制,可以采用压缩率、信息保持率等评价标准;当概要化是为了加速图形算法的查询效率,则评估的标准应是查询时间、准确度等;当概要化是为了图的可视化,则评价指标更加难以度量.本文调查表明,应用背景和目的需求相近时的图概要技术,才能依照统一的评价指标衡量算法的优劣,例如本文的实验针对空间压缩的应用需求,压缩率、信息保持率以及时间代价可以作为衡量指标.当前还没有统一的评价指标对各种图概要技术进行评价,考虑到概要技术的应用性,可以针对其概要技术提出一个多领域评估框架,囊括主流的概要技术,根据应用需求选择适应的评估方案,这也是图概要领域的研究者当前亟需确立的任务.
2) 基于动态图流的概要化[82].现实世界中的社交网络是基于时间维度的,对于这类图概要需要捕获随时间变化的结构和属性的模式[83].然而,针对动态图流的概要技术尚未得到充分的探索,当前部分模型通过嵌入技术将顶点投影到低维向量空间,并保持其顶点的结构相似性.现实生活中,Facebook用于发送消息所形成的社交网络、网络服务器之间的链接和消息流动、智能家居设备之间的信号传递都可以被视为动态图流.图流中每个顶点具有自己的邻接矩阵,通过矩阵的更新提取顶点随着时间变化的动态特征并进行个性化分析是图流概要化的核心技术.然而,增加时间维度将面临更多的挑战:如何描述随着时间推移而形成的动态图形的结构特征?如何滤除冗余的变化?如何根据实际应用需求捕捉合适的时间窗口,确定图流对时间的敏感度,这都是导致动态图概要研究进展缓慢的原因.动态图流的概要化无法用单一的概要图描述其空间特征和时间特征,而是需要一系列概要图序列描述其变化趋势.未来工作可以借助机器学习领域的Boosting思想,构建概要图序列,初始概要图代表初始时间窗口的特征(树),下一时刻概要图描述矫正信息(图流更新信息),通过一系列概要图序列拟合动态图流的变化趋势,描述并预测动态图流的结构特征.时间窗口的选取可通过偏方差和惩罚项制定损失函数,自适应地调整,避免过拟合,提升概要图序列对图流特征描述的泛化能力.
3) 异构信息网络的图概要[84].当前大多数关于网络科学、社交和信息网络的研究,普通是同构网络,即网络中的顶点都是相同实体类型的对象,并且链接都是相同类型的关系.这些研究获得了许多有趣的结果以及众多有重要影响的应用.然而,实际中大多数网络是异构的(heterogeneous)[85],即网络中的顶点和关系并不是相同类型的.例如,在一个医疗保健预测网络中,顶点可以是病人、医生、检查、疾病、药物、医院、治疗措施等,构建出顶点类型不同的异构网络.而现有的图概要技术多是基于相同顶点类型的同构网络,由于顶点实体类型的多样化和结构的复杂化,无法移植到异构网络中,但针对异构网络建模可以捕获真实世界中最根本的语义信息.有2种策略可以帮助建立异构网络的图概要,一是借鉴现有的属性与结构的相似性转化操作,将异构网络中不同的实体类型以增加属性域的方法转化为同一实体的不同属性,从而将异构网络转化为同构网络来处理;二是将异构网络拆分为多个同构网络分别进行概要化操作,提取隐藏的模式结构,揭示不同顶点之间的隐藏关系,不失为一种有效策略.目前针对异构网络的概要化技术尚未得到足够的关注.
4) 分布式图概要技术的扩展[86].当前的图概要技术,大多采取单个进程内存处理所有的任务.随着图数据规模的指数级增长和信息结构的复杂化,尤其在处理千亿个顶点和边时,单机的概要化技术往往陷入数据灾难.分布式环境能提供更多的存储内存,并行计算能极大地提高概要化效率.目前,分布式下的概要技术尚未得到重视,这主要取决于计算和通信成本的严峻挑战.首先顶点和边缘分布在不同的内存中,因此集中式图概要技术看似简单的操作,需要在分布式环境中跨越多个顶点进行消息传递和仔细协调.其次,单机的概要算法不需要考虑计算资源的分配,而一个优秀的分布式下图概要技术应该充分利用每一个机器,以实现高效的并行化计算,克服这些挑战.通过设计轻量级的过滤交互算法,在每一次迭代前对图数据进行预处理,可避免不必要的计算和通信开销,分布式下的概要技术更能胜任大图流下的计算分析,图概要领域的研究者更应重视这一方向的工作.
5) 图概要的低维嵌入表示[87].近年来以深度学习(deep learning)[88]为代表的表征学习方法在语音识别、图像理解以及机器翻译等任务上取得了巨大的成功.这些方法通过设计多层的非线性神经网络从原始数据提取有效特征,整个模型从数据的原始输入到目标任务的最终输出,实现了端到端的学习.由于深度学习等表征学习方法在多个领域的有效性,近年来涌现了大量的致力于面向网络结构数据的表征学习的工作.深度学习网络表征学习算法的目标是获得网络的低维稠密表示,对于大规模网络(如社会网络),网络表征学习的目标是把网络中的每个顶点表示成为一个低维稠密的向量并且保证在这个低维空间上能够很好地保留网络的拓扑结构.顶点表示能够当作顶点的特征用于顶点分类、顶点聚类、网络可视化、链接预测等不同的任务,本质上是通过保留网络的局部结构性来估计顶点的表示.概要技术可以引入其思想,将图数据的特征映射到低维向量空间中进行概要化,这种充满潜力的方案似乎更能解决大型复杂网络的概要化难点.
[1]Cheng Xueqi, Jin Xiaolong, Wang Yuanzhuo, et al. Survey on big data system and analytic technology[J]. Journal of Software, 2014, 25(9): 1889-1908 (in Chinese)(程学旗, 靳小龙, 王元卓, 等. 大数据系统和分析技术综述[J]. 软件学报, 2014, 25(9): 1889-1908)
[2]Zhang Yu, Liu Yanbing, Xiong Gang, et al. Survey on succinct representation of graph data[J]. Journal of Software, 2014, 25(9): 1937-1952 (in Chinese)(张宇, 刘燕兵, 熊刚, 等. 图数据表示与压缩技术综述[J]. 软件学报, 2014, 25(9): 1937-1952)
[3]Bonchi F, Castillo C, Gionis A, et al. Social network analysis and mining for business applications[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): No.22
[4]Kistler M, Perrone M, Petrini F. Cell multiprocessor communication network: Built for speed[J]. IEEE Micro, 2006, 26(3): 10-23
[5]Newman M E. The structure of scientific collaboration networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2000, 98(2): 404-409
[6]Crovella M E, Bestavros A. Self-similarity in world wide Web traffic: Evidence and possible causes[J]. ACM SIGMETRICS Performance Evaluation Review, 1996, 24(1): 160-169
[7]Holm D B, Eriksson K, Johanson J. Business networks and cooperation in international business relationships[J]. Journal of International Business Studies, 1996, 27(5): 1033-1053
[8]Nagurney A. A multiclass, multicriteria traffic network equilibrium model[J]. Mathematical & Computer Modelling, 2000, 32(3): 393-411
[9]Ruan Tong, Feng Donglei, Li Jing. Research on information filtering model based on Bayesian network[J]. Journal of Computer Research and Development, 2002, 39(12): 1564-1571 (in Chinese)(阮彤, 冯东雷, 李京. 基于贝叶斯网络的信息过滤模型研究[J]. 计算机研究与发展, 2002, 39(12): 1564-1571)
[10]Tan Lu, Jiang Lu. Systems biology and biological networks[J]. Complex Systems and Complexity Science, 2005, 2(4): 1-9 (in Chinese)(谭璐, 姜璐.系统生物学与生物网络研究[J]. 复杂系统与复杂性科学, 2005, 2(4): 1-9)
[11]Shen Jinping. Statistical report on Internet development in China[OL]. [2018-12-03]. http://www.techweb.com.cn/internet/2017-01-22/2478300.shtml(沈金萍. 中国互联网络发展状况统计报告[OL]. [2018-12-03]. http://www.techweb.com.cn/internet/2017-01-22/2478300.shtml)
[12]Tang Jie, Shen Huawei. Review and prospect of social network computing[OL]. [2018-12-03]. http://www.360doc.com/content/17/1122/10/49955868_706086795.shtml(唐杰, 沈华伟. 社会网络计算的回顾与展望[OL]. [2018-12-03]. http://www.360doc.com/content/17/1122/10/49955868_706086795.shtml)
[13]Seyyedi S H, Minaei-Bidgoli B. Estimator learning automata for feature subset selection in high-dimensional spaces, case study: Email spam detection[J]. International Journal of Communication Systems, 2018, 31(8): e3541
[14]Newman M E, Forrest S, Balthrop J. Email networks and the spread of computer viruses[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2002, 66(3): 035101
[15]Liu Yike, Safavi T, Dighe A, et al. Graph summarization methods and applications: A survey[J]. ACM Computing Surveys, 2018, 51(3): 62-64
[16]Aggarwal C, Wang H. Graph data management and mining: A survey of algorithms and applications[M] //Managing and Mining Graph Data. Berlin: Springer, 2010: 13-68
[17]Pan Qiuping, You Jinguo, Zhang Zhipeng, et al. Progress and challenges of graph aggregation and summarization techniques[J]. Journal of Software, 2015, 26(1): 167-177 (in Chinese)(潘秋萍, 游进国, 张志朋. 等. 图聚集技术的现状与挑战[J]. 软件学报, 2015, 26(1): 167-177)
[18]Shneiderman B, Dunne C. Interactive network exploration to derive insights: Filtering, clustering, grouping, and simplification[C] //Proc of the 20th Int Conf on Graph Drawing. Berlin: Springer, 2012: 2-18
[19]Escolano F, Curado M, Biasotti S, et al. Shape simplification through graph sparsification[C] //Proc of the 11th Int Workshop on Graph-Based Representations in Pattern Recognition. Berlin: Springer, 2017: 13-22
[20]Ahmed N K, Duffield N, Neville J, et al. Graph sample and hold: A framework for big-graph analytics[C] //Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2014: 1446-1455
[21]Kong Xiangnan, Wei Fan, Philip S. Dual active feature and sample selection for graph classification[C] //Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2011: 654-662
[22]Hao Yin, Benson A R, Leskovec J, et al. Local higher-order graph clustering[C] //Proc of the 23rd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2017: 555-564
[23]Schaeffer S E. Survey: Graph clustering[J]. Computer Science Review, 2007, 1(1): 27-64
[24]Abbe E. Graph compression: The effect of clusters[C] //Proc of the 54th Annual Allerton Conf on Communication, Control, and Computing. Piscataway, NJ: IEEE, 2016: 1-8
[25]Zhao Danfeng, Zhang Yiyi, Lin Junchen, et al. Query of marine big data based on graph compression and views[C] //Proc of the 2018 Int Conf on Data Mining Workshops (ICDMW). Piscataway, NJ: IEEE, 2018: 252-257
[26]Lin Shoude, Yeh M Y, Li Chengte. Sampling and summarization for social networks[OL]. [2018-12-03]. https://mslab.csie.ntu.edu.tw/tut-pakdd13/samsum-pakdd13.pdf
[27]Damnjanovic A, Montojo J, Wei Yongbin, et al. A survey on 3GPP heterogeneous networks[J]. Wireless Communications IEEE, 2011, 18(3): 10-21
[28]Toivonen H, Zhou F, Hartikainen A, et al. Compression of weighted graphs[C] //Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2011: 965-973
[29]Dhillon I, Guan Yuqiang, Kulis B. A fast kernel-based multilevel algorithm for graph clustering[C] //Proc of the 11th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2005: 629-634
[30]Stella X Y, Shi Jianbo. Multiclass spectral clustering[C] //Proc of the 9th IEEE Int Conf on Computer Vision. Los Alamitos: IEEE Computer Society, 2003: 313-326
[31]Krishna K, Murty M N. Genetic K-means algorithm[J]. IEEE Transactions on Systems, 1999, 29(3): 433-439
[32]Zhu Linhong, Ghasemi-Gol M, Szekely P, et al. Unsupervised entity resolution on multi-type graphs[C] //Proc of the Int Semantic Web Conf. Berlin: Springer, 2016: 649-667
[33]Barron A, Rissanen J, Yu Bin. The minimum description length principle in coding and modeling[J]. IEEE Transactions on Information Theory, 1998, 44(6): 2743-2760
[34]Navlakha S, Rastogi R, Shrivastava N. Graph summarization with bounded error[C] //Proc of the 2008 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2008: 419-432
[35]Khan K U, Nawaz W, Lee Y K. An efficient algorithm for MDL based graph summarization for dense graphs[J].Contemporary Engineering Sciences, 2014, 7(16): 791-796
[36]Lim Y, Kang U, Faloutsos C. SlashBurn: Graph compression and mining beyond caveman communities[J]. IEEE Transactions on Knowledge & Data Engineering, 2014, 26(12): 3077-3089
[37]Maccioni A, Abadi D J. Scalable pattern matching over compressed graphs via dedensification[C] //Proc of the 22nd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2016: 1755-1764
[38]Khan K U, Nawaz W, Lee Y K. Set-based unified approach for attributed graph summarization[C] //Proc of the 4th IEEE Int Conf on Big Data and Cloud Computing. Piscataway, NJ: IEEE, 2015: 378-385
[39]Dong Wei, Wang Zhe, Josephson W, et al. Modeling LSH for performance tuning[C] //Proc of the 17th ACM Conf on Information and Knowledge Management. New York: ACM, 2008: 669-678
[40]Wu Ye, Zhong Zhinong, Xiong Wei, et al. Graph summarization for attributed graphs[C] //Proc of the 2014 Int Conf on Information Science, Electronics and Electrical Engineering. Piscataway, NJ: IEEE, 2014: 503-507
[41]Liu Zheng, Yu Xu, Cheng Hong. Approximate homogeneous graph summarization[J]. Journal of Information Processing, 2012, 20(1): 77-88
[42]Seo H, Park K, Han Y, et al. An effective graph summarization and compression technique for a large-scaled graph[J]. Journal of Supercomputing, 2018, 10(12): 1-15
[43]LeFevre K, Terzi E. GraSS: Graph structure summarization[C] //Proc of the 2010 SIAM Int Conf on Data Mining. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2010: 454-465
[44]Riondato M, García-Soriano D, Bonchi F. Graph summarization with quality guarantees[J]. Data Mining and Knowledge Discovery, 2017, 31(2): 314-349
[45]Tian Yuanyuan, Hankins R A, Patel J M. Efficient aggregation for graph summarization[C] //Proc of the 2008 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2008: 567-580
[46]Zhang Ning, Tian Yuanyuan, Patel J M. Discovery-driven graph summarization[C] //Proc of the 26th Int Conf on Data Engineering. Piscataway, NJ: IEEE, 2010: 880-891
[47]Shoaran M, Thomo A, Weber-Jahnke J H. Zero-knowledge private graph summarization[C] //Proc of the 2013 IEEE Int Conf on Big Data. Piscataway, NJ: IEEE, 2013: 597-605
[48]Miao Qiguang, Wang Baoshu. Image fusion method based on improved Laplace pyramid transform[J]. Journal of Optics, 2007, 27(9): 1605-1610 (in Chinese) (苗启广, 王宝树. 基于改进的拉普拉斯金字塔变换的图像融合方法[J]. 光学学报, 2007, 27(9): 1605-1610)
[49]Hassanlou N, Shoaran M, Thomo A. Probabilistic graph summarization[C] //Proc of the 14th Int Conf on Web-Age Information Management. Berlin: Springer, 2013: 545-556
[50]Shrivastava A, Li Ping. In defense of minhash over SimHash[J]. arXiv preprint arXiv:1407.4416, 2014
[51]Cormode G, Muthukrishnan S. An improved data stream summary: The count-min sketch and its applications[J]. Journal of Algorithms, 2005, 55(1): 58-75
[52]Cohen E, Kaplan H. Tighter estimation using bottom k sketches[J]. Proceedings of the VLDB Endowment, 2008, 1(1): 213-224
[53]Zhao Peixiang, Aggarwal C C, Wang Min. gSketch: On query estimation in graph streams[J]. Proceedings of the VLDB Endowment, 2011, 5(3): 193-204
[54]Tang Nan, Chen Qing, Mitra P. On summarizing graph streams[J]. arXiv preprint arXiv:1510.02219, 2015
[55]Bandyopadhyay B, Fuhry D, Chakrabarti A, et al. Topological graph sketching for incremental and scalable analytics[C] //Proc of the 29th ACM Int on Conf on Information and Knowledge Management. New York: ACM, 2016: 1231-1240
[56]Lee B, Plaisant C, Parr C S, et al. Task taxonomy for graph visualization[C] //Proc of the 2006 AVI Workshop on Beyond Time and Errors: Novel Evaluation Methods for Information Visualization. New York: ACM, 2006: 1-5
[57]Shen Zeqian, Ma K L,Eliassiard T, et al.Visual analysis of large heterogeneous social networks by semantic and structural abstraction[J]. IEEE Transactions on Visuali-zation and Computer Graphics, 2006, 12(6): 1427-1439
[58]Barthelemy M, Chow E, Eliassirad T. Knowledge representation issues in semantic graphs for relationship detection[C] //Proc of the 2005 AI Technologies for Homeland Security. Menlo Park: AAAI, 2005: 91-98
[59]Li Chengte, Lin Shoude. Egocentric information abstraction for heterogeneous social networks[C] //Proc of the 2009 Int Conf on Advances in Social Network Analysis and Mining. Piscataway, NJ: IEEE, 2009: 255-260
[60]Buehrer G, Chellapilla K. A scalable pattern mining approach to Web graph compression with communities[C] //Proc of the 2008 Int Conf on Web Search and Data Mining. New York: ACM, 2008: 95-106
[61]Dunne C, Shneiderman B. Motif simplification: Improving network visualization readability with fan, connector, and clique glyphs[C] //Proc of the SIGCHI Conf on Human Factors in Computing Systems. New York: ACM, 2013: 3247-3256
[62]Koutra D, Kang U, Vreeken J, et al. Summarizing and understanding large graphs[J]. Statistical Analysis & Data Mining, 2015, 8(3): 183-202
[63]Shah N, Koutra D, Zou Tianmin, et al. TimeCrunch: Interpretable dynamic graph summarization[C] //Proc of the 21st ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2015: 1055-1064
[64]Qu Qiang, Liu Siyuan, Jensen C S, et al. Interestingness-driven diffusion process summarization in dynamic networks[M] //Machine Learning and Knowledge Discovery in Databases. Berlin: Springer, 2014: 597-613
[65]Lin Yuru, Sundaram H, Kelliher A. Summarization of social activity over time: People, actions and concepts in dynamic networks[C] //Proc of the 17th ACM Conf on Information and Knowledge Management. New York: ACM, 2008: 1379-1380
[66]Padilla P, Lopez M, Gorriz J M, et al. NMF-SVM based CAD tool applied to functional brain images for the diagnosis of Alzheimer’s disease[J]. IEEE Transactions on Medical Imaging, 2012, 31(2): 207-216
[67]Purohit M, Prakash B A, Kang C, et al. Fast influence-based coarsening for large networks[C] //Proc of the 20th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2014: 1296-1305
[68]Yu Jin, JaJa J F. Network summarization with preserved spectral properties[J]. arXiv preprint arXiv:1802.04447, 2018
[69]Lei Shi, Huang Tongtong, Tang Jie, et al. VEGAS: Visual influence graph summarization on citation networks[J]. IEEE Transactions on Knowledge & Data Engineering, 2015, 27(12): 3417-3431
[70]Maserrat H, Jian Pei. Neighbor query friendly compression of social networks[C] //Proc of the 16th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2010: 533-542
[71]Yongwook C, Wojciech S. Compression of graphical structures: Fundamental limits, algorithms, and experiments[J]. IEEE Transactions on Information Theory, 2012, 58(2): 620-638
[72]Boldi P, Vigna S. The webgraph framework I: Compression techniques[C] //Proc of the 13th Int Conf on World Wide Web. New York: ACM, 2004: 595-602
[73]Kang U, Tong Hanghang, Sun Jimeng, et al. Gbase: A scalable and general graph management system[C] //Proc of the 17th ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2011: 1091-1099
[74]Zhou Yang, Cheng Hong, Yuxu. Clustering large attributed graphs: An efficient incremental approach[C] //Proc of the 10th IEEE Int Conf on Data Mining. Piscataway, NJ: IEEE, 2011: 689-698
[75]Liu Xingjie,Tian Yuanyuan,He Qi, et al. Distributed graph summarization[C] //Proc of the 23rd ACM Int Conf on Information and Knowledge Management. New York: ACM, 2014: 799-808
[76]Kalavri V, Simas T, Logothetis D. The shortest path is not always a straight line: Leveraging semimetricity in graph analysis[J]. Proceedings of the VLDB Endowment, 2016, 9(9): 672-683
[77]Li Ronglu, Wang Jianhui, Chen Xiaoyun, et.al. Chinese text classification based on maximum entropy model[J]. Journal of Computer Research and Development, 2005, 42(1): 94-101(李荣陆, 王建会, 陈晓云, 等. 使用最大熵模型进行中文文本分类[J]. 计算机研究与发展, 2005, 42(1): 94-101)
[78]Ley M. The DBLP computer science bibliography: Evolution, research issues, perspectives[C] //Proc of the 9th Int Symp on String Processing and Information Retrieval. Berlin: Springer, 2002: 1-10
[79]Mehmood Y, Barbieri N, Bonchi F, et al. CSI: Community-level social influence analysis[C] //Proc of the 2013 Joint European Conf on Machine Learning and Knowledge Discovery in Databases. Berlin: Springer, 2013: 48-63
[80]You Jinguo, Pan Qiuping, Shi Wei, et al. Towards graph summary and aggregation: A survey[G] //Social Media Retrieval and Mining. Berlin: Springer, 2013: 3-12
[81]Pouriyeh S, Allahyari M, Liu Qingxia, et al. Graph-based ontology summarization: A survey[J]. arXiv preprint arXiv:1805.06051, 2018
[82]Fei Hao, Park D S. Sketch: A novel framework for capturing cliques from big graph[J]. The Journal of Supercomputing, 2018, 74(3): 1202-1214
[83]Cormode G, Cormode G, Muthukrishnan S. Summarizing and mining skewed data streams[C] //Proc of the 2005 SIAM Int Conf on Data Mining. Philadelphia, PA: SIAM, 2005: 44-55
[84]Yu Xiaodong, Chawla N V, Swami A. metapath2vec: Scalable representation learning for heterogeneous networks[C] //Proc of the 23rd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2017: 135-144
[85]Kong Xiangnan, Philip S Y. Graph classification in heterogeneous networks[G] //Encyclopedia of Social Network Analysis and Mining. Berlin: Springer, 2014: 641-648
[86]Khan A, Bhowmick S, Bonchi F, et al. Summarizing static and dynamic big graphs[J]. Proceedings of the VLDB Endowment, 2017, 10(12): 1981-1984
[87]Chuan Shi, Hu Binbin, Xin Zhao, et al. Heterogeneous information network embedding for recommendation[J]. arXiv preprint arXiv:1711.10730, 2017
[88]Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444



