聚类方法按照“物以”的原则将数据对象划分为不同的簇,并保持簇间数据元素间的距离尽可能地大、簇内数据元素间的距离尽可能地小,进而抽取数据对象中蕴含的模式结构.聚类分析无须借鉴数据的先验知识,仅根据数据的实际分布情况即可得到自然的数据划分,在认识数据中的不确定性和价值的隐蔽性方面具有重要的研究价值.然而,随着信息技术的迅猛发展和广泛应用,具有典型多源异构特性的跨媒体数据已经遍布生活的各个角落.跨媒体数据是指以不同模态、来源、空间等形式出现,但具有相似的高层语义的数据.如图1所示,相同的新闻可以用多种语言进行报道[1];同一幅图像可以在形状、纹理、颜色等特征空间上获得异构的描述[2];同一概念或事件可用图像、文本、视频、音频等不同类型的媒体共同表达[3];传统聚类方法在做数据分析时仅考虑单模态的数据信息,已经无法适应跨媒体数据的特征异构性.

Fig. 1 The typical cross-media data
图1 典型的跨媒体数据
跨媒体聚类(cross-media clustering, CMC)[4]是一种基于数据驱动的分析方法,旨在根据不同模态数据的分布相似性,同时聚类多个模态以揭示不同模态间的潜在关联.跨媒体聚类任务的核心问题在于捕捉多模态数据间的关联性,以实现信息的跨模态共享.针对此问题,较为直观的解决方法是寻找多模态数据的公共子空间.例如文献[5]提出基于典型关联分析(canonical correlation analysis, CCA)[6]的跨媒体聚类算法,该算法将多个模态的特征投影到低维的子空间上;文献[7]使用共享核嵌入、文献[8]使用高斯过程隐式变量模型学习多模态间的共享特征.然而,基于子空间的跨媒体聚类方法将各模态的特征映射到低维空间的同时,会破坏跨媒体数据的原始结构,导致一些重要信息的丢失.除了学习多模态共享子空间之外,近年来相关研究人员也提出了一些行之有效的跨媒体聚类策略.文献[9]使用层次模型[10](hierarchical model)自底向上地构建文本和视觉特征间的关联,进而在聚类过程中结合跨媒体特征;文献[11]首先将图像分割为区域的集合,此时,若将图像视为文档,则每个图像区域类似于文档中的单词,之后通过主题模型隐含狄利克雷分布(latent Drichlet allocation, LDA)[12]将文本与视觉信息转化为一种跨模态的向量表示;文献[2]提出多模态谱聚类算法,自动地结合图像数据的多种异构特征表示;文献[13]提出多视角联合矩阵分解方法,通过学习多视角数据的公共系数矩阵寻求多视角之间兼容的聚类划分;文献[14]提出鲁棒的多视角k-means方法,用来处理大规模数据的多种异构特征表示.然而,上述跨媒体数据聚类分析方法仅依赖各模态间的共享信息建立多模态数据的关联,忽略了各模态自身的私有信息,这显然与实际应用情况不符.
另外,机器学习领域中的集成聚类(consensus clustering, CC)方法可有效地处理多模态数据,引起了跨媒体研究人员的关注.集成聚类方法在处理跨媒体数据时,首先根据单模态的数据分布得到其自身的聚类划分(基聚类),之后按照特定的合并准则将不同模态的聚类划分进行合并,从而将多个模态的异构信息进行融合,得到最终的聚类划分.例如文献[15]设计基于相似簇、超图、集群3种一致性度量函数合并基聚类;文献[16]提出基于稀疏图表示和概率轨迹的聚类集成算法,同时根据基聚类的局部和全局信息获取最终的聚类划分;文献[17]在不考虑原始数据分布的情况下,通过局部密度估计方法对基聚类进行加权,进而区分基聚类的可依赖程度.然而,现有的集成聚类在处理跨媒体数据时忽略原始数据的特征分布,仅依赖基聚类构建最终的聚类划分,导致最终的聚类划分过度依赖基聚类的质量.
针对上述问题,本文提出共享和私有信息最大化(share and private information maximization, SPIM)的跨媒体聚类算法.如图2所示,该算法通过兼顾跨媒体数据间的共享信息和各媒体数据自身的私有信息进行聚类分析,以求得更加合理的聚类模式结构.首先,提出混合单词模型(hybrid words model, H-words)和聚类集成模型(clustering ensemble model, CE)构建跨媒体数据的2种共享信息,分别保持各模态底层特征的统计相似性和各模态的高层聚类划分间的相关性.其次,提出基于信息论的目标函数,将跨媒体数据的共享和私有信息融合在同一目标函数中.同时处理各模态自身的私有信息(原始特征)和聚类集成模型构建的共享信息(聚类划分),有助于克服集成聚类算法对基聚类的过度依赖.最后,采用顺序“抽取-合并”优化过程,保证SPIM算法的目标函数收敛到局部最优解.在6种跨媒体数据上的实验结果表明SPIM算法性能优于现有方法.本文的主要贡献总结为3个方面:
1) 提出共享和私有信息最大化的跨媒体聚类算法SPIM,该算法通过兼顾跨媒体数据的共享和私有信息,以求得更加合理的模式结构.
2) 提出2种跨媒体数据的共享信息构建模型:混合单词模型和聚类集成模型,分别保持各模态底层特征的统计相似性和各模态的高层聚类划分间的相关性.
3) 提出基于信息论的目标函数,并采用顺序“抽取-合并”优化策略对该目标函数进行优化,保证其收敛到局部最优解.
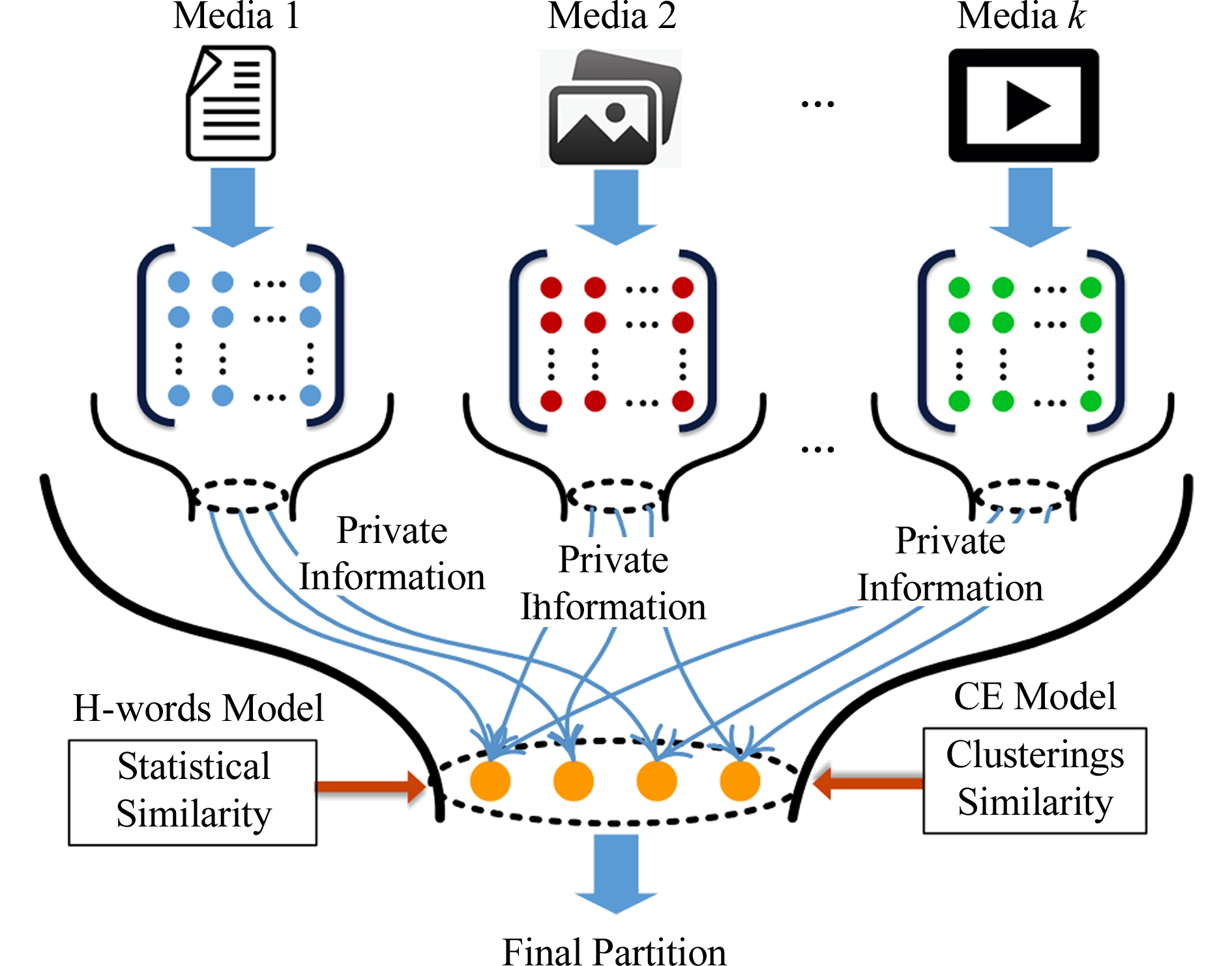
Fig. 2 The illustration of SPIM method
图2 SPIM方法示意图
本文工作与文献[18-19]中的多特征信息瓶颈(multi-feature information bottleneck, MfIB)算法、文献[20]中的多视角概念学习(multi-view concept learning, MCL)算法、文献[21]中的跨媒体社交图像聚类(cross-media social image clustering, CSIC)算法关联较为密切.其中MfIB算法是信息瓶颈(information bottlenede, IB)算法的扩展,该算法使用互信息量化聚类模式与多个特征间的信息量,然而,该算法要求多种特征表示来自同一数据分布,无法处理跨模态的异构特征.MCL算法和CSIC算法采用多模态数据的共享特征和独有特征进行跨模态分析.其中,MCL算法学习多模态数据的概念性隐式空间,并将该隐式空间分解为共享和独有2个部分.然而,该算法是半监督算法,无法处理聚类问题.CSIC算法将社交图像中视觉和社交标签信息的共享特征空间学习视为一个共轭词典学习问题,通过L1, 范数的正则项保证各模态的词典稀疏化,这种稀疏化使得各模态的独有特征得以保留.然而,该算法需要借助WordNet获得辅助的社交语义关系,仅适用图像和文本2种模态数据,无法处理更多模态.近年来,深度神经网络在跨媒体数据的一致性表征中取得了较好的结果,例如多层次跨模态关联学习[22]、多网络共享表征[23].深度神经网络需要大量已标注的训练数据,然而,数据标签信息的获取是费时费力的过程.
范数的正则项保证各模态的词典稀疏化,这种稀疏化使得各模态的独有特征得以保留.然而,该算法需要借助WordNet获得辅助的社交语义关系,仅适用图像和文本2种模态数据,无法处理更多模态.近年来,深度神经网络在跨媒体数据的一致性表征中取得了较好的结果,例如多层次跨模态关联学习[22]、多网络共享表征[23].深度神经网络需要大量已标注的训练数据,然而,数据标签信息的获取是费时费力的过程.
1 背景知识
IB算法[24-25]是一种典型的基于信息最大化的数据分析方法[18-19,26].给定源变量X与特征变量Y之间的联合概率分布p(X,Y),IB算法力图寻求源变量X的最优压缩表示T,同时使压缩变量T最大化地保存特征变量Y中蕴含的关于源变量X的信息量.如图3所示,源变量X与其特征变量Y之间的信息通过压缩变量T进行保存.IB算法可形式化描述为
(1)
其中,p(t|x)是源变量X到压缩变量T之间的编码方案,I(X;T)是变量之间的互信息,D是X到T之间所有可能的编码方案.从式(1)可知,IB算法是在信息保存程度满足I(T;Y)≥D的条件下,寻找能够最小化I(X;T)的一个编码方案p(t|x).文献[22]给出IB算法的目标函数:
(2)
其中,β是拉格朗日乘数因子,用来平衡数据对象的压缩与相关信息的保存.在聚类任务中,簇的个数M往往远远小于原始数据对象的数量,即M≪|X|,这意味着源变量X与其压缩变量T之间存在大幅度压缩.因此,实际应用中通常将β设置为无穷大.这种做法的有效性在多种数据类型的聚类任务中得到验证,例如文本[25]、图像[18]、视频[26].因此,IB算法的目标函数可改写为
(3)
其中,互信息I(T;Y)度量压缩变量T与特征变量Y之间的信息量.
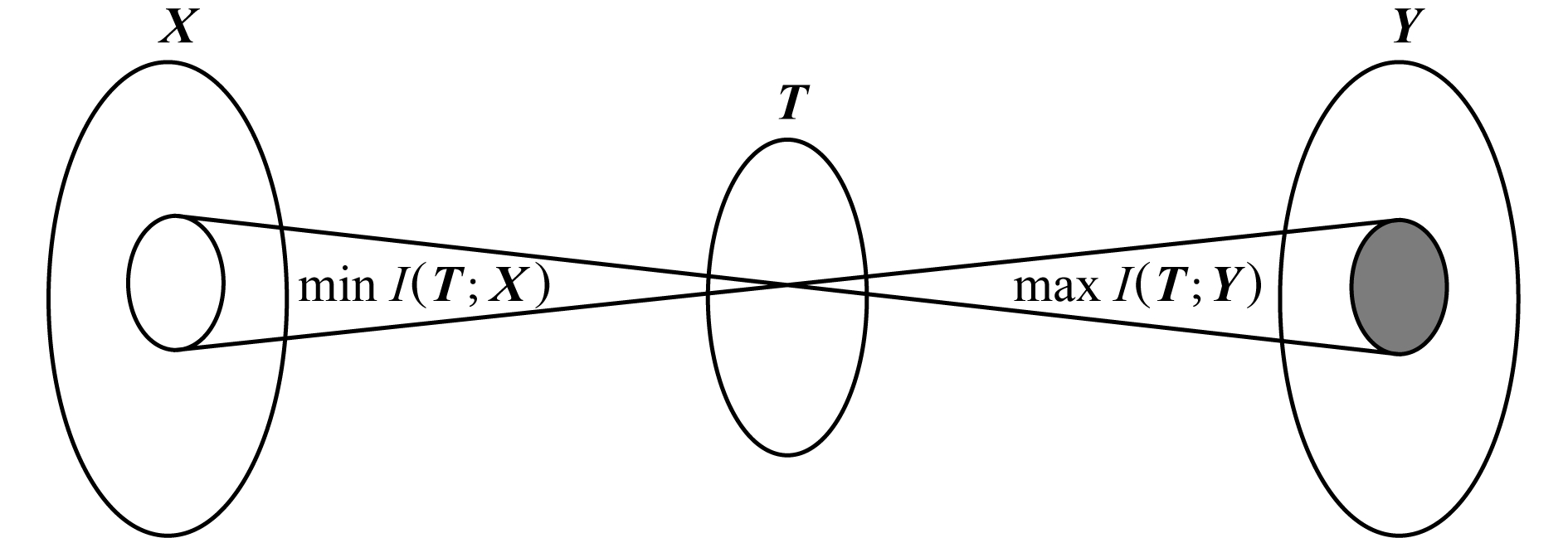
Fig. 3 The model of IB algorithm
图3 IB算法的模型图
2 共享和私有信息最大化的跨媒体聚类
本文提出共享和私有信息最大化的跨媒体聚类算法SPIM,该算法旨在兼顾跨模态数据间的共享信息和各模态自身的私有信息进行跨媒体聚类分析,以求得更加合理的模式结构.为了清晰地描述,本节首先给出SPIM算法的问题定义.
定义1. 使用源变量X=(x1,x2,…,xn)表示跨媒体数据对象的集合,使用私有变量Y1,Y2,…,Yk表示不同模态数据自身的私有信息(即各模态自身的特征表示,又称作源变量X的特征变量),使用共有变量S表示模态间的共享信息,其中,n是数据对象的数量,k是跨媒体数据的模态数量.SPIM算法的目标是寻求源变量X到压缩变量T的一种最优压缩表示p(t|x),在压缩过程中使压缩变量T同时最大化地保存与各模态自身的私有变量Y1,Y2,…,Yk和共有变量S间的信息.根据式(3),可给出SPIM目标函数:
(4)
其中,λ是控制私有信息与共享信息之间侧重程度的平衡参数.当λ=0且k=1时,SPIM算法回归至IB算法,因此,IB算法可视为SPIM算法的特例.
给定数据对象与其特征表示的联合概率分布,则压缩变量与各模态自身的私有变量之间的互信息![]() 是可计算的.为计算I(T;S),接下来首先给出2种跨媒体数据的共享信息构建模型.
是可计算的.为计算I(T;S),接下来首先给出2种跨媒体数据的共享信息构建模型.
2.1 混合单词模型
词库模型[27]是一种常用的数据表示方法,该方法可将跨媒体的各模态数据转换为单词或视觉单词出现频率的向量形式,例如一幅城市场景的图像可由高楼、街道、红绿灯等视觉单词出现频率表示;一则体育新闻可由比分、队员、场地等文字出现频率表示.在聚类任务中同时考虑不同模态数据的词频表示能在一定程度上刻画多模态间的关联性,但不同模态数据的词频向量在尺度上具有明显的差异,且存在较大的样本冗余.因此,本文提出混合单词H-words模型,首先将各模态的底层特征转换为统一的词频向量表示,然后使用自凝聚信息最大化方法自底向上地构建多模态的混合单词空间,抽取模态间的共享信息,最大化地保持各模态底层特征的统计相似性.

Fig. 4 The mutual information between two clusters of different modalities
图4 不同模态的聚类划分间的互信息
给定源变量X及其k个模态的私有变量Y1,Y2,…,Yk,其中,私有变量Yi的值域为![]() 为第i个模态的特征维度,
为第i个模态的特征维度,![]() 表示特征
表示特征![]() 在数据xj中出现的统计次数.因此,可以得到k个联合概率分布p(X,Y1),p(X,Y2),…,p(X,Yk).本文定义目标函数对混合单词空间
在数据xj中出现的统计次数.因此,可以得到k个联合概率分布p(X,Y1),p(X,Y2),…,p(X,Yk).本文定义目标函数对混合单词空间![]() 进行求解:
进行求解:
![]()
(5)
其中,![]() 是私有变量Yi到混合单词空间
是私有变量Yi到混合单词空间![]() 的映射.本文采用文献[26]中自底向上的层次模型对式(5)求解,该模型首先将每个数据元素视为单独的簇,即
的映射.本文采用文献[26]中自底向上的层次模型对式(5)求解,该模型首先将每个数据元素视为单独的簇,即![]() 其中
其中![]() 是混合单词空间的维度,|Yi|是第i个模态的特征个数.之后通过不断合并最相似的数据元素,可逐步降低
是混合单词空间的维度,|Yi|是第i个模态的特征个数.之后通过不断合并最相似的数据元素,可逐步降低![]() 的值,去除冗余特征.由于在自底向上的合并过程中最大化地保持各模态特征间的互信息,因此,我们称此过程为自凝聚信息最大化.假设yh,yg是私有变量Yi中的2个特征向量,则yh,yg合并前后式(5)的变化量计算为
的值,去除冗余特征.由于在自底向上的合并过程中最大化地保持各模态特征间的互信息,因此,我们称此过程为自凝聚信息最大化.假设yh,yg是私有变量Yi中的2个特征向量,则yh,yg合并前后式(5)的变化量计算为
(6)
其中,![]() 分别是将特征向量yh,yg合并前后式(5)的值.
分别是将特征向量yh,yg合并前后式(5)的值.
定义2. 合并yh,yg生成簇![]() 的概率计算为
的概率计算为
(7)
(8)
给出自凝聚信息最大化的详细执行过程:
1) 将每个特征点初始化为1个单独簇.
2) 计算所有特征对合并引起式(5)的改变量![]()
3) 合并满足![]() 的特征对.
的特征对.
4) 根据定义2更新![]() 直至达到事先给定的簇个数.
直至达到事先给定的簇个数.
2.2 聚类集成模型
为了进一步挖掘各模态间的关联关系,本文提出聚类集成CE模型,首先为各模态数据构建各自的聚类划分,然后使用互信息度量各模态高层聚类划分间的相关性,进而捕捉到多个模态的异构信息.
SPIM算法的目标是寻求源变量X中的压缩变量T,假设T中有M个簇T=(t1,t2,…,tM).根据源变量X的k个模态构建辅助聚类C=(C1,C2,…,Ck),并假设第l个模态的聚类划分Cl中同样具有M个簇![]() 假设ni为Cl中被划分至簇
假设ni为Cl中被划分至簇![]() 中的数据元素个数;nj为聚类划分T中划分到簇tj中数据元素个数;nij为同时属于簇
中的数据元素个数;nj为聚类划分T中划分到簇tj中数据元素个数;nij为同时属于簇![]() 和簇tj中数据元素个数,则聚类划分Cl和T之间的概率分布可计算为
和簇tj中数据元素个数,则聚类划分Cl和T之间的概率分布可计算为
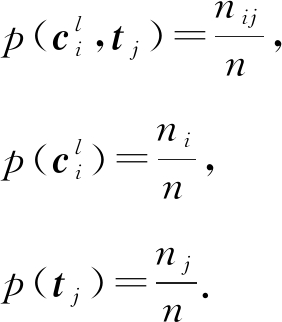
(9)
图4举例说明聚类集成模型中使用互信息度量各模态间高层聚类划分的相关性.图4中第i行第j列若为黑框,表示数据元素xj出现在簇ci中,否则表示不出现.另外,为了使展示更加清晰,该例中数据元素可被划分至多个簇中.图4(a)中聚类模式Cl和T高度相似,得到最高的互信息;图4(b)中Cl和T的相关性减弱,互信息也相应降低;图4(c)中Cl和T的相似度最弱,得到最低的互信息.因此,使用互信息可有效地度量跨模态高层聚类划分之间的相关性.
2.3 SPIM算法的目标函数
根据定义1可知,SPIM算法的目标是寻求源变量X到压缩变量T的一种最优压缩表示p(t|x),在压缩过程中使压缩变量T最大化地保存与各模态自身的私有变量Y1,Y2,…,Yk和共有变量S的信息量,其中共有变量由混合单词模型和聚类集成模型共同求得,因此,SPIM算法的目标函数可改写为
(10)
其中,![]() 度量压缩变量与各模态自身的私有变量之间的信息量;
度量压缩变量与各模态自身的私有变量之间的信息量;![]() 表示压缩变量与跨模态共享特征之间的信息量;
表示压缩变量与跨模态共享特征之间的信息量;![]() 度量压缩变量与跨模态的高层聚类划分之间的信息量;λ是控制私有信息与共享信息之间的侧重程度的平衡参数.
度量压缩变量与跨模态的高层聚类划分之间的信息量;λ是控制私有信息与共享信息之间的侧重程度的平衡参数.
2.4 SPIM算法目标函数的优化
本节使用顺序“抽取-合并”策略优化SPIM算法的目标函数,求解源变量X到压缩变量T之间的编码方案p(t|x).顺序“抽取-合并”优化方法包含3个步骤:
1) 将源变量X=(x1,x2,…,xn)随机划分至M个簇T=(t1,t2,…,tM);
2) 顺序地将每个数据元素x从当前簇told中抽取出来,作为单独簇{x};
3) 计算将单独簇{x}合并至其他簇中时SPIM算法目标函数中信息的损失量,并选取使得信息损失最小的簇tnew进行合并.
顺序抽取合并策略的核心问题是在迭代过程中选取合适的簇tnew对单独簇{x}进行合并.使用![]() 表示将x从簇told中抽取之前式(10)的值;使用
表示将x从簇told中抽取之前式(10)的值;使用![]() 表示抽取x之后目标函数的值;使用
表示抽取x之后目标函数的值;使用![]() 表示将单独簇{x}合并至tnew之后式(10)的值,tnew满足
表示将单独簇{x}合并至tnew之后式(10)的值,tnew满足![]() 其中,
其中,![]() 是{x}合并前后式(10)的改变量,在此称之为合并代价,其计算过程为
是{x}合并前后式(10)的改变量,在此称之为合并代价,其计算过程为
(11)
其中,![]() 分别是目标函数中
分别是目标函数中![]() 的合并代价.我们首先计算
的合并代价.我们首先计算![]() 假设单独簇{x}被合并到簇t形成新簇
假设单独簇{x}被合并到簇t形成新簇![]() 则:
则:
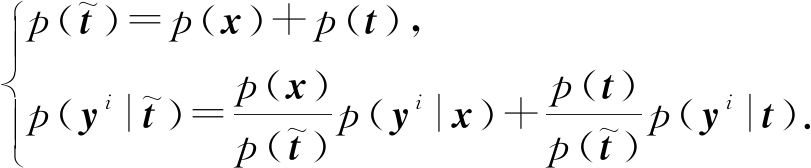
(12)
根据互信息的定义,可得:
把式(12)代入![]() 中可得:
中可得:
[p(x)+p(t)]·JSπ[p(Yi|x),p(Yi|t)],
其中,![]() 为2个概率分布之间的Jensen-Shannon距离.同理可知
为2个概率分布之间的Jensen-Shannon距离.同理可知![]() 的合并代价ΔIcom:
的合并代价ΔIcom:
(13)
在将{x}合并至簇t时,根据聚类集成模型中的式(9)可得到p(Tbef,Ci),p(Taft,Ci),因此可计算将{x}合并前后由I(T;Ci)引起的合并代价.综上所述,可计算将{x}合并至簇t的合并代价:
(14)
给出SPIM算法的实现过程:
算法1. SPIM算法.
输入:源变量X与多个模态的私有变量Y1,Y2,…,Yk之间的联合概率分布p(X,Y1),p(X,Y2),…,p(X,Yk);簇的个数M;平衡参数λ.
输出:X到T的编码方案p(t|x).
① 根据混合词库模型生成多个模态的混合单词空间![]() 并通过式(|Y1|+|Y2|+…+|Yk|)
并通过式(|Y1|+|Y2|+…+|Yk|) k确定
k确定![]() 的维度;
的维度;
② 根据聚类集成模型构建多个模态自身的聚类划分C1,C2,…,Ck;
③ 将源变量X随机划分为M个簇;
④ Repeat:
⑤ For every x∈X
⑥ 将x从当前簇told中抽取出来,作为单独簇{x};
⑦ 合并{x}至簇tnew,其中![]() 并根据式(14)计算合并代价;
并根据式(14)计算合并代价;
⑧ End For
⑨ Until p(t|x)不再发生变化.
2.5 算法分析
2.5.1 收敛性分析
定理1. SPIM算法可在有限迭代次数内收敛到局部最优解.
证明. 首先证明每次抽取合并过程都能够增加式(10)的值.使用![]() 表示将x从其原始簇told中抽取之前目标函数的值,使用
表示将x从其原始簇told中抽取之前目标函数的值,使用![]() 和
和![]() 表示合并单独簇{x}至
表示合并单独簇{x}至![]() 前后的目标函数值.合并过程有2种情况:1)tnew=told,意味着将{x}合并至其原本所在的簇told,此时,数据分布没有发生改变,则
前后的目标函数值.合并过程有2种情况:1)tnew=told,意味着将{x}合并至其原本所在的簇told,此时,数据分布没有发生改变,则![]() 意味着将{x}合并至其他簇tnew,因为
意味着将{x}合并至其他簇tnew,因为![]() 故将{x}合并至新簇tnew的合并代价Δ(x,tnew)一定小于将其合并至原始簇told的合并代价
故将{x}合并至新簇tnew的合并代价Δ(x,tnew)一定小于将其合并至原始簇told的合并代价![]() 即
即![]() 又因为
又因为![]() 故
故![]() 因此,每次抽取合并过程都有
因此,每次抽取合并过程都有![]()
证明SPIM算法的目标函数值有上界.压缩变量T是源变量X的一种压缩表示,则必有I(T;Yi)≤I(X;Yi)和![]() 当且仅当|X|=|Y|时,I(T;Yi)≤I(X;Yi)和
当且仅当|X|=|Y|时,I(T;Yi)≤I(X;Yi)和![]() 中的等号成立,此时X到T不存在压缩.另外,假设源变量X的正确划分为C,则I(T;Ci)≤I(T;C).综上所述,SPIM算法目标函数值的上界为
中的等号成立,此时X到T不存在压缩.另外,假设源变量X的正确划分为C,则I(T;Ci)≤I(T;C).综上所述,SPIM算法目标函数值的上界为![]() 因此SPIM算法可在有限迭代次数内收敛到局部最优解.
因此SPIM算法可在有限迭代次数内收敛到局部最优解.
证毕.
2.5.2 复杂度分析
预处理中步骤①可在![]() 的时间内构建多模态公共特征空间.预处理中步骤②的时间复杂度由构建基聚类所采用的聚类算法决定,本文使用顺序信息瓶颈(sequectial information bottleneck, sIB)算法,其时间复杂度为O(n log n).初始化过程可在O(1)时间内实现.在SPIM算法主循环中,抽取合并过程需要计算合并代价,时间复杂度为
的时间内构建多模态公共特征空间.预处理中步骤②的时间复杂度由构建基聚类所采用的聚类算法决定,本文使用顺序信息瓶颈(sequectial information bottleneck, sIB)算法,其时间复杂度为O(n log n).初始化过程可在O(1)时间内实现.在SPIM算法主循环中,抽取合并过程需要计算合并代价,时间复杂度为![]() 因此,SPIM算法的时间复杂度为
因此,SPIM算法的时间复杂度为![]() 其中M是最终聚类划分中簇的个数.
其中M是最终聚类划分中簇的个数.
3 实验与性能分析
3.1 数据集
本文在6种跨媒体数据集上验证SPIM算法的有效性:
1) Wikipedia数据集[28].该数据集包含2 866个文本图像对共计10个类,每幅图像的共生文本至少有70个单词.对于图像,本文采用文献[28]提供的128维SIFT[29]特征构建BoVW视觉特征表示;对于文本,首先构建500维BoW表示,然后通过LDA抽取100个话题的概率分布作为文本特征表示.
2) Pascal Sentence数据集[30].该数据集包含1 000个文本图像对共计20个类.对于图像,本文抽取1 024维的SIFT BoVW视觉特征表示;对于文本,首先构建300维BoW表示,然后通过LDA抽取100个话题的概率分布作为文本特征表示.
3) Pascal VOC 2007数据集[31].该数据集包含9 963个文本图像对共计20个类.本文采用文献[32]提供的798维基于标签排序的文本特征和776维的BoVW视觉特征.
4) X-Media[33-34]是针对检索任务[35]构建的跨媒体数据集,该数据集包含文本、图像、视频、音频、3维模型等多种模态的数据,共计20个类.我们使用5 000个文本、图像对评估算法性能.关于该数据集的特征描述,本文采用文献[33]提供的10维LDA文本特征、128维BoVW图像特征.
5) Reuters多语种数据集[1].该数据集由5种语言的新闻文档组成,包括西班牙语、意大利语、德语、法语和英语,每种语言的文档被分为6类:C15,CCAT,E21,ECAT,GCAT,M11.本文随机从每种语言类中挑取500个文档,并使用BoW模型抽取1 000个关键词,为每个语种构建1 000维BoW表示.
6) HMDB数据集[36].该数据集由51类共计6 849个人体动作视频序列组成,主要来源电影片段、网络视频等.本文提取视频序列3种异构描述子[37]:梯度直方图(histogram of oriented gradient, HOG)、光流直方图(histogram of optical flow, HOF)和空间时间特征(space-time interest points, STIP),分别构建视频序列的1 000维BoVW表示.
3.2 评价指标
为了公正地对聚类结果进行评估,本文使用2种指标[15]评估算法的聚类性能:
1) 聚类精度(clustering accuracy, ACC):
(15)
其中,li和ti分别表示数据对象的真实划分和聚类划分,n是数据集的大小.δ(x,y)为狄克拉函数,当x==y时,δ(x,y)=1,否则δ(x,y)=0.map(ti)是聚类划分ti与真实划分之间的映射函数.
2) 标准化互信息(normalized mutual information, NMI):
(16)
其中,T和C分别表示数据对象的聚类划分和真实划分,I(T;C)是T和C间的互信息,H(T)和H(C)分别表示聚类划分和真实划分的信息熵.ACC,NMI的值越大,聚类结果越好.
3.3 对比方法
为验证SPIM算法在跨媒体聚类任务中的有效性,本文将其与7种算法进行对比:
1) k-means算法.经典的单模态聚类算法.
2) IB算法[22].对各模态分别使用IB算法进行聚类,我们在所有图表中公布各模态中最好的聚类结果.
3) Concate -IB算法.将各模态的特征直接相连,然后使用IB算法进行聚类.
4) 典型关联分析(canonical correlation analysis, CCA)算法[6].采用CCA算法学习2个模态间的共享信息.对于Reuters和HMDB数据集,本文选择2种表现最优的模态作为CCA算法的输入.
5) CSPA(cluster-based similarity partitioning algorithm)算法[15].该算法是一种典型的聚类集成算法,首先根据基聚类的co-association矩阵生成图,其中顶点是数据对象,边的权重的数据对象间的co-association值,然后使用METIS算法进行聚类.
6) PTGP(probability trajectory graph parti-tioning)算法[16].该算法是基于稀疏图表示和概率轨迹的聚类集成算法,能够同时根据基聚类的局部和全局信息获取最终的聚类划分.
7) LWGP(locally weighted evidence accumu-lation)算法[17].该算法在不考虑原始数据分布的情况下,通过局部密度估计方法对基聚类进行加权,进而区分基聚类的可依赖程度.
表1给出算法的时间复杂度对比.其中,CCA算法的O(Md2)项为计算2个模态的协方差矩阵的时间复杂度,O(d3)项是特征分解的时间复杂度,d=max(|Yi|,|Yj|)是任意2个模态的特征维度的最大值.CSPA算法采用METIS算法[38]对基聚类的生成图进行划分,其时间复杂度为O(|X|2).LWGP算法首先构建数据对象X与基聚类之间的二分图(bipartite graph),之后使用TCut算法[39]图划分.与LWGP算不同,PTGP算法首先对数据对象X进行初步聚类生成中间簇Xmcluster,构建中间簇Xmcluster与基聚类的二分图,最后使用TCut算法进行二分图划分,其中|Xmcluster|是中间簇的数量.
Table 1 The Complexities of Different Baselines
表1 不同算法的时间复杂度对比
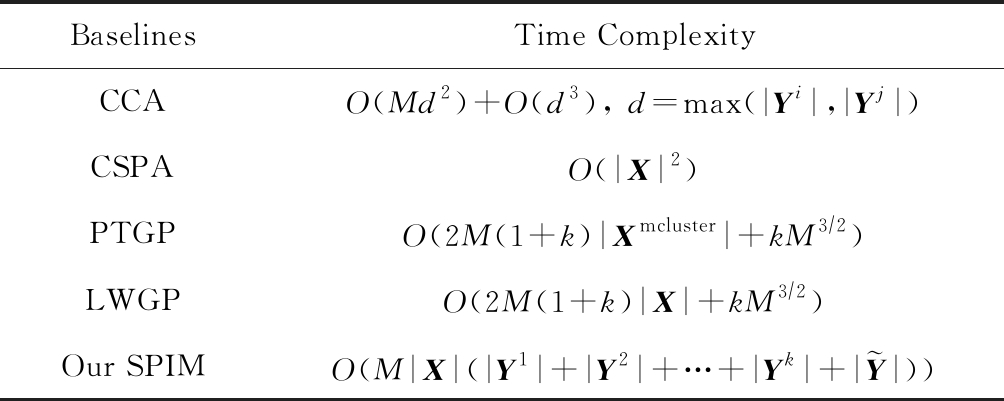
BaselinesTime ComplexityCCAO(Md2)+O(d3), d=max(|Yi|,|Yj|)CSPAO(|X|2)PTGPO(2M(1+k)|Xmcluster|+kM3∕2)LWGPO(2M(1+k)|X|+kM3∕2)Our SPIMO(M|X|(|Y1|+|Y2|+…+|Yk|+|Y|))
3.4 实验结果分析
为了验证数据不同模态表示能力的差异,图5给出IB算法在跨媒体数据不同模态上的聚类结果.图5中的实验结果表明:
1) IB算法在Wikipedia,Pascal Sentence和Pascal VOC 07数据集的文本、图像2种模态上的聚类结果具有较大的差异,且IB算法在文本模态上的聚类性能明显优于图像模态.这说明在跨模态的图像聚类任务中仅依赖图像信息很难获得较好的聚类结果,丰富的语义关系能够带来更加准确的语义相关性.因此,兼顾语义和视觉等模态信息有助于提升跨模态聚类任务的聚类性能.
2) IB算法在多语种数据集Reuters的各语种上和视频数据集HMDB的各异构特征空间上得到相近的聚类结果.这说明数据对象往往具有多个侧面的描述,例如相同的新闻可以用多种语言进行报道;包含相同人体动作的视频序列可以在梯度、光流、时空等特征空间上获得异构的描述.不同侧面的特征信息反映数据不同的内在特性,有效地组织和使用特征之间的互补作用以便确保高质量的聚类结果.
表2和表3展示了各种方法的对比结果.对于CCA算法,本文首先按照相关系数排序,并选取前d对典型得分作为特征向量进行聚类.我们在表2和表3中公布的是CCA算法聚类结果稳定后的值.为保证CSPA,PTGP,LWGP这3种集成聚类算法中基聚类间的差异性,我们对数据对象的各模态分别使用IB算法运行20次,然后使用聚类集成算法对所有模态的聚类成员进行合并,得到最终的聚类划分.根据原作者的建议,本文将PTGP算法中节点数量k设置为![]() 将LWEA算法中控制聚类不确定性(cluster uncertainty)的参数θ设置为0.4.另外,除CCA算法外,其他对比算法及本文提出的SPIM算法均受随机初始化的影响,因此,本文将这些算法运行10次,公布其平均结果(mean)及标准差(std).从表2和表3可知3点实验现象.
将LWEA算法中控制聚类不确定性(cluster uncertainty)的参数θ设置为0.4.另外,除CCA算法外,其他对比算法及本文提出的SPIM算法均受随机初始化的影响,因此,本文将这些算法运行10次,公布其平均结果(mean)及标准差(std).从表2和表3可知3点实验现象.
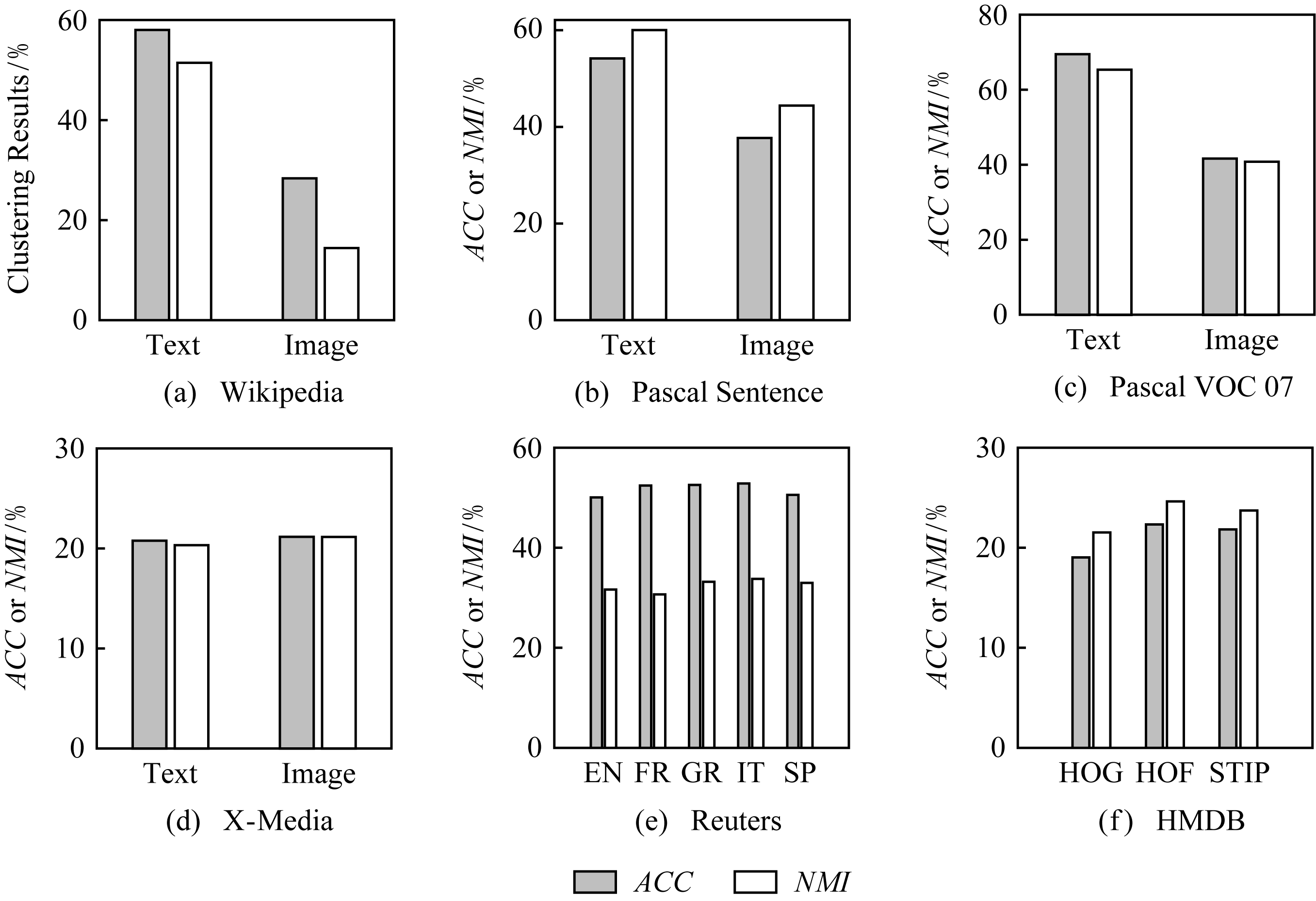
Fig. 5 Clustering results of IB on different media sources
图5 IB算法在不同媒体源上的聚类结果
Table 2 The ACC Comparison Results on 6 Cross-Media Datasets
表2 在6种跨媒体数据集上的ACC对比结果%

Datasetsk-meansIBConcate-IBmean±stdmean±stdmean±stdCCACSPAPTGPLWEASPIMmean±stdmean±stdmean±stdmean±stdWikipedia45.22±2.458.27±4.828.58±0.959.6760.09±5.162.07±1.062.86±0.865.50±2.3Pascal Sentence52.93±3.854.10±2.941.75±2.855.2055.15±2.057.83±0.859.67±0.763.02±1.5Pascal VOC 0764.99±3.569.53±3.262.77±2.369.0969.84±5.372.89±0.973.64±0.876.33±1.2X-Media20.55±0.621.16±0.521.31±0.523.5818.75±0.724.31±1.121.78±0.625.16±1.9Reuters53.16±1.453.12±3.153.43±3.450.9359.92±0.256.61±3.655.28±4.160.59±3.6HMDB18.46±0.922.31±2.223.35 ±1.325.3420.82±0.525.75±0.926.63±1.429.42±0.8Average42.5546.4138.5347.3047.4249.9149.9753.34
Note: The best clustering results in each case is boldfaced.
Table 3 The NMI Comparison Results on 6 Cross-Media Datasets
表3 在6种跨媒体数据集上的NMI对比结果 %
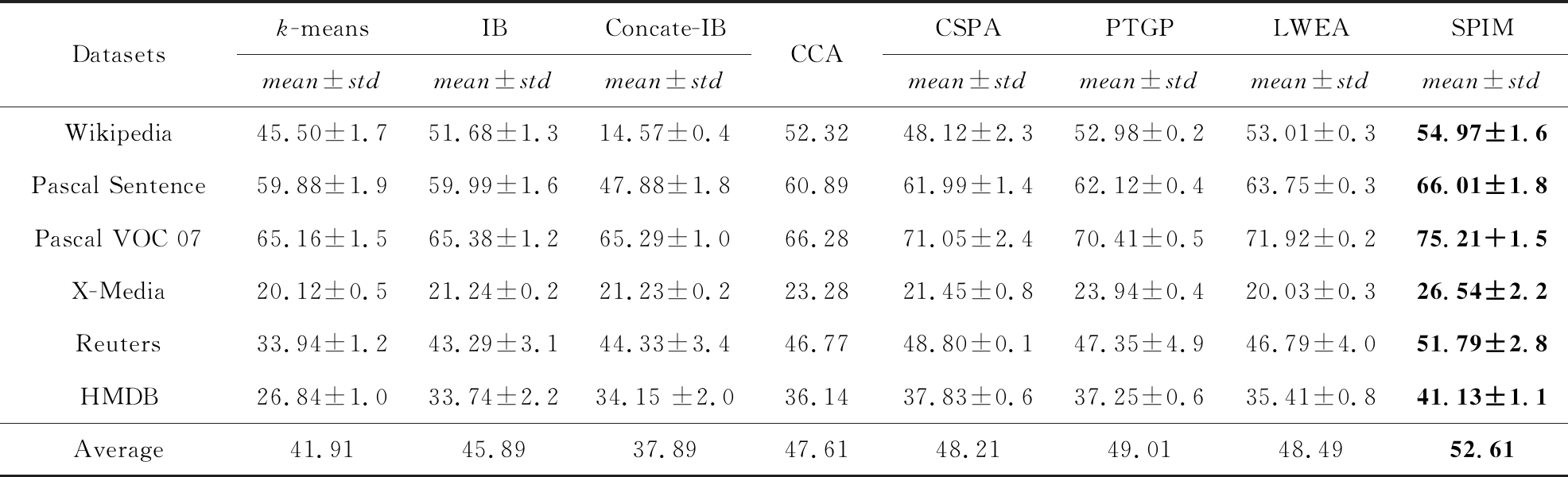
Datasetsk-meansIBConcate-IBmean±stdmean±stdmean±stdCCACSPAPTGPLWEASPIMmean±stdmean±stdmean±stdmean±stdWikipedia45.50±1.751.68±1.314.57±0.452.3248.12±2.352.98±0.253.01±0.354.97±1.6Pascal Sentence59.88±1.959.99±1.647.88±1.860.8961.99±1.462.12±0.463.75±0.366.01±1.8Pascal VOC 0765.16±1.565.38±1.265.29±1.066.2871.05±2.470.41±0.571.92±0.275.21+1.5X-Media20.12±0.521.24±0.221.23±0.223.2821.45±0.823.94±0.420.03±0.326.54±2.2Reuters33.94±1.243.29±3.144.33±3.446.7748.80±0.147.35±4.946.79±4.051.79±2.8HMDB26.84±1.033.74±2.234.15 ±2.036.1437.83±0.637.25±0.635.41±0.841.13±1.1Average41.9145.8937.8947.6148.2149.0148.4952.61
Note: The best clustering results in each case is boldfaced.
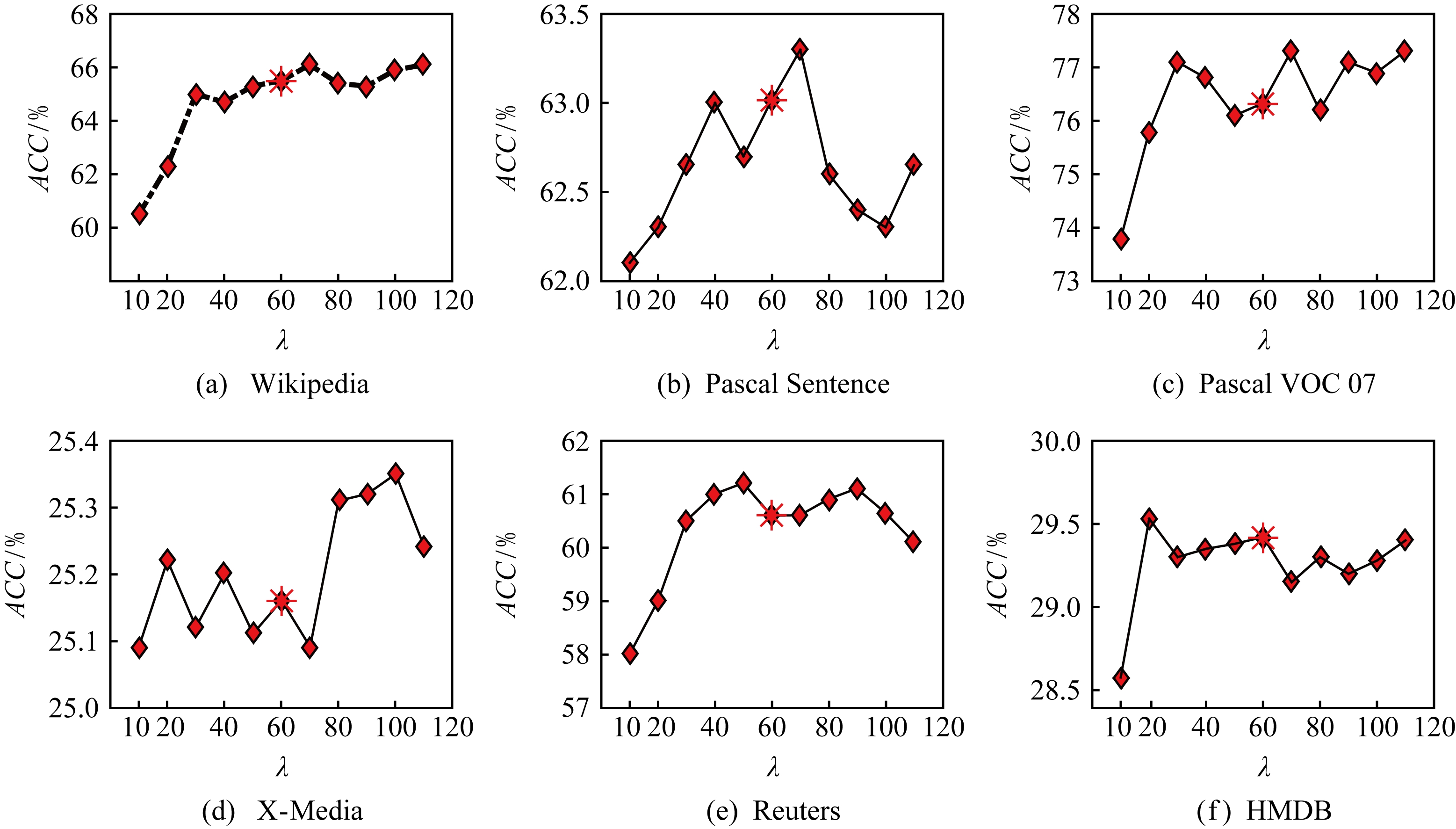
Fig. 6 The impact of λ on the performance of SPIM algorithm
图6 平衡参数λ对SPIM算法聚类结果的影响
1) 将各模态的特征直接相连不能有效地提升聚类性能.例如相比IB算法在单一模态上的最优结果,Concate-IB算法在Wikipedia,Pascal Sentence,Pascal VOC 07数据集上的ACC和NMI值出现下降.说明简单地连接多模态的特征信息不能稳定地提升算法的聚类质量.
2) 结合多模态信息的算法在聚类任务上的表现优于单模态聚类.从表2和表3可知,CCA,CSPA,PTGP,LWEA算法在本文使用的6种跨媒体数据上的平均聚类结果均优于k-means,IB等单模态聚类算法.这种现象验证了多模态之间的互补作用能够有效地提升聚类结果.
3) 相比于其他单模态和跨模态聚类算法,SPIM算法在本文使用的6种跨媒体数据集上的聚类结果均有提升.
3.5 参数分析
SPIM算法使用参数λ控制共享信息与私有信息间的侧重程度,因此,本节通过实验来观察不同参数值对聚类结果的影响.从图6可以看出,当λ取值较小时,SPIM算法得到较低的ACC值.随着λ值的增大,SPIM算法聚类效果逐渐变好,此时共享信息与私有信息的互补作用得以体现.随着λ值进一步增大,各模态的私有信息与共享信息达到平衡,SPIM算法的聚类结果也在一定程度上趋于稳定.注意,本文公布的SPIM算法的聚类结果对应参数取值为λ=60,聚类结果如图6中星号所示.
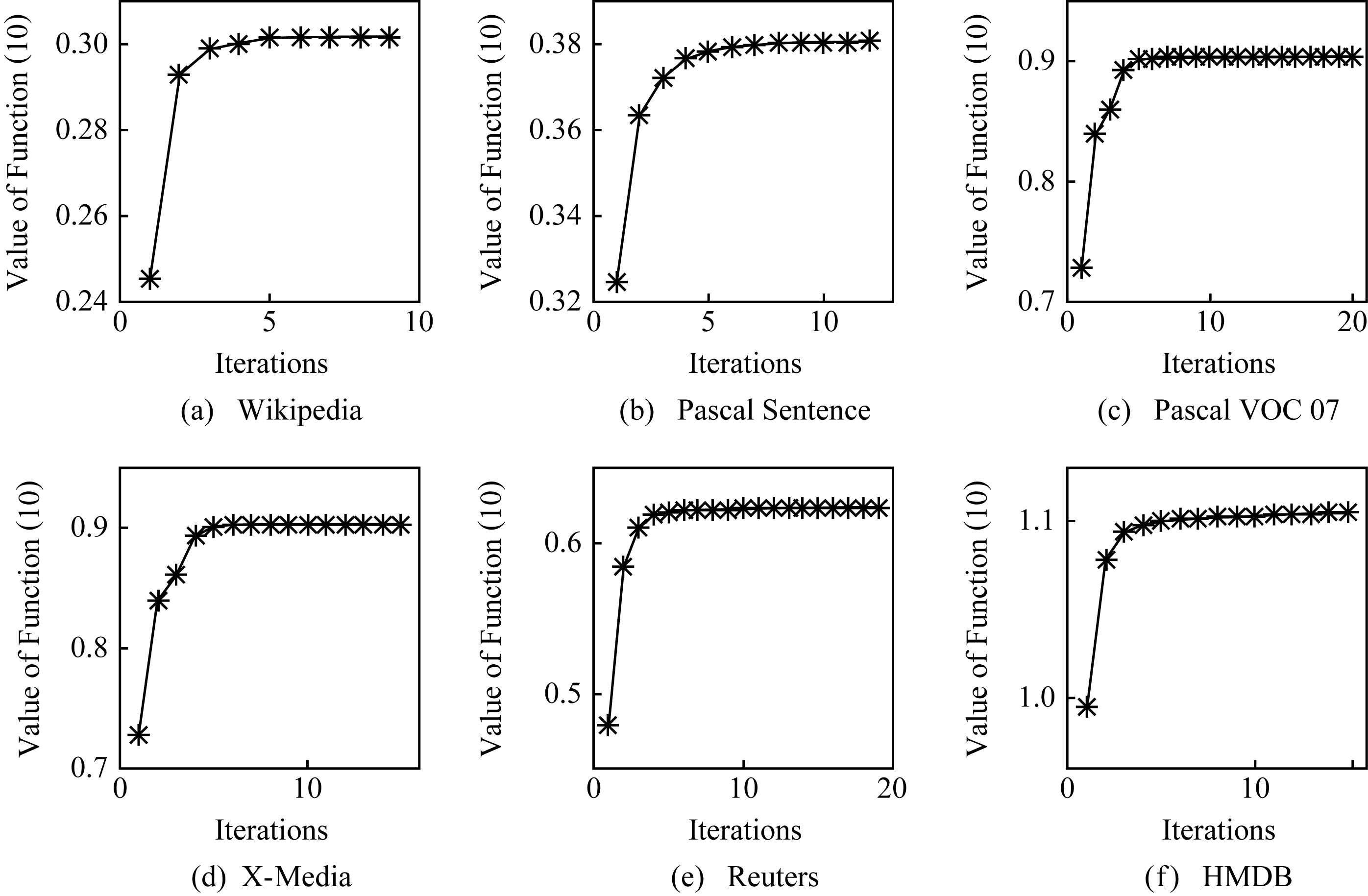
Fig. 7 The iteration number of SPIM on different datasets
图7 SPIM算法在不同数据集上达到收敛时的迭代次数
3.6 收敛性分析
SPIM算法的目标函数只能收敛到一个局部最优解,因此有必要对其收敛性进行经验性分析.图7给出SPIM算法每次迭代后式(10)的值.从图7可以看出,随着算法的运行,式(10)的值先是迅速上升,然后上升的幅度趋于平缓,最终得到目标函数的局部最优值,说明该算法具有较好的收敛性.

Fig. 8 Model ablation test of SPIM algorithm in terms of NMI
图8 SPIM算法在NMI指标上的模型简化测试
3.7 模型简化测试
SPIM算法通过混合单词模型和聚类集成模型对跨模态数据中各模态间的关联进行建模,分别保持各模态底层的统计相似性和各模态的高层聚类划分间的相关性.本节针对混合单词模型和聚类集成模型设计单独的实验,以验证单个模型的有效性.根据式(10)可知,SPIM算法在仅考虑单一混合单词模型和聚类集成模型时的目标函数可分别简化为
(17)
![]()
![]()
(18)
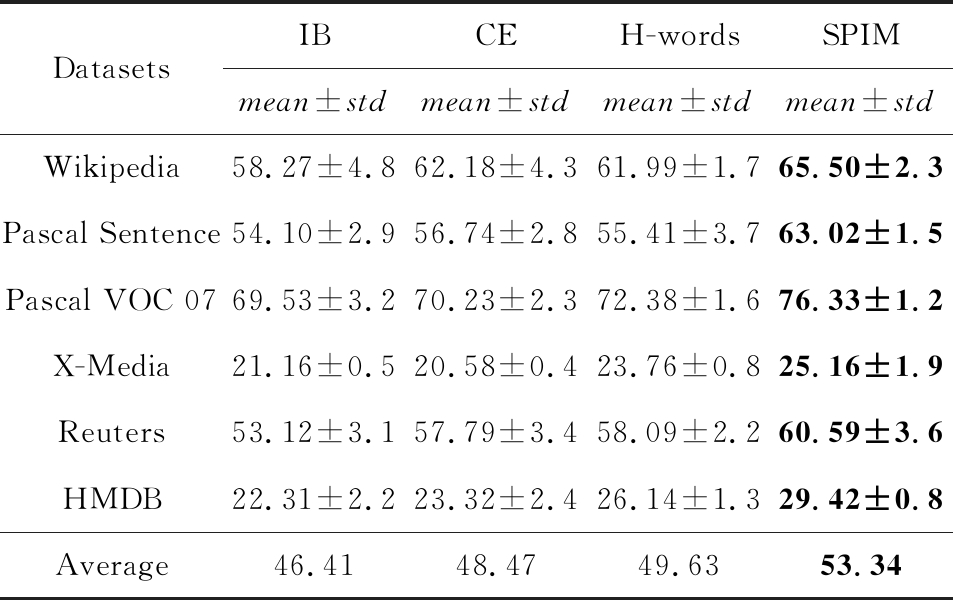
图8和表4给出分别考虑单一混合单词模型和聚类集成模型时SPIM算法的聚类精度和标准化互信息.从图8和表4可知:
1) SPIM算法在仅考虑单一模型时的聚类结果优于IB算法在单个模态中最优的聚类结果,验证SPIM算法中单一模型的有效性;
2) 在同时使用混合单词模型和聚类集成模型对共享信息建模时,SPIM算法的聚类结果进一步提升.例如,表4中SPIM算法在6种跨媒体数据集上的平均结果均优于IB算法、聚类集成模型和混合词库模型.
Table 4 Model Ablation test of SPIM Algorithm in Terms of ACC
表4 SPIM算法在ACC指标上的模型简化测试 %
DatasetsIBCEH-wordsSPIMmean±stdmean±stdmean±stdmean±stdWikipedia58.27±4.862.18±4.361.99±1.765.50±2.3Pascal Sentence54.10±2.956.74±2.855.41±3.763.02±1.5Pascal VOC 0769.53±3.270.23±2.372.38±1.676.33±1.2X-Media21.16±0.520.58±0.423.76±0.825.16±1.9Reuters53.12±3.157.79±3.458.09±2.260.59±3.6HMDB22.31±2.223.32±2.426.14±1.329.42±0.8Average46.4148.4749.6353.34
Note: The best clustering results in each case is boldfaced.
4 结 论
本文提出共享和私有信息最大化的跨媒体聚类算法SPIM,该算法能够使用跨模态数据间的共享信息和各模态自身的私有信息进行聚类分析.首先,提出2种跨媒体数据的共享信息构建模型,分别保持各模态底层特征的统计相似性和各模态的高层聚类划分间的相关性,其次,提出基于信息论的目标函数,将跨媒体数据的共享和私有信息融合在同一目标函数中.最后,采用顺序“抽取-合并”优化过程,保证SPIM的目标函数收敛到局部最优解.在6种跨媒体数据上的实验结果表明:本文提出的SPIM算法的优越性
[1]Kumar A, Daume H. A co-training approach for multi-view spectral clustering[C] //Proc of the 28th Int Conf on Machine Learning. New York: ACM, 2011: 393-400
[2]Cai Xiao, Nie Feiping, Huang Heng, et al. Heterogeneous image feature integration via multi-modal spectral clustering[C] //Proc of the 24th IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2011: 1977-1984
[3]Zhang Hong, Wu Fei, Zhuang Yueting. Cross-media correlation reasoning and retrieval[J]. Journal of Computer Research and Development, 2008, 45(5): 869-876 (in Chinese)(张鸿, 吴飞, 庄越挺. 跨媒体相关性推理与检索研究[J]. 计算机研究与发展, 2008, 45(5): 869-876)
[4]Zhang Lei, Zhao Yao, Zhu Zhenfeng. Advances in semantically shared subspace learning for cross-media data[J]. Chinese Journal of Computers, 2017, 40(6): 1394-1421 (in Chinese)(张磊, 赵耀, 朱振峰. 跨媒体语义共享子空间学习研究进展[J]. 计算机学报, 2017, 40(6): 1394-1421)
[5]Chaudhuri K, Kakade M, Livescu K, et al. Multi-view clustering via canonical correlation analysis[C] //Proc of the 26th Int Conf on Machine Learning. New York: ACM, 2009: 129-136
[6]Hardoon D R, Szedmak S, Shawe -Taylor J. Canonical correlation analysis: An overview with application to learning methods[J]. Neural Computation, 2004, 16(12): 2639-2664
[7]Sigal L, Memisevic R, Fleet D J. Shared kernel information embedding for discriminative inference[C] //Proc of the 22nd IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2009: 2852-2859
[8]Carl H, Phipip P, Lawrence N D. Gaussian process latent variable models for human pose estimation[C] //Proc of the 4th Machine Learning for Multimodal Interaction. Berlin: Springer, 2007: 132-143
[9]Barnard K, Forsyth D. Learning the semantics of words and pictures[C] //Proc of the 8th Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2001: 408-415
[10]Hofmann T. Learning and representing topic—A hierarchical mixture model for word occurrence in document databases[C] //Proc of the Workshop on Learning from Text and the Web. Pittsburgh, PA: CMU, 1998
[11]Barnard K, Duygulu P, Forsyth D, et al. Matching words and pictures[J]. Journal of Machine Learning Research, 2003, 3(2): 1107-1135
[12]Blei D M, Ng A Y, Jordan M I. Latent Dirichlet allocation[J]. Journal of Machine Learning Research, 2003, 3(1): 993-1022
[13]Gao Jing, Han Jiawei, Liu Jailu, et al. Multi-view clustering via joint nonnegative matrix factorization[C] //Proc of the 13th SIAM Int Conf on Data Mining. Philadelphia, PA: SIAM, 2013: 252-260
[14]Cai Xiao, Nie Feiping, Huang Heng. Multi-view k-means clustering on big data[C] //Proc of the 23rd Int Joint Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2013: 2598-2604
[15]Strehl A, Ghosh A. Cluster ensembles-a knowledge reuse framework for combining multiple partitions[J]. The Journal of Machine Learning Research, 2003 (3): 583-617
[16]Huang Dong, Lai Jianhuang, Wang Changdong. Robust ensemble clustering using probability trajectories[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(5): 1312-1326
[17]Huang Dong, Wang Changdong, Lai Jianhuang. Locally weighted ensemble clustering[J]. IEEE Transactions on Cybernetics, 2017, 48(5): 1460-1473
[18]Lou Zhengzheng, Ye Yangdong, Yan Xiaoqiang. The multi-feature information bottleneck with application to unsupervised image categorization[C] //Proc of the 23rd Int Joint Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2013: 1508-1515
[19]Yan Xiaoqiang, Ye Yangdong, Lou Zhengzheng. Unsuper-vised video categorization based on multivariate information bottleneck method[J]. Knowledge-Based Systems, 2015, 84(C): 34-45
[20]Luo Peng, Peng Jinye, Guan Ziyu, et al. Multi-view semantic learning for data representation[J]. IEEE Transactions on Knowledge and Data Engineering, 2015, 27(11): 3016-3028
[21]Zhao Qi, Li Zongmin, Cross-modal social image clustering[J]. Chinese Journal of Computers, 2018, 41(1): 98-111 (in Chinese)(赵其鲁, 李宗民. 跨模态社交图像聚类[J]. 计算机学报, 2018, 41(1): 98-111)
[22]Peng Yuxin, Qi Jinwei, Huang Xin, et al. CCL: Cross-modal correlation learning with multi-grained fusion by hierarchical network[J]. IEEE Transactions on Multimedia, 2018, 20(2): 405-420
[23]Peng Yuxin, Huang Xin, Qi Jinwei. Cross-media shared representation by hierarchical learning with multiple deep networks[C] //Proc of the 25th Int Joint Conf on Artificial Intelligence. Palo Alto, CA: AAAI, 2016: 3846-3853
[24]Tishby N, Pereira F, Bialek W. The information bottleneck method[C] //Proc of the 37th Allerton Conf on Communication, Control and Computing. Piscataway, NJ: IEEE, 1999: 368-377
[25]Slonim N. The information bottleneck: Theory and applications[D]. Hebrew, IL: Hebrew University, 2002
[26]Yan Xiaoqiang, Hu Shizhe, Ye Yangdong. Multi-task clustering of human actions by sharing information[C] //Proc of the 29th IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2017: 6401-6409
[27]Svetlana L, Cordelia S, Jean P. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories[C] //Proc of the 19th IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2006: 2169-2178
[28]Rasiwasia N, Pereira J C, Coviello E, et al. A new approach to cross-modal multimedia retrieval[C] //Proc of the 18th ACM Int Conf on Multimedia. New York: ACM, 2010: 251-260
[29]Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110
[30]Rashtchian C, Young P, Hodosh M, et al. Collecting image annotations using Amazon’s Mechanical Turk[C] //Proc of the Workshop on Creating Speech and Language Data with Amazon’s Mechanical Turk. Stroudsburg, PA: ACL, 2010: 139-147
[31]Everingham M, Gool L V, Williams C K I, et al. The pascal visual object classes (VOC) challenge[J]. International Journal of Computer Vision, 2010, 88(2): 303-338
[32]Hwang S J, Grauman K. Accounting for the relative importance of objects in image retrieval[C] //Proc of the British Machine Vision Conf. Berlin: Springer, 2010: 1-12
[33]Peng Yuxin, Zhai Xiaohua, Zhao Yunchao, et al. Semi-supervised cross-media feature learning with unified patch graph regularization[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2016, 26(3): 583-596
[34]Zhai Xiaohua, Peng Yuxin, Xiao Jianguo. Learning cross-media joint representation with sparse and semisupervised regularization[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2014, 24(6): 965-978
[35]Peng Yuxin, Huang Xin, Zhao Yunchao. An overview of cross-media retrieval: Concepts, methodologies, benchmarks and challenges[J]. IEEE Transactions on Circuits & Systems for Video Technology, 2017, 28(9): 2372-2385
[36]Kuehne H, Jhuang H, Garrote E, et al. HMDB: A large video database for human motion recognition[C] //Proc of the 13th IEEE Int Conf on Computer Vision. Piscataway, NJ: IEEE, 2011: 2556-2563
[37]Laptev I, Marszalek M, Schmid C, et al. Learning realistic human actions from movies[C] //Proc of the 21st IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2008: 1-8
[38]Karypis G, Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 359-392
[39]Chang Shifu, Wu Xiaoming, Li Zhenguo. Segmentation using superpixels: A bipartite graph partitioning approach[C] //Proc of the 25th IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2012: 789-796

