人才是指具有一定的专业技能,能进行创造性工作的劳动者,是推动社会经济发展的战略资源.随着经济全球化的发展,不同国家或地区间的人才交换日益频繁,人才流动的规模与方向均呈现出动态化和多样化的特点[1-2].一方面,人才流动对社会发展有一定的积极作用,例如相关研究表明:不同地区间的人才交换可促进知识和创新的传播,进而刺激地区经济和文化的发展[1].另一方面,过度的人才流失可能出现消极影响.例如相关研究发现:若发展中国家(或地区)的人才大量流向发达国家(或地区),易造成更广泛的发展不平衡现象[3-4].由此可见,人才流动对地区发展的影响较大,但自发的流动具有高度不确定性.因此,对人才流动进行观察、引导和调控,避免过度的人才流失,吸引亟需人才,促进人才结构平衡,是政府决策部门的重要职责.例如国家通过发布《国家中长期人才发展规划纲要(2010—2020年)》[5],为人才引流、调控和引进提供基本政策指导.
理解地区间人才流动的规律,是实现准确地观察和分析的前提.而精确地人才流动量预估,是制定和评估人才战略和干预政策的理论依据.因此,与人才流动问题相关的研究成果十分丰富[1-4],相关文献一般通过人口普查数据开展特定国家或地区范围内的人才流动分析.但人口流动与人才流动数据差异较大,因此分析结果一般无法直接反映人才流动规律.此外,人口普查数据更新周期长、时效性较差,基于该类数据开展的研究易缺乏准确及时的数据支撑.近年来,在线职业网络(online professional network, OPN)平台的发展,收集了大量职业变迁数据[6],其数据分布不受地理位置限制,为研究用人单位和地区间的人才流动提供了机会[7].OPN平台中的职业变迁数据包含平台用户的工作地点和时间信息,是较准确的人才流动数据样本.同时,OPN平台用户中的活跃群体对其职业信息的持续更新维护,也使得该数据样本相对人口普查样本有更好的时效性.
本文基于OPN平台中的职业变迁数据,研究地区间人才流动的模式分析和流动量预测问题.其中模式分析的目标是实现(定量的)地区间人才流动的空间和时间模式挖掘.流动量预测的目标是根据地区间历史人才流动量数据,预测未来地区间的人才流动量.模式分析和流动量预测均是人才流动研究的基础问题,但利用OPN数据解决这2个问题时面临着2方面挑战:
1) 数据稀疏性高.若地区数为n,则地区对数为n2.设有1 000个地区,则有约100万个(潜在的)人才流动方向,每个方向仅收集100人次流动量,即需约1亿条数据.此外,由于发达国家的大城市人口基数大且吸引力强,占据了主要人才流量,实际中约80%的地区间没有人才流动数据.稀疏性提高了大部分中小城市数据的方差,为分析和预测中小城市的人才流动量引入了不确定性.
2) 预测模型计算复杂度高.若地区数为n,给定时间长度为T(如5年)的历史数据,对于预测问题,共有Tn2个因变量和n2个预测目标,传统回归模型一般包含Tn4量级的参数.大量的参数使得模型易出现过拟合,模型训练的计算复杂度高.
为解决这2个挑战,本文利用参数重用的分析和预测方法,在缓解数据稀疏问题的同时降低模型复杂度.具体而言,本文构建了全球各地区间的人才流动网络,并用流动矩阵序列表示.基于流动矩阵序列,利用流量向量克服矩阵元素稀疏问题,分析各个地区的人才流动特点以及地区间人才交互的空间和时间模式.进一步分析该流动网络随时间动态改变的趋势,提出基于深度神经网络的人才流动预测模型,利用参数复用的卷积和循环神经网络结构,降低模型参数规模,预估未来时段地区间的人才流动量.本文的主要贡献有3个方面:
1) 提出了一种人才流动模式分析方法.本文用人才流动矩阵序列作为地区间人才流动的定量表示,为分析和预测提供数据结构支持,且提供了人才流动分析的一种量化的方法,并利用流量向量描述地区人才流动的特点,避免数据稀疏问题.
2) 提出了一种人才流动量预测模型.在人才流动矩阵序列的基础上,本文提出基于卷积和循环神经网络的预测模型,复用模型参数,分别提取静态和动态流动模式,对地区间人才流动进行预估.
3) 在大规模数据上,对所提出的模式分析和流量预测方法进行了实验验证.实验表明:本文提出的方法在预测问题上具有良好的性能.
1 相关工作
人才流动的相关文献主要关注人才流动现象的调研与分析,已有数十年研究历史.相关文献一般通过人工收集的调查数据来开展研究,如人口普查或问卷调查数据.相关研究内容包括:分析人才流动对社会的宏观影响,如知识和创新的传播[1-2];分析全球高技能人才交流的特点,并研究这类人才流动的定性问题,如是否应定性为人才流失或人才交换[3];提供应对人才流动的人才吸引政策、方案制定[4]等;分析科学技术人才的流失现象[6];研究发展中国家(如中国和印度等)的人才流动和区域发展之间的关联[8].这些研究或局限于定性分析,缺少定量研究成果,或受限于数据采集方案,可扩展性较差.
近年来,已有相关文献利用OPN数据开展人才流动相关研究.例如相关工作利用OPN数据分析美国对各行业专业工作者的吸引力[9-10].由于OPN数据规模大,不适合人工分析,因此相关工作一般利用机器学习技术来开展.例如针对网络的聚集特性,研究利用OPN数据为用人单位提供招聘指导[6-7],或利用人才数据分析企业特性[11]等.相关工作较关注为OPN平台运营方或其用户提供服务,而利用OPN数据对宏观模式的研究相对较少.
另一方面,交通流量预测问题[12]与人才流动预测问题相似.若将交通网络中的节点对应人才流动网络中的地区,则2个流量预测问题具有一定的相似性.近年来,深度神经网络在多个应用领域的成功[13],对交通流量预测领域产生了广泛影响.如相关研究利用多层稀疏自编码器(stacked auto encoders, SAEs)[12]预测一个时段的交通流量,取得了较好效果.交通流量的特点是空间上接近且互联的节点,其流量具有强关联性.与交通流量不同的是,人才流动不完全受空间位置限制,因为地缘接近关系一般只是促进工作变动的因素之一,而福利待遇、发展前景、文化和政治环境等对人才流动有较大影响.本文借鉴交通流量预测问题中采用的线性、非线性以及深度学习模型,作为所提出模型的性能评价基准.
2 人才流动的表示和模式分析
为形式化地表述人才流动模式分析及流动量预测任务,本节首先引入人才流动矩阵的概念,并在此基础上进一步详述人才流动的空间模式和时间模式分析方法.
2.1 人才流动矩阵
给定时间段 t∈(1,2,…,K),定义地区间人才流动矩阵Xt∈Rm×m,其元素![]() 为在该时间段内从地区i到地区j的人才流动量,m为地区数目.根据此定义,(X1,X2,…,Xk)为地区间人才流量的历史构成的矩阵序列.其中,地区内部的人才流量(即
为在该时间段内从地区i到地区j的人才流动量,m为地区数目.根据此定义,(X1,X2,…,Xk)为地区间人才流量的历史构成的矩阵序列.其中,地区内部的人才流量(即![]() 一般是地区间流量的数十倍,如图1所示,该流量一般与地区内劳动人口基数直接相关.图1为OPN样本中若干典型城市之间2016年前2个季度的人才流动量.流量矩阵是稀疏矩阵,实际数据中非零值率平均约为20%.图2示意性地展示了全球主要地区间的人才流动关系网络,其中节点表示地区,边表示地区间的人才流动关系.
一般是地区间流量的数十倍,如图1所示,该流量一般与地区内劳动人口基数直接相关.图1为OPN样本中若干典型城市之间2016年前2个季度的人才流动量.流量矩阵是稀疏矩阵,实际数据中非零值率平均约为20%.图2示意性地展示了全球主要地区间的人才流动关系网络,其中节点表示地区,边表示地区间的人才流动关系.
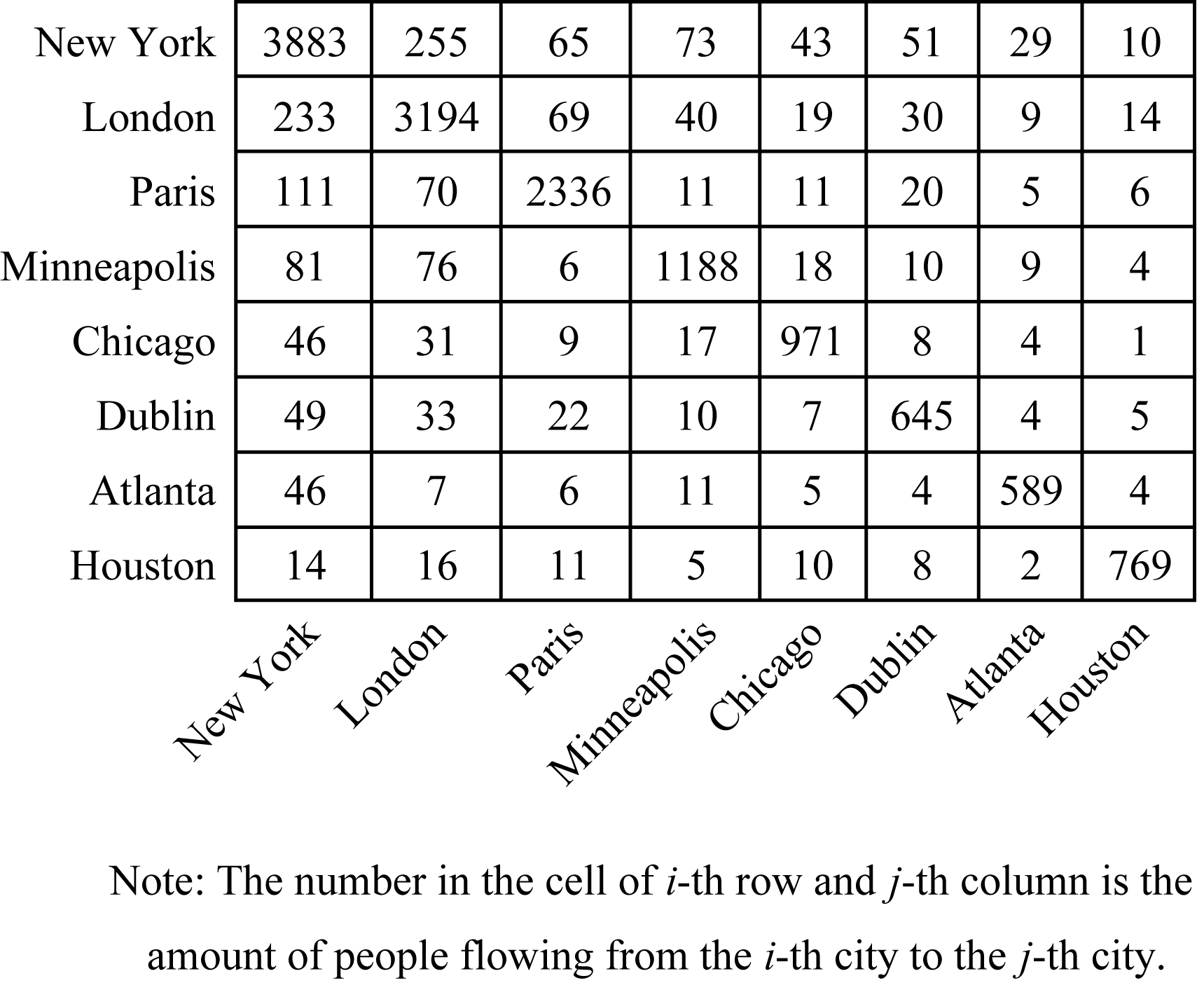
Fig. 1 Number of talent flows among several cities
图1 部分地区间人才流动量
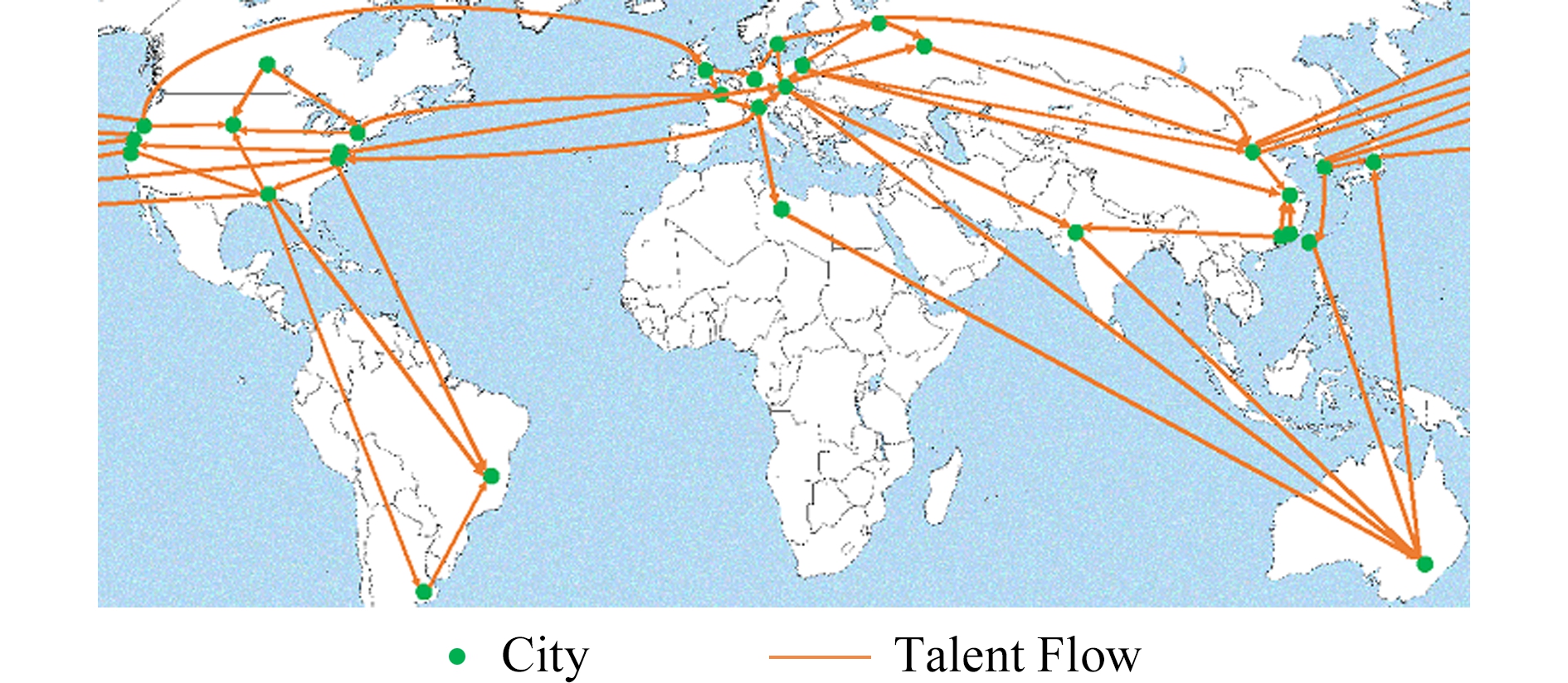
Fig. 2 Illustration of talent flow among cities
图2 人才流动示意图
为方便表述,引入符号![]() R1×m,表示人才流动矩阵的第i行,即地区i向其余地区输送的人才量,称为流出向量.引入符号
R1×m,表示人才流动矩阵的第i行,即地区i向其余地区输送的人才量,称为流出向量.引入符号![]() Rm×1表示人才流动矩阵的第j列,即地区j从其余地区吸引的人才量,称为流入向量.流出和流入向量统称为流量向量.图3为人才流动矩阵中流量向量的示意图.
Rm×1表示人才流动矩阵的第j列,即地区j从其余地区吸引的人才量,称为流入向量.流出和流入向量统称为流量向量.图3为人才流动矩阵中流量向量的示意图.
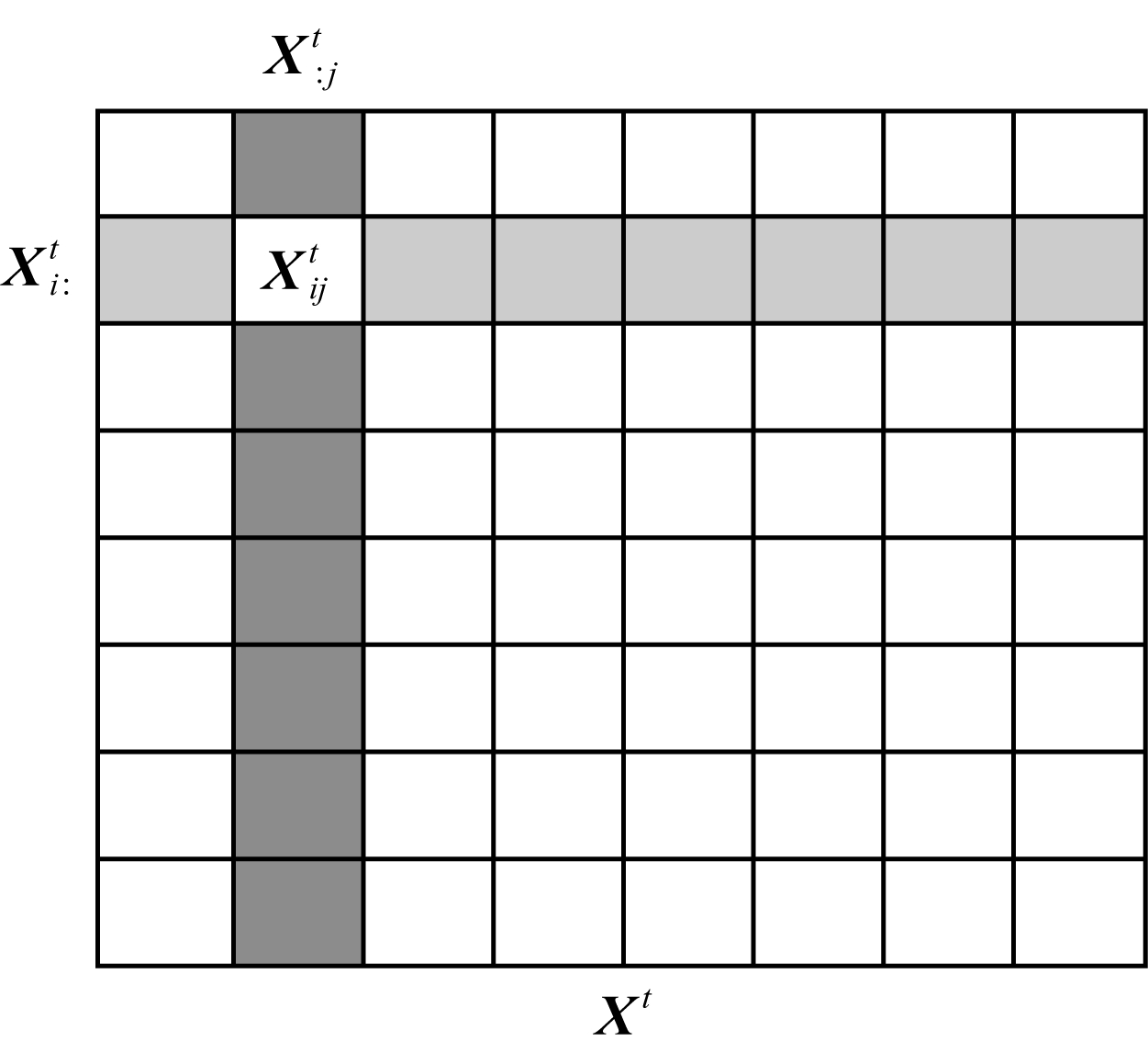
Fig. 3 An element of talent flow matrix
图3 人才流动矩阵示意图
对于给定的地区,其流量向量携带了该地区与其他地区间直接人才交换的完备信息.此外,由于流量矩阵稀疏,分析给定2个地区间的人才交互往往因缺乏数据而不可行,但对于给定地区,其流量向量平均含有约20%的非零项,其稀疏性相对较低,可以作为其人才吸引和流失的特征向量.因此,2.2节、2.3节通过分析流量向量的特点及向量间的关系,研究地区间人才流动的时空模式.
2.2 空间模式分析
2.2.1 地区人才吸引力模式
在给定的时间段t和给定的地区i,流量向量![]() 分别表示该地区向外部输送和从外部引入的人才流量.一般地,单个时间片中流量越大,该地区人才基数越大,或同等基数下人才活跃性越强.本文用
分别表示该地区向外部输送和从外部引入的人才流量.一般地,单个时间片中流量越大,该地区人才基数越大,或同等基数下人才活跃性越强.本文用![]() 分别表示地区流出和流入人才基数,其差值
分别表示地区流出和流入人才基数,其差值![]() 为地区净流入量.由于城市流入、流出量与劳动人口规模相关,本文用归一化后的净流入量
为地区净流入量.由于城市流入、流出量与劳动人口规模相关,本文用归一化后的净流入量![]() 表示相对吸引力程度,其数值称为人才净收益度.一般地,人才流入超过流出的地区是人才交换中的净受益者,净收益度为正值,反之为净流失者.由于发达国家和发展中国家的福利待遇和工业发展水平等差异明显,对人才的吸引力不对称,人才交换中的净受益者一般为发达国家的大中城市,而发展中国家的中小城市则往往是净流失者[8].
表示相对吸引力程度,其数值称为人才净收益度.一般地,人才流入超过流出的地区是人才交换中的净受益者,净收益度为正值,反之为净流失者.由于发达国家和发展中国家的福利待遇和工业发展水平等差异明显,对人才的吸引力不对称,人才交换中的净受益者一般为发达国家的大中城市,而发展中国家的中小城市则往往是净流失者[8].
表1是OPN数据中2016年净收益度最高以及最低的10个地区.从表1中可见,10个最大净流失地区中,有3个(Mumbai, Pune, Bangalore)来自发展中国家,其余地区多为发达国家的中小城市.10个最大净收益地区则均为人口密度大、工业发展水平高的城市.该结果说明净流入量是衡量人才吸引能力的一个良好指标.
Table 1 The Cities with Top Brain Drain or Gain in 2016
表1 2016年最大净流失和流入地区
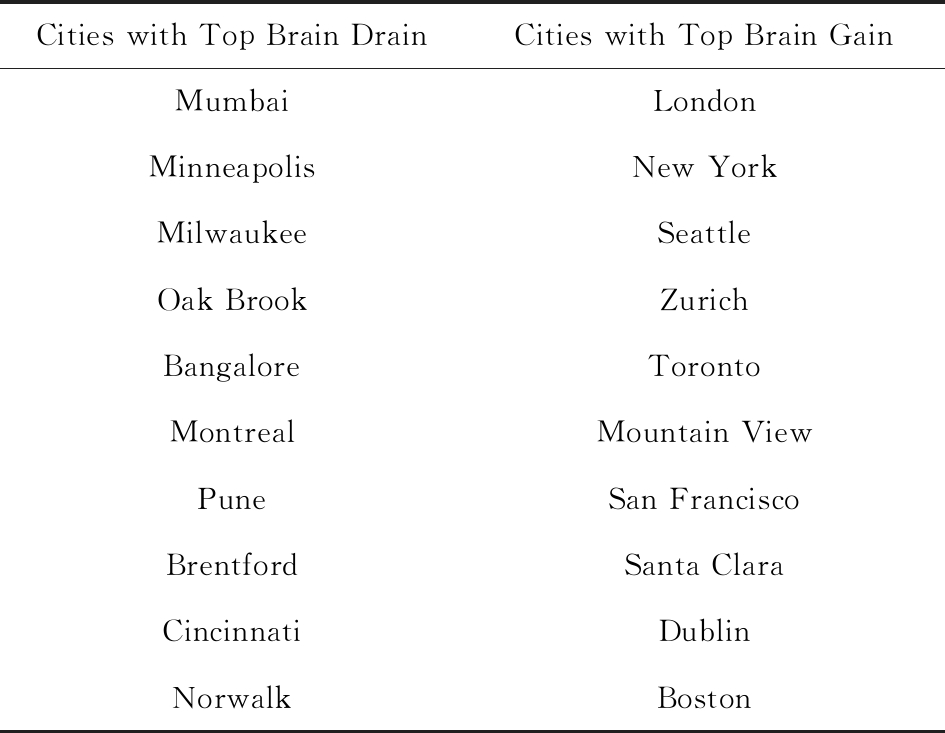
Cities with Top Brain DrainCities with Top Brain GainMumbaiLondonMinneapolisNew YorkMilwaukeeSeattleOak BrookZurichBangaloreTorontoMontrealMountain ViewPuneSan FranciscoBrentfordSanta ClaraCincinnatiDublinNorwalkBoston
除流量总量外,流量分布同样携带了有助于刻画地区人才吸引力的信息.具体而言,流入向量的零值越少、分布越均匀,则该地区人才流入渠道越丰富,即该地区的人才吸引力的区域多样性越强.同理,流出向量反映出地区人才供给多样性.本文引入流量分布的信息熵来刻画吸引力的多样性.
为方便表述,给定地区i,定义经过标准化后的流出向量,![]() 为流出分布,定义
为流出分布,定义![]() 为流入分布.流出和流入分布统称为流量分布.由于多样性主要由地区间人才交互关系来体现,而地区内部人才流量比地区间流量高数个量级,在数据中会掩盖地区间流量特点,因此计算信息熵值时忽略地区内部人才流量,即
为流入分布.流出和流入分布统称为流量分布.由于多样性主要由地区间人才交互关系来体现,而地区内部人才流量比地区间流量高数个量级,在数据中会掩盖地区间流量特点,因此计算信息熵值时忽略地区内部人才流量,即![]() 在该定义的基础上,人才流出分布的信息熵定义为
在该定义的基础上,人才流出分布的信息熵定义为
人才流入分布的信息熵定义为
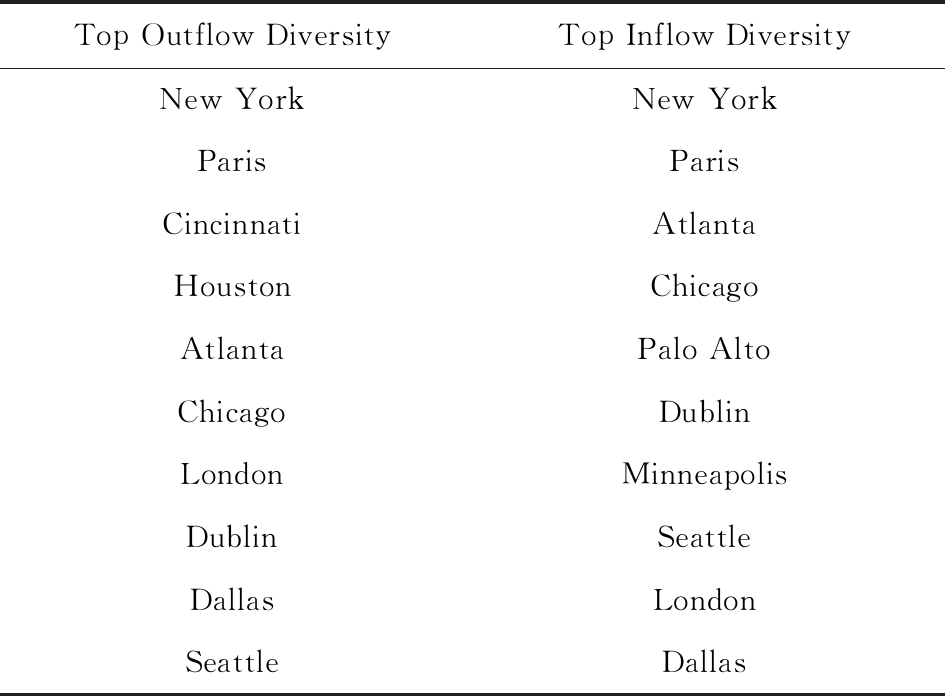
流入或流出分布的熵值越大,表明该地区流入或流出人才多样性越大.表2为OPN数据中2016年人才流入和流出多样性最高的10个地区.
从表2可见,高流出多样性地区和高流入多样性地区有明显的重叠,说明人才流失目标地区的分布与人才引入来源地区的分布有一定的对称性[8],这种对称性一般由地区的人才规模决定,规模大的地区倾向于更大的多样性.
Table 2 The Cities with Top Flow Diversity in 2016
表2 2016年流动多样性最大的城市
Top Outflow DiversityTop Inflow DiversityNew YorkNew YorkParisParisCincinnatiAtlantaHoustonChicagoAtlantaPalo AltoChicagoDublinLondonMinneapolisDublinSeattleDallasLondonSeattleDallas
另一方面,流入熵与流出熵的差值![]() 是地区人才吸引力的一个表征.一个地区的熵差
是地区人才吸引力的一个表征.一个地区的熵差![]() 小,表明该地区在该时段内的人才流失范围相对吸引力范围更广泛,因此人才流失更严重,反之则该地区更可能是净收益地区.图4是2类地区在2016年度熵差分布的盒图,其中si>0,si<0分别表示净流失地区和净受益地区.从图4可见,净流失地区的熵差多为负值且均值为负,反之为正.该结果说明熵差与人才流失程度呈正相关,即熵差大的地区,人才吸引能力强,反之亦然.
小,表明该地区在该时段内的人才流失范围相对吸引力范围更广泛,因此人才流失更严重,反之则该地区更可能是净收益地区.图4是2类地区在2016年度熵差分布的盒图,其中si>0,si<0分别表示净流失地区和净受益地区.从图4可见,净流失地区的熵差多为负值且均值为负,反之为正.该结果说明熵差与人才流失程度呈正相关,即熵差大的地区,人才吸引能力强,反之亦然.
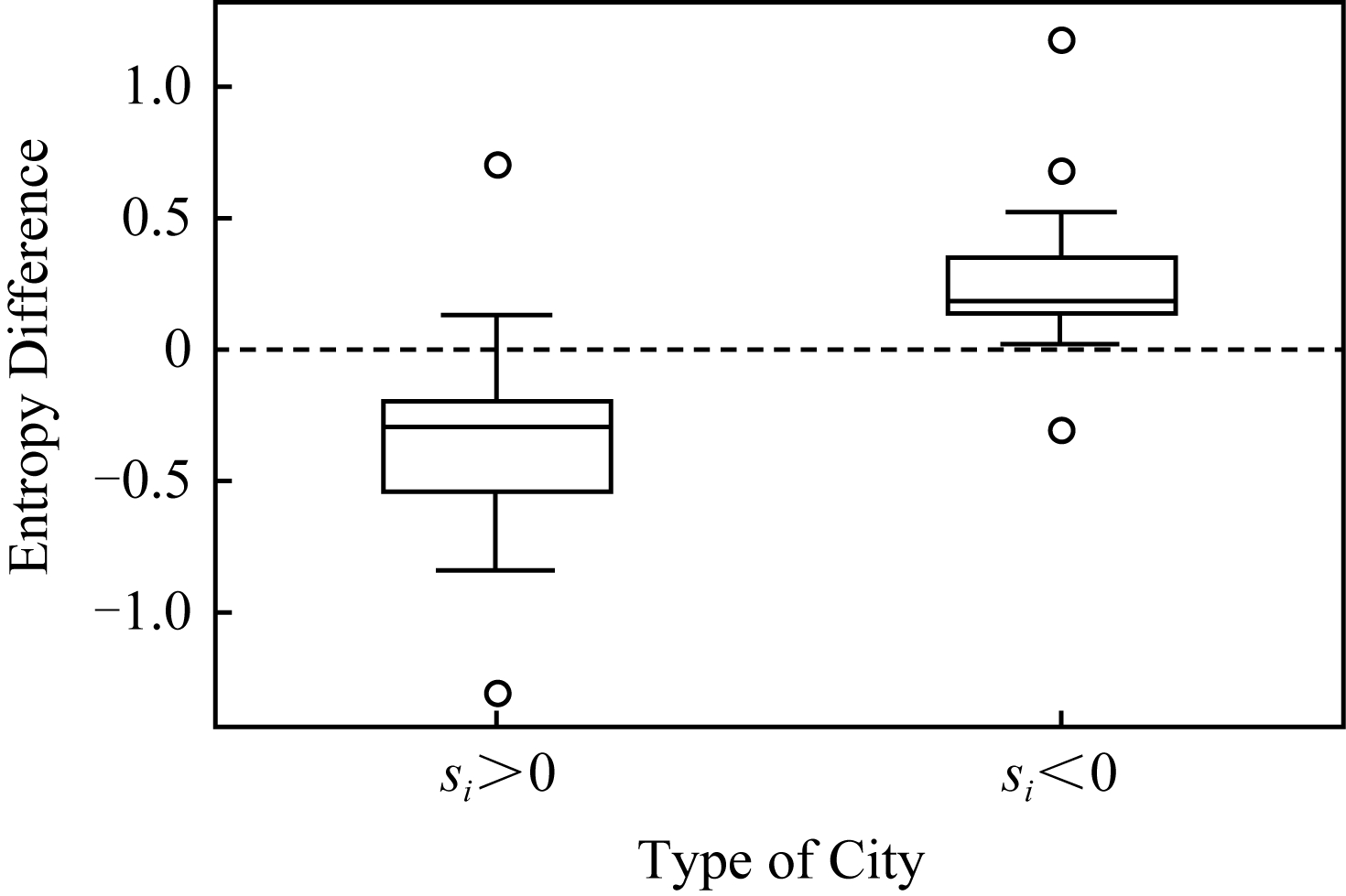
Fig. 4 The distribution of entropy difference
图4 熵差分布
2.2.2 流量模式的地区差异
2.2.1节分析表明地区的流量向量包含地区人才吸引力的特点,因此,通过比较流量向量,可以分析不同地区间人才吸引力的异同.
文献[7]根据人才交互进行用人单位间的关系分析.该研究工作应用在地区人才流量问题中,即根据地区i,j互相输送的人才类别和数量,对地区关系进行建模.与该文献不同,本文提出另一种地区间关系的度量方法,即通过比对地区间的人才流量向量的异同,分析地区间人才吸引力的差别.
由于地区流量向量可视为地区人才吸引力在一个时段内的空间分布,而具有相似吸引力空间分布的2个地区,在人才供需上有一定的共同点.因此,基于流量向量的相似性定义地区间关系,反映的是地区人才供需和地区人才吸引力方面的相似程度,即相似性大的地区间具有近似的人才吸引力.本文分别定义地区间的人才流入相似性和人才流出相似性为
![]()
(1)
![]()
(2)
与计算流入熵类似,在计算相似性时需排除地区内部人才流量的干扰,因此计算前将![]() 的第i个元素
的第i个元素![]() 和
和![]() 的第j个元素
的第j个元素![]() 置为0.
置为0.
该置零位置对应的![]() 为2个地区交互的人才量,其值越接近,表明2地区关系越近.置零后的差值(即
为2个地区交互的人才量,其值越接近,表明2地区关系越近.置零后的差值(即![]() 增大,进而减小相似性取值,在计算相似性时,需先互换
增大,进而减小相似性取值,在计算相似性时,需先互换![]() 的第j和第i个元素,使2个向量的零元素位置相同.图5示意性地展示了交换元素前后的流量向量.
的第j和第i个元素,使2个向量的零元素位置相同.图5示意性地展示了交换元素前后的流量向量.
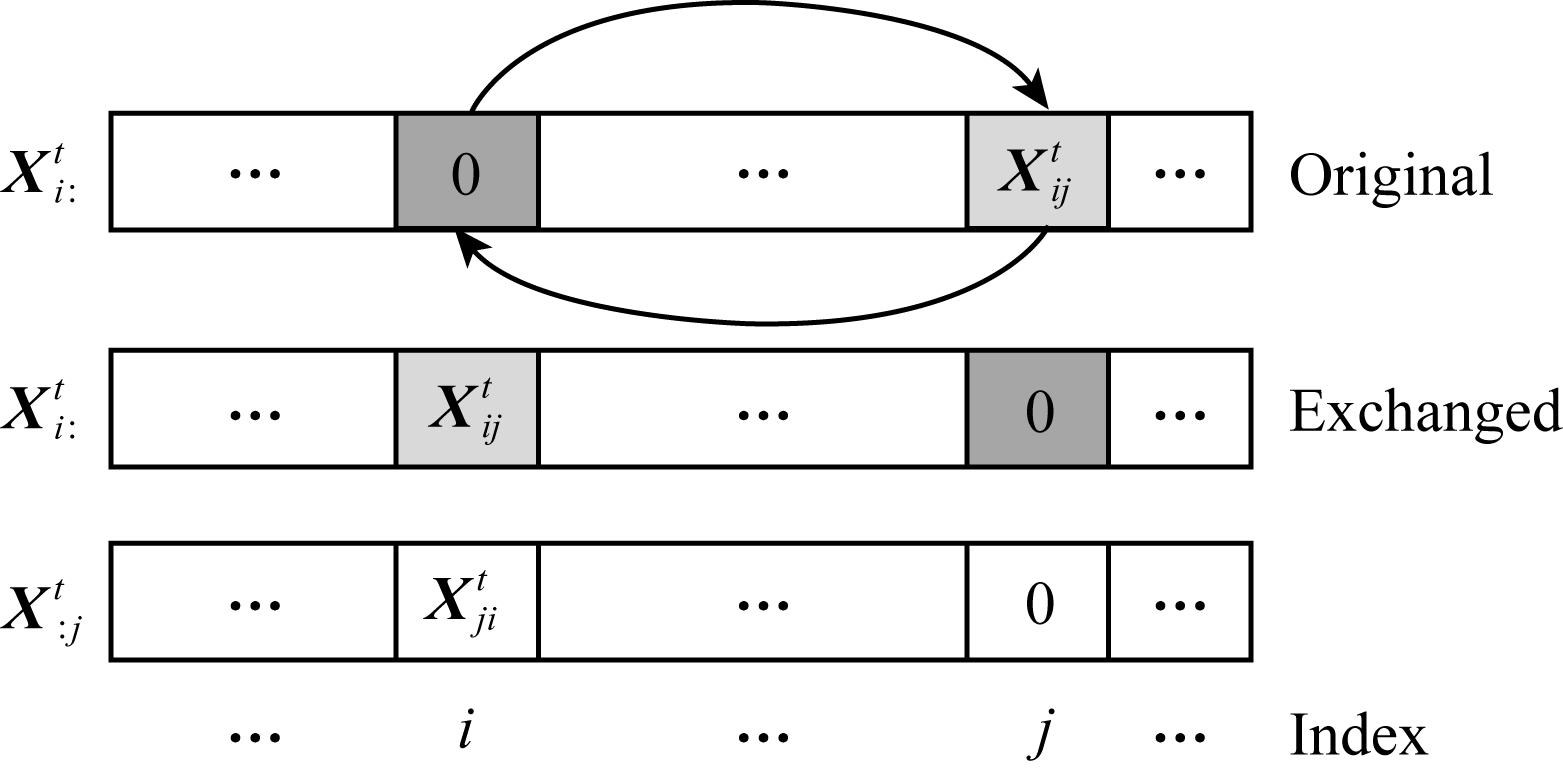
Fig. 5 Exchange the zero-elements in flow vectors
图5 不同流量向量的置零位置值交换示意图
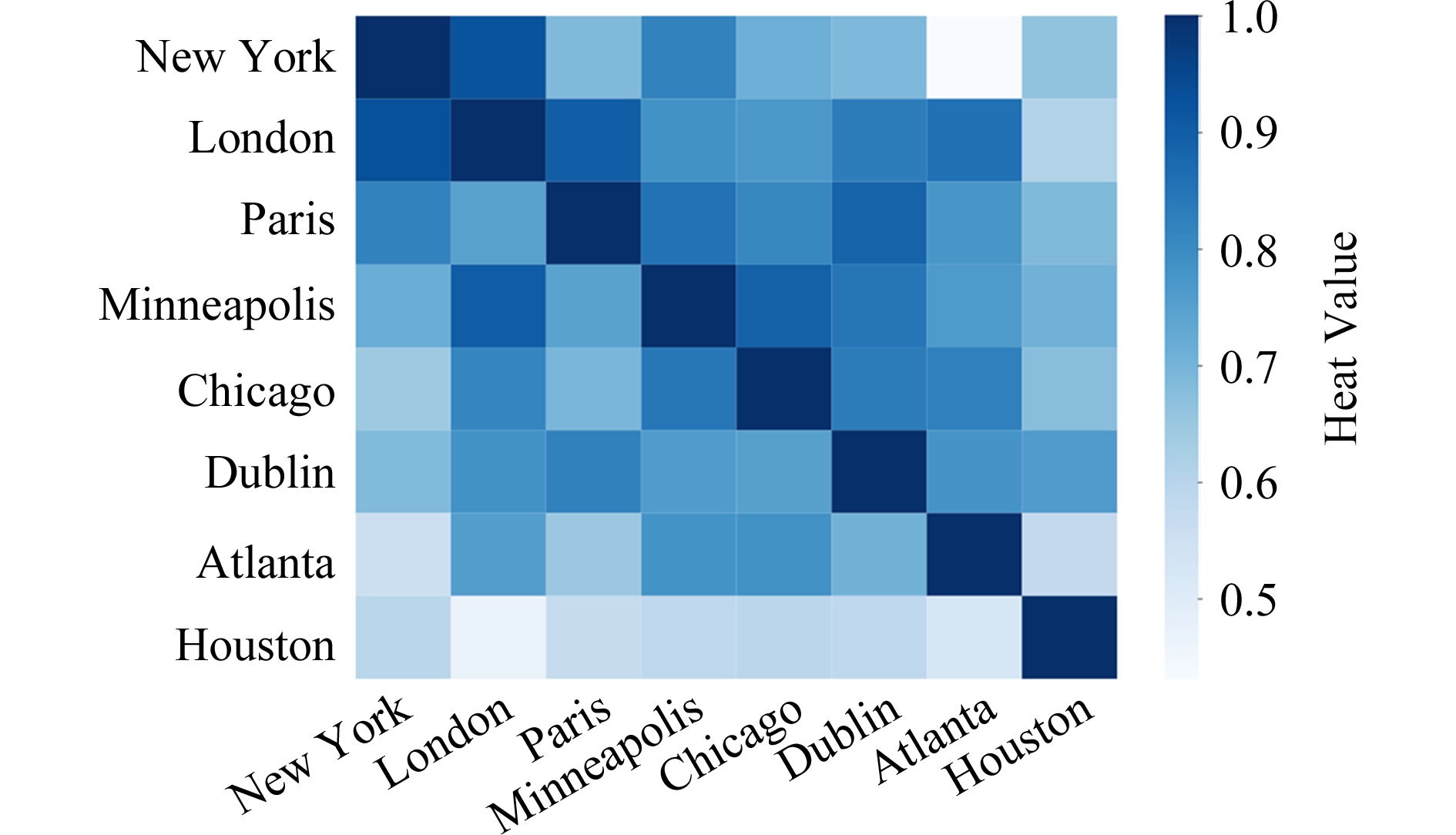
Fig. 6 Heat-map of similarities among cities
图6 城市人才流动量相似性热图
图6是根据2016年OPN数据计算的部分地区相似性的热力图,图6中矩形的上三角区域为根据流出向量计算的相似性,下三角区域为流入向量相似性.
从图6可以看出,流入和流出相似性存在一定的对称性,即存在部分地区对之间的流入相似性和流出相似性相同.例如London与Houston的流入和流出相似性均相对较低(图6中第2行和第2列),而与其余城市相似性均较高.但大部分城市对间的流入和流出相似性不完全一致,说明对应城市间的人才竞争力不均衡.因此,地区间相似性的对等程度是发现地区间吸引力相对强弱的方式之一.
2.2.3 基于人才流量的地区聚类
本节基于流量向量的地区间相似性,对地区进行聚类.该聚类与基于人才交换强弱关系的聚类[7]不同之处在于:聚类的结果中同一聚簇中的地点是具备类似人才吸引力模式的地区,而不是互相进行频繁人才交互的地区.该聚类结果是定位地区人才吸引力水平的一种方式,聚类结果具备潜在应用价值.一方面,求职者可以参考该结果,选择比当前所在地区吸引力更强的地区;另一方面,政策制定者可根据该结果选择合适的目标地区集合,以该目标地区集合中人才政策较优的地区作为本地区政策制定的参考.
本文采用层次聚类[14]方法进行地区聚类.具体而言,给定地区i,将其流出向量![]() 和流入向量
和流入向量![]() 拼接得到整体的流量向量,并定义S(i,j)为流量向量间的相似性,计算方式与式(1)相同.2个地区的距离定义为d(i,j)=1-S(i,j).聚类算法为自底向上的归并聚类[14],如算法1所示.
拼接得到整体的流量向量,并定义S(i,j)为流量向量间的相似性,计算方式与式(1)相同.2个地区的距离定义为d(i,j)=1-S(i,j).聚类算法为自底向上的归并聚类[14],如算法1所示.
算法1. 基于人才流动量的地区聚类.
输入:地点间的距离d(i,j);
输出:聚类结果C.
① 初始化归并队列l=∅,聚类队列C=∅;
② 将各个地区i∈(1,2,…,m),视为1个簇,加入l,C;
③ 计算每一对簇间的距离;
④ 选择l中距离最小的2个簇i,j,形成1个新的簇u,该新簇与已有簇v的距离定义为d(u,v)=(d(i,v)+d(j,v)) 2,将i,j从l中删除,并将u添加至l,C的队尾;
2,将i,j从l中删除,并将u添加至l,C的队尾;
⑤ 重复步骤④至l中的簇总数小于2;
⑥ 在C中,假设所有聚簇对间的最大距离为dm,将距离大于β×dm,(0<β<1)的聚簇分裂,得到聚类结果;
⑦ 算法结束.
算法1中超参数β∈(0,1)控制最终聚类的个数,其取值越大,聚类个数越少.图7是β=0.8时的聚类结果.观察该结果可知:聚类结果与地区的地缘关系存在差异性,可以归纳成3点:
1) 对一些发展中国家的城市而言,若城市在地缘上接近,则人才流量模式接近.例如印度(图7中的F类)和巴西(图7中的G类),不同城市人才流动模式互相接近,所以大部分出现在同一个聚类中.
2) 发达国家的大型城市与其他发达国家的大型城市更近似.如美国和北欧的大城市,尽管地缘上不接近,但均聚集在相同簇中.
3) 发达国家的中小城市与发展中国家的大城市更相似.如图7中的E类,是美国的普通中等城市,与北京等城市聚集在同一类中.
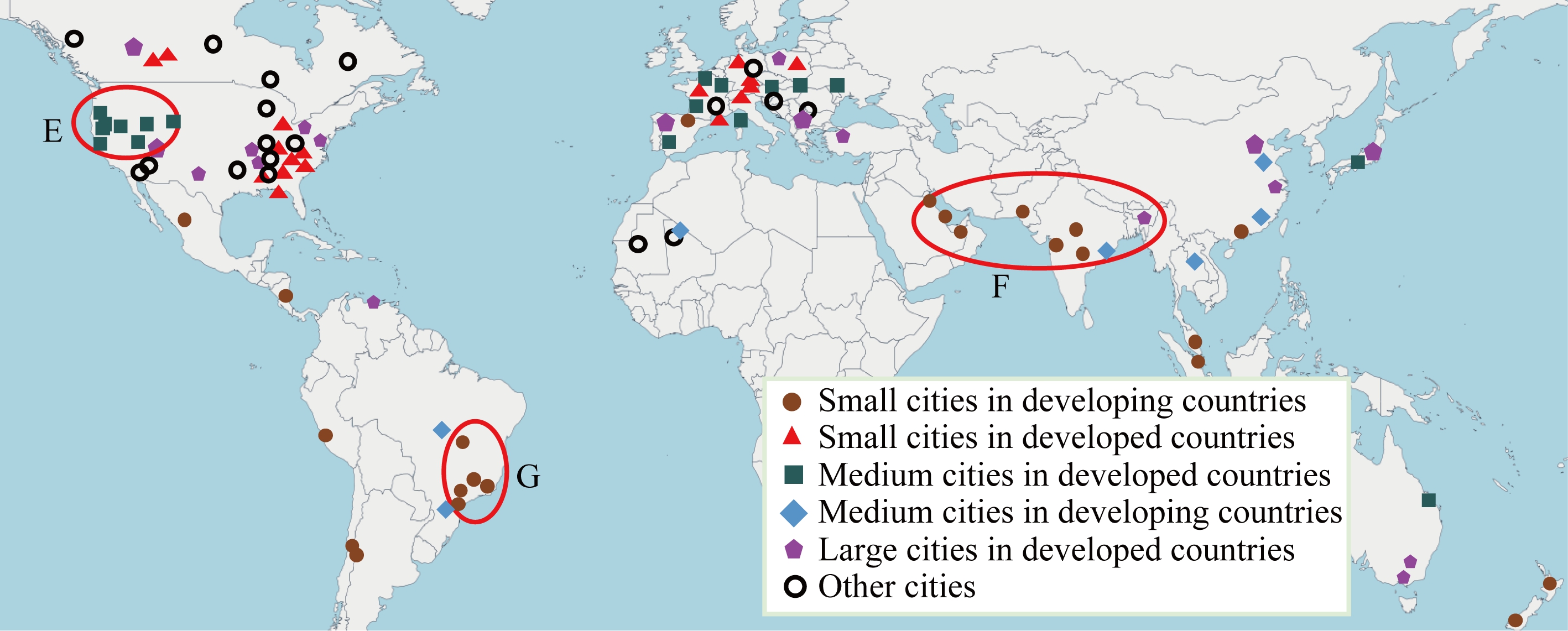
Fig. 7 Clustering results of several cities
图7 部分城市聚类结果
2.3 时间模式分析
本节基于人才流动矩阵序列,分析地区间人才流动呈现的时间模式.
一般而言,地区流出和流入人才基数(即![]() 的变化是各地区人口规模和地区人才吸引力等因素随时间变化共同作用的结果,也反映了地区整体人才活跃程度的变化.此外,经济、文化交流融合以及交通运输的发展,也可能促进人才流动基数的变化.
的变化是各地区人口规模和地区人才吸引力等因素随时间变化共同作用的结果,也反映了地区整体人才活跃程度的变化.此外,经济、文化交流融合以及交通运输的发展,也可能促进人才流动基数的变化.
图8和图9分别是OPN数据中10个典型城市流出和流入人才基数在1995—2016年的趋势曲线.需要指出的是,2016年的OPN数据由于采集过程中的干扰导致数据不完整,因此图8和图9中曲线在2015—2016年有下降趋势.整体上,从1995—2015年(除2009年外),流入和流出人才基数整体均逐年呈现上升趋势.一方面,由于这一趋势受OPN用户构成的影响,因此并不精确反映地区人才基数;另一方面,城市间的趋势对比可以反映竞争力的变化趋势,在同一时间窗口中,上升速度相对慢的城市,其竞争力相对下降.
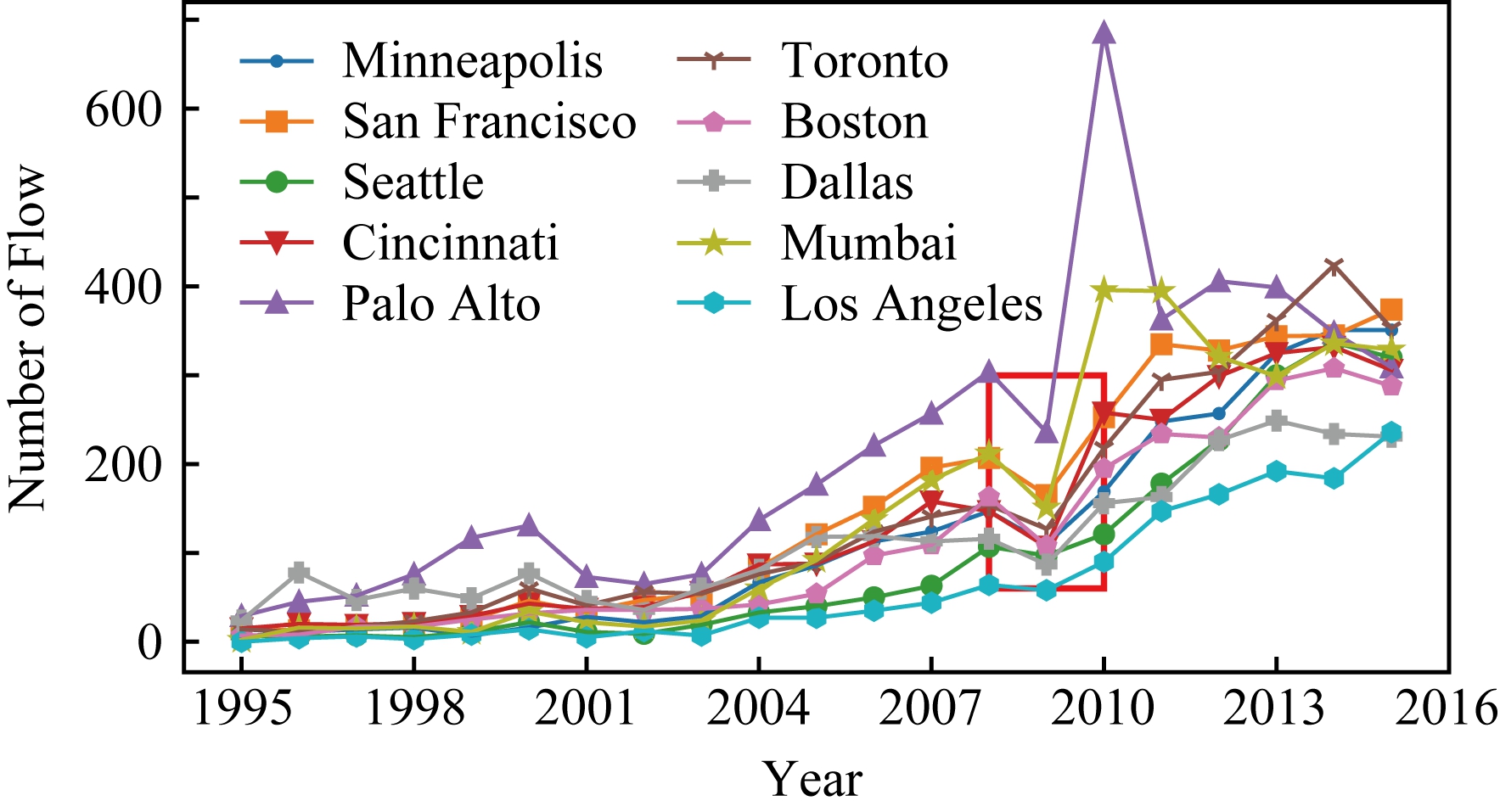
Fig. 8 The trend of out flow of several cities
图8 地区流出人才基数趋势图
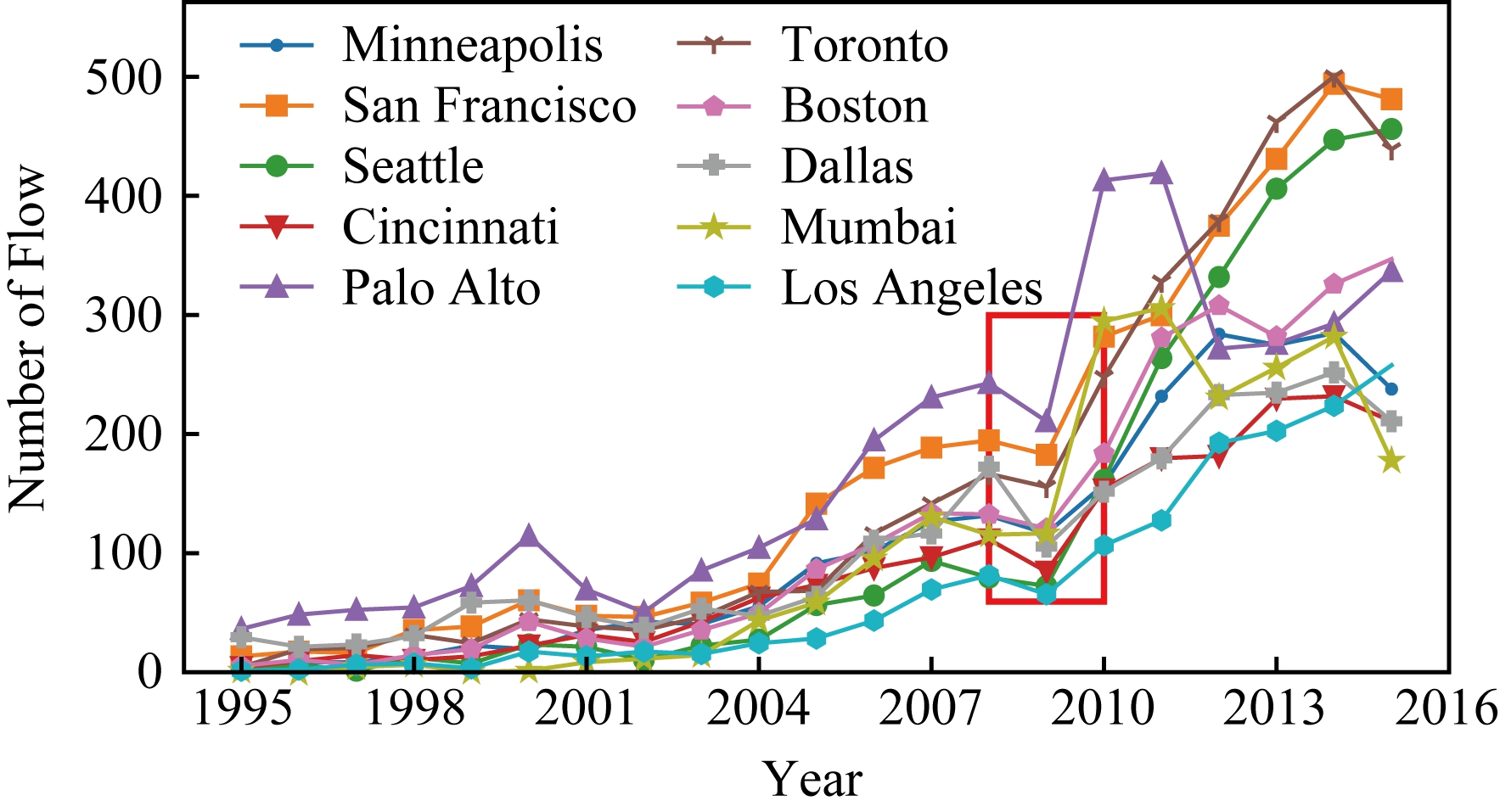
Fig. 9 The trend of in flow of several cities
图9 地区流入人才基数趋势图
图8和图9中,人口基数在2008—2009年出现了明显不符合增长趋势的下滑,但在2010年后继续保持增长.事实上,受2008年左右经济危机的影响,2009年全球就业市场表现低迷[15],其中大型金融和科技公司影响显著,所以代表性大城市的人员流动出现明显的下降.
流量分布的熵差是人才吸引力空间多样性的表征,而该熵差的变化则反映了这一多样性的变化趋势.图10是典型城市的熵差序列,其中的地区为图4所示的熵差中差值最大和最小的10个城市(地区).图10中圆点和叉点分别表示人才净流入地区(即si>0)和净流失地区(即si<0).
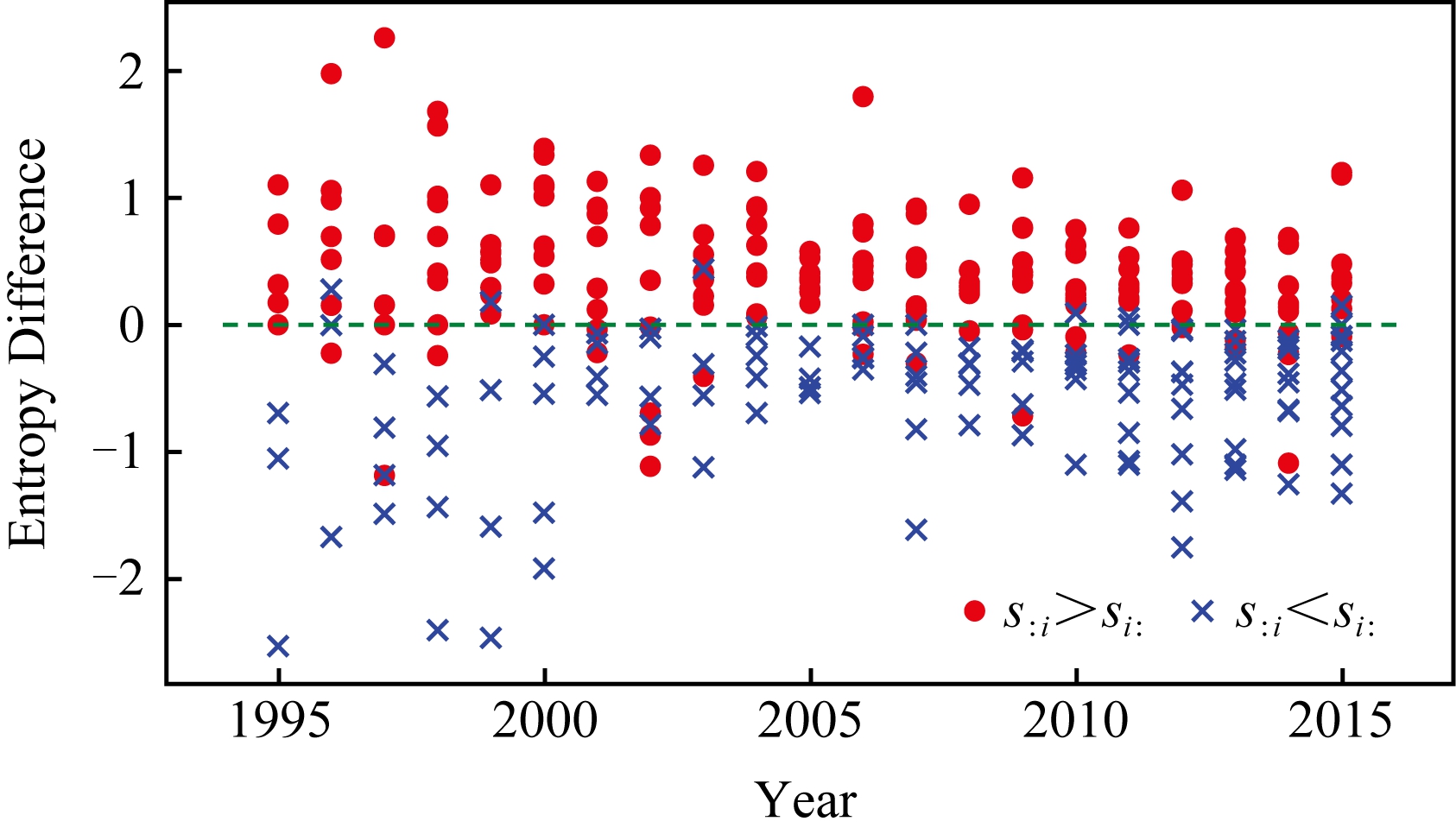
Fig. 10 The relation between entropy difference andtalent flow
图10 1995—2015年熵差与净流失
从图10可见,在1995—2015年间,净收益地区大部分保持较大的熵差,仅有小部分地区的熵差略有波动,反之亦然.这说明在人才竞争方面,具备竞争力的大城市其竞争力趋向保持高竞争力,而竞争力的弱小城市则长期不具备竞争优势.这种人才竞争力强者益强的现象,也是当前全球人才竞争力格局的体现.
3 人才流动量预测模型
本节首先定义人才流动量预测问题,然后详述预测模型设计的原则,以及基于卷积和循环神经网络的预测模型.
3.1 问题定义
人才流动量预测问题定义为:利用地区间人才流动量的历史数据,预估未来一个时间段地区间的人才流动量.借助人才流动矩阵,该问题可形式化地定义为:给定人才流动矩阵序列{Xt|t∈(1,2,…,K)},预估XK+1.
3.2 预测模型
从2.2节的分析可知,在单个时间片中,与人才流动模式相关的信息包含在流量向量中.同时,流动模式随时间逐渐演化,演化信息包含在连续的流量矩阵序列中.因此,一个良好定义的流动量预测模型应具备3个功能:
1) 可从流量向量中提取流量模式.模式提取以流量向量为基本单位,提取方法在不同流量向量间具备通用性.据此要求,可设计多元映射![]() Rk,从静态流出向量中提取模式,其中k为该映射输出维度,即流量模式空间的维度.同理,可设计映射
Rk,从静态流出向量中提取模式,其中k为该映射输出维度,即流量模式空间的维度.同理,可设计映射![]() Rm×1→Rk,从流入向量中提取模式.
Rm×1→Rk,从流入向量中提取模式.
2) 可对流量模式的动态演化趋势建模.模型应可捕获趋势在时间上的延续性,即保存当前时刻的趋势受过去时刻趋势的影响.据此要求,可设计时间上递归的多元映射![]() R2m+l→Rl(其中l为该映射的输出维度),基于流出模式f和流入模式g,以及历史累积趋势φt,获取演化趋势φt+1.
R2m+l→Rl(其中l为该映射的输出维度),基于流出模式f和流入模式g,以及历史累积趋势φt,获取演化趋势φt+1.
3) 可根据流量模式及其演化趋势对未来流动量进行预测.据此要求,设计输出映射O(φ1,φ2,…,φK):RKl→Rm×m预测下一时段人才流动矩阵XK+1.
对于满足上面3个功能的模型,由于有Tn2个因变量和n2个预测目标,模型一般包含Tn4量级的参数.但由于流量矩阵的稀疏性,流量模式在单个矩阵元素上表现不明显,因此在定义在流量向量上的流量模式规律性更强.本文提出在流量向量的基础上设计上述3类映射,同时在不同的流量向量上复用同一组模型参数,在利用流量向量携带的模式信息的同时缩小参数规模.
具体而言,对应上述3类映射,本文采用卷积神经网络(convolutional neural network, CNN)[16]实现映射f和g,采用循环神经网络(recurrent neural network, RNN)[17]实现映射φ,并采用全连接神经网络(full-connected neural network, FNN)[13]实现映射O,对XK+1进行预测.模型结构如图11所示,其中包含CNN部分(f,g)、RNN部分(φ)和全连接(O)部分,简记为CNN-RNN模型.
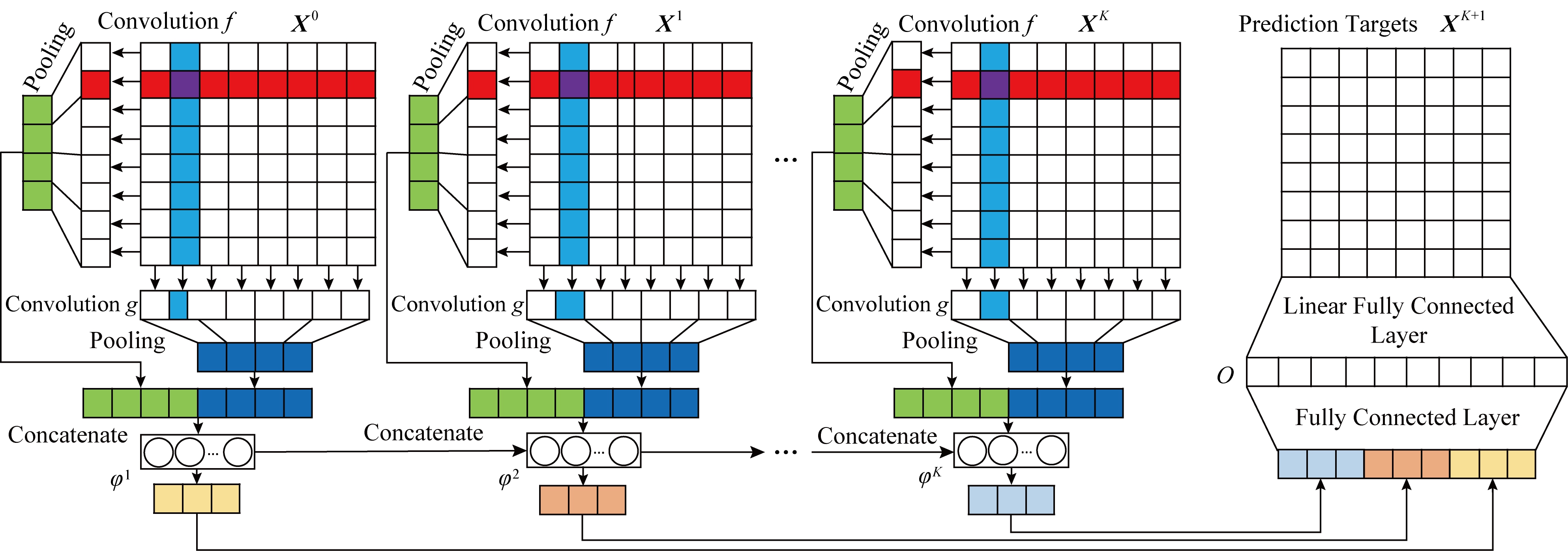
Fig. 11 The proposed model consisting of CNN, RNN and FNN
图11 CNN-RNN模型示意图
CNN模型利用较小的卷积核矩阵对流量矩阵做卷积.为实现从流量向量中提取流量模式的目标,本文采用与流量向量同型的矩阵作为卷积核,因此一个卷积操作对应从一个流量向量中提取模式.同时,同一卷积核作用在不同流量向量中实现了参数复用,减小了参数规模.RNN模型在时序上采用循环输入的策略,即当前时刻输出作为下一时刻输入的一部分.本文将CNN在矩阵序列中提取的流量模式序列作为RNN的输入,使流量模式在时序上具备连续性.FNN综合RNN在各时段的输出,经过全连接层后得到预测结果.
本节分别详述模型的CNN, RNN, FNN部分的计算细节.
1) CNN部分.该部分的输入为流量矩阵,输出为模式向量.首先从流出向量![]() 中提取静态模式,其卷积核大小与流出向量长度相同,该映射定义为
中提取静态模式,其卷积核大小与流出向量长度相同,该映射定义为
其中,Wf∈Rm×k是卷积核,k为卷积核数目,bf∈Rk是偏置项,二者均为可学习参数.σ(z)=1 (1+e-z)是Sigmoid激活函数.该卷积依次作用在Xt的每一行,得到卷积结果.该结果经过最大池化(max pooling)操作后得到空间模式向量
(1+e-z)是Sigmoid激活函数.该卷积依次作用在Xt的每一行,得到卷积结果.该结果经过最大池化(max pooling)操作后得到空间模式向量![]() R(m
R(m 2)×k,池化操作定义为
2)×k,池化操作定义为
其中,u=1,3,5,…,![]() m
m 2
2![]() .
.
同时,另一组CNN从流入向量![]() 中提取静态模式,其卷积核大小与流入向量大小相同,即:
中提取静态模式,其卷积核大小与流入向量大小相同,即:
其中,Wg∈Rk×m是卷积核,bg∈Rk是偏置项,均为可学习参数.对该卷积结果进行最大池化操作得到流入模式表示
拼接2次卷积并池化的结果,并展开成一维向量即得到CNN部分的输出![]() 其中pt∈Rmk,视为流量空间模式的向量表示.
其中pt∈Rmk,视为流量空间模式的向量表示.
2) RNN部分.该部分以pt为输入,实现φt+1(pt,γt)映射,实现时序循环结构.具体而言,RNN采用GRU(gated recurrent unit)结构,其计算过程:
zt=σ(Wzpt+Uzγt+bz), rt=σ(Wrpt+Urγt+br), ht+1=σ(Whpt+Uh(rt⊙γt)+bh), γt+1=(1-zt)⊙γt+zt⊙ht+1,
其中,W*∈Rl×mk,b*∈Rl分别为连接权重和偏置项参数;zt,rt是为防止参数学习过程中出现梯度消失问题[18]而设置的连接机制;初始化γ0=0.
3) FNN部分.该部分以拼接的γt为输入,并连接线性输出层,得到与Xt维度一致的输出,作为预测结果.具体而言,首先拼接RNN的输出γt得到γ=[γ1,γ2,…,γK],然后计算:
d=σ(Wdγ+bd), O=Wod+bo,
其中,Wd∈Rd×Kl,bd∈Rd,Wo∈Rmm×d,bo∈Rmm均为可学习参数.
模型的输出即为O∈Rmm,重新排列其维度为Rm×m,为下一时刻流量矩阵的预测值.
模型的目标函数为最小化预测结果O与实际流量矩阵XK+1的均方误差,即:
其中,θ为模型中可学习参数的集合,包括所有的连接权值和偏置,通过随机梯度下降方法训练[13].
3.3 模型复杂度分析
模型训练和预测时的计算量与可学习参数规模直接相关.本文提出的CNN-RNN模型中包含的可学习参数包括:网络层间连接权重项矩阵Wf,Wg,Wz,Wr,Wh,Uz,Ur,Uh,Wd,Wo等,共2mk+3mkl+3l2+dkl+dm2个参数,此外还包括偏置项bf,bg,bz,br,bh,bd,bo共2k+3l+d+m2项.其中k,l分别为卷积核个数和RNN神经元数,实验中设置为3,16,数值较小.而m为地区数量,约为1 200,因此m主要决定模型参数量,总参数量约为m2量级.
CNN-RNN的模型参数相对基准模型的参数规模较小.以线性拟合为例,有m2个预测目标,分别预测一对地区间的流量.模型包含Km2+1个输入项,对应K个历史矩阵,每个矩阵m2个参数和一个偏置项.因此,总参数个数为m2(Km2+1),约为m4量级,参数规模约为CNN-RNN模型的m2倍.
4 实验结果
4.1 实验数据
本文的实验数据来源为某大型在线职业平台[6],包括来自约6 000个用人单位的约500万就业记录,用人单位包括企业、高校和政府部门.数据中共包含1 200个地区,其中“地区”一般为对应国家的第3级行政区域,根据国家不同,分别为市、城镇或区,地区的空间分布如图6所示.本文采用这一数据集展示模式分析结果(见第3节),并评估人才流动预测模型的性能.
预测模型的训练和测试数据依据时间节点进行划分.具体而言,对于历史长度为K的预测实验,假设时间为(1,2,…,T),则训练集中的预训目标从t∈(K,K+1,…,![]() 0.8T
0.8T![]() )中选择,相应的测试目标从t∈{
)中选择,相应的测试目标从t∈{![]() 0.8T
0.8T![]() ,
,![]() 0.8T
0.8T![]() +1,…,T}中选择.给定目标矩阵,输入为对应目标前K个历史矩阵序列.由于单月和单季度数据不充分,实验中时间段按年度划分,即1个时段为1个自然年,流量为1年中流量的总和.
+1,…,T}中选择.给定目标矩阵,输入为对应目标前K个历史矩阵序列.由于单月和单季度数据不充分,实验中时间段按年度划分,即1个时段为1个自然年,流量为1年中流量的总和.
4.2 基准模型性能比较
本文共采用3个基准模型,包括绝对值约束的线性回归算法LASSO[19]、非线性回归算法SVR[20]以及多层稀疏编码器(stacked autoen-coders, SAEs)[12]模型.其中LASSO是有绝对值正则项的线性回归模型,在线性回归模型中性能表现较好且能较好地防止过拟合.SVR是有平方正则项的非线性回归模型,采用的核函数是径向基函数(radial basis function kernel),SVR是较先进的非线性回归模型.LASSO,SVR的正则系数通过在训练集中进行10折交叉验证进行选择.SAEs是由神经网络构成的自编码器,通过加入惩罚项来达到稀疏自编码的目的.训练好的SAEs模型在编码器后端加入前馈神经网络层来实现回归,该模型在交通流量预测问题中取得了较好的效果[12].LASSO, SVR, SAEs的输入均为实例向量,因此本文将输入(X1,X2,…,XK)展开为长度为Km2的向量,将输出展开为长度为m2的向量.此外,本文采用SVR的单目标变量模型,为实现多变量预测,分别为目标矩阵的每一个值项训练一个模型,共有m2个模型.
CNN-RNN模型的超参数通过在训练集中进行10折交叉验证进行选择.在本实验中,模型CNN部分的卷积核数k=3,RNN部分神经元数l=16,全连接层神经元数d=512.
本文采用的误差评价指标为实际流量和预测流量间的均方根误差(Es)和平均绝对值误差(Ea).分别定义为
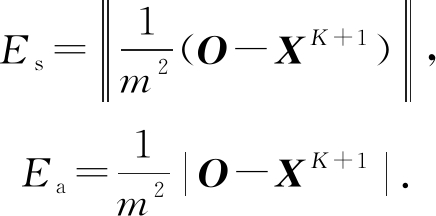
此外,由于流量矩阵是稀疏矩阵,在实际应用中关心的预测目标是非零位置的预测值,因此本文另外选择在非零元素上的均方误差(简记为Esn)和非零元素上的绝对值误差Ean作为评价指标.Es,Ea,Esn,Ean这4个指标均表示预测误差,误差值越小,表明模型预测效果越好.
图12为K=5的年度流量预测,即采用5年的历史数据,对下一年的流量数据进行预测的结果.
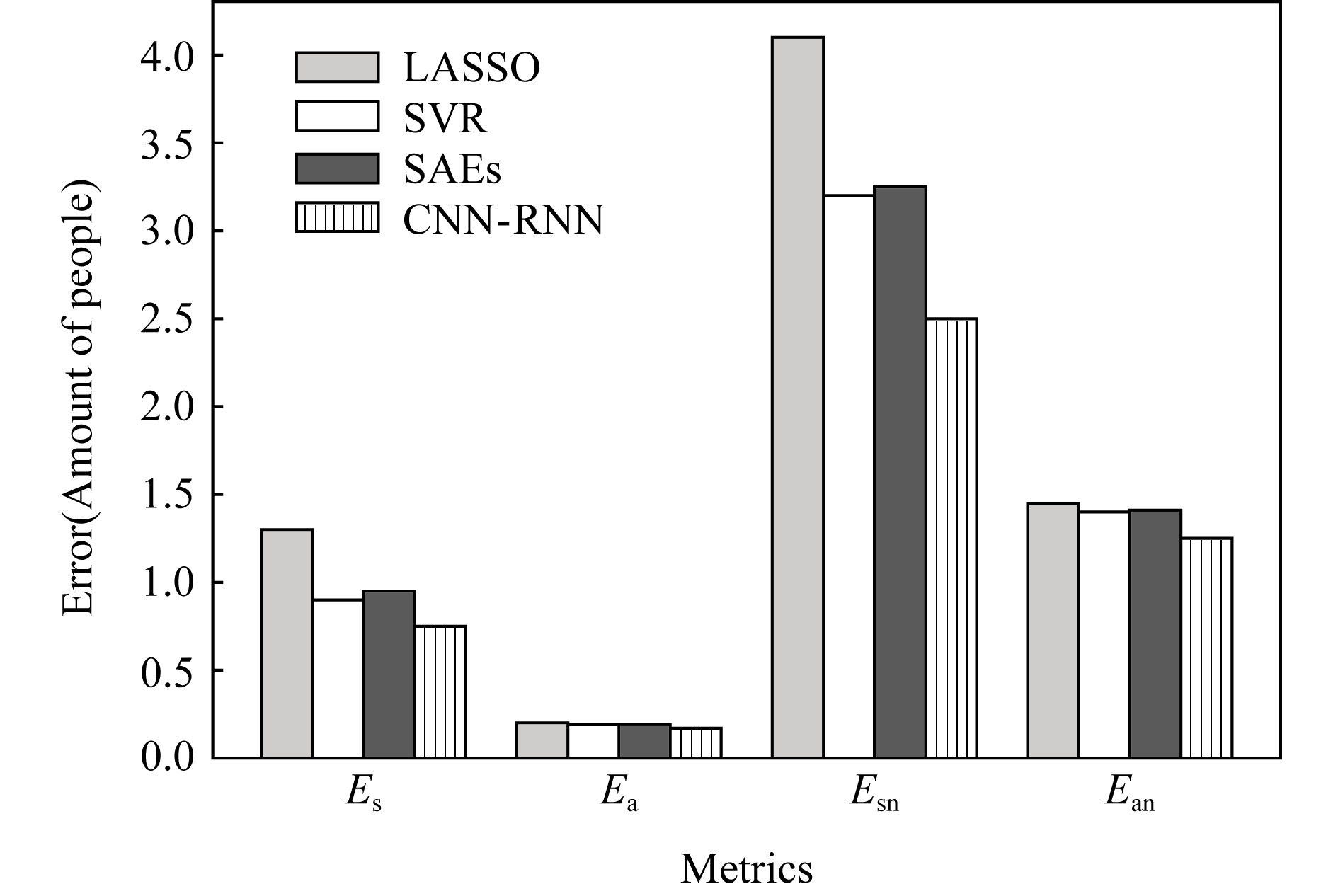
Fig. 12 Prediction errors of baselines
图12 基准模型预测误差
从图12中可见,CNN-RNN模型相对其他基准模型的4类误差均更小,其中Es,Ea,Esn,Ean相对最佳的基准模型SVR分别降低约20%,3%,24%,15%.此外,最佳的Es在1.0人次左右,Esn在2.5人次左右,即平均预测误差在1~3人次,而地区间人才流量平均约在50人次左右,因此预测结果较准确,较易满足一般预估任务的精度要求.最后,非零值位置平均误差绝对值相对较大,因此CNN-RNN模型在非零值位置的误差降低相对全局平均误差的降低幅度更大.该结果表明,本文提出的CNN-RNN模型的预测性能相对基准模型而言有明显的提高,且模型的绝对预测误差较低.
4.3 模型变体比较
CNN-RNN模型由多个部分组成,其中各部分均可独立作为模型完成预测任务.为评估模型各部分的预测能力,本节分别去除模型的CNN部分和RNN部分,利用剩余部分进行预测.各模型变体的实验设置与4.2节中的设置相同.为方便表述,本节分别用RNN表示去除CNN部分后的模型,用CNN表示去除RNN部分后的模型,用FNN表示同时去除RNN和CNN部分后的模型(即仅保留全连接部分的模型).
图13展示了各个模型变体的性能,其中RNN和CNN模型性能较相近,FNN模型性能相对较差.CNN-RNN模型的误差最小,相对变体中最佳的CNN降低约15%,2%,20%,13%.该结果表明CNN-RNN模型预测性能相对各模型变体单独预测的性能较好,但由于该模型复杂度更高,因此在实用中若考虑计算复杂性并不要求最小预测误差,则可用变体取代原模型.另一方面,模型的计算量集中在训练阶段,预测阶段计算量较小,因此在可离线训练的应用场景中CNN-RNN模型更具优势.
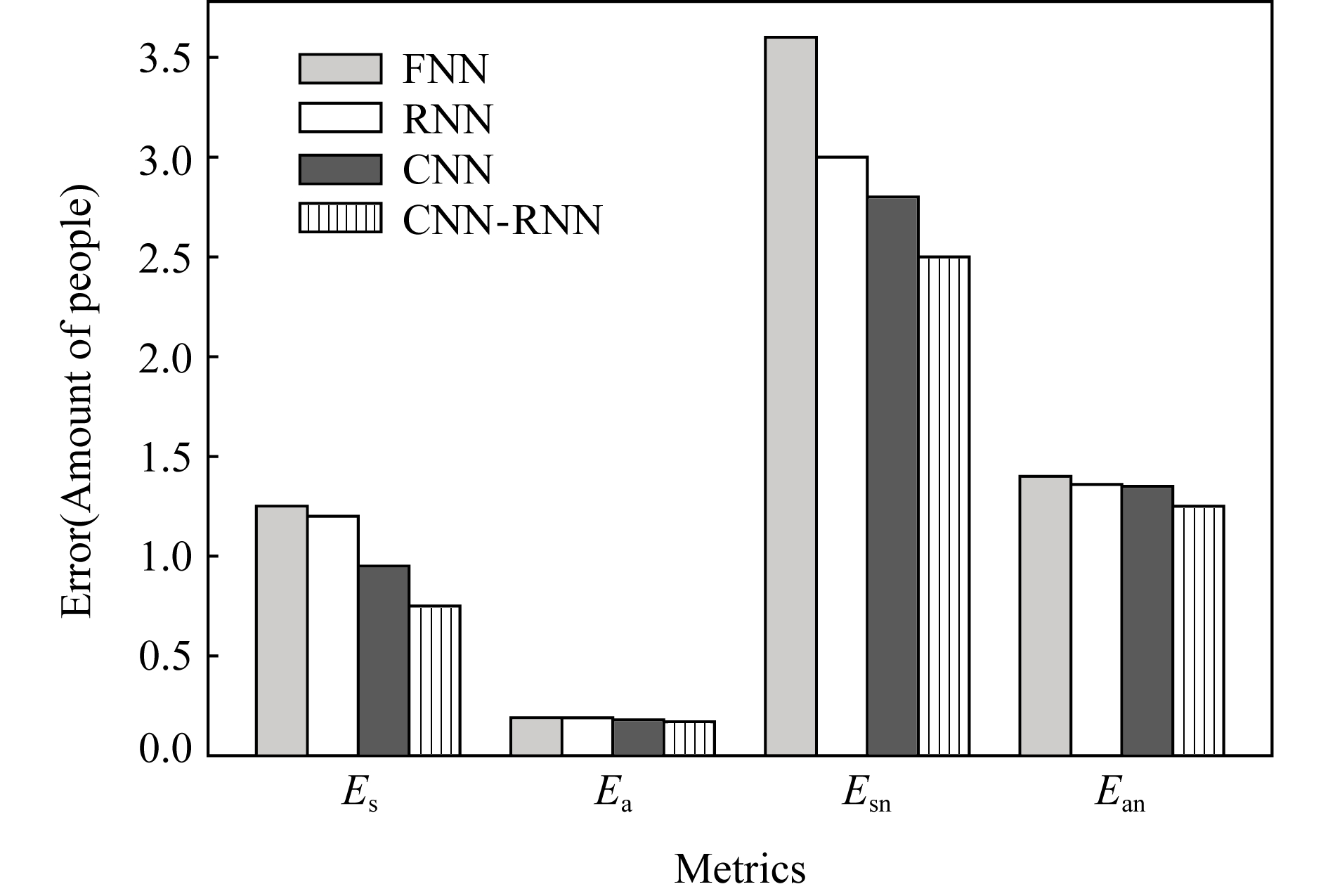
Fig. 13 Prediction errors of basic deep neural networks
图13 3种模型变体预测误差
4.4 数据历史长度影响
人才流动矩阵序列是预测模型的输入,所以不同的序列长度对模型的预测效果有直接影响.在实践中,数据收集成本随序列长度增加而增大,且收集大规模长时间的数据往往不可行.本节评估不同的数据历史K对结果影响,受数据集长度限制,实验中K分别取值为2~7,即采用2~7年的历史数据进行预测.
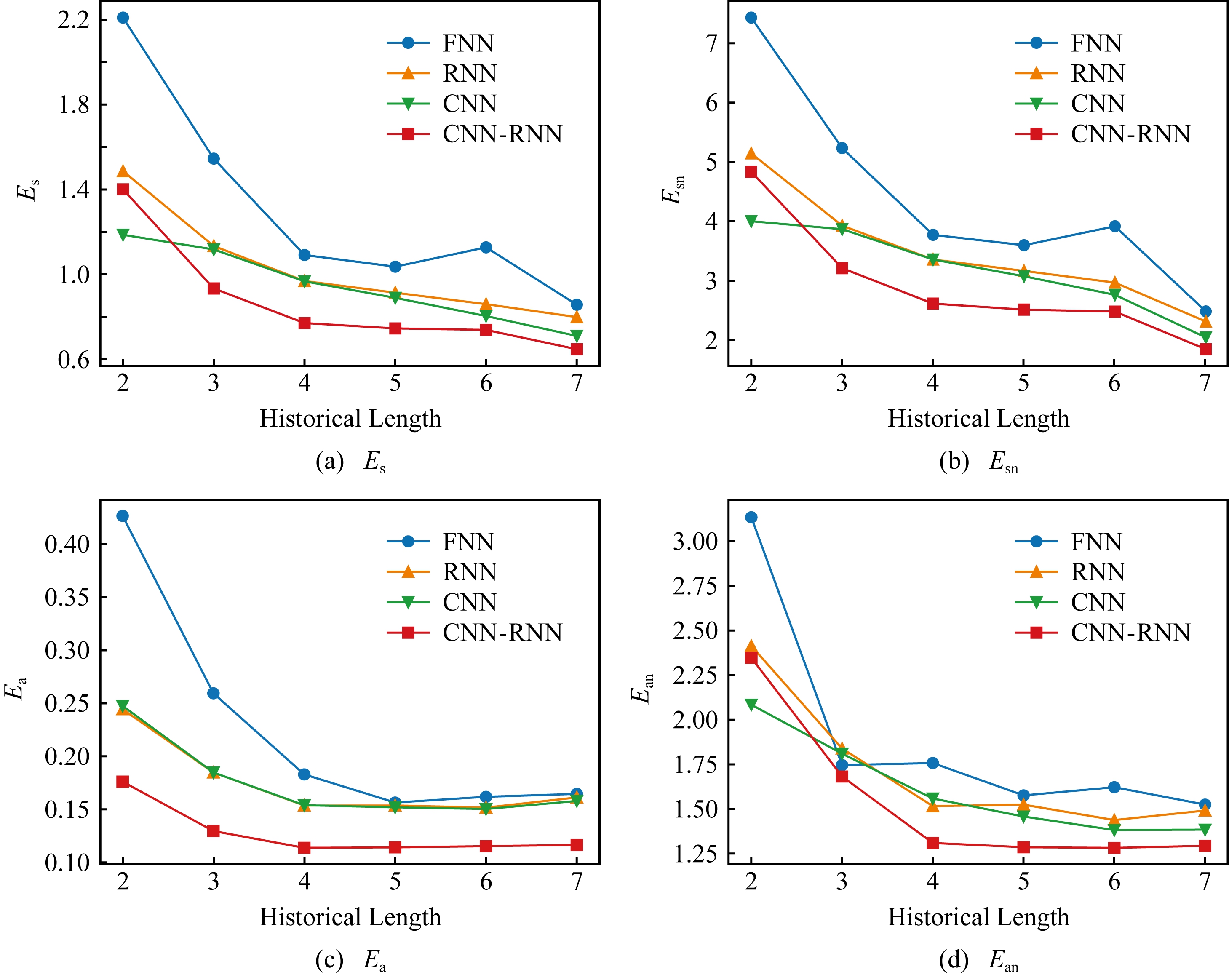
Fig. 14 Prediction error of models with different input lengths
图14 不同历史数据长度下的误差
图14是不同历史数据长度下的预测误差.图14 (a)~(d)分别表示4个评价指标的结果.该结果说明,CNN-RNN模型及其变体的预测误差随着历史数据长度的增加而呈现减小的趋势.预测误差在历史长度为2~4年时下降较快,在4~7年趋于稳定.此外,序列长度为2~3年和序列长度为5~6年的误差下降超过50%.该实验可以作为历史数据收集过程中的指导:历史数据长度至少需要达到一个最小的阈值,该阈值可以通过实验确定(如4年),更长的历史数据对于误差的减小效果较小.因此若收据收集的代价较高,则使用合适长度的历史数据即可.
5 结论与未来工作
本文提出人才流动矩阵序列,挖掘地区间人才流动的时空模式,并提出基于卷积和循环神经网络人才流动预测模型,通过大规模数据进行了模型性能验证.本文提出的模型可用于人才流动监控和分析,以及作为制定人才调控政策的参考.进一步,本文提出的方法可扩展应用在不同用人单位间的人才竞争模式发现任务等.此外,本文提出的基于矩阵序列的分析和预测模型,在类似场景中有一定应用潜力,如地区旅游人数建模与预估、区域商品供应量分配预估等.
[1]Williams A M. International labour migration and tacit knowledge transactions: A multi-level perspective[J]. Global Networks, 2007, 7(1): 29-50
[2]Williams A M. Listen to me, learn with me: International migration and knowledge transfer[J]. British Journal of Industrial Relations, 2007, 45(2): 361-382
[3]Guellec D, Cervantes M. International mobility of highly skilled workers: From statistical analysis to policy formulation[J]. International Mobility of the Highly Skilled, 2001, 1(1): 71-99
[4]Kofman E, Raghuram P. Gender and skilled migrants: Into and beyond the work place[J]. Geoforum, 2005, 36(2): 149-154
[5]Wang Yan, Fan Lihong. Using Multiple Measures to Train and Bring up Innovative Sci-tech Talents—Key Tasks Pointed out by “Outline of National Medium-and Long-term Program for Talent Development(2010—2020)”[J]. Bulletin of the Chinese Academy of Sciences, 2010, 25(6): 573-578 (in Chinese)(王艳, 樊立宏. 多头并举 培养造就创新型科技人才——《国家中长期人才发展规划纲要(2010—2020年)》解读[J]. 中国科学院院刊, 2010, 25(6): 573-578)
[6]Xu Huang, Yu Zhiwen, Xiong Hui, et al. Learning career mobility and human activity patterns for job change analysis[C] //Proc of IEEE Int Conf on Data Mining. Piscataway, NJ: IEEE, 2015: 1057-1062
[7]Xu Huang, Yu Zhiwen, Yang Jingyuan, et al. Talent circle detection in job transition networks[C] //Proc of the 22nd ACM SIGKDD Int Conf on Knowledge Discovery and Data Mining. New York: ACM, 2016: 655-664
[8]Saxenian A L. From brain drain to brain circulation: Transnational communities and regional upgrading in India and China[J]. Studies in Comparative International Development, 2005, 40(2): 35-61
[9]Rodriguez M, Helbing D, Zagheni E. Migration of professionals to the US[C] //Proc of Int Conf on Social Informatics. Berlin: Springer, 2014: 531-543
[10]Johnson J M, Regets M C. International mobility of scientists and engineers to the United States—brain drain or brain circulation?[J]. SRS Issue Brief, 1998, 1(6): 3-9
[11]Xu Huang, Yu Zhiwen, Guo Bin, et al. Extracting job title hierarchy from career trajectories: A Bayesian perspective[C] //Proc of the 27th Int Joint Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2018: 3599-3605
[12]Lu Yisheng, Duan Yanjie, Kang Wenwen, et al. Traffic flow prediction with big data: A deep learning approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 865-873
[13]Yu Kai, Jia Lei, Chen Yuqiang, et al. Deep learning: Yesterday, today, and tomorrow[J]. Journal of Computer Research and Development, 2013, 50(9): 1799-1804 (in Chinese)(余凯, 贾磊, 陈雨强, 等. 深度学习的昨天、今天和明天[J]. 计算机研究与发展, 2013, 50(9): 1799-1804)
[14]Zhang Gang, Liu Yue, Guo Jiafeng, et al. A hierarchical search result clustering method[J]. Journal of Computer Research and Development, 2008, 45(3): 542-547 (in Chinese)(张刚, 刘悦, 郭嘉丰, 等. 一种层次化的检索结果聚类方法[J]. 计算机研究与发展, 2008, 45(3): 542-547)
[15]Hipple S F. The labor market in 2009: Recession drags on[J]. Monthly Labor Review, 2010, 133(3): 3-22
[16]Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C] //Proc of Advances in Neural Information Processing Systems. New York: NIPS, 2012: 1097-1105
[17]Mikolov T, Karafiát M, Burget L, et al. Recurrent neural network based language mode[C] //Proc of the 11th Annual Conf of the Int Speech Communication Association. New York: ACM, 2010: 1045-1048
[18] Pascanu R, Mikolov T, Bengio Y. On the difficulty of training recurrent neural networks[C] //Proc of Int Conf on Machine Learning. New York: ACM, 2013: 1310-1318
[19]Tibshirani R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, 1996, 1(1): 267-288
[20]Liu Xiangdong, Luo Bin, Chen Zhaoqian. Optimal model selection for support vector machines[J]. Journal of Computer Research and Development, 2005, 42(4): 576-581 (in Chinese)(刘向东, 骆斌, 陈兆乾. 支持向量机最优模型选择的研究[J]. 计算机研究与发展, 2005, 42(4): 576-581)



