从地球、经济到人脑，在瞬态频率和复杂谐波的演化过程中形成了复杂系统.对于复杂系统的工作机理的探索一直是多学科研究的核心[1].随着数据采集技术和采集设备的飞速发展，复杂系统研究中对于数据处理的要求越来越高，所需处理数据的规模、维度及复杂性也在迅速增加.海量规模的时间序列大数据记录了复杂系统在时间和空间尺度上的演化.挖掘时间序列数据的潜在深度信息对于复杂系统过往数据分析和未来行为预测具有非常重要的意义[2].时间序列大数据包含了复杂系统中各个“个体单位”之间以及多个复杂系统间的相互联系.其外部表征具有数据相关性和多重数据属性，这一特性也决定了时间序列大数据具有较高的维度.
提取时间序列大数据潜在因子对研究复杂系统的整体机制起着至关重要的作用[3].高维科学数据中的一般潜在低维变量揭示了被观测系统动力学不断变化的整体机制.然而数据元素之间复杂的相互依赖关系、数据的高维度和海量的数据规模阻碍了其对整体机制的揭示.在小数据时代，时间序列大数据中低维特征的提取被认为是张量分解的数学问题.然而，直接采用传统的分析方法——独立成分分析[4](independent component analysis, ICA)及主成分分析[5-6](principal component analysis, PCA)——无法完整准确地提取出高维张量数据的潜在信息.这些方法使得维度之间的信息丢失和相关性破坏[7]，所提取的线性特征信息物理解释性较差.平行因子分析(parallel factor analysis， PARAFAC[8])和Tucker模型分解[9]适用于高维张量分解，其中因子化更新通常使用交替最小二乘法(alternating least squares， ALS)[10]或其他相关的替代算法[11-12]来解决.时间序列大数据具有动态增长的数据特征.数据规模不断增长，小数据时代的张量因子分解方法难以高效地应用于大规模、高维度的时间序列大数据.为保证原始关键信息提取的高效和完整，迫切需要开发一种面向大规模高维度的时间序列大数据分解分析方法，以实现快速有效的因子信息提取.
时间序列大数据的数据规模是巨大的，并且在空间中快速增长，无法保证对问题域有足够稳定的先验知识，这就导致无法确定张量分解的初始条件.良好的因子化分解初始条件和快速迭代的因子更新过程在大规模高维时间序列大数据分解过程中极其重要的.如何在缺失先验知识的前提下，适应大规模和超高维的数据特征，快速获取因子成为了时间序列大数据分析的重要研究挑战.为了解决上述挑战：1)基于贝叶斯因子化分解方法，本文提出一种在没有先验信息域和无需精确初始化过程即可快速获取收敛因子的海量并行贝叶斯因子化分析方法(the massively parallel Bayesian factorization approach， G -BF)；2)G -BF通过NVIDIA通用并行计算架构(compute unified device architecture， CUDA)[13]进行核函数映射，并行加速因子化迭代更新过程；3)G -BF使用高维数据映射方法完成对任意维度的时间序列大数据的分解要求；4)此外，G -BF结合粗粒度与细粒度2种并行方式应用于子因子融合框架(hierarchical-parallel factor analysis, H-PARAAC)[14]完成对超大规模张量的因子化分解.
为了评估G -BF的性能，本研究进行了一系列高维张量数据分析实验并与经过GPU加速的G -HALS算法对比探究G -BF的性能效率.实验结果表明：1)G -BF在Maxwell架构的GPU运行性能优于G -HALS；2)G -BF在处理高维数据规模、秩和维度等方面具有出色的可扩展性，可处理任意维度数据；3)此外，G -BF应用于现有的H-PARAFAC架构在处理超大规模高维张量时表现了优异的处理速度和性能，打破了可分析数据的规模限制.
本研究方法主要有3个方面优势：
1) G -BF能够在无需问题域的先验知识情况下快速准确地分解大规模时间序列大数据，获得低维特征因子信息；
2) G -BF针对高维时间序列大数据具有普适性，可分解数据维度可变，不限于3维或其他限定维度；
3) G -BF嵌入到H-PARAFAC架构中作为子张量因子分解过程的解决方案，在分解大规模张量时具有优越的性能，打破了处理数据规模大小的限制.
1 相关工作
针对大规模张量因子化分解问题，许多成功的方法和框架已经得到发展.大型矩阵及张量分解的性能已经成为研究的一大挑战.针对此问题的相关工作大致从优化分解过程和提高分解性能2个方面入手.
Bae等人[15]提出了一种高效多维并行可视化处理大规模科学数据算法(SMACOF).该算法利用集群消息传递接口并行矩阵操作和矩阵划分，实现了高维矩阵到低维欧氏空间的转换.
在线性分析问题中，特征值问题、奇异值问题以及QR分解(QR decomposition)问题极其重要.Agullo等人[16]提出了一种将矩阵分解为正交矩阵和上三角矩阵乘积的高效分解方法.该方法利用加速设备节点，采用CPU
GPU混合架构来加速QR分解过程.
Tan等人[17]提出了一个矩阵分解库(cuMF)来优化交替最小二乘法(ALS)方法以求解超大规模矩阵分解.cuMF在单个GPU节点上使用多种策略优化ALS中内存访问，同时将数据与模型并行化用于最小化GPU通信开销.
Zou等人[18]提出了一种并行张量分解算法(GPUTENSOR)加速大数据集的张量分解.该方法将大张量分成小块，利用图形处理单元(GPU)固有并行性及高存储带宽并行相关操作，同时使用零散方式优化计算策略，以避免中间数据爆炸而牺牲性能.
最近，Shin等人[19]提出了用坐标下降法更新参数的大规模高阶张量分解算法CDTF.该方法具有良好的数据可扩展性，运行在40个节点(Xeon 2.4 GHz)的Hadoop集群上时，可分解有10亿个可观测条目的5阶张量.
本研究的目标是在无需先验信息情况下高效分解大规模高维张量形式的时间序列大数据.所提出方法的研究包括：1)运行效率；2)分解的维度尺寸；3)可处理大型张量数据规模限制.
2 海量并行贝叶斯因子化分析方法(G -BF)
本节的主要内容包括4个部分：1)介绍贝叶斯分解算法(Bayesian factorization， BF)的理论知识；2)对本文提出的面向时间序列大数据海量并行贝叶斯因子化分析方法(G -BF)的算法设计和并行加速设计的描述；3)简要介绍G -BF和H-PARAFA框架的融合设计；4)对G -BF为满足处理任意维度分解需求采用的高维数据映射方法进行阐述.
2.1 贝叶斯分解算法
2.1.1 张量分解概率模型及贝叶斯先验
定义张量分解的线性模型表达式为
(1)
其中,Y表示大小为I1×I2×…×IN的N维张量，可以由因子张量X和噪声张量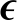
组成，∘表示外积，R表示因子矩阵秩，U(n)表示大小为In×R的因子矩阵集合，
表示第n个因子矩阵的第r行.
假设因子向量
和噪声张量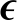均服从独立同分布的多维高斯分布
因此，无信息先验的分布表达式为
(2)
其中，大小为R×R的矩阵σ和标量λ为超参数.
2.1.2 基于变分贝叶斯推断的贝叶斯分解
概率模型在变分贝叶斯框架下采用确定性近似推理[20]，将自由能(Free)定义为p(Y)似然估计的边界下限:
(3)
其中，
表示任意概率分布，近似真实的后验分布
因子矩阵的后验分布p(U(n)|Y)(1≤n≤N)以及更新的超参数λ,σ在自由能最大化分析时获得.因子矩阵采用行向量的形式表示，沿每1行独立的行向量推导出其后验分布为
表示张量Y沿n-mode矩阵化张开矩阵的第i行向量.
通过变分贝叶斯推断求
的近似分布
(4)
其中，E{U(m)}(·)(1≤m≤N,m≠n)为由后验概率
的期望.通过计算
获得因子矩阵
(均值)和方差Ψ(n)：
(5)
符号⊕和⊙分别表示矩阵Hadamard和Khatri-Rao乘积，概率模型采用点估计更新超参数σ,λ.当所述自由能最大化时，求导计算
得到σ,λ更新公式
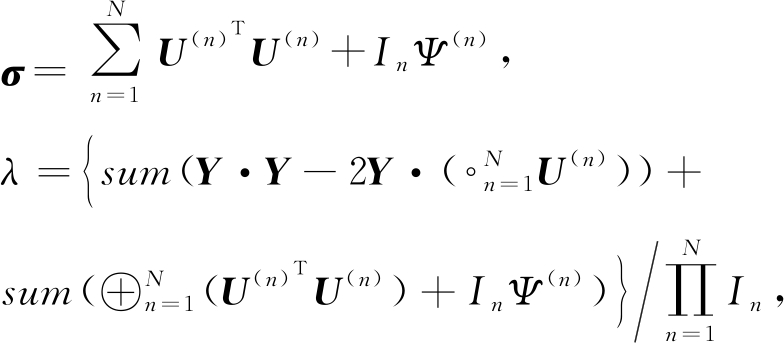
(6)
符号·表示内积.
2.2 海量并行贝叶斯因子化分解方法
2.2.1 G -BF并行加速设计策略
G -BF是基于BF算法理论可以在GPU节点上运行的大规模并行方法.在无需先验信息及精确因子初始化的情况下，G -BF算法可准确快速迭代地分解大规模张量获取因子矩阵.本方法涉及的大型矩阵运算操作主要包括Khatri-Rao乘积、Hadamard乘积、逐元除法和矩阵乘法等.利用CUDA进行密集矩阵运算并行加速，实现因子矩阵集的快速更新迭代求解.G -BF将运算过程作为设备并行模块映射到图1中CUDA核函数.G -BF分解大规模张量获取因子矩阵过程根据图1内容包含8个过程：
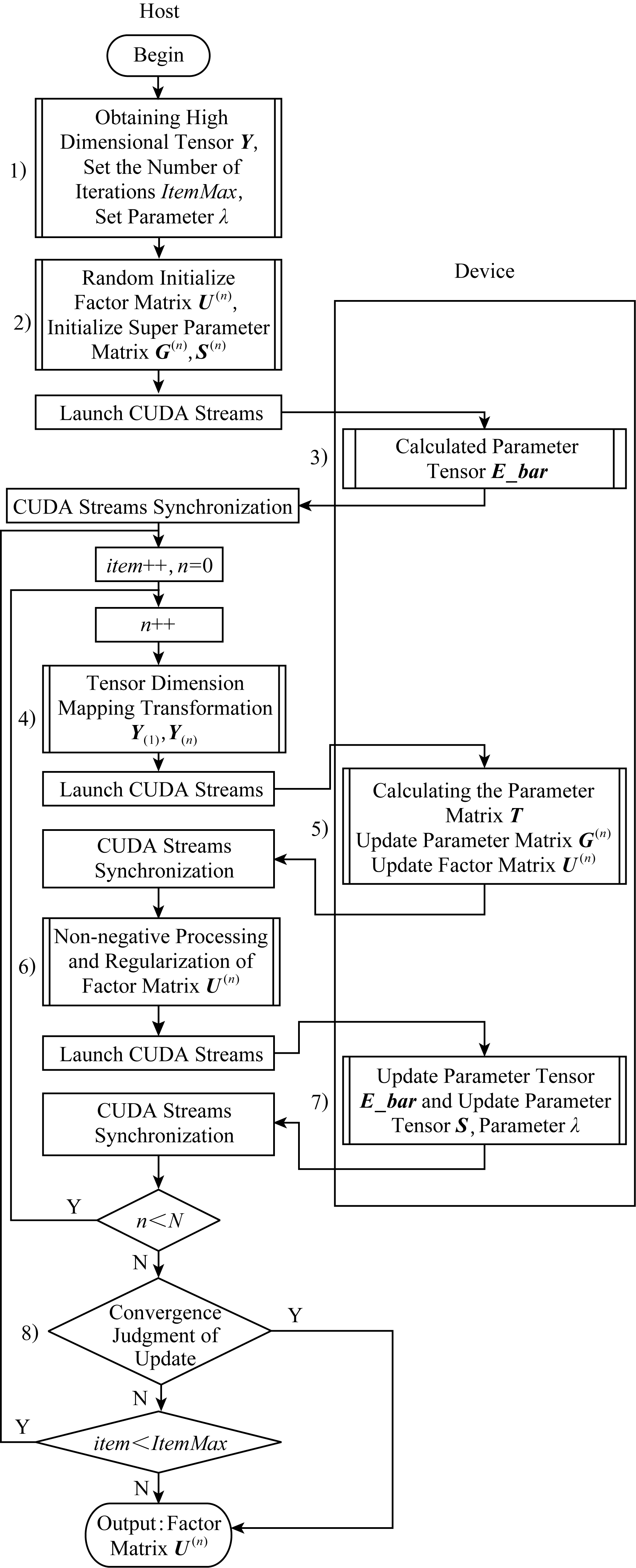
Fig. 1 G -BF method parallel acceleration design strategy diagram
图1 G -BF方法并行加速设计策略图
1) G -BF的第1步发生在主机端.首先，读取待处理张量Y，获取Y的维度大小N、因子化分析过程中表示因子集大小的参数R以及初始化超参数λ.定义G -BF最大迭代次数ItemMax.当迭代次数达到ItemMax时，无论是否达到收敛条件都将停止因子矩阵更新.此参数是限制整个因子化过程的总体耗时的重要参数，当不满足收敛条件时，ItemMax设定值越大，通过迭代分解获取的因子矩阵越接近最优解，但耗时也将更大.
2) 该过程初始化G -BF中各项参数矩阵及参数张量，此过程发生在主机端.首先将因子矩阵U(n)随机初始化大小为In×R的矩阵；S与G是3维张量，大小均为N×R×R,初始化方法为：当第2维和第3维的索引相同时，将值设为0.01，其余元素都设置为0.
3) 该过程在设备端负责计算初始化3维张量，其大小为N×R×R.E_Bar(n)的更新公式为
E_Bar(n)=U(n)TU(n)+InG(n),
这里涉及的运算操作包括矩阵乘法和矩阵加法.根据E_Bar(n)的更新公式可知，各个E_Bar(n)的更新过程相互独立.上角标n代表更新的不同维度.这里采用并行方式更新，调用cudaStreams执行多个维度的E_Bar(n)的并行更新，每1个cudaStream执行任务相同.第n个cudaStream的执行内容为：将对应第n维的因子矩阵U(n)和参数矩阵G(n)从主机端复制到设备端，主机端调用核函数在设备端计算E_Bar(n)，获得结果后拷贝回主机端.在完成上述准备后，开始迭代进行因子矩阵U(n)的维度更新，设置item=1，n=1，item表示G -BF实际迭代周期数，n表示G -BF当前更新维度.
4) 高维张量Y的存储映射.G -BF算法设计要求可分解任意维度张量，但NVIDIA的CUDA计算架构的数据管理固定为1维数据.在G -BF中将张量Y通过张量矩阵化展开方式映射为1维向量进行存储.当维度更新时，张量元素坐标根据维度间关系设定映射规则转换.该过程也可以在迭代更新之外完成，如此可减少维度转换的时间消耗，但这也将增加存储空间的负担.详细的维度映射方法将在2.2.4节给出.
5) G -BF的核心内容，其目的是更新每个迭代循环中各维度的因子矩阵U(n).大致分为3个部分：计算过程参数矩阵T、更新当前维度下参数矩阵G(n)、更新当前维度下因子矩阵U(n).
① 计算过程参数矩阵的主要内容为在主机端初始化过程参数矩阵T，其大小为R×R，数据值全部设为1λ.调用核函数更新设备端过程参数矩阵T，更新公式为T=T⊕U⊕-n,主要涉及的矩阵计算为Hadmard乘积.为减少核函数调用和数据传输带来的时间开销，将除当前维度之外的因子矩阵合并成1维向量与过程参数矩阵T一同作为Hadmard乘运算核函数的输入，输出结果为T的更新结果.
② 更新当前维度下参数矩阵G(n)更新规则为G(n)=(T+S(n)-1)-1，需要通过CUDA进行矩阵求逆和矩阵加法的GPU加速.
③ 更新当前维度下因子矩阵U(n)其更新公式为U(n)={(Y(n)λ)U⊙-n}G(n)，这部分发生在设备端，调用Khatri-Rao乘积核函数直接计算U⊙-n，将N-1个因子矩阵拷贝到1个一维向量作为核函数的输入参数以便一步直接计算U⊙-n，这样的方法减少了核函数的调用.(Y(n)λ)U⊙-n由于矩阵乘法特性以及输入矩阵规模过大导致本过程是整个G -BF中最耗时的步骤.调用设备端矩阵乘法核函数计算得到中间矩阵M，再次调用矩阵乘法核函数计算M×G(n)获得当前维度更新后的因子矩阵U(n).
6) 对当前更新维度的因子矩阵U(n)进行非负性和正则化处理.通过遍历将因子矩阵中的负数设为0或某一极小值以及将因子矩阵U(n)以列优先方式进行归一化.此操作目的是为减少计算复杂性以及满足H-PARAFAC框架.通过对因子矩阵附加约束，保证了结合H-PARAFAC框架后结果的唯一性.
7) 参数矩阵E_Bar(n)和参数张量S的更新.该更新计算过程在设备端运行.首先更新当前维度中的参数矩阵E_Bar(n)，更新规则为E_Bar(n)=U(n)TU(n)+G(n)，使用CUDA调用主机端的核函数，在设备端进行加速矩阵乘法和矩阵加法运算操作.接下来，更新参数张量S.张量S实际上是1组数量为N且大小为R×R的矩阵集，其中单个矩阵的更新规则为S(n)=E_Bar(n)In+G(n)，任何2个S(n)更新过程彼此独立，调用N个cudaStreams完成到设备端的并行传输并更新矩阵S(n).完成当前维度中的所有更新操作后，n增加1，更新下一个维度.
8) 判断G -BF是否达到收敛.通过FIT值大小来判断.FIT值的计算过程如下：
使用CUDA在设备端快速计算FIT值.G -BF的收敛条件设定为：如果FIT值小于超参数阈值或当迭代次数达到超参数迭代的最大次数时，迭代更新过程结束；G -BF最终输出张量Y的因子矩阵集U，否则“item+1”，重置“n=1”并返回4)，循环迭代更新.
当G -BF中收敛到全局最小值或迭代次数达到预设最大值时，输出的因子矩阵集为最优因子.
2.2.2 并行加速线程映射策略
G -BF模型中在GPU设备端进行的密集矩阵计算主要包括矩阵的Hadmard乘积、Khatri-Rao乘积、矩阵加减、逐元除法和矩阵乘法.G -BF中的矩阵运算根据线程管理和调用策略的不同分为：
1) 直接映射.输出矩阵的每个元素直接从输入矩阵中的单个元素确定.例如，在矩阵Hadmard乘积运算中，通过直接将2个输入矩阵的第i个元素相乘获得结果矩阵C的第i个元素，因此设备端线程直接映射到输入元素.如果输出矩阵有M个元素，并且核函数总共调用T个线程，那么每个线程最多负责计算(M+T-1)T元素.在G -BF中，Khatri-Rao乘积矩阵、Hadmard乘积矩阵、矩阵加减矩阵和逐元除法都属于直接映射.算法1以Hadmard乘积为例给出直接映射的代码设计.
算法1. 并行加速——矩阵Hadmard乘积.
输入：矩阵A大小(AX,AY)、矩阵B大小(AX,AY);
输出：矩阵C大小(AX,AY).
① row=blockIdx.y×blockDim.y+threadIdx.y；
② col=blockIdx.x×blockDim.x+threadIdx.x；
③ offsetX=gridDim.x×blockDim.x；
④ offsetY=gridDim.y×blockDim.y；
⑤ for i=col to AX step offsetX
⑥ for j=row to AY step offsetY
⑦ C[i×AY+j]=A[i×AY+j]×
B[i×AY+j];
⑧ end for
⑨ end for
2) 共享内存.输出矩阵的每个元素由输入矩阵的1行或1列获得.矩阵的乘法就是采用这种策略.矩阵乘法的输出矩阵C的索引(i,j)是输入矩阵A的第i行和输入矩阵B的第j列的对应元素乘积的和.若通过直接映射进行矩阵乘法，则每个线程需要将1列和1行元素从全局内存复制到局部内存，这会带来较高的时间开销，大大降低计算性能.
本文在G -BF中使用共享内存策略加快矩阵乘法的执行效率.设备端Block中共享存储器是线程共享的存储单元，与设备端的全局内存和局部内存相比，具有更高的带宽和更低的延迟.使用共享内存能够避免线程将数据从全局内存复制到本地内存的高额时间开销.在矩阵的乘法中，许多不同的线程使用相同的数据部分，而共享内存可以满足同一个Block中的线程可以共享数据.因此在对较大矩阵进行乘法运算时可以使用共享内存上的“分块矩阵”，每个块物理上对应于设备端的Block.假设2个输入矩阵A(m×l)和B(l×n)，将每个矩阵划分成一系列子矩阵(例如Aik和Bkj)，确保对应的子矩阵块的列等于行.
(7)
2.2.3 G -BF和H-PARAFAC
H-PARFAC框架是以大规模并行方式分解巨大稠密张量的一种解决方案，它使用现代并行和集群计算技术，实现了数据的近实时处理，并且使得提取任意大小和尺寸张量的全部因子成为可能.在大张量分解过程中，H-PARAFAC的分解和融合策略是非常有优势的.
G -BF在提取大规模高维数据低维信息时，具有优良的迭代效率和性能.该方法能有效分解一个庞大的稠密张量，并且不需要精确的初始化过程即可快速迭代出因子的全局最优解.将G -BF嵌入到H-PARAFAC框架中，它可以完成原来精确初始化模块中并行直接三线性分解(direct trilinear decomposition，DTLD[6])和子张量分解2个部分的工作，进而加速完成超大规模高维数据的低维因子化分解.图2展示了G -BF结合H-PARAFAC框架的完整设计.利用分解策略将原始高维张量变换为多个子张量；然后使用G -BF方法，将子张量因子化分解得到子因子矩阵；在子张量经G -BF分解后，利用H-PARAFAC方法将各维度的子因子矩阵进行融合，得到完整的原始张量的因子矩阵；最终完成超大规模高维时间序列张量大数据的分解.
Fig. 2 The design of H-PARAFAC framework with G -BF
图2 G -BF应用H-PARAFAC架构结合设计图
2.2.4 高维张量的数据存储映射
由于处理大规模时间序列大数据高维度分解设计目标的限制，张量Y的数据存储设计尤为重要.在分解过程中，几乎所有的运算都是矩阵运算和向量运算.在G -BF算法中，将张量Y扩展为矩阵Y(n)进行矩阵运算，其映射策略为：假设N维张量Y中任意元素的坐标为[i1,i2,…,iN]，张量每个维度的大小分别对应为I1,I2,…,IN，则映射到一维向量的元素位置为
(8)
由式(8)可知，张量中各元素的N维索引与一维矢量Y中的坐标是一一对应的，然后可以直接利用相应的元素进行计算.基于此映射策略来完成4)中提到的张量维度(Y(1)→Y(n))的转换.在嵌入G -BF的H-PARAFAC框架中子因子融合过程亦采用相似的维度转换映射规则.
3 实验结果与分析
本次实验对本文提出方法的性能进行了评估，并与G -HALS方法进行了对比.实验包括：1)使用CUDA8.0重新编译HALS算法G -HALS；2)使用CUDA8.0编译本文的G -BF算法.所有的实验都采用了相同的编译工具g++和nvcc.实验在1台装有NVIDIA GeForce TITAN X显卡(Maxwell archite-cture)的工作站上进行.具体的实验环境配置如表1所示:
Table 1 Configuration of Experimental Environment
表1 实验环境配置
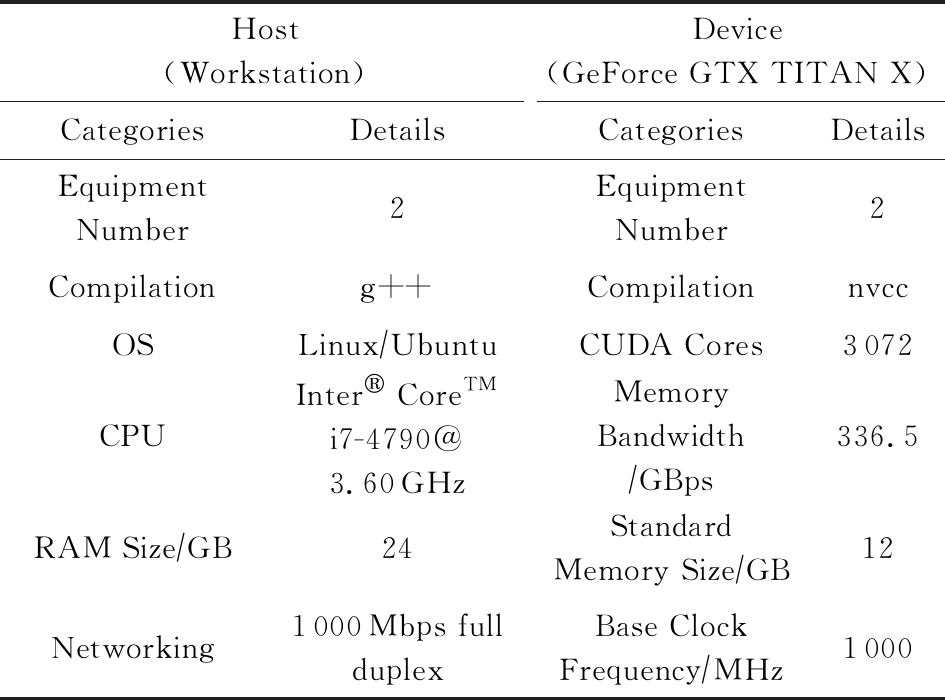
Host(Workstation)Device(GeForce GTX TITAN X)CategoriesDetailsCategoriesDetailsEquipmentNumber2Equipment Number2Compilationg++CompilationnvccOSLinux∕UbuntuCUDA Cores3072CPUInter CoreTMi7-4790@3.60GHzMemoryBandwidth∕GBps336.5RAM Size∕GB24StandardMemory Size∕GB12Networking1000Mbps fullduplexBase ClockFrequency∕MHz1000
3.1 运行效率
为了保持性能评估的一般性，本文实验数据均为由随机数组成的多通道数据集.在使用G -BF方法进行分析时，采用不同大小的数据集来测试该方法的适用性.随机生成不同大小的4阶张量，张量各个维度大小相同，包括40(404=2560000),50,60,70,80,90,100.
在所有的实验中，G -BF模型在每个张量上执行20次，每次实验的迭代次数设置为100次.G -BF模型单次迭代的执行时间如图3所示，G -HALS和G -BF的单次迭代执行时间随着数据量增大的变化趋势大致相同.
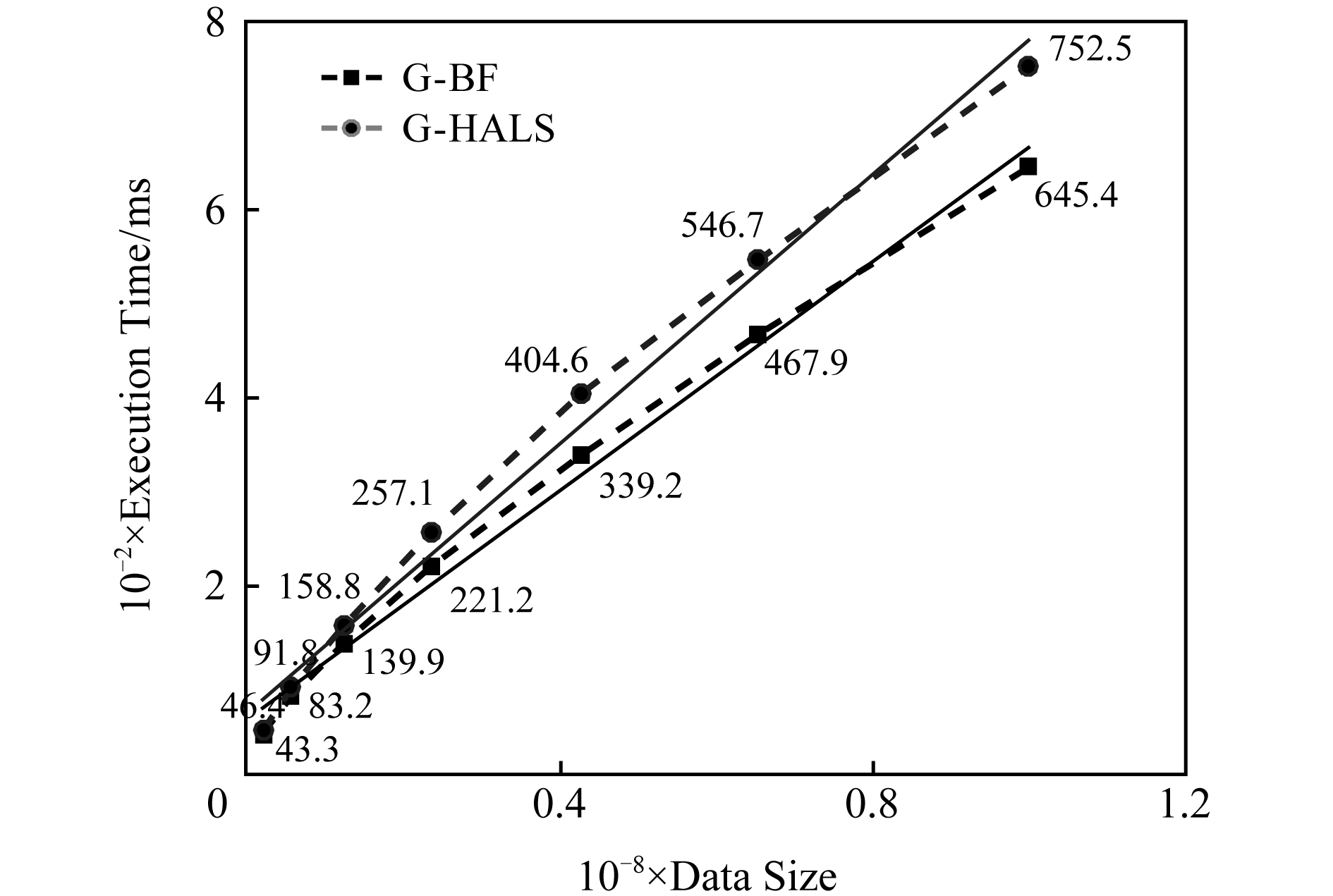
Fig. 3 The single execution time of G -HALS and G -BF processing the same tensor (order-4) with different sizes
图3 G -HALS和G -BF处理大小相同张量单次执行时间(4-阶)
G -BF的单次迭代时间范围为[43.3 ms,645.4 ms]，分别对应于最小体积和最大体积的张量.G -HALS对应的单次迭代时间值为[46.4 ms，752.5 ms].结果表明，G -BF和G -HALS单次迭代的性能都有相同的趋势.在处理相对小的张量时，由于GPU的基本通信时间和计算能力没有得到充分利用，G -BF的执行时间接近G -HALS.随着数据规模的增大，G -BF展现出性能上的优势，在数据规模非常大的情况下，G -BF在一定程度上能够减少执行时间.
G -BF处理不同尺寸张量的执行效率为(645.443.3-1)≈14倍，而数据尺度为38倍.在相同条件下，G -HALS的执行效率为(752.5/46.4-1)≈15倍.线性函数能很好地拟合了执行时间和数据大小，表明G -BF和G -HALS均能适应数据规模的变化.
使用相同的数据大小和截止条件来测试G -HALS和G -BF的迭代终止执行时间.图4显示了用G -HALS和G -BF过程分解张量的执行时间随数据量增长的变化趋势.在大多数情况下，G -BF的性能优于G -HALS，与上述单次迭代时的趋势一致.同时与单次迭代时间相比，性能改善更为明显，主要原因是G -BF在相同的条件下迭代次数较少.图5显示了张量分解中迭代次数的变化.相同条件下，在保证分解精度的同时G -BF算法的迭代次数更少，具有减少迭代次数的优点.
order-4:100×100×100×100 Fig. 4 The breakdown execution time of G -HALS andG -BF factoring analysis of tensor
图4 G -HALS和G -BF处理相同张量迭代终止时间
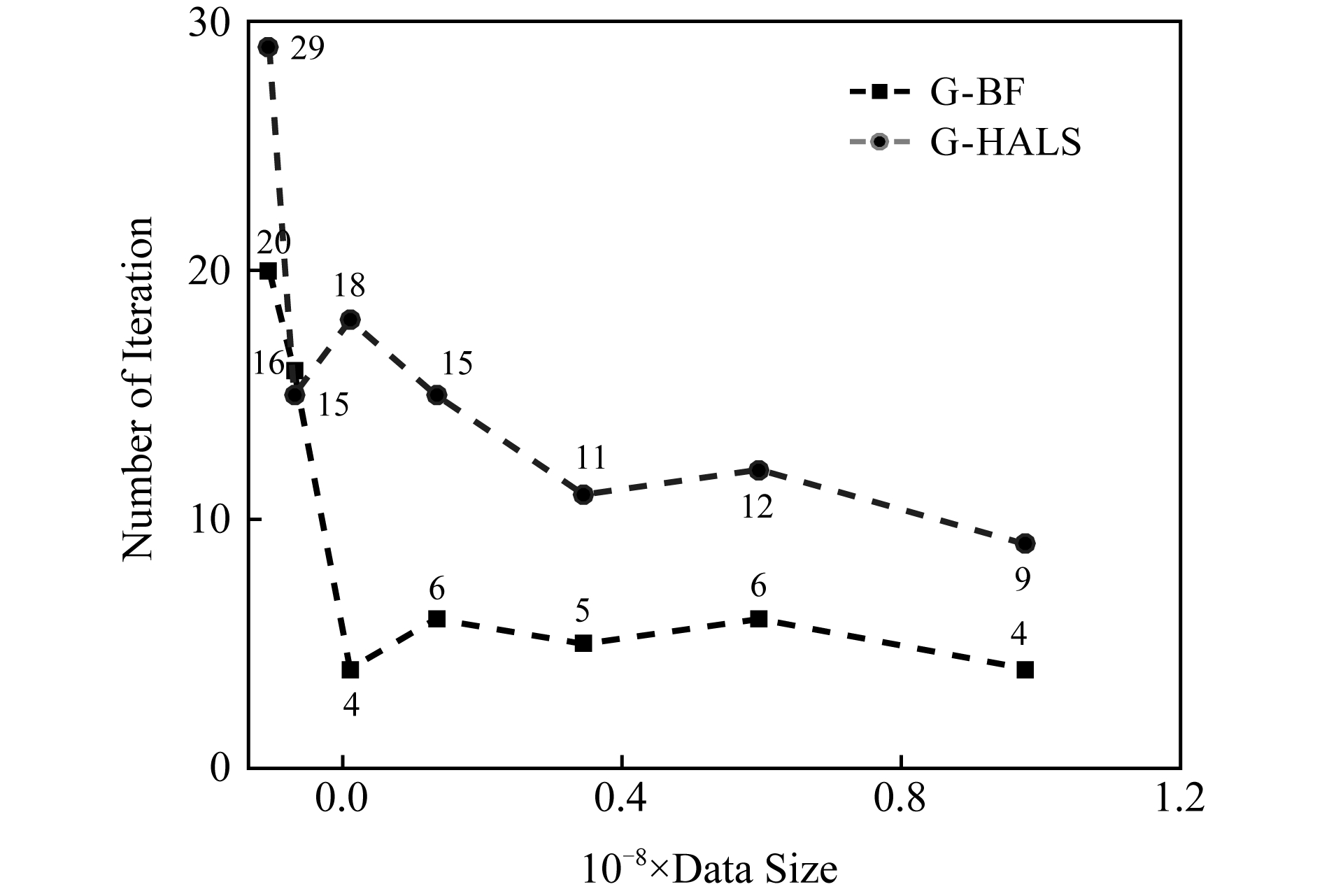
order-4:100×100×100×100 Fig. 5 The breakdown iterations of G -HALS andG -BF factoring analysis of tensor
图5 G -HALS和G -BF分解张量的迭代次数
3.2 可扩展性
图6显示了相同数据规模在不同因子数量的分解下单次迭代的执行时间.G -HALS算法的执行时间范围约为[725.3 ms，771.8 ms]，并且处理时间随着因子数量的增大而有增加的趋势.随着因子数量的增加，G -BF的执行时间[620.5 ms，673.3 ms]具有相同的变化趋势.以上实验结果表明：G -BF和G -HALS都具有良好的可扩展性.实验的数据集大小是固定的(1004=100 000 000)，因子数目作为唯一变量设置为4，8，12，16，20，24，28，32.
order-4:100×100×100×100 Fig. 6 The single execution time of G -HALS and G -BF processing the same tensor with different ranks
图6 不同秩下G -HALS和G -BF分解张量的单次执行时间
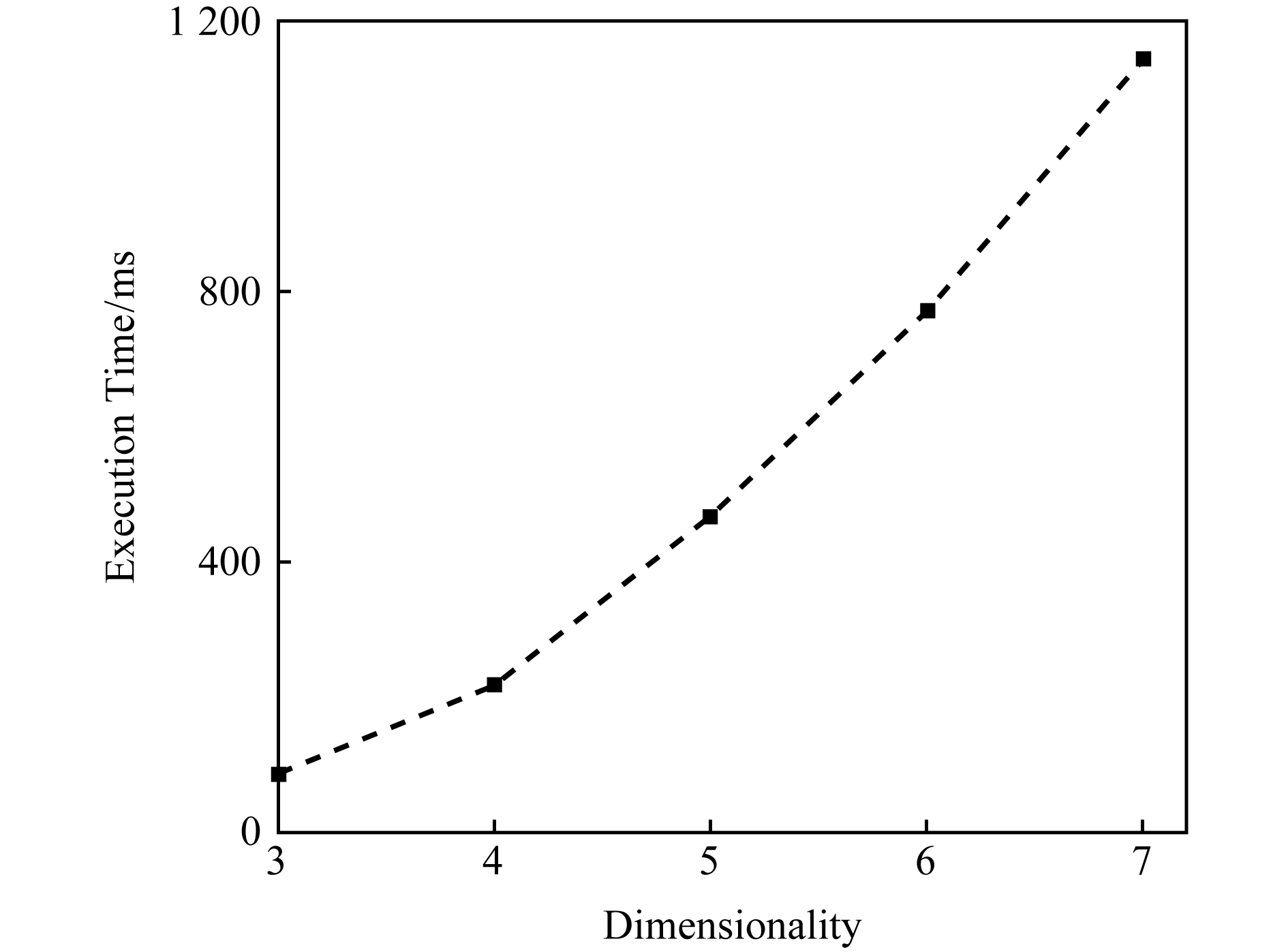
Fig. 7 The single execution time of G -BF processing the same volume (107) of different dimensionality
图7 G -BF处理不同维度张量(107)的单次执行时间
G -BF模型在数据维度上也表现出了良好的可扩展性.图7显示了G -BF模型在处理数据规模相同、维度不同时的单次迭代执行时间.随着张量维数的增加，单次迭代的执行时间也呈上升趋势.由于算法是基于维度数的迭代更新来求解最优因子，虽然数据量是固定的，但是维度数增长带来了更多的时间复杂度.实验表明：该方法适应于处理不同维度的数据，使得任意维张量的分解成为可能.
3.3 处理超大规模张量的性能探究
基于已有工作提出的H-PARAFAC框架[13]，探究G -BF可以处理超大规模的高维张量数据性能.G -BF可同时在多个节点上运行，图8示出了基于H-PARAFAC在2个计算节点使用G -BF进行张量分解的执行时间.
Fig. 8 Total execution time of H-PARAFAC with G -BF deriving sub-factors and full factors of simulated augmenting tensor (order-4) when data scale>108
图8 当数据规模>108时分解大张量总执行时间
图8上每个值表示处理张量的总时间.其中，数据规模从100×100×100×10增加到100×100×100×100 000,增加了10 000倍;而执行时间从10.3 s增加到16 346.2 s，时间开销增加了1 587倍.
GigaTensor[21]和CDTF[19]是与这项研究密切相关的2个优秀的张量分解框架.GigaTensor使用100个计算节点可以分解3阶稀疏张量(体积=109)，其时间开销比数据量的增加快得多.CDTF使用运行Hadoop的40个计算节点(Xeon 2.4 GHz)，可以分解具有109个数据元素的5阶张量，并且其开销随着数据量线性增加.作为对比，G -BF使用H-PARAFAC框架处理109个数据元素大小的4阶张量具有更高的效率.当时间大小相同时，结合H-PARAFAC的G -BF能够处理具有1011个数据元素的4阶张量.更重要的是，在处理海量数据时，G -BF打破了数据规模的限制.
4 总 结
先验知识的缺乏已成为分析高维大规模时间序列的主要挑战，大多数传统的因子分解方法不能适应数据的超高维和超大尺度.本文提出了一种海量并行贝叶斯分解方法(G -BF)来分析高维张量形式的时间序列大数据.这种方法具有3个优点：1)在没有先验信息的情况下获得因子矩阵；2)支持可变维度的张量分解；3)在处理大规模数据时保持性能和可扩展性的优势.
本研究使用GPU来加速密集矩阵的并行运算，高效的存储器配置方案和高维数据映射策略使得程序能够满足任意维度数据的大规模并行需求.同时，更新过程中的中间数据尽可能在设备存储器中创建和操作，显著降低了并行编程模型中主机与设备之间的通信消耗.
本文通过实验探究了G -BF方法在处理不同规模多维张量上的性能，与同一实验环境下HALS的并行优化算法(G -HALS)实验作为对比.由实验结果可得出3个结论：
1) 与G -HALS(常规因子分解算法)相比，G -BF具有更好的性能，并且随着数据量的增加，其优越性更加明显；
2) G -BF在数据规模、维度和因子数量等方面具有良好的可扩展性；
3) 将G -BF方法与已有的H-PARAFAC方法相结合，可以对超大张量(2个节点上的体积可达1011)进行因子分解，其性能相比传统方法显著提高.
总体而言，G -BF在对大规模多维张量的因子分解方面明显优于同类算法，针对时间序列大数据的因子降维分析方面具有很大的潜力.
[1]Goldenfeld N. Simple lessons from complexity[J]. Science, 1999, 284(5411): 87-89
[2]Wang Lizhe, Zhang Jiabin, Liu Peng, et al. Spectral-spatial multi-feature-based deep learning for hyperspectral remote sensing image classification[J]. Soft Computing, 2017, 21(1): 213-221
[3]Cunningham J P, Yu B M. Dimensionality reduction for large-scale neural recordings[J]. Nature Neuroscience, 2014, 17(11): 1500-1509
[4]Hyvarinen A, Oja E. Independent component analysis: Algorithms and applications[J]. Neural Networks, 2000, 13(4): 411-430
[5]Pearson K F R S. LIII. On lines and planes of closest fit to systems of points in space[J]. Philosophical Magazine, 1901, 2(11): 559-572
[6]Gu Yu, Xu Zongben, Sun Jian, et al. An intrusion detection ensemble system based on the features extracted by PCA and ICA[J]. Journal of Computer Research and Development, 2006, 43(4): 633-638 (in Chinese)(谷雨, 徐宗本, 孙剑, 等. 基于PCA与ICA特征提取的入侵检测集成分类系统[J]. 计算机研究与发展, 2006, 43(4): 633-638)
[7]Chen Dan, Li Xiaoli, Wang Lizhe, et al. Fast and scalable multi-way analysis of massive neural data[J]. IEEE Transactions on Computers, 2015, 64(3): 707-719
[8]Bro R. PARAFAC-tutorial and applications[J]. Chemometrics and Intelligent Laboratory Systems, 1997,38(2): 149-171
[9]Wang Juan, Li Xiaoli, Lu Chengbiao, et al. Characteristics of evoked potential multiple EEG recordings in patients with chronic pain by means of parallel factor analysis[J]. Computational and Mathematical Methods in Medicine, 2012, 26(2): 27-60
[10]Comon P, Luciani X, Almeida A L F D. Tensor decompositions, alternating least squares and other tales[J]. Journal of Chemometrics, 2009, 23(7/8): 393-405
[11]Phan A H, 
Cichocki A. Fast alternating LS algorithms for high order CANDECOMPPARAFAC tensor factorizations[J]. IEEE Transactions on Signal Processing, 2013, 61(19): 4834-4846
[12]Cichocki A, Zdunek R, Amari S I. Hierarchical ALS algorithms for nonnegative matrix and 3D tensor factorization[C] Proc of the 7th Int Conf on Independent Component Analysis and Signal Separation. Berlin: Springer, 2007: 169-176
[13]Fang Minquan, Zhang Weimin, Fang Jianbin, et al. GPU Programming and Code Optimization High Performance Computing for the Masses[M]. Beijing: Tsinghua University Press, 2016: 13-141 (in Chinese)(方民权, 张卫民, 方建滨, 等. GPU编程与优化——大众高性能计算[M]. 北京: 清华大学出版社, 2016: 13-141)
[14]Chen Dan, Hu Yangyang, Wang Lizhe, et al. H-PARAFAC: Hierarchical parallel factor analysis of multidimensional big data[J]. IEEE Transactions on Parallel & Distributed Systems, 2017, 28(4): 1091-1104
[15]Bae S H, Choi J Y, Qiu J, et al. Dimension reduction and visualization of large high-dimensional data via interpolation[C] Proc of the 19th ACM Int Symp on High Performance Distributed Computing. New York: ACM, 2010: 203-214
[16]Agullo E, Augonnet C, Dongarra J, et al. QR factorization on a multicore node enhanced with multiple GPU accelerators[C] Proc of the 25th IEEE Int Parallel & Distributed Processing Symp. Piscataway, NJ: IEEE, 2011: 932-943
[17]Tan Wei, Cao Liangliang, Fong Liana. Faster and cheaper: Parallelizing large-scale matrix factorization on GPUS[C] Proc of the 25th ACM Int Symp on High-Performance Parallel and Distributed Computing. New York: ACM, 2016: 219-230
[18]Zou Benyou, Li Cuiping, Tan Liwen, et al. GPUTENSOR: Efficient tensor factorization for context-aware recommenda-tions[J]. Information Sciences, 2015, 299(11): 159-177
[19]Shin Kijung, Lee S, Kang U. Fully scalable methods for distributed tensor factorization[J]. IEEE Transactions on Knowledge and Data Engineering, 2016, 29(1): 100-113
[20]Zhao Qibin, Zhang Liqing, Cichocki A. Bayesian CP factorization of incomplete tensors with automatic rank determination[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1751-1763
[21]Kang U, Papalexakis E, Harpale A, et al. GigaTensor: Scaling tensor analysis up by 100 times-algorithms and discoveries[C] Proc of the 21st ACM SIGKDD Int Conf on Knowledge Discovery & Data Mining. New York: ACM, 2012: 316-324
