多示例学习(multiple instance learning, MIL)在药物活性预测调查期间被首次提出[1].与传统的单示例学习不同,多示例学习的输入是一组标签为正或负的包,而不是一组标签为正或负的示例.在多示例学习中我们不会得到任何示例的标签信息.如今,多示例学习已经广泛地应用于各种领域,如图像分类检索、人脸识别、文本分类、计算机辅助医疗诊断等[2].在过去的时间里,已经提出了很多有效的MIL算法[3-5].
而近年来,深度神经网络也在各个领域都取得了很好的效果[6-8].其中MI-Net with DS和MI-Net with RC[9]是深度神经网络在多示例学习领域的成功应用,它使用了深度学习的技巧:深度监督和剩余连接,在图像领域的数据上取得了优异的成绩.然而在非图像任务上的性能并不像在图像任务上那么优秀.与大部分的深度神经网络模型一样,它也需要人工针对不同的数据集进行结构调整和参数选择.
最近几年,深度森林[10]进入了人们的视野.这是一种基于非可微模块构建的深度模型,具有比深度神经网络少得多的超参数,同时其模型复杂性可以通过数据相关的方式自动确定.实验表明,其性能对于超参数设置非常稳健,因此在大多数情况下,即使面对来自不同领域的不同数据,也可以通过使用相同的默认设置获得出色的性能.此外由于决策树的特性,深度森林在非图像的领域上也有着不错的效果.
因此在非图像任务上利用深度森林架构来解决多示例学习问题或许是一种更好的选择.Amores [2]指出包级别的算法通常比示例级的算法效果要好.但由于深度森林结构的限制,组成深度森林的每一个森林并不能直接被替换成包级别的森林,所以并不能把包级别的思想直接套用到深度森林框架上.这就使得我们需要提出一种新的深度森林结构来解决多示例学习问题.
本文提出了一种新的深度森林架构(multiple instance deep forest, MIDF),使用了包级的算法思想.在拼接时我们把包里的每个示例都看做是一个包,从而使得中间层的输出分布可以和包中的示例拼接成功,让级联结构依然有效.此外我们的架构由2个级联结构组成,一个使用k折交叉验证来帮助自动确定深度森林的层数,另一个根据所求的层数来计算最终的结果.实验结果表明:我们的方法在图像任务上的性能与擅长处理图像任务的MI-Net with DS和MI-Net with RC相当;而在文本数据上,我们的算法取得了比它们和其他基线算法更好的效果.
1 背景知识
本节主要介绍多示例学习问题的定义, 并回顾一个经典的基于包级别的多示例决策树算法ID3-MI[11].
多示例学习(MIL)问题最初在药物活性预测中提出.现在多示例学习已经被广泛应用于许多领域,并成为机器学习中的一个重要问题.在大量的多媒体数据中都包含着多示例(multiple instance, MI)结构,例如文本数据中的文章可以被分为多个段落,图像数据可以被划分成多个局部区域,基因表达数据包含着多个基因.多示例学习能够有效地处理这些多示例(MI)数据.
多示例学习(MIL)是一种弱监督学习(weakly supervised learning, WSL).在MIL中,每一个训练样本都是一个由许多示例组成的包.对于二分类问题,如果一个包中存在至少一个标签为正的示例,那么我们称这样的包是一个正包.如果一个包中的示例标签都为负,那么我们称这样的包是一个负包.尽管我们可以得到包的标签,但是所有示例的标签都是未知的.多示例学习的目标就是要在这样的假设下,训练出一个学习器能够很好地预测出包的标签.用形式化的语言来说:假设![]() 是一个示例空间,
是一个示例空间,![]() 是一个类别标签的集合.给定一个数据集{(X1,y1),(X2,y2),…,(Xi,yi),…,(XN,yN)},其中
是一个类别标签的集合.给定一个数据集{(X1,y1),(X2,y2),…,(Xi,yi),…,(XN,yN)},其中![]() 表示一个包,
表示一个包,![]() 表示Xi的标签,多示例学习的任务就是去寻找一个能够分类未知标签包的函数
表示Xi的标签,多示例学习的任务就是去寻找一个能够分类未知标签包的函数![]()
目前已经有许多算法被用来解决MIL问题.根据Amores的调查,MIL算法可以分为3个种类:示例空间(instance space, IS)范式、包空间(bag space, BS)范式和嵌入空间(embedded space, ES)范式.简而言之,对于IS范式,判别信息被认为是在示例级别上的,而在BS范式中,判别信息是在包级别上的.ES范式中的多示例学习算法明确或隐含地将每个包映射到单个特征向量上,该特征向量总结了关于整个包的相关信息.
ID3-MI算法就是一种包级多实例学习的算法,它遵循的是一种常见的分而治之的决策树方式.众所周知,决策树算法有着2个重要组成部分:1) 如何选择分割树节点的属性;2) 如何使用树进行预测.因此ID3-MI算法使用与标准决策树相同的方法来进行预测,也就是使用未知标签的包所落入的叶子节点的标签来确定该包的标签.显然ID3-MI算法的关键是如何定义一种衡量标准用来选择决策树的划分点.
对于传统的熵(entropy),不妨假设数据集D包含p个正例和n个负例,那么依据类别得到的D的熵可以写作:
![]()
![]()
(1)
如果选择在属性V上划分,并将D划分为{D1,D2,…,Dl},那么此时的熵可以写作:
(2)
此时的信息增益可以写作:
Gain(D,V)=Info(D)-Info(D,V)=
(3)
对于多示例学习,我们只需要考虑如何把计算正负例的个数转换成计算正负包的个数.假设![]() 和
和![]() 分别表示在数据集
分别表示在数据集![]() 中出现的正包和负包的个数.那么使用V来划分数据集D所得到的熵可以写作:
中出现的正包和负包的个数.那么使用V来划分数据集D所得到的熵可以写作:
Infomulti(D)=
(4)
Infomulti(D,V)=
(5)
使用相同思路可以得到多示例学习下的信息增益:
Gainmulti(D,V)=Infomulti(D)-
Infomulti(D,V)=Infomulti(D)-
(6)
算法1通过伪代码的形式给出了包级多实例决策树ID3-MI生成决策树过程的详细描述:
算法![]()
① if depth>max_depth或者![]() 标签相同 then
标签相同 then
② 将节点node置为叶子节点;
③ return;
④ end if
⑤ ![]()
⑥ 将左孩子节点中的包初始化![]()
⑦ 将右孩子节点中的包初始化![]()
⑧![]()
⑨ if ![]() 且
且![]()
threshold then
⑩![]()
 else
else
 end if
end if
 end for
end for
 node.left←DecisionNode(node,
node.left←DecisionNode(node,
node.depth+1);
 node.right←DecisionNode(node,
node.right←DecisionNode(node,
node.depth+1);
 end if
end if
2 多示例深度森林
多示例深度森林同时具有多示例森林和深度森林的优势.但是简单地将两者结合起来并不可行,我们需要更有效的结合方式.
2.1 多示例森林
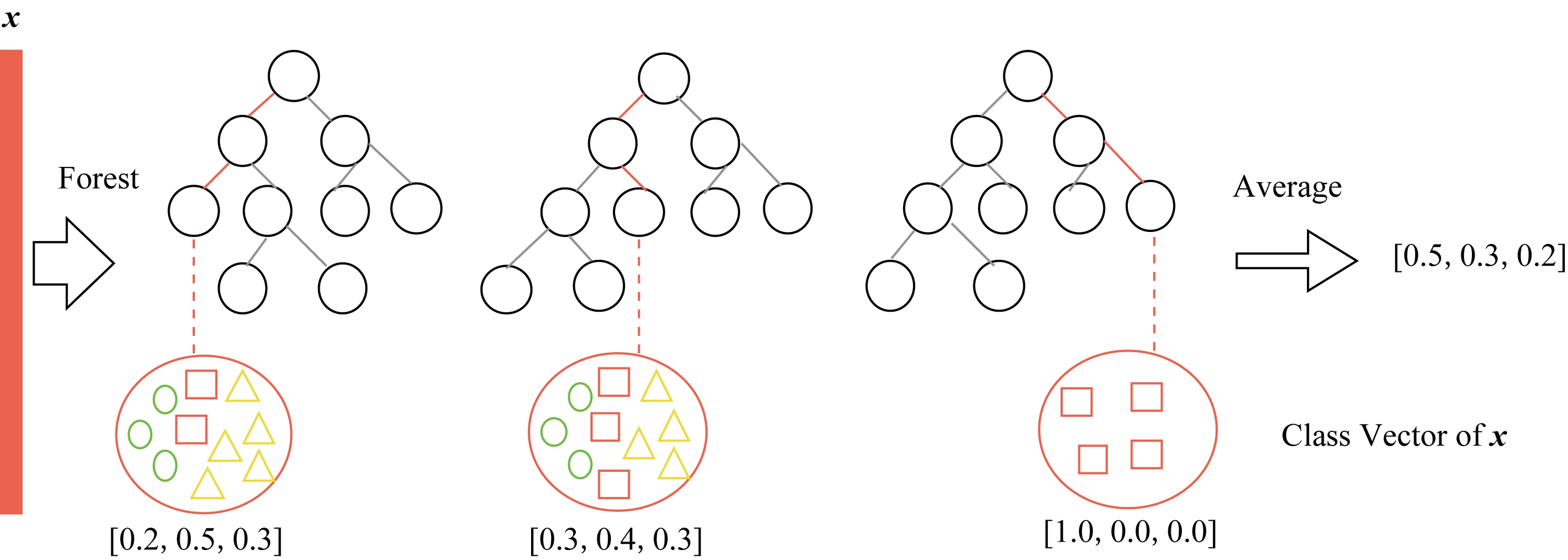
Fig. 1 The illustration of class vector generation
图1 类向量生成示意图
本节介绍2种多示例森林算法MIRF和BLRT[12] ,它们分别受到随机森林算法和极根随机树算法的启发.
随机森林(random forests, RFs)最初由Amit等人提出[13]并由Breiman[14]扩展.在随机森林中,每一棵树的训练集都是通过对原始训练集的有放回采样(自助采样法bootstrap)得到的.除此之外,在建树时对每个节点划分的选择也不再是对所有的属性计算一个最优化分,而是在属性集的一个随机子集中选择最优化分属性.如果我们假设所有的样本属性总数都是d,那么随机森林通常会挑出![]() 个属性用于选择最优化分.多示例随机森林(MIRF)使用了和随机森林类似的集成方法,它们之间的区别是MIRF集成的是包级多示例决策树ID3-MI而非传统的决策树.
个属性用于选择最优化分.多示例随机森林(MIRF)使用了和随机森林类似的集成方法,它们之间的区别是MIRF集成的是包级多示例决策树ID3-MI而非传统的决策树.
在极根随机树算法(ExtraTrees)[15]中,使用了更进一步的随机化步骤.与随机森林一样,极根随机树也是在候选特征的随机子集上来寻找划分,但不同的是极根随机树并非在每个属性上计算最优划分点,而是在这些属性上随机选择划分点.换言之这个值是在属性的经验范围内均匀随机选取的.在所有的随机划分点中,极根随机树会选择其中最优的作为该节点的划分点.BLRT受到了极根随机树的影响,并将传统的ExtraTree像ID3-MI那样推广成了包级多示例ExtraTree.
2.2 多示例深度森林
多示例深森林(MIDF)受到了深度森林的启发,它也具有级联结构,级联的每一层都是从其前一层接收特征,并将结果发送给下一层作为输入.MIDF的每一层都是MIRF和BLRT这2种不同多示例森林的集成,使用不同种类的森林集成可以增加MIDF算法的多样性.
在深度森林中,如果将示例提供给级联结构的某一层,则这一层中所有的森林都会预测出一个类别分布的估计值,并将这个分布估计值转化为类别向量,如图1所示.之后我们将类别向量与原始特征向量拼接起来,作为输入传递给下一层.但在MIDF中,得到该层中的每个森林所给出的包级预测后,我们不能简单地将长度为2的类别向量与大小为ni×d的原始特征矩阵直接拼接起来,因为他们在维度上并不相同.
为了解决拼接问题,我们将所有的森林都按包级进行训练(不妨假设每层由2个MIDF和2个BLRT组成).之后对于任意包![]() 将其中的每个示例
将其中的每个示例![]() 都看作一个包,这样会得到一个新的包集合
都看作一个包,这样会得到一个新的包集合![]() ,并把它提供给当前层的森林.森林会给出一个大小为
,并把它提供给当前层的森林.森林会给出一个大小为![]() 的类别向量的集合.此时训练集中的每个示例都可以与一个长度为2的类别向量进行拼接.在做好拼接之后,我们重新按照
的类别向量的集合.此时训练集中的每个示例都可以与一个长度为2的类别向量进行拼接.在做好拼接之后,我们重新按照![]() 将所有的示例划分成包,得到新的集合
将所有的示例划分成包,得到新的集合![]() 并把它作为输入传递给下一层.
并把它作为输入传递给下一层.![]() 中的每个示例
中的每个示例![]() 都有个d+8个属性.图2的级联结构中详细地给出了具体的拼接过程.
都有个d+8个属性.图2的级联结构中详细地给出了具体的拼接过程.
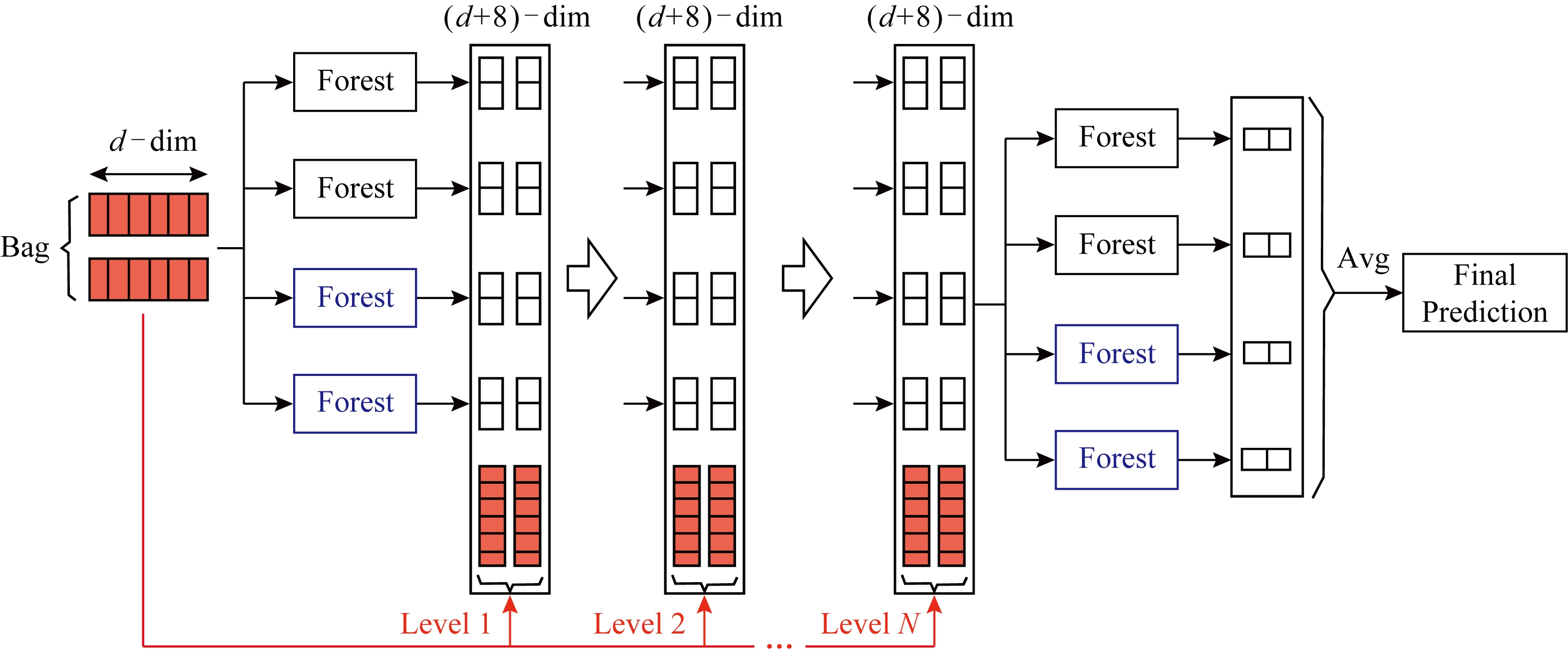
Fig. 2 The illustration of the cascade structure of multiple instance deep forest
图2 多示例深度森林级联示意图
本文算法由2个级联结构组成:1)用于确定MIDF的层数;2)用于计算最终预测结果.第1个级联中的每个森林所预测出的类别向量都是通过k折交叉验证得到的,这里我们通常取k=3.详细地,每个示例都会被用作训练数据k-1次,产生k-1个类别向量,然后对其取平均值以产生用于传递给下一层的增强特征.此外,在扩展一个新层之后,整个级联的性能将在验证集上进行评估,如果没有显著的性能增益,那么训练过程将会终止.因此,我们可以通过第1个级联结构来自动地确定级联的层数.第2个级联的每一层则使用了完整的训练数据,其训练的层数由第1个级联结构计算给出,并得到最终的预测结果.
3 实验测试
在本节中,我们分别在多个多示例学习基准数据集上进行实验,包括分子活动、图像识别以及文本分类数据集.并在这些数据集上对比多示例深度森林算法(MIDF)、Wang等人提出的多示例神经网络算法(MI-Net with DS和MI-Net with RC)以及MILES,miGraph, ID3-MI,MIRF等多示例学习算法的效果.
3.1 任务及其数据集
我们分别在3类任务上进行实验:
1) 药物激活预测.Musk数据集是1997年由Dietterich等人发布的关于预测分子是否具有麝香味的数据集.由于每个分子都可以被描述为它能够折叠成的不同形状(构象异构体),我们将每个分子对应为一个包,而包中的每一个示例则对应该分子的不同构象.其中,不同构象负责分子的不同性质,也就是它的气味.在实验里,如果至少包含一种能够让分子产生麝香味的构象,我们就将这个分子(包)标为正类,如果没有任何一种构象具有这种性质,我们就把这个分子标为负类.
2) 自动图像标注.在这一类任务中有3个比较有名的数据集,分别是Andrews等人于2002年提出的Fox,Tiger和Elephant数据集[3].在这类任务中,我们把图像本身作为包,图像的不同区域作为包中的示例.对于每个类别,如果图像包含该类动物,我们就把这个图像看作为正包,如果图像仅包含其他动物(来自其他类别的动物,不仅仅是Fox,Tiger和Elephant),那我们将其看作为负包.
3) 文本分类.我们从一个名为20 Newsgroups的语料库中生成了20个文本分类数据集,对于20个新闻类别中的每一个都生成了50个正包和50个负包.其中每个正包都包含了从目标类别中随机抽取的3%的示例,并从其他类别中随机均匀采样剩余示例,每个负包则只包含从其他类别中均匀采样的示例,并不包含本类别的数据.在所生成的包中的每个示例均拥有80维的特征.
3.2 实验设计
我们设计实验用来验证本文的多示例深度森林算法能够与深度神经网络以及其他算法在多个数据集上效果相当,并且在某些数据集上会取得更好的效果,同时我们的算法还能够更加容易地进行超参数的调整.在实验中,对于所有的数据集,我们都使用相同的级联结构(参数):每一层由2个包级多示例极跟随机树(BLRT)和2个包级多示例随机森林(MIRF)构成,其中每个森林均包含50棵树.
对于深度神经网络,我们使用Wang等人在2018年提出的MI-Net with DS和MI-Net with RC算法,这些算法都需要设定不同的学习率、权重衰减和动量值来获得在不同数据集上的高性能.因此,我们进行实验时在验证集上验证不同参数的效果,选择最佳的参数,并在训练集上重新训练得到最终的预测结果.
对于其余的多示例算法我们也使用了和MI-Net with DS和MI-Net with RC一样的方法来确定它们在不同数据集上的最优参数,并使用该参数得到最终的预测结果.
3.3 实验结果
我们通过10次10折交叉验证来比较ID3-MI、MIRF以及MIDF算法的性能(运行10次10折交叉验证,每次采取不同的随机数据划分).表1和表2展示了测试准确率的比较.
表1给出了在药物激活预测以及自动图像标注任务上的实验结果,表2给出了在文本分类任务上的实验结果,其中用黑体加粗来标注得到的最好结果.
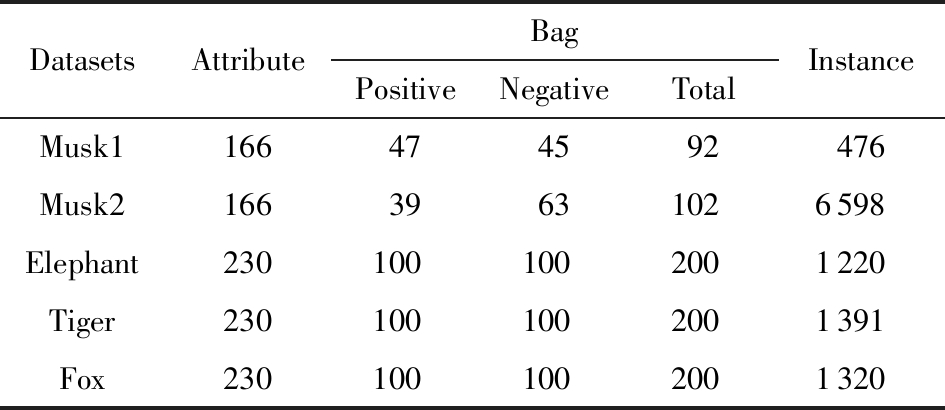
Table 1 Detailed Characteristics of Datasets
表1 数据集的具体信息
DatasetsAttributeBagPositiveNegativeTotalInstanceMusk1166474592476Musk216639631026598Elephant2301001002001220Tiger2301001002001391Fox2301001002001320
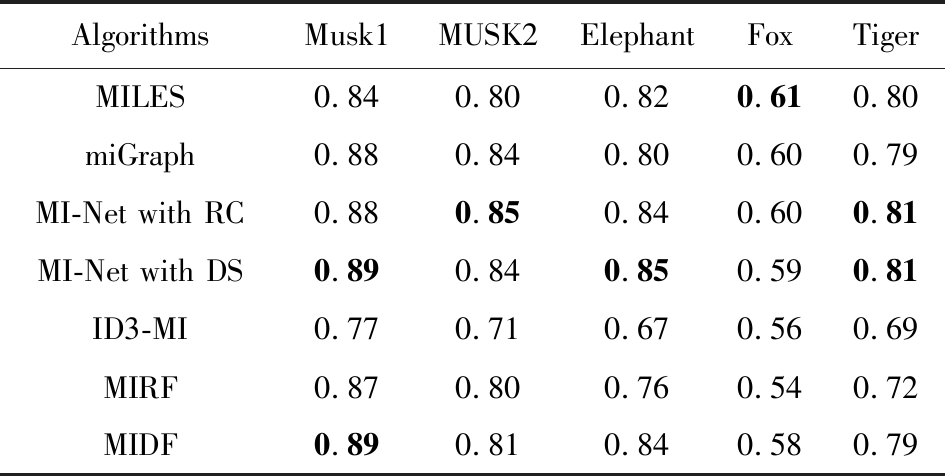
Table 2 Average Prediction Accuracy of Different Methods for Drug and Image Datasets
表2 药物和图片标注数据集上不同算法的平均预测准确率
AlgorithmsMusk1MUSK2ElephantFoxTigerMILES0.840.800.820.610.80miGraph0.880.840.800.600.79MI-Net with RC0.880.850.840.600.81MI-Net with DS0.890.840.850.590.81ID3-MI0.770.710.670.560.69MIRF0.870.800.760.540.72MIDF0.890.810.840.580.79
Note: The best results are in bold.
Table 3 Average Prediction Accuracy of Different Methods for Text Categorization Datasets
表3 文本分类数据集上不同算法的平均预测准确率

DatasetsMILESmiGraphMI-Net with RCMI-Net with DsID3-MIMIRFMIDFalt.atheism0.650.740.770.680.670.750.79comp.graphics0.640.800.790.740.730.810.81comp.os.ms-windows.misc0.570.570.640.580.560.600.61comp.sys.ibm.pc.hardware0.630.570.580.550.660.740.73comp.sys.mac.hardware0.590.730.740.680.670.750.79comp.windows.x0.740.770.700.560.730.780.77misc.forsale0.540.650.580.570.530.600.64rec.autos0.610.710.620.660.670.700.72rec.motorcycles0.650.780.840.800.760.790.81rec.sport.baseball0.710.740.790.700.690.780.82rec.sport.hockey0.780.790.740.600.710.770.80sci.crypt0.740.660.700.660.670.740.76sci.electronics.mat0.700.860.840.780.840.900.91sci.med0700.810.770.690.640.710.71sci.space0.610.670.730.670.630.690.74soc.religion.christian0.610.710.710.650.610.740.74talk.politics.guns0.700.620.720.630.650.690.71talk.politics.mideast0.710.620.640.640.730.790.80talk.politics.misc0.560.610.620.640.580.600.64talk.religion.misc0.600.640.630.620.590.670.68
Note: The best results are in bold.
MIDF在这些数据集上均展现了较好的效果,尤其是在处理文本分类任务时,我们在20个数据集中的12个数据集上取得了最优效果,并在其他8个数据集上同最优结果相当.同时在图像数据上我们同示例级的神经网络算法效果也相差不大.此外尽管其他算法在某些数据集上也展现了不错的效果,但他们往往需要针对不同数据集使用不同的超参数,这类超参数的选择十分困难且耗时.而我们的算法只需要使用相同的超参就可以得到很好的结果.
4 结束语
本文提出了一个新的深度森林框架MIDF来解决多示例学习问题.在这种新的框架下,拼接时会把包中的每个示例都看做是一个包,从而使得中间层的输出分布可以和包中的示例拼接成功,进而使得级联结构依然有效.另外,我们的架构由2个级联结构组成,其中一个使用k折交叉验证来帮助自动确定深度森林的层数,另一个根据所求的层数来计算最终的结果.实验结果表明:我们的方法在图像任务上的性能并不比擅长处理图像任务的MI-Nets差,而在在文本数据上,本文方法取得了比MI-Nets更好的效果.
[1]Dietterich T G, Lathrop R H, Lozano-Pérez T. Solving the multiple instance problem with axis-parallel rectangles[J]. Artificial Intelligence, 1997, 89(1/2): 31-71
[2]Amores J. Multiple instance classification: Review, taxonomy and comparative study[J]. Artificial Intelligence, 2013, 201: 81-105
[3]Andrews S, Tsochantaridis I, Hofmann T. Support vector machines for multiple-instance learning[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2003: 577-584
[4]Zhou Zhihua, Sun Yuyin, Li Yufeng. Multi-instance learning by treating instances as non-iid samples[C] //Proc of the 26th Annual Int Conf on Machine Learning. New York: ACM, 2009: 1249-1256
[5]Chen Yinxin, Bi Jinbo, Wang J Z. MILES: Multiple-instance learning via embedded instance selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(12): 1931-1947
[6]Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C] //Proc of the Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2012: 1097-1105
[7]Zeng Daojian, Liu Kang, Chen Yubo, et al. Distant supervision for relation extraction via piecewise convolutional neural networks[C] //Proc of the 2015 Conf on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2015: 1753-1762
[8]Goodfellow I, Bengio Y, Courville A. Deep Learning[M]. Cambridge, MA: MIT Press, 2016
[9]Wang Xinggang, Yan Yongluan, Tang Peng, et al. Revisiting multiple instance neural networks[J]. Pattern Recognition, 2018, 74(C): 15-24
[10]Zhou Zhihua, Feng Ji. Deep forest: Towards an alternative to deep neural networks[C] //Proc of the 26th Int Joint Conf on Artificial Intelligence. San Francisco, CA: Morgan Kaufmann, 2017: 3553-3559
[11]Chevaleyre Y, Zucker J D. Solving multiple-instance and multiple-part learning problems with decision trees and rule sets. Application to the mutagenesis problem[C] //Proc of the Conf of the Canadian Society for Computational Studies of Intelligence. Berlin: Springer, 2001: 204-214
[12]Komárek T, Somol P. Multiple instance learning with bag-level randomized trees[C] //Proc of the Joint European Conf on Machine Learning and Knowledge Discovery in Databases. Berlin: Springer, 2018: 259-272
[13]Amit Y, Geman D. Shape quantization and recognition with randomized trees[J]. Neural Computation, 1997, 9(7): 1545-1588
[14]Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32
[15]Geurts P, Ernst D, Wehenkel L. Extremely randomized trees[J]. Machine Learning, 2006, 63(1): 3-42


