近几年来,随着社会的发展,各行业和领域的数据量都在呈爆炸式增长,因而不断对存储系统提出挑战,云环境下的存储系统已逐步成为未来数据存储的发展趋势.云存储系统的一个重要目标就是无论系统发生什么样的故障,都必须保证数据的可用性,即云存储服务提供商总能够持续不断地向用户提供数据访问的服务,否则会直接影响上层应用给用户提供正常服务.2018年,Windows Azure云存储服务因故障中断时间超过24 小时,超过40个Azure 云应用服务因此而中断,造成不小的经济损失[1].因此,对云存储服务提供商和用户来说,数据可用性至关重要.
为了提高云存储的数据可用性,系统一般额外存储大量的冗余数据.冗余有2个常见的实现方式:复制和纠删码.复制是最简单的冗余方案,即一个文件拥有多个副本;而纠删码(一般采用Reed-Solomon码[2])是将一个文件等分成多个数据块,这些数据块再编码生成同样大小的若干个校验块,使得从所有数据块和校验块中任意下载原始文件大小的数据就可以重建出原始文件.与复制相比,纠删码可以大大提高数据可用性[3].可是,纠删码面临的一大挑战是当发生数据块丢失时,修复该数据块所需要的带宽消耗过大,即一个数据块丢失的话,需要下载多个块去重建出原始文件才能对单个数据块进行修复.这会使得数据修复性能偏低,从而导致云存储上的用户数据访问延迟过高,影响数据可用性.
为了降低纠删码的修复开销,不少云存储系统(Windows Azure[4], Facebook[5])开始使用一类新型的编码方法——局部修复码(locally repairable codes, LRC)[6].LRC设计特点是在Reed-Solomon码的基础上,将一个条带的所有数据块均分成若干个组,然后每个分组针对组内所有的数据块额外编码生成一个新的校验块,称之为该组的局部校验块.显然,任意一个数据块的丢失,都可以通过其组内的局部校验块和组内其他数据块来快速修复出来,而无须构建整个原始文件来对丢失的数据块进行修复.因此,比起Reed-Solomon码,LRC可以大大降低修复丢失的数据块所耗费的带宽,进而降低修复时间,从而优化云存储系统对于用户的访问延迟,提高数据的可用性.
我们发现,LRC蕴含了一个较强的假设:所有分组的长度是相同的.由于LRC修复一个数据块需要下载它所在组的所有块,那么这个假设就意味着修复任意一个数据块均需要下载同样多的块,耗费同样多的带宽.因此在这个假设下,想要LRC的修复效率得到比较好的保障,显然只有每个块丢失的概率较为均匀才比较公平;否则,如果块和块之间的丢失概率不同,但修复代价却相同,那么这对整个系统的修复效率就会产生公平性的影响.
但是,一些研究[7-8]表明:在云存储系统中,一些数据块的丢失概率其实远远大于其他数据块,这是因为这些数据块所在的磁盘可被预测出来将在近期内发生故障.实际上,磁盘是当前云存储系统中最主要的故障来源,磁盘故障占所有设备故障的78%[9].而磁盘故障大部分是由于诸如磨损之类的缓慢过程所导致的,这些过程通常会持续数月或数年,因此可以通过对磁盘历史状况不断监测而对其近期是否发生故障进行预测.这样的话,我们可以通过机器学习等方法提前预测到某些磁盘故障的发生,即近期内这些磁盘的故障概率远远高于其他磁盘——这意味着这些磁盘上的数据块的丢失概率也远远高于其他数据块.而这个现象和LRC码当前结构所蕴含的假设——“所有分组的长度相同,所有数据块修复代价一样”——是不匹配的.
因此,这启发我们将基于机器学习的磁盘故障预测技术运用到LRC中对其固定分组的假设进行改进,以进一步提高LRC的修复性能.需要注意的是,已有相关研究工作将磁盘故障预测技术应用到复制和纠删码技术中[8],但LRC拥有不同于复制和纠删码的“条带分组”的特点,因此需要我们专门针对该特点进行有效的设计.本文贡献有3个方面:
1) 将磁盘故障预测技术的结果和LRC参数结合,构造了一类基于预测的LRC(proactive LRC, pLRC)方案.pLRC通过磁盘故障预测方法,区分不同数据块的丢失概率,从而动态调整系统中的LRC分组大小.我们尽可能地让近期可能丢失的数据块所在分组的长度缩小,从而使得修复这些块所需的带宽降低;同时,对于近期不会丢失的数据块所在分组的长度变长,以保证pLRC的存储开销和LRC保持一致.
2) 理论上,我们利用MTTDL建模分析对比了LRC和pLRC,结果显示后者可以提高多达113%的可靠性.同时,我们还对pLRC的修复带宽进行了理论上的数值分析,结果显示后者修复带宽理论上可以降低48.1%.
3) 系统上,我们在Facebook的Hadoop HDFS RAID[10]平台中,通过修改HDFS RAID相关代码,实现了LRC和pLRC技术,并将其运行在真实云环境下(Amazon Web Sevice[11]).实验结果显示,比起LRC,pLRC的降级读性能提高了46.8%,磁盘修复时间缩短了47.5%.
1 研究背景和动机
1.1 云存储中编码研究现状
随着云业务大规模的落地实施,数据存储已脱离于单纯的存储介质,逐渐演变成一种云服务,即云存储.相比于传统的存储介质环境,云环境中数据量大、应用复杂,这使得云存储系统要满足海量的存储需求和动态的IO服务需求,因而必须提供高可用性的容错机制,即持续稳定的在线运行性能.对此,云存储系统通常采用数据冗余技术来进行保驾护航.传统的数据冗余技术主要包括副本、RAID等.副本,即存储同一份数据的多个相同拷贝;数据的副本越多、数据可靠性越高,但存储空间利用率也就越低.RAID,即把多块独立的存储磁盘按特定方式组合起来形成一个磁盘阵列;该技术提高了存储空间的利用率,但传统磁盘阵列存在着扩展性较差、弹性缺乏、容错数较低等缺陷.因此,副本和RAID较难满足云存储的海量存储和动态变化的服务需求.
针对传统数据冗余技术的不足,云存储系统中出现了一种更高效的数据冗余技术——纠删码,其基本思想是将一份数据划分为k个原始数据块,基于k个数据块编码获得r个校验块.以上k+r个块(即k个数据块和r个校验块,通常称为一个条带)中任意r块出错时,系统均可重构出k个原始数据块.常用纠删码为Reed-Solomon编码,通常记为(k,r) RS.与副本相比,纠删码可以大大提高数据可用性[3];另外,不同于弹性缺乏、容错数较低的RAID,纠删码还具有参数配置灵活、任意容错的特点(比如可以通过调整参数k和r来改变冗余度和容错数),因而可以根据存储服务需求的动态变化,自适应地来构建纠删码.在学术界,已有不少工作研究基于纠删码的云存储系统.比如,私有云存储(即企业内部数据中心):Facebook的f4[12]、IBM的Cleversafe[13]、Hitchhiker[14]、Giza[15]等;公有云存储:Azure[4],Hybris[16]等.在工业界,纠删码也逐渐成为云存储产品的标配之一,比如,国外云厂商Windows Azure采用(k,r)=(6,4)的纠删码[4],国内云厂商七牛云采用(k,r)=(28,4)的纠删码[17].
可是当某个数据块丢失时,纠删码需要下载所有k个块去重建出原始文件才能对这个块进行修复,这导致数据修复通常需耗费大量带宽,而对于存储集群来说,加速恢复是非常重要的[18].因此不少新型纠删码设计方案针对如何对修复带宽进行优化,主要分为再生码和局部修复码2类:
1) 再生码(regenerating codes, RC).Dimakis等人首次提出了再生码[19],比起传统纠删码降低了单节点修复带宽(即修复单节点故障所需的传输数据量),并将再生码分成两大类,分别为MSR码(minimal storage regenerating codes)和MBR码(minimal bandwidth regenerating codes).文献[20]采用随机线性编码[21]保证了在编码有限域足够大的条件下,再生码的解码成功率无限趋近于100%.随后的研究工作可以分成3类:1)由于随机线性编码很难满足精确修复特性,即并不保证原始丢失数据的恢复,因此一些工作[22-24]针对精确修复的再生码进行了广泛的研究;2)由于再生码最初只针对单节点修复,后续工作致力于多节点修复的再生码设计[25-26];3)还有一些研究专注于确定性再生码的设计[27-28].
2) 局部修复码(LRC).LRC[4-5]通过限制数据修复时所连接的节点数目,即将数据修复尽可能局限在较小的节点集合内,来大大降低数据传输和IO操作数.实际上,LRC引入了额外的存储消耗去达到局部修复的优点,即在理论上并没有做到存储效率的最优,但是由于其实现的简易性,不少云存储系统开始部署局部修复码,比如Azure[4],Facebook[5],Ceph[29-30]等.LRC是在参数为(k,r)的Reed-Solomon码的基础上,将一个条带的所有k个数据块均分成m组,每组有k m个数据块,然后每组将自己所有的k
m个数据块,然后每组将自己所有的k m个数据块通过异或额外生成一个新的校验块,称之为该组的局部校验块.与之对应,已有的r个校验块称之为全局校验块.
m个数据块通过异或额外生成一个新的校验块,称之为该组的局部校验块.与之对应,已有的r个校验块称之为全局校验块.
图1是(k,m,r) LRC的示例图,其中k=6,m=2,r=2.D1~D6是6个数据块,P1和P2是通过D1~D6编码生成的2个全局校验块.然后将所有数据块分为2组:D1~D3,D4~D6,每组异或编码生成一个新的局部校验块:Q1和Q2.我们可以发现,D1~D6中无论哪一个数据块丢失,都可以通过该块所在组的局部校验块快速修复出来.比如,假设数据块D1丢失,如果是基于Reed-Solomon编码,则需要下载D2~D6以及P1一共6个块将D1修复;而如果基于LRC,则仅需要下载D2,D3以及Q1一共3个块即可修复D1.因此,比起Reed-Solomon码,LRC可以降低大大降低修复一个丢失块的所需时间,从而优化云存储系统对于用户的访问性能.
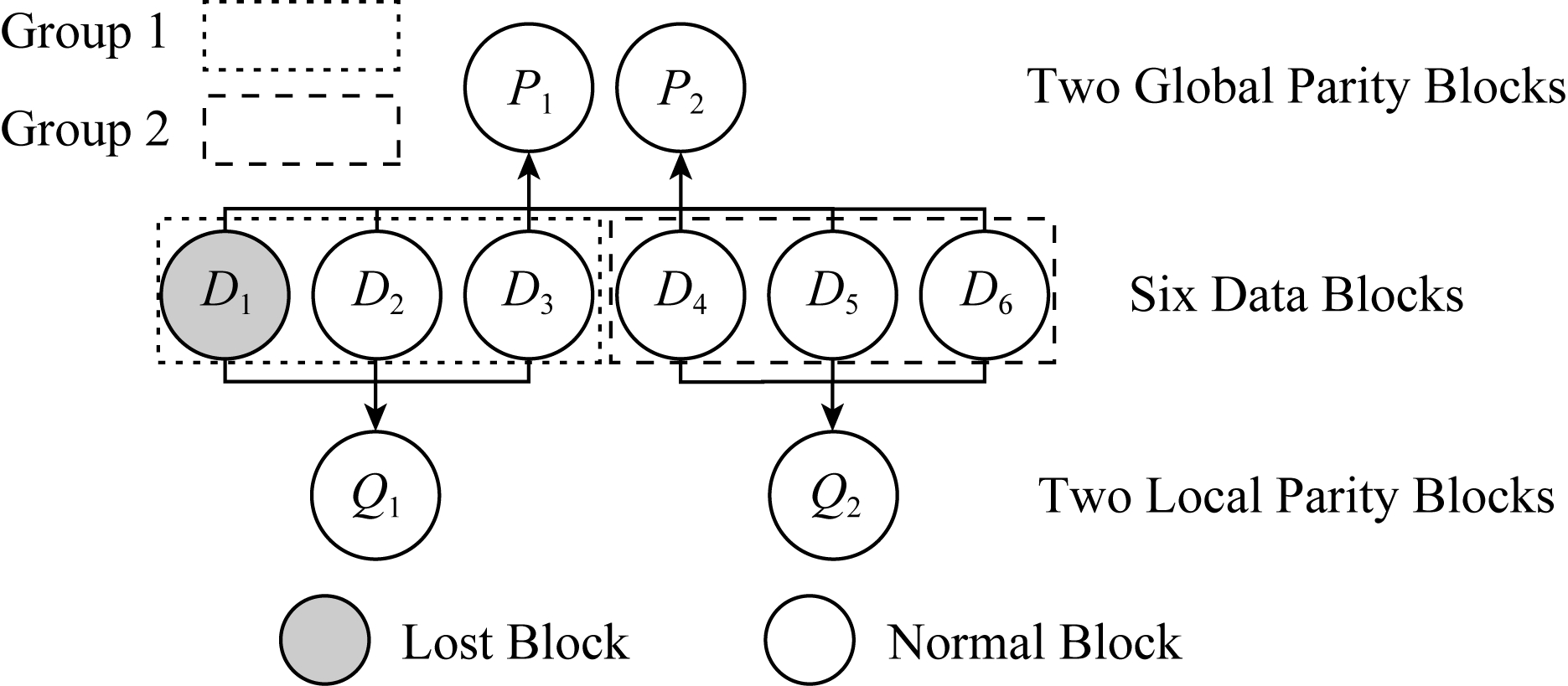
Fig. 1 An illustration of (6,2,2) LRC
图1 (6,2,2) LRC的示例图
1.2 云存储中磁盘故障预测研究现状
云存储系统发生服务中断的代价越来越高昂[31],服务中断最大的一个原因是磁盘设备发生故障[9,32].硬盘的故障一般分为2种:不可预测的和可预测的.前者发生几率不高,通常不可预测,比如人为不当操作造成的机械撞击等;但后者比如像轴承磨损、磁介质性能下降等都可以在几天甚至几周前就发现苗头从而进行规避.
基于此,1992年IBM在AS 400计算机的磁盘中使用了名为Predictive Failure Analysis(故障预警分析技术)的监控技术;不久,康柏、希捷、昆腾以及康纳共同提出了名为IntelliSafe的类似技术;1996年以上几家公司联合推出了一套硬盘状态检测与预警系统和规范,命名为S.M.A.R.T.(self-monitoring analysis and reporting technology), 即“自我检测分析与报告技术”,成为一种自动监控硬盘驱动器完好状况和报告潜在问题的技术标准.
400计算机的磁盘中使用了名为Predictive Failure Analysis(故障预警分析技术)的监控技术;不久,康柏、希捷、昆腾以及康纳共同提出了名为IntelliSafe的类似技术;1996年以上几家公司联合推出了一套硬盘状态检测与预警系统和规范,命名为S.M.A.R.T.(self-monitoring analysis and reporting technology), 即“自我检测分析与报告技术”,成为一种自动监控硬盘驱动器完好状况和报告潜在问题的技术标准.
SMART 技术通过在硬盘硬件内的检测指令对硬盘的各个硬件如磁头、马达、电路、盘片的运行情况进行监控,并与厂商所预设的安全值进行比较,若监控情况将超出或已超出预设安全值的安全范围时发出警报.但该方法只能预测出不到10%的硬盘故障[33].因此,有不少研究工作在SMART数据集上建立各种预测模型,以提高硬盘的故障率预测准确率.这些磁盘故障预测模型[7,34-37]通常有3个主要参数:
1) 准确率(false discovery rate, FDR),即故障磁盘中可以被准确预测出的比例.
2) 误报率(false alarm rate, FAR),即健康磁盘中被误报为故障磁盘的比例.
3) 提前预测时间(time in advance, TIA),即提前多长时间预测磁盘故障.
文献[33]提出了一种基于多实例学习框架和朴素贝叶斯分类器的故障预测算法,但仅使用了369个磁盘的SMART数据集.文献[35]采用贝叶斯方法对磁盘故障进行建模,数据集由1 936个磁盘组成,其中只有9个被标记为失败,同样也比较小.文献[36]利用统计检验相关方法(如多变量秩和检验)提高FDR和降低FAR,同样的数据集也相当小,只有347个磁盘器(其中36个故障).文献[34,37]采用人工神经网络和决策树等学习方法,数据集规模较大,包含来自企业级模型的总共23 395个磁盘(其中433个故障).该方法最好预测性能达到0.1%以下的FAR和95%以上的FDR,且TIA至少为一周以上,从而为故障处理预留了充足时间.文献[7]同样使用了一个包含超过20 000个磁盘的大型数据集,通过选择合适的SMART指标并调整预测模型,使得FDR高达98%.
1.3 本文研究动机
当前很少有工作将云存储系统中的编码技术和磁盘故障预测技术联系起来,文献[8]提出了一类基于磁盘故障预测技术的纠删码技术Procode.Procode的技术原理是把复制和纠删码结合起来,将预测的故障磁盘的数据块和校验块进行复制,使得这些块在丢失以后无须通过纠删码恢复,只用通过复制恢复即可,因此降低修复这些块所需要的时间.文献[8]的作者在其工作展望中希望有工作能将Procode的策略思想和新型的编码技术相结合起来.但是,如果直接将Procode对即将丢失的数据块进行简单复制的策略和新型编码技术LRC技术结合的话,那么将会破坏LRC的单一编码结构而造成副本一致性维护问题,并且还会引入额外的存储开销、增加磁盘个数而加大系统存储管理成本.
因此,这启发我们在LRC的编码结构和存储开销不变的前提下,将磁盘故障预测技术结果和LRC编码结合起来,构造了一类基于预测的LRC编码.pLRC算法首先通过文献[34]提供的一类磁盘故障预测方法以及相应的大型SMART数据集,区分一周的即将故障的磁盘(称为“坏盘”)和其他健康磁盘(称之为“好盘”);然后仅仅调整坏盘和好盘所拥有的数据块所在分组的大小,使得坏盘的数据块所在分组的长度变短,而这些分组为了保持存储量不变,同时将分组内其他好盘的数据块所在分组变长,并同步更新组内的校验块.这样的话,pLRC的编码结构依然和LRC保持一致,只是部分条带的分组组长不同;同时pLRC的存储开销和LRC也保持了一致.更重要的是,pLRC会对一周内大概率坏掉的磁盘进行快速修复,从而提高数据块修复性能.
图2是(6,2,2) LRC转变为pLRC的示例图.假设D1是坏盘的数据块,和图1相比,D1所在分组变短,其他分组变长,Q1和Q2因组长变化更新为![]() 和
和![]() 我们可以发现pLRC中仅仅只用D2和
我们可以发现pLRC中仅仅只用D2和![]() 共2个块即可修复D1.因此,比起图1中的LRC,pLRC存储开销保持不变的同时,降低修复带宽33%,从而缩短了修复坏盘数据块的所需时间,优化了云存储系统对于用户的数据在线访问性能.
共2个块即可修复D1.因此,比起图1中的LRC,pLRC存储开销保持不变的同时,降低修复带宽33%,从而缩短了修复坏盘数据块的所需时间,优化了云存储系统对于用户的数据在线访问性能.

Fig. 2 An illustration of pLRC from (6,2,2) LRC
图2 (6,2,2) LRC 转换为pLRC的示例图
2 pLRC的设计
在本节中,我们主要对pLRC的设计算法进行描述.
2.1 磁盘故障预测算法选择
当前有包括决策树、人工神经网络等机器学习算法可用于预测磁盘,我们的目标是在FDR和FAR之间找到一个较好的权衡.为了实现这一目标,我们对当前主流的2类分类算法:决策树[37]和人工神经网络[34]进行了比较.和文献[34]类似,我们在开源的SMART数据集[38]上针对12个特征(见表1)进行采样.SMART数据集包含23 395个磁盘(其中433个坏盘、22 962个好盘)在7天内的SMART记录,其中每个盘每小时都会生成一条SMART记录,因此每个好盘有168条记录,而坏盘记录到自己发生故障为止.然后,我们将采样数据集随机拆分为训练数据集(占总数据集的70%),并通过交叉验证测试数据集(占总数据集的30%).2个预测算法的性能如表2所示.
Table 1 Selected SMART Attributes
表1 所选的SMART属性

Attribute IDAttribute1Current Pending Sector Count2Current Pending Sector Count (raw value)3Hardware ECC Recovered4High Fly Writes5Raw Read Error Rate6Reallocated Sectors Count7Reallocated Sectors Count (raw value)8Reported Uncorrectable Errors9Seek Error Rate10Spin up Time11Temperature Celsius12Power on Hours
Table 2 Performance Comparison of Decision Tree and BP Neural Network
表2 决策树和人工神经网络的性能比较

AlgorithmFDR∕%FAR∕%TIA∕dDecision Tree930.487BP Neural Network952.877
从表2可以看出,决策树和人工神经网络都能达到良好的预测准确性;但人工神经网络的误报率较高,会导致pLRC错把不少的好盘上所保存的数据块也进行分组大小调整而耗费不小的带宽.因此,我们选择决策树作为我们的预测算法.
2.2 pLRC编码算法设计
pLRC编码算法有2个主要的设计目标:
1) 和LRC保持同样的存储开销和磁盘个数;
2) 比LRC拥有更低的数据块修复带宽.
针对这2个设计目标,pLRC的设计思想是对所有数据块进行“好”“坏”标记;然后在磁盘故障预测算法运行后,坏盘上的数据块标记为“坏块”;最后针对每个坏块所在的条带,缩短该坏块所在分组的组长,变长其他分组的组长,使得该条带所造成的存储开销和所需磁盘个数保持不变,并且坏块的修复所造成的带宽消耗降低.算法细节如下:
算法1. pLRC编码.
假设:系统有N个磁盘,每个磁盘拥有p个数据块,每个条带最多只包含一个坏块.
① 所有数据块都标为“好块”;
② 执行(k,m,r) LRC;
③ 运行Decision Tree算法,输出坏盘H1,H2,…,Hb;
④ H1,H2,…,Hb上所有数据块标为“坏块”,记为![]()
⑤![]()
![]() 所在的bp个条带记为S1,S2,…,Sbp;
所在的bp个条带记为S1,S2,…,Sbp;
⑥ for i=1 to bp
⑦ Si所有分组记为Gi,1,Gi,2,…Gi,m;
⑧![]() 所在分组记为Gi,1;
所在分组记为Gi,1;
⑨ Gi,1分组保留![]() 和任意一个数据块,将其他数据块随机转移到Gi,2,Gi,3,…,Gi,m;
和任意一个数据块,将其他数据块随机转移到Gi,2,Gi,3,…,Gi,m;
⑩ Gi,1,Gi,2,…,Gi,m更新校验块;
 end for
end for
算法1在初始状态时,所有数据块都标记为“好块”,然后执行LRC编码(行①②).在决策树预测算法过后,预测为坏盘所保存的数据块标记为“坏块”,然后找到所有坏块所在的条带(行③~⑤).最后对所有这些bp个条带进行分组大小调整:含有坏块的分组长度缩短为3(即原分组缩小为仅包含2个数据块和1个校验块的分组),即该分组为简单的(2,1) RS编码;然后该分组的其他块随机转移到其他分组,最后更新分组的校验块.
算法1的具体过程如图3所示,图3(a)是初始状态下的(12,3,2) LRC编码.图3(b)是预测算法后的(12,3,2) pLRC编码,![]() 标记为坏块,然后
标记为坏块,然后![]() 所在分组从4个数据块下降到2个数据块,其他2个数据D3和D4转移到另外分组,分组校验块
所在分组从4个数据块下降到2个数据块,其他2个数据D3和D4转移到另外分组,分组校验块
随之更新为:![]() 和
和![]() 坏块
坏块![]() 可以通过下载2个块就可以修复出来.
可以通过下载2个块就可以修复出来.
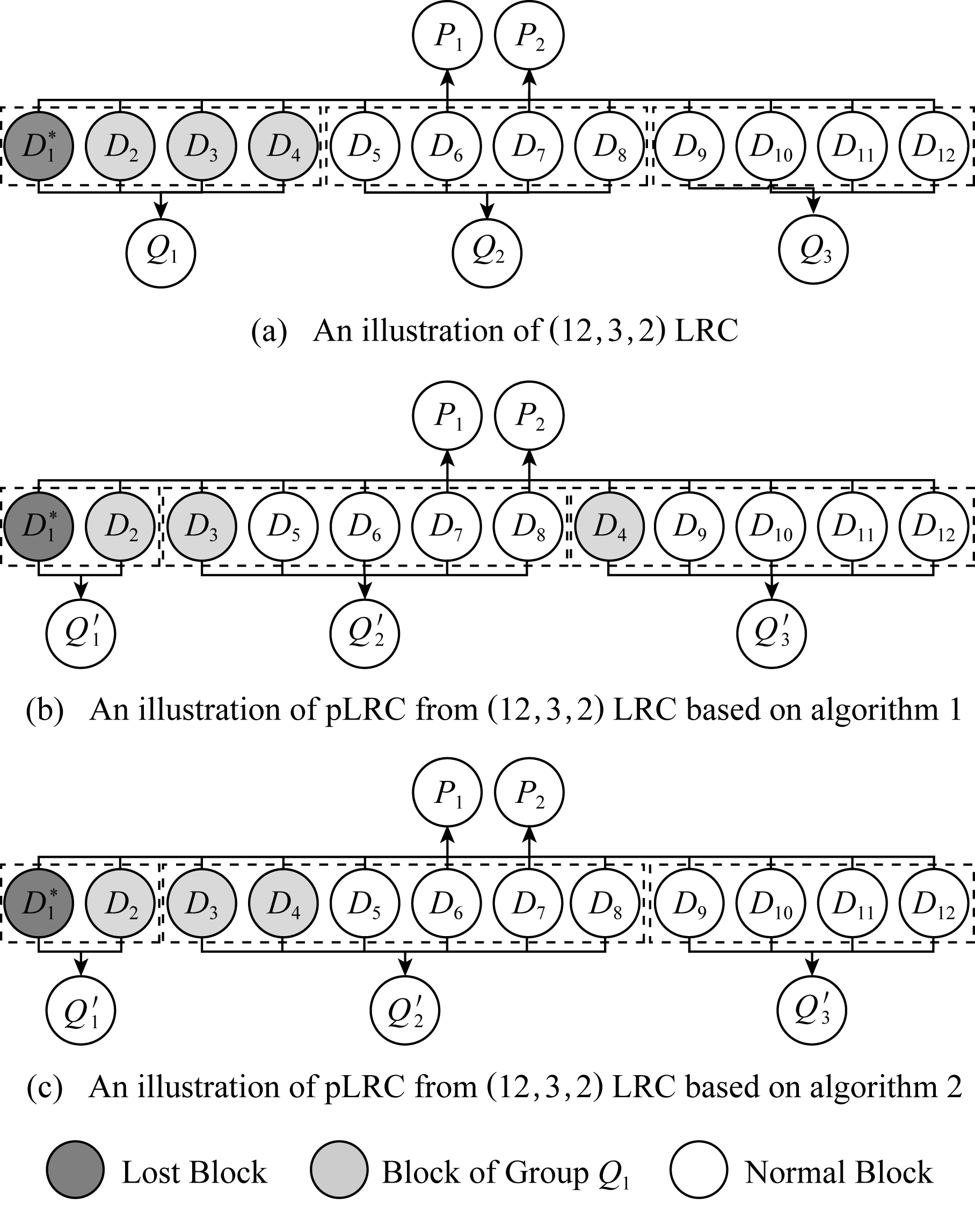
Fig. 3 Illustrations of pLRC
图3 pLRC的算法示例图
2.3 pLRC算法优化
当所有坏块被修复以后,pLRC应该回归LRC以等待下一次磁盘故障预测算法的执行.基于算法1的编码策略,我们可以发现需要对大量的局部校验块进行更新,将造成较大的传输开销.因此,我们对pLRC算法进行进一步的优化,优化思想是通过尽可能地减少局部校验块的更新个数来降低其更新所带来的开销.算法细节如下:
算法2. pLRC编码(优化).
①~⑧和算法1相同;
⑨ Gi,1分组保留di和任意一个数据块,将其他数据块全部转移到Gi,2;
⑩ Gi,1和Gi,2更新校验块;
 end for
end for
算法2将坏块所在分组需要转移的数据块全部放在另外一个分组内,使得需要更新的校验块永远只有2个.因此,在从pLRC回归到LRC时,只需要对2个校验块进行更新,这样可以将2个校验块的更新操作协同起来,从而降低传输开销.
举例说明,当从图3(b)的pLRC向图3(a)的LRC回归时,![]() 所在节点需要下载D3和D4更新回到
所在节点需要下载D3和D4更新回到![]() 所在节点需要下载D3回到
所在节点需要下载D3回到![]() 所在节点需要下载D4回到Q3,即系统总共需要下载4个数据块.与之对应的是,图3(c)的pLRC仅生产2个局部校验块
所在节点需要下载D4回到Q3,即系统总共需要下载4个数据块.与之对应的是,图3(c)的pLRC仅生产2个局部校验块![]() 和
和![]() 因此
因此![]() 所在节点首先下载D3和D4回到Q1之后,该节点可以额外生成一个D3和D4的异或块传输给
所在节点首先下载D3和D4回到Q1之后,该节点可以额外生成一个D3和D4的异或块传输给![]() 协助其回到Q2,从而系统总共只需要下载3个数据块.和算法1相比,算法2所造成的传输开销降低了25%.
协助其回到Q2,从而系统总共只需要下载3个数据块.和算法1相比,算法2所造成的传输开销降低了25%.
3 理论量化分析
在本节中,我们主要在理论上对pLRC的可靠性以及修复过程中消耗的带宽进行分析,并与LRC进行比较.
3.1 可靠性分析
可靠性是分布式系统中最重要的性质之一,下面对pLRC的可靠性进行分析.与之前的很多工作类似[4-5,39-42],我们使用马尔可夫模型来对平均无数据丢失时间(mean-time-to-data-loss, MTTDL)进行分析.与文献[4]相同,我们对一般化马尔可夫模型进行简单的扩展使其可以捕捉到LRC以及pLRC中的特殊状态变换.虽然基于马尔可夫的可靠性分析的有效性值得商榷[43],但我们认为它足以为本工作提供可靠性的初步见解.
1) 模型.将参数固定为k=6,m=2,r=2.图4为LRC和pLRC参数(k,m,r)=(6,2,2)的马尔可夫模型.假定我们将多个条带上的数据分布于k+m+r个节点上,每种状态代表可用节点的数量.比如状态10表示全部节点都是健康节点,而状态5则表示有数据丢失.在本文中,我们仅考虑独立故障,将单节点的故障率记为λ.因此,从状态i到状态i-1,1≤i≤n的状态转换率为iλ.
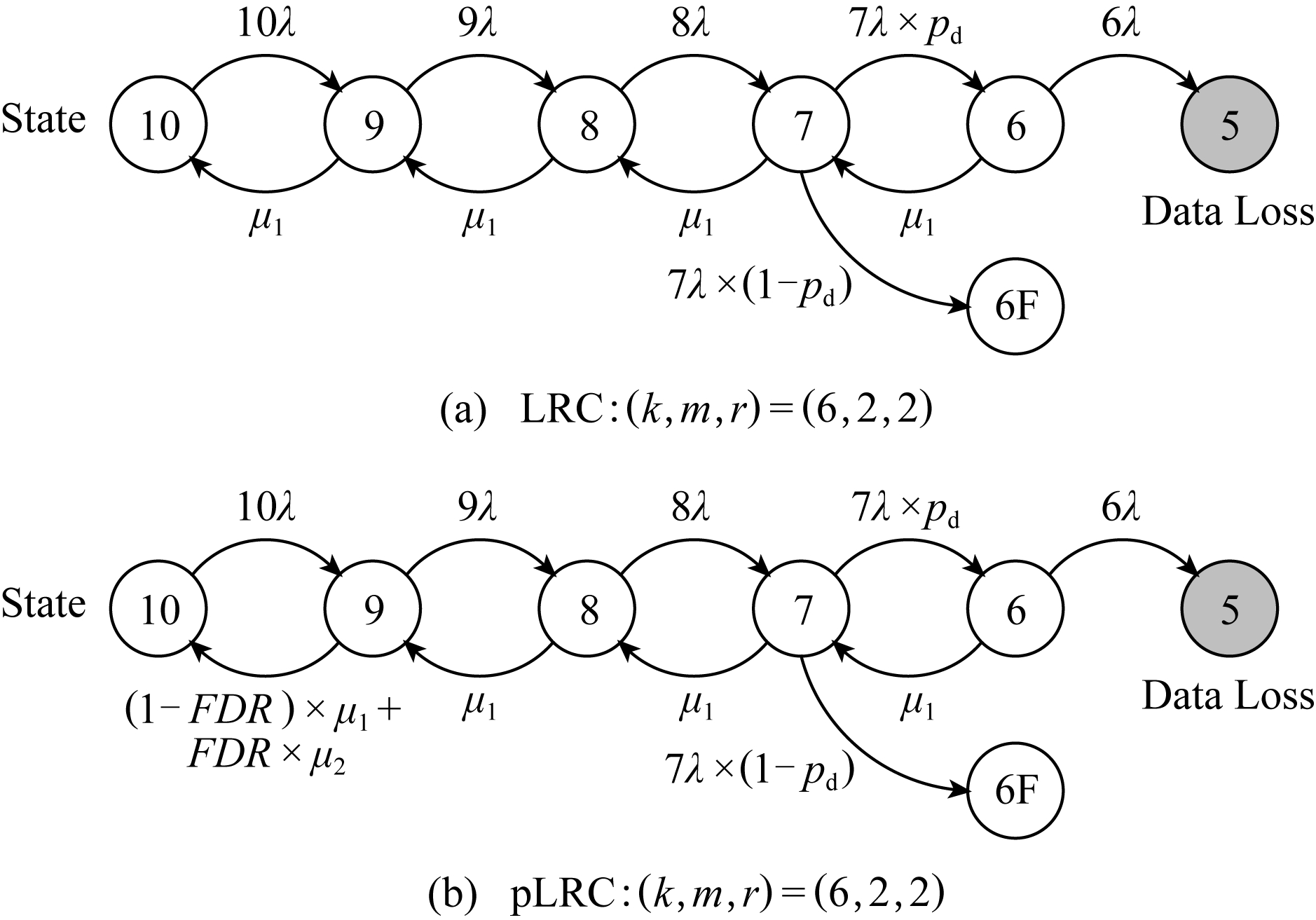
Fig. 4 Markov reliability model
图4 马尔可夫可靠性模型
马尔可夫模型中增加的扩展部分位于状态7,其可转换为2个拥有6个健康节点的状态.状态6代表了有4个可修复的故障,而状态6F则表示了有4个不可修复的故障.我们将在4个故障情形中可修复故障的比例记为pd,则从状态7到状态6的转换率为7λpd,而从状态7到状态6F的转换率为7λ(1-pd).
在反方向的修复模型上,我们将从状态i到状态i+1进行修复的修复率记为μ,其中在状态转换中使用LRC修复的修复率记为μ1,而对于pLRC从状态9到状态10的过程中使用(2,1) RS码的修复率记为μ2.在pLRC中,对于使用磁盘预测技术预测出的故障磁盘,我们将采用(2,1) RS码进行局部修复;对于未能预测出的故障磁盘,将仍使用LRC来进行修复.因此,pLRC中从状态9到状态10的修复率μ=(1-FDR)×μ1+FDR×μ2.
我们可以按如下方式配置参数:对于λ,我们假定一个节点的平均无故障时间(mean-time-to-failure, MTTF)为4年[5](也就是说,1 λ=4年).我们把节点间的可用带宽记为γ,集群中的节点数为M,单节点上的存储量记为S,修复每一单元数据所需要的修复开销记为C.例如,在(k,m,r)=(6,2,2)时,对于LRC来说,C=(3×8+6×2)
λ=4年).我们把节点间的可用带宽记为γ,集群中的节点数为M,单节点上的存储量记为S,修复每一单元数据所需要的修复开销记为C.例如,在(k,m,r)=(6,2,2)时,对于LRC来说,C=(3×8+6×2) 10=18
10=18 5,pd=86%[4],因此μ1=γ (M-1)
5,pd=86%[4],因此μ1=γ (M-1) (18S
(18S 5);而对于pLRC来说,C=(2×8+6×2)
5);而对于pLRC来说,C=(2×8+6×2) 10=14
10=14 5,因此μ2=γ(M-1)
5,因此μ2=γ(M-1) (14S
(14S 5).
5).
2) 分析.我们现在对LRC和pLRC策略下的MTTDL进行分析.采用2.1节所使用的SMART数据集,其中23 395个磁盘约30%作为测试集(M=7 019),使用一组经典的参数(S=16 TB,网络带宽利用率为0.1)[5]来对不同网络带宽下的两者的可靠性进行计算.结果如表3所示:
Table 3 MTTDLs of LRC and pLRC for Different Values of Bandwidth
表3 不同带宽下LRC和pLRC的MTTDL a

Bandwidth∕GbpsLRCpLRC13.02E+136.43E+1322.42E+145.14E+1438.16E+141.74E+1541.94E+154.11E+1553.78E+158.03E+1566.53E+151.39E+1671.04E+162.20E+1681.55E+163.29E+1692.20E+164.69E+16103.02E+166.43E+16
从表3中数据我们得到,在不同的网络带宽下,pLRC的MTTDL最多比LRC提高113%.主要的原因是pLRC提前预测了磁盘故障,并使用修复效率较高的(2,1) RS码进行局部修复,提升了系统的可靠性.我们还能看到,网络带宽越高,两者的MTTDL均越高.这是由于网络带宽越高,其余参数不变的情况下,修复率μ也越高,从而提升了可靠性.
3.2 修复带宽分析
对于(k,m,r) LRC和(k,m,r) pLRC,我们将LRC中修复每一单元所需的修复带宽记为CLRC,将pLRC中修复每一单元所需的修复带宽记为CpLRC.我们假定每个条带中最多含有一个坏盘上的块,通过对LRC进行分析得到:
(1)
注意:pLRC将预测将要坏掉的数据块使用(2,1)RS进行恢复,而未被预测中的块则仍使用原来的(k,m,r) LRC进行修复.同时,坏盘中的全局编码块也仍使用(k,m,r) LRC进行修复.因此,我们得到:
CpLRC=(1-FDR)×CLRC+FDR× ![]()
(2)

Fig. 5 Numerical results of recovery bandwidth for LRC and pLRC
图5 LRC和pLRC修复带宽的理论分析结果
通过计算式(1)、式(2)两个等式的差可以得到pLRC相对于LRC减少的修复带宽:
(3)
由式(3)可以得出,k m越大以及FDR越大,则CLRC-CpLRC越大,也就是pLRC相对于LRC来说,修复带宽减少得越多,修复带宽越小.
m越大以及FDR越大,则CLRC-CpLRC越大,也就是pLRC相对于LRC来说,修复带宽减少得越多,修复带宽越小.
如2.1节所示,根据基于决策树的磁盘预测算法的结果FDR≈93%,我们对(6,2,2) pLRC和(12,2,2) pLRC的修复带宽分别进行计算,并和相应的LRC进行比较,具体结果如图5所示:
从图5可以看出,对于(6,2,2) LRC和(6,2,2) pLRC,CLRC=3.6,CpLRC=2.86,且CLRC-CpLRC=0.74.也就是说,修复一个单元的数据,LRC需要3.6个单元的数据来进行修复,而pLRC仅需要2.86个单元即可修复,此时pLRC相对LRC的修复带宽下降了大约20.6%.同样地,在(k,m,r)=(12,2,2)时,pLRC相对LRC的修复带宽下降了大约48.1%.
我们发现,(12,2,2) pLRC对(6,2,2)pLRC的修复开销下降得更多,这是因为在FDR相同的情况下,(12,2,2) pLRC的k m=6大于(6,2,2) pLRC 的k
m=6大于(6,2,2) pLRC 的k m=3,由式(3)可知,前者的修复带宽下降更多.这说明条带越长,我们的算法效果越好,这符合实际云存储厂商为了降低存储成本采用大条带的事实[16].
m=3,由式(3)可知,前者的修复带宽下降更多.这说明条带越长,我们的算法效果越好,这符合实际云存储厂商为了降低存储成本采用大条带的事实[16].
3.3 pLRC更新开销分析
pLRC的更新开销包括2个部分:LRC重组成pLRC和pLRC回归为LRC时,算法2与算法1更新操作所造成的传输.下面我们对(k,m,r) pLRC的这2个算法在重组与回归过程中的更新造成的传输开销进行分析.
1) 对算法1的更新方式的传输开销进行分析.在重组过程中,其将一个分组中的k m个块除去坏块以及任意一个块,也就是将剩余的k
m个块除去坏块以及任意一个块,也就是将剩余的k m-2个块随机均匀转移到其余m-1组中去.算法1需要对这m-1个组中的编码块进行更新,同时也需要传输2个块(坏块以及任意一个块)来对第1个分组中的编码块进行更新,因而在重组过程中一共需要传输k
m-2个块随机均匀转移到其余m-1组中去.算法1需要对这m-1个组中的编码块进行更新,同时也需要传输2个块(坏块以及任意一个块)来对第1个分组中的编码块进行更新,因而在重组过程中一共需要传输k m个块.在回归过程中,算法1需要将之前重组出去的k
m个块.在回归过程中,算法1需要将之前重组出去的k m-2个块收集至第1个分组中以对第1个分组的编码块进行更新,并且这k
m-2个块收集至第1个分组中以对第1个分组的编码块进行更新,并且这k m-2个块需要对重组过程中更新的m-1个组的编码块进行更新.在回归过程中一共需要传输2(k
m-2个块需要对重组过程中更新的m-1个组的编码块进行更新.在回归过程中一共需要传输2(k m-2)个块.因此,我们可以得到算法1的更新方式的传输开销为
m-2)个块.因此,我们可以得到算法1的更新方式的传输开销为
(4)
2) 对算法2的更新方式的传输开销进行分析.在重组过程中,其将一个分组中剩余的k m-2个块均转移至第2个分组中,这样算法2可以先将2个块(坏块以及任意一个块)传至第1个分组中的编码块,以生成新的编码块.然后算法2利用第1个分组中旧的编码块与这2个块生成一个异或块,并将其传至第2个分组的编码块上对编码块进行更新.因而在重组过程中算法2一共需要传输3个块.在回归过程中,算法2需要将之前重组出去的k
m-2个块均转移至第2个分组中,这样算法2可以先将2个块(坏块以及任意一个块)传至第1个分组中的编码块,以生成新的编码块.然后算法2利用第1个分组中旧的编码块与这2个块生成一个异或块,并将其传至第2个分组的编码块上对编码块进行更新.因而在重组过程中算法2一共需要传输3个块.在回归过程中,算法2需要将之前重组出去的k m-2个块收集至第1个分组中以对第1个分组的编码块进行更新,同时,算法2利用收集的这k
m-2个块收集至第1个分组中以对第1个分组的编码块进行更新,同时,算法2利用收集的这k m-2个块生成一个更新块.然后算法2将这个更新块传至第2个分组的编码块上以对其进行更新.这样,在回归过程中一共需要传输k
m-2个块生成一个更新块.然后算法2将这个更新块传至第2个分组的编码块上以对其进行更新.这样,在回归过程中一共需要传输k m-2+1=k
m-2+1=k m-1个块.因此,我们可以得到算法2的更新方式的传输开销为
m-1个块.因此,我们可以得到算法2的更新方式的传输开销为
(5)
现在通过计算式(4)、式(5)两个等式的差来得到算法2相对于算法1减少的传输开销:
(6)
在LRC的算法中,分组中至少有3个块(2个数据块、1个编码块),因此k m≥3.通过式(6)我们发现算法2的更新方式的传输开销要小于等于算法1的开销,且k
m≥3.通过式(6)我们发现算法2的更新方式的传输开销要小于等于算法1的开销,且k m越大,算法2的传输开销相对于算法1来说越有优势.
m越大,算法2的传输开销相对于算法1来说越有优势.
根据式(4)(5),我们计算出不同分组内块数量下的算法传输开销,如图6所示:
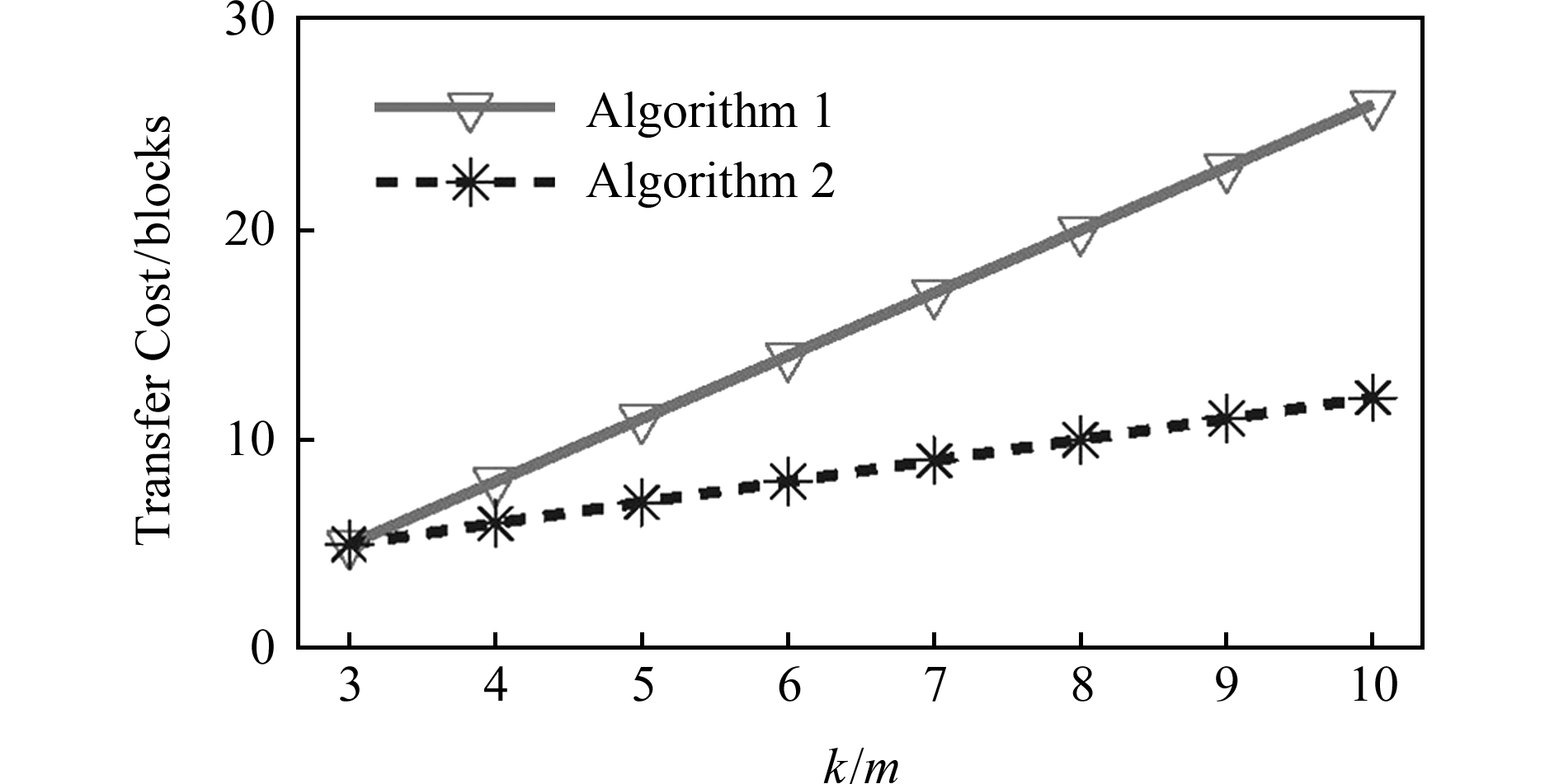
Fig. 6 Transfer cost of algorithm 1 and algorithm 2
图6 算法1和算法2更新方式的传输开销
从图6中我们可以看到,算法1的开销要大于算法2的开销,且2种算法的开销之差也随着分组内块的数量的增多而不断增加.
4 实验与结果
在本节中,我们在云上运行了实验,测试了pLRC的降级读性能以及修复性能,并将其与LRC进行对比.
4.1 实验部署环境
我们将pLRC部署在Facebook的HDFS[10]中,其通过整合HDFS-RAID[44]以在Hadoop Distributed File System (HDFS)[45]中支持纠删码.下面我们先对HDFS如何实现纠删码进行概述,然后介绍我们如何在HDFS中部署pLRC.
4.1.1 HDFS简概
HDFS是学术界和工业界部署应用最为广泛的分布式存储系统之一.它由2种类型的节点组成:一个执行管理操作并包含各种元数据的NameNode,以及多个包含数据的DataNode.HDFS将数据分为固定大小的块,这些块作为基本单元来进行读、写以及编码等操作.
HDFS-RAID引入了一个RaidNode来处理纠删码的相关操作如编码、修复等.RaidNode首先将数据存储为多个副本,并将这些副本分布在不同节点上.一段时间后,RaidNode通过使用MapReduce[46]来将这些块转换为编码过的块.具体来说,为了构建参数为(k,r)的纠删码,MapReduce作业中的map任务从不同的DataNode上收集k个编码块,然后将它们编码为r个校验块,并将这k+r个块分布至k+r个DataNode上.此外,RaidNode还会定期检查是否存在故障块,并触发修复操作来修复故障块.
4.1.2 pLRC部署
下面我们将解释如何扩展Facebook的HDFS以对pLRC进行支持.具体架构如图7所示:
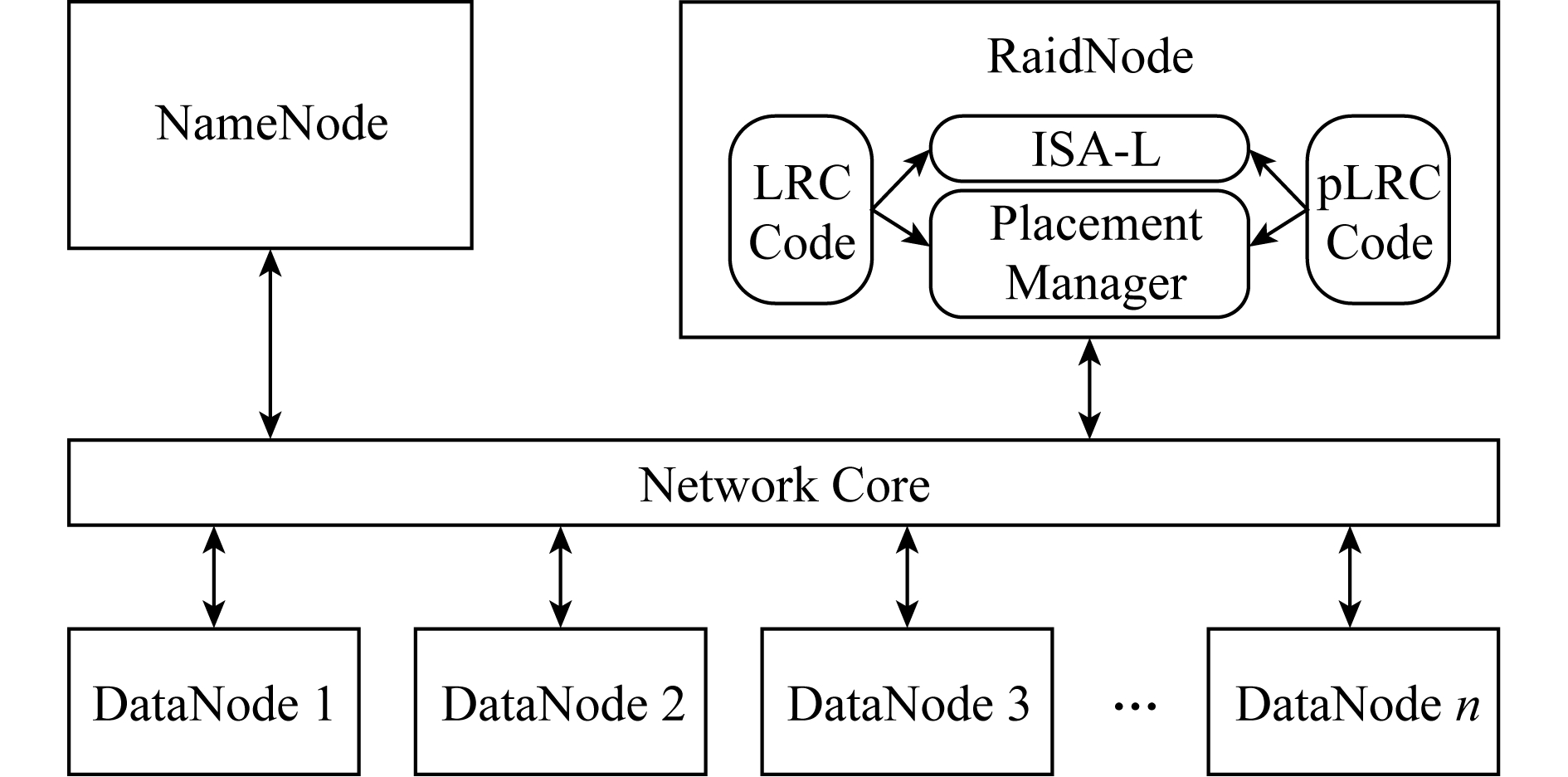
Fig. 7 Architecture of pLRC
图7 pLRC架构图
1) LRC和pLRC编码模块.我们在HDFS上增加了LRC编码,并实现了在预测到磁盘将要发生故障时将LRC编码转变为pLRC编码的相关模块.我们主要实现了LRC以及pLRC这2种编码的编解码以及修复操作.对于LRC,我们主要是增加了分组,计算出分组内的局部校验块,并通过Placement Manager模块指定其所有块的放置位置. LRC的分组信息、分组内局部校验块的信息以及块放置信息均存储于RaidNode上,以备修复过程及转换至pLRC时使用.对于pLRC, 我们首先在模块中增加getPredictingInfo API,通过此API从磁盘故障预测算法中获取预测的结果即坏盘;然后从NameNode获取坏盘中所有坏块相关的条带信息,从RaidNode获取分组、校验块信息以及块放置信息;最后通过传输块对分组校验块进行更新,使得坏块所在的条带从LRC编码转变为pLRC编码.
对于修复操作,我们主要关注单节点的故障修复.现在支持2类修复操作:①节点修复.指的是某个节点发生故障时,对其上所有丢失的数据块进行修复.由于每个丢失的数据块位于不同的条带中,因此利用条带中的其余数据对其进行修复.当RaidNode检测到节点故障时,RaidNode会调用pLRC的修复函数来进行节点修复,其先从NameNode获取相关所有条带信息.对每一个条带,pLRC从RaidNode上获取相关的分组信息及放置信息,然后利用这些信息调用相关的DataNode传输修复所需的块至新节点上以进行修复操作.②降级读.指的是修复某个当前不可用的数据块.我们对文件系统客户端进行了修改,当客户端读取数据发现不能获取某个块时,会触发块丢失故障异常.此时客户端将调用RaidNode上的pLRC从相关DataNode上读取分组中的相关块来对丢失块进行修复,并将修复出的块传给客户端,从而完成降级读操作.
2) ISA-L计算模块.以上的2种编码我们均通过使用Intel的ISA-L[47]硬件加速库来实现快速编解码.我们通过Java Native Interface (JNI)来将具体的编解码操作与Hadoop连接起来,从而极大地加速了编解码操作.我们主要使用2个ISA-L的API:用来指定编码系数的ec_init_tables以及用来具体执行编解码操作的ec_encode_data.这些ISA_L的API将基于硬件配置来自动对计算过程进行优化.
3) 数据布局.LRC及pLRC编码在编解码完成后需要考虑将数据块如何在集群中进行放置.因此我们将数据布局增添到HDFS中,通过对RaidNode中的数据布局管理模块进行更改,以此来指定条带中的数据具体是如何放置的.即如何把编码后的同一条带中的数据块与编码块随机地放置到集群中的不同节点上或是将解码后的数据块放置到特定的节点上.
4.2 实验配置与方法
1) 实验环境配置.我们的实验部署在Amazon EC2[11]上.使用位于美国东部(弗吉尼亚北部)区域的17个m4.4xlarge实例来进行实验,其中有1个实例用作管理节点NameNode及编解码节点RaidNode,其余16个实例用作数据节点DataNode.这些实例均基于Ubuntu 14.04的Linux平台,具体硬件配置为16核CPU、64 GB内存、2 TB SSD.
2) 实验方法.我们测试了4种不同参数下pLRC的降级读延迟以及单节点修复时间,并与LRC进行对比.这4组参数分别是:微软Azure[4]中采用的(6,2,2),(12,2,2),Faceook集群[5]中采用的(10,2,4),以及理论最优LRC[48]中采用的(6,2,3).
对于(6,2,2) pLRC,我们使用了总量为6 TB的数据来进行编码,生成4 TB的编码数据; 对于(12,2,2) pLRC我们使用了总量为12 TB的数据来进行编码,生成4 TB的编码数据; 对于(10,2,4) pLRC我们使用了总量为10 TB的数据来进行编码,生成6 TB的编码数据; 对于(6,2,3) pLRC我们使用了总量为6 TB的数据来进行编码,生成5 TB的编码数据.我们将这些数据分别均匀分布在10,16,16及11个数据节点上,每个数据节点存放1 T数据,取每个实验的5次平均运行结果.
4.3 实验结果
1) 数据块降级读性能.我们测试了当文件系统客户端读取一个不可用数据块的降级读性能.在系统中随机擦除掉一个数据块,然后让文件系统客户端通过降级读的方式来获取该数据块.降级读性能的测试结果如图8所示:
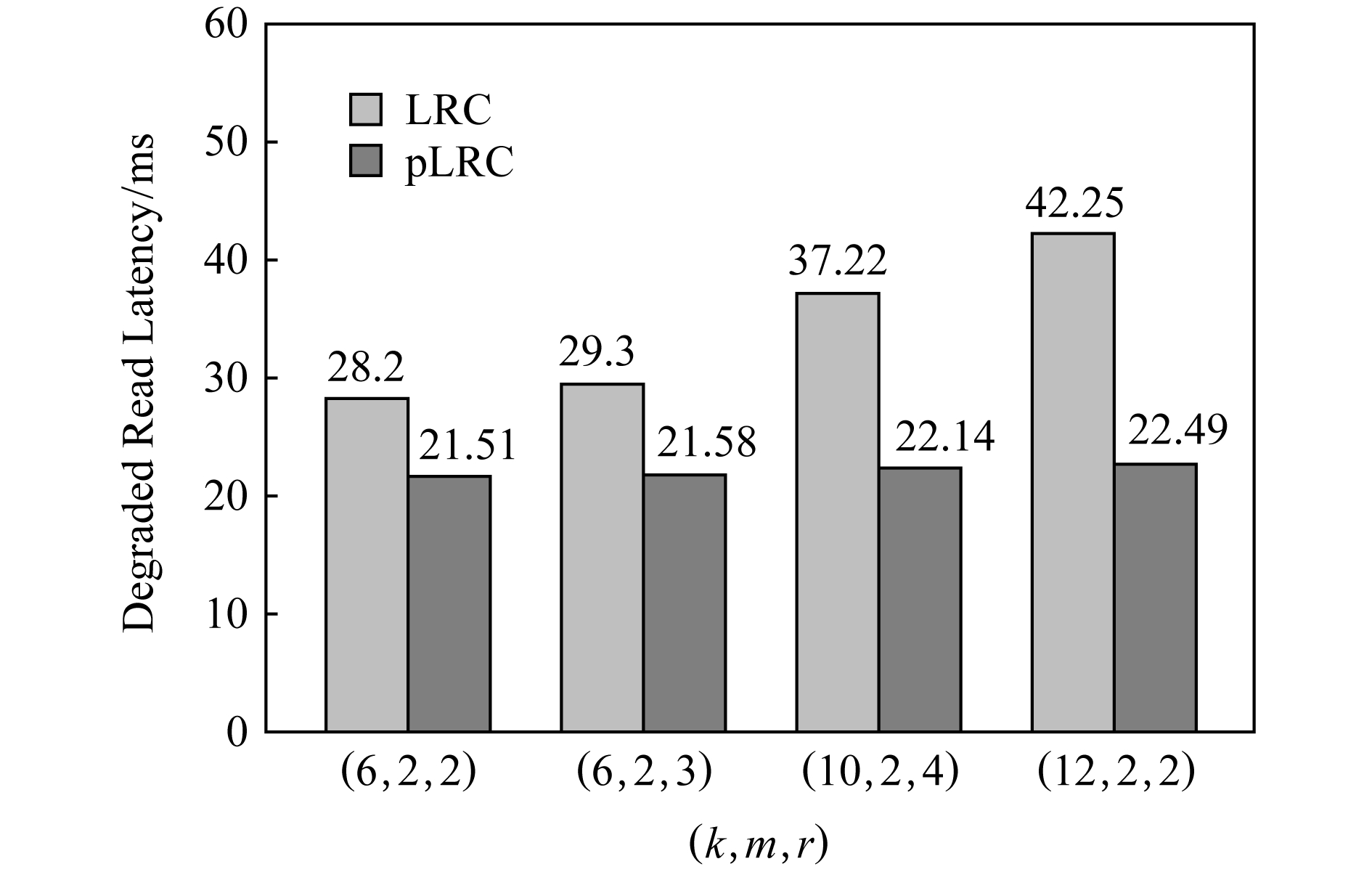
Fig. 8 Degraded read performance for LRC and pLRC
图8 LRC和pLRC的降级读性能
在图8中可以看到,在(k,m,r)=(12,2,2) 时,LRC的降级读时延为42.25 ms,pLRC的降级读时延为22.49 ms.pLRC相对于LRC来说减少了降级读的时延,降级读性能提升了大约46.8%.这主要是由于pLRC通过对预测到的坏盘使用(2,1) RS编码,大大减少了降级读时的修复开销,从而使得降级读性能得以提升.
我们还发现pLRC相对LRC来说,其在(k,m,r)=(12,2,2)情况下的降级读性能提升要比(k,m,r)=(6,2,2)大.和3.2节理论分析结果较为一致.
2) 节点修复性能.我们还测试了节点修复性能,即当某个节点发生故障时,系统对该节点上的多个数据块进行修复所消耗的时间.随机选取一个节点,擦除掉上面的所有块,然后分别使用pLRC和LRC来修复该节点上被擦除的所有块.节点修复性能的测试结果如图9所示:
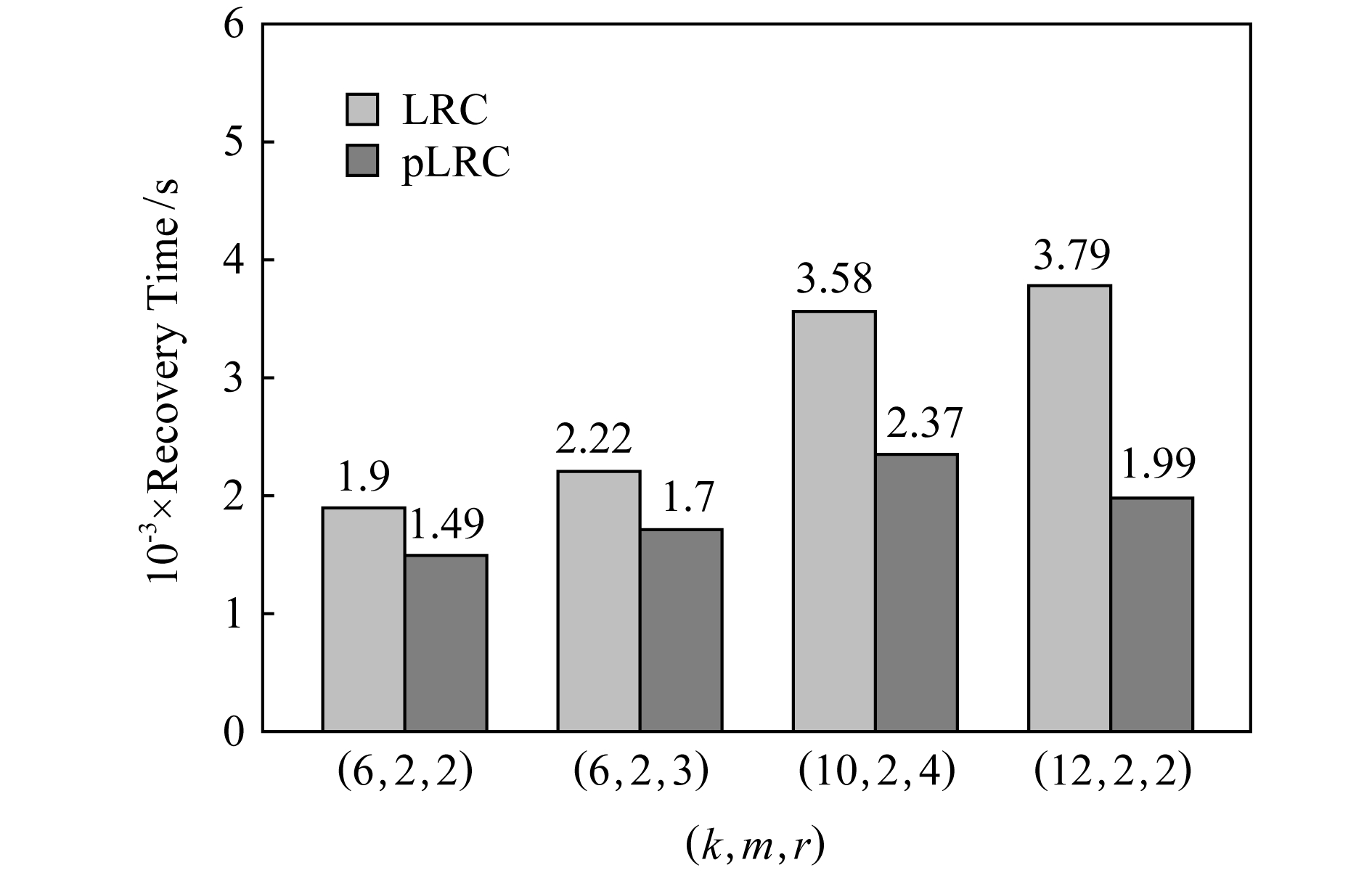
Fig. 9 Node repair performance for LRC and pLRC
图9 LRC和pLRC的节点修复性能
在图9中我们可以看到,在(k,m,r)=(12,2,2) 时,pLRC的节点修复时间为1.99×103 s,LRC的节点修复时间为3.79×103 s.pLRC相对于LRC修复时间下降了大约47.5%.在其余参数下情况类似.我们注意到(k,m,r)=(10,2,4)时,pLRC的节点修复时间相对LRC下降较少,主要是由于这种情况有较多的全局编码块,需要使用大量数据块来进行修复.
5 总 结
本文通过将基于机器学习的磁盘故障预测技术运用到LRC中以对其固定分组大小的假设进行改进,提出了一类基于预测的LRC编码方案pLRC,该方案通过动态调整系统中LRC的分组大小从而降低了修复带宽,并提升了系统的可靠性.
[1]Sebastian M. Microsoft Azure suffers outage after cooling issue[OL].[2019-01-05]https://www.datacenterdynamics.com/news/microsoft-azure-suffers-outage-after-cooling-issue/
[2]Reed I S, Solomon G. Polynomial codes over certain finite fields[J]. Journal of the Society for Industrial and Applied Mathematics, 1960, 8(2): 300-304
[3]Weatherspoon H, Kubiatowicz J D. Erasure coding vs. replication: A quantitative comparison[C] //Proc of Int Workshop on Peer-to-Peer Systems (IPTPS’02). Berlin: Springer, 2002: 328-337
[4]Huang Cheng, Simitci H, Xu Yikang, et al. Erasure coding in windows Azure storage[C] //Proc of the 2012 USENIX Conf on Annual Technical Conf (ATC’12). Berkeley, CA: USENIX Association, 2012: 15-26
[5]Sathiamoorthy M, Asteris M, Papailiopoulos D, et al. Xoring elephants: Novel erasure codes for big data[J]. Proceedings of International Conf on Very Large Data Bases Endowment, 2013, 6(5): 325-336
[6]Papailiopoulos D, Dimakis A G. Locally repairable codes[J]. IEEE Transactions on Information Theory, 2014, 60(10): 5843-5855
[7]Botezatu M M, Giurgiu I, Bogojeska J, et al. Predicting disk replacement towards reliable data centers[C] //Proc of the 22nd Int Conf on Knowledge Discovery and Data Mining (KDD’16). New York: ACM, 2016: 39-48
[8]Li Peng, Li Jing, Stones R J, et al. Procode: A proactive erasure coding scheme for cloud storage systems[C] //Proc of the 35th IEEE Symp on Reliable Distributed Systems (SRDS’16). Piscataway, NJ: IEEE, 2016: 219-228
[9]Schroeder B, Gibson G A. Disk failures in the real world: What does an mttf of 1 000 000 hours mean to you?[C] //Proc of the USENIX Conf on File and Storage Technologies (FAST’07). Berkeley, CA: USENIX Association, 2007: 1-16
[10]Facebook. Facebook’s Hadoop 20[OL].[2019-01-05]. https://github.com/facebookarchive/hadoop-20
[11]Amazon. Amazon elastic compute cloud (EC2)[OL].[2019-01-05]. http://aws.amazon.com/ec2/
[12]Muralidhar S, Lloyd W, Roy S, et al. f4: Facebook’s warm blob storage system[C] //Proc of the 11th USENIX Conf on Operating Systems Design and Implementation. Berkeley, CA: USENIX Association, 2014: 383-398
[13]IBM. IBM cloud[OL].[2019-01-05]. https://www.ibm.com/cloud/object-storage
[14]Rashmi K V, Shah N B, Gu Dikang, et al. A hitchhiker’s guide to fast and efficient data reconstruction in erasure-coded data centers[C] //Proc of the ACM Conf on Special Interest Group on Data Communication (SIGCOMM’14). New York: ACM, 2014: 331-342
[15]Chen Yulin, Mu Shuai, Li Jinyang, et al. Giza: Erasure coding objects across global data centers[C] //Proc of the 2017 USENIX Conf on Annual Technical Conf (ATC’17). Berkeley, CA: USENIX Association, 2017: 539-551
[16]Dobre D, Viotti P, Vukoli![]() M. Hybris: Robust hybrid cloud storage[C] //Proc of the ACM Symp on Cloud Computing. New York: ACM, 2014: 1-14
M. Hybris: Robust hybrid cloud storage[C] //Proc of the ACM Symp on Cloud Computing. New York: ACM, 2014: 1-14
[17]Qiniu Cloud. Qiniu Cloud[OL].[2019-01-05]. http://www.pingwest.com/qiniu/
[18]Luo Xianghong, Shu Jiwu. Summary of research for erasure code in storage system[J]. Journal of Computer Research and Development, 2012, 49(1): 1-11 (in Chinese)
(罗象宏, 舒继武. 存储系统中的纠删码研究综述[J]. 计算机研究与发展, 2012, 49(1): 1-11
[19]Dimakis A G, Godfrey P B, Wu Yunnan, et al. Network coding for distributed storage systems[J]. IEEE Transactions on Information Theory, 2010, 56(9): 4539-4551
[20]Shah N B, Rashmi K V, Kumar P V, et al. Interference alignment in regenerating codes for distributed storage: Necessity and code constructions[J]. IEEE Transactions on Information Theory, 2012, 58(4): 2134-2158
[21]Li S Y R, Yeung R W, Cai Ning. Linear network coding[J]. IEEE Transactions on Information Theory, 2003, 49(2): 371-381
[22]Hu Yuchong, Lee P P C, Shum K W. Analysis and construction of functional regenerating codes with uncoded repair for distributed storage systems[C] //Proc of the IEEE Int Conf on Computer Communication (INFOCOM’13). New York: IEEE Communications Society, 2013: 2355-2363
[23]Tamo I, Wang Zhiying, Bruck J. Zigzag codes: MDS array codes with optimal rebuilding[J]. IEEE Transactions on Information Theory, 2013, 59(3): 1597-1616
[24]Cadambe V R, Jafar S A, Maleki H, et al. Asymptotic interference alignment for optimal repair of MDS codes in distributed storage[J]. IEEE Transactions on Information Theory, 2013, 59(5): 2974-2987
[25]Hu Yuchong, Xu Yinlong, Wang Xiaozhao, et al. Cooperative recovery of distributed storage systems from multiple losses with network coding[J]. IEEE Journal on Selected Areas in Communications, 2010, 28(2): 68-276
[26]Shum K W, Hu Yuchong. Cooperative regenerating codes[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7229-7258
[27]Hu Yuchong, Li Xiaolu, Zhang Mi, et al. Optimal repair layering for erasure-coded data centers: From theory to practice[J]. ACM Transactions on Storage, 2017, 13(4): No.33
[28]Suh C, Ramchandran K. Exact-repair MDS code construction using interference alignment[J]. IEEE Transactions on Information Theory, 2011, 57(3): 1425-1442
[29]Ceph. Ceph[OL].[2019-01-05]. http://docs.ceph.com/docs/master/rados/operations/erasure-code-lrc/?highlight=locally
[30]Weil S A, Brandt S A, Miller E L, et al. Ceph: A scalable, high-performance distributed file system[C] //Proc of the 7th Symp on Operating Systems Design and Implementation (OSDI’06). Berkeley, CA: USENIX Association, 2006: 307-320
[31]Emerson. Data center downtime costs[OL].[2019-01-05]. http://www.emerson.com/en-us/News/Pages/Net-Power-Study-Data-Center.aspx
[32]Li Jing, Wang Gang, Liu Xiaoguang, et al. Review of reliability prediction for storage system[J]. Journal of Frontiers of Computer Science and Technology, 2017, 11(3):341-354 (in Chinese)
(李静, 王刚, 刘晓光, 等. 存储系统可靠性预测综述[J]. 计算机科学与探索, 2017, 11(3): 341-354)
[33]Murray J F, Hughes G F, Kreutz-Delgado K. Machine learning methods for predicting failures in hard drives: A multiple-instance application[J]. Journal of Machine Learning Research, 2005, 6(5): 783-816
[34]Zhu Bingpeng, Wang Gang, Liu Xiaoguang, et al. Proactive drive failure prediction for large scale storage systems[C] //Proc of the 29th IEEE Symp on Mass Storage Systems and Technologies (MSST’13). Piscataway, NJ: IEEE, 2013: 1-5
[35]Hamerly G, Elkan C. Bayesian approaches to failure prediction for disk drives[C] //Proc of the 18th Int Conf on Machine Learning (ICML’01). San Francisco, CA: Morgan Kaufmann, 2001: 202-209
[36]Hughes G F, Murray J F, Kreutz-Delgado K, et al. Improved disk-drive failure warnings[J]. IEEE Transactions on Reliability, 2002, 51(3): 350-357
[37]Li Jing, Ji Xinpu, Jia Yuhan, et al. Hard drive failure prediction using cassification and regression trees[C] //Proc of the 44th Annual IEEE/IFIP Int Conf on Dependable Systems and Networks (DSN’14). Los Alamitos, CA: IEEE Computer Society, 2014: 383-394
[38]Baidu. SMART dataset[OL].[2019-01-05]. http://pan.baidu.com/share/link?shareid=189977&uk=4278294944
[39]Cidon A, Escriva R, Katti S, et al. Tiered replication: A cost-effective alternative to full cluster geo-replication[C] //Proc of the 2012 USENIX Conf on Annual Technical Conf (ATC’15). Berkeley, CA: USENIX Association, 2015: 31-43
[40]Ford D, Labelle F, Popovici F I, et al. Availability in globally distributed storage systems[C] //Proc of the 7th Symp on Operating Systems Design and Implementation (OSDI’10). Berkeley, CA: USENIX Association, 2010: 1-7
[41]Silberstein M, Ganesh L, Wang Y, et al. Lazy means smart: Reducing repair bandwidth costs in erasure-coded distributed storage[C] //Proc of Int Conf on Systems and Storage (SYSTOR’14). New York: ACM, 2014: 1-7
[42]Mu Fei, Xue Wei, Shu Jiwu, et al. An analytical model for large-scale storage system with replicated data[J]. Journal of Computer Research and Development, 2009, 46(5): 756-761 (in Chinese)
(穆飞, 薛巍, 舒继武, 等. 一种面向大规模副本存储系统的可靠性模型[J]. 计算机研究与发展, 2009, 46(5): 756-761)
[43]Greenan K M, Plank J S, Wylie J J. Mean time to meaningless: MTTDL, Markov models, and storage system reliability[C] //Proc of the 2nd USENIX Conf on Hot Topics in Storage and File Systems (HotStorage’10). Berkeley, CA: USENIX Association, 2010: 1-5
[44]Apache. HDFS RAID[OL].[2019-01-05]. http://wiki.apache.org/hadoop/HDFS-RAID
[45]Shvachko K, Kuang H, Radia S, et al. The Hadoop distributed file system[C] //Proc of the 26th IEEE Symp Mass Storage Systems and Technologies (MSST’10). Piscataway, NJ: IEEE, 2010: 1-10
[46]Dean J, Ghemawat S. MapReduce: Simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113
[47]Intel. ISA-L[OL].[2019-01-05]. https://github.com/01org/isa-l
[48]Tamo I, Barg A. A family of optimal locally recoverable codes[J]. IEEE Transactions on Information Theory, 2014, 60(8): 4661-4676



 deep learning. (m201873224@hust.edu.cn)
deep learning. (m201873224@hust.edu.cn)