随着互联网时代的到来,信息过载问题也变得越来越严峻,用户很难在拥有众多信息的产品中挑选出自己的最爱.个性化推荐系统为解决这一问题应运而生.目前,个性化推荐算法大致可分为5类:基于内容的推荐[1-3]、基于关联规则的推荐[4]、基于知识的推荐[5]、协同过滤推荐[6]以及混合推荐[7].这其中,基于内容的推荐算法应用较为广泛.传统基于内容的推荐算法理论依据主要来源于信息检索和信息过滤,该算法需要了解项目的属性特征,通过分析用户历史行为记录,构建用户兴趣偏好向量.该算法的优点是推荐的结果比较直观,易于解释,但是对于项目的特征选择及复杂属性处理效果略逊一筹,并且需要分析属性间的依赖关系,还要面对新用户的冷启动等问题.针对以上不足,有学者从不同角度对这一算法给予改进和完善.李宇琦等人[1]提出一种基于网络表示学习的个性化商品推荐算法,在各项评测指标上均有显著提高.黄金超等人[2]则借助机器学习中分类算法的一些技巧,利用计算偏好分构造偏好度特征,提出一种基于偏好度特征的个性化推荐算法,具有一定的通用性,但仍存在矩阵稀疏、新用户冷启动等问题.
本文基于有序加权平均(ordered weighted aver-aging, OWA)及个性化建模思想,提出一种用户偏好诱导的模糊量词,并应用于个性化产品推荐.首先给定一组由多个备选方案构成的多属性样本数据,仅要求用户根据自己的态度偏好或主观评判,提供一个关于这组备选方案的优劣排序;根据这个排序序列,基于OWA思想并利用理想解法(technique for order preference by similarity to ideal solution, TOPSIS)方法,构造用户期望值提取模型,以获取特定偏好 态度条件下用户关于此样本信息的期望值,再从中抽取偏好、态度等个性化信息,生成针对该用户的个性化模糊量词;最后利用该量词对新产品属性值进行OWA数据集成,从而实现个性化产品推荐.值得注意,在所提方法中,为获取用户期望值,仅要求用户提供关于样本方案的主观排序(在个性化推荐应用中,样本方案的主观排序可从用户的历史浏览记录中获取),对用户的能力水平、专业知识、经历经验等差异性特质要求不高,目标模型构造精巧、实现简单、可操作性强,相比文献[8-10]的直接方法有极大优势,由此确定的个性化量词模型在实际应用中可面向不同层次、不同水平的用户进行针对性的产品推荐,具有较强的实用性和灵活性.迄今,未见与本文用户期望值提取模型相同或相似的研究文献或报告.
态度条件下用户关于此样本信息的期望值,再从中抽取偏好、态度等个性化信息,生成针对该用户的个性化模糊量词;最后利用该量词对新产品属性值进行OWA数据集成,从而实现个性化产品推荐.值得注意,在所提方法中,为获取用户期望值,仅要求用户提供关于样本方案的主观排序(在个性化推荐应用中,样本方案的主观排序可从用户的历史浏览记录中获取),对用户的能力水平、专业知识、经历经验等差异性特质要求不高,目标模型构造精巧、实现简单、可操作性强,相比文献[8-10]的直接方法有极大优势,由此确定的个性化量词模型在实际应用中可面向不同层次、不同水平的用户进行针对性的产品推荐,具有较强的实用性和灵活性.迄今,未见与本文用户期望值提取模型相同或相似的研究文献或报告.
1 相关工作
近年来,基于多属性决策的个性化推荐逐渐成为研究的热点.这类方法将决策思想及模型应用于个性化推荐中,得到一些较好的结果,比较典型的有混合多准则分析[11-15]、基于偏好的多属性信息评价[16-19]等.基于模糊量词的推荐模型并不多见,相关研究文献极少.李微娜[3]从用户偏好角度提出一种基于OWA算子的个性化推荐方法,利用Web用户反馈的不完全偏好信息并结合用户个性特征,实现待评价方案的OWA数据集成,进而计算出方案的优先顺序,得出最终的推荐方案.该方法将决策分析中经典的OWA算子引入个性化推荐中,对本文工作确有一定的启发作用.
事实上,Yager[20]提出OWA算子实现对数据排序位置加权,而非传统算子对指标或数据本身加权,集成过程能够灵活反映不同主体的偏好或态度,可直接应用于个性化推荐中.Yager[21]进一步强调OWA算子的集成效果依赖于OWA权重,并提出一种利用模糊语义量词获取OWA权重向量的有效方法.语义量词的概念最早由Zadeh[22]提出,并利用模糊子集形式化定义语义量词,将量词分成两大类:绝对量词和相对量词.绝对量词,如不多于5个、至少20个等;相对量词,如很少、大约一半、至多30%等.Yager[21]进一步将相对量词细分为3种:正则递增单调(regular increasing monotone, RIM)量词、正则递减单调(regular decreasing monotone, RDM)量词以及正则单峰单调(regular unimodal monotone, RUM)量词.注意到RDM量词是RIM量词的反义,而RUM量词可以表示为RIM与RDM这2种量词的交合,故应用中只考虑RIM量词即可.模糊量词在理论分析(计算机科学特别是人工智能)及实际应用中具有重要作用[20,23-31],而针对量词本身的研究文献却并不多见.Yager[23]介绍了一系列预定义的RIM量词函数,研究了参数分配与偏好态度之间的关系.注意多样的态度类型及特性并非通过简单的预定义量词及其参数分配就能够合理反映出来.Ying[24]提出一种量词的Sugeno积分语义,即量词由一系列模糊测度表示且其命题真值由Sugeno积分求得.Liu[32-33]提出一种带有生成函数的等差RIM量词,研究了该量词的数学性质及其潜在的应用.Guo[8]提出一种样本信息期望值诱导的个性化RIM量词,研究了其数学性质并应用于不确定性决策中.Guo[9],Guo & Xu[10]进一步研究并完善了这类量词的几何光滑、保形插值、逼近速度等数值特征,由此提出这类量词的多种函数表示形式.事实上,这类量词具有较强的个体针对性,能够很好地反映用户的主观偏好、决策态度等个性特征.注意到用于生成该类量词的关键数据信息,即用户期望值,是在设定的理想环境下采用一种比较直接的方法提取实现,在实际应用中可能会有一定的局限性.
2 理论基础
2.1 OWA算子
Yager[20]于1988年提出OWA集成算子的概念,定义为
(1)
其中,Y=(y1,y2,…,yn)T称为有序自变量参数向量,其分量yj是自变量参数xi∈R(i=1,2,…,n)中第j个最大值,Ω=(ω1,ω2,…,ωn)T称为OWA伴随权重向量,![]() 该算子的特点是对自变量参数xi(i=1,2,…,n)降序排列后加权集成,权重向量Ω只针对自变量参数的排序位置,与参数本身或其对应的指标无关.
该算子的特点是对自变量参数xi(i=1,2,…,n)降序排列后加权集成,权重向量Ω只针对自变量参数的排序位置,与参数本身或其对应的指标无关.
Yager[21]强调指出OWA集成效果依赖于伴随向量Ω,并提出一种利用模糊量词Q获得OWA权重向量的有效方法,即
(2)
其中,Q为RIM量词,表示为基本单位区间单调(basic unit-interval monotonic, BUM)函数,它满足3个条件:1)Q(0)=0; 2)Q(1)=1; 3)Q(x)≥Q(y),若x≥y.显然![]() 综合式(1)(2)可得:
综合式(1)(2)可得:
FQ(x1,x2,…,xn)=FΩ(x1,x2,…,xn)=
(3)
式(3)称为模糊量词诱导的OWA算子[21].
为考察OWA权重向量的分布所对应的态度值,Yager[20]引入态度特性(attitudinal character)的概念,定义为
(4)
易知,AC(Ω)∈[0,1].具体地,当Ω→(1,0,…,0)T,则AC(Ω)→1,表示用户更偏好于数值较大的参数,这显然是一种积极的态度;当Ω→(0,0,…,1)T,则AC(Ω)→0,表示用户更偏好于数值较小的参数,这显然是一种消极的态度;当Ω→(…,0,1,0,…)T或Ω→(1 n,1
n,1 n,…,1
n,…,1 n)T时,AC(Ω)≈0.5,表示用户既不偏好于较大的参数值也不偏好于较小的参数值,这是一种中庸态度.结合式(2)(4),可建立态度特性与模糊量词之间的关系,即:
n)T时,AC(Ω)≈0.5,表示用户既不偏好于较大的参数值也不偏好于较小的参数值,这是一种中庸态度.结合式(2)(4),可建立态度特性与模糊量词之间的关系,即:
(5)
进一步可得[23]:
(6)
Yager[21]进一步将量词诱导的OWA算子推广到更一般的环境,即参数值带有权重信息的情况.设A为m个备选方案集合,即A={a1,a2,…,am};c为具有不同权重信息的n个指标集合,即c={c1,c2,…,cn}.对于∀a∈A,ci(a)表示方案a关于指标ci的值,yj(a)为ci(a)(i=1,2,…,n)中第j个最大值,uj(a)是与yj(a)相对应的指标权重信息.此时,OWA权重可通过以下方式获得:

(7)
其中,![]() 于是有:
于是有:
FQ(c1(a),c2(a),…,cn(a))=
FΩ(c1(a),c2(a),…,cn(a))=
(8)
注意对于每个方案a,ci(a)(i=1,2,…,n)的排序都有可能不同,这将导致uj(a)(j=1,2,…,n)顺序的不同,进而有Sj(a)的不同,最终使得每个方案所对应的OWA权重也不同.这实际上体现了OWA数据集成的特点,即将主观偏好与客观数据有机结合,使得两者相辅相成、相得益彰.
2.2 TOPSIS方法
TOPSIS法又称为理想解法[34],是一种有效的多指标决策方法.在使用前,应先将指标值做标准化处理.设决策矩阵X=(xij)m×n,指标权重向量W=(w1,w2,…,wn)T,X的标准化矩阵Y=(yij)m×n,而
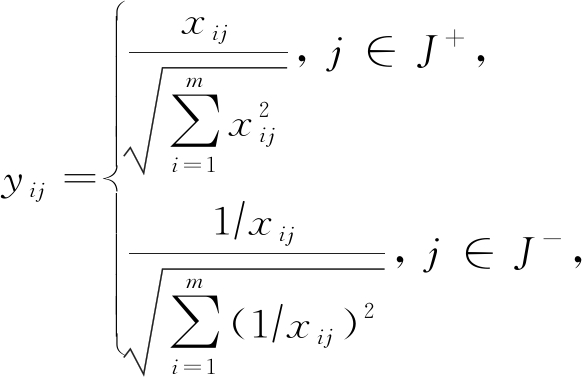
(9)
其中,i=1,2,…,m ,j=1,2,…,n;J+代表效益型指标集,J-代表成本型指标集.经过式(9)标准化后,矩阵Y中所有成本型指标值均转换成效益型值.
根据标准化矩阵Y,定义正、负理想解V+及V-分别为
(10)
(11)
定义方案ai到正、负理想解的距离分别为
(12)
(13)
则方案ai的相对贴进度可定义为
(14)
显然,当ai=V+,Ci=1;当ai=V-,Ci=0.Ci值越大,对应的方案越优良.
3 用户偏好诱导的模糊量词
3.1 样本数据的指标权重
为获取用户偏好诱导的模糊量词,需准备一组由多个备选方案组成的多属性样本数据.设该样本数据中方案ai关于指标cj的属性值为xij,i=1,2,…,m,j=1,2,…,n.所对应的决策矩阵X=(xij)m×n,待确定的指标权重向量W=(w1,w2,…,wn)T,X的标准化矩阵Y=(yij)m×n.由式(10)定义正理想解![]() 用各方案到V+的距离平方作为评价方案的准则[34],即:
用各方案到V+的距离平方作为评价方案的准则[34],即:
显然,di越小方案越优.为了确定指标权重wj,构造最优化模型
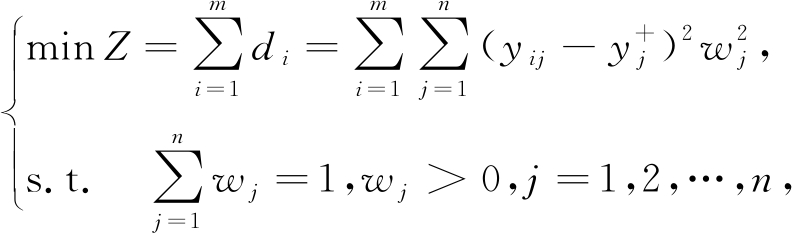
求解此模型,作拉格朗日函数:
令![]() 得:
得:
解得
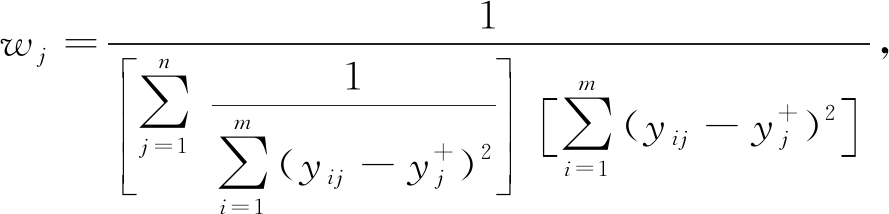
j=1,2,…,n.
(15)
3.2 基于偏好的用户期望值
对于3.1节给定的多属性样本数据,可利用TOPSIS方法中相对贴进度的定义,得到一组客观的方案排序序列.不失一般性,设样本各方案所对应的相对贴进度满足关系C1>C2>…>Cm,其中Ci是方案ai的相对贴进度,i=1,2,…,m,则样本方案ai的客观优劣排序为a1≻a2≻…≻am.显然,这是典型的传统排序方法所得到的结果.
下面考虑基于用户偏好的排序问题.假定用户根据自己的主观偏好或者决策态度,对该样本数据中方案的主观排序为b1≻b2≻…≻bm,其中bk表示样本方案ai(i=1,2,…,m)中用户第k个最满意方案,k=1,2,…,m,即对于该用户而言,b1即是最满意的方案,b2次之,bm是最不满意的方案.显然,这里考虑的主观排序序列依赖于用户的主观偏好 决策态度,与样本方案的客观优劣性无直接关系.
决策态度,与样本方案的客观优劣性无直接关系.
显而易见,不同排序序列中的方案表现出不同的重要性.为了表达并区分这种重要性,需要分配各方案相应的重要性权值.一方面,对于由传统TOPSIS方法得到的客观排序序列a1≻a2≻…≻am,可以使用相对贴进度表示这种重要性.在这种意义下,相对贴进度大者对应的方案具有较高重要性,相对贴进度小者对应的方案具有较低重要性.具体地,对于客观排序序列a1≻a2≻…≻am,a1所对应的贴进度值C1最大,客观上具有最高重要性,应该分配最大的权值,a2次之,am则最不重要,对应的权值应该最小.鉴于方案的客观重要性与其相对贴近度的一致性,可令weight(ai)=Ci,i=1,2,…,m.
另一方面,对于用户给出的主观偏好排序b1≻b2≻…≻bm,b1是该用户最满意的方案,主观上具有最高重要性,故应分配最大的权值,b2次之,bm对于该用户来说则最不重要,应该分配最小的权值.类似于上述客观排序序列中方案权值的分配策略,这里仍考虑使用相对贴进度实现主观偏好排序中各个方案的重要性权值的分配.此时的分配策略是,用户越满意的方案,赋予的相对贴进度值就越大,即令weight(bk)=Ck,其中bk是所有ai(i=1,2,…,m)中用户第k个最满意方案,Ck是ak(k=1,2,…,m)的相对贴进度,满足关系C1>C2>…>Cm.
综上显见,在同一个排序序列中,不同的方案具有不同的重要性,而对于同一个方案,在排序序列中所处位置不同,其重要性也不同.为进一步厘清备选方案的排序序列及其重要性权值分配策略之间的关系,需考察方案的不同排序序列中固有保持不变的因素.注意到上述2种主、客观方案排序序列中,已分配的方案的重要性权值均满足关系C1>C2>…>Cm,而C1,C2,…,Cm本质上可视为客观排序序列a1≻a2≻…≻am关于排序位置的重要性权值,即排序位置越靠前,该位置的重要性权值就越高.这意味着方案的重要性权值的分配与其所在排序序列中的具体位置紧密相关,更进一步,在用户的主观偏好排序意义下,方案重要性的分配并不依赖于方案本身,而依赖于它所在排序序列中的具体位置,位置越靠前,该位置上的方案就越重要,分配的重要性权值就越高,而对于某个排序序列的同一位置,不同的方案在该位置处应具有相同的重要性,应分配相同的重要性权值.
由此,可得出重要结论:用户的主观排序序列中各方案的重要性权值应与其所在位置的权值C1,C2,…,Cm相一致,即可令weight(bk)=weight(ak)=Ck,其中bk是所有ai(i=1,2,…,m)中用户第k个最满意方案,Ck是ak的相对贴进度,k=1,2,…,m,C1>C2>…>Cm.这一结论本质上与OWA权重向量的基本思想相一致.
为进一步阐明上述结论,方便后续的形式化操作,给出“备选方案-决策矩阵-重要性权值”的偏好有序结构为

(16)
其中,左侧方案列中,bk为所有ai(i=1,2,…,m)中用户第k个最满意方案,中间决策矩阵中,pkj是bk关于指标cj的标准化指标值,右侧权值列中,Ck(k=1,2,…,m)表示排序序列中第k个位置的权值,符号“↓”表示方案由优至劣,或权值由高到低.注意此时居中的决策矩阵P=(pkj)m×n已根据方案的主观偏好排序b1≻b2≻…≻bm对原标准化矩阵Y=(yij)m×n中的行向量重新做了相应的调整.
在这种偏好结构下,可计算用户关于各个指标cj的期望值,即:
(17)
其中,pkj是bk关于指标cj的属性值, 表示排序序列中第k(k=1,2,…,m)个位置的权值,可由式(14)确定.用户在此偏好结构下各指标的期望值可以记为向量
表示排序序列中第k(k=1,2,…,m)个位置的权值,可由式(14)确定.用户在此偏好结构下各指标的期望值可以记为向量![]()
由式(17)得到的![]() 显然满足关系
显然满足关系![]() 事实上,
事实上,![]() 值的大小总是依赖于用户关于备选方案的主观排序与客观排序的一致性.若这个主观排序与客观排序完全一致或基本一致,则
值的大小总是依赖于用户关于备选方案的主观排序与客观排序的一致性.若这个主观排序与客观排序完全一致或基本一致,则![]() 值较大;若主观排序与客观排序差异巨大甚至完全相反,则
值较大;若主观排序与客观排序差异巨大甚至完全相反,则![]() 值较小.
值较小.
用户期望值是构建个性化量词的重要数据信息,对个性化量词的性能起到决定性作用.文献[8-10]采用一种相对直接的方法获取用户期望值,即降序重排样本数据中各指标属性值后,要求用户根据自己的主观偏好直接选取一组关于各指标的期望值.为此,用户需要具有较丰富的领域知识和经历经验.相比之下,本文给出的模型只需用户参考样本数据,根据自己的偏好或态度提供一组关于样本方案的主观排序序列,由此提取用户的期望值,对用户的专业知识、能力水平、经历经验等差异性特质要求不高,具有更大的实用性和可操作性.
3.3 个性化模糊量词建立
现在利用3.2节得到的用户期望值,建立针对该用户的个性化量词.首先根据期望值向量![]() 并结合样本数据Y=(yij)m×n,抽取用户的偏好、态度信息,表示成OWA权重向量形式,记为
并结合样本数据Y=(yij)m×n,抽取用户的偏好、态度信息,表示成OWA权重向量形式,记为![]() 根据Guo[8],需对标准化决策矩阵Y=(yij)m×n中各列属性值做降序重排处理,重排后的矩阵记为
根据Guo[8],需对标准化决策矩阵Y=(yij)m×n中各列属性值做降序重排处理,重排后的矩阵记为![]() 本文考虑了样本数据中各指标权重信息,故生成si的公式,比较Guo[8]中的式(15)对si做修正:
本文考虑了样本数据中各指标权重信息,故生成si的公式,比较Guo[8]中的式(15)对si做修正:

(18)
其中,wj为指标cj的权重,由式(15)确定,![]() 表示用户关于cj的期望值,由式(17)确定.由此得到的用户态度向量S=(s1,s2,…,sm)T,各分量的分布依赖于样本方案的主观排序序列b1≻b2≻…≻bm与客观排序序列a1≻a2≻…≻am的一致性.当主观排序与客观排序完全一致或基本一致时,各个指标均有较大的用户期望值
表示用户关于cj的期望值,由式(17)确定.由此得到的用户态度向量S=(s1,s2,…,sm)T,各分量的分布依赖于样本方案的主观排序序列b1≻b2≻…≻bm与客观排序序列a1≻a2≻…≻am的一致性.当主观排序与客观排序完全一致或基本一致时,各个指标均有较大的用户期望值![]() 此时有影响的权重分量将集中分布在S的顶部位置附近,说明用户更偏好于数值较大的自变量参数,这是一种积极的态度;当主观排序与客观排序差异巨大甚至完全相反时,各个指标均有较小的用户期望值
此时有影响的权重分量将集中分布在S的顶部位置附近,说明用户更偏好于数值较大的自变量参数,这是一种积极的态度;当主观排序与客观排序差异巨大甚至完全相反时,各个指标均有较小的用户期望值![]() 此时有影响的权重分量集中分布在S的底部位置附近,说明用户更偏好于数值较小的自变量参数,这显然是一种消极的态度.
此时有影响的权重分量集中分布在S的底部位置附近,说明用户更偏好于数值较小的自变量参数,这显然是一种消极的态度.
利用上述结果S,进一步建立由用户偏好诱导的个性化量词[8]:

(19)
其中,si由式(18)确定.由式(6)可得量词Q≻的态度特性[8]:
(20)
其中si由式(18)确定.注意当S→(1,0,0,…,0)T时,有λQ≻→1-1 (2m),若m→∞,则λQ≻=1,这显然是积极的态度.当S→(0,0,…,0,1)T时,有λQ≻=1
(2m),若m→∞,则λQ≻=1,这显然是积极的态度.当S→(0,0,…,0,1)T时,有λQ≻=1 (2m),若m→∞,则λQ≻=0,这显然是消极的态度.当
(2m),若m→∞,则λQ≻=0,这显然是消极的态度.当![]() 或S→(1
或S→(1 m,1
m,1 m,…,1
m,…,1 m)T时,有λQ≻≈0.5,这是一种近似的中性态度,特别地,当S=(1
m)T时,有λQ≻≈0.5,这是一种近似的中性态度,特别地,当S=(1 m,1
m,1 m,…,1
m,…,1 m)T或
m)T或![]() 时,有λQ≻=0.5,这显然是完全的中性态度.
时,有λQ≻=0.5,这显然是完全的中性态度.
由此,本文提出一种较为新颖的模型用以提取用户关于样本信息的期望值,并据此建立针对此用户的个性化量词,称之为用户偏好诱导的模糊量词,简称偏好诱导量词.所提方法中用户期望值提取模型构造新颖精巧,实现简单方便,相比文献[8-10]中的直接方法有极大的优势.由此得到的量词模型,具有较强的个体针对性,能够很好地反映用户的偏好、态度等个性特征,为其追求主观偏好下的“最满意方案”而非一般意义下的“最优方案”提供一种切实可行的判决标准和分析工具,在需要特殊考虑主体偏好、态度等个性特征的复杂环境中,如不确定性决策、个性化产品推荐等应用中,具有较高的实用性、灵活性和可操作性.
关于模糊量词更多的函数表示、数学性质、一致性定理等内容,请参阅文献[8-10,20-21,23].
3.4 偏好诱导量词建模方法
综上,给出偏好诱导量词的建模方法为:
步骤0. 获取样本数据及用户偏好排序序列(个性化推荐应用中用户针对样本方案的主观排序可从其历史浏览记录中获取).
步骤1. 由式(15)获取样本信息指标权重向量.
步骤2. 由式(12) ~ (14)计算样本方案的相对贴近度,确定样本方案的客观排序序列.
步骤3. 根据用户偏好排序序列重排样本决策矩阵,由式(17)计算用户期望值.
步骤4. 降序重排决策矩阵中各列属性值,再由式(18)计算用户关于样本信息的态度向量.
步骤5. 利用所得态度向量,由式(19)建立个性化量词.
步骤6. 利用所得量词实现个性化推荐.
4 在个性化推荐中的应用
4.1 实例研究
本节应用3.3节所得的用户偏好诱导的模糊量词解决个性化产品推荐问题.算例中部分基础数据改编自李微娜[3].
假定某购物网站销售多个品牌笔记本电脑,显示其属性为价格c1、CPU速度c2、硬盘容量c3等3种,显然c1为成本型指标,c2和c3为效益型指标.
首先从用户网页历史浏览记录中获取用户偏好信息.用户通常通过点击进入笔记本电脑的产品信息页面,浏览一段时间后,可能会将感兴趣的产品放入购物车中.根据历史浏览记录,发现用户共浏览了5台笔记本电脑,其属性值标准化后如表1所示,其中,成本型指标c1的属性值利用式(9)已转换为效益型值.
Table 1 Specifications of Recently Visited Items
表1 已浏览商品明细

Visited Itemsc1c2c3a11.000.910.75a20.950.590.13a30.700.791.00a40.540.670.50a50.970.740.35
利用Shahabi等人[35]提出的客户追踪机制原理获取用户浏览该网站的起始时间、对商品的点击顺序和次数以及浏览该网站的结束时间等信息,得到用户关于以上产品的网页使用行为如表2所示:
Table 2 Usage Behaviors on Web Pages
表2 用户页面使用行为

Click SequenceVisited ItemsVisiting Time∕sInto Cart1a1712a5903a21004a5205a4706a330
由表2易知,用户共点击了6次有关笔记本电脑的信息页面:首先点击a1,用时7 s并将其放入购物车中,说明用户对a1非常感兴趣;然后点击a5,用时9 s但并没有放入购物车,说明对于a1和a5,用户对a1更感兴趣;接下来用户点击a2,用时10 s,可知此时对a5和a2,用户对a2更感兴趣;随后用户又再次点击a5,用时2 s,此时用户浏览a5共计11 s,因此相对于a2,a5是更理想的产品;同理可得用户对a4的态度较a3更感兴趣.
综上分析,可依据是否将商品放入购物车、累积浏览某一特定商品的时长等网页使用行为数据考察用户对商品的偏好程度,从而得到该用户对上述产品的主观偏好排序,即:
ζ:a1≻a5≻a2≻a4≻a3.
至此,可根据该主观偏好排序ζ,应用本文所提模型及方法建立针对该用户的个性化量词,其中,多属性样本信息已由表1给出.
步骤0. 已获取样本数据,即表1,以及用户偏好排序序列,即ζ.
步骤1. 根据表1,得到产品的标准化决策矩阵:
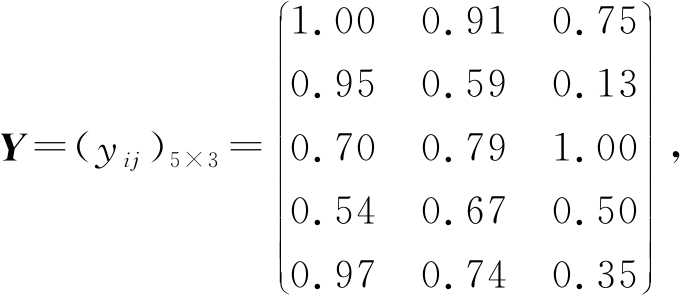
利用式(10)(11),定义正、负理想解分别为
再由式(15)得到指标权重向量:
W=(0.370,0.555,0.075)T.
步骤2. 利用式(12)(13),计算各产品到正、负理想解的距离,再利用式(14)计算各产品的相对贴进度为
C1=0.930, C2=0.444, C3=0.523, C4=0.193, C5=0.628,
据此得到产品的客观排序序列为
ο:a1≻a5≻a3≻a2≻a4.
相比较用户的主观偏好排序ζ:a1≻a5≻a2≻a4≻a3,两者有一定的差异.
步骤3. 根据用户的主观偏好排序ζ重排决策矩阵Y,定义“备选方案-决策矩阵-重要性权值”的偏好有序结构为
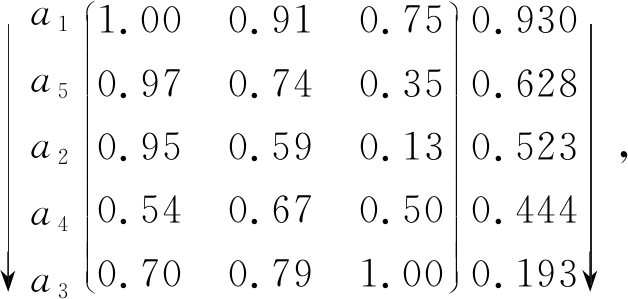
再利用式(17)计算用户的期望值,得到:
步骤4. 降序重排矩阵Y中各列属性值,得到新矩阵记为
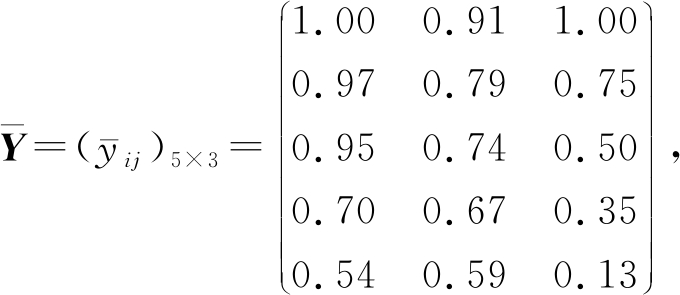
根据![]() 和
和![]() 利用式(18)计算态度向量:
利用式(18)计算态度向量:
S=(0.042,0.277,0.610,0.056,0.015)T.
可以看出,有影响的权重分量集中分布在S的中间位置偏上,说明用户稍微偏好数值较大的参数,对应于中性偏积极的态度.
步骤5. 利用获得的向量S及式(19),建立针对该用户的个性化量词,即:

进一步,利用式(20)得到对应的态度特征值:
λQ≻=0.555.
显然这是中性偏积极的态度.
步骤6. 下面使用所得量词Q≻通过OWA数据集成实现个性化产品推荐.假定该购物网站尚有未浏览待推荐的同类笔记本电脑5台,标准化后的各属性值如表3所示.类似地,成本型指标c1的属性值利用式(9)已转换为效益型值.
Table 3 Specifications of Items to be Recommended
表3 待推荐商品属性明细
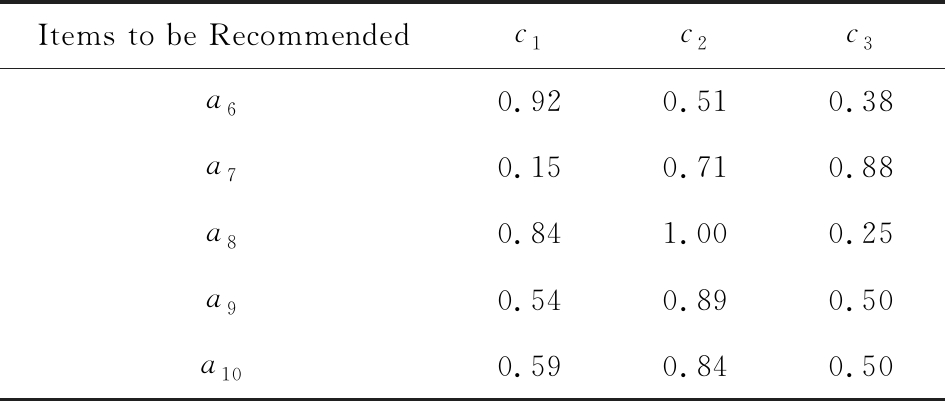
Items to be Recommendedc1c2c3a60.920.510.38a70.150.710.88a80.841.000.25a90.540.890.50a100.590.840.50
据此得到待推荐产品的标准化决策矩阵:
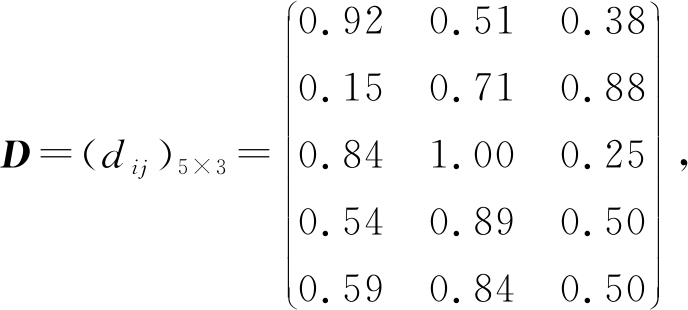
令:
Ua6=(0.92,0.51,0.38)T, Ua7=(0.15,0.71,0.88)T, Ua8=(0.84,1.00,0.25)T, Ua9=(0.54,0.89,0.50)T, Ua10=(0.59,0.84,0.50)T.
为实现每个待推荐产品的OWA数据集成,首先利用已得到的指标权重向量W=(0.370,0.555,0.075)T,由式(7)计算每个待推荐产品的OWA权重向量,即:
Ω(Ua6)=(0.278,0.716,0.006)T, Ω(Ua7)=(0.016,0.921,0.063)T, Ω(Ua8)=(0.791,0.203,0.006)T, Ω(Ua9)=(0.791,0.203,0.006)T, Ω(Ua10)=(0.791,0.203,0.006)T,
注意到每个待推荐产品的属性值的降序排列不同,导致其所对应的指标权重的顺序也不同,最终使得每个待推荐产品所对应的OWA权重也不同.最后利用所得量词Q≻及式(8)实现每个待推荐产品的OWA数据集成,即:
FQ≻(Ua6)=0.623, FQ≻(Ua7)=0.677, FQ≻(Ua8)=0.963, FQ≻(Ua9)=0.817, FQ≻(Ua10)=0.787,
显然,推荐的顺序为
a8≻a9≻a10≻a7≻a6.
即待推荐产品a6~a10中,a8为该用户偏好下的最满意产品,应优先推荐给该用户,而a6为最不满意产品,应最迟推荐给该用户.在李微娜[3]的结果中,推荐次序为a8≻a10≻a9≻a7≻a6,与本文结果基本一致,只是a9与a10互换了位置.事实上,李微娜[3]在计算的最后阶段,未考虑之前已获得的指标权重,直接使用式(2)获取OWA权重向量实现数据集成,而本文则自始至终充分考虑样本数据的指标权重,在最后阶段使用式(7)获取OWA权重向量,实现数据的加权集成,所得的推荐顺序更具可信性.
为进一步验证所提模型的有效性,以下将针对相同的样本数据(即表1),采用其他3种不同方法,分别考查其推荐结果并与本文模型所得结果作比较,具体如表4所示.表4中,文献[17,36-37]均假定用户具有理性中性态度(与本算例中态度特征值λQ≻=0.555相当),分别使用OWA算子、S-HARA效用函数、C-GOWA算子等模型及方法实现新产品序列的计算.显而易见,文献[36-37]中的2种方法所得结果和本文一致,而文献[17]方法所得结果和本文基本一致,只是a6和a7互换了位置.由此说明本文所提模型的有效性.
Table 4 Results from Different Methods
表4 不同方法得到的结果

MethodsSome Intermediate Results Final ResultsRanking List of RecommendationRef[17]a=0.740C1=0.603C2=0.273C3=0.124R(a6)=0.286R(a7)=0.262R(a8)=0.421R(a9)=0.357R(a10)=0.345a8≻a9≻a10≻a6≻a7Ref[36]W=(0.234,0.552,0.214)Tv6=-0.097v7=-0.069v8=0.046v9=0.016v10=0.012a8≻a9≻a10≻a7≻a6Ref[37]λ=(0.141,0.153,0.254,0.232,0.220)TZ6(v)=0.081Z7(v)=0.094Z8(v)=0.204Z9(v)=0.168Z10(v)=0.156a8≻a9≻a10≻a7≻a6
4.2 进一步讨论
下面进一步讨论样本方案的不同主观偏好排序对模糊量词及新产品推荐的作用.首先考察不同主观偏好排序对模糊量词的作用.
1) 假定之前用户针对产品a1~a5的主观偏好排序为ζⅠ:a1≻a5≻a3≻a2≻a4.显然这与4.1节所得的客观排序序列ο完全一致.此时,根据ζⅠ重新调整决策矩阵Y,定义“备选方案-决策矩阵-重要性权值”的偏好有序结构为

在此偏好结构下,可得用户期望值为
相比较4.1节所得的用户期望值:
显然![]() 中各分量数值较大,说明ζⅠ所对应的偏好或态度较前述ζ积极.进一步可得相应的态度向量为
中各分量数值较大,说明ζⅠ所对应的偏好或态度较前述ζ积极.进一步可得相应的态度向量为
SⅠ=(0.053,0.430,0.457,0.046,0.014)T,
注意到有影响的权重分量集中分布在SⅠ的偏上位置,说明该用户偏好数值较大的参数对应于积极的态度,所对应的量词函数为

其态度特征值为![]() 显然这是一种积极态度.
显然这是一种积极态度.
2) 假定用户针对a1~a5的主观偏好排序为ζⅡ:a4≻a2≻a3≻a5≻a1.显然这与4.1节客观排序序列ο完全相反.此时,根据ζⅡ重新调整决策矩阵Y,定义“备选方案-决策矩阵-重要性权值”的偏好有序结构为

在此偏好结构下,可得用户期望值为
相比较4.1节所得的用户期望值:
显然![]() 中各分量数值较小,说明ζⅡ所对应的偏好或态度较前述ζ消极.进一步可得相应的态度向量为
中各分量数值较小,说明ζⅡ所对应的偏好或态度较前述ζ消极.进一步可得相应的态度向量为
SⅡ=(0.034,0.090,0.150,0.664,0.062)T,
注意到有影响的权重分量集中分布在SⅡ的偏下位置,说明该用户偏好数值较小的参数,对应于消极的态度,所对应的量词函数为
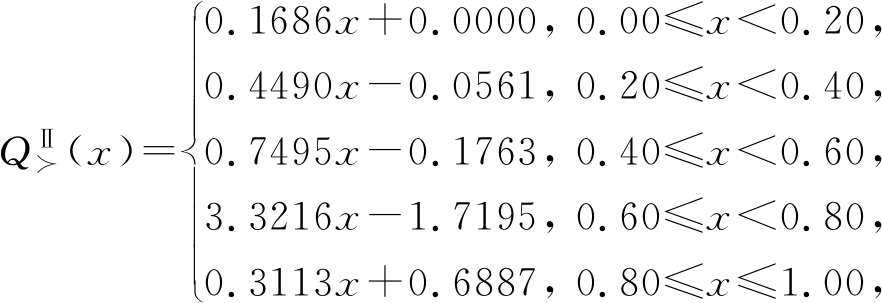
其态度特征值为![]() 显然这是一种消极态度.
显然这是一种消极态度.
综上易知,针对样本方案的不同主观排序能够反映用户不同的偏好及态度,进而对应于不同的用户期望值及量词函数,由此得到的个性化推荐序列也应该不同.为进一步表明上述观点,表5给出以上所得不同量词所对应的一些关键结果及其对新产品a6~a10的个性化推荐序列.同时,针对同一样本数据的不同偏好排序,亦给出使用李微娜[3]方法所得到的推荐序列.
Table 5 Some Key Results from Different Preference Rankings for Sample Alternatives
表5 不同偏好排序所对应的关键结果
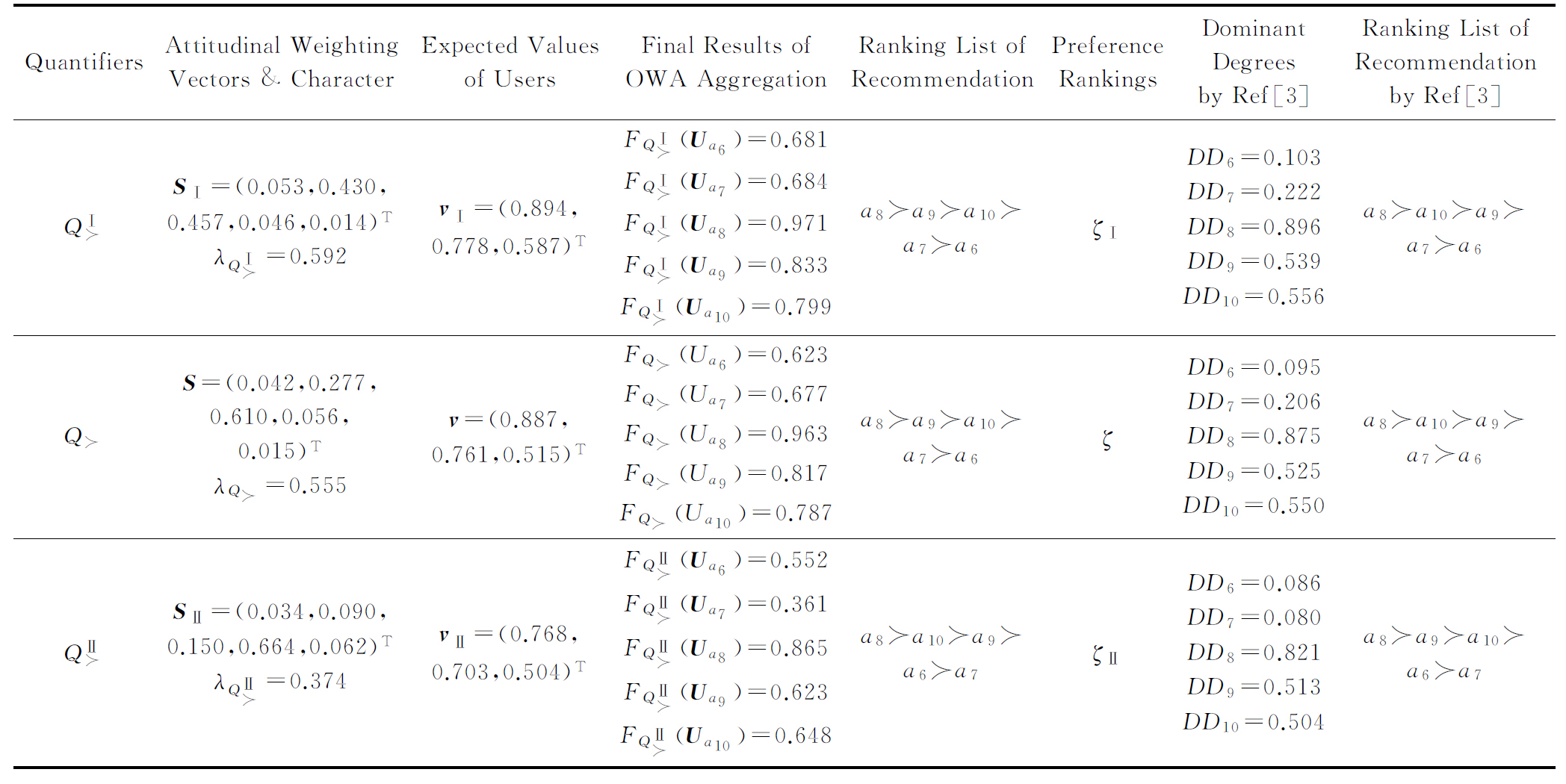
QuantifiersAttitudinal Weighting Vectors & CharacterExpected Values of UsersFinal Results of OWA AggregationRanking List of RecommendationPreference RankingsDominant Degrees by Ref[3]Ranking List of Recommendation by Ref[3]QⅠ≻SⅠ=(0.053,0.430,0.457,0.046,0.014)TλQⅠ≻=0.592vⅠ=(0.894,0.778,0.587)TFQⅠ≻(Ua6)=0.681FQⅠ≻(Ua7)=0.684FQⅠ≻(Ua8)=0.971FQⅠ≻(Ua9)=0.833FQⅠ≻(Ua10)=0.799a8≻a9≻a10≻a7≻a6ζⅠDD6=0.103DD7=0.222DD8=0.896DD9=0.539DD10=0.556a8≻a10≻a9≻a7≻a6Q≻S=(0.042,0.277,0.610,0.056,0.015)TλQ≻=0.555v=(0.887,0.761,0.515)TFQ≻(Ua6)=0.623FQ≻(Ua7)=0.677FQ≻(Ua8)=0.963FQ≻(Ua9)=0.817FQ≻(Ua10)=0.787a8≻a9≻a10≻a7≻a6ζDD6=0.095DD7=0.206DD8=0.875DD9=0.525DD10=0.550a8≻a10≻a9≻a7≻a6QⅡ≻SⅡ=(0.034,0.090,0.150,0.664,0.062)TλQⅡ≻=0.374vⅡ=(0.768,0.703,0.504)TFQⅡ≻(Ua6)=0.552FQⅡ≻(Ua7)=0.361FQⅡ≻(Ua8)=0.865FQⅡ≻(Ua9)=0.623FQⅡ≻(Ua10)=0.648a8≻a10≻a9≻a6≻a7ζⅡDD6=0.086DD7=0.080DD8=0.821DD9=0.513DD10=0.504a8≻a9≻a10≻a6≻a7
由表5可见,随着主观偏好排序与客观排序ο的差异性的增大(ζⅠ→ζ→ζⅡ),用户的偏好态度由积极转向中性再转至消极![]() 对应的态度特征值以及用户期望值均在逐渐减小,最终导致新产品推荐序列也不相同,所得推荐结果切实符合用户在某特定态度偏好下的个性特征.事实上,使用李微娜[3]的方法,每次用户的主观偏好排序发生变化时,均需要建立带有约束的高次非线性优化模型,计算复杂,求解困难;另外,随着样本方案增多,所需占优值矩阵及偏好强度矩阵也愈加复杂,更加不易观察,在实际应用中有一定局限性.其他典型方法,如最优化方法,通常根据客观数据建立最优化模型,单纯从数学角度求解,以得到所涉问题一般意义下的“最优方案”,并假定该最优结果适用于所有理性用户,有一种强烈的“逼迫感”,即代替用户决策并强制用户接受.这类方法未考虑用户本身的态度、偏好、意愿、倾向等个性特征及心理因素,从而使得这些所谓的“最优方案”显得过于刚性,在实际应用中明显缺乏因人而异的柔韧性和灵活性.
对应的态度特征值以及用户期望值均在逐渐减小,最终导致新产品推荐序列也不相同,所得推荐结果切实符合用户在某特定态度偏好下的个性特征.事实上,使用李微娜[3]的方法,每次用户的主观偏好排序发生变化时,均需要建立带有约束的高次非线性优化模型,计算复杂,求解困难;另外,随着样本方案增多,所需占优值矩阵及偏好强度矩阵也愈加复杂,更加不易观察,在实际应用中有一定局限性.其他典型方法,如最优化方法,通常根据客观数据建立最优化模型,单纯从数学角度求解,以得到所涉问题一般意义下的“最优方案”,并假定该最优结果适用于所有理性用户,有一种强烈的“逼迫感”,即代替用户决策并强制用户接受.这类方法未考虑用户本身的态度、偏好、意愿、倾向等个性特征及心理因素,从而使得这些所谓的“最优方案”显得过于刚性,在实际应用中明显缺乏因人而异的柔韧性和灵活性.
相比之下,本文模型及方法设计新颖精巧,可操作性强,可面向不同层次水平、不同知识结构的用户,利用他们的偏好信息反映其主观个性特性,同时与客观数据相结合,理性快捷地向其推荐相应态度偏好下的“最满意方案”而非一般意义下的“最优方案”,具有更大的实用性和灵活性.
5 结 论
本文研究了多属性样本方案的重要性与其主观偏好排序位置之间的关系,经形式化建模与分析后认为,用户的主观排序序列中各方案的重要性不依赖于方案本身的客观属性,而依赖于他们所在的主观排序位置,排序位置越靠前,对应方案越重要.基于这种理解,提出一种新颖的用户期望值提取模型,该模型构造精巧,实现简单,对用户的能力水平、专业知识、经历经验等差异性特质无特殊要求,具有较强的可操作性和灵活性.据此进一步建立由用户偏好信息诱导的模糊量词,该量词具有较强的个体针对性,能够很好地捕获并反映用户的偏好、态度等个性特征,为用户追求主观偏好下的“最满意方案”而非一般意义下的“最优方案”提供知识支持.最后将所得模型及方法应用于个性化推荐中,以解决典型的产品推荐问题.更一般地,在需要特殊考虑主体偏好、态度等个性特征的复杂环境中,如不确定性决策、情境感知计算、个性化商品定制等,本文模型及方法仍具有实际应用价值.下一步工作将深入分析多属性样本数据的分布特征与样本方案的主观偏好排序之间的关系及其对期望值的影响及作用机理,同时针对所得量词的几何特征做进一步研究,以期得到同时具有充分光滑、保形插值、快速收敛等优良性质的至善的个性化模糊量词.
[1]Li Yuqi, Chen Weizheng, Yan Hongfei, et al. Learning graph-based embedding for personalized product recommen-dation[J]. Chinese Journal of Computers, 2019, 42(8): 1767-1778 (in Chinese)(李宇琦, 陈维政, 闫宏飞, 等. 基于网络表示学习的个性化商品推荐[J]. 计算机学报, 2019, 42(8): 1767-1778)
[2]Huang Jinchao, Zhang Jiawei, Chen Ning, et al. Preference degree based personalized recommendation algorithm[J]. Journal of Shanghai Jiao Tong University, 2018, 52(7): 770-776 (in Chinese)(黄金超, 张佳伟, 陈宁, 等. 基于偏好度特征构造的个性化推荐算法[J]. 上海交通大学学报, 2018, 52(7): 770-776)
[3]Li Weina. Application of user preference-orented MADM method in personalized recommendation[D]. Harbin: Heilongjiang University, 2011 (in Chinese)(李微娜. 面向用户偏好的MADM方法在个性化推荐中的应用[D]. 哈尔滨: 黑龙江大学, 2011)
[4]Li Jie, Xu Yong, Wang Yunfeng, et al. Strongest association rules mining for personalized recommendation[J]. System Engineering-Theory & Practice, 2009, 29(8): 144-152 (in Chinese)(李杰, 徐勇, 王云峰, 等. 面向个性化推荐的强关联规则挖掘[J]. 系统工程理论与实践, 2009, 29(8): 144-152)
[5]Xie Zhenping, Jin Chen, Liu Yuan. Personalized knowledge recommendation model based on constructivist learning theory[J]. Journal of Computer Research and Development, 2018, 55(1): 125-138 (in Chinese)(谢振平, 金晨, 刘渊. 基于构建主义学习理论的个性化知识推荐模型[J]. 计算机研究与发展, 2018, 55(1): 125-138)
[6]Huang Xianying, Long Shuyan, Xie Jin. Collaborative filtering recommendation algorithm combined with user interest degree clustering[J]. Application on Research of Computers, 2019, 36(9): 2609-2612, 2617 (in Chinese)(黄贤英, 龙姝言, 谢晋. 结合用户兴趣度聚类的协同过滤推荐算法[J]. 计算机应用研究, 2019, 36(9): 2609-2612, 2617)
[7]Tao Yongcai, Huo Hao, Shi Lei, et al. Hybrid news recommendation based on time factor[J]. Journal of Chinese Computer Systems, 2018, 39(8): 1794-1798 (in Chinese)(陶永才, 火昊, 石磊, 等. 基于时间因子的个性化新闻混合推荐研研究[J]. 小型微型计算机系统, 2018, 39(8): 1794-1798)
[8]Guo Kaihong. Quantifiers induced by subjective expected value of sample information[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2014, 44(10): 1784-1794
[9]Guo Kaihong. Quantifiers induced by subjective expected value of sample information with Bernstein polynomials[J]. European Journal Operational Research, 2016, 254(1): 226-235
[10]Guo Kaihong, Xu Hao. Personalized quantifier by Bernstein polynomials combined with interpolation spline[J]. International Journal Intelligent Systems, 2018, 33(7): 1507-1533
[11]Vasto-Terrientes L D, Valls A, Zielniewicz P, et al. A hierarchical multi-criteria sorting approach for recommender systems[J]. Journal of Intelligent Information Systems, 2016, 46(2): 313-346
[12]Zhang Wenli. Hybrid multi-criteria recommendation systems combined with fuzzy mathematics and MODM methods[D]. Chengdu: University of Electronic Science and Technology of China, 2013 (in Chinese)(张文力. 结合模糊数学与多目标决策方法的混合多准则推荐系统[D]. 成都: 电子科技大学, 2013)
[13]Zhu Guowei, Zhou Li. Hybrid recommendation based on forgetting curve and domain nearest neighbor[J]. Journal of Management Sciences in China, 2012, 15(5): 55-64 (in Chinese)(朱国玮, 周利. 基于遗忘函数和邻域最近邻的混合推荐研究[J]. 管理科学学报, 2012, 15(5): 55-64)
[14]Soui M, Ghedira K, Abed M. A novel multi-criteria decision making approach for personalisation system[J]. Inter-national Journal of Services and Operations Management, 2014, 19(2): 191-211
[15]Nilashi M, Ibrahim O B, Ithnin N, et al. A multi-criteria recommendation system using dimensionality reduction and neuro-fuzzy techniques[J]. Soft Computing, 2015, 19(11): 3173-3207
[16]Wang Qian, Yang Liyun, Yang Deli. Collaborative filtering algorithm based on rating distribution of attributes faced user preference[J]. Journal of Systems Engineering, 2010, 25(4): 561-568 (in Chinese)(王茜, 杨莉云, 杨德礼. 面向用户偏好的属性值评分分布协同过滤算法[J]. 系统工程学报, 2010, 25(4): 561-568)
[17]Qin Jindong. Type-2 fuzzy decision making methods and the application in personalized recommendation[D]. Nanjing: Southeast University, 2016 (in Chinese)(秦晋栋. 二型模糊决策方法及其在个性化推荐中的应用[D]. 南京: 东南大学, 2016)
[18]Zhang Jin, You Tianhui, Fan Zhiping. Method for product purchasing recommendation ranking based on multi-attribute online ratings information[J]. Journal of Northeastern University:Natural Science, 2019, 40(1): 138-143 (in Chinese)(张瑾, 尤天慧, 樊治平. 基于多属性在线评价信息的商品购买推荐排序方法[J]. 东北大学学报:自然科学版, 2019, 40(1): 138-143)
[19]Liang Changyong, Leng Yajun, Wang Yongsheng, et al. Research on group recommendation in e-commerce recommender systems[J]. Chinese Journal of Management Science, 2013, 21(3): 153-158 (in Chinese)(梁昌勇, 冷亚军, 王勇胜, 等. 电子商务推荐系统中群体用户推荐问题研究[J]. 中国管理科学, 2013, 21(3): 153-158)
[20]Yager R R. On order weighted averaging aggregation operators in multi-criteria decision making[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1988, 18(1): 183-190
[21]Yager R R. Quantifier guide aggregation using operators[J]. International Journal Intelligent Systems, 1996, 11(1): 49-73
[22]Zadeh L A. A computational approach to fuzzy quantifiers in natural languages[J]. Computers & Mathematics with Applications, 1983, 9(1): 149-184
[23]Yager R R. OWA aggregation over a continuous interval argument with application to decision making[J]. IEEE Transactions on Systems, Man, and Cybernetics:Part B, 2004, 34(5): 1952-1963
[24]Ying Mingsheng. Linguistic quantifiers modeled by Sugeno integrals[J]. Artificial Intelligence, 2006, 170(6/7): 581-606
[25]Guo Kaihong. Amount of information and attitudinal based method for ranking Atanassov’s intuitionistic fuzzy values[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(1): 177-188
[26]Guo Kaihong, Li Wenli. An attitudinal-based method for constructing intuitionistic fuzzy information in hybrid MADM under uncertainty[J]. Information Sciences, 2012, 208: 28-38
[27]Guo Kaihong, Xu Hao. Knowledge measure for intuitionistic fuzzy sets with attitude towards non-specificity[J]. International Journal of Machine Learning and Cybernetics, 2019, 10(7): 1657-1669
[28]Guo Kaihong, Li Wenli. A unified framework for the key weights in MAGDM under uncertainty[J]. Soft Computing, 2017, 21(9): 2251-2262
[29]Guo Kaihong, Li Wenli. A C-OWA operator-based method for aggregating intuitionistic fuzzy information and its application to decision making under uncertainty[J]. International Journal of Digital Content Technology and Its Applications, 2010, 4(7): 140-147
[30]Guo Kaihong. Combination Rules for Uncertain Information and Approaches to Decision Factors under Group Decision Making Environment[M]. Shenyang: Liaoning University Publishing House, 2018 (in Chinese)(郭凯红. 群决策环境下不确定信息集成规则与决策要素获取方法[M]. 沈阳: 辽宁大学出版社, 2018)
[31]Shi Shengli, Liu Xuhua. Formalizing fuzzy quantifiers and reasoning[J]. Journal of Software, 1993, 4(3): 8-14 (in Chinese)(石生利, 刘叙华. 形式化模糊量词及推理[J]. 软件学报, 1993, 4(3): 8-14)
[32]Liu Xinwang. On the properties of equidifferent RIM quantifier with generating function[J]. International Journal of General Systems, 2005, 34(5): 579-594
[33]Liu Xinwang. Some properties of the weighted OWA operator[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2006, 36(1): 118-127
[34]Zhao Xinquan, Peng Yongxing. Management Decision Analysis[M]. 2th ed. Beijing: Science Press, 2008 (in Chinese)(赵新泉, 彭勇行. 管理决策分析 [M]. 2版. 北京: 科学出版社, 2008)
[35]Shahabi C, Zarkesh A M, Adibi J, et al. Knowledge discovery from users Web page navigation[C] //Proc of the 7th Int Workshop on Research Issues in Data Engineering. Piscataway, NJ: IEEE, 1997: 20-29
[36]Liu Huihui. Research of fuzzy multiple attributes decision making method based on S-shaped utility function[D]. Beijing: North China Electric Power University, 2017(in Chinese)(刘慧晖. S型效用函数下的模糊多属性决策方法研究[D]. 北京: 华北电力大学, 2017)
[37]Zhou Ligang. Some generalized information aggregation operators and their applications to multiple attribute decision making[D]. Hefei: Anhui University, 2013 (in Chinese)(周礼刚. 几类广义信息集成算子及其在多属性决策中的应用[D]. 合肥: 安徽大学, 2013)

